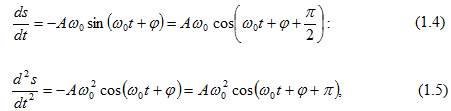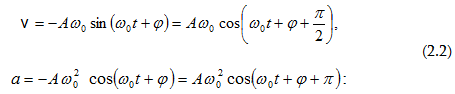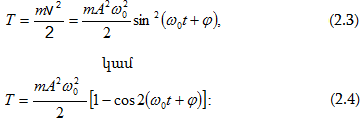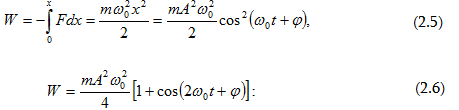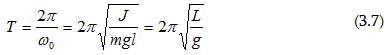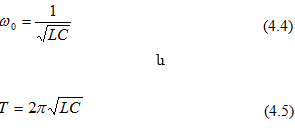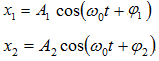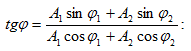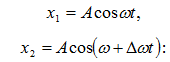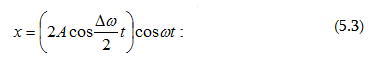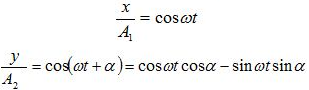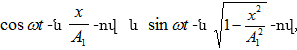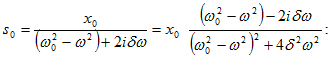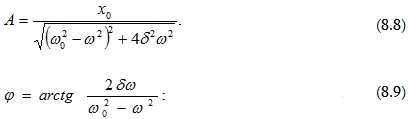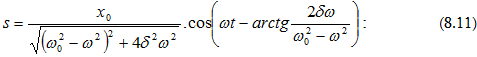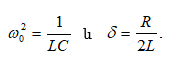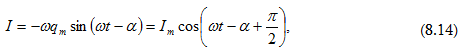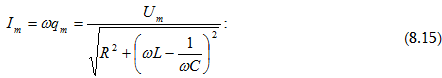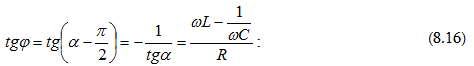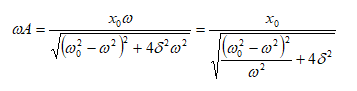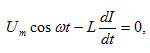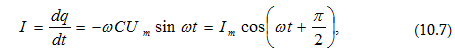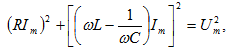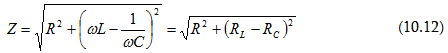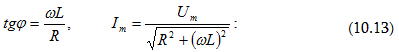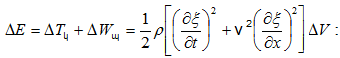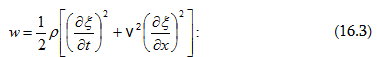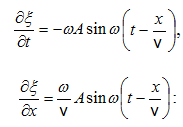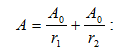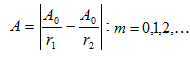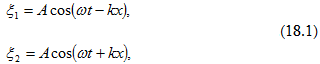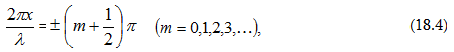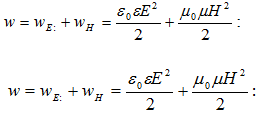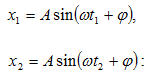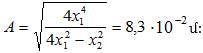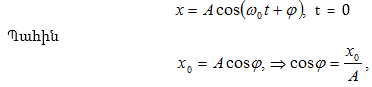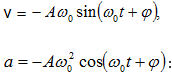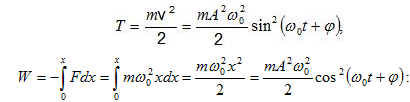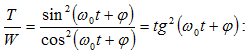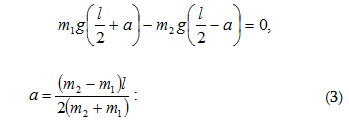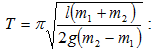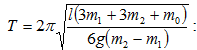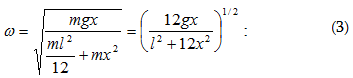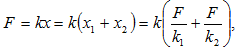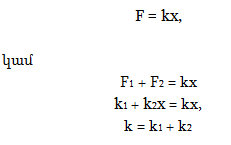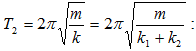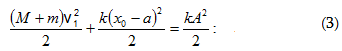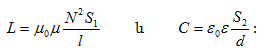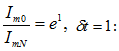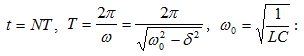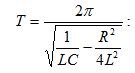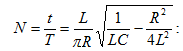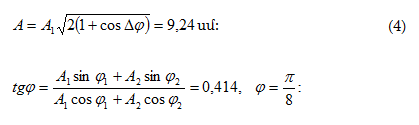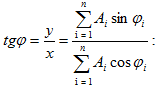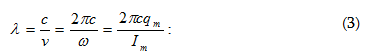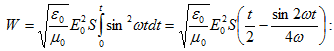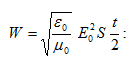ԳԼՈՒԽ 1
ՄԵԽԱՆԻԿԱԿԱՆ
ԵՎ
ԷԼԵԿՏՐԱՄԱԳՆԻՍԱԿԱՆ
ՏԱՏԱՆՈՒՄՆԵՐ
1.1.
Ներդաշնակ տատանումներ
և դրանց
բնութագրիչները
Տատանումներ
են կոչվում
այն շարժումները
կամ պրոցեսները,
որոնց
տարբերակիչ
առանձնահատկությունը
որոշ
աստիճանի
կրկնողականությունն
է: Կրկնողականության
այսպիսի
հատկությամբ
օժտըված
են, օրինակ,
ժամացույցի
ճոճանակի
տատանումները,
լարի
կամ կամերտոնի
ոտիկների
տատանումները,
փոփոխական
հոսանքը
և այլն: Ճոճանակի
տատանողական
շարժման
դեպքում
փոփոխվում
է նրա զանգվածի
կենտրոնի
կոորդինատը,
փոփոխական
հոսանքի
դեպքում
շղթայում
փոփոխվում
են լարումը
և հոսանքը:
Տատանողական
պրոցեսները
լայն
տարածում
են գտել բնության
մեջ և տեխնիկայում:
Շատ դեպքերում
դրանք
բացասական
դեր են խաղում:
Միաժամանակ
տատանողական
պրոցեսներն
ընկած
են տեխնիկայի
տարբեր
բնագավառների
հիմքում:
Այսպես`
տատանողական
պրոցեսների
վրա է հիմնված ամբողջ
ռադիոտեխնիկան:
Տատանումների
ֆիզիկական
բնույթը
կարող
է լինել
տարբեր,
ուստի
զանազանում
են հետևյալ
տատանումները`
մեխանիկական,
էլեկտրամագնիսական,
էլեկտրամեխանիկական
և այլն: Սակայն
տարբեր
տատանողական
պրոցեսներ
նկարագրվում
են միատեսակ
բնութագրիչներով
և միատեսակ
հավասարումներով:
Այստեղից
էլ հետևում
է տարբեր
ֆիզիկական
բնույթի
տատանումների
ուսումնասիրությանը
միատեսակ
մոտեցման
նպատակահարմարությունը:
Օրինակ,
մեխանիկական
և էլեկտրամագնիսական
տատանումներին
միատեսակ
մոտեցում
են ցուցաբերել
անգլիացի
ֆիզիկոս
Դ. Ռելեյը,
Ա. Ստոլետովը,Պ. Լեբեդևը: Տատանումների
տեսության
զարգացման
մեջ մեծ ավանդ
է դրել Լ. Մանդելշտամը:
Ազատ
կամ սեփական
են կոչվում
այն տատանումները,
որոնք
տեղի
են ունենում
ինքն
իրեն
թողնված
համակարգում`
հարված
հաղորդելուց
կամ իր հավասարակշռության
դիրքից
դուրս
բերելուց
հետո:
Օրինակ,
թելից
կախված
գնդիկի
(ճոճանակի)
տատանումները:
Տատանումներ
առաջացնել
կարելի
է կամ գնդիկին
էներգիա
հաղորդելով
կամ այն մի կողմ տանելուց
հետո
բաց թողնելով:
Տատանումների
պարզագույն
տեսակ
են ներդաշնակ
տատանումները:
Ֆիզիկական
մեծության`
ժամանակից
կախված
այնպիսի
պարբերական
փոփոխությունները,
որոնք
տեղի
են ունենում
սինուսի
կամ կոսինուսի
օրենքով,
կոչվում
են ներդաշնակ
տատանումներ:
Ներդաշնակ
տատանումների
դիտարկումը
կարևոր
է երկու
պատճառներով.
1) բնության
մեջ և տեխնիկայում
տատանումները
հաճախ
ունենում
են ներդաշնակ
տատանումներին
շատ մոտ բնույթ,
2) տարբեր
պարբերական
պրոցեսները
կարելի
է ներկայացնել
մի քանի ներդաշնակ
տատանումների
վերադրում:
s մեծության
ներդաշնակ
տատանումները
նկարագրվում
են հետևյալ
հավասարումով`

որտեղ
A-ն տատանվող
մեծության
առավելագույն
արժեքն է և
կոչվում է
տատանման
լայնույթ, 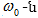 շրջանային
(ցիկլային)
հաճախությունն
է: Պարբերաբար
փոփոխվող
կոսինուսի
արգումենտը `
շրջանային
(ցիկլային)
հաճախությունն
է: Պարբերաբար
փոփոխվող
կոսինուսի
արգումենտը ` 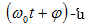 կոչվում
է տատանման
փուլ և
որոշում է
տատանվող
մեծության
շեղումը
հավասարակշռության
դիրքից ժամանակի
t պահին:
կոչվում
է տատանման
փուլ և
որոշում է
տատանվող
մեծության
շեղումը
հավասարակշռության
դիրքից ժամանակի
t պահին: 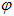 մեծությունը
ներդաշնակ
հավասարման
մեջ կոչվում է
սկզբնական
փուլ, և այն
որոշում է
տատանվող
մեծության
շեղումը
հավասարակշռության
դիրքից
ժամանակի t = 0 պահին:
մեծությունը
ներդաշնակ
հավասարման
մեջ կոչվում է
սկզբնական
փուլ, և այն
որոշում է
տատանվող
մեծության
շեղումը
հավասարակշռության
դիրքից
ժամանակի t = 0 պահին:
Սկզբնական
փուլի արժեքը
որոշվում է`
ժամանակի
հաշվարկման
սկիզբն
ընտրելով:
Քանի որ կոսինուսը
փոփոխվում է 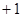 -ից
մինչև
-ից
մինչև 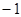 -ի
սահմաններում,
ապա s-ը կարող է
ընդունել +A-ից
մինչև -A
արժեքները:
Քանի որ
կոսինուսը
պարբերական ֆունկցիա
է 2π
պարբերությամբ,
ապա
ներդաշնակ տատանումներ
կատարող
համակարգի
տարբեր վիճակները
կրկնվում են
այնպիսի T
ժամանակից
հետո, որի
ընթացքում
տատանման
փուլը
ստանում է 2π-ի
հավասար աճ: T
ժամանակը
կոչվում է
տատանման պարբերություն:
Այն կարելի է
որոշել
հետևյալ
պայմանից`
-ի
սահմաններում,
ապա s-ը կարող է
ընդունել +A-ից
մինչև -A
արժեքները:
Քանի որ
կոսինուսը
պարբերական ֆունկցիա
է 2π
պարբերությամբ,
ապա
ներդաշնակ տատանումներ
կատարող
համակարգի
տարբեր վիճակները
կրկնվում են
այնպիսի T
ժամանակից
հետո, որի
ընթացքում
տատանման
փուլը
ստանում է 2π-ի
հավասար աճ: T
ժամանակը
կոչվում է
տատանման պարբերություն:
Այն կարելի է
որոշել
հետևյալ
պայմանից`
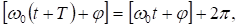
որտեղից

Միավոր
ժամանակում
կատարված
տատանումների
թիվը կոչվում
է
տատանումների
հաճախություն,
որը
նշանակում են
v-ով: Ակնհայտ է,
որ v հաճախությունը
մեկ տատաման T
տևողության
հետ կապված է
հետևյալ
առնչությամբ`

Որպես
հաճախության
միավոր
ընդունում են
այն տատանման
հաճախությունը,
որի
պարբերությունը
հավասար է 1 վ-ի:
Այս միավորը
կոչվում է հերց
(կրճատ` Հց):
Համեմատելով
(1.2) և (1.3)
արտահայտությունները`
կստանանք 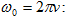
Այստեղից
հետևում
է, որ ցիկլային
հաճախությունը
թվապես
հավասար
է 2π վ-ում
մարմնի կատարած տատանումների
թվին:
Գտնենք
ներդաշնակորեն
տատանվող
մեծության
առաջին
և երրորդ
կարգի
ածանցյալները
ըստ ժամանակի.
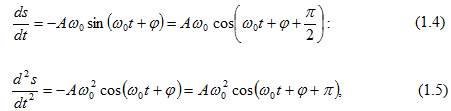
այսինքն
ստանում
ենք նույն
ցիկլային
հաճախությամբ
ներդաշնակ
տատանումներ:
(1.4) և (1.5) մեծությունների
լայնույթները
համապատասխանաբար
հավասար
են 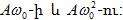 (1.4)
մեծության
փուլը (1.1)
մեծության
փուլից տարբերվում
է π/2-ով, իսկ
(1.5) մեծության
փուլը
(1.1) մեծության
փուլից
տարբերվում
է π-ով:
(1.4)
մեծության
փուլը (1.1)
մեծության
փուլից տարբերվում
է π/2-ով, իսկ
(1.5) մեծության
փուլը
(1.1) մեծության
փուլից
տարբերվում
է π-ով:
Հետևաբար,
ժամանակի այն
պահին, երբ s = 0 -ի,
ds/dt -ն ձեռք է
բերում առավելագույն
արժեք. երբ s-ը
հասնում է
բացասական
առավելագույն
արժեքին, ապա d2s
/dt2-ն ունի
առավելագույն
դրական
արժեք
(նկ.1, սկզբնական
փուլը`
φ = 0):
Արտահայտություն
(1.6) -ից հետևում
է ներդաշնակ
տատանումների
դիֆերենցիալ
հավասարումը

Այս
հավասարման
լուծումը (1.1)
արտահայտությունն
է:
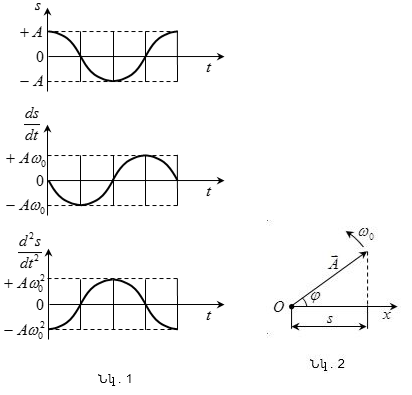
Ներդաշնակ
տատանումները
պատկերվում
են գրաֆիկորեն,
այսինքն`
հարթության
մեջ վեկտորների
տեսքով:
Այդպիսի
եղանակով
ստացված սխեման
կոչվում է վեկտորական
դիագրամ:
Վերցնենք x -ի
առանցքի վրա
կամայական O
կետից
տեղադրենք 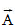 վեկտորը,
որի մոդուլը
հավասար է A
լայնույթին և
առանցքի հետ
կազմում է φ
անկյուն, որը
հավասար է
սկըզբնական
փուլին (նկ.2):
Եթե այդ
վեկտորը
պտտման մեջ
դնենք
վեկտորը,
որի մոդուլը
հավասար է A
լայնույթին և
առանցքի հետ
կազմում է φ
անկյուն, որը
հավասար է
սկըզբնական
փուլին (նկ.2):
Եթե այդ
վեկտորը
պտտման մեջ
դնենք 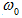 անկյունային
արագությամբ,
ապա վեկտորի
ծայրի
պրոյեկցիան կտեղափոխվի
x առանցքի վրա
–A-ից մինչև +A-ի
սահմաններում,
ընդ որում այս
պրոյեկցիայի
կոորդինատը
ժամանակի
ընթացքում
կփոփոխվի
անկյունային
արագությամբ,
ապա վեկտորի
ծայրի
պրոյեկցիան կտեղափոխվի
x առանցքի վրա
–A-ից մինչև +A-ի
սահմաններում,
ընդ որում այս
պրոյեկցիայի
կոորդինատը
ժամանակի
ընթացքում
կփոփոխվի 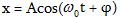 օրենքով:
Հետևաբար,
վեկտորի
ծայրի
պրոյեկցիան
առանցքի
վրա կըկատարի
ներդաշնակ
տատանում,
որի լայնույթը
հավասար
է վեկտորի
երկարությանը,
շրջանային
հաճախությունը`
վեկտորի
պտտման
անկյունային
արագությանը,
իսկ սկզբնական
փուլը`
ժամանակի
սկզբնական
պահին
առանցքի
հետ վեկտորի
կազմած
անկյանը:
օրենքով:
Հետևաբար,
վեկտորի
ծայրի
պրոյեկցիան
առանցքի
վրա կըկատարի
ներդաշնակ
տատանում,
որի լայնույթը
հավասար
է վեկտորի
երկարությանը,
շրջանային
հաճախությունը`
վեկտորի
պտտման
անկյունային
արագությանը,
իսկ սկզբնական
փուլը`
ժամանակի
սկզբնական
պահին
առանցքի
հետ վեկտորի
կազմած
անկյանը:
Ֆիզիկայում
հաճախ
օգտագործվում
է մի ուրիշ
մեթոդ,
որը տարբերվում
է վերևում
նկարագրված
մեթոդից:
Այդ մեթոդում
տատանվող
մեծությունը
ներկայացնում
են կոմպլեքս
թվով:
Համաձայն
Էյլերի
բանաձևի`
կոմպլեքս
թվերի
համար
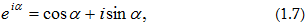
որտեղ
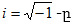 կեղծ
միավոր է:
Ուստի
ներդաշնակ
տատանումների
(1.1)
հավասարումը
կարելի է գրել
կոմպլեքս տեսքով.
կեղծ
միավոր է:
Ուստի
ներդաշնակ
տատանումների
(1.1)
հավասարումը
կարելի է գրել
կոմպլեքս տեսքով.

(1.8)
արտահայտության
իրական մասը`
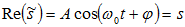
պայմանավորվում
ենք բաց
թողնել և (1.8)-ը
գրում ենք  տեսքով:
Տատանումների
տեսությունում
ընդունվում է,
որ տատանվող s
մեծությունը
հավասար է կոմպլեքս
արտահայտության
իրական
մասին, որը
կանգնած է այդ
հավասարության
աջ մասում:
տեսքով:
Տատանումների
տեսությունում
ընդունվում է,
որ տատանվող s
մեծությունը
հավասար է կոմպլեքս
արտահայտության
իրական
մասին, որը
կանգնած է այդ
հավասարության
աջ մասում:
>>
2.
Ներդաշնակ
մեխանիկական
տատանումներ
Դիցուք
նյութական
կետը
կատարում
է կոորդինատային
x առանցքի
երկայնքով
ուղղագիծ
ներդաշնակ
տատանումներ
հավասարակշռության
դիրքի
շուրջը,
որն ընդունվում
է կոորդինատների
սկիզբ:
Հետևաբար
x կոորդինատի
կախումը
t ժամանակից
տրվում
է (1.1) հավասարումով,
որտեղ
s = x.

Համաձայն
(1.4) և (1.5)
արտահայտությունների`
տատանվող կետի
արագությունը
և արագացումը
համապատասխանաբար
կլինեն`
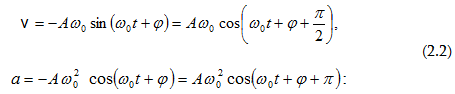
Նկատի
ունենալով (2.1)-ը
և (2.2)-ը m
զանգվածով
տատանվող
նյութական
կետի վրա
ազդող ուժը` 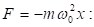

Հետևաբար,
ուժը
համեմատական
է հավասարակշռության
դիրքից
նյութական
կետի
շեղմանը
և ուղղված
է դեպի հավասարակշռության
դիրքը:
Ներդաշնակ
տատանումներ
կատարող
նյութական
կետի
կինետիկ
էներգիան`
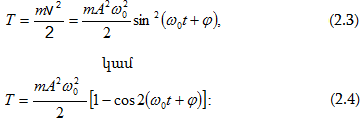
Առաձգական
F ուժի
ազդեցության
տակ ներդաշնակ
տատանումներ
կատարող
նյութական
կետի պոտենցիալ
էներգիան
հավասար է.
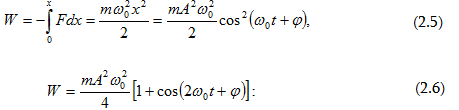
Գումարելով
(2.3) -ը և (2.5)-ը` լրիվ
էներգիայի
համար կստանանք`(2.7)

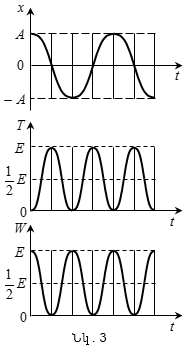
Այսպիսով,
ներդաշնակ
տատանումների
դեպքում լրիվ
մեխանիկական
էներգիան
պահպանվում է,
քանի որ
առաձգական
ուժը
կոնսերվատիվ
է: (2.4) և (2.6) բանաձևերից
հետևում է, որ
T-ն և W-ն
փոփոխվում են 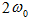 հաճախությամբ,
այսինքն`
այնպիսի
հաճախությամբ,
որը երկու
անգամ
գերազանցում
է ներդաշնակ
տատանումների
հաճախությանը:
Նկ.3-ում
պատկերված են
x-ի,T -ի և W-ի
ժամանակից
կախվածության
գրաֆիկները:
Քանի որ
հաճախությամբ,
այսինքն`
այնպիսի
հաճախությամբ,
որը երկու
անգամ
գերազանցում
է ներդաշնակ
տատանումների
հաճախությանը:
Նկ.3-ում
պատկերված են
x-ի,T -ի և W-ի
ժամանակից
կախվածության
գրաֆիկները:
Քանի որ
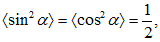
ապա (2.3),
(2.5) և (2.7) բանաձևերից
հետևում է, որ
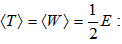
>>
3.
Ներդաշնակ
տատանակ,
ֆիզիկական և մաթեմատիկական
ճոճանակներ
Ներդաշնակ
տատանակ է
կոչվում այն
համակարգը,
որի
տատանումները
նկարագրվում
են (1.6) տեսքի հավասարումով.
(3.1)

Ներդաշնակ
տատանակի
տատանումները
պարբերական
շարժման
կարևոր
օրինակ են և
ծառայում են
ճշգրիտ կամ
մոտավոր
մոդել
քվանտային և
դասական
ֆիզիկայի շատ
խնդիրներում:
Ներդաշնակ
տատանակի
օրինակներ են
զսպանակավոր,
ֆիզիկական և
մաթեմատիկական
ճոճանակները,
տատանողական
կոնտուրը:
Զսպանակավոր
ճոճանակ:
Անկշիռ
առաձգական
զսպանակից և
նրան ամրացված
m զանգվածով
գնդիկից
կազմված
համակարգը կոչվում
է զսպանակավոր
ճոճանակ:
Այդպիսի
համակարգը
ներդաշնակ
տատանումներ
է կատարում F = - kx
առաձգական
ուժի ազդեցության
տակ, որտեղ k-ն
զսպանակի կոշտությունն
է: Շփման
ուժերի
բացակայության
դեպքում ճոճանակի
շարժման
հավասարումը`
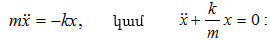
(3.1) -ից և
(1.1) -ից հետևում
է, որ զսպանակավոր
ճոճանակը
կատարում է
ներդաշնակ
տատանումներ
ըստ 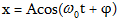 օրենքի
օրենքի

ցիկլիկ
հաճախությամբ
և
պարբերությամբ:

Զսպանակավոր
ճոճանակի
պոտենցիալ
էներգիան ըստ
(2.5) և (3.2)-ի հավասար
կլինի`
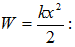
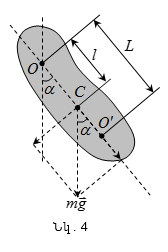
ֆիզիկական
ճոճանակ: Ֆիզիկական
ճոճանակ է
կոչվում այն
պինդ մարմինը,
որը կարող է
տատանվել նրա
իներցիայի
կենտրոնի հետ
չհամընկնող
անշարժ կետի
շուրջը: Հավասարակշռության
դիրքում
ճոճանակի
իներցիայի C
կենտրոնը
գտնվում է O
կախման կետի
տակ` նրա հետ
միասին
միևնույն
ուղղաձիգի
տակ (նկ.4): Եթե ճոճանակը
հավասարակշռությունից
շեղենք α անկյունով,
առաջանում է
պտտող մոմենտ,
որը ձգտում է
ճոճանակը
վերադարձնել
հավասարակշռության
դիրքը: Դրա
համար էլ
ինչպես
շեղմանը և առաձգական
ուժին, այնպես
էլ M մոմենտին
և α անկյունային
շեղմանը
վերագրում
ենք հակառակ
նշաններ: Այդ
մոմենտը`
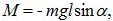
որտեղ
m-ը ճոճանակի
զանգվածն է, l-ը`
կախման կետի և
ճոճանակի
իներցիայի
կենտրոնի
միջև եղած
հեռավորությունը:
Նշանակելով
ճոճանակի
իներցիայի
մոմենտը կախման
կետով անցնող
առանցքի
նկատմամբ J-ով
և օգտվելով
պտտական
շարժման
դինամիկայի
օրենքից`
կարելի է գրել

Ճոճանակի
փոքր
տատանումների
դեպքում (հավասարակշռության
դիրքից
ճոճանակի
փոքր
անկյունային շեղումներ)
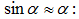
Հետևաբար,
(3.4)
հավասարումը
կարելի է գրել
հետևյալ
տեսքով` (3.5)
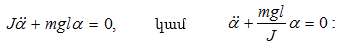
Ընդունելով

կստանանք
հետևյալ
հավասարումը`
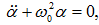
որը
նման է (2.1)
հավասարմանը,
որի լուծումը
մեզ հայտնի է.

(3.6)
արտահայտությունից
հետևում է, որ
հավասարակշռության
դիրքից փոքր
շեղումների
դեպքում
ֆիզիկական
ճոճանակը
կատարում է
ներդաշնակ
տատանումներ
ցիկլային
հաճախությամբ,
որը որոշվում
է (3.6) բանաձևով
և
պարբերությամբ:
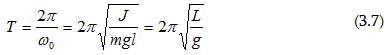
L =
J/ml-ը կոչվում է ֆիզիկական
ճոճանակի
բերված
երկարություն:
Կախման
կետն
իներցիայի
կենտրոնի հետ
միացնող
ուղղի վրա գտնվող
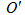 կետը,
որն ընկած է
պտտման
առանցքից
բերված երկարությանը
հավասար
հեռավորության
վրա, կոչվում
է ֆիզիկական
ճոճանակի
ճոճման
կենտրոն: Ըստ
Շտայների
թեորեմի` ճոճանակի
իներցիայի
մոմենտը
կախման կետով
անցնող առանցքի
նկատմամբ
որոշվում է
հետևյալ բանաձևով`
կետը,
որն ընկած է
պտտման
առանցքից
բերված երկարությանը
հավասար
հեռավորության
վրա, կոչվում
է ֆիզիկական
ճոճանակի
ճոճման
կենտրոն: Ըստ
Շտայների
թեորեմի` ճոճանակի
իներցիայի
մոմենտը
կախման կետով
անցնող առանցքի
նկատմամբ
որոշվում է
հետևյալ բանաձևով`

որտեղ
Jc - ն
իներցիայի մոմենտն
է ճոճանակի
իներցիայի
կենտրոնով
անցնող
առանցքի
նկատմամբ:
Նկատի
ունենալով
(3.8)-ը` բերված
երկարության
համար
կստանանք`
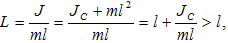
այսինքն
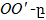 միշտ
մեծ է OC-ից,
այնպես, որ
կախման կետը և
ճոճման
կենտրոնը
գտնվում են
իներցիայի
կենտրոնի տարբեր
կողմերում:
միշտ
մեծ է OC-ից,
այնպես, որ
կախման կետը և
ճոճման
կենտրոնը
գտնվում են
իներցիայի
կենտրոնի տարբեր
կողմերում:
Կախման
կետը և ճոճման
կենտրոնն
օժտված են փոխադարձաբար
միմյանց
փոխարինելու
հատկությամբ,
այսինքն`
ճոճման կետը
կախման կետով
փոխարինելու
դեպքում
սկզբնական
կախման կետը
դառնում է
ճոճման կետ:
Հետևաբար,
հանգում ենք
այն
եզրակացության,
որ ճոճանակը
ճոճման
կենտրոնից
կախելու
դեպքում բերված
երկարությունը,
ինչպես նաև
ֆիզիկական ճոճանակի
տատանումների
պարբերությունը
կլինեն
այնպիսին,
ինչպես
նախորդ
դեպքում էին:
Մաթեմատիկական
ճոճանակ:
Մաթեմատիկական
ճոճանակ է
կոչվում
իդեալականացված
համակարգը,
որը բաղկացած
է զանգվածով
նյութական
կետից, որը
կախված է չձգվող
և անկշիռ
թելից: Իրական
ճոճանակը
կարելի է
համարել
մաթեմատիկական,
եթե թելի
երկարությունը
շատ մեծ է
կախված
մարմնի
չափերից, թելի
զանգվածը շատ
փոքր է մարմնի
զանգվածից, իսկ
թելի
դեֆորմացիաներն
այնքան փոքր
են, որ թելի
երկարությունը
կարելի է
համարել
անփոփոխ: Լավ
մոտավորությամբ
մաթեմատիկական
ճոճանակ է ոչ
մեծ ծանր
գնդիկը, որը
կախված է բարակ
երկար թելից:
Մաթեմատիկական
ճոճանակի
իներցիայի
մոմենտը`

որտեղ
l-ը ճոճանակի
երկարությունն
է:
Քանի
որ
մաթեմատիկական
ճոճանակը
կարելի է պատկերացնել
որպես
ֆիզիկական
ճոճանակի մասնավոր
դեպք,
ենթադրելով,
որ նրա ամբողջ
զանգվածը
կենտրոնացված
է զանգվածի
կենտրոնում, ապա
տեղադրելով (3.9)
արտահայտությունը
(3.7) բանաձևի մեջ` կստանանք
փոքր
տատանումների
համար մաթեմատիկական
ճոճանակի
տատանումների
պարբերությունը.

Համեմատելով
(3.7) և (3.10)
բանաձևերը`
տեսնում ենք,
որ եթե
ֆիզիկական
ճոճանակի
բերված
երկարությունը
հավասար է
մաթեմատիկական
ճոճանակի երկարությանը,
ապա այդ
ճոճանակների
պարբերությունները
իրար հավասար
են: Հետևաբար,
ֆիզիկական
ճոճանակի բերված
երկարությունն
այնպիսի
մաթեմատիկական
ճոճանակի
երկարությունն
է, որի
տատանումների
պարբերությունը
համընկնում է
տրված ֆիզիկական
ճոճանակի
պարբերության
հետ:
>>
4. Ազատ
ներդաշնակ
տատանումները
տատանողական
կոնտուրում
Տարբեր
ֆիզիկական
երևույթների
մեջ հատուկ տեղ
են գրավում
էլեկտրամագնիսական
տատանումները,
որոնց
դեպքում
էլեկտրական
մեծությունները
(լիցքերը,
հոսանքները)
պարբերաբար փոփոխվում
են, և որոնք
ուղեկցվում
են էլեկտրական
և մագնիսական
դաշտերի
փոխադարձ
փոխակերպումներով:
Էլեկտրամագնիսական
տատանումներ
գրգռելու և
պահպանելու
համար
օգտագործվում
է տատանողական
կոնտուր, մի
շղթա, որը
կազմված է
հաջորդաբար
միացված L ինդուկտիվության
կոճից, C
ունակության
կոնդենսատորից
և R
դիմադրությունից:
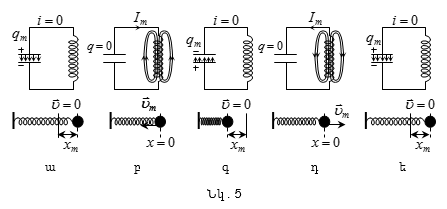
Քննարկենք
տատանողական
պրոցեսի
հաջորդական
փուլերը
իդեալական
կոնտուրում,
որի դիմադրությունն
աննշան փոքր է
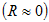 :Կոնտուրում
տատանումներ
գրգռելու
համար կոնդենսատորը
նախապես
լիցքավորում
են, հաղորդելով
նրա
շրջադիրներին
:Կոնտուրում
տատանումներ
գրգռելու
համար կոնդենսատորը
նախապես
լիցքավորում
են, հաղորդելով
նրա
շրջադիրներին
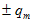 լիցք:
Այդ դեպքում
ժամանակի t = 0
սկզբնական
պահին (նկ. 5, ա)
կոնդենսատորի
շրջադիրների
միջև
առաջանում է
էլեկտրական
դաշտ, որի
էներգիան
հավասար է q2m /2C
: Եթե
կոնդենսատորը
փակենք
ինդուկտիվության
կոճով, այն
սկսում է
լիցքաթափվել,
և կոնտուրով
կանցնի
ժամանակի
ընթացքում
աճող I հոսանք:
Արդյունքում
էլեկտրական
դաշտի
էներգիան փոքրանում
է, իսկ կոճի
մագնիսական
դաշտի
էներգիան
լիցք:
Այդ դեպքում
ժամանակի t = 0
սկզբնական
պահին (նկ. 5, ա)
կոնդենսատորի
շրջադիրների
միջև
առաջանում է
էլեկտրական
դաշտ, որի
էներգիան
հավասար է q2m /2C
: Եթե
կոնդենսատորը
փակենք
ինդուկտիվության
կոճով, այն
սկսում է
լիցքաթափվել,
և կոնտուրով
կանցնի
ժամանակի
ընթացքում
աճող I հոսանք:
Արդյունքում
էլեկտրական
դաշտի
էներգիան փոքրանում
է, իսկ կոճի
մագնիսական
դաշտի
էներգիան 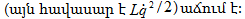
Քանի
որ 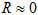 է,
ապա համաձայն
էներգիայի
պահպաման
օրենքի`
է,
ապա համաձայն
էներգիայի
պահպաման
օրենքի`
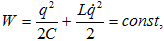
քանի
որ այն չի ծախսվում
տաքացման
վրա: t =
T/4 պահին,
երբ կոնդենսատորը
լրիվ
լիցքաթափվում
է, էլեկտրական
դաշտի
էներգիան
դառնում
է զրո, մագնիսական
դաշտի
էներգիան
և, հետևաբար
հոսանքը
հասնում
են առավելագույն
արժեքի
(նկ. 5, բ): Այդ պահից
սկսած`
հոսանքն
անցնում
է ինքնամակածման`
ԷլՇՈւ-ի հաշվին: Հետագայում
հոսանքը
փոքրանում
է, և երբ լիցքերը
կոնդենսատորի
շրջադիրների
վրա հասնում
են նախնական
մեծության,
հոսանքի
ուժը
հավասարվում
է զրոյի
(նկ. 5, գ): Վերալիցքավորման
արդյունքում
կոնդենսատորի
շրջադիրների
լիցքերը
փոխում
են իրենց
նշանները:
Դրանից
հետո
լիցքերը
սկսում
են շարժվել
հակառակ
ուղղությամբ:
Էլեկտրական
դաշտը
նորից
սկսում
է փոքրանալ,
և կոճի ներսում
դարձյալ
ի հայտ է գալիս մագնիսական
դաշտ:
Երբ էլեկտրական
դաշտը
լրիվ
անհետանում
է, մագնիսական
դաշտը
հասնում
է իր առավելագույն
արժեքին
(նկ. 5, դ):
Այնուհետև
կոճի
մագնիսական
դաշտը,
փոքրանալով,
դարձյալ
լիցքավորում
է կոնդենսատորը.
և համակարգը
վերադառնում
է իր սկըզբնական
վիճակին
(նկ. 5, ե): Այս պահից
սկսած`
ամբողջ
պրոցեսը
կրկնվում
է նորից
ու նորից:
Նկարագրված
պրոցեսի
ընթացքում
պարբերաբար
փոփոխվում
են (այսինքն
տատանվում
են)` շրջադիրների
վրա լիցքը,
կոնդենսատորում`
U լարումը
և ինդուկտիվության
միջով
անցնող
I հոսանքի
ուժը:
Տատանումները
ուղեկցվում
են էլեկտրական
և մագնիսական
դաշտերի
էներգիաների
փոխադարձ
փոխարկումներով:
Նկ.5-ում
կոնտուրում
կատարվող
տատանումներին
համադրված են
զսպանակավոր
ճոճանակի
տատանումները:
Կոնդենսատորի
շրջադիրներին
լիցք
հաղորդելուն
համապատասխանում
է ճոճանակը
արտաքին
ուժով
հավասարակշռության
վիճակից
հանելուն և
նրան
նախնական
շեղում հաղորդելուն:
Այդ դեպքում
առաջանում է
զսպանակի
առաձգական
դեֆորմացիայի
պոտենցիալ էներգիա,
որը հավասար է
kx2m/2:
Հաջորդ
փուլին
համապատասխանում
է ճոճանակի
անցումը
հավասարակշռության
վիճակով: Այդ պահին
քվազիառաձգական
ուժը հավասար
է զրոյի, և
ճոճանակը
սկսում է
շարժվել
իներցիայով:
Ճոճանակի
էներգիան
լրիվ փոխարկվում
է կինետիկ
էներգիայի և
որոշվում է 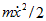 արտահայտությամբ:
Հետագա
փուլերի
համադրումը
թողնում ենք
ուսանողին:
Էլեկտրամագնիսական
և
մեխանիկական
տատանումների
համադրումից
հետևում է, որ
էլեկտրական
դաշտի q2/2C
էներգիան
համանման է
առաձգական
դեֆորմացիայի
պոտենցիալ
էներգիային,
իսկ
մագնիսական դաշտի
Ll2 / 2
էներգիան` կինետիկ
էներգիային: L
ինդուկտիվությունը
կատարում է m
զանգվածի
դերը,
ունակության
հակադարձ (1/C)
մեծությունը k
կոշտության
գործակցի
դերը,
կոնտուրի R
դիմադրության
դերը`
դիմադրության
ուժը:
Վերջապես, q
լիցքին համապատասխանում
է
հավասարակշռության
դիրքից
ճոճանակի x
շեղումը, իսկ
արտահայտությամբ:
Հետագա
փուլերի
համադրումը
թողնում ենք
ուսանողին:
Էլեկտրամագնիսական
և
մեխանիկական
տատանումների
համադրումից
հետևում է, որ
էլեկտրական
դաշտի q2/2C
էներգիան
համանման է
առաձգական
դեֆորմացիայի
պոտենցիալ
էներգիային,
իսկ
մագնիսական դաշտի
Ll2 / 2
էներգիան` կինետիկ
էներգիային: L
ինդուկտիվությունը
կատարում է m
զանգվածի
դերը,
ունակության
հակադարձ (1/C)
մեծությունը k
կոշտության
գործակցի
դերը,
կոնտուրի R
դիմադրության
դերը`
դիմադրության
ուժը:
Վերջապես, q
լիցքին համապատասխանում
է
հավասարակշռության
դիրքից
ճոճանակի x
շեղումը, իսկ 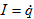 հոսանքի
ուժին`
հոսանքի
ուժին` 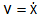 արագությունը:
Ինչպես
կտեսնենք
ստորև, էլեկտրական
և
մեխանիկական
տատանումների
համանմանությունը
տարածվում է
նաև դրանք
նկարագրող մաթեմատիկական
հավասարումների
վրա:
արագությունը:
Ինչպես
կտեսնենք
ստորև, էլեկտրական
և
մեխանիկական
տատանումների
համանմանությունը
տարածվում է
նաև դրանք
նկարագրող մաթեմատիկական
հավասարումների
վրա:
Համաձայն
Օհմի օրենքի, L
ինդուկտիվության
կոճ, C
ունակության
կոնդենսատոր
և R
դիմադրություն
ունեցող
կոնտուրի
համար`
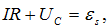
որտեղ
IR -ը լարումն է
դիմադրության
վրա, Uc = q/C - ն
լարումն է
կոնդենսատորի
վրա,
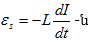
ինքնամակածման
ԷլՇՈւ-ն է, որն
առաջանում է
կոճում
փոփոխական
հոսանք
անցնելու
դեպքում: Հետևաբար`

Բաժանելով
(4.1) -ը L -ի և
տեղադրելով 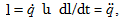 կստանանք
q լիցքի
տատանման
դիֆերենցիալ
հավասարումը.
կստանանք
q լիցքի
տատանման
դիֆերենցիալ
հավասարումը.

Տվյալ
տատանողական կոնտուրում
արտաքին
ԷլՇՈւ-ն
բացակայում է,
ուստի
դիտարկվող
տատանումները
ազատ տատանումներ
են: Եթե R
դիմադրությունը
հավասար է զրոյի,
կոնտուրում
էլեկտրամագնիսական
տատանումները
ներդաշնակ են:
Այդ դեպքում
(4.2)-ից կստանանք
կոնտուրում
լիցքի
ներդաշնակ
տատանումների
դիֆերենցիալ
հավասարումը.
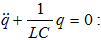
(3.1)
և (1.1)
արտահայտություններից
բխում է, որ q
լիցքը
կատարում է
ներդաշնակ
տատանումներ
ըստ հետևյալ
օրենքի`

որտեղ
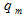 -ը
կոնդենսատորի
լիցքի
լայնույթի
տատանումներն
են
-ը
կոնդենսատորի
լիցքի
լայնույթի
տատանումներն
են 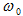 ցիկլային
հաճախությունով,
որն անվանում
են կոնտուրի
սեփական
հաճախություն,
այսինքն`
ցիկլային
հաճախությունով,
որն անվանում
են կոնտուրի
սեփական
հաճախություն,
այսինքն`
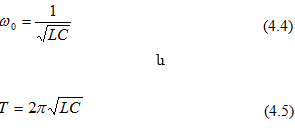
պարբերությամբ:
(4.5)
բանաձևը
առաջին անգամ
ստացել է
Թոմսոնը և կոչվում
է նրա
անունով:
Հոսանքի ուժը
տատանողական
կոնտուրում`
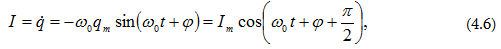
որտեղ
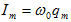 -ը
հոսանքի ուժի
լայնույթն է:
Լարումը
կոնդենսատորի
վրա`
-ը
հոսանքի ուժի
լայնույթն է:
Լարումը
կոնդենսատորի
վրա`
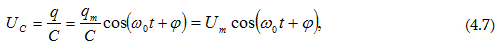
որտեղ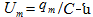 լարման
լայնույթն է:
լարման
լայնույթն է:
(4.3)
և (4.6)
արտահայտություններից
հետևում է, որ I
հոսանքի
տատանումները
q լիցքի
տատանումներից
առաջ են
ընկնում π/2
փուլով,
այսինքն, երբ
հոսանքը
հասնում է իր
առավելագույն
արժեքին, լիցքը
(ինչպես նաև
լարումը)
դառնում են
զրո և հակառակը:
>>
5.
Միևնույն
ուղղությունն
և միատեսակ
հաճախություններ
ունեցող
տատանումների
գումարումը:
Զարկումներ
Տատանվող
մարմինը
կարող է
մասնակցել
միաժամանակ
մի քանի
տատանումների:
Եթե, օրինակ,
զսպանակը, որի
ծայրին ամրացված
է գնդիկ,
կախենք այն
վագոնի
առաստաղից, որը
ճոճվում է
զսպանակների
վրա, ապա
գնդիկի շարժումը
Երկրի
մակերևույթի
նկատմամբ
բաղկացած
կլինի Երկրի
նկատմամբ
վագոնի
տատանումներից
և վագոնի
նկատմամբ
գնդիկի
տատանումներից:
Քննարկենք
միևնույն
ուղղություններով
և միատեսակ
հաճախություններով
կատարվող
երկու ներդաշնակ
տատանումների
գումարումը:
Տատանվող
մարմնի
արդյունարար x
շեղումը
հավասար
կլինի x1 և x2
շեղումների
գումարին,
որոնցից
յուրաքանչյուրը
տրվում է
հետևյալ
հավասարումներով`
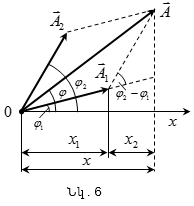
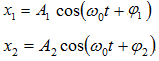
Oգտվելով
լայնույթի
վեկտորի
պտտման
մեթոդից`
կառուցենք
այդ
տատանումների
վեկտորական դիագրամը
(նկ.6): Քանի որ 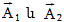 վեկտորները
պտտվում են
միևնույն
վեկտորները
պտտվում են
միևնույն 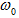 անկյունային
արագությամբ,
ապա նրանց
միջև
անկյունային
արագությամբ,
ապա նրանց
միջև 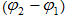 փուլերի
տարբերությունը
մնում է
հաստատուն:
Ակներև է, որ
արդյունարար
տատանումը
կլինի.
փուլերի
տարբերությունը
մնում է
հաստատուն:
Ակներև է, որ
արդյունարար
տատանումը
կլինի.
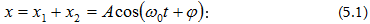
(5.1)
արտահայտության
մեջ A
լայնույթը և
սկզբնական φ
փուլը տրվում
են
համապատասխանաբար
հետևյալ
առնչություններով`
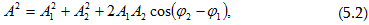
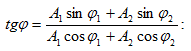
Այսպիսով,
մենք տեսնում
ենք, որ
արդյունարար տատանումը
նույնպես
ներդաշնակ
տատանում է,
որը տեղի է
ունենում
նույն
ուղղությամբ,
ինչ որ գումարվող
տատանումները
և կատարվում
են այդ տատանումների
հաճախությանը
հավասար
հաճախությամբ:
Վերլուծենք
(5.2)
արտահայտությունը`
կախված  փուլերի
տարբերությունից.
փուլերի
տարբերությունից.
1) եթե
գումարվող
տատանումների
փուլերի տարբերությունը`
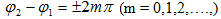
ապա
արդյունարար
տատանման A1 լայնույթը
հավասար է
գումարվող
տատանումների
A1 և A2
լայնույթների
գումարին
`A = A1 + A2 :
2)
եթե 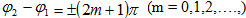 ապա
ապա
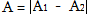 այսինքն`
արդյունարար
տատանման A
լայնույթը
հավասար է
գումարվող
տատանումների
A1 և A2 լայնույթների
տարբերության
բացարձակ արժեքին:
այսինքն`
արդյունարար
տատանման A
լայնույթը
հավասար է
գումարվող
տատանումների
A1 և A2 լայնույթների
տարբերության
բացարձակ արժեքին:
Գործնականում
հատուկ
հետաքրքրություն
է ներկայացնում
այն դեպքը,
երբ միևնույն
ուղղությամբ
կատարվող
երկու
ներդաշնակ
տատանումների
գումարման
դեպքում
դրանց
հաճախություններն
աննշան
տարբերվում
են իրարից:
Այդ տատանումների
գումարման
արդյունքում
ստացվում են
պարբերաբար
փոփոխվող
լայնույթով տատանումներ:
Տատանումների
լայնույթի
պարբերական
փոփոխությունները,
որոնք
առաջանում է
իրար մոտ
հաճախություններով
երկու ներդաշնակ
տատանումների
գումարման
դեպքում,
կոչվում են զարկումներ:
Դիցուք
գումարվող
տատանումների
A
լայնույթները
իրար հավասար
են,
հաճախությունները`
ω և ω + Δω և է, ընդ
որում Δω << ω:
Հաշվարկման
սկիզբն
ընտրենք
այնպես,
որպեսզի
երկու տատանումների
սկզբնական
փուլերը
հավասար լինեն
զրոյի.
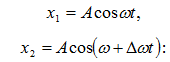
Գումարելով
այս
արտահայտությունները
և նկատի
ունենալով,
որ Δω/2 << ω -ից
ստանում ենք`
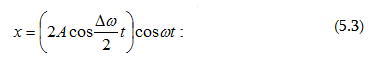
Արդյունարար
(5.3) տատանումը
կարելի է
դիտարկել
որպես ω
հաճախությամբ
ներդաշնակ
տատանում, որի
Aզարկ
լայնույթը փոփոխվում
է հետևյալ
պարբերական
օրենքով`

Aզարկ
-ի փոփոխման
հաճախությունը
երկու անգամ
մեծ է
կոսինուսի
փոփոխման
հաճախությունից
(քանի որ
վերցվում է
ըստ մոդուլի),
այսինքն`
զարկումների
հաճախությունը
հավասար է
գումարվող
տատանումների
հաճախությունների
տարբերությանը.
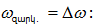
Զարկումների
պարբերությունը`
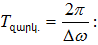
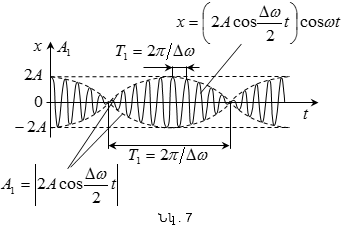
(5.3)-ի
կախվածության
բնույթը
ցույց է տրված
նկ.7-ում, որտեղ
անընդհատ
գծերը տալիս
են (5.3) արդյունարար
տատանման
գրաֆիկը, իսկ
նրանց
պարուրիչը
շտրիխներով`
լայնույթի
դանդաղ
փոփոխման գրաֆիկը
ըստ (5.4)
հավասարման:
Զարկումների
տոնի
հաճախության
որոշումը էտալոնային
և չափվող
տատանումների
միջև
գործնականում
օգտագործվող
ավելի լայն
կիրառելի
մեթոդ է`
համեմատելու
չափվող
մեծությունը
էտալոնայինի
հետ:
>>
6.
Փոխուղղահայաց
տատանումների
գումարումը
Դիտարկենք
միևնույն ω
հաճախություններով
երկու
ներդաշնակ
տատանումների
գումարման
արդյունքը,
որոնք տեղի են
ունենում
փոխուղղահայաց
ուղղություններով
x և y
առանցքների
երկայնքով:
Պարզության
համար
հաշվարկման
սկիզբն
ընդունենք այնպես,
որ առաջին
տատանման
սկզբնական
փուլը հավասար
լինի զրոյի և
գրենք.

Որտեղ
α-ն երկու տատանումների
փուլերի
տարբերությունն
է, A1 -ը և A2 -ը
գումարվող
տատանումների
լայնույթներն
են:
Արդյունարար
տատանումների
հետագծի
հավասարումը
ստանալու
համար պետք է (6.1)
հավասարումներից
արտաքսել t
պարամետրը:
Գումարվող
տատանումները
գրենք
հետևյալ տեսքով.
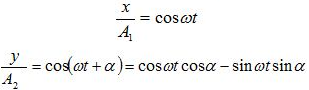
և
փոխարինելով
երկրորդ
հավասարման
մեջ
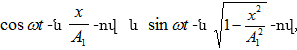
ոչ
բարդ
ձևափոխություններից
հետո կստանանք
էլիպսի
հավասարում,
որի
առանցքները
կոորդինատային
առանցքների
նկատմամբ
կողմնորոշված
են
կամայականորն.
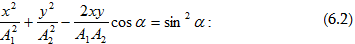
Քանի
որ
արդյունարար
տատանման
հետագիծն ունի
էլիպսի տեսք,
ապա այդպիսի
տատանումները
կոչվում են էլիպսաձև
բևեռացված:
Էլիպսի
կողմնորոշումը
և նրա չափերը
կախված են
գումարվող
տատանումների
լայնույթներից
և 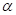 փուլերի
տարբերությունից:
Քննարկենք մի
քանի
մասնավոր
դեպքեր.
փուլերի
տարբերությունից:
Քննարկենք մի
քանի
մասնավոր
դեպքեր.
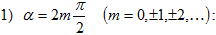
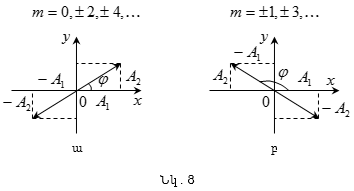
Տվյալ
դեպքոքում (6.2)
էլիպսի
հավասարումը
դառնում է
ուղղիղ
հավասարում.

որտեղ
«+» նշանը
համապատասխանում
է m-ի զրո և
զույգ արժեքներին
նկ. 8, ա), իսկ «-»-ը` m-ի
կենտ
արժեքներին (նկ.
8, բ): Արդյունարար
տատանումը ω
հաճախությամբ
և 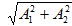 լայնույթով
տատանում է,
որը
կատարվում է (6.3)
ուղղի
երկայնքով x
առանցքի հետ
կազմելով φ = arctg (A2/A1)
անկյուն:
Տվյալ
դեպքում գործ
ունենք
գծային բևեռացված
տատանումների
հետ:
լայնույթով
տատանում է,
որը
կատարվում է (6.3)
ուղղի
երկայնքով x
առանցքի հետ
կազմելով φ = arctg (A2/A1)
անկյուն:
Տվյալ
դեպքում գործ
ունենք
գծային բևեռացված
տատանումների
հետ:
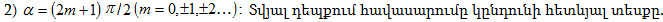

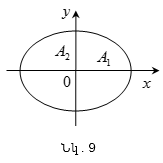
Այս
հավասարումը
էլիպսի
հավասարում է,
որի
առանցքները
համընկնում
են
կոորդինատային
առանցքների
հետ, իսկ
կիսաառանցքները
համապատասխանաբար
հավասար են
լայնույթներին
(նկ. 9):
A1
և A2
լայնույթների
հավասարության
դեպքում էլիպսը
վերածվում է
շրջանագծի:
Այդպիսի
տատանումները
կոչվում են
շրջանով բևեռացված
տատանումներ:
Եթե
փոխուղղահայաց
տատանումների
հաճախությունները
միատեսակ չեն,
արդյունարար
տատանման
հետագիծն
ունի
բավականին
բարդ տեսք. դրանք
կոչվում են
Լիսաժուի
պատկերներ:
Այդ կորերի
տեսքը կախված
է
լայնույթների,
հաճախությունների
հարաբերակցությունից
և վերադրվող տատանումների
փուլերի
տարբերությունից:
Նկ. 10-ում
բերված են
Լիսաժուի
պատկերները
տարբեր
հաճախությունների
(ցույց է
տրված ձախից)
հարաբերակցության
և փուլերի
տարբերության
ցույց է
տրված
վերևում,
փուլերի
տարբերությունը
ընդունվում է
հավասար α-ի
համար:
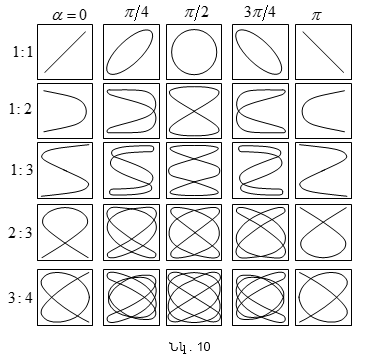
Ըստ
պատկերների
ձևի կարելի է
որոշել
անհայտ հաճախությունը
կամ որոշել
գումարվող
տատանումների
հաճախությունների
հարաբերությունը:
Ուստի
Լիսաժուի
պատկերների
վերլուծությունը
հաճախությունների
և գումարվող
տատանումների
փուլերի
տարբերության
հարաբերակցության,
ինչպես նաև
տատանումների
ձևի
հետազոտությունների
լայն օգտագործման
մեթոդ է:
>>
7.
Մեխանիկական
և
էլեկտրամագնիսական
մարող տատանումների
դիֆերենցիալ
հավասարումը
և
նրա լուծումը:
Ինքնատատանումներ
Քննարկենք
այն ազատ մարող
տատանումները,
որոնց
լայնույթները
իրական
տատանվող
համակարգում
էներգիայի
կորստի
պատճառով
ժամանակի
ընթացքում
փոքրանում
են: Տատանումների
էներգիայի
նվազման
պարզագույն
մեխանիզմը
մեխանիկական
տատանողական
համակարգերում
շփման
հետևանքով
նրա էներգիայի
փոխակերպումն
է ջերմաքանակի,
ինչպես
նաև էլեկտրական
տատանողական
համակարգերում
էլեկտրական
դաշտի
էներգիան
աստիճանաբար
փոխակերպվում
է հաղորդալարերի
ներքին
էներգիայի
(դրանք
տաքանում
են), որի պատճառով
տատանումները
մարում
են:
Տատանումների
մարման
օրենքը
որոշվում
է տատանողական
համակարգի
հատկություններով:
Սովորաբար
քննարկում
են գծային
համակարգեր`
իդեալականացված
իրական
համակարգեր,
որոնցում
համակարգի
ֆիզիկական
հատկությունները
որոշող
պարամետրերը
պրոցեսի
ընթացքում
չեն փոփոխվում:
Գծային
համակարգեր
են օրինակ,
զսպանակավոր
ճոճանակը
զսպանակի
փոքր
դեֆորմացիաների
դեպքում
(երբ ճիշտ է Հուկի օրենքը),
տատանողական
կոնտուրը,
որի ինդուկտիվությունը,
ունակությունը
և դիմադրությունը
կախված
չեն կոնտուրում
ոչ հոսանքից
և ոչ էլ լարումից:
Ըստ
իրենց
բնույթի
տարբեր
գծային
համակարգերը
նկարագըրվում
են համանման
գծային
դիֆերենցիալ
հավասարումներով,
ինչն
էլ հնարավորություն
է տալիս
տարբեր
ֆիզիկական
բնույթի
տատանումների
ուսումնասիրությանը
միատեսակ
մոտեցում
ցուցաբերել,
ինչպես
նաև կատարել
նրանց
մոդելավորում,
այդ թվում
և հաշվիչ
մեքենաներով:
Գծային
համակարգերի
ազատ
մարող
տատանումների
դիֆերենցիալ
հավասարումը
տրվում
է հետևյալ
տեսքով`
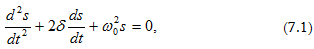
որտեղ
s-ը տատանվող
մեծությունն
է, որը նկարագրում
է այս կամ այն ֆիզիկական
պրոցես,
δ -ն մարման
գործակիցն է, 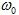 -ն
նույն
տատանողական
համակարգի
ազատ չմարող
տատանումների
ցիկլային
հաճախությունն
է, այսինքն δ = 0-ի
դեպքում
(էներգիայի
կորստի բացակայության
դեպքում)
կոչվում է
տատանողական
համակարգի
սեփական
հաճախություն:
(7.1) հավասարման
լուծումը
փնտրենք
հետևյալ
տեսքով`
-ն
նույն
տատանողական
համակարգի
ազատ չմարող
տատանումների
ցիկլային
հաճախությունն
է, այսինքն δ = 0-ի
դեպքում
(էներգիայի
կորստի բացակայության
դեպքում)
կոչվում է
տատանողական
համակարգի
սեփական
հաճախություն:
(7.1) հավասարման
լուծումը
փնտրենք
հետևյալ
տեսքով`

որտեղ
u = u(t):
Գտնելով
(7.2)
արտահայտության
առաջին և
երկրորդ
կարգի
ածանցյալները,
(7.1) -ի մեջ
տեղադրելուց
հետո
կստանանք`

(7.3)
հավասարման
լուծումը
կախված է
որոնելի մեծության
առաջ դրված
գործակցի
նշանից: Քննարկենք
այն դեպքը,
երբ այդ
գործակիցը
դրական է

Այդ
դեպքում
ստանում
ենք (3.1)
տեսքի
հավասարում,
որի լուծումը`
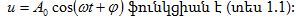
Այսպիսով,
(7.1) հավասարման
լուծումը
փոքր մարումների
դեպքում 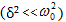 .
.
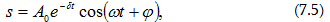
որտեղ

մարող
տատանումների
լայնույթն
է, A0-ն սկզբնական
լայնույթն
է: (7.5) կախվածության
գրաֆիկը
բերված
է նկ. 11-ում անընդհատ
գծով,
իսկ (7.6) կախվածությունը`
կետագծերով:
Գտնենք
այն τ
ժամանակը,
որի ընթացքում
լայնույթը
փոքրանում
է e անգամ:
Ըստ սահմանման
e-δτ = e-1, որտեղից
δτ=1: Հետևաբար,մարման
գործակցի
մեծությունը
հակադարձ
համեմատական
է այն ժամանակամիջոցին,
որի ընթացքում
լայնույթը
փոքրանում
է e անգամ:
τ-ն կոչվում է ռելաքսացիայի
ժամանակ:
Մարումը
խանգարում
է տատանումների
պարբերականությանը,
ուստի
մարող
տատանումները
պարբերական
չեն և, խիստ ասած, դրանց նկատմամբ
կիրառելի
չէ պարբերության
և հաճախության
հասկացությունը:
Սակայն,
եթե մարումը
փոքր
է, ապա պայմանականորեն
կարելի
է օգտվել
պարբերության
հասկացությունից
որպես
տատանվող
ֆիզիկական
մեծության
երկու
հաջորդական
առավելագույնների
(կամ նվազագույնների)
միջև
ժամանակի
միջակայք
(նկ.11): Ուստի
մարող
տատանումների
պարբերությունը,
նկատի
ունենալով
(7.4) բանաձևը,
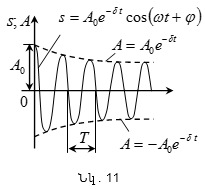
կստանանք`
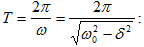
Մի
պարբերությամբ
իրարից
տարբերվող
ժամանակի
պահերին
համապատասխանող
լայնույթների
արժեքների
հարաբերությունը`
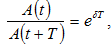
կոչվում
է մարման
դեկրեմենտ,
իսկ նրա
լոգարիթմը`
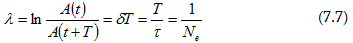
մարման
լոգարիթմական
դեկրեմենտ:
Ne -ն տատանումների
այն թիվն է, որը կատարվում
է այն ժամանակամիջոցում,
որի ընթացքում
տատանման
լայնույթը
փոքրանում
է е անգամ:
Տվյալ
համակարգի
համար
լոգարիթմական
դեկրեմենտը
հաստատուն
մեծություն
է:
Տատանողական
համակարգի
բնութագրման
համար
օգտագործում
են Q բարորակության
հասկացությունը,
որը լոգարիթմական
դեկրեմենտի
փոքր
արժեքների
դեպքում`
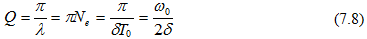
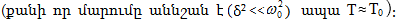
(7.8)
բանաձևից
հետևում է, որ
բարորակությունը
ուղիղ
համեմատական
է
տատանումների
այն Ne,
որը կատարում
է համակարգը
ռելաքսացիայի
ժամանակամիջոցում:
Արտածումները,
որոնք
ստացվեցին
գծային համակարգերի
համար,
կիրառելի են
տարբեր
բնույթի
ֆիզիկական
տատանումների
համար` մեխանիկական
(որպես օրինակ
կքննարկենք
ֆիզիկական
ճոճանակը) և
էլեկտրական
(որպես օրինակ
կքննարկենք
էլեկտրական
տատանողական
կոնտուրը):
ա)
զսպանակավոր
ճոճանակի
ազատ մարող
տատանումները: m
զանգվածով
զսպանակավոր
ճոճանակի
համար, որը
կատարում է
փոքր
տատանումներ F
= -kx առաձգական
ուժի
ազդեցության
տակ, շփման ուժը
համեմատական
է
արագությանը,
այսինքն`
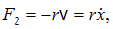
որտեղ
r-ը
դիմադրության
գործակիցն է,
բացասական
նշանը ցույց է
տալիս, որ
դիմադրության
ուժը և
արագությունն
ունեն
հակառակ
ուղղություններ:
Տվյալ
պայմանների
դեպքում ճոճանակի
շարժման
օրենքը
կունենա
հետևյալ տեսքը
(7.10)

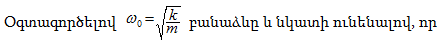

կստանանք
(7.1)-ին համանման
ճոճանակի
մարող տատանումների
դիֆերենցիալ
հավասարումը.
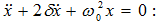
(7.1) և (7.5)
արտահայտություններից
հետևում է, որ
ճոճանակի
տատանումները
ենթարկվում
են հետևյալ
օրենքին`
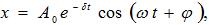
որտեղ
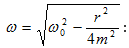
Զսպանակավոր
ճոճանակի
բարորակությունը
համաձայն (7.8) և
(7.10) բանաձևերի`
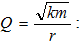
բ)
Ազատ մարող
տատանումները
էլեկտրական
տատանողական
կոնտուրում
Լիցքի
ազատ մարող
տատանումների
դիֆերենցիալ
հավասարումը (R
≠0)
դեպքում ըստ
(4.2)-ի
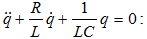
Նկատի
ունենալով
(4.4)-ը և
ընդունելով
մարման գործակիցը`

վերևի
դիֆերենցիալ
հավասարումը
կարելի է գրել
(7.1) հավասարման
նման.
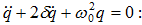
(7.1)
և (7.5)
արտահայտություններից
հետևում է, որ
լիցքի
տատանումները
կատարվում են
ըստ հետևյալ
օրենքի`(7.14)
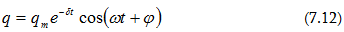
և
համաձայն (7.4)-ի

հաճախությունով,
որը փոքր է
կոնտուրի
սեփական 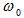 հաճախությունից:
R = 0 դեպքում (7.13)-ը
անցնում է (4.4)-ին:
հաճախությունից:
R = 0 դեպքում (7.13)-ը
անցնում է (4.4)-ին:
Մարման
լոգարիթմական
դեկրեմենտը
որոշվում է (7.7)
բանաձևով,
տատանողական
կոնտուրի
բարորակությունը
(տես (7.8))`

բանաձևով:
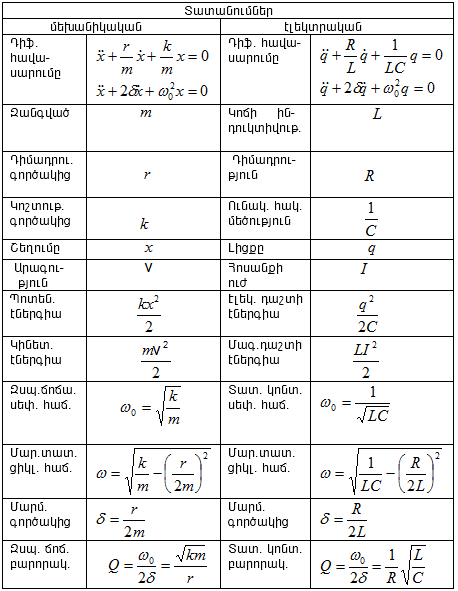
Աղյուսակ
1-ում կատարված
է տատանողական
կոնտուրում
և զսպանակավոր
ճոճանակում
մարող
տատանումների
համադրումը:
Աղյուսակ 1
Վերջում
նշենք,
որ δ
մարման գործակցի
մեծացման
դեպքում
մարող
տատանումների
պարբերությունը
մեծանում
է և 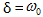 դեպքում
դառնում
է ∞, այսինքն
շարժումը
դառնում
է ոչ պարբերական:
Այս դեպքում
տատանվող
մեծությունը
ասիմպտոտորեն
մոտենում
է զրոյի,
երբ
դեպքում
դառնում
է ∞, այսինքն
շարժումը
դառնում
է ոչ պարբերական:
Այս դեպքում
տատանվող
մեծությունը
ասիմպտոտորեն
մոտենում
է զրոյի,
երբ 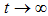 : Տվյալ
պրոցեսը
տատանողական
չէ, դառնում
է ապերիոդիկ:
: Տվյալ
պրոցեսը
տատանողական
չէ, դառնում
է ապերիոդիկ:
Տեխնիկայի
համար
մեծ հետաքրքրություն
ունի
չմարող
տատանումների
պահպանելու
հնարավորությունը:
Դրա համար
անհրաժեշտ
է համալրել
էներգիայի
կորուստը
իրական
տատանողական
համակարգում:
Հատկապես
կարևոր
և լայն կիրառական
է այսպես
կոչված
ինքնատատանումները`
չմարող
տատանումները,
որոնք
պահպանվում
են դիսիպատիվ
համակարգում
արտաքին
էներգիայի
աղբյուրի
հաշվին,
ընդ որում
այդ տատանումների
հատկությունները
որոշվում
է հենց իր` համակարգով:
Ինքնատատանումները,
ինչպես
և հարկադրական
տատանումները
ուղեկցվում
են տատանվող
համակարգի
վրա արտաքին
ուժերի
ազդեցությամբ,
սակայն
ժամանակի
այն պահերը,
երբ տեղի է ունենում
այս ազդեցությունները,
որոշվում
է հենց իր` տատանվող
համակարգի
կողմից,
այսինքն`
ինքը
տատանվող
համակարգն
է ղեկավարում
արտաքին
ազդեցությունները:
Օրինակ`
ժամացույցը,
որի մեջ ճոճանակը
հրվում
է վեր բարձրացրած
ծանրության
կամ ոլորված
զըսպանակի
էներգիայի
հաշվին,
ընդ որում
այս հրումները
տեղի
են ունենում
այն պահին,
երբ ճոճանակն
անցնում
է իր միջին
դիրքով:
Ինքնատատանողական
համակարգեր
են նաև ներքին
այրման
շարժիչները,
շոգետուրբինները,
լամպային
գեներատորները
և այլն:
>>
8.
Մեխանիկական
և
էլեկտրամագնիսակ
հարկադրական
տատանումների
դիֆերենցիալ
հավասարումը
և նրա
լուծումը
Որպեսզի
իրական
տատանողական
համակարգում ստացվեն
չմարող
տատանումներ
հարկավոր է կոմպենսացնել
էներգիայի
կորուստը:
Այդպիսի կոմպենսացումը
հնարավոր է
ինչ որ
պարբերաբար
ազդող X(t)
գործոնի
օգնությամբ,
որը փոփոխվում
է ներդաշնակ
օրենքով.
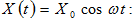
Եթե
դիտարկենք
մեխանիկական
տատանումները,
ապա X(t)-ի դերը
խաղում է
հարկադրող
ուժը`

հաշվի
արնելով (8.1)-ը
զսպանակավոր
ճոճանակի շարժման
օրենքի
համար (7.9)-ը
գրվում է
հետևյալ տեսքով`
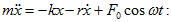
Օգտագործելով
(3.2)-ը և (7.10)-ը` գալիս
ենք հետևյալ
հավասարման`
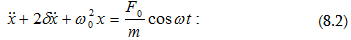
Եթե
դիտարկենք
էլեկտրական
տատանողական
կոնտուր,
ապա X(t)-ի դերը
խաղում
է կոնտուրին
մատուցվող
արտաքին
ըստ ներդաշնակ
օրենքով
պարբերաբար
փոփոխվող
ԷլՇՈւ-ն կամ փոփոխական
լարումը.

Այս
դեպքում (4.2)
հավասարումը
նկատի
ունենալով` (8.3)-ը
կարելի է գրել
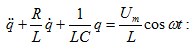
Օգտագործելով
(4.4)-ը և (7.11)-ը`
հանգում ենք
հետևյալ հավասարմանը`
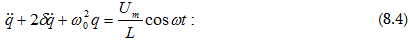
Այն
տատանումները,
որոնք
առաջանում են
արտաքին
պարբերաբար
փոփոխվող
ուժի կամ
արտաքին պարբերաբար
փոփոխվող
ԷլՇՈւ-ի
ազդեցության տակ,
համապատասխանաբար
կոչվում են հարկադրական
մեխանիկական
և
հարկադրական
էլեկտրամագնիսական
տատանումներ:
(8.2)
և (8.4)
հավասարումները
կարելի է
բերել
անհամասեռ
գծային
դիֆերենցիալ
հավասարման.
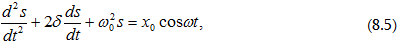
Կիրառելով
հավասարման
լուծումը
կոնկրետ ֆիզիկական
բնույթի
ստիպողական
տատանումների
համար
(մեխանիկական
տատանումների
դեպքում 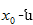 հավասար է F0
/ m-ի
էլետրամագնիսականի
դեպքում` Um /L ):
հավասար է F0
/ m-ի
էլետրամագնիսականի
դեպքում` Um /L ):
(8.5)
հավասարման
ընդհանուր
լուծումը
հավասար է (7.1)
համասեռ
հավասարման (7.5)
լուծման և
անհամասեռ
հավասարման
մասնակի
լուծումների
գումարին:
Մասնակի
լուծումը
գտնենք
կոմպլեքս տեսքով:
(8.5)
հավասարման
աջ մասը
փոխարինելով 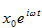 մեծությամբ
կստանանք`
մեծությամբ
կստանանք`

Այս
հավասարման
մասնակի
լուծումը
փնտրենք
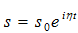 տեսքով:
Տեղադրելով
s-ի և նրա
ածանցյալների
արտահայտությունները
տեսքով:
Տեղադրելով
s-ի և նրա
ածանցյալների
արտահայտությունները
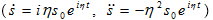 (8.6)
հավասարման
մեջ,
կստանանք`
(8.6)
հավասարման
մեջ,
կստանանք`
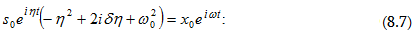
Քանի
որ այս
հավասարությունը
պետք է ճիշտ
լինի
ժամանակի
բոլոր
պահերին,
ուստի t
ժամանակը
նրանից պետք է
արտաքսել: Այստեղից
հետևում է, որ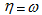 :
Վերջինը
նկատի
ունենալով`
(8.7)-ից կգտնենք S0
մեծությունը
և նրա
համարիչը և
հայտարարը բազմապատկելով
:
Վերջինը
նկատի
ունենալով`
(8.7)-ից կգտնենք S0
մեծությունը
և նրա
համարիչը և
հայտարարը բազմապատկելով
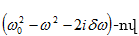 ստանում
ենք`
ստանում
ենք`
Քանի
որ այս
հավասարությունը
պետք է ճիշտ
լինի
ժամանակի
բոլոր
պահերին,
ուստի t
ժամանակը նրանից
պետք է
արտաքսել: Այստեղից
հետևում է, որ 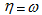 :
Վերջինը
նկատի
ունենալով`
(8.7)-ից կգտնենք s0
մեծությունը
և նրա
համարիչը և
հայտարարը
բազմապատկելով
:
Վերջինը
նկատի
ունենալով`
(8.7)-ից կգտնենք s0
մեծությունը
և նրա
համարիչը և
հայտարարը
բազմապատկելով
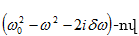 ստանում
ենք`
ստանում
ենք`
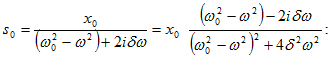
Այս
կոմպլեքս
թիվը հարմար է
ներկայացնել
էքսպոնենցիալ
տեսքով`
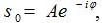
որտեղ
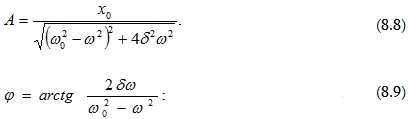
Հետևաբար,
(8.6) հավասարման
լուծումը
կոմպլեքս
ձևով
կընդունի
հետևյալ
տեսքը`
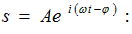
Նրա
իրական մասը,
որը (8.5)
հավասարման
լուծումն է,
հավասար է `

որտեղ
A-ն և φ-ն
համապատասխանաբար
տրվում են (8.8)-ով
և (8.9)-ով:
Այսպիսով
(8.5) անհամասեռ
հավասարման
մասնակի լուծումը
ունի հետևյալ
տեսքը`
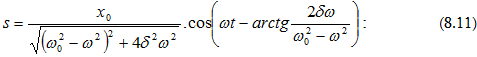
(8.5)
հավասարման
լուծումը
հավասար է
համասեռ հավասարման
լուծման.

և
(8.12) ու
(8.11) մասնակի
լուծման
գումարին:
(8.12)-ի գումարելին
զգալի
դեր է խաղում միայն
պրոցեսի
սկզբնական
փուլում,
այսպես
կոչված,
տատանումների
հաստատման
փուլում
(նկ. 12):
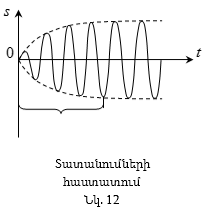
Ժամանակի
ընթացքում
e-δt էքսպոնենցիալ
արտադրիչի
առկայությամբ
(8.12) գումարելիի
դերն
առավել
փոքրանում
է, և բավականաչափ
ժամանակ
անցնելուց
հետո
այն կարելի
է անտեսել`
լուծման
մեջ պահպանելով
միայն
(8.11) գումարելին:
Այսպիսով,
(8.11) ֆունկցիան
նկարագրում
է հաստատված
հարկադրական
տատանումները:
Դրանք
ներդաշնակ
տատանումներ
են, որոնց
հաճախությունը
հավասար
է հարկադրող
ուժի
հաճախությանը:
Տատանումների
լայնույթը
և փուլը
որոշվում
են (8.8) և (8.9) արտահայտություններով:
Գրենք
(8.10), (8.8) և (8.9)
բանաձևերը
էլեկտրամագնիսական
տատաների
համար` հաշվի
առնելով, որ
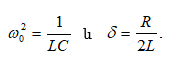

Դիֆերենցելով
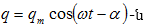 ըստ
ժամանակի`
կստանանք
կոնտուրում
կայունացված
տատանումների
դեպքում
հոսանքի ուժը.
ըստ
ժամանակի`
կստանանք
կոնտուրում
կայունացված
տատանումների
դեպքում
հոսանքի ուժը.
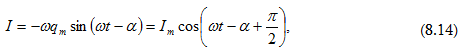
որտեղ
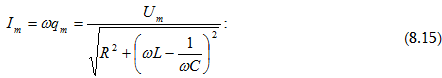
(8.14)
արտահայտությունը
կարելի է
գրել l = lm cos(ωt-φ)
տեսքով,
որտեղ φ = α – π/2 -ը
կիրառված
լարման և
հոսանքի միջև
փուլի շեղումն
է: (8.13)
հավասարման
համապատասխան`
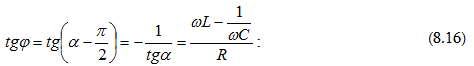
(8.16)
բանաձևից
հետևում է, որ
հոսանքը
լարումից փուլով
ետ է ընկնում
(φ > 0), եթե ωL > l/ωC և
լարումից առաջ
է ընկնում (φ < 0),
եթե ωL < l/ωC: (8.1) և (8.16) բանաձևերը
կարելի է
ստանալ նաև
վեկտորական դիագրամի
օգնությամբ:
>>
9.
Մեխանիկական
և
էլեկտրամագնիսական
հարկադրական
տատանումների
լայնույթը և
փուլը:
Ռեզոնանս
Քննարկենք
հարկադրական
տատանումների
A լայնույթիկախվածությունը
ω հաճախությունից:
Մեխանիկական
և էլեկտրամագնիսական
տատանումները
պետք է
քննարկենք միաժամանակ,
տատանվող
մեծություն
անվանելով
մերթ
տատանվող
մարմնի (x)
շեղումը
հավասարակշռության
դիրքից, մերթ
կոնդենսատորի
(q) լիցքը: (8.8)
բանաձևից
հետևում է, որ
շեղման
(լիցքի) A լայնույթը
ունի
առավելագույն
արժեք: Որպեսզի
որոշվի
ռեզոնանսային
ωռեզ
հաճախությունը,
որի դեպքում
շեղման
(լիցքի) A լայնույթը
հասնում է
առավելագույնի,
հարկավոր է
գտնել (8.8)
ֆունկցիայի
առավելագույնը
կամ, որ
նույնն է
արմատանշանի
տակ գտնվող
արտահայտության
նվազագույնը:
Ածանցելով
այդ
արտահայտությունն
ըստ ω-ի
և ստացված
արդյունքը
հավասարեցնելով
զրոյի,
կստանանք ωռեզ
որոշող
պայմանը.
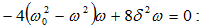
Այս
հավասարումը
ունի երեք
լուծում.
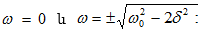
Զրոյի
հավասար
լուծումը
համապատասխանում
է հայտարարի
առավելագույնին:
Մնացած երկու լուծումներից
բացասականը
պետք է դեն
նետել, քանի
որ այն ոչ մի
ֆիզիկական
իմաստ չունի
(hաճախությունը
բացասական չի
կարող լինել):
Այսպիսով
ռեզոնանսային
հաճախության
համար
ստացվում է մեկ
արժեք,
այսինքն`

Հարկադրական
տատանումների
լայնույթի
կտրուկ աճի
երևույթը, երբ
հարկադրող
ուժի
(հարկադրող
փոփոխական
լարման
հաճախությունը)
հաճախությունը
մոտենում կամ
հավասարվում
է տատանվող
համակարգի
սեփական
հաճախությանը
կոչվում է
ռեզոնանս
(համապատասխանաբար
մեխանիկական
կամ
էլեկտրական):  պայմանի
դեպքում
գործնականում
ωռեզ -ը համընկնում
է
տատանողական
համակարգի ω0
հաճախության
հետ:
Տեղադրելով
(9.1)-ը (8.8)-ի մեջ կստանանք`
պայմանի
դեպքում
գործնականում
ωռեզ -ը համընկնում
է
տատանողական
համակարգի ω0
հաճախության
հետ:
Տեղադրելով
(9.1)-ը (8.8)-ի մեջ կստանանք`

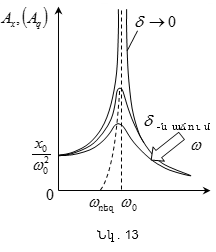
Նկ.
13-ում բերված
են տատանումների
լայնույթի
կախվածությունը
δ-ի
տարբեր արժեքների
դեպքում:
(9.1)-ից և (9.2)-ից հետևում
է, որ որքան
փոքր
է δ-ն այնքան բարձր
և աջ է ընկած տվյալ
կորի
առավելագույնը:
Երբ ω
→ 0 ապա
բոլոր
կորերը
հասնում
են միևնույն
զրոյից
տարբեր
սահմանային`
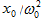 արժեքին,
որն անվանում
են ստատիկ
շեղում:
արժեքին,
որն անվանում
են ստատիկ
շեղում:
Մեխանիկական
տատանումների
դեպքում`
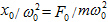 , իսկ
էլեկտրամագնիսական
տատանումների
դեպքում`
, իսկ
էլեկտրամագնիսական
տատանումների
դեպքում`
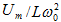 : Եթե
ω → ∞
ապա բոլոր
կորերը
ասիմպտոտորեն
ձգտում
են զրոյի:
Բերված
կորերի
ամբողջությունը
կոչվում
են ռեզոնանսային
կորեր:
: Եթե
ω → ∞
ապա բոլոր
կորերը
ասիմպտոտորեն
ձգտում
են զրոյի:
Բերված
կորերի
ամբողջությունը
կոչվում
են ռեզոնանսային
կորեր:
(9.2) բանաձևից
հետևում
է, որ փոքր մարումների
դեպքում
(δ2 << ω20 ) շեղման
(լիցքի)
ռեզոնանսային
լայնույթը`
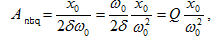
Որտեղ
Q -ն տատանվող
համակարգի
բարորակությունն
է: Այստեղից
հետևում
է, որ Q
բարորակությունը
բնութագրում
է տատանողական
համակարգի
ռեզոնանսային
հատկությունը:
Որքան
մեծ է Q -ն, այնքան
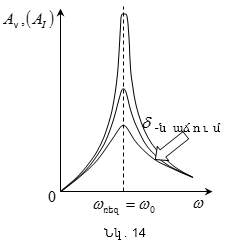
մեծ է Aռեզ –ը: Նկ. 14-ում
բերված
են ռեզոնանսային
կորերը
արագության
(հոսանքի)
լայնույթի
համար.
Արագության
(hոսանքի)
լայնույթը`
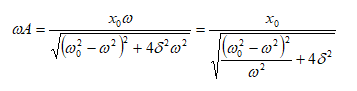
առավելագույնն
է ωռեզ = ω0
դեպքում և
հավասար է x0
/2δ, այսինքն`
որքան մեծ է δ
մարման
գործակիցը, այնքան
ցածր է
ռեզոնանսային
կորի
առավելագույնը:
Օգտագործելով
(7.10), (3.2) և (4.4), (7.11)-ը
մեխանիկական
ռեզոնանսի
դեպքում
կստանանք, որ
արագության լայնույթը`
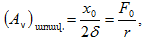
իսկ
էլեկտրական
ռեզոնանսի
դեպքում
հոսանքի
լայնույթը`
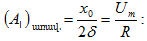
 արտահայտությունից
հետևում է, որ
եթե համակարգում
մարումը
բացակայում է
(δ = 0) ապա միայն այդ
դեպքում է, որ
տատանումները
և հարկադրող ուժը
(կիրառված
փոփոխական
լարումը)
ունեն միևնույն
փուլը, մնացած
բոլոր
դեպքերում φ≠0:
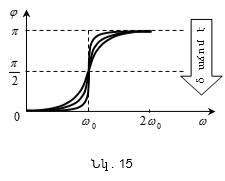
φ-ի կախվածությունը
ω-ից տարբեր
δմարuման
գործակիցների
դեպքում
գրաֆիկորեն
պատկերված է
նկ. 15-ում, որից
հետևում է, որ
ω-ի փոփոխության
դեպքում
փոփոխվում է
և φ փուլերի
շեղումը:
արտահայտությունից
հետևում է, որ
եթե համակարգում
մարումը
բացակայում է
(δ = 0) ապա միայն այդ
դեպքում է, որ
տատանումները
և հարկադրող ուժը
(կիրառված
փոփոխական
լարումը)
ունեն միևնույն
փուլը, մնացած
բոլոր
դեպքերում φ≠0:
φ-ի կախվածությունը
ω-ից տարբեր
δմարuման
գործակիցների
դեպքում
գրաֆիկորեն
պատկերված է
նկ. 15-ում, որից
հետևում է, որ
ω-ի փոփոխության
դեպքում
փոփոխվում է
և φ փուլերի
շեղումը:
(8.9)
բանաձևից
բխում է, որ ω = 0
դեպքում φ = 0
իսկ ω = ω0-ի
դեպքում
անկախ մարման
գործակցի
արժեքից φ=π/2
այսինքն`
ուժը
(լարումը) առաջ
է ընկնում ըստ
փուլի π/2-ով: ω-ի
հետագա
մեծացման
դեպքում
փուլերի
շեղումը
մեծանում է և
ω>>ω0
դեպքում φ → π այսինքն
տատանման
փուլը գրեթե հակառակ
է արտաքին
ուժի փուլին
(փոփոխական
լարման):
Նկ.15-ում
պատկերված
կորերի ընտանիքը,
կոչվում է
փուլային
ռեզոնանսային
կորեր:
Ռեզոնանսի
երևույթը
հարկավոր
է հաշվի
առնել
մեքենաներ
և տարբեր
տեսակի
կառույցներ
նախագծելիս:
Այդ սարքերի
տատանումների
սեփական
հաճախությունը
ոչ մի դեպքում
չպետք
է մոտ լինի հնարավոր
արտաքին
ազդեցությունների
հաճախությանը:
Այսպես,
նավի
կմախքի
կամ ինքնաթիռի
թևերի
թրթռումների
սեփական
հաճախությունը
պետք
է տարբերվի
այն տատանումների
հաճախությունից,
որոնք
կարող
են առաջանալ
թիապտուտակի
կամ պրոպելլերի
պտույտից:
Հակառակ
դեպքում
առաջանում
են թրթռումներ,
որոնք
կարող
են աղետների
պատճառ
դառնալ:
Հայտնի
են դեպքեր,
երբ կամուրջները
փլվել
են նրանց
վրայով
զինվորների
զորասյունը
համաքայլ
անցնելու
ժամանակ:
Այս դեպքերը
տեղի
են ունեցել
այն պատճառով,
որ կամրջի
տատանումների
սեփական
հաճախությունը
մոտ է եղել զորասյան
քայլելու
հաճախությանը:
Միաժամանակ
ռեզոնանսի
երևույթը
հաճախ
շատ օգտակար
է լինում
մանավանդ
ակուստիկայում,
ռադիոտեխնիկայում
և այլն:
>>
10.
Փոփոխական
հոսանք
Կայունացված
հարկադրական
էլեկտրամագնիսական
տատանումները
կարելի է
դիտարկել
որպես փոփոխական
հոսանքի
ընթացք`
դիմադրություն,
ինդուկտիվության
կոճ և
կոնդենսատոր
պարունակող
շղթայում:
Էլեկտրամագնիսական
գրգռումները
շղթայում
տարածվում են
հսկայական արագությամբ,
որը հավասար է
լույսի
արագությանը:
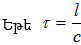
ժամանակի
ընթացքում,
անհրաժեշտ է
գրգռումը շղթայի
ամենահեռավոր
կետը
հաղորդելու
համար,
հոսանքի ուժը
փոխվում է
աննշան չափով,
ապա հոսանքի
ուժի
ակնթարթային
արժեքները
շղթայի բոլոր
կտրվածքներում
գործնականորեն
նույնը
կլինեն:
Այսպիսի
պայմանին
բավարարող
հոսանքները
կոչվում են քվազիստացիոնար:
Պարբերաբար
փոփոխվող
հոսանքների
համար քվազիստացիոնարության
պայմանը
կգրվի հետևյալ
կերպ`
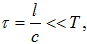
որտեղ
T-ն
պարբերությունն
է:
Քվազիստացիոնար
հոսանքների
ակնթարթային
արժեքների
համար
տեղի
ունի
Օհմի
օրենքը
և նրանից
բխող
Կիրխհովի
կանոնները:
Քննարկենք
հաջորդական
պրոցեսներ,
որոնք
ընթանում
են շղթայի
տեղամասում,
որը պարունակում
է դիմադրություն,
ինդուկտիվության
կոճ և կոնդենսատոր,
որի ծայրերին
կիրառված
է փոփոխական
լարում`

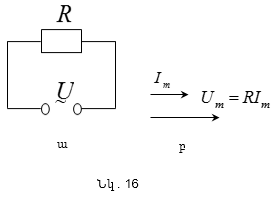
որտեղ
Um-ը լարման
լայնույթն է:
ա)
R դիմադրության
միջով հոսում
է փոփոխական
հոսանք (L → C, C → 0) (նկ.16,ա):
Քվազիստացիոնարության
պայմանը տեղի
ունենալու
դեպքում
դիմադրությունով
անցնող հոսանքը
որոշվում է
Օհմի օրենքով`
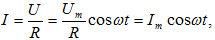
որտեղ
lm = Um / R-ը
հոսանքի ուժի
լայնույթն է:
Փոփոխական
հոսանքների և
լարումների
միջև եղած
առնչությունները
հատկապես
պարզ են
դառնում, եթե
օգտվենք
վեկտորական
դիագրամից:
Ընտրենք կամայական
ուղղություն,
որը
կանվանենք
հոսանքների
առանցք (նկ.16,բ):
Այդ
ուղղությամբ
տեղադրենք lm
հոսանքի
վեկտորը: Քանի
որ քննարկվող
դեպքում
լարումը և
հոսանքը
փոխվում են
համափուլ լարման
վեկտորը
նույնպես
ուղղված
կլինի հոսանքների
առանցքի
ուղղությամբ,
նրա
երկարությունը
հավասար է Rlm:Նկ.
16, բ-ում տրված է lm
հոսանքի ուժի
և
դիմադրության
վրա Um լարման
լայնույթների
դիագրամը
(փուլերի շեղումը
lm -ի և Um -ի
միջև հավասար
է զրոյի:)
բ) փոփոխական
հոսանքը
հոսում է L
ինդուկտիվության
կոճով
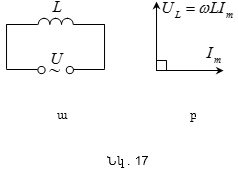
(R→0, C→0)
(նկ. 17, ա): Եթե
շղթային
կիրառված է
փոփոխական
լարում,ապա
նրանով
հոսում է
փոփոխական
հոսանք, որի
արդյունքում
առաջանում է
ինքնամակածման
ԷլՇՈւ`
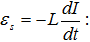
Ուստի
Օհմի օրենքը
դիտարկվող
տեղամասի
համար կգրվի հետևյալ
կերպ `
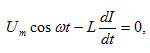
որտեղից

Քանի
որ արտաքին
լարումը
կիրառված է
ինդուկտիվության
կոճին, ապա

լարման
անկումն
է կոճի վրա: (10.2) հավասարումից
հետևում
է, որ
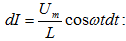
Ինտեգրումից
հետո, հաշվի
առնելով, որ
ինտեգրման
հաստատունը
հավասար է
զրոյի (քանի
որ բացակայում
է հոսանքի
հաստատուն
բաղադրիչը),
կստանանք`
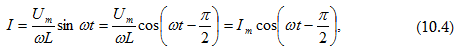
որտեղ
lm = Um /ωL:

մեծությունը
կոչվում է ռեակտիվ
ինդուկտիվ
դիմադրություն
կամ ինդուկտիվ
դիմադրություն:
(10.5)-ից հետևում
է, որ
հաստատուն
հոսանքի
համար(ω = 0)
ինդուկտիվության
կոճը
դիմադրություն
չունի: Um = ωLlm
տեղադրումը
(10.2)-ի մեջ, հաշվի
առնելով (10.3)-ը
բերում է ինդուկտիվության
կոճի վրա
լարման
անկման հետևյալ
արժեքին`

(10.4)
և (10.6)
արտահայտությունների
համեմատումից
բխում է, որ
ինդուկտիվության
վրա լարման
անկումը ինդուկտիվության
միջով անցնող
հոսանքից π / 2 փուլով
առաջ է
անցնում, որն
էլ ցույց է
տրված վեկտորային
դիագրամի վրա
(նկ.17,բ):
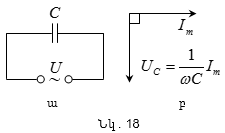
գ) փոփոխական
հոսանքը
հոսում է C ունակության
կոնդենսատորի
միջով (R→0, L→0)
(նկ.18,ա): Եթե
փոփոխական (10.1)
լարումը
կիրառված է կոնդենսատորին,
ապա այն
անընդհատ
վերալիցքավորվում
է, և շղթայով
անցնում է
անընդհատ
փոփոխական
հոսանք: Քանի
որ արտաքին
լարումը
կիրառված է
կոնդենսատորին,
իսկ մատուցող
հաղորդալարերի
դիմադրությունը
կարելի
անտեսել, ապա
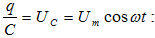
Հոսանքի
ուժը`
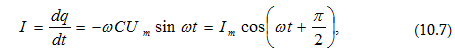
որտեղ
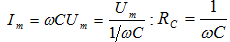
մեծությունը
կոչվում է ռեակտիվ
ունակային
դիմադրություն
կամ ունակային
դիմադրություն:
Հաստատուն
հոսանքի
համար (ω=0) Rc = ∞,
այսինքն
կոնդենսատորով
հաստատուն
հոսանք չի
կարող անցնել:
Լարման
անկումը
կոնդենսատորի
վրա`

Համեմատելով
(10.7) և (10.8)
արտահայտությունները`
տեսնում ենք,
որ
ունակության
վրա լարման
անկումը
կոնդենսատորով
անցնող հոսանքից
π/2 փուլով ետ է
մնում: Դա
ցույց է տրված
վեկտորային
դիագրամի վրա
(նկ. 18, բ):
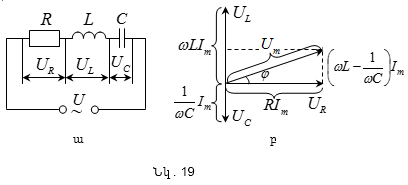
դ) ունակություն,
ինդուկտիվություն
և դիմադրություն
պարունակող
փոփոխական հոսանքի
շղթա: Նկ.
19ա-ում բերված
է շղթայի
տեղամաս, որը
պարունակում
է R
դիմադրություն,
L
ինդուկտիվության
կոճ, և C
ունակության
կոնդենսատոր,
որի ծայրերին
կիրառված է
փոփոխական
լարում է R
դիմադրություն,
L
ինդուկտիվության
կոճ, և C
ունակության
կոնդենսատոր,
որի
ծայրերին
կիրառված է
փոփոխական
լարում: Շղթայում
առաջանում է
փոփոխական
հոսանք, որն առաջ
է բերում
շղթայի բոլոր
տարրերի վրա
համապատասխան
լարման
անկումներ` UR, UL և UC: Նկ.19,
բ-ում
ներկայացված
է
դիմադրության,
կոճի և
կոնդենսատորի
վրա լարման
անկումերի լայնույթների
վեկտորական
դիագրամը:
Կիրառված
լարման Um
լայնույթը
պետք է
հավասար լինի
այդ լարման անկումների
լայնույթների
վեկտորական
գումարին:
Ինչպես
երևում է նկ.19,
բ-ից φ
անկյունը որոշում
է փուլերի
տարբերությունը
լարման և հոսանքի
միջև: Նկարից
երևում է, որ

Ուղղանկյուն
եռանկյունուց
ստանում ենք
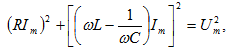
որտեղից
հոսանքի
լայնության
արժեքի համար ստացվուն
է`

որը
համընկնում է
(8.15)-հետ:
Հետևաբար, եթե
շղթայում
լարումը
փոփոխվում է
ըստ U = Um cosωt
օրենքի, ապա
շղթայով
հոսանք է
անցնում

որտեղ
φ-ն և Um -ը
որոշվում են
(10.9)-ով և (10.10)-ով:
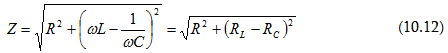
մեծությունը
կոչվում է
շղթայի լրիվ
դիմադրություն,
իսկ
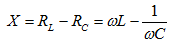
մեծությունը`
ռեակտիվ
դիմադրություն:
Դիտարկենք
մասնավոր
դեպք, երբ
շղթայում բացակայում
է
կոնդենսատորը:
Տվյալ
դեպքում UR և UL
լարման
անկումների
գումարը
հավասար է
կիրառված U
լարմանը: Այդ
դեպքի համար
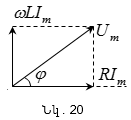
վեկտորական դիագրամը
պատկերված է
նկ. 20-ում, որից
հետևում է, որ
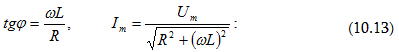
(10.9)
և (10.10)
արտահայտությունները
հաընկնում են
(10.13)-ի հետ, եթե
նրանցում 1 /ωC = 0
այսինքն`C = ∞:
Հետևաբար,
կոնդենսատորի
բացակայությունը
շղթայում
նշանակում է,
որ C = ∞ և ոչ թե C = 0
Տվյալ եզրակացությունը
կարելի է
մեկնաբանել
հետևյալ կերպ.
մոտեցնելով
կոնդենսատորի
շրջադիրները
մինչև նրանց
հպվելը`
կստանանք
շղթա, ուր
բացակայում է
կոնդենսատորը
(շրջադիրների
միջև հեռավորությունը
ձգտում է
զրոյի, իսկ
ունակությունը`
անսահմանության):
>>
11.
Լարումների
ռեզոնանս
Եթե
փոփոխական
հոսանքի
շղթան, որը
պարունակում
է հաջորդաբար
միացված
կոնդենսատոր,
ինդուկտիվության
կոճ և
դիմադրություն
(տես նկ.19),

ապա
հոսանքի և (10.9)
լարման միջև
փուլերի
շեղումը
դառնում է զրո
(φ = 0) այսինքն`
հոսանքի և
լարման փոփոխությունը
կատարվում է
համափուլ: (11.1)-ի
պայմանին բավարարում
է

հաճախությունը:
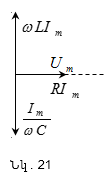
Տվյալ
դեպքում
շղթայի լրիվ Z
դիմադրությունը
դառնում է
նվազագույնը
և հավասար է R
ակտիվ դիմադրությանը,
և հոսանքը
որոշվում է
այդ դիմադրությունով,
ընդունելով առավելագույն
արժեք: Այդ
դեպքում
լարման անկումը
ակտիվ
դիմադրության
վրա հավասար է
շղթային
կիրառված
արտաքին
լարմանը (UR = U),
իսկ լարման
անկումը
կոնդենսատորի
և ինդուկտիվության
կոճի վրա
միատեսակ է
լայնույթով և
հակառակ` ըստ
փուլի: Այս
երևույթը
կոչվում է
լարումների
ռեզոնանս
(հաջորդական
ռեզոնանս), իսկ
(11.2)
հաճախությունը`
ռեզոնանսային
հաճախություն:
Լարումների
ռեզոնանսի
համար
վեկտորական դիագրամը
բերված է նկ.
21-ում, իսկ
հոսանքի
լայնության
կախվածությունը
ω-ից արդեն
տրվել է
նկ.14-ում:
Լարումների
ռեզոնանսի
դեպքում`
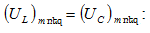
Տեղադրելով
այս բանաձևի
մեջ ռեզոնանսային
հաճախության
և լարման
լայնույթի
արժեքներն
իդուկտիվության
կոճի
և կոնդենսատորիվրա,
կստանանք`
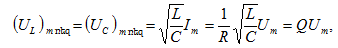
որտեղ
Q-ն կոնտուրի
բարորակությունն
է, որը
որոշվում է (7.14)
բանաձևով:
Քանի
որ սովորական
կոնտուրների համար
բարորակությունը
մեկից մեծ է,
ապա լարումը
ինչպես
ինդուկտիվության
կոճի, այնպես էլ
կոնդենսատորի
վրա
գերազանցում
է շղթային
կիրառված
լարմանը:
Ուստի
լարումների
ռեզոնանսի
երևույթը
օգտագործվում
է տեխնիկայում
որոշակի
հաճախության
լարման
տատանումները
ուժեղացնելու
համար:
Օրինակ,
կոնդենսատորի
վրա ռեզոնանսի
դեպքում
կարելի է
ստանալ QUm
լայնույթով
լարում (Q-ն
տվյալ
դեպքում
կոնտուրի
բարորակությունն
է, որը կարող է
մեծ լինել Um-ից):
Այդ լարման
ուժեղացումը
հնարավոր է
միայն
կոնտուրի
ռեզոնանսային
հաճախությանը
մոտ հաճախությունների
նեղ
միջակայքի
համար, որը
հնարավորություն
է տալիս
անջատելու
բազմաթիվ ազդանշաններից
որոշակի
հաճախությամբ
մեկ տատանում:
Լարումների
ռեզոնասի
երևույթը
անհրաժեշտ է
հաշվի առնել
էլեկտրական
գծերի
մեկուսացման
հաշվարկի
դեպքում,
որոնք պարունակում
են կոնդենսատորներ,
ինդուկտիվության
կոճեր, քանի
որ այլ կերպ
կարող է
դիտվել դրանց
ծակում:
>>
12.
Հոսանքների
ռեզոնանս
Քննարկենք
փոփոխական
հոսանքի շղթա,
որը պարունակում
է զուգահեռ
միացված C
ունակության կոնդենսատոր
և L
ինդուկտիվության
կոճ (նկ. 22):
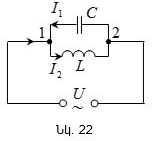
Պարզության
համար
ենթադրենք, որ
երկու ճյուղերի
ակտիվ
դիմադրությունները
այնքան փոքր
են, որ դրանք
կարելի է
անտեսել: Եթե
կիրառված
լարումը
փոփոխվում է
ըստ U = Umcosωt
համաձայն (10.11)
բանաձևի, 1C2
ճյուղով
անցնում է`
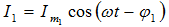
հոսանք,
որի
լայնույթը
որոշվում է (10.10)
բանաձևով, այն
պայմանով, որ R =
0, L = 0

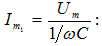

Այդ
հոսանքի
սկզբնական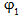 փուլը
ըստ (10.9) բանաձևի
որոշվում է
հետևյալ հավասարումով`
փուլը
ըստ (10.9) բանաձևի
որոշվում է
հետևյալ հավասարումով`
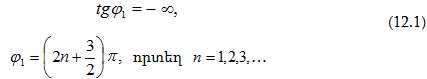
Նմանապես,
հոսանքը 1L2
ճյուղում`
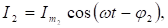
որի
լայնույթը
որոշվում է
(10.10)-ից, այն
պայմանով, որ R = 0,
C = ∞
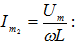
Այդ
հոսանքի
սկզբնական 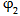 փուլը
ըստ (10.9)
բանաձևի`
փուլը
ըստ (10.9)
բանաձևի`
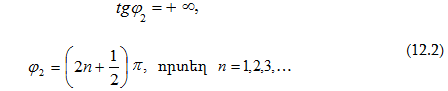
(12.1)
և (12.2)
արտահայտությունների
համեմատումից
բխում է, որ
հոսանքների
փուլերի
տարբերությունը
1C2 և 1L2
ճյուղերում
հավասար է` 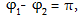 այսինքն`
ճյուղերում
հոսանքները
ըստ փուլի հակառակ
են: Հոսանքի
լայնույթը
արտաքին (չճյուղավորված)
շղթայում`
այսինքն`
ճյուղերում
հոսանքները
ըստ փուլի հակառակ
են: Հոսանքի
լայնույթը
արտաքին (չճյուղավորված)
շղթայում`
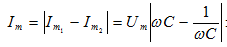

Եթե
ω = ωռեզ
= 1/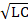 ապա lm1 = lm2 և lm = 0
: Արտաքին
շղթայում
հոսանքի ուժի
լայնույթի
կտրուկ
նվազումը, որը
սնում է զուգահեռ
միացված
ինդուկտիվության
կոճը և կոնդենսատորը,
կիրառված
լարման
ω հաճախության
մոտենալը
ωռեզ
ռեզոնանսային
հաճախությանը
կոչվում
է հոսանքների
ռեզոնանս
(զուգահեռ
ռեզոնանս):
Տվյալ
դեպքում
ռեզոնանսային
հաճախության
համար
ստացանք
նույնպիսի
արժեք,
ինչպիսին
և լարումների
ռեզոնանսի
դեպքում:
ապա lm1 = lm2 և lm = 0
: Արտաքին
շղթայում
հոսանքի ուժի
լայնույթի
կտրուկ
նվազումը, որը
սնում է զուգահեռ
միացված
ինդուկտիվության
կոճը և կոնդենսատորը,
կիրառված
լարման
ω հաճախության
մոտենալը
ωռեզ
ռեզոնանսային
հաճախությանը
կոչվում
է հոսանքների
ռեզոնանս
(զուգահեռ
ռեզոնանս):
Տվյալ
դեպքում
ռեզոնանսային
հաճախության
համար
ստացանք
նույնպիսի
արժեք,
ինչպիսին
և լարումների
ռեզոնանսի
դեպքում:
Հոսանքի
ուժի Im
լայնույթը
դարձավ
զրոյի
հավասար,
որովհետև
կոնտուրի
ակտիվ
դիմադրությունը
անտեսեցինք:
Եթե R դիմադրությունը
հաշվի
առնվի,
ապա փուլերի
φ1φ2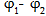 տարբերությունը
չի լինի հավասար
π, դրա
համար
էլ հոսանքների
ռեզոնանսի
դեպքում
հոսանքի
ուժի
Im լայնույթը
կլինի
զրոյից
տարբեր,
բայց
ընդունում
է հնարավոր
նվազագույն
արժեքը:
Այսպիսով,
հոսանքների
ռեզոնանսի
դեպքում
արտաքին
շղթայում
I1 և
I2 հոսանքներն
իրար
կոմպենսացնում
են, և I հոսանքի ուժը մատուցող
հաղորդալարերում
հասնում
է նվազագույն
արժեքին`
պայմանավորված
միայն
դիմադրության
միջով
անցնող
հոսանքով:
Հոսանքների
ռեզոնանսի
դեպքում
I1 և I2 հոսանքի
ուժերը
կարող
են աննշան
գերազանցել
I հոսանքի
ուժը:
Ուստի
դիտարկվող
կոնտուրը
ցույց
է տալիս
մեծ դիմադրություն
ռեզոնանսայինին
մոտ փոփոխական
հոսանքի
հաճախության
հետ: Հոսանքների
ռեզոնանսի
այս հատկությունն
օգտագործվում
է ռեզոնանսային
ուժեղացուցիչներում,
որոնք
հնարավորություն
են տալիս
բարդ
ձևի ազդանշանից
անջատել
մեկ որոշակի
տատանում:
Հոսանքների
ռեզոնանսը
օգտագործվում
է նաև ինդուկցիոն
վառարաններում,
որտեղ
մետաղների
տաքացումը
կատարվում
է մրրկային
հոսանքներով:
Նրանցում
կոնդենսատորը,
որը միացված
է զուգահեռ
տաքացնող
կոճին,
ընտրվում
է այնպես,
որպեսզի
գեներատորի
հաճախության
դեպքում
ստացվի
հոսանքների
ռեզոնանս,
որի արդյունքում
հոսանքի
ուժը
տաքացնող
կոճով
կլինի
ավելի
մեծ, քան հոսանքի
ուժը
մատուցող
հաղորդալարերում:
տարբերությունը
չի լինի հավասար
π, դրա
համար
էլ հոսանքների
ռեզոնանսի
դեպքում
հոսանքի
ուժի
Im լայնույթը
կլինի
զրոյից
տարբեր,
բայց
ընդունում
է հնարավոր
նվազագույն
արժեքը:
Այսպիսով,
հոսանքների
ռեզոնանսի
դեպքում
արտաքին
շղթայում
I1 և
I2 հոսանքներն
իրար
կոմպենսացնում
են, և I հոսանքի ուժը մատուցող
հաղորդալարերում
հասնում
է նվազագույն
արժեքին`
պայմանավորված
միայն
դիմադրության
միջով
անցնող
հոսանքով:
Հոսանքների
ռեզոնանսի
դեպքում
I1 և I2 հոսանքի
ուժերը
կարող
են աննշան
գերազանցել
I հոսանքի
ուժը:
Ուստի
դիտարկվող
կոնտուրը
ցույց
է տալիս
մեծ դիմադրություն
ռեզոնանսայինին
մոտ փոփոխական
հոսանքի
հաճախության
հետ: Հոսանքների
ռեզոնանսի
այս հատկությունն
օգտագործվում
է ռեզոնանսային
ուժեղացուցիչներում,
որոնք
հնարավորություն
են տալիս
բարդ
ձևի ազդանշանից
անջատել
մեկ որոշակի
տատանում:
Հոսանքների
ռեզոնանսը
օգտագործվում
է նաև ինդուկցիոն
վառարաններում,
որտեղ
մետաղների
տաքացումը
կատարվում
է մրրկային
հոսանքներով:
Նրանցում
կոնդենսատորը,
որը միացված
է զուգահեռ
տաքացնող
կոճին,
ընտրվում
է այնպես,
որպեսզի
գեներատորի
հաճախության
դեպքում
ստացվի
հոսանքների
ռեզոնանս,
որի արդյունքում
հոսանքի
ուժը
տաքացնող
կոճով
կլինի
ավելի
մեծ, քան հոսանքի
ուժը
մատուցող
հաղորդալարերում:
>>
13.
Փոփոխական
հոսանքի
շղթայում
անջատված
հզորությունը
Փոփոխական
հոսանքի
ակնթարթային
հզորությունը
հավասար է
լարման և
հոսանքի ակնթարթային
արժեքների
արտադրյալին.
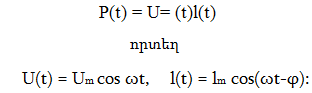
Բացելով
cos(ωt –φ)-ն
կստանանք`
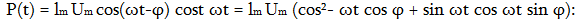
Գործնականում
հետաքրքրություն
է ներկայացնում
հզորության
ոչ թե
ակնթարթային
արժեքը, այլ
նրա միջին
արժեքը
տատանման մեկ
պարբերության
ընթացքում:
Հաշվի
առնելով, որ
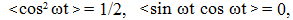

Վեկտորական
դիագրամից
(տես նկ.18)
հետևում է, որ
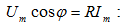
Հետևաբար`<
P > = 1/2 Rl2m: Այսպիսի
հզորություն
է զարգացնում
նաև l = lm/√2
հաստատուն
հոսանքը:
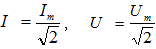
մեծությունները
կոչվում են
համապատասխանաբար
հոսանքի և
լարման
գործող (կամ էֆեկտիվ)
արժեքներ:
Փոփոխական
հոսանքի բոլոր
ամպերմետրերը
և
վոլտմետրերը
սովորաբար աստիճանավորում
են այնպես, որ
դրանք ցույց են
տալիս
հոսանքի ուժի
ու լարման
գործող արժեքները:
Գործող
արժեքների
միջոցով
միջին հզորության
(13.1) բանաձևին
կարելի է տալ
հետևյալ տեսքը`

որտեղ
cos φ բազմապատկիչը
կոչվում
է հզորության
գործակից:
(13.2) բանաձևը
ցույց
է տալիս,
որ փոփոխական
հոսանքի
շղթայում
անջատված
հզորությունը
ընդհանուր
դեպքում
կախված
է ոչ միայն
հոսանքից
և լարումից,
այլ նաև նրանց
միջև
փուլերի
շեղումից:
Եթե շղթայում
ռեակտիվ
դիմադրությունը
բացակայում
է, ապա cosφ = 1 և P = IU: Եթե շղթան
պարունակում
է միայն
ռեակտիվ
դիմադրություն
(R = 0), ապա
cos φ = 0 և միջին հզորությունը
հավասար
է զրոյի:
Տեխնիկայում
ձգտում
են cosφ-ն հնարավորին
չափ մեծ վերցնել:
Փոքր
cosφ -ի դեպքում
շղթայում
անհրաժեշտ
հզորությունը
անջատելու
համար
պետք
է մեծ հոսանքի
ուժ բաց թողնել:
Այդ դեպքում
մեծանում
են կորուստները
հաղորդալարերում,
և հարկ է լինում մեծացնել
նրանց
կտրվածքը,
որը բարձրացնում
է էլեկտրահաղորդման
գծի գինը: Դրա համար
գործնականում
միշտ
ձգտում
են մեծացնել
cosφ, որի թույլատրելի
ամենափոքր
արժեքը
արդյունաբերական
կայանքների
համար
կազմում
է մոտավորապես
0.85:
>>
ԳԼՈՒԽ 2
ԱՌԱՁԳԱԿԱՆ
ԱԼԻՔՆԵՐ
14.
Ալիքային
պրոցեսներ:
Երկայնական և
լայնական
ալիքներ
Տատանումները,
որոնք
գրգռվում
են միջավայրի
(պինդ,
հեղուկ
կամ գազային)
որևէ
կետում
տարածվում
են նրա մեջ վերջավոր
արագությամբ,
որը կախված
է միջավայրի
հատկություններից`
փոխանցվելով
միջավայրի
մի կետից
մյուսին:
Որքան
միջավայրի
մասնիկները
հեռու
են դասավորված
տատանման
աղբյուրից,
այնքան
ավելի
ուշ են տատանվում:
Այլ կերպ ասած` միջավայրի
մասնիկների
և աղբյուրի
տատանումների
փուլը
մեկը
մյուսից
այնքան
ավելի
շատ են տարբերվում,
որքան
մեծ է այդ հեռավորությունը:
Տատանումների
տարածման
ուսումնասիրության
դեպքում
հաշվի
չի առնվում
միջավայրի
ընդհատ
(մոլեկուլային)
կառուցվածքը,
և միջավայրը
դիտարկվում
է որպես
անընդհատ,
այսինքն`
տարածության
մեջ անընդհատ
բաշխված
և օժտըված
առաձգական
հատկություններով:
Անընդհատ
միջավայրում
տատանումների
տարածման
պրոցեսը
կոչվում
է ալիքային
պրոցես
(կամ ալիք):
Ալիքի
տարածման
դեպքում
միջավայրի
մասնիկները
ալիքի
հետ միասին
չեն շարժվում,
այլ տատանվում
են իրենց
հավասարակշռության
դիրքի
շուրջը:
Ալիքի
հետ միասին
միջավայրի
մի մասնիկից
մյուսին
հաղորդվում
է միայն
տատանողական
շարժման
վիճակը
և նրա էներգիան:
Ուստի
բոլոր
ալիքների
հիմնական
հատկությունը,
անկախ
նրանց
բնույթից,
էներգիայի
տեղափոխությունն
է առանց
նյութի
տեղափոխության:
Ալիքի
տարածան
ուղղության
նկատմամբ
մասնիկների
տատանումների
ուղղություններից
կախված
տարբերում
են երկայնական
և լայնական
ալիքներ:
Երկայնական
են կոչվում
այն ալիքները,
որոնց տարածման
ուղղությունը
համընկնում է
միջավայրի
մասնիկների
տատանումների
ուղղությանը:
Լայնական
են կոչվում
այն ալիքները,
որոնց տարածման
ուղղությունն
ուղղահայաց է
միջավայրի
մասնիկների
տատանման
ուղղությանը:
Միջավայրում
մեխանիկական
ալիքներն
առաջանում են
առաձգականության
ուժերի
շնորհիվ:
Երկայնական
ալիքների
տարածման
ժամանակ տեղի
են ունենում
միջավայրի խտացումներ
և
նոսրացումներ,
իսկ լայնական
ալիքների
տարածման
ժամանակ`
միջավայրի
շերտերի սահք
միմյանց
նկատմամբ:
Սեղմման և
ձգման դեֆորմացիաների
դեպքում միշտ
առաջանում են
առաձգական
ուժեր, իսկ
սահքի
դեֆորմացիաներն
առաջ են բերում
առաձգական
ուժեր միայն
պինդ
մարմիններում:
Հեղուկներում
և գազերում
շերտերի սահքի
դեպքում
առաձգականության
ուժեր չեն առաջանում:
Ուստի
երկայնական
ալիքները
կարող են
տարածվել
բոլոր
միջավայրերում`
և պինդ մարմիններում,
և
հեղուկներում,
և գազերում,
իսկ լայնական
ալիքները`
միայն պինդ
մարմիններում:
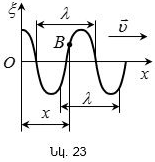
Առաձգական
ալիքը
կոչվում է
ներդաշնակ,
եթե նրան
համապատասխանող
միջավայրի
մասնիկների
տատանումները
նույնպես
ներդաշնակ են:
Նկ. 23-ում
պատկերված է
ներդաշնակ
լայնական
ալիք, որը
տարածվում է
x-ի առանցքի
երկայնքով v
արագությամբ,
այսինքն
բերված է
ալիքային
պրոցեսին մասնակցող
միջավայրի
մասնիկի 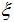 շեղման
և այդ
մասնիկների
(օրինակ B
մասնիկ) x հեռավորության
կախվածությունը
տատանման O աղբյուրից
ինչ-որ
ֆիքսված
ժամանակի t
պահի hամար: Բերված
շեղման
և այդ
մասնիկների
(օրինակ B
մասնիկ) x հեռավորության
կախվածությունը
տատանման O աղբյուրից
ինչ-որ
ֆիքսված
ժամանակի t
պահի hամար: Բերված
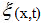 ֆունկցիայի
գրաֆիկը
հիշեցնում է
ներդաշնակ
տատանման
գրաֆիկը,
սակայն ըստ
էության դրանք
տարբեր են:
Ալիքի
գրաֆիկը
տալիս է
միջավայրի
բոլոր
մասնիկների
շեղումները
մինչև տատանումների
աղբյուրը
եղած
հեռավորություններից
ժամանակի
տվյալ պահին,
իսկ
տատանումների
գրաֆիկը
տալիս է
մասնիկի
շեղման
կախվածությունը
ժամանակից
(տես նկ.2)
Միևնույն
փուլով տատանվող
ամենամոտ
կետերի միջև
եղած հեռավորությունը
կոչվում է
ալիքի
ֆունկցիայի
գրաֆիկը
հիշեցնում է
ներդաշնակ
տատանման
գրաֆիկը,
սակայն ըստ
էության դրանք
տարբեր են:
Ալիքի
գրաֆիկը
տալիս է
միջավայրի
բոլոր
մասնիկների
շեղումները
մինչև տատանումների
աղբյուրը
եղած
հեռավորություններից
ժամանակի
տվյալ պահին,
իսկ
տատանումների
գրաֆիկը
տալիս է
մասնիկի
շեղման
կախվածությունը
ժամանակից
(տես նկ.2)
Միևնույն
փուլով տատանվող
ամենամոտ
կետերի միջև
եղած հեռավորությունը
կոչվում է
ալիքի 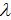 երկարություն
(նկ. 23): Ակնհայտ
է, որ ալիքի
երկարությունը
հավասար է այն
հեռավորությանը,
որն անցնում է
ալիքըմեկ
պարբերության
ընթացքում,
այսինքն`
երկարություն
(նկ. 23): Ակնհայտ
է, որ ալիքի
երկարությունը
հավասար է այն
հեռավորությանը,
որն անցնում է
ալիքըմեկ
պարբերության
ընթացքում,
այսինքն`
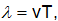
կամ
նկատի
ունենալով, որ
T = 1/υ, որտեղ υ -ն
տատանման
հաճախությունն
է,
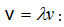
Իրականում
տատանվում
են ոչ միայն
x առանցքի
վրա դասավորված
մասնիկները,
այլև
որոշ
ծավալում
պարփակված
մասնիկների
ամբողջությունը:
Տարածվելով
տատանումների
աղբյուրից,
ալիքային
պրոցեսն
ընդգրկում
է տարածության
ավելի
ու ավելի
նոր մասեր:
Այն կետերի
երկրաչափական
տեղը,
որոնց
հասնում
են տատանումները
ժամանակի
t պահին
կոչվում
է ալիքի
ճակատ:
Միատեսակ
փուլերով
տատանվող
կետերի
երկրաչափական
տեղը
կոչվում
է ալիքային
մակերևույթ:
Ալիքային
մակերևույթը
կարելի
է անցկացնել
ալիքային
պրոցեսով
ընդգրկված
տարածության
ցանկացած
կետով:
Հետևաբար,
գոյություն
ունեն
անսահման
բազմությամբ
ալիքային
մակերևույթներ,
այն դեպքում,
երբ ժամանակի
յուրաքանչյուր
պահի
համար
գոյություն
ունի
միայն
մեկ ալիքային
ճակատ:
Ալիքային
մակերևույթները
լինում
են ցանկացած
ձևի: Պարզագույն
դեպքում
դրանք
ունեն
հարթության
կամ գնդային
մակերևույթի
ձև: Համապատասխանաբար,
այս դեպքերում
ալիքը
կոչվում
է հարթ կամ սֆերիկ:
Ալիքային
մակերևույթները
հարթ
ալիքում
իրար
զուգահեռ
հարթությունների
ամբողջություն
է, իսկ սֆերիկ
ալիքում`
համակենտրոն
գնդային
մակերևույթների
ամբողջություն:
>>
15.
Վազող ալիքի
հավասարումը:
Փուլային
արագություն:
Ալիքային
հավասարում
Վազող
ալիքներ են
կոչվում այն
ալիքները,
որոնք
տարածության
մեջ
տեղափոխում
են էներգիա:
Ալիքի
էներգիայի
տեղափոխությունը
քանակապես
բնութագրվում
է էներգիայի
հոսքի
խտության
վեկտորով:
Առաձգական
ալիքների
համար այդ
վեկտորը կոչվում
է Ումովի
վեկտոր:
Ումովի
վեկտորի
ուղղությունը
համընկնում է
էներգիայի
փոխադրման
ուղղության
հետ, իսկ նրա
մոդուլը
թվապես
հավասար է
այն
էներգիային,
որը
տեղափոխում է
ալիքը
տեղափոխմանը
ուղղահայաց
միավոր մակերեսով
միավոր
ժամանակում:
Ալիքի
հավասարում է
կոչվում այն
արտահատությունը,
որը տալիս է
տատանվող
կետի շեղումը
որպես
ֆունկցիա նրա x,
y, z
կոորդինատներից
և t ժամանակից`
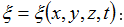
Գտնենք
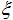 ֆունկցիայի
տեսքը հարթ
ալիքի
դեպքում, ենթադրելով,
որ
տատանումները
կրում են
ներդաշնակ
բնույթ:
Պարզության
համար
կոորդինատային
առանցքներն
ուղղենք
այնպես,
որպեսզի x
առանցքը
համընկնի
ալիքի
տարածման
ուղղության
հետ: Այդ
դեպքում
ալիքային
մակերևույթները
ուղղահայաց
կլինեն x
առանցքին, և
քանի որ
ալիքային
մակերևույթի
բոլոր կետերը
միատեսակ են
տատանվում,
ֆունկցիայի
տեսքը հարթ
ալիքի
դեպքում, ենթադրելով,
որ
տատանումները
կրում են
ներդաշնակ
բնույթ:
Պարզության
համար
կոորդինատային
առանցքներն
ուղղենք
այնպես,
որպեսզի x
առանցքը
համընկնի
ալիքի
տարածման
ուղղության
հետ: Այդ
դեպքում
ալիքային
մակերևույթները
ուղղահայաց
կլինեն x
առանցքին, և
քանի որ
ալիքային
մակերևույթի
բոլոր կետերը
միատեսակ են
տատանվում, 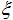 շեղումը
կախված կլինի
միայն x-ից և
t-ից, այսինքն`
շեղումը
կախված կլինի
միայն x-ից և
t-ից, այսինքն`
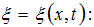
Նկ.
23-ում
դիտարկենք
միջավայրի
որևէ B մասնիկ, որը
գտնվում է
տատանման O աղբյուրից
x
հեռավորության
վրա: Դիցուք x = 0
հարթության
մեջ գտնվող
կետերի
տատանումները
ունեն
հետևյալ
տեսքը`
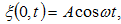
ապա
միջավայրի B
մասնիկը
տատանվում է
նույն օրենքով,
բայց նրա
տատանումները
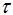 ժամանակով
ետ կընկնեն
աղբյուրի
տատանումներից,
քանի որ x
հեռավորությունն
ալիքը
անցնելու
համար
կպահանջվի τ = x/v
ժամանակ,
որտեղ v -ն
ալիքի
տարածման
արագությունն
է: Այդ
դեպքում x
հարթության
մեջ ընկած
մասնիկի տատանման
հավասարումը
կունենա
հետևյալ տեսքը`
ժամանակով
ետ կընկնեն
աղբյուրի
տատանումներից,
քանի որ x
հեռավորությունն
ալիքը
անցնելու
համար
կպահանջվի τ = x/v
ժամանակ,
որտեղ v -ն
ալիքի
տարածման
արագությունն
է: Այդ
դեպքում x
հարթության
մեջ ընկած
մասնիկի տատանման
հավասարումը
կունենա
հետևյալ տեսքը`

որտեղից
հետևում է, որ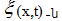 ոչ
միայն
ժամանակի
պարբերական
ֆունկցիա է, այլ
նաև
պարբերական
ֆունկցիա է
ըստ x կոորդինատի:
(15.1)
հավասարումը
վազող ալիքի
հավասարումն
է: Եթե հարթ
ալիքը տարածվում
է հակառակ
ուղղությամբ,
ապա
ոչ
միայն
ժամանակի
պարբերական
ֆունկցիա է, այլ
նաև
պարբերական
ֆունկցիա է
ըստ x կոորդինատի:
(15.1)
հավասարումը
վազող ալիքի
հավասարումն
է: Եթե հարթ
ալիքը տարածվում
է հակառակ
ուղղությամբ,
ապա
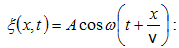
Ընդհանուր
դեպքում
էներգիան
չկլանող միջավայրում
x-ի առանցքի դրական
ուղղությամբ
տարածվող
հարթ ալիքի հավասարումը
կգրվի
հետևյալ
ձևով`(15.1) (15.2)-ն
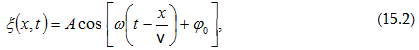
Որտեղ
A = const-ը ալիքի
լայնույթն է,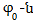 ալիքի
սկզբնական
փուլն է, որն
ընդհանուր
դեպքում
որոշվում է x-ի
և t-ի
հաշվարկման սկզբի
ընտրությամբ.
ալիքի
սկզբնական
փուլն է, որն
ընդհանուր
դեպքում
որոշվում է x-ի
և t-ի
հաշվարկման սկզբի
ընտրությամբ.
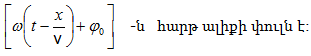
Ալիքի
բնութագրման
համար
օգտագործվում
է ալիքային
թիվը`

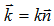 վեկտորը,
որն ըստ
մոդուլի
հավասար է
վեկտորը,
որն ըստ
մոդուլի
հավասար է 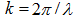 ալիքային
թվին
և ուղղված
է ալիքային
մակերևույթի
նորմալի
ուղղությամբ,
կոչվում
է ալիքային
վեկտոր:
ալիքային
թվին
և ուղղված
է ալիքային
մակերևույթի
նորմալի
ուղղությամբ,
կոչվում
է ալիքային
վեկտոր:
Նկատի
ունենալով
(15.3)-ը (15.2) հավասարմանը`
կարելի
տալ հետևյալ
տեսքը`
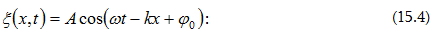
x-ի
առանցքի
բացասական
ուղղության
երկայնքով
տարածվող
ալիքի
հավասարումը
(15.4)-ից տարբերվում
է միայն kx-ի
նշանով:
Հիմնվելով
Էյլերի (1.7)
բանաձևի վրա`
հարթ ալիքի հավասարումը
կարելի է գրել
հետևյալ
տեսքով`
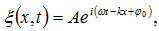
որտեղ
ֆիզիկական
իմաստ
ունի
միայն
իրական
մասը:
Ենթադրենք,
որ ալիքային
պրոցեսի
դեպքում
փուլը
հաստատուն
է, այսինքն
`
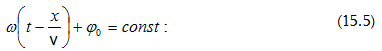
Ածանցելով
(15.5)
արտահայտությունը
և կրճատելով
ω-ի վրա կստանանք`
dt – 1/v dx = 0 որտեղից`

Հետևաբար,
ալիքի
տարածման
արագությունը
(15.6) հավասարման
մեջ ոչ այլ
ինչ է, եթե ոչ
ալիքի փուլի
տեղափոխման
արագությունը,
և այն
կոչվում է փուլային
արագություն:
Եթե
բոլոր
ուղղություններով
ալիքի տարածման
արագությունը
նույնն է, ապա
կետային աղբյուրով
ստեղծված
ալիքը կլինի
սֆերիկ:
Սֆերիկ ալիքի
հավասարումը
գրվում է
հետևյալ
տեսքով`
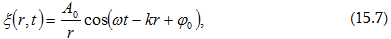
Որտեղ
r-ը աղբյուրի
կենտրոնից
մինչև
տարածության
տվյալ կետն
ընկած
հեռավորությունն
է:
Սֆերիկ
ալիքի
դեպքում, եթե
նույնիսկ
ալիքի էներգիան
չի կլանվում
միջավայրում,
տատանումների
լայնույթը
հաստատուն չի
մնում և
աղբյուրից հեռանալու
հետ միասին
փոքրանում է
1/r
օրենքով:
(15.3)-ից
երևում է, որ
փուլային
արագությունը`

Եթե
ալիքների
փուլային
արագությունը
միջավայրում
կախված է
հաճախությունից,
այդ երևույթը
կոչվում է ալիքների
դիսպերսիա,
իսկ
միջավայրը,
ուր դիտվում է
ալիքների դիսպերսիա,
կոչվում է դիսպերսող
միջավայր:
Ալիքների
տարածումը
համասեռ
իզոտրոպ միջավայրում
ընդհանուր
դեպքում
նկարագրվում
է մասնակի
ածանցյալներով
դիֆերենցիալ
հավասարումով,
որը կոչվում է
ալիքային
հավասարում
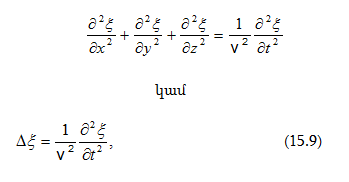
որտեղ
v-ն փուլային
արագությունն
է, 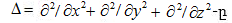 Լապլասի
օպերատորն է:(15.9)
Լապլասի
օպերատորն է:(15.9)
Ցանկացած
ալիքի
հավասարում
(15.9)-ի
հավասարման լուծումն
է:
Համապատասխան
տեղադրումով
կարելի է
համոզվել, որ
(15.9)-ի
հավասարմանը
բավարարում է,
մասնավորապես
(15.2) հարթ ալիքը
և (15.7) սֆերիկ
ալիքը: Հարթ
ալիքի համար,
որը
տարածվում է
x-ի առանցքի երկայնքով,
ալիքային
հավասարումն
ունի հետևյալ
տեսքը.

Հաշվարկները
ցույց են
տալիս, որ
երկայնական ալիքների
փուլային
արագությունը
որոշվում է
հետևյալ բանաձևով`

Այսպիսով,
երկայնական
առաձգական
ալիքների փուլային
արագությունը
հավասար է
Յունգի մոդուլի
և միջավայրի
խտության
հարաբերության
քառակուսի
արմատին:
Լայնական
ալիքների
համար
կատարված
հաշվարկները
հանգեցնում
են հետևյալ
արտահայտությանը`

որտեղ
G-ն սահքի
մոդուլն է:
Վերադրման
սկզբունքը:
Խմբային
արագություն: Եթե
միջավայրը,
որի մեջ
տարածվում են
միաժամանակ
մի քանի
ալիքներ
գծային է,
այսինքն` նրա հատկությունը
չի փոփոխվում
ալիքով
ստեղծվող
գրգըռումների
ազդեցության
տակ, ապա նրան կիրառելի
է վերադրման
սկզբունքը:
Գծային
միջավայրում
մի քանի ալիքների
տարածման
դեպքում,
նրանցից
յուրաքանչյուրը
տարածվում է
այնպես,
կարծես թե մյուս
ալիքները
բացակայում
են, իսկ
միջավայրի մասնիկի
արդյունարար
շեղումը
ժամանակի ցանկացած
պահին
հավասար է
շեղումների
երկրաչափական
գումարին,
որոնք
ստանում են
մասնիկները`
մասնակցելով
գումարվող
պրոցեսներից
յուրաքանչյուրին:
Ելնելով
վերադրման
սկզբունքից և
Ֆուրյեի վերլուծությունից`
ցանկացած
ալիք կարելի է
ներկայացնել
ներդաշնակ
ալիքների
գումարի տեսքով,
այսինքն`
ալիքային
ծրարի տեսքով
կամ ալիքների
խմբով:
Ալիքային
ծրար
է կոչվում
ալիքների
վերադրումը,
որոնք իրարից
տարբերվում
են աննշան
հաճախություններով,
զբաղեցնելով
ժամանակի
յուրաքանչյուր
պահին
տարածության
սահմանափակ
տիրույթ:
Քննարկենք
ալիքների
պարզագույն
խումբ, որը ստացվում
է x-ի դրական
առանցքի երկայնքով
տարածվող
միատեսակ
լայնույթներով,
իրար մոտ
հաճախություններով
և ալիքային
թվերով, ընդ
որում`dω<<ω և dk<<
k երկու
ներդաշնակ
ալիքների
վերադրման
արդյունքում:
Այդ դեպքում
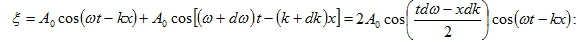
Այս
ալիքը
ներդաշնակից
տարբերվում է
նրանով, որ
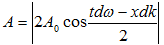
լայնույթը
դանդաղ
փոփոխվող ֆունկցիա
է x
կոորդինատից
և t ժամանակակից:
Ոչ ներդաշնակ
ալիքի
(ալիքային
ծրարի) տարածման
արագություն
ընդունում են
ալիքի
լայնույթի
առավելագույնի
տեղափոխությունը,
դիտարկելով
ինքը
առավելագույնը
որպես ալիքային
ծրարի
կենտրոն: tdω – xdk = const
պայմանի
դեպքում ստանում
ենք`

որտեղ
u-ն խմբային
արագությունն
է: Այն կարելի
է սահմանել
որպես
ալիքների
խմբի
շարժման
արագություն,
կազմելով
ժամանակի
յուրաքանչյուր
պահին
տարածության
մեջ տեղայնացված
ալիքային
ծրար:
(15.13) արտահայտությունը
ստացվել
է պարզագույն
ալիքների
խմբի
համար
երկու
բաղադրիչներից,
սակայն
այն ճիշտ է նաև շատ
ալիքների
վերադրման
համար:
Քննարկենք
խմբային`u = dω/dk և
փուլային` v = ω / k արագությունների
միջև կապը:
Հաշվի
արնելով, որ 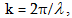 կստանանք`
կստանանք`
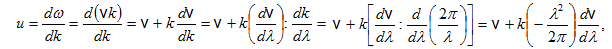
կամ

(15.14)-ից
բխում է, որ u-ն
կարող է
լինել v-ից ինչպես
փոքր, այնպես
էլ մեծ`
կախված 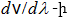 նշանից:
Չդիսպերսող
միջավայրում`
նշանից:
Չդիսպերսող
միջավայրում`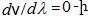 և
խմբային
արագությունը
համընկնում է
փուլայինի
հետ:
և
խմբային
արագությունը
համընկնում է
փուլայինի
հետ:
Խմբային
արագության
հասկացությունը
շատ կարևոր է
ռադիոլոկացիայում.
տիեզերական
օբյեկտների
ղեկավարման
համակարգերում
և այլ դեպքերում
հեռավորությունների
չափմանը հենց
ինքն է
մասնակցում:
Հարաբերականության
տեսությունում
ապացուցվում
է, որ խմբային
արագությունը
` u << c, մինչդեռ
փուլային
արագության
համար սահմանափակում
գոյություն
չունի:
>>
16.
Առաձգական
ալիքի
էներգիան
Երկայնական
ալիքի
տարածման
միջավայրում
առանձնացնենք
այնքան փոքր
տարրական 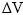 ծավալ,
որ
դեֆորմացիաները
և շարժման
արագությունները
այս ծավալի
բոլոր
կետերում
կարելի լինի
համարել
միատեսակ
համապատասխանաբար
հավասար`
ծավալ,
որ
դեֆորմացիաները
և շարժման
արագությունները
այս ծավալի
բոլոր
կետերում
կարելի լինի
համարել
միատեսակ
համապատասխանաբար
հավասար`
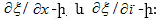
Առանձնացված
ծավալը
օժտված է
առաձգական
դեֆորմացիայի
պոտենցիալ
էներգիայով,
որը որոշվում
է հետևյալ
արտահայտությամբ

Քննարկնող
ծավալն
օժտված կլինի
նաև կինետիկ
էներգիայով`

որտեղ
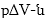 ծավալի
զանգվածն է,
իսկ
ծավալի
զանգվածն է,
իսկ 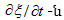 նրա
արագությունը:
(16.1) և (16.2)
արտահայտությունների
գումարը
տալիս է լրիվ
էներգիան`
նրա
արագությունը:
(16.1) և (16.2)
արտահայտությունների
գումարը
տալիս է լրիվ
էներգիան`
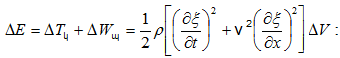
Բաժանելով
ΔE էներգիան ΔV
ծավալին,
որտեղ այն տեղայնացված
է, կստանանք
էներգիայի
ծավալային
խտությունը`
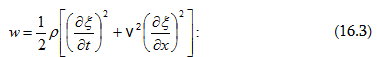
Ածանցելով
հարթ ալիքի (15.1)
հավասարումը
ըստ t-ի և x -ի,
կստանանք`
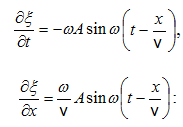
Տեղադրելով
այս
արտահայտությունները
(16.3)-ի բանաձևի
մեջ, կստանանք
`
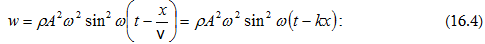
Լայնական
ալիքների
դեպքում
էներգիայի
ծավալային
խտության
համար
ստացվում է
նույնպիսի
արտահայտություն
Ինչպես
հետևում է (16.4)-ից,
էներգիայի
խտությունը
ժամանակի
յուրաքանչյուր
պահին
տարածության
տարբեր կետերում
տարբեր է:
Միևնույն
կետում
էներգիայի խտությունը
ըստ ժամանակի
փոփոխվում է
սինուսի
քառակուսի
աստիճանի
օրենքով: Քանի
որ սինուսի
քառակուսի
աստիճանի
միջին արժեքը
հավասար է 1/2-ի,
ապա
էներգիայի
խտության
միջին արժեքը
ըստ ժամանակի
միջավայրի
յուրաքանչյուր
կետում կլինի`

(16.4)
էներգիայի
խտությունը
և նրա միջին (16.5)
արժեքը համեմատական
են միջավայրի
p խտությանը, ω
հաճախության քառակուսուն
և ալիքի A
լայնույթի
քառակուսուն:
Այսպիսով,
միջավայրը,
որտեղ
առաջանում է
ալիքը, օժտված
է էներգիայի
լրացուցիչ
պաշարով: Այս
էներգիան
տատանումների
աղբյուրից
դեպի միջավայրի
տարբեր
կետերն է
տարածվում
ալիքի
միջոցով,
հետևաբար,
ալիքը իր հետ
տանում է էներգիա:
Միավոր
ժամանակում
որևէ
մակերեսով ալիքի
միջոցով
տեղափոխվող
էներգիայի
քանակը
կոչվում է
էներգիայի
հոսք:
Էներգիայի
հոսքը
միջավայրի
տարբեր
կետերում
օժտված է տարբեր
ինտենսիվությամբ:
Էներգիայի
հոսքը տարածության
տարբեր
կետերում
բնութագրելու
համար
օգտվում են մի
վեկտորական
մեծությունից,
որը կոչվում է
էներգիայի
հոսքի
խտության
վեկտոր: Այս
մեծությունը
թվապես
հավասար է
տվյալ կետով
անցնող և
էներգիայի
տեղափոխությանն
ուղղահայաց
միավոր
մակերեսով
անցնող
էներգիայի
հոսքին:
Էներգիայի
հոսքի
խտության
վեկտորի ուղղությունը
համընկնում է
էներգիայի
փոխադրման
ուղղության
հետ:
Էներգիայի
հոսքի
խտության
վեկտորը որոշվում
է հետևյալ
բանաձևով`

որտեղ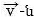 փուլային
արագության
վեկտորն է:
Էներգիայի հոսքի
խտության
վեկտորը
առաջին անգամ
մտցրել է Ա.
Ումովը և
կոչվում է
Ումովի
վեկտոր:
փուլային
արագության
վեկտորն է:
Էներգիայի հոսքի
խտության
վեկտորը
առաջին անգամ
մտցրել է Ա.
Ումովը և
կոչվում է
Ումովի
վեկտոր:
>>
17.
Ալիքների
ինտերֆերենցիան
Կոհերենտություն
է կոչվում մի
քանի տատանողական
կամ ալիքային
պրոցեսների
համաձայնեցված
ընթացքը
ժամանակի և
տարածության
մեջ: Եթե
ալիքների
գրգռված
տատանումների
փուլերի
տարբերությունը
ժամանակի
ընթացքում
մնում է
հաստատուն,
ալիքները
կոչվում են կոհերենտ:
Այդպիսի
ալիքների
աղբյուրները
նույնպես կոչվում
են կոհերենտ:
Տարածության
մեջ երկու
(կամ մի քանի)
կոհերենտ
ալիքների
վերադրման
դեպքում նրա
տարբեր կետերում,
կախված
ալիքների
փուլերի միջև
եղած
հարաբերակցությունից,
ստացվում է
արդյունարար
ալիքի
ուժեղացում
կամ
թուլացում:
Դիտարկենք
երկու
կոհերենտ
սֆերիկ
ալիքների
վերադրումը,
որոնք
գրգռվում են S1
և S2 կետային
աղբյուրներով,
տատանվում են
միևնույն A0 լայնույթով,
ω
հաճախությամբ
և հաստատուն
փուլերի տարբերությամբ:
Համաձայն (15.7)-ի,
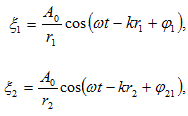
որտեղ
r1-ը և r2-ը
ալիքների
աղբյուրներից
մինչև
ընտրված B կետը
եղած
հեռավորություններն
են, k-ն
ալիքային թիվն
է, 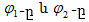 դիտարկվող
երկու սֆերիկ
ալիքների
սկզբնական
փուլերն են:
դիտարկվող
երկու սֆերիկ
ալիքների
սկզբնական
փուլերն են:
Արդյունարար
ալիքի
լայնույթը B
կետում ըստ (5.2)-ի
հավասար է`
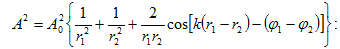
Քանի
որ կոհերենտ
աղբյուրների
համար սկզբնական
փուլերի
տարբերությունը`
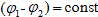 է, ապա
երկու
ալիքների
վերադրման
արդյունքը կախված
է Δ = r1- r2
տարբերությունից,
որը կոչվում
է ալիքների
ընթացքի
տարբերություն:
է, ապա
երկու
ալիքների
վերադրման
արդյունքը կախված
է Δ = r1- r2
տարբերությունից,
որը կոչվում
է ալիքների
ընթացքի
տարբերություն:
Այն
կետերում,
որտեղ
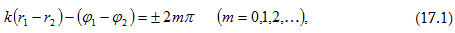
դիտվում
է ինտերֆերենցիոն
առավելագույն:
Արդյունարար
տատանման
լայնույթը`
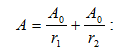
Այն
կետերում,
որտեղ
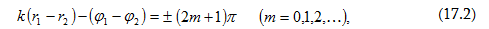
դիտվում
է ինտերֆերենցիոն
նվազագույն:
Արդյունարար
տատանման
լայնույթը`
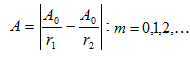
կոչվում
է ինտերֆերենցիոն
առավելագույնի
կամ նվազագույնի
կարգ: (17.1) և (17.2)
պայմանները
բերում են նրան,
որ

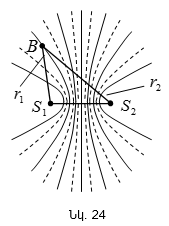
(17.3)
արտահայտությունը
հիպերբոլի
հավասարում է,
որի
կիզակետերը
գտնվում են S1
և S2 կետերում:
Այսպիսով, այն
կետերի
երկրաչափական
տեղը, որտեղ
տատանումները
ուժեղացնում
կամ
թուլացնում
են միմյանց,
ներկայացնում
են հիպերբոլների
ընտանիք (տես
նկ.24,
համապատասխանով
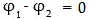 պայմանին):
Հոծ գծերով
ցույց են
տրված այն տեղերը,
որտեղ
տատանումներն
ուժեղացնում են
միմյանց, իսկ
կետագծերով`
այն տեղերը,
որտեղ
տատանումները
թուլացնում
են միմյանց:
պայմանին):
Հոծ գծերով
ցույց են
տրված այն տեղերը,
որտեղ
տատանումներն
ուժեղացնում են
միմյանց, իսկ
կետագծերով`
այն տեղերը,
որտեղ
տատանումները
թուլացնում
են միմյանց:
>>
18.
Կանգուն
ալիքներ
Ալիքների
ինտերֆերենցիայի
արդյունքի
հատուկ
օրինակ են
այսպես
կոչված
կանգուն
ալիքները,
որոնք
առաջանում են
միատեսակ
լայնույթներ
և հաճախություններ
ունեցող
հանդիպակաց
հարթ
ալիքների
վերադրման
հետևանքով:
Կանգուն
ալիքի
հավասարումը
արտածելու
համար
ենթադրենք, որ
երկու հարթ
ալիքներ
տարածվում են
միջավայրում
առանց մարման
իրար ընդառաջ
x-ի առանցքի
երկայնքով,
ընդ որում`
երկու ալիքներն
էլ բնութագրվում
են միատեսակ
հաճախություններով
և լայնույթներով:
Բացի դրանից,
կոորդինատների
սկիզբը
ընտրենք այն
կետում, ուր
երկու ալիքներն
էլ ունեն
միատեսակ
սկզբնական
փուլեր, ժամանակի
հաշվարկը
սկսում ենք
այն պահից,
երբ երկու
ալիքների
սկըզբնական
փուլերը
հավասար են
զրոյի, որից
հետո երկու
ալիքների
հավասարումները
կարելի է գրել
հետևյալ
տեսքով.
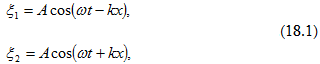
Գումարելով
հավասարումները
և նկատի ունենալով,
որ 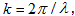 կստանանք
կանգուն
ալիքի
հավասարումը.
կստանանք
կանգուն
ալիքի
հավասարումը.
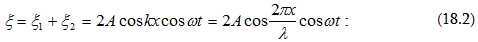
Կանգուն
ալիքի (18.2)
հավասարումից
հետևում է, որ այդ
ալիքի
յուրաքանչյուր
կետում տատանումները
կատարվում են
նույն ω
հաճախությամբ,
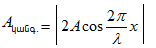
լայնույթով,
որը կախված
է դիտարկվող
կետի x
կոորդինատից:
Միջավայրի
այն կետերում,
որտեղ
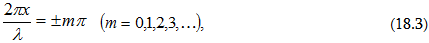
տատանման
լայնույթը
հասնում
է իր առավելագույն
արժեքին,
հավասար
է 2A-ի:
Միջավայրի
այն կետերում,
որտեղ
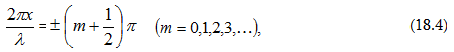
տատանման
լայնույթը
դառնում
է զրո: Այսպիսով,
որոշակի
կետերում
կանգուն
ալիքի
լայնույթը
հավասար
է երկու
գումարվող
ալիքների
լայնույթների
գումարին,
այդպիսի
կետերը
կոչվում
են փնջվածքներ,
այլ կետերում
արդյունարար
լայնույթը
հավասար
է զրոյի,
այդ կետերը
կոչվում
են հանգույցներ:
Հանգույցներում
գտնվող
միջավայրի
կետերը
տատանումներ
չեն կատարում:
(18.3) և
(18.4) արտահայտություններից
կստանանք
համապատասխանաբար
փնջվածքների
և հանգույցների
կոորդինատները
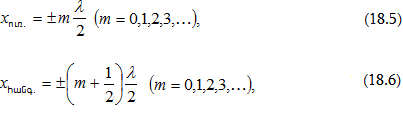
(18.5)
և (18.6)
բանաձևերից
հետևում է, որ
երկու հարևան փնջվածքների
և երկու
հարևան
հանգույցների
միջև
հեռավորությունը
միատեսակ է և
հավասար է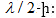 Կանգուն
ալիքի հարևան
փնջվածքի և հանգույցի
միջև
հեռավորությունը
հավասար է
Կանգուն
ալիքի հարևան
փնջվածքի և հանգույցի
միջև
հեռավորությունը
հավասար է 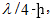 այսինքն`
հանգույցները
և
փնջվածքները
միմյանցից
հեռացած են
ալիքի
երկարության
մեկ քառորդի
չափով: Ի
տարբերություն
վազող ալիքի,
որի բոլոր
կետերը
կատարում են
միատեսակ
լայնույթով,
բայց ըստ
փուլի
ուշացումով
տատանումներ,
կանգուն ալիքի
բոլոր կետերը
երկու
հանգույցների
միջև
տատանվում են
տարբեր
լայնույթներով,
բայց միատեսակ
փուլերով:
Հանգույցով
անցնելու դեպքում
`
այսինքն`
հանգույցները
և
փնջվածքները
միմյանցից
հեռացած են
ալիքի
երկարության
մեկ քառորդի
չափով: Ի
տարբերություն
վազող ալիքի,
որի բոլոր
կետերը
կատարում են
միատեսակ
լայնույթով,
բայց ըստ
փուլի
ուշացումով
տատանումներ,
կանգուն ալիքի
բոլոր կետերը
երկու
հանգույցների
միջև
տատանվում են
տարբեր
լայնույթներով,
բայց միատեսակ
փուլերով:
Հանգույցով
անցնելու դեպքում
` 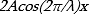 բազմապատկիչը
փոխում է իր
նշանը, ուստի
տատանման
փուլը
հանգույցից
տարբեր
կողմերում
տարբերվում է
π-ով այսինքն
կետերը, որոնք
ընկած են
հանգույցից
տարբեր
կողմերում,
տատանվում են
հակափուլով:
բազմապատկիչը
փոխում է իր
նշանը, ուստի
տատանման
փուլը
հանգույցից
տարբեր
կողմերում
տարբերվում է
π-ով այսինքն
կետերը, որոնք
ընկած են
հանգույցից
տարբեր
կողմերում,
տատանվում են
հակափուլով:
Կանգուն
ալիքի
առաջացումը
սովորաբար
դիտվում է
վազող ալիքի և
անդրադարձած
ալիքի ինտերֆերենցիայի
դեպքում:
Օրինակ, եթե
պարանի ծայրն
անշարժ ամրացվի,
ապա պարանի
ամրացման
տեղում
անդրադարձած
ալիքը կինտերֆերենցվի
առաջ վազող
ալիքի հետ և
կառաջացնի
կանգուն ալիք:
Այդ դեպքում
անշարժ մնացող
հանգուցային
կետերը
միմյանցից
գտնվում են
վազող ալիքի
երկարության
կեսին հավասար
հեռավորությունների
վրա, պարանի
ամրացման
կետում, այսինքն`
այն
սահմանում,
որտեղ տեղի է
ունենում ալիքի
անդրադարձումը,
ստացվում է
հանգույց:
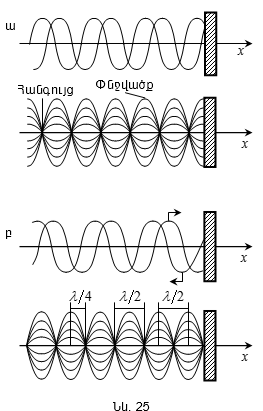
Ընդհանրապես,
անդրադարձման
սահմանում
կարող է
առաջանալ կամ
հանգույց, կամ
փնջվածք, որը
կախված է
միջավայրի
խտությունների
հարաբերակցությունից:
Եթե
միջավայրը,
որից տեղի է ունենում
անդրադարձումը,
ավելի պակաս
խիտ է, քան այն
միջավայրը,
ուր
տարածվում է
ալիքը, ապա
սահմանում
առաջանում է
փնջվածք (նկ.25, ա):
Եթե այն
միջավայրը,
որից
կատարվում է
անդրադարձումը,
ավելի խիտ է,
քան այն
միջավայրը,
ուր տեղի է
ունենում
ալիքի
տարածումը,
ապա սահմանում
առաջանում է
հանգույց (նկ. 25,
բ):
Ավելի
խիտ
միջավայրից
անդրադառնալու
ժամանակ
սահմանում
հանգույցի
առաջանալը
բացատրվում է
նրանով, որ
ալիքը
անդրադառնալով
ավելի խիտ
միջավայրից,
անդրադարձման
տեղում իր փուլը
փոխում է
հակադիր
փուլի, այդ
ժամանակ սահմանում
գումարվում
են հակադիր
ուղղության
տատանումներ,
որը և
հանգեցնում է
հանգույցի
առաջացմանը:
Քանի
որ փուլը
փոխվում է
հակադիր
փուլի ալիքի
երկարության
կեսին
հավասար
տարածության
վրա, ապա այդ
փաստն
ընդունված է
անվանել «կես
ալիքի կորուստ»:
Եթե ալիքն
անդրադառնում
է ավելի նոսր
միջավարից`
անդրադարձման
տեղում,
ալիքը չի
փոխում փուլը,
այդ պատճառով
կես ալիքի
կորուստ տեղի
չի ունենում,
որի շնորհիվ ընկնող
և
անդրադարձող
ալիքների
փուլերը սահմանում
միատեսակ են,
և այդ տեղում
միևնույն փուլի
տատանումների
գումարման
հետևանքով առաջանում
է փնջվածք:
Եթե
դիտարկվի
վազող ալիքը,
ապա նրա
տարածման ուղղությամբ
տեղափոխվում
է էներգիա:
Կանգուն
ալիքի
դեպքում
էներգիայի
տեղափոխում
չկա, քանի որ
հակառակ
ուղղություններով
միատեսակ
լայնույթներով
ընկնող և
անդրադարձնող
ալիքները
կրում են
միատեսակ
էներգիա: Ուստի
արդյունարար
կանգուն
ալիքի
էներգիան
երկու
հանգուցային
կետերի
սահմաններում
մնում է
հաստատուն:
Միայն ալիքի
երկարության
կեսին
հավասար
սահմանային
հեռավորությունների
վրա
կատարվում է
կինետիկ
էներգիայի փոխակերպում
պոտենցիալի և
հակառակը:
>>
19.
Ձայնային
ալիքներ
Առաձգական
միջավայրում
տարածվող
ալիքները,
որոնց
հաճախոթյուններն
ընկա են 16-20000 Հց
սահմաններում,
կոչվում են ձայնային
ալիքներ: 20
Հց-ից փոքր
հաճախություն
ունեցող
առաձգական
ալիքները
կոչվում են ինֆրաձայն,
իսկ 20000Հց-ից
ավելի հաճախություն
ունեցող
առաձգական
ալիքները` ուլտրաձայն:
Ինֆրաձայները
և
ուլտրաձայները
մարդու ականջը
չի լսում:
Գազերում
և
հեղուկներում
ձայնային
ալիքը լինում
է միայն
երկայնական և
բաղկացած է
միջավայրի
իրար
հաջորդող
սեղմումներից
և նոսրացումներից:
Պինդ
մարմիններում
կարող են
տարածվել
ինչպես
երկայնական,
այնպես էլ
լայնական
ալիքներ:
Ձայնի
ինտենսիվություն
է կոչվում այն
մեծությունը,
որը որոշվում
է ըստ
ժամանակի
էներգիայի
միջին
արժեքով, որը
տեղափոխում է
ձայնային
ալիքը միավոր
ժամանակում
ալիքի տարածման
ուղղությանը
ուղղահայաց
միավոր
մակերեսով.
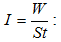
Ինտենսիվության
միավորը
ՄՀ-ում Վտ/մ2
է:
Տարբեր
հաճախությունների
համար մարդու
ականջի
զգայնությունը
տարբեր է:
Ձայնային զգացողություն
առաջացնելու
համար ալիքը
պետք է օժտված
լինի որոշ
նվազագույն
ինտենսիվությամբ,
որը կոչվում է
լսելիության
շեմ:
Լսելիության
շեմը տարբեր
մարդկանց
համար տարբեր
է և խիստ
կախում ունի
ձայնի
հաճախությունից:
Մեծ
ինտենսիվությունների
դեպքում ալիքը
դադարում է
որպես ձայն
ընկալվելուց,
և ականջում
առաջացնում է ցավի
զգացում: Նկ.
26-ում բերված է
լսելիության
շեմի և ցավի
զգացողության
կախվածությունը
ձայնի
հաճախությունից:
Այն տիրույթը,
որն ընկած է երկու
կորերի միջև,
լսելիության
տիրույթն է:
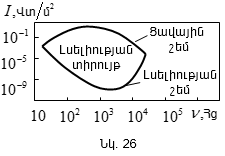
Եթե
ձայնի
ինտենսիվությունը
մի մեծություն
է, որը
օբյեկտիվորեն
բնութագրում
է ալիքային
պրոցեսը, ապա
ձայնի
սուբյեկտիվ բնութագիրը,
կապված նրա
ինտենսիվության
հետ ձայնի
ուժգնությունն
է, որը կախված
է հաճախությունից:
Համաձայն
Վեբեր-Ֆեխների
ֆիզոլոգիական
օրենքի` ձայնի
ինտենսիվության
մեծացման հետ
ուժգնությունը
աճում է
լոգարիթմական
օրենքով: Դրա
հիման վրա
ներմուծվում
է ձայնի
ուժգնության
օբյեկտիվ
գնահատականը
ըստ նրա ինտենսիվության
չափման
արժեքի.
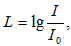
որտեղ
I0-ն ձայնի
ինտենսիվությունն
է լսելիության
շեմի
վրա, որը բոլոր
ձայների
համար
ընդունվում
է հավասար`
10-12 Վտ/մ2:
L մեծությունը
կոչվում
է ձայնի
ինտենսիվության
մակարդակ
և չափվում
է բելերով
(ի պատիվ
հեռախոսի
գյուտարար
Բելի):
Սովորաբար
օգտվում
են 10 անգամ
ավելի
փոքր
միավորից,
որը կոչվում
է դեցիբել
(դԲ):
Ձայնի
ֆիզոլոգիական
բնութագիրը
ուժգնության
մակարդակն
է որն արտահայտվում
է ֆոներով
(ֆոն):
1000 Հց (մաքուր
տոնի
ստանդարտ
հաճախությունը)
հավասար
է ֆոնի, եթե նրա ինտենսիվության
մակարդակը
հավասար
է 1 դԲ-ի: Օրինակ, մետրոյի
վագոնում
մեծ արագությունների
դեպքում
աղմուկին
համապատասխանում
է 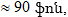 իսկ 1մ հեռավորության
վրա շշուկին`
իսկ 1մ հեռավորության
վրա շշուկին`
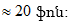
Իրական
ձայնը
հաճախությունների
մեծ հավաքածուով
ներդաշնակ
տատանումների
վերադրում է,
այսինքն
ձայնը օժտված
է ակուստիկ
սպեկտրով,
որը կարող է
լինել անընդհատ
(որոշակի
միջակայքում
մասնակցում
են բոլոր հաճախությունների
տատանումներ)
և գծային (մասնակցում
են իրարից բաժանված
որոշակի
տատանումներ):
Ձայնը,
բացի
ուժգնությունից,
բնութագրվում
է նաև
բարձրությունով
և տեմբրով:
Ձայնի բարձրությունը
բնութագրում
է ձայնի
որակը: Հաճախության
մեծացման հետ
ձայնի
բարձրությունը
մեծանում է:
Ակուստիկ
սպեկտրի
բնույթը և էներգիայի
բաշխումը հաճախությունների
միջև որոշում
է ձայնային
զգացողության
առանձնահատկությունը,
որը կոչվում է
ձայնի տեմբր:
Այսպես,
տարբեր
երգիչներ
վերցնելով
միևնույն
նոտան,
ունենում են
տարբեր
ակուստիկ
սպեկտր,
այսինքն
նրանց ձայնն
ունի տարբեր
տեմբր:
Ձայնի
աղբյուր
կարող է լինել
յուրաքանչյուր
մարմին, որը
տատանվում է
առաձգական
միջավայրում
ձայնային
հաճախությամբ
(օրինակ,
լարային
գործիքներում
ձայնի աղբյուրը
լարն է, որը
միացված է
գործիքի
իրանին):
Մարմինը,
կատարելով
տատանումներ,
առաջ է բերում
նույն
հաճախությամբ
իրեն հարող
միջավայրի մասնիկների
տատանումներ:
Տատանողական
շարժման
վիճակը
հաջորդաբար
հաղորդվում է
մարմնից
ավելի հեռու
գտնվող
միջավայրի
մասնիկներին,
այսինքն`
միջավայրում
տարածվում է
աղբյուրի
հաճախությանը
հավասար
տատանման
հաճախությամբ
ալիք, որոշակի
արագությամբ,
որը կախված է
միջավայրի
խտությունից
և առաձգական
հատկություններից:
Ձայնային
ալիքի
տարածման
արագությունը
գազերում
որոշվում է
հետևյալ
բանաձևով`(19.1)

որտեղ
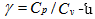 գազի
մոլային
ջերմունակությունների
հարաբերությունն
է հաստատուն
ճնշման և
հաստատուն
ծավալի
դեպքում, R -ը
մոլային
գազային հաստատունն
է, T-ն
ջերմադինամիկական
ջերմաստիճանը,
M-ը` մոլային
զանգվածը: (19.1)
բանաձևից
հետևում է, որ
ձայնի
արագությունը
գազում
կախված չէ p
ճնշումից,
բայց աճում է
ջերմաստիճանի
բարձրացումով:
Որքան մեծ է
գազի մոլային
զանգվածը,
այնքան փոքր է
նրանում ձայնի
արագությունը:
Օրինակ, T=273Կ
դեպքում
ձայնի արագությունը
օդում
գազի
մոլային
ջերմունակությունների
հարաբերությունն
է հաստատուն
ճնշման և
հաստատուն
ծավալի
դեպքում, R -ը
մոլային
գազային հաստատունն
է, T-ն
ջերմադինամիկական
ջերմաստիճանը,
M-ը` մոլային
զանգվածը: (19.1)
բանաձևից
հետևում է, որ
ձայնի
արագությունը
գազում
կախված չէ p
ճնշումից,
բայց աճում է
ջերմաստիճանի
բարձրացումով:
Որքան մեծ է
գազի մոլային
զանգվածը,
այնքան փոքր է
նրանում ձայնի
արագությունը:
Օրինակ, T=273Կ
դեպքում
ձայնի արագությունը
օդում  (18.1) բանաձևը
համապատասխանում
է փորձի
տվյալներին:
(18.1) բանաձևը
համապատասխանում
է փորձի
տվյալներին:
Մթնոլորտում
ձայնի
տարածման
դեպքում ամհրաժեշտ
է հաշվի առնել
մի շարք
գործոններ.
քամու
արագությունը
և
ուղղությունը,
օդի խոնավությունը,
գազային
միջավայրի
մոլեկուլային
կառուցվածքը,
ձայնի
անդրադարձման
և բեկման
երևույթը
երկու միջավայրերի
սահմանի վրա:
Բացի դրանից,
ցանկացած
իրական
միջավայր
օժտված է
մածուցիկությամբ,
դրա համար էլ
ձայնը մարում
է, այսինքն` տեղի
է ունենում
լայնույթի
փոքրացում,
հետևաբար ձայնային
ալիքի
տարածմանը
զուգընթաց
նրա ինտենսիվությունը
փոքրանում է:
Ձայնի մարումը
նշանակալի
չափով
պայմանավորված
է միջավայրում
նրա
կլանումով,
կապված
ձայնային էներգիայի
ոչ դարձելի
անցումով
էներգիայի
այլ ձևերի
(հիմնականում
ջերմայինի):
Շենքի
ակուստիկայի
համար մեծ
նշանակություն
ունի ձայնի
ռեվերբերացիան`
ձայնի
աստիճանաբար
մարման
պրոցեսը փակ շենքերում
նրա աղբյուրի
անջատումից
հետո: Եթե
շենքը դատարկ
է, ապա տեղի է
ունենում
ձայնի դանդաղ
մարում և
շենքում
թնդյուն է
առաջանում:
Եթե ձայները
մարում են
արագ
(ձայնակլանիչ նյութերի
օգտագործման
դեպքում), ապա
նրանք ընկալվում
են խլացումով:
Ռեվերբերացիայի
ժամանակամիջոցը
այն է. որի
ընթացքում
ձայնի ինտենսիվությունը
շենքում
թուլանում է
միլիոն անգամ,
իսկ նրա
մակարդակը`
60դԲ-ով: Շենքն
ունի լավ
ակուստիկա,
եթե
ռեվերբերացիայի
ժամանակը կազմում
է 0,5-1,5 վ:
>>
20.
Դոպլերի
էֆեկտը
ակուստիկայում
Դոպլերի
էֆեկտ է
կոչվում
ընդունիչի
կողմից ընկալվող
տատանման
հաճախության
փոփոխությունը
այդ
տատանումների
աղբյուրի և
ընդունիչի`
միմյանց
նկատմամբ շարժման
դեպքում:
Օրինակ,
փորձից
հայտնի է, որ
գնացքի
սուլոցի
ձայնը
կառամատույցին
մոտենալիս
բարձրանում է,
և ցածրանում է
հեռանալիս,
այսինքն
տատանումների
աղբյուրի
շարժումը
ընդունիչի
նկատմամբ
փոխում է
գրանցվող տատանումների
հաճախությունը:
Դոպլերի
էֆեկտը
քննարկելու
համար
ենթադրենք, որ
ձայնի
աղբյուրը և ընդունիչը
շարժվում են
նրանց
միացնող
ուղղի երկայնքով.
vաղբ և vընդ -ը համապատասխանաբար`
աղբյուրի և
ընդունիչի
շարժման
արագություններն
են, ընդ որում
դրանք դրական
են, եթե աղբյուրը
(ընդունիչը)
մոտենում է
ընդունիչին
(աղբյուրին), և
բացասական,
եթե հեռանում
են: Աղբյուրի
տատանման
հաճախությունը
հավասար է:
Քննարկենք
հետևյալ
դեպքերը:
1. Աղբյուրը և
ընդունիչը
միջավայրի
նկատմամբ
անշարժ են, այսինքն`
vաղբ = vընդ =
0: Եթե u-ն
ալիքի
տարածման
արագությունն
է դիտարկվող
միջավայրում,
ապա ալիքի
երկարությունը`
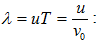
Ալիքը
տարածվելով
միջավայրում`
հասնում է ընդունիչին
և առաջ է
բերում նրա
ձայնազգայուն
տարրի
տատանումներ
հետևյալ
հաճախությամբ`
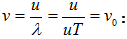
Հետևաբար,
ձայնի v
հաճախությունը,
որը գրանցում
է ընդունիչը,
հավասար է այն
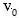 հաՃախությանը,
որով
աղբյուրից
ճառագայթվում
է ձայնային
ալիքը:
հաՃախությանը,
որով
աղբյուրից
ճառագայթվում
է ձայնային
ալիքը:
2.
Ընդունիչը
մոտենում է
աղբյուրին,
աղբյուրն անշարժ
է, այսինքն vընդ
> 0, vաղբ = 0:
Տվյալ
դեպքում
ալիքի
տարածման
արագությունը
ընդունիչի
նկատմամբ
դառնում է
հավասար` u + vընդ
: Քանի որ
ալիքի
երկարությունն
այդ դեպքում չի
փոխվում, ապա
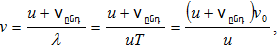
այսինքն`
ընդունիչով
ընկալվող
հաճախությունը (u + vընդ)/u անգամ
մեծ է
աղբյուրի
տատանման
հաճախությունից:
3.
Աղբյուրը
մոտենում է ընդունիչին,
իսկ
ընդունիչն
անշարժ է,
այսինքն` vաղբ
> 0 և vընդ > 0:
Տատանումների
արագությունը
կախված է
միայն
միջավայրի հատկություններից,
դրա համար էլ
աղբյուրի տատանումների
պարբերությանը
հավասար
ժամանակամիջոցում
ճառագայթված
ալիքը
ընդունիչի ուղղությամբ
անցնում է uT
հեռավորություն
(հավասար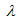 ալիքի
երկարությանը),
անկախ այն
բանից` աղբյուրը
շարժվում է,
թե անշարժ է:
Այդ նույն
ժամանակամիջոցում
աղբյուրն
անցնում է
ալիքի ուղղությամբ
vաղբT
հեռավորություն
(նկ.27), այսինքն`
ալիքի երկարությունը
շարժման
ուղղությամբ
կրճատվում և
դառնում է
հավասար`
ալիքի
երկարությանը),
անկախ այն
բանից` աղբյուրը
շարժվում է,
թե անշարժ է:
Այդ նույն
ժամանակամիջոցում
աղբյուրն
անցնում է
ալիքի ուղղությամբ
vաղբT
հեռավորություն
(նկ.27), այսինքն`
ալիքի երկարությունը
շարժման
ուղղությամբ
կրճատվում և
դառնում է
հավասար`
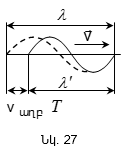
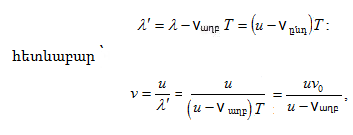
այսինքն,
տատանման v
հաճախությունը,
որն ընկալվում
է ընդունիչի
կողմից,
մեծանում է u/(u – vաղբ)
անգամ: 2 և 3
կետերում
նշված
դեպքերում,
եթե vաղբ < 0 և vընդ
< 0,
նշանը կդառնա
հակառակ:
4.
Աղբյուրը և
ընդունիչը
շարժվում են
միմյանց նկատմամբ:
Օգտագործելով
և դեպքերում
ստացված
արդյունքները`
կարելի է
գրել
ընդունիչով
գրանցվող տատանման
հաճախության
համար
հետևյալ արտահայտությունը
`

ընդ որում`
վերին
նշանը
վերցվում
է, եթե աղբյուրի
կամ ընդունիչի
շարժման
դեպքում
տեղի
է ունենում
դրանց
մոտեցում,
ներքևի
նշանը`
դրանց
փոխադարձաբար
հեռանալու
դեպքում:
Բերված
բանաձևերից
հետևում
է, որ Դոպլերի
էֆեկտը
տարբեր
է կախված
այն բանից
թե շարժվում
է աղբյուրը
կամ ընդունիչը:
Եթե արագությունների
ուղղությունները
չեն համընկնում
աղբյուրով
և ընդունիչով
անցնող
ուղղի
հետ, ապա այդ արագությունների
փոխարեն
(20.1) բանաձևում
պետք
է վերցնել
նրանց
պրոյեկցիաները
այդ ուղղի
ուղղության
վրա:
>>
21.
Ուլտրաձայն
և նրա կիրառությունը
Իր
բնույթով
ուլտրաձայնը
առաձգական
ալիքներ են, և
դրանով այն
չի
տարբերվում
ձայնից: Սակայն
ուլտրաձայնը,
ունենալով
մեծ հաճախություններ
( v > 20 կՀց, և
հետևաբար,
ալիքի փոքր
երկարություններ,
բնութագրվում
է
առանձնահատուկ
հատկություններով:
Ուլտրաձայնային
ալիքները
փոքր
երկարության
շնորհիվ, ինչպես
և լուսային
ալիքները,
կարող են
ստացվել խիստ
ուղղորդված
փնջերի
տեսքով:
Ուլտրաձայնային
ալիքների
գրգռման
համար ներկայումս
հիմնականում
օգտվում են
երկու երևույթներից.
հակադարձ
պիեզոէլեկտրական
էֆեկտից և
մագնիսաստրիկցիայից:
Հակադարձ
պիեզոէլեկտրական
էֆեկտն այն է,
որ որոշ
բյուրեղներից
(օրինակ,
քվարցից,
սեգնետյան
աղից,
բարիումի
տիտանատից և
այլն) որևէ
ձևով կտրված
թիթեղը
էլեկտրական
դաշտի
ազդեցության
տակ
դեֆորմացվում
է. դաշտի մի
ուղղության
դեպքում
երկարում է,
իսկ հակառակ ուղղության
դաշտի
դեպքում`
սեղմվում:
Տեղավորելով
թիթեղը
մետաղական
շրջադիրների
միջև, որոնց
միացված է
բարձր
հաճախության
փոփոխական
լարման
աղբյուրը,
կարելի է այդ
թիթեղում
առաջացնել
հարկադրական
տատանումներ:
Այդ տատանումների
լայնույթները
հատկապես մեծ են
դառնում այն
դեպքում, երբ
լարման
փոփոխությունների
հաճախությունը
համընկնում է
թիթեղի սեփական
տատանումների
հաճախության
հետ: Թիթեղի տատանումները
հաղորդվում
են նրան
շրջապատող
հեղուկ կամ
գազային
միջավայրին,
առաջացնելով
նրա մեջ
ուլտրաձայնային
ալիք:
Մագնիսաստրիկցիայի
երևույթն այն
է, որ ֆեռոմագնիսական
նյութերը
(երկաթ, նիկել,
որոշ համաձուլվածքներ
և այլն)
մագնիսական
դաշտի ազդեցությունից
դեֆորմացվում
են: Ուստի
ֆերրոմագնիսական
ձողը
փոփոխական
մագնիսական դաշտում
տեղավորելով
(օրինակ,
այնպիսի կոճի
մեջ, որով
անցնում է
փոփոխական
հոսանք),
կարելի է
առաջացնել
մեխանիկական
տատանումներ,
և դարձյալ
դրանք
առանձնապես
ուժգին
կլինեն
ռեզոնանսի
դեպքում:
Ուղղորդված
ուլտրաձայնային
փնջերը լայն կիրառությում
են գտել
տեխնիկայում,
օրինակ, ուղղորդված
ստորջրյա
որոշակի
կողմեր ազդանշաններ
տալու համար,
ստորջրյա
առարկաները
հայտնաբերելու
և խորությունները
որոշելու
համար
(էխոլոտ):
Էխոլոտի
կազմության
սկզբունքը
հետևյալն է.
ուլտրաձայների
աղբյուրից
ջրի մեջ
ուղղաձիգ
դեպի ներքև
ուղարկվում է
ձայնային
ալիք, որը
հասնելով
հատակին,
անդրադառնում
է նրանից և ետ
վերադառնում:
Իմանալով
ձայնի
տարածման
արագությունը
ջրում, ըստ
ուլտրաձայնային
ազդանշանի առաքման
և նրա
վերադարձի
(արձագանքը
նկատելու)
միջև ընկած
ժամանակամիջոցի,
հեշտ է հաշվել
խորությունը:
Արձագանքի
ընկալումը
կատարվում է
նաև պիեզոքվարցի
միջոցով:
Ձայնային
ալիքները հասնելով
պիեզոքվարցին,
նրա մեջ
առաջացնում են
առաձգական
տատանումներ,
որոնց
հետևանքով
քվարցի
հակադիր
մակերևույթների
վրա առաջանում
են
էլեկտրական
լիցքեր, որոնք
համապատասխան
էլեկտրական
սարքավորման
միջոցով կարող
են
հայտնաբերվել
և չափվել:
Եթե
ուլտրաձայնային
ազդանշանը
բաց թողնվի
հետազոտվող
դետալի միջով,
ապա ըստ փնջի
ցրման
բնույթի և
ուլտրաձայնային
ստվերի
առաջացման
կարելի է
նրանում հայտնաբերել
արատները:
Այդ
սկզբունքի
հիման վրա
ստեղծվել է
տեխնիկայի
ամբողջ մի
ճյուղ`
ուլտրաձայնային
արատադիտում,
որի սկիզբը
դրվել է Սոկոլովի
կողմից:
Ուլտրաձայնի
կիրառությունն
ընկած է նաև
ակուստիկայի
նոր
բնագավառի` ձայնագիտական
էլեկտրոնիկայի
հիմքում, որը
հնարավորություն
է տալիս դրա
հիման վրա
մշակել
սարքեր
միկրոռադիոէլեկտրոնիկայում
ազդանշանների
ինֆորմացիայի
մշակման
համար: Բժշկության
մեջ փոքր
հզորության
ուլտրաձայնն
օգտագործվում
է որպես
ախտորոշման,
իսկ մեծ
հզորության ուլտրաձայնը
կիրառվում է
վիրաբուժական
նպատակներով:
Ուլտրաձայնը
կիրառվում է
նաև շատ կոշտ
և շատ փխրուն
մարմինների
մեխանիկական մշակման
համար,
քիմիայում
(էմուլսիաների,
սուսպենզիաների
ստացում),
մետաղաձուլման
գործում, երկրաբանության
մեջ
(ուլտրաձայնային
կարոտաժ), ինչպես
և
տեխնոլոգիական
տարբեր
պրոցեսներում:
>>
ԳԼՈՒԽ 3
ԷԼԵԿՏՐԱՄԱԳՆԻՍԱԿԱՆ
ԱԼԻՔՆԵՐ
22. Էլեկտրամագնիսական
ալիքների
փորձնական
Ստացումը
Մաքսվելի
տեսությունից
բխող
բազմաթիվ
կարևոր
հետևություններից
ամենաէականը
էլեկտրամագնիսական
ալիքների
գոյության
կանխատեսումն
է: Համաձայն
այդ տեսության`
փոփոխական
մագնիսական
դաշտը
ստեղծում
է մրրկային
էլեկտրական
դաշտ,
իսկ փոփոխական
էլեկտրական
դաշտը`
մագնիսական
դաշտ:
Եթե տարածության
որևէ
կետում
ստեղծվում
է փոփոխական
մագնիսական
դաշտ
(դա կարող
է տեղի ունենալ,
օրինակ,
հաղորդչում
հոսանքի
ուժի
փոփոխության
հետևանքով),
ապա այն տարածության
հարևան
կետերում
ստեղծում
է փոփոխական
մագնիսական
դաշտ:
Վերջինս
իր հերթին
այլ կետերում
ստեղծում
է փոփոխական
էլեկտրական
դաշտ
և այսպես
շարունակ:
Այսպիսով,
նկարագրված
պրոցեսը
չի տեղայնացվում
իր ծագման
տեղում,
այլ ժամանակի
ընթացքում,
ընդգրկելով
ավելի
ու ավելի
մեծ տիրույթներ,
տարածվում
է տարածության
մեջ` առաջացնելով
էլեկտրամագնիսական
ալիք:
Փոփոխական
էլեկտրամագնիսական
դաշտի
տարածումը
տարածության
մեջ
կոչվում
է էլեկտրամագնիսական
ալիք:
Մաքսվելի
տեսության
հաստատման
համար
կարևոր
դեր խաղացին
Հերցի
փորձերը,
որոնց
համաձայն
էլեկտրական
և մագնիսական
դաշտերը
տարածվում
են ալիքների
տեսքով,
որոնց
վարքը
լրիվ
նկարագրվում
է Մաքսվելի
հավասարումներով:
Էլեկտրամագնիսական
ալիքների
իրական
աղբյուրներ
կարող
է լինել
ցանկացած
տատանողական
կոնտուր
կամ հաղորդիչ,
որով
հոսում
է փոփոխական
հոսանք,
քանի
որ էլեկտրամագնիսական
ալիքների
գրգռման
համար
անհրաժեշտ
է տարածության
մեջ ստեղծել
փոփոխական
էլեկտրական
դաշտ
(շեղման
հոսանք)
կամ համապատասխանաբար
փոփոխական
մագնիսական
դաշտ:
Սակայն
աղբյուրի
ճառագայթման
ընդունակությունը
որոշվում
է նրա ձևով, չափերով
և տատանման
հաճախությամբ:
Որպեսզի
ճառագայթումը
էական
դեր խաղա անհրաժեշտ
է մեծացնել
տարածության
այն ծավալը
ուր ստեղծվում
է էլեկտրամագնիսական
դաշտը:
Ուրեմն
էլեկտրամագնիսական
ալիքների
ստացման
համար
փակ տատանողական
կոնտուրները
պիտանի
չեն, քանի որ էլեկտրական
դաշտը
հիմնականում
կենտրոնացված
է կոնդենսատորի
ներսում,
իսկ մագնիսական
դաշտը`
կոճի
ներսում:
Կոնտուրից
հեռու
տիրույթներում
էլեկտրամագնիսական
դաշտը
գործնականում
բացակայում
է:
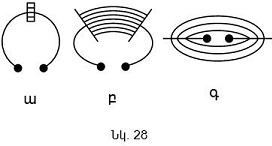
Հ.
Հերցը
իր փորձերում,
փոքրացնելով
կոճի
գալարների
թիվը
և կոնդենսատորի
շրջադիրների
մակերեսը,
միաժամանակ
հեռացնելով
շրջադիրները
իրարից
(նկ. 28, ա, բ)` անցում
կատարեց
փակ տատանողական
կոնտուրից
բաց
տատանողական
կոնտուրի
(Հերցի
վիբրատորին):
Այդպիսի
կոնտուրում
առաջացած
էլեկտրամագնիսական
տատանումները
չեն տեղայնացվում
սահմանափակ
տիրույթում,
այլ տարածվում
են տարածության
մեջ որպես
էլեկտրամագնիսական
ալիք:
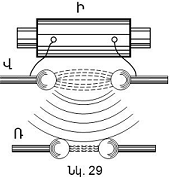
Բաց
տատանողական
կոնտուրն
օժտված
է համեմատաբար
փոքր
էլեկտրաունակությամբ
և ինդուկտիվությամբ,
ուստի
նրանում
ծագող
տատանումների
հաճախությունը,
հետևաբար
ճառագայթված
ալիքի
ինտենսիվությունը
էապես
գերազանցում
է փակ կոնտուրի
առաքած
ինտենսիվությունը:
Հերցի
տատանակը
(վիբրատորը)
կազմված
է երկու
ուղիղ
հաղորդալարերից,
որոնց
ծայրերն
իրարից
բաժանված
են օդային
նեղ տարածությամբ
(կայծային
արանքով,
նկ.28, գ): Հերցը ձողերի
ծայրերին
ամրացնում
էր տարբեր
չափերի
մետաղե
գնդեր,
որոնց
օգնությամբ
փոխում
էր տատանակի
էլեկտրաունակությունը:
Էլեկտրամագնիսական
ալիքներ
գրգռելու համար
Հերցի
տատանակը
միացվում է Ի ինդուկտորին
(նկ. 29): Երբ
լարումը
գերազանցում էր
որոշակի
սահմանային
արժեքը,
հաղորդալարերի
արանքում
կայծ էր
առաջանում,
տատանակի շղթան
փակվում էր, և
պարպման
ընթացքում
շղթայում
ծագում էին
բարձր
հաճախության
էլեկտրամագնիսական
տատանումներ:
Մարման
հետևանքով
(ճառագայթում,
ջերմային
կորուստներ)
լարումը
փոքրանում էր,
և պարպումը
դադարում էր:
Այնուհետև
ինդուկտորը
նորից
լիցքավորում
էր
կոնդենսատորը,
նորից կայծ էր
առաջանում, և
այսպես
շարունակ դիտվում
էին
տատանումներ:
Էլեկտրամագնիսական
ալիքների
գրանցման
համար Հերցը
ճառագայթող
տատանակից
որոշ
հեռավորության
վրա
տեղադրում էր
երկրորդ
տատանակը` Ռ
ռեզոնատորը,
որի
տատանումների
սեփական հաճախությունը
հավասար էր
ճառագայթող
տատանակի
հաճախությանը,
այսինքն
համալրված է
ռեզոնանսով
տատանակի հետ:
Հերցը
ոչ միայն
ստացավ և
գրանցեց
էլեկտրամագնիսական
ալիքները,
այլև պարզեց
դրանց հիմնական
հատկությունները:
Նա պարզեց, որ
էլեկտրամագնիսական
ալիքները
տարածվում են
դիէլեկտրական
միջավայրում:
Փորձերով նա
պարզեց նաև,
որ
էլեկտրամագնիսական
ալիքներն
անդրադառնում
են մետաղի
մակերևույթից:
Ուսումնասիրելով
տատանակից
եկող և մետաղե
թիթեղից
անդրադարձած
ալիքների
վերադրման
երևույթը`
Հերցը
հայտնաբերեց,
որ տարածության
մեջ
առաջանում են
ալիքի
էներգիայի բաշխման
առավելագույններ
և
նվազագույններ:
Որոշելով
հարևան
առավելագույնների
դիրքերը նա
կարողացավ c = λv բանաձևով
որոշել
էլեկտրամագնիսական
ալիքի
տարածման
արագությունը:
Պարզվեց, որ
այն հավասար է
վակուումում
լույսի
տարածման
արագությանը`
c = 3 · 108 կմ/վ:
Այսպիսով
Հերցի
կատարած
փորձերով
փայլուն
կերպով
ապացուցվեց
Մաքսվելի
տեսության
ճշմարտացիությունը:
Չմարող
տատանումնր
ստանալու
համար անհրաժեշտ
է ստեղծել
ինքնատատանողական
համակարգ, որն
ապահովում է
էներգիայի
հաղորդումը
մի հաճախությամբ,
որը հավասար է
կոնտուրի
սեփական
տատանումների
հաճախությանը:
Ուստի 20-րդ դարում
անցում
կատարվեց
էլեկտրամագնիսական
ալիքների գրգըռմանը
էլեկտրոնային
լամպերի
օգնությամբ:
Լամպային
գեներատորները
հնարավորություն
են տալիս
ստանալու
(գործնականորեն
ցանկացած)
տրված
հզորության և
սինուսոիդային
ձևի
տատանումներ:
Էլեկտրամագնիսական
ալիքները
օժտված
լինելով հաճախությունների
լայն
տիրույթով
(կամ λ = c / v ալիքի
երկարություններով,
որտեղ c-ն էկեկտրամագնիսական
ալիքների արագությունն
է վակուումում),
մեկը մյուսից
տարբերվում
են իրենց
գրգռման և
գրանցման
եղանակներով,
ինչպես նաև
հատկություններով:
Լույսի
էլեկտրամագնիսական
բնույթի
պարզաբանումը
թույլ տվեց
բոլոր տիպի
էլեկտրամագնիսկան
ճառագայթումները
դասակարգել և
միավորել
էլեկտրամագնիսական
ալիքների
սանդղակում: Էլեկտրամագնիսական
ալիքները
ընդունված է
բաժանել
ցածրահաճախային
ճառագայթման,
ռադիոալիքների,
ինֆրակարմիր
ճառագայթման, տեսանելի
լույսի,
ուլտրամանուշակագույն
ճառագայթման, ռենտգենյան
ճառագայթման
և
գամմա-ճառագայթման:
Էլեկտրամագնիսական
ալիքների
կլանման, անդրադարձման
և այլ
հատկություններն
էապես կախված
են նրանց
ալիքի երկարությունից:
Քննարկենք
էլեկտրամագնիսական
ալիքների
հիմնական խմբին
այս
տեսանկյունից:
Ցածրհաճախական
ճառագայթման
ալիքները այն էլեկտրամագնիսական
ալիքներն են,
որոնք
գրգռվում են
մեծ ինդուկտիվությամբ
և
էլեկտրաունակությամբ
սարքերում:
Օրինակ` Հց
հաճախությամբ
փոփոխական
հոսանքի գեներատորներում
ստեղծվում են
Հց
հաճախությամբ
փոփոխական
հոսանքի գեներատորներում
ստեղծվում են 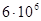 մ երկարությամբ
ալիքներ,
որոնք
գործնականում
չեն ճառագայթվում:
մ երկարությամբ
ալիքներ,
որոնք
գործնականում
չեն ճառագայթվում:
Ռադիոալիքները
ստեղծվում են
բաց
տատանողական կոնտուրներում:
Ըստ ալիքի
երկարության
ռադիոալիքները
բաժանվում են
երկար (3 · 103 մ <
λ < 3 · 104 մ),
միջին (2 · 102 նմ-ից
մինչև 3 · 103 մ ),
կարճ (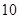 մ-ից
մինչև
մ-ից
մինչև 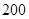 մ)
և գերկարճ
ռադիոալիքներ
(λ < 10մ): Որքան
ալիքը երկար
է, այնքան նրա`
Երկրի
մակերևույթը
շրջանցելու հատկությունն
ուժեղ է
արտահայտված:
մ)
և գերկարճ
ռադիոալիքներ
(λ < 10մ): Որքան
ալիքը երկար
է, այնքան նրա`
Երկրի
մակերևույթը
շրջանցելու հատկությունն
ուժեղ է
արտահայտված:
Ցանկացած
տաք մարմին
առաքում է
էլեկտրամագնիսական
ալիքներ,
որոնք
կոչվում են իֆրակարմիր
ալիքներ:
Ինֆրակարմիր
ալիքներ են
առաքու վառած
վառարանը,
բնակարանի
ջեռուցման
մարտկոցները
և այլն: Այդ
ալիքները,
կլանվելով,
նկատելիորեն տաքացնում
են շրջապատի
մարմինները:
Այդ պատճառով
ինֆրակարմիր
ալիքները
հաճախ
անվանում են
ջերմային
ալիքներ: Էլեկտրամագնիսական
ալիքների սանդղակում
ինֆրակարմիր
ալիքները զբաղեցնում
են
գերկարճալիք
ռադիոալիքների
(10-3մ)
տիրույթից
մինչև տեսանելի
լույսի
կարմիր
գույնի (7,6 · 10-7մ)
տիրույթը:
Ինֆրակարմիր
ճառագայթման աղբյուրներն
են Արեգակը,
աստղերը և
մոլորակները:
Օրինակ` արեգակնային
ճառագայթման
էներգիայի
մոտ 50%-ը հասնում
է Երկիր ինֆրակարմիր
ճառագայթման
տեսքով:
Ինֆրակարմիր
ալիքները մեծ
կիրառություններ
ունեն. դրանք օգտագործվում
են լաքի և
ներկի
ծածկույթներ,
մրգեր և բանջարեղեն
չորացնելու
համար: Հայտնի
են
ինֆրակարմիր
ճառագայթային
դիակները,
որոնց
միջոցով
կարելի է
գիշերը
շրջապատի առարկաները
տարբերել
միմյանցից:
Ինֆրակարմիր
ճառագայթներն
օգտագործվում
են նաև թույլ
մառախուղի
ժամանակ լուսանկարելիս,
երբ
սովորական լուսանկարչական
ապարատներով
ստացվում են
ոչ հստակ լուսանկարներ:
Տեսանելի
լույսն
էլեկտրամագնիսական
սանդղակում
զբաղեցնում է
չափազանց նեղ
տիրույթ: Նրա
ալիքի
երկարությունը
փոփոխվում է 7.6
· 10 -7մ (կարմիր
լույս) մինչև 30.8
· 10-7մ
(մանուշակագույն
լույս):
Շիկացման
լամպի էներգիայի
միայն 3 – 4%
է վերածվում
լույսի,
մնացածը
վերածվում է
ինֆրակարմիր
ճառագայթման:
Էլեկտրամագնիսական
ալիքների
սանդղակում ուլտրամանուշակագույն
ալիքները
զբաղեցնում
են տեսանելի
լույսի
մանուշակագույն
(3.8 · 10-7մ)
տիրույթից
մինչև
ռենտգենյան
ալիքների (10-8 մ)
տիրույթը: Այդ
ճառագայթման
բնական
աղբյուրներ
են Արեգակը,
աստղերը
միգամածությունները:
Օրինակ`
արեգակնային
ճառագայթման
էներգիայի
մոտ 10% կազմում
է
ուլտրամանուշակագույն
ճառագայթումը:
Ուլտրամանուշակագույն
ճառագայթումը
կարելի է
նկատել
լյումինեսցենց
առաջացնող նյութով
պատած էկրանի
միջոցով:Էկրանի
այն մասը, որի
վրա ընկնում է
ուլտրամանուշակագույն
ճառագայթում,
սկսում է
լուսարձակել:
Ուլտրամանուշակագույն
ճառագայթները,
ինչպես և ինֆրակարմիր
ճառագայթները
աչքի համար
անտեսանելի
են:
Ուլտրամանուշակագույն
ճառագայթներն
օգտագործում
են
բժշկության
մեջ`
մանրէները
ոչնչացնելու
համար,
քրեագիտության
մեջ և
կերպարվեստի
ստեղծագործությունների
իսկությունը
պարզելու
համար:
Ռենտգենյան
ճառագայթները
հայտնագործել
է գերմանացի
ֆիզիկոս
Վ. Ռենտգենը
1895թ., երբ ուսումնասիրում
էր գազապարպիչ
խողովակում
կաթոդի
արձակած
ճառագայթումը,
որն այն ժամանակ
հայտնի
էր կաթոդային
ճառագայթներ
անվամբ:
Ռենտգենյան
ճառագայթները
ստանում
են հատուկ
խողովակներում,
որանք
կոչվում
են ռենտգենյան
խողովակներ,
որոնցում
էլեկտրոնները
պոկվելով
շիկացած
կաթոդից,
հարվածում
են անոդին,
որից
էլ արձակվում
են ռենտգենյան
ճառագայթներ:
Ռենտգենյան
ճառագայթները
ներգործում
են լուսանկարչական
թիթեղի
վրա, առաջ են բերում
օդի իոնացում:
Ռենտգենյան
ճառագայթների
ալիքի
երկարությունը
շատ փոքր է (10-12 - 10-8
մ), ընդ որում,
այնքան
փոքր
է, որքան
մեծ է անոդին բախվող
էլեկտրոնների
կինետիկ
էներգիան:
Ռենտգենյան
ճառագայթների
մեծ թափանցելիությունը
պայմանավորված
է նրա փոքր ալիքի
երկարությամբ:
Ռենտգենյան
ճառագայթները
մեծ կիրառությոն
ունեն
բժշկության
մեջ: Նրանք
կիրառվում
են հիվանդությունները
ճիշտ
ախտորոշելու,
ոսկորների
կոտրվածքները
նկարելու,
ինչպես
նաև քաղցկեղային
հիվանդությունները
բուժելու
համար:
Ռենտգենյան
ճառագայթները
լայնորեն
կիրառվում
են տարբեր
նյութերի
քիմիական
բարդ
մոլեկուլների
և միացությունների
բաղադրության
և կառուցվածքի
հետազոտություններում:
γ ճառագայթները
կարճ ` 10-13 - 10-10 մ
ալիքի
երկարությամբ
էլեկտրամագնիսական
ալիքներ են:
>>
23.
էլեկտրամագնիսական
ալիքի
դիֆերենցիալ
հավասարումը
Ինչպես
արդեն նշել
ենք, Մաքսվելի
հավասարումների
կարևոր
հետևություններից
մեկը էլեկտրամագնիսական
ալիքների
գոյության
փաստն է,
այսինքն
Մաքսվելի
հավասարումներից
հետևում է, որ
համասեռ և
իզոտրոպ
միջավայրերի
համար
լիցքերից և
հոսանքներից
հեռու, որոնք
ստեղծում են
էլեկտրամագնիսական
դաշտը,
փոփոխական
էլեկտրամագնիսական
դաշտի 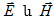 լարվածությունների
վեկտորները
բավարարում
են (15.10) տիպի
ալիքային
հավասարմանը
լարվածությունների
վեկտորները
բավարարում
են (15.10) տիպի
ալիքային
հավասարմանը

որտեղ
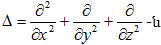
Լապլասի
օպերատորն է,
v-ն փուլային
արագությունը:
Յուրաքանչյուր
ֆունկցիա, որը
բավարարում է
(23.1) և (23.2)
հավասարումներին
նկարագրում է
որևէ ալիք: Հետևաբար
էլեկտրամագնիսական
դաշտերը,
իրոք, կարող
են
գոյություն
ունենալ
էլեկտրամագնիսական
ալիքների
տեսքով:
Էլեկտրամագնիսական
ալիքների
փուլային
արագությունը
որոշվում է
հետևյալ
բանաձևով`
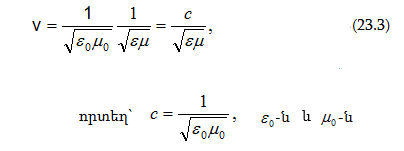
համապատասխանաբար
էլեկտրական
և մագնիսական
հաստատուններն
են, ε-ը և μ-ն
համապատասխանաբար
միջավայրի
դիէլեկտրական
և մագնիսական
թափանցելիություններն
են:
Վակուումում
(ε = 1 և μ = 1
դեպքում)
էլեկտրամագնիսական
ալիքների
տարածման
արագությունը
համընկնում
է արագության
հետ: Նյութի
մեջ εμ
> 1-ից ուստի էլեկտրամագնիսական
ալիքների
տարածման
արագությունը
նյութում
միշտ
փոքր
է քան վակուումում:
Էլեկտրամագնիսական
դաշտի
տարածման
արագությունը
(23.3) բանաձևով
որոշելու
դեպքում
ստացված
արդյունքը
բավականին
լավ համընկնում
է փորձի
տվյալների
հետ, եթե հաշվի
առնվի
ε-ի և μ-ի հաճախությունից
կախվածությունը:
Էլեկտրամագնիսական
ալիքների
տարածման
արագության
համընկումը
վակուումում
լույսի
տարածման
արագության
հետ ցույց
է տալիս
էլեկտրամագնիսական
և օպտիկական
երևույթների
միջև
եղած
խորը
կապը,
որը Մաքսվելին
հնարավորություն
տվեց
ստեղծել
լույսի
էլեկտրամագնիսական
տեսությունը,
համաձայն
որի լույսը
էլեկտրամագնիսական
ալիք
է:
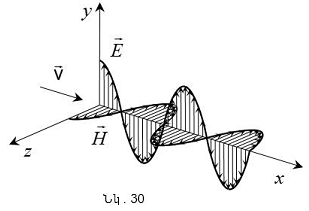
Մաքսվելի
տեսության
հետևություններից
է էլեկտրամագնիսական
ալիքների
լայնական լինելը:
Էլեկտրական և
մագնիսական
դաշտերի լարվածությունների
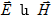 վեկտորները
փոխուղղահայաց
են (նկ. 30-ում
ցույց է տրված
հարթ
էլեկտրամագնիսական
ալիքի ակնթարթային
«լուսանկարը»)
և ընկած են
ալիքի տարածման
վեկտորները
փոխուղղահայաց
են (նկ. 30-ում
ցույց է տրված
հարթ
էլեկտրամագնիսական
ալիքի ակնթարթային
«լուսանկարը»)
և ընկած են
ալիքի տարածման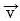 արագության
վեկտորին
ուղղահայաց
հարթության
մեջ, ընդ
որում
արագության
վեկտորին
ուղղահայաց
հարթության
մեջ, ընդ
որում 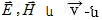 վեկտորները
կազմում են աջ
պտուտակային
համակարգ: Ըստ
Մաքսվելի
հավասա E-ի և H-ի
ակնթարթային
արժեքները
ցանկացած
կետում
կապված են
հետևյալ
առնչությամբ`
վեկտորները
կազմում են աջ
պտուտակային
համակարգ: Ըստ
Մաքսվելի
հավասա E-ի և H-ի
ակնթարթային
արժեքները
ցանկացած
կետում
կապված են
հետևյալ
առնչությամբ`

Հետևաբար,
E-ն և H-ը
միաժամանակ
հասնում են
առավելագույնի,
միաժամանկ
դառնում են
զրո և այլն: (23.1) և
(23.2)
հավասարումներից
կարելի է
անցնել `

հավասարումներին,
որտեղ
համապատասխանաբար
y և z ինդեքսները
E-ի և H-ի դեպքում
ընդգծում են
այն, որ 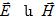 վեկտորները
ուղղված են
փոխուղղահայաց
y և z առանցքներով:
վեկտորները
ուղղված են
փոխուղղահայաց
y և z առանցքներով:
(23.5)
և (23.6)
հավասարումներին
բավարարում
են մասնավորապես
հարթ
մեներանգ
էլեկտրամագնիսական
ալիքները
(խիստ մեկ որոշակի
հաճախության
էլեկտրամագնիսական
ալիքները),
որոնք նկարագրվում
են հետևյալ
հավասարումներով`
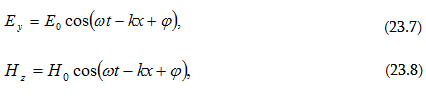
Որտեղ
E0 –ն և H0 -ն
համապատասխանաբար
ալիքի
էլեկտրական և
մագնիսական
դաշտերի
լարվածությունների
լայնույթներն
են, ω-ն ալիքի
շրջանային
հաճախությունն
է, k-ն ալիքային թիվն
է, φ-ն
տատանումների
սկզբնական
փուլերն են x = 0
կոորդինատով
կետերում: (23.7) և
(23.8) հավասարումներում
φ-ն միատեսակ
է, քանի որ
էլեկտրական և մագնիսական
վեկտորների
տատանումները
էլեկտրամագնիսական
ալիքում
կատարվում են
միատեսակ
փուլերով:
>>
24.
Էլեկտրամագնիսական
ալիքի
էներգիան և
իմպուլսը
Էլեկտրամագնիսական
ալիքների
դիտման հնարավորությունը
ցույց է
տալիս, որ
դրանք էներգիա
են
տեղափոխում:
Էլեկտրամագնիսական
ալիքի
էներգիայի w
ծավալային խտությունը
հավասար է
էլեկտրական
դաշտի
էներգիայի
ծավալային
խտության որը
որոշվում է
(որը որոշվում
է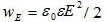 բանաձևով) և
մագնիսական
դաշտի
էներգիայի ծավալային
խտության (որը
որոշվում է
բանաձևով) և
մագնիսական
դաշտի
էներգիայի ծավալային
խտության (որը
որոշվում է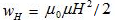 բանաձևով)
գումարին.
բանաձևով)
գումարին.
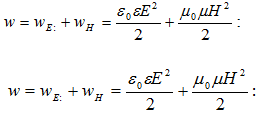
Նկատի
ունենալով (23.4)
արտահայտությունը`
կստանանք, որ էլեկտրական
և մագնիսական
դաշտերի
էներգիաները
ժամանակի յուրաքանչյուր
պահին նույնն
են, ուստի
կարելի է գրել
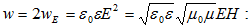
Բազմապատկելով
էներգիայի w
խտությունը
միջավայրում
ալիքի տարածման
v արագությամբ
(տես (23.3)
բանաձևը)
կստանանք էներգիայի
հոսքի
խտության
մոդուլը.
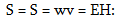
Քանի
որ 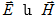 վեկտորները
փոխադարձաբար
ուղղահայաց
են և ալիքի
տարածման
ուղղության
հետ կազմում
են աջ պտուտակային
համակարգ, ապա
վեկտորները
փոխադարձաբար
ուղղահայաց
են և ալիքի
տարածման
ուղղության
հետ կազմում
են աջ պտուտակային
համակարգ, ապա
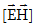 վեկտորի
ուղղությունը
համընկնում է
էներգիաայի
տեղափոխման
ուղղության
հետ, իսկ այդ վեկտորի
մոդուլը հավասար
է EH-ի (քանի որ sin α =
1):
վեկտորի
ուղղությունը
համընկնում է
էներգիաայի
տեղափոխման
ուղղության
հետ, իսկ այդ վեկտորի
մոդուլը հավասար
է EH-ի (քանի որ sin α =
1):
Հետևաբար,
էներգիայի
հոսքի
խտության
վեկտորը
կարելի է ներկայացնել
որպես 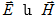 վեկտորների
վեկտորական
արտադրյալ.
վեկտորների
վեկտորական
արտադրյալ.
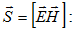
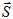 վեկտորը
կոչվում է
Պոյնտինգի
վեկտոր:
վեկտորը
կոչվում է
Պոյնտինգի
վեկտոր: 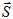 վեկտորն
ուղղված է
էլեկտրամագնիսական
ալիքի
տարածման
կողմը, նրա
մոդուլը
հավասար է այն
էներգիային,
որը
տեղափոխում է էլեկտրամագնիսական
ալիքը միավոր
ժամանակում
ալիքի
տարածման
ուղղությանն
ուղղահայաց
միավոր
մակերեսով:
վեկտորն
ուղղված է
էլեկտրամագնիսական
ալիքի
տարածման
կողմը, նրա
մոդուլը
հավասար է այն
էներգիային,
որը
տեղափոխում է էլեկտրամագնիսական
ալիքը միավոր
ժամանակում
ալիքի
տարածման
ուղղությանն
ուղղահայաց
միավոր
մակերեսով:
Եթե
էլեկտրամագնիսական
ալիքները
կլանվում կամ
անդրադառնում
են
մարմիններից
(այդ երևույթները
հատատվել են
Հերցի
փորձերով),
ապա Մաքսվելի
տեսությունից
հետևում է, որ
էլեկտրամագնիսական
ալիքները
պետք է ճնշում
գործադրեն
մարմինների
վրա:
Էլեկտրամագնիսական
ալիքների
ճնշումը բացատրվում
է նրանով, որ
ալիքի
էլեկտրական
դաշտի
ազդեցության
տակ նյութի
լիցքավորված
մասնիկները
սկսում են
կարգավորված
շարժվել և ալիքի
մագնիսական
դաշտի կողմից
ենթարկվում
են Լորենցի
ուժի
ազդեցությանը:
Սակայն
ճնշման այդ
արժեքն
աննշան փոքր
է: Կարելի է
գնահատել, որ
արեգակնային
ճառագյթման
միջին
հզորության
դեպքում, որը
հասնում է
Երկրին,
բացարձակ
կլանող
մարմնի համար
ճնշումը
կազմում է
մոտավորապես 5
մկՊա:
Էլեկտրամագնիսական
ալիքների
ճնշման
գոյությունը
բերում է այն
եզրակացության,
որ նրանց
հատուկ է մեխանիկական
իմպուլսը:
Էլեկտրամագնիսական
ալիքը, որը
կրում է W
էներգիա,
օժտված է p = W/c
իմպուլսով:
>>
25.
Դիպոլի
ճառագայթումը
Էլեկտրամագնիսական
ալիքների
կիրառությունը
Էլեկտրամագնիսական
ալիքների
պարզագույն ճառագայթիչ
է էլեկտրական
դիպոլը, որի
էլեկտրական
մոմենտը
փոփոխվում է
ըստ ժամանակի
ներդաշնակ
օրենքով`
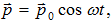
որտեղ
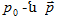 վեկտորի
լայնույթն է:
վեկտորի
լայնույթն է:
Նման
դիպոլի
օրինակ է այն
համակարգը,
որը կազմված է
անշարժ +q
լիցքից և նրա
մոտ 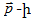 ուղղության
երկայնքովω
հաճախությամբ
տատանվող -q
լիցքից:
ուղղության
երկայնքովω
հաճախությամբ
տատանվող -q
լիցքից:
Դիպոլի
ճառագայթման
խնդիրը
ճառագայթող
համակարգերի
տեսության
մեջ կարևոր
նշանակություն
ունի, քանի որ
ամեն մի
իրական
ճառագայթող
համակարգ
(օրինակ
անտենան)
կարելի է
հաշվարկել`
քննարկելով դիպոլի
ճառագայթումը:
Բացի դրանից,
նյութի և ճառագայթման
փոխազդեցության
հետ կապված շատ
հարցեր
կարելի է
բացատրել
դասական
տեսության
հիման վրա,
քննարկելով
ատոմները
որպես լիցքերի
համակարգ,
որոնցում
էլեկտրոնները
կատարում են
իրենց
հավասարակշռության
դիրքի շուրջը
ներդաշնակ
տատանումներ:
Դիպոլի
էլեկտրամագնիսական
դաշտի
բնույթը կախված
է քննարկվող
կետի դիրքից:
Հատուկ հետաքրքրություն
է
ներկայացնում,
այսպես կոչված,
դիպոլի
ալիքային
գոտին`
տարածության
կետեր, որոնք
հեռացված են
դիպոլից, r
այնպիսի հեռավորությունների
վրա, որոնք
գերազանցում
են ալիքի
երկարությունը
(r >> λ) քանի որ
նրանում
դիպոլի
էլեկտրամագնիսական
դաշտի
պատկերը խիստ
պարզեցվում է:
Եթե
ալիքը
տարածվում է
համասեռ
իզոտրոպ միջավայրում,
ապա այն
ժամանակը, որի
ընթացքում ալիքները
անցնում են
մինչև այն
կետերը որոնք հեռացված
են դիպոլից r
hեռավորության
վրա միատեսակ
է: Ուստի
սֆերայի
բոլոր
կետերում,
որի կենտրոնը
համընկնում է
դիպոլի հետ,
տատանումների
փուլը կլինի
միատեսակ,
այսինքն`
ալիքային
գոտում ալիքային
ճակատը կլինի
սֆերա, և
հետևաբար, ալիքը,
որը
ճառագայթում
է դիպոլը,
կլինի սֆերիկ
ալիք:
Յուրաքանչյուր
կետում
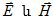 վեկտորները
տատանվում
են ըստ cos(ωt – kr)
օրենքի: Այդ վեկտորների
լայնույթները
ուղիղ
համեմատական
են 1/r sin
θ (վակուումում),
այսինքն`
կախված
են մինչև
ճառագայթիչը
եղած r
հեռավորությունից
և շառավիղ-վեկտորի
ուղղությունով
և դիպոլի
առանցքով
կազմված
θ
անկյունից: Այստեղից
հետևում
է, որ դիպոլի
ճառագայթման
ինտենսիվությունը
ալիքային
գոտում
`
վեկտորները
տատանվում
են ըստ cos(ωt – kr)
օրենքի: Այդ վեկտորների
լայնույթները
ուղիղ
համեմատական
են 1/r sin
θ (վակուումում),
այսինքն`
կախված
են մինչև
ճառագայթիչը
եղած r
հեռավորությունից
և շառավիղ-վեկտորի
ուղղությունով
և դիպոլի
առանցքով
կազմված
θ
անկյունից: Այստեղից
հետևում
է, որ դիպոլի
ճառագայթման
ինտենսիվությունը
ալիքային
գոտում
`

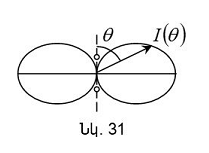
(25.1)
կախվածությունը
θ-ից r-ի տրված
արժեքի դեպքում
բերված
բևեռային
կոորդինատներով
(նկ. 31), կոչվում է
դիպոլի
ճառագայթման ուղղորդվածության
դիագրամ:
(25.1)
բանաձևից
բխում է, որ
ալիքի
ինտենսիվությունը
ճառագայթի
ուղղությամբ
(երբ θ = const)
փոխվում է
ճառագայթիչից
ունեցած
հեռավորության
քառակուսուն
հակադարձ
համեմատական: Բացի
այդ կախում
ունի θ
անկյունից:
Ամենից ավելի
ուժեղ դիպոլը
ճառագայթում
է իր առանցքին
ուղղահայաց
ուղղություններով
(θ = π/2):
Իր
առանցքի
երկայնքով (θ = 0
և θ = π) դիպոլն
ընդհանրապես
չի
ճառագայթում:
Դիպոլի
ճառագայթման
ուղղորդվածության
դիագրամը
հնարավորություն
է տալիս
կազմավորել
ճառագայթումը
որոշ
բնութագրիչներով
և օգտագործվում
է անտենաների
նախագծման
դեպքում:
Էլեկտրամագնիսական
ալիքները
առաջինն օգտագործվեցին
Հերցի
փորձերից յոթ
տարի հետո: Ա. Պոպովը
1895թ. Ռուսական
ֆիզիկաքիմիական
ընկերության
նիստում
առաջին անգամ
ցուցադրեց էլեկտրամագնիսական
ալիքների
օգնությամբ
ազդանշաններ
հաղորդող և
ընդունող մի
սարք, որը
փաստորեն
ժամանակակից
ռադիոյի
նախատիպն էր:
Այդ սարքը
հնարավորություն
էր տալիս
հեռավորության
վրա առանց
հաղորդալարերի
հաղորդել կարճատև
հեռագրական
ազդանշաններ:
Ռադիոյի հայտնագործման
սկզբնական
շրջանում
կապն իրականացվում
էր միայն փոքր
հեռավորությունների
վրա Մորզեի
այբուբենի
(պայմանական
նշանների`
կետերի և գծիկների
համակարգ)
միջոցով:
Էլեկտրոնային
լամպի
հայտնագործումից
հետո
էլեկտրոնային
ուժեղարարների
օգնությամբ
հաջողվեց էապես
մեծացնել
ռադիոկապի
հեռավորությունը:
Ռադիոյի
զարգացման
հաջորդ
փուլում
հնարավոր
դարձավ խոսքի,
երաժշտության
հաղորդումը:
Աշխարհի շատ
գիտնականների
և
ճարտարագետների
ջանքերով
ռադիոն
կատարելագործվեց
այն աստիճանի,
որ ներկայումս
ռադիոհաղորդիչ
կայանները և
ռադիոընդունիչները
շատ քիչ են
հիշեցնում
Պոպովի ստեղծած
սարքը:
Սանտիմետրային
և
միլիմետրային
տիրույթի էլեկտրամագնիսական
ալիքներն,
իրենց
ճանապարհին
հանդիպելով
արգելքների,
նրանցից
անդրադառնում
են: Այս
երևույթն
ընկած է
ռադիոլոկացիայի
հիմքում`
առարկաների
հայտնաբերումը
(օրինակ,
ինքնաթիռների,
տիեզերանավերի
և այլն) մեծ
հեռավորությունների
վրա և նրանց
դիրքի ճշգրիտ
որոշումը:
Բացի դրանից,
ռադիոլոկացիայի
մեթոդները
օգտագործվում
են ամպերի
անցումը և
կազմավորումը,
մթնոլորտի
վերին
շերտերում
մետեորիտների
շարժումը
դիտելու
համար և այլն:
Էլեկտրամագնիսական
ալիքների
համար բնութագրական
է դիֆրակցիայի
երևույթը`
այսինքն
ալիքների
կողմից տարբեր
արգելքների
շըրջանցումը:
Հենց ռադիոալիքների
դիֆրակցիայի
շնորհիվ է
հնարավոր իրականացնել
հեռու
կայանների
միջև կայուն ռադիոկապը,
որոնք
բաժանված են
իրարից Երկրի ուռուցիկությամբ:
Երկար
ալիքները
(հարյուր և
հազարավոր մետր)
կիրառվում են
լուսահեռագրության
մեջ, կարճ
ալիքները (մի
քանի մետրեր և
պակաս) կիրառվում
են
հեռուստատեսության
մեջ
պատկերների
հաղորդման
համար ոչ մեծ
հեռավորությունների
վրա (փոքր-ինչ
մեծ ուղիղ
տեսանելիության
սահմաններում):
Էլեկտրամագնիսական
ալիքները
օգտագործվում
են նաև
ռադիոգեոդեզիայում
ճշգրիտ որոշելու
հեռավորությունները
ռադիոազդանշանների
օգնությամբ,
ռադիոաստղագիտության
մեջ երկնային
մարմինների
ռադիոճառագայթման
հետազոտությունների
համար և այլն:
Էլեկտրամագնիսական
ալիքների
կիրառությունների
լրիվ
նկարագիրը
գործնականորեն
տալ հնարավոր
չէ, քանի որ
չկա գիտության
և տեխնիկայի
մի բնագավառ,
որտեղ դրանք չօգտագործվեն:
>>
26.
Խնդիրների
լուծման
օրինակներ
Խնդիր
1. Կետը
կատարում է
ներդաշնակ
տատանումներ:
Ժամանակի 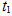 պահին շեղումը`
պահին շեղումը`
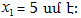 Փուլը
երկու անգամ
մեծացնելու
դեպքում կետի
շեղումը
դարձավ
Փուլը
երկու անգամ
մեծացնելու
դեպքում կետի
շեղումը
դարձավ 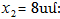 Գտնել
տատանման
լայնույթը:
Գտնել
տատանման
լայնույթը:
Լուծում: Գրենք
երկու
դեպքում
շեղումների
հավասարումները.
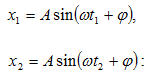
Համաձայն
խնդրի
պայմանի`
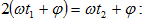
Կատարենք
նշանակում`
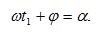
այդ
դեպքում
շեղումների
համար
հավասարումները
կարող են
ներկայացվել
հետևյալ
տեսքով`
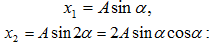
Երկու
հավասարումները
բարձրացնելով
քառակուսի,
նրանցից
երկրորդը
բաժանելով
չորսի և առաջինից
հանելով
երկրորդը
կստանանք`
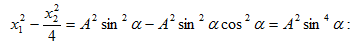
Հաշվի
առնելով, որ 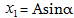 կստանանք`
կստանանք`
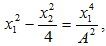
որտեղից
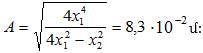
>>
Խնդիր
2. Նյութական
կետը
կատարում
է A = 0,04մ լայնույթով
և T = 2 վ պարբերությամբ
ներդաշնակ
տատանումներ:
Գրել
կետի
շարժման
հավասարումը,
եթե նրա շարժումը
սկսվում
է x0 = 0,02
մ դիրքից:
Լուծում:
Ներդաշնակ
տատանումների
դեպքում
շեղումը
փոփոխվում
է, կախված
ժամանակից
հետևյալ
օրենքով`
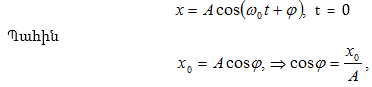
որտեղից
հետևում է, որ
φ = π / 3: Քանի որ ω0 =
2π / T = πվ-1, կետի
շարժման
հավասարումը
կընդունի
հետևյալ
տեսքը`
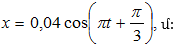
>>
Խնդիր
3. m =10-2կգ
զանգվածով
նյութական
կետը
կատարում
է ներդաշնակ
տատանումներ
ըստ 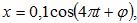 մ
օրենքի: Որոշել վերադարձնող
ուժի
և կինետիկ
էներգիայի
առավելագույն
արժեքները:
մ
օրենքի: Որոշել վերադարձնող
ուժի
և կինետիկ
էներգիայի
առավելագույն
արժեքները:
Լուծում:
x = 0,1 cos(4πt + φ)
ներդաշնակ
տատանման
հավասարումից
հետևում
է, որ լայնույթը`
A = 0,1 մ, ω0 = 4π վ-1:
Արագության
և արագացման
համար
ստանում
ենք`
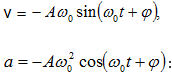
Քանի
որ 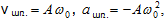 կունենանք`
կունենանք`
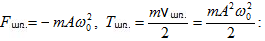
Տեղադրելով
թվային
արժեքները` կստանանք`
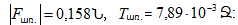
>>
Խնդիր
4.
Որոշել
ներդաշնակ
տատանումներ
կատարող կետի
T կինետիկ
էներգիայի և
նրա W
պոտենցիալ
էներգիայի
հարաբերությունը,
եթե
սկզբնական փուլը
հայտնի է:
Լուծում:
Գտնենք x = Acos (ω0t +
φ) ֆունկցիայի
ըստ ժամանակի
առաջին և
երկրորդ
կարգի
ածանցյալները.
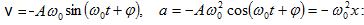
Կինետիկ
և պոտենցիալ
էներգիաների
համար
համապատասխանաբար
կստանանք`
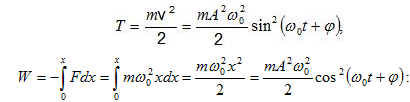
Բաժանելով
վերջին
հավասարումները
իրար` կստանանք`
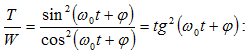
>>
Խնդիր
5. k = 900 Ն/մ կոշտությամբ
հորիզոնական
զսպանակին
ամրացված
M = 4կգ զանգվածով
գունդը
գտնվում
է ողորկ
սեղանի
վրա, որի վրայով
այն կարող
է առանց
շփման
սահել:
m = 10կգ
զանգվածով
գնդակը
թռչելով
հորիզոնական
ուղղությամբ`
v0 = 600 մ/վ արագությամբ
և հարվածի
պահին
ունենալով
զսպանակի
երկայնքով
ուղղված
արագություն`
մխրճվում
է գնդի մեջ: Անտեսելով
զսպանակի
զանգվածը
և օդի դիմադրության
ուժը`
որոշել
գնդի
տատանման
լայնույթը
և պարբերությունը:
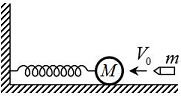
Լուծում:
Օգտվելով
իմպուլսի
պահպանման
օրենքից` կարող
ենք գրել`

որտեղ
v-ն գնդի և
գնդակի
արագությունն
է հարվածից հետո:

Համաձայն
էներգիայի
պահպանման
օրենքի`

(2)-ը
տեղադրելով (
3)-ի մեջ`
լայնույթի
համար կստանանք`

Նկատի
ունենալով, որ
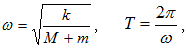
պարբերության
համար
ստանում ենք`

Տեղադրելով
(4) և (5) –ի մեջ
մտնող
մեծությունների
թվային
արժեքները
կստանանք`A=0,1մ: T=0,419վ:
>>
Խնդիր
6. α և β
թեքության
անկյուն
ունեցող
երկու թեք
հարթություններ
միացված են
հիմքի մոտ
(տես նկ.): Փոքրիկ
մարմինը այդ
հարթություններով
իր շարժման
ընթացքում
կատարում է
տատանումներ`
սահելով
ներքև-վերև:
Մարմինը
շարժումն
սկսում է այդ
հարթություններից
որևէ մեկի
վրայից և
գտնվում է
հիմքից h բարձրության
վրա: Գտնել
մարմնի
տատանումների
պարբերությունը:
Շփումն
անտեսել:
Հարթությունից
հարթություն
անցումը
սահուն է և
հարթ:
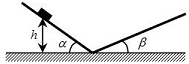
Լուծում: Եթե
մարմինը
սահում է h
բարձրությունից,
ապա այն ներքև
է իջնում 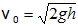 արագությամբ:
Նրա հետագա
շարժումը թեք
հարթությամբ
դեպի վեր
կլինի
դանդաղող
արագությամբ:
Նրա հետագա
շարժումը թեք
հարթությամբ
դեպի վեր
կլինի
դանդաղող 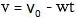 արագությամբ,
որտեղ w-ն այն
արագացումն
է, որը հաղորդում
է գլորող
ուժը.
արագությամբ,
որտեղ w-ն այն
արագացումն
է, որը հաղորդում
է գլորող
ուժը.
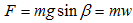
Աջ
հարթությունով
շարժման
դեպքում`
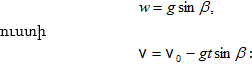
Մարմինը
կշարժվի դեպի
վեր մինչև նրա
արագության
զրո դառնալը,
այսինքն`
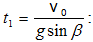
Նույն
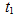 ժամանակում
մարմինը
շարժվում է
ներքև: Շարժման
լրիվ
ժամանակը աջ
թեք
հարթությունով
կլինի`
ժամանակում
մարմինը
շարժվում է
ներքև: Շարժման
լրիվ
ժամանակը աջ
թեք
հարթությունով
կլինի`
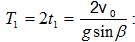
Համանմանորեն
ձախ թեք
հարթության
համար կարող
ենք գրել`
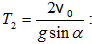
Մարմնի
լրիվ
տատանման պարբերությունը`
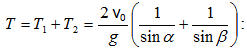
Տեղադրելով
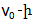 համար
արտահայտությունը`
կստանանք
համար
արտահայտությունը`
կստանանք
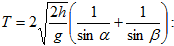
>>
Խնդիր
7.
Անկշիռ բարակ
l
երկարության
ձողի
ծայրերին ամրացված
են m1 և m2 զանգվածներով
փոքրիկ
բեռներ: Ձողը
տատանվում է
իր մեջտեղով
անցնող
հորիզոնական
առանցքի
շուրջը (տես
նկ.): Որոշել
ձողի կատարած
տատանումների
պարբերությունը,
հետյալ
դեպքերի համար
ա) ձողը
անկշիռ է, բ)
ձողի
զանգվածը
հավասար է m0-ի:
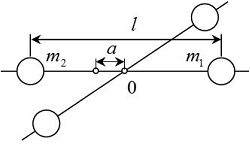
Լուծում:
Ֆիզիկական
ճոճանակի
տատանման
պարբերությունը`

որտեղ
J-ն ճոճանակի
իներցիայի
մոմենտն է, m-ը`
նրա զանգվածը,
α-ն
ծանրության
կենտրոնից
մինչև պտտման
առանցքը եղած հեռավորությունն
է, g -ն ազատ
անկման
արագացումն է:
ա)
Ճոճանակի
իներցիայի
մոմենտը, երբ
ձողը անկշիռ
է, հավասար է
բեռների
իներցիայի
մոմենտների գումարին
` J = J1 + J2:
Անտեսելով
բեռների
չափերը,
այսինքն
դրանք ընդունելով
որպես
նյութական
կետեր,
կստանանք`
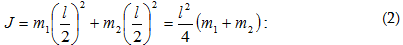
Ճոճանակի
զանգվածը` m = m1+m2:
α
հեռավորությունը
գտնելու
համար գրենք
բեռների
հավասարակշռության
պայմանը.
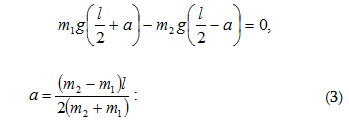
Տեղադրելով
(1)-ի մեջ (2)-ը և (3)-ը`
պարբերության
համար
կստանանք`
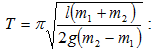
բ)
Եթե ձողի
զանգվածը 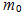 է, ապա
ճոճանակի
իներցիայի
մոմենտը`
է, ապա
ճոճանակի
իներցիայի
մոմենտը`
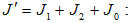
Նկատի
ունենալով, որ
ձողի
իներցիայի
մոմենտը ձողի
մեջտեղով
անցնող
առանցքի
նկատմամբ հավասար
է 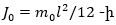 կստանանք`
կստանանք`
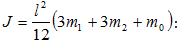
Ճոճանակի
զանգվածը` m = m1+m2
+m0:
Հավասարակշռության
պայմանը`
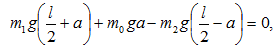
որտեղից
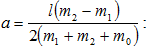
Տատանման
պարբերության
համար
ստանում ենք`
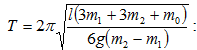
>>
Խնդիր
8.
Ֆիզիկական
ճոճանակը l = 0,35մ
երկարության
համասեռ
բարակ ձող է:
Զանգվածի
կենտրոնից
ի՞նչ x հեռավորության
վրա պետք է
լինի կախման
կետը, որպեսզի
տատանման
հաճախությունը
լինի առավելագույնը:
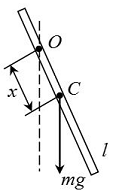
Լուծում:
Ֆիզիկական
ճոճանակի
տատանման
պարբերությունը
որոշվում է հետևյալ
բանաձևով`
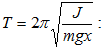
Քանի
որ

Օգտվելով
Շտայների
թեորեմից`
ձողի
իներցիայի
մոմենտը
O կետով
անցնող
առանցքի
նկատմամբ
հավասար
կլինի`

Տեղադրելով
(2)-ը (1)-ի մեջ` ω
հաճախության
համար կստանանք
հետևյալ
արտահայտությունը`
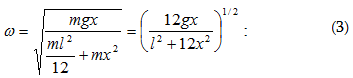
Ածանցելով
(3)-ը ըստ x-ի և հավասարեցնելով
զրոյի`
ստանում ենք`
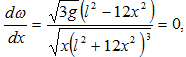
որտեղից
հետևում է.
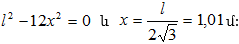
>>
Խնդիր
9. k1
և k2
կոշտություն
ունեցող
երկու
զսպանակներ
միացված են
մի դեպքում
հաջորդաբար,
մյուս դեպքում
զուգահեռ:
Ինչպիսի՞ն է
բեռների
ուղղաձիգ
տատանումների
պարբերությունների
հարաբերությունը
այդպիսի
զսպանակների
վրա (տես նկ.):
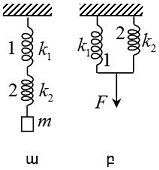
Lուծում: ա)
Զսպանակներից
յուրաքանչյուրը
F ուժի
ազդեցության
տակ ձգվում է
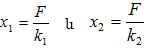
երկարությամբ:
Զսպանակների
համակարգի
համար կարելի
է գրել`
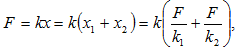
որտեղից
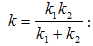
m
զանգվածով
բեռի
տատանման
պարբերությունը`
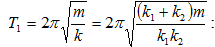
բ)
F ուժը, որն
ազդում է զսպանակների
համակարգի
վրա, կարելի է
բաժանել
երկու `F1 և F2
բաղադրիչների,
որոնցից մեկը
կիրաոված է 1
զսպանակի վրա,
մյուսը` 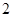 զսպանակի
վրա: Երկու
զսպանակներն
էլ ձգվում են
միատեսակ x
երկարությամբ:
զսպանակի
վրա: Երկու
զսպանակներն
էլ ձգվում են
միատեսակ x
երկարությամբ:
Յուրաքանչյուր
զսպանակի
համար կարելի
է գրել`
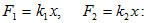
Զսպանակների
համակարգի
համար`
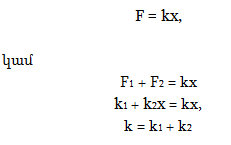
Հետևաբար,
m զանգվածով
բեռի
տատանման
պարբերությունը`
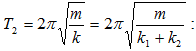
Արդյունքում
կստանանք`
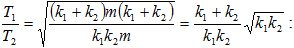
>>
Խնդիր 10. Երկու մաթեմատիկական ճոճանակներ ունեն հավասար զանգվածներ, երկարություններով տարբերվում են n=1,5 անգամ և տատանվում են միևնույն անկյունային լայնույթով: Որոշել թե ո՞ր ճոճանակն է օժտըված ավելի մեծ էներգիայով և քանի անգամ:
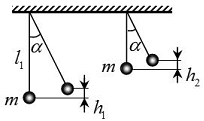
Լուծում:
մաթեմատիկական
ճոճանակի
լրիվ
էներգիան հավասար
է պոտենցիալ
էներգիայի
առավելագույնին.
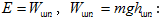
Նկարից
երևում է, որ 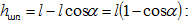 Հետևաբար,
կարող ենք
գրել`
Հետևաբար,
կարող ենք
գրել`
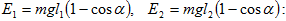
Հավասարումները
բաժանելով
իրար` ստանում
ենք`
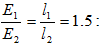
>>
Խնդիր
11. M
զանգվածով
սկավառակն
ամրացված է k
կոշտություն
ունեցող
զսպանակին
(տես նկ.): Երբ h
բարձրությունից
m զանգվածով
օղակն
ընկնում է
սկավառակի
վրա, նըրանք
կատարում են
ներդաշնակ
տատանումներ:
Ընդունելով
օղակի
հարվածը
սկավառակին
բացարձակ ոչ
առաձգական,
որոշել տատանումների
պարբերությունը:
Զսպանակի զանգվածն
անտեսել:
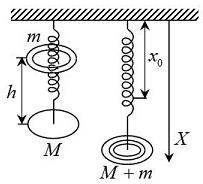
Լուծում: h
բարձրությունից
ազատ անկման
դեպքում օղակը
ձեռք է
բերում`
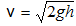
արագություն:
Բացարձակ
ոչ առաձգական
հարվածից
հետո սկավառակը
և օղակը
ժամանակի սկզբնական
պահին ձեռք են
բերում v1
արագություն,
որը կգտնենք
իմպուլսի
պահպանման
օրենքից.

որտեղից
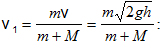
Սկավառակը
մտնելով
շարժման մեջ`
զսպանակը ձգում
է այնքան,
մինչև սկավառակի
և օղակի
շարժման
ամբողջ
էներգիան
չփոխարկվի ձգված
զսպանակի
պոտենցիալ
էներգիային: Այնուհետև
համակարգը
պետք է կատարի
ներդաշնակ
տատանումներ
ինչոր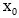 հավասարակշռության
դիրքի
նկատմամբ:
հավասարակշռության
դիրքի
նկատմամբ:
Քանի
որ մինչև
օղակի
ընկնելը
զսպանակը
սկավառակի Mg
կշռի
ազդեցության
տակ ձգվում է
մինչև a
երկարությունը,
ապա a
օրդինատը
հանդիսանում
է տատանվող
համակարգի սկզբնական
դիրքը:
Ակներև
է, որ
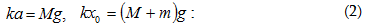
Գրենք
տատանվող
պրոցեսի
համար
էներգիայի պահպանման
օրենքը`
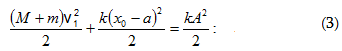
(1)
և (2)
բանաձևերից
որոշելով 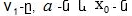 և
դրանք
տեղադրելով
(3)-ի` մեջ
լայնույթի
համար ստանում
ենք հետևյալ
արտահայտությունը`
և
դրանք
տեղադրելով
(3)-ի` մեջ
լայնույթի
համար ստանում
ենք հետևյալ
արտահայտությունը`
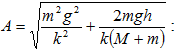
>>
Խնդիր
12. k
=Ն/մ
կոշտություն
ունեցող
զսպանակից
կախված m = 0,6կգ
զանգվածով
մարմինը
ինչ-որ
միջավայրում
կատարում է
առաձգական
տատանումներ:
Տատանումների
մարման
լոգարիթմական
դեկրեմենտը`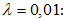 1)
որոշել այն
ժամանակամիջոցը,
որի
ընթացքում
տատանումների
լայնույթը
փոքրանում է 3
անգամ, 2) բեռի
լրիվ
տատանումների
այն թիվը, որի
դեպքում
կատարվում է
լայնույթի
նման
փոքրացում:
1)
որոշել այն
ժամանակամիջոցը,
որի
ընթացքում
տատանումների
լայնույթը
փոքրանում է 3
անգամ, 2) բեռի
լրիվ
տատանումների
այն թիվը, որի
դեպքում
կատարվում է
լայնույթի
նման
փոքրացում:
Լուծում: Մարող
տատանումների
դեպքում`
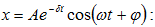
Լոգարիթմելով
ստանում ենք`
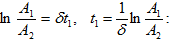
Հաշվի
առնելով, որ
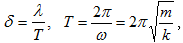
կստանանք`
Ըստ
խնդրի
պայմանի 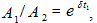 որտեղ
δ -ն մարման
գործակիցն է:
որտեղ
δ -ն մարման
գործակիցն է:
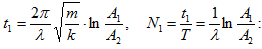
Տեղադրելով
վերջին երկու
բանաձևերի
մեջ մտնող
մեծությունների
թվային
արժեքները`
կստանանք` 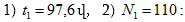
>>
Խնդիր
13. m =
0,1կգ
զանգվածով
մարմինը,
կատարելով
մարող տատանումներ,
τ = 60վ-ում
կորցրեց իր
էներգիայի 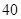 %-ը:
Որոշել r դիմադրության
գործակիցը:
%-ը:
Որոշել r դիմադրության
գործակիցը:
Լուծում:
Դիմադրության
գործակիցը
որոշվում է
հետևյալ
բանաձևով`

Մարող
տատանումների
դեպքում
տատանումների
լայնույթ`

Քանի
որ էներգիան
համեմատական
է լայնույթի
քառակուսուն,
կարող ենք
գրել`
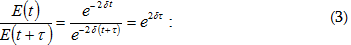
Ըստ
խնդրի
պայմանի E(t) / E(t + τ) = 1 /
0,6: Հետևաբար, 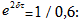 Վերջինից
հետևում է, որ
δ = 1 / 2τ ln 1/ 0,6: Հետևաբար,
r = m / τ ln 1 / 0,6:
Վերջինից
հետևում է, որ
δ = 1 / 2τ ln 1/ 0,6: Հետևաբար,
r = m / τ ln 1 / 0,6:
Տեղադրելով
վերջին
բանաձևի մեջ
մտնող մեծությունների
թվային արժեքները`
ստանում ենք. r =
8,51 · 10-4 կգ/վ:
>>
Խնդիր
14.
Տատանողական
կոնտուրը
պարունակում
է սոլենոիդ,
որի
երկարությունը`
l = 0,05մ, լայնական
հատույթի
կտրվածքը` S1 = 1,5
· 10-4մ2,
գալարների
թիվը` N = 500 և
կոնդենսատոր, որի
շրջադիրների
հեռավորությունը`
d = 1,5 · 10-3 մ է,
շրջադիրների մակերեսը`
S2 = 10-6մ2:
Որոշել
կոնտուրի
սեփական
տատանումների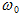 հաճախությունը:
հաճախությունը:
Լուծում:
Կոնտուրի
սեփական
հաճախությունը`

որտեղ
L-ը և C-ն
համապատասխանաբար
կոնտուրի ինդուկտիվությունն
ու ունակությունն
է, որոնք
որոշվում են
հետևյալ բանաձևով`
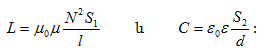
Նկատի
ունենալով, որ
օդի համար` ε = μ =
1-ի L-ի և C-ի արժեքները
տեղադրելով
(1)-ի մեջ
կստանանք`

Քանի
որ
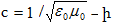 ,
,
վերջինը
նկատի
ունենալով
(2)-ից ստանում
ենք`

Տեղադրելով
(3)-ի մեջ մտնող
մեծությունների
թվային արժեքները
ստանում ենք` 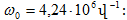
>>
Խնդիր
15. Երբ
տատանողական
կոնտուրում
եղել է  կոնդենսատորը,
սեփական
տատանումները
կատարվել են
կոնդենսատորը,
սեփական
տատանումները
կատարվել են 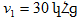 հաճախությամբ:
Երբ 1
կոնդենսատորը
փոխարինվել է
2 կոնդենսատորով,
սեփական
տատանումների
հաճախությունը
դարձել է
հավասար`
հաճախությամբ:
Երբ 1
կոնդենսատորը
փոխարինվել է
2 կոնդենսատորով,
սեփական
տատանումների
հաճախությունը
դարձել է
հավասար` 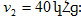 Ինչպիսի՞ն
կլինի այդ
հաճախությունը
1 և 2 կոնդենսատորների
զուգահեռ
միացման
դեպքում:
Ինչպիսի՞ն
կլինի այդ
հաճախությունը
1 և 2 կոնդենսատորների
զուգահեռ
միացման
դեպքում:
Լուծում:1 և 2
կոնդենսատորների
համար տրված
հաճախությունները`

Կոնդենսատորների
զուգահեռ
միացման
դեպքում
որոնելի հաճախությունը`
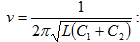
Գրված
առնչություններից
ստանում ենք`
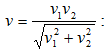
Տեղադրելով
թվային
արժեքները
ստանում ենք` v =
24 կՀց:
>>
Խնդիր
16.
Տատանողական
կոնտուրում
ազատ չմարող տատանումների
էներգիան
հավասար է` W1 = 2
· 10-4Ջ-ի:
Կոնդենսատորի
շրջադիրները
դանդաղ
հեռացնելով`
տատանման
հաճախությունը
մեծացավ n = 2
անգամ: Որոշել
էլեկտրական
ուժերի դեմ
կատարված աշխատանքը:
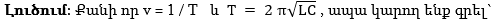
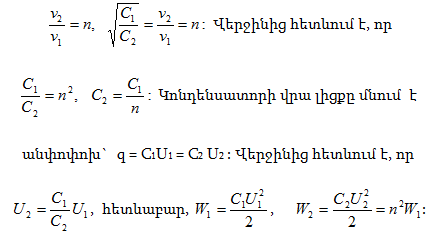
Կատարված
աշխատանքը
հավասար է
կոնդենսատորի
էներգիայի
փոփոխությանը`
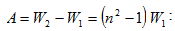
Տեղադրելով
թվային
արժեքները
ստանում ենք` A = 6
· 10-7 Ջ:
>>
Խնդիր
17.
Ինչի՞ է
հավասար
տատանողական
կոնտուրի մագնիսական
դաշտի
էներգիայի և
նրա
էլեկտրական դաշտի
էներգիայի հարաբերությունը
ժամանակի T/8
պահին:
Lուծում:
Տատանողական
կոնտուրի
կոնդենսատորի
վրա լարումը
փոփոխվում է
հետևյալ
օրենքով`

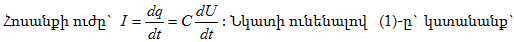
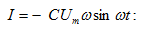
Հետևաբար,
մագնիսական
դաշտի
էներգիայի
համար
կունենանք`
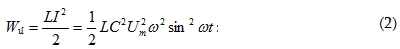
Էլեկտրական
դաշտի
էներգիան`
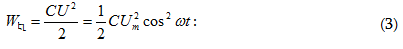
Բաժանելով
(3)-ը (2)-ի վրա
կստանանք`
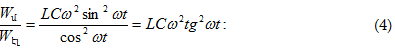
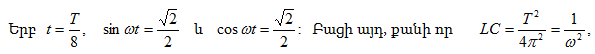
ապա
վերջնականապես
ստանում ենք`
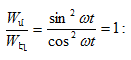
>>
Խնդիր
18.
Տատանողական
կոնտուրը
բաղկացած է L = 10
մՀն ինդուկտիվության
կոճից, C = 0,1մկՖ
ունակության
կոնդենսատորից
և R = 20 Օմ
դիմադրությունից:
Ի՞նչ թվով
տատանումներից
հետո հոսանքի
լայնույթը
կոնտուրում
կփոքրանա e
անգամ:
Լուծում:
Տատանողական
կոնտուրում
հոսանքի
լայնույթը
փոփոխվում է
հետևյալ
օրենքով.
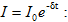
Ըստ
խնդրի
պայմանի
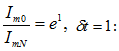
Քանի
որ մարման
գործակիցը` δ = R /
2L ստանում ենք t
= 1/ δ = 2L / R : Մյուս
կողմից
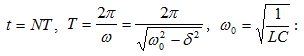
Պարբերության
համար
ստանում ենք`
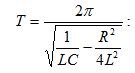
Հետևաբար,
տատանումների
լրիվ թվի
համար կստանանք`
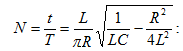
Տեղադրելով
թվային
արժեքները`
ստանում ենք` N =
50:
>>
Խնդիր
19.
Այն
ժամանակամիջոցը,
որի
ընթացքում
համակարգը կատարում
է N = 50 լրիվ
տատանում,
լայնույթը
փոքրանում է 2
անգամ: Որոշել
համակարգի Q
բարորակությունը:
Լուծում:
Համակարգի
բարորակությունը
որոշվում է հետևյալ
բանաձևով` Q = π / λ,
որտեղ λ-ն
մարման
լոգարիթմական
դեկրեմենտն է:
Տատանման
լայնույթի
համար կարող
ենք գրել`
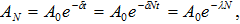

որտեղից
հետևում է, որ
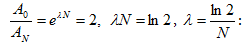
Վերջինը
նկատի
ունենալով,
բարորակության
համար
կստանանք` Q = πN / ln2 =
227:
>>
Խնդիր
20. Գտնել
այն
ժամանակամիջոցը,
որի դեպքում Q բարորակություն
ունեցող
կոնտուրում
հոսանքի
տատանման լայնույթը
փոքրանում է η
անգամ, եթե
մարող
տատանումների
հաճախությունը
հավասար է ω -ի:
Լուծում: Քանի
որ հոսանքի
լայնույթը` 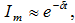 ապա
այն τ ժամանակամիջոցը,
որի դեպքում
լայնույթը
փոքրանում է η
անգամ, որոշվում
է η = eδt
հավասարումով,
որտեղից
ապա
այն τ ժամանակամիջոցը,
որի դեպքում
լայնույթը
փոքրանում է η
անգամ, որոշվում
է η = eδt
հավասարումով,
որտեղից

Մյուս
կողմից
կոնտուրի Q
բարորակությունը
δ -ի հետ
կապված է.

Արտաքսելով
(1) և (2)
հավասարումներից
δ -ն, կստանանք`
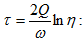
>>
Խնդիր
21.
Միևնույն
ուղղությամբ
տեղի ունեցող
տատանումների
գումարման
դեպքում
արդյունարար
տատանումը
նկարագրվում
է x = A costcosωt
հավասարման
տեսքով:
Որոշել վերադրվող
տատանումների`
1) շրջանային
հաճախությունները,
2)
արդյունարար տատանման
զարկումների
պարբերությունը:
Լուծում:
Արդյունարար
տատանումը`
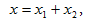
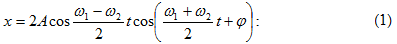
Ըստ
խնդրի պայմանի

(1)-ը
համեմատելով
(2)-ի հետ` գալիս
ենք այն
հետևության,
որ
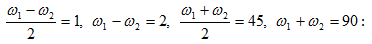
Երկրորդ
և չորրորդ
հավասարուների
համատեղ լուծումից
ստանում ենք` 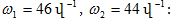 Քանի
որ
Քանի
որ 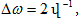 ուստի
պարբերության
համար
կստանանք`
ուստի
պարբերության
համար
կստանանք`
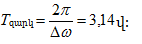
>>
Խնդիր
22.
Նույն
պարբերություն`
T = 4վ և A1 = A2 = 5սմ լայնույթով
միևնույն
ուղղություն
ունեցող
երկու ներդաշնակ
տատանումների
փուլերի
տարբերությունը
կազմում է π/4:
Գրել այդ տատանումների
գումարման
դեպքում
ստացվող
արդյունարար տատանման
շարժման
հավասարումը,
եթե տատանումներից
մեկի
սկզբնական փուլը
հավասար է
զրոյի:
Լուծում: Գրենք
տատանումների
հավասարումները.


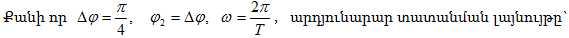
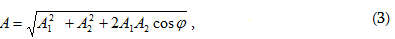
ապա
հաշվի
առնելով
խնդրի
պայմանները,
ստանում ենք`
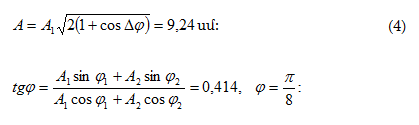
Այսպիսով,
արդյունարար
տատանման
շարժման հավասարման
համար
ստանում ենք`
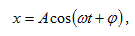
կամ
տեղադրելով
վերջինի մեջ
մտնող
մեծությունների
թվային արժեքները,
կստանանք`
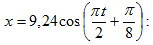
>>
Խնդիր
23.
Կետը
միաժամանակ
մասնակցում է
n թվով միևնույն
ուղղություն
ունեցող,
նույն
հաճախություններով
տատանումների.
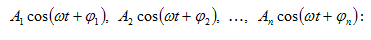
Օգտվելով
վեկտորական
դիագրամից`
որոշել
արդյունարար
տատանման համար
լայնույթը և
սկզբնական
փուլը:
Լուծում:
Ըստ
տատանումների
վերադրման
սկզբունքի` գտնենք
արդյունարար
տատանումը
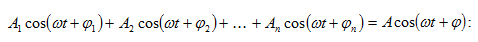
Օգտվենք
վեկտորական
դիագրամից:
Արդյունարար
տատանման վեկտորի
պրոյեկցիաները
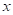 և
և 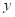 առանցքների
վրա հավասար
են առանձին
տատանումների
պրոյեկցիաների
գումարին.
առանցքների
վրա հավասար
են առանձին
տատանումների
պրոյեկցիաների
գումարին.
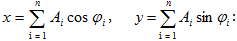
Արդյունարար
տատանման
լայնույթը`
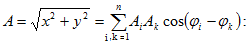
Արդյունարար
տատանման
փուլի համար
կունենանք`
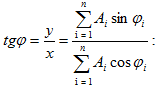
>>
Խնդիր
24. Հարթ
սինուսոիդային
ալիքը
տարածվում է
էներգիան չկլանող
միջավայրում
ուղղի
երկայնքով,
որը համընկնում
է x-ի դրական
առանցքի
ուղղության
հետ v = 10մ/վ
արագությամբ:
Այդ ուղղի վրա
երկու կետեր,
գտնվելով
տատանումների
աղբյուրից 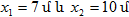 հեռավորությունների
վրա,
տատանվում են
հեռավորությունների
վրա,
տատանվում են 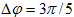 փուլերի
տարբերությամբ:
Ալիքի
լայնույթը` A =
5սմ: Որոշել
ալիքի երկարությունը,
ալիքի
հավասարումը,
երկրորդ կետի
փուլերի
տարբերությամբ:
Ալիքի
լայնույթը` A =
5սմ: Որոշել
ալիքի երկարությունը,
ալիքի
հավասարումը,
երկրորդ կետի
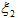 շեղումը
ժամանակի`
շեղումը
ժամանակի` 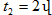 պահին:
պահին:
Լուծում:
Տատանվող
կետերի
փուլերի
տարբերությունը`
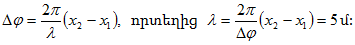
Ալիքի
հավասարումը`
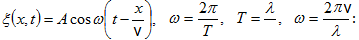
Երկրորդ
կետի շեղումը`
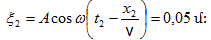
Ալիքի
հավասարման
համար
ստանում ենք`
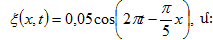
>>
Խնդիր
25. Գտնել 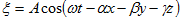 տեսք
ունեցող
ալիքի
տեսք
ունեցող
ալիքի 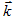 ալիքային
վեկտորը և v
արագությունը:
ալիքային
վեկտորը և v
արագությունը:
Լուծում:
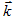 ալիքային
վեկտորը
ներկայացնենք
իր պրոյեկցիաներով`
ալիքային
վեկտորը
ներկայացնենք
իր պրոյեկցիաներով`

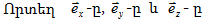
միավոր
վեկտորներ են
x, y, և z կոորդինատային
առանցքների
վրա: Ալիքի
հավասարումից
հետևում է, որ

Նկատի
ունենալով (2)-ը`
(1)-ից ալիքային
վեկտորի համար
ստանում ենք`

Ալիքի
արագությունը,
հաճախությունը
և ալիքային
վեկտորի
մոդուլը իրար
հետ կապված են
հետևյալ բանաձևով`

Ալիքային
վեկտորի
մոդուլի
համար (3)-ից
ստանում ենք`

Հաշվի
առնելով (5)-ը`
(4)-ից ստանում
ենք`
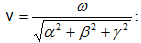
>>
Խնդիր
26. Նորմալ
մթնոլորտային
ճնշման
դեպքում (p = 1,01 · 105
Պա) երկատոմ
գազի
խտությունը` p =1,78
կգ/մ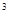 :
Որոշել այդ պայմանների
դեպքում
ձայնի արագությունը
գազում:
:
Որոշել այդ պայմանների
դեպքում
ձայնի արագությունը
գազում:
Լուծում:
Ձայնի
արագությունը
գազում
որոշվում է
հետևյալ
բանաձևով`

որտեղ
R -ը գազային
հաստատունն է,
M-ը` գազի մոլային
զանգվածը է, T-ն
բացարձակ
ջերմաստիճանը,
γ -ն ադիաբատի
ցուցիչն է և որոշվում
է γ = I + 2/ i
բանաձևով, i-ն
գազի
մոլեկուլի
ազատության աստիճանների
թիվն է:
Երկատոմ գազի
համար i = 5 :
Իդեալական
գազի վիճակի
հավասարումից`

Նկատի
ունենալով (2)-ը`
(1)-ից ստանում
ենք`
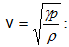
Տեղադրելով
թվային
արժեքները`
ստանում ենք` v =
282 մ/վ:
>>
Խնդիր
27.
Որոշել
էլեկտրամագնիսական
ալիքի
երկարությունը
վակուումում,
որին
համալրված է
տատանողական
կոնտուրը, եթե
կոնդենսատորի
շրջադիրների
վրա
առավելագույն
լիցքը` 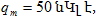 իսկ
հոսանքի
առավելագույն
արժեքը
կոնտուրում` Im
=1.5 Ա է: Կոնտուրի
ակտիվ
դիմադրությունն
անտեսել:
իսկ
հոսանքի
առավելագույն
արժեքը
կոնտուրում` Im
=1.5 Ա է: Կոնտուրի
ակտիվ
դիմադրությունն
անտեսել:
Լուծում:
Տատանողական
կոնտուրում
կոնդենսատորի
վրա լիցքի տատանումները
տեղի են
ունենում
հետևյալ
օրենքով`

Ածանցելով
(1) -ը ըստ
ժամանակի`
հոսանքի
համար կստանանք`

որտեղ
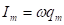 -ը
հոսանքի
լայնույթային
արժեքն է,
-ը
հոսանքի
լայնույթային
արժեքն է, 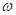 -ն` կոնտուրի
սեփական
հաճախությունը:
Ալիքի
երկարությունը`
-ն` կոնտուրի
սեփական
հաճախությունը:
Ալիքի
երկարությունը`
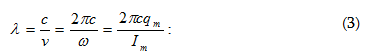
Տեղադրելով
(3)-ի մեջ մտնող
մեծությունների
թվային
արժեքները` կստանանք`
λ = 62,8 մ:
>>
Խնդիր
28. v = 5
ՄՀց
հաճախության
էլեկտրամագնիսական
ալիքը ε = 2
դիէլետրական
թափանցելիություն
ունեցող ոչ
մագնիսական
միջավայրից
անցնում է
վակուում:
Որոշել ալիքի
երկարության
աճը:
Լուծում:
Վակուումում
էլեկտրամագնիսական
ալիքի երկարությունը`

որտեղ
c -ն լույսի արագությունն
է
վակուումում:
Միջավայրում ալիքի
երկարությունը`

Որտեղ
v-ն
էլեկտրամագնիսական
ալիքի
արագությունն
է միջավայրում,
n-ը` միջավայրի
բացարձակ
բեկման
ցուցիչը, μ -ն` մագնիսական
թափանցելիությունը
(μ = 1):
Ալիքի
երկարության
աճի համար,
օգտվելով (1)-ից
և (2)-ից, ստանում
ենք`
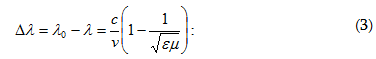
Տեղադրելով
(3)-ի մեջ մտնող
մեծությունների
թվային
արժեքները`
կունենանք` 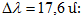
>>
Խնդիր
29.
Վակուումում
x-ի առանցքի
երկայնքով
տարածվում է
հարթ
էլեկտրամագնիսական
ալիք: Ալիքի
էլեկտրական
դաշտի լարվածության
լայնույթը` E0
= 10Վ/մ: Որոշել
ալիքի
մագնիսական
դաշտի լարվածության
լայնույթը:
Լուծում:
Էլեկտրամագնիսական
ալիքում
ժամանակի ցանկացած
պահին ալիքի
յուրաքանչյուր
կետում E-ն և H-ը
կապված են
իրար հետ
հետևյալ
առնչությամբ`
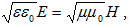
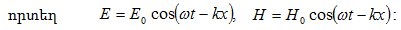
Վակուումի
դեպքում` ε = μ = 1,
հետևաբար,
կստանանք`
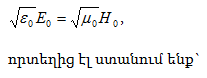
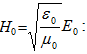
Տեղադրելով
թվային
արժեքները
կստանանք` 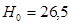 Ա/մ:
Ա/մ:
>>
Խնդիր
30. Որոշել
վակուումում
տարածվող
հարթ սինուսոիդային
ալիքի
տեղափոխած
էներգիան t =
1վ-ում, ալիքի
տարածման ուղղությանն
ուղղահայաց
մակերևույթի S
=1մ մակերեսով:
Ալիքի էլեկտրական
դաշտի
լարվածության
լայնույթը`E0 =
5 մՎ/մ: Ալիքի պարբերությունը`
T<< t
մակերեսով:
Ալիքի էլեկտրական
դաշտի
լարվածության
լայնույթը`E0 =
5 մՎ/մ: Ալիքի պարբերությունը`
T<< t
Լուծում:
Էլեկտրամագնիսական
ալիքի
էներգիայի
հոսքի
խտությունը
որոշվում է
Պոյնտինգի
վեկտորով.
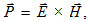
որտեղ
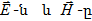 էլեկտրամագնիսական
ալիքի
էլեկտրական և մագնիսական
դաշտերի
լարվածության
վեկտորներն
են: Նկատի ունենալով,
որ
էլեկտրամագնիսական
ալիքի
էլեկտրական և մագնիսական
դաշտերի
լարվածության
վեկտորներն
են: Նկատի ունենալով,
որ 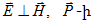 մոդուլի
համար
ստանում ենք`
մոդուլի
համար
ստանում ենք`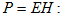 Քանի
որ E և H
մեծությունները
էլեկտրամագնիսական
ալիքի յուրաքանչյուր
կետում
ժամանակի
ցանկացած
պահին
փոփոխվում են
սինուսի
օրենքով,
գտնվելով
միևնույն փուլերում,
ապա P
մեծության ակնթարթային
արժեքը
հավասար է`
Քանի
որ E և H
մեծությունները
էլեկտրամագնիսական
ալիքի յուրաքանչյուր
կետում
ժամանակի
ցանկացած
պահին
փոփոխվում են
սինուսի
օրենքով,
գտնվելով
միևնույն փուլերում,
ապա P
մեծության ակնթարթային
արժեքը
հավասար է`
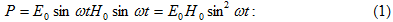
Այսպիսով,
P մեծությունը
ժամանակի
ֆունկցիա է:
Համաձայն էներգիայի
հոսքի
խտության
վեկտորի
սահմանման
կունենանք`

որտեղ
dW -ն ալիքով
տեղափոխված
էներգիան է dt
ժամանակում:
(2) և (1)
արտահայտություններից
ունենք`
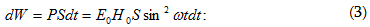
dW
-ի որոշման
համար պետք է
հայտնի լինի H0
մեծությունը,
որը կարելի է
գտնել 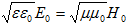 առնչությունից:
Այստեղից
առնչությունից:
Այստեղից
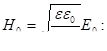
Ըստ
պայմանի, ` ε = μ = 1
հետևաբար`

(4)
-ը
տեղադրելով
(3)-ի մեջ`
ստանում ենք`
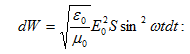
Ալիքի
տեղափոխած
էներգիան t
ժամանակի
ընթացքում`
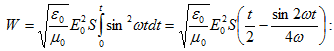
Ըստ
խնդրի
պայմանի T << t ,
ուստի t / 2 >> sin2ωt /4ω
և sin2ωt /4ω անդամը
կարելի է
անտեսել:
Հետևաբար`
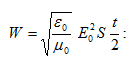
Տեղադրելով
բանաձևի մեջ
մտնող
մեծությունների
թվային արժեքները`
ստանում ենք` W = 3,
25 · 10-8Ջ:
>>
ԳՐԱԿԱՆՈՒԹՅՈՒՆ
1.
И.
В. Савельев.
Курс общей
физики. Книга
1. Механика,Москва:
Издательство
Астрель 2005.
2.
И.
В. Савельев.
Курс общей физики.
Книга 2.
Электричество
и магнетизм. Москва:
Издательство
Астрель 2001.
3.
А. А.
Детлаф, Б.М.
Яворский.
Курс физики.
т.1, Москва:
Высшая школа,
2002.
4.
А. А.
Детлаф, Б.М.
Яворский.
Курс физики.
т.2, Москва:
Высшая школа,
2002.
5.
Д.В.Сивухин.
Общий курс физики.
Механика,Москва:
Наука 1985.
Արսեն
Հովհաննեսի
Աբոյան
Տատանումներ
և ալիքներ
Ուսումնական
ձեռնարկ
Խմբագիր`
Ն. Ա.
Խաչատրյան
Համակարգչային
շարվածքը
և
ձևավորումը`
Զ. Չթչյան
Նկարները`
Թ. Մադոյան