

ԳՄԴ 535.231.2:539.18
Ա.Հ. Աբոյան
Օպտիկա: Ճառագայթման քվանտային բնույթը և ատոմի Բորի տեսությունը: Ուսումնական ձեռնարկ. - ՀՊՃՀ, Երևան, 2006թ.:
Ձեռնարկում շարադրված նյութը համապատասխանում է ճարտարագիտական մասնագիտությունների ընդհանուր ֆիզիկայի դասընթացի գործող ծրագրին: Բացի տրադիցիոն բաժիններից ձեռնարկում արտացոլված են օպտիկայում ձեռք բերված խոշոր նվաճումները (լազերներ, հոլոգրաֆիա, ռենտգենյան ինտերֆերաչափեր) և անհրաժեշտ ուշադրություն է դարձված գիտափորձին: Ձեռնարկում մանրամասն նկարագրված են լույսի դիֆրակցիայի, ինտերֆերենցիայի, բևեռացման, դիսպերսիայի, լույսի ցրման ու կլանման, ջերմային ճառագայթման երևույթները, ինչպես նաև քվանտային մեխանիկայի տարրերը, ատոմի կառուցվածքը և Բորի տեսությունը:
Ձեռնարկը նախատեսված է ՀՊՃՀ-ի բոլոր դեպատամենտների ուսանողների համար: Այն կարող է օգտակար լինել նաև դասախոսներին և այլ բուհերի ուսանողներին:
Գրախոսներ՝ ֆիզ. մաթ. գիտ. դոկտոր, պրոֆեսոր
Ռ© Կարախանյան
ֆիզ. մաթ. գիտ. թեկնածու, դոցենտ
Ս. Մանուկյան

ԳԼՈՒԽ 1. ՕՊՏԻԿԱՅԻ ՀԻՄՆԱԿԱՆ ՕՐԵՆՔՆԵՐԸ
1.1 Օպտիկական տեսությունների զարգացման գլխավոր փուլերը
1. Անդրադարձման օրենքի արտածումը
ԳԼՈՒԽ 2. ԼՈՒՅՍԻ ԻՆՏԵՐՖԵՐԵՆՑԻԱՆ
2.1 Գծային օպտիկայի վերադրման սկզբունքը
2.2 Լույսի էլեկտրամագնիսական բնույթը: Լուսային հոսք
2.3 Էլեկտրամագնիսական ալիքների տարածումը: Փուլային և խմբային արագություններ
2.4 Տատանումների գումարումը: Լուսային ալիքների ինտերֆերենցիան: Կոհերենտություն
2.5 Լույսի երկու կոհերենտ աղբյուրներից ստացվող ինտերֆերենցիոն պատկերի հաշվարկը
2.6 Կոհերենտ փնջերի ստացման եղանակները օպտիկայում
2.7 Լույսի ինտերֆերենցիան բարակ թաղանթներում
2.8 Հավասար հաստության շերտեր: Նյուտոնի օղակները
2.9 Լույսի ինտերֆերենցիայի կիրառությունները
2.10 Ռենտգենյան ինտերֆերաչափեր
3.1 Հյուգենս-Ֆրենելի սկզբունքը
3.3 ֆրենելի դիֆրակցիան պարզագույն արգելքներից
3. Ֆրաունհոֆերյան դիֆրակցիան ճեղքից
4.
Դիֆրակցիան ![]() ճեղքերից
(դիֆրակցիոն ցանց)
ճեղքերից
(դիֆրակցիոն ցանց)
3.4 Դիֆրակցիան տարածական ցանցում: Վուլֆ-Բրեգի բանաձևը
3.5 Վուլֆ-Բրեգի բանաձևի ճշգրտումը բեկման հաշվառմամբ
3.6 Գաղափար հոլոգրաֆիայի մասին
4.1 Բնական և բևեռացված լույս: Մալյուսի օրենքը
4.3 Բևեռացումը կրկնակի ճառագայթաբեկման դեպքում
4.6 Արհեստական կրկնակի ճառագայթաբեկում: Քերի երևույթը
5.2 Էլեկտրամագնիսական ալիքների փոխազդեցությունը նյութի հետ: Լույսի դիսպերսիայի դասական տեսությունը
5.5 Վավիլով-Չերենկովի երևույթը
ԳԼՈՒԽ 6. ՃԱՌԱԳԱՅԹՄԱՆ ՔՎԱՆՏԱՅԻՆ ԲՆՈՒՅԹԸ
6.1 Ջերմային ճառագայթում: Ջերմային ճառագայթման առանձնահատկությունները
6.2 Մարմինների ճառագայթման և կլանման ընդունակությունը
6.5 Ստեֆան-Բոլցմանի օրենքի արտածումը
6.9 Ստեֆան-Բոլցմանի օրենքի արտածումը Պլանկի բանաձևից
6.10 Օպտիկական հրաչափություն (պիրոմետրիա)
ԳԼՈՒԽ 7. ՔՎԱՆՏԱՕՊՏԻԿԱԿԱՆ ԵՐԵՎՈՒՅԹՆԵՐ
7.3 Այնշտայնի վարկածը և լուսաէֆեկտի հավասարումը
ԳԼՈՒԽ 8. ԱՏՈՄԻ ԲՈՐԻ ՏԵՍՈՒԹՅՈՒՆԸ
8.1 Օրինաչափություններ ատոմային սպեկտրներում Բալմերի ընդհանրացրած բանաձևը
8.5 Շրջանային ուղեծրերի քվանտացումը և ջրածնի ատոմի տեսությունը
ԳԼՈՒԽ 9. ՋՐԱԾՆԻ ԱՏՈՄԻ ՔՎԱՆՏԱՄԵԽԱՆԻԿԱԿԱՆ ՏԵՍՈՒԹՅՈՒՆԸ
9.1 Դը Բրոյլի վարկածը: Նյութի ալիքային հատկությունները
9.3 Հայզենբերգի անորոշությունների առնչությունները
9.4 Ալիքային ֆունկցիան և նրա վիճակագրական իմաստը
9.6 Մասնիկն անվերջ խոր միաչափ փոսում
9.8 Ջրածնի ատոմը` ըստ Շրյոդինգերի տեսության: Քվանտային թվեր
9.9 Էլեկտրոնի սպինը: Սպինային քվանտային թիվ: Պաուլիի սկզբունքը
9.11 Անընդհատ սպեկտրով ռենտգենյան ճառագայթների առաջացումը
9.12 Գծային սպեկտրով ռենտգենյան ճառագայթների առաջացումը
9.13 Ստիպողական ճառագայթում: Լազերներ
Օպտիկան ֆիզիկայի այն բաժինն է, որն ուսումնասիրում է լույսի բնույթը, առաքման և կլանման օրենքները, տարածումը տարբեր միջավայրերում, ինչպես նաև նյութի հետ լույսի փոխազդեցության ժամանակ առաջացող երևույթները:
Օպտիկական երևույթները մարդկությանը հետաքրքրել են շատ վաղուց, սակայն օպտիկայի տեսության սկիզբը պետք է համարել 17-րդ դարը: Օպտիկայի զարգացումը պատմականորեն կարելի է բաժանել հետևյալ փուլերի. առաջին փուլ` Նյուտոնի, Հյուգենսի ժամանակներից մինչև 19-րդ դարի սկիզբը` ալիքային և մասնիկային պատկերացումների վրա հիմնված, միմյանց բացառող տեսությունների բուռն պայքարի դարաշրջանը, որն ավարտվեց ալիքային տեսության հաղթանակով: Երկրորդ փուլը Ֆրենելի, Յունգի ժամանակներից մինչև լուսային մասնիկների` քվանտների գաղափարի հաստատման և նրանց տեսության զարգացման դարաշրջանն է, իսկ երրորդն արդի փուլն է, որը կապված է հատկապես օպտիկական քվանտային գեներատորների հայտնագործման հետ:
Սկզբնական շրջանում օպտիկան սահմանափակվում էր էլեկտրամագնիսական ալիքների սպեկտրի տեսանելի մասով: Ժամանակակից օպտիկան ուսումնասիրում է էլեկտրամագնիսական ալիքների սպեկտրի ինչպես տեսանելի, այնպես էլ նրան հարող ուլտրամանուշակագույն և ինֆրակարմիր տիրույթները: Օպտիկական երևույթների մի մեծ խումբ կարելի է քննարկել առանց լույսի ալիքային բնույթը հաշվի առնելու, ընդունելով, որ լուսային էներգիան փոխանցվում է ճառագայթի երկայնքով: Այս պատկերացումը և լույսի անդրադարձման ու բեկման օրենքները միասին կազմում են երկրաչափական օպտիկայի հիմքը: Երկրաչափական օպտիկայի օրենքները խախտվում են, երբ միջավայրում կան կտրուկ անհամասեռություններ կամ փնջի կտրուկ սահմանափակումներ: Այս դեպքում հանդես են գալիս լույսի ալիքային հատկությունները: Օպտիկական այն երևույթները (լույսի դիֆրակցիա, ինտերֆերենցիա, բևեռացում), որոնք կարող են բացատրվել միայն լույսի մասին ալիքային պատկերացումներով, կազմում են ալիքային օպտիկայի ուսումնասիրության առարկան: Լույսի ալիքային հատկությունները նկարագրելու համար անհրաժեշտ է հենվել լույսի ֆենոմենոլոգիական էլեկտրամգնիսական տեսության տրված եզրային պայմաններում Մաքսվելի հավասարումների լուծման վրա: Այս տեսության մեջ միջավայրը նկարգրվում է մակրոսկոպիկ մեծություններով` նյութական հաստատուններով (դիէլեկտրական և մագնիսական թափանցելիություններ, հաղորդականություն և այլն), և այդ իմաստով տեսության արդյունքներն անկախ են միջավայրի մոլեկուլային կառուցվածքի այս կամ այն պատկերացումներից: Մյուս կողմից, այդ մակրոսկոպիկ մեծությունները որոշվում են միջավայրը կազմող ատոմների և մոլեկուլների հատկություններով, այնպես որ օպտիկական երևույթները տեղեկություն են պարունակում միջավայրի ատոմական և մոլեկուլային կառուցվածքի մասին: Սովորաբար այդ երևույթներն ուսումնասիրվում են մոլեկուլային օպտիկա բաժնում:
Միջավայրի նկարագրումը մակրոսկոպիկ հաստատուններով հնարավոր է միայն թույլ էլեկտրամագնիսական դաշտերում: Ուժեղ դաշտերում միջավայրի հաստատունները փոխվում են` կախված էլեկտրական և մագնիսական դաշտի լարվածությունների մեծություններից: Այս երեվույթները կազմում են ոչ գծային օպտիկայի ուսումնասիրման առարկան: Այս բնագավառի ուսումնասիրությունները նոր թափ են ստացել օպտիկական քվանտային գեներատորների` լազերների հայտնագործումից հետո:
Սպեկտրոսկոպիան օպտիկայի կարևորագույն բաժիններից է, որը զբաղվում է ինչպես ատոմների և մոլեկուլների կլանման ու ճառագայթման, այնպես էլ կոմբինացիոն ցրման սպեկտրների ուսումնասիրությամբ:
Օպտիկական չափումները, ուսումնասիրման մեթոդները և գործիքները լայն կիրառություն ունեն կյանքի ամենատարբեր ոլորտներում, թե° գիտական և թե° գործնական խնդիրների լուծման համար: Լույսի արագության որոշման փորձերը վակուումում և տարբեր միջավայրերում (Մայքելսոնի փորձ, Ֆիզոյի փորձ) էական նշանակություն են ունեցել հարաբերական հատուկ տեսության զարգացման համար:
Օպտիկայի բնագավառում ՀՀ-ում կատարվող աշխատանքները հիմնականում վերաբերում են օպտիկական քվանտային գեներատորների հետազոտությանը, նոր տեսակի գեներատորների մշակմանը, լուսային ճառագայթի և նյութի գծային ու ոչ գծային փոխազդեցությունների ուսումնասիրությանը:
ՕՊՏԻԿԱՅԻ ՀԻՄՆԱԿԱՆ ՕՐԵՆՔՆԵՐԸ
1.1. Օպտիկական տեսությունների զարգացման գլխավոր փուլերը
Օպտիկական երևույթների մի շարք օրինաչափություններ հայտնի են դեռ հին ժամանակներից: Փորձով սահմանվել են այնպիսի օրենքներ, ինչպիսիք են լույսի ուղղագիծ տարածման օրենքը, լուսային փնջերի անկախության օրենքը, լույսի անդրադարձման օրենքը, լույսի բեկման օրենքը:
Համասեռ միջավայրում լույսը ուղղագիծ է տարածվում: Դա բխում է նրանից, որ ոչ թափանցիկ առարկաները փոքր չափերի լույսի աղբյուրներով լուսավորելիս տալիս են կտրուկ եզրագծված ստվերներ: Լույսի ուղղագիծ տարածման օրենքը մոտավոր է. շատ փոքր անցքերով անցնելու դեպքում նկատվում են շեղումներ ուղղագիծ տարածման օրենքից և որքան փոքր է անցքը, այնքան մեծ են շեղումները:
 Լուսային
փնջերի անկախությունն
այն է, որ հատվելիս
դրանք չեն փոխազդում
միմյանց հետ: Փնջերի
հատվելը դրանցից
յուրաքանչյուրին
չի խանգարում
իրարից անկախ
տարածվելուն:
Լուսային
փնջերի անկախությունն
այն է, որ հատվելիս
դրանք չեն փոխազդում
միմյանց հետ: Փնջերի
հատվելը դրանցից
յուրաքանչյուրին
չի խանգարում
իրարից անկախ
տարածվելուն:
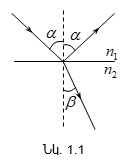
Երկու թափանցիկ միջավայրերի սահմանն անցնելիս ընկնող ճառագայթը բաժանվում է երկու ճառագայթի` անդրադարձած և բեկված (նկ.1.1): Այդ ճառագայթների ուղղությունները որոշվում են լույսի անդրադարձման և բեկման օրենքներով: Լույսի անդրադարձման օրենքը ձևակերպվում է հետևյալ կերպ.
1. Անդրադարձած ճառագայթը գտնվում է այն հարթության մեջ, որի մեջ գտնվում են ընկնող ճառագայթը և անկման կետում անդրադարձնող մակերևույթին կանգնեցրած ուղղահայացը:
2. Անդրադարձման անկյունը հավասար է անկման անկյանը:
Փորձերի հիման վրա սահմանվել են լույսի բեկման հետևյալ օրենքները:
1. Բեկված ճառագայթը գտնվում է այն նույն հարթության մեջ, ուր գտնվում են ընկնող ճառագայթը և այն ուղղահայացը, որը կանգնեցված է երկու միջավայրերի բաժանման սահմանին` ճառագայթի անկման կետում:
2. Անկման և բեկման անկյունների բոլոր փոփոխությունների դեպքում անկման անկյան սինուսի և բեկման անկյան սինուսի հարաբերությունը տվյալ երկու միջավայրերի համար հաստատուն մեծություն է, որը կոչվում է երկրորդ միջավայրի բեկման ցուցիչ` առաջինի նկատմամբ:
Այդ օրենքը մաթեմատիկորեն կարելի է արտահայտել հետևյալ բանաձևով`

որտեղ
![]() -ն անկման
անկյունն է,
-ն անկման
անկյունն է,![]() -ն` բեկման
անկյունը և
-ն` բեկման
անկյունը և ![]() -ը` հարաբերական
բեկման ցուցիչը:
Տվյալ նյութի բեկման
ցուցիչը վակուումի
նկատմամբ կոչվում
է նյութի բացարձակ
բեկման ցուցիչ:
Երկու նյութերի
համեմատության
դեպքում այն նյութը,
որն ունի ավելի
մեծ բեկման ցուցիչ,
կոչվում է օպտիկապես
ավելի խիտ: Բեկան
ցուցիչ հասկացությունը
խոր ֆիզիկական
բովանդակություն
ունի: Բեկման բացարձակ
n ցուցիչը ցույց
է տալիս, թե լույսի
արագությունը
վակուումի մեջ
քանի անգամ է մեծ
լույսի արագությունից
տվյալ նյութում,
այսինքն`
-ը` հարաբերական
բեկման ցուցիչը:
Տվյալ նյութի բեկման
ցուցիչը վակուումի
նկատմամբ կոչվում
է նյութի բացարձակ
բեկման ցուցիչ:
Երկու նյութերի
համեմատության
դեպքում այն նյութը,
որն ունի ավելի
մեծ բեկման ցուցիչ,
կոչվում է օպտիկապես
ավելի խիտ: Բեկան
ցուցիչ հասկացությունը
խոր ֆիզիկական
բովանդակություն
ունի: Բեկման բացարձակ
n ցուցիչը ցույց
է տալիս, թե լույսի
արագությունը
վակուումի մեջ
քանի անգամ է մեծ
լույսի արագությունից
տվյալ նյութում,
այսինքն` ![]()
Առաջին պարզորոշ ձևակերպված տեսակետը լույսի բնույթի մասին պատկանում է Նյուտոնին: Ելնելով լույսի ուղղագիծ տարածման օրենքից` Նյուտոնը գտնում էր, որ լույսը ներկայացնում է հատուկ մասնիկների` կորպուսկուլների հոսք: Լույսի արագությունն այն արագությունն է, որով շարժվում են լույսի կորպուսկուլները: Ենթադրելով, որ նրանց շարժման արագությունը տարբեր միջավայրերում տարբեր է, Նյուտոնը դրա հիման վրա կարողացավ բացատրել լույսի ճառագայթների բեկման և անդրադարձման օրենքները:
Հյուգենսն առաջ քաշեց ալիքային տեսությունը, ըստ որի լույսը դիտվում էր որպես տիեզերական եթերում տարածվող առաձգական ալիք: Հարյուրից ավելի տարիներ կորպուսկուլյար տեսությունը անհամեմատ ավելի շատ կողմնակիցներ ուներ, քան ալիքայինը: Սակայն 19-րդ դարի սկզբում Ֆրենելին հաջողվեց ալիքային պատկերացումների հիման վրա բացատրել` այն ժամանակ հայտնի բոլոր օպտիկական երևույթները: Արդյունքում ալիքային տեսությունը ստացավ համընդհանուր ճանաչում, իսկ կորպուսկուլյար տեսությունը մոռացվեց համարյա մեկ հարյուրամյակ:
Նշենք, որ Նյուտոնի և Հյուգենսի տեսությունները հանգեցնում են բեկման ցուցչի և նյութում լույսի տարածման արագության միջև տարբեր կախումների:
Ըստ
Նյուտոնի, լուսային
ճառագայթը մոտենում
է մակերևույթի
ուղղահայացին
այն պատճառով,
որ երկրորդ միջավայրում
լույսը տարածվում
է ավելի մեծ արագությամբ,
քան առաջին միջավայրում:
Լույսի արագությունն
առաջին միջավայրում
նշանակենք ![]() իսկ երկրորդում`
իսկ երկրորդում`
![]() Նյուտոնի
կարծիքով, արագության
փոփոխությունը
հետևանք է այն
բանի, որ լույսի
կորպուսկուլները
երկրորդ միջավայրի
մոլեկուլների
կողմից ձգվում
են ավելի մեծ ուժով,
քան առաջին միջավայրի
մոլեկուլների
կողմից: Քանի որ
ձգողական ուժերի
համազորն ունի
երկու միջավայրերի
բաժանման սահմանին
տարված ուղղահայացի
ուղղությունը,
ուստի բաժանման
սահմանից անցնելիս
լուսային հոսքի
արագության նորմալ
բաղադրիչը փոխվում
է: Լույսի արագության
համապատասխան
արժեքները նկ.1.2-ում
պատկերված են
Նյուտոնի
կարծիքով, արագության
փոփոխությունը
հետևանք է այն
բանի, որ լույսի
կորպուսկուլները
երկրորդ միջավայրի
մոլեկուլների
կողմից ձգվում
են ավելի մեծ ուժով,
քան առաջին միջավայրի
մոլեկուլների
կողմից: Քանի որ
ձգողական ուժերի
համազորն ունի
երկու միջավայրերի
բաժանման սահմանին
տարված ուղղահայացի
ուղղությունը,
ուստի բաժանման
սահմանից անցնելիս
լուսային հոսքի
արագության նորմալ
բաղադրիչը փոխվում
է: Լույսի արագության
համապատասխան
արժեքները նկ.1.2-ում
պատկերված են ![]() վեկտորներով:
Այդ վեկտորների
նորմալ բաղադրիչները`
OA1 -ը և OB1-ը
իրարից տարբեր
են: Լույսի արագության
OA2 բաղադրիչը,
որն ուղղված է
բաժանման սահմանի
երկայնքով, չի
փոխվում: Համադրելով
OA1A և OB1B եռանկյունները`
գտնում ենք.
վեկտորներով:
Այդ վեկտորների
նորմալ բաղադրիչները`
OA1 -ը և OB1-ը
իրարից տարբեր
են: Լույսի արագության
OA2 բաղադրիչը,
որն ուղղված է
բաժանման սահմանի
երկայնքով, չի
փոխվում: Համադրելով
OA1A և OB1B եռանկյունները`
գտնում ենք.
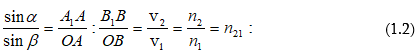
Վերջինից
հետևում է, որ հարաբերական
բեկման ցուցիչն
ըստ Նյուտոնի
հավասար է երկրորդ
և առաջին միջավայրերում
լույսի տա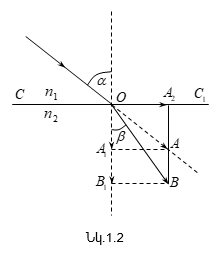 րածման
արագությունների
հարաբերությանը:
Եթե
րածման
արագությունների
հարաբերությանը:
Եթե ![]() ապա
լուսային ճառագայթն
այդ միջավայրերի
բաժանման սահմանն
անցնելիս մոտենում
է նորմալին
ապա
լուսային ճառագայթն
այդ միջավայրերի
բաժանման սահմանն
անցնելիս մոտենում
է նորմալին ![]() Եթե
Եթե ![]() ապա լուսային
ճառագայթը բաժանման
սահմանից անցնելիս
հեռանում է նորմալից:
ապա լուսային
ճառագայթը բաժանման
սահմանից անցնելիս
հեռանում է նորմալից:
Նյուտոնի ժամանակներում լույսի տարածման արագությունը տարբեր միջավայրերում որոշված չէր, ուստի և Նյուտոնի վարկածն անմիջական ստուգման ենթարկել հնարավոր չէր:
Հյուգենսը, որը Նյուտոնի ժամանակակիցն էր, այլ տեսակետ ուներ լույսի բնույթի մասին: Նա գտնում էր, որ լույսը ալիքային պրոցես է, և հատուկ լուսային կորպուսկուլներ գոյություն չունեն: Ինչպես Նյուտոնին, այնպես էլ Հյուգենսին հաջողվեց, ելնելով իր վարկածից, տալ լույսի անդրադարձման և բեկման օրենքների բացատրությունը: Հյուգենսը, ինչպես և Նյուտոնը, լույսի բեկման պատճառը տեսնում էր այն բանում, որ լույսը տարբեր արագություններով է տարածվում տարբեր միջավայրերում, սակայն Հյուգենսի եզրակացությունն այդ արագությունների հարաբերակցության վերաբերյալ Նյուտոնի եզրակացության ճիշտ հակառակն էր:
Լույսի բեկման երևույթն ալիքային տեսակետից քննության առնելիս օգտվենք Հյուգենսի սկզբունքից, որն ասում է.
Միջավայրի յուրաքանչյուր կետ, որին հասնում է լուսային գրգիռը, ինքն իր հերթին դառնում է լուսային երկրորդային ալիքների աղբյուր, ալիքներ, որոնց պարուրիչը ժամանակի յուրաքանչյուր տվյալ պահին ներկայացնում է տարածվող ալիքի ճակատը (մակերևույթը): Քանի որ ալիքների տարածման ուղղությունն ուղղահայաց է ալիքի մակերևույթին, ապա իմանալով ալիքային մակերևույթը, կարող ենք որոշել լույսի տարածման ուղղությունը:
 Քննարկենք
հարթ ալիքի բեկումը
երկու միջավայրերի,
ընդ որում` ալիքի
արագությունն
առաջին միջավայրում
նշանակենք
Քննարկենք
հարթ ալիքի բեկումը
երկու միջավայրերի,
ընդ որում` ալիքի
արագությունն
առաջին միջավայրում
նշանակենք ![]()
Դիցուք
![]() ալիքի
ճակատի OC ուղղահայացով
և բեկող միջավայրի
մակերևույթի OD
ուղղահայացով
կազմված անկյունն
է (նկ.1.3): Ենթադրենք,
որ t=0 պահին ալիքի
ճակատի C կետը,
հասնելով բեկող
միջավայրին, համընկել
է O կետի հետ: Այն
ալիքի
ճակատի OC ուղղահայացով
և բեկող միջավայրի
մակերևույթի OD
ուղղահայացով
կազմված անկյունն
է (նկ.1.3): Ենթադրենք,
որ t=0 պահին ալիքի
ճակատի C կետը,
հասնելով բեկող
միջավայրին, համընկել
է O կետի հետ: Այն
![]() ժամանակը,
որը պահանջվում
է, որպեսզի ալիքի
ճակատի A կետը
հասնի երկրորդ
միջավայրին (B
կետը) O կետից, որպես
կենտրոնից, երկրորդային
ալիքը կտարածվի
որոշ OF շառավղով:
Երկրորդային ալիքները,
որոնց կենտրոններն
O1, O2 և այլ կետերում
են, այդ նույն պահին
տարածված կլինեն
համապատասխան
հեռավորություններով,
առաջացնելով երկրորդ
միջավայրում տարրական
սֆերիկ ալիքներ`F1,F2,...:
Համաձայն Հյուգենսի
սկզբունքի, ալիքային
ճակատի իսկական
դիրքը տրվում է
տարրական ալիքների
պարուրիչով, այսինքն`
BF2F1F հարթությամբ:
Պարզ է,որ
ժամանակը,
որը պահանջվում
է, որպեսզի ալիքի
ճակատի A կետը
հասնի երկրորդ
միջավայրին (B
կետը) O կետից, որպես
կենտրոնից, երկրորդային
ալիքը կտարածվի
որոշ OF շառավղով:
Երկրորդային ալիքները,
որոնց կենտրոններն
O1, O2 և այլ կետերում
են, այդ նույն պահին
տարածված կլինեն
համապատասխան
հեռավորություններով,
առաջացնելով երկրորդ
միջավայրում տարրական
սֆերիկ ալիքներ`F1,F2,...:
Համաձայն Հյուգենսի
սկզբունքի, ալիքային
ճակատի իսկական
դիրքը տրվում է
տարրական ալիքների
պարուրիչով, այսինքն`
BF2F1F հարթությամբ:
Պարզ է,որ
![]() Տեղադրելով այստեղ
Տեղադրելով այստեղ
![]() արժեքները`
կստանանք
արժեքները`
կստանանք ![]() կամ
կամ

Այսպիսով,
ըստ Հյուգենսի,
անկման անկյան
և բեկման անկյան
սինուսների հարաբերությունը
հավասար է առաջին
միջավայրում լույսի
տարածման արագության`
![]() և
երկրորդ միջավայրում
նրա ունեցած արագության`
և
երկրորդ միջավայրում
նրա ունեցած արագության`
![]() հարաբերությանը
(այլ ոչ թե
հարաբերությանը
(այլ ոչ թե ![]() ինչպես
Նյուտոնն էր ենթադրում):
Ըստ Հյուգենսի,
այն փաստը, որ մի
միջավայրից մյուսի
մեջ անցնելիս լույսի
ճառագայթը բեկվելով
մոտենում է ուղղահայացին,
հետևում է, որ լույսի
արագությունը
երկրորդ միջավայրում
ավելի փոքր է, քան
առաջինում: Այնինչ,
ըստ Նյուտոնի,
ինչպես տեսանք,
բեկումն այդպիսի
բնույթ կարող է
ունենալ միայն
այն դեպքում, եթե
լույսի արագությունը
երկրորդ միջավայրում
ավելի մեծ է, քան
առաջինում: Լույսի
արագությունների
իրական հարաբերակցությունը,
որը համապատասխանում
է
ինչպես
Նյուտոնն էր ենթադրում):
Ըստ Հյուգենսի,
այն փաստը, որ մի
միջավայրից մյուսի
մեջ անցնելիս լույսի
ճառագայթը բեկվելով
մոտենում է ուղղահայացին,
հետևում է, որ լույսի
արագությունը
երկրորդ միջավայրում
ավելի փոքր է, քան
առաջինում: Այնինչ,
ըստ Նյուտոնի,
ինչպես տեսանք,
բեկումն այդպիսի
բնույթ կարող է
ունենալ միայն
այն դեպքում, եթե
լույսի արագությունը
երկրորդ միջավայրում
ավելի մեծ է, քան
առաջինում: Լույսի
արագությունների
իրական հարաբերակցությունը,
որը համապատասխանում
է ![]() արժեքին,
հաստատվեց միայն
1850 թվականին, երբ
Ֆուկոն իրագործեց
լույսի արագության
չափումը ջրում:
Ֆուկոյի չափումները
ցույց տվեցին,
որ իրոք, լույսի
արագութունը ջրում
ավելի փոքր է, քան
օդում, և դրանով
իսկ նպաստեցին
լույսի վերաբերյալ
ալիքային պատկերացումների
հաստատմանը:
արժեքին,
հաստատվեց միայն
1850 թվականին, երբ
Ֆուկոն իրագործեց
լույսի արագության
չափումը ջրում:
Ֆուկոյի չափումները
ցույց տվեցին,
որ իրոք, լույսի
արագութունը ջրում
ավելի փոքր է, քան
օդում, և դրանով
իսկ նպաստեցին
լույսի վերաբերյալ
ալիքային պատկերացումների
հաստատմանը:
Ալիքային տեսությունն իր հետագա զարգացումը ստացավ Յունգի և Ֆրենելի տեսություններում: Յունգն առաջ քաշեց ինտերֆերենցի սկզբունքը, որի օգնությամբ բացատրեց բարակ թաղանթներում գույների ծագումը: Ֆրենելն ընդհանրացրեց Հյուգենսի սկզբունքը` այն լրացնելով Յունգի ինտերֆերենցի սկզբունքով և քննության առավ դիֆրակցիայի երևույթը: Միայն դրանից հետո էր, որ լույսի ալիքային տեսությունը կարելի էր ձևակերպված համարել:
Մաքսվելի տեսական հետազոտությունները (1865թ.) ցույց տվեցին, որ էլեկտրական և մագնիսական դաշտերի փոփոխությունը տեղայնացված չէ տարածության մեջ, այլ տարածվում է լույսի արագությանը հավասար արագությամբ: Այդ տեսական եզրակացությունը ավելի ուշ հաստատվեց Հ.Հերցի և Պ.Լեբեդևի փորձերով: Ըստ Ջ. Մաքսվելի լույսը էլեկտրամագնիսական ալիք է, որը տարածվում է միջավայրում`

արագությամբ,
որտեղ c -ն լույսի
արագությունն
է վակուումում,
![]() լույսի
արագությունն
է միջավայրում,
որի հարաբերական
դիէլեկտրական
թափանցելիությունը
և հարաբերական
մագնիսական թափանցելիությունը
համապատասխանաբար
լույսի
արագությունն
է միջավայրում,
որի հարաբերական
դիէլեկտրական
թափանցելիությունը
և հարաբերական
մագնիսական թափանցելիությունը
համապատասխանաբար
![]() և
և
![]() է:
է:
Ըստ սահմանման, միջավայրի բեկման ցուցիչը`
![]()
Այս
առնչությունը
կապ է հաստատում
նյութի օպտիկական,
էլեկտրական և
մագնիսական հաստատունների
միջև: Բայց այս
առնչությունից
չի երևում, որ n-ը
պետք է կախում
ունենա լուսային
ալիքի ![]() երկարությունից,
իսկ փորձից հայտնի
է, որ գոյություն
ունի լույսի դիսպերսիա,
այսինքն, n-ը փոփոխվում
է լուսային ալիքի
երկարության փոփոխմանը
զուգընթաց`
երկարությունից,
իսկ փորձից հայտնի
է, որ գոյություն
ունի լույսի դիսպերսիա,
այսինքն, n-ը փոփոխվում
է լուսային ալիքի
երկարության փոփոխմանը
զուգընթաց` ![]() Մաքսվելի
տեսությունը, որը
նյութի էլեկտրամագնիսական
հատկությունները
բնութագրելու
համար սահմանափակվում
է միայն մակրոսկոպիկ
պարամետրերով
Մաքսվելի
տեսությունը, որը
նյութի էլեկտրամագնիսական
հատկությունները
բնութագրելու
համար սահմանափակվում
է միայն մակրոսկոպիկ
պարամետրերով
![]() այս
փաստի բացատրությունը
տալ չկարողացավ:
Անհրաժեշտ էր նյութի
և լույսի փոխազդեցության
պրոցեսների ավելի
մանրազնին դիտարկում,
որը հենված լիներ
նյութի կառուցվածքի
մասին խորացված
պատկերացման վրա:
Այն կատարեց Լորենցը`
ստեղծելով դիսպերսիայի
էլեկտրոնային
տեսությունը (1896թ.):
Ատոմների բաղադրության
մեջ մտնող և նրանցում
որոշակի պարբերությամբ
տատանումներ կատարող
էլեկտրոնների
պատկերացումը
հնարավորություն
տվեց բացատրել
թե´ լույսի առաքման
և կլանման երևույթները
նյութերում և թե´
նյութի մեջ լույսի
տարածման առանձնահատկությունները:
Մասնավորապես
հասկանալի դարձավ
նաև լույսի դիսպերսիայի
երևույթը, պարզվեց,
որ
այս
փաստի բացատրությունը
տալ չկարողացավ:
Անհրաժեշտ էր նյութի
և լույսի փոխազդեցության
պրոցեսների ավելի
մանրազնին դիտարկում,
որը հենված լիներ
նյութի կառուցվածքի
մասին խորացված
պատկերացման վրա:
Այն կատարեց Լորենցը`
ստեղծելով դիսպերսիայի
էլեկտրոնային
տեսությունը (1896թ.):
Ատոմների բաղադրության
մեջ մտնող և նրանցում
որոշակի պարբերությամբ
տատանումներ կատարող
էլեկտրոնների
պատկերացումը
հնարավորություն
տվեց բացատրել
թե´ լույսի առաքման
և կլանման երևույթները
նյութերում և թե´
նյութի մեջ լույսի
տարածման առանձնահատկությունները:
Մասնավորապես
հասկանալի դարձավ
նաև լույսի դիսպերսիայի
երևույթը, պարզվեց,
որ ![]() դիէլեկտրական
թափանելիությունը
էլեկտրոնային
տեսակետից կախում
ունի էլեկտրամագնիսական
դաշտի հաճախությունից,
այսինքն`
դիէլեկտրական
թափանելիությունը
էլեկտրոնային
տեսակետից կախում
ունի էլեկտրամագնիսական
դաշտի հաճախությունից,
այսինքն` ![]() ալիքի երկարությունից:
Սակայն շուտով
պարզվեց, որ էլեկտրոնային
տեսությամբ կարող
են մեկնաբանվել
ոչ բոլոր փորձնական
փաստերը:
ալիքի երկարությունից:
Սակայն շուտով
պարզվեց, որ էլեկտրոնային
տեսությամբ կարող
են մեկնաբանվել
ոչ բոլոր փորձնական
փաստերը:
Այս դժվարությունները բացատրվեցին լույսի քվանտային տեսությունով, որը առաջ քաշվեց Պլանկի կողմից 1900թ.: Պլանկի տեսությունը հիմնվում էր բոլոր պրոցեսների, այդ թվում և լույսի առաքման օպտիկական պրոցեսների դիսկրետության գաղափարի վրա, որը հնարավորություն տվեց բացատրել Լորենցի տեսությանը հակասող երեվույթները: Հետագայում լույսի քվանտային տեսությունն իրենց աշխատանքներում զարգացրին Ա.Այնշտայնը, Ն.Բորը, Վ.Հայզենբերգը, Է.Շրյոդինգերը, Պ.Դիրակը և ուրիշները:
Ժամանակակից պատկերացումների հիման վրա լույսն ունի մասնիկաալիքային բնույթ (մասնիկաալիքային երկակի բնույթ). մի կողմից այն օժտված է ալիքային հատկություններով (ինտերֆերենցիայի երեվույթը, դիֆրակցիա, բևեռացում), մյուս կողմից լույսը զրոյական հանգստի զանգվածով և վակուումում լույսի արագությամբ շարժվող մասնիկների` ֆոտոնների հոսք է:
Հետագայում պարզվեց, որ մասնիկաալիքային երկակի բնույթը հատուկ է ոչ միայն լույսին, այլ նաև նյութի փոքրագույն մասնիկներին` էլեկտրոններին, պրոտոններին, նեյտրոններին և այլն:
 Համաձայն երկրաչափական
օպտիկայի հիմնական
օրենքների լույսը
համասեռ միջավայրում
տարածվում է ուղղագիծ:
Ինչպիսին կլինի
լույսի տարածումն
այն միջավայրում,
որի բեկման ցուցիչն
անընդհատ փոփոխվում
է: Անհամասեռ միջավայրում
լուսային ճառագայթները
կորանում են: Անհամասեռ
միջավայրում լույսի
տարածման ճանապարհը
կարելի է գտնել
ֆրանսիացի մաթեմատիկոս
Ֆերմայի`
հայտնագործած
սկզբունքով (1679թ.):
Համաձայն այդ սկզբունքի՝
լույսը մի
կետից մյուսը
տարածվում է այնպիսի
ճանապարհով, որի
համար պահանջվում
է նվազագույն ժամանակ:
Համաձայն Ֆերմայի,
այդ սկզբունքը
ճիշտ է այն
ճառագայթների
համար, որոնք անդրադառնում
կամ բեկվում են
հարթ մակերևույթների
վրա:
Հետագայուն Ֆերմայի
սկզբունքը կատարելագործվել
է այնպես, որ նրանից
կարելի է օգտվել`
անկախ անդրադարձնող
և բեկող մակերևույթների
ձևից: Ֆերմայի
սկզբունքի
մաթեմատիկական
արտահայտությունը
տալու համար օգտվենք
ճանապարհի օպտիկական
երկարություն
հասկացությունից:
Համաձայն երկրաչափական
օպտիկայի հիմնական
օրենքների լույսը
համասեռ միջավայրում
տարածվում է ուղղագիծ:
Ինչպիսին կլինի
լույսի տարածումն
այն միջավայրում,
որի բեկման ցուցիչն
անընդհատ փոփոխվում
է: Անհամասեռ միջավայրում
լուսային ճառագայթները
կորանում են: Անհամասեռ
միջավայրում լույսի
տարածման ճանապարհը
կարելի է գտնել
ֆրանսիացի մաթեմատիկոս
Ֆերմայի`
հայտնագործած
սկզբունքով (1679թ.):
Համաձայն այդ սկզբունքի՝
լույսը մի
կետից մյուսը
տարածվում է այնպիսի
ճանապարհով, որի
համար պահանջվում
է նվազագույն ժամանակ:
Համաձայն Ֆերմայի,
այդ սկզբունքը
ճիշտ է այն
ճառագայթների
համար, որոնք անդրադառնում
կամ բեկվում են
հարթ մակերևույթների
վրա:
Հետագայուն Ֆերմայի
սկզբունքը կատարելագործվել
է այնպես, որ նրանից
կարելի է օգտվել`
անկախ անդրադարձնող
և բեկող մակերևույթների
ձևից: Ֆերմայի
սկզբունքի
մաթեմատիկական
արտահայտությունը
տալու համար օգտվենք
ճանապարհի օպտիկական
երկարություն
հասկացությունից:
Ճանապարհի
օպտիկական երկարություն
է կոչվում լույսի
տարածման համասեռ
միջավայրում
ճառագայթի երկրաչափական
l ճանապարհի և
միջավայրի n բեկման
ցուցչի արտադրյալը`
![]() որտեղ
որտեղ
![]() ճանապարհի
օպտիկական երկարությունն
է: Եթե լույսի տարածման
միջավայրը անհամասեռ
է, ապա ճառագայթի
ճանապարհը պետք
է բաժանել այնպիսի
փոքր տեղամասերի,
որոնցից յուրաքանչյուրի
սահմաններում
բեկման ցուցիչը
կարելի է ընդունել
հաստատուն: Այս
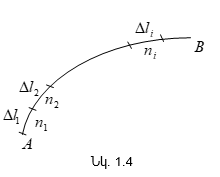
դեպքում (AB) ճանապարհի
օպտիկական երկարությունը
կարելի է ներկայացնել
հետևյալ տեսքով
(նկ.1.4).
ճանապարհի
օպտիկական երկարությունն
է: Եթե լույսի տարածման
միջավայրը անհամասեռ
է, ապա ճառագայթի
ճանապարհը պետք
է բաժանել այնպիսի
փոքր տեղամասերի,
որոնցից յուրաքանչյուրի
սահմաններում
բեկման ցուցիչը
կարելի է ընդունել
հաստատուն: Այս
դեպքում (AB) ճանապարհի
օպտիկական երկարությունը
կարելի է ներկայացնել
հետևյալ տեսքով
(նկ.1.4).
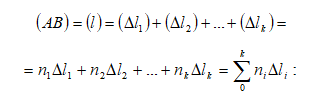
Սահմանում գումարն անցնում է ինտեգրալի.
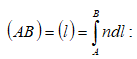
dl հեռավորության վրա լույսի տարածման համար անհրաժեշտ ժամանակը նշանակենք dt-ով: Կունենանք`
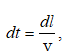
որտեղ
![]() բեկման
ցուցիչ ունեցող
միջավայրում լույսի
տարածման արագությունն
է: A կետից B կետը
լույսի տարածման
համար անհրաժեշտ
ժամանակամիջոցը
կլինի.
բեկման
ցուցիչ ունեցող
միջավայրում լույսի
տարածման արագությունն
է: A կետից B կետը
լույսի տարածման
համար անհրաժեշտ
ժամանակամիջոցը
կլինի.
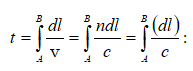
Համաձայն Ֆերմայի նվազագույն ժամանակի սկզբունքի` ինտեգրալի վարիացիան, որով որոշվում է լույսի տարածման ժամանակամիջոցը, պետք է դառնա զրո.
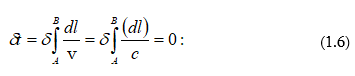
Սա Ֆերմայի սկզբունքի մաթեմատիկական արտահայտությունն է:
(1.6)-ը
ավելի ընդհանուր
արտահայտություն
է, քան Ֆերմայի
սկզբունքը` ձևակերպված
իր սկզբնական տեսքով:
Բանն այն է, որ ![]() պայմանը
միայն նվազագույնի
պայման չէ. դա էքստրեմումի
պայման է, այսինքն`
նվազագույնի, առավելագույնի
կամ ստացիոնարության,
հետևաբար, լույսը
երկու կետերի միջև
տարածվելու դեպքում
կարող է «ընտրել»
ոչ միայն այն ճանապարհը,
որը պահանջում
է անցման նվազագույն
ժամանակ, այլ նաև
այն, որը կպահանջի
առավելագույն
ժամանակ, կամ էլ
այնպիսի ճանապարհներ,
որոնք կպահանջեն
միևնույն ժամանակներ:
Բոլոր վերևը նշված
դեպքերը պարզ կդառնան
հետևյալ օրինակներով:
պայմանը
միայն նվազագույնի
պայման չէ. դա էքստրեմումի
պայման է, այսինքն`
նվազագույնի, առավելագույնի
կամ ստացիոնարության,
հետևաբար, լույսը
երկու կետերի միջև
տարածվելու դեպքում
կարող է «ընտրել»
ոչ միայն այն ճանապարհը,
որը պահանջում
է անցման նվազագույն
ժամանակ, այլ նաև
այն, որը կպահանջի
առավելագույն
ժամանակ, կամ էլ
այնպիսի ճանապարհներ,
որոնք կպահանջեն
միևնույն ժամանակներ:
Բոլոր վերևը նշված
դեպքերը պարզ կդառնան
հետևյալ օրինակներով:
Լույսի ուղղագիծ տարածման օրենքը համասեռ միջավայրում, որպես Ֆերմայի սկզբունքի հետևանք:
Նկատի ունենալով, որ երկու կետերի միջև նվազագույն հեռավորությունն այդ կետերը միացնող ուղիղ գիծն է, համասեռ միջավայրում լույսի ուղղագիծ տարածումը Ֆերմայի սկզբունքի հետևանք է:
Լույսի անդրադարձման և բեկման օրենքները բխում են Ֆերմայի սկզբունքից:
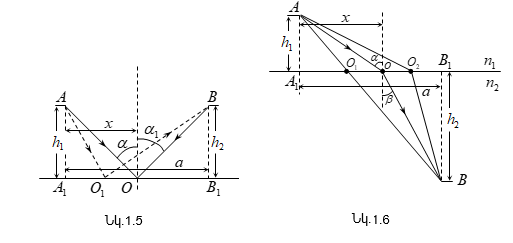 1. Անդրադարձման
օրենքի արտածումը: Լուսային ճառագայթը
A կետից ուղղենք
հայելային մակերևույթի
վրա (նկ.1.5): Հայելուց
անդրադարձած
ճառագայթը հասնում
է B կետը: Ելնելով
Ֆերմայի սկզբունքից՝
որոշենք նվազագույն
ժամանակ պահանջող
A կետից B կետը
լույսի անցած ճանապարհը:
A և B կետերից տանենք
հայելային մակերևույթի
նորմալները: Կատարենք
նշանակումներ.
1. Անդրադարձման
օրենքի արտածումը: Լուսային ճառագայթը
A կետից ուղղենք
հայելային մակերևույթի
վրա (նկ.1.5): Հայելուց
անդրադարձած
ճառագայթը հասնում
է B կետը: Ելնելով
Ֆերմայի սկզբունքից՝
որոշենք նվազագույն
ժամանակ պահանջող
A կետից B կետը
լույսի անցած ճանապարհը:
A և B կետերից տանենք
հայելային մակերևույթի
նորմալները: Կատարենք
նշանակումներ.
![]() A կետից B
կետը լույսի տարածման
համար պահանջվող
ժամանակը, հայելային
մակերևույթից
անդրադառնալու
պայմանով, կլինի.
A կետից B
կետը լույսի տարածման
համար պահանջվող
ժամանակը, հայելային
մակերևույթից
անդրադառնալու
պայմանով, կլինի.
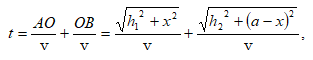
որտեղ
![]() լույսի
տարածման արագությունն
է: Ինչպես տեսնում
ենք, լույսի տարածման
ժամանակը կախված
է O կետի դիրքից,
այսինքն`
լույսի
տարածման արագությունն
է: Ինչպես տեսնում
ենք, լույսի տարածման
ժամանակը կախված
է O կետի դիրքից,
այսինքն`![]() փոփոխականից:
փոփոխականից:
Համաձայն Ֆերմայի սկզբունքի կունենանք`
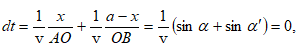
![]() Բացասական
նշանը ցույց է
տալիս, որ
Բացասական
նշանը ցույց է
տալիս, որ ![]() անկյունները
դասավորված են
մակերևույթի նորմալի
տարբեր կողմերում:
Հետևաբար, ինչպես
բխում է Ֆերմայի
սկզբունքից, նվազագույնը
կլինի այն ճանապարհը,
որի դեպքում տեղի
ունի մեզ հայտնի
անդրադարձման
օրենքը:
անկյունները
դասավորված են
մակերևույթի նորմալի
տարբեր կողմերում:
Հետևաբար, ինչպես
բխում է Ֆերմայի
սկզբունքից, նվազագույնը
կլինի այն ճանապարհը,
որի դեպքում տեղի
ունի մեզ հայտնի
անդրադարձման
օրենքը:
2. Բեկման
օրենքի արտածումը: Դիցուք ունենք
![]() բեկման
ցուցիչներով
իրար սահմանակցող
երկու միջավայրեր
(նկ.1.6): Առաջին միջավայրի
A կետից դուրս
եկող ճառագայթը
բաժանման սահմանի
վրա բեկվելուց
հետո տարածվում
է OB ուղղությամբ:
Ելնելով Ֆերմայի
սկզբունքից` ապացուցենք,
որ լույսի ճառագայթը
A կետից B կետը
կտարածվի բեկման
օրենքին համապատասխան`
բեկման
ցուցիչներով
իրար սահմանակցող
երկու միջավայրեր
(նկ.1.6): Առաջին միջավայրի
A կետից դուրս
եկող ճառագայթը
բաժանման սահմանի
վրա բեկվելուց
հետո տարածվում
է OB ուղղությամբ:
Ելնելով Ֆերմայի
սկզբունքից` ապացուցենք,
որ լույսի ճառագայթը
A կետից B կետը
կտարածվի բեկման
օրենքին համապատասխան`
![]()
Ինչպես
նախորդ դեպքում,
նշանակենք. ![]()
![]()
Այն ժամանակը, որը պահանջվում է, որպեսզի լույսը տարածվի A կետից B կետը, հավասար է`
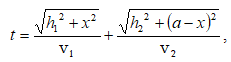
Որտեղ
![]() լույսի
տարածման արագություններն
են` համապատասխանաբար
առաջին և երկրորդ
միջավայրերում:
Լույսի տարածման
ժամանակը կախված
է O կետի դիրքից:
Համաձայն Ֆերմայի
սկզբունքի լույսի
ճառագայթը բոլոր
հնարավոր ճանապարհներից
( AOB, AO1B, AO2B և այլն)
«ընտրում» է այն,
որը պահանջում
է տարածման նվազագույն
ժամանակ, այսինքն`
իրական կլինի այն
ճանապարհը, որի
համար տեղի ունի`dt
= 0: Հետևաբար,
լույսի
տարածման արագություններն
են` համապատասխանաբար
առաջին և երկրորդ
միջավայրերում:
Լույսի տարածման
ժամանակը կախված
է O կետի դիրքից:
Համաձայն Ֆերմայի
սկզբունքի լույսի
ճառագայթը բոլոր
հնարավոր ճանապարհներից
( AOB, AO1B, AO2B և այլն)
«ընտրում» է այն,
որը պահանջում
է տարածման նվազագույն
ժամանակ, այսինքն`
իրական կլինի այն
ճանապարհը, որի
համար տեղի ունի`dt
= 0: Հետևաբար,
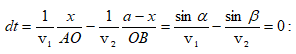
Այսպիսով, հանգում ենք
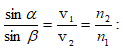
առնչությանը, որն արտահայտում է բեկման օրենքը:
Օրվա տևողության «մեծացումը»: Օրվա «երկարացումը» 7-8 րոպեով նույնպես բացատրվում է Ֆերմայի սկզբունքով: Ինչպես հայտնի է, Երկրի մակերևույթից հեռանալիս տեղի է ունենում մթնոլորտային ճնշման փոքրացում` համաձայն բարոմետրական բանաձևի.
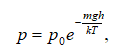
որտեղ
![]() ճնշումն
է Երկրի մակերևույթի
վրա, p-ն` h բարձրության
վրա, k-ն Բոլցմանի
հաստատունն է,
T-ն` բացարձակ ջերմաստիճանը,
m-ը` օդի մոլեկուլի
զանգվածը: Համանման
ձևով տեղի է ունենում
օդի բեկման ցուցչի
նվազում` Երկրի
մակերևույթից
հեռանալուն զուգընթաց:
Ուստի արեգակնային
ճառագայթներն
արևածագի և արևամուտի
դեպքում տարածվում
են ոչ թե ուղիղ
գծերով, այլ մթնոլորտի
խիտ շերտերում
ավելի կտրուկ կոր
ճանապարհներով`
կրճատելով այդ
շերտերում իրենց
ճանապարհը: Քանի
որ առարկան միշտ
երևում է նրանից
դուրս եկող ճառագայթի
ուղղագիծ շարունակության
ուղղությամբ,
ուստի արևածագի
դեպքում մենք դիտում
ենք Արեգակը մի
քանի րոպե շուտ,
իսկ արևամուտի
դեպքում` Արեգակը
մնում է տեսանելի
մի քանի րոպե ավելի
երկար` մինչև մայրամուտ:
Նշված երևույթների
հաշվին օրվա «երկարացումը»
կազմում է 7-8 րոպե:
ճնշումն
է Երկրի մակերևույթի
վրա, p-ն` h բարձրության
վրա, k-ն Բոլցմանի
հաստատունն է,
T-ն` բացարձակ ջերմաստիճանը,
m-ը` օդի մոլեկուլի
զանգվածը: Համանման
ձևով տեղի է ունենում
օդի բեկման ցուցչի
նվազում` Երկրի
մակերևույթից
հեռանալուն զուգընթաց:
Ուստի արեգակնային
ճառագայթներն
արևածագի և արևամուտի
դեպքում տարածվում
են ոչ թե ուղիղ
գծերով, այլ մթնոլորտի
խիտ շերտերում
ավելի կտրուկ կոր
ճանապարհներով`
կրճատելով այդ
շերտերում իրենց
ճանապարհը: Քանի
որ առարկան միշտ
երևում է նրանից
դուրս եկող ճառագայթի
ուղղագիծ շարունակության
ուղղությամբ,
ուստի արևածագի
դեպքում մենք դիտում
ենք Արեգակը մի
քանի րոպե շուտ,
իսկ արևամուտի
դեպքում` Արեգակը
մնում է տեսանելի
մի քանի րոպե ավելի
երկար` մինչև մայրամուտ:
Նշված երևույթների
հաշվին օրվա «երկարացումը»
կազմում է 7-8 րոպե:
Միրաժ: Ամռանը օդի ջերմաստիճանը ծովի մակերևույթի վրա ավելի ցածր է, քան նրա մակերևույթից ավելի հեռու կետերում. այլ բառերով` օդի ջերմաստիճանը ծովի մակերևույթից հեռանալուն զուգընթաց մեծանում է: Օդի տաքացումն առաջ է բերում նրա ընդարձակումը, իսկ ընդարձակումն իր հերթին` բեկման ցուցչի փոքրացման:
 Քանի
որ լույսը տաք
շերտերում ավելի
արագ է անցնում,
քան սառը շերտերում,
դրա հետևանքով
այն տարածվում
է կոր հետագծով
նվազագույն ժամանակում:
Ահա թե ինչու ամռանը
ծովում լողացող
առարկայից, օրինակ`
նավակից եկող լուսային
ճառագայթի ճանապարհը
ծռվում է, որի պատճառով
էլ նավակը թվում
է օդում կախված
(նկ.1.7ա): Այդ նույն
պատճառով էլ ամռանը,
երբ օդի ջերմաստիճանը
Երկրի մակերևույթից
հեռանալուն զուգընթաց,
նվազում է, խճուղու
վրա տեսնում ենք
«ջուր» (իրականում`
կապույտ երկինք),
որն անհետանում
է տվյալ տեղին
մոտենալու դեպքում
(նկ.1.7բ):
Քանի
որ լույսը տաք
շերտերում ավելի
արագ է անցնում,
քան սառը շերտերում,
դրա հետևանքով
այն տարածվում
է կոր հետագծով
նվազագույն ժամանակում:
Ահա թե ինչու ամռանը
ծովում լողացող
առարկայից, օրինակ`
նավակից եկող լուսային
ճառագայթի ճանապարհը
ծռվում է, որի պատճառով
էլ նավակը թվում
է օդում կախված
(նկ.1.7ա): Այդ նույն
պատճառով էլ ամռանը,
երբ օդի ջերմաստիճանը
Երկրի մակերևույթից
հեռանալուն զուգընթաց,
նվազում է, խճուղու
վրա տեսնում ենք
«ջուր» (իրականում`
կապույտ երկինք),
որն անհետանում
է տվյալ տեղին
մոտենալու դեպքում
(նկ.1.7բ):
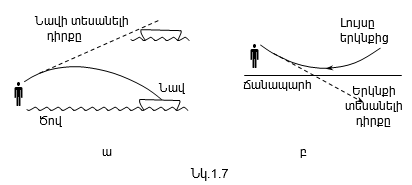
 Ժամանակի
ստացիոնարության
արժեքը: Լույսի կետային
աղբյուրը տեղադրենք
էլիպսաձև հայելու
կիզակետում, օրինակ`
O կետում (նկ.1.8): Լույսը
դուրս գալով այդ
կիզակետով, հայելուց
անդրադառնալուց
հետո անկախ էլիպսի
մակերևույթի M
կետի դիրքից, միշտ
ընկնում է մյուս
O1 կիզակետը:
Դա կապված է այն
բանի հետ, որ էլիպսի
համար նրա մակերևույթի
ցանկացած կետի
հեռավորությունների
գումարը երկու
կիզակետերից մնում
է հաստատուն մեծություն,
այսինքն`
Ժամանակի
ստացիոնարության
արժեքը: Լույսի կետային
աղբյուրը տեղադրենք
էլիպսաձև հայելու
կիզակետում, օրինակ`
O կետում (նկ.1.8): Լույսը
դուրս գալով այդ
կիզակետով, հայելուց
անդրադառնալուց
հետո անկախ էլիպսի
մակերևույթի M
կետի դիրքից, միշտ
ընկնում է մյուս
O1 կիզակետը:
Դա կապված է այն
բանի հետ, որ էլիպսի
համար նրա մակերևույթի
ցանկացած կետի
հեռավորությունների
գումարը երկու
կիզակետերից մնում
է հաստատուն մեծություն,
այսինքն` ![]() Լրիվ ճանապարհների
երկարությունների
հավասարութունը
բերում է ժամանակների
հավասարության,
ինչն էլ ստացիոնարության
պայմանն է:
Լրիվ ճանապարհների
երկարությունների
հավասարութունը
բերում է ժամանակների
հավասարության,
ինչն էլ ստացիոնարության
պայմանն է:
Համանման երևութ նկատվում է նաև այն դեպքում, երբ լույսի զուգահեռ փունջն անդրադառնում է պարաբոլական հայելուց (նկ.1.8): Պարաբոլական հայելու մակերևույթի վրա ընկնող լույսի զուգահեռ ճառագայթներն անդրադառնալուց հետո հավաքվում են միևնույն O կետում, որը կոչվում է կիզակետ: Հեշտ կարելի է ապացուցել, որ այդ դեպքում ճառագայթներն անցնում են միատեսակ ճանապարհներ: Տանենք MN հարթությունը, որն ուղղահայաց է զուգահեռ ճառագայթների ուղղությանը: Մինչև այդ հարթությունը` բոլոր ճառագայթներն անցնում են միատեսակ ճանապարհներ: Համաձայն պարաբոլական մակերևույթի հատկության` պետք է տեղի ունենա հետևյալ պայմանը`
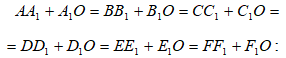
Քանի որ բոլոր ճառագայթները տարածվում են նույն միջավայրում, ուստի լույսը բոլոր ճանապարհներն անցնում է միևնույն ժամանակում: Պարաբոլական հայելու կիզակետող հատկությունը հնարավորություն է տալիս այն օգտագործել աստղերը դիտելու նպատակով: Դրա համար էլ այդ հայելիները լայն կիրառություն ունեն աստղադիտակներում:
Ելնելով վերը շարադրվածից` հանգում ենք այն եզրակացության, որ Ֆերմայի սկզբունքը հնարավորություն է տալիս ստանալ երկրաչափական օպտիկայի հետևյալ օրենքներն ու դրույթները.
· Լույսի ուղղագիծ տարածման օրենքը համասեռ միջավայրում:
· Անդրադարձման և բեկման օրենքներն երկու միջավայրերի բաժանման սահմանի վրա:
· Անհամասեռ միջավայրում լույսի ճանապարհի որոշումը:
Հեշտությամբ կարելի է համոզվել, որ Ֆերմայի սկզբունքից նույնպես բխում է լուսային ճանապարհի դարձելիության (շրջելիության) օրենքը: Իրոք, (1.6) արտահայտության մեջ ինտեգրման սահմանների փոխելը չի խանգարում նրա ճիշտ լինելուն, քանի որ, եթե A-ից մինչև B ինտեգրման դեպքում ինտեգրալի վարիացիան հավասար է զրոյի, ապա այն հավասար է զրոյի նաև B -ից մինչև A ինտեգրման դեպքում:
ԼՈՒՅՍԻ ԻՆՏԵՐՖԵՐԵՆՑԻԱՆ
2.1. Գծային օպտիկայի վերադրման սկզբունքը
Լույսի ինտերֆերենցիան վերաբերում է այն երևույթներին, որոնք էական դեր են խաղացել լույսի բնույթը բացահայտելուն: Հենց այս երևույթը Արագոյին և Ֆրենելին թույլ տվեց ոչ միայն հաստատելու լույսի ալիքային բնույթը, այլ նաև լուսային ալիքների լայնական լինելը:
Լուսային
փնջերի անկախության
օրենքը նշանակում
է, որ լուսային
փնջերն իրար հանդիպելիս,
իրար վրա չեն ազդում:
Այդ դրույթը պարզորեն
ձևակերպված է Հյուգենսի
կողմից: Նա գրել
է. «Լույսի հրաշալի
հատկություններից
մեկն այն է, որ երբ
այն գալիս է տարբեր,
նույնիսկ հակառակ
ուղղություններից,
նրա ճառագայթները
կատարում են իրենց
գործողությունը`
առանց որևէ խոչընդոտի
անցնելով մեկը
մյուսի միջով:
Դրանով է պայմանավորված
այն, որ մի քանի
դիտողներ միաժամանակ
միևնույն անցքից
կարող են տեսնել
տարբեր առարկաներ…»:
Մաթեմատիկորեն
դա նշանակում է,
որ դաշտի ![]() լարվածությունը,
որը ստեղծվում
է տարածության
տվյալ կետում
լույսի երկու աղբյուրներով,
հավասար է
լարվածությունը,
որը ստեղծվում
է տարածության
տվյալ կետում
լույսի երկու աղբյուրներով,
հավասար է ![]() լարվածությունների
վեկտորական գումարին,
որոնք նրանք ստեղծում
են առանձին-առանձին,
այսինքն
լարվածությունների
վեկտորական գումարին,
որոնք նրանք ստեղծում
են առանձին-առանձին,
այսինքն ![]() Սա էլ հենց,
այսպես կոչված,
վերադրման սկզբունքի
բովանդակությունն
է:
Սա էլ հենց,
այսպես կոչված,
վերադրման սկզբունքի
բովանդակությունն
է:
Վերադրման
սկզբունքը հետևանք
է այն բանի, որ լուսային
ալիքները նկարագրվում
են Մաքսվելի գծային
համասեռ և նյութական
գծային հավասարումներով:
Այլ բառերով ասած,
միջավայրի հատկությունները,
որի մեջ տարածվում
է լույսը, կախված
չեն տարածվող լուսային
ալիքի ինտենսիվությունից:
Դա, ինչպես մեզ
այժմ հայտնի է,
տեղի ունի միայն
թույլ դաշտերի
դեպքում: Թույլ
դաշտերի դեպքում
նյութական հավասարումներն
ունեն հետևյալ
տեսքը. ![]() Ուժեղ
դաշտերում այդ
հավասարումները
դառնում են ոչ
գծային, այսինքն`
Ուժեղ
դաշտերում այդ
հավասարումները
դառնում են ոչ
գծային, այսինքն`
![]() արդեն
արդեն
![]() լարվածություններից
կախված գծային
ֆունկցիաներ չեն:
Հետևաբար, վերադրման
սկզբունքը ճիշտ
կլինի միայն թույլ
դաշտերի համար,
այսինքն` վերադրման
սկզբունքը գծային
օպտիկայի սկզբունք
է: Լազերային
ճառագայթման
հզոր փնջի տարածումն
ուղեկցվում է միջավայրում
տարբեր
երևույթներով.
տեղի է ունենում
Էլեկտրաստրիկցիա,
առաջացած
ուժեղ
լուսային դաշտի
ազդեցությամբ
առաջանում է ոչ
գծային էլեկտրոնային
բևեռացում, տեղի
է ունենում միջավայրի
տաքացում` լուսային
ալիքի էներգիայի
ցրման հաշվին,
տեղի է ունենում
դաշտում մոլեկուլների
«դասավորություն»
(հեղուկ միջավայրերում)
և այլն: Բոլոր այդ
երևույթները փոփոխում
են միջավայրի հատկությունները:
Մասնավորապես,
Էլեկտրաստրիկցիան
ուժեղ լուսային
դաշտում առաջ է
բերում լուսային
դաշտի լարվածության
քառակուսուն համեմատական
ճնշման առաջացում,
իսկ սա իր հերթին
փոխում է միջավայրի
խտությունը և
առաջացնում բեկման
ցուցչի համապատասխան
փոփոխություններ:
Դաշտի ուղղությամբ
մոլեկուլների
«դասավորության»
արդյունքում
միջավայրը դառնում
է անհամասեռ, իսկ
նրա միջին բեկման
ցուցիչը կողմնորոշված
դաշտի համար աճում
է: Միջավայրի հատկությունների
համանման բոլոր
փոփոխություններն
առաջ են բերում
բեկման ցուցչի
և կլանման գործակցի
կախվածություն
լույսի ինտենսիվությունից:
Հետեվաբար, լույսի
հզոր փունջը տարածվելով
միջավայրում`
փոփոխում է նրա
հատկությունները,
ստեղծելով նախորդից
տարբեր պայմաններ
իր տարածման համար:
Lույսի այդպիսի
ազդեցությունն
իր վրա` միջավայրի
շնորհիվ, ընդունված
է անվանել ինքնազդեցության
երևույթ: Ինքնազդեցության
պրոցեսը առաջ է
բերում լույսի
ինտենսիվության
փոփոխություն,
բևեռացում և այլն:
Ակներև է, որ այդ
պայմաններում
երկու հզոր ալիքներ,
տարածվելով ոչ
գծային միջավայրում,
հնարավոր չէ, որ
իրար հետ չփոխազդեն:
Այսպիսով, վերադրման
սկզբունքն ուժեղ
լուսային դաշտերում,
որոնք տարածվում
են միջավայրում,
արդեն տեղի ունենալ
չի կարող:
լարվածություններից
կախված գծային
ֆունկցիաներ չեն:
Հետևաբար, վերադրման
սկզբունքը ճիշտ
կլինի միայն թույլ
դաշտերի համար,
այսինքն` վերադրման
սկզբունքը գծային
օպտիկայի սկզբունք
է: Լազերային
ճառագայթման
հզոր փնջի տարածումն
ուղեկցվում է միջավայրում
տարբեր
երևույթներով.
տեղի է ունենում
Էլեկտրաստրիկցիա,
առաջացած
ուժեղ
լուսային դաշտի
ազդեցությամբ
առաջանում է ոչ
գծային էլեկտրոնային
բևեռացում, տեղի
է ունենում միջավայրի
տաքացում` լուսային
ալիքի էներգիայի
ցրման հաշվին,
տեղի է ունենում
դաշտում մոլեկուլների
«դասավորություն»
(հեղուկ միջավայրերում)
և այլն: Բոլոր այդ
երևույթները փոփոխում
են միջավայրի հատկությունները:
Մասնավորապես,
Էլեկտրաստրիկցիան
ուժեղ լուսային
դաշտում առաջ է
բերում լուսային
դաշտի լարվածության
քառակուսուն համեմատական
ճնշման առաջացում,
իսկ սա իր հերթին
փոխում է միջավայրի
խտությունը և
առաջացնում բեկման
ցուցչի համապատասխան
փոփոխություններ:
Դաշտի ուղղությամբ
մոլեկուլների
«դասավորության»
արդյունքում
միջավայրը դառնում
է անհամասեռ, իսկ
նրա միջին բեկման
ցուցիչը կողմնորոշված
դաշտի համար աճում
է: Միջավայրի հատկությունների
համանման բոլոր
փոփոխություններն
առաջ են բերում
բեկման ցուցչի
և կլանման գործակցի
կախվածություն
լույսի ինտենսիվությունից:
Հետեվաբար, լույսի
հզոր փունջը տարածվելով
միջավայրում`
փոփոխում է նրա
հատկությունները,
ստեղծելով նախորդից
տարբեր պայմաններ
իր տարածման համար:
Lույսի այդպիսի
ազդեցությունն
իր վրա` միջավայրի
շնորհիվ, ընդունված
է անվանել ինքնազդեցության
երևույթ: Ինքնազդեցության
պրոցեսը առաջ է
բերում լույսի
ինտենսիվության
փոփոխություն,
բևեռացում և այլն:
Ակներև է, որ այդ
պայմաններում
երկու հզոր ալիքներ,
տարածվելով ոչ
գծային միջավայրում,
հնարավոր չէ, որ
իրար հետ չփոխազդեն:
Այսպիսով, վերադրման
սկզբունքն ուժեղ
լուսային դաշտերում,
որոնք տարածվում
են միջավայրում,
արդեն տեղի ունենալ
չի կարող:
2.2. Լույսի էլեկտրամագնիսական բնույթը: Լուսային ալիք
Այժմ
լույս ասելով`
հասկանում են էլեկտրամագնիսական
ճառագայթումը,
որն ընկալվում
է մարդու աչքի
կողմից: Ընկալվող
էլեկտրամագնիսական
ճառագայթման ալիքի
երկարություններն
ընկած են 0,38 մկմ-ից
մինչև 0.76 մկմ միջակայքում:
Ֆիզիկայում հաճախ
լույս են անվանում
նաև անտեսանելի
էլեկտրամագնիսական
ալիքները, որոնք
ընկած են 0,01 մկմ-ից
մինչև 340 մկմ (վերևում
նշված միջակայքի
սահմաններից դուրս):
Դա կապված է այն
բանի հետ, որ այդ
էլեկտրամագնիսական
ալիքների ֆիզիկական
հատկությունները
մոտ են լուսային
ալիքների հատկություններին:
Մաքսվելը տվեց
հավասարումներ,
որոնք կապ են հաստատում
տարածության յուրաքանչյուր
կետում ժամանակի
ցակացած պահին
էլեկտրական դաշտի
![]() լարվածության
և մագնիսական դաշտի
լարվածության
և մագնիսական դաշտի
![]() ինդուկցիայի,
էլեկտրական հոսանքների
ինդուկցիայի,
էլեկտրական հոսանքների
![]() խտությունների
և լիցքերի միջև:
Մաքսվելի տեսությունից
բխում է, որ էլեկտրական
և մագնիսական դաշտերի
փոփոխությունները
փոխկապակցված
են: Այդ տեսության
հիմքում ձևակերպվեց
ֆիզիկայում կարևոր
հասկացություններից
մեկը` էլեկտրամագնիսական
դաշտ հասկացությունը:
Մաքսվելի հավասարումների
մեջ մտնում է արագությունը,
որով պետք է տարածվեն
տարածության մեջ
փոփոխվող էլեկտրական
և մագնիսական դաշտերը,
այսինքն` էլեկտրամագնիսական
ալիքը: Այդ արագությունը
հավասար է լույսի
արագությանը: Իր
տեսական հետազոտությունների
հիման վրա Մաքսվելը
եզրակացրեց. «լույսն
ունի էլեկտրամագնիսական
բնույթ»: Լույսի
էլեկտրամագնիսական
տեսության փորձարարական
հաստատումը կատարվեց
Հերցի փորձերով,
որոնք ցույց տվեցին,
որ էլեկտրամագնիսական,
ինչպես և լուսային
ալիքները երկու
միջավայրերի բաժանման
սահմանի վրա ենթարկվում
են անդրադարձման
և բեկման: Դրա հետ
մեկտեղ հաստատվեց,
որ լուսային և
էլեկտրամագնիսական
ալիքների տարածման
արագությունները
նույնն են: Հարթ
էլեկտրամագնիսական
ալիքը, որը տարածվում
է, օրինակ,
խտությունների
և լիցքերի միջև:
Մաքսվելի տեսությունից
բխում է, որ էլեկտրական
և մագնիսական դաշտերի
փոփոխությունները
փոխկապակցված
են: Այդ տեսության
հիմքում ձևակերպվեց
ֆիզիկայում կարևոր
հասկացություններից
մեկը` էլեկտրամագնիսական
դաշտ հասկացությունը:
Մաքսվելի հավասարումների
մեջ մտնում է արագությունը,
որով պետք է տարածվեն
տարածության մեջ
փոփոխվող էլեկտրական
և մագնիսական դաշտերը,
այսինքն` էլեկտրամագնիսական
ալիքը: Այդ արագությունը
հավասար է լույսի
արագությանը: Իր
տեսական հետազոտությունների
հիման վրա Մաքսվելը
եզրակացրեց. «լույսն
ունի էլեկտրամագնիսական
բնույթ»: Լույսի
էլեկտրամագնիսական
տեսության փորձարարական
հաստատումը կատարվեց
Հերցի փորձերով,
որոնք ցույց տվեցին,
որ էլեկտրամագնիսական,
ինչպես և լուսային
ալիքները երկու
միջավայրերի բաժանման
սահմանի վրա ենթարկվում
են անդրադարձման
և բեկման: Դրա հետ
մեկտեղ հաստատվեց,
որ լուսային և
էլեկտրամագնիսական
ալիքների տարածման
արագությունները
նույնն են: Հարթ
էլեկտրամագնիսական
ալիքը, որը տարածվում
է, օրինակ, ![]() առանցքի
ուղղությամբ, նկարագրվում
է հետևյալ հավասարումներով`
առանցքի
ուղղությամբ, նկարագրվում
է հետևյալ հավասարումներով`
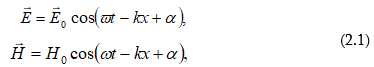
 որտեղ
որտեղ
![]() վեկտորների
լայնույթային
արժեքներն են,
k-ն ալիքային վեկտորի
մոդուլն է,
վեկտորների
լայնույթային
արժեքներն են,
k-ն ալիքային վեկտորի
մոդուլն է, ![]() սկզբնական
փուլն է: Էլեկտրամագնիսական
ալիքում տատանվում
են երկու վեկտորներ`
էլեկտրական դաշտի
և մագնիսական դաշտի
լարվածությունների
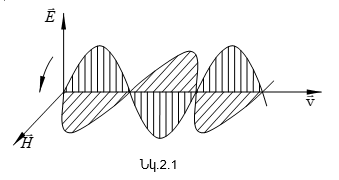
վեկտորները (նկ.2.1):
Փորձերը ցույց
են տվել, որ լույսի
ֆիզոլոգիական,
ֆոտոքիմիական,
ֆոտոէլեկտրական
և այլ ազդեցություններն
առաջանում են
էլեկտրական վեկտորի
տատանումներով:
Դրան համապատասխան
հետագայում խոսելու
ենք լուսային վեկտորի
(էլեկտրական դաշտի
լաածության վեկտոր)
մասին: Լուսային
ալիքի մագնիսական
վեկտորին համարյա
չենք անդրադառնալու:
սկզբնական
փուլն է: Էլեկտրամագնիսական
ալիքում տատանվում
են երկու վեկտորներ`
էլեկտրական դաշտի
և մագնիսական դաշտի
լարվածությունների
վեկտորները (նկ.2.1):
Փորձերը ցույց
են տվել, որ լույսի
ֆիզոլոգիական,
ֆոտոքիմիական,
ֆոտոէլեկտրական
և այլ ազդեցություններն
առաջանում են
էլեկտրական վեկտորի
տատանումներով:
Դրան համապատասխան
հետագայում խոսելու
ենք լուսային վեկտորի
(էլեկտրական դաշտի
լաածության վեկտոր)
մասին: Լուսային
ալիքի մագնիսական
վեկտորին համարյա
չենք անդրադառնալու:
Եթե
լուսային ալիքի
երկարությունը
վակուումում ![]() է, ապա n բեկման
ցուցիչ ունեցող
միջավայրում ալիքների
երկարությունները
կլինեն այլ:
է, ապա n բեկման
ցուցիչ ունեցող
միջավայրում ալիքների
երկարությունները
կլինեն այլ: ![]() հաճախության
տատանումների
դեպքում ալիքի
երկարությունը
վակուումում կլինի
հաճախության
տատանումների
դեպքում ալիքի
երկարությունը
վակուումում կլինի
![]() Եթե
միջավայրում լուսային
ալիքի փուլային
արագությունը`
Եթե
միջավայրում լուսային
ալիքի փուլային
արագությունը`
![]() է,
ալիքի երկարությունը
կունենա
է,
ալիքի երկարությունը
կունենա ![]() արժեքը:
Այսպիսով, n բեկման
ցուցիչ ունեցող
միջավայրում
լուսային ալիքի
երկարությունը
կապված է վակուումում
ալիքի երկարության
հետ հետևյալ առնչությամբ`
արժեքը:
Այսպիսով, n բեկման
ցուցիչ ունեցող
միջավայրում
լուսային ալիքի
երկարությունը
կապված է վակուումում
ալիքի երկարության
հետ հետևյալ առնչությամբ`
![]()
Էլեկտրամագնիսական ալիքի տարածումը կապված է էներգիայի տեղափոխության հետ: Էլեկտրամագնիսական ալիքով տեղափոխվող էներգիան որոշելու համար, պետք է գործ ունենանք էներգիայի ծավալային խտության հետ: Էլեկտրամագնիսական դաշտի էներգիայի ծավալային խտությունը (միավոր ծավալին ընկնող էներգիայի քանակը) հավասար է էլեկտրական դաշտի էներգիայի ծավալային խտության և մագնիսական դաշտի էներգիայի ծավալային խտության գումարին.
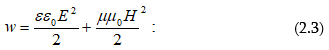
Եթե
նկատի ունենանք,
որ տարածության
տվյալ կետում
![]() վեկտորները
փոփոխվում են միևնույն
փուլով, կարող
ենք օգտվել հետևյալ
առնչությունից`
վեկտորները
փոփոխվում են միևնույն
փուլով, կարող
ենք օգտվել հետևյալ
առնչությունից`
![]()
Նկատի
ունենալով (2.4)-ը` ըստ
(2.3)-ի էլեկտրական
և մագնիսական
դաշտերի էներգիաների
ծավալային խտությունը
ժամանակի յուրաքանչյուր
պահին նույնն է`
![]() Ուստի
կարելի է գրել`
Ուստի
կարելի է գրել`
![]() Օգտվելով
(2.4)-ից` էլեկտրամագնիսական
ալիքի էներգիայի
խտության արտահայտությանը
կարելի է տալ հետևյալ
տեսքը`
Օգտվելով
(2.4)-ից` էլեկտրամագնիսական
ալիքի էներգիայի
խտության արտահայտությանը
կարելի է տալ հետևյալ
տեսքը`
![]()
Էլեկտրամագնիսական ալիքի արագությունը որոշվում է հետևյալ բանաձևով`

Բազմապատկելով
էներգիայի ![]() խտությունը
խտությունը
![]() արագությամբ,
կստանանք էներգիայի
հոսքի խտությունը`
արագությամբ,
կստանանք էներգիայի
հոսքի խտությունը`
![]()
![]() վեկտորները
փոխադարձաբար
ուղղահայաց են
և ալիքի տարածման
ուղղության հետ
կազմում են աջ-պտուտակային
համակարգ: Այդ
պատճառով
վեկտորները
փոխադարձաբար
ուղղահայաց են
և ալիքի տարածման
ուղղության հետ
կազմում են աջ-պտուտակային
համակարգ: Այդ
պատճառով ![]() վեկտորի
ուղղությունը
համընկնում է
էներգիայի տեղափոխման
ուղղության հետ,
իսկ այդ վեկտորի
մոդուլը հավասար
է EH-ի
վեկտորի
ուղղությունը
համընկնում է
էներգիայի տեղափոխման
ուղղության հետ,
իսկ այդ վեկտորի
մոդուլը հավասար
է EH-ի ![]() Հետևաբար
էներգիայի հոսքի
խտության վեկտորը
կարելի է ներկայացնել
որպես
Հետևաբար
էներգիայի հոսքի
խտության վեկտորը
կարելի է ներկայացնել
որպես ![]() վեկտորների
վեկտորական արտադրյալ.
վեկտորների
վեկտորական արտադրյալ.
![]()
![]() վեկտորը
կոչվում է Պոյնտինգի
վեկտոր: Էլեկտրամագնիսական
ալիքի ինտենսիվություն
է կոչվում այն
մեծությունը, որը
հավասար է միավոր
ժամանակամիջոցում
ալիքի տարածման
ուղղությանն ուղղահայաց
մակերևույթի միավոր
մակերեսով անցած
միջին էներգիային:
Էլեկտրամագնիսական
ալիքի ինտենսիվությունը
հավասար է Պոյնտինգի
վեկտորի մոդուլի
միջին արժեքին
մեկ լրիվ տատանման
T պարբերությանը
հավասար ժամանակամիջոցի
ընթացքում.
վեկտորը
կոչվում է Պոյնտինգի
վեկտոր: Էլեկտրամագնիսական
ալիքի ինտենսիվություն
է կոչվում այն
մեծությունը, որը
հավասար է միավոր
ժամանակամիջոցում
ալիքի տարածման
ուղղությանն ուղղահայաց
մակերևույթի միավոր
մակերեսով անցած
միջին էներգիային:
Էլեկտրամագնիսական
ալիքի ինտենսիվությունը
հավասար է Պոյնտինգի
վեկտորի մոդուլի
միջին արժեքին
մեկ լրիվ տատանման
T պարբերությանը
հավասար ժամանակամիջոցի
ընթացքում.
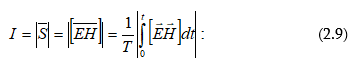
Այս
դեպքում, ենթադրվում
է, որ T << 1 վ, այսինքն`
էլեկտրամագնիսական
ալիքի հաճախությունը`
![]() Հարթ
մեներանգ ալիքի
համար (2.9)-ից և (2.1)-ից
հետևում է, որ
Հարթ
մեներանգ ալիքի
համար (2.9)-ից և (2.1)-ից
հետևում է, որ
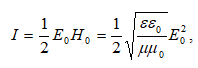
քանի
որ ![]() միջին
արժեքը
միջին
արժեքը ![]() ժամանակի
ընթացքում 1/2 է:
ժամանակի
ընթացքում 1/2 է:
2.3 էլեկտրամագնիսական ալիքների տարածումը
Փուլային և խմբային արագություններ
Վերևը ծանոթացանք էլեկտրամագնիսական ալիքների որոշ հատկություններին: Այժմ ավելի մանրամասն դիտարկենք էլեկտրամագնիսական ալիքների տարածումը և ծանոթանանք փուլային և խմբային արագությունների հասկացություններին:
Դիտարկենք հարթ մեներանգ լուսային ալիքը, որը տարածվում է համասեռ միջավայրում x-երի առանցքի դրական ուղղությամբ.
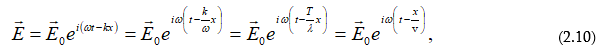
Որտեղ
![]() : Կարելի
է ապացուցել, որ
v-ն հավասար փուլերի
մակերևույթի (ալիքային
մակերևույթի)
տեղափոխման արագությունն
է: Իրոք, հավասար
փուլերի մակերևույթի
հավասարումն ունի
հետևյալ տեսքը.
: Կարելի
է ապացուցել, որ
v-ն հավասար փուլերի
մակերևույթի (ալիքային
մակերևույթի)
տեղափոխման արագությունն
է: Իրոք, հավասար
փուլերի մակերևույթի
հավասարումն ունի
հետևյալ տեսքը.

Դիֆերենցելով այդ արտահայտությունն ըստ t ժամանակի` կգտնենք ալիքային մակերևույթի տեղափոխման արագությունը x -երի առանցքի երկայնքով, որը կոչվում է փուլային արագություն.
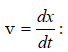
Օգտագործելով
փուլի արտահայտությունը`
k ալիքային թվի
միջոցով կարելի
է ստանալ բանաձև
փուլային արագությունը
որոշելու համար:
Դիֆերենցելով
![]() արտահայտությունն
ըստ t ժամանակի`
կստանանք.
արտահայտությունն
ըստ t ժամանակի`
կստանանք.

 Հետևաբար,
մեներանգ ալիքը
կարելի է բնութագրել
միայն փուլային
արագությամբ:
Հետևաբար,
մեներանգ ալիքը
կարելի է բնութագրել
միայն փուլային
արագությամբ:
Խմբային
արագություն: Կարելի էր սահմանափակվել
միայն փուլային
արագությունով,
եթե մեներանգ
ալիքներ իրականում
գոյություն ունենային:
Սակայն առանձին
ատոմներն իրականում
ճառագայթում են
ոչ անվերջ ըստ
ժամանակի մեներանգ
ալիքներ, այլ իրենց
տեսակի լուսային
իմպուլսներ: Նման
«լուսային իմպուլսը»
կարող է մոդուլացվել
![]() տևողության
մեներանգ ալիքի
տեսքով, ինչպես
ցույց է տրված
նկ.2.2-ում: Լուսային
ալիքի ոչ մեներանգությունը
հիմնականում
պայմանավորված
է մեներանգ ալիքի
ընդհատումով:
տևողության
մեներանգ ալիքի
տեսքով, ինչպես
ցույց է տրված
նկ.2.2-ում: Լուսային
ալիքի ոչ մեներանգությունը
հիմնականում
պայմանավորված
է մեներանգ ալիքի
ընդհատումով:
Վերջավոր
իմպուլսները կարելի
է ներկայացնել
տարբեր լայնույթներով,
հաճախություններով
և փուլերով ներդաշնակ
տատանումների
համախմբի տեսքով:
Դիցուք ![]() այն միջակայքն
է, որի սահմաններում
ընկած են հիշատակված
հաճախությունները:
այն միջակայքն
է, որի սահմաններում
ընկած են հիշատակված
հաճախությունները:
![]() միջակայքի
լայնությունը
կախված է իմպուլսի
տևողությունից:
Կարելի է ապացուցել,
որ հաճախությունների
միջակայքը հակադարձ
համեմատական է
իմպուլսի տևողությանը,
այսինքն`
միջակայքի
լայնությունը
կախված է իմպուլսի
տևողությունից:
Կարելի է ապացուցել,
որ հաճախությունների
միջակայքը հակադարձ
համեմատական է
իմպուլսի տևողությանը,
այսինքն` ![]()
Իմպուլսի ձևը որոշվում է իր ներդաշնակ բաղադրիչների հաճախություններով, լայնույթներով և փուլերով: Եթե այդ բոլոր բաղադրիչների արագությունները միատեսակ են, ապա նրանց փուլային հարաբերակցությունը տարածման դեպքում չի փոփոխվում, և հետևաբար իմպուլսի ձևը նույնպես մնում է անփոփոխ: Այս դեպքում իմպուլսի տեղափոխման արագությունը համընկնում իր ներդաշնակ բաղադրիչի արագության հետ: Այն միջավայրը, որում ներդաշնակ ալիքի փուլային արագությունը կախված չէ հաճախությունից, կոչվում է չդիսպերսող: Եթե ներդաշնակ ալիքների արագությունները կախված են հաճախություններից, նրանց միջև փուլային հարաբերակցությունները փոփոխվում են դրանց տարածմանը զուգընթաց, որը բերում է իմպուլսի ձևի փոփոխության: Այստեղից հետևում է, որ իմպուլսի տեղափոխման արագությունը և նրա ներդաշնակ բաղադրիչների փուլային արագությունը չեն համընկնում: Այս դեպքում իմպուլսի տարածումը բնութագրվում է, այսպես կոչված, խմբային արագության օգնությամբ: Այն միջավայրը, ուր փուլային արագությունը կախված է հաճախությունից, կոչվում է դիսպերսող: Ներմուծենք խմբային արագությունը պարզագույն խմբի դեպքի համար, որը բաղկացած է միատեսակ լայնույթներով, աննշան տարբերվող հաճախությունով և x -երի առանցքի երկայնքով տարածվող երկու ներդաշնակ բաղադրիչներից:
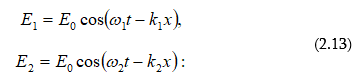
Արդյունարար ալիքը կունենա հետևյալ տեսքը`
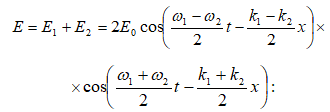
Ըստ
պայմանի` ![]() Նկատի ունենալով
վերջինը` կստանանք.
Նկատի ունենալով
վերջինը` կստանանք.
![]()
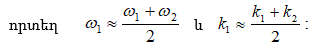
Ստացված
(2.14)-ը բարդ ալիքի
համար կարելի
է մոտավորապես
ընդունել ![]() հաճախությունով,
k1 ալիքային թվով
և դանդաղ փոփոխվող
(մոդուլացված)
հաճախությունով,
k1 ալիքային թվով
և դանդաղ փոփոխվող
(մոդուլացված)
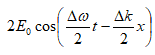
լայնույթով
մեներանգ ալիքի
հավասարում: Եթե
ըստ լայնույթի
մոդուլացված այդպիսի
իմպուլսն ընդունվում
է սպեկտրային սարքով,
ապա այն գրանցում
է երկու հաճախություններ`
![]() Մոդուլացված
լայնույթը բնութագրում
է ալիքների խումբ:
Ուստի իմպուլսի
տարածումը կարելի
է բնութագրել մոդուլացված
լայնույթի որոշակի
արժեքի տարածման
արագությամբ: Այդ
արագությունն
անվանում են ալիքների
խմբային արագություն:
Քանի որ փորձում
հարմար է գրանցել
առավելագույն
լայնույթը, ուստի
խմբային արագության
տակ հասկանում
են ալիքի լայնույթի
տեղափոխման արագությունը:
Հետևաբար, խմբային
արագությունը
որոշվում է հետևյալ
պայմանից`
Մոդուլացված
լայնույթը բնութագրում
է ալիքների խումբ:
Ուստի իմպուլսի
տարածումը կարելի
է բնութագրել մոդուլացված
լայնույթի որոշակի
արժեքի տարածման
արագությամբ: Այդ
արագությունն
անվանում են ալիքների
խմբային արագություն:
Քանի որ փորձում
հարմար է գրանցել
առավելագույն
լայնույթը, ուստի
խմբային արագության
տակ հասկանում
են ալիքի լայնույթի
տեղափոխման արագությունը:
Հետևաբար, խմբային
արագությունը
որոշվում է հետևյալ
պայմանից`
![]()
որտեղ m-ը ցանկացած ամբողջ թիվ է : (2.15)-ը դիֆերենցելով ըստ t-ի` կստանանք.
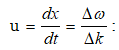
Սահմանում կարելի է անցնել դիֆերենցիալի.

Ելնելով (2.16)-ից և (2.12)-ից` կարելի է գտնել փուլային և խմբային արագությունների միջև եղած կապը.
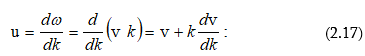
Քանի
որ ![]() և
այստեղից
և
այստեղից ![]() ապա (2.17)-ից
կունենանք`
ապա (2.17)-ից
կունենանք`
![]()
Ստացված արտահայտությունը կոչվում է Ռելեի բանաձև: Նրա կողմից է առաջինը ներմուծվել խմբային արագության հասկացությունը:
2.4. Տատանումների
գումարումը:
Լուսային ալիքների
ինտերֆերենցիան:
Կոհերենտություն
Դիցուք տարածության որևէ կետում հանդիպում են միևնույն հաճախության, տարբեր սկզբնական փուլերով և տարբեր լայնույթներով երկու տատանումներ: Պարզության համար ընդունում ենք, որ երկու տատանումներն էլ տեղի են ունենում միևնույն ուղղի երկայնքով: Հետևաբար կունենանք`
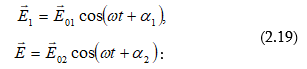
Ժամանակի
հաշվարկման սկիզբը
կարելի է ընտրել
այնպես, որ տատանումներից
մեկի սկզբնական
փուլը հավասար
լինի զրոյի: Այս
դեպքում մյուս
տատանման սկզբնական
փուլը հավասար
կլինի վերադրվող
տատանումների
սկզբնական փուլերի
տարբերությանը:
Սակայն, որպեսզի
չխանգարվի քննարկման
ընդհանրությունը,
ընդունենք, որ
ինչպես ![]() -ը,
այնպես էլ
-ը,
այնպես էլ ![]() -ը զրոյից
տարբեր են: Որոշակիության
համար ընդունենք,
որ
-ը զրոյից
տարբեր են: Որոշակիության
համար ընդունենք,
որ ![]() Գումարման
արդյունքում կստանանք`
Գումարման
արդյունքում կստանանք`
![]()
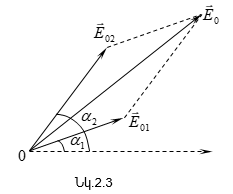
Հետևաբար, միևնույն հաճախության երկու ներդաշնակ տատանումների գումարման դեպքում, որոնք տեղի են ունենում միևնույն ուղղի երկայնքով, առաջանում է նույն հաճախության արդյունարար ներդաշնակ տատանում նույն ուղղի երկայնքով, որի լայնույթը և սկզբնական փուլը որոշվում են վեկտորային դիագրամից (նկ.2.3).
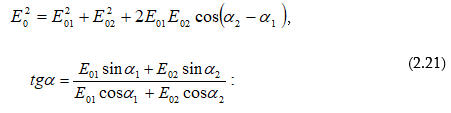
Քանի որ ինտենսիվությունն ուղիղ համեմատական է լայնույթի քառակուսուն, (2.21) հավասարումների համակարգի առաջին հավասարումից ինտենսիվության համար կստանանք`
![]()
որտեղ I1 -ը և I2 -ը գումարվող տատանումների ինտենսիվություններն են, իսկ I-ն` արդյունարար ինտենսիվությունը:
 Էլեկտրամագնիսական
ալիքների ճառագայթումը
կապված է ատոմների
տատանումների
հետ, որոնք ներդաշնակ
չեն, յուրաքանչյուր
տատանման ակտ տեղի
է ունենում 10-8վ
կարգի ժամանակի
ընթացքում: Միևնույն
ատոմի տատանման
տարբեր ակտերը,
ինչպես նաև տարբեր
ատոմների միաժամանակյա
տատանումները
տեղի են ունենում
մեկը մյուսից անկախ,
այսինքն համապատասխան
տատանումները
կապված չեն ըստ
փուլի և օժտված
են տարբեր սկզբնական
փուլերով: Հետևաբար,
տվյալ դեպքում
(2.22) վերադրման արդյունքը
պետք է կախված
լինի ժամանակից:
Ինտենսիվության
փոփոխության մեծ
հաճախության պատճառով
ոչ վիզուալ, և ոչ
էլ օպտիկական սարքերի
օգնությամբ հնարավոր
չէ հետևել այդպիսի
արագ փոփոխությունների:
Ուստի անհրաժեշտ
է (2.22)-ը միջինացնել
ըստ դիտման ժամանակամիջոցի,
այսինքն`
Էլեկտրամագնիսական
ալիքների ճառագայթումը
կապված է ատոմների
տատանումների
հետ, որոնք ներդաշնակ
չեն, յուրաքանչյուր
տատանման ակտ տեղի
է ունենում 10-8վ
կարգի ժամանակի
ընթացքում: Միևնույն
ատոմի տատանման
տարբեր ակտերը,
ինչպես նաև տարբեր
ատոմների միաժամանակյա
տատանումները
տեղի են ունենում
մեկը մյուսից անկախ,
այսինքն համապատասխան
տատանումները
կապված չեն ըստ
փուլի և օժտված
են տարբեր սկզբնական
փուլերով: Հետևաբար,
տվյալ դեպքում
(2.22) վերադրման արդյունքը
պետք է կախված
լինի ժամանակից:
Ինտենսիվության
փոփոխության մեծ
հաճախության պատճառով
ոչ վիզուալ, և ոչ
էլ օպտիկական սարքերի
օգնությամբ հնարավոր
չէ հետևել այդպիսի
արագ փոփոխությունների:
Ուստի անհրաժեշտ
է (2.22)-ը միջինացնել
ըստ դիտման ժամանակամիջոցի,
այսինքն`
![]()
Վերևի գիծը նշանակում է համապատասխան մեծությունների միջինացում ըստ ժամանակի:
Ընդունելով,
որ E01-ը և E02 -ը
կախված չեն ժամանակից,
կունենանք ![]() և
և ![]() Հետևաբար`
Հետևաբար`
![]()
Որպեսզի որոշվի ինտենսիվության միջին արժեքը, բավական է տվյալ դեպքում գտնել փուլերի տարբերության կոսինուսի միջին արժեքը.
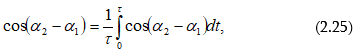
որտեղ
![]() դիտման
ժամանակն է: Ինչպես
հետևում է (2.24)-ից
և (2.25)-ից, ինտենսիվության
միջին արժեքը կախված
է վերադրվող տատանումների
փուլերի տարբերությունից:
Դիտարկենք երկու
մասնավոր դեպքեր
:
դիտման
ժամանակն է: Ինչպես
հետևում է (2.24)-ից
և (2.25)-ից, ինտենսիվության
միջին արժեքը կախված
է վերադրվող տատանումների
փուլերի տարբերությունից:
Դիտարկենք երկու
մասնավոր դեպքեր
:
1.
Ենթադրենք
![]() Համաձայն
(2.25)-ի կունենանք`
Համաձայն
(2.25)-ի կունենանք`
հետևաբար,
![]()
այսինքն`
![]()
(2.26) արտահայտությունը նշանակում է, որ վերադրվող տատանումների հաստատուն փուլերի տարբերության դեպքում արդյունարար ինտենսիվությունը կլինի տարբեր (մեծ կամ փոքր կախված որոշակի փուլերի տարբերության արժեքից) առանձին տատանանումների ինտենսիվությունների գումարից:
Եթե ալիքների գրգռված տատանումների փուլերի տարբերությունը ժամանակի ընթացքում մնում է հաստատուն, ալիքները կոչվում են կոհերենտ: Այդպիսի աղբյուրները նույնպես կոչվում են կոհերենտ:
Այսպիսով,
կոհերենտ լուսային
ալիքների վերադրման
ժամանակ տեղի է
ունենում լուսային
հոսքի վերաբաշխում
տարածության մեջ,
որի հետևանքով
որոշ տեղերում
առաջանում են ինտենսիվության
առավելագույններ,
այլ տեղերում`
նվազագույններ:
Այս երևույթը կոչվում
է ինտերֆերենցիա:
Ինտերֆերեցիան
պայմանավորված
է (2.26)-ի` ![]() երրորդ
անդամով, որն անվանում
են ինտերֆերենցիոն
անդամ: Այն բնութագրում
է գումարվող տատանումների
կորելացիան:
երրորդ
անդամով, որն անվանում
են ինտերֆերենցիոն
անդամ: Այն բնութագրում
է գումարվող տատանումների
կորելացիան:
2. Վերադրվող
տատանումների
փուլերի տարբերությունը
փոփոխվում է անկանոն
ձևով: Այս դեպքում
![]() փուլերի
տարբերությունը
անընդհատ փոփոխվում
է` հավասար հավանականությամբ
ընդունելով միատեսակ
դրական և բացասական
արժեքներ, որի
հետևանքով ըստ
ժամանակի
փուլերի
տարբերությունը
անընդհատ փոփոխվում
է` հավասար հավանականությամբ
ընդունելով միատեսակ
դրական և բացասական
արժեքներ, որի
հետևանքով ըստ
ժամանակի ![]() Հետևաբար`
Հետևաբար`
![]()
Ինչպես երևում է (2.28)-ից, փուլերի տարբերության քաոսային փոփոխության դեպքում ալիքներից ստացվող արդյունարար ինտենսիվությունը հավասար է յուրաքանչյուր ալիքից առանձին ստեղծված ինտենսիվությունների գումարին: Նման ալիքները կոչվում են ոչ կոհերենտ:
Նշենք, որ ինտերֆերենցիան հատկապես պարզորոշ կերպով ի հայտ է գալիս այն դեպքում, երբ երկու ալիքների ինտենսիվությունները նույնն են` I1 = I2 : Այդ դեպքում (2.26) բանաձևի համաձայն նվազագույնի կետերում I = 0, իսկ առավելագույնի կետերում I = 4I1 : Ոչ կոհերենտ ալիքների համար նույն պայմանի դեպքում ամենուրեք ստացվում է միատեսակ լուսավորվածություն`I = 2I1 (տես (2.28) բանաձևը):
Վերևում շարադրվածից բխում է, որ որևէ մակերևույթ մի քանի լույսի աղբյուրներով (օրինակ, երկու լամպերով) լուսավորելիս թվում է, թե պետք է դիտվի ինտերֆերենցիոն պատկեր նրա համար բնորոշ առավելագույնների և նվազագունների հերթագայությամբ: Սակայն ամենօրյա փորձից հայտնի է, որ նշված դեպքում մակեևույթի լուսավորվածությունը մոնոտոն կերպով նվազում է լույսի աղբյուրից հեռանալուն զուգընթաց, և ոչ մի ինտերֆերենցիոն պատկեր չի դիտվում: Դա բացատրվում է նրանով, որ լույսի բնական աղբյուրները կոհերենտ չեն: Առանձին ատոմի ճառագայթումը տևում է 10-8 վ: Այդ ժամանակամիջոցում հասցնում է առաջանալ ալիքների լծաշարքի մոտ երեք մետր երկարություն ունեցող հաջորդականություն: Ատոմը «մարելով»` որոշ ժամանակից հետո նորից գրգռվում է և ճառագայթում է նոր ալիքների լծաշարք: Սակայն ալիքների նոր լծաշարքի փուլը ոչ մի կերպ կապված չէ նախորդ լծաշարքի փուլի հետ: Միաժամանակ գրգռվում են մեծ թվով ատոմներ: Նրանց գրգռած ալիքների լծաշարքերը, իրար վրա վերադրվելով, առաջացնում են մարմնի արձակած լուսային ալիքը: Այդ ալիքում ատոմների մի խմբի ճառագայթումը 10-8 վ կարգի ժամանակից հետո փոխարինվում է մի այլ խմբի ճառագայթումով, ընդ որում` ալիքի փուլը կրում է պատահական թռիչքաձև փոփոխություն:
Կոհերենտությունը
բնութագելու համար
հարմար է ներմուծել
կոհերենտության
![]() ժամանակի
կամ
կոհերենտության
երկարություն
հասկացությունը`
ժամանակի
կամ
կոհերենտության
երկարություն
հասկացությունը`
![]()
Կոհերենտության ժամանակը լծաշարքի տևողությունն է, իսկ կոհերենտության երկարությունը` լծաշարքի տարածական երկարությունը:
Լույսի
բնական աղբյուրի
ճառագայթման մասին
վերն ասվածից պարզ
է, որ այդպիսի աղբյուրի
արձակած լուսային
ալիքի կոհերենտության
ժամանակը 10-8 վ
է: ![]() ժամանակում
ալիքն անցնում
է
ժամանակում
ալիքն անցնում
է ![]() ճանապարհ,
որը համաձայն
(2.19)-ի կոհերենտության
երկարությունն
է, այն կազմում
է մոտ 3 մ: Լազերային
աղբյուրների դեպքում
կոհերենտության
երկարությունը
հասնում է 1000մ և ավելի:
ճանապարհ,
որը համաձայն
(2.19)-ի կոհերենտության
երկարությունն
է, այն կազմում
է մոտ 3 մ: Լազերային
աղբյուրների դեպքում
կոհերենտության
երկարությունը
հասնում է 1000մ և ավելի:
Ինտերֆերենցիոն պատկերների տեսանելիության կախվածությունը ընթացքների տարբերությունից, իսկ վերջինը` կոհերենտության երկարությունից, հնարավորություն է տալիս փորձով որոշել կոհերենտության երկարությունը և ժամանակը: Այդ մեթոդի էությունն սահմանային ընթացքների տարբերության որոշումն է, որի դեպքում ինտերֆերենցիան դիտվում է: Գտնված սահմանային ընթացքների տարբերությունը մեզ տալիս է կոհերենտության երկարությունը, որտեղից էլ կարելի է որոշել կոհերենտության ժամանակը (2.29)-ով:
Ամփոփելով
կարող ենք ասել,
որ կոհերենտություն
է կոչվում մի քանի
տատանողական կամ
ալիքային պրոցեսների
համաձայնեցված
ընթացքը: Եթե երկու
տատանումների
![]() փուլերի
տարբերությունը
ժամանակի ընթացքում
մնում է անփոփոխ
տարածության տվյալ
կետում, կոչվում
է ժամանակային
կոհերենտություն:
Համաձայնեցվածությունը,
այսինքն, երբ հաստատուն
է մնում
ալիքային
մակերևույթի
տարբեր կետերում
կատարվող տատանումների
փուլերի տարբերությունը,
կոչվում է տարածական
կոհերենտություն:
փուլերի
տարբերությունը
ժամանակի ընթացքում
մնում է անփոփոխ
տարածության տվյալ
կետում, կոչվում
է ժամանակային
կոհերենտություն:
Համաձայնեցվածությունը,
այսինքն, երբ հաստատուն
է մնում
ալիքային
մակերևույթի
տարբեր կետերում
կատարվող տատանումների
փուլերի տարբերությունը,
կոչվում է տարածական
կոհերենտություն:
2.5. Լույսի երկու կոհերենտ աղբյուրներից ստացվող
ինտերֆերենցիոն պատկերի հաշվարկը
Պարզվեց, որ լույսի բնական աղբյուրները կոհերենտ չեն: Կոհերենտ լուսային ալիքներ կարելի է ստանալ` միևնույն աղբյուրի ճառագայթած ալիքը անդրադարձումների կամ բեկումների միջոցով երկու մասի բաժանելով: Եթե երկու ալիքներն անցնեն տարբեր օպտիկական ճանապարհներ և հետո վերադրվեն իրար վրա` կդիտվի ինտերֆերենցիա: Ինտերֆերենցվող ալիքների անցած օպտիկական ճանապարհների երկարությունների տարբերությունը չպետք է շատ մեծ լինի, որովհետև գումարվող ալիքները պետք է պատկանեն ալիքների միևնույն լծաշարքին: Եթե այդ տարբերությունը լինի 3 մ-ից մեծ, կվերադրվեն տարբեր լծաշարքերի համապատասխանող տատանումները, նրանց միջև փուլերի տարբերությունն անընդհատ կփոփոխվի քաոսային ձևով, և ինտերֆերենցիա չի դիտվի:
Ընդունենք,
որ երկու կոհերենտ
ալիքների բաժանումը
տեղի է ունենում
O կետում (նկ.2.4): Դիցուք
ինտերֆերենցիայի
ենթակա ալիքներից
մեկն անցնում
է ![]() ճանապարհ
այն միջավայրում,
որի բեկման ցուցիչը
ճանապարհ
այն միջավայրում,
որի բեկման ցուցիչը
![]() է,
իսկ լույսի տարածման
արագությունը
է,
իսկ լույսի տարածման
արագությունը
![]() է:
Երկրորդ ալիքն
անցնում է
է:
Երկրորդ ալիքն
անցնում է ![]() ճանապարհ
երկրորդ միջավայրում,
որի բեկման ցուցիչը
ճանապարհ
երկրորդ միջավայրում,
որի բեկման ցուցիչը
![]() է,
իսկ լույսի տարածման
արագությունը`
է,
իսկ լույսի տարածման
արագությունը`
![]() Եթե
O կետում տատանման
փուլը
Եթե
O կետում տատանման
փուլը ![]() է,
ապա վերադրման
P կետում առաջին
ալիքը կգրգռի
է,
ապա վերադրման
P կետում առաջին
ալիքը կգրգռի
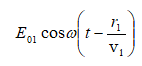
տատանում, իսկ երկրորդը ալիքը`
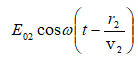
տատանում,
որտեղ ![]() առաջին և երկրորդ
ալիքների փուլային
արագություններն
են: Ուստի P կետում
ալիքների գրգռած
տատանումների
փուլերի տարբերությունը`
առաջին և երկրորդ
ալիքների փուլային
արագություններն
են: Ուստի P կետում
ալիքների գրգռած
տատանումների
փուլերի տարբերությունը`
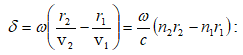
![]() փոխարինելով
փոխարինելով
![]() (
(![]() ալիքի երկարությունն
է վակուումում),
փուլերի տարբերության
արտահայտությանը
կարելի է տալ հետևյալ
տեսքը`
ալիքի երկարությունն
է վակուումում),
փուլերի տարբերության
արտահայտությանը
կարելի է տալ հետևյալ
տեսքը`

որտեղ
![]()
մեծությունը հավասար է ալիքների անցած ճանապարհների օպտիկական երկարությունների տարբերությանը և կոչվում է ընթացքի օպտիկական տարբերություն:
(2.31) բանաձևից
հետևում է, որ եթե
![]() ընթացքի
օպտիկական տարբերությունը
հավասար է վակուումում
ամբողջ թվով ալիքի
երկարությունների`
ընթացքի
օպտիկական տարբերությունը
հավասար է վակուումում
ամբողջ թվով ալիքի
երկարությունների`
![]()
ապա
![]() փուլերի
տարբերությունը
ստացվում է
փուլերի
տարբերությունը
ստացվում է ![]() բազմապատիկը,
և երկու ալիքների`
P կետում առաջացրած
տատանումները
կկատարվեն նույն
փուլով: Հետևաբար,
(2.32) պայմանը ինտեֆերենցիոն
առավելագույնի
պայմանն է: k թիվը
կոչվում է ինտերֆերենցիայի
կարգ:
բազմապատիկը,
և երկու ալիքների`
P կետում առաջացրած
տատանումները
կկատարվեն նույն
փուլով: Հետևաբար,
(2.32) պայմանը ինտեֆերենցիոն
առավելագույնի
պայմանն է: k թիվը
կոչվում է ինտերֆերենցիայի
կարգ:
Եթե
![]() վակուումում
հավասար է կենտ
թվով կիսաալիքի
երկարությունների`
վակուումում
հավասար է կենտ
թվով կիսաալիքի
երկարությունների`
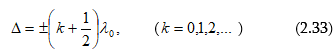
ապա
![]() այնպես,
որ P կետում տատանումները
գտնվում են հակափուլում:
Ուստի (2.33) պայմանը
ինտերֆերենցիոն
նվազագույնի
պայմանն է:
այնպես,
որ P կետում տատանումները
գտնվում են հակափուլում:
Ուստի (2.33) պայմանը
ինտերֆերենցիոն
նվազագույնի
պայմանն է:
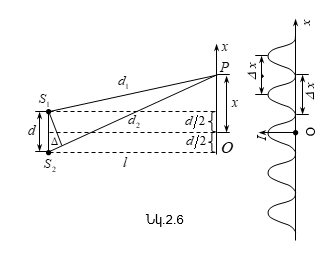
Դիցուք երկու կոհերենտ լուսային ալիքներ, որոնք դուրս են գալիս նեղ ճեղքերի տեսք ունեցող S1 և S2 իրական կամ կեղծ աղբյուրներից (նկ.2.5): OAB տիրույթը, որտեղ այդ ալիքները վերադրվում են, կոչվում է ինտերֆերենցիայի դաշտ: Այդ ամբողջ տիրույթում դիտվում է լույսի առավելագույն և նվազագույն ինտենսիվության տեղերի հերթագայություն: Եթե ինտերֆերենցիայի դաշտի մեջ մտցվի էկրանը, ապա նրա վրա կերևա ինտերֆերենցիոն պատկեր, որը կունենա իրար հաջորդող լուսավոր և խավար ուղղագիծ շերտերի տեսք: Հաշվենք շերտերի լայնությունը` ենթադրելով, որ էկրանը զուգահեռ է S1 և S2 աղբյուրներով անցնող հարթությանը: էկրանի վրա կետի դիրքը կբնորոշենք S1 և S2 գծերին ուղղահայաց ուղղությամբ հաշվվող x կոորդինատով (նկ.2.6): Էկրանի կենտրոնից (O կետից) հեռանալուն զուգընթաց դիտվում է մութ և լուսավոր շետերի հերթագայություն: Որպեսզի պարզվի թե ինչ կլինի P կետում, որոշենք S1 և S2 աղբյուրներից ընթացքի տարբերությունը: Նկ. 2.6-ից հետևում է, որ
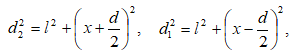
որտեղից`
![]()
Հստակ
ինտերֆերենցիոն
պատկեր ստանալու
համար աղբյուրների
միջև եղած d հեռավորությունը
պետք է զգալիորեն
փոքր լինի մինչև
էկրանը եղած![]() հեռավորությունից:
հեռավորությունից:
![]() հեռավորությունը,
որի սահմաններում
առաջանում են ինտերֆերենցիոն
շերտեր, նույնպես
զգալիորեն փոքր
է լինում
հեռավորությունը,
որի սահմաններում
առաջանում են ինտերֆերենցիոն
շերտեր, նույնպես
զգալիորեն փոքր
է լինում ![]() Նշված պայմանների
դեպքում կարելի
է ընդունել
Նշված պայմանների
դեպքում կարելի
է ընդունել ![]() բեկման
ցուցիչ ունեցող
միջավայրում d2
– d1 տարբերությունը
տալիս է ընթացքի
օպտիկական տարբերությունը:
Հետևաբար կարելի
է գրել`
բեկման
ցուցիչ ունեցող
միջավայրում d2
– d1 տարբերությունը
տալիս է ընթացքի
օպտիկական տարբերությունը:
Հետևաբար կարելի
է գրել`

Տեղադրելով
(2.34)-ը (2.32)-ի մեջ` կստանանք,
որ ինտենսիվության
առավելագույններ
կդիտվեն ![]() այն արժեքների
դեպքում, որոնք
հավասար են`
այն արժեքների
դեպքում, որոնք
հավասար են`
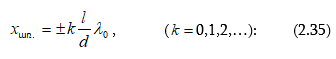
(2.35)-ը տեղադրելով (2.33)-ի մեջ` կստանանք ինտենսիվության նվազագույնների կոորդինատները.
![]()
Երկու
հարևան նվազագույների
միջև եղած ![]() հեռավորությունը
կոչվում է ինտերֆերենցիոն
շերտի լայնություն:
(2.36) բանաձևից հետևում
է, որ շերտի լայնությունը`
հեռավորությունը
կոչվում է ինտերֆերենցիոն
շերտի լայնություն:
(2.36) բանաձևից հետևում
է, որ շերտի լայնությունը`

Ինտենսիվության
երկու հարևան առավելագույնների
միջև եղած հեռավորությունը
կոչվում է ինտերերֆերենցիոն
շերտերի միջև հեռավորություն:
(2.36) արտահայտությունից
հետևում է, որ շերտերի
միջև հեռավորությունը
նույնպես որոշվում
է (2.37) բանաձևով: Ինչպես
հետևում է (2.37)-ից,
ինտերֆերենցիոն
շերտի լայնությունը
կախված չէ ինտերֆերենցիայի
կարգից և հաստատուն
է տվյալ ![]() դեպքում:
Հաստատուն
դեպքում:
Հաստատուն ![]() դեպքում
աղբյուրների միջև
եղած d հեռավորության
փոքրացումը բերում
է ինտերֆերենցիոն
շերտի լայնության
մեծացում, այսինքն`
պատկերը դառնում
է ավելի ցայտուն:
Քանի որ տեսանելի
լույսի համար
դեպքում
աղբյուրների միջև
եղած d հեռավորության
փոքրացումը բերում
է ինտերֆերենցիոն
շերտի լայնության
մեծացում, այսինքն`
պատկերը դառնում
է ավելի ցայտուն:
Քանի որ տեսանելի
լույսի համար
![]() ուստի
ցայտուն ինտերֆերենցիոն
պատկերը տեսանելի
դիտման համար հասանելի
է, եթե տեղի ունի
ուստի
ցայտուն ինտերֆերենցիոն
պատկերը տեսանելի
դիտման համար հասանելի
է, եթե տեղի ունի
![]() պայմանը:
Այդ դեպքում կոհերենտ
աղբյուրների ստացման
բոլոր մեթոդներում
անհրաժեշտ է հնարավորին
չափով d -ն փոքր
վերցնել: Ինչպես
վերևում նշեցինք,
ինտերֆերենցիոն
շերտերի լայնությունը
կախված է
պայմանը:
Այդ դեպքում կոհերենտ
աղբյուրների ստացման
բոլոր մեթոդներում
անհրաժեշտ է հնարավորին
չափով d -ն փոքր
վերցնել: Ինչպես
վերևում նշեցինք,
ինտերֆերենցիոն
շերտերի լայնությունը
կախված է ![]() ալիքի երկարությունից:
Միայն պատկերի
մեջտեղում, որտեղ
x = 0, բոլոր ալիքների
երկարությունների
առավելագույնները
համընկնում են:
Պատկերի կենտրոնից
հեռանալուն զուգընթաց
տարբեր գույների
առավելագույններն
իրար նկատմամբ
ավելի ու ավելի
են տեղաշարժվում:
Դա հանգեցնում
է նրան, որ սպիտակ
լույսի դեպքում
ինտերֆերենցիոն
պատկերը ճապաղվում
է: Մեներանգ լույսի
դեպքում ինտերֆերենցիոն
շերտերի թիվն աճում
է: Նկ.2.6-ի աջ կողմում
ցույց է տրված
լույսի I ինտենսիվության
կախումն x կոորդինատից`
մեներանգ լույսի
դեպքում: Չափելով
շերտերի միջև եղած
ալիքի երկարությունից:
Միայն պատկերի
մեջտեղում, որտեղ
x = 0, բոլոր ալիքների
երկարությունների
առավելագույնները
համընկնում են:
Պատկերի կենտրոնից
հեռանալուն զուգընթաց
տարբեր գույների
առավելագույններն
իրար նկատմամբ
ավելի ու ավելի
են տեղաշարժվում:
Դա հանգեցնում
է նրան, որ սպիտակ
լույսի դեպքում
ինտերֆերենցիոն
պատկերը ճապաղվում
է: Մեներանգ լույսի
դեպքում ինտերֆերենցիոն
շերտերի թիվն աճում
է: Նկ.2.6-ի աջ կողմում
ցույց է տրված
լույսի I ինտենսիվության
կախումն x կոորդինատից`
մեներանգ լույսի
դեպքում: Չափելով
շերտերի միջև եղած
![]() հեռավորությունը
և իմանալով
հեռավորությունը
և իմանալով ![]() և d-ն` կարելի
է (2.37) բանաձևով հաշվել
և d-ն` կարելի
է (2.37) բանաձևով հաշվել
![]() ալիքի
երկարությունը:
Հենց լույսի ինտերֆերենցիայի
փորձերից են առաջին
անգամ որոշվել
տարբեր գույնի
լուսային ճառագայթների
ալիքի երկարությունները:
ալիքի
երկարությունը:
Հենց լույսի ինտերֆերենցիայի
փորձերից են առաջին
անգամ որոշվել
տարբեր գույնի
լուսային ճառագայթների
ալիքի երկարությունները:
Լուսավոր և խավար շերտերի ինտենսիվությունները նշանակենք Iառ. և Iնվ.-ով: Ներմուծենք մի պարամետր, որը որոշում է ինտերֆերենցիոն շերտերի տեսանելիությունը (հստակությունը).

Եթե
մութ շերտի ինտենսիվությունը
հավասար է զրոյի,
ապա V = 1 այսինքն`
տեսանելիությունն
ամենամեծն է: Հավասարաչափ
լուսավորվածության
դեպքում Iառ.=Iնվ.
հետևաբար ![]() այսինքն`
ինտերֆերենցիոն
պատկերի հստակությունն
ամենափոքրն է:
Այսպիսով շերտերի
տեսանելիության
արժեքը գտնվում
է
այսինքն`
ինտերֆերենցիոն
պատկերի հստակությունն
ամենափոքրն է:
Այսպիսով շերտերի
տեսանելիության
արժեքը գտնվում
է ![]() սահմաններում:
սահմաններում:
2.6. Կոհերենտ փնջերի ստացման եղանակներն օպտիկայում
Մաքսվելը,
իր պատրաստած ինտերֆերաչափով
փորձեր կատարելով
կադմիումի կարմիր
գծի համար, եկավ
այն եզրակացության,
որ ինտերֆերենցիոն
պատկերը պահպանում
է իր տեսանելիությունը
ընդհուպ միչև
![]() ընթացքների
տարբերությունը
(նկ.2.7): Լազերային
ճառագայթումն
օժտված է բարձր
կոհերենտությամբ:
Դրանում կարելի
է համոզվել, եթե
կատարվի լազերային
ճառագայթումով,
այսպես կոչված,
Յունգի փորձը:
ընթացքների
տարբերությունը
(նկ.2.7): Լազերային
ճառագայթումն
օժտված է բարձր
կոհերենտությամբ:
Դրանում կարելի
է համոզվել, եթե
կատարվի լազերային
ճառագայթումով,
այսպես կոչված,
Յունգի փորձը:
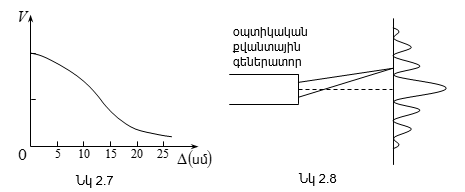
Դրա համար լազերային ճառագաթումը բաց թողնենք լազերի ելքի կտրվածքի երկու անցքերով և այն ուղղենք էկրանի վրա, որը դրված է աղբյուրից որոշակի հեռավորության վրա: Ինչպես ցույց է տալիս փորձը, էկրանի վրա դիտվում է ըստ ժամանակի կայուն հստակ ինտերֆերենցիոն պատկեր (նկ.2.8), որը վկայում է լազերային աղբյուրի տարածականորեն բաժանված երկու կետերից դուրս եկող ճառագայթման բարձր կոհերետության մասին: Լազերային ճառագայթների օգնությամբ հնարավոր է դիտել ինտեֆերենցիոն պատկեր, որը պարունակում է 108 շերտ: Դա կապված է այն բանի հետ, որ լազերից ստացված երկու ճառագայթները մնում են կոհերենտ և ինտերֆերենցվում են կիլոմետրերի հասնող ընթացքի տարբերության դեպքում: Այդպիսի կոհերենտ լույսի աղբյուրների տեսակը, ինչպես հայտնի է, սկսեցին ստեղծել 1960 թվականից: Ստորև մենք կծանոթանանք կոհերենտ ճառագայթման ստացման տարբեր մեթոդներին լույսի ոչ լազերային աղբյուրների դեպքում: Կոհերենտությունն իրականացնելու համար անհրաժեշտ է լուսային փունջը բաժանել երկու փնջերի և ստիպել, որ դրանք նորից հանդիպեն այնպես, որպեսզի ինտերֆերենցվող փնջերի ընթացքի տարբերությունը լինի կոհերենտության երկարությունից փոքր: Գոյություն ունի կոհերենտ «աղբյուրների» ստացման երկու տարբեր` ալիքային ճակատի բաժանման և լայնույթի բաժանման մեթոդներ:
Ալիքային ճակատի բաժանան մեթոդը, որը հարմար է միայն բավականին փոքր աղբյուրների համար, աղբյուրից դուրս եկող փունջը բաժանվում է երկու փնջերի. մե´րթ անցնելով երկու իրար մոտ դասավորված անցքերով, մե´րթ անդրադառնալով հայելային մակերևույթներից և այլն: Երկրորդ մեթոդը, որը հարմար է ինչպես փոքր, այնպես էլ մեծ աղբյուրների համար, փունջը բաժանվում է կիսաթափանցիկ մակերևույթից անցման և անդրադարձման ճանապարհով: Երկրորդ մեթոդի հիմնական առավելությունը մեծ ինտենսիվության փնջի ստացումն է:
Նշված մեթոդների օգնությամբ կարելի է իրականացնել ինտերֆերենցիա, ինչպես երկու, այնպես էլ շատ փնջերով: Այս դեպքում առաջացած ինտերֆերենցիան համապատասխանաբար կոչվում է երկճառագայթ և բազմաճառագայթ:
Քննարկենք երկու ինտերֆերենցիայի ստացման սխեմաներ, որոնցից մեկում լուսային ալիքը երկու մասի բաժանելու համար օգտագործվում է անդրադարձումը, իսկ մյուսում` բեկումը:
Ֆրենելի
հայելիներ: Երկու հպվող
A1O և A2O հարթ
հայելիներ դրվում
են այնպես, որ դրանց
անդրադարձնող
մակերևույթները
կազմեն 180°-ին մոտ
անկյուն (նկ.2.9): Նկարում
![]() անկյունը
շատ փոքր է: Կետային
S աղբյուրից ճառագայթած
լույսը երկու
հայելիներից անդրադառնալուց
հետո տարածվում
է երկու փնջերի
տեսքով S1 և S2
կենտրոններից,
որոնք S աղբյուրի
կեղծ պատկերներն
են հայելիներում:
անկյունը
շատ փոքր է: Կետային
S աղբյուրից ճառագայթած
լույսը երկու
հայելիներից անդրադառնալուց
հետո տարածվում
է երկու փնջերի
տեսքով S1 և S2
կենտրոններից,
որոնք S աղբյուրի
կեղծ պատկերներն
են հայելիներում:
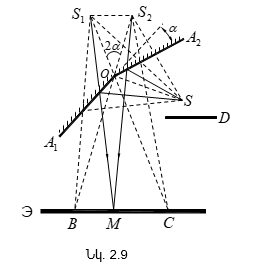
Այդ
փնջերը կոհերենտ
են և վերադրման
դեպքում էկրանի
վրա տալիս են ինտերֆերենցիոն
պատկեր (BC տիրույթը):
Ինտերֆերենցիայի
արդյունքը էկրանի
որևէ M կետում
կախված է լույսի
ալիքի երկարությունից,
լույսի կոհերենտ
S1 և S2 կեղծ աղբյուրներից
մինչև M կետը եղած`
![]() երկրաչափակական
ընթացքի տարբերությունից:
Ուստի ինտերֆերենցիոն
առավելագույնների
և նվազագույնների
պայմանները համապատասխան
(2.23) և (2.24) բանաձևերի
կունենան հետևյալ
տեսքը`
երկրաչափակական
ընթացքի տարբերությունից:
Ուստի ինտերֆերենցիոն
առավելագույնների
և նվազագույնների
պայմանները համապատասխան
(2.23) և (2.24) բանաձևերի
կունենան հետևյալ
տեսքը`

k մեծությունը կոչվում է ինտերֆերենցիայի կարգ:
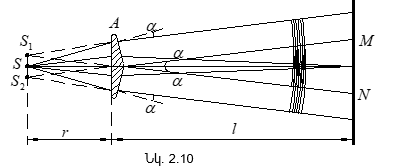
Ֆրենելի երկպրիզմա: Ապակու մի կտորից պատրաստված և ընդհանուր հիմք ունեցող երկու պրիզմաներ են, որոնց բեկող անկյունը փոքր է (նկ. 2.10): Լույսի S աղբյուրը տեղադրված է պրիզմաներից r հեռավորության վրա: Լույսի S աղբյուրից դուրս եկող ալիքային ճակատը պրիզմաների օգնությամբ բաժանվում է երկու մասի, որոնք հանդիպում են պրիզմաների հետևում:
Քանի
որ երկու ճառագայթներն
առաջացել են միևնույն
աղբյուրից, վերածածկման
տիրույթում առաջանում
է ինտերֆերենցիոն
պատկեր: Գտնվելով
էկրանի տեղադրված
տեղում, դիտողին
թվում է, թե ճառագայթները
գալիս են երկու
S1 և S2 աղբյուրներից:
Հետևաբար, տվյալ
դեպքում կոհերենտ
աղբյուրների
դերը կատարում
են S1 և S2 աղբյուրները,
որոնք S կետի կեղծ
պատկերներն են:
Ֆրենելի երկպրիզմայով
փորձում բեկող
անկյունների
փոքրության հետևանքով
ինտերֆերենցի
ապերտուրան գործնականում
չի տարբերվում
ծածկող փնջերի
ապերտուրայից,
որն էլ առաջ է բերում
ինտերֆերենցիոն
պատկերի ընդհանուր
լուսավորվածության
փոքրացում: d = S1S2
հեռավորությունը
փոքրացնելու համար
պրիզմաների բեկող
![]() ակյունները
վերցնում են փոքր:
ակյունները
վերցնում են փոքր:
Յունգի մեթոդը: Ըստ այս մեթոդի (նկ.2.11) լույսի կոհերենտ ալիքներն անթափանց էկրանի վրա S1 և S2 երկու նեղ ճեղքերն են: Լույսի սկզբնական աղբյուր է ծառայում պայծառ լուսավորված S ճեղքը, որը զուգահեռ է S1 և S2 ճեղքերին և գտնվում է նրանցից միևնույն հեռավորության վրա: Ինտերֆերենցիոն պատկերի հաշվարկը էկրանի վրա, որը ստացվում է Ֆրենելի երկպրիզմայով կամ Յունգի մեթոդով, չի տարբերվում Ֆրենելի հայելիների համար վերևում դիտարկվածից:
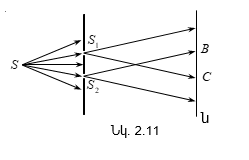
2.7. Լույսի ինտերֆերենցիան բարակ թաղանթներում
Լույսի ինտերֆերենցիան բավական հաճախ նկատվում է բարակ թաղանթներում: Բարակ թափանցիկ թաղանթների ներկվածքը, գունավոր նախշանկարները բենզինի, կերոսինի, յուղի բարակ թաղանթների վրա, այս ամենը լույսի ճառագայթների ինտերֆերենցիայի հետևանք են: Տեսնենք, թե ինչպես են առաջանում ինտերֆերենցիոն պատկերները բարակ թաղանթներում:
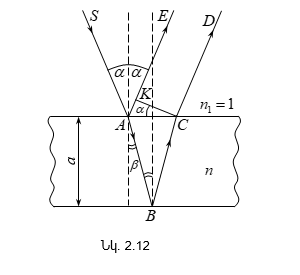
Դիցուք
թափանցիկ հարթ-զուգահեռ
d հաստության
բարակ թաղանթի
վրա ընկնում է
հարթ լուսային
ալիք, որը նորմալի
ուղղության հետ
կազմում է ![]() անկյուն
(նկ.2.12): Քննարկենք
թաղանթից անդրադարձած
ճառագայթներում
ինտերֆերենցի
արդյունքը: SA ճառագայթն
ընկնելով A կետը`
մասամբ անդրադառնում
է (AE), մասամբ բեկվում(AB):
Բեկված AB ճառագայթն
անդրադառնում
է թաղանթի ներքևի
մակերևույթի B
կետից և բեկվելով
C կետում` դուրս
է գալիս թաղանթից
(CD) : AE և CD ճառագայթները
կոհերենտ են, քանի
որ առաջացել են
մեկ A ճառագայթից:
Գտնենք AE և CD ճառագայթների
ընթացքի օպտիկական
տարբերությունը:
Դրա համար C կետից
AE և CD ճառագայթներին
տանենք CK նորմալը:
AE և CD ճառագայթների
օպտիկական ճանապարհները
CK նորմալից մինչև
նրանց վերադրման
տեղը նույնն են:
Քանի որ AE ճառագայթն
առաջին միջավայրում,
որի բեկման ցուցիչը`
անկյուն
(նկ.2.12): Քննարկենք
թաղանթից անդրադարձած
ճառագայթներում
ինտերֆերենցի
արդյունքը: SA ճառագայթն
ընկնելով A կետը`
մասամբ անդրադառնում
է (AE), մասամբ բեկվում(AB):
Բեկված AB ճառագայթն
անդրադառնում
է թաղանթի ներքևի
մակերևույթի B
կետից և բեկվելով
C կետում` դուրս
է գալիս թաղանթից
(CD) : AE և CD ճառագայթները
կոհերենտ են, քանի
որ առաջացել են
մեկ A ճառագայթից:
Գտնենք AE և CD ճառագայթների
ընթացքի օպտիկական
տարբերությունը:
Դրա համար C կետից
AE և CD ճառագայթներին
տանենք CK նորմալը:
AE և CD ճառագայթների
օպտիկական ճանապարհները
CK նորմալից մինչև
նրանց վերադրման
տեղը նույնն են:
Քանի որ AE ճառագայթն
առաջին միջավայրում,
որի բեկման ցուցիչը`
![]() (օդ)
անցնում է AK օպտիկական
ճանապարհ, իսկ
CD ճառագայթը երկրորդ
միջավայրում (թաղանթում),
որի բեկման ցուցիչը
n է, անցնում է (AB
+ BC)n օպտիկական
ճանապարհ, հետևաբար`
(օդ)
անցնում է AK օպտիկական
ճանապարհ, իսկ
CD ճառագայթը երկրորդ
միջավայրում (թաղանթում),
որի բեկման ցուցիչը
n է, անցնում է (AB
+ BC)n օպտիկական
ճանապարհ, հետևաբար`
![]()
Ըստ
նկ. 2.12-ի` ![]() իսկ
իսկ ![]() բայց
բայց ![]() հետևաբար
հետևաբար
![]() Կատարելով
այդ եռանկյունաչափական
ձևափոխությունները
երկու ճառագայթների
ընթացքի տարբերության
համար` կստանանք.
Կատարելով
այդ եռանկյունաչափական
ձևափոխությունները
երկու ճառագայթների
ընթացքի տարբերության
համար` կստանանք.
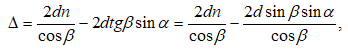
քանի որ
![]() հետևաբար`
հետևաբար`
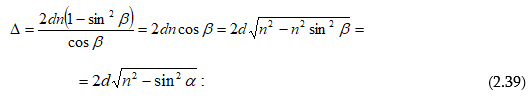
Վերջնական
ընթացքի տարբերությունը
ստանալու համար
անհրաժեշտ է հաշվի
առնել, որ լուսային
ալիքներն անդրադառնալով
օպտիկապես խիտ
միջավայրից (մեծ
բեկման ցուցչով)`
փուլը փոխում
են ![]() այսինքն
ստանում են հավասար
այսինքն
ստանում են հավասար
![]() լրացուցիչ
ընթացքի տարբերություն:
Այս դեպքում (2.39)-ը
կարելի է գրել.
լրացուցիչ
ընթացքի տարբերություն:
Այս դեպքում (2.39)-ը
կարելի է գրել.
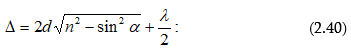
Ընթացքի
տարբերությունը
կախված է թաղանթի
d հաստությունից,
նյութի n բեկման
ցուցչից, ճառագայթների
անկման![]() անկյունից
և լուսային
անկյունից
և լուսային![]() ալիքի երկարությունից:
Այսպիսով, բարակ
թաղանթներից անդրադարձած
լույսում ինտերֆերենցիայի
արդյունքը որոշվում
է հետևյալ պայմաններով`
արտահայտված ընթացքի
տարբերության
միջոցով.
ալիքի երկարությունից:
Այսպիսով, բարակ
թաղանթներից անդրադարձած
լույսում ինտերֆերենցիայի
արդյունքը որոշվում
է հետևյալ պայմաններով`
արտահայտված ընթացքի
տարբերության
միջոցով.
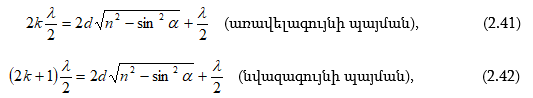
Վերլուծելով (2.41) և (2.42) արտահայտությունները` հանգում ենք հետևյալ եզրակացությունների:
![]() Եթե բարակ
թաղանթի վրա ընկնում
է մեներանգ ճառագայթում,
օրինակ
Եթե բարակ
թաղանթի վրա ընկնում
է մեներանգ ճառագայթում,
օրինակ ![]() կարմիր
գույնի լույս,
ապա այն անդրադարձող
լույսում կլինի
մե´րթ կարմիր (2.41),
մե´րթ մութ (2.42):
կարմիր
գույնի լույս,
ապա այն անդրադարձող
լույսում կլինի
մե´րթ կարմիր (2.41),
մե´րթ մութ (2.42):
![]() Եթե բարակ
թաղանթի վրա ընկնում
է սպիտակ լույս,
ապա այն կունենա
համապատասխան
Եթե բարակ
թաղանթի վրա ընկնում
է սպիտակ լույս,
ապա այն կունենա
համապատասխան
![]() գունավորում,
որի համար տեղի
ունի (2.41) պայմանը:
Համասեռ գունավորում
կստացվի այն դեպքում,
երբ թաղանթի հաստությունն
ամենուրեք նույնն
է, հակառակ դեպքում
գունավորումը
տարբեր տեղերում
կլինի տարբեր:
գունավորում,
որի համար տեղի
ունի (2.41) պայմանը:
Համասեռ գունավորում
կստացվի այն դեպքում,
երբ թաղանթի հաստությունն
ամենուրեք նույնն
է, հակառակ դեպքում
գունավորումը
տարբեր տեղերում
կլինի տարբեր:
Ինտերֆերենցիոն պատկեր դիտվում է նաև անցնող լույսում, բայց քանի որ անցնող լույսում կես ալիքի կորուստ չկա, ուստի ամբողջ ինտերֆերենցիոն պատկերը փոխվում է հակառակի:
2.8. Հավասար հաստության շերտեր: Նյուտոնի օղակները
Օդային
սեպում ինտերֆերենցիոն
շերտեր կարելի
է դիտել, եթե հարթ-զուգահեռ
թիթեղը դրվի մյուսի
վրա և վերևի թիթեղի
ծայրերից մեկի
տակ դրվի մի ոչ
մեծ առարկա այնպես,
որ նրանց միջև
առաջանա օդային
սեպ (նկ.2.13): Այս դեպքում
ճառագայթների
ընթացքի տարբերությունը
որոշվում է (2.41) և
(2.42)-ով: Ենթադրենք,
որ 1-4 ճառագայթներն
ընկնում են սեպի
վրա ուղղահայաց
![]() և
օդի բեկման ցուցիչը`
n=1, այդ դեպքում`
և
օդի բեկման ցուցիչը`
n=1, այդ դեպքում`
![]()
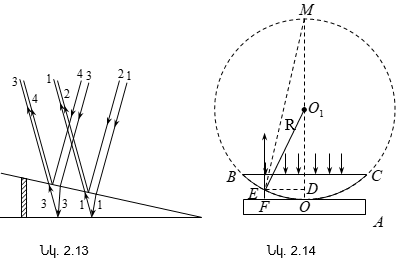
Սահմանի
վրա, որտեղ հպվում
են թիթեղները ![]() և (2.40)-ից հետևում
է, որ
և (2.40)-ից հետևում
է, որ ![]() ուստի
դիտվում է մութ
շերտ: Առաջին լուսավոր
շերտը (k=1) առաջանում
է, եթե
ուստի
դիտվում է մութ
շերտ: Առաջին լուսավոր
շերտը (k=1) առաջանում
է, եթե ![]() քանի
որ
քանի
որ ![]() դրա
համար էլ
դրա
համար էլ ![]() Այստեղից
ստանում ենք, որ
այս տեղում օդային
սեպի հաստությունը`
Այստեղից
ստանում ենք, որ
այս տեղում օդային
սեպի հաստությունը`
![]() Հենց
այդպիսի օդային
բացակն անցնում
է հպման նիստին
զուգահեռ, և լուսավոր
շերտն ունի ուղիղ
գծի տեսք:
Հենց
այդպիսի օդային
բացակն անցնում
է հպման նիստին
զուգահեռ, և լուսավոր
շերտն ունի ուղիղ
գծի տեսք:
Երկրորդ
լուսավոր շերտը
գտնվում է այնտեղ,
որտեղ օդային սեպի
հաստությունը
հասնում է ![]() քանի որ
այդ դեպքում`
քանի որ
այդ դեպքում`
Այդ շերտերը, որոնցից յուրաքանչյուրին համապատասխանում է սեպի որոշակի հաստություն, կամ դրանք զուգահեռ են թիթեղին, կոչվում են հավասար հաստության շերտեր: Հավասար հաստության շերտերը կարող են լինել ուղիղ գծեր, համակենտրոն շրջանագծեր և ունենալ ցանկացած այլ ձև, կախված կետերի դասավորությունից, որոնք համապատասխանում են d=const պայմանին: Սեպի անկյունը պետք է լինի շատ փոքր, հակառակ դեպքում` հավասար հաստության շերտերը իրար վրա կընկնեն և հնարավոր չի լինի զատել դրանք:
Հավասար հաստության շերտեր կարելի է ստանալ, եթե մեծ կորության R շառավղով հարթ ուռուցիկ ոսպնյակը դրվի հարթ-զուգահեռ A թիթեղի վրա (նկ.2.14): Այս դեպքում հավասար հաստության շերտերն ունեն օղակների տեսք, որոնք կոչվում են Նյուտոնի օղակներ: Եթե ոսպնյակի BC հարթ մակերևույթի վրա ընկնում են լույսի զուգահեռ ճառագայթներ, ապա ալիքները, որոնք անդրադառնում են օդային բացակի վերին և ներքին սահմանից, ինտերֆերենցում են իրար հետ` առաջացնելով հավասար հաստության իտերֆերենցիոն օղակներ: Այդ օղակների տեսքը մեներանգ լույսի դեպքում ցույց է տրված նկ.2.15ա-ում: Կենտրոնում գտնվում է մութ օղակը (զրոյական կարգի նվազագույն): Այն շրջապատված է իրար հաջորդող լուսավոր և մութ օղակներով, որոնց լայնությունն և ինտենսիվությունը, կենտրոնական բծից հեռանալուն զուգընթաց, աստիճանաբար նվազում է: Անցնող լույսի մեջ դիտվում է լրացուցիչ պատկեր` կենտրոնական օղակը լուսավոր է, հաջորդ օղակը մութ է և այլն (նկ.2.15բ):
Ընթացքի օպտիկական տարբերությունը ճառագայթների միջև, որոնք անդրադարձել են օդային բացակի վերին և ներքևի մակերևույթներից O կետից կամայական r=DE հեռավորության վրա, կլինի`
որտեղ
օդի բեկման ցուցիչն
ընդունվել է հավասար
մեկի, իսկ ![]() անդամը
հաշվի է առնում
փուլի շեղումը
անդամը
հաշվի է առնում
փուլի շեղումը
![]() թիթեղի
մակերևույթից
լույսի անդրադարձման
դեպքում: EOD և EDM
ուղղանկյուն եռանկյունների
նմանությունից
հետևում է, որ
թիթեղի
մակերևույթից
լույսի անդրադարձման
դեպքում: EOD և EDM
ուղղանկյուն եռանկյունների
նմանությունից
հետևում է, որ
![]()
որտեղ
DO=EF, DE=r և ![]() քանի
որ
քանի
որ
![]()
Այսպիսով`
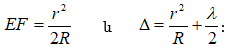
Այս
առնչությունից,
ինչպես նաև ![]() պայմաններից
հետևում է, որ անդրադարձած
լույսում Նյուտոնի
k-րդ լուսավոր
և խավար օղակների
շառավիղները համապատասխանաբար
կլինեն.
պայմաններից
հետևում է, որ անդրադարձած
լույսում Նյուտոնի
k-րդ լուսավոր
և խավար օղակների
շառավիղները համապատասխանաբար
կլինեն.
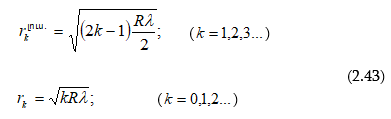
Ակներև է, որ անցնող լույսում`
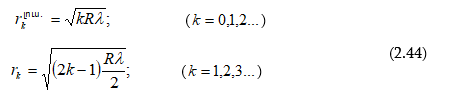
Նյուտոնի օղակների ձևը հեշտությամբ աղավաղվում է ուռուցիկ ոսպնյակի և հարթ թիթեղի մակերևույթների մշակման աննշան արատների դեպքում: Ուստի Նյուտոնի օղակների ձևի դիտումը հնարավորություն է տալիս իրականացնել ոսպնյակների և հարթ թիթեղների մակերևույթների մշակման որակի արագ և ճշգրիտ ստուգում:
2.9. Լույսի ինտերֆերենցիայի կիրառությունները
Լույսի ինտեֆերենցի երևույթը լայն կիրառություն է գտել գիտության և տեխնիկայի տարբեր բնագավառներում: Այն օգտագործվում է գազանման նյութերի բեկման ցուցիչը որոշելու, ալիքի երկարությունների և անկյունների ճշգրիտ չափումների, մարմինների միկրոսկոպիկ չափերը, մակերևույթների մշակման որակի ստուգման և այլնի համար:
Էլեկտրամագնիսական ճառագայթման ռենտգենյան տիրույթում ինտերֆերենցիան բյուրեղային մարմինների բյուրեղային ցանցի ռենտգենակառուցվածքային անալիզի հիմքն է: Այդ նպատակին են ծառայում տարբեր կոնստրուկցիայի սարքեր, որոնք կոչվում են ինտերֆերաչափեր: Յուրաքանչյուր ինտերֆերաչափով չափվող պարամետրը փոփոխական մեծություն է, իսկ մնացած բոլորը` հաստատուն:
1. Առաջին
ինտերֆերաչափն
առաջարկվել է
Ա.Մայքելսոնի կողմից:
Մեներանգ լույսի
ուղղաձիգ ճառագայթը
S աղբյուրից ![]() անկյան
տակ ընկնում է
հարթ-զուգահեռ
A թիթեղի վրա, որի
հետևի մակերևույթը
պատված է արծաթի
կիսաթափանց բարակ
շերտով (նկ.2.16): Լույսի
մի մասն այդ շերտից
անդրադառնում
է (հորիզոնական
1 ճառագայթը), մյուս
մասն անցնում է
նրանով (ուղղաձիգ
2 ճառագայթը): 1 ճառագայթն
անդրադառնում
է M2 ուղղաձիգ
հարթ հայելուց,
մասամբ անցնում
է A թիթեղով (
անկյան
տակ ընկնում է
հարթ-զուգահեռ
A թիթեղի վրա, որի
հետևի մակերևույթը
պատված է արծաթի
կիսաթափանց բարակ
շերտով (նկ.2.16): Լույսի
մի մասն այդ շերտից
անդրադառնում
է (հորիզոնական
1 ճառագայթը), մյուս
մասն անցնում է
նրանով (ուղղաձիգ
2 ճառագայթը): 1 ճառագայթն
անդրադառնում
է M2 ուղղաձիգ
հարթ հայելուց,
մասամբ անցնում
է A թիթեղով (![]() ճառագայթ):
2 ճառագայթն անդրադառնում
է հորիզոնական
M2 հարթ հայելուց
և վերադառնում
է A թիթեղ, կրկնակի
անցնելով B ապակյա
թիթեղով, որը զուգահեռ
է
ճառագայթ):
2 ճառագայթն անդրադառնում
է հորիզոնական
M2 հարթ հայելուց
և վերադառնում
է A թիթեղ, կրկնակի
անցնելով B ապակյա
թիթեղով, որը զուգահեռ
է ![]() թիթեղին
և նրանից տարբերվում
է միայն նրանով,
որ արծաթի շերտով
պատված չէ: Այդ
ճառագայթը
թիթեղին
և նրանից տարբերվում
է միայն նրանով,
որ արծաթի շերտով
պատված չէ: Այդ
ճառագայթը ![]() մասամբ
անդրադառնում
է
մասամբ
անդրադառնում
է ![]() թիթեղի
արծաթապատված
մակերևույթից:
թիթեղի
արծաթապատված
մակերևույթից:
![]() ճառագայթները
կոհերենտ են: Նրանց
ինտերֆերենցիայի
արդյունքը կախված
է 1 և 2 ճառագայթների
օպտիկական ընթաքի
տարբերությունից:
Շնորհիվ
ճառագայթները
կոհերենտ են: Նրանց
ինտերֆերենցիայի
արդյունքը կախված
է 1 և 2 ճառագայթների
օպտիկական ընթաքի
տարբերությունից:
Շնորհիվ![]() թիթեղի
նրանց ճանապարհները
նույնն են, դրա
համար
թիթեղի
նրանց ճանապարհները
նույնն են, դրա
համար ![]() թիթեղը
կոչվում է կոմպենսատոր:
Այսպիսով,
թիթեղը
կոչվում է կոմպենսատոր:
Այսպիսով, ![]() ճառագայթների
օպտիկական ընթացքի
տարբերությունը`
ճառագայթների
օպտիկական ընթացքի
տարբերությունը`
![]()
որտեղ
![]() օդի
բացարձակ բեկման
ցուցիչն է,
օդի
բացարձակ բեկման
ցուցիչն է, ![]() և
և ![]() Օ կետից
մինչև M1 և M2
հայելիներն ընկած
հեռավորություններն
են: Եթե
Օ կետից
մինչև M1 և M2
հայելիներն ընկած
հեռավորություններն
են: Եթե ![]() դիտվում
է ինտերֆերենցիոն
առավելագույն:
Հայելիներից մեկը
շեղելով
դիտվում
է ինտերֆերենցիոն
առավելագույն:
Հայելիներից մեկը
շեղելով ![]() հեռավորությամբ,
առաջացնում է
ինտերֆերենցիոն
նվազագույն: Այսպիսով,
ըստ ինտերֆերենցիոն
պատկերի փոփոխության`
կարելի է դատել
հայելիներից մեկի
փոքր տեղափոխության
մասին և դրանով
Մայքելսոնի ինտերֆերաչափն
օգտագործել երկարության
ճշգրիտ չափման
համար:
հեռավորությամբ,
առաջացնում է
ինտերֆերենցիոն
նվազագույն: Այսպիսով,
ըստ ինտերֆերենցիոն
պատկերի փոփոխության`
կարելի է դատել
հայելիներից մեկի
փոքր տեղափոխության
մասին և դրանով
Մայքելսոնի ինտերֆերաչափն
օգտագործել երկարության
ճշգրիտ չափման
համար:
2. Ժամենի
ինտեֆերաչափը: Նկ.2.17-ում պատկերված
է Ժամենի ինտերֆերաչափի
սխեման, որն օգտագործվում
է գազերի բեկման
ցուցիչները և նրանց
կախվածությունը
ջերմաստիճանից,
ճնշումից և խոնավությունից
ճշգրտորեն չափելու
համար: Երկու միատեսակ
հաստ հարթ-զուգահեռ
A և B ապակյա թիթեղներ
տեղադրված են համարյա
միմյանց զուգահեռ:
Մեներանգ լույսի
S աղբյուրից ճառագայթներն
ընկնում են A թիթեղի
մակերևույթի վրա
տարբեր` ![]() մոտ
մոտ ![]() անկյունների
տակ: Նկ.2.17-ում ցույց
է տրված մեկ ընկնող
ճառագայթ: Թիթեղի
երկու մակերևույթներից
նրանց անդրադարձման
հետևանքով, նրանից
դուրս են գալիս
երկու կոհերենտ
1 և 2 զուգահեռ ճառագայթներ:
Այդ ճառագայթներն
անցնելով ապակյա
միատեսակ փակ K1
և K2 կյուվետներով,
երկրորդ B թիթեղից
անդրադառնալուց
հետո հավաքվում
են L ոսպնյակով
և ինտերֆերենցում
են: Հավասար թեքության
ինտերֆերենցիոն
շերտերը դիտվում
են օկուլյարի օգնությամբ,
որը նկարում ցույց
չի տրված: Եթե կյուվետներից
K1 -ը լցված է հայտնի
անկյունների
տակ: Նկ.2.17-ում ցույց
է տրված մեկ ընկնող
ճառագայթ: Թիթեղի
երկու մակերևույթներից
նրանց անդրադարձման
հետևանքով, նրանից
դուրս են գալիս
երկու կոհերենտ
1 և 2 զուգահեռ ճառագայթներ:
Այդ ճառագայթներն
անցնելով ապակյա
միատեսակ փակ K1
և K2 կյուվետներով,
երկրորդ B թիթեղից
անդրադառնալուց
հետո հավաքվում
են L ոսպնյակով
և ինտերֆերենցում
են: Հավասար թեքության
ինտերֆերենցիոն
շերտերը դիտվում
են օկուլյարի օգնությամբ,
որը նկարում ցույց
չի տրված: Եթե կյուվետներից
K1 -ը լցված է հայտնի
![]() բացարձակ
բեկման ցուցիչ
ունեցող գազով,
երկրորդը` այն
գազով, որի
բացարձակ
բեկման ցուցիչ
ունեցող գազով,
երկրորդը` այն
գազով, որի ![]() բեկման
ցուցիչը պետք է
որոշել: Ինտերֆերենցվող
ճառագայթների
միջև ընթացքի
տարբերությունը`
բեկման
ցուցիչը պետք է
որոշել: Ինտերֆերենցվող
ճառագայթների
միջև ընթացքի
տարբերությունը`
![]() Հետևաբար`
Հետևաբար`
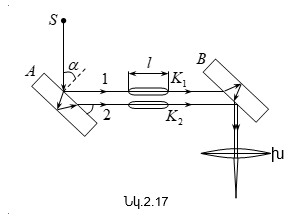
![]()
որտեղ
k-ն ինտերֆերենցիոն
առավելագույնի
կարգն է: ![]() տարբերության
փոփոխությունն
առաջացնում է ինտերֆերենցիոն
շերտերի տեղաշարժ:
l =5 սմ և
տարբերության
փոփոխությունն
առաջացնում է ինտերֆերենցիոն
շերտերի տեղաշարժ:
l =5 սմ և ![]() դեպքում շերտերի
շեղումը կազմում
է նրանց լայնության
0,1 մասը, որը դեռևս
կարելի է բավարար
համարել գրանցելու
համար և համապատասխանում
է
դեպքում շերտերի
շեղումը կազմում
է նրանց լայնության
0,1 մասը, որը դեռևս
կարելի է բավարար
համարել գրանցելու
համար և համապատասխանում
է ![]() տարբերության
աննշան փոփոխությանը.
տարբերության
աննշան փոփոխությանը.
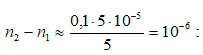
2.10. Ռենտգենյան ինտերֆերաչափեր
Ինպես վերևում նշեցինք, կոհերենտ են այն ալիքները, որոնք պատկանում են տվյալ ատոմի արձակման միևնույն ակտին: Ուրեմն կոհերենտ ալիքներ ստանալու նպատակով անհրաժեշտ է արձակված ճառագայթումը բաժանել երկու հոսքերի և ստիպել, որ դրանք հանդիպեն այն բանից հետո, երբ կանցնեն տարբեր ճանապարհներ: Բոլոր օպտիկական ինտերֆերաչափերն իրականացվել են ըստ այդ սկզբունքի: Ակներև է, որ նույն սկզբունքով կարելի է պատրաստել ռենտգենյան ինտերֆերաչափեր: Սակայն ռենտգենյան ճառագայթների հայտնագործումից հետո դեռևս երկար ժամանակ չիրականացվեց ռենտգենյան ինտերֆերաչափերի պատրաստումը բյուրեղներից: Դա բացատրվում է նրանով, որ ռենտգենյան ալիքների փոքր երկարության պատճառով (ռենտգենյան ալիքների երկարությունները երեք կարգով փոքր են, քան լուսային ալիքներինը), այդ ալիքների ինտերֆերաչափերին ներկայացվում էին ավելի խիստ պայմաններ, և հարկավոր էր հաղթահարել հետևյալ դժվարությունները.
· Հստակ ինտերֆերենցիոն պատկեր ստանալու համար անհրաժեշտ է, վերադրվող ալիքները լինեն խիստ հարթ-զուգահեռ և մեներանգ, որին իրական բյուրեղներում դժվար է հասնել:
· Քանի որ ռենտգենյան ճառագայթների հայելային անդրադարձումն ստացվում է շատ փոքր սահքի անկյունների տիրույթում, ուստի առաջնային փնջի տրոհումը գործնականորեն հնարավոր է միայն ատոմական հարթություններից բրեգյան անդրադարձման օգնությամբ, որը պահանջում է ինտերֆերաչափի առանձին բյուրեղների բավականին ճիշտ կողմնորոշումներ:
· Ինտերֆերենցիոն պատկեր գործնականում չի դիտվում, երբ վերադրվող ալիքների լայնույթներն իրարից զգալիորեն տարբերվում են: Մյուս կողմից, առաջնային փնջի տրոհումն ալիքների, որոնք լայնույթներով քիչ են տարբերվում, նույնպես դյուրին խնդիր չէ:
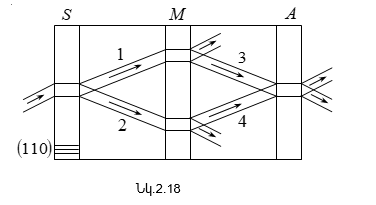
Կատարյալ բյուրեղների աճեցման տեխնիկայի զարգացման և ռենտգենյան ճառագայթների անոմալ կլանման երևույթի հայտնագործման շնորհիվ հնարավոր եղավ հաղթահարել վերևը նշված դժվարությունները և իրականացնել ռենտգենյան ինտերֆերաչափերի պատրաստումը:
Առաջին եռաբյուրեղ ինտերֆերաչափը սիլիցիումի միաբյուրեղից պատրաստվել է Երևանի պետական համալսարանի պինդ մարմնի ֆիզիկայի ամբիոնի գիտահետազոտական լաբորատորիայում: Պատրաստվել են նաև նոր տեսակի ռենտգենյան տարածաչափական ինտերֆերաչափեր Հայաստանի պետական ճարտարագիտական համալսարանի ֆիզիկայի ամբիոնի ռենտգենյան լաբորատորիայում: Այդ ինտերֆերաչափերով ստացվել են մուարի շերտեր և գնահատվել նրա զգայունությունը: Ցույց է տրված, որ ռենտգենյան ինտերֆերաչափի միջոցով կարելի է բաղդատել ատոմական հարթությունների հարյուրերորդական վայրկյանի կարգի ապակողմնորոշումները:
Ռենտգենյան ինտերֆերաչափերի տեսությունը հիմնված է ռենտգենյան ճառագայթների դինամիկ տեսության վրա: Համառոտակի նկարագրենք ինտերֆերաչափի աշխատանքի երկրաչափությունը, այսպես կոչված, Լաուեի տիպի ինտերֆերաչափերը:
Լաուեի
տիպի ամենագործածական
ինտերֆերաչափերից
մեկն ունի հետևյալ
կառուցվածքը: Սիլիցիումի
բարձր կատարելություն
ունեցող միաբյուրեղից
կտրվում են միևնույն
հիմքի վրա գտնվող
բյուրեղներ «ա»
տառի ձևով (նկ.2.18):
Այդ ամբողջ սարքը
փաստորեն մի միաբյուրեղ
է, ուր բոլոր բյուրեղագիտական
հարթություններն
իրար զուգահեռ
են: Եզրերի բյուրեղները
միջին բյուրեղից
գտնվում են հնարավորին
ճշգրիտ միևնույն
հեռավորության
վրա: Հաշվարկները
ցույց են տալիս,
որ ինտերֆերաչափում
բյուրեղների հեռավորությունների
ճշտությունը պետք
է լինի ![]() ոչ
ավելի: Երեք բյուրեղներն
էլ ունեն միևնույն
հաստությունը:
Անդրադարձնող
հարթություններն
ուղղահայաց են
բյուրեղների մեծ
մակերևույթներին
և ինտերֆերաչափի
հիմքի մակերևույթին:
ոչ
ավելի: Երեք բյուրեղներն
էլ ունեն միևնույն
հաստությունը:
Անդրադարձնող
հարթություններն
ուղղահայաց են
բյուրեղների մեծ
մակերևույթներին
և ինտերֆերաչափի
հիմքի մակերևույթին:
Ռենտգենյան
ճառագայթների
փունջը բյուրեղներին
զուգահեռ և հիմքին
ուղղահայաց ճեղքից
ընկնում է առաջին
բյուրեղի անդրադարձնող
հարթության վրա
![]() Բրեգի
անկյան տակ և բաժանվում
է երկու մասի` անկման
և անդրադարձման
ուղղությամբ: Ռենտգենյան
ճառագայթների
դինամիկ տեսության
համաձայն, ընկնող
ռենտգենյան ալիքի
էներգիան բյուրեղի
մեջ, եթե այն բավականաչափ
հաստ է, հոսում
է ատոմական հարթություններով
և բյուրեղից դուրս
գալիս ճեղքվում
է երկու հավասար
ինտենսիվություններ
և միևնույն փուլեր
ունեցող փնջերի,
որոնք միջբյուրեղային
տարածություններում
տարածվում են
անկման և անդրադարձման
ուղղություններով
(նկարում 1 և 2): Առաջին
բյուրեղը կոչվում
է պառակտիչ (S)
: Առաջին բյուրեղից
դուրս եկող 1 և
2 փնջերն ընկնում
են երկրորդ բյուրեղի
վրա և ենթարկվելով
Լաուեի անդրադարձման,
սկիզբ են տալիս
3 և 4 միևնույն
փուլերով ու միևնույն
ինտենսիվությամբ
փնջերին: Երկրորդ
բյուրեղը կոչվում
է հայելի (M): Այդ
3 և 4 փնջերն ընկնում
են ճիշտ իրար վրա
երրորդ բյուրեղի
ներսի (առաջին)
մակերևույթին:
Նրանց էներգիաները
երրորդ բյուրեղի
մեջ հոսում են
իրար զուգահեռ
անդրադարձնող
հարթություններով,
և տեղի է ունենում
ինտերֆերենցիա:
Երրորդ բյուրեղից
դուրս գալիս, այդ
վերադրված փունջը
ճեղքվում է երկու`
իրար հավասար փուլերով
և ինտենսիվություններով
փնջերի, որոնք
տարածվում են
սկզբնական անկման
և անդրադարձման
ոււղղություններով,
և որոնց հետքերը
կարելի է ստանալ
ինտերֆերաչափի
բյուրեղներին
զուգահեռ դրված
ռենտգենյան ֆոտոթիթեղի
վրա: Երրորդ բյուրեղը
կոչվում է վերլուծիչ
(A)` վերադրման և
ինտերֆերենցման
բյուրեղ:
Բրեգի
անկյան տակ և բաժանվում
է երկու մասի` անկման
և անդրադարձման
ուղղությամբ: Ռենտգենյան
ճառագայթների
դինամիկ տեսության
համաձայն, ընկնող
ռենտգենյան ալիքի
էներգիան բյուրեղի
մեջ, եթե այն բավականաչափ
հաստ է, հոսում
է ատոմական հարթություններով
և բյուրեղից դուրս
գալիս ճեղքվում
է երկու հավասար
ինտենսիվություններ
և միևնույն փուլեր
ունեցող փնջերի,
որոնք միջբյուրեղային
տարածություններում
տարածվում են
անկման և անդրադարձման
ուղղություններով
(նկարում 1 և 2): Առաջին
բյուրեղը կոչվում
է պառակտիչ (S)
: Առաջին բյուրեղից
դուրս եկող 1 և
2 փնջերն ընկնում
են երկրորդ բյուրեղի
վրա և ենթարկվելով
Լաուեի անդրադարձման,
սկիզբ են տալիս
3 և 4 միևնույն
փուլերով ու միևնույն
ինտենսիվությամբ
փնջերին: Երկրորդ
բյուրեղը կոչվում
է հայելի (M): Այդ
3 և 4 փնջերն ընկնում
են ճիշտ իրար վրա
երրորդ բյուրեղի
ներսի (առաջին)
մակերևույթին:
Նրանց էներգիաները
երրորդ բյուրեղի
մեջ հոսում են
իրար զուգահեռ
անդրադարձնող
հարթություններով,
և տեղի է ունենում
ինտերֆերենցիա:
Երրորդ բյուրեղից
դուրս գալիս, այդ
վերադրված փունջը
ճեղքվում է երկու`
իրար հավասար փուլերով
և ինտենսիվություններով
փնջերի, որոնք
տարածվում են
սկզբնական անկման
և անդրադարձման
ոււղղություններով,
և որոնց հետքերը
կարելի է ստանալ
ինտերֆերաչափի
բյուրեղներին
զուգահեռ դրված
ռենտգենյան ֆոտոթիթեղի
վրա: Երրորդ բյուրեղը
կոչվում է վերլուծիչ
(A)` վերադրման և
ինտերֆերենցման
բյուրեղ:

Եթե բյուրեղի բյուրեղային ցանցերը թերություններ չունեն, իրար խիստ զուգահեռ են և ունեն միևնույն միջհարթությունային հեռավորությունը, ինտերֆերաչափից դուրս եկած փնջերի հետքերը կլինեն ճեղքի սև պատկերները` համասեռ ինտենսիվությամբ: Իսկ եթե կա տարբեր բյուրեղների կամ միևնույն բյուրեղի տարբեր մասերի միջհարթությունային հեռավորությունների տարբերություն կամ էլ հարթությունների պտույտ իրար նկատմամբ, հետքերի մեջ առաջ կգան մթին և լուսավոր շերտեր, որոնք կոչվում են մուարի պատկերներ: Մուարի շերտերը կլինեն անդրադարձնող հարթություններին ուղղահայաց, եթե առաջացել են հարթությունների` իրար նկատմամբ պտույտի հետևանքով (նկ.2.19ա), իսկ եթե առաջացել են միջհարթությունային հեռավորությունների տարբերության պատճառով` կլինեն անդրադարձնող հարթություններին զուգահեռ (նկ.2.19բ): Եթե ինտերֆերաչափի բյուրեղների ցանցերը միաժամանակ պարունակում են և´ հարթությունների պտույտ, և´ միջհարթությունային հեռավորությունների տարբերություն, մուարի շերտերը կստացվեն թեք` նշված երկու մասնավոր դեպքերի զուգորդումից տարբեր կետերում (կախված հարթությունների պտույտների և հեռավորությունների տարբերությունների մեծությունից կունենան տարբեր ուղղություններ (նկ.2.19գ): Դիսլոկացիաների առկայության դեպքում համապատասխան տեղերում մուարի պատկերները կաղավաղվեն (նկ.2.19դ):
Մեծ զգայնությունը, որով օժտված են ռենտգենյան ինտերֆերաչափերը, տալիս են հետևյալ հնարավորությունները.
1. Ինտերֆերաչափական համակարգերում մուարի պատկերներով աննշան դիլատացիոն և ռոտացիոն խանգարումների ճշգրիտ չափումը:
Եռաբյուրեղ
ինտերֆերաչափը
կարելի է օգտագործել
բյուրեղների կատարելության
աստիճանը հետազոտելու
նպատակով: Այդպիսի
հետազոտության
օրինակ ներկայացված
է մուարի տեղագրության
վրա (նկ.2.20), որն ստացվել
է բարձր կատարելության
սիլիցիումի միաբյուրեղից
պատրաստված ինտերֆերաչափից
220 անդրադարձումով:
Այս դեպքում ինտերֆերաչափի
առանցքը (S-A) դասավորված
է բյուրեղի աճեցման
առանցքի երկայնքով:
Հետևաբար մուարի
պատկերը պետք է
ցույց տա աճեցման
հնարավոր անհամասեռությունները:
Քանի որ տեղագրության
վրա ![]() անդրադարձնող
հարթությունը
դասավորված է
ուղղաձիգ, ապա
մուարի ուղղաձիգ
շերտերը տեղագրության
վերին մասում պատկանում
են դիլատացիոն
մուարին: Պարզվում
է, որ հարաբերական
դեֆորմացիաները`
անդրադարձնող
հարթությունը
դասավորված է
ուղղաձիգ, ապա
մուարի ուղղաձիգ
շերտերը տեղագրության
վերին մասում պատկանում
են դիլատացիոն
մուարին: Պարզվում
է, որ հարաբերական
դեֆորմացիաները`
![]() է,
իսկ ցանցի տեղային
պտույտը`
է,
իսկ ցանցի տեղային
պտույտը` ![]() Այսպիսով,
բյուրեղը, որից
պատրաստված է ինտերֆերաչափը,
համարյա կատարյալ
է և դիսլոկացիաներ
չունի:
Այսպիսով,
բյուրեղը, որից
պատրաստված է ինտերֆերաչափը,
համարյա կատարյալ
է և դիսլոկացիաներ
չունի:
2. Ռենտգենյան ճառագայթման հաճախության լայն միջակայքում բյուրեղային և ամորֆ նյութերի, ինչպես նաև հեղուկների բեկման ցուցչի ճշգրիտ չափումը: Դրա համար հարկավոր է սեպաձև նմուշը տեղադրել ինտերֆերաչափի M և A բյուրեղների միջև, այնպես, որ բեկող կողը զուգահեռ լինի բյուրեղներին և ուղղահայաց` ինտերֆերաչափի հիմքին:
3. Բյուրեղային ցանցի պարամետրերի բացարձակ որոշումը:
4. Կառուցվածքային գործոնի չափումը մեծ ճշտությամբ:
5. Տարբեր տեսակի արատներով և դեֆորմացիաներով առաջացացած բյուրեղային ցանցի կառուցվածքային խանգարումների ուսումնասիրություն: Հնարավոր է նաև ըստ ստացվող ինտերֆերենցիոն պատկերի տեսքի` որոշել բարակ թաղանթների որակը:
ԼՈՒՅՍԻ ԴԻՖՐԱԿՑԻԱՆ
3.1 Հյուգենս - ֆրենելի սկզբունքը
Լույսի ինտերֆերենցի երևույթները, իրենց ամբողջ բազմազանությամբ, լուսային պրոցեսների ալիքային բնույթ ունենալու ամենահամոզիչ ապացույցն են: Սակայն ալիքային պատկերացման վերջնական հաղթանակն անհնարին կլիներ, եթե ալիքային տեսակետից չմեկնաբանվեր հիմնական և փորձով լավ հաստատվող լույսի ուղղագիծ տարածման օրենքը:
Լույսի դիֆրակցիա է կոչվում այն երևույթների համախումբը, որոնք դիտվում են խիստ անհամասեռություններ ունեցող միջավայրում լույսի տարածման ժամանակ և կապված են երկրաչափական օպտիկայից եղած շեղումների հետ: Մասնավորապես, դիֆրակցիան հանգեցնում է լուսային ալիքների կողմից արգելքների շրջանցմանը և լույսի թափանցմանը երկրաչափական ստվերի տիրույթը: Դիֆրակցիայի դիտման հնարավորությունը կախված է լուսային ալիքի և անհամասեռությունների չափերի հարաբերակցությունից: Դիֆրակցիայի երևույթը բացատրվում է Ֆրենելի կողմից առաջարկված մեթոդով` օգտագործելով Հյուգենսի սկզբունքը:
Համաձայն Հյուգենսի` ալիքի ճակատի յուրաքանչյուր կետ կարելի է դիտարկել որպես տատանումների ինքնուրույն աղբյուր: Հյուգենսի սկզբունքը հնարավորություն է տալիս լուծել միայն լուսային ալիքի ճակատի տարածման ուղղության խնդիրը և ըստ էության չի շոշափում տարբեր ուղղությամբ տարածվող ալիքների ինտենսիվության հարցը: Այդ պակասը լրացրեց Ֆրենելը, որը Հյուգենսի սկզբունքի մեջ ֆիզիկական իմաստ մտցրեց, լրացնելով այն ինտերֆերենցիայի գաղափարով: Դրա շնորհիվ տարրական ալիքների պարուրիչը, որը Հյուգենսը զուտ ձևականորեն էր մտցրել, ստացավ պարզ ֆիզիկական բովանդակություն, որպես մի մակերևույթ, որտեղ տարրական ալիքների փոխադարձ ինտերֆերենցի շնորհիվ արդյունարար ալիքն ունի զգալի ինտենսիվություն: Այսպես ձևափոխված Հյուգենս-Ֆրենելի սկզբունքն ալիքային օպտիկայի հիմնական սկզբունքն է դառնում և հնարավորություն է տալիս հետազոտել արդյունարար ալիքի տարբեր ուղղությամբ ունեցած ինտենսիվությունների հարցերը, այսինքն` լուծել լույսի դիֆրակցիայի վերաբերյալ խնդիրներ: Դրան համապատասխան լուծվեց լույսի ուղղագիծ տարածման օրենքի կիրառելիության սահմանի վերաբերյալ խնդիրը, և Հյուգենս-Ֆրենելի սկզբունքը դարձավ կիրառելի` ցանկացած երկարության ալիքի տարածման օրենքը պարզելու համար:
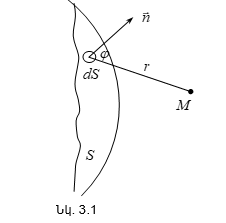
Արդյունարար ալիքի լայնույթը (ինտենսիվությունը) գտնելու համար, համաձայն Ֆրենելի` Հյուգենսի սկզբունքը պետք է ձևակերպել հետւյալ կերպ: Դիցուք S-ը որևէ աղբյուրից արտածվող լույսի ալիքային մակերևույթներից մեկն է (նկ.3.1): Այդ մակերևույթի առջևում գտնվող M կետում լուսային ալիքի երևույթը կարելի է որոշել ըստ Ֆրենելի սկզբունքի` հետևյալ նկատառումներով: Մակերևույթի յուրաքանչյուր տարր ծառայում է որպես երկրորդային սֆերիկ ալիքի աղբյուր, որի լայնույթը համեմատական է տարրի մեծությանը: Սֆերիկ ալիքի լայնույթը նվազում է աղբյուրից ունեցած r հեռավորության հետ 1/r օրենքով: Հետևաբար, ալիքային մակերևույթի յուրաքանչյուր dS տեղամասից M կետն է գալիս այսպիսի տատանում`
![]()
որտեղ
![]() տատանման
փուլն է S ալիքային
մակերևույթի գտնված
տեղում, k-ն ալիքային
թիվն է, r -ը մակերևույթի
dS տարրի հեռավորությունն
է M կետից:
տատանման
փուլն է S ալիքային
մակերևույթի գտնված
տեղում, k-ն ալիքային
թիվն է, r -ը մակերևույթի
dS տարրի հեռավորությունն
է M կետից: ![]() մեծությունը
որոշվում է dS -ի
գտնված տեղում
լուսային տատանումների
լայնույթով: Համեմատականության
K գործակիցը Ֆրենելն
ընդունում էր նվազող,
երբ dS-ի
մեծությունը
որոշվում է dS -ի
գտնված տեղում
լուսային տատանումների
լայնույթով: Համեմատականության
K գործակիցը Ֆրենելն
ընդունում էր նվազող,
երբ dS-ի ![]() նորմալի
և dS -ից դեպի M կետը
ուղղության միջև
կազմված
նորմալի
և dS -ից դեպի M կետը
ուղղության միջև
կազմված ![]() անկյունը
մեծանում և դառնում
զրո, երբ
անկյունը
մեծանում և դառնում
զրո, երբ ![]()
Արդյունարար տատանումն M կետում ստացվում է որպես (3.1) տատանումների վերադրում, որոնք վերցվում են ամբողջ S ալիքային մակերևույթի համար.
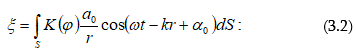
(3.2) բանաձևը Հյուգենս-Ֆրենելի սկզբունքի անալիտիկ արտահայտությունն է: Ընդհանուր դեպքում (3.2)-ով հաշվումները շատ դժվար են: Սակայն Ֆրենելը, դիտարկելով երկրորդային ալիքների փոխադարձ ինտերֆերենցիան, օգտագործեց մի վերին աստիճանի մատչելի մեթոդ, որը փոխարինում է բարդ հաշվարկները և ալիքների տարածման խնդիրը վերլուծելիս ունի ընդհանուր նշանակություն: Այս մեթոդը ստացավ ֆրենելյան գոտիների մեթոդ անվանումը:
Հյուգենս-Ֆրենելի սկզբունքից օգտվելով` գտնենք լուսային ալիքի տատանման լայնույթը, որը հարուցվում է համասեռ միջավայրում S կետային լույսի աղյուրից տարածվող սֆերիկ ալիքով M կետում (նկ.3.2): Այդպիսի ալիքի ալիքային մակերևույթը համաչափ է SM ուղղի նկատմամբ:
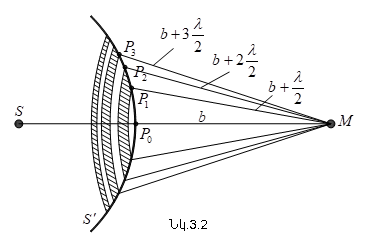
Ֆրենելն
ալիքային մակերևույթը
բաժանեց օղակային
գոտիների, որոնք
կառուցված են այնպես,
որ դրանց եզրերի
հեռավորությունները
մինչև B կետը իրարից
տարբերվեն ![]()
![]() ալիքի երկարությունն
է այն միջավայրում,
որտեղ տարածվում
է ալիքը: Դժվար
չէ տեսնել, որ m-րդ
գոտու արտաքին
եզրից մինչև M
կետը եղած
ալիքի երկարությունն
է այն միջավայրում,
որտեղ տարածվում
է ալիքը: Դժվար
չէ տեսնել, որ m-րդ
գոտու արտաքին
եզրից մինչև M
կետը եղած ![]() հեռավորությունը
կարելի է ներկայացնել
հետևյալ տեսքով`
հեռավորությունը
կարելի է ներկայացնել
հետևյալ տեսքով`
![]()
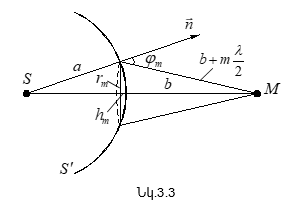
որտեղ
b-ն ալիքային մակերևույթի
P0 գագաթի հեռավորությունն
է M կետից: Երկու
հարևան գոտիների
այն կետերից, որոնք
գտնվում են գոտիների
արտաքին եզրերի
մոտ կամ գոտիների
մեջտեղում, M կետը
եկող տատանումները
կլինեն հակափուլում:
Հետևաբար, ամբողջապես
վերցրած յուրաքանչյուր
գոտուց առաջացած
արդյունարար
տատանումները
ևս հարևան գոտիների
համար ըստ փուլի`
կտարբերվեն ![]() Ֆրենելի
գոտիներով ստեղծվող
տատանումների
լայնույթը գնահատելու
համար որոշենք
այդ գոտիների մակերեսները:
m-րդ գոտու արտաքին
եզրով ալիքային
մակերևույթից
առանձնացվում
է
Ֆրենելի
գոտիներով ստեղծվող
տատանումների
լայնույթը գնահատելու
համար որոշենք
այդ գոտիների մակերեսները:
m-րդ գոտու արտաքին
եզրով ալիքային
մակերևույթից
առանձնացվում
է ![]() բարձրության
գնդային սեգմենտ
(նկ.3.3): m-րդ սեգմենտի
մակերեսը հավասար
է`
բարձրության
գնդային սեգմենտ
(նկ.3.3): m-րդ սեգմենտի
մակերեսը հավասար
է` ![]() իսկ
(m-1)-րդինը`
իսկ
(m-1)-րդինը` ![]() Այդ դեպքում
m-րդ գոտու մակերեսը
կարելի է ներկայացնել
հետևյալ տեսքով.
Այդ դեպքում
m-րդ գոտու մակերեսը
կարելի է ներկայացնել
հետևյալ տեսքով.
![]()
Նկ.3.3-ից հետևում է`
![]()
որտեղ
![]() ալիքային
մակերևույթի շառավիղն
է,
ալիքային
մակերևույթի շառավիղն
է, ![]() m-րդ գոտու
արտաքին եզրի շառավիղը:
Քառակուսի բարձրացնելով
փակագծերի միջի
արտահայտությունները`
կստանանք
m-րդ գոտու
արտաքին եզրի շառավիղը:
Քառակուսի բարձրացնելով
փակագծերի միջի
արտահայտությունները`
կստանանք
![]()
որտեղից
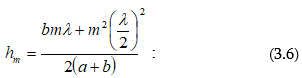
Սահմանափակվելով
ոչ շատ մեծ m-երի
դիտարկումով` ![]() փոքրության
պատճառով կարելի
է անտեսել
փոքրության
պատճառով կարելի
է անտեսել ![]() պարունակող
գումարելին, որի
դեպքում (3.6)-ից կստանանք`
պարունակող
գումարելին, որի
դեպքում (3.6)-ից կստանանք`

Հետևաբար

իսկ Ֆրենելի m-րդ գոտու մակերեսը`
![]()
Ստացված արտահայտությունը կախում չունի m-ից: Հետևաբար, մեծ m -ի դեպքում Ֆրենելի գոտիների մակերեսները մոտավորապես նույնն են: Գնահատենք Ֆրենելի գոտիների շառավիղները:
Ըստ
(3.5)-ի` ![]() Ոչ
շատ մեծ m -ի դեպքում
սեգմենտի բարձրությունը`
Ոչ
շատ մեծ m -ի դեպքում
սեգմենտի բարձրությունը`
![]() ուստի
կարելի է ընդունել,
որ
ուստի
կարելի է ընդունել,
որ ![]() Տեղադրելով
վերջինի մեջ
Տեղադրելով
վերջինի մեջ ![]() համար (3.7)
արտահայտութjունը`
կգտնենք Ֆրենելի
m -րդ գոտու շառավիղը.
համար (3.7)
արտահայտութjունը`
կգտնենք Ֆրենելի
m -րդ գոտու շառավիղը.

Եթե
ընդունենք, որ
![]() ապա
առաջին (կենտրոնական)
գոտու շառավղի
համար ստացվում
է
ապա
առաջին (կենտրոնական)
գոտու շառավղի
համար ստացվում
է ![]() արժեքը:
Հաջորդ գոտիների
շառավիղներն աճում
են
արժեքը:
Հաջորդ գոտիների
շառավիղներն աճում
են ![]() համեմատական:
համեմատական:
Քանի
որ հարևան գոտիներով
դիտման կետը եկած
տատանումների
փուլերը տարբերվում
են ![]() -ով, ուստի
M կետում արդյունարար
տատաման E լայնույթը
կարելի է գտնել
հանրահաշվորեն.
-ով, ուստի
M կետում արդյունարար
տատաման E լայնույթը
կարելի է գտնել
հանրահաշվորեն.
![]()
Գոտիների
ուղարկած լուսային
տատանումների
լայնույթները
նվազում են ինչպես
ալիքային մակերևույթի
նորմալով և դիտման
կետը գնացող ուղղությունով
կազմած ![]() անկյան
մեծացմամբ, այնպես
էլ գոտու համարի
մեծացումով, ինչպես
1/r Հետևաբար, կարելի
գրել
անկյան
մեծացմամբ, այնպես
էլ գոտու համարի
մեծացումով, ինչպես
1/r Հետևաբար, կարելի
գրել
![]()
(3.11) –ից
հետևում է, որ ![]()
(3.11)–ը ներկայացնենք հետևյալ տեսքով`
![]()
![]() մոնոտոն
նվազման հետևանքով
կարելի է ընդունել,
որ
մոնոտոն
նվազման հետևանքով
կարելի է ընդունել,
որ
![]()
Ուրեմն` (3.14) պայմանի դեպքում փակագծերի միջի արտահայտությունները հավասար կլինեն զրոյի, և (3.13)-ը կնդունի հետևյալ տեսքը`
![]()
Վերջինից հետևում է, որ M կետում սֆերիկ ալիքային մակերևույթի ստեղծած լայնույթը հավասար է միայն կենտրոնական գոտու ստեղծած լայնույթի կեսին: Ըստ վերը նշված գնահատման` կենտրոնական գոտին ունի միլիմետրերի մասերի կարգի չափեր: Հետևաբար, լույսը S կետից M կետն է տարածվում կարծես թե նեղ, ուղիղ կանալով, այսինքն` գործնականորեն ուղղագիծ:
Եթե ալիքի ճանապարհին դնենք ոչ թափանցիկ էկրան, որն ունի Ֆրենելի միայն կենտրոնական գոտին բաց պահող անցք, ապա M կետում լայնույթը հավասար կինի E1-ի, այսինքն` երկու անգամ կգերազանցի (3.15) լայնույթին: Այտեղից էլ հետևում է, որ լույսի ինտենսիվությունն M կետում չորս անգամ ավելի մեծ կլինի, քան S և M կետերի միջև արգելք չլինելու դեպքում:
3.3. Ֆրենելի դիֆրակցիան պարզագույն արգելքներից
Տարբերում են դիֆրակցիայի երկու դեպք: Եթե լույսի S աղբյուրը և M դիտման կետը դասավորված են արգեքից այնքան հեռու, որ արգելքի վրա ընկնող և դեպի M կետը գնացող ճառագայթները գործնականորեն առաջացնում են զուգահեռ փնջեր, ասում են Ֆրաունհոֆերի դիֆրակցիա կամ դիֆրակցիա զուգահեռ ճառագայթներում: Հակառակ դեպքում ասում են Ֆրենելի դիֆրակցիա: Լայնույթների գումարման հանրահաշվական եղանակը, որը քննարկվեց վերևում, թույլ է տալիս լուծելու դիֆրակցիայի պարզագույն խնդիրները:
1. Դիֆրակցիան
կլոր անցքից: S աղբյուրից
տարածվող գնդային
ալիքի ճանապարհին
տեղադրենք ոչ թափանցիկ
էկրան, որի վրա
բացված է ![]() շառավղով փոքր
անցք (նկ.3.4):
շառավղով փոքր
անցք (նկ.3.4):
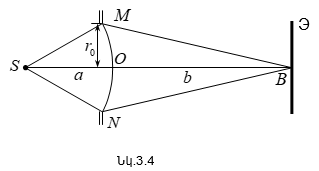
Եթե ![]() և b հեռավորությունները
բավարարում են
հետևյալ պայմանին`
և b հեռավորությունները
բավարարում են
հետևյալ պայմանին`

ապա անցքը բացված կթողնի Ֆրենելի առաջին m գոտիները: (3.16)-ը լուծելով m -ի նկատմամբ` կստանանք Ֆրենելի բաց գոտիների թիվը.

(3.11)-ին համաձայն B կետում տատանման լայնույթը`
![]()
(3.18) արտահայտությունը գրելով (3.13)-ի տեսքով` կարելի է ցույց տալ, որ
![]()
Ստացված արտահայտության մեջ «+» նշանը վերցվում է կենտ գոտիների համար, «-» նշանը` զույգ գոտիների համար:
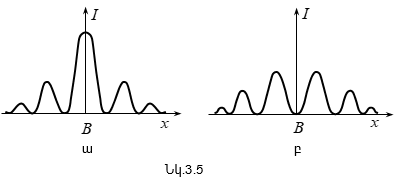
(3.19)-ից
հետևում է, որ եթե
անցքի մեջ տեղավորվում
են զույգ թվով
գոտիներ, ապա B
կետում կլինի խավար,
քանի որ B կետի
հեռավորությունները
հարևան գոտիների
համապատասխան
մասերից տարբերվում
են ![]() և
հետևաբար տատանումները
փոխադարձաբար
իրար մարում են:
Կենտ գոտիների
դեպքում B կետում
կլինի լույս: Այսպիսով,
կլոր անցքից ստացվող
դիֆրակցիոն պատկերը
իրար հաջորդող
լուսավոր և խավար
համակենտրոն օղակներ
են: Պատկերենք
լույսի ինտենսիվության
բաշխվածությունը
կլոր անցքով դիֆրակցիայի
համար: B կետը էկրանի
կենտրոնն է, x-ը`
դիֆրակցիոն պատկերի
կենտրոնից եղած
հեռավորությունը:
Նկ.3.5ա-ի համար m -ը
կենտ է, նկ.3.5բ-ի դեպքում
m-ը զույգ է:
և
հետևաբար տատանումները
փոխադարձաբար
իրար մարում են:
Կենտ գոտիների
դեպքում B կետում
կլինի լույս: Այսպիսով,
կլոր անցքից ստացվող
դիֆրակցիոն պատկերը
իրար հաջորդող
լուսավոր և խավար
համակենտրոն օղակներ
են: Պատկերենք
լույսի ինտենսիվության
բաշխվածությունը
կլոր անցքով դիֆրակցիայի
համար: B կետը էկրանի
կենտրոնն է, x-ը`
դիֆրակցիոն պատկերի
կենտրոնից եղած
հեռավորությունը:
Նկ.3.5ա-ի համար m -ը
կենտ է, նկ.3.5բ-ի դեպքում
m-ը զույգ է:
2. Դիֆրակցիան
կլոր սկավառակից: Լույսի
S կետային աղբյուրի
և B դիտակետի
միջև տեղադրենք![]() շառավղով
ոչ թափանցիկ կլոր
սկավառակ (նկ.3.6)
այնպես, որ այն
փակի Ֆրենելի m
առաջին գոտիները:
Հանրահաշվական
գումարման ճանապարհով
B կետում արդյունարար
լայնույթի համար
կստանանք`
շառավղով
ոչ թափանցիկ կլոր
սկավառակ (նկ.3.6)
այնպես, որ այն
փակի Ֆրենելի m
առաջին գոտիները:
Հանրահաշվական
գումարման ճանապարհով
B կետում արդյունարար
լայնույթի համար
կստանանք`
![]()
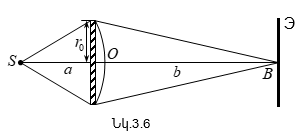
Քանի որ փակագծերի միջի արտահայտությունները մոտ են զրոյի, ստանում ենք.
![]()
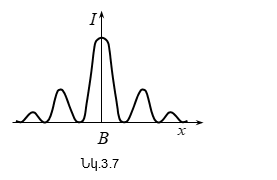
Այսպիսով, անթափանց սկավառակի հետևում դրված էկրանի կենտրոնում լուսավորվածությունը միշտ զրոյից տարբեր է, և դիֆրակցիոն պատկերն ունենում է իրար հաջորդող լուսավոր և խավար օղակների տեսք: Պատկերի կենտրոնում ցանկացած m-ի դեպքում (ինչպես զույգ, այնպես էլ կենտ) ստացվում է լուսավոր բիծ: Լույսի I ինտեսիվության կախումը պատկերի կենտրոնից ունեցած x հեռավորությունից բերված է նկ.3.7-ում:
3.
Ֆրաունհոֆերի
դիֆրակցիան ճեղքից: Դիտարկենք
![]() լայնության
նեղ ճեղքը, որը
լուսավորված
է
լայնության
նեղ ճեղքը, որը
լուսավորված
է ![]() ալիքի երկարության
զուգահեռ մեներանգ
ճառագայթների
փնջով (նկ.3.8): Հյուգենսի
սկզբունքի համաձայն`
ճեղքի յուրաքանչյուր
լուսավորված կետ
տատանման աղբյուր
է, այսինքն` նոր
երկրորդային սֆերիկ
ալիքների կենտրոն:
Այդ կոհերենտ ալիքները
ճեղքի մյուս կողմում
տարածվում են բոլոր
ուղղություններով:
L ոսպնյակի կիզակետային
հարթության մեջ
տեղավորված էկրանի
յուրաքանչյուր
կետում կհավաքվեն
ճեղքի տարբեր կետերից
եկող զուգահեռ
ճառագայթները,
որոնք կունենան
ընթացքների տարբերություն,
հեևաբար կառաջացնեն
ինտերֆերենցիոն
պատկեր: Էկրանի
վրա կարող են հանդիպել
միևնույն փուլերով
ալիքներ, այդ դեպքում
տեղի է ունենում
տատանումների
ուժեղացում, հակառակ
փուլերի դեպքում`
տատանումների
թուլացում:
ալիքի երկարության
զուգահեռ մեներանգ
ճառագայթների
փնջով (նկ.3.8): Հյուգենսի
սկզբունքի համաձայն`
ճեղքի յուրաքանչյուր
լուսավորված կետ
տատանման աղբյուր
է, այսինքն` նոր
երկրորդային սֆերիկ
ալիքների կենտրոն:
Այդ կոհերենտ ալիքները
ճեղքի մյուս կողմում
տարածվում են բոլոր
ուղղություններով:
L ոսպնյակի կիզակետային
հարթության մեջ
տեղավորված էկրանի
յուրաքանչյուր
կետում կհավաքվեն
ճեղքի տարբեր կետերից
եկող զուգահեռ
ճառագայթները,
որոնք կունենան
ընթացքների տարբերություն,
հեևաբար կառաջացնեն
ինտերֆերենցիոն
պատկեր: Էկրանի
վրա կարող են հանդիպել
միևնույն փուլերով
ալիքներ, այդ դեպքում
տեղի է ունենում
տատանումների
ուժեղացում, հակառակ
փուլերի դեպքում`
տատանումների
թուլացում:
Օրինակ`
դիտարկենք նորմալի
հետ ![]() անկյուն
կազմող ճառագայթների
տարածումը և որոշենք
ինտերֆերենցի
արդյունքը: B կետից
1 ճառագայթի վրա
իջեցնենք ուղղահայաց:
Ակնհայտ է, որ
անկյուն
կազմող ճառագայթների
տարածումը և որոշենք
ինտերֆերենցի
արդյունքը: B կետից
1 ճառագայթի վրա
իջեցնենք ուղղահայաց:
Ակնհայտ է, որ
![]() Նկ.3.8-ից երևում
է
Նկ.3.8-ից երևում
է ![]() լայնության
ճեղքի եզրերից
դուրս եկած ճառագայթների
ընթացքների տարբերությունը`
լայնության
ճեղքի եզրերից
դուրս եկած ճառագայթների
ընթացքների տարբերությունը`
![]()
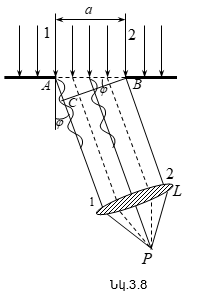
Ալիքային
մակերևույթի բաց
մասը տրոհենք հավասար
լայնության գոտիների
այնպես, որ հարևան
գոտիների եզրերից
մինչև դիտարկվող
P կետը ընթացքի
տարբերությունը
լինի ![]() Ընթացքի
տարբերությունը
փուլերի տարբերության
հետ կապված է
Ընթացքի
տարբերությունը
փուլերի տարբերության
հետ կապված է ![]() առնչությամբ:
Տվյալ դեպքում
հարևան երկու գոտիների
համար
առնչությամբ:
Տվյալ դեպքում
հարևան երկու գոտիների
համար ![]() և այդ գոտիներից
եկած ճառագայթներն
էկրանի P կետում
հանդիպում են հակառակ
փուլերով և միմյանց
մարում են: Տվյալ`
և այդ գոտիներից
եկած ճառագայթներն
էկրանի P կետում
հանդիպում են հակառակ
փուլերով և միմյանց
մարում են: Տվյալ`
![]() ընթացքի
տարբերության
դեպքում գոտիների
k թիվը ճեղքում
հավասար կլինի
ընթացքի
տարբերության
դեպքում գոտիների
k թիվը ճեղքում
հավասար կլինի
![]()
Եթե
k-ն զույգ թիվ է
(k=2m), ապա հարևան
գոտիների յուրաքանչյուր
զույգի կողմից
առաքված տատանումները,
P կետում վերադրվելով,
փոխադարձաբար
կմարեն միմյանց,
և արդյունարար
լայնույթը հավասար
կլինի զրոյի: Գոտիների
կենտ թվի դեպքում
(k=2m+1) գոտիներից
մեկի ազդեցությունը
մնում է չկոմպենսացված,
և P կետում դիտվում
է տատանումների
ուժեղացում: Այսպիսով,
![]() լայնություն
ունեցող մեկ ճեղքի
համար ինտերֆերենցիոն
նվազագույնի պայմանը
կլինի.
լայնություն
ունեցող մեկ ճեղքի
համար ինտերֆերենցիոն
նվազագույնի պայմանը
կլինի.
![]()
իսկ առավելագույնի պայմանը`
![]()
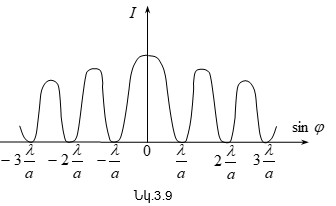
Լույսի
ինտենսիվության
բաշխումը ոսպնյակի
կիզակետային հարթության
մեջ ցույց է տրված
նկ.3.9-ում: Դիֆրակցիոն
շերտերի դիրքը
որոշող ![]() մեծությունը,
իսկ փոքր անկյունների
դեպքում իրենք`
մեծությունը,
իսկ փոքր անկյունների
դեպքում իրենք`
![]() անկյունները,
համեմատական են
ալիքի երկարություններին:
Հետևաբար, ալիքի
տարբեր երկարություն
ունեցող ճառագայթների
համար էկրանի վրա
լուսավոր շերտերն
իրար վրա չեն վերադրվի,
այլ կդասավորվեն
իրար զուգահեռ`
ալիքի երկարության
մեծացման կարգով:
Սպիտակ լույսը
ճեղքով անցնելու
դեպքում տարրալուծվում
է բաղադրիչ մասերի`
էկրանի վրա առաջացնելով
դիֆրակցիոն պատկեր:
Նկատենք, որ դիֆրակցիան
դիտելու համար
անհրաժեշտ է գոնե
առաջին մաքսիմումի
անկյունները,
համեմատական են
ալիքի երկարություններին:
Հետևաբար, ալիքի
տարբեր երկարություն
ունեցող ճառագայթների
համար էկրանի վրա
լուսավոր շերտերն
իրար վրա չեն վերադրվի,
այլ կդասավորվեն
իրար զուգահեռ`
ալիքի երկարության
մեծացման կարգով:
Սպիտակ լույսը
ճեղքով անցնելու
դեպքում տարրալուծվում
է բաղադրիչ մասերի`
էկրանի վրա առաջացնելով
դիֆրակցիոն պատկեր:
Նկատենք, որ դիֆրակցիան
դիտելու համար
անհրաժեշտ է գոնե
առաջին մաքսիմումի
![]() առկայությունը:
առկայությունը:
4. Դիֆրակցիան N ճեղքերից (դիֆրակցիոն ցանց): Դիֆրակցիոն ցանցը միանման, անթափանց միջնորմներով բաժանված, միևնույն լայնությունն ունեցող ճեղքերի շարք է: Ապակու մակերևույթի վրա, իրարից միևնույն հեռավորության վրա` կտրիչով գծում են զուգահեռ շտրիխների շարք: Գծված մասերը լույսը ցրում են և գործնականորեն անթափանց են: Չվնասված մասերը շատ նեղ դիֆրակցիոն ճեղքեր են: Ներկայումս պատրաստվող լավ դիֆրակցիոն ցանցերը մեկ միլիմետրի վրա ունենում են մինչև 1700 ճեղք: Այդպիսի ցանցերի պատկերները պատրաստվում են ժելատինի կամ պլաստմասսայի վրա պատճենահանելու ճանապարհով: Ոչ մեծ թվով շտրիխներ ունեցող դիֆրակցիոն ցանցերը պատրաստվում են լուսանկարչական մեթոդով:
Դիտարկենք
դիֆրակցիան N
ճեղքերից: Միանման
ճեղքերի համակարգով
լույսի անցման
դեպքում (դիֆրակցիոն
ցանց) դիֆրակցիոն
պատկերը բավականաչափ
բարդանում է: Այդ
դեպքում առանձին
ճեղքերից դիֆրակցիայի
ենթարկվող ճառագայթները
ոսպնյակի կիզակետային
հարթության մեջ
վերադրվում են
և տալիս ինտերֆերենցիոն
պատկեր: Եթե ճեղքերի
թիվը N է, ապա իրար
հետ ինտերֆերենցվում
են N փնջեր: Դիցուք
![]() ալիքի երկարություն
ունեցող լույսը
նորմալի ուղղությամբ
ընկնում է ցանցի
վրա (նկ.3.10):
ալիքի երկարություն
ունեցող լույսը
նորմալի ուղղությամբ
ընկնում է ցանցի
վրա (նկ.3.10):
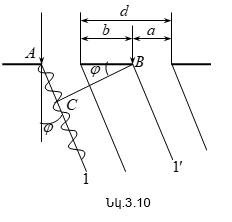
Ճեղքերի
մյուս կողմում,
շնորհիվ դիֆրակցիայի,
ճառագայթները
կտարածվեն տարբեր
ուղղություններով:
Դիտարկենք այն
ճառագայթները,
որոնք ցանցի նորմալի
հետ կազմում են![]() անկյուն:
անկյուն:
![]() ճառագայթների
միջև ընթացքների
տարբերությունը
հավասար է`
ճառագայթների
միջև ընթացքների
տարբերությունը
հավասար է`
![]()
որտեղ
![]() կոչվում
է ցանցի հաստատուն
կամ պարբերություն:
կոչվում
է ցանցի հաստատուն
կամ պարբերություն:
Ընթացքի
այդ տարբերությանը
համապատասխանում
է այդ ճառագայթների
միջև փուլերի հետևյալ
տարբերությունը`
![]()
Եթե
![]() նշանակում
է, որ
նշանակում
է, որ ![]() ճառագայթները
գալիս են միևնույն
փուլերով և ուժեղացնում
են միմյանց: Այդ
դեպքում առավելագույնների
առաջացման պայմանը
կունենա հետևյալ
տեսքը`
ճառագայթները
գալիս են միևնույն
փուլերով և ուժեղացնում
են միմյանց: Այդ
դեպքում առավելագույնների
առաջացման պայմանը
կունենա հետևյալ
տեսքը`
![]()
![]()
Առավելագույնները, որոնք բավարարում են (4) պայմանին, կոչվում են գլխավոր: Ակնհայտ է, որ նախկին նվազագույնների դիրքերը չեն փոխվի, քանի որ այն ուղղությունները, որոնցով ճեղքերից ոչ մեկը լույս չի ուղարկում, այն չի ստանում նաև N ճեղքերի դեպքում: Ինչպես մեկ ճեղքի, այնպես էլ N ճեղքերի համար նվազագույնի պայմանը նույնն է`
![]()
Երկու հարևան գլխավոր առավելագույնների միջև եղած միջակայքերում կան (N-1)-ական լրացուցիչ նվազագույններ, որոնք բաժանված են երկրորդային առավելագույններով (նկ.3.11), որոնց ինտենսիվությունները զգալիորեն փոքր են գլխավոր առավելագույնների ինտենսիվություններից:
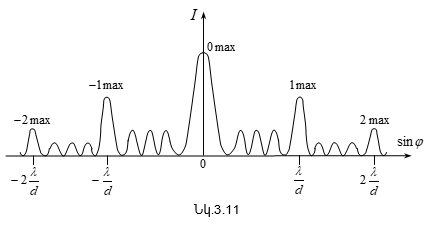
Այդ նվազագույններն առաջանում են այն ուղղություններով, որոնց համար առանձին ճեղքերից առաջացած տատանումները փոխադարձաբար մարում են իրար: Լրացուցիչ նվազագույնների ուղղությունները որոշվում են հետևյալ պայմանից`
![]()
(3.24)
պայմանից հետևում
է, որ n=0-ի դեպքում
![]() Էկրանի վրա
ստացվում է դիֆրակցիոն
առավելագույն,
որը կոչվում է
զրոյական: Երբ
Էկրանի վրա
ստացվում է դիֆրակցիոն
առավելագույն,
որը կոչվում է
զրոյական: Երբ
![]() զրոյական
առավելագույնի
երկու կողմերում
առաջանում են առավելագույններ,
որոնք կոչվում
են առաջին կարգի:
Դիֆրակցիոն ցանցը
սպիտակ լույսով
լուսավորելիս
էկրանի վրա միագույն
լուսավոր շերտի
փոխարեն երևում
են խավար շերտերով
բաժանված սպեկտրներ:
Այդ պատճառով յուրաքանչյուր
առավելագույն
համապատասխան
կարգի սպեկտր է,
բացի զրոյական
նվազագույնից:
Առավելագույնների
ինտենսիվությունները,
կարգի աճմանը զուգընթաց,
աստիճանաբար նվազում
են (նկ.3.11): Դիֆրակցիոն
առավելագույնների
թիվը սահմանափակ
է և որոշվում է
հետևյալ պայմանից`
զրոյական
առավելագույնի
երկու կողմերում
առաջանում են առավելագույններ,
որոնք կոչվում
են առաջին կարգի:
Դիֆրակցիոն ցանցը
սպիտակ լույսով
լուսավորելիս
էկրանի վրա միագույն
լուսավոր շերտի
փոխարեն երևում
են խավար շերտերով
բաժանված սպեկտրներ:
Այդ պատճառով յուրաքանչյուր
առավելագույն
համապատասխան
կարգի սպեկտր է,
բացի զրոյական
նվազագույնից:
Առավելագույնների
ինտենսիվությունները,
կարգի աճմանը զուգընթաց,
աստիճանաբար նվազում
են (նկ.3.11): Դիֆրակցիոն
առավելագույնների
թիվը սահմանափակ
է և որոշվում է
հետևյալ պայմանից`
![]()
Որքան մեծ է ցանցի հաստատունը, այնքան մեծ թվով դիֆրակցիոն մաքսիմումներ կարելի է դիտել, այդ դեպքում դիֆրակցիոն առավելագույնները դառնում են ավելի նեղ ու պայծառ:
(3.24) բանաձևից հետևում է, որ տարբեր երկարության ալիքների ճառագայթներն առավելագույններ ունեն տարբեր ուղղություններով: Հետևաբար, եթե ցանցի վրա ընկնում է սպիտակ լույս, ապա այն վերլուծում է սպեկտրի:
Այսպիսով, դիֆրակցիոն ցանցը սպեկտրային սարք է և բնութագրվում է անկյունային ու լուծող ընդունակությունով: D անկյունային դիսպերսիան որոշում է սպեկտրի անկյունային լայնությունը: Գլխավոր առավելագույնները որոշվում են (3.24) բանաձևով: Այդ բանաձևից հետևում է, որ անկյան սինուսի շեղումը հավասար է`
![]()
Գործնականում
սովորաբար ![]() անկյունները
մեծ չեն
անկյունները
մեծ չեն ![]() ուստի
այդ պայմանը կարելի
է ներկայացնել
հետևյալ տեսքով.
ուստի
այդ պայմանը կարելի
է ներկայացնել
հետևյալ տեսքով.
![]()
Երկու տարբեր ալիքի երկարությունների համար`
![]()
որտեղից
![]()
Ստացված առնչությունից հետևում է, որ երկու առավելագույնների միջև անկյունը, որը համապատասխանում է երկու տարբեր ալիքների երկարություններին, ուղիղ համեմատական է սպեկտրի կարգին և հակադարձ համեմատական է ցանցի հաստատունին, այսինքն` անկյունային դիսպերսիան այնքան մեծ է, որքան մեծ է սպեկտրի կարգը և որքան փոքր է ցանցի հաստատունը: Ցանցի ճեղքերը մեծացնելով` գլխավոր առավելագույնները դառնում են ավելի նեղ (նկ.3.11):
Դիֆրակցիոն
ցանցի R լուծող
ընդունակությունը
բնութագրում է
երկու հավասար
ինտենսիվությաբ
![]() մեներանգ
ալիքների նվազագույն
հեռավորությունը,
որոնք առանձին
կարելի է դիտել
սպեկտրում.
մեներանգ
ալիքների նվազագույն
հեռավորությունը,
որոնք առանձին
կարելի է դիտել
սպեկտրում.
![]()
Համաձայն Ռելեի, երկու սպեկտրալ գծեր համարվում են լուծելի, եթե ալիքներից մեկի գլխավոր առավելագույնն ընկնում է երկրորդ մոտակա գծի նվազագույնի վրա: Դա տեղի է ունենում հետևյալ պայմանի դեպքում.
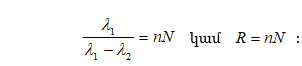
Այսպիսով, ցանցի լուծող ընդունակությունը հավասար է ցանցի ճեղքերի N քանակի և սպեկտրի n կարգի արտադրյալին:
3.4. Դիֆրակցիան տարածական ցանցում:
Վուլֆ- Բրեգի բանաձևը
Դիֆրակցիոն
ցանցում երկրորդային
ալիքների աղբյուրները`
ճեղքերը, դասավորված
են մի գծի վրա: Այդպիսի
դիֆրակցիոն ցանցը
հաճախ կոչվում
է գծային դիֆրակցիոն
ցանց: Դրան հակառակ
տարածական կամ
ծավալային ցանց
անվանում են այն
մարմինը, որի մեջ
երկրորդային ալիքների
աղբյուրները կանոնավոր
կերպով, միմյանցից
որոշակի հեռավորությամբ
դասավորված են
կոորդինատային
բոլոր երեք առանցքների
վրա: Երկրորդային
ալիքների աղբյուրներն
անվանում են դիֆրակցիոն
ցանցի հանգույցներ,
իսկ հանգույցների
իրարից ունեցած
հեռավորությունը`
ցանցի հաստատուն
կամ պարբերություն:
Որպես տարածական
դիֆրակցիոն ցանցեր
կարող են օգտագործվել
բյուրեղները: Ինչպես
հայտնի է, բյուրեղների
մեջ ատոմները դասավորված
են կանոնավոր կերպով,
միմյանցից որոշակի
հեռավորության
վրա ![]() Երբ բյուրեղի
միջով անցնում
են էլեկտրամագնիսական
ալիքներ, նրանց
մեջ գտնվող ատոմները
դառնում են երկրորդային
ալիքների աղբյուրներ:
Երկրորդային ալիքների
վերադրումը առաջ
է բերում դիֆրակցիոն
առավելագույններ:
Այդ առավելագույնների
դիրքը կախված է
ատոմների իրարից
ունեցած հեռավորությունից:
Երբ բյուրեղի
միջով անցնում
են էլեկտրամագնիսական
ալիքներ, նրանց
մեջ գտնվող ատոմները
դառնում են երկրորդային
ալիքների աղբյուրներ:
Երկրորդային ալիքների
վերադրումը առաջ
է բերում դիֆրակցիոն
առավելագույններ:
Այդ առավելագույնների
դիրքը կախված է
ատոմների իրարից
ունեցած հեռավորությունից:
Քանի
որ դիֆրակցիոն
երևույթները նկատվում
են միայն այն դեպքերում,
երբ ընկնող ճառագայթման
ալիքի երկարությունը
փոքր է դիֆրակցիոն
ցանցի հաստատունից,
ապա բյուրեղային
ցանցերից ստացվող
դիֆրակցիան դիտելու
համար տեսանելի
լույսը պիտանի
չէ, տեսանելի լույսի
ալիքի երկարությունը
![]() չափազանց
մեծ է դրա համար:
Պինդ մարմիններում
դիֆրակցիայի երևույթը
դիտելու համար
անհրաժեշտ է այնպիսի
ճառագայթում, որի
ալիքի երկարությունը
լինի 10-11 …10-10: Ալիքի
այդպիսի երկարությամբ
ճառագայթում առաջանում
է, երբ զանազան
նյութեր ռմբակոծվում
են մի քանի տասնյակ
հազար էլեկտրոն-վոլտ
կինետիկ էներգիայով
օժտված էլեկտրոններով:
Այդպիսի ճառագայթումը
հայտնի է ռենտգենյան
անունով: Դիֆրակցիան
պինդ մարմիններից
դիտելու համար
օգտագործում են
ռենտգենյան ճառագայթները:
չափազանց
մեծ է դրա համար:
Պինդ մարմիններում
դիֆրակցիայի երևույթը
դիտելու համար
անհրաժեշտ է այնպիսի
ճառագայթում, որի
ալիքի երկարությունը
լինի 10-11 …10-10: Ալիքի
այդպիսի երկարությամբ
ճառագայթում առաջանում
է, երբ զանազան
նյութեր ռմբակոծվում
են մի քանի տասնյակ
հազար էլեկտրոն-վոլտ
կինետիկ էներգիայով
օժտված էլեկտրոններով:
Այդպիսի ճառագայթումը
հայտնի է ռենտգենյան
անունով: Դիֆրակցիան
պինդ մարմիններից
դիտելու համար
օգտագործում են
ռենտգենյան ճառագայթները:
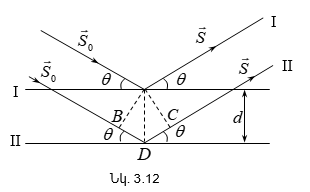
Վուլֆը
և Բրեգը բյուրեղը
դիտել են որպես
ատոմական հարթությունների
համակարգ, հարթություններ,
որոնցից յուրաքանչյուրը
ռենտգենյան ճառագայթներն
անդրադարձնում
է ճիշտ այնպես,
ինչպես հայելին
լույսի ճառագայթները:
Ենթադրենք բյուրեղը
բաղկացած է իրարից
d հեռավորության
վրա գտնվող ատոմական
հարթություններից,
և այդ հարթությունների
վրա ընկնում է
ռենտգենյան ճառագայթների
![]() ալիքի երկարության
մեներանգ և զուգահեռ
փունջ, որը հարթությունների
հետ կազմում է
ալիքի երկարության
մեներանգ և զուգահեռ
փունջ, որը հարթությունների
հետ կազմում է
![]() անկյուն:
Ատոմական հարթություններից
յուրաքանչյուրն
այդ ճառագայթները
կանդրադարձնի
անկյուն:
Ատոմական հարթություններից
յուրաքանչյուրն
այդ ճառագայթները
կանդրադարձնի
![]() անկյան տակ,
սակայն տարբեր
հարթություններից
անդրադարձած ճառագայթների
միջև դիտման կետում
(նկ.3.12) կառաջանա փուլերի
տարբերություն:
Անդրադարձած
գումար ալիքի լայնույթը
կախված է այդ փուլերի
տարբերությունից,
դիտման կետում
կընդունի առավելագույն
կամ նվազագույն
արժեք: Քանի որ
հարևան հարթություններն
իրարից գտնվում
են միևնույն d
հեռավորության
վրա, այդ պատճառով,
երբ հարևան երկու
հարթություններից
անդրադարձած ճառագայթներն
իրար ուժեղացնեն,
ապա իրար կուժեղացնեն
նաև այդ համակարգին
պատկանող բոլոր
հարթություններից
անդրադարձած ճառագայթները:
Ուստի, երբ մենք
ցանկանում ենք
որոշել, թե հարթությունների
տվյալ համակարգից
անդրադարձած ճառագայթը
որ դիրքում կընդունի
առավելագույն
արժեք, բավական
է որոշել, թե երկու
հարևան հարթություններից
անդրադարձած
ճառագայթներն
երբ իրար կուժեղացնեն:
անկյան տակ,
սակայն տարբեր
հարթություններից
անդրադարձած ճառագայթների
միջև դիտման կետում
(նկ.3.12) կառաջանա փուլերի
տարբերություն:
Անդրադարձած
գումար ալիքի լայնույթը
կախված է այդ փուլերի
տարբերությունից,
դիտման կետում
կընդունի առավելագույն
կամ նվազագույն
արժեք: Քանի որ
հարևան հարթություններն
իրարից գտնվում
են միևնույն d
հեռավորության
վրա, այդ պատճառով,
երբ հարևան երկու
հարթություններից
անդրադարձած ճառագայթներն
իրար ուժեղացնեն,
ապա իրար կուժեղացնեն
նաև այդ համակարգին
պատկանող բոլոր
հարթություններից
անդրադարձած ճառագայթները:
Ուստի, երբ մենք
ցանկանում ենք
որոշել, թե հարթությունների
տվյալ համակարգից
անդրադարձած ճառագայթը
որ դիրքում կընդունի
առավելագույն
արժեք, բավական
է որոշել, թե երկու
հարևան հարթություններից
անդրադարձած
ճառագայթներն
երբ իրար կուժեղացնեն:
Նկարում
ցույց տրված առաջին
և երկրորդ հարթություններից
անդրադարձած
ճառագայթների
միջև ընթացքի ![]() տարբերությունը
կլինի .
տարբերությունը
կլինի . ![]() Մյուս
կողմից հայտնի
է, որ երկու կոհերենտ
ալիքներ իրար կուժեղացնեն,
եթե նրանց ճանապարհների
տարբերությունը
հավասար է զրոյի
կամ ամբողջ թվով
ալիքի երկարության,
ուստի համաձայն
վերը նշվածի, բյուրեղից
անդրադարձած ճառագայթների
լայնույթը կընդունի
առավելագույն
արժեք, եթե բավարարվի
հետևյալ պայմանը.
Մյուս
կողմից հայտնի
է, որ երկու կոհերենտ
ալիքներ իրար կուժեղացնեն,
եթե նրանց ճանապարհների
տարբերությունը
հավասար է զրոյի
կամ ամբողջ թվով
ալիքի երկարության,
ուստի համաձայն
վերը նշվածի, բյուրեղից
անդրադարձած ճառագայթների
լայնույթը կընդունի
առավելագույն
արժեք, եթե բավարարվի
հետևյալ պայմանը.
![]()
որտեղ`
![]()
(3.26)-ը կոչվում է Վուլֆ-Բրեգի բանաձև` ի պատիվ ռուս ֆիզիկոս Վուլֆի և անգլիացի ֆիզիկոս Բրեգի, որոնք իրարից անկախ արտածել են այդ բանաձևը:
Այսպիսով,
համաձայն (3.26) բանաձևի,
հարթությունների
տվյալ համակարգից
անդրադարձող ճառագայթ
կառաջանա, եթե
սահքի անկյունը`
![]() միջհարթությունային
հեռավորությունը`
d-ն և ռենտգենյան
սկզբնական ճառագայթների
ալիքի երկարությունը
բավարարեն (3.26) պայմանին:
միջհարթությունային
հեռավորությունը`
d-ն և ռենտգենյան
սկզբնական ճառագայթների
ալիքի երկարությունը
բավարարեն (3.26) պայմանին:
Այդ
պայմանին բավարարելու
համար հարմար է
տվյալ d-ի և ![]() դեպքում
ընտրել համապատասխան
դեպքում
ընտրել համապատասխան
![]() Այսպիսով
ստացվում է, որ
Վուլֆ-Բրեգի եղանակով
ինտերֆերենցիոն
առավելագույններ
ստանալու համար
պետք է վերցնել
մեներանգ ճառագայթներ
(որոշակի
Այսպիսով
ստացվում է, որ
Վուլֆ-Բրեգի եղանակով
ինտերֆերենցիոն
առավելագույններ
ստանալու համար
պետք է վերցնել
մեներանգ ճառագայթներ
(որոշակի ![]() ), ատոմային
հարթությունների
որոշակի համակարգ
(որոշակիd) և համաձայն
(3.26) բանաձևի ընտրել
), ատոմային
հարթությունների
որոշակի համակարգ
(որոշակիd) և համաձայն
(3.26) բանաձևի ընտրել
![]() Եթե
Եթե ![]() ընտրված
է այնպես, որ (3.26)-ի
մեջ m=1-ի, ապա անդրադարձումը
կկոչվի առաջին
կարգի, իսկ երբ
m=2, անդրադարձումը
կկոչվի երկրորդ
կարգի և այլն: (3.26)-ի
մեջ m=0 համապատասխանում
է սկզբնական ճառագայթների
ուղղությամբ կատարվող
անդրադարձմանը
(ցրում սկզբնական
ճառագայթի ուղղությամբ):
ընտրված
է այնպես, որ (3.26)-ի
մեջ m=1-ի, ապա անդրադարձումը
կկոչվի առաջին
կարգի, իսկ երբ
m=2, անդրադարձումը
կկոչվի երկրորդ
կարգի և այլն: (3.26)-ի
մեջ m=0 համապատասխանում
է սկզբնական ճառագայթների
ուղղությամբ կատարվող
անդրադարձմանը
(ցրում սկզբնական
ճառագայթի ուղղությամբ):
Ռենտգենյան ճառագայթումը բավական ուժեղ ազդեցություն է ունենում լուսանկարչական թիթեղի վրա, ուստի և դիֆրակցիոն պատկերը, որն առաջանում է, երբ ռենտգենյան ճառագայթներն անցնում են բյուրեղային մարմնի միջով, կարելի է հեշտությամբ սևեռել լուսանկարչական թիթեղի վրա:
Ռենտգենյան ճառագայթների դիֆրակցիան դիտելու համար բյուրեղներն օգտագործելու միտքը պատկանում է Լաուեին: 1912թ. Լաուեն, Ֆրեդերիխը և Կիպինգը հայտնաբերեցին, որ քարաղի բյուրեղների միջով ռենտգենյան ճառագայթներ բաց թողնելիս նկատվում է պարզորոշ դիֆրակցիոն պատկեր:
Ռենտգենյան ճառագայթների դիֆրակցիայի երևույթը ծառայում է որպես ռենտգենակառուցվածքային անալիզի հիմք, որի օգնությամբ հետազոտվում է նյութերի ատոմային կառուցվածքը: Ռենտգենակառուցվածքային անալիզում ուսումնասիրվում են միաբյուրեղների, բազմաբյուրեղների և այնպիսի օբյեկտների դիֆրակցիոն պատկերները, որոնք չունեն խիստ եռաչափ պարբերականություն` պոլիմերներ, ամորֆ նյութեր, հեղուկներ, գազեր:
3.5.Վուլֆ-Բրեգի բանաձևի ճշգրտումը բեկման հաշվառմամբ
Վուլֆ-Բրեգի
(3.26) բանաձևն արտածելիս
ենթադրվում է,
որ ռենտգենյան
ճառագայթների
բեկման ցուցիչը
հավասար է մեկի,
այսինքն` ռենտգենյան
ճառագայթները
միջավայր մտնելիս
չեն բեկվում: Քանի
որ ռենտգենյան
ճառագայթների
բեկման ցուցիչը
մեկից շատ քիչ
է տարբերվում
(![]() որտեղ
որտեղ
![]() կոչվում
է բեկման ցուցչի
միավոր դեկրեմենտ,
այն
կոչվում
է բեկման ցուցչի
միավոր դեկրեմենտ,
այն ![]() կարգի
մեծություն է),
սովորաբար, առանց
մեծ սխալ գործելու
կարելի է ընդունել,
որ այն հավասար
է մեկի: Սակայն
երբ կարիք է զգացվում
անդրադարձման
ուղղությունը
որոշել մեծ ճշտությամբ,
անհրաժեշտ է հաշվի
առնել բեկման ցուցչի`
մեկից տարբեր
լինելը:
կարգի
մեծություն է),
սովորաբար, առանց
մեծ սխալ գործելու
կարելի է ընդունել,
որ այն հավասար
է մեկի: Սակայն
երբ կարիք է զգացվում
անդրադարձման
ուղղությունը
որոշել մեծ ճշտությամբ,
անհրաժեշտ է հաշվի
առնել բեկման ցուցչի`
մեկից տարբեր
լինելը:
Մեր նպատակն է Վուլֆ-Բրեգի բանաձևի ճշգրտումը կատարել բեկման ցուցչի` մեկից տարբեր լինելու հաշվառմամբ:

Ենթադրենք
հարթ զուգահեռ
ռենտգենյան ալիքը
![]() սահքի
անկյան տակ ընկնում
է բյուրեղի վրա
և մտնելով բյուրեղի
մեջ բեկվում է:
Քանի որ ռենտգենյան
ճառագայթների
բեկման ցուցիչը
մեկից փոքր է, ուստի
բեկվելիս նրանք
հեռանում են նորմալից,
և անկման սահքի
անկյունը մեծ
է լինում բեկման
սահքի անկյունից
սահքի
անկյան տակ ընկնում
է բյուրեղի վրա
և մտնելով բյուրեղի
մեջ բեկվում է:
Քանի որ ռենտգենյան
ճառագայթների
բեկման ցուցիչը
մեկից փոքր է, ուստի
բեկվելիս նրանք
հեռանում են նորմալից,
և անկման սահքի
անկյունը մեծ
է լինում բեկման
սահքի անկյունից
![]() Նկար
3.13-ից երևում է, որ
առաջին և երկրորդ
ատոմական հարթություններից
անդրադարձած
ճառագայթների
(1 և 2 ճառագայթներ)
միջև ճանապարհների
տարբերությունը`
Նկար
3.13-ից երևում է, որ
առաջին և երկրորդ
ատոմական հարթություններից
անդրադարձած
ճառագայթների
(1 և 2 ճառագայթներ)
միջև ճանապարհների
տարբերությունը`
![]()
որտեղ
n-ը միջավայրի
բեկման ցուցիչն
է: Քանի որ ![]() իսկ
իսկ ![]() ուստի
ուստի ![]() համար կստանանք`
համար կստանանք`
![]() Նկատի
ունենալով, որ
բեկման ցուցիչը`
Նկատի
ունենալով, որ
բեկման ցուցիչը`
![]() կստանանք`
կստանանք`
![]()
Առավելագույն անդրադարձում ստանալու համար պետք է հարևան հարթություններից անդրադարձած ալիքների օպտիկական ճանապարհների տարբերությունը հավասար լինի ամբողջ թվով ալիքի երկարության`
![]()
Բեկման
ցուցչի ![]() արտահայտությունից
կստանանք
արտահայտությունից
կստանանք ![]() նկատի ունենալով
նաև այն, որ բեկման
ցուցչի քառակուսին
մեծ ճշտությամբ
կարելի է արտահայտել
նկատի ունենալով
նաև այն, որ բեկման
ցուցչի քառակուսին
մեծ ճշտությամբ
կարելի է արտահայտել
![]() տեսքով,
(3.27)-ը կընդունի հետևյալ
տեսքը`
տեսքով,
(3.27)-ը կընդունի հետևյալ
տեսքը`
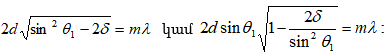
Օգտվելով
![]() փոքրությունից`
կարող ենք կատարել
հետևյալ ձևափոխությունները`
փոքրությունից`
կարող ենք կատարել
հետևյալ ձևափոխությունները`
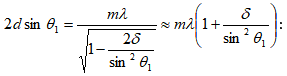
Այսպիսով, հաշվի առնելով ռենտգենյան ճառագայթների բեկումը« Վուլֆ-Բրեգի բանաձևի փոխարեն կստանանք հետևյալ ճշգրտված բանաձևը`
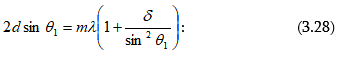
Ինչպես երևում է (3.28)-ից, անդրադարձման մեծ անկյունների դեպքում ուղղումը չնչին է, ուստի ուղղված բանաձևից իմաստ ունի օգտվել միայն սահքի փոքր անկյունների դեպքում:
Այժմ տեսնենք, թե բեկման ցուցչի` մեկից տարբեր լինելը հաշվի առնելու պատճառով ինչքանով է փոփոխվում Վուլֆ-Բրեգի պայմանին բավարարող անկյունը: Այդ նպատակով կազմենք Վուլֆ-Բրեգի ճշգրտված (3.28) և (3.26) չճշգրտված բանաձևերի տարբերությունը.
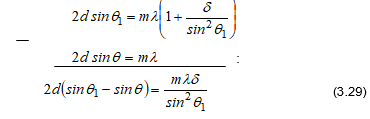
Առանց
մեծ սխալ գործելու
վերջին արտահայտության
մեջ կարող ենք
2d-ն փոխարինել
![]() իսկ
իսկ
![]() տարբերությունը`
տարբերությունը`
![]() որտեղ
որտեղ
![]() Վուլֆ-Բրեգի
ճշգրտված և չճշգրտված
բանաձևերին համապատասխանող
անկյունների տարբերությունն
է: Այդ դեպքում
(3.29) արտահայտությունը
կընդունի հետևյալ
տեսքը`
Վուլֆ-Բրեգի
ճշգրտված և չճշգրտված
բանաձևերին համապատասխանող
անկյունների տարբերությունն
է: Այդ դեպքում
(3.29) արտահայտությունը
կընդունի հետևյալ
տեսքը`
![]()
Քանի
որ ![]() շատ
փոքր է, ուստի
շատ
փոքր է, ուստի ![]() անկյունային
վայրկյանի կարգի
մեծություն է,
և կարիք է լինում
հաշվի առնել անդրադարձման
ուղղությունը
մեծ ճշտությամբ
որոշելիս:
անկյունային
վայրկյանի կարգի
մեծություն է,
և կարիք է լինում
հաշվի առնել անդրադարձման
ուղղությունը
մեծ ճշտությամբ
որոշելիս:
3.6. Գաղափար օպտիկական հոլոգրաֆիայի մասին
Հոլոգրաֆիան առարկայական և նրա հետ կոհերենտ հենակետային ալիքով առաջացած ինտերֆերենցիոն պատկերում ինտենսիվության բաշխվածության գրանցման վրա հիմնված ալիքների գրառման և վերականգնման եղանակ է: Գրանցված ինտերֆերենցիոն պատկերը կոչվում է հոլոգրամ: Էլեկտրամագնիսական դաշտերի կառուցվածքի գրառման վերարտադրման գաղափարն առաջին անգամ արտահայտել և ցուցադրել է Դ. Հաբորը 1948թ.: Նա էլ հեց մտցրել է «հոլոգրամ» տերմինը (այն է` «լրիվ գրառում»): Սակայն Հաբորի աշխատանքները մինչև լազերների ստեղծումը լայն տարածում չգտան, որովհետև հոլոգրաֆիայի համար անհրաժեշտ են տարածական և ժամանակային բարձր կոհերենտությամբ լույսի աղբյուրներ, որոնց հզորությանը ներկայացվող պահանջներն անհամատեղելի են լույսի սովորական աղբյուրների հնարավորությունների հետ: Հոլոգրաֆիան, որպես օպտիկայի ինքնուրույն բաժին, ստեղծվեց ամերիկացի ֆիզիկոսներ Լեյթի և Ուպաթնիեքսի աշխատություններից հետո (1960-1963): Նրանք առաջինը ցուցադրեցին երկչափ և եռաչափ օբյեկտների բարձրորակ հոլոգրամներ: 1962-1963թթ. նրանցից անկախ, Դենիսյուկը հրապարակեց ծավալային հոլոգրամների մասին փորձնականորեն հաստատված գաղափար, որոնք սկզբունքային առավելություններ ունեն մինչ այդ հայտնի հոլոգրամների նկատմամբ: Որն է հոլոգրաֆիայի սկզբունքը: Ինչպես կարելի է գրանցել և վերականգնել առարկայի մասին ամբողջ ինֆորմացիան:
Իր ծագումով հոլոգրոֆիան պարտական է ալիքայի օպտիկայի` ինտերֆերենցիայի և դիֆրակցիայի հիմնական օրենքներին:
Ալիքը գրանցելու և վերականգնեու համար, անհրաժեշտ է գրանցել և վերականգնել առարկայից եկող ալիքի լայնույթը և փուլը: Այդ հնարավորությունը տալիս է լայնույթային և փուլային ինֆորմացիա պարունակող հետևյալ բանաձևը.
![]()
Ինչպես հետևում է (3.31)-ից, ինտերֆերենցիոն պատկերում ինտենսիվության բաշխվածությունը, բացի ինտերֆերենցող ալիքների լայնույթներից, որոշվում է նաև նրանց փուլերի տարբերությամբ: Հետևաբար, ինչպես փուլային, այնպես էլ լայնույթային ինֆորմացիան գրանցելու համար անհրաժեշտ է, բացի առարկայից եկող ալիքից (առարկայական կամ ազդանշանային ալիք), ունենալ նաև նրա հետ կոհերենտ ալիք, որը կոչվում է հենակետային ալիք:
Այսպիսով, եզրակացությունը հետևյալն է. առարկայով դիֆրակցված ալիքի գրանցման և վերականգման համար, անհրաժեշտ է ստիպել նրան ինտերֆերենցվել հայտնի փուլով կոհերենտ հենակետային ալիքի հետ, այնուհետև հենակետային ալիքի օգնությամբ ընդհանուր ինտերֆերենցիոն պատկերից դուրս բերել առարկայական ալիքը: Հենց սա էլ հոլոգրաֆիայի գաղափարն է: Այն գործնականում կարելի է իրականացնել հետևյալ ձևով: Հետազոտվող օբյեկտը լուսավորում են օպտիկական սարքի միջոցով նախապես լայնացված լազերային լույսի փնջով: Օբյեկտի վրա ցրված լուսային ալիքը և հայելուց անդրադարձած սկզբնական (հենակետային) ալիքն ընկնում են լուսանկարչական թիթեղի վրա (նկ .3.14ա), որի վրա գրանցվում է առաջացող ինտերֆերենցիոն պատկերը: Լուսանկարչական թիթեղը հայտածվում է և սևեռակվում սովորական եղանակով. այն կրում է հետազոտվող առարկայի վերաբերյալ եղած ամբողջ ինֆորմացիան: Այդպիսի թիթեղը կոչվում է հոլոգրամ: Արտաքուստ այն ոչնչով չի տարբերվում սովորական հավասարաչափ լուսավորված թիթեղից: Եվ միայն մանրադիտակով դիտելիս, ամենապարզ դեպքերում, կարելի է նկատել կարգավորված միկրոկառուցվածք, որն առաջանում է երկու լուսային ալիքների ինտերֆերենցի հետևանքով:
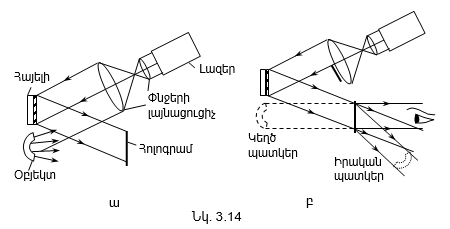
Ալիքը վերականգնելու համար hեռացնում են հետազոտվող առարկան և այն տեղում, որտեղ գտնվում էր լուսանկարչական թիթեղը լուսանկարման պահին, տեղադրում են հոլոգրամը և լուսավորում են հենակետային փնջով: Հենակետային փունջը հոլոգրամի վրա ենթարկվում է դիֆրակցիայի, որի հետևանքով առաջանում է ճիշտ այնպիսի կառուցվածքով ալիք, ինչպիսին էր առարկայից անդրադաձած ալիքը: Այդ ալիքը տալիս է առարկայի կեղծ պատկերը, որն ընկալում է դիտողի աչքը (նկ. 3.14բ): Կեղծ պատկերը կազմավորող ալիքի հետ մեկտեղ դիֆրակցիայի ժամանակ առաջանում է ևս մի ալիք, որը կազմավորում է առարկայի իրական պատկերը:
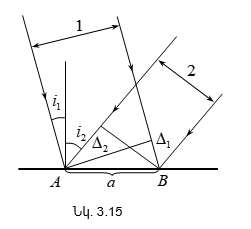
Տարրական
հաշվարները ցույց
են տալիս, որ հոլոգրամն
իրեն առաջացնող
ալիքներից վերականգնում
է այն ալիքը, որը
բացակայում է ալիքային
ճակատի վերականգնման
դեպքում: Դիցուք
ֆոտոթիթեղի վրա
վերադրվում են
երկու կոհերենտ
հարթ ալիքներ (նկ.3.15):
Առաջին և երկրորդ
ալիքների անկման
անկյունները նշանակենք
համապատասխանաբար
![]() Երկու կոհերենտ
ալիքների ինտերֆերենցիայի
արդյունքում ֆոտոթիթեղի
վրա առաջանում
է ինտերֆերենցիոն
շերտերի համակարգ:
Դիցուք A և B կետերը
համապատասխանում
են երկու հարևան
շերտերի դիրքերին:
Քանի որ, A-ից B անցելիս
1 և 2 փնջերի ընթացքի
տարբերությունը
փոխվում է
Երկու կոհերենտ
ալիքների ինտերֆերենցիայի
արդյունքում ֆոտոթիթեղի
վրա առաջանում
է ինտերֆերենցիոն
շերտերի համակարգ:
Դիցուք A և B կետերը
համապատասխանում
են երկու հարևան
շերտերի դիրքերին:
Քանի որ, A-ից B անցելիս
1 և 2 փնջերի ընթացքի
տարբերությունը
փոխվում է ![]() ապա
ապա
![]() որտեղ
որտեղ ![]() երկու
շերտերի կենտրոնների
հեռավորությունն
է: Նման ձևով գրանցված
հոլոգրամը ներկայացնում
է
երկու
շերտերի կենտրոնների
հեռավորությունն
է: Նման ձևով գրանցված
հոլոգրամը ներկայացնում
է ![]() հաստատունով
դիֆրակցիոն ցանց
և որոշվում է հետևյալ
բանաձևով.
հաստատունով
դիֆրակցիոն ցանց
և որոշվում է հետևյալ
բանաձևով.
![]()
Եթե
ենթադրվի, որ ըստ
լայնույթի թիթեղի
բացթողման գործակիցը
նրա վրա ընկնող
լույսի ինտենսիվությունից
կախված է գծայնորեն,
ապա ստացված շերտերի
համակարգը, ինչպես
հետևում է (3.31) բանաձևից,
կունենա բացթողման
սինուսոիդային
բաշխում: Հոլոգրամի
(սինուսոիդային
դիֆրակցիոն ցանց)
վրա ուղղենք փնջերից
մեկը, որը մասնակցում
է նրա առաջացմանը,
օրինակ 1 փունջը:
Եթե դիֆրակցիոն
ցանցի վրա ճառագայթի
անկման անկյունը
նշանակենք ![]() իսկ
դիֆրակցիայի անկյունը
իսկ
դիֆրակցիայի անկյունը
![]() ապա, ինչպես
հայտնի է, նրանք
կապված են հետևյալ
առնչությամբ`
ապա, ինչպես
հայտնի է, նրանք
կապված են հետևյալ
առնչությամբ`
![]()
որտեղ m-ը սպեկտրի կարգն է: Սինուսոիդային ցանցի համար m=1, ուստի (3.32)-ից`
![]()
Քանի
որ մեր դեպքում
անկման անկյունը
![]() է, ապա տեղադրելով
է, ապա տեղադրելով
![]() և նկատի ունենալով,
որ
և նկատի ունենալով,
որ ![]() կստանանք`
կստանանք`
![]() որտեղից
որտեղից
![]() այսինքն,
հոլոգրամը 1 փնջով
լուսավորելիս
վերականգնվում
է 2 փունջը: Եթե հոլոգրամի
լուսավորումը
կատարվի 2 փնջով,
ապա կվերականգնվի
1 փունջը, այսինքն`
հենակետային և
առարկայական փնջերն
օժտված են փոխադարձ
դարձելիության
հատկություններով:
այսինքն,
հոլոգրամը 1 փնջով
լուսավորելիս
վերականգնվում
է 2 փունջը: Եթե հոլոգրամի
լուսավորումը
կատարվի 2 փնջով,
ապա կվերականգնվի
1 փունջը, այսինքն`
հենակետային և
առարկայական փնջերն
օժտված են փոխադարձ
դարձելիության
հատկություններով:
Հոլոգրաֆիական
մեթոդը կիրառվում
է գիտության և
տեխնիկայի տարբեր
բնագավառներում
և ապագայում կունենա
մեծ առաջընթաց:
Թվարկենք կիրառություններից
մի քանիսը: Հոլոգրաֆիական
մեթոդը հնարավորություն
է տալիս ֆոտոէմուլսիայի
տրված փոքր տեղամասի
վրա գրառելու տպագրական
տեքստի ![]() անգամ
ավելի շատ էջեր,
քան սովորական
միկրոլուսանկարչական
մեթոդները: Ուստի
հոլոգրաֆիան լայնորեն
կիրառվում է ինֆորմացիայի
գրառման և պահպանման
մեջ: Լայն ճակատով
աշխատանքներ
են կատարվում նաև
հոլոգրաֆիական
կինոյի և հեռուստատեսության
ստեղծման ասպարեզում:
անգամ
ավելի շատ էջեր,
քան սովորական
միկրոլուսանկարչական
մեթոդները: Ուստի
հոլոգրաֆիան լայնորեն
կիրառվում է ինֆորմացիայի
գրառման և պահպանման
մեջ: Լայն ճակատով
աշխատանքներ
են կատարվում նաև
հոլոգրաֆիական
կինոյի և հեռուստատեսության
ստեղծման ասպարեզում:
ԼՈՒՅՍԻ ԲԵՎԵՌԱՑՈՒՄԸ
4.1. Բնական և բևեռացված լույս: Մալյուսի օրենքը
Ինտերֆերենցիայի և դիֆրակցիայի երևույթները դիտվում են ինչպես լայնական, այնպես էլ երկայնական ալիքների համար: Դրա հետ մեկտեղ գոյություն ունեն երևույթներ, որոնց համար լուսային ալիքների լայնականությունն ունի սկզբունքային նշանակություն: Այդպիսի երևույթների շարքին է դասվում լույսի բևեռացման երևույթը:
Ըստ Մաքսվելի տեսության լույսը էլեկտրամագնիսական ալիք է. լուսային ալիքում էլեկտրական և մագնիսական վեկտորները տատանվում են ալիքի տարածման ուղղությանն ուղղահայաց:
Ատոմների գրգռած ալիքների լծաշարքերն իրար վրա վերադրվելով` առաջացնում են մարմնի արձակած լուսային ալիքը: Յուրաքանչյուր լծաշարքի համար տատանումների հարթությունը կողմնորոշված է պատահական ձևով: Ուստի արդյունարար ալիքում տարբեր ուղղությունների տատանումները ներկայացված են հավասար հավանականությամբ:
Եթե
լուսային ալիքում
էլեկտրական դաշտի
լարվածության
![]() վեկտորի
տատանումները
տեղի են ունենում
բոլոր հնարավոր
ուղղություններով
ճառագայթի տարածման
ուղղությանն ուղղահայաց
հարթության մեջ,
ապա լույսը կոչվում
է բնական:
վեկտորի
տատանումները
տեղի են ունենում
բոլոր հնարավոր
ուղղություններով
ճառագայթի տարածման
ուղղությանն ուղղահայաց
հարթության մեջ,
ապա լույսը կոչվում
է բնական:
Այն
լույսը, ուր ![]() վեկտորի
տատանումների
ուղղությունը
որևէ ձևով կարգավորված
է, կոչվում է բևեռացված
լույս:
վեկտորի
տատանումների
ուղղությունը
որևէ ձևով կարգավորված
է, կոչվում է բևեռացված
լույս:
Եթե
![]() վեկտորի
տատանումները
տեղի են ունենում
միայն մեկ ուղղությամբ`
ճառագայթի տարածման
ուղղությանն ուղղահայաց,
ապա լույսը կոչվում
է հարթ բևեռացված
կամ գծային բևեռացված:
Այն լույսը, ուր
տատանումները
մի ուղղությամբ
գերակշռում են
այլ ուղղությունների
տատանումներին,
կոչվում է մասնակի
բևեռացված:
վեկտորի
տատանումները
տեղի են ունենում
միայն մեկ ուղղությամբ`
ճառագայթի տարածման
ուղղությանն ուղղահայաց,
ապա լույսը կոչվում
է հարթ բևեռացված
կամ գծային բևեռացված:
Այն լույսը, ուր
տատանումները
մի ուղղությամբ
գերակշռում են
այլ ուղղությունների
տատանումներին,
կոչվում է մասնակի
բևեռացված:
Այն
հարթությունը,
որն անցնում է
![]() վեկտորի
տատանումների
ուղղությամբ
և ճառագայթով,
անվանում են բևեռացման
հարթություն
(նկ. 4.1-ի վրա A հարթությունը):
վեկտորի
տատանումների
ուղղությամբ
և ճառագայթով,
անվանում են բևեռացման
հարթություն
(նկ. 4.1-ի վրա A հարթությունը):
Այն
հարթությունը,
որն անցնում է
ճառագայթով և ուղղահահայաց
է ![]() վեկտորի
տատանումների
ուղղությանը (B
հարթություն),
ուր տատանվում
է
վեկտորի
տատանումների
ուղղությանը (B
հարթություն),
ուր տատանվում
է ![]() վեկտորը,
անվանում են տատանումների
հարթություն:
վեկտորը,
անվանում են տատանումների
հարթություն:
Տատանումների հարթությունը և բևեռացման հարթությունը միշտ իրար փոխուղղահայաց են:
Հարթ բևեռացած լույս կարելի է ստանալ բնական լույսից` բևեռացուցիչ կոչվող սարքերի միջոցով:
Այդ սարքերը բաց են թողնում այն տատանումները, որոնք զուգահեռ են մի հարթության, որն անվանում են բևեռացուցչի հարթություն և լրիվ կասեցնում են այդ հարթությանն ուղղահայաց տատանումները:
Դիտարկենք
հետևյալ փորձը:
Լույսն ուղղենք
տուրմալինի T1
բյուրեղի մակերևույթին
ուղղահայաց, որը
կտրված է, այսպես
կոչված, OO օպտիկական
առանցքին զուգահեռ
(նկ.4.2): Օպտիկական
առանցքի սահմանումը
կտրվի այս գլխի
4.3 բաժնում: Պտտելով
T1 բյուրեղը ճառագայթի
առանցքի շուրջը`
հետևենք նրանով
անցնող լույսի
ինտենսիվության
փոփոխությանը:
Ինչպես ցույց է
տալիս փորձը, բյուրեղի
այդպիսի պտույտն
անցնող լույսի
ինտենսիվության
փոփոխություն
առաջ չի բերում:
Եթե ճառագայթի
ճանապարհին դրվի
երկրորդ նույնատիպ
և առաջինին զուգահեռ
T2 տուրմալինի
բյուրեղը (նկ.4.3), ապա
նրանցից մեկի պտտումը
ճառագայթի առանցքի
շուրջն այդ թիթեղներով
անցած լույսի ինտենսիվությունը
կախված բյուրեղների
OO և O1O1 առանցքների
միջև կազմված ![]() անկյունից,
փոփոխվում է համաձայն
Մալյուսի կողմից
սահմանած օրենքի`
անկյունից,
փոփոխվում է համաձայն
Մալյուսի կողմից
սահմանած օրենքի`
![]()
որտեղ
Io-ն և ![]() -ն համապատասխանաբար
երկրորդ բյուրեղի
վրա ընկնող և նրանից
դուր եկող լույսի
ինտենսիվություններն
են:
-ն համապատասխանաբար
երկրորդ բյուրեղի
վրա ընկնող և նրանից
դուր եկող լույսի
ինտենսիվություններն
են:
Դիտվող երևույթները կարելի է բացատրել, եթե ենթադրվի, որ 1) լույսը լայնական ալիք է, 2) տուրմալինի բյուրեղը բաց է թողնում միայն այն լույսը, որի էլեկտրական վեկտորի տատանումներն ուղղված են բյուրեղի օպտիկական առանցքին զուգահեռ և լրիվ կլանում է լույսը այն դեպքում, երբ էլեկտրական վեկտորի տատանումներն ուղղված են բյուրեղի օպտիկական առանցքին ուղղահայաց: Իրոք, քանի որ T1 բյուրեղի մակերևույթի վրա ընկնող լուսային ալիքներում էլեկտրական վեկտորը տատանվում է բոլոր հնարավոր ուղղություններով, ապա T1 բյուրեղը ճառագայթի առանցքի շուրջը պտտելիս, միշտ տատանումներ կգտնվեն բյուրեղի բացթողնման ուղղության երկայնքով, և հետևաբար բյուրեղի միջով անցնող լույսի ինտենսիվությունը չի փոփոխվի: Բյուրեղից դուրս եկող լույսի մեջ էլեկտրական վեկտորի տատանումները տեղի են ունենում նույն ուղղությամբ: Այդպիսի լույսը, ինչպես վերևը նշեցինք, կոչվում է գծային կամ հարթ բևեռացված:
Ենթադրենք,
թե առաջին բյուրեղից
դուրս եկող լուսային
ճառագայթում
էլեկտրական ![]() վեկտորն
ուղղված է այնպես,
ինչպես ցույց է
տրված նկ.4.4-ում: Ակներև
է, որ լույսի էլեկտրական
վեկտորի մեծությունը,
որն անցնում է
երկրորդ բյուրեղով`
վեկտորն
ուղղված է այնպես,
ինչպես ցույց է
տրված նկ.4.4-ում: Ակներև
է, որ լույսի էլեկտրական
վեկտորի մեծությունը,
որն անցնում է
երկրորդ բյուրեղով`
![]() Քանի որ ինտենսիվությունն
ուղիղ համեմատական
է լայնույթի քառակուսուն
Քանի որ ինտենսիվությունն
ուղիղ համեմատական
է լայնույթի քառակուսուն
![]() ապա կստանանք
ապա կստանանք
![]() առնչությունը,
որն էլ արտահայտում
է Մալյուսի օրենքը:
Հետաքրքիր է նշել,
որ Մալյուսն իր
օրենքը արտածել
է միանգամայն
այլ եղանակով`
հիմնվելով լույսի
մասնիկային բնույթի
մասին պատկերացումների
վրա: Արագոյի կողմից
կատարված լուսաչափական
փորձերը հաստատեցին
Մալյուսի (4.1) բանաձևը:
առնչությունը,
որն էլ արտահայտում
է Մալյուսի օրենքը:
Հետաքրքիր է նշել,
որ Մալյուսն իր
օրենքը արտածել
է միանգամայն
այլ եղանակով`
հիմնվելով լույսի
մասնիկային բնույթի
մասին պատկերացումների
վրա: Արագոյի կողմից
կատարված լուսաչափական
փորձերը հաստատեցին
Մալյուսի (4.1) բանաձևը:
Նշենք, որ տուրմալինի առաջին բյուրեղի T1 թիթեղը, որը բնական լույսը փոխակերպում է գծային-հարթ բևեռացված լույսի, կոչվում է բևեռացուցիչ: Երկրորդ տուրմալինի բյուրեղի T2 թիթեղը, որը կատարում է առաջին բյուրեղից դուրս եկող լույսի վերլուծությունը, կոչվում է վերլուծիչ:
Եթե
մասնակի բևեռացված
լույսն անցկացնենք
բևեռացուցչի միջով,
ապա սարքը ճառագայթի
ուղղության շուրջը
պտտելիս անցած
լույսի ինտենսիվությունը
կփոփոխվի Iառ.-ից
մինչև Iնվ-ի սահմաններում,
ընդ որում` անցումն
այս արժեքներից
մեկից մյուսին
կկատարվի ![]() անկյունով
պտտելիս, և մեկ
լրիվ պտույտի դեպքում
երկու անգամ կստանանք
ինտենսիվության
առավելագույն
արժեք և երկու
անգամ` ինտենսիվության
նվազագույն:
անկյունով
պտտելիս, և մեկ
լրիվ պտույտի դեպքում
երկու անգամ կստանանք
ինտենսիվության
առավելագույն
արժեք և երկու
անգամ` ինտենսիվության
նվազագույն:
Բևեռացման աստիճան է կոչվում հետևյալ արտահայտությունը`

Հարթ
բևեռացված լույսի
համար ![]() բնական
լույսի համար
բնական
լույսի համար
![]()
Քննարկենք երկու կոհերենտ հարթ բևեռացված լուսային ալիքներ, որոնց տատանումների հարթությունները փոխուղղահայաց են: Դիցուք մի ալիքում տատանումները կատարվում են x առանցքի ուղղությամբ (նկ.4.5), երկրորդում` y առանցքի ուղղությամբ: Այդ ալիքների լուսային վեկտորների պրոյեկցիաները համապատասխան առանցքների վրա փոփոխվում են հետևյալ օրենքով`
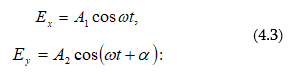
![]() մեծությունները
մեծությունները
![]() արդյունարար
լուսային վեկտորի
ծայրի կոորդինատներն
են (նկ.4.5): Արդյունարար
տատանման հետագիծը
ստանալու համար
այս հավասարումներից
պետք է արտաքսել
ժամանակը: Վերևում
գրված առնչությունները
տալիս են`
արդյունարար
լուսային վեկտորի
ծայրի կոորդինատներն
են (նկ.4.5): Արդյունարար
տատանման հետագիծը
ստանալու համար
այս հավասարումներից
պետք է արտաքսել
ժամանակը: Վերևում
գրված առնչությունները
տալիս են`
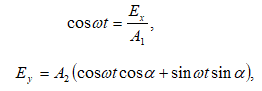
կամ
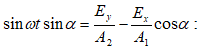
Քառակուսի բարձրացնելով և գումարելով
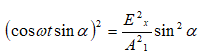
արտահայտությանը, կստանանք`
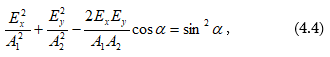
այսինքն`
էլիպսի հավասարում
(մասնավորապես
կարող է ստացվել
շարժում ուղղի
հատվածով կամ շրջանագծով):
(4.3) կոորդինատներն
ունեցող կետը,
այսինքն` ![]() վեկտորի
ծայրը, շարժվում
է էլիպսով: Այսպիսով,
երկու կոհերենտ
հարթ
բևեռացված լուսային
ալիքներ, որոնց
տատանումների
հարթությունները
փոխուղղահայաց
են, վերադրվելիս
տալիս են մի ալիք,
ուր լուսային վեկտորը
(
վեկտորի
ծայրը, շարժվում
է էլիպսով: Այսպիսով,
երկու կոհերենտ
հարթ
բևեռացված լուսային
ալիքներ, որոնց
տատանումների
հարթությունները
փոխուղղահայաց
են, վերադրվելիս
տալիս են մի ալիք,
ուր լուսային վեկտորը
(![]() վեկտորը)
ժամանակի ընթացքում
փոփոխվում է այնպես,
որ նրա ծայրը գծում
է էլիպս: Այդպիսի
լույսը կոչվում
է էլիպսաձև բևեռացված:
վեկտորը)
ժամանակի ընթացքում
փոփոխվում է այնպես,
որ նրա ծայրը գծում
է էլիպս: Այդպիսի
լույսը կոչվում
է էլիպսաձև բևեռացված:
Այն
դեպքում, երբ ![]() (4.4)
հավասարումն ընդունում
է
(4.4)
հավասարումն ընդունում
է

տեսքը,
այսինքն` մի էլիպս,
որը կողմնորոշված
է գլխավոր առանցքների
նկատմամբ: Եթե
![]() էլիպսը վերածվում
է ուղղի հատվածի
և ստացվում է հարթ
բևեռացված լույս:
Երբ փուլերի տարբերությունը`
էլիպսը վերածվում
է ուղղի հատվածի
և ստացվում է հարթ
բևեռացված լույս:
Երբ փուլերի տարբերությունը`
![]() և գումարվող
ալիքների լայնությունները
հավասար են, էլիպսը
վերածվում է շրջանագծի:
Այդ դեպքում ստացվում
է շրջանով բևեռացված
լույս:
և գումարվող
ալիքների լայնությունները
հավասար են, էլիպսը
վերածվում է շրջանագծի:
Այդ դեպքում ստացվում
է շրջանով բևեռացված
լույս:
4.2. Լույսի բևեռացումը երկու դիէլեկտրիկների սահմանի
վրա անդրադարձման և բեկման դեպքում
Բրյուստերի օրենքը
Եթե բնական լույսի փունջն ուղղենք երկու դիէլեկտրիկների սահմանի վրա (օրինակ, օդ և ապակի), ապա լույսի մի մասն անդրադառնում է, մյուս մասը բեկվելով տարածվում է երկրորդ միջավայրում:
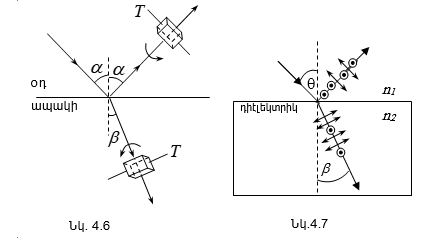
Տեղադրելով
վերլուծիչը (օրինակ,
տուրմալինի բյուրեղը)
ճառագայթի ճանապարհին`
կարելի է հետազոտել
անդրադարձած և
բեկված ճառագայթների
բևեռացումը (նկ.4.6):
Այդպիսի հետազոտություն
կատարվել է 1810թ. Մալյուսի
կողմից: Պարզվել
է, որ եթե լույսի
անկման անկյունը
![]() բեկան
ցուցիչ ունեցող
երկու դիէլեկտրիկների
սահմանի վրա հավասար
չէ զրոյի, ապա անդրադարձած
և բեկված ճառագայթները
մասնակի բևեռացված
են: Անդրադարձած
ճառագայթում գերակշռում
են այն տատանումները,
որոնք ուղղահայաց
են անկման հարթությանը
(նկ.4.7-ում այդ տատանումները
նշված են կետերով),
իսկ բեկված ճառագայթում
տատանումները
զուգահեռ են անկման
հարթությանը (նկարում
դրանք պատկերված
են երկկողմ սլաքներով):
Բևեռացման աստիճանը
կախված է անկման
բեկան
ցուցիչ ունեցող
երկու դիէլեկտրիկների
սահմանի վրա հավասար
չէ զրոյի, ապա անդրադարձած
և բեկված ճառագայթները
մասնակի բևեռացված
են: Անդրադարձած
ճառագայթում գերակշռում
են այն տատանումները,
որոնք ուղղահայաց
են անկման հարթությանը
(նկ.4.7-ում այդ տատանումները
նշված են կետերով),
իսկ բեկված ճառագայթում
տատանումները
զուգահեռ են անկման
հարթությանը (նկարում
դրանք պատկերված
են երկկողմ սլաքներով):
Բևեռացման աստիճանը
կախված է անկման
![]() անկյունից:
անկյունից:
![]()
պայմանի
դեպքում, որտեղ
![]() երկրորդ
միջավայրի բեկման
ցուցիչն է առաջինի
նկատմամբ, անդրադարձած
ճառագայթը լրիվ
բևեռացված է, իսկ
բեկված ճառագայթի
բևեռացման աստիճանը
հասնում է ամենամեծ
արժեքի, սակայն
այդ ճառագայթը
բևեռացված է մնում
մասնակիորեն:
երկրորդ
միջավայրի բեկման
ցուցիչն է առաջինի
նկատմամբ, անդրադարձած
ճառագայթը լրիվ
բևեռացված է, իսկ
բեկված ճառագայթի
բևեռացման աստիճանը
հասնում է ամենամեծ
արժեքի, սակայն
այդ ճառագայթը
բևեռացված է մնում
մասնակիորեն:
(4.6) առնչությունը
կոչվում է Բրյուստերի
օրենք: ![]() անկյունը
կոչվում է Բրյուստերի
անկյուն կամ լրիվ
բևեռացման անկյուն:
անկյունը
կոչվում է Բրյուստերի
անկյուն կամ լրիվ
բևեռացման անկյուն:
Ցույց տանք, որ երբ լույսն ընկնում է Բրյուստերի անկյան տակ, անդրադարձած և բեկված ճառագայթները դառնում են փոխուղղահայաց:
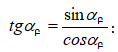
Ըստ բեկման օրենքի՝
![]()
որտեղ ![]() բեկման
անկյունն է: Բրյուստերի
օրենքից և այս
երկու առնչություններից
հետևում է, որ
բեկման
անկյունն է: Բրյուստերի
օրենքից և այս
երկու առնչություններից
հետևում է, որ ![]()
Հետևաբար`
![]()
4.3. Բևեռացումը կրկնակի ճառագայթաբեկման դեպքում
1670թ.
Է. Բարտոլոմինը
դիտեց հետաքրքիր
մի երևույթ. իսլանդական
սպաթի (ածխաթթվական
կալցիումի` ![]() մի
տարատեսակը, հեքսագոնալային
համակարգի բյուրեղ)
բյուրեղի միջով
լույսի անցման
դեպքում լուսային
ճառագայթը բաժանվում
է երկու ճառագայթների:
Այս երևույթը կոչվում
է կրկնակի ճառագայթաբեկում:
Պարզվեց, որ բյուրեղից
դուրս եկող երկու
ճառագայթները
զուգահեռ են միմյանց
և բյուրեղի մակերևույթի
վրա ընկնող ճառագայթին
(նկ.4.8), գծային բևեռացված
են փոխուղղահայաց
հարթություններում
և օժտված են տարբեր
ինտենսիվություններով:
Այդ ճառագայթներից
մեկը բավարարում
է սովորական բեկման
օրենքին և կոչվում
է սովորական ճառագայթ
և գծագրերում
նշանակվում է
օ տառով: Երկրորդ
ճառագայթը կոչվում
է ոչ սովորական,
չի ենթարկվում
բեկման օրենքին
և գծագրերում
նշանակվում է
e տառով:
մի
տարատեսակը, հեքսագոնալային
համակարգի բյուրեղ)
բյուրեղի միջով
լույսի անցման
դեպքում լուսային
ճառագայթը բաժանվում
է երկու ճառագայթների:
Այս երևույթը կոչվում
է կրկնակի ճառագայթաբեկում:
Պարզվեց, որ բյուրեղից
դուրս եկող երկու
ճառագայթները
զուգահեռ են միմյանց
և բյուրեղի մակերևույթի
վրա ընկնող ճառագայթին
(նկ.4.8), գծային բևեռացված
են փոխուղղահայաց
հարթություններում
և օժտված են տարբեր
ինտենսիվություններով:
Այդ ճառագայթներից
մեկը բավարարում
է սովորական բեկման
օրենքին և կոչվում
է սովորական ճառագայթ
և գծագրերում
նշանակվում է
օ տառով: Երկրորդ
ճառագայթը կոչվում
է ոչ սովորական,
չի ենթարկվում
բեկման օրենքին
և գծագրերում
նշանակվում է
e տառով:
Միառանցք և երկառանցք բյուրեղներ: Կատարված փորձերը ցույց են տալիս, որ իսլանդական սպաթի բյուրեղում կա մի ուղղություն, որի երկայնքով կրկնակի ճառագայթաբեկում տեղի չի ունենում: Այդպիսի բյուրեղները կոչվում են միառանցք բյուրեղներ, իսկ այն ուղղությունը, որի երկայնքով կրկնակի ճառագայթաբեկում տեղի չի ունենում, ընդունված է անվանել բյուրեղի օպտիկական առանցք:
Իսլանդական սպաթը միակ բյուրեղը չէ, որ օժտված է երկբեկման հատկությամբ: Տուրմալինը, քվարցը և այլ բյուրեղներ (ընդհանրապես բոլոր բյուրեղները, որոնք պատկանում են տրիգոնալային, տետրագոնալային և հեքսագոնալային համակարգերին) նույնպես օժտված են այդպիսի հատկությամբ և միառանցք են: Իսլանդական սպաթում երկճառագայթաբեկման հատկությունը համեմատած ուրիշ նյութերի բյուրեղների հետ, ավելի ուժեղ է արտահայտվում: Ահա թե ինչու երկճառագայթաբեկման երևույթն առաջինը հայտնաբերվել է իսլանդական սպաթի բյուրեղներում:
Հետագա հետազոտությունները ցույց են տվել, որ գոյություն ունեն բյուրեղներ (որոնք պատկանում են ռոմբիկային, մոնոկլինային և տրիկլինային համակարգերին), որոնցում կան երկու ուղղություններ, որոնց երկայնքով տեղի չի ունենում երկճառագայթաբեկում: Այդպիսի բյուրեղները կոչվում են երկառանցք (փայլարը, գիպսը և այլն): Խորանարդային համակարգի բյուրեղներում երկճառագայթաբեկում չի դիտվում:
Միառանցք բյուրեղի օպտիկական առանցքով անցնող ցանկացած հարթություն կոչվում է բյուրեղի գլխավոր հատույթ կամ գլխավոր հարթություն: Երկառանցք բյուրեղներում գլխավոր հատույթի տակ հասկացվում է այն հարթությունը, որն անցնում է երկու օպտիկական առանցքներով:
Երկբեկումը
բացատրվում է բյուրեղների
անիզոտրոպությամբ:
Որոշ բյուրեղներում
ուղղությունից
կախվածություն
է ի հայտ գալիս,
մասնավորապես
![]() դիէլեկտրական
թափանցելիության
համար: Քանի որ
դիէլեկտրական
թափանցելիության
համար: Քանի որ
![]() հետևաբար
անիզոտրոպությունից
բխում է, որ
հետևաբար
անիզոտրոպությունից
բխում է, որ ![]() վեկտորի
տատանումների
տարբեր ուղղություններ
ունեցող էլեկտրամագնիսական
ալիքներին համապատասխանում
են
վեկտորի
տատանումների
տարբեր ուղղություններ
ունեցող էլեկտրամագնիսական
ալիքներին համապատասխանում
են ![]() բեկման
ցուցչի տարբեր
արժեքներ: Ուստի
բյուրեղում լուսային
ալիքի արագությունը
կախում կունենա
բեկման
ցուցչի տարբեր
արժեքներ: Ուստի
բյուրեղում լուսային
ալիքի արագությունը
կախում կունենա
![]() լուսային
վեկտորի տատանումների
ուղղությունից:
լուսային
վեկտորի տատանումների
ուղղությունից:
Սովորական և ոչ սովորական ճառագայթներ: Սովորական և ոչ սովորական ճառագայթների հետազոտությունը ցույց է տվել, որ երկու ճառագայթներն էլ լրիվ բևեռացված են փոխուղղահայաց ուղղություններով (նկ.4.7):
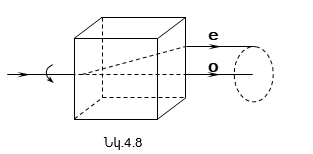
Սովորական ճառագայթում լուսային վեկտորի տատանումները կատարվում են գլխավոր հատույթին ուղղահայաց հարթության մեջ, ոչ սովորական ճառագայթում լուսային վեկտորի տատանումները տեղի են ունենում գլխավոր հատույթին համընկնող հարթության մեջ:
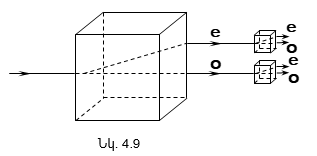
Եթե
ճառագայթներից
մեկը (սովորական
կամ ոչ սովորական)
ուղղվի երկբեկող
միառանցք բյուրեղի
վրա, ապա նրանցից
յուրաքանչյուրը
կրկնապատկվում
է (նկ.4.9): Հետևաբար,
երկճառագայթաբեկումը
առաջանում է բյուրեղի
վրա ինչպես բնական,
այնպես էլ հարթ
բևեռացված լույս
ընկնելու դեպքում:
Տարբերությունը
միայն այն է, որ
եթե առաջին դեպքում
երկու ճառագայթների
ինտենսիվությունները
իրար հավասար են,
ապա երկրորդ դեպքում
ինտենսիվությունները
տարբեր են և կախված
են ընկնող հարթ
բևեռացած լույսի
տատանումների
հարթությունով
և բյուրեղի գլխավոր
հատույթի հարթությամբ
կազմված անկյունից:
Դրանում համոզվելու
համար, բյուրեղի
վրա ուղղենք E
լայնույթով գծային
բևեռացված լույս:
Ընկնող լույսի
տատանումների
հարթության և բյուրեղի
գլխավոր հատույթի
միջև անկյունը
նշանակենք ![]() Ակներև
է, որ ոչ սովորական
և սովորական ճառագայթների
էլեկտրական վեկտորներն
ընկնող գծային
բևեռացված լույսի
տատանումների
հարթության հետ
կազմում են համապատասխանաբար
Ակներև
է, որ ոչ սովորական
և սովորական ճառագայթների
էլեկտրական վեկտորներն
ընկնող գծային
բևեռացված լույսի
տատանումների
հարթության հետ
կազմում են համապատասխանաբար
![]() անկյուններ:
Ուստի սովորական
և ոչ սովորական
ճառագայթների
համար էեկտրական
վեկտորի լայնույթի
տատանումները
համապատասխանաբար
կլինեն`
անկյուններ:
Ուստի սովորական
և ոչ սովորական
ճառագայթների
համար էեկտրական
վեկտորի լայնույթի
տատանումները
համապատասխանաբար
կլինեն`
![]()
Ինտենսիվությունների հարաբերության համար կունենանք`

Ինչպես
հետևում է (4.6)-ից
միայն ![]() դեպքում
դեպքում
![]() (4.6) բանաձևը
հաստատվում է փորձի
տվյալներով:
(4.6) բանաձևը
հաստատվում է փորձի
տվյալներով:
![]() մեծությունը
կոչվում է սովորական
ճառագայթի բեկման
ցուցիչ,
մեծությունը
կոչվում է սովորական
ճառագայթի բեկման
ցուցիչ, ![]() մեծությունը`
ոչ սովորական ճառագայթի
բեկման ցուցիչ:
Կախված նրանից,
թե արագություններից
որն է ավելի մեծ`
vo-ն, թե ve-ն տարբերում
են դրական և բացասական
միառանցք բյուրեղներ:
Դրական բյուրեղների
համար
մեծությունը`
ոչ սովորական ճառագայթի
բեկման ցուցիչ:
Կախված նրանից,
թե արագություններից
որն է ավելի մեծ`
vo-ն, թե ve-ն տարբերում
են դրական և բացասական
միառանցք բյուրեղներ:
Դրական բյուրեղների
համար ![]() (դա նշանակում
է, որ
(դա նշանակում
է, որ ![]() ): Բացասական
բյուրեղների համար
): Բացասական
բյուրեղների համար
![]()
Բնական լույսը գծային բևեռացված լույսի փոխակերպելու համար օգտագործում են բևեռացնող սարքեր (բևեռացուցիչներ): Մենք արդեն ծանոթ ենք հարթ բևեռացված լույսի ստացման որոշ մեթոդների: Երկու դիէլեկտրիկների բաժանման սահմանից Բրյուստերի անկման անկյան տակ ընկած լույսի անդրադաձման դեպքում տեղի է ունենում լրիվ բևեռացում: Շատ թիթեղներից կազմելով կույտ` կարելի է ստանալ գործնականորեն լրիվ գծային բևեռացում նաև բեկման դեպքում: Սակայն բևեռացված լույսի ինտենսիվության ուժեղ թուլացումն այդ մեթոդները դարձնում է անհարմար:
Ինչպես
հայտնի է, սովորական
և ոչ սովորական
ճառագայթները
գծային բևեռացված
են: Եթե դրանք բաժանվեն
մեկը մյուսից բավարար
հեռավորության
վրա, կարելի է ստանալ
երկու գծային բևեռացված
ճառագայթներ:
Այդ նպատակի համար
ընտրում են այնպիսի
բյուրեղ, որի no
և ne բեկման ցուցիչները
մեծությամբ իրարից
շատ են տարբերվում:
Այդ առումով լավագույն
բյուրեղ է իսլանդական
սպաթը, որի համար
![]()
Որոշ բյուրեղներում ճառագայթներից մեկը մյուսից ավելի ուժեղ է կլանվում: Այդ երևույթը կոչվում է երկգունություն (դիքրոիզմ): Տեսանելի ճառագայթներում շատ ուժեղ դիքրոիզմ ունի տուրմալինի բյուրեղը: Նրա մեջ սովորական ճառագայթը գործնականորեն լրիվ կլանվում է 1մմ երկարության վրա:
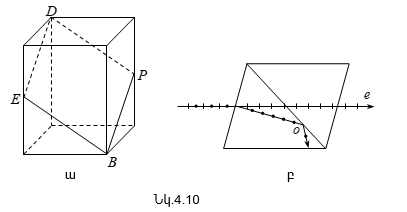
Մեծ
տարածում է ստացել
Նիկոլի պրիզմա
(կամ պարզապես
նիկոլ) կոչվող
բևեռացուցիչը:
Այն իսլանդական
սպաթից պատրաստված
զուգահեռանիստի
ձև ունեցող բյուրեղ
է (նկ.4.10ա): Բյուրեղը
BEDP թեք հարթությամբ
կտրվում է երկու
մասի, այնուհետև
սոսնձվում է կանադական
բալզամով: Կանադական
բալզամ է կոչվում
խեժանման նյութը,
որը ստացվում է
կանադական սոճուց:
Այդ նյութի բեկման
ցուցիչը մոտ է
ապակու բեկման
ցուցչին, այդ պատճառով
կանադական բալզամը
կիրառվում է օպտիկական
գործիքների ապակե
մասերը սոսնձելու
համար: Կանադական
բալզամի ![]() բեկման
ցուցիչը գտնվում
է բյուրեղի սովորական
և ոչ սովորական
ճառագայթների
no և ne բեկման
ցուցիչների միջև
բեկման
ցուցիչը գտնվում
է բյուրեղի սովորական
և ոչ սովորական
ճառագայթների
no և ne բեկման
ցուցիչների միջև
![]() Դիցուք բնական
ճառագայթն ընկնում
է պրիզմայի ներքին
նիստի վրա (4.10բ): Անկման
անկյունն այնպիսին
է, որ սովորական
ճառագայթը միջնաշերտում
կրում է լրիվ ներքին
անդրադարձում
և շեղվում դեպի
մի կողմ, ընկնելով
պրիզմայի կողմնային
նիստի վրա, որը
ծածկված է լույսի
համար անթափանց
նյութի շերտով,
այնտեղ կլանվում
է, իսկ ոչ սովորական
ճառագայթն ազատ
անցնում է միջնաշերտի
միջով և դուրս
է գալիս պրիզմայից
(նկ.4.10բ): Այսպիսով,
Նիկոլի պրիզմայի
միջով անցնում
է միայն ոչ սովորական
ճառագայթը:
Դիցուք բնական
ճառագայթն ընկնում
է պրիզմայի ներքին
նիստի վրա (4.10բ): Անկման
անկյունն այնպիսին
է, որ սովորական
ճառագայթը միջնաշերտում
կրում է լրիվ ներքին
անդրադարձում
և շեղվում դեպի
մի կողմ, ընկնելով
պրիզմայի կողմնային
նիստի վրա, որը
ծածկված է լույսի
համար անթափանց
նյութի շերտով,
այնտեղ կլանվում
է, իսկ ոչ սովորական
ճառագայթն ազատ
անցնում է միջնաշերտի
միջով և դուրս
է գալիս պրիզմայից
(նկ.4.10բ): Այսպիսով,
Նիկոլի պրիզմայի
միջով անցնում
է միայն ոչ սովորական
ճառագայթը:
Բևեռացնող նյութերի գործածությունը հնարավորություն է տալիս խուսափել դիմացից եկող մեքենաների լույսի կուրացուցիչ ազդեցությունից և մեծ չափով մեծացնում է երթևեկության անվտանգությունը: Դրա համար պահանջվում է գտնել էժան բևեռացնող նյութեր պատրաստելու մեծ թվով եղանակներ:
Որոշ բյուրեղների և օրգանական միացությունների լուծույթների միջով հարթ բևեռացված լույսի անցման դեպքում նկատվում է բևեռացման հարթության պտտում: Այդպիսի ունակությամբ օժտված նյութերը կոչվում են օպտիկապես ակտիվ: Դրանց թվին են պատկանում բյուրեղներից` քվարցը, զուտ հեղուկներից` սկիպիդարը և օպտիկապես ակտիվ նյութերի լուծույթները ոչ ակտիվ լուծիչներում` գինեթթվի և շաքարի ջրային լուծույթները:
Երկու
նիկոլներով լույսի
անցման դեպքում,
որոնց բևեռացման
հարթությունները
փոխուղղահայաց
են, տեսողության
դաշտը կլինի մութ,
քանի որ երկրորդ
նիկոլն իր միջով
անցնող տատանումները
բաց չի թողնում:
Նիկոլների միջև
տեղադրենք քվարցե
բարակ բյուրեղը,
որը կտրված է օպտիկական
առանցքին ուղղահայաց:
Տեսողական դաշտը
դառնում է լուսավոր:
Բայց նիկոլներից
մեկը պտտելով
որոշ անկյան տակ`
տեսողության դաշտը
նորից կարելի է
դարձնել մութ:
Այս փորձը ցույց
է տալիս, որ քվարցե
թիթեղով լույսի
անցման դեպքում
այն մնում է բևեռացված,
բայց նրա բևեռացման
հարթությունը
պտտվել է որևէ
![]() անկյունով:
Այս երևույթը ստացել
է բևեռացման հարթության
պտտում անվանումը:
Պինդ մարմիններում
բևեռացման հարթության
պտտման անկյունը
համեմատական է
բյուրեղում լուսային
ճառագայթի անցած
անկյունով:
Այս երևույթը ստացել
է բևեռացման հարթության
պտտում անվանումը:
Պինդ մարմիններում
բևեռացման հարթության
պտտման անկյունը
համեմատական է
բյուրեղում լուսային
ճառագայթի անցած
![]() ճանապարհին.
ճանապարհին.
![]()
![]() գործակիցը
կոչվում է պտտման
հաստատուն, կախված
է նյութի տեսակից,
ջերմաստիճանից
և ալիքի երկարությունից:
գործակիցը
կոչվում է պտտման
հաստատուն, կախված
է նյութի տեսակից,
ջերմաստիճանից
և ալիքի երկարությունից:
Լուծույթներում
բևեռացման հարթության
պտտման անկյունը
համեմատական է
լուծույթում ճառագայթի
անցած ![]() ճանապարհին
և ակտիվ նյութի
կոնցենտրացիային`
ճանապարհին
և ակտիվ նյութի
կոնցենտրացիային`
![]()
որտեղ
![]() մեծությունը
կոչվում է պտտման
տեսակարար հաստատուն,
C-ն օպտիկապես
ակտիվ նյութի կոնցենտրացիան
է:
մեծությունը
կոչվում է պտտման
տեսակարար հաստատուն,
C-ն օպտիկապես
ակտիվ նյութի կոնցենտրացիան
է:
Պտտման տեսակարար հաստատունը կախված է օպտիկապես ակտիվ նյութի բնույթից, ջերմաստիճանից և ալիքի երկարությունից:
Բևեռացման հարթության պտտման ուղղությունից կախված օպտիկապես ակտիվ նյութերը բաժանվում են աջ և ձախ պտտողների: Եթե նայենք ճառագայթին ընդառաջ, աջ պտտող նյութերում բևեռացման հարթությունը կպտտվի ժամսլաքի ուղղությամբ, ձախ պտտող նյութերում` ժամսլաքին հակառակ ուղղությամբ: Այսպիսով, ճառագայթի ուղղությունը և պտտման ուղղությունը աջ պտտող նյութերում կազմում են ձախ պտուտակային համակարգ, իսկ ձախ պտտող նյութերում` աջ պտուտակային համակարգ: Պտտման ուղղությունը կախում չունի օպտիկապես ակտիվ միջավայրում ճառագայթի ուղղությունից:
Բևեռացման հարթության պտտումը բացատրելու համար Ֆրենելը ենթադրեց, որ օպտիկապես ակտիվ նյութերում շրջանով դեպի աջ և դեպի ձախ բևեռացված ճառագայթները տարածվում են տարբեր արագություններով:
Շրջանային բևեռացման տարբեր ուղղություններ ունեցող լույսի արագությունների տարբերությունը պայմանավորված է մոլեկուլների անհամաչափափությամբ կամ բյուրեղում ատոմների անհամաչափ դասավորությամբ:
Բևեռացման հարթության պտտման երևույթն իր կիրառությունն է գտել լուծույթում ակտիվ նյութի կոնցենտրացիան որոշելու համար: Քանի որ պտտման անկյունը համեմատական է ակտիվ նյութի կոնցենտրացիային և շերտի հաստությանը, օգտագործելով (4.8) առնչությունը կարելի է որոշել կոնցենտրացիան: Այդ սկզբունքի վրա է հիմնված շաքարաչափ սարքի կառուցվածքը` լուծույթում շաքարի կոնցենտրացիան որոշելու համար:
4.6. Արհեստական կրկնակի ճառագայթաբեկում
Քերի երևույթը
1875թ. Ջ. Քերը հայտնաբերեց, որ եթե իզոտրոպ դիէլեկտրիկները (ինչպես պինդ, այնպես էլ հեղուկ) տեղավորենք էլեկտրական դաշտում, ապա այդ նյութերը դառնում են անիզոտրոպ: Հետագայում Քերի երևույթը դիտվեց նաև գազերում: Նկ.4.11-ում պատկերված է հեղուկներում Քերի երևույթը դիտելու սխեման: Սարքը կազմված է Քերի բջջից, որը տեղադրված է խաչված P բևեռաչուցչի և A անալիզատորի միջև: Քերի բջիջը հեղուկով լցված հերմետիկ անոթ է, որի մեջ մտցված են կոնդենսատորի թիթեղները: Տեխնիկայում կիրառվող Քերի բջիջները լցվում են նիտրոբենզոլով: Էլեկտրական դաշտի բացակայության դեպքում հեղուկը իզոտրոպ է, լույսի անցումը նրա միջով չի փոխում նրա բևեռացման աստիճանը: Տեսադաշտն այս դեպքում խավար է: Եթե կոնդենսատորին կիրառենք լարում, դիէլեկտրիկը դառնում է անիզոտրոպ, և նրանում առաջանում է կրկնակի ճառագայթաբեկում, հետևաբար հեղուկը ձեռք է բերում միառանցք բյուրեղի հատկություն, որի առանցքը կողմնորոշված է դաշտի ուղղությամբ, ինչի շնորհիվ էլ տեսադաշտը դառնում է լուսավոր: Ուսումնասիրելով երկբեկումը տարբեր երկարություն ունեցող լուսային ալիքների համար տարբեր հեղուկներում և տարբեր դաշտերում, Քերը հաստատեց, որ սովորական և ոչ սովորական ճառագայթների բեկման ցուցիչների no-ne տարբերության վրա ազդում են ինչպես էլեկտրական դաշտի մեծությունը, այնպես էլ լույսի ճառագայթների ալիքի երկարության չափը: no և ne բեկման ցուցիչների տարբերությունը համեմատական է դաշտի լարվածության քառակուսուն`
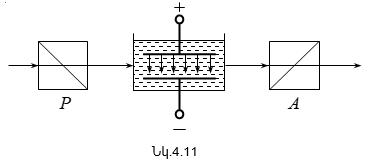
![]()
որտեղ
![]() գործակիցը
կախված է միայն
նյութի տեսակից
և նրա վիճակից,
ինչպես նաև լուսային
ալիքի
գործակիցը
կախված է միայն
նյութի տեսակից
և նրա վիճակից,
ինչպես նաև լուսային
ալիքի ![]() երկարությունից:
Ոչ սովորական և
սովորական ճառագայթների
միջև փուլերի տարբերությունը
կոնդենսատորի
միջով անցնելուց
հետո կլինի`
երկարությունից:
Ոչ սովորական և
սովորական ճառագայթների
միջև փուլերի տարբերությունը
կոնդենսատորի
միջով անցնելուց
հետո կլինի`
![]()
որտեղ
![]() նյութի շերտի
հաստությունն
է, իսկ
նյութի շերտի
հաստությունն
է, իսկ ![]() այսպես
կոչված, Քերի հաստատունն
է: Այն մեծանում
է ալիքի փոքրացման
դեպքում և խիստ
փոքրանում է ջերմաստիճանի
բարձրացման հետ:
այսպես
կոչված, Քերի հաստատունն
է: Այն մեծանում
է ալիքի փոքրացման
դեպքում և խիստ
փոքրանում է ջերմաստիճանի
բարձրացման հետ:
(4.9)
և (4.10) բանաձևերի
մեջ մտնում է դաշտի
լարվածության
քառակուսին: Այդ
պատճառով (no-ne ) տարբերության,
ինչպես նաև![]() փուլերի
տարբերության
նշանը չի փոխվում`
դաշտի ուղղությունը
փոխելիս: Հայտնի
հեղուկներից ամենամեծ
Քերի հաստատուն
ունի նիտրոբենզոլը
(C6H5NO2): Նրա համար
փուլերի
տարբերության
նշանը չի փոխվում`
դաշտի ուղղությունը
փոխելիս: Հայտնի
հեղուկներից ամենամեծ
Քերի հաստատուն
ունի նիտրոբենզոլը
(C6H5NO2): Նրա համար
![]() Եթե
Եթե ![]() և
E=104 Վ/սմ, (4.10) բանաձևով
նիտրոբենզոլի
համար ստացվում
է
և
E=104 Վ/սմ, (4.10) բանաձևով
նիտրոբենզոլի
համար ստացվում
է ![]()
Քերի երևույթի բացատրությունը տվել են Պ. Լանժեվենը և Մ. Բորնը: Հեղուկ դիէլեկտրիկի յուրաքանչյուր մոլեկուլ օժտված է անիզոտրոպ օպտիկական հատկություններով, բայց քանի որ մոլեկուլների շարժումը քաոսային է, ապա հեղուկը ամբողջությամբ իզոտրոպ է: Էլեկտրական դաշտի ազդեցությամբ մոլեկուլները ձեռք են բերում լրացուցիչ դիպոլային մոմենտ, իսկ դիպոլային մոմենտ ունեցողները կողմնորոշվում են դաշտի ուղղությամբ, և հեղուկն ամբողջությամբ դառնում է անիզոտրոպ մարմին: Մոլեկուլների կողմնորոշումը էլեկտրական դաշտում ավերում է ջերմային շարժումը, ուստի ջերմաստիճանի բարձրացումը բերում է Քերի հաստատունի փոքրացման: Այն ժամանակամիջոցը, որի ընթացքում հաստատվում (դաշտը միացնելիս) կամ վերանում է (դաշտն անջատելիս) մոլեկուլների գերակշռող կողմնորոշումը, կազմում է մոտ 10-10 վ: Մոլեկուլների կողմնորոշման և ապակողմնորոշման մեծ արագությունը հնարավորություն է տալիս Քերի երևույթը դիտել ոչ միայն փոփոխական էլեկտրական դաշտում, այլև հզոր լազերային լույսի դաշտում: Այսպիսով, խաչված բևեռացուցիչների միջև տեղավորված Քերի բջիջը կարող է ծառայել որպես գործնականորեն լրիվ ոչ իներցիոն փական: Կոնդենսատորի թիթեղների վրա լարման բացակայության դեպքում փականը փակ է լինում:
Քերի երևույթը լայնորեն օգտագործվում է տեխնիկայում: Քերի կոնդենսատորը (Քերի բջիջը) օգտագործվում է որպես ոչ իներցիոն լուսային փական` ձայնային կինոյում լույսը մոդուլացնելու համար, ինչպես նաև հատուկ սաքերում և հետազոտությունների համար:
ԼՈՒՅՍԻ ԴԻՍՊԵՐՍԻԱՆ
5.1. Նորմալ և անոմալ դիսպերսիա
![]()
Հայտնի
է, որ սպիտակ լույսի
նեղ փունջը ապակյա
պրիզմայով անցկացնելու
դեպքում պրիզմայի
ետևում տեղադրված
էկրանի վրա դիտվում
են ծիածանագույն
շերտեր (նկ.5.1), որոնք
կոչվում են պրիզմատիկ
սպեկտր կամ դիսպերսիոն
սպեկտր: Առաջին
անգամ այս երևույթը
հայտնաբերել է
Ի. Նյուտոնը 1666թ.:
Էկրանի վրա սպեկտրը
դիտվում է նաև
այն դեպքում, երբ
լույսի աղբյուրը,
պրիզման և էկրանը
տեղադրված են
փակ անոթում, որից
օդը հանված է: Հետևաբար,
պրիզմատիկ սպեկտրի
առաջանալը վկայությունն
է այն բանի, որ ապակու
բացարձակ n բեկման
ցուցիչը կախված
է լույսի ![]() հաճախությունից
կամ ալիքի երկարությունից.
հաճախությունից
կամ ալիքի երկարությունից.
![]() Ինչպես ցույց
են տվել փորձերը,
n-ի կախումը
Ինչպես ցույց
են տվել փորձերը,
n-ի կախումը ![]() հատուկ
է բոլոր նյութերին:
Միջավայրի բեկման
ցուցչի կախումը
լույսի հաճախությունից
(կամ ալիքի երկարությունից)
կոչվում է դիսպերսիա:
հատուկ
է բոլոր նյութերին:
Միջավայրի բեկման
ցուցչի կախումը
լույսի հաճախությունից
(կամ ալիքի երկարությունից)
կոչվում է դիսպերսիա:
Լույսի
դիսպերսիան միջավայրում
կոչվում է նորմալ,
եթե հաճախության
մեծացմանը զուգընթաց
միջավայրի n բացարձակ
բեկման ցուցիչը
նույնպես աճում
է. ![]() Այդպիսի
կապ դիտվում է
հաճախությունների
այն միջակայքում,
որոնց համար միջավայրը
թափանցիկ է: Օրինակ,
սովորական ապակին
թափանցիկ է տեսանելի
լույսի համար և
այդ հաճախությունների
միջակայքում օժտված
է նորմալ դիսպերսիայով
(տես նկ. 5.1):
Այդպիսի
կապ դիտվում է
հաճախությունների
այն միջակայքում,
որոնց համար միջավայրը
թափանցիկ է: Օրինակ,
սովորական ապակին
թափանցիկ է տեսանելի
լույսի համար և
այդ հաճախությունների
միջակայքում օժտված
է նորմալ դիսպերսիայով
(տես նկ. 5.1):
Լույսի
դիսպերսիան միջավայրում
կոչվում է անոմալ,
եթե հաճախության
մեծացմանը զուգընթաց
միջավայրի բացարձակ
բեկման ցուցիչը
փոքրանում է. ![]()
Անոմալ դիսպերսիան դիտվում է հաճախությունների այն տիրույթում, որոնք համապատասխանում են նյութի կողմից լույսի ինտենսիվ կլանման շերտերին:
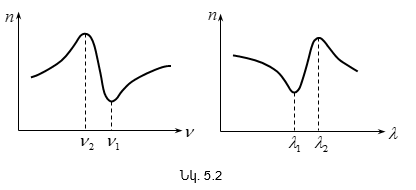
Ապակու
համար այդ շերտերը
գտնվում են սպեկտրի
ուլտրամանուշակագույն
և ինֆրակարմիր
տիրույթներում:
Նկ. 5.2-ում ցույց է
տրված n-ի ![]() կախվածության
ընթացքը: Անոմալ
դիսպերսիան համապատասխանում
է
կախվածության
ընթացքը: Անոմալ
դիսպերսիան համապատասխանում
է ![]() մինչև
մինչև ![]() հաճախությունների
միջակայքին: Կախված
դիսպերսիայի բնույթից`
լույսի խմբային
արագությունը
նյութում կարող
է լինել ինչպես
մեծ, այնպես էլ
փոքր փուլային
հաճախությունների
միջակայքին: Կախված
դիսպերսիայի բնույթից`
լույսի խմբային
արագությունը
նյութում կարող
է լինել ինչպես
մեծ, այնպես էլ
փոքր փուլային![]() արագությունից:
Իրոք,
արագությունից:
Իրոք,
![]()
այնպես
որ 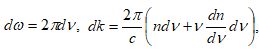 խմբային
արագությունը`
խմբային
արագությունը`

Նորմալ
դիսպերսիայի դեպքում
![]() Անոմալ դիսպերսիայի
դեպքում`
Անոմալ դիսպերսիայի
դեպքում` ![]() և
մասնավորապես,
եթե
և
մասնավորապես,
եթե ![]() ապա
ապա ![]()
Համաձայն հարաբերականության տեսության և փորձերի տվյալների` լուսային ազդանշանի տարածման արագությունը ցանկացած նյութում չի կարող գերազանցել վակուումում լույսի արագությանը: Ուստի վերևում ստացված արդյունքը վկայում է, որ անոմալ դիսպերսիայի տիրույթում խմբային արագությունը չի համընկնում ալիքների խմբի էներգիայի տեղափոխման արագության հետ:
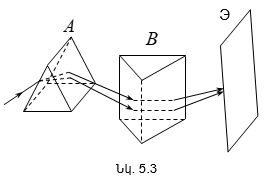
Ազդանշանի նկարագրման հնարավորությունը խմբային արագության օգնությամբ հիմնվում է այն ենթադրության վրա, որ միջավայրում ազդանշանի տարածման պրոցեսում պահպանվում է ազդանշանի «ձևը», այսինքն` լայնույթի և էներգիայի բաշխումը նրա երկարությամբ: Խիստ ասած, այդ պայմանը տեղի ունի միայն վակուումի համար: Բոլոր այլ միջավայրերի համար այն տեղի ունի մոտավոր, և որքան նեղ է ազդանշանի հաճախության սպեկտրը, այնքան այն ավելի ճշգրիտ է: Կլանման շերտերին մոտ նյութում լույսի դիսպերսիան այնքան մեծ է, որ ազդանշանի «ձևը» նյութի մեջ նրա տարածմանը զուգընթաց արագ փոփոխվում է:
Նորմալ և անոմալ դիսպերսիաները կարելի է դիտել Նյուտոնի կողմից առաջարկված խաչաձև պրիզմաների մեթոդով: Այդ մեթոդի էությունն այն է, որ լույսը հաջորդաբար անցնում է երկու պրիզմաների միջով, որոնց բեկող կողերը իրար ուղղահայաց են դասավորված (նկ.5.3): A-ն ապակյա պրիզմա է, իսկ B պրիզման պատրաստված է այն նյութից, ուր հետազոտվում է լույսի դիսպերսիան: A պրիզման լուսավորվում է սպիտակ լույսի զուգահեռ փնջով: Լույսի ճառագայթներն անցնելով A և B պրիզմաների միջով` շեղվում են դեպի պրիզմաների հիմքերը: Լույսի տարբեր երկարության ալիքների համար որքան մեծ են համապատասխանաբար պրիզմաների բեկման ցուցիչների արժեքները, այնքան մեծ են շեղման անկյունները:
Եթե B պրիզման չլիներ, ապա էկրանի վրա կդիտվեր ապակու մեջ լույսի նորմալ դիսպերսիայով պայմանավորված սպեկտրը, որը կունենար ծիածանագույն ուղղանկյուն շերտիկի տեսք (նկ.5.4ա): Երկրորդ պրիզմայում լույսի դիսպերսիայի հետևանքով սպեկտրն էկրանի վրա ծռվում է: Նրա տեսքը B պրիզմայում նորմալ դիսպերսիայի դեպքում, տեսանելի լույսի ալիքի երկարությունների ամբողջ միջակայքում պատկերված է նկ.5.4բ-ում: Վերջապես նկ.5.4գ-ում պատկերված սպեկտրը համապատասխանում է այն դեպքին, երբ B պրիզմայի նյութի կողմից լույսի կլանման շերտերից մեկը գտնվում է տեսանելի լույսի տիրույթում: Սպեկտրի ներքևի կեսի շեղումը վերևինի նկատմամբ դեպի ձախ պայմանավորված է կլանման շերտերի սահմաններում անոմալ դիսպերսիայով:
5.2. Էլեկտրամագնիսական ալիքների փոխազդեցությունը
նյութի հետ: Լույսի դիսպերսիայի դասական
տեսությունը
Լույսի դիսպերսիան էլեկտրմագնիսական ալիքների և նյութի կազմի մեջ մտնող լիցքավորված մասնիկների փոխազդեցության արդյունք է: Դրա համար էլ Մաքսվելի մակրոսկոպիկ էլեկտրամագնիսական տեսությունը չկարողացավ բացատրել այդ երևույթը: Դիսպերսիայի դասական տեսությունը մշակվեց միայն Լորենցի կողմից ստեղծված նյութի կառուցվածքի էլեկտրոնային տեսությունից հետո:
Մաքսվելի տեսությունից հետևում է, որ միջավայրի բացարձակ բեկման ցուցիչն արտահայվում է հետևյալ բանաձևով`
![]()
որտեղ
![]() միջավայրի
հարաբերական դիէլեկտրական
թափանցելիությունն
է: (5.1) բանաձևը ստանում
ենք (1.5)-ից` ընդունելով,
որ բոլոր թափանցիկ
նյութերի
միջավայրի
հարաբերական դիէլեկտրական
թափանցելիությունն
է: (5.1) բանաձևը ստանում
ենք (1.5)-ից` ընդունելով,
որ բոլոր թափանցիկ
նյութերի ![]() մագնիսական
թափանցելիությունը
հավասար է մեկի:
Առաջին հայացքից
կարող է թվալ, որ
այս բանաձևը ճիշտ
չէ: Օրինակ, ջրի
համար
մագնիսական
թափանցելիությունը
հավասար է մեկի:
Առաջին հայացքից
կարող է թվալ, որ
այս բանաձևը ճիշտ
չէ: Օրինակ, ջրի
համար ![]() իսկ
իսկ ![]() Սակայն
նկատի պետք է ունենալ,
որ
Սակայն
նկատի պետք է ունենալ,
որ ![]() արժեքը ստացվել
է էլեկտրաստատիկ
չափումներից:
Արագ փոփոխվող
էլեկտրական դաշտերում
ստացվում է
արժեքը ստացվել
է էլեկտրաստատիկ
չափումներից:
Արագ փոփոխվող
էլեկտրական դաշտերում
ստացվում է ![]() այլ
արժեք, որը կախում
ունի դաշտի տատանման
հաճախությունից:
Դրանով է բացատրվում
լույսի դիսպերսիան,
այսինքն` բեկման
ցուցչի կախումը
հաճախությունից
(կամ ալիքի երարությունից):
(5.1)-ում համապատասխան
հաճախության համար
ստացված
այլ
արժեք, որը կախում
ունի դաշտի տատանման
հաճախությունից:
Դրանով է բացատրվում
լույսի դիսպերսիան,
այսինքն` բեկման
ցուցչի կախումը
հաճախությունից
(կամ ալիքի երարությունից):
(5.1)-ում համապատասխան
հաճախության համար
ստացված ![]() արժեքի
տեղադրումը հանգեցնում
է n-ի ճիշտ արժեքին:
արժեքի
տեղադրումը հանգեցնում
է n-ի ճիշտ արժեքին:
Բեկման ցուցչի կախումն ալիքի երկարությունից արտածելու համար գտնենք, թե դիէլեկտրական թափանցելիությունը ինչպես է կախված փոփոխական էլեկտրական դաշտի հաճախությունից, և ապա (5.1) առնչության հիման վրա անցնենք n-ին:
Էլեկտրոնային
տեսության համաձայն`
դիէլեկտրիկի մոլեկուլները
կամ ատոմները ընդունենք
որպես այնպիսի
համակարգեր, որոնց
կազմի մեջ մտնում
են ատոմի ներսում
հավասարակշռության
վիճակում գտնվող
էլեկտրոնները:
Արտաքին դաշտի
ազդեցության տակ
այդ լիցքերը տեղաշարժվում
են հավասարակշռության
վիճակից ![]() հեռավորության
վրա` ատոմը դարձնելով
էլեկտրական դիպոլ
(երկբևեռ):
հեռավորության
վրա` ատոմը դարձնելով
էլեկտրական դիպոլ
(երկբևեռ):
Էլեկտրականության դասընթացից հայտնի է, որ
![]()
որտեղ
![]() միջավայրի
դիէլեկտրական
ընկալունակությունն
է,
միջավայրի
դիէլեկտրական
ընկալունակությունն
է, ![]() էլեկտրական
հաստատունն է,
իսկ Pe–ն բևեռացման
վեկտորի պրոյեկցիան
է էլեկտրական դաշտի
լարվածության
էլեկտրական
հաստատունն է,
իսկ Pe–ն բևեռացման
վեկտորի պրոյեկցիան
է էլեկտրական դաշտի
լարվածության
![]() վեկտորի
ուղղության վրա:
վեկտորի
ուղղության վրա:
Այսպիսով`

Լուսային ալիքի մեծ հաճախության շնորհիվ միջավայրի բևեռացումը պայմանավորված է միայն էլեկտրոնների շեղումով (էլեկտրոնային բևեռացում): Հետևաբար, համասեռ միջավայրի համար`
![]()
որտեղ
![]() -ն միավոր
ծավալում ատոմների
թիվն է,
-ն միավոր
ծավալում ատոմների
թիվն է, ![]() ատոմի
դիպոլային մոմենտն
է: Առաջին մոտավորությամբ
կարելի է ընդունել,
որ
ատոմի
դիպոլային մոմենտն
է: Առաջին մոտավորությամբ
կարելի է ընդունել,
որ ![]() մեծությունը
որոշվում է միայն
ատոմի միջուկի
հետ ավելի թույլ
կապված էլեկտրոններով:
Այդ էլեկտրոնները
կոչվում են օպտիկական
էլեկտրոններ:
մեծությունը
որոշվում է միայն
ատոմի միջուկի
հետ ավելի թույլ
կապված էլեկտրոններով:
Այդ էլեկտրոնները
կոչվում են օպտիկական
էլեկտրոններ:
Ակներև է, որ մեկ օպտիկական էլեկտրոնով ատոմների համար
![]()
որտեղ
![]() էլեկտրոնի
լիցքի բացարձակ
մեծությունն է,
r -ը էլեկտրոնի
շեղումն է լուսային
ալիքի էլեկտրական
դաշտի ազդեցության
տակ: Բացասական
նշանը ցույց է
տալիս, որ
էլեկտրոնի
լիցքի բացարձակ
մեծությունն է,
r -ը էլեկտրոնի
շեղումն է լուսային
ալիքի էլեկտրական
դաշտի ազդեցության
տակ: Բացասական
նշանը ցույց է
տալիս, որ ![]() և
և
![]() վեկտորները
հակառակ են բացասական
լիցքավորված էլեկտրոնի
վեկտորները
հակառակ են բացասական
լիցքավորված էլեկտրոնի
![]() շեղման ուղղությանը:
(5.2) և (5.3)-ից հետևում
է, որ
շեղման ուղղությանը:
(5.2) և (5.3)-ից հետևում
է, որ

Այսպիսով, խնդիրը հանգեցվում է r-ի և E-ի կապը գտնելուն:
Թափանցիկ նյութերի համար առաջին մոտավորությամբ կարելի է ընդունել, որ տատանվող օպտիկական էլեկտրոնի վրա ազդում են հետևյալ ուժերը.
ա) գրգռող (ստիպող) ուժը
![]()
որտեղ
E0-ն E լարվածության
լայնույթն է, ![]() լուսային
ալիքի շրջանային
հաճախությունը:
լուսային
ալիքի շրջանային
հաճախությունը:
բ) օպտիկական էլեկտրոնի վրա ազդող և հավասարակշռության դիրքն ուղղված քվազիառաձգական ուժը`
![]()
որտեղ
k-ն քվազիառաձգական
ուժի գործակիցն
է, որը էլեկտրոնի
m զանգվածի և ![]() ցիկլային
հաճախության հետ
կապված է
ցիկլային
հաճախության հետ
կապված է ![]() առնչությամբ,
այնպես, որ
առնչությամբ,
այնպես, որ
![]()
Էլեկտրոնի ստիպողական տատանումների դիֆերենցիալ հավասարումն ունի հետևյալ տեսքը`
![]()
որտեղից
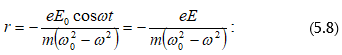
(5.4)-ից և (5.8)-ից հետևում է`
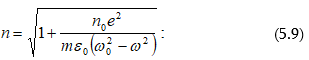
Այսպիսով
(5.9)-ի համաձայն բեկման
ցուցիչը կախում
ունի արտաքին
դաշտի հաճախությունից,
այսինքն ` գտած
բանաձևը տալիս
է լույսի դիսպերսիան.
ճիշտ է, այն ստացվեց
որոշ պարզեցումներ
ընդունելուց
հետո, որոնք հետագայում
պետք է վերացվեն:
![]() -ի կախվածության
գրաֆիկը
-ի կախվածության
գրաֆիկը ![]() -ից
ըստ (5.9) բանաձևի բերված
է նկ.5.5-ում:
-ից
ըստ (5.9) բանաձևի բերված
է նկ.5.5-ում:
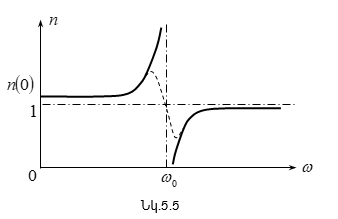
Ինչպես
երևում է (5.9) բանաձևից,
![]() մինչև
մինչև ![]() տիրույթում
տիրույթում
![]() և աճում է
և աճում է
![]() աճման հետ
միասին (նորմալ
դիսպերսիա): Երբ
աճման հետ
միասին (նորմալ
դիսպերսիա): Երբ
![]() բեկման ցուցիչը`
բեկման ցուցիչը`
![]()
![]() մինչև
մինչև
![]() տիրույթում
տիրույթում
![]() և նույնպես
աճում
և նույնպես
աճում![]()
![]() մինչև
1 (նորմալ դիսպերսիա):
Բեկման ցուցչի
մինչև
1 (նորմալ դիսպերսիա):
Բեկման ցուցչի
![]() անվերջություն
դառնալը ֆիզիկական
իմաստ չունի և
ստացվել է այն
պարզեցված ենթադրության
արդյունքում,
որ բացակայում
է մարումը պայմանավորող
շարժման դիմադրության
ուժը, այսինքն`
մենք ուշադրություն
չդարձրինք էներգիայի
կորստին, որը պայմանավորված
է երկրորդային
էլեկտրամագնիսական
ալիքների ճառագայթմամբ,
ճառագայթող ատոմների
բախումներով
և այլ պատճառներով:
Բոլոր այդ կորուստները
կարելի է մոտավորապես
հաշվի առնել, եթե
ենթադրվի, որ տատանվող
էլեկտրոնի վրա
ազդում է լրացուցիչ
դիմադրության
ուժ, որը համեմատական
է արագությանը.
անվերջություն
դառնալը ֆիզիկական
իմաստ չունի և
ստացվել է այն
պարզեցված ենթադրության
արդյունքում,
որ բացակայում
է մարումը պայմանավորող
շարժման դիմադրության
ուժը, այսինքն`
մենք ուշադրություն
չդարձրինք էներգիայի
կորստին, որը պայմանավորված
է երկրորդային
էլեկտրամագնիսական
ալիքների ճառագայթմամբ,
ճառագայթող ատոմների
բախումներով
և այլ պատճառներով:
Բոլոր այդ կորուստները
կարելի է մոտավորապես
հաշվի առնել, եթե
ենթադրվի, որ տատանվող
էլեկտրոնի վրա
ազդում է լրացուցիչ
դիմադրության
ուժ, որը համեմատական
է արագությանը.
![]()
որտեղ
![]() -ն դիմադրության
գործակիցն է: Ուստի
(5.7)-ից ավելի ճշգրիտ,
ստիպողական տատանումներ
կատարող օպտիկական
էլեկտրոնի դիֆերենցիալ
հավասարումը կունենա
հետևյալ տեսքը.
-ն դիմադրության
գործակիցն է: Ուստի
(5.7)-ից ավելի ճշգրիտ,
ստիպողական տատանումներ
կատարող օպտիկական
էլեկտրոնի դիֆերենցիալ
հավասարումը կունենա
հետևյալ տեսքը.
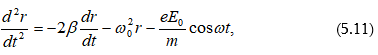
որտեղ
![]() կոչվում
է մարման գործակից:
կոչվում
է մարման գործակից:
Կարելի է ցույց տալ, որ այդ հավասարման լուծումը բերում է գազի բեկման ցուցչի համար հետևյալ արտահայտությանը.
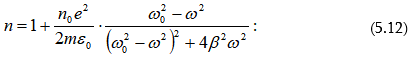
Մարման
ազդեցությունը
n-ի ![]() կախվածության
վրա էական է դառնում
միայն
կախվածության
վրա էական է դառնում
միայն ![]() հաճախությունների
այն տիրույթում,
որը մոտ է
հաճախությունների
այն տիրույթում,
որը մոտ է ![]() Այդ
տիրույթի սահմաններից
դուրս
Այդ
տիրույթի սահմաններից
դուրս ![]() և (5.12) և (5.9)-ը
բանաձևերը լրիվ
համարժեք են: (5.12)
բանաձևին համապատասխանող
n-ի
և (5.12) և (5.9)-ը
բանաձևերը լրիվ
համարժեք են: (5.12)
բանաձևին համապատասխանող
n-ի ![]() կախվածության
գրաֆիկը
կախվածության
գրաֆիկը ![]() մոտ
ցույց է տրված
նկ.5.5-ում կետագծային
կորով: (5.12) բանաձևից
հետևում է, որ
մոտ
ցույց է տրված
նկ.5.5-ում կետագծային
կորով: (5.12) բանաձևից
հետևում է, որ ![]() դեպքում`
n=1:
դեպքում`
n=1:
Մինչ
այժմ հիմնվում
էինք այն ենթադրության
վրա, որ յուրաքանչյուր
նյութի համար կա
օպտիկական էլեկտրոնների
ազատ տատանումների
մեկ բնութագրական
![]() շրջանային
հաճախություն:
Իրականում, ինչպես
ցույց է տալիս
փորձը, ցանկացած
գազային նյութով
լույսի անցման
դեպքում դիտվում
են այդ նյութի
համար բնութագրական
մի շարք գծեր կամ
կլանման շերտեր:
Հետևաբար, յուրաքանչյուր
նյութ բնութագրվում
է տարբեր
շրջանային
հաճախություն:
Իրականում, ինչպես
ցույց է տալիս
փորձը, ցանկացած
գազային նյութով
լույսի անցման
դեպքում դիտվում
են այդ նյութի
համար բնութագրական
մի շարք գծեր կամ
կլանման շերտեր:
Հետևաբար, յուրաքանչյուր
նյութ բնութագրվում
է տարբեր ![]() շրջանային
հաճախությունների
հավաքածուով:
Դրա համար էլ լույսի
դիսպերսիայի դասական
տեսությունում
ներմուծվում է
այն ենթադրությունը,
որ նյութի յուրաքանչյուր
ատոմ (մոլեկուլ)
կարելի է դիտարկել
որպես տարբեր
էֆեկտիվ
շրջանային
հաճախությունների
հավաքածուով:
Դրա համար էլ լույսի
դիսպերսիայի դասական
տեսությունում
ներմուծվում է
այն ենթադրությունը,
որ նյութի յուրաքանչյուր
ատոմ (մոլեկուլ)
կարելի է դիտարկել
որպես տարբեր
էֆեկտիվ ![]() լիցքերով
և
լիցքերով
և ![]() զանգվածներով
լիցքավորված մասնիկների
ներդաշնակ տատանակների
համակարգ, որոնք
կատարում են
զանգվածներով
լիցքավորված մասնիկների
ներդաշնակ տատանակների
համակարգ, որոնք
կատարում են ![]() շրջանային
հաճախություններով
ազատ չմարող տատանումներ:
Լուսային ալիքի
Էլեկտրական դաշտի
ազդեցության տակ
բոլոր այդ տատանակները
կատարում են ստիպողական
տատանումներ և
մտցնում իրենց
ներդրումը նյութի
բևեռացման, հետևաբար
և նրա բեկման ցուցչի
արտահայտության
մեջ: Եթե i-րդ տատանակի
մարման գործակիցը,
որը
շրջանային
հաճախություններով
ազատ չմարող տատանումներ:
Լուսային ալիքի
Էլեկտրական դաշտի
ազդեցության տակ
բոլոր այդ տատանակները
կատարում են ստիպողական
տատանումներ և
մտցնում իրենց
ներդրումը նյութի
բևեռացման, հետևաբար
և նրա բեկման ցուցչի
արտահայտության
մեջ: Եթե i-րդ տատանակի
մարման գործակիցը,
որը ![]() շրջանային
հաճախության
համար հավասար
է
շրջանային
հաճախության
համար հավասար
է ![]() ապա գազի
համար (5.12)-ի փոխարեն
բեկման ցուցչի
հաճախությունից
կախվածության
համար ստացվում
է հետևյալ արտահայտությունը`
ապա գազի
համար (5.12)-ի փոխարեն
բեկման ցուցչի
հաճախությունից
կախվածության
համար ստացվում
է հետևյալ արտահայտությունը`
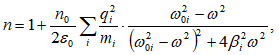
կամ
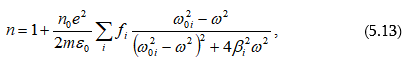
որտեղ
գումարումը կատարվում
է ըստ ![]() բոլոր
արժեքների: Չափայնություն
չունեցող`
բոլոր
արժեքների: Չափայնություն
չունեցող`
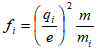
գործակիցը
կոչվում է i-րդ
տատանակի ուժ:
Այն բնութագրում
է նյութի կողմից
![]() շրջանային
հաճախության լույսի
կլանումը: n-ի
շրջանային
հաճախության լույսի
կլանումը: n-ի ![]() կախվածության
գրաֆիկն ըստ (5.13)
բանաձևի բերված
է նկ. 5.6-ում, որը լավ
համաձայնեցվում
է սովորական պայմաններում
կատարված փորձերի
տվյալների հետ:
Վերևում բերված
արտածումներում
մենք միշտ ընդունում
էինք, որ տատանակների
վրա ազդում է միայն
լուսային ալիքի
արտաքին էլեկտրական
դաշտը: Իրականում
դրանք ենթարկվում
են նաև ներքին
էլեկտրական դաշտի
ազդեցությանը,
որը ստեղծվում
է նյութը շրջապատող
մոլեկուլներով,
որոնք բևեռացվում
են լուսային ալիքի
դաշտում: Այլ հավասար
պայմաններում
այդ դաշտի ազդեցությունն
այնքան էական
է, որքան փոքր են
մոլեկուլների
միջև եղած միջին
հեռավորությունները:
կախվածության
գրաֆիկն ըստ (5.13)
բանաձևի բերված
է նկ. 5.6-ում, որը լավ
համաձայնեցվում
է սովորական պայմաններում
կատարված փորձերի
տվյալների հետ:
Վերևում բերված
արտածումներում
մենք միշտ ընդունում
էինք, որ տատանակների
վրա ազդում է միայն
լուսային ալիքի
արտաքին էլեկտրական
դաշտը: Իրականում
դրանք ենթարկվում
են նաև ներքին
էլեկտրական դաշտի
ազդեցությանը,
որը ստեղծվում
է նյութը շրջապատող
մոլեկուլներով,
որոնք բևեռացվում
են լուսային ալիքի
դաշտում: Այլ հավասար
պայմաններում
այդ դաշտի ազդեցությունն
այնքան էական
է, որքան փոքր են
մոլեկուլների
միջև եղած միջին
հեռավորությունները:
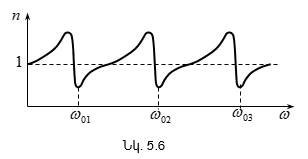
Սեղմված գազերում, ինչպես նաև հեղուկներում և պինդ մարմիններում այն բավականաչափ մեծ է:
Ռենտգենյան
ճառագայթների
դիսպերսիան: Ռենտգենյան
ճառագայթների
դեպքում լուսային
ալիքի դաշտի հաճախությունը
սովորաբար զգալիորեն
ավելի մեծ է, քան
ատոմի սեփական
տատանումների
հաճախությունը:
Այդ պատճառով ![]() համեմատությամբ
համեմատությամբ
![]() մեծությունը
կարելի է անտեսել,
և դիսպերսիայի
(5.9) բանաձևն առանց
մարումը հաշվի
առնելու կընդունի
հետևյալ տեսքը`
մեծությունը
կարելի է անտեսել,
և դիսպերսիայի
(5.9) բանաձևն առանց
մարումը հաշվի
առնելու կընդունի
հետևյալ տեսքը`

Այսպիսով,
ռենտգենյան ճառագայթների
համար բեկման ցուցիչը
ստացվում է 1-ից
փոքր, թեպետ, ![]() չափազանց
մեծ լինելու հետևանքով
մեկից շատ քիչ
է տարբերվում:
Ռենտգենյան ճառագայթների
բեկման ցուցիչը
հաջողվեց չափել`
դիտելով ճառագայթների
շեղումը տարբեր
նյութերից պատրաստած
պրիզմաների մեջ:
Ապակու համար,
եթե ալիքի երկարությունը
մոտ է 10-10 մ-ին, ստացվում
է n=1-10-6 :
չափազանց
մեծ լինելու հետևանքով
մեկից շատ քիչ
է տարբերվում:
Ռենտգենյան ճառագայթների
բեկման ցուցիչը
հաջողվեց չափել`
դիտելով ճառագայթների
շեղումը տարբեր
նյութերից պատրաստած
պրիզմաների մեջ:
Ապակու համար,
եթե ալիքի երկարությունը
մոտ է 10-10 մ-ին, ստացվում
է n=1-10-6 :
Այն
հանգամանքը, որ
![]() հնարավորություն
տվեց իրականացնել
ռենտգենյան ճառագայթներով
լրիվ ներքին անդրադարձման
երևույթը օդ-ապակի
սահմանի վրա: Հետագայում
հետազոտություններ
կատարվեցին նաև
այլ նյութերով,
որոնք օգտագործվեցին
ռենտգենյան ճառագայթների
բեկման ցուցչի
մեծությունը ճշգրիտ
չափելու համար:
Փոփոխելով ռենտգենյան
ճառագայթների
ալիքի երկարությունը`
կարելի է նյութի
բնութագրական
հաճախությունների
մոտ դիտել նաև
ռենտգենյան ճառագայթների
անոմալ դիսպերսիան:
հնարավորություն
տվեց իրականացնել
ռենտգենյան ճառագայթներով
լրիվ ներքին անդրադարձման
երևույթը օդ-ապակի
սահմանի վրա: Հետագայում
հետազոտություններ
կատարվեցին նաև
այլ նյութերով,
որոնք օգտագործվեցին
ռենտգենյան ճառագայթների
բեկման ցուցչի
մեծությունը ճշգրիտ
չափելու համար:
Փոփոխելով ռենտգենյան
ճառագայթների
ալիքի երկարությունը`
կարելի է նյութի
բնութագրական
հաճախությունների
մոտ դիտել նաև
ռենտգենյան ճառագայթների
անոմալ դիսպերսիան:
Լույսի անցումը նյութի միջով, ալիքի էլեկտրամագնիսական դաշտի ազդեցությամբ, առաջացնում է միջավայրի էլեկտրոնների տատանումներ. միաժամանակ տեղի է ունենում այդ ալիքի էներգիայի կորուստ, որը ծախսվում է էլեկտրոնների տատանումները գրգռելու վրա: Այդ էներգիան մասամբ նորից վերադառնում է ճառագայթմանը այն երկրորդային ալիքների տեսքով, որոնք առաքվում են էլեկտրոնների կողմից, մասամբ էլ այն կարող է էներգիայի այլ ձևերի անցնել:
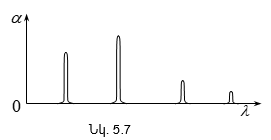
Այսպիսով, նյութի միջով լույսն անցնելիս ինտենսիվությունը փոքրանում է` լույսը կլանվում է նյութում: Էլեկտրոնների ստիպողական տատանումները, հետևաբար նաև լույսի կլանումը, հատկապես ինտենսիվ են դառնում ռեզոնանսային հաճախության դեպքում (տես նկ. 5.6-ի կետագծով պատկերված կլանման կորը):
Դեռ
18-րդ դարում Բուգերը
և Լամբերտը փորձով
ցույց են տվել,
որ ![]() ճանապարհի
վրա լույսի ինտենսիվության
փոփոխությունը
համեմատական
է այդ ճանապարհի
և իր` ինտենսիվության
մեծությանը.
ճանապարհի
վրա լույսի ինտենսիվության
փոփոխությունը
համեմատական
է այդ ճանապարհի
և իր` ինտենսիվության
մեծությանը.
![]()
որտեղ
![]() կլանման
գործակիցն է և
կախված է լույսի
ալիքի երկարությունից,
նյութի քիմիական
բնույթից և վիճակից:
Կարևոր է նշել,
որ կլանման գործակիցը
կախում չունի լույսի
ինտենսիվությունից:
Բացասական նշանը
ցույց է տալիս,
որ dI-ն և
կլանման
գործակիցն է և
կախված է լույսի
ալիքի երկարությունից,
նյութի քիմիական
բնույթից և վիճակից:
Կարևոր է նշել,
որ կլանման գործակիցը
կախում չունի լույսի
ինտենսիվությունից:
Բացասական նշանը
ցույց է տալիս,
որ dI-ն և ![]() ունեն
տարբեր նշաններ:
ունեն
տարբեր նշաններ:
Դիցուք
կլանող շերտի մուտքում
լույսի ինտենսիվությունը
Io է: Գտնենք ![]() hաստություն
ունեցող նյութի
շերտն անցած լույսի
ինտենսիվությունը:
Ինտեգրելով (5.15) արտահայտությունը
( նախապես անջատելով
փոփոխականները)`
կարող ենք գրել`
hաստություն
ունեցող նյութի
շերտն անցած լույսի
ինտենսիվությունը:
Ինտեգրելով (5.15) արտահայտությունը
( նախապես անջատելով
փոփոխականները)`
կարող ենք գրել`
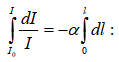
Արդյունքում կստանանք`
![]()
Ստացված
առնչությունը
կրում է Բուգերի
օրենք անունը:
Համաձայն այդ
օրենքի կլանող
նյութում լույսի
ինտենսիվությունը
նվազում է էքսպոնենցիալ
օրենքով: Երբ ![]() , I
ինտենսիվությունը
դառնում է Io-ից
e անգամ ավելի
փոքր: Այսպիսով,
կլանման գործակիցը
մի մեծություն
է` հակադարձ այն
շերտի հաստությանը,
որով լույսն անցնելիս
ինտենսիվությունը
նվազում է e=2,72 անգամ:
, I
ինտենսիվությունը
դառնում է Io-ից
e անգամ ավելի
փոքր: Այսպիսով,
կլանման գործակիցը
մի մեծություն
է` հակադարձ այն
շերտի հաստությանը,
որով լույսն անցնելիս
ինտենսիվությունը
նվազում է e=2,72 անգամ:
Դիէլեկտրիկներում չկան ազատ էլեկտրոններ, և լույսի կլանումը սերտորեն կապված է ատոմներում էլեկտրոնների և դիէլեկտիկի մոլեկուլներում ատոմների հարկադրական տատանումների ժամանակ ռեզոնանսի երևույթի հետ: Դրա համար էլ դիէլեկտրիկները լույսը կլանում են ավել կամ պակաս ընտրողական` կախված լույսի հաճախությունից: Կլանումը մեծ է միայն հաճախությունների այն տիրույթում, որոնք մոտ են ատոմներում էլեկտրոնների և մոլեկուլներում ատոմների սեփական տատանումների հաճախություններին: Լույսի մնացած բոլոր հաճախությունների համար դիէլեկտրիկը գործնականորեն թափանցիկ է, այսինքն նրա կլանման գործակիցը մոտ է զրոյի: Այդ ռեզոնանսային կլանման երևույթն ավելի ցայտուն է հայտնաբերվում միատոմ նոսր գազերում, որոնք օժտված են կլանման գծային սպեկտրով (նկ.5.7): Ինտենսիվ կլանման դիսկրետ հաճախությունները համընկնում են այդ գազերի գրգռված ատոմների սեփական ճառագայթման հաճախությունների հետ:
Պինդ մարմինները, հեղուկները և մեծ ճնշումների տակ գտնվող գազերը տալիս են կլանման լայն շերտեր:
Մետաղները
գործնականորեն
անթափանց են լույսի
համար, նրանց համար
![]() 10-4սմ-1 կարգի
մեծություն է:
Համեմատության
համար նշենք, որ
ապակու համար
10-4սմ-1 կարգի
մեծություն է:
Համեմատության
համար նշենք, որ
ապակու համար
![]() Դա պայմանավորված
է մետաղներում
ազատ էլեկտրոնների
առկայությամբ:
Լուսային ալիքի
էլեկտրական դաշտի
ազդեցության տակ
ազատ էլեկտրոնները
շարժման մեջ են
դրվում` մետաղում
առաջանում են արագ
փոփոխվող հոսանքներ,
որոնք ուղեկցվում
են ջոուլ-լենցյան
ջերմաքանակի անջատումով:
Արդյունքում լուսային
ալիքի էներգիան
նվազում է` փոխարկվելով
մետաղի ներքին
էներգիայի:
Դա պայմանավորված
է մետաղներում
ազատ էլեկտրոնների
առկայությամբ:
Լուսային ալիքի
էլեկտրական դաշտի
ազդեցության տակ
ազատ էլեկտրոնները
շարժման մեջ են
դրվում` մետաղում
առաջանում են արագ
փոփոխվող հոսանքներ,
որոնք ուղեկցվում
են ջոուլ-լենցյան
ջերմաքանակի անջատումով:
Արդյունքում լուսային
ալիքի էներգիան
նվազում է` փոխարկվելով
մետաղի ներքին
էներգիայի:
Լույսի ցրման պրոցեսի էությունն այն է, որ նյութի միջով անցնող լույսն ատոմներում առաջացնում է էլեկտրոնների տատանումներ: Տատանվող էլեկտրոնները դառնում են բոլոր ուղղություններով տարածվող երկրորդային ալիքների աղբյուրներ: Թվում է, թե այս երևույթը բոլոր դեպքերում պետք է հանգեցնի լույսի ցրմանը: Սակայն երկրորդային ալիքները կոհերենտ են, այնպես որ անհրաժեշտ է հաշվի առնել նրանց փոխադարձ ինտերֆերենցիան:
Հաշվարկները ցույց են տալիս, որ համասեռ միջավայրի դեպքում երկրորդային ալիքները բոլոր ուղղություններում լրիվ իրար մարում են, բացի առաջնային ալիքի տարածման ուղղությունից: Այդ պատճառով լույսի վերաբաշխում ըստ ուղղությունների, այսինքն` լույսի ցրում չի լինում: Լույսի ցրումն առաջանում է միայն անհամասեռ միջավայրում: Դիֆրակցվելով միջավայրի անհամասեռությունների վրա` լուսային ալիքները տալիս են մի դիֆրակցիոն պատկեր, որը բնութագրվում է բոլոր ուղղություններով բավականաչափ հավասար բաշխմամբ: Փոքր անհամասեռությունների վրա կատարվող այդպիսի դիֆրակցիան անվանում են լույսի ցրում: Ակնհայտորեն արտահայտված օպտիկական անհամասեռություններով միջավայրերը կոչվում են պղտոր միջավայրեր: Դրանց թվին են պատկանում` 1) ծուխը, այսինքն` մանրագույն պինդ մասնիկների կախույթները գազերում, 2) մառախուղը` հեղուկի մանրագույն կաթիլների կախույթները գազերում, 3) կախույթները կամ սուսպենզիաները, որոնք առաջանում են հեղուկում լողացող պինդ մասնիկներից, 4) էմուլսիաները, այսինքն` մեկ հեղուկի մանրագույն կաթիլների կախույթները մեկ ուրիշի մեջ, որը չի լուծում առաջինին (էմուլսիայի օրինակ կարող է ծառայել կաթը, որը յուղի կաթիլների կախույթ է ջրի մեջ) և այլն:
Կողմնային
ուղղություններով
ցրվելու հետևանքով
լույսի ինտենսիվությունը
տարածման ուղղությամբ
ավելի արագ է նվազում,
քան միայն կլանման
դեպքում: Այդ պատճառով
պղտոր նյութի համար
(5.16) արտահայտության
մեջ իրական կլանման
![]() գործակցի
հետ մեկտեղ պետք
է լինի նաև լրացուցիչ
գործակցի
հետ մեկտեղ պետք
է լինի նաև լրացուցիչ
![]() գործակից,
որը պայմանավորված
է ցրումով.
գործակից,
որը պայմանավորված
է ցրումով.
![]()
![]() հաստատունը
կոչվում է լուսաթուլացման
գործակից: Եթե
անհամասեռությունների
չափերը փոքր են
լուսային ալիքի
երկարության հետ
համեմատած (ոչ
ավելի քան
հաստատունը
կոչվում է լուսաթուլացման
գործակից: Եթե
անհամասեռությունների
չափերը փոքր են
լուսային ալիքի
երկարության հետ
համեմատած (ոչ
ավելի քան ![]() ցրված
լույսի I ինտենսիվությունը
համեմատական է
հաճախության չորրորդ
կամ հակադարձ համեմատական`
ալիքի երկարության
չորրորդ աստիճանին.
ցրված
լույսի I ինտենսիվությունը
համեմատական է
հաճախության չորրորդ
կամ հակադարձ համեմատական`
ալիքի երկարության
չորրորդ աստիճանին.
![]()
Այս
կախվածությունը
կրում է Ռելեյի
օրենք անունը:
Նրա ծագումը հեշտ
է հասկանալ, երե
հաշվի առնենք,
որ էլեկտրամագնիսական
տեսության համաձայն
երկրորդային ալիքների
ինտենսիվությունը
համեմատական է
ճառագայթող էլեկտրոնի
արագացման քառակուսուն:
Էլեկտրոնի շարժումը
կատարվում է ներդաշնակ
օրենքով` ![]() Այս
դեպքում արագացումը
համեմատական է
Այս
դեպքում արագացումը
համեմատական է
![]() Հետևաբար,
ճառագայթման ինտենսիվությունը
համեմատական կլինի
Հետևաբար,
ճառագայթման ինտենսիվությունը
համեմատական կլինի
![]()
Բնական
լույսի ցրման դեպքում,
լույսի ![]() ինտենսիվությունը,
որը ցրվում է առաջնային
փնջի ուղղության
հետ
ինտենսիվությունը,
որը ցրվում է առաջնային
փնջի ուղղության
հետ ![]() անկյան տակ,
որոշվում է հետևյալ
բանաձևով`
անկյան տակ,
որոշվում է հետևյալ
բանաձևով`
![]()
որտեղ
![]() -ը լույսի
ինտենսիվությունն
է
-ը լույսի
ինտենսիվությունն
է ![]() ցրման անկյան
տակ, այսինքն` առաջնային
փնջի ուղղությանն
ուղղահայաց: Եթե
ցրող նյութի մոլեկուլները
էլեկտրականապես
իզոտրոպ են (ոչ
բևեռային մոլեկուլներ),
ապա լույսը, որը
ցրվում է
ցրման անկյան
տակ, այսինքն` առաջնային
փնջի ուղղությանն
ուղղահայաց: Եթե
ցրող նյութի մոլեկուլները
էլեկտրականապես
իզոտրոպ են (ոչ
բևեռային մոլեկուլներ),
ապա լույսը, որը
ցրվում է ![]() անկյան
տակ լրիվ բևեռացված
է մի հարթության
մեջ, որն անցնում
է ընկնող և ցրվող
ճառագայթներով:
անկյան
տակ լրիվ բևեռացված
է մի հարթության
մեջ, որն անցնում
է ընկնող և ցրվող
ճառագայթներով:
Եթե անհամասեռությունների չափերը համեմատելի են ալիքի երկարությունների հետ, անհամասեռության տարբեր տեղերում գտնվող էլեկտրոնները տատանվում են նկատելիորեն շեղված փուլերով: Այս հանգամանքը բարդացնում է երևույթը և հանգեցնում այլ օրինաչափությունների: Ցրված լույսի ինտենսիվությունը դառնում է համեմատական հաճախության քառակուսուն (hակադարձ համեմատական ալիքի երկարության քառակուսուն):
Նույնիսկ կողմնակի խառնուրդներից և աղտոտություններից խնամքով մաքրված հեղուկներն ու գազերը, որոնց չի կարելի համարել պղտոր միջավայրեր, որոշ չափով ցրում են լույսը: Լ. Մանդելշտամը և Մ. Սմոլուխովսկին բացահայտել են, որ այս դեպքում օպտիկական անհամասեռությունների հայտնվելու պատճառը խտության ֆլուկտուացիաներն են (այսինքն` փոքր ծավալների սահմաններում դիտվող խտության շեղումներ նրա միջին արժեքից): Այդ ֆլուկտուացիաներն առաջանում են նյութի մոլեկուլների քաոսային շարժման հետևանքով: Այդ պատճառով նրանցով պայմանավորված լույսի ցրումը կոչվում է մոլեկուլային:
Ա. Այնշտայնը հիմնվելով Մ. Սմոլուխովսկու գաղափարների վրա` 1910թ. ստեղծեց լույսի մոլեկուլային ցրման տեսությունը:
Մոլեկուլային ցրումով է բացատրվում երկնքի կապույտ գույնը: Մոլեկուլների քաոսային շարժման հետևանքով մթնոլորտում անընդհատ առաջացող օդի խիտ և նոսր տեղերը ցրում են արեգակնային լույսը: Համաձայն Ռելեի օրենքի` կապույտ և երկնագույն ճառագաթներն ավելի ուժեղ են ցրվում, քան դեղիններն ու կարմիրները` պայմանավորելով երկնքի կապույտ գույնը: Երբ Արեգակը գտնվում է հորիզոնի մոտ, նրանից անմիջականորեն տարածվող ճառագայթներն անցնում են ցրող միջավայրի ավելի հաստ շերտ, որի հետևանքով նրանք հարստանում են ավելի երկար ալիքներով: Այդ պատճառով երկինքը արշալույսին ներկվում է կարմրագույն երանգով:
Խտության
զգալի ֆլուկտուացիաներ
առաջանալու բարենպաստ
պայմաններ կան
հատկապես նյութի
կրիտիկական վիճակի
մոտակայքում
(կրիտիկական կետում
![]() Այս ֆլուկտուացիաներն
այնքան ուժեղ
են ցրում լույսը,
որ նյութով լցված
ապակե սրվակը լույսի
դիմաց թվում է
բոլորովին սև:
Այս երևույթը կոչվում
է կրիտիկական
օպալեսցենցիա:
Այս ֆլուկտուացիաներն
այնքան ուժեղ
են ցրում լույսը,
որ նյութով լցված
ապակե սրվակը լույսի
դիմաց թվում է
բոլորովին սև:
Այս երևույթը կոչվում
է կրիտիկական
օպալեսցենցիա:
5.5. Վավիլով- Չերենկովի երևույթը
1934թ.
Պ. Չերենկովը հայտնաբերեց
հեղուկների լուսարձակման
մի տեսակ, որն առաջանում
է ռադոնի ![]() ճառագայթների
ազդեցության տակ:
Ս. Վավիլովը ենթադրեց,
որ ճառագայթման
աղբյուրը
ճառագայթների
ազդեցության տակ:
Ս. Վավիլովը ենթադրեց,
որ ճառագայթման
աղբյուրը ![]() ճառագայթներով
առաջացած արագ
էլեկտրոններն
են: Վավիլով - Չերենկովի
էֆեկտ անվանումն
ստացած այս երևույթի
բացատրությունը
տվեցին 1937թ. Ի.Տամմը
և Ի.Ֆրանկը, որոնք
էլ 1958թ. արժանացան
Նոբելյան մրցանակի:
ճառագայթներով
առաջացած արագ
էլեկտրոններն
են: Վավիլով - Չերենկովի
էֆեկտ անվանումն
ստացած այս երևույթի
բացատրությունը
տվեցին 1937թ. Ի.Տամմը
և Ի.Ֆրանկը, որոնք
էլ 1958թ. արժանացան
Նոբելյան մրցանակի:
Էլեկրտրամագնիսական
տեսությունից
հայտնի է, որ առանց
արագացման շարժվող
լիցքը էլեկտրամագնիսական
ալիքներ չի ճառագայթում:
Սակայն, Տամմը
և Ֆրանկը ցույց
տվեցին, որ դա ճիշտ
է միայն այն դեպքում,
երբ լիցքավորված
մասնիկի![]() արագությունը
չի գերազանցում
էլեկտրամագնիսական
ալիքների c/n փուլային
արագությանն այն
միջավայրում, որտեղ
շարժվում է մասնիկը:
Հիշեցնենք, որ
համաձայն հարաբերականության
տեսության մասնիկի
արագությունը
չի կարող ոչ միայն
գերազանցել, այլև
հավասարվել դատարկության
մեջ լույսի արագության
արժեքին: Ուստի,
եթե լիցքը վակուումում
շարժվում է ուղղագիծ
և հավասարաչափ,
իրոք չի ճառագայթում
էլեկտրամագնիսական
ալիքներ: Թափանցիկ
նյութի մեջ տեսանելի
լույսի փուլային
արագությունը
փոքր է
արագությունը
չի գերազանցում
էլեկտրամագնիսական
ալիքների c/n փուլային
արագությանն այն
միջավայրում, որտեղ
շարժվում է մասնիկը:
Հիշեցնենք, որ
համաձայն հարաբերականության
տեսության մասնիկի
արագությունը
չի կարող ոչ միայն
գերազանցել, այլև
հավասարվել դատարկության
մեջ լույսի արագության
արժեքին: Ուստի,
եթե լիցքը վակուումում
շարժվում է ուղղագիծ
և հավասարաչափ,
իրոք չի ճառագայթում
էլեկտրամագնիսական
ալիքներ: Թափանցիկ
նյութի մեջ տեսանելի
լույսի փուլային
արագությունը
փոքր է ![]() -ից:
Այն հավասար է
ինչպես վերևում
նշեցինք`c/n-ի, որտեղ
-ից:
Այն հավասար է
ինչպես վերևում
նշեցինք`c/n-ի, որտեղ
![]() նյութի
բացարձակ բեկման
ցուցիչն է: Հետեվաբար,
նյութի մեջ լիցքը
կարող է շարժվել
«գերլուսային»
արագությամբ
նյութի
բացարձակ բեկման
ցուցիչն է: Հետեվաբար,
նյութի մեջ լիցքը
կարող է շարժվել
«գերլուսային»
արագությամբ
![]() Այն դեպքում,
երբ լիցքավորված
մասնիկը նյութի
մեջ շարժվում է
գերլուսային արագությամբ`
նույնիսկ հավասարաչափ,
ապա պետք է ճառագայթի
էլեկտրամագնիսական
ալիքներ: Այսպիսով,
բացատրվեց Վավիլով-Չերենկովի
էֆեկտը և ցույց
տրվեցին նրա առաջացման
պայմանները:
Այն դեպքում,
երբ լիցքավորված
մասնիկը նյութի
մեջ շարժվում է
գերլուսային արագությամբ`
նույնիսկ հավասարաչափ,
ապա պետք է ճառագայթի
էլեկտրամագնիսական
ալիքներ: Այսպիսով,
բացատրվեց Վավիլով-Չերենկովի
էֆեկտը և ցույց
տրվեցին նրա առաջացման
պայմանները:
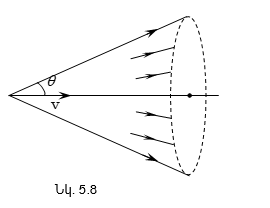
Հարկավոր է նշել, որ Վավիլով-Չերենկովյան ճառագայթման պրոցեսում ճառագայթող ազատ մասնիկի էներգիան և շարժման արագությունը իհարկե փոքրանում են, այսինքն` մասնիկն արգելակվում է: Սակայն շատ էական է, որ ի տարբերություն արգելակման ճառագայթման, որը մասնիկի արագության փոփոխության հետևանք է, Վավիլով-Չերենկովի էֆեկտի դեպքում մասնիկի արագության փոքրացումը ինքն է ճառագայթման հետևանք: Եթե ճառագայթման հաշվին կատարվող էներգիայի կորուստը լրացվի ինչ-որ եղանակով, հավասարաչափ արագությամբ շարժվող մասնիկն, այնուամենայնիվ, կլինի ճառագայթման աղբյուր:
Վավիլով-Չերենկովի
ճառագայթման
մեջ գերակշռում
են կարճ ալիքները,
որի շնորհիվ ճառագայթումն
ունի երկնագույն
երանգավորում:
Ճառագայթման
բնորոշ հատկությունն
այն է, որ այն ճառագայթվում
է ոչ թե բոլոր ուղղություններով,
այլ մի կոնի ծնիչներով,
որի առանցքը համընկնում
է մասնիկի արագության
ուղղության հետ
(նկ.5.8): Ճառագայթման
տարածման
ուղղությունների
և մասնիկի արագության
վեկտորի միջև կազմված
![]() անկյունը
որոշվում է հետևյալ
առնչությամբ`
անկյունը
որոշվում է հետևյալ
առնչությամբ`
![]()
Որքան մեծ է բեկման ցուցիչը, այնքան փոքր է մասնիկի արագությունը: Ուստի հեղուկ և պինդ նյութերում ճառագայթումը առաջանում է մասնիկների ավելի փոքր արագությունների դեպքում, քան գազերի մեջ: Ավելի արագ մասնիկները կարող են այդ էֆեկտն առաջացնել օդում, որն օգտագործում են տիեզերական ճառագայթումը դիտելու համար:
Վավիլով-Չերենկովի էֆեկտը փորձով դիտվել է հեղուկ և պինդ միջավայրերում շարժվող էլեկտրոնների համար:
Վավիլով-Չերենկովի
էֆեկտը լայն կիրառություն
է գտել միջուկային
ֆիզիկայում և բարձր
էներգիաների ֆիզիկայում:
Այսպես կոչված
Չերենկովի հաշվիչներում
արագաշարժ մասնիկով
հարուցված լուսային
բռնկումը լուսաբազմապատկիչի
օգնությամբ վերածվում
է հոսանքի իմպուլսի:
Որպեսզի այդպիսի
հաշվիչն աշխատի,
մասնիկի էներգիան
պետք է գերազանցի
![]() պայմանով
որոշվող շեմային
արժեքը: Այդ պատճառով
չերենկովյան հաշվիչները
հնարավորություն
են տալիս ոչ միայն
գրանցել մասնիկները,
այլև որոշել մասնիկի
արագության մեծությունն
և ուղղությունը,
դատել նրանց էներգիայի
մասին, ինչպես
նաև որոշել նրա
լիցքը:
պայմանով
որոշվող շեմային
արժեքը: Այդ պատճառով
չերենկովյան հաշվիչները
հնարավորություն
են տալիս ոչ միայն
գրանցել մասնիկները,
այլև որոշել մասնիկի
արագության մեծությունն
և ուղղությունը,
դատել նրանց էներգիայի
մասին, ինչպես
նաև որոշել նրա
լիցքը:
ՃԱՌԱԳԱՅԹՄԱՆ ՔՎԱՆՏԱՅԻՆ ԲՆՈՒՅԹԸ
6.1. Ջերմային
ճառագայթում:
Ջերմային ճառագայթման
առանձնահատկությունները
Ջերմային ճառագայթման տեսությունը սկսվում է 1859թ., երբ Կիրխհոֆը տվեց ջերմային ճառագայթման հիմնական օրենքը: Նա առաջարկեց բացարձակ սև մարմնի կոնցեպցիան և տվեց նրա մոդելը: Այդ ժամանակից մինչև 20-րդ դարի սկիզբը բացարձակ սև մարմնի ճառագայթման քննարկումը ֆիզիկայում եղել է ամենակարևոր հրատապ հիմնախնդիրը: Սակայն ճառագայթման դասական տեսությունը չկարողացավ տալ մոլեկուլների և ատոմների սպեկտրների, ջերմային ճառագայթման օրենքների բավարար նկարագրությունները: Այս խնդիրները հնարավոր եղավ լուծել ճառագայթման քվանտային տեսության շրջանակներում: Առաջին աշխատանքը, որը դրեց ճառագայթման քվանտային տեսության սկիզբը, պատկանում է Մ. Պլանկին (1900թ.), որը բանաձև արտածեց հավասարակշիռ ջերմային ճառագայթման սպեկտրում էներգիայի բաշխման վերաբերյալ, առաջինը ընդունեց, որ ատոմային համակարգերը էլեկտրամագնիսական ալիքներ են արձակում ոչ թե անընդհատ, այլ բաժիններով` քվանտներով: Ճառագայթման քվանտային տեսության հիմքը դրեցին Ա. Այնշտայնը, Ն. Բորը, Լ. դը Բրոյլը և այլք:
Առաջին անգամ լույսի վերաբերյալ ալիքային պատկերացումների անբավարարությունը երևան եկավ` բացարձակ սև մարմինների ջերմային ճառագայթման օրենքներն ուսումնասիրելիս:
Ի՞նչ ենք հասկանում` ջերմային ճառագայթում ասելով:
Մարմինների ճառագայթումն ուղեկցվում է էներգիայի կորստով: Որպեսզի ճառագայթումը տևական լինի, պետք է լրացնել մարմնի էներգիայի կորուստը: Ըստ լուսարձակման բնույթի` էներգիայի համալրումը կատարվում է զանազան պրոցեսներով:
Օդում օքսիդացող ֆոսֆորը լուսարձակում է քիմիական փոխակերպումների ժամանակ անջատվող էներգիայի հաշվին: Լուսարձակման այս տեսակը կոչվում է քեմիլյումինեսցենտում: Տարբեր տեսակի գազային ինքնուրույն պարպումների ժանամակ առաջացող լուսարձակումը կրում է էլեկտրալյումինեսցենտում անվանումը: Պինդ մարմինների՝ էլեկտրոնների ռմբակոծումով առաջացած լուսարձակումը կոչվում է կաթոդալյումինեսցենտում: Որոշ մարմիններ իրենք են սկսում լուսարձակել անմիջականորեն ճառագայթման ազդեցությամբ: Այդպիսի պրոցեսները միավորվում են ֆոտոլյումինեսցենտում անվան տակ: Այս դեպքում լույսը գրգռում է նյութի ատոմները, մեծացնում է նրանց ներքին էներգիան, որից հետո դրանք սկսում են իրենք լուսարձակել: Օրինակ, այն լուսարձակող ներկերը, որոնցով պատում են տոնածառի շատ խաղալիքներ, նախապես ճառագայթվելուց հետո լույս են արձակում:
Մարմինների ամենատարածված լուսարձակումը պայմանավորված է դրանց տաքացումով: Ջերմային է կոչվում այն ճառագայթումը, որն առաջանում է մարմինների տաքացման հետևանքով: Ջերմային ճառագայթումը կարելի է պահպանել անփոփոխ, եթե մարմնին անընդհատ հաղորդվի համապատասխան քանակությամբ ջերմաքանակ: Ջերմային ճառագայթումը կարող է լինել հավասարակշիռ: Պարզաբանենք, թե ինչ պետք է հասկանալ` հավասարակշիռ ճառագայթում ասելով:
Ենթադրենք, թե ճառագայթող մարմինը շրջապատված է իդեալական հայելային թաղանթով: Այդ դեպքում պատերից ճառագայթման անդրադարձման հետևանքով այդ ճառագայթումը չի ցրվի տարածության մեջ, այլ կմնա հայելային խոռոչի սահմաններում՝ մասամբ կլանվելով ճառագայթող մարմնի կողմից: Վերը նշված պայմաններում քննարկվող համակարգում, այն է՝ հայելային խոռոչում և ճառագայթող մարմնում, էներգիայի կորուստ տեղի չի ունենում:
Համակարգի վիճակը կոչվում է հավասարակշիռ, եթե էներգիայի բաշխումը մարմնի (կամ մարմինների) և ճառագայթման միջև ժամանակի ընթացքում մնում է անփոփոխ: Ջերմային ճառագայթման համար այդպիսի հավասարակշիռ վիճակ ստեղծվում է ավտոմատորեն: Տեղադրենք խոռոչի մեջ մի մարմին, որը ճառագայթում է ավելի մեծ քանակությամբ ջերմաքանակ, քան կլանում է: Այդ մարմինն սկսում է կորցնել իր էներգիան՝ սառչելով (հովանալով): Այդ պատճառով նրա ճառագայթումն աստիճանաբար թուլանում է, և այս պրոցեսը շարունակվում է այնքան ժամանակ, մինչև որ հավասարակշռություն է հաստատվում: Ընդհակառակը, եթե ներս մտցված մարմինը ճառագայթում է ավելի քիչ էներգիա, քան կլանում է, ապա այն սկսում է տաքանալ, ընդ որում նրա ճառագայթումն ուժեղանում է, մինչև որ հաստատվում է հավասարակշռության վիճակ: Այդպիսի հավասարակշռությունը կլինի կայուն: Եթե պատահաբար մարմինը կլանի ավելի մեծ կամ փոքր քանակությամբ ճառագայթում, ապա, համապատասխանաբար, ճառագայթման ինտենսիվության մեծացման կամ փոքրացման ճանապարհով (հետևանքով) կրկին վերահաստատվում է սկզբնական վիճակը:
Վերևում թվարկված ճառագայթման բոլոր մյուս տեսակները, բացառությամբ ջերմայինի, չեն կարող հավասարակշիռ լինել: Հավասարակշիռ վիճակների և պրոցեսների նկատմամբ կիրառելի են ջերմադինամիկայի օրենքները: Հետևաբար, ջերմային ճառագայթումը նույնպես պետք է ենթարկվի ջերմադինամիկայի սկզբունքներից բխող ընդհանուր օրինաչափություններին:
6.2. Մարմինների ճառագայթման և կլանման ընդունակությունը
Նախքան ջերմային ճառագայթման հիմնական օրենքների շարադրմանն անցնելը, ծանոթանանք որոշ անհրաժեշտ հասկացությունների:
Ճառագայթման
ընդունակություն: Հաճախությունների
միավոր միջակայքում
մարմնի մակերևույթի
միավոր մակերեսից
ճառագայթման հզորությունը
կոչվում է մարմնի
ճառագայթման ընդունակություն:
Եթե ճառագայթման
հզորությունը
միավոր մակերեսից
հաճախությունների
![]() միջակայքում
նշանակենք
միջակայքում
նշանակենք ![]() ապա ճառագայթման
ընդունակությունը
կարող է գրվել
հետևյալ տեսքով՝
ապա ճառագայթման
ընդունակությունը
կարող է գրվել
հետևյալ տեսքով՝
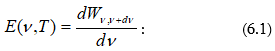
Քանի որ ճառագայթման ընդունակությունը, բացի ջերմաստիճանից, կախված է նաև հաճախությունից, ապա այն կոչվում է մակերևութային ճառագայթման սպեկտրային խտություն:
Կլանման
ընդունակություն: Մարմինների
վրա ընկած ճառագայթման
կլանումը բնութագրելու
համար ներմուծվում
է կլանման ընդունակություն
հասկացությունը:
Մարմնի կլանման
ընդունակության
տակ հասկացվում
է հաճախությունների
![]() միջակայքում
մարմնի մակերևույթի
կլանած էներգիայի
քանակության և
ընկած ճառագայթման
ընդհանուր քանակության
հարաբերությունը
միևնույն հաճախությունների
միջակայքում.
միջակայքում
մարմնի մակերևույթի
կլանած էներգիայի
քանակության և
ընկած ճառագայթման
ընդհանուր քանակության
հարաբերությունը
միևնույն հաճախությունների
միջակայքում.
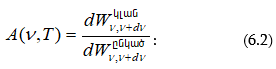
A-ի, ինչպես
և E-ի կախվածությունը
![]() և
T-ից հաստատվում
են փորձերի տվյալներով:
և
T-ից հաստատվում
են փորձերի տվյալներով:
Ինչպես
հետևում է (6.1) և (6.2)-ից,
![]() չափայնություն
չունեցող մեծություն
է, իսկ
չափայնություն
չունեցող մեծություն
է, իսկ ![]() չափվում
է Ջ/մ2վ : Ընդունված
սահմանման համաձայն
չափվում
է Ջ/մ2վ : Ընդունված
սահմանման համաձայն
![]() միշտ կանոնավոր
կոտորակ է և
միշտ կանոնավոր
կոտորակ է և ![]() առավելագույն
արժեքը մեկ է:
առավելագույն
արժեքը մեկ է:
Բացարձակ
սև մարմին: Բոլոր հաճախությունների
և ջերմաստիճանների
դեպքում, այն մարմինները,
որոնց ![]() Կիրխհոֆն անվանեց
բացարձակ սև
կամ բացարձակ
կլանող: Բնության
մեջ բացարձակ
սև մարմիններ գոյություն
չունեն: Բայց կարելի
է գտնել մարմին,
որն իր հատկություններով
շատ մոտ է բացարձակ
սև մարմիններին
(մուրը, սև թավիշը):
Թվարկված նյութերի
ուժեղ կլանման
հատկությունը
բացատրվում է
դրանց ծակոտկենությամբ:
Կիրխհոֆն անվանեց
բացարձակ սև
կամ բացարձակ
կլանող: Բնության
մեջ բացարձակ
սև մարմիններ գոյություն
չունեն: Բայց կարելի
է գտնել մարմին,
որն իր հատկություններով
շատ մոտ է բացարձակ
սև մարմիններին
(մուրը, սև թավիշը):
Թվարկված նյութերի
ուժեղ կլանման
հատկությունը
բացատրվում է
դրանց ծակոտկենությամբ:
Կարելի է ստեղծել մի հարմարանք, որն իր հատկություններով մոտ լինի բացարձակ սև մարմնին: Բացարձակ սև մարմնի նմանակ է սնամեջ գունդը, որն իր մակերևույթի վրա ունի մարմնի չափերի համեմատությամբ շատ փոքր անցք (նկ. 6.1):
Անցքից ներս թափանցած լույսի ճառագայթներն այնտեղից դուրս գալ չեն կարող` առանց անոթի պատից բազմաթիվ անգամ անդրադառնալու: Յուրաքանչյուր անդրադարձման ժամանակ էներգիայի մի մասը կլանվում է, որի հետևանքով այդպիսի խոռոչը գործնականորեն կլանում է ցանկացած հաճախության ամբողջ ճառագայթումը: Այսպիսով, սնամեջ մարմնի վրայի փոքրիկ անցքը կատարում է բացարձակ սև մարմնի դեր:
Պրևոյի կանոնը: Համաձայն Պրևոյի կանոնի (1809թ.), եթե երկու մարմիններ տարբեր քանակությամբ էներգիա են կլանում, ապա նրանց ճառագայթումները նույնպես պետք է տարբեր լինեն:
Պրևոյի կանոնը հաստատվում է փորձերի տվյալներով: Հարկավոր է նշել, որ միևնույն ջերմաստիճանի դեպքում, տարբեր մարմինների ճառագայթման սպեկտրային կազմը նույնպես կլինի տարբեր: Եթե վերցվի միևնույն ձևի երկու մարմին, օրինակ՝ քվարցի և պողպատի ձողեր, միևնույն 800oC ջերմաստիճանի դեպքում քվարցե ձողը չի ճառագայթում տեսանելի ճառագայթներ, մինչդեռ միևնույն ժամանակ շիկացած պողպատը ճառագայթում է պայծառ կարմիր-բալագույն լույս:
Կիրխհոֆի օրենքը: Պրևոյի կանոնը ճառագայթման և կլանման մասին տալիս է միայն որակական պատկերացում: Կես դար հետո (1859) Կիրխհոֆն այդ կանոնին տվեց խիստ քանակական օրենքի տեսք, որը ջերմային ճառագայթման բոլոր հարցերում խաղում է հիմնական դեր:
Կիրխհոֆի
օրենքը վերաբերում
է ![]() միջև եղած առնչությանը
և ասում է, որ մարմնի
ճառագայթման և
կլանման ընդունակությունների
հարաբերությունը
կախում չունի մարմնի
բնույթից, այսինքն՝
միջև եղած առնչությանը
և ասում է, որ մարմնի
ճառագայթման և
կլանման ընդունակությունների
հարաբերությունը
կախում չունի մարմնի
բնույթից, այսինքն՝
![]() հարաբերությունը
բոլոր մարմինների
համար հաճախության
և ջերմաստիճանի
մի ունիվերսալ
ֆունկցիա է, մինչդեռ
հարաբերությունը
բոլոր մարմինների
համար հաճախության
և ջերմաստիճանի
մի ունիվերսալ
ֆունկցիա է, մինչդեռ
![]() առանձին վերցրած
մեկ մարմնից մյուսին
անցնելիս կարող
են շատ մեծ չափով
փոխվել.
առանձին վերցրած
մեկ մարմնից մյուսին
անցնելիս կարող
են շատ մեծ չափով
փոխվել.
![]()
![]() ֆունկցիան
անվանում են Կիրխհոֆի
ֆունկցիա:
ֆունկցիան
անվանում են Կիրխհոֆի
ֆունկցիա:
Կիրխհոֆն իր օրենքը սահմանեց՝ հենվելով ջերմադինամիկայի երկրորդ օրենքի վրա, որից բխում է, որ մեկուսացված համակարգում հաստատված ջերմային հավասարակշռությունը նրա մասերի միջև տեղի ունեցող ջերմության հասարակ փոխանակումների միջոցով չի խախտվում:
Կիրխհոֆի
օրենքը կիրառենք
բացարձակ սև մարմնի
նկատմամբ: Եթե
բացարձակ սև մարմինների
համար ճառագայթման
ընդունակությունը
նշանակենք ![]() ապա քանի
որ
ապա քանի
որ ![]() կստանանք`
կստանանք`
![]()
այսինքն`
![]() հետևաբար Կիրխհոֆի
ունիվերսալ ֆունկցիան
ոչ այլ ինչ է, եթե
ոչ բացարձակ սև
մարմնի ճառագայթման
ընդունակություն:
հետևաբար Կիրխհոֆի
ունիվերսալ ֆունկցիան
ոչ այլ ինչ է, եթե
ոչ բացարձակ սև
մարմնի ճառագայթման
ընդունակություն:
Այժմ Կիրխհոֆի օրենքը կարելի է գրել հետևյալ տեսքով՝
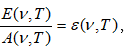
այսինքն` բոլոր մամինների համար, միևնույն հաճախության և ջերմաստիճանի դեպքում, ճառագայթման ընդունակությունների և կլանման ընդունակությունների հարաբերությունը հավասար է բացարձակ սև մարմնի ճառագայթման ընդունակությանը:
Այսպիսով,
![]() ունիվերսալ մեծություն
է, և նրա բացահայտ
կախվածության
որոշումը հաճախությունից
և ջերմաստիճանից
ջերմային ճառագայթման
տեսության հիմնական
խնդիրն է:
ունիվերսալ մեծություն
է, և նրա բացահայտ
կախվածության
որոշումը հաճախությունից
և ջերմաստիճանից
ջերմային ճառագայթման
տեսության հիմնական
խնդիրն է:
Կիրխհոֆի օրենքի արտածումը: Արտածենք Կիրխհոֆի օրենքը՝ ելնելով ջերմադինամիկական նկատառումներից: Դիցուք էլեկտրամագնիսական ալիքների համար անթափանց իդեալական անդրադարձնող պատերով խոռոչի ներսում գտնվում են երկու մարմիններ՝ M բացարձակ սև մարմինը և կամայական (ոչ սև) N մարմինը (նկ. 6.2): Ակներև է, որ ժամանակի ընթացքում խոռոչի ներսում ճառագայթման և M ու N մարմինների միջև, որոնք ընդունում են միևնույն ջերմաստիճանը, կվերականգնվի դինամիկ հավասարակշռություն, այլ խոսքով, յուրաքանչյուր մարմին կկլանի այնքան էներգիա, որքան ճառագայթում է:

Քանի որ
M բացարձակ սև
մարմինը միավոր
մարկերևույթից
միավոր ժամանակում
հաճախությունների
![]() միջակայքում
ճառագայթում է
միջակայքում
ճառագայթում է
![]() էներգիա, ապա
ակներև է, որ մարմիններից
յուրաքնաչյուրի
միավոր մակերևույթի
վրա նույն հաճախությունների
միջակայքում ընկնում
է էներգիայի
էներգիա, ապա
ակներև է, որ մարմիններից
յուրաքնաչյուրի
միավոր մակերևույթի
վրա նույն հաճախությունների
միջակայքում ընկնում
է էներգիայի ![]() քանակություն:
Եթե N մարմնի ճառագայթման
և կլանման ընդունակությունները
համապատասխանաբար
նշանակենք
քանակություն:
Եթե N մարմնի ճառագայթման
և կլանման ընդունակությունները
համապատասխանաբար
նշանակենք ![]() ապա միավոր
մակերևույթից
միավոր ժամանակում
հաճախությունների
ապա միավոր
մակերևույթից
միավոր ժամանակում
հաճախությունների
![]() լայնության
միջակայքում ճառագայթման
և կլանման էներգիաները
համապատասխանաբար
կլինեն՝
լայնության
միջակայքում ճառագայթման
և կլանման էներգիաները
համապատասխանաբար
կլինեն՝ ![]()
![]() Դինամիկ
հավասարակշռության
վերականգնման
դեպքում էներգիայի
այս քանակությունները
կլինեն հավասար,
այսինքն՝
Դինամիկ
հավասարակշռության
վերականգնման
դեպքում էներգիայի
այս քանակությունները
կլինեն հավասար,
այսինքն՝
![]()
որտեղից էլ`
![]()
Այսպիսով, Կիրխհոֆի օրենքն ապացուցված է ցանկացած մարմնի համար:
Ստեֆանը, իր փորձերի չափումները (1879թ.), ինչպես և ուրիշ հետազոտողների չափումները վերլուծելով, եկավ այն եզրակացության, որ մարմինների ինտեգրալ ճառագայթման ընդունակությունն ուղիղ համեմատական է բացարձակ ջերմաստիճանի չորրորդ աստիճանին.
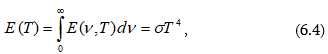
որտեղ
![]() հաստատուն մեծություն
է:
հաստատուն մեծություն
է:
Ստեֆանն իր օրենքը ձևակերպել էր ցանկացած մարմնի ճառագայթման համար, սակայն հետագա չափումները ցույց տվեցին, որ նրա եզրակացությունները սխալ են: 1884 թվականին Բոլցմանն, ըստ ջերմադինամիկական դատողությունների, նկատի ունենալով, որ ըստ դասական էլեկտրադինամիկայի գոյություն ունի էներգիայի խտությանը համեմատական ճառագայթային էներգիայի ճնշում, տեսականորեն ցույց տվեց, որ բացարձակ սև մարմնի գումարային ճառագայթումը պետք է լինի համեմատական ջերմաստիճանի չորրորդ աստիճանին, այսինքն՝
![]()
Այսպիսով,
Ստեֆանի եզրակացությունը
ճիշտ է միայն բացարձակ
սև մարմինների
համար, որոնցով
նա փորձ չէր կատարել:
Խնամքով կատարված
փորձերը հնարավորություն
տվեցին հաստատելու
(6.5) օրենքը և որոշելու
այդ օրենքի ![]() հաստատունը:
Ժամանակակից չափումների
համաձայն
հաստատունը:
Ժամանակակից չափումների
համաձայն ![]() (6.5) արտահայտությունն
ստացավ Ստեֆան-Բոլցմանի
օրենք անվանումը:
Այսպիսով, Ստեֆան-Բոլցմանի
օրենքը գործում
է միայն բացարձակ
սև մարմնի համար:
Այն մարմինը, որի
համար
(6.5) արտահայտությունն
ստացավ Ստեֆան-Բոլցմանի
օրենք անվանումը:
Այսպիսով, Ստեֆան-Բոլցմանի
օրենքը գործում
է միայն բացարձակ
սև մարմնի համար:
Այն մարմինը, որի
համար ![]() կոչվում
է գորշ: Իրական
մարմինն իր հատկությամբ
կարող է մոտ լինել
գորշ մարմնին համեմատաբար
ոչ մեծ ճառագայթման
հաճախությունների
միջակայքում: Այս
դեպքում նույնպես
մարմնի ինտեգրալ
ճառագայթման ընդունակությունը
հաճախ գրում են
(6.5) տեսքով, այսինքն`
կոչվում
է գորշ: Իրական
մարմինն իր հատկությամբ
կարող է մոտ լինել
գորշ մարմնին համեմատաբար
ոչ մեծ ճառագայթման
հաճախությունների
միջակայքում: Այս
դեպքում նույնպես
մարմնի ինտեգրալ
ճառագայթման ընդունակությունը
հաճախ գրում են
(6.5) տեսքով, այսինքն`
![]()
Չափայնություն
չունեցող ![]() գործակիցը
կոչվում է մարմնի
սևության աստիճան:
գործակիցը
կոչվում է մարմնի
սևության աստիճան:
6.5. Ստեֆան - Բոլցմանի օրենքի արտածումը
Ելնելով ջերմադինամիկական նկատառումներից՝ արտածենք բանաձև (6.5)-ը: Դիտարկենք հավասարակշիռ ճառագայթում, որը գտնվում է էլեկտրամագնիսական ալիքների համար անթափանց պատերով գլանի ներսում: Գլանի մեջ մխոցի առկայությունը մեզ հնարավորություն է տալիս փոփոխել ճառագայթումով զբաղեցրած ծավալը: Ճառագայթումը սկզբնական վիճակում բնութագրվում է V ծավալով, P ճնշումով և T ջերմաստիճանով:
Դիտարկվող ճառագայթմանը կիրառենք ջերմադինամիկայի հայտնի հավասարումը.
![]()
որը ջերմադինամիկայի առաջին և երկրորդ օրենքների ընդհանրացված արտահայտությունն է: Այստեղ dS-ը, dU-ն և dV-ն համապատասխանաբար համակարգի էնտրոպիայի, ներքին էներգիայի և ծավալի փոփոխություններն են: Քանի որ ներքին էներգիան ծավալի և ջերմաստիճանի ֆունկցիա է, կունենանք՝
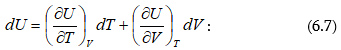
Տեղադրելեվ (6.6) – ը (6.7) – ի մեջ՝ կստանանք՝
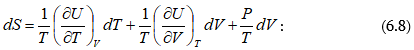
Այստեղից՝
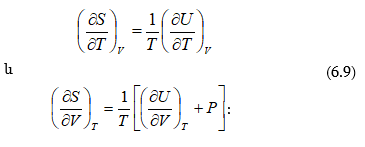
Եթե վերցնենք (6.9)-ի առաջին հավասարման ածանցյալն ըստ V-ի, և (6.9)-ի երկրորդ հավասարման ածանցյալն ըստ T-ի, ապա հավասարումների ձախ մասերի հավասարության շնորհիվ աջ մասերի համար կստանանք՝
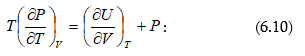
Ծավալի
իզոթերմ փոփոխության
դեպքում ճառագայթման
էներգիայի խտությունը
չի փոփոխվում,
այսինքն՝ U=U(T): Ուստի
ծավալի տվյալ արժեքի
դեպքում ճառագայթման
էներգիան կդառնա՝
U=w(T)V: Նկատի ունենալով
ճառագայթման իզոտրոպությունը՝
գործադրած ճնշումը
գլանի պատերի վրա
կլինի՝ ![]() Նկատի
ունենալով վերջինը՝
(6.10)-ի մեջ կստանանք՝
Նկատի
ունենալով վերջինը՝
(6.10)-ի մեջ կստանանք՝
![]()
որտեղից
![]()
ինտեգրելով (6.11)-ը՝ կստանանք.
![]()
և
![]()
Քանի որ ճառագայթման ծավալային խտությունը մի մեծություն է, որն ուղիղ համեմատական է ճառագայթման ընդունակությանը, ապա (6.12) -ից ստանում ենք.
![]()
այսինքն՝ հանգում ենք Ստեֆան - Բոլցմանի օրենքին:
Ստեֆան-Բոլցմանի
օրենքը որոշում
է բացարձակ սև
մարմնի ինտեգրալ
ճառագայթման ընդունակության
և ջերմաստիճանի
կապը, սակայն որևէ
տեղեկություն
չի տալիս ճառագայթման
էներգիայի հաճախության
հետ կապի մասին,
այսինքն՝ անհայտ
է մնում Կիրխհոֆի
ունիվերսալ ֆունկցիայի
բացահայտ տեսքը:Այդ
ուղղությամբ կարևոր
առաջընթաց քայլ
էր, այսպես կոչված,
Վինի օրենքը: 1893թ.
Վինը, հիմնվելով
ջերմադինամիկայի
և էլեկտրադինամիկայի
օրենքների վրա,
որոշեց բացարձակ
սև մարմնի ճառագայթման
ընդունակության
կախվածությունը
հաճախությունից
և ջերմաստիճանից:
Համաձայն Վինի
օրենքի` բացարձակ
սև մարմինների
ճառագայթման ընդունակությունն
ուղիղ համեմատական
է հաճախության
խորանարդին և
![]() հարաբերության
ֆունկցիա է.
հարաբերության
ֆունկցիա է.
![]()
որտեղ ![]() հաստատուն
մեծություն է,
F-ը մի ֆունկցիա
է, որի տեսքը Վինին
հայտնի չէր: Չնայած
Վինի (6.14) օրենքը չի
տալիս
հաստատուն
մեծություն է,
F-ը մի ֆունկցիա
է, որի տեսքը Վինին
հայտնի չէր: Չնայած
Վինի (6.14) օրենքը չի
տալիս ![]() բացահայտ
տեսքը, կախված
հաճախությունից
և ջերմաստիճանից,
նրանից բխում
են մի շարք կարևոր
հետևություններ.
բացահայտ
տեսքը, կախված
հաճախությունից
և ջերմաստիճանից,
նրանից բխում
են մի շարք կարևոր
հետևություններ.
Շեղման օրենքը: Վինի կողմից շեղման օրենքը սահմանվում է հետևյալ կերպ. ալիքի երկարությունը, որը համապատասխանում է ճառագայթման ընդունակության առավելագույնին, հակադարձ համեմատական է բացարձակ ջերմաստիճանին:
Նախքան
այդ ապացուցելը`
ներմուծենք ![]() ֆունկցիան:
Ակներև է, որ
ֆունկցիան:
Ակներև է, որ ![]() լուսային
հոսքերն են, որոնք
համապատասխանում
են հաճախությունների
լուսային
հոսքերն են, որոնք
համապատասխանում
են հաճախությունների
![]() միջակայքին կամ
համապատասխան
ալիքների երկարությունների
միջակայքին կամ
համապատասխան
ալիքների երկարությունների
![]() միջակայքին:
միջակայքին:
Քանի որ
![]() ապա ստանում
ենք՝
ապա ստանում
ենք՝
![]()
Նկատի
ունենալով, որ
![]() (c- ն լույսի արագությունն
է), ապա
(c- ն լույսի արագությունն
է), ապա
![]()
Տեղադրելով (16)-ը (15)-ի մեջ՝ կստանանք
![]()
Բացասական
նշանը բաց թողնվեց
այն պարզ պատճառով,
որ այն ցույց է
տալիս միայն ![]() մեծանալու
դեպքում
մեծանալու
դեպքում ![]() փոքրանալը:
փոքրանալը:
Ըստ (6.17)-ի`
![]() կորից
կորից
![]() կորին անցնելիս
կորի ձևը տրանսֆորմացիայի
է ենթարկվում:
Մասնավորապես
մեկ և մյուս կորում
առավելագույնների
դիրքերը համապատասխանում
են տարբեր հաճախությունների
(ալիքների երկարություններին):
Այդ պատճառով
պետք է միշտ նշել,
թե կորերից որ
մեկն ի նկատի ունենք:
Տեսական հաշիվներում
ավելի հաճախ հանդիպում
է
կորին անցնելիս
կորի ձևը տրանսֆորմացիայի
է ենթարկվում:
Մասնավորապես
մեկ և մյուս կորում
առավելագույնների
դիրքերը համապատասխանում
են տարբեր հաճախությունների
(ալիքների երկարություններին):
Այդ պատճառով
պետք է միշտ նշել,
թե կորերից որ
մեկն ի նկատի ունենք:
Տեսական հաշիվներում
ավելի հաճախ հանդիպում
է ![]() կորը, փորձարարական
չափումների արդյունքում
ավելի հաճախ՝
կորը, փորձարարական
չափումների արդյունքում
ավելի հաճախ՝
![]()
Տեղադրելով (6.14)-ը (6.17)-ի մեջ՝ կստանանք
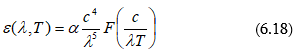
(6.18) արտահայտությունը Վինի օրենքն է` գրված ալիքի երկարություններով:
Որպեսզի
գտնենք ![]() այն արժեքը,
որի դեպքում ինտեգրալ
ճառագայթման ընդունակությունը
դառնում է առավելագույն,
պետք է (6.18)-ը դիֆերենցենք
ըստ
այն արժեքը,
որի դեպքում ինտեգրալ
ճառագայթման ընդունակությունը
դառնում է առավելագույն,
պետք է (6.18)-ը դիֆերենցենք
ըստ ![]() և արդյունքը
հավասարեցնենք
զրոյի.
և արդյունքը
հավասարեցնենք
զրոյի.

որտեղից՝
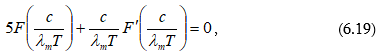
որտեղ
![]()
![]() այն արժեքն
է, որի դեպքում
ճառագայթման ընդունակությունը
դառնում է առավելագույն:
(6.19) հավասարումն
առաջին կարգի դիֆերենցիալ
հավասարում է,
որի լուծումը հանգեցնում
է հետևյալ արդյունքին՝
այն արժեքն
է, որի դեպքում
ճառագայթման ընդունակությունը
դառնում է առավելագույն:
(6.19) հավասարումն
առաջին կարգի դիֆերենցիալ
հավասարում է,
որի լուծումը հանգեցնում
է հետևյալ արդյունքին՝
![]()
Այսպիսով,
![]()
որտեղ b-ն
ջերմաստիճանից
կախում չունեցող
հաստատուն է: Փորձնական
կորերը հաստատում
են այդ եզրակացությունը
և հնարավորություն
են տալիս հաշվելու
b-ն ![]() Վինի օրենքը
նշված տեսքով կրում
է շեղման օրենք
անվանումը, այն
ցույց է տալիս,
որ
Վինի օրենքը
նշված տեսքով կրում
է շեղման օրենք
անվանումը, այն
ցույց է տալիս,
որ ![]() ֆունկցիայի առավելագույնը
ջերմաստիճանի
բարձրացման հետ
շեղվում է դեպի
կարճ ալիքների
տիրույթը:
ֆունկցիայի առավելագույնը
ջերմաստիճանի
բարձրացման հետ
շեղվում է դեպի
կարճ ալիքների
տիրույթը:
Օգտվելով
(6.20) բանաձևից` կարելի
է որոշել ալիքի
այն երկարությունները,
որոնցում տարբեր
ջերմաստիճանների
դեպքում ընկնում
են ճառագայթման
էներգիայի առավելագույնները:
Օրինակ 4000Կ ջերմաստիճանից
ցածրերի դեպքում,
բացարձակ սև մարմնի
ճառագայթման ընդունակության
առավելագույնները
ընկած են տեսանելի
տիրույթի սահմաններից
դուրս՝ պատկանելով
ինֆրակարմիր ճառագայթման
տիրույթին: T=300Կ-ի
դեպքում ![]() 5000Կ ջերմաստիճանի
դեպքում ճառագայթման
առավելագույնը
համապատասխանում
է դեղին-կանաչ
5000Կ ջերմաստիճանի
դեպքում ճառագայթման
առավելագույնը
համապատասխանում
է դեղին-կանաչ
![]() գույնին: 6000Կ ջերմաստիճանից
բարձրերի դեպքում
առավելագույնը
տեղափոխվում է
սպեկտրի ուլտրամանուշակագույն
տիրույթ (նկ.6.3):
գույնին: 6000Կ ջերմաստիճանից
բարձրերի դեպքում
առավելագույնը
տեղափոխվում է
սպեկտրի ուլտրամանուշակագույն
տիրույթ (նկ.6.3):
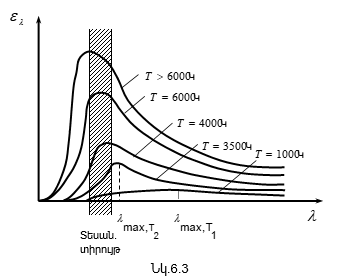
Մաքսիմալ ճառագայթման ընդունակություն: Վինի օրենքից հետևում է, որ ճառագայթման ընդունակության առավելագույնն ուղիղ համեմատական է բացարձակ ջերմաստիճանի հինգերորդ աստիճանին: Իրոք, տեղադրելով (6.20)-ը (6.18) -ի մեջ՝ կստանանք
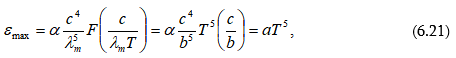
որտեղ
![]() հաստատուն մեծություն
է:
հաստատուն մեծություն
է:
Վերևում
դիտարկված բոլոր
դեպքերում ջերմային
ճառագայթման ուսումնասիրության
նկատմամբ մոտեցումը
եղել է ջերմադինամիկական:
Ռելեյը և Ջինսը
փորձել են որոշել
![]() ֆունկցիան՝ ելնելով
ըստ ազատության
աստիճանների էներգիայի
հավասարաչափ բաշխման
դասական վիճակագրության
թեորեմից: Նրանք
ենթադրեցին, որ
յուրաքանչյուր
էլեկտրամագնիսական
տատանմանը միջին
հաշվով բաժին
է ընկնում թվով
երկու կես kT-ի հավասար
էներգիա՝ մեկ կեսը
ալիքի էլեկտրական,
մյուսը՝ մագնիսական
էներգիային: Ռելեյը
բացարձակ սև մարմնի
ճառագայթման ընդունակության
համար ստացավ հետևյալ
արտահայտությունը.
ֆունկցիան՝ ելնելով
ըստ ազատության
աստիճանների էներգիայի
հավասարաչափ բաշխման
դասական վիճակագրության
թեորեմից: Նրանք
ենթադրեցին, որ
յուրաքանչյուր
էլեկտրամագնիսական
տատանմանը միջին
հաշվով բաժին
է ընկնում թվով
երկու կես kT-ի հավասար
էներգիա՝ մեկ կեսը
ալիքի էլեկտրական,
մյուսը՝ մագնիսական
էներգիային: Ռելեյը
բացարձակ սև մարմնի
ճառագայթման ընդունակության
համար ստացավ հետևյալ
արտահայտությունը.
![]()
որտեղ k-ն Բոլցմանի հաստատունն է: Ջինսը կատարելով ճշգրիտ հաշվարկ և որոշելով համեմատականության գործակիցը՝ գտավ, որ
![]()
(6.22) բանաձևը ստացավ Ռելեյ-Ջինսի օրենք անունը: Ռելեյ-Ջինսի բանաձևը փորձարարական տվյալների հետ համաձայնության մեջ է միայն մեծ ալիքի երկարությունների (փոքր հաճախությունների) և բարձր ջերմաստիճանների տիրույթում: Բացի դրանից, պարզվեց, որ Ռելեյ-Ջինսի բանաձևից փորձել ստանալ Ստեֆան-Բոլցմանի օրենքը, հանգեցնում է անհեթեթության: Էրենֆեստի կողմից այն անվանվել է «ուլտրամանուշակագույն աղետ»: Իրոք
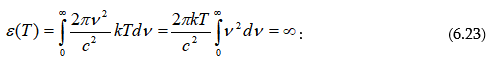
Ինտեգրալ ճառագայթման ընդունակության անսահմանության հավասարվելը նշանակում է, որ մարմնի և ճառագայթման միջև հավասարակշռությունը վերականգնվում է միայն մարմինների այնպիսի ջերմաստիճանի դեպքում, որը հավասար է բացարձակ զրոյի: Սա հակասում է փորձի տվյալներին, քանի որ մարմինը ճառագայթման հետ գտնվում է հավասարակշռության մեջ կամայական՝ զրոյից տարբեր ջերմաստիճանում:
Բացարձակ
սև մարմնի ճառագայթման
օրենքը տեսականորեն
հաստատելու բազմաթիվ
փորձերը, որոնք
ինչպես տեսանք,
հանգեցրին մի շարք
կարևոր մասնավոր
օրենքների դրսևորմանը,
չկարողացան տալ
խնդրի ընդհանուր
լուծումը: Դրանք
հանգեցնում էին
այնպիսի եզրակացությունների,
որոնք փորձի հետ
համաձայնեցվում
էին T-ի և ![]() միայն
սահմանափակ միջակայքում:
Այդ անհաջողությունների
պատճառը շատ խորն
էր: Պարզվում է,
որ դասական էլեկտրադինամիկայի
այն օրենքները,
որոնց հիման վրա
կատարվում են այդ
բոլոր հետազոտությունները,
միայն մոտավոր
ճշտություն ունեն
և տալիս են սխալ
արդյունքներ, երբ
դիտարկվում են
ջերմային ճառագայթումը
պայմանավորող
տարրական պրոցեսները:
միայն
սահմանափակ միջակայքում:
Այդ անհաջողությունների
պատճառը շատ խորն
էր: Պարզվում է,
որ դասական էլեկտրադինամիկայի
այն օրենքները,
որոնց հիման վրա
կատարվում են այդ
բոլոր հետազոտությունները,
միայն մոտավոր
ճշտություն ունեն
և տալիս են սխալ
արդյունքներ, երբ
դիտարկվում են
ջերմային ճառագայթումը
պայմանավորող
տարրական պրոցեսները:
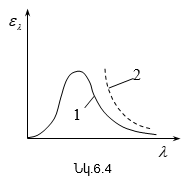
Նկար 6.4-ում
ցույց են տրված
բացարձակ սև մարմնի
ճառագայթման էներգիայի
սպեկտրային բաշխման
փորձարարական
կորը (1 անընդհատ
կորը) և Ռելեյ-Ջինսի
տեսական կորը (2
կետագծերով կորը):
Ինչպես մենք տեսանք,
դասական ֆիզիկայի
շրջանակներում
չի հաջողվում տեսականորեն
լրիվ նկարագրել
փորձարարական
կորը. այսինքն`
անհնարին է գտնել
Կիրխհոֆի ֆունկցիայի
բացահայտ տեսքը
ցանկացած ջերմաստիճանի
և հաճախության
դեպքում: 1900թ. Պլանկին
հաջողվեց գտնել
![]() ֆունկցիայի տեսքը,
որը ճշտորեն համապատասխանում
է փորձարարական
տվյալներին: Այդ
ֆունկցիայի տեսքը
գտնելու համար
անհրաժեշտ էր
անել մի վարկած,
որն արմատապես
հակասում է դասական
ֆիզիկայի ներկայացրած
ամբողջ համակարգին,
այն է` վարկած այն
մասին, որ միկրոսկոպիկ
համակարգի (ատոմներ,
մոլեկուլներ)
էներգիան կարող
է ընդունել միայն
որոշակի, դիսկրետ
արժեքներ: Պլանկն
իր բանաձևի արտածման
համար ճառագայթող
նյութական կենտրոնները
սխեմայացրեց` դիտելով
դրանք որպես գծային
ներդաշնակ տատանակներ
(օսցիլյատորներ),
որոնք կրում են
էլեկտրական լիցք,
որի շնորհիվ նրանք
կարող են էներգիայի
փոխանակություն
կատարել շրջապատող
էլեկտրամագնիսական
դաշտի հետ: Այդ
վարկածը, որը Պլանկը
դրեց իր բանաձևի
արտածման հիմքում,
ժամանակակից, ավելի
ճշգրիտ ձևակերպմամբ
այսպիսին է. տատանակները
կարող են գտնվել
միայն որոշակի
վիճակներում, որոնցում
նրանց էներգիան
էներգիայի ամենափոքրագույն
E0 քանակության
ամբողջ բազմապատիկն
է`
ֆունկցիայի տեսքը,
որը ճշտորեն համապատասխանում
է փորձարարական
տվյալներին: Այդ
ֆունկցիայի տեսքը
գտնելու համար
անհրաժեշտ էր
անել մի վարկած,
որն արմատապես
հակասում է դասական
ֆիզիկայի ներկայացրած
ամբողջ համակարգին,
այն է` վարկած այն
մասին, որ միկրոսկոպիկ
համակարգի (ատոմներ,
մոլեկուլներ)
էներգիան կարող
է ընդունել միայն
որոշակի, դիսկրետ
արժեքներ: Պլանկն
իր բանաձևի արտածման
համար ճառագայթող
նյութական կենտրոնները
սխեմայացրեց` դիտելով
դրանք որպես գծային
ներդաշնակ տատանակներ
(օսցիլյատորներ),
որոնք կրում են
էլեկտրական լիցք,
որի շնորհիվ նրանք
կարող են էներգիայի
փոխանակություն
կատարել շրջապատող
էլեկտրամագնիսական
դաշտի հետ: Այդ
վարկածը, որը Պլանկը
դրեց իր բանաձևի
արտածման հիմքում,
ժամանակակից, ավելի
ճշգրիտ ձևակերպմամբ
այսպիսին է. տատանակները
կարող են գտնվել
միայն որոշակի
վիճակներում, որոնցում
նրանց էներգիան
էներգիայի ամենափոքրագույն
E0 քանակության
ամբողջ բազմապատիկն
է`
![]()
Ճառագայթման և կլանման ժամանակ տատանակներն այդ վիճակներից մեկից մյուսն անցնում են թռիչքով` բացառելով միջանկյալ վիճակները:
Չարտածելով բանաձևը` ներկայացնենք Պլանկի հայտնի բանաձևը բացարձակ սև մարմնի ճառագայթման ընդունակության համար
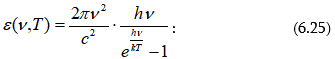
Հաճախություններից անցնելով ալիքի երկարություններին՝ գրենք Պլանկի բանաձևն անպիսի տեսքով, որը հարմար է փորձի տվյալների հետ բաղդատելու համար՝
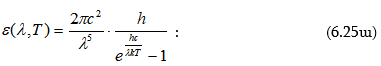
Ստացվեց,
որ (6.25ա) բանաձևը հիանալիորեն
համապատասխանում
է վերը քննարկված
փորձնական կորին:
Ալիքի երկարության
փոքրացման հետ
![]() չի ձգտում անվերջության,
այլ ունի առավելագույն`
որոշ
չի ձգտում անվերջության,
այլ ունի առավելագույն`
որոշ ![]() արժեքի դեպքում:
Եթե
արժեքի դեպքում:
Եթե ![]() ապա Պլանկի
բանաձևը կանխագուշակում
է
ապա Պլանկի
բանաձևը կանխագուշակում
է ![]() էքսպոնենցիալ
անկում, որը նույնպես
լիովին համապատասխանում
է փորձի տվյալներին:
էքսպոնենցիալ
անկում, որը նույնպես
լիովին համապատասխանում
է փորձի տվյալներին:
Քանի որ Պլանկի բանաձևը ճիշտ է ցանկացած հաճախությունների և ջերմաստիճանների դեպքում, ապա նրանից պետք է ստացվեն ջերմային ճառագայթման հայտնի բոլոր օրենքները: Համոզվենք դրանում:
6.9. Ստեֆան - Բոլցմանի օրենքի արտածումը Պլանկի բանաձևից
Ելնելով Պլանկի բանաձևից՝ որոշենք բացարձակ սև մարմնի ինտեգրալ ճառագայթման ընդունակությունը.

Կատարենք
փոփոխականի փոխարինում,
նշանակենք ![]()
կստանանք՝
![]()
որտեղ
 :
:
Քանի որ
![]() ուստի կստանանք՝
ուստի կստանանք՝
![]()
Հետևաբար,
մենք ոչ միայն
ստացանք Ստեֆան-Բոլցմանի
օրենքը, այլև մի
արտահայտություն
![]() հաստատունի համար,
որի օգնությամբ
կարելի է հաշվել
այդ հաստատունը:
հաստատունի համար,
որի օգնությամբ
կարելի է հաշվել
այդ հաստատունը:
Հարկավոր է նշել, որ ըստ (6.25) բանաձևի, յուրաքանչյուր ազատության աստիճանին բաժին ընկնող օսցիլյատորի միջին էներգիան իրականում հաստատուն մեծություն չէ. այն կախված է հաճախությունից: Հաճախության մեծացումով այդ էներգիան փոքրանում է, որն էլ վերևում նշված «ուլտրամանուշակագույն աղետի» պատճառն է:
Ռելեյ–Ջինսի
օրենքի արտածումը
Պլանկի բանաձևից: Դիտարկենք
փոքր հաճախությունների
և մեծ ջերմաստիճանների
տիրույթը, այսինքն`
ընդունենք ![]() (6.25)-ի մեջ
էքսպոնենտը կարելի
է վերածել շարքի
ըստ
(6.25)-ի մեջ
էքսպոնենտը կարելի
է վերածել շարքի
ըստ ![]() աստիճանների
և սահմանափակվել
առաջին աստիճանով,
այսինքն՝
աստիճանների
և սահմանափակվել
առաջին աստիճանով,
այսինքն՝
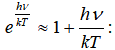
Վերջինը տեղադրելով (6.25)-ի հայտարարում կստանանք՝
![]()
Սա էլ հենց Ռելեյ-Ջինսի օրենքն է (տես (6.22)):
Վերջում նշենք, որ 1916թ. Այնշտայնը տվեց Պլանկի բանաձևի մի պարզ և ուսանելի արտածում: Այդ արտածման մեջ առաջին անգամ մտցվում է ստիպողական ճառագայթում հասկացությունը:
6.10. Օպտիկական հրաչափություն (պիրոմետրիա)
Բացարձակ
սև մարմինների
ճառագայթման օրենքներն
օգտագործվում
են շիկացած մարմինների
ջերմաստիճանը
չափելու համար:
Բարձր ջերմաստիճանների
դեպքում ![]() ջերմաէլեմենտների
և բոլոմետրերի
օգնությամբ կատարվող
չափումները բավարար
չափով ստույգ չեն,
իսկ շատ դեպքերում
ընդհանրապես անհնարին
են, ուստի ճառագայթման
օրենքներն, ըստ
էության, այս բնագավառում
միակ հիմքն են
ջերմաստիճանները
չափելու համար:
Այն սարքերը, որոնք
ծառայում են նշված
ջերմաստիճանների
չափման համար,
կոչվում են հրաչափեր:
Ըստ ջերմաստիճանի
չափման
սկզբունքի` հրաչափերը
բաժանվում
են երեք խմբի` ռադիացիոն,
պայծառային
և գունային: Ռադիացիոն
հրաչափում օգտագործվում
է Ստեֆան-Բոլցմանի
օրենքը: Ոչ սև մարմնի
համար ռադիացիոն
հրաչափի ցուցմունքները
տալիս են ոչ թե
իրական T ջերմաստիճանը,
այլ ջերմաստիճանի
այն Tռադ արժեքը,
որի դեպքում բացարձակ
սև մարմնի ինտեգրալ
ճառագայթման
ընդունակությունը
հավասար է հետազոտվող
մարմնի ինտեգրալ
ճառագայթման
ընդունակությանը:
(6.5) և (6.5ա) բանաձևերից
հետևում է, որ հետազոտվող
մարմնի իրական
ջերմաստիճանը
գտնելու համար
անհրաժեշտ է գիտենալ
նրա սևության
աստիճանը: Տեղեկատուներում
տարբեր ճառագայթիչների
համար կան
ջերմաէլեմենտների
և բոլոմետրերի
օգնությամբ կատարվող
չափումները բավարար
չափով ստույգ չեն,
իսկ շատ դեպքերում
ընդհանրապես անհնարին
են, ուստի ճառագայթման
օրենքներն, ըստ
էության, այս բնագավառում
միակ հիմքն են
ջերմաստիճանները
չափելու համար:
Այն սարքերը, որոնք
ծառայում են նշված
ջերմաստիճանների
չափման համար,
կոչվում են հրաչափեր:
Ըստ ջերմաստիճանի
չափման
սկզբունքի` հրաչափերը
բաժանվում
են երեք խմբի` ռադիացիոն,
պայծառային
և գունային: Ռադիացիոն
հրաչափում օգտագործվում
է Ստեֆան-Բոլցմանի
օրենքը: Ոչ սև մարմնի
համար ռադիացիոն
հրաչափի ցուցմունքները
տալիս են ոչ թե
իրական T ջերմաստիճանը,
այլ ջերմաստիճանի
այն Tռադ արժեքը,
որի դեպքում բացարձակ
սև մարմնի ինտեգրալ
ճառագայթման
ընդունակությունը
հավասար է հետազոտվող
մարմնի ինտեգրալ
ճառագայթման
ընդունակությանը:
(6.5) և (6.5ա) բանաձևերից
հետևում է, որ հետազոտվող
մարմնի իրական
ջերմաստիճանը
գտնելու համար
անհրաժեշտ է գիտենալ
նրա սևության
աստիճանը: Տեղեկատուներում
տարբեր ճառագայթիչների
համար կան ![]() արժեքների
աղյուսակներ:
Հետևաբար կարող
ենք գրել`
արժեքների
աղյուսակներ:
Հետևաբար կարող
ենք գրել`
![]()
կամ

![]()
Վոլֆրամի
համար 1500Կ իրական
ջերմաստիճանի
դեպքում ![]() իսկ 3000Կ-ի
դեպքում`
իսկ 3000Կ-ի
դեպքում` ![]() Այսպիսով,
վոլֆրամի 3000Կ իրական
ջերմաստիճանի
դեպքում ռադիացիոն
ջերմաչափը ցույց
կտա հետևյալ ջերմաստիճանը`
Այսպիսով,
վոլֆրամի 3000Կ իրական
ջերմաստիճանի
դեպքում ռադիացիոն
ջերմաչափը ցույց
կտա հետևյալ ջերմաստիճանը`
![]()
Պայծառային
հրաչափով ջերմաստիճանի
որոշման մեթոդը
հիմնված է սպեկտրի
միևնույն որոշակի
![]() նեղ տեղամասում
լուսարձակող մարմնի
և բացարձակ սև
մարմնի ճառագայթումների
համեմատության
վրա: Այդ ձևով չափված
ջերմաստիճանը
կոչվում է պայծառային:
նեղ տեղամասում
լուսարձակող մարմնի
և բացարձակ սև
մարմնի ճառագայթումների
համեմատության
վրա: Այդ ձևով չափված
ջերմաստիճանը
կոչվում է պայծառային:
Վինի շեղման
օրենքի օգնությամբ
կարելի է որոշել
մարմնի ջերմաստիճանը,
եթե հայտնի է նրա
էներգիայի սպեկտրային
բաշխումը: Չափված
![]() ալիքի երկարությամբ
(6.20) հավասարման օգնությամբ
կարելի է որոշել
մարմնի ջերմաստիճանը:
ալիքի երկարությամբ
(6.20) հավասարման օգնությամբ
կարելի է որոշել
մարմնի ջերմաստիճանը:
Մարմնի
ջերմաստիճանը,
որը չափվում է
Վինի օրենքի հիման
վրա, կոչվում է
գունային ջերմաստիճան:
Արեգակի ճառագայթման
սպեկտրի առավելագույնն
ընկնում է ![]() ալիքի
երկարության վրա:
Տեղադրումը (6.20)-ում
Արեգակի գունային
ջերմաստիճանի
համար կստանանք`
ալիքի
երկարության վրա:
Տեղադրումը (6.20)-ում
Արեգակի գունային
ջերմաստիճանի
համար կստանանք`

Արեգակի ջերմաստիճանը ստացվում է մոտ 5800Կ: Գունային և ռադիացիոն ջերմաստիճանների միջև եղած փոքր տարբերությունը վկայում է, որ Արեգակի մակերևույթն իր հատկություններով մոտ է բացարձակ սև մարմնին:
Այսպիսով, ըստ դիտումների, օպտիկական ճանապարհով որոշվում է երեք պայմանական ջերմաստիճաններից մեկը` ռադիացիոն Tռադ, գունային Tգուն և պայծառային Tպայծ : Tռադ և Tպայծ միշտ փոքր են իսկական ջերմաստիճանից:
Շիկացած
մարմինների լուսարձակումն
օգտագործվում
է լույսի աղբյուրների
ստեղծման համար:
Առաջին շիկացման
լամպերը ստեղծվել
են Ա. Լոդիգինի
կողմից 1873թ., իսկ առաջին
աղեղային լամպերը`
Պ. Յաբլոչկովի
կողմից 1876թ.: Լույսի
աղբյուրի կարևորագույն
բնութագրիչը
նրա ճառագայթման
բաղադրությունը
և լուսային արգասիքն
են, որը հավասար
է լուսային հոսքի
և լույսի աղբյուրի
սպառած հզորության
հարաբերությանը:
Լուսային արգասիքը
չափվում է լմ/Վտ-ով:
Ներկա ժամանակում
օգտագործվում
են վոլֆրամի թելիկով
շիկացման լամպեր:
Վոլֆրամի օգտագործումը
թելերի պատրաստման
համար պայմանավորված
է երկու պատճառներով:
Առաջինը, որ դժվարահալ
է և դիմացկուն
բարձր ջերմաստիճանների
դեպքում փոշիացման
նկատմամբ: Երկրորդ`
նրա ջերմային ճառագայթման
ընտրողականը.
վոլֆրամի էներգիայի
բաժինը, որն ընկնում
է տեսանելի լույսի
ճառագայթման
վրա զգալիորեն
մեծ է, քան բացարձակ
սև մարմնինը, որը
տաքացված է մինչև
նույն ջերմաստիճանը:
Ուստի վոլֆրամե
թելիկի լուսային
արգասիքը ավելի
մեծ է, քան բացարձակ
սև մարմնինը: Վոլֆրամե
թելիկով լամպերում
թելիկի տաքացման
ջերմաստիճանը
չպետք է գերազանցի
2500Կ, քանի որ հակառակ
դեպքում լամպն
արագ շարքից դուրս
կգա` թելիկի փոշիացման
հետևանքով: Այդ
ջերմաստիճանի
դեպքում առավելագույն
ճառագայթումը
համապատասխանում
է 1100նմ ալիքի երկարության,
այսինքն` գտնվում
է ինֆրակարմիր
ճառագայթման
տիրույթում: Ուստի
լամպի լուսային
արգասիքը մեծացնելու
և նրա լույսի սպեկտրային
բաղադրութունը
ցերեկային լույսի
![]() բաղադրությանը
մոտեցնելու համար
անհրաժեշտ է մեծացնել
շիկացման թելիկի
ջերմաստիճանը:
Դա հաջողվեց լամպերը
իներտ գազով լցնելու
շնորհիվ (արգոնով
կամ ազոտով` ավելացրած
կրիպտոնի և քսենոնի
խառնուրդ): Իներտ
գազի առկայությունը
փոքրացնում է
վոլֆրամի արագ
փոշիացումը:
բաղադրությանը
մոտեցնելու համար
անհրաժեշտ է մեծացնել
շիկացման թելիկի
ջերմաստիճանը:
Դա հաջողվեց լամպերը
իներտ գազով լցնելու
շնորհիվ (արգոնով
կամ ազոտով` ավելացրած
կրիպտոնի և քսենոնի
խառնուրդ): Իներտ
գազի առկայությունը
փոքրացնում է
վոլֆրամի արագ
փոշիացումը:
ՔՎԱՆՏԱՕՊՏԻԿԱԿԱՆ ԵՐԵՎՈՒՅԹՆԵՐ
7.1. Լուսային քվանտներ
Լույսը ճառագայթվելիս և կլանվելիս իրեն պահում է այն մասնիկների հոսքի նման, որոնց էներգիան կախված է հաճախությունից: Անսպասելիորեն պարզվեց, որ լույսի բաժինը շատ նման է այն բանին, ինչը ընդունված է անվանել մասնիկ: Լույսի ճառագայթման և կլանման ժամանակ դրսևորվող հասկացությունները կոչվում են կորպուսկուլյար հասկացություններ (կորպուսկուլ բառը նշանակում է մասնիկ): Իսկ մասնիկն ինքը կոչվեց ֆոտոն կամ լուսային քվանտ: Լույսի քվանտներին հատուկ են մասնիկների շատ առանաձնահատկություններ: Այս պատճառով լույսի քվանտները հաճախ կոչվում են ֆոտոններ` նպատակ ունենալով ընդգծել դրանց նմանությունը նյութական մասնիկների:
Քվանտ-ֆոտոնների
հիմնական բնութագիրը
դրանց մեջ կենտրոնացած
էներգիայի քանակությունն
է: Այդ էներգիայի
մեծությունը նշանակելու
ենք ![]() Քվանտի էներգիայի
մեծությամբ որոշվում
են ճառագայթման
հատկությունները:
Մեներանգ լուսային
հոսքը բաղկացած
է միատեսակ էներգիայով
օժտված քվանտներից:
Ճառագայթման տարբեր
տեսակները, համաձայն
քվանտային պատկերացումների,
իրարից զանազանվում
են հենց քվանտների
էներգիայով:
Քվանտի էներգիայի
մեծությամբ որոշվում
են ճառագայթման
հատկությունները:
Մեներանգ լուսային
հոսքը բաղկացած
է միատեսակ էներգիայով
օժտված քվանտներից:
Ճառագայթման տարբեր
տեսակները, համաձայն
քվանտային պատկերացումների,
իրարից զանազանվում
են հենց քվանտների
էներգիայով:
Ըստ ալիքային
տեսության` ճառագայթման
տարբեր տեսակները
միմյանցից տարբերվում
են էլեկտրամագնիսական
տատանումների
հաճախությամբ՝
![]() Համաձայն ալիքային
պատկերացումների`
տատանումների
հաճախությունն
է այն հիմնական
պարամետրը, որով
որոշում են ճառագայթման
հատկությունները:
Համաձայն ալիքային
պատկերացումների`
տատանումների
հաճախությունն
է այն հիմնական
պարամետրը, որով
որոշում են ճառագայթման
հատկությունները:
Ակներև
է, որ այս երկու
մեծությունների՝
քվանտի ![]() էներգիայի
և տատանման
էներգիայի
և տատանման ![]() հաճախության
միջև պետք է լինի
որոշակի կապ, նկատի
ունենալով, որ
այս տարբեր պարամետրերը
բնութագրում են
միևնույն
երևույթի՝ ճառագայթման
հատկությունները:
հաճախության
միջև պետք է լինի
որոշակի կապ, նկատի
ունենալով, որ
այս տարբեր պարամետրերը
բնութագրում են
միևնույն
երևույթի՝ ճառագայթման
հատկությունները:
Պլանկը
ենթադրեց, որ քվանտի
էներգիայի՝ ![]() հաճախության
միջև գոյություն
ունի ուղիղ համեմատականություն.
հաճախության
միջև գոյություն
ունի ուղիղ համեմատականություն.
![]()
h մեծությունը
ստացել է Պլանկի
հաստատուն անվանումը:
h-ի թվային արժեքը
հավասար է ![]() Առնչություն
(7.1)-ից հետևում է.
Առնչություն
(7.1)-ից հետևում է.
![]()
Այսպիսով,
լուսային հոսքը,
որը սրանից առաջ
բնութագրվում
էր որպես ![]() հաճախությամբ
մեներանգ ալիք,
ըստ քվանտային
պատկերացումների`
քվանտների հոսք
է, որոնց էներգիան՝
հաճախությամբ
մեներանգ ալիք,
ըստ քվանտային
պատկերացումների`
քվանտների հոսք
է, որոնց էներգիան՝
![]() Լուսային հոսքի
ինտենսիվությունը՝
I (լուսային էներգիայի
այն քանակը, որն
անցնում է 1սմ2
մակերեսով 1վ-ում),
որոշվում է քվանտների
այն քանակով, որոնք
1վ-ում անցնում
են տվյալ մակերեսի
մեկ քառակուսի
սանտիմետրի միջով.
Լուսային հոսքի
ինտենսիվությունը՝
I (լուսային էներգիայի
այն քանակը, որն
անցնում է 1սմ2
մակերեսով 1վ-ում),
որոշվում է քվանտների
այն քանակով, որոնք
1վ-ում անցնում
են տվյալ մակերեսի
մեկ քառակուսի
սանտիմետրի միջով.
![]()
որտեղ
N-ը ցույց է տալիս
1վ-ում 1սմ2 մակերեսով
անցնող քվանտների
քանակությունը:
Քանի որ լուսային
հոսքը ստացվում
է որպես առանձին
քվանտների գումար,
ապա մարմինները
կարող են արձակել
(առաքել) և կլանել
լույսը միայն
![]() բազմապատիկ քանակություններով:
բազմապատիկ քանակություններով:
Հավասարակշիռ
ջերմային ճառագայթման
սպեկտրում էներգիայի
բաշխումը բացատրելու
համար Պլանկը ենթադրեց,
որ լույսն առաքվում
է միայն ![]() բաժիններով:
Լուսաէֆեկտը բացատրելու
համար բավական
է ենթադրել, որ
լույսը կլանվում
է նույնպիսի բաժիններով:
Սակայն Այնշտայնը
զգալիորեն հեռու
գնաց: Նա առաջ քաշեց
այն վարկածը, որ
լույսը տարածվում
է առանձին մասնիկների
ձևով, որոնց սկզբում
կոչվեցին լուսային
քվանտներ: Հետագայում
այդ մասնիկները
ստացան ֆոտոններ
անվանումը:
բաժիններով:
Լուսաէֆեկտը բացատրելու
համար բավական
է ենթադրել, որ
լույսը կլանվում
է նույնպիսի բաժիններով:
Սակայն Այնշտայնը
զգալիորեն հեռու
գնաց: Նա առաջ քաշեց
այն վարկածը, որ
լույսը տարածվում
է առանձին մասնիկների
ձևով, որոնց սկզբում
կոչվեցին լուսային
քվանտներ: Հետագայում
այդ մասնիկները
ստացան ֆոտոններ
անվանումը:
Այնշտայնի վարկածը հաստատվեց մի շարք փորձերով: Ամենաանմիջական հաստատումը տվեց Բոտեյի փորձը:
Ֆոտոնն օժտված է

էներգիայով,
որը որոշվում է
միայն ![]() հաճախությամբ
կամ
հաճախությամբ
կամ ![]() ալիքի երկարությամբ:
h-ի և c-ի արժեքների
տեղադրումը հանգեցնում
է
ալիքի երկարությամբ:
h-ի և c-ի արժեքների
տեղադրումը հանգեցնում
է

բանաձևին,
որտեղ ![]() արտահայտված
է էլեկտրոն-Վոլտով,
իսկ
արտահայտված
է էլեկտրոն-Վոլտով,
իսկ ![]() անգստրեմով:
անգստրեմով:
![]() ալիքի երկարությանը
համապատասխանում
է ֆոտոնի
ալիքի երկարությանը
համապատասխանում
է ֆոտոնի ![]() էներգիա:
էներգիա:
Նկատի
ունենալով, որ
ֆոտոնն օժտված
է ![]() էներգիայով,
համաձայն հարաբերականության
տեսության, այն
պետք է օժտված
լինի նաև զանգվածով՝
էներգիայով,
համաձայն հարաբերականության
տեսության, այն
պետք է օժտված
լինի նաև զանգվածով՝
![]()
Ֆոտոնը լույսի արագությամբ շարժվող մասնիկ է: Ֆոտոնի դադարի mo զանգվածը հավասար է զրոյի: Այսպիսով կարելի է ասել, որ ֆոտոնը մի մասնիկ է, որը էապես տարբերվում է այնպիսի մասնիկներից, ինչպիսիք են՝ էլեկտրոնը, պրոտոնը և նեյտրոնը, որոնք ունեն զրոյից տարբեր հանգստի զանգված և կարող են գտնվել հանգստի վիճակում: Ֆոտոնը չունի հանգստի զանգված և կարող է գոյություն ունենալ` միայն c արագությամբ շարժվելով:
Քանի որ ֆոտոնը տեղափոխվում է լույսի c արագությանը հավասար արագությամբ, ապա այն օժտված է իմպուլսով՝

Ֆոտոնի իմպուլսն ուղղված է ճառագայթի ուղղությամբ:
Որքան մեծ է հաճախությունը, այնքան մեծ են ֆոտոնի էներգիան և իմպուլսը, և այնքան ավելի որոշակի կերպով են արտահայտված լույսի կորպուսկուլյար հատկությունները:
Այն բազմազան երևույթների մեջ, որոնցում արտահայտվում է լույսի ազդեցությունը նյութի վրա, ամենակարևոր տեղը զբաղեցնում է ֆոտոէլեկտրական էֆեկտը (լուսաէֆեկտ), այսինքն՝ լույսի ազդեցության շնորհիվ` էլեկտրոնների առաքումը: Այս երևույթն էր, որ առաջինը հանգեցրեց լուսային քվանտների պատկերացմանը և չափազանց կարևոր դեր խաղաց ժամանակակից տեսական պատկերացումների զարգացման մեջ: Մյուս կողմից՝ ֆոտոէֆեկտն օգտագործվում է լուսաէլեկտրական տարրերում, որոնք բացառիկ լայն կիրառում են ստացել գիտության և տեխնիկայի ամենաբազմազան բնագավառներում, և որոնք ունեն օգտագործման ավելի հարուստ հեռանկարներ:
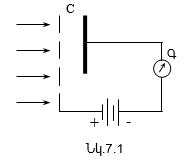
Ֆոտոէֆեկտի երևույթը 1887թ. հայտնագործել է Հերցը: Նա նկատել է, որ պարպիչի ցինկե գնդիկների միջև կայծի ստեղծումը զգալիորեն հեշտանում է` գնդիկներից մեկը լուսավորելիս ուլտրամանուշակագույն ճառագայթներով:
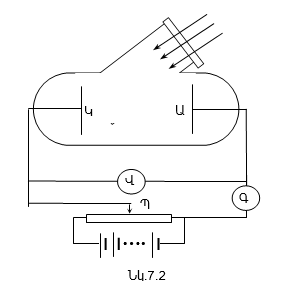
Ֆոտոէֆեկտը դիտելու` Ստոլետովի փորձի սխեման պատկերված է նկ.7.1-ում: Էլեկտրական շղթան կազմված է էլեմենտների մարտկոցից և C կոնդենսատորից, որի դրական լիցքավորված թիթեղը պատրաստված է լարային ցանցի ձևով: Լույսն անցնում է լարային էլեկտրոդի բջիջների միջով և ընկնում բացասական լիցքավորված հոծ թիթեղի վրա: Արդյունքում, առաջացած լուսահոսանքն արձանագրվում է Գ գալվանոմետրի միջոցով: Ստոլետովի հետազոտությունների հիմնական արդյունքները, որոնք իրենց արժեքը պահպանել են մինչև օրս, եղել են հետևյալ եզրակացությունները.
ա) Ամենամեծ ազդեցություն ունեն ուլտրամանուշակագույն ճառագայթները:
բ) Ֆոտոհոսանքի ուժը համեմատական է թիթեղի վրա ընկնող լույսի ինտենսիվությանը:
գ) Լույսի ազդեցության տակ առաքվող լիցքերն ունեն բացասական նշան:
10 տարի անց
(1898թ.) Լենարդը և Թոմսոնը
կատարեցին առաքվող
լիցքերի ![]() հարաբերության
չափումը` էլեկտրական
և մագնիսական դաշտերում
նրանց շեղման միջոցով:
Այդ չափումները
հարաբերության
չափումը` էլեկտրական
և մագնիսական դաշտերում
նրանց շեղման միջոցով:
Այդ չափումները
![]() համար տվին
համար տվին ![]() արժեքը,
դրանով ապացուցելով,
որ լույսի միջոցով
առաքվող բացասական
լիցքերն էլեկտրոններն
են:
արժեքը,
դրանով ապացուցելով,
որ լույսի միջոցով
առաքվող բացասական
լիցքերն էլեկտրոններն
են:
Ֆոտոէֆեկտի մասին ավելի ամբողջական պատկերացում կազմելու համար պետք է պարզել, թե ինչի՞ց է կախված նյութի մակերևույթից լույսի պոկած էլեկտրոնների (լուսաէլեկտրոնների) թիվը և ինչով է որոշվում նրանց արագությունը;
Այդպիսի հետազոտություններ կատարելու համար փորձը պետք է կատարել վակուումում (նկ. 7.2):
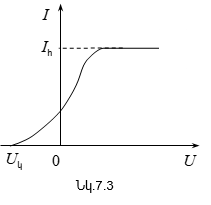
Քվարցային պատուհանից լույսը թափանցում է օդահանված բալոնի մեջ և լուսավորում ուսումնասիրվող նյութից պատրաստված Կ կաթոդը: Լուսաէֆեկտի հետևանքով առաքված էլեկտրոններն էլեկտրական դաշտի ազդեցության տակ շարժվում են դեպի Ա անոդը` առաջացնելով լուսահոսանք, որը չափվում է Գ գալվանոմետրով:
Լարումը անոդի և կաթոդի միջև կարելի է փոփոխել Պ պոտենցիոմետրի միջոցով և չափել Վ վոլտմետրով:
Չփոխելով լուսային հոսքը, մեծացնելով U անոդային լարումը` հոսանքի ուժը կաճի: Որոշակի լարման դեպքում այն հասնում է առավելագույն արժեքի, որից հետո այլևս չի մեծանում:
Նկ.7.3-ում
պատկերված է վոլտ-ամպերային
բնութագիծը, այսինքն`
կոր, որը ցույց
է տալիս I ֆոտոհոսանքի
կախվածությունն
էլեկտրոդների
միջև եղած U լարումից
լույսի անփոփոխ
![]() հոսքի
դեպքում: Կորից
երևում է, որ որոշ
ոչ շատ մեծ լարման
դեպքում ֆոտոհոսանքը
հասնում է հագեցման,
կաթոդից առաքված
բոլոր էլեկտրոնները
հասնում են անոդին:
Հետևաբար, հագեցման
հոսանքի Ih արժեքը
որոշվում է լույսի
ազդեցության տակ
միավոր ժամանակում
կաթոդից առաքված
էլեկտրոնների
թվով:
հոսքի
դեպքում: Կորից
երևում է, որ որոշ
ոչ շատ մեծ լարման
դեպքում ֆոտոհոսանքը
հասնում է հագեցման,
կաթոդից առաքված
բոլոր էլեկտրոնները
հասնում են անոդին:
Հետևաբար, հագեցման
հոսանքի Ih արժեքը
որոշվում է լույսի
ազդեցության տակ
միավոր ժամանակում
կաթոդից առաքված
էլեկտրոնների
թվով:
Այս փորձում,
փոփոխելով լուսային
հոսքի մեծությունը,
հաջողվեց սահմանել
պարզ կախում. մեկ
վայրկյանում մետաղի
մակերևույթից
լույսի պոկած էլեկտրոնների
թիվն ուղիղ համեմատական
է լուսային ալիքի
ինտենսիվությանը
կամ կաթոդի վրա
ընկնող լույսի
անփոփոխ սպեկտրային
բաղադրության
դեպքում հագեցման
հոսանքի ուժը համեմատական
է լուսային ![]() հոսքին.
հոսքին.
![]()
Այս փաստն անվանում են Ստոլետովի օրենք:
U=0 դեպքում լուսահոսանքը չի անհետանում: Սա վկայում է, որ էլեկտրոնները կատոդից հեռանում են զրոյից տարբեր արագությամբ: Որպեսզի ֆոտոհոսանքը դառնա զրո, պետք է կիրառել Uկ կասեցնող լարում (կամ կասեցնող պոտենցիալ):
Այդպիսի
լարման դեպքում
էլեկտրոններից
ոչ մեկը, նույնիսկ
կաթոդից դուրս
թռչելու ամենամեծ
![]() արագությունն
ունեցողը, չի կարողանում
հաղթահարել կասեցնող
դաշտը և հասնել
անոդին:
արագությունն
ունեցողը, չի կարողանում
հաղթահարել կասեցնող
դաշտը և հասնել
անոդին:
Uկ կասեցնող լարման մեծությունը կախված է լույսի պոկած էլեկտրոնների ունեցած առավելագույն կինետիկ էներգիայից: Չափելով կասեցնող լարումը և կիրառելով էներգիայի պահպանման օրենքը` կարելի է գտնել էլեկտրոնների կինետիկ էներգիայի առավելագույն արժեքը.

Փորձերը ցույց տվեցին, որ լույսի ինտենսիվությունը փոխելիս, կասեցնող լարումը չի փոխվում: Դա նշանակում է, որ էլեկտրոնների կինետիկ էներգիան չի փոխվում: Լույսի ալիքային տեսակետից այս փաստն անհասկանալի է: Չէ՞ որ, որքան մեծ է լույսի ինտենսիվությունը, այնքան ավելի մեծ ուժեր են ազդում էլեկտրոնների վրա լուսային ալիքի էլեկտրամագնիսական դաշտի կողմից, և թվում է, թե ավելի մեծ էներգիա պետք է հաղորդվի էլեկտրոններին:
Սակայն
փորձերի ընթացքում
պարզվեց, որ լույսի
պոկած էլեկտրոնների
կինետիկ էներգիան
կախված է միայն
լույսի հաճախությունից:
Ֆոտոէլեկտրոնների
առավելագույն
կինետիկ էներգիան
լույսի հաճախության
աճին զուգընթաց
աճում է գծայնորեն
և կախված չէ լույսի
ինտենսիվությունից:
Եթե լուսային ալիքի
հաճախությունը
փոքր է տվյալ նյութի
համար որոշակի
![]() նվազագույն հաճախությունից,
ապա լուսաէֆեկտ
տեղի չի ունենում:
նվազագույն հաճախությունից,
ապա լուսաէֆեկտ
տեղի չի ունենում:
7.3. Այնշտայնի վարկածը և ֆոտոէֆեկտի հավասարումը
Ֆոտոէֆեկտի երևույթը բացատրելու բոլոր փորձերը Մաքսվելի էլեկտրադինամիկայի օրենքների հիման վրա, ըստ որոնց լույսը տարածության մեջ աընդհատ բաշխված էլեկտրամագնիսական ալիք է, անարդյունք մնացին: Հնարավոր չէր հասկանալ, թե ֆոտոէլեկտրոնների էներգիան ինչու է միայն լույսի հաճախությամբ որոշվում, և ինչու միայն փոքր ալիքի երկարությամբ լույսն է էլեկտրոններ պոկում:
Ֆոտոէֆեկտի երևույթը և նրա բոլոր օրինաչափությունները լավ բացատրվում են լույսի քվանտային տեսության հիման վրա, որն էլ հաստատում է լույսի քվանտային բնույթը:
1905թ. Այնշտայնը
ցույց է տվել, որ
ֆոտոէֆեկտի բոլոր
օրինաչափությունները
հեշտությամբ բացատրվում
են, եթե ենթադրենք,
որ լույսը կլանվում
է նույնպիսի ![]() բաժիններով
(քվանտներով), ինչպիսի
բաժիններով այն,
ըստ Պլանկի ենթադրության,
առաքվում է, որոնց
էներգիան և իմպուլսը՝
բաժիններով
(քվանտներով), ինչպիսի
բաժիններով այն,
ըստ Պլանկի ենթադրության,
առաքվում է, որոնց
էներգիան և իմպուլսը՝

Մետաղներում ֆոտոէֆեկտի երևույթի նկատմամբ կիրառելով էներգիայի պահպանման օրենքը՝ Այնշտայնն առաջարկեց հետևյալ բանաձևը՝

որտեղ A-ն մետաղից էլեկտրոնի ելքի աշխատանքն է, v-ն՝ ֆոտոէլեկտրոնի արագությունը: Ըստ Այնշտայնի, յուրաքանչյուր քվանտ կլանվում է միայն մեկ էլեկտրոնի կողմից, ընդ որում` ընկած ֆոտոնի էներգիան ծախսվում է A ելքի աշխատանք կատարելու վրա: Այն նվազագույն աշխատանքը, որն անհրաժեշտ է էլեկտրոնը նյութից պոկելու համար, կոչվում է ելքի աշխատանք:
Հավասարում (7.10)-ը բացատրում է ֆոտոէֆեկտին վերաբերող հիմնական փաստերը: Ըստ Այնշտայնի` լույսի ինտենսիվությունը համեմատական է լուսային փնջի էներգիայի քվանտների թվին, որի պատճառով էլ որոշում է մետաղից պոկված էլեկտրոնների թիվը: Իսկ էլեկտրոնների արագությունն ըստ (7.10)-ի որոշվում է միայն լույսի հաճախությամբ և ելքի աշխատանքով, որը կախված է մետաղի տեսակից և նրա մակերևույթի վիճակից: Արագությունը կախված չէ լույսի ինտենսիվությունից:
Ցանկացած
նյութից ֆոտոէֆեկտ
դիտվում է այն
դեպքում, երբ լույսի
![]() հաճախությունը
մեծ է
հաճախությունը
մեծ է ![]() փոքրագույն
արժեքից: Չէ՞ որ
մետաղից էլեկտրոն
պոկելու համար,
նույնիսկ առանց
նրան կինետիկ էներգիա
հաղորդելու, պետք
է կատարել A ելքի
աշխատանք: Հետևաբար,
քվանտի էներգիան
պետք է մեծ լինի
այդ աշխատանքից.
փոքրագույն
արժեքից: Չէ՞ որ
մետաղից էլեկտրոն
պոկելու համար,
նույնիսկ առանց
նրան կինետիկ էներգիա
հաղորդելու, պետք
է կատարել A ելքի
աշխատանք: Հետևաբար,
քվանտի էներգիան
պետք է մեծ լինի
այդ աշխատանքից.
![]()
![]() սահմանային
հաճախությունը
կոչվում է ֆոտոէֆեկտի
կարմիր սահման:
Այն արտահայտվում
է այսպես.
սահմանային
հաճախությունը
կոչվում է ֆոտոէֆեկտի
կարմիր սահման:
Այն արտահայտվում
է այսպես.
![]()
Քանի որ
A ելքի աշխատանքը
կախված է նյութի
տեսակից, այդ պատճառով
էլ ֆոտոէֆեկտի
![]() սահմանային հաճախությունը
(կարմիր սահմանը)
տարբեր նյութերի
համար այլ է:
սահմանային հաճախությունը
(կարմիր սահմանը)
տարբեր նյութերի
համար այլ է:
Այնշտայնի
բանաձևի օգնությամբ
կարելի է բացատրել
ֆոտոէֆեկտի այլ
օրինաչափություններ:
Ընդունենք, որ
անոդի և կաթոդի
միջև գոյություն
ունի կասեցնող
պոտենցիալ: Եթե
էլեկտրոնների
կինետիկ էներգիան
բավարար է, ապա
դրանք, հաղթահարելով
կասեցնող պոտենցիալը,
ստեղծում են լուսահոսանք:
Ֆոտոհոսանքում
առկա են այն էլեկտրոնները,
որոնց բավարարում
է ![]() պայմանը: Կասեցնող
պոտենցիալը որոշվում
է հետևյալ պայմանից՝
պայմանը: Կասեցնող
պոտենցիալը որոշվում
է հետևյալ պայմանից՝

որտեղ
![]() պոկված էլեկտրոնների
առավելագույն
արագությունն
է: Տեղադրելով
(7.12)-ը (7.9)-ի մեջ՝ կստանանք
պոկված էլեկտրոնների
առավելագույն
արագությունն
է: Տեղադրելով
(7.12)-ը (7.9)-ի մեջ՝ կստանանք
![]()
որտեղից

Այսպիսով, կասեցնող պոտենցիալը կախված չէ ինտենսիվությունից, այն կախված է միայն ընկնող լույսի հաճախությունից: Մետաղի էլեկտրոնի ելքի աշխատանքը և Պլանկի հաստատունը կարելի է գտնել՝ կառուցելով Uկ -ի կախման գրաֆիկն ընկնող լույսի հաճախությունից (նկ.7.4):
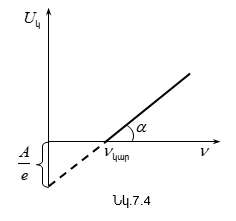
Ինչպես
երևում է գրաֆիկից, ![]() և
պոտենցիալի առանցքից
կտրած հատվածը
տալիս է A/e-ն Քանի որ լույսի
ինտենսիվությունը
ուղիղ համեմատական
է ֆոտոնների քանակին,
ուստի ընկնող լույսի
ինտենսիվության
մեծացումը հանգեցնում
է պոկված էլեկտրոնների
թվի, այսինքն՝
ֆոտոհոսանքի մեծացմանը:
Նշենք, որ ինչպես
ցույց է տալիս
փորձը, քվանտների
միայն մի փոքր
մասն է իր էներգիան
հաղորդում ֆոտոէլեկտրոններին:
Մնացած քվանտների
էներգիան ծախսվում
է լույսը կլանող
նյութի տաքացման
վրա:
և
պոտենցիալի առանցքից
կտրած հատվածը
տալիս է A/e-ն Քանի որ լույսի
ինտենսիվությունը
ուղիղ համեմատական
է ֆոտոնների քանակին,
ուստի ընկնող լույսի
ինտենսիվության
մեծացումը հանգեցնում
է պոկված էլեկտրոնների
թվի, այսինքն՝
ֆոտոհոսանքի մեծացմանը:
Նշենք, որ ինչպես
ցույց է տալիս
փորձը, քվանտների
միայն մի փոքր
մասն է իր էներգիան
հաղորդում ֆոտոէլեկտրոններին:
Մնացած քվանտների
էներգիան ծախսվում
է լույսը կլանող
նյութի տաքացման
վրա:
Բացի մեր
դիտարկած արտաքին
ֆոտոէֆեկտից, գոյություն
ունի նաև ներքին
ֆոտոէֆեկտ, որը
դիտվում է դիէլեկտրիկներում
և կիսահաղորդիչներում:
Դրա էությունն
այն է, որ լույսի
ազդեցությամբ
տեղի է ունենում
էլեկտրոնների
վերաբաշխում ըստ
էներգետիկ մակարդակների:
Եթե քվանտի ![]() էներգիան
գերազանցում է
արգելված գոտու
լայնությանը, քվանտ
կլանած էլեկտրոնը
վալենտական գոտուց
անցնում է հաղորդականության
գոտի: Արդյունքում,
հանդես է գալիս
հոսանքակիր լրացուցիչ
զույգ` էլեկտրոն
և խոռոչ, որը մեծացնում
է նյութի էլեկտրահաղորդականությունը:
էներգիան
գերազանցում է
արգելված գոտու
լայնությանը, քվանտ
կլանած էլեկտրոնը
վալենտական գոտուց
անցնում է հաղորդականության
գոտի: Արդյունքում,
հանդես է գալիս
հոսանքակիր լրացուցիչ
զույգ` էլեկտրոն
և խոռոչ, որը մեծացնում
է նյութի էլեկտրահաղորդականությունը:
Ֆոտոէֆեկտի հայտնագործումը շատ մեծ նշանակություն ունեցավ լույսի բնույթի ավելի խորը ըմբռնման համար: Բայց գիտության արժեքը միայն այն չէ, որ պարզաբանում է շրջապատող աշխարհի բարդ, բազմապիսի կառուցվածքը, այլև այն, որ մեզ տալիս է միջոցներ, որոնք օգտագործելով, կարելի է կատարելագործել արտադրությունը, բարելավել հասարակության նյութական և մշակութային կյանքի պայմանները:
Ֆոտոէֆեկտի միջոցով «սկսեց խոսել» կինոն: Նրա շնորհիվ է, որ այժմ կարելի է շարժվող պատկերներ հաղորդել: Ֆոտոէլեկտրոնային սարքերի կիրառությունը հնարավորություն տվեց ստեղծել հաստոցներ, որոնք առանց մարդու մասնակցության, տրված գծագրերով դետալներ են պատրաստում: Ֆոտոէֆեկտի վրա հիմնված սարքերը ցանկացած մարդուց լավ են ստուգում արտադրանքի չափերը, ժամանակին միացնում ու անջատում փարոսները, փողոցների լուսավորությունը և այլն:
Այս բոլորը հնարավոր դարձավ շատ կատարյալ սարքերի` ֆոտոէլեմենտների գյուտի շնորհիվ, որոնց մեջ լուսային էներգիան ղեկավարում է էլեկտրական հոսանքի էներգիան կամ փոխարկվում է դրան:
Նյութի վրա լույսի կողմից կատարվող տարբեր ազդեցությունների մեջ լույսի ճնշումը շատ կարևոր դեր է խաղում: Այն մեծ նշանակություն ունեցավ լույսի էլեկտրամագնիսական տեսության զարգացման գործում: Լույսի բնույթի նկատմամբ, ընդհանուր փիլիսոփայական տեսակետից, ճնշումը մեծ հետաքրքրություն է ներկայացնում, վերջապես այն ունի կարևոր տիեզերական կիրառություններ:
Այն միտքը, որ լույսը պետք է ճնշում գործադրի լուսավորված մարմինների վրա, արտահայտել է դեռ Կեպլերը: Նա դրանով էր բացատրում գիսաստղերի պոչերի ձևը:
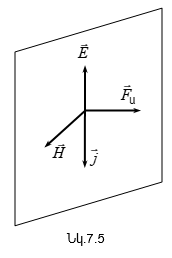
Լույսի ճնշումը կարելի է բացատրել՝ ելնելով էլեկտրամագնիսական տեսությունից: Իրոք, ընդունենք, որ լուսային հարթ ալիքը նորմալի ուղղությամբ ընկնում է մետաղի վրա, որը համընկնում է նկարի հարթության հետ (նկ.7.5): Ակներև է, որ էլեկտրական և մագնիսական վեկտորները կդասավորվեն այն մակերևույթի հարթության մեջ, որի վրա ընկնում է լույսը:
Ազատ էլեկտրոնները,
էլեկտրական վեկտորի
ազդեցության տակ
շարժվելով ![]() հակառակ,
ստեղծում են
հակառակ,
ստեղծում են ![]() խտության
հոսանք: Համաձայն
Ամպերի օրենքի`
լուսային դաշտի
մագնիսական վեկտորի
կողմից ազդում
է
խտության
հոսանք: Համաձայն
Ամպերի օրենքի`
լուսային դաշտի
մագնիսական վեկտորի
կողմից ազդում
է ![]() ուժը, որն ուղղված
է մետաղի մակերևույթին
ուղղահայաց: Ուժը,
որն ազդում է մակերևույթի
միավոր մակերեսի
վրա, առաջացնում
է լուսային ճնշում:
Համանման ձևով
կարելի է բացատրել
լույսի ճնշումը
դիէլեկտրիկների
վրա: Այս դեպքում
ընկնող ճառագայթման
էլեկտրական դաշտը
գրգռում է փոփոխական
բևեռացում, իսկ
նրա մագնիսական
դաշտը բևեռացման
դեպքում ազդելով
շարժվող լիցքերի
վրա, առաջացնում
է ճնշում:
ուժը, որն ուղղված
է մետաղի մակերևույթին
ուղղահայաց: Ուժը,
որն ազդում է մակերևույթի
միավոր մակերեսի
վրա, առաջացնում
է լուսային ճնշում:
Համանման ձևով
կարելի է բացատրել
լույսի ճնշումը
դիէլեկտրիկների
վրա: Այս դեպքում
ընկնող ճառագայթման
էլեկտրական դաշտը
գրգռում է փոփոխական
բևեռացում, իսկ
նրա մագնիսական
դաշտը բևեռացման
դեպքում ազդելով
շարժվող լիցքերի
վրա, առաջացնում
է ճնշում:
Մաքսվելը, ելնելով էլեկտրամագնիսական տեսությունից, հաշվեց հարթ էլեկտրամագնիսական ալիքի ճանապարհին գտնվող մարմնի վրա P ճնշման մեծությունը.
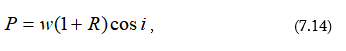
որտեղ w-ն դաշտի էներգիայի ծավալային խտությունն է, R-ը` անդրադարձման գործակիցը, i-ն ալիքի` մարմնի վրա անկման անկյունն է:
Շատ գիտնականների
երազանքն էր փորձարարական
ճանապարհով որոշել
լույսի ճնշումը:
Սակայն մեծաթիվ
փորձերն այդ ուղղությամբ
չտվեցին դրական
արդյունքներ: Պատճառն
այն է, որ ինչպես
այժմ մեզ հայտնի
է, արեգակնային
լույսի ճնշումը
երկրի մակերևույթի
վրա շատ փոքր մեծություն
է ![]() Այդպիսի աննշան
ճնշումը չափելու
համար հարկավոր
էր օգտվել գերզգայուն
չափողական սարքավորումից:
Այդպիսի աննշան
ճնշումը չափելու
համար հարկավոր
էր օգտվել գերզգայուն
չափողական սարքավորումից:
Լույսի ճնշումը փորձով հայտնաբերվել և առաջին անգամ չափվել է Լեբեդևի կողմից, իր ժամանակի համար փորձնական մեծ հմտություն պահանջող եզակի սարքավորումով:
Լույսի ճնշման հարցը քննարկենք քվանտային տեսակետից: Քանի որ լույսի քվանտներն օժտված են իմպուլսով, ապա ընդհարվելով որևէ մարմնի հետ, պետք է նրան իմպուլս հաղորդեն: Մեկ վայրկյանի ընթացքում մարմնին հաղորդված իմպուլսը ներկայացնում է մարմնի վրա ազդող ուժը: Ճնշման մեծությունը չափվում է այն ուժով, որն ազդում է մակերևույթի 1սմ2-ու վրա: Այսպիսով, ըստ քվանտային պատկերացումների, լույսի ճնշման պատճառն այն է, որ քվանտներն օժտված են իմպուլսով:
Դիցուք ֆոտոնների հոսքի խտությունը (միավոր ժամանակում միավոր մակերևույթի վրա ընկնող ֆոտոնների թիվը) հավասար է N-ի: Լուսային էներգիայի հոսքը հավասար է՝
![]()
Ֆոտոնների
այս քանակությունից
RN-ը կանդրադառնա
մակերևույթից,
իսկ (1-R)N-ը կկլանվի
մակերևույթի կողմից:
Յուրաքանչյուր
կլանված ֆոտոն
մարմնին կհաղորդի
![]() իմպուլս,
յուրաքանչյուր
անդրադարձածը,
նկատի ունենալով,
որ այս դեպքում
ֆոտոնի իմպուլսը
իմպուլս,
յուրաքանչյուր
անդրադարձածը,
նկատի ունենալով,
որ այս դեպքում
ֆոտոնի իմպուլսը
![]() վերածվում է
վերածվում է
![]() , հաղորդում
է մարմնին
, հաղորդում
է մարմնին ![]() իմպուլս
իմպուլս
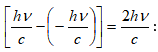 Մարմնի մակերևույթի
վրա ընկնող բոլոր
N ֆոտոնները մեկ
վայրկյանում նրան
կհաղորդեն իմպուլս,
որը կլինի՝
Մարմնի մակերևույթի
վրա ընկնող բոլոր
N ֆոտոնները մեկ
վայրկյանում նրան
կհաղորդեն իմպուլս,
որը կլինի՝
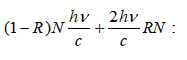
Այդ իմպուլսը վերագրելով 1սմ2-ուն, լույսի ճնշման համար կստանանք հետևյալ արտահայտությունը՝
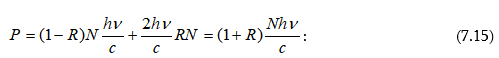
Ֆոտոնների
հոսքի N խտությունը
կարելի է ներկայացնել
որպես ֆոտոնների
n խտության (միավոր
ծավալում ֆոտոնների
քանակի) և նրանց
c արագության
արտադրյալ, այսինքն՝
N=nc: Այնուհետև նկատի
ունենալով, որ
![]() արտադրյալը տալիս
է միավոր ծավալում
գտնվող ֆոտոնների
w էներգիան (Էներգիայի
խտությունը), կարելի
է գրել
արտադրյալը տալիս
է միավոր ծավալում
գտնվող ֆոտոնների
w էներգիան (Էներգիայի
խտությունը), կարելի
է գրել
![]()
որը համընկնում է ճնշման համար էլեկտրամագնիսական տեսությունից ստացվող Մաքսվելի (7.14) բանաձևի հետ:
Եթե մարմինը հայելային ձևով (ամբողջապես) անդրադարձնում է իր վրա ընկած լույսը, ապա R=1, և
![]()
Եթե մարմինն ամբողջովին կլանում է լույսը (բացարձակ սև մարմին), ապա R=0, և
![]()
Լույսի ճնշումը բացարձակ սև մարմնի վրա երկու անգամ ավելի փոքր է, քան՝ հայելային ձևով անդրադարձնող մարմնի վրա:
Լուսային ճնշման երևույթը քվանտային կամ ալիքային տեսակետից ինչպես էլ մեկնաբանված լինի, նրա՝ փորձով հաստատված լինելու փաստը մեծ նշանակություն ունի: Այս փաստն ապացուցում է, որ լույսն ունի ոչ միայն էներգիա, այլև իմպուլս, որն անկասկած վկայում է լույսի նյութականության մասին, այն մասին, որ լույսը, ինչպես նյութը, մատերիայի ձևերից մեկն է:
Դիտարկվեցին մի շարք երևույթներ, որոնցում լույսն իրեն պահում է որպես մասնիկների (ֆոտոնների) հոսք: Սակայն չպետք է մոռանալ, որ այնպիսի երևույթներ, ինչպիսիք են լույսի ինտերֆերենցիան ու դիֆրակցիան, կարող են բացատրվել միայն ալիքային պատկերացումների հիման վրա: Այսպիսով, լույսն ի հայտ է բերում մասնիկաալիքային երկակիություն. որոշ երևույթներում ի հայտ է գալիս նրա ալիքային բնույթը, և նա իրեն պահում է որպես էլեկտրամագնիսական ալիք, իսկ այլ երևույթներում դրսևորվում է լույսի մասնիկային (կորպուսկուլային) բնույթը, և նա իրեն պահում է որպես ֆոտոնների հոսք:
Նշենք, որ մասնիկաալիքային երկակիությունը հատուկ է ոչ միայն լուսային մասնիկներին, այլև նյութի մասնիկներին (էլեկտրոններին, պրոտոններին, ատոմներին և այլն):
Ալիքային և կորպուսկուլյար շարժման այդպիսի զուգակցումը շատ ընդհանուր բնույթ ունի և հատուկ է մատերիայի այն բոլոր ձևերին, որոնց ուսումնասիրությունը կազմում է ֆիզիկայի, որպես գիտության, առարկան և բովանդակությունը:
Ռենտգենյան ճառագայթների ցրման հետազոտությունը 1923 թվականին Կոմպտոնին բերեց կարևոր երևույթի հայտնագործման, որը զգալի չափով խորացնում է մեր պատկերացումները ֆոտոնների մասին: Կոմպտոնի երևույթը ռենտգենյան ճառագայթների ալիքի երկարության փոփոխությունն է այն պահին, երբ տեղի է ունենում նրանց ցրումը թեթև ատոմներով: Հետագայում այդ երևույթը հայտնաբերվեց նաև ծանր ատոմներով ցրման դեպքում, ընդ որում, այդ վերջին դեպքում երևույթը շատ ավելի է բարդանում:
Ռենտգենյան ճառագայթների ցրումը կապված է նյութի էլեկտրոնների ստիպողական տատանումների հետ, այնպես որ ցրվող լույսի հաճախությունը պետք է հավասար լինի ընկնող լույսի հաճախությանը: Սակայն Կոմպտոն խնամքով կատարած չափումները ցույց տվեցին, որ ալիքի անփոփոխ երկարության ճառագայթման շարքում, ցրված ռենտգենյան լույսում երևան են գալիս քիչ ավելի մեծ ալիքի երկարությամբ ռենտգենյան ճառագայթներ:
Կոմպտոնի
փորձի սխեման ցույց
է տրված նկ.7.6-ում:
Դ1 և Դ2 դիաֆրագմաների
միջոցով անջատված
ռենտգենյան ճառագայթների
նեղ փունջը ցրվում
է թեթև ատոմներ
ունեցող նյութի
միջով (ածուխ, պարաֆին
և այլն): Ցրված լույսն
ուսումնասիրվում
է ռենտգենյան ճառագայթների
սպեկտրոգրաֆի
միջոցով (լուսանկարման
կամ իոնացման
խցիկի օգնությամբ):
Սկզբնական փունջն
այնպես է ընտրվում,
որ այն պարունակում
է ![]() ալիքի
երկարության մեներանգ
ռենտգենյան լույս:
Ցրված լույսի մեջ
ալիքի
երկարության մեներանգ
ռենտգենյան լույս:
Ցրված լույսի մեջ
![]() հետ միասին հայտնաբերվում
է և
հետ միասին հայտնաբերվում
է և ![]() ավելի մեծ ալիքի
երկարություն:
Ալիքի երկարության`
դիտվող փոփոխությունը՝
ավելի մեծ ալիքի
երկարություն:
Ալիքի երկարության`
դիտվող փոփոխությունը՝
![]() կախում չունի
ցրման ենթարկվող
ռենտգենյան ճառագայթների
ալիքի երկարությունից,
ինչպես և ցրող
մարմնի նյութից,
բայց կախում ունի
ցրման ուղղությունից:
Եթե
կախում չունի
ցրման ենթարկվող
ռենտգենյան ճառագայթների
ալիքի երկարությունից,
ինչպես և ցրող
մարմնի նյութից,
բայց կախում ունի
ցրման ուղղությունից:
Եթե ![]() նշանակենք
սկզբնական ճառագայթի
և ցրված ճառագայթի
ուղղություններով
կազմված անկյունը,
ապա
նշանակենք
սկզբնական ճառագայթի
և ցրված ճառագայթի
ուղղություններով
կազմված անկյունը,
ապա ![]() կախումն
այդ անկյունից
արտահայտվում
է հետևյալ բանաձևով՝
կախումն
այդ անկյունից
արտահայտվում
է հետևյալ բանաձևով՝

որտեղ
![]() փորձից գտած
հաստատուն է, որը
ցույց է տալիս
ալիքի երկարության
փոփոխության մեծությունը,
երբ ցրումը կատարվում
է ուղիղ անկյան
տակ:
փորձից գտած
հաստատուն է, որը
ցույց է տալիս
ալիքի երկարության
փոփոխության մեծությունը,
երբ ցրումը կատարվում
է ուղիղ անկյան
տակ:
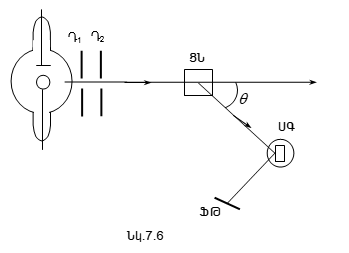
Կոմպտոնի երևույթը բացատրվում է լույսի քվանտային տեսության հիման վրա: Քվանտային տեսության արդյունքների համընկնումը փորձերի տվյալների հետ, խոսում է հօգուտ լույսի քվանտային տեսության: Հետևաբար, Կոմպտոնի երևույթը փորձարարական փաստերից այն մեկն է, որը հաստատում է լույսի քվանտային տեսությունը: Կոմպտոնի էֆեկտը գնահատելի է նաև նրանով, որ ֆոտոնների մասնակցության պրոցեսում նրանով ստուգվում է ոչ միայն էներգիայի պահպանման օրենքը, (ինչպես դա տեղի էր ունենում լուսաէֆեկտի դեպքում), այլ նաև իմպուլսի պահպանման օրենքը:
Համառոտակի շարադրենք Կոմպտոնի երևույթի քվանտային տեսությունը:
Դիտարկենք ռենտգենյան ճառագայթման փոխազդեցությունը նյութի հետ՝ որպես ռենտգենյան ֆոտոնների և ազատ էլեկտրոնների բախման պրոցես: Ֆոտոնի բախումն ազատ էլեկտրոնների հետ ընդունում ենք բացարձակ առաձգական: Դիտարկումը տանենք էներգիայի և իմպուլսի պահպանման օրենքների հիման վրա:
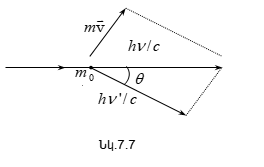
Դիցուք
mo հանգստի զանգվածով
էլեկտրոնի վրա
ընկնում է ![]() էներգիայով
ռենտգենյան ճառագայթման
քվանտ: Դադարի
էլեկտրոնի հետ
ռենտգենյան ֆոտոնի
առաձգական բախման
արդյունքում էլեկտրոնը
ձեռք է բերում
էներգիայով
ռենտգենյան ճառագայթման
քվանտ: Դադարի
էլեկտրոնի հետ
ռենտգենյան ֆոտոնի
առաձգական բախման
արդյունքում էլեկտրոնը
ձեռք է բերում
![]() իմպուլս, և տեղի
է ունենում
իմպուլս, և տեղի
է ունենում ![]() էներգիայով
ֆոտոնի ցրում
էներգիայով
ֆոտոնի ցրում
![]() անկյան տակ (նկ.7.7):
Կիրառելով էներգիայի
և իմպուլսի պահպանման
օրենքները` կստանանք
անկյան տակ (նկ.7.7):
Կիրառելով էներգիայի
և իմպուլսի պահպանման
օրենքները` կստանանք
![]()

Էներգիայի պահպանման օրենքը գրելիս պետք է նկատի ունենալ էլեկտրոնի զանգվածի կախումն արագությունից:
Արտագրենք (7.20)-ը հետևյալ տեսքով`
![]()
և հանենք նրանից (7.21)-ը: Նախապես այդ հավասարման բոլոր անդամները բերելով ընդհանուր հայտարարի` կստանանք.
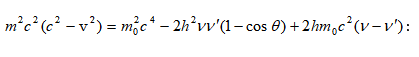
Քանի որ
![]() ,
ապա կստանանք
,
ապա կստանանք
![]()
Անցնելով
հաճախություններից
ալիքի երկարություններին
![]() (7.22)-ից կստանանք՝
(7.22)-ից կստանանք՝
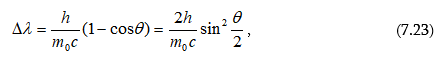
որտեղ
![]()
Բանաձև
(7.23)-ը համընկնում
է երևույթի օրենքը
սահմանող փորձարարական
բանաձև (7.19)-ի հետ:
Իրոք, տեղադրելով
h-ի, mo-ի և c-ի թվային
արժեքները՝ կգտնենք,
որ ![]() ,
որը համապատասխանում
է փորձի տվյալներին:
,
որը համապատասխանում
է փորձի տվյալներին:
Ատոմների
հետ ամուր կապված
էլեկտրոնների
վրա ֆոտոնների
ցրման դեպքում
էներգիայի և իմպուլսի
փոխանակումը ատոմի
հետ կատարվում
է որպես մի ամբողջություն:
Քանի որ ատոմի
զանգվածը շատ է
գերազանցում էլեկտրոնի
զանգվածին, կոմպտոնյան
շեղումն այս դեպքում
աննշան է, և ![]() գործնականորեն
համընկնում է
գործնականորեն
համընկնում է ![]() հետ:
հետ:
ԱՏՈՄԻ ԲՈՐԻ ՏԵՍՈՒԹՅՈՒՆԸ
8.1. Օրինաչափություններ ատոմային սպեկտրներում:
Բալմերի ընդհանրացրած բանաձևը
Նորմալ վիճակում ջրածինը չի ճառագայթում: Սակայն կարելի է ջրածնի մեջ ճառագայթում գրգռել, եթե նրա ատոմներին հաղորդենք լրացուցիչ ներքին էներգիա:
Ջրածնի այն ատոմները, որոնք օժտված են լրացուցիչ ներքին էներգիայով, կոչվում են գրգռված ատոմներ: Ատոմների այդպիսի գրգռում իրագործվում է, օրինակ գազային պարպման մեջ` նրանց ընդհարումների հետևանքով այնպիսի իոնների և հատկապես էլեկտրոնների հետ, որոնք օժտված են բավականաչափ կինետիկ էներգիայով: Ատոմական ջրածնի սպեկտրը գծային է: Այդ սպեկտրը կարելի է բաժանել գծերի խմբերի, որոնք կոչվում են սերիաներ: Ատոմական ջրածնի սպեկտրային գծերն իրենց հաջորդականության մեջ պարզ օրինաչափություն են ցուցաբերում, որն արտահայտվում է պարզ առնչությամբ: Այսպես, սպեկտրի տեսանելի և մոտիկ ուլտրամանուշակագույն մասերում դասավորված են մի շարք պայծառ գծեր, որոնց ալիքների երկարությունները կարելի է ճշգրիտ ներկայացնել շվեյցարացի ֆիզիկոս Բալմերի տված հետևյալ առնչությամբ.

որտեղ
![]() հաստատուն
է, n-ը` 3, 4, 5 և այլ արժեքներ
ընդունող ամբողջ
թիվ: Զուգորդելով
(8.1)-ը ալիքների երկարությունների`
փորձով գտնված
տվյալների հետ`
որոշված է, որ
հաստատուն
է, n-ը` 3, 4, 5 և այլ արժեքներ
ընդունող ամբողջ
թիվ: Զուգորդելով
(8.1)-ը ալիքների երկարությունների`
փորձով գտնված
տվյալների հետ`
որոշված է, որ ![]()
Բալմերյան
սերիայի գծերի
դասավորությունը
բերված է նկ.8.1-ում,
որտեղ ![]() պայմանանշաններով
նշանակված են այն
գծերը, որոնք գտնվում
են տեսանելի տիրույթում:
պայմանանշաններով
նշանակված են այն
գծերը, որոնք գտնվում
են տեսանելի տիրույթում:
![]() ցույց է տալիս
սերիայի սահմանը:
Յուրաքանչյուր
գծի վերևում տրված
է նրա ալիքի երկարությունն`
անգստրեմներով:
ցույց է տալիս
սերիայի սահմանը:
Յուրաքանչյուր
գծի վերևում տրված
է նրա ալիքի երկարությունն`
անգստրեմներով:
Բանաձև
(8.1)-ով արտահայտվող
օրինաչափությունը
դառնում է հատկապես
դիտելի, եթե այն
ներկայացվի այն
տեսքով, որից սովորաբար
օգտվում են այժմ:
Այդ նպատակով այս
բանաձևն անհրաժեշտ
է ձևափոխել այնպես,
որ այն հնարավորություն
տա հաշվել ոչ թե
ալիքի երկարությունները,
այլ հաճախությունները
կամ ալիքային թվերը:
Համաձայն հայտնի
բանաձևի` հաճախությունը
(տատանումների
թիվը 1 վայրկյանում)
արտահայտվում
է ![]() տեսքով, որտեղ
c-ն լույսի արագությունն
է դատարկության
մեջ, իսկ
տեսքով, որտեղ
c-ն լույսի արագությունն
է դատարկության
մեջ, իսկ ![]() ալիքի
երկարությունն
է նունպես դատարկության
մեջ: Ալիքային
թիվը ալիքի երկարության
հակադարձն է կամ
1սմ-ի մեջ տեղավորվող
ալիքների թիվը.
ալիքի
երկարությունն
է նունպես դատարկության
մեջ: Ալիքային
թիվը ալիքի երկարության
հակադարձն է կամ
1սմ-ի մեջ տեղավորվող
ալիքների թիվը.

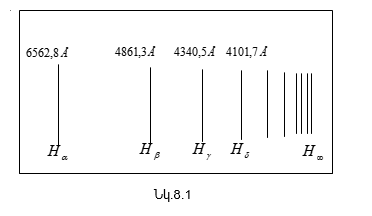
Սպեկտրաչափության մեջ գերադասում են օգտվել ալիքային թվերից, որովհետև ներկայումս ալիքի երկարությունները որոշվում են մեծ ճշտությամբ և, հետևապես, այդպիսի ճշտությամբ էլ հայտնի են ալիքային թվերն այն ժամանակ, երբ լույսի արագությունը, ուրեմն և հաճախությունը, որոշված են զգալիորեն փոքր ճշտությամբ: Եթե (8.1)-ը ձևափոխենք ալիքային թվի համար, կստացվի
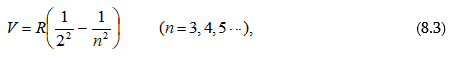
բանաձևը,
որտեղ R տառով
նշանակված է ![]() հավասար
հաստատունը: Այս
հաստատունը, ի
պատիվ շվեդ սպեկտրոսկոպիստի,
անվանում են Ռիդբերգի
հաստատուն`
հավասար
հաստատունը: Այս
հաստատունը, ի
պատիվ շվեդ սպեկտրոսկոպիստի,
անվանում են Ռիդբերգի
հաստատուն`
![]()
Բանաձև (8.3)-ը կոչվում է Բալմերի բանաձև, իսկ ջրածնի ատոմի սպեկտրային գծերի համապատասխան սերիան` Բալմերի սերիա:
Հետագա հետազոտությունները ցույց են տվել, որ բացի Բալմերի սերիայից, ատոմական ջրածնի սպեկտրի մեջ կան ևս մի քանի սերիաներ, որոնք ներկայացվում են միևնույն բանաձևերով: Այսպես, սպեկտրի ուլտրամանուշակագույն մասում գտնվում է Լայմանի սերիան: Մնացած սերիաները ինֆրակարմիր տիրույթում են: Այս սերիաների գծերը կարող են ներկայացվել բանաձև (8.3)-ի տեսքով.
|
Լայմանի սերիա` |
|
|
Պաշենի սերիա` |
|
|
Բրեկետի սերիա` |
|
|
Պֆունդի սերիա` |
|
Այստեղից երևում է, որ ատոմական ջրածնի բոլոր հայտնի սերիաները կարելի է ներկայացնել մեկ բանաձևով.
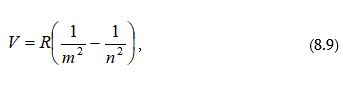
որտեղ
m-ը 1 արժեք ունի
Լայմանի սերիայի
համար, 2 արժեք` Բալմերի
սերիայի համար
և այլն: Տվյալ m-ի
դեպքում n թիվն
ընդունում է բոլոր
ամբողջ արժեքները`
սկսած (m+1)-ից: Բանաձև
(8.9)-ը կոչվում է Բալմերի
ընդհանրացրած
բանաձև: n-ի աճման
հետ գծի ալիքային
թիվը յուրաքանչյուր
սերիայում ձգտում
է ![]() սահմանային արժեքին,
որը կոչվում է
սերիայի սահման
(նկ.8.1-ում
սահմանային արժեքին,
որը կոչվում է
սերիայի սահման
(նկ.8.1-ում ![]() պայմանանշանով
նշված է Բալմերի
սերիայի սահմանը):
պայմանանշանով
նշված է Բալմերի
սերիայի սահմանը):
(8.5)-(8.8)
բանաձևերն իրար
հետ համեմատելով
հեշտ է նկատել,
որ այդ բանաձևերից
յուրաքանչյուրի
առաջին հաստատուն
անդամը մյուսի
փոփոխական անդամներից
մեկն է: Օրինակ,
Պաշենի սերիայի
բանաձևի ![]() հաստատուն
անդամը Բալմերի
սերիայի հնարավոր
փոփոխական անդամներից
առաջինն է և Լայմանի
սերիայի բանաձևի
համար` երկրորդը:
Բալմերի սերիայի
հաստատուն անդամն
իր հերթին Լայմանի
սերիայի բանաձևի
մեջ փոփոխական
անդամներից մեկն
է և այլն: Այս փաստն
առանձնապես պարզ
երևում է Բալմերի
ընդհանրացրած
(8.9) բանաձևից, որը
ցույց է տալիս,
որ ջրածնի սպեկտրի
ցանկացած սպեկտրային
գծի ալիքային թիվը
կարելի է ներկայացնել
որպես
հաստատուն
անդամը Բալմերի
սերիայի հնարավոր
փոփոխական անդամներից
առաջինն է և Լայմանի
սերիայի բանաձևի
համար` երկրորդը:
Բալմերի սերիայի
հաստատուն անդամն
իր հերթին Լայմանի
սերիայի բանաձևի
մեջ փոփոխական
անդամներից մեկն
է և այլն: Այս փաստն
առանձնապես պարզ
երևում է Բալմերի
ընդհանրացրած
(8.9) բանաձևից, որը
ցույց է տալիս,
որ ջրածնի սպեկտրի
ցանկացած սպեկտրային
գծի ալիքային թիվը
կարելի է ներկայացնել
որպես ![]() տիպի երկու
անդամների տարբերություն,
m-ի ցանկացած երկու
ամբողջ արժեքների
դեպքում: Մտցնելով
տիպի երկու
անդամների տարբերություն,
m-ի ցանկացած երկու
ամբողջ արժեքների
դեպքում: Մտցնելով
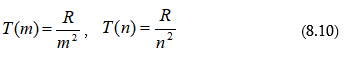
նշանակումները, մենք կարող ենք (8.9)-ը գրել երկու ամբողջ թվերի ֆունկցիաների տարբերության տեսքով.
![]()
T(m), T(n) թվերը կոչվում են սպեկտրային կամ ուղղակի թերմեր: Ջրածնի համար թերմերի ամբողջ համակարգը ստացվում է մի ընդհանուր բանաձևից`
![]()
(8.12)-ից հետևում է, որ գիտենալով տվյալ ատոմի թերմերի համակարգը` կարող ենք ստանալ ցանկացած սպեկտրային գծի ալիքային թիվը, որպես այդ համակարգի երկու անդամների տարբերություն:
![]()
Ատոմի բարդ կառուցվածքի հայտնագործումը ժամանկակից ֆիզիկայի կազմավորման կարևոր փուլն է, որն իր հետքն է թողել նրա ողջ հետագա զարգացման վրա: Ատոմի կառուցվածքի քանակական տեսության, որը թույլ տվեց բացատրել ատոմային սպեկտրները, ստեղծման ընթացքում հայտնագործվեցին միկրոմասնիկների շարժման նոր` քվանտային մեխանիկայի օրենքները:
Գիտնականները
միանգամից չէ,
որ հանգեցին ատոմի
կառուցվածքի մասին
ճիշտ պատկերացումների:
Ատոմի առաջին մոդելը
առաջարկել է Թոմսոնը
1903թ.: Ըստ Թոմսոնի
մոդելի` ատոմը
դրական լիցքով
հավասարաչափ լիցքավորված
գունդ է, ուր գտնվում
են էլեկտրոնները:
Պարզագույն ատոմտ`
ջրածնի ատոմը,
մոտավորապես ![]() շառավղով
դրական լիցքավորված
գունդ է, որի ներսում
գտնվում է էլեկտրոնը:
Ավելի բարդ ատոմներում`
դրական լիցքավորված
գնդում, գտնվում
են մի քանի էլեկտրոններ,
այնպես, որ ատոմը
նման է կեքսի, որի
մեջ չամչի հատիկների
դերը խաղում են
էլեկտրոնները:
շառավղով
դրական լիցքավորված
գունդ է, որի ներսում
գտնվում է էլեկտրոնը:
Ավելի բարդ ատոմներում`
դրական լիցքավորված
գնդում, գտնվում
են մի քանի էլեկտրոններ,
այնպես, որ ատոմը
նման է կեքսի, որի
մեջ չամչի հատիկների
դերը խաղում են
էլեկտրոնները:
Ըստ Թոմսոնի մոդելի էլեկտրոններն ատոմում գտնվում են հանգստի վիճակում, և միայն ատոմի գրգռման ժամանակ են նրանք սկսում տատանվել, ինչն էլ, դասական ֆիզիկայի օրենքների համաձայն, պատճառ է դառնում լույսի ճառագայթման:
Թեև
Թոմսոնի մոդելը
ճիշտ չէր, բայց
գիտության պատմության
մեջ այն դրական
դեր խաղաց: Մասնավորապես
ատոմի մասին այդպիսի
պատկերացումը
շատ արդյունավետ
եղավ քիմիայում:
Թոմսոնը վերլուծեց
էլեկտրոնի հավասարակշռության
պայմանները ատոմներում
և ցույց տվեց, որ
էլեկտրոնների
թվից կախված` ստացվում
են կայուն կամ
անկայուն կոնֆիգուրացիաներ:
Այդ պատկերացումները
հնարավորություն
տվեցին մոտենալ
տարրերի հատկությունների
պարբերականության
հարցի բացատրությանը
և դրանք պահպանվեցին
ատոմի նոր տեսությունում:
Այսպիսով, Թոմսոնի
մոդելն օգնում
էր բացատրել որոշ
երևույթներ, բայց
սպեկտրային օրինաչափությունները
բացատրելու համար
այն պիտանի չէր:
Ավելին, Թոմսոնի
դատողությունները,
թե ինչպես են ատոմում
բաշխված դրական
և բացասական լիցքերը,
որևէ փորձնական
հիմք չունեին:
Այդ պատճառով պետք
է կարևոր քայլ
համարել անմիջապես
ատոմի ներսը թափանցելու
փորձը, որի նպատակն
էր պարզել, թե ատոմում
լիցքերը տարածականորեն
ինչպես են բաշխված:
Նման տեսակի փորձերի
կատարումը ձեռնարկեց
Ռեզերֆորդը: Ռեզերֆորդն
իր առաջ նպատակ
դրեց ստուգել ատոմի`
Թոմսոնի մոդելի
ճիշտ լինելը: Դրական
լիցքի, հետևաբար,
և զանգվածի բաշխումը
ատոմի մեջ փորձնականորեն
ուսումնասիրելու
համար Ռեզերֆորդը
1906թ. առաջարկեց ատոմի
զոնդում ալֆա մասնիկների
(![]() մասնիկների)
միջոցով: Հիշեցնենք,
որ ալֆա մասնիկը
(
մասնիկների)
միջոցով: Հիշեցնենք,
որ ալֆա մասնիկը
(![]() մասնիկը) հելիումի
իոնացված (առանց
էլեկտրոնների)
ատոմ է, որի զանգվածը
մոտավորապես 8000
անգամ մեծ է էլեկտրոնի
զանգվածից, իսկ
դրական լիցքը հավասար
է էլեկտրոնի լիցքի
բացարձակ արժեքի
կրկնապատիկին:
Ալֆա մասնիկների
(
մասնիկը) հելիումի
իոնացված (առանց
էլեկտրոնների)
ատոմ է, որի զանգվածը
մոտավորապես 8000
անգամ մեծ է էլեկտրոնի
զանգվածից, իսկ
դրական լիցքը հավասար
է էլեկտրոնի լիցքի
բացարձակ արժեքի
կրկնապատիկին:
Ալֆա մասնիկների
(![]() մասնիկների) արագությունը
շատ մեծ է. այն կազմում
է լույսի արագության
1/15 մասը:
մասնիկների) արագությունը
շատ մեծ է. այն կազմում
է լույսի արագության
1/15 մասը:
Ռեզերֆորդը
ռադիոակտիվ պատրաստուկից
արձակված ![]() մասնիկներով
ռմբակոծում էր
ծանր տարրերի ատոմները:
մասնիկներով
ռմբակոծում էր
ծանր տարրերի ատոմները:
![]() մասնիկների
փունջն առանձնացվում
էր դիաֆրագմայով
և հետո ընկնում
հետազոտվող նյութի
(ոսկի, պղինձ և այլն)
նրբաթիթեղի վրա:
Ցրվելուց հետո
մասնիկների
փունջն առանձնացվում
էր դիաֆրագմայով
և հետո ընկնում
հետազոտվող նյութի
(ոսկի, պղինձ և այլն)
նրբաթիթեղի վրա:
Ցրվելուց հետո
![]() մասնիկներն ընկնում
են ցինկի սուլֆիդով
պատված էկրանի
վրա: Էկրանի հետ
ամեն մի մասնիկի
բախմանն ուղեկցում
էր լույսի բռնկում
(սցինտիլյացիա),
որը կարելի էր
տեսնել մանրադիտակով:
Ռեզերֆորդն ու
իր աշխատակիցները,
հաշվելով տարբեր
անկյուններով
ցրված
մասնիկներն ընկնում
են ցինկի սուլֆիդով
պատված էկրանի
վրա: Էկրանի հետ
ամեն մի մասնիկի
բախմանն ուղեկցում
էր լույսի բռնկում
(սցինտիլյացիա),
որը կարելի էր
տեսնել մանրադիտակով:
Ռեզերֆորդն ու
իր աշխատակիցները,
հաշվելով տարբեր
անկյուններով
ցրված ![]() մասնիկների
թիվը, կարողացան
գնահատել միջուկի
չափերը: Պարըվեց,
որ միջուկի տրամագիծը
մասնիկների
թիվը, կարողացան
գնահատել միջուկի
չափերը: Պարըվեց,
որ միջուկի տրամագիծը
![]() կարգի է (տարբեր
միջուկների տրամագծերը
տարբեր են): Հետագայում
հաջողվեց որոշել
նաև միջուկի լիցքը:
Էլեկտրոնի լիցքը,
որպես միավոր ընդունելու
դեպքում, միջուկի
լիցքը ճիշտ հավասար
է տվյալ քիմիական
տարրի կարգաթվին
Մենդելեևի աղյուսակում:
կարգի է (տարբեր
միջուկների տրամագծերը
տարբեր են): Հետագայում
հաջողվեց որոշել
նաև միջուկի լիցքը:
Էլեկտրոնի լիցքը,
որպես միավոր ընդունելու
դեպքում, միջուկի
լիցքը ճիշտ հավասար
է տվյալ քիմիական
տարրի կարգաթվին
Մենդելեևի աղյուսակում:
Ընդհանրացնելով փորձերում ստացված արդյունքները` 1911թ. Ռեզերֆորդն առաջարկեց ատոմի նոր` միջուկային մոդելը: Ըստ այդ մոդելի` ատոմի կենտրոնում գտնվում է 10-15-10-14 մ շառավիղ ունեցող միջուկը, որտեղ կենտրոնացված է ատոմի գրեթե ամբողջ զանգվածը, որը և լիցքավորված է դրական լիցքով, իսկ միջուկի շուրջը դասավորվում են Z էլեկտրոններ, որոնք բաշխված են ատոմի գրաված ամբողջ ծավալում: Ատոմի չափերը համարում ենք այն տիրույթի չափերը, որտեղ դասավորված են ատոմին պատկանող էլեկտրոնները: Այդպիսի համակարգը չի կարող կայուն հավասարակշռության մեջ գտնվել, եթե լիցքերն անշարժ են (էլեկտրաստատիկայի ընդհանուր դրույթը): Այդ պատճառով անհրաժեշտ է ենթադրել, որ էլեկտրոնները պտտվում են միջուկի շուրջն այնպես, ինչպես մոլորակներն Արեգակնային համակարգում` գծելով Արեգակի շուրջը փակ հետագծեր: Այսպես ծագեց Ռեզերֆորդի ատոմի միջուկային մոդելը:
Ըստ Ռեզերֆորդի մոդելի` ջրածնի ատոմը բաղկացած է միջուկից և նրա շուրջը պտտվող մեկ էլեկտրոնից (նկ.8.2):
Ռեզերֆորդի
առաջարկած մոդելը
հիմնված է հավաստի
փորձնական տվյալների
վրա, որոնք ստացվել
են ![]() մասնիկների ցրման
փորձերից: Բայց
միաժամանակ այն
ոչ միայն չի բացատրում
սպեկտրային օրինաչափությունները,
այլև, եթե այդպիսի
համակարգում պրոցեսները
նկարագրենք` հենվելով
դասական մեխանիկայի
և էլեկտրադինամիկայի
օրենքների վրա,
հնարավոր չի լինի
բացատրել ատոմի
կողմից մեներանգ
ճառագայթների
առաքման փաստը:
մասնիկների ցրման
փորձերից: Բայց
միաժամանակ այն
ոչ միայն չի բացատրում
սպեկտրային օրինաչափությունները,
այլև, եթե այդպիսի
համակարգում պրոցեսները
նկարագրենք` հենվելով
դասական մեխանիկայի
և էլեկտրադինամիկայի
օրենքների վրա,
հնարավոր չի լինի
բացատրել ատոմի
կողմից մեներանգ
ճառագայթների
առաքման փաստը:
Իրոք, էլեկտրոնների շրջանագծով կամ առհասարակ կորագիծ ուղեծրով շարժվելն արագացող շարժում է և ըստ Մաքսվելի էլեկտրադինամիկայի օրենքների` պետք է ուղեկցվի համապատասխան հաճախության լույսի ճառագայթումով:
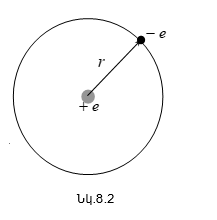
Մասնավորապես, երբ պտույտը կատարվում է շրջանագծով և հավասարաչափ է, ապա ճառագայթման հաճախությունը պետք է հավասար լինի պտտման հաճախությանը. ավելի բարդ պարբերական շարժումների դեպքում ճառագայթումն ըստ Ֆուրյեի թեորեմի, կպարունակի մի շարք մեներանգ բաղադրիչներ: Ճառագայթման հետևանքով կփոքրանա ատոմային համակարգի էներգիան և դրա հետ միասին կփոքրանա էլեկտրոնի հեռավորությունը միջուկի կենտրոնից, հետևաբար, կփոքրանա նաև պտտման պարբերությունը: Այսպիսով, պտտման հաճախությունը և հետևաբար նաև ճառագայթման հաճախությունն անընդհատ մեծանում են` ատոմը կարձակի անընդհատ սպեկտր: Միաժամանակ էլեկտրոնն անընդհատ մոտենալով միջուկին` աննշան (10-8վ) ժամանակից հետո պետք է որ ընկնի միջուկի վրա, և դրանից հետո ատոմը` որպես այդպիսին, կդադարի գոյություն ունենալուց:
Ուրեմն, համաձայն դասական էլեկտրադինամիկայի օրենքների` Ռեզերֆորդի ատոմը պետք է անկայուն լինի և իր գոյության ամբողջ ընթացքում պետք է ճառագայթի անընդհատ սպեկտր: Այս երկու եզրակացություններն էլ խիստ հակասում են փորձին:
Ճառագայթման վրա ծախսված էներգիայի կորստի պատճառով ատոմի անխուսափելի կործանման մասին հետևության չհամընկնելը փորձի հետ` դասական ֆիզիկայի օրենքները ներատոմային երևույթների նկատմամբ կիրառելու արդյունք է: Այստեղից հետևում է, որ ատոմի հետ կապված երևույթների նկատմամբ դասական ֆիզիկայի օրենքները կիրառելի չեն:
Այս դժվարությունից դուրս գալու ելքն առաջարկվեց Բորի կողմից (1913թ.), որը հրաժարվեց ատոմի նկատմամբ դասական էլեկտրադինամիկայի օրենքների կիրառումից: Հենվելով Պլանկի քվանտային տեսության գաղափարների վրա` Բորը Ռեզերֆորդի մոդելի մեկնաբանությանը մոտեցավ այդ նոր պատկերացումների տեսանկյունից: Սակայն պետք է նշել, որ Պլանկի տեսությունն ընդունելով, որ տարրական տատանակի (օսցիլյատորի) նկատմամբ դասական էլեկտրադինամիկան կիրառելի չէ, դրա փոխարեն առաջ չքաշեց մշակված քվանտային էլեկտրադինամիկա: Դրան համապատասխան, Բորն էլ չէր կարող տալ Ռեզերֆորդի ատոմի բարդ խնդրի մի այնպիսի լուծում, որը լիներ նոր ֆիզիկայի օրենքների հետևողական կիրառումը: Նա ստիպված էր կանխադրույթների (պոստուլատների) միջոցով նոր ֆիզիկայի ոգով ձևակերպել որոշ հաստատումներ` առանց այդ կանխադրույթների կիրառման դեղատոմսի որևէ ռացիոնալ հիմնավորում տալու: Սակայն այդ ակնհայտ ոչ կատարյալ ուղու վրա ստացվեցին այնպիսի զարմանալի արդյունքներ, որ Բորի ենթադրության ճշտությունը ակներև դարձավ:
Քվանտային տեսության հետևողական զարգացումը հանգեցրեց քվանտային մեխանիկայի և քվանտային էլեկտրադինամիկայի ստեղծմանը: Այժմ քվանտային մեխանիկայի և քվանտային էլեկտրադինամիկայի օգնությամբ հաջողվել է տալ խնդրի ավելի ճշգրիտ լուծումը:
Բորը Պլանկի գաղափարներն ավելի ընդհանրացրեց, ենթադրելով, որ Ռեզերֆորդի ատոմի դեպքում էլ դասական էլեկտրադինամիկայի պահանջած անըդհատ ճառագայթումը տեղի չի ունենում: Նման ատոմի սպեկտրի գծային լինելը մեկնաբանելու համար պետք է ենթադրել, որ ատոմային համակարգի ճառագայթումն այլ ձևով է կատարվում, քան պետք է տեղի ունենար ըստ սովորական մակրոսկոպիկ պատկերացումների, որի շնորհիվ այդ պատկերացումների հիման վրա ճառագայթման հաճախությունը որոշել հնարավոր չէ:
Բորը
ենթադրեց, որ ճառագայթումն
ունի այնպիսի ![]() հաճախություն,
որը որոշվում է
հաճախության հետևյալ
պայմանով.
հաճախություն,
որը որոշվում է
հաճախության հետևյալ
պայմանով.

որտեղ En
-ը և Em-ը համակարգի
էներգիաներն են
նախքան ճառագայթելը
և ճառագայթելուց
հետո: Այսպիսով,
ճառագայթման![]() հաճախությունն
ընդհանրապես կապված
չէ ատոմային համակարգի
շարժումների հաճախություններից
և ոչ մեկի հետ:
հաճախությունն
ընդհանրապես կապված
չէ ատոմային համակարգի
շարժումների հաճախություններից
և ոչ մեկի հետ:
Ելնելով այս օրենքից` կարող ենք եզրակացնել, որ սպեկտրները մեզ չեն տալիս ատոմներում մասնիկների շարժման պատկերը, ինչպես դա ընդունված է ճառագայթման սովորական տեսության մեջ: Սպեկտրները միայն հնարավորություն են տալիս դատելու էներգիայի այն փոփոխությունների մասին, որոնք տեղի են ունենում ատոմներում տարբեր հնարավոր պրոցեսների ընթացքում: Այսպիսի մոտեցման համաձայն սպեկտրային գծերի ընդհատ լինելու բնույթը վկայում է, որ գոյություն ունեն էներգիայի որոշակի, դիսկրետ արժեքներ, որոնք համապատասխանում են ատոմի առանձնահատուկ վիճակներին: Այդ վիճակները տեղին է անվանել ստացիոնար, որովհետև ենթադրվում է, որ ատոմը դրանցից յուրաքանչյուրում կարող է մի որոշ ժամանակ մնալ և դուրս գալով այդ վիճակից, ընկնել մի ուրիշ, նոր ստացիոնար վիճակի մեջ` փոխելով իր էներգիան վերջնական արժեքով:
Այս նկատառումները Բորը ձևակերպեց երկու կանխադրույթների ձևով.
1. Ատոմները և ատոմային համակարգերը երկար ժամանակ կարող են գտնվել միայն որոշակի վիճակներում` կայուն (ստացիոնար) վիճակներում, որոնց մեջ գտնվելիս, չնայած նրանց մեջ տեղի ունեցող էլեկտրոնների շարժմանը, չեն ճառագայթում և չեն կլանում էներգիա: Այդ վիճակներում ատոմների էներգիաները կազմում են E1,E2,…En ընդհատ (դիսկրետ) շարք: Այդ վիճակները բնորոշվում են իրենց կայունությամբ: Էներգիայի ամեն մի փոփոխություն կլանման, էլեկտրամագնիսական ճառագայթման կամ բախումների հետևանքով կարող է տեղի ունենալ միայն մի վիճակից մյուսը լրիվ տեղափոխման դեպքում (թռիչքով):
2.
Մի կայուն վիճակից
մյուսին անցնելու
ժամանակ ատոմներն
արձակում կամ կլանում
են խիստ որոշակի
հաճախության ճառագայթում:
Ճառագայթումը,
որն արձակվում
կամ կլանվում է
En վիճակից
Em վիճակին
անցնելիս, մեներանգ
է, և նրա հաճախությունը
որոշվում է ![]() պայմանից
(Բորի հաճախությունների
պայման):
պայմանից
(Բորի հաճախությունների
պայման):
Ամենափոքր E1 էներգիայով վիճակն անվանում են հիմնական վիճակ, իսկ ավելի մեծ էներգիաներով (E2, E3, …) վիճակները` գրգռված վիճակներ: Այս երկու կանխադրույթներն էլ խիստ հակասում են դասական էլեկտրադինամիկայի պահանջներին, որովհետև ըստ առաջին կանխադրույթի ատոմները չեն ճառագայթում, չնայած` նրանց մեջ մտնող էլեկտրոնները կատարում են արագացումով շարժում, իսկ ըստ երկրորդի` առաքված հաճախությունները ոչ մի կապ չունեն էլեկտրոնների պարբերական շարժման հաճախության հետ, այլ վկայում են միայն ատոմի էներգիայի փոփոխության մասին:
Ֆրանկի և Հերցի փորձերի նպատակն էր փորձարարական ճանապարհով ստուգել Բորի կանխադրույթները ստացիոնար վիճակների գոյության մասին: Այդ փորձերի ժամանակ չափվում էր այն էներգիայի քանակությունը, որը հաղորդվում է ատոմներին էլեկտրոնների հետ փոխհարվածի ժամանակ:
Եթե գազային միջավայրով անցնում է որոշակի էնեգիայով օժտված էլեկտրոնների հոսք, ապա այդ միջավայրով շարժվելիս էլեկտրոններն ընդհարվում են ատոմների հետ (ենթարկվում են փոխհարվածի), որի հետևանքով էլեկտրոնների սկզբնական էներգիան փոփոխվում է:
Նկատի
ունենալով, որ
էլեկտրոնների
զանգվածը փոքր
է` ատոմների զանգվածի
հետ համեմատած,
առաձգական հարվածի
ժամանակ էլեկտրոնի
կինետիկ էներգիան
փոփոխվում է չափազանց
աննշան չափով`
մոտավորապես ![]() կարգի
մեծությամբ, որտեղ
me-ն էլեկտրոնի
զանգվածն է, իսկ
Eկ-ն` էլեկտրոնի
կինետիկ էներգիան:
Ուստի կարելի է
ընդունել, որ առաձգական
հարվածի դեպքում
էլեկտրոնը հանդիպակաց
ատոմին չի տալիս
իր էներգիան: Մինչդեռ
ոչ առաձգական
հարվածի ժամանակ
այն կարող է ամբողջությամբ
կամ զգալի չափով
իր էներգիան փոխանցել
ատոմի էլեկտրոններից
մեկին:
կարգի
մեծությամբ, որտեղ
me-ն էլեկտրոնի
զանգվածն է, իսկ
Eկ-ն` էլեկտրոնի
կինետիկ էներգիան:
Ուստի կարելի է
ընդունել, որ առաձգական
հարվածի դեպքում
էլեկտրոնը հանդիպակաց
ատոմին չի տալիս
իր էներգիան: Մինչդեռ
ոչ առաձգական
հարվածի ժամանակ
այն կարող է ամբողջությամբ
կամ զգալի չափով
իր էներգիան փոխանցել
ատոմի էլեկտրոններից
մեկին:
Ըստ մեխանիկայի օրենքների` փոխհարվածի ժամանակ ատոմի կողմից էլեկտրոններին հաղորդվող էներգիան կախված է ընդհարման պայմաններից, մասնավորապես` նշանառության պարամետրի մեծությունից: Քանի որ այդ պարամետրը կարող է ունենալ ցանկացած արժեք և ընդհարումից ընդհարում կարող է փոխվել կամայական ձևով, ապա փոխանցվող էներգիայի քանակությունն էլ կարող է լինել խիստ բազմապիսի:
Նկատի ունենալով, որ երբ մեծ թվով էլեկտրոններ են անցնում, կարող են տեղի ունենալ փոխհարվածի ամեն տեսակի դեպք, ապա համաձայն մեխանիկայի օրենքների, էլեկտրոնների հոսքում պետք է տեղի ունենան էներգիայի ամեն տեսակի կորուստներ: Սակայն, եթե ատոմների մեջ գոյություն ունի ստացիոնար վիճակ, ապա էներգիայի փոփոխությունը ատոմային էլեկտրոնների մեջ չի կարող կամայական լինել: Այն կարող է հավասար լինել միայն ստացիոնար վիճակների էներգիաների միջև եղած տարբերությանը: Ուստի, արտաքին էլեկտրոնների մեջ ոչ առաձգական հարվածների ժամանակ էներգիայի կորուստն էլ կամայական լինել չի կարող, այն պետք է հավասար լինի ատոմների ստացիոնար վիճակների էներգիաների միջև եղած տարբերությանը:
Այսպիսով, եթե ստացիոնար վիճակներ իրոք գոյություն ունեն, ապա էլեկտրոնները, բախվելով ատոմների հետ, պետք է էներգիան կորցնեն դիսկրետ ձևով, այսինքն` որոշակի բաժիններով: Եթե ստացիոնար վիճակներ չկան, ապա ընդհարման ժամանակ էներգիայի կորուստները կարող են կամայական լինել:
Էլեկտրոնների ոչ առաձգական ընդհարումներն ատոմների հետ գրանցելու և այս դեպքում ատոմին փոխանցված էներգիայի մեծությունը որոշելու համար, Ֆրանկը և Հերցը կիրառեցին, այսպես կոչված, կասեցնող պոտենցիալի մեթոդը: Նրանց սարքի սխեման պատկերված է նկ. 8.3-ում: Այդ նկարում Կ տառով նշանակված է կաթոդը, որը տաքացվում է մինչև այն ջերմաստիճանը, որի ժամանակ առաջանում է ջերմաէլեկտրոնային էմիսիա:
Մ1 մարտկոցով Կ կաթոդի և Ց ցանցի միջև ստեղծվում է էլեկտրական դաշտ, որն արագացնում է էլեկտրոնները: Եթե էլեկտրոնները ԿՑ տարածության մեջ փոխհարվածների չեն ենթարկվում և էներգիա չեն կորցնում, ապա Ց ցանցն անցնելուց հետո նրանք կունենան eU էներգիա, որտեղ U-ն պոտենցիալների տարբերությունն է կաթոդի և ցանցի միջև: Ց ցանցի և Ա անոդի միջև, ընդհակառակը, Մ2 մարտկոցով ստեղծվում է թույլ դաշտ, որն արգելակում է էլեկտրոնները: Դրա համար անոդի վրա ստեղծվում է ավելի փոքր պոտենցիալ, քան Ց-ի վրա, այն հաշվով, որ Ց-ի և Ա-ի միջև պոտենցիալների տարբերությունը հավասար լինի 0,5Վ-ի: Այդ դաշտը թույլ չի տալիս էլեկտրոններին հասնել անոդին: Իսկ եթե Կ-ից մինչև Ա ընկած ճամապարհին էլեկտրոններն անոթում գտնվող գազի մոլեկուլների ոչ առաձգական ընդհարումների հետևանքով կորցնեն իրենց էներգիան, ապա նրանք չեն կարողանա անցնել ՑԱ կասեցնող դաշտի միջով և կընկնեն Ց ցանցի վրա:
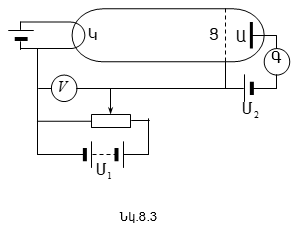
Ուստի նկ.8.3-ում պատկերված սխեմայով կարելի է, ըստ Գ գալվանոմետրի ցուցմունքների, գրանցել այն էլեկտրոնները, որոնք ոչ առաձգական հարվածի հետևանքով կորցրել են իրենց էներգիան: Երբ էլեկտրոնները կորցնում են իրենց էներգիան, դրանք կասեցվում են արգելակող դաշտի կողմից և չեն անցնում գալվանոմետրի միջով: Ուստի և Գ գալվանոմետրը ցույց է տալիս հոսանքի անկում:
Ֆրանկի և Հերցի փորձերում որպես գազային մարմին, ծառայում էին սնդիկի գոլորշիները: Սնդիկի գոլորշիներով լցնում էին անոթը, որից նախօրոք օդը հանում և անոթը գազազրկում էին: Հետազոտությունների նպատակն էր որոշել Գ գալվանոմետրի միջով անցնող I հոսանքի ուժի կախումն այն էլեկտրոնների կինետիկ էներգիայից, որոնք դուրս էին գալիս ԿԱ տարածության մեջ: Հետազոտությունների արդյունքները ներկայացված են նկ.8.4-ում մի կորի տեսքով, որը ցույց է տալիս հոսանքի կախումն էլեկտրոնների կինետիկ էներգիայից: Կորը շատ բնորոշ տեսք ունի: Վերլուծության ենթարկենք այն, ցույց տալու համար, թե ինչի հետևանք է նրա յուրահատուկ տեսքը:
Սկզբում էլեկտրոնների կինետիկ էներգիայի աճմանը զուգընթաց, Գ գալվանոմետրի միջով անցնող հոսանքն աճում է: Այդ աճը, որը սովորական է ջերմաէլեկտրական սարքերի համար, տեղի է ունենում հետեվյալ օրենքով`

և հետևանք է այն բանի, որ էներգիայի աճմանը զուգընթաց էլեկտրոնների ավելի ու ավելի մեծ քանակություն է անցնում Ց ցանցի բջիջների միջով: Սակայն հոսանքի այդ աճը տեղի է ունենում միայն մինչև այն պահը, երբ էներգիան հավասարվում է 4,9էՎ-ի:
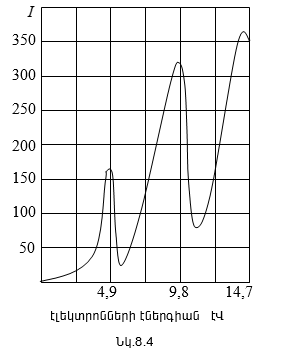
Այնուհետև, երբ էլեկտրոնների կինետիկ էներգիան շարունակում է մեծանալ, հոսանքը չի մեծանում, ինչպես պետք էր սպասել ըստ (8.14) առնչության, այլ շեշտակի ընկնում է: Դրանից հետո էլեկտրոնների էներգիայի աճման հետ հոսանքը դարձյալ շարունակում է աճել և հետո, երբ էլեկտրոնների կինետիկ էներգիան հավասար է դառնում 9,8էՎ-ի, կրկին շեշտակի ընկնում է: Հոսանքի հաջորդ անկումը վրա է հասնում այն ժամանակ, երբ էլեկտրոնների էներգիան հասնում է 14,7էՎ-ի:
Հոսանքի
աճն (մինչև մաքսիմումը)
այն պահին, երբ
էլեկտրոնների
կինետիկ էներգիան
4,9էՎ է, նշանակում
է, որ քանի դեռ էլեկտրոնի
էներգիան չի հավասարվել
4,9էՎ-ի, էլեկտրոնները
ԿՑ տարածության
մեջ ոչ առաձգական
հարվածների չեն
ենթարկվում: Տեղի
են ունենում միայն
առաձգական փոխհարվածներ,
որոնց հետևանքով
էլեկտրոնները
էներգիա չեն կորցնում,
ուստի այն բոլոր
էլեկտրոնները,
որոնք անցնում
են Ց ցանցի բջիջների
միջով հասնում
են անոդին և ապա
անցնում Գ գալվանոմետրի
միջով: Երբ էլեկտրոնների
կինետիկ էներգիան
հասնում է 4,9էՎ-ի,
դրանք ընդհարվելով
սնդիկի ատոմների
հետ, ենթարկվում
են ոչ առաձգական
հարվածի` համարյա
ամբողջությամբ
կորցնելով իրենց
էներգիան: Դրա
հետևանքով չեն
կարողանում հասնել
Ա էլեկտրոդին:
Երբ էլեկտրոնների
էներգիան դառնում
է 5,4էՎ-ից ավելի մեծ,
հոսանքը նորից
սկսում է աճել:
Այս աճը տեղի է
ունենում այն պատճառով,
որ ոչ առաձգական
հարվածի հետևանքով
էներգիան կորցրած
էլեկտրոնը դեռ
ունենում է այնքան
էներգիա, որն անհրաժեշտ
է տարածության
մեջ գործող դաշտի
ուժերի դեմ աշխատանք
կատարելու համար:
Քանի որ պետք է
հաղթահարել պոտենցիալների
0,5էՎ տարբերություն,
ապա հոսանքի աճն
այն պահին, երբ
էլեկտրոնի կինետիկ
էներգիան հավասարվում
է 5,4էՎ-ի, նշանակում
է, որ էլեկտրոնները
ոչ առաձգական հարվածի
ժամանակ կորցրել
են 4,9էՎ էներգիա:
Հոսանքի անկումն
այն ժամանակ, երբ
էներգիան հասնում
է 9,8էՎ-ի, համապատասխանում
է այն դեպքերին,
երբ էլեկտրոնը
սնդիկի ատոմների
հետ մի շարք ընդհարումներ
ունենալու հետևանքով
ենթարկվել է մի
շարք ոչ առաձգական
փոխհարվածների,
որոնցից յուրաքանչյուրի
ժամանակ կորցրել
է 4,9էՎ: Երրորդ մաքսիմումը
համապատասխանում
է այն դեպքին, երբ
էլեկտրոնը ԿՑ
ճանապարհն անցնելիս
ենթարկվել է երեք
ոչ առաձգական հարվածների,
որոնցից յուրաքանչյուրի
ժամանակ այն կորցրել
է 4,9-ական էՎ: Այսպիսով
մենք կարող ենք
եզրակացնել, որ
սնդիկի ատոմների
հետ ընդհարվելիս
էլեկտրոններն
իրենց էներգիան
կորցնում են բաժիններով,
յուրաքանչյուրը`
4,9էՎ: Այս եզրակացության
ճշմարտացիությունը
հաստատվում է նաև
այն բանով, որ 4,9 Վ
լարման դեպքում
սնդիկի գոլորշիներն
սկսում են ճառագայթել:
Ճառագայթման հաճախությունը,
որը որոշվում է
![]() բանաձևով, համընկնում
է փորձնականորեն
դիտվածի հետ: Դա
նշանակում է, որ
սնդիկի գրգռված
ատոմներն այնուհետև
անցնում են ստորին
էներգետիկ վիճակին
և ճառագայթում
են լուսային քվանտներ`
Բորի երկրորդ կանխադրույթին
համապատասխան:
բանաձևով, համընկնում
է փորձնականորեն
դիտվածի հետ: Դա
նշանակում է, որ
սնդիկի գրգռված
ատոմներն այնուհետև
անցնում են ստորին
էներգետիկ վիճակին
և ճառագայթում
են լուսային քվանտներ`
Բորի երկրորդ կանխադրույթին
համապատասխան:
Համանման փորձեր կատարվեցին նաև ուրիշ գազային նյութերով: Այդ փորձերի ընթացքում պարզվեց, որ կալիումի գոլորշիներում ոչ առաձգական հարվածի հետևանքով էլեկտրոնները էներգիան կորցնում են 1,63 էՎ-ի հավասար բաժիններով, նատրիումի գոլորշիների մեջ` 2,12 էվ, գազային հելիումի մեջ էլեկտրոններն իրենց էներգիան կորցնում են 21 էՎ-ի հավասար բաժիններով:
Ֆրանկի և Հերցի փորձերը ցույց են տալիս, որ ատոմի հետ ընդհարվելիս էլեկտրոնն իր էներգիան փոխանցում է ատոմին միայն որոշակի բաժիններով: Հետևաբար այս փորձերն ապացուցում են Բորի միտքն ատոմների ստացիոնար վիճակների մասին:
8.5. Շրջանային ուղեծրերի քվանտացումը և
ջրածնի ատոմի Բորի տարրական տեսությունը
Ֆրանկի և Հերցի փորձերը ցույց տվեցին, որ, իրոք, ատոմների ստացիոնար վիճակներ գոյություն ունեն: Իսկ ի՞նչ եղանակով կարելի է հաշվել ստացիոնար վիճակների էներգիան, էներգիայի E1,E2,…,Ei արժեքների դիսկրետ շարքը: Քանի որ Բորի կանխադրույթները հակասում են դասական մեխանիկայի օրենքներին, ակներև է, որ ստացիոնար ուղեծրի էներգիան հաշվելու համար չի կարելի օգտվել մեխանիկայի օրենքներից: Իրոք, երբ Բորի կանխադրույթները պահանջում են էներգիայի մակարդակների դիսկրետ հաջորդականություն, որոնց ատոմի մեջ համապատասխանում է քվանտացված ուղեծրերի ընտրյալ շարք, դասական ֆիզիկան բերում է ուղեծրերի անընդհատ բազմության: Այս հակասությունն ունի շատ ընդհանուր բնույթ: Փաստերի միակցությունը միարժեք կերպով ցույց է տալիս, որ ատոմական աշխարհի երևույթների մեջ հանդես է գալիս ընդհատություն, որը բնորոշվում է Պլանկի հաստատունի վերջավոր արժեքով (զրոյի հավասար չլինելով): Հակառակը, մակրոսկոպիկ երևույթների համար, այսինքն մեծ մասշտաբի երևույթների համար, բնորոշ է հենց անընդհատությունը:
Այսպիսով, մենք գալիս ենք այն եզրակացության, որ դասական ֆիզիկան, իր անըդհատ փոփոխվող մեծություններով, ատոմական երևույթների նկատմամբ կիրառելի չէ: Հետագայում պարզվեց, որ էլեկտրոնների շարժումն ատոմի մեջ ենթարկվում է ալիքային մեխանիկայի օրենքներին, սակայն այդ օրենքները հաստատվեցին տասներկու տարի հետո այն ժամանակից, երբ Բորը բանաձևեց իր կանխադրույթները:
Ուստի, ատոմային մեխանիկայի զարգացման առաջին շրջանում հարկ եղավ օգտագործել մի մեթոդ, որը տրամաբանորեն հակասական էր, բայց հնարավորություն էր տալիս ստանալու ճիշտ արդյունքներ` ատոմային մեխանիկայի մի շարք խնդիրներ լուծելիս: Ըստ այդ մեթոդի ենթադրվում էր, որ ատոմների ստացիոնար վիճակներին համապատասխանող էլեկտրոնների ուղեծրերը դասական մեխանիկայի տեսակետից հնարավոր ուղեծրեր են, ուստի ատոմի մեջ էլեկտրոնների ուղեծրերը գտնելու խնդիրը լուծվում է դասական մեխանիկայի սովորական մեթոդներով:
Այնուհետև, միայն ուղեծրերի անընդհատ բազմությունից, որոնք հնարավոր են ըստ դասական մեխանիկայի, ընտրվում են նրանք, որոնք համապատասխանում են ատոմի ստացիոնար վիճակներին: Ատոմների ստացիոնար վիճակներին համապատասխանող ուղեծրերի ընտրության այս մեթոդն էլ ստացել է քվանտացման մեթոդ անվանումը:
Բորի
առաջարկած քվանտացման
մեթոդը դարձավ
Պլանկի արտահայտած
գաղափարի նպատակահարմար
ընդհանրացումը:
Ըստ Պլանկի` մարմինների
և ճառագայթման
դաշտի միջև էներգիայի
փոխանակության
քվանտային բնույթն
արտահայտվում
է Պլանկի h հաստատունի
օգնությամբ [h-ի
չափայնությունը
(էներգիա![]() ժամանակ)]:
Ընդունելով, որ
Պլանկի այդ նույն
հաստատունն արտահայտում
է ներատոմային
պրոցեսների քվանտային
բնույթը, մենք
կարող ենք եզրակացնել,
որ ատոմային մեխանիկայում
այս հաստատուն
մեծությունները,
որոնք ունեն (էներգիա
ժամանակ)]:
Ընդունելով, որ
Պլանկի այդ նույն
հաստատունն արտահայտում
է ներատոմային
պրոցեսների քվանտային
բնույթը, մենք
կարող ենք եզրակացնել,
որ ատոմային մեխանիկայում
այս հաստատուն
մեծությունները,
որոնք ունեն (էներգիա![]() ժամանակ)
չափայնությունը,
չեն կարող ունենալ
կամայական արժեքներ,
այլ պետք է լինեն
Պլանկի h հաստատունի
բազմապատիկները:
Եվ հենց այդ շարժումներն
էլ, որոնց համար
այդ մեծությունները
կհանդիսանան h
-ի բազմապատիկները,
կհամապատասխանեն
ստացիոնար վիճակներին:
ժամանակ)
չափայնությունը,
չեն կարող ունենալ
կամայական արժեքներ,
այլ պետք է լինեն
Պլանկի h հաստատունի
բազմապատիկները:
Եվ հենց այդ շարժումներն
էլ, որոնց համար
այդ մեծությունները
կհանդիսանան h
-ի բազմապատիկները,
կհամապատասխանեն
ստացիոնար վիճակներին:
Առաջին անգամ քվանտացման մեթոդը Բորի կողմից առաջարկվեց ջրածնի ատոմի ստացիոնար վիճակներին համապատասխանող շրջանային ուղեծրերի ընտրման համար:
Ըստ
Բորի` ջրածնի ատոմի
ստացիոնար վիճակներին
համապատասխանում
են էլեկտրոնների
այնպիսի ուղեծրեր,
որոնց համար իմպուլսի
մոմենտը հավասար
է Պլանկի h հաստատունի
և ![]() -ի հարաբերության
ամբողջ բազմապատիկին.
-ի հարաբերության
ամբողջ բազմապատիկին.

որտեղ
me-ն էլեկտրոնի
զանգվածն է, v-ն`
նրա արագությունը,
r-ը` այն շրջանագծի
շառավիղը, որով
շարժվում է էլեկտրոնը,
n-ը ամբողջ թիվ
է և կոչվում է գլխավոր
քվանտային թիվ,
![]()
Դժվար
չէ նկատել, որ mevr
մեծությունն ունի
(էներգիա![]() ժամանակ)
չափայնություն:
Բորի (8.15) պայմանը
հնարավորություն
տվեց լուծելու
ջրածնի ատոմի մեջ
էլեկտրոնների
հնարավոր ուղեծրերը:
ժամանակ)
չափայնություն:
Բորի (8.15) պայմանը
հնարավորություն
տվեց լուծելու
ջրածնի ատոմի մեջ
էլեկտրոնների
հնարավոր ուղեծրերը:
Իր կանխադրույթները Բորը կիրառեց պարզագույն համակարգի` ջրածնի ատոմի տեսության կառուցման համար:
Դիտարկենք Ze լիցք ունեցող ատոմային միջուկի դաշտում շարժվող էլեկտրոնը: Այդպիսի համակարգը Z=1 դեպքում համապատասխանում է ջրածնի ատոմին, այլ Z -երի դեպքում` ջրածնանման իոններին, այսինքն Z կարգային համարով ատոմին, որից հեռացել են բոլոր էլեկտրոնները, բացի մեկից:
Էլեկտրոնի արագության և ուղեծրի շառավղի միջև կապ կա, որը բխում է Նյուտոնի երկրորդ օրենքից: Ուղեծրում էլեկտրոնին կենտրոնաձիգ արագացում հաղորդում է կուլոնյան ուժը: Հետևաբար`

(8.15) և (8.16)-ից արտաքսելով v-ն` ստանում ենք, որ ատոմում էլեկտրոնային ուղեծրերի շառավիղը կարող է ընդունել միայն մի շարք դիսկրետ արժեքներ`

Բորի ուղեծրերի շառավիղները փոփոխվում են ընդհատ կերպով, n թվի փոփոխության հետ միասին: Պլանկի հաստատունը, էլեկտրոնի զանգվածը և լիցքը որոշում են էլեկտրոնային ուղեծրերի հնարավոր արժեքները:
Ջրածնային ատոմի առաջին ուղեծրի շառավղի համար (Z=1, n=1) ստացվում է.
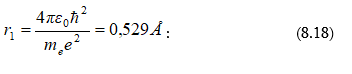
Նկատի ունենալով (8.17)-ը` (8.15)-ից գտնում ենք էլեկտրոնի շարժման արագությունը ստացիոնար ուղեծրում.

Տալով n-ին (8.19) առնչությունում բնական թվերի շարքի արժեքները` կստանանք էլեկտրոնների շարժման արագություններն այդ ուղեծրերով: Ստացված առնչությունները, սակայն, մատչելի չեն փորձնական ստուգման համար, որովհետև ոչ էլեկտրոնի շառավիղը և ոչ էլ էլեկտրոնի շարժման արագությունն այդ ուղեծրով անմիջականորեն չափել հնարավոր չէ: Տեսության ստուգման համար պետք է հաշվել այնպիսի մեծություններ, որոնք կարելի է փորձով անմիջականորեն չափել:
Այդպիսի մեծություն է այն էներգիան, որը ճառագայթվում կամ կլանվում է ջրածնի ատոմների կողմից: Այդ էներգիայի արժեքը մեծ ճշտությամբ որոշվում է սպեկտրային չափումներով: Հայտնի է, որ ջրածնի ատոմի ճառագայթման էներգիայի արժեքն արտահայտվում է Բալմերի ընդհանրացրած բանաձև (8.9)-ով: Ըստ Բորի երկրորդ կանխադրույթի, ատոմների ճառագայթած և կլանած էներգիան հավասար է ատոմների ստացիոնար վիճակների էներգիաների տարբերությանը: Ուստի, Բորի տեսությունը ստուգելու համար պետք է բաղդատել ստացիոնար վիճակների էներգիաների հաշվարկված տարբերությունները ջրածնի ատոմի ճառագայթած էներգիայի հետ:
Ատոմի ներքին էներգիան էլեկտրոնի կինետիկ էներգիայի և էլեկտրոնի ու միջուկի փոխազդեցության պոտենցիալ էներգիայի գումարն է.
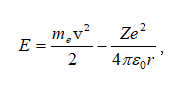
(8.16)-ից հետևում է, որ
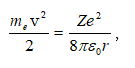
հետևաբար`
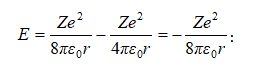
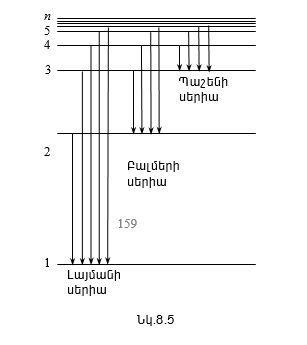
E մեծության բացասական նշանը պայմանավորված է նրանով, որ մենք իրարից անսահման հեռավորության վրա գտնվող երկու լիցքերի պոտենցիալ էներգիայի մեծությունն ընդունեցինք հավասար զրոյի:
Վերջապես հաշվի առնելով r-ի` (8.17)-ով տրվող արժեքները, կստանանք ատոմի ներքին էներգիայի թույլատրելի արժեքները.
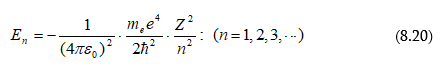
(8.20)-ով որոշվող էներգետիկ մակարդակների սխեման տրված է նկ.8.5-ում:
Ստորին էներգետիկ վիճակում (n=1, Z=1)
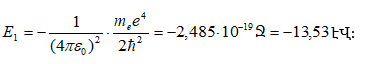
Այդ վիճակում ատոմը կարող է գտնվել ցանկացած չափով տևական ժամանակ: Ջրածնի ատոմը իոնացնելու (նրանից էլեկտրոն պոկելու) համար ատոմին անհրաժեշտ է հաղորդել 12,53էՎ էներգիա: Այդ էներգիան կոչվում է իոնացման էներգիա: n=2,3,4,… բոլոր վիճակները համապատասխանում են գրգռված ատոմին: Այդ վիճակներում կյանքի տևողությունը 10-8վ կարգի է:
Ըստ Բորի, երբ ջրածնի ատոմը (Z=1) n վիճակից անցնում է m վիճակին, ճառագայթում է լույսի քվանտ: Ճառագայթման հաճախությունն արտահայտվում է հետևյալ առնչությամբ.
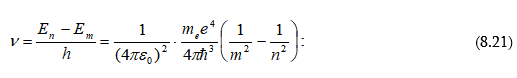
Ալիքային թիվը`
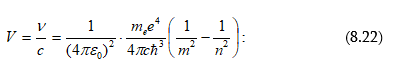
(8.22) առնչությունը ցույց է տալիս, որ ալիքային թվերն արտահայտվում են երկու գումարելիների` թերմերի տարբերությամբ: Հետևաբար, Բորի տեսությունը ճիշտ է որոշում ջրածնային ատոմների ճառագայթման բնույթը: Ավելին, ալիքային թվերի արժեքները, որոնք որոշվում են բանաձև (8.22)-ով, ճշգրտորեն համընկնում են փորձնական տվյալների հետ: (8.22)-ի մեջ
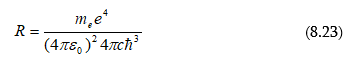
հաստատուն մեծությունը ներկայացնում է Ռիդբերգի հաստատունը:
Այսպիսով, հանգեցինք Բալմերի ընդհանրացրած բանաձևին: Եթե (8.23)-ի մեջ տեղադրենք նրա մեջ մտնող հաստատունների արժեքները, կստանանք մի մեծություն, որը համաձայնության մեջ է Ռիդբերգի հաստատունի փորձնական արժեքի հետ:
Այսպիսով, Բորի տեսությունը ոչ միայն քանակապես, այլև որակապես մեծ ճշտությամբ որոշում է ջրածնի ատոմի ալիքային թվերի մեծությունը:
Քանի որ Բորի տեսությունը դասական և քվանտային ֆիզիկաների արհեստական միավորման արդյունք էր, ապա բնական է, որ այն չէր կարող քանակապես բացատրել բոլոր ատոմների ճառագայթման սպեկտրները: Իսկապես, հելիումի ատոմի համար քանակական արդյունքները չհամընկան փորձնական արդյունքների հետ. հնարավոր էր միայն կատարել որակական եզրակացություններ: Պատճառն այն է, որ Բորի տեսությունը քվանտային տեսություն չէր. միայն կանխադրույթներն էին քվանտային, մանավանդ որևէ տեղից չէին բխում: Սակայն Բորի տեսությունը խթանեց քվանտային մեխանիկայի զարգացումը, որից Բորի կանխադրույթները բխում են արդեն որպես հետևանք:
Այսպիսով, Բորի տեսությունը խոշոր քայլ էր ատոմի տեսության զարգացման ուղղությամբ: Այն ողջ հստակությամբ ցույց տվեց ներատոմային երևույթների նկատմամբ դասական ֆիզիկայի կիրառման անհնարինությունը և քվանտային օրենքների առաջնային նշանակությունը միկրոաշխարհում:
ՔՎԱՆՏԱՅԻՆ ՄԵԽԱՆԻԿԱՅԻ ՏԱՐՐԵՐԸ
9.1. Դը Բրոյլի վարկածը
Նյութի ալիքային հատկությունները
Բորի տեսությունը հանդիսացավ դասական պատկերացումների և 1923թ. ձևավորված ալիքային մեխանիկայի նոր գաղափարների միջանկյալ օղակը: Այդ գաղափարների հաստատման պատճառ հանդիսացավ ճառագայթման մասնիկաալիքային երկակիությունը: Պատկերացումն այն մասին, որ էլեկտրոններն օժտված են ալիքային հատկություններով, պատկանում է ֆրանսիացի ֆիզիկոս դը Բրոյլին: Դը Բրոյլը ելնում էր մինչ այդ ստեղծված այն պատկերացումներից, որոնց համաձայն լույսը ներկայացնում է այնպիսի մասնիկների (քվանտների) հոսք, որոնք միաժամանակ իրենց մեջ զուգակցում են նաև ալիքային շարժման հատկությունները: Դը Բրոյլը ենթադրեց, որ էլեկտրոնների հոսքի հետ կապված է որոշ ալիքային պրոցես, որն ազդեցություն է գործում էլեկտրոնների վարքի վրա և պայմանավորում է նրանց մի շարք հատկությունները, որոնք անհամատեղելի են մասնիկների հատկությունների հետ:
Դը
Բրոյլը, համանմանություն
անցկացնելով ![]() էներգիա
ունեցող քվանտի
և
էներգիա
ունեցող քվանտի
և ![]() իմպուլսի միջև,
ենթադրեց, որ էլեկտրոնի
կամ հանգստի զանգված
ունեցող որևէ այլ
մասնիկի շարժումը
կապված է ալիքային
պրոցեսի հետ: Այդ
պրոցեսին համապատասխանում
է ալիք, որի երկարությունը`
իմպուլսի միջև,
ենթադրեց, որ էլեկտրոնի
կամ հանգստի զանգված
ունեցող որևէ այլ
մասնիկի շարժումը
կապված է ալիքային
պրոցեսի հետ: Այդ
պրոցեսին համապատասխանում
է ալիք, որի երկարությունը`

Որտեղ p=mv -ն շարժվող մասնիկի իմպուլսն է, v-ն նրա արագությունը, h-ը` Պլանկի հաստատունը:
(9.1) առնչությամբ որոշվող ալիքի երկարությունն ընդունված է անվանել դը բրոյլյան ալիքի երկարություն:
Հետաքրքրական է նշել, որ դը Բրոյլին հաջողվեց որոշ չափով հիմնավորել Բորի առաջին կանխադրույթը: Դը Բրոյլը ենթադրեց, որ ստացիոնար են էլեկտրոնների այն վիճակները, որոնց ժամանակ նրանց ուղեծրի երկարության վրա տեղավորվում են ամբողջ թվով դը բրոյլյան ալիքներ:
Դը Բրոյլի պայմանը`

զուգակցելով (9.1) -ի հետ, հանգեցնում է հետևյալ առնչությանը`

կամ
![]() այսինքն՝ պարզվեց,
որ դը Բրոյլի կողմից
բանաձևված պայմանները
ստացիոնար վիճակների
համար համընկնում
են Բորի կողմից
բանաձևված (8.15) պայմանի
հետ:
այսինքն՝ պարզվեց,
որ դը Բրոյլի կողմից
բանաձևված պայմանները
ստացիոնար վիճակների
համար համընկնում
են Բորի կողմից
բանաձևված (8.15) պայմանի
հետ:
Դը Բրոյլի գաղափարները խթան հանդիսացան ալիքային մեխանիկան ստեղծելու համար, որը էլեկտրոնների վիճակը հաշվի առնելով նկարագրում է նրանց ալիքային հատկությունները, և մեծ դեր խաղացին ատոմների կառուցվածքի վերաբերյալ ուսմունքի զարգացման գործում:
Դը Բրոյլի առաջադրած պատկերացումն էլեկտրոնի ալիքային հատկությունների մասին սկզբնական շրջանում ֆիզիկոսների հավանությանը չարժանացավ: Միայն 1928 թվականին, երբ Դեվիսոնը և Ջերմերը ցույց տվին, որ էլեկտրոնային հոսքի համար դիֆրակցիայի երևույթ գոյություն ունի, էլեկտրոնների ալիքային հատկությունների իրական լինելու մասին եղած կասկածները փարատվեցին:
9.2. Դևիսոնի և Ջերմերի փորձերը
1927թ. Դևիսոնն ու Ջերմերն ուսումնասիրում էին նիկելի միաբյուրեղի վրա էլեկտրոնների ցրումը նկ.9.1-ում պատկերված սարքի օգնությամբ: Սարքը բաղկացած էր միաէներգիական էլեկտրոնների նեղ փնջի աղբյուր հանդիսացող 1 էլեկտրոնային թնդանոթից: Էլեկտրոնների փունջն ուղղվում է նիկելե 2 թիթեղի վրա, որից անդրադառնում է տարբեր ուղղություններով: 3 էլեկտրոնները որսվում են գալվանոմետրի հետ միացված շարժվող գլանային 4 էլեկտրոդի օգնությամբ: Անդրադարձած փնջի ինտենսիվությունը որոշվում է գալվանոմետրով անցած հոսանքի ուժով: Փորձերը ցույց տվեցին, որ անկման տվյալ անկյան դեպքում, էլեկտրոնները բյուրեղի մակերեվույթից անդրադառնում են տարբեր անկյունների տակ, ընդ որում, որոշ ուղղություններով դիտվում է անդրադարձած էլեկտրոնների առավելագույն թվաքանակ, իսկ այլ ուղղություններով` նվազագույն, այսինքն` դիտվում է դիֆրակցիոն պատկեր: Այս երևույթը դիտվում է, երբ Դը Բրոյլի ալիքն ունենում է բյուրեղի միջատոմական հեռավորություների կարգի երկարություն:
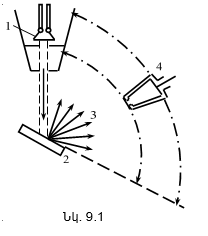
Էլեկտրոնների հետ կապված ալիքի երկարությունը ռենտգենյան ճառագայթների ալիքի երկարության կարգի է:
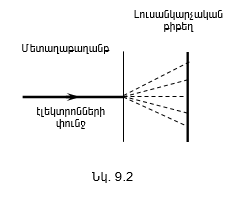
Ռենտգենյան
ճառագայթների
փունջն ուղղելով
բյուրեղի վրա`
կարելի է ստանալ
դիֆրակցիոն պատկեր:
Ելնելով սրանից`
կարելի էր սպասել,
որ համանման երևույթ
կդիտվի նաև էլեկտրոնների
համար: Քանի որ
տարբեր բյուրեղների
կառուցվածքը,
մասնավորապես`
նիկելի, ուսումնասիրվել
է, ապա Վուլֆ-Բրեգի
![]() բանաձևով կարելի
է որոշել բրեգյան
ալիքի երկարությունը
և համեմատել այն
դը Բրոյլի ալիքի
երկարության հետ
(9.1):
բանաձևով կարելի
է որոշել բրեգյան
ալիքի երկարությունը
և համեմատել այն
դը Բրոյլի ալիքի
երկարության հետ
(9.1):

Թոմսոնը և նրանից անկախ Տարտակովսկին հայտնաբերեցին, որ բյուրեղային թիթեղից ցրվող էլեկտրոնների փունջը տալիս է դիֆրակցիոն պատկեր: Փորձն իրականացվել է հետևյալ կերպ: Մի քանի տասնյակ կիլովոլտ կարգի պոտենցիալների տարբերությունով արագացվող էլեկտրոնների փունջն անցնում է բարակ մետաղաթաղանթի միջով և ընկնում է լուսանկարչական թիթեղի վրա (նկ.9.2): Վերջինիս հարվածելիս էլեկտրոնը նրա վրա ազդում է այնպես, ինչպես ֆոտոնը: Ոսկու` այդ եղանակով ստացված էլեկտրոնագիրը (նկ.9.3ա) համադրված է ալյումինինիումի` նման պայմաններում ստացված ռենտգենագրի հետ (նկ.9.3բ): Երկու պատկերների նմանությունը ապշեցուցիչ է:
Դևիսոնի և Ջերմերի փորձերը հաստատեցին, որ էլեկտրոնները դիֆրակցվել են որպես ալիքներ, այդ ալիքների երկարությունը ճշտորեն համընկնում է այն ալիքի երկարության հետ, որը տալիս են ալիքային մեխանիկայի բանաձևերը, այսինքն դը բրոյլյան և բրեգյան ալիքների երկարություններն իրար հավասար են: Այնպես, ինչպես էլեկտրոնների համար, նույն կերպ դիֆրակցիոն երևույթներ են դրսևորում նաև ատոմների և մոլեկուկների փնջերը:
Ալիքների և մասնիկների միջև եղած կապը բնության օրենք է, այդ երկակիությունը սերտ կապի մեջ է Պլանկի հաստատունի գործողության քվանտի գոյության հետ:
Ալիքային հատկությունները բնութագրական են ոչ միայն շարժվող մասնիկների փնջի, այլև առանձին շարժվող մասնիկի համար: Ֆաբրիկանտը, Բիբերմանը և Սուշկինը փորձնական ճանապարհով հայտնաբերեցին միայնակ էլեկտրոնների դիֆրակցիայի երևույթը: Մետաղական թիթեղը միայնակ էլեկտրոններով ռմբակոծելու դեպքում դիտվում է նույնպիսի դիֆրակցիոն պատկեր, ինչպիսին դիտվում է էլեկտրոնների փնջի անցման ժամանակ:
Այսպիսով, էլեկտրոնները ֆոտոնների նման ունեն մասնիկաալիքային երկակի բնույթ: Մասնիկային և ալիքային հատկանիշները միմյանց հետ կապված են Պլանկի հաստատունով.
![]()
Դը Բրոյլի ալիքների ֆիզիկական իմաստը կարելի է հասկանալ` վերլուծելով մասնիկների և լույսի ալիքային ու մասնիկային հատկությունների միջև եղած կապը: Դիֆրակցիոն առավելագույնները համապատասխանում են տարածության այն կետերին, որտեղ ընկնում են ամենամեծ թվով մասնիկներ: Այդ կետերը բնութագրվում են ալիքի առավելագույն լայնույթով: Այսպիսով, տարածության տվյալ կետում դը Բրոյլի ալիքի լայնույթի քառակուսին տարածության տվյալ կետում մասնիկի հայտնաբերման հավանականության չափանիշն է:
9.3. Հայզենբերգի անորոշությունների առնչությունները
Պարզվեց, որ Բորի տեսությունը բավարար չէ միկրոաշխարհի` օրինակ, բազմաէլեկտրոն ատոմների, մոլեկուլների կառուցվածքի, քիմիական կապի և այլ շատ երևույթների բացատրման համար: Դը Բրոյլի գաղափարները և նյութի մասնիկների ալիքային հատկությունների փորձնական բացահայտումը խթան հանդիսացան սկզբունքորեն նոր, միկրոմասնիկների վարքը նրանց ալիքային հատկությունների հաշվառման հետ նկարագրող տեսության ստեղծման համար: Այդ տեսությունը քվանտային (ալիքային) մեխանիկան է, որի հիմունքները ստեղծվել էին 1925-1926թթ. Վ. Հայզենբերգի և Է. Շրյոդինգերի կողմից:
Քվանտային մեխանիկան բացահայտում է նյութի երկու հիմնական հատկությունները՝ ներատոմային պրոցեսների քվանտայնությունն ու մասնիկների ալիքային բնույթը:
Քվանտային մեխանիկան զուրկ է ակներևությունից, որը բնութագրական է դասական մեխանիկայի համար:
Մեզ համար սովորական մակրոաշխարհի պատկերները դառնում են ոչ պիտանի միկրոաշխարհում կատարվող երևույթների նկարագրման համար:
Մակրոաշխարհում տեղի ունեցող երևույթների ուսումնասիրության ժամանակ, օգտվում էինք դասական ֆիզիկայի օրենքներից, որոնք մնում են անսասան, եթե սահմանափակվի դրանց կիրառման տիրույթը: Որպեսզի լուծվի այն հարցը, թե մեխանիկայի (դասական և ռելյատիվիստական) ինչպիսի օրենքներից է անհրաժեշտ օգտվել քննարկվող տվյալ երևույթի նկարագրման համար, անհրաժեշտ է իմանալ, թե ինչպիսի արագությամբ է շարժվում հետազոտվող մարմինը: Եթե նրա արագությունը համեմատելի է վակուումում լույսի արագության հետ, ապա պետք է կիրառել հարաբերականության տեսության բանաձևերը: Լույսի արագությունը վակուումում դասական օրենքների կիրառելիության սահմանի որոշման չափանիշն է, քանի որ այն ազդանշանների հաղորդման առավելագույն արագությունն է:
Հարց է առաջանում, գոյություն ունի արդյո՞ք նման չափանիշ մասնիկաալիքային երկակիությամբ օժտված նյութի մասնիկների վարքի նկարագրման համար: Այո, այդպիսի չափանիշ գոյություն ունի. դա Պլանկի հաստատունն է:
Ցանկացած մասնիկի վարքը նկարագրելու համար անհրաժեշտ է որոշել նրա x կոորդինատը, p իմպուլսը, E էներգիան և այլն: Դասական մեխանիկայում չկան սահմանափակումներ, որոնք արգելեն ճշտության ցանկացած աստիճանով միաժամանակ չափել օրինակ x կոորդինատը և px իմպուլսի համապատասխան պրոյեկցիան: Քվանտային մեխանիկայում դրությունը սկզբունքորեն այլ է:
Քանի որ շարժվող մասնիկն օժտված է մասնիկաալիքային երկակիությամբ, ապա x կոորդինատի և px իմպուլսի միաժամանակյա ճշգրիտ որոշումն անհնարին է:
Հայզենբերգի
կողմից միկրոմասնիկների
վարքի մանրակրկիտ
վերլուծությունը
ցույց տվեց, որ
գոյություն ունի
նշված մեծությունների
չափումների ճշտության
սկզբունքային
սահման: Եթե ![]() նշանակենք
կոորդինատների
որոշման անճշտությունները
(անորոշությունները),
իսկ
նշանակենք
կոորդինատների
որոշման անճշտությունները
(անորոշությունները),
իսկ ![]() իմպուլսի
համապատասխան
պրոյեկցիաների
որոշման անորոշությունները,
ապա այդ մեծությունները
միմյանց հետ կապված
են հետևյալ կախվածություններով.
իմպուլսի
համապատասխան
պրոյեկցիաների
որոշման անորոշությունները,
ապա այդ մեծությունները
միմյանց հետ կապված
են հետևյալ կախվածություններով.
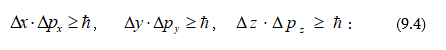
Այս
կախումն անվանում
են Հայզենբերգի
անորոշությունների
առնչություն,
ըստ որի, որքան
ճշգրիտ է որոշված
կոորդինատը ![]() , այնքան
ավելի փոքր ճշտությամբ
է որոշվում իմպուլսը
, այնքան
ավելի փոքր ճշտությամբ
է որոշվում իմպուլսը
![]() և
հակառակը:
և
հակառակը:
Այսպիսով,
անորոշությունների
առնչությունը
տալիս է այն սահմանները,
որոնցից դուրս
դասական ֆիզիկայի
դրույթները դառնում
են անընդունելի:
Եթե ![]() արտադրյալը համեմատելի
է
արտադրյալը համեմատելի
է ![]() հետ, ապա մասնիկի
վարքը նկարագրվում
է քվանտային մեխանիկայի
օրենքներով: Եթե
հետ, ապա մասնիկի
վարքը նկարագրվում
է քվանտային մեխանիկայի
օրենքներով: Եթե
![]() համեմատությամբ,
ապա մասնիկի վարքը
նկարագրվում է
դասական ֆիզիկայի
օրենքներով:
համեմատությամբ,
ապա մասնիկի վարքը
նկարագրվում է
դասական ֆիզիկայի
օրենքներով:
Որպեսզի հասկանանք, թե ինչու փորձն ավելի մեծ ճշտություն չի տալիս, քան թույլ է տալիս անորոշությունների առնչությունը, ենթադրենք, որ անհրաժեշտ է ճշգրտորեն որոշել v արագությամբ և p իմպուլսով փնջում թռչող էլեկտրոնի դիրքը (նկ. 9.4):
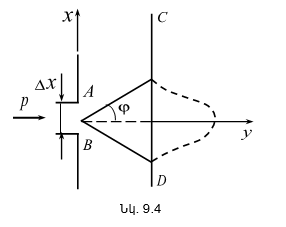
Փնջի
ճանապարհին գտնվում
է ![]() լայնությամբ
AB ճեղքը: Ճեղքի
հետևում գտնվում
է CD էկրանը, որի
վրա դիտվում է
դիֆրակցիոն պատկերը
(էլեկտրոնների
համար ճեղքի
լայնությամբ
AB ճեղքը: Ճեղքի
հետևում գտնվում
է CD էկրանը, որի
վրա դիտվում է
դիֆրակցիոն պատկերը
(էլեկտրոնների
համար ճեղքի ![]() լայնությունը
համեմատելի է դը
Բրոյլի ալիքի երկարության
հետ):
լայնությունը
համեմատելի է դը
Բրոյլի ալիքի երկարության
հետ):
Կետագծերով
ցույց է տրված
հավանականության
խտությունը կենտրոնական
առավելագույնի
(մաքսիմումի ) համար:
Դիֆրակցիայի ժամանակ
մեկ ճեղքից բարձր
կարգի առավելագույնների
ինտենսիվությունը
կարելի է անտեսել`
կենտրոնական առավելագույնի
ինտենսիվության
համեմատությամբ:
Կենտրոնական առավելագույնի
դիրքը որոշվում
է առաջին կարգի
նվազագույնների
(մինիմումների)
ուղղությամբ,այսինքն
![]() առնչությունով
որոշվող
առնչությունով
որոշվող ![]() անկյունով:
k=1-ի դեպքում՝
անկյունով:
k=1-ի դեպքում՝ ![]()
որտեղ

Քանի
որ փնջում յուրաքանչյուր
էլեկտրոն մինչև
ճեղքը շարժվում
է ճեղքի հարթությանն
ուղղահայաց, ապա
իմպուլսի բաղադրիչը՝
![]() սակայն
էլեկտրոնի x կոորդինատն
անորոշ է:
սակայն
էլեկտրոնի x կոորդինատն
անորոշ է:
Ճեղքով
անցման պահին էլեկտրոնն
ունի ճեղքի կոորդինատին
հավասար կոորդինատ:
Էլեկտրոնի կոորդինատի
որոշման մեջ պարունակվում
է ճեղքի չափերից
կախված ![]() անորոշություն:
անորոշություն:
Դիֆրակցիայի
ժամանակ ի հայտ
է գալիս իմպուլսի
![]() բաղադրիչը,
իմպուլսի բաղադրիչի
անորոշությունը
կախված է
բաղադրիչը,
իմպուլսի բաղադրիչի
անորոշությունը
կախված է ![]() անկյունից:
անկյունից:
![]()
Հաշվի առնելով (9.5)-ը, կստանանք
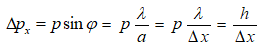
կամ
![]()
Եթե հաշվի առնվի երկրորդ դիֆրակցիոն առավելագույնի առկայությունը, ապա իմպուլսի որոշման մեջ անորոշությունը կմեծանա, դրա համար (9.7) արտահայտությունը կարելի է գրել հետևյալ տեսքով.
![]()
(9.8)-ի նման առնչություն տեղի ունի նաև ժամանակի և էներգիայի համար.
![]()
Այս
առնչությունը
դիտարկենք` այն
կիրառելով ատոմի
գրգռված վիճակի
նկատմամբ: Եթե
![]() ատոմի
գրգռված վիճակի
կյանքի միջին տևողությունն
է, իսկ
ատոմի
գրգռված վիճակի
կյանքի միջին տևողությունն
է, իսկ ![]() նրա էներգետիկ
մակարդակի միջև
լայնությունը
(վիճակի էներգիայի
անորոշություն),
ապա ինչքան կարճ
է համակարգի որևէ
վիճակի գոյության
ժամանակամիջոցը,
այնքան ավելի անորոշ
է նրա էներգիայի
արժեքը:
նրա էներգետիկ
մակարդակի միջև
լայնությունը
(վիճակի էներգիայի
անորոշություն),
ապա ինչքան կարճ
է համակարգի որևէ
վիճակի գոյության
ժամանակամիջոցը,
այնքան ավելի անորոշ
է նրա էներգիայի
արժեքը:
Գրգռված
վիճակից նորմալ
վիճակի անցնելիս`
ատոմը ճառագայթում
է էներգիայի քվանտ,
որը բնութագրվում
է ճառագայթման
սպեկտրային գծի
ճապաղման որոշակի
![]() հաճախությամբ,
ինչը բերում է
սպեկտրային գծերի
լայնացման:
հաճախությամբ,
ինչը բերում է
սպեկտրային գծերի
լայնացման:
Հայզենբերգն ու Բորը ցույց տվեցին, որ ոչ մի չափում չի կարող տալ անորոշությունների առնչություններին հակասող արդյունքներ: Այդ առնչությունները քվանտային մեխանիկայի հիմնարար դրույթներից են:
Ատոմում էլեկտրոնի շարժման ժամանակ անորոշությունների առնչությունը նշանակալի փոփոխություններ է մտցնում էլեկտրոնի հետագծի մասին պատկերացումների, այսինքն` նրա ուղեծրի մեջ:
Ջրածնի
ատոմի Բորի առաջին
ուղեծրի շառավիղը`
![]() Էլեկտրոնի արագությունը
ուղեծրի վրա՝
Էլեկտրոնի արագությունը
ուղեծրի վրա՝
![]() Եթե ենթադրենք,
որ արագությունը
որոշվել է ընդամենը
10%-ի ճշտությամբ,
այսինքն՝
Եթե ենթադրենք,
որ արագությունը
որոշվել է ընդամենը
10%-ի ճշտությամբ,
այսինքն՝ ![]() ապա կոորդինատի
անորոշությունը
`
ապա կոորդինատի
անորոշությունը
`
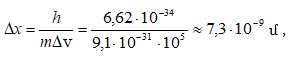
ինչը համարյա
150 անգամ գերազանցում
է ուղեծրի շառավղին:
Այսպիսով, ատոմում
էլեկտրոնի համար
հետագծի (ուղեծրի)
դասական պատկերացումը
կորցնում է իր
իմաստը: Ուղեծրի
հասկացության
քվանտամեխանիկական
իմաստի մասին կխոսվի
ստորև: Մակրոսկոպական
մարմինների համար
Հայզենբերգի անորոշությունների
առնչությամբ վերադրվող
սահմանափակումները
բացարձակապես
էական չեն: Օրինակ,
![]() տրամագծով
v=10 մ/վրկ արագությամբ
շարժվող (1%-ի ճշտությամբ
չափված, այսինքն`
տրամագծով
v=10 մ/վրկ արագությամբ
շարժվող (1%-ի ճշտությամբ
չափված, այսինքն`
![]() ) փոքրիկ կաթիլի
համար կոորդինատի
անորոշությունը
`
) փոքրիկ կաթիլի
համար կոորդինատի
անորոշությունը
`

ինչը 1020 անգամ փոքր է կաթիլի տրամագծից:
Իմպուլս-կոորդինատ անորոշությունների առնչությունը հնարավորություն է տալիս բացատրել ատոմների կայունությունը:
Իրոք, յուրաքանչյուր ատոմ կազմված է միջուկից և էլեկտրոններից: Միջուկի և էլեկտրոնների միջև գործում են կուլոնյան ձգողության ուժերը: Դրա համար էլ էլեկտրոնի իմպուլսը չի պահպանվում: Այս դեպքում, համաձայն ճառագայթման ոչ քվանտային օրենքների, էլեկտրոնը պետք է կորցնի էներգիա` առաքելով էլեկտրամագնիսական ալիքներ: Արդյունքում էլեկտրոնի շարժումը պետք է արագանա, և այն պետք է մոտենա միջուկին, և, ի վերջո, ընկնի նրա վրա: Միջուկի վրա էլեկտրոնների ընկնելուց հետո, ատոմները դառնում են ատոմային միջուկների չափերի կարգի էլեկտրաչեզոք մասնիկներ: Նյութը դառնում է շատ նոսր փոշի, և պինդ մարմինը քայքայվում է: Այդ պրոցեսները տեղի չեն ունենում, որովհետև նրանք անորոշությունների առնչություններով արգելված են: Այսպես, եթե էլեկտրոնը մոտենում է միջուկին, ապա էլեկտրոնի կոորդինատների արժեքներում անորոշությունները պետք է փոքրանան: Այդ դեպքում համաձայն (9.8)-ի պետք է աճի էլեկտրոնի իմպուլսի անորոշությունը և նրա արագությունը պետք է մեծանա: Իրոք, էլեկտրոնի կոորդինատները և իմպուլսը միատեսակ ցրվում են իրենց միջին արժեքների շրջակայքում:
Ատոմի
էլեկտրոնի համար
բնական կոորդինատային
համակարգ է այն
համակարգը, որը
կոշտ կապված է
ատոմի միջուկի
հետ: Կոորդինատային
այդ համակարգում
էլեկտրոնի իմպուլսի
և նրա կոորդինատների
միջին արժեքները
զրո են, ուստի ![]() Քանի որ
ատոմում էլեկտրոնի
շարժումը ոչ ռելյատիվիստական
է, ապա
Քանի որ
ատոմում էլեկտրոնի
շարժումը ոչ ռելյատիվիստական
է, ապա ![]() այնպես, որ
այնպես, որ
![]() և այլն: Դրա համար
էլ իմպուլսի անորոշության
աճման հետ համեմատականորեն
աճում է էլեկտրոնի
արագությունը:
Միաժամանակ մեծանում
է էլեկտրոնի էներգիան,
որի արդյունքում
այն միջուկից հեռանում
է: Այսպիսով, ատոմում
անորոշությունների
առնչություններ
դրսևորվում են
փոքր հեռավորությունների
վրա վանողական
ուժերին համանման:
Իր բարդ քվանտային
շարժումով էլեկտրոնը
գտնվում է միջուկից
միջին հաշվով այնպիսի
հեռավորությունների
վրա, որ վանողական
և կուլոնյան ձգողության
ուժերի ազդեցությունները
կոմպենսացվում
են, այնպես որ էլեկտրոնի
էներգիան չի փոփոխվում,
և այն էլեկտրամագնիսական
ալիքներ չի ճառագայթում:
և այլն: Դրա համար
էլ իմպուլսի անորոշության
աճման հետ համեմատականորեն
աճում է էլեկտրոնի
արագությունը:
Միաժամանակ մեծանում
է էլեկտրոնի էներգիան,
որի արդյունքում
այն միջուկից հեռանում
է: Այսպիսով, ատոմում
անորոշությունների
առնչություններ
դրսևորվում են
փոքր հեռավորությունների
վրա վանողական
ուժերին համանման:
Իր բարդ քվանտային
շարժումով էլեկտրոնը
գտնվում է միջուկից
միջին հաշվով այնպիսի
հեռավորությունների
վրա, որ վանողական
և կուլոնյան ձգողության
ուժերի ազդեցությունները
կոմպենսացվում
են, այնպես որ էլեկտրոնի
էներգիան չի փոփոխվում,
և այն էլեկտրամագնիսական
ալիքներ չի ճառագայթում:
Իմպուլս-կոորդինատ
անորոշությունների
առնչությունը
հնարավորություն
է տալիս գնահատել
ջրածնի ատոմի գծային
չափերը և էլեկտրոնի
նվազագույն էներգիան
այդ ատոմում: Գնահատումը
կատարվում է հետևյալ
կերպ: Ջրածնի ատոմի
միակ էլեկտրոնի
էներգիան ընդունվում
է հավասար ![]() , որտեղ
r-ը էլեկտրոնի
հեռավորությունն
է միջուկից, p-ն`
էլեկտրոնի իմպուլսը:
, որտեղ
r-ը էլեկտրոնի
հեռավորությունն
է միջուկից, p-ն`
էլեկտրոնի իմպուլսը:
Համաձայն
անորոշությունների
առնչության` կոորդինատի
և իմպուլսի համար
p և r մեծությունները
միաժամանակ գոյություն
չունեն: Քանի որ
ջրածնի ատոմի միջուկի
հետ կապված կոորդինատային
համակարգում ![]() իսկ
իսկ ![]() ապա
ապա ![]() արտադրյալի
նվազագույն արժեքը
հավասար է
արտադրյալի
նվազագույն արժեքը
հավասար է ![]() Ուստի
նվազագույն էներգիան
գնահատելու համար
կարելի է ընդունել`
Ուստի
նվազագույն էներգիան
գնահատելու համար
կարելի է ընդունել`
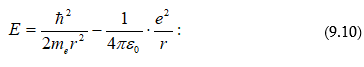
Գտնենք r-ի արժեքը , որի դեպքում E-ն նվազագույնն է: Ածանցելով (9.10) ֆունկցիան ըստ r-ի և ածանցյալը հավասարեցնելով զրոյի` կստանանք`
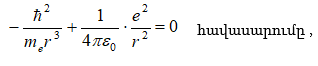
որտեղից հետևում է

Միջուկի և էլեկտրոնի միջև այդպիսի նվազագույն հեռավորության դեպքում նվազագույն էներգիան՝
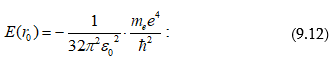
Տեղադրելով
(9.11) և (9.12) բանաձևերի
մեջ էլեկտրական
հաստատունը ![]() Պլանկի
հաստատունը՝
Պլանկի
հաստատունը՝
![]() էլեկտրոնի
զանգվածը՝
էլեկտրոնի
զանգվածը՝ ![]() և նրա լիցքը`
և նրա լիցքը`
![]() կստանանք`
կստանանք`
![]()
Այս արժեքները լավ համընկնում են փորձի տվյալների հետ, որն էլ համոզիչ կերպով հաստատում է անորոշությունների առնչությունը:
9.4. Ալիքային ֆունկցիան և նրա վիճակագրական իմաստը
Քվանտային մեխանիկայի օրենքները ստացան հավանական մեկնաբանություն. նրանք որոշում են այս կամ այն պատահարի առաջացման հավանականությունը:
Այսպես, էլեկտրոնների դիֆրակցիայի փորձում, էլեկտրոնի ընկնելը ֆոտոթիթեղի որոշակի կետում կարելի է գուշակել միայն հավանականության որոշակի աստիճանով: Միկրոմասնիկների դիֆրակցիոն պատկերը վիճակագրական (հավանական) օրինաչափության դրսևորումն է, որի համաձայն մասնիկներն ընկնում են ֆոտոթիթեղի այն մասերի վրա, որտեղ դը Բրոյլի ալիքների ինտենսիվությունն ամենամեծն է:
Միկրոաշխարհի
երևույթների հավանական
մեկնաբանությունը
քվանտային մեխանիկայի
բնորոշ հատկանիշն
է: Քանի որ միկրոմասնիկներին
վերագրում են ալիքային
պրոցես, որը համապատասխանում
է նրա շարժմանը,
ապա քվանտային
մեխանիկայում
մասնիկի վիճակը
նկարագրում են
ալիքային ֆունկցիայով,
որը կախված է x, y,
z կոորդինատներից
և t ժամանակից`
![]() (x,
y, z, t):
(x,
y, z, t): ![]() ֆունկցիայի (փսի
ֆունկցիայի) կոնկրետ
տեսքը որոշվում
է մասնիկի վիճակով,
նրա վրա ազդող
ուժերի բնույթով:
Եթե մասնիկի վրա
ազդող ուժային
դաշտը ստացիոնար
է, այսինքն կախված
չէ ժամանակից,
ապա
ֆունկցիայի (փսի
ֆունկցիայի) կոնկրետ
տեսքը որոշվում
է մասնիկի վիճակով,
նրա վրա ազդող
ուժերի բնույթով:
Եթե մասնիկի վրա
ազդող ուժային
դաշտը ստացիոնար
է, այսինքն կախված
չէ ժամանակից,
ապա ![]() ֆունկցիան
կարելի է ներկայացնել
երկու բազմապատկիչների
արտադրյալի տեսքով,
որոնցից մեկը կախված
է ժամանակից, մյուսը՝
կոորդինատից.
ֆունկցիան
կարելի է ներկայացնել
երկու բազմապատկիչների
արտադրյալի տեսքով,
որոնցից մեկը կախված
է ժամանակից, մյուսը՝
կոորդինատից.
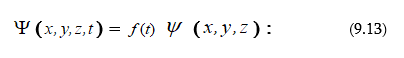
Հետագայում
կքննարկենք միայն
ստացիոնար վիճակները:![]() ֆունկցիան
մասնիկի հավանական
վիճակի բնութագիրն
է, որը պարզաբանելու
համար, մտովի առանձնացնենք
բավականաչափ փոքր
ֆունկցիան
մասնիկի հավանական
վիճակի բնութագիրն
է, որը պարզաբանելու
համար, մտովի առանձնացնենք
բավականաչափ փոքր
![]() ծավալը, որի սահմաններում
ծավալը, որի սահմաններում
![]() ֆունկցիայի արժեքները
կհամարենք միևնույնը:
Այդ դեպքում մասնիկի
տվյալ ծավալում
գտնվելու dW հավանականությունը
համեմատական է
ծավալին և կախված
է
ֆունկցիայի արժեքները
կհամարենք միևնույնը:
Այդ դեպքում մասնիկի
տվյալ ծավալում
գտնվելու dW հավանականությունը
համեմատական է
ծավալին և կախված
է![]() ֆունկցիայի
մոդուլի քառակուսուց
(դը Բրոյլի ալիքի
լայնույթի քառակուսուց).
ֆունկցիայի
մոդուլի քառակուսուց
(դը Բրոյլի ալիքի
լայնույթի քառակուսուց).
![]()
Այստեղից հետևում է ալիքային ֆունկցիայի ֆիզիկական իմաստը.

Ալիքային ֆունկցիայի մոդուլի քառակուսին ունի հավանականության խտության իմաստ, այսինքն որոշում է x, y, z կոորդինատներով որոշվող կետի շրջակայքի միավոր ծավալում մասնիկի գտնվելու հավանականությունը: Ինտեգրելով (9.15) արտահայտությունն ըստ ծավալի` կորոշենք մասնիկի գտնվելու հավանականությունն այդ ծավալում ստացիոնար դաշտի պայմաններում.

Եթե հայտնի է, որ մասնիկը գտնվում է V ծավալի սահմաններում, ապա (9.16) արտահայտության ինտեգրալն ըստ ծավալի պետք է հավասար լինի մեկի.

(9.17)-ը
![]() ֆունկցիայի նորմավորման
պայմանն է: Ինտեգրումը
կատարվում է x,
y և z փոփոխականների
փոփոխման ամբողջ
տիրույթով: (9.17) ինտեգրալն
ծավալի բոլոր հնարավոր
տարրերում մասնիկի
գտնվելու հավանականությունների
գումարն է, այսինքն`տարածության
որևէ տեղում մասնիկի
հայտնաբերման
հավանականությունը:
Այս հավանականությունը
ստույգ պատահարի
հավանականություն
է և, հետեվաբար,
պետք է հավասար
լինի մեկի:
ֆունկցիայի նորմավորման
պայմանն է: Ինտեգրումը
կատարվում է x,
y և z փոփոխականների
փոփոխման ամբողջ
տիրույթով: (9.17) ինտեգրալն
ծավալի բոլոր հնարավոր
տարրերում մասնիկի
գտնվելու հավանականությունների
գումարն է, այսինքն`տարածության
որևէ տեղում մասնիկի
հայտնաբերման
հավանականությունը:
Այս հավանականությունը
ստույգ պատահարի
հավանականություն
է և, հետեվաբար,
պետք է հավասար
լինի մեկի:
Որպեսզի ալիքային ֆունկցիան դառնա միկրոմասնիկի վիճակի օբյեկտիվ (իրական) բնութագիրը, այն պետք է լինի վերջավոր, միարժեք, անընդհատ, քանի որ հավանականությունը չի կարող լինել մեկից մեծ, չի կարող լինել ոչ միարժեք մեծություն և չի կարող փոփոխվել թռիչքաձև:
![]() ֆունկցիայի
վերլուծական արտահայտությունը
յուրաքանչյուր
կոնկրետ դեպքում
կարելի է ստանալ
քվանտային մեխանիկայի
հիմնական հավասարման
լուծման ճանապարհով,
որն առաջարկել
է Շրյոդինգերը
1926 թվին:
ֆունկցիայի
վերլուծական արտահայտությունը
յուրաքանչյուր
կոնկրետ դեպքում
կարելի է ստանալ
քվանտային մեխանիկայի
հիմնական հավասարման
լուծման ճանապարհով,
որն առաջարկել
է Շրյոդինգերը
1926 թվին:
Ինչպես Նյուտոնի դինամիկայի հավասարումները չեն կարող ստացվել տեսականորեն և մեծ թվով փորձարական փաստերի ընդհանրացում են, այնպես էլ Շրյոդինգերի հավասարումը չի կարելի արտածել նախապես հայտնի որևէ առնչությունից: Այն պետք է դիտարկել որպես ելակետային հիմնական ենթադրություն, որի ճշմարտացիությունը ապացուցվում է այն հանգամանքով, որ նրանից բխող բոլոր հետևություններն ամենաճշգրիտ ձևով համաձայնում են փորձարական փաստերի հետ:
Շրյոդինգերի ժամանակային հավասարումը ունի հետևյալ տեսքը
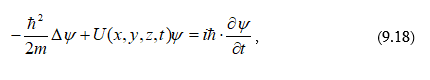
որտեղ
m-ը մասնիկի զանգվածն
է, ![]() Լապլասի
օպերատորը.
Լապլասի
օպերատորը.
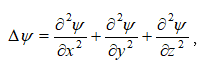
i-ն կեղծ միավորը, U(x,y,z,t)-ն՝ մասնիկի պոտենցիալ էներգիան ուժային դաշտում, որտեղ այն շարժվում է:
Այս
հավասարումը ճիշտ
է v<<c արագությամբ
շարժվող ցանկացած
մասնիկի համար:
Այն ժամանակից
կախված ընդհանուր
հավասարում է:
Շրյոդինգերի հավասարումը
![]() ֆունկցիան կապում
է միկրոմասնիկի
m զանգվածի, նրա
E լրիվ էներգիայի
և U պոտենցիալ
էներգիայի հետ:
Պոտենցիալ էներգիան
որոշվում է ուժային
դաշտով, որում
գտնվում է մասնիկը,
և ստացիոնար դեպքի
համար ժամանակից
կախված չէ:
ֆունկցիան կապում
է միկրոմասնիկի
m զանգվածի, նրա
E լրիվ էներգիայի
և U պոտենցիալ
էներգիայի հետ:
Պոտենցիալ էներգիան
որոշվում է ուժային
դաշտով, որում
գտնվում է մասնիկը,
և ստացիոնար դեպքի
համար ժամանակից
կախված չէ:
Շրյոդինգերի հավասարումը ստացիոնար վիճակների համար ունի հետևյալ տեսքը.

![]() ֆունկցիան իր
իմաստով պետք է
բավարարի հետևյալ
պահանջներին. լինի
միարժեք, անընդհատ,
վերջավոր ամբողջ
տարածության մեջ,
ունենա անընդհատ
ածանցյալներ: Օբյեկտիվորեն
գոյություն ունեցող
մասնիկի համար
պետք է իրականացվի
նորմավորման պայմանը,
այսինքն` մասնիկի
գտնվելու հավանականությունը
տարածության որևէ
մասում հավասար
է մեկի (ստույգ
պատահար): Այն տեղերում,
որտեղ մասնիկը
չի կարող գտնվել
ֆունկցիան իր
իմաստով պետք է
բավարարի հետևյալ
պահանջներին. լինի
միարժեք, անընդհատ,
վերջավոր ամբողջ
տարածության մեջ,
ունենա անընդհատ
ածանցյալներ: Օբյեկտիվորեն
գոյություն ունեցող
մասնիկի համար
պետք է իրականացվի
նորմավորման պայմանը,
այսինքն` մասնիկի
գտնվելու հավանականությունը
տարածության որևէ
մասում հավասար
է մեկի (ստույգ
պատահար): Այն տեղերում,
որտեղ մասնիկը
չի կարող գտնվել
![]() Վերևում
թվարկված պայմաններն
անվանվել են ստանդարտ:
Վերևում
թվարկված պայմաններն
անվանվել են ստանդարտ:
Եթե մասնիկը տեղափոխվում է միայն որևէ ուղղի, օրինակ x առանցքի երկայնքով, ապա Շրյոդինգերի հավասարումը պարզեցվում է և ստանում հետևյալ տեսքը.
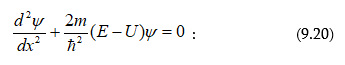
Շրյոդինգերի հավասարման մեջ որպես պարամետր մտնում է մասնիկի E լրիվ էներգիան: Դիֆերենցիալ հավասարումների տեսությունից հետևում է, որ Շրյոդինգերի հավասարումը ստանդարտ պայմաններին բավարարող լուծում ունի ոչ թե E էներգիայի ցանկացած արժեքների, այլ միայն որոշ ընտրված արժեքների դեպքում, որոնք կոչվում են սեփական արժեքներ: E էներգիայի սեփական արժեքներին համապատասխանող լուծումները կոչվում են խնդրի սեփական ֆունկցիաներ:
9.6. Մասնիկն անվերջ խոր միաչափ պոտենցիալ փոսում
Մասնիկի
համար էներգիայի
սեփական արժեքների
և դրանց համապատասխանող
ֆունկցիաների
որոշման ավելի
պարզ օրինակը միմյանցից![]() հեռավորությամբ
անվերջ բարձր պատերով
միաչափ «պոտենցիալ
փոսում» մասնիկի
շարժման մասին
խնդրի լուծումն
է: Ենթադրենք` մասնիկը
կարող է շարժվել
միայն x առանցքի
երկայնքով, փոսի
լայնության սահմաններում`
հեռավորությամբ
անվերջ բարձր պատերով
միաչափ «պոտենցիալ
փոսում» մասնիկի
շարժման մասին
խնդրի լուծումն
է: Ենթադրենք` մասնիկը
կարող է շարժվել
միայն x առանցքի
երկայնքով, փոսի
լայնության սահմաններում`
![]()
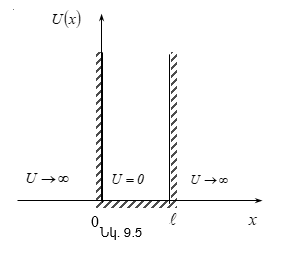
Քանի
որ փոսի պատերն
անվերջ բարձր են,
ապա մասնիկը նրա
սահմաններից դուրս
գալ չի կարող, դրա
համար էլ ![]() ֆունկցիան
փոսի սահմաններից
դուրս հավասար
է զրոյի:
ֆունկցիան
փոսի սահմաններից
դուրս հավասար
է զրոյի:
Անընդհատության
պայմանից հետևում
է, որ ![]() ֆունկցիան
պետք է զրո լինի
նաև փոսի սահմանների
վրա.
ֆունկցիան
պետք է զրո լինի
նաև փոսի սահմանների
վրա.
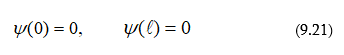
Այս արտահայտություններն էլ որոշում են այն պայմանները, որոնց պետք է բավարարեն Շրյոդինգերի հավասարման ֆիզիկական իմաստ ունեցող լուծումները:
Փոսի
ներսում ![]() ֆունկցիան
զրոյից տարբեր
է: Քանի որ
ֆունկցիան
զրոյից տարբեր
է: Քանի որ ![]() տիրույթում
ուժային դաշտերը
չեն ազդում մասնիկի
վրա, ապա U պոտենցիալ
էներգիան այս դեպքում
ունի նկ. 9.5-ում բերված
տեսքը:
տիրույթում
ուժային դաշտերը
չեն ազդում մասնիկի
վրա, ապա U պոտենցիալ
էներգիան այս դեպքում
ունի նկ. 9.5-ում բերված
տեսքը:
Այն
հավասար է զրոյի
(0<![]() <
<![]() ) դեպքում
և ձգտում է անվերջության
(
) դեպքում
և ձգտում է անվերջության
(![]() < 0 և
< 0 և ![]() >
>![]() )
դեպքում: Քննարկվող
տիրույթի համար,
որտեղ
)
դեպքում: Քննարկվող
տիրույթի համար,
որտեղ ![]() ֆունկցիան
զրոյից տարբեր
է, (9.20) հավասարումը
կընդունի հետևյալ
տեսքը.
ֆունկցիան
զրոյից տարբեր
է, (9.20) հավասարումը
կընդունի հետևյալ
տեսքը.

Մտցնելով
![]()
նշանակումը, կստանանք մի հավասարում, որը լավ հայտնի է տատանումների տեսությունից.

(9.24) հավասարման լուծումը
![]()
ֆունկցիան է:
![]() հաստատունների
ընտրությունը
պետք է բավարարի
(9.21) պայմաններին.
հաստատունների
ընտրությունը
պետք է բավարարի
(9.21) պայմաններին.
![]() պայմանից
ունենք
պայմանից
ունենք ![]() որտեղից
հետևում է,
որտեղից
հետևում է, ![]() պայմանից
ունենք
պայմանից
ունենք ![]() Այս առնչությունը
ճիշտ է, եթե
Այս առնչությունը
ճիշտ է, եթե
![]()
(![]() =0 դեպքն անիմաստ
է, քանի որ ստացվում
է
=0 դեպքն անիմաստ
է, քանի որ ստացվում
է ![]() այսինքն`
մասնիկը ոչ մի
տեղ չի գտնվում):
այսինքն`
մասնիկը ոչ մի
տեղ չի գտնվում):
Հաշվի առնելով (9.25)-ը և (9.26)-ը` պոտենցիալ փոսում գտնվող մասնիկի համար ալիքային ֆունկցիան ունի հետևյալ տեսքը.
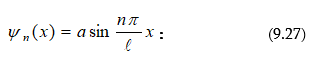
![]() որոշման համար
օգտվենք նորմավորման
պայմանից`
որոշման համար
օգտվենք նորմավորման
պայմանից`
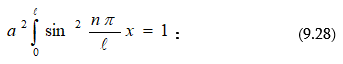
Ինտեգրման
միջակայքի եզրերում
ենթաինտեգրալ
ֆունկցիան դառնում
է զրո: Ուստի, ինտեգրալի
արժեքը կարելի
է ստանալ՝ բազմապատկելով
![]() միջին
արժեքը, (որը ինչպես
հայտնի է, հավասար
է 1/2-ի ) միջակայքի
միջին
արժեքը, (որը ինչպես
հայտնի է, հավասար
է 1/2-ի ) միջակայքի
![]() երկարությամբ:
Արդյունքում կստանանք
երկարությամբ:
Արդյունքում կստանանք
![]()
որտեղից
![]() Վերջինը տեղադրելով
(9.27)-ի մեջ` կստանանք
խնդրի սեփական
ֆունկցիաների
տեսքը:
Վերջինը տեղադրելով
(9.27)-ի մեջ` կստանանք
խնդրի սեփական
ֆունկցիաների
տեսքը:
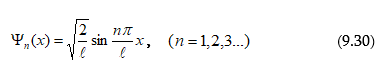

Պոտենցիալ
փոսում ազատ մասնիկի
![]() ֆունկցիայի`
n-ից կախման գրաֆիկները
պատկերված են նկ.
9.6 ա և նկ. 9.6 բ-ում:
ֆունկցիայի`
n-ից կախման գրաֆիկները
պատկերված են նկ.
9.6 ա և նկ. 9.6 բ-ում:
(9.30)-ը
քառակուսի բարձրացնելով`
կորոշենք պոտենցիալ
հորի տարբեր կետերում
մասնիկի գտնվելու
![]() հավանականության
խտությունը:
հավանականության
խտությունը: ![]() -ու x-ից
կախվածությունը
n-ի տարբեր արժեքների
դեպքում պատկերված
է նկ. 9.6 բ-ում: Նկարից
երևում է` n=2 դեպքում
փոսի մեջտեղում
մասնիկի գտնվելու
հավանականությունը
հավասար է զրոյի:
Համաձայն դասական
ֆիզիկայի օրենքների,
պոտենցիալ փոսում
մասնիկի բոլոր
վիճակները (դիրքերը)
հավասարահավանական
են: (9.23)-ի և (9.26)-ի համատեղ
լուծումը թույլ
է տալիս որոշել
մասնիկի էներգիայի
սեփական արժեքները.
-ու x-ից
կախվածությունը
n-ի տարբեր արժեքների
դեպքում պատկերված
է նկ. 9.6 բ-ում: Նկարից
երևում է` n=2 դեպքում
փոսի մեջտեղում
մասնիկի գտնվելու
հավանականությունը
հավասար է զրոյի:
Համաձայն դասական
ֆիզիկայի օրենքների,
պոտենցիալ փոսում
մասնիկի բոլոր
վիճակները (դիրքերը)
հավասարահավանական
են: (9.23)-ի և (9.26)-ի համատեղ
լուծումը թույլ
է տալիս որոշել
մասնիկի էներգիայի
սեփական արժեքները.
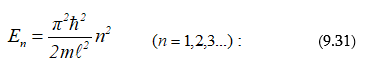
Շրյոդինգերի հավասարման լուծումը հնարավորություն տվեց որոշել էներգիայի սեփական արժեքները, այդ արժեքները քվանտացված են և առաջացնում են ընդհատ սպեկտր: n ամբողջ թիվը, որը բնորոշում է մասնիկի էներգիան, կոչվում է գլխավոր քվանտային թիվ:
Որոշենք երկու հարևան մակարդակների էներգիաների տարբերությունը.
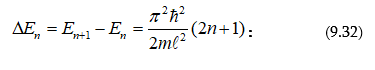
(9.32) հավասարումից երևում է, որ ինչքան փոքր են մասնիկի զանգվածը և պոտենցիալ փոսի չափերը, այնքան մեծ է ընդհատությունը, այսինքն` երկու իրար հարևան մակարդակների էներգիաների տարբերությունը:
Ենթադրենք,
թե մասնիկի զանգվածը
10-26 կգ է (մոլեկուլի
զանգվածի կարգի),
իսկ պոտենցիալ
հորի չափերը ![]() , n=1, այդ
դեպքում
, n=1, այդ
դեպքում
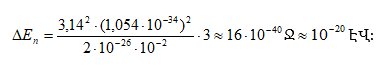
![]() այսպիսի արժեքների
դեպքում էներգետիկ
մակարդակներն
ընդունվում են`
որպես էներգիայի
անընդհատ սպեկտր:
Եթե
այսպիսի արժեքների
դեպքում էներգետիկ
մակարդակներն
ընդունվում են`
որպես էներգիայի
անընդհատ սպեկտր:
Եթե ![]() (էլեկտրոնի
զանգվածի կարգի)
պոտենցիալ փոսի
միևնույն չափերի
դեպքում`
(էլեկտրոնի
զանգվածի կարգի)
պոտենցիալ փոսի
միևնույն չափերի
դեպքում` ![]() , n=1, ապա
, n=1, ապա
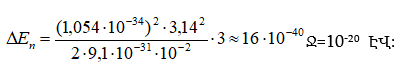
Վերևը քննարկված օրինակներում էներգիայի քվանտացումը, թեկուզև սկզբունքորեն, տեղի կունենա, բայց մասնիկների շարժման բնույթի վրա ազդեցություն չի թողնի:
Էներգետիկ մակարդակների ընդհատությունը դառնում է նկատելի, երբ պոտենցիալ փոսի չափերը ատոմային չափերի կարգի են:
![]()

Պոտենցիալ
փոսում մասնիկը
չի կարող ունենալ
![]() -ից փոքր էներգիա:
Այդ էներգիան զրոյից
տարբեր է: Այդպիսի
էներգիայի առկայությունը
բխում է անորոշությունների
հետևյալ առնչությունից՝
-ից փոքր էներգիա:
Այդ էներգիան զրոյից
տարբեր է: Այդպիսի
էներգիայի առկայությունը
բխում է անորոշությունների
հետևյալ առնչությունից՝
![]()
![]() լայնությամբ
փոսում մասնիկի
կոորդինատի անորոշությունը
հավասար է
լայնությամբ
փոսում մասնիկի
կոորդինատի անորոշությունը
հավասար է ![]() այդ դեպքում
իմպուլսի անորոշությունը՝
այդ դեպքում
իմպուլսի անորոշությունը՝
![]() Իմպուլսի այդպիսի
անորոշությանը
համապատասխանում
է
Իմպուլսի այդպիսի
անորոշությանը
համապատասխանում
է ![]() կինետիկ
էներգիային: Մնացած
բոլոր մակարդակներն
(n>1) ունեն այդ նվազագույն
արժեքից մեծ էներգիա:
Ինչպես հետևվում
է (9.31) և (9.32) առնչություններից
(n>>1) մեծ քվանտային
թվերի դեպքում
կինետիկ
էներգիային: Մնացած
բոլոր մակարդակներն
(n>1) ունեն այդ նվազագույն
արժեքից մեծ էներգիա:
Ինչպես հետևվում
է (9.31) և (9.32) առնչություններից
(n>>1) մեծ քվանտային
թվերի դեպքում
![]()
Այսպիսով, հարևան մակարդակներն այնքան իրար մոտիկ դասավորված կլինեն, ինչքան մեծ է n-ը: Եթե n -ը շատ մեծ է, ապա էներգետիկ մակարդակներն ընկալվում են որպես էներգիայի անընդհատ սպեկտր, այսինքն` ընդհատությունը հարթվում է: Այդպիսի արդյունքը Բորի համապատասխանության սկզբունքի մասնավոր դեպքն է, որի համաձայն քվանտային թվերի մեծ արժեքների դեպքում քվանտային մեխանիկայի օրենքները վերածվում են դասական մեխանիկայի օրենքների: Նմանապես v<<c դեպքում հարաբերականության հատուկ տեսության բանաձևերը վերածվում են դասական մեխանիկայի Գալիլեյ-Նյուտոնի բանաձևերի: Այսպիսով, համաձայն համապատասխանության սկզբունքի, ցանկացած ավելի ընդհանուր նոր տեսություն հանդիսանում է դասականի զարգացումը, սակայն լրիվ չի ժխտում, միայն ցույց է տալիս նրա կիրառելիության սահմանները: Որոշակի սահմանային դեպքերում նոր տեսությունն անցնում է հնին:
Քննարկենք ներդաշնակ տատանակը (օցիլյատոր), այսինքն` մի մասնիկ, որը գտնվում է f=-kx քվազիառաձգական ուժի ազդեցության տակ: Այդպիսի մասնիկի պոտենցիալ էներգիան՝

Մտցնելով
դասական ներդաշնակ
տատանակի ![]() սեփական
հաճախությունը,
կարելի է գրել
սեփական
հաճախությունը,
կարելի է գրել
![]()
Հետևաբար, Շրյոդինգերի հավասարումը ներդաշնակ տատանակի համար ունի հետևյալ տեսքը`
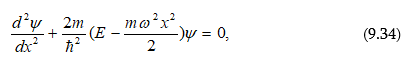
որտեղ E-ն տատանակի լրիվ էներգիան է: Այս հավասարումն ունի վերջավոր, միարժեք և անընդհատ լուծումներ E պարամետրի
![]()
արժեքների դեպքում: n թիվը, որը կոչվում է տատանողական քվանտային թիվ, կարող է ընդունել 0,1,2, և այլ արժեքներ:
Ներդաշնակ
տատանակի էներգետիկ
մակարդակների
սխեման տրված է
նկ. 9.7-ում: ![]()
![]()
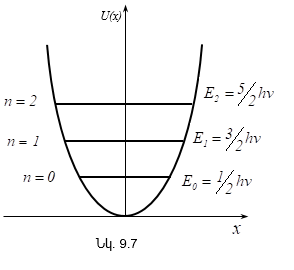
Մակարդակները ներգծված են U պոտենցիալ էներգիայի կորի մեջ: (9.35) բանաձևից հետևում է, որ տատանակն ունի միմյանցից միևնույն էներգետիկ հեռավորությունների վրա դասավորված E1,E2,…, էներգիայի արժեքների ընդհատ սպեկտր:
![]() ամենափոքր
էներգիան, որը կարող է
ունենալ ներդաշնակ
տատանակը, կոչվում
է զրոյական էներգիա:
E0 մեծությունը
երբեք չի դառնում
զրո, այդ թվում
նաև` T=0 Կ-ի դեպքում:
ամենափոքր
էներգիան, որը կարող է
ունենալ ներդաշնակ
տատանակը, կոչվում
է զրոյական էներգիա:
E0 մեծությունը
երբեք չի դառնում
զրո, այդ թվում
նաև` T=0 Կ-ի դեպքում:
Զրոյական էներգիայի գոյությունը հաստատվում է ցածր ջերմաստիճաններում բյուրեղների կողմից լույսի ցրման ուսումնասիրության վերաբերյալ կատարված փորձերով: Պարզվում է, որ ջերմաստիճանը նվազելիս ցրված լույսի ինտենսիվությունը ձգտում է ոչ թե զրոյի, այլ վերջավոր արժեքի` վկայելով, որ բյուրեղային ցանցում ատոմների տատանումները չեն դադարում նաև բացարձակ զրոյում:
9.8. Ջրածնի ատոմն` ըստ Շրյոդինգերի տեսության
Քվանտային թվեր
Ըստ Շրյոդինգերի` ջրածնի ատոմի մեջ էլեկտրոնի շարժման վիճակը որոշվում է (9.19) հավասարումով: Ջրածնի ատոմում կամ ջրածնանման իոնում էլեկտրոնի պոտենցիալ էներգիան՝

Որտեղ
![]() միջուկի
լիցքն է, r-ը՝ միջուկի
և էլեկտրոնի միջև
եղած հեռավորությունը,
միջուկի
լիցքն է, r-ը՝ միջուկի
և էլեկտրոնի միջև
եղած հեռավորությունը,
![]() էլեկտրական
հաստատունը: Այս
դեպքում Շրյոդինգերի
հավասարումն ունի
հետևյալ տեսքը.
էլեկտրական
հաստատունը: Այս
դեպքում Շրյոդինգերի
հավասարումն ունի
հետևյալ տեսքը.
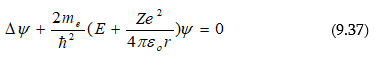
Քանի
որ դաշտը կենտրոնական-համաչափ
է, նպատակահարմար
է օգտվել սֆերիկ
կոորդինատների
համակարգից՝ ![]()
(9.37)-ում տեղադրելով Լապլասի օպերատորի արտահայտությունը սֆերիկ կոորդինատներով` կստանանք
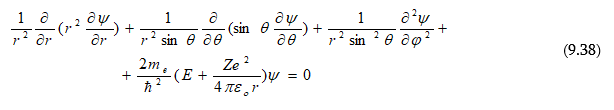
(9.38) հավասարումը լուծվում է փոփոխականների անջատման եղանակով: Կարելի է ցույց տալ, որ (9.38) հավասարումը պահանջվող միարժեք, վերջավոր և անընդհատ լուծումներ ունի հետևյալ դեպքերում՝ ա) E-ի ցանկացած դրական արժեքների դեպքում, բ) էներգիայի բացասական արժեքների դեպքում, որոնք, հավասար են՝
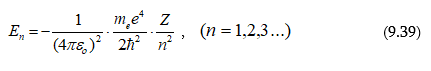
E>0 դեպքը համապատասխանում է ազատ էլեկտրոնի վիճակին: E<0 դեպքը համապատասխանում է ատոմի սահմաններում գտնվող էլեկտրոնին: (9.39)-ի և (8.20)-ի համեմատությունը ցույց է տալիս, որ քվանտային մեխանիկան հանգեցնում է ջրածնային ատոմի էներգիայի նույնպիսի արժեքներին, ինչպիսիք ստացվում էին Բորի տեսությունում: Սակայն քվանտային մեխանիկայում այդ արժեքները ստացվում են տրամաբանական ճանապարհով՝ այն հիմնական ենթադրությունից, որ միկրոմասնիկների շարժումը նկարագրվում է Շրյոդինգերի հավասարումով: Այդպիսի արդյունք ստանալու համար Բորը ստիպված մտցրեց հատուկ լրացուցիչ ենթադրություններ:
(9.38)
հավասարման սեփական
ֆունկցիաները
պարունակում են
ամբողջաթիվ պարամետրեր:
Դրանցից մեկը համընկնում
է էներգիայի մակարդակի
n համարի հետ, մյուս
երկուսը ընդունված
է նշանակել ![]() Այս թվերը
կոչվում են քվանտային.
n-գլխավոր քվանտային
թիվ,
Այս թվերը
կոչվում են քվանտային.
n-գլխավոր քվանտային
թիվ,![]() -ուղեծրային
քվանտային թիվ,
m-մագնիսական
քվանտային թիվ:
Այդ թվերի որոշման
համար կանխադրույթներ
չի պահանջվում:
-ուղեծրային
քվանտային թիվ,
m-մագնիսական
քվանտային թիվ:
Այդ թվերի որոշման
համար կանխադրույթներ
չի պահանջվում:
![]() քվանտային
թվերը որոշվում
են
քվանտային
թվերը որոշվում
են ![]() ֆունկցիայի հատկություններից,
այն է`
ֆունկցիայի հատկություններից,
այն է` ![]() ֆունկցիան
անընդհատ է, միարժեք
և վերջավոր ամբողջ
ծավալում: Ջրածնի
ատոմում էլեկտոնի
վիճակը կախված
է
ֆունկցիան
անընդհատ է, միարժեք
և վերջավոր ամբողջ
ծավալում: Ջրածնի
ատոմում էլեկտոնի
վիճակը կախված
է ![]() երեք քվանտային
թվերից, ընդ որում`
գլխավոր քվանտային
թվի՝ n -ի արժեքը
որոշում է վիճակի
էներգիան: Բնական
է ենթադրել, որ
երկու մյուս քվանտային
թվերը նույնպես
որոշում են որևէ
ֆիզիկական մեծություն:
Իրոք, քվանտային
մեխանիկայում
ապացուցվում է,
որ ուղեծրային
քվանտային թիվը՝
երեք քվանտային
թվերից, ընդ որում`
գլխավոր քվանտային
թվի՝ n -ի արժեքը
որոշում է վիճակի
էներգիան: Բնական
է ենթադրել, որ
երկու մյուս քվանտային
թվերը նույնպես
որոշում են որևէ
ֆիզիկական մեծություն:
Իրոք, քվանտային
մեխանիկայում
ապացուցվում է,
որ ուղեծրային
քվանտային թիվը՝
![]() որոշում է ատոմում
էլեկտրոնի իմպուլսի
մոմենտի մեծությունը,
որը կարող է ունենալ
միայն դիսկրետ
արժեքներ և որոշվում
է հետևյալ բանաձևով`
որոշում է ատոմում
էլեկտրոնի իմպուլսի
մոմենտի մեծությունը,
որը կարող է ունենալ
միայն դիսկրետ
արժեքներ և որոշվում
է հետևյալ բանաձևով`
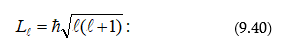
Տրված n-ի արժեքների դեպքում ուղեծրային քվանտային թիվը կարող է ընդունել՝ 0,1,2,…,n-1,… արժեքներ: Մագնիսական քվանտային թիվը՝ m-ը որոշում է էլեկտրոնի ուղեծրային իմպուլսի մոմենտի պրոյեկցիան արտաքին մագնիսական դաշտի կամավոր ընտրված որևէ z ուղղության վրա: Տրված ուղղության վրա իմպուլսի մոմենտի պրոյեկցիան հավասար է.
![]()
Տրված
![]() արժեքների դեպքում
m քվանտային թիվն
ընդունում է
արժեքների դեպքում
m քվանտային թիվն
ընդունում է ![]() այսինքն՝
ընդամենը
այսինքն՝
ընդամենը ![]() տարբեր
արժեքներ:
տարբեր
արժեքներ:
(9.40)
և (9.41) առնչությունները
ցույց են տալիս,
որ ատոմում էլեկտրոնի
իմպուլսի մոմենտը
և այդ մոմենտի
պրոյեկցիան էներգիայի
նման քվանտացված
մեծություններ
են:![]() հաստատունը
կարելի է դիտել
որպես իմպուլսի
մոմենտի բնական
միավոր:
հաստատունը
կարելի է դիտել
որպես իմպուլսի
մոմենտի բնական
միավոր:
Յուրաքանչյուր
En-ին (բացի E1-ից)
համապատասխանում
են մի քանի ալիքային
ֆունկցիաներ՝
![]() որոնք
իրարից տարբերվում
են
որոնք
իրարից տարբերվում
են ![]() քվանտային
թվերի արժեքներով:
Դա նշանակում է,
որ ջրածնի ատոմը
կարող է էներգիայի
միևնույն արժեքն
ունենալ՝ գտնվելով
մի քանի տարբեր
վիճակներում:
Միատեսակ էներգիա
ունեցող վիճակները
կոչվում են այլասերված,
իսկ էներգիայի
որևէ արժեք ունեցող
տարբեր վիճակների
թիվը կոչվում
է համապատասխան
էներգետիկ մակարդակի
այլասերման բազմապատիկություն:
Ջրածնի ատոմի մակարդակների
այլասերման բազմապատիկությունը
հեշտ է հաշվել՝
ելնելով
քվանտային
թվերի արժեքներով:
Դա նշանակում է,
որ ջրածնի ատոմը
կարող է էներգիայի
միևնույն արժեքն
ունենալ՝ գտնվելով
մի քանի տարբեր
վիճակներում:
Միատեսակ էներգիա
ունեցող վիճակները
կոչվում են այլասերված,
իսկ էներգիայի
որևէ արժեք ունեցող
տարբեր վիճակների
թիվը կոչվում
է համապատասխան
էներգետիկ մակարդակի
այլասերման բազմապատիկություն:
Ջրածնի ատոմի մակարդակների
այլասերման բազմապատիկությունը
հեշտ է հաշվել՝
ելնելով ![]() հնարավոր
արժեքներից:
հնարավոր
արժեքներից:![]() քվանտային թվի n-ի արժեքներից
յուրաքանչյուրին
համապատասխանում
է m քվանտային
թվի
քվանտային թվի n-ի արժեքներից
յուրաքանչյուրին
համապատասխանում
է m քվանտային
թվի ![]() արժեք: Հետևաբար,
տրված n- ին համապատասխանող
տարբեր վիճակների
թիվը՝
արժեք: Հետևաբար,
տրված n- ին համապատասխանող
տարբեր վիճակների
թիվը՝
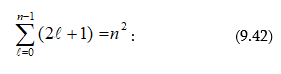
Այսպիսով, ջրածնի ատոմի յուրաքանչյուր էներգետիկ մակարդակ ունի այլասերման n բազմապատիկություն:
Ատոմային
ֆիզիկայում կիրառվում
են իմպուլսի մոմենտի
տարբեր արժեքներ
ունեցող էլեկտրոնի
վիճակների՝ սպեկտրասկոպիայից
փոխառնված պայմանական
նշանակումներ.
![]() վիճակում
գտնվող էլեկտրոնն
անվանում են s
էլեկտրոն (համապատասխան
վիճակը՝ s վիճակ),
վիճակում
գտնվող էլեկտրոնն
անվանում են s
էլեկտրոն (համապատասխան
վիճակը՝ s վիճակ),
![]() դեպքում՝p էլեկտրոն,
դեպքում՝p էլեկտրոն,
![]() դեպքում
d էլեկտրոն,
դեպքում
d էլեկտրոն, ![]() դեպքում՝
f էլեկտրոն, ապա
հետևում են g, h
և այլն, ըստ այբուբենի:
Գլխավոր քվանտային
թվի արժեքը նշվում
է
դեպքում՝
f էլեկտրոն, ապա
հետևում են g, h
և այլն, ըստ այբուբենի:
Գլխավոր քվանտային
թվի արժեքը նշվում
է ![]() քվանտային
թվի պայմանական
նշանակումից առաջ:
Այսպիսով,
քվանտային
թվի պայմանական
նշանակումից առաջ:
Այսպիսով, ![]() վիճակում
գտնվող էլեկտրոնը
նշանակվում է 3p
պայմանանշանով
և այլն:
վիճակում
գտնվող էլեկտրոնը
նշանակվում է 3p
պայմանանշանով
և այլն:
Քանի
որ ![]() միշտ
փոքր է n-ից, հնարավոր
են էլեկտրոնի
հետևյալ վիճակները
միշտ
փոքր է n-ից, հնարավոր
են էլեկտրոնի
հետևյալ վիճակները
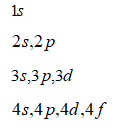
և այլն:
Հայտնի
է, որ լույսի առաքումն
ու կլանումը կատարվում
են էլեկտրոնի՝
մեկ մակարդակից
մյուսին անցնելու
դեպքում: Քվանտային
մեխանիկայում
ապացուցվում է,
որ հնարավոր են
միայն այնպիսի
անցումներ, որոնց
ժամանակ ![]() քվանտային
թիվը փոփոխվում
է մեկ միավորով.
քվանտային
թիվը փոփոխվում
է մեկ միավորով.
![]()
(9.43)
առնչությամբ արտահայտված
պայմանը անվանում
են ընտրության
կանոն: Ընտրության
կանոնի գոյությունը
պայմանավորված
է նրանով, որ ֆոտոնն
օժտված է իմպուլսի
սեփական մոմենտով
(սպինով), որը մոտավորապես
հավասար է ![]() Ճառագայթվելիս
ֆոտոնը ատոմից
տանում է, իսկ կլանվելիս՝
բերում է այդ մոմենտը,
այնպես, որ ընտրության
կանոնը պարզապես
իմպուլսի մոմենտի
պահպանման օրենքի
հետևանքն է:
Ճառագայթվելիս
ֆոտոնը ատոմից
տանում է, իսկ կլանվելիս՝
բերում է այդ մոմենտը,
այնպես, որ ընտրության
կանոնը պարզապես
իմպուլսի մոմենտի
պահպանման օրենքի
հետևանքն է:
9.9. Էլեկտրոնի սպինը: Սպինային քվանտային թիվ
Պաուլիի սկզբունքը
Ալկալիական
մետաղների սպեկտրների
ուսումնասիրությունը
մեծ լուծող ուժ
ունեցող սարքերի
օգնությամբ ցույց
տվեց, որ այդ սպեկտրներից
յուրաքանչյուր
գիծ կրկնակի է
(դուբլետ): Այսպես,
նատրիումին բնորոշ
![]() դեղին գիծը բաղկացած
է
դեղին գիծը բաղկացած
է ![]() և
և ![]() ալիքի
երկարության երկու
գծերից: Գծերի
տրոհումը պայմանավորված
է մագնիսական դաշտի
ազդեցության ատոմի
էներգետիկ մակարդակների
տրոհումով: Սպեկտրի
այն կառուցվածքը,
որն արտացոլում
է գծերի տրոհումը
բաղադրիչների,
կոչվում է նուրբ
կառուցվածք: Մի
քանի բաղադրիչներից
բաղկացած բարդ
գծերը ստացել
են մուլտիպլետներ
անվանումը:
ալիքի
երկարության երկու
գծերից: Գծերի
տրոհումը պայմանավորված
է մագնիսական դաշտի
ազդեցության ատոմի
էներգետիկ մակարդակների
տրոհումով: Սպեկտրի
այն կառուցվածքը,
որն արտացոլում
է գծերի տրոհումը
բաղադրիչների,
կոչվում է նուրբ
կառուցվածք: Մի
քանի բաղադրիչներից
բաղկացած բարդ
գծերը ստացել
են մուլտիպլետներ
անվանումը:
Բացի ալկալիական մետաղներից, նուրբ կառուցվածք են ցույց տալիս նաև այլ տարրեր, ընդ որում` բաղադրիչների թիվը մուլտիպլետում կարող է հավասար լինել երկուսի (դուբլետներ), երեքի (տրիպլետներ), չորսի (կվարտետներ), հինգի (կվինտետներ) և այլն:
Սպեկտրների
մուլտիպլետային
կառուցվածքը բացատրելու
համար հոլանդացի
ֆիզիկոսներ Գաուդսմիտը
և Ուլենբեկը 1925թ.
առաջարկեցին այն
վարկածը, որ էլեկտրոնն
օժտված է իմպուլսի
սեփական մոմենտով՝
![]() ,
որը կապված չէ
տարածության մեջ
էլեկտրոնի շարժման
հետ: Այդ սեփական
մոմենտը կոչվեց
սպին: Սպինը
պետք է համարել
էլեկտրոնին հատուկ
ներքին հատկություն,
ինչպես հատուկ
են լիցքը և զանգվածը:
Էլեկտրոնի սպինի
մասին ենթադրությունը
հաստատվել է մեծ
թվով փորձարարական
փաստերով: Պարզվել
է նաև, որ սպինի
առկայությունը
և նրա բոլոր հատկություններն
ինքնըստինքյան
բխում են քվանտային
մեխանիկայի՝ Դիրակի
ստացած հավասարումից,
որը բավարարում
է հարաբերականության
տեսության պահանջներին:
Այսպիսով պարզվեց,
որ էլեկտրոնի սպինը
միաժամանակ և
քվանտային, և ռելյատիվիստական
հատկություն է:
Ներկայումս ապացուցված
է նաև, որ սպին ունեն
և մյուս տարրական
մասնիկները՝ պրոտոնները,
նեյտրոնները, ֆոտոնները:
,
որը կապված չէ
տարածության մեջ
էլեկտրոնի շարժման
հետ: Այդ սեփական
մոմենտը կոչվեց
սպին: Սպինը
պետք է համարել
էլեկտրոնին հատուկ
ներքին հատկություն,
ինչպես հատուկ
են լիցքը և զանգվածը:
Էլեկտրոնի սպինի
մասին ենթադրությունը
հաստատվել է մեծ
թվով փորձարարական
փաստերով: Պարզվել
է նաև, որ սպինի
առկայությունը
և նրա բոլոր հատկություններն
ինքնըստինքյան
բխում են քվանտային
մեխանիկայի՝ Դիրակի
ստացած հավասարումից,
որը բավարարում
է հարաբերականության
տեսության պահանջներին:
Այսպիսով պարզվեց,
որ էլեկտրոնի սպինը
միաժամանակ և
քվանտային, և ռելյատիվիստական
հատկություն է:
Ներկայումս ապացուցված
է նաև, որ սպին ունեն
և մյուս տարրական
մասնիկները՝ պրոտոնները,
նեյտրոնները, ֆոտոնները:
Էլեկտրոնի սեփական իմպուլսի մոմենտի մեծությունը որոշվում է քվանտային մեխանիկայի ընդհանուր օրենքներով (տես (9.40) բանաձևը), այսպես կոչված, սպինային քվանտային թվով՝ s, որը հավասար է 1/2-ի.
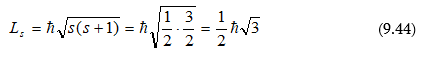
Մեխանիկական
մոմենտի բաղադրիչը
տրված ուղղությամբ
կարող է ընդունել
![]() տարբերվող
քվանտացված արժեքներ.
տարբերվող
քվանտացված արժեքներ.
![]()
որտեղ
![]()
Ատոմում
յուրաքանչյուր
էլեկտրոն առաջին
մոտավորությամբ
շարժվում է ոչ
կուլոնյան կենտրոնահամաչափ
դաշտում: Այդ դեպքում
էլեկտրոնի վիճակը
որոշվում է երեք
քվանտային թվերով՝
![]() ,
որոնց ֆիզիկական
իմաստը պարզաբանվեց
վերևում: Էլեկտրոնի
սպինի գոյության
կապակցությամբ
նշված քվանտային
թվերին պետք է
ավելացնել
,
որոնց ֆիզիկական
իմաստը պարզաբանվեց
վերևում: Էլեկտրոնի
սպինի գոյության
կապակցությամբ
նշված քվանտային
թվերին պետք է
ավելացնել ![]() քվանտային
թիվը, որը կարող
է ընդունել
քվանտային
թիվը, որը կարող
է ընդունել ![]() արժեքներ
և որոշում է սպինի
բաղադրիչը տրված
ուղղությամբ:
արժեքներ
և որոշում է սպինի
բաղադրիչը տրված
ուղղությամբ:
Մագնիսական
քվանտային թվի
համար m-ի փոխարեն
մենք օգտվելու
ենք ![]() նշանակումից՝
ընդգծելու համար
այն հանգամանքը,
որ այդ թիվը որոշում
է ուղեծրային
մոմենտի բաղադրիչը,
որի մեծությունը
տրվում է
նշանակումից՝
ընդգծելու համար
այն հանգամանքը,
որ այդ թիվը որոշում
է ուղեծրային
մոմենտի բաղադրիչը,
որի մեծությունը
տրվում է ![]() քվանտային
թվով:
քվանտային
թվով:
Այսպիսով,
ատոմում յուրաքանչյուր
էլեկտրոնի վիճակը
բնորոշվում է
չորս քվանտային
թվերով. գլխավոր
![]() ուղեծրային
ուղեծրային
![]() մագնիսական
մագնիսական
![]() սպինային
սպինային
![]() Վիճակի էներգիան
հիմնականում կախում
ունի
Վիճակի էներգիան
հիմնականում կախում
ունի ![]() թվերից: Որոշ
բացառություններով`
վիճակի էներգիան
ավելի արագ աճում
է n թվի, քան
թվերից: Որոշ
բացառություններով`
վիճակի էներգիան
ավելի արագ աճում
է n թվի, քան ![]() մեծացման
հետ: Այդ պատճառով
որպես կանոն, ավելի
մեծ n-ով վիճակը,
անկախ
մեծացման
հետ: Այդ պատճառով
որպես կանոն, ավելի
մեծ n-ով վիճակը,
անկախ ![]() արժեքից,
օժտված է ավելի
մեծ էներգիայով:
արժեքից,
օժտված է ավելի
մեծ էներգիայով:
Ատոմի
նորմալ (չգրգռված)
վիճակում էլեկտրոնները
պետք է դասավորվեն
իրենց մատչելի
ամենացածր էներգետիկ
մակարդակներում:
Այդ պատճառով
թվում է, թե ցանկացած
ատոմում նորմալ
վիճակում բոլոր
էլեկտրոնները
պետք է գտնվեն
1s վիճակում ![]() փորձը
ցույց է տվել, որ
դա այդպես չէ:
փորձը
ցույց է տվել, որ
դա այդպես չէ:
Քվանտային
մեխանիկայի օրենքներից
մեկի համաձայն,
որը
կոչվում է Պաուլիի
սկզբունք, միևնույն
ատոմում կամ որևէ
քվանտային համակարգում
չեն կարող լինել
![]() չորս քվանտային
թվերի միատեսակ
համախմբությամբ
օժտված երկու
էլեկտրոններ:
Այլ խոսքով, նույն
վիճակում միաժամանակ
չեն կարող գտնվել
երկու էլեկտրոններ:
չորս քվանտային
թվերի միատեսակ
համախմբությամբ
օժտված երկու
էլեկտրոններ:
Այլ խոսքով, նույն
վիճակում միաժամանակ
չեն կարող գտնվել
երկու էլեկտրոններ:
Ռենտգենյան ճառագայթները հայտնագործվել են 1895թ. գերմանական Վյուրցբուրգ համալսարանական քաղաքում Վ. Ռենտգենի կողմից:
Ռենտգենյան
ճառագայթներն
առաջանում են նյութի
կողմից արագ էլեկտրոնների
արգելակման դեպքում:
Ռենտգենյան ճառագայթների
ստացման համար
օգտագործում են
հատուկ էլեկտրավակուումային
սարքեր` ռենտգենյան
խողովակներ, որոնք
կազմված են վակուումային
ապակյա կամ մետաղական
իրանից, որում
մեկը մյուսից որոշակի
հեռավորության
վրա գտնվում են
կաթոդը և անոդը
(հակակաթոդը), որոնք
միացվում են բարձր
լարման ցանցին:
Ռենտգենյան խողովակներում
կաթոդը ծառայում
է որպես էլեկտրոնների
աղբյուր, իսկ անոդը
` ռենտգենյան ճառագայթների
աղբյուր: Կաթոդի
և անոդի միջև ստեղծվում
է ուժեղ էլեկտրական
դաշտ, որն էլեկտրոններին
հաղորդում է մինչև
104…105Էվ էներգիա:
Էլեկտրոններին
այդքան բարձր էներգիա
հաղորդելու համար
ռենտգենյան խողովակներում
ստեղծվում է վակուումում
![]() : Ժամանակակից
արագացուցչային
սարքավորումներում
(բետատրոններում
և սինքրոտրոններում)
ռենտգենյան ճառագայթներ
առաջանում են
: Ժամանակակից
արագացուցչային
սարքավորումներում
(բետատրոններում
և սինքրոտրոններում)
ռենտգենյան ճառագայթներ
առաջանում են
![]() ՄէՎ և ավելի
էներգիայով էլեկտրոնների
արգելակման դեպքում:
ՄէՎ և ավելի
էներգիայով էլեկտրոնների
արգելակման դեպքում:
Ռենտգենյան
ճառագայթները,
ինչպես և լույսը,
էլեկտրամագնիսական
ալիքներ են, որոնց
ալիքի երկարությունը
10-10…10-13մ կարգի է:
Հիշեցնենք, որ
աչքի կողմից ընկալվող
ամենակարճ ալիքի
երկարությունը
մանուշակագույն
ճառագայթների
համար ![]() մ է: Տարբերում
են երկու տեսակի
ռենտգենյան ճառագայթներ`
անընդհատ սպեկտրով
և գծային սպեկտրով:
մ է: Տարբերում
են երկու տեսակի
ռենտգենյան ճառագայթներ`
անընդհատ սպեկտրով
և գծային սպեկտրով:
9.11. Անընդհատ սպեկտրով ռենտգենյան ճառագայթների առաջացումը
Դասական
տեսության համաձայն`
անընդհատ սպեկտրով
ռենտգենյան ճառագայթներ
առաջանում են,
երբ արագ էլեկտրոններն
արգելակվում են
անոդի նյութի կողմից:
Արգելակվող էլեկտրոնը
շարժվում է բացասական
արագացմամբ և ինչ-որ
![]() պահից
պահից![]() պահն
իր արագությունը
փոխում է
պահն
իր արագությունը
փոխում է ![]() մինչև
մինչև
![]() ժամանակամիջոցում
առաքում է ալիքների
մի «ծրար»: Այդ «ծրարի»
մեջ ալիքի երկարությունը
փոփոխվում է անընդհատ:
Ալիքների այդ
«ծրարը» սպեկտրային
սարքի միջոցով
վերածելով սպեկտրի
(«ծրարի» էներգիան
բաշխելով ըստ
ալիքի երկարության),
կստանանք նկ.9.8-ի
կորը: Այդ կորից
երևում է, որ ռենտգենյան
ճառագայթների
անընդհատ սպեկտրը
կարճ ալիքների
կողմից կտրուկ
սահմանափակված
է:
ժամանակամիջոցում
առաքում է ալիքների
մի «ծրար»: Այդ «ծրարի»
մեջ ալիքի երկարությունը
փոփոխվում է անընդհատ:
Ալիքների այդ
«ծրարը» սպեկտրային
սարքի միջոցով
վերածելով սպեկտրի
(«ծրարի» էներգիան
բաշխելով ըստ
ալիքի երկարության),
կստանանք նկ.9.8-ի
կորը: Այդ կորից
երևում է, որ ռենտգենյան
ճառագայթների
անընդհատ սպեկտրը
կարճ ալիքների
կողմից կտրուկ
սահմանափակված
է:

Ռենտգենյան
ճառագայթների
անընդհատ սպեկտրի
մեջ չկան ճառագայթներ,
որոնց ալիքի երկարությունը
փոքր լինի սահմանային
![]() ալիքի
երկարությունից:
Այդ կորից երևում
է նաև, որ ինչ-որ
մի ալիքի երկարությամբ,
որը մենք կնշանակենք
ալիքի
երկարությունից:
Այդ կորից երևում
է նաև, որ ինչ-որ
մի ալիքի երկարությամբ,
որը մենք կնշանակենք
![]() առաքվում են
մեծագույն ինտենսիվությամբ
ռենտգենյան ճառագայթներ
(նկ.9.8): Փորձը ցույց
է տալիս, որ արգելակվող
էլեկտրոնների
սկզբնական արագությունը
մեծացնելիս
առաքվում են
մեծագույն ինտենսիվությամբ
ռենտգենյան ճառագայթներ
(նկ.9.8): Փորձը ցույց
է տալիս, որ արգելակվող
էլեկտրոնների
սկզբնական արագությունը
մեծացնելիս ![]() շեղվում
են կարճ ալիքների
կողմը: Նկ.9.9-ում բերված
է անընդհատ սպեկտրով
ռենտգենյան ճառագայթների
էներգիայի բաշխումն
ըստ ալիքի երկարության`
ռենտգենյան խողովակի
վրա կիրառված
տարբեր լարումների
դեպքում: Այդ կորերը
ցույց են տալիս,
որ ռենտգենյան
խողովակի վրա
կիրառված լարման
մեծացման հետ
անընդհատ սպեկտրով
ռենտգենյան ճառագայթների
ինտենսիվությունը
մեծանում է, և կարճ
ալիքային սահմանն
ու ինտենսիվության
առավելագույնը
շեղվում են կարճ
ալիքների կողմը:
շեղվում
են կարճ ալիքների
կողմը: Նկ.9.9-ում բերված
է անընդհատ սպեկտրով
ռենտգենյան ճառագայթների
էներգիայի բաշխումն
ըստ ալիքի երկարության`
ռենտգենյան խողովակի
վրա կիրառված
տարբեր լարումների
դեպքում: Այդ կորերը
ցույց են տալիս,
որ ռենտգենյան
խողովակի վրա
կիրառված լարման
մեծացման հետ
անընդհատ սպեկտրով
ռենտգենյան ճառագայթների
ինտենսիվությունը
մեծանում է, և կարճ
ալիքային սահմանն
ու ինտենսիվության
առավելագույնը
շեղվում են կարճ
ալիքների կողմը:
Դասական
տեսությունը չի
կարող բացատրել
ռենտգենյան ճառագայթների
անընդհատ սպեկտրի
կարճ ալիքային
սահմանի գոյությունը
և այդ սահմանի
շեղումը կարճ ալիքների
կողմը` ըստ ռենտգենյան
խողովակի վրա
կիրառված լարման
մեծացման: Դասական
էլեկտրադինամիկայի
տեսության համաձայն`
ռենտգենյան ճառագայթների
անընդհատ սպեկտրը
պետք է տարածվի
![]() տիրույթում,
մինչդեռ փորձը
ցույց է տալիս,
որ էլեկտրոնների
արգելակման ժամանակ
առաջացած ռենտգենյան
ճառագայթների
անընդհատ սպեկտրը
տարածվում է
տիրույթում,
մինչդեռ փորձը
ցույց է տալիս,
որ էլեկտրոնների
արգելակման ժամանակ
առաջացած ռենտգենյան
ճառագայթների
անընդհատ սպեկտրը
տարածվում է ![]() տիրույթում,
և որքան մեծ է ռենտգենյան
խողովակում էլեկտրոններին
արագացնող լարումը,
այնքան
տիրույթում,
և որքան մեծ է ռենտգենյան
խողովակում էլեկտրոններին
արագացնող լարումը,
այնքան ![]() փոքր է,
(չնայած ասում
ենք, որ ռենտգենյան
ճառագայթների
սպեկտրը տարածվում
է մինչև
փոքր է,
(չնայած ասում
ենք, որ ռենտգենյան
ճառագայթների
սպեկտրը տարածվում
է մինչև ![]() բայց
բավականաչափ երկար
ալիքներն արդեն
ռենտգենյան ալիքների
հատկություն
չեն ունենում):
բայց
բավականաչափ երկար
ալիքներն արդեն
ռենտգենյան ալիքների
հատկություն
չեն ունենում):
Այս
դժվարությունները
կարելի է հաղթահարել`
դիմելով քվանտային
մեխանիկային` ընդունելով,
որ ռենտգենյան
ճառագայթները
քվանտների հոսք
են: Հայտնի է, որ
քվանտի էներգիան`
![]() որտեղ h-ը Պլանկի
հաստատունն է,
իսկ
որտեղ h-ը Պլանկի
հաստատունն է,
իսկ ![]() հաճախությունը:
Կարելի է պատկերացնել,
որ արագ էլեկտրոնը
արգելակվելիս
իր կինետիկ էներգիան
արձակում է որպես
ռենտգենյան ճառագայթների
քվանտներ: Եթե
էլեկտրոնն իր ամբողջ
կինետիկ էներգիան
արձակում է որպես
մեկ քվանտ, այդ
դեպքում քվանտի
էներգիան, ինչպես
և հաճախությունը,
կլինի մեծագույնը,
իսկ նրան համապատասխանող
ալիքի երկարությունը`
նվազագույնը, որը
և կլինի ռենտգենյան
ճառագայթների
անընդհատ սպեկտրի
կարճ ալիքային
սահմանը:
հաճախությունը:
Կարելի է պատկերացնել,
որ արագ էլեկտրոնը
արգելակվելիս
իր կինետիկ էներգիան
արձակում է որպես
ռենտգենյան ճառագայթների
քվանտներ: Եթե
էլեկտրոնն իր ամբողջ
կինետիկ էներգիան
արձակում է որպես
մեկ քվանտ, այդ
դեպքում քվանտի
էներգիան, ինչպես
և հաճախությունը,
կլինի մեծագույնը,
իսկ նրան համապատասխանող
ալիքի երկարությունը`
նվազագույնը, որը
և կլինի ռենտգենյան
ճառագայթների
անընդհատ սպեկտրի
կարճ ալիքային
սահմանը:
Ռենտգենյան
ճառագայթների
կարճալիքային
սահմանին համապատասխանող
ալիքի ![]() երկարությունը
կարելի է գտնել
հետևյալ կերպ:
Ենթադրենք ռենտգենյան
խողովակի վրա կիրառված
լարումը, որի շնորհիվ
շիկացած կաթոդից
դուրս եկած էլեկտրոնները
մինչև անոդին հասնելը
արագանում են,
U է: Շիկացած կաթոդից
էլեկտրոնները
դուրս են գալիս
ինչ-որ սկզբնական
արագությամբ, որը
տարբեր էլեկտրոնների
համար կարող է
տարբեր մեծություն
ունենալ, բայց
այդ սկզբնական
արագությունները
ռենտգենյան խողովակի
էլեկտրական դաշտում
էլեկտրոնների
ձեռք բերած արագության
նկատմամբ չնչին
են (սովորաբար
U-ն մի քանի տասնյակ
հազարից մինչև
հարյուր հազարավոր
վոլտ է), և առանց
զգալի սխալ կատարելու
կարելի է առաջինը
վերջինի նկատմամբ
անտեսել: Այսպիսով,
կարելի է պնդել,
որ շիկացած կաթոդից
դուրս եկած, ռենտգենյան
խողովակում արագացված
և անոդին հասած
բոլոր էլեկտրոններն
ունեն միևնույն
v արագությունը,
որը որոշվում է
հետևյալ պայմանից.
երկարությունը
կարելի է գտնել
հետևյալ կերպ:
Ենթադրենք ռենտգենյան
խողովակի վրա կիրառված
լարումը, որի շնորհիվ
շիկացած կաթոդից
դուրս եկած էլեկտրոնները
մինչև անոդին հասնելը
արագանում են,
U է: Շիկացած կաթոդից
էլեկտրոնները
դուրս են գալիս
ինչ-որ սկզբնական
արագությամբ, որը
տարբեր էլեկտրոնների
համար կարող է
տարբեր մեծություն
ունենալ, բայց
այդ սկզբնական
արագությունները
ռենտգենյան խողովակի
էլեկտրական դաշտում
էլեկտրոնների
ձեռք բերած արագության
նկատմամբ չնչին
են (սովորաբար
U-ն մի քանի տասնյակ
հազարից մինչև
հարյուր հազարավոր
վոլտ է), և առանց
զգալի սխալ կատարելու
կարելի է առաջինը
վերջինի նկատմամբ
անտեսել: Այսպիսով,
կարելի է պնդել,
որ շիկացած կաթոդից
դուրս եկած, ռենտգենյան
խողովակում արագացված
և անոդին հասած
բոլոր էլեկտրոններն
ունեն միևնույն
v արագությունը,
որը որոշվում է
հետևյալ պայմանից.

որտեղ e-ն և m-ը էլեկտրոնի լիցքն ու զանգվածն են: Մյուս կողմից, եթե արգելակման ժամանակ էլեկտրոնն իր ամբողջ կինետիկ էներգիան անոդի վրա արձակում է որպես մեկ ռենտգենյան քվանտ, ապա`

որտեղ
![]() ռենտգենյան
անընդհատ սպեկտրի
կարճալիքային
սահմանին համապատախանող
հաճախությունն
է, որն այդ սպեկտրում
ամենամեծն է: Օգտվելով
(9.46) և (9.47)-ից` կստանանք
ռենտգենյան
անընդհատ սպեկտրի
կարճալիքային
սահմանին համապատախանող
հաճախությունն
է, որն այդ սպեկտրում
ամենամեծն է: Օգտվելով
(9.46) և (9.47)-ից` կստանանք
![]()
Նկատի
ունենալով, որ
![]() (c-ն լույսի
արագությունն
է վակուումում),
կստանանք.
(c-ն լույսի
արագությունն
է վակուումում),
կստանանք.

(9.48) արտահայտությունից պարզ է դառնում անընդհատ սպեկտրի կարճ ալիքային սահմանի գոյությունը և այդ սահմանի դեպի կարճ ալիքների կողմը շեղվելը, երբ էլեկտրոնների արագությունը մեծացվում է:
(9.48)-ից
երևում է, որ տրված
U-ի դեպքում, այսինքն`
էլեկտրոնների
տրված արագության
դեպքում, ռենտգենյան
ճառագայթների
անընդհատ սպեկտրում
![]() փոքր երկարությամբ
ալիք գոյություն
ունենալ չի կարող
և որ U -ն մեծացնելիս,
արգելակվող էլեկտրոնների
արագությունը
մեծացնելիս
փոքր երկարությամբ
ալիք գոյություն
ունենալ չի կարող
և որ U -ն մեծացնելիս,
արգելակվող էլեկտրոնների
արագությունը
մեծացնելիս ![]() -ն փոքրանում
է, այսինքն` կարճ
ալիքային սահմանը
շեղվում է դեպի
կարճ երկարության
ալիքները: Մեծ
երկարության ալիքներ
ստացվում են այն
դեպքում, երբ արգելակվող
էլեկտրոնի կինետիկ
էներգիան արձակվում
է մեկից ավելի
ռենտգենյան քվանտներով,
և որքան էլեկտրոնի
արձակած քվանտների
թիվը մեծ լինի,
այնքան այդ քվանտների
էներգիան և հաճախությունը
փոքր կլինեն, իսկ
ալիքի երկարությունը`
մեծ, որի պատճառով,
ռենտգենյան ճառագայթների
անընդհատ սպեկտրը
երկար ալիքների
կողմից սահմանափակված
չպետք է լինի:
-ն փոքրանում
է, այսինքն` կարճ
ալիքային սահմանը
շեղվում է դեպի
կարճ երկարության
ալիքները: Մեծ
երկարության ալիքներ
ստացվում են այն
դեպքում, երբ արգելակվող
էլեկտրոնի կինետիկ
էներգիան արձակվում
է մեկից ավելի
ռենտգենյան քվանտներով,
և որքան էլեկտրոնի
արձակած քվանտների
թիվը մեծ լինի,
այնքան այդ քվանտների
էներգիան և հաճախությունը
փոքր կլինեն, իսկ
ալիքի երկարությունը`
մեծ, որի պատճառով,
ռենտգենյան ճառագայթների
անընդհատ սպեկտրը
երկար ալիքների
կողմից սահմանափակված
չպետք է լինի: ![]() մեծ երկարության
ալիքներ կստացվեն
նաև այն պատճառով,
որ էլեկտրոնը
կարող է իր կինետիկ
էներգիայի մի
մասն արձակել
որպես ռենտգենյան
քվանտ, իսկ մյուս
մասը ծախսել այլ
պրոցեսների վրա:
Այսպիսով, հասկանալի
է դառնում նաև
արգելակման ռենտգենյան
ճառագայթման սպեկտրի
անընդհատ լինելը:
Եթե (9.48)-ի մեջ տեղադրենք
h-ի, c-ի, e-ի արժեքները
և U -ն արտահայտենք
կիլովոլտերով,
իսկ
մեծ երկարության
ալիքներ կստացվեն
նաև այն պատճառով,
որ էլեկտրոնը
կարող է իր կինետիկ
էներգիայի մի
մասն արձակել
որպես ռենտգենյան
քվանտ, իսկ մյուս
մասը ծախսել այլ
պրոցեսների վրա:
Այսպիսով, հասկանալի
է դառնում նաև
արգելակման ռենտգենյան
ճառագայթման սպեկտրի
անընդհատ լինելը:
Եթե (9.48)-ի մեջ տեղադրենք
h-ի, c-ի, e-ի արժեքները
և U -ն արտահայտենք
կիլովոլտերով,
իսկ ![]() անգստրեմներով,
ապա
անգստրեմներով,
ապա ![]() համար կստանանք
հետևյալ առնչությունը`
համար կստանանք
հետևյալ առնչությունը`

U=100կՎ-ի
դեպքում անընդհատ
սպեկտրում ամենակարճ
ալիքի երկարությունը`
0.123ժ է: Պետք է ավելացնել,
որ արգելակման
սպեկտրի սահմանի`
![]() ալիքի փորձով
որոշված երկարությամբ
հնարավոր է որոշել
Պլանկի h հաստատունի
արժեքը: Պլանկի
հաստատունի որոշումը
արգելակման ռենտգենյան
սպեկտրի սահմանային
ալիքի երկարության
միջոցով, այդ հաստատունը
որոշելու ամենից
ավելի հուսալի
և ճշգրիտ եղանակներից
մեկն է:
ալիքի փորձով
որոշված երկարությամբ
հնարավոր է որոշել
Պլանկի h հաստատունի
արժեքը: Պլանկի
հաստատունի որոշումը
արգելակման ռենտգենյան
սպեկտրի սահմանային
ալիքի երկարության
միջոցով, այդ հաստատունը
որոշելու ամենից
ավելի հուսալի
և ճշգրիտ եղանակներից
մեկն է:
Անընդհատ սպեկտրով ռենտգենյան ճառագայթները կարևոր կիրառություն ունեն տեխնիկայում, բժշկության, ռենտգենակառուցվածքային հետազոտությունների ու ռենտգենասպեկտրային հետազոտությունների բնագավառներում: Անընդհատ սպետրով ռենտգենյան ճառագայթները տեխնիկայում լայնորեն կիրառվում են դետալների ներքին անտեսանելի թերությունները հայտնաբերելու համար: Բժշկության մեջ այդ ճառագայթներով լուսավորում են մարդկանց ներքին օրգանները` հիվանդությունները հայտնաբերելու նպատակով (ախտորոշում): Ռենտգենակառուցվածքային անալիզի մեջ անընդհատ սպեկտրով ռենտգենյան ճառագայթները կիրառվում են Լաուեի եղանակով բյուրեղների կառուցվածքը հետազոտելու, իսկ ռենտգենասպեկտրային անալիզի մեջ այդ ճառագայթները կիրառվում են կլանման սպեկտրները հետազոտելու նպատակով:
9.12. Գծային սպեկտրով ռենտգենյան ճառագայթների առաջացումը
Երբ ռենտգենյան խողովակի վրա կիրառված պոտենցիալների տարբերությունն աստիճանաբար մեծացնելիս այն գերազանցում է տվյալ նյութից պատրաստված անոդի համար մի որոշակի Uo արժեքը, ապա անընդհատ սպեկտրով ռենտգենյան ճառագայթների հետ միասին առաջանում են նաև գծային սպեկտրով ռենտգենյան ճառագայթներ: Այդ դեպքում կաթոդից դեպի անոդ գնացող արագացված էլեկտրոնների մի մասն իր էներգիան տալիս է անոդի ատոմների միջուկներին մոտ գտնվող էլեկտրոններին: Վերջիններս, ստանալով վերոհիշյալ էներգիան` հեռանում են ատոմից կամ էլ գրավում են ազատ մակարդակներ: Այսպիսով, անոդի ատոմների միջուկներին մոտ առաջանում են էլեկտրոններից ազատ մակարդակներ: Ազատ մակարդակներ առաջանալուց հետո ( 10-8 վ-ի ընթացքում), հեռավոր մակարդակներից այդ ազատ մակարդակներն են տեղափոխվում էլեկտրոններ, որոնք իրենց առաջին և վերջին մակարդակներում ունեցած էներգիաների տարբերությունն արձակում են որպես ռենտգենյան ճառագայթներ:
Քանի
որ միջուկին մոտ
գտնվող էլեկտրոնին
ատոմից դուրս հանելու
համար անհրաժեշտ
է որոշակի Eo-ի
հավասար կամ նրանից
մեծ էներգիա, ապա
գծային սպեկտրով
ռենտգենյան ճառագայթներ
առաջացնելու համար
ռենտգենյան խողովակի
վրա կիրառված լարումը
պետք է բավարարի
հետևյալ պայմանին`
![]() որտեղ e-ն էլեկտրոնի
լիցքն է, իսկ U-ն`
ռենտգենյան խողովակի
վրա կիրառված լարումը:
Ուրեմն, ռենտգենյան
խողովակի անոդը
ռմբակոծող էլեկտրոնների
ազդեցության տակ
անոդի ատոմները
գրգռվում են և,
երբ անցնում են
նորմալ վիճակի,
արձակում են ռենտգենյան
ճառագայթներ:
Սակայն քանի որ
ատոմը կլանում
և արձակում է էներգիայի
միայն որոշակի
բաժիններ, այդ
պատճառով էլ նրա
արձակած ռենտգենյան
ճառագայթներն
ունենում են գծային
սպեկտր, որը բաղկացած
է որոշակի ընդհատ
գծերից:
որտեղ e-ն էլեկտրոնի
լիցքն է, իսկ U-ն`
ռենտգենյան խողովակի
վրա կիրառված լարումը:
Ուրեմն, ռենտգենյան
խողովակի անոդը
ռմբակոծող էլեկտրոնների
ազդեցության տակ
անոդի ատոմները
գրգռվում են և,
երբ անցնում են
նորմալ վիճակի,
արձակում են ռենտգենյան
ճառագայթներ:
Սակայն քանի որ
ատոմը կլանում
և արձակում է էներգիայի
միայն որոշակի
բաժիններ, այդ
պատճառով էլ նրա
արձակած ռենտգենյան
ճառագայթներն
ունենում են գծային
սպեկտր, որը բաղկացած
է որոշակի ընդհատ
գծերից:
Տարբեր տեսակի ատոմների կլանած և արձակած էներգիայի բաժինների մեծությունները տարբեր են լինում, ուստի և տարբեր կլինեն տարբեր ատոմների արձակած ռենտգենյան ալիքների հաճախությունները: Այսպիսով, ռենտգենյան խողովակում առաջացած գծային սպեկտրով ռենտգենյան ճառագայթների սպեկտրային բնույթը (հաճախությունները) բնորոշվում է անոդի ատոմների տեսակով: Այդ նկատառումով էլ ռենտգենյան ճառագայթներն անվանում են բնութագրական ճառագայթներ: Նրանք բնորոշվում են անոդի նյութի տեսակով և հակառակը` իրենք են բնորոշում անոդի նյութի տեսակը:
Ռենտգենյան սպեկտրոսկոպիայում գլխավոր քվանտային թվի տարբեր արժեքներին համապատասխանող էլեկտրոնային թաղանթները նշանակվում են հետևյալ կերպ.
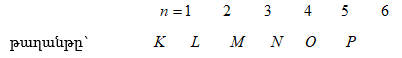
Այսինքն առաջին թաղանթը (n=1) նշանակվում է K տառով, երկրորդը (n=2)L տառով, երրորդը (n=3)M տառով և այլն:
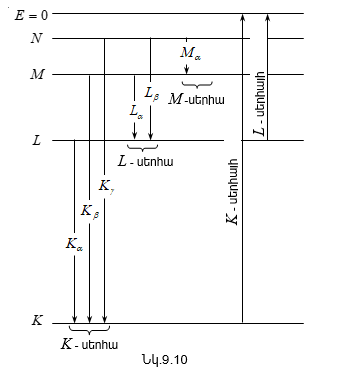
Ալիքների
երկարության աճման
կարգով բնութագրական
ռենտգենյան ճառագայթների
սերիաները համապատասխանաբար
կոչվում են ![]()
![]()
![]()
![]()
![]()
![]() սերիաներ:
Այդ անվանումները,
ինչպես ցույց կտրվի
ներքևում, կապված
են այդ սերիաների
գծերի ծագման
հետ: Ռենտգենյան
սպեկտրների առաջացման
սխեման տրված է
նկ.9.10-ում: Դիագրամի վրա
սլաքներով ցույց
են տրված այն անցումները,
որոնք առաջանում
են K, L և M սերիաները
կազմող առանձին
մեներանգ գծերը:
Ատոմը գրգռվում
է, եթե ներքին էլեկտրոններից
մեկը հեռանում
է: Եթե, օրինակ, էլեկտրոնը
հեռանում է ատոմի
ամենաներքին
K թաղանթից արագ
էլեկտրոնի կամ
առաջնային կոշտ
ճառագայթման ազդեցության
տակ, ապա ազատված
տեղը կարող է զբաղեցնել
որևէ էլեկտրոն
L, M, N և ուրիշ թաղանթներից:
Այդպիսի անցումը
կապված է որոշակի
էներգիայով քվանտների
արձակման և K սերիայի
ռենտգենյան գծերի
առաջացման հետ:
Յուրաքանչյուր
ատոմի համար գոյություն
ունի K սերիայի
գրգռման որոշակի
սահման: Օրինակ,
սնդիկի համար
(Z=80) այն կազմում
է մոտ 82կէՎ: Էլեկտրոնի
անցումն L թաղանթից
K թաղանթի վրա
համապատասխանում
է ռենտգենյան
բնութագրական
ճառագայթման K
սերիայի
սերիաներ:
Այդ անվանումները,
ինչպես ցույց կտրվի
ներքևում, կապված
են այդ սերիաների
գծերի ծագման
հետ: Ռենտգենյան
սպեկտրների առաջացման
սխեման տրված է
նկ.9.10-ում: Դիագրամի վրա
սլաքներով ցույց
են տրված այն անցումները,
որոնք առաջանում
են K, L և M սերիաները
կազմող առանձին
մեներանգ գծերը:
Ատոմը գրգռվում
է, եթե ներքին էլեկտրոններից
մեկը հեռանում
է: Եթե, օրինակ, էլեկտրոնը
հեռանում է ատոմի
ամենաներքին
K թաղանթից արագ
էլեկտրոնի կամ
առաջնային կոշտ
ճառագայթման ազդեցության
տակ, ապա ազատված
տեղը կարող է զբաղեցնել
որևէ էլեկտրոն
L, M, N և ուրիշ թաղանթներից:
Այդպիսի անցումը
կապված է որոշակի
էներգիայով քվանտների
արձակման և K սերիայի
ռենտգենյան գծերի
առաջացման հետ:
Յուրաքանչյուր
ատոմի համար գոյություն
ունի K սերիայի
գրգռման որոշակի
սահման: Օրինակ,
սնդիկի համար
(Z=80) այն կազմում
է մոտ 82կէՎ: Էլեկտրոնի
անցումն L թաղանթից
K թաղանթի վրա
համապատասխանում
է ռենտգենյան
բնութագրական
ճառագայթման K
սերիայի ![]() գծի ամենաերկար
ալիքին:
գծի ամենաերկար
ալիքին: ![]() գիծը
համապատասխանում
է M թաղանթից էլեկտրոնի
անցմանը
գիծը
համապատասխանում
է M թաղանթից էլեկտրոնի
անցմանը ![]() թաղանթի
վրա,
թաղանթի
վրա, ![]() գիծը` N թաղանթից
K թաղանթի վրա
անցմանը:
գիծը` N թաղանթից
K թաղանթի վրա
անցմանը: ![]() գծերի
համախումբը կազմում
է K սերիան:
գծերի
համախումբը կազմում
է K սերիան: ![]() անցման
դեպքում գծերի
հաճախություններն
աճում են: Հակառակը,
անցման
դեպքում գծերի
հաճախություններն
աճում են: Հակառակը,
![]() գծերին
անցման դեպքում,
գծերի ինտենսիվությունները
նվազում են, քանի
որ L թաղանթից
K թաղանթին անցումների
հավանականությունը
ավելի մեծ է, քան
L, M և ուրիշ ավելի
հեռու թաղանթներից:
Նման ձևով առաջանում
են նաև մյուս սերիաները:
K սերիան պարտադիր
կարգով ուղեկցվում
է մյուս սերիաներով,
քանի որ նրա գծերի
առաքմամբ L, M և
N այլ շերտերում
ազատվում են մակարդակներ,
որոնք իրենց հերթին
լցվում են ավելի
բարձր շերտերի
էլեկտրոններով:
գծերին
անցման դեպքում,
գծերի ինտենսիվությունները
նվազում են, քանի
որ L թաղանթից
K թաղանթին անցումների
հավանականությունը
ավելի մեծ է, քան
L, M և ուրիշ ավելի
հեռու թաղանթներից:
Նման ձևով առաջանում
են նաև մյուս սերիաները:
K սերիան պարտադիր
կարգով ուղեկցվում
է մյուս սերիաներով,
քանի որ նրա գծերի
առաքմամբ L, M և
N այլ շերտերում
ազատվում են մակարդակներ,
որոնք իրենց հերթին
լցվում են ավելի
բարձր շերտերի
էլեկտրոններով:
Մոզլին, 1914թ. ուսումնասիրելով քիմիական տարրերի ռենտգենյան սպեկտրները, սահմանեց մի պարզ օրենք, որը սպեկտրային գծի հաճախությունները կապում է դրանք ճառագայթող տարրի ատոմական համարի հետ.
![]()
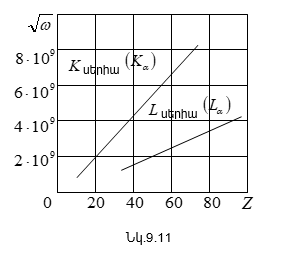
Մոզլիի
օրենքը կարելի
է ձևակերպել հետևյալ
կերպ. հաճախության
քառակուսի արմատը
գծային ֆունկցիա
է տարրի Z ատոմական
համարից: ![]() հաստատունը
միևնույն սերիայի
սահմաններում
պահպանում իր
արժեքը բոլոր տարրերի
համար, բայց փոփոխվում
է մեկ սերիայից
մյուսին անցնելիս:
Մոզլիի չափումներով
հաստատունը
միևնույն սերիայի
սահմաններում
պահպանում իր
արժեքը բոլոր տարրերի
համար, բայց փոփոխվում
է մեկ սերիայից
մյուսին անցնելիս:
Մոզլիի չափումներով
![]() K սերիայի
և
K սերիայի
և ![]() L սերիայի
համար: Թե որքանով
է ճշգրիտ Մոզլիի
օրենքը, կարելի
է դատել նկ.9.11-ում
պատկերված դիագրամից,
(որն անվանում
են Մոզլիի դիագրամ):
Մոզլիի սահմանած
օրենքը թույլ է
տալիս ռենտգենյան
գծերի չափված ալիքի
երկարությամբ
ճշգրիտ որոշել
տվյալ տարրի ատոմական
համարը: Այն մեծ
դեր խաղաց տարրերը
պարբերական համակարգում
դասավորելու հարցում:
Մոզլին իր գըտած
օրենքին տվեց
պարզ տեսական բացատրություն:
Նա գտավ, որ
L սերիայի
համար: Թե որքանով
է ճշգրիտ Մոզլիի
օրենքը, կարելի
է դատել նկ.9.11-ում
պատկերված դիագրամից,
(որն անվանում
են Մոզլիի դիագրամ):
Մոզլիի սահմանած
օրենքը թույլ է
տալիս ռենտգենյան
գծերի չափված ալիքի
երկարությամբ
ճշգրիտ որոշել
տվյալ տարրի ատոմական
համարը: Այն մեծ
դեր խաղաց տարրերը
պարբերական համակարգում
դասավորելու հարցում:
Մոզլին իր գըտած
օրենքին տվեց
պարզ տեսական բացատրություն:
Նա գտավ, որ ![]() գծի համար
(6.5) բանաձևում C
հաստատունն ունի
գծի համար
(6.5) բանաձևում C
հաստատունն ունի
![]() արժեքը,
որտեղ R-ը Ռիդբերգի
հաստատունն է:
Հետևաբար այդ գծի
համար (9.50) բանաձևը
կարելի է գրել
հետևյալ տեսքով`
արժեքը,
որտեղ R-ը Ռիդբերգի
հաստատունն է:
Հետևաբար այդ գծի
համար (9.50) բանաձևը
կարելի է գրել
հետևյալ տեսքով`
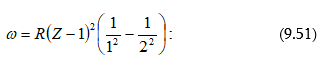
Այդպիսի հաճախության գիծ է ստացվում, երբ (Z-1)e լիցքի դաշտում գտնվող էլեկտրոնը n=2 մակարդակից անցնում է n=1 մակարդակը: Մյուս գծերի համար (9.51) բանաձևին կարելի է տալ հետևվյալ տեսքը.
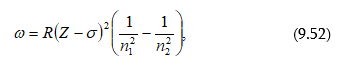
որտեղ
![]() նույն
սերիաների սահմաններում
հաստատուն մեծություն
է:
նույն
սերիաների սահմաններում
հաստատուն մեծություն
է: ![]() հաստատունի
իմաստը հեշտ է
հասկանալ. ռենտգենյան
ճառագայթներ արձակելիս
անցումներ կատարող
էլեկտրոնները
գտնվում են միջուկի
ներգործության
տակ, որի ձգողականությունը
նրան շրջապատող
մյուս էլեկտրոնների
ազդեցությամբ
մի փոքր թուլանում
է: Դա այսպես կոչված,
էկրանավորող ազդեցություն
է, որն արտահայտվում
է Z-ից ինչ-որ
հաստատունի
իմաստը հեշտ է
հասկանալ. ռենտգենյան
ճառագայթներ արձակելիս
անցումներ կատարող
էլեկտրոնները
գտնվում են միջուկի
ներգործության
տակ, որի ձգողականությունը
նրան շրջապատող
մյուս էլեկտրոնների
ազդեցությամբ
մի փոքր թուլանում
է: Դա այսպես կոչված,
էկրանավորող ազդեցություն
է, որն արտահայտվում
է Z-ից ինչ-որ![]() մեծություն
հանելու անհրաժեշտությամբ:
մեծություն
հանելու անհրաժեշտությամբ:
Մոզլիի կողմից ստացած տվյալները հաստատեցին, որ մի տարրից մյուսին անցնելիս միջուկի լիցքը մեծանում է մեկ միավորով, և որ Մենդելեևի պարբերական համակարգում տարրերը դասավորված են միջուկի լիցքի մեծացման կարգով:
9.13. Ստիպողական ճառագայթում: Լազերներ
Գրգռված վիճակներից հիմնական վիճակի ատոմներն անցնում են ինքնակամ (սպոնտան), ընդ որում` անցումների հետևանքով ճառագայթված բոլոր ֆոտոններն ունեն ալիքի տարբեր հաճախություններ, փուլեր և բևեռացում: Այդպիսի ճառագայթումը կոչվում է ոչ կոհերենտ և ինտերֆերենցիոն պատկեր չի տալիս: 1917թ. Ա. Այնշտայնը ցույց տվեց, որ բացի մեկ էներգետիկ մակարդակից մյուսին ատոմների ինքնակամ անցումներից, դիտվում են նաև ստիպողական (կամ ինդուկտված) անցումներ, որոնք պայմանավորված են ատոմի վրա ընկնող ճառագայթման ներգործությամբ: Ինքնակամ անցումները կարող են իրականանալ միայն մեկ ուղղությամբ` առավել բարձր էներգետիկ մակարդակներից դեպի ավելի ցածրերը: Ստիպողական անցումները կարող են հավասար հավանականությամբ տեղի ունենալ ինչպես մեկ, այնպես էլ մյուս ուղղությամբ: Ավելի բարձր մակարդակի անցնելու դեպքում ատոմը կլանում է իր վրա ընկնող ճառագայթումը: Որևէ գրգռված մակարդակից ավելի ցածր էներգետիկ մակարդակի ստիպողական անցման դեպքում ատոմը ճառագայթում է ֆոտոն` ի լրումն այն ֆոտոնի, որի ներգործությամբ տեղի է ունեցել անցումը: Այդ լրացուցիչ ճառագայթումը կոչվում է ստիպողական (կամ ինդուկտված):
Ստիպողական ճառագայթումն օժտված է խիստ կարևոր հատկություններով: Նրա տարածման ուղղությունը ճշտորեն համընկնում է անցումը հարուցած արտաքին ճառագայթման տարածման ուղղության հետ: Նույնը վերաբերում է ստիպողական և արտաքին ճառագայթումների հաճախությանը, փուլին և բևեռացմանը: Այսպիսով, ստիպողական և արտաքին ճառագայթումները կոհերենտ են: Ստիպողական ճառագայթման այս առանձնահատկությունն ընկած է լազերներ կոչվող լույսի ուժեղացուցիչների և գեներատորների գործողության հիմքում: Նշենք, որ ստիպողական ճառագայթումը լույսի կլանման պրոցեսի շրջումն է: Ստիպողական ճառագայթման հաշվին լույսը ուժեղացնելու սկզբունքը առաջին անգամ առաջարկել է Վ. Ֆաբրիկանտը 1940թ.: Ստիպողական ճառագայթման օգտագործումը միկրոալիքային տիրույթում էլեկտրամագնիսական ալիքների ուժեղացման համար 1953թ. իրարից անկախ առաջարկել են ռուս գիտնականներ Ն. Բասովն ու Ա. Պրոխորովը և ամերիկացի գիտնականներ Տաունսն ու Վեբերը: Սանտիմետրանոց ալիքների տիրույթում աշխատող համապատասխան սարքերը ստացել են մազերներ անվանումը: «Մազեր» բառն առաջացել է անգլերեն անվանման բառերի առաջին տառերից` Mikrowave Amplification by stimulated Emission of Radiation (միկրոալիքների ուժեղացումը ստիպողական ճառագայթման օգնությամբ): 1960թ. Տ. Մեյմանը (ԱՄՆ) ստեղծեց օպտիկական տիրույթում աշխատող առաջին համանման սարքը` լազերը (Light Amplification by stimulated of Radiation - Լույսի ուժեղացումը ստիպողական ճառագայթման օգնությամբ): Երբեմն լազերներն անվանում են օպտիկական քվանտային գեներատորներ:
Նյութի
վրա ընկնող լույսը
, որի ![]() հաճախությունը
համընկնում է նյութի
ատոմների (En-Em)/h
հաճախություններից
որևէ մեկի հետ
հաճախությունը
համընկնում է նյութի
ատոմների (En-Em)/h
հաճախություններից
որևէ մեկի հետ
![]() հարուցում է
երկու պրոցես.
1) ատոմների անցում
Em էներգիայով
վիճակից En էներգիայով
վիճակի, 2) ատոմների
ստիպողական անցում
n վիճակից m վիճակի:
Առաջին պրոցեսը
հանգեցնում է
լույսի կլանմանը
և ընկնող փնջի
ինտենսիվության
թուլացմանը, երկրորդը`
ընկնող փնջի ինտենսիվության
մեծացմանը: Լուսային
փնջի ինտենսիվության
արդյունարար փոփոխությունը
կախում ունի այն
բանից, թե երկու
պրոցեսներից որն
է գերակշռում:
հարուցում է
երկու պրոցես.
1) ատոմների անցում
Em էներգիայով
վիճակից En էներգիայով
վիճակի, 2) ատոմների
ստիպողական անցում
n վիճակից m վիճակի:
Առաջին պրոցեսը
հանգեցնում է
լույսի կլանմանը
և ընկնող փնջի
ինտենսիվության
թուլացմանը, երկրորդը`
ընկնող փնջի ինտենսիվության
մեծացմանը: Լուսային
փնջի ինտենսիվության
արդյունարար փոփոխությունը
կախում ունի այն
բանից, թե երկու
պրոցեսներից որն
է գերակշռում:
Ջերմադինամիկական հավասարակշռության դեպքում ատոմների բաշխումն ըստ տարբեր էներգետիկ վիճակների որոշվում է Բոլցմանի օրենքով.
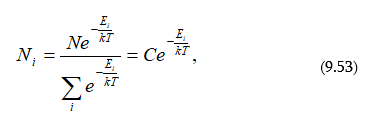
որտեղ N-ը ատոմների ընդհանուր թիվն է, Ni -ն T ջերմաստիճանում Ei էներգիայով վիճակում գտնվող ատոմների թիվն է:
(9.53) բանաձևից հետևում է, որ վիճակի էներգիայի մեծացման համեմատ մակարդակի բնակեցվածությունը, այսինքն` ատոմների թիվը տվյալ վիճակում, նվազում է: Երկու մակարդակների միջև անցումների թիվը համեմատական է ելակետային մակարդակի բնակեցվածությանը: Հետևաբար, ջերմադինամիկական հավասարակշռությունում գտնվող ատոմների համակարգում ընկնող լուսային ալիքի կլանումը կգերակշռի ստիպողական ճառագայթմանը, այնպես, որ նյութի միջով անցնելիս ընկնող ալիքը թուլանում է: Ընկնող ալիքի ուժեղացում ստանալու համար պետք է որևէ եղանակով շրջել էներգետիկ մակարդակների բնակեցվածությունը, այսինքն` անել այնպես, որ En ավելի մեծ էներգիա ունեցող վիճակում գտնվեն ավելի մեծ թվով ատոմներ, քան Em ավելի փոքր էներգիայով վիճակում: Այդ դեպքում ասում են, որ ատոմների տվյալ համախումբն ունի ինվերսային բնակեցվածություն: (9.53) բանաձևի համաձայն
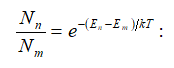
Ինվերսային
բնակեցվածության
դեպքում ![]() Այս դեպքի
վրա ձևականորեն
տարածելով (9.53) բաշխումը,
T-ի համար կստանանք
բացասական արժեք:
Այդ պատճառով
էլ ինվերսային
բնակեցվածությամբ
վիճակները կոչվում
են բացասական
ջերմաստիճանով
վիճակներ: Բայն
այն է, որ ինվերսային
բնակեցվածությամբ
վիճակներն անհավասարակշիռ
են: Մինչդեռ ջերմաստիճանի
հասկացությունը
կիրառելի է միայն
հավասարակշիռ
վիճակներում:
Այս դեպքի
վրա ձևականորեն
տարածելով (9.53) բաշխումը,
T-ի համար կստանանք
բացասական արժեք:
Այդ պատճառով
էլ ինվերսային
բնակեցվածությամբ
վիճակները կոչվում
են բացասական
ջերմաստիճանով
վիճակներ: Բայն
այն է, որ ինվերսային
բնակեցվածությամբ
վիճակներն անհավասարակշիռ
են: Մինչդեռ ջերմաստիճանի
հասկացությունը
կիրառելի է միայն
հավասարակշիռ
վիճակներում:
Էներգետիկ մակարդակների ինվերսային բնակեցվածություն ունեցող նյութում ստիպողական ճառագայթումը կարող է գերազանցել ատոմների կողմից լույսի կլանումը, որի հետևանքով ընկնող լույսը նյութի միջով անցնելիս կուժեղանա: Լույսի ինտենսիվության փոփոխությունը կլանող միջավայրով անցնելիս տրվում է հետևյալ բանաձևով (տես (5.16))`
![]()
Ընկնող
փնջի ուժեղացման
դեպքում երևույթն
ընթանում է այնպես,
ինչպես, եթե (9.54) բանաձևում
![]() կլանման գործակիցը
լիներ բացասական:
Համապատասխանաբար,
ինվերսիոն բնակեցվածությամբ
ատոմների համախումբը
կարելի է դիտարկել
որպես բացասական
կլանման գործակցով
միջավայր:
կլանման գործակիցը
լիներ բացասական:
Համապատասխանաբար,
ինվերսիոն բնակեցվածությամբ
ատոմների համախումբը
կարելի է դիտարկել
որպես բացասական
կլանման գործակցով
միջավայր:
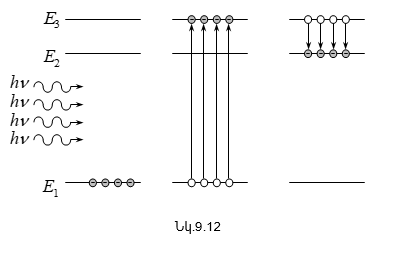
Լազերի գործնական իրականացումը հնարավոր դարձավ այն բանից հետո, երբ գտնվեցին որոշ նյութերում մակարդակների ինվերսային բնակեցվածություն իրականացնելու եղանակները: Որպեսզի ստացվի ինվերսիոն բնակեցվածություն, հարկավոր է օգտագործել ակտիվ միջավայրի երեք կամ ավելի էներգետիկ մակարդակներ: Այդ նպատակով սովորաբար օգտագործում են ատոմներ, որոնց գրգռված վիճաների կյանքի տևողություններն էապես տարբերվում են միմյանցից: Կան գրգռված մակարդակներ, որտեղ ատոմները կարող են գտնվել համեմատաբար երկար ժամանակ: Այդ մակարդակներին կոչվում են մետաստաբիլ (hամարյա կայուն): Այդպիսի մակարդակ ունի սուտակի բյուրեղում (Al2O3) խառնուրդի ձևով առկա քրոմի ատոմը (նկ.9.12): Բացի 1 հիմնական վիճակից, այն ունի երկու գրգռված վիճակ, որոնց կյանքի տևողությունները տարբերվում են 105 անգամ` 3 մակարդակում այն 10-8վ կարգի է, իսկ 2-ում` 10-3վ կարգի:
Եթե
լույսի ազդեցությամբ
ատոմը գրգռվում
է, այսինքն` կլանելով
էներգիա`1 վիճակից
անցնում է 3 վիճակ,
ապա մոտ 10-8վ անց
այն անցնում է
2 մակարդակ: E3
էներգիայով մակարդակից
E2 էներգիայով
մակարդակ անցնելիս
լույս չի արձակվում:
Էներգիաների այդ
տարբերությունը
հաղորդվում է բյուրեղին,
որից բյուրեղը
տաքանում է: Եթե
անընդհատ ճառագայթենք
բյուրեղը, ապա
մեծ քանակությամբ
ատոմներ կունենանք
«բնակեցված» 2 վիճակում:
Եթե ![]() էներգիայով
մեկ ֆոտոն հայտնվի
բյուրեղում, ապա
ատոմներից մեկը
հարկադրված կճառագայթի
նմանատիպ ֆոտոն:
Այնուհետև այդ
երկու ֆոտոնները
հարկադրում են
ևս երկու ատոմի
ճառագայթել, և
այսպես շարունակ:
Ֆոտոնների թիվն
անընդհատ կրկնապատկվում
է: Այսպիսով լույսն
ուժեղանում է,
ընդ որում բոլոր
ֆոտոններն ունենում
են նույն հաճախությունը,
փուլը և բևեռացումը:
Ստացվում է լույսի
ուժեղ կոհերենտ
փունջ (նկ.9.13):
էներգիայով
մեկ ֆոտոն հայտնվի
բյուրեղում, ապա
ատոմներից մեկը
հարկադրված կճառագայթի
նմանատիպ ֆոտոն:
Այնուհետև այդ
երկու ֆոտոնները
հարկադրում են
ևս երկու ատոմի
ճառագայթել, և
այսպես շարունակ:
Ֆոտոնների թիվն
անընդհատ կրկնապատկվում
է: Այսպիսով լույսն
ուժեղանում է,
ընդ որում բոլոր
ֆոտոններն ունենում
են նույն հաճախությունը,
փուլը և բևեռացումը:
Ստացվում է լույսի
ուժեղ կոհերենտ
փունջ (նկ.9.13):
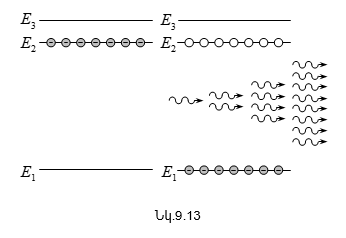
Ինչպես
վերևում նշեցինք
լույսի առաջին
գեներատորը ստեղծվել
է Տ. Մեյմանի կողմից:
Գեներատորի բանող
մարմինը վարդագույն
սուտակից պատրաստված
գլանն է, որում
խառնուրդի (մոտ
0,05%) տեսքով կան քրոմի
իոններ (նկ.9.14 ): Գլանի
տրամագիծը 1սմ
կարգի է, երկարությունը`
մոտ 5սմ: Սուտակի
բյուրեղի ձողի
ճակատներից մեկը
հայելային է, իսկ
մյուսը պատված
է արծաթի այնպիսի
շերտով, որն անցկացնում
է իր վրա ընկած
էներգիայի 8%-ը: Որքան
մեծ է քրոմի կոնցենտրացիան,
այնքան ուժեղ է
բյուրեղի երանգավորւմը:
Լույսը կլանելիս
քրոմի իոնները`
![]() (քրոմն այս ձևով
է հանդես գալիս
սուտակի բյուրեղում),
անցնում են գրգռված
վիճակի: Լազերում
սուտակը լուսավորվում
է իմպուլսային
քսենոնային լամպով
(նկ.9.14), որը տալիս
է լայնաշերտ հաճախության
լույս: Լամպի բավարար
հզորության դեպքում
քրոմի իոնների
մեծ մասը տեղափոխվում
է գրգռված վիճակի:
Ատոմները գրգռված
վիճակի տեղափոխելու
համար լազերի բանող
մարմնին էներգիա
հաղորդելու պրոցեսը
կոչվում է ներմղում:
Լամպի ճառագայթման
ազդեցությամբ
ատոմներն անցնում
են 3 մակարդակ
և, կարճ ժամանակ
մնալով այնտեղ`
իջնում են 2 մակարդակ:
(քրոմն այս ձևով
է հանդես գալիս
սուտակի բյուրեղում),
անցնում են գրգռված
վիճակի: Լազերում
սուտակը լուսավորվում
է իմպուլսային
քսենոնային լամպով
(նկ.9.14), որը տալիս
է լայնաշերտ հաճախության
լույս: Լամպի բավարար
հզորության դեպքում
քրոմի իոնների
մեծ մասը տեղափոխվում
է գրգռված վիճակի:
Ատոմները գրգռված
վիճակի տեղափոխելու
համար լազերի բանող
մարմնին էներգիա
հաղորդելու պրոցեսը
կոչվում է ներմղում:
Լամպի ճառագայթման
ազդեցությամբ
ատոմներն անցնում
են 3 մակարդակ
և, կարճ ժամանակ
մնալով այնտեղ`
իջնում են 2 մակարդակ:
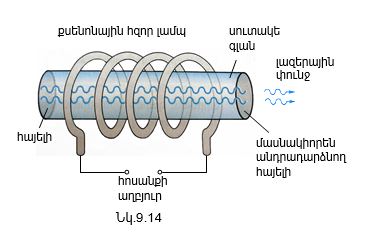
Քանի
որ 2 մակարդակում
գտնվելու կյանքի
տևողությունը
անհամեմատ մեծ
է 3 մակարդակում
կյանքի տևողությունից,
ապա այնտեղ մեծ
թվով ատոմներ
են կուտակվում:
Բավականաչափ հզոր
ներմղման դեպքում
2 մակարդակում
գտնվող քրոմի իոնների
թիվը դառնում
է 1 մակարդակի
իոնների թվից մեծ:
Հետևաբար, տեղի
է ունենում 1 և
2 մակարդակների
ինվերսիա: Ինքնաբերաբար
տեղի ունեցող
![]() անցումների
հետևանքով
սկսում են բոլոր
ուղղություններով
ֆոտոններ ճառագայթվել:
Այն ֆոտոնները,
որոնք բյուրեղի
առանցքի նկատմամբ
անկյան տակ են
շարժվում, նրանից
դուրս են գալիս
և հետագա պրոցեսներում
ոչ մի դեր չեն խաղում:
Իսկ այն ֆոտոնները,
որոնք շարժվում
են բյուրեղի առանցքի
ուղղությամբ, իրենց
շարժման ժամանակ
առաջ են բերում
նոր ատոմների
հարկադրական ճառագայթումներ,
և ֆոտոնների թիվը
շատ արագ ավելանում
է: Ճառագայթները
հասնելով հայելուն,
անդրադառնում
են` ճանապարհին
անընդհատ ավելանալով:
Հասնելով թափանցիկ
հայելուն` նրանց
մեծ մասը բյուրեղից
դուրս է գալիս
կոհերենտ, վառ
կարմիր գույնի
փնջի տեսքով:
անցումների
հետևանքով
սկսում են բոլոր
ուղղություններով
ֆոտոններ ճառագայթվել:
Այն ֆոտոնները,
որոնք բյուրեղի
առանցքի նկատմամբ
անկյան տակ են
շարժվում, նրանից
դուրս են գալիս
և հետագա պրոցեսներում
ոչ մի դեր չեն խաղում:
Իսկ այն ֆոտոնները,
որոնք շարժվում
են բյուրեղի առանցքի
ուղղությամբ, իրենց
շարժման ժամանակ
առաջ են բերում
նոր ատոմների
հարկադրական ճառագայթումներ,
և ֆոտոնների թիվը
շատ արագ ավելանում
է: Ճառագայթները
հասնելով հայելուն,
անդրադառնում
են` ճանապարհին
անընդհատ ավելանալով:
Հասնելով թափանցիկ
հայելուն` նրանց
մեծ մասը բյուրեղից
դուրս է գալիս
կոհերենտ, վառ
կարմիր գույնի
փնջի տեսքով:
Նկարագրված պրոցեսները սխեմատիկորեն պատկերված են նկ.9.15-ում: Մինչև իմպուլսի սկիզբը քրոմի իոնները գտնվում են հիմնական վիճակում (սև շրջանակները նկ.9.15ա-ում): Ներմղման լույսը (հոծ սլաքները նկ.9.15բ-ում) իոնների մեծ մասը տեղափոխում է գրգռված վիճակի (բաց շրջանակներ): Հեղեղը սկսում է զարգանալ, երբ գրգռված իոնները բյուրեղի առանցքին զուգահեռ ուղղությամբ ինքնակամորեն առաքում են ֆոտոններ (կետագծային սլաքները նկ.9.15գ-ում):

Ֆոտոնները բազմանում են ի հաշիվ ստիպողական ճառագայթման: Այս պրոցեսը զարգանում է (նկ.9.15, դ և ե), քանի որ ֆոտոնները բազմիցս անցնում են բյուրեղի երկայնքով` անդրադառնալով նրա կտրվածքներից: Երբ փունջը դառնում է բավականաչափ ինտենսիվ, նրա մի մասը դուրս է գալիս բյուրեղի կիսաթափանցիկ կտրվածքից (նկ.9.15զ):
Սուտակե լազերներն աշխատում են իմպուլսային ռեժիմով (կրկնվելու հաճախությունը րոպեում մի քանի իմպուլսի կարգի է): Բյուրեղի ներսում անջատվում է մեծ քանակությամբ ջերմաքանակ: Ուստի հարկ է լինում այն ինտենսիվորեն սառեցնել, որն իրակնացվում է հեղուկ օդի օգնությամբ:
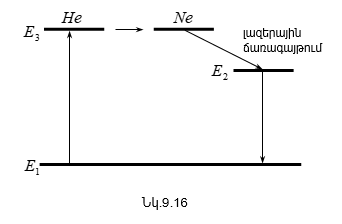
1961թ. ստեղծվեց Ջավանի առաջարկած գազային լազերը, որն աշխատում է հելիումի և նեոնի խառնուրդով: Նրանում ներմղումն իրականացվում է էլեկտրական մարմանդ պարպման հաշվին: Պարպման խողովակը լցվում է 1մմ սնդ. սյան ճնշման տակ գտնվող հելիումի և 0,1մմ սնդ. սյան ճնշման տակ գտնվող նեոնի խառնուրդով: Խողովակի ծայրերին կան հարթ-զուգահեռ հայելիներ, որոնցից մեկը կիսաթափանցիկ է: Հելիումի ատոմներն էլեկտրոնների հետ հարվածների հաշվին անցնում են E3 գրգռված վիճակի: Գրգռված հելիումի ատոմները նեոնի ատոմների հետ բախումների արդյունքում, վերջինները նույնպես գրգռվում են և անցնում են նեոնի վերին մակարդակներից մեկը, որը մոտ է դասավորված համապատասխան հելիումի մակարդակին: Նեոնի ատոմների անցումն այդ մակարդակից E2 ներքևի մակարդակներից մեկն ուղեկցվում է լազերի ճառագայթումով: Նկ.9.16-ում պատկերված է այդպիսի լազերի երեք էներգետիկ մակարդակով պարզագույն դիագրամը: Ակտիվ միջավայրում ձնահյուսի նման լույսի ինտենսիվության ուժեղացումը նշանակում է, որ այդպիսի միջավայրը գործում է որպես էլեկտրամագնիսական ալիքների ուժեղացուցիչ: Գազային լազերներն աշխատում են անընդհատ ռեժիմով և ինտենսիվ սառեցման կարիք չեն զգում:
Լազերները լայն կիրառություն են գտել կենցաղում և ժամանակակից տեխնիկայում: Լազերային ճառագայթումն աչքի է ընկնում մի շարք առանձնահատկություններով: Նրան բնորոշ են.1) ժամանակային և տարածական կոհերենտությունը, 2) խիստ մեներանգությունը, 3) մեծ ինտենսիվությունը և 4) փնջի նեղությունը:
Ճառագայթման
բարձր կոհերենտությունը
լազերների օգտագործման
լայն հեռանկարներ
է բացում ռադիոկապի
նպատակների, մասնավորապես
տիեզերքում` ուղղված
ռադիոկապի համար:
Եթե գտնվի լույսը
մոդուլացնելու
և ապամոդուլացնելու
մեթոդ, ապա կարելի
կլինի հաղորդել
հսկայական ծավալի
տեղեկատվություն:
Կիրառության ուղղություններից
մեկը կապված է
այն հանգամանքի
հետ, որ հնարավոր
է լինում լույսի
նեղ փնջում կենտրոնացնել
մեծ հզորություն
(մինչև տասնյակ
մեգավատտ): Հզորության
այդքան բարձր խտության
լուսային փնջերը
կարելի է օգտագործել
մեխնիկական մշակման
և զոդման համար,
քիմիական ռեակցիաների
ընթացքի վրա ազդելու
համար: Լազերային
ճառագայթով գեոդեզիայում
կատարում են հեռավորությունների,
ինքնաթիռների,
նավերի, հրթիռների
արագությունների
չափումներ և շարժման
ուղղությունների
շտկումներ: Օրինակ,
1970թ. նոյեմբերի 17-ին
«Լուսին -17» ավտոմատ
կայանը Լուսնի
մակերևույթի
վրա հասցրեց «Լուսնագնաց-1»
շարժական լաբորատորիան:
Լուսնագնացի վրա
տեղադրված էր լազերային
անդրադարձիչ: Ըստ
լազերային ճառագայթի
վազքի ժամանակի,
որն ուղարկվում
էր Երկրից և անդրադառնում
էր լուսնագնացի
անդրադարձչից,
ճշգրիտ չափվել
է Երկրից մինչև
Լուսին եղած հեռավորությունը:
Լազերների օգնությամբ
կարելի է չափել
ոչ միայն աստղագիտական,
այլ նաև փոքր հեռավորությունները:
Փոքր հեռավորությունները
չափելու համար
ստեղծվել է մի
հետաքրքիր սարք`
լազերային ինտերֆերաչափը,
որի օգնությամբ
չափվել է երկրակեղևի
դեֆորմացիան ![]() մ սխալի
ճշտությամբ: Լազերային
ճառագայթի միջոցով
կարելի է կատարել
վիրահատություններ,
օրինակ` «եռակցել»
աչքի հատակի շերտազատված
ցանցաթաղանթը,
կտրել-հեռացնել
ուռուցքները: Լազերներն
օգտագործվում
են ձայնի, հեռուստատեսային
պատկերների բարձրորակ
տեսագրությունների
ժամանակ: Լազերային
ճառագայթումն
իր կիրառությունն
է գտել հոլոգրաֆիայում:
մ սխալի
ճշտությամբ: Լազերային
ճառագայթի միջոցով
կարելի է կատարել
վիրահատություններ,
օրինակ` «եռակցել»
աչքի հատակի շերտազատված
ցանցաթաղանթը,
կտրել-հեռացնել
ուռուցքները: Լազերներն
օգտագործվում
են ձայնի, հեռուստատեսային
պատկերների բարձրորակ
տեսագրությունների
ժամանակ: Լազերային
ճառագայթումն
իր կիրառությունն
է գտել հոլոգրաֆիայում:
Վերը ասվածն ամենևին չի սպառում լազերի բոլոր հնարավորությունները: Դա լույսի աղբյուրի միանգամայն նոր տեսակ է, և առայժմ դժվար է պատկերացնել նրա կիրառման բոլոր հնարավոր ասպարեզները:
1. Լույսի ինտերֆերենցիա
Խնդիր
1.1. Երկու
զուգահեռ լուսային
փնջեր, որոնք գտնվում
են իրարից d=5սմ
հեռավորության
վրա, ընկնում են
![]() բեկող անկյուն
ունեցող քվարցե
պրիզմայի վրա:
Որոշել այդ փնջերի
բեկող անկյուն
ունեցող քվարցե
պրիզմայի վրա:
Որոշել այդ փնջերի
![]() ընթացքի
օպտիկական տարբերությունը:
Պրիզմայի բեկման
ցուցիչը` n=1,49:
ընթացքի
օպտիկական տարբերությունը:
Պրիզմայի բեկման
ցուցիչը` n=1,49:
Լուծում: Ընթացքի օպտիկական տարբերությունը`
![]()
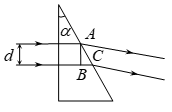
Նկարից
երևում է, որ ![]() հետեվաբար`
հետեվաբար`
![]() Տեղադրելով վերջինի
մեջ մտնող մեծությունների
թվային արժեքները`
կստանանք
Տեղադրելով վերջինի
մեջ մտնող մեծությունների
թվային արժեքները`
կստանանք ![]()
Խնդիր
1.2. Յունգի
փորձում ճեղքերի
միջև հեռավորությունը`d=1մմ-ի,
իսկ ճեղքերից մինչև
էկրանը եղած ![]() հեռավորությունը
3մ է : Որոշել
հեռավորությունը
3մ է : Որոշել
1) առաջին լուսավոր շերտի դիրքը,
2) երրորդ
մութ շերտի դիրքը,
եթե ճեղքերը լուսավորվում
են ![]() ալիքի երկարության
մեներանգ լույսով:
ալիքի երկարության
մեներանգ լույսով:
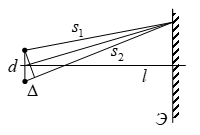
Լուծում: Օգտվենք ինտերֆերենցիոն մաքսիմումի`
![]()
և մինիմումի պայմաններից
![]()
Ընթացքների
տարբերությունը`
![]() Նկարից օգտվելով`
դժվար չէ ցույց
տալ, որ
Նկարից օգտվելով`
դժվար չէ ցույց
տալ, որ

(1)-ը և (3)-ը հավասարեցնելով իրար կստանանք`
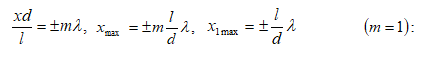
Համանմանորեն (2)-ից և (3)-ից կստանանք`
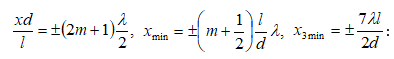
Տեղադրելով
վերջինների մեջ
մտնող մեծությունների
թվային արժեքները`
կստանանք. ![]()
Խնդիր
1.3. Ֆրենելի
հայելիներով փորձում
լույսի աղբյուրի
կեղծ պատկերների
միջև հեռավորությունը`
d=0.5մմ է, իսկ նրանցից
մինչև էկրանը
եղած հեռավորությունը`
![]() է: Դեղին լույսում
ինտերֆերենցիոն
շերտի լայնությունը`
է: Դեղին լույսում
ինտերֆերենցիոն
շերտի լայնությունը`
![]() Գտնել դեղին
լույսի ալիքի
երկարությունը:
Գտնել դեղին
լույսի ալիքի
երկարությունը:
Լուծում: Օգտվենք ինտեֆերենցիոն մաքսիմումի պայմանից`
![]()
Մյուս կողմից`
![]()
Հավասարեցնելով
(1) և (2) հավասարումները`
ստանում ենք ![]() որտեղից
որտեղից
![]() Ինտերֆերենցիոն
շերտի լայնության
համար կստանանք`
Ինտերֆերենցիոն
շերտի լայնության
համար կստանանք`
![]() որտեղից էլ ալիքի
երկարության համար
կունենանք`
որտեղից էլ ալիքի
երկարության համար
կունենանք` ![]() Թվային
արժեքները տեղադրելով`
ստանում ենք`
Թվային
արժեքները տեղադրելով`
ստանում ենք` ![]()
Խնդիր1.4. Որոշել,
թե Ֆրենելի հայելիներով
փորձում քանի անգամ
կփոփոխվի ինտերֆերենցիոն
շերտերի լայնությունը,
եթե մանուշակագույն
![]() լուսազտիչը փոխարինվի
կարմիրով
լուսազտիչը փոխարինվի
կարմիրով ![]()
Լուծում: Դարձյալ օգտվենք մաքսիմումի պայմանից`
![]()
Վերջինից օգտվելով` ինտերֆերենցիոն շերտի լայնության համար ստանում ենք`
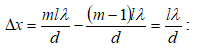
Հետևաբար`
![]()
Խնդիր1.5. Ֆրենելի
բիպրիզմայից մինչև
նեղ ճեղքերը և
էկրանը եղած հեռավորությունը
համապատասխանաբար`
![]() Երկպրիզման
ապակուց է, որի
բեկող անկյունը`
Երկպրիզման
ապակուց է, որի
բեկող անկյունը`
![]() Որոշել լույսի
ալիքի երկարությունը,
եթե ինտերֆերենցիոն
Որոշել լույսի
ալիքի երկարությունը,
եթե ինտերֆերենցիոն
շերտերի
լայնությունը`
![]()
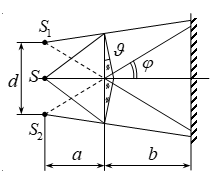
Լուծում:
Պրիզմայում
ճառագայթի շեղումը
որոշվում է` ![]() պայմանից:
Ինտերֆերենցիոն
շերտի լայնությունը`
պայմանից:
Ինտերֆերենցիոն
շերտի լայնությունը`
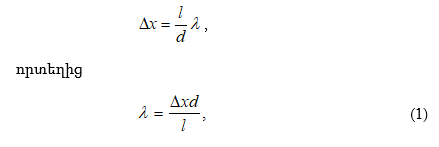
որտեղ
![]() Նկարից հետևում
է, որ
Նկարից հետևում
է, որ
![]()
Նկատի ունենալով (2)-ը` (1)-ից կստանանք`

![]()
Տեղադրելով
(3)-ի մեջ մտնող մեծությունների
թվային արժեքները,
ալիքի երկարության
համար ստանում
ենք` ![]()
2. Լույսի դիֆրակցիան
Խնդիր
2.1. Լույսի
![]() կետային աղբյուրը
տեղադրված է d=2մմ
տրամագծով կլոր
անցքով դիաֆրագմայի
առաջ
կետային աղբյուրը
տեղադրված է d=2մմ
տրամագծով կլոր
անցքով դիաֆրագմայի
առաջ ![]() հեռավորության
վրա: Որոշել դիաֆրագմայից
մինչև դիտման կետը
եղած b հեռավորությունը,
եթե անցքը բաց
է թողնում Ֆրենելի
երեք գոտիները:
հեռավորության
վրա: Որոշել դիաֆրագմայից
մինչև դիտման կետը
եղած b հեռավորությունը,
եթե անցքը բաց
է թողնում Ֆրենելի
երեք գոտիները:
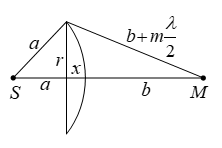
Լուծում: Նկարից երևում է, որ գոտու շառավիղը`
![]()
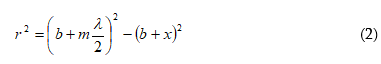
(1)-ը հավասարեցնելով (2)-ին և լուծելով x-ի նկատմամբ` կստանանք`

Նկատի ունենալով (3)-ը` (1)-ից ստանում ենք`
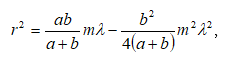
Քանի որ
![]() շատ փոքր է
շատ փոքր է ![]() փոքր լինելու
պատճառով, ուստի
կարող ենք գրել.
փոքր լինելու
պատճառով, ուստի
կարող ենք գրել.

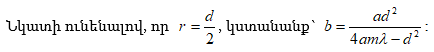
Վերջինի մեջ տեղադրելով թվային արժեքները ստանում ենք` b=2մ:
Խնդիր
2.2. Որոշել
Ֆրենելի երրորդ
գոտու շառավիղը
հարթ ալիքի համար:
Ալիքային մակերևույթից
մինչև դիտման կետը
եղած հեռավորությունը`
b=1.5մ է: Ալիքի երկարությունը`
![]()
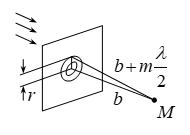
Լուծում: Նկարից օգտվելով` կարող ենք գրել.
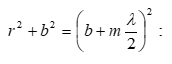
Փակագծերը բացելով և որոշ ձևափոխություններ կատարելով` ստանում ենք`
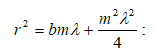
Քանի
որ ![]() հետևաբար
հետևաբար ![]() Տեղադրելով
թվային արժեքները
ստանում ենք` r=1,64մմ:
Տեղադրելով
թվային արժեքները
ստանում ենք` r=1,64մմ:
Խնդիր
2.3. Մեներանգ
լույսի ![]() դիֆրակցիան
դիտվում է կետային
աղբյուրից
դիֆրակցիան
դիտվում է կետային
աղբյուրից ![]() հեռավորության
վրա: Լույսի աղբյուրի
և էկրանի մեջտեղում
գտնվում է d=5մմ
տրամագծով կլոր
անթափանց սկավառակ:
հեռավորության
վրա: Լույսի աղբյուրի
և էկրանի մեջտեղում
գտնվում է d=5մմ
տրամագծով կլոր
անթափանց սկավառակ:

Որոշել
![]() հեռավորությունը,
եթե սկավառակը
փակում է Ֆրենելի
կենտրոնական գոտին:
հեռավորությունը,
եթե սկավառակը
փակում է Ֆրենելի
կենտրոնական գոտին:
Լուծում: Օգտվելով նկարից կարող ենք գրել`
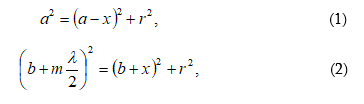
(1)-ից և (2)-ից հետևում է.
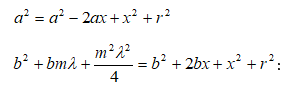
Նկատի
ունենալով, որ
![]() շատ փոքր են և
հաշվի առնելով,որ
շատ փոքր են և
հաշվի առնելով,որ
![]() վերջին
երկու հավասարումներից
կստանանք`
վերջին
երկու հավասարումներից
կստանանք`
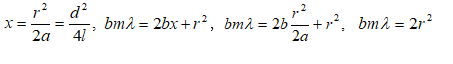
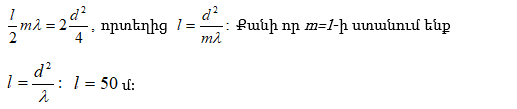
Խնդիր
2.4. ![]() մմ լայնության
նեղ ճեղքի վրա
ուղղահայաց ընկնում
է
մմ լայնության
նեղ ճեղքի վրա
ուղղահայաց ընկնում
է ![]() նմ ալիքի
երկարության
մեներանգ լույս:
Որոշել լույսի
ուղղությունը
(լույսի սկզբնական
ուղղության նկատմամբ)
երկրորդ դիֆրակցիոն
շերտի վրա:
նմ ալիքի
երկարության
մեներանգ լույս:
Որոշել լույսի
ուղղությունը
(լույսի սկզբնական
ուղղության նկատմամբ)
երկրորդ դիֆրակցիոն
շերտի վրա:
Լուծում:
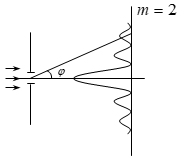
Օգտվենք մեկ ճեղքի դեպքում դիֆրակցիոն առավելագույնի պայմանից.
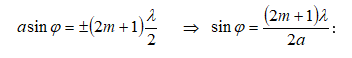
![]() Տեղադրելով
թվային արժեքները`
ստանում ենք`
Տեղադրելով
թվային արժեքները`
ստանում ենք` ![]()
Խնդիր
2.5. Դիֆրակցիոն
ցանցի վրա ուղղահայաց
ընկնում է ![]() ալիքի
երկարության մեներանգ
լույս: Որոշել
այդ ցանցով սպեկտրի
ամենամեծ կարգը,
երե ցանցի հաստատունը
` d=2մկմ:
ալիքի
երկարության մեներանգ
լույս: Որոշել
այդ ցանցով սպեկտրի
ամենամեծ կարգը,
երե ցանցի հաստատունը
` d=2մկմ:
Լուծում:
Դիֆրակցիոն ցանցում
առավելագույնի
պայմանը որոշվում
է հետևյալ բանաձևով`
![]()
![]()
Խնդիր
2.6. ![]() երկարության
դիֆրակցիոն ցանցի
վրա, որը պարունակում
է N=3000 գծեր, ուղղահայաց
ընկնում է
երկարության
դիֆրակցիոն ցանցի
վրա, որը պարունակում
է N=3000 գծեր, ուղղահայաց
ընկնում է ![]() ալիքի
երկարության մեներանգ
լույս: Որոշել
1) առավելագույնների
թիվը, որը դիտվում
է դիֆրակցիոն ցանցի
սպեկտրում, 2) վերջին
առավելագույնին
համապատասխանող
անկյունը:
ալիքի
երկարության մեներանգ
լույս: Որոշել
1) առավելագույնների
թիվը, որը դիտվում
է դիֆրակցիոն ցանցի
սպեկտրում, 2) վերջին
առավելագույնին
համապատասխանող
անկյունը:
Լուծում: Օգտվենք դիֆրակցիոն առավելագույնի պայմանից.
![]()
Դիֆրակցիոն
ցանցի հաստատունը`
![]()
Առավելագույնների
թիվը` ![]() Վերջին
առավելագույնին
համապատասխանող
անկյունը կարող
ենք գտնել հետևյալ
պայմանից`
Վերջին
առավելագույնին
համապատասխանող
անկյունը կարող
ենք գտնել հետևյալ
պայմանից`
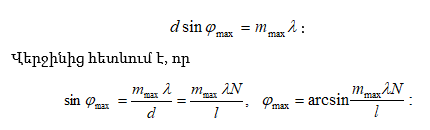
Թվային արժեքները տեղադրելով` ստանում ենք`
![]()
Խնդիր
2.7. ![]() ալիքի
երկարության ռենտգենյան
ճառագայթման նեղ
փունջը
ալիքի
երկարության ռենտգենյան
ճառագայթման նեղ
փունջը![]() սահքի
անկյան տակ ընկնում
է բնական
սահքի
անկյան տակ ընկնում
է բնական ![]() միաբյուրեղի
նիստի վրա, որի
խտությունը`
միաբյուրեղի
նիստի վրա, որի
խտությունը` ![]() Որոշել
սահքի անկյունը,
եթե այդ նիստից
հայելային անդրադարձման
դեպքում դիտվում
է երկրորդ կարգի
առավելագույն:
Որոշել
սահքի անկյունը,
եթե այդ նիստից
հայելային անդրադարձման
դեպքում դիտվում
է երկրորդ կարգի
առավելագույն:
Լուծում: Տարածական ցանցում դիֆրակցիոն առավելագույնները որոշվում են Վուլֆ-Բրեգի բանաձևով`
![]()
![]() Յուրաքանչյուր
իոն մտնում է 8 բջջի
մեջ: Մեկ մոլում
կան
Յուրաքանչյուր
իոն մտնում է 8 բջջի
մեջ: Մեկ մոլում
կան ![]() բջիջ:
բջիջ:
Դիֆրակցիոն
ցանցի հաստատունը`
![]() որտեղ
որտեղ ![]() Նկատի
ունենալով վերջինները`
ստանում ենք`
Նկատի
ունենալով վերջինները`
ստանում ենք`
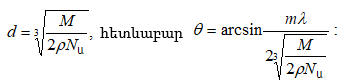
Տեղադրելով
թվային արժեքները`
![]()
3. Լույսի բևեռացումը
Խնդիր
3.1. Որոշել
ապակու բեկման
ցուցիչը , եթե նրանից
լույսն անդրադառնալիս
անդրադարձած ճառագայթը
![]() բեկման անկյան
դեպքում լրիվ բևեռացված
է:
բեկման անկյան
դեպքում լրիվ բևեռացված
է:
Լուծում:
Համաձայն
լույսի բեկման
օրենքի` ![]()
Լրիվ բևեռացման
դեպքում անկման
անկյունը հավասար
է Բրյուստերի անկյանը`
![]()

Խնդիր 3.2. Որոշել մասնակի բևեռացած լույսի բևեռացման աստիճանը, եթե նրան համապատասխանող լույսի առավելագույն ինտենսիվությանը համապատասխանող լուսային վեկտորի լայնույթը երեք անգամ մեծ է ինտնսիվության նվազագույնին համապատասխանող լայնույթից:
Լուծում: Բևեռացման աստիճանը որոշվում է հետևյալ բանաձևով`
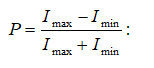
Քանի
որ ![]() կստանանք`
կստանանք`
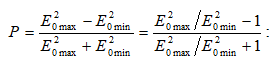
Կատարելով հաշվարկը` ստանում ենք` P=0,8:
Խնդիր 3.3. Բևեռացուցչի և վերլուծիչի գլխավոր հարթություններով կազմած անկյունը 300 է: Որոշել նրանց միջով անցնող լույսի ինտենսիվության փոփոխությունը, եթե նրանց գխավոր հարթությունների միջև անկյունը 450 է:
Լուծում: Համաձայն Մալյուսի օրենքի` առաջին դեպքում անալիզատորով դուրս եկած լույսի ինտենսիվությունը`
![]()
Համանմանորեն երկրորդ դեպքում`
![]()
Բաժանելով (1)-ը (2)-ի վրա` կստանանք.
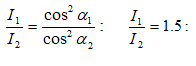
Խնդիր
3.4. Որոշել,
թե քանի անգամ
կթուլանա երկու
նիկոլներով անցնող
լույսի ինտենսիվությունը,
որոնք դասավորված
են այնպես, որ նրանց
գլխավոր հարթությունների
միջև անկյունը`
![]() եթե նիկոլներից
յուրաքանչյուրում
կորչում է ընկնող
լույսի 8%-ը:
եթե նիկոլներից
յուրաքանչյուրում
կորչում է ընկնող
լույսի 8%-ը:
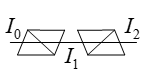
Լուծում: Առաջին նիկոլով անցնող լույսի ինտենսիվությունը`
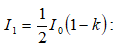
Համաձայն Մալյուսի օրենքի` երկրորդ նիկոլով անցնող լույսի ինտենսիվությունը`
![]()
Նկատի ունենալով արժեքը` կունենանք.
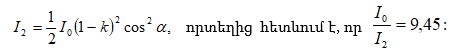
4. Էլետրամագնիսական ալիքի փոխազդեցությունը նյութի հետ
Խնդիր
4.1. Ապացուցել,
որ եթե մեներանգ
լույսի փունջն
ընկնում է n բեկման
ցուցիչ ունեցող
պրիզմայի նիստի
վրա փոքր անկյան
տակ, ապա պրիզմայի
փոքր բեկող ![]() անկյան
դեպքում ճառագայթների
շեղման
անկյան
դեպքում ճառագայթների
շեղման ![]() անկյունը
կախում չունի անկման
անկյունից և հավասար
է
անկյունը
կախում չունի անկման
անկյունից և հավասար
է ![]()
Լուծում: Լույսի
մեներանգ փունջն
անցնելով պրիզմայի
միջով` լույսի
ճառագայթները
ենթարկվում են
բեկման, որի հետևանքով
ճառագայթը պրիզմայից
դուրս գալիս խոտորված
է լինում ![]() անկյունով.
անկյունով.
![]()
Դժվար չէ նկարում տեսնել, որ
![]()
Oգտվելով բեկման օրենքից` կարող ենք գրել`

Երբ
պրիզմայի բեկող
անկյունը փոքր
է, և փոքր է նմանապես
անկման ![]() անկյունը,
շեղման անկյան
արտահայտությունը
պարզ տեսք է ստանում,
որովհետև մնացած
բոլոր անկյուններն
էլ`
անկյունը,
շեղման անկյան
արտահայտությունը
պարզ տեսք է ստանում,
որովհետև մնացած
բոլոր անկյուններն
էլ` ![]() նույնպես
փոքր կլինեն, և
այդ անկյունների
սինուսների փոխարեն
կարելի է վերցնել
հենց իրենց անկյունների
արժեքները: Այդ
դեպքում (3)-ից կստանանք`
նույնպես
փոքր կլինեն, և
այդ անկյունների
սինուսների փոխարեն
կարելի է վերցնել
հենց իրենց անկյունների
արժեքները: Այդ
դեպքում (3)-ից կստանանք`
![]() Վերջիններից
հետևում է, որ
Վերջիններից
հետևում է, որ ![]() Նկատի
ունենալով (2)-ը` կարող
ենք գրել`
Նկատի
ունենալով (2)-ը` կարող
ենք գրել`
![]()
Նկատի ունենալով (4)-ը` (1)-ից կստանանք
![]()
Այսպիսով`
![]()
Խնդիր
4.2. ![]() հաճախության
էլեկտրամագնիսական
ալիքը տարածվում
է նոսրացված պլազմայում:
Ազատ էլեկտրոնների
կոնցենտրացիան
պլազմայի մեջ
հաճախության
էլեկտրամագնիսական
ալիքը տարածվում
է նոսրացված պլազմայում:
Ազատ էլեկտրոնների
կոնցենտրացիան
պլազմայի մեջ ![]() է: Որոշել
պլազմայի
է: Որոշել
պլազմայի ![]() դիէլեկտրական
թափանցելիության
կախումը
դիէլեկտրական
թափանցելիության
կախումը ![]() հաճախությունից:
Ալիքների փոխազդեցությունը
պլազմայի իոնների
հետ անտեսել:
հաճախությունից:
Ալիքների փոխազդեցությունը
պլազմայի իոնների
հետ անտեսել:
Լուծում: Դիէլեկտրական թափանցելիությունը կարելի որոշել հետեվյալ բանաձևով`
![]() P-ն բևեռացման
վեկտորի պրոեկցիան
է
P-ն բևեռացման
վեկտորի պրոեկցիան
է ![]() ուղղության վրա,
ուղղության վրա,
![]() դաշտի լարվածությունն
է:
դաշտի լարվածությունն
է: ![]() հետևաբար
հետևաբար

Նկատի
ունենալով, որ
![]() Լուծելով էլեկտրոնի
համար հետևյալ
դիֆերենցիալ հավասարումը`
Լուծելով էլեկտրոնի
համար հետևյալ
դիֆերենցիալ հավասարումը`
![]() A-ի
համար ստանում
ենք`
A-ի
համար ստանում
ենք`
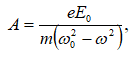
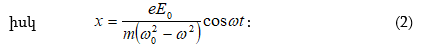
Նկատի ունենալով (2)-ը և E-ի արժեքը` կստանանք.
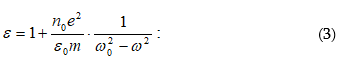
Ընդունելով
![]()
Խնդիր 4.3. Ինչ-որ նյութի միջով լույսն անցնելով x ճանապարհ` ինտենսիվությունը փոքրացավ 3 անգամ: Որոշել, թե քանի անգամ կփոքրանա լույսի ինտենսիվությունը 2x ճանապարհն անցնելու դեպքում:
Լուծում: Լույս
նյութի միջով անցնելիս
նրա ինտենսիվությունը
փոփոխվում է հետևյալ
օրենքով` ![]()
![]() Ըստ խնդրի
պայմանի
Ըստ խնդրի
պայմանի ![]() որտեղից
հետևում է, որ
որտեղից
հետևում է, որ ![]()
2x
ճանապարհի
վրա ![]()
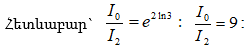
Խնդիր
4.4. Լույսն
ընկնում է ուղղահայաց
հաջորդաբար միևնույն
նյութից պատրաստված
երկու թիթեղների
վրա, որոնք համապատասխանաբար
ունեն ![]() և
և ![]() հաստություններ:
Որոշել այդ նյութի
կլանման գործակիցը,
եթե առաջին թիթեղով
անցնող լույսի
ինտենսիվությունը
կազմում է սկզբնական
լույսի ինտենսիվության
82%-ը, իսկ երկրորդով`
67%-ը:
հաստություններ:
Որոշել այդ նյութի
կլանման գործակիցը,
եթե առաջին թիթեղով
անցնող լույսի
ինտենսիվությունը
կազմում է սկզբնական
լույսի ինտենսիվության
82%-ը, իսկ երկրորդով`
67%-ը:
Լուծում: Ինտենսիվությունների փոփոխությունները, երբ լույսն անցնում է առաջին և երկրորդ թիթեղներով`
![]()
Հավասարումները բաժանելով իրար` կստանանք

![]()
5. Ճառագայթման քվանտային բնույթը
Խնդիր 5.1. Մուֆելային վառարանի ներքին ջերմաստիճանը S=30սմ2 մակերեսով բաց անցքի դեպքում` T=1300Կ: Ընդունելով, որ վառարանի անցքը ճառագայթում է որպես բացարձակ սև մարմին` որոշել, թե հզորության որ մասն է ցրվում պատերի կողմից, եթե վառարանի պահանջվող հզորությունը կազմում է`P=1500Վտ:
Լուծում: Ճառագայթած
հզորությունը`
![]() Պատերի կողմից
ցրված հզորությունը`
Պատերի կողմից
ցրված հզորությունը`
![]() Այսպիսով`
Այսպիսով`
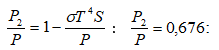
Խնդիր
5.2. Որոշել
թե ինչպես և քանի
անգամ կփոփոխվի
բացարձակ սև մարմնի
ճառագայթման հզորությունը,
եթե ալիքի երկարությունը,
որը համապատասխանում
է նրա էներգետիկ
լուսատվության
խտության առավելագույնին,
շեղվում է ![]()
Լուծում: Համաձայն Վինի շեղման օրենքի` կարող ենք գրել
![]()
Ճառագայթման հզորությունները`
![]()
Վերջին երկու հավասարումներից հետևում է.
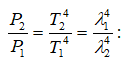
Տեղադրելով
թվային արժեքները`
ստանում ենք` ![]()
Խնդիր
5.3. Ընդունելով,
որ ջերմային կորուստները
պայմանավորված
են միայն ճառագայթումով,
որոշել թե ինչպիսի
հզորություն է
անհրաժեշտ մատուցել
d=2սմ տրամագծով
պղնձյա գնդիկին,
որպեսզի շրջապատող
միջավայրի To=260կ
ջերմաստիճանի
դեպքում նրա ջերմաստիճանը
պահպանվի հավասար
T=290Կ: Պղնձի կլանման
ընդունակությունը
ընդունել` ![]()
Լուծում: Ճառագայթման և կլանման հզորությունները որոշվում են հետևյալ բանաձևերով`
![]()
Քանի
որ ![]() պահանջվող
հզորությունը`
պահանջվող
հզորությունը`
![]()
Տեղադրելով մեծությունների թվային արժեքները` ստանում ենք` P=0,107Վտ:
Խնդիր:
5.4. Նիկելի
համար լուսաէֆեկտի
կարմիր սահմանը`
![]() Գտնել նիկելե
էլեկտրոդի վրա
ընկնող լույսի
ալիքի երկարությունը,
եթե լուսահոսանքը
դադարում է U=1,5Վ
արգելակող պոտենցիալների
տարբերության
դեպքում:
Գտնել նիկելե
էլեկտրոդի վրա
ընկնող լույսի
ալիքի երկարությունը,
եթե լուսահոսանքը
դադարում է U=1,5Վ
արգելակող պոտենցիալների
տարբերության
դեպքում:
Լուծում: Համաձայն արտաքին լուսաէֆեկտի համար Այնշտայնի հավասարման

որտեղ
h-ը Պլանկի հաստատունն
է, c-ն` լույսի արագությունը,
![]() լույսի ալիքի
երկարությունը,
A-ն` մետաղից էլեկտրոնի
ելքի աշխատանքը,
լույսի ալիքի
երկարությունը,
A-ն` մետաղից էլեկտրոնի
ելքի աշխատանքը,
![]() լուսաէլեկտրոնների
առավելագույն
կինետիկ էներգիան:
լուսաէլեկտրոնների
առավելագույն
կինետիկ էներգիան:
Լուսաէֆեկտի կարմիր սահմանը որոշվում է հետևյալ պայմանից`

Լուսաէլեկտրոնների
առավելագույն
կինետիկ էներգիան
կարող է որոշվել
արգելակող ![]() պոտենցիալների
տարբերության
միջոցով.
պոտենցիալների
տարբերության
միջոցով.
![]()
որտեղ e-ն էլեկտրոնի լիցքն է:
Տեղադրելով (2) և (3) արտահայտությունները (1)-ի մեջ` կստանանք`

(4) հավասարումից կգտնենք լույսի ալիքի երկարությունը.
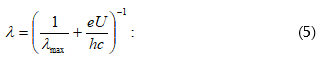
Տեղադրելով
(5) -ի մեջ մտնող մեծությունների
թվային արժեքները`
կստանանք` ![]()
Խնդիր
5.5. ![]() ալիքի
երկարության մեներանգ
լույսի ճնշումը
ճառագայթների
անկմանն ուղղահայաց
դասավորված սևացրած
մակերևույթի վրա
հավասար է` p=0,12մկՊա:
Որոշել յուրաքանչյուր
վայրկյանում 1մ2
մակերևույթի վրա
ընկնող ֆոտոնների
թիվը:
ալիքի
երկարության մեներանգ
լույսի ճնշումը
ճառագայթների
անկմանն ուղղահայաց
դասավորված սևացրած
մակերևույթի վրա
հավասար է` p=0,12մկՊա:
Որոշել յուրաքանչյուր
վայրկյանում 1մ2
մակերևույթի վրա
ընկնող ֆոտոնների
թիվը:
Լուծում: Մակերևույթի վրա ուղղահայաց ընկնող լույսի ճնշումը որոշվում է հետևյալ բանաձևով`

որտեղ
![]() էներգետիկ
լուսավորվածությունն
է, c-ն` լույսի արագությունը,
R-ն մակերևույթի
անդրադարձման
գործակիցն է, որը
տվյալ դեպքում
հավասար է զրոյի:
էներգետիկ
լուսավորվածությունն
է, c-ն` լույսի արագությունը,
R-ն մակերևույթի
անդրադարձման
գործակիցն է, որը
տվյալ դեպքում
հավասար է զրոյի:
![]() հետևաբար
վերջինը տեղադրելով
(1)-ի մեջ կստանանք`
հետևաբար
վերջինը տեղադրելով
(1)-ի մեջ կստանանք`
![]() Ընդունելով,
որ R=0` վերջինից
ֆոտոնների թվի
համար ստանում
ենք`
Ընդունելով,
որ R=0` վերջինից
ֆոտոնների թվի
համար ստանում
ենք`
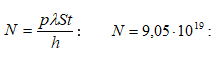
Խնդիր
5.6. ![]() էներգիայով
ֆոտոնի ցրման անկյունը
ազատ էլեկտրոնի
վրա`
էներգիայով
ֆոտոնի ցրման անկյունը
ազատ էլեկտրոնի
վրա` ![]() Գտնել ցրված
ֆոտոնի ալիքի երկարությունը,
էլեկտրոնի էներգիան:
Էլեկտրոնի կինետիկ
էներգիան մինչև
բախումը անտեսել:
Գտնել ցրված
ֆոտոնի ալիքի երկարությունը,
էլեկտրոնի էներգիան:
Էլեկտրոնի կինետիկ
էներգիան մինչև
բախումը անտեսել:
Լուծում: Ֆոտոնի ալիքի երկարության փոփոխությունը կոմպտոնյան ցրման դեպքում հավասար է.

որտեղ
![]() ընկնող
և ցրված ֆոտոնի
ալիքի երկարություններն
են, h-ը Պլանկի հաստատունն
է, mo-ն էլեկտրոնի
հանգստի զանգվածն
է, c-ն լույսի արագությունն
է վակուումում,
ընկնող
և ցրված ֆոտոնի
ալիքի երկարություններն
են, h-ը Պլանկի հաստատունն
է, mo-ն էլեկտրոնի
հանգստի զանգվածն
է, c-ն լույսի արագությունն
է վակուումում,
![]() կոմպտոնյան
ալիքի երկարությունն
է,
կոմպտոնյան
ալիքի երկարությունն
է, ![]() ցրման անկյունը
:
ցրման անկյունը
:
Նկարում
![]() ընկնող և ցրված
ֆոտոնների իմպուլսներն
են:
ընկնող և ցրված
ֆոտոնների իմպուլսներն
են:
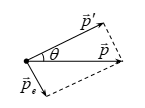
(1) բանաձևից հետևում է.
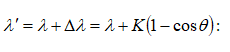

Էլեկտրոնի
էներգիան, համաձայն
էներգիայի պահպանան
օրենքի, հավասար
է ![]() Ալիքի երկարության
փոփոխությունը
արտահայտենք հաճախության
փոփոխությամբ.
Ալիքի երկարության
փոփոխությունը
արտահայտենք հաճախության
փոփոխությամբ.
![]()
Հաշվի առնելով (1)-ը կարելի է գրել`
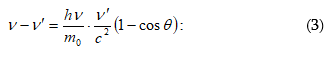
Բազմապատկելով
(3) արտահայտությունը
h-ով և նկատի ունենալով,
![]()

Էլեկտրոնի
հանգստի էներգիան`
![]()
(2)-ի
և (4)-ի մեջ տեղադրելով
մեծությունների
թվային արժեքները`
ստանում ենք` ![]()
6. Ջրածնի ատոմը` ըստ Բորի տեսության
Խնդիր 6.1. Որոշել ֆոտոնի էներգիան, որն առաքվում է, երբ էլեկտրոնը ջրածնի ատոմում երրորդ (n=3) էներգետիկ մակարդակից անցնում է երկրորդին (m=2):
Լուծում: Համաձայն Բորի` երկրորդ կանխադրույթի`
![]()
Մյուս կողմից`
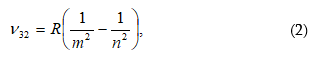
որտեղ
![]() Ռիդբերգի
հաստատունն է:
(2) հավասարման աջ
և ձախ մասերը բազմապատկելով
h-ով` կստանանք`
Ռիդբերգի
հաստատունն է:
(2) հավասարման աջ
և ձախ մասերը բազմապատկելով
h-ով` կստանանք`
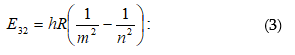
Տեղադրելով
(2)-ի մեջ մտնող մեծությունների
թվային արժեքները`
կստանանք` ![]() էՎ:
էՎ:
Խդիր
6.2. Լայմանի
սերիայի ջրածնային
սպեկտրային գծերի
առավելագույն
ալիքի երկարությունը`
![]() Ընդունելով,
որ Ռիդբերգի հաստատունը
հայտնի է, որոշել
Բալմերի սերիայի
գծերի ամենամեծ
ալիքի երկարությունը:
Ընդունելով,
որ Ռիդբերգի հաստատունը
հայտնի է, որոշել
Բալմերի սերիայի
գծերի ամենամեծ
ալիքի երկարությունը:

Լուծում: Օգտվենք Բալմերի ընդհանրացված բանաձևից`

Լայմանի սերիայի համար m=1, Բալմերի սերիայի համար m=2:: Տված m-ի դեպքում n թիվն ընդունում է բոլոր ամբողջ արժեքները` սկսած (m+1)-ից: Այսպիսով, օգտվելով (1)-ից, Լայմանի և Բալմերի սերիաների համար կարող ենք գրել`
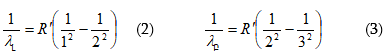
(2) և (3) արտահայտություններից հետևում է, որ
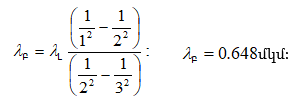
Խնդիր 6.3. Օգտագործելով Բորի տեսությունը` որոշել ջրածնի ատոմի երրորդ ուղեծրով շարժվող էլեկտրոնի ուղեծրային մագնիսական մոմենտը:
Լուծում: Էլեկտրոնի մագնիսական մոմենտը որոշվում է հետևյալ բանաձևով`
![]()
Նկատի
ունենալով, որ
հոսանքի ուժը`
![]() որտեղ
e-ն էլեկտրոնի
լիցքն է, T-ն պարբերությունն
է, S-ը ուղեծրի մակերեսն
է, կարող ենք գրել`
որտեղ
e-ն էլեկտրոնի
լիցքն է, T-ն պարբերությունն
է, S-ը ուղեծրի մակերեսն
է, կարող ենք գրել`
![]() Վեջինները նկատի
ունենալով` (1)-ից
կստանանք`
Վեջինները նկատի
ունենալով` (1)-ից
կստանանք`
![]()
Բորի քվանտացման պայմանից`
![]()
(2) և (3) արտահայտություններից հետևում է, որ

Խնդիր
6.4. Էլեկտրոնը
գրգռված վիճակից
հիմնական վիճակի
անցման դեպքում
արձակում է ![]() ալիքի
երկարության
ֆոտոն: Որոշել
էլեկտրոնի ուղեծրային
մեխանիկական մոմենտի
փոփոխությունը:
ալիքի
երկարության
ֆոտոն: Որոշել
էլեկտրոնի ուղեծրային
մեխանիկական մոմենտի
փոփոխությունը:
Լուծում: Օգտվենք Բորի քվանտացման պայմանից`
![]()
որտեղ
![]() էլեկտրոնի ուղեծրային
մեխանիկական մոմենտն
է: Էլեկտրոնի ուղեծրային
մեխանիկական մոմենտի
փոփոխության համար
կարող ենք գրել`
էլեկտրոնի ուղեծրային
մեխանիկական մոմենտն
է: Էլեկտրոնի ուղեծրային
մեխանիկական մոմենտի
փոփոխության համար
կարող ենք գրել`
![]()
Համաձայն Բալմերի ընդհանրացված բանաձևի`

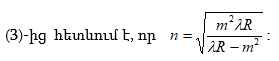
Վերջինը նկատի ունենալով (2)-ից` կստանանք`
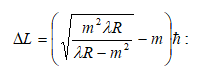
Տեղադրելով
ստացված արտահայտության
մեջ ![]()
7. Քվանտային մեխանիկայի տարրերը
Խնդիր 7.1. Որոշել ջրածնի ատոմի մեջ երրորդ ուղեծրում գտնվող էլեկտրոնի դը բրոլյան ալիքի երկարությունը:
Լուծում: Դը բրոլյան ալիքի երկարությունը որոշվում է հետևյալ բանաձևով`

Ըստ Բորի քվանտացման պայմանի`
![]()
Ջրածնի ատոմում կուլոնյան ուժը էլեկտրոնին հաղորդում է կենտրոնաձիգ արագացում.

Օգտվելով (2)-ից և (3)-ից` էլեկտրոնի արագության համար կստանանք`

(4)-ը տեղադրելով (1)-ի մեջ` ստանում ենք`
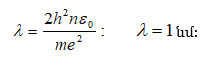
Խնդիր 7.2. Էլեկտրոնի կինետիկ էներգիան` T=1,02ՄէՎ-ի: Որոշել այդ էլեկտրոնի` դը Բրոյլի ալիքի երկարությունը:
Լուծում: Դը Բրոյլի ալիքի երկարությունը որոշվում է հետևյալ բանաձևով.

որտեղ
![]() իմպուլսով մասնիկին
համապատասխանող
ալիքի երկարությունն
է, h-ը Պլանկի հաստատունն
է: Ըստ խնդրի պայմանի
էլեկտրոնի կինետիկ
էներգիան երկու
անգամ մեծ է նրա
հանգստի էներգիայից,
այսինքն`
իմպուլսով մասնիկին
համապատասխանող
ալիքի երկարությունն
է, h-ը Պլանկի հաստատունն
է: Ըստ խնդրի պայմանի
էլեկտրոնի կինետիկ
էներգիան երկու
անգամ մեծ է նրա
հանգստի էներգիայից,
այսինքն`
![]()
Հետևաբար, շարժվող էլեկտրոնը ռելյատիվիստական մասնիկ է: Ռելյատիվիստական մասնիկի իմպուլսը`
![]()
կամ նկատի ունենալով (2) առնչությունը`
![]()
Տեղադրելով (4)-ը (1)-ի մեջ` ստանում ենք`
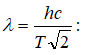

Խնդիր
7.3. Օգտագործելով
Հայզենբերգի անորոշությունների
առնչությունը,
ցույց տալ, որ ատոմների
միջուկները չեն
կարող պարունակել
էլեկտրոններ: Ընդունել
միջուկի շառավիղը`
![]()
Լուծում: Օգտվենք Հայզենբերգի անորոշությունների առնչությունից.
![]()
որտեղ
![]() կոորդինատի
անորոշությունն
է,
կոորդինատի
անորոշությունն
է, ![]() իմպուլսի
անորոշությունն
է, h-ը Պլանկի հաստատունն
է:
իմպուլսի
անորոշությունն
է, h-ը Պլանկի հաստատունն
է:
Եթե
կոորդինատի անորոշությունը
ընդունենք հավասար
միջուկի շառավղին,
այսինքն ![]() ապա էլեկտրոնի
իմպուլսի անորոշությունը`
ապա էլեկտրոնի
իմպուլսի անորոշությունը`
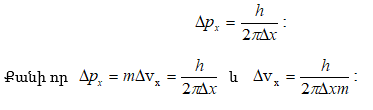
Վերջինից
էլեկտրոնի արագության
անորոշության
համար ստացվում
է` ![]()
Համեմատելով
արագության ստացված
արժեքը վակուումում
լույսի արագության
հետ` տեսնում ենք,
որ ![]() իսկ դա հնարավոր
չէ, հետևաբար, միջուկը
էլեկտրոն չի պարունակում:
իսկ դա հնարավոր
չէ, հետևաբար, միջուկը
էլեկտրոն չի պարունակում:
Խնդիր
7.4. Ինչ-որ
մասնիկի ալիքային
ֆունկցիան ունի
![]() տեսքը, որտեղ
r-ը մասնիկից մինչև
ուժային կենտրոնը
եղած հեռավորությունն
է,
տեսքը, որտեղ
r-ը մասնիկից մինչև
ուժային կենտրոնը
եղած հեռավորությունն
է, ![]() հաստատուն է:
Օգտագործելով
հավանականությունների
նորմավորման պայմանը`
որոշել նորմավորման
A գործակիցը:
հաստատուն է:
Օգտագործելով
հավանականությունների
նորմավորման պայմանը`
որոշել նորմավորման
A գործակիցը:
Լուծում: Նորմավորման պայմանն ունի հետևյալ տեսքը`

Նկարում
երևում է, որ ծավալի
տարրը` ![]()
Վերջինը տեղադրելով (1)-ի մեջ` կստանանք`
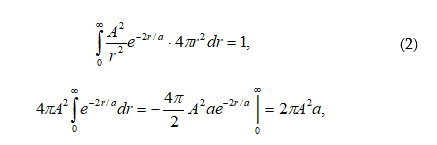
հետևաբար
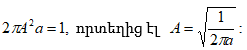
Խնդիր
7.5. Ջրածնի
ատոմի մեջ էլեկտրոնի
հիմնական վիճակը
նկարագրող ալիքային
ֆունկցիան ունի
![]() տեսքը, որտեղ
r-ը էլեկտրոնի
հեռավորությունն
է միջուկից,
տեսքը, որտեղ
r-ը էլեկտրոնի
հեռավորությունն
է միջուկից, ![]() Բորի
առաջին ուղեծրի
շառավիղն է: Որոշել
էլեկտրոնի ամենահավանական
հեռավորությունը
միջուկից:
Բորի
առաջին ուղեծրի
շառավիղն է: Որոշել
էլեկտրոնի ամենահավանական
հեռավորությունը
միջուկից:
Լուծում: Էլեկտրոնի
ծավալի տվյալ տարրում
գտնվելու հավանականությունը
որոշվում է. ![]()
Վերջինը նկատի ունենալով, կստանանք`
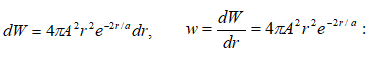
Ածանցելով վերջին արտահայտությունը ըստ r-ի և հավասարեցնելով զրոյի` կստանանք`
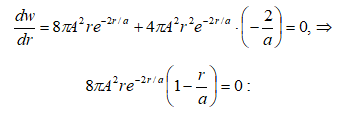
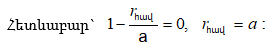
Խնդիր
7.6. E էներգիայով
մասիկը շարժվում
է x-ի առանցքի դրական
ուղղությամբ և
իր ճանապարհին
հանդիպում է անվերջ
լայն ուղղանկյուն
U բարձրությամբ
պոտենցիալ արգելքի,
ընդ որում ![]() Գրել
Շրյոդինգերի
հավասարումը 1
և 2 տիրույթների
համար:
Գրել
Շրյոդինգերի
հավասարումը 1
և 2 տիրույթների
համար:

Լուծում: Շրյոդինգերի հավասարումը 1 և 2 տիրույթների համար կգրվի հետևալ տեսքերով`
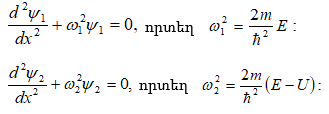
Խնդիր
7.7. Ապացուցել,
որ ![]() ֆունկցիան m
զանգվածով և քվազիառաձգական
ուժի k հաստատունով
ներդաշնակ տատանակի
համար Շրյոդինգերի
հավասարման լուծումն
է: Որոշել տատանակի
լրիվ էներգիայի
սեփական արժեքը:
ֆունկցիան m
զանգվածով և քվազիառաձգական
ուժի k հաստատունով
ներդաշնակ տատանակի
համար Շրյոդինգերի
հավասարման լուծումն
է: Որոշել տատանակի
լրիվ էներգիայի
սեփական արժեքը:
Լուծում: Շրյոդինգերի հավասարումը ներդաշնակ տատանակի համար ունի հետևյալ տեսքը.
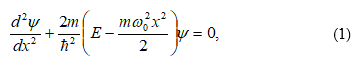
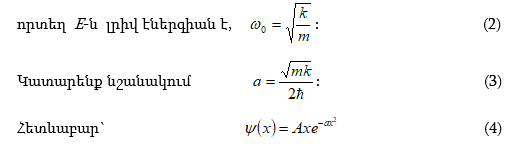
(4)-ը ածանցելով ըստ x-ի` կստանանք`
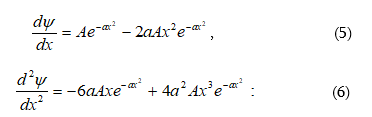
Նկատի ունենալով (5)-ը և (6)-ը` (1)-ց կստանանք`
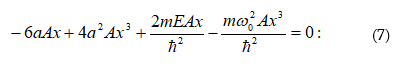
Հաշվի առնելով (2)-ը` (7)-ը կընդունի հետևյալ տեսքը`
![]()
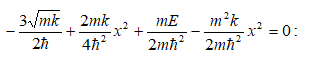
Վերջինից հետևում է, որ
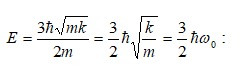
Խնդիր
7.8. Մաթեմատիկական
ճոճանակը ընդունելով
որպես ներդաշնակ
տատանակ` որոշել
Երկրի ձգողական
դաշտում գտնվող
![]() երկարություն
ունեցող ճոճանակի
զրոյական էներգիան`
արտահայտված
էլեկտրոն վոլտերով:
երկարություն
ունեցող ճոճանակի
զրոյական էներգիան`
արտահայտված
էլեկտրոն վոլտերով:
Լուծում: Տատանակի
զրոյական էներգիան
որոշվում է հետևյալ
բանաձևով` ![]()
Մաթեմատիկական ճոճանակի տատանման պարբերությունը`
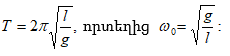
Վերջինը նկատի ունենալով` կստանանք`
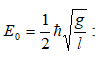
Տեղադրելով
թվային արժեքները`
ստանում ենք` ![]()
Խնդիր
7.9. Որոշել,
թե ![]() վիճակում գտնվող
էլեկտրոնի
վիճակում գտնվող
էլեկտրոնի ![]() ուղեծրային
իմպուլսի մոմենտը
քանի անգամ մեծ
կլինի p վիճակում
գտնվող էլեկտրոնի
ուղեծրային իմպուլսի
մոմենտից:
ուղեծրային
իմպուլսի մոմենտը
քանի անգամ մեծ
կլինի p վիճակում
գտնվող էլեկտրոնի
ուղեծրային իմպուլսի
մոմենտից:
Լուծում: Էլեկտրոնի ուղեծրային իմպուլսի մոմենտը`
![]()
![]() վիճակում
գտնվող էլեկտրոնի
համար
վիճակում
գտնվող էլեկտրոնի
համար ![]() ուստի (1)-ից
ստանում ենք`
ուստի (1)-ից
ստանում ենք`
![]()
Համանմանորեն
p վիճակում գտնվող
էլեկտրոնի համար
![]() կարող ենք
գրել`
կարող ենք
գրել`
![]()
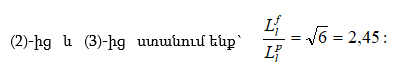
Խնդիր 7.10. Որոշել ռենտգենյան անընդհատ սպեկտրի կարճ ալիքային սահմանի ալիքի երկարությունը, եթե ռենտգենյան խողովակի անոդը ռմբակոծող էլեկտրոնի արագությունը` v=0,8c:
Լուծում: Էլեկտրոնի կինետիկ էներգիան որոշվում է հետևյալ պայմանից`
![]()
որտեղ e-ն էլեկտրոնի լիցքն է, U-ն ռենտգենյան խողովակին կիրառված լարումն է: Կարճ ալիքային սահմանին համապատասխանող ալիքի երկարությունը որոշվում է հետևյալ բանաձևով`

Էլեկտրոնի կինետիկ էներգիան`
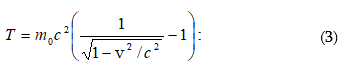
Նկատի ունենալով (2)-ը և (3)-ը` (1)-ից կստանանք`
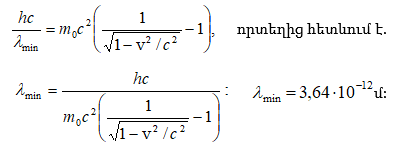
Խնդիր
7.11. Որոշել
Մենդելեևի պարբերական
համակարգի տարրի
կարգաթիվը, եթե
ռենտգենյան բնութագրական
ճառագայթման ալիքի
երկարությունը
![]() գծի համար`
գծի համար` ![]()
Լուծում: Օգտվելով Մոզլիի օրենքից` կարող ենք գրել.
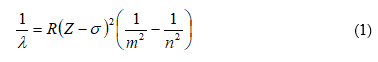
որտեղ
R-ը Ռիդբերգի հաստատունն
է ![]() էկրանացման
գործակիցն է, որը
էկրանացման
գործակիցն է, որը
![]() -սերիայի
համար`
-սերիայի
համար`![]() (1) առնչությունից
հետևում է.
(1) առնչությունից
հետևում է.

Լուծելով Z-ի նկատմամբ` ստանում ենք`
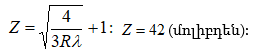
Խնդիր
7.12. Որոշել
ռենտգենյան ճառագայթման
L սերիայի համար
![]() էկրանացման
հաստատունը, եթե
վոլֆրամի ատոմում
(Z=1)M թաղանթից L
թաղանթին անցնելու
դեպքում առաքված
ֆոտոնի ալիքի երկարությունը`
էկրանացման
հաստատունը, եթե
վոլֆրամի ատոմում
(Z=1)M թաղանթից L
թաղանթին անցնելու
դեպքում առաքված
ֆոտոնի ալիքի երկարությունը`
![]()
Լուծում: ![]() գծի համար
m=3, n=3: Մոզլիի օրենքից`
գծի համար
m=3, n=3: Մոզլիի օրենքից`
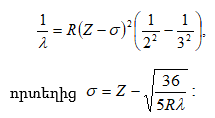
Վերջինի
մեջ տեղադրելով
թվային արժեքները`
ստանում ենք` ![]()
1. Р. Дичберн. Физическая оптика Москва. Наука 1967.
2. М. Борн и Э. Вольф. Основы оптики. Москва. Наука 1973.
3. М. Франсон С. Сланский. Когерентность в оптике. Москва, Наука, 1973.
4. И. В. Савельев. Курс общей физики, т.3. Москва: Астрель, АСТ 2005.
5. Г. Ландсберг. Оптика. Москва Изд. Тех. Лит. 1957.
6. А. А. Детлаф, Б. М. Яворский Курс физики. т.3, Москва: Выс-шая школа, 2002.
7. Д.В. Сивухин. Общий курс физики. Оптика, Москва: Наука 1985.
1. Р. Дичберн. Физическая оптика Москва. Наука 1967.
