
ԳԼՈՒԽ 10. ԻԴԵԱԼԱԿԱՆ ԳԱԶԵՐԻ ՄՈԼԵԿՈՒԼԱՅԻՆ-ԿԻՆԵՏԻԿ ՏԵՍՈՒԹՅՈՒՆԸ
10.1 Հետազոտությունների վիճակագրական և ջերմադինամիկական մեթոդներ
10.2 Նյութի քանակ: Ավոգադրոյի օրենքը
10.3 Միջմոլեկուլային փոխազդեցության ուժերը և էներգիան
10.4 Իդեալական գազ: Իդեալական գազի վիճակի պարամետրերը
10.5 Իդեալական գազի փորձարարական օրենքները
10.6 Իդեալական գազի վիճակի հավասարումը
10.7 Իդեալական գազերի մոլեկուլային-կինետիկ տեսության հիմնական հավասարումը
10.8 Մոլեկուլների բաշխումն ըստ արագությունների
10.9 Բարոմետրական բանաձև: Բոլցմանի բաշխումը
10.10 Մոլեկուլների ազատ վազքի միջին երկարությունը
10.11 Փոխանցման երևույթները գազերում
ԳԼՈՒԽ 11. ՋԵՐՄԱԴԻՆԱՄԻԿԱՅԻ ՀԻՄՈՒՆՔՆԵՐԸ
11.1 Ջերմադինամիկական համակարգ: Ջերմադինամիկական պրոցես: Դարձելի և ոչ դարձելի պրոցեսներ
11.2 Համակարգի ներքին էներգիան: Իդեալական գազի ներքին էներգիան
11.3 Էներգիայի հավասարաչափ բաշխման օրենքն ըստ մոլեկուլի ազատության աստիճանների
11.4 Աշխատանքն ու ջերմաքանակը որպես էներգիայի փոխանցման ձևեր
11.5 Գազի կատարած աշխատանքը ծավալի փոփոխության դեպքում
11.6 Ջերմադինամիկայի առաջին օրենքը
11.7 Ջերմադինամիկայի առաջին օրենքի կիրառումը իզոպրոցեսների նկատմամբ
11.9 Ադիաբատ պրոցես: Ադիաբատի հավասարումը
11.11 Ցիկլ: Դարձելի և ոչ դարձելի պրոցեսներ
11.12 Կառնոյի ցիկլը և նրա Օ.Գ.Գ.-ը
11.13 Ջերմադինամիկայի երկրորդ օրենքը
11.14 Էնտրոպիան և նրա հատկությունները
11.15 Ջերմադինամիկայի երկրորդ օրենքի վիճակագրական մեկնաբանությունը
ԳԼՈՒԽ 12. ԻՐԱԿԱՆ ԳԱԶԵՐ, ՀԵՂՈՒԿՆԵՐ ԵՎ ՊԻՆԴ ՄԱՐՄԻՆՆԵՐ
12.2 Վան - դեր - Վաալսի հավասարումը: Իրական գազերի վիճակի հավասարումը
12.3 Վան - դեր - Վաալսի իզոթերմերը: Նյութի կրիտիկական վիճակ
12.4 Կրիտիկական մեծությունների որոշումը
12.5 Իրական գազի ներքին էներգիան
12.7 Հեղուկների հատկությունները: Մակերևութային լարվածություն
12.9 Ճնշումը հեղուկի կորացած մակերևույթի տակ
12.11 Պինդ մարմիններ: Միաբյուրեղներ և բազմաբյուրեղներ
12.12 Բյուրեղային պինդ մարմինների տեսակները
12.13 Բյուրեղային ցանցի արատների դասակարգումը
12.14 Պինդ մարմնի ջերմունակությունը
12.15 Գոլորշիացում, սուբլիմում, հալում և բյուրեղացում: Ամորֆ մարմիններ
12.16 Առաջին և երկրորդ կարգի փուլային անցումներ
12.17 Վիճակի դիագրամը: Եռակի կետ
12.18 Ֆիզիկական մեծությունների միավորները
Մոլեկուլային ֆիզիկան ֆիզիկայի այն բաժինն է, որը մարմինների մոլեկուլային կառուցվածքի դիտարկման հիման վրա ուսումնասիրում է դրանց ֆիզիկական հատկությունները տարբեր ագրեգատային վիճակներում: Մոլեկուլային ֆիզիկայի խնդիրները, որոնք կապված են ֆիզիկական մարմինները կազմող մասնիկների (ատոմների, իոնների, մոլեկուլների) շարժման և փոխազդեցության ուսումնասիրման հետ, լուծվում են վիճակագրական ֆիզիկայի, ջերմադինամիկայի և ֆիզիկական կինետիկայի մեթոդներով: Մոլեկուլային ֆիզիկայի առաջին ավարտուն բաժինը գազերի կինետիկ տեսությունն է: Այդ տեսությունը զարգացնող աշխատությունների շնորհիվ ստեղծվեց դասական վիճակագրական ֆիզիկան (Ջ. Մաքսվել, Լ. Բոլցման, Ջ. Գիբս): Մոլեկուլային ուժերի (մոլեկուլային փոխազդեցության) մասին քանակական պատկերացումներն սկսեցին զարգանալ մազական երևույթների տեսության մեջ: Այս բնագավառում կատարված հիմնարար աշխատանքներով սկիզբ դրվեց մակերևութային երևույթների տեսությանը: Միջմոլեկուլային փոխազդեցությունները հաշվի առնվեցին նաև իրական գազերի և հեղուկների ֆիզիկական հատկությունները բացատրելիս ( Յ. Վան-դեր-Վաալս):
20 -րդ դարի սկզբին մոլեկուլային ֆիզիկան թևակոխեց զարգացման նոր շրջան, որը բնորոշվում է մարմինների իրական մոլեկուլային կառուցվածքի ապացույցներով: Այս շրջանում կատարված աշխատանքները վերաբերում են միկրոմասնիկների բրոունյան շարժմանը (Ժ. Պերեն, Մ. Սմոլուխովսկի, Ա. Այնշտայն): Նյութերի մոլեկուլային կառուցվածքի հետազոտման նպատակով ռենտգենյան ճառագայթների դիֆրակցիայի, հետագայում նաև էլեկտրոնների և նեյտրոնների դիֆրակցիայի կիրառությունը հնարավորություն տվեց ճշգրիտ տվյալներ ստանալու բյուրեղական պինդ մարմինների և հեղուկների կառուցվածքի մասին (Մ. Լաուե, Ու.Հ. Բրեգ, Ու.Լ. Բրեգ,Գ. Վուլֆ, Ա.Ի. Իոֆֆե, Ջ. Բեռնալ, Վ. Ի. Դանիլով և ուրիշներ):
Մոլեկուլային ֆիզիկայի ընդգրկած պրոբլեմների շրջանակը շատ ընդարձակ է, այստեղ դիտարկվում են այնպիսի հարցեր, ինչպիսիք են` գազերի, հեղուկների և պինդ մարմինների կառուցվածքը, դրանց փոփոխությունը արտաքին պայմանների (ճնշում, ջերմաստիճան, էլեկտրական, մագնիսական դաշտեր) ազդեցությամբ, փոխանցման երևույթները (դիֆուզիա, ջերմահաղորդականություն, ներքին շփում), փուլային հավասարակշռությունը և փուլային անցումների պրոցեսները (բյուրեղացում և հալում, գոլորշիացում և կոնդենսացում), նյութի կրիտիկական վիճակը, տարբեր փուլերի բաժանման սահմանում դիտվող մակերևութային երևույթները:
Մոլեկուլային ֆիզիկայի բազմակողմնակի և բուռն զարգացման հետևանքով դրանից անջատվեցին մի շարք խոշոր ինքնուրույն բաժիններ` վիճակագրական ֆիզիկան, պինդ մարմնի ֆիզիկան, ֆիզիկական քիմիան, մոլեկուլային կենսաբանությունը, մետաղաֆիզիկան, պոլիմերների ֆիզիկան, բյուրեղաֆիզիկան, ֆիզիկաքիմիական մեխանիկան և այլք: Արդի գիտության մեջ և տեխնիկայում օգտագործվող բազմաթիվ նոր նյութերի կառուցվածքի բացահայտված առանձնահատկությունները խթանեցին հետազոտման զանազան գիտական մոտեցումների զարգացումը: Չնայած հետազոտման օբյեկտների ու մեթոդների բազմազանությանը, պահպանվում է մոլեկուլային ֆիզիկայի հիմնական դրույթը` նկարագրել նյութի մակրոսկոպիկ հատկությունները, ելնելով նրա կառուցվածքի միկրոսկոպիկ (մոլեկուլային) պատկերի առանձնահատկություններից:
ԳԼՈՒԽ 10. ԻԴԵԱԼԱԿԱՆ ԳԱԶԵՐԻ ՄՈԼԵԿՈՒԼԱՅԻՆ-ԿԻՆԵՏԻԿ ՏԵՍՈՒԹՅՈՒՆԸ
10.1. ՀԵՏԱԶՈՏՈՒԹՅՈՒՆՆԵՐԻ ՎԻՃԱԿԱԳՐԱԿԱՆ ԵՎ ՋԵՐՄԱԴԻՆԱՄԻԿԱԿԱՆ ՄԵԹՈԴՆԵՐ
Մոլեկուլային-կինետիկ տեսության հիմնական դրույթները: Մոլեկուլային ֆիզիկան ֆիզիկայի այն բաժինն է, որն ուսումնասիրում է նյութերի կառուցվածքը և հատկությունները՝ ելնելով, այսպես կոչված, մոլեկուլայինկինետիկ պատկերացումներից: Այդ պատկերացումների համաձայն.
1. Բոլոր մարմինները բաղկացած են մեծ թվով չափազանց փոքր առանձին մասնիկներից՝ ատոմներից, մոլեկուլներից, որոնց կազմի մեջ մտնում են առավել մանր տարրական մասնիկներ (էլեկտրոններ, պրոտոններ, նեյտրոններ): Ցանկացած նյութի կառուցվածք ընդհատ է:
2. Նյութի ատոմներն ու մոլեկուլները մշտապես գտնվում են անընդհատ քաոսային շարժման մեջ, որը կոչվում է ջերմային շարժում:
3. Ցանկացած նյութի մասնիկների միջև առկա են փոխազդեցության ուժեր՝ ձգողական և վանողական: Այդ ուժերի բնույթը էլեկտրամագնիսական է:
Այս դրույթները հաստատվում են դիֆուզիայի, բրոունյան շարժման երևույթներով, գազերի, հեղուկների, պինդ մարմինների հատկություններով ու կառուցվածքային առանձնահատկություններով, ինչպես նաև այլ երևույթներով:
Մոլեկուլային-կինետիկ տեսության հիմքում ընկած փորձնական տվյալները մոլեկուլային շարժման և այդ շարժման ջերմաստիճանից կախվածության ակնառու ապացույցն են: Ի տարբերություն մեխանիկական շարժման, մարմինների տաքացումը կամ սառեցումը կարող է առաջ բերել նրանց ֆիզիկական հատկությունների փոփոխություն: Այսպես, ուժեղ սառեցման պայմաններում ջուրը վերածվում է սառույցի, իսկ մետաղի տաքացումը մինչև բարձր ջերմաստիճաններ, առաջ է բերում նրա վերածվելը ոչ միայն հեղուկի, այլև գազի:
Ջերմային պրոցեսների ընթացքն անմիջականորեն կապված է նյութի կառուցվածքի հետ: Դրա համար էլ ջերմային երևույթները կարող են օգտագործվել նյութի կառուցվածքի բացատրության նպատակով, իսկ նյութի կառուցվածքն, իր հերթին, մեզ պատկերացում է տալիս ջերմային երևույթների ֆիզիկական էության մասին: Որպեսզի հնարավոր լինի բացատրել այդ պրոցեսները և սովորել կառավարել դրանք, անհրաժեշտ է սահմանել օրենքներ, որոնց ենթարկվում են ջերմության ազդեցության տակ մարմինների հետ կատարվող փոփոխությունները: Այդ օրենքները նկարագրում են մատերիայի շարժման ջերմային ձևը:
Ջերմային երևույթների նկարագրման համար, ֆիզիկայում օգտագործում են երկու հիմնական մեթոդներ՝ մոլեկուլային-կինետիկ (վիճակագրական) և ջերմադինամիկական: Մոլեկուլային-կինետիկ մեթոդը հիմնված է այն պատկերացման վրա, որ բոլոր նյութերը բաղկացած են քաոսային շարժման մեջ գտնվող մոլեկուլներից: Քանի որ մոլեկուլների թիվը չափազանց մեծ է, հետևաբար, կիրառելով վիճակագրության օրենքները, կարելի է գտնել որոշակի օրինաչափություններ միմիայն ամբողջական նյութի համար:
Մարմինների տարբեր հատկությունները և նյութի վիճակի փոփոխություններն ուսումնասիրվում են նաև ջերմադինամիկայում: Սակայն, ի տարբերություն մոլեկուլային-կինետիկ տեսության, ջերմադինամիկայում ուսումնասիրվում են մարմինների և բնության երևույթների մակրոսոպիկ հատկությունները, առանց նրանց միկրոսկոպիկ հատկությունները նկատի ունենալու: Ջերմադինամիկայի հիմքում ընկած են մի քանի հիմնական օրենքներ, որոնք սահմանվել են մեծ թվով փորձնական փաստերի ընդհանրացման հիման վրա: Այդ պատճառով ջերմադինամիկայի եզրակացությունները կըրում են շատ ընդհանուր բնույթ:
Ուսումնասիրելով նյութի վիճակի փոփոխությունները տարբեր տեսանկյուններից, ջերմադինամիկան և մոլեկուլային-կինետիկ տեսությունը լրացնում են միմյանց` ըստ էության կազմելով մի ամբողջություն:
10.2. ՆՅՈՒԹԻ ՔԱՆԱԿ: ԱՎՈԳԱԴՐՈՅԻ ՕՐԵՆՔԸ
Մոլեկուլների չափերը: Բոլոր մարմինները բաղկացած են հսկյական քանակությամբ մոլեկուլներից և ատոմներից: Քանի որ ատոմների ու մոլեկուլների չափերը շատ փոքր են, ապա դրանք անզեն աչքով տեսնել անհնար է: 30000 և ավելի անգամ խոշորացնող էլեկտրոնային մանրադիտակի օգնությամբ նկարահանվել են առանձին խոշոր մոլեկուլներ: Ռենտգենակառուցվածքային անալիզի մեթոդով մեծ ճշտությամբ կարելի է որոշել մոլեկուլների չափերը: Ռենտգենակառուցվածքային անալիզի արդյունքները ցույց են տալիս, որ թթվածնի երկատոմ մոլեկուլի գծային չափերը 4•10-10 մ կարգի է, այդպիսի չափեր ունեն նաև ազոտի մոլեկուլները:
Վերջին ժամանակներում նյութի կառուցվածքի ուսումնասիրության բնագավառում ձեռք բերված մեծ հաջողությունների շնորհիվ մեր առջև բացվեց մի նոր աշխարհ՝ մանր մասնիկների աշխարհը: Այդ աշխարհը ստացավ միկրոաշխարհ անվանումը, ի տարբերություն խոշոր մարմինների աշխարհի՝ մակրոաշխարհի: Պարզվեց, որ միկրոաշխարհը չափազանց բարդ է: Ցանկացած մարմնի մոլեկուլները բաղկացած են ավելի մանր մասնիկներից՝ ատոմներից, որոնք էլ իրենց հերթին բաղկացած են էլեկտրոններից և միջուկներից: Ատոմների միջուկները կազմված են պրոտոններից և նեյտրոններից: Ատոմ անվանում են տվյալ քիմիական տարրի ամենափոքր մասնիկը: Յուրաքանչյուր քիմիական տարրի համապատասխանում են միանգամայն սահմանված ատոմներ, որոնք պահպանում են տվյալ տարրի քիմիական հատկությունները: Մոլեկուլ կոչվում է տվյալ նյութի ամենափոքր կայուն մասնիկը, որն օժտված է այդ նյութի հիմնական քիմիական հատկություններով:
Մոլեկուլի զանգվածը: Առանձին մոլեկուլների և ատոմների զանգվածները շատ փոքր են: Օրինակ, ջրի մոլեկուլի զանգվածի բացարձակ արժեքը 3•10-26 կգ կարգի մեծություն է: Առանձին մոլեկուլների զանգվածները փորձնականորեն որոշում են հատուկ սարքի օգնությամբ՝ զանգվածասպեկտրաչափով:
Մոլեկուլային
ֆիզիկայում ընդունված
է ատոմների և մոլեկուլների
զանգվածը բնութագրել
ոչ թե իրենց բացարձակ
արժեքներով (կիլոգրամներով),
այլ հարաբերական
և չափայնություն
չունեցող մեծությամբ,
որն անվանում են
![]() հարաբերական
ատոմային զանգված
կամ
հարաբերական
ատոմային զանգված
կամ ![]() հրաբերական
մոլեկուլային
զանգված: Միջազգային
համաձայնագրով,
որպես ատոմական
զանգվածի միավոր,
ընդունվում է ածխածնի
12C իզոտոպի զանգվածի
1/12 մասը՝
հրաբերական
մոլեկուլային
զանգված: Միջազգային
համաձայնագրով,
որպես ատոմական
զանգվածի միավոր,
ընդունվում է ածխածնի
12C իզոտոպի զանգվածի
1/12 մասը՝ ![]()
Հարաբերական մոլեկուլային զանգվածը կարելի է որոշել, մոլեկուլի զանգվածի և զանգվածի ատոմային միավորի (1,66 •10-27կգ) հարաբերությամբ
![]()
Նույն ձևով
որոշվում է նաև
հարաբերական ատոմային
զանգվածը՝ ![]()
Նյութի քանակ: Մակրոսկոպական մարմինները բաղկացած են հսկայական թվով մոլեկուլներից: Քանի որ առանձին մոլեկուլների զանգվածներն իրարից տարբեր են, ապա տարբեր նյութերի միևնույն թվով մոլեկուլներն ունեն տարբեր զանգվածներ, օրինակ, ջրածնի 1028 մոլեկուլներն ունեն 33,45կգ, իսկ 1028 թթվածնի մոլեկուլները՝ 531.45կգ զանգված: Այդ պատճառով ընդունված է տվյալ նյութի մեջ մոլեկուլների և ատոմների թիվը համեմատել 0,012կգ ածխածնում պարունակվող ատոմների թվի հետ: Մակրոսկոպական մարմնում պարունակվող ատոմների հարաբերական քանակը բնութագրվում է մի ֆիզիկական մեծությամբ, որը կոչվում է նյութի v քանակ:
Տվյալ մակրոսկոպական
մարմնում նյութի
քանակը N մոլեկուլների
(ատոմների) և 0,012կգ
ածխածնում պարունակվող
![]() (Ավոգադրոյի
թիվ) ատոմների
հարաբերությունն
է
(Ավոգադրոյի
թիվ) ատոմների
հարաբերությունն
է
![]()
Որպես նյութի քանակի չափման միավոր ընդունված է մոլը:
Մեկ մոլն այն նյութի քանակն է, որը պարունակում է այնքան մոլեկուլ (ատոմ), որքան մոլեկուլ (ատոմ) է պարունակում 0,012կգ ածխածինը: Ըստ սահմանման ցանկացած նյութի մոլը պարունակում է նույն թվով մոլեկուլներ (ատոմներ): Այդ թիվը կոչվում է Ավոգադրոյի թիվ:
Որոշենք
Ավոգադրոյի ![]() թվի
արժեքը: Դրա համար
անհրաժեշտ է ածխածնի
մեկ մոլի զանգվածը`
0,012կգ/մոլ մեծությունը
բաժանել ածխածնի
մեկ ատոմի
թվի
արժեքը: Դրա համար
անհրաժեշտ է ածխածնի
մեկ մոլի զանգվածը`
0,012կգ/մոլ մեծությունը
բաժանել ածխածնի
մեկ ատոմի ![]() զանգվածին: Ճշգրիտ
չափումների համաձայն
զանգվածին: Ճշգրիտ
չափումների համաձայն ![]() հետևաբար`
հետևաբար`
![]()
Այսպիսով,
ցանկացած նյութի
մեկ մոլը պարունակում
է միևնույն` ![]() թվով մոլեկուլ (Ավոգադրոյի
օրենք): Այս օրենքը
տեղի ունի ինչպես
գազերի, այնպես
էլ հեղուկների
և պինդ մարմինների
համար:
թվով մոլեկուլ (Ավոգադրոյի
օրենք): Այս օրենքը
տեղի ունի ինչպես
գազերի, այնպես
էլ հեղուկների
և պինդ մարմինների
համար:
Մոլային զանգված: Մոլեկուլային ֆիզիկայում օգտվում են նաև M մոլային զանգված հասկացությունից, որը սահմանվում է որպես 1 մոլ նյութի զանգված`
![]()
Ցանկացած
նյութի զանգվածը`
![]()
Մոլային զանգվածի միավորն է կիլոգրամը բաժանած մոլի (կգ/մոլ):
Հայտնի
է, որ գազի մեկ մոլը
նորմալ պայմաններում
զբաղեցնում է ![]() ծավալ: Հետևաբար,նորմալ
պայմաններում
ցանկացած գազի
1մ3-ը պարունակում
է հավասար թվով
մոլեկուլներ՝
ծավալ: Հետևաբար,նորմալ
պայմաններում
ցանկացած գազի
1մ3-ը պարունակում
է հավասար թվով
մոլեկուլներ՝
![]()
Այս թիվն ստացել է Լոշմիդտի հաստատուն անունը:
10.3. ՄԻՋՄՈԼԵԿՈՒԼԱՅԻՆ ՓՈԽԱԶԴԵՑՈՒԹՅԱՆ ՈՒժԵՐԸ ԵՎ ԷՆԵՐԳԻԱՆ
Նյութի կառուցվածքի ուսումնասիրության դեպքում հաստատվել է, որ մոլեկուլների միջև միաժամանակ գործում են ձգողական և վանողական ուժեր, որոնք կոչվում են մոլեկուլային ուժեր: Ձգման նկատմամբ պինդ մարմինների դիմադրությունը, հեղուկի մակերևույթի առանձնահատկությունները և այլ երևույթներ հանգեցնում են այն եզրակացության, որ մոլեկուլների միջև գործում են ձգողական ուժեր: Շատ խիտ գազերի և հատկապես հեղուկ ու պինդ մարմինների փոքր սեղմելիությունը նշանակում է, որ մոլեկուլների միջև գոյություն ունեն վանողական ուժեր: Պինդ և հեղուկ մարմիններում վանողական և ձգողական ուժերը գործում են միաժամանակ: Եթե դա չլիներ, ապա մարմինները կայուն չէին լինի կամ մասերի կբաժանվեին, կամ էլ կկպչեին իրար: Մոլեկուլային փոխազդեցության ուժերն իրենց բնույթով համարվում են էլեկտրամագնիսական ծագում ունեցող ուժեր:
Մոլեկուլների կազմության մեջ մտնող ատոմները բացասական լիցք ունեցող էլեկտրոններից և դրական լիցք ունեցող միջուկներից բաղկացած լիցքավորված մասնիկների բարդ համակարգեր են: Ատոմում էլեկտրոնները միջուկի մոտ պահվում են տարանուն լիցքերի փոխազդեցության կուլոնյան ձգողական ուժերով: Ատոմն ամբողջությամբ էլեկտրաչեզոք է: Մոլեկուլները բաղկացած են ատոմներից: Մոլեկուլում ատոմները միասին պահող ուժերն իրենց բնույթով նույնպես էլեկտրական են, սակայն դրանց առաջացումը փոքրինչ բարդ է: Մոլեկուլային ուժերի խիստ տեսությունը տրվում է քվանտային մեխանիկայի տեսանկյունից:
Մոլեկուլային փոխազդեցությունը էլեկտրականապես չեզոք մոլեկուլների կամ ատոմների փոխազդեցությունն է:
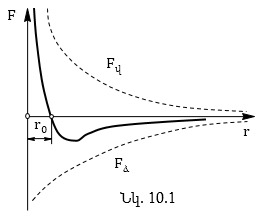
Փոխազդեցության
ուժերը կախված
են մոլեկուլների
միջև եղած հեռավորությունից:
Մոլեկուլների
չափերը մի քանի
անգամ գերազանցող
հեռավորությունների
վրա նրանց փոխազդեցությունը
գործնականորեն
հավասար է զրոյի:
Նկ.10.1-ում ցույց է
տրված երկու մոլեկուլների
փոխազդեցության
ուժի կախումը նրանց
միջև եղած հեռավորությունից:
Մի մոլեկուլի էլեկտրոնների
և մյուս մոլեկուլի
ատոմային միջուկների
միջև գործում են
![]() ձգողության ուժերը,
որոնք պայմանականորեն
ընդունված է համարել
բացասական: Միաժամանակ
մոլեկուլների
էլեկտրոնների,
ինչպես նաև նրանց
միջուկների միջև
գործում են
ձգողության ուժերը,
որոնք պայմանականորեն
ընդունված է համարել
բացասական: Միաժամանակ
մոլեկուլների
էլեկտրոնների,
ինչպես նաև նրանց
միջուկների միջև
գործում են ![]() վանողական
ուժերը, որոնք
պայմանականորեն
ընդունվում են
դրական: Ինչպես
երևում է նկ.10.1-ում,
վանողական
ուժերը, որոնք
պայմանականորեն
ընդունվում են
դրական: Ինչպես
երևում է նկ.10.1-ում,
![]() հեռավորության
վրա արդյունարար
ուժը հավասար է
զրոյի
հեռավորության
վրա արդյունարար
ուժը հավասար է
զրոյի ![]() , այսինքն՝
ձգողական ուժերը
հավասարակշռում
են վանողական ուժերին:
Դրան համապատասխանում
է փոխազդող մոլեկուլների
ամենամեծ կայուն
վիճակը:
, այսինքն՝
ձգողական ուժերը
հավասարակշռում
են վանողական ուժերին:
Դրան համապատասխանում
է փոխազդող մոլեկուլների
ամենամեծ կայուն
վիճակը: ![]() դեպքում
ձգողական ուժը
գերազանցում է
վանողական ուժին,
իսկ
դեպքում
ձգողական ուժը
գերազանցում է
վանողական ուժին,
իսկ ![]() դեպքում՝
հակառակը: Քանի
որ ձգողական և
վանողական ուժերը
գործում են միաժամանակ,
ապա կարելի է որոշել
դրանց համազորը,
որը բնութագրում
է մոլեկուլների
միջև փոխազդեցության
ուժը: Փոխազդեցության
ուժը բնութագրող
կորը թույլ է տալիս
կատարել մարմինների
սեղմման և ձգման
ժամանակ առաձգական
ուժերի առաջացման
որակական բացատրությունը:
դեպքում՝
հակառակը: Քանի
որ ձգողական և
վանողական ուժերը
գործում են միաժամանակ,
ապա կարելի է որոշել
դրանց համազորը,
որը բնութագրում
է մոլեկուլների
միջև փոխազդեցության
ուժը: Փոխազդեցության
ուժը բնութագրող
կորը թույլ է տալիս
կատարել մարմինների
սեղմման և ձգման
ժամանակ առաձգական
ուժերի առաջացման
որակական բացատրությունը:
Պինդ մարմնի
սեղմման ժամանակ
տեղի է ունենում
մասնիկների մոտեցում:
![]() փոքր հեռավորության
վրա առաջանում
է մասնիկների մոտեցմանն
արգելակող և մասնիկներին
նախնական դիրքը
վերադարձնող ուժ:
Պինդ մարմնի ձգման
ժամանակ տեղի է
ունենում մասնիկների
հեռացում մեկը
մյուսից
փոքր հեռավորության
վրա առաջանում
է մասնիկների մոտեցմանն
արգելակող և մասնիկներին
նախնական դիրքը
վերադարձնող ուժ:
Պինդ մարմնի ձգման
ժամանակ տեղի է
ունենում մասնիկների
հեռացում մեկը
մյուսից ![]() հեռավորության
վրա, այս դեպքում
մասնիկների միջև
սկսում են գործել
ձգողական ուժերը,
որոնք ձգտում են
մասնիկը վերադարձնել
իր ելման վիճակին
հեռավորության
վրա, այս դեպքում
մասնիկների միջև
սկսում են գործել
ձգողական ուժերը,
որոնք ձգտում են
մասնիկը վերադարձնել
իր ելման վիճակին![]() : Ատոմներն
ու մոլեկուլները
փոխազդում են,
հետևաբար օժտված
են
: Ատոմներն
ու մոլեկուլները
փոխազդում են,
հետևաբար օժտված
են ![]() պոտենցիալ էներգիայով:
Ցույց տանք մոլեկուլների
փոխազդեցության
պոտենցիալ էներգիայի
և նրանց հեռավորության
միջև եղած կախման
մոտավոր բնութագիրը:
Պոտենցիալ էներգիան
դրական է համարվում
մոլեկուլների՝
իրար վանելու դեպքում,
իսկ բացասական՝
միմյանց ձգելու
դեպքում: Միմյանից
անվերջ հեռու գտնվող
մարմինների ձգողության
պոտենցիալ էներգիան
պայմանականորեն
ընդունում են հավասար
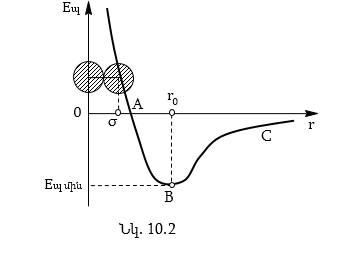
զրոյի: Մոլեկուլները
իրար մոտենալու
դեպքում (նկ.10.2) դրանց
պոտենցիալ էներգիան
կփոքրանա, և
պոտենցիալ էներգիայով:
Ցույց տանք մոլեկուլների
փոխազդեցության
պոտենցիալ էներգիայի
և նրանց հեռավորության
միջև եղած կախման
մոտավոր բնութագիրը:
Պոտենցիալ էներգիան
դրական է համարվում
մոլեկուլների՝
իրար վանելու դեպքում,
իսկ բացասական՝
միմյանց ձգելու
դեպքում: Միմյանից
անվերջ հեռու գտնվող
մարմինների ձգողության
պոտենցիալ էներգիան
պայմանականորեն
ընդունում են հավասար
զրոյի: Մոլեկուլները
իրար մոտենալու
դեպքում (նկ.10.2) դրանց
պոտենցիալ էներգիան
կփոքրանա, և ![]() դեպքում
այն կհասնի իր
նվազագույն արժեքին
դեպքում
այն կհասնի իր
նվազագույն արժեքին
![]() : Մոլեկուլների
հետագա մոտեցումը
հնարավոր է միայն
վանողական ուժերի
դեմ կատարվող աշխատանքի
հաշվին: Այդ դեպքում
մոլեկուլների
պոտենցիալ էներգիան
կսկսի կտրուկ աճել:
Այսպիսով, մոլեկուլների
փոխազդեցության
պոտենցիալ էներգիան
նվազագույնն է
: Մոլեկուլների
հետագա մոտեցումը
հնարավոր է միայն
վանողական ուժերի
դեմ կատարվող աշխատանքի
հաշվին: Այդ դեպքում
մոլեկուլների
պոտենցիալ էներգիան
կսկսի կտրուկ աճել:
Այսպիսով, մոլեկուլների
փոխազդեցության
պոտենցիալ էներգիան
նվազագույնն է
![]() դեպքում: Հետևաբար,
մոլեկուլների
կայուն հավասարակշռության
վիճակը համապատասխանում
է նրանց պոտենցիալ
էներգիայի նվազագույնին:
դեպքում: Հետևաբար,
մոլեկուլների
կայուն հավասարակշռության
վիճակը համապատասխանում
է նրանց պոտենցիալ
էներգիայի նվազագույնին:
Մոլեկուլների
փոխազդեցության
պոտենցիալ էներգիայի
կախվածության
գրաֆիկը նրանց
միջև եղած հեռավորությունից
անվանում են պոտենցիալ
կոր, ABC տեղամասը՝
պոտենցիալ փոս,
![]() պոտենցիալ փոսի
խորություն, σ-ն՝
մոլեկուլի էֆեկտիվ
տրամագիծ, որը
որոշում է այն
տիրույթի չափերը,
ուր այլ մոլեկուլ
մուտք գործել չի
կարող: Որպես կանոն,
միջմոլեկուլային
փոխազդեցությունը
նկարագրվում է
փոխազդեցության
պոտենցիալ էներգիայով,
քանի որ հատկապես
փոխազդեցության
միջին պոտենցիալ
էներգիան է որոշում
նյութի վիճակն
ու նրա շատ հատկություններ:
Ատոմներն ու մոլեկուլները
գտնվում են շարժման
մեջ և, հետևաբար,
օժտված են որոշակի
կինետիկ էներգիայով:
Ջերմային քաոսային
շարժման միջին
պոտենցիալ փոսի
խորություն, σ-ն՝
մոլեկուլի էֆեկտիվ
տրամագիծ, որը
որոշում է այն
տիրույթի չափերը,
ուր այլ մոլեկուլ
մուտք գործել չի
կարող: Որպես կանոն,
միջմոլեկուլային
փոխազդեցությունը
նկարագրվում է
փոխազդեցության
պոտենցիալ էներգիայով,
քանի որ հատկապես
փոխազդեցության
միջին պոտենցիալ
էներգիան է որոշում
նյութի վիճակն
ու նրա շատ հատկություններ:
Ատոմներն ու մոլեկուլները
գտնվում են շարժման
մեջ և, հետևաբար,
օժտված են որոշակի
կինետիկ էներգիայով:
Ջերմային քաոսային
շարժման միջին
![]() կինետիկ էներգիայի
և նվազագույն
կինետիկ էներգիայի
և նվազագույն ![]() պոտենցիալ
էներգիայի միջև
եղած առնչությունը
որոշում է նյութի
այս կամ այն ագրեգատային
վիճակի գոյության
հնարավորությունը՝
գազանման, պինդ
և հեղուկ:
պոտենցիալ
էներգիայի միջև
եղած առնչությունը
որոշում է նյութի
այս կամ այն ագրեգատային
վիճակի գոյության
հնարավորությունը՝
գազանման, պինդ
և հեղուկ:

10.4. ԻԴԵԱԼԱԿԱՆ ԳԱԶ: ԻԴԵԱԼԱԿԱՆ ԳԱԶԻ ՎԻՃԱԿԻ
ՊԱՐԱՄԵՏՐԵՐԸ
Մոլեկուլային ֆիզիկայում և ջերմադինամիկայում քննարկվում են մեծ քանակությամբ մասնիկներից բաղկացած համակարգեր, այսինքն՝ մակրոսկոպական համակարգեր: Առանձին վերցրած մեկ մասնիկի համար չի կարելի ցույց տալ նրա կոորդինատն ու շարժման ուղղությունը, որոշել ջերմաստիճանն ու ճնշումը: Չափելի են միայն մոլեկուլների համախմբի վիճակի պարամետրերը, այսինքն՝ մակրոսկոպական բնութագրերը: Սկզբում պարզենք, թե ինչպիսի՞ օրինաչափությունների է ենթարկվում գազային վիճակում գտնվող նյութի վարքը: Այդ նպատակով դիտարկենք իրական գազերի իդեալականացված մոդելը՝ իդեալական գազը:
Իդեալական կոչվում է այնպիսի գազը, որի մեջ կարելի է անտեսել մոլեկուլների չափերը, միջմոլեկուլային փոխազդեցության ուժերը: Այդպիսի գազում մոլեկուլների բախումները տեղի են ունենում առաձգական գնդերի բախման օրենքով: Իրական գազերն իրենց պահում են իդեալականի նման, երբ մոլեկուլների միջև եղած միջին հեռավորությունը շատ անգամ մեծ է նրանց չափերից, այսինքն՝ բավականաչափ մեծ նոսրացումների դեպքում:
Գազային նյութի որոշակի զանգվածի վիճակը բնութագրվում է միմյանցից կախված ֆիզիկական մեծություններով, որոնք կոչվում են վիճակի պարամետրեր: Դրանք են՝ p ճնշումը,V ծավալը, և T ջերմաստիճանը: Գազի ծավալը միշտ համապատասխանում է այն անոթի ծավալին, որի մեջ այն լցված է: Ծավալի միավորը խորանարդ մետրն է (մ3): Ճնշումն այն ֆիզիկական մեծությունն է, որը հավասար է մակերևույթի տարրի վրա ուղղահայաց ազդող F ուժի և այդ տարրի մակերեսի հարաբերությանը
![]()
Ճնշման միավորը պասկալն է (1Պա =1Ն/մ2): Ինչպե՞ս է առաջանում գազի ճնումը: Գազի յուրաքանչյուր մոլեկուլ, հարվածելով անոթի պատին, որի մեջ գտնվում է, փոքր ժամանակամիջոցում ազդում է պատի վրա որոշակի ուժով: Անկանոն հարվածների արդյունքում, պատի միավոր մակերեսի վրա բոլոր մոլեկուլների կողմից գործադրված ուժը ժամանակի ընթացքում որոշակի միջին մեծության նկատմամբ արագորեն փոփոխվում է: Ճնշումը չափող սարքերը կոչվում են մանոմետրեր: Մանոմետրերն արձանագրում են նրա զգայուն տարրի (մեմբրանի) կամ ճնշման այլ ընդունիչի միավոր մակերեսին ընկնող միջինացված ճնշման ուժն ըստ ժամանակի: Մոլեկուլային ֆիզիկայում ջերմաստիճանի հասկացությունը ամենակարևորներից մեկն է: Ջերմաստիճանի քանակական որոշումը հաստատելու համար անհրաժեշտ է մտցնել ջերմային հավասարակշռության հասկացությունը: Պարզաբանենք այդ: Վերցնենք մի քանի մարմիններ (մարմինների համակարգ)՝ տաքացրած երկաթ (A մարմին), սենյակային ջերմաստիճանի ջուր (B մարմին) և սառույց (C մարմին):
Կատարենք պայմանական գրանցում, որը ցույց կտա, թե այդ մարմինների միջև ջերմափոխանակության դեպքում ինչպես է կատարվում մարմինների էներգիայի փոփոխությունը.
![]()
Սլաքների ուղղությունը ցույց է տալիս, թե ջերմափոխանակության ժամանակ ո՞ր մարմնից որին է փոխանցվում էներգիան: Ջերմափոխանակության դեպքում էներգիան միշտ ավելի բարձր ջերմաստիճան ունեցող մարմնից փոխանցվում է ավելի ցածր ջերմաստիճան ունեցող մարմնին: Ի վերջո, վրա է հասնում մարմինների համակարգի մի վիճակ, որի դեպքում համակարգի մարմինների միջև ջերմափոխանակությունը կբացակայի: Այդպիսի վիճակն անվանում են ջերմային հավասարակշռություն: Ջերմային հավասարակշռության մեջ գտնվող մարմիններն ունեն միևնույն ջերմաստիճանը:
Եթե մարմինների համակարգը գտնվում է ջերմային հավասարակըշռության մեջ, ապա նրա մասերի ծավալը, ջերմաստիճանն ու վիճակի այլ բնութագրիչները ժամանակի ընթացքում չեն փոփոխվում: Մարմինների միջև ջերմափոխանակության ուղղությունը որոշելու`ջերմաստիճանի հատկությունը ջերմադինամիկայում ամենակարևորն է:
Ջերմաստիճանի փոփոխության դեպքում փոփոխվում են մարմինների չափերը, նրանց ծավալները, էլեկտրական դիմադրությունը և այլ հատկություններ: Ընդհանրապես, բոլոր ֆիզիկական և քիմիական երևույթների մեծ մասի մեջ դիտվում է կախում ջերմաստիճանից: Այդպիսով, ջերմաստիճանը կարելի է որոշել տվյալ նյութի չափման համար հարմար որևէ ֆիզիկական հատկության փոփոխության միջոցով: Ջերմաստիճանի միարժեք որոշման համար անհրաժեշտ է ջերմաչափական մարմնի և ջերմաստիճանային պարամետրերի ընտրությունը:
Ջերմաստիճանային որոշակի միջակայքերի համար որպես ջերմաչափական մարմին կարելի է ընտրել գազ (օրինակ ջրածին) կամ հեղուկ (սնդիկ, սպիրտ): Դրանց ջերմաստիճանային պարամետրը ծավալն է: Ջերմաստիճանային պարամետրեր կարող են լինել մի քանի կիսահաղորդիչների և հաղորդիչների դիմադրությունները, ճառագայթման ինտենսիվությունը և այլն: Ջերմաստիճանային պարամետրը պետք է ջերմաստիճանի փոփոխման հետ փոփոխվի անընդհատ և մոնոտոն, այսինքն՝ այն տարբեր ջերմաստիճաններում չպետք է ունենա միևնույն արժեքները:
Ներկայումս
կիրառում են միայն
ջերմաստիճանային
երկու սանդղակ՝
ջերմադինամիկական,
որն աստիճանավորված
է կելվիններով
(Կ) և Միջազգային
գործնական՝ աստիճանավորված
Ցելսիուսի աստիճաներով
![]() Ջերմադինամիկական
ջերմաստիճանը
(T) և ջերմաստիճանն
ըստ Միջազգային
գործնական սանդղակի
(t) կապված են հետևյալ
առնչությամբ՝
Ջերմադինամիկական
ջերմաստիճանը
(T) և ջերմաստիճանն
ըստ Միջազգային
գործնական սանդղակի
(t) կապված են հետևյալ
առնչությամբ՝
![]()
Ջերմաստիճանի ֆիզիկական իմաստի հասկացությունը կբացահայտվի գազերի մոլեկուլայինկինետիկ տեսության և ջերմադինամիկայի հիմունքների ուսումնասիրությանը զուգընթաց: p, V, T պարամետրերի միջև գոյություն ունի միարժեք հարաբերակցություն: Ընդհանուր տեսքով դա վիճակի հավասարումն է: Պարզ համակարգերի համար այն կարող է գրվել հետևյալ ձևով. f(p,V,T): Վիճակի հավասարման օգնությամբ միշտ երկու պարամետրերով կարելի է որոշել երրորդը:
10.5. ԻԴԵԱԼԱԿԱՆ ԳԱԶԻ ՓՈՐՁԱՐԱՐԱԿԱՆ ՕՐԵՆՔՆԵՐԸ
Իզոթերմպրոցես: Բոյլ-Մարիոտի օրենքը: Գազի վիճակի ցանկացած փոփոխություն կոչվում է ջերմադինամիկական պրոցես: Ցանկացած ջերմադինամիկական պրոցեսում փոփոխվում են գազի վիճակը բնորոշող պարամետրերը: Չկա որևէ պրոցես, որի դեպքում փոփոխվի միայն մեկ պարամետր: Մեկ պարամետրի փոփոխությունը հանգեցնում է մնացածների փոփոխությանը: Այն պրոցեսը, որի դեպքում պարամետրերից մեկը մնում է հաստատուն, իսկ մյուս երկուսըփոփոխվում են, կոչվում է իզոպրոցես:
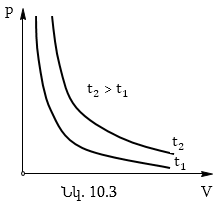
Գազում ընթացող պրոցեսը, որի դեպքում ջերմաստիճանը մնում է հաստատուն, կոչվում է իզոթերմ (հունարեն «իզոս» - հավասար, «թերմոս» - տաք):
18 -րդ դարում ֆրանսիացի գիտնական Է. Մարիոտը և անգլիացի գիտնական Ռ. Բոյլը համարյա միաժամանակ ցույց են տվել, որ հաստատուն ջերմաստիճանում գազի ճնշումը կախված է նրա ծավալից. տրված զանգվածով գազի ճնշումը հաստատուն ջերմաստիճանում փոփոխվում է նրա ծավալին հակադարձ համեմատական (Բոյլ-Մարիոտի օրենք): Այս օրենքը կարելի է սահմանել այլ կերպ. տրված զանգվածով գազի ճնշման և ծավալի արտադրյալը հաստատուն մեծություն է:
![]()
p,V կոորդինատական համակարգում այս օրենքը գրաֆիկորեն արտահայտվում է իզոթերմ կոչվող կորով (նկ.10.3): Գազի միևնույն զանգվածի համար տարբեր իզոթերմերը համապատասխանում են տարբեր ջերմաստիճաններում տեղի ունեցող պրոցեսներին:
Իզոբար պրոցես: Գեյ-Լյուսակի օրենքը: Գազում ընթացող այն պրոցեսը, որի ժամանակ ճնշումը մնում է հաստատուն, կոչվում է իզոբար («բարոս» - ծանր):
Գազի ծավալի կախումը նրա ջերմաստիճանից հաստատուն ճնշման դեպքում հաստատվել է ֆրանսիացի ֆիզիկոս Լ.Գեյ - Լյուսակի կողմից: Նրա կատարած փորձերը ցույց տվեցին, որ գազի ծավալի մեծացումն ուղիղ համեմատական է ջերմաստիճանի աճին:
Տրված զանգվածով գազի ծավալը հաստատուն ճնշման դեպքում ջերմաստիճանի մեծացմանը զուգընթաց աճում է գծայնորեն (Գեյ - Լյուսակի օրենք):
![]()
որտեղ V -ն
գազի ծավալն է
t ջերմաստիճանում,
V0 -ն նրա ծավալը՝
00C-ում, ![]() - մեծությունը
կոչվում է ծավալային
ընդարձակման ջերմաստիճանային
գործակից: Բոլոր
գազերի համար
α = 1/2730 C-1:
- մեծությունը
կոչվում է ծավալային
ընդարձակման ջերմաստիճանային
գործակից: Բոլոր
գազերի համար
α = 1/2730 C-1:
Հետևաբար

Ծավալի գրաֆիկական կախումը ջերմաստիճանից արտահայտվում է ուղիղ գծով՝ իզոբարով (նկ.10.4): Չափազանց ցածր ջերմաստիճանների դեպքում (-2730C-ին մոտ) Գեյ-Լյուսակի օրենքը չի գործում, այդ պատճառով էլ գրաֆիկի վրա հոծ գիծը փոխարինվում է կետագծերով:
Իզոխոր պրոցես: Շառլի օրենքը: Գազում ընթացող այն պրոցեսը, որի դեպքում ծավալը մնում է հաստատուն, կոչվում է իզոխոր («խորեմ»-տարողություն): Տրված զանգվածով գազի ճնշման կախումը ջերմաստիճանից անփոփոխ ծավալի դեպքում առաջին անգամ ուսումնասիրվել է 1787թ. ֆրանսիացի ֆիզիկոս Ժ. Շառլի կողմից: Նա հաստատել է, որ տրված զանգվածով գազի ճնշումը, հաստատուն ծավալի դեպքում, ջերմաստիճանի մեծացման հետ աճում է գծայնորեն (Շառլի օրենք).
![]()
Որտեղ p-ն
գազի ճնշումն է
t0C ջերմաստիճանում,
![]() նրա ճնշումը՝
00C -ում: γ մեծությունը
կոչվում է ճնշման
ջերմաստիճանային
գործակից: Նրա
արժեքը կախված
չէ գազի բնույթից:
Բոլոր գազերի համար
γ = 1 / 2730C-1: Այսպիսով,
նրա ճնշումը՝
00C -ում: γ մեծությունը
կոչվում է ճնշման
ջերմաստիճանային
գործակից: Նրա
արժեքը կախված
չէ գազի բնույթից:
Բոլոր գազերի համար
γ = 1 / 2730C-1: Այսպիսով,

Ճնշման գրաֆիկական կախումը ջերմաստիճանից արտահայտվում է ուղիղ գծով՝ իզոխորով (նկ.10.5):
Եթե իզոխորը (նկ.10.5) շարունակենք դեպի բացասական ջերմաստիճանների տիրույթ, ապա աբսցիսների առանցքի հետ հատման կետում կունենանք՝
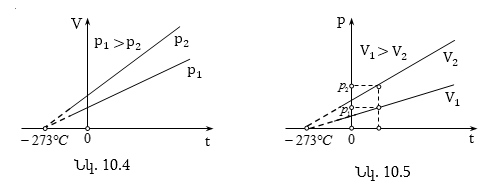

Այստեղից t = -2730C (ավելի ճիշտ-273,160C ), ինչը և համապատասխանում է ջերմադինամիկական սանդղակի զրոյին: Այս ջերմաստիճանը անվանում են Կելվինի զրո կամ բացարձակ զրո:
Ջերմաստիճանների ջերմադինամիկական սանդղակն առաջարկվել է անգլիացի գիտնական Կելվինի կողմից: Այդ սանդղակի վրա որպես հաշվարկման սկիզբ, ընդունվել է 0Կ-ը: Կելվինի զրոն այն սահմանային ջերմաստիճանն է, որի դեպքում իդեալական գազի ճնշումը հավասար է զրոյի:
Ջերմադինամիկական սանդղակով, որպես ջերմաստիճանային միավոր, ընդունված է Կելվինը (Կ), որը համապատասխանում է 10C-ին:
Ջերմաստիճանների ջերմադինամիկական սանդղակով հաշվարկված ջերմաստիճանը նշանակվում է T-ով: Այն կոչվում է ջերմադինամիկական ջերմաստիճան: Քանի որ նորմալ մթնոլորտային ճնշման դեպքում սառույցի հալման ջերմաստիճանն ընդունված 00C-ում հավասար է 273,16Կ-1 ապա
![]()
Այժմ (10.8) և (10.9) հավասարումների մեջ Ցելսիուսի սանդղակով հաշվարկված ջերմաստիճանը փոխարինելով ջերմադինամիկական ջերմաստիճանով` Գեյ-Լյուսակի և Շառլի օրենքներին կարելի է տալ ավելի հարմար տեսք.

Գազի ծավալները
T1 և T2 ջերմաստիճաններում
նշանակելով V1-ով
և V2-ով, իսկ ճնշումները
համապատասխանաբար`![]() կարող
ենք գրել`
կարող
ենք գրել`
![]()
p = const, m = const դեպքում և
![]()
V = const, m = const դեպքում:
Գեյ-Լյուսակի (10.12) և Շառլի (10.13) օրնեքների այդպիսի գրառումներում ավելի լիարժեք է բացահայտվում դրանց ֆիզիկական իմաստը: Գազի տրված զանգվածի համար նրա ծավալն իզոբար կամ ճնշումն իզոխոր պրոցեսների դեպքում համեմատական է ջերմադինամիկական ջերմաստիճանին:
Գազային օրենքները մեծ ճշտությամբ տեղի ունեն ոչ շատ բարձր ճնշումների և ոչ շատ ցածր ջերմաստիճանների դեպքում:
10.6. ԻԴԵԱԼԱԿԱՆ ԳԱԶԻ ՎԻՃԱԿԻ ՀԱՎԱՍԱՐՈՒՄԸ
Իզոպրոցեսները քննարկելիս մինչև այժմ ենթադրում էինք, որ վիճակի երեք պարամետրերից մեկը մնում էր հաստատուն: Գործնականում շատ հաճախ բախվում ենք այնպիսի դեպքերի, երբ միաժամանակ փոփոխվում են վիճակի երեք պարամետրերը: Այդ պարամետրերի միջև գոյություն ունի որոշակի կապ, այն անվանում են վիճակի հավասարում, որն ընդհանուր տեսքով տրվում է`
![]()
արտահայտությամբ, որտեղ փոփոխականներից յուրաքանչյուրը մյուս երկուսի ֆունկցիա է:
Ֆրանսիացի
ֆիզիկոս և ճարտարագետ
Բ. Կլապեյրոնը
(1799-1864) արտածեց իդեալական
գազի վիճակի հավասարումը`
միացնելով Բոյլ-Մարիոտի
և Գեյ-Լյուսակի
օրենքները: Ենթադրենք,
թե գազի սկզբնական
վիճակը m = const դեպքում
բնութագրվում
է ![]() իսկ
վերջնականը՝ համապատասխանաբար
իսկ
վերջնականը՝ համապատասխանաբար
![]() պարամետրերով
(նկ.10.6):
պարամետրերով
(նկ.10.6):
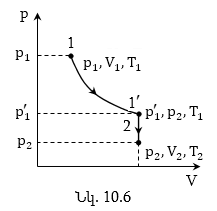
Դիցուք սկզբնական վիճակից անցումը վերջնական վիճակին կատարվում է հաջորդաբար երկու տեսակի պրոցեսներով.
![]()
Բոյլ-Մարիոտի (10.6) և Շառլի (10.13) օրենքներին համապատասխան կարող ենք գրել`

Արտաքսելով
(10.14) և (10.15) հավասարումներից
![]() կստանանք
կստանանք
![]()
Քանի որ ընտրվել են կամայական և վիճակները, ապա տվյալ զանգվածով գազի համար` pV/ T մեծությունը մնում է հաստատուն, այն է`
![]()
(10.17) արտահայտությունը կոչվում է Կլապեյրոնի հավասարում: (10.17) հավասարման մեջ B հաստատունի արժեքը կախված է գազի զանգվածից և մոլեկուլային զանգվածից, ինչպես նաև ճնշման, ծավալի և ջերմաստիճանի միավորների ընտրությունից: Հաշվենք այդ հաստատունը մեկ մոլ քանակությամբ նյութի համար: Ինչպես հետևում է Ավոգադրոյի օրենքից, ցանկացած գազի մեկ մոլը միևնույն ջերմաստիճանի և ճնշման միևնույն արժեքների դեպքում զբաղեցնում է միևնույն ծավալը:
![]()
Պա պայմաններում
1 մոլ ցանկացած
գազ զբաղեցնում
է ![]() ծավալ:
ծավալ:
Այս տվյալները տեղադրելով (10.17) հավասարման մեջ՝ կստանանք նրա մեջ մտնող հաստատունի արժեքը, ընդ որում ցանկացած գազի մեկ մոլի համար այդ արժեքը նույնն է: Այն ստացել է ունիվերսալ գազային հաստատուն անվանումը և նշանակվում է R-ով: Գտնենք R-ի թվային արժեքը ՄՀ համակարգում:
![]()
(10.17) հավասարումը 1 մոլ գազի համար կարելի է գրել այսպես
![]()
(10.18)-ից հեշտությամբ
կարելի է ստանալ
հավասարում գազի
ցանկացած զանգվածի
համար: m զանգվածով
գազը կգրավի ![]() ծավալ,
որտեղ M-ը մեկ մոլ
գազի զանգվածն
է, n / M-ը՝ գազի մոլերի
թիվը: (10.18) հավասարման
երկու մասերը բազմապատկելով
m/M-ով՝ կստանանք
ծավալ,
որտեղ M-ը մեկ մոլ
գազի զանգվածն
է, n / M-ը՝ գազի մոլերի
թիվը: (10.18) հավասարման
երկու մասերը բազմապատկելով
m/M-ով՝ կստանանք
![]()
![]()
![]()
որը Մենդելեև-Կլապեյրոնի հավասարումն է գազի ցանկացած զանգվածի համար:
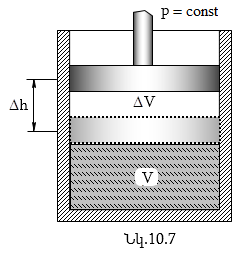
Այժմ պարզաբանենք գազային հաստատունի ֆիզիկական իմաստը: Ենթադրենք՝ գլանում մխոցի տակ T ջերմաստիճանում գտնվում է մեկ մոլ գազ (նկ.10.7), որի ծավալը V է: Այն տաքացնենք իզոբար ձևով (p = cosnt) 1Կ- ով, այդ դեպքում մխոցը կբարձրանա Δh բարձրության վրա, իսկ գազի ծավալը կմեծանա ΔV-ով: Գրենք (10.18) հավասարումը տաքացած գազի համար՝
![]()
և նրանից հանենք
![]() հավասարումը,
որը համապատասխանում
է գազի վիճակին
մինչև տաքացումը.
հավասարումը,
որը համապատասխանում
է գազի վիճակին
մինչև տաքացումը.
և նրանից հանենք հավասարումը, որը համապատասխանում է գազի վիճակին մինչև տաքացումը.
![]()
Տեղադրելով (10.20) -ի մեջ ΔV= SΔh -ը, որտեղ s- ը գլանի հիմքի մակերեսն է, կստանանք՝
![]()
Սակայն F = pS ուժն է, իսկ A = FΔh մխոցի տեղաշարժով պայմանավորված աշխատանքն է, որը կատարում է F ուժը արտաքին ուժերի դեմ գազի ընդարձակման ժամանակ: Հետևաբար, R = A, այսինքն՝ գազային հաստատունը որոշվում է այն աշխատանքով, որը կատարում է մեկ մոլ գազը, երբ այն իզոբար տաքացվում է 1Կ-ով:
10.7. ԻԴԵԱԼԱԿԱՆ ԳԱԶԵՐԻ ՄՈԼԵԿՈՒԼԱՅԻՆ-ԿԻՆԵՏԻԿ ՏԵՍՈՒԹՅԱՆ ՀԻՄՆԱԿԱՆ ՀԱՎԱՍԱՐՈՒՄԸ
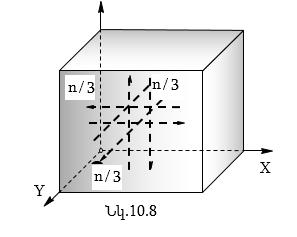
Ճնշումն առաջանում է անոթի պատերին մոլեկուլների հարվածների հետևանքով: Քննարկենք խորանարդաձև անոթում (նկ.10.8) գտնվող, կամայականորեն ընտրված իդեալական գազի I մոլեկուլի վարքը:
Դիցուք ![]() անոթի
պատին ուղղահայաց
ուղղված նրա արագությունն
է, իսկ
անոթի
պատին ուղղահայաց
ուղղված նրա արագությունն
է, իսկ ![]() զանգվածը:
Առաձգական հարվածի
դեպքում մոլեկուլն
անոթի պատին հաղորդում
է
զանգվածը:
Առաձգական հարվածի
դեպքում մոլեկուլն
անոթի պատին հաղորդում
է ![]() իմպուլս,
հարվածից հետո
նրա իմպուլսը հավասար
կլինի
իմպուլս,
հարվածից հետո
նրա իմպուլսը հավասար
կլինի ![]() Հետևաբար,
մոլեկուլի իմպուլսը
կփոփոխվի
Հետևաբար,
մոլեկուլի իմպուլսը
կփոփոխվի ![]() Ըստ
Նյուտոնի երկրորդ
օրենքի
Ըստ
Նյուտոնի երկրորդ
օրենքի
![]()
Եթե խորանարդի
մեջ, որի կողի երկարությունը
![]() է, գտնվում
է n թվով մոլեկուլ,
ապա մոլեկուլների
անկանոն շարժման
և բոլոր ուղղությունների
հավասարահավանականության
հետևանքով կարելի
է համարել, որ n/3 մոլեկուլներ
շարժվում են x-երի
առանցքի ուղղությամբ,
n/3 մոլեկուլներ
y-ների առանցքի
ուղղությամբ, n/3՝
z-երի առանցքի ուղղությամբ:
Գազի ճնշման միջին
ուժը գտնելու համար
հարկավոր է հաշվել
որոշակի ժամանակամիջոցում
պատի և հարվածող
բոլոր մոլեկուլների
իմպուլսների գումարը:
Նույն պատի վրա
(նիստի) մեկ հարվածից
մինչև հաջորդ հարվածը
մոլեկուլն անցնում
է միջինը
է, գտնվում
է n թվով մոլեկուլ,
ապա մոլեկուլների
անկանոն շարժման
և բոլոր ուղղությունների
հավասարահավանականության
հետևանքով կարելի
է համարել, որ n/3 մոլեկուլներ
շարժվում են x-երի
առանցքի ուղղությամբ,
n/3 մոլեկուլներ
y-ների առանցքի
ուղղությամբ, n/3՝
z-երի առանցքի ուղղությամբ:
Գազի ճնշման միջին
ուժը գտնելու համար
հարկավոր է հաշվել
որոշակի ժամանակամիջոցում
պատի և հարվածող
բոլոր մոլեկուլների
իմպուլսների գումարը:
Նույն պատի վրա
(նիստի) մեկ հարվածից
մինչև հաջորդ հարվածը
մոլեկուլն անցնում
է միջինը ![]() հավասար
ճանապարհ: Այդ
երկու հարվածների
միջև ընկած ժամանակամիջոցը`
հավասար
ճանապարհ: Այդ
երկու հարվածների
միջև ընկած ժամանակամիջոցը`
![]() Այժմ
որոշենք այն միջին
ուժը, որով ազդում
է մեկ մոլեկուլը
պատերից որևէ մեկի
վրա: (10.22) հավասարման
մեջ
Այժմ
որոշենք այն միջին
ուժը, որով ազդում
է մեկ մոլեկուլը
պատերից որևէ մեկի
վրա: (10.22) հավասարման
մեջ ![]() ժամանակամիջոցի
փոխարեն տեղադրենք
իր արժեքը`
ժամանակամիջոցի
փոխարեն տեղադրենք
իր արժեքը`
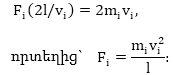
Գազի մոլեկուլները
շարժվում են տարբեր
արագություններով
![]() հետևաբար
նրանք անոթի պատերին
կհաղորդեն տարբեր
ինպուլսներ: Ընտրենք
մոլեկուլների
շարժման որևէ ուղղություն,
օրինակ, x-երի առանցքի
ուղղությունը:
Այդ ուղղությամբ
խորանարդի երկու՝
իրար դեմ հանդիման
նիստերի միջև շարժվում
է բոլոր մոլեկուլների
1/3 - ը, և մեկ նիստի
վրա հարվածի գումարային
ուժը
հետևաբար
նրանք անոթի պատերին
կհաղորդեն տարբեր
ինպուլսներ: Ընտրենք
մոլեկուլների
շարժման որևէ ուղղություն,
օրինակ, x-երի առանցքի
ուղղությունը:
Այդ ուղղությամբ
խորանարդի երկու՝
իրար դեմ հանդիման
նիստերի միջև շարժվում
է բոլոր մոլեկուլների
1/3 - ը, և մեկ նիստի
վրա հարվածի գումարային
ուժը
![]()
Իդեալական
գազում ![]() ուստի
ուստի
![]()
(10.23) հավասարման աջ մասը բազմապատկենք n-ով և բաժանենք n-ի, կստանանք
![]()
Փակագծերում գտնվող արտահայտությունը` <v2քառ> մոլեկուլների շարժման միջին քառակուսային արագության քառակուսին է: Այսպիսով,
![]()
![]()
![]()
![]()
Այսպիսով՝
![]()
(10.25)-ը մոլեկուլային-կինետիկ
տեսության հիմնական
հավասարումն է:
Այն արտահայտում
է մակրոսկոպիկ
մեծությունը՝
գազի ճնշումը մոլեկուլների
![]() կոնցենտրացիայի
միջոցով, առանձին
մոլեկուլների
m զանգվածով և նրանց
շարժման <vքառ>
միջին քառակուսային
արագությամբ: Եթե
կոնցենտրացիայի
միջոցով, առանձին
մոլեկուլների
m զանգվածով և նրանց
շարժման <vքառ>
միջին քառակուսային
արագությամբ: Եթե
![]() միջոցով
արտահայտենք որևէ
մոլեկուլի համընթաց
շարժման միջին
կինետիկ էներգիան,
ապա (10.25) հավասարումը
կարելի է գրել
հետևյալ տեսքով
միջոցով
արտահայտենք որևէ
մոլեկուլի համընթաց
շարժման միջին
կինետիկ էներգիան,
ապա (10.25) հավասարումը
կարելի է գրել
հետևյալ տեսքով
![]()
Գազի ճնշումը հավասար է այն բոլոր մոլեկուլների համընթաց շարժման միջին կինետիկ էներգիայի 2/3-ին, որոնք պարունակվում են գազի միավոր ծավալում:
Այժմ անցնենք գազերի մոլեկուլային-կինետիկ տեսության հիմնական հավասարումից բխող կարևոր հետևություններին:
Վերցնենք
1 մոլ գազ, որն զբաղեցնում
է ![]() ծավալ:
Գազի մոլեկուլների
խտությունը՝
ծավալ:
Գազի մոլեկուլների
խտությունը՝ ![]() և (10.26) հավասարումը
կարելի է գրել
հետևյալ տեսքով.
և (10.26) հավասարումը
կարելի է գրել
հետևյալ տեսքով.
![]()
Սակայն մեկ
մոլի համար ճիշտ
է ![]() վիճակի
հավասարումը,
վիճակի
հավասարումը,
![]()
Ճնշման այս արտահահայտությունը տեղադրելով (10.27) հավասարման մեջ և լուծելով այն T-ի կամ <E>-ի նկատմամբ՝ կստանանք մոլեկուլային-կինետիկ տեսության առաջին դրույթը.
![]()
Ըստ (10.28) հավասարման` ջերմադինամիկական ջերմաստիճանն ուղիղ համեմատական է գազի մոլեկուլների քաոսային շարժման միջին կինետիկ էներգիային: Ինչքան արագ են շարժվում մոլեկուլները, այնքան բարձր է ջերմաստիճանը: (10.28)-ից գտնում ենք
![]()
ցանկացած գազի համար, որից բխում է գազերի մոլեկուլային տեսության երկրորդ դրույթը. միևնույն ջերմաստիճանում գտնվող տարբեր գազերի մոլեկուլների միջին կինետիկ էներգիաները հավասար են միմյանց: Գազային մոլեկուլների միջին կինետիկ էներգիաների հավասարությունից հետևում է, որ միևնույն ջերմաստիճանն ունեցող տարբեր գազերի խառնվելու դեպքում, մի գազի մոլեկուլներից մյուս գազի մոլեկուլներին էներգիայի զգալի փոխանցում տեղի չի ունենում:
![]() մեծությունը
ստացել է Բոլցմանի
հաստատուն անվանունը
և ներկայացնում
է մեկ մոլեկուլին
վերագրվող գազային
հաստատունը.
մեծությունը
ստացել է Բոլցմանի
հաստատուն անվանունը
և ներկայացնում
է մեկ մոլեկուլին
վերագրվող գազային
հաստատունը.
![]()
Հետևաբար (8.28ա) արտահայտությունը կարելի է ներկայացնել
![]()
տեսքով: (10.29) -ը տեղադրելով (10.26) -ի մեջ, կգտնենք գազի ճնշման արտահայտությունը.
![]()
Գազի ճնշումն ուղիղ հանմեմատական է միավոր ծավալում մոլեկուլների թվի և նրա ջերմադինամիկական ջերմաստիճանի արտադրյալին:
(10.29) հավասարման վերլուծությունը ցույց է տալիս, որ T = 0Կ-ի դեպքում մոլեկուլների համընթաց շարժման կինետիկ էներգիան՝ <E> =0, հետևաբար <vքառ>=0: Այսպիսով բացակայում է մոլեկուլների համընթաց շարժումը: Սակայն դա չի նշանակում, որ T = 0Կ -ի դեպքում շարժումն ընդհանրապես դադարում է: Պահպանվում են ատոմների և մոլեկուլների պըտըտական ու տատանողական շարժումները: Ժամանակակից պատկերացումներով T = 0Կ-ի դեպքում ատոմներում, նաև` ավելի մանր մասնիկներում մնում է որոշակի էներգիա, որն անվանում են զրոյական: Այժմ (10.29) բանաձևը ներկայացնենք հետևյալ տեսքով՝
![]()
որտեղից միջին քառակուսային արագությունը`
![]()
Այստեղից հետևում է մոլեկուլային-կինետիկ տեսության երրորդ դրույթը. մոլեկուլների միջին քառակուսային արագությունն ուղիղ համեմատական է ջերմադինամիկական ջերմաստիճանի քառակուսի արմատին: Այսպիսով, իմանալով գազի ջերմաստիճանը, կարելի է գտնել մոլեկուլների շարժման միջին քառակուսային արագությունը: (10.29) արտահայտության հիման վրա կարելի է տալ ջերմաստիճանի սահմանումը. ջերմադինամիկական ջերմաստիճանը, մինչև հաստատուն բազմապատկչի ճշտությամբ, հավասար է իդեալական գազի մոլեկուլի համընթաց շարժման միջին կինետիկ էներգիային:
Եթե ունենք մի քանի գազերի խառնուրդ, ապա ըստ զանգվածի` տարբեր մոլեկուլներ կունենան տարբեր միջին արագություններ, բայց մոլեկուլների միջին էներգիան կլինի նույնը: Այս դեպքում ճնշումը կլինի
![]()
որտեղ ![]() և այլն
առաջին, երկրորդ
և այլ տեսակի մոլեկուլների
քանակն է միավոր
ծավալում: (10.32) արտահայտությունը
կարելի է ներկայացնել
հետևյալ տեսքոով`
և այլն
առաջին, երկրորդ
և այլ տեսակի մոլեկուլների
քանակն է միավոր
ծավալում: (10.32) արտահայտությունը
կարելի է ներկայացնել
հետևյալ տեսքոով`
![]()
Բայց ![]() այն
այն ![]() նշումն
է, որը կլիներ անոթում
միայն առաջին տեսակի
մոլեկուլների
առկայության դեպքում,
նշումն
է, որը կլիներ անոթում
միայն առաջին տեսակի
մոլեկուլների
առկայության դեպքում,
![]() այն
այն
![]() ճնշումն
է, որը կլիներ անոթում
միայն երկրորդ
տեսակի մոլեկուլների
առկայության դեպքում
և այլն: Այն ճնշումը,
որը պայմանավորված
է որևէ տեսակի
մոլեկուլներով,
այն պայմանով,
որ միայն դրանք
են գտնվում անոթում,
ընդ որում այն
քանակով, ինչ քանակով
նրանք գտնվում
են խառնուրդում,
կոչվում է գազի
խառնուրդի համապատասխան
բաղադրամասի պարցիալ
ճընշում: Մտցնելով
պարցիալ ճնշումները`
(10.32) հիման վրա կարելի
է գրել
ճնշումն
է, որը կլիներ անոթում
միայն երկրորդ
տեսակի մոլեկուլների
առկայության դեպքում
և այլն: Այն ճնշումը,
որը պայմանավորված
է որևէ տեսակի
մոլեկուլներով,
այն պայմանով,
որ միայն դրանք
են գտնվում անոթում,
ընդ որում այն
քանակով, ինչ քանակով
նրանք գտնվում
են խառնուրդում,
կոչվում է գազի
խառնուրդի համապատասխան
բաղադրամասի պարցիալ
ճընշում: Մտցնելով
պարցիալ ճնշումները`
(10.32) հիման վրա կարելի
է գրել
![]()
(10.33) բանաձևը ներկայացնում է այսպես կոչված Դալտոնի օրենքը. իդեալական գազերի դեպքում պարցիալ ճնշումների գումարը հավասար է ամբողջ գազային խառնուրդի ճնշմանը:
Խնդիր 1: ![]() զանգվածով
և
զանգվածով
և ![]() մոլային
զանգվածով գազը
խառնել են
մոլային
զանգվածով գազը
խառնել են ![]() զանգվածով
և
զանգվածով
և ![]() մոլային
զանգվածով գազի
հետ: Գտնել խառնուրդի
մոլային զանգվածը
և խտությունը,
եթե խառնուդի ջերմաստիճանը
հավասար է T-ի, ճնշումը
p-ի:
մոլային
զանգվածով գազի
հետ: Գտնել խառնուրդի
մոլային զանգվածը
և խտությունը,
եթե խառնուդի ջերմաստիճանը
հավասար է T-ի, ճնշումը
p-ի:
Լուծում:
Գազերի խառնուրդի
ճնշումը կարելի
է որոշել Դալտոնի
օրենքից, որի համաձայն
![]() որտեղ
որտեղ
![]() պարցիալ
ճնշումներն են:
պարցիալ
ճնշումներն են:
Գրենք յուրաքանչյուր գազի համար վիճակի հավասարումը` նկատի ունենալով, որ գազերը գտնվում են նույն ջերմաստիճանում և զբաղեցնում են միատեսակ ծավալ.
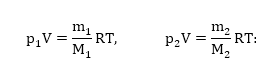
Այս հավասարումները գումարելով իրար կստանանք`
![]()
Մյուս կողմից վիճակի հավասարումը m զանգվածով խառնուրդի համար
![]()
Համեմատելով (1) և (2) հավասարումներն իրար հետ` խառնուրդի մոլային զանգվածի համար կստանանք`

(2)-ից խառնուրդի խտության համար ստանում ենք`
![]()
Նկատի ունենալով (3)-ը (4)-ից կստանանք`
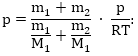
10.8. ՄՈԼԵԿՈՒԼՆԵՐԻ ԲԱՇԽՈՒՄՆ ԸՍՏ ԱՐԱԳՈՒԹՅՈՒՆՆԵՐԻ
Մաքսվելի օրենքը: Գազերի ուսումնասիրության դեպքում ընդունվում է մի հիմնական մոդել՝ իդեալական գազի մոդելը, որպես անկանոն ջերմային շարժմանն անընդհատ մասնակցող չփոխազդող մասնիկների մի մեծ համախումբ: Մասնիկների այդ համախմբի համար կիրառելի է հավանականությունների մաթեմատիկական տեսության՝ միջին, միջին քառակուսային և մասնիկների վարքը համախմբում բնութագրող առավել հավանական պարամետրերի մասին հասկացությունների վրա հիմնված վիճակագրական մեթոդը:
Քննարկենք Մաքսվելի բաշխումը կամ մոլեկուլների բաշխումն ըստ արագությունների:
Գազի մոլեկուլների
արագություններն
ունեն տարբեր արժեքներ
և ուղղություններ,
ընդ որում, յուրաքանչյուր
առանձին մոլեկուլի
արագության ինչպես
մեծությունը, այնպես
էլ ուղղությունը
փոփոխվում է բախումների
արդյունքում, դրա
համար էլ հնարավոր
չէ որոշել ժամանակի
տվյալ ակնթարթին
ճշտորեն տրված
արագություն ունցող
մոլեկուլների
թիվը, բայց կարելի
է հաշվել այն մոլեկուլների
թիվը, որոնց արագություններն
ընկած են ![]() միջակայքում:
միջակայքում:
Միաժամանակ ենթադրվում է, որ գազում գոյություն չունեն ճիշտ միևնույն արագությունն ունեցող մոլեկուլներ, և dN մոլեկուլների թիվը, որոնց արագություններն ընկած են v-ի և v+dv-ի միջև ընկած նեղ միջակայքում, ուղիղ համեմատական է N մոլեկուլների ընդհանուր թվին, dv միջակայքի լայնությանը և կախված է v արագությունից: Այդպիսի տեսական կախվածությունը հաստատվել է Մաքսվելի կողմից հավանականությունների տեսության հիման վրա:
![]()
Արագությունների dv միջակայքում գտնվող v արագություն ունեցող մոլեկուլների հարաբերական թիվը ցույց տվող
![]()
ֆունկցիան անվանում են գազի մոլեկուլների բաշխման ֆունկցիա ըստ արագությունների կամ Մաքսվելի բաշխման ֆունկցիա:

Այդ ֆունկցիան
գրաֆիկորեն պատկերված
է նկ.10.9ա -ում: Ստվերագծված
f(v)dv մակերեսը հավասար
է dN/N -ի, այսինքն՝
գազի մոլեկուլների
այն հարաբերական
թվին, որոնց արագություններն
ընկած են v-ից v+dv միջակայքում:
Բաշխման կորի առավելագույնը
(մաքսիմումը) համապատասխանում
է մոլեկուլների
առավել հավանական
![]() արագությանը,
որը կարելի է գտնել՝
լուծելով f (v) ֆունկցիայի
մաքսիմումը գըտնելու
խնդիրը:
արագությանը,
որը կարելի է գտնել՝
լուծելով f (v) ֆունկցիայի
մաքսիմումը գըտնելու
խնդիրը:
Վերցնելով
![]()
ածանցյալն ըստ արագության և հավասարեցնելով այն զրոյի՝ կստանանք՝
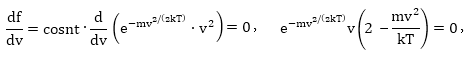
Այս հավասարմանը
բավարարող v=0 և v=
∞ արժեքները համապատասխանում
են f(v)-ի մինիմումին:
Փակագծերում գտնվող
արտահայտությունը
զրոյի վերածող
v-ի արժեքը որոնելի
![]()
![]()
Նշենք որ f(v) ֆունկցիայի տեսքը կախված է գազի տեսակից (մոլեկուլների զանգվածից) ու T ջերմաստիճանից: Գազի ճնշումն ու ծավալը չեն ազդում մոլեկուլների՝ ըստ արագությունների բաշխման վրա:
Ջերմաստիճանի
բարձրացման դեպքում
![]() մեծանում
է, այդ պատճառով
մոլեկուլների՝
ըստ արագությունների
բաշխման կորի առավելագույնը
տեղաշարժվում
է մեծ արագություների
կողմը՝
մեծանում
է, այդ պատճառով
մոլեկուլների՝
ըստ արագությունների
բաշխման կորի առավելագույնը
տեղաշարժվում
է մեծ արագություների
կողմը՝ ![]() Հետևաբար
ջերմաստիճանի
աճին զուգընթաց
մեծանում է մեծ
արագությամբ օժտված
մոլեկուլների
հարաբերական թիվը:
1 և 2 կորերով սահմանափակված
մակերեսները (նկ.10.9բ)
պետք է միմյանց
հավասար լինեն,
քանի որ նրանց
մեծությունը համեմատական
է մոլեկուլների
ընդհանուր թվին,
որը երկու դեպքում
էլ մնում է անփոփոխ:
Գազի մոլեկուլների
մեծ մասը շարժվում
է ամենամեծ հավանական
արագությամբ այն
դեպքում, երբ շատ
փոքր և շատ մեծ
արագություն ունեցող
մոլեկուլների
թիվը փոքր է: Բացի
առավել հավանական
արագությունից,
գազի մոլեկուլների
շարժումը բնորոշում
է նաև <v> միջին թվաբանական
արագությունը,
որը որոշվում է
Հետևաբար
ջերմաստիճանի
աճին զուգընթաց
մեծանում է մեծ
արագությամբ օժտված
մոլեկուլների
հարաբերական թիվը:
1 և 2 կորերով սահմանափակված
մակերեսները (նկ.10.9բ)
պետք է միմյանց
հավասար լինեն,
քանի որ նրանց
մեծությունը համեմատական
է մոլեկուլների
ընդհանուր թվին,
որը երկու դեպքում
էլ մնում է անփոփոխ:
Գազի մոլեկուլների
մեծ մասը շարժվում
է ամենամեծ հավանական
արագությամբ այն
դեպքում, երբ շատ
փոքր և շատ մեծ
արագություն ունեցող
մոլեկուլների
թիվը փոքր է: Բացի
առավել հավանական
արագությունից,
գազի մոլեկուլների
շարժումը բնորոշում
է նաև <v> միջին թվաբանական
արագությունը,
որը որոշվում է
![]() բանաձևով:
բանաձևով:
Միջին թվաբանական արագության ընդհանուր սահմանումից v-ի ընդհատ արժեքների համար ունենք
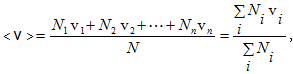
որտեղ N-ը ![]() արագություն
ունեցող մասնիկների
թիվն է: Անընդհատ
սպեկտրի դեպքում
արագության արժեքը՝
արագություն
ունեցող մասնիկների
թիվն է: Անընդհատ
սպեկտրի դեպքում
արագության արժեքը՝
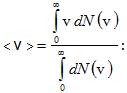
Սակայն լրիվ մասնիկների թիվը՝
![]()
հետևաբար
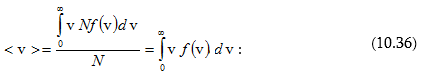
(10.36) -ի մեջ տեղադրելով f(v)-ի արժեքը և ինտեգրելով ստացված արտահայտությունը՝ կգտնենք
![]()
Համանման ձևով միջին քառակուսային արագության համար կստանանք՝
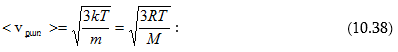
Միջին քառակուսային արագությունը հավասար է արագության քառակուսու միջինի քառակուսի արմատին: Եթե բոլոր մոլեկուլների զանգվածները հավասար են, ապա
![]()
Կիրառելով իդեալական գազի մոլեկուլների բաշխումն ըստ արագու թյունների
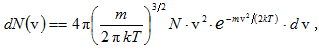
գտնենք գազի մոլեկուլների բաշխումն ըստ էներգիաների:
Իդեալական գազի մոլեկուլներն օժտված են կինետիկ էներգիայով՝
![]()
որտեղից հետևում
է, որ ![]() v փոփոխականից
անցնելով E փոփոխականին՝
կստանանք
v փոփոխականից
անցնելով E փոփոխականին՝
կստանանք
![]()
Որտեղ dN(E)-ն այն մոլեկուլների թիվն է, որոնց կինետիկ էներգիայի արժեքները գտնվում են E-ից մինչև E + dE միջակայքում: Մոլեկուլների բաշխման ֆունկցիան ըստ էներգիաների ունի հետևյալ տեսքը
![]()
Իդեալական գազի մոլեկուլի <E> միջին կինետիկ էներգիան որոշվում է (10.36)-ի համանման ինտեգրալով՝
![]()
Անհրաժեշտ է նշել, որ Մաքսվելի սահմանած մոլեկուլների՝ ըստ արագությունների բաշխման օրենքը և նրանից բխող հետևանքները իրավացի են միայն հավասարակշռված վիճակում գտնվող գազի համար: Այս օրենքը իրավացի է ցանկացած N թվի համար, եթե այդ թիվը բավականին մեծ է: Մաքսվելի օրենքը վիճակագրական է, իսկ վիճակագրական օրենքներն այնքան ճիշտ են տեղի ունենում, որքան ավելի մեծ թվով միատեսակ օբյեկտների վրա է այդ օրենքը տարածվում: Փոքր թվով օբյեկտների դեպքում կարող են դիտվել զգալի շեղումներ վիճակագրական կանխագուշակումներից: Ըստ արագության և էներգիայի մոլեկուլների բաշխման Մաքսվելի օրենքն առաջին անգամ փորձնականորեն հաստատվել է Շտեռնի փորձերով:
10.9. ԲԱՐՈՄԵՏՐԱԿԱՆ ԲԱՆԱՁԵՎ: ԲՈԼՑՄԱՆԻ ԲԱՇԽՈՒՄԸ
Մաքսվելի բաշխման օրենքի քննարկման ժամանակ ենթադրվում էր, որ մոլեկուլները հավասարաչափ բաշխվում են անոթի ամբողջ ծավալով, ինչը ճիշտ է, եթե անոթի ծավալը մեծ չէ: Մեծ ծավալներում մոլեկուլների բաշխման հավասարաչափությունը խախտվում է ծանրության ուժի ազդեցության հետևանքով, որի պատճառով խտությունը, հետևաբար նաև միավոր ծավալում մոլեկուլների թիվը կլինի ոչ միատեսակ: Դիտարկենք Երկրի ձգողական դաշտում գտնվող գազի մոլեկուլները:
Պարզաբանենք
մթնոլորտային
ճնշման կախումը
Երկրի մակերևույթից
ունեցած բարձրությունից:
Ենթադրենք՝ մթնոլորտային
ճնշումը Երկրի
մակերևույթի վրա
![]() է: hբարձրության
վրա այն հավասար
է p-ի: Բարձրությունը
dh-ով մեծացնելու
դեպքում ճնշումը
կփոքրանա dp-ով:
է: hբարձրության
վրա այն հավասար
է p-ի: Բարձրությունը
dh-ով մեծացնելու
դեպքում ճնշումը
կփոքրանա dp-ով:
![]()
որտեղ p-ն օդի
խտությունն է տվյալ
բարձրության վրա,
![]() m-ը մոլեկուլի
զանգվածն է,
m-ը մոլեկուլի
զանգվածն է, ![]() մոլեկուլների
կոնցենտրացիան:
մոլեկուլների
կոնցենտրացիան:
Կիրառելով
![]() արտահայտությունը,
կստանանք
արտահայտությունը,
կստանանք
![]()
այդ դեպքում
![]()
Ենթադրելով, որ որոշակի h բարձրության վրա T = const, g = const, անջատելով փոփոխականները, ինտեգրենք (10.43) արտահայտությունը.
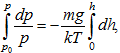
կստանանք բարոմետրական բանաձևը՝
![]()
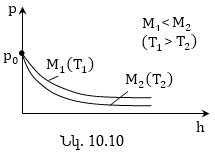
Բարոմետրական բանաձևը ցույց է տալիս գազի ճնշման կախումը Երկրի մակերևույթից ունեցած բարձրությունից: Բանաձևից հետևում է, որ ճնշումը բարձրության հետ նվազում է այնքան արագ, որքան ավելի ծանր է գազը (որքան ավելի մեծ է m-ն և որքան ավելի ցածր է ջերմաստիճանը) (նկ.10.10): Բարոմետրական բանաձևը հնարավորություն է տալիս գտնել ճնշումը կախված բարձրությունից, կամ չափելով ճնշումը գտնել բարձրությունը: Երկրի մակերևույթից հաշված բարձրությունը որոշելու համար ծառայող սարքը կոչվում է բարձրաչափ կամ ալտիմետր:
Եթե հաշվի առնենք, որ օդի մոլեկուլների կոնցենտրացիան մթնոլորտում որոշում է ճընշումը, ապա (10.44) բանաձևը կարելի է գրել հետևյալ տեսքով.
![]()
(10.45) բանաձևից
հետևում է, որ մասնիկների
թիվը զրոյից տարբեր
բարձրությունների
վրա ջերմաստիճանի
իջեցման հետ նվազում
է, և T = 0Կ-ի դեպքում
դառնում է զրո,
այսինքն 0Կ-ի դեպքում
բոլոր մոլեկուլները
կդասավորվեն Երկրի
մակերևույթի վրա:
Քանի որ մոլեկուլների
պոտենցիալ էներգիան
տարբեր բարձրությունների
վրա տարբեր է և
h բարձրության
վրա որոշվում է
![]() բանաձևով,
ապա (տես՝ (10.45)) կստանանք`
բանաձևով,
ապա (տես՝ (10.45)) կստանանք`
![]()
(10.46)-ից հետևում է, որ մոլեկուլները մեծ խտությամբ տեղավորվում են այնտեղ, որտեղ ավելի փոքր է նրանց պոտենցիալ էներգիան և հակառակը՝ ավելի փոքր խտությամբ այնտեղ, որտեղ նրանց պոտենցիալ էներգիան ավելի մեծ է: (10.46)-ը Բոլցմանի օրենքն է, որը ցույց է տալիս ջերմային շարժմանը մասնակցող մոլեկուլների բաշխումն ուժերի պոտենցիալային դաշտում, մասնավորապես` ծանրության ուժի դաշտում:
Բոլցմանի օրենքն ունիվերսալ է, այն ճիշտ է ուժերի պոտենցիալային դաշտում ցանկացած թվով մասնիկների համար: Այն արտահայտում է մասնիկների առավելագույն ցրմանը ձգտող ջերմային շարժման և Երկրի մակերևույթին մոտ գտնվող մասնիկների առավելագույն խտացմանը ձգտող ծանրության ուժերի միջև հավասարակշռության պայմանը:
Այն դեպքում, երբ Մաքսվելի օրենքը տալիս է մասնիկների բաշխումն ըստ կինետիկ էներգիայի արժեքների, Բոլցմանի օրենքը տալիս է մասնիկների բաշխումն ըստ պոտենցիալ էներգիայի արժեքների: Երկու բաշխուների համար էլ բնորոշ է էքսպոնենցիալ արտադրիչի առկայությունը, որի ցուցիչում գտնվում է մեկ մոլեկուլի կինետիկ կամ, համապատասխանաբար, պոտենցիալ էներգիայի և մոլեկուլի ջերմային շարժման միջին էներգիան որոշող մեծության հարաբերությունը:
Բոլցմանի բաշխման ճշմարտացիությունը փորձարարական ճանապարհով հաստատվեց Ավոգադրոյի հաստատունի որոշման ժամանակ: Ավոգադրոյի հաստատունը որոշվել է երկու անկախ եղանակներով: Առաջին եղանակը հիմնված է հավասարակշռության վիճակում գտնվող էմուլսիաների և սուսպենզիաների բարոմետրական բանաձևի կիրառման վրա: Մյուս եղանակն առաջարկվել է Ժ.Պերրենի կողմից և հիմնված է բրոունայն շարժման դիտման վրա: Այդ երկու եղանակները տվեցին միևնույն արդյունքները: Ավոգադրոյի հաստատունը՝ այսինքն մեկ մոլ նյութի մեջ մոլեկուլների թիվը, հավասար է 6,023գ1023 մոլ-1:
Խնդիր 1: Օգտագործելով
իդեալական գազի
մոլեկուլների`
ըստ արագությունների
բաշխման ֆունկցիան,
գտնել մոլեկուլների
բաշխման օրենքն
ըստ հարաբերական
արագությունների
![]()
Լուծում: Մոլեկուլների բաշխման ֆունկցիան ըստ արագությունների ունի հետևյալ տեսքը`

Մոլեկուլի հավանական արագությունը որոշվում է
![]()
բանաձևով,
մոլեկուլի հարաբերական
արագությունը`
![]() , որտեղ
v-ն տրված արագությունն
է:
, որտեղ
v-ն տրված արագությունն
է: ![]()
![]()
Վերջին երկուսից հետևում է`
![]()
Նկատի ունենալով (1)-ը (2)-ից կստանանք`

Այսպիսով ստանում ենք`
![]()
Խնդիր 2: Թթվածնի մոլեկուլների ո՞ր մասն է 273Կ ջերմաստիճանում օժտված 100մ/վ-ից մինչև 110մ/վ արագությամբ:
Լուծում: Մոլեկուլների բաշխումն ըստ հարաբերական արագությունների տրվում է

բանաձևով,
որտեղ u-ն հարաբերական
արագությունն
է: Մեր դեպքում
v=100մ/վ և dv=10մ/վ: Ամենահավանական
արագությունը
![]() Հետևաբար,
հարաբերական արագությունը`
Հետևաբար,
հարաբերական արագությունը`
![]()
Նկատի ունենալով վերջինները (1) բանաձևը տալիս է`

Խնդիր 3: Որոշել
![]() բարձրության
վրա օդի ճնշման
հարաբերությունը
բարձրության
վրա օդի ճնշման
հարաբերությունը
![]() խորության
հորատանցքի հատակի
ճնշմանը: Երկրի
մակերևույթի վրա
օդը գտնվում է
նորմալ պայմաններում,
և նրա ջերմաստիճանը
կախում չունի բարձրությունից:
խորության
հորատանցքի հատակի
ճնշմանը: Երկրի
մակերևույթի վրա
օդը գտնվում է
նորմալ պայմաններում,
և նրա ջերմաստիճանը
կախում չունի բարձրությունից:
Լուծում: Օգտվելով բարոմետրական բանաձևից` կարող ենք գրել.

որտեղ M-ը օդի մոլային զանգվածն է, R-ը գազային հաստատունն է, T-ն օդի բացարձակ ջերմաստիճանն է: (1) և (2) արտահայտություններից հետևում է `
![]()
Տեղադրելով
(3)-ի մեջ մտնող մեծությունների
թվային աժեքները
կստանանք `![]()
Խդիր 4: Ուղղաձիգ
երկար անոթի մեջ
գտնվում է գազ,
որը կազմված է
![]() զանգվածներով
երկու տարբեր գազերի
մոլեկուլներից,
ընդ որում
զանգվածներով
երկու տարբեր գազերի
մոլեկուլներից,
ընդ որում ![]() Անոթի
հատակին այդ մոլեկուլների
կոնցենտրացիաները
համապատասխանաբար
Անոթի
հատակին այդ մոլեկուլների
կոնցենտրացիաները
համապատասխանաբար
![]() Նկատի
ունենալով, որ
ամբողջ բարձրությամբ
T ջերմաստիճանը
մնում է անփոփոխ,
գտնել h բարձրությունը,
որի վրա այդ գազերի
մոլեկուլների
կոնցենտրացիաները
կլինեն միատեսակ:
Նկատի
ունենալով, որ
ամբողջ բարձրությամբ
T ջերմաստիճանը
մնում է անփոփոխ,
գտնել h բարձրությունը,
որի վրա այդ գազերի
մոլեկուլների
կոնցենտրացիաները
կլինեն միատեսակ:
Լուծում: Առաջին և երկրորդ գազերի համար ըստ Բոլցմանի բաշխման կարող ենք գրել`

![]()
![]()
որտեղից ստանում ենք
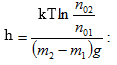
10.10. ՄՈԼԵԿՈՒԼՆԵՐԻ ԱԶԱՏ ՎԱԶՔԻ ՄԻՋԻՆ ԵՐԿԱՐՈՒԹՅՈՒՆԸ
Գազի մոլեկուլի միջին արագությունը շատ մեծ է: Այն կազմում է հարյուրավոր, նույնիսկ հազարավոր մետրեր վայրկյանում: Սակայն, կատարելով անկանոն շարժում, գազի մոլեկուլները նորմալ պայմաններում մեկ վայրկյանում ենթարկվում են հսկայական թվով բախումների, և մի կետից մինչև մյուս կետը նրանց անցած տարածությունն ավելի մեծ է լինում, քան L տեղափոխությունը: Ենթադրենք, թե մոլեկուլը շարժվում է A-ից B կետը (նկ.10.11):
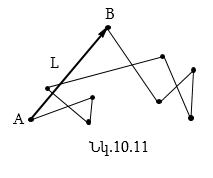
Այդ մոլեկուլի հետագիծը, այլ մոլեկուլների հետ նրա բախումների հետևանքով, բեկյալ գիծ է: Ճշտորեն հետևել A-ից B կետն անցած մասնիկի ճիշտ հետագծին անհնար է, դրա համար գազում մոլեկուլի իրական տեղաշարժը գնահատվում է դիֆուզիայի արագությամբ (A և B կետերի միջև մոլեկուլի L տեղափոխության հարաբերությունն այն ժամանակամիջոցին, որի ընթացքում տեղի է ունեցել այդ տեղափոխությունը): Մոլեկուլի դիֆուզիայի արագությունը զգալիորեն փոքր է նրա մոլեկուլային շարժման միջին արագությունից:
Մոլեկուլների
դիֆուզիայի արագության
գնահատման համար
ներմուծվում է
ազատ վազքի ![]() միջին
երկարություն
հասկացությունը:
Դա այն ճանապարհն
է, որը մոլեկուլն
անցնում է իրար
հաջորդող հարվածների
միջև ընկած ժամանակի
ընթացքում: Ենթադրենք,
որ միավոր ծավալում
պարունակվում
է
միջին
երկարություն
հասկացությունը:
Դա այն ճանապարհն
է, որը մոլեկուլն
անցնում է իրար
հաջորդող հարվածների
միջև ընկած ժամանակի
ընթացքում: Ենթադրենք,
որ միավոր ծավալում
պարունակվում
է ![]() մոլեկուլ,
որոնցից յուրաքանչյուրը
կարելի է ներկայացնել
r շառավղով գնդիկի
տեսքով (նկ.10.12): Ենթադրենք՝
տվյալ A մոլեկուլի
հետագիծն ուղիղ
գիծ է (չնայած դա
այդպես չէ), իսկ
նրա ճանապարհին
հանդիպած բոլոր
մոլեկուլներն
անշարժ են:
մոլեկուլ,
որոնցից յուրաքանչյուրը
կարելի է ներկայացնել
r շառավղով գնդիկի
տեսքով (նկ.10.12): Ենթադրենք՝
տվյալ A մոլեկուլի
հետագիծն ուղիղ
գիծ է (չնայած դա
այդպես չէ), իսկ
նրա ճանապարհին
հանդիպած բոլոր
մոլեկուլներն
անշարժ են:
A մոլեկուլն
իր ճանապարհին
մի քանի անգամ
կբախվի այլ մոլեկուլների,
օրինակ B-ին, որոնց
կենտրոնները նրա
շարժման հետագծից
գտնվում են 2r-ից
ոչ հեռու: Հետևաբար,
կարելի է ենթադրել,
որ այն տիրույթը,
ուր կատարվում
է տվյալ մոլեկուլի
փոխազդեցությունը
մյուսների հետ,
մի գլան է, որի շառավիղը
2r է: Շարժվող մոլեկուլը
մեկ վայրկյանում
կբախվի այն մոլեկուլներին,
որոնք գտնվում
են գլանի ներսում
և կանցնի իր <v> արագությանը
թվապես հավասար
ճանապարհ: Գլանի
ծավալը թվապես
հավասար է![]() իսկ
A մոլեկուլի բախումների
միջին թիվը գլանի
ծավալում գտնվող
մոլեկուլների
հետ կլինի`
իսկ
A մոլեկուլի բախումների
միջին թիվը գլանի
ծավալում գտնվող
մոլեկուլների
հետ կլինի`
![]()
(10.47) բանաձևից
<z>-ի որոշման ժամանակ
ելնում ենք նրանից,
որ բոլոր մոլեկուլները,
բացի մեկից, անշարժ
են: Իրականում
բոլոր մոլեկուլները
գտնվում են քաոսային
շարժման մեջ: Այդ
պատճառով բանաձևի
մեջ մտցվում է
![]() հավասար
ուղղման գործակից,
որը ցույց է տալիս,
որ իրականում բախումների
թիվն ավելի մեծ
է՝
հավասար
ուղղման գործակից,
որը ցույց է տալիս,
որ իրականում բախումների
թիվն ավելի մեծ
է՝
![]()
որտեղ![]() մոլեկուլների
կոնցենտրացիան
է: Մոլեկուլի ազատ
վազքի միջին երկարությունը
հավասար է 1վրկ-ում
մոլեկուլի անցած
ճանապարհի և այդ
ժամանակամիջոցում
կատարված բախումների
թվի հարաբերությանը
մոլեկուլների
կոնցենտրացիան
է: Մոլեկուլի ազատ
վազքի միջին երկարությունը
հավասար է 1վրկ-ում
մոլեկուլի անցած
ճանապարհի և այդ
ժամանակամիջոցում
կատարված բախումների
թվի հարաբերությանը
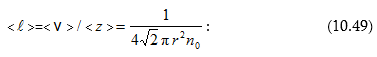
(10.49) արտահայտությունից
հետևում է, որ ![]() կախված
չէ գազի ջերմաստիճանից,
քանի որ ջերմաստիճանի
բարձրացման հետ
աճում են <v> արագությունն
ու <z> բախումների
թիվը: Տրված գազի
համար, անփոփոխ
ջերմաստիճանի
դեպքում, ազատ
վազքի միջին երկարությունը
հակադարձ համեմատական
է գազի ճնշմանը
(10.30):
կախված
չէ գազի ջերմաստիճանից,
քանի որ ջերմաստիճանի
բարձրացման հետ
աճում են <v> արագությունն
ու <z> բախումների
թիվը: Տրված գազի
համար, անփոփոխ
ջերմաստիճանի
դեպքում, ազատ
վազքի միջին երկարությունը
հակադարձ համեմատական
է գազի ճնշմանը
(10.30):
Փոխազդեցության
ժամանակ մոլեկուլները
կարող են մոտենալ
մինչև որոշակի
![]() ամենափոքր
հեռավորության
վրա, որը կոչվում
է մոլեկուլի էֆեկտիվ
տրամագիծ: Եթե
ամենափոքր
հեռավորության
վրա, որը կոչվում
է մոլեկուլի էֆեկտիվ
տրամագիծ: Եթե
![]() ապա
(10.49)-ից կունենանք
ապա
(10.49)-ից կունենանք
(10.49) և (10.50) բանաձևերը կարող են օգտագործվել գազի մոլեկուլների էֆեկտիվ տրամագծի, ազատ վազքի միջին երկարության և կոնցենտրացիայի որոշման համար:
Գազի վիճակը,
որի դեպքում ազատ
վազքի միջին ![]() երկարությունը
համեմատելի է անոթի
երկարությունը
համեմատելի է անոթի
![]() չափերի
հետ, որի մեջ լցված
է գազը, կոչվում
է վակուում: Տարբերակում
են վակուումի հետևյալ
աստիճանները՝
գերբարձր
չափերի
հետ, որի մեջ լցված
է գազը, կոչվում
է վակուում: Տարբերակում
են վակուումի հետևյալ
աստիճանները՝
գերբարձր![]() ճնշումը՝
133•10-8 Պա և ցածր), բարձր
(
ճնշումը՝
133•10-8 Պա և ցածր), բարձր
( ![]() ճնշումը՝
133•10-3 Պա, միջին
ճնշումը՝
133•10-3 Պա, միջին![]() ճնշումը՝
(1÷133)•10-3 Պա), ցածր
ճնշումը՝
(1÷133)•10-3 Պա), ցածր ![]() ճնշումը՝
(133÷1,01)•10-5 Պա]:
ճնշումը՝
(133÷1,01)•10-5 Պա]:
10.11. ՓՈԽԱՆՑՄԱՆ ԵՐԵՎՈՒՅԹՆԵՐԸ ԳԱԶԵՐՈՒՄ
Մոլեկուլների անկանոն ջերմային շարժումները, դրանց միջև անընդհատ բախումները հանգեցնում են այն երևույթին, որ մոլեկուլները, թեկուզ և համեմատաբար դանդաղ, տեղափոխվում են տարածության մի կետից մյուսը: Բախումների արդյունքում փոխվում են մոլեկուլների արագությունների ուղղությունն ու մոդուլը, որը հանգեցնում է իմպուլսի և էներգիայի փոխանցման: Այդ պատճառով, եթե գազային միջավայրում դիտարկենք միջավայրի առանձին մասերի անվերջ փոքր ծավալները, ինքնաբերաբար առաջ են գալիս գազի խտության (կոնցենտրացիայի), ջերմաստիճանի և ճնշման ֆլուկտուացիաներ, որոնք ակնթարթորեն անհետանում են: Եթե տվյալ անհամասեռությունները հարուցվել են կողմնակի աղբյուրի կողմից և հաստատուն բնույթ են կրում, ապա մոլեկուլների քաոսային շարժումը ձգտում է վերացնել այդ անհամասեռությունները:
Այդ դեպքում գազում առաջանում են առանձնահատուկ՝ փոխանցման երևույթներ: Դրանք են՝ դիֆուզիան, ջերմահաղորդականությունը և ներքին շփումը:
Եթե տեղայնացված ծավալում բաշխված է մի այլ գազի խառնուկ կամ մեծացվել է տվյալ գազի ճնշումը, մոլեկուլների քաոսային շարժումը կնպաստի գազային մոլեկուլների կոնցենտրացիայի հավասարեցմանը: Գազային մոլեկուլների կոնցենտրացիայի հավասարեցման պրոցեսը (ինչպես նաև հեղուկ և պինդ մարմինների մոլեկուլներինը) կոչվում է դիֆուզիա:
Գազի տարբեր մասերում ջերմաստիճանի ոչ միատեսակության դեպքում, այն մոլեկուլները, որոնք գտնվում են ավելի տաք տիրույթներում, միջին հաշվով ունենում են ավելի մեծ կինետիկ էներգիա, քան ավելի սառը տիրույթում գտնվող մոլեկուլները: Այստեղ մոլեկուլային շարժումն ուղեկցվում է գումարային տեղափոխությամբ դեպի գազի ավելի սառը մասերի ուղղությամբ, որի հետևանքով տեղի է ունենում ջերմաստիճանի հավասարեցում: Այս պրոցեսն անվանում են ջերմահաղորդականություն:
Կարող է տեղի ունենալ նաև գազի շերտերի արագությունների հավասարեցում, եթե դրանք շարժվում են տարբեր արագություններով: Միջինում այդպիսի շերտերի մոլեկուլների իմպուլսները տարբեր են, ավելի արագ շերտերի մոլեկուլներն ունեն իմպուլսի ավելի մեծ արժեք: Ավելի արագ շերտերից մոլեկուլի անցումն ավելի դանդաղ շերտ ուղեկցվում է իմպուլսի փոխանցումով և հարուցում է դանդաղ շերտը արագացնող ուժերի իմպուլսի ազդեցությունը: Հակառակ ազդեցությունն են գործում դանդաղ շերտի մոլեկուլները, որոնք անցնում են ավելի արագ շերտ. այս դեպքում առաջանում են արգելակող ուժեր: Սրանց գումարային արդյունքը շերտերի արագությունների հավասարեցումն է: Այս երևույթն անվանում են ներքին շփում կամ մածուցիկություն: Բոլոր այս երեք տարբեր ֆիզիկական երևույթների հիմքում ընկած է միևնույն մոլեկուլային մեխանիզմը՝ ջերմային շարժումը և մոլեկուլների միախառնումը: Քննարկենք փոխանցման երևույթները և բերենք այն օրինաչափությունները, որոնց նրանք ենթարկվում են:
Դիֆուզիա: Ենթադրենք՝ համասեռ գազի p խտությունը կամ n կոնցենտրացիան փոփոխվում է x-առանցքի ուղղությամբ, ընդ որում x-ի առանցքին ուղղահայաց ΔS փոքր մակերեսի սահմաններում (խտությունը կամ կոնցենտրացիան ընդունվում է գործնականորեն հաստատուն):
Եթե գազի կոնցենտրացիան մակերեսի մի կողմում (օրինակ՝ ձախից) ավելի մեծ է, քան մյուս կողմում, ապա ձախից աջ անցնող մոլեկուլների թիվը կլինի ավելի մեծ, քան հակառակը: Հետևաբար, կարելի է խոսել որոշակի ուղղությամբ գազի զանգվածի դիֆուզիայի մասին:
Արված ենթադրությունների դեպքում կոնցենտրացիայի փոփոխությունը Δx երկարության վրա հավասար է Δn-ի, այսինքն՝ կոնցենտրացիայի գրադիենտը Δn/Δx է, կամ խտության գրադիենտը հավասար է Δp/Δx: Փորձնական տվյալների հիման վրա շվեյցարացի ֆիզիկոս Ա.Ֆիկի կողմից հաստատվել է, որ դիֆուզիայի ժամանակ Δt ժամանակամիջոցում ΔS մակերեսի միջով փոխանցված զանգվածը որոշվում է հետևյալ բանաձևով.

որտեղ D-ն դիֆուզիայի գործակիցն է, բացասական նշանը ցույց է տալիս, որ դիֆուզիայի դեպքում մոլեկուլների կամ զանգվածի տեղափոխությունը միշտ տեղի է ունենում կոնցենտրացիայի կամ խտության նվազման ուղղությամբ: (10.51) բանաձևը կոչվում է դիֆուզիայի հավասարում կամ Ֆիկի օրենք և ավելի խիստ դիֆերենցիալ տեսքով գրվում է հետևյալ կերպ՝
![]()
Դիֆուզիայի գործակցի միավորը՝ քառ. մետրը բաժանած վայրկ. (մ2/վրկ): Եթե ներմուծվի զանգվածի հոսքի խտության հասկացությունը որպես նյութի այն զանգվածով որոշվող մեծություն, որը դիֆուզվում է x-երի առանցքին ուղղահայաց միավոր մակերեսով միավոր ժամանակամիջոցում, ապա Ֆիկի օրենքը կունենա հետևյալ տեսքը.

Դիֆուզիայի գործակիցը թվապես հավասար է զանգվածի հոսքի խտությանը՝ խտության միավոր գրադիենտի դեպքում: Ֆիկի օրենքը դիֆուզիայի երևույթը դիտարկում է մակրոսկոպական տեսանկյունից:
Ցույց տանք Ֆիկի օրենքի արտածումը մոլեկուլային-կինետիկ տեսանկյունից, հաշվի առնելով, որ քիմիապես համասեռ գազի բոլոր մոլեկուլներն ունեն մոլեկուլների ջերմային շարժման միջին արագությանը հավասար <v > արագություն, և գազի մոլեկուլների շարժման ցանկցած հնարավոր ուղղություն հավասարահավանական է:
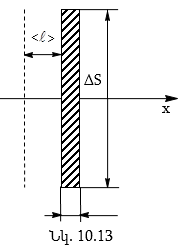
Ենթադրենք, որ n կոնցենտրացիան փոփոխվում է x-երի առանցքի ուղղությամբ, և x-երի առանցքին ուղղահայաց ΔS փոքր մակերեսի սահմաններում կոնցենտրացիան մնում է հաստատուն (նկ.10.13)
ΔS մակերեսով
մոլեկուլների
հոսքը պետք է անցնի
ինչպես աջ, այնպես
էլ ձախ, քանի որ
մոլեկուլները
քաոսային շարժում
են կատարում: Քանի
որ մոլեկուլների
կոնցենտրացիան
x-երի առանցքի երկայնքով
նվազում է ձախից
աջ, այսինքն՝ ![]() հետևաբար
կգերակշռի մոլեկուլների
անցումը ձախից
աջ: Քանի որ տարածության
մեջ բոլոր երեք
ուղղություններով
միջին հաշվով տեղաշարժվում
են հավասար թվով
մոլեկուլներ, ապա
x-երի առանցքի երկայնքով
կշարժվի մոլեկուլների
1/3 մասը, նրանց կեսը
(բոլոր մոլեկուլների
1/6 մասը) կշարժվի
ձախից աջ, իսկ մյուս
կեսը՝ աջից ձախ:
Աջից և ձախից« մինչև
ΔS մակերեսն առանց
բախվելու մյուսների
հետ կհասնեն միայն
այն մոլեկուլները,
որոնք գտնվում
են
հետևաբար
կգերակշռի մոլեկուլների
անցումը ձախից
աջ: Քանի որ տարածության
մեջ բոլոր երեք
ուղղություններով
միջին հաշվով տեղաշարժվում
են հավասար թվով
մոլեկուլներ, ապա
x-երի առանցքի երկայնքով
կշարժվի մոլեկուլների
1/3 մասը, նրանց կեսը
(բոլոր մոլեկուլների
1/6 մասը) կշարժվի
ձախից աջ, իսկ մյուս
կեսը՝ աջից ձախ:
Աջից և ձախից« մինչև
ΔS մակերեսն առանց
բախվելու մյուսների
հետ կհասնեն միայն
այն մոլեկուլները,
որոնք գտնվում
են ![]() ազատ
վազքի միջին երկարությանը
հավասար հեռավորության
վրա: Հաշվի առնելով
արված ենթադրությունները
ΔS մակերեսով Δt
ժամանակամիջոցում
ձախից աջ կանցնեն
ազատ
վազքի միջին երկարությանը
հավասար հեռավորության
վրա: Հաշվի առնելով
արված ենթադրությունները
ΔS մակերեսով Δt
ժամանակամիջոցում
ձախից աջ կանցնեն
![]() մոլեկուլներ.
մոլեկուլներ.
![]()
որտեղ ![]() մոլեկուլների
կոնցենտրացիան
է ΔS մակերեսից
ձախ
մոլեկուլների
կոնցենտրացիան
է ΔS մակերեսից
ձախ ![]() հեռավորության
վրա: Աջից ձախ կանցնեն
հեռավորության
վրա: Աջից ձախ կանցնեն
![]() մոլեկուլներ
մոլեկուլներ
![]()
Դիֆուզիայի հետևանքով առավելապես ձախից աջ տեղափոխվող մոլեկուլների քանակը՝
![]()
![]() կոնցենտրացիաների
տարբերությունն
է
կոնցենտրացիաների
տարբերությունն
է ![]() հեռավորության
վրա գտնվող կետերի
միջև: Եթե կոնցենտրացիայի
գրադիենտը
Δn/Δx, ապա
հեռավորության
վրա գտնվող կետերի
միջև: Եթե կոնցենտրացիայի
գրադիենտը
Δn/Δx, ապա![]() և (8.54) արտահայտությունը
կնդունի հետևյալ
տեսքը՝
և (8.54) արտահայտությունը
կնդունի հետևյալ
տեսքը՝
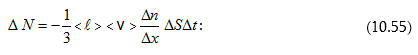
Այս հավասարման երկու կողմերը բազմապատկելով մոլեկուլի զանգվածով՝ կստանանք`
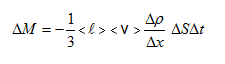
կամ դիֆերենցիալ տեսքով
![]()
(10.56) հավասարումը համեմատելով Ֆիկի օրենքի (10.52) հետ՝ որոշում ենք դիֆուզիայի գործակիցը մոլեկուլայինկինետիկ տեսության հիման վրա.
![]()
Հետևաբար, դիֆուզիայի
գործակիցն ուղիղ
համեմատական է
![]() ազատ
վազքի միջին երկարությանն
ու մոլեկուլի
<v> միջին արագությանը:
ազատ
վազքի միջին երկարությանն
ու մոլեկուլի
<v> միջին արագությանը:
Հաշվի առնելով,
որ ![]() հակադարձ
համեմատական է
գազի ճընշմանը,
իսկ <v>-ը կախված
է ջերմաստիճանից
ու գազի բնույթից.
հակադարձ
համեմատական է
գազի ճընշմանը,
իսկ <v>-ը կախված
է ջերմաստիճանից
ու գազի բնույթից.
![]()
ապա դիֆուզիայի պրոցեսի ինտենսիվությունը մեծանում է ջերմաստիճանի բարձրացմանն ու ճնշման փոքրացմանը զուգընթաց և կախված է գազի տեսակից:
Ջերմահաղորդականություն:
Ենթադրենք՝ ջերմաստիճանի
փոփոխությունը
կատարվում է x-երի
առանցքի երկայնքով
և էներգիայի փոխադրումը
ջերմության տեսքով
կատարվում է x-երի
առանցքին ուղղահայաց
ΔS փոքր մակերեսով:
Քննարկենք մակերեսին
մոտ, նրանից աջ
և ձախ հավասար
հեռավորության
վրա գտնվող, նրան
զուգահեռ գազի
շերտերը: Այդ շերտերի
հեռավորությունը
հավասար է Δx-ի: Դիցուք
ձախ մասում տեղավորված
շերտի ջերմաստիճանը![]() է, իսկ
աջ մասինը՝
է, իսկ
աջ մասինը՝ ![]() և
և![]() Արված
ենթադրությունների
պայմաններում
ջերմաստիճանի
գրադիենտը հավասար
է ΔT/Δx:
Արված
ենթադրությունների
պայմաններում
ջերմաստիճանի
գրադիենտը հավասար
է ΔT/Δx:
Փորձնական տվյալների հիման վրա ֆրանսիացի ֆիզիկոս Շ.Ֆուրյեի կողմից հաստատվել է, որ ջերմահաղորդականության հետևանքով Δt ժամանակամիջոցում ΔS մակերեսով անցնող էներգիան որոշվում է հետևյալ բանաձևով
![]()
որտեղ ![]() ջերմահաղորդականության
գործակիցն է:
(10.58) բանաձևի բացասական
նշանը ցույց է
տալիս, որ ջերմության
հոսքն ուղղված
է ջերմաստիճանի
նվազման կողմը:
(10.58) բանաձևը կոչվում
է ջերմահաղորդականության
հավասարում կամ
Ֆուրյեի օրենք
և ավելի խիստ դիֆերենցիալ
տեսքով գրվում
է`
ջերմահաղորդականության
գործակիցն է:
(10.58) բանաձևի բացասական
նշանը ցույց է
տալիս, որ ջերմության
հոսքն ուղղված
է ջերմաստիճանի
նվազման կողմը:
(10.58) բանաձևը կոչվում
է ջերմահաղորդականության
հավասարում կամ
Ֆուրյեի օրենք
և ավելի խիստ դիֆերենցիալ
տեսքով գրվում
է`
![]()
Եթե մտցնենք
ջերմային հոսքի
![]() խտության
հասկացությունը՝
որպես միավոր ժամանակում
x-երի առանցքին
ուղղահայաց միավոր
մակերեսով ջերմության
ձևով տեղափոխվող
էներգիայով որոշվող
մեծություն, ապա
Ֆուրյեի օրենքը
կընդունի հետևյալ
տեսքը՝
խտության
հասկացությունը՝
որպես միավոր ժամանակում
x-երի առանցքին
ուղղահայաց միավոր
մակերեսով ջերմության
ձևով տեղափոխվող
էներգիայով որոշվող
մեծություն, ապա
Ֆուրյեի օրենքը
կընդունի հետևյալ
տեսքը՝
![]()
![]() ջերմահաղորդականության
գործակիցը թվապես
հավասար է ջերմային
հոսքի խտությանը,
երբ ջերմաստիճանի
գրադիենտը հավասար
է միավորի: Ջերմահաղորդականության
գործակցի միավորը
Վտ/(մ.Կ) է: Կարելի
է ցույց տալ, որ
ջերմահաղորդականության
գործակիցը թվապես
հավասար է ջերմային
հոսքի խտությանը,
երբ ջերմաստիճանի
գրադիենտը հավասար
է միավորի: Ջերմահաղորդականության
գործակցի միավորը
Վտ/(մ.Կ) է: Կարելի
է ցույց տալ, որ
![]()
որտեղ ![]() գազի
տեսակարար ջերմունակությունն
է հաստատուն ծավալի
դեպքում:
գազի
տեսակարար ջերմունակությունն
է հաստատուն ծավալի
դեպքում:
Ներքին շփում: Այս երևույթն առաջանում է գազի երկու հարևան շերտերի միջև դրանց հարաբերական շարժման ժամանակ: Հայտնի է, որ գազի մոլեկուլներն իրենց շարժման ժամանակ կատարում են ոչ միայն կանոնավոր, այլև անկանոն ջերմային շարժում` անցնելով մի շերտից մյուսը և հակառակը: Յուրաքանչյուր m զանգված ունեցող մոլեկուլ, անցնելով մի շերտից մյուս շերտը, փոփոխում է իր իմպուլսը m v-ով: Այս դեպքում առաջանում է հարևան շերտերի կողմից տվյալ շերտի վրա ազդող շփման ուժ: Այդ ուժն ուղիղ համեմատական է գազի երկու շերտերի հպման հարթության մեջ գտնվող ΔS մակերեսին, արագության Δv/Δx գրադիենտին և շերտերի բաժանման մակերեսին ազդում է շոշափողով: Ներքին շփման օրենքը սահմանել է Նյուտոնը, և այն ունի հետևյալ տեսքը՝

որտեղ ![]() ներքին
շփման գործակիցն
է (դինամիկ մածուցիկությունը):
Ներքին շփման գործակիցը
թվապես հավասար
է միավոր մակերեսի
վրա ազդող ուժին,
երբ արագության
գրադիենտը հավասար
է միավորի: Ներքին
շփման գործակցի
միավորը պասկալ•վայրկյանն
է (Պա•վրկ): Արագության
գրադիենտն ուղղված
է ΔS մակերեսին
ուղղահայաց, որի
աջ և ձախ մասերում
շերտերը շարժվում
են
ներքին
շփման գործակիցն
է (դինամիկ մածուցիկությունը):
Ներքին շփման գործակիցը
թվապես հավասար
է միավոր մակերեսի
վրա ազդող ուժին,
երբ արագության
գրադիենտը հավասար
է միավորի: Ներքին
շփման գործակցի
միավորը պասկալ•վայրկյանն
է (Պա•վրկ): Արագության
գրադիենտն ուղղված
է ΔS մակերեսին
ուղղահայաց, որի
աջ և ձախ մասերում
շերտերը շարժվում
են ![]() տարբեր
արագություններով:
Բացասական նշանը
ցուց է տալիս, որ
իմպուլսը փոխանցվում
է արագության նվազման
ուղղությամբ: Դինամիկ
մածուցիկության
գործակիցը որոշվում
է
տարբեր
արագություններով:
Բացասական նշանը
ցուց է տալիս, որ
իմպուլսը փոխանցվում
է արագության նվազման
ուղղությամբ: Դինամիկ
մածուցիկության
գործակիցը որոշվում
է
![]()
բանաձևով: (10.57),
(10.61) և (10.63) արտահայտությունների
համեմատությունից
հետևում է, որ ![]() միջև
գոյություն ունեն
հետևյալ առնչությունները.
միջև
գոյություն ունեն
հետևյալ առնչությունները.
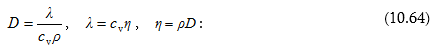
Ստացված բանաձևերի վերլուծությունը ցույց է տալիս, որ ջերմահաղորդականության` ինչպես նաև մածուցիկության գործակիցները կախված չեն գազի ճնշումից, այլ կախված են միայն ջերմաստիճանից: Դա բխում է այն բանից, որ խտությունն ուղիղ համեմատական, իսկ ազատ վազքի միջին երկարությունը` հակադարձ համեմատական են ճնշմանը. մոլեկուլների արագությունը և գազի տեսակարար ջերմունակությունը ճնշումից կախում չունեն: Սակայն շատ ցածր ճնշումների դեպքում ջերմահաղոդականության գործակիցը ճնշումից կախված է:
Խնդիր 1: Որոշել
![]() ճնշման
տակ գտնվող ազոտի
դիֆուզիայի և ներքին
շփման գործակիցները:
ճնշման
տակ գտնվող ազոտի
դիֆուզիայի և ներքին
շփման գործակիցները:
Լուծում: Դիֆուզիայի գործակիցը `
![]()
որտեղ <v>-ն մոլեկուլների միջին թվաբանական արագությունն է և հավասար է`

![]() մոլեկուլի
ազատ վազքի միջին
երկարությունն
է: Ազոտի մոլեկուլների
ազատ վազքի միջին
երկարությունը
որոշվում է`
մոլեկուլի
ազատ վազքի միջին
երկարությունն
է: Ազոտի մոլեկուլների
ազատ վազքի միջին
երկարությունը
որոշվում է`
![]()
d-ն ազոտի մոլեկուլի էֆեկտիվ տրամագիծն է, n-ը մոլեկուլների թիվն է միավոր ծավալում և որոշվում է` n = p/kT հավասարումով: Վեջինը տեղադըրելով (3) հավասարման մեջ կստանանք`

Տեղադրելով (3) և (4)-ը (1) արտահայտության մեջ կունենանք`
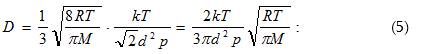
Ներքին շփման գործակիցը`
![]()
որտեղ p-ն գազի խտությունն է 300Կ և 105 Պա ճնշման դեպքում:
p -ն գտնելու
համար օգտվենք
իդեալական գազի
վիճակի հավասարումից:
Գրենք այն ազոտի
երկու վիճակների
համար նորմալ պայմանների
դեպքում ![]()
որտեղ p-ն գազի խտությունն է 300Կ և 05 Պա ճնշման դեպքում:
![]()
![]()
![]()
Ներքին շփման գործակիցը կարելի է արտահայտել դիֆուզիայի գործակցի միջոցով`
![]()
Տեղադրելով (5) և (9) արտահայտությունների մեջ մտնող մեծությունների թվային արժեքները` ստացվում է
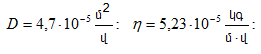
Խնդիր 2. Միևնույն
ջերմաստիճանի
և ճնշման դեպքում
քանի անգամ են
ածխաթթու գազի
և ազոտի ներքին
շփման ![]() գործակիցները
տարբերվում իրարից:
Գազերի մոլեկուլների
էֆեկտիվ տրամագծերը
հավասար են:
գործակիցները
տարբերվում իրարից:
Գազերի մոլեկուլների
էֆեկտիվ տրամագծերը
հավասար են:
Լուծում: Ներքին շփման գործակիցը և մոլեկուլի միջին արագությունը`
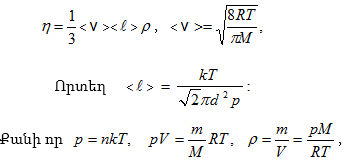
ուստի ածխաթթու գազի և ազոտի ներքին շփման գործակիցների համար ստանում ենք`
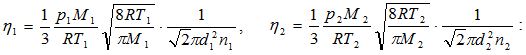
![]()
![]()
ԳԼՈՒԽ 11. ՋԵՐՄԱԴԻՆԱՄԻԿԱՅԻ ՀԻՄՈՒՆՔՆԵՐԸ
11.1. ՋԵՐՄԱԴԻՆԱՄԻԿԱԿԱՆ ՀԱՄԱԿԱՐԳ, ՋԵՐՄԱԴԻՆԱՄԻԿԱԿԱՆ ՊՐՈՑԵՍ:
ԴԱՐՁԵԼԻ ԵՎ ՈՉ ԴԱՐՁԵԼԻ ՊՐՈՑԵՍՆԵՐ
Ջերմադինամիկան պատկանում է ֆիզիկայի բացառիկ տեսությունների շարքին, որոնք ունեն հետևյալ ընդհանուր գծերը. այն չի դիտարկում նյութի ատոմային կառուցվածքը, կիրառում է մեծություններ, որոնք սահմանվում են միայն մակրոսկոպական համակարգերի նկատմամբ, տեսության շարադրումը (կառուցվածքը) հիմնվում է հայտնի փորձնական տվյալների վրա: Նյութի հատկություններն արտահայտվում են բնութագրական պարամետրերով (խտություն, մածուցիկություն և այլն): Ջերմադինամիկան ուսումնասիրում է մակրոսկոպական համակարգերի ջերմային հատկությունները`չառնչվելով համակարգը կազմող մարմինների միկրոսկոպիկ կառուցվածքին: Այն կառուցվում է ջերմադինամիկայի մի քանի հիմնական սկզբունքների վրա, որոնք հայտնի բազմաթիվ փորձնական տվյալների ընդհանրացումն են: Նյութի հատկությունների տեսական ուսումնասիրությամբ զբաղվում է վիճակագրական ֆիզիկան, որը տվել է ջերմադինամիկայի օրենքների հիմնավորումն ու որոշել նրանց կիրառման սահմանը: Ջերմադինամիկայի հիմունքների ուսումնասիրության ժամանակ անհրաժեշտ է հիշել հետևյալ սահմանումները:
Ջերմային շարժման և միմյանց վրա փոխազդեցության հետևանքով էներգիայի փոխանակում կատարող մեծ քանակությամբ մասնիկներից (ատոմներից և մոլեկուլներից) բաղկացած ֆիզիկական համակարգը կոչվում է ջերմադինամիկական համակարգ:
Ջերմադինամիկական համակարգի վիճակը որոշվում է մակրոսկոպական պարամետրերով, օրինակ, տեսակարար ծավալով, ճնշումով, ջերմաստիճանով: Ջերմադինամիկական պրոցես կոչվում է մակրոսկոպական համակարգի անցումը մի ջերմադինամիկական վիճակից մյուսին: Պրոցեսները լինում են դարձելի և ոչ դարձելի: Դարձելի կոչվում է այնպիսի պրոցեսը, որի դեպքում հնարավոր է համակարգի ետդարձը վերջնական վիճակից նախնականին նույն միջանկյալ վիճակների միջով այնպես, որ շրջապատող մարմիններում ոչ մի փոփոխություն չկատարվի: Դարձելի պրոցեսը ֆիզիկական աբստրակցիա է: Դարձելիությանը մոտեցող պրոցեսի օրինակը երկար կախոցով ծանր ճոճանակի տատանումն է: Այս դեպքում կինետիկ էներգիան գործնականորեն լրիվ վերածվում է պոտենցիալ էներգիայի և հակառակը: Տատանումները տեղի են ունենում երկար ժամանակ առանց լայնույթի նկատելի փոփոխության, միջավայրի դիմադրության և շփման ուժերի աննշան լինելու հետևանքով:
Շփումով կամ տաք մարմնից սառը մարմնին ջերմատվությամբ ուղեկցվող ցանկացած պրոցես ոչ դարձելի է: Ոչ դարձելի պրոցեսի օրինակ է գազի ընդարձակումը (նույնիսկ իդեալական) դատարկության մեջ: Ընդարձակվելով գազը չի հաղթահարում միջավայրի դիմադրությունը, աշխատանք չի կատարում, սակայն, որպեսզի գազի բոլոր մոլեկուլները հավաքվեն նախկին ծավալում, այսինքն` գազը բերվի սկզբնական (նախնական) վիճակին, անհրաժեշտ է աշխատանք կատարել: Այսպիսով, բոլոր իրական պրոցեսները ոչ դարձելի են:
11.2. ՀԱՄԱԿԱՐԳԻ ՆԵՐՔԻՆ ԷՆԵՐԳԻԱՆ: ԻԴԵԱԼԱԿԱՆ ԳԱԶԻ ՆԵՐՔԻՆ ԷՆԵՐԳԻԱՆ
Ջերմադինամիկական համակարգը, որպես ատոմների ու մոլեկուլների բազմություն, օժտված է U ներքին էներգիայով:
Ներքին էներգիան մոլեկուլային փոխազդեցության և մոլեկուլների ջերմային շարժման էներգիաների գումարն է:
Համակարգի ներքին էներգիան կախված է միայն նրա վիճակից և համարվում է վիճակի միարժեք ֆունկցիա:
Համակարգի վիճակի փոփոխությունը բնութագրվում է վիճակի p,V,T, պարամետրերով: Համակարգի միևնույն վիճակին համապատասխանում է U ներքին էներգիայի որոշակի արժեք: Գազի տաքացման ժամանակ մեծանում է մոլեկուլների ու ատոմների շարժման արագությունը, ինչը հանգեցնում է ներքին էներգիայի մեծացման, հետևաբար ներքին էներգիան կախված է ջերմաստիճանից: Ճնշման կամ տեսակարար ծավալի փոփոխության հետևանքով փոփոխվում են միջմոլեկուլային հեռավորությունները, այսինքն` ատոմների ու մոլեկուլների փոխազդեցության պոտենցիալ էներգիան նույնպես փոփոխվում է: Դա նշանակում է, որ փոփոխվում է նաև ներքին էներգիան:
Ներքին էներգիայի հաշվարկի սկիզբ համարվում է համակարգի այն վիճակը, որի դեպքում ներքին էներգիան հավասար է զրոյի: Սովորաբար համարում են, որ ներքին էներգիան հավասար է զրոյի T = 0Կ-ի դեպքում: Համակարգի մի վիճակից մյուսին անցման ժամանակ գործնական հետաքըրքրություն ներկայացնում է ներքին էներգիայի ΔU փոփոխությունը, այդ պատճառով ներքին էներգիայի հաշվարկի նախնական ընտրությունը նշանակություն չունի:
Քանի որ համակարգի ներքին էներգիան կախված է համակարգի բոլոր մասնիկների փոխազդեցությունից, ապա նրա ավելի խիստ սահմանման համար անհրաժեշտ է նաև հաշվի առնել իոնների և ատոմների էլեկտրոնային թաղանթներում շարժվող էլեկտրոնների էներգիան և ներմիջուկային էներգիան: Այդ պատճառով հաճախ ներքին էներգիայի հասկացությունը գործածելիս, հարմարության համար, նկատի են ունենում ոչ թե տվյալ համակարգի ամբողջ ներքին էներգիան, այլ միայն նրա այն մասը, որը էական է այդ երևույթի դիտարկման համար: Օրինակ, մարմնի մասնիկները գտնվում են շարժման մեջ, այսինքն` ունեն կինետիկ էներգիա: Մասնիկների միջև գործում են ձգողական և վանողական ուժեր, հետևաբար մասնիկներն օժտված են նաև պոտենցիալ էներգիայով: Հսկայական քանակությամբ մասնիկների քաոսային շարժման էներգիան հաշվել, առավել ևս հաշվառել նրանցից յուրաքանչյուրի պոտենցիալ էներգիան հնարավոր չէ: Այսպիսով, բոլոր մասնիկների էներգիան գումարվում է մի ընդհանուր գումարի մեջ, որը որոշում է մարմնի ներքին էներգիան: Պարզ է, որ չափել կարելի է սոսկ ներքին էներգիայի փոփոխությունը և ոչ թե մարմնի ամբողջ էներգիան: Էներգիայի հասկացությունը միշտ վերաբերում է մարմինների համակարգին:
Չի կարելի համարել, որ էներգիա կարող է ունենալ մեկ մարմինը կամ մեկ մասնիկը, առանց մյուս մարմինների և ուրիշ մասնիկների հետ կապ ունենալու: Մարմնի ձևի կամ ծավալի ցանկացած փոփոխության ժամանակ փոփոխվում է մարմնի ներքին էներգիան: Եթե այդ դեպքում ջերմաստիճանը չի փոխվում (մասնիկների կինետիկ էներգիան), ապա փոփոխվում է մարմնի մասնիկների պոտենցիալ էներգիան: Գերակշռող դեպքերում միաժամանակ փոփոխվում են մարմնի մասերի և' կինետիկ« և' պոտենցիալ էներգիաները:
Ոչ թե մոլեկուլներից, այլ առանձին ատոմներից բաղկացած գազը կոչվում է միատոմ: Միատոմ գազերի թվին են պատկանում իներտ գազերը՝ հելիումը, նեոնը, արգոնը: Իդեալական գազերի դեպքում անտեսում են մոլեկուլների փոխազդեցության ուժերը, այսինքն` դրանց պոտենցիալ էներգիան պետք է հավասար լինի զրոյի, որի համար իդեալական գազի ներքին էներգիան մոլեկուլների ջերմային շարժման կինետիկ էներգիան է:
Ցույց է տրվել (10.29), որ մոլեկուլի (միատոմ) համընթաց
շարժման միջին կինետիկ էներգիան հավասար է՝
![]()
Մեկ մոլը պարունակում
է ![]() թվով
ատոմներ, m զանգվածով
գազը պարունակում
է v = m/M մոլ, դրա համար
միատոմ իդեալական
գազի ներքին էներգիան`
թվով
ատոմներ, m զանգվածով
գազը պարունակում
է v = m/M մոլ, դրա համար
միատոմ իդեալական
գազի ներքին էներգիան`
![]()
քանի որ ![]() Իդեալական
գազի ներքին էներգիան
ուղիղ համեմատական
է գազի զանգվածին
ու նրա ջերմադինամիկական
ջերմաստիճանին:
Իդեալական
գազի ներքին էներգիան
ուղիղ համեմատական
է գազի զանգվածին
ու նրա ջերմադինամիկական
ջերմաստիճանին:
11.3. ԷՆԵՐԳԻԱՅԻ ՀԱՎԱՍԱՐԱՉԱՓ ԲԱՇԽՄԱՆ ՕՐԵՆՔՆ ԸՍՏ ՄՈԼԵԿՈՒԼԻ
ԱԶԱՏՈւԹՅԱՆ ԱՍՏԻՃԱՆՆԵՐԻ
Մոլեկուլի միջին էներգիայի համար ստացած <E>=3kt/2 բանաձևը հաշվի է առնում մոլեկուլի միայն համընթաց շարժման էներգիան: Սակայն համընթաց շարժման հետ մեկտեղ հնարավոր են նաև մոլեկուլի պտույտը և մոլեկուլի կազմի մեջ մտնող ատոմների տատանումներ: Շարժման բոլոր տեսակներին պատկանող էներգիան հաշվելու համար անհրաժեշտ է մտցնել ազատության աստիճանների թիվ հասկացությունը: Մարմնի ազատության աստիճանների թիվ կոչվում է այն անկախ մեծությունների քանակը, որոնց օգնությամբ որոշվում է մարմնի դիրքը տարածության մեջ: Այսպես, օրինակ, նյութական կետի դիրքը տարածության մեջ որոշվում է` երեք կոորդինատների (դեկարտյան x,y,z կոորդինատների) արժեքները տալով: Սրան համապատասխան` նյութական կետն ունի երեք ազատության աստիճան:
Բացարձակ պինդ մարմնի դիրքը կարելի է որոշել` տալով նրա իներցիայի կենտրոնի երեք կոորդինատները (x,y,z) և երկու` θ ու φ անկյունները, որոնք ցույց են տալիս մարմնի հետ կապված և նրա իներցիայի կենտրոնով անցնող որևէ առանցքի ուղղությունը (նկ.11.1), և վերջապես, նորից մարմնի հետ կապված ու առաջին առանցքին ուղղահայաց երկրորդ առանցքի ուղղությունը որոշող Ψ անկյունը: Այսպիսով, բացարձակ պինդ մարմինն ունի վեց ազատության աստիճաններ: Ընդ որում վեց ազատության աստիճաններից երեքը համընթաց են, իսկ մյուս երեքը` պտտական:
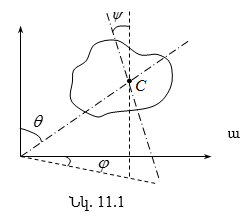
Գազերի ջերմունակությունը չափելու փորձերից պարզվում է, որ մոլեկուլների ազատության աստիճանների թիվը որոշելիս ատոմները պետք է դիտել որպես նյութական կետեր: Հետևաբար, միատոմ մոլեկուլին պետք է վերագրել երեք համընթաց ազատության աստիճան, երկատոմ մոլեկուլին, նրա ատոմների միջև գոյություն ունեցող կապի բնույթից կախված` կամ երեք համընթաց և երկու պտտական ազատության աստիճաններ (կոշտ կապի դեպքում), կամ այս հինգից բացի մեկ տատանողական ազատության աստիճան ևս (առաձգական կապի դեպքում), կոշտ կապով եռատոմ մոլեկուլին` երեք համընթաց և երեք պտտական ազատության աստիճաններ և այլն:
Մոլեկուլը ինչ թվով ազատության աստիճաններ էլ որ ունենա, երեքը համընթաց են: Քանի որ մոլեկուլի համընթաց ազատության աստիճաններից ոչ մեկը մյուսների նկատմամբ առավելություն չունի, նրանցից յուրաքանչյուրին հասնում է միջին հաշվով միատեսակ էներգիա, որը հավասար է 1/kT-ի: Բնական է ենթադրել, որ շարժման տեսակներից ոչ մեկը առավելություն չունի մյուսների նկատմամբ, հետևաբար, ցանկացած համընթաց, պտտական և տատանողական ազատության աստիճանին պետք է հասնի միջին հաշվով միևնույն` ավելի ճիշտ, կինետիկ էներգիան, որը հավասար է kT/2-ի: Այս դրույթը հայտնի է ըստ ազատության աստիճանների` էներգիայի հավասարաչափ բաշխման դրույթ անվան տակ:
Հավասարաչափ բաշխման դրույթի համաձայն մեկ մոլեկուլի <E> էներգիայի միջին արժեքը (միևնույն ջերմաստիճանի դեպքում) մեծ կլինի այնքան, որքան ավելի բարդ է մոլեկուլը և որքան ավելի շատ ազատության աստիճաններ ունի այն:
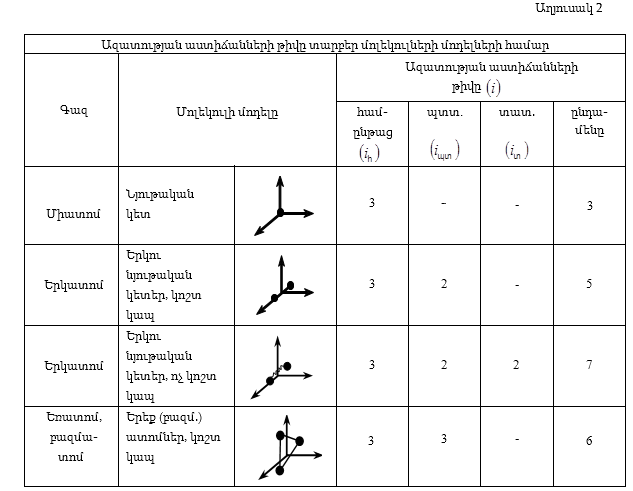
<E>-ը որոշելիս պետք է նկատի ունենալ, որ տատանողական ազատության աստիճանը պետք է օժտված լինի երկու անգամ ավելի մեծ էներգետիկ ունակությամբ` համընթաց կամ պտտական ազատության աստիճանների համեմատությամբ: Դա բացատրվում է նրանով, որ մոլեկուլի համընթաց և պտտական շարժումները կապված են միայն կինետիկ էներգիայի առկայության հետ, մինչդեռ տատանողական շարժումը կապված է թե կինետիկ և թե պոտենցիալ էներգիայի առկայության հետ, ընդ որում ներդաշնակ տատանակի համար ստացվում է, որ կինետիկ և պոտենցիալ էներգիաների միջին արժեքները հավասար են: Ուստի յուրաքանչյուր տատանողական ազատության աստիճանին պետք է բաժին ընկնի միջին հաշվով kT-ի երկու կես. մեկ կեսը կինետիկ էներգիայի տեսքով, մյուս կեսը` պոտենցիալ էներգիայի տեսքով: Այսպիսով, մոլեկուլի միջին էներգիան`
![]()
որտեղ i-ն մոլեկուլի համընթաց, պտտական և կրկնապատկված տատանողական ազատության ատիճանների թվերի գումարն է:
Բազմատոմ իդեալական գազի զանգվածի ներքին էներգիան`
![]()
11.4. ԱՇԽԱՏԱՆՔՆ ՈՒ ՋԵՐՄԱՔԱՆԱԿԸ` ՈՐՊԵՍ ԷՆԵՐԳԻԱՅԻ
ՓՈԽԱՆՑՄԱՆ ՁԵՎԵՐ
Մարմնի ներքին էներգիան կարելի է փոփոխել տարբեր եղանակներով: Դիտարկենք ներքին էներգիայի փոփոխման երկու եղանակ:
Մեխանիկական եղանակ: Շարժական մխոցով գլանի մեջ գտնվում է իդեալական գազ: Դիցուք մխոցի վրա ազդում է արտաքին ուժը, որն արագորեն սեղմում է գազը և գազի դիմադրության ուժերը հաղթահարելու համար կատարում է աշխատանք: Գազի սեղմման ժամանակ նրա ներքին էներգիան մեծանում է մխոցի կողմից մեխանիկական աշխատանք կատարելու հաշվին: Գազի ընդարձակման ժամանակ նրա ներքին էներգիան փոքրանում է` վերածվելով շարժվող մխոցի մեխանիկական էներգիայի:
Ջերմափոխանակություն: Տարբեր ջերմաստիճան ունեցող երկու մարմիններ դնենք շփման մեջ: Դիցուք առաջին մարմնի ջերմաստիճանն ավելի բարձր է, քան երկրորդինը: Էներգիաների փոխանակման արդյունքում առաջին մարմնի ջերմաստիճանը նվազում է, իսկ երկրորդինը՝ մեծանում: Քննարկվող օրինակում առաջին մարմնի մոլեկուլների քաոսային շարժման կինետիկ էներգիան վերածվում է երկրորդ մարմնի մոլեկուլների քաոսային շարժման կինետիկ էներգիայի:
Ներքին էներգիայի փոխանցման պրոցեսն, առանց մեխանիկական աշխատանք կատարելու, անվանում են ջերմափոխանակություն: Ջերմափոխանակության պրոցեսում որպես մարմնի ստացած կամ տված էներգիայի չափ ծառայում է ջերմաքանակ կոչվող ֆիզիկական մեծությունը:
Ջերմաքանակն ու աշխատանքը ոչ թե էներգիայի տեսակներ են, այլ նրա հաղորդման ձևերը: Դրանք գոյություն ունեն միայն էներգիայի հաղորդման պրոցեսում:
11.5. ԳԱԶԻ ԿԱՏԱՐԱԾ ԱՇԽԱՏԱՆՔԸ ԾԱՎԱԼԻ
ՓՈՓՈԽՈՒԹՅԱՆ ԴԵՊՔՈՒՄ
Հաշվենք գազի կատարած աշխատանքը իզոբար ընդարձակման ժամանակ: Դիցուք գլանում մխոցի տակ գտնվում է V ծավալ զբաղեցնող գազ p ճնշման տակ: Մխոցի մակերեսը S է: Մխոցի վրա գազի գործադրած ուժը՝ F = pS: Գազի ընդարձակման ժամանակ մխոցը բարձրանում է dh բարձրության վրա, այդ դեպքում գազը կկատարի δA = Fdh = pSdh աշխատանքը: Սակայն Sdh = dV-ն գազի ծավալի մեծացումն է: Հետևաբար տարրական աշխատանքը
![]()
Եթե dV > 0, ապա δA > 0, և աշխատանքը համարվում է դրական (գազն ընդարձակվում է):
Եթե dV < 0, ապա δA < 0, և աշխատանքը համարվում է բացասական (գազը սեղմվում է):
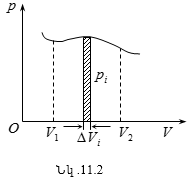
Մարմնի ծավալի փոփոխման պրոցեսը պատկերենք (pV) դիագրամում (նկ.11.2):
![]() տարրական
աշխատանքին համապատասխանում
է գրաֆիկի վրա
ստվերագծված նեղ
մակերեսը: Ակնհայտ
է, որ V առանցքով,
p = f(V) կորով և
տարրական
աշխատանքին համապատասխանում
է գրաֆիկի վրա
ստվերագծված նեղ
մակերեսը: Ակնհայտ
է, որ V առանցքով,
p = f(V) կորով և ![]() ուղիղներով
սահմանափակված
մակերեսը թվապես
հավասար է այն
աշխատանքին, որը
կատարվում է ծավալը
ուղիղներով
սահմանափակված
մակերեսը թվապես
հավասար է այն
աշխատանքին, որը
կատարվում է ծավալը
![]() մինչև
մինչև
![]() փոփոխվելու
դեպքում:
փոփոխվելու
դեպքում:
Գազի կատարած
A լրիվ աշխատանքը
նրա ծավալի ![]() փոփոխության
դեպքում գտնում
ենք (11.4) բանաձևի ինտեգրումով.
փոփոխության
դեպքում գտնում
ենք (11.4) բանաձևի ինտեգրումով.
![]()
Ինտեգրման արդյունքը կախված է գազում ընթացող պրոցեսից:
Որոշենք գազի կատարած աշխատանքը տարբեր պրոցեսներում ընդարձակման դեպքում:
Իզոխոր պրոցեսի դեպքում V = const, հետևաբար dV = 0 և A = 0:
Իզոբար պրոցեսի դեպքում p = const, այդ դեպքում
![]()
Գազի իզոբար ընդարձակման ժամանակ կատարված աշխատանքը հավասար է գազի ճնշման ու նրա ծավալի մեծացման արտադրյալին: p,V դիագրամի վրա (նկ.11.3ա) գազի իզոբար ընդարձակման աշխատանքը որոշվում է abcd ուղղանկյան մակերեսով: Իզոթերմ պրոցեսում T = const:
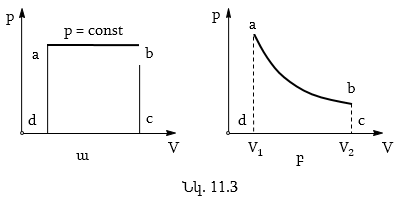
Ելնելով վիճակի (10.19) հավասարումից` որոշենք ճնշումը՝
![]()
Տեղադրելով այս արտահայտությունը (11.6) բանաձևի մեջ՝ կստանանք

Քանի որ պրոցեսն
իզոթերմ է, ![]()
![]()
p,Vդիագրամի վրա (նկ.11.3բ) իզոթերմ ընդարձակման աշխատանքը գրաֆիկորեն արտահայտվում է abcd պատկերի մակերեսով:
Ջերմաքանակ: Ջերմունակություն: Ջերմափոխանակության ճանապարհով գազին փոխանցված էներգիան (առանց նրա վրա աշխատանք կատարելու) կոչվում է Q ջերմաքանակ: Ջերմաքանակի միավորը ջոուլն է (Ջ): Համակարգին անվերջ փոքր ջերմաքանակ (δQ) հաղորդելիս նրա ջերմաստիճանը փոխվում է dT-ով: Համակարգի ջերմունակություն C կոչվում է համակարգին հաղորդված δQ ջերմաքանակի և ջերմաստիճանի dT փոփոխության հարաբերությունը. C = δQ/dT:
Ջերմունակության միավորը ջոուլի և կելվինի հարաբերությունն է (Ջ/Կ): Տարբերում են տեսակարար ջերմունակությունը (1կգ նյութի ջերմունակությունը)
![]()
և մոլային ջերմունակությունը (մեկ մոլ նյութի ջերմունակությունը)
![]()
Ջերմադինամիկական համակարգերում ընթացող տարբեր պրոցեսների ժամանակ ջերմունակությունները տարբեր կլինեն: Եթե պրոցեսն ընթանում է որևէ հաստատուն x պարամետրի դեպքում, ապա այս պրոցեսում տեսակարար ջերմունակությունը
![]()
Իմանալով համակարգի տեսակարար կամ մոլային ջերմունակությունը` կարելի է որոշել համակարգի ստացած ջերմաքանակը.
![]()
Ջերմաքանակը, ներքին էներգիան և աշխատանքը ՄՀ-ում չափվում են ջոուլներով (Ջ):
11.6. ՋԵՐՄԱԴԻՆԱՄԻԿԱՅԻ ԱՌԱՋԻՆ ՕՐԵՆՔԸ
Ջերմադինամիկայի հիմքը կազմում են երկու օրենքներ (սկզբունքներ): Ջերմադինամիկայի առաջին սկզբունքի ձևակերպման մեջ կարևոր պատմական դեր են խաղացել մարդու անհաջող փորձերը կառուցելու այնպիսի մեքենա, որն օգտագործելով էներգիայի համարժեք քանակություն, աշխատանք պետք է կատարեր: Այդպիսի մեքենան անվանեցին առաջին կարգի հավերժական շարժիչ (լատիներեն` պերպետուում մոբիլե):
Ջերմադինամիկայի առաջին սկզբունքը ձևակերպում են հետևյալ պընդման տեսքով. անհնար է կառուցել առաջին կարգի հավերժական շարժիչ:
Ջերմադինամիկայի առաջին սկզբունքը էներգիայի պահպանման և փոխակերպման օրեքն է. բնության մեջ ընթացող զանազան պրոցեսների ժամանակ էներգիան ոչնչից չի առաջանում և չի անհետանում, այլ մի ձևից անցնում է մի այլ ձևի:
Ջերմադինամիկայի առաջին սկզբունքը մաթեմատիկական տեսքով գրառելու նպատակով դիտարկենք, թե ինչպես է ընթանում համակարգի ներքին էներգիայի փոփոխությունը:
Մարմնի ներքին էներգիան ընդհանրապես կարող է աճել ինչպես արտաքին ուժերի մեխանիկական աշխատանքի արդյունքում, այնպես էլ ջերմափոխանակության հետևանքով:
Շրջապատող մարմինների հետ էներգիայի փոխանակման դեպքում, հանգամանքներից ելնելով« մարմնի ներքին էներգիան կարող է ինչպես աճել, այնպես էլ նվազել: δQ-ի նշանը ցույց է տալիս ջերմափոխանակության ուղղությունը: Եթե ջերմափոխանակության ժամանակ շրջապատող մարմինները տաքանում են, այսինքն` քննարկվող մարմնից էներգիա են խլում, ապա δQ<0: Եթե մարմնի ներքին էներգիայի dU փոփոխության դեպքում շրջապատող մարմինների դեմ կատարվում է δA աշխատանք, ապա այդ աշխատանքը համարվում է դրական (+δA), իսկ եթե շրջապատող ուժերը աշխատանք են կատարում դիտարկվող մարմնի դեմ, ապա այդ աշխատանքը բացասական է (-δA ):
Քանի որ համակարգի ներքին էներգիան ընդհանրապես փոփոխվում է ինչպես մարմնին ջերմաքանակ հաղորդելիս, այնպես էլ նրա դեմ աշխատանք կատարելիս, հաշվի առնելով նշանների կանոնը, տեղի ունեցող պրոցեսի նկատմամբ կիրառելի էներգիայի պահպանման օրենքը կարելի է ձևակերպել այլ կերպ.
Համակարգի ներքին էներգիայի փոփոխությունը հավասար է համակարգին հաղորդված ջերմաքանակի և նրա դեմ կատարված մեխանի-կական աշխատանքի տարբերությանը.
![]()
կամ համակարգին հաղորդված ջերմաքանակը ծախսվում է նրա ներքին էներգիայի մեծացման և համակարգի կողմից արտաքին մարմինների դեմ աշխատանք կատարելու վրա.
![]()
Եթե տարբեր նախնական ջերմաստիճան ունեցող մի քանի մարմիններից բաղկացած փակ համակարգում տեղի է ունենում ջերմափոխանակություն, ապա համակարգի ներսում ոչ մի աշխատանք չի կատարվում:
Քանի որ համակարգը փակ է, ապա համակարգի ներքին էներգիայի փոփոխությունը հավասար է զրոյի: Համաձայն ջերմադինամիկայի առաջին սկզբունքի, համակարգի մարմինների ներքին էներգիայի փոփոխությունը հավասար է համակարգի ներսում մինչև ջերմային հավասարակշռությունն այդ մարմինների կողմից տրված կամ ստացած ջերմության քանակությանը, այսինքն` մի վիճակ, որի դեպքում ջերմաստիճանը դադարում է փոփոխվելուց:
11.7. ՋեՐՄԱԴԻՆԱՄԻԿԱՅԻ
ԱՌԱՋԻՆ ՕՐԵՆՔԻ
ԿԻՐԱՌՈՒՄԸ ԻԶՈՊՐՈՑԵՍՆԵՐԻ
ՆԿԱՏՄԱՄԲ
Իզոխոր պրոցես: Դիտարկենք հաստատուն ծավալում կատարվող 1մոլ գազի տաքացումը: Քանի որ V=const, ապա dV=0, հետևաբար δA=pdV=0: Ջերմադինամիկայի առաջին սկզբունքից (11.14) հետևում է, որ իզոխոր պրոցեսի դեպքում գազին հաղորդված ամբողջ ջերմաքանակը ծախսվում է նրա ներքին էներգիան մեծացնելու վրա:
![]()
![]()
![]()
որտեղ ![]() գազի
մոլային ջերմունակությունն
է հաստատուն ծավալի
դեպքում: Եթե գազն
իդեալական է, ապա
գազի
մոլային ջերմունակությունն
է հաստատուն ծավալի
դեպքում: Եթե գազն
իդեալական է, ապա
![]() ջերմաստիճանից
կախված չէ և հաստատուն
մեծություն է:
ջերմաստիճանից
կախված չէ և հաստատուն
մեծություն է:
(11.16) արտահայտությունը ցույց է տալիս, որ իդեալական գազի ներքին էներգիան ջերմաստիճանի միարժեք ֆունկցիա է:
Ինտեգրելով (11.16) արտահայտությունը՝ կունենանք
![]()
(9.17)-ը կոչվում
է Ջոուլի օրենք:
Ջոուլի և ըստ ազատության
աստիճանների էներգիայի
հավասարաչափ բաշխման
օրենքներից բխում
է ![]() միջև
հետևյալ առնչությունը.
միջև
հետևյալ առնչությունը.
![]()
Իզոբար պրոցես: Քննարկենք մեկ մոլ գազի տաքացումը հաստատուն ճնշման դեպքում (p = const): Այս դեպքում փոփոխվում են ծավալն ու ջերմաստիճանը, հետևաբար կատարվում է δA = pdV աշխատանք, և փոփոխվում է dU ներքին էներգիան: Այս պրոցեսի համար ջերմադինամիկայի առաջին սկզբունքն ունի հետևյալ տեսքը
![]()
Իզոբար պրոցեսի
ժամանակ ![]() այդ պատճառով
ջերմադինամիկայի
առաջին սկզբունքն
ընդունում է հետևյալ
տեսքը
այդ պատճառով
ջերմադինամիկայի
առաջին սկզբունքն
ընդունում է հետևյալ
տեսքը
![]()
կամ, քանի որ
ներքին էներգիան
միայն ջերմաստիճանի
ֆունկցիա է ՝ ![]() ապա
ապա
![]()
Գրենք վիճակի հավասարումը մեկ մոլ իդեալական գազի համար. pV = RT:
Իզոբար պրոցեսի համար այս հավասարումը ստանում է հետևյալ տեսքը. pdV = RdT:
Այս արտահայտությունը տեղադրենք (11.19) բանաձևի մեջ
![]()
որտեղից
![]()
(11.20) առնչությունն
անվանում են Մայերի
հավասարում: (9.18) հավասարումից
![]() արժեքը
տեղադրելով Մայերի
հավասարման մեջ՝
կունենանք
արժեքը
տեղադրելով Մայերի
հավասարման մեջ՝
կունենանք
![]()
որտեղից՝
![]()
Իզոթերմ պրոցես: T=const դեպքում dU=0 դրա համար էլ համակարգին հաղորդված ամբողջ ջերմաքանակը ծախսվում է արտաքին ուժերի դեմ աշխատանք կատարելու վրա`δQ = δA:
11.8. ԳԱԶԵՐԻ ՋԵՐՄՈՒՆԱԿՈՒԹՅՈՒՆԸ
Ըստ (11.18) և (11.21) բանաձևերի`
գազերի ջերմունակությունը
չպետք է կախում
ունենա ջերմաստիճանից:
Հատկապես ապշեցնում
են տեսության և
փորձի միջև գոյություն
ունեցող անհամապատասխանությունները`
ջերմունակության
կախումը ջերմաստիճանից
քննարկելիս: Նկ.11.4-ում
բերված է մոլի
![]() ջերմունակության
կախումը ջերմաստիճանից
պատկերող կորը,
որը փորձնական
եղանակով ստացվել
է ջրածնի համար:
ջերմունակության
կախումը ջերմաստիճանից
պատկերող կորը,
որը փորձնական
եղանակով ստացվել
է ջրածնի համար:
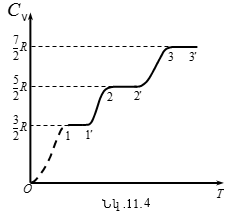
Տեսության համաձայն` ջերմունակությունը չպետք է կախում ունենա ջերմաստիճանից: Ինչպես երևում է նկարից, դա իրավացի է միայն ջերմաստիճանային առանձին միջակայքերի սահմաններում, ընդ որում տարբեր միջակայքերում ջերմունակությունն ունի մոլեկուլի ազատության աստիճանների տարբեր թվերին համապատասխանող արժեքներ:
Այսպես ![]() տեղամասում
տեղամասում
![]() հավասար
է 3/2R-ի: Դա նշանակում
է, որ մոլեկուլը
իրեն պահում է
միայն համընթաց
ազատության աստիճաններով
օժտված համակարգի
նման:
հավասար
է 3/2R-ի: Դա նշանակում
է, որ մոլեկուլը
իրեն պահում է
միայն համընթաց
ազատության աստիճաններով
օժտված համակարգի
նման: ![]() տեղամասում
տեղամասում
![]() հավասար
է 5/2R-ի: Հետևաբար,
այս տեղամասին
համապատասխանող
ջերմաստիճաններում
մոլեկուլի` ավելի
ցածր ջերմաստիճանների
դեպքում ունեցած
երեք համընթաց
ազատության աստիճաններին
ավելանում են երկու
պտտական ազատության
աստիճաններ ևս:
Վերջապես, բավականաչափ
բարձր ջերմաստիճանների
դեպքում
հավասար
է 5/2R-ի: Հետևաբար,
այս տեղամասին
համապատասխանող
ջերմաստիճաններում
մոլեկուլի` ավելի
ցածր ջերմաստիճանների
դեպքում ունեցած
երեք համընթաց
ազատության աստիճաններին
ավելանում են երկու
պտտական ազատության
աստիճաններ ևս:
Վերջապես, բավականաչափ
բարձր ջերմաստիճանների
դեպքում ![]() հավասարվում
է 7/2R-ի, որը վկայում
է այս ջերմաստիճանների
դեպքում մոլեկուլի
տատանումների
առկայության մասին:
Նշված միջակայքերի
միջև ջերմունակությունը
մոնոտոն աճում
է ջերմաստիճանի
հետ միասին, այսինքն`
համապատասխանում
է կարծես թե ազատության
աստիճանների ոչ
ամբողջ փոփոխական
թվի:
հավասարվում
է 7/2R-ի, որը վկայում
է այս ջերմաստիճանների
դեպքում մոլեկուլի
տատանումների
առկայության մասին:
Նշված միջակայքերի
միջև ջերմունակությունը
մոնոտոն աճում
է ջերմաստիճանի
հետ միասին, այսինքն`
համապատասխանում
է կարծես թե ազատության
աստիճանների ոչ
ամբողջ փոփոխական
թվի:
Այսպիսով,
մոլեկուլի ազատության
աստիճանների թիվը,
որը դրսևորվում
է ջերմունակությունում,
կախում ունի ջերմաստիճանից:
Ցածր ջերմաստիճանների
դեպքում նկատվում
է մոլեկուլների
միայն համընթաց
շարժում: Ավելի
բարձր ջերմաստիճանների
դեպքում համընթաց
շարժման հետ մեկտեղ
նկատվում է նաև
մոլեկուլների
պտտում: Եվ վերջապես,
առավել բարձր ջերմաստիճանների
դեպքում շարժման
առաջին երկու տեսակներին
ավելանում են նաև
մոլեկուլների
տատանումները:
Ընդ որում, ինչպես
հետևում է ջերմունակության
կորի մոնոտոն ընթացքից,
ոչ բոլոր մոլեկուլներն
են, որ միաժամանակ
են ներգրավվում
պտտական, այնուհետև`
տատանողական շարժման
մեջ: Օրինակ` սկզբում
պտույտը նկատվում
է մոլեկուլների
ոչ մեծ մասի մոտ:
Ջերմաստիճանի
բարձրացման հետ
միասին այս մոլեկուլների
քանակն աճում է
և, վերջին հաշվով,
որոշակի ջերմաստիճանի
դեպքում պըտըտական
շարժման մեջ ներգրավվում
են գործնականորեն
բոլոր մոլեկուլները:
Համանման պրոցես
տեղի է ունենում
նաև մոլեկուլների
տատանողական շարժման
դեպքում: Ջերմունակության
այսպիսի վարքի
բացատրությունը
տրվում է քվանտային
մեխանիկայում:
Ինչպես ցույց է
տրվում քվանտային
մեխանկայում, մոլեկուլների
պտտական և տատանողական
շարժումների էներգիան
քվանտացած է: Դա
նշանակում է, որ
մոլեկուլի պտտական
և տատանողական
էներգիաները չեն
կարող ցանկացած
արժեքներ ստանալ,
այլ ստանում են
միայն դիսկրետ,
այսինքն` առանձին,
իրարից վերջավոր
մեծությամբ տարբերվող
արժեքներ: Հետևաբար,
այս տեսակի շարժումների
հետ կապված էներգիան
կարող է փոփոխվել
միայն թռիչքներով:
Համընթաց շարժման
էներգիայի համար
այսպիսի սահմանափակում
չկա, այն կարող
է փոփոխվել անընդհատ`ինչքան
ասես փոքր բաժիններով:
Էներգիայի առանձին
թույլատրելի արժեքների
միջև գոյություն
ունեցող միջակայքերը
կամ, ինչպես ընդունված
է ասել, էներգիական
մակարդակների
միջև գոյություն
ունեցող միջակայքերը
տատանումների
համար մոտավորապես
մեկ կարգով ավելի
մեծ են, քան պտտման
համար: Գազի մոլեկուլներն
ըստ էներգիայի
արժեքների բաշխված
են այնպես, որ դրանց
գերակշռող մասն
օժտված է միջին
<E>-ին մոտ էներգիաներով,
և մոլեկուլների
միայն փոքր մասն
է, որ ունի <E>-ը զգալիորեն
գերազանցող էներգիա:
Ուստի, որպեսզի
մոլեկուլների
զգալի մասը ներգրավվի
պտտական կամ տատանողական
շարժման մեջ, պետք
է, որ նրանց միջին
էներգիան բավականաչափ
մեծ լինի` համապատասխան
էներգիայի թույլատրված
մակարդակների
միջև գոյություն
ունեցող հեռավորության
հետ համեմատած:
Ջերմաստիճանի
փոքր փոփոխությունները
կհանգեցնեն միայն
համընթաց շարժման
էներգիայի փոփոխությունների,
որին համապատասխան
գազի ջերմունակությունը
հավասարվում է
3/2R-ի (նկ.11.4-ում պատկերված
կորի ![]() տեղամասը):
Ջերմաստիճանի
բարձրացումն ուղեկցվում
է միջին էներգիայի
աճով, որի հետևանքով
ավելի մեծ թվով
մոլեկուլներ են
ներգրավվում պտտական
շարժման մեջ: Այս
պրոցեսին համապատասխանում
է կորի
տեղամասը):
Ջերմաստիճանի
բարձրացումն ուղեկցվում
է միջին էներգիայի
աճով, որի հետևանքով
ավելի մեծ թվով
մոլեկուլներ են
ներգրավվում պտտական
շարժման մեջ: Այս
պրոցեսին համապատասխանում
է կորի ![]() տեղամասը:
Բոլոր մոլեկուլները
պտտական շարժման
մեջ ներգրավվելուց
հետո սկսվում է
տեղամասը:
Բոլոր մոլեկուլները
պտտական շարժման
մեջ ներգրավվելուց
հետո սկսվում է
![]() hորիզոնական
տեղամասը: Այս
տեղամասին համապատասխանող
ջերմաստիճանների
դեպքում միջին
էներգիան դեռևս
զգալիորեն փոքր
է տատանողական
էներգիայի թույլատրելի
մակարդակների
միջև գոյություն
ունեցող հեռավորությունից,
որի հետևանքով
մոլեկուլների
տատանումները
գործնականորեն
բացակայում են:
Ջերմաստիճանի
հետագա բարձրացման
դեպքում ավելի
մեծ թվով մոլեկուլներ
կսկսեն ներգրավվել
տատանողական շարժման
մեջ, որին համապատասխանում
է անցման
hորիզոնական
տեղամասը: Այս
տեղամասին համապատասխանող
ջերմաստիճանների
դեպքում միջին
էներգիան դեռևս
զգալիորեն փոքր
է տատանողական
էներգիայի թույլատրելի
մակարդակների
միջև գոյություն
ունեցող հեռավորությունից,
որի հետևանքով
մոլեկուլների
տատանումները
գործնականորեն
բացակայում են:
Ջերմաստիճանի
հետագա բարձրացման
դեպքում ավելի
մեծ թվով մոլեկուլներ
կսկսեն ներգրավվել
տատանողական շարժման
մեջ, որին համապատասխանում
է անցման ![]() տեղամասը
ջերմունակության
կորի վրա: Վերջապես,
բավականաչափ բարձր
ջերմաստիճանի
դեպքում բոլոր
մոլեկուլները
կներգրավվեն տատանողական
շարժման մեջ, որի
հետևանքով ջերմունակությունը
կհավասարվի 7/2R-ի:
Վերադառնալով
ջերմունակության
դասական տեսությանը`
կարելի է ասել,
որ նրա արդյունքները
ճիշտ են առանձին
ջերմաստիճանային
միջակայքերի համար,
ընդ որում` յուրաքանչյուր
միջակայքին համապատասխանում
է մոլեկուլի` իրեն
հատկանշական ազատության
աստիճանների թիվ:
տեղամասը
ջերմունակության
կորի վրա: Վերջապես,
բավականաչափ բարձր
ջերմաստիճանի
դեպքում բոլոր
մոլեկուլները
կներգրավվեն տատանողական
շարժման մեջ, որի
հետևանքով ջերմունակությունը
կհավասարվի 7/2R-ի:
Վերադառնալով
ջերմունակության
դասական տեսությանը`
կարելի է ասել,
որ նրա արդյունքները
ճիշտ են առանձին
ջերմաստիճանային
միջակայքերի համար,
ընդ որում` յուրաքանչյուր
միջակայքին համապատասխանում
է մոլեկուլի` իրեն
հատկանշական ազատության
աստիճանների թիվ:
Խնդիր 1: Որոշել
օդի ![]() տեսակարար
ջերմունակությունները`
նկատի ունենալով,
որ նրա բաղադրության
մեջ 20% -ը թթվածին
է, իսկ 80% -ը` ջրածին:
տեսակարար
ջերմունակությունները`
նկատի ունենալով,
որ նրա բաղադրության
մեջ 20% -ը թթվածին
է, իսկ 80% -ը` ջրածին:
Լուծում: Իդեալական գազի ջերմունակությունները որոշվում են`
![]()
բանաձևերով, որտեղ i-ն մոլեկուլների ազատության աստիճանների թիվն է (թթվածնի և ազոտի համար i=5): Թթվածնի տեսակարար ջերմունակությունները հաստատուն ծավալի և հաստատուն ճնշման դեպքում արտահայտվում են`
![]()
բանաձևերով,
որտեղ ![]() թթվածնի
մոլային զանգվածն
է, R-ը` գազային հաստատունը:
թթվածնի
մոլային զանգվածն
է, R-ը` գազային հաստատունը:
Համանմանորեն ազոտի տեսակարար ջերմունակությունների համար կունենանք`
![]()
որտեղ ![]() ազոտի
մոլային զանգվածն
է:
ազոտի
մոլային զանգվածն
է:
m զանգվածով օդը հաստատուն ծավալի դեպքում 1Կ-ով տաքացնելու համար պահանջվող ջերմաքանակը հավասար է
![]()
Հետևաբար
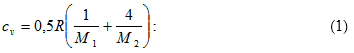
m զանգվածով օդը հաստատուն ճնշման դեպքում 1Կ-ով տաքացնելու համար պահանջվող ջերմաքանակը`
![]()
որտեղից
![]()
(1) և (2) արտահայտությունների մեջ մտնող մեծությունների թվային արժեքները տեղադրելով՝
![]()
կստանանք`
![]()
Խնդիր 2: m = 16
· 10-2 կգ զանգվածով
թթվածինը տաքացվել
է հաստատուն ճնշման
տակ ![]() Որոշել
գազին հաղորդված
ջերմաքանակը, ներքին
էներգիայի փոփոխությունը,
գազի ընդարձակման
աշխատանքը:
Որոշել
գազին հաղորդված
ջերմաքանակը, ներքին
էներգիայի փոփոխությունը,
գազի ընդարձակման
աշխատանքը:
Լուծում: Հաստատուն ճնշման տակ գազը տաքացնելու համար անհրաժեշտ ջերմաքանակը`
![]()
որտեղ ![]() գազի
տեսակարար և մոլային
ջերմունակություններն
են հաստատուն ճնշման
դեպքում, M = 32 · 10-3
կգ/մոլ թթվածնի
մոլային զանգվածն
է:
գազի
տեսակարար և մոլային
ջերմունակություններն
են հաստատուն ճնշման
դեպքում, M = 32 · 10-3
կգ/մոլ թթվածնի
մոլային զանգվածն
է:
Բոլոր երկատոմ
գազերի համար`
![]() Գազի
ներքին էներգիայի
փոփոխությունը`
Գազի
ներքին էներգիայի
փոփոխությունը`
![]()
որտեղ ![]() գազի մոլային
ջերմունակությունն
է հաստատուն ծավալի
դեպքում: Բոլոր
երկատոմ գազերի
համար`
գազի մոլային
ջերմունակությունն
է հաստատուն ծավալի
դեպքում: Բոլոր
երկատոմ գազերի
համար` ![]()
Գազի ընդարձակման
աշխատանքն իզոբար
պրոցեսի դեպքում`
![]() գազի
ծավալի փոփոխությունն
է, որը կարելի է
գտնել Կլապեյրոն
- Մենդելեևի հավասարումից:
գազի
ծավալի փոփոխությունն
է, որը կարելի է
գտնել Կլապեյրոն
- Մենդելեևի հավասարումից:

(4)-ից հանելով (3)-ը` կստանանք`
![]()
հետևաբար`
![]()
Տեղադրելով (1), (2) և (5) արտահայտությունների մեջ մտնող մեծությունների թվային արժեքները` ստանում ենք`
![]()
11.9. ԱԴԻԱԲԱՏ ՊՐՈՑԵՍ: ԱԴԻԱԲԱՏԻ ՀԱՎԱՍԱՐՈՒՄԸ
Պրոցեսը, որն ընթանում է առանց շրջակա միջավայրի հետ ջերմափոխանակության, կոչվում է ադիաբատ (δQ = 0):
Ադիաբատին մոտ պրոցես հնարավոր է իրականացնել միայն այն դեպքում, եթե գազը գտնվում է շատ լավ ջերմամեկուսացնող հատկություններով թաղանթի ներսում:
Ադիաբատ կարելի է համարել շատ արագ ընթացող պրոցեսները: Գազի շատ արագ սեղմման ժամանակ ծախսվում է ներքին էներգիայի մեծացմանն ու ջերմաստիճանի բարձրացմանը հանգեցնող աշխատանք: Մարմինները, որոնց ջերմաստիճանը բարձր է, պետք է որոշ ջերմաքանակ փոխանցեն շրջապատող միջավայրին, սակայն ջերմափոխանակության պրոցեսը պահանջում է որոշակի ժամանակ, դրա համար արագ սեղմման (կամ ընդարձակման) դեպքում ջերմաքանակը չի հասցնում տվյալ ծավալից անջատվել, այսինքն δQ = 0, և պրոցեսը կարելի է դիտել որպես ադիաբատ: Այդպիսի պրոցեսի օրինակ կարող է ծառայել տաք խառնուրդի պայթյունը ներքին այրման շարժիչի աշխատանքի ժամանակ:
Ջերմադինամիկայի առաջին սկզբունքը ադիաբատ պրոցեսի համար ունի հետևյալ տեսքը.
![]()
Ադիաբատ պրոցեսի դեպքում աշխատանքը կատարվում է միայն գազի ներքին էներգիայի փոփոխության հաշվին, այսինքն`
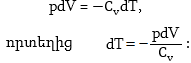
Ադիաբատ ընդարձակման ժամանակ գազն աշխատանք է կատարում և նրա ներքին էներգիան, հետևաբար նաև ջերմաստիճանը նվազում են:
Ադիաբատ սեղմման ժամանակ գազի կատարած աշխատաքը բացասական է և, նրա ներքին էներգիան հետևաբար նաև ջերմաստիճանն աճում են: Ադիաբատ ընդարձակման ժամանակ գազի սառեցման երևույթը լայնորեն կիրառվում է տեխնիկայում, օրինակ` սառնարանային կայանքներում: Մեկ մոլ գազի համար ճիշտ է Մենդելեև - Կլապեյրոնի հավասարումը` pV = R:
Այս հավասարումից,
երբ փոփոխվում
են բոլոր երեք
պարամետրերը
(P,V,T), կունենանք pdV +
Vdp = RdT: Հաշվի առնելով,
որ ![]() կստանանք`
կստանանք`
![]()
Օգտագործելով Մայերի (11.20) հավասարումը` կարող ենք գրել
![]()
Այս հավասարումը
բաժանենք ![]() և ներմուծենք
և ներմուծենք![]() նշանակումը:
Այդ դեպքում
նշանակումը:
Այդ դեպքում
![]()
Ինտեգելով այս արտահայտությունը, կստանանք`
ln p + γ lnV = const, որտեղ const -ն ինտեգրման հաստատունն է. այսպիսով,
![]()
Սա Պուասոնի հավասարումն է: Այն կապ է հաստատում գազի վիճակի պարամետրերի միջև ադիաբատ պրոցեսի դեպքում:
Օգտվելով (11.22)-ից` կարելի է անցնել T և V փոփոխականներով հավասարմանը, փոխարինելով p-ն T-ով և V ով` իդեալական գազի վիճակի (10.19) հավասարմանը համապատասխան, այսինքն`
![]()
Տեղադրելով այս արտահայտությունը (11.22)-ի մեջ և նկատի ունենալով, որ m-ը, M-ն և R-ը հաստատուններ են, կստանանք
![]()
(11.23) առնչությունն իդեալական գազի ադիաբատի հավասարումն է` T և V փոփոխականներով:
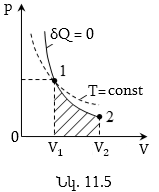
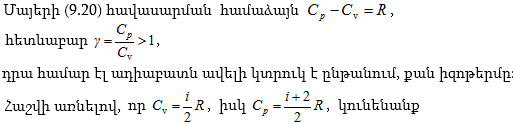
![]()
![]()
![]()
որտեղ γ-ն կոչվում
է ադիաբատի ցուցիչ,
կամ Պուասոնի գործակից:
Միատոմ գազերի
համար (Ne, He և այլն),
որոնք բավականին
լավ են բավարարում
իդեալականության
պայմանին, i=3, γ=1,67: Երկատոմ
գազերի համար ![]() γ-ի արժեքները,
հաշված ըստ (11.24) բանաձևի,
լավ հաստատվում
են փորձերով:
γ-ի արժեքները,
հաշված ըստ (11.24) բանաձևի,
լավ հաստատվում
են փորձերով:
Հաշվենք ադիաբատ պրոցեսում իդեալական գազի կատարած աշխատանքը
![]()
![]()
ուրեմն`
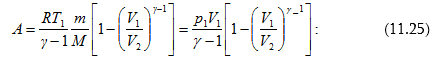
Պոլիտրոպիկ են կոչվում այն պրոցեսները, որոնց ընթացքում մարմնի ջերմունակությունը մնում է հաստատուն: Հետևաբար, պոլիտրոպիկ պրոցեսում գազը, բացի վիճակի հավասարումից, ենթարկվում է նաև լրացուցիչ պայմանի`
![]()
Որպեսզի ստանանք պոլիտրոպի հավասարումը իդեալական գազի համար` օգտվենք ջերմադինամիկայի առաջին օրենքից`
![]()
![]()
![]()
Ձևափոխենք այս առնչությունը հետևյալ ձևով.
![]()
(հավասարման երկու մասերը բազմապատկեցինք R-ով):
Վիճակի հավասարումը դիֆերենցելով` գալիս ենք հետևյալ հավասարման`
![]()
Այսպիսի փոխարինում կատարելով (11.29) հավասարման մեջ` ստանում ենք հետևյալ հավասարումը `
![]()
Բաժանելով այս հավասարումը pV-ի և նկատի ունենալով, որ
![]()
արդյունքում կստանանք
![]()
Ներմուծելով
![]()
մեծությունը (11.30) հավասարմանը կարելի է տալ հետևյալ տեսքը`
![]()
Այս հավասարման լուծումը տալիս է`
![]()
Ստացված հավասարումը
իդեալական գազի
պոլիտրոպի հավասարումն
է: (11.31) արտահայտության
մեջ n մեծությունը
կոչվում է պոլիտրոպի
ցուցիչ: (11.33) հավասարումը
նման է ադիաբատի
(11.22) հավասարմանը,
միայն ![]() փոխարինված
է n-ով: Պոլիտրոպի
հավասարումը T
և V փոփոխականներով
կստանանք (11.23) հավասարումից`
դարձյալ
փոխարինված
է n-ով: Պոլիտրոպի
հավասարումը T
և V փոփոխականներով
կստանանք (11.23) հավասարումից`
դարձյալ ![]() փոխարինելով
n -ով.
փոխարինելով
n -ով.
![]()
Լուծելով (11.31) հավասարումը C -ի նկատմամբ` կստանանք պոլիտրոպիկ պրոցեսի դեպքում ջերմունակությունն արտահայտող բանաձևը պոլիտրոպի n ցուցչով.
![]()
Աղյուսակում տրված են n -ի այն արժեքները, որոնց դեպքում պոլիտրոպիկ պրոցեսը նույնական է մեզ արդեն հայտնի պրոցեսներից մեկի հետ:
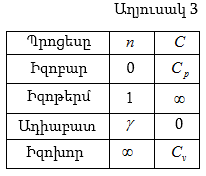
Աղյուսակի առաջին երեք տողերն ակնհայտ են: Չորրորդ տողի իրավացիության մեջ համոզվելու համար պոլիտրոպի (11.33) hավասարումը գրենք հեևյալ տեսքով`
![]()
որտեղ 1 և 2 ինդեքսները վերաբերում են երկու կամավոր կերպով վերցված վիճակներին: (11.36)-ից հանենք n աստիճանի արմատ`
![]()
n-ը ձգտեցնելով + ∞ կամ - ∞ կհանգենք հետևյալ պայմանին`
![]()
որը բնութագրում
է իզոխոր պրոցեսը:
n=0 դեպքում (11.33) հավասարումը
վերածվում է p =
const իզոբարի (10.13) հավասարմանը:
n = γ դեպքում (11.33) հավասարումը
վերածվում է ադիաբատի
(11.22) հավասարմանը:
Վերջապես, n=1 դեպքում
ստացվում է իզոթերմի
(10.6) հավասարումը:
Իզոթերմ պրոցեսի
դեպքում (11.35) բանաձևը
ջերմունակության
համար տալիս է
![]() արժեքը:
Սա նշանակում է,
որ մարմնին հաղորդելով
δQ =0 ջերմաքանակ,
ջերմաստիճանի`
dT = 0 փոփոխություն
չի բերում: Ադիաբատ
պրոցեսի դեպքում
(10.35) հավասարումը
ջերմունակության
համար տալիս է
արժեքը:
Սա նշանակում է,
որ մարմնին հաղորդելով
δQ =0 ջերմաքանակ,
ջերմաստիճանի`
dT = 0 փոփոխություն
չի բերում: Ադիաբատ
պրոցեսի դեպքում
(10.35) հավասարումը
ջերմունակության
համար տալիս է
![]() արժեքը:
Ջերմունակության
այդպիսի արժեքը
պայմանավորված
է նրանով, որ δQ = 0 սակայն
dT -ն նույն ժամանակում
զրոյից տարբեր
է:
արժեքը:
Ջերմունակության
այդպիսի արժեքը
պայմանավորված
է նրանով, որ δQ = 0 սակայն
dT -ն նույն ժամանակում
զրոյից տարբեր
է:
11.11 ՑԻԿԼ: ԴԱՐՁԵԼԻ ԵՎ ՈՉ ԴԱՐՁԵԼԻ ՊՐՈՑԵՍՆԵՐ
Էներգիայի ցանկացած տեսակ կարող է լրիվ փոխարկվել ջերմության, սակայն մոլեկուլների ու ատոմների քաոսային շարժման էներգիան չի կարող լրիվ սպառվել և վերածվել էներգիայի մի այլ տեսակի, քանի որ մոլեկուլների անկանոն շարժումը նյութի բնական վիճակն է:

Բանող մարմին կոչվում է էներգիայի մի տեսակը մի այլ տեսակի փոխարկելու պրոցեսն իրականացնող ջերմադինամիկական համակարգը: Բանող մարմինը պրոցեսի սկզբում ու վերջում գտնվում է տարբեր վիճակներում: Նրա վիճակը բնորոշող պարամետրերը կարող են ունենալ տարբեր արժեքներ: Ջերմադինամիկայում կարևոր նշանակություն ունեն այնպիսի պրոցեսները, երբ ջերմադինամիկական համակարգը պրոցեսի վերջում գալիս է սկզբնական վիճակին, և այդ վիճակը բնորոշող պարամետրերն ընդունում են նախնական արժեքները: Այդպիսի պրոցեսները կոչվում են փակ (շրջանային) պրոցեսներ կամ ցիկլեր: Եթե համակարգն անցնելով մի շարք վիճակներով` վերադառնում է իր սկզբնական վիճակին, ապա ասում են, որ տվյալ համակարգը կատարում է ցիկլ:
Նկ.11.6-ում ցույց
է տրված երկու
իզոբարերից (ab,cd) և
երկու իզոխորերից
(bc,da)բաղկացած ցիկլ:
ab -ով ընդարձակման
դեպքում բանող
մարմնի կողմից
կատարվում է ![]() դրական
աշխատանք, որը
չափվում է
դրական
աշխատանք, որը
չափվում է ![]() պատկերի
մակերեսով: cd-ով
սեղման դեպքում
արտաքին ուժերը
կատարում են
պատկերի
մակերեսով: cd-ով
սեղման դեպքում
արտաքին ուժերը
կատարում են ![]() աշխատանք,
որը չափվում է
աշխատանք,
որը չափվում է
![]() պատկերի
մակերեսով: Բանող
մարմինը մեկ ցիկլի
ընթացքում կատարում
է abcd ստվերագծված
մակերեսով չափվող
պատկերի
մակերեսով: Բանող
մարմինը մեկ ցիկլի
ընթացքում կատարում
է abcd ստվերագծված
մակերեսով չափվող
![]() դրական
աշխատանքը: Պրոցեսն
ավանում են դարձելի,
եթե նրա ավարտից
հետո համակարգը
վերադառնում է
իր սկզբնական վիճակին:
Միաժամանակ սկզբնական
վիճակին են վերադառնում
նրա հետ փոխազդող
բոլոր մարմինները:
Օրինակ ABCD անոթի
մի մասում (I) պարփակված
գազը (նկ.11.7) MN միջնորմի
հեռացումից հետո
ընդարձակվում
է վակուումում
և գրավում ամբողջ
անոթի ծավալը
(I և II): Գազի մոլեկուլները,
կատարելով քաոսային
շարժում, կարո՞ղ
են արդյոք նորից
հավաքվել անոթի
մեկ մասի մեջ:
դրական
աշխատանքը: Պրոցեսն
ավանում են դարձելի,
եթե նրա ավարտից
հետո համակարգը
վերադառնում է
իր սկզբնական վիճակին:
Միաժամանակ սկզբնական
վիճակին են վերադառնում
նրա հետ փոխազդող
բոլոր մարմինները:
Օրինակ ABCD անոթի
մի մասում (I) պարփակված
գազը (նկ.11.7) MN միջնորմի
հեռացումից հետո
ընդարձակվում
է վակուումում
և գրավում ամբողջ
անոթի ծավալը
(I և II): Գազի մոլեկուլները,
կատարելով քաոսային
շարժում, կարո՞ղ
են արդյոք նորից
հավաքվել անոթի
մեկ մասի մեջ:
Գործնականում
դա տեղի չի ունենում:
Կարելի է գազը
նորից սեղմել և
ստիպել, որ այն
գրավի իր նախկին
ծավալը, սակայն
այդ դեպքում շրջապատող
մարմիններում
տեղի կունենան
փոփոխություններ:
Ուրեմն գազի ընդարձակումը
վակուումում ոչ
դարձելի է: Հետևաբար,
ոչ դարձելի պրոցեսները
մի ուղղությամբ
ընթանում են ինքնաբերաբար,
իսկ հակառակ ուղղությամբ
իրականացնել կարելի
է միայն արտաքին
ուժերի աշխատանքի
արդյունքով: Այդ
պրոցեսների բնութագրական
առանձնահատկությունն
այն է, որ դրանք
ընթանում են հավասարակշռության
վիճակի կողմը,
այսինքն` այնպիսի
վիճակի, որի դեպքում
համակարգի պարամետրերն
ունեն հնարավորին
չափ երկար ժամանակ
անփոփոխ մնացող
որոշակի արժեքներ:
Ոչ դարձելի է այնպիսի
պրոցեսը, որը համակարգին
տեղափոխում է փոքր
հավանական վիճակից
ավելի մեծ հավանական
վիճակի: Շրջանային
պրոցեսը, որի մեջ
համակարգը կատարում
է ![]() դրական
աշխատանք, կոչվում
է ուղիղ ցիկլ:
(pV) դիագրամի վրա
ուղիղ ցիկլը ցույց
է տրվում ժամացույցի
սլաքի շարժման
ուղղությամբ «
փակ կորի տեսքով
(նկ.11.8ա):
դրական
աշխատանք, կոչվում
է ուղիղ ցիկլ:
(pV) դիագրամի վրա
ուղիղ ցիկլը ցույց
է տրվում ժամացույցի
սլաքի շարժման
ուղղությամբ «
փակ կորի տեսքով
(նկ.11.8ա):
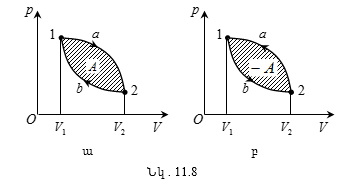
Շրջանային պրոցեսը, որի մեջ համակարգի կողմից կատարվող աշխատանքը բացասական է
![]()
կոչվում է հակադարձ ցիկլ: (p,V) դիագրամի վրա հակադարձ ցիկլը ցույց է տրվում ժամացույցի սլաքի շարժման հակառակ ուղղությամբ փակ կորի տեսքով (նկ.11.8բ):
Ուղիղ ցիկլը օգտագործվում է ջերմային շարժիչներում, պարբերաբար գործող շարժիչներում, որոնք դրսից ստացած ջերմաքանակի հաշվին աշխատանք են կատարում:
Ջերմային շարժիչը վառելանյութի ներքին էներգիան մեխանիկականի վերածող համակարգ է: Վառելանյութի այրման ժամանակ անջատված էներգիան ջերմափոխանակության ճանապարհով փոխանցվում է գազին: Գազն ընդարձակվելով` շարժման մեջ է դնում մեխանիզմը և աշխատանք է կատարում արտաքին ուժերի դեմ: Ջերմային շարժիչի աշխատանքի սխեման բերված է նկ.11.9-ում:
Ցանկացած
ջերմային շարժիչ
բաղկացած է երեք
հիմնական մասերից.
բանող մարմին,
ջեռուցիչ ու սառնարան:
Բանող մարմինը
(գազը կամ գոլորշին)
ընդարձակվելիս
ջեռուցչից ստանալով
որոշակի ![]() ջերմաքանակ՝
կատարում է աշխատանք:
Ի հաշիվ վառելիքի
այրման ջեռուցչի
ջերմաքանակ՝
կատարում է աշխատանք:
Ի հաշիվ վառելիքի
այրման ջեռուցչի
![]() ջերմաստիճանը
մնում է հաստատուն:
ջերմաստիճանը
մնում է հաստատուն:
Սեղմման ժամանակ
բանող մարմինը
ջերմության որոշ
![]() քանակություն
տալիս է
քանակություն
տալիս է ![]() ջերմաստիճան
ունեցող սառնարանին:
Ջերմային շարժիչը
պետք է աշխատի
պարբերաբար (ցիկլերով):
Ցիկլի ավարտին
բանող մարմինը
վերադառնում է
իր սկզբնական վիճակին,
նրա ներքին էներգիան
ընդունում է իր
նախնական արժեքը:
ջերմաստիճան
ունեցող սառնարանին:
Ջերմային շարժիչը
պետք է աշխատի
պարբերաբար (ցիկլերով):
Ցիկլի ավարտին
բանող մարմինը
վերադառնում է
իր սկզբնական վիճակին,
նրա ներքին էներգիան
ընդունում է իր
նախնական արժեքը:

Դրա համար էլ ցիկլի աշխատանքը կարող է կատարվել` միայն բանող մարմնին արտաքին աղբյուրների հաշվին ջերմաքանակ մատուցելով: Իրական ջերմային շարժիչներն աշխատում են բաց ցիկլերով, այսինքն ընդարձակումից հետո գազն արտանետվում է, իսկ մեքենայի մեջ մտցվում ու սեղմվում է գազի նոր բաժին:
![]()
η մեծությունը կոչվում է շրջանային պրոցեսի օգտակար գործողության գործակից:
Հակադարձ
ցիկլն օգտագործվում
է սառնարանային
մեքենաներում,
պարբերաբար գործող
սարքերում, որոնցում
արտաքին ուժերի
աշխատանքի հաշվին
ջերմաքանակը տեղափոխվում
է ավելի բարձր
ջերմաստիճան ունեցող
մարմնին (նկ. 11.10): Սառնարանային
մեքենան ավելի
ցածր ![]() ջեմաստիճանով
մարմնից պետք է
խլի
ջեմաստիճանով
մարմնից պետք է
խլի ![]() ջերմաքանակ
և ավելի տաք
ջերմաքանակ
և ավելի տաք ![]() ջերմաստիճան
ունեցող մարմնին
հաղորդի
ջերմաստիճան
ունեցող մարմնին
հաղորդի ![]() ջերմաքանակ:
Սառեցման գործակիցը
որոշվում է հետևյալ
առնչությամբ`
ջերմաքանակ:
Սառեցման գործակիցը
որոշվում է հետևյալ
առնչությամբ`
![]()
11.12. ԿԱՌՆՈՅԻ ՑԻԿԼԸ ԵՎ ՆՐԱ ՕԳԳ–Ն
Դիտարկելով ջերմային մեքենաների օգտակար գոծողության գործակցի մասին հարցը՝ Կառնոն ցույց է տվել, որ առավելագույն ՕԳԳ կարելի է ստանալ իրար հաջորդող երկու հավասարակշիռ իզոթերմ և երկու հավասարակշիռ ադիաբատ պրոցեսներից բաղկացած դարձելի շրջանային պրոցեսի դեպքում: Հավասարակշիռ կոչվում է այն պրոցեսը, որի մեջ գազն անցնում է իրար հաջորդող մի շարք հավասարակշռված վիճակներով:
Այդպիսի իրար հարևան երկու վիճակների պարամետրերն միմյանցից տարբերվում են անվերջ փոքր մեծությամբ: Կառնոյի ցիկլով աշխատող իդեալական մեքենայում բացակայում են ջերմահաղորդականության, շփման, և այլ գործընթացների վրա կատարվող կորուստները: Որպես բանող նյութ ընտրվում է իդեալական գազը:
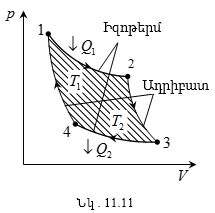
pV դիագրամում
(նկ.11.11) սկզբնական
վիճակը պատկերված
է 1 կետով, որը բնութագրվում
է ![]() պարամետրերով
(
պարամետրերով
(![]() ջեռուցչի ջերմաստիճանն
է): Իզոթերմ ընդարձակման
պրոցեսը պատկերված
է 1 - 2 իզոթերմով, այս
պրոցեսի դեպքում
ջեռուցչից համակարգը
ստանում է
ջեռուցչի ջերմաստիճանն
է): Իզոթերմ ընդարձակման
պրոցեսը պատկերված
է 1 - 2 իզոթերմով, այս
պրոցեսի դեպքում
ջեռուցչից համակարգը
ստանում է ![]() ջերմաքանակ:
Կետ 2-ը բնութագրվում
է
ջերմաքանակ:
Կետ 2-ը բնութագրվում
է ![]() պարամետրերով:
Հետագա ընդարձակումը
կատարվում է ադիաբատորեն
(2 - 3):
պարամետրերով:
Հետագա ընդարձակումը
կատարվում է ադիաբատորեն
(2 - 3):
Կետ 3 - ը բնութագրվում
է ![]() (
(![]() սառնարանի
ջերմաստիճանն
է) պարամետրերով:
3 - 4 իզոթերմ սեղմման
դեպքում համակարգը
սառնարանին տալիս
է
սառնարանի
ջերմաստիճանն
է) պարամետրերով:
3 - 4 իզոթերմ սեղմման
դեպքում համակարգը
սառնարանին տալիս
է ![]() ջերմաքանակ`
անցնելով
ջերմաքանակ`
անցնելով ![]() պարամետրերով
բնութագրվող վիճակի
(կետ 4): Հետագա սեղմումը
տեղի է ունենում
ադիաբատորեն, որն
ուղեկցվում է ջերմաստիճանի
բարձրացումով:
Պրոցեսն ավարտվում
է, երբ համակարգը
վերադառնում է
ելային 1 վիճակին:
Այս ցիկլի կատարման
ընթացքում բանող
մարմինը ջեռուցչից
ստանում է
պարամետրերով
բնութագրվող վիճակի
(կետ 4): Հետագա սեղմումը
տեղի է ունենում
ադիաբատորեն, որն
ուղեկցվում է ջերմաստիճանի
բարձրացումով:
Պրոցեսն ավարտվում
է, երբ համակարգը
վերադառնում է
ելային 1 վիճակին:
Այս ցիկլի կատարման
ընթացքում բանող
մարմինը ջեռուցչից
ստանում է ![]() ջերմաքանակ,
ջերմաքանակի
ջերմաքանակ,
ջերմաքանակի ![]() մասը
տալիս է սառնարանին:
Այդ ջերմաքանակների
մասը
տալիս է սառնարանին:
Այդ ջերմաքանակների
![]() տարբերության
հաշվին կատարվում
է աշխատանք:
տարբերության
հաշվին կատարվում
է աշխատանք:
Դիցուք բանող մարմինը իդեալական գազի 1 մոլն է: Ջերմադինամիկայի առաջին սկզբունքի համաձայն.
![]()
1-2 իզոթերմ պրոցեսի
դեպքում իդեալական
գազի ներքին էներգիան
չի փոփոխվում,
հետևաբար δQ = δA, այսինքն
1 վիճակից 2 վիճակին
անցման դեպքում
![]() ջերմաքանակը
հավասար է իզոթերմ
ընդարձակման աշխատանքին.
ջերմաքանակը
հավասար է իզոթերմ
ընդարձակման աշխատանքին.
![]()
2 - 3 և 4 - 1 ադիաբատ պրոցեսների դեպքում համակարգը ջերմաքանակ չի ստանում՝ δQ = 0, և ընդարձակման աշխատանքը կատարվում է ներքին էներգիայի նվազման հաշվին՝ δA = - dU:
3 - 4 իզոթերմ սեղղման
դեպքում գազի տված
![]() ջերմաքանակը
սառնարանին հավասար
է սեղման
ջերմաքանակը
սառնարանին հավասար
է սեղման ![]() աշխատանքին
աշխատանքին
![]()
Մեկ ցիկլի ընթացքում կատարված օգտակար աշխատանքը հավասար է ջեռուցչից բանող մարմնի ստացած ջերմաքանակի և սառնարանին տրված ջերմաքանակի տարբերությանը.
![]()
Ցույց տանք,
որ ![]() :
Այդ նպատակով գրենք
ադիաբատի հավասարումը
2 - 3 և 4 -1 ադիաբատների
համար, կստանանք
:
Այդ նպատակով գրենք
ադիաբատի հավասարումը
2 - 3 և 4 -1 ադիաբատների
համար, կստանանք
![]()
որտեղից
![]()
Հաշվենք օգտակար գործողության գործակիցը իդեալական ջերմային մեքենայի համար
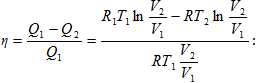
![]()
![]()
Այստեղից պարզ է, որ իդեալական գազով Կառնոյի ցիկլի ՕԳԳ-ն կախված է միայն ջեռուցչի և սառնարանի ջերմաստիճաններից: (9.41) hավասարումից հետևում է.
ա) ջերմային մեքենայի ՕԳԳ-ն մեծացնելու համար անհրաժեշտ է բարձրացնել ջեռուցչի ջերմաստիճանը և իջեցնել սառնարանի ջերմաստիճանը,
բ) ջերմային մեքենայի ՕԳԳ-ն միշտ փոքր է մեկից:
Պարբերաբար
գործող բոլոր ջերմային
մեքենաներից, որոնք
ունեն ջեռուցիչների
![]() և
և ![]() սառնարանների
միատեսակ ջերմաստիճաններ,
ամենամեծ ՕԳԳ-ով
օժտված են դարձելի
մեքենաները: Այդ
դեպքում դարձելի
մեքենաների ՕԳԳ-ները,
որոնք աշխատում
են ջեռուցիչների
և սառնարանների
միատեսակ ջերմաստիճանների
դեպքում, հավասար
են իրար և կախում
չունեն բանող նյութի
տեսակից և որոշվում
են միայն ջեռուցչի
և սառնարանի ջերմաստիճաններով:
Այս պնդումը, կոչվում
է Կառնոյի թեորեմ:
սառնարանների
միատեսակ ջերմաստիճաններ,
ամենամեծ ՕԳԳ-ով
օժտված են դարձելի
մեքենաները: Այդ
դեպքում դարձելի
մեքենաների ՕԳԳ-ները,
որոնք աշխատում
են ջեռուցիչների
և սառնարանների
միատեսակ ջերմաստիճանների
դեպքում, հավասար
են իրար և կախում
չունեն բանող նյութի
տեսակից և որոշվում
են միայն ջեռուցչի
և սառնարանի ջերմաստիճաններով:
Այս պնդումը, կոչվում
է Կառնոյի թեորեմ:
Կառնոյի ցիկլը դարձելի է, քանի որ նրա բոլոր բաղադրիչ մասերը հավասարակշիռ պրոցեսներ են: Դրա համար էլ Կառնոյի ցիկլով աշխատող մեքենան կարող է աշխատել նաև որպես սառնարանային մեքենա: Օրինակ, դիցուք ցիկլի 1 կետում (նկ.11.11) իզոթերմի փոխարեն սկսվում է ադիաբատ ընդարձակում, որի արդյունքում բանող մարմինն անցնում է կետ 4 -ը, այնուհետև կատարվում է իզոթերմ ընդարձակում մինչև կետ 3-ը, դրանից հետո հաջորդում են ադիաբատ և իզոթերմ պրոցեսներն ընդհուպ մինչև 1 կետը: Այդ կերպ հակադարձ ցիկլն ավարտվում է:
Կարելի է ցույց տալ, որ ցանկացած ոչ դարձելի ցիկլի ՕԳԳ-ը միշտ փոքր է Կառնոյի դարձելի ցիկլի ՕԳԳ-ից
![]()
Ընդ որում, հավասարության նշանը համապատասխանում է դարձելի ցիկլին, որտեղից
![]()
Կառնոյի թեորեմը
հիմք ծառայեց ջերմաստիճանների
ջերմադինամիկական
սանդղակի սահմանման
համար. այսինքն
![]() ջերմաստիճանների
համեմատման համար
անհրաժեշտ է իրականացնել
Կառնոի ցիկլ, ուր
մարմիններից մեկն
օգտագործվում
է որպես ջեռուցիչ,
մյուսը` որպես
սառնարան: Ըստ
(11.42) հավասարման մարմինների
ջերմաստիճանների
հարաբերությունը
հավասար է ցիկլում
տված ջերմաքանակի
և ստացած ջերմաքանակի
հարաբերությանը:
Համաձայն Կառնոյի
թեորեմի` բանող
մարմնի քիմիական
բաղադրությունը
ջերմաստիճանների
համեմատման արդյունքի
վրա չի ազդում,
դրա համար էլ այդպիսի
ջերմադինամիկական
սանդղակը կապված
չէ որևէ մարմնի
ջերմաչափական
հատկությունների
հետ:
ջերմաստիճանների
համեմատման համար
անհրաժեշտ է իրականացնել
Կառնոի ցիկլ, ուր
մարմիններից մեկն
օգտագործվում
է որպես ջեռուցիչ,
մյուսը` որպես
սառնարան: Ըստ
(11.42) հավասարման մարմինների
ջերմաստիճանների
հարաբերությունը
հավասար է ցիկլում
տված ջերմաքանակի
և ստացած ջերմաքանակի
հարաբերությանը:
Համաձայն Կառնոյի
թեորեմի` բանող
մարմնի քիմիական
բաղադրությունը
ջերմաստիճանների
համեմատման արդյունքի
վրա չի ազդում,
դրա համար էլ այդպիսի
ջերմադինամիկական
սանդղակը կապված
չէ որևէ մարմնի
ջերմաչափական
հատկությունների
հետ:
11.13. ՋԵՐՄԱԴԻՆԱՄԻԿԱՅԻ ԵՐԿՐՈՐԴ ՍԿԶԲՈՒՆՔԸ
Ջերմադինամիկայի առաջին սկզբունքով քանակական առնչություն է ստեղծվում ջերմաքանակի, աշխատանքի և մարմնի ներքին էներգիայի փոփոխության միջև, սակայն այն չի որոշում պրոցեսների ընթացքի ուղղությունը: Ջերմադինամիկայի առաջին սկզբունքով էներգիայի անցումը ջերմության ձևով միանման հնարավոր է ինչպես ավելի տաք մարմնից ավելի սառը մարմնին, այնպես էլ հակառակը: Ջերմադինամիկայի երկրորդ օրենքով որոշվում է բնության մեջ ընթացող և էներգիայի փոխակերպման հետ կապված պրոցեսների ուղղությունը: Ջերմության փոխակերպումը աշխատանքի հնարավոր է միայն ջեռուցչի և սառնարանի առկայության դեպքում: Բոլոր ջերմային մեքենաներում օգտակար կերպով օգտագործվում է միայն ջեռուցչից սառնարանին տրված էներգիայի մի մասը: Այլ կերպ ասած, ոչ մի ջերմային շարժիչ չի կարող տալ մեկի հավասար ՕԳԳ:
Իդեալական ջերմային մեքենայի ՕԳԳ-ն որոշվում է միայն ջեռուցչի և սառնարանի ջերմաստիճաններով (Ս.Կառնո):
Բնության մեջ անհնար է որևէ պրոցես, որի միակ արդյունքը լինի ջերմության լրիվ փոխակերպումը աշխատանքի (Մ.Պլանկ):
Ջերմությունը չի կարող ինքնաբերաբար փոխանցվել ավելի ցածր ջերմաստիճանով մարմնից ավելի բարձր ջերմաստճանով մարմնին (Ռ.Կլաուզիուս): Երկրորդ օրենքով բացառվում է որևէ աղբյուրի ներքին էներգիայի պաշարների օգտագործման հնարավորություն առանց` նրա ավելի ցածր ջերմաստիճանային մակարդակի փոխադրության, այսինքն՝ առանց սառնարանի: Օրինակ, օվկիանոսների ներքին էներգիայի անսահման պաշարները գործնականորեն հնարավոր չէ լրիվ օգտագործել: Հենց որ օվկիանոսի ջերմաստիճանն ավելի ցածր դառնա շրջապատող միջավայրի ջերմաստիճանից, նրա ջերմաքանակի օգտագործումը կհանգեցնի այնպիսի մի պրոցեսի, որի մեջ պետք կլինի իրագործել ջերմության անցումը սառը մարմնից ավելի տաք մարմնին, իսկ այդպիսի պրոցեսն ինքնաբերաբար ընթանալ չի կարող: Այսպիսով, ջերմադինամիկայի երկրորդ սկզբունքը հաստատում է երկրորդ կարգի հավերժական շարժիչի կառուցման անհնարինությունը, այսինքն մի շարժիչի, որն աշխատում է մի այլ մարմնի սառեցման հաշվին:
11.14. ԷՆՏՐՈՊԻԱՆ ԵՎ ՆՐԱ ՀԱՏԿՈւԹՅՈՒՆՆԵՐԸ
Էնտրոպիայի հասկացությունը մտցվել է 1865թ. Ռ. Կլաուզիուսի կողմից: Այդ հասկացության ֆիզիկական բովանդակությունը պարզելու համար մըտցվում է բերված ջերմության գաղափարը:
Այն մեծությունը, որը հավասար է իզոթերմ պրոցեսի ժամանակ մարմնի ստացած ջերմաքանակի և այն ջերմաստիճանի հարաբերությանը, որի դեպքում կատարվում է ջերմափոխանցումը, կոչվում է բերված ջերմություն (Q/T):
(11.42) արտահայտության
մեջ ![]() ը
ջեռուցչի կողմից
մարմնին տված ջերմաքանակն
է,
ը
ջեռուցչի կողմից
մարմնին տված ջերմաքանակն
է, ![]() բանող
մարմնից սառնարանի
ստացած ջերմաքանակն
է: Եթե Q-ի տակ հասկանանք
հանրահաշվական
մեծություն, ապա
կարելի է համարել,
որ բանող մարմինը
սառնարանից ստանում
է (-Q) ջերմաքանակ:
Այդ դեպքում (11.42)
-ը կընդունի հետևյալ
տեսքը.
բանող
մարմնից սառնարանի
ստացած ջերմաքանակն
է: Եթե Q-ի տակ հասկանանք
հանրահաշվական
մեծություն, ապա
կարելի է համարել,
որ բանող մարմինը
սառնարանից ստանում
է (-Q) ջերմաքանակ:
Այդ դեպքում (11.42)
-ը կընդունի հետևյալ
տեսքը.
![]()
կամ ընդհանուր տեսքով՝
![]()
այսինքն՝ Կառնոյի դարձելի ցիկլի համար բերված ջերմությունների հանրահաշվական գումարը հավասար է զրոյի: Ընդհանուր դեպքում համակարգի վիճակի ցանկացած փոփոխություն կարելի է ներկայացնել որպես անսահման մեծ թվով անսահման փոքր փոփոխությունների արդյունք: Յուրաքանչյուր այդպիսի անսահման փոքր փոփոխության դեպքում համակարգը կամ կլանում, կամ անջատում է անսահման փոքր δQ ջերմաքանակ (եթե պրոցեսն ադիաբատ չէ): Եթե համակարգը կլանում է ջերմաքանակ, ապա δQ > 0, իսկ եթե անջատում է, ապա δQ < 0: (11.44) արտահայտությունն ամբողջ ցիկլի համար ավելի խիստ կարելի է գրել ինտեգրալի միջոցով.
![]()
Քանի որ փակ կոնտուրով ինտեգրալը հավասար է զրոյի, ապա δQ/T ինտեգրալատակ արտահայտությունն ինչ-որ ֆունկցիայի լրիվ դիֆերենցիալն է, որը կախված չէ այն ճանապարհից, որով համակարգը հասել է այդ վիճակին: Վիճակի ֆունկցիան, որի դիֆերենցիալը δQ/T- ն է, կոչվում է էնտրոպիա և նշանակվում է S-ով: Կամ կարելի է ասել, որ ջերմադինամիկական փակ համակարգում ինքնաբերաբար ընթացող պրոցեսների ուղղությունը բնութագրող ֆունկցիան անվանում են էնտրոպիա.
![]()
Էնտրոպիայի միավորն է ջոուլը բաժանած Կելվինի կամ (Ջ/Կ): Մարմնի յուրաքանչյուր վիճակին համապատասխանում է էնտրոպիայի մի որոշակի արժեք, ուրեմն էնտրոպիան վիճակի միարժեք ֆունկցիա է: Դիցուք մարմինը դարձելի ճանապարհով A վիճակից անցնում է B վիճակին, այդ դեպքում
![]()
Էնտրոպիան ադիտիվ մեծություն է: Դա նշանակում է, որ համակարգի էնտրոպիան հավասար է համակարգի մեջ մտնող մարմինների էնտրոպիաների գումարին:
Շրջանային դարձելի պրոցեսի դեպքում էնտրոպիայի ΔS փոփոխությունը հավասար է զրոյի: Ոչ դարձելի պրոցեսի համար
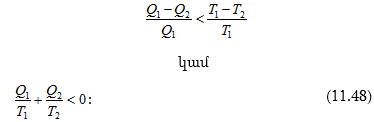
Դարձելի և ոչ դարձելի պրոցեսների համար այս առնչությունը գրվում է Կլաուզիուսի անհավասարության տեսքով.
![]()
Կարելի է ենթադրել, որ n մարմինների հետ համակարգի ջերմափոխանակության դեպքում պետք է բավարարի (11.44)-ին համանման պայման.
![]()
Այսպիսով, ցանկացած ցիկլի համար բերված ջերմությունների գումարը չի կարող զրոյից մեծ լինել: (11.50)-ի ավելի խիստ արտահայտությունը պետք է գրվի հետևյալ տեսքով
![]()
Էնտրոպիայի
փոփոխությունը
տեղի է ունեում
միայն բանող մարմնի
և ջերմության աղբյուրի
միջև ջերմափոխանակության
դեպքում: Եթե մարմինն
աղբյուրից (ջեռուցչից
կամ սառնարանից)
ստացել է δQ ջերմաքանակ,
ուրեմն նրա էնտրոպիան
փոփոխվել է ![]() չափով,
որտեղ T-ն մարմնի
ջերմաստիճանն
է: Այս դեպքում
ջերմության աղբյուրը
տվել է (կորցրել
է) նույնպիսի
չափով,
որտեղ T-ն մարմնի
ջերմաստիճանն
է: Այս դեպքում
ջերմության աղբյուրը
տվել է (կորցրել
է) նույնպիսի ![]() ջերմաքանակ:
Ակներև է, որ
ջերմաքանակ:
Ակներև է, որ ![]() այս
դեպքում աղբյուրի
էնտոպիան փոփոխվել
է
այս
դեպքում աղբյուրի
էնտոպիան փոփոխվել
է ![]() որտեղ
T-ն աղբյուրի ջերմաստիճանն
է: Քանի որ պրոցեսը
դարձելի է, ուրեմն
պետք է պահպանվի
հետևյալ հավասարությունը.
որտեղ
T-ն աղբյուրի ջերմաստիճանն
է: Քանի որ պրոցեսը
դարձելի է, ուրեմն
պետք է պահպանվի
հետևյալ հավասարությունը.
![]()
Փակ, այսինքն`
այլ մարմինների
հետ ջերմաքանակ
չփոխանակող (ΔQ
= 0) համակարգի էնտրոպիայի
փոփոխությունը
հավասար է զրոյի.
![]() Հետևաբար,
ցանկացած դարձելի
պրոցեսի դեպքում
փակ համակարգի
ներսում էնտրոպիան
մնում է անփոփոխ
Հետևաբար,
ցանկացած դարձելի
պրոցեսի դեպքում
փակ համակարգի
ներսում էնտրոպիան
մնում է անփոփոխ
![]()
Ոչ դարձելի պրոցեսի դեպքում փակ համակարգում
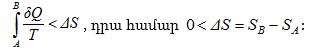
Այսպիսով,
![]()
Ընդհանրացնելով (9.52) և (9.53)-ը` կարելի է պնդել, որ փակ համակարգի էնտրոպիան իր փոփոխության ժամանակ չի կարող փոքրանալ.
![]()
Ինչպես ցույց են տալիս տեսությունն ու փորձը, փակ համակարգերում ոչ դարձելի պրոցեսների համար էնտրոպիան միշտ աճում է: Փակ համակարգերի էներգիան պահպանվում է, այդ պատճառով փակ համակարգում տեղի ունեցող ցանկացած փոփոխության դեպքում՝ պրոցեսի սկզբում ու վերջում էներգիան նույնն է, և հնարավոր չէ էներգիայի արժեքով սկզբնական վիճակը տարբերել վերջնականից: Էնտրոպիայի արժեքով կարելի է դատել, թե պրոցեսի որ ուղղությունն է հնարավոր (այսինքն՝ որ վիճակն է սկզբնականը և որը` վերջնականը): Դա պայմանավորված է նրանով, որ բնականոն ընթացող պրոցեսներում էնտրոպիան մեծանում է: Տրված համակարգի համար էնտոպիայի աճը հնարավոր է մինչև որոշակի արժեք, որը համապատասխանում է հավասարակշռության վիճակին: Հավասարակշռության վիճակում էնտրոպիայի արժեքն առավելագույնն է: Այսպիսով, փակ համակարգում չեն կարող ընթանալ այնպիսի պրոցեսներ, որոնք հանգեցնում են համակարգի էնտրոպիայի փոքրացմանը:
Եթե համակարգը կատարում է հավասարակշիռ անցում վիճակից վիճակին, ապա համաձայն (11.46)-ի, էնտրոպիայի փոփոխությունը`

որտեղ ենթաինտեգրալ արտահայտությունը և ինտեգրման սահմանները որոշվում են ուսումնասիրվող պրոցեսը բնութագրող մեծությունների միջոցով: Էնտրոպիան որոշվում է մինչև ադիտիվ հաստատունի ճշտությամբ: Հաստատունի արժեքը, որով որոշվում է էնտրոպիան, դեր չի խաղում, քանի որ ֆիզիկական իմաստ ունի, ոչ թե ինքը էնտրոպիան, այլ էնտրոպիայի տարբերությունը: Ելնելով (11.55) արտահայտությունից` գտնենք էնտրոպիայի փոփոխությունը իդեալական գազի պրոցեսներում: Քանի որ
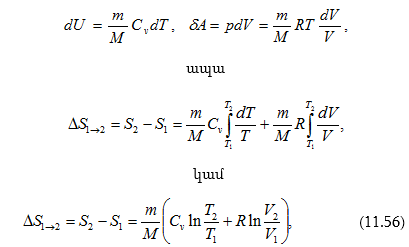
այսինքն, իդեալական
գազի էնտրոպիայի
փոփոխությունը
1 վիճակից 2 վիճակին
անցման դեպքում
կախված չէ ![]() պրոցեսի
անցման տեսակից:
Քանի որ ադիաբատ
պրոցեսի համար
δQ = 0 և, հետևաբար
S= const, այսինքն` ադիաբատ
դարձելի պրոցեսն
ընթանում է հաստատուն
էնտրոպիայի դեպքում:
(11.56) բանաձևից հետևում
է, որ իզոթերմ պրոցեսի
դեպքում`
պրոցեսի
անցման տեսակից:
Քանի որ ադիաբատ
պրոցեսի համար
δQ = 0 և, հետևաբար
S= const, այսինքն` ադիաբատ
դարձելի պրոցեսն
ընթանում է հաստատուն
էնտրոպիայի դեպքում:
(11.56) բանաձևից հետևում
է, որ իզոթերմ պրոցեսի
դեպքում`
![]()
իզոխոր պրոցեսի դեպքում՝
![]()
11.15. ՋԵՐՄԱԴԻՆԱՄԻԿԱՅԻ ԵՐԿՐՈՐԴ ՕՐԵՆՔԻ
ՎԻՃԱԿԱԳՐԱԿԱՆ ՄԵԿՆԱԲԱՆՈՒԹՅՈՒՆԸ
Ջերմադինամիկայի կողմից ուսումնասիրվող պրոցեսներն ու հասկացությունները քննարկենք վիճակագրական ֆիզիկայի տեսանկյունից: Ինչ-պես հայտնի է, ջերմադինամիկական (p,V,T) պարամետրերով որոշվող համակարգի վիճակը կոչվում է մակրովիճակ, որն էլ դիտվում է փորձով: Վիճակագրական ֆիզիկայում համակարգի տվյալ մակրովիճակն իրականացնող միկրովիճակների թիվը կոչվում է W ջերմադինամիկական հավանականություն:
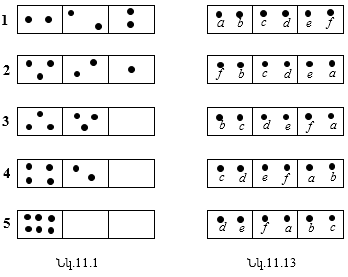
Պարզաբանենք
օրինակով: Դիցուք
անոթում գտնվում
են գազի վեց մոլեկուլներ՝
a,b,c,d,e,f: Մտովի, անոթը
բաժանենք երեք
հավասար մասերի:
Անկանոն կերպով
խառնվելով` մոլեկուլներն
առաջացնում են
մակրոբաշխումներ:
Դրանցից մի քանիսը
ցույց են տրված
նկ.11.12-ում: Ցանկացած
մակրոբաշխում,
օրինակ 1-ը, կարող
է իրագործվել մի
շարք միկրոբաշխումներով:
1 մակրոբաշխումը
տվող մի շարք միկրոբաշխումներ
տըրված են նկ.11.13-ում:
Տեսական ֆիզիկայում
ապացուցվում է,
որ ջերմադինամիկական
հավանականությունը,
այսինքն N մասնիկների
միկրոբաշխումներն
n վիճակներով (վեց
մասնիկ անոթի երեք
մասերում) որոշվում
է![]() բանաձևով,
որտեղ
բանաձևով,
որտեղ ![]() մասնիկների
թիվն է առաջին
վիճակում (անոթի
առաջին մասում),
մասնիկների
թիվն է առաջին
վիճակում (անոթի
առաջին մասում),
![]() մասնիկների
թիվը երկրորդ վիճակում
(անոթի երկրորդ
մասում),
մասնիկների
թիվը երկրորդ վիճակում
(անոթի երկրորդ
մասում), ![]() մասնիկների
թիվը երրորդ վիճակում
(անոթի երրորդ
մասում):
մասնիկների
թիվը երրորդ վիճակում
(անոթի երրորդ
մասում):
Հաշվենք նկ.11.12 - ում բերված 1,2,3,4,5 մակրովիճակների ջերմադինամիկական հավանականությունները:

Հավասարաչափ բաշխման ամենամեծ ջերմադինամիկական հավանականությունը կարող է իրագործվել եղանակների ամենամեծ թվով:
Էնտրոպիայի կապը ջերմադինամիկական հավանականության հետ սահմանել է Բոլցմանը: Էնտրոպիան ուղիղ համեմատական է ջերմադինամիկական հավանականության լոգարիթմին.
![]()
որտեղ k-ն Բոլցմանի հաստատունն է: Էնտրոպիայի հասկացության վիճակագրական իմաստն այն է, որ մեկուսացած համակարգի էնտրոպիայի մեծացումը կախված է այդ համակարգի ավելի քիչ հավանական վիճակից ավելի մեծ հավանական վիճակի անցման հետ:
Յուրաքանչյուր մարմին, որպես կանոն, բացարձակ զրո ջերմաստիճանում գտնվում է մի վիճակում, որի ջերմադինամիկական հավանականությունը հավասար է մեկի: Համաձայն (11.57) բանաձևի` այդ դեպքում էնտրոպիան հավասար է զրոյի, որից էլ` ցանկացած մարմնի էնտրոպիան ձըգտում է զրոյի, եթե ջերմաստիճանը ձգտում է զրոյի.
![]()
Այս պնդումն անվանում են Ներնստի թեորեմ կամ ջերմադինամիկայի երրորդ սկզբունք:
Ջերմադինամիկայի երկրորդ օրենքի վիճակագրական բնութագիրը բացահայտող ձևակերպումներից մեկը Բոլցմանի ձևակերպումն է. բնության մեջ բոլոր պրոցեսներն ընթանում են վիճակի հավանականության մեծացումն առաջացնող ուղղությամբ: Օրինակ, գազերում դիֆուզիայի պրոցեսն ընթանում է այն պատճառով, որ մոլեկուլների հավասարաչափ բաշխումն ամբողջ ծավալով վիճակագրորեն ավելի հավանական կլինի: Ջերմադինամիկայի երկրորդ օրենքը շատ թվով մասնիկներից բաղկացած փակ համակարգերի համար իրագործվող վիճակագրական օրենք է: Երկրորդ օրենքը կիրառելի չէ անվերջ թվով մասնիկներից բաղկացած համակարգերի համար, քանի որ այդպիսի համակարգերի համար բոլոր վիճակները հավասարահավանական են:
Խնդիր 1: Ջերմային
մեքենայի ջեռուցչի
ջերմաստիճանը
![]() է, սառնարանի
ջերմաստիճանը`
է, սառնարանի
ջերմաստիճանը`
![]() Որոշել
ջերմային մեքենայի
օ.գ.գ-ը և լրիվ հզորությունը,
եթե ջեռուցիչը
յուրաքանչյուր
վայրկյանում նրան
տալիս է 1675Ջ ջերմաքանակ:
Որոշել
ջերմային մեքենայի
օ.գ.գ-ը և լրիվ հզորությունը,
եթե ջեռուցիչը
յուրաքանչյուր
վայրկյանում նրան
տալիս է 1675Ջ ջերմաքանակ:
Լուծում: Ջերմային մեքենայի օ.գ.գ-ը որոշվում է` հետևյալ բանաձևով:
![]()
Մյուս կողմից
![]()
(1) և (2) արտահայտություններից գտնում ենք`
![]()
Մեքենայի լրիվ հզորությունը`
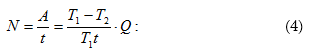
Տեղադրելով
(1)-ի և (4)-ի մեջ մտնող
մեծությունների
թվային արժեքները`
ստանում ենք` ![]()
Խնդիր 2: Գտնել
էնտրոպիայի փոփոխությունը`
![]() ջերմաստիճան
ունեցող m = 0,01կգ սառույցը
ջերմաստիճան
ունեցող m = 0,01կգ սառույցը
![]() ջերմաստիճանի
գոլորշու փոխարկելիս:
ջերմաստիճանի
գոլորշու փոխարկելիս:
Լուծում: Էնտրոպիայի փոփոխությունը որոշվում է

բանաձևով,
որտեղ ![]() էնտրոպիայի
արժեքներն են համապատասխանաբար
առաջին և երկրորդ
վիճակներում: Էնտրոպիայի
լրիվ փոփոխությունը
տվյալ դեպքում
ստացվում է որպես
առանձին պրոցեսների
ժամանակ նրա փոփոխությունների
գումար:
էնտրոպիայի
արժեքներն են համապատասխանաբար
առաջին և երկրորդ
վիճակներում: Էնտրոպիայի
լրիվ փոփոխությունը
տվյալ դեպքում
ստացվում է որպես
առանձին պրոցեսների
ժամանակ նրա փոփոխությունների
գումար:
1) m զանգված
ունեցող սառույցի
տաքացումը ![]() ջերմաստիճանից
մինչև
ջերմաստիճանից
մինչև ![]() ջերմաստիճանը:
Քանի որ այդ դեպքում
ջերմաստիճանը:
Քանի որ այդ դեպքում
![]() , որտեղ
, որտեղ
![]() սառույցի
տեսակարար ջերմունակությունն
է, ապա (1) բանաձևից
գտնում ենք.
սառույցի
տեսակարար ջերմունակությունն
է, ապա (1) բանաձևից
գտնում ենք.
![]()
2) m զանգված
ունեցող սառույցի
հալումը ![]() ջերմաստիճանում:
Քանի որ
ջերմաստիճանում:
Քանի որ ![]() որտեղ
λ-ն հալման տեսակարար
ջերմությունն
է, ապա, համաձայն
(1) բանաձևի՝
որտեղ
λ-ն հալման տեսակարար
ջերմությունն
է, ապա, համաձայն
(1) բանաձևի՝
![]()
3) m զանգված
ունեցող ջրի տաքացումը![]() մինչև
մինչև
![]()
![]()
![]()
որտեղ ![]() ջրի
տեսակարար ջերմունակությունն
է:
ջրի
տեսակարար ջերմունակությունն
է:
4) m զանգվածով
ջրի գոլորշիացումը
![]() ջերմաստիճանում
ջերմաստիճանում
![]()
որտեղ r -ը գոլորշիացման տեսակարար ջերմությունն է:
Էնտրոպիայի լրիվ փոփոխությունը`
![]()
![]()
Տեղադրելով այս տվյալները վերը ստացված արտահայտության մեջ` կստանանք`
![]()
Խնդիր 3. v =2 մոլ երկատոմ իդեալական գազի տաքացման դեպքում նրա ջերմաստիճանը բարձրացավ n =2 անգամ: Որոշել էնտրոպիայի փոփոխությունը, եթե տաքացումը տեղի է ունեցել. 1) իզոխոր, 2) իզոբար:
Լուծում: 1) Իզոխոր պրոցեսի դեպքում`
![]()
որտեղ ![]() մոլային
ջերմունակությունն
է հաստատուն ծավալի
դեպքում, i-ն մոլեկուլի
ազատության աստիճանների
թիվն է, R-ը ունիվերսալ
գազային հաստատունը:
Այս դեպքում էնտրոպիայի
փոփոխությունը`
մոլային
ջերմունակությունն
է հաստատուն ծավալի
դեպքում, i-ն մոլեկուլի
ազատության աստիճանների
թիվն է, R-ը ունիվերսալ
գազային հաստատունը:
Այս դեպքում էնտրոպիայի
փոփոխությունը`
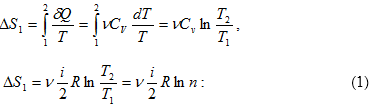
2) Իզոբար պրոցեսի դեպքում`
![]()
որտեղ ![]() մոլային
ջերմունակությունն
է հաստատուն ճնշման
դեպքում:
մոլային
ջերմունակությունն
է հաստատուն ճնշման
դեպքում:
Այս դեպքում էնտրոպիայի փոփոխությունը՝
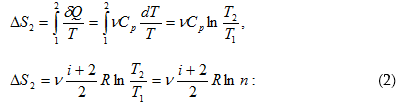
Տեղադրելով (1)-ի և (2)-ի մեջ մտնող մեծությունների թվային արժեքները կստանանք.
![]()
ԳԼՈՒԽ 12. ԻՐԱԿԱՆ ԳԱԶԵՐ, ՀԵՂՈՒԿՆԵՐ ԵՎ ՊԻՆԴ ՄԱՐՄԻՆՆԵՐ
12.1. ՄԻՋՄՈԼԵԿՈՒԼԱՅԻՆ ՈՒԺԵՐ
Միջմոլեկուլային փոխազդեցության ուժերի առկայությունն ու մոլեկուլների վերջավոր չափերը իրական և իդեալական գազերի հիմնական տարբերություններն են: Այդ տարբերություններն անընդհատ մեծանում են ճընշման մեծացմանը զուգընթաց: Ցանկացած գազի մոլեկուլների միջև գործող միջմոլեկուլային փոխազդեցության ուժերն էլեկտրամագնիսական և քվանտային բնույթ ունեն: 10-9-10-10 մետր կարգի հեռավորության վրա ի հայտ եկող փոխազդեցության ուժերը կոչվում են վան-դեր-վաալսյան:
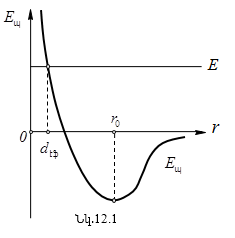
Մոլեկուլն իր էլեկտրական հատկություններով մոտավորապես կարելի է դիտարկել որպես էլեկտրական երկբևեռ, եթե այն միատոմ է, կամ քառաբևեռ, եթե մոլեկուլը բազմատոմ է: Երկբևեռի դաշտի լարվածությունը փոփոխվում է հեռավորության երրորդ աստիճանին հակադարձ համեմատական: Քառաբևեռի դաշտի լարվածությունը, կախված հեռավորությունից, փոփոխվում է ավելի արագ, քան երկբևեռինը: 10-9-10-10մ կարգի հեռավորության վրա մոտեցող մոլեկուլների միջև գործում են ինչպես տարանուն լիցքերի ձգողական ուժերը, այնպես էլ նույնանուն լիցքերի վանողական ուժերը: Միջմոլեկուլային փոխազդեցության ուժերը կարճազդու են: Ձգողական ուժերն ընդունված է համարել բացասական, իսկ վանողական ուժերը՝ դրական: Սրան համապատասխան իրար ձգող լիցքերի պոտենցիալ էներգիան համարում են բացասական, իսկ իրար վանող լիցքերի պոտենցիալ էներգիան՝ դրական:
Մոլեկուլների միջև, հեռավորությունից կախված, վանողական ուժերը փոփոխվում են ավելի արագ, քան ձգողական ուժերը: Հետևաբար, մոտեցող մոլեկուլների դրական պոտենցիալ էներգիան հեռավորության հետ փոփոխվում է ավելի արագ, քան ձգողական բացասական էներգիան:
Ձգողական
և վանողական ուժերի
միաժամանակյա
ազդեցությունը
ցույց է տալիս,
որ մոլեկուլի վրա
ազդում է միջմոլեկուլային
ուժերի փոխազդեցության
համազորը, այսինքն`
համակարգի լրիվ
պոտենցիալ էներգիան
հավասար է մոլեկուլների
դրական վանողական
էներգիայի և ձգողական
բացասական էներգիայի
գումարին: Փոխազդեցության
լրիվ էներգիայի
կախումը հեռավորությունից
գրաֆիկորեն ներկայացված
է նկ.10.1-ում: Ինչպես
երևում է նկարից,
փոխազդեցության
լրիվ էներգիան
ունի «պոտենցիալ
փոսի» տեսք: Համակարգի
կայուն վիճակը
համապատասխանում
է պոտենցիալ էներգիայի
նվազագույն պաշարին,
այսինքն` ![]() դեպքում:
Մոլեկուլների
կենտրոնների միջև
դեպքում:
Մոլեկուլների
կենտրոնների միջև
![]() հեռավորության
վրա ձգողական և
վանողական ուժերն
իրար հավասար են:
Մոլեկուլների
հետագա մոտենալու
դեպքում վանողական
ուժերը շատ արագ
մեծանում են, որը
համապատասխանում
է կորի անցմանը
դրական տիրույթ
(նկ.12.1):
հեռավորության
վրա ձգողական և
վանողական ուժերն
իրար հավասար են:
Մոլեկուլների
հետագա մոտենալու
դեպքում վանողական
ուժերը շատ արագ
մեծանում են, որը
համապատասխանում
է կորի անցմանը
դրական տիրույթ
(նկ.12.1): ![]() փոքր
հեռավորության
վրա միջմոլեկուլային
փոխազդեցությունն
ունի քվանտային
փոխանակային բնույթ,
որը հանգեցնում
է կամ ուժեղ ձգողական
(քիմիական կապ),
կամ վանողական
զգալի ուժերի ծագմանը:
Մոլեկուլներն
ամենամեծ մերձեցման
հասնում են
փոքր
հեռավորության
վրա միջմոլեկուլային
փոխազդեցությունն
ունի քվանտային
փոխանակային բնույթ,
որը հանգեցնում
է կամ ուժեղ ձգողական
(քիմիական կապ),
կամ վանողական
զգալի ուժերի ծագմանը:
Մոլեկուլներն
ամենամեծ մերձեցման
հասնում են ![]() հեռավորության
վրա, որի դեպքում
մոլեկուլների
ամբողջ կինետիկ
էներգիան ծախսվում
է վանողական ուժերի
դեմ աշխատանք կատարելու
վրա: Այս դեպքում
պոտենցիալ էներգիան
հավասար է երկու
մոլեկուլներից
կազմված համակարգի
լրիվ էներգիային
(Eլրիվ = E): E գիծն
(նկ.12.1) արտահայտում
է ամբողջ համակարգի
լրիվ էներգիան,
այսինքն` մոլեկուլի
պոտենցիալ և կինետիկ
էներգիաների գումարը:
հեռավորության
վրա, որի դեպքում
մոլեկուլների
ամբողջ կինետիկ
էներգիան ծախսվում
է վանողական ուժերի
դեմ աշխատանք կատարելու
վրա: Այս դեպքում
պոտենցիալ էներգիան
հավասար է երկու
մոլեկուլներից
կազմված համակարգի
լրիվ էներգիային
(Eլրիվ = E): E գիծն
(նկ.12.1) արտահայտում
է ամբողջ համակարգի
լրիվ էներգիան,
այսինքն` մոլեկուլի
պոտենցիալ և կինետիկ
էներգիաների գումարը:
![]() հեռավորությունը
մոլեկուլի էֆեկտիվ
տրամագիծն է, այսինքն`
որոշում է այն
տիրույթի գծային
չափերը, որի մեջ
մյուս մոլեկուլը
թափանցել չի կարող:
հեռավորությունը
մոլեկուլի էֆեկտիվ
տրամագիծն է, այսինքն`
որոշում է այն
տիրույթի գծային
չափերը, որի մեջ
մյուս մոլեկուլը
թափանցել չի կարող:
12.2. ՎԱՆ-ԴԵՐ-ՎԱԱԼՍԻ ՀԱՎԱՍԱՐՈՒՄԸ: ԻՐԱԿԱՆ ԳԱԶԵՐԻ
ՎԻՃԱԿԻ ՀԱՎԱՍԱՐՈՒՄԸ
Գազերի մոլեկուլային-կինետիկ մոդելում գազը պատկերվում է` բաղկացած առաձգական գնդերին նմանեցվող անկանոն շարժվող մոլեկուլներից: Մոլեկուլների միջև ուժերը գործում են միայն հարվածի պահին, ընդ որում դրանք վանման առաձգական ուժեր են: Մոլեկուլների չափերը համարվում են մոլեկուլների միջև եղած հեռավորության համեմատությամբ այնքան փոքր, որ դրանց չափերը կարելի է անտեսել: Այս մոդելը համապատասխանում է իդեալական գազին, այսինքն` այնպիսի գազին, որը ճշտորեն ենթարկվում է Բոյլ-Մարիոտի և Գեյ-Լյուսակի օրենքներին: Սակայն իրական գազերը, ինչպես գիտենք, այդ օրենքներին ենթարկվում են միայն որոշ մոտավորությամբ: Մեծ ճնշումների դեպքում բոլոր գազերը բացահայտորեն շեղվում են Բոյլ-Մարիոտի օրենքից: Համարելով մոլեկուլերը գնդիկներ` մենք պետք է դրանց շառավիղներն ընունենք 10-10մ կարգի մեծություններ: Այստեղից մեկ մոլեկուլի ծավալը կլինի`
![]()
Նորմալ պայմաններում
գազի 1մ3-ում գտնվում
են ![]() թվով
մոլեկուլներ, որտեղից
բոլոր մոլեկուլների
սեփական ծավալը
կլինի
թվով
մոլեկուլներ, որտեղից
բոլոր մոլեկուլների
սեփական ծավալը
կլինի
![]() այսինքն`
1 մթնոլորտ ճնշման
և 00C ջերմաստիճանի
դեպքում գազի ծավալի
չնչին մասն է բաժին
ընկնում մոլեկուլների
սեփական ծավալին:
5000մթ ճնշման դեպքում,
ըստ Բոյլ-Մարիոտի
օրենքի, սկզբնական
1մ3 ծավալը պետք
է փոքրանա մինչև
այսինքն`
1 մթնոլորտ ճնշման
և 00C ջերմաստիճանի
դեպքում գազի ծավալի
չնչին մասն է բաժին
ընկնում մոլեկուլների
սեփական ծավալին:
5000մթ ճնշման դեպքում,
ըստ Բոյլ-Մարիոտի
օրենքի, սկզբնական
1մ3 ծավալը պետք
է փոքրանա մինչև
![]() այդ
դեպքում գազի գրաված
ծավալի կեսը բաժին
է ընկնում մոլեկուլների
սեփական ծավալին:
Ակնհայտ է,որ այս
դեպքում գազի հիշատակված
մոդելը պիտանի
չէ, և իրական գազերի
հատկությունների
շեղումը Բոյլ-Մարիոտի
օրենքից հասկանալի
է: Այսպիսով, իդեալական
գազերի հատկություններից
գազերի շեղման
պատճառը նախ` պետք
է պայմանավորված
լինի մոլեկուլների
սեփական չափերի
գոյությամբ, երկրորդ`
նրանով, որ մոլեկուլների
միջև փոխազդեցության
ուժերի բնույթը
շատ ավելի բարդ
է, քան առաձգական
գնդերի միջև: Այս
երկու պատճառն
էլ հաշվի է առնված
Վան-դեր-Վաալսի
կողմից:
այդ
դեպքում գազի գրաված
ծավալի կեսը բաժին
է ընկնում մոլեկուլների
սեփական ծավալին:
Ակնհայտ է,որ այս
դեպքում գազի հիշատակված
մոդելը պիտանի
չէ, և իրական գազերի
հատկությունների
շեղումը Բոյլ-Մարիոտի
օրենքից հասկանալի
է: Այսպիսով, իդեալական
գազերի հատկություններից
գազերի շեղման
պատճառը նախ` պետք
է պայմանավորված
լինի մոլեկուլների
սեփական չափերի
գոյությամբ, երկրորդ`
նրանով, որ մոլեկուլների
միջև փոխազդեցության
ուժերի բնույթը
շատ ավելի բարդ
է, քան առաձգական
գնդերի միջև: Այս
երկու պատճառն
էլ հաշվի է առնված
Վան-դեր-Վաալսի
կողմից:
Առաջին պատճառը` մոլեկուլի սեփական չափերը, արտահայտվում է նրանով, որ գազը պարունակող անոթում մոլեկուլները շարժվում են ոչ այնպես ազատ, ինչպես կշարժվեին, եթե դրանք լինեին կետային: Ազատ շարժման համար մոլեկուլներին տրամադրված ծավալը փոքր է անոթի երկրաչափական V ծավալից ինչ-որ b մեծությամբ: Մոլեկուլների սեփական ծավալի հետ կապված այդ b մեծությունը կարելի է գազի տվյալ քանակի համար ընդունել հաստատուն: Այդ պատճառով էլ վիճակի հավասարման մեջ V ծավալը պետք է փոխարինել V-b մեծութամբ:
Իդեալական գազի մեկ մոլի համար տեղի ունի հետևյալ հավասարումը`
![]()
Հաշվի առնելով
մոլեկուլների
սեփական ծավալի
դերը` պետք է մոլի
ծավալը` ![]() փոխարինել
փոխարինել
![]() մեծությամբ`
մեծությամբ`
![]()
(12.1) հավասարումից
հետևում է, որ ![]() դեպքում
գազի ծավալը`
դեպքում
գազի ծավալը` ![]() այսինքն`
գազն անսահման
սեղմելու դեպքում
նրա ծավալը կձգտի
զրոյի, որն անհնար
է: Գազի սեղմումը
տեղի է ունենում
ի հաշիվ միջմոլեկուլային
ազատ տարածության,
այստեղից` շատ
մեծ ճնշումների
դեպքում մոլեկուլները
կդասավորվեն բավականին
խիտ, որից հետո
գազի սեղմելիությունը
պետք է լինի չափազանց
փոքր:
այսինքն`
գազն անսահման
սեղմելու դեպքում
նրա ծավալը կձգտի
զրոյի, որն անհնար
է: Գազի սեղմումը
տեղի է ունենում
ի հաշիվ միջմոլեկուլային
ազատ տարածության,
այստեղից` շատ
մեծ ճնշումների
դեպքում մոլեկուլները
կդասավորվեն բավականին
խիտ, որից հետո
գազի սեղմելիությունը
պետք է լինի չափազանց
փոքր:
Ըստ (12. 2 ) բանաձևի
![]() դեպքում
գազի ծավալը`
դեպքում
գազի ծավալը` ![]() այսպիսով,
b մեծությունն
այն ծավալն է, որին
ձգտում է մոլի
այսպիսով,
b մեծությունն
այն ծավալն է, որին
ձգտում է մոլի
![]() ծավալը
շատ մեծ ճնշումների
դեպքում: Այն հավասար
է մեկ մոլում պարունակվող
բոլոր մոլեկուլների
զբաղեցրած ծավալին`
խիտ դասավորման
դեպքում:
ծավալը
շատ մեծ ճնշումների
դեպքում: Այն հավասար
է մեկ մոլում պարունակվող
բոլոր մոլեկուլների
զբաղեցրած ծավալին`
խիտ դասավորման
դեպքում:
Երկրորդ պատճառը`
մոլեկուլների
միջև փոխազդեցության
ուժերի առկայությունը
հանգեցնում է այն
բանին, որ միմյանցից
որոշ հեռավորության
վրա գտնվող մոլեկուլները
փոխադարձաբար
ձգվում են: Այդ
ձգողական ուժերը
միայն մոլեկուլների
շատ փոքր հեռավորությունների
դեպքում (հարվածի
պահին) փոխարինվում
են ավելի ինտենսիվ
վանողական ուժերով:
Միջմոլեկուլային
ձգողական ուժերի
հետևանքով գազը
զբաղեցնում է ավելի
փոքր V ծավալ, քան
այն բխում է Բոյլ-Մարիոտի
օրենքից, կարծես
թե նա գտնվելիս
լինի ավելի մեծ
![]() ճնշման
տակ, քան այն արտաքին
p ճնշումը, որը նրա
վրա գործադրում
են անոթի պատերը:
Այսպիսով, (8.18) հավասարման
մեջ արտաքին p ճնշումը
պետք է փոխարինել
ճնշման
տակ, քան այն արտաքին
p ճնշումը, որը նրա
վրա գործադրում
են անոթի պատերը:
Այսպիսով, (8.18) հավասարման
մեջ արտաքին p ճնշումը
պետք է փոխարինել
![]() մեծությամբ,
որտեղից կստանանք
մեծությամբ,
որտեղից կստանանք
![]()
![]() մեծությունը
կոչվում է գազի
ներքին ճնշում:
Միջմոլեկուլային
փոխազդեցությունը
տեղի է ունենում
մոլեկուլային
ազդեցության շառավղի
սահմաններում:
մեծությունը
կոչվում է գազի
ներքին ճնշում:
Միջմոլեկուլային
փոխազդեցությունը
տեղի է ունենում
մոլեկուլային
ազդեցության շառավղի
սահմաններում:
Իրական գազի
մոլեկուլային
ազդեցության շառավղի
կարգի չափեր ունեցող
երկու տարրական
ծավալների ձգողության
ուժը համեմատական
է ինչպես մեկ, այնպես
էլ, մյուս ծավալով
գազի կոնցենտրացիային,
հետևաբար նաև խտության
քառակուսուն կամ
հակադարձ համեմատական
է ծավալի քառակուսուն,
ուստի ներքին ![]() ճնշումը`
ճնշումը`
![]()
որտեղ n-ը կոնտրենցիան է, p-ն` խտությունը:
Այսպիսով, իրական գազում ընդհանուր ճնշումը հաստատվում է արտաքին և ներքին ճնշումներից.
![]()
Մոլեկուլի
![]() ծավալի
և b ուղղման միջև
կախվածությունը
կարելի է ստանալ
հետևյալ ճանապարհով:
Երկու մոլեկուլներ
կարող են իրար
մոտենալ իրենց
շառավիղների գումարից
ոչ փոքր հեռավորության
վրա: Այդ դեպքում
գազի զբաղեցրած
ամբողջ ծավալից
հարկավոր է հանել
նրա որոշակի b մասը,
որը համեմատական
է բախվող մոլեկուլների
շառավիղների գումարին
հավասար շառավղով
գծված գնդի (սֆերայի)
ծավալին և բախվող
մոլեկուլների
թվին.
ծավալի
և b ուղղման միջև
կախվածությունը
կարելի է ստանալ
հետևյալ ճանապարհով:
Երկու մոլեկուլներ
կարող են իրար
մոտենալ իրենց
շառավիղների գումարից
ոչ փոքր հեռավորության
վրա: Այդ դեպքում
գազի զբաղեցրած
ամբողջ ծավալից
հարկավոր է հանել
նրա որոշակի b մասը,
որը համեմատական
է բախվող մոլեկուլների
շառավիղների գումարին
հավասար շառավղով
գծված գնդի (սֆերայի)
ծավալին և բախվող
մոլեկուլների
թվին.
![]()
որտեղ համասեռ
գազի դեպքում,
![]() մեկ
մոլեկուլի ծավալն
է: Ընդունենք k գործակիցը
հավասար 1/2-ի, հիմնվելով
այն բանի վրա, որ
շատ դեպքերում
միաժամանակ բախվում
են երկու մոլեկուլներ,
այլ ոչ թե մեծ թվով
մոլեկուլներ: Եռակի,
քառակի և այլ բախումներ
տեղի են ունենում
հազվադեպ: Հետևաբար
(12.3) հավասարությունը
կընդունի հետևյալ
տեսքը`
մեկ
մոլեկուլի ծավալն
է: Ընդունենք k գործակիցը
հավասար 1/2-ի, հիմնվելով
այն բանի վրա, որ
շատ դեպքերում
միաժամանակ բախվում
են երկու մոլեկուլներ,
այլ ոչ թե մեծ թվով
մոլեկուլներ: Եռակի,
քառակի և այլ բախումներ
տեղի են ունենում
հազվադեպ: Հետևաբար
(12.3) հավասարությունը
կընդունի հետևյալ
տեսքը` ![]() Այսպիսով
մոլեկուլների
ծավալի հաշվառման
հետևանքով ստացված
b ուղղումը մոտավորապես
հավասար է մոլեկուլների
սեփական ծավալի
քառապատիկին:
a և b հաստատունները
յուրաքանչյուր
գազի համար կարող
են որոշվել կրիտիկական
պարամետրերով
փորձնական ճանապարհով:
Այսպիսով
մոլեկուլների
ծավալի հաշվառման
հետևանքով ստացված
b ուղղումը մոտավորապես
հավասար է մոլեկուլների
սեփական ծավալի
քառապատիկին:
a և b հաստատունները
յուրաքանչյուր
գազի համար կարող
են որոշվել կրիտիկական
պարամետրերով
փորձնական ճանապարհով:
Այսպիսով,
նկատի ունենալով
![]() արժեքը,
մեկ մոլ իրական
գազի համար կստանանք
հետևյալ հավասարումը,
որն ստացել է Վան
-դեր - Վաալսը.
արժեքը,
մեկ մոլ իրական
գազի համար կստանանք
հետևյալ հավասարումը,
որն ստացել է Վան
-դեր - Վաալսը.

Եթե վեցնենք m /M մոլերի քանակով գազ, ապա (10.4) փոխարեն կստանանք`
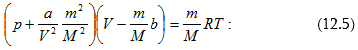
12.3. ՎԱՆ-ԴԵՐ-ՎԱԱԼՍԻ ԻԶՈԹԵՐՄԵՐԸ: ՆՅՈՒԹԻ ԿՐԻՏԻԿԱԿԱՆ ՎԻՃԱԿԸ
Վան-դեր-Վաալսի հավասարումը`
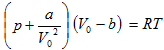
երրորդ աստիճանի
հանրահաշվական
հավասարում է`
![]() նկատմամբ:
Այդ պատճառով էլ,
կախված p-ի և T-ի արժեքներից,
նկատմամբ:
Այդ պատճառով էլ,
կախված p-ի և T-ի արժեքներից,
![]() մոլային
ծավալի համար այն
տալիս է կամ մեկ,
կամ երեք տարբեր
արժեքներ: Իրական
գործակիցներով
և ազատ անդամով
հանրահաշվական
երրորդ աստիճանի
հավասարումը միշտ
ունի երեք լուծում,
սակայն դրանցից
երկուսը կարող
են կոմպլեքս լինել:
Քանի որ
մոլային
ծավալի համար այն
տալիս է կամ մեկ,
կամ երեք տարբեր
արժեքներ: Իրական
գործակիցներով
և ազատ անդամով
հանրահաշվական
երրորդ աստիճանի
հավասարումը միշտ
ունի երեք լուծում,
սակայն դրանցից
երկուսը կարող
են կոմպլեքս լինել:
Քանի որ ![]() ծավալն
իրական մեծություն
է, ապա
ծավալն
իրական մեծություն
է, ապա ![]() համար
կունենանք կամ
մեկ, կամ երեք տարբեր
լուծումներ: Գրաֆիկորեն
պատկերելով p-ի
կախումը
համար
կունենանք կամ
մեկ, կամ երեք տարբեր
լուծումներ: Գրաֆիկորեն
պատկերելով p-ի
կախումը ![]() տարբեր
ջերմաստիճանների
համար` կստանանք
մի շարք իզոթերմեր
(նկ.12.2):
տարբեր
ջերմաստիճանների
համար` կստանանք
մի շարք իզոթերմեր
(նկ.12.2):
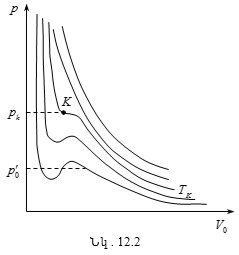
Իզոթերմերից
յուրաքանչյուրը
համապատասխանում
է որոշակի T ջերմաստիճանի:
Ինչքան ջերմաստիճանը
բարձր է, այնքան
նկ.12.2-ում իզոթերմերն
ավելի բարձր և
աջ են ընկած: Նկարից
երևում է, որ միայն
բարձր T ջերմաստիճանների
դեպքում ![]() ծավալի
փոքրացման հետ
իզոթերմը մոնոտոն
կերպով է աճում`
հիշեցնելով Բոյլ-Մարիոտի
օրենքին համապատասխանող
իզոթերմը: Այդպիսի
իզոթերմի վրա
p ճնշման յուրաքանչյուր
արժեքին համապատասխանում
է
ծավալի
փոքրացման հետ
իզոթերմը մոնոտոն
կերպով է աճում`
հիշեցնելով Բոյլ-Մարիոտի
օրենքին համապատասխանող
իզոթերմը: Այդպիսի
իզոթերմի վրա
p ճնշման յուրաքանչյուր
արժեքին համապատասխանում
է ![]() մոլային
ծավալի մեկ արժեք,
այնպես, ինչպես
այդ տեղի ունի
Մենդելեև-Կլապեյրոնի
բանաձևին ենթարկվելու
դեպքում: Ավելի
ցածր ջերմաստիճաններում
իզոթերմերը ծավալի
և ճնշման որոշակի
տիրույթում տալիս
են սապատներ: Այդ
տիրույթում, ընդհանրապես,
յուրաքանչյուր
p ճնշմանը համապատասխանում
են
մոլային
ծավալի մեկ արժեք,
այնպես, ինչպես
այդ տեղի ունի
Մենդելեև-Կլապեյրոնի
բանաձևին ենթարկվելու
դեպքում: Ավելի
ցածր ջերմաստիճաններում
իզոթերմերը ծավալի
և ճնշման որոշակի
տիրույթում տալիս
են սապատներ: Այդ
տիրույթում, ընդհանրապես,
յուրաքանչյուր
p ճնշմանը համապատասխանում
են ![]() ծավալի
երեք արժեքներ:
Առաջին հայացքից
բավականին տարօրինակ
այս կախման իմաստը
պարզաբանելու
համար, պետք է փորձին
դիմել: Նկ.12.3-ում բերված
են ածխաթթու գազի
համար փորձով ստացված
իզոթերմերը: Բարձր
T ջերմաստիճանների
դեպքում ածխաթթու
գազի իզոթերմերը
հիշեցնում են իդեալական
գազի իզոթերմեր:
ծավալի
երեք արժեքներ:
Առաջին հայացքից
բավականին տարօրինակ
այս կախման իմաստը
պարզաբանելու
համար, պետք է փորձին
դիմել: Նկ.12.3-ում բերված
են ածխաթթու գազի
համար փորձով ստացված
իզոթերմերը: Բարձր
T ջերմաստիճանների
դեպքում ածխաթթու
գազի իզոթերմերը
հիշեցնում են իդեալական
գազի իզոթերմեր:
Ավելի ցածր ջերմաստիճանների դեպքում իզոթերմերի բնույթը բոլորովին այլ է:
Այդպիսի ցածր ջերմաստիճանին համապատասխանող իզոթերմը սխեմատիկ պատկերված է նկ.12.4-ում:
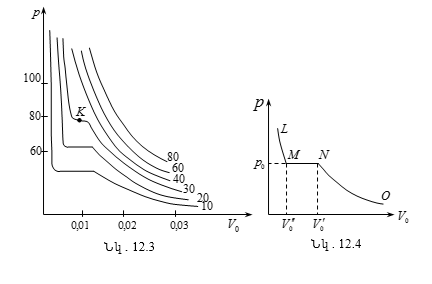
Պարզության
համար նշենք այն
փորձի սխեման,
որի օգնությամբ
որոշվել է ![]() մոլային
ծավալի կախումը
ճնշումից ածխաթթու
գազի համար:
մոլային
ծավալի կախումը
ճնշումից ածխաթթու
գազի համար:
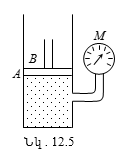
Այդ փորձի
սխեման (նկ.12.5) հետևյալն
է` հաստ պատեր ունեցող
A գլանում B մխոցի
տակ գտնվում է
մեկ մոլ ածխաթթու
գազ, որի T ջերմաստիճանը
ամբողջ փորձի ընթացքում
պահպանվում է հաստատուն:
Ածխաթթու գազի
գրաված ![]() ծավալը
մխոցի տարբեր դիրքերի
համար կարող է
չափվել: Այդ տարբեր
ծավալներին համապատասխանող
ճընշումները չափվում
են M մանոմետրով:
Մեծ
ծավալը
մխոցի տարբեր դիրքերի
համար կարող է
չափվել: Այդ տարբեր
ծավալներին համապատասխանող
ճընշումները չափվում
են M մանոմետրով:
Մեծ ![]() ծավալների
դեպքում B մխոցի
իջեցման ժամանակ
ածխաթթու գազի
ճնշումն աճում
է մոնոտոն կերպով,
պրոցեսի այդ մասին
համապատասխանում
է նկ.12.4-ում պատկերված
իզոթերմի ON ճյուղը:
Այստեղ ածխաթթու
գազի հատկությունները
նման են իդեալական
գազի հատկություններին,
թեպետ և նա որոշ
չափով ավելի մեծ
սեղմելիություն
է ցուցաբերում,
քան պահանջվում
է Բոյլ-Մարիոտի
օրենքի համաձայն:
Որոշ
ծավալների
դեպքում B մխոցի
իջեցման ժամանակ
ածխաթթու գազի
ճնշումն աճում
է մոնոտոն կերպով,
պրոցեսի այդ մասին
համապատասխանում
է նկ.12.4-ում պատկերված
իզոթերմի ON ճյուղը:
Այստեղ ածխաթթու
գազի հատկությունները
նման են իդեալական
գազի հատկություններին,
թեպետ և նա որոշ
չափով ավելի մեծ
սեղմելիություն
է ցուցաբերում,
քան պահանջվում
է Բոյլ-Մարիոտի
օրենքի համաձայն:
Որոշ ![]() ճնշման
հասնելու դեպքում,
որին համապատասխանում
է
ճնշման
հասնելու դեպքում,
որին համապատասխանում
է ![]() ծավալ
(իզոթերմի N կետը),
ածխաթթու գազի
վարքագիծը խիստ
փոխվում է. մխոցի
հետագա իջեցման
դեպքում
ծավալ
(իզոթերմի N կետը),
ածխաթթու գազի
վարքագիծը խիստ
փոխվում է. մխոցի
հետագա իջեցման
դեպքում ![]() ճնշումը
մնում է հաստատուն,
սկսվում է ածխաթթու
գազի հեղուկացումը:
ճնշումը
մնում է հաստատուն,
սկսվում է ածխաթթու
գազի հեղուկացումը:
Ինչքան ավելի
է մխոցը իջնում,
այնքան գազի (այս
պայմաններում
այն ընդունված
է անվանել հագեցած
գոլորշի) ավելի
շատ քանակություն
է հեղուկի վերածվում:
![]() ճընշումով
և
ճընշումով
և ![]() ծավալով
բնորոշվող իզոթերմի
M կետը համապատասխանում
է մխոցի տակ գտնված
ածխաթթու գազի`
ամբողջ քանակության
հեղուկ վիճակի
անցնելուն: Այդ
դեպքում մխոցի
տակ միայն հեղուկ
կլինի. մխոցի հետագա
առաջընթացը չափազանց
մեծ ջանք կպահանջի,
քանի որ հեղուկը
քիչ սեղմելի է:
Իզոթերմի ML ճյուղը
համապտասխանում
է ածխաթթու գազի
հեղուկ վիճակին:
Այն
ծավալով
բնորոշվող իզոթերմի
M կետը համապատասխանում
է մխոցի տակ գտնված
ածխաթթու գազի`
ամբողջ քանակության
հեղուկ վիճակի
անցնելուն: Այդ
դեպքում մխոցի
տակ միայն հեղուկ
կլինի. մխոցի հետագա
առաջընթացը չափազանց
մեծ ջանք կպահանջի,
քանի որ հեղուկը
քիչ սեղմելի է:
Իզոթերմի ML ճյուղը
համապտասխանում
է ածխաթթու գազի
հեղուկ վիճակին:
Այն ![]() ճնշումը,
որի դեպքում տեղի
է ունենում հեղուկացումը,
կոչվում է հագեցած
գոլորշու
ճնշումը,
որի դեպքում տեղի
է ունենում հեղուկացումը,
կոչվում է հագեցած
գոլորշու ![]() առաձգականություն
տվյալ T ջերմաստիճանում:
առաձգականություն
տվյալ T ջերմաստիճանում:
Հագեցած գոլորշիների
առաձգականությանը
հավասար p ճնշման
դեպքում նյութի
տվյալ քանակությունը
կարող է ունենալ
![]() ծավալների
միջև ընկած ցանկացած
մոլային ծավալ:
Այդ տիրույթում
նյութը գոյություն
ունի միաժամանակ
երկու ագրեգատային
վիճակներում (ինչպես
ասում են` երկու
փուլերում)` հեղուկ
և գազային: Ինչքան
ծավալի արժեքը
մոտ է
ծավալների
միջև ընկած ցանկացած
մոլային ծավալ:
Այդ տիրույթում
նյութը գոյություն
ունի միաժամանակ
երկու ագրեգատային
վիճակներում (ինչպես
ասում են` երկու
փուլերում)` հեղուկ
և գազային: Ինչքան
ծավալի արժեքը
մոտ է ![]() այնքան
նյութի ավելի շատ
մասն է գտնվում
հեղուկ վիճակում
և այնքան ավելի
քիչ մասն է բաժին
ընկնում գազային
(գոլորշի) վիճակին:
Ճիշտ նույն տիպի
իզոթերմեր են ստացվում
նաև բոլոր այլ
նյութերի համար
այն ջերմաստիճանների
տիրույթում, որոնց
դեպքում դրանք
կարող են սեղմման
միջոցով գազանման
վիճակից անցնել
հեղուկ վիճակի:
այնքան
նյութի ավելի շատ
մասն է գտնվում
հեղուկ վիճակում
և այնքան ավելի
քիչ մասն է բաժին
ընկնում գազային
(գոլորշի) վիճակին:
Ճիշտ նույն տիպի
իզոթերմեր են ստացվում
նաև բոլոր այլ
նյութերի համար
այն ջերմաստիճանների
տիրույթում, որոնց
դեպքում դրանք
կարող են սեղմման
միջոցով գազանման
վիճակից անցնել
հեղուկ վիճակի:
Փորձնական
իզոթերմերի համեմատությունը
Վան-դեր-Վաալսի
տեսական իզոթերմերի
հետ, ցույց է տալիս,
որ սապատների տիրույթը
Վան-դեր-Վաալսի
իզոթերմերի վրա
վերաբերում է նյութի
գազանման վիճակից
հեղուկ վիճակին
կամ հակառակը անցնելուն:
Սակայն այդ դեպքում
նյութի անցումը
գազանման վիճակից
հեղուկ վիճակին
և հակառակը իրականում
տեղի է ունենում
ոչ թե ծռումներ
ունեցող կորով,
այլ ուղիղ գծով
(MN ուղիղը նկ.12.4-ում)
հաստատուն ![]() ճնշման
տակ: Այսպիսով,
Վան-դեր-Վաալսի
իզոթերմերը ոչ
միայն ավելի ճշգրիտ
են արտահայտում
գազի վարքագիծը,
քան իդեալական
գազի իզոթերմերը,
այլև ընդգրկում
են գազի հեղուկացման
պրոցեսը, ինչպես
նաև արտահայտում
են հեղուկի այն
հատկությունը,
որը հանդես է գալիս
նրա նվազ սեղմելիության
մեջ: Ջերմաստիճանի
բարձրացման հետ
մեկտեղ սապատների
տիրույթը Վան-դեր-Վաալսի
իզոթերմերի վրա
նեղանում է, այսինքն`
ճնշման
տակ: Այսպիսով,
Վան-դեր-Վաալսի
իզոթերմերը ոչ
միայն ավելի ճշգրիտ
են արտահայտում
գազի վարքագիծը,
քան իդեալական
գազի իզոթերմերը,
այլև ընդգրկում
են գազի հեղուկացման
պրոցեսը, ինչպես
նաև արտահայտում
են հեղուկի այն
հատկությունը,
որը հանդես է գալիս
նրա նվազ սեղմելիության
մեջ: Ջերմաստիճանի
բարձրացման հետ
մեկտեղ սապատների
տիրույթը Վան-դեր-Վաալսի
իզոթերմերի վրա
նեղանում է, այսինքն`
![]() ծավալների
տարբերությունը
նվազում է, որտեղ
ծավալների
տարբերությունը
նվազում է, որտեղ
![]() այն
ծավալն է, որի դեպքում
նյութը
այն
ծավալն է, որի դեպքում
նյութը ![]() ճնշման
ներքո ամբողջությամբ
գտնվում է գազային
վիճակում (գոլորշու
տեսքով), իսկ
ճնշման
ներքո ամբողջությամբ
գտնվում է գազային
վիճակում (գոլորշու
տեսքով), իսկ ![]() այն
ծավալն է, երբ նյութը
նույն
այն
ծավալն է, երբ նյութը
նույն ![]() ճընշման
դեպքում ամբողջությամբ
վերածվելէ է հեղուկ
վիճակի: Նկ.12.6-ում
համեմատված են
իրական իզոթերմերը
տարբեր ջերմաստիճանների
համար: Չնրբագծված
տիրույթը վերաբերում
է նյութի գազանման
վիճակին, կետագծերով
նշված տիրույթը
երկփուլ վիճակին`
գազանման և հեղուկ,
իսկ նրբագծված
տիրույթը` նյութի
հեղուկ վիճակին:
ճընշման
դեպքում ամբողջությամբ
վերածվելէ է հեղուկ
վիճակի: Նկ.12.6-ում
համեմատված են
իրական իզոթերմերը
տարբեր ջերմաստիճանների
համար: Չնրբագծված
տիրույթը վերաբերում
է նյութի գազանման
վիճակին, կետագծերով
նշված տիրույթը
երկփուլ վիճակին`
գազանման և հեղուկ,
իսկ նրբագծված
տիրույթը` նյութի
հեղուկ վիճակին:
Վան-դեր-Վաալսի
իզոթերմերի մեջ
կա այնպիսի իզոթերմ,
որը սապատավոր
իզոթերմերն առանձնացնում
է այն իզոթերմերից,
որոնք սապատ չունեն:
Այդ իզոթերմը կոչվում
է կրիտիկական,
իսկ դրան համապատասխանող
ջերմաստիճանը
կրիտիկական ![]() ջերմաստիճան
(տես նկ.12.3 և նկ.12.6):
ջերմաստիճան
(տես նկ.12.3 և նկ.12.6):
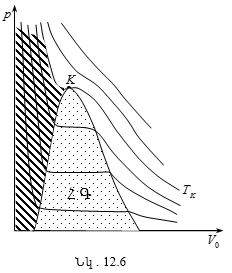
Կրիտիկական
իզոթերմը սապատների
փոխարեն ունի միայն
շրջման K կետ. այդ
կետում նրան տարած
շոշափողը զուգահեռ
է աբսցիսների առանցքին:
K կետը կոչվում
է կրիտիկական կետ,
իսկ նրան համապատասխանող
![]() ծավալը
և
ծավալը
և ![]() ճնշումը`
կրիտիկական ծավալ
և կրիտիկական
ճնշում: Յուրաքանչյուր
տվյալ նյութի համար
իր կրիտիկական
ջերմաստիճանը,
մոլային ծավալը
և ճնշումն ունեն
որոշակի արժեքներ:
ճնշումը`
կրիտիկական ծավալ
և կրիտիկական
ճնշում: Յուրաքանչյուր
տվյալ նյութի համար
իր կրիտիկական
ջերմաստիճանը,
մոլային ծավալը
և ճնշումն ունեն
որոշակի արժեքներ:
Կրիտիկական
ջերմաստիճանի
հասկացությունը
առաջին անգամ մըտցրել
է Մենդելեևը 1865թ.:
Մենդելեևն իր հետազոտություններում
կրիտիկական ջերմաստիճանն
անվանել է հեղուկի
բացարձակ եռման
ջերմաստիճան, որի
դեպքում անհետանում
են հարակցական
ուժերը մոլեկուլների
միջև, և հեղուկը
վերածվում է գոլորշու`
անկախ ճնշումից
և տեսակարար ծավալից:
Կրիտիկական ջեմաստիճանի
այս հասկացությունը
միանգամայն համապատասխանում
է հեղուկ վիճակից
գազային վիճակին
անցնելու վերաբերյալ
ժամանակակից պատկերացմանը:
Իրոք, նկ.12.6-ում սահմանազատված
են գազանման և
հեղուկ վիճակները
և հեղուկացման
տիրույթը, գրաֆիկից
երևում է` կրիտիկական
![]() ջերմաստիճանից
բարձր ջերմաստիճանում
նյութը կարող է
գոյություն ունենալ
միայն գազային
վիճակում:
ջերմաստիճանից
բարձր ջերմաստիճանում
նյութը կարող է
գոյություն ունենալ
միայն գազային
վիճակում:
Գազը, որի T ջերմաստիճանը
բարձր է ![]() ջերմաստիճանից,
ոչ մի տեսակի սեղմումով
չի կարող անցնել
հեղուկ վիճակի:
Կրիտիկականից
ցածր ջերմաստիճանների
դեպքում նյութը,
կախված ճնշումից,
կարող է գոյություն
ունենալ կամ գազանման,
կամ հեղուկ վիճակում
և կամ միաժամանակ
երկու փուլերում`
հեղուկի և հագեցած
գոլորշու: Հագեցած
գոլորշու
ջերմաստիճանից,
ոչ մի տեսակի սեղմումով
չի կարող անցնել
հեղուկ վիճակի:
Կրիտիկականից
ցածր ջերմաստիճանների
դեպքում նյութը,
կախված ճնշումից,
կարող է գոյություն
ունենալ կամ գազանման,
կամ հեղուկ վիճակում
և կամ միաժամանակ
երկու փուլերում`
հեղուկի և հագեցած
գոլորշու: Հագեցած
գոլորշու ![]() առաձգականությունը
չի կարող ավելի
մեծ արժեք ունենալ,
քան տվյալ նյութի
կրիտիկական
առաձգականությունը
չի կարող ավելի
մեծ արժեք ունենալ,
քան տվյալ նյութի
կրիտիկական ![]() ճնշումը:
Նյութի ծավալը
հեղուկ վիճակում
չի կարող ունենալ
ավելի մեծ արժեք,
քան այդ նյութի
տվյալ քանակի կրիտիկական
ծավալը: Նշենք,
որ hելիումի համար
կրիտիկական ջերմաստիճանը
-2690C Է, իսկ ջրի համար`
3740C: Ջրի համար կրիտիկական
ճնշումը 218 մթ. է, իսկ
կրիտիկական ծավալը,
այսինքն այն ծավալը,
որը զբաղեցնում
է 1 գ ջուրը կրիտիկական
ճնշման և կրիտիկական
ջերմաստիճանի
դեպքում, 3սմ3 է:
ճնշումը:
Նյութի ծավալը
հեղուկ վիճակում
չի կարող ունենալ
ավելի մեծ արժեք,
քան այդ նյութի
տվյալ քանակի կրիտիկական
ծավալը: Նշենք,
որ hելիումի համար
կրիտիկական ջերմաստիճանը
-2690C Է, իսկ ջրի համար`
3740C: Ջրի համար կրիտիկական
ճնշումը 218 մթ. է, իսկ
կրիտիկական ծավալը,
այսինքն այն ծավալը,
որը զբաղեցնում
է 1 գ ջուրը կրիտիկական
ճնշման և կրիտիկական
ջերմաստիճանի
դեպքում, 3սմ3 է:
12.4. ԿՐԻՏԻԿԱԿԱՆ ՄԵԾՈՒԹՅՈՒՆՆԵՐԻ ՈՐՈՇՈՒՄԸ
Վան-դեր-Վաալսի
հավասարման քննարկումը
հնարավորություն
է տալիս կապ հաստատել
![]() կրիտիկական
ջերմաստիճանի,
կրիտիկական
ջերմաստիճանի,
![]() մոլային
ծավալի,
մոլային
ծավալի, ![]() ճնշման
և a ու b ուղղումների
միջև:
ճնշման
և a ու b ուղղումների
միջև:
Ձևափոխենք Վան-դեր-Վաալսի
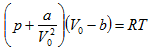
հավասարումը,
բազմապատկելով
աջ և ձախ մասերը
![]() բաց
անելով փակագծերը
և հավաքելով
բաց
անելով փակագծերը
և հավաքելով ![]() նույն
աստիճան ունեցող
անդամները, կստանանք`
նույն
աստիճան ունեցող
անդամները, կստանանք`
![]()
Այստեղից
անմիջականորեն
երևում է, որ Վան-դեր-Վաալսի
հավասարումը ![]() նկատմամբ
երրորդ աստիճանի
հավասարում է:
նկատմամբ
երրորդ աստիճանի
հավասարում է:![]() կրիտիկական
ջերմաստիճանի
համար Վան-դեր-Վաալսի
կրիտիկական
ջերմաստիճանի
համար Վան-դեր-Վաալսի
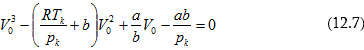
հավասարումը
K կրիտիկական կետում
ունի շրջման կետ
(նկ.12.2): Այդ պատճառով
այդ կետում այն
ունի մեկ եռակի
![]() արմատ
և կարելի է այն
ներկայացնել հետևյալ
տեսքով`
արմատ
և կարելի է այն
ներկայացնել հետևյալ
տեսքով`
![]()
կամ, եթե կատարենք աստիճան բարձրացնելու գործողությունը, կստանանք
![]()
(12.7) և (12.8) հավասարումները
նույնաբար պետք
է համընկնեն, որը
հնարավոր է ![]() նույն
աստիճանների գործակիցների
հավասարության
պարագայում, որտեղից
կունենանք`
նույն
աստիճանների գործակիցների
հավասարության
պարագայում, որտեղից
կունենանք`
![]()
Լուծելով
այս երեք հավասարումները
![]() երեք
անհայտների նկատմամբ
կստանանք`
երեք
անհայտների նկատմամբ
կստանանք`
![]()
![]()
![]()
Այսպիսով,
![]() կրիտիկական
մեծություններն
արտահայտվում
են Վան-դեր-Վաալսի
a և b ուղղումների
միջոցով:
կրիտիկական
մեծություններն
արտահայտվում
են Վան-դեր-Վաալսի
a և b ուղղումների
միջոցով:
12.5. ԻՐԱԿԱՆ ԳԱԶԻ ՆԵՐՔԻՆ ԷՆԵՐԳԻԱՆ
Ի տարբերություն իդեալական գազերի, որտեղ ներքին էներգիան սոսկ մոլեկուլների շարժման կինետիկ էներգիան է, որը կախված է ջերմաստիճանից և կախված չէ գազի զբաղեցրած ծավալից, քանի որ գազում բացակայում են միջմոլեկուլային փոխազդեցությունները, իրական գազերում միջմոլեկուլային փոխազդեցությունները կարևոր դեր են խաղում: Այդ պատճառով իրական գազի ներքին էներգիան որոշվում է մոլեկուլների փոխազդեցության պոտենցիալ էներգիայի և դրանց շարժման կինետիկ էներգիայի գումարով:
Քանի որ մելեկուլների փոխազդեցության պոտենցիալ էներգիան կախված է դրանց փոխադարձ դիրքից, ապա այն պետք է փոփոխվի գազի ծավալի փոփոխության դեպքում: Մոլեկուլների փոխազդեցության պոտենցիալ էներգիան մոլ գազի համար կարելի է հաշվել հետևյալ բանաձևով՝
![]()
որտեղ ![]() լրացուցիչ
ներքին ճնշումն
է, որը մտնում է
Վան-դեր-Վաալսի
հավասարման մեջ:
լրացուցիչ
ներքին ճնշումն
է, որը մտնում է
Վան-դեր-Վաալսի
հավասարման մեջ:
![]() արժեքը
տեղադրելով (12.9) հավասարման
մեջ՝ կունենանք.
արժեքը
տեղադրելով (12.9) հավասարման
մեջ՝ կունենանք. ![]()
Այս էներգիան ունի բացասական նշան, քանի որ ներքին ճնշում առաջացնող մոլեկուլային ուժերը ձգողական ուժեր են: Օգտագործելով Ջոուլի օրենքը` կարելի է հաշվել իրական գազի ներքին էներգիան
![]()
(12.10) բանաձևով որոշվում է 1 մոլ իրական գազի ներքին էներգիան: v մոլ գազի ներքին էներգիան որոշվում է հետևյալ բանաձևով`
![]()
![]()
Իրական գազի ներքին էներգիան կախված է ինչպես ջերմաստիճանից, այնպես էլ ծավալից: Քննարկենք իրական գազի ընդարձակումը դատարկության մեջ: Այս դեպքում արտաքին ճնշումը հավասար է զրոյի, դրա համար էլ գազը արտաքին ուժերի դեմ աշխատանք չի կատարում: Սակայն իրական գազում գործում են միջմոլեկուլային փոխազդեցության ուժեր, և գազի ընդարձակման ժամանակ աշխատանք է կատարվում այդ ուժերի հաղթահարման դեմ՝ գազի ներքին էներգիայի հաշվին: Սրա հետևանքով դատարկության մեջ ընդարձակման դեպքում իրական գազի ջերմաստիճանը պետք է իջնի:
Սակայն դա այդպես չէ. որոշ դեպքերում կարող է տեղի ունենալ ջերմաստիճանի բարձրացում: Իրական գազը ընդարձակման ժամանակ սառչում է այն դեպքում, երբ գերակշռում է ձգողական ուժերի ազդեցությունը գազի մոլեկուլների միջև: Այդ դեպքում գազի մոլեկուլները ձգողական ուժերի դեմ աշխատանք են կատարում իրենց կինետիկ էներգիայի հաշվին, որի հետևանքով կինետիկ էներգիան փոքրանում է, այսինքն` ջերմաստիճանն իջնում է: Եթե գերակշռում է վանողական ուժերի ազդեցությունը գազի մոլեկուլների միջև, ընդարձակման դեպքում մոլեկուլների արագությունը չի փոքրանում, այլ մեծանում է, այսինքն` ջերմաստիճանը բարձրանում է:
Հետևաբար, կախված այն բանից, թե ինչն է գերակշռում մոլեկուլների միջև՝ ձգողական ուժերը, թե՝ վանողական, գազի դատարկության մեջ ընդարձակման ժամանակ կարող է տեղի ունենալ գազի տաքացում կամ սառեցում:
Իրական գազերի ընդարձակման դեպքում ներքին էներգիայի փոփոխությունն ընկած է գազերը սեղմող մեքենայի գործողության սկզբունքի հիմքում:
Խնդիր 1: v = 1մոլ
թթվածինը (իրական
գազ) ![]() ջերմաստիճանում
զբաղեցնում է
ջերմաստիճանում
զբաղեցնում է ![]() ծավալ
և իզոթերմ ընդաձակվում
է մինչև
ծավալ
և իզոթերմ ընդաձակվում
է մինչև ![]()
1) ընդարձակման աշխատանքը
2) գազի ներքին էներգիայի փոփոխությունը: a և b ուղղումներն ընդունել համապատասխանաբար հավասար
![]()
Լուծում: Օգտվենք Վան-դեր-Վաալսի հավասարումից գրված կամայական զանգվածով գազի համար
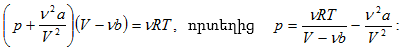
Աշխատանքը`
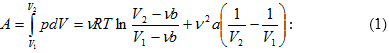
Գազի ներքին էներգիայի փոփոխությունը`
![]()
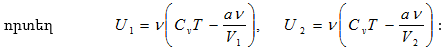
Նկատի ունենալով վերջինները` (2)-ից կստանանք`
![]()
Տեղադրելով
(1)-ի և (3)-ի մեջ մտնող
մեծությունների
թվային արժեքները
կստանանք` ![]()
12.6. ՋՈՈՒԼ-ԹՈՄՍՈՆԻ ԷՖԵԿՏԸ
Եթե իդեալական գազը ադիաբատորեն ընդարձակվում է և այդ դեպքում կատարում է աշխատանք, այն սառչում է, քանի որ տվյալ դեպքում աշխատանքը կատարվում է իր ներքին էներգիայի նվազման հաշվին: Նույնպիսի պրոցեսը, բայց իրական գազի հետ` իրական գազի ադիաբատիկ ընդարձակումը արտաքին ուժերով դրական աշխատանքի կատարումը իրականացրին անգլիացի ֆիզիկոսներ Ջոուլը (1818-1889) և Ու. Թոմսոնը (1824-1907):
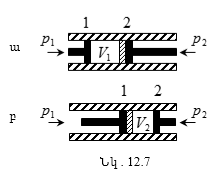
Քննարկենք
Ջոուլ-Թոմսոնի
էֆեկտը: Նկ. 12.7-ում
բերված է նրանց
փորձի սխեման:
Ծակոտկեն միջնորմով
ջերմամեկուսիչ
խողովակում գտնվում
են երկու մխոցներ,
որոնք կարող են
տեղափոխվել առանց
շփման: Դիցուք
սկզբում միջնորմից
ձախ 1 մխոցի տակ
գազը գտնվում է
![]() ճնշման
տակ և զբաղեցնում
է
ճնշման
տակ և զբաղեցնում
է ![]() ծավալ
ծավալ
![]() ջերմաստիճանում
(նկ.12.7ա), իսկ միջնորմի
աջ մասում գազը
բացակայում է
(2 մխոցը մոտեցված
է միջնորմին): Ծակոտկեն
միջնորմի միջով
գազի անցնելուց
հետո աջ մասում
գազը բնութագրվում
է
ջերմաստիճանում
(նկ.12.7ա), իսկ միջնորմի
աջ մասում գազը
բացակայում է
(2 մխոցը մոտեցված
է միջնորմին): Ծակոտկեն
միջնորմի միջով
գազի անցնելուց
հետո աջ մասում
գազը բնութագրվում
է ![]() պարամետրերով
(նկ.12.7բ):
պարամետրերով
(նկ.12.7բ):
![]() ճնշումները
պահպանվում են
հաստատուն
ճնշումները
պահպանվում են
հաստատուն ![]()
Քանի որ գազի ընդարձակումը տեղի է ունենուն շրջապատող միջավայրի հետ առանց ջերմափոխանակության, ապա ջերմադինամիկայի առաջին օրենքի հիման վրա
![]()
Գազի կատարած
արտաքին աշխատանքը
կազմված է դրական
աշխատանքից 2 մխոցը
շարժելու դեպքում
![]() և բացասական`
1 մխոցի շարժվելու
դեպքում
և բացասական`
1 մխոցի շարժվելու
դեպքում ![]() այսինքն`
այսինքն`
![]() Տեղադրելով
(12.12) բանաձևի մեջ
աշխատանքների
համար արտահայտությունները,
կստանանք`
Տեղադրելով
(12.12) բանաձևի մեջ
աշխատանքների
համար արտահայտությունները,
կստանանք`
![]()
Այսպիսով,
Ջոուլ-Թոմսոնի
փորձում պահպանվում
է (մնում է հաստատուն)
![]() մեծությունը:
Այն վիճակի ֆունկցիա
է և կոչվում է էնթալպիա:
մեծությունը:
Այն վիճակի ֆունկցիա
է և կոչվում է էնթալպիա:
Պարզության համար դիտարկենք 1 մոլ գազ: Տեղադրելով (12.13) բանաձևի մեջ
![]()
արտահայտությունները
և Վան-դեր-Վալսի
(12.4) հավասարումից
նախորոշված ![]() արժեքները
և կատարելով տարրական
ձևափոխություններ,
կստանանք`
արժեքները
և կատարելով տարրական
ձևափոխություններ,
կստանանք`

(12.14) արտահայտությունից
հետևում է, որ![]() տարբերության
նշանը կախված է
նրանից, թե Վան-դեր-Վաալսի
ուղղումներից
որն է մեծ դեր խաղում:
Վերլուծենք տվյալ
արտահայտությունը`
ենթադրություն
անելով, որ և
տարբերության
նշանը կախված է
նրանից, թե Վան-դեր-Վաալսի
ուղղումներից
որն է մեծ դեր խաղում:
Վերլուծենք տվյալ
արտահայտությունը`
ենթադրություն
անելով, որ և ![]()
1) ![]() այսինքն
հաշվի չենք առնում
մոլեկուլների
միջև ձգողության
ուժերը, հաշվի
ենք առնում միայն
մոլեկուլների
սեփական չափերը:
Այս դեպքում
այսինքն
հաշվի չենք առնում
մոլեկուլների
միջև ձգողության
ուժերը, հաշվի
ենք առնում միայն
մոլեկուլների
սեփական չափերը:
Այս դեպքում
![]()
այսինքն` տվյալ դեպքում գազը տաքանում է:
2) ![]() այսինքն
հաշվի չենք առնում
մոլեկուլների
չափերը, հաշվի
ենք առնում միայն
մոլեկուլների
միջև ձգողության
ուժերը:
այսինքն
հաշվի չենք առնում
մոլեկուլների
չափերը, հաշվի
ենք առնում միայն
մոլեկուլների
միջև ձգողության
ուժերը:

այսինքն տվյալ դեպքում գազը սառչում է.
3) երկու ուղղումներն
էլ հաշվի ենք առնում:
Տեղադրելով (12.14) արտահայտության
մեջ Վան-դեր-Վալսի
(12.7) հավասարումից
նախորոշված ![]() արժեքը,
կունենանք`
արժեքը,
կունենանք`
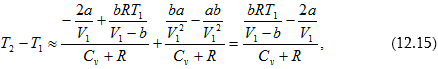
այսինքն` ջերմաստիճանների
տարբերության
նշանը կախված է
սկզբնական ![]() ծավալի
և սկզբնական
ծավալի
և սկզբնական ![]() ջերմաստիճանի
արժեքներից: Իրական
գազի ջերմաստիճանի
փոփոխությունը
նրա ադիաբատ ընդարձակման
կամ, ինչպես ասում
են, ադիաբատ դրոսելման
արդյունքում, գազի
դանդաղ անցումը
դրոսելով (օրինակ,
ծակոտկեն միջնորմով)
ճնշման անկման
ազդեցության տակ
կոչվում է Ջոուլ-Թոմսոնի
էֆեկտ: Ջոուլ-Թոմսոնի
էֆեկտը ընդունված
է անվանել դրական,
եթե գազը դրոսելման
պրոցեսում սառչում
է
ջերմաստիճանի
արժեքներից: Իրական
գազի ջերմաստիճանի
փոփոխությունը
նրա ադիաբատ ընդարձակման
կամ, ինչպես ասում
են, ադիաբատ դրոսելման
արդյունքում, գազի
դանդաղ անցումը
դրոսելով (օրինակ,
ծակոտկեն միջնորմով)
ճնշման անկման
ազդեցության տակ
կոչվում է Ջոուլ-Թոմսոնի
էֆեկտ: Ջոուլ-Թոմսոնի
էֆեկտը ընդունված
է անվանել դրական,
եթե գազը դրոսելման
պրոցեսում սառչում
է ![]() և
բացասական, եթե
գազը տաքանում
է
և
բացասական, եթե
գազը տաքանում
է ![]()
Կախված դրոսելման պայմանից` միևնույն գազի համար Ջոուլ-Թոմսոնի էֆեկտը կարող է լինել ինչպես դրական, այնպես էլ բացասական: Ջերմաստիճանը, որի դեպքում (տվյալ ճնշման համար) տեղի ունի Ջոուլ-Թոմսոնի էֆեկտի նշանի փոփոխություն, կոչվում է ինվերսիայի ջերմաստիճան: Նրա կախվածությունը ծավալից կստանանք` հավասարեցնելով (12.15) արտահայտությունը զրոյի.
![]()
(12.16) հավասարումով որոշվող կորը` ինվերսիայի կորը, բերված է նկ.12.8-ում: Այդ կորի վերևի տիրույթը համապատասխանում է Ջոուլ-Թոմսոնի բացասական էֆեկտին, կորից ներքևի տիրույթը` դրականին:
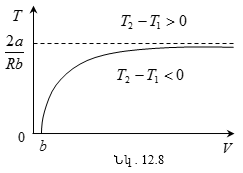
Նշենք, որ ճնշման
մեծ անկումների
դեպքում դրոսելում
գազի ջերմաստիճանը
նշանակալից չափով
փոփոխվում է: Այսպես,
20-ից մինչև 0,1ՄՊա
170C սկզբնական
ջերմաստիճանի
դրոսելման դեպքում
օդը սառչում է
350C -ով: Ջոուլ-Թոմսոնի
էֆեկտը պայմանավորված
է գազի շեղումով
իդեալականից: Իրոք,
մեկ մոլ իդեալական
գազի համար ![]() ուստի
(12.13) արտահայտությունը
կընդունի հետևյալ
տեսքը`
ուստի
(12.13) արտահայտությունը
կընդունի հետևյալ
տեսքը`
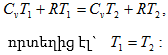
12.7. ՀԵՂՈՒԿՆԵՐԻ ՀԱՏԿՈՒԹՅՈՒՆՆԵՐԸ: ՄԱԿԵՐԵՎՈՒԹԱՅԻՆ
ԼԱՐՎԱԾՈՒԹՅՈՒՆ
Հեղուկ վիճակը
միջանկյալ վիճակ
է գազային և պինդ
վիճակների միջև
և նմանություն
ունի ինչպես մեկի,
այնպես էլ մյուսի
հետ: Հեղուկները
պինդ մարմինների
նման ունեն որոշակի
ծավալ և ընդունում
են այն անոթի ձևը,
որի մեջ նրանք
գտնվում են: Գազի
մոլեկուլները
գործնականում
կապված չեն միմյանց
հետ միջմոլեկուլային
փոխազդեցության
ուժերով, և տվյալ
դեպքում գազի մոլեկուլների
ջերմային շարժման
միջին էներգիան
ավելի մեծ է մոլեկուլների
ձգողությամբ պայմանավորված
միջին պոտենցիալ
էներգիայից, ուստի
գազի մոլեկուլները
թռչում են տարբեր
կողմեր, և գազը
զբաղեցնում է իրեն
տրամադրված ամբողջ
ծավալը: Պինդ և
հեղուկ մարմիններում
մոլեկուլների
միջև փոխազդեցության
ուժերը արդեն էական
են և պահում են
մոլեկուլներին
միմյանցից որոշակի
հեռավորության
վրա: Այս դեպքում
մոլեկուլների
քաոսային (ջերմային)
շարժման միջին
էներգիան փոքր
է մոլեկուլների
փոխազդեցության
ուժերով պայմանավորված
միջին պոտենցիալ
էներգիայից, և
այն բավարար չէ
մոլեկուլների
միջև ձգողական
ուժերը հաղթահարելու
համար, դրա համար
էլ պինդ մարմինները
և հեղուկները որոշակի
ծավալ են ունենում:
Հեղուկների ռենտգենակառուցվածքային
անալիզը ցույց
է տվել, որ հեղուկների
մասնիկների դասավորության
բնույթը միջանկյալ
է հեղուկների և
պինդ մարմինների
միջև: Գազերում
մոլեկուլները
շարժվում են քաոսայնորեն,
ուստի նրանց փոխադարձ
դասավորության
ոչ մի օրինաչափություն
չկա: Պինդ մարմինների
համար դիտվում
է մասնիկների դասավորության,
այսպես կոչված,
հեռակա կարգ,
այսինքն` մասնիկների
կարգավորված դասավորություն,
որը կրկնվում է
մեծ հեռավորությունների
վրա: Հեղուկներում
գոյություն ունի
այսպես կոչված
մոտակա կարգ,
այսինքն` մասնիկների
կարգավորված դասավորություն,
կրկնվելով միջատոմային
հեռավորությունների
հետ համեմատելի
հեռավորությունների
վրա: Մինչև ներկա
ժամանակները հեղուկների
լրիվ տեսություն
չի տրվել: Հեղուկների
հատկությունների
ուսումնասիրության
մի շարք հիմնախնդիրների
մշակումը պատկանում
է Յ. Ֆրենկելին
(1894-1952):Ֆրենկելը մշակել
է տեսություն,
որի համաձայն հեղուկի
մոլեկուլը որոշակի
ժամանակի ընթացքում
տատանվում է իր
հավասարակշռության
դիրքի շուրջը,
կարծես թե գտնվելով
բյուրեղային ցանցի
հանգույցում: Հեղուկի
մոլեկուլի նստակյաց
կյանքի տևողությունը
շատ փոքր է ![]() որից
հետո հեղուկի մոլեկուլը
թռիչքով անցնում
է հավասարակշռության
նոր դիրք (նոր հանգույց):
Պարզագույն դեպքերում
հեղուկի մոլեկուլների
վազքը համընկնում
է ցանցի հաստատունի
հետ (երկու հարևան
հանգույցների
միջև եղած հեռավորության
հետ): Մոլեկուլը,
գտնվելով ցանցի
հանգույցում` կատարում
է ցանցի հաստատունից
փոքր լայնույթով
ջերմային տատանումներ:
Դա թույլ է տալիս
ընդունել, որ հեղուկը
ունի քվազիբյուրեղային
կառուցվածք: Այսպիսով,
հեղուկի մոլեկուլները
բավականին դանդաղ
տեղափոխվում են
հեղուկի ամբողջ
զանգվածով, և դիֆուզիան
տեղի է ունենում
ավելի դանդաղ,
քան գազերում:
Հեղուկի ջերմաստիճանը
բարձրացնելով
տատանողական շարժման
հաճախությունը`
կտրուկ մեծանում
է, աճում է մոլեկուլների
շարժունակությունը,
որն էլ իր հերթին
դառնում է հեղուկի
մածուցիկության
փոքրացման պատճառ:
որից
հետո հեղուկի մոլեկուլը
թռիչքով անցնում
է հավասարակշռության
նոր դիրք (նոր հանգույց):
Պարզագույն դեպքերում
հեղուկի մոլեկուլների
վազքը համընկնում
է ցանցի հաստատունի
հետ (երկու հարևան
հանգույցների
միջև եղած հեռավորության
հետ): Մոլեկուլը,
գտնվելով ցանցի
հանգույցում` կատարում
է ցանցի հաստատունից
փոքր լայնույթով
ջերմային տատանումներ:
Դա թույլ է տալիս
ընդունել, որ հեղուկը
ունի քվազիբյուրեղային
կառուցվածք: Այսպիսով,
հեղուկի մոլեկուլները
բավականին դանդաղ
տեղափոխվում են
հեղուկի ամբողջ
զանգվածով, և դիֆուզիան
տեղի է ունենում
ավելի դանդաղ,
քան գազերում:
Հեղուկի ջերմաստիճանը
բարձրացնելով
տատանողական շարժման
հաճախությունը`
կտրուկ մեծանում
է, աճում է մոլեկուլների
շարժունակությունը,
որն էլ իր հերթին
դառնում է հեղուկի
մածուցիկության
փոքրացման պատճառ:
Հեղուկի յուրաքանչյուր մոլեկուլի վրա շրջապատող մոլեկուլների կողմից ազդում են հեռավորության հետ արագ նվազող ձգողության ուժեր: Հետևաբար, սկսած որոշակի նվազագույն հեռավորությունից, մոլեկուլների միջև ձգողության ուժերը կարելի է անտեսել: Այդ r հեռավորությունը (10-9 մ կարգի) կոչվում է մոլեկուլային ազդեցության շառավիղ, իսկ r շառավղով գնդոլորտը` մոլեկուլային ազդեցության ոլորտ:
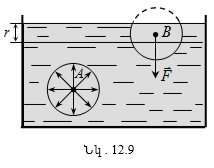
եղուկին ներսում մտովի առանձնացնենք որևէ A մոլեկուլ, դրա շուրջը տանենք r շառավղով գնդոլորտ` A մոլեկուլի ազդեցության ոլորտը (նկ. 12.9): Վեջինիս մեջ գտնվող մոլեկուլները ձգվում են A մոլեկուլի կողմից, իսկ նրանից դուրս գտնվողները չեն փոխազդում A-ի հետ: Ազդեցության ոլորտում կգտնվեն մեծ թվով մոլեկուլներ, և դրանց կողմից A մոլեկուլի վրա ազդող միջին ուժը հավասար կլինի զրոյի:
Եթե B մոլեկուլը
գտնվում է հեղուկի
մակերևույթին,
ապա նրա ազդեցության
ոլորտի ստորին
կեսը լցնում են
հեղուկի, իսկ վերին
կեսը` հեղուկից
վեր գտնվող գազի
(գոլորշու) մոլեկուլները:
Քանի որ գոլորշու
խտությունը շատ
անգամ փոքր է հեղուկի
խտությունից, ապա
B մոլեկուլի ազդեցության
ոլորտի վերին կեսում
մոլեկուլների
թիվը շատ փոքր
կլինի ստորին կեսում
մոլեկուլների
թվից: Հետևաբար,
B մոլեկուլի վրա
ազդող ձգողության
ուժերի ![]() համազորն
ուղղված կլինի
հեղուկի մակերևույթին
ուղղահայաց` դեպի
հեղուկի խորքը:
Այսպիսով, մակերևութային
շերտի բոլոր մոլեկուլների
արդյունարար ուժերը
հեղուկի վրա գործադրում
են ճնշում, որն
անվանում են մոլեկուլային
(կամ ներքին) ճնշում:
Հեղուկի խորքում
գտնվող A մոլեկուլի
և մակերևութային
շերտում գտնվող
B մոլեկուլի վիճակների
տարբերությունը
պարզորոշ է դրսևորվում
հատկապես էներգիական
տեսանկյունից:
Հեղուկի ողջ ծավալում
հաստատուն ջերմաստիճանում
մոլեկուլների
միջին կինետիկ
էներգիան միևնույնն
է: Սակայն եթե համեմատենք
մոլեկուլների
պոտենցիալ էներգիաները,
ապա կհամոզվենք,
որ դրանք միևնույնն
են միայն հեղուկի
խորքում գտնվող
մոլեկուլների
համար: Մակերևութային
շերտի մոլեկուլներն
ունեն ավելի մեծ
պոտենցիալ էներգիա
խորքում գտնվողների
համեմատությամբ,
քանի որ մոլեկուլը
հեղուկի խորքից
մակերևութային
շերտ մտցնելու
համար անհրաժեշտ
է կատարել որոշակի
աշխատանք ձգողության
ուժերի համազորի
դեմ: Որքան մեծ
է հեղուկի մակերևույթի
մակերեսը, այնքան
շատ մոլեկուլներ
են օժտված այդ
հավելուրդային
պոտենցիալ էներգիայով:
Հետևաբար` տրված
զանգվածով հեղուկի
մակերևույթի մակերեսը
մեծանալիս (օրինակ`
հեղուկի մեծ կաթիլը
մանր կաթիլների
տրոհելիս) հեղուկի
ներքին էներգիան
մեծանում է: Ներքին
էներգիայի մեջ
մակերևութային
շերտի բաժինը համեմատական
է մակերևութային
շերտի մակերեսին,
ուստի այն անվանում
են մակերևութային
էներգիա: Մակերևութային
էներգիան`
համազորն
ուղղված կլինի
հեղուկի մակերևույթին
ուղղահայաց` դեպի
հեղուկի խորքը:
Այսպիսով, մակերևութային
շերտի բոլոր մոլեկուլների
արդյունարար ուժերը
հեղուկի վրա գործադրում
են ճնշում, որն
անվանում են մոլեկուլային
(կամ ներքին) ճնշում:
Հեղուկի խորքում
գտնվող A մոլեկուլի
և մակերևութային
շերտում գտնվող
B մոլեկուլի վիճակների
տարբերությունը
պարզորոշ է դրսևորվում
հատկապես էներգիական
տեսանկյունից:
Հեղուկի ողջ ծավալում
հաստատուն ջերմաստիճանում
մոլեկուլների
միջին կինետիկ
էներգիան միևնույնն
է: Սակայն եթե համեմատենք
մոլեկուլների
պոտենցիալ էներգիաները,
ապա կհամոզվենք,
որ դրանք միևնույնն
են միայն հեղուկի
խորքում գտնվող
մոլեկուլների
համար: Մակերևութային
շերտի մոլեկուլներն
ունեն ավելի մեծ
պոտենցիալ էներգիա
խորքում գտնվողների
համեմատությամբ,
քանի որ մոլեկուլը
հեղուկի խորքից
մակերևութային
շերտ մտցնելու
համար անհրաժեշտ
է կատարել որոշակի
աշխատանք ձգողության
ուժերի համազորի
դեմ: Որքան մեծ
է հեղուկի մակերևույթի
մակերեսը, այնքան
շատ մոլեկուլներ
են օժտված այդ
հավելուրդային
պոտենցիալ էներգիայով:
Հետևաբար` տրված
զանգվածով հեղուկի
մակերևույթի մակերեսը
մեծանալիս (օրինակ`
հեղուկի մեծ կաթիլը
մանր կաթիլների
տրոհելիս) հեղուկի
ներքին էներգիան
մեծանում է: Ներքին
էներգիայի մեջ
մակերևութային
շերտի բաժինը համեմատական
է մակերևութային
շերտի մակերեսին,
ուստի այն անվանում
են մակերևութային
էներգիա: Մակերևութային
էներգիան`
![]()
որտեղ ![]() հեղուկի
մակերևութային
լարվածությունն
է:
հեղուկի
մակերևութային
լարվածությունն
է:
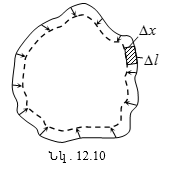
Քանի որ հավասարակշիռ վիճակը բնութագրվում է պոտենցիալ էներգիայի նվազագույնով, ապա հեղուկը արտաքին ուժերի բացակայության դեպքում պետք է ընդունի այնպիսի ձև, որպեսզի տրված ծավալի դեպքում ունենա նվազագույն մակերևույթ, այսինքն` գնդի ձև: Դիտելով օդում կախված փոքրագույն մանիկները` կարող ենք տեսնել, որ իրոք դրանք ունեն գնդիկների տեսք, բայց փոքր-ինչ աղավաղված են ձգողության ուժի ազդեցության հետևանքով: Ցանկացած հեղուկի կաթիլը անկշռելության պայմաններում, անկախ նրա չափերից, ունի սֆերիկ ձև, որն ապացուցվել է տիեզերանավերում կատարված փորձերով:
Այսպիսով, հեղուկի կայուն հավասարկշիռ պայմանը մակերևութային էներգիայի նվազագույն լինելն է: Սա նշանակում է, որ տրված ծավալի դեպքում հեղուկը պետք է ունենա մակերևույթի ամենափոքր մակերես, այսինքն` հեղուկը ձգտում է փոքրացնել ազատ մակերևույթի մակերեսը: Այս դեպքում հեղուկի մակերևութային շերտը կարելի է նմանեցնել ձգված առաձգական թաղանթի, ուր ազդում են լարվածության ուժերը:
Դիտարկենք փակ կոնտուրով սահմանափակված հեղուկի մակերևույթը (նկ.12.10): Մակերևութային ուժերի ազդեցության տակ (ուղղված են հեղուկի մակերևույթին շոշափողով և ուղղահայաց են կոնտուրի տեղամասին, որի վրա նրանք ազդում են) հեղուկի մակերևույթը կրճատվում է, և դիտարկվող կոնտուրը տեղափոխվում է նոր դիրք (նկարում նշված են սլաքներով): Առանձնացված տեղամասի կողմից ազդող ուժերը նրան սահմանակից տեղամասերի վրա կատարում են աշխատանք.
![]()
որտեղ ![]() մակերևութային
լարվածության
ուժն է, որն ազդում
է հեղուկի մակերևույթի
կոնտուրի միավոր
երկարության վրա:
մակերևութային
լարվածության
ուժն է, որն ազդում
է հեղուկի մակերևույթի
կոնտուրի միավոր
երկարության վրա:
![]()
![]()
Այս աշխատանքը կատարվում է մակերևութային էներգիայի նվազման հաշվին, այսինքն
![]()
(12.17) - (12.19) արտահայտությունների համեմատությունից հետևում է, որ
![]()
այսինքն` մակերևութային
լարվածությունը
հավասար է մակերևույթը
սահմանափակող
կոնտուրի միավոր
երկարությանն
ընկնող մակերևութային
լարվածության
ուժին: ![]() կարելի
է սահմանել որպես
հեղուկի մակերևույթի
մակերեսը հաստատուն
ջերմաստիճանում
միավոր մակերեսով
մեծացնելու համար
պահանջվող աշխատանք:
Մակերևութային
լարվածության
միավորը Ն/մ3 կամ
Ջ/մ3 է:
կարելի
է սահմանել որպես
հեղուկի մակերևույթի
մակերեսը հաստատուն
ջերմաստիճանում
միավոր մակերեսով
մեծացնելու համար
պահանջվող աշխատանք:
Մակերևութային
լարվածության
միավորը Ն/մ3 կամ
Ջ/մ3 է:
Հեղուկների
մեծամասնության
համար 300Կ ջերմաստիճանի
դեպքում մակերևութային
լարվածությունը
10-2-10-1 Ն/մ կարգի
է: Ջերմաստիճանը
բարձրացնելիս
մակերևութային
լարվածությունը
փոքրանում է, քանի
որ մեծանում է
հեղուկի մոլեկուլների
միջև միջին հեռավորությունը:
Մակերևութային
լարվածությունը
կախված է հեղուկի
տեսակից և հեղուկում
խառնուրդների
առկայությունից:
Այն նյութերը,
որոնք թուլացնում
են հեղուկի մակերևութային
լարվածությունը
կոչվում են մակերևութաակտիվ:
Ջրի նկատմամբ ավելի
հայտնի մակերևութաակտիվ
նյութ է օճառը:
Այն շատ է փոքրացնում
նրա մակերևութային
լարվածությունը
![]() Մակերևութաակտիվ
նյութեր են սպիրտները,
եթերը, նավթը և
այլն, որոնք թուլացնում
են ջրի մակերևութային
լարվածությունը:
Գոյություն ունեն
նյութեր (շաքար,
աղ), որոնք մեծացնում
են հեղուկի մակերևութային
լարվածությունը,
շնորհիվ այն բանի,
որ դրանց մոլեկուլները
ավելի ուժեղ են
փոխազդում հեղուկի
մոլեկուլների
հետ, քան հեղուկի
մոլեկուլները
միմյանց հետ: Մակերևութային
լարվածությունը
կախված չէ հեղուկի
մակերևույթի մակերեսից:
Մակերևութաակտիվ
նյութեր են սպիրտները,
եթերը, նավթը և
այլն, որոնք թուլացնում
են ջրի մակերևութային
լարվածությունը:
Գոյություն ունեն
նյութեր (շաքար,
աղ), որոնք մեծացնում
են հեղուկի մակերևութային
լարվածությունը,
շնորհիվ այն բանի,
որ դրանց մոլեկուլները
ավելի ուժեղ են
փոխազդում հեղուկի
մոլեկուլների
հետ, քան հեղուկի
մոլեկուլները
միմյանց հետ: Մակերևութային
լարվածությունը
կախված չէ հեղուկի
մակերևույթի մակերեսից:
Գործնականում հայտնի է, որ ջրի կաթիլը տարածվում է ապակու վրա և ընդունում է նկ. 10.11-ում պատկերված ձևը, միևնույն ժամանակ նույն մակերևույթի վրա սնդիկը փոխարկվում է տափակած կաթիլի (նկ.10.12): Առաջին դեպքում ասում են, որ հեղուկը թրջում է պինդ մակերևույթը, երկրորդում` չի թրջում: Թրջումը կախված է հպվող միջավայրերի մակերևույթների շերտերի մոլեկուլների միջև ազդող ուժերի բնույթից: Թրջող հեղուկների համար հեղուկի և պինդ մարմնի մոլեկուլների միջև գործող ուժերը գերազանցում են հեղուկի մոլեկուլների միջև գործող ձգողության ուժերը: Չթրջող հեղուկների համար հեղուկ-պինդ մարմին ձգողությունը չի գերազանցում հեղուկի մոլեկուլների ձգողությունը, հեղուկը ձգտում է ընդունել գնդի ձև:
Երեք միջավայրերի
հպման գծին (O կետը,
նրա հատումն է
նկարի հարթության
հետ) կիրառված
են մակերևութային
լարվածության
երեք ուժեր, որոնք
ուղղված են շոշափողով
համապատասխան
երկու հպվող միջավայրերի
մակերևույթների
ներսը (նկ.12.11 և 12.12): Այդ
ուժերը վերագրված
հպման գծի միավոր
երկարությանը,
հավասար են համապատասխան
մակերևութային
լարվածություններին`![]() Հեղուկի
մակերևույթին
տարված շոշափող
հարթության և պինդ
մարմնի մակերևույթով
կազմված
Հեղուկի
մակերևույթին
տարված շոշափող
հարթության և պինդ
մարմնի մակերևույթով
կազմված ![]() անկյունը
կոչվում է եզրային
անկյուն: Կաթիլի
հավասարակշռության
պայմանի դեպքում
(նկ.12.11) պինդ մարմնի
մակերևույթի շոշափողի
ուղղության վրա
լարվածության
ուժերի պրոյեկցիաների
գումարը պետք է
հավասար լինի զրոյի,
այսինքն`
անկյունը
կոչվում է եզրային
անկյուն: Կաթիլի
հավասարակշռության
պայմանի դեպքում
(նկ.12.11) պինդ մարմնի
մակերևույթի շոշափողի
ուղղության վրա
լարվածության
ուժերի պրոյեկցիաների
գումարը պետք է
հավասար լինի զրոյի,
այսինքն`
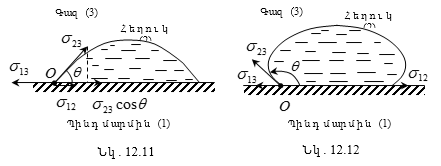
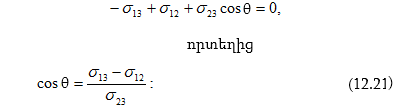
(12.21) պայմանից
բխում է, որ եզրային
անկյունը, կախված
![]() արժեքներից,
կարող է լինել
սուր անկյուն կամ
բութ անկյուն:
արժեքներից,
կարող է լինել
սուր անկյուն կամ
բութ անկյուն:
![]()
այսինքն հեղուկը թրջում է պինդ մակերևույթը:
![]()
այսինքն` հեղուկը չի թրջում պինդ մակերևույթը: Եզրային անկյունը բավարարում է (12.21) պայմանին, եթե
![]()
Եթե (12.22) պայմանը
տեղի չունի, ապա
հեղուկի կաթիլը
![]() ոչ մի
արժեքի դեպքում
չի կարող գտնվել
հավասարակշռության
մեջ: Եթե
ոչ մի
արժեքի դեպքում
չի կարող գտնվել
հավասարակշռության
մեջ: Եթե ![]() հեղուկը
տարածվում է պինդ
մարմնի մակերևույթով,
ծածկելով այն բարակ
շերտով (օրինակ,
կերոսինը ապակու
մակերևույթի վրա),
այս դեպքում տեղի
ունի լրիվ թրջում
(տվյալ դեպքում
հեղուկը
տարածվում է պինդ
մարմնի մակերևույթով,
ծածկելով այն բարակ
շերտով (օրինակ,
կերոսինը ապակու
մակերևույթի վրա),
այս դեպքում տեղի
ունի լրիվ թրջում
(տվյալ դեպքում
![]() ): Եթե
): Եթե
![]() հեղուկը
դառնում է գնդային
կաթիլ, սահմանում
ունենալով հպման
միայն մի կետ (օրինակ,
ջրի կաթիլը պարաֆինի
մակերևույթի վրա),
այս դեպքում տեղի
ունի ոչ լրիվ թրջում
(տվյալ դեպքում`
հեղուկը
դառնում է գնդային
կաթիլ, սահմանում
ունենալով հպման
միայն մի կետ (օրինակ,
ջրի կաթիլը պարաֆինի
մակերևույթի վրա),
այս դեպքում տեղի
ունի ոչ լրիվ թրջում
(տվյալ դեպքում`
![]() ):
):
Թրջումը և չթրջումը հարաբերական հասկացություններ են, այսինքն հեղուկը թրջելով մեկ պինդ մակերևույթ, չի թրջում մյուսը. օրինակ, ջուրը թրջում է ապակին, բայց չի թրջում պարաֆինը. սնդիկը չի թրջում ապակին, բայց թրջում է մաքուր մետաղների մակերևույթները:
Թրջելու և չթրջելու երևույթն ունի մեծ գործնական նշանակություն: Այն օգտագործվում է ներկման, զոդման և այլ գործընթացներում և հատկապես հանքարդյունաբերության մեջ` հանքանյութի հարստացման համար: Հարըստացման պրոցեսում օգտագործվում է տարբեր խառնուրդների միջոցով հեղուկի մակերևույթին լարվածության փոփոխման և հեղուկի կողմից տարբեր պինդ մարմիններ` ոչ միևնույն ձևով թրջելու հատկությունը: Օգտակար հանածո պարունակող հանքանյութը աղալով վերածում են 0.1- 0.01 մմ չափի հատիկներով փոշու և խառնում ջրի հետ: Այնուհետև ջրի մեջ կաթեցնում են որևէ հեղուկ (օրինակ, յուղ), որը թրջում է մետաղի հատիկները, սակայն չի թրջում դատարկ ապարը: Ջրի և փոշու խառնուրդի մեջ օդ է մղվում և ինտենսիվորեն խառնվում: Օդի պղպջակները կպչում են յուղի բարակ շերտով պատված մետաղի հատիկներին: Մետաղի հատիկի և նրան կպած օդի պղպջակի միջին խտությունը ջրի խտությունից ավելի փոքր է ստացվում, ուստի մետաղահատիկը լողում է դեպի վեր: Դատարկ ապարի հատիկները չեն կպչում օդի պղպջակներին և իջնում են ներքև` հավաքվելով անոթի հատակին: Այս եղանակով օգտակար հանածոն անջատում են դատարկ ապարներից և ստանում օգտակար հանածոյով հարուստ և հետագա մշակման համար պիտանի խտանյութ:
12. 9. ՃՆՇՈՒՄԸ ՀԵՂՈՒԿԻ ԿՈՐԱՑԱԾ ՄԱԿԵՐԵՎՈՒՅԹԻ ՏԱԿ
Եթե հեղուկի մակերևույթը հարթ չէ, այլ` կորացած, ապա այն հեղուկի վրա գործադրում է հավելուրդային (լրացուցիչ) ճնշում: Այդ ճնշումը պայմանավորված է մակերևութային ուժերով, ընդ որում ուռուցիկ մակերևույթի համար դրական է, իսկ գոգավորի համար` բացասական:
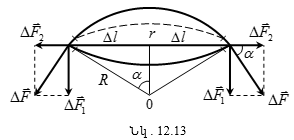
Հավելուրդային
ճնշման հաշվարկի
համար, ենթադրենք,
որ հեղուկի ազատ
մակերևույթը ունի
R շառավղով սֆերայի
ձև, որից մտովի
կտրված է գնդային
սեգմենտ, որը հենված
է ![]() շառավղով
շրջանագծի վրա
(նկ.12.13): Այդ կոնտուրի
յուրաքանչյուր
անվերջ փոքր
շառավղով
շրջանագծի վրա
(նկ.12.13): Այդ կոնտուրի
յուրաքանչյուր
անվերջ փոքր ![]() երկարության
տարրի վրա ազդում
է սֆերայի մակերևույթին
շոշափող` մակերևութային
լարվածության
երկարության
տարրի վրա ազդում
է սֆերայի մակերևույթին
շոշափող` մակերևութային
լարվածության
![]() ուժը:
ուժը:
![]() վերլուծելով
երկու բաղադրիչների
վերլուծելով
երկու բաղադրիչների
![]() տեսնում
ենք, որ
տեսնում
ենք, որ ![]() ուժերի
երկրաչափական
գումարը հավասար
է զրոյի, քանի որ
կոնտուրի հակադիր
կողմերում այդ
ուժերն ուղղված
են հակառակ ուղղություններով
և միմյանց փոխադարձաբար
հավասարակշռում
են: Ուստի կտրված
սեգմենտի վրա ազդող
մակերևութային
լարվածության
ուժերի համազորը
հեղուկի ներսում
ուղղված է հարթության
կտրվածքին ուղղահայաց
և հավասար է
ուժերի
երկրաչափական
գումարը հավասար
է զրոյի, քանի որ
կոնտուրի հակադիր
կողմերում այդ
ուժերն ուղղված
են հակառակ ուղղություններով
և միմյանց փոխադարձաբար
հավասարակշռում
են: Ուստի կտրված
սեգմենտի վրա ազդող
մակերևութային
լարվածության
ուժերի համազորը
հեղուկի ներսում
ուղղված է հարթության
կտրվածքին ուղղահայաց
և հավասար է ![]() բաղադրիչ
ուժերի հանրահաշվական
գումարին.
բաղադրիչ
ուժերի հանրահաշվական
գումարին.
![]()
Բաժանելով
այդ ուժը սեգմենտի
հիմքի ![]() մակերեսին`
կհաշվենք հավելուրդային
ճնշումը հեղուկի
վրա, որն առաջացնում
են մակերևութային
լարվածության
ուժերը` պայմանավորված
մակերևույթի կորությամբ.
մակերեսին`
կհաշվենք հավելուրդային
ճնշումը հեղուկի
վրա, որն առաջացնում
են մակերևութային
լարվածության
ուժերը` պայմանավորված
մակերևույթի կորությամբ.
![]()
Եթե հեղուկի մակերևույթը գոգավոր է, ապա կարելի է ապացուցել, որ մակերևութային լարվածության ուժն ուղղված է հեղուկից դեպի վեր և հավելուրդային ճնշումը`
![]()
Հետևաբար,
հեղուկի ներսում
գոգավոր մակերևույթի
տակ ճնշումը ![]() ավելի
փոքր է, քան գազում:
ավելի
փոքր է, քան գազում:
(12.23) և (12.24) բանաձևերը Լապլասի բանաձևի մասնավոր դեպքերն են, որով որոշվում է հավելուրդային ճնշումը երկակի կորությամբ հեղուկի կամայական մակերևույթի համար.

որտեղ ![]() տվյալ
կետում հեղուկի
երկու ցանկացած
փոխադարձաբար
ուղղահայաց նորմալ
մակերևույթների
կորության շառավիղներն
են:
տվյալ
կետում հեղուկի
երկու ցանկացած
փոխադարձաբար
ուղղահայաց նորմալ
մակերևույթների
կորության շառավիղներն
են:
Կորության շառավիղը դրական է, եթե համապատասխան կտրվածքի կորության կենտրոնը գտնվում է հեղուկի ներսում և բացասական, եթե կորության կենտրոնը գտնվում է հեղուկից դուրս:
Սֆերիկ կոր
մակերևույթների
համար ![]() (12.25) արտահայտությունը
փոխակերպվում
է (12.24)-ի, գլանայինի
համար
(12.25) արտահայտությունը
փոխակերպվում
է (12.24)-ի, գլանայինի
համար ![]() հավելուրդային
ճնշումը`
հավելուրդային
ճնշումը`
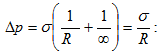
Հարթ մակերևույթի
դեպքում ![]() մակերևութային
լարվածության
ուժերը հավելուրդային
ճնշում չեն առաջացնում:
մակերևութային
լարվածության
ուժերը հավելուրդային
ճնշում չեն առաջացնում:
Եթե նեղ խողովակի (մազախողովակ) մի ծայրը իջեցնենք լայն անոթի մեջ, որը լցված է հեղուկով, ապա մազախողովակի պատերը հեղուկի թրջման կամ չթրջման հետևանքով, հեղուկի մակերևույթի կորությունը մազախողովակում դառնում է նշանակալից: Եթե հեղուկը թրջում է խողովակի պատերը, ապա հեղուկի մակերևույթը ընդունում է գոգավոր ձև (նկ. 12.14), իսկ չթրջող հեղուկինը` ուռուցիկ: Հեղուկի նման ձևի կորացած մակերևույթները կոչվում են մենիսկ:
Հեղուկի գոգավոր մակերևույթի տակ առաջանում է (12.24) բանաձևով որոշվող հավելուրդային բացասական ճնշում: Այս ճնշման առկայությունը հանգեցնում է նրան, որ մազախողովակում հեղուկը բարձրանում է, քանի որ լայն անոթում հեղուկի հարթ մակերևույթի տակ հավելուրդային ճնշում չկա: Եթե հեղուկը չի թրջում մազախողովակի պատերը, ապա դրական հավելուրդային ճնշումը բերում է մազախողովակում հեղուկի իջեցմանը:
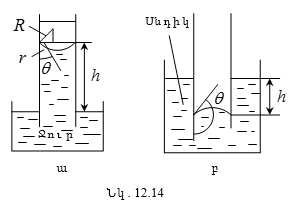
Մազախողովակներում
հեղուկի մակարդակի
փոփոխության երևույթը
կոչվում է մազականություն:
Հեղուկը մազախողովակում
բարձրանում կամ
իջնում է այնպիսի
h բարձրության
վրա, որի դեպքում
հեղուկի սյան ![]() hիդրոստատիկ
ճնշումը հավասարակշռվում
է հավելուրդային
hիդրոստատիկ
ճնշումը հավասարակշռվում
է հավելուրդային
![]() ճնշումով,
այսինքն`
ճնշումով,
այսինքն`
![]()
որտեղ p-ն հեղուկի խտությունն է, g-ն` ազատ անկման արագացումը:
Եթե r-ը մազախողովակի
շառավիղն է, ![]() եզրային
անկյունը, ապա
նկ. 12.14-ից հետևում
է, որ
եզրային
անկյունը, ապա
նկ. 12.14-ից հետևում
է, որ

Համապատասխան այն երևույթի, որ թրջող հեղուկը մազախողովակում բարձրանում է, (12.26) բանաձևից կստանանք h-ի դրական արժեքներ`
![]()
![]()
(12.26) արտահայտությունից
նույնպես հետևում
է, որ մազախողովակում
հեղուկի բարձրանալը
(իջնելը) հակադարձ
համեմատական է
նրա շառավղին:
Բարակ մազախողովակներում
հեղուկը բարձրանում
է բավականին բարձր:
Այսպես, լրիվ թրջման
դեպքում ![]() ջուրը
ջուրը
![]() 10մկմ
տրամագծով մազախողովակում
բարձրանում է
10մկմ
տրամագծով մազախողովակում
բարձրանում է ![]()
Մազական երևույթները մեծ դեր են խաղում բնության մեջ, լայնորեն կիրառվում են տեխնիկայում, կենցաղում: Այսպես, բույսերի արմատներում, ցողուններում և տերևներում առկա մազանոթային համակարգի միջոցով ջուրը և սննդանյութերի ջրային լուծույթները թափանցում և տարածվում են բույսերում: Ջուրը գետնի վերին շերտերն է բարձրանում մազականության շնորհիվ:
Շինարարության մեջ օգտագործվող շինանյութերում (քար, աղյուս բետոն, փայտ և այլն) կան բազմաթիվ մազանոթներ, որոնցով ջուրը շինության հիմքից բարձրանում է վեր` խոնավացնելով կառույցը: Ուստի կառույցները խոնավությունից պաշտպանելու նպատակով կիրառում են ջրամեկուսացում` դրանց հիմքերը պատելով տաք բիտումով, ջրամերժ ցեմենտով և այլ ջրամեկուսիչ նյութերով:
12.11. ՊԻՆԴ ՄԱՐՄԻՆՆԵՐ: ՄԻԱԲՅՈՒՐԵՂՆԵՐ
ԵՎ ԲԱԶՄԱԲՅՈՒՐԵՂՆԵՐ
Պինդ մարմինները (բյուրեղները) բնութագրվում են նշանակալից միջմոլեկուլային փոխազդեցության ուժերի առկայությամբ և պահպանում են ոչ միայն իրենց ծավալը, այլև` ձևը: Բյուրեղներն ունեն կանոնավոր երկրաչափական ձև, որը ինչպես ցույց են տվել գերմանացի ֆիզիկոս Մ. Լաուեի (1879-1960) կողմից կատարված ռենտգենագրական հետազոտությունները, մասնիկների (ատոմներ, մոլեկուլներ, իոններ) կարգավորված դասավորության արդյունք է, կազմելով բյուրեղը:
Կառուցվածքը, որի համար բնութագրական է մասնիկների կանոնավոր պարբերական կրկնողությունը երեք չափումներով, կոչվում է բյուրեղական ցանց: Այն կետերը, որոնցում դասավորված են մասնիկները, ավելի ճիշտ միջին հավասարակշիռ դիրքերը, որոնց շուրջը մասնիկները կատարում են տատանումներ, կոչվում են բյուրեղային ցանցի հանգույցներ:
Բյուեղային մարմինները կարելի է բաժանել երկու խմբի. միաբյուրեղների և բազմաբյուրեղների: Միաբյուրեղները` պինդ մարմիններ են, որոնց մասնիկները առաջացնում են միասնական բյուրեղային ցանց: Միաբյուրեղների կառուցվածքը հայտնաբերվում է ըստ նրանց արտաքին ձևի:
Միաբյուրեղներ են բազմաթիվ հանքատեսակները: Սակայն խոշոր բնական միաբյուրեղները հանդիպում են բավականին հազվադեպ (օրինակ, սառույց, կերակրի աղ, իսլանդական շպատ): Ներկայումս շատ միաբյուրեղներ արհեստականորեն աճեցվում են լաբորատորիաներում: Խոշոր միաբյուրեղների աճեցման պայմանը (մաքուր լուծույթ, դանդաղ սառեցում և այլն) հաճախ չեն բավարարում, ուստի պինդ մարմինների մեծ մասն ունի մանրբյուրեղային կառուցվածք. դրանք բաղկացած են միաբյուրեղի փոքր կտորներից` բյուրեղիկներից, որոնք միմյանց նկատմամբ պատահական դիրքեր ունեն և սերտաճած են: Այդպիսի պինդ մարմինները կոչվում են բազմաբյուրեղներ (շատ լեռնային ապարներ, մետաղների համաձուլվածքներ): Բազմաբյուրեղի բյուրեղիկները կարելի է դիտել մանրադիտակի օգնությամբ, իսկ թարմ կոտրվածքների վրա` երբեմն անզեն աչքով:
Ի տարբերություն միաբյուրեղների, որոնք անիզոտրոպ են, բազմաբյուրեղների ֆիզիկական հատկությունները (մեխանիկական, ջերմային, էլեկտրական, օպտիկական) կախված չեն ուղղությունից. բազմաբյուրեղները իզոտրոպ են: Բազմաբյուրեղներում անիզոտրուպությունն առկա է յուրաքանչյուր բյուրեղիկում, սակայն վերջիններիս` իրար նկատմամբ պատահական կողմնորոշման հետևանքով մարմինը, որպես ամբողջություն, դրսեվորում է իզոտրոպություն: Բազմաբյուրեղները չունեն նաև միաբյուրեղներին բնորոշ արտաքին կանոնավոր ձև:
Բյուրեղային վիճակում միևնույն քիմիական բաղադրությունն ունեցող շատ նյութեր, կախված պայմաններից, կարող են գոյություն ունենալ մի քանի տարբեր ձևերով: Այս հատկությունը հայտնի է որպես բազմաձևություն (պոլիմորֆիզմ): Օրինակ հայտնի է սառույցի տարատեսակ, ածխածինը գոյություն ունի գրաֆիտի և ալմաստի ձևով:
12.12. ԲՅՈՒՐԵՂԱՅԻՆ ՊԻՆԴ ՄԱՐՄԻՆՆԵՐԻ ՏԵՍԱԿՆԵՐԸ
Գոյություն ունի բյուրեղների դասակարգման երկու հայտանիշ.
1) բյուրեղագիտական, 2) ֆիզիկական (մասնիկների բնույթը, դասավորված բյուրեղային ցանցի հանգույցներում և դրանց միջև ուժերի փոխազդեցության բնույթը):
1. Բյուրեղների բյուրեղագիտական հայտանիշը: Տվյալ դեպքում կարևոր է միայն մասնիկների դասավորության տարածական պարբերականությունը, ուստի կարելի է շեղվել դրանց կառուցվածքից` դիտարկելով մասնիկները որպես երկրաչափական կետեր: Բյուրեղային ցանցը կարող է լինել տարբեր համաչափության տարբեր տեսակների:
Բյուրեղային ցանցի համաչափությունը նրա հատկությունն է համատեղվել ինքն իր հետ որոշ տարածական տեղափոխությունների, օրինակ, զուգահեռ տեղափոխությունների, պտույտների, անդրադարձումների կամ դրանց համակցումների դեպքում: Բյուրեղային ցանցում, ինչպես ցույց է տվել ռուս բյուրեղագետ Ե. Ֆեոդորովը (1853-1919), հատուկ է համաչափության տարրերի համակցում, կամ տարբեր տարածական խմբեր: Եռաչափ տարածության մեջ տեղափոխման համաչափության հետ կապում են եռաչափ պարբերական կառուցվածքի հասկացությունը` տարածական ցանցերը կամ Բրավեի ցանցերը, որոնց մասին պատկերացումը մտցրել է
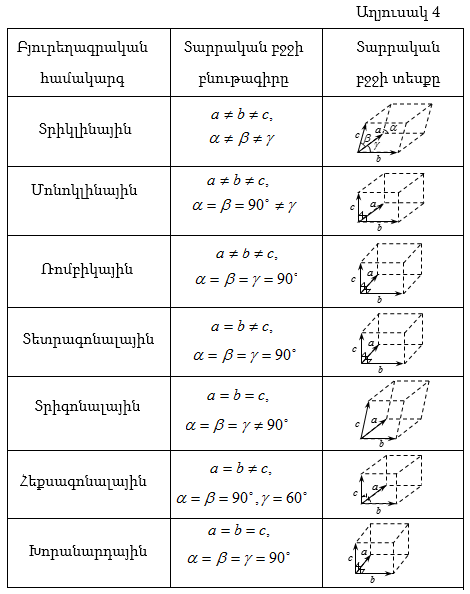
ֆրանսիացի բյուրեղագետ Օ. Բրավեն (1811-1863):
Ամեն մի տարածական ցանց կարող է ստեղծել միևնույն կառուցվածքի տարրը` տարրական բջիջը կրկնվելով երեք տարբեր ուղղություններով: Գոյություն ունի ընդամենը 14 տեսակի Բրավեի ցանց, որոնք տարբերվում են տեղափոխության համաչափությամբ: Դրանք բաժանվում են յոթ բյուրեղագիտական համակարգերի կամ սինգոնիաների` ներկայացվելով համաչափության կարգի մեծացումով (աղյուսակ 4):
Տարրական
բջիջը նկարագրելու
համար օգտվում
են բյուրեղագիտական
կոորդինատային
առանցքներից, որոնք
տարվում են տարրական
բջիջի կողերին
զուգահեռ, իսկ
կոորդինատների
սկիզբն ընտրում
են տարրական բջջի
առաջնային նիստի
ձախ անկյունում:
Բյուրեղային տարրական
բջիջը զուգահեռանիստ
է կառուցված a, b, c
կողերի վրա, որոնց
միջև անկյունները`
![]() է (տես
վերևում բերված
աղյուսակը):
է (տես
վերևում բերված
աղյուսակը): ![]() մեծությունները
միարժեք բնութագրում
են տարրական բջիջը
և կոչվում են
նրա պարամետրեր:
մեծությունները
միարժեք բնութագրում
են տարրական բջիջը
և կոչվում են
նրա պարամետրեր:
2. Բյուրեղների ֆիզիկական հայտանիշը: Կախված մասնիկների տեսակից բյուրեղական ցանցի հանգույցներում դասավորությունից, և նրանց միջև փոխազդեցության ուժերի բնույթից` բյուրեղները բաժանվում են չորս տեսակի. իոնային, ատոմային, մետաղական և մոլեկուլային:
Իոնային բյուրեղներ:
Բյուրեղային ցանցի
հանգույցներում
հաջորդաբար դասավորվում
են հակառկ նշանի
իոնները: Տիպիկ
իոնային բյուրեղներ
են ալկալիական
մետաղների հալոգենային
միացությունները
(NaCl, CsCl, KBr և այլն), ինչպես
նաև տարբեր տարրերի
օքսիդները (MgO, CaO և
այլն): Առավել բնութագրական
է երկու իոնային
բյուրեղների ցանցերի
կառուցվածքը`NaCl-ի
(միմյանց վրա դրված
երկու միատեսակ
նիստակենտրոնացված
խորանարդային
ցանցեր են. այդ
ցանցերից մեկի
հանգույցներում
գտնվում են ![]() իոնները,
մյուսի հանգույցներում`
իոնները,
մյուսի հանգույցներում`
![]() իոնները)
և CsCl-ի (ծավալակենտրոնացված
խորանարդային
ցանց, որի յուրաքանչյուր
տարրական բջիջի
կենտրոնում գտնվում
է իոն) ցույց է տրված
նկ.12.15-ում:
իոնները)
և CsCl-ի (ծավալակենտրոնացված
խորանարդային
ցանց, որի յուրաքանչյուր
տարրական բջիջի
կենտրոնում գտնվում
է իոն) ցույց է տրված
նկ.12.15-ում:
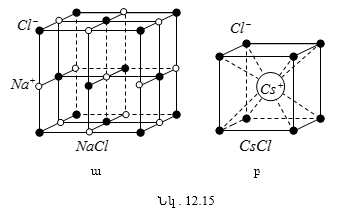
Իոնների միջև փոխազդեցության ուժերը հիմնականում էլեկտրաստատիկ (կուլոնյան) բնույթի են: Տարանուն լիցքավորված իոնների միջև փոխազդեցության ձգողական կուլոնյան ուժերով պայմանավորված կապը կոչվում է իոնային (կամ տարաբևեռ): Իոնային ցանցում չի կարելի անջատել առանձին մոլեկուլներ. բյուրեղը կարծես թե մի հսկա մոլեկուլ է:
Ատոմային բյուրեղներ: Բյուրեղային ցանցի հանգույցներում տեղավորվում են չեզոք ատոմները, որոնք ցանցի հանգույցներում պահվում են նմանաբևեռ կամ կովալենտ կապով: Կովալենտ կապի դեպքում փոխազդեցության ուժերը նույնպես ունեն էլեկտրական (բայց ոչ կուլոնյան) բնույթ: Այս ուժերի բնույթի բացատրությունը տրվում է քվանտային մեխանիկայում:
Նմանաբևեռ կապն իրականացվում է էլեկտրոնային զույգերով: Այդ նշանակում է, որ երկու ատոմների միջև կապը ապահովելու համար յուրաքանչյուր ատոմից մասնակցում է մեկական էլեկտրոն: Այդ պատճառով նմանաբևեռ կապն ունի ուղղորդված բնույթ: Ատոմային բյուրեղներ են ալմաստը և գրաֆիտը (ածխածնի երկու տարբեր վիճակներ), որոշ անօրգանական միացություններ (ZnS, BeO և այլն), ինչպես նաև տիպիկ կիսահաղորդիչներ գերմանիումը (Ge) և սիլիցիումը (Si): Ալմաստի ցանցի կառուցվածքը բերված է նկ.12.16 -ում, որտեղ ածխածնի յուրաքանչյուր ատոմ շրջապատված է այնպիսի չորս ատոմներով, որոնք տեղավորված են դրանից միատեսակ հեռավորությունների վրա քառանիստի գագաթներում:
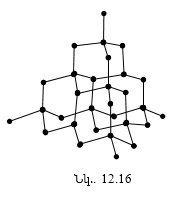
Ինչպես նշեցինք, վալենտական կապը իրականցվում է զույգ էլեկտրոններով, որոնք շարժվում են երկու ատոմներն ընդգրկող ուղեծրերով և կրում են ուղղորդված բնույթ. կովալենտ ուժերն ուղղված են կենտրոնական ատոմից դեպի քառանիստի գագաթները: Ի տարբերություն գրաֆիտի` ալմաստի ցանցը հարթ շերտեր չի պարունակում, որի պատճառով հնարավոր չէ շեղել բյուրեղի առանձին մասերը, դրա համար էլ ալմաստը ամուր միացություն է:
Մետաղական բյուրեղներ: Բյուրեղային ցանցի բոլոր հանգույցներում տեղավորված են մետաղի դրական իոններ: Բյուրեղական ցանցի առաջացման դեպքում ատոմների հետ համեմատաբար թույլ կապված էլեկտրոնները բաժանվում են ատոմներից և կոլեկտիվացվում. դրանք պատկանում են արդեն ոչ թե մեկ ատոմին, ինչպես իոնային կապի դեպքում, այլ ամբողջապես ամբողջ բյուրեղին: Այսպիսով, մետաղներում դրական իոնների միջև, քաոսայնորեն, գազի մոլեկուլների նման շարժվում են «ազատ» էլեկտրոնները, որոնց առկայությունն ապահովում է մետաղի լավ հաղորդականությունը: Այդ էլեկտրոնները կատարում են «ցեմենտի» դեր և միատեղ են պահում դրական իոնները. հակառակ դեպքում` ցանցը իոնների միջև գոյություն ունեցող վանողական ուժերի ազդեցության տակ կքայքայվեր: Սրա հետ միասին էլեկտրոններն էլ իոնների կողմից պահվում են բյուրեղային ցանցի սահմաններում և չեն կարող հեռանալ այնտեղից: Քանի որ մետաղական կապը ուղղորդված ազդեցություն չունի և ցանցի դրական իոնները միատեսակ են ըստ հատկության, ապա մետաղները պետք է ունենան համաչափության բարձր կարգ: Իրոք, մետաղների մեծամասնությունն ունի ծավալակենտրոնացված խորանարդային (Li, Na, K, Rb, Cs) և նիստակենտրոնացված խորանարդային (Cu, Ag, Pt, Au) ցանցեր: Մետաղները հանդիպում են բազմաբյուրեղների տեսքով:
Մոլեկուլային
բյուրեղներ: Բյուրեղային
ցանցի հանգույցներում
տեղավորված են
նյութի չեզոք մոլեկուլները,
որոնց միջև փոխազդեցության
ուժերը պայմանավորված
են ատոմների էլեկտրոնային
թաղանթներում
էլեկտրոնների
փոխադարձ աննշան
շեղումներով: Այդ
ուժերը կոչվում
են Վան-դեր-վաալսյան,
քանի որ ունեն
նույն բնույթը,
ինչ որ մոլեկուլների
միջև փոխազդեցության
ուժերը, որոնք
գազերը շեղում
են իդեալական վիճակից:
Մոլեկուլային
բյուրեղներ են,
օրինակ, օրգանական
միացություններից
շատերը (պարաֆին,
սպիրտ, ռետինը
և այլն), իներտ գազերը
(![]() գազերը
պինդ վիճակում,
սառույցը, ինչպես
նաև բրոմի
գազերը
պինդ վիճակում,
սառույցը, ինչպես
նաև բրոմի ![]() և յոդի
և յոդի
![]() բյուրեղները:
Վան-դեր-վաալսյան
ուժերը բավականին
թույլ են, դրա համար
էլ մոլեկուլային
բյուրեղները հեշտ
դեֆորմացվում
են:
բյուրեղները:
Վան-դեր-վաալսյան
ուժերը բավականին
թույլ են, դրա համար
էլ մոլեկուլային
բյուրեղները հեշտ
դեֆորմացվում
են:
Որոշ պինդ մարմիններում միաժամանակ կարող են իրականացվել մի քանի կապերի տեսակները: Որպես օրինակ կարող է ծառայել գրաֆիտը:
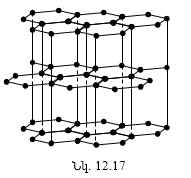
Գրաֆիտի ցանցը (նկ.12.17) կազմված է մի շարք զուգահեռ հարթություններից, որոնցում ածխածնի ատոմները տեղավորված են կանոնավոր վեցանկյան գագաթներում: Հարթությունների միջև եղած հեռավորությունը ավելի քան երկու անգամ գերազանցում է վեցանկյան ատոմների միջև առկա հեռավորությունը: Հարթ շերտերը իրար հետ կապված են վան-դեր-վաալսյան ուժերով: Շերտի սահմաններում երեք վալենտական էլեկտրոնները կազմում են վալենտական կապ հարևան ածխածնի ատոմների հետ, իսկ չորրորդ էլեկտրոնը մնալով «ազատ» կոլեկտիվացվում է, բայց ոչ ամբողջ ցանցի համար, ինչպես մետաղների դեպքում, այլ մեկ շերտի սահմաններում: Դրանով է բացատրվում գրաֆիտի փափկությունը, քանի որ նրա շերտերը կարող են սահել միմյանց նկատմամբ: Ածխածնի երկու տարատեսակների` գրաֆիտի և ալմաստի ցանցերի կառուցվածքի տարբերությունը բնորոշում է նրանց ֆիզիկական հատկությունների տարբերությունը. գրաֆիտի փափկությունը և ալմաստի կարծրությունը: Գրաֆիտը էլեկտրականության հաղորդիչ է, ալմաստը` դիէլեկտրիկ է (չկան ազատ լիցքեր): Բյուրեղներում ատոմների դասավորությունը բնութագրվում է կոորդինացիոն թվով, այսինքն`տվյալ ատոմին ամենամոտ բյուրեղային ցանցում միատեսակ հարևան ատոմների կամ մոլեկուլային բյուրեղներում մոլեկուլների թվով:
12.13. ԲՅՈՒՐԵՂԱՅԻՆ ՑԱՆՑԻ ԱՐԱՏՆԵՐԻ ԴԱՍԱԿԱՐԳՈՒՄԸ
Ինչպես բնության մեջ հանդիպող, այնպես էլ արհեստականորեն ստացված բոլոր իրական բյուրեղները իդեալական չեն: Դրանցում միշտ առկա են կառուցվածքային խախտումներ, որոնք ընդունված է կոչել անկատարելություններ կամ արատներ: Բյուրեղների ծավալային հատկությունները գործնականորեն կախված չեն դրանցում առկա արատներից: Սակայն կառուցվածքային արատներն էապես ազդում են բյուրեղների մի շարք այլ հատկությունների վրա: Այսպես, բազմաթիվ բյուրեղների և, մասնավորապես, կիսահաղորդիչների էլեկտրահաղորդականությունը կարող է ամբողջությամբ կախված լինել քիմիապես օտար խառնուրդների առկայությունից: Շատ բյուրեղների գունավորումը հետևանք է դրանցում առկա արատների: Դիֆուզիայի երևույթն էապես արագանում է արատների առկայության պատճառով: Պինդ մարմինների մեխանիկական և պլաստիկ հատկությունները պայմանավորված են արատներով: Թվարկած, ինչպես նաև բյուրեղի շատ այլ հատկություններ, զգալիորեն կախված են նրա կատարելության աստիճանից, ուստի կոչվում են կառուցվածքային:
Բյուրեղական կառուցվածքի արատներից բացի, կարևոր նշանակություն ունեն այլ տիպի անկատարելություններ` էլեկտրոնային կառուցվածքի խախտումները, որոնք հատկապես ազդում են բյուրեղների կարևորագույն էլեկտրական և մագնիսական հատկությունների վրա:
Սովորաբար արատ են անվանում բյուրեղի ցանկացած տիրույթ, որտեղ միկրոսկոպական մակարդակով մասնիկների (ատոմների, իոնների, մոլեկուլների) դասավորությունը կտրուկ տարբերվում է իդեալական բյուրեղին բնորոշ դասավորությունից:
Բյուրեղային արատները լինում են` կետային (զրոյաչափ), գծային (միաչափ), մակերևույթներ կազմող (երկչափ) և ծավալային (եռաչափ):
Կետային արատ է կոչվում բյուրեղական ցանցի աղավաղումը, որը տեղայնացված է ատոմական ծավալի կարգի մեծության տիրույթում:
Կետային արատներն իրենց հերթին լինում են` էներգիական, էլեկտրոնային և ատոմային: Կետային էներգիական արատների առաջացման պատճառը ջերմային տատանումների քվանտների` ֆոնոնների էներգիայի տեղային ֆլուկտուացիաներն են: Էլեկտրոնային արատներից են էքսիտոնները (էլեկտրոններից և խոռոչներից կազմված արատներ), էլեկտրոնների պակասը կամ ավելցուկը: Ատոմային արատները հետևանք են ատոմների պարբերական դասավորության խախտումների:
Եթե ատոմների կանոնավոր դասավորությունը խախտվում է միայն որոշակի գծի փոքր տիրույթում, ապա այդպիսի արատը կոչվում է գծային: Եթե ատոմների կանոնավոր դասավորությունը խախտվում է որոշակի մակերեվույթի փոքր շրջակայքում, ընդգրկելով միջատոմական հեռավորությունների կարգի շերտ, այդպիսի արատը կոչվում է մակերևութային: Եռաչափ (կամ ծավալային) արատ է կոչվում բյուրեղական ցանցի ցանկացած աղավաղում, որը տարածական երեք ուղղություններով էլ ունի մակրոսկոպական չափեր:
Արատի ազդեցությունը բյուրեղի ֆիզիկական հատկությունների վրա կարող է դրսևորվել երկու ճանապարհով: Նախ՝ արատին հարող տիրույթում բյուրեղը խաթարված է, և արատը հանդես է գալիս որպես բյուրեղի տեղային անհամասեռություն: Երկրորդ` արատի առկայությունը հանգեցնում է արատից զգալի հեռավորությունների վրա բյուրեղական ցանցի ստացիոնար աղավաղումների, ինչը, վերջին հաշվով, հանգում է ատոմների` իդեալական բյուրեղին բնորոշ հավասարակշռության դիրքերից շեղումների: Այսպիսով, բյուրեղում արատը կատարում է նաև շեղումների դաշտի աղբյուրի դեր: Արատի շուրջ ծագող շեղումների դաշտը կախված է բյուրեղական ցանցի (մատրիցի) վրա արատի ազդեցության բնույթից:
Ծանոթանանք բյուրեղական տարբեր կառուցվածքային արատների կոնկրետ օրինակների: Պարզագույն կետային արատներ են «սեփական», այսինքն` տվյալ բյուրեղական կառուցվածքին պատկանող միջհանգուցային ատոմները: Ինչպես բխում է անվանումից, միջհանգուցային ատոմը տեղադրված է իդեալական ցանցի ատոմների հավասարակշռության դիրքերի միջև (նկ.12.17 ա): Եթե բյուրեղական ցանցի հանգույցը զբաղեցված չէ ատոմի կողմից, թափուր է, ապա այդպիսի արատն անվանում են թափուրք (նկ.12.17 բ):
Եթե տվյալ բյուրեղական կառուցվածքի միջհանգուցային դիրքում գտնվում է այլ քիմիական տարրի ատոմ, ապա այդպիսի արատը կոչվում է խառնուկ (նկ.12.18 ա), իսկ եթե այլ քիմիական տարրի ատոմը զբաղեցնում է «սեփական» (մատրիցի) ատոմի հանգույցը, ապա այդպիսի արատը կոչ-վում է տեղակալման խառնուկ (նկ.12.18բ):
Ատոմը կարող է պոկվել իր տեղից (հանգույցից) և անցնել բյուրեղի մակերևույթ` առաջացնելով Շոտկիի արատ (նկ.12.19.), իսկ երբ ատոմը, պոկվելով ցանցի հանգույցից, գրավում է միջհանգուցային դիրք (այսպես կոչված, միջհանգույց), ստեղծվում է Ֆրենկելի արատ (նկ.12.20):
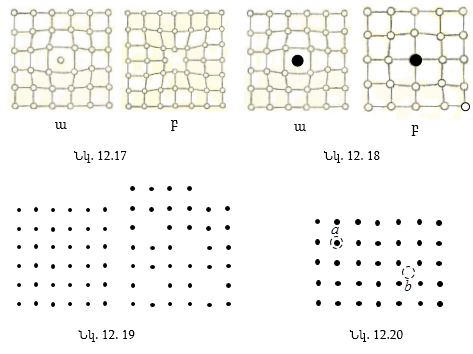
Գծային արատները` դիսլոկացիաները, ավելի բարդ կառուցվածքային արատներ են. պարզագույն տեսակներն են եզրային և պտուտակային դիսլոկացիաները: Եզրային դիսլոկացիաները պայմանավորված են «ավելորդ» ատոմային հարթության գոյությամբ (նկ.12.21-ում այն համընկում է y-ի առանցքով անցնող վերին կիսահարթության հետ): Բյուրեղի վերին կեսում տեղի է ունեցել սեղմում, ներքին կեսում` ձգում:
Պտուտակային դիսլոկացիայի դեպքում ատոմային հարթությունները չեն եզրափակվում բյուրեղի ներսում. դրանք իրար կապակցվում են այնպես, որ կազմում են բյուրեղի մի եզրից սկսվող և մյուսում վերջացող պտուտակային մակերևույթ: Պտուտակային դիսլոկացիայի (նկ.12.22) առանձնահատկությունն այն է, որ բյուրեղի տեղաշարժված և չտեղաշարժված մասերը բաժանող սահմանը զուգահեռ է սահքի ուղղությանը (եզրային դիսլոկացիայի դեպքում սահմանն ուղղահայաց է սահքի ուղղությանը): Արատավոր բյուրեղի դիսլոկացիայի գծի շուրջը ցանցի տրանսլյացիայի վեկտորներից կազմված կոնտուրը կտրված է. այն փակող վեկտորը կոչվում է տվյալ դիսլոկացիայի Բյուրգերսի վեկտոր: Դիսլոկացիայի բնույթը որոշվում է Բյուրգերսի վեկտորի մեծությամբ և ուղղությամբ: Դիսլոկացիաները, ինչպես և կետային արատները, կարող են տեղաշարժվել բյուրեղական ցանցում: Բյուրեղների պլաստիկ դեֆորմացիաները սովորաբար պայմանավորված են ատոմների հենց այդպիսի կոլեկտիվ տեղաշարժերով:
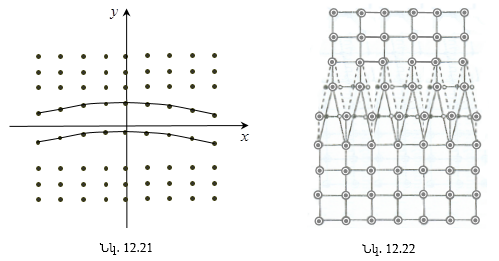
Մակերևույթներ կազմող արատների շարքին են դասվում կրկնորդ բյուրեղների սահմանները, գծային դիսլոկացիաների շարքերը, բյուրեղի հատիկների սահմանները: Բյուրեղի մակերևույթը ևս կարելի է համարել այդպիսի արատ: Շերտավոր ցանցերում գոյություն ունեն շերտերի վերադրման հաջորդականության խախտումով պայմանավորված արատներ: Ծավալային արատներից են թափուր տեղերի կուտակումը, տարբեր արատների վրա հավաքվող մասնիկները, խառնուրդների կուտակումը աճի գոտիների և սեկտորների տեսքով: Փոխազդեցությունները թվարկված տարրական արատների միջև հանգեցնում են նոր, ավելի բարդ կառուցածքներով արատների առաջացման: Դրանց թվին են պատկանում, օրինակ, գունավորման F, V կենտրոնները: Գոյություն ունեն բյուրեղների արատների (հիմնականում մետաղների արատների) հայտնաբերման տարբեր մեթոդներ և եղանակներ: Բյուրեղների ֆիզիկական հատկություններն էապես կախված են արատների առկայությունից: Այդ արատների տեսակով և քանակով են պայմանավորված բյուրեղների պլաստիկությունը, առաձգականության սահմանը, ամրությունը, ջերմային և էլեկտրական հատկությունները:
12.14. ՊԻՆԴ ՄԱՐՄԻՆՆԵՐԻ ՋԵՐՄՈՒՆԱԿՈՒԹՅՈՒՆԸ
Որպես պինդ
մարմնի մոդել քննարկենք
ճշգրիտ կառուցված
բյուրեղային ցանցը,
որի հանգույցներում
մասնիկները (ատոմները,
մոլեկուլները)
ընդունելով որպես
նյութական կետեր
տատանվում են իրենց
հավասարակշռության
դիրքի շուրջը:
Բյուրեղային ցանցի
հանգույցներում
մասնիկների դասավորությունը
համապատասխանում
է դրանց փոխադարձ
պոտենցիալ էներգիայի
նվազագույնին:
Հավասարակշռության
դիրքից ցանկացած
ուղղությամբ մասնիկների
շեղման դեպքում
առաջանում է մի
ուժ, որը ձգտում
է մասնիկը վերադարձնել
սկզբնական դիրքը,
որի հետևանքով
առաջանում են մասնիկի
տատանումներ: Կամայական
ուղղությամբ կատարվող
տատանումները
կարելի է ներկայացնել
որպես երեք փոխուղղահայաց
ուղղություններով
կատարվող տատանումների
վերադրում: Այսպիսով,
բյուրեղում յուրաքանչյուր
մասնիկի պետք է
վերագրել ազատության
երեք տատանողական
աստիճաններ: Ինչպես
հայտնի է, ազատության
յուրաքանչյուր
տատանողական աստիճանին
միջին հաշվով բաժին
է ընկնում kT-ի երկու
կեսերին հավասար
էներգիա, որոնցից
մեկը կինետիկ էներգիա
է, իսկ մյուսը` պոտենցիալ:Հետևաբար,
յուրաքանչյուր
մասնիկի, օրինակ,
ատոմի` ատոմային
ցանցում, իոնի`
իոնային կամ մետաղական
ցանցում, միջին
հաշվով բաժին է
ընկնում 3kT-ի հավասար
էներգիա: Բյուրեղային
վիճակում գտընվող
նյութի մեկ մոլի
ներքին էներգիան
կարելի է որոշել`
մեկ մասնիկի միջին
էներգիան բազմապատկելով
բյուրեղային ցանցի
հանգույցներում
գտնվող մասնիկների
թվով, որը համընկնում
է Ավոգադրոյի ![]() թվի
հետ, միայն քիմիապես
պարզ նյութերի
դեպքում:
թվի
հետ, միայն քիմիապես
պարզ նյութերի
դեպքում:
Այսպիսով, մեկ մոլ պինդ մարմնի ներքին էներգիայի համար`
![]()
որտեղ k-ն Բոլցմանի հաստատունն է, R-ը` մոլային գազային հաստատունը: Պինդ մարմնի մոլային ջերմունակության համար ստանում ենք`
![]()
Ըստ (12.27)-ի հետևում
է, որ քիմիապես
պարզ մարմինների
բյուրեղային վիճակում
մոլային ջերմունակությունը
միատեսակ է բոլոր
մարմինների համար
և հավասար է 3R-ի և
կախում չունի ջերմաստիճանից:
Այս օրենքը փորձնական
ճանապարհով հայտնաբերել
են ֆրանսիացի գիտնականներ
Պ. Դյուլոնգը
(1785-1838) և Լ. Պտին (1791-1820) և կրում
է Դյուլոնգի և
Պտիի օրենք անվանունը:
Այս օրենքը բավականին
լավ մոտավորությամբ
տեղի ունի շատ
պինդ մարմինների
համար սենյակային
ջերմաստիճանում:
Սակայն ալմաստը,
օրինակ, սենյակային
ջերմաստիճանում
ունի Ջ/(մոլ.Կ) ջերմունակություն:
Ավելին, (12.27)-ին հակառակ
բյուրեղների ջերմունակությունը
կախում ունի ջերմաստիճանից,
ընդ որում կախումն
ունի նկ.12.23-ում ցույց
տրված բնույթը:
Բոլոր մարմինների
ջերմունակությունները
բացարձակ զրոյի
մոտակայքում համեմատական
են ![]() ,
և միայն յուրաքանչյուր
մարմնի համար բնորոշ
բավական բարձր
ջերմաստիճանում
սկսում է տեղի
ունենալ (12.27) -ը:
,
և միայն յուրաքանչյուր
մարմնի համար բնորոշ
բավական բարձր
ջերմաստիճանում
սկսում է տեղի
ունենալ (12.27) -ը:
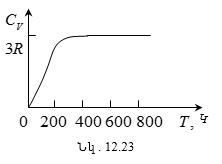
Մարմիններից մեծ մասի մոտ այդ տեղի է ունենում սենյակային ջերմաստիճանում, իսկ ալմաստի ջերմունակությունը հասնում է (12.27) արժեքին միայն 10000C-ի կարգի ջերմաստիճանում: Այնշտայնի և Դեբայի ստեղծած պինդ մարմինների ջերմունակության ճշգրիտ տեսությունը առաջին հերթին հաշվի է առնում տատանողական շարժման էներգիայի քվանտացումը: Երկրորդ` տեսությունը հաշվի է առնում այն, որ բյուրեղային ցանցում կատարվող մասնիկների տատանումները իրարից անկախ չեն: Բյուրեղների ջերմունակության քվանտային տեսությունը լավ համաձայնեցվում է փորձնական տվյալների հետ, մասնավորապես, բարձր ջերմաստիճանների համար այն հանգեցնում է (12.27) արտահայտությանը:
12.15. ԳՈԼՈՐՇԻԱՑՈՒՄ, ՍՈՒԲԼԻՄՈՒՄ, ՀԱԼՈՒՄ ԵՎ ԲՅՈՒՐԵՂԱՑՈՒՄ
ԱՄՈՐՖ ՄԱՐՄԻՆՆԵՐ
Ինչպես հեղուկներում, այնպես էլ պինդ մարմիններում միշտ կան որոշակի թվով մոլեկուլներ, որոնց էներգիան բավարար է հաղթահարելու այլ մոլեկուլների ձգողությունը, և որոնք ընդունակ են պոկվել հեղուկի կամ պինդ մարմնի մակերևույթից և անցնել դրանց շրջապատող տարածություն: Այդ պրոցեսը հեղուկների համար կոչվում է գոլորշացում (կամ շոգեգոյացում), պինդ մարմինների համար` սուբլիմում (կամ ցնդում): Հեղուկների գոլորշացումը տեղի է ունենում ցանկացած ջերմաստիճանում, սակայն նրա ինտենսիվությունը ջերմաստիճանի բարձրացմանը զուգընթաց աճում է: Գոլորշացման պրոցեսին զուգընթաց տեղի ունի հակառակ պրոցեսը` գոլորշու կոնդենսացումը հեղուկի: Եթե հեղուկի միավոր մակերևույթից միավոր ժամանակում դուրս եկած մոլեկուլների քանակը հավասար է նույն ժամանակում գոլորշուց հեղուկ վերադարձող մոլեկուլների քանակին, ապա հեղուկի և գոլորշու միջև հաստատված հավասարակշռությունն ընդունված է անվանել շարժուն (դինամիկ), քանի որ այն հավասար արագություններով և հակառակ ուղղություններով ընթացող երկու պրոցեսների` գոլորշացման և խտացման արդյունք է: Այն գոլորշին, որն իր հեղուկի հետ գտնվում է դինամիկ հավասարակշռության մեջ, կոչվում է հագեցած:
Պինդ մարմինների մեծամասնության համար սուբլիմումի պրոցեսը սովորական ջերմաստիճանների դեպքում աննշան է, և գոլորշու ճնշումը պինդ մարմնի մակերևույթից վեր փոքր է: Ինտենսիվ սուբլիմում են նաֆթալինը, կամֆորան, որոնք հայտնաբերվում են յուրահատուկ խիստ հոտով: Հատկապես սուբլիմումը ինտենսիվ է կատարվում վակուումում: Սուբլիմումի հայտնի օրինակ է սառույցի փոխակերպումը գոլորշու, թաց սպիտակեղենի չորանալը սառնամանիքին:
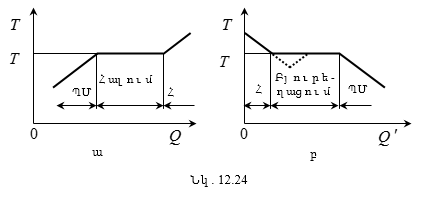
Եթե պինդ պինդ
մարմինը տաքացվում
է, նրա ներքին էներգիան
աճում է: Ջերմաստիճանի
բարձրացման դեպքում
մասնիկների տատանումների
լայնույթը մեծանում
է: Արդյունքում
մեծանում են միջմասնիկային
հեռավորությունները,
և, հետևաբար, թուլանում
են ձգողության
ուժերը: Որոշակի
(հալման) ջերմաստիճանում
այդ ուժերն այլևս
ի վիճակի չեն պահելու
մասնիկներին հանգույցների
մոտ, և բյուրեղային
ցանցը քայքայվում
է: Նկ.12.24 ա-ում պատկերված
է մարմնի T(Q) կախվածությունը,
որտեղ Q-ն մարմնի
ստացած ջերմաքանակն
է հալման դեպքում:
Պինդ մարմնին ջերմաքանակ
հաղորդելուն զուգընթաց
նրա ջերմաստիճանը
բարձրանում է,
և ![]() հալման
ջերմաստիճանի
դեպքում սկսվում
է մարմնի պինդ
վիճակից անցումը
հեղուկի:
հալման
ջերմաստիճանի
դեպքում սկսվում
է մարմնի պինդ
վիճակից անցումը
հեղուկի: ![]() ջերմաստիճանը
մնում է հաստատուն
մինչև ամբողջ բյուրեղի
հալվելը, և միայն
այդ դեպքում հեղուկի
ջերմաստիճանը
նորից սկսում է
բարձրանալ: Հալման
պրոցեսում մարմնին
հաղորդված ջերմաքանակը
ծախսվում է բյուրեղային
ցանցի քայքայման
աշխատանք կատարելու
վրա, ուստի
ջերմաստիճանը
մնում է հաստատուն
մինչև ամբողջ բյուրեղի
հալվելը, և միայն
այդ դեպքում հեղուկի
ջերմաստիճանը
նորից սկսում է
բարձրանալ: Հալման
պրոցեսում մարմնին
հաղորդված ջերմաքանակը
ծախսվում է բյուրեղային
ցանցի քայքայման
աշխատանք կատարելու
վրա, ուստի ![]() մինչև
ամբողջ բյուրեղի
հալումը: Այնուհետև
մատուցված ջերմաքանակը
նորից ծախսվում
է հեղուկի մասնիկների
էներգիայի մեծացման
վրա, և նրա ջերմաստիճանը
սկսում է բարձրանալ:
Այն ջերմաքանակը,
որն անհրաժեշտ
է կգ զանգվածով
բյուրեղային նյութը
հաստատուն ջերմաստիճանում
հեղուկի փոխակերպելու
համար, կոչվում
է հալման տեսակարար
ջերմություն:
Եթե հեղուկը սառեցվում
է, հակառակ ուղղությամբ
է ընթանում պրոցեսը:
(նկ.12.24 բ.
մինչև
ամբողջ բյուրեղի
հալումը: Այնուհետև
մատուցված ջերմաքանակը
նորից ծախսվում
է հեղուկի մասնիկների
էներգիայի մեծացման
վրա, և նրա ջերմաստիճանը
սկսում է բարձրանալ:
Այն ջերմաքանակը,
որն անհրաժեշտ
է կգ զանգվածով
բյուրեղային նյութը
հաստատուն ջերմաստիճանում
հեղուկի փոխակերպելու
համար, կոչվում
է հալման տեսակարար
ջերմություն:
Եթե հեղուկը սառեցվում
է, հակառակ ուղղությամբ
է ընթանում պրոցեսը:
(նկ.12.24 բ. ![]() բյուրեղացան
դեպքում մարմնի
տված ջերմաքանակն
է): Սկզբում հեղուկի
ջերմաստիճանն
ընկնում է, այնուհետև
բյուրեղացան
դեպքում մարմնի
տված ջերմաքանակն
է): Սկզբում հեղուկի
ջերմաստիճանն
ընկնում է, այնուհետև
![]() հալմանը
հավասար հաստատուն
ջերմաստիճանի
դեպքում սկսվում
է բյուրեղացումը,
որի ավարտից հետո
բյուրեղի ջերմաստիճանն
սկսում է ընկնել:
հալմանը
հավասար հաստատուն
ջերմաստիճանի
դեպքում սկսվում
է բյուրեղացումը,
որի ավարտից հետո
բյուրեղի ջերմաստիճանն
սկսում է ընկնել:
Նյութի բյուրեղացման համար անհրաժեշտ է այսպես կոչված բյուրեղացման կենտրոնների առկայությունը` բյուրեղային սաղմեր, որոնք կարող են լինել ոչ միայն առաջացող նյութի բյուրեղիկներ, այլ նաև խառնուրդներ: Բյուրեղացման կենտրոնների բացակայությունը մաքուր հեղուկում խոչընդոտում է միկրոսկոպական բյուրեղիկների առաջացմանը, և նյութը մնալով հեղուկ վիճակում` սառչում է մինչև այն ջերմաստիճանը, որը փոքր է բյուրեղացման ջերմաստիճանից, այդ դեպքում առաջանում է գերսառեցրած հեղուկ (նկ.12.24 բ-ում համապատասխանում է կետագծային կորը): Ուժեղ գերսառեցման դեպքում սկսվում է բյուրեղացման կենտրոնների սպոնտան առաջացումը, և նյութը բավականին արագ բյուրեղանում է: Սովորաբար հալույթի գերսառեցումը կատարվում է մի քանի աստիճանից մինչև տասնյակ աստիճաններ, բայց մի շարք նյութերի համար կարող է հասնել հարյուրավոր աստիճանների: Մեծ մածուցիկության շնորհիվ ուժեղ գերսառեցրած հեղուկները կորցնում են հոսունությունը, պահպանելով, ինչպես և պինդ մարմինները, իրենց ձևը: Այդ մարմինները ստացել են ամորֆ մարմիններ անվանումը. դրանցից են ապակին, ձյութը, մոմը, զմուռսը: Այսպիսով, ամորֆ մարմինները, լինելով գերսառեցրած հեղուկներ, ի տարբերություն բյուրեղների, իզոտրոպ են, այսինքն` դրանց ֆիզիկական հատկությունները բոլոր ուղղություններով միատեսակ են: Այս փաստը վկայում է, որ ամորֆ մամինները չունեն կանոնավոր ներքին կառուցվածք: Դրանց, ինչպես և հեղուկների համար բնութագրական է մասնիկների դասավորության մոտակա կարգը: Ի տարբերություն հեղուկների` ամորֆ մարմիններում մասնիկների շարժունակությունը բավականին փոքր է: Ամորֆ մարմինների ներքին կանոնավոր կառուցվածքի բացակայության անմիջական հետևանք է այն, որ դրանք չունեն հալման ջերմաստիճան: Եթե ամորֆ մարմինը տաքացնենք, ապա ջերմաքանակ հաղորդելուն զուգընթաց նրա ջերմաստիճանն անընդհատ կբարձրանա, այն աստիճանաբար կփափկի և կվերածվի հեղուկի: Եթե այդ հեղուկից ջերմաքանակ վերցնենք, ապա նրա ջերմաստիճանը անընդհատ կնվազի, և հեղուկը կանցնի պինդ ամորֆ վիճակի: Ամորֆ նյութերից են նաև պոլիմերները` նյութեր, որոնք կազմված են հսկայական թվով միատեսակ օղակներից` մոնոմերներից: Օղակները միմյանց հետ կապված են ամուր քիմիական կապերով` կազմելով երկար շղթայիկներ: Պոլիմերների շարքից են, ինչպես բնական (կրախմալ, սպիտակուցներ, կաուչուկ, կաշի, փայտ և այլն), այնպես էլ արհեստական (պլաստմասսաներ, պոլիստիրոլ, կապրոն, լավսան և այլն) օրգանական նյութերը:
Պոլիմերներին հատուկ է ամրությունը և էլաստիկությունը: Որոշ պոլիմերներ դիմանում են 5-10 անգամ իրենց սկզբնական երկարությունը գերազանցող երկարացումը:
12.16. ԱՌԱՋԻՆ ԵՎ ԵՐԿՐՈՐԴ ՍԵՌԻ ՓՈՒԼԱՅԻՆ ԱՆՑՈՒՄՆԵՐ
Փուլ է կոչվում նյութի ջերմադինամիկական հավասարակշիռ վիճակը, որը տարբերվում է նույն նյութի այլ հնարավոր հավասարակշիռ վիճակներից ֆիզիկական հատկություններով: Եթե օրինակ, փակ անոթում ջուր կա, ուրեմն այդ համակարգը երկփուլ է. հեղուկ փուլը` ջուրն է, գազային փուլը` օդի խառնուրդը ջրային գոլորշիների հետ: Եթե ջրի մեջ գցենք սառույցի կտորներ, այդ համակարգը կդառնա եռափուլ:
Հաճախ «փուլ» հասկացությունը օգտագործվում է ագրեգատային վիճակի իմաստով, սակայն հարկավոր է հաշվի առնել, որ այն ավելի լայն է քան «ագրեգատային վիճակ» հասկացությունը: Մեկ ագրեգատային վիճակի սահմաններում նյութը կարող է գտնվել մի քանի փուլերում, տարբերվելով իր հատկություններով, բաղադրությունով և կառուցվածքով (օրինակ, սառույցը հանդիպում է հինգ տարբեր ձևափոխություններով` փուլերով):
Նյութի անցումը մի փուլից մյուսին` փուլային անցումը միշտ կապված է նյութի հատկությունների որակական փոփոխությունների հետ: Փուլային անցման օրինակ կարող է ծառայել նյութի ագրեգատային վիճակի փոփոխությունը կամ անցումները, կապված բաղադրության փոփոխության, կառուցվածքի և նյութի հատկությունների (օրինակ, բյուրեղային նյութի անցումը մի ձևափոխությունից մյուսին) հետ: Տարբերում են երկու սեռի փուլային ացումներ. փուլային անցումները, որոնք կապված են (օրինակ, հալում, բյուրեղացում) ջերմաքանակի կլանման կամ անջատման հետ, կոչվում են երկրորդ սեռի փուլային անցումներ: Առաջին սեռի փուլային անցումը բնութագրվում է ջերմաստիճանի հաստատունությամբ, ծավալի և էնտրոպիայի փոփոխություններով: Դրա բացատրությունը կարելի է տալ հետևյալ ձևով: Օրինակ, մարմնի հալման դեպքում հարկավոր է հաղորդել որոշակի ջերմաքանակ, որպեսզի առաջանա բյուրեղային ցանցի քայքայում: Հալման դեպքում մատուցված ջերմաքանակը գնում է ոչ թե մարմնի տաքացման, այլ միջատոմային կապերը խզելու վրա, դրա համար էլ հալումն ընթանում է հաստատուն ջերմաստիճանի դեպքում: Նման անցումներում` ավելի կարգավորված բյուրեղային վիճակից ավելի փոքր կարգավորված հեղուկ վիճակին, անկանոնության աստիճանը մեծանում է, այսինքն` համաձայն ջերմադինամիկայի երկրորդ օրենքի, այդ պրոցեսը կապված է համակարգի էնտրոպիայի աճման հետ: Եթե պրոցեսը տեղի է ունենում հակառակ ուղղությամբ (բյուրեղացում), ապա համակարգն անջատում է ջերմաքանակ:
Փուլային անցումները, որոնք կապված չեն ջերմաքանակի կլանման կամ անջատման և ծավալի փոփոխության հետ, կոչվում են երկրորդ սեռի փուլային անցումներ:
Այդ անցումները բնութագրվում են ծավալի և էնտրոպիայի հաստատունությամբ, բայց թռիչքաձև ջերմունակության փոփոխությամբ: Երկրորդ սեռի փուլային անցման ընդհանուր մեկնաբանությունը առաջարկվել է Լ. Լանդաուի (1908-1968) կողմից: Համաձայն այդ մեկնաբանության, երկրորդ կարգի փուլային անցումները կապված են համաչափության փոփոխության հետ. անցման բարձր կետում, որպես կանոն, համակարգը օժտված է ավելի բարձր համաչափությամբ, քան անցման ցածր կետում: Երկրորդ սեռի փուլային անցման օրինակներ են ֆերոմագնիսական նյութերի (երկաթ, նիկել) անցումը որոշակի ճնշման և ջերմաստիճանի դեպքում պարամագնիսական վիճակի, որոշ համաձուլվածքների և մետաղների անցումը 0Կ-ին մոտ ջերմաստիճանի դեպքում գերհաղորդականության վիճակին, որը բնութագրվում է թռիչքաձև էլեկտրական դիմադրության փոքրացումով` մինչև զրո:
12.17. ՎԻՃԱԿԻ ԴԻԱԳՐԱՄԸ: ԵՌԱԿԻ ԿԵՏ
Եթե համակարգը բաղկացած է քիմիապես համասեռ նյութից կամ նրա միացությունից, ապա փուլի հասկացությունը համընկնում է ագրեգատային վիճակի հասկացության հետ:
Հալման, բյուրեղացման, գոլորշիացման պրոցեսները կոչվում են առաջին սեռի փուլային անցումներ: Որպեսզի նկարագրվի նյութի վիճակը և նրանում կատարվող փուլային անցումները, պետք է օգտվել վիճակի դիագրամից: Սովորաբար այդ դիագրամները կառուցվում են p, T (ճնշում, ջերմաստիճան) կոորդինատներով: Դիագրամի վրա յուրաքանչյուր կետ պատկերում է նյութի որոշակի վիճակ: Որպես օրինակ, քննարկենք ջրի վիճակի դիագրամը (նկ.12.25): Հեղուկը իրեն սահմանակից գոլորշու հետ կարող է գտնվել դինամիկ հավասարակշռության մեջ: Այդ վիճակը դիագրամի վրա պատկերված է AM կորով:
Եթե առանց փոխելու համակարգի ծավալը նրանից աստիճանաբար հեռացնենք ջերմաքանակ, այդ պրոցեսը կուղեկցվի նյութի ջերմաստիճանի իջեցումով և ճնշման համապատասխան փոքրացումով: Ջերմաստիճանը ընկնում է մինչև բյուրեղացման ջերմաստիճանի արժեքին հասնելը:
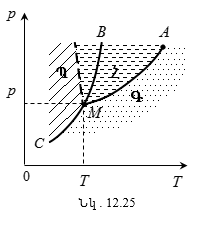
Բյուրեղացման դեպքում ջերմաստիճանը և ճնշումը մնում են հաստատուն: Դիագրամի վրա AM-ից ներքև ընկած տիրույթը (ավելի ցածր ճնշում կամ ավելի բարձր ջերմաստիճան) գազային վիճակի տիրույթն է, AM-ից բարձր ընկած տիրույթը նյութի հեղուկ վիճակի տիրույթն է: BM կորը համապատասխանում է պինդ մարմին հեղուկ (սառույց և ջուր) հավասարակըշռության վիճակին, այսինքն` ներկայացնում է պինդ մարմնի հալման կորը, երբ պինդ մարմինը (սառույցի բյուրեղները) և հեղուկը (ջուրը) գտնվում են հավասարակըշռության մեջ: CM կորն արտահայտում է պինդ մարմին-գազ հավասարակշռության վիճակը, այսինքն ներկայացնում է սուբլիմումի կորը: CMA տիրույթում ջուրը կարող է գտնվել միայն գազային վիճակում (ջրի գոլորշիներ): CMB տիրույթում ջուրը գտնվում է պինդ վիճակում և ներկայացնում է սառույցի ձևափոխություններից մեկը:
Հավասարակշռության
երեք կորերը հատվում
են մեկ M կետում,
որը կոչվում է
եռակի կետ: Այն
բնութագրվում
է նրանով, որ ջերմաստիճանի
![]() և ճնշման
և ճնշման
![]() արժեքների
դեպքում կարող
են հավասարակշռության
վիճակում գտընվել
նյութի երեք փուլերը`
պինդ, հեղուկ և
գազանման: Ջրի
համար
արժեքների
դեպքում կարող
են հավասարակշռության
վիճակում գտընվել
նյութի երեք փուլերը`
պինդ, հեղուկ և
գազանման: Ջրի
համար ![]()
Յուրաքանչյուր նյութի համար վիճակի դիագրամը կառուցվում է փորձի տվյալներով: Ըստ վիճակի դիագրամի` կարելի է որոշել, թե որ վիճակում է գտնվում նյութը տրված պարամետրերի դեպքում (ճնշման և ջերմաստիճանի):
Ջերմադինամիկան տալիս է միևնույն նյութի երկու փուլերի հավասարակշռության կորերի հաշվարկման մեթոդ: Համաձայն Կլապեյրոն–Կլաուզիուսի հավասարման ըստ ջերմաստիճանի, հավասարակշռության ճնշման ածանցյալը հավասար է`
![]()
որտեղ L-ը փուլային
ացման ջերմաքանակն
է, T-ն` անցման ջերմաստիճանը,
![]() նյութի
ծավալի փոփոխությունն
է նրա առաջին փուլից
երկրորդին անցնելիս:
նյութի
ծավալի փոփոխությունն
է նրա առաջին փուլից
երկրորդին անցնելիս:
Կլապեյրոն-Կլաուզիուսի
հավասարումը հնարավորություն
է տալիս որոշել
հավասարակշռության
կորերի թեքությունը:
Քանի որ L և T-ն դրական
են, թեքությունը
տրվում է ![]() նշանով:
Հեղուկների գոլորշացման
և պինդ մարմինների
սուբլիմումի դեպքում
նյութի ծավալը
միշտ աճում է, ուստի
համաձայն (12.28)-ի, dp/dT
> 0, հետևաբար, այդ
պրոցեսներում
ջերմաստիճանի
բարձրացումը առաջ
է բերում ճնշման
մեծացում, և հակառակը:
նշանով:
Հեղուկների գոլորշացման
և պինդ մարմինների
սուբլիմումի դեպքում
նյութի ծավալը
միշտ աճում է, ուստի
համաձայն (12.28)-ի, dp/dT
> 0, հետևաբար, այդ
պրոցեսներում
ջերմաստիճանի
բարձրացումը առաջ
է բերում ճնշման
մեծացում, և հակառակը:
Նյութերի
մեծամասնության
հալման դեպքում,
որպես կանոն, ծավալն
աճում է, այսինքն`
dp/dT > 0, հետևաբար, ճնշման
մեծացումը առաջ
է բերում հալման
ջերմաստիճանի
բարձրացում (նկ.12.25,
հոծ գիծը): Որոշ
նյութերի համար
![]() հեղուկ
փուլի ծավալը փոքր
է պինդ փուլի ծավալից,
այսինքն` dp/dT< 0 հետևաբար,
ճնշման մեծացումն
ուղեկցվում է հալման
ջերմաստիճանի
ցածրացումով (նկ.12.25,
կետագիծը:)
հեղուկ
փուլի ծավալը փոքր
է պինդ փուլի ծավալից,
այսինքն` dp/dT< 0 հետևաբար,
ճնշման մեծացումն
ուղեկցվում է հալման
ջերմաստիճանի
ցածրացումով (նկ.12.25,
կետագիծը:)
12.18. ՖԻԶԻԿԱԿԱՆ ՄԵԾՈՒԹՅՈՒՆՆԵՐԻ ԻԱՎՈՐՆԵՐԸ
Ֆիզիկան փորձարարական գիտություն է, որի պատճառով էլ ֆիզիկական պրոցեների դիտման և տարբեր ֆիզիկական մեծությունների չափման հմտությունը ստանում է հատուկ նշանակություն: Բոլոր փոփոխությունները, որոնք տեղի են ունենում ֆիզիկական երևույթներում, գնահատվում են քանակական չափման միջոցով:
Չափել որևէ մեծություն նշանակում է այն համեմատել նրան համասեռ մի այլ մեծության հետ` պայմանականորեն ընդունելով որպես միավոր:
Համասեռ ֆիզիկական մեծություններ կոչվում են այն մեծությունները, որոնք բնութագրում են մարմնի միևնույն հատկությունը և կարող են տարբերվել միայն թվապես: 5 մետրը և 15 սանտիմետրը համասեռ մեծություններ են. դրանք երկուսն էլ բնութագրում են մարմնի տարածականությունը, օրինակ` որևէ մարմնի երկարությունը:
Կարելի է ընտրել Ֆիզիկական մեծությունների կամայական, միավորներ, սակայն կծագեն դժվարություններ դրանց համեմատության դեպքում: Ուստի նպատակահարմար է ներմուծել միավորների համակարգ, ընդգրկելով բոլոր ֆիզիկական միավորները: Միավորների համակարգը կառուցելու համար կամայականորեն ընտրվում են մի քանի` միմյանցից անկախ ֆիզիկական մեծությունների համար միավորներ: Այդ միավորները կոչվում են հիմնական: Բոլոր մնացած ֆիզիկական մեծությունները, որոնք արտահայտվում են հիմնական միավորների միջոցով, կոչվում են համակարգի ածանցյալ միավորներ:
Գիտական, ինչպես նաև ուսումնական գրականության մեջ պարտադիր է կիրառել միջազգային համակարգը (ՄՀ), որը կառուցվում է յոթ հիմնական միավորների վրա` մետր, կիլոգրամ, վայրկյան, ամպեր, կելվին, մոլ, կանդելա և երկու լրացուցիչ` ռադիան և ստեռադիան:
Մետրը` վակուումում լույսի անցած ճանապարհի երկարությունն է 1/299792458 վ-ում:
Կիլոգրամը` զանգվածի միավորը, ներկայացվում է որպես միջազգային կիլոգրամի նախատիպի զանգվածը: Որպես զանգվածի չափանմուշ ընդունված է պլատինի և իրիդիումի համաձուլվածքից հատուկ պատրաստված մոտ 39մմ տրամագծով և նույնքան բարձրությամբ գլանի զանգվածը: Զանգվածի չափանմուշը պահվում է չափերի և կշիռների միջազգային բյուրոյում` Ֆրանսիայի Սևր քաղաքում:
Վայրկյանը` ժամանակի միավորը, հավասար է 9192631770 ճառագայթման պարբերությանը, որը համապատասխանում է ցեզիումի -133 ատոմի հիմնական վիճակի երկու գերնուրբ մակարդակների միջև անցմանը:
Ամպերն այն
չփոփոխվող հոսանքի
ուժն է, որն անցնելով
երկու զուգահեռ,
ուղղագիծ, անվերջ
երկար և աննշան
շրջանային կտրվածք
ունեցող հաղորդիչների
միջով, որոնք վակուումում
դասավորված են
իրարից 1մ հեռավորության
վրա, նրանցից յուրաքանչյուրի
1մ երկարությամբ
հատվածի վրա մյուսի
կողմից ազդում
է ![]()
Կելվինը հավասար է ջրի եռակի կետի ջերմադինամիկական ջերմաստիճանի 1/273,16 մասին: Ջրի եռակի կետն այն ջերմաստիճանն է, որի ժամանակ ջրի երեք փուլերը (պինդ, հեղուկ և գազային) գտնվում են հավասառակշռության մեջ:
Մոլը համակարգի նյութի այն քանակն է, որը պարունակում է այնքան կառուցվածքային տարրեր, որքան ատոմներ պարունակում է 0,012 կգ ածխածինը:
Կանդելան`
աղբյուրի լույսի
ուժն է տրված ուղղությամբ,
որն առաքում է
մեներանգ ճառագայթում
![]() հաճախությամբ,
որի էներգիական
լույսի ուժը այդ
ուղղությամբ կազմում
է 1/683 Վտ/սռ:
հաճախությամբ,
որի էներգիական
լույսի ուժը այդ
ուղղությամբ կազմում
է 1/683 Վտ/սռ:
Ռադիանը շրջանի երկու շառավիղների միջև ընկած անկյունն է, որը շրջանագծից հատում է շառավղին հավասար երկարություն ունեցող աղեղ:
Ստեռադիանը այն մարմնային անկյունն է, որի գագաթը գտնվում է գնդի կենտրոնում, և որը գնդի մակերևույթի վրա անջատում է մի մակերես, որը հավասար է այն քառակուսու մակերեսին, որի կողմը հավասար է գնդի շառավղին:
1. И. В. Савельев. Курс общей физики. Механика. Москва: Астрель. АСТ, 2005.
2. А. А. Детлаф., Б. М. Яворский., Л. Б. Милковская. Курс общей физики. Т. 1, – М.: Высшая школа, 1973.
3. Д. В. Сивухин Общий курс физики. Т. 1, 3. – М.: Наука, 1974.
4. Н. В. Александров., А. Я. Яшкин. Курс общей физики. Механика. – М.: Просвещение, 1973.
5. И. В. Савельев. Курс общей физики. Молекулярная физика и термодинамика. Москва: Астрель. АСТ, 2004.
6. И. В. Савельев. Курс общей физики. Волны. Оптика. Москва: Астрель. АСТ, 2005.
7. А. А. Детлаф., Б. М. Яворский. Курс физики. – М: Высшая школа. 2002.
