ԳՄԴ  531+539.1                            Տպագրված է համաձայն 2010թ.

հրատարակչական պլանի

 (հաստատված 30.01.2010թ. ԳԽ նիստում)

 Ուսումնական ձեռնարկ.Եր.: Ճարտարագետ, 2010.- 317 էջ:

Ուսումնական ձեռնարկը բաղկացած է տասներկու գլուխներից, որոնցում շարադրված են մեխանիկայի ֆիզիկական հիմունքները, մեխանիկական տատանումներին և ալիքներին, մոլեկուլային ֆիզիկային և ջերմադինամիկային, իրական գազերին, հեղուկներին և պինդ մարմիններին վերաբերող հարցերը, որոնք անհրաժեշտ են տեսական ֆիզիկայի և այլ ֆիզիկային վերաբերող առարկաների ուսումնասիրման համար:

Ձեռնարկի հիմնական նպատակն առաջին հերթին ուսանողներին ֆիզիկայի հիմնական գաղափարներին և մեթոդներին ծանոթացնելն է: Հատուկ ուշադրություն է դարձվել ֆիզիկական օրենքների իմաստի բացատրմանը և դրանց կիրառմանը:

Ձեռնարկը նախատեսված է ՀՊՃՀ-ի բոլոր ֆակուլտետների առաջին կուրսերի ուսանողների համար: Այն կարող է օգտակար լինել նաև հեռակա բաժնի ուսանողներին:

Ուսումնական ձեռնարկը գրված է ընդհանուր ֆիզիկայի դասընթացի գործող ծրագրին համապատասխան` տեխնիկական և բնագիտական մասնագիտությունների ուսանողների համար:

Գրախոսներ՝

  ֆիզ.մաթ. գիտ. դոկտոր, պրոֆեսոր       

Տեխ. գիտ. դոկտոր, պրոֆեսոր

ԲՈՎԱՆԴԱԿՈՒԹՅՈՒՆ

Ներածություն

Ֆիզիկայի առարկան և նրա կապը այլ գիտությունների հետ

           ՄԵԽԱՆԻԿԱՅԻ ՖԻԶԻԿԱԿԱՆ ՀԻՄՈՒՆՔՆԵՐԸ

ԳԼՈՒԽ 1. ԿԻՆԵՄԱՏԻԿԱՅԻ ՏԱՐՐԵՐԸ

1.1 Հաշվարկման համակարգ: Հետագիծ, ճանապարհ, տեղափոխության վեկտոր

1.2 Արագություն և արագացում

1.3 Արագացման տանգենցիալ և նորմալ բաղադրիչներ

1.4 Արագության և արագացման պրոյեկցիաները կոորդի նատային առանցքների վրա

1.5 Անկյունային արագություն և անկյունային արագացում

ԳԼՈՒԽ 2. ՆՅՈՒԹԱԿԱՆ ԿԵՏԻ ԵՎ ՆՅՈՒԹԱԿԱՆ ԿԵՏԵՐԻ ՀԱՄԱԿԱՐԳԻ ԴԻՆԱՄԻԿԱ

2.1 Փոխազդեցություն և իներտություն: Հիմնարար փոխազդեցության տեսակները

2.2 Նյուտոնի օրենքները

2.3 Շփման ուժեր

2.4 Պինդ մարմնի դեֆորմացիան

2.5 Մեխանիկական համակարգի զանգվածների (իներցիայի) կենտրոն և նրա շարժման հավասարումը

2.6 Իմպուլսի պահպանման օրենքը

2.7 Փոփոխական զանգվածով մարմնի շարժման հավասարումը

ԳԼՈՒԽ 3. ԱՇԽԱՏԱՆՔ ԵՎ ԷՆԵՐԳԻԱ

3.1 Էներգիա, աշխատանք, հզորություն

3.2 Կինետիկ և պոտենցիալ էներգիաներ

3.3 Մեխանիկական էներգիայի պահպանման օրենքը

3.4 Մարմինների բացարձակ առաձգական և բացարձակ ոչ առաձգական հարված

ԳԼՈՒԽ 4. ՊԻՆԴ ՄԱՐՄՆԻ ՊՏՏԱԿԱՆ ՇԱՐԺՄԱՆ ԴԻՆԱՄԻԿԱ

4.1 Ուժի մոմենտը կետի և առանցքի նկատմամբ: Նյութական կետի իմպուլսի մոմենտը կետի և առանցքի նկատմամբ

4.2 Պտտական շարժման դինամիկայի հավասարումը

4.3 Մարմնի իներցիայի մոմենտն անշարժ առանցքի նկատ մամբ

4.4 Շտայների թեորեմը

4.5 Իմպուլսի մոմենտի պահպանման օրենքը

4.6 Պինդ մարմնի պտտական շարժման կինետիկ էներգիան

ԳԼՈՒԽ 5. ՁԳՈՂՈՒԹՅՈՒՆ: ԴԱՇՏԻ ՏԵՍՈՒԹՅԱՆ ՏԱՐՐԵՐԸ

5.1 Կեպլերի օրենքները: Տիեզերական ձգողության օրենքը

5.2 Ծանրության ուժ և կշիռ: Անկշռություն

5.3 Ձգողական դաշտ և նրա լարվածությունը

5.4 Աշխատանքը ձգողության դաշտում: Ձգողության դաշտի պոտենցիալը

5.5 Տիեզերական արագություններ

ԳԼՈՒԽ 6. ՀԵՂՈՒԿՆԵՐԻ ՄԵԽԱՆԻԿԱՅԻ ՏԱՐՐԵՐԸ

6.1 Հեղուկի և գազի ճնշումը

6.2 Անխզելիության հավասարումը

6.3 Բեռնուլիի հավասարումը

6.4 Մածուցիկ հեղուկի շարժումը: Հեղուկների հոսքի լամինար և տուրբուլենտ ռեժիմներ

6.5 Մածուցիկության որոշման մեթոդները

6.6 Մարմինների շարժումը հեղուկներում և գազերում

ԳԼՈՒԽ 7. ՀԱՐԱԲԵՐԱԿԱՆՈՒԹՅԱՆ ՀԱՏՈՒԿ ՏԵՍՈՒԹՅԱՆ ՏԱՐՐԵՐԸ

7.1 Գալիլեյի ձևափոխությունները

7.2 Հարաբերականության հատուկ տեսության կանխադրույթները

7.3 Լորենցի ձևափոխությունները

7.4 Հետևություններ Լորենցի ձևափոխություններից

1. Երկարության ռելյատիվիստական կրճատումը

2. Ժամանակի ընթացքի ռելյատիվիստական դանդաղումը

3. Ժամացույցների կամ երկվորյակների պարադոքսը

7.5 Միջակայք (ինտերվալ) և նրա ինվարիանտությունը

7.6 Արագությունների գումարման ռելյատիվիստական օրենքը

7.7 Ռելյատիվիստական դինամիկայի տարրերը: Ռելյատիվիստական իմպուլսը և զանգվածը

7.8 Ռելյատիվիստական էներգիա: Էներգիայի և զանգվածի կապը

7.9 էներգիայի կապը իմպուլսի հետ

ԳԼՈՒԽ 8. ՄԵԽԱՆԻԿԱԿԱՆ ՏԱՏԱՆՈՒՄՆԵՐ

8.1. Ներդաշնակ տատանումներ և դրանց բնութագրիչները

8.2. Ներդաշնակ մեխանիկական տատանումներ

8.3. Ներդաշնակ տատանակ: Զսպանակավոր, ֆիզիկական և մաթեմատիկական ճոճանակներ

8.4.Միևնույն ուղղությունը և միատեսակ հաճախություններ ունեցող տատանումների գումարումը: Զարկեր

8.5. Փոխուղղահայաց տատանումների գումարումը

8.6 Մեխանիկական մարող տատանումների դիֆերենցիալ հավասարումը և նրա լուծումը: Ինքնատատանումներ

8.7 Մեխանիկական հարկադրական տատանումների դիֆերենցիալ հավասարումը և նրա լուծումը

8.8 Մեխանիկական հարկադրական տատանումների լայնույթը և փուլը: Ռեզոնանս

ԳԼՈՒԽ 9. ԱՌԱՁԳԱԿԱՆ ԱԼԻՔՆԵՐ

9.1 Ալիքային պրոցեսներ: Երկայնական և լայնական ալիքներ

9.2 Վազող ալիքի հավասարումը: Փուլային արագություն: Ալիքային հավասարում

9.3. Առաձգական ալիքի էներգիան

9.4. Ալիքների ինտերֆերենցիան

9.5 Կանգուն ալիքներ

9.6 Ձայնային ալիքներ

9.7. Դոպլերի էֆեկտը ակուստիկայում

9.8. Ուլտրաձայն և նրա կիրառությունը

ՆԵՐԱԾՈՒԹՅՈՒՆ

ՖԻԶԻԿԱՅԻ ԱՌԱՐԿԱՆ ԵՎ ՆՐԱ ԿԱՊԸ ԱՅԼ ԳԻՏՈՒԹՅՈՒՆՆԵՐԻ ՀԵՏ

Ֆիզիկան բնական այլ գիտությունների հետ միասին ուսումնասիրում է մեզ շրջապատող նյութական աշխարհի օբյեկտիվ հատկությունները:

Ֆիզիկան ուսումնասիրում է մատերիայի շարժման ամենաընդհանուր ձևերը (մեխանիկական, ջերմային, էլեկտրամագնիսական և այլն) և դրանց փոխադարձ փոխարկումները: Ֆիզիկայի ուսումնասիրած շարժման ձևերը առկա են շարժման բոլոր բարձր և ավելի բարդ ձևերում (քիմիական, կենսաբանական և այլ պրոցեսներում) և անբաժան են նրանցից, թեև ամենևին էլ չեն սպառում դրանք: Այսպես, ֆիզիկայի հայտնաբերած տիեզերական ձգողության օրենքին ենթարկվում են հայտնի բոլոր մարմինները` երկրային և երկնային, անկախ այն բանից` դրանք քիմիապես պարզ նյութեր են, թե` բարդ, կենդանի, թե` մեռած: Ֆիզիկայի սահմանած էներգիայի պահպանման օրենքին ենթարկվում են բոլոր պրոցեսները, անկախ այն բանից, կրու՞մ են դրանք առանձնահատուկ քիմիական, կենսաբանական և այլ բնույթ, թե՞ ոչ: Ֆիզիկան բնագիտության հիմքն է:

Ֆիզիկայի և բնական մի շարք այլ գիտությունների միջև չի կարելի կտրուկ սահման դնել: Ֆիզիկայի և քիմիայի միջև գոյություն ունեն սահմանամերձ ընդարձակ շրջաններ, նույնիսկ առաջ են եկել հատուկ գիտություններ` ֆիզիկական քիմիա և քիմիական ֆիզիկա: Գիտելիքների բնագավառներ, որտեղ ֆիզիկայի մեթոդները կիրառվում են ավելի կամ պակաս չափով մասնակի հարցերը ուսումնասիրելու համար, նույնպես միանում, կազմում են հատուկ գիտություններ. այդպես է առաջ եկել, օրինակ, աստղաֆիզիկան, որն ուսումնասիրում է երկնային օբյեկտներում ընթացող ֆիզիկական երեվույթները, և երկրաֆիզիկան, որն ուսումնասիրում է Երկրի մթնոլորտում և երկրագնդի կեղևի մեջ ընթացող ֆիզիկական երևույթները: Ֆիզիկայում հայտնագործությունները հաճախ խթան են հանդիսացել այլ գիտությունների զարգացմանը: Մանրադիտակի և հեռադիտակի գյուտերն արագացրել են կենսաբանության և աստղագիտության զարգացումը: Ֆիզիկոսների հայտնաբերած սպեկտրային անալիզը դարձավ աստղաֆիզիկայի հիմնական մեթոդը և այլն:

Ֆիզիկայի, ինչպես և այլ գիտությունների զարգացմանը խթան են հանդիսացել մադկանց գործնական պահանջները: Հին եգիպտացիների և հույների մեխանիկան առաջ է եկել անմիջականորեն այն պահանջների կապակցությամբ, որ առաջադրում էր այն ժամանակվա կառուցողական և ռազմական տեխնիկան: Նմանապես զարգացող տեխնիկայի և ռազմական գործի ազդեցության տակ գիտական մեծ հայտնագործություններ կատարվեցին 17-րդ դարի և 18-րդ դարի սկզբին:

Ռուս գիտնական Մ. Լոմոնոսովն իր գիտական աշխատանքը զուգակցում էր գործնականի պահանջներին: Նրա բազմաթիվ և բազմազան հետազոտությունները պինդ և հեղուկ մարմինների բնույթի, օպտիկայի, օդերևութաբանության, մթնոլորտային էլեկտրականության ուղղությամբ կապված էին այս կամ այն գործնական հարցերի հետ:

19-րդ դարի սկզբին շոգեմեքենայի կիրառությունը անհրաժեշտ դարձրեց ամենաշահավետ կերպով ջերմաքանակը մեխանիկական աշխատանքի փոխարկելու հարցի լուծումը:

1831 թվականին Ֆարադեյի կողմից էլեկտրամագնիսական մակածման երևույթի հայտնագործումը հնարավոր դարձրեց էլեկտրական երևույթների գործնական լայն կիրառությունը:

1869 թվականին Դ. Մենդելեևի կողմից հայտնաբերված պարբերական օրենքը ոչ միայն բացառիկ դեր խաղաց ատոմների ու քիմիական երևույթների մասին ուսմունքի զարգացման, այլև քիմիայի ու ֆիզիկայի բազմաթիվ գործնական խնդիրների լուծման մեջ:

Ժամանակակից գիտատեխնիկական առաջընթացը օրգանապես կապված է ֆիզիկայի հետ: Ռադիոտեխնիկայում, միջուկային էներգետիկայում, հրթիռային և կիսահաղորդչային տեխնիկայում, ավտոմատիկայում և հեռուստամեխանիկայում, հաշվողական և ստուգիչ-չափողական և տեխնիկայի այլ բնագավառներում լայն կիրառություն ունեն ֆիզիկայի նվաճումները:

Ֆիզիկայի բուռն թափով զարգացումը, նրա աճող կապը տեխնիկայի հետ, ցույց է տալիս ընդհանուր ֆիզիկայի նշանակալից աճող դերը բարձրագույն տեխնիկական ուսումնական հաստատությունում` որպես հիմնարար բազա, ճարտարագետի տեսական պատրաստվածության համար, առանց որի նրա հաջող գործնեությունը անհնարին է:

>>

1.1. ՀԱՇՎԱՐԿՄԱՆ ՀԱՄԱԿԱՐԳ: ՀԵՏԱԳԻԾ, ՃԱՆԱՊԱՐՀԻ ԵՐԿԱՐՈՒԹՅՈՒՆ,
ՏԵՂԱՓՈԽՈՒԹՅԱՆ ՎԵԿՏՈՐ

Մեխանիկան ֆիզիկայի այն բաժինն է, որն ուսումնասիրում է մեխանիկական շարժումների օրինաչափությունները և այդ շարժումներն առաջացնող կամ փոփոխող պատճառները: Մեխանիկական շարժում է կոչվում ժամանակի ընթացքում տարածության մեջ մարմնի դիրքի փոփոխությունն այլ մարմինների նկատմամբ կամ մարմնի մասերի դիրքերի փոփոխությունը իրար նկատմամբ:

Որպես գիտություն, մեխանիկայի զարգացումն սկսվում է 3-րդ դարից, երբ հույն գիտնական Արքիմեդը (287-212 մինչև մ. թ.) ձևակերպեց լծակի հավասարակշռության օրենքը և լողացող մարմինների հավասարակշռության պայմանները: Մեխանիկայի հիմնական օրենքները սահմանվել են իտալացի ֆիզիկոս և աստղագետ Գ. Գալիլեյի (1564-1642) և վերջնական ձևակերպումն են ստացել անգլիացի գիտնական Ի. Նյուտոնի (1643-1727) կողմից:

Գալիլեյ-Նյուտոնի մեխանիկան կոչվում է դասական մեխանիկա: Դասական մեխանիկան ձևավորվել է միայն սահմանափակ տիպի շարժումների դիտումների հիման վրա, ինչպիսիք են` մարդու մարմնի չափերի հետ համեմատելի (նետված քարը) կամ նրա համեմատությամբ շատ խոշոր (մոլորակների շարժումը) և ոչ շատ մեծ արագություններով օժտված մարմինների շարժումը: Այստեղից էլ բխում է դասական մեխանիկայի մոտավոր բնույթը: Գիտության հետագա զարգացումը ցույց տվեց, որ դասական մեխանիկան իրականության հիանալի մոտավորությունն է, քանի դեռ մենք գործ ունենք մեծ թվով ատոմներից բաղկացած (մակրոսկոպիկ) մարմինների շարժման հետ, մարմիններ, որոնց արագությունները, համեմատած լույսի c արագության հետ, փոքր են: Լույսի արագության հետ համեմատելի արագությամբ շարժվող մարմինների շարժման օրենքները ուսումնասիրվում են ռելյատիվիստական մեխանիկայում` հիմնված հարաբերականության հատուկ տեսության վրա, որը սահմանել է Ա. Այնշտայնը (1879-1955): Միկրոսկոպիկ մարմինների (առանձին ատոմներ և տարրական մասնիկներ) շարժումը նկարագրելու համար դասական մեխանիկայի օրենքները կիրառելի չեն` դրանք փոխարինվում են քվանտային մեխանիկայի օրենքներով:

Ռելյատիվիստական մեխանիկայի հավասարումներից սահմանում (v<<c) անցում է կատարվում դասական մեխանիկայի բանաձևերին, քվանտային մեխանիկայի հավասարումները սահմանում (զանգվածների համար, որոնք շատ մեծ են ատոմների զանգվածների հետ համեմատած) նույնպես անցնում են դասական մեխանիկայի հավասարումներին: Սա ցույց է տալիս դասական մեխանիկայի կիրառելիության սահմանափակումը` մարմինների մեծ զանգվածների մեխանիկայի (համեմատած ատոմների զանգվածների հետ), որոնք շարժվում են փոքր արագություններով (համեմատած լույսի արագության հետ):

Մեխանիկան բաժանվում է երեք բաժինների` կինեմատիկայի, դինամիկայի և ստատիկայի: Կինեմատիկան ուսումնասիրում է մարմինների շարժումները, առանց քննարկելու այդ շարժումները պայմանավորող պատճառները: Դինամիկան ուսումնասիրում է մարմինների շարժման օրենքները և պատճառները, որոնք առաջ են բերում կամ փոփոխում են այդ շարժումը: Ստատիկան ուսումնասիրում է մարմինների համակարգի հավասարակշռության օրենքները: Եթե հայտնի են մարմինների շարժման օրենքները, ապա դրանցից կարելի է ստանալ հավասարակշռության օրենքները: Դրա համար էլ ստատիկայի օրենքները դինամիկայի օրենքներից անկախ չեն քննարկվում:

Մեխանիկայում մարմինների շարժումների նկարագրման համար կախված խնդիրների կոնկրետ պայմաններից օգտագործում են տարբեր ֆիզիկական մոդելներ: Պարզագույն մոդել է նյութական կետը` այնպիսի մարմին, որի չափերը և ձևը տվյալ խնդրի մեջ կարելի է անտեսել: Նյութական կետ հասկացությունը վերացարկում (աբստրակցիա) է, բայց նրա ներմուծումը հեշտացնում է գործնական խնդիրների լուծումը: Օրինակ` ուսումնասիրելով մոլորակների շարժումը Արեգակի շուրջը ուղեծրերով` կարելի է դրանք ընդունել նյութական կետեր:

Կամայական մակրոսկոպիկ մարմինը կամ մարմինների համակարգը կարելի է մտովի բաժանել միմյանց հետ փոխազդող փոքր մասերի, որոնցից յուրաքանչյուրը դիտարկվում է որպես նյութական կետ: Ուստի կամայական մարմինների շարժման ուսումնասիրությունը բերվում է նյութական կետերի համակարգի ուսումնասիրությանը:

Մարմինները միմյանց փոխազդեցության հետևանքով կարող են դեֆորմացվել, այսինքն` փոխել իրենց ձևն ու չափերը: Դրա համար էլ մեխանիկայում մտցվում է նորից մի մոդել` բացարձակ պինդ մարմնի մոդելը: Բացարձակ պինդ մարմին է կոչվում այն մարմինը, որը ոչ մի պայմանի դեպքում չի կարող դեֆորմացվել, այսինքն` փոփոխել իր ձևն ու չափերը, և բոլոր պայմանների դեպքում այդ մարմնի երկու կետերի միջև (կամ ավելի ճիշտ երկու մասնիկների միջև) հեռավորությունը մնում է հաստատուն:

Պինդ մարմնի ցանկացած շարժում կարելի է ներկայացնել որպես երկու` համընթաց և պտտական շարժումների համակցում:

Համընթաց կոչվում է այն շարժումը, որի ժամանակ ցանկացած երկու կետեր միացնող ուղիղը շարժման ընթացքում մնում է ինքն իրեն զուգահեռ: Պտտական կոչվում է մարմնի այն շարժումը, որի ժամանակ նրա բոլոր կետերը շարժվում են շրջանագծերով, որոնց կենտրոնները գտնվում են մեկ ուղղի` պտտման առանցքի վրա:

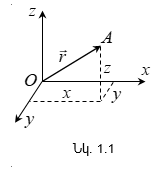
Մարմինների շարժումը կատարվում է տարածության և ժամանակի մեջ: Ուստի նյութական կետի շարժման նկարագրման համար պետք է իմանալ, տարածության որ մասերում և ժամանակի ինչ պահերին այդ կետը գտնվել է այս կամ այն դիրքում: Ուստի, որպեսզի հնարավոր լինի բնութագրել որևէ մարմնի շարժումը, ամենից առաջ անհրաժեշտ է պայմանավորվել, թե ինչ այլ մարմնի նկատմամբ պետք է հաշվել տվյալ մարմնի տեղափոխությունը: Այդ մարմինը կոչվում է հաշվարկման մարմին, որի հետ կապում են կոորդինատային հաշվարկման որևէ համակարգ և ժամանակը չափող սարք, օրինակ, կոորդինատների ուղղանկյուն համակարգ և ժամացույց:

Ավելի հաճախ օգտագործվող դեկարտյան համակարգում A կետի դիրքը ժամանակի տվյալ պահին նշված համակարգի նկատմամբ որոշվում է երեք կոորդինատներով` x, y և z կամ  շառավիղ-վեկտորով, որը տարվում է կոորդինատների հաշվարկման սկզբից մինչև տվյալ կետը (նկ.1.1):

Նյութական կետի շարժման ժամանակ նրա կոորդինատները ժամանակի ընթացքում փոփոխվում են: Ընդհանուր դեպքում նրա շարժումը որոշվում է երեք սկալյար հավասարումներով`

որը համարժեք է հետևյալ վեկտորական հավասարմանը`

 (1.1) և (1.2) հավասարումները կոչվում են նյութական կետի շարժման կինեմատիկական հավասարումներ:

Այն անկախ մեծությունների թիվը, որոնք լրիվ որոշում են կետի դիրքը տարածության մեջ, կոչվում է ազատության աստիճանների թիվ: Եթե նյութական կետը ազատ շարժվում է տարածության մեջ, ապա այն օժտված է երեք ազատության աստիճաններով (x, y և z), եթե այն շարժվում է ինչ-որ մակերևույթով` երկու ազատության աստիճաններով, եթե ինչ-որ գծի երկայնքով` մեկ ազատության աստիճանով:

Արտաքսելով (1.1) և (1.2) հավասարումներից t ժամանակը` կստանանք նյութական կետի շարժման հետագծի հավասարումը: Հետագիծ կոչվում է այն կետերի երկրաչափական տեղը, որոնցով տվյալ հաշվարկման համակարգում հաջորդաբար անցնում է նյութական կետը շարժման ժամանակ: Կախված հետագծի ձևից` շարժումները կարող են լինել ուղղագիծ և կորագիծ:

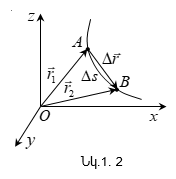
Քննարկենք նյութական կետի շարժումը կամայական հետագծի երկայնքով (նկ.1.2): Ժամանակի հաշվարկման սկիզբ ընդունում ենք այն պահը, երբ կետը գտնվել է A դիրքում: Հետագծի AB տեղամասի երկարությունը, որն անցնում է նյութական կետը ժամանակի հաշվարկման սկզբնական պահից, կոչվում է ճանապարհի երկարություն, և այն ժամանակից կախված սկալյար ֆունկցիա է.  Շարժվող նյութական կետի սկզբնական դիրքից ժամանակի տվյալ պահին նրա ունեցած դիրքին տարված` վեկտորը (կետի շառավիղ վեկտորի աճը դիտարկվող ժամանակի ընթացքում) կոչվում է տեղափոխություն:

Ուղղագիծ շարժման դեպքում տեղափոխության վեկտորը համընկնում է հետագծի համապատասխան տեղամասի հետ, և տեղափոխության մոդուլը հավասար է  անցած ճանապարհին:

>>

1.2. ԱՐԱԳՈՒԹՅՈՒՆ ԵՎ ԱՐԱԳԱՑՈՒՄ

Նյութական կետի շարժման բնութագրման համար օգտագործվում է վեկտորական մի մեծություն` արագությունը, որով որոշվում է ինչպես շարժման թափը, այնպես էլ նրա ուղղությունը ժամանակի տվյալ պահին:

Դիցուք նյութական կետը շարժվում է ինչ-որ կորագիծ հետագծով, այնպես, որ ժամանակի t պահին նրան համապատասխանում է  շառավիղ-վեկտորը (նկ.1.3):

Փոքր  ժամանակամիջոցի ընթացքում կետն անցնում է  ճանապարհ և ստանում տարրական  (անվերջ փոքր)  տեղափոխություն:

Միջին արագության վեկտոր է կոչվում շառավիղ-վեկտորի  աճի և  ժամանակամիջոցի հարաբերությունը.

Միջին արագության վեկտորի ուղղությունը համընկնում է  ուղղության հետ:  անսահման փոքրացնելու դեպքում միջին արագությունը ձգտում է սահմանային արժեքին, որն անվանում են  ակնթարթային արագություն.

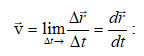
Այսպիսով, ակնթարթային արագությունը վեկտորական մեծություն է և որոշվում է շարժվող կետիշառավիղ-վեկտորի առաջին կարգի ածանցյալով ըստ ժամանակի: Քանի որ հատողը սահմանում համընկնում է շոշափողի հետ, ապա  արագության վեկտորն ուղղված է հետագծի շոշափողով դեպի շարժման կողմը (նկ.1.3):  փոքրացումով  ճանապարհի երկարությունը ավելի է մոտենում  ուստի ակնթարթային արագության մոդուլը`

Այսպիսով, ակնթարթային արագության մոդուլը հավասար է ճանապարհի առաջին կարգի ածանցյալին ըստ ժամանակի.

Անհավասարաչափ շարժման դեպքում ակնթարթային արագության մոդուլը ժամանակի ընթացքում փոփոխվում է: Տվյալ դեպքում օգտագործում են < v > սկալյար մեծությունը` անհավասարաչափ շարժման միջին արագությունը`

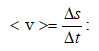
Նկ.1.3-ից հետևում է, որ < v >-ը մեծ է  քանի որ  և միայն ուղղագիծ շարժման դեպքում`

Եթե ds=vdt արտահայտությունը ինտեգրվի ըստ ժամանակի t-ից մինչև  սահմաններում, կարելի է գտնել  ժամանակում կետի անցած ճանապարհը.

Հավասարաչափ շարժման դեպքում ակնթարթային արագության թվային արժեքը հաստատուն է, ուստի (1.5) արտահայտությունը կընդունի հետևյալ տեսքը`

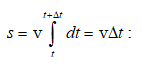
Կետի անցած ճանապարհը  ժամանակամիջոցի ընթացքում որոշվում է հետևյալ ինտեգրալով

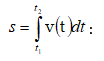
Անհավասարաչափ շարժման դեպքում կարևոր է իմանալ, թե որքան արագ է փոփոխվում արագությունը ժամանակի ընթացքում: Այն ֆիզիկական մեծությունը, որը բնութագրում է արագության փոփոխությունը ըստ մոդուլի և ուղղության, կոչվում է արագացում:

>>

1.3. ԱՐԱԳԱՑՄԱՆ ՏԱՆԳԵՆՑԻԱԼ ԵՎ ՆՈՐՄԱԼ ԲԱՂԱԴՐԻՉՆԵՐ

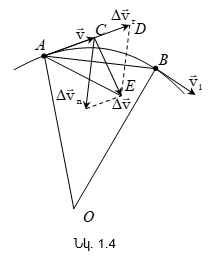
Քննարկենք հարթ շարժումը, այսինքն այն շարժումը, որի դեպքում հետագծի բոլոր տեղամասերում կետերը ընկած են մեկ հարթության մեջ: Դիցուք  վեկտորը տալիս է կետի արագությունը ժամանակի t պահին A դիրքում:  ժամանակում կետն անցել է B դիրքը և ձեռք է բերել  տարբեր` ինչպես ըստ մոդուլի, այնպես էլ ուղղությամբ  հավասար արագություն: Տեղափոխենք  վեկտորը A կետը և գտնենք  (նկ.1.4):

Անհավասարաչափ շարժման միջին արագացում t-ից մինչև  միջակայքում կոչվում է այն վեկտորական մեծությունը, որը հավասար է արագության  փոփոխության և  ժամանակի միջակայքի հարաբերությանը.

Նյութական կետի ակնթարթային արագացումը ժամանակի t պահին հավասար է միջին արագացման սահմանին`

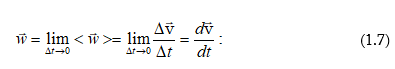
Այսպիսով, արագացումը վեկտորական մեծություն է և հավասար է արագության առաջին կարգի ածանցյալին ըստ ժամանակի:

վեկտորը վերածենք երկու բաղադրիչների: Դրա համար A կետից (տես նկ.1.4)  արագության ուղղությամբ տեղադրենք վեկտորը, որը մոդուլով հավասար է  Ակներև է, որ վեկտորը հավասար է  և որոշում է ժամանակամիջոցում արագության փոփոխությունը ըստ մոդուլի:  վեկտորի երկրորդ  բաղադրիչը բնութագրում է արագության փոփոխությունը ըստ ուղղության ժամանակամիջոցում:

Արագացման տանգենցիալ բաղադրիչը`

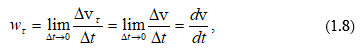
այսինքն հավասար է արագության մոդուլի ածանցյալին ըստ ժամանակի: Այն բնութագրում է արագության փոփոխությունը ըստ մոդուլի:

Գտնենք արագացման երկրորդ բաղադրիչը: Ենթադրենք` B կետը բավականին մոտ է A կետին, ուստի  կարելի է ընդունել ինչ-որ r շառավղով շրջանագծի աղեղ, որը քիչ է տարբերվում AB լարից: AOB և EAD եռանկյունների նմանությունից հետևում է`

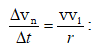
Սահմանում, երբ  կստանանք`  Քանի որ  EAD անկյունը ձգտում է զրոյի, հետևաբար EAD եռանկյունը հավասարակողմ է, ապա  միջև կազմած EAD անկյունը ձգտում է 90⁰ -ի: Հետևաբար, երբ  վեկտորները դառնում են իրար փոխուղղահայաց: Քանի որ արագության վեկտորն ուղղված է հետագծի շոշափողով, ապա  վեկտորն ուղղահայաց է արագության վեկտորին և ուղղված է կորության կենտրոն:

Արագացման

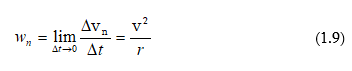
բաղադրիչը կոչվում է նորմալ արագացում կամ կենտրոնաձիգ արագացում:

Տանգենցիալ և նորմալ բաղադրիչների երկրաչափական գումարը տալիս է մարմնի լրիվ արագացումը (նկ.1.5):

Ամփոփելով կարող ենք ասել, որ կորագիծ անհավասարաչափ շարժման դեպքում լրիվ արագացումը բաժանվում է երկու բաղադրիչների  տանգենցիալ արագացման, որը բնորոշում է արագության փոփոխությունն ըստ մոդուլի, և նորմալ արագացման, որը բնորոշում է արագության փոփոխությունն ըստ ուղղության:

 բաղադրիչները միմյանց ուղղահայաց են: Կախված տանգենցիալ և նորմալ արագացումների բաղադրիչներից` շարժումը կարելի է դասակարգել հետևյալ ձևով.

1) եթե  ապա շարժումը ուղղագիծ հավասարաչափ է:

2) եթե  ապա շարժումը ուղղագիծ հավասարաչափ արագացող է: Այդպիսի շարժման դեպքում`

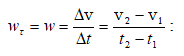
Եթե ժամանակի սկզբնական պահին t₁=0, իսկ սկզբնական արագությունը`  ապա ընդունելով  կստանանք`

Ինտեգրելով այս արտահայտությունը զրոյից մինչև ժամանակի կամայական t պահը` կստանանք կետի անցած ճանապարհը հավասար փոփոխական շարժման դեպքում.

3)  ապա փոփոխական արագացումով ուղղագիծ շարժում է:

4)  դեպքում արագությունը փոփոխվում է միայն ըստ ուղղության:  բանաձևից հետևում է, որ կորության շառավիղը պետք է լինի հաստատուն: Հետևաբար, շարժումը շրջանագծով հավասարաչափ է:

>>

1.4. ԱՐԱԳՈՒԹՅԱՆ ԵՎ ԱՐԱԳԱՑՄԱն ՊՐՈՅԵԿՑԻԱՆԵՐԸ
 ԿՈՈՐԴԻՆԱՏԱՅԻՆ ԱՌԱՆՑՔՆԵՐԻ ՎՐԱ

Կետի դիրքը որոշող շառավիղ-վեկտորը դեկարտյան ուղղանկյուն կոորդինատային համակարգում կարելի է ներկայացնել կոորդինատային առանցքներով ուղղված երեք վեկտորների գումարի տեսքով.

 շառավիղ-վեկտորի պրոյեկցիաներն են համապատասխան կոորդինատային առանցքների վրա: Ածանցելով (1.6)-ը ըստ ժամանակի` կստանանք շարժվող կետի համար արագության արտահայտությունը.

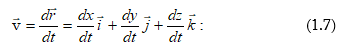
(1.7)-ից հետևում է, որ արագության վեկտորի պրոյեկցիաները կոորդինատային առանցքների վրա հավասար են համապատասխան կոորդինատների ածանցյալներին

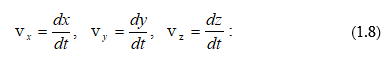
Կետի շարժման նկարագրման կոորդինատային եղանակի դեպքում տրվում են  ֆունկցիաները: Դրանք կարելի է դիտարկել որպես  պրոյեկցիաներ համապատասխան առանցքների վրա: Վեկտորի  ֆունկցիաների ածանցյալներն ըստ ժամանակի տալիս են արագության պրոյեկցիաները կոորդինատային առանցքների վրա: Ինչ վերաբերում է արագացմանը, դժվար չէ տեսնել, որ նրա պրոյեկցիաները կոորդինատային առանցքների վրա հավասար են արագության վեկտորի պրոյեկցիաների ածանցյալներին ըստ ժամանակի կամ շառավիղ-վեկտորի պրոյեկցիաների երկրորդ կարգի ածանցյալներին ըստ ժամանակի.

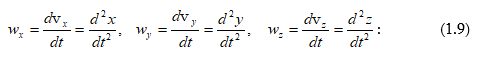
Կոորդինատային եղանակը հնարավորություն է տալիս որոշել արագության և արագացման մոդուլներն ու ուղղությունը` գտնելու շարժման հետագիծը: Արագության մոդուլը որոշվում է այսպես.

Արագության ուղղությունը կարելի է որոշել` տալով ուղղորդ կոսինուսները` այսինքն կոորդինատային առանցքների հետ վեկտորի կազմած անկյունների կոսինուսները:

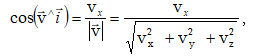
համանմանորեն արտահայտվում է արագացման մոդուլը`

և արագացման ուղղորդ կոսինուսները

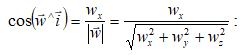
Եթե հարթ շարժումը տրված է կոորդինատային տեսքով, այսինքն` տրված են

ֆունկցիաները, ապա հետագծի հավասարումը կստանանք, եթե (1.10) հավասարումների համակարգից արտաքսենք t ժամանակը: Արդյունքում ստացվում է առնչություն, որը պարունակում է միայն x և y որն էլ հարթ կորի հավասարումն է:

>>

1.5. ԱՆԿՅՈՒՆԱՅԻՆ ԱՐԱԳՈՒԹՅՈՒՆ ԵՎ ԱՆԿՅՈՒՆԱՅԻՆ ԱՐԱԳԱՑՈՒՄ

Դիտարկենք պինդ մարմին, որը պտտվում է աշարժ առանցքի շուրջը: Պինդ մարմնի առանձին կետերը գծում են տարբեր շառավիղներով շրջանագծեր, որոնց կենտրոնները ընկած են պտտման առանցքի վրա: Դիցուք որևէ կետ պտտվում է R շառավիղ ունեցող շրջանագծով (նկ.1.6): Նրա դիրքը  ժամանակամիջոցում տրվում է  անկյունով:

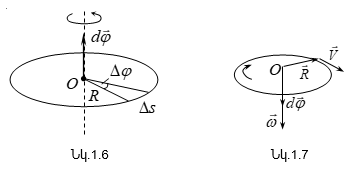
Տարրական (անվերջ փոքր) պտույտները կարելի է դիտարկել որպես վեկտորներ վեկտորի մոդուլը հավասար է պտույտի անկյանը, իսկ նրա ուղղությունը համընկնում է պտուտակի սայրի համընթաց շարժման հետ, որի գլխիկը պտտվում է շրջանագծով կետի շարժման ուղղությամբ, այսինքն ենթարկվում է աջ պտուտակի կանոնին (նկ.1.6): Այն վեկտորները, որոնց ուղղությունները կապված են պտտման ուղղության հետ, կոչվում են կեղծ կամ աքսիալ վեկտորներ: Այդ վեկտորները չունեն որոշակի կիրառման կետեր, դրանք կարող են տեղադրվել պտտման առանցքի ցանկացած կետից:

Անկյունային արագություն է կոչվում այն վեկտորական մեծությունը, որը հավասար է մարմնի պտույտի անկյան առաջին կարգի ածանցյալին ըստ ժամանակի.

վեկտորն, ինչպես և վեկտորն ուղղված է ըստ աջ պտուտակի կանոնի պտտման առանցքի երկայնքով, (նկ.1.7): Կետի գծային արագությունը (նկ.1. 7)`

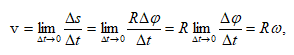
 այսինքն`

Գծային արագության համար ստացված բանաձևը կարելի է գրել վեկտորական արտադրյալի տեսքով.

Այս դեպքում վեկտորական արտադրյալի մոդուլը, ըստ սահմանման, հավասար է  իսկ ուղղությունը համընկնում է աջ պտուտակի համընթաց շարժման ուղղության հետ,  նրա պտտման դեպքում:

Անկյունային արագության վեկտորի մոդուլը հավասար է  Հաստատուն անկյունային արագություն ունեցող պտույտը կոչվում է հավասարաչափ, ընդ որում`  Այսպիսով, հավասարաչափ պտույտի դեպքում  ցույց է տալիս, թե ինչ անկյունով է պտտվում մարմինը միավոր ժամանակի ընթացքում: Անկյունային արագության միավորը ՄՀ-ում ռադ/վ է:

Հավասարաչափ պտույտը կարելի է բնութագրել T պտտման պարբերությամբ, որը այն ժամանակն է, որի ընթացքում մարմինը կատարում է մեկ պտույտ, այսինքն` պտտվում է  անկյունով: Քանի որ  ժամանակամիջոցին համապատասխանում է  պտտման անկյունը, ապա

որտեղից

Պտույտների լրիվ թիվը, որը կատարում է շրջանագծով շարժվող մարմինը միավոր ժամանակամիջոցում, կոչվում է պտտման հաճախություն.

որտեղից

Մարմնի անհավասարաչափ պտույտը բնութագրելու համար ներմուծվում է անկյունային արագացման հասկացությունը: Անկյունային արագացում կոչվում է այն վեկտորական մեծությունը, որը հավասար է անկյունային արագության ածանցյալին ըստ ժամանակի.

Անշարժ առանցքի շուրջը մարմնի պտտման դեպքում անկյունային արագացման վեկտորն ուղղված է պտտման առանցքի երկայնքով անկյունային արագության վեկտորի տարրական աճի կողմը: Արագացող շարժման դեպքում  վեկտորը համագիծ է  վեկտորին (նկ.1.8 ա), իսկ դանդաղող շարժման դեպքում հակառակ է նրան (նկ.1.8 բ): Անկյունային արագացման միավորը ռադ/վ² է:

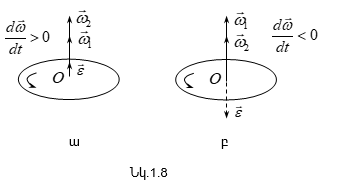
Արագացման տանգենցիալ բաղադրիչը`

Արագացման նորմալ բաղադրիչը`

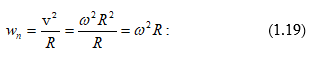
Լրիվ արագացման համար ստանում ենք`

Այսպիսով, կապը գծային (s ճանապարհի երկարություն, որն անցնում է կետը R շառավղով շրջանագծի աղեղը, v գծային արագություն,  տանգենցիալ արագացում,  նորմալ արագացում) և անկյունային (պտույտի անկյուն,  անկյունային արագություն,  անկյունային արագացում) մեծությունների միջև արտահայտվում է հետևյալ բանաձևերով`

Կետի շրջանագծով հավասարաչափ արագացող շարժման դեպքում

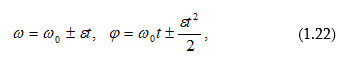
որտեղ  սկզբնական անկյունային արագությունն է:

Խնդիր 1: A մասնիկի դիրքը բնութագրող շառավիղ-վեկտորը O անշարժ կետի նկատմամբ ըստ ժամանակի փոփոխվում է  օրենքով, որտեղ  հաստատուն վեկտորներ են, ընդ որում`  ուղղահայաց է  դրական հաստատուն է: Գտնել մասնիկի  արագացումը և հետագծի y(x) հավասարումը` ընդունելով, որ x և y առանցքները համըկնում են  վեկտորների ուղղության հետ:

Լուծում: Ածանցելով  ըստ ժամանակի երկու անգամ կստանանք`

այսինքն  միշտ ուղղված է դեպի O կետը, և նրա մոդուլը համեմատական է մասնիկից մինչև այդ կետը եղած հեռավորությանը: Գտնենք հետագծի հավասարումը: Պրոյեկտելով  առանցքների վրա կստանանք`

Արտաքսելով ստացված հավասարումներից  գտնում ենք`

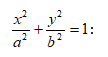
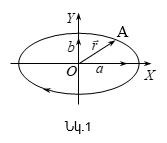
Ստացված հավասարումը էլիպսի հավասարում է,  նրա կիսաառանցքներն են (նկ.1): Սլաքով ցույց է տրված A մասնիկի շարժման ուղղությունը:

Խնդիր 2: Կետը շարժվում է հարթ հետագծով այնպես, որ նրա տանգենցիալ արագացումը`  իսկ նորմալ արագացումը`  որտեղ  դրական հաստատուններ են, t-ն` ժամանակը: t=0 պահին կետը սկսում է շարժվել:

Գտնել կետի հետագծի կորության R շառավիղը և նրա w լրիվ արագացումը` կախված կետի անցած s ճանապարհից:

Լուծում: Կետի արագության տարրական աճը` dv=wdt: Ինտեգրելով այս հավասարումը կստանանք`

Անցած ճանապարհը`

Հետագծի կորության շառավիղը որոշվում է

բանաձևով: Քանի որ  (3)-ից կստանանք`

>>

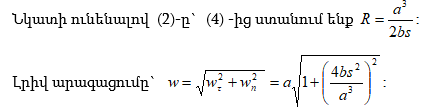
ԳԼՈՒԽ 2. ՆՅՈՒԹԱԿԱՆ ԿԵՏԻ ԵՎ ՆՅՈՒԹԱԿԱՆ ԿԵՏԵՐԻ ՀԱՄԱԿԱՐԳԻ ԴԻՆԱՄԻԿԱ

2.1. ՓՈԽԱԶԴԵՑՈՒԹՅՈՒՆ ԵՎ ԻՆԵՐՏՈՒԹՅՈՒՆ: ՀԻՄՆԱՐԱՐ ՓՈԽԱԶԴԵՑՈՒԹՅԱՆ ՏԵՍԱԿՆԵՐԸ

Ուժը վեկտորական ֆիզիկական մեծություն է, որը տալիս է այլ մարմինների կողմից տվյալ մարմնի վրա մեխանիկական ազդեցության չափը: Այս ազդեցությունն ի հայտ է գալիս շարժվող մարմնի արագության կամ մարմնի ձևի և չափերի փոփոխության դեպքում: Ուժը, ինչպես և ցանկացած վեկտորական մեծություն, համարվում է տրված, եթե հայտնի են նրա թվային արժեքը, ուղղությունը և կիրառման կետը: Մարմնի հանգստի կամ ուղղագիծ հավասարաչափ շարժման վիճակը պահպանելու հատկությունը կոչվում է իներտություն: Մարմնի համընթաց շարժման դեպքում մարմնի իներտության չափը բնութագրվում է մի ֆիզիկական մեծությամբ, որը կոչվում է զանգված: Դասական մեխանիկայում (v<<c) մարմնի զանգվածը համարվում է հաստատուն և հավասար է հանգստի զանգվածին  Մարմնի զանգվածը ադիտիվ մեծություն է, այսինքն` այն հավասար է բոլոր մասնիկների (նյութական կետերի) զանգվածների գումարին, որոնցից կազմված է մարմինը:

Ժամանակակից ֆիզիկայում ապացուցված է, որ բնության մեջ գոյություն ունեցող բոլոր ուժերը չորս տեսակի փոխազդեցությունների առանձին դրսևորումներ են:

Առաջինը գրավիտացիոն փոխազդեցությունն է, որն իրականացվում է զանգված ունեցող ցանկացած մասնիկների միջև: Փոխազդեցության ուժը ձգողական է, այն հեռազդեցության բնույթ ունի, այսինքն` ազդում է նաև մեծ հեռավորությունների վրա: Այս փոխազդեցությամբ է պայմանավորված, օրինակ, Արեգակնային համակարգի գոյությունը: Տարրական մասնիկների գրավիտացիոն փոխազդեցության ուժը չնչին է դրանց փոքր զանգվածների պատճառով:

Երկրորդը էլեկտրամագնիսական փոխազդեցությունն է, որը նույնպես հեռազդեցության բնույթ ունի: Այս փոխազդեցությունը գործում է լիցքավորված մասնիկների միջև և, դրանց լիցքերի նշանից կախված, կարող է ունենալ ձգողական կամ վանողական բնույթ: Այս ուժերով է պայմանավորված, օրինակ, ատոմի գոյությունը: Լիցքավորված տարրական մասնիկների միջև գործող էլեկտրամագնիսական փոխազդեցության ուժերն անհամեմատ մեծ են նրանց միջև գործող գրավիտացիոն ուժերից: Օրինակ` երկու անշարժ պրոտոնների միջև գործող էլեկտրամագնիսական կուլոնյան ուժը մոտ  անգամ մեծ է դրանց միջև գործող գրավիտացիոն ուժից:

Փոխազդեցության մյուս տեսակն ուժեղ փոխազդեցությունն է: Փոխազդեցության այս տեսակն անվանում են նաև միջուկային, քանի որ հենց այս փոխազդեցությամբ է պայմանավորված միջուկի գոյությունը: Միջուկային փոխազդեցության ուժերը գործում են միջուկի չափերի կարգի`  հեռավորությունների վրա: Այդ հեռավորությունների վրա միջուկային ուժերը կուլոնյան ուժերից մոտ հարյուր անգամ մեծ են: Ավելի մեծ հեռավորությունների վրա միջուկային ուժերը շատ արագ ձգտում են զրոյի: Սա նշանակում է, որ դրանք կարճազդու են: Ուժեղ փոխազդեցությամբ փոխազդող տարրական մասնիկները կոչվում են հադրոններ (հունարեն «հադրոս»` մեծ, ուժեղ բառից), դրանցից են նաև նուկլոնները` պրոտոնը և նեյտրոնը:

Չորրորդ տիպի փոխազդեցությունը կոչվում է թույլ փոխազդեցություն: Այսպիսի ուժերը նույնպես կարճազդու են, գործում են և ավելի փոքր հեռավորությունների վրա: Այս փոխազդեցությամբ են պայմանավորված մի խումբ տարրական մասնիկների միջև տեղի ունեցող ռեակցիաները և փոխակերպումները: Դրանցից են լեպտոնները (հունարեն «լեպտոս»`բարակ, թեթև բառից): Լեպտոններ են` էլեկտրոնը, նեյտրինոյի տեսակները, մյուոնը և դրանց հակամասնիկները:

>>

2.2. ՆՅՈՒՏՈՆԻ ՕՐԵՆՔՆԵՐԸ

Մինչև այժմ դիտարկվել է միայն մարմինների տեղափոխությունը` կախված ժամանակից, առանց դրանց առաջացման պատճառների քննարկման, այսինքն՝ դիտարկվել է կինեմատիկայի խնդիրները: Իսկ այն հարցերը, որոնք կապված են մարմինների փոխազդեցությունների հետ և առաջացնում են շարժման վիճակի փոփոխություն, չեն շոշափվել: Այդ հարցերը վերաբերում են դինամիկայի բնագավառին: Դինամիկայի հիմնական դրույթները ձևակերպվել են Նյուտոնի կողմից իր «Բնական փիլիսոփայության մաթեմատիկական սկզբունքները» աշխատության մեջ (1687), որի առանցքը կազմում են երեք օրենքները: Նյուտոնի առաջին օրենքը կարելի է ձևակերպել հետևյալ կերպ. յուրաքանչյուր մարմին պահպանում է իր հանգստի կամ հավասարաչափ և ուղղագիծ շարժման վիճակը, քանի դեռ այլ մարմինների կողմից ազդեցությունը չի ստիպել նրան փոխելու այդ վիճակը:

Նյուտոնի առաջին օրենքից բխում է, որ մարմինն իր հանգստի կամ հավասարաչափ ուղղագիծ շարժման վիճակը միայն այն դեպքում կարող է փոխել, երբ նրա վրա ազդում են այլ մարմիններ:

Նյուտոնի առաջին օրենքը հնարավոր չէ սովորական փորձով ստուգել, քանի որ մեզ շրջապատող իրական պայմաններում հնարավոր չէ մարմիններն այնպիսի պայմաններում դնել, որ նրանց վրա բոլորովին չազդեն այլ մարմիններ: Սակայն Նյուտոնի առաջին օրենքի իրավացի լինելու մեջ համոզվում ենք մի շարք փաստերի ընդհանրացման միջոցով: Սովորաբար մեզ շրջապատող առարկաների հանգստի վիճակը պայմանավորված է նրանով, որ տարբեր մարմինների ազդեցությունները համակշռում են միմյանց, ինչպես օրինակ, դադարի վիճակում գտնվող մարմինների դեպքում՝ Երկրի կողմից ձգողականությունը և հենարանի կամ կախոցի հակազդեցությունը: Շարժման դեպքում մարմինն այնքան երկար է պահպանում իր արագությունը, որքան նրա վրա թույլ են ազդում այլ մարմիններ. հարթ հորիզոնական մակերևույթով նետված քարն այնքան ավելի երկար կշարժվի, որքան հարթ է այդ մակերևույթը, այսինքն՝ որքան փոքր է նրա վրա այլ մարմինների դիմադրող ազդեցությունը: Նյուտոնի առաջին օրենքի ճշտության մեջ վերջնականապես համոզվում ենք անուղղակի ձևով. նրանից բխող բոլոր հետևանքների և փորձնական տվյալների համընկնումով: Դիտումները ցույց են տալիս, որ Նյուտոնի առաջին օրենքը ճիշտ է հաշվարկման ոչ բոլոր համակարգերի նկատմամբ: Արդեն նշվել է, որ շարժման բնույթը կախված է հաշվարկման համակարգի ընտրությունից: Քննարկենք հաշվարկման երկու համակարգեր, որոնք շարժվում են իրար նկատմամբ որևէ արագացումով: Եթե դրանցից մեկի նկատմամբ մարմինը հանգստի վիճակում է, ապա ակնհայտ է, որ մյուսի նկատմամբ այն կշարժվի արագացումով: Հետևաբար, Նյուտոնի առաջին օրենքը չի կարող տեղի ունենալ այդպիսի երկու համակարգերում միաժամանակ: Հաշվարկման այն համակարգը, որտեղ իրագործվում է Նյուտոնի առաջին օրենքը, կոչվում է իներցիալ:

Փորձնական ճանապարհով հաստատված է, որ հաշվարկման այն համակարգը, որի սկիզբը համընկնում է Արևի կենտրոնի հետ, իսկ առանցքներն ուղղված են դեպի համապատասխան ձևով ընտրված աստղերը, կարելի է համարել իներցիալ: Այդ համակարգը կոչվում է արևակենտրոն (հելիոցենտրիկ) հաշվարկման համակարգ: Ցանկացած հաշվարկման համակարգ, որը շարժվում է հավասարաչափ և ուղղագիծ արևակենտրոն կամ որևէ այլ իներցիալ համակարգի նկատմամբ, նույնպես իներցիալ է: Իսկ ամեն մի համակարգ, որը իներցիալ համակարգերից մեկի նկատմամբ ունի արագացում, ինքը իներցիալ չի լինի:

Այսպիսով, Նյուտոնի առաջին օրենքը հաստատում է, որ բնության մեջ գոյություն ունեն իներցիալ հաշվարկման համակարգեր, այսինքն` այնպիսի համակարգեր, որոնց նկատմամբ ազատ շարժվող մարմինը պահպանում է իր արագությունը:

Նյուտոնի երկրորդ օրենքում հանդես են գալիս կինեմատիկայում չօգտագործվող երեք նոր ֆիզիկական մեծություններ՝ ուժ, զանգված և իմպուլս: Ուժը տալիս է տվյալ մարմնի վրա այլ մարմինների ազդեցության ուղղությունը և քանակական բնութագիրը: Զանգվածը տալիս է այդ ազդեցություների նկատմամբ մարմնի «զգայունության» քանակական բնութագիրը, այսինքն` մարմնի իներտության չափը:  իմպուլսը համընթաց շարժում կատարող մարմնի հիմնական դինամիկական բնութագիրն է:

Նյուտոնի ձևակերպմամբ երկրորդ օրենքն ասում է. մարմնի իմպուլսի փոփոխության արագությունը հավասար է մարմնի վրա ազդող  արդյունարար ուժին.

(2.1) հավասարումը կոչվում է մարմնի համընթաց շարժման դինամիկայի հավասարում: Փոխարինելով  և ենթադրելով, որ մարմնի զանգվածը հաստատուն է, (2.1) առնչությունը կարելի է ներկայացնել՝

տեսքով, որտեղ  Այսպիսով, հանգում ենք Նյուտոնի երկրորդ օրենքի այլ ձևակերպման, որը դեռ Նյուտոնից առաջ տվել էր Գալիլեյը: Մարմնի զանգվածի և արագացման արտադրյալը հավասար է մարմնի վրա ազդող համազոր ուժին: Նշենք, որ Նյուտոնի օրենքը բազմաթիվ փորձերի ընդհանրացման արդյունք է: Այս օրենքը, ինչպես և Նյուտոնի առաջին օրենքը, իրավացի է միայն հաշվարկման իներցիալ համակարգերում: Մասնավոր դեպքում, երբ ուժը հավասար է զրոյի (մարմնի վրա այլ մարմինների ազդեցության բացակայության դեպքում), արագացումը, ինչպես հետևում է (2.2)-ից, նույնպես հավասար կլինի զրոյի  որը և համընկնում է Նյուտոնի առաջին օրենքի պնդման հետ: Դրա համար կարող է թվալ, թե առաջին օրենքը մտնում է երկրորդ օրենքի մեջ՝ որպես նրա մասնավոր դեպք: Չնայած դրան` առաջին օրենքը ձևակերպվում է երկրորդից անկախ, քանի որ, ըստ էության, այն պարունակում է հաշվարկման իներցիալ համակարգերի գոյության մասին կանխադրույթը:

Նյուտոնի երրորդ օրենքը լրացնում է երկրորդ օրենքի բովանդակությունը և ընդգծում այն հանգամանքը, որ մարմինների շարժման վիճակների փոփոխություն առաջ բերող ազդեցությունները կրում են փոխազդեցության բնույթ: Եթե A մարմինը ազդում է B մարմնի վրա որևէ ուժով, ապա միևնույն ժամանակի ընթացքում B մարմինն ազդում է A մարմնի վրա ուժով:

Դիտարկենք հետևյալ օրինակը.  զանգվածներով երկու մարմիններ, որոնք մեկուսացված են արտաքին ազդեցությունից, ձգում կամ վանում են իրար որևէ բնույթի ուժով (նկ. 2.1)

 ուժերի ազդեցության տակ մարմինները համապատասխանաբար ձեռք են բերում հակառակ ուղղված  արագացումներ: Պարզվում է, որ այս արագացումների արժեքները հակադարձ համեմատական են մարմինների զանգվածներին՝

որտեղից հետևում է հավասարությունը, հետևաբար նաև ուժերի մոդուլների հավասարությունը՝  Ակնհայտ է, որ ուժերի ուղղությունները հակառակ են:

Նյուտոնի երրորդ օրենքը փորձնական փաստերի ընդհանրացում է, որը կարելի է ձևակերպել հետևյալ կերպ. մարմինների` միմյանց վրա ունեցած յուրաքանչյուր ազդեցություն կրում է փոխազդեցության բնույթ. ուժերը, որոնցով մարմիններն ազդում են միմյանց վրա, միշտ ունեն նույն բնույթը և ազդման գիծը, հավասար են ըստ մեծության և հակառակ՝ ըստ ուղղության: Օգտվելով նկ.2.1-ում օգտագործված նշանակումներից` երրորդ օրենքի էությունը կարելի է գրել հետևյալ տեսքով՝

Ըստ վերը նշվածի` ուժերը միշտ առաջանում են զույգ-զույգ, ամեն մի ուժին, որը կիրառված է որևէ մարմնի վրա, հակադրվում է նրան մեծությամբ հավասար և հակառակ ուղղված մի այլ ուժ, որը կիրառված է տվյալ մարմնի հետ փոխազդող մի այլ մարմնի վրա: Ակնառու է, որ այդ ուժերը չեն համակշռում իրար:

Նյուտոնի երրորդ օրենքը, ինչպես և առաջին երկու օրենքները, ճիշտ են հաշվարկման իներցիալ համակարգերում: Նշենք նաև, որ լույսի արագության հետ համեմատած արագություններով շարժվելու դեպքում նկատվում են շեղումներ (2.3) օրենքից:

>>

2.3. ՇՓՄԱՆ ՈՒԺԵՐ

Փորձից հայտնի է, որ ամեն մի մարմին շարժվելով մի ուրիշ մարմնի հորիզոնական մակերևույթով, նրա վրա այլ ուժերի ազդեցության բացակայության դեպքում ժամանակի ընթացքում դանդաղեցնում է իր շարժումը, և, վերջիվերջո, կանգ է առնում: Դա կարելի է բացատրել շփման ուժի գոյությամբ, որը խոչընդոտում է հպվող մարմինների` սահքին միմյանց նկատմամբ: Շփման ուժերը կախված են մարմինների հարաբերական արագություններից, նրանց ազդեցության արդյունքում մեխանիկական էներգիան միշտ փոխակերպվում է հպվող մարմինների ներքին էներգիայի, այսինքն` մասնիկների ջերմային էներգիայի:

Տարբերում են արտաքին (չոր) և ներքին շփում (հեղուկ կամ մածուցիկ) շփում: Այդ բաժանումը ունի պայմանական բնույթ: Արտաքին կոչվում է այն շփումը, որն առաջանում է երկու հպվող մարմինների շոշափող հարթության մեջ դրանց հարաբերական տեղափոխության դեպքում: Եթե հպվող մարմինները միմյանց նկատմամբ անշարժ են, խոսում են դադարի շփման ուժի մասին, եթե կատարվում է այդ մարմինների հարաբերական տեղափոխություն, ապա կախված դրանց հարաբերական շարժման բնույթից, խոսում են սահքի և գլորման շփման ուժի մասին:

Ներքին շփում կոչվում է այն շփումը, որն առաջանում է միևնույն մարմնի մասերի, օրինակ, հեղուկի կամ գազի տարբեր շերտերի միջև, որոնց արագությունները շերտից շերտ փոխվում են: Ի տարբերություն արտաքին շփման` այստեղ բացակայում է դադարի շփումը:

 Եթե մարմինները սահում են միմյանց նկատմամբ և բաժանված են մածուցիկ հեղուկի միջնաշերտով (քսուքներ), ապա շփումն առաջանում է քսուքի շերտում: Այսպիսի դեպքում խոսում են հիդրոդինամիկական շփման (քսուքի շերտը բավականաչափ հաստ է) և եզրային շփման (քսուքային միջնաշերտի հաստությունը կազմում է մոտ 0,1 մկմ և ավելի փոքր) մասին: Շփման ուժերը որոշվում են նյութի մոլեկուլների միջև փոխազդեցության բնույթով և ըստ իրենց բնույթի էլեկտրամագնիսական ուժեր են: Այդ ուժերը նկարագրվում են փորձնական ճանապարհով ստացված օրինաչափություններով:

Քննարկենք արտաքին շփման որոշ օրինաչափություններ: Այդ շփումը պայմանավորված է հպվող մակերևույթների խորդուբորդություններով, իսկ շատ ողորկ մակերևույթների դեպքում` միջմոլեկուլային ուժերի ձգողությամբ:

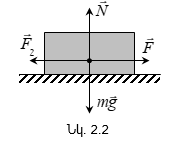
Դիտարկենք հարթության վրա գտնվող մարմինը (նկ.2.2), որի նկատմամբ կիրառված է հորիզոնական  ուժը: Մարմինը գտնվում է շարժման մեջ միայն այն դեպքում, երբ կիրառված  ուժը մեծ է  շփման ուժից: Ֆրանսիացի ֆիզիկոսներ Գ. Ամոնտոնը (1663-1705) և Շ. Կուլոնը (1736-1806) փորձնական ճանապարհով սահմանեցին հետևյալ օրենքը. սահքի  շփման ուժը համեմատական է N նորմալ ճնշման ուժին, որով մի մարմինն ազդում է մյուսի վրա.

որտեղ  սահքի շփման գործակիցն է և կախված է հպվող մակերևույթների հատկությունից:

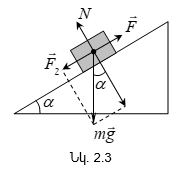
Գտնենք շփման գործակցի արժեքը: Եթե մարմինը գտնվում է թեք հարթության վրա (նկ.2.3), որի թեքման անկյունը է, ապա այն գտնվում է շարժման մեջ միայն այն դեպքում, երբ ծանրության  տանգենցիալ բաղադրիչը մեծ է  Հետևաբար, սահմանային դեպքում (մարմնի սահքի սկիզբ)  կամ

որտեղից

Այսպիսով, շփման գործակիցը հավասար է  անկյան տանգենսին, որի դեպքում սկսվում է մարմնի սահքը թեք հարթությունով:

Ողորկ մակերևույթների համար որոշակի դեր է սկսում խաղալ միջմոլեկուլային ձգողությունը: Դրանց համար կիրառվում է սահքի շփման օրենքը`

որտեղ  սահքի իրական շփման գործակիցն է, S-ը մարմինների միջև հպման մակերեսը,  լրացուցիչ ճնշումն է` պայմանավորված միջմոլեկուլային ձգողական ուժերով, որոնք արագ նվազում են` մասնիկների միջև հեռավորությունը մեծացնելով:

Շփման ուժերը էապես փոքրացնելու համար հարկավոր է սահքի շփման ուժը փոխարինել գլորման շփման ուժով (գնդիկային և հոլովակային առանցկակալներ և այլն):

Գլորման շփման ուժը որոշվում է Կուլոնի կողմից տրված օրենքով.

որտեղ  գլորման շփման գործակիցն է, r-ը` գլորվող մարմնի շառավիղը: Գլորման շփման ուժը հակադարձ համեմատական է գլորվող մարմնի շառավղին:

Շփումը բնության մեջ և տեխնիկայում մեծ դեր է խաղում: Շփման շնորհիվ շարժվում է տրանսպորտը, պահվում է պատին խփված մեխը: Որոշ դեպքերում շփման ուժերը վտանգավոր ազդեցություն են թողնում և հետևաբար, հարկավոր է դրանք փոքրացնել: Ուստի հպվող մակերևույթները պատում են քսուքով (շփման ուժը փոքրանում է մոտ 10 անգամ), որը լցնում է այդ մակերևույթների միջև խորդուբորդությունները և բաշխվում է դրանց միջև բարակ շերտով, այնպես, որ կարծես թե մակերևույթները դադարում են միմյանց հետ շփվելուց, և հեղուկի առանձին շերտեր սահում են միմյանց նկատմամբ: Այսպիսով, պինդ մարմինների արտաքին շփումը փոխարինվում է նշանակալից փոքր հեղուկի ներքին շփումով:

>>

2. 4. ՊԻՆԴ ՄԱՐՄՆԻ ԴԵՖՈՐՄԱՑԻԱՆ

Դիտարկելով պինդ մարմնի մեխանիկան, օգտվեցինք բացարձակ պինդ մարմնի հասկացությունից: Սակայն բնության մեջ բացարձակ պինդ մարմիններ չկան, քանի որ բոլոր իրական մարմինները ուժի ազդեցության տակ փոխում են իրենց ձևը և չափերը, այսինքն` դեֆորմացվում են:

Դեֆորմացիան կոչվում է առաձգական, եթե արտաքին ուժերը վերացնելուց հետո մարմինն ընդունում է սկզբնական ձևը և չափերը: Այն դեֆորմացիաները, որոնք պահպանվում են մարմնում արտաքին ուժերը վերացնելուց հետո, կոչվում են պլաստիկ (կամ մնացորդային):

Իրական մարմնի դեֆորմացիաները միշտ պլաստիկ են, քանի որ դրանք արտաքին ուժերի վերացման դեպքում, երբեք լրիվ չեն անհետանում: Սակայն, եթե մնացորդային դեֆորմացիաները փոքր են, ապա դրանք կարելի է անտեսել և դիտարկել առաձգական դեֆորմացիաները: Առաձգականության տեսությունում ապացուցվում է, որ բոլոր տեսակի դեֆորմացիաները (ձգում կամ սեղմում, սահք, ծռում, պտտում) կարող են տեղեկացնել միաժամանակ կատարվող ձգման կամ սեղմման և սահքի դեֆորմացիաների մասին:

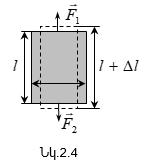
Դիտարկենք l երկարություն և S լայնական հատույթի մակերեսով համասեռ ձող (նկ.2.4), որի ծայրերին կիրառված են նրա առանցքով ուղղված  ուժեր  արդյունքում ձողի երկարությունը փոխվում է մեծությամբ: Բնական է, որ ձգման դեպքում  դրական է, իսկ սեղմման դեպքում` բացասական:

Մարմնի դեֆորմացիայի դեպքում ծագում են առաձգականության ուժեր: Այն ֆիզիկական մեծությունը, որը թվապես հավասար է մարմնի լայնական հատույթի միավոր մակերեսի վրա ազդող առաձգականության ուժի մոդուլին, կոչվում է մեխանիկական լարում և որոշվում է

բանաձևով: Բանաձևից հետևում է, որ մեխանիկական լարման չափման միավորը պասկալն է (Պա):

Եթե ուժը ուղղված է մակերևույթի նորմալով, լարումը կոչվում է նորմալ, եթե ուղղված է մակերևույթին շոշափողով` տանգենցիալ լարում:

Մարմնի դեֆորմացիայի քանակական չափը բնութագրվում է հարաբերական դեֆորմացիայով: Այսպես, ձողի հարաբերական երկարացումը (երկայնական դեֆորմացիա)`

հարաբերական լայնական սեղմումը (լայնական դեֆորմացիա)`

որտեղ d-ն ձողի տրամագիծն է:

 դեֆորմացիաները միշտ ունեն տարբեր նշաններ (ձգման դեպքում  դրական է, իսկ  բացասական, սեղմման դեպքում  բացասական է, իսկ  դրական): Փորձից հետևում է  փոխադարձ կապը.

որտեղ  նյութի հատկություններից կախված դրական մեծություն է և կոչվում է Պուասոնի գործակից:

 Անգլիացի ֆիզիկոս Ռ. Հուկը (1635-1703) փորձարարական ճանապարհով հայտնաբերեց, որ փոքր դեֆորմացիաների դեպքում հարաբերական երկարացումը և լարումը համեմատական են միմյանց

որտեղ E համեմատականության գործակիցը կոչվում է Յունգի մոդուլ: (2.12) արտահայտությունից երևում է, որ Յունգի մոդուլը որոշվում է այն լարումով, որն առաջացնում է միավորի հավասար հարաբերական դեֆորմացիա: (2.9), (2.12) և (2.8) բանաձևերից հետևում է, որ

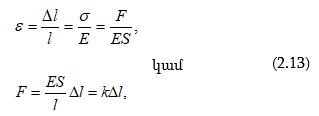
որտեղ k-ն առաձգականության գործակիցն է: (2.13) արտահայտությունը նույնպես որոշում է Հուկի օրենքը, համաձայն որի ձողի երկարացումը առաձգական դեֆորմացիայի դեպքում համեմատական է ձողի վրա ազդող ուժին: Պինդ մարմինների դեֆորմացիաները ենթարկվում են Հուկի օրենքին մինչև հայտնի սահմանը: Դեֆորմացիայի և լարման միջև կապը բերված է լարման դիագրամի տեսքով, որի որակական ընթացքը կդիտարկենք մետաղական նմուշի վրա (նկ.2.5):

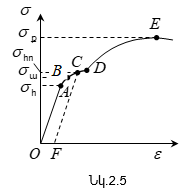
Նկարից երևում է, որ  գծային կախվածությունը, որը տվել է Հուկը, կատարվում է շատ նեղ տիրույթում, մինչև այսպես կոչված համեմատականության սահմանը  Լարման հետագա մեծացման դեպքում դեֆորմացիան դեռ առաձգական է (չնայած  կախվածությունը արդեն ոչ գծային է), և մինչև առաձգականության սահմանը  մնացորդային դեֆորմացիաներ չեն առաջանում:

Առաձգականության սահմանից դուրս մարմնում առաջանում են մնացորդային դեֆորմացիաներ և ուժի ազդեցությունը վերացնելուց հետո, մարմընի վերադարձը սկզբնական վիճակին նկարագրող գրաֆիկը պատկերվում ոչ թե BO կորով, այլ OA-ին զուգահեռ CF ուղղով:

Այն լարումը, որի դեպքում առաջ է գալիս նկատելի մնացորդային դեֆորմացիա  կոչվում է հոսունության սահման  կորի վրա` C կետը: CD տիրույթում դեֆորմացիան աճում է առանց լարման մեծացման, այսինքն` մարմինը կարծես թե «հոսում» է: Այդ տիրույթը կոչվում է հոսունության տիրույթ կամ պլաստիկ դեֆորմացիաների տիրույթ:

Այն նյութերը, որոնց համար հոսունության տիրույթը նշանակալից է, կոչվում են մածուցիկ, իսկ այն նյութերը, որոնցում հոսունությունը գործնականորեն բացակայում է, կոչվում են փխրուն: Հետագա ձգման դեպքում (D կետին մոտ) տեղի է ունենում մարմնի քայքայում: Այն առավելագույն լարումը, որն առաջանում է մարմնում մինչև նրա քայքայումը, կոչվում է ամրության սահման  Լարման դիագրամը տարբեր պինդ մարմինների համար կախված է տարբեր գործոններից: Միևնույն պինդ մարմինը կարող է ուժի կարճատև ազդեցության դեպքում հադես գալ որպես փխրուն, իսկ երկարատև, բայց թույլ ուժերի դեպքում` հոսելի:

Հաշվենք առաձգական ձգված ձողի պոտենցիալ էներգիան, որը հավասար է դեֆորմացիայի դեպքում արտաքին ուժերի կատարած աշխատանքին.

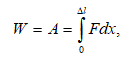
որտեղ x-ը ձողի բացարձակ երկարացումն է, որը դեֆորմացիայի դեպքում փոփոխվում է 0-ից մինչև  Համաձայն Հուկի (2.13) օրենքի`

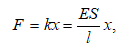
ուստի

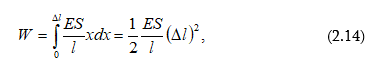
այսինքն` առաձգականորեն ձգված ձողի պոտենցիալ էներգիան համեմատական է դեֆորմացիայի քառակուսուն:

>>

2.5. ՄԵԽԱՆԻԿԱԿԱՆ ՀԱՄԱԿԱՐԳԻ ԶԱՆԳՎԱԾՆԵՐԻ (ԻՆԵՐՑԻԱՅԻ)
ԿԵՆՏՐՈՆ ԵՎ ՆՐԱ ՇԱՐԺՄԱն ԴԻՆԱՄԻԿԱՅԻ ՕՐԵՆՔԸ

Դիտարկենք մեխանիկական համակարգ, որը բաղկացած է n թվով նյութական կետերից:

Համակարգի իներցիայի կենտրոն է կոչվում այն կետը, որի դիրքը տարածության մեջ որոշվում է  շառավիղ-վեկտորով, որը որոշվում է հետևյալ արտահայտությամբ՝

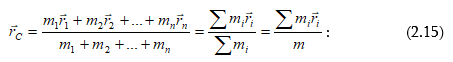
 նյութական կետի զանգվածն է,  տարածության մեջ այդ կետի դիրքը որոշող շառավիղ-վեկտորը, m-ը` համակարգի գումարային զանգվածը:

Իներցիայի կենտրոնի դեկարտյան կոորդինատները հավասար են  պրոյեկցիաներին (կոորդինատների առանցքների վրա), այսինքն՝

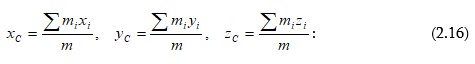
Նշենք, որ համասեռ գրավիտացիոն դաշտում իներցիայի կենտրոնը համընկնում է համակարգի ծանրության կենտրոնի հետ:

Ածանցելով  ըստ ժամանակի` կստանանք իներցիայի կենտրոնի արագությունը՝

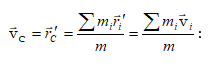
Այսպիսով, համակարգի իմպուլսը հավասար է համակարգի զանգվածի և նրա իներցիայի կենտրոնի արագության արտադրյալին: Ածանցելով (2.6)-ը ըստ ժամանակի` կստանանք՝

Ըստ (2.18) հավասարության մարմնի զանգվածի կենտրոնը շարժվում է այնպես, ինչպես շարժվում է մարմնի զանգվածին հավասար զանգված ունեցող նյութական կետն այնպիսի ուժի ազդեցության տակ, որը հավասար է արտաքին ուժերի վեկտորական գումարին: Եթե արտաքին ուժերի արդյունարար վեկտորը հավասար է զրոյի, ապա մարմնի զանգվածի կենտրոնը կմնա հանգստի վիճակում կամ կշարժվի ուղղագիծ և հավասարաչափ: Ներքին ուժերը չեն կարող փոխել զանգվածի կենտրոնի արագությունը:

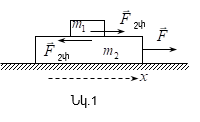
Խնդիր 1:  զանգվածով չորսուն գտնվում է  զանգվածով տախտակի վրա, որը գտնվում է հորիզոնական հարթության մեջ (նկ.1):

Տախտակի և չորսուի մակերևույթների միջև շփման գործակիցը  է: Տախտակին կիրառված է հորիզոնական F ուժ, որը կախված է ժամանակից  օրենքով, որտեղ  հաստատուն է: Գտնել. 1) ժամանակի այն  պահը, որի դեպքում տախտակը կսկսի սահել չորսուի տակից, 2) չորսուի և տախտակի  արագացումները շարժման պրոցեսում: Գծել այդ կախվածությունների գրաֆիկները:

Լուծում: 1) Գրենք դինամիկայի հիմնական հավասարումը չորսուի և տախտակի համար` վերցնելով x-ի առանցքի դրական ուղղությունը, ինչպես ցույց է տրված նկ.1-ում:

F ուժի աճի դեպքում սկսում է աճել նաև շփման ուժը (սկզբում այն դադարի շփման ուժ է): Բայց F_շփ շփման ուժն ունի սահման`

Քանի դեռ F_շփ-ն այդ սահմանին չի հասել, երկու մարմիններն էլ կշարժվեն որպես մեկ ամբողջություն միևնույն արագացումներով: Երբ F_շփ ուժը հասնում է իր սահմանին, տախտակն սկսում է սահել չորսուի տակից, այսինքն

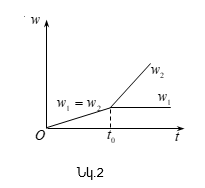
Տեղադրելով  (1)-ից (2)-ի մեջ, հաշվի առնելով, որ

 որտեղ «-» նշանը համապատասխանում է t=t₀ պահին: Որտեղից

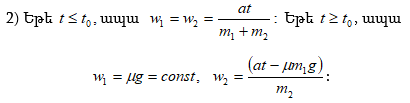
 կախվածությունների գրաֆիկները բերված են նկ.2-ում:

>>

2.6. ԻՄՊՈՒԼՍԻ ՊԱՀՊԱՆՄԱՆ ՕՐԵՆՔԸ

Փակ համակարգի համար գոյություն ունեն համակարգը կազմող մասնիկների կոորդինատների և արագությունների այնպիսի ֆունկցիաներ, որոնք շարժման դեպքում իրենց արժեքները պահպանում են հաստատուն: Այդ ֆունկցիաները կոչվում են շարժման ինտեգրալներ: Շարժման ինտեգրալների թվին են պատկանում իմպուլսը, էներգիան և իմպուլսի մոմենտը: Դրան համապատասխան առկա են հետևյալ պահպանման օրենքները՝ էներգիայի պահպանման օրենքը, իմպուլսի պահպանման օրենքը և իմպուլսի մոմենտի պահպանման օրենքը:

Նախ քննարկենք իմպուլսի պահպանման օրենքը: Դիցուք ունենք n թվով նյութական կետերի մեխանիկական համակարգ: Համակարգը կարող է լինել կամ փակ, կամ բաց: Համակարգը կոչվում է փակ, եթե նրանում գործում են միայն ներքին ուժեր: Ներքին կոչվում է այն ուժը, որին, ըստ Նյուտոնի երրորդ օրենքի, հակազդող ուժը գտնվում է համակարգի ներսում: Քանի որ ներքին ուժերը զույգ առ զույգ թվապես հավասար են, ազդում են նույն գծով և իրար հակառակ են ուղղված, ապա բոլոր ներքին ուժերի վեկտորական գումարը հավասար է զրոյի: Համակարգը կոչվում է բաց, եթե, բացի ներքին ուժերից, նրանում գործում են արտաքին ուժեր: Արտաքին կոչվում է այն ուժը, որին, ըստ Նյուտոնի երրորդ օրենքի, հակազդող ուժը գտնվում է համակարգից դուրս: Ինչպես գիտենք, նյութական կետի իմպուլս է կոչվում նրա զանգվածի և արագության արտադրյալը՝  Ըստ Նյուտոնի երկրորդ օրենքի` իմպուլսի փոփոխությունը միավոր ժամանակում հավասար է նյութական կետի վրա ազդող ուժերի համազորին.

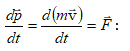
Միանգամայն պարզ է, որ մեկ նյութական կետի իմպուլսը կմնա հաստատուն, եթե նրա վրա ազդող ուժերի համազորը՝

Եթե ունենք նյութական կետերի մեխանիկական որևէ համակարգ, համակարգի մեջ մտնող յուրաքանչյուր նյութական կետի վրա ազդում են ինչպես ներքին, այնպես էլ արտաքին ուժեր (եթե համակարգը բաց է): Հետեվաբար, յուրաքանչյուր նյութական կետի իմպուլսը համակարգի ներսում փոփոխվում է: Մեզ հետաքրքրում է՝ փոփոխվու՞մ է արդյոք այդ դեպքում համակարգի իմպուլսը, թե` ոչ: Համակարգի իմպուլսը`

Ամբողջ համակարգի իմպուլսի փոփոխությունը միավոր ժամանակում հավասար է նրա մեջ մտնող նյութական կետերի՝ միավոր ժամանակում իմպուլսների փոփոխությունների վեկտորական գումարին:

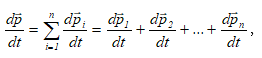
որտեղ

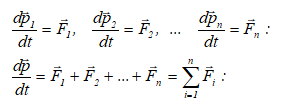
Համակարգի  իմպուլսը կմնա հաստատուն, թե կփոփոխվի, կախված է նրանից, թե  գումարը ինչի՞ է հավասար: Այդ գումարը հաշվելու համար սովորաբար դիմում են Նյուտոնի երրորդ օրենքին: Եթե համակարգը փակ է, ապա արտաքին ուժերը բացակայում են, և գործում են միայն ներքին ուժերը, որոնց վեկտորական գումարը հավասար կլինի զրոյի, և խնդիրը միանգամից կլուծվի:

Այսպիսով, փակ համակարգի դեպքում  հետևաբար, ներքին ուժերը փակ համակարգի իմպուլսը փոխել չեն կարող: Փակ համակարգ կազմող մարմինների իմպուլսների վեկտորական գումարը մնում է հաստատուն այդ համակարգի մարմինների ցանկացած փոխազդեցության դեպքում.

Բաց համակարգի դեպքում՝

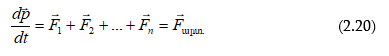
Այսպիսով կարող ենք ասել, որ համակարգի իմպուլսը փոխել կարող են միայն արտաքին ուժերը:

Վեկտորական (2.20) հավասարումը համարժեք է երեք սկալյար հավասարումների

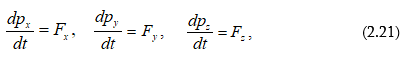
որոնք ստացվում են (2.20) հավասարումից, դեկարտյան կոորդինատային համակարգի անշարժ առանցքների վրա պրոյեկտման ճանապարհով: (2.21) հավասարումներից հետևում է իմպուլսի պրոյեկցիայի պահպանման օրենքը. եթե արտաքին ուժերի արդյունարար վեկտորի պրոյեկցիան որևէ առանցքի վրա հավասար է զրոյի, ապա համակարգի իմպուլսի վեկտորի պրոյեկցիան այդ առանցքի վրա կախված չէ ժամանակից: Օրինակ, եթե

Իմպուլսի պահպանման օրենքը կարելի է ստանալ նաև Նյուտոնի երրորդ օրենքի փոխարեն օգտվելով տարածության համասեռության հատկությունից: Ենթադրենք համակարգը փակ է: Այն 1 դիրքից մտովի տեղափոխենք 2 դիրքն այնպես, որ բոլոր նյութական կետերը կրեն միատեսակ տեղափոխություններ, և նրանց արագությունները ուղղությամբ և թվային արժեքով մնան նույնը: Ըստ տարածության համասեռության, եթե մարմինների համակարգը զուգահեռ տեղափոխենք 1 դիրքից 2 դիրքը և մարմինները դնենք նույն պայմանների մեջ, ապա դա չի ազդի դեպքերի ընթացքի վրա: Այդ նշանակում է, որ նման տեղափոխության ժամանակ նյութական կետերի փոխազդեցության պոտենցիալ և շարժման կինետիկ էներգիաները փոփոխություն չեն կրի, այսինքն` E=T+U=const (համակարգի լրիվ մեխանիկական էնեգիան մնում է հաստատուն): Հետևաբար, համակարգի նման տեղափոխության ժամանակ աշխատանք չի կատարվում (A=0) :

այսինքն` փակ համակարգի իմպուլսը պահպանվում է:

>>

2.7. ՓՈՓՈԽԱԿԱՆ ԶԱՆԳՎԱԾՈՎ ՄԱՐՄՆԻ ՇԱՐԺՄԱՆ ՀԱՎԱՍԱՐՈՒՄԸ

Որոշ մարմինների շարժումն ուղեկցվում է նրանց զանգվածի փոփոխությամբ, օրինակ հրթիռի զանգվածը փոքրանում է գազերի արտահոսքի հետևանքով, որոնք առաջանում են վառելիքի այրման դեպքում:

Արտածենք փոփոխական զանգվածով մարմնի շարժման հավասարումը հրթիռի շարժման օրինակով: Եթե ժամանակի t պահին հրթիռի զանգվածը m է, նրա արագությունըէ, ապա dt ժամանակում արտահոսքի պատճառով նրա զանգվածը նվազում է` դառնալով m-dm, իսկ արագությունը`  Համակարգի իմպուլսի փոփոխությունը dt ժամանակում`

որտեղ  գազերի արտահոսքն է հրթիռի նկատմամբ:

Հետևաբար` (հաշվի առանք, որ  անվերջ փոքր է մյուսների համեմատ): Եթե համակարգի վրա ազդում են արտաքին ուժեր, ապա ուստի

կամ

(2.22) հավասարման աջ մասի երկրորդ գումարելին կոչվում է ռեակտիվ ուժ`  Եթե  հակառակ է արագության ուղղությանը, ապա հրթիռն արագացվում է, իսկ եթե համընկնում է  հետ, արգելակվում է:

Այսպիսով, ստացվում է փոփոխական զանգվածով մարմնի շարժման հավասարումը`

որն առաջին անգամ ստացել է Ի. Մեշչերսկին (1859-1935):

Կիրառենք (2.23) հավասարումը հրթիռի շարժման դեպքում, որի վրա չեն ազդում արտաքին ուժեր: Ընդունելով, որ  և նկատի ունենալով, որ դուրս մղվող գազերի արագությունը հրթիռի նկատմամբ հաստատուն է (հրթիռը շարժվում է ուղղագիծ), կստանանք`

որտեղից

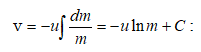
Ինտեգրման C հաստատունի արժեքը որոշենք սկզբնական պայմաններից: Եթե ժամանակի սկզբնական պահին հրթիռի արագությունը զրո է, իսկ նրա մեկնարկային զանգվածը`

Հետևաբար`

Այս առնչությունը կոչվում է Ցիոլկովսկու բանաձև: Այն ցույց է տալիս, որ. 1) ինչքան մեծ է հրթիռի վերջնական m զանգվածը, այնքան մեծ պետք է լինի հրթիռի մեկնարկային  զանգվածը, 2) որքան մեծ է գազերի արտահոսքի u արագությունը հրթիռի տվյալ մեկնարկային  զանգվածի դեպքում, այնքան մեծ կարող է լինել վերջնական զանգվածը: Հաշվարկի համաձայն, եթե u=2000մ/վ, ապա առաջին տիեզերական արագություն (v=8000մ/վ) ստանալու համար անհրաժեշտ է, որ վառելիքի զանգվածը մոտ 54 անգամ գերազանցի հրթիռի վերջնական զանգվածը:

 (2.23) և (2.24) արտահայտությունները ստացվել են ոչ ռելյատիվիստական շարժումների համար, այսինքն այն դեպքերի համար, երբ v և u արագությունները փոքր են վակուումում լույսի տարածման արագության համեմատ:

>>

ԳԼՈՒԽ 3. ԱՇԽԱՏԱՆՔ ԵՎ ԷՆԵՐԳԻԱ

3.1. ԷՆԵՐԳԻԱ, ԱՇԽԱՏԱՆՔ, ՀԶՈՐՈՒԹՅՈՒՆ

Էներգիան տարբեր շարժումների ձևերի և փոխազդեցությունների ունիվերսալ չափն է: Մատերիայի շարժման ձևերի հետ կապում են էներգիայի տարբեր տեսակներ. մեխանիկական, ջերմային, էլեկտրամագնիսական, միջուկային և այլն: Որոշ երևույթներում մատերիայի շարժման ձևը չի փոփոխվում (օրինակ, տաք մարմինը տաքացնում է սառը մարմինը), ուրիշներում` անցնում է այլ ձևի (օրինակ, շփման արդյունքում մեխանիկական շարժումը փոխակերպվում է ջերմայինի): Սակայն էական է, որ բոլոր դեպքերում էներգիան, որը տրվում է (այս կամ այն ձևով) մեկ մարմնից մյուսին, հավասար է վերջին մարմնի ստացած էներգիային:

Մարմնի մեխանիկական շարժման փոփոխությունը առաջ է գալիս այլ մարմինների կողմից նրա վրա ազդող ուժերով:

Որպեսզի քանակապես բնութագրվի էներգիայի փոխանակման պրոցեսը, փոխազդող մարմինների միջև մեխանիկայում ներմուծվում է ուժի աշխատանքի հասկացությունը:

Մեխանիկական աշխատանք կոչվում է այն սկալյար մեծությունը, որը բնութագրում է այնպիսի ֆիզիկական պրոցես, երբ տեղի ունի էներգիայի փոխանցում մի մարմնից մյուսին (մյուսներին) կամ փոխակերպում մի տեսակից այլ տեսակի (տեսակների)՝ ուժի ազդեցության տակ մարմնի տեղափոխության հետևանքով:

Եթե մարմինը շարժվում է ուղղագիծ և նրա վրա ազդում է հաստատուն ուժ, որը տեղափոխության ուղղության հետ կազմում է անկյուն, ապա այդ ուժի աշխատանքը հավասար է տեղափոխության ուղղության վրա ուժի F_S պրոյեկցիայի  և ուժի կիրառման կետի տեղափոխության արտադրյալին.

Ուժը կարող է փոփոխվել ինչպես ըստ մոդուլի, այնպես էլ ըստ ուղղության, ուստի ընդհանուր դեպքում (3.1) բանաձևից օգտվել չի կարելի: Սակայն, եթե դիտարկենք տարրական տեղափոխությունը, ապա  կարող ենք ընդունել հաստատուն, իսկ նրա կիրառման կետի շարժումը` ուղղագիծ:  ուժի տարրական աշխատանք տեղափոխության վրա կոչվում է`

սկալյար մեծությունը, որտեղ  վեկտորների միջև անկյունն է,  տարրական ճանապարհն է,  վեկտորի պրոյեկցիան է  վեկտորի վրա (նկ. 3.1 ):

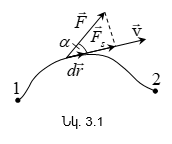
Ուժի աշխատանքը հետագծի 1 կետից մինչև 2 կետը տեղամասի վրա հավասար է ճանապարհի անվերջ փոքր առանձին տեղամասերում տարրական աշխատանքների հանրահաշվական գումարին: Այդ գումարը բերվում է ինտեգրալի`

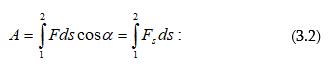
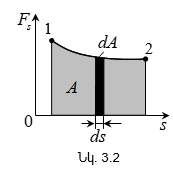
Ինտեգրալի հաշվման համար հարկավոր է գիտենալ  կախվածությունը s ճանապարհից 1-2 հետագծի երկայնքով: Այդ կախվածությունը ներկայացված է գրաֆիկորեն (նկ. 3.2): Որոնելի A աշխատանքը գրաֆիկի վրա որոշվում է ստվերագծված պատկերի մակերեսով: Եթե, օրինակ, մարմինը շարժվում է ուղղագիծ, ուժը`  ապա կստանանք`

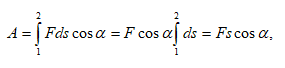
որտեղ s-ը մարմնի անցած ճանապարհն է:

(3.1) բանաձևից հետևում է, որ  դեպքում ուժի աշխատանքը դրական է, այս դեպքում բաղադրիչը ուղղությամբ համընկնում է շարժման արագության վեկտորի ուղղության հետ (տես նկ.3.1): Եթե  ապա ուժի աշխատանքը բացասական է:  դեպքում (ուժն ուղղահայաց է տեղափոխությանը) ուժի աշխատանքը հավասար է զրոյի: Վերջին հանգամանքը պարզորոշ ցույց է տալիս, որ աշխատանք հասկացությունը մեխանիկայում հիմնովին տարբերվում է աշխատանքի մասին եղած առօրյա պատկերացումից: Առօրյա հասկացության համաձայն, յուրաքանչյուր ճիգ, մասնավորապես մկանային լարվածություն, միշտ ուղեկցվում է աշխատանքի կատարումով: Օրինակ՝ կանգնած տեղում (անշարժ) ծանր բեռը բռնելու ժամանակ բեռնակիրը մեծ ճիգ է գործադրում, այսինքն՝ «կատարում է աշխատանք»: Սակայն աշխատանքը, որպես մեխանիկական մեծություն, այս դեպքում հավասար է զրոյի:

Աշխատանքի միավորը ջոուլն է (Ջ): 1Ջ-ն այն աշխատանքն է, որը կատարում է 1Ն ուժը 1մ ճանապարհի վրա:

Որպեսզի բնութագրվի աշխատանքի կատարման արագությունը, ներմուծվում է հզորության հասկացությունը.

 dt ժամանակում  ուժը կատարում է  աշխատանք, և այդ ուժով զարգացրած հզորությունը ժամանակի տվյալ պահին`

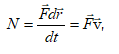
այսինքն` հավասար է ուժի վեկտորի և արագության վեկտորի սկալյար արտադրյալին: N-ը սկալյար մեծություն է: Հզորության միավորը վատն (Վտ) է: 1Վտ-ն այն հզորությունն է, որի դեպքում 1վ-ում կատարվում է 1Ջ աշխատանք:

Խնդիր 1: m զանգվածով քարը Երկրի մակերևույթից  սկզբնական արագությամբ նետվել է հորիզոնի նկատմամբ անկյան տակ: Անտեսելով օդի դիմադրությունը` գտնել ծանրության ուժի հզորությունը շարժումը սկսելուց t վայրկյան անց, ինչպես նաև այդ ուժի աշխատանքը շարժման առաջին t վայրկյանում: Գծել N(t) և A(t) կախվածությունների գրաֆիկները:

Լուծում: Քարի արագությունը շարժման սկզբից t վայրկյան անց`  Ծանրության  ուժի զարգացրած հզորությունն այդ պահին`

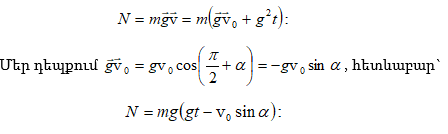
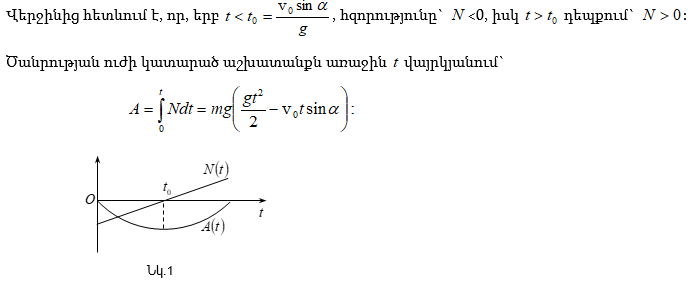
N(t) և A(t) կախվածությունների գրաֆիկները ցույց են տրված նկ.1-ում:

Խնդիր 2: Յուրաքանչյուրը m զանգվածով և +q լիցքով լիցքավորված միատեսակ երեք մասնիկներ տեղադրել են կողմ ունեցող հավասարակողմ եռանկյան գագաթներում: Այնուհետև, մասնիկները միաժամանակ ազատվում են, որից հետո դրանք վանողական կուլոնյան ուժերի ազդեցության տակ սիմետրիկորեն թռչում են: Գտնել.

1) Յուրաքանչյուր մասնիկի արագության կախումը նրանց միջև եղած r հեռավորությունից:

2) Այն աշխատանքը, որը կատարում են կուլոնյան ուժերը ազդելով յուրաքանչյուր մասնիկի վրա, երբ մասնիկները թռչում են միմյանցից շատ մեծ հեռավորությունների վրա:

Լուծում: Քանի որ տվյալ համակարգը փակ է, ուստի նրա համար կինետիկ էներգիայի աճը հավասար է պոտենցիալ էներգիայի նվազմանը, այսինքն`

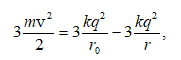
որտեղից կստանանք`  Վերջինից հետևում է,որ երբ  յուրաքանչյուր մասնիկի արագությունը ձգտում է սահմանային արժեքին` Բոլոր փոխազդեցության ուժերի կատարած աշխատանքը համակարգի կոնֆիգուրացիայի փոփոխության դեպքում հավասար է համակարգի պոտենցիալ էներգիայի նվազմանը.

որտեղ հաշվի է առնված, որ վերջնական դիրքում  Այստեղից էլ որոնելի աշխատանքը`

>>

3.2. ԿԻՆԵՏԻԿ ԵՎ ՊՈՏԵՆՑԻԱԼ ԷՆԵՐԳԻԱՆԵՐ

Մեխանիկական համակարգի կինետիկ էներգիա է կոչվում այդ համակարգի մեխանիկական շարժման էներգիան: Կինետիկ էներգիան որոշվում է դիտարկվող համակարգի մարմինների զանգվածներով և արագություններով:

Հանգստի վիճակում գտնվող մարմնի վրա ազդողուժը, առաջ բերելով նրա շարժումը, կատարում է աշխատանք, իսկ շարժվող մարմնի էներգիան աճում է ծախսված աշխատանքի մեծությամբ: Այսպիսով,  ուժի dA աշխատանքը ճանապարհի վրա, որը մարմինն անցնում է մի ժամանակում, որի ընթացքում արագությունն աճում է 0-ից մինչև v, գնում է մարմնի կինետիկ էներգիայի մեծացման վրա, այսինքն`

Oգտագործելով Նյուտոնի երկրորդ օրենքը`  և բազմապատկելով  տեղափոխությունով, կստանանք`

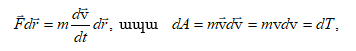
որտեղից`

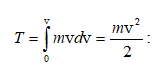
Այսպիսով, v արագությամբ շարժվող m զանգվածով մարմինն օժտված է կինետիկ էներգիայով.

(3.4) բանաձևից երևում է, որ կինետիկ էներգիան կախված է միայն մարմնի զանգվածից և արագությունից, այսինքն` համակարգի կինետիկ էներգիան նրա մեխանիկական շարժման վիճակի ֆունկցիա է:

(3.4) բանաձևի արտածման դեպքում ենթադրվեց, որ շարժումը դիտարկվում է հաշվարկման իներցիալ համակարգում, քանի որ այլ կերպ չէինք կարող օգտագործել Նյուտոնի օրենքները: Տարբեր իներցիալ հաշվարկման համակարգերում, որոնք շարժվում են միմյանց նկատմամբ, մարմնի արագությունը, հետևաբար և նրա կինետիկ էներգիան կլինեն տարբեր: Այսպիսով, կինետիկ էներգիան կախված է հաշվարկման համակարգի ընտրությունից:

Մեխանիկական համակարգի կինետիկ էներգիան հավասար է համակարգի մեջ մտնող մարմինների կինետիկ էներգիաների գումարին: Այսպես, n թվով նյութական կետերից կազմված մեխանիկական համակարգի կինետիկ էներգիան`

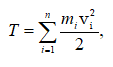
որտեղ  զանգվածով i-րդ նյութական կետի արագությունն է:

Դիցուք մարմինների փոխազդեցությունը իրականացվում է ուժային դաշտերի (օրինակ, առաձգական ուժերի դաշտ, գրավիտացիոն ուժերի դաշտ) միջոցով: Այդ փոխազդեցությունը բնութագրվում է նրանով, որ ազդող ուժերի կատարած աշխատանքը մարմնի տեղափոխության դեպքում մեկ դիրքից մյուսը կախված չէ այն բանից, թե ինչպիսի հետագծով է կատարվել այդ տեղափոխությունը, այլ կախված է միայն սկզբնական և վերջնական դիրքերից: Այդպիսի դաշտերը կոչվում են պոտենցիալային, իսկ դրանցում գործող ուժերը` կոնսերվատիվ: Եթե ուժի կատարած աշխատանքը կախված է մարմնի մի կետից մյուսը տեղափոխության հետագծից, այդպիսի ուժը կոչվում է դիսսիպատիվ, դրա օրինակն է շփման ուժը: Այն ուժերը, որոնք կախված են փոխազդող մասնիկների միջև եղած հեռավորությունից և ուղղված են մասնիկների զանգվածների կենտրոնները միացնող ուղղի երկայնքով, կոչվում են կենտրոնական ուժեր: Այն դաշտը, որի լարվածությունը բոլոր կետերում մնում է անփոփոխ, կոչվում է համասեռ դաշտ:

Մարմինը, գտնվելով պոտենցիալային դաշտում, օժտված է պոտենցիալ էներգիայով: Կարելի է ասել, որ մեխանիկական համակարգի պոտենցիալ էներգիա է կոչվում էներգիայի այն մասը, որը կախված է համակարգի մասնիկների փոխադարձ դասավորությունից և արտաքին ուժային դաշտում նրանց դիրքից:

Կոնսերվատիվ ուժերի աշխատանքը համակարգի կոնֆիգուրացիայի տարրական (անվերջ փոքր) փոփոխության դեպքում հավասար է պոտենցիալ էնեգիայի աճին վերցրած «-» նշանով (աշխատանքը կատարվում է պոտենցիալ էներգիայի նվազման հաշվին).

dA աշխատանքն արտահայտվում է որպեսուժի և  տեղափոխության սկալյար արտադրյալ, հետևաբար (3.5) արտահայտությունը կարելի է գրել հետևյալ տեսքով`

Ուրեմն, եթե հայտնի է  ֆունկցիան, (3.6) բանաձևից կարելի է գտնել  ուժի մոդուլը և ուղղությունը: Համաձայն (3.6) բանաձևի, պոտենցիալ էներգիան`

որտեղ C-ն ինտեգրման հաստատուն է, այսինքն` պոտենցիալ էներգիան որոշվում է մինչև ինչ-որ հաստատունի ճշտությամբ: Սակայն դա էական չէ, քանի որ ֆիզիկական առնչությունների մեջ մտնում է կամ երկու կետերի պոտենցիալ էներգիաների տարբերությունը, կամ U ֆունկցիայի ածանցյալը` ըստ կոորդինատների: Ուստի մարմնի պոտենցիալ էներգիան ինչ-որ որոշակի դիրքում պայմանականորեն ընդունում են հավասար զրոյի (ընտրում են հաշվարկի զրոյական մակարդակ), իսկ մարմնի պոտենցիալ էներգիան այլ դիրքերում հաշվում են զրոյական մակարդակի նկատմամբ:

Կոնսերվատիվ ուժերի համար

կամ վեկտորական տեսքով`

որտեղ

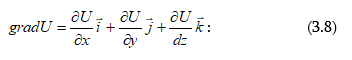
 կոորդինատային առանցքների ուղղությամբ միավոր վեկտորներ են): (3.8) արտահայտությամբ վեկտորը կոչվում է U սկալյարի գրադիենտ: grandU ընդունված է նշանակել նաև  նշանակում է սիմվոլիկ վեկտոր, որը կոչվում է Համիլտոնի օպերատոր կամ «նաբլա» օպերատոր.

U ֆունկցիայի կոնկրետ տեսքը կախված է ուժային դաշտի բնույթից: Օրինակ, երկրագնդի մակերևույթից h բարձրության վրա բարձրացված m զանգվածով մարմնի պոտենցիալ էներգիան`

որտեղ h բարձրությունը հաշվարկվում է զրոյական մակարդակից, որի համար U=0: (3.10) արտահայտությունը բխում է անմիջականորեն նրանից, որ պոտենցիալ էներգիան հավասար է ծանրության ուժի աշխատանքին երկրագնդի մակերևույթի վրա h բարձրությունից մարմնի անկման դեպքում:

Քանի որ հաշվարկման սկիզբն ընտրվում է կամայական, ապա պոտենցիալ էներգիան կարող է ունենալ բացասական արժեք (կինետիկ էներգիան միշտ դրական է): Եթե Երկրագնդի մակերևույթի վրա գտնվող մարմնի պոտենցիալ էներգիան ընդունվի հավասար զրոյի, ապա մարմնի պոտենցիալ էներգիան հանքահորի հատակին

Գտնենք առաձգական դեֆորմացված մարմնի (զսպանակի) պոտենցիալ էներգիան: Առաձգական ուժը համեմատական է դեֆորմացիային.

որտեղ  առաձգական ուժի պրոյեկցիան է x առանցքի վրա, k-ն զսպանակի կոշտությունն է, իսկ բացասական նշանը ցույց է տալիս, որ  ուղղված է x դեֆորմացիային հակառակ: Ըստ Նյուտոնի երրորդ օրենքի` դեֆորմացնող ուժը ըստ մոդուլի հավասար է առաձգականության ուժին և ուղղված է նրան հակառակ, այսինքն`

ուժով կատարված տարրական dA աշխատանքն ավերջ փոքր dx դեֆորմացիայի դեպքում`

իսկ լրիվ աշխատանքը`

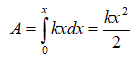
ծախսվում է զսպանակի պոտենցիալ էներգիայի մեծացման վրա: Այսպիսով, առաձգական դեֆորմացված մարմնի պոտենցիալ էներգիան`

Համակարգի պոտենցիալ էներգիան համակարգի վիճակի ֆունկցիա է: Այն կախված է համակարգի կոնֆիգուրացիայից և արտաքին մարմինների նկատմամբ ունեցած նրա դիրքից:

Համակարգի լրիվ մեխանիկական էներգիան հավասար է կինետիկ և պոտենցիալ էներգիաների գումարին` E=T+U:

Խնդիր 1: Ուժային դաշտում գտնվող մասնիկի պոտենցիալ էներգիայի կախումը կոորդինատներից ունի հետևյալ տեսքը  որտեղ  Որոշել մասնիկի վրա ազդող ուժի մոդուլը (2,1,1)մ կոորդինատներով կետում:

Լուծում: Օգտվենք մասնիկի վրա ազդող ուժի և պոտենցիալ էներգիայի կապից.

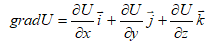
Ուժի վեկտորը`

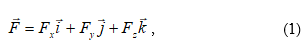
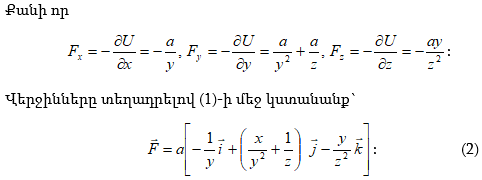
(2)-ից ուժի մոդուլի համար կստանանք հետևյալ արտահայտությունը`

>>

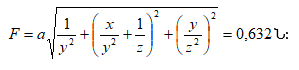
3.3. ՄԵԽԱՆԻԿԱԿԱՆ ԷՆԵՐԳԻԱՅԻ ՊԱՀՊԱՆՄԱՆ ՕՐԵՆՔԸ

Էներգիայի պահպանման օրենքը բազմաթիվ փորձերի տվյալների ընդհանրացումների արդյունք է: Այս օրենքի գաղափարը պատկանում է Մ. Լոմոնոսովին (1711-1765), շարադրելով էներգիայի և մատերիայի շարժման պահպանման օրենքը, իսկ էներգիայի պահպանման օրենքի քանակական ձևակերպումը տրվել է գերմանացի բժիշկ Մայերի (1814-1878) և գերմանացի բնագետ Գ. Հելմոլցի (1821-1894) կողմից:

Քննարկենք զանգվածներով նյութական կետերի համակարգ, որոնք շարժվում են արագություններով: Դիցուք ներքին կոնսերվատիվ ուժերի արդյունարարներն են, որոնք ազդում են այդ կետերից յուրաքանչյուրի վրա, իսկ արտաքին ուժերի արդյունարարներն են, որոնք նույնպես ընդունում ենք, որ կոնսերվատիվ են: Բացի դրանից, ընդունում ենք, որ նյութական կետերի վրա ազդում են ոչ կոնսերվատիվ արտաքին ուժեր: Այդ ուժերի արդյունարարները, որոնք ազդում են նյութական կետերից յուրաքանչյուրի վրա, նշանակենք

 Քանի որ v<<c դեպքում նյութական կետերի զանգվածները հաստատուն են, այդ կետերի համար գրենք Նյուտոնի երկրոդ օրենքի հավասարումները`

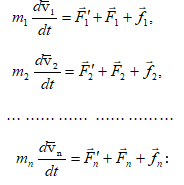
Համակարգի նյութական կետերը ուժերի ազդեցության տակ dt ժամանակի ընթացքում կատարում են համապատասխանաբար հավասար տեղափոխություններ: Բազմապատկելով հավասարումներից յուրաքանչյուրը սկալյարորեն համապատասխան տեղափոխությամբ և հաշվի արնելով, որ կստանանք`

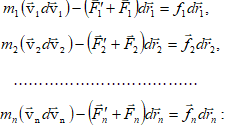
Գումարելով այս հավասարումները կստանանք`

 (3.12) հավասարման ձախ մասի առաջին գումարելին`

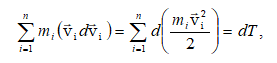
որտեղ dT-ն համակարգի կինետիկ էներգիայի աճն է:

Երկրորդ գումարելին`  հավասար է ներքին և արտաքին կոնսերվատիվ ուժերի տարրական աշխատանքին, վերցրած «-» նշանով, այսինքն` հավասար է համակարգի տարրական պոտենցիալ էներգիայի dU աճին:

 (3.12) հավասարության աջ մասը տալիս է համակարգի վրա ազդող արտաքին ոչ կոնսերվատիվ ուժերի աշխատանքը: Այսպիսով, կունենանք`

Համակարգի 1 վիճակից 2 վիճակին անցման դեպքում`

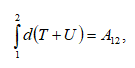
Այսինքն` համակարգի լրիվ մեխանիկական էներգիայի փոփոխությունը մի վիճակից մյուսին անցման դեպքում հավասար է արտաքին ոչ կոնսերվատիվ ուժերի կատարած աշխատանքին: Եթե արտաքին ոչ կոնսերվատիվ ուժերը բացակայում են, ապա (3.13) -ից հետևում է.

որտեղից

Այսինքն համակարգի լրիվ մեխանիկական էներգիան մնում է հաստատուն: (3.14)-ը արտահայտում է մեխանիկական էներգիայի պահպանման օրենքը. միմյանց վրա միայն կոնսերվատիվ ուժերով ազդող մարմիններից բաղկացած փակ համակարգի լրիվ մեխանիկական էներգիան մնում է հաստատուն, այսինքն` ժամանակի ընթացքում չի փոփոխվում:

Մեխանիկական համակարգերը, որոնց մարմինների վրա ազդում են միայն կոնսերվատիվ (արտաքին և ներքին ուժեր), կոչվում են կոնսերվատիվ համակարգեր: Մեխանիկական էներգիայի պահպանման օրենքը կարելի է ձևակերպել հետևյալ կերպ. Կոնսերվատիվ համակարգերում լրիվ մեխանիկական էներգիան պահպանվում է:

Էներգիայի պահպանման օրենքը կարելի է ստանալ նաև` օգտվելով ժամանակի համասեռության հատկությունից:

Ժամանակի համասեռություն նշանակում է, որ ժամանակի տարբեր պահերին, եթե փակ համակարգի բոլոր մարմինները դնենք նույն պայմանների մեջ, սկսած այդ պահից բոլոր երևույթները կընթանան նույն ձևով:

Մեխանիկայից փոխ վերցնենք Նյուտոնի երկրորդ օրենքի այն հետևանքը, որ համազոր ուժի կատարած աշխատանքը հավասար է նրա կինետիկ էներգիայի փոփոխությանը.

Մեր հետագա դատողությունները կկատարենք մեկ նյութական կետի համար:

Նյութական կետերի համակարգի դեպքում ամեն ինչ կլինի նույն ձևով, միայն կփոխվի այն արգումենտների թիվը, որոնցից կախված է պոտենցիալային ֆունկցիան: Ընդհանուր դեպքում փոփոխվող պոտենցիալային դաշտում  Նյութական կետի վրա ազդող ուժերի աշխատանքը, երբ այն ինչ-որ հետագծով տեղափոխվում է 1 դիրքից 2 դիրքը, կարտահայտվի հետևյալ ինտեգրալով՝

Ձևափոխենք այս արտահայտությունը՝ գումարելով և հանելով  կստանանք՝

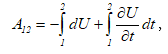
որտեղ

dU-ն կլինի լրիվ դիֆերենցիալ:

Ինտեգրելուց հետո կունենանք՝

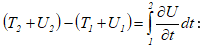
Ստացված արտահայտությունը ճիշտ է նաև նյութական կետերի համակարգի համար: Այժմ օգտվենք համակարգի փակության պայմանից և ժամանակի համասեռության հատկությունից: Եթե համակարգը փակ է, և ժամանակը՝ համասեռ, ապա պոտենցիալ էներգիան ժամանակից բացահայտ կախված լինել չի կարող և Արդյունքում՝

Այսինքն, փակ կոնսերվատիվ համակարգի լրիվ մեխանիկական էներգիան մնում է անփոփոխ:

Եթե փակ համակարգի կոնսերվատիվ ուժերից բացի, գործում են նաև ոչ կոնսերվատիվ ուժեր, օրինակ, շփման ուժերը, ապա համակարգի լրիվ մեխանիկական էներգիան չի պահպանվում: Ոչ կոնսերվատիվ ուժերը դիտելով որպես արտաքին ուժեր, կարելի է գրել՝

որտեղ A_{ոչ կոն.}-ը ոչ կոնսերվատիվ ուժերի կատարած աշխատանքն է:

Շփման ուժերը հիմնականում կատարում են բացասական աշխատանք: Ուստի, փակ համակարգում շփման ուժերի դեմ կատարված աշխատանքը ժամանակի ընթացքում հանգեցնում է նրա լրիվ մեխանիկական էներգիայի փոքրացմանը և փոխարկմանը և ոչ մեխանիկական էներգիայի ձևերին: Այս դեպքում առկա է էներգիայի պահպանման ավելի ընդհանուր հետևյալ օրենքը. ցանկացած արտաքին ազդեցություններից մեկուսացված համակարգի բոլոր ձևերի էներգիաների (ներառյալ նաև ոչ մեխանիկական) գումարը մնում է հաստատուն:

Դիտարկենք էներգիայի և իմպուլսի պահպանման օրենքների համատեղ կիրառության վերաբերյալ խնդիրների լուծման օրինակներ:

Խնդիր 1: Նույն m զանգվածն ունեցող երկու առաձգական գնդեր կրում են ոչ կենտրոնական հարված: Հարվածից առաջ առաջին գնդի արագությունը  է, երկրորդ գնդինը՝ 0 (անշարժ է), իսկ հարվածից հետո համապատասխանաբար՝ Ցույց տալ, որ հարվածից հետո (նկ.1.) գնդերը կթռչեն իրար նկատմամբ ուղիղ անկյան տակ: Էներգիայի կորուստը և պտույտն անտեսել:

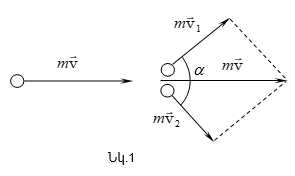
Լուծում: Քանի որ էներգիայի կորուստ չկա, ապա այդպիսի համակարգի համար գործում է ինչպես մեխանիկական էներգիայի պահպանման, այնպես էլ իմպուլսի պահպանման օրենքները:

Հաշվի առնելով այն, որ բացարձակ առաձգական հարվածից անմիջապես հետո մարմինների պոտենցիալ էներգիաները գրեթե նույնն մնում են և փոխվում են միայն կինետիկ էներգիաները, կարող ենք գրել՝

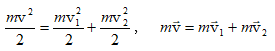
կամ

Քանի որ վեկտորական գումարն է, ապա նրա մոդուլը կորոշվի կոսինուսների թեորեմով՝

որտեղ (3.23) և (3.24) հավասարումների համեմատումից հետևում է, որ  բայց, քանի որ  հետևաբար

Խնդիր 2: m զանգվածով գնդիկը թռչում է դեպի հանգստի վիճակում գտնվող M զանգվածով գնդիկը: Ինչպե՞ս է կախված գնդիկների զանգվածների հարաբերությունից այն էներգիան, որը կորցնում է թռչող գնդիկն առաձգական հարվածի դեպքում:

Լուծում: Թռչող գնդիկի արագությունը մինչև հարվածը նշանակենք  հարվածից հետո՝  դադարի վիճակում գտնվող գնդիկի արագությունը հարվածից հետո՝

Օգտվելով էներգիայի և իմպուլսի պահպանման օրենքներից` կարող ենք գրել.

Համատեղ լուծելով այս համակարգը, կստանանք՝ որտեղ գնդիկների զանգվածների հարաբերությունն է:

Գտնենք M զանգվածով գնդիկին հաղորդված էներգիան.

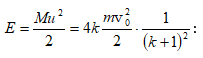
Քանի որ թռչող գնդիկի սկզբնական էներգիան է,ապա

Հետազոտենք ստացված արտահայտությունը: Ակնհայտ է, որ երբ Քանի որ ֆունկցիան անընդհատ է, ապա k-ի որոշակի արժեքի դեպքում այն կունենա առավելագույն արժեք:

E-ի առաջին կարգի ածանցյալը հավասարեցնելով զրոյի` լուծում ենք ստացված հավասարումը և գտնում նրա արմատը՝ k=1: Հետևաբար, թռչող գնդիկը կորցնում է իր կինետիկ էներգիայի առավելագույն մասը՝ նույն զանգվածով գնդիկին հարվածելիս: E(k) կախվածության գրաֆիկը ցույց է տրված նկ.3.3-ում:

Այստեղից պարզ է, որ նեյտրոնների շարժումը դանդաղեցնելու նրանցից էներգիայի հնարավոր առավելագույն մասը խլելու համար անհրաժեշտ է, որ նեյտրոնները հարվածի ենթարկվեն իրենց զանգվածին մոտ զանգվածներով ատոմների, ավելի լավ է` ջրածնի ատոմների միջուկների կողմից: Այդ պատճառով էլ նեյտրոններից պաշտպանվելու նպատակով օգտագործում են ջրածին պարունակող նյութեր:

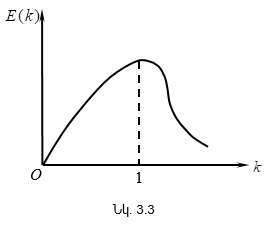
(3.27) բանաձևը հնարավորություն է տալիս հասկանալ այն հիմնական դժվարություններից մեկը, որին բախվում է կառավարվող ջերմամիջուկային սինթեզի իրականացումը: Որպեսզի այդպիսի սինթեզը հնարավոր դառնա, դեյտերիումի կամ դեյտերիումտրիտիումի պլազման պետք է տաքացված լինի մինչև մի քանի հարյուր միլիոն Կելվին (10⁸-10⁹ Կ): Համապատասխան էներգիա պետք է ունենան դեյտերիումի և տրիտիումի իոնները: Լիցքավորված մարմինների էներգիայի մեծացման ամենահասարակ միջոցը նրանց վրա էլեկտրական դաշտով ազդելն է: Բայց այդ դեպքում գործնականում ամբողջ էներգիան կլանվում է ազատ վազքի մեծ երկարություն ունեցող էլեկտրոնների կողմից: Իհարկե, էլեկտրոնների և իոնների էներգիաները հետագայում պետք է աստիճանաբար հավասարվեն: Սակայն զանգվածների մեծ տարբերության պատճառով յուրաքանչյուր հարվածի ժամանակ էլեկտրոնն իոնին հաղորդում է շատ փոքր էներգիա, այդ իսկ պատճառով ջերմային հավասարակշռության հաստատման ժամանակը շատ ավելի մեծ է, քան պլազմայի պահպանման ժամանակը:

>>

3.4 ՄԱՐՄԻՆՆԵՐԻ ԲԱՑԱՐՁԱԿ ԱՌԱՁԳԱԿԱՆ ԵՎ ԲԱՑԱՐՁԱԿ ՈՉ ԱՌԱՁԳԱԿԱՆ ՀԱՐՎԱԾ

Հարված (կամ բախում) է կոչվում երկու կամ ավելի մարմինների հարվածը, որի դեպքում փոխազդեցությունն կարճատև է: Առավել հետաքրքրություն են ներկայացնում բացարձակ առաձգական և բացարձակ ոչ առաձգական բախումները:

Այն ուղիղը, որն անցնում է մարմինների հպման կետով և ուղղահայաց է նրանց հպման մակերևույթներին, կոչվում է հարվածի գիծ: Հարվածը կոչվում է կենտրոնական, եթե մարմինները մինչև բախումը շարժվում են այն ուղղի երկայնքով, որն անցնում է նրանց զանգվածների կենտրոնով: Այստեղ դիտարկվելու են միայն կենտրոնական բացարձակ առաձգական և բացարձակ ոչ առաձգական հարվածները:

Բացարձակ առաձգական է կոչվում այն հարվածը, որի դեպքում մարմինների մեխանիկական էներգիայի կորուստ տեղի չի ունենում, և բախվող մարմինների ներքին էներգիան մնում է անփոփոխ: Այսպիսի հարվածի դեպքում կինետիկ էներգիան լրիվ կամ մասնակի փոխարկվում է առաձգական դեֆորմացիայի պոտենցիալ էներգիայի: Այնուհետև, մարմիններն իրար հրելով` նորից ստանում են իրենց սկզբնական ձևը:

Բախվող մարմինների միջև փոխազդեցության ուժերը (հարվածային կամ ակնթարթային ուժերը) այնքան մեծ են, որ նրանց վրա ազդող արտաքին ուժերը կարելի է անտեսել: Դա թույլ է տալիս բախման պրոցեսում մարմինների համակարգը դիտարկել որպես մոտավորապես փակ համակարգ և նրա համար կիրառել պահպանման օրենքները:

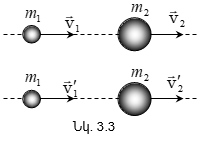
զանգվածներով գնդերի արագությունները մինչև հարվածը նշանակենք հարվածից հետո` (նկ.3.3): Կենտրոնական ուղիղ հարվածի դեպքում գնդերի արագությունների վեկտորները մինչև հարվածը և հարվածից հետո ընկած են նրանց կենտրոնները միացնող ուղղի վրա: Արագությունների վեկտորների պրոյեկցիաները այդ ուղղի վրա հավասար են արագությունների մոդուլներին: Նրանց ուղղությունները հաշվի կառնենք նշաններով. դրական արժեք կվերագրենք աջ շարժվողին, բացասական` ձախ շարժվողին:

Նշված ենթադրությունների դեպքում պահպանման օրենքները կունենան հետևյալ տեսքը.

Կատարելով համապատասխան ձևափոխություններ (3.15) և (3.16) արտահայտություններում կստանանք`

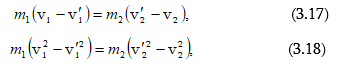
որտեղից

Լուծելով (3.17) և (3.19) հաասարումները, կգտնենք`

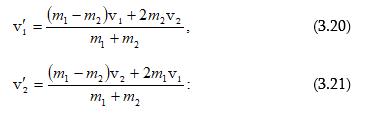
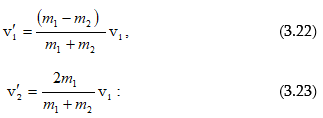
Վերլուծենք (3.22) և (3.23) արտահայտությունները տարբեր զանգվածներով երկու գնդերի համար.

Առաջին գունդը շարունակում է շարժվել այն ուղղությամբ, ինչ, որ մինչև հարվածը, բայց փոքր արագությամբ Հարվածից հետո երկրորդ գնդի արագությունն ավելի հետո մեծ է, քան առաջին գնդինը (նկ.3.4):

Առաջին գնդի շարժման ուղղությունը հարվածի դեպքում փոխվում է, գունդը ետ է թռչում: Երկրորդ գունդը շարժվում է նույն կողմը, ուր շարժվում էր առաջին գունդը մինչև հարվածը, բայց փոքր արագությամբ, այսինքն`  (նկ.3.5):

(օրինակ, գնդի բախումը պատի հետ): (3.22) և (3.23) հետևում է, որ

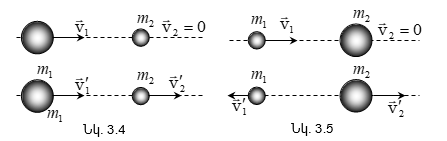
2.  դեպքում (3.20) և (3.21) արտահայտություններից ստանում ենք`

այսինքն` հավասար զանգվածներով գնդերը փոխանակում են արագությունները:

Մարմինների բախումը կոչվում է բացարձակ ոչ առաձգական, եթե միմյանց հետ բախվելուց հետո մարմինները միանում են իրար, այնուհետև շարժվում են որպես մի ամբողջություն:

Բացարձակ ոչ առաձգական հարվածը բնորոշ է նրանով, որ այս դեպքում դեֆորմացիայի պոտենցիալ էներգիա չի առաջանում, մարմինների կինետիկ էներգիան լրիվ կամ մասամբ փոխարկվում է ներքին էներգիայի: Հարվածից հետո մարմինները շարժվում են նույն արագությամբ կամ մնում են հանգստի վիճակում: Բացարձակ ոչ առաձգական հարվածի դեպքում առկա է միայն իմպուլսի պահպանման օրենքը, իսկ մեխանիկական էներգիայի պահպանման օրենքը տեղի չի ունենում. առկա է տարբեր տեսակների` մեխանիկական և ներքին էնեգիաների գումարի պահպանման օրենքը:

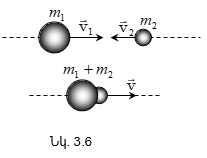
Բացարձակ ոչ առաձգական հարվածը կարելի է ցուցադրել պլաստիլինից պատրաստված գնդերի օգնությամբ, որոնք շարժվում են իրար ընդառաջ (նկ.3.6): Եթե գնդերի զանգվածները  է, իսկ արագությունները մինչև հարվածը`  օգտագործելով իմպուլսի պահպանման օրենքը, կարելի է գրել`

որտեղ գնդերի շարժման արագությունն է հարվածից հետո: Այդ դեպքում

Եթե գնդերը շարժվում են իրար ընդառաջ, դրանք միմյանց հետ կշարունակեն շարժվել այն կողմը, որ կողմը շարժվում էր մեծ իմպուլսով օժտված գունդը: Մասնավոր դեպքում, եթե գնդիկների զանգվածները հավասար են,

Պարզենք, թե ինչպես է փոխվում գնդերի կինետիկ էներգիան կենտրոնական բացարձակ ոչ առաձգական հարվածի դեպքում: Քանի որ գնդերի փոխհարվածի պրոցեսում նրանց միջև ազդող ուժեր կան, որոնք կախված են ոչ թե գնդերի դեֆորմացիաներից, այլ` արագություններից, ուստի մենք գործ ունենք այնպիսի ուժերի հետ, որոնք համանման են շփման ուժերին, դրա համար էլ մեխանիկական էներգիան չպետք է պահպանվի: Դեֆորմացիայի հետևանքով տեղի է ունենում կինետիկ էներգիայի «կորուստ», փոխարկվելով ջերմային կամ այլ տեսակի էներգիաների: Էներգիայի այդ «կորուստը» կարելի է որոշել մինչև հարվածը և հարվածից հետո մարմինների կինետիկ էներգիաների տարբերությամբ.

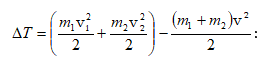
Օգտագործելով (3.24) -ը, կստանանք`

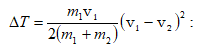
Եթե հարվածվող մարմինը սկզբում անշարժ էր ուրեմն`

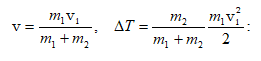
Երբ (անշարժ մարմնի զանգվածը շատ մեծ է), ապա և մարմնի համարյա ամբողջ կինետիկ էներգիան անցնում է էներգիայի այլ ձևերի: Այդ նպատակով էլ, օրինակ, նշանակալից դեֆորմացիա ստանալու համար զնդանը պետք է մուրճից ավելի զանգվածեղ լինի: Ընդհակառակը, մեխը պատի մեջ խփելու դեպքում մուրճի զանգվածը շատ ավելի մեծ պետք է լինի այդ դեպքում  և գործնականորեն ամբողջ էներգիան ծախսվում է մեխի հնարավոր մեծ տեղափոխության, և ոչ թե պատի մնացորդային դեֆորմացիայի վրա: Բացարձակ ոչ առաձգական հարվածը օրինակն է այն երևույթի, թե ինչպես է տեղի ունենում մեխանիկական էներգիայի «կորուստը» դիսսիպատիվ ուժերի ազդեցության տակ:

>>

ԳԼՈՒԽ 4. ՊԻՆԴ ՄԱՐՄՆԻ ՊՏՏԱԿԱՆ ՇԱՐԺՄԱՆ

 ԴԻՆԱՄԻԿԱ

Ինչպես հայտնի է, պինդ մարմնի մեխանիկական շարժումը կարելի է պատկերացնել համընթաց և պտտական համակցված շարժումների միջոցով: Քանի որ համընթաց շարժման դեպքում մարմնի բոլոր կետերը կատարում են միատեսակ շարժում, ապա տվյալ հաշվարկման XYZ համակարգի նկատմամբ մարմնի համընթաց շարժումը կարելի է նկարագրել նրա որևէ կետի կոորդինատների՝ ժամանակից կախումն արտահայտող x=x(t), y=y(t) և z=z(t) հավասարումներով (նկ.4.1):

O կետի շուրջը մարմնի պտտական շարժումը նկարագրվում է այդ կետով տարված OX, OY, OZ առանցքների շուրջը մարմնի պտտման անկյունների՝ ժամանակից կախումն արտահայտող հավասարումներով, որոնք x=x(t), y=y(t), z=z(t) հավասարումների հետ միասին կազմում են մարմնի շարժման հավասարումների լրիվ համակարգը (նկ.4.2):

 Յուրաքանչյուր OX, OY և OZ առանցքի շուրջը մարմնի պտտական շարժումը նկարագրվում է այն նույն կինեմատիկական մեծություններով, որոնց միջոցով նկարագրվում է կետի շարժումը շրջանագծով` անկյուններով,  անկյունային արագություններով, անկյունային արագացումներով, պտտման հաճախությամբ և պարբերությամբ: Այդ մեծությունները միատեսակ են պինդ մարմնի բոլոր կետերի համար:

 Քննարկենք մեկ անշարժ առանցքի շուրջը մարմնի պտտական շարժումն առաջացնող գործոնը:

>>

4.1. ՈՒԺԻ ՄՈՄԵՆՏԸ ԿԵՏԻ ԵՎ ԱՌԱՆՑՔԻ ՆԿԱՏՄԱՄԲ:

ՆՅՈՒԹԱԿԱՆ ԿԵՏԻ ԻՄՊՈՒԼՍԻ ՄՈՄԵՆՏԸ ԿԵՏԻ և ԱՌԱՆՑՔԻ ՆԿԱՏՄԱՄԲ: ՈՒԺԱԶՈՒՅԳ

Մեխանիկայի հիմնական օրենքները կապված են ուժի մոմենտ և իմպուլսի մոմենտ հասկացությունների հետ: Հարկավոր է տարբերել այդ վեկտորների մոմենտները կետի ու առանցքի նկատմամբ և երբեք չշփոթել միմյանց հետ: Վեկտորի մոմենտը կետի նկատմամբ և առանցքի նկատմամբ տարբեր հասկացություններ են, չնայած` դրանք փոխկապակցված են: Վեկտորի մոմենտը կետի նկատմամբ ինքը վեկտոր է: Նույն վեկտորի մոմենտը առանցքի նկատմամբ, կետի նկատմամբ իր մոմենտի պրոյեկցիան է նույն առանցքի վրա: Այսպիսով, վեկտորի մոմենտն առանցքի նկատմամբ արդեն վեկտոր չէ: Սկսենք մոմենտների դիտարկումը կետի նկատմամբ: Դիցուք O-ն որևէ կետ է, որի նկատմամբ դիտարկվում է ուժի վեկտորի և իմպուլսի վեկտորի մոմենտը: Այն կոչվում է սկիզբ կամ բևեռ:

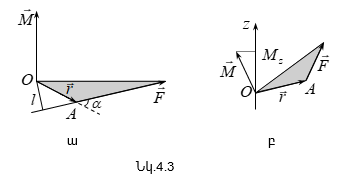
Եթե նյութական կետի վրա ազդում է  ուժ, ապա O կետի նկատմամբ ուժի մոմենտ է կոչվում շառավիղ-վեկտորի և  ուժի վեկտորական արտադրյալը (նկ. 4.3ա):

Նկարից երևում է, որ ուժի մոմենտի մոդուլը կարելի է ներկայացնել

տեսքով, որտեղ ուժի բազուկն է O կետի նկատմամբ:                        

պրոյեկցիան որևէ z առանցքի վրա, որն անցնում է O կետով և որի նկատմամբ որոշվում է  կոչվում է ուժի մոմենտ այդ առանցքի նկատմամբ (նկ.4.3բ).

Եթե ապա վեկտորական արտադրյալի հայտնի հատկության հիման վրա կարելի է գրել.

Այստեղից հետևում է, որ երկու կամ մի քանի ուժերի արդյունարար մոմենտը O կետի նկատմամբ հավասար է բաղադրիչ ուժերի մոմենտների երկրաչափական գումարին նույն O կետի նկատմամբ:

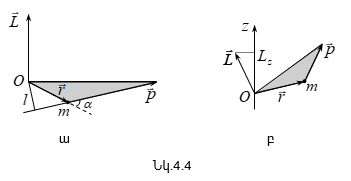
Դիցուք զանգվածով նյութական կետը շարժվում է O կետի շուրջը: Նյութական կետի O կետի նկատմամբ իմպուլսի մոմենտ է կոչվում  շառավիղ-վեկտորի և իմպուլսի վեկտորական արտադրյալը (նկ.4.4ա)

Քանի որ  վեկտորն ուղղահայաց է կազմված հարթությանը, ուստի նրա հաստատուն լինելը նշանակում է, որ շարժումը տեղի է ունենում միշտ նույն հարթությունում:  վեկտորը սովորական  վեկտորներից տարբերվում է: Այս վեկտորները բևեռային են, այսինքն` ունեն կիրառման կետ (ինչպես ասում են բևեռ ունեն): Իսկ իմպուլսի մոմենտը, որը որոշվում է երկու վեկտորների օգնությամբ, կիրառման կետ ունենալ չի կարող: Այդպիսի վեկտորները, ինչպես  բնութագրվում են նրանով, որ դրանց սկզբները կարելի է տեղափոխել վեկտորի ուղղությամբ: Այդպիսի վեկտորները, որոնք որոշակի կիրառման կետ չունեն, կոչվում են սահող կամ աքսիալ:

(4.5) վեկտորի պրոյեկցիան որևէ z առանցքի վրա, կոչվում է նյութական կետի իմպուլսի մոմենտ այդ առանցքի նկատմամբ (նկ.4.4բ).                        

Նկար 4.4ա-ից երևում է, որ նյութական կետի իմպուլսի մոմենտի մոդուլը`

որտեղ կետից ուղղի վրա իջեցրած ուղղահայացի երկարությունն է, որի երկայնքով ուղղված է մասնիկի իմպուլսը: Այդ երկարությունը կոչվում է O կետի նկատմամբ իմպուլսի բազուկ:

Ուժազույգ է կոչվում մեծությամբ իրար հավասար և հակառակ ուղղված երկու ուժեր, որոնք չեն ազդում միևնույն ուղղի երկայնքով (նկ.4.5):

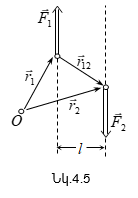
Այն ուղիղների միջև եղած հեռավորությունը, որոնց երկարությամբ ազդում են ուժերը, կոչվում է ուժազույգի բազուկ: Ուժազույգ կազմող ուժերի արդյունարար մոմենտը`

Նկատի ունենալով, որ  կարելի է գրել`

որտեղ  մի վեկտոր է, որը տարված է  ուժի կիրառման կետից  ուժի կիրառման կետը: (4.8) արտահայտությունը կախում չունի O կետի ընտրությունից, հետևաբար, ուժազույգի մոմենտը ցանկացած կետի նկատմամբ մնում է նույնը: Այսպիսով, ուժազույգի մոմենտն ուղղահայաց է այն հարթությանը, որի վրա գտնվում են ուժերը, և թվապես հավասար է այդ ուժերից մեկի մոդուլի և բազկի արտադրյալին:

Իմպուլսի մոմենտի և ուժի մոմենտի հասկացությունների ներմուծման նպատակահարմարությունն արդարացվում է նրանով, որ դրանք կապված են իրար հետ կարևոր առնչությամբ, որն այժմ կարտածենք` օգտվելով Նյուտոնի երկրորդ օրենքից:

Ենթադրում ենք, որ O կետն անշարժ է: Դիֆերենցելով (4.5)-ը ըստ ժամանակի` կստանանք

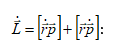
Քանի որ, ըստ ենթադրության, O կետն անշարժ է, ապա  ածանցյալը նյութական կետի արագությունն է, որը կապված է նրա իմպուլսի հետ  առնչությամբ: Ուստի, առաջին գումարելին հավասար է զրոյի, որպես երկու  միագիծ վեկտորների վեկտորական արտադրյալ: Երկրորդ գումարելին կարելի է ձևափոխել Նյուտոնի հավասարման օգնությամբ, այն է  Այդ դեպքում կստացվի

Այս առնչությունն էլ հենց մենք ուզում էինք ստանալ: Վերջինից հետևում է, որ O կետի նկատմամբ նյութական կետի իմպուլսի մոմենտի ածանցյալն ըստ ժամանակի հավասար է այդ կետի նկատմամբ նյութական կետի վրա ազդող ուժի մոմենտին: Սա Նյուտոնի երկրորդ օրենքի գրության այլ ձև է պտտական շարժման համար: Այն կոչվում է նաև մոմենտների հավասարում: Միանգամայն պարզ է, որ եթե մեկ նյութական կետի վրա ազդող ուժի մոմենտը O կետի նկատմամբ հավասար է զրոյի, ապա նյութական կետի իմպուլսի մոմենտը O կետի նկատմամբ կմնա հաստատուն:

Արտածման դեպքում չենթադրվեց, որ m զանգվածը մնում է հաստատուն: Ուստի, (4.8) հավասարումը ճիշտ է նաև ռելյատիվիստական մեխանիկայում, այն է` նյութական կետի այնպիսի մեծ արագությունների դեպքում, որը թույլատրվում է հարաբերականության տեսությամբ:

(4.8) մոմենտների հավասարումը կարելի է ընդհանրացնել նյութական կետերի կամայական համակարգի դեպքի համար: Նյութական կետերի համակարգի իմպուլսի մոմենտ O կետի նկատմամբ կոչվում է համակարգի բոլոր նյութական կետերի իմպուլսների մոմենտների վեկտորական գումարը նույն O կետի նկատմամբ: Համանմանորեն, բոլոր ուժերի մոմենտը, որն ազդում է նյութական կետերի համակարգի վրա, որոշվում է որպես առանձին ուժերի մոմենտների վեկտորական գումար: Բոլոր ուժերի մոմենտները գումարելու փոխարեն, նկատի ունենալով (4.4) առնչությունը, կարելի է գտնել այդ ուժերի արդյունարարը, այնուհետև հաշվել նրա մոմենտը: Այդպես կարելի է վարվել նաև նյութական կետերի համակարգի իմպուլսը գտնելու դեպքում. սկզբում վեկտորապես գումարել բոլոր նյութական կետերի իմպուլսները, այնուհետև գտնել դիտարկվող կետի նկատմամբ ստացված վեկտորի մոմենտը:

Ենթադրենք O բևեռն անշարժ է: Գրենք մոմենտների հավասարումը յուրաքանչյուր նյութական կետի համար, այնուհետև դրանք վեկտորապես գումարենք: Կրկին հանգում ենք (4.8) առնչությանը, սակայն` արդեն նյութական կետերի համակարգի համար: Այդ դեպքում տակ պետք է հասկանալ, ինչպես արտաքին, այնպես էլ ներքին բոլոր ուժերի մոմենտը: Սակայն ներքին ուժերին չպետք է ուշադրություն դարձնել, քանի որ ցանկացած կետի նկատմամբ նրանց լրիվ մոմենտը հավասար է զրոյի: Դա բացատրվում է նրանով, որ ներքին ուժերը միշտ հանդես են գալիս զույգ-զույգ ուժին, որով k-րդ նյութական կետն ազդում է i-րդ կետի վրա, համապատասխանում է հավասար և հակառակ ուղղված  ուժը, որով i-րդ կետն ազդում է k-րդի վրա: Այդ երկու ուժերն ուղղված են միևնույն ուղղի երկայնքով: Մոմենտները հաշվելիս, դրանց կիրառման կետերը կարելի է տեղափոխել այդ ուղղի վրա` միևնույն կետը: Արդյունքում ուժերը փոխադարձաբար իրար կոմպենսացնում են, իսկ դրանց արդյունարար մոմենտը հավասարվում է զրոյի:

Այսպիսով Նյուտոնի երրորդ օրենքը հնարավորություն է տալիս (4.8) հավասարումից բացառել ներքին ուժերը: (4.8) հավասարման փոխարեն ստացվում է ՝

Այսինքն` կամայական անշարժ կետի նկատմամբ նյութական կետերի համակարգի իմպուլսի մոմենտի ածանցյալն ըստ ժամանակի հավասար է նույն կետի նկատմամբ բոլոր արտաքին ուժերի մոմենտների երկրաչափական գումարին:

Վեկտորական (4.9) հավասարումը համարժեք է երեք սկալյար հավասարումների.

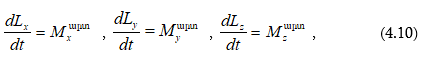
որոնք ստացվում են (4.9) հավասարումից, դեկարտյան կոորդինատային համակարգի անշարժ առանցքների վրա պրոյեկտման ճանապարհով:

 Ինդեքս «արտ»-ը ցույց է տալիս, որ ուժերի մոմենտները հաշվելիս ներքին ուժերին կարելի է ուշադրություն չդարձնել:

Այսպիսով, մոմենտների հավասարման մեջ տակ միշտ պետք է նկատի ունենալ արտաքին ուժերի մոմենտը:  մեծությունները համապատասխանաբար կոչվում են իմպուլսի մոմենտ և ուժի մոմենտ X-երի առանցքի նկատմամբ: Նույնն ասում են իմպուլսի և ուժի մոմենտների մասին Y և Z կոորդինատային առանցքների նկատմամբ: Ընդհանրապես,  իմպուլսի և ուժի մոմենտները կամայական X-երի առանցքի նկատմամբ անվանում են վեկտորների պրոյեկցիաներ այդ առանցքի վրա, ենթադրելով, որ O բևեռը գտնվում է դիտարկվող առանցքի վրա.

(4.11) հավասարումը կոչվում է մոմենտների հավասարում անշարժ X առանցքի նկատմամբ:

>>

4.2. ՊՏՏԱԿԱՆ ՇԱՐԺՄԱՆ ԴԻՆԱՄԻԿԱՅԻ ՀԱՎԱՍԱՐՈՒՄԸ

Դիտարկենք պտտական շարժումը՝ կիրառելով առանցքի նկատմամբ մոմենտների հավասարումը: Որպես մոմենտների անշարժ առանցք հարմար է ընտրել պտտման առանցքը: Եթե նյութական կետը պտտվում է r շառավիղ ունեցող շրջանագծով (նկ.4.6), ապա նրա իմպուլսի մոմենտը O առանցքի նկատմամբ կլինի L=mvr:

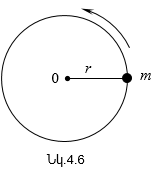
Եթե պտտման անկյունային արագությունն է, ապա  և, հետևաբար,  Եթե O կետի շուրջը պտտվում է նյութական կետերի համակարգ միևնույն անկյունային արագությամբ, ապա որտեղ գումարումը կատարվում է ըստ համակարգի բոլոր նյութական կետերի: Քանի որ,մեծությունը բոլոր նյութական կետերի համար նույնն է, ապա այն կարելի է դուրս բերել գումարի նշանի տակից: Այդ դեպքում կստանանք՝

որտեղ

I մեծությունը, որը հավասար է նյութական կետերի զանգվածների և պտտման առանցքից նրանց ունեցած հեռավորությունների քառակուսիների արտադրյալների գումարին, կոչվում է առանցքի նկատմամբ համակարգի իներցիայի մոմենտ:

 (4.12) հավասարումը ցույց է տալիս, որ համակարգի պտտման դեպքում նրա իմպուլսի մոմենտը պտտման առանցքի նկատմամբ հավասար է նույն առանցքի նկատմամբ իներցիայի մոմենտի և անկյունային արագության արտադրյալին:

Եթե նյութական կետերի համակարգի պտտական շարժման վրա վերադրվում է նրանց շառավղային, ինչպես նաև առանցքին զուգահեռ շարժումը, ապա այդպիսի շարժումների առկայությունը չի անդրադառնում (4.12) բանաձևի ճշտության վրա: Դա բխում է նրանից, որ նյութական կետի իմպուլսի մոմենտն իր  արագությունից կախված է գծայնորեն: Երբ  արագությունն ուղղված է շառավղով կամ զուգահեռ է պտտման առանցքին, այդ առանցքի նկատմամբ իմպուլսի մոմենտը հավասար է զրոյի: Հետևաբար, այդպիսի շարժումներն անմիջականորեն չեն ազդի պտտման առանցքի նկատմամբ համակարգի իմպուլսի և նրա անկյունային արագության միջև եղած կապի տեսքի վրա: Դրանց ազդեցությունն ուղղակի է, այսինքն` I իներցիայի մոմենտը դադարում է հաստատուն մեծություն լինելուց և փոխվում է ժամանակի ընթացքում համակարգի կոնֆիգուրացիայի ակնթարթային փոփոխությանը համապատասխան: Այս դեպքում (4.11) հավասարումը կընդունի հետևյալ տեսքը.                       

որտեղ M-ը արտաքին ուժերի մոմենտն է առանցքի նկատմամբ: (4.14)-ը անշարժ առանցքի շուրջը պտտական շարժման դինամիկայի հիմնական հավասարումն է: Այն հիշեցնում է նյութական կետի շարժման համար Նյուտոնի հավասարումը: Զանգվածի դերը կատարում է I իներցիայի մոմենտը, արագության դերը՝ անկյունային արագությունը, ուժի դերը՝ M ուժի մոմենտը, իմպուլսի դերը՝ L իմպուլսի մոմենտը:

Համընթաց և պտտական շարժումների գրառման համանմանությունները բերված են աղյուսակ 1-ում:

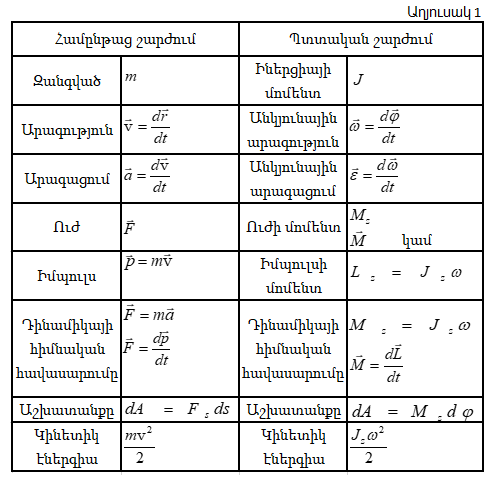
Հաճախ L իմպուլսի մոմենտն անվանում են համակարգի պտտական իմպուլս: Օգտվելով այս տերմինաբանությունից` կարելի է ասել, որ համակարգի պտտական իմպուլսի ածանցյալն ըստ ժամանակի հավասար է պտտման առանցքի նկատմամբ արտաքին ուժերի մոմենտին:

Եթե պտտման առանցքի նկատմամբ արտաքին ուժերի M մոմենտը հավասար է զրոյի, ապա  պտտական իմպուլսը պահպանվում է:

Կարևոր մասնավոր դեպք է նյութական կետերի չփոփոխվող համակարգի կամ պինդ մարմնի պտույտն անշարժ առանցքի շուրջը: Այս դեպքում I իներցիայի մոմենտը պտտման ժամանակ մնում է հաստատուն և (4.14) հավասարումն ընդունում է հետևյալ տեսքը.

Այսինքն` պտտման անշարժ առանցքի նկատմամբ պինդ մարմնի իներցիայի մոմենտի և  անկյունային արագացման արտադրյալը հավասար է նույն առանցքի նկատմամբ արտաքին ուժերի մոմենտին:

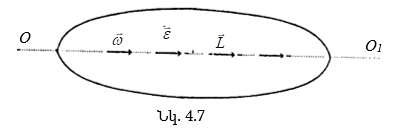
Հարկ է մեկ անգամ ևս նշել, որ ի տարբերություն  բևեռային վեկտորների, որոնք ունեն իրենց կիրառման կետը, առանցքային սահող վեկտորներ են, այսինքն, դրանց սկիզբը կարելի է տեղափոխել վեկտորի ուղղության հետ համընկնող առանցքի երկայնքով: Այս վեկտորների ուղղությունները որոշվում են աջ պտուտակի կանոնով (նկ. 4.7):

>>

4.3. ՄԱՐՄՆԻ ԻՆԵՐՑԻԱՅԻ ՄՈՄԵՆՏՆ ԱՆՇԱՐԺ

ԱՌԱՆՑՔԻ ՆԿԱՏՄԱՄԲ

Համընթաց շարժման դեպքում մարմնի իներտության չափը զանգվածն է, իսկ պտտական շարժման դեպքում՝ իներցիայի մոմենտը:

Իներցիայի մոմենտը զանգվածի նման ադիտիվ մեծություն է, այսինքն՝ մեխանիկական համակարգի (նկ.4.8) իներցիայի մոմենտն անշարժ առանցքի նկատմամբ հավասար է համակարգի բոլոր n նյութական կետերի իներցիայի մոմենտների գումարին: Համակարգի իներցիայի մոմենտը հավասար է այդ կետերի  զանգվածների և տվյալ առանցքից դրանց  հեռավորությունների քառակուսիների արտադրյալների գումարին՝

որտե i-րդ կետի ցանգվածն է,  պտտման առանցքից դրա հեռավորությունն է, իսկ դրա իներցիայի մոմենտը առանցքի նկատմամբ:

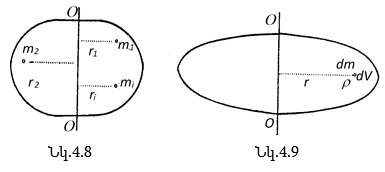
Հոծ մարմնի դեպքում (նկ.4.9) իներցիայի մոմենտը հաշվելու համար բաժանենք այն անվերջ փոքր dV ծավալների: Հաշվի առնելով, որ OO առանցքից r հեռավորության վրա գտնվող խտությամբ dV ծավալի զանգվածը հավասար է՝  հոծ մարմնի իներցիայի մոմենտը կարելի է հաշվել հետևյալ բանաձևով՝

(4.17) բանաձևը հնարավորություն է տալիս հաշվել մարմնի իներցիայի մոմենտը ցանկացած առանցքի նկատմամբ, եթե հայտնի է առանցքի նկատմամբ մարմնի ներսում նյութի խտության բաշխման օրենքը՝ Ինչպես տեսնում ենք, մամնի իներցիայի մոմենտը կախված է ոչ միայն մարմնի զանգվածից և նրա չափերից, այլև՝ առանցքի նկատմամբ մարմնի ներսում նյութի խտության բաշխումից: Ի տարբերություն զանգվածի, մարմնի իներցիայի մոմենտը չի ենթարկվում պահպանման օրենքին: Մարմնի ձևի և առանցքի նկատմամբ դիրքի փոփոխությունը կարող է փոխել մարմնի իներցիայի մոմենտն այդ առանցքի նկատմամբ:

>>

4.4. ՇՏԱՅՆԵՐԻ ԹԵՈՐԵՄԸ

Տեղադրենք մարմնի C զանգվածի կենտրոնում որևէ XYZ կոորդինատային համակարգի սկիզբը և դրանից որոշ հեռավորության վրա տեղադրենք մի այլ  կոորդինատային համակարգ, որի առանցքներն ուղղված են XYZ համակարգի առանցքներին զուգահեռ այնպես, ինչպես պատկերված է նկ.4.10-ում առանցքներն ուղղահայաց են նկարի հարթությանը):

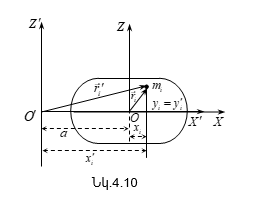
Ակնհայտ է, որ մարմնի զանգվածի կենտրոնի կոորդինատները հավասար են զրոյի:

Այժմ բաժանելով մարմինը փոքր մասերի` հաշվենք նրա իներցիայի մոմենտը  առանցքի նկատմամբ:

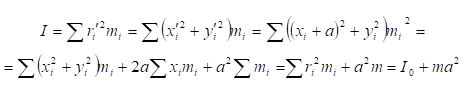
Այսպիսով, եթե հայտնի է m զանգված ունեցող մարմնի C իներցիայի կենտրոնով անցնող  առանցքի նկատմամբ  իներցիայի մոմենտը, ապա այդ առանցքից հեռավորության վրա գտնվող զուգահեռ  առանցքի նկատմամբ (նկ.4.11) մարմնի I իներցիայի մոմենտը`

Շատ դեպքերում իներցիայի մոմենտների հաշվարկը կարելի է պարզեցնել` օգտագործելով համաչափության և նմանության նկատառումները, Շտայների թեորեմը, ինչպես նաև որոշ այլ ընդհանուր առնչություններ, որոնց մասին կխոսվի ստորև:

Դիտարկենք երկու միանման և պտտման առանցքի նկատմամբ նույն կերպ տեղադրված, միևնույն խտությունն ունեցող  և  մարմինները: Այդ մարմինների լրիվ և տարրական զանգվածներն իրար հարաբերում են այնպես, ինչպես դրանց գծային չափերի խորանարդները:

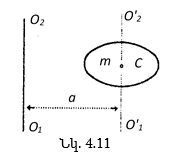
Քանի որ տարրական զանգվածները բազմապատկվում են մինչև պտտման առանցքն ունեցած իրենց հեռավորությունների քառակուսիներով, ապա A և B մարմինների իներցիայի մոմենտները կլինեն համեմատական նույն չափերի հինգերորդ աստիճաններին: Այդպիսով կամ  տակ պետք է հասկանալ մարմնի որևէ բնութագրական չափ կամ պտտման առանցքից նրա որևէ բնութագրական կետի հեռավորություն: Համեմատականության k գործակիցը կախված է միայն մարմնի ձևից և պտտման առանցքի նկատմամբ նրա դասավորությունից:

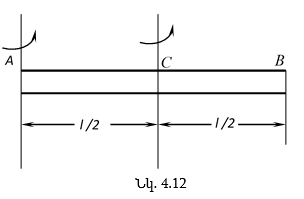
Բերենք իներցիայի մոմենտի հաշվման օրինակ:

Օգտվելով Շտայների թեորեմից` հաշվենք բարակ համասեռ ձողի իներցիայի մոմենտը նրան ուղղահայաց առանցքի նկատմամբ:

Դիցուք առանցքն անցնում է ձողի A ծայրով (նկ.4.12): Իներցիայի մոմենտի համար կարելի է գրել

որտեղ  ձողի երկարությունն է: Ձողի C կենտրոնը նրա զանգվածների կետրոնն է: Ըստ Շտայների թեորեմի

մեծությունը կարելի է ներկայացնել երկու՝ CA և CB ձողերի իներցիայի մոմենտների գումարի տեսքով: Յուրաքանչյուր ձողի երկարությունը հավասար է զանգվածը՝  հետևաբար, իներցիայի մոմենտը հավասար կլինի

Տեղադրելով այս արտահայտությունները նախորդ բանաձևի մեջ` կստանանք.

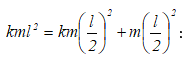
Լուծելով ստացած հավասարումը` կստանանք k=1/3: Արդյունքում, ձողի A ծայրով անցնող առանցքի նկատմամբ իներցիայի մոմենտի համար կստանանք.  իսկ զանգվածների C կենտրոնով անցնող առանցքի նկատմամբ իներցիայի մոմենտը կլինի՝

Վերջում նշենք, որ համասեռ սկավառակի իներցիայի մոմենտը նրա կենտրոնով անցնող առանցքի նկատմամբ` որտեղ R-ը սկավառակի շառավիղն է, իսկ m-ը` նրա զանգվածը:

R շառավիղ ունեցող համասեռ գնդի իներցիայի մոմենտը նրա կենտրոնով անցնող առանցքի նկատմամբ ՝

>>

4.5. ԻՄՊՈՒԼՍԻ ՄՈՄԵՆՏԻ ՊԱՀՊԱՆՄԱՆ ՕՐԵՆՔԸ

Դիցուք ունենք n թվով նյութական կետերից բաղկացած որևէ մեխանիկական համակարգ:

Եթե համակարգը փակ է, ապա նյութական կետերի վրա ազդում են միայն ներքին ուժեր, բաց համակարգի դեպքում՝ նաև արտաքին ուժեր: Անկախ այնհանգամանքից ուժերը ներքին են, թե արտաքին, դրանք առաջացնում են նյութական կետերի իմպուլսների մոմենտների փոփոխություն: Մեզ նորից հետաքրքրում է ամբողջ համակարգի իմպուլսի մոմենտը՝ փոխվու՞մ է, թե` ոչ: Ամբողջ համակարգի իմպուլսի մոմենտի փոփոխությունը միավոր ժամանակում հավասար է առանձին նյութական կետերի իմպուլսների մոմենտների միավոր ժամանակում փոփոխությունների վեկտորական գումարին.

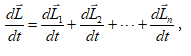
քանի որ

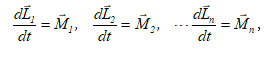
որտեղ համապատասխան նյութական կետերի վրա ազդող ուժերի մոմենտներն են:

Նորից նկատում ենք, որ վարքը կախված է  գումարից: Եթե համակարգը փակ է, այս դեպքում ուժերը կլինեն ներքին ուժեր, և ըստ Նյուտոնի երրորդ օրենքի ոչ միայն դրանց գումարն է հավասար զրոյի, այլ նաև` դրանց մոմենտների գումարը:

Փակ համակարգի համար՝

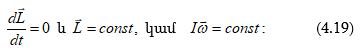
Ստացված առնչությունն արտահայտում է իմպուլսի մոմենտի պահպանման օրենքը՝ ցանկացած փոխազդեցությունների դեպքում փակ համակարգի ներսում գտնվող մարմինների իմպուլսների մոմենտների վեկտորական գումարը մնում է հաստատուն:

Նշենք, որ իմպուլսի մոմենտի պահպանման օրենքը բնության հիմնարար օրենք է:

Եթե արտաքին ուժերի բացակայության դեպքում իներցիայի մոմենտը փոխվում է, ապա սկսում է փոխվել և  անկյունային արագությունը, այնպես, որ արտադրյալը մնում է հաստատուն: Եթե I իներցիայի մոմենտն աճում է, այդ դեպքում նվազում է  անկյունային արագությունը և հակառակը:

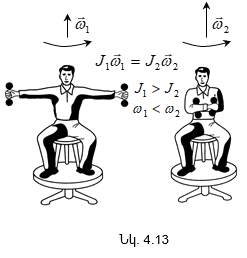
Իմպուլսի մոմենտի պահպանման օրենքը կարելի է ցուցադրել Ժուկովսկու նստարանի օգնությամբ, որը կարող է առանց շփման պտտվել ուղղաձիգ առանցքի շուրջը: Դիցուք նստարանի վրա նստած մարդը պարզած ձեռքերում պահած ծանրոցներով (նկ.4.13) պտտվում է նստարանի հետ միասին  անկյունային արագությամբ: Այդ դեպքում համակարգն ունի  որոշակի իմպուլսի մոմենտ: Եթե մարդը ծանրոցները սեղմի իրեն, համակարգի իներցիայի մոմենտը կփոքրանա: Քանի որ արտաքին ուժերի մոմենտը հավասար է զրոյի, համակարգի իմպուլսի մոմենտը պահպանվում է, և հետևաբար,  անկյունային արագությունը աճում է, այնպես որ

Եթե համակարգը բաց է, ապա գումարը հավասար կլինի արտաքին ուժերի մոմենտների գումարին, որը հավասար չէ զրոյի, այս դեպքում  կփոխվի և

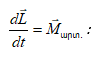
Իմպուլսի մոմենտի պահպանման օրենքը կարելի է ստանալ` օգտվելով ոչ թե Նյուտոնի երրորդ օրենքից, այլ տարածության իզոտրոպությունից: Ըստ տարածության իզոտրոպության հատկության, եթե մարմինների փակ համակարգը շրջենք փոքր  անկյունով այնպես, որ չփոխվեն մարմինների փոխադարձ դիրքը և արագությունները, ապա դրանց փոխազդեցության պոտենցիալ էներգիան և շարժման կինետիկ էներգիան նույնպես չեն փոխվի, իսկ դա նշանակում է, որ այդպիսի շրջման համար չի պահանջվի արտաքին ուժերի աշխատանք:

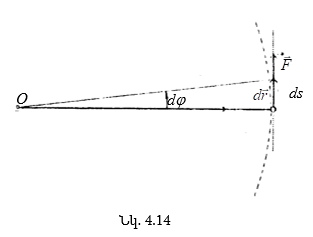
Նյութական կետի անվերջ փոքր տեղափոխության ժամանակ (նկ.4.14) նրա հետագծի շոշափողով ուղղված  ուժի dA աշխատանքը՝

Նյութական կետերի համակարգի դեպքում՝  

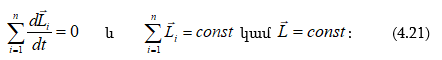
Այժմ դիտարկենք իմպուլսի մոմենտի պահպանման օրենքի կիրառության օրինակ:

Դիցուք նյութական կետը շարժվում է փակ հետագծով (նկ.4.15): Ներմուծենք սեկտորիալ արագության գաղափարը: Հետագծի վրա նյութա կան կետի (մասնիկի) դիրքը որոշվում է  շառավիղ-վեկտորով: Ենթադրենք` մասնիկը dt ժամանակամիջոցում A կետից տեղափոխվում է B կետը, կրելով  տեղափոխություն:

Ներմուծենք մակերեսի  քվազիվեկտորի հասկացությունը, որը թվապես հավասար է շառավիղ-վեկտորի գծած եռանկյան մակերեսին և ուղղահայաց է նրան.

Այդ վեկտորի ածանցյալն ըստ ժամանակի՝  կոչվում է սեկտորիալ արագություն և թվապես հավասար է միավոր ժամանակում շառավիղ-վեկտորի գծած մակերեսին՝

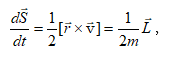
որտեղ m-ը մասնիկի զանգվածն է,  իմպուլսի մոմենտը: Այս դեպքում ենթադրում ենք, որ շառավղային ուղղությամբ  չի փոփոխվում: Եթե m զանգվածով մասնիկը շարժվում է կենտրոնական (կուլոնյան, գրավիտացիոն) ուժերի ազդեցության տակ, ապա ակնհայտ է, որ այդ ուժերի մոմենտները հավասար են զրոյի՝  Օգտվելով Նյուտոնի երկրորդ օրենքից` պտտական շարժման համար՝

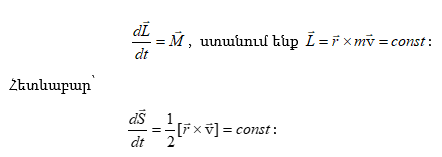
Այսպիսով, կենտրոնական ուժային դաշտում շարժվող մարմնի իմպուլսի մոմենտը և նրա շառավիղ-վեկտորի սեկտորիալ արագությունը մնում են հաստատուն:

Հայտնի է, որ մոլորակներն Արեգակի շուրջը շարժվում են փակ կորերով՝ էլիպսներով (նկ.4.16):

Քանի որ Արեգակի և մոլորակների փոխազդեցության ուժերը կենտրոնական են, ապա

Հետևաբար՝  այսինքն՝ հետագծով մոլորակի շարժման ժամանակ ինչքան փոքրանում է նրա դիրքի շառավիղ-վեկտորը, այնքան մեծանում է նրա շարժման արագությունը:

>>

4.6. ՊԻՆԴ ՄԱՐՄՆԻ ՊՏՏԱԿԱՆ ՇԱՐԺՄԱՆ ԿԻՆԵՏԻԿ ԷՆԵՐԳԻԱՆ

Դիտարկենք 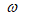 անկյունային արագությամբ անշարժ առանցքի շուրջը պտտվող մարմինը (նկ.4.17):

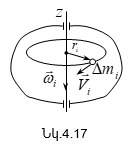
Նրա i-րդ տարրի կինետիկ էներգիան կլինի՝

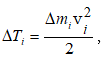
որտեղ  տարրի զանգվածն է նրա գծային արագությունը: Քանի որ  ապա

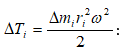
Ամբողջ մարմնի կինետիկ էներգիան բաղկացած է այդ մարմնի առանձին մասերի կինետիկ էներգիաներից, այսինքն՝

Այս առնչության աջ մասի գումարը մարմնի իներցիայի մոմենտն է պտտման առանցքի նկատմամբ: Այսպիսով, անշարժ առանցքի շուրջը պտտվող մարմնի կինետիկ էներգիան՝

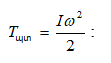
Ստացված արտահայտությունը համանման է համընթաց շարժվող մարմնի կինետիկ էներգիայի համար ստացված  արտահայտությանը: Պտտական շարժման ժամանակ զանգվածի դերում հանդես է գալիս իներցիայի մոմենտը, իսկ գծային արագության դերում՝ անկյունային արագությունը:

Ընդհանուր դեպքում պինդ մարմնի շարժումը կարելի է պատկերացնել որպես երկու շարժումների վերադրում, մարմնի իներցիայի (զանգվածի) կենտրոնի արագությամբ համընթաց և զանգվածի կենտրոնով անցնող առանցքի շուրջ անկյունային արագությամբ պտտական շարժումների: Այդպիսի պատկերացման համաձայն մարմնի լրիվ կինետիկ էներգիան կարող է որոշել Քյոնիգի թեորեմի հիման վրա՝

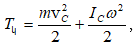
որտեղ  մարմնի իներցիայի մոմենտն է նրա զանգվածի կենտրոնով անցնող ակնթարթային պտտման առանցքի նկատմամբ: Նշենք, որ ընդհանուր դեպքում ակնթարթային առանցքը տեղափոխվում է մարմնի նկատմամբ, և  իներցիայի մոմենտը փոխվում է ժամանակի ընթացքում: Մասնավոր դեպքում, երբ մարմինը կատարում է հարթ շարժում,  մնում է հաստատուն: Այսպիսով հարթ շարժման դեպքում մարմնի T_կ լրիվ կինետիկ էներգիան հավասար է T_համ. համընթաց և T_պտ. պտտական շարժումների կինետիկ էներգիաների գումարին՝ T_կ= T_համ.+ T_պտ. :

Խնդիր 1:  զանգվածով և R շառավղով համասեռ գլանը կարող է առանց շփման պտտվել O կետով անցնող հորիզոնական անշարժ առանցքի շուրջը: Գլանի վրա միաշարք փաթաթված է l երկարությամբ և m զանգվածով չձգվող ճկուն բարակ պարան (նկ.1):

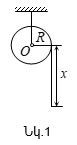
Որոշել գլանի անկյունային արագացման կախումը պարանի կախված մասի x երկարությունից: Ընդունել, որ սահքը բացակայում է, և պարանի փաթաթված մասի ծանրության կենտրոնը գտնվում է գլանի առանցքի վրա:

Լուծում: Օգտվենք մոմենտների հավասարումից O կետով անցնող առանցքի նկատմամբ.

Նույն առանցքի նկատմամբ իմպուլսի մոմենտը` քանի որ համասեռ գլանի համար

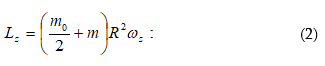
Ծանրության ուժի մոմենտն առանցքի նկատմամբ

Դիֆերենցելով (2)-ն ըստ ժամանակի կստանանք`

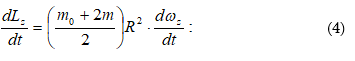
Նկատի ունենալով (3)-ը և (4) - ը` (1)-ից կստանանք.

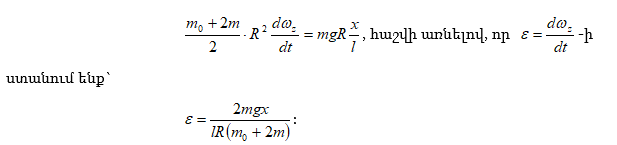
Խնդիր 2:  զանգվածով հորիզոնական հարթակը պտտվում է իր կենտրոնով անցնող ուղղաձիգ առանցքի շուրջը, կատարելով 0,2պտ/վ: Հարթակի եզրին կանգնած է 60 կգ զանգված ունեցող մարդը: Ի՞նչ արագությամբ կսկսի պտտվել հարթակը, եթե մարդը հարթակի եզրից տեղափոխվի դեպի նրա կենտրոնը: Հարթակը համարել կլոր համասեռ սկավառակ, իսկ մարդուն` նյութական կետ:

Լուծում: Իմպուլսի մոմենտի պահպանման օրենքի հիման վրա ունենք`

որտեղ  հարթակի իներցիայի մոմենտն է մարդու հետ, երբ վերջինս կանգնած է հարթակի եզրում, հարթակի անկյունային արագություններն են համապատասխանաբար մարդու առաջին և երկրորդ դիրքերում: Այդ դեպքում`

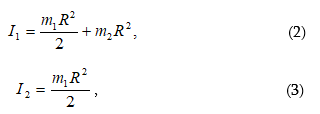
որտեղ R-ը հարթակի շառավիղն է,  հարթակի զանգվածն է  մարդու զանգվածը: Տեղադրելով (2)-ը և (3)-ը (1)-ի մեջ և հաշվի առնելով, որ որտեղ  հարթակի պտույտների թիվն է մեկ վայրկյանում, կստանանք`

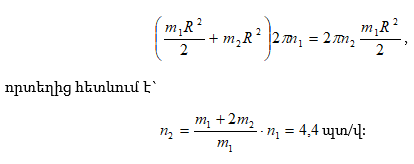
Խնդիր 3: Երկու թափանիվների հոլովակները միացված են փոկով: Հոլովակների շառավիղները հապատասխանաբար  են: Թափանիվների իներցիայի մոմենտներն իրենց կենտրոնով անցնող առանցքների նկատմամբ համապատասխանաբար I₁ և I₂ են (նկ.2):

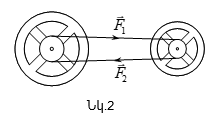
Պահելով երկրորդ թափանիվը և փոկն անշարժ` առաջինը պտտեցվում է մինչև  անկյունային արագությունը, որի հետևանքով փոկանվի եզրակետերի և փոկի միջև առաջանում է սահք: Այնուհետև փոկն ու երկրորդ թափանիվը բաց են թողնվում: Անտեսելով բոլոր շփման ուժերը, բացի փոկի և փոկանիվների միջև սահքի շփումից, որոշել թափանիվների կայունացված պտտման  անկյունային արագությունները սահքը դադարելուց հետո: Գտնել նաև կինետիկ էներգիայի կորուստը սահքի շփման վրա: Փոկի զանգվածն անտեսել:

Լուծում: Շնորհիվ սահքի շփման, փոկի F₁ լարվածությունը վերևում և F₂ լարվածությունը ներքևում կլինեն տարբեր: Գրելով թափանիվների շարժման հավասարումները կստանանք`

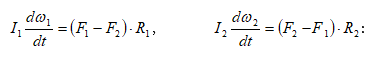
Գրված հավասարումները բաժանելով համապատասխանաբար R₁ և R₂-ի, այնուհետև գումարելով իրար` կստանանք.

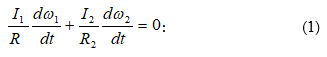
Ինտեգրելով (1)-ը կստանանք`

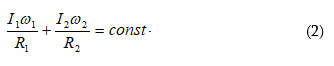
const-ի արժեքը կգտնենք, ընդունելով, որ սկզբնական պահին  (2)-ից կստանանք. Այսպիսով,

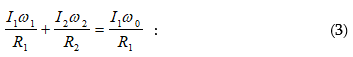
Երբ սահքը բացակայում է,

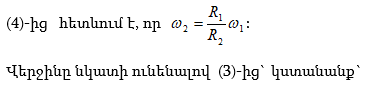
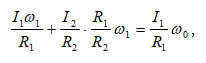
որտեղից

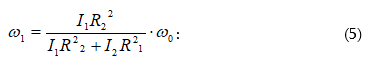
Նկատի ունենալով (5)-ը` (4)-ից ստանում ենք.

Շփման վրա կինետիկ էներգիայի կորուստը`

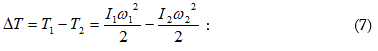
Նկատի ունենալով (5)-ը և (6)-ը` (7)-ից կստանանք`

>>

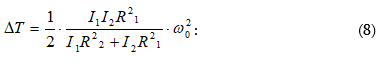
ԳԼՈՒԽ 5. ՁԳՈՂՈՒԹՅՈՒՆ: ԴԱՇՏԻ ՏԵՍՈՒԹՅԱՆ ՏԱՐՐԵՐԸ

5.1. ԿԵՊԼԵՐԻ ՕՐԵՆՔՆԵՐԸ: ՏԻԵԶԵՐԱԿԱՆ ՁԳՈՂՈՒԹՅԱՆ ՕՐԵՆՔԸ

Դեռ խորն անցյալում հայտնի էր, որ ի տարբերություն աստղերի, որոնք տարածության մեջ իրենց փոխադարձ դիրքը պահպանում են հարյուրամյակների ընթացքում անփոփոխ, մոլորակները աստղերի միջև գծում են բարդ հետագծեր: Մոլորակների օղակաձև շարժումը նկարագրելու համար հույն գիտնական Կ. Պտղոմեոսը (մ.թ.2-րդ դար), հաշվի առնելով, որ Երկիրը տեղավորված է Տիեզերքի կենտրոնում, ենթադրեց, որ մոլորակներից յուրաքանչյուրը շարժվում է փոքր շրջանով, որի կենտրոնը հավասարաչափ շարժվում է մեծ շրջանով, իսկ այդ կենտրոնում գտնվում է Երկիրը: Այդ կոնցեպցիան ստացավ աշխարհի պտղոմեոսյան երկրակենտրոն համակարգ անվանումը:

16-րդ դարի սկզբում լեհ աստղագետ Ն. Կոպեռնիկոսի (1473-1543) կողմից հիմնավորվեց արևակենտրոն համակարգը, որի համաձայն երկնային մարմինների շարժումը բացատրվում է Երկրի (ինչպես նաև այլ մոլորակների) շարժումով Արեգակի շուրջը և Երկրի օրական պտույտով: Կոպեռնիկոսի տեսությունը և դիտումները ընդունվեցին որպես հետաքրքրաշարժ երևակայություն (ֆանտազիա): 17-րդ հարյուրամյակի սկզբին մեծաթիվ գիտնականներ համոզվեցին աշխարհի արևակենտրոն համակարգի ճիշտ լինելու մեջ: Գերմանացի գիտնական Ի. Կեպլերը (1571-1630), մշակելով և ճշգրտելով դանիացի աստղագետ Տ. Բրագեի (1546-1601) բազմաթիվ դիտումների արդյունքները, տվեց մոլորակների շարժման երեք օրենքները.

1. Բոլոր մոլորակները շարժվում են էլիպսներով, որոնց կիզակետերից մեկում գտնվում է Արեգակը:

2. Մոլորակի շառավիղ-վեկտորը հավասար ժամանակամիջոցներում հավասար մակերեսներ է գծում:

3. Արեգակի շուրջը մոլորակների պտտման պարբերությունների քառակուսիները հարաբերում են իրար այնպես, ինչպես դրանց ուղեծրերի մեծ կիսառանցքների խորանարդները:

Ի. Նյուտոնը, ուսումնասիրելով երկնային մարմինների շարժումը Կեպլերի օրենքների և դինամիկայի հիմնական օրենքների հիման վրա հայտնագործեց տիեզերական ձգողության օրենքը. ցանկացած երկու նյութական կետերի միջև գործում է փոխադարձ ձգողության ուժ, որն ուղիղ համեմատական է այդ կետերի զանգվածների արտադրյալին և հակադարձ համեմատական է դրանց միջև եղած r հեռավորության քառակուսուն.

Այդ ուժը կոչվում է գրավիտացիոն (կամ տիեզերական ձգողության ուժ): Գրավիտացիոն ուժերը միշտ ձգողական են և ուղղված են այն ուղղի երկայնքով, որն անցնում է փոխազդող մարմիններով: Համեմատականության G գործակիցը կոչվում է գրավիտացիոն հաստատուն:

Տիեզերական ձգողության օրենքը ճիշտ է միայն այն մարմինների համար, որոնք կարելի է ընդունել որպես նյութական կետեր, այսինքն որոնց չափերը շատ փոքր են` դրանց միջև եղած հեռավորության համեմատ: Վերջավոր չափեր ունեցող մարմինների միջև փոխազդեցության ուժը գտնելու համար մարմիններից յուրաքանչյուրը պետք է բաժանել տարրական զանգվածների, որպեսզի դրանք կարելի լինի համարել նյութական կետեր, այնուհետև գտնել տարբեր մարմիններին պատկանող նյութական կետերի յուրաքանչյուր զույգի փոխազդեցության ուժը և երկրաչափորեն գումարել, որը բավականին դժվար մաթեմատիկական խնդիր է:

Առաջին անգամ տիեզերական օրենքի փորձնական ապացույցը երկրային մարմինների, ինչպես նաև G գրավիտացիոն հաստատունի թվային արժեքը որոշելու համար կատարվել է անգլիացի ֆիզիկոս Գ. Կավենդիշի (1731-1810) կողմից:

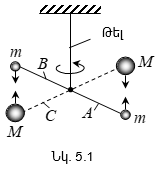
Կավենդիշի փորձի սկզբունքային սխեման բերված է նկ.5.1-ում, օգտագործելով ոլորակշեռքի խիստ զգայուն մեթոդը: Թեթև A կշռալծակը երկու հավասար m=729գ զանգվածներով միատեսակ գնդիկների հետ միասին կախված է առաձգական B թելից: C կշռալծակի վրա նույն բարձրության վրա ամրացված են M=158կգ զանգվածներով երկու գնդեր: Պտտելով C կշռալծակը ուղղաձիգ առանցքի շուրջը կարելի է փոփոխել m և M զանգվածներով գնդերի միջև հեռավորությունը: M զանգվածներով գնդիկների կողմից m զանգվածներով գնդիկներին կիրառված ուժազույգի ազդեցության տակ, A կշռալծակը պտտվում է հորիզոնական հարթության մեջ, պտտելով B թելը մինչև առաձգական ուժի մոմենտի` ձգողական ուժի մոմենտին հավասարակշռելը: Իմանալով թելի առաձգականության հատկությունները, կարելի է ըստ պտույտի անկյան չափման գտնել առաջացած ձգողական ուժը և գնդիկների հայտնի զանգվածներով հաշվել G-ի արժեքը:

G-ի արժեքը հիմնարար ֆիզիկական հաստատուն է, ընդունվում է հավասար  Այսպիսով, 1կգ զանգված ունեցող երկու գնդերը, որոնց կենտրոններն իրարից հեռացած են 1մ-ով, փոխադարձաբար ձգում են  ուժով: G մեծության շատ փոքր լինելը ցույց է տալիս, որ գրավիտացիոն փոխազդեցության ուժը կարող է լինել նշանակալից միայն մեծ զանգվածների դեպքում:

>>

5.2. ԾԱՆՐՈՒԹՅԱՆ ՈՒԺ ԵՎ ԿՇԻՌ: ԱՆԿՇՌՈՒԹՅՈՒՆ

Երկրի մակերևույթի մոտ բոլոր մարմինները ընկնում են նույն արագացումով, որը ստացել է ազատ անկման  արագացում անվանումը: Այսպիսով, Երկրի հետ կապված հաշվարկման համակարգում ամեն մի m զանգվածով մարմնի վրա ազդում է  ուժը, որն անվանում են ծանրության ուժ: Համաձայն Գալիլեյի ընդհանրացած հիմնարար ֆիզիկական օրենքի, բոլոր մարմինները միևնույն ձգողության դաշտում ընկնում են նույն արագացումներով: Հետևաբար, եկրագնդի տվյալ վայրում ազատ անկման արագացումը նույնն է բոլոր մարմինների համար:

Փորձերը ցույց են տալիս, որ Երկրի մակերևույթին չափված ազատ անկման արագացումը բևեռներում մոտավորապես հավասար է 9.832մ/վ², հասարակածում 9.780մ/վ², իսկ 45⁰ լայնության վրա` 9.81մ/վ²: Սա պայմանավորված է մի կողմից իր առանցքի շուրջը Երկրի օրական պտույտի և Երկրի ոչ լրիվ գնդաձև լինելու հանգամանքով (հասարակածային և բևեռային շառավիղները համապատասխանաբար հավասար են 6378 և 6357կմ): Բերված թվերը ցույց են տալիս, որ ազատ անկման արագացման արժեքները երկրագնդի տարբեր շրջաններում շատ քիչ են տարբերվում իրարից, ուստի ազատ անկման արագացումը, որն օգտագործվում է գործնական խնդիրների լուծման դեպքում, ընդունվում է հավասար 9.81մ/վ²:

Եթե անտեսվի իր առանցքի շուրջը Երկրի օրական պտույտը, ապա ծանրության ուժը և գրավիտացիոն ձգողության ուժը իրար հավասար են.

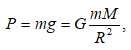
որտեղ M-ը Երկրի զանգվածն է, R-ը Երկրի կենտրոնից մինչև մարմին ընկած հեռավորությունն է: Այս բանաձևը տրված է այն դեպքի համար, երբ մարմինը գտնվում է Երկրի մակերևույթի վրա:

Եթե մարմինը գտնվում է Երկրի մակերևույթից h բարձրության վրա, ապա

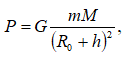
այսինքն` Երկրի մակերևույթից հեռանալով` ծանրության ուժը փոքրանում է: R₀-ն Երկրի շառավիղն է:

Մարմնի կշիռ կոչվում է այն ուժը, որով մարմինը Երկրի գրավիտացիոն ձգողության հետևանքով ազդում է հորիզոնական հենարանի կամ ուղղաձիգ կախոցի վրա: Մարմնի կշիռը հանդես է գալիս միայն այն ժամանակ, երբ մարմինը շարժվում է g-ից տարբեր արագացումով, այսինքն, երբ մարմնի վրա, բացի ծանրության ուժից, ազդում են նաև այլ ուժեր: Մարմնի վիճակը, որի դեպքում այն շարժվում է միայն ծանրության ուժի ազդեցության տակ, կոչվում է անկշռելության վիճակ:

Այսպիսով, ծանրության ուժը միշտ ազդում է, իսկ կշիռը հանդես է գալիս միայն այն դեպքում, երբ մարմնի վրա, բացի ծանրության ուժից, ազդում են նաև այլ ուժեր, որի հետևանքով մարմինը շարժվում է  տարբեր  արագացումով: Եթե մարմինը շարժվում է Երկրի ձգողության դաշտում  արագացումով, ապա այդ մարմնին կիրառված է լրացուցիչ  ուժ, որը բավարարում է հետևյալ պայմանին`

Այդ դեպքում մարմնի կշիռը`

Այսինքն, եթե մարմինը գտնվում է դադարի վիճակում կամ շարժվում է ուղղագիծ և հավասարաչափ, ապա  Եթե մարմինը ազատ շարժվում է ձգողության դաշտում ցանկացած հետագծով և ցանկացած ուղղությամբ, ապա  այսինքն` մարմինը անկշիռ է: Անկշռության վիճակ դիտվում է տիեզերանավում, երբ այն շարժվում է ազատ անկման արագացմամբ, անկախ նրա շարժման ուղղությունից: Երկրի մթնոլորտից դուրս անջատված շարժիչով տիեզերանավի վրա ազդում է միայն գրավիտացիոն ձգողության ուժը: Այդ ուժի ազդեցությամբ տիեզերանավը և նրանում գտնվող բոլոր մարմինները շարժվում են նույն արագացմամբ, ուստի գտնվում են անկշության վիճակում:

>>

5.3. ՁԳՈՂԱԿԱՆ ԴԱՇՏ ԵՎ ՆՐԱ ԼԱՐՎԱԾՈՒԹՅՈՒՆԸ

Նյուտոնի (5.1) տիեզերական ձգողության օրենքով որոշվում է ձգողության ուժի կախումը փոխազդող մարմինների զանգվածներից և դրանց միջև հեռավորությունից, սակայն ցույց չի տալիս, թե ինչպես է իրականացվում այդ փոխազդեցությունը: Ձգողությունը պատկանում է փոխազդեցության հատուկ խմբի: Ձգողության ուժերը կախված չեն այն բանից, թե փոխազդող մարմինները ինչպիսի միջավայրում են գտնվում: Ձգողությունը գոյություն ունի և վակուումում:

Մարմինների միջև գրավիտացիոն փոխազդեցությունը իրականացվում է ձգողության դաշտի կամ գրավիտացիոն դաշտի օգնությամբ: Այդ դաշտը հարուցվում է մարմիններով, և այն մատերիայի գոյության ձևերից մեկն է: Ձգողական դաշտի հիմնական հատկությունն այն է, որ ամեն մի m զանգվածով մարմնի վրա, որը գտնվում է այդ դաշտում, ազդում է ձգողության ուժը, այսինքն`

 վեկտորը կախում չունի m-ից և կոչվում է ձգողության դաշտի լարվածություն: Ձգողության դաշտի լարվածությունը որոշվում է այն ուժով, որն ազդում է դաշտի կողմից միավոր զանգնվածով նյութական կետի վրա և ուղղությամբ համընկնում է ազդող ուժի հետ: Լարվածութունը ձգողական դաշտի ուժային բնութագիրն է:

Եթե դաշտը ստեղծվել է մի քանի աղբյուրներով, ապա դաշտի արդյունարար լարվածությունը նրա ցանկացած կետում որոշվում է դաշտերի վերադրման սկզբունքով`

Ձգողության դաշտը կոչվում է համասեռ, եթե նրա լարվածությունը դաշտի բոլոր կետերում նույնն է, և կենտրոնական, եթե դաշտի բոլոր կետերում լարվածության վեկտորներն ուղղված են այն ուղիղների երկայնքով, որոնք հատվում են միևնույն A կետում, որն անշարժ է ինչ-որ իներցիալ հաշվարկման համակարգի նկատմամբ (նկ.5.2):

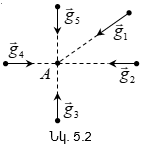
Ուժային դաշտի գրաֆիկական պատկերման համար օգտագործում են ուժագծերը (լարվածության գծերը): Ուժագծերն ընտրվում են այնպես, որ դաշտի լարվածության վեկտորը յուրաքանչյուր կետում ուղղված լինի ուժագծերին տարված շոշափողով:

>>

5.4. ԱՇԽԱՏԱՆՔԸ ՁԳՈՂՈՒԹՅԱՆ ԴԱՇՏՈՒՄ: ՁԳՈՂՈՒԹՅԱՆ

ԴԱՇՏԻ ՊՈՏԵՆՑԻԱԼԸ

Որոշենք այն աշխատանքը, որը կատարում են ձգողական դաշտի ուժերը m զանգվածով նյութական կետի տեղափոխման վրա: Հաշվենք, օրինակ, ինչպիսի աշխատանք է անհրաժեշտ կատարել m զանգվածով մարմինը Երկրից հեռացնելու համար: R հեռավորության վրա (նկ.5.3) տվյալ մարմնի վրա ազդում է`  ուժը, որտեղ M-ը Երկրի զանգվածն է:

Այդ մարմնի տեղափոխության դեպքում dR հեռավորության վրա կատարվում է հետևյալ աշխատանքը`

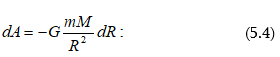
Բացասական նշանը ցույց է տալիս, որ ուժը և տեղափոխությունը տվյալ դեպքում ուղղություններով հակառակ են (տես նկ. 5.3):

Եթե մարմինը տեղափոխվի R₁ հեռավորությունից մինչև R₂, ապա աշխատանքը`

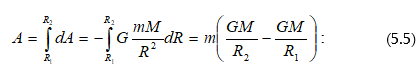
Ստացված արտահայտությունից բխում է, որ ձգողության դաշտում աշխատանքը կախում չունի տեղափոխության հետագծից. այն կախված է մարմնի սկզբնական և վերջնական դիրքից, այսինքն` ձգողության ուժերը կոնսերվատիվ ուժեր են, իսկ ձգողական դաշտը` պոտենցիալային է:

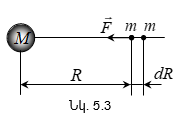
Համաձայն dA=-dW բանաձևի` կոնսերվատիվ ուժերով կատարված աշխատանքը հավասար է համակարգի պոտենցիալ էներգիայի փոփոխությանը` վերցրած «-» նշանով, այսինքն`

բանաձևից ստանում ենք`

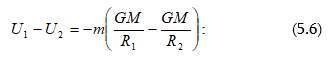
Քանի որ բանաձևի մեջ մտնում է միայն պոտենցիալների տարբերությունը երկու վիճակներում, ապա  ձգտելու դեպքում, հարմարության համար պոտենցիալ էներգիան ընդունում են հավասար զրոյի: Այդ դեպքում (5.6) արտահայտությունը կգրվի հետևյալ տեսքով.

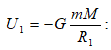
Քանի որ առաջին կետը ընտրվել էր կամայական, ապա

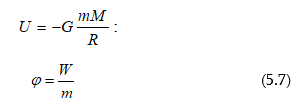
մեծությունը ձգողական դաշտի էներգետիկ բնութագիրն է և կոչվում է պոտենցիալ: Ձգողական դաշտի պոտենցիալը սկալյար մեծություն է, որոշվում է դաշտի տվյալ կետում միավոր զանգվածով մարմնի պոտենցիալ էներգիայով կամ այն աշխատանքով, որը կատարում են դաշտի ուժերը միավոր զանգվածը դաշտի տվյալ կետից մինչև անվերջություն տեղափոխելու համար: Այսպիսով, ձգողական դաշտի պոտենցիալը, որը ստեղծում է M զանգվածով մարմինը`

որտեղ R-ը այդ մարմնից մինչև դիտարկվող կետը եղած հեռավորությունն է:

 (5.8) բանաձևից հետևում է, որ միևնույն պոտենցիալով կետերի երկրաչափական տեղը կազմում է սֆերիկ մակերևույթ (R=const): Այն մակերևույթը, որի համար պոտենցիալը հաստատուն է, կոչվում է համապոտենցիալ:

Քանի որ դաշտի պոտենցիալը սկալյար մեծություն է, ապա արդյունարար պոտենցիալի արժեքը որոշվում է պարզ գումարումով`

Քննարկենք փոխադարձ կապը ձգողական դաշտի պոտենցիալի և նրա g լարվածության միջև: (5.3) և (5.6) արտահայտություններից հետևում է, որ դաշտի ուժերով m զանգածով մարմնի փոքր տեղափոխության դեպքում կատարված տարրական dA աշխատանքը`

Մյուս կողմից dA=Fdl, որտեղ dl-ը տարրական տեղափոխությունն է: Հաշվի առնելով, որ F=mg կստանանք dA=mgdl, այսինքն`

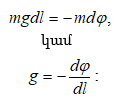
մեծությունը բնութագրում է ձգողության դաշտում տեղափոխության ուղղությամբ պոտենցիալի փոփոխությունը միավոր երկարության վրա: Կարելի է ապացուցել, որ

(5.10) բանաձևի մեջ բացասական նշանը ցույց է տալիս, որ  լարվածության վեկտորն ուղղված է պոտենցիալի նվազման կողմը:

Ելնելով ձգողության տեսության պատկերացումներից` որպես մասնավոր օրինակ, քննարկենք մարմնի պոտենցիալ էներգիան, որը գտնվում է Երկրի նկատմամբ h բարձրության վրա.

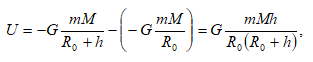
որտեղ R₀-ն Երկրի շառավիղն է:

Քանի որ

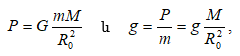
ապա նկատի ունենալով  պայմանը, կստանանք`

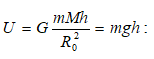
Այսպիսով, ստացանք մեզ ծանոթ պոտենցիալ էներգիայի բանաձևը:

>>

5.5 ՏԻԵԶԵՐԱԿԱՆ ԱՐԱԳՈՒԹՅՈՒՆՆԵՐ

Տիեզերական տարածության մեջ հրթիռներ արձակելու համար, նպատակադրվածությունից կախված, հարկավոր է դրանց հաղորդել որոշակի սկզբնական արագություններ, որոնք կոչվում են տիեզերական արագություններ:

Առաջին տիեզերական արագություն է կոչվում այն նվազագույն արագությունը, որն անհրաժեշտ է հաղորդել մարմնին, որպեսզի այն շարժվի Երկրի շուրջը շրջանային ուղեծրով, այսինքն` դառնա Երկրի արհեստական արբանյակ: r շառավիղ ունեցող շրջանային ուղեծրով շարժվող արբանյակի վրա ազդում է Երկրի ձգողության ուժը` հաղորդելով նրան  կենտրոնաձիգ արագացում: Ըստ Նյուտոնի օրենքի`

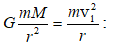
Եթե արբանյակը շարժվում է Երկրի մակերևույթին մոտ, ապա  ուստի Երկրի մակերևույթին մոտ`

Սակայն  արագությունը բավարար չէ Երկրագնդի ձգողության դաշտից մարմինը դուրս բերելու համար, այսինքն` մարմինը Երկրագնդից այնպիսի հեռավորության վրա տանելու համար, որտեղ Երկրագնդի ձգողությունը դադարում է էական դեր խաղալ: Այս իրագործելու համար անհրաժեշտ արագությունը կոչվում է երկրորդ տիեզերական արագություն: Այս արագության դեպքում մարմինը դառնում է Արեգակի արբանյակ:

Որպեսզի մարմինը կարողանա հաղթահարել Երկրագնդի ձգողությունը և հեռանա տիեզերական տարածություն, անհրաժեշտ է, որ նրա կինետիկ էներգիան հավասար դառնա ձգողության ուժերի դեմ կատարված աշխատանքին.

Տիեզերական երրորդ արագություն կոչվում է այն արագությունը, որն անհրաժեշտ է հաղորդել Երկրի վրա մարմնին, որպեսզի այն հեռանա Արեգակնային համակարգի սահմաններից` հաղթահարելով Արեգակի ձգողությունը: Երրորդ տիեզերական արագությունը`  Մարմիններին այսպիսի արագությունների հաղորդումը դժվար տեխնիկական խնդիր է:

Առաջին անգամ տիեզերական արագություններ ստացել են ԽՍՀՄ-ում: 1957թ. հոկտեմբերի 4-ին մարդկության պատմության մեջ առաջին անգամ իրագործվեց Երկրագնդի արհեստական արբանյակի հաջող իրագործումը: 1959թ. հունվարի 2-ին հաղթահարվեց երկրորդ սահմանը: Այդ օրը արձակվեց տիեզերական հրթիռ, որը դուրս եկավ Երկրագնդի ձգողության դաշտից և դարձավ Արեգակնային համակարգի առաջին արհեստական մոլորակը: 1961թ. ապրիլի 12-ին ԽՍՀՄ-ում իրագործվեց աշխարհում առաջին անգամ մարդու թռիչքը տիեզերական տարածության մեջ: Առաջին տիեզերագնացը` Յ.Գագարինը, թռիչք կատարեց Երկրագնդի շուրջը և բարեհաջող վայրէջք կատարեց:

>>

ԳԼՈՒԽ 6. ՀԵՂՈՒԿՆԵՐԻ ՄԵԽԱՆԻԿԱՅԻ ՏԱՐՐԵՐԸ

6.1. ՀԵՂՈՒԿԻ ԵՎ ԳԱԶԻ ՃՆՇՈՒՄԸ

Գազի մոլեկուլները, կատարելով անկանոն քաոսային շարժում, կապված չեն կամ թույլ են կապված փոխազդեցության ուժերով, որի պատճառով դրանք ազատ շարժվում են և բախման արդյունքում ձգտում են թռչել ամեն կողմ, լցնելով իրենց տրամադրված ամբողջ ծավալը. այսինքն` գազի ծավալը որոշվում է այն անոթի ծավալով, որը զբաղեցնում է գազը:

Հեղուկը, ունենալով որոշակի ծավալ, ընդունում է այն անոթի ձևը, որի մեջ այն գտնվում է: Բայց ի տարբերություն գազերի` հեղուկներում մոլեկուլների միջին հեռավորությունը գործնականում մնում է հաստատուն, ուստի հեղուկի ծավալը գործնականում անփոփոխ է:

Հեղուկների և գազերի հատկություններն իրարից բավականին տարբերվում են, սակայն մի շարք մեխանիկական երևույթներում դրանց վարքը որոշվում է միատեսակ պարամետրերով և նույնական հավասարումներով: Ուստի հիդրոաերոմեխանիկան մեխանիկայի այն բաժինն է, որն ուսումնասիրում է հեղուկների և գազերի հավասարակշռությունը և շարժումը, դրանց միջև փոխազդեցությունը և դրանցով պինդ մարմինների շրջահոսումը` կիրառելով հեղուկների և գազերի ուսումնասիրման միասնական մոտեցում:

Մեխանիկայում մեծ ճշտությամբ հեղուկները և գազերը դիտարկվում են որպես հոծ անընդհատ բաշխված` դրանցով զբաղեցրած տարածության մի մասը: Գազերի խտությունը էապես կախված է ճնշումից: Հեղուկների սեղմելիությունը շատ խնդիրներում կարելի է անտեսել և օգտվել հեղուկի անսեղմելիության միակ հասկացությունից, այն հեղուկների համար, որոնց խտությունը միատեսակ է և ժամանակի ընթացքում չի փոփոխվում:

 Եթե հանգստի վիճակում հեղուկի մեջ տեղադրվի բարակ թիթեղ, ապա հեղուկի մասերը գտնվելով թիթեղի տարբեր կողմերում, պետք է ազդեն նրա յուրաքանչյուր  տարրի վրա  ուժերով, որոնք, անկախ թիթեղի կողմնորոշումից, կլինեն մոդուլով հավասար և ուղղված`  մակերեսին ուղղահայաց, քանի որ շոշափող ուժերի առկայությունը առաջ կբերեր հեղուկի մասնիկների շարժում (նկ.6.1):

Այն ֆիզիկական մեծությունը, որը որոշվում է հեղուկի կողմից միավոր մակերեսի վրա ազդող նորմալ ուժով, կոչվում է հեղուկի ճնշում.

Ճնշման միավորը պասկալն է (Պա):

Հեղուկների (գազերի) հավասարակշռության դեպքում ճնշումը ենթարկվում է Պասկալի օրենքին. հեղուկի մակերևույթի վրա ճնշումը, որը գործադրվում է արտաքին ուժերով, հաղորդվում է հեղուկին բոլոր ուղղություններով միատեսակ: Հեղուկի հավասարկշռության դեպքում ճնշումը ըստ հորիզոնականի միատեսակ է: Դրա համար էլ հեղուկի հանգստի ազատ մակերևույթը պատերից հեռու միշտ հորիզոնական է: Եթե հեղուկը անսեղմելի է, նրա խտությունը կախված չէ ճնշումից: Այդ դեպքում կտրվածքով հեղուկի սյունը, որի բարձրությունը h է և խտությունը`  նրա կշիռը`  իսկ ճնշումը ներքին հիմքի վրա`

այսինքն` ճնշումը, կախված բարձրությունից, փոփոխվում է գծայնորեն:  ճնշումը կոչվում է հիդրոստատիկ ճնշում: Համաձան (6.1) բանաձևի, ճնշման ուժը հեղուկի ներքևի շերտերի վրա ավելի մեծ է, քան վերին շերտերում, դրա համար էլ հեղուկի մեջ ընկղմված մարմնի վրա ազդում է այնպիսի ուժ, որը որոշվում է Արքիմեդի օրենքով. հեղուկի (գազի) մեջ ընկղմված մարմնի վրա ազդում է դեպի վեր ուղղված արտամղող ուժ, որը հավասար է մարմնի ծավալով արտամղած հեղուկի (գազի) կշռին.

որտեղ  հեղուկի խտությունն է, V-ն` հեղուկի մեջ մարմնի ընկղմված ծավալը:

>>

6.2. ԱՆԽԶԵԼԻՈՒԹՅԱՆ ՀԱՎԱՍԱՐՈՒՄԸ

Հեղուկների շարժումը կոչվում է հոսանք, իսկ հեղուկի մասնիկների շարժումը` հոսք: Յուրաքանչյուր մասնիկին համապատասխանում է իր արագությունը: Ամբողջ հեղուկը, ինչպես ընդունված է ասել, արագության վեկտորի դաշտ է: Արագության վեկտորի դաշտում կարող ենք տանել գծեր, որոնց շոշափողները յուրաքանչյուր կետում համընկնում են այդ կետում հեղուկի մասնիկների արագության ուղղության հետ (նկ. 6.2): Այդպիսի գծերը կոչվում են հոսանքի գծեր:

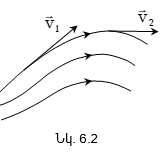
Ընդունված է հոսանքի գծերը տանել այնպես, որ դրանց խտությունը մեծ լինի այնտեղ, ուր ավելի մեծ է հեղուկի հոսանքի արագությունը և փոքր այնտեղ, ուր հեղուկն ավելի դանդաղ է հոսում: Կայունացած (ստացիոնար) հոսանքի դեպքում հեղուկի արագությունը յուրաքանչյուր կետում, ըստ ժամանակի, մնում է հաստատուն: Այդ դեպքում հոսանքի գծերը նույնպես անփոփոխ կմնան և կհամընկնեն հեղուկի առանձին մասնիկների հետագծերին: Հոսանքի գծերը կարելի է տեսանելի դարձնել` հեղուկում թողնելով ներկի շիթ կամ խառնելով ինչ-որ նկատելի կախված մասնիկներ: Հոսանքի գծերով սահմանափակված հեղուկի մասը կոչվում է հոսանքի խողովակ: Բոլոր մասնիկները, որոնք գտնվում են հոսանքի խողովակի որոշ կտրվածքում, շարժվելիս շարունակում են ընթանալ հոսանքի խողովակի ներսում և դուրս չեն գալիս նրանից: Նմանապես դրսից ոչ մի մասնիկ չի թափանցի հոսանքի խողովակի ներսը: Դիտարկենք հոսանքի խողովակը և ընտրենք նրա որևէ երկու S<sub>1</sub> և S<sub>2</sub> նորմալ հատույթներ (նկ.6.3): Միավոր ժամանակում S<sub>1</sub> հատույթով կհոսի  ծավալով հեղուկ, որտեղ  հեղուկի հոսանքի արագությունն է S<sub>1</sub> կտրվածքում: Միավոր ժամանակում S<sub>2</sub> հատույթով կհոսի  ծավալով հեղուկ, որտեղ  հեղուկի հոսանքի արագությունն է S<sub>2</sub> հատույթում: Անսեղմելի հեղուկի համար S<sub>2</sub> հատույթից հոսում է հեղուկի նույնպիսի ծավալ, ինչպիսին հոսել է S<sub>1</sub> հատույթից, այսինքն`

Հետևաբար, անսեղմելի հեղուկի հոսանքի արագության և հոսանքի խողովակի լայնական հատույթի արտադրյալը հաստատուն մեծություն է հոսանքի տրված խողովակի համար: (6.2) առնչությունը կոչվում է անխզելիության հավասարում անսեղմելի հեղուկի համար:

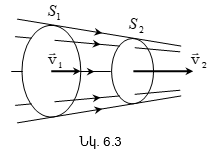
Անսեղմելի հեղուկի որևէ իրական խողովակով ստացիոնար հոսանքի դեպքում, այդ խողովակի ծավալը կհամընկնի հոսանքի խողովակի հետ: Այստեղից էլ, ըստ անխզելիության հավասարման, այն տեղերում, ուր խողովակը լայն է, հեղուկը կհոսի դանդաղ, իսկ այն տեղերում, որտեղ խողովակը նեղ է, հեղուկը կհոսի արագ:

>>

6.3. ԲԵՌՆՈՒԼԻԻ ՀԱՎԱՍԱՐՈՒՄԸ

Իրական հեղուկներում հոսքի առանձին շերտերի միջև առաջանում են ներքին շփման ուժեր, որոնք արգելակում են շերտերի հարաբերական շեղումները: Սակայն մի շարք դեպքերում դրանք կարելի է անտեսել: Ուստի մի շարք օրինաչափություններ արտածելու համար օգտվում են իդեալական հեղուկի մոդելից, երևակայական մի հեղուկ, ուր ներքին շփումը լրիվ կարելի է անտեսել:

Ստացիոնար հոսող անսեղմելի իդեալական հեղուկում անջատենք հոսանքի խողովակ, որը սահմանափակված է S₁ և S₂ հատույթներով, որոնցով ձախից աջ հոսում է հեղուկ (նկ.6.4):

Հեղուկի արագությունը S₁ հատույթի տեղում նշանակենք  ճնշումը`  իսկ արագությունն ու ճնշումը S<sub>2</sub> հատույթում` համապատասխանաբար  Ենթադրենք` հոսանքի խողովակը տեղավորված է ոչ թե հորիզոնական, այլ որոշ չափով թեք դիրքով. բարձրութունը, որի վրա գտնվում է S<sub>1</sub>-ը, նշանակենք h<sub>1</sub>-ով, իսկ հատույթի բարձրությունը` h₂-ով:  փոքր ժամանակի ընթացքում հեղուկը տեղափոխվում է S₁ հատույթից  հատույթը, S₂-ից`

Համաձայն էներգիայի պահպանման օրենքի` իդեալական անսեղմելի հեղուկի էներգիայի (E₂ - E₁) փոփոխությունը պետք է հավասար լինի m զանգվածով հեղուկի տեղափոխության համար արտաքին ուժերի կատարած A աշխատանքին.

որտեղ E₁-ը և E₂-ը m զանգվածով հեղուկի լրիվ էներգիաներն են համապատասխանաբար S₁ և S₂ հատույթների տեղերում: Մյուս կողմից A-ն այն աշխատանքն է, որը կատարվում է դիտարկվող փոքր ժամանակամիջոցի ընթացքում S₁ և S₂ հատույթների միջև պարփակված ամբողջ հեղուկի տեղափոխության համար: m զանգվածը S₁-ից մինչև  տեղաշարժելու դեպքում հեղուկը պետք է տեղափոխվի  համապատասխանաբար`  հեռավորության վրա:

Նշենք, որ  այնքան փոքր են, որ նկ.6.4-ում ներկանշված ծավալների բոլոր կետերին վերագրվում է արագության, ճնշման և բարձրության հաստատուն արժեքներ:

Հետևաբար`

որտեղ  (բացասական է, քանի որ ուղղված է հեղուկի հոսքին հակառակ): E₁ և E₂ լրիվ էներգիաները պետք է գումարվեն m զանգվածով հեղուկի կինետիկ և պոտենցիալ էներգիաներից.

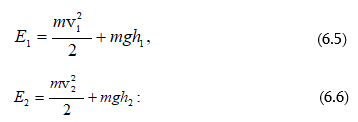
Տեղադրելով (6.5) և (6.6)-ը (6.3)-ի մեջ և հավասարեցնելով (6.3)-ը (6.4)-ին, կստանանք`

Համաձայն անսեղմելի հեղուկի (6.2) անխզելիության հավասարման` հեղուկի զբաղեցրած ծավալը մնում է հաստատուն, այսինքն`

Բաժանելով (6.7) արտահայտությունը  կստանանք`

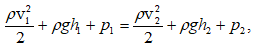
որտեղ  հեղուկի խտությունն է:

Քանի որ ընտրել ենք կամայական հատույթ, ապա կարող նք գրել`

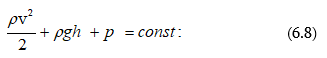
(6.8) հավասարումն առաջին անգամ արտածվել է շվեյցարացի ֆիզիկոս Դ. Բեռնուլիի (1700-1782) կողմից և կոչվում է Բեռնուլիի հավասարում:

Չնայած այս հավասարումը ստացվել է իդեալական հեղուկի համար, այն կիրառելի է նաև իրական հեղուկների դեպքում, որոնց ներքին շփումը շատ մեծ չէ:

(6.8) բանաձևի մեջ մտնող p մեծությունը կոչվում է ստատիկ ճնշում (հեղուկի ճնշումն է իր կողմից շրջահոսող մարմնի մակերևույթի վրա), դինամիկ ճնշումն է, հիդրոստատիկ ճնշումը:

Հորիզոնական հոսանքի խողովակի համար  (6.8) արտահայտությունն ընդունում է հետևյալ տեսքը`

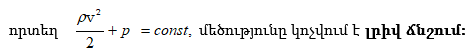
Հորիզոնական հոսանքի խողովակի համար Բեռնուլիի (6.9) հավասարումից և (6.2) անխզելիության հավասարումից հետևում է, որ հորիզոնական խողովակով հեղուկի հոսելու դեպքում, որն ունի տարբեր կտրվածքներ, հեղուկի արագությունը մեծ է նեղ մասերում, իսկ ստատիկ ճնշումը մեծ է լայն տեղերում, այսինքն` այն տեղերում, ուր արագությունը փոքր է: Դա կարելի է ցուցադրել` խողովակի երկայնքով տեղադրելով մանոմետրեր (նկ.6.6): Բեռնուլիի հավասարման համապատասխան փորձը ցույց է տալիս, որ մանոմետրական B խողովակում, որն ամրացված է խողովակի նեղ մասում, հեղուկի մակարդակն ավելի ցածր է, քան A և C մանոմետրական խողովակներում, որոնք ամրացված են խողովակի լայն մասերում:

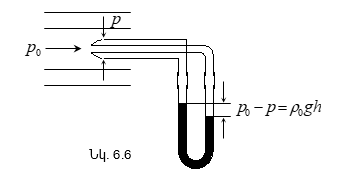
Քանի որ դինամիկ ճնշումը կապված է հեղուկի (գազի) արագության հետ, Բեռնուլիի հավասարումը հնարավորություն է տալիս չափել հեղուկի հոսքի արագությունը: Այդ նպատակով օգտագործվում է Պիտոյի խողովակը (նկ.6.6): Սարքը կազմված է երկու ուղիղ անկյան տակ ծռված խողովակներից, որոնց հակառակ ծայրերը միացված են մանոմետրին: Խողովակներից մեկով չափվում է լրիվ ճնշումը  մյուսի օգնությամբ` ստատիկ ճնշումը (p): Մանոմետրով չափվում է ճնշումների տարբերությունը.

որտեղ  հեղուկի խտությունն է մանոմետրում: Մյուս կողմից` համաձայն Բեռնուլիի հավասարման, լրիվ և ստատիկ ճնշումների տարբերությունը հավասար է դինամիկ ճնշմանը.

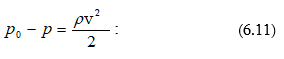
(6.10) և (6.11) բանաձևերից ստանում ենք հեղուկի հոսքի որոնելի արագությունը`

Ստատիկ ճնշման փոքրացումը այն կետերում, որտեղ հոսքի արագությունը մեծ է, դրված է ջրաշիթային պոմպի աշխատանքի հիմքում (նկ.6.7): Ջրի շիթը մտնում է մթնոլորտի հետ անմիջական կապ ունեցող խողովակը, որտեղից դուրս գալու պահին նրա ճնշումը հավասարվում է մթնոլորտային ճնշմանը: Խողովակն ունի նեղ տեղամաս, որով ջուրը հոսում է ավելի մեծ արագությամբ, որի հետևանքով այդ տեղամասում ճնշումը մթնոլորտայինից ավելի փոքր է: Այդպիսի ճնշում առաջանում է նաև խողովակն ընդգրկող պոմպի խցիկում, որը հաղորդակցվում է խողովակի հետ նրա նեղ մասում եղած խզվածքով: Պոմպի խցիկին միացնելով մի ծավալ` կարելի է օդը (կամ որևէ գազ) նրանից դուրս քաշել, ճնշումն այնտեղ իջեցնելով մինչև 100մմ սնդիկի սյան կարգի: Հանվող օդը ներծծվում է ջրի շիթով և ուղարկվում դեպի մթնոլորտ:

Բեռնուլիի հավասարումը օգտագործվում է` հեղուկի հոսքի արագությունը անոթի հատակի կամ պատի անցքի միջով գտնելու համար: Դիտարկենք հեղուկով լցված գլանային անոթ, որի կողմնային պատի վրա հեղուկի մակերևույթից ներքև կա փոքր անցք (նկ. 6.8): Քննարկենք երկու հատույթներ (անոթի մեջ հեղուկի ազատ մակերևույթի h₁ մակարդակի վրա և անցքից նրա ելքի h₂ մակարդակի վրա) և գրենք Բեռնուլիի հավասարումը.

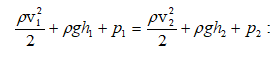
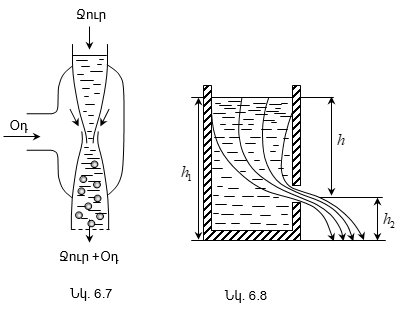
Քանի որ հեղուկի  ճնշումները առաջին և երկրորդ մակարդակների վրա հավասար են մթնոլորտայինին, այսինքն`  ապա հավասարումը կընդունի հետևյալ տեսքը`

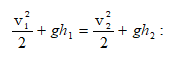
Անխզելիության (6.2) հավասարումից հետևում է, որ  որտեղ S₁-ը և S₂-ը անոթի և անցքի լայնական հատույթների մակերեսներն են: Եթե S₁ >>S₂, ապա  գումարելին կարելի է անտեսել: Այդ դեպքում կստանանք`

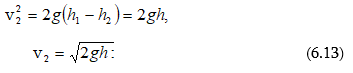
Այս բանաձևը կոչվում է Տորիչելիի բանաձև: (6.13) բանաձևից հետևում է, որ այն արագությունը, որը ձեռք է բերում հեղուկի շիթը h բարձրությունից հոսելիս, հավասար է նույն բարձրությունից ազատ անկման դեպքում մարմնի ձեռք բերած արագությանը:

>>

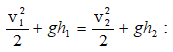
6.4. ՄԱԾՈՒՑԻԿ ՀԵՂՈՒԿԻ ՇԱՐԺՈՒՄԸ: ՀԵՂՈՒԿՆԵՐԻ

ՀՈՍՔԻ ԼԱՄԻՆԱՐ ԵՎ ՏՈՒՐԲՈՒԼԵՆՏ ՌԵԺԻՄՆԵՐ

Բոլոր իրական հեղուկներում, առանձին շերտերը մյուսների նկատմամբ տեղափոխվելիս, առաջ են գալիս ավելի կամ պակաս չափով զգալի շփման ուժեր: Ավելի արագ շարժվող շերտի կողմից դանդաղ շարժվող շերտի վրա արագացնող ուժ է ազդում: Ընդհակառակը, դանդաղ շարժվող շերտի կողմից արագ շարժվող շերտի վրա ազդում է դանդաղեցնող ուժ: Այս ուժերը, որոնք կոչվում են ներքին շփման ուժեր, ուղղված են շերտերի մակերևույթի շոշափողով: Բոլոր իրական հեղուկներին և գազերին բնորոշ է մածուցիկությունը (ներքին շփումը):

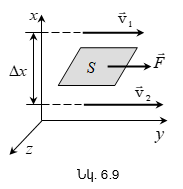
Ներքին շփման ուժը նույնքան մեծ է, որքան մեծ է դիտարկվող շերտի մակերևույթի S մակերեսը (նկ. 6.9) և կախում ունի այն բանից, թե որքան արագ է փոխվում հեղուկի հոսանքի արագությունը` մի շերտից մյուսին անցնելիս: Նկարում ներկայացված են երկու շերտեր, որոնք գտնվում են իրարից  հեռավորության վրա և շարժվում են  արագություններով: Այս դեպքում,  Այն ուղղությունը, որից հաշվում են շերտերի միջև եղած  հեռավորությունը, ուղղահայաց է շերտերի հոսանքի արագությանը:  մեծությունը, որը ցույց է տալիս, թե x-ի ուղղությամբ որքան արագ է փոխվում արագությունը շերտից շերտ անցնելիս, կոչվում է արագության գրադիենտ: Այսպիսով, ներքին շփման ուժի մոդուլը`

որտեղհամեմատականության գործակիցը կախված է հեղուկի բնույթից և կոչվում է դինամիկ մածուցիկություն (կամ պարզապես մածուցիկություն): Մածուցիկության միավորը (Պա.վ) է: Որքան մեծ է մածուցիկությունը, այնքան հեղուկը խիստ կտարբերվի իդեալականից, նույնքան էլ ներքին շփման մեծ ուժեր են առաջանում նրա մեջ: Մածուցիկությունը կախված է ջերմաստիճանից, ընդ որում այդ կախվածությունը հեղուկների և գազերի համար տարբեր է, հեղուկների համար ջերմաստիճանի մեծացման դեպքում  փոքրանում է, գազերի մոտ հակառակը` մեծանում է, որն էլ ցույց է տալիս նրանցում ներքին շփման մեխանիզմների տարբերությունը: Հատկապես, ջերմաստիճանից շատ ուժեղ կախված է յուղի մածուցիկությունը: Օրինակ, գերչակի յուղի մածուցիկությունը 18-40⁰C ջերմաստիճանային միջակայքում ընկնում է չորս անգամ: Ակադեմիկոս Պ. Կապիցան (1894-1984) հայտնագործեց, որ 2.17Կ ջերմաստիճանի դեպքում հեղուկ հելիումը անցնում է գերհաղորդականության վիճակի, որտեղ նրա մածուցիկությունը հավասար է զրոյի:

Գոյություն ունի հեղուկների հոսքի երկու ռեժիմ: Մի դեպքում հեղուկը կարծես բաժանվում է այնպիսի շերտերի, որոնք իրար նկատմամբ սահում են առանց իրար խառնվելու: Այդպիսի հոսանքը կոչվում է լամինար (շերտավոր): Եթե լամինար հոսանքի մեջ մտցնենք ներկված շիթ, այն առանց տարածվելու կպահպանվի հոսքի ամբողջ երկարությամբ, որովհետև լամինար հոսանքում հեղուկի մասնիկները չեն անցնում մի շերտից մյուսը: Լամինար հոսանքը ստացիոնար է:

Հեղուկը խողովակով շարժվելու ժամանակ, արագությունը մեծացնելիս, հոսանքը կորցնում է իր լամինար բնույթը և դառնում է անկանոն: Առաջ են գալիս խողովակի առանցքին ուղղահայաց բաղադրիչ արագություններ: Հեղուկի յուրաքանչյուր կետում տեղի են ունենում արագության վեկտորի անկանոն շեղումներ իր միջին արժեքից: Այդպիսի շարժումը կոչվում է տուրբուլենտ: Երբ մարմինը շրջահոսվում է մածուցիկ հեղուկով, արագության մեծացման հետ հոսանքը փոխում է իր բնույթը և դառնում է մրրկային:

Նկ. 6.10ա-ում ցույց տրված հոսանքի արագության փոփոխման բնույթը խողովակի առանցքից ունեցած հեռավորությունից վերաբերում է լամինար հոսանքի դեպքին (արագությունների պրոֆիլը պարաբոլային է): Տուրբուլենտ հոսանքի դեպքում կարելի է խոսել խողովակի հատույթի յուրաքանչյուր կետին համապատասխանող միջին (ըստ ժամանակի) արագության մասին: Միջին արագությունների պրոֆիլը տուրբուլենտ հոսանքի դեպքում պատկերված է նկ.6.10բ-ում: Այս դեպքում խողովակի պատերի մոտ արագությունը փոփոխվում է անհամեմատ ավելի արագ, քան լամինար հոսանքի դեպքում, իսկ կտրվածքի մյուս մասում արագության փոփոխությունն ավելի փոքր է:

Նկ. 6.10ա-ում ցույց տրված հոսանքի արագության փոփոխման բնույթը խողովակի առանցքից ունեցած հեռավորությունից վերաբերում է լամինար հոսանքի դեպքին (արագությունների պրոֆիլը պարաբոլային է): Տուրբուլենտ հոսանքի դեպքում կարելի է խոսել խողովակի հատույթի յուրաքանչյուր կետին համապատասխանող միջին (ըստ ժամանակի) արագության մասին:

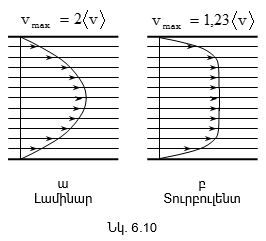
Միջին արագությունների պրոֆիլը տուրբուլենտ հոսանքի դեպքում պատկերված է նկ. 6.10բ-ում: Այս դեպքում խողովակի պատերի մոտ արագությունը փոփոխվում է անհամեմատ ավելի արագ, քան լամինար հոսանքի դեպքում, իսկ կտրվածքի մյուս մասում արագության փոփոխությունն ավելի փոքր է: Հոսանքի բնույթը կախված է չափայնություն չունեցող մեծությունից, որը կոչվում է Ռեյնոլդսի թիվ.

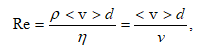
որտեղ  հեղուկի խտությունն է, <v>-ը հեղուկի միջին արագությունն է խողովակի հատույթով, d-ն` լայնական հատույթը բնորոշող չափը, օրինակ` խողովակի տրամագիծը,  կինեմատիկական մածուցիկությունը:

Ռեյնոլդսի թվի փոքր արժեքների դեպքում  դիտվում է լամինար հոսանք, անցումը լամինար հոսանքից անցումը տուրբուլենտին կատարվում է  տիրույթում, իսկ Re=2300 դեպքում (ողորկ խողովակների համար) հոսանքը տուրբուլենտ է: Եթե Ռեյնոլդսի թիվը միատեսակ է, ապա տարբեր հեղուկների (գազերի) հոսանքի ռեժիմը տարբեր կտրվածքներով խողովակներում միատեսակ է:

>>

6.5. ՄԱԾՈՒՑԻԿՈՒԹՅԱՆ ՈՐՈՇՄԱՆ ՄԵԹՈԴՆԵՐԸ

1. Ստոքսի մեթոդը: Մածուցիկության որոշման այս եղանակը հիմնված է հեղուկի մեջ դանդաղ շարժվող սֆերիկ ձև ունեցող մարմնի արագությունը չափելու վրա:

Հեղուկի մեջ ուղղաձիգ ցած ընկնող գնդիկի վրա ազդում են երեք ուժեր. ծանրության ուժը`  գնդիկի խտությունն է), Արքիմեդի ուժը`  հեղուկի խտությունն է) և դիմադրության ուժը, որը փորձնականորեն որոշել է Ստոքսը և ունի հետևյալ տեսքը`  (r-ը գնդիկի շառավիղն է): Գնդիկի հավասարաչափ շարժման դեպքում

կամ

որտեղից

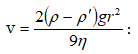
Չափելով գնդիկի հավասարաչափ շարժման արագությունը` կարելի է որոշել հեղուկի (գազի) մածուցիկությունը:

2. Պուազեյլի մեթոդը: Պուազեյլը, ուսումնասիրելով հեղուկի լամինար շարժումը կլոր խողովակում, գտավ արագության փոփոխության կախումը խողովակի առանցքից ունեցած r հեռավորությունից: Հեղուկում մտովի անջատենք r շառավղով և dr հաստության գլանային ծավալ (նկ.6.11):

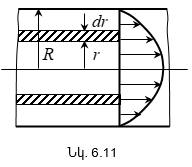
Ներքին շփման ուժը, որն ազդում է այդ ծավալի կողմնային մակերևույթի վրա

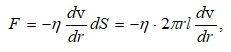
որտեղ dS-ը գլանային շերտի կողմնային մակերևույթն է, բացասական նշանը ցույց է տալիս, որ շառավղի աճի դեպքում արագությունը նվազում է: Հեղուկի կայունացած հոսանքի դեպքում գլանի կողմնային մակերևույթի վրա ազդող ներքին շփման ուժը հավասարակշռվում է նրա վրա ազդող ճնշման ուժով.

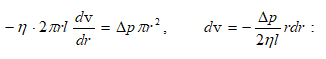
Ինտեգրելուց հետո ենթադրելով, որ պատերի մոտ տեղի ունի հեղուկի կպչում, այսինքն առանցքից R հեռավորության վրա արագությունը հավասար է զրոյի, կստանանք`

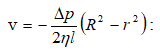
Այստեղից հետևում է, որ հեղուկի մասնիկների արագությունը բաշխվում է ըստ պարաբոլային օրենքի, ընդ որում` պարաբոլի գագաթը ընկած է խողովակի առանցքի վրա (նկ.6.10): t ժամանակում խողովակով կհոսի հեղուկ, որի ծավալը`

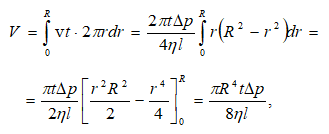
որտեղից մածուցիկությունը `

(6.15) բանաձևը կոչվում է Պուազեյլի բանաձև: Մածուցիկությունը որոշելու համար օգտագործվող սարքերը կոչվում են մածուցիկաչափեր:

>>

6.6. ՄԱՐՄԻՆՆԵՐԻ ՇԱՐԺՈՒՄԸ ՀԵՂՈՒԿՆԵՐՈՒՄ ԵՎ ԳԱԶԵՐՈՒՄ

Աերոդինամիկայի և հիդրոդինամիկայի կարևոր խնդիրներից մեկը հեղուկներում և գազերում պինդ մարմինների շարժման ուսումնասիրությունն է, մասնավորապես այն ուժերի ուսումնասիրությունը, որոնցով միջավայրը ազդում է շարժվող մարմինների վրա:

Այդ հիմնախնդիրը մեծ նշանակություն ունի` կապված ավիացիայի բուռն զարգացման և ծովային նավերի շարժման արագության մեծացման հետ:

Հեղուկի կամ գազի մեջ շարժվող մարմնի վրա ազդում են երկու ուժեր (նրանց արդյունարարը նշանակենք R-ով), որոնցից մեկը` ճակատային դիմադրությունը  ուղղված է մարմնի շարժման հակառակ կողմը (հոսքի կողմը), իսկ երկրորդը` վերամբարձ ուժը  ուղղահայաց այդ ուղղությանը (նկ.6.12):

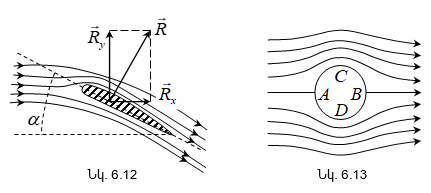
Եթե մարմինը համաչափ է, և նրա համաչափության առանցքը համընկնում է արագության ուղղության հետ, ապա նրա վրա ազդում է միայն ճակատային դիմադրությունը, այս դեպքում վերամբարձ ուժը հավասար է զրոյի: Կարելի է ապացուցել, որ իդեալական հեղուկում հավասարաչափ շարժումը կատարվում է առանց ճակատային դիմադրության: Եթե դիտարկենք գլանի շարժումը այդպիսի հեղուկի մեջ (նկ.6.13), ապա հոսանքի գծերի պատկերը համաչափ է ինչպես A և B կետերով անցնող ուղղի նկատմամբ, այնպես էլ C և D կետերով անցնող ուղղի նկատմամբ, այսինքն արդյունարար ճնշման ուժը գլանի մակերևույթի վրա հավասար է զրոյի:

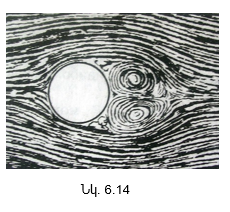
Այլ է պատկերը մածուցիկ հեղուկում մարմնի շարժման դեպքում (հատկապես շրջահոսման արագությունը մեծացնելու դեպքում): Միջավայրի մածուցիկության հետևանքով մարմնի մակերևույթի մերձակա տիրույթում առաջանում է մասնիկների սահմանային շերտ, որոնք շարժվում են փոքր արագություններով: Սահմանային շերտում գործում են շփման ուժերը, որոնք վերջին հաշվով ստացվում են կիրառված մարմնի նկատմամբ և առաջացնում են ճակատային դիմադրություն: Սահմանային շերտի առկայությունն արմատապես փոխում է մարմնի` հեղուկով շրջահոսման բնույթը: Այդ դեպքում լրիվ շրջահոսումը դառնում է անհնար: Մակերևութային շերտում շփման ուժերի ազդեցությունը հանգեցնում է այն բանին, որ հոսքը անջատվում է մարմնի մակերևույթից, որի հետևանքով մարմնի հետևում առաջանում են մրրիկներ (նկ. 6.14, որտեղ պատկերված է գլանի շրջահոսումը մածուցիկ հեղուկով): Մարմնի հետևում առաջացած մրրիկային տեղամասում ճնշումն ավելի ցածր է, ուստի ճնշման ուժերի արդյունարարը հավասար չի լինի զրոյի` իր հերթին պայմանավորելով ճակատային դիմադրությունը: Մարմնի տվյալ չափերի դեպքում ճնշման դիմադրությունը խիստ կախված է մարմնի ձևից: Այդ պատճառով այն կոչվում է նաև ձևի դիմադրություն: Ճնշման ամենափոքր դիմադրությամբ օժտված են շրջահոսելի, կաթիլաձև մարմինները (նկ.6.12): Աշխատում են այդպիսի ձև տալ ինքնաթիռի թևերին: Շնորհիվ ինքնաթիռի թևի` նկ.6.12-ում պատկերված ձևի, շարժվող թևի շուրջը առաջանում է օդի շրջապտույտ` ուղղված ժամցույցի սլաքի շարժման ուղղությամբ: Թևի վերևում շրջապտույտի  արագությունը և հանդիպակաց օդի v արագությունը գումարվում են, իսկ թևի տակ` հանվում: Ուստի օդի հարաբերական արագությունը թևից վեր  գերազանցում է թևի տակի հարաբերական արագությանը  այսինքն  Հետևաբար, համաձայն Բեռնուլիի հավասարման, ճնշումը թևի տակ ավելի մեծ է, քան ճնշումը թևից վեր  Ճնշումների  տարբերության հաշվին առաջանում է ինքնաթիռի թևի  վերամբարձ ուժը:

Ճակատային դիմադրությունը, ինչպես վերը նշվեց կախված է մարմնի ձևից և հոսքի նկատմամբ նրա դիրքից, որը հաշվի է առնվում չափայնություն չունեցող C_x դիմադրության գործակցով, որը որոշվում է փորձով.

որտեղ  միջավայրի խտությունն է, v-ն` մարմնի շարժման արագությունն է, S-ը մարմնի ամենամեծ լայնական հատույթը:

R_x բաղադրիչը կարելի է բավականաչափ փոքրացնել, ընտրելով մարմնի այնպիսի ձև, որը չի նպաստում մրրիկների առաջացմանը: Վերամբարձ ուժը կարող է որոշվել (6.16) համանման բանաձևով.

որտեղ C_y -ը վերամբարձ ուժի չափայնություն չունեցող գործակից է:

Ինքնաթիռի թևի համար պահանջվում է մեծ վերամբարձ ուժ փոքր ճակատային դիմադրության դեպքում (այդ պայմանը կատարվում է փոքր գրոհման անկյունների դեպքում, նկ.6.13):

Թևը այնքան լավ է բավարարում այդ պայմանին, որքան մեծ է  մեծությունը, որը կոչվում է թևի որակ:

Թևի պահանջվող պրոֆիլի նախագծման և մարմնի երկրաչափական ձևի ազդեցությունը վերամբարձ ուժի գործակցի ուսումնասիրության մեջ մեծ ծառայություններ է ունեցել Ն. Ժուկովսկին (1847-1921):

>>

ԳԼՈՒԽ 7. ՀԱՐԱԲԵՐԱԿԱՆՈՒԹՅԱՆ ՀԱՏՈՒԿ ՏԵՍՈՒԹՅԱՆ ՏԱՐՐԵՐԸ

Հարաբերականության հատուկ տեսությունը տարածության և ժամանակի արդիական ֆիզիկական տեսություն է, որը հիմնել է Այնշտայնը՝ վակուումում լույսի տարածման արագության հետ համեմատելի արագությամբ շարժվող մարմինների մոտ առաջացող յուրահատուկ ռելյատիվիստական հատկությունների ու երևույթների ուսումնասիրության համար:

Հարաբերականության հատուկ տեսությունը երբեմն անվանում են հարաբերականության մասնավոր տեսություն կամ ռելյատիվիստական տեսություն՝ լատինական «relativus»` հարաբերական բառից:

Հարաբերականության տեսությունում, ինչպես և նյուտոնյան մեխանիկայում, ենթադրվում է, որ ժամանակը համասեռ է, իսկ տարածությունը համասեռ և իզոտրոպ, սակայն, ի տարբերություն նյուտոնյան մեխանիկայի, հարաբերականության տեսությունում ընդունվում է, որ տարբեր հաշվարկման համակարգերում ժամանակն ընթանում է տարբեր ձևով: Տարածությունն ու ժամանակն ստացվում են փոխադարձաբար կապված` առաջացնելով մատերիայի գոյության «ժամանակ-տարածություն» միասնական ձևը:

>>

7.1. ԳԱԼԻԼԵՅԻ ՁԵՎԱՓՈԽՈՒԹՅՈՒՆՆԵՐԸ

 Նյուտոնյան դասական մեխանիկայում Գալիլեյի ձևափոխություններ են կոչվում կոորդինատների և ժամանակի փոփոխման բանաձևերը, որոնք կիրառվում են K(x,y,z,t) մի իներցիալ համակարգից մի այլ 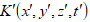 համակարգի անցման դեպքում: Գալիլեյի ձևափոխությունները հիմնվում են ժամանակի և երկարության հատվածների բացարձակության դրույթների վրա: Առաջին դրույթը պնդում է, որ ժամանակի ընթացքը միատեսակ է բոլոր իներցիալ համակարգերում,  Երկրորդ դրույթի համաձայն մարմինների չափերը կախված չեն դրանց շարժման արագությունից և համակարգերի ընտրությունից,

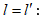
Ընդհանուր դեպքում, երբ 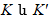 հաշվարկման համակարգերի կոորդինատների առանցքները t=0 պահին համընկնում են, իսկ  արագությունն ունի կամայական ուղղություն (նկ.7.1), M կետի կոորդինատների համար Գալիլեյի ձևափոխություններն ունեն հետևյալ տեսքը՝

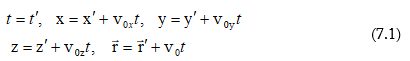
Այն դեպքում, երբ  արագությունն ուղղված է OX առանցքով (նկ. 7.2),

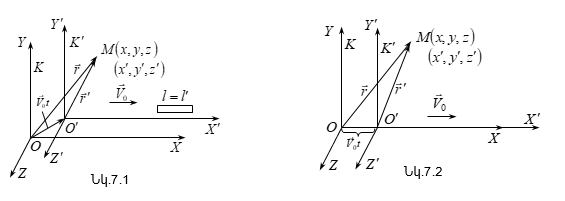
Գալիլեյի ձևափոխություններն ունեն հետևյալ տեսքը՝

կամ

Ածանցելով (7.3) արտահայտությունը` ստանում ենք արագությունների գումարման դասական օրենքը՝

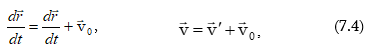
իսկ ածանցելով (7.4) արտահայտությունը՝ հանգում ենք այն եզրակացության, որ նյութական կետի արագացումը նույնն է բոլոր իներցիալ հաշվարկման համակարգերում: Այլ կերպ ասած, արագացումը ինվարիանտ է Գալիլեյի ձևափոխությունների նկատմամբ՝

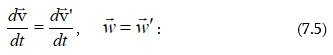
Այստեղից բխում է, որ եթե K համակարգը իներցիալ է, այսինքն` այդ համակարգում ազատ մարմինը շարժվում է հաստատուն արագությամբ՝  առանց արագացման՝  ապա  համակարգը ևս իներցիալ է, քանի որ այդ համակարգում նույն մարմինը շարժվում է նույնպես հաստատուն արագությամբ՝  առանց արագացման  Այսպիսով, որևէ իներցիալ հաշվարկման համակարգի նկատմամբ հաստատուն արագությամբ շարժվող այլ հաշվարկման համակարգերը նույնպես իներցիալ են:

Գալիլեյի հարաբերականության մեխանիկական սկզբունքը պնդում է, որ բոլոր իներցիալ հաշվարկման համակարգերում մեխանիկական երևույթները նույն սկզբնական պայմանների դեպքում ընթանում են միատեսակ, իսկ մեխանիկայի օրենքները սահմանվում նույն կերպ, այսինքն՝ մեխանիկայի բոլոր օրենքների բանաձևերն ինվարիանտ են Գալիլեյի ձևափոխությունների նկատմամբ և ունեն նույն մաթեմատիկական տեսքը: Այլ կերպ ասած, գտնվելով իներցիալ փակ համակարգի ներսում, ոչ մի մեխանիկական փորձով հնարավոր չէ որոշել իներցիալ համակարգի արագությունը և անգամ հայտնաբերել նրա շարժման որևէ վկայություն: Քանի որ ըստ Նյուտոնի` ցանկացած մարմնի զանգվածը նույնն է բոլոր իներցիալ համակարգերում՝ m=const, ապա Նյուտոնի երկրորդ օրենքը ինվարիանտ է Գալիլեյի ձևափոխությունների նկատմամբ՝

Թվում է` կարելի է եզրակացնել, որ ոչ միայն մեխանիկայի, այլև օպտիկայի օրենքներն ինվարիանտ են Գալիլեյի ձևափոխությունների նկատմամբ, քանի որ, ըստ Նյուտոնի, լույսը մասնիկների (կորպուսկուլների) մեխանիկական շարժում է, իսկ, ըստ Քրիստիան Հյուգենսի (1629-1695), լույսը՝ մեխանիկական ալիք է: Սակայն Ալբերտ Մայքելսոնը (1852-1931) փորձով ապացուցեց, որ լույսի տարածման արագությունը վակուումում տարբեր իներցիալ հաշվարկման համակարգերում ինվարիանտ չէ նյուտոնյան մեխանիկայում ընդունված Գալիլեյի ձևափոխությունների նկատմամբ:

Այնշտայնը եկավ այն եզրակացության, որ նյուտոնյան մեխանիկայի օրենքները, ինչպես նաև Գալիլեյի ձևափոխությունները, կիրառելի են միայն այն դեպքում, երբ մարմինների և համակարգերի շարժման արագությունները զգալիորեն փոքր են վակուումում լույսի տարածման արագությունից: Այն դեպքում, երբ մարմինները և հաշվարկման համաարգերը շարժվում են լույսի արագությանը մոտ արագություններով, ենթարկվում են հարաբերականության հատուկ տեսության օրենքներին:

Օգտվելով Գալիլեյի հարաբերականության սկզբունքից` ցույց տանք, որ երկու  զանգվածներով մարմինների ոչ առաձգական բախման ժամանակ կազմավորված մարմնի զանգվածը՝

Դիտարկենք բախման պրոցեսը որևէ K իներցիալ հաշվանքի հանակարգում: նշանակենք մարմինների արագությունները մինչև բախումը, իսկ  ընդհանուր մարմնի արագությունը բախումից հետո: Իմպուլսի պահպանման օրենքի համաձայն՝

Դիտարկենք նույն պրոցեսը հաշվարկման համակարգում, որը շարժվում է K համակարգի նկատմամբ ուղղագիծ և հավասարաչափ  արագությամբ: Հարաբերականության սկզբունքի համաձայն, իմպուլսի պահպանման օրենքը ճիշտ է նաև  համակարգում և ունի հետևյալ տեսքը՝

Հաշվարկման իներցիալ համակարգերի համարժեքությունից հետևում է, որ բոլոր մարմինների զանգվածները  համակարգում նույնպիսին են, ինչպիսին էին K համակարգում:

Առաջին հավասարումից հանելով երկրորդը և հաշվի առնելով, որ

ստանում ենք

կամ

Այսպիսով, մարմնի ընդհանուր զանգվածը հավասար է բաղադրիչ մարմինների զանգվածների գումարին: Այդ հատկությունն անվանում են զանգվածի ադիտիվություն:

Ապացույցը կարելի է ընդհանրացնել, և բոլորովին անհրաժեշտ չէ, որ մարմինները բախվեն: Կարելի է վերցնել կամայական քիմիական ռեակցիա, և ռեակցիայի արդյունքում կստացվի, որ նյութերի զանգվածների գումարը մինչ ռեակցիան հավասար է նյութերի զանգվածների գումարին ռեակցիայից հետո: Դա զանգվածի պահպանման օրենքն է: Այդ օրենքը, որ մենք ստացանք որպես Գալիլեյի հարաբերականության սկզբունքի հետևանք, ճիշտ է նյուտոնյան մեխանիկայի համար, բայց Գալիլեյի հարաբերականության սկզբունքը բնության ոչ լիովին ճշգրիտ օրենքն է. այն մոտավոր սահմանային դեպք է Այնշտայնի հարաբերականության սկզբունքի համար: Դրանից ելնելով, ստացվում է, որ զանգվածի և էներգիայի պահպանման օրենքները, որոնք ոչ ռելյատիվիստական ֆիզիկայում համարվում էին բնության երկու անկախ, ճշգրիտ օրենքներ, ռելյատիվիստական ֆիզիկայում կորցնում են իրենց անկախությունը և ընդգրկվում զանգված - էներգիա մեկ ընդհանուր պահպանման օրենքի մեջ:

Ցանկացած էներգիա օժտված է այնպիսի զանգվածով, որը հավասար է էներգիայի քանակի հարաբերությանը վակուումում լույսի արագության քառակուսուն՝

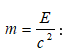
Դա Այնշտայնի հիմնարար օրենքն է զանգվածի և էներգիայի փոխադարձ կապի մասին:

Զանգվածի հաշվեկշռի մեջ պետք է հաշվի առնվեն ոչ միայն նյութի, այլ նաև առաքվող և կլանվող էներգիայի զանգվածները: Բնության բոլոր պրոցեսներում նյութի զանգվածների և էներգիայի գումարը մնում է հաստատուն:

>>

7.2. ՀԱՐԱԲԵՐԱԿԱՆՈՒԹՅԱՆ ՀԱՏՈՒԿ ՏԵՍՈՒԹՅԱՆ

ԿԱՆԽԱԴՐՈՒՅԹՆԵՐԸ

Հարաբերականության հատուկ տեսության հիմքը կազմում են Այնշտայնի կողմից 1905 թ. ձևակերպված երկու կանխադրույթները:

1. Այնշտայնի հարաբերականության սկզբունքը

Հաշվարկման բոլոր իներցիալ համակարգերում միևնույն սկզբնական պայմանների դեպքում բնության երևույթները միատեսակ են ընթանում, իսկ ֆիզիկական օրենքներն արտահայտող հավասարումներն ինվարիանտ են կոորդինատների և ժամանակի նկատմամբ, այսինքն՝ գրվում են նույն տեսքով: Այլ կերպ ասած, գտնվելով փակ իներցիալ համակարգում, ոչ մի փորձով հնարավոր չէ որոշել նրա արագությունը: Այսպիսով, առաջին կանխադրույթը Գալիլեյի հարաբերականության սկզբունքը տարածում է բոլոր ֆիզիկական երևույթների և օրենքների վրա:

2. Լույսի արագության հաստատուն լինելու սկզբունքը

Լույսի c արագությունը վակուումում բոլոր իներցիալ հաշվարկման համակարգերում հաստատուն է, կախված չէ աղբյուրների և ընդունիչների շարժումից ու լույսի տարածման ուղղությունից:

Երկրորդ կանխադրույթից բխում է, որ Գալիլեյի և Նյուտոնի կողմից նկարագրված տիեզերքի (աշխարհի) ֆիզիկական պատկերը չի համապատասխանում իրականությանը, այսինքն՝ գոյություն չունեն իրարից անկախ բացարձակ տարածություն ու բացարձակ ժամանակ: Ըստ Այնշտայնի, տարածության տարբեր մասերում կատարված իրադարձությունների միաժամանակության հասկացությունը հարաբերական է, այսինքն, որևէ մի համակարգում երկու տարատեղ միաժամանակյա երևույթներն ուրիշ հաշվարկման համակարգի նկատմամբ միաժամանակ չեն կատարվում: Դա բխում է նրանից, որ t ժամանակն x,y,z կոորդինատները միասին կազմում են քառաչափ տարածություն (x,y,z): Հարաբերականության տեսության երկրորդ կանխադրույթի օգնությամբ բացատրվեց 1871թ. կատարված Մայքելսոնի փորձերի «բացասական արդյունքը», այսինքն՝ Երկրի շարժման բացարձակ արագության որոշման անհնարինությունը տարբեր ուղղություններով լույսի տարածման արագության չափման միջոցով:

>>

7.3. ԼՈՐԵՆՑԻ ՁԵՎԱՓՈԽՈՒԹՅՈՒՆՆԵՐԸ

Դիտարկենք մի օրինակ: Դիցուք, երբ անշարժ K համակարգը պահին լիովին համընկնում է շարժական  համակարգի հետ, նրանց կոորդինատների ընդհանուր սկզբնակետում տեղի է ունենում լույսի բռնկում, և այդ պահից լույսը սկսում է տարածվել բոլոր ուղղություններով c արագությամբ, իսկ  համակարգը սկսում է շարժվել OX առանցքի ուղղությամբ` հաստատուն  արագությամբ (նկ. 7.3):

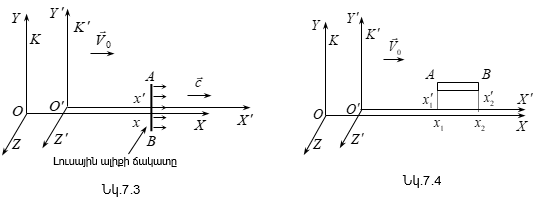
Որոշ ժամանակից հետո լուսային ալիքի AB ճակատի կոորդինատները համակարգերում համապատասխանաբար կլինեն՝

Քանի որ այսինքն՝ իներցիալ հաշվարկման տարբեր համակարգերում ժամանակի ընթացքը տարբեր է:

Տարածության և ժամանակի մասին եղած դասական պատկերացումների սնանկության պատճառն այն սխալ ենթադրությունն է, թե փոխազդեցություններն ու ազդանշանները կարելի է ակնթարթորեն հաղորդել տարածության մի կետից մյուսը: Սակայն դա այդպես չէ: Այդ նշանակում է, որ Գալիլեյի ձևափոխությունների մեջ անհրաժեշտ է մտցնել համապատասխան փոփոխություններ՝

որտեղ չափայնություն չունեցող համեմատականության գործակիցներ են: Իներցիալ հաշվարկման բոլոր համակարգերի իրավահավասարությունից բխում է, որ (7.7) կոորդինատների ձևափոխությունները պետք է իրարից տարբերվեն միայն հաշվարկման համակարգերի շարժման հարաբերական  արագության նշանով, իսկ համեմատականության գործակիցները պետք է լինեն նույնը՝

Որպեսզի գտնենք գործակիցը, տեղադրենք (7.6) առնչությունները (7.7) արտահայտությունների մեջ և, բազմապատկելով դրանք իրար հետ, կստանանք՝

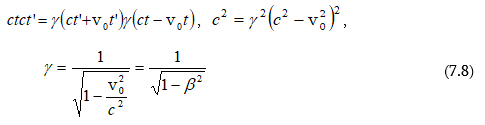
որտեղ  Տեղադրելով  (7.8) արտահայտությունը (7.7) հավասարումների մեջ, կստանանք Լորենցի ձևափոխությունները  կոորդինատների համար՝

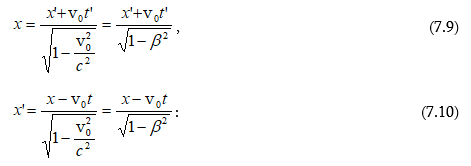
Քանի որ մեր օրինակում y օրդինատների և z ապլիկատների առանցքների ուղղությամբ  հաշվարկման համակարգերի հարաբերական արագությունը հավասար է զրոյի, ապա

Որպեսզի ստանանք Լորենցի ձևափոխությունները ժամանակի համար, տեղադրենք (7.6) առնչությունները (7.9) և (7.10) արտահայտությունների մեջ՝

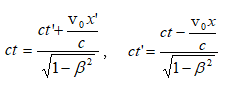
ստանում ենք՝

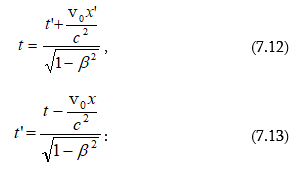
Լորենցի ձևափոխություններից բխում է, որ շարժական մի իներցիալ համակարգից որևէ այլ անշարժ իներցիալ համակարգի անցնելիս և հակառակը, կոորդինատները և ժամանակը կարող են հաշվարկվել (7.9), (7.10), (7.11), (7.12) և (7.13) բանաձևերի օգնությամբ այն դեպքերում, երբ մարմնի շարժման  արագությունը փոքր է վակուումում լույսի տարածման c արագությունից՝  Դրանից կարելի է եզրակացնել, որ, ըստ հարաբերականության հատուկ տեսության, բացառությամբ որոշ տարրական մասնիկների, օրինակ՝ ֆոտոնների, որոնց արագությունը ցանկացած իներցիալ հաշվարկման համակարգերում հավասար է c -ի, բոլոր մարմինների շարժման արագությունները միշտ փոքր են վակուումում լույսի տարածման արագությունից:

Երբ  Լորենցի ձևափոխությունները վերածվում են Գալիլեյի ձևափոխությունների:

Այսպիսով, Այնշտայնի կանխադրույթներից բխում են Լորենցի ձևափոխությունները և մի շարք հետևություններ, որոնք անսովոր են նյուտոնյան մեխանիկայի տեսակետից՝

1) հաշվարկման տարբեր համակարգերում ժամանակի անհավասարությունը,

2) ժամանակի և կոորդինատների փոխադարձ կապը,

3) բնության գոյությունը քառաչափ ժամանակ-տարածության մեջ,

4) բոլոր մարմինների շարժման արագության փոքր լինելը վակուումում լույսի տարածման արագությունից:

>>

7.4. ՀԵՏԵՎՈՒԹՅՈՒՆՆԵՐ ԼՈՐԵՆՑԻ ՁԵՎԱՓՈԽՈՒԹՅՈՒՆՆԵՐԻՑ

1. Երկարության ռելյատիվիստական կրճատումը

Համեմատենք ժամանակի որոշակի պահին AB ձողի  երկարությունները համապատասխանաբար անշարժ K և շարժական  համակարգերում, երբ ձողն անշարժ վիճակում գտնվում է  համակարգում առանցքին զուգահեռ (նկ.7.4), այսինքն շարժվում է  համակարգի հետ միասին,  արագությամբ (K համակարգի նկատմամբ):

Ձողի երկարությունը համակարգում՝

որտեղ ձողի A և B ծայրակետերի կոորդինատներն են ժամանակի որևէ t պահին: Համաձայն (7.10)-ի,  համակարգում դադարի վիճակում գտնվող ձողի երկարությունը՝

Հաշվի առնելով, որ  հանգում ենք այն եզրակացության, որ շարժվող մարմնի չափը կախված է նրա արագությունից և կրճատվում է նրա շարժման ուղղությամբ  Այս երևույթն այլ կերպ կոչվում է լորենցյան կամ ֆիցջերալդյան կրճատում: Նշենք, որ քննարկվող դեպքում x և z առանցքների ուղղությամբ ձողի չափերը նույնն են, ինչ որ  առանցքների ուղղությամբ: Երբեմն մարմնի երկարությունն այն համակարգում, որի նկատմամբ մարմինը գտնվում է դադարի վիճակում, անվանում են մարմնի սեփական երկարություն: Դա մարմնի առավելագույն երկարությունն է:

Լորենցյան կրճատումը տարածության և ժամանակի միջև եղած փոխադարձ կապի հետևանքն է: Բանն այն է, որ երբ  համակարգում ձողի ծայրակետերում նույն պահն է, K համակարգում նույն ձողի ծայրակետում ժամանակները տարբերվում են իրարից և հակառակը, երբ  Համաձայն (7.12)-ի

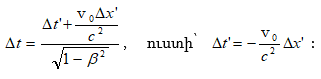
Ստացվածից և (7.14) ու (7.9) առնչություններից հետևում է նույնը՝

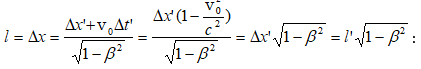
2. Ժամանակի ընթացքի ռելյատիվիստական դանդաղումը

Քննարկենք հետևյալ հարցը, ինչպիսի՞ն է որևէ կետում տեղի ունեցած պատահարի տևողությունը երկու տարբեր իներցիալ համակարգերի նկատմամբ: Դիցուք համակարգի նկատմամբ դադարի վիճակում գտնվող x կետում էլեկտրական լամպը լիցքավորված կոնդենսատորին միացնելիս լույս արձակեց որոշ ժամանակամիջոցի ընթացքում`

K համակարգում այդ լուսարձակման ժամանակամիջոցը ՝

Գտնենք կապը  ժամանակամիջոցների միջև.

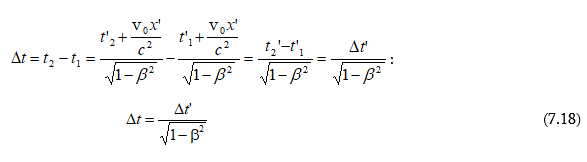
Ստացված (7.18) արտահայտությունից բխում է. ցանկացած K համակարգում դիտարկվող պատահարի  տևողությունն ավելի մեծ է, քան նրա սեփական ժամանակը համակարգում, այսինքն՝ այն համակարգում, որի նկատմամբ պատահարի օբյեկտը գտնվում է դադարի վիճակում, այսինքն՝ անշարժ K համակարգի նկատմամբ շարժվող  համակարգում տեղի է ունենում ժամանակի դանդաղում: Համաձայն հարաբերականության տեսության առաջին կանխադրույթի՝ սեփական ժամանակը ինվարիանտ է, այսինքն՝ հաստատուն մեծություն է բոլոր իներցիալ հաշվարկման համակարգերում: Նշանակում է, եթե լամպը և լիցքավորված կոնդենսատորը գտնվեն դադարի վիճակում K համակարգի նկատմամբ, ապա այդ համակարգի նկատմամբ լուսարձակման տևողությունը կլինի նույնը, ինչ որ նախորդ դեպքում  համակարգի նկատմամբ: Հաճախ սեփական ժամանակը  փոխարեն նշանակվում է

(7.19) առնչության ճշտությունը և  սեփական ժամանակի ինվարիանտությունը բազմիցս հաստատվել են փորձերով: Բերենք մի օրինակ: Տիեզերական ճառագայթների կազմում կան մեզոններ կամ մյուոններ կոչվող տարրական մասնիկներ: Այդ մասնիկներն անկայուն են, և նրանց կյանքի միջին տևողությունը, այսինքն գոյության միջին սեփական ժամանակը, չափված այնպիսի հաշվարկման համակարգի նկատմամբ, որում նրանք անշարժ են, կազմում է ընդամենը մոտ Կարող է թվալ, որ նույնիսկ լույսի արագությամբ շարժվելիս մյուոնները կարող են անցնել ոչ ավելի, քան 600 մ ճանապարհ՝

Սակայն, ինչպես ցույց են տալիս հետազոտությունները, տիեզերական ճառագայթների ազդեցության հետևանքով մյուոններն առաջանում են մթնոլորտում, 20-30կմ բարձրության վրա և զգալի քանակությամբ հասնում են Երկրի մակերևույթին: Հետևաբար, մյուոնի կյանքի տևողությունը մեծանում է հաշվարկման այն համակարգում, որի նկատմամբ այն շարժվում է: Երկրի հետ կապված համակարգում c-ին մոտ արագությամբ շարժվող մյուոնն ապրում է մի քանի անգամ ավելի երկար, քան իր հետ կապված «սեփական» հաշվարկման համակարգում, որում մյուոնն անշարժ է:

 Նշենք, որ իրադարձության (պատահարի) ընթացքի դանդաղումը, ինչպես և մարմնի չափերի կրճատումը նկատելի չէ, երբ մարմինները և իներցիալ հաշվարկման համակարգերը շարժվում են միմյանց նկատմամբ լույսի տարածման c արագության համեմատությամբ զգալիորեն փոքր արագությամբ՝ v<<c: Այդ դեպքում պետք է համարել, որ մարմնի չափերը և պատահարի տևողությունը գրեթե բացարձակ նույնն են նշված համակարգում, այսինքն՝  Իսկ այն դեպքում, երբ պայմանականորեն անշարժ K համակարգի նկատմամբ որևէ համակարգ շարժվում է լույսի արագությանը շատ մոտ արագությամբ, K համակարգի նկատմամբ համակարգում տեղի է ունենում չափերի կրճատում և ժամանակի դանդաղում:

 3. «Ժամացույցների» կամ «երկվորյակների» պարադոքսը

Պարադոքսի էությունն այն է, որ  համակարգերում գտնվող դիտողները, հավասարապես օգտվելով Լորենցի ձևափոխություններից, հանգում են հակասական եզրակացության. յուրաքանչյուր դիտող համարում է, որ իր ժամանակն ավելի արագ է ընթանում, և իր ժամացույցն ավելի առաջ է, քան մյուսինը: Սակայն ժամացույցների պարադոքսը վերանում է, երբ դիտարկում ենք որոշակի դեպք: Օրինակ, Երկրից թռչող տիեզերանավը որոշ ժամանակից հետո կատարում է շրջադարձ և վերադառնում է Երկիր, երկրացիները և տիեզերագնացները իրավահավասար չեն. տիեզերանավի և Երկրի վրա գտնվող արագացումը չափող գործիքները կարող են նշել, թե այդ մարմիններից ո՞րն է որից հեռացել՝ տիեզերանավը Երկրի՞ց, թե` հակառակը: Այսպիսով, ի տարբերրություն Այնշտայնի հարաբերականության սկզբունքի, անգամ իներցիալ համակարգերը որոշ առումով հավասարազոր չեն: Տիեզերանավի վերադարձից հետո անպայման կպարզվի, որ տիեզերանավի ժամացույցի ցուցմունքն ավելի փոքր է, քան Երկրինը, այսինքն՝ թռչող տիեզերանավում անցած ժամանակը ավելի կարճատև է: Դա արդեն ստույգ հաստատված է փորձով:

>>

7.5. ՄԻՋԱԿԱՅՔԸ (ԻՆՏԵՐՎԱԼ) ԵՎ ՆՐԱ ԻՆՎԱՐԻԱՆՏՈՒԹՅՈՒՆԸ

Տարբեր իներցիալ հաշվարկման համակարգերում վակուումում լույսի տարածման արագության հաստատուն լինելը ոչ միայն Այնշտայնի տեսական գուշակումն է, այլ նաև փորձնական փաստ: Այն վկայում է փոխադարձ կապի մասին, որն առկա է տարածության և ժամանակի միջև:

Ժամանակի և տարածության միասնականությունը կազմում է քառաչափ ժամանակտարածությունը: Այսպիսի ոչ էվկլիդյան ժամանակ-տարածության մեջ կետը կոչվում է տիեզերական կետ: Նրա (t,x,y,z) կոորդինատները ցույց են տալիս այդ կետում կատարված որևէ պատահարի տեղն ու ժամանակը, օրինակ, մասնիկի տրոհումը: Յուրաքանչյուր մեխանիկական պրոցեսին քառաչափ ժամանակ-տարածության մեջ համապատասխանում է գիծ, որը կոչվում է տիեզերական գիծ: Դադարում գտնվող մասնիկի վիճակը նկարագրող տիեզերական գիծն ուղիղ գիծ է, որը զուգահեռ է ժամանակի առանցքին:

Քառաչափ ժամանակ-տարածության մեջ երկու տիեզերական կետերի միջև  հեռավորությունը կոչվում է միջակայք (ինտերվալ)՝

որտեղ  եռաչափ տարածության մեջ երկու կետերի միջև հեռավորությունն է:

Ցույց տանք, որ նկ.7.4-ում պատկերված  համակարգերի դեպքում միջակայքն ինվարիանտ է Լորենցի ձևափոխությունների նկատմամբ, այսինքն՝

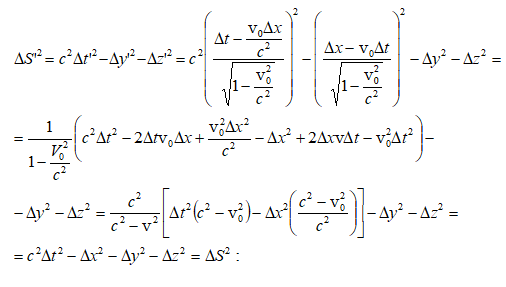
Այսինքն` ինչպես վակուումում լույսի տարածման c արագությունը, այնպես էլ միջակայքը ինվարիանտ են և կախված չեն հաշվարկման համակարգից: Այս արդյունքին կարելի է գալ ավելի կարճ եղանակով, եթե օգտվենք սեփական ժամանակի ինվարիանտությունից: Դիցուք մասնիկը  արագությամբ ժամանակամիջոցում տեղափոխվել է  հեռավորության վրա: Այդ իրադարձության միջակայքը`

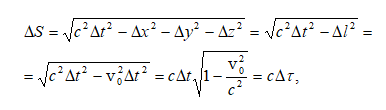
որտեղ պատահարի սեփական ժամանակն է: Քանի որ c-ն և  ինվարիանտներ են, ապա ինվարիանտ է նաև նրանց արտադրյալը, ուստի, ինվարիանտ է և միջակայքը՝

Երբ միջակայքի արժեքը իրական է՝  այն կոչվում է ժամանականման:

Դրանով հաստատվում է, որ միևնույն տիեզերական կետում կամ երկու տարբեր  տիեզերական կետերում կատարված պատահարների միջև կարող է լինել պատճառահետևանքային կապ: Օրինակ, երբ տվյալ կետում տեղի է ունենում որևէ երևույթի սկիզբն ու վերջը,

Միջակայքի զրոյական արժեքը՝  համապատասխանում է վակուումում լույսի տարածմանը, քանի որ այդ դեպքում

Երբ միջակայքի արժեքը կեղծ է`  այն կոչվում է տարածանման: Դա վկայում է, որ երկու  տիեզերական կետերում կատարված պատահարները պատճառահետևանքային կապի մեջ չեն գտնվում, քանի որ ոչ մի ազդեցություն կամ ազդանշան չի կարող տարածվել c-ից մեծ արագությամբ:

>>

7.6. ԱՐԱԳՈՒԹՅՈՒՆՆԵՐԻ ԳՈՒՄԱՐՄԱՆ ՌԵԼՅԱՏԻՎԻՍՏԱԿԱՆ ՕՐԵՆՔԸ

Օգտվելով Լորենցի ձևափոխություններից` կարող ենք գրել

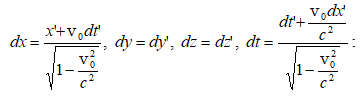
Գտնենք նկ.7.2-ում պատկերված  համակարգերի նկատմամբ շարժվող M մասնիկի  արագությունների՝  պրոյեկցիաների միջև կապը:

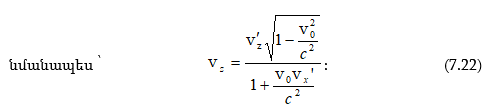
Եթե  արագություններն ուղղված են առանցքներին զուգահեռ՝ ապա, համաձայն 7.20-ի,

(7.23) առնչությունն արտահայտում է արագությունների գումարման ռելյատիվիստական օրենքը, որի համաձայն ոչ մի իներցիալ հաշվարկման համակարգի նկատմամբ մարմնի արագությունը չի կարող գերազանցել լույսի տարածման c արագությանը վակուումում:

Հետևություններ.

1) եթե  ապա v<<c: Դա նշանակում է, որ եթե հաշվարկման որևէ համակարգում մարմինը շարժվում է  արագությամբ, ապա ցանկացած ուրիշ համակարգում նրա արագությունը չի գերազանցի և նույնիսկ չի հասնի լույսի արագությանը:

2) եթե  ապա և v<c: Համոզվելու համար (7.23) բանաձևի մեջ տեղադրենք

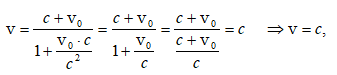
այսինքն՝ վակուումում լույսի արագությունն ունի նույն արժեքը հաշվարկման բոլոր իներցիալ համակարգերում:

3) եթե  ապա, պարզեցնելով (7.23) բանաձևը, կստանանք արագությունների գումարման օրենքը նյուտոնյան մեխանիկայում՝

>>

7.7. ՌԵԼՅԱՏԻՎԻՍՏԱԿԱՆ ԴԻՆԱՄԻԿԱՅԻ ՏԱՐՐԵՐԸ

Ռելյատիվիստական իմպուլսը և զանգվածը

Հարաբերականության հատուկ տեսության առաջին կանխադրույթի համաձայն, բոլոր պահպանման օրենքները ցանկացած իներցիալ համակարգում պետք է գործեն նույնությամբ, իսկ այդ օրենքներին վերաբերող ֆիզիկական մեծությունները պետք է ինվարիանտ լինեն Լորենցի ձևափոխությունների նկատմամբ: Այս պայմանին բավարարում է ռելյատիվիստական իմպուլսի հետևյալ արտահայտությունը.

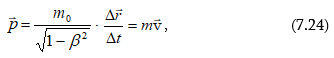
որտեղ  ներկայացնում է մարմնի դադարի զանգվածը, որն, ինչպես և  մարմնի սեփական ժամանակը, որոշվում է այն հաշվարկման համակարգում, որտեղ մարմինը և չափիչ գործիքները գտնվում են դադարի վիճակում, իսկ m-ը մեկնաբանվում է որպես  արագությամբ շարժվող մարմնի ռելյատիվիստական զանգված`

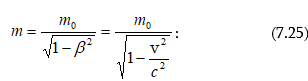
(7.25) առնչությունից բխում է,որ զանգվածի կախումը արագությունից զգացնել է տալիս միայն այն դեպքում, երբ մարմինը շարժվում է վակուումում լույսի տարածման c արագությանը մոտ արագությամբ:

 Ինչպես նյուտոնյան մեխանիկայում, այնպես էլ ռելյատիվիստական մեխանիկայում, զանգվածն իներտության չափն է: Սակայն մարմնի իներտությունը հաստատուն չի մնում, այլ մեծանում է շարժման արագության աճին զուգընթաց (նկ.7.5):

Ֆիզիկորեն դա նշանակում է, որ ինչքան մեծ է շարժման արագությունը, այնքան «դժվար» է փոխել այդ արագությունը: Լույսի արագությանը մոտ արագությունների դեպքում մարմնի իներտությունն այնքան արագ է աճում, որ արագության հետագա մեծացումը դառնում է անհնարին:  դեպքում զանգվածի անվերջ աճով էլ բացատրվում է լույսի արագությանը անհասանելիության հանգամանքը:

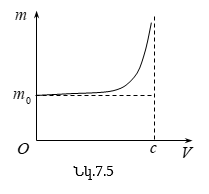
Այստեղից հետևում է, որ ոչ մի մարմին, որն օժտված է ոչ զրոյական  հանգստի զանգվածով, չի կարող շարժվել վակուումում լույսի արագությանը հավասար արագությամբ:

Հարաբերականության տեսությունը չի բացառում այնպիսի մասնիկների գոյությունը, որոնք շարժվում են լույսի արագությամբ: Այդպիսի մասնիկներ են ֆոտոնները, որոնց հանգստի զանգվածը հավասար է զրոյի: Ֆոտոնները վակուումում շարժվում են միշտ լույսի արագությանը հավասար արագությամբ: Հաշվի առնելով իմպուլսի (7.24) ռելյատիվիստական արտահայտությունը և տեղադրելով այն Նյուտոնի երկրորդ օրենքի (2.1) բանաձևի մեջ` կստանանք համընթաց շարժման դինամիկայի ռելյատիվիստական օրենքը՝

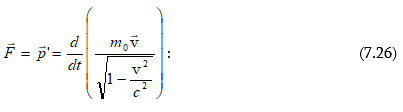
Ռելյատիվիստական դինամիկայի հիմնական օրենքից հետևում է, որ

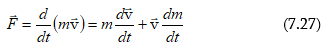
(7.27) -ից արագացման համար ստանում ենք

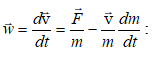
Նկատի ունենալով զանգվածի կախումը արագությունից` կարելի է ապացուցել, որ նյութական կետի արագացման և այն առաջացնող ուժի միջև կապն ունի հետևյալ տեսքը.

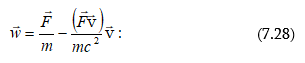
Ի տարբերություն դասական մեխանիկայի, ռելյատիվիստական մեխանիկայում արագացումն ընդհանուր դեպքում չի համընկնում այն առաջացնող ուժի ուղղության հետ: Միայն երկու դեպքում է, որ արագացման վեկտորը միագիծ է ուժի վեկտորին:

1. Նյութական կետի վրա ազդում է լայնական ուժ, որն առաջացնում է արագության փոփոխություն միայն ըստ ուղղության, արագության մոդուլը և ռելյատիվիստական զանգվածը չեն փոփոխվում:  ուստի Հետևաբար

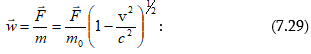
2. Նյութական կետի վրա ազդում է երկայնական ուժ, որն առաջ է բերում արագության մոդուլի և զանգվածի փոփոխություն.

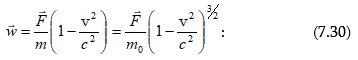
Մոդուլով հավասար ուժերից լայնական ուժը նյութական կետին հաղորդում է ավելի մեծ արագացում, քան երկայնական ուժը: Այս օրինաչափությունը հաշվի է առնվում լիցքավորված մասնիկների գծային և ցիկլային արագացուցիչների հաշվարկման դեպքում:

>>

7.8. ՌԵԼՅԱՏԻՎԻՍՏԱԿԱՆ ԷՆԵՐԳԻԱ: ԷՆԵՐԳԻԱՅԻ

ԵՎ ԶԱՆԳՎԱԾԻ ԿԱՊԸ

Էներգիայի ռելյատիվիստական արտահայտությունը գտնելու համար (7.26) hավասարումը բազմապատկենք  տեղափոխությամբ: Արդյունքում կստանանք

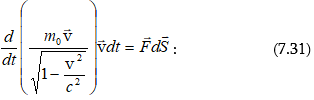
Այս առնչության աջ մասը տալիս է dA աշխատանքը, որը dt ժամանակում ծախսվում է մասնիկի վրա: Համաձայն կինետիկ էներգիայի թեորեմի` բոլոր ուժերի համազորի աշխատանքը ծախսվում է մասնիկի կինետիկ էներգիայի փոփոխության վրա: Հետևաբար, (7.31) առնչության ձախ մասը պետք է մեկնաբանվի որպես մասնիկի T կինետիկ էներգիայի աճ dt ժամանակում: Այսպիսով,

Ձևափոխելով ստացված արտահայտությունը և նկատի ունենալով, որ

կստանանք`

Ստացված առնչության ինտեգրումից ստացվում է.

Ինտեգրման հաստատունը որոշենք` ելնելով այն պայմանից, որ երբ v=0, մարմնի կինետիկ էներգիան ևս հավասար է զրոյի (T=0): (7.33) առնչությունից ստանում ենք.

Այդ դեպքում կինետիկ էներգիայի ռելյատիվիստական արտահայտությունն ունենում է հետևյալ տեսքը`

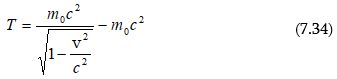
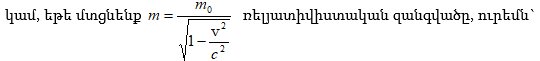
Այսպիսով, կինետիկ էներգիան հանդես է գալիս որպես էներգիաների տարբերություն, որոնցով օժտված է մարմինը շարժման և դադարի վիճակներում: Շարժվող մարմինն օժտված է էներգիայով, որը կախված է ռելյատիվիստական զանգվածից: Եզրակացությունը հետևյալն է, ինչպիսի վիճակում էլ որ գտնվի մարմինը, այն օժտված է լրիվ ռելյատիվիստական էներգիայով, այսինքն.

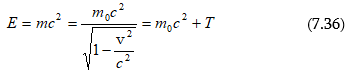
Եթե մարմինը հանգստի վիճակում է (v=0), էներգիան`

(7.37) հանգստի էներգիայի առկայությունը թույլ է տալիս յուրաքանչյուր մարմին դիտարկել որպես պոտենցիալ էներգիայի ինչ-որ ամբար, որը կարող է փոխարկվել էներգիայի ցանկացած այլ տեսակների: Այս դեպքում ոչ մի նշանակություն չունի մարմնի ներքին կառուցվածքը. այն կարող է լինել պարզ (տարրական մասնիկ) կամ բարդ (ատոմ, բյուրեղ, մարմինների համակարգ): Ո՞րն է (7.37) բանաձևի իմաստը:

 Այս բանաձևը ցույց է տալիս այն առավելագույն էներգիան, որը կարող է ստացվել  հանգստի զանգված ունեցող մարմնից, եթե այդ մարմինն ամբողջովին փոխակերպվում է հանգստի զանգվածից զրկված նյութական օբյեկտի, այսինքն՝ մարմնի էլեկտրամագնիսական ճառագայթման:

Այսպիսով, նշված օրենքը ցույց է տալիս նյութի հետ կապված էներգիայի անցման սկզբունքային հնարավորությունը և հակառակը:

Այսպիսի ուղիղ անցման դասական օրինակ է էլեկտրոնի միացման ռեակցիան պոզիտրոնի հետ (միևնույն հանգստի զանգվածով երկու մասնիկներ), որի արդյունքում էլեկտրոնը և պոզիտրոնը դադարում են գոյություն ունենալուց՝ փոխարկվելով էլեկտրամագնիսական ճառագայթման, ընդ որում, ճառագայթման էներգիան ճշտորեն հավասար է երկու մասնիկների հանգստի էներգիաների գումարին (ենթադրվում է, որ մասնիկները կինետիկ էներգիա չունեն):

Հակառակ անցման օրինակ է էլեկտրոն-պոզիտրոն զույգի առաջացումը էլեկտրամագնիսական ճառագայթման քվանտներից:

Եթե  հանգստի զանգվածով մարմինն անջատում  էներգիա, ապա դրանից հետո մարմնի հանգստի զանգվածը պետք է փոքրանա  ընդ որում, հանգստի էներգիան հանգստի զանգվածի հետ դարձյալ պետք է կապված լինի

առնչությամբ: Այստեղից հետևում է, որ

 մեծությունը կոչվում է զանգվածի պակասորդ: Այն ցույց է տալիս, թե որքանով կփոքրանա մարմնի հանգստի զանգվածը, եթե այն տալիս է  էներգիա, կամ հակառակը, որքանով կմեծանա մարմնի հանգստի զանգվածը, եթե այն կլանել է  էներգիա: Այս պնդումը կոչվում է ռելյատիվիստական զանգվածի և էներգիայի փոխադարձ կապի օրենք:

Գտնենք ոչ ռելյատիվիստական կինետիկ էներգիայի արտահայտությունը (7.36) հավասարությունից.

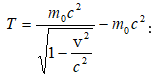
Երբ մարմնի արագությունը շատ մեծ չէ (v<<c) ,

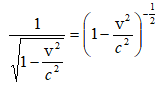
արտահայտությունը կարելի է ներկայացնել

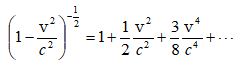
տեսքով, և, սահմանափակվելով այս վերլուծության առաջին երկու անդամներով, T-ի համար կստանանք.

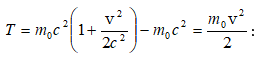
Իսկ սա սովորական (ոչ ռելյատիվիստական) կինետիկ էներգիայի բանաձևն է: Այսպիսով, պարզվում է, որ կինետիկ էներգիայի համար սովորական բանաձևը ճիշտ է միայն փոքր արագությունների դեպքում: T-ի ճշգրիտ արժեքը ցանկացած արագությունների դեպքում  հաշվվում է (7.34) ռելյատիվիստական բանաձևով:

>>

7.9. ԷՆԵՐԳԻԱՅԻ ԿԱՊԸ ԻՄՊՈՒԼՍԻ ՀԵՏ

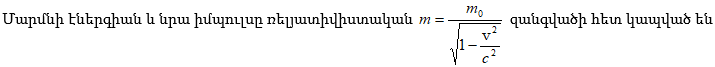
առնչություններով, որտեղ  մարմնի արագությունն է: Երկու հավասարումները բարձրացնելով քառակուսի, որից հետո երկրորդ հավասարումը բազմապատկելով  կստանանք՝

Առաջին հավասարումից հանելով երկրորդը, ստանում ենք.

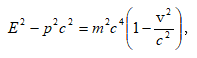
կամ

Մենք ստացանք էներգիայի որոնելի կապը իմպուլսի հետ.

Մարմնի  հանգստի զանգվածը և լույսի c արագությունը վակուումում բոլոր իներցիալ համակարգերում ունեն անփոփոխ արժեք: Այս մեծությունները ինվարիանտ են Լորենցի ձևափոխությունների նկատմամբ: Ինչ վերաբերում է E-ին և p-ին, մի իներցիալ համակարգից մյուսին անցնելիս այդ մեծություններն, ընդհանրապես, փոփոխվում են: Բայց, ինչպես հետեվում է (7.39)-ից,  տարբերությունը բոլոր իներցիալ համակարգերում պահպանվում է: Այսպիսով,  մեծությունը ինվարիանտ է Լորենցի ձևափոխությունների նկատմամբ: Այս է  միջև գտնված կապի կարևոր յուրահատկությունը: (7.39)-ից գտնենք E ռելյատիվիստական էներգիան.

Այստեղից հետևում է, որ ռելյատիվիստական էներգիայով օժտված են նաև այնպիսի մարմինները (նյութական օբյեկտները), որոնք չունեն հանգստի զանգված Ներկայումս հայտնի են երկու այդպիսի մասնիկներ. ֆոտոնը և նեյտրինոն: Այդ մասնիկների էներգիան`

իսկ իմպուլսը՝

Սա նշանակում է, որ ֆոտոնների, ինչպես նաև նեյտրինոների հոսքերը պետք է ճնշում գործադրեն: Լույսի ճնշումը չափվել է Լեբեդևի կողմից:

Նշենք, որ հարաբերականության հատուկ տեսության բոլոր բանաձևերը վերածվում են նյուտոնյան մեխանիկայի բանաձևերի, երբ մարմինները շարժվում են վակուումում լույսի տարածման արագությունից զգալիորեն փոքր արագությամբ՝ v<<c: Դրանով ապացուցվում է, որ նյուտոնյան մեխանիկան ռելյատիվիստական մեխանիկայի մասնավոր դեպքն է: Այսինքն՝ հարաբերականության հատուկ տեսությունն ընդգրկում է իր մեջ նյուտոնյան մեխանիկան և դասական մեխանիկայի ընդհանուր տեսությունն է:

Խնդիր1: Որոշել v=0.9c արագությամբ շարժվող էլեկտրոնի իմպուլսը և կինետիկ էներգիան:

Լուծում: Մասնիկի իմպուլս է կոչվում մասնիկի զանգվածի և արագության արտադրյալը.

Քանի որ էլեկտրոնի արագությունը մոտ է լույսի արագությանը, անհրաժեշտ է հաշվի առնել զանգվածի կախումը արագությունից, որը որոշվում է

բանաձևով, որտեղ m-ը շարժվող մասնիկի զանգվածն է,  մասնիկի հանգստի զանգվածը,  Փոխարինելով (1)-ի մեջ m զանգվածը իր (2) արտահայտությամբ և նկատի ունենալով, որ  կստանանք`

 Տեղադրելով (3) բանաձևի մեջ մտնող մեծությունների թվային արժեքները կստանանք`

Ռելյատիվիստական մեխանիկայում մասնիկի T կինետիկ էներգիան որոշվում է, որպես մասնիկի E լրիվ էներգիայի և  հանգստի էներգիայի տարբերություն, այսինքն

Քանի որ  ապա հաշվի առնելով զանգվածի կախումը արագությունից, ստանում ենք`

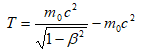
կամ

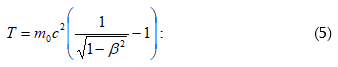
Տեղադրելով թվային արժեքները ստանում ենք`

Խնդիր 2. Մասնիկի կինետիկ էներգիան հավասար է իր հանգստի էներգիային: Որոշել մասնիկի արագությունը:

Լուծում: Մասնիկի կինետիկ էներգիան`  որտեղ E-ն մասնիկի շարժման էներգիան է և որոշվում է

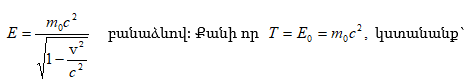
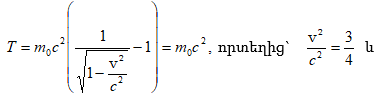
Խնդիր 3. Ինչպիսի արագացնող պոտենցիալների տարբերություն պետք է անցնի էլեկտրոնը, որպեսզի նրա երկայնական չափերը փոքրանան երկու անգամ:

Լուծում: Լորենցի ձևափոխություններից բխում է, որ

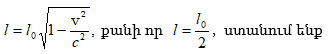
Խնդիր 4: Որոշել  զանգվածով մասնիկի արագության կախումը ժամանակից, եթե շարժումը միաչափ է, ուժը հաստատուն է, և շարժման հավասարումը ռելյատիվիստական է:

Լուծում: Ըստ Նյուտոնի օրենքի

>>

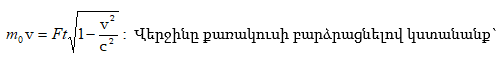
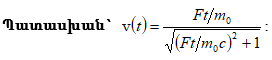
ԳԼՈՒԽ 8. ՄԵԽԱՆԻԿԱԿԱՆ ՏԱՏԱՆՈՒՄՆԵՐ

8.1. ՆԵՐԴԱՇՆԱԿ ՏԱՏԱՆՈՒՄՆԵՐ ԵՎ ԴՐԱՆՑ ԲՆՈՒԹԱԳՐԻՉՆԵՐԸ

Տատանումներ են կոչվում այն շարժումները կամ պրոցեսները, որոնց տարբերակիչ առանձնահատկությունը որոշ աստիճանի կրկնողականությունն է: Կրկնողականության այսպիսի հատկությամբ օժտված են, օրինակ, ժամացույցի ճոճանակի տատանումները, լարի կամ կամերտոնի ոտիկների տատանումները, փոփոխական հոսանքը և այլն: Ճոճանակի տատանողական շարժման դեպքում փոփոխվում է նրա զանգվածի կենտրոնի կոորդինատը, փոփոխական հոսանքի դեպքում շղթայում փոփոխվում են լարումը և հոսանքը: Տատանողական պրոցեսները լայն տարածում են գտել բնության մեջ և տեխնիկայում: Շատ դեպքերում դրանք բացասական դեր են խաղում: Միաժամանակ տատանողական պրոցեսներն ընկած են տեխնիկայի տարբեր բնագավառների հիմքում: Այսպես` տատանողական պրոցեսների վրա է հիմնված ամբողջ ռադիոտեխնիկան:

Տատանումների ֆիզիկական բնույթը կարող է լինել տարբեր, ուստի զանազանում են հետևյալ տատանումները` մեխանիկական, էլեկտրամագնիսական, էլեկտրամեխանիկական և այլն: Սակայն տարբեր տատանողական պրոցեսներ նկարագրվում են միատեսակ բնութագրիչներով և միատեսակ հավասարումներով: Այստեղից էլ հետևում է տարբեր ֆիզիկական բնույթի տատանումների ուսումնասիրությանը միատեսակ մոտեցման նպատակահարմարությունը: Օրինակ, մեխանիկական և էլեկտրամագնիսական տատանումներին միատեսակ մոտեցում են ցուցաբերել անգլիացի ֆիզիկոս Դ. Ռելեյը, Ա. Ստոլետովը,Պ. Լեբեդևը: Տատանումների տեսության զարգացման մեջ մեծ ավանդ է դրել Լ. Մանդելշտամը:

Ազատ կամ սեփական են կոչվում այն տատանումները, որոնք տեղի են ունենում ինքն իրեն թողնված համակարգում` հարված հաղորդելուց կամ իր հավասարակշռության դիրքից դուրս բերելուց հետո: Օրինակ, թելից կախված գնդիկի (ճոճանակի) տատանումները: Տատանումներ առաջացնել կարելի է` կամ գնդիկին էներգիա հաղորդելով կամ այն մի կողմ տանելուց հետո բաց թողնելով:

Տատանումների պարզագույն տեսակ են ներդաշնակ տատանումները: Ֆիզիկական մեծության` ժամանակից կախված այնպիսի պարբերական փոփոխությունները, որոնք տեղի են ունենում սինուսի կամ կոսինուսի օրենքով, կոչվում են ներդաշնակ տատանումներ: Ներդաշնակ տատանումների դիտարկումը կարևոր է երկու պատճառով. 1) բնության մեջ և տեխնիկայում տատանումները հաճախ ունենում են ներդաշնակ տատանումներին շատ մոտ բնույթ, 2) տարբեր պարբերական պրոցեսները կարելի է ներկայացնել մի քանի ներդաշնակ տատանումների վերադրումով: s մեծության ներդաշնակ տատանումները նկարագրվում են հետևյալ հավասարումով`

որտեղ A-ն տատանվող մեծության առավելագույն արժեքն է և կոչվում է տատանման լայնույթ,  շրջանային (ցիկլային) հաճախությունն է: Պարբերաբար փոփոխվող կոսինուսի արգումենտը`  կոչվում է տատանման փուլ և որոշում է տատանվող մեծության շեղումը հավասարակշռության դիրքից ժամանակի t պահին:  մեծությունը ներդաշնակ հավասարման մեջ կոչվում է սկզբնական փուլ, և այն որոշում է տատանվող մեծության շեղումը հավասարակշռության դիրքից ժամանակի t=0 պահին:

Սկզբնական փուլի արժեքը որոշվում է` ժամանակի հաշվարկման սկիզբն ընտրելով: Քանի որ կոսինուսը փոփոխվում է +1-ից մինչև -1 սահմաններում, ապա s-ը կարող է ընդունել +A-ից մինչև -A արժեքները: Քանի որ կոսինուսը պարբերական ֆունկցիա է  պարբերությամբ, ապա ներդաշնակ տատանումներ կատարող համակարգի տարբեր վիճակները կրկնվում են այնպիսի T ժամանակից հետո, որի ընթացքում տատանման փուլը ստանում է  հավասար աճ: T ժամանակը կոչվում է տատանման պարբերություն: Այն կարելի է որոշել հետևյալ պայմանից`

որտեղից

Միավոր ժամանակում կատարված տատանումների թիվը կոչվում է տատանումների հաճախություն, որը նշանակում են  Ակնհայտ է, որ  հաճախությունը մեկ տատաման T տևողության հետ կապված է հետևյալ առնչությամբ`

 Որպես հաճախության միավոր ընդունում են այն տատանման հաճախությունը, որի պարբերությունը հավասար է 1վ-ի: Այս միավորը կոչվում է հերց (կրճատ`Հց): Համեմատելով (8.2) և (8.3) արտահայտությունները` կստանանք Այստեղից հետևում է, որ ցիկլային հաճախությունը թվապես հավասար է  մարմնի կատարած տատանումների թվին:

Գտնենք ներդաշնակորեն տատանվող s մեծության առաջին և երկրորդ կարգի ածանցյալներն ըստ ժամանակի.

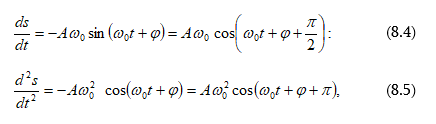
այսինքն ստանում ենք նույն ցիկլային հաճախությամբ ներդաշնակ տատանումներ: (8.4) և (8.5) մեծությունների լայնույթները համապատասխանաբար հավասար են  (8.4) մեծության փուլը (8.1) մեծության փուլից տարբերվում է  իսկ (8.5) մեծության փուլը (8.1) մեծության փուլից տարբերվում է Հետևաբար, ժամանակի այն պահին, երբ  ձեռք է բերում առավելագույն արժեք. երբ s-ը հասնում է բացասական առավելագույն արժեքին, ապա  ունի առավելագույն դրական արժեք (նկ.8.1, սկզբնական փուլը`

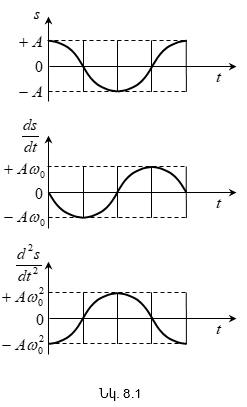
Արտահայտություն (8.5) -ից հետևում է ներդաշնակ տատանումների դիֆերենցիալ հավասարումը

Այս հավասարման լուծումը (8.1) արտահայտությունն է :

 Ներդաշնակ տատանումները պատկերվում են գրաֆիկորեն, այսինքն` հարթության մեջ վեկտորների տեսքով: Այդպիսի եղանակով ստացված սխեման կոչվում է վեկտորական դիագրամ: Վերցնենք x-ի առանցքի վրա կամայական O կետից տեղադրենք  վեկտորը, որի մոդուլը հավասար է A լայնույթին և առանցքի հետ կազմում է  անկյուն, որը հավասար է սկզբնական փուլին (նկ.8.2): Եթե այդ վեկտորը պտտման մեջ դնենք  անկյունային արագությամբ, ապա վեկտորի ծայրի պրոյեկցիան կտեղափոխվի x առանցքի վրա –A-ից մինչև +A-ի սահմաններում, ընդ որում այս պրոյեկցիայի կոորդինատը ժամանակի ընթացքում կփոփոխվի  օրենքով: Հետևաբար, վեկտորի ծայրի պրոյեկցիան առանցքի վրա կկատարի ներդաշնակ տատանում, որի լայնույթը հավասար է վեկտորի երկարությանը, շրջանային հաճախությունը` վեկտորի պտտման անկյունային արագությանը, իսկ սկզբնական փուլը` ժամանակի սկզբնական պահին առանցքի հետ վեկտորի կազմած անկյանը:

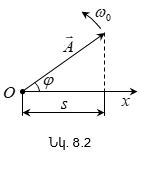
Ֆիզիկայում հաճախ օգտագործվում է մի ուրիշ մեթոդ, որը տարբերվում է վերը նկարագրված մեթոդից: Այդ մեթոդում տատանվող մեծությունը ներկայացնում են կոմպլեքս թվով: Համաձայն Էյլերի բանաձևի` կոմպլեքս թվերի համար

որտեղ  կեղծ միավոր է: Ուստի ներդաշնակ տատանումների (8.1) հավասարումը կարելի է գրել կոմպլեքս տեսքով.

(8.8) արտահայտության իրական մասը`

պայմանավորվում ենք բաց թողնել և (8.8)-ը գրում ենք  տեսքով: Տատանումների տեսությունում ընդունվում է, որ տատանվող s մեծությունը հավասար է կոմպլեքս արտահայտության իրական մասին, որը կանգնած է այդ հավասարության աջ մասում:

>>

8.2. ՄԵԽԱՆԻԿԱԿԱՆ ՆԵՐԴԱՇՆԱԿ ՏԱՏԱՆՈՒՄՆԵՐ

Դիցուք նյութական կետը կատարում է կոորդինատային x առանցքի երկայնքով ուղղագիծ ներդաշնակ տատանումներ հավասարակշռության դիրքի շուրջը, որն ընդունվում է կոորդինատների սկիզբ:

Հետևաբար x կոորդինատի կախումը t ժամանակից տրվում է (8.1) հավասարումով, որտեղ s=x.

Համաձայն (8.4) և (8.5) արտահայտությունների` տատանվող կետի v արագությունը և արագացումը համապատասխանաբար կլինեն`

Նկատի ունենալով (8.9)-ը և (8.10)-ը` m զանգվածով տատանվող նյութական կետի վրա ազդող ուժը`

Հետևաբար, ուժը համեմատական է հավասարակշռության դիրքից նյութական կետի շեղմանը և ուղղված է դեպի հավասարակշռության դիրքը:

Ներդաշնակ տատանումներ կատարող նյութական կետի կինետիկ էներգիան`

կամ

Առաձգական F ուժի ազդեցության տակ ներդաշնակ տատանումներ կատարող նյութական կետի պոտենցիալ էներգիան հավասար է.

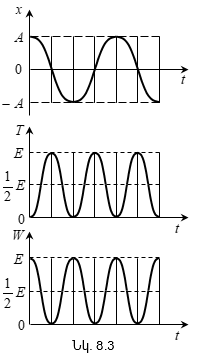
Այսպիսով, ներդաշնակ տատանումների դեպքում լրիվ մեխանիկական էներգիան պահպանվում է, քանի որ առաձգական ուժը կոնսերվատիվ է:

 (8.12) և (8.14) բանաձևերից հետևում է, որ T-ն և W- ն փոփոխվում են  հաճախությամբ, այսինքն` այնպիսի հաճախությամբ, որը երկու անգամ գերազանցում է ներդաշնակ տատանումների հաճախությանը: Նկ. 8.3-ում պատկերված են x-ի, T-ի և W-ի ժամանակից կախվածության գրաֆիկները:

>>

8.3. ՆԵՐԴԱՇՆԱԿ ՏԱՏԱՆԱԿ, ՖԻԶԻԿԱԿԱՆ ԵՎ

ՄԱԹԵՄԱՏԻԿԱԿԱՆ ՃՈՃԱՆԱԿՆԵՐ

Ներդաշնակ տատանակ է կոչվում այն համակարգը, որի տատանումները նկարագրվում են (8.6) տեսքի հավասարումով.

Ներդաշնակ տատանակի տատանումները պարբերական շարժման կարևոր օրինակ են և ծառայում են ճշգրիտ կամ մոտավոր մոդել քվանտային և դասական ֆիզիկայի շատ խնդիրներում: Ներդաշնակ տատանակի օրինակներ են զսպանակավոր, ֆիզիկական և մաթեմատիկական ճոճանակները, տատանողական կոնտուրը:

Զսպանակավոր ճոճանակ: Անկշիռ առաձգական զսպանակից և նրան ամրացված m զանգվածով գնդիկից կազմված համակարգը կոչվում է զսպանակավոր ճոճանակ: Այդպիսի համակարգը ներդաշնակ տատանումներ է կատարում F=-kx առաձգական ուժի ազդեցության տակ, որտեղ k-ն զսպանակի կոշտությունն է: Շփման ուժերի բացակայության դեպքում ճոճանակի շարժման հավասարումը`

 (8.16)-ից և (8.1)-ից հետևում է, որ զսպանակավոր ճոճանակը կատարում է ներդաշնակ տատանումներ ըստ

ցիկլիկ հաճախությամբ և

պարբերությամբ:

Զսպանակավոր ճոճանակի պոտենցիալ էներգիան ըստ (8.13) և (8.17)-ի կլինի`

Ֆիզիկական ճոճանակ: Ֆիզիկական ճոճանակ է կոչվում այն պինդ մարմինը, որը կարող է տատանվել նրա իներցիայի կենտրոնի հետ չհամընկնող անշարժ կետի շուրջը: Հավասարակշռության դիրքում ճոճանակի իներցիայի C կենտրոնը գտնվում է O կախման կետի տակ` նրա հետ միասին միևնույն ուղղաձիգի տակ (նկ.8.4):

Եթե ճոճանակը հավասարակըշռությունից շեղենք անկյունով, առաջանում է պտտող մոմենտ, որը ձգտում է ճոճանակը վերադարձնել հավասարակշռության դիրքը: Դրա համար էլ ինչպես շեղմանը և առաձգական ուժին, այնպես էլ M մոմենտին և անկյունային շեղմանը վերագրում ենք հակառակ նշաններ: Այդ մոմենտը`

որտեղ m-ը ճոճանակի զանգվածն է,  կախման կետի և ճոճանակի իներցիայի կենտրոնի միջև եղած հեռավորությունը: Նշանակելով ճոճանակի իներցիայի մոմենտը կախման կետով անցնող առանցքի նկատմամբ J-ով և օգտվելով պտտական շարժման դինամիկայի օրենքից` կարելի է գրել

Ճոճանակի փոքր տատանումների դեպքում (հավասարակշռության դիրքից ճոճանակի փոքր անկյունային շեղումներ)  Հետևաբար, (8.19) հավասարումը կարելի է գրել հետևյալ տեսքով`

Ընդունելով

կստանանք հետևյալ հավասարումը`

որը նման է (8.9) հավասարմանը, որի լուծումը մեզ հայտնի է.

(8.21) արտահայտությունից հետևում է, որ հավասարակշռության դիրքից փոքր շեղումների դեպքում ֆիզիկական ճոճանակը կատարում է ներդաշնակ տատանումներ ցիկլային հաճախությամբ, որը որոշվում է (8.20) բանաձևով և

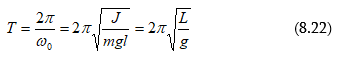
Կախման կետն իներցիայի կենտրոնի հետ միացնող ուղղի վրա գտնվող  կետը, որն ընկած է պտտման առանցքից բերված երկարությանը հավասար հեռավորության վրա, կոչվում է ֆիզիկական ճոճանակի ճոճման կենտրոն:

Ըստ Շտայների թեորեմի` ճոճանակի իներցիայի J մոմենտը կախման կետով անցնող առանցքի նկատմամբ որոշվում է հետևյալ բանաձևով`

որտեղ  իներցիայի մոմենտն է ճոճանակի իներցիայի կենտրոնով անցնող առանցքի նկատմամբ:

Նկատի ունենալով (8.23)-ը` բերված երկարության համար կստանանք`

այսինքն  միշտ մեծ է CO-ից, այնպես, որ կախման կետը և ճոճման կենտրոնը գտնվում են իներցիայի կենտրոնի տարբեր կողմերում: Կախման կետը և ճոճման կենտրոնն օժտված են փոխադարձաբար միմյանց փոխարինելու հատկությամբ, այսինքն` ճոճման կետը կախման կետով փոխարինելու դեպքում սկզբնական կախման կետը դառնում է ճոճման կետ: Հետևաբար, հանգում ենք այն եզրակացության, որ ճոճանակը ճոճման կենտրոնից կախելու դեպքում բերված երկարությունը, ինչպես նաև ֆիզիկական ճոճանակի տատանումների պարբերությունը կլինեն այնպիսին, ինչպիսին նախորդ դեպքում էին:

Մաթեմատիկական ճոճանակ: Մաթեմատիկական ճոճանակ է կոչվում իդեալականացված համակարգը, որը բաղկացած է m զանգվածով նյութական կետից, որը կախված է չձգվող և անկշիռ թելից: Իրական ճոճանակը կարելի է համարել մաթեմատիկական, եթե թելի երկարությունը շատ մեծ է կախված մարմնի չափերից, թելի զանգվածը շատ փոքր է մարմնի զանգվածից, իսկ թելի դեֆորմացիաներն այնքան փոքր են, որ թելի երկարությունը կարելի է համարել անփոփոխ: Լավ մոտավորությամբ մաթեմատիկական ճոճանակ է ոչ մեծ ծանր գնդիկը, որը կախված է բարակ երկար թելից:

Մաթեմատիկական ճոճանակի իներցիայի մոմենտը`

Քանի որ մաթեմատիկական ճոճանակը կարելի է պատկերացնել որպես ֆիզիկական ճոճանակի մասնավոր դեպք, ենթադրելով, որ նրա ամբողջ զանգվածը կենտրոնացված է զանգվածի կենտրոնում, ապա տեղադրելով (8.24) արտահայտությունը (8.22) բանաձևի մեջ` կստանանք փոքր տատանումների համար մաթեմատիկական ճոճանակի տատանումների պարբերությունը.

Համեմատելով (8.22) և (8.25) բանաձևերը` տեսնում ենք, որ եթե ֆիզիկական ճոճանակի բերված L երկարությունը հավասար է մաթեմատիկական ճոճանակի երկարությանը, ապա այդ ճոճանակների պարբերությունները իրար հավասար են: Հետևաբար, ֆիզիկական ճոճանակի բերված երկարությունն այնպիսի մաթեմատիկական ճոճանակի երկարությունն է, որի տատանումների պարբերությունը համընկնում է տրված ֆիզիկական ճոճանակի պարբերության հետ:

>>

8.4. ՄԻԵՎՆՈՒՅՆ ՈՒՂՂՈՒԹՅՈՒՆԸ ԵՎ ՄԻԵՎՆՈՒՅՆ

ՀԱՃԱԽՈՒԹՅՈՒՆՆԵՐ ՈՒՆԵՑՈՂ ՏԱՏԱՆՈՒՄՆԵՐԻԳՈՒՄԱՐՈՒՄԸ: ԶԱՐԿԵՐ

Տատանվող մարմինը կարող է մասնակցել միաժամանակ մի քանի տատանումների: Եթե, օրինակ, զսպանակը, որի ծայրին ամրացված է գնդիկ, կախենք այն վագոնի առաստաղից, որը ճոճվում է զսպանակների վրա, ապա գնդիկի շարժումը Երկրի մակերևույթի նկատմամբ բաղկացած կլինի Երկրի նկատմամբ վագոնի տատանումներից և վագոնի նկատմամբ գնդիկի տատանումներից:

Քննարկենք միևնույն ուղղություններով և միատեսակ հաճախություններով կատարվող երկու ներդաշնակ տատանումների գումարումը: Տատանվող մարմնի արդյունարար x շեղումը հավասար կլինի  շեղումների գումարին, որոնցից յուրաքանչյուրը տրվում է հետևյալ հավասարումներով`

Oգտվելով լայնույթի վեկտորի պտտման մեթոդից` կառուցենք այդ տատանումների վեկտորական դիագրամը (նկ.8.5): Քանի որ  վեկտորները պտտվում են միևնույն  անկյունային արագությամբ, ապա նրանց միջև  փուլերի տարբերությունը մնում է հաստատուն: Ակներև է, որ արդյունարար տատանումը կլինի.

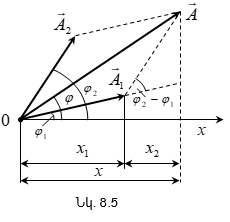
(8.26) արտահայտության մեջ A լայնույթը և սկզբնական փուլը տրվում են համապատասխանաբար հետևյալ առնչություններով`

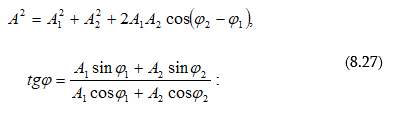
Այսպիսով, արդյունարար տատանումը նույնպես ներդաշնակ տատանում է, որը տեղի է ունենում նույն ուղղությամբ, ինչ որ գումարվող տատանումները և կատարվում են այդ տատանումների հաճախությանը հավասար հաճախությամբ:

Վերլուծենք (8.27) արտահայտությունը` կախված  փուլերի տարբերությունից.

1) եթե գումարվող տատանումների փուլերի տարբերությունը`  ապա արդյունարար տատանման A լայնույթը հավասար է գումարվող տատանումների A<sub>1</sub> և A<sub>2</sub> լայնույթների գումարին`A= A₁ + A₂:

2)  այսինքն` արդյունարար տատանման A լայնույթը հավասար է գումարվող տատանումների A₁ և A₂ լայնույթների տարբերության բացարձակ արժեքին:

Գործնականում հատուկ հետաքրքրություն է ներկայացնում այն դեպքը, երբ միևնույն ուղղությամբ կատարվող երկու ներդաշնակ տատանումների գումարման դեպքում դրանց հաճախություններն աննշան տարբերվում են իրարից: Այդ տատանումների գումարման արդյունքում ստացվում են պարբերաբար փոփոխվող լայնույթով տատանումներ: Տատանումների լայնույթի պարբերական փոփոխությունները, որոնք առաջանում են իրար մոտ հաճախություններով երկու ներդաշնակ տատանումների գումարման դեպքում, կոչվում են Դիցուք գումարվող տատանումների A լայնույթները իրար հավասար են, հաճախությունները`  ընդ որում  Հաշվարկման սկիզբն ընտրենք այնպես, որպեսզի երկու տատանումների սկզբնական փուլերը հավասար լինեն զրոյի.

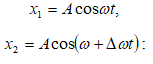
 Գումարելով այս արտահայտությունները և նկատի ունենալով, որ  ստանում ենք`

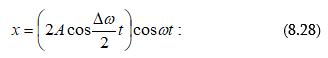
Արդյունարար (8.28) տատանումը կարելի է դիտարկել որպես  հաճախությամբ ներդաշնակ տատանում, որի  լայնույթը փոփոխվում է հետևյալ պարբերական օրենքով`

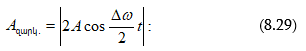
 փոփոխման հաճախությունը երկու անգամ մեծ է կոսինուսի փոփոխման հաճախությունից (քանի որ վերցվում է ըստ մոդուլի), այսինքն` զարկումների հաճախությունը հավասար է գումարվող տատանումների հաճախությունների տարբերությանը.

Զարկումների պարբերությունը`

(8.28)-ի կախվածության բնույթը ցույց է տրված նկ. 8.6-ում, որտեղ անընդհատ գծերը տալիս են (8.28) արդյունարար տատանման գրաֆիկը, իսկ, նրանց պարուրիչը շտրիխներով` լայնույթի դանդաղ փոփոխման գրաֆիկը ըստ (8.29) հավասարման:

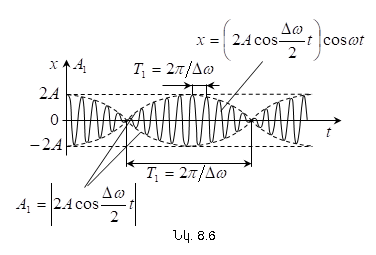
Զարկումների տոնի հաճախության որոշումը էտալոնային և չափվող տատանումների միջև գործնականում օգտագործվող ավելի լայն կիրառելի մեթոդ է` համեմատելու չափվող մեծությունը էտալոնայինի հետ:

>>

8.5. ՓՈԽՈՒՂՂԱՀԱՅԱՑ ՏԱՏԱՆՈՒՄՆԵՐԻ ԳՈՒՄԱՐՈՒՄԸ

 Դիտարկենք միևնույն  հաճախություններով երկու ներդաշնակ տատանումների գումարման արդյունքը, որոնք տեղի են ունենում փոխուղղահայաց ուղղություններով x և y առանցքների երկայնքով: Պարզության համար հաշվարկման սկիզբն ընդունենք այնպես, որ առաջին տատանման սկզբնական փուլը հավասար լինի զրոյի և գրենք.

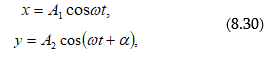
որտեղ  երկու տատանումների փուլերի տարբերությունն է,  գումարվող տատանումների լայնույթներն են:

Արդյունարար տատանումների հետագծի հավասարումը ստանալու համար պետք է (8.30) հավասարումներից արտաքսել t պարամետրը:

Գումարվող տատանումները գրենք հետևյալ տեսքով.

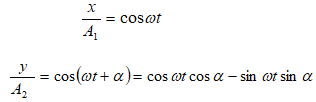
և փոխարինելով երկրորդ հավասարման մեջ  ոչ բարդ ձևափոխություններից հետո կստանանք էլիպսի հավասարում, որի առանցքները կոորդինատային առանցքների նկատմամբ կողմնորոշված են կամայականորեն.

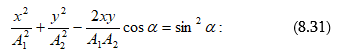
Քանի որ արդյունարար տատանման հետագիծն ունի էլիպսի տեսք, ապա այդպիսի տատանումները կոչվում են Էլիպսի կողմնորոշումը և նրա չափերը կախված են գումարվող տատանումների լայնույթներից և  փուլերի տարբերությունից: Քննարկենք մի քանի մասնավոր դեպքեր.

որտեղ «+» նշանը համապատասխանում է m-ի զրո և զույգ արժեքներին նկ. 8.7, ա), իսկ «-»-ը` m-ի կենտ արժեքներին (նկ. 8.7, բ)

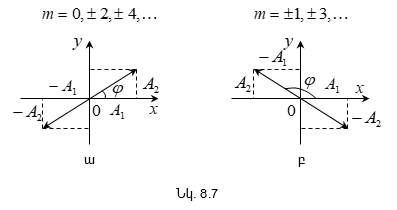
Արդյունարար տատանումը  հաճախությամբ և  լայնույթով տատանում է, որը կատարվում է (8.32) ուղղի երկայնքով x առանցքի հետ կազմելով  անկյուն: Տվյալ դեպքում գործ ունենք գծային բևեռացված տատանումների հետ:

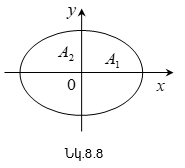
Այս հավասարումը էլիպսի հավասարում է, որի առանցքները համընկնում են կոորդինատային առանցքների հետ, իսկ կիսաառանցքները համապատասխանաբար հավասար են լայնույթներին (նկ. 8.8):  լայնույթների հավասարության դեպքում էլիպսը վերածվում է շրջանագծի: Այդպիսի տատանումները կոչվում են շրջանով բևեռացված տատանումներ:

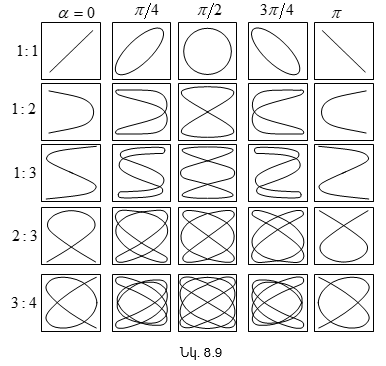
Եթե փոխուղղահայաց տատանումների հաճահաճախուխությունները միատեսակ չեն, արդյունարար տատանման հետագիծն ունի բավականին բարդ տեսք. դրանք կոչվում են Լիսաժուի պատկերներ: Այդ կորերի տեսքը կախված է լայնույթների, հաճախությունների հարաբերակցությունից և վերադրվող տատանումների փուլերի տարբերությունից: Նկ. 8.9-ում բերված են Լիսաժուի պատկերները տարբեր հաճախությունների (ցույց է տրված ձախից) հարաբերակցության և փուլերի տարբերության ցույց է տրված վերևում, փուլերի տարբերությունը ընդունվում է հավասար  համար:

Ըստ պատկերների ձևի կարելի է որոշել անհայտ հաճախությունը կամ որոշել գումարվող տատանումների հաճախությունների հարաբերությունը: Ուստի Լիսաժուի պատկերների վերլուծությունը հաճախությունների և գումարվող տատանումների փուլերի տարբերության հարաբերակցության, ինչպես նաև տատանումների ձևի հետազոտությունների լայն օգտագործման մեթոդ է:

>>

8.6. ՄԵԽԱՆԻԿԱԿԱՆ ՄԱՐՈՂ ՏԱՏԱՆՈՒՄՆԵՐԻ ԴԻՖԵՐԵՆՑԻԱԼ

ՀԱՎԱՍԱՐՈՒՄԸ ԵՎ ՆՐԱ ԼՈՒԾՈՒՄԸ: ԻՆՔՆԱՏԱՏԱՆՈՒՄՆԵՐ

Քննարկենք այն ազատ մարող տատանումները, որոնց լայնույթները իրական տատանվող համակարգում էներգիայի կորստի պատճառով ժամանակի ընթացքում փոքրանում են: Տատանումների էներգիայի նվազման պարզագույն մեխանիզմը մեխանիկական տատանողական համակարգերում շփման հետևանքով նրա էներգիայի փոխակերպումն է ջերմաքանակի, ինչպես նաև էլեկտրական տատանողական համակարգերում էլեկտրական դաշտի էներգիան աստիճանաբար փոխակերպվում է հաղորդալարերի ներքին էներգիայի (դրանք տաքանում են), որի պատճառով տատանումները մարում են: Տատանումների մարման օրենքը որոշվում է տատանողական համակարգի հատկություններով: Սովորաբար քննարկում են իդեալականացված իրական համակարգեր, որոնցում համակարգի ֆիզիկական հատկությունները որոշող պարամետրերը պրոցեսի ընթացքում չեն փոփոխվում: Գծային համակարգեր են օրինակ, զսպանակավոր ճոճանակը զսպանակի փոքր դեֆորմացիաների դեպքում (երբ ճիշտ է Հուկի օրենքը), տատանողական կոնտուրը, որի ինդուկտիվությունը, ունակությունը և դիմադրությունը կախված չեն կոնտուրում ոչ հոսանքից և ոչ էլ լարումից:

Ըստ իրենց բնույթի տարբեր գծային համակարգերը նկարագրվում են համանման գծային դիֆերենցիալ հավասարումներով, ինչն էլ հնարավորություն է տալիս տարբեր ֆիզիկական բնույթի տատանումների ուսումնասիրությանը միատեսակ մոտեցում ցուցաբերել, ինչպես նաև կատարել նրանց մոդելավորում, այդ թվում և հաշվիչ մեքենաներով:

Գծային համակարգերի ազատ մարող տատանումների դիֆերենցիալ հավասարումը տրվում է հետևյալ տեսքով`

որտեղ s-ը տատանվող մեծությունն է, որը նկարագրում է այս կամ այն ֆիզիկական պրոցես,  մարման գործակիցն է,  նույն տատանողական համակարգի ազատ չմարող տատանումների ցիկլային հաճախությունն է, այսինքն  դեպքում (էներգիայի կորստի բացակայության դեպքում) կոչվում է տատանողական համակարգի սեփական հաճախություն:

(8.34) հավասարման լուծումը փնտրենք հետևյալ տեսքով`

Գտնելով (8.35) արտահայտության առաջին և երկրորդ կարգի ածանցյալները, (8.34) -ի մեջ տեղադրելուց հետո կստանանք`

(8.36) հավասարման լուծումը կախված է որոնելի մեծության առաջ դրված գործակցի նշանից: Քննարկենք այն դեպքը, երբ այդ գործակիցը դրական է.

Այդ դեպքում ստանում ենք (8.16) տեսքի հավասարում, որի լուծումը`  ֆունկցիան է (տես (8.1)): Այսպիսով, (8.34) հավասարման լուծումը փոքր մարումների դեպքում

որտեղ

մարող տատանումների լայնույթն է, A₀-ն սկզբնական լայնույթն է: (8.38) կախվածության գրաֆիկը բերված է նկ. 8.10-ում անընդհատ գծով, իսկ (8.39) կախվածությունը` կետագծերով:

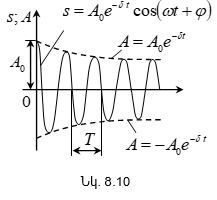
Գտնենք այն ժամանակը, որի ընթացքում լայնույթը փոքրանում է e անգամ: Ըստ սահմանման  որտեղից  Հետևաբար, մարման գործակցի մեծությունը հակադարձ համեմատական է այն ժամանակամիջոցին, որի ընթացքում լայնույթը փոքրանում է e անգամ:  կոչվում է ռելաքսացիայի ժամանակ: Մարումը խանգարում է տատանումների պարբերականությանը, ուստի մարող տատանումները պարբերական չեն և, խիստ ասած, դրանց նկատմամբ կիրառելի չէ պարբերության և հաճախության հասկացությունը: Սակայն, եթե մարումը փոքր է, ապա պայմանականորեն կարելի է օգտվել պարբերության հասկացությունից որպես տատանվող ֆիզիկական մեծության երկու հաջորդական առավելագույնների (կամ նվազագույնների) միջև ժամանակի միջակայք (նկ.8.10): Ուստի մարող տատանումների պարբերությունը, նկատի ունենալով (8.37) բանաձևը, կստանանք`

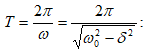
Մի պարբերությամբ իրարից տարբերվող ժամանակի պահերին համապատասխանող լայնույթների արժեքների հարաբերությոնը`

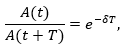
կոչվում է մարման դեկրեմենտ, իսկ նրա լոգարիթմը`

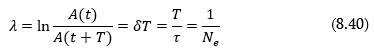
մարման լոգարիթմական դեկրեմենտ: N_e-ն տատանումների այն թիվն է, որը կատարվում է այն ժամանակամիջոցում, որի ընթացքում տատանման լայնույթը փոքրանում է e անգամ: Տվյալ համակարգի համար լոգարիթմական դեկրեմենտը հաստատուն մեծություն է:

Տատանողական համակարգի բնութագրման համար օգտագործում են Q բարորակության հասկացությունը, որը լոգարիթմական դեկրեմենտի փոքր արժեքների դեպքում`

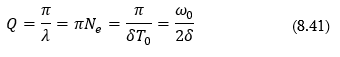
(քանի որ մարումը աննշան է  (8.41) բանաձևից հետևում է, որ բարորակությունը ուղիղ համեմատական է տատանումների այն N_e թվին, որը կատարում է համակարգը ռելաքսացիայի ժամանակամիջոցում:

Արտածումները, որոնք ստացվեցին գծային համակարգերի համար, կիրառելի են տարբեր բնույթի ֆիզիկական տատանումների համար` մեխանիկական և էլեկտրական (որպես օրինակ կքննարկենք ֆիզիկական ճոճանակը): Զանգվածով զսպանակավոր ճոճանակի համար, որը կատարում է փոքր տատանումներ F=-kx առաձգական ուժի ազդեցության տակ, շփման ուժը համեմատական է արագությանը, այսինքն`

որտեղ r-ը դիմադրության գործակիցն է, բացասական նշանը ցույց է տալիս, որ դիմադրության ուժը և արագությունն ունեն հակառակ ուղղություններ: Տվյալ պայմանների դեպքում ճոճանակի շարժման օրենքը կունենա հետևյալ տեսքը`

Oգտագործելով  բանաձևը և նկատի ունենալով, որ

կստանանք (8.34)-ին համանման ճոճանակի մարող տատանումների դիֆերենցիալ հավասարումը.

(8.34) և (8.38) արտահայտություններից հետևում է, որ ճոճանակի տատանումները ենթարկվում են հետևյալ օրենքին`

որտեղ

Զսպանակավոր ճոճանակի բարորակությունը համաձայն (8.41) և (8.43) բանաձևերի`

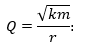
Վերջում նշենք, որ մարման գործակցի մեծացման դեպքում մարող տատանումների պարբերությունը մեծանում է և  դեպքում դառնում է  այսինքն շարժումը դառնում է ոչ պարբերական: Այս դեպքում տատանվող մեծությունը ասիմպտոտիկորեն մոտենում է զրոյի, երբ  Տվյալ պրոցեսը տատանողական չէ, դառնում է ապերիոդիկ:

Տեխնիկայի համար մեծ հետաքրքրություն ունի չմարող տատանումների պահպանելու հնարավորությունը: Դրա համար անհրաժեշտ է համալրել էներգիայի կորուստը իրական տատանողական համակարգում: Հատկապես կարևոր և լայն կիրառական է այսպես կոչված չմարող տատանումները որոնք պահպանվում են դիսիպատիվ համակարգում արտաքին էներգիայի աղբյուրի հաշվին, ընդ որում այդ տատանումների հատկությունները որոշվում է հենց իր` համակարգով: Ինքնատատանումները, ինչպես և հարկադրական տատանումները ուղեկցվում են տատանվող համակարգի վրա արտաքին ուժերի ազդեցությամբ, սակայն ժամանակի այն պահերը, երբ տեղի է ունենում այս ազդեցությունները, որոշվում է հենց իր` տատանվող համակարգի կողմից, այսինքն` ինքը տատանվող համակարգն է ղեկավարում արտաքին ազդեցությունները: Օրինակ` ժամացույցը, որի մեջ ճոճանակը հրվում է վեր բարձրացրած ծանրության կամ ոլորված զսպանակի էներգիայի հաշվին, ընդ որում այս հրումները տեղի են ունենում այն պահին, երբ ճոճանակն անցնում է իր միջին դիրքով:

Ինքնատատանողական համակարգեր են նաև ներքին այրման շարժիչները, շոգետուրբինները, լամպային գեներատորները և այլն:

>>

8.7. ՄԵԽԱՆԻԿԱԿԱՆ ՀԱՐԿԱԴՐԱԿԱՆ ՏԱՏԱՆՈՒՄՆԵՐԻ

ԴԻՖԵՐԵՆՑԻԱԼ ՀԱՎԱՍԱՐՈՒՄԸ ԵՎ ՆՐԱ ԼՈՒԾՈՒՄԸ

Որպեսզի իրական տատանողական համակարգում ստացվեն չմարող տատանումներ հարկավոր է կոմպենսացնել էներգիայի կորուստը: Այդպիսի կոմպենսացումը հնարավոր է ինչ որ պարբերաբար ազդող X(t) գործոնի օգնությամբ, որը փոփոխվում է ներդաշնակ օրենքով.

Եթե դիտարկենք մեխանիկական տատանումները, ապա X(t)-ի դերը խաղում է հարկադրող ուժը`

հաշվի արնելով (8.44)-ը զսպանակավոր ճոճանակի շարժման օրենքի համար (8.42)-ը գրվում է հետևյալ տեսքով`

Օգտագործելով (8.17)-ը և (8.43)-ը` գալիս ենք հետևյալ հավասարման`

Այն տատանումները, որոնք առաջանում են արտաքին պարբերաբար փոփոխվող ուժի ազդեցության տակ, կոչվում են (8.45) հավասարուը կարելի է բերել անհամասեռ գծային դիֆերենցիալ հավասարման.

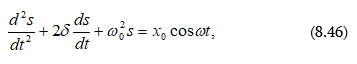
Կիրառելով հավասարման լուծումը կոնկրետ ֆիզիկական բնույթի ստիպողական տատանումների համար (մեխանիկական տատանումների դեպքում  հավասար է

(8.46) հավասարման ընդհանուր լուծումը հավասար է (8.34) համասեռ հավասարման (8.38) լուծման և անհամասեռ հավասարման մասնակի լուծումների գումարին: Մասնակի լուծումը գտնենք կոմպլեքս տեսքով:

(8.46) հավասարման աջ մասը փոխարինելով  մեծությամբ կստանանք`

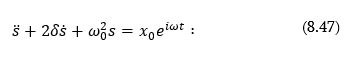
 Այս հավասարման մասնակի լուծումը փնտրենք  տեսքով: Տեղադրելով s-ի և նրա ածանցյալների արտահայտությունները`  հավասարման մեջ, կստանանք`

Քանի որ այս հավասարությունը պետք է ճիշտ լինի ժամանակի բոլոր պահերին, ուստի t ժամանակը նրանից պետք է արտաքսել: Այստեղից հետևում է, որ  Վերջինը նկատի ունենալով` (8.48)-ից կգտնենք  մեծությունը և նրա համարիչը և հայտարարը բազմապատկելով  ստանում ենք`

Այս կոմպլեքս թիվը հարմար է ներկայացնել էքսպոնենցիալ տեսքով`

որտեղ

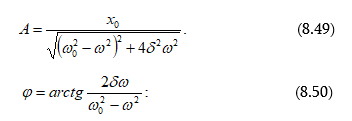
Հետևաբար, (8.47) հավասարման լուծումը կոմպլեքս ձևով կընդունի հետևյալ տեսքը`

Նրա իրական մասը, որը (8.46) հավասարման լուծումն է, հավասար է`

որտեղ  համապատասխանաբար տրվում են (8.49)-ով և (8.50)-ով:

Այսպիսով (8.46) անհամասեռ հավասարման մասնակի լուծումը ունի հետևյալ տեսքը`

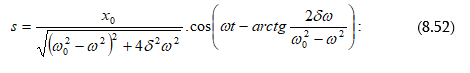
(8.46) հավասարման լուծումը հավասար է ընդհանուր համասեռ հավասարման լուծման (տես (8.38))

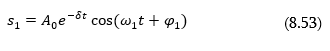
և (8.52) մասնակի լուծման գումարին: (8.53)-ի գումարելին զգալի դեր է խաղում միայն պրոցեսի սկզբնական փուլում, այսպես կոչված, տատանումների հաստատման փուլում (նկ. 8.12):

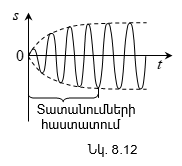
Ժամանակի ընթացքում  էքսպոնենցիալ արտադրիչի առկայությամբ (8.53) գումարելիի դերն առավել փոքրանում է, և բավականաչափ ժամանակ անցնելուց հետո այն կարելի է անտեսել` լուծման մեջ պահպանելով միայն (8.51) գումարելին:

Այսպիսով, (8.52) ֆունկցիան նկարագրում է հաստատված հարկադրական տատանումները: Դրանք ներդաշնակ տատանումներ են, որոնց հաճախությունը հավասար է հարկադրող ուժի հաճախությանը:

>>

8.8. ՄԵԽԱՆԻԿԱԿԱՆ ՀԱՐԿԱԴՐԱԿԱՆ ՏԱՏԱՆՈՒՄՆԵՐԻ

ԼԱՅՆՈՒՅԹԸ ԵՎ ՓՈՒԼԸ: ՌԵԶՈՆԱՆՍ

Քննարկենք հարկադրական տատանումների A լայնույթի կախվածությունը հաճախությունից: (8.49) բանաձևից հետևում է, որ շեղման A լայնույթը ունի առավելագույն արժեք: Որպեսզի որոշվի ռեզոնանսային  հաճախությունը, որի դեպքում շեղման A լայնույթը հասնում է առավելագույնի, հարկավոր է գտնել (8.49) ֆունկցիայի առավելագույնը կամ, որ նույնն է արմատանշանի տակ գտնվող արտահայտության նվազագույնը: Ածանցելով այդ արտահայտությունն ըստ  և ստացված արդյունքը հավասարեցնելով զրոյի, կստանանք  որոշող պայմանը.

Զրոյի հավասար լուծումը համապատասխանում է հայտարարի առավելագույնին: Մնացած երկու լուծումներից բացասականը պետք է դեն նետել, քանի որ այն ոչ մի ֆիզիկական իմաստ չունի (hաճախությունը բացասական չի կարող լինել): Այսպիսով ռեզոնանսային հաճախության համար ստացվում է մեկ արժեք, այսինքն`

Հարկադրական տատանումների լայնույթի կտրուկ աճի երևույթը, հաճախությունը մոտենում կամ հավասարվում է տատանվող համակարգի սեփական հաճախությանը կոչվում է ռեզոնանս: պայմանի դեպքում գործնականում  համընկնում է տատանողական համակարգի  հաճախության հետ: Տեղադրելով (8.54)-ը (8.49)-ի մեջ կստանանք`

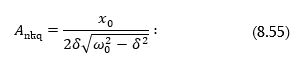
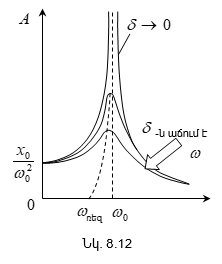
Նկ. 8.12-ում բերված են տատանումների լայնույթի կախվածությունը  տարբեր արժեքների դեպքում: (8.54)-ից և (8.55)-ից հետևում է, որ որքան փոքր է  այնքան բարձր և աջ է ընկած տվյալ կորի առավելագույնը: Երբ  ապա բոլոր կորերը հասնում են միևնույն զրոյից տարբեր սահմանային`  արժեքին, որն անվանում են Մեխանիկական տատանումների դեպքում` Եթե ապա բոլոր կորերը ասիմպտոտիկորեն ձգտում են զրոյի: Բերված կորերի ամբողջությունը կոչվում են ռեզոնանսային կորեր: (8.55) բանաձևից հետևում է, որ փոքր մարումների դեպքում  շեղման ռեզոնանսային լայնույթը`

(8.55) բանաձևից հետևում է, որ փոքր մարումների դեպքում  շեղման ռեզոնանսային լայնույթը`

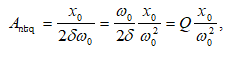
որտեղ Q-ն տատանվող համակարգի բարորակությունն է: Այստեղից հետևում է, որ Q բարորակությունը բնութագրում է տատանողական համակարգի ռեզոնանսային հատկությունը: Որքան մեծ է Q-ն, այնքան մեծ է

Նկ. 8.13-ում բերված են ռեզոնանսային կորերը արագության լայնույթի համար: Արագության լայնույթը`

առավելագույնն է  դեպքում և հավասար է  այսինքն` որքան մեծ էմարման գործակիցը, այնքան ցածր է ռեզոնանսային կորի առավելագույնը: Օգտագործելով (8.43) և (8.17)-ը մեխանիկական ռեզոնանսի դեպքում կստանանք, որ արագության լայնույթը`

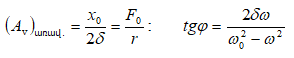
արտահայտությունից հետևում է, որ եթե համակարգում մարումը բացակայում է  ապա միայն այդ դեպքում է, որ տատանումները և հարկադրող ուժը ունեն միևնույն փուլը, մնացած բոլոր դեպքերում  կախվածությունը  տարբեր մարման գործակիցների դեպքում գրաֆիկորեն պատկերված է նկ.8.14-ում, որից հետեվում է, որ  փոփոխության դեպքում փոփոխվում է և փուլերի շեղումը: (8.50) բանաձևից բխում է, որ  դեպքում  դեպքում անկախ մարման գործակցի արժեքից  այսինքն` ուժը առաջ է ընկնում ըստ փուլի  հետագա մեծացման դեպքում փուլերի շեղումը մեծանում է և  դեպքում  այսինքն տատանման փուլը համարյա հակառակ է արտաքին ուժի փուլին: Նկ.8.14-ում պատկերված կորերի ընտանիքը, կոչվում է փուլային ռեզոնանսային կորեր:

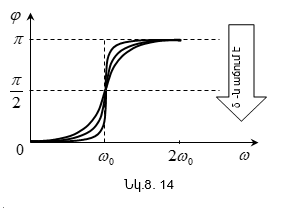
Ռեզոնանսի երևութը հարկավոր է հաշվի առնել մեքենաներ և տարբեր տեսակի կառույցներ նախագծելիս: Այդ սարքերի տատանումների սեփական հաճախությունը ոչ մի դեպքում չպետք է մոտ լինի հնարավոր արտաքին ազդեցությունների հաճախությանը: Այսպես, նավի կմախքի կամ ինքնաթիռի թևերի թրթռումների սեփական հաճախությունը պետք է տարբերվի այն տատանումների հաճախությունից, որոնք կարող են առաջանալ թիապտուտակի կամ պրոպելլերի պտույտից: Հակառակ դեպքում առաջանում են թրթռումներ, որոնք կարող են աղետների պատճառ դառնալ: Հայտնի են դեպքեր, երբ կամուրջները փլվել են նրանց վրայով զինվորների զորասյունը համաքայլ անցնելու ժամանակ: Այս դեպքերը տեղի են ունեցել այն պատճառով, որ կամրջի տատանումների սեփական հաճախությունը մոտ է եղել զորասյան քայլելու հաճախությանը: Միաժամանակ ռեզոնանսի երևույթը հաճախ շատ օգտակար է լինում մանավանդ ակուստիկայում, ռադիոտեխնիկայում և այլն:

>>

ԳԼՈՒԽ 9. ԱՌԱՁԳԱԿԱՆ ԱԼԻՔՆԵՐ

9.1. ԱԼԻՔԱՅԻՆ ՊՐՈՑԵՍՆԵՐ: ԵՐԿԱՅՆԱԿԱՆ ԵՎ ԼԱՅՆԱԿԱՆ

ԱԼԻՔՆԵՐ

Տատանումները, որոնք գրգռվում են միջավայրի (պինդ, հեղուկ կամ գազային) որևէ կետում տարածվում են նրա մեջ վերջավոր արագությամբ, որը կախված է միջավայրի հատկություններից` փոխանցվելով միջավայրի մի կետից մյուսին: Որքան միջավայրի մասնիկները հեռու են դասավորված տատանման աղբյուրից, այնքան ավելի ուշ են տատանվում: Այլ կերպ ասած` միջավայրի մասնիկների և աղբյուրի տատանումների փուլը մեկը մյուսից այնքան ավելի շատ են տարբերվում, որքան մեծ է այդ հեռավորությունը: Տատանումների տարածման ուսումնասիրության դեպքում հաշվի չի առնվում միջավայրի ընդհատ (մոլեկուլային) կառուցվածքը, և միջավայրը դիտարկվում է որպես անընդհատ, այսինքն` տարածության մեջ անընդհատ բաշխված և օժտված առաձգական հատկություններով:

Անընդհատ միջավայրում տատանումների տարածման պրոցեսը կոչվում է ալիքային պրոցես (կամ ալիք): Ալիքի տարածման դեպքում միջավայրի մասնիկները ալիքի հետ միասին չեն շարժվում, այլ տատանվում են իրենց հավասարակշռության դիրքի շուրջը: Ալիքի հետ միասին միջավայրի մի մասնիկից մյուսին հաղորդվում է միայն տատանողական շարժման վիճակը և նրա էներգիան: Ուստի բոլոր ալիքների հիմնական հատկությունը, անկախ նրանց բնույթից, էներգիայի տեղափոխությունն է առանց նյութի տեղափոխության:

Ալիքի տարածան ուղղության նկատմամբ մասնիկների տատանումների ուղղություններից կախված տարբերում են երկայնական և լայնական ալիքներ: Երկայնական են կոչվում այն ալիքները, որոնց տարածման ուղղությունը համընկնում է միջավայրի մասնիկների տատանումների ուղղությանը:

Լայնական են կոչվում այն ալիքները, որոնց տարածման ուղղությունն ուղղահայաց է միջավայրի մասնիկների տատանման ուղղությանը:

Միջավայրում մեխանիկական ալիքներն առաջանում են առաձգականության ուժերի շնորհիվ: Երկայնական ալիքների տարածման ժամանակ տեղի են ունենում միջավայրի խտացումներ և նոսրացումներ, իսկ լայնական ալիքների տարածման ժամանակ` միջավայրի շերտերի սահք միմյանց նկատմամբ: Սեղմման և ձգման դեֆորմացիաների դեպքում միշտ առաջանում են առաձգական ուժեր, իսկ սահքի դեֆորմացիաներն առաջ են բերում առաձգական ուժեր միայն պինդ մարմիններում: Հեղուկներում և գազերում շերտերի սահքի դեպքում առաձգականության ուժեր չեն առաջանում: Ուստի երկայնական ալիքները կարող են տարածվել բոլոր միջավայրերում` և պինդ մարմիններում, և հեղուկներում, և գազերում, իսկ լայնական ալիքները` միայն պինդ մարմիններում:

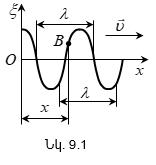
Առաձգական ալիքը կոչվում է ներդաշնակ, եթե նրան համապատասխանող միջավայրի մասնիկների տատանումները նույնպես ներդաշնակ են: Նկ. 9.1-ում պատկերված է ներդաշնակ լայնական ալիք, որը տարածվում է x-ի առանցքի երկայնքով v արագությամբ, այսինքն բերված է ալիքային պրոցեսին մասնակցող միջավայրի մասնիկի  շեղման և այդ մասնիկների (օրինակ B մասնիկ) x հեռավորության կախվածությունը տատանման O աղբյուրից ինչ-որ ֆիքսված ժամանակի t պահի hամար: Բերված  ֆունկցիայի գրաֆիկը հիշեցնում է ներդաշնակ տատանման գրաֆիկը, սակայն ըստ էության դրանք տարբեր են: Ալիքի գրաֆիկը տալիս է միջավայրի բոլոր մասնիկների շեղումները մինչև տատանումների աղբյուրը եղած հեռավորություններից ժամանակի տվյալ պահին, իսկ տատանումների գրաֆիկը տալիս է մասնիկի շեղման կախվածությունը ժամանակից (տես նկ.9.1) Միևնույն փուլով տատանվող ամենամոտ կետերի միջև եղած հեռավորությունը կոչվում է ալիքի երկարություն (նկ. 9.1): Ակնհայտ է, որ ալիքի երկարությունը հավասար է այն հեռավորությանը, որն անցնում է ալիքը մեկ պարբերության ընթացքում, այսինքն`

կամ նկատի ունենալով, որ  որտեղ  տատանման հաճախությունն է,

Իրականում տատանվում են ոչ միայն x առանցքի վրա դասավորված մասնիկները, այլև որոշ ծավալում պարփակված մասնիկների ամբողջությունը: Տարածվելով տատանումների աղբյուրից, ալիքային պրոցեսն ընդգրկում է տարածության ավելի ու ավելի նոր մասեր: Այն կետերի երկրաչափական տեղը, որոնց հասնում են տատանումները ժամանակի t պահին կոչվում է ալիքի ճակատ:

Միատեսակ փուլերով տատանվող կետերի երկրաչափական տեղը կոչվում է ալիքային մակերևույթ: Ալիքային մակերևույթը կարելի է անցկացնել ալիքային պրոցեսով ընդգրկված տարածության ցանկացած կետով: Հետևաբար, գոյություն ունեն անսահման բազմությամբ ալիքային մակերևույթներ, այն դեպքում, երբ ժամանակի յուրաքանչյուր պահի համար գոյություն ունի միայն մեկ ալիքային ճակատ: Ալիքային մակերևույթները լինում են ցանկացած ձևի: Պարզագույն դեպքում դրանք ունեն հարթության կամ գնդային մակերևույթի ձև: Համապատասխանաբար, այս դեպքերում ալիքը կոչվում է հարթ կամ սֆերիկ: Ալիքային մակերևույթները հարթ ալիքում իրար զուգահեռ հարթությունների ամբողջություն է, իսկ սֆերիկ ալիքում` համակենտրոն գնդային մակերևույթների ամբողջություն:

>>

9.2. ՎԱԶՈՂ ԱԼԻՔԻ ՀԱՎԱՍԱՐՈՒՄԸ: ՓՈՒԼԱՅԻՆ

 ԱՐԱԳՈՒԹՅՈՒՆ: ԱԼԻՔԱՅԻՆ ՀԱՎԱՍԱՐՈՒՄ

Վազող ալիքներ են կոչվում այն ալիքները, որոնք տարածության մեջ տեղափոխում են էներգիա: Ալիքի էներգիայի տեղափոխությունը քանակապես բնութագրվում է էներգիայի հոսքի խտության վեկտորով: Առաձգական ալիքների համար այդ վեկտորը կոչվում է Ումովի վեկտոր: Ումովի վեկտորի ուղղությունը համընկնում է էներգիայի փոխադրման ուղղության հետ, իսկ նրա մոդուլը թվապես հավասար է այն էներգիային, որը տեղափոխում է ալիքը տեղափոխմանը ուղղահայաց միավոր մակերեսով միավոր ժամանակում:

Ալիքի հավասարում է կոչվում այն արտահատությունը, որը տալիս է տատանվող կետի շեղումը որպես ֆունկցիա նրա x, y, z կոորդինատներից և t ժամանակից`

Գտնենք  ֆունկցիայի տեսքը հարթ ալիքի դեպքում, ենթադրելով, որ տատանումները կրում են ներդաշնակ բնույթ: Պարզության համար կոորդինատային առանցքներն ուղղենք այնպես, որպեսզի x առանցքը համընկնի ալիքի տարածման ուղղության հետ: Այդ դեպքում ալիքային մակերևույթները ուղղահայաց կլինեն առանցքին, և քանի որ ալիքային մակերևույթի բոլոր կետերը միատեսակ են տատանվում,  շեղումը կախված կլինի միայն x-ից և t-ից, այսինքն`

Նկ. 9.1-ում դիտարկենք միջավայրի որևէ B մասնիկ, որը գտնվում է տատանման O աղբյուրից x հեռավորության վրա: Դիցուք x=0 հարթության մեջ գտնվող կետերի տատանումները ունեն հետևյալ տեսքը`

 ապա միջավայրի B մասնիկը տատանվում է նույն օրենքով, բայց նրա տատանումները  ժամանակով ետ կընկնեն աղբյուրի տատանումներից, քանի որ հեռավորությունն ալիքը անցնելու համար կպահանջվի ժամանակ, որտեղ v-ն ալիքի տարածման արագությունն է: Այդ դեպքում x հարթության մեջ ընկած մասնիկի տատանման հավասարումը կունենա հետևյալ տեսքը`

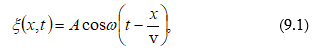
որտեղից հետևում է, որ  ոչ միայն ժամանակի պարբերական ֆունկցիա է, այլ նաև պարբերական ֆունկցիա է ըստ x կոորդինատի: (9.1) հավասարումը վազող ալիքի հավասարումն է: Եթե հարթ ալիքը տարածվում է հակառակ ուղղությամբ, ապա

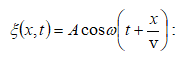
Ընդհանուր դեպքում էներգիան չկլանող միջավայրում x-ի առանցքի դրական ուղղությամբ տարածվող հարթ ալիքի հավասարումը կգրվի հետևյալ ձևով`

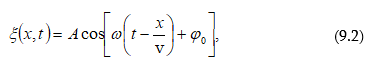
որտեղ A=const -ը ալիքի լայնույթն է,  ալիքի սկզբնական փուլն է, որն ընդհանուր դեպքում որոշվում է x-ի և t-ի հաշվարկման սկզբի ընտրությամբ.

Ալիքի բնութագրման համար օգտագործվում է ալիքային թիվը`

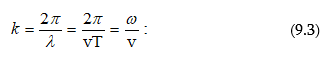
վեկտորը, որն ըստ մոդուլի հավասար է  ալիքային թվին և ուղղված է ալիքային մակերևույթի նորմալի ուղղությամբ, կոչվում է ալիքային վեկտոր:

Նկատի ունենալով (9.3)-ը (9.2) հավասարմանը` կարելի տալ հետևյալ տեսքը`

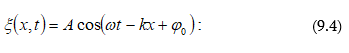
x-ի առանցքի բացասական ուղղության երկայնքով տարածվող ալիքի հավասարումը (9.4)-ից տարբերվում է միայն kx-ի նշանով:

Հիմնվելով Էյլերի (8.7) բանաձևի վրա` հարթ ալիքի հավասարումը կարելի է գրել հետևյալ տեսքով`

որտեղ ֆիզիկական իմաստ ունի միայն իրական մասը:

Ենթադրենք, որ ալիքային պրոցեսի դեպքում փուլը հաստատուն է, այսինքն`

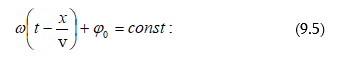
Ածանցելով (9.5) արտահայտությունը և կրճատելով  վրա կստանանք` որտեղից`

Հետևաբար, ալիքի տարածման v արագությունը (9.6) հավասարման մեջ ոչ այլ ինչ է, եթե ոչ ալիքի փուլի տեղափոխման արագությունը, և այն կոչվում է փուլային արագություն:

Եթե բոլոր ուղղություններով ալիքի տարածման արագությունը նույնն է, ապա կետային աղբյուրով ստեղծված ալիքը կլինի սֆերիկ: Սֆերիկ ալիքի հավասարումը գրվում է հետևյալ տեսքով`

որտեղ r-ը աղբյուրի կենտրոնից մինչև տարածության տվյալ կետն ընկած հեռավորությունն է:

Սֆերիկ ալիքի դեպքում, եթե նույնիսկ ալիքի էներգիան չի կլանվում միջավայրում, տատանումների լայնույթը հաստատուն չի մնում և աղբյուրից հեռանալու հետ միասին փոքրանում է  օրենքով:

(9.3)-ից երևում է, որ փուլային արագությունը`

Եթե ալիքների փուլային արագությունը միջավայրում կախված է հաճախությունից, այդ երևույթը կոչվում է ալիքների դիսպերսիա, իսկ միջավայրը, ուր դիտվում է ալիքների դիսպերսիա, կոչվում է դիսպերսող միջավայր: Ալիքների տարածումը համասեռ իզոտրոպ միջավայրում ընդհանուր դեպքում նկարագրվում է մասնակի ածանցյալներով դիֆերենցիալ հավասարումով, որը կոչվում է ալիքային հավասարում

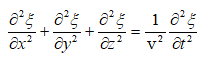
կամ

Ցանկացած ալիքի հավասարում (9.9)-ի հավասարման լուծումն է: Համապատասխան տեղադրումով կարելի է համոզվել, որ (9.9)-ի հավասարմանը բավարարում է, մասնավորապես (9.2) հարթ ալիքը և (9.7) սֆերիկ ալիքը: Հարթ ալիքի համար, որը տարածվում է x-ի առանցքի երկայնքով, ալիքային հավասարումն ունի հետևյալ տեսքը.

Հաշվարկները ցույց են տալիս, որ երկայնական ալիքների փուլային արագությունը որոշվում է հետևյալ բանաձևով`

Այսպիսով, երկայնական առաձգական ալիքների փուլային արագությունը հավասար է Յունգի մոդուլի և միջավայրի խտության հարաբերության քառակուսի արմատին:

Լայնական ալիքների համար կատարված հաշվարկները հանգեցնում են հետևյալ արտահայտությանը`

որտեղ G-ն սահքի մոդուլն է:

Վերադրման սկզբունքը: Խմբային արագություն: Եթե միջավայրը, որի մեջ տարածվում են միաժամանակ մի քանի ալիքներ գծային է, այսինքն` նրա հատկությունը չի փոփոխվում ալիքով ստեղծվող գրգռումների ազդեցության տակ, ապա նրան կիրառելի է վերադրման սկզբունքը: Գծային միջավայրում մի քանի ալիքների տարածման դեպքում, նրանցից յուրաքանչյուրը տարածվում է այնպես, կարծես թե մյուս ալիքները բացակայում են, իսկ միջավայրի մասնիկի արդյունարար շեղումը ժամանակի ցանկացած պահին հավասար է շեղումների երկրաչափական գումարին, որոնք ստանում են մասնիկները` մասնակցելով գումարվող պրոցեսներից յուրաքանչյուրին:

Ելնելով վերադրման սկզբունքից և Ֆուրյեի վերլուծությունից` ցանկացած ալիք կարելի է ներկայացնել ներդաշնակ ալիքների գումարի տեսքով, այսինքն` ալիքային ծրարի տեսքով կամ ալիքների խմբով:

Ելնելով վերադրման սկզբունքից և Ֆուրյեի վերլուծությունից` ցանկացած ալիք կարելի է ներկայացնել ներդաշնակ ալիքների գումարի տեսքով, այսինքն` ալիքային ծրարի տեսքով կամ ալիքների խմբով:

Ալիքային ծրար է կոչվում ալիքների վերադրումը, որոնք իրարից տարբերվում են աննշան հաճախություններով, զբաղեցնելով ժամանակի յուրաքանչյուր պահին տարածության սահմանափակ տիրույթ:

Քննարկենք ալիքների պարզագույն խումբ, որը ստացվում է x-ի դրական առանցքի երկայնքով տարածվող միատեսակ լայնույթներով, իրար մոտ հաճախություններով և ալիքային թվերով, ընդ որում`  երկու ներդաշնակ ալիքների վերադրման արդյունքում: Այդ դեպքում

Այս ալիքը ներդաշնակից տարբերվում է նրանով, որ

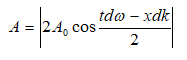
լայնույթը դանդաղ փոփոխվող ֆունկցիա է x կոորդինատից և t ժամանակից: Ոչ ներդաշնակ ալիքի (ալիքային ծրարի) տարածման արագություն ընդունում են ալիքի լայնույթի առավելագույնի տեղափոխությունը, դիտարկելով առավելագույնը որպես ալիքային ծրարի կենտրոն:  պայմանի դեպքում ստանում ենք`

որտեղ u-ն խմբային արագությունն է: Այն կարելի է սահմանել որպես ալիքների խմբի շարժման արագություն, կազմելով ժամանակի յուրաքանչյուր պահին տարածության մեջ տեղայնացված ալիքային ծրար:

(9.13) արտահայտությունը ստացվել է պարզագույն ալիքների խմբի համար երկու բաղադրիչներից, սակայն այն ճիշտ է նաև շատ ալիքների վերադրման համար:

Քննարկենք խմբային`  և փուլային`  արագությունների միջև կապը: Հաշվի առնելով, որ  կստանանք`

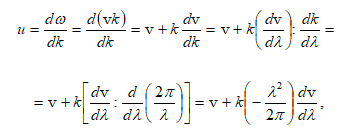
կամ

(9.14)-ից բխում է, որ u-ն կարող է լինել v-ից ինչպես փոքր, այնպես էլ մեծ` կախված  նշանից: Չդիսպերսող միջավայրում`  և խմբային արագությունը համընկնում է փուլայինի հետ:

Խմբային արագության հասկացությունը շատ կարևոր է ռադիոլոկացիայում. տիեզերական օբյեկտների ղեկավարման համակարգերում և այլ դեպքերում հեռավորությունների չափմանը հենց ինքն է մասնակցում: Հարաբերական տեսությունում ապացուցվում է, որ խմբային արագությունը` u<<c, մինչդեռ փուլային արագության համար սահմանափակում գոյություն չունի:

>>

9.3. ԱՌԱՁԳԱԿԱՆ ԱԼԻՔԻ ԷՆԵՐԳԻԱՆ

Երկայնական ալիքի տարածման միջավայրում առանձնացնենք այնքան փոքր տարրական  ծավալ, որ դեֆորմացիաները և շարժման արագությունները այս ծավալի բոլոր կետերում կարելի լինի համարել միատեսակ համապատասխանաբար հավասար`

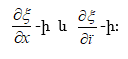
Առանձնացված ծավալն օժտված է առաձգական դեֆորմացիայի պոտենցիալ էներգիայով, որը որոշվում է հետևյալ արտահայտությամբ

Քննարկվող ծավալն օժտված կլինի նաև կինետիկ էներգիայով`

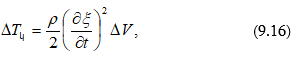
որտեղ  ծավալի զանգվածն է, իսկ  նրա արագությունը:

(9.15) և (9.16) արտահայտությունների գումարը տալիս է լրիվ էներգիան`

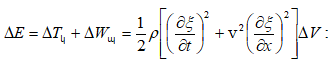
Բաժանելով  էներգիան  ծավալին, որտեղ այն տեղայնացված է, կստանանք էներգիայի ծավալային խտությունը`

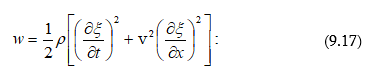
Ածանցելով հարթ ալիքի (9.1) հավասարումը ըստ t-ի և x-ի, կստանանք`

Տեղադրելով այս արտահայտությունները (9.17) բանաձևի մեջ, կստանանք`

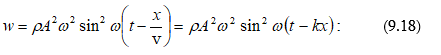
Լայնական ալիքների դեպքում էներգիայի ծավալային խտության համար ստացվում է նույնպիսի արտահայտություն:

Ինչպես հետևում է (9.18)-ից, էներգիայի խտությունը ժամանակի յուրաքանչյուր պահի տարածության տարբեր կետերում տարբեր է: Միևնույն կետում էներգիայի խտությունը ըստ ժամանակի փոփոխվում է սինուսի քառակուսի աստիճանի օրենքով: Քանի որ սինուսի քառակուսի աստիճանի միջին արժեքը 1/2 է, ապա էներգիայի խտության միջին արժեքը ըստ ժամանակի միջավայրի յուրաքանչյուր կետում կլինի`

(9.18) էներգիայի խտությունը և նրա միջին (9.19) արժեքը համեմատական են միջավայրի խտությանը,  հաճախության քառակուսուն և ալիքի A լայնույթի քառակուսուն:

Այսպիսով, միջավայրը, որտեղ առաջանում է ալիքը, օժտված է էներգիայի լրացուցիչ պաշարով: Այս էներգիան տատանումների աղբյուրից դեպի միջավայրի տարբեր կետերն է տարածվում ալիքի միջոցով, հետևաբար, ալիքն իր հետ տանում է էներգիա: Միավոր ժամանակում որևէ մակերեսով ալիքի միջոցով տեղափոխվող էներգիայի քանակը կոչվում է էներգիայի հոսք: Էներգիայի հոսքը միջավայրի տարբեր կետերում օժտված է տարբեր ինտենսիվությամբ: Էներգիայի հոսքը տարածության տարբեր կետերում բնութագրելու համար օգտվում են մի վեկտորական մեծությունից, որը կոչվում է էներգիայի հոսքի խտության վեկտոր: Այս մեծությունը թվապես հավասար է տվյալ կետով անցնող և էներգիայի տեղափոխությանն ուղղահայաց միավոր մակերեսով անցնող էներգիայի հոսքին: Էներգիայի հոսքի խտության վեկտորի ուղղությունը համընկնում է էներգիայի փոխադրման ուղղության հետ: Էներգիայի հոսքի խտության վեկտորը որոշվում է հետևյալ բանաձևով`

որտեղ  փուլային արագության վեկտորն է: Էներգիայի հոսքի խտության վեկտորը առաջին անգամ մտցրել է Ա. Ումովը և կոչվում է Ումովի վեկտոր:

>>

9.4. ԱԼԻՔՆԵՐԻ ԻՆՏԵՐՖԵՐԵՆՑԻԱՆ

Կոհերենտություն է կոչվում մի քանի տատանողական կամ ալիքային պրոցեսների համաձայնեցված ընթացքը ժամանակի և տարածության մեջ: Եթե ալիքների գրգռված տատանումների փուլերի տարբերությունը ժամանակի ընթացքում մնում է հաստատուն, ալիքները կոչվում են կոհերենտ: Այդպիսի ալիքների աղբյուրները նույնպես կոչվում են կոհերենտ:

Տարածության մեջ երկու (կամ մի քանի) կոհերենտ ալիքների վերադրման դեպքում նրա տարբեր կետերում, կախված ալիքների փուլերի միջև եղած հարաբերակցությունից, ստացվում է արդյունարար ալիքի ուժեղացում կամ թուլացում:

Դիտարկենք երկու կոհերենտ սֆերիկ ալիքների վերադրումը, որոնք գրգռվում են  կետային աղբյուրներով, տատանվում են միևնույն լայնույթով,  հաճախությամբ և հաստատուն փուլերի տարբերությամբ: Համաձայն (9.7)-ի,

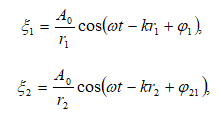
որտեղ  ալիքների աղբյուրներից մինչև ընտրված B կետը եղած հեռավորություններն են, k-ն ալիքային թիվն է,  դիտարկվող երկու սֆերիկ ալիքների սկզբնական փուլերն են:

Արդյունարար ալիքի լայնույթը B կետում ըստ (8.27)-ի կլինի`

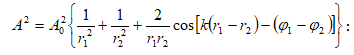
Քանի որ կոհերենտ աղբյուրների համար սկզբնական փուլերի տարբերությունը`  ապա երկու ալիքների վերադրման արդյունքը կախված է  տարբերությունից, որը կոչվում է ալիքների ընթացքի տարբերություն:

Այն կետերում, որտեղ

դիտվում է ինտերֆերենցիոն առավելագույն: Արդյունարար տատանման լայնույթը`

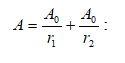
Այն կետերում, որտեղ

դիտվում է ինտերֆերենցիոն նվազագույն: Արդյունարար տատանման լայնույթը`

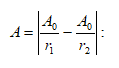
 կոչվում է ինտերֆերենցիոն առավելագույնի կամ նվազագույնի կարգ: (9.21) և (9.22) պայմանները բերում են նրան, որ

(9.23) արտահայտությունը հիպերբոլի հավասարում է, որի կիզակետերը գտնվում են  կետերում: Այսպիսով, այն կետերի երկրաչափական տեղը, որտեղ տատանումները ուժեղացնում կամ թուլացնում են միմյանց, ներկայացնում են հիպերբոլների ընտանիք (տես նկ.9.2, համապատասխանով  պայմանին): Հոծ գծերով ցույց են տրված այն տեղերը, որտեղ տատանումներն ուժեղացնում են միմյանց, իսկ կետագծերով` այն տեղերը, ուր տատանումները թուլացնում են միմյանց:

>>

9.5. ԿԱՆԳՈՒՆ ԱԼԻՔՆԵՐ

Ալիքների ինտերֆերենցիայի արդյունքի հատուկ օրինակ են այսպես կոչված կանգուն ալիքները, որոնք առաջանում են միատեսակ լայնույթներ և հաճախություններ ունեցող հանդիպակաց հարթ ալիքների վերադրման հետևանքով:

Կանգուն ալիքի հավասարումը արտածելու համար ենթադրենք, որ երկու հարթ ալիքներ տարածվում են միջավայրում առանց մարման իրար ընդառաջ x-ի առանցքի երկայնքով, ընդ որում` երկու ալիքներն էլ բնութագրվում են միատեսակ հաճախություններով և լայնույթներով: Բացի դրանից, կոորդինատների սկիզբն ընտրենք այն կետում, ուր երկու ալիքներն էլ ունեն միատեսակ սկզբնական փուլեր, ժամանակի հաշվարկը սկսում ենք այն պահից, երբ երկու ալիքների սկզբնական փուլերը հավասար են զրոյի, որից հետո երկու ալիքների հավասարումները կարելի է գրել հետևյալ տեսքով.

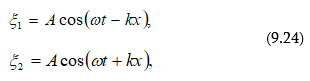
Գումարելով հավասարումները և նկատի ունենալով, որ  կստանանք կանգուն ալիքի հավասարումը.

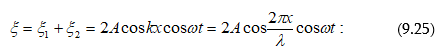
Կանգուն ալիքի (9.25) հավասարումից հետևում է, որ այդ ալիքի յուրաքանչյուր կետում տատանումները կատարվում են նույն  հաճախությամբ,  լայնույթով, որը կախված է դիտարկվող կետի x կոորդինատից:

Միջավայրի այն կետերում, որտեղ

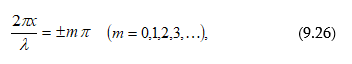
տատանման լայնույթը հասնում է իր առավելագույն արժեքին, հավասար է 2A-ի:

 Միջավայրի այն կետերում, որտեղ

տատանման լայնույթը դառնում է զրո: Այսպիսով, որոշակի կետերում կանգուն ալիքի լայնույթը հավասար է երկու գումարվող ալիքների լայնույթների գումարին, այդպիսի կետերը կոչվում են փնջվածքներ, այլ կետերում արդարդյունարար լայնույթը հավասար է զրոյի, այդ կետերը կոչվում են հանգույցներ: Հանգույցներում գտնվող միջավայրի կետերը տատանումներ չեն կատարում:

 (9.26) և (9.27) արտահայտություններից կստանանք համապատասխանաբար փնջվածքների և հանգույցների կոորդինատները`

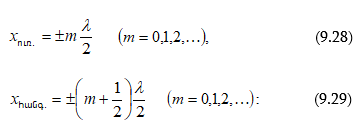
(9.28) և (9.29) բանաձևերից հետևում է, որ երկու հարևան փնջվածքների և երկու հարևան հանգույցների միջև հեռավորությունը միատեսակ է և հավասար է  Կանգուն ալիքի հարևան փնջվածքի և հանգույցի միջև հեռավորությունը հավասար է  այսինքն` հանգույցները և փնջվածքները միմյանցից հեռացած են ալիքի երկարության մեկ քառորդի չափով: Ի տարբերություն վազող ալիքի, որի բոլոր կետերը կատարում են միատեսակ լայնույթով, բայց ըստ փուլի ուշացումով տատանումներ, կանգուն ալիքի բոլոր կետերը երկու հանգույցների միջև տատանվում են տարբեր լայնույթներով, բայց միատեսակ փուլերով: Հանգույցով անցնելու դեպքում  բազմապատկիչը փոխում է իր նշանը, ուստի տատանման փուլը հանգույցից տարբեր կողմերում տարբերվում է  այսինքն կետերը, որոնք ընկած են հանգույցից տարբեր կողմերում, տատանվում են հակափուլով:

Կանգուն ալիքի առաջացումը սովորաբար դիտվում է վազող ալիքի և անդրադարձած ալիքի ինտերֆերենցի դեպքում: Օրինակ, եթե պարանի ծայրն անշարժ ամրացվի, ապա պարանի ամրացման տեղում անդրադարձած ալիքը կինտերֆերենցվի առաջ վազող ալիքի հետ և կառաջացնի կանգուն ալիք: Այդ դեպքում անշարժ մնացող հանգուցային կետերը միմյանցից գտնվում են վազող ալիքի երկարության կեսին հավասար հեռավորությունների վրա, պարանի ամրացման կետում, այսինքն` այն սահմանում, որտեղ տեղի է ունենում ալիքի անդրադարձումը, ստացվում է հանգույց:

Ընդհանրապես, անդրադարձման սահմանում կարող է առաջանալ կամ հանգույց, կամ փնջվածք, որը կախված է միջավայրի խտությունների հարաբերակցությունից: Եթե միջավայրը, որից տեղի է ունենում անդրադարձումը, ավելի պակաս խիտ է, քան այն միջավայրը, ուր տարածվում է ալիքը, ապա սահմանում առաջանում է փնջվածք (նկ.9.3, ա): Եթե այն միջավայրը, որից կատարվում է անդրադարձումը, ավելի խիտ է, քան այն միջավայրը, ուր տեղի է ունենում ալիքի տարածումը, ապա սահմանում առաջանում է հանգույց (նկ. 9.3, բ):

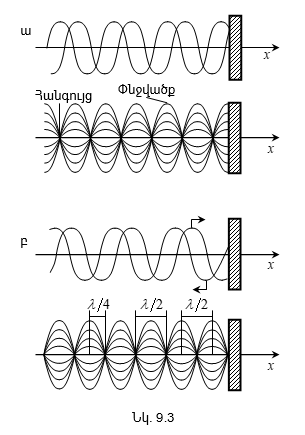
Ավելի խիտ միջավայրից անդրադառնալու ժամանակ սահմանում հանգույցի առաջանալը բացատրվում է նրանով, որ ալիքը անդրադառնալով ավելի խիտ միջավայրից, անդրադարձման տեղում իր փուլը փոխում է հակադիր փուլի, այդ ժամանակ սահմանում գումարվում են հակադիր ուղղության տատանումներ, որը և հանգեցնում է հանգույցի առաջացմանը:

Քանի որ փուլը փոխվում է հակադիր փուլի ալիքի երկարության կեսին հավասար տարածության վրա, ապա այդ փաստն ընդունված է անվանել «կես ալիքի կորուստ»: Եթե ալիքն անդրադառնում է ավելի նոսր միջավարից` անդրադարձման տեղում, ալիքը չի փոխում փուլը, այդ պատճառով կես ալիքի կորուստ տեղի չի ունենում, որի շնորհիվ ընկնող և անդրադարձող ալիքների փուլերը սահմանում միատեսակ են, և այդ տեղում միևնույն փուլի տատանումների գումարման հետևանքով առաջանում է փնջվածք:

Եթե դիտարկվի վազող ալիքը, ապա նրա տարածման ուղղությամբ տեղափոխվում է էներգիա: Կանգուն ալիքի դեպքում էներգիայի տեղափոխում չկա, քանի որ հակառակ ուղղություններով միատեսակ լայնույթներով ընկնող և անդրադարձնող ալիքները կրում են միատեսակ էներգիա: Ուստի արդյունարար կանգուն ալիքի էներգիան երկու հանգուցային կետերի սահմաններում մնում է հաստատուն: Միայն ալիքի երկարության կեսին հավասար սահմանային հեռավորությունների վրա կատարվում է կինետիկ էներգիայի փոխակերպում պոտենցիալի և հակառակը:

>>

9.6. ՁԱՅՆԱՅԻՆ ԱԼԻՔՆԵՐ

Առաձգական միջավայրում տարածվող ալիքները, որոնց հաճախություններն ընկած են 16-20000 Հց սահմաններում, կոչվում են ձայնային ալիքներ: 20 Հց-ից փոքր հաճախություն ունեցող առաձգական ալիքները կոչվում են ինֆրաձայն, իսկ 20000Հց-ից ավելի հաճախություն ունեցող առաձգական ալիքները` ուլտրաձայն: Ինֆրաձայները և ուլտրաձայները մարդու ականջը չի լսում:

Գազերում և հեղուկներում ձայնային ալիքը լինում է միայն երկայնական և բաղկացած է միջավայրի իրար հաջորդող սեղմումներից և նոսրացումներից: Պինդ մարմիններում կարող են տարածվել ինչպես երկայնական, այնպես էլ լայնական ալիքներ:

Ձայնի ինտենսիվություն է կոչվում այն մեծությունը, որը որոշվում է ըստ ժամանակի էներգիայի միջին արժեքով, որը տեղափոխում է ձայնային ալիքը միավոր ժամանակում ալիքի տարածման ուղղությանը ուղղահայաց միավոր մակերեսով.

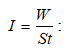
Ինտենսիվության միավորը ՄՀ-ում Վտ/մ² է:

Տարբեր հաճախությունների համար մարդու ականջի զգայնությունը տարբեր է: Ձայնային զգացողություն առաջացնելու համար ալիքը պետք է օժտված լինի որոշ նվազագույն ինտենսիվությամբ, որը կոչվում է լսելիության շեմ: Լսելիության շեմը տարբեր մարդկանց համար տարբեր է և խիստ կախում ունի ձայնի հաճախությունից: Մեծ ինտենսիվությունների դեպքում ալիքը դադարում է որպես ձայն ընկալվելուց, և ականջում առաջացնում է ցավի զգացում: Նկ.9.4-ում բերված է լսելիության շեմի և ցավի զգացողության կախվածությունը ձայնի հաճախությունից: Այն տիրույթը, որն ընկած է երկու կորերի միջև, լսելիության տիրույթն է:

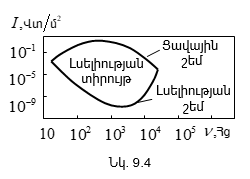
Եթե ձայնի ինտենսիվությունը մի մեծություն է, որը օբյեկտիվորեն բնութագրում է ալիքային պրոցեսը, ապա ձայնի սուբյեկտիվ բնութագիրը, կապված նրա ինտենսիվության հետ, ձայնի ուժգնությունն է, որը կախված է հաճախությունից: Համաձայն Վեբեր-Ֆեխների ֆիզոլոգիական օրենքի` ձայնի ինտենսիվության մեծացման հետ ուժգնությունն աճում է լոգարիթմական օրենքով: Դրա հիման վրա ներմուծվում է ձայնի ուժգնության օբյեկտիվ գնահատականը ըստ նրա ինտենսիվության չափման արժեքի.

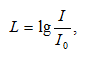
որտեղ  ձայնի ինտենսիվությունն է լսելիության շեմի վրա, որը բոլոր ձայների համար ընդունվում է հավասար` 10^-12 Վտ/մ² : L մեծությունը կոչվում է ձայնի ինտենսիվության մակարդակ և չափվում է բելերով (ի պատիվ հեռախոսի գյուտարար Բելի): Սովորաբար օգտվում են 10 անգամ ավելի փոքր միավորից, որը կոչվում է դեցիբել (դԲ):  

Ձայնի ֆիզոլոգիական բնութագիրը ուժգնության մակարդակն է, որն արտահայտվում է ֆոներով (ֆոն): 1000Հց (մաքուր տոնի ստանդարտ հաճախությունը) հավասար է 1 ֆոնի, եթե նրա ինտենսիվության մակարդակը հավասար է 1դԲ -ի: Օրինակ, մետրոյի վագոնում մեծ արագությունների դեպքում աղմուկին համապատասխանում է  ֆոն, իսկ 1մ հեռավորության վրա շշուկին`

Իրական ձայնը հաճախությունների մեծ հավաքածուով ներդաշնակ տատանումների վերադրում է, այսինքն ձայնը օժտված է ակուստիկական սպեկտրով, որը կարող է լինել անընդհատ (որոշակի միջակայքում մասնակցում են բոլոր հաճախությունների տատանումներ) և գծային (մասնակցում են իրարից բաժանված որոշակի տատանումներ):

Ձայնը, բացի ուժգնությունից, բնութագրվում է նաև բարձրությամբ և տեմբրով: Ձայնի բարձրությունը բնութագրում է ձայնի որակը: Հաճախության մեծացման հետ ձայնի բարձրությունը մեծանում է: Ակուստիկական սպեկտրի բնույթը և էներգիայի բաշխումը հաճախությունների միջև որոշում է ձայնային զգացողության առանձնահատկությունը, որը կոչվում է ձայնի տեմբր: Այսպես, տարբեր երգիչներ վերցնելով միևնույն նոտան, ունենում են տարբեր ակուստիկական սպեկտր, այսինքն` նրանց ձայնն ունի տարբեր տեմբրեր:

Ձայնի աղբյուր կարող է լինել յուրաքանչյուր մարմին, որը տատանվում է առաձգական միջավայրում ձայնային հաճախությամբ (օրինակ, լարային գործիքներում ձայնի աղբյուրը լարն է, որը միացված է գործիքի իրանին):

Մարմինը, կատարելով տատանումներ, առաջ է բերում նույն հաճախությամբ իրեն հարող միջավայրի մասնիկների տատանումներ: Տատանողական շարժման վիճակը հաջորդաբար հաղորդվում է մարմնից ավելի հեռու գտնվող միջավայրի մասնիկներին, այսինքն` միջավայրում տարածվում է աղբյուրի հաճախությանը հավասար տատանման հաճախությամբ ալիք, որոշակի արագությամբ, որը կախված է միջավայրի խտությունից և առաձգական հատկություններից:

Ձայնային ալիքի տարածման արագությունը գազերում որոշվում է հետևյալ բանաձևով`

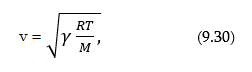
որտեղ  գազի մոլային ջերմունակությունների հարաբերությունն է հաստատուն ճնշման և հաստատուն ծավալի դեպքում, R-ը մոլային գազային հաստատունն է, T-ն ջերմադինամիկական ջերմաստիճանը, M-ը` մոլային զանգվածը: (9.30) բանաձևից հետևում է, որ ձայնի արագությունը գազում կախված չէ p ճնշումից, բայց աճում է ջերմաստիճանի բարձրացումով: Որքան մեծ է գազի մոլային զանգվածը, այնքան փոքր է նրանում ձայնի արագությունը: Օրինակ, T=273Կ դեպքում ձայնի արագությունը օդում (M=29•10^-3 կգ/մոլ, v=331մ/վ, ջրածնում (M=2•10^-3կգ/մոլ) v=1260մ/վ): (9.30) բանաձևը համապատասխանում է փորձի տվյալներին:

Մթնոլորտում ձայնի տարածման դեպքում ամհրաժեշտ է հաշվի առնել մի շարք գործոններ. քամու արագությունը և ուղղությունը, օդի խոնավությունը, գազային միջավայրի մոլեկուլային կառուցվածքը, ձայնի անդրադարձման և բեկման երևույթը երկու միջավայրերի սահմանի վրա: Բացի դրանից, ցանկացած իրական միջավայր օժտված է մածուցիկությամբ, դրա համար էլ ձայնը մարում է, այսինքն` տեղի է ունենում լայնույթի փոքրացում, հետևաբար ձայնային ալիքի տարածմանը զուգընթաց նրա ինտենսիվությունը փոքրանում է: Ձայնի մարումը նշանակալի չափով պայմանավորված է միջավայրում նրա կլանումով, կապված ձայնային էներգիայի ոչ դարձելի անցումով էներգիայի այլ ձևերի (հիմնականում ջերմայինի) հետ:

Շենքի ակուստիկայի համար մեծ նշանակություն ունի ձայնի ռեվերբերացիան` ձայնի աստիճանաբար մարման պրոցեսը փակ շենքերում նրա աղբյուրի անջատումից հետո: Եթե շենքը դատարկ է, ապա տեղի է ունենում ձայնի դանդաղ մարում, և շենքում թնդյուն է առաջանում: Եթե ձայները մարում են արագ (ձայնակլանիչ նյութերի օգտագործման դեպքում), ապա դրանք ընկալվում են խլացումով: Ռեվերբերացիայի ժամանակամիջոցը այն է. որի ընթացքում ձայնի ինտենսիվությունը շենքում թուլանում է միլիոն անգամ, իսկ նրա մակարդակը` 60դԲ -ով: Շենքն ունի լավ ակուստիկա, եթե ռեվերբերացիայի ժամանակը կազմում է 0.5-1.5 վ:

>>

9.7. ԴՈՊԼԵՐԻ էՖԵԿՏԸ ԱԿՈՒՍՏԻԿԱՅՈՒՄ

Դոպլերի էֆեկտ է կոչվում ընդունիչի կողմից ընկալվող տատանման հաճախության փոփոխությունը այդ տատանումների աղբյուրի և ընդունիչի` միմյանց նկատմամբ շարժման դեպքում: Օրինակ, փորձից հայտնի է, որ գնացքի սուլոցի ձայնը կառամատույցին մոտենալիս բարձրանում է, և ցածրանում է հեռանալիս, այսինքն տատանումների աղբյուրի շարժումը ընդունիչի նկատմամբ փոխում է գրանցվող տատանումների հաճախությունը: Դոպլերի էֆեկտը քննարկելու համար ենթադրենք, որ ձայնի աղբյուրը և ընդունիչը շարժվում են նրանց միացնող ուղղի երկայնքով.  համապատասխանաբար` աղբյուրի և ընդունիչի շարժման արագություններն են, ընդ որում դրանք դրական են, եթե աղբյուրը (ընդունիչը) մոտենում է ընդունիչին (աղբյուրին), և բացասական, եթե հեռանում են: Աղբյուրի տատանման հաճախությունը հավասար է  Քննարկենք հետևյալ դեպքերը:

1. Աղբյուրը և ընդունիչը միջավայրի նկատմամբ անշարժ են, այսինքն`  Եթե u-ն ալիքի տարածման արագությունն է դիտարկվող միջավայրում, ապա ալիքի երկարությունը`

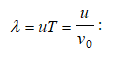
Ալիքը տարածվելով միջավայրում` հասնում է ընդունիչին և առաջ է բերում նրա ձայնազգայուն տարրի տատանումներ հետևյալ հաճախությամբ`

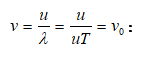
Հետևաբար, ձայնի  հաճախությունը, որը գրանցում է ընդունիչը, հավասար է այն  հաՃախությանը, որով աղբյուրից ճառագայթվում է ձայնային ալիքը:

2. Ընդունիչը մոտենում է աղբյուրին, աղբյուրն անշարժ է, այսինքն

Տվյալ դեպքում ալիքի տարածման արագությունը ընդունիչի նկատմամբ դառնում է հավասար`  Քանի որ ալիքի երկարությունն այդ դեպքում չի փոխվում, ապա

այսինքն` ընդունիչով ընկալվող հաճախությունը  անգամ մեծ է աղբյուրի տատանման հաճախությունից:

3. Աղբյուրը մոտենում է ընդունիչին, իսկ ընդունիչն անշարժ է, այսինքն`

Տատանումների արագությունը կախված է միայն միջավայրի հատկություններից, դրա համար էլ աղբյուրի տատանումների պարբերությանը հավասար ժամանակամիջոցում ճառագայթված ալիքը ընդունիչի ուղղությամբ անցնում է uT հեռավորություն (հավասար ալիքի երկարությանը), անկախ այն բանից` աղբյուրը շարժվում է, թե անշարժ է: Այդ նույն ժամանակամիջոցում աղբյուրն անցնում է ալիքի ուղղությամբ  հեռավորություն (նկ.9.5), այսինքն` ալիքի երկարությունը շարժման ուղղությամբ կրճատվում և դառնում է`

Հետևաբար`

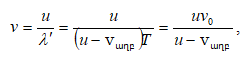
այսինքն, տատանման հաճախությունը, որն ընկալվում է ընդունիչի կողմից, մեծանում է  անգամ: 2 և 3 կետերում նշված դեպքերում, եթե  նշանը կդառնա հակառակ:

4. Աղբյուրը և ընդունիչը շարժվում են միմյանց նկատմամբ: Օգտագործելով և դեպքերում ստացված արդյունքները` կարելի է գրել ընդունիչով գրանցվող տատանման հաճախության համար հետևյալ արտահայտությունը`

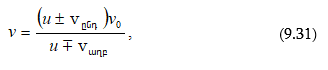
ընդ որում` վերին նշանը վերցվում է, եթե աղբյուրի կամ ընդունիչի շարժման դեպքում տեղի է ունենում դրանց մոտեցում, ներքևի նշանը` դրանց փոխադարձաբար հեռանալու դեպքում:

Բերված բանաձևերից հետևում է, որ Դոպլերի էֆեկտը տարբեր է, կախված այն բանից` շարժվում է աղբյուրը, թե՞ ընդունիչը: Եթե արագությունների ուղղությունները չեն համընկնում աղբյուրով և ընդունիչով անցնող ուղղի հետ, ապա այդ արագությունների փոխարեն (9.31) բանաձևում պետք է վերցնել դրանց պրոյեկցիաները այդ ուղղի ուղղության վրա:

>>

9.8. ՈՒԼՏՐԱՁԱՅՆ ԵՎ ԴՐԱ ԿԻՐԱՌՈՒԹՅՈՒՆԸ

Իր բնույթով ուլտրաձայնը առաձգական ալիքներ են, և դրանով այն չի տարբերվում ձայնից: Սակայն ուլտրաձայնը, ունենալով մեծ հաճախություններ  և հետևաբար, ալիքի փոքր երկարություններ, բնութագըրվում է առանձնահատուկ հատկություններով: Ուլտրաձայնային ալիքները փոքր երկարության շնորհիվ, ինչպես և լուսային ալիքները, կարող են ստացվել խիստ ուղղորդված փնջերի տեսքով:

Ուլտրաձայնային ալիքների գրգռման համար ներկայումս հիմնականում օգտվում են երկու երևույթներից. հակադարձ պիեզոէլեկտրական էֆեկտից և մագնիսաստրիկցիայից: Հակադարձ պիեզոէլեկտրական էֆեկտն այն է, որ որոշ բյուրեղներից (օրինակ, քվարցից, սեգնետյան աղից, բարիումի տիտանատից և այլն) որևէ ձևով կտրված թիթեղը էլեկտրական դաշտի ազդեցության տակ դեֆորմացվում է. դաշտի մի ուղղության դեպքում երկարում է, իսկ հակառակ ուղղության դաշտի դեպքում` սեղմվում: Տեղավորելով թիթեղը մետաղական շրջադիրների միջև, որոնց միացված է բարձր հաճախության փոփոխական լարման աղբյուրը, կարելի է այդ թիթեղում առաջացնել հարկադրական տատանումներ: Այդ տատանումների լայնույթները հատկապես մեծ են դառնում այն դեպքում, երբ լարման փոփոխությունների հաճախությունը համընկնում է թիթեղի սեփական տատանումների հաճախության հետ: Թիթեղի տատանումները հաղորդվում են նրան շրջապատող հեղուկ կամ գազային միջավայրին` առաջացնելով նրա մեջ ուլտրաձայնային ալիք:

Մագնիսաստրիկցիայի երևույթն այն է, որ ֆերոմագնիսական նյութերը (երկաթ, նիկել, որոշ համաձուլվածքներ և այլն) մագնիսական դաշտի ազդեցությունից դեֆորմացվում են: Ուստի ֆերոմագնիսական ձողը փոփոխական մագնիսական դաշտում տեղավորելով (օրինակ, այնպիսի կոճի մեջ, որով անցնում է փոփոխական հոսանք), կարելի է առաջացնել մեխանիկական տատանումներ, և դարձյալ դրանք առանձնապես ուժգին կլինեն ռեզոնանսի դեպքում:

Ուղղորդված ուլտրաձայնային փնջերը լայն կիրառությում են գտել տեխնիկայում, օրինակ, ուղղորդված ստորջրյա որոշակի կողմեր ազդանշաններ տալու համար, ստորջրյա առարկաները հայտնաբերելու և խորությունները որոշելու համար (էխոլոտ): Էխոլոտի կազմության սկզբունքը հետևյալն է. ուլտրաձայների աղբյուրից ջրի մեջ ուղղաձիգ դեպի ներքև ուղարկվում է ձայնային ալիք, որը հասնելով հատակին, անդրադառնում է նրանից և ետ վերադառնում: Իմանալով ձայնի տարածման արագությունը ջրում, ըստ ուլտրաձայնային ազդանշանի առաքման և նրա վերադարձի (արձագանքը նկատելու) միջև ընկած ժամանակամիջոցի, հեշտ է հաշվել ջրի խորությունը: Արձագանքի ընկալումը կատարվում է նաև պիեզոքվարցի միջոցով: Ձայնային ալիքները հասնելով պիեզոքվարցին, նրա մեջ առաջացնում են առաձգական տատանումներ, որոնց հետևանքով քվարցի հակադիր մակերևույթների վրա առաջանում են էլեկտրական լիցքեր, որոնք համապատասխան էլեկտրական սարքավորման միջոցով կարող են հայտնաբերվել և չափվել:

Եթե ուլտրաձայնային ազդանշանը բաց թողնվի հետազոտվող դետալի միջով, ապա ըստ փնջի ցրման բնույթի և ուլտրաձայնային ստվերի առաջացման կարելի է նրանում հայտնաբերել արատները:

 Այդ սկզբունքի հիման վրա ստեղծվել է տեխնիկայի ամբողջ մի ճյուղ` ուլտրաձայնային արատադիտում, որի սկիզբը դրվել է Սոկոլովի կողմից: Ուլտրաձայնի կիրառությունն ընկած է նաև ակուստիկայի նոր բնագավառի` ձայնագիտական էլեկտրոնիկայի հիմքում, որը հնարավորություն է տալիս դրա հիման վրա մշակել սարքեր միկրոռադիոէլեկտրոնիկայում ազդանշանների ինֆորմացիայի մշակման համար: Բժշկության մեջ փոքր հզորության ուլտրաձայնն օգտագործվում է որպես ախտորոշման, իսկ մեծ հզորության ուլտրաձայնը կիրառվում է վիրաբուժական նպատակներով: Ուլտրաձայնը կիրառվում է նաև շատ կոշտ և շատ փխրուն մարմինների մեխանիկական մշակման համար, քիմիայում (էմուլսիաների, սուսպենզիաների ստացում), մետաղաձուլման գործում, երկրաբանության մեջ (ուլտրաձայնային կարոտաժ), ինչպես և տեխնոլոգիական տարբեր պրոցեսներում:

>>

Խնդիրների լուծման օրինակներ

Մեխանիկական տատանումներ և ալիքներ

 Խնդիր 1. Կետը կատարում է ներդաշնակ տատանումներ: Ժամանակի  պահին շեղումը`  է: Փուլը երկու անգամ մեծացնելու դեպքում կետի շեղումը դարձավ  Գտնել տատանման լայնույթը:

Լուծում: Գրենք երկու դեպքում շեղումների հավասարումները.

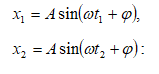
Համաձայն խնդրի պայմանի`  Կատարենք նշանակում`  այդ դեպքում շեղումների համար հավասարումները կարող են ներկայացվել հետևյալ տեսքով`

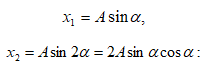
Երկու հավասարումները բարձրացնելով քառակուսի, նրանցից երկրորդը բաժանելով չորսի և առաջինից հանելով երկրորդը կստանանք`

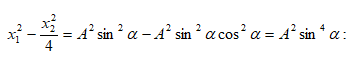
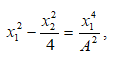
որտեղից

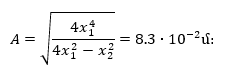
Խնդիր 2. Նյութական կետը կատարում է A=0.04մ լայնույթով և T=2վ պարբերությամբ ներդաշնակ տատանումներ: Գրել կետի շարժման հավասարումը, եթե նրա շարժումը սկսվում է  դիրքից:

Լուծում: Ներդաշնակ տատանումների դեպքում շեղումը փոփոխվում է, կախված ժամանակից հետևյալ օրենքով`

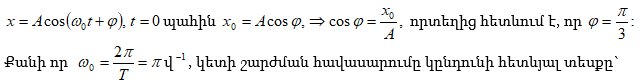
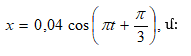
Խնդիր 3.  զանգվածով նյութական կետը կատարում է ներդաշնակ տատանումներ ըստ  օրենքի: Որոշել վերադարձնող ուժի և կինետիկ էներգիայի առավելագույն արժեքները:

Լուծում:  ներդաշնակ տատանման հավասարումից հետևում է, որ լայնույթը`  Արագության և արագացման համար ստանում ենք`

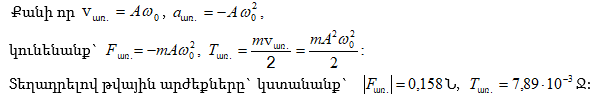
Խնդիր 4. Որոշել ներդաշնակ տատանումներ կատարող կետի T կինետիկ էներգիայի և նրա W պոտենցիալ էներգիայի հարաբերությունը, եթե սկզբնական փուլը հայտնի է:

Լուծում: Գտնենք  ֆունկցիայի ըստ ժամանակի առաջին և երկրորդ կարգի ածանցյալները.

Կինետիկ և պոտենցիալ էներգիաների համար համապատասխանաբար կստանանք`

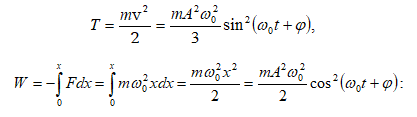
Բաժանելով վերջին հավասարումները իրար` կստանանք`

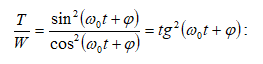
Խնդիր 5. k=900 Ն/մ կոշտությամբ հորիզոնական զսպանակին ամրացված M=4կգ զանգվածով գունդը գտնվում է ողորկ սեղանի վրա, որի վրայով այն կարող է առանց շփման սահել: m=10կգ զանգվածով գնդակը թռչելով հորիզոնական ուղղությամբ`  արագությամբ և հարվածի պահին ունենալով զսպանակի երկայնքով ուղղված արագություն` մխրճվում է գնդի մեջ: Անտեսելով զսպանակի զանգվածը և օդի դիմադրության ուժը` որոշել գնդի տատանման լայնույթը և պարբերությունը:

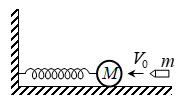
Լուծում: Օգտվելով իմպուլսի պահպանման օրենքից` կարող ենք գրել`

որտեղ v-ն գնդի և գնդակի արագությունն է հարվածից հետո:

Համաձայն էներգիայի պահպանման օրենքի`

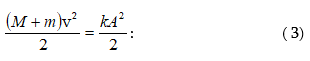
 (2)- ը տեղադրելով ( 3)-ի մեջ` լայնույթի համար կստանանք`

Նկատի ունենալով, որ

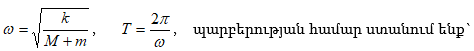
 Տեղադրելով (4) և (5)-ի մեջ մտնող մեծությունների թվային արժեքները կստանանք` A=0.1մ: T=0.419վ:

Խնդիր 6.  թեքության անկյուն ունեցող երկու թեք հարթություններ միացված են հիմքի մոտ (տես նկ.): Փոքրիկ մարմինը այդ հարթություններով իր շարժման ընթացքում կատարում է տատանումներ` սահելով ներքև-վերև: Մարմինը շարժումն սկսում է այդ հարթություններից որևէ մեկի վրայից և գտնվում է հիմքից h բարձրության վրա: Գտնել մարմնի տատանումների պարբերությունը: Շփումն անտեսել: Հարթությունից հարթություն անցումը սահուն է և հարթ:

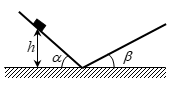
Լուծում: Եթե մարմինը սահում է h բարձրությունից, ապա այն ներքև է իջնում  արագությամբ: Նրա հետագա շարժումը թեք հարթությամբ դեպի վեր կլինի դանդաղող  արագությամբ, որտեղ w-ն այն արագացումն է, որը հաղորդում է գլորող ուժը.

Աջ հարթությունով շարժման դեպքում`

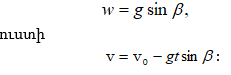
Մարմինը կշարժվի դեպի վեր մինչև նրա արագության զրո դառնալը, այսինքն`

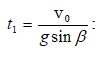
Նույն  ժամանակում մարմինը շարժվում է ներքև: Շարժման լրիվ ժամանակը աջ թեք հարթությունով կլինի`

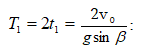
Համանմանորեն ձախ թեք հարթության համար կարող ենք գրել`

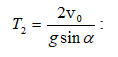
Մարմնի լրիվ տատանման պարբերությունը`

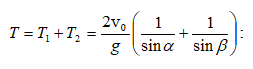
Տեղադրելով  համար արտահայտությունը` կստանանք

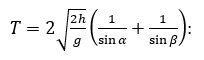
Խնդիր 7. Անկշիռ բարակ երկարության ձողի ծայրերին ամրացված են  զանգվածներով փոքրիկ բեռներ: Ձողը տատանվում է իր մեջտեղով անցնող հորիզոնական առանցքի շուրջը (տես նկ.): Որոշել ձողի կատարած տատանումների պարբերությունը, հետևյալ դեպքերի համար ա) ձողը անկշիռ է, բ) ձողի զանգվածը հավասար է

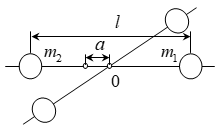
Լուծում: Ֆիզիկական ճոճանակի տատանման պարբերությունը`

որտեղ J-ն ճոճանակի իներցիայի մոմենտն է, m-ը` նրա զանգվածը,  ծանրության կենտրոնից մինչև պտտման առանցքը եղած հեռավորությունն է, g-ն ազատ անկման արագացումն է:

ա) Ճոճանակի իներցիայի մոմենտը, երբ ձողը անկշիռ է, հավասար է բեռների իներցիայի մոմենտների գումարին`  Անտեսելով բեռների չափերը, այսինքն դրանք ընդունելով որպես նյութական կետեր, կստանանք`

Ճոճանակի զանգվածը`  հեռավորությունը գտնելու համար գրենք բեռների հավասարակշռության պայմանը.

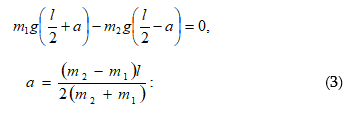
Տեղադրելով (1)-ի մեջ (2)-ը և (3)-ը` պարբերության համար կստանանք`

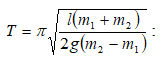
բ) Եթե ձողի զանգվածը  է, ապա ճոճանակի իներցիայի մոմենտը`

Նկատի ունենալով, որ ձողի իներցիայի մոմենտը ձողի մեջտեղով անցնող առանցքի նկատմամբ հավասար է  կստանանք`

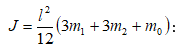
Ճոճանակի զանգվածը`  Հավասարակշռության պայմանը`

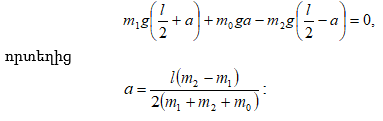
Տատանման պարբերության համար ստանում ենք`

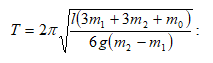
Խնդիր 8. Ֆիզիկական ճոճանակը  երկարության համասեռ բարակ ձող է: Զանգվածի կենտրոնից ի՞նչ x հեռավորության վրա պետք է լինի կախման կետը, որպեսզի տատանման հաճախությունը լինի առավելագույնը:

Լուծում: Ֆիզիկական ճոճանակի տատանման պարբերությունը որոշվում է հետևյալ բանաձևով`

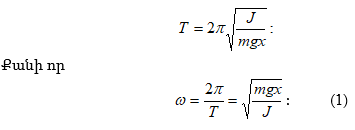
Օգտվելով Շտայների թեորեմից` ձողի իներցիայի մոմենտը O կետով անցնող առանցքի նկատմամբ հավասար կլինի`

 Տեղադրելով (2)-ը (1)-ի մեջ` հաճախության համար կստանանք հետևյալ արտահայտությունը`

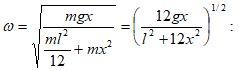
Ածանցելով (3)-ը ըստ x-ի և հավասարեցնելով զրոյի` ստանում ենք`

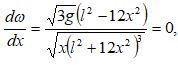
Խնդիր 9.  կոշտություն ունեցող երկու զսպանակներ միացված են մի դեպքում հաջորդաբար, մյուս դեպքում զուգահեռ: Ինչպիսի՞ն է բեռների ուղղաձիգ տատանումների պարբերությունների հարաբերությունը այդպիսի զսպանակների վրա (տես նկ.):

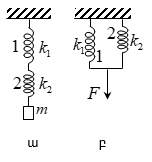
Lուծում: ա) Զսպանակներից յուրաքանչյուրը F ուժի ազդեցության տակ ձգվում է

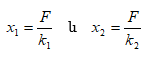
երկարությամբ: Զսպանակների համակարգի համար կարելի է գրել`

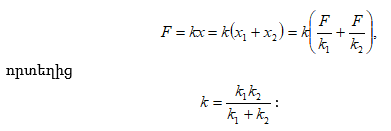
 m զանգվածով բեռի տատանման պարբերությունը`

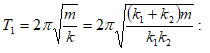
բ) F ուժը, որն ազդում է զսպանակների համակարգի վրա, կարելի է բաժանել երկու`  բաղադրիչների, որոնցից մեկը կիրաոված է 1 զսպանակի վրա, մյուսը` 2 զսպանակի վրա: Երկու զսպանակներն էլ ձգվում են միատեսակ x երկարությամբ:

Յուրաքանչյուր զսպանակի համար կարելի է գրել`

Զսպանակների համակարգի համար`

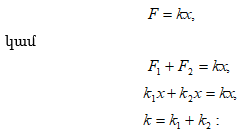
Հետևաբար, m զանգվածով բեռի տատանման պարբերությունը`

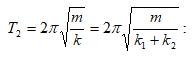
Արդյունքում կստանանք`

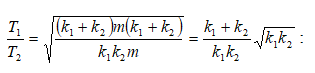
Խնդիր 10. k=30Ն/մ կոշտություն ունեցող զսպանակից կախված m=0.6կգ զանգվածով մարմինը ինչ-որ միջավայրում կատարում է առաձգական տատանումներ: Տատանումների մարման լոգարիթմական դեկրեմենտը`  1) որոշել այն ժամանակամիջոցը, որի ընթացքում տատանումների լայնույթը փոքրանում է 3 անգամ, 2) բեռի լրիվ տատանումների այն թիվը, որի դեպքում կատարվում է լայնույթի նման փոքրացում:

Լուծում: Մարող տատանումների դեպքում`

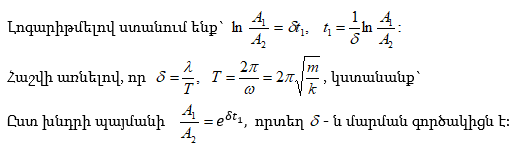
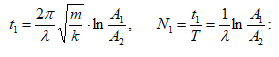
Տեղադրելով վերջին երկու բանաձևերի մեջ մտնող մեծությունների թվային արժեքները` կստանանք`

Խնդիր 11. m=0.1կգ զանգվածով մարմինը, կատարելով մարող տատանումներ,  կորցրեց իր էներգիայի 40%-ը: Որոշել r դիմադրության գործակիցը:

Լուծում: Դիմադրության գործակիցը որոշվում է հետևյալ բանաձևով`

Մարող տատանումների դեպքում տատանումների լայնույթը`

Քանի որ էներգիան համեմատական է լայնույթի քառակուսուն, կարող ենք գրել`

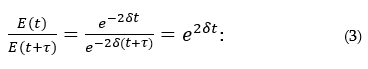
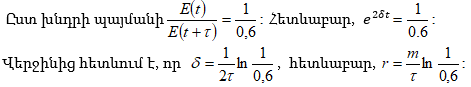
Տեղադրելով վերջին բանաձևի մեջ մտնող մեծությունների թվային արժեքները` ստանում ենք.

Խնդիր 12. Այն ժամանակամիջոցը, որի ընթացքում համակարգը կատարում է N=50 լրիվ տատանում, լայնույթը փոքրանում է 2 անգամ: Որոշել համակարգի Q բարորակությունը:

Լուծում: Համակարգի բարորակությունը որոշվում է հետևյալ բանաձևով`  որտեղ  մարման լոգարիթմական դեկրեմենտն է: Տատանման լայնույթի համար կարող ենք գրել`

որտեղից հետևում է, որ

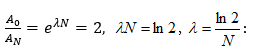
Վերջինը նկատի ունենալով, բարորակության համար կստանանք`

Խնդիր 13. Հարթ սինուսոիդային ալիքը տարածվում է էներգիան չկլանող միջավայրում ուղղի երկայնքով, որը համընկնում է x-ի դրական առանցքի ուղղության հետ v=10մ/վ արագությամբ: Այդ ուղղի վրա երկու կետեր, գտնվելով տատանումների աղբյուրից  հեռավորությունների վրա, տատանվում են  փուլերի տարբերությամբ: Ալիքի լայնույթը` A=5սմ: Որոշել ալիքի երկարությունը, ալիքի հավասարումը, երկրորդ կետի  շեղումը ժամանակի`  պահին:

Լուծում: Տատանվող կետերի փուլերի տարբերությունը`

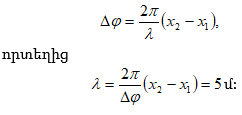
Ալիքի հավասարումը`

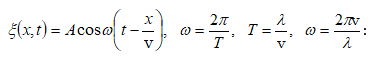
Երկրորդ կետի շեղումը`

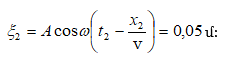
Ալիքի հավասարման համար ստանում ենք`

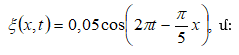
Խնդիր 14. Գտնել  տեսք ունեցող ալիքի  ալիքային վեկտորը և v արագությունը:

Լուծում:  ալիքային վեկտորը ներկայացնենք իր պրոյեկցիաներով`

որտեղ միավոր վեկտորներ են x, y և z կոորդինատային առանցքների վրա: Ալիքի հավասարումից հետևում է, որ

Նկատի ունենալով (2)-ը` (1)-ից ալիքային վեկտորի համար ստանում ենք`

Ալիքի արագությունը, հաճախությունը և ալիքային վեկտորի մոդուլը իրար հետ կապված են հետևյալ բանաձևով`

Ալիքային վեկտորի մոդուլի համար (3)-ից ստանում ենք`

Հաշվի առնելով (5)-ը` (4)-ից ստանում ենք`