


Ա.Հ.Աբոյան
Ա 152 Էլեկտրամագնիսականության հիմնական օրենքները: Ուսումնական ձեռնարկ. - Եր.: ճարտարագետ, 2008թ.:
Ձեռնարկի հիմնական նպատակն է ուսանողներին ծանոթացնել ամենից առաջ ֆիզիկայի հիմնական գաղափարների և մեթոդների հետ: Հատուկ ուշադրություն է դարձվում ֆիզիկական օրենքների իմաստի բացատրման և նրանց գիտակցական օգտագործման վրա: Չնայած համեմատաբար փոքր ծավալին, ձեռնարկը պարունակում է էլեկտրամագնիսականության մասին ուսմունքի այն բոլոր հարցերի շարադրումը, որոնք անհրաժեշտ են տեսական ֆիզիկայի և այլ ֆիզիկական առարկաների ուսումնասիրման համար:
Ուսումնական ձեռնարկը գրված է ֆիզիկայի դասընթացի գործող ծրագրին համապատասխան տեխնիկական մասնագիտությունների ուսանողների համար:
Նախատեսված է ՀՊՃՀ-ի բոլոր դեպարտամենտների առաջին կուրսերի, ինչպես նաև հեռակա բաժնի ուսանողների համար: Այն կարող է օգտակար լինել նաև դասախոսներին և այլ բուհերի ուսանողներին:
Գրախոսներ`
Ֆիզ.մաթ.գիտ. դոկտոր, պրոֆեսոր
Ռ. Կարախանյան
Տեխ. գիտ. դոկտոր, պրոֆեսոր
Հ. Դրմեյան
Խմբագիր` Ն. Խաչատրյան

1.1 Էլեկտրական լիցք: Էլեկտրական լիցքի քվանտային բնույթը: Տարրական լիցք: Լիցքի պահպանման օրենքը:
1.4 Էլեկտրական դաշտի գրաֆիկական պատկերումը:
1.7 Էլեկտրաստատիկ դաշտի պոտենցիալ: Պոտենցիալների տարբերություն: Համապոտենցիալ մակերևույթներ:
1.8 Լարվածության և պոտենցիալների տարբերության կապը:
1.9 Էլեկտրական դիպոլ (երկբևեռ): Դիպոլի էլեկտրաստատիկ դաշտի պոտենցիալի և լարվածության հաշվարկը:
1.10 Երկբևեռի վարքը և պոտենցիալային էներգիան արտաքին էլեկտրաստատիկ դաշտում:
ԳԼՈՒԽ 2. ԷԼԵԿՏՐԱԿԱՆ ԴԱՇՏԸ ԴԻԷԼԵԿՏՐԻԿՆԵՐՈՒՄ
2.1 Դիէլեկտրիկներ: Դրանց տարատեսակները:
2.2 Դիէլեկտրիկներն արտաքին էլեկտրաստատիկ դաշտում: Դիէլեկտրիկների բևեռացման մեխանիզմը:
ԳԼՈՒԽ 3. ՀԱՂՈՐԴԻՉՆԵՐՆ ԷԼԵԿՏՐԱԿԱՆ ԴԱՇՏՈՒՄ
3.2 Հաղորդիչն արտաքին էլեկտրական դաշտում:
3.3 Մեկուսացված հաղորդչի էլեկտրաունակությունը:
3.4 Կոնդենսատորներ: Դրանց տարատեսակները:
3.5 Կոնդենսատորների զուգահեռ և հաջորդական միացումը:
ԳԼՈՒԽ 4. ՀԱՍՏԱՏՈՒՆ ԷԼԵԿՏՐԱԿԱՆ ՀՈՍԱՆՔ
4.1 Էլեկտրական հոսանք: Նրա գոյության պայմանները: Հոսանքի ուժ և խտություն:
4.2 Անընդհատության հավասարումը ինտեգրալ և դիֆերենցիալ տեսքով:
4.3 Օհմի օրենքը շղթայի համասեռ տեղամասի համար: Էլեկտրական դիմադրություն:
4.5 Հոսանքի աշխատանքը և հզորությունը: Ջոուլ Լենցի օրենքը:
4.6 Օհմի օրենքը շղթայի անհամասեռ տեղամասի համար:
ԳԼՈՒԽ 5. ԷԼԵԿՏՐԱԿԱՆ ՀՈՍԱՆՔԸ ՄԵՏԱՂՆԵՐՈՒՄ,ՎԱԿՈՒՈՒՄՈՒՄ ԵՎ ԳԱԶԵՐՈՒՄ
5.1 Մետաղների հաղորդականության դասական տեսությունը:
5.2 Մետաղների հաղորդականության դասական տեսությունը:
5.3 Էլեկտրոնի ելքի աշխատանքը մետաղից:
5.4 Էմիսիոն երևույթներ և նրանց կիրառությունները:
5.5 Գազերի իոնացումը: Ոչ ինքնուրույն և ինքնուրույն գազային պարպումներ:
5.6 Պլազմա և նրա հատկությունները:
ԳԼՈՒԽ 6. ՄԱԳՆԻՍԱԿԱՆ ԴԱՇՏԸ ՎԱԿՈՒՈՒՄՈՒՄ
6.1 Մագնիսական դաշտ: Մագնիսական դաշտի ինդուկցիայի վեկտոր:
6.2 Մագնիսական դաշտի գրաֆիկական պատկերումը:
6.4 Ուղիղ և շրջանային հոսանքների դաշտերը:
6.5 Շարժվող էլեկտրական լիցքի մագնիսական դաշտը
6.6 Գաուսի թեորեմը մագնիսական դաշտի ինդուկցիայի վեկտորի համար ինտեգրալային և դիֆերենցիալ տեսքով:
6.7 Մագնիսական դաշտի ինդուկցիայի վեկտորի շրջապտույտի թեորեմը և նրա կիրառությունները:
ԳԼՈՒԽ 7. ՄԱԳՆԻՍԱԿԱՆ ԴԱՇՏԻ ԱԶԴԵՑՈՒԹՅՈՒՆԸ ՀՈՍԱՆՔՆԵՐԻ և ԼԻՑՔԵՐԻ ՎՐԱ
7.2 Երկու անվերջ երկար զուգահեռ հոսանքակիր հաղորդիչների փոխազդեցության ուժը:
7.4 Մագնիսական դաշտում հոսանքակիր հաղորդչի տեղափոխման վրա կատարվող աշխատանքը:
7.5 Լիցքավորված մասնիկների շարժումը համասեռ մագնիսական դաշտում:
ԳԼՈՒԽ 8. ՄԱԳՆԻՍԱԿԱՆ ԴԱՇՏԸ ՆՅՈՒԹԻ ՄԵՋ
8.1 Մագնիսական դաշտի նկարագրումը մագնետիկում:
8.2 Մագնիսացման մեխանիզմը: Մագնիսացման վեկտոր:
8.3 Մագնիսական դաշտի լարվածության վեկտորը և շրջապտույտի թեորեմը վեկտորի համար:
ԳԼՈՒԽ 9. ԷԼԵԿՏՐԱՄԱԳՆԻՍԱԿԱՆ ՄԱԿԱԾՈՒՄ
9.1 Էլեկտրամագնիսական մակածման երևույթը:
9.2 Մակածման հոսանքի ուղղությունը: Լենցի կանոնը:
9.3 Էլեկտրամագնիսական մակածման օրենքի արտածումը երկու եղանակով:
9.5 Անվերջ երկար սոլենոիդի ինդուկտիվությունը:
9.6 Անջատման և միացման հոսանքներ:
9.8 Մագնիսական դաշտի էներգիան և էներգիայի ծավալային խտությունը:
ԳԼՈՒԽ 10. ԷԼԵԿՏՐԱՄԱԳՆԻՍԱԿԱՆ ԴԱՇՏ
10.1 Վեկտորական դաշտի ռոտոր: Շրջապտույտի թեորեմը դիֆերենցիալ տեսքով:
10.2 Մրրկային էլեկտրական դաշտ:
10.4 Մաքսվելի հավասարումներն ինտեգրալ և դիֆերենցիալ տեսքով:
Մենք սկսում ենք ֆիզիկայի մի նոր բաժնի՝ «Էլեկտրադինամիկայի», ուսումնասիրությունը: Ինքը՝ անվանումը, ցույց է տալիս, որ խոսքն այն երևույթների մասին է, որոնք որոշվում են էլեկտրականապես լիցքավորված մասնիկների շարժմամբ և փոխազդեցությամբ: Այդպիսի փոխազդեցությունը կոչվում է էլեկտրամագնիսական: Այդ փոխազդեցության բնույթի ուսումնասիրությունը մեզ կհանգեցնի ֆիզիկայի հիմնական հասկացություններից մեկին՝ էլեկտրամագնիսական դաշտի հասկացությանը, որի միջոցով էլ իրագործվում է ինչպես երկու առանձին, էլեկտրականապես լիցքավորված մասնիկների փոխազդեցությունը, այնպես էլ երկու լիցքավորված մարմիններինը:
Գիտության կողմից հայտնագործված չորս տիպի փոխազդեցությունների մեջ, որոնք են գրավիտացիոն, էլեկտրամագնիսական, միջուկային և թույլ, հատկապես, էլեկտրամագնիսական փոխազդեցություններն են գրավում առաջին տեղն իրենց դրսևորումների ծավալով և բազմազանությամբ: Առօրյա կյանքում և տեխնիկայում ամենից հաճախ հանդիպում ենք էլեկտրամագնիսական ուժերի տարբեր տեսակների: Էլեկտրամագնիսական փոխազդեցության դրսևորման ձևեր են առաձգականության և շփման ուժերը:
Էլեկտրամագնիսական փոխազդեցություններն են, որ հնարավորություն են տալիս ձեզ` տեսնելու և կարդալու գիրքը, քանի որ լույսն էլեկտրամագնիսական դաշտի ձևերից մեկն է: Ինքը՝ կյանքն անիմաստ է առանց այդ ուժերի: Կենդանի էակները, ինչպես ցույց են տվել տիեզերագնացների թռիչքները, ընդունակ են երկար ժամանակ գտնվելու անկշռելության վիճակում, երբ տիեզերական ձգողության ուժերը չեն դրսևորվում: Բայց եթե մի ակնթարթ դադարի էլեկտրամագնիսական ուժերի ազդեցությունը, ապա միանգամից կանհետանա նաև կյանքը:
Մասնիկների փոխազդեցության պրոցեսում բնության ամենափոքր համակարգերում՝ ատոմային միջուկներում և տիեզերական մարմինների փոխազդեցություններում, էլեկտրամագնիսական ուժերը կարևոր դեր են խաղում, մինչդեռ միջուկային, թույլ և գրավիտացիոն փոխազդեցությունները որոշում են պրոցեսները կամ շատ փոքր, կամ միայն տիեզերական մասշտաբներով: Ատոմային թաղանթի կազմությունը, ատոմների հարակցումը մոլեկուլներ կազմելու համար (քիմիական ուժեր) և նյութի կտորների գոյացումը որոշվում են բացառապես էլեկտրամագնիսական ուժերով: Դժվար է, համարյա անհնար ցույց տալ մի երևույթ, որը կապված չլինի էլեկտրամագնիսական ուժերի ազդեցության հետ:
Էլեկտրադինամիկայի ստեղծումն արդյունք է պատահական հայտնագործությունների և գիտական հետազոտությունների մի երկար շղթայի՝ սկսած մետաքսի հետ շփված սաթի՝ թեթև առարկաներ իրեն ձգելու հատկության հայտնագործումից և վերջացրած անգլիացի մեծ գիտնական Ջ. Մաքսվելի վարկածով այն մասին, որ մագնիսական դաշտը ծնունդ է առնում փոփոխական էլեկտրական դաշտից: Միայն էլեկտրադինամիկայի ստեղծումից հետո, XIX դարի երկրորդ կեսին, սկսվեց էլեկտրամագնիսական երևույթների գործնական լայն օգտագործումը: Ռադիոյի գյուտը Ա.Պոպովի կողմից նոր տեսության սկզբունքների առաջին կարևոր կիրառություններից մեկն է: Էլեկտրադինամիկայի զարգացման ընթացքում առաջին անգամ գիտական հետազոտությունները նախորդեցին տեխնիկայի կիրառություններին: Եթե շոգեմեքենան կառուցվեց ջերմային պրոցեսների տեսության ստեղծումից շատ և շատ առաջ, ապա էլեկտրաշարժիչի կամ ռադիոընդունիչի կառուցումը հնարավոր դարձավ միայն էլեկտրադինամիկայի օրենքների հայտնագործումից և ուսումնասիրությունից հետո:
Էլեկտրամագնիսական երևույթների գործնական բազմաթիվ կիրառությունները կերպարանափոխեցին մարդկանց կյանքն ամբողջ երկրագնդի վրա: Ժամանակակից քաղաքակրթությունն անիմաստ է առանց էլեկտրական հոսանքի էներգիայի ամենալայն օգտագործման:
Մեր խնդիրն է ուսումնասիրել էլեկտրամագնիսական փոխազդեցությունների հիմնական օրենքները:
ԳԼՈՒԽ 1. ԷԼԵԿՏՐԱԿԱՆ ԴԱՇՏԸ ՎԱԿՈՒՈՒՄՈՒՄ
1.1. ԷԼԵԿՏՐԱԿԱՆ ԼԻՑՔ: ԷԼԵԿՏՐԱԿԱՆ ԼԻՑՔԻ ՔՎԱՆՏԱՅԻՆ ԲՆՈՒՅԹԸ: ՏԱՐՐԱԿԱՆ ԼԻՑՔ: ԼԻՑՔԻ ՊԱՀՊԱՆՄԱՆ ՕՐԵՆՔԸ
Մի քանի դար մեր թվարկությունից առաջ հին Հունաստանի գիտնականները հայտնաբերեցին այն փաստը, որ սաթե առարկաները շփելուց հետո դեպի իրենց են ձգում թեթև մարմիններ: Հունարեն սաթը կոչվում է էլեկտրոն. այդ բառից էլ ծագել է «էլեկտրականություն» անունը:
16-րդ դարի վերջին անգլիացի բժիշկ Ջիլբերտը հայտնագործեց, որ շփելիս, բացի սաթից, թեթև մարմիններ ձգելու հատկություն են ձեռք բերում նաև մի շարք ուրիշ նյութեր, օրինակ` ապակին, խեժը: Մարմինների վրա այդպիսի հատկությունների առաջացման երևույթն անվանեցին էլեկտրականացում: Մարմինների էլեկտրականացումը բացատրում էին մարմնի վրա էլեկտրական լիցքի երևան գալով:
Եթե մարմինն օժտված է էլեկտրամագնիսական փոխազդեցության մեջ մտնելու հատկությամբ, ապա ասում են, որ այն կրում է էլեկտրական լիցք կամ լիցքավորված է: Էլեկտրական լիցքը մարմնի` էլեկտրական փոխազդեցության մեջ մտնելու հատկության քանակական չափն է: Այն սկալյար ֆիզիկական մեծություն է:
Բնության մեջ բոլոր մարմինները միմյանց հետ փոխազդում են տիեզերական ձգողության (գրավիտացիոն) ուժերով: Այդ փոխազդեցությունն իրականացվում է տարածության մեջ մարմինների ստեղծած գրավիտացիոն դաշտերի միջոցով: Նյութը կազմող տարրական մասնիկների՝ էլեկտրոնների, պրոտոնների և նեյտրոնների միջև գործող գրավիտացիոն փոխազդեցության ուժերը շատ փոքր են, այդ պատճառով դրանք էական դեր չեն խաղում միկրոաշխարհում: Այդ ուժերն էական են դառնում միայն այն դեպքում, երբ փոխազդող մարմիններից գոնե մեկն օժտված է բավականաչափ մեծ զանգվածով, ինչը բնորոշ է երկնային մարմիններին՝ աստղերին, մոլորակներին:
Գրավիտացիոն փոխազդեցության ուժերն իրարից որոշ հեռավորության վրա գտնվող մարմինների (մասնիկների) միջև գործող միակ ուժերը չեն: Տարրական մասնիկների զգալի մասը, այդ թվում նաև էլեկտրոններն ու պրոտոնները, օժտված են մեկ այլ, այսպես կոչված, էլեկտրամագնիսական փոխազդեցության մեջ մտնելու հատկությամբ: Փոխազդեցության այս տեսակը թե՞ իր բնույթով և թե՞ իր ինտենսիվությամբ էապես տարբերվում է գրավիտացիոն փոխազդեցությունից: Էլկտրամագնիսական փոխազդեցության ժամանակ կարող են ծագել ինչպես ձգողական, այնպես էլ վանողական ուժեր:
Էլեկտրական լիցքի մասին հայտնի փորձարարական տվյալները թույլ են տալիս անել հետևյալ եզրակացությունները:
1. Լիցքավորված մարմինները կարող են ինչպես ձգել, այնպես էլ վանել միմյանց: Բնության մեջ գոյություն ունեն երկու տեսակի էլեկտրական լիցքեր՝ դրական և բացասական: Որպես դրական լիցք ընդունվում է այն, որն առաջանում է ապակե ձողիկը մետաքսով շփելով էլեկտրականացնելու ժամանակ: Իսկ այն լիցքը, որը երևան է գալիս խեժի (կամ կաուչուկի) ձողիկի վրա, երբ այն շփում են մորթով, անվանել են բացասական լիցք: Բոլոր նույնանուն լիցքերն իրար վանում են, իսկ տարանուն լիցքերը՝ ձգում: Ատոմները կազմող տարրական մասնիկներից պրոտոնի լիցքն անվանում են դրական, իսկ էլեկտրոնինը՝ բացասական:
1.
Ամերիկացի
ֆիզիկոս
Միլլիկենը
փորձով ցույց
է տվել, որ
էլեկտրական
լիցքը կարող է
ընդունել
միայն ընդհատ արժեքներ:
Բնության մեջ
գոյություն
ունի լիցքի
որոշակի
նվազագույն
քանակ, որը չի
մասնատվում
էլ ավելի փոքր
քանակների:
Լիցքի այդ
նվազագույն
քանակն
անվանում են
տարրական
լիցք:
Կամայական
մարմնի լիցքը
տարրական
լիցքի
բազմապատիկն
է: Տարրական
դրական լիցք է
կրում
պրոտոնը, իսկ
մոդուլով այդ
լիցքին
հավասար,
սակայն
բացասական
տարրական
լիցք կրում է
էլեկտրոնը: ![]() Մարմինն
էլեկտրականապես
չեզոք է, այսինքն`
նրա լիցքը
հավասար է 0-ի,
եթե նրանում Ne
էլեկտրոնների
թիվը հավասար
է Np պրոտոնների
թվին:
Ընդհանուր
դեպքում
Մարմինն
էլեկտրականապես
չեզոք է, այսինքն`
նրա լիցքը
հավասար է 0-ի,
եթե նրանում Ne
էլեկտրոնների
թիվը հավասար
է Np պրոտոնների
թվին:
Ընդհանուր
դեպքում ![]()
2. Էլեկտրական
լիցքի մյուս
կարևոր
հատկությունն
այն է, որ փակ
համակարգում
տեղի ունեցող
ցանկացած
պրոցեսում՝
համակարգը
կազմող բոլոր
(մասնիկների)
մարմինների
լիցքերի հանրահաշվական
գումարը
մնում է
անփոփոխ: Այս
պնդումը
հայտնի է
որպես Էլեկտրական
լիցքի
պահպանման
օրենք:
Համակարգը համարվում
է փակ, եթե նրա
մեջ
արտաքինից
չեն մտնում և
նրանից դուրս
չեն գալիս
լիցքավորված
մարմիններ
(մասնիկներ):
Եթե
համակարգը
կազմող
մասնիկների
լիցքերը
նշանակենք ![]() ,
ապա համաձայն
լիցքի
պահպանման
օրենքի
,
ապա համաձայն
լիցքի
պահպանման
օրենքի ![]() Էլեկտրական
լիցքի
պահպանման
օրենքը նույնպիսի
հիմնարար
ֆիզիկական
օրենք է,
ինչպիսիք
էներգիայի և
իմպուլսի
պահպանման օրենքները:
Էլեկտրական
լիցքի
պահպանման
օրենքը նույնպիսի
հիմնարար
ֆիզիկական
օրենք է,
ինչպիսիք
էներգիայի և
իմպուլսի
պահպանման օրենքները:
3. Էլեկտրական լիցքը մնում է ինվարիանտ, նրա մեծությունը կախված չէ հաշվարկման համակարգից, այսինքն` կախված չէ այն բանից` շարժվում է այն, թե գտնվում է դադարի վիճակում:
Մոլեկուլային ֆիզիկայից հայտնի է, որ բոլոր նյութերը, անկախ իրենց ագրեգատային վիճակից, բաղկացած են մոլեկուլներից և ատոմներից: Նշենք, որ ատոմն իր հերթին կազմված է դրական լիցքավորված միջուկից և նրա շուրջը պտտվող բացասական լիցքավորված էլեկտրոններից:
Ակնհայտ է դառնում, որ մարմինը լիցքավորելու համար անհրաժեշտ է խախտել մարմինը կազմող ատոմներում դրական և բացասական լիցքերի հավասարակշռությունը:
Լիցքերի միջև հավասարակշռության (հավասարության) խախտումն ընդունված է անվանել մարմնի լիցքավորում:
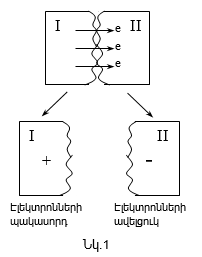
Դրական և բացասական լիցքերի միջև առկա հավասարակշռությունը ատոմներում հիմնականում խախտվում է էլեկտրոնների թվի փոփոխությունից, որովհետև միջուկում դրական մասնիկների` պրոտոնների թվի փոփոխությունը պահանջում է ավելի մեծ էներգիա (աշխատանք): Հասկանալով լիցքավորման պրոցեսը` դժվար չէ տալ լիցքավորման եղանակները: Օրինակ` լիցքավորում տարբեր մարմինների շփման միջոցով (նկ.1): Տարբեր մարմինների փոխադարձ շփման ժամանակ դիտվում է մակերևույթների այն աստիճանի մոտեցում (որոշ տիրույթներում), որ տեղի է ունենում էլեկտրոնների անցում մի մարմնից մյուսը: Արդյունքում մարմիններից մեկում առաջանում է էլեկտրոնների պակասորդ, որը լիցքավորվում է դրական, իսկ մյուսում` էլեկտրոնների ավելցուկ, և այն լիցքավորվում է բացասական: Մարմնի լիցքավորումը կարող է իրականացվել զանազան արտաքին ազդակների` իոնարարների, լույսի, ջերմաստիճանի, ճառագայթման և այլ ազդեցությունների միջոցով: Վերը բերված լիցքավորման մեխանիզմների նկարագրությունից հետևում է, որ ցանկացած մեծության լիցք պետք է լինի տարրական լիցքի՝ պրոտոնի կամ էլեկտրոնի լիցքի բազմապատիկը: Այս փաստը հաստատված է փորձով:
Կախված ազատ լիցքերի կոնցենտրացիայից` մարմինները բաժանվում են հաղորդիչների, դիէլեկտրիկների և կիսահաղորդիչների:
Հաղորդիչներ են կոչվում այն մարմինները, որոնցում էլեկտրական լիցքերը կարող են տեղաշարժվել նրա ամբողջ ծավալով: Հաղորդիչները բաժանվում են երկու խմբերի. 1) առաջին սեռի հաղորդիչներ (մետաղներ), որոնցում լիցքերի (ազատ էլեկտրոնների) տեղափոխությունը չի ուղեկցվում քիմիական փոխակերպումներով, 2) երկրորդ սեռի հաղորդիչներ (օրինակ, հալված աղերը, թթուների լուծույթները), որոնցում լիցքերի (դրական և բացասական իոնների) տեղափոխությունը առաջացնում է քիմիական փոփոխություններ:
Դիէլեկտրիկներ են կոչվում այն մարմինները, որոնցում գործնականում բացակայում են ազատ լիցքերը (օրինակ, ապակին, պլաստմասաները):
Կիսահաղորդիչները (օրինակ, գերմանիում, սիլիցիում) զբաղեցնում են միջանկյալ դիրք հաղորդիչների և դիէլեկտրիկների միջև:
Մարմինների նշված բաժանումը բացարձակ պայմանական է, սակայն նրանցում ազատ լիցքերի կոնցենտրացիաների մեծ տարբերությամբ է պայմանավորված նրանց վարքի հսկայական տարբերությունները, որի պատճառով էլ արդարացվում է մարմինների բաժանումը հաղորդիչների, դիէլեկտրիկների և կիսահաղորդիչների:
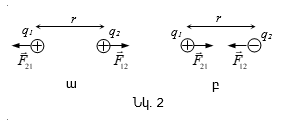
Փորձերը ցույց են տալիս, որ լիցքավորված մարմինները միմյանց հետ միշտ փոխազդում են. նույնանուն լիցքերը միմյանց վանում են (նկ.2ա), իսկ տարանուն լիցքերը՝ իրար ձգում (նկ.2բ): Մասնավոր դեպքում, տվյալ հաշվարկման համակարգում անշարժ կետային լիցքերի միջև փոխազդեցության օրենքը քանակապես որոշվել է Կուլոնի (1736-1806) կողմից` 1785թ. փորձով, ոլորակշեռքի օգնությամբ: Ելնելով այդ օրենքի հիմնարար բնույթից՝ այն անվանում են նաև էլեկտրաստատիկայի հիմնական օրենք: Կուլոնի օրենքը սահմանվում է կետային լիցքերի համար: Լիցքը կոչվում է կետային, եթե այն կրող մարմինը տվյալ խնդրում կարելի է համարել նյութական կետ:
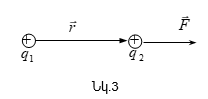
Կուլոնի օրենքն ունի հետևյալ տեսքը`
![]() ,
(1.1)
,
(1.1)
որտեղ
![]() -ն
համեմատականության
գործակից է,
-ն
համեմատականության
գործակից է, ![]() -ը
-ը ![]() և
և ![]() -ը`
կետային լիցքերի
միջև եղած
հեռավորությունը
(նկ.3):
-ը`
կետային լիցքերի
միջև եղած
հեռավորությունը
(նկ.3):
Կուլոնի
օրենքն
արտահայտող (1.1)
բանաձևում ![]() համեմատականության
գործակիցն
ունի հետևյալ
ֆիզիկական
իմաստը. այն
թվապես
հավասար է
միավոր
հեռավորության
վրա գտնվող
միավոր
լիցքերի փոխազդեցության
ուժին: k
գործակցի
թվային արժեքը
կախված է
միավորների
ընտրությունից
և որոշվում է
փորձնական
եղանակով:
Փորձը ցույց է
տալիս, որ
համեմատականության
գործակիցն
ունի հետևյալ
ֆիզիկական
իմաստը. այն
թվապես
հավասար է
միավոր
հեռավորության
վրա գտնվող
միավոր
լիցքերի փոխազդեցության
ուժին: k
գործակցի
թվային արժեքը
կախված է
միավորների
ընտրությունից
և որոշվում է
փորձնական
եղանակով:
Փորձը ցույց է
տալիս, որ
![]() Ն.մ
Ն.մ![]() /Կլ
/Կլ![]() :
:
Կուլոնի
օրենքից բխող
մի շարք
առնչություններ
առավել պարզ
տեսք են
ընդունում,
երբ ![]() հաստատունը
ներկայացվում
է հետևյալ տեսքով.
հաստատունը
ներկայացվում
է հետևյալ տեսքով.
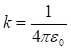
![]() մեծությունը
կոչվում է
էլեկտրական
հաստատուն:
Այն պատկանում
է հիմնարար
ֆիզիկական
հաստատունների
թվին և
հավասար է`
մեծությունը
կոչվում է
էլեկտրական
հաստատուն:
Այն պատկանում
է հիմնարար
ֆիզիկական
հաստատունների
թվին և
հավասար է`
![]() Կլ
Կլ![]() /Ն.մ
/Ն.մ![]() :
:
Այսպիսով, Կուլոնի օրենքը կընդունի հետևյալ տեսքը՝
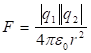 : (1.2)
: (1.2)
Կուլոնի օրենքը կարելի է գրել վետորական տեսքով.
![]() , (1.3)
, (1.3)
Այս
արտահայության
մեջ ![]() -ը
մի վեկտոր է,
որը տարված է
մեկ լիցքից
մյուսը և
ուղղված է
դեպի այն
լիցքը, որի
նկատմամբ կիրառված
է
-ը
մի վեկտոր է,
որը տարված է
մեկ լիցքից
մյուսը և
ուղղված է
դեպի այն
լիցքը, որի
նկատմամբ կիրառված
է ![]() ուժը
(նկ.3):
ուժը
(նկ.3):
Ցանկացած երկու անշարժ կետային լիցքերի փոխազդեցության ուժը վակուումում ուղիղ համեմատական է լիցքերի մոդուլների արտադրյալին, հակադարձ համեմատական նրանց միջև եղած հեռավորության քառակուսուն և ուղղված է այդ լիցքերը միացնող ուղղի երկայնքով:
Կուլոնի օրենքը ճիշտ է ոչ միայն կետային լիցքերի, այլև լիցքավորված գնդաձև մարմինների համար, որոնց լիցքերը հավասարաչափ բաշխված են նրանց ամբողջ ծավալով կամ մակերևույթով: Այդ դեպքում որպես մարմինների հեռավորություն պետք է ընդունել գնդերի կենտրոնների միջև եղած հեռավորությունը:
Գիտենալով կետային լիցքերի փոխազդեցության օրենքը` կարելի է հաշվել վերջավոր չափեր ունեցող մարմինների վրա կենտրոնացված լիցքերի փոխազդեցության ուժը: Այդ ուժի որոշման համար մարմիններից յուրաքանչյուրը պետք է դիտել որպես կետային լիցքերի համակարգ, գտնել տարբեր մարմիններին պատկանող կետային լիցքերի յուրաքանչյուր զույգի փոխազդեցության ուժը և հաշվել այդ բոլոր ուժերի համազորը:
Կուլոնի
օրենքի
իրագործման
ճշտությունը
մեծ
հեռավորությունների
վրա, ընդհուպ
մինչև ![]() մ
հաստատվել է
մերձերկրյա
տարածության
մեջ արբանյակների
օգնությամբ
մագնիսական
դաշտի
ուսումնասիրության
դեպքում: Նրա
իրագործումը
փոքր հեռավորությունների
վրա, ընդհուպ
մինչև
մ
հաստատվել է
մերձերկրյա
տարածության
մեջ արբանյակների
օգնությամբ
մագնիսական
դաշտի
ուսումնասիրության
դեպքում: Նրա
իրագործումը
փոքր հեռավորությունների
վրա, ընդհուպ
մինչև ![]() մ,
ստուգվել է
տարրական
մասնիկների
փոխազդեցության
փորձերով:
մ,
ստուգվել է
տարրական
մասնիկների
փոխազդեցության
փորձերով:
ՄՀ-ում
լիցքի
միավորը
կուլոնն է: 1
Կլ-ը այն լիցքն
է, որը 1 վ-ում
անցնում է
հաղորդչի
լայնական հատույթով,
երբ նրանում
հաստատուն
հոսանքի ուժը
1 Ա է: Բնության
մեջ գոյություն
ունեցող
ամենափոքր՝
տարրական լիցքի
մոդուլը՝ ![]() Կլ:
Կլ:
1.3. ԷԼԵԿՏՐԱՍՏԱՏԻԿ ԴԱՇՏ: ԷԼԵԿՏՐԱՍՏԱՏԻԿ ԴԱՇՏԻ ԼԱՐՎԱԾՈՒԹՅՈՒՆ: ԷԼԵԿՏՐԱՍՏԱՏԻԿ ԴԱՇՏԵՐԻ
ՎԵՐԱԴՐՄԱՆ ՍԿԶԲՈՒՆՔԸ
Ցանկացած
![]() լիցք
իր շուրջը
ստեղծում է
էլեկտրական
դաշտ, որի
գոյությունը
հաստատվում է
որևէ այլ`
լիցք
իր շուրջը
ստեղծում է
էլեկտրական
դաշտ, որի
գոյությունը
հաստատվում է
որևէ այլ` ![]() փորձնական
լիցքի վրա ազդող
ուժի
առկայությամբ
(նկ.4):
փորձնական
լիցքի վրա ազդող
ուժի
առկայությամբ
(նկ.4):
Համաձայն մերձազդեցության տեսության՝ նույնիսկ մեկ լիցքը շրջակա տարածության մեջ առաջացնում է որոշակի փոփոխություն: Յուրաքանչյուր լիցք իր շրջակա տարածությունն օժտում է յուրահատուկ ֆիզիկական հատկություններով, այլ խոսքով, ասում ենք, որ լիցքն իր շուրջն ստեղծում է էլեկտրական դաշտ, որն էլ ազդում է դաշտում տեղադրված ցանկացած այլ լիցքի վրա: Այսպիսով, երկու լիցքեր միմյանց վրա անմիջականորեն չեն ազդում, նրանցից յուրաքանչյուրն իր շուրջը ստեղծում է էլեկտրական դաշտ, և մի լիցքի դաշտն ազդում է մյուս լիցքի վրա, և հակառակը:
Լիցքերի միջև փոխազդեցությունն իրականացվում է մատերիայի հատուկ գոյաձևի` լիցքերից յուրաքանչյուրի ստեղծած էլեկտրական դաշտի շնորհիվ: Դաշտի գաղափարն առաջին անգամ տվել է անգլիացի գիտնական Մ. Ֆարադեյը (1791-1867):
Դիտարկվող
հաշվարկման
համակարգում
անշարժ լիցքի
ստեղծած
դաշտը`
էլեկտրաստատիկ
դաշտը,
բնութագրվում
է ![]() էլեկտրաստատիկ
դաշտի
լարվածությամբ:
Այն
էլեկտրական
դաշտի
ուժային
բնութագիրն է,
որով կարելի է
հաշվել դաշտի
յուրաքանչյուր
կետում
տեղադրված
կամայական
լիցքի վրա
ազդող ուժի
մեծությունն
ու
ուղղությունը:
Եթե
էլեկտրական
դաշտի տվյալ
կետում հերթով
տեղադրենք
տարբեր
մեծության
փորձնական լիցքեր՝
էլեկտրաստատիկ
դաշտի
լարվածությամբ:
Այն
էլեկտրական
դաշտի
ուժային
բնութագիրն է,
որով կարելի է
հաշվել դաշտի
յուրաքանչյուր
կետում
տեղադրված
կամայական
լիցքի վրա
ազդող ուժի
մեծությունն
ու
ուղղությունը:
Եթե
էլեկտրական
դաշտի տվյալ
կետում հերթով
տեղադրենք
տարբեր
մեծության
փորձնական լիցքեր՝
![]() , և
ամեն անգամ
չափենք
լիցքերի վրա
ազդող
, և
ամեն անգամ
չափենք
լիցքերի վրա
ազդող ![]() ուժերը,
ապա կհամոզվենք,
որ բոլոր
լիցքերի
համար ազդող
ուժի և լիցքի
հարաբերությունը
կախված չէ
լիցքի
մեծությունից
և այդ կետում
ունի
հաստատուն
ուղղություն
և
մեծություն՝
ուժերը,
ապա կհամոզվենք,
որ բոլոր
լիցքերի
համար ազդող
ուժի և լիցքի
հարաբերությունը
կախված չէ
լիցքի
մեծությունից
և այդ կետում
ունի
հաստատուն
ուղղություն
և
մեծություն՝ ![]() ,
հետեվաբար՝
կարող է
ծառայել
որպես
էլեկտրական դաշտի
բնութագիր:
Այն կոչվում
է էլեկտրական
դաշտի
լարվածություն
և նշանակվում
է
,
հետեվաբար՝
կարող է
ծառայել
որպես
էլեկտրական դաշտի
բնութագիր:
Այն կոչվում
է էլեկտրական
դաշտի
լարվածություն
և նշանակվում
է ![]() տառով:
Էլեկտրաստատիկ
դաշտի
լարվածությունը
այն
ֆիզիկական
մեծությունն
է, որը թվապես հավասար
է դաշտի տվյալ
կետում
միավոր փորձնական
դրական լիցքի
վրա ազդող
ուժին.
տառով:
Էլեկտրաստատիկ
դաշտի
լարվածությունը
այն
ֆիզիկական
մեծությունն
է, որը թվապես հավասար
է դաշտի տվյալ
կետում
միավոր փորձնական
դրական լիցքի
վրա ազդող
ուժին.
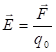 : (1.4)
: (1.4)
(1.4)
բանաձևից
հետևում է, որ
էլեկտրական
դաշտի
լարվածությունը
վեկտորական
մեծություն է:
Տրված ![]() լարվածությամբ
էլեկտրական
դաշտի կողմից
կամայական
լարվածությամբ
էլեկտրական
դաշտի կողմից
կամայական ![]() լիցքի
վրա ազդող
լիցքի
վրա ազդող ![]() ուժը
որոշվում է (1.4)
բանաձևից.
ուժը
որոշվում է (1.4)
բանաձևից.
![]() : (1.5)
: (1.5)
Լարվածությունն
էլեկտրական
դաշտի ուժային
բնութագիրն է.
այն որոշում է
![]() լիցքի
վրա ազդող
ուժը:
լիցքի
վրա ազդող
ուժը: ![]() վեկտորի
ուղղությունը
համընկնում է
դրական լիցքի
վրա ազդող
ուժի
ուղղության
հետ և հակառակ
է բացասական
լիցքի վրա
ազդող ուժի
ուղղությանը:
վեկտորի
ուղղությունը
համընկնում է
դրական լիցքի
վրա ազդող
ուժի
ուղղության
հետ և հակառակ
է բացասական
լիցքի վրա
ազդող ուժի
ուղղությանը:
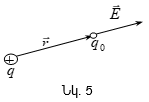
Հաշվենք
![]() կետային
լիցքի դաշտի
լարվածությունը
տարածության
կամայական
կետում: Դրա
համար, ըստ (1.4)
սահմանման,
պետք է այդ
կետում
տեղադրել
որևէ
կետային
լիցքի դաշտի
լարվածությունը
տարածության
կամայական
կետում: Դրա
համար, ըստ (1.4)
սահմանման,
պետք է այդ
կետում
տեղադրել
որևէ ![]() կետային
լիցք, որոշել
նրա վրա ազդող
կետային
լիցք, որոշել
նրա վրա ազդող
![]() ուժը
և այն բաժանել
այդ լիցքի վրա
(նկ. 5):
ուժը
և այն բաժանել
այդ լիցքի վրա
(նկ. 5):
Օգտվելով
Կուլոնի
օրենքից`
լարվածության
վեկտորի ![]() մոդուլի
համար
կստանանք՝
մոդուլի
համար
կստանանք՝
![]() : (1.6)
: (1.6)
Այսպիսով,
կետային
լիցքի էլեկտրական
դաշտի
լարվածության
մոդուլը
ուղիղ
համեմատական
է ![]() լիցքի
մեծությանը և
հակադարձ համեմատական`
լիցքից մինչև
դաշտի տվյալ
կետը եղած
լիցքի
մեծությանը և
հակադարձ համեմատական`
լիցքից մինչև
դաշտի տվյալ
կետը եղած ![]() եռավորության
քառակուսուն:
եռավորության
քառակուսուն:
Դաշտի
![]() լարվածությունը
չափվում է
լարվածությունը
չափվում է ![]()
![]() միավորով:
միավորով:
Գործնականում
էլեկտրաստատիկ
դաշտը պայմանավորված
է լինում ոչ
թե մեկ, այլ`
մեկից ավելի
անշարժ
լիցքերով: Այդ
դեպքում
էլեկտրաստատիկ
դաշտի
լարվածության
սահմանման
համաձայն ![]() -ն
կորոշվի
հետևյալ
բանաձևով.
-ն
կորոշվի
հետևյալ
բանաձևով.
![]() ,
,
![]() , (1.7)
, (1.7)
որտեղ
![]() -ն
-ն ![]() -րդ
լիցքի
ստեղծած
դաշտի լարվածությունն
է դաշտի
դիտարկվող
կետում:
-րդ
լիցքի
ստեղծած
դաշտի լարվածությունն
է դաշտի
դիտարկվող
կետում:
Այսպիսով,
տարածության
տվյալ կետում
լիցքերի
համակարգի
ստեղծած
արդյունարար
դաշտի լարվածությունը
հավասար է
առանձին
լիցքերի ստեղծած
դաշտերի լարվածությունների
վեկտորական
գումարին: Այս
փաստը
ֆիզիկայում
ընդունված է
անվանել էլեկտրաստատիկ
դաշտերի
վերադրման
սկզբունք, որն
իր հերթին
հետևանք է
դաշտի գծային
հատկության:
Նշենք, որ վերադրման
սկզբունքը
փորձերի ընդհանրացման
արդյունք է և,
հնարավոր է`
խանգարվում է
փոքր հեռավորությունների
(![]() մ)
վրա:
մ)
վրա:
1.4. ԷԼԵԿՏՐԱԿԱՆ ԴԱՇՏԻ ԳՐԱՖԻԿԱԿԱՆ ՊԱՏԿԵՐՈՒՄԸ
Էլեկտրական
դաշտը
գրաֆիկորեն`
լարվածության
վեկտորներով
պատկերելը
կբերեր
վեկտորների
խայտաբղետ
դասավորված
հավաքածուի:
Այդ
դժվարությունը
հաղթահարվեց
Ֆարադեյի
կողմից, որն
առաջարկեց
դաշտը պատկերել
լարվածության
գծերի
(ուժագծերի)
միջոցով: Տանք
լարվածության
գծի (ուժագծի)
սահմանումը:
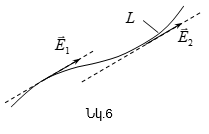
Այն երևակայական
![]() գիծը
(նկ.6), որի
ցանկացած
կետում տարած
շոշափողը
համընկնում է
այդ նույն
կետում
լարվածության
վեկտորի հետ,
կոչվում է
լարվածության
գիծ (ուժագիծ):
գիծը
(նկ.6), որի
ցանկացած
կետում տարած
շոշափողը
համընկնում է
այդ նույն
կետում
լարվածության
վեկտորի հետ,
կոչվում է
լարվածության
գիծ (ուժագիծ):
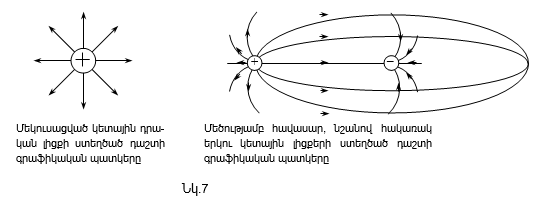
Նկ.7-ում բերված են էլեկտրաստատիկ դաշտերի գրաֆիկական պատկերման առանձին օրինակներ:
Եթե էլեկտրաստատիկ դաշտի լարվածությունը տարբեր կետերում տարբեր է, դաշտը կոչվում է անհամասեռ: Եթե էլեկտրաստատիկ դաշտի լարվածության վեկտորը հաստատուն է դաշտի բոլոր կետերի համար, ապա այդպիսի դաշտը կոչվում է համասեռ (նկ.8): Համասեռ դաշտի օրինակ է միմյանց զուգահեռ, մեծությամբ հավասար, նշանով հակառակ լիցքերով հավասարաչափ լիցքավորված հարթությունների ստեղծած դաշտը եզրերից հեռու տիրույթում (նկ.8):
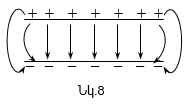
Համասեռ դաշտը գրաֆիկորեն պատկերվում է միմյանց զուգահեռ և միմյանցից հավասարահեռ լարվածության գծերի տեսքով:
Նշենք լարվածության գծերի հատկություններից մի քանիսը.
Լարվածության գծերը սկսվում են դրական լիցքերից և վերջանում կամ բացասական լիցքերի վրա, կամ` անվերջությունում: Քանի որ լարվածության վեկտորը տարածության յուրաքանչյուր կետում ունի որոշակի ուղղություն, բացառությամբ այն կետերի, որտեղ լարվածությունը հավասար է զրոյի, ապա այդ կետով կարող է անցնել միայն մեկ ուժագիծ: Այստեղից հետևում է, որ ուժագծերը չեն հատվում, նրանք միայն զուգամիտում են լիցքերի վրա:
1.5. ԷԼԵԿՏՐԱՍՏԱՏԻԿ ԴԱՇՏԻ ԼԱՐՎԱԾՈՒԹՅԱՆ ՎԵԿՏՈՐԻ ՀՈՍՔ:
ԳԱՈՒՍԻ ԹԵՈՐԵՄԸ ԻՏԵԳՐԱԼԱՅԻՆ ԵՎ ԴԻՖԵՐԵՆՑԻԱԼ ՏԵՍՔՈՎ
Որպեսզի
լարվածության
գծերի
օգնությամբ հնարավոր
լինի
բնութագրել
ոչ միայն
էլեկտրաստատիկ
դաշտի ![]() լարվածության
ուղղությունը,
այլ նաև արժեքը,
պայմանավորվում
են դրանք
տանել որոշակի
խտությամբ
(նկ.9):
Լարվածության
գծերի խտությունն
ընտրվում է
այնպես, որ
դրանց
ուղղահայաց
մակերեսի
միավոր մակերևույթը
հատող գծերի
թիվը հավասար
լինի
լարվածության
ուղղությունը,
այլ նաև արժեքը,
պայմանավորվում
են դրանք
տանել որոշակի
խտությամբ
(նկ.9):
Լարվածության
գծերի խտությունն
ընտրվում է
այնպես, որ
դրանց
ուղղահայաց
մակերեսի
միավոր մակերևույթը
հատող գծերի
թիվը հավասար
լինի ![]() վեկտորի
թվային
արժեքին: Այդ
դեպքում
լարվածության
գծերի
պատկերի միջոցով
կարելի է
դատել
տարածության
տարբեր
կետերում
վեկտորի
թվային
արժեքին: Այդ
դեպքում
լարվածության
գծերի
պատկերի միջոցով
կարելի է
դատել
տարածության
տարբեր
կետերում ![]() վեկտորի
ուղղության և
մեծության
մասին:
վեկտորի
ուղղության և
մեծության
մասին:
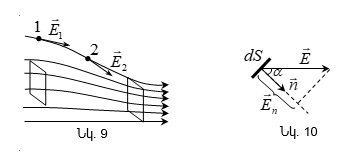
Լարվածության
գծերի այն
թիվը որոնք
թափանցում են
տարրական ![]() մակերեսը,
որի
մակերեսը,
որի ![]() նորմալը
նորմալը ![]() վեկտորի հետ
կազմում է
վեկտորի հետ
կազմում է ![]() անկյուն
հավասար է
անկյուն
հավասար է ![]() , որտեղ
, որտեղ ![]() -ը
-ը ![]() վեկտորի
պրոյեկցիան է
վեկտորի
պրոյեկցիան է ![]() նորմալի
վրա (նկ.10):
նորմալի
վրա (նկ.10):
![]()
![]() մեծությունը
կոչվում է լարվածության
վեկտորի հոսք
dS մակերեսի
միջով: Այստեղ
մեծությունը
կոչվում է լարվածության
վեկտորի հոսք
dS մակերեսի
միջով: Այստեղ
![]() -ը
վեկտոր է, որի
մոդուլը
հավասար է dS-ի,
իսկ ուղղությունը
համընկնում է
մակերեսի
-ը
վեկտոր է, որի
մոդուլը
հավասար է dS-ի,
իսկ ուղղությունը
համընկնում է
մակերեսի ![]() նորմալի
ուղղության
հետ:
նորմալի
ուղղության
հետ: ![]() վեկտորի
(հետևաբար և
վեկտորի
(հետևաբար և ![]() -ի)
ուղղության
ընտրությունը
պայմանական է,
քանի որ այն
կարելի է
ուղղել
ցանկացած
կողմ: Էլեկտրաստատիկ
դաշտի
լարվածության
վեկտորի հոսքի
միավորը` վոլտմետրն
է ( Վ.մ):
Կամայական
փակ S
մակերևույթի
համար
լարվածության
վեկտորի
հոսքն այդ
մակերևույթով
-ի)
ուղղության
ընտրությունը
պայմանական է,
քանի որ այն
կարելի է
ուղղել
ցանկացած
կողմ: Էլեկտրաստատիկ
դաշտի
լարվածության
վեկտորի հոսքի
միավորը` վոլտմետրն
է ( Վ.մ):
Կամայական
փակ S
մակերևույթի
համար
լարվածության
վեկտորի
հոսքն այդ
մակերևույթով
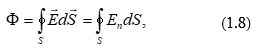
որտեղ ինտեգրալը վերցվում է S փակ մակերևույթով:
(1.8)
բանաձևի
համաձայն
որևէ
մակերևույթով
![]() վեկտորի
հոսքը թվապես
հավասար է այդ
մակերևույթը
հատող
վեկտորի
հոսքը թվապես
հավասար է այդ
մակերևույթը
հատող ![]() -ի
գծերի թվին:
-ի
գծերի թվին: ![]() վեկտորի
հոսքը
հանրահաշվական
մեծություն է.
կախված է ոչ
միայն
վեկտորի
հոսքը
հանրահաշվական
մեծություն է.
կախված է ոչ
միայն ![]() դաշտի
կոնֆիգուրացիայից,
այլ նաև
դաշտի
կոնֆիգուրացիայից,
այլ նաև ![]() -ի
ուղղության
ընտրությունից:
Փակ մակերևույթների
համար
նորմալի
դրական
ուղղություն է
ընտրվում
արտաքին
նորմալը,
այսինքն այն
նորմալը, որն
ուղղված է
մակերևույթով
ընդգրկված
տիրույթից
դուրս: Այդ
պատճառով այն
տեղերում,
որտեղ
-ի
ուղղության
ընտրությունից:
Փակ մակերևույթների
համար
նորմալի
դրական
ուղղություն է
ընտրվում
արտաքին
նորմալը,
այսինքն այն
նորմալը, որն
ուղղված է
մակերևույթով
ընդգրկված
տիրույթից
դուրս: Այդ
պատճառով այն
տեղերում,
որտեղ ![]() վեկտորն
ուղղված է
դուրս
(այսինքն`
վեկտորն
ուղղված է
դուրս
(այսինքն`![]() գիծը
դուրս է գալիս
մակերևույթով
սահմանափակված
ծավալից),
գիծը
դուրս է գալիս
մակերևույթով
սահմանափակված
ծավալից), ![]() և,
համապատասխանաբար
և,
համապատասխանաբար
![]() -ը,
կլինեն
դրական, իսկ
այն տեղերում,
որտեղ
-ը,
կլինեն
դրական, իսկ
այն տեղերում,
որտեղ ![]() վեկտորն
ուղղված է
ներս
(այսինքն`
վեկտորն
ուղղված է
ներս
(այսինքն` ![]() գիծը
մտնում է
մակերևույթով
սահմանափակված
ծավալի մեջ),
գիծը
մտնում է
մակերևույթով
սահմանափակված
ծավալի մեջ), ![]() և
և ![]() -ը,
կլինեն
բացասական:
-ը,
կլինեն
բացասական:
Էլեկտրական լիցքերի համակարգի դաշտի լարվածության հաշվարկը էլեկտրական դաշտերի վերադման սկզբունքի օգնությամբ կարելի է էականորեն պարզեցնել` կիրառելով գերմանացի գիտնական Կ. Գաուսի (1777-1855) կողմից արտածված թեորեմը:
Գաուսի թեորեմը մաթեմատիկական կապ է հաստատում փակ մակերևույթով լարվածության վեկտորի հոսքի և այդ մակերևույթով ընդգրկված ծավալում գտնվող ամբողջ լիցքի միջև: Ստանանք այդ կապը:
(1.8)
բանաձևին
համապատասխան
լարվածության
վեկտորի
հոսքը ![]() լիցքն
ընդգրկող
լիցքն
ընդգրկող ![]() շառավիղ
ունեցող
սֆերիկ մակերևույթով,
որը գտնվում է
նրա
կենտրոնում (նկ.11),
կլինի`
շառավիղ
ունեցող
սֆերիկ մակերևույթով,
որը գտնվում է
նրա
կենտրոնում (նկ.11),
կլինի`
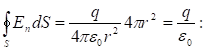
Այս արդյունքը ճիշտ է ցանկացած ձևի փակ մակերևույթի համար: Իրոք, եթե սֆերան շրջափակենք կամայական փակ մակերևույթով (նկ.11), ապա սֆերան թափանցող լարվածության յուրաքանչյուր գիծ անցնում է և այդ մակերևույթի միջով:
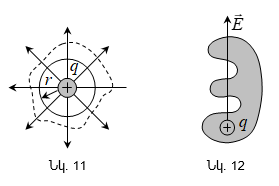
Կնճիռներ
ունեցող
մակերևույթի
միջով անցնող
հոսքը
հաշվելիս (նկ.12,
որտեղ ցույց է
տրված ![]() -ի`
-ի` ![]() թվով
գծերից մեկը),
պետք է հաշվի
առնել, որ քննարկվող
դեպքում
թվով
գծերից մեկը),
պետք է հաշվի
առնել, որ քննարկվող
դեպքում ![]() -ի
տվյալ գծի
հատումների
թիվը
մակերևույթի
հետ կարող է
միայն կենտ
լինել, ընդ
որում այդ հատումները
ընդհանուր
հոսքի մեջ հաջորդաբար
կմտցնեն մերթ
դրական, մերթ
բացասական
ներդրում: Հանրագումարում,
քանի անգամ էլ
որ տվյալ գիծը
հատի
մակերևույթը,
արդյունարար
հոսքի մեջ հավասար
կլինի կամ
-ի
տվյալ գծի
հատումների
թիվը
մակերևույթի
հետ կարող է
միայն կենտ
լինել, ընդ
որում այդ հատումները
ընդհանուր
հոսքի մեջ հաջորդաբար
կմտցնեն մերթ
դրական, մերթ
բացասական
ներդրում: Հանրագումարում,
քանի անգամ էլ
որ տվյալ գիծը
հատի
մակերևույթը,
արդյունարար
հոսքի մեջ հավասար
կլինի կամ ![]() -ի
(այն գծերի
համար, որոնք
վերջին
հաշվով դուրս
են գալիս), կամ -1-ի
(այն գծերի
համար, որոնք
ներս են
մտնում):
Մասնավորապես,
եթե
մակերևույթի
ներսում
լիցքեր չկան,
հոսքը
հավասար է
զրոյի: Այսպիսով,
ինչպիսին էլ
լինի կետային
լիցք պարունակող
փակ մակերևույթի
ձևը,
-ի
(այն գծերի
համար, որոնք
վերջին
հաշվով դուրս
են գալիս), կամ -1-ի
(այն գծերի
համար, որոնք
ներս են
մտնում):
Մասնավորապես,
եթե
մակերևույթի
ներսում
լիցքեր չկան,
հոսքը
հավասար է
զրոյի: Այսպիսով,
ինչպիսին էլ
լինի կետային
լիցք պարունակող
փակ մակերևույթի
ձևը, ![]() վեկտորի
հոսքը այդ
մակերևույթի
միջով
հավասար է
վեկտորի
հոսքը այդ
մակերևույթի
միջով
հավասար է ![]() -ի,
այսինքն`
-ի,
այսինքն`
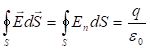 :
(1.9)
:
(1.9)
Հոսքի
նշանը
համընկնում է ![]() լիցքի
նշանի հետ:
լիցքի
նշանի հետ:
Ինչպես երևում է, ինտեգրումը կախված չէ մակերևույթի ձևից (նրանում կնճիռների առկայությունից):
Այսպիսով, ստացանք որոնելի մաթեմատիկական կապը, որի ֆիզիկական իմաստը հետևյալն է:
Փակ
մակերևույթով
էլեկտրական
դաշտի լարվածության
վեկտորի
հոսքը
վակուումում
հավասար է այդ
մակերևույթով
ընդգրկված ![]() լիցքի
և
լիցքի
և ![]() -ի
հարաբերությանը:
Դժվար չէ
ցույց տալ, որ
ընդհանուր
դեպքում, եթե
փակ
մակերևույթով
ընդգրկված են
-ի
հարաբերությանը:
Դժվար չէ
ցույց տալ, որ
ընդհանուր
դեպքում, եթե
փակ
մակերևույթով
ընդգրկված են ![]() թվով
լիցքեր,
համաձայն
դաշտերի
վերադրման
սկզբունքի
բոլոր
լիցքերով
ստեղծված արդյունարար
դաշտի
թվով
լիցքեր,
համաձայն
դաշտերի
վերադրման
սկզբունքի
բոլոր
լիցքերով
ստեղծված արդյունարար
դաշտի ![]() լարվածությունը
հավասար է
յուրաքանչյուր
առանձին
լիցքով
ստեղծված
լարվածությունը
հավասար է
յուրաքանչյուր
առանձին
լիցքով
ստեղծված ![]() դաշտերի
լարվածությունների
վեկտորական գումարին`
դաշտերի
լարվածությունների
վեկտորական գումարին`![]() Ուստի
Ուստի
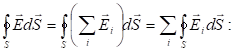
Համաձայն
(1.9)-ի գումարի
նշանի տակ
գտնվող
յուրաքանչյուր
ինտեգրալ
հավասար է ![]() -ի,
հետևաբար`
-ի,
հետևաբար`
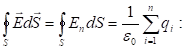 (1.10)
(1.10)
(1.10) բանաձևն արտահայտում է Գաուսի թեորեմը ինտեգրալային տեսքով վակուումում էլեկտրաստատիկ դաշտի համար.
էլեկտրաստատիկ
դաշտի
լարվածության
վեկտորի
հոսքը
վակուումում
կամայական
փակ մակերևույթի
միջով
հավասար է այդ
մակերևույթի
ներսում
գտնվող
լիցքերի
հանրահաշվական
գումարին`
բաժանած ![]() -ի:
-ի:
Այս թեորեմը մաթեմատիկորեն արտածվել է ցանկացած բնույթի վեկտորական դաշտի համար Մ. Օստրոգրադսկու կողմից, այնուհետև անկախ նրանից Գաուսի կողմից` կիրառվել է էլեկտրաստատիկ դաշտի համար:
Ընդհանուր
դեպքում
էլեկտրական
լիցքերը կարող
են բաշխված
լինել
տարածության
տարբեր կետերում
տարբեր ![]() ծավալային
խտությամբ:
Ուստի փակ
ծավալային
խտությամբ:
Ուստի փակ ![]() մակերևույթով
սահմանափակված
մակերևույթով
սահմանափակված
![]() ծավալում
գտնվող
գումարային
լիցքը կլինի
ծավալում
գտնվող
գումարային
լիցքը կլինի ![]() :
Օգտագործելով
այս
արդյունքը`
Գաուսի (1.10) թեորեմը
կարելի է
գրել`
:
Օգտագործելով
այս
արդյունքը`
Գաուսի (1.10) թեորեմը
կարելի է
գրել`
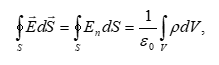
որտեղ
աջ մասի
ինտեգրալը
վերցվում է S
մակերևույթով
պարփակված V
ծավալով:
Ինչպես
տեսնում ենք,
Գաուսի
թեորեմի
ստացման հիմքում
ընկած էր այն
փաստը, որ ![]() Հետևաբար
Գաուսի
թեորեմի
ֆիզիկական
հիմքը Կուլոնի
օրենքն է,
ուրեմն
կարելի է
նշել, որ Գաուսի
թեորեմը
Կուլոնի
օրենքի
ինտեգրալ արտահայտությունն
է:
Հետևաբար
Գաուսի
թեորեմի
ֆիզիկական
հիմքը Կուլոնի
օրենքն է,
ուրեմն
կարելի է
նշել, որ Գաուսի
թեորեմը
Կուլոնի
օրենքի
ինտեգրալ արտահայտությունն
է:
Գաուսի թեորեմը մի շարք դեպքերում թույլ է տալիս դաշտի լարվածությունը գտնել շատ ավելի պարզ միջոցներով, քան կետային լիցքի լարվածության համար (1.6) բանաձևը, և դաշտերի վերադրման սկզբունքը օգտագործելով:
Գաուսի թեորեմը դիֆերենցիալ տեսքով: Էլեկտրական դաշտի կարևոր հատկությունը, որն արտահայտում է Գաուսի թեորեմը, հարկադրում է այն ներկայացնել այլ տեսքով, որն ընդլայնում է թեորեմի հնարավորությունները՝ որպես հետազոտությունների և հաշվարկի միջոց:
Ի
տարբերություն
(1.9) տեսքի, որը
կոչվում է
ինտեգրալային,
մենք
կփնտրենք
Գաուսի
թեորեմի
դիֆերենցիալ
տեսքը, որով
կապ է հաստատվում
լիցքի ![]() ծավալային
խտության և
տարածության
տվյալ կետի
շրջակայքում
ծավալային
խտության և
տարածության
տվյալ կետի
շրջակայքում ![]() լարվածության
փոփոխությունների
միջև: Դրա համար
սկզբում
պատկերացնենք
լարվածության
փոփոխությունների
միջև: Դրա համար
սկզբում
պատկերացնենք
![]() լիցքը
լիցքը
![]() փակ
մակերևույթով
պարփակված
փակ
մակերևույթով
պարփակված ![]() ծավալում,
երբ
ծավալում,
երբ ![]() որտեղ
որտեղ
![]() -ն
-ն ![]() ծավալում
լիցքի
ծավալային
խտության
միջին արժեքն
է: Այնուհետև
այս
արտահայտությունը
տեղադրենք (1.9)
հավասարման
մեջ և նրա
երկու մասերը
բաժանենք
ծավալում
լիցքի
ծավալային
խտության
միջին արժեքն
է: Այնուհետև
այս
արտահայտությունը
տեղադրենք (1.9)
հավասարման
մեջ և նրա
երկու մասերը
բաժանենք ![]() -ի:
Արդյունքում
կստանանք.
-ի:
Արդյունքում
կստանանք.
![]() : (1.11)
: (1.11)
V ծավալը
ձգտեցնելով
դաշտի` մեզ
հետաքրքրող կետին`
այն ձգտեցնենք
զրոյի:
Ակնհայտ է, որ
այդ դեպքում ![]() -ն դաշտի
տվյալ կետում
կձգտի
-ն դաշտի
տվյալ կետում
կձգտի ![]() արժեքին,
այսինքն` (1.11)
հավասարման
ձախ մասի արժեքը
կձգտի
արժեքին,
այսինքն` (1.11)
հավասարման
ձախ մասի արժեքը
կձգտի ![]() : Այն
մեծությունը,
որը
: Այն
մեծությունը,
որը ![]() -ի և
-ի և ![]() ծավալի
հարաբերության
սահմանն է,
երբ
ծավալի
հարաբերության
սահմանն է,
երբ ![]() , կոչվում է
, կոչվում է
![]() դաշտի
դիվերգենցիա
և նշանակվում`
դաշտի
դիվերգենցիա
և նշանակվում`![]() : Այսպիսով,
ըստ
սահմանման՝
: Այսպիսով,
ըստ
սահմանման՝
![]() : (1.12)
: (1.12)
Համանման ձևով որոշվում է ցանկացած այլ վեկտորական դաշտի դիվերգենցիան:
(1.12)
առնչությունից
հետևում է, որ
դիվերգենցիան
կոորդինատների
սկալյար
ֆունկցիա է: ![]() դաշտի
դիվերգենցիայի
արտահայտությունը
ստանալու
համար, պետք է
ըստ (1.12)-ի
վերցնել
անվերջ փոքր
դաշտի
դիվերգենցիայի
արտահայտությունը
ստանալու
համար, պետք է
ըստ (1.12)-ի
վերցնել
անվերջ փոքր ![]() ծավալ, որոշել
ծավալ, որոշել
![]() վեկտորի
հոսքը այդ
ծավալը
պարփակող փակ
մակերևույթի
միջով և գտնել
այդ հոսքի և
ծավալի հարաբերությունը:
վեկտորի
հոսքը այդ
ծավալը
պարփակող փակ
մակերևույթի
միջով և գտնել
այդ հոսքի և
ծավալի հարաբերությունը:
Դիվերգենցիայի համար ստացված արտահայտությունը կախված է կոորդինատների համակարգի ընտրությունից (կոորդինատների տարբեր համակարգերում այն կլինի տարբեր): Օրինակ, կոորդինատների դեկարտյան համակարգում
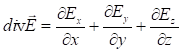 : (1.13)
: (1.13)
Այսպիսով,
պարզեցինք, որ
երբ ![]() , (1.11)
արտահայտության
աջ մասը
ձգտում է
, (1.11)
արտահայտության
աջ մասը
ձգտում է ![]() , իսկ ձախ
մասը՝
, իսկ ձախ
մասը՝ ![]() , հետևաբար,
, հետևաբար,
![]() դաշտի
դիվերգենցիան
նույն կետում
լիցքի խտության
հետ կապված է
հետևյալ
հավասարումով`
դաշտի
դիվերգենցիան
նույն կետում
լիցքի խտության
հետ կապված է
հետևյալ
հավասարումով`
![]() : (1.14)
: (1.14)
Այս
հավասարումն
արտահայտում
է Գաուսի
թեորեմը
դիֆերենցիալ
տեսքով:
Վեկտորական
անալիզի
բանաձևերի գրառումն
ու դրանցով
գործողությունները
զգալիորեն հեշտանում
են, եթե
մտցվում է
վեկտորական
դիֆերենցիալ
օպերատոր, որը
նշանակվում է ![]() (նաբլա) սիմվոլով
և կոչվում է
նաբլա օպերատոր
կամ
Համիլտոնի
օպերատոր: Այդ
օպերատորը
պատկերվում է
որպես
այնպիսի
վեկտոր, որի
բաղադրիչներն
են
(նաբլա) սիմվոլով
և կոչվում է
նաբլա օպերատոր
կամ
Համիլտոնի
օպերատոր: Այդ
օպերատորը
պատկերվում է
որպես
այնպիսի
վեկտոր, որի
բաղադրիչներն
են ![]() և
և ![]() :
:
Հետևաբար՝
![]() ,
(1.15)
,
(1.15)
որտեղ
![]() -ն միավոր
վեկտորներ են
-ն միավոր
վեկտորներ են ![]() առանցքների
ուղղությամբ:
առանցքների
ուղղությամբ:
Ինքնըստինքյան
այդ վեկտորը
իմաստ չունի:
Այն իմաստ է
ստանում
սկալյար կամ
վեկտորական ֆունկցիայի
հետ
զուգակցված,
որով այն
սիմվոլիկ
կերպով
բազմապատկվում
է: Այսպես, եթե ![]() վեկտորը
սկալյարորեն
բազմապատկվի
վեկտորը
սկալյարորեն
բազմապատկվի ![]() վեկտորով,
ապա
կստանանք՝
վեկտորով,
ապա
կստանանք՝
![]() ,
,
իսկ
սա ոչ այլ ինչ
է, քան ![]() -ն:
Այսպիսով,
-ն:
Այսպիսով, ![]() դաշտի
դիվերգենցիան
կարելի է գրել
կամ
դաշտի
դիվերգենցիան
կարելի է գրել
կամ ![]() կամ
կամ ![]() , երկու
դեպքում էլ
կարդացվում է «դիվերգենցիա
, երկու
դեպքում էլ
կարդացվում է «դիվերգենցիա
![]() »: Օգտվելով
երկրորդ
նշանակումից`
Գաուսի թեորեմը
կունենա
հետևյալ
տեսքը.
»: Օգտվելով
երկրորդ
նշանակումից`
Գաուսի թեորեմը
կունենա
հետևյալ
տեսքը.
![]() : (1.16)
: (1.16)
Գաուսի
թեորեմը
դիֆերենցիալ
տեսքով լոկալ
(տեղային)
թեորեմ է. ![]() դաշտի
դիվերգենցիան
տվյալ կետում
կախված է միայն
նույն կետում
էլեկտրական
լիցքի
դաշտի
դիվերգենցիան
տվյալ կետում
կախված է միայն
նույն կետում
էլեկտրական
լիցքի ![]() խտությունից:
Սա
էլեկտրական
դաշտի կարևոր
հատկություններից
մեկն է: Այն
կետերում,
որտեղ
խտությունից:
Սա
էլեկտրական
դաշտի կարևոր
հատկություններից
մեկն է: Այն
կետերում,
որտեղ ![]() , ունենք
դաշտի
աղբյուրներ (դրական
լիցքեր), իսկ
այն կետերում,
որտեղ
, ունենք
դաշտի
աղբյուրներ (դրական
լիցքեր), իսկ
այն կետերում,
որտեղ ![]() , ունենք
դաշտի
հոսարաններ
(բացասական
լիցքեր):
, ունենք
դաշտի
հոսարաններ
(բացասական
լիցքեր): ![]() վեկտորի
գծերը դուրս
են գալիս
դաշտի
աղբյուրներից,
իսկ
հոսարանների
տեղում դրանք
վերջանում են:
վեկտորի
գծերը դուրս
են գալիս
դաշտի
աղբյուրներից,
իսկ
հոսարանների
տեղում դրանք
վերջանում են:
Գաուսի թեորեմի կիրառությունները: Գաուսի թեորեմի (1.9) տեսքից հետևում է, որ հեշտությամբ հնարավոր է հաշվել միայն հավասարաչափ լիցքավորված համաչափ մարմինների ստեղծած դաշտերի լարվածությունները:
1.
Համասեռ
լիցքավորված
անվերջ
հարթության դաշտը
(նկ.13): Անվերջ
հարթությունը
(նկ.13)
լիցքավորված
է ![]() հաստատուն
մակերևութային
խտությամբ (
հաստատուն
մակերևութային
խտությամբ (![]() -ը միավոր
մակերևույթին
ընկնող լիցքն
է): Խնդրի համաչափությունից
հետևում է, որ
լարվածության
գծերը
ուղղահայաց
են դիտարկվող
հարթությանը
և ուղղված են
նրանից աջ և
ձախ: Իրոք,
քանի որ
հարթությունն
անվերջ է և
համասեռ
լիցքավորված,
ոչ մի հիմք
չկա, որ
-ը միավոր
մակերևույթին
ընկնող լիցքն
է): Խնդրի համաչափությունից
հետևում է, որ
լարվածության
գծերը
ուղղահայաց
են դիտարկվող
հարթությանը
և ուղղված են
նրանից աջ և
ձախ: Իրոք,
քանի որ
հարթությունն
անվերջ է և
համասեռ
լիցքավորված,
ոչ մի հիմք
չկա, որ ![]() վեկտորը
հարթության
նորմալից այս
կամ այն կողմ
կշեղվի:
Ակնհայտ է, որ
հարթության
նկատմամբ
համաչափ
կետերում դաշտի
լարվածությունը
նույնն է ըստ
մեծության և
հակադիր` ըստ
ուղղության:
վեկտորը
հարթության
նորմալից այս
կամ այն կողմ
կշեղվի:
Ակնհայտ է, որ
հարթության
նկատմամբ
համաչափ
կետերում դաշտի
լարվածությունը
նույնն է ըստ
մեծության և
հակադիր` ըստ
ուղղության:
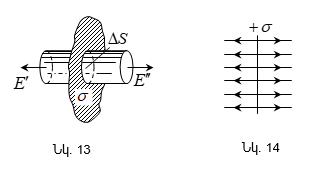
Մտովի
պատկերացնենք
գլանային
մակերևույթ,
որի հիմքերը
զուգահեռ են
լիցքավորված
հարթությանը,
իսկ առանցքն
ուղղահայաց է
նրան: Այդ
մակերևույթի
նկատմամբ
կիրառենք
Գաուսի
թեորեմը: Քանի
որ գլանի
ծնիչները
զուգահեռ են
լարվածության
գծերին (![]() ), ապա
լարվածության
վեկտորի
հոսքը գլանի
կողմնային
մակերևույթով
հավասար է
զրոյի, քանի
որ նրա
յուրաքանչյուր
կետում
), ապա
լարվածության
վեկտորի
հոսքը գլանի
կողմնային
մակերևույթով
հավասար է
զրոյի, քանի
որ նրա
յուրաքանչյուր
կետում ![]() -ի,
իսկ լրիվ
հոսքը գլանի
միջով
հավասար է նրա
հիմքերի
միջով անցնող
հոսքերի
գումարին:
Հիմքերի համար
-ի,
իսկ լրիվ
հոսքը գլանի
միջով
հավասար է նրա
հիմքերի
միջով անցնող
հոսքերի
գումարին:
Հիմքերի համար
![]() -ը
համընկնում է
-ը
համընկնում է
![]() -ի
հետ: Ըստ
համաչափության
նկատառումների`
-ի
հետ: Ըստ
համաչափության
նկատառումների`![]() Հետևաբար,
մակերևույթի
միջով
գումարային հոսքը
հավասար
կլինի
Հետևաբար,
մակերևույթի
միջով
գումարային հոսքը
հավասար
կլինի ![]() Կառուցված
գլանի
ներսում
գտնվող լիցքը
Կառուցված
գլանի
ներսում
գտնվող լիցքը ![]() է:
Համաձայն
Գաուսի (1.10)
թեորեմի`
է:
Համաձայն
Գաուսի (1.10)
թեորեմի`
![]()
որտեղից
![]() :
(1.17)
:
(1.17)
Ըստ
ստացված
բանաձևի`
անվերջ
հավասարաչափ
լիցքավորված
հարթության
դաշտի
լարվածությունը
կախված չէ
գլանի
երկարությունից:
Հարթությունից
ցանկացած հեռավորությունների
վրա դաշտի
լարվածությունն
ըստ
մեծության
նույնն է:
Այսինքն` այդ
դաշտը
համասեռ է:
Բացասական
լիցքավորված
հարթության
համար
արդյունքը
կլինի նույնը,
միայն թե ![]() վեկտորը
և լարվածության
գծերը
կունենան
հակառակ
ուղղություն:
վեկտորը
և լարվածության
գծերը
կունենան
հակառակ
ուղղություն:
2.
Տարանուն
լիցքերով հավասարաչափ
լիցքավորված
երկու
զուգահեռ հարթությունների
դաշտը:
Դիցուք
հարթությունները
լիցքավորված
են
հավասարաչափ
տարանուն ![]() և
և ![]() մակերևութային
խտություններով
(նկ.15): Նկարում
վերին
սլաքները
համապատասխանում
են
դրականապես
լիցքավորված
հարթության
դաշտին, ներքևինները`
բացասականապես
լիցքավորվածին:
մակերևութային
խտություններով
(նկ.15): Նկարում
վերին
սլաքները
համապատասխանում
են
դրականապես
լիցքավորված
հարթության
դաշտին, ներքևինները`
բացասականապես
լիցքավորվածին:
Հարթություններով սահմանափակված ծավալից դուրս գումարվող դաշտերն ունեն հակառակ ուղղություններ, այնպես որ արդյունարար լարվածությունը հավասար է զրոյի: Հարթությունների միջև ընկած տիրույթում`
![]() որտեղ
որտեղ
![]() և
և ![]() -ը
որոշվում են (1.17)
բանաձևով:
Հետևաբար
արդյունարար
լարվածությունը`
-ը
որոշվում են (1.17)
բանաձևով:
Հետևաբար
արդյունարար
լարվածությունը`
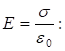 (1.18)
(1.18)
Այսպիսով, արդյունարար դաշտի լարվածությունը հարթությունների միջև եղած տիրույթում նկարագրվում է (1.18) բանաձևով, հարթություններով սահմանափակված ծավալից դուրս հավասար է զրոյի: Հարթությունների ներսում դաշտը համասեռ է:
3.
Հավասարաչափ
լիցքավորված,
անվերջ երկար
գլանի դաշտը: Դիտարկենք
այն դաշտը,
որն
առաջանում է ![]() հաստատուն
գծային
խտությամբ
լիցքավորված
հաստատուն
գծային
խտությամբ
լիցքավորված ![]() շառավղով
գլանային
անվերջ մակերևույթի
կողմից:
Համաչափության
նկատառումներով
դաշտի լարվածությունը
ցանկացած
կետում պետք է
լինի գլանի
առանցքին ուղղահայաց
շառավղային
ուղիղների
ուղղությամբ,
իսկ
լարվածության
մոդուլը
կարող է կախում
ունենալ
միայն գլանի
առանցքից
եղած
շառավղով
գլանային
անվերջ մակերևույթի
կողմից:
Համաչափության
նկատառումներով
դաշտի լարվածությունը
ցանկացած
կետում պետք է
լինի գլանի
առանցքին ուղղահայաց
շառավղային
ուղիղների
ուղղությամբ,
իսկ
լարվածության
մոդուլը
կարող է կախում
ունենալ
միայն գլանի
առանցքից
եղած ![]() հեռավորությունից:
Մտովի
պատկերացնենք
լիցքավորված
մակերևույթի
հետ
համառանցք մի
փակ գլանային
մակերևույթ`
հեռավորությունից:
Մտովի
պատկերացնենք
լիցքավորված
մակերևույթի
հետ
համառանցք մի
փակ գլանային
մակերևույթ`![]() շառավղով
և
շառավղով
և ![]() բարձրությամբ
(նկ.16):
բարձրությամբ
(նկ.16):
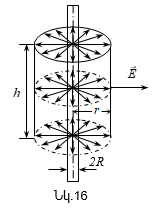
Այս
գլանի
հիմքերի
համար ![]() ,
կողմնային
մակերևույթի
համար`
,
կողմնային
մակերևույթի
համար`![]() (լիցքը
դրական ենք
համարում):
Հետևաբար
(լիցքը
դրական ենք
համարում):
Հետևաբար ![]() վեկտորի
հոսքը այդ փակ
մակերևույթի
միջով հավասար
վեկտորի
հոսքը այդ փակ
մակերևույթի
միջով հավասար
![]() : Եթե
: Եթե ![]() , մակերևույթի
մեջ լիցքը
հավասար է`
, մակերևույթի
մեջ լիցքը
հավասար է` ![]() :
Կիրառելով
Գաուսի
թեորեմը`
ստանում ենք
:
Կիրառելով
Գաուսի
թեորեմը`
ստանում ենք
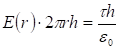 ,
,
որտեղից
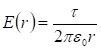 : (1.19)
: (1.19)
Այսպիսով,
անվերջ,
հավասարաչափ
լիցքավորված
գլանի
էլեկտրաստատիկ
դաշտի
լարվածությունն
ուղղված է շառավղով
և հակադարձ
համեմատական
է գլանի առանցքից
ունեցած ![]() հեռավորությանը:
հեռավորությանը:
Եթե
![]() , փակ
մակերևույթը
լիցք չի
պարունակում,
որի
հետևանքով
, փակ
մակերևույթը
լիցք չի
պարունակում,
որի
հետևանքով ![]() :
Այսպիսով,
անվերջ երկար
լիցքավորված
գլանային
մակերեվույթի
ներսում
դաշտը
բացակայում է:
Բացասականորեն
լիցքավորված
գլանի դաշտը
դրականորեն
լիցքավորված
գլանի դաշտից
տարբերվում է
միայն
:
Այսպիսով,
անվերջ երկար
լիցքավորված
գլանային
մակերեվույթի
ներսում
դաշտը
բացակայում է:
Բացասականորեն
լիցքավորված
գլանի դաշտը
դրականորեն
լիցքավորված
գլանի դաշտից
տարբերվում է
միայն ![]() վեկտորի
ուղղությամբ:
վեկտորի
ուղղությամբ:
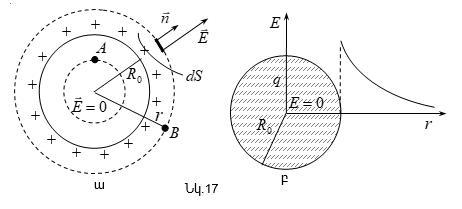
4.
Հավասարաչափ
լիցքավորված
գնդային
մակերևույթի
դաշտը:
Դիցուք տրված
է ![]() լիցքով
և
լիցքով
և ![]() շառավղով
հավասարաչափ
լիցքավորված
գնդային
մակերևույթը
(նկ.17 ա):
շառավղով
հավասարաչափ
լիցքավորված
գնդային
մակերևույթը
(նկ.17 ա):
![]() լարվածությունը
լարվածությունը
![]() կետում
հաշվելու
համար
կետում
հաշվելու
համար ![]() կետով
տանենք տրված
գնդային
մակերևույթին
համակենտրոն
գնդային մակերևույթ
և գրենք
Գաուսի
թեորեմն այդ
մակերևույթի
համար.
կետով
տանենք տրված
գնդային
մակերևույթին
համակենտրոն
գնդային մակերևույթ
և գրենք
Գաուսի
թեորեմն այդ
մակերևույթի
համար.
![]() : (1.20)
: (1.20)
Հավասարման
աջ մասը հավասար
է զրոյի, քանի
որ այդ մակերևույթով
ընդգրկված
լիցք չկա:
Ուրեմն`
լիցքավորված
մակերևույթի
ներսում
էլեկտրաստատիկ
դաշտը
բացակայում է`![]() :
:
![]() կետում
դաշտի
լարվածությունը
հաշվելու
համար
կետում
դաշտի
լարվածությունը
հաշվելու
համար ![]() կետով
տանենք տրված
գնդին
համակենտրոն
գնդային
մակերևույթ և
գրենք Գաուսի
թեորեմն այդ
մակերևույթի
համար.
կետով
տանենք տրված
գնդին
համակենտրոն
գնդային
մակերևույթ և
գրենք Գաուսի
թեորեմն այդ
մակերևույթի
համար.
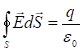 :
:
Խնդրի
համաչափության
պատճառով ![]() ,
, ![]() փակ
մակերևույթի
ցանկացած
փակ
մակերևույթի
ցանկացած ![]() տարրի
վրա,
հետևաբար`
տարրի
վրա,
հետևաբար`
![]() ,
,
որտեղից
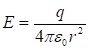 : (1.21)
: (1.21)
Այսպիսով,
հավասարաչափ
լիցքավորված
գնդային
մակերևույթից
դուրս դաշտի
լարվածությունը
որոշվում է
նույն
բանաձևով, ինչ
որ ![]() կետային
լիցքի դաշտի
լարվածությունը,
եթե այդ լիցքը
գտնվեր
դիտարկվող
գնդային
մակերևույթի
կենտրոնում:
կետային
լիցքի դաշտի
լարվածությունը,
եթե այդ լիցքը
գտնվեր
դիտարկվող
գնդային
մակերևույթի
կենտրոնում:
Նկ.17
բ-ում բերված
է նաև լիցքավորված
գնդային
մակերևույթի
դաշտի
լարվածության
մեծության
կախումը
կենտրոնից
ունեցած ![]() հեռավորությունից:
հեռավորությունից:
5.
Հավասարաչափ
ծավալով
լիցքավորված
գնդի դաշտը:
Դիցուք տրված
է ![]() շառավղով
և
շառավղով
և ![]() լիցքի
ծավալային
խտությամբ
հավասարաչափ
լիցքավորված
գունդ (նկ.18 ա):
Հաշվենք
լիցքավորված
գնդի դաշտի
լարվածությունը
լիցքի
ծավալային
խտությամբ
հավասարաչափ
լիցքավորված
գունդ (նկ.18 ա):
Հաշվենք
լիցքավորված
գնդի դաշտի
լարվածությունը
![]() կետում
(գնդի
ներսում) և
կետում
(գնդի
ներսում) և ![]() կետում
(գնդից դուրս):
կետում
(գնդից դուրս):
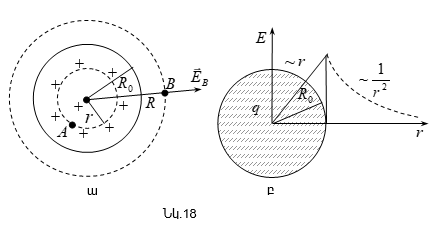
![]() կետում
դաշտի
լարվածությունը
հաշվելու համար
կետում
դաշտի
լարվածությունը
հաշվելու համար
![]() կետով
տանենք տրված
գնդին
համակենտրոն
գնդային
կետով
տանենք տրված
գնդին
համակենտրոն
գնդային ![]() մակերևույթ
(նկ.18ա) և դրա
համար գրենք
Գաուսի թեորեմը.
մակերևույթ
(նկ.18ա) և դրա
համար գրենք
Գաուսի թեորեմը.
 ,
,
որտեղ
![]() -ը
-ը ![]() շառավղով
գնդի մեջ առկա
լիցքն է`
շառավղով
գնդի մեջ առկա
լիցքն է`
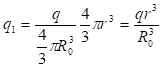 :
:
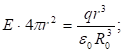
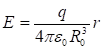 : (1.22)
: (1.22)
![]() կետում
դաշտի
լարվածությունը
հաշվելու
համար գրենք
Գաուսի
թեորեմն այն
գնդային
մակերևույթի
համար, որն
անցնում է B
կետով և
համակենտրոն
է տրված
գնդին.
կետում
դաշտի
լարվածությունը
հաշվելու
համար գրենք
Գաուսի
թեորեմն այն
գնդային
մակերևույթի
համար, որն
անցնում է B
կետով և
համակենտրոն
է տրված
գնդին.
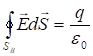 ,
,
![]()
որտեղից
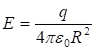 : (1.23)
: (1.23)
Ինչպես երևում է, ծավալով հավասարաչափ լիցքավորված գնդի դաշտի լարվածությունը գնդից դուրս կետերի համար համարժեք է գնդի կենտրոնում տեղադրված (նույն մեծությամբ) կետային լիցքի դաշտի լարվածությանը:
Այսպիսով,
ծավալով
լիցքավորված
գնդի դաշտի լարվածության
կախումը գնդի
կենտրոնից
ունեցած հեռավորությունից
գնդի ներսում
և նրանից դուրս
տարբեր է,
գնդի ներսում
![]() իսկ
գնդից դուրս`
իսկ
գնդից դուրս` ![]() :
Նկ.18 բ-ում
բերված է նաև
ծավալով
լիցքավորված գնդի
դաշտի
լարվածության
մեծության
կախումը
կենտրոնից
ունեցած
:
Նկ.18 բ-ում
բերված է նաև
ծավալով
լիցքավորված գնդի
դաշտի
լարվածության
մեծության
կախումը
կենտրոնից
ունեցած ![]() հեռավորությունից:
հեռավորությունից:
1.6. ԷԼԵԿՏՐԱՍՏԱՏԻԿ ԴԱՇՏԻ ՈՒԺԵՐԻ ԿԱՏԱՐԱԾ
ԱՇԽԱՏԱՆՔԸ: ԷԼԵԿՏՐԱՍՏԱՏԻԿ ԴԱՇՏԻ ԼԱՐՎԱԾՈՒԹՅԱՆ
ՎԵԿՏՈՐԻ ՇՐՋԱՊՏՈՒՅՏԻ ԹԵՈՐԵՄԸ
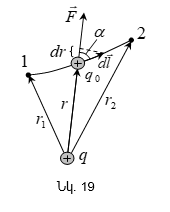
Դիցուք
![]() լիցքը
լիցքը
![]() կետային
լիցքի
դաշտում
տեղափոխվում
է
կետային
լիցքի
դաշտում
տեղափոխվում
է ![]() շառավիղ-վեկտորով
որոշվող
դիրքից
շառավիղ-վեկտորով
որոշվող
դիրքից ![]() դիրքը
(նկ.19):
դիրքը
(նկ.19): ![]() լիցքի
վրա ազդող
էլեկտրական
ուժի կատարած
տարրական
աշխատանքը
որոշվում է
հետևյալ կերպ.
լիցքի
վրա ազդող
էլեկտրական
ուժի կատարած
տարրական
աշխատանքը
որոշվում է
հետևյալ կերպ.
![]() ,
,
![]() :
:
Ինտեգրելով
ստացված
արտահայտությունը
ճանապարհի 1-2
տեղամասում ![]() -ից
մինչև
-ից
մինչև ![]() սահմաններում`
աշխատանքի
համար
կստանանք`
սահմաններում`
աշխատանքի
համար
կստանանք`
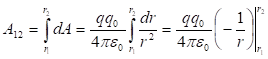 ,
,
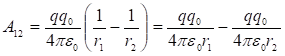 : (1.24)
: (1.24)
Աշխատանքի համար ստացված (1.24) բանաձևից երևում է, որ այն կախված չէ այն հետագծի ձևից, որով էլեկտրական դաշտում տեղափոխվել է լիցքը, այլ կախված է միայն այդ լիցքի սկզբնական և վերջնական դիրքերից: Այդպիսի հատկությամբ օժտված դաշտերն ընդունված է անվանել պոտենցիալային, իսկ նրանցում գործող ուժերը` կոնսերվատիվ ուժեր:
Պոտենցիալային դաշտում կոնսերվատիվ ուժերի կատարած աշխատանքը փակ հետագծով հավասար է զրոյի: Դա դաշտի պոտենցիալային բնույթի սահմանումն է: Մաթեմատիկորեն այդ փաստը գրվում է այսպես.
![]() կամ
կամ ![]() , (1.25)
, (1.25)
որը
ճիշտ է
ցանկացած փակ
կոնտուրի
համար: Պետք է
նկատի
ունենալ, որ
բանաձևը ճիշտ
է միայն էլեկտրաստատիկ
դաշտի համար:
Հետագայում
ցույց կտրվի,
որ շարժվող
լիցքերի
դաշտը
այսինքն՝
ժամանակի
ընթացքում
փոփոխվող
դաշտը պոտենցիալային
չէ, հետևաբար (1.25)
պայմանը այդ
դաշտի համար
տեղի չունի: ![]() տեսքի
արտահայտությունը
կոչվում է
տեսքի
արտահայտությունը
կոչվում է ![]() վեկտորի
շրջապտույտ
փակ
կոնտուրով:
Այսպիսով,
ցանկացած փակ
կոնտուրով
էլեկտրաստատիկ
դաշտի
լարվածության
վեկտորի շրջապտույտը
զրո է: Այս
պնդումն անվանում
են շրջապտույտի
թեորեմ:
վեկտորի
շրջապտույտ
փակ
կոնտուրով:
Այսպիսով,
ցանկացած փակ
կոնտուրով
էլեկտրաստատիկ
դաշտի
լարվածության
վեկտորի շրջապտույտը
զրո է: Այս
պնդումն անվանում
են շրջապտույտի
թեորեմ:
1.7. ԷԼԵԿՏՐԱՍՏԱՏԻԿ ԴԱՇՏԻ ՊՈՏԵՆՑԻԱԼ: ՊՈՏԵՆՑԻԱԼՆԵՐԻ ՏԱՐԲԵՐՈՒԹՅՈՒՆ:
ՀԱՄԱՊՈՏԵՆՑԻԱԼ ՄԱԿԵՐԵՎՈՒՅԹՆԵՐ
Ուժերի
պոտենցիալային
դաշտում
գտնվող
մարմինն
օժտված է պոտենցիալ
էներգիայով,
որի հաշվին
դաշտի
ուժերով
կատարվում է
աշխատանք:
Հետևաբար, (1.24) աշխատանքը
կարող է ներկայացվել
որպես
պոտենցիալ
էներգիայի այն
արժեքների
տարբերություն,
որոնցով ![]() լիցքն
օժտված էր
լիցքն
օժտված էր ![]() լիցքի
դաշտի 1 և 2
կետերում.
լիցքի
դաշտի 1 և 2
կետերում.
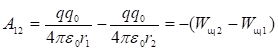 , (1.26)
, (1.26)
Ըստ
ստացված
արտահայտության`
![]() լիցքի
դաշտում
լիցքի
դաշտում ![]() լիցքի
փոխազդեցության
պոտենցիալ
էներգիան
որոշվում է
հետևյալ
բանաձևով`
լիցքի
փոխազդեցության
պոտենցիալ
էներգիան
որոշվում է
հետևյալ
բանաձևով`
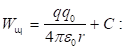
Պոտենցիալ
էներգիայի
արտահայտության
մեջ ![]() հաստատունի
արժեքը
սովորաբար
ընտրվում է այնպես,
որ լիցքը
մինչև
անվերջություն
հեռացնելիս
հաստատունի
արժեքը
սովորաբար
ընտրվում է այնպես,
որ լիցքը
մինչև
անվերջություն
հեռացնելիս ![]() պոտենցիալ
էներգիան
դառնա զրո:
Այս պայմանի դեպքում
ստացվում է`
պոտենցիալ
էներգիան
դառնա զրո:
Այս պայմանի դեպքում
ստացվում է`
![]() (1.27)
(1.27)
Նույնանուն
լիցքերի
համար ![]() և
դրանց
փոխազդեցության
(վանողական)
պոտենցիալ
էներգիան
դրական է,
տարանուն լիցքերի
համար
և
դրանց
փոխազդեցության
(վանողական)
պոտենցիալ
էներգիան
դրական է,
տարանուն լիցքերի
համար ![]() և
փոխազդեցության
(ձգողական)
պոտենցիալ
էներգիան` բացասական:
Եթե դաշտը
ստեղծվել է
և
փոխազդեցության
(ձգողական)
պոտենցիալ
էներգիան` բացասական:
Եթե դաշտը
ստեղծվել է ![]() թվով
թվով
![]() կետային
լիցքերի
համակարգով,
էլեկտրաստատիկ
ուժերի
կատարած
աշխատանքը
կետային
լիցքերի
համակարգով,
էլեկտրաստատիկ
ուժերի
կատարած
աշխատանքը ![]() լիցքի
վրա հավասար է
առանձին
ուժերի
կատարած
աշխատանքների
հանրահաշվական
գումարին`
պայմանավորված
յուրաքանչյուր
առանձին
լիցքով:
Ուստի
լիցքի
վրա հավասար է
առանձին
ուժերի
կատարած
աշխատանքների
հանրահաշվական
գումարին`
պայմանավորված
յուրաքանչյուր
առանձին
լիցքով:
Ուստի ![]() լիցքի
լիցքի
![]() պոտենցիալ
էներգիան այդ
դաշտում
հավասար է
առանձին
լիցքերի
պոտենցիալ
էներգիան այդ
դաշտում
հավասար է
առանձին
լիցքերի ![]() պոտենցիալ
էներգիաների
գումարին`
պոտենցիալ
էներգիաների
գումարին`
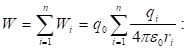 (1.28)
(1.28)
Ըստ
(1.27) և (1.28)
բանաձևերի` ![]() հարաբերությունը
կախում չունի
հարաբերությունը
կախում չունի ![]() լիցքից
և կոչվում է
դաշտի
պոտենցիալ
տվյալ կետում.
լիցքից
և կոչվում է
դաշտի
պոտենցիալ
տվյալ կետում.
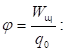 (1.29)
(1.29)
Պոտենցիալը դաշտի էներգետիկ բնութագիրն է:
Ըստ
(1.29)-ի`
պոտենցիալը
թվապես
հավասար է այն
պոտենցիալ
էներգիային,
որով օժտված է
միավոր
դրական լիցքը
դաշտի տվյալ
կետում: Ըստ (1.27)
և (1.29) բանաձևերի`
դաշտի պոտենցիալը,
որը ստեղծվում
է ![]() կետային
լիցքով,
կլինի.
կետային
լիցքով,
կլինի.
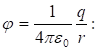 (1.30)
(1.30)
Եթե
դաշտը
ստեղծվում է ![]() թվով
կետային
լիցքերի
համակարգով,
ապա այդպիսի
դաշտի որևէ
կետում
պոտենցիալը
որոշվում է
վերադրման
սկզբունքի
համաձայն: Այս
դեպքում
օգտվելով (1.28) և
(1.29) բանաձևերից`
լիցքերի համակարգի
պոտենցիալի
համար
կստանանք`
թվով
կետային
լիցքերի
համակարգով,
ապա այդպիսի
դաշտի որևէ
կետում
պոտենցիալը
որոշվում է
վերադրման
սկզբունքի
համաձայն: Այս
դեպքում
օգտվելով (1.28) և
(1.29) բանաձևերից`
լիցքերի համակարգի
պոտենցիալի
համար
կստանանք`
![]() կամ
կամ ![]() (1.31)
(1.31)
Պոտենցիալը սկալյար մեծություն է: Դրական լիցքի պոտենցիալը դրական է, բացասական լիցքինը` բացասական: Այսպիսով, լիցքերի համակարգով ստեղծվող դաշտի պոտենցիալը ցանկացած կետում հավասար է առանձին լիցքերով ստեղծվող պոտենցիալների հանրահաշվական գումարին: Դաշտերը վերադրելիս դաշտի լարվածությունները գումարվում են վեկտորապես, մինչդեռ պոտենցիալները գումարվում են հանրահաշվորեն: Այդ պատճառով պոտենցիալների հաշվարկը, սովորաբար, շատ ավելի պարզ է լինում, քան էլեկտրական դաշտի լարվածությունների հաշվարկը:
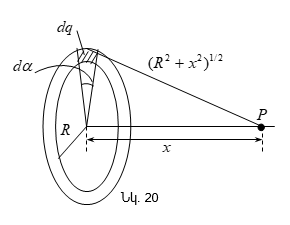
Որպես
օրինակ
հաշվենք ![]() լիցքով
հավասարաչափ
լիցքավորված,
լիցքով
հավասարաչափ
լիցքավորված, ![]() շառավղով
բարակ օղակի
դաշտի
պոտենցիալը
օղակի
առանցքի վրա`
կենտրոնից
շառավղով
բարակ օղակի
դաշտի
պոտենցիալը
օղակի
առանցքի վրա`
կենտրոնից ![]() հեռավորության
վրա
հեռավորության
վրա ![]() կետում
(նկ.20): Օղակը
բաժանենք
տարրական
մասերի`
յուրաքանչյուրի
վրա
կետում
(նկ.20): Օղակը
բաժանենք
տարրական
մասերի`
յուրաքանչյուրի
վրա ![]() լիցքով:
Տարրական
լիցքը` որպես
կետային լիցք,
օղակի
կենտրոնից
լիցքով:
Տարրական
լիցքը` որպես
կետային լիցք,
օղակի
կենտրոնից ![]() հեռավորության
վրա կստեղծի
հեռավորության
վրա կստեղծի ![]() պոտենցիալը:
Վերադրման
սկզբունքի
համաձայն,
օգտվելով (1.31)-ից,
ամբողջ օղակի
պոտենցիալը
պոտենցիալը:
Վերադրման
սկզբունքի
համաձայն,
օգտվելով (1.31)-ից,
ամբողջ օղակի
պոտենցիալը ![]() կետում
կորոշվի`
կետում
կորոշվի`
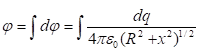
![]()
![]()
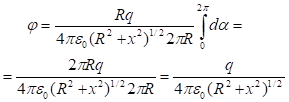 (1.32)
(1.32)
![]() լիցքի
սկզբնական դիրքից
վերջնական դիրքը
տեղափոխելու
լիցքի
սկզբնական դիրքից
վերջնական դիրքը
տեղափոխելու ![]() աշխատանքը,
արտահայտված
տեղափոխման
սկզբնական և
վերջնական
դիրքերի
պոտենցիալներով,
կլինի.
աշխատանքը,
արտահայտված
տեղափոխման
սկզբնական և
վերջնական
դիրքերի
պոտենցիալներով,
կլինի.
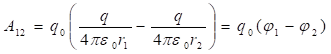 :
(1.33)
:
(1.33)
![]() պոտենցիալների
տարբերությունն
է
պոտենցիալների
տարբերությունն
է ![]() կետերի
համար, որի
ֆիզիկական
իմաստը բխում
է հենց
աշխատանքի
համար
ստացված
վերջին (1.33) բանաձևից.
կետերի
համար, որի
ֆիզիկական
իմաստը բխում
է հենց
աշխատանքի
համար
ստացված
վերջին (1.33) բանաձևից.
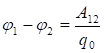 : (1.34)
: (1.34)
Պոտենցիալների տարբերությունը դաշտի երկու կետերի համար թվապես հավասար է էլեկտրաստատիկ ուժերի կատարած այն աշխատանքին, որն անհրաժեշտ է միավոր դրական լիցքը դաշտի մի կետից մյուս կետը տեղափոխելու համար:
Հաճախ պոտենցիալների տարբերությունն անվանում են լարում տրված երկու կետերի միջև:
Դաշտի
ուժերի
կատարած
աշխատանքը ![]() լիցքը
1 կետից 2 կետը
տեղափոխելու
դեպքում
կարելի է գրել
նաև հետևյալ
տեսքով`
լիցքը
1 կետից 2 կետը
տեղափոխելու
դեպքում
կարելի է գրել
նաև հետևյալ
տեսքով`
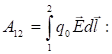 (1.35)
(1.35)
Հավասարեցնելով (1.33) և (1.35)-ը իրար պոտենցիալների տարբերության համար հանգում ենք հետևյալ արտահայտությանը`
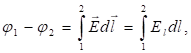 (1.36)
(1.36)
որտեղ
ինտեգրումը
կարելի է
կատարել
ցանկացած գծի
երկայնքով,
որը միացնում
է սկզբնական և
վերջնական
կետերը, քանի
որ
էլեկտրաստատիկ
դաշտի ուժերի
կատարած
աշխատանքը
կախում չունի
տեղափոխման
հետագծից: Եթե
![]() լիցքը
լիցքը
![]() պոտենցիալ
ունեցող
կետից
տեղափոխվում
է անվերջություն
(որտեղ ըստ
պայմանի
պոտենցիալը
զրո է), ապա դաշտի
ուժերի
աշխատանքը
կլինի`
պոտենցիալ
ունեցող
կետից
տեղափոխվում
է անվերջություն
(որտեղ ըստ
պայմանի
պոտենցիալը
զրո է), ապա դաշտի
ուժերի
աշխատանքը
կլինի`
![]() (1.37)
(1.37)
Այստեղից պարզ է է, որ պոտենցիալը թվապես հավասար է այն աշխատանքին, որը կատարում են դաշտի ուժերը միավոր դրական լիցքի վրա, երբ այն տվյալ կետից հեռացվում է դեպի անվերջություն: Ըստ մեծության այդպիսի աշխատանք էլ անհրաժեշտ է կատարել էլեկտրական ուժերին հակառակ` միավոր դրական լիցքը անվերջությունից դաշտի տվյալ կետը տեղափոխելու համար:
Լարումը, ինչպես և պոտենցիալների տարբերությունը, չափվում է վոլտով (Վ):
![]() :
:
1 Վ-ն այնպիսի երկու կետերի պոտենցիալների տարբերությունն է, որոնց միջև 1 Կլ լիցք տեղափոխելիս դաշտը կատարում է 1 Ջ աշխատանք:
Էլեկտրաստատիկ
դաշտը
գրաֆիկորեն
պատկերելու
համար հաճախ
օգտվում են ոչ
միայն լարվածության
գծերից, այլև`
համապոտենցիալ
մակերևույթներից
(գծերից):
Կետերի այն
բազմությունը,
որին
համապատասխանում
է պոտենցիալի
միևնույն
արժեքը,
անվանում են
համապոտենցիալ
մակերևույթներ
(գծեր): Եթե
դաշտը
ստեղծվում է ![]() կետային
լիցքով, ապա
նրա
պոտենցիալը
համաձայն (1.30)-ի,
կլինի
կետային
լիցքով, ապա
նրա
պոտենցիալը
համաձայն (1.30)-ի,
կլինի ![]() Այսպիսով
տվյալ
դեպքում
համապոտենցիալ
մակերեվույթները
համակենտրոն
գնդոլորտներ
են: Հետևաբար,
լարվածության
գծերը
կետային
լիցքի դեպքում
ուղղահայաց
են
համապոտենցիալ
մակերևույթներին:
Այսպիսով
տվյալ
դեպքում
համապոտենցիալ
մակերեվույթները
համակենտրոն
գնդոլորտներ
են: Հետևաբար,
լարվածության
գծերը
կետային
լիցքի դեպքում
ուղղահայաց
են
համապոտենցիալ
մակերևույթներին:
Լարվածության
գծերը միշտ
ուղղահայաց
են
համապոտենցիալ
մակերևույթներին:
Իրոք,
համապոտենցիալ
մակերևույթի
բոլոր կետերը ունեն
նույն
պոտենցիալը,
ուստի լիցքի
տեղափոխության
աշխատանքը
համապոտենցիալ
մակերևույթի
երկայնքով
հավասար է
զրոյի,
այսինքն լիցքերի
վրա ազդող
էլեկտրաստատիկ
ուժերը միշտ
ուղղված են
համապոտենցիալ
մակերևույթների
նորմալների
ուղղությամբ:
Հետևաբար, ![]() վեկտորը
միշտ
ուղղահայաց է
համապոտենցիալ
մակերևույթներին,
դրա համար էլ
վեկտորը
միշտ
ուղղահայաց է
համապոտենցիալ
մակերևույթներին,
դրա համար էլ ![]() վեկտորի
գծերը
օրթոգոնալ են
այդ
մակերևույթներին:
վեկտորի
գծերը
օրթոգոնալ են
այդ
մակերևույթներին:
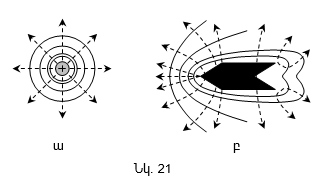
Յուրաքանչյուր լիցքի և յուրաքանչյուր լիցքերի համակարգի շուրջը կարելի է տանել անթիվ բազմությամբ համապոտենցիալ մակերևույթներ: Սակայն դրանք, սովորաբար, տարվում են այնպես, որ ցանկացած երկու հարևան համապոտենցիալ մակերևույթների միջև պոտենցիալների տարբերությունը լինի նույնը: Այդ դեպքում համապոտենցիալ մակերևույթների խտությունն ակնառու բնութագրում է դաշտի լարվածությունը տարբեր կետերում: Այնտեղ, որտեղ այդ մակերևույթները խիտ են դասավորված, դաշտի լարվածությունը մեծ է:
Այսպիսով, գիտենալով էլեկտրաստատիկ դաշտի լարվածության գծերի դասավորությունը, կարելի է կառուցել համապոտենցիալ մակերևույթները և, հակառակը հայտնի համապոտենցիալ մակերևույթների դասավորությամբ կարելի է որոշել դաշտի յուրաքանչյուր կետում դաշտի լարվածության մոդուլը և ուղղությունը: Նկ.21ա-ում,որպես օրինակ, ցույց են տրված կետային դրական լիցքի լարվածության գծերի տեսքը (կետագծային գծեր) և համապոտենցիալ մակերևույթների հատույթը (հոծ գծեր), իսկ նկ.21 բ-ում` լիցքավորված մետաղական գլանը, որը մի ծայրում ունի ելուստ, մյուս ծայրում` փոս:
1.8. ԷԼԵԿՏՐԱՍՏԱՏԻԿ ԴԱՇՏԻ ԼԱՐՎԱԾՈՒԹՅԱՆ ԵՎ
ՊՈՏԵՆՑԻԱԼԻ ԿԱՊԸ
Ստանանք
լարվածության
և պոտենցիալի
կապը: ![]() լիցքի
ստեղծած
էլեկտրաստատիկ
դաշտում ընտրենք
կամայական
լիցքի
ստեղծած
էլեկտրաստատիկ
դաշտում ընտրենք
կամայական ![]() ուղղություն
(նկ.22):
ուղղություն
(նկ.22): ![]() լիցքն
լիցքն
![]() երկայնքով
տեղափոխելիս
դաշտի ուժերի
կատարած
տարրական
աշխատանքը
կորոշվի
երկայնքով
տեղափոխելիս
դաշտի ուժերի
կատարած
տարրական
աշխատանքը
կորոշվի
![]()
բանաձևով,
որտեղ ![]() -ը
լարվածության
-ը
լարվածության
![]() վեկտորի
պրոյեկցիան է
վեկտորի
պրոյեկցիան է
![]() ուղղությամբ:
ուղղությամբ:
Հաշվի
առնելով` ![]() :
:
Ներմուծեցինք
![]() մասնակի
ածանցյալը,
որովհետև
մասնակի
ածանցյալը,
որովհետև ![]() փոփոխվում
է ոչ միայն
փոփոխվում
է ոչ միայն ![]() ուղղությամբ:
Այսպիսով`
ուղղությամբ:
Այսպիսով`
![]() :
(1.38)
:
(1.38)
![]() -ի
պրոյեկցիան
-ի
պրոյեկցիան ![]() ուղղությամբ
հավասար է այդ
ուղղությամբ
պոտենցիալի
նվազման
արագությանը:
ուղղությամբ
հավասար է այդ
ուղղությամբ
պոտենցիալի
նվազման
արագությանը:
Որպես
![]() ուղղություն
վերցնելով
ուղղություն
վերցնելով ![]() կոորդինատային
առանցքները`
կոորդինատային
առանցքները`![]() -ի համապատասխան
բաղադրիչների
համար կստանանք.
-ի համապատասխան
բաղադրիչների
համար կստանանք.
![]() ,
, ![]() ,
, ![]() :
:
Քանի որ
![]() ,
,
որտեղ
![]() -ն
միավոր վեկտորներն
են
համապատասխանաբար`
-ն
միավոր վեկտորներն
են
համապատասխանաբար`
![]() առանցքների
ուղղություններով:
առանցքների
ուղղություններով:
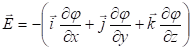
փակագծերում
գտնվող
արտահայտությունը
կոչվում է ![]() սկալյարի
գրադիենտ
(նշանակվում է
սկալյարի
գրադիենտ
(նշանակվում է
![]() ):
Օգտագործելով
գրադիենտի
նշանակումը`
կարելի է
գրել՝
):
Օգտագործելով
գրադիենտի
նշանակումը`
կարելի է
գրել՝
![]()
![]() կամ
կամ ![]() :
(1.39)
:
(1.39)
Այսպիսով,
էլեկտրական
դաշտի
լարվածությունը
հավասար է
պոտենցիալի
գրադիենտին`
հակառակ
նշանով:
Բացասական
նշանը ցույց է
տալիս, որ
դաշտի ![]() լարվածության
վեկտորն
ուղղված է
պոտենցիալի նվազման
կողմը:
լարվածության
վեկտորն
ուղղված է
պոտենցիալի նվազման
կողմը:
![]() 1.9.
ԷԼԵԿՏՐԱԿԱՆ
ԴԻՊՈԼ
(ԵՐԿԲԵՎԵՌ):
1.9.
ԷԼԵԿՏՐԱԿԱՆ
ԴԻՊՈԼ
(ԵՐԿԲԵՎԵՌ):
ԴԻՊՈԼԻ ԷԼԵԿՏՐԱՍՏԱՏԻԿ ԴԱՇՏԻ ՊՈՏԵՆՑԻԱԼԻ ԵՎ ԼԱՐՎԱԾՈՒԹՅԱՆ ՀԱՇՎԱՐԿԸ
Էլեկտրական
դիպոլ
(երկբևեռ)
կոչվում է մեծությամբ
հավասար
երկու
այնպիսի ![]() և
և ![]() տարանուն
կետային
լիցքերի
համակարգը, որոնց
միջև եղած
տարանուն
կետային
լիցքերի
համակարգը, որոնց
միջև եղած![]() հեռավորությունը
զգալիորեն
ավելի փոքր է,
քան մինչև այն
կետերը եղած
հեռավորությունը,
որոնցում
որոշվում է համակարգի
դաշտը (նկ.23):
հեռավորությունը
զգալիորեն
ավելի փոքր է,
քան մինչև այն
կետերը եղած
հեռավորությունը,
որոնցում
որոշվում է համակարգի
դաշտը (նկ.23):
Էլեկտրական դիպոլը բնութագրվում է դիպոլային մոմենտով`
![]() ,
(1.40)
,
(1.40)
որտեղ
![]() լիցքից
դեպի
լիցքից
դեպի ![]() -ն ուղղված
-ն ուղղված
![]() վեկտորը
կոչվում է
դիպոլի
բազուկ և
մեծությամբ
հավասար է
լիցքերի միջև
եղած
հեռավորությանը:
վեկտորը
կոչվում է
դիպոլի
բազուկ և
մեծությամբ
հավասար է
լիցքերի միջև
եղած
հեռավորությանը:
Հաշվենք
էլեկտրական
դիպոլի դաշտի
պոտենցիալը ![]() կետում
(նկ.24):
Վերադրման
սկզբունքի
համաձայն
կետում
(նկ.24):
Վերադրման
սկզբունքի
համաձայն ![]() կետում
պոտենցիալը
կորոշվի
հետևյալ կերպ.
կետում
պոտենցիալը
կորոշվի
հետևյալ կերպ.
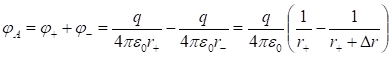 ,
,
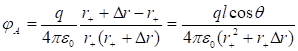 :
:
Հաշվի
առնելով այն,
որ ![]() դիպոլի
մոմենտն է,
կստանանք`
դիպոլի
մոմենտն է,
կստանանք`
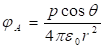 :
:
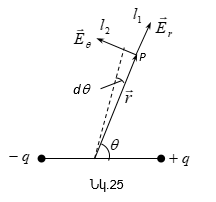
Ստացված արտահայտությունը կարելի է ներկայացնել հետևյալ տեսքով`
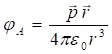 :
(1.41)
:
(1.41)
![]() անկյունների
տիրույթում
անկյունների
տիրույթում ![]() ,
, ![]() անկյունների
տիրույթում
անկյունների
տիրույթում ![]() :
:
Այժմ հաշվենք էլեկտրական դիպոլի դաշտի լարվածությունը: Դիպոլի դաշտի լարվածությունը հաշվելու համար օգտվենք լարվածության և պոտենցիալի միջև եղած կապից ու վերը ստացված (1.36) պոտենցիալի բանաձևից.
![]() և
և ![]() :
:
Նախ
հաշվենք ![]() -ի
բաղադրիչները
դիտարկվող
-ի
բաղադրիչները
դիտարկվող ![]() կետում
փոխուղղահայաց
կետում
փոխուղղահայաց
![]() ուղղություններով
(նկ.25),
համապատասխանաբար
նշանակելով
ուղղություններով
(նկ.25),
համապատասխանաբար
նշանակելով
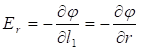 և
և ![]() .
.
 ,
, ![]() :
:
![]() և
և ![]() վեկտորները
դիպոլի
առանցքի հետ
գտնվում են միևնույն
հարթության
մեջ:
Դիտարկվող
կետում
երկբևեռի
դաշտի
արդյունարար
լարվածությունը`
վեկտորները
դիպոլի
առանցքի հետ
գտնվում են միևնույն
հարթության
մեջ:
Դիտարկվող
կետում
երկբևեռի
դաշտի
արդյունարար
լարվածությունը`
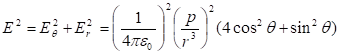 ,
,
վերջինս ձևափոխելով` կունենանք`
![]() : (1.42)
: (1.42)
Ստացվեց դիպոլի էլեկտրական դաշտի լարվածության բանաձևն ընդհանուր դեպքի համար, որից բխում են հետևյալ մասնավոր դեպքերը`
ա)
Լարվածությունը
դիպոլի
առանցքի վրա,
երբ ![]() ստացվում
է
ստացվում
է
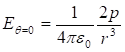 , (1.43)
, (1.43)
ուղղությամբ
համընկնում է
երկբևեռի ![]() մոմենտի
հետ:
մոմենտի
հետ:
բ)
Երբ ![]() -ի
լարվածությունը
դիպոլի միջնուղղահայացի
վրա,
ստացվում է`
-ի
լարվածությունը
դիպոլի միջնուղղահայացի
վրա,
ստացվում է`
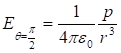 ,
(1.44)
,
(1.44)
ուղղությամբ
հակառակ է ![]() մոմենտին:
Դիպոլից
ունեցած
հեռավորության
համեմատ
լարվածությունը
նվազում է
ինչպես
մոմենտին:
Դիպոլից
ունեցած
հեռավորության
համեմատ
լարվածությունը
նվազում է
ինչպես ![]() ,
այսինքն՝
ավելի արագ,
քան կետային
լիցքի դաշտի
լարվածությունը,
(որը նվազում
է ինչպես
,
այսինքն՝
ավելի արագ,
քան կետային
լիցքի դաշտի
լարվածությունը,
(որը նվազում
է ինչպես ![]() ):
):
1.10. ԵՐԿԲԵՎԵՌԻ ՎԱՐՔԸ ԵՎ ՊՈՏԵՆՑԻԱԼԱՅԻՆ ԷՆԵՐԳԻԱՆ ԱՐՏԱՔԻՆ ԷԼԵԿՏՐԱՍՏԱՏԻԿ ԴԱՇՏՈՒՄ
Նախ դիտարկենք երկբևեռի վրա ազդող ուժերը համասեռ էլեկտրաստատիկ դաշտում (նկ.26):
Ակնհայտ
է, որ
երկբևեռը
կազմող
լիցքերի վրա կազդեն
մեծությամբ
հավասար,
ուղղությամբ
հակադիր
երկու ուժեր` ![]() և
և ![]() :
Այդ ուժերը
կազմում են
ուժազույգ,
որի բազուկը
հավասար է
:
Այդ ուժերը
կազմում են
ուժազույգ,
որի բազուկը
հավասար է ![]() ուժազույգի
մոմենտը`
ուժազույգի
մոմենտը`
![]() ,
,
որտեղ
![]() դիպոլային
մոմենտն է:
Ուժազույգի
դիպոլային
մոմենտն է:
Ուժազույգի ![]() մոմենտի
ուղղությունը
որոշվում է`
մոմենտի
ուղղությունը
որոշվում է`
![]() ,
(1.45)
,
(1.45)
վեկտորական արտադրյալով:
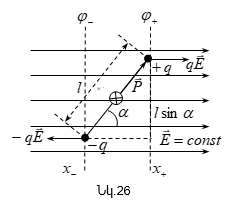
Այսպիսով,
համասեռ
էլեկտրաստատիկ
դաշտում երկբևեռը
կպտտվի և
կձգտի գրավել
![]() դիրք:
Անհամասեռ
էլեկտրական
դաշտում, բացի
պտտվելուց,
լիցքերի վրա
ազդող ուժերի
տարբերության
պատճառով
երկբևեռը
կձգվի ուժեղ
դաշտի կողմը:
դիրք:
Անհամասեռ
էլեկտրական
դաշտում, բացի
պտտվելուց,
լիցքերի վրա
ազդող ուժերի
տարբերության
պատճառով
երկբևեռը
կձգվի ուժեղ
դաշտի կողմը:
Երկբևեռն էլեկտրաստատիկ դաշտում օժտված է պոտենցիալ էներգիայով: Հաշվենք այդ էներգիան`
![]() ,
,
որտեղ ![]() դաշտի
պոտենցիալներն
են
դաշտի
պոտենցիալներն
են ![]() լիցքերի
գտնվելու
կետերում:
լիցքերի
գտնվելու
կետերում:
Համասեռ
էլեկտրաստատիկ
դաշտում
պոտենցիալը
որոշվում է ![]() բանաձևով:
բանաձևով:
![]() այն
առանցքն է,
որով ուղղված
է
այն
առանցքն է,
որով ուղղված
է ![]() -ն:
Հետևաբար,
երկբևեռի
էներգիան
էլեկտրաստատիկ
դաշտում
արտահայտվում
է (նկ.26) հետևյալ
առնչությունով.
-ն:
Հետևաբար,
երկբևեռի
էներգիան
էլեկտրաստատիկ
դաշտում
արտահայտվում
է (նկ.26) հետևյալ
առնչությունով.
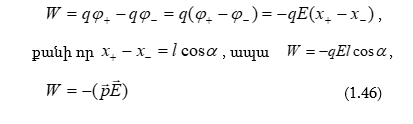
բանաձևով:
Ստացված
բանաձևն
արտահայտում
է ![]() էլեկտրական
մոմենտով
երկբևեռի
պոտենցիալ էներգիան
էլեկտրական
մոմենտով
երկբևեռի
պոտենցիալ էներգիան
![]() լարվածության
էլեկտրական
դաշտում:
Ստացված
բանաձևից
հետևում է, որ
երկբևեռի
էներգիան նվազագույնն
է, երբ
լարվածության
էլեկտրական
դաշտում:
Ստացված
բանաձևից
հետևում է, որ
երկբևեռի
էներգիան նվազագույնն
է, երբ ![]() (այսինքն
(այսինքն
![]() ),
իսկ
),
իսկ ![]() հավասար
ամենամեծ
արժեքը այն
դեպքում, երբ
հավասար
ամենամեծ
արժեքը այն
դեպքում, երբ ![]() -ն
ուղղված է
-ն
ուղղված է ![]() վեկտորին
հակառակ:
վեկտորին
հակառակ:
Անհամասեռ
դաշտում
դիպոլի
լիցքերի վրա
ազդող ուժերը,
ընդհանուր
առմամբ,
մեծությամբ
նույնը չեն:
Դիպոլի փոքր
չափերի
դեպքում ![]() ուժերը
կարելի է
մոտավորապես
համարել միագիծ
(նկ. 27):
Ենթադրենք, թե
դաշտն ամենից
արագ փոխվում
է
ուժերը
կարելի է
մոտավորապես
համարել միագիծ
(նկ. 27):
Ենթադրենք, թե
դաշտն ամենից
արագ փոխվում
է ![]() ուղղությամբ,
որը դիպոլի
տեղավորված
տեղում
համընկնում է
ուղղությամբ,
որը դիպոլի
տեղավորված
տեղում
համընկնում է ![]() ուղղության
հետ: Դիպոլի
դրական լիցքը
բացասականի
նկատմամբ
ուղղության
հետ: Դիպոլի
դրական լիցքը
բացասականի
նկատմամբ ![]() ուղղությամբ
շեղված է
ուղղությամբ
շեղված է ![]() մեծությամբ:
Ուստի, դաշտի
լարվածությունն
այն կետերում,
որտեղ
գտնվում են
լիցքերը, տարբերվում
է`
մեծությամբ:
Ուստի, դաշտի
լարվածությունն
այն կետերում,
որտեղ
գտնվում են
լիցքերը, տարբերվում
է`
![]()
չափով:
Հետևաբար,
դիպոլի վրա
ազդող ուժերի ![]() համազորը
կլինի զրոյից
տարբեր: Պարզ
է, որ
համազորը
կլինի զրոյից
տարբեր: Պարզ
է, որ ![]() առանցքի
վրա այդ համազորի
պրոյեկցիան
կլինի.
առանցքի
վրա այդ համազորի
պրոյեկցիան
կլինի.
![]() (1.47)
(1.47)
Այսպիսով,
անհամասեռ
դաշտում
դիպոլի վրա,
բացի պտտող (1.40)
մոմենտից,
ազդում է նաև
(1.46) ուժը: Այս
ուժի
ազդեցության
տակ դիպոլը
կամ
ներքաշվում է
ավելի ուժեղ
դաշտի
տիրույթը, երբ
![]() անկյունը
սուր է, կամ
նրանից դուրս
է մղվում, երբ
անկյունը
սուր է, կամ
նրանից դուրս
է մղվում, երբ ![]() անկյունը
բութ է:
անկյունը
բութ է:
ԳԼՈՒԽ 2: ԷԼԵԿՏՐԱԿԱՆ ԴԱՇՏԸ ԴԻԷԼԵԿՏՐԻԿՆԵՐՈՒՄ
2.1. ԴԻԷԼԵԿՏՐԻԿՆԵՐ: ԴՐԱՆՑ ՏԱՐԱՏԵՍԱԿՆԵՐԸ
Այն նյութերը, որոնցում բացակայում են ազատ լիցքերը (ի տարբերություն մետաղների), կոչվում են դիէլեկտրիկներ (մեկուսիչներ): Բնականաբար, դիէլեկտրիկներում էլեկտրական դաշտի առկայությունը չի ուղեկցվի լիցքերի (էլեկտրոնների) կարգավորված շարժմամբ: Նշենք, որ դիէլեկտրիկները հոսանք չեն հաղորդում, այն պարզ պատճառով, որ նրանցում չկան ազատ լիցքեր: Բոլոր լիցքերն ատոմներում և մոլեկուլներում կապված վիճակում են: Տարբերում են դիէլեկտրիկների հետևյալ տարատեսակները (նկ.28):
1. Բևեռային դիէլեկտրիկներ: Դիէլեկտրիկները կոչվում են բևեռային, եթե կազմված են բևեռային մոլեկուլներից` մոլեկուլներ, որոնք ունեն սեփական դիպոլային մոմենտ, պայմանավորված նրանով, որ նրանցում դրական և բացասական լիցքերի ծանրության կենտրոնները միմյանցից շեղված են դիպոլի բազկի չափով: Օրինակ` HCl, H2O, NH3 :
2.
Ոչ բևեռային
դիէլեկտրիկներ:
Ոչ բևեռային
կոչվում են
այն
դիէլեկտրիկները,
որոնցում
դրական և
բացասական
լիցքերի ծանրության
կենտրոնները
համընկնում
են: Հետևաբար, ![]() դիպոլային
մոմենտները
ոչ բևեռային
դիէլեկտրիկներում
հավասար են
զրոյի:
Օրինակ` H2, N2, O2,
CCl4 և այլն:
դիպոլային
մոմենտները
ոչ բևեռային
դիէլեկտրիկներում
հավասար են
զրոյի:
Օրինակ` H2, N2, O2,
CCl4 և այլն:
3. Իոնային դիէլեկտրիկներ: Այս տիպին են պատկանում այն դիէլեկտրիկները, որոնք ունեն բյուրեղային կառուցվածք և կարելի է ներկայացնել որպես երկու ենթաբյուրեղային ցանցեր` կազմված միայն դրական և բացասական իոններից:
4.
Սեգնետաէլեկտրիկներ:
Այս նյութերը
արտաքին
էլեկտրական
դաշտի բացակայության
դեպքում
օժտված են
սպոնտան (ինքնակամ)
բևեռացումով:
Այս երևույթն
առաջին անգամ
հայտնաբերվել
է սեգնետյան
աղի համար,
այդ կապակցությամբ
բոլոր նման
նյութերը
կոչվում են սեգնետաէլեկտրիկներ:
Սեգնետաէլեկտրիկները
մնացած
դիէլեկտրիկներից
տարբերվում
են մի շարք
բնորոշ
հատկություններով.
սովորական
դիէլեկտրիկների
դիէլեկտրական
թափանցելիությունը
հավասար է մի
քանի միավորի,
սեգնետաէլեկտրիկների
դիէլեկտրական
թափանցելիությունը
մի քանի
հազարի կարգի
է: ![]() կախումը
կախումը
![]() -ից
գծային չէ և, հետևաբար,
դիէլեկտրական
թափանցելիությունը
կախված է
դաշտի
լարվածությունից:
-ից
գծային չէ և, հետևաբար,
դիէլեկտրական
թափանցելիությունը
կախված է
դաշտի
լարվածությունից:
2.2. ԴԻԷԼԵԿՏՐԻԿՆԵՐՆ ԱՐՏԱՔԻՆ ԷԼԵԿՏՐԱՍՏԱՏԻԿ ԴԱՇՏՈՒՄ
ԴԻԷԼԵԿՏՐԻԿՆԵՐԻ ԲԵՎԵՌԱՑՄԱՆ ՄԵԽԱՆԻԶՄԸ
Բոլոր դիէլեկտրիկները, անկախ տարատեսակից, արտաքին էլեկտրական դաշտում բևեռանում են, որի արդյունքում ստեղծում են սեփական էլեկտրական դաշտ` պայմանավորված դիէլեկտրիկի մակերեվույթի վրա առաջացած մակերևութային կապված լիցքերով: Այդ դաշտն ուղղությամբ հակադիր է արտաքին դաշտին, որի պատճառով դիէլեկտրիկի առկայությունը տարածության այս կամ այն տիրույթում հանգեցնում է այդ տիրույթում դաշտի առկա լարվածության փոքրացմանը` կախված դիէլեկտրիկի տեսակից: Դիէլեկտրիկի բևեռացման մեխանիզմը կախված է նրա տարատեսակից:
1. Բևեռային
դիէլեկտրիկների
բևեռացման
մեխանիզմը:
Հայտնի է, որ
բևեռային
դիէլեկտրիկը
կազմված է
սեփական
դիպոլային
մոմենտներով
օժտված բևեռային
մոլեկուլներից:
Արդեն
վերևում դիտարկել
ենք երկբևեռի
վարքն
արտաքին
էլեկտրական
դաշտում:
Պարզել ենք,
որ
երկբևեռներն
արտաքին
դաշտում
ձգտում են
կողմնորոշվել
այնպես, որ
նրանց
մոմենտները
համուղղվեն
արտաքին դաշտի
ուղղությամբ:
Երկբևեռների
կողմնորոշմանն
ակներևաբար
կխանգարեն
ջերմային
շարժումն ու
միջմոլեկուլային
փոխազդեցությունները:
Երկբևեռների
կողմնորոշումը,
կախված
արտաքին դաշտի
լարվածությունից,
հանգում է
դիէլեկտրիկի
մակերևույթի
վրա կապված
(բևեռային)
լիցքերի
առաջացմանը,
որոնք էլ
պայմանավորում
են արտաքին
դաշտի ուղղությանը
հակադիր
սեփական
դաշտը` ![]() լարվածությամբ:
Վերը նշված
բևեռացման
մեխանիզմն
անվանում են կողմնորոշիչ
(նկ.29):
լարվածությամբ:
Վերը նշված
բևեռացման
մեխանիզմն
անվանում են կողմնորոշիչ
(նկ.29):
2. Ոչ բևեռային դիէլեկտրիկների բևեռացման մեխանիզմը:
Նախ քննարկենք ոչ բևեռային մոլեկուլի (ատոմի) վարքն արտաքին էլեկտրաստատիկ դաշտում (նկ.30):
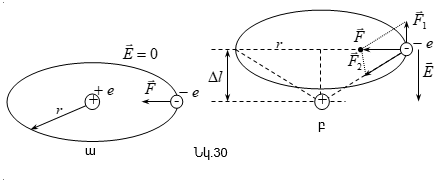
Նկ.30-ում բերված է ջրածնի ատոմը. ա) արտաքին դաշտի բացակայության և բ) արտաքին դաշտի առկայության դեպքում:
ա)
դեպքում, երբ ![]() էլեկտրոնին
էլեկտրոնին
![]() շառավղով
ուղեծրի վրա
պահող միակ
ուժը կուլոնյան
ուժն է.
շառավղով
ուղեծրի վրա
պահող միակ
ուժը կուլոնյան
ուժն է.
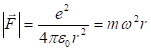 , (2.1)
, (2.1)
որտեղ
![]() էլեկտրոնի
զանգվածն է,
էլեկտրոնի
զանգվածն է, ![]() անկյունային
արագությունը,
անկյունային
արագությունը,
![]() -ը
էլեկտրոնի
ուղեծրի
շառավիղը:
-ը
էլեկտրոնի
ուղեծրի
շառավիղը:
բ)
դեպքում, երբ ![]() էլեկտրոնի
ուղեծիրը
(էլեկտրոնային
ամպը) դեֆորմացվում
է: Առաջին
մոտավորությամբ
էլեկտրոնային
ուղեծրի
դեֆորմացիան
կարելի է դիտել
որպես նրա
շեղում
էլեկտրոնի
ուղեծիրը
(էլեկտրոնային
ամպը) դեֆորմացվում
է: Առաջին
մոտավորությամբ
էլեկտրոնային
ուղեծրի
դեֆորմացիան
կարելի է դիտել
որպես նրա
շեղում ![]() ուղղությանը
հակառակ`
ուղղությանը
հակառակ` ![]() չափով,
քանի որ
չափով,
քանի որ ![]() Այս
դեպքում
կենտրոնաձիգ
ուժի դերը
կկատարի
էլեկտրոնի
վրա արտաքին
դաշտի կողմից
ազդող
Այս
դեպքում
կենտրոնաձիգ
ուժի դերը
կկատարի
էլեկտրոնի
վրա արտաքին
դաշտի կողմից
ազդող ![]() և միջուկի
կողմից ազդող
և միջուկի
կողմից ազդող ![]() ուժերի
համազորը:
ուժերի
համազորը:
![]() ,
,
որտեղ
![]() Նկ.
30բ-ից հետևում
է, որ
Նկ.
30բ-ից հետևում
է, որ
![]() ,
որտեղից
,
որտեղից ![]() :
:
Էլեկտրոնային
ուղեծրի
(ամպի)
շեղումը ![]() հետևաբար,
բացասական
լիցքի
ծանրության
կենտրոնի
շեղումը
միջուկի`
դրական լիցքի
ծանրության
կենտրոնի
նկատմամբ
ուղեկցվում է
մոլեկուլում
(ատոմում)
առաձգական
երկբևեռի
մակածմամբ,
որի դիպոլային
մոմենտը`
հավասար է.
հետևաբար,
բացասական
լիցքի
ծանրության
կենտրոնի
շեղումը
միջուկի`
դրական լիցքի
ծանրության
կենտրոնի
նկատմամբ
ուղեկցվում է
մոլեկուլում
(ատոմում)
առաձգական
երկբևեռի
մակածմամբ,
որի դիպոլային
մոմենտը`
հավասար է.
![]() (2.2)
(2.2)
կամ,
օգտվելով (2.1)
բանաձևից, ![]()
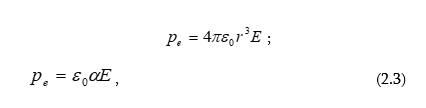
որտեղ
![]() կոչվում
է
բևեռացվելիություն,
որը բնութագրում
է
էլեկտրոնային
ամպի
դեֆորմացվելու
ընդունակությունն
արտաքին
կոչվում
է
բևեռացվելիություն,
որը բնութագրում
է
էլեկտրոնային
ամպի
դեֆորմացվելու
ընդունակությունն
արտաքին ![]() դաշտի
ազդեցությամբ:
դաշտի
ազդեցությամբ:
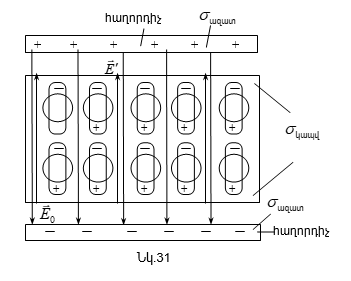
Պարզելով ոչ բևեռային մոլեկուլի վարքն արտաքին էլեկտրական դաշտում` արդեն դժվար չէ մեկնաբանել ոչ բևեռային դիէլեկտրիկի բևեռացման մեխանիզմը (նկ.31): Իրոք, արտաքին դաշտի ազդեցությամբ ոչ բևեռային դիէլեկտրիկի մոլեկուլները դեֆորմացվելով ձեռք են բերում որոշակի դիպոլային մոմենտ (առաձգական), այնուհետև, ինչպես և կոշտ դիպոլների դեպքում, ձգտում են կողմնորոշվել արտաքին դաշտի ազդեցությամբ: Բևեռացման նման մեխանիզմը հասկանալի պատճառներով անվանում են դեֆորմացիոն կամ առաձգական:
3. Իոնային (բյուրեղային) դիէլեկտրիկի դեֆորմացման մեխանիզմը: Բյուրեղային դիէլեկտրիկի բևեռացումն արտաքին դաշտի ազդեցությամբ հանգում է բացասական իոններով ենթացանցի նկատմամբ դրական իոններով ենթացանցի շեղմանը: Արդյունքում դիէլեկտրիկի մակերևույթի վրա առաջանում են նորից կապված բևեռային լիցքեր, որոնք ստեղծում են իրենց սեփական դաշտը, որն ուղղությամբ հակառակ է արտաքին դաշտին: Բևեռացման նշված տարատեսակն անվանում են իոնային բևեռացում:
Անկախ
բևեռացման
մեխանիզմից և
դիէլեկտրիկի
տարատեսակից,
որպես
բևեռացման
աստիճանի քանակական
չափանիշ
ընդունվում է
դիէլեկտրիկի
միավոր
ծավալում
առկա
մոլեկուլների
դիպոլային
մոմենտների
գումարը` ![]() բևեռացման
վեկտորը.
բևեռացման
վեկտորը.
![]() , (2.4)
, (2.4)
որտեղ
![]() -ը
-ը ![]() ծավալում
դիպոլների
թիվն է,
ծավալում
դիպոլների
թիվն է, ![]() առանձին
մոլեկուլի
դիպոլային
մոմենտը:
առանձին
մոլեկուլի
դիպոլային
մոմենտը:
Եթե
դիէլեկտրիկն
ամբողջ
ծավալով
համասեռ է, ապա
![]() բևեռացման
վեկտորը
հաստատուն է և
հավասար է.
բևեռացման
վեկտորը
հաստատուն է և
հավասար է.
![]()
որտեղ
![]() միավոր
ծավալում
մոլեկուլների
(դիպոլների) թիվն
է: Հաշվի
առնելով վերը
նշվածը`
միավոր
ծավալում
մոլեկուլների
(դիպոլների) թիվն
է: Հաշվի
առնելով վերը
նշվածը`
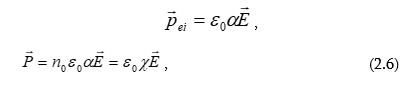
որտեղ
![]() միավոր
ծավալի
բևեռացվելիությունն
է և կրում է դիէլեկտրական
ընկալունակություն
անվանումը:
միավոր
ծավալի
բևեռացվելիությունն
է և կրում է դիէլեկտրական
ընկալունակություն
անվանումը:
Դիէլեկտրիկի
բևեռացման
ժամանակ նրա
մեջ ընդհանուր
դեպքում
կարող են
առաջանալ և´ ծավալային
(եթե
դիէլեկտրիկը
անիզոտրոպ է),
և´
մակերևութային
կապված
լիցքեր: ![]() վեկտորի
դաշտն օժտված
է հիանալի և
կարևոր
հատկությամբ:
Պարզվում է,
որ
վեկտորի
դաշտն օժտված
է հիանալի և
կարևոր
հատկությամբ:
Պարզվում է,
որ ![]() վեկտորի
հոսքը
կամայական
փակ S
մակերևույթով
հավասար է այդ
մակերևույթով
սահմանափակված
դիէլեկտրիկի
ծավալում եղած
կապված
լիցքերի
հանրահաշվական
գումարին` հակառակ
նշանով.
վեկտորի
հոսքը
կամայական
փակ S
մակերևույթով
հավասար է այդ
մակերևույթով
սահմանափակված
դիէլեկտրիկի
ծավալում եղած
կապված
լիցքերի
հանրահաշվական
գումարին` հակառակ
նշանով.
![]() : (2.7)
: (2.7)
Այս
հավասարումն
արտահայտում
է Գաուսի թեորեմը
![]() վեկտորի
համար
ինտեգրալային
տեսքով: Գաուսի
թեորեմը
վեկտորի
համար
ինտեգրալային
տեսքով: Գաուսի
թեորեմը ![]() վեկտորի
դաշտի համար
դիֆերենցիալ
տեսքով`
վեկտորի
դաշտի համար
դիֆերենցիալ
տեսքով`
![]() , (2.8)
, (2.8)
այսինքն`
դաշտի որևէ
կետում ![]() վեկտորի
դիվերգենցիան
հակառակ
նշանով հավասար
է այդ նույն
կետում
ավելցուկային
կապված լիցքի
ծավալային
խտությանը:
վեկտորի
դիվերգենցիան
հակառակ
նշանով հավասար
է այդ նույն
կետում
ավելցուկային
կապված լիցքի
ծավալային
խտությանը:
Դեբայը (1884-1966) ցույց է տվել, որ թույլ էլեկտրական դաշտերում (2.6) բանաձևը ճիշտ է և բևեռային, և ոչ բևեռային դիէլեկտրիկների համար, որոնց դեպքում
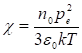 , (2.9)
, (2.9)
որտեղ
![]() մոլեկուլների
թիվն է
դիէլեկտրիկի
միավոր ծավալում,
մոլեկուլների
թիվն է
դիէլեկտրիկի
միավոր ծավալում,
![]() կոշտ
դիպոլային
մոմենտն է, k-ն`
Բոլցմանի
հաստատունը, T-ն`
բացարձակ
ջերմաստիճանը:
կոշտ
դիպոլային
մոմենտն է, k-ն`
Բոլցմանի
հաստատունը, T-ն`
բացարձակ
ջերմաստիճանը:
Նկ.32-ում
բերված է
բևեռացման
վեկտորի
մեծության
կախումն
արտաքին
դաշտի
լարվածության
մեծությունից:
Նկարից պարզ
երևում է, որ
սկսած ![]()
![]() մնում
է հաստատուն`
բոլոր երկբևեռները
կողմնորոշվել
են դաշտի
ուղղությամբ
և բևեռացման
վեկտորի
արժեքն
առավելագույնն
է:
մնում
է հաստատուն`
բոլոր երկբևեռները
կողմնորոշվել
են դաշտի
ուղղությամբ
և բևեռացման
վեկտորի
արժեքն
առավելագույնն
է:
Արտաքին դաշտի լարվածության հետագա աճը կարող է ուղեկցվել մոլեկուլի քայքայումով` ազատ լիցքերի առաջացումով, հետևաբար, դիէլեկտրիկի ծակվելով: Դիէլեկտրիկը կդադարի մեկուսիչ լինելուց և կվերածվի հաղորդչի:
Նկ.33-ում բերված է դիէլեկտրական ընկալունակության կախումը 1/T-ից (ա) բևեռային և (բ) ոչ բևեռային դիէլեկտրիկների համար:
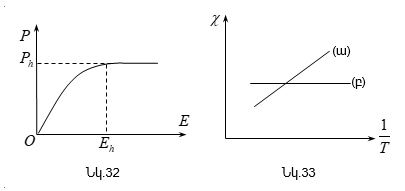
Բևեռային
դիէլեկտրիկներում
դիտվում է ոչ
միայն
կողմնորոշիչ,
այլ նաև`
դեֆորմացիոն
(էլեկտրոնային)
բևեռացում: Ոչ
մեծ դաշտերի
դեպքում
բևեռացման ![]() վեկտորի և
վեկտորի և ![]() լարվածության
վեկտորի միջև
պահպանվում է
ուղիղ
համեմատական
կապ (նկ.32):
Այդպիսի
դիէլեկտրիկները
կոչվում են գծային
(իզոտրոպ):
լարվածության
վեկտորի միջև
պահպանվում է
ուղիղ
համեմատական
կապ (նկ.32):
Այդպիսի
դիէլեկտրիկները
կոչվում են գծային
(իզոտրոպ):
Եթե
դիէլետրիկներում
![]() դիէլեկտրական
ընկալունակությունը
կախված է
դիէլեկտրիկում
ընտրված
ուղղությունից,
դիէլեկտրիկը
կոչվում է ոչ
գծային կամ անիզոտրոպ:
Դիէլեկտրիկներից
շատերի համար
դիէլեկտրական
ընկալունակությունը
կախված է
դիէլեկտրիկում
ընտրված
ուղղությունից,
դիէլեկտրիկը
կոչվում է ոչ
գծային կամ անիզոտրոպ:
Դիէլեկտրիկներից
շատերի համար ![]() դիէլեկտրական
ընկալունակությունը
չի գերազանցում
մեկ արժեքը:
Սակայն
գոյություն
ունի
դիէլեկտրիկների
մի խումբ,
որոնց մոտ
դիէլեկտրական
ընկալունակությունը
հասնում է մեծ
արժեքների:
դիէլեկտրական
ընկալունակությունը
չի գերազանցում
մեկ արժեքը:
Սակայն
գոյություն
ունի
դիէլեկտրիկների
մի խումբ,
որոնց մոտ
դիէլեկտրական
ընկալունակությունը
հասնում է մեծ
արժեքների:
Օրինակ`
ջրի համար ![]() սպիրտի
համար`
սպիրտի
համար` ![]() Սեգնետաէլեկտրիկների
համար այն
հասնում է մի
քանի հազարի:
Սեգնետաէլեկտրիկների
համար այն
հասնում է մի
քանի հազարի:
2.4. ԷԼԵԿՏՐԱԿԱՆ ԻՆԴՈՒԿՑԻԱՅԻ (ՇԵՂՄԱՆ) ՎԵԿՏՈՐ:
ԳԱՈՒՍԻ ԹԵՈՐԵՄԸ ԻՆԴՈՒԿՑԻԱՅԻ ՎԵԿՏՈՐԻ ՀԱՄԱՐ
ԴԻԷԼԵԿՏՐԱԿԱՆ ԹԱՓԱՆՑԵԼԻՈՒԹՅՈՒՆ
Դիէլեկտրիկում
![]() մակրոսկոպիկ
դաշտն
առաջանում է
երկու դաշտերի
վերադրման հետևանքով.
ազատ
լիցքերով
ստեղծված
մակրոսկոպիկ
դաշտն
առաջանում է
երկու դաշտերի
վերադրման հետևանքով.
ազատ
լիցքերով
ստեղծված ![]() դաշտի,
այսինքն`
այնպիսի
լիցքերով,
որոնք մեկ մարմնից
մյուսը կարող
են հաղորդվել
նրանց հպման
դեպքում և
կապված
լիցքերի
դաշտի,
այսինքն`
այնպիսի
լիցքերով,
որոնք մեկ մարմնից
մյուսը կարող
են հաղորդվել
նրանց հպման
դեպքում և
կապված
լիցքերի ![]() դաշտի:
Դաշտերի
վերադրման
սկզբունքի
համաձայն
դաշտի:
Դաշտերի
վերադրման
սկզբունքի
համաձայն
![]() : (2.10)
: (2.10)
Դիէլեկտրիկի
բևեռացումը
պայմանավորված
է (2.10)
գումարային
դաշտի
ազդեցությամբ:
Հետևաբար, հենց
այս ![]() -ն
է, որ պետք է
տեղադրել (2.6)
բանաձևի մեջ:
-ն
է, որ պետք է
տեղադրել (2.6)
բանաձևի մեջ:
Կապված
լիցքերը ազատ
լիցքերից
տարբերվում են
միայն նրանով,
որ չեն կարող
դուրս գալ այն
մոլեկուլների
(ատոմների) սահմաններից,
որոնց
կազմության
մեջ նրանք մտնում
են: Իսկ
մնացածում
նրանց
հատկություններն
այնպիսին են,
ինչպիսին`
բոլոր մյուս
լիցքերինը:
Մասնավորապես,
կապված
լիցքերի վրա
են սկսվում
կամ
վերջանում ![]() վեկտորի
վեկտորի
![]() թվով
լարվածության
գծերը: Այդ
պատճառով Գաուսի
թեորեմը (2.10)
արտահայտությամբ
որոշվող
թվով
լարվածության
գծերը: Այդ
պատճառով Գաուսի
թեորեմը (2.10)
արտահայտությամբ
որոշվող ![]() վեկտորի
համար պետք է
գրել հետևյալ
կերպ.
վեկտորի
համար պետք է
գրել հետևյալ
կերպ.
![]() : (2.11)
: (2.11)
Այսինքն`
![]() վեկտորի՝
փակ
մակերևույթի
միջով անցնող
հոսքը
հաշվելիս
պետք է հաշվի
առնել
մակերևույթի
ներսում
գտնվող ոչ
միայն ազատ,
այլև կապված
լիցքերի
հանրահաշվական
գումարը:
Դիէլեկտրիկում
դաշտը
գտնելու
համար (2.11)
բանաձևը դառնում
է քիչ պիտանի:
Այն անհայտ
վեկտորի՝
փակ
մակերևույթի
միջով անցնող
հոսքը
հաշվելիս
պետք է հաշվի
առնել
մակերևույթի
ներսում
գտնվող ոչ
միայն ազատ,
այլև կապված
լիցքերի
հանրահաշվական
գումարը:
Դիէլեկտրիկում
դաշտը
գտնելու
համար (2.11)
բանաձևը դառնում
է քիչ պիտանի:
Այն անհայտ ![]() մեծության
հատկություններն
արտահայտում
է
մեծության
հատկություններն
արտահայտում
է ![]() լիցքերի
միջոցով,
որոնք իրենց
հերթին որոշվում
են
լիցքերի
միջոցով,
որոնք իրենց
հերթին որոշվում
են ![]() անհայտ
դաշտով: Այդ
դժվարությունը
կարելի է
շրջանցել, եթե
անհայտ
դաշտով: Այդ
դժվարությունը
կարելի է
շրջանցել, եթե
![]() լիցքերն
արտահայտենք
(2.7) բանաձևով
որոշվող
լիցքերն
արտահայտենք
(2.7) բանաձևով
որոշվող ![]() վեկտորի
հոսքի
միջոցով: Այդ
դեպքում (2.11)
արտահայտությունը
կարելի է
ձևափոխել
հետևյալ
տեսքով.
վեկտորի
հոսքի
միջոցով: Այդ
դեպքում (2.11)
արտահայտությունը
կարելի է
ձևափոխել
հետևյալ
տեսքով.
![]() : (2.12)
: (2.12)
Ինտեգրալի
նշանի տակ
փակագծերի
մեջ գտնվող
մեծությունը
նշանակում են ![]() տառով:
Այսպիսով,
մենք գտանք
օժանդակ
տառով:
Այսպիսով,
մենք գտանք
օժանդակ ![]() վեկտորը.
վեկտորը.
![]()
![]() մեծությունը
կոչվում է
էլեկտրական
շեղում կամ
էլեկտրական
ինդուկցիա,
որի հոսքը
կամայական
փակ
մակերևույթի
միջով հավասար
է այդ
մակերևույթի
ներսում
գտնվող ազատ
լիցքերի
հանրահաշվական
գումարին.
մեծությունը
կոչվում է
էլեկտրական
շեղում կամ
էլեկտրական
ինդուկցիա,
որի հոսքը
կամայական
փակ
մակերևույթի
միջով հավասար
է այդ
մակերևույթի
ներսում
գտնվող ազատ
լիցքերի
հանրահաշվական
գումարին.
![]() : (2.14)
: (2.14)
Այս
պնդումն
անվանում են
Գաուսի
թեորեմ ![]() դաշտի
համար: Եթե
ազատ լիցքերը
փակ մակերևույթի
ներսում
դաշտի
համար: Եթե
ազատ լիցքերը
փակ մակերևույթի
ներսում ![]() ծավալային
խտությամբ
բաշխված են
անընդհատ, ապա
(2.14) բանաձևն
ընդունում է
հետևյալ
տեսքը.
ծավալային
խտությամբ
բաշխված են
անընդհատ, ապա
(2.14) բանաձևն
ընդունում է
հետևյալ
տեսքը.
![]() : (2.15)
: (2.15)
Էլեկտրական շեղման վեկտորի հոսքի միավորը կուլոնն է:
Տեղադրելով
(2.13) բանաձևում ![]() -ի
համար գրված (2.6)
արտահայտությունը`
կստանանք՝
-ի
համար գրված (2.6)
արտահայտությունը`
կստանանք՝
![]()
Չափայնություն չունեցող
![]()
մեծությունը
կոչվում է
հարաբերական
դիէլեկտրական
թափանցելիություն
կամ,
պարզապես, միջավայրի
դիէլեկտրական
թափանցելիություն:
![]() դիէլեկտրական
թափանցելիությունը
(ինչպես նաև
դիէլեկտրական
թափանցելիությունը
(ինչպես նաև ![]() -ն)
դիէլեկտրիկի
էլեկտրական
բնութագիրն է:
Բոլոր
նյութերի
համար
-ն)
դիէլեկտրիկի
էլեկտրական
բնութագիրն է:
Բոլոր
նյութերի
համար ![]() վակուումի
համար՝
վակուումի
համար՝ ![]() արժեքները
կախված են
դիէլեկտրիկի
բնույթից և
տատանվում են
մեկից քիչ
տարբերվող
մեծությունից
(գազեր) մինչև
մի քանի հազար
(որոշ
հախճապակիներ):
արժեքները
կախված են
դիէլեկտրիկի
բնույթից և
տատանվում են
մեկից քիչ
տարբերվող
մեծությունից
(գազեր) մինչև
մի քանի հազար
(որոշ
հախճապակիներ):
![]() -ի
մեծ արժեք
ունի ջուրը
-ի
մեծ արժեք
ունի ջուրը ![]()
(2.16) արտահայտությունը կարելի է գրել հետևյալ տեսքով
![]()
Ըստ (2.18)-ի
իզոտրոպ
դիէլեկտրիկներում
![]() վեկտորը
համագիծ է
վեկտորը
համագիծ է ![]() վեկտորին:
Անիզոտրոպ
դիէլեկտրիկներում
այդ
վեկտորները
համագիծ չեն:
վեկտորին:
Անիզոտրոպ
դիէլեկտրիկներում
այդ
վեկտորները
համագիծ չեն:
(2.14) հավասարումը կարելի է ներկայացնել դիֆերենցիալ տեսքով՝
![]()
այսինքն`
![]() վեկտորի
դիվերգենցիան
որևէ կետում
հավասար է այդ
նույն կետում
ազատ լիցքերի
ծավալային
խտությանը:
վեկտորի
դիվերգենցիան
որևէ կետում
հավասար է այդ
նույն կետում
ազատ լիցքերի
ծավալային
խտությանը:
Այն
կետերում,
որտեղ
դիվերգենցիան
դրական է,
ունենք ![]() դաշտի
աղբյուրներ
դաշտի
աղբյուրներ ![]() իսկ
այն կետերում,
որտեղ այն
բացասական է՝
իսկ
այն կետերում,
որտեղ այն
բացասական է՝ ![]() դաշտի
հոսարաններ
դաշտի
հոսարաններ ![]()
![]() վեկտորները,
ըստ
բովանդակության,
կարելի է
մեկնաբանել
այսպես:
վեկտորները,
ըստ
բովանդակության,
կարելի է
մեկնաբանել
այսպես: ![]() դաշտի
լարվածությունը
պայմանավորված
է թե´ ազատ և թե´
կապված
լիցքերով:
դաշտի
լարվածությունը
պայմանավորված
է թե´ ազատ և թե´
կապված
լիցքերով: ![]() շեղման
վեկտորը
պայմանավորված
է միայն ազատ
լիցքերով, իսկ
շեղման
վեկտորը
պայմանավորված
է միայն ազատ
լիցքերով, իսկ
![]() բևեռացման
վեկտորը
կապված է
միայն
մակածված կամ
կապված
լիցքերի հետ:
Այսպիսով,
դաշտի հիմնական
բնութագիրն է
վեկտորը, իսկ
բևեռացման
վեկտորը
կապված է
միայն
մակածված կամ
կապված
լիցքերի հետ:
Այսպիսով,
դաշտի հիմնական
բնութագիրն է
վեկտորը, իսկ ![]() և
և ![]() վեկտորները
դաշտի
օժանդակ
օգտակար
բնութագրեր
են:
վեկտորները
դաշտի
օժանդակ
օգտակար
բնութագրեր
են:
Սեգնետաէլեկտրիկները
այն
դիէլեկտրիկներն
են որոնք
որոշակի
ջերմաստիճանային
միջակայքում
արտաքին
էլեկտրական
դաշտի
բացակայության
դեպքում
օժտված են
ինքնակամ (բևեռացումով)
բևեռացվելիությամբ:
Սեգնետաէլեկտրիկներին
են պատկանում,
օրինակ Ի.
Կուրչատովի և
Պ. Կոբեկի
կողմից
մանրակրկիտ
ուսումնասիրված
սեգնետյան
աղը` գինեթթվի
նատրիումկալիումական
կրկնակի աղն
է` ![]() (նրանից
էլ եկել է այդ
անվանումը) և
բարիումի տիտանատը`
(նրանից
էլ եկել է այդ
անվանումը) և
բարիումի տիտանատը`
![]() Սեգնետաէլեկտրիկ
ները մնացած
դիէլեկտրիկներից
տարբերվում
են մի շարք
բնորոշ
հատկություններով:
Սեգնետաէլեկտրիկ
ները մնացած
դիէլեկտրիկներից
տարբերվում
են մի շարք
բնորոշ
հատկություններով:
Սովորական
դիէլեկտրիկների
![]() -ը հավասար
է մի քանի
միավորի,
որպես
բացառություն
հասնելով մի
քանի
տասնյակի
(օրինակ ջրի համար
-ը հավասար
է մի քանի
միավորի,
որպես
բացառություն
հասնելով մի
քանի
տասնյակի
(օրինակ ջրի համար
![]() ),
սեգնետաէլեկտրիկների
դիէլեկտրական
թափանցելիությունը
լինում է մի
քանի հազարի
կարգի:
),
սեգնետաէլեկտրիկների
դիէլեկտրական
թափանցելիությունը
լինում է մի
քանի հազարի
կարգի:
D-ի կախումը E-ից գծային չէ և, հետևաբար, դիէլեկտրական թափանցելիությունը կախված է լինում դաշտի լարվածությունից (նկ.34- ում կորի առաջին ճյուղը):
Դաշտի փոփոխությունների դեպքում բևեռացման P վեկտորի (և, հետևաբար նաև D-ի) արժեքները հետ են մնում դաշտի E լարվածությունից, որի պատճառով P-ն և D-ն որոշվում են E-ի ոչ միայն տվյալ պահին ունեցած մեծությամբ, այլև E-ի նախորդ արժեքներով, այսինքն` կախում ունեն դիէլեկտրիկի նախապատմությունից: Այս երևույթը կոչվում է հիստերեզիս:
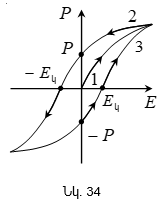
Արտաքին էլեկտրական դաշտի E լարվածությունը մեծացնելով (նկ. 34) P բևեռացվելիությունը աճում է`հասնելով հագեցման (1 կորը): P-ի փոքրացումը E-ի փոքրացումով տեղի է ունենում 2 կորով, և E=0-ի դեպքում սեգնետաէլեկտրիկը պահպանում է Pմն. մնացորդային բևեռացում, այսինքն` սեգնետաէլեկտրիկը մնում է բևեռացված արտաքին էլեկտրական դաշտի բացակայության դեպքում: Որպեսզի վերացվի մնացորդային բևեռացումը, հարկավոր է կիրառել հակառակ ուղղությամբ դաշտ (- Eկ): Eկ մեծությունը կոչվում է կոէրցիտիվ ուժ: E-ի հետագա փոփոխության դեպքում ստացվում է հիստերեզիսի օղակի 3 ճյուղը:
Սեգնետաէլեկտրիկների բևեռացման վարքագիծը նման է ֆերոմագնիսների վարքագծին: Այդ պատճառով սեգնետաէլեկտրիկները երբեմն կոչվում են ֆերոէլեկտրիկներ: Սեգնետաէլեկտրիկներ կարող են լինել միայն բյուրեղային նյութերը, ընդ որում այնպիսիները, որոնք համաչափության կենտրոն չունեն:
Արտաքին էլեկտրական դաշտի բացակայության դեպքում սեգնետաէլեկտրիկը ներկայացնում է տարբեր ուղղություններով ինքնակամ բևեռացման տիրույթներ, որոնք կոչվում են դոմեններ:
Դա
գծապատկեով
ցույց է տրված
բարիումի
տիտանատի
օրինակով (նկ.35),
որտեղ
սլաքները և ![]() նշանները
ցույց են
տալիս
նշանները
ցույց են
տալիս ![]() վեկտորի
ուղղությունը:
Քանի որ
հարևան դոմեններում
այդ
ուղղությունները
տարբեր են, ապա
ամբողջությամբ
դիէլեկտրիկի
դիպոլային մոմենտը
հավասար է
զրոյի:
Սեգնետաէլեկտրիկը
արտաքին դաշտ
մտցնելու
դեպքում տեղի
է ունենում
դոմենների
դիպոլային
մոմենտների
կողմնորոշում
դաշտի
ուղղությամբ,
ուստի
դոմենների
գումարային
էլեկտրական
դաշտը պետք է
պահպանի
նրանց որոշակի
կողմնորոշումը
արտաքին
դաշտը վերանալուց
հետո: Դրա
համար էլ
սեգնետաէլեկտրիկները
ունեն անոմալ
մեծ
դիէլեկտրական
թափանցելիության
արժեքներ
(սեգնետյան
աղի համար, օրինակ,
վեկտորի
ուղղությունը:
Քանի որ
հարևան դոմեններում
այդ
ուղղությունները
տարբեր են, ապա
ամբողջությամբ
դիէլեկտրիկի
դիպոլային մոմենտը
հավասար է
զրոյի:
Սեգնետաէլեկտրիկը
արտաքին դաշտ
մտցնելու
դեպքում տեղի
է ունենում
դոմենների
դիպոլային
մոմենտների
կողմնորոշում
դաշտի
ուղղությամբ,
ուստի
դոմենների
գումարային
էլեկտրական
դաշտը պետք է
պահպանի
նրանց որոշակի
կողմնորոշումը
արտաքին
դաշտը վերանալուց
հետո: Դրա
համար էլ
սեգնետաէլեկտրիկները
ունեն անոմալ
մեծ
դիէլեկտրական
թափանցելիության
արժեքներ
(սեգնետյան
աղի համար, օրինակ,
![]() ):
):
Սեգնետաէլեկտրական
հատկությունները
մեծապես
կախված են
ջերմաստիճանից:
Տարբեր
նյութերի
համար տարբեր ![]() որոշակի
արժեքից
բարձր
ջերմաստիճանների
դեպքում
սեգնետաէլեկտրական
հատկություններն
անհետանում
են, և
սեգնետաէլեկտրական
նյութը
դառնում է
սովորական
դիէլեկտրիկ: Այդ
ջերմաստիճանը
կոչվում է Կյուրիի
կետ, ի պատիվ
Կյուրիի, որը
երկաթի և նրա
նման նյութերի
(ֆերոմագնիսներ)
մագնիսական
հատկություններն
ուսումնասիրելիս,
առաջինը
հայտնաբերեց
այդ
կրիտիկական
ջերմաստիճանի
գոյությունը:
Որոշ
դեպքերում,
ինչպես,
օրինակ, սեգնետյան
աղի մոտ,
գոյություն
ունի Կյուրիի
երկու
ջերմաստիճան (
+22.50C և -150C), և
սեգնետաէլեկտրական
հատկությունները
դիտվում են
միայն այդ
երկու կետերի
միջև ընկած ջերմաստիճանային
միջակայքում:
Մեկ կամ մի քանի
Կյուրիի
կետերի
գոյությունը
բոլոր սեգնետաէլեկտրիկական
նյութերի չորրորդ
բնորոշ
հատկությունն
է: Գործնականորեն
կարևոր
սեգնետաէլեկտրիկ
է բարիումի մետատիտանատը`
BaTiO3 : Նրա
Կյուրիի կետն
ընկած է 1250C
մոտակայքում,
իսկ
դիէլեկտրական
թափանցելիության
առավելագույն
արժեքը
հասնում է 6000-7000-ի:
որոշակի
արժեքից
բարձր
ջերմաստիճանների
դեպքում
սեգնետաէլեկտրական
հատկություններն
անհետանում
են, և
սեգնետաէլեկտրական
նյութը
դառնում է
սովորական
դիէլեկտրիկ: Այդ
ջերմաստիճանը
կոչվում է Կյուրիի
կետ, ի պատիվ
Կյուրիի, որը
երկաթի և նրա
նման նյութերի
(ֆերոմագնիսներ)
մագնիսական
հատկություններն
ուսումնասիրելիս,
առաջինը
հայտնաբերեց
այդ
կրիտիկական
ջերմաստիճանի
գոյությունը:
Որոշ
դեպքերում,
ինչպես,
օրինակ, սեգնետյան
աղի մոտ,
գոյություն
ունի Կյուրիի
երկու
ջերմաստիճան (
+22.50C և -150C), և
սեգնետաէլեկտրական
հատկությունները
դիտվում են
միայն այդ
երկու կետերի
միջև ընկած ջերմաստիճանային
միջակայքում:
Մեկ կամ մի քանի
Կյուրիի
կետերի
գոյությունը
բոլոր սեգնետաէլեկտրիկական
նյութերի չորրորդ
բնորոշ
հատկությունն
է: Գործնականորեն
կարևոր
սեգնետաէլեկտրիկ
է բարիումի մետատիտանատը`
BaTiO3 : Նրա
Կյուրիի կետն
ընկած է 1250C
մոտակայքում,
իսկ
դիէլեկտրական
թափանցելիության
առավելագույն
արժեքը
հասնում է 6000-7000-ի:
Սեգնետաէլեկտրիկներն ունեն կարևոր գործնական կիրառություններ: Սեգնետաէլեկտրիկներից բարդ դիէլեկտրիկներ պատրաստելով և դրանց տարբեր խառնուրդներ ավելացնելով` կարելի է ստանալ բարձր որակի մեծ ունակության, բայց փոքր չափերի կոնդենսատորներ: Բարիումի տիտանատը իր քիմիական կայունության և, բարձր մեխանիկական ամրության, ինչպես նաև սեգնետաէլեկտրական հատկությունները ջերմաստիճանային լայն միջակայքում պահպանելու շնորհիվ գտել է գիտատեխնիկական մեծ կիրառություն (օրինակ, որպես ուլտրաձայնային ալիքների գեներատոր և ընդունիչ): Ներկա ժամանակում հայտնի են ավելի քան հարյուրավոր սեգնետաէլեկտրիկներ, չհաշված դրանց պինդ լուծույթները:
ԳԼՈՒԽ 3. ՀԱՂՈՐԴԻՉՆԵՐՆ ԷԼԵԿՏՐԱԿԱՆ ԴԱՇՏՈՒՄ
3.1. ԷԼԵԿՏՐԱԿԱՆ ԴԱՇՏԸ ԼԻՑՔԱՎՈՐՎԱԾ ՀԱՂՈՐԴՉԻ
Հաղորդիչներ կոչվում են այն նյութերը, որոնցում կան ազատ լիցքեր, այսինքն` լիցքեր, որոնք էլեկտրական դաշտի ազդեցությամբ ընդունակ են կարգավորված շարժվելու հաղորդչի ներսում: Հաղորդիչների դասին են պատկանում մետաղները, որոնցում որպես ազատ լիցքեր հանդես են գալիս բյուրեղային ցանցը կազմող ատոմներից պոկված և ընդհանրացված էլեկտրոնները: Հաղորդիչներում լիցք կրողներն ընդունակ են տեղաշարժվել ցանկացած չափով փոքր ուժի ազդեցության տակ: Ուստի, լիցքերի հավասարակշռությունը հաղորդչի վրա կարող է դիտվել միայն հետևյալ պայմանների բավարարման դեպքում.
1. Դաշտի լարվածությունը հաղորդչի ներսում ամենուրեք պետք է հավասար լինի զրոյի՝
![]()
Համապատասխան
(1.34)-ի դա
նշանակում է,
որ հաղորդչի
ներսում
պոտենցիալը
պետք է լինի
հաստատուն ![]()
2. Դաշտի լարվածությունը հաղորդչի մակերևույթի վրա յուրաքանչյուր կետում պետք է ուղղված լինի մակերևույթի նորմալի ուղղությամբ՝
![]()
Հետևաբար, լիցքերի հավասարակշռության դեպքում հաղորդչի մակերևույթը կլինի համապոտենցիալ:
Եթե
հաղորդիչ
մարմնին
հաղորդենք
որևէ q լիցք,
ապա այն
կբաշխվի
այնպես, որ
հավասարակշռության
պայմանները
պահպանվեն:
Մտովի պատկերացնենք
մի կամայական
փակ
մակերևույթ,
որը ամբողջությամբ
գտնվում է
մարմնի
սահմաններում:
Քանի որ լիցքի
հավասարակշռության
ժամանակ հաղորդչի
մեջ
յուրաքանչյուր
կետում դաշտը
բացակայում է,
ուստի
էլեկտրական
շեղման վեկտորի
հոսքը
մակերևույթի
միջով
հավասար է
զրոյի: Գաուսի
թեորեմի
համաձայն
լիցքերի
հանրահաշվական
գումարը
մակերևույթի
ներսում
նույնպես
հավասար
կլինի զրոյի:
Սա ճիշտ է
հաղորդչի
ներսում կամայականորեն
տարված
ցանկացած
չափի մակերևույթի
համար:
Հետևաբար,
հավասարակշռության
դեպքում
հաղորդչի ոչ
մի մասում
ավելցուկային
լիցքեր չեն
լինի: Դրանք
բոլորը որևէ ![]() խտությամբ
կբաշխվեն
հաղորդչի
մակերևույթով:
խտությամբ
կբաշխվեն
հաղորդչի
մակերևույթով:
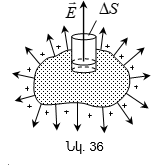
Քանի որ հավասարակշռության վիճակում հաղորդչի մեջ ավելցուկային լիցքեր չկան, ուստի հաղորդչի ներսում վերցրած որևէ ծավալից նյութի հեռացումը երբեք չի անդրադառնա լիցքերի հավասարակշիռ բաշխման վրա: Այսպիսով, ավելցուկային լիցքը սնամեջ հաղորդչի վրա բաշխվում է այնպես, ինչպես հոծ հաղորդչի վրա, այսինքն՝ նրա արտաքին մակերևույթով: Հավասարակշռության վիճակում ավելցուկային լիցքերը խոռոչի մակերևույթի վրա չեն կարող դասավորվել: Այս հետեվությունը բխում է նաև այն բանից, որ տվյալ q լիցքը կազմող նույնանուն տարրական լիցքերը փոխադարձաբար վանվում են, հետևաբար, ձգտում են դասավորվել իրարից ամենամեծ հեռավորության վրա:
Քննարկենք
մի ոչ մեծ
գլանային
մակերևույթ՝ կազմված
հաղորդչի մակերևույթին
տարած
նորմալներով
և ![]() մեծության
հիմքերով,
որոնցից մեկը
դասավորված է
հաղորդչի
ներսում, իսկ
մյուսը՝
նրանից դուրս
(նկ. 36): Այդ
մակերևույթի
միջով էլեկտրական
շեղման
վեկտորի
հոսքը
հավասար է
մեծության
հիմքերով,
որոնցից մեկը
դասավորված է
հաղորդչի
ներսում, իսկ
մյուսը՝
նրանից դուրս
(նկ. 36): Այդ
մակերևույթի
միջով էլեկտրական
շեղման
վեկտորի
հոսքը
հավասար է ![]() որտեղ
D-ն շեղման
վեկտորի
մեծությունն
է հաղորդչի մակերևույթի
անմիջական
մոտակայքում:
Իրոք, հոսքը
գլանային
մակերևույթի
ներքին մասով
հավասար է
զրոյի, քանի
որ հաղորդչի
ներսում
որտեղ
D-ն շեղման
վեկտորի
մեծությունն
է հաղորդչի մակերևույթի
անմիջական
մոտակայքում:
Իրոք, հոսքը
գլանային
մակերևույթի
ներքին մասով
հավասար է
զրոյի, քանի
որ հաղորդչի
ներսում ![]() -ն,
հետևաբար նաև
D-ն, զրո է:
Հաղորդչից
դուրս՝ նրա
անմիջական մոտակայքում
դաշտի
-ն,
հետևաբար նաև
D-ն, զրո է:
Հաղորդչից
դուրս՝ նրա
անմիջական մոտակայքում
դաշտի ![]() լարվածությունն
ուղղված է
հաղորդչի
մակերևույթի
նորմալի
ուղղությամբ:
Հետևաբար,
գլանի դուրս ցցված
կողմնային
մակերևույթի
համար
լարվածությունն
ուղղված է
հաղորդչի
մակերևույթի
նորմալի
ուղղությամբ:
Հետևաբար,
գլանի դուրս ցցված
կողմնային
մակերևույթի
համար ![]() իսկ
արտաքին
հիմքի համար
իսկ
արտաքին
հիմքի համար ![]() (ենթադրվում
է, որ արտաքին
հիմքը շատ մոտ
է դասավորված
հաղորդչի
մակերևույթին):
Գլանի մեջ
ընկնում է
(ենթադրվում
է, որ արտաքին
հիմքը շատ մոտ
է դասավորված
հաղորդչի
մակերևույթին):
Գլանի մեջ
ընկնում է ![]() ազատ լիցք (
ազատ լիցք (![]() -ն
հաղորդչի
մակերևույթի
տվյալ կետում
լիցքի խտությունն
է): Գլանային
մակերևույթի
նկատմամբ
կիրառելով
Գաուսի
թեորեմը` կստանանք
-ն
հաղորդչի
մակերևույթի
տվյալ կետում
լիցքի խտությունն
է): Գլանային
մակերևույթի
նկատմամբ
կիրառելով
Գաուսի
թեորեմը` կստանանք
![]() , այսինքն՝
, այսինքն՝ ![]() Այստեղից,
հաղորդչի
մակերևույթի
մոտակայքում
դաշտի
լարվածության
համար
ստանում ենք՝
Այստեղից,
հաղորդչի
մակերևույթի
մոտակայքում
դաշտի
լարվածության
համար
ստանում ենք՝
![]() , (3.3)
, (3.3)
որտեղ
![]() -ը
հաղորդիչը
շրջապատող
միջավայրի
հարաբերական
դիէլեկտրական
թափանցելիությունն
է (համեմատեք
այս
արդյունքը
վակուումում
գտնվող գլանի
և գնդի համար
գրված
բանաձևերի
հետ): Քննարկենք
նկ. 37-ում
պատկերված
լիցքավորված
հաղորդչով
ստեղծված
դաշտը:
Հաղորդչից
մեծ հեռավորությունների
վրա
համապոտենցիալ
մակերևույթներն
ունեն
կետային
լիցքին
բնորոշ
գնդային մակերեվույթի
ձև (տեղ
տնտեսելու
համար նկարում
գնդային
մակերևույթը
պատկերված է
հաղորդչից ոչ
մեծ
հեռավորության
վրա,
կետագծերով ցույց
են տրված
դաշտի
լարվածության
գծերը):
-ը
հաղորդիչը
շրջապատող
միջավայրի
հարաբերական
դիէլեկտրական
թափանցելիությունն
է (համեմատեք
այս
արդյունքը
վակուումում
գտնվող գլանի
և գնդի համար
գրված
բանաձևերի
հետ): Քննարկենք
նկ. 37-ում
պատկերված
լիցքավորված
հաղորդչով
ստեղծված
դաշտը:
Հաղորդչից
մեծ հեռավորությունների
վրա
համապոտենցիալ
մակերևույթներն
ունեն
կետային
լիցքին
բնորոշ
գնդային մակերեվույթի
ձև (տեղ
տնտեսելու
համար նկարում
գնդային
մակերևույթը
պատկերված է
հաղորդչից ոչ
մեծ
հեռավորության
վրա,
կետագծերով ցույց
են տրված
դաշտի
լարվածության
գծերը):
Հաղորդչին
մոտենալու
համեմատ`
համապոտենցիալ
մակերևույթներն
ավելի ու
ավելի նման են
դառնում հաղորդչի
մակերևույթին,
որը, ինչպես
գիտենք, համապոտենցիալ
է: Ելուստների
մոտակայքում
համապոտենցիալ
մակերևույթները
դասավորվում
են ավելի խիտ,
ուստի դաշտի
լարվածությունն
այստեղ ավելի
մեծ է:
Այստեղից, (3.3)-ի
համաձայն,
ստացվում է,
որ լիցքերի
խտությունը
ելուստների
վրա առավել մեծ
է: Այդ նույն
հետևությանը
կարելի է
հանգել` հաշվի
առնելով, որ
փոխադարձաբար
վանվելու պատճառով
լիցքերը
ձգտում են,
որքան կարելի
է, իրարից
հեռու
դասավորվել:
Հաղորդչում
եղած
փոսիկների
մոտակայքում
(նկ.38) համապոտենցիալ
մակերևույթները
դասավորված
են ավելի
նոսր:
Համապատասխանաբար,
այդ տեղերում
դաշտի
լարվածությունն
ու լիցքերի
խտությունն
ավելի փոքր
կլինեն:
Ընդհանրապես,
հաղորդչի տվյալ
պոտենցիալի
դեպքում
լիցքերի
խտությունը
որոշվում է
մակերևույթի
կորությամբ,
այն աճում է դրական
կորության
(ուռուցիկության)
մեծացման հետ
և նվազում՝
բացասական
կորության (գոգավորության)
մեծացման հետ:
Լիցքերի
խտությունը
հատկապես մեծ
է լինում
սայրերին, այդ
պատճառով
դաշտի
լարվածությունը
սայրերի
մոտակայքում
կարող է
այնքան մեծ
լինել, որ
տեղի կունենա
հաղորդիչը
շրջապատող
գազի
մոլեկուլների
իոնացում: ![]() -ից տարբեր
նշան ունեցող
իոնները
ձգվում են դեպի
հաղորդիչը և
չեզոքացնում
նրա լիցքը:
-ից տարբեր
նշան ունեցող
իոնները
ձգվում են դեպի
հաղորդիչը և
չեզոքացնում
նրա լիցքը: ![]() -ի նշանն
ունեցող
իոններն
սկսում են
հեռանալ հաղորդչից՝
իրենց հետ
տանելով գազի
չեզոք մոլեկուլներ:
Որպես
արդյունք
առաջանում է գազի
նկատելի
շարժում, որը
կոչվում է
էլեկտրական
քամի:
Հաղորդչի
լիցքը
փոքրանում է.
այն կարծես
հոսում է
սայրերից և
քշվում
տարվում է քամու
միջոցով: Դրա
համար
այդպիսի
երևույթն անվանում
են լիցքի հոսք
սայրերից:
-ի նշանն
ունեցող
իոններն
սկսում են
հեռանալ հաղորդչից՝
իրենց հետ
տանելով գազի
չեզոք մոլեկուլներ:
Որպես
արդյունք
առաջանում է գազի
նկատելի
շարժում, որը
կոչվում է
էլեկտրական
քամի:
Հաղորդչի
լիցքը
փոքրանում է.
այն կարծես
հոսում է
սայրերից և
քշվում
տարվում է քամու
միջոցով: Դրա
համար
այդպիսի
երևույթն անվանում
են լիցքի հոսք
սայրերից:
3.2. ՀԱՂՈՐԴԻՉՆ ԱՐՏԱՔԻՆ ԷԼԵԿՏՐԱԿԱՆ ԴԱՇՏՈՒՄ
Չլիցքավորված
հաղորդիչն
էլեկտրական
դաշտ մտցնելիս
լիցք
կրողները
դրվում են
շարժման մեջ՝
դրականները ![]() վեկտորի,
բացասականները՝
հակառակ
ուղղությամբ
(նկ.39ա): Դրա
հետևանքով
հաղորդչի
ծայրերին
առաջանում են
հակառակ
նշաններով
լիցքեր, որոնք
կոչվում են
մակածված: Նկ.
39-ում հոծ գծերով
ցույց են
տրված
արտաքին դաշտի
լարվածության
գծերը: Այդ
լիցքերի
դաշտն ունի
արտաքին
դաշտին
հակառակ
ուղղություն:
Այսպիսով,
լիցքերի
կուտակումը
հաղորդչի
ծայրերին
հանգեցնում է
նրանում
դաշտի
թուլացման:
Լիցքը
կրողները
վերաբաշխվում
են այնքան
ժամանակ,
մինչև որ տեղի
են ունենում (3.1)
և (3.2) պայմանները,
այսինքն՝
քանի դեռ
դաշտի լարվածությունը
հաղորդչի
ներսում չի
հավասարվել
զրոյի, իսկ
լարվածության
գծերը
հաղորդչից
դուրս
ուղղահայաց
չեն նրա մակերևույթին
(նկ.39բ): Հետևաբար,
էլեկտրական
դաշտ մտցված
չեզոք հաղորդիչն
ընդհատում է
լարվածության
գծերի մի մասը.
դրանք
վերջանում են
բացասական
մակածված
լիցքերի վրա և
կրկին
սկսվում են
դրականների
վրա:
վեկտորի,
բացասականները՝
հակառակ
ուղղությամբ
(նկ.39ա): Դրա
հետևանքով
հաղորդչի
ծայրերին
առաջանում են
հակառակ
նշաններով
լիցքեր, որոնք
կոչվում են
մակածված: Նկ.
39-ում հոծ գծերով
ցույց են
տրված
արտաքին դաշտի
լարվածության
գծերը: Այդ
լիցքերի
դաշտն ունի
արտաքին
դաշտին
հակառակ
ուղղություն:
Այսպիսով,
լիցքերի
կուտակումը
հաղորդչի
ծայրերին
հանգեցնում է
նրանում
դաշտի
թուլացման:
Լիցքը
կրողները
վերաբաշխվում
են այնքան
ժամանակ,
մինչև որ տեղի
են ունենում (3.1)
և (3.2) պայմանները,
այսինքն՝
քանի դեռ
դաշտի լարվածությունը
հաղորդչի
ներսում չի
հավասարվել
զրոյի, իսկ
լարվածության
գծերը
հաղորդչից
դուրս
ուղղահայաց
չեն նրա մակերևույթին
(նկ.39բ): Հետևաբար,
էլեկտրական
դաշտ մտցված
չեզոք հաղորդիչն
ընդհատում է
լարվածության
գծերի մի մասը.
դրանք
վերջանում են
բացասական
մակածված
լիցքերի վրա և
կրկին
սկսվում են
դրականների
վրա:
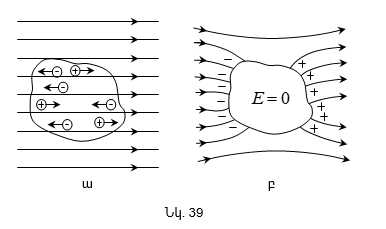
Մակածված լիցքերը բաշխվում են հաղորդչի արտաքին մակերևույթով: Եթե հաղորդչի ներսում խոռոչ կա, ապա մակածված լիցքերի հավասարակշիռ բաշխման դեպքում դաշտը նրա ներսում նույնպես դառնում է զրո: Սրա վրա է հիմնված էլեկտրաստատիկ պաշտպանությունը: Որևէ սարք արտաքին դաշտերի ներգործությունից պաշտպանելու համար, այն շրջապատում են հաղորդիչ պատյանով (էկրանով): Արտաքին դաշտն էկրանի ներսում չեզոքանում է նրա մակերևույթի վրա առաջացող մակածված լիցքերով: Նման էկրանը լավ է գործում նաև այն դեպքում, եթե այն պատրաստված է ոչ թե հոծ, այլ խիտ ցանցի ձևով:
3.3. ՄԵԿՈՒՍԱՑՎԱԾ ՀԱՂՈՐԴՉԻ ԷԼԵԿՏՐԱՈՒՆԱԿՈՒԹՅՈՒՆԸ
Դիտարկենք մեկուսացված հաղորդիչ, այսինքն հաղորդիչ, որը գտնվում է շրջապատի մարմիններից այնքան մեծ հեռավորության վրա, որ դրանց էլեկտրական ազդեցությունը կարելի է անտեսել: Նրա պոտենցիալը համաձայն (1.30) բանաձևի, համեմատական է լիցքին:
Փորձից պարզվում է, որ երբ տարբեր հաղորդիչներ լիցքավորված են միատեսակ, դրանք ունեն տարբեր պոտենցիալներ: Ուստի մեկուսացված հաղորդչի համար կարելի է գրել`
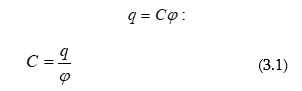
մեծությունը կոչվում է մեկուսացված հաղորդչի էլեկտրաունակություն (կամ պարզապես ունակություն): Մեկուսացված հաղորդչի ունակությունը թվապես հավասար է այն լիցքին, որի հաղորդումը հաղորդչին նրա պոտենցիալը մեծացնում է մեկ միավորով: Էլեկտրաունակությունը բնութագրում է հաղորդչի` լիցք կուտակելու ունակությունը:
Հաղորդչի էլեկտրաունակությունը կախված է նրա չափերից և ձևից, բայց կախված չէ հաղորդչի նյութի տեսակից և զանգվածից, ագրեգատային վիճակից, հաղորդչի ներսի խոռոչի ձևից և չափերից: Դա կապված է այն բանի հետ, որ ավելցուկային լիցքերը բաշխվում են հաղորդչի արտաքին մակերևույթի վրա: Ունակությունը կախված չէ նաև հաղորդչի լիցքից և պոտենցիալից:
Մասնավորապես,
![]() շառավղով
մեկուսացված
գունդը, որը
գտնվում է
շառավղով
մեկուսացված
գունդը, որը
գտնվում է ![]() դիէլեկտրական
թափանցելիություն
ունեցող համասեռ
միջավարում
նրա
պոտենցիալը`
դիէլեկտրական
թափանցելիություն
ունեցող համասեռ
միջավարում
նրա
պոտենցիալը`
![]() :
:
Վերջինը նկատի ունենալով` (3.1)-ից գնդի ունակության համար կստանանք`
![]()
Որպես
![]() ունակության
միավոր ՄՀ-ում
ընդունված է
ֆարադը (Ֆ):
ունակության
միավոր ՄՀ-ում
ընդունված է
ֆարադը (Ֆ):
Դա
այնպիսի
առանձնացված
հաղորդչի
էլեկտրաունակությունն
է, որ
պոտենցիալը 1Վ-ով
փոխելու
համար
պահանջվում է
նրան հաղորդել
1Կլ լիցք: (3.2)
բանաձևից
երևում է, որ 1Ֆ
էլեկտրաունակությամբ
օժտված է այն
լիցքավորված
գունդը
վակուումում ![]() որի շառավիղը
հավասար է`
որի շառավիղը
հավասար է`
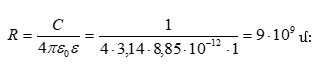
Ինչպես երևում է, 1Ֆ էլեկտրաունակությունը համապատասխանում է չափազանց մեծ երկրաչափական չափերով գնդի, հետևաբար, այն էլեկտրաունակության մեծ միավոր է:
Այդ պատճառով գործնականում օգտագործվում են էլեկտրաունակության ավելի փոքր հետևյալ միավորները`
1 միկրոֆարադ (մկՖ) = 10-6Ֆ, 1 պիկոֆարադ (պկՖ) = 10-12 Ֆ: Օրինակ` Երկրագնդի ունակությունը` R = 6400 կմ, C = 711 մկՖ: Գործնականում հաղորդչի մեկուսացումը գրեթե անհնար է: Հետևաբար, նրա ունակությունը, կախված հարևան հաղորդիչների դիրքից և չափերից, կլինի փոփոխական: Այդ պատճառով ռադիոտեխնիկայում լայն կիրառություն ունեն այնպիսի սարքեր` կոնդենսատորներ, որոնց էլեկտրաունակությունն ունի որոշակի արժեք` անկախ շրջապատում առկա հաղորդիչներից:
3.4 ԿՈՆԴԵՆՍԱՏՈՐՆԵՐ: ԴՐԱՆՑ ՏԱՐԱՏԵՍԱԿՆԵՐԸ
Երկու
կամ ավելի
հաղորդիչների
(շրջադիրների)
այնպիսի համակարգը,
որի
էլեկտրաունակությունը
կախված է
միմիայն
դրանց փոխադարձ
դիրքից,
չափերից, ձևից
և միմյանցից
բաժանող միջավայրի
![]() դիէլեկտրական
թափանցելիությունից,
կոչվում է
կոնդենսատոր:
դիէլեկտրական
թափանցելիությունից,
կոչվում է
կոնդենսատոր:
Ավելի հաճախ կոնդենսատորը կազմված է երկու հաղորդիչներից` շրջադիրներից: Կախված շրջադիրների ձևից` տարբերում են հարթ, գլանային և գնդային կոնդենսատորներ:
Անկախ ձևից (տարատեսակից)` կոնդենսատորի էլեկտրաունակությունը որոշվում է հետևյալ բանաձևով`
![]() , (3.3)
, (3.3)
որտեղ
![]() -ը
շրջադիրների
միջև այն
պոտենցիալների
տարբերությունն
է, որն
առաջանում է
շրջադիրների
վրա
-ը
շրջադիրների
միջև այն
պոտենցիալների
տարբերությունն
է, որն
առաջանում է
շրջադիրների
վրա ![]() լիցքի
առկայությամբ:
լիցքի
առկայությամբ:
Կոնդենսատորը
լիցքավորելիս
շրջադիրներից
մեկը ստանում
է ![]()
Բանաձև (3.3)-ից երևում է, որ կոնդենսատորի էլեկտրաունակությունը ֆիզիկական մեծություն է, որը թվապես հավասար է այն լիցքին, որն անհրաժեշտ է հաղորդել շրջադիրներին, որպեսզի նրանց միջև պոտենցիալների տարբերությունը հավասարվի 1Վ-ի:
Կոնդենսատորի էլեկտրաունակությունը կախված է նրա շրջադիրների երկրաչափական չափերից, ձևից և փոխադարձ դասավորությունից, ինչպես նաև շրջադիրների միջև գտնվող նյութի դիէլեկտրական թափանցելիությունից:
Հաշվենք
հարթ
կոնդենսատորի
էլեկտրաունակությունը:
Հարթ կոնդենսատորն
միմյանց
զուգահեռ,
իրարից ![]() հեռավորության
վրա գտնվող,
հեռավորության
վրա գտնվող, ![]() դիէլեկտրական
թափանցելիություն
ունեցող դիէլեկտրիկով
բաժանված,
միմյանց
ընդգրկող S
մակերեսներով
հաղորդիչ
հարթություններ
են (նկ.40):
դիէլեկտրական
թափանցելիություն
ունեցող դիէլեկտրիկով
բաժանված,
միմյանց
ընդգրկող S
մակերեսներով
հաղորդիչ
հարթություններ
են (նկ.40):
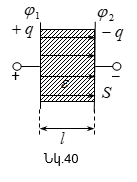
Կոնդենսատորի
էլեկտրաունակության
սահմանման
համաձայն` ![]() Օգտվելով
Օգտվելով
![]() կապից`
կստանանք.
կապից`
կստանանք.
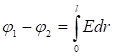 : (3.4)
: (3.4)
Գաուսի
թեորեմի
կիրառություններից
հայտնի է, որ ![]() Տեղադրելով
(3.4)-ում`
կստանանք.
Տեղադրելով
(3.4)-ում`
կստանանք.
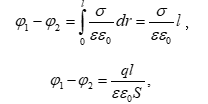
որտեղից հետևում է, որ

Ինչպես երևում է, հարթ կոնդենսատորի ունակությունն, իրոք, կախված է միայն չափերից, ձևից և միջավայրի դիէլեկտրական թափանցելիությունից:
Համանման ձևով կարելի է հաշվել գլանային և գնդային կոնդենսատորների էլեկտրաունակությունները:
(1.19)
բանաձևում ![]() -ն
փոխարինելով
-ն
փոխարինելով ![]() (
(![]() շրջադիրների
երկարությունն
է) և հաշվի
առնելով
դիէլեկտրիկի
գոյության
հնարավորությունը,
գլանային
կոնդենսատորի
շրջադիրների
միջև դաշտի
լարվածության
համար
կստանանք
հետևյալ
արտահայտությունը`
շրջադիրների
երկարությունն
է) և հաշվի
առնելով
դիէլեկտրիկի
գոյության
հնարավորությունը,
գլանային
կոնդենսատորի
շրջադիրների
միջև դաշտի
լարվածության
համար
կստանանք
հետևյալ
արտահայտությունը`
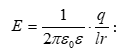
Շրջադիրների
միջև
պոտենցիալների
տարբերությունը
ստանում ենք
օգտվելով ![]() բանաձևից:
Տեղադրելով
բանաձևից:
Տեղադրելով ![]() -ի արժեքը
վերջինի մեջ
կստանանք.
-ի արժեքը
վերջինի մեջ
կստանանք.
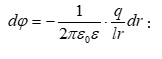
Շրջադիրների միջև պոտենցիալների տարբերությունը ստանում ենք ինտեգրելով.
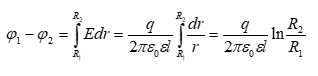
(R1
և R2 - ը ներքին
և արտաքին
շրջադիրների
շառավիղներն
են):
Բաժանելով ![]() գտած
արժեքին,
կստանանք
գլանային
կոնդենսատորի
ունակությունը.
գտած
արժեքին,
կստանանք
գլանային
կոնդենսատորի
ունակությունը.
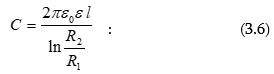
Եթե շրջադիրների միջև եղած բացակը համեմատաբար փոքր է, այսինքն` տեղի ունի d = R2 – R1 << R1 պայմանը, (3.6) բանաձևի հայտարարը կարելի է ձևափոխել հետևյալ կերպ`
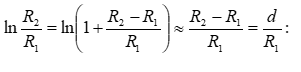
![]() արտահայտությունը
տալիս է
շրջադիրների S
մակերեսը:
Այսպիսով,
փոքր բացակի
դեպքում գլանային
կոնդենսատորի
ունակությունը
կարելի է
մոտավոր
հաշվել (3.5)
բանաձևով:
Ստանանք գնդային
կոնդենսատորի
ունակության
բանաձևը: Գնդային
կոնդենսատորի
շրջադիրների
միջև դաշտի
լարվածությունը
հավասար է՝
արտահայտությունը
տալիս է
շրջադիրների S
մակերեսը:
Այսպիսով,
փոքր բացակի
դեպքում գլանային
կոնդենսատորի
ունակությունը
կարելի է
մոտավոր
հաշվել (3.5)
բանաձևով:
Ստանանք գնդային
կոնդենսատորի
ունակության
բանաձևը: Գնդային
կոնդենսատորի
շրջադիրների
միջև դաշտի
լարվածությունը
հավասար է՝
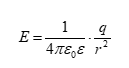
(ինչպես և նախորդ դեպքում, հաշվի է առնված դիէլեկտրիկի առկայության հնարավորությունը շրջադիրների միջև եղած բացակում):
Գտնենք պոտենցիալների տարբերությունը.
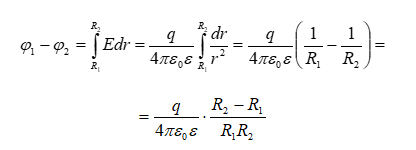
(R1
և R2 - ը ներքին
և արտաքին
շրջադիրների
շառավիղներն
են):
Բաժանելով ![]() գտած
արժեքին,
կստանանք
գնդային
կոնդենսատորի
ունակությունը.
գտած
արժեքին,
կստանանք
գնդային
կոնդենսատորի
ունակությունը.
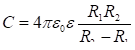 : (3.7)
: (3.7)
Այն
դեպքում, երբ ![]() գնդաձև
կոնդենսատորի
ունակությունը
նույնպես
կարելի է
հաշվել հարթ
կոնդենսատորի
բանաձևով:
Իրոք, այս
դեպքում
գնդաձև
կոնդենսատորի
ունակությունը
նույնպես
կարելի է
հաշվել հարթ
կոնդենսատորի
բանաձևով:
Իրոք, այս
դեպքում ![]() մեծությունը
մոտավորապես
հավասար է
շրջադիրներից
մեկի S
մակերեսին:
Այդ պատճառով
(3.7) բանաձևը
կարելի է մոտավորապես
գրել (3.5) տեսքով:
մեծությունը
մոտավորապես
հավասար է
շրջադիրներից
մեկի S
մակերեսին:
Այդ պատճառով
(3.7) բանաձևը
կարելի է մոտավորապես
գրել (3.5) տեսքով:
(3.5), (3.6) և (3.7) արտահայտություններից պարզ է, թե ինչու շրջադիրների միջև սեգնետաէլեկտրական շերտ մտցնելը (օրինակ բարիումի մետատիտանատ) թույլ է տալիս կոնդենսատորի ոչ մեծ չափերի դեպքում ստանալ մեծ ունակություն:
Բացի ունակությունից, յուրաքանչյուր կոնդենսատոր բնութագրվում է Uառ. սահմանային լարումով, որը կարելի է կիրառել կոնդենսատորի շրջադիրներին, չվախենալով նրա ծակվելուց: Այս լարումը գերազանցելիս, տեղի է ունենում շրջադիրների մեջ գտնվող դիէլեկտրիկի ծակում (միջավայրի ատոմների իոնացման շնորհիվ այն դառնում է հաղորդիչ), և կոնդենսատորն արագորեն պարպվում է: Դրանից հետո այն դառնում է օգտագործման համար ոչ պիտանի:
3.5 ԿՈՆԴԵՆՍԱՏՈՐՆԵՐԻ ԶՈՒԳԱՀԵՌ ԵՎ ՀԱՋՈՐԴԱԿԱՆ ՄԻԱՑՈՒՄԸ
Ունենալով մի շարք կոնդենսատորներ` կարելի է զգալիորեն ընդլայնել ունակության և աշխատանքային լարման հնարավոր արժեքների թիվը, եթե կոնդենսատորները միացնելով` կազմենք մարտկոց: Կոնդենսատորները կարելի է միացնել տարբեր եղանակներով: Գործնականում դա հաճախ կատարվում է, երբ արդյունարար ունակությունը կախված է լինում միացման եղանակից: Տարբերում են միացման երկու հիմնական եղանակ` զուգահեռ և հաջորդական (նկ.41 ա,բ):
Որոշենք
մարտկոցի
էլեկտրաունակությունը
զուգահեռ
միացման
դեպքում (նկ.41,ա):
Լիցքի պահպանման
օրենքի
համաձայն ![]() գումարային
լիցքը
գումարային
լիցքը ![]() հանգույցում
բաշխվում է
ըստ
կոնդենսատորների
շրջադիրների`
հանգույցում
բաշխվում է
ըստ
կոնդենսատորների
շրջադիրների`
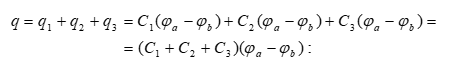
Համարժեք
կոնդենսատորի
էլեկտրաունակությունը,
որն ի վիճակի
է կուտակել ![]() լիցք,
նույն
լիցք,
նույն ![]() պոտենցիալների
տարբերության
դեպքում`
պոտենցիալների
տարբերության
դեպքում`
![]()
որից ստացվում է`
![]()
Կոնդենսատորների զուգահեռ
միացման դեպքում
մարտկոցի ընդհանուր
էլեկտրաունակությունը
հավասար է առանձին
կոնդենսատորների
էլեկտրաունակությունների
գումարին:
Մասնավորապես,
C0 էլեկտրաունակությամբ
![]() կոնդենսատորների
զուգահեռ
միացման դեպքում
մարտկոցի
էլեկտրաունակությունը՝
C = nC0:
կոնդենսատորների
զուգահեռ
միացման դեպքում
մարտկոցի
էլեկտրաունակությունը՝
C = nC0:
Որոշենք մարտկոցի էլեկտրաունակությունը հաջորդական միացման դեպքում (նկ.41,բ): Պոտենցիալների տարբերության ֆիզիկական իմաստից ելնելով`
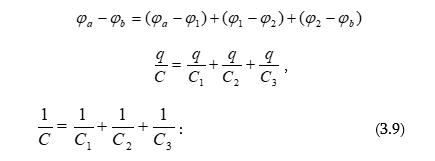
Կոնդենատորների
հաջորդական
միացման դեպքում
մարտկոցի
էլեկտրաունակության
հակադարձ
մեծությունը
հավասար է
առանձին
կոնդենսատորների
էլեկտրաունակությունների
հակադարձ
մեծությունների
գումարին:
Մասնավորապես, C0 էլեկտրաունակությամբ
![]() կոնդենսատորների
հաջորդական
միացման
դեպքում՝ C = C0/n:
կոնդենսատորների
հաջորդական
միացման
դեպքում՝ C = C0/n:
3.6. ԼԻՑՔԱՎՈՐՎԱԾ ՀԱՂՈՐԴՉԻ ԷՆԵՐԳԻԱՆ: ԼԻՑՔԱՎՈՐՎԱԾ ԿՈՆԴԵՆՍԱՏՈՐԻ ԷՆԵՐԳԻԱՆ,
ԷԼԵԿՏՐԱՍՏԱՏԻԿ ԴԱՇՏԻ ԷՆԵՐԳԻԱՆ ԵՎ ԷՆԵՐԳԻԱՅԻ ԾԱՎԱԼԱՅԻՆ ԽՏՈՒԹՅՈՒՆԸ
Հաղորդիչը լիցքավորելիս, նույնանուն լիցքերի միջև վանողական կուլոնյան ուժերը հաղթահարելու համար, անհրաժեշտ է կատարել որոշակի աշխատանք: Այդ աշխատանքը ծախսվում է լիցքավորված հաղորդչի էներգիայի աճի վրա:
Դիցուք
համասեռ,
իզոտրոպ
միջավայրում
ունենք ![]() ունակության
հաղորդիչ,
որին
ունակության
հաղորդիչ,
որին ![]() լիցք
հաղորդելիս
այն ձեռք է
բերում
լիցք
հաղորդելիս
այն ձեռք է
բերում ![]() պոտենցիալ
(նկ.42):
պոտենցիալ
(նկ.42):
Անվերջությունից
![]() հաղորդչի
վրա
հաղորդչի
վրա ![]() լիցք
տեղափոխելիս
կատարվում է
հետևյալ տարրական
աշխատանքը.
լիցք
տեղափոխելիս
կատարվում է
հետևյալ տարրական
աշխատանքը.
![]()
Որպեսզի
հաղորդիչը
լիցքավորենք
![]()
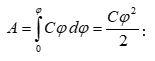
Հասկանալի է, որ լիցքավորված հաղորդչի էներգիան հավասար է այն աշխատանքին, որը պետք է կատարել այն լիցքավորելու համար:
Ստացված բանաձևը ոչ այլ ինչ է, եթե ոչ լիցքավորված հաղորդչի էներգիան.
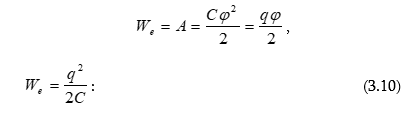
![]() ընդունված
է անվանել
լիցքավորված
հաղորդչի սեփական
էներգիա:
ընդունված
է անվանել
լիցքավորված
հաղորդչի սեփական
էներգիա:
Կոնդենսատորը լիցքավորելու ժամանակ էլեկտրաստատիկ ուժերի դեմ կատարվում է մի շրջադիրից մյուսը լիցքի տեղափոխման աշխատանք: Այս դեպքում
![]() , (3.11)
, (3.11)
որտեղ
![]()
Օգտագործելով
(3.10)
արտահայտությունը`
կարելի է
գտնել
մեխանիկական
(պոնդերոմոտորային)
ուժը, որով
իրար ձգում են
կոնդենսատորի
թիթեղները:
Ենթադրենք, որ
թիթեղների
միջև եղած
սկզբնական ![]() հեռավորությունը
մեծացնում
ենք
հեռավորությունը
մեծացնում
ենք ![]() -ով:
Այդ դեպքում
թիթեղին
կիրառված
ուժը կատարում
է
-ով:
Այդ դեպքում
թիթեղին
կիրառված
ուժը կատարում
է ![]() աշխատանք
համակարգի
պոտենցիալ
էներգիայի
նվազման
հաշվին.
աշխատանք
համակարգի
պոտենցիալ
էներգիայի
նվազման
հաշվին. ![]() որտեղից
որտեղից

Տեղադրելով (3.10)-ի մեջ (3.5) արտահայտությունը, կստանանք`
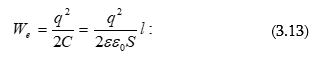
Կատարելով ածանցում էներգիայի կոնկրետ արժեքի դեպքում (տես (3.12) և (3.13)), կստանանք որոնելի ուժը.
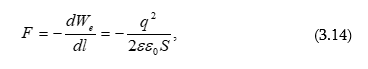
որտեղ ,
«-»
նշանը ցույց է
տալիս, որ ![]() ուժը
ձգողական ուժ
է: Հաղորդչի
ուժը
ձգողական ուժ
է: Հաղորդչի ![]() պոտենցիալի
մեծացումը
առաջ է բերում
համապատասխանաբար
նրա
էլեկտրաստատիկ
դաշտի ուժեղացում:
Բնականաբար
պետք է
ենթադրել, որ
լիցքավորված
մարմնի
սեփական
էներգիան ոչ
այլ ինչ է, քան
իր
էլեկտրաստատիկ
դաշտի
էներգիան: Այդ
ենթադրությունը
ստուգենք
հարթ կոնդենսատորի
համասեռ
էլեկտրաստատիկ
դաշտի օրինակով:
Եթե
էլեկտրական
դաշտն օժտված
է էլեկտրական
էներգիայով,
ապա այդ
էներգիան
պետք է բաշխված
լինի դաշտի
ծավալով, ընդ
որում` որքան
ուժեղ է դաշտը,
այնքան ավելի
մեծ կլինի
էներգիան:
Էլեկտրաստատիկ
դաշտի միավոր
ծավալում
պարփակված
էներգիան`
այսպես
կոչված
էներգիայի
ծավալային
խտությունը,
համասեռ
դաշտի բոլոր
կետերում
պետք է լինի
միատեսակ, իսկ
լրիվ էներգիան`
համեմատական
նրա ծավալին:
Ապացուցելով,
որ լիցքավորված
հարթ
կոնդենսատորի
սեփական էներգիան
համեմատական
է իր
էլեկտրաստատիկ
դաշտի
ծավալին
(տվյալ
դեպքում`
կոնդենսատորի
շրջադիրների
միջև եղած
տարածության
ծավալին), դրանով
մենք
ապացուցած
կլինենք, որ
էլեկտրաստատիկ
դաշտն օժտված
է էներգիայով:
պոտենցիալի
մեծացումը
առաջ է բերում
համապատասխանաբար
նրա
էլեկտրաստատիկ
դաշտի ուժեղացում:
Բնականաբար
պետք է
ենթադրել, որ
լիցքավորված
մարմնի
սեփական
էներգիան ոչ
այլ ինչ է, քան
իր
էլեկտրաստատիկ
դաշտի
էներգիան: Այդ
ենթադրությունը
ստուգենք
հարթ կոնդենսատորի
համասեռ
էլեկտրաստատիկ
դաշտի օրինակով:
Եթե
էլեկտրական
դաշտն օժտված
է էլեկտրական
էներգիայով,
ապա այդ
էներգիան
պետք է բաշխված
լինի դաշտի
ծավալով, ընդ
որում` որքան
ուժեղ է դաշտը,
այնքան ավելի
մեծ կլինի
էներգիան:
Էլեկտրաստատիկ
դաշտի միավոր
ծավալում
պարփակված
էներգիան`
այսպես
կոչված
էներգիայի
ծավալային
խտությունը,
համասեռ
դաշտի բոլոր
կետերում
պետք է լինի
միատեսակ, իսկ
լրիվ էներգիան`
համեմատական
նրա ծավալին:
Ապացուցելով,
որ լիցքավորված
հարթ
կոնդենսատորի
սեփական էներգիան
համեմատական
է իր
էլեկտրաստատիկ
դաշտի
ծավալին
(տվյալ
դեպքում`
կոնդենսատորի
շրջադիրների
միջև եղած
տարածության
ծավալին), դրանով
մենք
ապացուցած
կլինենք, որ
էլեկտրաստատիկ
դաշտն օժտված
է էներգիայով:
Ըստ հարթ կոնդենսատորի ունակության (3.5) բանաձևի`
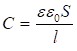 ,
,
իսկ պոտենցիալների տարբերությունը նրա շրջադիրների միջև`
![]()
Տեղադրելով
![]() -ի և
-ի և ![]() -ի
համար
արտահայտությունները
(3.11) բանաձևի մեջ`
կստանանք.
-ի
համար
արտահայտությունները
(3.11) բանաձևի մեջ`
կստանանք.
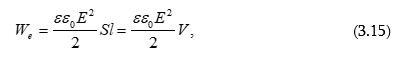
որտեղ ![]() -ը
կոնդենսատորների
շրջադիրների միջև
էլեկտրաստատիկ
դաշտի ծավալն
է:
-ը
կոնդենսատորների
շրջադիրների միջև
էլեկտրաստատիկ
դաշտի ծավալն
է:
Այսպիսով,
իրոք,
լիցքավորված
հարթ
կոնդենսատորի
էներգիան
համեմատական
է նրա
ծավալին,
հետևաբար,
կոնդենսատորի
համասեռ
էլեկտրական
դաշտի
էներգիայի ![]() ծավալային
խտությունը
հաստատուն է.
ծավալային
խտությունը
հաստատուն է.
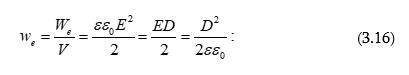
Այստեղ
հաշվի առնվեց,
որ ![]() :
:
Այսպիսով,
համասեռ էլեկտրաստատիկ
դաշտի
էներգիայի
ծավալային
խտությունը
որոշվում է
նրա ![]() լարվածությամբ
կամ
լարվածությամբ
կամ ![]() շեղման
վեկտորի
մոդուլով:
շեղման
վեկտորի
մոդուլով:
Կամայական լիցքավորված մարմինների ստեղծած անհամասեռ էլեկտրական դաշտերի հետազոտությունները ցույց են տվել, որ դրանց համար (3.15) բանաձևը կիրառելի չէ, մինչդեռ (3.16) արտահայտությունը մնում է ճիշտ և որոշում է ցանկացած էլեկտրական դաշտի յուրաքանչյուր կետում էներգիայի ծավալային խտությունը:
Ուստի
դաշտի անվերջ
փոքր ![]() ծավալի
ծավալի
![]() էներգիան
կլինի.
էներգիան
կլինի.
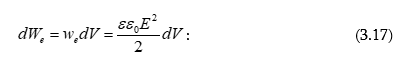
Ինտեգրելով
(10)-ը դաշտի
ամբողջ ![]() ծավալով`
գտնում ենք
էլեկտրաստատիկ
դաշտի լրիվ
էներգիան.
ծավալով`
գտնում ենք
էլեկտրաստատիկ
դաշտի լրիվ
էներգիան.

Կարելի է ցույց տալ, որ ցանկացած լիցքավորված հաղորդչի էլեկտրական դաշտի էներգիան, ինչպես և հարթ կոնդենսատորի դեպքում, հավասար է այդ մարմնի սեփական էներգիային.

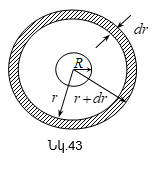
(3.16)
արտահայտության
ճիշտ լինելը
ապացուցենք ![]() շառավղով
և
մակերևույթով
հավասարաչափ
շառավղով
և
մակերևույթով
հավասարաչափ ![]() լիցքով
լիցքավորված
գնդի
անհամասեռ
էլեկտրաստատիկ
դաշտի
օրինակով (նկ.43):
Լիցքավորված գնդի
կենտրոնից
լիցքով
լիցքավորված
գնդի
անհամասեռ
էլեկտրաստատիկ
դաշտի
օրինակով (նկ.43):
Լիցքավորված գնդի
կենտրոնից ![]() հեռավորության
վրա դաշտի
լարվածությունը`
հեռավորության
վրա դաշտի
լարվածությունը` ![]() Հաշվենք
ըստ (3.18) բանաձևի
դաշտի
Հաշվենք
ըստ (3.18) բանաձևի
դաշտի ![]() էներգիան,
որը բաժին է
ընկնում
անվերջ բարակ
գնդային
շերտին, որն
ընկած է
էներգիան,
որը բաժին է
ընկնում
անվերջ բարակ
գնդային
շերտին, որն
ընկած է
![]() և
և ![]() շառավիղներով
գնդոլորտների
միջև (նկ.43): Այդպիսի
շերտի ծավալը
կլինի.
շառավիղներով
գնդոլորտների
միջև (նկ.43): Այդպիսի
շերտի ծավալը
կլինի.
![]()
Տեղադրելով
![]() -ի և
-ի և ![]() -ի արժեքները
(3.14) բանաձի մեջ`
կստանանք.
-ի արժեքները
(3.14) բանաձի մեջ`
կստանանք.

Ինտեգրելով (3.20)-ը` կստանանք լիցքավորված գնդի դաշտի լրիվ էներգիան.
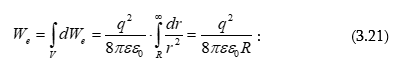
Նկատի
ունենալով, որ
լիցքավորված
գնդի ունակությունը
որոշվում է ![]() բանաձևով`
նրա
էլեկտրաստատիկ
դաշտի էներգիայի
համար (3.21)
արտահայտությունը
կընդունի
բանաձևով`
նրա
էլեկտրաստատիկ
դաշտի էներգիայի
համար (3.21)
արտահայտությունը
կընդունի
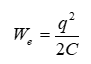
տեսքը, այսինքն` լիցքավորված գնդի էլեկտրաստատիկ դաշտի էներգիան հավասար է իր սեփական էներգիային (3.10):
Այս արդյունքը լրիվ հասկանալի է. լիցքավորված մարմինն օժտըված է էլեկտրական էներգիայով, քանի որ նրա լիցքավորման դեպքում ստեղծվող էլեկտրական դաշտի ուժերի դեմ կատարվում է աշխատանք:
(3.10) բանաձևը կոնդենսատորի էներգիան կապում է նրա շրջադիրների վրա եղած լիցքերի հետ, (3.16) բանաձևը` դաշտի լարվածության հետ: Տրամաբանական է այսպիսի հարց առաջադրել. իսկ որտե՞ղ է կենտրոնացված էներգիան, որո՞նք են էներգիայի կրողները` լիցքերը, թե՞ դաշտը: Էլեկտրաստատիկայի շրջանակներում, որն ուսումնասիրում է անշարժ լիցքերի` ժամանակի ընթացքում հաստատուն դաշտերը, անհնար է այս հարցին պատասխանել: Հաստատուն դաշտերը և նրանց պայմանավորող լիցքերը չեն կարող իրարից մեկուսացված գոյություն ունենալ: Սակայն ժամանակի ընթացքում փոփոխվող դաշտերը կարող են գոյություն ունենալ նրանց հարուցող լիցքերից անկախ և տարածության մեջ տարածվել որպես էլեկտրամագնիսական ալիքներ: Փորձը ցույց է տվել, որ էլեկտրամագնիսական ալիքները տեղափոխում են էներգիա: Մասնավորապես, այն էներգիան, որի հաշվին կյանքը Երկրի վրա գոյություն ունի, Արեգակից հասնում է էլեկտրամագնիսական (լուսային) ալիքների միջոցով, ռադիոընդունիչին հնչել ստիպող էներգիան հաղորդող կայանից գալիս է էլեկտրամագնիսական ալիքների միջոցով և այլն: Այս փաստերը ստիպում են ընդունել, որ էներգիան կրողը դաշտն է:
ԳԼՈՒԽ 4. ՀԱՍՏԱՏՈՒՆ ԷԼԵԿՏՐԱԿԱՆ ՀՈՍԱՆՔ
4.1. ԷԼԵԿՏՐԱԿԱՆ ՀՈՍԱՆՔ: ՆՐԱ ԳՈՅՈՒԹՅԱՆ
ՊԱՅՄԱՆՆԵՐԸ: ՀՈՍԱՆՔԻ ՈՒԺ ԵՎ ԽՏՈՒԹՅՈՒՆ
Նախորդ
գլխում
քննարկեցինք
էլեկտրաստատիկայի
հիմնական
հարցերը: Այժմ
քննարկենք
շարժվող
լիցքերի հետ
կապված երևույթները:
Շարժվող
էլեկտրական
լիցքերի հետ
կապված
երևույթները
և պրոցեսները
կազմում են
էլեկտրականության
մասին
ուսմունքի հատուկ
մի բաժին, որն
անվանում են
էլեկտրադինամիկա:
Լիցքավորված
մասնիկների
ուղղորդված
շարժումը, որի
արդյունքում
տեղի է ունենում
լիցքի տեղափոխություն,
կոչվում է
էլեկտրական
հոսանք: Էլեկտրական
հոսանքը, որն
առաջանում է
հաղորդչում`
նրանում
էլեկտրական
դաշտ
ստեղծվելու հետևանքով,
կոչվում է
հաղորդականության
հոսանք:
Լիցքերի
շարժման
ժամանակ
խանգարվում է
նրանց
հավասարակշիռ
բաշխումը.
հաղորդչի մակերևույթն
արդեն
համապոտենցիալ
մակերևույթ
չէ, և էլեկտրական
դաշտի
ուժագծերը
նրան
ուղղահայաց չեն,
քանի որ
էլեկտրական
լիցքերի
շարժման համար
անհրաժեշտ է,
որպեսզի
հաղորդչի
մակերևույթի
վրա
էլեկտրական
դաշտի
լարվածության
տանգենցիալ
բաղադրիչը
հավասար
չլինի զրոյի ![]()
Որպես փորձերից բխող հետևանք, հիմնավորվել է, որ էլեկտրական հոսանքը պայմանավորված է մետաղական հաղորդիչներում էլեկտրոնների, էլեկտրոլիտներում` դրական և բացասական իոնների (անիոնների և կատիոնների), գազերում` էլեկտրոնների և իոնների ուղղորդված շարժումով: Որպես հոսանքի ուղղություն պայմանականորեն ընդունվում է դրական լիցքերի տեղափոխման ուղղությունը: Եթե հոսանքը պայմանավորված է բացասական լիցքերի շարժումով, ինչպես մետաղներում է, ապա հոսանքի ուղղությունը հակառակ է լիցքերի ուղղորդված շարժման ուղղությանը:
Հաղորդականության հոսանքի առաջացման և գոյության համար անհրաժեշտ են երկու պայմաններ. առաջին՝ անհրաժեշտ է, որ միջավայրում լինեն լիցքավորված ազատ մասնիկներ, այլ խոսքով` անհրաժեշտ է, որ միջավայրը լինի հաղորդիչ: Երկրորդ՝ անհրաժեշտ է տվյալ միջավայրում էլեկտրական դաշտի առկայություն. նրա էներգիան ծախսվում է էլեկտրական լիցքերի տեղափոխման վրա: Որպեսզի հոսանքը երկարատև լինի, էլեկտրական դաշտի էներգիան պետք է ժամանակի ընթացքում համալրել, այլ խոսքով` հարկավոր է այնպիսի մի սարք, որում էներգիայի ինչ-որ տեսակը անընդհատ փոխակերպվի էլեկտրական դաշտի էներգիայի: Այդպիսի սարքը կոչվում է հոսանքի աղբյուր:
Էլեկտրական լիցքերի ուղղորդված շարժում կարելի է իրականացնել նաև այլ եղանակներով՝ տարածության մեջ լիցքավորված մարմինների (հաղորդիչ կամ դիէլեկտրիկ) տեղափոխումով: Այդպիսի էլեկտրական հոսանքը կոչվում է կոնվեկցիոն: Օրինակ, ուղեծրով շարժվող Երկիրը, որն օժտված է ավելցուկային բացասական լիցքով, կարելի է դիտարկել որպես կոնվեկցիոն հոսանք: Էլեկտրական հոսանքի գոյության մասին կարելի է դատել այն ազդեցություններով, որոնք տեղի են ունենում հաղորդչով հոսանք անցնելիս: Հաղորդչով էլեկտրակական հոսանք անցնելիս այն ունենում է ջերմային, քիմիական և մագնիսական ազդեցություններ:
Էլեկտրական
հոսանքը
քանակապես
բնութագրելու
համար
ներմուծվում ![]() հոսանքի
ուժը, որը
հավասար է
հաղորդչի
լայնական
հատույթով
միավոր
ժամանակում
անցած լիցքին.
հոսանքի
ուժը, որը
հավասար է
հաղորդչի
լայնական
հատույթով
միավոր
ժամանակում
անցած լիցքին.
![]()
Եթե հոսանքի ուժն ու նրա ուղղությունը ժամանակի ընթացքում չեն փոփոխվում, հոսանքը կոչվում է հաստատուն: Հաստատուն հոսանքի ուժը որոշվում է հետևյալ բանաձևով.

Միավորների ՄՀ-ում հոսանքի ուժի միավորը մեկ ամպերն է (1 Ա), որը հիմնական միավոր է և սահմանվում է հոսանքակիր հաղորդիչների մագնիսական փոխազդեցության հիման վրա:
Հոսանքի
ուժը հավասար
է 1 ամպերի, եթե
վակուումում
իրարից 1մ
հեռավորության
վրա գտնվող երկու
անվերջ երկար
և անվերջ
բարակ
հաղորդալարերով
անցնելիս՝ նրանցից
յուրաքանչյուրի
1մ
երկարությամբ
հատվածի վրա
մյուսի
կողմից
ազդում է ![]()
Էլեկտրական
հոսանքի
բաշխվածությունը
հաղորդչի
լայնական
հատույթով
բնութագրելու
համար
մտցվում է
հոսանքի
խտության ![]() վեկտորը,
որն ուղղված է
հոսանքի
ուղղությամբ
և թվապես
հավասար է
հոսանքի
ուղղությանն
ուղղահայաց
միավոր
վեկտորը,
որն ուղղված է
հոսանքի
ուղղությամբ
և թվապես
հավասար է
հոսանքի
ուղղությանն
ուղղահայաց
միավոր ![]() մակերեսով
անցնող
հոսանքի
ուժին.
մակերեսով
անցնող
հոսանքի
ուժին.

որտեղ
![]() -ն հոսանքի
ուժն է
-ն հոսանքի
ուժն է ![]() տարրական
մակերեսի
միջով, որը
տեղադրված է
տարրական
մակերեսի
միջով, որը
տեղադրված է ![]() վեկտորի
ուղղությանն
ուղղահայաց:
Միավորների
ՄՀ-ում
հոսանքի
տության
միավորն է`
վեկտորի
ուղղությանն
ուղղահայաց:
Միավորների
ՄՀ-ում
հոսանքի
տության
միավորն է` ![]() Ա/մ2:
Ա/մ2:
(4.3)
բանաձևը
կարելի է ընդհանրացնել:
Եթե ![]() մակերեսը
տարված է
կամայականորեն
այնպես, որ
նրա նորմալը
մակերեսը
տարված է
կամայականորեն
այնպես, որ
նրա նորմալը ![]() վեկտորի
հետ կազմում է
վեկտորի
հետ կազմում է
![]() անկյուն,
ապա նրան
համապատասխանող
անկյուն,
ապա նրան
համապատասխանող
![]() մակերեսը,
որն
ուղղահայաց է
մակերեսը,
որն
ուղղահայաց է ![]() վեկտորին,
հավասար է.
վեկտորին,
հավասար է.
![]()
Տեղադրելով այս արտահայտությունը (4.3)-ի մեջ՝ կստանանք
կամ

որտեղ
![]() վեկտորի
պրոյեկցիան է dS
մակերեսի նորմալի
ուղղության
վրա: (4.4)
բանաձևից
հետևում է, որ
հաղորդչում
լրիվ հոսանքի
ուժը՝
վեկտորի
պրոյեկցիան է dS
մակերեսի նորմալի
ուղղության
վրա: (4.4)
բանաձևից
հետևում է, որ
հաղորդչում
լրիվ հոսանքի
ուժը՝

որտեղ ինտեգրումը տարածվում է հաղորդչի ամբողջ S հատույթով:
Հետագայում
մենք
կդիտարկենք
հաղորդչի միայն
այնպիսի
լայնական
հատույթներ,
որոնց համար ![]() ուստի
ուստի

Փորձերը
ցույց են
տվել, որ
համասեռ
հաղորդչի ամբողջ
լայնական ![]() հատույթով
հաստատուն
հոսանքի
խտությունը նույնն
է: Հետևաբար,
հաստատուն
հոսանքի համար
(4.6) բանաձևը
կարելի է գրել
հետևյալ
տեսքով.
հատույթով
հաստատուն
հոսանքի
խտությունը նույնն
է: Հետևաբար,
հաստատուն
հոսանքի համար
(4.6) բանաձևը
կարելի է գրել
հետևյալ
տեսքով.
![]()
Հաստատուն հոսանքի շղթայում, որը կազմված է փոփոխական լայնույթով հատույթի մակերեսներից (նկ. 44), հոսանքի խտությունները տարբեր S1 և S2 հատույթներում հակադարձ համեմատական են հատույթների մակերեսներին.
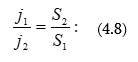
Կարելի
է ցույց տալ,
որ հոսանքի
ուժը կախված է
հոսանքն առաջացնող
լիցքակիրների
ուղղորդված
շարժման ![]() միջին
արագությունից,
միջին
արագությունից,
![]() կոնցենտրացիայից,
յուրաքանչյուր
մասնիկի լիցքի
կոնցենտրացիայից,
յուրաքանչյուր
մասնիկի լիցքի ![]() մեծությունից
և հաղորդչի
լայնական
հատույթի
մեծությունից
և հաղորդչի
լայնական
հատույթի ![]() մակերեսից:
Արտածենք այդ
կախումն
արտահայտող
բանաձևը:
մակերեսից:
Արտածենք այդ
կախումն
արտահայտող
բանաձևը:
Դիցուք
գլանաձև
հաղորդչում
լիցքավորված
մասնիկներն
ուղղորդված
շարժման ![]() միջին
արագությամբ
տեղափոխվում
են
միջին
արագությամբ
տեղափոխվում
են ![]() լայնական
հատույթով
ձախից աջ (նկ.45): Հաղորդչի
S լայնույթով
լայնական
հատույթով
ձախից աջ (նկ.45): Հաղորդչի
S լայնույթով
![]() ժամանակում
կանցնեն այն բոլոր
լիցքերը,
որոնք
գտնվում են S-ից
ոչ հեռու, քան
ժամանակում
կանցնեն այն բոլոր
լիցքերը,
որոնք
գտնվում են S-ից
ոչ հեռու, քան ![]() հեռավորությունն
է, այսինքն՝ 1 և 2
հատույթներով
սահմանափակված
գլանի
ներսում, որի
ծավալը
հեռավորությունն
է, այսինքն՝ 1 և 2
հատույթներով
սահմանափակված
գլանի
ներսում, որի
ծավալը ![]() է
(նկ.43): Այդ
ծավալում
եղած
մասնիկների
թիվը
է
(նկ.43): Այդ
ծավալում
եղած
մասնիկների
թիվը ![]() է:
Դրանց
ընդհանուր
լիցքը
հավասար է՝
է:
Դրանց
ընդհանուր
լիցքը
հավասար է՝
![]()
Տեղադրելով (4.9)-ը (4.1)-ի մեջ` կստանանք.
![]()
Հոսանքի խտության համար կստանանք
![]()
(4.10) բանաձևը թույլ է տալիս հաշվել լիցքավորված մասնիկների ուղղորդված շարժման միջին արագությունը:
4.2. ԱՆԸՆԴՀԱՏՈՒԹՅԱՆ ՀԱՎԱՍԱՐՈՒՄՆ ԻՆՏԵԳՐԱԼԱՅԻՆ
ԵՎ ԴԻՖԵՐԵՆՑԻԱԼ ՏԵՍՔՈՎ
Դիտարկենք
որևէ
կամայական ![]() փակ
մակերևույթ,
որով հոսում է
հոսանք:
փակ
մակերևույթ,
որով հոսում է
հոսանք:
![]() ինտեգրալն
ըստ
ինտեգրալն
ըստ ![]() փակ մակերևույթի
պետք է
հավասար լինի
այն հոսանքների
ուժերի
հանրահաշվական
գումարին, որոնք
անցնում են
այդ
մակերևույթի
առանձին
փակ մակերևույթի
պետք է
հավասար լինի
այն հոսանքների
ուժերի
հանրահաշվական
գումարին, որոնք
անցնում են
այդ
մակերևույթի
առանձին ![]() տարրերի
միջով, այսինքն՝
այն պետք է հավասար
լինի լիցքի
այն քանակությանը,
որը դուրս է
գալիս միավոր
ժամանակում
տարրերի
միջով, այսինքն՝
այն պետք է հավասար
լինի լիցքի
այն քանակությանը,
որը դուրս է
գալիս միավոր
ժամանակում ![]() մակերևույթով
սահմանափակված
մակերևույթով
սահմանափակված
![]() ծավալից:
ծավալից:
Մյուս
կողմից` լիցքի
պահպանման
օրենքի
համաձայն, V ծավալի
սահմաններից
դուրս եկող
լիցքի քանակը
մեկ
վայրկյանում
հավասար
կլինի ![]() այսինքն՝
այդ ծավալի
ներսում
գտնվող
այսինքն՝
այդ ծավալի
ներսում
գտնվող ![]() լիցքի
նվազմանն այդ
նույն
ժամանակամիջոցում
(նկ.46): Այսպիսով,
մենք հանգում
ենք՝
լիցքի
նվազմանն այդ
նույն
ժամանակամիջոցում
(նկ.46): Այսպիսով,
մենք հանգում
ենք՝

հավասարությանը: Այս առնչությունը կոչվում է անընդհատության հավասարում ինտեգրալային տեսքով: Ըստ էության, այն էլեկտրական լիցքի պահպանման օրենքի արտահայտությունն է:
Ներկայացնենք
![]() լիցքը
լիցքը ![]() տեսքով,
կստանանք.
տեսքով,
կստանանք.
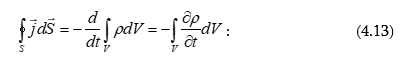
Ինտեգրալի
տակ վերցված
է ![]() -ի մասնակի
ածանցյալն
ըստ
-ի մասնակի
ածանցյալն
ըստ ![]() -ի, քանի որ
լիցքի
խտությունը
կարող է
կախված լինել
ոչ միայն
ժամանակից,
այլ նաև
կոորդինատներից:
-ի, քանի որ
լիցքի
խտությունը
կարող է
կախված լինել
ոչ միայն
ժամանակից,
այլ նաև
կոորդինատներից:
Ձևափոխենք (4.13) հավասարման ձախ մասը` օգտվելով Գաուս-Օստրոգրադսկու` մակերևութային և ծավալային ինտեգրալների կապն արտահայտող թեորեմից`

Արդյունքում կստանանք՝

Ստացված
հավասարումը
ճիշտ է
կամայական
ընտրված ![]() ծավալի
դեպքում, որով
վերցվում են
ինտեգրալները:
Դա հնարավոր է
միայն այն
դեպքում, երբ
տարածության
յուրաքանչյուր
կետում տեղի
ունի
ծավալի
դեպքում, որով
վերցվում են
ինտեգրալները:
Դա հնարավոր է
միայն այն
դեպքում, երբ
տարածության
յուրաքանչյուր
կետում տեղի
ունի

(4.16) առնչությունն անընդհատության հավասարումն է դիֆերենցիալ տեսքով: Այն, (ինչպես և (4.13)-ը), արտահայտում է լիցքի պահպանման օրենքը:
Հաստատուն հոսանքի դեպքում տարբեր կետերում պոտենցիալը, լիցքի խտությունը և ուրիշ մեծություններ չեն փոփոխվում: Հետևաբար, հաստատուն հոսանքի դեպքում՝
![]()
Այս հավասարումը ամենաընդհանուր արտահայտությունն է այն փաստի, որ հաստատուն հոսանքի գծերը միշտ փակ են կամ գնում են անվերջություն:
4.3. ՕՀՄԻ ՕՐԵՆՔԸ ՇՂԹԱՅԻ ՀԱՄԱՍԵՌ ՏԵՂԱՄԱՍԻ ՀԱՄԱՐ:
ԷԼԵԿՏՐԱԿԱՆ ԴԻՄԱԴՐՈՒԹՅՈՒՆ
Էլեկտրական հոսանքը շղթայում (հաղորդչում) պայմանավորված է հաղորդչի ծայրերում պոտենցիալների տարբերությամբ, որը կարող է ստեղծվել գալվանական մարտկոցի միջոցով:
Գերմանացի ֆիզիկոս Օհմը փորձով ցույց է տվել, որ համասեռ մետաղական հաղորդչով անցնող հոսանքի ուժն ուղիղ համեմատական է հաղորդչի ծայրերում պոտենցիալների տարբերությանը (լարմանը) և հակադարձ համեմատական է նրա դիմադրությանը.

Համասեռ
է կոչվում այն
տեղամասը, ուր
կողմնակի
ուժեր չեն
գործում: ![]() էլեկտրական
դիմադրությունն
իր հերթին կախված
է նյութի
տեսակից,
չափերից և
ջերմաստիճանից`
էլեկտրական
դիմադրությունն
իր հերթին կախված
է նյութի
տեսակից,
չափերից և
ջերմաստիճանից`

որտեղ
![]() -ն հաղորդչի
տեսակարար
դիմադրությունն
է,
-ն հաղորդչի
տեսակարար
դիմադրությունն
է, ![]() -ը
հաղորդչի
երկարությունն
է,
-ը
հաղորդչի
երկարությունն
է, ![]() -ը
հաղորդչի
լայնական
հատույթի
մակերեսն է,
-ը
հաղորդչի
լայնական
հատույթի
մակերեսն է, ![]() -ը
դիմադրությունն
է
-ը
դիմադրությունն
է ![]() ջերմաստիճանում,
R0-ն
դիմադրությունն
է
ջերմաստիճանում,
R0-ն
դիմադրությունն
է ![]() -ում,
-ում, ![]() -ն`
դիմադրության
ջերմաստիճանային
գործակիցը:
Մաքուր մետաղների
համար
-ն`
դիմադրության
ջերմաստիճանային
գործակիցը:
Մաքուր մետաղների
համար ![]()
Դիմադրությունը հաղորդչի էլեկտրական հատկությունները բնութագրող հիմնական մեծություններից է: Այն հաղորդչի կողմից ազատ լիցքակիրների ուղղորդված շարժմանը ցույց տրվող դիմադրության քանակական չափն է:
ՄՀ-ում
դիմադրության
միավորը Օմ-ն
է: Այն սահմանվում
է ըստ Օհմի
օրենքի՝ ![]() 1Վ/1Ա=1
Օմ: 1 Օմ-ն այն
հաղորդչի
դիմադրությունն
է, որի ծայրերին
1Վ լարում
կիրառելիս
նրանով
անցնող հոսանքի
ուժը 1Ա է:
1Վ/1Ա=1
Օմ: 1 Օմ-ն այն
հաղորդչի
դիմադրությունն
է, որի ծայրերին
1Վ լարում
կիրառելիս
նրանով
անցնող հոսանքի
ուժը 1Ա է:
Օհմի
օրենքը
կարելի է գրել
դիֆերենցիալ
տեսքով:
Հաղորդչի
ներսում որևէ կետի
շրջակայքում
մտովի
անջատենք մի
տարրական
գլանաձև
ծավալ, որի
ծնիչները
զուգահեռ են
տվյալ կետում
հոսանքի խտության
![]() վեկտորին:
Գլանի
լայնական
հատույթով
անցնում է
վեկտորին:
Գլանի
լայնական
հատույթով
անցնում է ![]() ուժի
հոսանք: Գլանի
նկատմամբ
կիրառված
լարումը
հավասար է
ուժի
հոսանք: Գլանի
նկատմամբ
կիրառված
լարումը
հավասար է ![]() ,
որտեղ
,
որտեղ ![]() -ն
դաշտի
լարվածությունն
է տվյալ
կետում:
-ն
դաշտի
լարվածությունն
է տվյալ
կետում:
Գլանի
դիմադրությունը,
(4.19) բանաձևի
համաձայն, հավասար
է ![]() Այս
արժեքները
տեղադրելով
(4.18)-ի մեջ`
կստանանք`
Այս
արժեքները
տեղադրելով
(4.18)-ի մեջ`
կստանանք`
Լիցք
կրողները
յուրաքանչյուր
կետում շարժվում
են ![]() վեկտորի
ուղղությամբ:
Այդ պատճառով
վեկտորի
ուղղությամբ:
Այդ պատճառով
![]() և
և ![]() վեկտորների
ուղղությունները
համընկնում են:
Այսպիսով,
կարող ենք
գրել`
վեկտորների
ուղղությունները
համընկնում են:
Այսպիսով,
կարող ենք
գրել`
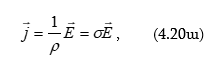
որտեղ
![]() մեծությունը,
կոչվում է
տեսակարար
էլեկտրահաղորդականություն:
(4.20ա) բանաձևը
Օհմի օրենքն
արտահայտում
է
դիֆերենցիալ
տեսքով:
մեծությունը,
կոչվում է
տեսակարար
էլեկտրահաղորդականություն:
(4.20ա) բանաձևը
Օհմի օրենքն
արտահայտում
է
դիֆերենցիալ
տեսքով:
Տեսակարար
դիմադրության
կախումը
ջերմաստիճանից
բերված է
նկ.47-ում: 1 կորը
համապատասխանում
է սովորական մետաղական
հաղորդիչներից
շատերին: ![]() մնացորդային
դիմադրության
մեծությունը
խստորեն
կախված է
նյութի
մաքրությունից
և նմուշում
մնացորդային
մեխանիկական
լարումների
առկայությունից:
Այդ պատճառով
ջերմամշակումից
հետո
մնացորդային
դիմադրության
մեծությունը
խստորեն
կախված է
նյութի
մաքրությունից
և նմուշում
մնացորդային
մեխանիկական
լարումների
առկայությունից:
Այդ պատճառով
ջերմամշակումից
հետո ![]() նկատելիորեն
փոքրանում է:
Իդեալական
կանոնավոր
բյուրեղային
ցանց ունեցող
բացարձակ
մաքուր
մետաղի համար,
բացարձակ
զրոյում
նկատելիորեն
փոքրանում է:
Իդեալական
կանոնավոր
բյուրեղային
ցանց ունեցող
բացարձակ
մաքուր
մետաղի համար,
բացարձակ
զրոյում![]()
Մետաղների
և
համաձուլվածքների
մի մեծ խմբի համար
Կելվինի մի
քանի
աստիճանի
կարգի ջերմաստիճանի
դեպքում
դիմադրությունը
թռիչքաձև
դառնում է զրո
( 2 կորը նկ. 47-ում):
Գերհաղորդականություն
կոչվող այս
երևույթը
սնդիկի համար
առաջինը
հայտնաբերել
է Կամերլինգ-Օննեսը
1911թ.-ին:
Սառեցնելիս
սնդիկի դիմադրությունը
սկզբում
աստիճանաբար
փոքրանում է,
իսկ հետո՝ ![]() 4,1Կ
ջերմաստիճանում
կտրուկ,
թռիչքաձև դառնում
է զրո:
Հետագայում
գերհաղորդականություն
հայտնաբերվեց
կապարի,
անագի, ցինկի
և այլ
մետաղների,
ինչպես նաև մի
շարք համաձուլվածքներում:
4,1Կ
ջերմաստիճանում
կտրուկ,
թռիչքաձև դառնում
է զրո:
Հետագայում
գերհաղորդականություն
հայտնաբերվեց
կապարի,
անագի, ցինկի
և այլ
մետաղների,
ինչպես նաև մի
շարք համաձուլվածքներում:
1986 թվականին շվեյցարացի գիտնականներ Բեդնորցը և Մյուլերը հայտնագործեցին բարձրջերմաստիճանային գերհաղորդականությունը: Հաջողվեց ստանալ նյութեր (լանթանի, բարիումի և այլ տարրերի բարդ օքսիդային միացություններ), որոնք գերհաղորդիչ վիճակի են անցնում բավականաչափ բարձր՝ 100 Կ-ին մոտ ջերմաստիճաններում: Ներկայումս սինթեզվել են նյութեր, որոնք գերհաղորդիչ վիճակի են անցնում 162 Կ ջերմաստիճանում:
Եթե գերհաղորդիչ վիճակում գտնվող օղակում ստեղծվի հոսանք, ապա այն կպահպանվի գործնականորեն անվերջ երկար ժամանակ, քանի որ դիմադրության բացակայության հետևանքով ջերմային կորուստները բացակայում են: Այս հատկությունների շնորհիվ գերհաղորդիչները լայն կիրառություն են գտել տեխնիկայում:
4.4 ԿՈՂՄՆԱԿԻ ՈՒԺԵՐ: ԷԼՇՈՒ
Հաստատուն էլեկտրական հոսանք առաջանալու համար անհրաժեշտ է հաղորդչի ծայրերում ստեղծել պոտենցիալների հաստատուն տարբերություն: Պարզենք, թե ինչպես կարելի է ստեղծել պոտենցիալների հաստատուն տարբերություն: Վերցնենք երկու A և B հաղորդիչ գնդեր: Գնդերը լիցքավորենք մոդուլով հավասար, տարանուն լիցքերով (նկ.48ա): Էլեկտրական դաշտի ազդեցությամբ բացասական լիցքավորված A գնդի հավելուրդային էլեկտրոնները հաղորդալարով կշարժվեն դեպի B գունդը և կչեզոքացնեն նրա դրական լիցքը: Կարճ ժամանակամիջոցում գնդերի պոտենցիալները կհավասարվեն, և հոսանքը կընդհատվի: Որպեսզի հաղորդալարում պահպանվի երկարատև հոսանք, անհրաժեշտ է միշտ համալրել գնդերի լիցքերը: Դա կարելի է անել B գնդից էլեկտրոնները մեկ այլ ճանապարհով անընդհատ տեղափոխելով դեպի A գունդ (նկ.48բ):

Էլեկտրոնների նման տեղափոխությունն ինքնակամ տեղի ունենալ չի կարող, քանի որ այդ տեղամասում էլեկտրական դաշտը խանգարում է դրանց շարժմանը: Անհրաժեշտ են ոչ էլեկտրական ուժեր, որոնք էլեկտրոններին կարող են տեղափոխել էլեկտրական ուժերին հակառակ ուղղությամբ: Իրոք, էլեկտրաստատիկ դաշտը պոտենցիալային է (էլեկտրաստատիկ դաշտի լարվածության վեկտորի շրջապտույտը հավասար է զրոյի), ուստի լիցքը փակ շղթայով տեղափոխելիս դաշտի կատարած աշխատանքը հավասար է զրոյի: Մինչդեռ էլեկտրական հոսանքի անցումն ուղեկցվում է էներգիայի անջատմամբ (հաղորդիչները տաքանում են): Լիցքավորված մասնիկներին ուղղորդված շարժման մեջ դնող, դրական և բացասական լիցքերն իրարից անջատող ոչ էլեկտրաստատիկ բնույթի ուժերը կոչվում են կողմնակի ուժեր: Այն սարքը, որտեղ կողմնակի ուժերն առաջացնում են լիցքերի բաժանում, կոչվում է հոսանքի աղբյուր: Կողմնակի ուժերի ազդեցությամբ հոսանքի աղբյուրի ներսում լիցքավորված մասնիկները շարժվում են կուլոնյան ուժերին հակառակ, որի արդյունքում աղբյուրի բևեռների միջև պահպանվում է պոտենցիալների տարբերություն: Շղթայի մնացած տեղամասերում լիցքավորված մասնիկները շարժվում են էլեկտրական դաշտի ազդեցությամբ:

Վերոհիշյալը ավելի լավ հասկանալու համար դիմենք հաղորդչով անցնող էլեկտրական հոսանքի և խողովակով ընթացող հեղուկի հոսքի համանմանությանը: Հորիզոնական խողովակի ցանկացած տեղամասում հեղուկը հոսում է այդ տեղամասի ծայրերում եղած ճնշման տարբերության հաշվին: Հեղուկը տեղափոխվում է դեպի ճնշման փոքրացման կողմը: Բայց ճնշման ուժը հեղուկի մեջ առաձգականության ուժերի այն տեսակն է, որոնք կուլոնյան ուժերի նման պոտենցիալային ուժեր են: Ուստի այդ ուժերի աշխատանքը փակ ճանապարհի վրա հավասար է զրոյի, և միայն այդ ուժերը ընդունակ չեն առաջացնել հեղուկի երկարատև շրջանառություն խողովակի միջով: Շփման ուժերի ազդեցության հետևանքով հեղուկի հոսքն ուղեկցվում է էներգիայի կորուստներով: Ջրի շրջանառության համար անհրաժեշտ է պոմպ: Այդ պոմպի մխոցն ազդում է հեղուկի մասնիկների վրա և պոմպի մուտքում ու ելքում ստեղծում ճնշումների հաստատուն տարբերություն (նկ. 49.): Դրա շնորհիվ հեղուկը հոսում է խողովակի միջով: Պոմպը հոսանքի աղբյուրի համանմանությունն է, իսկ կողմնակի ուժերի դերը կատարում է շարժվող մխոցի կողմից ջրի վրա ազդող ուժը: Պոմպի ներսում հեղուկը հոսում է փոքր ճնշում ունեցող տեղամասերից դեպի մեծ ճնշում ունեցող տեղամասերը: Ճնշումների տարբերությունը համանման է լարմանը:
Կողմնակի ուժերը կարող են պայմանավորված լինել քիմիական պրոցեսներով, լիցքը կրողների դիֆուզիայով, որը կատարվում է համասեռ միջավայրում կամ երկու տարասեռ նյութերի սահմանի միջով, ժամանակի ընթացքում փոփոխվող մագնիսական դաշտերով առաջացած էլեկտրական (բայց ոչ էլեկտրաստատիկ) դաշտերով և այլն:
Առաջին հոսանքի աղբյուրների (1800թ.) հեղինակներն են Ա. Վոլտան (1745-1827) և Լ.Գալվանին (1737-1798): Մեզ հայտնի Վոլտայի և գալվանական էլեմենտներում կողմնակի ուժերն ունեն քիմիական բնույթ:
Հոսանքի աղբյուրը բնութագրվում է ԷլՇՈՒ-ով` (էլեկտրաշարժ ուժ)`

Հոսանքի աղբյուրի էլեկտրաշարժ ուժը (ԷլՇՈՒ) ֆիզիկական մեծություն է, որը թվապես հավասար է կողմնակի ուժերի կատարած այն աշխատանքին, որն անհրաժեշտ է միավոր դրական լիցքը աղբյուրի մի բևեռից մյուսը (կամ փակ շղթայով) տեղափոխելու համար: ԷլՇՈՒ-ն չափվում է նույն միավորներով, ինչ միավորներով չափվում է պոտենցիալը, այն է` վոլտերով:
![]() լիցքի
վրա ազդող
լիցքի
վրա ազդող ![]() կողմնակի
ուժը կարելի է
ներկայացնել
կողմնակի
ուժը կարելի է
ներկայացնել ![]() որտեղ
որտեղ ![]() -ն
կողմնակի
ուժերի դաշտի
լարվածությունն
է:
-ն
կողմնակի
ուժերի դաշտի
լարվածությունն
է: ![]() լիցքի
տեղափոխման
վրա կողմնակի
ուժերի կատարած
աշխատանքը
փակ շղթայի
ամբողջ
երկայնքով
լիցքի
տեղափոխման
վրա կողմնակի
ուժերի կատարած
աշխատանքը
փակ շղթայի
ամբողջ
երկայնքով

Բաժանելով
(4.22)-ը ![]() կստանանք
շղթայում գործող
ԷլՇՈՒ-ի արտահայտությունը`
կստանանք
շղթայում գործող
ԷլՇՈՒ-ի արտահայտությունը`

Այսպիսով, փակ շղթայում գործող ԷլՇՈՒ-ն որոշվում է որպես կողմնակի ուժերի դաշտի լարվածության վեկտորի շրջապտույտ:
Ակնհայտ
է, որ ![]() տեղամասում
գործող
ԷլՇՈՒ-ն
հավասար է`
տեղամասում
գործող
ԷլՇՈՒ-ն
հավասար է`

Բացի
կողմնակի
ուժերից,
լիցքի վրա
ազդում են էլեկտրաստատիկ
դաշտի ![]() ուժերը:
Հետևաբար,
շղթայի
յուրաքանչյուր
կետում
ուժերը:
Հետևաբար,
շղթայի
յուրաքանչյուր
կետում ![]() լիցքի վրա
ազդող
համազոր ուժը
հավասար է`
լիցքի վրա
ազդող
համազոր ուժը
հավասար է`

![]() լիցքի
վրա
արդյունարար
ուժի
աշխատանքը
շղթայի 1-2
տեղամասում
տրվում է
հետևյալ
արտահայտությամբ`
լիցքի
վրա
արդյունարար
ուժի
աշխատանքը
շղթայի 1-2
տեղամասում
տրվում է
հետևյալ
արտահայտությամբ`

Oգտագործելով (4.23) և (1.35)-ը` կարող ենք գրել`
![]()
Փակ
շղթայի համար
էլեկտրաստատիկ
ուժերի
կատարած
աշխատանքը
հավասար է
զրոյի,
այնպես, որ ![]()
Այն
մեծությունը,
որը հավասար է
էլեկտրաստատիկ
և կողմնակի
ուժերով
միավոր
դրական լիցքը
տեղափոխելու
վրա կատարված
աշխատանքին,
կոչվում է
լարման անկում
կամ պարզապես ![]() լարում
շղթայի տվյալ
տեղամասում:
Այսպիսով, (4.24)
բանաձևի
համաձայն
լարում
շղթայի տվյալ
տեղամասում:
Այսպիսով, (4.24)
բանաձևի
համաձայն
![]()
Կողմնակի
ուժերի
բացակայության
դեպքում ![]() լարումը
հաընկնում է
պոտենցիալների
լարումը
հաընկնում է
պոտենցիալների
![]() տարբերության
հետ:
տարբերության
հետ:
4.5 ՀՈՍԱՆՔԻ ԱՇԽԱՏԱՆՔԸ ԵՎ ՀԶՈՐՈՒԹՅՈՒՆԸ
ՋՈՈՒԼ-ԼԵՆՑԻ ՕՐԵՆՔԸ
Քննարկենք
համասեռ
հաղորդիչ, որի
ծայրերին
կիրառված է ![]() լարում:
լարում: ![]() ժամանակում
հաղորդչի
լայնական
հատույթի
միջով
տեղափոխվում
է`
ժամանակում
հաղորդչի
լայնական
հատույթի
միջով
տեղափոխվում
է`![]() լիցք: Այս
դեպքում
էլեկտրաստատիկ
դաշտի ուժերը
և կողմնակի
ուժերը
կատարում են
աշխատանք.
լիցք: Այս
դեպքում
էլեկտրաստատիկ
դաշտի ուժերը
և կողմնակի
ուժերը
կատարում են
աշխատանք.
![]()
Եթե
հաղորդչի
դիմադրությունը
![]() է, ապա
օգտագործելով
Օհմի օրենքը,
կստանանք, որ
հոսանքի
աշխատանքը`
է, ապա
օգտագործելով
Օհմի օրենքը,
կստանանք, որ
հոսանքի
աշխատանքը`

(4.24) և (4.25)-ից հետևում է, որ հոսանքի հզորությունը`

Եթե հոսանքն արտահայտվում է ամպերներով, լարումը` վոլտերով, դիմադրությունը` օմերով, ապա աշխատանքն արտահայտվում է ջոուլներով, իսկ հզորությունը` վատտերով:
Եթե հոսանքն անցնում է անշարժ մետաղական հաղորչով, ապա ամբողջ աշխատանքը գնում է նրա տաքացման վրա և ըստ էներգիայի պահպանման օրենքի`
![]()
Այսպիսով, օգտագործելով (4.26 բ), (4.24) և (4.25) արտահայտությունները, կստանանք`

(4.27) արտահայտությունը Ջոուլ-Լենցի օրենքն է, որը փորձնական ճանապարհով տրվել է միմյանցից ակախ անգլիացի ֆիզիկոս Ջոուլի և ռուս ֆիզիկոս Լենցի կողմից:
Հաղորդչում
անջատենք
տարրական
գլանային ![]() ծավալ
(գլանի
առանցքը
համընկնում է
հոսանքի
ուղղության
հետ), որի դիմադրությունը`
ծավալ
(գլանի
առանցքը
համընկնում է
հոսանքի
ուղղության
հետ), որի դիմադրությունը`
![]() : Ըստ
Ջոուլ-Լենցի
օրենքի այդ
ծավալում
ժամանակում
անջատվում է
ջերմաքանակ.
: Ըստ
Ջոուլ-Լենցի
օրենքի այդ
ծավալում
ժամանակում
անջատվում է
ջերմաքանակ.

Միավոր ժամանակում, միավոր ծավալում անջատված ջերմաքանակը կոչվում է հոսանքի տեսակարար ջերմային հզորություն: Այն հավասար է`
![]()
Օգտագործելով
Օհմի օրենքը դիֆերենցիալ
տեսքով ![]() առնչությունը,
կստանանք`
առնչությունը,
կստանանք`
![]()
(4.28) և (4.29) բանաձևերը Ջոու-Լենցի օրենքի ընդհանրացված արտահայտություններն են դիֆերենցիալ տեսքով:
Հոսանքի ջերմային ազդեցությունը լայնորեն կիրառվում է տեխնիկայում, որն սկսվում է Լոդիգինի կողմից կատարած շիկացման լամպի հայտնագործումով: էլեկտրական հոսանքով հաղորդիչների տաքացման վրա է հիմնված մուֆելային վառարանների, էլեկտրական աղեղի, կոնտակտային էլեկտրաեռակցումը, կենցաղային էլեկտրաջեռուցման սարքերը և այլն:
4.6. ՕՀՄԻ ՕՐԵՆՔԸ ՇՂԹԱՅԻ ԱՆՀԱՄԱՍԵՌ
ՏԵՂԱՄԱՍԻ ՀԱՄԱՐ
Օհմի
օրենքը (4.18)
տեսքով ճիշտ է
շղթայի
համասեռ տեղամասի
համար,
այսինքն
այնպիսի
տեղամասի, ուր
ԷլՇՈՒ չի
գործում
(կողմնակի
ուժեր չեն գործում):
Դիտարկենք
անհամասեռ
շղթայի տեղամաս,
որտեղ 1-2
տեղամասում
գործող
ԷլՇՈՒ-ն
նշանակենք ![]() իսկ
տեղամասի
ծայրերում
պոտենցիալների
տարբերությունը`
իսկ
տեղամասի
ծայրերում
պոտենցիալների
տարբերությունը`![]() (նկ. 50):
(նկ. 50):
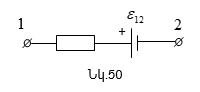
Եթե հոսանք անցնում է 1-2 տեղամասը կազմող անշարժ հաղորդիչներով, ապա հոսանքի անցման միակ արդյունքը կլինի հաղորդիչների տաքացումը: Այդ պատճառով բոլոր ուժերի (էլեկտրաստատիկ և կողմնակի) կատարած աշխատանքը լիցք կրողների վրա պետք է հավասար լինի անջատվող ջերմաստիճանին: dt ժամանակում հաղորդիչով տեղափոխվում է dq=Idt լիցք: (4.24)-ի համաձայն այդ լիցքի վրա կատարվող աշխատանքը՝
![]()
dt ժամանակում անջատվում է
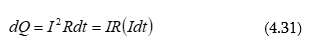
ջերմաքանակ: Էներգիայի պահպանման օրենքի համաձայն (4.30) և (4.31) բանաձևերից կստանանք`
![]()
որտեղից՝
![]()
(4.32) և (4.33) բանաձևերն արտահայտում են Օհմի օրենքը շղթայի անհամասեռ տեղամասի համար ինտեգրալային տեսքով:
Եթե
շղթայի տվյալ
տեղամասում հոսանքի
աղբյուրը
բացակայում է
(![]() ), (4.33)-ից
հանգում ենք
Օհմի օրենքին
շղթայի
համասեռ
տեղամասի
համար (4.18).
), (4.33)-ից
հանգում ենք
Օհմի օրենքին
շղթայի
համասեռ
տեղամասի
համար (4.18).

(կողմնակի
ուժերի
բացակայության
դեպքում տեղամասի
ծայրերում
լարումը
հավասար է
պոտենցիալների
տարբերությանը):
Եթե էլեկտրական
շղթան փակ է,
ապա ընտրված 1
և 2 կետերը
համընկնում
են, ![]() ուստի (4.33)-ից
ստանում ենք
Օհմի օրենքը
փակ շղթայի
համար.
ուստի (4.33)-ից
ստանում ենք
Օհմի օրենքը
փակ շղթայի
համար.
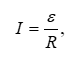
որտեղ
![]() -ը
շղթայում
գործող
ԷլՇՈՒ-ն է,
-ը
շղթայում
գործող
ԷլՇՈՒ-ն է, ![]() -ը` ամբողջ
շղթայի
գումարային
դիմադրությունը:
-ը` ամբողջ
շղթայի
գումարային
դիմադրությունը:
Ընդհանուր
դեպքում ![]() (
(![]() -ը հոսանքի
աղբյուրի
ներքին դիմադրությունն
է,
-ը հոսանքի
աղբյուրի
ներքին դիմադրությունն
է, ![]() -ը` արտաքին
շղթայի
դիմադրությունը):
Ուստի, Օհմի
օրենքը փակ
շղթայի համար
կունենա
հետևյալ
տեսքը:
-ը` արտաքին
շղթայի
դիմադրությունը):
Ուստի, Օհմի
օրենքը փակ
շղթայի համար
կունենա
հետևյալ
տեսքը:

Եթե
շղթան բաց է, և
հետևաբար
նրանում
հոսանքը
բացակայում է ![]() ապա
Օհմի (4.33)
օրենքից
կստանանք, որ
ապա
Օհմի (4.33)
օրենքից
կստանանք, որ ![]() այսինքն`
բաց շղթայում
գործող
ԷլՇՈՒ-ն հավասար
է
պոտենցիալների
տարբերությանը
նրա ծայրերում:
Հետևաբար,
հոսանքի
աղբյուրի
ԷլՇՈՒ-ն
որոշելու
համար,
հարկավոր է
չափել նրա
սեղմակներում
պոտենցիալների
տարբերությունը
բաց շղթայի
դեպքում:
այսինքն`
բաց շղթայում
գործող
ԷլՇՈՒ-ն հավասար
է
պոտենցիալների
տարբերությանը
նրա ծայրերում:
Հետևաբար,
հոսանքի
աղբյուրի
ԷլՇՈՒ-ն
որոշելու
համար,
հարկավոր է
չափել նրա
սեղմակներում
պոտենցիալների
տարբերությունը
բաց շղթայի
դեպքում:
Ճյուղավորված շղթաներում (առանձին տեղամասերում) հաճախ միայն Օհմի օրենքի կիրառմամբ հնարավոր չէ բոլոր ճյուղերում հաշվել հոսանքի ուժն ու լարման անկումները:
Գերմանացի
ֆիզիկոս
Հուստավ
Կիրխհոֆը (1824-1887)
ձևակերպեց
լիցքի և
էներգիայի
պահպանման
օրենքների
վրա հիմնված
երկու կանոն,
որոնց կիրառումը
հնարավորություն
է տալիս
հաշվել շղթայի
բոլոր
ճյուղերում
(տեղամասերում)
![]() հոսանքի
ուժերն ու
հոսանքի
ուժերն ու ![]() լարման
անկումները:
լարման
անկումները:
Կիրխհոֆի առաջին կանոնը: Ճյուղավորված շղթաների հաշվարկը զգալիորեն պարզեցվում է, եթե օգտվում ենք Կիրխհոֆի ձևակերպած կանոններից: Դրանցից առաջինը վերաբերում է շղթայի հանգույցներին: Հանգույց է կոչվում այն կետը, որտեղ հատվում են երկուսից ավելի հաղորդիչներ (նկ.51): Կիրխհոֆի առաջին կանոնն ասում է. հաստատուն հոսանքի շղթայի ցանկացած հանգույցում հոսանքների հանրահաշվական գումարը հավասար է զրոյի:
![]()
կամ

որտեղ
![]() -ը
հանգույցը
կազմող
ճյուղերի
թիվն է:
Հանգույց
մտնող և
հանգույցից
դուրս եկող
հոսանքներին
վերագըրվում
են հակառակ
նշաններ:
-ը
հանգույցը
կազմող
ճյուղերի
թիվն է:
Հանգույց
մտնող և
հանգույցից
դուրս եկող
հոսանքներին
վերագըրվում
են հակառակ
նշաններ:

Այս
արդյունքի
իրավացիությունը
բխում է հետևյալ
նկատառումից.
եթե
հոսանքների
հանրահաշվական
գումարը
զրոյից
տարբեր լիներ,
հանգույցում
տեղի
կունենար
լիցքի
կուտակում կամ
նվազում, որն
իր հերթին
կառաջացներ
հանգույցի
պոտենցիալի և շղթայով
անցնող
հոսանքների
փոփոխում: Այսպիսով,
որպեսզի շղթայում
հոսանքները
հաստատուն լինեն,
պետք է տեղի
ունենա (4.27)
պայմանը: (4.27)
հավասարումը
կարելի է գրել
շղթայի ![]() հանգույցներից
յուրաքանչյուրի
համար: Սակայն
անկախ են
միայն
հանգույցներից
յուրաքանչյուրի
համար: Սակայն
անկախ են
միայն ![]() հավասարումները,
իսկ
հավասարումները,
իսկ ![]() -րդը
կլինի դրանց
հետևանքը:
-րդը
կլինի դրանց
հետևանքը:
Կիրխհոֆի
երկրորդ
կանոնը: Շղթայի
յուրաքանչյուր
փակ կոնտուրում
լարման
անկումների
հանրահաշվական
գումարը
հավասար է այդ
կոնտուրում
առկա ![]() ԷլՇՈՒ-ների
հանրահաշվական
գումարին.
ԷլՇՈՒ-ների
հանրահաշվական
գումարին.

որտեղ
![]() -ը
դիտարկվող
փակ
կոնտուրում
տեղամասերի
թիվն է:
-ը
դիտարկվող
փակ
կոնտուրում
տեղամասերի
թիվն է:
(4.28) հավասարումը կազմելու համար տրված փակ կոնտուրում կամայականորեն ընտրում ենք կոնտուրի շրջանցման ուղղությունը, տեղամասերից յուրաքանչյուրում` նշում հոսանքի ուղղությունը (պայմանականորեն):

Տվյալ տեղամասում լարման անկմանը վերագրվում է դրական նշան, եթե նրանում հոսանքի ուղղությունը համընկնում է կոնտուրի շրջանցման ուղղության հետ, հակառակ դեպքում` լարման անկմանն այդ տեղամասում վերագրվում է բացասական նշան:
Դիտարկվող փակ կոնտուրում գործող ԷլՇՈՒ-ներին վերագրվում է դրական նշան, եթե նրանով պայմանավորված հոսանքի ուղղությունը համընկնում է կոնտուրի շրջանցման ուղղության հետ, հակառակ դեպքում` ԷլՇՈՒ-ին վերագրվում է բացասական նշան:
Կիրխհոֆի երկրորդ կանոնը նկ.52-ում բերված կոնտուրի համար կունենա հետևյալ տեսքը.
![]()
![]() թվով
տեղամասերից
և
թվով
տեղամասերից
և ![]() հանգույցներից
կազմված
շղթայի համար Կիրխհոֆի
առաջին օրենքին
համապատասխանող
անկախ հավասարումների
թիվը
հանգույցներից
կազմված
շղթայի համար Կիրխհոֆի
առաջին օրենքին
համապատասխանող
անկախ հավասարումների
թիվը ![]() է: Իսկ
Կիրխհոֆի
երկրորդ
կանոնին համապատասխանող
անկախ
հավասարումների
թիվը`
է: Իսկ
Կիրխհոֆի
երկրորդ
կանոնին համապատասխանող
անկախ
հավասարումների
թիվը` ![]() :
:
Հարկ է նշել, որ յուրաքանչյուր փակ կոնտուր մյուսից պետք է տարբերվի գոնե մեկ տեղամասով:
ԳԼՈՒԽ 5. ԷԼԵԿՏՐԱԿԱՆ ՀՈՍԱՆՔԸ ՄԵՏԱՂՆԵՐՈՒՄ, ՎԱԿՈՒՈՒՄՈՒՄ ԵՎ ԳԱԶԵՐՈՒՄ
5.1 ՄԵՏԱՂՆԵՐԻ ՀԱՂՈՐԴԱԿԱՆՈՒԹՅԱՆ ԴԱՍԱԿԱՆ
ՏԵՍՈՒԹՅՈՒՆԸ
Մինչ այժմ էլեկտրական հոսանքը դիտարկվում էր զուտ մակրոսկոպիկ տեսանկյունից, գիտենալով միայն, որ մետաղական հաղորդիչներում այն ազատ էլեկտրոնների, իսկ լուծույթներում` դրական և բացասական իոնների ուղղորդված շարժում է:
Մետաղների
հաղորդականության
էլեկտրոնային
տեսությունն
առաջին անգամ
տրվել է
Դրուդեի
կողմից 1900թ.
այնուհետև իր
հետագա
զարգացումն է
ստացել Հ.
Լորենցի
աշխատանքներում:
Այդ պատճառով
այն
ֆիզիկայում
հայտնի է
որպես
Դրուդե-Լորենցի
դասական
էլեկտրոնային
տեսություն:
Ըստ դասական
էլեկտրոնային
տեսության`
մետաղների բարձր
էլեկտրահաղորդականությունը
պայմանավորված
է նրանցում
առկա
հսկայական
թվով (![]() )
հաղորդականության
էլեկտրոններով,
որոնք շարժվում
են հաղորդչի
ամբողջ
ծավալով:
Դրուդեն
ենթադրեց, որ
մետաղի մեջ
էլեկտրոնները
կարելի է ընդունել
որպես
էլեկտրոնային
գազ, որի
նկատմամբ կիրառելի
են միատոմ
իդեալական
գազի օրենքները:
Էլեկտրոններն
իրենց
շարժման
ընթացքում
բախվում են
մետաղի
բյուրեղային
ցանցի իոններին,
հետևաբար
դրանց ազատ
վազքի
)
հաղորդականության
էլեկտրոններով,
որոնք շարժվում
են հաղորդչի
ամբողջ
ծավալով:
Դրուդեն
ենթադրեց, որ
մետաղի մեջ
էլեկտրոնները
կարելի է ընդունել
որպես
էլեկտրոնային
գազ, որի
նկատմամբ կիրառելի
են միատոմ
իդեալական
գազի օրենքները:
Էլեկտրոններն
իրենց
շարժման
ընթացքում
բախվում են
մետաղի
բյուրեղային
ցանցի իոններին,
հետևաբար
դրանց ազատ
վազքի ![]() միջին
երկարությունն
ընդունվում է
նույն կարգի,
ինչ որ
բյուրեղային
ցանցի
հաստատունը` 10-10մ:
միջին
երկարությունն
ընդունվում է
նույն կարգի,
ինչ որ
բյուրեղային
ցանցի
հաստատունը` 10-10մ:
Ըստ Դրուդե-Լորենցի տեսության էլեկտրոններն օժտված են նույնպիսի ջերմային էներգիայով, ինչպիսին և միատոմանի գազի մոլեկուլները: Ուստի, օգտագործելով մոլեկուլային կինետիկ տեսության եզրակացությունները`կարելի է գտնել էլեկտրոնների ջերմային շարժման միջին արագությունը`

որը
![]() Կ
ջերմաստիճաի
համար
հավասար է
Կ
ջերմաստիճաի
համար
հավասար է ![]() մ/վ-ի: Էլեկտրոնների
ջերմային
շարժումն իր
քաոսայնության
հետևանքով չի
կարող
էլետրական
հոսանք առաջացնել:
մ/վ-ի: Էլեկտրոնների
ջերմային
շարժումն իր
քաոսայնության
հետևանքով չի
կարող
էլետրական
հոսանք առաջացնել:
Մետաղական հաղորդչում էլեկտրական դաշտի ազդեցության տակ էլեկտրոնները կատարում են ուղղորդված շարժում` ստեղծելով էլեկտրական հոսանք:
![]() բանաձևով
կարելի է
հաշվել
էլեկտրոնների
կարգավորված
շարժման
միջին արագությունը:
Մեկուսացված
պղնձե հաղորդալարի
համար, որի կտրվածքը
1մմ2 է,
հոսանքի
առավելագույն
թույլատրելի
խտությունը
բանաձևով
կարելի է
հաշվել
էլեկտրոնների
կարգավորված
շարժման
միջին արագությունը:
Մեկուսացված
պղնձե հաղորդալարի
համար, որի կտրվածքը
1մմ2 է,
հոսանքի
առավելագույն
թույլատրելի
խտությունը ![]() Հաշվի
առնելով, որ
էլեկտրոնի
լիցքի
մեծությունը՝
Հաշվի
առնելով, որ
էլեկտրոնի
լիցքի
մեծությունը՝
![]() Կլ է, իսկ
պղնձում ազատ
էլեկտրոնների
կոնցենտրացիան՝
Կլ է, իսկ
պղնձում ազատ
էլեկտրոնների
կոնցենտրացիան՝
![]() մ-3 կարգի
մեծություն է,
ուղղորդված
շարժման միջին
արագության
համար
ստացվում է
մ-3 կարգի
մեծություն է,
ուղղորդված
շարժման միջին
արագության
համար
ստացվում է ![]() Էլեկտրոնների
ուղղորդված
շարժման
արագության
այսպիսի փոքր
արժեքը բնավ
չի հակասում
այն փաստին,
որ հոսանքը
հաղորդչում
առաջանում է
շատ արագ, գրեթե
ակնթարթորեն:
Դա
բացատրվում է
նրանով, որ չնայած
էլեկտրոնների
փոքր
արագություններին,
էլեկտրական
դաշտը հաղորդչում
տարածվում է
լույսի
արագությանը
մոտ
արագությամբ:
Քանի որ հաղորդչի
ամբողջ
ծավալում կան
ազատ
էլեկտրոններ,
ապա նրանք
բոլորը դաշտի
ազդեցության
տակ սկսում են
ուղղորդված
շարժվել գործնականորեն
միաժամանակ:
Էլեկտրոնների
ուղղորդված
շարժման
արագության
այսպիսի փոքր
արժեքը բնավ
չի հակասում
այն փաստին,
որ հոսանքը
հաղորդչում
առաջանում է
շատ արագ, գրեթե
ակնթարթորեն:
Դա
բացատրվում է
նրանով, որ չնայած
էլեկտրոնների
փոքր
արագություններին,
էլեկտրական
դաշտը հաղորդչում
տարածվում է
լույսի
արագությանը
մոտ
արագությամբ:
Քանի որ հաղորդչի
ամբողջ
ծավալում կան
ազատ
էլեկտրոններ,
ապա նրանք
բոլորը դաշտի
ազդեցության
տակ սկսում են
ուղղորդված
շարժվել գործնականորեն
միաժամանակ:
Ուղղորդված
շարժման ![]() միջին
արագությունը
ջերմային
շարժման ֆոնի
վրա անվանում են
դրեյֆի`
հոսընթացի
արագություն:
միջին
արագությունը
ջերմային
շարժման ֆոնի
վրա անվանում են
դրեյֆի`
հոսընթացի
արագություն:
Էլեկտրոնները մետաղական հաղորդիչներում ենթարկվում են Մաքսվել-Բոլցմանի վիճակագրությանը, էլեկտրական դաշտի բացակայության դեպքում ենթարկվում են Մաքսվելի բաշխմանը:
Դրուդե-Լորենցի տեսությունն անվանում են դասական (ոչ քվանտային), որովհետև այստեղ անտեսվում են էլեկտրոնի` միկրոմասնիկի ալիքային հատկությունները, և նրա նկատմամբ կիրառվում են դասական մեխանիկայի օրենքները:
5.2. ՕՀՄԻ ԵՎ ՋՈՈՒԼ-ԼԵՆՑԻ ՕՐԵՆՔՆԵՐԸ:
ԴՐԱՆՑ ԴԻՖԵՐԵՆՑԻԱԼ ՏԵՍՔԸ ԵՎ ԱՐՏԱԾՈՒՄՆ ԸՍՏ ԴԱՍԱԿԱՆ ՏԵՍՈՒԹՅԱՆ
Մետաղների հաղորդականության դասական էլեկտրոնային տեսության հիմնական խնդիրն է տեսականորեն արտածել էլեկտրական հոսանքի հիմնական օրենքները՝ Օհմի և Ջոուլ-Լենցի օրենքները, որոնք հայտնաբերվել են փորձով:
Դիտարկենք
մետաղական հաղորդիչը,
ուր, համաձայն
վերը նշված
դասական
էլեկտրոնային
տեսության,
բյուրեղական
ցանցի միջև
ընկած ազատ
էլեկտրոններն
էլեկտրական
դաշտի
ազդեցությամբ
սկսում են
կատարել
ուղղորդված
շարժում`
առաջացնելով
էլեկտրական
հոսանք:
Պարզության
համար նկ.53-ում
բերված է
միաչափ
բյուրեղային
ցանց, ուր ![]() զանգվածով,
զանգվածով,
![]() լիցքով
էլեկտրոնը
լիցքով
էլեկտրոնը ![]() ուժի
ազդեցության
տակ կկատարի
հավասարաչափ
արագացող
շարժում`
ուժի
ազդեցության
տակ կկատարի
հավասարաչափ
արագացող
շարժում` ![]() արագացումով:
արագացումով:

Օգտվելով Նյուտոնի երկրորդ օրենքից՝
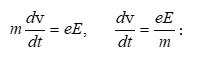
Էլեկտրոնը,
ազատ վազքի
ընթացքում
անցնելով բյուրեղային
ցանցի
հաստատունի
կարգի ![]() ազատ
վազքի միջին
երկարություն,
ձեռք է բերում`
ազատ
վազքի միջին
երկարություն,
ձեռք է բերում`
![]() արագություն,
որտեղ
արագություն,
որտեղ ![]() -ն
ազատ վազքի
միջին
տևողությունն
է.
-ն
ազատ վազքի
միջին
տևողությունն
է.
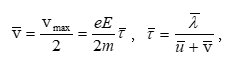
որտեղ ![]() -ն
ջերմային
շարժման
միջին
արագությունն
է,
-ն
ջերմային
շարժման
միջին
արագությունն
է, ![]() -ն`
ուղղորդված
շարժման
միջին
արագությունը:
Հայտնի է, որ
-ն`
ուղղորդված
շարժման
միջին
արագությունը:
Հայտնի է, որ ![]() ,
հետևաբար.
,
հետևաբար.
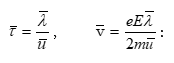
Օգտվելով
հոսանքի
խտության ![]() արտահայտությունից`
արտահայտությունից`
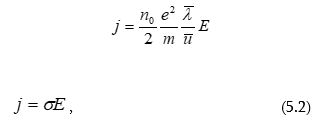
որտեղ ![]() կոչվում
է տեսակարար
էլեկտրահաղորդականություն,
իսկ
կոչվում
է տեսակարար
էլեկտրահաղորդականություն,
իսկ ![]() տեսակարար
դիմադրություն:
Հաշվի
առնելով, որ
տեսակարար
դիմադրություն:
Հաշվի
առնելով, որ ![]() և
և ![]() վեկտորներն
ունեն
միևնույն
ուղղությունը
վեկտորներն
ունեն
միևնույն
ուղղությունը
![]() : (5.3)
: (5.3)
Ստացանք
Օհմի օրենքը
դիֆերենցիալ
տեսքով: Համոզվենք,
որ այն իրոք
Օհմի օրենքն
է` մեզ արդեն
հայտնի տեսքով:
Օգտվենք
հետևյալ
հայտնի
առնչություններից`
![]() Դրանք
տեղադրելով
(5.3)-ի մեջ՝
կստանանք`
Դրանք
տեղադրելով
(5.3)-ի մեջ՝
կստանանք`

շղթայի
համասեռ
տեղամասի
համար Օհմի
օրենքը
ինտեգրալային
տեսքով:
Ուրեմն ![]() օրենքը
մեզ հայտնի
Օհմի օրենքն
է: Իսկ այժմ պատասխանենք
այն հարցին`
թե ինչու է
այն կոչվում
դիֆերենցիալ
տեսքով, երբ
նրանում
նույնիսկ
բացակայում է
d
դիֆերենցիալի
նշանը:
օրենքը
մեզ հայտնի
Օհմի օրենքն
է: Իսկ այժմ պատասխանենք
այն հարցին`
թե ինչու է
այն կոչվում
դիֆերենցիալ
տեսքով, երբ
նրանում
նույնիսկ
բացակայում է
d
դիֆերենցիալի
նշանը:
![]() տեսքով
գրված օրենքն
ընդունված է
անվանել դիֆերենցիալ
տեսքով,
որովհետև այն
ճիշտ է անվերջ
փոքր
տեղամասի`
շղթայի
ցանկացած
կետի համար, ի
տարբերություն
տեսքով
գրված օրենքն
ընդունված է
անվանել դիֆերենցիալ
տեսքով,
որովհետև այն
ճիշտ է անվերջ
փոքր
տեղամասի`
շղթայի
ցանկացած
կետի համար, ի
տարբերություն
![]() տեսքի,
որտեղ
տեսքի,
որտեղ ![]() -ն
լարումն է
վերջավոր
հեռավորության
վրա գտնվող
երկու կետերի
միջև:
-ն
լարումն է
վերջավոր
հեռավորության
վրա գտնվող
երկու կետերի
միջև:
Այժմ ստանանք Ջոուլ-Լենցի օրենքը դիֆերենցիալ տեսքով: Էլեկտրոնային դասական տեսությամբ հաշվենք միավոր ժամանակում միավոր ծավալում անջատված էներգիան: Այդ էներգիան պայմանավորված է էլեկտրոնների` դաշտի ուժերի ազդեցությամբ արագացմամբ շարժվելիս ձեռք բերած կինետիկ էներգիայի հաղորդմամբ բյուրեղային ցանցին, այդ ցանցի հանգույցների հետ բախվելիս:
Միավոր ժամանակում ցանցի հանգույցների հետ էլեկտրոնների բախումների միջին թիվը նշանակենք.

Միավոր
ծավալում
էլեկտրոնների
թիվը
նշանակենք ![]() -ով,
յուրաքանչյուր
բախման
հետևանքով
ցանցին
էլեկտրոնի
կողմից
հաղորդված
կինետիկ
էներգիան կլինի.
-ով,
յուրաքանչյուր
բախման
հետևանքով
ցանցին
էլեկտրոնի
կողմից
հաղորդված
կինետիկ
էներգիան կլինի.

Նկ. 54-ում
բերված է
էլեկտրոնի
արագության
փոփոխությունը
հաջորդական
բախումների
միջև եղած ![]() ազատ
վազքի
տիրույթներում:
ազատ
վազքի
տիրույթներում:

Միավոր ժամանակում, միավոր ծավալում ցանցին հաղորդած էներգիան (անջատված էներգիան).
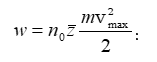
Հաշվի
առնելով, որ ![]()
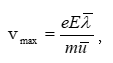
կստանանք`

![]() ,
(5.4)
,
(5.4)
որտեղ ![]() տեսակարար
էլեկտրահաղորդականությունն
է:
տեսակարար
էլեկտրահաղորդականությունն
է:
![]() -ն
Ջոուլ-Լենցի
օրենքն է
դիֆերենցիալ
տեսքով:
-ն
Ջոուլ-Լենցի
օրենքն է
դիֆերենցիալ
տեսքով:
Համոզվենք, որ այս օրենքն իրոք դեռևս ֆիզիկայի դպրոցական դասընթացից մեզ հայտնի Ջուլ-Լենցի օրենքն է:
Օգտվելով

Ստացանք հոսանքատար հաղորդչում անջատված ջերմաքանակի համար դպրոցական դասընթացից հայտնի Ջոուլ-Լենցի օրենքը:
Վիդեման-Ֆրանցի
օրենքը: 1853թ.
Վիդեմանի և
Ֆրանցի
կողմից փորձնականորեն
ստացվել է ![]() ջերմահաղորդականության
և
ջերմահաղորդականության
և ![]() տեսակարար
էլեկտրահաղորդականության
գործակիցների
միջև հետևյալ
առնչությունը`
տեսակարար
էլեկտրահաղորդականության
գործակիցների
միջև հետևյալ
առնչությունը`

որը հայտնի է որպես Վիդեման-Ֆրանցի օրենք: Փորձի հիման վրա ստացված այս օրենքը հիմնավորվում է էլեկտրոնային տեսությամբ: Իրոք`

որտեղ ![]() -ն
Բոլցմանի
հաստատունն է:
-ն
Բոլցմանի
հաստատունն է:

Դրուդեի տեսությամբ

Ստացված
![]() հաստատունի
թվային
արժեքը մեծ
ճշտությամբ
համընկնում է
փորձից
ստացված թվային
արժեքի հետ:
հաստատունի
թվային
արժեքը մեծ
ճշտությամբ
համընկնում է
փորձից
ստացված թվային
արժեքի հետ:
Այսպիսով, դասական տեսությունը կարողացավ բացատրել Օհմի և Ջոուլ-Լենցի օրենքները, ինչպես նաև տվեց Վիդեման-Ֆրանցի օրենքի որակական բացատրությունը: Դրա հետ մեկտեղ այդ տեսությունը հանդիպեց էական դժվարությունների: Դրանցից հիմնականը երկուսն են.
•  բանաձևից
բխում է, որ
մետաղների
դիմադրությունը
(այսինքն՝
բանաձևից
բխում է, որ
մետաղների
դիմադրությունը
(այսինքն՝ ![]() -ի
հակադարձ
մեծությունը)
պետք է աճի
-ի
հակադարձ
մեծությունը)
պետք է աճի ![]() -ին
համեմատականորեն:
Իրոք, ոչ մի
հիմք չկա ենթադրելու,
որ
-ին
համեմատականորեն:
Իրոք, ոչ մի
հիմք չկա ենթադրելու,
որ ![]() և
և
![]() մեծությունները
կախում ունեն
ջերմաստիճանից:
Իսկ ջերմային
շարժման
արագությունը
համեմատական
է
մեծությունները
կախում ունեն
ջերմաստիճանից:
Իսկ ջերմային
շարժման
արագությունը
համեմատական
է ![]() -ին:
Տեսության
այս
եզրակացությունը
հակասում է
փորձնական
տվյալներին,
որոնց
համաձայն մետաղների
էլեկտրական
դիմադրությունն
աճում է
-ին:
Տեսության
այս
եզրակացությունը
հակասում է
փորձնական
տվյալներին,
որոնց
համաձայն մետաղների
էլեկտրական
դիմադրությունն
աճում է ![]() -ի
առաջին
աստիճանին
համեմատական,
այսինքն՝ ավելի
արագ, քան
-ի
առաջին
աստիճանին
համեմատական,
այսինքն՝ ավելի
արագ, քան ![]() -ն:
-ն:
• Դասական
տեսության
երկրորդ
դժվարությունն
այն է, որ
էլեկտրոնային
գազը պետք է
ունենա 3R/2
մոլային
ջերմունակություն:
Այս
մեծությունը
ավելացնելով
բյուրեղային
ցանցի ջերմունակությանը
(որը կազմում
է ![]() )`
մետաղի
մոլային
ջերմունակության
համար կստանանք
9R/2 արժեք:
Այսպիսով,
դասական
էլեկտրոնային
տեսության
համաձայն
մետաղների
մոլային ջերմունակությունը
պետք է 1,5 անգամ
ավելի մեծ
լինի, քան
դիէլեկտրիկներինը:
Մինչդեռ,
իրականում
մետաղների
մոլային
ջերմունակությունը
նկատելիորեն
չի
տարբերվում
ոչ մետաղական
բյուրեղների
ջերմունակությունից:
Այսպիսի
անհամապատասխանության
բացատրությունը
կարողացավ
տալ միայն
մետաղների
քվանտային
տեսությունը:
)`
մետաղի
մոլային
ջերմունակության
համար կստանանք
9R/2 արժեք:
Այսպիսով,
դասական
էլեկտրոնային
տեսության
համաձայն
մետաղների
մոլային ջերմունակությունը
պետք է 1,5 անգամ
ավելի մեծ
լինի, քան
դիէլեկտրիկներինը:
Մինչդեռ,
իրականում
մետաղների
մոլային
ջերմունակությունը
նկատելիորեն
չի
տարբերվում
ոչ մետաղական
բյուրեղների
ջերմունակությունից:
Այսպիսի
անհամապատասխանության
բացատրությունը
կարողացավ
տալ միայն
մետաղների
քվանտային
տեսությունը:
5.3 ԷԼԵԿՏՐՈՆՆԵՐԻ ԵԼՔԻ ԱՇԽԱՏԱՆՔԸ ՄԵՏԱՂԻՑ
Ինչպես ցույց է տալիս փորձը, ազատ էլեկտրոնները սովորական ջերմաստիճանների դեպքում ինքնակամորեն չեն կարող հեռանալ մետաղից: Հետևաբար, մետաղի մակերևութային շերտում պետք է լինի արգելակող էլեկտրական դաշտ, որը խոչընդոտում է էլեկտրոնի` մետաղից դուրս գալուն վակուում: Այն աշխատանքը, որն անհրաժեշտ է ծախսել էլեկտրոնը մետաղից վակուում հեռացնելու համար, կոչվում է ելքի աշխատանք: Նշենք ելքի աշխատանքի գոյության երկու հավանական պատճառները:
1. Եթե էլեկտրոնը ինչ-որ պատճառով հեռանում է մետաղից, ապա այն տեղը, որը էլեկտրոնը թողեց, առաջանում է ավելցուկային դրական լիցք, և էլեկտրոնը ձգվում է իրենով մակածված դրական լիցքը:
2.
Առանձին
էլեկտրոնները,
թողնելով
մետաղը,
հեռանում են
նրանից
ատոմային
կարգի
հեռավորությունների
վրա և
ստեղծում են
մետաղի
մակերևույթի
վերևում «էլեկտրոնային
ամպ», որի
խտությունը
արագ նվազում
է հեռավորության
հետ: Այդ ամպը
ցանցի դրական
իոնների ներքին
շերտի հետ
միասին
ստեղծում է
կրկնակի էլեկտրական
շերտ, որի դաշտը
նման է հարթ
կոնդենսատորի
դաշտին: Այդ
շերտի
հաստությունը
հավասար է մի
քանի միջատոմային
հեռավորությունների
(![]() մ): Այն
արտաքին
տարածության
մեջ
էլեկտրական դաշտ
չի ստեղծում,
բայց
խոչընդոտում
է ազատ էլեկտրոնների`
մետաղից
դուրս գալուն:
մ): Այն
արտաքին
տարածության
մեջ
էլեկտրական դաշտ
չի ստեղծում,
բայց
խոչընդոտում
է ազատ էլեկտրոնների`
մետաղից
դուրս գալուն:
Այսպիսով, մետաղից էլեկտրոնը դուրս թռչելու դեպքում պետք է հաղթահարի նրան արգելակող կրկնակի շերտի էլեկտրական դաշտը: Այդ դեպքում պոտենցիալների տարբերությունը, որը կոչվում է պոտենցիալի մակերևութային թռիչք, որոշվում է մետաղից էլեկտրոնի ելքի A աշխատանքով`

որտեղ
![]() -ն
էլեկտրոնի լիցքն
է:
-ն
էլեկտրոնի լիցքն
է:
Քանի
որ կրկնակի
շերտից դուրս
էլեկտրական դաշտը
բացակայում է,
ապա
միջավայրի
պոտենցիալը
հավասար է
զրոյի, իսկ
մետաղի
ներսում պոտենցիալը
դրական է և
հավասար է ![]() -ի: Ազատ
էլեկտրոնի
պոտենցիալ
էներգիան
մետաղի
ներսում
հավասար է
-ի: Ազատ
էլեկտրոնի
պոտենցիալ
էներգիան
մետաղի
ներսում
հավասար է ![]() -ի և
վակուումի
նկատմամբ բացասական
է: Ելնելով
սրանից`
կարելի է
ընդունել, որ
ամբողջ
մետաղի
ծավալը
հաղորդականության
էլեկտրոնների
համար
ներկայացնում
է հարթ հատակով
պոտենցիալային
փոս, որի
խորությունը
հավասար է
ելքի
-ի և
վակուումի
նկատմամբ բացասական
է: Ելնելով
սրանից`
կարելի է
ընդունել, որ
ամբողջ
մետաղի
ծավալը
հաղորդականության
էլեկտրոնների
համար
ներկայացնում
է հարթ հատակով
պոտենցիալային
փոս, որի
խորությունը
հավասար է
ելքի ![]() աշխատանքին:
աշխատանքին:
Ելքի
աշխատանքն
արտահայտվում
է էլեկտրոն-վոլտերով
(էՎ). 1էՎ-ը
հավասար է այն
աշխատանքին,
որը կատարում
են դաշտի
ուժերը
տարրական
էլեկտրական
լիցքի (էլեկտրոնի
լիցքին
հավասար
լիցքը)
տեղափոխության
դեպքում, երբ
այն անցնում
է Վ
պոտենցիալների
տարբերություն:
Քանի որ
էլեկտրոնի
լիցքը ![]() Կլ է, ապա
Կլ է, ապա ![]() Ելքի
աշխատանքը
կախված է
մետաղների
քիմիական
բնույթից և
նրանց
մակերևույթների
մաքրությունից
և տատանվում է
մի քանի էլեկտրոն-վոլտի
սահմաններում
(օրինակ,
կալիումի
համար
Ելքի
աշխատանքը
կախված է
մետաղների
քիմիական
բնույթից և
նրանց
մակերևույթների
մաքրությունից
և տատանվում է
մի քանի էլեկտրոն-վոլտի
սահմաններում
(օրինակ,
կալիումի
համար ![]() էՎ,
պլատինի
համար
էՎ,
պլատինի
համար ![]() էՎ):
Ընտրելով
մակերևույթի
ծածկույթը
որոշակի ձևով`
կարելի է
էականորեն
փոքրացնել
ելքի աշխատանքը:
Օրինակ, եթե
վոլֆրամի (
էՎ):
Ընտրելով
մակերևույթի
ծածկույթը
որոշակի ձևով`
կարելի է
էականորեն
փոքրացնել
ելքի աշխատանքը:
Օրինակ, եթե
վոլֆրամի (![]() էՎ)
մակերևույթը
ծածկվի
հողալկալիական
մետաղի (Ca, Sr, Ba) օքսիդի
շերտով, ապա ելքի
աշխատանքը
նվազում է
մինչև 2էՎ:
էՎ)
մակերևույթը
ծածկվի
հողալկալիական
մետաղի (Ca, Sr, Ba) օքսիդի
շերտով, ապա ելքի
աշխատանքը
նվազում է
մինչև 2էՎ:
5.4. ԷՄԻՍԻՈՆ ԵՐԵՎՈՒՅԹՆԵՐ ԵՎ ՆՐԱՆՑ ԿԻՐԱՌՈՒԹՅՈՒՆՆԵՐԸ
Եթե մետաղներում էլեկտրոններին հաղորդվի էներգիա, որն անհրաժեշտ է ելքի աշխատանքը հաղթահարելու համար, ապա էլեկտրոնների մի մասը կարող է հեռանալ մետաղից, որի արդյունքում դիտվում է էլեկտրոնների առաքման երևույթ կամ էլեկտրոնային էմիսիա:
Կախված էլեկտրոններին էներգիա հաղորդելու եղանակից` տարբերում են ջերմաէլեկտրոնային, լուսաէլեկտրոնային, երկրորդական էլեկտրոնային և ինքնաէլեկտրոնային էմիսիաներ:
1. Ջերմաէլեկտրոնային էմիսիա է կոչվում էլեկտրոնների արձակումը տաքացրած պինդ և հեղուկ մարմիններից: Այս բաժնում մեզ հետաքրքրելու են միայն մետաղները:

Ազատ էլեկտրոնների կոնցենտրացիան մետաղներում բավականին բարձր է, դրա համար էլ նույնիսկ միջին ջերմաստիճանների դեպքում էլեկտրոնների` ըստ արագությունների (ըստ էներգիաների) բաշխման հետևանքով որոշ էլեկտրոններ` օժտված լինելով բավականաչափ էներգիայով, հաղթահարում են մետաղի մակերևույթի սահմանում պոտենցիալային պատնեշը: Ջերմաստիճանը բարձրացնելիս այդպիսի էլեկտրոնների թիվը կտրուկ աճում է և դառնում է միանգամայն նկատելի:
Ջերմաէլեկտրոնային
էմիսիայի
օրինաչափությունների
հետազոտությունը
կարելի
կատարել
երկէլեկտրոդ
էլեկտրոնային
լամպի օգնությամբ,
որը կոչվում է
վակուումային
դիոդ (նկ.55): Դա
օդը խնամքով
հանված
մետաղական
կամ ապակե
բալոն է, որի
ներսում կան
երկու էլեկտրոդներ`![]() կաթոդը և
կաթոդը և ![]() անոդը:
Պարզագույն
դեպքում
կաթոդն ունի
բարակ
դժվարահալ
ուղիղ լարի,
իսկ անոդը`
նրան համառանցք
գլանի ձև:
անոդը:
Պարզագույն
դեպքում
կաթոդն ունի
բարակ
դժվարահալ
ուղիղ լարի,
իսկ անոդը`
նրան համառանցք
գլանի ձև:
Կաթոդը
տաքացվում է ![]() շիկացման
մարտկոցի
հոսանքով:
Շիկացման ջերմաստիճանը
կարելի է
փոփոխել`
կարգավորելով
հոսանքի ուժը
շիկացման
մարտկոցի
հոսանքով:
Շիկացման ջերմաստիճանը
կարելի է
փոփոխել`
կարգավորելով
հոսանքի ուժը ![]() ռեոստատով:
Անոդային
լարման
ռեոստատով:
Անոդային
լարման ![]() մեծությունը
կարելի է
փոփոխել
մեծությունը
կարելի է
փոփոխել ![]() պոտենցիոմետրի
միջոցով և
չափել
պոտենցիոմետրի
միջոցով և
չափել ![]() վոլտմետրով
(
վոլտմետրով
(![]() -ն
համարվում է
դրական, եթե
անոդի
պոտենցիալը
ավելի բարձր է
կաթոդի
պոտենցիալից):
-ն
համարվում է
դրական, եթե
անոդի
պոտենցիալը
ավելի բարձր է
կաթոդի
պոտենցիալից):
![]() միլիամպերմետրը
նախատեսված է
հոսանքի ուժը
չափելու
համար:
միլիամպերմետրը
նախատեսված է
հոսանքի ուժը
չափելու
համար:

Եթե
շիկացած
կաթոդի
ջերմաստիճանը
պահենք հաստատուն
և հանենք
անոդային ![]() հոսանքի
կախումը
անոդային
հոսանքի
կախումը
անոդային ![]() լարումից` վոլտ-ամպերային
բնութագիծը
(նկ. 56), ապա
պարզվում է,
որ այն գծային
չէ, այսինքն
վակուումային
դիոդի համար
Օհմի օրենքը
տեղի չունի:
Ջերմաէլեկտրոնային
էմիսիայի
լարումից` վոլտ-ամպերային
բնութագիծը
(նկ. 56), ապա
պարզվում է,
որ այն գծային
չէ, այսինքն
վակուումային
դիոդի համար
Օհմի օրենքը
տեղի չունի:
Ջերմաէլեկտրոնային
էմիսիայի ![]() հոսանքի
կախվածությունը
անոդային
լարումից
փոքր դրական
հոսանքի
կախվածությունը
անոդային
լարումից
փոքր դրական ![]() -ի
արժեքների
տիրույթում
նկարագրվում
է երեք
երկրորդի
օրենքով, որը տրվել
է ռուս ֆիզիկոս
Ս. Բոգուսլավսկու
և ամերիկացի
ֆիզիկոս Ի.
Լենգմյուրի
կողմից.
-ի
արժեքների
տիրույթում
նկարագրվում
է երեք
երկրորդի
օրենքով, որը տրվել
է ռուս ֆիզիկոս
Ս. Բոգուսլավսկու
և ամերիկացի
ֆիզիկոս Ի.
Լենգմյուրի
կողմից.
![]()
որտեղ
![]() -ն
գործակից է,
որը կախված է
էլեկտրոդների
ձևից և չափերից,
ինչպես նաև
դրանց
փոխադարձ
դասավորությունից:
-ն
գործակից է,
որը կախված է
էլեկտրոդների
ձևից և չափերից,
ինչպես նաև
դրանց
փոխադարձ
դասավորությունից:
Անոդային
լարման
մեծացման
դեպքում
հոսանքն
աճում է մինչև
որոշակի ![]() առավելագույն
արժեքը, որը
կոչվում է
հագեցման
հոսանք: Դա նշանակում
է, որ համարյա
բոլոր
էլեկտրոնները,
թողնելով
կաթոդը,
հասնում են
անոդ,
առավելագույն
արժեքը, որը
կոչվում է
հագեցման
հոսանք: Դա նշանակում
է, որ համարյա
բոլոր
էլեկտրոնները,
թողնելով
կաթոդը,
հասնում են
անոդ, ![]() -ի հետագա
աճը չի կարող
մեծացնել
ջերմաէլեկտրոնային
էմիսիայի
հոսանքը:
Հետևաբար,
հագեցման
հոսանքի
խտությունը
բնութագրում
է կաթոդի
նյութի
էմիսիոն
ընդունակությունը:
Հագեցման
հոսանքի
խտությունը որոշվում
է
Ռիչարդսոն-Դեշմանի
բանաձևով, որը
արտածվել է
տեսականորեն
քվանտային
վիճակագրության
հիման վրա.
-ի հետագա
աճը չի կարող
մեծացնել
ջերմաէլեկտրոնային
էմիսիայի
հոսանքը:
Հետևաբար,
հագեցման
հոսանքի
խտությունը
բնութագրում
է կաթոդի
նյութի
էմիսիոն
ընդունակությունը:
Հագեցման
հոսանքի
խտությունը որոշվում
է
Ռիչարդսոն-Դեշմանի
բանաձևով, որը
արտածվել է
տեսականորեն
քվանտային
վիճակագրության
հիման վրա.

որտեղ
![]() -ն էլեկտրոնի
ելքի
աշխատանքն է
կաթոդից,
-ն էլեկտրոնի
ելքի
աշխատանքն է
կաթոդից, ![]() -ն ջերմադինամիկական
ջերմաստիճանն
է, C-ն մետաղից
կախում
չունեցող
հաստատուն է,
որի տեսական
արժեքը
հավասար է
-ն ջերմադինամիկական
ջերմաստիճանն
է, C-ն մետաղից
կախում
չունեցող
հաստատուն է,
որի տեսական
արժեքը
հավասար է ![]() Սա չի
հաստատվում
փորձով,
փորձնական
արժեքները
ստացվում են
մոտավորապես
երկու անգամ ավելի
փոքր, քան
տեսականը,
որը ըստ
էության բացատրվում
է
մակերևութային
էֆեկտներով:
Ելքի
աշխատանքի
փոքրացումը
առաջ է բերում
հագեցման
հոսանքի
խտության
կտրուկ մեծացում:
Դրա համար էլ
օգտագործվում
են օքսիդային
կաթոդներ
(օրինակ,
նիկելը
ծածկվում է հողալկալիական
մետաղի
օքսիդով),
որոնց ելքի աշխատանքը
Սա չի
հաստատվում
փորձով,
փորձնական
արժեքները
ստացվում են
մոտավորապես
երկու անգամ ավելի
փոքր, քան
տեսականը,
որը ըստ
էության բացատրվում
է
մակերևութային
էֆեկտներով:
Ելքի
աշխատանքի
փոքրացումը
առաջ է բերում
հագեցման
հոսանքի
խտության
կտրուկ մեծացում:
Դրա համար էլ
օգտագործվում
են օքսիդային
կաթոդներ
(օրինակ,
նիկելը
ծածկվում է հողալկալիական
մետաղի
օքսիդով),
որոնց ելքի աշխատանքը
![]() էՎ է:
էՎ է:
Նկ.56-ում
ներկայացված
է
վոլտ-ամպերային
բնութագծերը
կաթոդի երկու ![]() և
և ![]() ջերմաստիճանների
համար, ընդ
որում
ջերմաստիճանների
համար, ընդ
որում ![]() :
Կաթոդի
ջերմաստիճանի
մեծացման հետ
կաթոդից
էլեկտրոնների
արձակումը
մեծանում է,
այդ դեպքում
մեծանում է և
հագեցման
հոսանքը: Երբ
:
Կաթոդի
ջերմաստիճանի
մեծացման հետ
կաթոդից
էլեկտրոնների
արձակումը
մեծանում է,
այդ դեպքում
մեծանում է և
հագեցման
հոսանքը: Երբ ![]() կաթոդից
պոկված
էլեկտրոնները
նրա շուրջն առաջացնում
են բացասական
տարածական
լիցք` էլեկտրոնային
ամպ: Այդ ամպը
վանում է
կաթոդից
դուրս թռչող
էլեկտրոններին,
և նրանց մեծ
մասը
վերադառնում
է կաթոդ:
Այնուամենայնիվ,
ոչ մեծ թվով
էլեկտրոնների
հաջողվում է
թռչել մինչև
անոդ, որի հետևանքով
անոդային
շղթայում
անցնում է
թույլ հոսանք:
Անոդի վրա
էլեկտրոնների
ընկնելը լրիվ
դադարեցնելու,
այսինքն`
կաթոդից
պոկված
էլեկտրոնները
նրա շուրջն առաջացնում
են բացասական
տարածական
լիցք` էլեկտրոնային
ամպ: Այդ ամպը
վանում է
կաթոդից
դուրս թռչող
էլեկտրոններին,
և նրանց մեծ
մասը
վերադառնում
է կաթոդ:
Այնուամենայնիվ,
ոչ մեծ թվով
էլեկտրոնների
հաջողվում է
թռչել մինչև
անոդ, որի հետևանքով
անոդային
շղթայում
անցնում է
թույլ հոսանք:
Անոդի վրա
էլեկտրոնների
ընկնելը լրիվ
դադարեցնելու,
այսինքն` ![]() -ն զրո
դարձնելու
համար
անհրաժեշտ է
կաթոդի և անոդի
միջև
առաջացնել
որոշ
բացասական
լարում:
Հետևաբար,
դիոդի
վոլտ-ամպերային
բնութագիծը
սկսվում է ոչ
թե զրոյից,
այլ
կոորդինատների
սկզբնակետից
մի փոքր ձախ
ընկած կետից:
-ն զրո
դարձնելու
համար
անհրաժեշտ է
կաթոդի և անոդի
միջև
առաջացնել
որոշ
բացասական
լարում:
Հետևաբար,
դիոդի
վոլտ-ամպերային
բնութագիծը
սկսվում է ոչ
թե զրոյից,
այլ
կոորդինատների
սկզբնակետից
մի փոքր ձախ
ընկած կետից:
Ջերմաէլեկտրոնային էմիսիայի երևույթը օգտագործվում է այնպիսի սարքերում, որոնցում անհրաժեշտ է ստանալ էլեկտրոնների հոսք վակուումում, օրինակ էլեկտրոնային լամպերում, ռենտգենյան խողովակներում, էլեկտրոնային մանրադիտակներում և այլն: Էլեկտրոնային լամպերը լայն կիրառություն ունեն ռադիոտեխնիկայում, ավտոմատիկայում և հեռուստամեխանիկայում փոփոխական հոսանքները ուղղելու, փոփոխական հոսանքները և էլեկտրական ազդանշանները ուժեղացնելու, էլեկտրամագնիսական տատանումները կայունացնելու համար և այլն: Լայն կիրաություն են ստացել նաև այնպիսի լամպերը, որոնցում մի բալոնի մեջ համատեղված է էլեկտրոդների երկու համակարգ: Ամեն մի այդպիսի լամպ կատարում է երկու լամպի դեր:
2. Լուսաէլեկտրոնային էմիսիա է կոչվում մետաղներից էլեկտրոնների էմիսիան լույսի, ինչպես նաև կարճալիքային էլեկտրամագնիսական ճառագայթման (օրինակ, ռենտգենյան) ազդեցության տակ
3. Երկրորդային էլեկտրոնային էմիսիա է կոչվում էլեկտրոնների արձակումը մետաղների, կիսահաղորդիչների կամ դիէլեկտրիկների մակերևույթներից, դրանք էլեկտրոնների փնջով ռմբակոծելու դեպքում: Երկրորդային էլեկտրոնային հոսքը կազմված է մակերևույթից անդրադարձած էլեկտրոններով (առաձգական և ոչ առաձգական անդրադարձած էլեկտրոնները), և «իրական» երկրորդային էլեկտրոնները` էլեկտրոններ, որոնք պոկվել են մետաղից, կիսահաղորդիչից և դիէլեկտրիկից առաջնային էլետրոններով:
Երկրորդային
էլեկտրոնների
![]() թվի
հարաբերությունը
էմիսիան առաջացնող
սկզբնական
էլեկտրոնների
թվի
հարաբերությունը
էմիսիան առաջացնող
սկզբնական
էլեկտրոնների
![]() թվին
կոչվում է
երկրորդային
էլեկտրոնային
էմիսիայի
գործակից.
թվին
կոչվում է
երկրորդային
էլեկտրոնային
էմիսիայի
գործակից.


![]() գործակիցը
կախված է
նյութի
մակերևույթի
բնույթից,
ռմբակոծող
մասնիկների
էներգիայից և
մակերևույթի
վրա անկման
անկյունից:
Կիսահաղորդիչներում
և
դիէլեկտրիկներում
գործակիցը
կախված է
նյութի
մակերևույթի
բնույթից,
ռմբակոծող
մասնիկների
էներգիայից և
մակերևույթի
վրա անկման
անկյունից:
Կիսահաղորդիչներում
և
դիէլեկտրիկներում
![]() -ն ավելի
մեծ է, քան
մետաղներում:
Դա բացատրվում
է նրանով, որ
մետաղներում
ուր
հաղորդականության
էլեկտրոնների
կոնցենտրացիան
մեծ է,
երկրորդային
էլեկտրոնները
հաճախ
բախվելով
նրանց հետ,
կորցնում են
իրենց
էներգիան և
չեն կարող
դուրս գալ
մետաղից:
Կիսահաղորդիչներում
և դիէլեկտրիկներում
հաղորդականության
էլեկտրոնների
կոնցենտրացիայի
փոքր լինելու
պատճառով, երկրորդային
էլեկտրոնների
բախումը
նրանց հետ
կատարվում է
հաճախակի, և
երկրորդային
էլեկտրոնների
դուրս գալը
էմիտերից
աճում է մի
քանի անգամ:
Օրինակ,
նկ.57-ում
բերված է
երկրորդային
էլեկտրոնային
էմիսիայի
-ն ավելի
մեծ է, քան
մետաղներում:
Դա բացատրվում
է նրանով, որ
մետաղներում
ուր
հաղորդականության
էլեկտրոնների
կոնցենտրացիան
մեծ է,
երկրորդային
էլեկտրոնները
հաճախ
բախվելով
նրանց հետ,
կորցնում են
իրենց
էներգիան և
չեն կարող
դուրս գալ
մետաղից:
Կիսահաղորդիչներում
և դիէլեկտրիկներում
հաղորդականության
էլեկտրոնների
կոնցենտրացիայի
փոքր լինելու
պատճառով, երկրորդային
էլեկտրոնների
բախումը
նրանց հետ
կատարվում է
հաճախակի, և
երկրորդային
էլեկտրոնների
դուրս գալը
էմիտերից
աճում է մի
քանի անգամ:
Օրինակ,
նկ.57-ում
բերված է
երկրորդային
էլեկտրոնային
էմիսիայի ![]() գործակցի
որակական
կախումը
ընկնող
էլեկտրոնների
գործակցի
որակական
կախումը
ընկնող
էլեկտրոնների
![]() էներգիայից
էներգիայից
![]() -ի համար: Էլեկտրոնների
էներգիայի
մեծացմամբ
-ի համար: Էլեկտրոնների
էներգիայի
մեծացմամբ ![]() -ն աճում է,
քանի որ
առաջնային
էլեկտրոններն
ավելի խորն են
թափանցում
բյուրեղային
ցանցի մեջ և,
հետևաբար,
պոկում են
ավելի շատ
երկրորդային
էլեկտրոններ:
Սակայն
առաջնային
էլեկտրոնների
որոշ
էներգիայի
դեպքում
-ն աճում է,
քանի որ
առաջնային
էլեկտրոններն
ավելի խորն են
թափանցում
բյուրեղային
ցանցի մեջ և,
հետևաբար,
պոկում են
ավելի շատ
երկրորդային
էլեկտրոններ:
Սակայն
առաջնային
էլեկտրոնների
որոշ
էներգիայի
դեպքում ![]() -ն սկսում է
փոքրանալ: Դա
կապված է այն
բանի հետ, որ
առաջնային էլեկտրոնների
թափանցման
խորության
մեծացմանը
զուգընթաց
երկրորդայիններին
ավելի դժվար է
պոկվել դեպի
մակերևույթ:
-ն սկսում է
փոքրանալ: Դա
կապված է այն
բանի հետ, որ
առաջնային էլեկտրոնների
թափանցման
խորության
մեծացմանը
զուգընթաց
երկրորդայիններին
ավելի դժվար է
պոկվել դեպի
մակերևույթ: ![]() -ի համար
-ի համար ![]() -ի արժեքը
հասնում է
-ի արժեքը
հասնում է ![]() -ի, (մաքուր
մետաղների
համար այն չի
գերազանցում 2-ը):
Երկրորդային
էլեկտրոնային
էմիսիան օգտագործվում
է լուսաէլեկտրոնային
բազմապատկիչներում,
որոնք
կիրառվում են
թույլ
էլեկտրական
հոսանքները
ուժեղացնելու
համար:
-ի, (մաքուր
մետաղների
համար այն չի
գերազանցում 2-ը):
Երկրորդային
էլեկտրոնային
էմիսիան օգտագործվում
է լուսաէլեկտրոնային
բազմապատկիչներում,
որոնք
կիրառվում են
թույլ
էլեկտրական
հոսանքները
ուժեղացնելու
համար:
4.
Ինքնաէլեկտրոնային
էմիսիա է
կոչվում
էլեկտրոնների
էմիսիան
մետաղների
մակեևույթներից
արտաքին
ուժեղ
էլեկտրական
դաշտի
ազդեցության
տակ: Այս երևույթները
կարելի է
դիտել օդը
հանված
խողովակներում,
որի
էլեկտրոդների
կոնֆիգուրացիան
(կաթոդը սուր
է, իսկ անոդը`
խողովակի
ներքին մակերևույթն
է) թույլ է
տալիս
մոտավորապես ![]() Վ լարման
դեպքում
ստանալ
Վ լարման
դեպքում
ստանալ ![]() Վ/մ
լարվածության
էլեկտրական
դաշտեր:
Լարման
աստիճանաբար
մեծացման
դեպքում
արդեն կաթոդի
մակերևույթի
մոտ մոտավորապես
Վ/մ
լարվածության
էլեկտրական
դաշտեր:
Լարման
աստիճանաբար
մեծացման
դեպքում
արդեն կաթոդի
մակերևույթի
մոտ մոտավորապես
![]() Վ/մ դաշտի
լարվածության
դեպքում
առաջանում է
թույլ հոսանք`
պայմանավորված
կաթոդից արձակված
էլեկտրոններով:
Այդ հոսանքի
ուժը մեծանում
է` խողովակի
վրա լարումը
բարձրացնելով:
Հոսանքներն
առաջանում են
սառը կաթոդի դեպքում,
ուստի
նկարագրված
երևույթը
կոչվում է
նաև սառը
էմիսիա: Այդ
երևույթի
բացատրությունը
կարելի է տալ
միայն
քվանտային
տեսությամբ:
Վ/մ դաշտի
լարվածության
դեպքում
առաջանում է
թույլ հոսանք`
պայմանավորված
կաթոդից արձակված
էլեկտրոններով:
Այդ հոսանքի
ուժը մեծանում
է` խողովակի
վրա լարումը
բարձրացնելով:
Հոսանքներն
առաջանում են
սառը կաթոդի դեպքում,
ուստի
նկարագրված
երևույթը
կոչվում է
նաև սառը
էմիսիա: Այդ
երևույթի
բացատրությունը
կարելի է տալ
միայն
քվանտային
տեսությամբ:
5.5 ԳԱԶԵՐԻ ԻՈՆԱՑՈՒՄԸ: ՈՉ ԻՆՔՆՈՒՐՈՒՅՆ ԵՎ ԻՆՔՆՈՒՐՈՒՅՆ ԳԱԶԱՅԻՆ ՊԱՐՊՈՒՄՆԵՐ
Գազերը
ոչ շատ բարձր
ջերմաստիճանների
և մթնոլորտայինին
մոտ
ճնշումների
դեպքում լավ մեկուսիչներ
են: Եթե
մթնոլորտային
չոր օդում
տեղադրվի լավ
մեկուսացված
լիցքավորված
էլեկտրաչափը,
ապա նրա լիցքը
կմնա երկար
ժամանակ
անփոփոխ: Դա
բացատրվում է
նրանով, որ
սովորական
պայմաններում
գազերը
կազմված են
չեզոք
ատոմներից և մոլեկուլներից
և չեն
պարունակում
ազատ լիցքեր (էլեկտրոններ
և իոններ):
Գազը դառնում
է էլեկտրականության
հաղորդիչ, եթե
նրա
մոլեկուլների
մի մասը
իոնացվում է,
այսինքն` տեղի
է ունենում
չեզոք
ատոմների և
մոլեկուլների
ճեղքում`
իոնների և
ազատ
էլեկտրոնների:
Դրա համար գազը
հարկավոր է
ենթարկել ինչ
որ իոնարարի
ազդեցությանը
(օրինակ,
մոտեցնելով
լիցքավորված
էլեկտրաչափին
մոմի բոցը,
նկատում ենք
նրա լիցքի
անկում.
այստեղ գազի
հաղորդականությունը
առաջ է գալիս
տաքացումով):
Այսպիսով, գազերի
իոնացման
դեպքում
իոնարարի
ազդեցության
տակ ատոմների
և
մոլեկուլների
էլեկտրոնային
թաղանթներից
կատարվում է
մեկ կամ մի
քանի
էլեկտրոնների
պոկում, որը
հանգեցնում է
ազատ էլեկտրոնների
և դրական
իոնների
առաջացմանը
(նկ. 58): Էլեկտրոնները
կարող են
միանալ չեզոք
ատոմներին և
մոլեկուլներին
փոխարկելով
դրանք բացասական
իոնների: Գազի
միջով
էլեկտրական
հոսանք անցնելու
պրոցեսն
անվանում են գազային
պարպում:
Գազերը
կարելի է
իոնացնել
էլեկտրոնային
փնջերի,
ուլտրամանուշակագույն,
ռենտգենյան, ռադիոակտիվ
և զանազան այլ
ճառագայթումներով:
Որպեսզի
մոլեկուլից
(ատոմից) մեկ
էլեկտրոն հեռացվի`
անհրաժեշտ է
ծախսել
որոշակի
էներգիա, որը
կոչվում է իոնացման
էներգիա, որի
արժեքները
տարբեր
նյութերի
ատոմների համար
ընկած են ![]() էՎ-ի
սահմաններում:
էՎ-ի
սահմաններում:
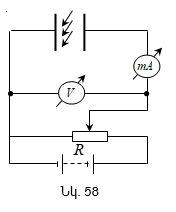
Գազում իոնացման պրոցեսին զուգընթաց տեղի է ունենում նաև վերամիավորման պրոցես: Դրական իոններն ու էլեկտրոնները, հանդիպելով միմյանց, վերամիավորվում են` առաջացնելով չեզոք ատոմ կամ մոլեկուլ: Այսպիսով, մի կողմից` իոնարարն անընդհատ ստեղծում է ազատ էլեկտրոններ և իոններ, մյուս կողմից` դրանք վերամիավորվում են` առաջացնելով չեզոք ատոմներ և մոլեկուլներ: Եթե իոնարարի ազդեցությունն անփոփոխ է, ապա այդ երկու պրոցեսների միջև հաստատվում է շարժուն հավասարակշռություն, այսինքն` միավոր ժամանակում իոնացման արդյունքում ծնված մասնիկների թիվը հավասարվում է վերամիավորման հետևանքով չեզոքացող մասնիկների թվին:
Արտաքին էլեկտրական դաշտի բացակայությամբ իոնարարի ազդեցությամբ առաջացած իոններն ու ազատ էլեկտրոնները գազում կատարում են քաոսային շարժում: Էլեկտրական դաշտ կիրառելիս ջերմային շարժման հետ մեկտեղ առաջանում է էլեկտրոնների և իոնների կարգավորված շարժում, այսինքն` էլեկտրական հոսանք: Այսպիսով, հոսանքը գազերում պայմանավորված է իոնների և էլեկտրոնների ուղղորդված շարժմամբ, այսինքն` իոնացված գազն օժտված է էլեկտրոնային և իոնային էլեկտրահաղորդականությամբ:
Քննարկենք գազային միջակայք պարունակող շղթա (նկ.56), որն անընդհատ ենթարկվում է ինտենսիվությունով հաստատուն իոնարարի ազդեցությանը: Իոնարարի ազդեցության արդյունքում գազը ձեռք է բերում որոշակի հաղորդականություն և շղթայով անցնում է հոսանք, որի կախումը կիրառված լարումից բերված է նկ.59-ում:
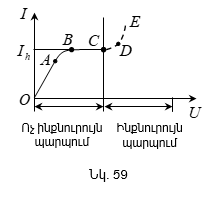
OA կորի
տեղամասում
հոսանքի ուժն
աճում է լարմանը
համեմատական,
այսինքն` տեղի
ունի Օհմի օրենքը:
Լարման
հետագա մեծացման
դեպքում Օհմի
օրենքը խանգարվում
է. հոսանքի
աճը
դանդաղում է (AB
տեղամաս), և
վերջապես (BC
տեղամաս)
հոսանքի ուժն
ընդունում է
իր առավելագույն
արժեքը և
լարման
հետագա
մեծացման դեպքում
դադարում է
աճելուց:
Հոսանքի ուժի
այդ ![]() առավելագույն
արժեքը
կոչվում է
հագեցման
հոսանք: Եթե AC տեղամասում
կիրառված
լարման որևէ
արժեքի դեպքում
իոնարարի
ազդեցությունը
դադարեցվի,
ապա կարճ
ժամանակամիջոցում
հոսանքի ուժը կհավասարվի
զրոյի: Այդ
ընթացքում
գազում առկա
բոլոր
լիցքավորված
մասնիկները
կամ կհասնեն
էլեկտրոդներին,
կամ
կվերամիավորվեն,
և պարպումը
կդադարի: Այդ
պատճառով
միայն
արտաքին
իոնարարի ազդեցությամբ
տեղի ունեցող
պարպումն
անվանում են ոչ
ինքնուրույն
պարպում:
Էլեկտրոդների
միջև լարման
հետագա
մեծացման
դեպքում
հոսանքի ուժը
սկզբում
դանդաղ (CD
տեղամաս),
այնուհետև
կտրուկ (DE
տեղամաս)
աճում է:
առավելագույն
արժեքը
կոչվում է
հագեցման
հոսանք: Եթե AC տեղամասում
կիրառված
լարման որևէ
արժեքի դեպքում
իոնարարի
ազդեցությունը
դադարեցվի,
ապա կարճ
ժամանակամիջոցում
հոսանքի ուժը կհավասարվի
զրոյի: Այդ
ընթացքում
գազում առկա
բոլոր
լիցքավորված
մասնիկները
կամ կհասնեն
էլեկտրոդներին,
կամ
կվերամիավորվեն,
և պարպումը
կդադարի: Այդ
պատճառով
միայն
արտաքին
իոնարարի ազդեցությամբ
տեղի ունեցող
պարպումն
անվանում են ոչ
ինքնուրույն
պարպում:
Էլեկտրոդների
միջև լարման
հետագա
մեծացման
դեպքում
հոսանքի ուժը
սկզբում
դանդաղ (CD
տեղամաս),
այնուհետև
կտրուկ (DE
տեղամաս)
աճում է:
Եթե արտաքին իոնարարի ազդեցությունը վերացնելուց հետո գազում պարպումը պահպանվում է, կոչվում է ինքնուրույն պարպում:
Քննարկենք ինքնուրույն պարպան առաջացման պայմանը: Ինչպես վերևում ցույց տրվեց, գազային միջակայքի էլեկտրոդների միջև մեծ լարումների դեպքում (տես նկ. 59) հոսանքն ուժեղ աճում է (CD և DE տեղամասեր նկ. 59): Արտաքին իոնիզատորի ազդեցության տակ մեծ լարումների դեպքում առաջացած էլեկտրոնները, որոնք արագացվում են էլեկտրական դաշտով, բախվելով գազի չեզոք մոլեկուլների հետ, նրանց իոնացնում են, որի արդյունքում առաջանում են երկրորդային էլեկտրոններ և դրական իոններ (նկ. 60,1 պրոցես): Դրական իոնները շարժվում են դեպի կաթոդ, իսկ էլեկտրոնները` դեպի անոդ: Երկրորդային էլեկտրոնները նորից իոնացնում են գազի մոլեկուլները, և, հետևաբար, էլեկտրոնների և իոնների ընդհանուր քանակը պետք է աճի էլեկտրոնների շարժումով դեպի անոդ հեղեղանման, որն էլ հոսանքի մեծացման պատճառն է CD տեղամասում (տես նկ. 59): Նկարագրված պրոցեսը կոչվում է հարվածային իոնացում:

Սակայն հարվածային իոնացումը էլեկտրոնների ազդեցության տակ բավարար չէ պարպումը պահպանելու համար արտաքին իոնարարը հեռացնելու դեպքում: Այդ դեպքում անհրաժեշտ էլեկտրոնների հեղեղները «վերարտադրվեն», այսինքն, որպեսզի գազում ինչ-որ պրոցեսների ազդեցության տակ առաջաջանան նոր էլեկտրոններ: Այդպիսի պրոցեսները սխեմատիկորեն ցույց են տրված նկ. 60-ում.
1) էլեկտրական դաշտով արագացված դրական իոնները, հարվածելով կաթոդին, նրանից պոկում են էլեկտրոններ (2 պրոցես), 2) դրական իոնները, բախվելով գազի մոլեկուլների հետ, բերում են գրգռված վիճակի, այդպիսի մոլեկուլների անցումը նորմալ վիճակի ուղեկցվում է ֆոտոնի արձակումով (3 պրոցես), 3) ֆոտոնը, կլանվելով չեզոք մոլեկուլով, նրան իոնացնում է, տեղի է ունենում այսպես կոչված մոլեկուլների ֆոտոնային իոնացման պրոցես (4 պրոցես), 4) էլեկտրոնների պոկում կաթոդից ֆոտոններով (5 պրոցես):
Վերջապես,
գազային
միջակայքի
էլեկտրոդների
միջև նշանակալի
լարումների
դեպքում,
գալիս է մի
պահ, երբ
դրական
իոնները,
օժտված
լինելով
ավելի փոքր
ազատ վազքի
երկարությամբ
քան էլեկտրոնները,
ձեռք են
բերում
էներգիա, որը
բավարար է գազի
մոլեկուլները
իոնացնելու
համար (6
պրոցես), և
դեպի
բացասական
թիթեղ
ուղղելու
իոնների հեղեղները:
Երբ բացի
էլեկտրոնների
հեղեղներից
առաջանում են
նաև իոնային
հեղեղներ, արդեն
հոսանքի ուժը
աճում է
գործնականորեն
առանց
լարումը
մեծացնելու (![]() տեղամաս
նկ. 59):
Նկարագրված (1-6)
պրոցեսների
արդյունքում
իոնների և
էլեկտրոնների
թիվը գազի
ծավալում
հեղեղանման
աճում է և
պարպումը
դառնում է
ինքնուրույն,
այսինքն
պարպումը
պահպանվում է
արտաքին
իոնարարի
ազդեցությունը
վերացնելուց հետո:
Այն լարումը
որի դեպքում
առաջանում է ինքնուրույն
պարպում,
կոչվում է ծակման
լարում: Կախված
գազի
ճնշումից,
էլեկտրոդների
կոնֆիգուրացիայից,
արտաքին
շղթայի
պարամետրերից,
կարելի է
խոսել չորս
տեսակի
ինքնուրույն
պարպումների
մասին.
մարմրող,
կայծային,
աղեղային և պսակաձև:
տեղամաս
նկ. 59):
Նկարագրված (1-6)
պրոցեսների
արդյունքում
իոնների և
էլեկտրոնների
թիվը գազի
ծավալում
հեղեղանման
աճում է և
պարպումը
դառնում է
ինքնուրույն,
այսինքն
պարպումը
պահպանվում է
արտաքին
իոնարարի
ազդեցությունը
վերացնելուց հետո:
Այն լարումը
որի դեպքում
առաջանում է ինքնուրույն
պարպում,
կոչվում է ծակման
լարում: Կախված
գազի
ճնշումից,
էլեկտրոդների
կոնֆիգուրացիայից,
արտաքին
շղթայի
պարամետրերից,
կարելի է
խոսել չորս
տեսակի
ինքնուրույն
պարպումների
մասին.
մարմրող,
կայծային,
աղեղային և պսակաձև:
1. Մարմրող պարպումը աrաջանում է ցածր ճնշումների դեպքում:
Եթե
30-50 սմ
երկարության
ապակե
խողովակում
ներզոդված էլեկտրոդներին
կիրառվի մի
քանի հարյուր
վոլտ հաստատուն
լարում, աստիճանաբար
խողովակից օդը
դուրս մղելով,
ապա ![]() կՊա ճնշումների
դեպքում
առաջանում է
պարպում` անոդը
կաթոդի հետ
միացնող
լուսավոր
ծուռումուռ բարակ
քուղի տեսքով:
Ճնշումը ցածրացնելուն
զուգընթաց
քուղը
հաստանում է և
կՊա ճնշումների
դեպքում
առաջանում է
պարպում` անոդը
կաթոդի հետ
միացնող
լուսավոր
ծուռումուռ բարակ
քուղի տեսքով:
Ճնշումը ցածրացնելուն
զուգընթաց
քուղը
հաստանում է և
![]() Պա ճնշման
դեպքում
լցնում է
ամբողջ
խողովակի
կտրվածքը.
ստացվում է
մարմրող
պարպում: Նրա հիմնական
մասերը ցույց
են տրված նկ.
61-ում: Կաթոդի
մոտ ստեղծվում
է լուսավոր
շերտ, որը
կոչվում է
կաթոդային լուսավոր
թաղանթ (1):
Կաթոդի և
լուսավոր
շերտի միջև
գտնվում է մութ
շերտը (2), որն
անվանում են կաթոդային
մութ
տարածություն:
Այս շերտը
փոխվում է
լուսավոր
տիրույթի, որն
անվանում են մարմրող
լուսարձակում
(3), որն
առաջանում է
էլեկտրոնների
ռեկոմբինացիայով
դրական
իոնների հետ:
Մարմրող
լուսարձակմանը
սահմանակից է
մի մութ
միջակայք` ֆարադեյան
մութ
տարածությունը
(4): Դրանց միջև
սահմանը աղավաղված
է: Խողովակի
մնացած
ամբողջ մասը
լցված է լուսավոր
գազով և
կոչվում է դրական
սյուն (5):
Ճնշումը
ցածրացնելիս
պարպման կաթոդային
մասը և
ֆարադեյան
մութ տարածությունը
լայնանում են,
իսկ դրական սյունը
կարճանում: 133Պա
ճնշման
դեպքում
դրական
սյունը
տրոհվում է մի
շարք իրար
հաջորդող
մութ և
լուսավոր ծռված
շերտերի:
Մարմրող
պարպման
պահպանման համար
հատուկ
նշանակություն
ունեն նրա
երկու մասերը`
կաթոդային
մութ տարածությունը
և մարմրող
լուսարձակումը:
Կաթոդային
մութ տարածության
մեջ տեղի է
ունենում
էլեկտրոնների
և դրական
իոնների
ուժեղ
արագացում, որի
արդյունքում
կաթոդից
պոկվում են
էլեկտրոններ
(երկրորդային
էմիսիա):
Մարմրող լուսարձակման
տիրույթում
տեղի է
ունենում գազի
մոլեկուլների
էլեկտրոնների
հարվածային
իոնացում: Այս
դեպքում առաջացած
դրական
իոնները
սլանում են
կաթոդ, և
նրանից
պոկում են նոր
էլեկտրոններ,
որոնք իրենց
հերթին նորից
իոնացնում են
գազը և այսպես
շարունակ:
Այսպիսով
անընդհատ
պահպանվում է
մարմրող
պարպումը:
Պա ճնշման
դեպքում
լցնում է
ամբողջ
խողովակի
կտրվածքը.
ստացվում է
մարմրող
պարպում: Նրա հիմնական
մասերը ցույց
են տրված նկ.
61-ում: Կաթոդի
մոտ ստեղծվում
է լուսավոր
շերտ, որը
կոչվում է
կաթոդային լուսավոր
թաղանթ (1):
Կաթոդի և
լուսավոր
շերտի միջև
գտնվում է մութ
շերտը (2), որն
անվանում են կաթոդային
մութ
տարածություն:
Այս շերտը
փոխվում է
լուսավոր
տիրույթի, որն
անվանում են մարմրող
լուսարձակում
(3), որն
առաջանում է
էլեկտրոնների
ռեկոմբինացիայով
դրական
իոնների հետ:
Մարմրող
լուսարձակմանը
սահմանակից է
մի մութ
միջակայք` ֆարադեյան
մութ
տարածությունը
(4): Դրանց միջև
սահմանը աղավաղված
է: Խողովակի
մնացած
ամբողջ մասը
լցված է լուսավոր
գազով և
կոչվում է դրական
սյուն (5):
Ճնշումը
ցածրացնելիս
պարպման կաթոդային
մասը և
ֆարադեյան
մութ տարածությունը
լայնանում են,
իսկ դրական սյունը
կարճանում: 133Պա
ճնշման
դեպքում
դրական
սյունը
տրոհվում է մի
շարք իրար
հաջորդող
մութ և
լուսավոր ծռված
շերտերի:
Մարմրող
պարպման
պահպանման համար
հատուկ
նշանակություն
ունեն նրա
երկու մասերը`
կաթոդային
մութ տարածությունը
և մարմրող
լուսարձակումը:
Կաթոդային
մութ տարածության
մեջ տեղի է
ունենում
էլեկտրոնների
և դրական
իոնների
ուժեղ
արագացում, որի
արդյունքում
կաթոդից
պոկվում են
էլեկտրոններ
(երկրորդային
էմիսիա):
Մարմրող լուսարձակման
տիրույթում
տեղի է
ունենում գազի
մոլեկուլների
էլեկտրոնների
հարվածային
իոնացում: Այս
դեպքում առաջացած
դրական
իոնները
սլանում են
կաթոդ, և
նրանից
պոկում են նոր
էլեկտրոններ,
որոնք իրենց
հերթին նորից
իոնացնում են
գազը և այսպես
շարունակ:
Այսպիսով
անընդհատ
պահպանվում է
մարմրող
պարպումը:

Խողովակում
գազի հետագա
նոսրացման
դեպքում (![]() Պա) գազի
լուսարձակումը
թուլանում է,
և սկսում են
լուսարձակել
խողովակի
պատերը:
Դրական իոններով
կաթոդից
պոկված
էլեկտրոններն
այդպիսի
նոսրացումների
դեպքում
հաճախ են ընդհարվում
գազի
մոլեկուլների
հետ և դրա
համար էլ
արագացվում
են դաշտով,
հարվածելով
ապակուն առաջ
են բերում նրա
լուսարձակումը,
այպես կոչված,
կաթոդային
լյումինեսցենտում:
Էլեկտրոնների
այդ հոսքը
պատմականորեն
ստացել է կաթոդային
ճառագայթներ
անունը: Եթե
կաթոդի վրա
բացվեն փոքր
անցքեր, ապա
կաթոդը
ռմբակոծող
դրական
իոնները,
անցնելով
անցքերով,
թափանցում են
կաթոդի մոտի
տարածությունը
և առաջացնում
են կտրուկ
սահմանափակ
փունջ, որն
ստացել է կանալային
(կամ դրական) ճառագայթներ
անվանումը:
Պա) գազի
լուսարձակումը
թուլանում է,
և սկսում են
լուսարձակել
խողովակի
պատերը:
Դրական իոններով
կաթոդից
պոկված
էլեկտրոններն
այդպիսի
նոսրացումների
դեպքում
հաճախ են ընդհարվում
գազի
մոլեկուլների
հետ և դրա
համար էլ
արագացվում
են դաշտով,
հարվածելով
ապակուն առաջ
են բերում նրա
լուսարձակումը,
այպես կոչված,
կաթոդային
լյումինեսցենտում:
Էլեկտրոնների
այդ հոսքը
պատմականորեն
ստացել է կաթոդային
ճառագայթներ
անունը: Եթե
կաթոդի վրա
բացվեն փոքր
անցքեր, ապա
կաթոդը
ռմբակոծող
դրական
իոնները,
անցնելով
անցքերով,
թափանցում են
կաթոդի մոտի
տարածությունը
և առաջացնում
են կտրուկ
սահմանափակ
փունջ, որն
ստացել է կանալային
(կամ դրական) ճառագայթներ
անվանումը:
Մարմրող պարպումը լայն կիրառություն է գտել տեխնիկայում: Քանի որ դրական սյան լուսարձակումը յուրաքանչյուր գազի համար ունի բնութագրական գույն, ապա այն օգտագործում են գազալուսային խողովակներում լուսավոր մակագրերի և գովազդների համար (օրինակ, նեոնային գազապարպման խողովակները տալիս են կարմիր լուսարձակում, արգոնայինը` կապույտ-կանաչ լուսարձակում): Ցերեկային լույսի լամպերում, որոնք ավելի շահավետ են, քան շիկացման լամպերը, մարմրող պարպման ճառագայթումը տեղի ունենալով սնդիկի գոլորշիների վրա, կլանվում է խողովակի ներքին մակերևույթը ծածկելով ֆլուորենցող նյութով (լյումինոֆորով), որը կլանված ճառագայթման ազդեցության տակ սկսում է լուսարձակել: Լուսարձակման սպեկտրը համապատասխան լյումինոֆորների ընտրման դեպքում մոտ է արեգակնային ճառագայթման սպեկտրին: Մարմրող պարպումը օգտագործվում է մետաղների կաթոդային փոշեպատման համար: Նյութի կաթոդը մարմրող պարպման մեջ դրական իոնների ռմբակոծման հետևանքով ուժեղ տաքանում է` անցնելով գոլորշիացման վիճակի: Տեղադրելով կաթոդի մոտ տարբեր առարկաներ` դրանք կարելի է ծածկել մետաղի հավասարաչափ շերտով:
2.
Կայծային
պարպումն
առաջանում է,
երբ
էլեկտրական
դաշտի
լարվածությունը
հասնում է տվյալ
գազի համար
ծակման ![]() արժեքին:
արժեքին:
![]() -ի
մեծությունը
կախում ունի
գազի
ճնշումից. օդի
համար
մթնոլորտային
ճնշման
դեպքում այն կազմում
է մոտ
-ի
մեծությունը
կախում ունի
գազի
ճնշումից. օդի
համար
մթնոլորտային
ճնշման
դեպքում այն կազմում
է մոտ ![]() Վ/մ: Ճնշման
մեծացման
համեմատ
Վ/մ: Ճնշման
մեծացման
համեմատ ![]() -ն աճում է:
Պաշենի
փորձարարական
օրենքի համաձայն
դաշտի
ծակման
լարվածության
և ճնշման հարաբերությունը
մոտավորապես
հաստատուն է.
-ն աճում է:
Պաշենի
փորձարարական
օրենքի համաձայն
դաշտի
ծակման
լարվածության
և ճնշման հարաբերությունը
մոտավորապես
հաստատուն է.

Կայծային
պարպումն
ուղեկցվում է
պայծառ լույս
արձակող
ծուռումուռ,
ճյուղավորված
կանալի
առաջացումով
որով անցնում
է մեծ հոսանքի
ուժի կարճատև
իմպուլս: Գազի
ջերմաստիճանը
կայծային կանալում
լինում է շատ
բարձր` մինչև ![]() Կ: Գազի
արագ ուժեղ
տաքացումը ճնշումը
կտրուկ
բարձրացնում
է և
առաջացնում հարվածային
և ձայնային
ալիքներ: Այդ
պատճառով
կայծային
պարպումն
ուղեկցվում է
ձայնային
երևույթներով`
թույլ
ճարճատյունից`
փոքր հզորության
կայծի
դեպքում,
մինչև
ամպրոպի դղրդյունը,
որ լսվում է
կայծակից
հետո: Կայծի
առաջացմանը
նախորդում է
գազում ուժեղ
իոնացված կանալի
ստեղծումը,
որը կոչվում է
ստրիմեր: Այդ
կանալը
առաջանում է
կայծի
ճանապարհին առաջացող
էլեկտրոնային
հեղեղները
իրար ծածկելու
միջոցով:
Յուրաքանչյուր
հեղեղի
նախահայր է
ծառայում
լուսաիոնացման
միջոցով
առաջացած
էլեկտրոնը:
Ստրիմերի
զարգացման
սխեման ցույց
է տրված նկ.
62-ում: Դաշտի
լարվածությունն
այնպիսին է,
որ որևէ
պրոցեսի
հետևանքով
կաթոդից
դուրս թռած
էլեկտրոնը
ազատ վազքի
երկարության
վրա ձեռք է
բերում
իոնացման
համար
բավականաչափ
էներգիա:Այդ
պատճառառով
տեղի է
ունենում
էլեկտրոնների
բազմացում`
առաջանում է
հեղեղ (այդ
դեպքում
առաջացող
դրական իոնները
էական դեր չեն
խաղում շատ
ավելի փոքր
շարժունակության
հետևանքով:
Նրանք
պայմանավորում
են տարածական
լիցքը, որն
առաջացնում է
պոտենցիալի
վերաբաշխում):
Ատոմը, որից
իոնացման ժամանակ
պոկվում է ներքին
էլեկտրոններից
մեկը,
արձակում է
ճառագայթում
(այդ
ճառագայթումը
նկարում
ցույց է տրված
ծուռումուռ
գծերով), որն
առաջացնում է
մոլեկուլների
լուսաիոնացում,
ընդ որում`
առաջացող
էլեկտրոնները
ծնում են
նորանոր հեղեղներ:
Հեղեղները,
իրար
ծածկելով,
առաջացնում են
լավ հաղորդող
կանաչ`ստրիմեր,
որով կաթոդից
դեպի անոդն է
սլանում
էլեկտրոնների
հզոր հոսք`
տեղի է ունենում
ծակում:
Կ: Գազի
արագ ուժեղ
տաքացումը ճնշումը
կտրուկ
բարձրացնում
է և
առաջացնում հարվածային
և ձայնային
ալիքներ: Այդ
պատճառով
կայծային
պարպումն
ուղեկցվում է
ձայնային
երևույթներով`
թույլ
ճարճատյունից`
փոքր հզորության
կայծի
դեպքում,
մինչև
ամպրոպի դղրդյունը,
որ լսվում է
կայծակից
հետո: Կայծի
առաջացմանը
նախորդում է
գազում ուժեղ
իոնացված կանալի
ստեղծումը,
որը կոչվում է
ստրիմեր: Այդ
կանալը
առաջանում է
կայծի
ճանապարհին առաջացող
էլեկտրոնային
հեղեղները
իրար ծածկելու
միջոցով:
Յուրաքանչյուր
հեղեղի
նախահայր է
ծառայում
լուսաիոնացման
միջոցով
առաջացած
էլեկտրոնը:
Ստրիմերի
զարգացման
սխեման ցույց
է տրված նկ.
62-ում: Դաշտի
լարվածությունն
այնպիսին է,
որ որևէ
պրոցեսի
հետևանքով
կաթոդից
դուրս թռած
էլեկտրոնը
ազատ վազքի
երկարության
վրա ձեռք է
բերում
իոնացման
համար
բավականաչափ
էներգիա:Այդ
պատճառառով
տեղի է
ունենում
էլեկտրոնների
բազմացում`
առաջանում է
հեղեղ (այդ
դեպքում
առաջացող
դրական իոնները
էական դեր չեն
խաղում շատ
ավելի փոքր
շարժունակության
հետևանքով:
Նրանք
պայմանավորում
են տարածական
լիցքը, որն
առաջացնում է
պոտենցիալի
վերաբաշխում):
Ատոմը, որից
իոնացման ժամանակ
պոկվում է ներքին
էլեկտրոններից
մեկը,
արձակում է
ճառագայթում
(այդ
ճառագայթումը
նկարում
ցույց է տրված
ծուռումուռ
գծերով), որն
առաջացնում է
մոլեկուլների
լուսաիոնացում,
ընդ որում`
առաջացող
էլեկտրոնները
ծնում են
նորանոր հեղեղներ:
Հեղեղները,
իրար
ծածկելով,
առաջացնում են
լավ հաղորդող
կանաչ`ստրիմեր,
որով կաթոդից
դեպի անոդն է
սլանում
էլեկտրոնների
հզոր հոսք`
տեղի է ունենում
ծակում:

Կայծային պարպումը օգտագործվում է ներքին այրման շարժիչներում վառելանյութի խառնուրդի բոցավառման համար և էլեկտրահաղորդման գծերի ապահովման համար գերլարումներից (կայծային պարպիչներ): Փոքր պարպումային միջակայքի երկարության դեպքում կայծային պարպումն առաջացնում է մետաղի մակերևույթի քայքայում (էրոզիա), ուստի այն օգտագործվում է մետաղների էլեկտրակայծային ճշգրիտ մշակման համար (կտրում, շաղափում): Այն օգտագործվում է սպետրային անալիզում լիցքավորված մասնիկները գրանցելու համար (կայծային պարպիչներ):
3.
Աղեղային
պարպում: Եթե
հզոր
աղբյուրից
կայծային
պարպման բռնկումից
հետո
աստիճանաբար
փոքրացվի
էլեկտրոդների
միջև
հեռավորությունը,
ապա պարպումը դառնում
է անընդհատ`
առաջանում է
աղեղային պարպում:
Այս դեպքում
հոսանքի ուժը
կտրուկ աճում
է` դառնալով
հարյուրավոր
ամպեր, իսկ
լարումը պարպման
միջակայքում
ընկնում է
մինչև մի քանի
տասնյակ վոլտ:
1802թ. Պետրովը
հայտնաբերեց,
որ եթե ցածր
լարման
աղբյուրին
միացրած ածխե
էլեկտրոդները,
որոնք
նախապես
հպված են
միմյանց, իրարից
հեռացվեն, ապա
էլեկտրոդների
միջև բռնկվում
է
կուրացուցիչ
լուսարձակում:
Էլեկտրոդների
հորիզոնական
դասավորության
դեպքում տաքացած
լուսավոր
գազը
կորանում է
աղեղի տեսքով,
որի
հետևանքով
հայտնագործած
երևույթը կոչվում
է վոլտյան
(կամ
էլեկտրական
աղեղ): Մթնոլորտային
ճնշման
դեպքում
կաթոդի
ջերմաստիճանը
մոտավորապես
հավասար է ![]() Կ:
Էլեկտրոնների
հզոր հոսանքով
ռմբակոծվող
անոդը ավելի է
տաքանում: Դա
հանգեցնում է
նրան, որ
անոդը
ինտենսիվորեն
գոլորշիանում
է, և նրա
մակերևույթի
վրա առաջանում
է փոս`
խառնարան:
Խառնարանը
աղեղի ամենապայծառ
տեղն է:
Կ:
Էլեկտրոնների
հզոր հոսանքով
ռմբակոծվող
անոդը ավելի է
տաքանում: Դա
հանգեցնում է
նրան, որ
անոդը
ինտենսիվորեն
գոլորշիանում
է, և նրա
մակերևույթի
վրա առաջանում
է փոս`
խառնարան:
Խառնարանը
աղեղի ամենապայծառ
տեղն է:
Ժամանակակից պատկերացումներով, աղեղային պարպումը պահպանվում է կաթոդի բարձր ջերմաստիճանի, ինտենսիվ ջերմաէլեկտրոնային էմիսիայի, ինչպես նաև մոլեկուլների ջերմաստիճանային իոնացման հաշվին, պայմանավորված գազի բարձր ջերմաստիճանով:
Աղեղային
պարպումն
ունի լայն
կիրառություն
մետաղների կտրման
և եռակցման,
բարձրորակ
պողպատներ
(աղեղային վառարան)
ստանալու և
լուսավորության
համար (լուսարձակներ,
պրոյեկցիոն
սարքեր):
Էլեկտրական աղեղը
կիրառվում է
որպես լույսի
հզոր աղբյուր:
Գերբարձր
ճնշման
աղեղային
լամպերում (ԳԲՃ
լամպեր)
պարպումը
տեղի է
ունենում
վոլֆրամե
էլեկտրոդների
միջև` սնդիկի
գոլորշիների
մթնոլորտում
և մինչև ![]() Պա
ճնշման տակ,
կամ իներտ
գազում
(նեոնում, արգոնում,
կրիպտոնում
կամ
քսենոնում)`
մինչև
Պա
ճնշման տակ,
կամ իներտ
գազում
(նեոնում, արգոնում,
կրիպտոնում
կամ
քսենոնում)`
մինչև ![]() Պա ճնշման
տակ: Քանի որ
ԳԲՃ լամպը շատ
ուժեղ տաքանում
է, նրա բալոնը
պատրաստում
են քվարցից
(որը ավելի
բարձր
ջերմաստիճանում
է փափկում,
քան ապակին):
Սնդիկի գոլորշիներում
վառվող աղեղը
արձակում է
ուլտրամանուշակագույն
ճառագայթման
հզոր հոսք: Քվարցե
բալոնով
սնդիկային
լամպերը
(քվարցը անցկացնում
է
ուլտրամանուշակագույն
ճառագայթները,
սովորական
ապակին
կլանում է
դրանք) որպես
ուլտրամանուշակագույն
ճառագայթների
աղբյուր օգտագործվում
են
բժշկության
մեջ գիտական
հետազոտություններում:
Պա ճնշման
տակ: Քանի որ
ԳԲՃ լամպը շատ
ուժեղ տաքանում
է, նրա բալոնը
պատրաստում
են քվարցից
(որը ավելի
բարձր
ջերմաստիճանում
է փափկում,
քան ապակին):
Սնդիկի գոլորշիներում
վառվող աղեղը
արձակում է
ուլտրամանուշակագույն
ճառագայթման
հզոր հոսք: Քվարցե
բալոնով
սնդիկային
լամպերը
(քվարցը անցկացնում
է
ուլտրամանուշակագույն
ճառագայթները,
սովորական
ապակին
կլանում է
դրանք) որպես
ուլտրամանուշակագույն
ճառագայթների
աղբյուր օգտագործվում
են
բժշկության
մեջ գիտական
հետազոտություններում:
4.
Պսակաձև
պարպումը
բարձրավոլտ
էլեկտրական
պարպում է
բարձր ճնշման
(օրինակ,
մթնոլորտային)
մեծ
կորություն ունեցող
էլեկտրոդների
մակերևույթի
մոտ (օրինակ,
սայրը) կտրուկ
անհամասեռ
դաշտի դեպքում:
Երբ դաշտի
լարվածությունը
սայրի մոտ
հասնում է ![]() կՎ-ի, ապա
նրա շուրջը
ծագում է
լուսարձակում,
ունենալով
պսակի տեսք,
որով էլ
պայմանավորված
է այդ տեսակի
պարպման
անունը: Պսակաձև
պարպման
դեպքում
մոլեկուլների
իոնացումը և
գրգռումը
տեղի է
ունենում ոչ
ամբողջ միջէլեկտրոդային
տարածությունում,
այլ միայն փոքր
կորության
շառավիղ
ունեցող
էլեկտրոդի
մոտակայքում,
որտեղ
լարվածությունը
հասնում է
կՎ-ի, ապա
նրա շուրջը
ծագում է
լուսարձակում,
ունենալով
պսակի տեսք,
որով էլ
պայմանավորված
է այդ տեսակի
պարպման
անունը: Պսակաձև
պարպման
դեպքում
մոլեկուլների
իոնացումը և
գրգռումը
տեղի է
ունենում ոչ
ամբողջ միջէլեկտրոդային
տարածությունում,
այլ միայն փոքր
կորության
շառավիղ
ունեցող
էլեկտրոդի
մոտակայքում,
որտեղ
լարվածությունը
հասնում է ![]() -ին
հավասար կամ
նրան
գերազանցող
արժեքների: Պսակ
առաջացնող
էլեկտրոդի
նշանից
կախված` տարբերում
են դրական կամ
բացասական
պսակ: Պսակ
առաջացնող
շերտի և պսակ
չառաջացնող
էլեկտրոդի
միջև գտնվում
է պսակի
արտաքին
տիրույթը:
Ծակման ռեժիմ
-ին
հավասար կամ
նրան
գերազանցող
արժեքների: Պսակ
առաջացնող
էլեկտրոդի
նշանից
կախված` տարբերում
են դրական կամ
բացասական
պսակ: Պսակ
առաջացնող
շերտի և պսակ
չառաջացնող
էլեկտրոդի
միջև գտնվում
է պսակի
արտաքին
տիրույթը:
Ծակման ռեժիմ ![]() գոյություն
ունի միայն
պսակ
առաջացնող
շերտի
սահմաններում:
Այդ պատճառով
կարելի է ասել,
որ պսակային
պարպումը
գազային
միջակայքի ոչ
լրիվ ծակումն
է: Բացասական
պսակի
դեպքում կաթոդի
վրա դիտվող
երևույթները
նման են մարմրող
պարպման
կաթոդի վրա
դիտվող
երևույթներին:
Ուժեղ դաշտի
միջոցով
արագացված
դրական իոնները
կաթոդից
պոկում են
էլեկտրոններ,
որոնք
առաջացնում
են
մոլեկուլների
իոնացում և
գրգռում պսակ
առաջացնող
շերտում:
Պսակի արտաքին
տիրույթում
դաշտը
բավական չէ,
որպեսզի
էլեկտրոններին
հաղորդի
իոնացման
համար անհրաժեշտ
էներգիա: Այդ
պատճառով այս
տիրույթը
թափանցած
էլեկտրոնները
դաշտի
միջոցով
տարվում են դեպի
անոդ:
Էլեկտրոնների
մի մասը խլում
են մոլեկուլները,
որի
հետևանքով
առաջանում են
բացասական
իոններ:
Այսպիսով,
արտաքին
տիրույթում
հոսանքը
պայմանավորված
է միայն
բացասական
իոններով: Այս
տիրույթում
պարպումն
ունի ոչ
ինքնուրույն
բնույթ:
Դրական
պսակում
էլեկտրոնային
հեղեղները
ծնվում են
պսակի
արտաքին
սահմանի մոտ և
սլանում են
դեպի պսակ
առաջացնող
էլեկտրոդը`
անոդը:
Հեղեղները
ծնող
էլեկտրոնների
գոյացումը
պայմանավորված
է
լուսաիոնացումով,
որն
առաջանում է
պսակ
առաջացնող
շերտի
ճառագայթումից:
Պսակի
արտաքին
տիրույթում
հոսանք կրողները
դրական
իոններն են,
որոնք դաշտի
ազդեցության
տակ շարժվում
են դեպի անոդ:
գոյություն
ունի միայն
պսակ
առաջացնող
շերտի
սահմաններում:
Այդ պատճառով
կարելի է ասել,
որ պսակային
պարպումը
գազային
միջակայքի ոչ
լրիվ ծակումն
է: Բացասական
պսակի
դեպքում կաթոդի
վրա դիտվող
երևույթները
նման են մարմրող
պարպման
կաթոդի վրա
դիտվող
երևույթներին:
Ուժեղ դաշտի
միջոցով
արագացված
դրական իոնները
կաթոդից
պոկում են
էլեկտրոններ,
որոնք
առաջացնում
են
մոլեկուլների
իոնացում և
գրգռում պսակ
առաջացնող
շերտում:
Պսակի արտաքին
տիրույթում
դաշտը
բավական չէ,
որպեսզի
էլեկտրոններին
հաղորդի
իոնացման
համար անհրաժեշտ
էներգիա: Այդ
պատճառով այս
տիրույթը
թափանցած
էլեկտրոնները
դաշտի
միջոցով
տարվում են դեպի
անոդ:
Էլեկտրոնների
մի մասը խլում
են մոլեկուլները,
որի
հետևանքով
առաջանում են
բացասական
իոններ:
Այսպիսով,
արտաքին
տիրույթում
հոսանքը
պայմանավորված
է միայն
բացասական
իոններով: Այս
տիրույթում
պարպումն
ունի ոչ
ինքնուրույն
բնույթ:
Դրական
պսակում
էլեկտրոնային
հեղեղները
ծնվում են
պսակի
արտաքին
սահմանի մոտ և
սլանում են
դեպի պսակ
առաջացնող
էլեկտրոդը`
անոդը:
Հեղեղները
ծնող
էլեկտրոնների
գոյացումը
պայմանավորված
է
լուսաիոնացումով,
որն
առաջանում է
պսակ
առաջացնող
շերտի
ճառագայթումից:
Պսակի
արտաքին
տիրույթում
հոսանք կրողները
դրական
իոններն են,
որոնք դաշտի
ազդեցության
տակ շարժվում
են դեպի անոդ:
Բարձր լարման հարմարանքներում, մասնավորապես բարձր լարման հաղորդալարերում, պսակաձև պարպումը հանգեցնում է հոսանքի վնասակար կորուստների: Այդ պատճառով հարկ է լինում միջոցներ ձեռնարկել նրա վերացման համար: Այդ նպատակով բարձր լարման հաղորդալարերը վերցնում են բավականաչափ մեծ տրամագծով` այնքան մեծ, ինչքան մեծ է գծի լարումը: Պսակաձև պարպումը օգտագործվում է էլեկտրազտիչներում, որոնք կիրառվում են արդյունաբերական գազերը խառնուրդներից մաքրելու համար:
5.6 ՊԼԱԶՄԱ ԵՎ ՆՐԱ ՀԱՏԿՈՒԹՅՈՒՆՆԵՐԸ
Պլազմա է
կոչվում
ուժեղ
իոնացված
գազը, ուր
դրական և
բացասական
լիցքերի
կոնցենտրացիաները
գործնականում
միատեսակ են:
Պլազման
էլեկտրոններից,
իոններից և չեզոք
ատոմներից
կազմված
էլեկտրաչեզոք
համակարգ է:
Պլազմա
կարելի է
ստանալ ոչ
միայն գազի
տաքացման,
այլև տարբեր
իոնարարների
(զանազան
ճառագայթումների,
լիցքավորված
մասնիկների)
ազդեցությամբ:
Տարբերում են բարձրջերմաստիճանային
պլազմա, որն
առաջանում է
գերբարձր
ջերմաստիճանների
դեպքում, և գազապարպման
պլազմա, որն
առաջանում է
գազային
պարպման
դեպքում: Պլազման
բնութագրվում
է ![]() իոնացման
աստիճանով, որը
լիցքավորված
մասնիկների
կոնցենտրացիայի
և մասնիկների
լրիվ
կոնցենտրացիայի
հարաբերությունն
է: Թույլ
իոնացված
պլազմայում
իոնացման
աստիճանը
իոնացման
աստիճանով, որը
լիցքավորված
մասնիկների
կոնցենտրացիայի
և մասնիկների
լրիվ
կոնցենտրացիայի
հարաբերությունն
է: Թույլ
իոնացված
պլազմայում
իոնացման
աստիճանը ![]() կարգի
մեծություն է,
իսկ լրիվ
իոնացված
պլազմայում
կարգի
մեծություն է,
իսկ լրիվ
իոնացված
պլազմայում ![]()
Լիցքավորված
մասնիկները
(էլեկտրոնները,
իոնները),
գազապարպման
պլազմայում
գտնվելով արագացնող
էլեկտրական
դաշտում,
ունեն տարբեր
միջին
կինետիկ
էներգիաներ:
Սա նշանակում
է, որ
էլեկտրոնային
գազի ![]() ջերմաստիճանը
և իոնային
գազի
ջերմաստիճանը
և իոնային
գազի ![]() ջերմաստիճանը
տարբեր են,
ընդ որում
ջերմաստիճանը
տարբեր են,
ընդ որում ![]() Այդ
ջերմաստիճանների
անհամապատասխանությունը
ցույց է
տալիս, որ
գազապարպման
պլազման անհվասարակշիռ
է, դրա համար
էլ այն
կոչվում է ոչ
իզոթերմիկ:
Գազապարպման
պլազմայում
ռեկոմբինացիայի
պրոցեսում
լիցքավորված
մասնիկների
նվազումը
լրացվում է
էլեկտրական
դաշտով
արագացված էլեկտրոնների
հարվածային
իոնացումով:
Էլեկտրական
դաշտի
վերացումը
առաջ է բերում
գազապարպման
պլազմայի
անհետացում:
Բարձրջերմաստիճանային
պլազման
հավասարակշիռ
և իզոթերմիկ
է, այսինքն
որոշակի
ջերմաստիճանի
դեպքում
լիցքավորված
մասնիկների
նվազումը լրացվում
է ջերմաստիճանային
իոնացման
արդյունքով:
Այդպիսի պլազմայում
պահպանվում է
պլազման
կազմող տարբեր
մասնիկների
միջին
կինետիկ
էներգիաների
հավասարությունը:
Նման
պլազմայի
վիճակում են
գտնվում
աստղերը,
աստղային
մթնոլորտը,
Արեգակը:
Նրանց
ջերմաստիճանը
հասնում է
տասնյակ
միլիոն աստիճանի:
Պլազմայի
գոյության
պայմանը
լիցքավորված
մասնիկների
որոշ
նվազագույն
խտությունն է,
որից սկսած
կարելի է
խոսել
պլազմայի մասին:
Այդ
խտությունը
որոշվում է
ֆիզիկայում
պլազմայի
Այդ
ջերմաստիճանների
անհամապատասխանությունը
ցույց է
տալիս, որ
գազապարպման
պլազման անհվասարակշիռ
է, դրա համար
էլ այն
կոչվում է ոչ
իզոթերմիկ:
Գազապարպման
պլազմայում
ռեկոմբինացիայի
պրոցեսում
լիցքավորված
մասնիկների
նվազումը
լրացվում է
էլեկտրական
դաշտով
արագացված էլեկտրոնների
հարվածային
իոնացումով:
Էլեկտրական
դաշտի
վերացումը
առաջ է բերում
գազապարպման
պլազմայի
անհետացում:
Բարձրջերմաստիճանային
պլազման
հավասարակշիռ
և իզոթերմիկ
է, այսինքն
որոշակի
ջերմաստիճանի
դեպքում
լիցքավորված
մասնիկների
նվազումը լրացվում
է ջերմաստիճանային
իոնացման
արդյունքով:
Այդպիսի պլազմայում
պահպանվում է
պլազման
կազմող տարբեր
մասնիկների
միջին
կինետիկ
էներգիաների
հավասարությունը:
Նման
պլազմայի
վիճակում են
գտնվում
աստղերը,
աստղային
մթնոլորտը,
Արեգակը:
Նրանց
ջերմաստիճանը
հասնում է
տասնյակ
միլիոն աստիճանի:
Պլազմայի
գոյության
պայմանը
լիցքավորված
մասնիկների
որոշ
նվազագույն
խտությունն է,
որից սկսած
կարելի է
խոսել
պլազմայի մասին:
Այդ
խտությունը
որոշվում է
ֆիզիկայում
պլազմայի ![]() անհավասարությունից,
որտեղ
անհավասարությունից,
որտեղ ![]() -ը
լիցքավորված
մասնիկների
համակարգի
գծային չափն
է,
-ը
լիցքավորված
մասնիկների
համակարգի
գծային չափն
է, ![]() -ն այսպես
կոչված
դեբայեվյան
էկրանացման
շառավիղն է`
այն
հեռավորությունը,
որի վրա տեղի
ունենում
պլազմայի
ցանկացած
լիցքի կուլոնյան
դաշտի
էկրանացումը:
-ն այսպես
կոչված
դեբայեվյան
էկրանացման
շառավիղն է`
այն
հեռավորությունը,
որի վրա տեղի
ունենում
պլազմայի
ցանկացած
լիցքի կուլոնյան
դաշտի
էկրանացումը:
Պլազման
օժտված է
հետևյալ
հիմնական
հատկություններով.
գազի բարձր
աստիճանի
իոնացումով,
սահմանում
լրիվ
իոնացումով,
արդյունարար
տարածական
լիցքի զրոյի
հավասարվելով,
(պլազմայում
դրական և
բացասական լիցքերի
կոնցենտրացիաները
գործնականում
միատեսակ են),
բարձր
էլեկտրահաղորդականությամբ,
ընդ որում`
հոսանքը
պլազմայում
հիմնականում
ստեղծվում է
էլեկտրոններով,
որպես ավելի
շարժուն մասնիկներ,
էլեկտրական և
մագնիսական
դաշտերի
ուժեղ
փոխազդեցությամբ,
պլազմայում
էլեկտրոնների
բարձր հաճախության
տատանումներով
(![]()
![]() Հց): Այս
հատկությունները
որոշում են
պլազմայի որակական
յուրահատկությունը
թույլ տալով պլազման
ընդունել
որպես նյութի
չորրորդ վիճակ:
Հց): Այս
հատկությունները
որոշում են
պլազմայի որակական
յուրահատկությունը
թույլ տալով պլազման
ընդունել
որպես նյութի
չորրորդ վիճակ:
Պլազմայի
ֆիզիկական
հատկությունների
ուսումնասիրությունը
հնարավորություն
է տալիս մի
կողմից
լուծելու
աստղագիտության
շատ հիմնախնդիրներ,
քանի որ
տիեզերական
տարածության
մեջ նյութի
ամենատարածված
վիճակը պլազման
է, իսկ մյուս
կողմից
բացում է
սկզբունքային
հնարավորություններ`
կառավարվող
ջերմամիջուկային
ռեակցիաներ
իրականացնելու:
Կառավարվող
ջերմամիջուկային
ռեակցիայի
ուսումնասիրության
հիմնական
օբյեկտը
բարձրջերմաստիճանային
պլազման է`
դեյտերիումից
և տրիտիից (![]() Կ):
Կ):
Ցածրջերմաստիճանային
պլազման (<![]() Կ)
կիրառվում է
գազային լազերներում,
ջերմաէլեկտրոնային
փոխարկիչներում
և մագնիսահիդրոդինամիկական
գեներատորներում,
անմիջականորեն
ջերմային
էներգիան
էլեկտրականի
փոխարինող
սարքերում,
պլազմային հրթիռային
շարժիչներում,
որոնք
հեռանկարային
են երկարատև
տիեզերական
թռիչքների
համար:
Կ)
կիրառվում է
գազային լազերներում,
ջերմաէլեկտրոնային
փոխարկիչներում
և մագնիսահիդրոդինամիկական
գեներատորներում,
անմիջականորեն
ջերմային
էներգիան
էլեկտրականի
փոխարինող
սարքերում,
պլազմային հրթիռային
շարժիչներում,
որոնք
հեռանկարային
են երկարատև
տիեզերական
թռիչքների
համար:
Ցածրջերմաստիճանային պլազման, որը ստանում են պլազմատրոններում, օգտագործվում են մետաղների կտրման և եռակցման, որոշ քիմիական միացություններ ստանալու համար (օրինակ, իներտ գազերի հալոգենիդներ), որոնք չի կարելի ստանալ այլ եղանակներով:
ԳԼՈՒԽ 6. ՄԱԳՆԻՍԱԿԱՆ ԴԱՇՏԸ ՎԱԿՈՒՈՒՄՈՒՄ
6.1. ՄԱԳՆԻՍԱԿԱՆ ԴԱՇՏ: ՄԱԳՆԻՍԱԿԱՆ ԴԱՇՏԻ
ԻՆԴՈՒԿՑԻԱՅԻ ՎԵԿՏՈՐ
1820թ. դանիացի ֆիզիկոս Էրստեդը (1777-1851) փորձնականորեն հայտնաբերեց, որ էլեկտրական հոսանքն իր շուրջը ստեղծում է մագնիսական դաշտ: Վերջինս հայտնաբերվում է մագնիսական սլաքի վրա թողած ազդեցությամբ (նկ.63): Հարկ է նշել, որ մագնիսական սլաքի վրա ազդեցությունը (տվյալ դեպքում` սլաքի պտույտը) կախված է հոսանքի մեծությունից, ուղղությունից և հոսանքի ու մագնիսական սլաքի փոխադարձ դիրքից:

Այսպիսով, շարժվող լիցքերը (հոսանքները) փոփոխում են իրենց շրջապատող տարածության հատկությունները՝ նրա մեջ ստեղծելով մագնիսական դաշտ: Դաշտը դրսևորվում է նրանով, որ նրա մեջ շարժվող լիցքերի վրա ուժեր են ազդում:
Ինչպես էլեկտրական դաշտն ուսումնասիրելու համար օգտագործեցինք փորձնական կետային լիցք, այնպես էլ մագնիսական դաշտը ուսումնասիրելու համար կիրառենք փորձնական հոսանք, որն անցնում է շատ փոքր չափեր ունեցող հարթ փակ կոնտուրով: Տարածության մեջ կոնտուրի կողմնորոշումը կբնութագրենք այդ կոնտուրին տարած այնպիսի նորմալի ուղղության միջոցով, որը հոսանքի ուղղության հետ կապված է աջ պտուտակի կանոնով: Այդպիսի նորմալը կանվանենք դրական (նկ.64):

Եթե
փորձնական
կոնտուրը
մտցնենք
մագնիսական
դաշտ,
կտեսնենք, որ
դաշտը
կոնտուրի վրա
թողնում է
կողմնորոշող
ազդեցություն՝
դասավորելով
նրան իր
դրական
նորմալի
նկատմամբ որոշակի
ուղղությամբ:
Այդ
ուղղությունը
ընդունում
ենք որպես
դաշտի ուղղություն
տվյալ կետում:
Եթե կոնտուրը
շրջենք
այնպես, որ
նորմալի և
դաշտի
ուղղությունները
չհամընկնեն,
ապա կառաջանա
մի պտտող մոմենտ,
որը կձգտի
կոնտուրը
վերադարձնել
իր հավասարակշռության
դիրքը:
Մոմենտի
մեծությունը
կախված է
նորմալի և
դաշտի
ուղղության
միջև եղած ![]() անկյունից,
ընդ որում իր
ամենամեծ Mmax
արժեքին է
հասնում, երբ
անկյունից,
ընդ որում իր
ամենամեծ Mmax
արժեքին է
հասնում, երբ ![]() (
(![]() դեպքում
մոմենտը
հավասար է
զրոյի):
դեպքում
մոմենտը
հավասար է
զրոյի):
Պտտող մոմենտը կախում ունի ինչպես տվյալ կետում դաշտի հատկություններից, այնպես էլ կոնտուրի հատկություններից: Եթե դաշտի նույն կետում տարբեր փորձնական կոնտուրներ տեղադրենք, կտեսնենք, որ Mmax -ի մեծությունը համեմատական է կոնտուրում եղած հոսանքի ուժին ու կոնտուրի S մակերեսին և կախում չունի կոնտուրի ձևից: Այսպիսով, հոսանքակիր հարթ կոնտուրի վրա մագնիսական ազդեցությունը որոշվում է
![]() (6.1)
(6.1)
մեծությամբ, որն անվանում են կոնտուրի մագնիսական մոմենտ:
Բացի հոսանքի ուժից և մակերեսից, կոնտուրը բնութագրվում է նաև մագնիսական դաշտում իր ունեցած կողմնորոշումով: Այդ պատճառով մագնիսական մոմենտը պետք է դիտել որպես մի վեկտոր, որի ուղղությունը համընկնում է կոնտուրի դրական նորմալի ուղղությանը՝
![]() , (6.2)
, (6.2)
որտեղ ![]() -ը
միավոր
վեկտոր է:
-ը
միավոր
վեկտոր է:
![]() -ի
տարբեր
արժեքներ
ունեցող
տարբեր
փորձնական
կոնտուրների
վրա դաշտի
տվյալ կետում
ազդում են
տարբեր
մեծության Mmax
պտտող
մոմենտներ:
Սակայն
-ի
տարբեր
արժեքներ
ունեցող
տարբեր
փորձնական
կոնտուրների
վրա դաշտի
տվյալ կետում
ազդում են
տարբեր
մեծության Mmax
պտտող
մոմենտներ:
Սակայն ![]() հարաբերությունը
բոլոր
կոնտուրների
համար դաշտի
տվյալ կետում
նույնը կլինի
և կարող է ընդունվել
դաշտը
քանակապես
բնութագրելու
համար: Այդ
հարաբերությունը
նշանակում են
B-ով և
անվանում են
մագնիսական
դաշտի
ինդուկցիա.
հարաբերությունը
բոլոր
կոնտուրների
համար դաշտի
տվյալ կետում
նույնը կլինի
և կարող է ընդունվել
դաշտը
քանակապես
բնութագրելու
համար: Այդ
հարաբերությունը
նշանակում են
B-ով և
անվանում են
մագնիսական
դաշտի
ինդուկցիա.

Մագնիսական
ինդուկցիան
մի վեկտոր է,
որի ուղղությունը
համընկնում է
փորձնական
կոնտուրի
դրական
նորմալի
ուղղության
հետ (նրա հավասարակշռված
դիրքում մենք
այն անվանեցինք
դաշտի
ուղղություն):
(6.3) բանաձևը
որոշում է վեկտորի
չափը:
Մագնիսական
դաշտի
ինդուկցիան ՄՀ-ում
չափվում է [![]() ] = 1 Ն/Ամ = 1 Տլ
(տեսլայով):
] = 1 Ն/Ամ = 1 Տլ
(տեսլայով):
Կարող
ենք ասել, որ ![]() -ն
բնութագրում
է մագնիսական
դաշտի
ազդեցությունը
հոսանքի վրա
և, հետևաբար,
էլեկտրական
դաշտի
-ն
բնութագրում
է մագնիսական
դաշտի
ազդեցությունը
հոսանքի վրա
և, հետևաբար,
էլեկտրական
դաշտի ![]() լարվածության
նմանակն է,
որը
բնութագրում
է էլեկտրական
դաշտի
ուժային
ազդեցությունը
լիցքի վրա:
լարվածության
նմանակն է,
որը
բնութագրում
է էլեկտրական
դաշտի
ուժային
ազդեցությունը
լիցքի վրա:
Մագնիսական դաշտը, ինչպես և էլեկտրական դաշտը, ենթարկվում է վերադրման սկզբունքին: Եթե մագնիսական դաշտը ստեղծվում է մի քանի հոսանքներով կամ շարժվող լիցքերով, ապա արդյունարար դաշտի մագնիսական ինդուկցիայի վեկտորը դաշտի որևէ կետում հավասար է հոսանքների կամ շարժվող լիցքերից յուրաքանչյուրի ստեղծած դաշտերի ինդուկցիաների վեկտորական գումարին.

որտեղ
![]() -ն
-ն ![]() -րդ
հոսանքի
ինդուկցիայի
վեկտորն է
դիտարկվող
կետում:
-րդ
հոսանքի
ինդուկցիայի
վեկտորն է
դիտարկվող
կետում:
6.2. ՄԱԳՆԻՍԱԿԱՆ ԴԱՇՏԻ ԳՐԱՖԻԿԱԿԱՆ ՊԱՏԿԵՐՈՒՄԸ
Մագնիսական
դաշտի
ակնառու
պատկերը
կարելի է
ստանալ,
այսպես
կոչված,
մագնիսական
ինդուկցիայի
գծերի
կառուցմամբ:
Մագնիսական
ինդուկցիայի
գծեր են
կոչվում այն
գծերը, որոնց
յուրաքանչյուր
կետում
տարված
շոշափողներն
ունեն նույն
ուղղությունը,
ինչ որ ![]() վեկտորը
դաշտի տվյալ
կետում (նկ.65):
Այդ տեսակետից
մագնիսական
ինդուկցիայի
գծերը նման են
էլեկտրաստատիկ
դաշտի
լարվածության
գծերին:
վեկտորը
դաշտի տվյալ
կետում (նկ.65):
Այդ տեսակետից
մագնիսական
ինդուկցիայի
գծերը նման են
էլեկտրաստատիկ
դաշտի
լարվածության
գծերին:

Կառուցենք մագնիսական ինդուկցիայի գծերը ուղղագիծ հոսանքակիր հաղորդչի մագնիսական դաշտի համար: Կատարված փորձերից հետևում է, որ մագնիսական դաշտի ինդուկցիայի գծերը կլինեն հոսանքակիր հաղորդչին ուղղահայաց հարթության մեջ գտնվող համակենտրոն շրջանագծեր: Շրջանագծի կենտրոնը գտնվում է հաղորդչի առանցքի վրա (նկ.66): Գծերի վրա եղած սլաքները ցույց են տալիս, թե որ կողմն է ուղղված մագնիսական դաշտի ինդուկցիայի վեկտորը` տվյալ գծին տարված շոշափողը: Այդ ուղղությունը կարելի է որոշել խցանահանի կանոնով: Եթե խցանահանի սայրի համընթաց շարժման ուղղությունը համընկնի հաղորդչում հոսանքի ուղղությանը, ապա նրա բռնակի պտտման ուղղությունը կհամընկնի մագնիսական ինդուկցիայի վեկտորի ուղղության հետ: Ինչպես և էլեկտրական դաշտի լարվածության գծերի դեպքում, մագնիսական ինդուկցիայի գծերը տանում են այնպես, որ որքան ավելի ուժեղ է դաշտը, այնքան ավելի մեծ լինի նրանց խտությունը: Մագնիսական դաշտը կարելի է էապես ուժեղացնել, եթե հոսանքակիր հաղորդիչը փաթաթվի պարույրի տեսքով: Արդյունքում ստացված հոսանքակիր կոճն անվանում են սոլենոիդ: Սոլենոիդի մագնիսական դաշտի ինդուկցիայի գծերը պատկերված են նկար 67-ում: Եթե կոճի երկարությունը շատ մեծ է նրա լայնական չափերից, ապա նրա ներսում դաշտը գործնականում կարելի է համարել համասեռ (ինդուկցիայի գծերը միմյանց զուգահեռ և նույն խտությամբ գծեր են):

Մագնիսական ինդուկցիայի գծերի կարևոր առանձնահատկությունն այն է, որ նրանք ո´չ սկիզբ ունեն, ո´չ էլ վերջ: Դրանք միշտ փակ են: Հիշենք, որ էլեկտրական դաշտում դրությունն այլ է: Էլեկտրաստատիկ դաշտի ուժագծերը բոլոր դեպքերում սկիզբ են առնում դրական լիցքերից և վերջանում բացասականների վրա: Փակ ուժագծերով դաշտերը կոչվում են մրրկային: Մագնիսական դաշտը մրրկային դաշտ է: Մագնիսական ինդուկցիայի գծերի փակ լինելը մագնիսական դաշտի հիմնական հատկությունն է, որից հետևում է, որ մագնիսական դաշտը աղբյուրներ չունի: Բնության մեջ էլեկտրական լիցքերի նման մագնիսական լիցքեր գոյություն չունեն:
Բիո-Սավար-Լապլաս
գիտնականների
եռյակը համատեղ
տվել է մի
օրենք, որի
օգնությամբ
հնարավորություն
է ընձեռվում
դաշտի
ցանկացած
կետում
հաշվել
ցանկացած ձևի
հոսանքատար
հաղորդչի
ստեղծած
մագնիսական
դաշտի
ինդուկցիան:
Նրանք
վերլուծելով
փորձնական
տվյալները`
գտան, որ
ցանկացած
հոսանքի
մագնիսական
դաշտը կարելի
է հաշվել
որպես այնպիսի
դաշտերի
վեկտորական
գումար, որոնք
ստեղծվում են
հոսանքի
առանձին
տարրական
տեղամասերով:
Հոսանքի ![]() տարրով
ստեղծված
դաշտի
մագնիսական
ինդուկցիայի
համար նրանք
տվեցին
հետևյալ
բանաձևը՝
տարրով
ստեղծված
դաշտի
մագնիսական
ինդուկցիայի
համար նրանք
տվեցին
հետևյալ
բանաձևը՝

որտեղ
![]() -ն
համեմատականության
գործակից է,
որը կախված է
չափման
միավորների
ընտրությունից,
-ն
համեմատականության
գործակից է,
որը կախված է
չափման
միավորների
ընտրությունից,
![]() -ն հոսանքի
ուժն է,
-ն հոսանքի
ուժն է, ![]() -ը մի
վեկտոր է, որը
համընկնում է
հոսանքի տարրական
տեղամասի հետ
և ունի
հոսանքի
ուղղությունը
(նկ. 68),
-ը մի
վեկտոր է, որը
համընկնում է
հոսանքի տարրական
տեղամասի հետ
և ունի
հոսանքի
ուղղությունը
(նկ. 68), ![]() -ը մի
վեկտոր է, որը
հոսանքի
տարրից
տարված է մինչև
այն կետը,
որտեղ
որոշվում է
-ը մի
վեկտոր է, որը
հոսանքի
տարրից
տարված է մինչև
այն կետը,
որտեղ
որոշվում է ![]() -ն, իսկ
-ն, իսկ ![]() -ը այդ
վեկտորի չափն
է: (6.5)
առնչությունը
կոչվում է
Բիո-Սավար-Լապլասի
օրենք:
-ը այդ
վեկտորի չափն
է: (6.5)
առնչությունը
կոչվում է
Բիո-Սավար-Լապլասի
օրենք: ![]() վեկտորն
ուղղահայաց է
վեկտորն
ուղղահայաց է ![]() -ով և այն
կետով անցնող
հարթությանը,
որտեղ որոշվում
է դաշտը, ընդ որում
ուղղված է
այնպես, որ
-ով և այն
կետով անցնող
հարթությանը,
որտեղ որոշվում
է դաշտը, ընդ որում
ուղղված է
այնպես, որ ![]() -ի շուրջը
կատարվող
պտույտը
-ի շուրջը
կատարվող
պտույտը ![]() -ի
ուղղությամբ
-ի
ուղղությամբ ![]() -ի հետ
կապված է աջ պտուտակի
կանոնով:
-ի հետ
կապված է աջ պտուտակի
կանոնով: ![]() -ի չափի
համար կարող
ենք գրել.
-ի չափի
համար կարող
ենք գրել.

որտեղ
![]() -ն
-ն ![]() և
և ![]() վեկտորների
միջև կազմված
անկյունն է:
վեկտորների
միջև կազմված
անկյունն է:

Ռացիոնալացված ձևով Բիո-Սավար-Լապլասի օրենքը գրվում է հետևյալ կերպ.

այսինքն՝
ընդունվում է ![]()
![]() Հն/մ-ը
մագնիսական
հաստատունն է:
Հն/մ-ը
մագնիսական
հաստատունն է:
6.4. ՈՒՂԻՂ ԵՎ ՇՐՋԱՆԱՅԻՆ ՀՈՍԱՆՔՆԵՐԻ ԴԱՇՏԵՐԸ
Բիո-Սավար-Լապլասի օրենքը կիրառենք պարզագույն հոսանքների դաշտերը հաշվելու համար:

Դիցուք
տրված է ![]() վերջավոր
երկարությամբ
լարը, որով
նշված
ուղղությամբ
հոսում է
վերջավոր
երկարությամբ
լարը, որով
նշված
ուղղությամբ
հոսում է ![]() հոսանքը:
Անհրաժեշտ է
գտնել
մագնիսական
դաշտի
ինդուկցիան
լարից
հոսանքը:
Անհրաժեշտ է
գտնել
մագնիսական
դաշտի
ինդուկցիան
լարից ![]() հեռավորության
վրա որևէ O
կետում (նկ.69):
Համաձայն
Բիո-Սավար-Լապլասի`
լարը
բաժանենք
հեռավորության
վրա որևէ O
կետում (նկ.69):
Համաձայն
Բիո-Սավար-Լապլասի`
լարը
բաժանենք ![]() հոսանքի
տարրերի և
նրանցից յուրաքանչյուրի
համար գրենք
Բիո-Սավար-Լապլասի
օրենքը.
հոսանքի
տարրերի և
նրանցից յուրաքանչյուրի
համար գրենք
Բիո-Սավար-Լապլասի
օրենքը.

Ակնհայտ
է, որ ![]() կետում
ամբողջ լարի
առանձին
կետում
ամբողջ լարի
առանձին ![]() մասերը
կստեղծեն
միևնույն
ուղղությամբ
մասերը
կստեղծեն
միևնույն
ուղղությամբ ![]() դաշտեր,
ուստի դրանց
վեկտորական
վերադրումը
կբերի
մեծությունների
թվաբանական գումարմանը,
դաշտեր,
ուստի դրանց
վեկտորական
վերադրումը
կբերի
մեծությունների
թվաբանական գումարմանը,
![]() տարրի
մագնիսական
դաշտի
ինդուկցիայի
մեծությունը
կլինի
տարրի
մագնիսական
դաշտի
ինդուկցիայի
մեծությունը
կլինի

Տարբեր
![]() -երի
համար տարբեր
են ինչպես
-երի
համար տարբեր
են ինչպես ![]() անկյունը,
այնպես էլ
անկյունը,
այնպես էլ ![]() -ը:
Նշված երկու
փոփոխականներից
անցնենք մեկին`
-ը:
Նշված երկու
փոփոխականներից
անցնենք մեկին`
![]() -ին: C
կետից
-ին: C
կետից ![]() -ին
իջեցնենք
-ին
իջեցնենք ![]() ուղղահայացը
և օգտվենք
հետևյալ
ակնհայտ առնչություններից.
ուղղահայացը
և օգտվենք
հետևյալ
ակնհայտ առնչություններից.

![]() և dl-ի
վերջին
արտահայտությունները
տեղադրելով
(6.9)-ի մեջ` կստանանք
և dl-ի
վերջին
արտահայտությունները
տեղադրելով
(6.9)-ի մեջ` կստանանք
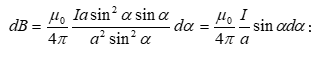
MN
վերջավոր
երկարությամբ
լարի ստեղծած
ինդուկցիան
հաշվելու
համար ![]() սահմաններում
կատարենք
ինտեգրում.
սահմաններում
կատարենք
ինտեգրում.

Անվերջ
ուղիղ
հոսանքի
բոլոր
տարրական
մասերի համար ![]() անկյունը
փոփոխվում է 0-ից
մինչև
անկյունը
փոփոխվում է 0-ից
մինչև ![]() ,
հետևաբար,
կստանանք.
,
հետևաբար,
կստանանք.
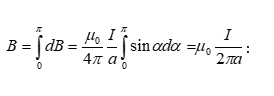
Այսպիսով, անվերջ ուղիղ հոսանքի մագնիսական դաշտի ինդուկցիան որոշվում է հետևյալ բանաձևով.

Քննարկենք այն դաշտը, որը ստեղծվում է R շառավղով շրջանագծի ձև ունեցող բարակ լարով անցնող հոսանքով (շրջանային հոսանք): Որոշենք մագնիսական դաշտի ինդուկցիան շրջանային հոսանքի կենտրոնում (նկ. 70):

Հոսանքի
յուրաքանչյուր
տարր
կենտրոնում ստեղծում
է ![]() ինդուկցիա,
որն ունի
կոնտուրին
տարած դրական
նորմալի
ուղղությունը:
Բոլոր
ինդուկցիա,
որն ունի
կոնտուրին
տարած դրական
նորմալի
ուղղությունը:
Բոլոր ![]() վեկտորների
գումարումը
հանգում է
նրանց մոդուլների
գումարմանը: Համաձայն
Բիո-Սավար-Լապլասի
օրենքի
վեկտորների
գումարումը
հանգում է
նրանց մոդուլների
գումարմանը: Համաձայն
Բիո-Սավար-Լապլասի
օրենքի
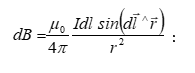
Մեր
դիտարկած
դեպքի համար ![]() շառավիղ
վեկտորը
ուղղահայաց է
հոսանքի
շառավիղ
վեկտորը
ուղղահայաց է
հոսանքի ![]() տարրին,
իսկ ըստ
մոդուլի
հավասար է
գալարի շառավղին,
այնպես, որ
տարրին,
իսկ ըստ
մոդուլի
հավասար է
գալարի շառավղին,
այնպես, որ ![]() և r =R :
Ուստի
կստանանք`
և r =R :
Ուստի
կստանանք`

Արդյունարար դաշտի ինդուկցիան գալարի կենտրոնում կստանանք, եթե (6.13)-ը ինտեգրենք

Այժմ
հաշվենք
մագնիսական
դաշտի
ինդուկցիան
շրջանային
հոսանքի
առանցքին
կոնտուրի հարթությունից
![]() հեռավորության
վրա: Դիցուք
տրված է
հեռավորության
վրա: Դիցուք
տրված է ![]() շառավղով
շառավղով
![]() հոսանքատար
գալարը (նկ.71):
հոսանքատար
գալարը (նկ.71):

Համաձայն
Բիո-Սավար-Լապլասի
օրենքի`
գալարը բաժանենք
![]() հոսանքի
տարրերի:
Գծագրում
ցույց տանք տրամագծորեն
հակադիր
երկու
հոսանքի
տարրերի:
Գծագրում
ցույց տանք տրամագծորեն
հակադիր
երկու ![]() տարրերին
համապատասխանող
տարրերին
համապատասխանող
![]() ինդուկցիաները:
ինդուկցիաները:
![]() -ը և
-ը և ![]() -ը համապատասխանաբար
-ը համապատասխանաբար
![]() և
և ![]() տարրերի
ինդուկցիաներն
են: Դժվար չէ
նկատել, որ
նրանցից
յուրաքանչյուրի
հորիզոնական
բաղադրիչները
իրար
կչեզոքացնեն:
Այդ պատճառով
կարելի է
հաշվել
ցանկացած
տարրերի
ինդուկցիաներն
են: Դժվար չէ
նկատել, որ
նրանցից
յուրաքանչյուրի
հորիզոնական
բաղադրիչները
իրար
կչեզոքացնեն:
Այդ պատճառով
կարելի է
հաշվել
ցանկացած ![]() տարրի
ստեղծած
տարրի
ստեղծած ![]() վեկտորի
միայն
ուղղաձիգ
բաղադրիչը.
վեկտորի
միայն
ուղղաձիգ
բաղադրիչը.
![]() ,
,
որտեղ
![]() -ն,
համաձայն
Բիո-Սավար-Լապլասի
օրենքի (քանի որ
-ն,
համաձայն
Բիո-Սավար-Լապլասի
օրենքի (քանի որ
![]() )`
)`
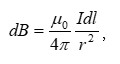
հետևաբար`
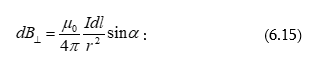
r-ը և ![]() -ն
արտահայտենք h-ով.
-ն
արտահայտենք h-ով.

Ինտեգրելով ամբողջ կոնտուրով`

Ինչպես
և պետք էր
սպասել, (6.16)
բանաձևը ![]() դեպքում
վերածվում է
շրջանային
հոսանքի
կենտրոնում
մագնիսական
ինդուկցիայի
համար
ստացված (6.14)
բանաձևին:
դեպքում
վերածվում է
շրջանային
հոսանքի
կենտրոնում
մագնիսական
ինդուկցիայի
համար
ստացված (6.14)
բանաձևին:
(6.16)
առնչության
համարիչում
գտնվող ![]() մեծությունը
հավասար է
կոնտուրի pm
մագնիսական
մոմենտին:
Կոնտուրից
մեծ հեռավորության
վրա
հայտարարում
մեծությունը
հավասար է
կոնտուրի pm
մագնիսական
մոմենտին:
Կոնտուրից
մեծ հեռավորության
վրա
հայտարարում ![]() -ն
-ն ![]() -ու համեմատ
կարելի է
անտեսել: Այդ
դեպքում (6.16) բանաձևը
կստանա
հետևյալ
տեսքը`
-ու համեմատ
կարելի է
անտեսել: Այդ
դեպքում (6.16) բանաձևը
կստանա
հետևյալ
տեսքը`

որը
համանման է
դիպոլի
առանցքի վրա
դաշտի լարվածության
համար
ստացված (1.38)
արտահայտությանը:
Հաշվի
առնելով, որ
շրջանային
հոսանքի առանցքի
վրա ![]() -ն
և
-ն
և ![]() -ը
ուղղված են
կոնտուրին
տարած
նորմալի
ուղղությամբ,
կարող ենք
գրել.
-ը
ուղղված են
կոնտուրին
տարած
նորմալի
ուղղությամբ,
կարող ենք
գրել.

6.5. ՇԱՐԺՎՈՂ ԷԼԵԿՏՐԱԿԱՆ ԼԻՑՔԻ ՄԱԳՆԻՍԱԿԱՆ ԴԱՇՏԸ
Իոֆֆեի կողմից էլեկտրոնային փնջերի հետ կատարված փորձերն ապացուցում են շարժվող էլեկտրական լիցքերի շուրջը մագնիսական դաշտի գոյությունը: Բիո-Սավար-Լապլասի օրենքը թույլ է տալիս գտնել շարժվող էլեկտրական լիցքի ստեղծած մագնիսական դաշտի ինդուկցիայի և լարվածության վեկտորների արտահայտությունները: Եթե միջավայրը համասեռ և իզոտրոպ է, ապա Բիո-Սավար-Լապլասի օրենքը կարելի է գրել հետևյալ տեսքով՝

որտեղ
![]() -ն
չափայնություն
չունեցող
մեծություն է,
որը
բնութագրում
է միջավայրի
մագնիսական
հատկությունները
և կոչվում է
միջավայրի
հարաբերական
մագնիսական
թափանցելիություն:
Այն կախված չէ
միավորների
համակարգի
ընտրությունից
և
վակուումում
հավասար է
մեկի:
-ն
չափայնություն
չունեցող
մեծություն է,
որը
բնութագրում
է միջավայրի
մագնիսական
հատկությունները
և կոչվում է
միջավայրի
հարաբերական
մագնիսական
թափանցելիություն:
Այն կախված չէ
միավորների
համակարգի
ընտրությունից
և
վակուումում
հավասար է
մեկի:
Բիո-Սավար-Լապլասի օրենքը ներկայացնենք՝

տեսքով:
Համասեռ
հաղորդչում
հաստատուն
հոսանքի ուժը
հոսանքի ![]() խտության
հետ կապված է
խտության
հետ կապված է ![]() առնչությունով,
որտեղ S-ը
հաղորդչի
լայնական
հատույթի
մակերեսն է:
Ուստի՝
առնչությունով,
որտեղ S-ը
հաղորդչի
լայնական
հատույթի
մակերեսն է:
Ուստի՝
![]() : (6.20)
: (6.20)
Հոսանքի խտության վեկտորը հավասար է.
![]() , (6.21)
, (6.21)
որտեղ
![]() -ն մասնիկի
լիցքն է:
Լիցքերի
-ն մասնիկի
լիցքն է:
Լիցքերի ![]() միջին
արագությամբ
կարգավորված շարժումը
հաղորդչում
ստեղծում է
միջին
արագությամբ
կարգավորված շարժումը
հաղորդչում
ստեղծում է ![]() էլեկտրական
հոսանք,
էլեկտրական
հոսանք, ![]() -ն հաղորդչի
միավոր
ծավալում
լիցքավորված
մասնիկների
թիվն է:
-ն հաղորդչի
միավոր
ծավալում
լիցքավորված
մասնիկների
թիվն է:
![]() -ի
արտահայտությունը
(6.21)-ից
տեղադրելով
(6.20)-ի մեջ՝ կստանանք.
-ի
արտահայտությունը
(6.21)-ից
տեղադրելով
(6.20)-ի մեջ՝ կստանանք.
![]() ,
,
![]() արտադրյալը
լիցքավորված
մասնիկների
լրիվ թիվն է,
որոնք գտնվում
են հաղորդչի
երկարության dl
տեղամասի
ծավալում, դրա
համար
արտադրյալը
լիցքավորված
մասնիկների
լրիվ թիվն է,
որոնք գտնվում
են հաղորդչի
երկարության dl
տեղամասի
ծավալում, դրա
համար
![]() : (6.22)
: (6.22)
Տեղադրելով
![]() -ի
արտահայտությունը
(6.19)-ի մեջ`
կստանանք.
-ի
արտահայտությունը
(6.19)-ի մեջ`
կստանանք.

կամ

Բոլոր
![]() թվով
թվով ![]() լիցքերը
շարժվում են
միևնույն
ուղղությամբ
և միատեսակ
արագությամբ:
Ուստի,
յուրաքանչյուր
լիցքով
ստեղծված
մագնիսական
դաշտի
լիցքերը
շարժվում են
միևնույն
ուղղությամբ
և միատեսակ
արագությամբ:
Ուստի,
յուրաքանչյուր
լիցքով
ստեղծված
մագնիսական
դաշտի ![]() ինդուկցիան
ինդուկցիան
![]() արդյունարար
ինդուկցիայից
dn անգամ փոքր
կլինի.
արդյունարար
ինդուկցիայից
dn անգամ փոքր
կլինի.
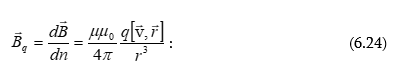
![]() արագությամբ
շարժվող
արագությամբ
շարժվող ![]() լիցքի
մագնիսական
դաշտի
լարվածությունը`
լիցքի
մագնիսական
դաշտի
լարվածությունը`
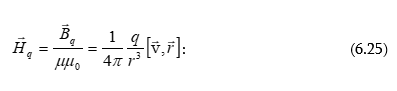

(6.24) և (6.25)
բանաձևերից
հետևում է, որ
շարժվող
լիցքի մագնիսական
դաշտի ![]() ինդուկցիան
և
ինդուկցիան
և ![]() լարվածությունը
կամայական
լարվածությունը
կամայական ![]() կետում
ուղղահայաց
են
կետում
ուղղահայաց
են ![]() լիցքի
լիցքի
![]() արագությունով
և
արագությունով
և ![]() շառավիղ-վեկտորով
կազմված
հարթությանը:
շառավիղ-վեկտորով
կազմված
հարթությանը:
Եթե ![]() , ապա
, ապա
![]() և
և ![]() վեկտորների
ծայրերից
նայելիս
կարճագույն պտույտը
վեկտորների
ծայրերից
նայելիս
կարճագույն պտույտը
![]() -ից
դեպի
-ից
դեպի ![]() տեղի
է ունենում
ժամացույցի
սլաքի
հակառակ ուղղությամբ
(նկ. 72ա):
տեղի
է ունենում
ժամացույցի
սլաքի
հակառակ ուղղությամբ
(նկ. 72ա):
Եթե
լիցքը՝ ![]() ,
ապա
,
ապա ![]() և
և
![]() վեկտորներն
ուղղված են
հակառակ
կողմը (նկ. 72բ):
վեկտորներն
ուղղված են
հակառակ
կողմը (նկ. 72բ):
Շարժվող
լիցքի
մագնիսական
դաշտը
տարածության
յուրաքանչյուր
կետում
կախված է
ժամանակից,
քանի որ լիցքի
շարժման
պրոցեսում
փոփոխվում է ![]() շառավիղվեկտորի
ինչպես
թվային
արժեքը, այնպես
էլ
ուղղությունը:
շառավիղվեկտորի
ինչպես
թվային
արժեքը, այնպես
էլ
ուղղությունը:
Շարժվող
լիցքի մագնիսական
դաշտի թվային
արժեքը ![]() կետում
հավասար է.
կետում
հավասար է.

(6.26)
բանաձևից
հետևում է, որ
շարժվող
լիցքի մագնիսական
դաշտի ![]() ինդուկցիան
ցանկացած
կետում ուղիղ
համեմատական
է լիցքի
մեծությանը,
նրա
արագությանն ու
միջավայրի
մագնիսական
թափանցելիությանը
և հակադարձ
համեմատական
է դաշտի տվյալ
կետից լիցքի
ունեցած հեռավորության
քառակուսուն:
ինդուկցիան
ցանկացած
կետում ուղիղ
համեմատական
է լիցքի
մեծությանը,
նրա
արագությանն ու
միջավայրի
մագնիսական
թափանցելիությանը
և հակադարձ
համեմատական
է դաշտի տվյալ
կետից լիցքի
ունեցած հեռավորության
քառակուսուն: ![]() ինդուկցիան
կախված է
ինդուկցիան
կախված է ![]() և
և ![]() վեկտորների
կազմած
անկյունից:
Այն առավելագույնն
է հարթության
այն կետերում,
որոնք տարված
են
վեկտորների
կազմած
անկյունից:
Այն առավելագույնն
է հարթության
այն կետերում,
որոնք տարված
են ![]() լիցքով
լիցքով ![]() արագության
վեկտորին
ուղղահայաց:
Ենթադրվում է,
որ լիցքի
արագությունը
շատ անգամ
փոքր է լույսի
արագությունից:
Դաշտի բոլոր
այն կետերում,
որոնք գտնվում
են լիցքի
շարժման
արագության
վեկտորին
ուղղահայաց:
Ենթադրվում է,
որ լիցքի
արագությունը
շատ անգամ
փոքր է լույսի
արագությունից:
Դաշտի բոլոր
այն կետերում,
որոնք գտնվում
են լիցքի
շարժման ![]() արագության
վեկտորի հետ
համընկնող
ուղղի վրա,
մագնիսական
դաշտի
ինդուկցիան
հավասար է զրոյի:
արագության
վեկտորի հետ
համընկնող
ուղղի վրա,
մագնիսական
դաշտի
ինդուկցիան
հավասար է զրոյի:
Այսպիսով, շարժվող լիցքի մագնիսական դաշտը, ի տարբերություն անշարժ լիցքերի էլեկտրաստատիկ դաշտի, համաչափ չէ (կետային լիցքի էլեկտրաստատիկ դաշտն օժտված է կենտրոնական համաչափությամբ):
6.6. ԳԱՈՒՍԻ ԹԵՈՐԵՄԸ ՄԱԳՆԻՍԱԿԱՆ ԴԱՇՏԻ ԻՆԴՈՒԿՑԻԱՅԻ ՎԵԿՏՈՐԻ
ՀԱՄԱՐ ԻՆՏԵԳՐԱԼԱՅԻՆ ԵՎ ԴԻՖԵՐԵՆՑԻԱԼ ՏԵՍՔՈՎ
Դիտարկենք
մագնիսական
դաշտ, որի
յուրաքանչյուր
կետում ![]() վեկտորը
նույնն է:
Տանենք այդ
դաշտում
կամայական
վեկտորը
նույնն է:
Տանենք այդ
դաշտում
կամայական ![]() հարթություն,
որի
հարթություն,
որի ![]() նորմալը
նորմալը ![]() -ի հետ
կազմում է
-ի հետ
կազմում է ![]() անկյուն
(նկ. 73):
անկյուն
(նկ. 73):
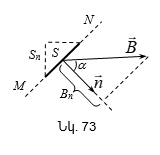
Հարթության
վրա առանձնացնենք
![]() մակերեսով
տեղամաս: S հարթ
մակերևույթի
միջով
մակերեսով
տեղամաս: S հարթ
մակերևույթի
միջով ![]() վեկտորի
հոսք է կոչվում
հետևյալ
մեծությունը.
վեկտորի
հոսք է կոչվում
հետևյալ
մեծությունը.
![]() : (6.27)
: (6.27)
(6.27) բանաձևը կարելի է գրել նաև հետևյալ տեսքով.
![]() , (6.28)
, (6.28)
որտեղ
![]() -ն
-ն ![]() վեկտորի
պրոյեկցիան է
վեկտորի
պրոյեկցիան է ![]() նորմալի
վրա, իսկ
նորմալի
վրա, իսկ ![]() -ն
-ն ![]() մակերևույթի
մակերեսի
պրոյեկցիան է
մակերևույթի
մակերեսի
պրոյեկցիան է ![]() վեկտորին
ուղղահայաց
հարթության
մեջ:
վեկտորին
ուղղահայաց
հարթության
մեջ:
Քանի որ մագնիսական դաշտը գրաֆիկորեն պատկերելիս ինդուկցիայի գծերի խտությունը սովորաբար ընտրվում է այնպես, որ այն համեմատական լինի ինդուկցիայի վեկտորի մեծությանը, ապա կարող ենք պնդել, որ որևէ մակերևույթով մագնիսական հոսքը համեմատական է մագնիսական ինդուկցիայի գծերի թվին, որոնք թափանցում են այդ մակերևույթը:
Ընդհանուր
դեպքում ![]() մակերևույթը
կարող է
ունենալ
կամայական ձև,
իսկ
մակերևույթը
կարող է
ունենալ
կամայական ձև,
իսկ ![]() -ն
նրա տարբեր
կետերում
կարող է
տարբեր լինել ինչպես
մոդուլով,
այնպես էլ`
ուղղությամբ:
Սակայն
մակերևույթի
յուրաքանչյուր
-ն
նրա տարբեր
կետերում
կարող է
տարբեր լինել ինչպես
մոդուլով,
այնպես էլ`
ուղղությամբ:
Սակայն
մակերևույթի
յուրաքանչյուր
![]() տարրի
սահմաններում
այն կարելի է
ընդունել հարթ,
իսկ դաշտը՝
համասեռ:
Ուստի, մակերևույթի
տարրի
սահմաններում
այն կարելի է
ընդունել հարթ,
իսկ դաշտը՝
համասեռ:
Ուստի, մակերևույթի
![]() մակերես
ունեցող
տեղամասով
տարրական
մակերես
ունեցող
տեղամասով
տարրական ![]() հոսքը`
հոսքը`
![]() , (6.29)
, (6.29)
որտեղ ![]() -ը
-ը ![]() մակերեսի
նորմալի
միավոր
վեկտորն է: (6.29)
բանաձևը
կարող ենք
ներկայացնել
նաև հետևյալ
տեսքով՝
մակերեսի
նորմալի
միավոր
վեկտորն է: (6.29)
բանաձևը
կարող ենք
ներկայացնել
նաև հետևյալ
տեսքով՝
![]() : (6.30)
: (6.30)
Եթե (6.30)-ը ինտեգրենք, կստանանք լրիվ հոսքը S մակերևույթով.

Միավորների
ՄՀ-ում մագնիսական
հոսքի
միավորը
վեբերն է (1Վբ):
1Վբ
մագնիսական
հոսք
առաջացնում է
1Տլ ինդուկցիայով
համասեռ
մագնիսական
դաշտը` մագնիսական
դաշտի ![]() վեկտորին
ուղղահայաց 1մ2
մակերես
ունեցող
մակերևույթով:
վեկտորին
ուղղահայաց 1մ2
մակերես
ունեցող
մակերևույթով:
Էլեկտրադինամիկայում
մագնիսական
դաշտի համար
ապացուցվում
է Գաուսի
հետևյալ
թեորեմը. ![]() վեկտորի
հոսքը
կամայական
փակ
մակերևույթով
հավասար է
զրոյի.
վեկտորի
հոսքը
կամայական
փակ
մակերևույթով
հավասար է
զրոյի.

(6.32)-ը Գաուսի թեորեմն է՝ գրված ինտեգրալային տեսքով: Գաուսի (6.32) թեորեմը կարելի է գրել նաև դիֆերենցիալ տեսքով.
![]() կամ
կամ ![]() : (6.33)
: (6.33)
Այսինքն,
![]() դաշտի
դիվերգենցիան
ամենուրեք
հավասար է զրոյի:
Սա նշանակում
է, որ
մագնիսական
դաշտը աղբյուրներ
(մագնիսական
լիցքեր)
չունի: Մագնիսական
դաշտ
ստեղծում են
ոչ թե
մագնիսական
լիցքերը
(որոնք
բնության մեջ
չկան), այլ`
էլեկտրական
հոսանքները:
Ցանկացած
մագնիսական
դաշտի ինդուկցիայի
գծերը փակ
գծեր են: (6.33)-ը
հիմնարար օրենք
է. այն ճիշտ է
ոչ միայն
հաստատուն,
այլև փոփոխական
մագնիսական
դաշտերի
համար:
դաշտի
դիվերգենցիան
ամենուրեք
հավասար է զրոյի:
Սա նշանակում
է, որ
մագնիսական
դաշտը աղբյուրներ
(մագնիսական
լիցքեր)
չունի: Մագնիսական
դաշտ
ստեղծում են
ոչ թե
մագնիսական
լիցքերը
(որոնք
բնության մեջ
չկան), այլ`
էլեկտրական
հոսանքները:
Ցանկացած
մագնիսական
դաշտի ինդուկցիայի
գծերը փակ
գծեր են: (6.33)-ը
հիմնարար օրենք
է. այն ճիշտ է
ոչ միայն
հաստատուն,
այլև փոփոխական
մագնիսական
դաշտերի
համար:
6.7.ՄԱԳՆԻՍԱԿԱՆ ԴԱՇՏԻ ԻՆԴՈՒԿՑԻԱՅԻ ՎԵԿՏՈՐԻ ՇՐՋԱՊՏՈՒՅՏԻ
ԹԵՈՐԵՄԸ ԵՎ ՆՐԱ ԿԻՐԱՌՈՒԹՅՈՒՆՆԵՐԸ
Մագնիսական
դաշտը, ի
տարբերություն
էլեկտրաստատիկ
դաշտի, ոչ
պոտենցիալային
է: ![]() վեկտորի
շրջապտույտը
փակ կոնտուրի
երկայնքով
հավասար չէ
զրոյի և
կախված չէ
կոնտուրի ընտրությունից:
Դրանում
համոզվելու
համար որպես
օրինակ
դիտարկենք վակուումում
գտնվող
անվերջ երկար
հոսանքակիր
հաղորդչի
մագնիսական
դաշտը: Այդ
դաշտի ինդուկցիայի
գծերը
համակենտրոն
շրջանագծեր են,
որոնց
հարթություններն
ուղղահայաց
են հաղորդչին,
իսկ
կենտրոններն
ընկած են նրա
առանցքի վրա
(նկ. 74): Նկարում
դրանք պատկերված
են կետագծերով:
Գտնենք
վեկտորի
շրջապտույտը
փակ կոնտուրի
երկայնքով
հավասար չէ
զրոյի և
կախված չէ
կոնտուրի ընտրությունից:
Դրանում
համոզվելու
համար որպես
օրինակ
դիտարկենք վակուումում
գտնվող
անվերջ երկար
հոսանքակիր
հաղորդչի
մագնիսական
դաշտը: Այդ
դաշտի ինդուկցիայի
գծերը
համակենտրոն
շրջանագծեր են,
որոնց
հարթություններն
ուղղահայաց
են հաղորդչին,
իսկ
կենտրոններն
ընկած են նրա
առանցքի վրա
(նկ. 74): Նկարում
դրանք պատկերված
են կետագծերով:
Գտնենք ![]() վեկտորի
շրջապտույտը
մագնիսական
ինդուկցիայի
վեկտորի
շրջապտույտը
մագնիսական
ինդուկցիայի ![]() շառավղով
շրջանագծի
կամայական
ինդուկցիայի
գծի
երկայնքով:
շառավղով
շրջանագծի
կամայական
ինդուկցիայի
գծի
երկայնքով:


Ինդուկցիայի
գծի բոլոր
կետերում ![]() վեկտորը
մոդուլով
հավասար է
հետևյալ
արտահայտությանը՝
վեկտորը
մոդուլով
հավասար է
հետևյալ
արտահայտությանը՝

և
ուղղված է այդ
գծի
շոշափողով
այնպես, որ ![]() : Հետևաբար՝
: Հետևաբար՝

(6.36)-ից կարելի է անել հետևյալ եզրակացությունները.
ա)
ուղիղ
հոսանքի
մագնիսական
դաշտը
մրրկային է,
քանի որ
նրանում ![]() վեկտորի
շրջապտույտը
մագնիսական
ինդուկցիայի
գծի
երկայնքով
հավասար չէ
զրոյի,
վեկտորի
շրջապտույտը
մագնիսական
ինդուկցիայի
գծի
երկայնքով
հավասար չէ
զրոյի,
բ)
ուղիղ
հոսանքի
դաշտի ![]() վեկտորի
շրջապտույտը
վակուումում
նույնն է
ցանկացած
մագնիսական
ինդուկցիայի
գծի
երկայնքով.
հավասար է
մագնիսական հաստատունի
և հոսանքի
ուժի
արտադրյալին:
Ցույց տանք,
որ (6.36) բանաձևը
ճիշտ է
կամայական
ձևի փակ
վեկտորի
շրջապտույտը
վակուումում
նույնն է
ցանկացած
մագնիսական
ինդուկցիայի
գծի
երկայնքով.
հավասար է
մագնիսական հաստատունի
և հոսանքի
ուժի
արտադրյալին:
Ցույց տանք,
որ (6.36) բանաձևը
ճիշտ է
կամայական
ձևի փակ ![]() կոնտուրի
համար, որն
ընդգրկում է
անվերջ երկար
հոսանքակիր
հաղորդիչը
(նկ. 75):
կոնտուրի
համար, որն
ընդգրկում է
անվերջ երկար
հոսանքակիր
հաղորդիչը
(նկ. 75):

L կոնտուրի A
կետում B
վեկտորն ուղղահայաց
է ![]() շառավիղ-վեկտորին:
Ուստի, կարելի
է ընդունել,
որ
շառավիղ-վեկտորին:
Ուստի, կարելի
է ընդունել,
որ ![]() -ի
պրոյեկցիան
-ի
պրոյեկցիան ![]() վեկտորի
ուղղության
վրա հավասար
է՝
վեկտորի
ուղղության
վրա հավասար
է՝
![]()
և
համընկնում է ![]() շառավղով
շրջանագծի
փոքր աղեղի
հետ, այսինքն՝
շառավղով
շրջանագծի
փոքր աղեղի
հետ, այսինքն՝

որտեղ
![]() -ն
կենտրոնական
անկյունն է,
որի տակ
երևում է
-ն
կենտրոնական
անկյունն է,
որի տակ
երևում է ![]() կոնտուրի
կոնտուրի ![]() տարրը
շրջանագծի
կենտրոնից:
(6.36)-ից և (6.37)-ից հետևում
է, որ
տարրը
շրջանագծի
կենտրոնից:
(6.36)-ից և (6.37)-ից հետևում
է, որ

(6.38)-ը
ինտեգրելով
ամբողջ փակ L
կոնտուրի
երկայնքով և
հաշվի
առնելով, որ
այս դեպքում ![]() անկյունը
փոփոխվում է 0-ից
մինչև
անկյունը
փոփոխվում է 0-ից
մինչև ![]() ,
կստանանք՝
,
կստանանք՝

Այսպիսով, ապացուցվեց, որ անկախ այդ կոնտուրի ձևից, (6.39) բանաձևը ճիշտ է հաղորդիչն ընդգրկող ցանկացած փակ կոնտուրի համար:

Ենթադրենք`
փակ ![]() կոնտուրը
չի ընդգրկում
իր մեջ
հոսանքակիր հաղորդիչը
(նկ. 76)
կոնտուրը
չի ընդգրկում
իր մեջ
հոսանքակիր հաղորդիչը
(նկ. 76)
Այս դեպքում՝

որտեղ
![]() և
և ![]()
![]() կոնտուրի
տեղամասերն են:
Փոխարինելով
ենթաինտեգրալային
արտահայտությունները
(6.38) բանաձևով`
կստանանք
կոնտուրի
տեղամասերն են:
Փոխարինելով
ենթաինտեգրալային
արտահայտությունները
(6.38) բանաձևով`
կստանանք
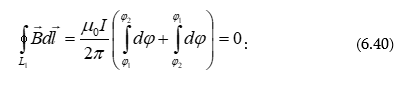
Այսպիսով,
եթե կոնտուրը
չի ընդգրկում
հոսանքակիր
հաղորդիչը, ![]() վեկտորի
շրջապտույտը
հավասար է
զրոյի:
վեկտորի
շրջապտույտը
հավասար է
զրոյի:
Եթե
կոնտուրն
ընդգրկում է
մի քանի
հոսանքներ, ![]() վեկտորի
շրջապտույտը
հավասար է
նրանց
հանրահաշվական
գումարի և
մագնիսական
հաստատունի
արտադրյալին՝
վեկտորի
շրջապտույտը
հավասար է
նրանց
հանրահաշվական
գումարի և
մագնիսական
հաստատունի
արտադրյալին՝

Հոսանքների գումարը հաշվելիս դրական պետք է համարել այն հոսանքը, որի ուղղությունը կոնտուրով շրջանցելու ուղղության հետ կապված է աջ պտուտակի կանոնով: Հակառակ ուղղության հոսանքը կլինի բացասական:
(6.41) արտահայտությունը ճիշտ է միայն վակուումում առկա դաշտի համար: Նյութում եղած դաշտի համար (6.41) բանաձևում, բացի լարերով անցնող հաղորդականության հոսանքներից (մակրոհոսանքներից), անհրաժեշտ է հաշվի առնել նաև մոլեկուլային հոսանքները:
Օգտվելով
![]() բանաձևից՝
(6.39)-ը կարող ենք
գրել
բանաձևից՝
(6.39)-ը կարող ենք
գրել

տեսքով,
որտեղ S-ը
տվյալ
կոնտուրի վրա
հենվող
կամայական
մակերևույթ է:
![]() և
և ![]() մեծությունները
համապատասխան
դաշտերի ուժային
բնութագրիչներն
են:
մեծությունները
համապատասխան
դաշտերի ուժային
բնութագրիչներն
են: ![]() շրջապտույտի
համար (1.25) և (6.36)
արտահայտությունների
համադրումը
թույլ է տալիս
եզրակացնել,
որ այդ երկու
դաշտերի միջև
սկզբունքային
տարբերություն
կա: Էլեկտրաստատիկ
դաշտի
լարվածության
վեկտորի
շրջապտույտը
միշտ հավասար
է զրոյի, և
հետևաբար, էլեկտրաստատիկ
դաշտը
պոտենցիալային
է: Մագնիսական
ինդուկցիայի
շրջապտույտը
զրոյից տարբեր
է, եթե այն
կոնտուրը,
որով
հաշվվում է
շրջապտույտը,
ընդգրկում է
հոսանք:
Այսպիսի հատկությամբ
օժտված
դաշտերը
կոչվում են
մրրկային կամ
սոլենոիդային:
Այնուհետև
էլեկտրաստատիկ
դաշտի
լարվածության
գծերը
սկսվում և վերջանում
են լիցքերի
վրա: Փորձը
ցույց է տվել, որ
մագնիսական
դաշտի
ինդուկցիայի
գծերը, հակառակը,
միշտ փակ են:
Սա նշանակում
է, որ բնության
մեջ
մագնիսական
լիցքեր չկան:
շրջապտույտի
համար (1.25) և (6.36)
արտահայտությունների
համադրումը
թույլ է տալիս
եզրակացնել,
որ այդ երկու
դաշտերի միջև
սկզբունքային
տարբերություն
կա: Էլեկտրաստատիկ
դաշտի
լարվածության
վեկտորի
շրջապտույտը
միշտ հավասար
է զրոյի, և
հետևաբար, էլեկտրաստատիկ
դաշտը
պոտենցիալային
է: Մագնիսական
ինդուկցիայի
շրջապտույտը
զրոյից տարբեր
է, եթե այն
կոնտուրը,
որով
հաշվվում է
շրջապտույտը,
ընդգրկում է
հոսանք:
Այսպիսի հատկությամբ
օժտված
դաշտերը
կոչվում են
մրրկային կամ
սոլենոիդային:
Այնուհետև
էլեկտրաստատիկ
դաշտի
լարվածության
գծերը
սկսվում և վերջանում
են լիցքերի
վրա: Փորձը
ցույց է տվել, որ
մագնիսական
դաշտի
ինդուկցիայի
գծերը, հակառակը,
միշտ փակ են:
Սա նշանակում
է, որ բնության
մեջ
մագնիսական
լիցքեր չկան:
1.
Անվերջ երկար
սոլենոիդի
մագնիսական
դաշտի ինդուկցիայի
հաշվարկը:
Սոլենոիդը
կհամարենք
անվերջ երկար,
եթե նրա տրամագիծը
շատ անգամ
փոքր է նրա
երկարությունից
(![]() ): Իր
ստեղծած
դաշտի
տեսակետից
սոլենոիդը
համարժեք է
ընդհանուր
ուղիղ առանցք
ունեցող
միատեսակ
շրջանային
հոսանքների համակարգին:
Անվերջ երկար
սոլենոիդն իր
առանցքին
ուղղահայաց
ցանկացած
հարթության
նկատմամբ
համաչափ է:
Այդպիսի
հարթության
նկատմամբ
զույգ-զույգ
համաչափ
վերցրած
փաթույթները
ստեղծում են
մի դաշտ, որի
մագնիսական
ինդուկցիան
հարթությանն
ուղղահայաց է:
): Իր
ստեղծած
դաշտի
տեսակետից
սոլենոիդը
համարժեք է
ընդհանուր
ուղիղ առանցք
ունեցող
միատեսակ
շրջանային
հոսանքների համակարգին:
Անվերջ երկար
սոլենոիդն իր
առանցքին
ուղղահայաց
ցանկացած
հարթության
նկատմամբ
համաչափ է:
Այդպիսի
հարթության
նկատմամբ
զույգ-զույգ
համաչափ
վերցրած
փաթույթները
ստեղծում են
մի դաշտ, որի
մագնիսական
ինդուկցիան
հարթությանն
ուղղահայաց է:
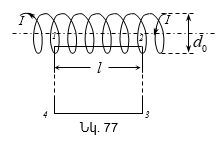
Հետևաբար,
սոլենոիդի
ներսում և
նրանից դուրս
ցանկացած
կետում ![]() վեկտորը
կարող է
ունենալ
միայն
առանցքին զուգահեռ
ուղղություն:
Հոսանքատար
սոլենոիդի
ստեղծած
մագնիսական
դաշտի ինդուկցիան
հաշվելու
համար
օգտվենք
վեկտորը
կարող է
ունենալ
միայն
առանցքին զուգահեռ
ուղղություն:
Հոսանքատար
սոլենոիդի
ստեղծած
մագնիսական
դաշտի ինդուկցիան
հաշվելու
համար
օգտվենք ![]() վեկտորի
շրջապտույտի
(6.41) բանաձևից.
վեկտորի
շրջապտույտի
(6.41) բանաձևից. ![]() կոնտուրն
ընտրենք 1-2-3-4-1
ուղղանկյան
տեսքով (նկ.77):
կոնտուրն
ընտրենք 1-2-3-4-1
ուղղանկյան
տեսքով (նկ.77): ![]() վեկտորի
շրջապտույտն
այդ
կոնտուրով
կարող ենք
ներկայացնել
հետևյալ կերպ.
վեկտորի
շրջապտույտն
այդ
կոնտուրով
կարող ենք
ներկայացնել
հետևյալ կերպ.

Աջ մասի
չորս
ինտեգրալներից
երկրորդը և
չորրորդը
հավասար են
զրոյի, քանի
որ ![]() վեկտորն
ուղղահայաց է
կոնտուրի այն
տեղամասերին,
որոնցով
դրանք
վերցվում են (
վեկտորն
ուղղահայաց է
կոնտուրի այն
տեղամասերին,
որոնցով
դրանք
վերցվում են (![]() ): 3-4
տեղամասը
սոլենոիդից
մեծ
հեռավորության
վրա
վերցնելով
(որտեղ դաշտը
շատ փոքր է)`
երրորդ
գումարելին
կարող ենք
անտեսել՝
): 3-4
տեղամասը
սոլենոիդից
մեծ
հեռավորության
վրա
վերցնելով
(որտեղ դաշտը
շատ փոքր է)`
երրորդ
գումարելին
կարող ենք
անտեսել՝ ![]() :
Հետևաբար
կարող ենք
ընդունել, որ
:
Հետևաբար
կարող ենք
ընդունել, որ

որտեղ ![]() -ն
դաշտի մագնիսական
ինդուկցիան է
այն կետերում,
որտեղ դասավորված
է կոնտուրի 1-2 տեղամասը,
-ն
դաշտի մագնիսական
ինդուկցիան է
այն կետերում,
որտեղ դասավորված
է կոնտուրի 1-2 տեղամասը,
![]() -ը
այդ տեղամասի
երկարությունն
է: Եթե 1-2
տեղամասը
սոլենոիդի
ներսում
անցնում է նրա
առանցքից
ցանկացած
հեռավորության
վրա, ապա
կոնտուրն
ընդգրկում է
-ը
այդ տեղամասի
երկարությունն
է: Եթե 1-2
տեղամասը
սոլենոիդի
ներսում
անցնում է նրա
առանցքից
ցանկացած
հեռավորության
վրա, ապա
կոնտուրն
ընդգրկում է ![]() գումարային
հոսանք, որտեղ
գումարային
հոսանք, որտեղ
![]() -ը
սոլենոիդի
միավոր
երկարությանն
ընկնող
գալարների
թիվն է,
-ը
սոլենոիդի
միավոր
երկարությանն
ընկնող
գալարների
թիվն է, ![]() -ն՝
հոսանքի ուժը
սոլենոիդում:
Ուստի, (6.44)-ի
համաձայն
-ն՝
հոսանքի ուժը
սոլենոիդում:
Ուստի, (6.44)-ի
համաձայն

որտեղից

Պետք է
նշել, որ
ստացված
արդյունքը
կախում չունի
այն բանից, թե
առանցքից
ի՞նչ
հեռավորության
վրա է
դասավորվում
1-2 տեղամասը:
Եթե այդ տեղամասը
գտնվում է
սոլենոիդից
դուրս, ապա
կոնտուրով ընդգրկված
հոսանքը հավասար
է զրոյի, որի
հետևանքով ![]() :
Այսպիսով,
անվերջ երկար
սոլենոիդից
դուրս մագնիսական
ինդուկցիան
հավասար է
զրոյի, ներսում
ամենուրեք
նույնն է և
որոշվում է (6.45)
բանաձևով:
:
Այսպիսով,
անվերջ երկար
սոլենոիդից
դուրս մագնիսական
ինդուկցիան
հավասար է
զրոյի, ներսում
ամենուրեք
նույնն է և
որոշվում է (6.45)
բանաձևով:
2.
Տորոիդի
մագնիսական դաշտի
ինդուկցիան:
Տորոիդ է
կոչվում
օղակաձև կոճը,
որի գալարները
փաթաթված են
տորաձև
միջուկի վրա
(նկ.78): Այն համարժեք
է միատեսակ
շրջանային
հոսանքների համակարգին,
որոնց
կենտրոնները
դասավորված
են
շրջանագծով:
Վերցնենք ![]() շառավղով
շրջանաձև մի
կոնտուր, որի
կենտրոնը
համընկնում է
տորոիդի
կենտրոնի հետ:
Համաչափության
շնորհիվ
շառավղով
շրջանաձև մի
կոնտուր, որի
կենտրոնը
համընկնում է
տորոիդի
կենտրոնի հետ:
Համաչափության
շնորհիվ ![]() վեկտորը
յուրաքանչյուր
կետում պետք է
ունենա
կոնտուրին
տարված
շոշափողի
ուղղությունը:
Հետևաբար՝
վեկտորը
յուրաքանչյուր
կետում պետք է
ունենա
կոնտուրին
տարված
շոշափողի
ուղղությունը:
Հետևաբար՝

որտեղ
![]() -ն
մագնիսական
ինդուկցիան է
այն կետերում,
որոնցով
անցնում է
կոնտուրը:
-ն
մագնիսական
ինդուկցիան է
այն կետերում,
որոնցով
անցնում է
կոնտուրը:

Եթե
կոնտուրն
անցնում է
տորոիդի
ներսով, ապա
այն
ընդգրկում է ![]() հոսանք (
հոսանք (![]() -ը տորոիդի
շառավիղն է,
-ը տորոիդի
շառավիղն է, ![]() -ը`
գալարների
թիվը նրա
միավոր
երկարության
վրա): Այս
դեպքում`
-ը`
գալարների
թիվը նրա
միավոր
երկարության
վրա): Այս
դեպքում`
![]()
որտեղից

Տորոիդից
դուրս անցնող
կոնտուրը
հոսանքներ չի
ընդգրկում,
ուստի նրա
համար ![]() -ն
հավասար է
զրոյի:
Այսպիսով,
մագնիսական
ինդուկցիան
տորոիդից
դուրս
հավասար է
զրոյի: Այն
տորոիդի
համար, որի
-ն
հավասար է
զրոյի:
Այսպիսով,
մագնիսական
ինդուկցիան
տորոիդից
դուրս
հավասար է
զրոյի: Այն
տորոիդի
համար, որի ![]() շառավիղը
զգալիորեն
գերազանցում
է փաթույթի
շառավղին,
շառավիղը
զգալիորեն
գերազանցում
է փաթույթի
շառավղին, ![]() հարաբերությունը
տորոիդի
ներսում
գտնվող բոլոր
կետերի համար
մեկից քիչ է
տարբերվում և
(6.48)-ի փոխարեն
ստացվում է
այնպիսի
բանաձև,
ինչպիսին
անվերջ երկար
սոլենոիդի
համար էր.
հարաբերությունը
տորոիդի
ներսում
գտնվող բոլոր
կետերի համար
մեկից քիչ է
տարբերվում և
(6.48)-ի փոխարեն
ստացվում է
այնպիսի
բանաձև,
ինչպիսին
անվերջ երկար
սոլենոիդի
համար էր.

Այս
դեպքում
տորոիդի
կտրվածքներից
յուրաքանչյուրում
դաշտը կարելի
է համարել
համասեռ:
Տարբեր
կտրվածքներում
դաշտն ունի
տարբեր ուղղություն:
Այդ պատճառով
ամբողջ
տորոիդի սահմաններում
դաշտի
համասեռության
մասին կարելի
է խոսել միայն
պայմանականորեն`
նկատի
ունենալով ![]() վեկտորի
չափը:
վեկտորի
չափը:
ԳԼՈՒԽ 7. ՄԱԳՆԻՍԱԿԱՆ ԴԱՇՏԻ ԱԶԴԵՑՈՒԹՅՈՒՆԸ
ՀՈՍԱՆՔՆԵՐԻ ԵՎ ԼԻՑՔԵՐԻ ՎՐԱ
7.1. ԱՄՊԵՐԻ ՕՐԵՆՔԸ
Հաղորդիչները, որոնցով անցնում է էլեկտրական հոսանք, իրենց շուրջն ստեղծում են մագնիսական դաշտ և ազդում են իրենց մոտ գտնվող հաստատուն մագնիսների վրա: Իր հերթին` մագնիսական դաշտն ազդում է հոսանքակիր հաղորդչի վրա: Հոսանքակիր հաղորդչի վրա մագնիսական դաշտի ազդեցությունը դիտվել է Էրստեդի և Ամպերի կողմից: Ամպերը, մանրամասնորեն ուսումնասիրելով այդ երևույթը, եկավ այն եզրակացության, որ հոսանքակիր հաղորդչի ուղիղ տեղամասի վրա համասեռ մագնիսական դաշտն ազդում է այնպիսի ուժով, որի մոդուլը հավասար է մագնիսական ինդուկցիայի վեկտորի մոդուլի, հոսանքի ուժի, տեղամասի երկարության և ինդուկցիայի վեկտորի ու հաղորդչի տեղամասի կազմած անկյան սինուսի արտադրյալին՝

Ամպերի
(7.1) օրենքը
կարելի է
ընդհանրացնել
անհամասեռ
մագնիսական
դաշտի և
կամայական
ձևի հաղորդչի
դեպքի համար:
Իրոք,
կամայական
ձևի հաղորդչի
անվերջ փոքր ![]() տարրը
կարելի է
ընդունել ուղղագիծ,
իսկ
տարրը
կարելի է
ընդունել ուղղագիծ,
իսկ ![]() տարրի
զբաղեցրած
տիրույթում
մագնիսական դաշտը՝
համասեռ:
Ուստի,
ընդհանուր
դեպքում Ամպերի
օրենքն ունի
տարրի
զբաղեցրած
տիրույթում
մագնիսական դաշտը՝
համասեռ:
Ուստի,
ընդհանուր
դեպքում Ամպերի
օրենքն ունի

տեսքը:
Ամպերի
օրենքը
հնարավորություն
է տալիս որոշել
մագնիսական
ինդուկցիայի
թվային արժեքը:
Ենթադրենք
հոսանքի ![]() տարրն
ուղղահայաց է
մագնիսական դաշտի
ուղղությանը
տարրն
ուղղահայաց է
մագնիսական դաշտի
ուղղությանը ![]() :
Ամպերի
օրենքը
կարելի է գրել
:
Ամպերի
օրենքը
կարելի է գրել

(7.3)-ից
հետևում է, որ ![]() մագնիսական
ինդուկցիան
թվապես
հավասար է դաշտի
կողմից
միավոր
երկարության
հաղորդչի վրա
ազդող ուժին,
որով անցնում
է միավոր ուժի
հոսանք, ընդ
որում`
հաղորդիչը
դասավորված է
մագնիսական
դաշտի
ուղղությանն
ուղղահայաց: Այսպիսով,
մագնիսական
ինդուկցիան
մագնիսական
դաշտի
ուժային
բնութագիրն է:
մագնիսական
ինդուկցիան
թվապես
հավասար է դաշտի
կողմից
միավոր
երկարության
հաղորդչի վրա
ազդող ուժին,
որով անցնում
է միավոր ուժի
հոսանք, ընդ
որում`
հաղորդիչը
դասավորված է
մագնիսական
դաշտի
ուղղությանն
ուղղահայաց: Այսպիսով,
մագնիսական
ինդուկցիան
մագնիսական
դաշտի
ուժային
բնութագիրն է:
![]() ուժի
ուղղությունը
հոսանքի
երկու
ուղղությունների
համար
ուժի
ուղղությունը
հոսանքի
երկու
ուղղությունների
համար ![]() -ի
դեպքում
ցույց է տրված
նկ.69 ա, բ-ում: Այն
կարելի է
որոշել ձախ
ձեռքի
կանոնով: Եթե
ձախ ձեռքը պահենք
այնպես, որ
ինդուկցիայի
-ի
դեպքում
ցույց է տրված
նկ.69 ա, բ-ում: Այն
կարելի է
որոշել ձախ
ձեռքի
կանոնով: Եթե
ձախ ձեռքը պահենք
այնպես, որ
ինդուկցիայի ![]() վեկտորը
մտնի ափի մեջ,
իսկ պարզած
չորս մատներն
ուղղված
լինեն
հոսանքի
ուղղությամբ,
ապա
վեկտորը
մտնի ափի մեջ,
իսկ պարզած
չորս մատներն
ուղղված
լինեն
հոսանքի
ուղղությամբ,
ապա ![]() -ով
բացված
բթամատը
ցույց կտա
տեղամասի վրա
ազդող Ամպերի
ուժի
ուղղությունը
(նկ.79ա,բ):
-ով
բացված
բթամատը
ցույց կտա
տեղամասի վրա
ազդող Ամպերի
ուժի
ուղղությունը
(նկ.79ա,բ):
Ամպերի օրենքը կարելի է գրել վեկտորական տեսքով՝

![]() և
և
![]() վեկտորների
փոխադարձ
դասավորությունը
պատկերված է
նկ. 80 -ում:
վեկտորների
փոխադարձ
դասավորությունը
պատկերված է
նկ. 80 -ում:

Կանգ առնենք
էլեկտրամագնիսական
փոխազդեցության
ուժերի էական
առանձնահատկության
վրա, որն արտահայտվում
է Ամպերի
օրենքում:
Էլեկտրաստատիկայում
մենք գործ
ունեինք
կենտրոնական
ուժերի հետ,
քանի որ երկու
կետային
լիցքերի միջև
փոխազդեցության
ուժն ուղղված
է լիցքերը միացնող
ուղղի
երկայնքով:
Կենտրոնական
ուժերի օրինակ
են նաև
ձգողական
(գրավիտացիոն)
ուժերը: ![]() լարվածության
էլեկտրաստատիկ
դաշտում
տեղադրված
լարվածության
էլեկտրաստատիկ
դաշտում
տեղադրված ![]() կետային
լիցքի վրա
ազդող
կետային
լիցքի վրա
ազդող ![]() ուժն
իր
մեծությամբ և
ուղղությամբ
համընկնում է
ուժն
իր
մեծությամբ և
ուղղությամբ
համընկնում է ![]() վեկտորի
հետ, այսինքն`
ուղղված է
էլեկտրաստատիկ
դաշտի
ուժագծի
շոշափողով:
վեկտորի
հետ, այսինքն`
ուղղված է
էլեկտրաստատիկ
դաշտի
ուժագծի
շոշափողով:
Էլեկտրամագնիսական փոխազդեցության ուժերը, ինչպես երևում է Ամպերի օրենքից, կենտրոնական չեն: Դրանք միշտ ուղղահայաց են մագնիսական ինդուկցիայի գծերին:
7.2. ԵՐԿՈՒ ԱՆՎԵՐՋ ԵՐԿԱՐ ԶՈՒԳԱՀԵՌ ՀՈՍԱՆՔԱԿԻՐ
ՀԱՂՈՐԴԻՉՆԵՐԻ ՓՈԽԱԶԴԵՑՈՒԹՅԱՆ ՈՒԺԸ
Դիտարկենք
երկու բարակ,
երկար,
ուղղագիծ և զուգահեռ
հաղորդիչներ,
որոնք
գտնվում են
իրարից ![]() հեռավորության
վրա: Փորձը
ցույց է
տալիս, որ երբ
հաղորդիչներով
հոսում են
հոսանքներ, նրանց
միջև
առաջանում են
փոխազդեցության
ուժեր: Եթե
հեռավորության
վրա: Փորձը
ցույց է
տալիս, որ երբ
հաղորդիչներով
հոսում են
հոսանքներ, նրանց
միջև
առաջանում են
փոխազդեցության
ուժեր: Եթե ![]() և
և ![]() հոսանքներն
ունեն
միևնույն
ուղղությունը`
հաղորդիչներն
իրար ձգում են
(նկ. 81 ա) և վանում
են, եթե
հոսանքները
հակառակ են
(նկ. 81 բ):
հոսանքներն
ունեն
միևնույն
ուղղությունը`
հաղորդիչներն
իրար ձգում են
(նկ. 81 ա) և վանում
են, եթե
հոսանքները
հակառակ են
(նկ. 81 բ):

Ըստ
Ամպերի (7.4)
օրենքի, ![]() հոսանքով
երկրորդ
հաղորդչի
հոսանքով
երկրորդ
հաղորդչի ![]() տարրի
վրա ազդում է
տարրի
վրա ազդում է ![]() ուժը,
որտեղ
ուժը,
որտեղ ![]() -ը
-ը ![]() հոսանքով
առաջին
հաղորդչի
մագնիսական
դաշտի
ինդուկցիան է:
հոսանքով
առաջին
հաղորդչի
մագնիսական
դաշտի
ինդուկցիան է:
Եթե
հաղորդիչների
երկարությունները
շատ անգամ մեծ
են նրանց միջև
եղած b
հեռավորությունից,
ապա ![]() -ի
որոշման
դեպքում
առաջին
հաղորդիչը
կարելի է
ընդունել
անվերջ երկար:
-ի
որոշման
դեպքում
առաջին
հաղորդիչը
կարելի է
ընդունել
անվերջ երկար:
Հետևաբար`

Համանմանորեն`
![]() հոսանքով
առաջին
հաղորդչի
հոսանքով
առաջին
հաղորդչի ![]() տարրի
վրա ազդում է
տարրի
վրա ազդում է ![]() ուժը,
որի մոդուլը`
ուժը,
որի մոդուլը`

Այսպիսով,
![]() և
և
![]() ուժերի
մոդուլների
համար կարելի
է գրել ընդհանուր
բանաձև.
ուժերի
մոդուլների
համար կարելի
է գրել ընդհանուր
բանաձև.

Այս բանաձևը օգտագործվում է միավորների ՄՀ-ում միավորը` ամպերը, սահմանելու համար:
Մագնիսական
դաշտն ազդում
է ոչ միայն
հոսանքակիր
հաղորդչի, այլ
նաև առանձին
շարժվող էլեկտրական
լիցքի վրա:
Դրանում
կարելի է
համոզվել
էլեկտրոնային
փնջերի հետ
վակուումում
կատարված
փորձերով: Եթե
մագնիսական
դաշտ չկա, ապա
էլեկտրոնները
վակուումային
խողովակում
շարժվում են
ուղղագիծ: Եթե
խողովակը
տեղադրենք
ուժեղ
մագնիսական
դաշտում, ապա
էլեկտրոնների
հետագծերը
շեղվում են:
Փորձը ցույց է
տալիս, որ արտաքին
մագնիսական
դաշտում
էլեկտրոնները
շեղվում են
մագնիսական
դաշտի ![]() ինդուկցիային
և
էլեկտրոնների
շարժման
ինդուկցիային
և
էլեկտրոնների
շարժման ![]() արագությանն
ուղղահայաց
ուղղությամբ:
Այսպիսով,
մագնիսական
դաշտում
շարժվող
էլեկտրոնի
վրա ազդում է
ուժ, որն ուղղված
է այն կողմը,
որ կողմն
ուղղված է
արագությանն
ուղղահայաց
ուղղությամբ:
Այսպիսով,
մագնիսական
դաշտում
շարժվող
էլեկտրոնի
վրա ազդում է
ուժ, որն ուղղված
է այն կողմը,
որ կողմն
ուղղված է ![]() վեկտորական
արտադրյալը:
վեկտորական
արտադրյալը:
Մագնիսական
դաշտում
դրական և
բացասական իոնների
շարժման
դիտարկումը
ցույց է տվել,
որ դրանց վրա
նույնպես
ազդում են
ուժեր, որոնք
ուղղված են ![]() և
և ![]() վեկտորներին
ուղղահայաց:
Պարզվել է, որ
դրական
լիցքավորված
մասնիկների
համար ուժի
ուղղությունը
համընկնում է
վեկտորներին
ուղղահայաց:
Պարզվել է, որ
դրական
լիցքավորված
մասնիկների
համար ուժի
ուղղությունը
համընկնում է ![]() վեկտորի
ուղղության
հետ, իսկ
բացասական
լիցքավորված
մասնիկների
համար՝
վեկտորի
ուղղության
հետ, իսկ
բացասական
լիցքավորված
մասնիկների
համար՝ ![]() վեկտորի
ուղղության
հետ:
վեկտորի
ուղղության
հետ:
Գտնենք
մագնիսական
դաշտում
շարժվող
լիցքի վրա
ազդող ուժի
արտահայտությունը:
Ըստ Ամպերի (7.2)
օրենքի ![]() հոսանքով
հաղորդչի
հոսանքով
հաղորդչի ![]() տարրի վրա,
որը գտնվում է
մագնիսական
դաշտում,
ազդում է
տարրի վրա,
որը գտնվում է
մագնիսական
դաշտում,
ազդում է ![]() ուժը՝
ուժը՝
![]()
Եթե
հաղորդչում ![]() հոսանքը
պայմանավորված
է մասնիկների
շարժումով,
որոնց լիցքը
հավասար է
հոսանքը
պայմանավորված
է մասնիկների
շարժումով,
որոնց լիցքը
հավասար է ![]() -ի, ապա ըստ (6.22)
բանաձևի՝
-ի, ապա ըստ (6.22)
բանաձևի՝

որտեղ
![]() -ը
-ը ![]() երկարություն
ունեցող
հաղորդչի
ծավալում մասնիկների
թիվն է,
երկարություն
ունեցող
հաղորդչի
ծավալում մասնիկների
թիվն է, ![]() -ն՝
նրանց
կարգավորված
շարժման
արագությունը:
Ուստի՝
-ն՝
նրանց
կարգավորված
շարժման
արագությունը:
Ուստի՝

Բաժանելով
(7.7) հավասարման
աջ և ձախ
մասերը ![]() մասնիկների
թվին, կգտնենք
մասնիկների
թվին, կգտնենք
![]() ուժը, որն
ազդում է
յուրաքանչյուր
լիցքի վրա
ուժը, որն
ազդում է
յուրաքանչյուր
լիցքի վրա

(7.8)
առնչությունն
առաջինը
ստացել է
Լորենցը: Դրա
համար էլ
մագնիսական
դաշտում
շարժվող ![]() լիցքի վրա
ազդող
լիցքի վրա
ազդող ![]() ուժը
կոչվում է
Լորենցի ուժ:
Լորենցի ուժի
ուղղությունը,
որը որոշվում
է (7.8) բանաձևով,
համաձայնեցվում
է վերևում
նշված
փորձերի
արդյունքների
հետ:
ուժը
կոչվում է
Լորենցի ուժ:
Լորենցի ուժի
ուղղությունը,
որը որոշվում
է (7.8) բանաձևով,
համաձայնեցվում
է վերևում
նշված
փորձերի
արդյունքների
հետ:
Նկար
82 ա,բ-ում ցույց
է տրված ![]() ,
, ![]() և
և ![]() վեկտորների
փոխադարձ
դասավորությունը
դրական և
բացասական
լիցքերի
համար:
Լորենցի ուժի
թվային
արժեքը`
վեկտորների
փոխադարձ
դասավորությունը
դրական և
բացասական
լիցքերի
համար:
Լորենցի ուժի
թվային
արժեքը`

որտեղ
![]() -ն
-ն ![]() և
և ![]() վեկտորների
կազմած
անկյունն է:
վեկտորների
կազմած
անկյունն է:

Լորենցի ուժը միշտ ուղղահայաց է լիցքի շարժման արագությանը և նրան հաղորդում է կենտրոնաձիգ արագացում: Լորենցի ուժն աշխատանք չի կատարում: Այն միայն փոխում է մագնիսական դաշտում շարժվող լիցքի արագության ուղղությունը: Մագնիսական դաշտում լիցքի արագության բացարձակ մեծությունը և նրա կինետիկ էներգիան շարժման ժամանակ չեն փոփոխվում:
Ընդհանուր
դեպքում՝
շարժվող
էլեկտրական լիցքի
վրա, բացի ![]() ինդուկցիա
ունեցող
մագնիսական
դաշտից, կարող
է ազդել նաև
էլեկտրական
դաշտը, որի
լարվածությունը
հավասար է
ինդուկցիա
ունեցող
մագնիսական
դաշտից, կարող
է ազդել նաև
էլեկտրական
դաշտը, որի
լարվածությունը
հավասար է ![]() -ի:
Այդ դեպքում
լիցքի վրա ազդող
արդյունարար
ուժը հավասար
է էլեկտրական դաշտի
կողմից լիցքի
վրա ազդող
-ի:
Այդ դեպքում
լիցքի վրա ազդող
արդյունարար
ուժը հավասար
է էլեկտրական դաշտի
կողմից լիցքի
վրա ազդող ![]() ուժի
և Լորենցի
ուժի
վեկտորական
գումարին.
ուժի
և Լորենցի
ուժի
վեկտորական
գումարին.

(7.10) արտահայտությունը կոչվում է Լորենցի բանաձև:
7.4. ՄԱԳՆԻՍԱԿԱՆ ԴԱՇՏՈՒՄ ՀՈՍԱՆՔԱԿԻՐ
ՀԱՂՈՐԴՉԻ ՏԵՂԱՓՈԽՄԱՆ ՎՐԱ ԿԱՏԱՐՎՈՂ ԱՇԽԱՏԱՆՔԸ
Ընդունենք, որ հոսանքակիր հաղորդիչը կարող է արտաքին մագնիսական դաշտում ազատորեն տեղաշարժվել: Դա կարելի է իրականացնել հաղորդալարերի ծայրերի և փակ շղթայի մնացած մասերի միջև եղած սահող կոնտակտների օգնությամբ (նկ.83):

Ենթադրենք` արտաքին դաշտը համասեռ է և ուղղահայաց է կոնտուրի հարթությանը: Հոսանքի և դաշտի` նկարում ցույց տրված ուղղությունների դեպքում ուժն ուղղված կլինի դեպի աջ և կլինի
![]()
որտեղ
![]() -ը
հոսանքի
տեղաշարժվող
տեղամասի
երկարությունն
է:
-ը
հոսանքի
տեղաշարժվող
տեղամասի
երկարությունն
է: ![]() ճանապարհի
վրա այդ ուժը հաղորդչի
վրա կկատարի
հետևյալ
աշխատանքը`
ճանապարհի
վրա այդ ուժը հաղորդչի
վրա կկատարի
հետևյալ
աշխատանքը`

![]() արտադրյալը
հավասար է
ստվերագծված
մակերեսին
(նկ. 81),
արտադրյալը
հավասար է
ստվերագծված
մակերեսին
(նկ. 81),
իսկ ![]() -ը`
այդ մակերեսի
միջով անցնող
մագնիսական
ինդուկցիայի
-ը`
այդ մակերեսի
միջով անցնող
մագնիսական
ինդուկցիայի ![]() հոսքին:
Այդ պատճառով
կարող ենք
գրել
հոսքին:
Այդ պատճառով
կարող ենք
գրել

որտեղ
![]() -ն
մագնիսական
ինդուկցիայի
հոսքն է, որը
հատում է
շարժվող
հաղորդիչը:
Ստացած
արդյունքը հեշտությամբ
կարելի է
ընդհանրացնել
անհամասեռ
դաշտի համար:
Այդ նպատակով
հաղորդիչը պետք
է տրոհել
-ն
մագնիսական
ինդուկցիայի
հոսքն է, որը
հատում է
շարժվող
հաղորդիչը:
Ստացած
արդյունքը հեշտությամբ
կարելի է
ընդհանրացնել
անհամասեռ
դաշտի համար:
Այդ նպատակով
հաղորդիչը պետք
է տրոհել ![]() հատվածների
և
յուրաքանչյուր
հատվածի վրա կատարվող
տարրական
աշխատանքները
գումարել (
հատվածների
և
յուրաքանչյուր
հատվածի վրա կատարվող
տարրական
աշխատանքները
գումարել (![]()
![]() յուրաքանչյուր
փոքր
մակերեսի
սահմաններում
մագնիսական
ինդուկցիան
կարելի է
համարել
հաստատուն):
յուրաքանչյուր
փոքր
մակերեսի
սահմաններում
մագնիսական
ինդուկցիան
կարելի է
համարել
հաստատուն):
Եթե ![]() վեկտորը
կոնտուրին
տարած
նորմալի հետ
կազմում է
զրոյից
տարբեր
վեկտորը
կոնտուրին
տարած
նորմալի հետ
կազմում է
զրոյից
տարբեր ![]() անկյուն,
ապա ուժի
ուղղությունը
տեղաշարժման
ուղղության
հետ նույնպես
կկազմի
անկյուն,
ապա ուժի
ուղղությունը
տեղաշարժման
ուղղության
հետ նույնպես
կկազմի ![]() անկյուն
(
անկյուն
(![]() -ը
ուղղահայաց է
-ը
ուղղահայաց է ![]() -ին) և
-ին) և

որտեղ
![]() -ն
-ն ![]() վեկտորի
բաղադրիչն է
վեկտորի
բաղադրիչն է ![]() մակերեսի
նորմալի
ուղղությամբ:
մակերեսի
նորմալի
ուղղությամբ: ![]() արտադրյալը
հաղորդչով
հատվող
արտադրյալը
հաղորդչով
հատվող ![]() հոսքըն
է: Այսպիսով,
այս դեպքում
ևս մենք հանգում
ենք (7.11)
բանաձևին:
հոսքըն
է: Այսպիսով,
այս դեպքում
ևս մենք հանգում
ենք (7.11)
բանաձևին:
Կարելի է ցույց տալ, որ երբ փակ կոնտուրը տեղափոխվում է անհամասեռ մագնիսական դաշտում, կոնտուրի տեղափոխման վրա կատարված աշխատանքը որոշվում է դարձյալ (7.11) բանաձևով:
7.5. ԼԻՑՔԱՎՈՐՎԱԾ ՄԱՍՆԻԿՆԵՐԻ ՇԱՐԺՈՒՄԸ ՀԱՄԱՍԵՌ
ՄԱԳՆԻՍԱԿԱՆ ԴԱՇՏՈՒՄ
Վերը ստացած Լորենցի ուժի (7.8) արտահայտությունը հնարավորություն է տալիս սահմանել մագնիսական դաշտում լիցքավորված մասնիկների շարժման մի շարք օրինաչափություններ, որոնք ընկած են էլեկտրոնային մանրադիտակի, զանգվածասպեկտրագրիչի և լիցքավորված մասնիկների արագացուցիչների աշխատանքի հիմքում:
Դիտարկենք լիցքավորված մասնիկների շարժումը համասեռ մագնիսական դաշտում: Ենթադրում ենք, որ մասնիկի վրա չեն ազդում էլեկտրական դաշտեր:
Սկսենք
պարզագույն
դեպքից.
լիցքավորված
մասնիկը
շարժվում է
մագնիսական
ինդուկցիայի գծի
երկայնքով:
Այդպիսի
շարժման
դեպքում ![]() և
և ![]() վեկտորների
միջև
անկյունը՝
վեկտորների
միջև
անկյունը՝ ![]() կամ
կամ ![]() : Ըստ (7.9)
բանաձևի`
Լորենցի ուժը
: Ըստ (7.9)
բանաձևի`
Լորենցի ուժը ![]() է, այսինքն՝
մագնիսական
դաշտը
մասնիկի վրա չի
ազդում:
Մասնիկը
շարժվում է
իներցիայով՝
ուղղագիծ և
հավասարաչափ:
է, այսինքն՝
մագնիսական
դաշտը
մասնիկի վրա չի
ազդում:
Մասնիկը
շարժվում է
իներցիայով՝
ուղղագիծ և
հավասարաչափ:

Դիտարկենք
այն դեպքը,
երբ ![]() լիցք
ունեցող
մասնիկը
շարժվում է
ինդուկցիայի
գծերին
ուղղահայաց
լիցք
ունեցող
մասնիկը
շարժվում է
ինդուկցիայի
գծերին
ուղղահայաց ![]() :
Հետևաբար,
Լորենցի ուժը
թվապես
հավասար է.
:
Հետևաբար,
Լորենցի ուժը
թվապես
հավասար է.

և
ուղղահայաց է
![]() և
և ![]() վեկտորներին
(նկ.84): Այս
դեպքում
մասնիկը շարժվում
է մագնիսական
ինդուկցիայի
վեկտորին ուղղահայաց
հարթության
մեջ, ընդ
որում` Լորենցի
ուժը մասնիկին
հաղորդում է
կենտրոնաձիգ
արագացում՝
վեկտորներին
(նկ.84): Այս
դեպքում
մասնիկը շարժվում
է մագնիսական
ինդուկցիայի
վեկտորին ուղղահայաց
հարթության
մեջ, ընդ
որում` Լորենցի
ուժը մասնիկին
հաղորդում է
կենտրոնաձիգ
արագացում՝

որտեղ
![]() -ը
լիցքավորված
մասնիկի
զանգվածն է,
իսկ
-ը
լիցքավորված
մասնիկի
զանգվածն է,
իսկ ![]() -ը` նրա հետագծի
կորության
շառավիղը:
-ը` նրա հետագծի
կորության
շառավիղը:
Հավասարեցնելով (7.12) և (7.13) արտահայտությունների աջ մասերը` կստանանք հետագծի կորության շառավիղը.

Քանի
որ համասեռ
դաշտում ![]() , իսկ
մագնիսական
դաշտում
լիցքի
արագության
թվային
արժեքը չի փոփոխվում,
ապա այդ լիցքի
հետագծի
կորության շառավիղը
մնում է
հաստատուն:
Հետևաբար,
լիցքավորված
մասնիկը
կշարժվի
շրջանագծով,
որի հարթությունն
ուղղահայաց է
մագնիսական
դաշտին, իսկ
շառավիղն ուղիղ
համեմատական
է մասնիկի
արագությանը
և հակադարձ համեմատական՝
նրա q/m
տեսակարար
լիցքի ու
մագնիսական
դաշտի
, իսկ
մագնիսական
դաշտում
լիցքի
արագության
թվային
արժեքը չի փոփոխվում,
ապա այդ լիցքի
հետագծի
կորության շառավիղը
մնում է
հաստատուն:
Հետևաբար,
լիցքավորված
մասնիկը
կշարժվի
շրջանագծով,
որի հարթությունն
ուղղահայաց է
մագնիսական
դաշտին, իսկ
շառավիղն ուղիղ
համեմատական
է մասնիկի
արագությանը
և հակադարձ համեմատական՝
նրա q/m
տեսակարար
լիցքի ու
մագնիսական
դաշտի ![]() ինդուկցիայի
արտադրյալին:
Լորենցի ուժի
և նրա կողմից
մագնիսական
դաշտում
լիցքավորված
մասնիկի
առաջացրած
շեղման
ուղղությունները
կախված են
մասնիկի
ինդուկցիայի
արտադրյալին:
Լորենցի ուժի
և նրա կողմից
մագնիսական
դաշտում
լիցքավորված
մասնիկի
առաջացրած
շեղման
ուղղությունները
կախված են
մասնիկի ![]() լիցքի նշանից:
Եթե մասնիկը
շարժվում է
ձախից աջ, իսկ
մագնիսական
դաշտն
ուղղված է
նկ.84-ում ցույց
տրված
ուղղությամբ,
ապա
լիցքի նշանից:
Եթե մասնիկը
շարժվում է
ձախից աջ, իսկ
մագնիսական
դաշտն
ուղղված է
նկ.84-ում ցույց
տրված
ուղղությամբ,
ապա ![]() դեպքում
մասնիկը
շեղվում է
ներքև, իսկ
դեպքում
մասնիկը
շեղվում է
ներքև, իսկ ![]() դեպքում՝
վերև:
Այսպիսով,
մագնիսական
դաշտում
մասնիկի
շեղման
բնույթից
կարելի է
դատել նրա
լիցքի նշանի
մասին:
Մասնիկը
դեպքում՝
վերև:
Այսպիսով,
մագնիսական
դաշտում
մասնիկի
շեղման
բնույթից
կարելի է
դատել նրա
լիցքի նշանի
մասին:
Մասնիկը ![]() շառավիղ
ունեցող
շրջանագծով
շարժվում է հավասարաչափ:
Մասնիկի
պտտման
պարբերությունը,
այսինքն` այն
շառավիղ
ունեցող
շրջանագծով
շարժվում է հավասարաչափ:
Մասնիկի
պտտման
պարբերությունը,
այսինքն` այն ![]() ժամանակը,
որը ծախսում է
մեկ լրիվ
պտույտի համար,
ինչպես
երևում է (7.14)
բանաձևից,
հավասար է.
ժամանակը,
որը ծախսում է
մեկ լրիվ
պտույտի համար,
ինչպես
երևում է (7.14)
բանաձևից,
հավասար է.

Պտտման պարբերությունը կախում չունի մասնիկի արագությունից:
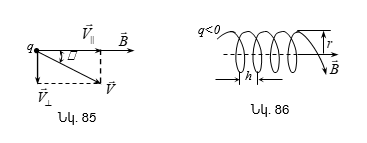
Այժմ
դիտարկենք
համասեռ
մագնիսական
դաշտում
շարժվող
լիցքավորված
մասնիկի
շարժման ընդհանուր
դեպքը, երբ
նրա ![]() արագությունը
ուղղված է
դաշտի
ինդուկցիայի
արագությունը
ուղղված է
դաշտի
ինդուկցիայի ![]() վեկտորի
նկատմամբ
կամայական
վեկտորի
նկատմամբ
կամայական ![]() սուր
անկյան տակ
(նկ.85):
Արագության
սուր
անկյան տակ
(նկ.85):
Արագության ![]() վեկտորը
վերածենք
վեկտորը
վերածենք ![]() վեկտորին
զուգահեռ
վեկտորին
զուգահեռ ![]() և նրան ուղղահայաց
և նրան ուղղահայաց
![]() երկու բաղադրիչների.
երկու բաղադրիչների.

Մագնիսական
դաշտում ![]() -ը չի
փոխվում:
Շնորհիվ
-ը չի
փոխվում:
Շնորհիվ ![]() -ի` մասնիկը
շարժվում է
շրջանագծով,
որի
հարթությունն
ուղղահայաց է
-ի` մասնիկը
շարժվում է
շրջանագծով,
որի
հարթությունն
ուղղահայաց է ![]() վեկտորին,
իսկ
վեկտորին,
իսկ ![]() շառավիղն
ըստ (7.14) բանաձևի
հավասար է
շառավիղն
ըստ (7.14) բանաձևի
հավասար է

Մասնիկը
միաժամանակ
մասնակցում է
երկու շարժումների.
այն
հավասարաչափ
պտտվում է ![]() արագությամբ
արագությամբ
![]() շառավիղ
ունեցող
շրջանագծով և
շարժվում է
շառավիղ
ունեցող
շրջանագծով և
շարժվում է ![]() հաստատուն
արագությամբ
համընթաց
պտտման հարթությանն
ուղղահայաց:
Ուստի
լիցքավորված
մասնիկի
շարժման
հետագիծը
պարուրագիծ է,
որի առանցքը
համընկնում է
մագնիսական
դաշտի ինդուկցիայի
գծին (նկ. 86):
Գալարների
հաստատուն
արագությամբ
համընթաց
պտտման հարթությանն
ուղղահայաց:
Ուստի
լիցքավորված
մասնիկի
շարժման
հետագիծը
պարուրագիծ է,
որի առանցքը
համընկնում է
մագնիսական
դաշտի ինդուկցիայի
գծին (նկ. 86):
Գալարների ![]() շառավիղը
որոշվում է (7.17)
բանաձևով, իսկ
հարևան
գալարների միջև
եղած h
հեռավորությունը
(պարուրագծի
քայլը)`
շառավիղը
որոշվում է (7.17)
բանաձևով, իսկ
հարևան
գալարների միջև
եղած h
հեռավորությունը
(պարուրագծի
քայլը)`

Փոխարինելով
T–ն ըստ (7.15)
բանաձևի, իսկ ![]() -ն ըստ (7.16)
բանաձևի
կստանանք`
-ն ըստ (7.16)
բանաձևի
կստանանք`
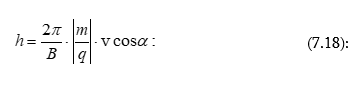
7.6. ՀՈԼԼԻ ԵՐԵՎՈՒՅԹԸ
Դիտարկենք
ուղղանկյուն
կտրվածք
ունեցող ոսկուց
պատրաստված
հաղորդիչ,
որում ![]() խտության
հոսանք կա (նկ. 87):
Այդպիսի
թիթեղի ներսում
համապոտենցիալ
մակերևույթները
կլինեն
հոսանքի
ուղղությանն
ուղղահայաց
հարթություններ,
և հետևաբար,
այդ
հարթություններում
գտնվող 1 և 2
մետաղյա
զոնդերի միջև
պոտենցիալների
տարբերությունը
հավասար
կլինի զրոյի:
Սակայն եթե
նմուշի մեջ
ստեղծենք
հոսանքին ու զոնդերին
ուղղահայաց
մագնիսական
դաշտ, ապա զոնդերի
միջև
կառաջանա
պոտենցիալների
տարբերություն,
որը ցույց
կտա, որ
մագնիսական
դաշտի
առկայության
դեպքում
համապոտենցիալ
հարթությունները
դառնում են
թեք:
խտության
հոսանք կա (նկ. 87):
Այդպիսի
թիթեղի ներսում
համապոտենցիալ
մակերևույթները
կլինեն
հոսանքի
ուղղությանն
ուղղահայաց
հարթություններ,
և հետևաբար,
այդ
հարթություններում
գտնվող 1 և 2
մետաղյա
զոնդերի միջև
պոտենցիալների
տարբերությունը
հավասար
կլինի զրոյի:
Սակայն եթե
նմուշի մեջ
ստեղծենք
հոսանքին ու զոնդերին
ուղղահայաց
մագնիսական
դաշտ, ապա զոնդերի
միջև
կառաջանա
պոտենցիալների
տարբերություն,
որը ցույց
կտա, որ
մագնիսական
դաշտի
առկայության
դեպքում
համապոտենցիալ
հարթությունները
դառնում են
թեք:
Պոտենցիալների այս լայնակի տարբերության առաջացումն էլ կազմում է Հոլլի երևույթի էությունը:

Պոտենցիալների այս լայնակի տարբերության առաջացումն էլ կազմում է Հոլլի երևույթի էությունը:
Հոլլի
երևույթը
դիտելու
համար նմուշը
տեղավորում
են ուժեղ
էլեկտրամագնիսի
բևեռների միջև,
որն ստեղծում
է 1Տլ կարգի
ինդուկցիա,
իսկ առաջացող
պոտենցիալների
տարբերությունը
չափում են կամ
զգայուն
գալվանոմետրի
օգնությամբ,
կամ էլ կոմպենսացիոն
եղանակով`
պոտենցիոմետրի
օգնությամբ:
Փորձը ցույց է
տալիս, որ
պոտենցիալների
լայնակի ![]() տարբերությունը
համեմատական
է հոսանքի
տարբերությունը
համեմատական
է հոսանքի ![]() խտությանը,
խտությանը,
![]() մագնիսական
ինդուկցիային
և զոնդերի
միջև եղած
մագնիսական
ինդուկցիային
և զոնդերի
միջև եղած ![]() հեռավորությանը՝
հեռավորությանը՝

որտեղ
![]() -ը նյութի
տեսակից
կախված
հաստատուն է:
Այն ստացել է
Հոլլի
հաստատուն
անվանումը:
-ը նյութի
տեսակից
կախված
հաստատուն է:
Այն ստացել է
Հոլլի
հաստատուն
անվանումը:
Հետագա ուսումնասիրությունները ցույց տվեցին, որ Հոլլի երևույթը դիտվում է բոլոր հաղորդիչներում և կիսահաղորդիչներում` անկախ նրանց նյութի տեսակից: Հոսանքի կամ մագնիսական դաշտի ուղղության փոփոխությունը առաջ է բերում պոտենցիալների տարբերության նշանի փոփոխություն: Հոլլի R հաստատունի մեծությունը կախված է թիթեղի նյութի տեսակից, ընդ որում` այդ գործակիցը որոշ նյութերի համար դրական է, իսկ այլ նյութերի համար` բացասական:
Հոլլի
երևույթը
հեշտությամբ
բացատրվում է էլեկտրոնային
տեսությամբ և
Լորենցի ուժի
առկայության
հետևանք է:
Որպեսզի այդ
երևույթի
ֆիզիկական
էությունը
ավելի լավ
պարզաբանվի,
կսահմանափակվենք
միայն նրա
պարզեցված
տեսությամբ և
մոտավորապես
կհամարենք, որ
բոլոր
էլեկտրոնները
շարժվում են
հաստատուն
արագությամբ,
որը հավասար է
նրանց
կարգավորված
շարժման
միջին ![]() արագությանը:
Այդ դեպքում
յուրաքանչյուր
էլեկտրոնի
վրա ազդում է
Լորենցի ուժը,
որն ուղղահայաց
է հոսանքի
ուղղությանն
ու
մագնիսական
դաշտին և
հավասար է
արագությանը:
Այդ դեպքում
յուրաքանչյուր
էլեկտրոնի
վրա ազդում է
Լորենցի ուժը,
որն ուղղահայաց
է հոսանքի
ուղղությանն
ու
մագնիսական
դաշտին և
հավասար է ![]() -ի:
-ի:
Այդ
ուժի
ազդեցության
տակ
էլեկտրոնները
կտեղաշարժվեն
այնպես, որ
թիթեղի
նիստերից մեկը
կլիցքավորվի
բացասական
լիցքով,
մյուսը՝ դրական,
և թիթեղի
ներսում
կառաջանա
հոսանքի ու
մագնիսական
դաշտի
նկատմամբ
լայնակի ![]() էլեկտրական
դաշտ:
Հավասարակշռության
դեպքում
էլեկտրական
դաշտի կողմից
էլեկտրոնների
վրա ազդող
ուժը հավասար
է Լորենցի
ուժին՝
էլեկտրական
դաշտ:
Հավասարակշռության
դեպքում
էլեկտրական
դաշտի կողմից
էլեկտրոնների
վրա ազդող
ուժը հավասար
է Լորենցի
ուժին՝
![]()
Հետևաբար, պոտենցիալների լայնակի տարբերությունը՝
![]()
Այս
արտահայտության
մեջ
էլեկտրոնների
միջին ![]() արագությունը
կարելի է
արտահայտել
հոսանքի
արագությունը
կարելի է
արտահայտել
հոսանքի ![]() խտությամբ.
քանի որ
խտությամբ.
քանի որ
![]()
ապա՝
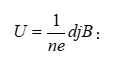
Ստացված արտահայտությունը համընկնում է (6.19) բանաձևի հետ և, այսպիսով, էլեկտրոնային տեսությունը բացատրում է Հոլլի երևույթը ոչ միայն որակապես, այլև՝ քանակապես: Հոլլի հաստատունը՝

Այն
կախված է էլեկտրոնների
![]() կոնցենտրացիայից:
Հետևաբար,
չափելով
Հոլլի հաստատունը,
կարելի է
որոշել
հաղորդչում
էլեկտրոնների
կոնցենտրացիան:
(7.20) բանաձևից
երևում է, որ Հոլլի
հաստատունի
նշանը
համընկնում է
կոնցենտրացիայից:
Հետևաբար,
չափելով
Հոլլի հաստատունը,
կարելի է
որոշել
հաղորդչում
էլեկտրոնների
կոնցենտրացիան:
(7.20) բանաձևից
երևում է, որ Հոլլի
հաստատունի
նշանը
համընկնում է ![]() լիցքակրի
նշանի հետ:
Ուստի
կիսահաղորդչի
համար Հոլլի
հաստատունի
չափման հիման
վրա կարելի
դատել նրա
հաղորդականության
մասին:
Էլեկտրոնային
հաղորդականության
դեպքում
լիցքակրի
նշանի հետ:
Ուստի
կիսահաղորդչի
համար Հոլլի
հաստատունի
չափման հիման
վրա կարելի
դատել նրա
հաղորդականության
մասին:
Էլեկտրոնային
հաղորդականության
դեպքում ![]() , իսկ
անցքայինի
դեպքում`
, իսկ
անցքայինի
դեպքում` ![]() Եթե
կիսահաղորդչում
միաժամանակ
իրականացվում
են երկու
տեսակի
հաղորդականություններն
էլ, ապա ըստ
Հոլլի
հաստատունի
նշանի կարելի
է դատել, թե
նրանցից որն է
գերակշռողը:
Պարզվեց, որ
միավալենտ
մետաղների
համար
հաղորդականության
էլեկտրոնների
կոնցենտրացիան
համընկնում է
ատոմների
կոնցենտրացիայի
հետ:
Եթե
կիսահաղորդչում
միաժամանակ
իրականացվում
են երկու
տեսակի
հաղորդականություններն
էլ, ապա ըստ
Հոլլի
հաստատունի
նշանի կարելի
է դատել, թե
նրանցից որն է
գերակշռողը:
Պարզվեց, որ
միավալենտ
մետաղների
համար
հաղորդականության
էլեկտրոնների
կոնցենտրացիան
համընկնում է
ատոմների
կոնցենտրացիայի
հետ:
Էլեկտրոնային
հաղորդիչների
համար Հոլլի հաստատունի
արժեքը
հնարավորություն
է տալիս
գնահատել
էլեկտրոնների
ազատ վազքի
միջին
երկարությունը:
Պարզվել է, որ
մետաղներում
էլեկտրոնների
ազատ վազքի
միջին երկարությունը
հասնում է
հարյուրավոր
միջհանգուցային
հեռավորության
(![]() սմ):
սմ):
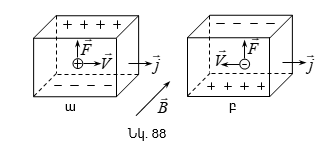
Հեշտ է նաև տեսնել, որ պոտենցիալների լայնակի տարբերության նշանը կախված է էլեկտրահաղորդականությունը պայմանավորող շարժվող մասնիկների լիցքի նշանից: Իրոք, ենթադրենք հաղորդող թիթեղում հոսանքը հոսում է ձախից աջ (նկ. 88ա): Եթե հաղորդչում շարժվող մասնիկները կրում են դրական լիցք, ապա այդ մասնիկների արագությունը կունենա նույն ուղղությունը, ինչ հոսանքը, և մագնիսական դաշտի նշված ուղղության դեպքում Լորենցի ուժը ուղղված կլինի ներքևից վերև: Այդ դեպքում թիթեղի վերին նիստը կլիցքավորվի դրական լիցքով, իսկ ներքևինը՝ բացասական: Իսկ եթե մասնիկները լիցքավորված են բացասականորեն, ապա նրանց արագությունն ուղղված կլինի հոսանքին հակառակ (նկ. 88բ): Քանի որ Լորենցի ուժը կախված է մասնիկների և´ լիցքից, և´ արագությունից, ապա նրա ուղղությունը չի փոխվի, և ուրեմն, լիցքավորված մասնիկները դարձյալ կկուտակվեն վերին նիստի մոտ: Սակայն, որովհետև մասնիկները լիցքավորված են բացասականորեն, վերին նիստը կլիցքավորվի բացասականորեն, իսկ ներքևինը՝ դրականորեն, այսինքն՝ Հոլլի երևույթը կունենա հակառակ նշան:
Հոլլի երևույթում պոտենցիալների լայնակի տարբերության նշանը կախված է հոսանքակիրների նշանից:
ԳԼՈՒԽ 8. ՄԱԳՆԻՍԱԿԱՆ ԴԱՇՏԸ ՆՅՈՒԹԻ ՄԵՋ
8.1. ՄԱԳՆԻՍԱԿԱՆ ԴԱՇՏԻ ՆԿԱՐԱԳՐՈՒՄԸ ՄԱԳՆԵՏԻԿՈՒՄ
Նախորդ բաժինններում ենթադրվում էր, որ հաղորդիչները, որոնցով հոսում են մագնիսական դաշտ ստեղծող հոսանքները, գտնվում են վակուումում:
Եթե
հոսանք կրող
հաղորդիչները
գտնվում են որևէ
միջավայրում,
մագնիսական
դաշտն էապես
փոխվում է: Դա
բացատրվում է
նրանով, որ
ամեն մի նյութ
մագնետիկ է,
այսինքն՝
ընդունակ է
մագնիսական
դաշտի
ազդեցության
տակ
մագնիսական
մոմենտ ձեռք
բերելու
(մագնիսանալու):
Մագնիսացված
նյութը
ստեղծում է իր
![]() մագնիսական
դաշտը, որը
գումարվում է
հաղորդականության
հոսանքներով
պայմանավորված
մագնիսական
դաշտը, որը
գումարվում է
հաղորդականության
հոսանքներով
պայմանավորված
![]() դաշտին:
Երկու
դաշտերը
միասին տալիս
են
դաշտին:
Երկու
դաշտերը
միասին տալիս
են ![]() արդյունարար
դաշտը:
արդյունարար
դաշտը: ![]() դաշտը,
ինչպես նաև
հաղորդականության
հոսանքների
դաշտը,
ինչպես նաև
հաղորդականության
հոսանքների ![]() դաշտը,
չունի
աղբյուրներ
(մագնիսական
լիցքեր):
Ուստի
մագնետիկի
առկայության
դեպքում
արդյունարար
դաշտի համար
ճիշտ է Գաուսի
թեորեմը՝
դաշտը,
չունի
աղբյուրներ
(մագնիսական
լիցքեր):
Ուստի
մագնետիկի
առկայության
դեպքում
արդյունարար
դաշտի համար
ճիշտ է Գաուսի
թեորեմը՝
![]()
Սա
նշանակում է,
որ ![]() վեկտորի
գծերն
անընդհատ և
փակ են նաև
մագնետիկի
առկայության
դեպքում:
վեկտորի
գծերն
անընդհատ և
փակ են նաև
մագնետիկի
առկայության
դեպքում:
8.2. ՄԱԳՆԻՍԱՑՄԱՆ ՄԵԽԱՆԻԶՄԸ: ՄԱԳՆԻՍԱՑՄԱՆ ՎԵԿՏՈՐ
Մարմինների
մագնիսացումը
բացատրելու
համար Ամպերը
ենթադրեց, որ
նյութի
մոլեկուլներում
շրջանառություն
են կատարում
շրջանային
հոսանքներ:
Յուրաքանչյուր
այդպիսի
հոսանք
օժտված է
մագնիսական
մոմենտով և
շրջապատող
տարածության
մեջ ստեղծում
է մագնիսական
դաշտ:
Մոլեկուլային
հոսանքներն
արտաքին դաշտի
բացակայության
դեպքում
ունեն
քաոսային կողմնորոշում,
որի
հետևանքով
նրանցով պայմանավորված
արդյունարար
դաշտը զրո է:
Քաոսային
կողմնորոշման
պատճառով
մարմնի
գումարային
մագնիսական
մոմենտը
նույպես զրո
է: Եթե նյութը
տեղադրենք
արտաքին
մագնիսական
դաշտում, ապա
դաշտի
ազդեցության
տակ
մոլեկուլների
մագնիսական
մոմենտները
գերադասելի
կողմնորոշում
են ձեռք
բերում մի
ուղղությամբ,
որի
հետևանքով մագնետիկը
մագնիսանում
է, նրա
գումարային մագնիսական
մոմենտը
դառնում է
զրոյից տարբեր:
Առանձին
մոլեկուլային
հոսանքների
մագնիսական
դաշտերն այս
դեպքում
արդեն իրար
չեն
հավասարակշռում,
և առաջանում է
![]() դաշտը:
դաշտը:
Այլ
կերպ է տեղի
ունենում այն
նյութերի
մագնիսացումը,
որոնց
մոլեկուլները
մագնիսական դաշտի
բացակայության
դեպքում
չունեն մագնիսական
մոմենտներ:
Այդպիսի
նյութերն
արտաքին
մագնիսական
դաշտ
մտցնելիս
մոլեկուլներում
մակածվում են
տարրական շրջանային
հոսանքներ, և
մոլեկուլները
ու նրանց հետ
մեկտեղ
ամբողջ
նյութը ձեռք
են բերում մագնիսական
մոմենտ, որը
նույնպես ![]() դաշտ է
առաջացնում:
դաշտ է
առաջացնում:
Նյութերի մեծամասնությունը մագնիսական դաշտ մտցնելու դեպքում թույլ են մագնիսացվում: Ուժեղ մագնիսական հատկություններով են օժտված միայն ֆերոմագնիսները` երկաթը, նիկելը, կոբալտը, դրանց շատ համաձուլվածքներ և այլն:
Մագնետիկի
մագնիսացման
աստիճանը
բնութագրվում
է միավոր
ծավալի
մագնիսական
մոմենտով: Այս
մեծությունը
կոչվում է
մագնիսացման
վեկտոր և նշանակվում
է ![]() տառով: Եթե
մագնետիկն
անհամասեռ է
մագնիսացված,
մագնիսացման
վեկտորը
տվյալ կետում
որոշվում է
հետևյալ
առնչությամբ՝
տառով: Եթե
մագնետիկն
անհամասեռ է
մագնիսացված,
մագնիսացման
վեկտորը
տվյալ կետում
որոշվում է
հետևյալ
առնչությամբ՝

որտեղ
![]() -ն տվյալ
կետի
շրջակայքում
վերցրած
ֆիզիկորեն
անվերջ փոքր
ծավալ է,
-ն տվյալ
կետի
շրջակայքում
վերցրած
ֆիզիկորեն
անվերջ փոքր
ծավալ է, ![]() -ը՝
առանձին
մոլեկուլի
մագնիսական
մոմենտը: Գումարումը
կատարվում է
ամբողջ
-ը՝
առանձին
մոլեկուլի
մագնիսական
մոմենտը: Գումարումը
կատարվում է
ամբողջ ![]() ծավալում
գտնվող բոլոր
մոլեկուլների
համար: (8.2)
հավասարման
աջ մասի համարիչը
և հայտարարը
բազմապատկենք
ծավալում
գտնվող բոլոր
մոլեկուլների
համար: (8.2)
հավասարման
աջ մասի համարիչը
և հայտարարը
բազմապատկենք
![]() -ով,
կստանանք՝
-ով,
կստանանք՝

որտեղ
![]() -ը
մոլեկուլների
թիվն է
-ը
մոլեկուլների
թիվն է ![]() ծավալում,
ծավալում, ![]() -ը՝ միջին
մագնիսական
մոմենտը:
-ը՝ միջին
մագնիսական
մոմենտը:
Ինչպես
վերևում
ասվեց, նյութի
մագնիսացումը
պայմանավորված
է մագնիսական
մոմենտների կամ
մոլեկուլներում
մակածված
մագնիսական մոմենտների
մեկ
ուղղությամբ
գերադասելի կողմնորոշումով:
Դա կարելի է
ասել նաև
յուրաքանչյուր
մոլեկուլի
հետ կապված
տարրական շրջանային
հոսանքների
վերաբերյալ:
Դրանք կոչվում
են մոլեկուլային
հոսանքներ:
Մոլեկուլային
հոսանքների այդպիսի
վարքն
առաջացնում է ![]() մակրոսկոպիկ
հոսանքներ,
որոնց
անվանում են մագնիսացման
հոսանքներ:
մակրոսկոպիկ
հոսանքներ,
որոնց
անվանում են մագնիսացման
հոսանքներ:
Կարելի
է ցույց տալ,
որ
մագնիսացման
վեկտորի
շրջապտույտը
կամայական
փակ կոնտուրով
հավասար է
մագնիսացման ![]() հոսանքների
հանրահաշվական
գումարին.
հոսանքների
հանրահաշվական
գումարին.

որտեղ
![]() , ընդ որում
ինտեգրումը
կատարվում է
կոնտուրի վրա
հենված
կամայական
մակերևույթով:
, ընդ որում
ինտեգրումը
կատարվում է
կոնտուրի վրա
հենված
կամայական
մակերևույթով:
8.3.
ՄԱԳՆԻՍԱԿԱՆ
ԴԱՇՏԻ
ԼԱՐՎԱԾՈՒԹՅԱՆ
![]() ՎԵԿՏՈՐԸ
ԵՎ
ՎԵԿՏՈՐԸ
ԵՎ
ՇՐՋԱՊՏՈՒՅՏԻ
ԹԵՈՐԵՄԸ ![]() ՎԵԿՏՈՐԻ
ՀԱՄԱՐ
ՎԵԿՏՈՐԻ
ՀԱՄԱՐ
Արտաքին
մագնիսական
դաշտում
տեղավորված մագնետիկներում
առաջանում են
մագնիսացման հոսանքներ,
ուստի ![]() վեկտորի
շրջապտույտը
կորոշվի ոչ
միայն հաղորդականության
հոսանքներով,
այլ նաև
մագնիսացման
հոսանքներով,
այսինքն՝
վեկտորի
շրջապտույտը
կորոշվի ոչ
միայն հաղորդականության
հոսանքներով,
այլ նաև
մագնիսացման
հոսանքներով,
այսինքն՝

որտեղ
![]() -ն և
-ն և ![]() -ը
կոնտուրով
ընդգրկված
հաղորդականության
և
մագնիսացման
հոսանքներն
են: Նկատի
ունենալով, որ
ընդհանուր
դեպքում
-ը
կոնտուրով
ընդգրկված
հաղորդականության
և
մագնիսացման
հոսանքներն
են: Նկատի
ունենալով, որ
ընդհանուր
դեպքում ![]() հոսանքների
գտնելը բարդ
խնդիր է, (8.5)
բանաձևը գործնականորեն
դառնում է քիչ
պիտանի:
Պարզվում է,
որ կարելի է
գտնել մի
օժանդակ
վեկտոր, որի
շրջապտույտը որոշվում
է միայն
հաղորդականության
հոսանքներով:
Իրոք, մենք
գիտենք, որ
հոսանքների
գտնելը բարդ
խնդիր է, (8.5)
բանաձևը գործնականորեն
դառնում է քիչ
պիտանի:
Պարզվում է,
որ կարելի է
գտնել մի
օժանդակ
վեկտոր, որի
շրջապտույտը որոշվում
է միայն
հաղորդականության
հոսանքներով:
Իրոք, մենք
գիտենք, որ ![]() -ը կապված է
մագնիսացման
վեկտորի
շրջապտույտի
հետ հետևյալ
բանաձևով.
-ը կապված է
մագնիսացման
վեկտորի
շրջապտույտի
հետ հետևյալ
բանաձևով.

Ենթադրելով,
որ ![]() և
և ![]() վեկտորների
շրջապտույտը
վերցվում է միևնույն
կոնտուրով, (8.5)-ի
մեջ
վեկտորների
շրջապտույտը
վերցվում է միևնույն
կոնտուրով, (8.5)-ի
մեջ ![]() -ը
ներկայացնենք
(8.6) բանաձևով՝
-ը
ներկայացնենք
(8.6) բանաձևով՝

Ինտեգրալի
նշանի տակ
փակագծերում
գտնվող
արտահայտությունն
էլ հենց մեր
որոնած
օժանդակ
վեկտորն է:
Այն
նշանակվում է ![]() տառով և
կոչվում
մագնիսական
դաշտի
լարվածություն:
Այսպիսով,
մագնիսական
դաշտի լարվածություն
է կոչվում այն
ֆիզիկական
մեծությունը,
որը որոշվում
է
տառով և
կոչվում
մագնիսական
դաշտի
լարվածություն:
Այսպիսով,
մագնիսական
դաշտի լարվածություն
է կոչվում այն
ֆիզիկական
մեծությունը,
որը որոշվում
է

առնչությամբ:
Օգտագործելով (8.8)-ը՝ (8.7) բանաձևը կարելի է գրել հետևյալ տեսքով՝

Եթե
մակրոսկոպիկ
հոսանքները
տարածության
մեջ բաշխված
են ![]() խտությամբ,
ապա (8.9) բանաձևը
ձևափոխվում է
հետևյալին՝
խտությամբ,
ապա (8.9) բանաձևը
ձևափոխվում է
հետևյալին՝

(S-ը
կամայական
մակերևույթ է,
սահմանափակված
այն կոնտուրով,
որով
վերցվում է
շրջապտույտը):
(8.9) և (8.10)
բանաձևերն
արտահայտում
են ![]() վեկտորի
շրջապտույտի
թեորեմը:
Մագնիսական դաշտի
լարվածության
վեկտորի
շրջապտույտը որևէ
կոնտուրով
հավասար է այդ
կոնտուրով ընդգրկված
մակրոսկոպիկ
հոսանքների
հանրահաշվական
գումարին:
Վերը ասվածից
բխում է, որ
մագնիսական
դաշտի
վեկտորի
շրջապտույտի
թեորեմը:
Մագնիսական դաշտի
լարվածության
վեկտորի
շրջապտույտը որևէ
կոնտուրով
հավասար է այդ
կոնտուրով ընդգրկված
մակրոսկոպիկ
հոսանքների
հանրահաշվական
գումարին:
Վերը ասվածից
բխում է, որ
մագնիսական
դաշտի ![]() լարվածությունը
լարվածությունը
![]() էլեկտրական
շեղման
նմանակն է:
էլեկտրական
շեղման
նմանակն է:
![]() և
և ![]() վեկտորների
կապը:
Ընդունված է
վեկտորների
կապը:
Ընդունված է ![]() մագնիսացման
վեկտորը
կապել ոչ թե
մագնիսական
ինդուկցիայի,
այլ դաշտի
լարվածության
հետ: Այժմ
սահմանափակվենք
միայն
այնպիսի մագնետիկների
դիտարկումով,
որոնց համար
մագնիսացման
վեկտորը
կապել ոչ թե
մագնիսական
ինդուկցիայի,
այլ դաշտի
լարվածության
հետ: Այժմ
սահմանափակվենք
միայն
այնպիսի մագնետիկների
դիտարկումով,
որոնց համար ![]() -ի
կախումը
-ի
կախումը ![]() -ից
ունի գծային
բնույթ,
այսինքն՝
-ից
ունի գծային
բնույթ,
այսինքն՝

որտեղ
![]() -ն
տվյալ
մագնետիկին
բնորոշ
մեծություն է,
որը կոչվում է
մագնիսական
ընկալունակություն:
-ն
տվյալ
մագնետիկին
բնորոշ
մեծություն է,
որը կոչվում է
մագնիսական
ընկալունակություն:
![]() -ի
չափայնությունը
համընկնում է
-ի
չափայնությունը
համընկնում է
![]() -ի
չափայնության
հետ:
Հետևաբար
-ի
չափայնության
հետ:
Հետևաբար ![]() -ն
չափայնություն
չունեցող
մեծություն է:
-ն
չափայնություն
չունեցող
մեծություն է:
Տեղադրելով
 բանաձևի
մեջ
բանաձևի
մեջ ![]() -ի
արտահայտությունը`
կստանանք՝
-ի
արտահայտությունը`
կստանանք՝ 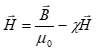
այսինքն՝

Չափայնություն
չունեցող ![]() մեծությունը
կոչվում է
նյութի
հարաբերական
մագնիսական
թափանցելիություն
կամ պարզապես՝
մագնիսական
թափանցելիություն:
մեծությունը
կոչվում է
նյութի
հարաբերական
մագնիսական
թափանցելիություն
կամ պարզապես՝
մագնիսական
թափանցելիություն:
Ի
տարբերություն
դիէլեկտրական
![]() ընկալունակության,
որն
ընդունում է
միայն դրական
արժեքներ
(իզոտրոպ
միջավայրում՝
դիէլեկտրիկում),
բևեռացման
ընկալունակության,
որն
ընդունում է
միայն դրական
արժեքներ
(իզոտրոպ
միջավայրում՝
դիէլեկտրիկում),
բևեռացման ![]() վեկտորը
միշտ ուղղված
է
վեկտորը
միշտ ուղղված
է ![]() դաշտի
ուղղությամբ:
Մագնիսական
ընկալունակությունը
կարող է լինել
ինչպես
դրական, այնպես
էլ`
բացասական:
Այդ պատճառով
մագնիսական թափանցելիությունը
կարող է լինել
ինչպես մեկից
մեծ, այնպես
էլ մեկից
փոքր:
Մագնետիկները,
որոնք
ենթարկվում
են
դաշտի
ուղղությամբ:
Մագնիսական
ընկալունակությունը
կարող է լինել
ինչպես
դրական, այնպես
էլ`
բացասական:
Այդ պատճառով
մագնիսական թափանցելիությունը
կարող է լինել
ինչպես մեկից
մեծ, այնպես
էլ մեկից
փոքր:
Մագնետիկները,
որոնք
ենթարկվում
են ![]() կախվածությանը,
բաժանվում են
պարամագնիսների
(
կախվածությանը,
բաժանվում են
պարամագնիսների
(![]() >0)
և
դիամագնիսների
(
>0)
և
դիամագնիսների
(![]() <0):
Պարամագնիսներում
<0):
Պարամագնիսներում
![]() դիամագնիսներում
դիամագնիսներում
![]() :
Նշենք, որ
բացի այս
մագնետիկներից
գոյություն
ունեն
ֆերոմագնիսներ,
որոնցում
:
Նշենք, որ
բացի այս
մագնետիկներից
գոյություն
ունեն
ֆերոմագնիսներ,
որոնցում ![]() կախվածությունն
ունի բարդ
բնույթ: Այն
գծային չէ. և
դիտվում է, այսպես
կոչված,
հիստերեզիսը,
այսինքն
կախվածությունն
ունի բարդ
բնույթ: Այն
գծային չէ. և
դիտվում է, այսպես
կոչված,
հիստերեզիսը,
այսինքն ![]() -ը
կախված է
մագնետիկի
նախապատմությունից:
-ը
կախված է
մագնետիկի
նախապատմությունից:
Մագնետիկների
համար, որոնք
ենթարկվում
են (8.11) կախվածությանը
(8.8)
արտահայտությունն
ընդունում է ![]() տեսքը:
Որտեղից`
տեսքը:
Որտեղից`
![]()
Պարամագնիսների
մոտ ![]() ,
դիամագնիսների
մոտ
,
դիամագնիսների
մոտ ![]() ,
ընդ որում
երկու
դեպքում էլ
,
ընդ որում
երկու
դեպքում էլ ![]() -ն
1-ից շատ քիչ է
տարբերվում,
այսինքն` այդ
մագնետիկների
մագնիսական
հատկություններն
արտահայտվում
են շատ թույլ:
Համառոտակի
նկարագրենք
ֆերոմագնիսների
հատկությունները:
Ֆերոմագնիսներ
են կոչվում
այն նյութերը,
որոնցում
ներքին
(սեփական)
մագնիսական
դաշտը
հարյուր և
հազարավոր անգամներ
կարող է
գերազանցել
իրեն
առաջացնող արտաքին
մագնիսական
դաշտին: Դրանց
թվին են պատկանում
երկաթը,
նիկելը,
կոբալտը,
դրանց համաձուլվածքներն
ու
միացությունները:
-ն
1-ից շատ քիչ է
տարբերվում,
այսինքն` այդ
մագնետիկների
մագնիսական
հատկություններն
արտահայտվում
են շատ թույլ:
Համառոտակի
նկարագրենք
ֆերոմագնիսների
հատկությունները:
Ֆերոմագնիսներ
են կոչվում
այն նյութերը,
որոնցում
ներքին
(սեփական)
մագնիսական
դաշտը
հարյուր և
հազարավոր անգամներ
կարող է
գերազանցել
իրեն
առաջացնող արտաքին
մագնիսական
դաշտին: Դրանց
թվին են պատկանում
երկաթը,
նիկելը,
կոբալտը,
դրանց համաձուլվածքներն
ու
միացությունները:

Ֆերոմագնիսները
ուժեղ
մագնիսական
նյութեր են,
որոնց
մագնիսացումը
շատ (մինչև 1010)
անգամ
գերազանցում
է
դիամագնիսների
և պարամագնիսների
մագնիսացմանը,
որոնք
պատկանում են
թույլ
մագնիսական
նյութերի
դասին: Թույլ
մագնիսական
նյութերի
մագնիսացումը
դաշտի
լարվածության
հետ
փոփոխվում է
գծայնորեն: Ֆերոմագնիսների
մագնիսացումը
![]() -ից
բարդ կախում
ունի: 100 Ա/մ
կարգի
դաշտերում
մագնիսացումը`
-ից
բարդ կախում
ունի: 100 Ա/մ
կարգի
դաշտերում
մագնիսացումը`
![]() -ն, հասնում
է հագեցման
(նկ.89):
Մագնիսացման
հիմնական
կորը
-ն, հասնում
է հագեցման
(նկ.89):
Մագնիսացման
հիմնական
կորը ![]() դիագրամի
վրա բերված է
նկ.90-ում:
Հիշեցնենք, որ
դիագրամի
վրա բերված է
նկ.90-ում:
Հիշեցնենք, որ
![]() , այդ
պատճառով
հագեցման հասնելիս
, այդ
պատճառով
հագեցման հասնելիս
![]() -ն
-ն
![]() -ին զուգընթաց
շարունակում
է աճել,
-ին զուգընթաց
շարունակում
է աճել, ![]() գծային
օրենքով,
որտեղ
գծային
օրենքով,
որտեղ ![]() :
Ֆերոմագնիսների
մոտ
:
Ֆերոմագնիսների
մոտ ![]() -ն
կախված է արտաքին
մագնիսական
դաշտից, քանի
որ
-ն
կախված է արտաքին
մագնիսական
դաշտից, քանի
որ ![]() -ի
և
-ի
և ![]() -ի միջև
գոյություն
ունի ոչ
գծային
կախվածություն:
Մագնիսացման
դեպքում
ֆերոմագնիսի
ներսում
մագնիսական
դաշտի
լարվածությունն
աճում է 0-ից
մինչև H-ի
որոշակի
արժեք (նկ.91):
Ֆերոմագնիսում
ինդուկցիայի
փոփոխությունը
բնութագրվում
է
-ի միջև
գոյություն
ունի ոչ
գծային
կախվածություն:
Մագնիսացման
դեպքում
ֆերոմագնիսի
ներսում
մագնիսական
դաշտի
լարվածությունն
աճում է 0-ից
մինչև H-ի
որոշակի
արժեք (նկ.91):
Ֆերոմագնիսում
ինդուկցիայի
փոփոխությունը
բնութագրվում
է ![]() կորով:
Եթե
կորով:
Եթե ![]() -ը
փոքրացվի, ապա
ինդուկցիայի
փոփոխությունը
պատկերվում է
-ը
փոքրացվի, ապա
ինդուկցիայի
փոփոխությունը
պատկերվում է ![]() կորով:
Դաշտի
լարվածության`
կորով:
Դաշտի
լարվածության`
![]() արժեքի
դեպքում
ինդուկցիան
տարբեր է
զրոյից:
Ֆերոմագնիսն
այս վիճակում
հաստատուն
մագնիս է:
Որպեսզի
վերացվի
մնացորդային մագնիսացումը,
հարկավոր է
ստեղծել
արժեքի
դեպքում
ինդուկցիան
տարբեր է
զրոյից:
Ֆերոմագնիսն
այս վիճակում
հաստատուն
մագնիս է:
Որպեսզի
վերացվի
մնացորդային մագնիսացումը,
հարկավոր է
ստեղծել ![]() դաշտը,
որն ուղղված է
սկզբնականին
հակառակ: Մագնիսական
դաշտի այն
լարվածությունը,
որի դեպքում B = 0, անվանում
են Hկ
կոէրցիտիվ
ուժ: Դաշտի
լարվածության
հետագա փոփոխության
դեպքում
ինդուկցիան
փոփոխվում է`
կազմելով,
ինչպես ցույց
է տրված
նկ.91-ում, հիստերեզիսի
օղակը: Կախված
կոէրցիտիվ
ուժի արժեքներից`
ֆերոմագնիսները
լինում են
փափուկ և
կոշտ: Փափուկ
ֆերոմագնիսներն
ունեն հիստերեզիսի
նեղ օղակ և
կոէրցիտիվ
ուժի փոքր
արժեքներ:
Կոշտ
ֆերոմագնիսներին
բնութագրական
են
հիստերեզիսի
լայն օղակը և,
համապատասխանաբար`
կոէրցիտիվ
ուժի մեծ
արժեքները:
Փափուկ ֆերոմագնիսներից
են երկաթը,
պերմալոն և
այլ նյութեր:
դաշտը,
որն ուղղված է
սկզբնականին
հակառակ: Մագնիսական
դաշտի այն
լարվածությունը,
որի դեպքում B = 0, անվանում
են Hկ
կոէրցիտիվ
ուժ: Դաշտի
լարվածության
հետագա փոփոխության
դեպքում
ինդուկցիան
փոփոխվում է`
կազմելով,
ինչպես ցույց
է տրված
նկ.91-ում, հիստերեզիսի
օղակը: Կախված
կոէրցիտիվ
ուժի արժեքներից`
ֆերոմագնիսները
լինում են
փափուկ և
կոշտ: Փափուկ
ֆերոմագնիսներն
ունեն հիստերեզիսի
նեղ օղակ և
կոէրցիտիվ
ուժի փոքր
արժեքներ:
Կոշտ
ֆերոմագնիսներին
բնութագրական
են
հիստերեզիսի
լայն օղակը և,
համապատասխանաբար`
կոէրցիտիվ
ուժի մեծ
արժեքները:
Փափուկ ֆերոմագնիսներից
են երկաթը,
պերմալոն և
այլ նյութեր:
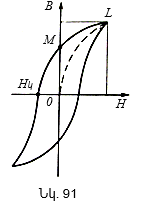
Հիստերեզիսի օղակը բնութագրում է այն աշխատանքը, որն անհրաժեշտ է ծախսել ֆերոմագնիսի վերամագնիսացման վրա: Եթե ըստ աշխատանքի պայմանի` ֆերոմագնիսը պետք է վերամագնիսացվի փոփոխական մագնիսական դաշտում, ապա նպատակահարմար է օգտագործել փափուկ ֆերոմագնիսներ, որոնց հիստերեզիսի օղակը փոքր է: Փափուկ ֆերոմագնիսներից պատրաստում են տրանսֆորմատորի, գեներատորների, էլեկտրաշարժիչների միջուկները: Կոշտ ֆերոմագնիսներից, որոնցից են պողպատը և նրա համաձուլվածքները, պատրաստում են հաստատուն մագնիսներ:

Ֆերոմագնիսականության
տեսությունը
ստեղծել են
Յա. Ֆրենկելը
և Վ. Հայզենբերգը:
Մագնիսամեխանիկական
երևույթների
ուսումնասիրության
փորձերից
հետևում է, որ
ֆերոմագնիսների
մագնիսական
հատկությունները
պայմանավորված
են
էլեկտրոնների
սեփական (սպինային)
մագնիսական
մոմենտներով:
Որոշակի պայմաններում
բյուրեղներում
կարող են առաջանալ
այնպիսի ուժեր
(կոչվում են
փոխանակային),
որոնք
էլեկտրոնների
մագնիսական
մոմենտներին
ստիպում են իրար
զուգահեռ
դասավորվել:
Դրա
հետևանքով առաջանում
են
մագնիսացման
ինքնակամ
(սպոնտան) տիրույթներ,
որոնք
կոչվում են
դոմեններ: Յուրաքանչյուր
դոմենի
սահմաններում
ֆերոմագնիսը
սպոնտան
կերպով
մագնիսացված
է մինչև
հագեցման աստիճանը
և օժտված է
որոշակի
մագնիսական
մոմենտով: Այս
մոմենտների
ուղղությունները
տարբեր
դոմենների
համար տարբեր
են (նկ.92), այնպես,
որ արտաքին
դաշտի
բացակայության
դեպքում ամբողջ
մարմնի
գումարային
մոմենտը
հավասարվում
է զրոյի:
Դոմեններն
ունեն ![]() սմ
կարգի չափեր:
Դաշտի
ազդեցության
դեպքում տեղի
է ունենում
դոմենների
մագնիսական
մոմենտների
շրջադարձ: Ընդ
որում`
էլեկտրոնների
մոմենտները
դոմենի
սահմաններում
միաժամանակ
շրջվում են
առանց իրար
նկատմամբ
ունեցած
զուգահեռությունը
խախտելու (նկ.93):
Այս
պրոցեսները
դարձելի չեն,
ինչը և դառնում
է
հիստերեզիսի
պատճառ:
Յուրաքանչյուր
ֆերոմագնիսի
համար
գոյություն
ունի որոշակի
սմ
կարգի չափեր:
Դաշտի
ազդեցության
դեպքում տեղի
է ունենում
դոմենների
մագնիսական
մոմենտների
շրջադարձ: Ընդ
որում`
էլեկտրոնների
մոմենտները
դոմենի
սահմաններում
միաժամանակ
շրջվում են
առանց իրար
նկատմամբ
ունեցած
զուգահեռությունը
խախտելու (նկ.93):
Այս
պրոցեսները
դարձելի չեն,
ինչը և դառնում
է
հիստերեզիսի
պատճառ:
Յուրաքանչյուր
ֆերոմագնիսի
համար
գոյություն
ունի որոշակի ![]() ջերմաստիճան,
որի ժամանակ
սպոնտան
մագնիսացման
տիրույթները
քայքայվում
են և նյութը կորցնում
է
ֆերոմագնիսական
հատկությունները:
Այդ
ջերմաստիճանը
կոչվում է
Կյուրիի կետ:
Երկաթի համար
այն հավասար է
ջերմաստիճան,
որի ժամանակ
սպոնտան
մագնիսացման
տիրույթները
քայքայվում
են և նյութը կորցնում
է
ֆերոմագնիսական
հատկությունները:
Այդ
ջերմաստիճանը
կոչվում է
Կյուրիի կետ:
Երկաթի համար
այն հավասար է
![]() ,
նիկելի համար`
,
նիկելի համար`
![]() :
Կյուրիի
կետից բարձր
նջերմաստիճանի
դեպքում
ֆերոմագնիսը
դառնում է
սովորական
պարամագնիս:
Կյուրիի
կետից ցած
սառեցնելիս,
ֆերոմագնիսում
նորից
առաջանում են
դոմեններ:
:
Կյուրիի
կետից բարձր
նջերմաստիճանի
դեպքում
ֆերոմագնիսը
դառնում է
սովորական
պարամագնիս:
Կյուրիի
կետից ցած
սառեցնելիս,
ֆերոմագնիսում
նորից
առաջանում են
դոմեններ:
ԳԼՈՒԽ 9. ԷԼԵԿՏՐԱՄԱԳՆԻՍԱԿԱՆ ՄԱԿԱԾՈՒՄ
9.1. ԷԼԵԿՏՐԱՄԱԳՆԻՍԱԿԱՆ ՄԱԿԱԾՄԱՆ ԵՐԵՎՈՒՅԹԸ
Էլեկտրամագնիսական մակածման երևույթը հայտնագործել է Ֆարադեյը 1831 թ.: Այդ հայտնագործությունը պատկանում է 19-րդ դարի առաջին կեսի ամենանշանավոր գիտական նվաճումների թվին:
Էլեկտրամագնիսական մակածման երևույթի հիման վրա ստեղծվեցին էլեկտրական էներգիայի հզոր գեներատորներ, որոնց կատարելագործմանը մասնակցեցին տարբեր երկրների ու ժողովուրդների գիտնականներն ու տեխնիկները: Նրանց թվում էին նաև ռուս գիտնականներ` Լենցը, Յակոբին, Յաբլոչկովը և ուրիշներ, որոնք մեծ ավանդ ներդրեցին էլեկտրատեխնիկայի զարգացման գործում:
Էլեկտրամագնիսական մակածման երևույթի հայտնագործումով վերջնականապես անխզելի կապ հաստատվեց էլեկտրական հոսանքի և մագնիսական դաշտի միջև:
Էլեկտրամագնիսական մակածման երևույթի հայտնագործումը պատահական չէր: Ֆարադեյը և շատ այլ գիտնականներ գիտակցորեն փնտրում էին հետևյալ խնդրի լուծումը. «Եթե հոսանքը ստեղծում է մագնիսական դաշտ, ապա գոյություն չունի՞ արդյոք երևույթի հակառակ կողմը, չի՞ կարելի արդյոք մագնիսական դաշտի միջոցով ստանալ էլեկտրական հոսանք», այս միտքն էր հետաքրքրում գիտնականներին իրենց հետազոտություններում:
Ֆարադեյը շատ աշխատանք թափեց և մեծ հնարագիտություն ցուցաբերեց, մինչև որ գալվանոմետրի շեղված սլաքն առաջինը ցույց տվեց, որ նա իր ենթադրություններում չի սխալվել:
Էլեկտրամագնիսական մակածման երևույթի էությունը լուսաբանելու համար դիտարկենք հետևյալ փորձերը: Մետաղալարե փաթույթով կոճից և նրա ծայրերին միացված գալվանոմետրից կազմենք շղթա, որը չի պարունակում հոսանքի աղբյուր: Եթե կոճին մոտեցվում է հաստատուն մագնիս (նկ.94 ա), ապա գալվանոմետրի սլաքը շեղվում է` ցույց տալով կոճի շղթայում մակածված հոսանքի առաջացումը: Կոճից մագնիսը հեռացնելիս գալվանոմետրի սլաքը դարձյալ շեղվում է, բայց այս անգամ հակառակ ուղղությամբ (նկ. 94բ):
Հենց որ մագնիսի շարժումը կոճի նկատմամբ ընդհատվում է, հոսանքն էլ դադարում է: Հետևաբար, կոճի շղթայում հոսանք գոյություն ունի միայն այն ժամանակ, երբ մագնիսը շարժվում է կոճի նկատմամբ:

Կարելի է փորձը ձևափոխել՝ կոճը հագցնել անշարժ մագնիսին և դուրս հանել այն: Հիմա էլ կարելի է հայտնաբերել, որ մագնիսի նկատմամբ կոճի շարժվելու ժամանակ շղթայում նորից հոսանք է առաջանում:

Դիտարկենք
մեկ այլ փորձ:
Մետաղալարե
փաթույթով ![]() կոճը
միացնենք
գալվանոմետրին,
իսկ
կոճը
միացնենք
գալվանոմետրին,
իսկ ![]() կոճը`
հոսանքի
աղբյուրին
(նկ.95): Երբ
կոճերը միմյանց
նկատմամբ
անշարժ են,
գալվանոմետրը
կոճը`
հոսանքի
աղբյուրին
(նկ.95): Երբ
կոճերը միմյանց
նկատմամբ
անշարժ են,
գալվանոմետրը
![]() կոճում
հոսանք չի
գրանցի, որքան
էլ որ մեծ լինի
կոճում
հոսանք չի
գրանցի, որքան
էլ որ մեծ լինի
![]() կոճով
անցնող
հոսանքի ուժը
(հետևաբար` և
նրա ստեղծած
մագնիսական
դաշտը): Եթե
կոճով
անցնող
հոսանքի ուժը
(հետևաբար` և
նրա ստեղծած
մագնիսական
դաշտը): Եթե ![]() կոճը շարժենք,
ապա կնկատենք,
որ
գալվանոմետրը
հոսանք է
ցույց տալիս:
Այդ հոսանքն
առաջանում է
միայն
շարժման
ժամանակ: Ընդ
որում, որքան
արագ է շարժվում
կոճը, այնքան
ուժեղ է
հոսանքը:
Հոսանքն
առաջանում է
կոճը և´
մոտեցնելիս, և´
հեռացնելիս,
սակայն այդ
դեպքերում
հոսանքներն
ունեն
հակառակ
ուղղություններ:
Հոսանք առաջանում
է նաև այն
դեպքում, երբ
կոճը շարժենք,
ապա կնկատենք,
որ
գալվանոմետրը
հոսանք է
ցույց տալիս:
Այդ հոսանքն
առաջանում է
միայն
շարժման
ժամանակ: Ընդ
որում, որքան
արագ է շարժվում
կոճը, այնքան
ուժեղ է
հոսանքը:
Հոսանքն
առաջանում է
կոճը և´
մոտեցնելիս, և´
հեռացնելիս,
սակայն այդ
դեպքերում
հոսանքներն
ունեն
հակառակ
ուղղություններ:
Հոսանք առաջանում
է նաև այն
դեպքում, երբ ![]() կոճն ենք
թողնում
անշարժ և
շարժում ենք
կոճն ենք
թողնում
անշարժ և
շարժում ենք ![]() կոճը:
կոճը:
![]() կոճում
մակածման
հոսանք
կարելի է
առաջացնել
նաև կոճի
հոսանքը
փոփոխելով:
կոճում
մակածման
հոսանք
կարելի է
առաջացնել
նաև կոճի
հոսանքը
փոփոխելով:
Մի փորձ էլ կատարենք: Պայտաձև մագնիսի մագնիսական դաշտում տեղավորենք հարթ կոճը, որի ծայրերը միացնենք գալվանոմետրին: Կոճի շրջման ժամանակ գալվանոմետրը նշում է նրա մեջ մակածման հոսանքի առաջացումը:
Մեր քննարկած փորձերի հիման վրա կարելի է նկատել, որ մակածման հոսանքի ծագման բոլոր դեպքերում տեղի է ունենում մագնիսական հոսքի փոփոխություն, երբ հոսքը թափանցում է հաղորդիչն ընդգրկող մակերեսի ներսը:
Իրոք, երբ մագնիսը շարժվում է գալվանոմետրին միացրած կոճի նկատմամբ կամ կոճը՝ մագնիսի նկատմամբ, կոճի գալարների ներսը թափանցող մագնիսական հոսքը փոխվում է. երբ մագնիսը շարժվում է դեպի ներքև, այն մեծանում է, իսկ երբ շարժվում է դեպի վերև՝ փոքրանում է: Երկու դեպքում էլ կոճի գալարներում առաջանում է հոսանք:
Նշենք սակայն`ոչ միշտ է, որ մագնիսական դաշտի փոփոխությունը հաղորդիչ կոնտուրում հոսանք է մակածում: Եթե գալվանոմետրին միացված հարթ, հաղորդիչ կոնտուրն անհամասեռ մագնիսական դաշտում տեղափոխենք այնպես, որ նրանով սահմանափակված մակերևույթը շարժման ընթացքում մնա ինդուկցիայի գծերին զուգահեռ, այսինքն` ինդուկցիայի գծերը չհատեն այդ մակերևույթը, ապա նրանում հոսանք չի առաջանա:
Ուրեմն՝ փակ հաղորդիչ կոնտուրի մեջ թափանցող մագնիսական հոսքի ամեն մի փոփոխության ժամանակ հաղորդչում ծագում է էլեկտրական հոսանք, որը գոյություն ունի մագնիսական հոսքի փոփոխության ամբողջ պրոցեսի ընթացքում:
Այս է բնության կարևորագույն օրենքներից մեկը՝ էլեկտրամագնիսական մակածման օրենքը:
Մակածման ժամանակ հաղորդչում ծագող էլեկտրաշարժ ուժն ընդունված է անվանել մակածման էլեկտրաշարժ ուժ:
Նկատենք, որ էլեկտրամագնիսական մակածման երևույթի համար բնորոշ մեծությունը մակածման ԷլՇՈՒ-ն է, և ոչ` մակածման հոսանքը, որը կախված է հաղորդչի դիմադրությունից: Երկու միևնույն չափերի և ձևի հաղորդիչներում, միևնույն պայմաններում, ԷլՇՈՒ-ն կլինի նույնը, իսկ մակածման հոսանքը մեծ կլինի այն հաղորդիչում, որի դիմադրությունը փոքր է:
Մտցնելով մակածման ԷլՇՈՒ-ի հասկացությունը` կարելի է էլեկտրամագնիսական մակածման օրենքն արտահայտել ավելի ընդհանուր ձևով:
Հաղորդիչ կոնտուրի մեջ թափանցող մագնիսկան հոսքի ամեն մի փոփոխության դեպքում հաղորդչում ծագում է մակածման ԷլՇՈՒ:
Էլեկտրամագնիսական մակածման երևույթը նկատվում է նաև բաց հաղորդիչներում: Այն դեպքում, երբ հաղորդիչը հատում է մագնիսական ուժագծերը, նրա ծայրերում առաջանում է պոտենցիալների տարբերություն, որի հայտնվելու պատճառը մակածման նույն այդ ԷլՇՈՒ-ն է:
9.2. ՄԱԿԱԾՄԱՆ ՀՈՍԱՆՔԻ ՈՒՂՂՈՒԹՅՈՒՆԸ: ԼԵՆՑԻ ԿԱՆՈՆԸ
Հաղորդչում մակածման հոսանքը, ըստ նրա ծագման պայմանների, ունի տարբեր ուղղություններ, որի վերաբերյալ կարող ենք դատել գալվանոմետրի սլաքի շեղման համաձայն. վերևում նկարագրված մի քանի փորձերում այն շեղվում էր մի կողմ, իսկ մյուս փորձերում՝ մյուս կողմ: Մակածման հոսանքի ուղղության հարցը ամենաընդհանուր ձևով լուծել է Լենցը: Նախքան Լենցի կանոնի ձևակերպելը քննարկենք հոսանքի ուղղությունը մի քանի մասնավոր դեպքերում: Վերցնենք ալյումինե երկու թեթև օղակներ, որոնք գտնվում են պատվանդանի ծայրին (նկ.96):

Օղակներից
մեկը՝ ![]() -ն,
փակ է,
մյուսը՝ B-ն,
ունի կտրվածք:
Եթե մագնիսը
մոտեցնենք և հեռացնենք
կտրվածք
ունեցող
օղակից, ապա
կարելի է
նկատել, որ
այն չի
փոխազդում
մագնիսի հետ,
քանի որ
օղակում
մակածման
հոսանք չի
ծագում:
Սակայն
շարժելով
մագնիսը փակ
օղակի
նկատմամբ` կհայտնաբերենք,
որ մագնիսը
մոտեցնելու
ժամանակ
օղակը նրանից
վանվում է,
իսկ հեռացնելու
ժամանակ`
ձգվում: Նկար
97-ում
գծապատկերով
ցույց է տրված
կոճում ծագող
մակածման
հոսանքի
ուղղությունը
այն դեպքում,
երբ մագնիսը
շարժժվում է
կոճի
նկատմամբ:
Նկարում
ուղղաձիգ սլաքները
ցույց են
տալիս
մագնիսի
շարժման ուղղությունը
կոճի
նկատմամբ, իսկ
գալարների վրա
գտվող
սլաքները՝
այդ դեպքում
կոճում ծագող մակածման
հոսանքի
ուղղությունը:
97ա նկարում ցույց
է տրված, որ
երբ մագնիսի
հյուսիսային
բևեռը
մոտենում է
կոճին,
նրանում
ծագում է մակածման
հոսանք, այն
դառնում է
էլեկտրամագնիս՝
մագնիսին
ավելի մոտ
գտընվող կոճի
ծայրում ծագում
է
էլեկտրամագնիսի
հյուսիսային
բևեռ (եթե
նայենք
հյուսիսային
բևեռի կողմից,
մակածման
հոսանքն
անցնում է
կոճի
գալարներով
ժամացույցի
սլաքի
հակառակ
ուղղությամբ):
Իսկ երբ
մագնիսի
հյուսիսային
բևեռը
հեռանում է կոճից
(նկ.97բ), կոճին
ավելի մոտ
գտնվող
ծայրում ծագում
է հարավային
բևեռ:
Համանման
ձևով, երբ մագնիսի
հարավային
բևեռը
մոտենում է
կոճին (նկ. 97գ),
մագնիսին
ավելի մոտ
գտնվող կոճի
ծայրում ծագում
է հարավային
բևեռ, իսկ երբ
մագնիսը հեռանում
է (նկ. 97դ), ապա
այդ ծայրում
ծագում է հյուսիսային
բևեռ:
-ն,
փակ է,
մյուսը՝ B-ն,
ունի կտրվածք:
Եթե մագնիսը
մոտեցնենք և հեռացնենք
կտրվածք
ունեցող
օղակից, ապա
կարելի է
նկատել, որ
այն չի
փոխազդում
մագնիսի հետ,
քանի որ
օղակում
մակածման
հոսանք չի
ծագում:
Սակայն
շարժելով
մագնիսը փակ
օղակի
նկատմամբ` կհայտնաբերենք,
որ մագնիսը
մոտեցնելու
ժամանակ
օղակը նրանից
վանվում է,
իսկ հեռացնելու
ժամանակ`
ձգվում: Նկար
97-ում
գծապատկերով
ցույց է տրված
կոճում ծագող
մակածման
հոսանքի
ուղղությունը
այն դեպքում,
երբ մագնիսը
շարժժվում է
կոճի
նկատմամբ:
Նկարում
ուղղաձիգ սլաքները
ցույց են
տալիս
մագնիսի
շարժման ուղղությունը
կոճի
նկատմամբ, իսկ
գալարների վրա
գտվող
սլաքները՝
այդ դեպքում
կոճում ծագող մակածման
հոսանքի
ուղղությունը:
97ա նկարում ցույց
է տրված, որ
երբ մագնիսի
հյուսիսային
բևեռը
մոտենում է
կոճին,
նրանում
ծագում է մակածման
հոսանք, այն
դառնում է
էլեկտրամագնիս՝
մագնիսին
ավելի մոտ
գտընվող կոճի
ծայրում ծագում
է
էլեկտրամագնիսի
հյուսիսային
բևեռ (եթե
նայենք
հյուսիսային
բևեռի կողմից,
մակածման
հոսանքն
անցնում է
կոճի
գալարներով
ժամացույցի
սլաքի
հակառակ
ուղղությամբ):
Իսկ երբ
մագնիսի
հյուսիսային
բևեռը
հեռանում է կոճից
(նկ.97բ), կոճին
ավելի մոտ
գտնվող
ծայրում ծագում
է հարավային
բևեռ:
Համանման
ձևով, երբ մագնիսի
հարավային
բևեռը
մոտենում է
կոճին (նկ. 97գ),
մագնիսին
ավելի մոտ
գտնվող կոճի
ծայրում ծագում
է հարավային
բևեռ, իսկ երբ
մագնիսը հեռանում
է (նկ. 97դ), ապա
այդ ծայրում
ծագում է հյուսիսային
բևեռ:
Հայտնի է, որ միմյանց նկատմամբ նույնանուն բևեռներով դասավորված մագնիսները վանվում են, իսկ տարանուն բևեռներովները` ձգվում են: Հետևաբար, երբ կոճում մակածման հոսանքը ծագում է նրան մագնիս մոտեցնելու հետևանքով, ապա մագնիսի և մակածված հոսանքների միջև եղած փոխազդեցության ուժերը մագնիսին վանում են կոճից (նկ. 97ա): Իսկ երբ մագնիսը հեռանում է կոճից, ապա դրանք միմյանց ձգում են (նկ. 97բ):

Քննարկված փորձերից կարելի է անել հետևյալ եզրակացությունը. հաղորդչում ծագող մակածման հոսանքն ուղղված է այնպես, որ իր մագնիսական դաշտով հակազդում է մագնիսի և հաղորդչի` միմյանց նկատմամաբ շարժվելուն:
Քննարկենք այն դեպքը, երբ B կոճում մակածման հոսանքը ծագում է A կոճում հոսանքը փոփոխելու հետևանքով: Այդ դեպքը գծապատկերով ներկայացված է նկար 98-ում, որտեղ A և B կոճերից յուրաքանչյուրը պատկերված է մի գալարի ձևով: Փորձը ցույց է տալիս, որ A կոճում հոսանքն մեծացնելիս, այսինքն՝ մագնիսական դաշտն ուժեղացնելիս, B կոճում մակածման հոսանքն ունի մի ուղղություն, որը հակառակ է A կոճի հոսանքին (նկ. 98ա): Իսկ A կոճում հոսանքը փոքրացնելիս, այսինքն՝ մագնիսական դաշտը թուլացնելիս, B կոճում մակածման հոսանքն ունի այն նույն ուղղությունը, ինչ A կոճում (նկ.98բ): Առաջին դեպքում B կոճի մակածման հոսանքի մագնիսական դաշտն ուղղված է դեպի A կոճի մագնիսական դաշտի հակառակ կողմը՝ հակազդելով նրա ուժեղացմանը: Երկրորդ դեպքում ընդհակառակը, B կոճի մակածման հոսանքի մագնիսական դաշտն ուղղված է դեպի այն նույն կողմը, ինչ որ A կոճի դաշտը` հակազդելով նրա թուլացմանը:
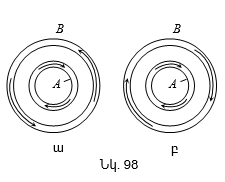
Մակածման հոսանքի` մեր քննարկած բոլոր դեպքերը լիովին համապատասխանում են Լենցի կանոնին, որն ամենաընդհանուր ձևով կարելի է ձևակերպել հետևյալ կերպ. փակ հաղորդիչ կոնտուրում առաջացած մակածման հոսանքը միշտ ունի այնպիսի ուղղություն, որի դեպքում նրա մագնիսական դաշտը հակազդում է այդ հոսանքն առաջացնող մագնիսական հոսքի փոփոխմանը:
Մակածման հոսանքը, ինչպես և ամեն մի հոսանք, օժտված է էներգիայով: Հետևաբար, ստանալով մակածման հոսանք, մենք դրանով էլ ստանում ենք էլեկտրական էներգիա: Էներգիայի պահպանման և փոխակերպման օրենքի համաձայն` էներգիան կարող է ստացվել որևէ այլ տեսակի էներգիայի համարժեք քանակության հաշվին: Երբ մագնիսը մենք մոտեցնում ենք, օրինակ, կոճին (նկ.97ա), ապա կոճում ծագող մակածման հոսանքն իր մագնիսական դաշտով վանում է մագնիսը: Մագնիսը շարժելով` հաղթահարում ենք վանման այդ ուժերը, այսինքն՝ աշխատանք ենք կատարում, որի շնորհիվ մեխանիկական էներգիան փոխարկվում է մակածման հոսանքի էներգիայի: Մագնիսը կոճից դուրս հանելիս (նկ. 97բ) կատարվում է կոճի ձգողության ուժի հաղթահարման աշխատանք: Այստեղ մեխանիկական էներգիան նույնպես փոխարկվում է մակածման հոսանքի էներգիայի:
Այսպիսով, Լենցի կանոնը լիովին համապատասխանում է էներգիայի պահպանման և փոխակերպման օրենքին:
Մակածման ԷլՇՈՒ-ի մեծությունը: Վերևում ծանոթացանք այն պայմաններին, որոնց դեպքում հաղորդչում ծագում է մակածման ԷլՇՈՒ: Քննարկենք, թե ինչից է կախված մակածման ԷլՇՈՒ-ի մեծությունը: Մակածման ԷլՇՈՒ-ի մեծության մասին կարելի է դատել մակածման հոսանքով, որը ծագում է փակ կոնտուրում: Այդ հոսանքի մեծությունը, ըստ Օհմի օրենքի, որոշվում է ԷլՇՈՒ-ի մեծությամբ և շղթայի դիմադրությամբ: Տվյալ հաղորդչում որքան մեծ է մակածման հոսանքը, այնքան մեծ է նրանում ծագած մակածման ԷլՇՈՒ-ն:
Մակածմանը վերաբերող նկարագրված փորձերում կարելի է նշել հետևյալ շատ կարևոր հանգամանքը. որքան արագ է փոփոխվում հաղորդիչ կոնտուրի մեջ թափանցող մագնիսական հոսքը, այնքան ավելի մեծ հոսանք է անցնում հաղորդչով, հետևաբար, ավելի մեծ մակածման ԷլՇՈՒ է ծագում նրանում:
Այսպես, օրինակ, որքան արագ է շարժվում մագնիսը կոճի նկատմամբ (տես նկ.94), այնքան մեծ է այն անկյունը, որով գալվանոմետրի սլաքը շեղվում է, հետևաբար, կոճում ավելի զգալի մեծության մակածման ԷլՇՈՒ է ծագում: Մագնիսի դանդաղ շարժման ժամանակ մագնիսական հոսքը, որն ընդգրկում է կոճի գալարները, դանդաղորեն է փոփոխվում, և կոճում ծագող ԷլՇՈՒ-ն մեծությամբ փոքր է լինում: Այսպիսով, դանդաղորեն կամ արագորեն փոփոխելով մագնիսական հոսքը` հաղորդչում կարելի է ստանալ տարբեր մեծության ԷլՇՈՒ-ներ:
Մագնիսական հոսքի զանազան փոփոխությունների դեպքում տարբեր հաղորդիչների հետ կատարված չափումները ցույց են տալիս, որ հաղորդչում ծագող մակածման ԷլՇՈՒ-ի մեծությունը համեմատական է մագնիսական հոսքի փոփոխման արագությանը:
Նշանակելով
մակածման
ԷլՇՈՒ-ն ![]() տառով`
կարելի է
գրել՝
տառով`
կարելի է
գրել՝

որտեղ
![]() -ն
համեմատականության
գործակից է,
որի թվային
արժեքը
կախված է նրանից,
թե ինչպիսի միավորներով
են չափվել (9.1)
հավասարման
մեջ մտնող
մյուս
մեծություննները:
-ն
համեմատականության
գործակից է,
որի թվային
արժեքը
կախված է նրանից,
թե ինչպիսի միավորներով
են չափվել (9.1)
հավասարման
մեջ մտնող
մյուս
մեծություննները:
Մակածման
ԷլՇՈՒ-ի (9.1)
բանաձևում
բացասական նշանը
ցույց է
տալիս, որ երբ
հաղորդիչ
կոնտուրի մեջ
ներթափանցող
մագնիսական
հոսքն աճում է
(այսինքն, երբ ![]() ),
մակածման
ԷլՇՈՒ-ն կլինի
բացասական,
այն ստեղծում
է մակածման
հոսանք, որն
իր ստեղծած
մագնիսական
հոսքով
փոքրացնում է
իրեն առաջացնող
հոսքը: Երբ
մագնիսական
հոսքը
նվազում է (այսինքն,
երբ
),
մակածման
ԷլՇՈՒ-ն կլինի
բացասական,
այն ստեղծում
է մակածման
հոսանք, որն
իր ստեղծած
մագնիսական
հոսքով
փոքրացնում է
իրեն առաջացնող
հոսքը: Երբ
մագնիսական
հոսքը
նվազում է (այսինքն,
երբ ![]() ),
ԷլՇՈՒ-ն
դրական է և
մակածման
հոսանքն իր
ստեղծած մագնիսական
հոսքով պետք է
խանգարի
մագնիսական
հոսքի
նվազմանը:
),
ԷլՇՈՒ-ն
դրական է և
մակածման
հոսանքն իր
ստեղծած մագնիսական
հոսքով պետք է
խանգարի
մագնիսական
հոսքի
նվազմանը:
Միավորների
ՄՀ-ում
ԷլՇՈՒ-ն
չափվում է
վոլտերով,
ինդուկցիայի
հոսքը՝
վեբերներով,
ժամանակը՝
վայրկյաններով,
հետևաբար` (9.1)
բանաձևում համեմատականության
գործակիցը` ![]() ,
կստանանք՝
,
կստանանք՝

(9.2)-ը արտահայտում է էլեկտրամագնիսական մակածման օրենքը, որը կարելի է ձևակերպել հետևյալ կերպ. էլեկտրամագնիսական մակածման ԷլՇՈՒ-ն փակ հաղորդիչ կոնտուրում հավասար է մագնիսական հոսքի փոփոխության արագությանը՝ վերցրած հակառակ նշանով:
Էլեկտրամագնիսական մակածման օրենքը ձևակերպվում է հենց ԷլՇՈՒ-ի համար, բայց ոչ հոսանքի ուժի համար: Այդպիսի ձևակերպման դեպքում օրենքն արտահայտում է երևույթի էությունը, որը կախում չունի այն հաղորդիչների հատկություններից, որոնց մեջ առաջանում է մակածման հոսանք: Էլեկտրամագնիսական մակածման օրենքում հաշվի է առնված մակածման հոսանքի ուղղությունը (կամ մակածման ԷլՇՈՒ-ի նշանը)` Լենցի կանոնին համապատասխան:
9.3. ԷԼԵԿՏՐԱՄԱԳՆԻՍԱԿԱՆ ՄԱԿԱԾՄԱՆ ՕՐԵՆՔԻ ԱՐՏԱԾՈՒՄԸ ԵՐԿՈՒ ԵՂԱՆԱԿՈՎ
Գոյություն ունի մագնիսական դաշտում ԷլՇՈՒ-ի առաջացման երկու մեխանիզմ. երբ հաղորդիչն անշարժ վիճակում գտնվում է ժամաակի ընթացքում փոփոխվող մագնիսական դաշտում, նրանում ԷլՇՈՒ-ի առաջացման պատճառը մրրկային էլեկտրական դաշտի ի հայտ գալն է:
ԷլՇՈՒ կարող է առաջանալ նաև այն դեպքում, երբ հաղորդիչը շարժվում է ժամանակի ընթացքում անփոփոխ մագնիսական դաշտում: Այս դեպքում ԷլՇՈՒ-ի առաջացման պատճառը հաղորդչում գտնվող ազատ լիցքերի վրա մագնիսական դաշտի կողմից ազդող Լորենցի ուժն է:

Դիտարկենք
մակածման
ԷլՇՈՒ-ի
առաջացումը,
հետևաբար` նաև
մակածման
հոսանքի
ծագումը: Դիցուք
առանց
հոսանքի ![]() երկարության
հաղորդիչը
շարժվում է
մագնիսական
դաշտում
երկարության
հաղորդիչը
շարժվում է
մագնիսական
դաշտում ![]() արագությամբ:
Մագնիսական
դաշտը
համասեռ է: Մագնիսական
ինդուկցիայի
վեկտորն
ուղղված է մեզնից
դեպի
հարթությունը`
նրան
ուղղահայաց
(նկ. 99):
արագությամբ:
Մագնիսական
դաշտը
համասեռ է: Մագնիսական
ինդուկցիայի
վեկտորն
ուղղված է մեզնից
դեպի
հարթությունը`
նրան
ուղղահայաց
(նկ. 99):
Հաղորդչի`
դեպի աջ
շարժման
դեպքում
նրանում գտնվող
ազատ
էլեկտրոնները
նույնպես
կշարժվեն
դեպի աջ,
այսինքն՝
կառաջանա
կոնվեկցիոն
հոսանք: Այդ
հոսանքի
ուղղությունը
հակառակ է
էլեկտրոնների
շարժման ուղղությանը:
Մագնիսական
դաշտի կողմից
յուրաքանչյուր
շարժվող
էլեկտրոնի
վրա ազդում է
Լորենցի ուժ:
Էլեկտրոնի
լիցքը
բացասական է,
այդ պատճառով
Լորենցի ![]() ուժն
ուղղված է
դեպի ներքև:
Հետևաբար,
էլեկտրոններն
այդ ուժի
ազդեցության
տակ շարժվում են
դեպի ներքև, և
ուժն
ուղղված է
դեպի ներքև:
Հետևաբար,
էլեկտրոններն
այդ ուժի
ազդեցության
տակ շարժվում են
դեպի ներքև, և ![]() երկարության
հաղորդչի
ներքևի
մասում կկուտակվեն
բացասական
լիցքերը, իսկ
վերին մասում՝
դրականները:
Սրա
արդյունքում
կառաջանա պոտենցիալների
երկարության
հաղորդչի
ներքևի
մասում կկուտակվեն
բացասական
լիցքերը, իսկ
վերին մասում՝
դրականները:
Սրա
արդյունքում
կառաջանա պոտենցիալների
![]() տարբերություն:
Այսպիսով,
հաղորդչում
կծագի
տարբերություն:
Այսպիսով,
հաղորդչում
կծագի ![]() լարվածությամբ
էլեկտրական
դաշտ, որը
կարգելակի
էլեկտրոնների
հետագա
տեղաշարժը:
Լիցքերը
կդադարեն
տեղաշարժվել
էլեկտրական
դաշտի
այնպիսի
լարվածությամբ
էլեկտրական
դաշտ, որը
կարգելակի
էլեկտրոնների
հետագա
տեղաշարժը:
Լիցքերը
կդադարեն
տեղաշարժվել
էլեկտրական
դաշտի
այնպիսի ![]() լարվածության
դեպքում, երբ
էլեկտրական
դաշտի կողմից
գործող
լարվածության
դեպքում, երբ
էլեկտրական
դաշտի կողմից
գործող ![]() ուժը
կլինի
մոդուլով
հավասար, բայց
ուղղությամբ`
հակառակ
մագնիսական
դաշտի կողմից
ազդող
ուժը
կլինի
մոդուլով
հավասար, բայց
ուղղությամբ`
հակառակ
մագնիսական
դաշտի կողմից
ազդող ![]() ուժին.
ուժին.
![]()
![]() երկարություն
ունեցող
շարժվող
հաղորդչի էլեկտրական
դաշտի E լարվածությունը
և
երկարություն
ունեցող
շարժվող
հաղորդչի էլեկտրական
դաշտի E լարվածությունը
և ![]() պոտենցիալների
տարբերությունը
միմյանց հետ
կապված են
հետևյալ
առնչությամբ.
պոտենցիալների
տարբերությունը
միմյանց հետ
կապված են
հետևյալ
առնչությամբ.
![]()
Եթե
այսպիսի
հաղորդիչը
փակվի, ապա
շղթայով հոսանք
կանցնի:
Այսպիսով,
համասեռ
մագնիսական ![]() դաշտում
դաշտում
![]() արագությամբ
շարժվող
արագությամբ
շարժվող ![]() երկարության
հաղորդչի
ծայրերում
կմակածվի
ԷլՇՈՒ.
երկարության
հաղորդչի
ծայրերում
կմակածվի
ԷլՇՈՒ.
![]()
Հաշվի
առնելով, որ ![]() ձևափոխենք
(8.3)
հավասարումը.
ձևափոխենք
(8.3)
հավասարումը.
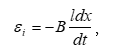
որտեղ
![]() -ը
կոնտուրի`
-ը
կոնտուրի` ![]() ժամանակամիջոցում
ժամանակամիջոցում
![]() երկարության
հաղորդչով
շարժման
ժամանակ գծված
մակերեսն է:
Այս դեպքում
երկարության
հաղորդչով
շարժման
ժամանակ գծված
մակերեսն է:
Այս դեպքում
![]() ,
,
որտեղ՝
![]() :
:
Հետևաբար,

Մակածման ԷլՇՈՒ-ն կոնտուրում հավասար է կոնտուրով սահմանափակված մակերեսի միջով մագնիսական հոսքի փոփոխման արագությանը (էլեկտրամագնիսական մակածման օրենք, կամ Ֆարադեյի օրենք): Կիրառելով Օհմի օրենքը լրիվ շղթայի համար և Ֆարադեյի օրենքը` կստանանք մակածման հոսանքի համար հետևյալ արտահայտությունը.

(9.5) հավասարումից հետևում է, որ մակածման հոսանքը կախված է կոնտուրի դիմադրությունից:
Շղթայում էլեկտրաշարժ ուժը հետևանք է կողմնակի, այսինքն՝ ոչ էլեկտրական ծագում ունեցող ուժերի ազդեցության: Մագնիսական դաշտում հաղորդչի շարժման ժամանակ կողմնակի ուժերի դերը կատարում է Լորենցի ուժը, որի ազդեցության տակ տեղի է ունենում լիցքերի բաժանում, ինչի արդյունքում հաղորդչի ծայրերում ի հայտ է գալիս պոտենցիալների տարբերություն: Հաղորդչում մակածման ԷլՇՈՒ-ն այն աշխատանքն է, որը ծախսվում է միավոր դրական լիցքը հաղորդչի երկայնքով տեղափոխելիս:
Այսպիսով,
փոփոխական
մագնիսական
դաշտն առաջ է
բերում մակածված
էլեկտրական
դաշտ: Այդ
դաշտը ոչ
պոտենցիալային
է, քանի որ փակ
շղթայով
միավոր
դրական լիցքի
տեղափոխության
ժամանակ այդ
դաշտում կատարված
աշխատանքը
հավասար է
մակածման ԷլՇՈՒ-ին,
այլ ոչ` զրոյի: Այդպիսի
դաշտերն
անվանում են
մրրկային: Մրրկային
էլեկտրական
դաշտի
ուժագծերը, ի
տարբերություն
էլեկտրաստատիկ
դաշտի
լարվածության
գծերի, փակ են:
Եթե փակ
կոնտուրը
պարունակում
է հաջորդաբար
միացված ![]() գալարներ
(օրինակ՝ կոճ
կամ սոլենոիդ),
ապա մակածման
ԷլՇՈՒ-ն
հավասար է
առանձին
գալարների
ԷլՇՈՒ-ների
գումարին.
գալարներ
(օրինակ՝ կոճ
կամ սոլենոիդ),
ապա մակածման
ԷլՇՈՒ-ն
հավասար է
առանձին
գալարների
ԷլՇՈՒ-ների
գումարին.

որտեղ
![]() -ն
հոսքահարակցումն
է, այսինքն՝
գումարային մագնիսական
հոսքը
-ն
հոսքահարակցումն
է, այսինքն՝
գումարային մագնիսական
հոսքը ![]() գալարների
միջով:
գալարների
միջով:
Ֆարադեյի
օրենքը
կարելի է
ստանալ նաև
էներգիայի
պահպանման
օրենքից:
Դիցուք ![]() հոսանքով
հաղորդիչը
տեղավորված է
կոնտուրի
հարթությանն
ուղղահայաց
համասեռ
մագնիսական
դաշտում և կարող
է ազատ
տեղաշարժվել:
հոսանքով
հաղորդիչը
տեղավորված է
կոնտուրի
հարթությանն
ուղղահայաց
համասեռ
մագնիսական
դաշտում և կարող
է ազատ
տեղաշարժվել:
Ամպերի
ուժի
ազդեցության
տակ հաղորդիչը
կտեղափոխվի dx
հատվածով: Հետևաբար,
Ամպերի ուժը
կկատարի ![]() աշխատանք: Կոնտուրի
լրիվ
դիմադրությունը
աշխատանք: Կոնտուրի
լրիվ
դիմադրությունը
![]() է, և
համաձայն
էներգիայի
պահպանման
օրենքի,
հոսանքի
աղբյուրի
է, և
համաձայն
էներգիայի
պահպանման
օրենքի,
հոսանքի
աղբյուրի ![]() էներգիան
էներգիան
![]() ժամանակամիջոցում
կծախսվի
մագնիսական
դաշտում
ժամանակամիջոցում
կծախսվի
մագնիսական
դաշտում ![]() ջոուլ-լենցյան
ջերմության և
հաղորդչի
տեղաշարժման
ջոուլ-լենցյան
ջերմության և
հաղորդչի
տեղաշարժման ![]() էներգիայի
վրա.
էներգիայի
վրա.
![]()
որտեղից՝

որտեղ
![]() արտահայտում
է Ֆարադեյի
օրենքը:
արտահայտում
է Ֆարադեյի
օրենքը:
Յուրաքանչյուր հաղորդիչ կոնտուր, որով հոսանք է անցնում, գտնվում է այդ հոսանքի ստեղծած մագնիսական դաշտում: Երբ կոնտուրում հոսանքի ուժը փոփոխվում է, փոփոխվում է նաև այդ դաշտը: Մագնիսական դաշտի փոփոխությունը հանգեցնում է կոնտուր թափանցող մագնիսական հոսքի փոփոխության, ինչը կոնտուրում ծնում է մակածման ԷլՇՈՒ: Այն երևույթը, երբ կոնտուրով անցնող փոփոխվող հոսանքն այդ նույն կոնտուրում ստեղծում է մակածման ԷլՇՈՒ, կոչվում է ինքնամակածում, իսկ առաջացած ԷլՇՈՒ-ն` ինքնամակածման ԷլՇՈՒ:
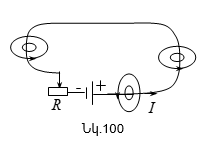
Վերջինս
կարող է իրականացվել
կոնտուրում
հոսանքի
փոփոխման
հետևանքով
(փոխելով ![]() դիմադրությունը)
(նկ.100): Իրոք,
մագնիսական
ինդուկցիայի
դիմադրությունը)
(նկ.100): Իրոք,
մագնիսական
ինդուկցիայի ![]() մոդուլը,
որը ցանկացած
փակ
կոնտուրում
ստեղծվում է
հոսանքի
կողմից,
համեմատական
է հոսանքի
ուժին: Քանի
որ
մոդուլը,
որը ցանկացած
փակ
կոնտուրում
ստեղծվում է
հոսանքի
կողմից,
համեմատական
է հոսանքի
ուժին: Քանի
որ ![]() մագնիսական
հոսքը
համեմատական
է B-ին, ապա
մագնիսական
հոսքը
համեմատական
է B-ին, ապա ![]() :
:
Հետևաբար, կարելի է պնդել, որ
![]()
որտեղ
![]() -ը
համեմատականության
գործակից է.
այն կախված է
կոնտուրի
ձևից,
չափերից,
միջավայրի
-ը
համեմատականության
գործակից է.
այն կախված է
կոնտուրի
ձևից,
չափերից,
միջավայրի ![]() մագնիսական
թափանցելիությունից
և կոչվում է
կոնտուրի
ինդուկտիվություն:
Էլեկտրամագնիսական
մակածման
օրենքն
ինքնամակածման
երևույթի
դեպքում
կընդունի
հետևյալ
տեսքը.
մագնիսական
թափանցելիությունից
և կոչվում է
կոնտուրի
ինդուկտիվություն:
Էլեկտրամագնիսական
մակածման
օրենքն
ինքնամակածման
երևույթի
դեպքում
կընդունի
հետևյալ
տեսքը.

եթե
![]() ,
ինդուկտիվությունն
իր իմաստով
արտահայտում
է հաղորդչի
իներտությունը
հոսանքի
փոփոխման
նկատմամբ:
Ինդուկտիվության
ֆիզիկական
իմաստը և
չափման
միավորը
կարելի է տալ
ինքնամակածման
երևույթն արտահայտող
օրենքի
օգնությամբ:
,
ինդուկտիվությունն
իր իմաստով
արտահայտում
է հաղորդչի
իներտությունը
հոսանքի
փոփոխման
նկատմամբ:
Ինդուկտիվության
ֆիզիկական
իմաստը և
չափման
միավորը
կարելի է տալ
ինքնամակածման
երևույթն արտահայտող
օրենքի
օգնությամբ:

Ինդուկտիվությունը
այն
ֆիզիկական
մեծությունն
է, որը թվապես
հավասար է
ինքնամակածման
ԷլՇՈՒ-ին, որն
առաջանում է
փակ հաղորդիչ
կոնտուրում,
երբ հոսանքի
ուժը նրանում
1վ-ում փոփոխվում
է 1Ա-ով:
Ինդուկտիվության
միավորը հենրին
է (Հն): 1Հն-ն
այնպիսի հաղորդիչ
կոնտուրի ինդուկտիվությունն
է, որում 1վ-ում
1Ա հոսանքի փոփոխությունը
մակածում է 1Վ
ԷլՇՈՒ:
Ինքնամակածման
երևույթի
դրսևորումը
կարելի է դիտել
պարզ
փորձերով:
Նկար 101ա-ում
ցույց է տրված
երկու
միատեսակ
լամպերի
զուգահեռ
միացման սխեմա:
Նրանցից մեկը R
դիմադրության
ռեզիստորով
միացված է
հոսանքի
աղբյուրին,
իսկ երկրորդը`
երկաթե
միջուկ
ունեցող ![]() կոճին
հաջորդաբար:
Առաջին լամպը
բռնկվում է գործնականորեն
բանալին
փակելուց
անմիջապես
հետո, իսկ
երկրորդը`
զգալի
ուշացմամբ:
Վերջին լամպի
շղթայում
ինքնամակածման
ԷլՇՈՒ-ն մեծ է,
և հոսանքի
ուժը
միանգամից չի
հասնում իր
առավելագույն
արժեքին: Այն
շղթայի
սխեման, որը
թույլ է տալիս
դիտել
ինքնամակածման
ԷլՇՈՒ-ի երևան
գալը շղթան
անջատելիս,
ցույց է տրված
նկ. 101 բ-ում: Երբ
բաց ենք անում
կոճին
հաջորդաբար:
Առաջին լամպը
բռնկվում է գործնականորեն
բանալին
փակելուց
անմիջապես
հետո, իսկ
երկրորդը`
զգալի
ուշացմամբ:
Վերջին լամպի
շղթայում
ինքնամակածման
ԷլՇՈՒ-ն մեծ է,
և հոսանքի
ուժը
միանգամից չի
հասնում իր
առավելագույն
արժեքին: Այն
շղթայի
սխեման, որը
թույլ է տալիս
դիտել
ինքնամակածման
ԷլՇՈՒ-ի երևան
գալը շղթան
անջատելիս,
ցույց է տրված
նկ. 101 բ-ում: Երբ
բաց ենք անում
![]() բանալին,
բանալին, ![]() կոճի մեջ
առաջանում է
ինքնամակածման
ԷլՇՈՒ, որը
պահպանում է
սկզբնական
հոսանքը:
Արդյունքը
լինում է այն,
որ անջատման
պահին
գալվանոմետրի
միջով անցնում
է հոսանք
(կետագիծ
սլաքը), որն
ուղղված է
մինչև
անջատումը
շղթայում
գոյություն
ունեցող
սկզբնական
հոսանքին
հակառակ (հոծ
սլաքը): Ընդ
որում` այդ
հոսանքի ուժն
ավելի մեծ է, քան
գալվանոմետրի
միջով անցնող
հոսանքի ուժը,
երբ K
բանալին փակ
է: Դա
նշանակում է,
որ ինքնամակածման
ԷլՇՈՒ-ն մեծ է
մարտկոցի
ԷլՇՈՒ-ից`
կոճի մեջ
առաջանում է
ինքնամակածման
ԷլՇՈՒ, որը
պահպանում է
սկզբնական
հոսանքը:
Արդյունքը
լինում է այն,
որ անջատման
պահին
գալվանոմետրի
միջով անցնում
է հոսանք
(կետագիծ
սլաքը), որն
ուղղված է
մինչև
անջատումը
շղթայում
գոյություն
ունեցող
սկզբնական
հոսանքին
հակառակ (հոծ
սլաքը): Ընդ
որում` այդ
հոսանքի ուժն
ավելի մեծ է, քան
գալվանոմետրի
միջով անցնող
հոսանքի ուժը,
երբ K
բանալին փակ
է: Դա
նշանակում է,
որ ինքնամակածման
ԷլՇՈՒ-ն մեծ է
մարտկոցի
ԷլՇՈՒ-ից` ![]() >
>![]() :
:
9.5. ԱՆՎԵՐՋ ԵՐԿԱՐ ՍՈԼԵՆՈԻԴԻ ԻՆԴՈՒԿՏԻՎՈՒԹՅՈՒՆԸ
Արդեն
նշել ենք, որ
գլանաձև
հաղորդիչ
փաթույթն
ընդունված է
անվանել
սոլենոիդ:
Սոլենոիդը
կանվանենք
անվերջ երկար,
եթե նրա
երկարությունը
շատ անգամ մեծ
է գալարի
տրամագծի
չափերից` ![]() :
:
Սոլենոիդով
![]() հոսանք
անցնելիս
սոլենոիդի
ներսում
առաջանում է
համասեռ
մագնիսական դաշտ,
որի
մագնիսական
ինդուկցիան՝
հոսանք
անցնելիս
սոլենոիդի
ներսում
առաջանում է
համասեռ
մագնիսական դաշտ,
որի
մագնիսական
ինդուկցիան՝ ![]() :Հոսքը
գալարներից
յուրաքանչյուրի
միջով կլինի
:Հոսքը
գալարներից
յուրաքանչյուրի
միջով կլինի ![]() , իսկ
սոլենոիդում
հարակցվող
լրիվ
մագնիսական
հոսքը՝
, իսկ
սոլենոիդում
հարակցվող
լրիվ
մագնիսական
հոսքը՝
![]()
որտեղ
![]() -ը
սոլենոիդի
լայնական
հատույթի
մակերեսն է,
-ը
սոլենոիդի
լայնական
հատույթի
մակերեսն է, ![]() -ը՝
գալարների
թիվը միավոր
երկարության
վրա (
-ը՝
գալարների
թիվը միավոր
երկարության
վրա (![]() արտադրյալը
տալիս է
գալարների
արտադրյալը
տալիս է
գալարների ![]() լրիվ թիվը):
լրիվ թիվը):
Համադրելով (9.7)-ը և (9.9)-ը` երկար սոլենոիդի ինդուկտիվության համար ստանում ենք հետևյալ արտահայտությունը.
![]()
որտեղ
![]() -ը
սոլենոիդի
ծավալն է:
-ը
սոլենոիդի
ծավալն է:
Այսպիսով, իրոք, սոլենոիդի ինդուկտիվությունը կախված է նրա չափերից (երկարաչափական ձևից) և միջավայրի մագնիսական թափանցելիությունից:
9.6. ԱՆՋԱՏՄԱՆ ԵՎ ՄԻԱՑՄԱՆ ՀՈՍԱՆՔՆԵՐ
Դիտարկենք ![]() դիմադրությունից,
դիմադրությունից,
![]() ինդուկտիվությունից,
ինդուկտիվությունից,
![]() ԷլՇՈՒ-ով
հոսանքի
աղբյուրից և
ԷլՇՈՒ-ով
հոսանքի
աղբյուրից և ![]() բանալուց
կազմված փակ
շղթա:
բանալուց
կազմված փակ
շղթա: ![]() բանալին
փակելու
դեպքում
շղթայում
առաջանում է
հոսանք, որը
որոշվում է
Օհմի օրենքով`
բանալին
փակելու
դեպքում
շղթայում
առաջանում է
հոսանք, որը
որոշվում է
Օհմի օրենքով`

որտեղ
![]() -ն
ինքնամակածման
ԷլՇՈՒ-ն է:
-ն
ինքնամակածման
ԷլՇՈՒ-ն է:

Փոփոխականների անջատման միջոցով լուծենք ստացված գծային դիֆերենցիալ հավասարումը.
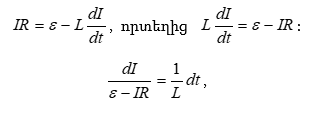
ստացված հավասարումը ներկայացնենք հետևյալ տեսքով

Ընդունելով,
որ ![]()
![]() և
և ![]() -ը
հաստատուն են,
վերջին
արտահայտությունը
ինտեգրենք,
կստանանք.
-ը
հաստատուն են,
վերջին
արտահայտությունը
ինտեգրենք,
կստանանք.

որտեղ
![]() -ն
ինտեգրման
կամայական
հաստատուն է:
Պոտենցումից
հետո
կստանանք.
-ն
ինտեգրման
կամայական
հաստատուն է:
Պոտենցումից
հետո
կստանանք.

Ժամանակի
![]() սկզբնական
պահին
հոսանքի ուժը
նշանակենք
սկզբնական
պահին
հոսանքի ուժը
նշանակենք ![]() -ով:
Հետևաբար`
-ով:
Հետևաբար`
![]()
C-ի արժեքը տեղադրելով (9.12)-ի մեջ` կստանանք.

Ձևափոխոխելով վերջին արտահայտությունը` կստանանք.

(9.13)
բանաձևը
հնարավորութուն
է տալիս գտնել
շղթան
հաստատուն ![]() ԷլՇՈՒ
ունեցող
աղբյուրին
միացնելու և
անջատելու
դեպքում
հոսանքի
փոփոխման
օրենքները
այն փակ
շղթայում, որն
օժտված է հաստատուն
ԷլՇՈՒ
ունեցող
աղբյուրին
միացնելու և
անջատելու
դեպքում
հոսանքի
փոփոխման
օրենքները
այն փակ
շղթայում, որն
օժտված է հաստատուն
![]() դիմադրությամբ
և
դիմադրությամբ
և ![]() ինդուկտիվությամբ:
ինդուկտիվությամբ:
Դիտարկենք միացման (շղթան փակելու) և անջատման (շղթան անջատելու) դեպքերն առանձին-առանձին:
1. Հոսանքի
աղբյուրի
միացման
դեպքում
սկզբնական
հոսանքը` ![]() , և (9.13)
բանաձևը
կընդունի
հետևյալ
տեսքը.
, և (9.13)
բանաձևը
կընդունի
հետևյալ
տեսքը.

Գրաֆիկորեն
այն
արտահայտված
է նկ.102-ում: Ինչպես
երևում է ![]() կորից,
հոսանքն իր
վերջնական
արժեքին
հասնում է
որոշ
կորից,
հոսանքն իր
վերջնական
արժեքին
հասնում է
որոշ ![]() ժամանակ
անց: Հոսանքի
մեծացումը
տեղի է ունենում
այնքան արագ,
ինչքան մեծ է
ժամանակ
անց: Հոսանքի
մեծացումը
տեղի է ունենում
այնքան արագ,
ինչքան մեծ է ![]() հարաբերությունը,
այսինքն`
որքան փոքր է
շղթայի
ինդուկտիվությունը,
և մեծ է նրա
դիմադրությունը:
հարաբերությունը,
այսինքն`
որքան փոքր է
շղթայի
ինդուկտիվությունը,
և մեծ է նրա
դիմադրությունը:

2. Հոսանքի
աղբյուրը
անջատելու
դեպքում ![]() և (9.13)-ից
կստանանք
և (9.13)-ից
կստանանք

Գրաֆիկորեն
այն
պատկերված է
նկ.103-ում:
Ինչպես երևում
է, հոսանքն իր
զրոյական
արժեքին հասնելու
համար
պահանջում է
որոշ ![]() ժամանակ:
Հոսանքը
նվազում է
այնքան արագ,
որքան մեծ է
շղթայի
դիմադրությունը,
և փոքր է նրա
ինդուկտիվությունը:
ժամանակ:
Հոսանքը
նվազում է
այնքան արագ,
որքան մեծ է
շղթայի
դիմադրությունը,
և փոքր է նրա
ինդուկտիվությունը:
Նշված
փաստը փորձով
հիմնավորվում
է նկ.102-ում պատկերված
սխեմայի
միջոցով: Հարկ
է նշել, որ հաճախ
ինքնամակածման
երևույթով
պայմանավորված
ինքնամակածման
ԷլՇՈՒ-ն կարող
է շատ անգամ
գերազանցել
սկզբնական ![]() ԷլՇՈՒ-ին:
Իրոք,
գնահատենք
ինքնամակածման
ԷլՇՈՒ-ն, որն
առաջանում է
դիմադրության
կտրուկ
մեծացմամբ
ԷլՇՈՒ-ին:
Իրոք,
գնահատենք
ինքնամակածման
ԷլՇՈՒ-ն, որն
առաջանում է
դիմադրության
կտրուկ
մեծացմամբ ![]() -ից
-ից ![]() :
Ենթադրենք
շղթայում
գործում է
:
Ենթադրենք
շղթայում
գործում է ![]() ԷլՇՈՒ
և հաստատված է
ԷլՇՈՒ
և հաստատված է
![]() հոսանք:
Ածանցենք
հոսանք:
Ածանցենք ![]() (9.13)
առնչությունը
ըստ
(9.13)
առնչությունը
ըստ ![]() -ի և
ստացված
հավասարման աջ
և ձախ մասերը
բազմապատկելով
(
-ի և
ստացված
հավասարման աջ
և ձախ մասերը
բազմապատկելով
(![]() )-ով,
ինքնամակածման
ԷլՇՈՒ-ի համար
կստանանք հետևյալ
արտահայտությունը`
)-ով,
ինքնամակածման
ԷլՇՈՒ-ի համար
կստանանք հետևյալ
արտահայտությունը`

որտեղից

Ստացված
բանաձևից
հետևում է, որ
շղթայի դիմադրության
կտրուկ
մեծացման
դեպքում` ![]() որն
օժտված է մեծ
ինդուկտիվությամբ
որն
օժտված է մեծ
ինդուկտիվությամբ
![]() ինքնամակածման
ԷլՇՈՒ-ն կարող
է շատ անգամ
գերազանցել
շղթային
միացված
ինքնամակածման
ԷլՇՈՒ-ն կարող
է շատ անգամ
գերազանցել
շղթային
միացված ![]() ԷլՇՈՒ-ին:
Կենցաղում
հաճախ շղթան
անջատելիս նկատելի
է էլեկտրական
լամպի
շիկացման
թելիկի
այրումը
(կտրվելը):
ԷլՇՈՒ-ին:
Կենցաղում
հաճախ շղթան
անջատելիս նկատելի
է էլեկտրական
լամպի
շիկացման
թելիկի
այրումը
(կտրվելը):
![]()
Դիտարկենք
անշարժ իրար
նկատմամբ ոչ
շատ հեռու
դասավորված
երկու
կոնտուր` (1) և (2) (նկ.104):
Եթե 1
կոնտուրով
անցնում է ![]() հոսանք,
ապա այդ
հոսանքով
ստեղծած
մագնիսական
հոսքը
(նկարում այդ
հոսքը
ստեղծող
դաշտը պատկերված
է հոծ գծերով),
համեմատական
է
հոսանք,
ապա այդ
հոսանքով
ստեղծած
մագնիսական
հոսքը
(նկարում այդ
հոսքը
ստեղծող
դաշտը պատկերված
է հոծ գծերով),
համեմատական
է ![]() -ին:
Նշանակենք
-ին:
Նշանակենք![]() -ով հոսքի
այն մասը, որը
թափանցում է 2
կոնտուրը:
Հետևաբար`
-ով հոսքի
այն մասը, որը
թափանցում է 2
կոնտուրը:
Հետևաբար`
![]()
որտեղ
![]() -ը
համեմատականության
գործակից է:
-ը
համեմատականության
գործակից է:

Եթե
![]() հոսանքը
փոփոխվում է,
ապա 2 կոնտուրում
մակածվում է
հոսանքը
փոփոխվում է,
ապա 2 կոնտուրում
մակածվում է ![]() ԷլՇՈՒ, որը
ըստ Ֆարադեյի
օրենքի
հավասար և նշանով
հակառակ է
երկրորդ
կոնտուր
թափանցող և առաջին
կոնտուրում
հոսանքով
ստեղծած մագնիսական
ԷլՇՈՒ, որը
ըստ Ֆարադեյի
օրենքի
հավասար և նշանով
հակառակ է
երկրորդ
կոնտուր
թափանցող և առաջին
կոնտուրում
հոսանքով
ստեղծած մագնիսական
![]() հոսքի
փոփոխության
արագությանը.
հոսքի
փոփոխության
արագությանը.
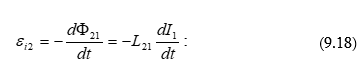
Համանմանորեն,
երկրորդ
կոնտուրով ![]() հոսանքի
անցման դեպքում
մագնիսական
հոսքը (նկ.104-ում
նրա դաշտը պատկերված
է կետագծերով)
թափանցում է
առաջին
կոնտուր: Եթե
հոսանքի
անցման դեպքում
մագնիսական
հոսքը (նկ.104-ում
նրա դաշտը պատկերված
է կետագծերով)
թափանցում է
առաջին
կոնտուր: Եթե ![]() -ը հոսքի
այն մասն է,
որը
թափանցում է 1
կոնտուր, ապա
-ը հոսքի
այն մասն է,
որը
թափանցում է 1
կոնտուր, ապա

Եթե
![]() հոսանքը փոփոխվում
է, ապա 1
կոնտուրում
մակածվում է
հոսանքը փոփոխվում
է, ապա 1
կոնտուրում
մակածվում է ![]() ԷլՇՈՒ, որը
հավասար և
նշանով
հակառակ է
առաջին կոնտուր
թափանցող և
երկրորդ
կոնտուրում
հոսանքով
ստեղծած
մագնիսական
ԷլՇՈՒ, որը
հավասար և
նշանով
հակառակ է
առաջին կոնտուր
թափանցող և
երկրորդ
կոնտուրում
հոսանքով
ստեղծած
մագնիսական ![]() հոսքի
փոփոխության
արագությանը.
հոսքի
փոփոխության
արագությանը.

(1) և (2) կոնտուրները կոչվում են կապակցված, իսկ կոնտուրներից մեկում հոսանքի ուժի փոփոխությունների ժամանակ մյուսում ԷլՇՈՒ-ի առաջացման երևույթը կոչվում է փոխադարձ ինդուկցիա:
![]() և
և ![]() համեմատականության
գործակիցները
կոչվում են
կոնտուրների
փոխադարձ
ինդուկտիվություններ:
Փորձերով
հաշվարկները
հաստատում են,
որ
համեմատականության
գործակիցները
կոչվում են
կոնտուրների
փոխադարձ
ինդուկտիվություններ:
Փորձերով
հաշվարկները
հաստատում են,
որ

![]() և
և ![]() գործակիցները կախված
են
կոնտուրների
ձևից, չափերից
և փոխադարձ
դասավորությունից,
ինչպես նաև`
կոնտուրները
շրջապատող
միջավայրի
մագնիսական
թափանցելիությունից:
Փոխադարձ
ինդուկտիվության
միավորը
նույնն է, ինչ
որ ինդուկտիվության
համար` հենրին
(Հն):
գործակիցները կախված
են
կոնտուրների
ձևից, չափերից
և փոխադարձ
դասավորությունից,
ինչպես նաև`
կոնտուրները
շրջապատող
միջավայրի
մագնիսական
թափանցելիությունից:
Փոխադարձ
ինդուկտիվության
միավորը
նույնն է, ինչ
որ ինդուկտիվության
համար` հենրին
(Հն):
Հաշվենք
ընդհանուր
տորոիդային
միջուկի վրա
փաթաթված
երկու կոճերի
փոխադարձ
ինդուկտիվությունը:
Այս դեպքն
գործնական
մեծ նշանակություն
ունի (նկ. 105): ![]() գալարների
թվով,
գալարների
թվով, ![]() hոսանքով
և
hոսանքով
և ![]() մագնիսական
թափանցելիություն ունեցող
առաջին կոճով
ստեղծված
մագնիսական
դաշտի ինդուկցիան`
մագնիսական
թափանցելիություն ունեցող
առաջին կոճով
ստեղծված
մագնիսական
դաշտի ինդուկցիան`

որտեղ
![]() -ը
միջուկի
երկարությունն
է միջին գծով:
Երկրորդ կոճի
մեկ գալարով
մագնիսական
հոսքը`
-ը
միջուկի
երկարությունն
է միջին գծով:
Երկրորդ կոճի
մեկ գալարով
մագնիսական
հոսքը`
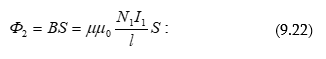
Լրիվ
մագնիսական
հոսքը
(հոսքահարակցումը)
![]() գալարներ
պարունակող
երկրորդային
փաթույթի
միջով`
գալարներ
պարունակող
երկրորդային
փաթույթի
միջով`
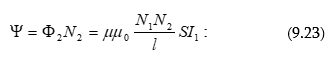
![]() հոսքը
ստեղծվում է
հոսքը
ստեղծվում է ![]() հոսանքով,
ուստի
համաձայն (9.17)-ի,
կստանանք`
հոսանքով,
ուստի
համաձայն (9.17)-ի,
կստանանք`
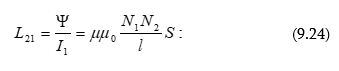
Եթե
հաշվենք 1 կոճի
միջով
մագնիսական
հոսքը, որն
ստեղծվում է 2
կոճով, ապա ![]() -ի համար
կստանանք (9.24)
բանաձևին
համապատասխան
արտահայտություն:
Այսպիսով,
երկու կոճերի
փոխադարձ
ինդուկտիվությունը,
որոնք
փաթաթված են
տորոիդային
ընդհանուր միջուկի
վրա`
-ի համար
կստանանք (9.24)
բանաձևին
համապատասխան
արտահայտություն:
Այսպիսով,
երկու կոճերի
փոխադարձ
ինդուկտիվությունը,
որոնք
փաթաթված են
տորոիդային
ընդհանուր միջուկի
վրա`
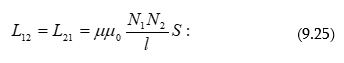
9.8. ՄԱԳՆԻՍԱԿԱՆ ԴԱՇՏԻ ԷՆԵՐԳԻԱՆ ԵՎ ԷՆԵՐԳԻԱՅԻ
ԾԱՎԱԼԱՅԻՆ ԽՏՈՒԹՅՈՒՆԸ
Փակ
հաղորդիչ
կոնտուրում
էլեկտրական
հոսանքի
անցման
դեպքում
առաջանում է
ինքնամակածման
ԷլՇՈՒ, որը
հակազդում է
հոսանքի
մեծացմանը:
Ըստ Օհմի
օրենքի՝ ![]() դիմադրություն
և
դիմադրություն
և ![]() ինդուկտիվություն
ունեցող
կոնտուրում
հոսանքի
ուժը՝
ինդուկտիվություն
ունեցող
կոնտուրում
հոսանքի
ուժը՝

որտեղ
![]() -ը
հոսանքի
աղբյուրի
ԷլՇՈՒ-ն է,
-ը
հոսանքի
աղբյուրի
ԷլՇՈՒ-ն է, ![]() -ը
ինքնամակածման
ԷլՇՈՒ-ն, որը
հավասար է՝
-ը
ինքնամակածման
ԷլՇՈՒ-ն, որը
հավասար է՝ ![]()
Այսպիսով՝

Էլեկտրական
էներգիայի աղբյուրի
կատարած
աշխատանքը ![]() ժամանակում՝
ժամանակում՝

(9.26) հավասարման աջ մասի առաջին գումարելին սովորական ջոուլ-լենցյան աշխատանքն է, որը ծախսվում է հաղորդչի տաքացման վրա, իսկ երկրորդը` լրացուցիչ աշխատանքն է` պայմանավորված մակածման երևույթներով: Լրացուցիչ աշխատանքը, որը ծախսվում է կոնտուրում հոսանքի ուժը 0-ից մինչև I մեծացնելու վրա՝

որտեղ
![]() հոսանքի
սեփական
էներգիան է L ինդուկտիվություն
ունեցող
կոնտուրում:
հոսանքի
սեփական
էներգիան է L ինդուկտիվություն
ունեցող
կոնտուրում:
Հաղորդչում հոսանքի ուժի մեծացումը առաջ է բերում համապատասխան մագնիսական դաշտի ուժեղացում: Հետևաբար, բնականաբար ենթադրվում է, որ հոսանքի սեփական էներգիան ոչ այլ ինչ է, քան նրա մագնիսական դաշտի էներգիան:
Որպես օրինակ` դիտարկենք երկար սոլենոիդի համասեռ մագնիսական դաշտը: Սոլենոիդի ինդուկտիվությունը՝
![]()
որտեղ
![]() -ը
սոլենոիդի
միավոր
երկարության
վրա փաթույթի
գալարների
թիվն է,
-ը
սոլենոիդի
միավոր
երկարության
վրա փաթույթի
գալարների
թիվն է, ![]() -ն՝
սոլենոիդի
ներսում
համասեռ
դաշտի ծավալը:
Այդ դաշտի
մագնիսական
ինդուկցիան՝
-ն՝
սոլենոիդի
ներսում
համասեռ
դաշտի ծավալը:
Այդ դաշտի
մագնիսական
ինդուկցիան՝
![]()
որտեղից

Տեղադրելով
![]() -ի և
-ի և ![]() -ի
արտահայտությունները
(9.27)-ի մեջ` կստանանք
երկար սոլենոիդի
մագնիսական
դաշտի
էներգիան.
-ի
արտահայտությունները
(9.27)-ի մեջ` կստանանք
երկար սոլենոիդի
մագնիսական
դաշտի
էներգիան.

Քանի
որ դաշտը
համասեռ է,
նրա ![]() էներգիան
բաշխված է դաշտի
ամբողջ
էներգիան
բաշխված է դաշտի
ամբողջ ![]() ծավալով
հավասարաչափ՝
ծավալով
հավասարաչափ՝

ծավալային խտությամբ:
Քանի
որ
մագնիսական
դաշտի
ինդուկցիան և
լարվածությունը
կապված են ![]() առնչությամբ,
ապա
մագնիսական
դաշտի էներգիայի
ծավալային
խտությունը
կարելի է գրել
հետևյալ երեք
համարժեք
բանաձևերով՝
առնչությամբ,
ապա
մագնիսական
դաշտի էներգիայի
ծավալային
խտությունը
կարելի է գրել
հետևյալ երեք
համարժեք
բանաձևերով՝
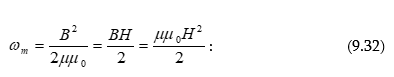
(9.32) արտահայտությունը ճիշտ է միայն այնպիսի միջավայրերի համար, որոնցում B-ի կախվածությունը H-ից գծային է, այսինքն` այն վերաբերվում է պարամագնիսներին և դիամագնիսներին:
Կամայական
ձևի
կոնտուրով
անցնող ![]() հոսանքի
անհամասեռ
մագնիսական
դաշտի էներգիան
բաշխված է
անհավասարաչափ:
Անվերջ փոքր dV ծավալի
սահմաններում
դաշտը կարելի
է համարել
համասեռ,
ուստի դաշտի
հոսանքի
անհամասեռ
մագնիսական
դաշտի էներգիան
բաշխված է
անհավասարաչափ:
Անվերջ փոքր dV ծավալի
սահմաններում
դաշտը կարելի
է համարել
համասեռ,
ուստի դաշտի ![]() ծավալի
ծավալի ![]() էներգիան՝
էներգիան՝

Ինտեգրելով
(9.33)
հավասարումը
դաշտի ամբողջ ![]() ծավալով`
գտնում ենք
մագնիսական
դաշտի
ծավալով`
գտնում ենք
մագնիսական
դաշտի ![]() լրիվ
էներգիան.
լրիվ
էներգիան.

Կարելի է ցույց տալ, որ

Այսպիսով, ելնելով (9.35)-ից, կարելի է տալ ինդուկտիվության էներգետիկ սահմանումը. կոնտուրի ինդուկտիվությունը թվապես հավասար է կոնտուրով անցնող միավոր ուժի հոսանքով ստեղծված մագնիսական դաշտի էներգիայի կրկնապատիկին:
Հարաբերականության
տեսությունում
ապացուցվում
է, որ
ցանկացած
շարժվող
օբյեկտի
երկու կարևորագույն
բնութագրիչների`
![]() զանգվածի
և
զանգվածի
և ![]() լրիվ
էներգիայի
միջև
գոյություն
ունի հետևյալ
կապը`
լրիվ
էներգիայի
միջև
գոյություն
ունի հետևյալ
կապը`
![]()
որտեղ
c-ն լույսի
արագությունն
է
վակուումում:
Ուստի մագնիսական
դաշտն օժտված
է ոչ միայն W էներգիայով,
այլ նաև ![]() զանգվածով.
զանգվածով.

Իրականում հարկավոր է դիտարկել շարժվող լիցքերով ստեղծված միասնական էլեկտրամագնիսական դաշտը: Այդ դաշտի լրիվ էներգիան հավասար է լիցքերով ստեղծված էլեկտրական և մագնիսական դաշտերի էներգիաների գումարին.
![]()
(9.36) և (9.37)
բանաձևերից
հետևում է, որ
էլեկտրամագնիսական
դաշտն օժտված
է ![]() զանգվածով.
զանգվածով.

Էլեկտրամագնիսական դաշտն այնքան նյութական է, ինչպես և նյութը: Այն մատերիայի ձևերից մեկն է և իր գոյության համար այլ միջավայրի կարիք չի զգում:
ԳԼՈՒԽ 10. ԷԼԵԿՏՐԱՄԱԳՆԻՍԱԿԱՆ ԴԱՇՏ
10.1. ՎԵԿՏՈՐԱԿԱՆ ԴԱՇՏԻ ՌՈՏՈՐ: ՇՐՋԱՊՏՈՒՅՏԻ ԹԵՈՐԵՄԸ ԴԻՖԵՐԵՆՑԻԱԼ ՏԵՍՔՈՎ
Մագնիսական
դաշտի կարևոր
հատկությունը,
որն
արտահայտում
է ![]() վեկտորի
շրջապտույտի
մասին
թեորեմը,
հարկադրում է
այդ թեորեմը
ևս
ներկայացնել
դիֆերենցիալ
տեսքով, որն
ընդլայնում է
նրա հնարավորությունները
որպես
հետազոտությունների
և հաշվարկի
միջոց: Այդ
նպատակի
համար դիտարկենք
վեկտորի
շրջապտույտի
մասին
թեորեմը,
հարկադրում է
այդ թեորեմը
ևս
ներկայացնել
դիֆերենցիալ
տեսքով, որն
ընդլայնում է
նրա հնարավորությունները
որպես
հետազոտությունների
և հաշվարկի
միջոց: Այդ
նպատակի
համար դիտարկենք
![]() վեկտորի
շրջապտույտի
և կոնտուրով
սահմանափակված
վեկտորի
շրջապտույտի
և կոնտուրով
սահմանափակված
![]() մակերեսի
հարաբերությունը:
մակերեսի
հարաբերությունը:
Պարզվում
է, որ եթե ![]() , այդ
հարաբերությունը
ձգտում է որոշ
սահմանի, ընդ
որում այդ
սահմանը
կախված է
տարածության
տվյալ կետում
կոնտուրի
կողմնորոշումից:
Կոնտուրի
կողմնորոշումը
տրվում է
կոնտուրի
հարթության
նորմալի
, այդ
հարաբերությունը
ձգտում է որոշ
սահմանի, ընդ
որում այդ
սահմանը
կախված է
տարածության
տվյալ կետում
կոնտուրի
կողմնորոշումից:
Կոնտուրի
կողմնորոշումը
տրվում է
կոնտուրի
հարթության
նորմալի ![]() վեկտորով,
ընդ որում`
վեկտորով,
ընդ որում` ![]() -ի
ուղղությունը
կապված է
կոնտուրի
շրջանցման ուղղության
հետ` աջ
պտուտակի
կանոնով:
Նշված գործողության
դեպքում
ստացվող
սահմանը սկալյար
մեծություն է,
որն իրեն
պահում է
կոնտուրի
հարթության
-ի
ուղղությունը
կապված է
կոնտուրի
շրջանցման ուղղության
հետ` աջ
պտուտակի
կանոնով:
Նշված գործողության
դեպքում
ստացվող
սահմանը սկալյար
մեծություն է,
որն իրեն
պահում է
կոնտուրի
հարթության ![]() նորմալի
ուղղության
վրա որպես
ինչ-որ վեկտորի
պրոյեկցիա,
որով
վերցվում է
շրջապտույտը: Այդ
վեկտորն անվանում
են
նորմալի
ուղղության
վրա որպես
ինչ-որ վեկտորի
պրոյեկցիա,
որով
վերցվում է
շրջապտույտը: Այդ
վեկտորն անվանում
են ![]() դաշտի
ռոտոր և
նշանակում են
դաշտի
ռոտոր և
նշանակում են ![]() : Այսպիսով,
: Այսպիսով,
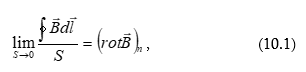
որտեղ
աջ մասը ![]() վեկտորի
պրոյեկցիան է
վեկտորի
պրոյեկցիան է ![]() նորմալի
վրա: Ուրեմն`
նորմալի
վրա: Ուրեմն` ![]() վեկտորի
դաշտի
յուրաքանչյուր
կետում առկա է
վեկտորի
դաշտի
յուրաքանչյուր
կետում առկա է
![]() վեկտոր,
որի
ուղղությունն
ու մոդուլը
տվյալ կետում
կապված են իր`
դաշտի հատկությունների
հետ:
վեկտոր,
որի
ուղղությունն
ու մոդուլը
տվյալ կետում
կապված են իր`
դաշտի հատկությունների
հետ: ![]() վեկտորի
ուղղությունը
որոշվում է
վեկտորի
ուղղությունը
որոշվում է ![]() մակերեսի
մակերեսի ![]() նորմալի
այն
ուղղությամբ,
որի դեպքում (10.1)
մեծության
արժեքը
հասնում է
առավելագույնի`
միաժամանակ
հանդիսանալով
նորմալի
այն
ուղղությամբ,
որի դեպքում (10.1)
մեծության
արժեքը
հասնում է
առավելագույնի`
միաժամանակ
հանդիսանալով
![]() վեկտորի մոդուլ:
Մաթեմատիկայում
վեկտորի մոդուլ:
Մաթեմատիկայում
![]() -ի
արտահայտությունը
ստանում են
կոորդինատային
ներկայացմամբ:
Մեր նպատակների
համար կարևոր
է այլ բան.
պարզվում է, որ
-ի
արտահայտությունը
ստանում են
կոորդինատային
ներկայացմամբ:
Մեր նպատակների
համար կարևոր
է այլ բան.
պարզվում է, որ
![]() -ն
ձևականորեն
կարելի է
դիտարկել
որպես նաբլա`
-ն
ձևականորեն
կարելի է
դիտարկել
որպես նաբլա` ![]() օպերատորի
և
օպերատորի
և ![]() վեկտորի
վեկտորական
արտադրյալ,
այսինքն՝
վեկտորի
վեկտորական
արտադրյալ,
այսինքն՝ ![]() : Որպես
ավելի հարմար
նշանակում,
պետք է օգտվել
վերջինից: Այն
հնարավորություն
է տալիս վեկտորական
արտադրյալը
գրել որոշիչի
օգնությամբ.
: Որպես
ավելի հարմար
նշանակում,
պետք է օգտվել
վերջինից: Այն
հնարավորություն
է տալիս վեկտորական
արտադրյալը
գրել որոշիչի
օգնությամբ.
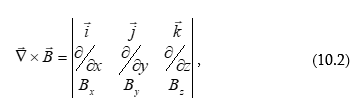
որտեղ
![]() -ն
դեկարտյան
կոորդինատների
առանցքների
միավոր
վեկտորներն
են: (10.2) արտահայտությունը
ճիշտ է ոչ
միայն
-ն
դեկարտյան
կոորդինատների
առանցքների
միավոր
վեկտորներն
են: (10.2) արտահայտությունը
ճիշտ է ոչ
միայն ![]() դաշտի
ռոտորի, այլև
ցանկացած
վեկտորական
դաշտի համար,
մասնավորապես,
նաև
դաշտի
ռոտորի, այլև
ցանկացած
վեկտորական
դաշտի համար,
մասնավորապես,
նաև ![]() դաշտի
համար:
դաշտի
համար: ![]() վեկտորի
շրջապտույտի
թեորեմից՝
վեկտորի
շրջապտույտի
թեորեմից՝
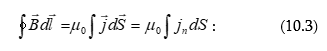
Համաձայն (10.1)-ի` (10.3) հավասարումը կարելի է ներկայացնել հետևյալ կերպ՝

որտեղից
![]()
Սա
էլ ![]() վեկտորի
շրջապտույտի
թեորեմն է`
դիֆերենցիալ
տեսքով:
վեկտորի
շրջապտույտի
թեորեմն է`
դիֆերենցիալ
տեսքով:
(10.4)-ից
երևում է, որ
դաշտի ռոտորը
ուղղությամբ
տվյալ կետում
համընկնում է
հոսանքի
խտության ![]() վեկտորի
ուղղության
հետ, իսկ
վեկտորի
ուղղության
հետ, իսկ ![]() -ի
մոդուլը
-ի
մոդուլը ![]() է:
է:
Էլեկտրաստատիկ
դաշտում ![]() վեկտորի
շրջապտույտը
զրո է, ուստի
վեկտորի
շրջապտույտը
զրո է, ուստի
![]()
Այն վեկտորական դաշտը, որի ռոտորն ամենուրեք հավասար է զրոյի, պոտենցիալային դաշտ է, հակառակ դեպքում՝ դաշտը կոչվում է սոլենոիդային: Հետևաբար, էլեկտրաստատիկ դաշտը պոտենցիալային է, իսկ մագնիսական դաշտը՝ սոլենոիդային:
10.2. ՄՐՐԿԱՅԻՆ ԷԼԵԿՏՐԱԿԱՆ ԴԱՇՏ
Վերլուծելով էլեկտրամագնիսական մակածման երևույթը` Մաքսվելը եզրակացրեց, որ մակածման ԷլՇՈՒ-ի հանդես գալու պատճառը էլեկտրական դաշտի ծագումն է (նկ. 106): Այդ դեպքում հաղորդիչները երկրորդական դեր են խաղում և միայն այդ դաշտը հայտնաբերող յուրատեսակ սարք են: Դաշտի ազդեցության տակ հաղորդականության էլեկտրոնները հաղորդալարում շարժման մեջ են դրվում և, եթե հաղորդալարը փակ է, նրա մեջ ծագում է մակածման հոսանք:
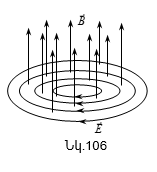
Դիտարկվող երևույթի էական հատկությունն այն է, որ ծագող էլեկտրական դաշտը էլեկտրաստատիկ չէ: Էլեկտրաստատիկ դաշտի ուժագծերը միշտ բաց են. դրանք սկսվում և վերջանում են էլեկտրական լիցքերի վրա, որին համապատասխան` էլեկտրաստատիկ դաշտում լարվածության վեկտորի շրջապտույտը փակ կոնտուրով միշտ հավասար է զրոյի: Այդ պատճառով էլեկտրաստատիկ դաշտը չի կարող օժանդակել լիցքերի փակ շարժմանը, հետևաբար, չի կարող հանգեցնել ԷլՇՈՒ-ի ծագմանը: Ընդհակառակը, էլեկտրամագնիսական մակածման դեպքում ծագող էլեկտրական դաշտն ունի փակ ուժագծեր, այսինքն՝ մրրկային դաշտ է: Այդպիսի դաշտը հաղորդալարում առաջացնում է փակ հետագծերով էլեկտրոնների շարժում և հանգեցնում է ԷլՇՈՒ-ի ծագման: Այդ դեպքում կողմնակի ուժեր են մրրկային էլեկտրական դաշտի ուժերը: Այդ դաշտում էլեկտրական լարվածության վեկտորի շրջապտույտը փակ կոնտուրով հավասար չէ զրոյի: Նրա արժեքը որևէ երկու կետերի միջև արդեն չի որոշվում միայն այդ կետերի դիրքով, ինչպես դա էլեկտրաստատիկ դաշտի դեպքում էր, այլ կախված է նաև տվյալ կետերը միացնող կոնտուրի (հաղորդչի) ձևից:

Այսպիսով, էլեկտրամագնիսական ինդուկցիայի երևույթի լուրջ մեկնաբանումը հանգեցնում է Մաքսվելի տեսության առաջին հիմնական դրույթն արտահայտող հետևյալ եզրակացությանը՝ մագնիսական դաշտի ամեն մի փոփոխություն առաջացնում է մրրկային էլեկտրական դաշտ (նկ. 107):
Ստացված արդյունքը կարելի է արտահայտել քանակական ձևով: Համաձայն էլեկտրամագնիսական մակածման երևույթի հիմնական օրենքի` մակածման ԷլՇՈՒ-ն հավասար է մագնիսական հոսքի փոփոխման արագությանը՝

որտեղ
![]() -ն
մագնիսական
ինդուկցիայի
-ն
մագնիսական
ինդուկցիայի ![]() վեկտորի
հոսքն է
դիտարկվող
վեկտորի
հոսքն է
դիտարկվող ![]() կոնտուրով
սահմանափակված
կոնտուրով
սահմանափակված
![]() մակերեսով
(նկ. 107)՝
մակերեսով
(նկ. 107)՝

Մյուս
կողմից, որևէ ![]() կոնտուրում
գործող ԷլՇՈՒ
-ն՝
կոնտուրում
գործող ԷլՇՈՒ
-ն՝

որտեղ
![]() կողմնակի
ուժերի դաշտի
լարվածությունն
է: Տվյալ
դեպքում
կողմնակի
ուժերի դաշտի
լարվածությունն
է: Տվյալ
դեպքում ![]() -ը
մրրկային
էլեկտրական
-ը
մրրկային
էլեկտրական ![]() դաշտի
լարվածությունն
է: Այդ
պատճառով,
(10.8)-ում ենթադրելով,
որ
դաշտի
լարվածությունն
է: Այդ
պատճառով,
(10.8)-ում ենթադրելով,
որ ![]() ,
և (10.8)-ը
տեղադրելով
(10.6)-ի մեջ,
կունենանք՝
,
և (10.8)-ը
տեղադրելով
(10.6)-ի մեջ,
կունենանք՝

Մյուս կողմից`

որտեղ ինտեգրալը վերցվում է կոնտուրին հենված կամայական մակերևույթով: Քանի որ կոնտուրն անշարժ է, ըստ ժամանակի ածանցման և մակերևույթով ինտեգրման գործողությունների տեղերը կարելի է փոխել.

![]() վեկտորը
կախում ունի
ինչպես
ժամանակից,
այնպես էլ
կոորդինատներից:
(10.11) հավասարման
աջ մասում
նկատի է
առնվում
վեկտորը
կախում ունի
ինչպես
ժամանակից,
այնպես էլ
կոորդինատներից:
(10.11) հավասարման
աջ մասում
նկատի է
առնվում ![]() -ի
ածանցյալն
ըստ
ժամանակի՝
մակերևույթի
համապատասխան
անփոփոխ
կետում: Այդ
պատճառով ենթաինտեգրալ
արտահայտության
մեջ օգտագործված
է ըստ
ժամանակի
մասնակի
ածանցյալի
սիմվոլը:
-ի
ածանցյալն
ըստ
ժամանակի՝
մակերևույթի
համապատասխան
անփոփոխ
կետում: Այդ
պատճառով ենթաինտեգրալ
արտահայտության
մեջ օգտագործված
է ըստ
ժամանակի
մասնակի
ածանցյալի
սիմվոլը:
(10.9) և (10.11) արտահայտություններն իրար հավասարեցնելով` կստանանք`
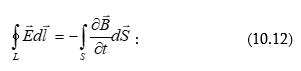
Ձախ մասում ինտեգրալը վերցվում է կամայական փակ կոնտուրով, իսկ աջ մասում՝ այդ կոնտուրի վրա հենված կամայական մակերևույթով:
Ստացված (10.12) առնչությունն արտահայտում է փոփոխական մագնիսական դաշտի ու մրրկային էլեկտրական դաշտի միջև քանակական կապը և Մաքսվելի տեսության հիմնական հավասարումներից մեկն է:
Նախորդ բաժիններում դիտարկումներից պարզվեց, որ ամեն մի փոփոխական մագնիսական դաշտ առաջացնում է մրրկային էլեկտրական դաշտ: Վերլուծելով տարբեր էլեկտրամագնիսական պրոցեսներ` Մաքսվելը եկավ այն եզրակացության, որ պետք է գոյություն ունենա նաև հակադարձ երևույթ՝ էլեկտրական դաշտի ամեն մի փոփոխություն առաջացնում է մրրկային մագնիսական դաշտ: Այդ պնդումն արտահայտում է էլեկտրամագնիսական դաշտի կարևորագույն հատկությունը, և Մաքսվելի տեսության երկրորդ հիմնական դրույթն է:
Քանի որ մագնիսական դաշտն ամեն մի հոսանքի հիմնական, անհրաժեշտ հատկանիշն է, ապա Մաքսվելը, ի տարբերություն լիցքավորված մասնիկների (էլեկտրոնների և իոնների) շարժումով պայմանավորված հաղորդականության հոսանքի, փոփոխական էլեկտրական դաշտն անվանեց շեղման հոսանք: Շեղման հոսանքի հասկացությունը կարելի է պարզել նկ.108-ում պատկերված փորձի օգնությամբ: Կազմենք մետաղական հաղորդիչ, կոնդենսատոր, մարտկոց և փոխարկիչ պարունակող կոնտուր: Կոնտուրում առկա հոսանքի մասին գաղափար կազմելու համար նրան միացնենք ցուցադրական ամպերմետրի դեր կատարող շիկացման ոչ մեծ լամպ: Ստանում ենք բաց կոնտուր, որը խզվում է կոնդենսատորով: Ինչպես գիտենք, հաստատուն հոսանքն այդպիսի բաց կոնտուրով չի անցնում, և մարտկոցի երկարատև միացման դեպքում լամպը ոչ մի շիկացում ցույց չի տալիս:

Այլ է պատկերը մարտկոցի միացմանը հաջորդող ակնթարթներին: Կոնդենսատորը կլիցքավորվի, և մետաղյա հաղորդալարում կծագի կարճատև լիցքավորման հոսանք: Եթե լիցքավորման ավարտից հետո մարտկոցը փոխարկիչի օգնությամբ փոխարկենք, ապա կոնդենսատորը կվերալիցքավորվի, և այդ ընթացքում հաղորդալարում նորից կծագի հոսանք, բայց այժմ` հակառակ ուղղության: Մարտկոցի յուրաքանչյուր փոխարկման ժամանակ հաղորդալարում կծագի հոսանքի իմպուլս, և լամպը կտա կարճատև բռնկում:
Եթե փոխարկիչին միացված հաղորդալարի ծայրերը միացնենք փոփոխական հոսանքի լուսավորության ցանցին, ապա կոնդենսատորի վերալիցքավորումներն անընդհատ կհետևեն մեկը մյուսին՝ վայրկյանում 100 անգամ հաճախությամբ, և կոնտուրում երկար ժամանակ գոյություն կունենա փոփոխական հոսանք: Այս դեպքում լամպի առանձին բռնկումներն արդեն նկատելի չեն լինի, և այն կշիկանա հավասարաչափ:
Տեսնում ենք, որ, ի տարբերություն հաստատուն հոսանքի, փոփոխվող կամ փոփոխական հոսանքները կարող են գոյություն ունենալ նաև բաց կոնտուրներում: Այդ դեպքում, ամեն անգամ, երբ բաց կոնտուրով հոսանք է անցնում, նրա ծայրերի (կոնդենսատորի թիթեղների) միջև ստանում ենք ժամանակի ընթացքում փոփոխվող էլեկտրական դաշտ կամ շեղման հոսանք: Այսպիսով, մետաղյա հաղորդչի հաղորդականության հոսանքները փակվում են դիէլեկտրիկների շեղման հոսանքներով:
Համաձայն Մաքսվելի՝ կոնդենսատորում էլեկտրական դաշտը ցանկացած պահի ստեղծում է այնպիսի մագնիսական դաշտ, ինչպիսին կլիներ, եթե թիթեղների միջև գոյություն ունենար մետաղյա հաղորդալարերում եղած հոսանքի ուժին հավասար ուժ ունեցող հաղորդականության հոսանք: Կամ, այլ կերպ ասած, մեր բաց կոնտուրի մագնիսական դաշտը այնպիսին է, ինչպիսին այն փակ կոնտուրի դեպքում էր:
Դա թույլ է տալիս որոշել փոփոխվող էլեկտրական դաշտի և նրա կողմից հարուցված մագնիսական դաշտի միջև եղած քանակական կապը: Իսկապես, եթե էլեկտրական շեղումը կոնդենսատորում է, լիցքի մակերևութային խտությունը թիթեղների վրա կլինի՝
![]()
Ուրեմն` թիթեղներից յուրաքանչյուրի վրա լրիվ լիցքը՝
![]()
որտեղ
![]() -ը
թիթեղների
մակերեսն է:
Եթե
-ը
թիթեղների
մակերեսն է:
Եթե ![]() ժամանակի
ընթացքում
լիցքը
փոփոխվում է
ժամանակի
ընթացքում
լիցքը
փոփոխվում է ![]() -ով, ապա
հաղորդալարում
հոսանքի
ուժը՝
-ով, ապա
հաղորդալարում
հոսանքի
ուժը՝
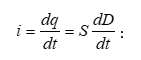
Այն
միարժեք
կերպով
կապված է
էլեկտրական
դաշտի
ինդուկցիայի
փոփոխման
արագության
հետ: Այստեղից
հետևում է, որ
կոնդենսատորի
փոփոխվող
դաշտն
առաջացնում է
նույնպիսի
մագնիսական
դաշտ, ինչպես ![]() ուժ կամ
ուժ կամ

խտություն ունեցող հոսանքը: Այս մեծությունն ստացել է շեղման հոսանքի խտություն անվանումը:
Օգտվելով
այս
հասկացությունից`
Մաքսվելի երկրորդ
դրույթը
կարելի է
արտահայտել
հետևյալ
քանակական
տեսքով՝
ժամանակի
ընթացքում փոփոխական
էլեկտրական
դաշտն առաջացնում
է նույնպիսի
մագնիսական
դաշտ, ինչպիսին
(10.13) բանաձևով
որոշվող ![]() խտություն
ունեցող
հաղորդականության
հոսանքը:
խտություն
ունեցող
հաղորդականության
հոսանքը:
Ընդհանուր դեպքում էլեկտրական դաշտը կարող է լինել անհամասեռ և կարող է կախված լինել ոչ միայն ժամանակից, այլև` կոորդինատներից: Այդ դեպքում շեղման հոսանքի խտության համար արտահայտությունը կլինի՝

որտեղ մասնակի ածանցյալի նշանը ցույց է տալիս, որ մագնիսական դաշտը կախված է դաշտի յուրաքանչյուր կետում ինդուկցիայի փոփոխման արագությունից ըստ ժամանակի:

Հարկ
կա ընդգծել,
որ շեղման
հոսանքը
որոշվում է ![]() վեկտորի
ածանցյալով,
բայց ոչ հենց
այդ վեկտորով:
Այսպես,
օրինակ, հարթ
կոնդենսատորի
դաշտում
վեկտորի
ածանցյալով,
բայց ոչ հենց
այդ վեկտորով:
Այսպես,
օրինակ, հարթ
կոնդենսատորի
դաշտում ![]() վեկտորն
ուղղված է
դրական
թիթեղից դեպի
բացասականը:
Եթե
էլեկտրական
դաշտը
մեծանում է, ապա
վեկտորն
ուղղված է
դրական
թիթեղից դեպի
բացասականը:
Եթե
էլեկտրական
դաշտը
մեծանում է, ապա
![]() ,
հետևաբար, նաև
շեղման
հոսանքն
այնպես է ուղղված,
ինչպես ցույց
է տրված նկ. 109ա-ում:
Եթե
Էլեկտրական
դաշտը
նվազում է,
ապա
,
հետևաբար, նաև
շեղման
հոսանքն
այնպես է ուղղված,
ինչպես ցույց
է տրված նկ. 109ա-ում:
Եթե
Էլեկտրական
դաշտը
նվազում է,
ապա ![]() -ն
ուղղված է
բացասական
թիթեղից դեպի
դրականը, և
մագնիսական
դաշտը
հակառակ է
առաջինին (նկ.
109բ): Եթե որևէ
հաղորդչում
կա փոփոխական
հոսանք, ուրեմն
հաղորդչի
ներսում
գոյություն
ունի փոփոխական
էլեկտրական
դաշտ: Ուստի, հաղորդչի
ներսում
ունենում ենք
թե´
հաղորդականության,
թե´ շեղման
հոսանք, և
հաղորդչի
մագնիսական
դաշտը
որոշվում է
նրանց
գումարով,
այսինքն՝
լրիվ հոսանքով:
Լրիվ հոսանքի
խտությունը՝
-ն
ուղղված է
բացասական
թիթեղից դեպի
դրականը, և
մագնիսական
դաշտը
հակառակ է
առաջինին (նկ.
109բ): Եթե որևէ
հաղորդչում
կա փոփոխական
հոսանք, ուրեմն
հաղորդչի
ներսում
գոյություն
ունի փոփոխական
էլեկտրական
դաշտ: Ուստի, հաղորդչի
ներսում
ունենում ենք
թե´
հաղորդականության,
թե´ շեղման
հոսանք, և
հաղորդչի
մագնիսական
դաշտը
որոշվում է
նրանց
գումարով,
այսինքն՝
լրիվ հոսանքով:
Լրիվ հոսանքի
խտությունը՝

Միջավայրի էլեկտրահաղորդականությունից և դաշտի փոփոխման արագությունից (փոփոխական հոսանքի հաճախությունից) կախված` (10.15)-ում երկու գումարելիները տարբեր դեր են խաղում: Լավ հաղորդող նյութերում (մետաղներում) ու ցածր հաճախությունների դեպքում շեղման հոսանքի խտությունը փոքր է, և հաղորդականության հոսանքի համեմատ շեղման հոսանքը կարելի է անտեսել: Ուստի, մետաղներում փոփոխական հոսանքի արտամղման երևույթի մեջ (սկինէֆեկտ) շեղման հոսանքը զգալի դեր չի խաղում: Ընդհակառակը, վատ հաղորդող միջավայրերում (մեկուսիչներ) և բարձր հաճախությունների դեպքում շեղման հոսանքը հիմնական դեր է խաղում:
(10.15) բանաձևի երկու անդամները կարող են ունենալ թե´ միևնույն, թե´ հակառակ նշաններ: Այդ պատճառով լրիվ հոսանքը կարող է հաղորդականության հոսանքից ինչպես մեծ, այնպես էլ փոքր լինել և, մասնավոր դեպքում, նույնիսկ վերածվել զրոյի:
Այսպիսով, ընդհանուր դեպքում փոփոխվող հոսանքների մագնիսական դաշտը որոշվում է ոչ թե հաղորդականության հոսանքով, այլ` լրիվ հոսանքով: Եթե մենք ունենք բաց կոնտուր, ապա հաղորդչի ծայրերում ընդհատվում է միայն հաղորդականության հոսանքը: Իսկ դիէլեկտրիկում հաղորդչի ծայրերի միջև ունենք շեղման հոսանք, որը փակում է հաղորդականության հոսանքը: Ուստի, եթե էլեկտրական հոսանքի տակ հասկանանք (10.15) բանաձևով որոշվող լրիվ հոսանքը, ապա կստացվի, որ բնության մեջ բոլոր էլեկտրական հոսանքները փակ են: Այդ կարևոր եզրակացությունը ևս ստացել է Մաքսվելը:
Հաղորդականության
հոսանքին
հատուկ բոլոր
ֆիզիկական
հատկություններից
շեղման
հոսանքին Մաքսվելը
վերագրեց
միայն մեկ՝
շրջապատող
տարածության
մեջ
մագնիսական
դաշտ ստեղծելու
ունակությունը:
Ըստ Մաքսվելի`
մագնիսական
դաշտերը
հաշվարկելիս
բանաձևերի մեջ
պետք է
տեղադրել
հոսանքի լրիվ
խտությունը, որը
հաղորդականության
հոսանքի
խտության և
շեղման
հոսանքի խտության
գումարն է:
Մասնավորապես,
![]() վեկտորի
շրջապտույտը
ցանկացած
կոնտուրով [տես
(6.39) բանաձևը]
պետք է
հավասար
լինի՝
վեկտորի
շրջապտույտը
ցանկացած
կոնտուրով [տես
(6.39) բանաձևը]
պետք է
հավասար
լինի՝

(10.16) հավասարումը Մաքսվելի տեսության երկրորդ հիմնական հավասարումն է:
10.4. ՄԱՔՍՎԵԼԻ ՀԱՎԱՍԱՐՈՒՄՆԵՐՆ ԻՆՏԵԳՐԱԼԱՅԻՆ ԵՎ
ԴԻՖԵՐԵՆՑԻԱԼ ՏԵՍՔՈՎ
Շեղման հոսանքի ներմուծումով փայլուն կերպով ավարտվեց էլեկտրամագնիսական դաշտի մակրոսկոպիկ տեսությունը: Շեղման հոսանքի հայտնաբերումը Մաքսվելին հնարավորություն տվեց ստեղծել էլեկտրական և մագնիսական երևույթների միասնական տեսություն:
Մաքսվելի տեսությունը բացատրեց այդ ժամանակ հայտնի բոլոր փորձնական փաստերը և կանխագուշակեց մի շարք նոր երևույթներ, որոնց գոյությունը հաստատվեց հետագայում, մասնավորապես, էլեկտրամագնիսական ալիքների, այսինքն՝ տարածության մեջ վերջավոր արագությամբ տարածվող փոփոխական էլեկտրամագնիսական դաշտի գոյությունը: Դրանից հետո էլեկտրամագնիսական ալիքների հատկությունների տեսական ուսումնասիրությունը Մաքսվելին հանգեցրեց լույսի էլեկտրամագնիսական տեսության ստեղծմանը, որի համաձայն լույսը նույնպես էլեկտրամագնիսական ալիք է: Հետագայում էլեկտրամագնիսական ալիքները, իրոք, փորձով ստացվեցին, իսկ ավելի ուշ լույսի էլեկտրամագնիսական տեսությունը և դրա հետ նաև Մաքսվելի ամբողջ տեսությունը լրիվ և փայլուն ապացույց ստացան: Տեսության հիմքը կազմում են Մաքսվելի հավասարումները: Այդ հավասարումները չորսն են (մենք դրանցից յուրաքանչյուրին ծանոթացել ենք առանձին-առանձին նախորդ բաժիններում): Այժմ այդ ամենը ի մի բերենք:
Մաքսվելի հավասարումների առաջին զույգը (10.12) և (8.1) հավասարումներն են.

Մաքսվելի հավասարումների երկրորդ զույգն են կազմում (10.16) և (2.15) -ը.

որտեղ
![]() -ն
հաղորդականության
հոսանքի
խտությունն
է,
-ն
հաղորդականության
հոսանքի
խտությունն
է, ![]() -ն՝ ազատ
լիցքերի
ծավալային
խտությունը:
-ն՝ ազատ
լիցքերի
ծավալային
խտությունը:
Այս հավասարումները սեղմ տեսքով արտահայտում են մեր տեղեկությունները էլեկտրամագնիսական դաշտի մասին: Այդ հավասարումների բովանդակությունը հետևյալն է.
1.
![]() վեկտորի
շրջապտույտը
կամայական
փակ
կոնտուրով
հավասար է այդ
կոնտուրով սահմանափակված
ցանկացած
մակերևույթով
մագնիսական
հոսքի
ածանցյալին
ըստ ժամանակի՝
վերցրած
հակառակ
նշանով: (10.17)-ը,
ըստ էության,
էլեկտրամագնիսական
մակածման
օրենքի
արտահայտությունն
է:
վեկտորի
շրջապտույտը
կամայական
փակ
կոնտուրով
հավասար է այդ
կոնտուրով սահմանափակված
ցանկացած
մակերևույթով
մագնիսական
հոսքի
ածանցյալին
ըստ ժամանակի՝
վերցրած
հակառակ
նշանով: (10.17)-ը,
ըստ էության,
էլեկտրամագնիսական
մակածման
օրենքի
արտահայտությունն
է:
2.
![]() վեկտորի
հոսքը
կամայական
փակ
մակերևույթով
միշտ հավասար
է զրոյի: (10.18)-ը
արտահայտում
է
վեկտորի
հոսքը
կամայական
փակ
մակերևույթով
միշտ հավասար
է զրոյի: (10.18)-ը
արտահայտում
է ![]() վեկտորի
այն հատկությունը,
որ նրա գծերը
փակ են
(բնության մեջ
մագնիսական
լիցքեր
գոյություն
չունեն):
վեկտորի
այն հատկությունը,
որ նրա գծերը
փակ են
(բնության մեջ
մագնիսական
լիցքեր
գոյություն
չունեն):
3.
![]() վեկտորի
շրջապտույտը
ցանկացած փակ
կոնտուրով
հավասար է այդ
կոնտուրով
սահմանափակված
կամայական
մակերևույթի
միջով անցնող
լրիվ
հոսանքին
(հաղորդականության
և շեղման
հոսանքին):
վեկտորի
շրջապտույտը
ցանկացած փակ
կոնտուրով
հավասար է այդ
կոնտուրով
սահմանափակված
կամայական
մակերևույթի
միջով անցնող
լրիվ
հոսանքին
(հաղորդականության
և շեղման
հոսանքին):
4.
![]() վեկտորի
հոսքը
կամայական
փակ
մակերևույթով
հավասար է այդ
մակերևույթով
պարփակված
ազատ լիցքերի հանրահաշվական
գումարին: (10.20)-ը
ցույց է
տալիս, որ
վեկտորի
հոսքը
կամայական
փակ
մակերևույթով
հավասար է այդ
մակերևույթով
պարփակված
ազատ լիցքերի հանրահաշվական
գումարին: (10.20)-ը
ցույց է
տալիս, որ ![]() վեկտորի
գծերը կարող
են սկսվել և
վերջանալ
լիցքերի վրա:
վեկտորի
գծերը կարող
են սկսվել և
վերջանալ
լիցքերի վրա:
(10.17)
- (10.20)
հավասարումները
Մաքսվելի
հավասարումներն
են ինտեգրալային
տեսքով: Դրանք
որևէ
կոնտուրի երկայնքով
![]() -ի և
-ի և ![]() -ի
արժեքները
կապում են նրա
վրա հենված
մակերևույթի
կետերում
-ի
արժեքները
կապում են նրա
վրա հենված
մակերևույթի
կետերում ![]() -ի
(համապատասխանաբար`
-ի
(համապատասխանաբար`
![]() -ի)
արժեքներին:
-ի)
արժեքներին:
Ստացիոնար
դաշտերի
համար (![]() և
և ![]() ) Մաքսվելի
հավասարումները
ընդունում են
հետևյալ տեսքը`
) Մաքսվելի
հավասարումները
ընդունում են
հետևյալ տեսքը`

այսինքն տվյալ դեպքում էլեկտրական դաշտի աղբյուրները միայն էլեկտրական լիցքերն են, իսկ մագնիսական դաշտինը` հաղորդականության հոսանքները: Այս դեպքում էլեկտրական և մագնիսական դաշտերը իրարից անկախ են, որն էլ հնարավորություն է տալիս հաստատուն էլեկտրական և մագնիսական դաշտերն ուսումնասիրել առանձին-առանձին:
Վեկտորական
անալիզի
թեորեմների
միջոցով ինտեգրալային
տեսքով
հավասարումներից
կարելի է
անցնել
դիֆերենցիալ
տեսքով
հավասարումների,
որոնք ![]() -ի
կամ
-ի
կամ ![]() -ի
արժեքները
որևէ կետում
կապում են տարածության
նույն կետում
-ի
արժեքները
որևէ կետում
կապում են տարածության
նույն կետում ![]() -ի
(համապատասխանաբար
-ի
(համապատասխանաբար
![]() -ի)
հետ:
-ի)
հետ:
Ստոքսի
թեորեմը:
Գիտենալով ![]() վեկտորի
ռոտորը
վեկտորի
ռոտորը ![]() մակերևույթի
որևէ կետում`
կարելի է
հաշվել այդ
վեկտորի շրջապտույտը
մակերևույթի
որևէ կետում`
կարելի է
հաշվել այդ
վեկտորի շրջապտույտը
![]() մակերեվույթը
սահմանափակող
մակերեվույթը
սահմանափակող
![]() կոնտուրով:
կոնտուրով:

Գաուս-Օստրոգրադսկու
թեորեմը: Գիտենալով
![]() վեկտորի
դիվերգենցիան
տարածության
յուրաքանչյուր
կետում`
կարելի է
հաշվել այդ
վեկտորի
հոսքը
վերջավոր
չափերով
կամայական
վեկտորի
դիվերգենցիան
տարածության
յուրաքանչյուր
կետում`
կարելի է
հաշվել այդ
վեկտորի
հոսքը
վերջավոր
չափերով
կամայական ![]() փակ
մակերևույթով:
փակ
մակերևույթով:

Կիրառենք
Ստոքսի (10.21)
թեորեմը (10.17)
բանաձևի ձախ
մասի
նկատմամբ՝
վերցնելով
որպես
մակերևույթ,
որով
կատարվում է ![]() ֆունկցիայի
ինտեգրումը,
այն նույն
մակերևույթը,
որով
վերցվում է
ինտեգրալը աջ
մասում: Այդ դեպքում
(10.17)
հավասարումը
կստանա
հետևյալ տեսքը՝
ֆունկցիայի
ինտեգրումը,
այն նույն
մակերևույթը,
որով
վերցվում է
ինտեգրալը աջ
մասում: Այդ դեպքում
(10.17)
հավասարումը
կստանա
հետևյալ տեսքը՝

Երկու ինտեգրալներն էլ վերցվում են նույն մակերևույթով: Ուստի, ստացված հավասարությունը կարելի է գրել հետևյալ կերպ՝

Այս հավասարությունը
պետք է տեղի
ունենա
ինտեգրման
կամայական
ընտրված ![]() մակերևույթի
համար, որն
ակներևորեն
հնարավոր է
միայն այն
դեպքում, երբ
ենթաինտեգրալ
արտահայտությունը
տարածության
ցանկացած կետում
և
կամայականորեն
կողմնորոշված
մակերևույթի
համար, որն
ակներևորեն
հնարավոր է
միայն այն
դեպքում, երբ
ենթաինտեգրալ
արտահայտությունը
տարածության
ցանկացած կետում
և
կամայականորեն
կողմնորոշված
![]() մակերեսի
համար
հավասար լինի
զրոյի: Այսպիսով,
հանգում ենք
այն
եզրակացության,
որ
տարածության
յուրաքանչյուր
կետում տեղի է
ունենում
հետևյալ
հավասարությունը՝
մակերեսի
համար
հավասար լինի
զրոյի: Այսպիսով,
հանգում ենք
այն
եզրակացության,
որ
տարածության
յուրաքանչյուր
կետում տեղի է
ունենում
հետևյալ
հավասարությունը՝

Կիրառելով Ստոքսի թեորեմը (10.19) բանաձևի նկատմամբ և կրկնելով նույն դատողությունները` կստանանք.

Այժմ կիրառենք Գաուս-Օստրոգրադսկու (10.22) թեորեմը (10.20) բանաձևի ձախ մասի նկատմամբ: Որպես արդյունք կստանանք հետեվյալ հավասարումը՝

Եթե ծավալը, որով կատարվում է ինտեգրումը, ընտրված է կամայականորեն, ստացված առնչությունը տեղի կունենա միայն այն պայմանի դեպքում, երբ հավասարության երկու մասերում էլ ենթաինտեգրալ արտահայտությունները տարածության յուրաքանչյուր կետում ունեն միատեսակ արժեքներ, այսինքն՝
![]()
Գաուս-Օստրոգրադսկու թեորեմի կիրառումը (10.18) բանաձևի նկատմամբ տալիս է
![]()
Այսպիսով, Մաքսվելի հավասարումները դիֆերենցիալ տեսքով կարտահայտվեն հետևյալ բանաձևերով՝

Պետք է նշել, որ այս հավասարումների մեջ մտնող տարբեր մեծություններն անկախ չեն, և նրանց միջև գոյություն ունեն հետևյալ կապերը՝
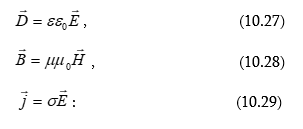
Մաքսվելի հավասարումները դիֆերենցիալ տեսքով բնութագրում են դաշտը տարածության յուրաքանչյուր կետում: Մաքսվելի հավասարումների ֆիզիկական իմաստը դիֆերենցիալ տեսքով նույնն է, ինչ որ ինտեգրալային տեսքով:
(10.23) - (10.29)
հավասարումները
կազմում են
Մաքսվելի հավասարումների
համակարգը:
Դրանք դադարի
վիճակում
գտնվող
միջավայրերի
էլեկտրական և
մագնիսական
դաշտերի
համար առավել
ընդհանուր հավասարումներ
են: Նշենք, որ ![]()
![]() և
և ![]() մեծությունները
Մաքսվելի
հավասարումների
մեջ մտնում են
որպես նյութական
հաստատուններ,
այսինքն՝
որպես նյութի
հատկությունները
բնութագրող
տրված մեծություններ:
մեծությունները
Մաքսվելի
հավասարումների
մեջ մտնում են
որպես նյութական
հաստատուններ,
այսինքն՝
որպես նյութի
հատկությունները
բնութագրող
տրված մեծություններ:
Մաքսվելի հավասարումները էլեկտրամագնիսականության մասին ուսմունքում նույն դերն են կատարում, ինչ որ Նյուտոնի օրենքները մեխանիկայում կամ հիմնական օրենքները (սկզբունքները) ջերմադինամիկայում:
Մաքսվելի հավասարումներից հետևում է, որ փոփոխական մագնիսական դաշտը միշտ կապված է իրենով հարուցված էլեկտրական դաշտի հետ, իսկ փոփոխական էլեկտրական դաշտը միշտ կապված է իրենով հարուցված մագնիսական դաշտի հետ, այսինքն էլեկտրական և մագնիսական դաշտերը անխզելիորեն կապված են մեկը մյուսի հետ` այսինքն ստեղծում են միասնական էլեկտրամագնիսական դաշտ:
Մաքսելի տեսությունը, հանդիսանալով էլեկտրական և մագնիսական երևույթների հիմնական օրենքների ընդհանրացումը, ոչ միայն կարողացավ բացատրել արդեն հայտնի փորձարարական փաստերը, այլ նաև կանխագուշակեց նոր երևույթներ: Այդ տեսության կարևոր եզրակացություններից մեկը շեղման հոսանքներով մագնիսական դաշտի գոյությունն է, որը Մաքսվելին հնարավորություն տվեց գուշակելու էլեկտրամագնիսական ալիքների` փոփոխական էլեկտրամագնիսական դաշտի գոյությունը, որը տարածության մեջ տարածվում է վերջավոր արագությամբ:
Էլեկտրամագնիսական
դաշտին
կիրառելի է
միայն
Այնշտայնի
հարաբերականության
սկզբունքը,
քանի որ վակուումում
էլեկտրամագնիսական
ալիքների տարածման
փաստը
հաշվարկման
բոլոր
իներցիալ
համակարգերում
միևնույն ![]() արագությամբ
անհամատեղելի
է Գալիլեյի
հարաբերականության
սկզբունքի
հետ:
արագությամբ
անհամատեղելի
է Գալիլեյի
հարաբերականության
սկզբունքի
հետ:
Համաձայն
Այնշտայնի
հարաբերական
տեսության`
մեխանիկական,
օպտիկական և
էլեկտրամագնիսական
երևութները
հաշվարկման
բոլոր իներցիալ
համակարգերում
ընթանում են
միատեսակ,
այսինքն`
նկարագրվում
են միատեսակ
հավասարումներով:
Մաքսվելի
հավասարումները
ինվարիանտ են
Լորենցի
ձևափոխությունների
նկատմամբ.
նրանց տեսքը
չի փոխվում մի
հաշվարկման
իներցիալ
համակարգից մյուսին
անցնելու
դեպքում,
չնայած ![]()
![]()
![]()
![]() մեծությունները
նրանցում
ձևափոխվում
են որոշակի
կանոններով:
մեծությունները
նրանցում
ձևափոխվում
են որոշակի
կանոններով:
Այսպիսով, Մաքսվելի տեսությունը, նրա փորձառական հաստատումը, ինչպես նաև Այնշտայնի հարաբերականության սկզբունքը բերում են էլեկտրական, մագնիսական և օպտիկական երևույթների միասնական տեսության` հիմնվելով էլեկտրամագնիսական դաշտի պատկերացումների վրա:
Բուհում ֆիզիկայի ուսումնասիրության ընթացքում կարևոր նշանակություն ունի ուսանողների կողմից տեսական գիտելիքների գործնական կիրառումը, հատկապես, խնդիրների լուծման ժամանակ: Ստորև բերված են խնդիրների լուծման օրինակներ, որոնք նույնատիպ են ձևակերպված. տվյալների վերածում ՄՀ-ի, անհրաժեշտ հավասարումների գրանցում, դրանց լուծումներն ընդհանուր տեսքով, թվային արժեքների տեղադրում վերջնական բանաձևի մեջ, պատասխանի գրանցում: Որոշ խնդիրների լուծումներ բերվում են առանց բացատրությունների, քանի որ նախ հարկավոր է մանրամասն ուսումնասիրել տվյալ թեմայի տեսական նյութը, այնուհետև կատարել խնդրի լուծման սեփական վերլուծությունը, լուծել խնդիրը և միայն արդյունքների համեմատման համար անդրադառնալ պատրաստի լուծմանը, որն, ըստ էության, միշտ չէ, որ միակ լուծումն է:
Խնդիր
1. ![]() կգ
զանգվածով
երկու փոքրիկ
գնդիկներ
կախված են
կգ
զանգվածով
երկու փոքրիկ
գնդիկներ
կախված են ![]() սմ
երկարության
մետաքսյա
թելերից,
որոնք ամրացված
են միևնույն
կետում: Երբ
գնդիկներին հաղորդում
են միատեսակ
մեծությամբ և
նշանով
սմ
երկարության
մետաքսյա
թելերից,
որոնք ամրացված
են միևնույն
կետում: Երբ
գնդիկներին հաղորդում
են միատեսակ
մեծությամբ և
նշանով ![]() լիցքեր,
թելերը
հեռանում են
լիցքեր,
թելերը
հեռանում են ![]() անկյունով:
Որոշել լիցքի
մեծությունը:
անկյունով:
Որոշել լիցքի
մեծությունը:
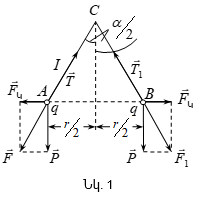
Լուծում: Նկարից`

Ըստ Կուլոնի օրենքի կետային լիցքերի փոխազդեցության ուժը`

որտեղ
![]()
(1)-ը, (2) -ը և (3)-ը համատեղ լուծելով, կստանանք`

Պատասխան`
![]() Կլ:
Կլ:
Խնդիր 2.
Չորս
միատեսակ ![]() կետային
լիցքեր
տեղավորված
են քառանկյան
գագաթներում:
Ինչպիսի՞
տարանուն
կետային
լիցքեր
տեղավորված
են քառանկյան
գագաթներում:
Ինչպիսի՞
տարանուն ![]() լիցք
պետք է
տեղավորել
քառանկյան
կենտրոնում,
որպեսզի այդ
լիցքերի
համակարգը
գտնվի հավասարակշռության
մեջ:
լիցք
պետք է
տեղավորել
քառանկյան
կենտրոնում,
որպեսզի այդ
լիցքերի
համակարգը
գտնվի հավասարակշռության
մեջ:
Լուծում:
Համակարգը
կգտնվի
հավասարակշռության
մեջ, եթե
յուրաքանչյուր
գագաթում
տեղավորված ![]() լիցքի
վրա ազդող
ուժերի
համազորը`
մյուս երեք
գագաթներում
տեղավորված
լիցքերի
կողմից, հավասարակշռվի
կենտրոնում տեղավորված
լիցքի
վրա ազդող
ուժերի
համազորը`
մյուս երեք
գագաթներում
տեղավորված
լիցքերի
կողմից, հավասարակշռվի
կենտրոնում տեղավորված
![]() տարանուն
լիցքի ձգողական
ուժի հետ ( նկ. 2)`
տարանուն
լիցքի ձգողական
ուժի հետ ( նկ. 2)`
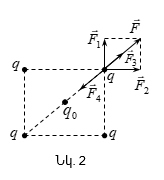
![]()
Եթե
քառանկյան
կողմը
նշանակենք ![]() -ով,
ապա
կունենանք`
-ով,
ապա
կունենանք`

Հետևաբար`
![]()
![]() և
և ![]() ուժերի
համազորը
կլինի`
ուժերի
համազորը
կլինի`

Հավասարակշռության պայմանից`

Պատասխան` ![]()
![]()
Խնդիր 3.
Բարակ ուղիղ ![]() երկարության
լարը
հավասարաչափ
լիցքավորված
է
երկարության
լարը
հավասարաչափ
լիցքավորված
է ![]() լիցքով:
Գտնել դաշտի
լիցքով:
Գտնել դաշտի ![]() լարվածությունը
այն կետում,
որը լարի
կենտրոնից
գտնվում է
լարվածությունը
այն կետում,
որը լարի
կենտրոնից
գտնվում է ![]() հեռավորության
վրա և
սիմետրիկ է
դասավորված
լարի ծայրերի
նկատմամբ:
Դիտարկել
հեռավորության
վրա և
սիմետրիկ է
դասավորված
լարի ծայրերի
նկատմամբ:
Դիտարկել ![]() դեպքը:
դեպքը:
Լուծում:

Այս արտահայտությունը ինտեգրելով ստանում ենք`
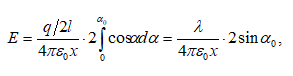
որտեղ![]() -ն
-ն ![]() անկյան
առավելագույն
արժեքն է, ընդ
որում`
անկյան
առավելագույն
արժեքն է, ընդ
որում`

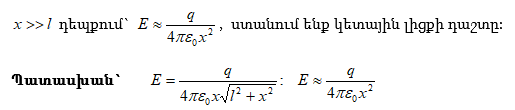
Խնդիր 4.
![]() մ
շառավղով
օղակը
հավասարաչափ
լիցքավորված
է
մ
շառավղով
օղակը
հավասարաչափ
լիցքավորված
է ![]() Կլ/մ
գծային
լիցքով:
Որոշել դաշտի
լարվածությունը
օղակի
կենտրոնով
անցնող
առանցքի վրա
Կլ/մ
գծային
լիցքով:
Որոշել դաշտի
լարվածությունը
օղակի
կենտրոնով
անցնող
առանցքի վրա ![]() կետում,
որը հեռացված
է օղակի
կենտրոնից
կետում,
որը հեռացված
է օղակի
կենտրոնից ![]() մ-ով:
Դիտարկել
մ-ով:
Դիտարկել ![]() դեպքը:
դեպքը:
Լուծում:

Օղակի լիցքը`

Եթե
![]() , ապա
ստանում ենք
կետային
լիցքի դաշտի
լարվածությունը
, ապա
ստանում ենք
կետային
լիցքի դաշտի
լարվածությունը
![]()
Պատասխան` ![]() կՎ/մ:
կՎ/մ:
Խնդիր 5.
![]() մ
շառավղով
մետաղական
գնդի վրա
գտնվում է
մ
շառավղով
մետաղական
գնդի վրա
գտնվում է ![]() նԿլ
լիցք: Որոշել էլեկտրաստատիկ
դաշտի
լարվածությունը.
նԿլ
լիցք: Որոշել էլեկտրաստատիկ
դաշտի
լարվածությունը.
1)
գնդի
կենտրոնից ![]() սմ
հեռավորության
վրա 2) գնդի
մակերևույթի
վրա 3) գնդի
կենտրոնից
սմ
հեռավորության
վրա 2) գնդի
մակերևույթի
վրա 3) գնդի
կենտրոնից ![]() սմ
հեռավորության
վրա: Կառուցել
սմ
հեռավորության
վրա: Կառուցել
![]() կախվածության
գրաֆիկը:
կախվածության
գրաֆիկը:

Լուծում: Օգտվենք Գաուսի թեորեմից`


Խնդիր 6.
Էլեկտրական
դաշտի
լարվածությունը
կախված է
միայն ![]() և
և
![]() կոորդինատներից`
կոորդինատներից`
![]() օրենքով,
որտեղ
օրենքով,
որտեղ ![]() -ն
հաստատուն
մեծություն
է,
-ն
հաստատուն
մեծություն
է, ![]() և
և ![]() -ն
-ն ![]() և
և ![]() առանցքների
միավոր
վեկտորներն
են: Գտնել լիցքը
առանցքների
միավոր
վեկտորներն
են: Գտնել լիցքը
![]() շառավղով
գնդի ներսում,
որի կենտրոնը
կոորդինատների
սկզբնակետն է:
շառավղով
գնդի ներսում,
որի կենտրոնը
կոորդինատների
սկզբնակետն է:

Lուծում:
Նշենք,
որ ![]() դաշտը
առանցքասիմետրիկ
է, որտեղից էլ
գալիս ենք այն
եզրակացության,
որ հոսքը
դաշտը
առանցքասիմետրիկ
է, որտեղից էլ
գալիս ենք այն
եզրակացության,
որ հոսքը ![]() շառավղով
գնդային
մակերևույթով
հավասար է
նույն
շառավղով և
շառավղով
գնդային
մակերևույթով
հավասար է
նույն
շառավղով և ![]() բարձրությամբ
գլանի
կողմնային
մակերևույթով
հոսքին:
Հետևաբար,
Գաուսի
թեորեմի
համաձայն`
բարձրությամբ
գլանի
կողմնային
մակերևույթով
հոսքին:
Հետևաբար,
Գաուսի
թեորեմի
համաձայն`
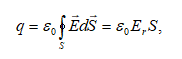
որտեղ
![]() և
և ![]() Վերջնականապես
կստանանք`
Վերջնականապես
կստանանք`
Պատասխան`
![]()
Խնդիր 7.
Համակարգը
կազմված է ![]() շառավղով
հավասարաչափ
լիցքավորված
գնդից և
շրջապատող
միջավայրից,
որը լցված է
շառավղով
հավասարաչափ
լիցքավորված
գնդից և
շրջապատող
միջավայրից,
որը լցված է ![]() ծավալային
խտության
լիցքով, որտեղ
ծավալային
խտության
լիցքով, որտեղ
![]() -ն
դրական
հաստատուն է,
-ն
դրական
հաստատուն է, ![]() -ը
գնդի
կենտրոնից
հեռավորությունն
է: Գտնել գնդի
այն լիցքը,
որի դեպքում
գնդից դուրս
էլեկտրական
դաշտի
-ը
գնդի
կենտրոնից
հեռավորությունն
է: Գտնել գնդի
այն լիցքը,
որի դեպքում
գնդից դուրս
էլեկտրական
դաշտի ![]() լարվածությունը
կախված չի
լինի
լարվածությունը
կախված չի
լինի ![]() -ից:
Ի՞նչի է
հավասար
-ից:
Ի՞նչի է
հավասար ![]() -ն:
-ն:
Լուծում:
Դիցուք
որոնելի
լիցքը
հավասար է ![]() -ի:
Օգտվելով
Գաուսի
թեորեմից` այն
գրենք
-ի:
Օգտվելով
Գաուսի
թեորեմից` այն
գրենք ![]() շառավղով
գնդային
մակերևույթի
համար.
շառավղով
գնդային
մակերևույթի
համար.

Ինտեգրելով (1)-ը կստանանք`

![]() լարվածությունը
կախված չի
լինի
լարվածությունը
կախված չի
լինի ![]() -ից
այն պայմանով,
երբ (2)
հավասարման
փակագծերի միջի
արտահայտությունը
հավասար է
զրոյի,
որտեղից`
-ից
այն պայմանով,
երբ (2)
հավասարման
փակագծերի միջի
արտահայտությունը
հավասար է
զրոյի,
որտեղից` ![]()
![]() -ի
համար
ստանում ենք`
-ի
համար
ստանում ենք` ![]()

Խնդիր 8: Սնամեջ
գունդն իր վրա
կրում է
հավասարաչափ
բաշխված լիցք:
Որոշել գնդի
շառավիղը, եթե
գնդի կենտրոնում
պոտենցիալը` ![]() Վ է,
իսկ գնդի
կենտրոնից
Վ է,
իսկ գնդի
կենտրոնից ![]() սմ
հեռավորության
վրա`
սմ
հեռավորության
վրա` ![]() Վ:
Վ:

Լուծում: Օգտվելով կետային լիցքի պոտենցիալի բանաձևից`
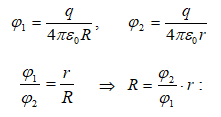
Պատասխան` ![]() սմ:
սմ:
Խնդիր 9. Լիցքավորված
գնդի դաշտի
պոտենցիալը
կախված է
միայն մինչև
գնդի կենտրոնը
եղած ![]() հեռավորությունից`
ըստ
հեռավորությունից`
ըստ ![]() օրենքի,
որտեղ
օրենքի,
որտեղ ![]() -ն
և
-ն
և ![]() -ն
հաստատուններ
են: Գտնել
գնդի ներսում
լիցքի
-ն
հաստատուններ
են: Գտնել
գնդի ներսում
լիցքի ![]() ծավալային
խտությունը:
ծավալային
խտությունը:
Լուծում:
Սկզբում
գտնենք դաշտի
լարվածությունը.
համաձայն ![]() -ի
կստանանք`
-ի
կստանանք`
![]()
Համաձայն
Գաուսի
թեորեմի` ![]() Դիֆերենցելով
այս արտահայտությունը,
կստանանք
Դիֆերենցելով
այս արտահայտությունը,
կստանանք

որտեղ
![]() -ն
-ն ![]() և
և ![]() շառավիղներով
գնդերի միջև
լիցքն է:
Արդյունքում
ստանում ենք
շառավիղներով
գնդերի միջև
լիցքն է:
Արդյունքում
ստանում ենք

որտեղից

Տեղադրելով (1)-ը (2)-ի մեջ, կստանանք`

(3)-ից հետևում է, որ գնդի ներսում լիցքը բաշխված է հավասարաչափ:
Պատասխան`
![]()
Խնդիր 10.
Գտնել ![]() և
և
![]() մոմենտներով
երկու
կետային
դիպոլների
փոխազդեցության
ուժը, եթե
մոմենտներով
երկու
կետային
դիպոլների
փոխազդեցության
ուժը, եթե ![]() և
և ![]() վեկտորներն
ուղղված են
դիպոլները
միացնող ուղղի
երկայնքով, և
վերջինների
միջև հեռավորությունը
հավասար է
վեկտորներն
ուղղված են
դիպոլները
միացնող ուղղի
երկայնքով, և
վերջինների
միջև հեռավորությունը
հավասար է ![]() -ի:
-ի:
Լուծում: Դիպոլի վրա ազդող ուժը`

որտեղ
![]() -ն
-ն ![]() դիպոլի
դաշտի
լարվածությունն
է և որոշվում է
դիպոլի
դաշտի
լարվածությունն
է և որոշվում է

Գտնելով
(2) արտահայտության
ածանցյալն
ըստ ![]() -ի և
արդյունքը
տեղադրելով
(1)-ի մեջ,
-ի և
արդյունքը
տեղադրելով
(1)-ի մեջ, ![]() -ի
համար
կստանանք`
-ի
համար
կստանանք`

Նշենք,
որ
դիպոլներն
իրար կձգեն,
եթե ![]() , և
կվանեն, եթե
, և
կվանեն, եթե ![]()

Խնդիր 11.
Ինչ-որ
էլեկտրաստատիկ
դաշտի
պոտենցիալն
ունի ![]() տեսքը,
որտեղ
տեսքը,
որտեղ ![]() -ն
և
-ն
և ![]() -ն
հաստատուններ
են: Գտնել
դաշտի
լարվածության
մոդուլը և
ուղղությունը:
-ն
հաստատուններ
են: Գտնել
դաշտի
լարվածության
մոդուլը և
ուղղությունը:
Լուծում:


Խնդիր 12. Գտնել
դաշտի
լարվածությունը,
որի պոտենցիալն
ունի հետևյալ
տեսքը. 1) ![]()
![]() -ն
հաստատուն է, 2)
-ն
հաստատուն է, 2) ![]()
![]() -ն
հաստատուն
վեկտոր է,
-ն
հաստատուն
վեկտոր է, ![]() -ը մեզ
հետաքրքրող
կետում
շառավիղ-վեկտորն
է:
-ը մեզ
հետաքրքրող
կետում
շառավիղ-վեկտորն
է:
Լուծում: 1) օգտվելով

արտահայտությունից,
կստանանք ` ![]()
2) ![]() որտեղ
որտեղ
![]()
![]() և
և ![]() -ը հաստատուններ
են: (1)-ից
օգտվելով
ստանում ենք`
-ը հաստատուններ
են: (1)-ից
օգտվելով
ստանում ենք`
![]() Այստեղից
հետևում է, որ
տվյալ
դեպքում
դաշտը համասեռ
է:
Այստեղից
հետևում է, որ
տվյալ
դեպքում
դաշտը համասեռ
է:
Պատասխան`
![]()
![]()
Խնդիր 13.
Էլեկտրական
դաշտը
ստեղծվում է ![]() սմ
շառավիղ
ունեցող
ծավալային
սմ
շառավիղ
ունեցող
ծավալային ![]() Կլ/մ3
խտությամբ
հավասարաչափ
լիցքավորված
գնդով: Որոշել
դաշտի երկու
կետերի միջև
պոտենցիալների
տարբերությունը,
որոնք ընկած
են գնդի
կենտրոնից
Կլ/մ3
խտությամբ
հավասարաչափ
լիցքավորված
գնդով: Որոշել
դաշտի երկու
կետերի միջև
պոտենցիալների
տարբերությունը,
որոնք ընկած
են գնդի
կենտրոնից ![]() սմ և
սմ և ![]() սմ հեռավորությունների
վրա:
սմ հեռավորությունների
վրա:
Լուծում: Ըստ Գաուսի թեորեմի

![]()
Խնդիր 14.
Էլեկտրաստատիկ
դաշտը
ստեղծվել է
հաստատուն ![]() Կլ/մ
գծային
խտության
լիցքով
դրական
լիցքավորված
անվերջ երկար
լարով:
Ինչպի՞սի
արագություն
է ձեռք բերում
էլեկտրոնը
արտաքին ուժերի
ազդեցության
տակ`
մոտենալով
լարվածության
գծի
երկայնքով
Կլ/մ
գծային
խտության
լիցքով
դրական
լիցքավորված
անվերջ երկար
լարով:
Ինչպի՞սի
արագություն
է ձեռք բերում
էլեկտրոնը
արտաքին ուժերի
ազդեցության
տակ`
մոտենալով
լարվածության
գծի
երկայնքով ![]() սմ-ից
մինչև
սմ-ից
մինչև ![]() սմ:
սմ:
Լուծում: Արտաքին ուժերի կատարած աշխատանքը ծախսվում է էլեկտրոնին կինետիկ էներգիա հաղորդելու վրա.

որտեղից արագության համար ստանում ենք`

Պատասխան`
![]() մ/վ:
մ/վ:
Խնդիր 15.
Հորիզոնի հետ ![]() անկյուն
կազմող թեք
հարթությամբ
անկյուն
կազմող թեք
հարթությամբ ![]() բարձրությունից
սահում է
բարձրությունից
սահում է ![]() լիցքով
լիցքավորված
փոքր մարմինը:
Մարմնի սկզբնական
դիրքից
տարված
ուղղաձիգ
հարթության և
թեք
հարթության
հիմքի հատման
կետում գտնվում
է
լիցքով
լիցքավորված
փոքր մարմինը:
Մարմնի սկզբնական
դիրքից
տարված
ուղղաձիգ
հարթության և
թեք
հարթության
հիմքի հատման
կետում գտնվում
է ![]() լիցք:
Որոշել ի՞նչ
արագությամբ
կհասնի
մարմինը թեք
հարթության
հիմքին:
Շփումն անտեսել:
Մարմնի
զանգվածը
լիցք:
Որոշել ի՞նչ
արագությամբ
կհասնի
մարմինը թեք
հարթության
հիմքին:
Շփումն անտեսել:
Մարմնի
զանգվածը ![]() է:
է:

Լուծում:
Համաձայն
էներգիայի
պահպանման
օրենքի ![]() կետում
մարմնի
պոտենցիալ
էներգիան
(երկրի և լիցքի
ստեղծած
դաշտերի)
հավասար է
կետում
մարմնի
պոտենցիալ
էներգիան
(երկրի և լիցքի
ստեղծած
դաշտերի)
հավասար է ![]() կետում
կինետիկ և
լիցքերի
փոխազդեցության
պոտենցիալ
էներգիաների
գումարին (տես
նկ.8)`
կետում
կինետիկ և
լիցքերի
փոխազդեցության
պոտենցիալ
էներգիաների
գումարին (տես
նկ.8)`

Այստեղից

Խնդիր 16.
Միատեսակ
լիցք ունեցող
երկու գնդեր
գտնվում են
իրարից ![]() հեռավորության
վրա ուղղաձիգ
ուղղությամբ: Ներքևի
գունդն ամրացված
է, իսկ վերևի
գունդը
հեռավորության
վրա ուղղաձիգ
ուղղությամբ: Ներքևի
գունդն ամրացված
է, իսկ վերևի
գունդը ![]() սկզբնական
արագությամբ
ընկնում է
առաջինի վրա:
Ներքևի գնդից
ի՞նչ
սկզբնական
արագությամբ
ընկնում է
առաջինի վրա:
Ներքևի գնդից
ի՞նչ ![]() նվազագույն
հեռավորության
վրա վերևի
գունդը կանգ
կառնի:
նվազագույն
հեռավորության
վրա վերևի
գունդը կանգ
կառնի:

Lուծում: Էներգիայի պահպանման օրենքի համաձայն`

որտեղ
![]() -ը
գնդիկի
զանգվածն է:
Գրված
արտահայտությունից
հետևում է`
-ը
գնդիկի
զանգվածն է:
Գրված
արտահայտությունից
հետևում է`

որի լուծումը կլինի`

Դրական
նշանը
համապատասխանում
է ![]() -ի առավելագույն
արժեքին, երբ
-ի առավելագույն
արժեքին, երբ ![]() -ն
ուղղված լինի
ուղղաձիգ
դեպի վեր:
-ն
ուղղված լինի
ուղղաձիգ
դեպի վեր:
Խնդիր 17. ![]() Վ/մ
լարվածության
էլեկտրաստատիկ
դաշտում, դաշտին
ուղղահայաց
տեղադրում են
անվերջ հարթ
զուգահեռ
ապակյա թիթեղ
Վ/մ
լարվածության
էլեկտրաստատիկ
դաշտում, դաշտին
ուղղահայաց
տեղադրում են
անվերջ հարթ
զուգահեռ
ապակյա թիթեղ ![]() :
Որոշել. 1)
էլեկտրաստատիկ
դաշտի
լարվածությունը
թիթեղի ներսում,
2) էլեկտրական
շեղումը
թիթեղի
ներսում, 3) ապակու
բևեռացածությունը,
4) կապված
լիցքերի մակերևութային
խտությունն
ապակու վրա:
:
Որոշել. 1)
էլեկտրաստատիկ
դաշտի
լարվածությունը
թիթեղի ներսում,
2) էլեկտրական
շեղումը
թիթեղի
ներսում, 3) ապակու
բևեռացածությունը,
4) կապված
լիցքերի մակերևութային
խտությունն
ապակու վրա:
Լուծում: Էլեկտրական դաշտի լարվածությունը դիէլեկտրիկում`


Խնդիր 18. Հարթ
կոնդենսատորի
թիթեղների
միջև հեռավորությունը`
![]() սմ:
Կոնդենսատորի
լիցքավորումից
հետո մինչև
սմ:
Կոնդենսատորի
լիցքավորումից
հետո մինչև ![]() Վ
պոտենցիալների
տարբերությունը
թիթեղների
միջև մտցնում
են ապակե
թիթեղ(
Վ
պոտենցիալների
տարբերությունը
թիթեղների
միջև մտցնում
են ապակե
թիթեղ(![]() ):
Որոշել. 1)
ապակու
դիէլեկտրիկ
ընկալունակությունը,
2) կապված
լիցքերի մակերևութային
խտությունը
ապակե թիթեղի
վրա:
):
Որոշել. 1)
ապակու
դիէլեկտրիկ
ընկալունակությունը,
2) կապված
լիցքերի մակերևութային
խտությունը
ապակե թիթեղի
վրա:
Լուծում: Դիէլեկտրիկ ընկալունակությունը

![]()
Խնդիր 19.
Հարթ
կոնդենսատորի
շրջադիրների
միջև եղած տարածությունը
լցված է
փայլարով ![]() :
Կոնդենսատորի
շրջադիրների
մակերեսը`
:
Կոնդենսատորի
շրջադիրների
մակերեսը` ![]() սմ3: Որոշել
կապված
լիցքերի
մակերևութային
խտությունը
փայլարում,
եթե
շրջադիրները
մեկը մյուսին
ձգում են
սմ3: Որոշել
կապված
լիցքերի
մակերևութային
խտությունը
փայլարում,
եթե
շրջադիրները
մեկը մյուսին
ձգում են ![]() Ն
ուժով:
Ն
ուժով:
Լուծում: Կոնդենսատորի լիցքը`

![]()
Խնդիր 20. ![]() սմ և
սմ և ![]() սմ
շառավիղներով
երկու համակենտրոն
հաղորդիչ
գնդեր
լիցքավորված
են համապատասխանաբար
միատեսակ`
սմ
շառավիղներով
երկու համակենտրոն
հաղորդիչ
գնդեր
լիցքավորված
են համապատասխանաբար
միատեսակ` ![]() նԿլ
լիցքերով: Որոշել
այդ գնդերի
միջև
պարփակված
էլեկտրաստատիկ
դաշտի
էներգիան:
նԿլ
լիցքերով: Որոշել
այդ գնդերի
միջև
պարփակված
էլեկտրաստատիկ
դաշտի
էներգիան:

Լուծում: Էլեկտրաստատիկ դաշտի էներգիայի ծավալային խտությունը`

Պատասխան`
![]() մկՋ:
մկՋ:
Խնդիր 21.
![]() սմ
շառավղով հոծ
էբոնիտե
սմ
շառավղով հոծ
էբոնիտե ![]() գունդը
հավասարաչափ
լիցքավորված
է
գունդը
հավասարաչափ
լիցքավորված
է ![]() նԿլ/մ3
ծավալային
խտությամբ
լիցքով:
Որոշել գնդի ներսում
էլեկտրաստատիկ
դաշտի
էներգիան:
նԿլ/մ3
ծավալային
խտությամբ
լիցքով:
Որոշել գնդի ներսում
էլեկտրաստատիկ
դաշտի
էներգիան:
Լուծում:
Տարրական ![]() ծավալի
էներգիան`
ծավալի
էներգիան`

Պատասխան`
![]() պկՋ:
պկՋ:
Խնդիր 22. Գնդային
թաղանթը, որը
լիցքավորված
է ![]() լիցքով,
նրա
կենտրոնում
գտնվում է
լիցքով,
նրա
կենտրոնում
գտնվում է ![]() լիցքը:
Գտնել
էլեկտրական
ուժերի
աշխատանքը
թաղանթի
ընդարձակման
դեպքում, երբ
թաղանթի
շառավիղը
մեծանում է
լիցքը:
Գտնել
էլեկտրական
ուժերի
աշխատանքը
թաղանթի
ընդարձակման
դեպքում, երբ
թաղանթի
շառավիղը
մեծանում է ![]() -ից
մինչև
-ից
մինչև ![]() :
:

Լուծում: Էլեկտրական ուժերի կատարած աշխատանքը հավասար է համակարգի էլեկտրական էներգիայի նվազմանը.
![]()
![]() տարբերությունը
գտնելու
համար, պետք է
նշենլ, որ
թաղանթի
ընդարձակման
դեպքում
էլեկտրական
դաշտը և
հետևաբար
նրանում
տեղայնացված
էներգիան փոփոխվում
են միայն
ստվերագծված
գնդային շերտում:
Հետևաբար`
տարբերությունը
գտնելու
համար, պետք է
նշենլ, որ
թաղանթի
ընդարձակման
դեպքում
էլեկտրական
դաշտը և
հետևաբար
նրանում
տեղայնացված
էներգիան փոփոխվում
են միայն
ստվերագծված
գնդային շերտում:
Հետևաբար`

որտեղ
![]() -ը և
-ը և ![]() -ը դաշտերի
լարվածություններն
են (ստվերագծված
շերտում
համակարգի
կենտրոնից
-ը դաշտերի
լարվածություններն
են (ստվերագծված
շերտում
համակարգի
կենտրոնից ![]() հեռավորության
վրա) թաղանթի
մինչև
ընդարձակումը
և
ընդարձակումից
հետո:
Օգտվելով
Գաուսի
թեորեմից`
կարելի է
գտնել
հեռավորության
վրա) թաղանթի
մինչև
ընդարձակումը
և
ընդարձակումից
հետո:
Օգտվելով
Գաուսի
թեորեմից`
կարելի է
գտնել ![]() -ը
և
-ը
և ![]() -ը:
-ը:

![]()

Խնդիր 23.
Հարթ օդային
կոնդենսատորի
շրջադիրներին
կիրառված է ![]() Վ
պոտենցիալների
տարբերություն:
Շրջադիրների
մակերեսը`
Վ
պոտենցիալների
տարբերություն:
Շրջադիրների
մակերեսը` ![]() սմ2,
նրանց միջև
եղած
հեռավորությունը`
սմ2,
նրանց միջև
եղած
հեռավորությունը`
![]() մմ:
Շրջադիրները
իրարից
հեռացրին
մինչև
մմ:
Շրջադիրները
իրարից
հեռացրին
մինչև ![]() մմ
հեռավորությունը:
Գտնել
կոնդենսատորի
մմ
հեռավորությունը:
Գտնել
կոնդենսատորի
![]() և
և ![]() էներգիաները
մինչև
հեռացումը և
հեռացնելուց
հետո, եթե լարման
աղբյուրը
տեղաշարժից
առաջ. 1)
անջատված էր, 2)
անջատված չէր:
էներգիաները
մինչև
հեռացումը և
հեռացնելուց
հետո, եթե լարման
աղբյուրը
տեղաշարժից
առաջ. 1)
անջատված էր, 2)
անջատված չէր:
Լուծում: Կոնդենսատորի ունակությունները`

![]()

![]()

Խնդիր 24. Շրջադիրների
![]() և
և ![]() շառավիղներով
գնդային
կոնդենսատորը
(
շառավիղներով
գնդային
կոնդենսատորը
(![]() <
<![]() )
լցված է
իզոտրոպ, բայց
անհամասեռ
դիէլեկտրիկով,
որի
դիէլեկտրական
թափանցելիությունը
կախված է
մինչև
համակարգի
կենտրոնը
եղած
)
լցված է
իզոտրոպ, բայց
անհամասեռ
դիէլեկտրիկով,
որի
դիէլեկտրական
թափանցելիությունը
կախված է
մինչև
համակարգի
կենտրոնը
եղած ![]() հեռավորությունից
հեռավորությունից
![]() օրենքով,
օրենքով,
![]() Որոշել
այդպիսի կոնդենսատորի
ունակությունը:
Որոշել
այդպիսի կոնդենսատորի
ունակությունը:
Լուծում:
Համաձայն
կոնդենսատորի
ունակության
սահմանման` ![]() :
:
Խնդիրը
հանգում է
տրված ![]() -ի
դեպքում
-ի
դեպքում ![]() պոտենցիալների
տարբերության
որոշման.
պոտենցիալների
տարբերության
որոշման.

որտեղ
ենթադրվում է,
որ ներքին շրջադիրն
ունի![]() լիցք:
Որոշենք
լիցք:
Որոշենք ![]() -ն
գրելով
Գաուսի
թեորեմը
-ն
գրելով
Գաուսի
թեորեմը ![]() վեկտորի
համար.
վեկտորի
համար.

Վերջին արտահայտությունը (1)-մեջ տեղադրելուց և համապատասխան ինտեգրումից կստանանք`
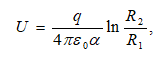
որտեղից ստանում ենք`

Խնդիր 25. S=0.8
մմ
կտրվածքով
պղնձյա
հաղորդչով
անցնում է I=80
մԱ հոսանք:
Գտնել
հաղորդչի
երկայնքով
էլեկտրոնների
կարգավորված
շարժման
միջին
արագությունը,
ընդունելով,
որ պղնձի
յուրաքանչյուր
ատոմին
ընկնում է մեկ
ազատ
էլեկտրոն:
Պղնձի խտությունը`
![]() գ/սմ3:
գ/սմ3:
Լուծում: Հոսանքի խտությունը`

Պատասխան` ![]() մ/վ:
մ/վ:
Խնդիր 26.
Որոշել
էլեկտրոնների
գումարային
իմպուլսը ![]() մ
երկարության
ուղիղ
հաղորդալարում,
որով անցնում
է
մ
երկարության
ուղիղ
հաղորդալարում,
որով անցնում
է ![]() Ա
հոսանք:
Ա
հոսանք:
Լուծում: Էլեկտրոնների գումարային իմպուլսը`
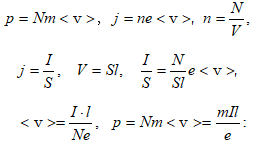
Պատասխան`
![]() կգմ/վ:
կգմ/վ:
Խնդիր 27.
![]() մմ2
կտրվածքով
ալյումինե
հաղորդալարով
անցնում է
մմ2
կտրվածքով
ալյումինե
հաղորդալարով
անցնում է ![]() Ա
հոսանք:
Որոշել այն
ուժը, որով
ազդում է էլեկտրական
դաշտը
առանձին էլեկտրոնների
վրա:
Ա
հոսանք:
Որոշել այն
ուժը, որով
ազդում է էլեկտրական
դաշտը
առանձին էլեկտրոնների
վրա:
Լուծում: էլեկտրոնի վրա ազդող ուժը`
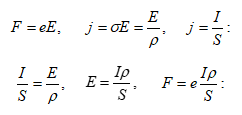
Պատասխան`
![]() Ն:
Ն:
Խնդիր 28.
Կլոր
կտրվածքով S
մակերեսով
երկար
հաղորդիչը
պատրաստված է
նյութից, որի
տեսակարար
դիմադրությունը
կախված է
միայն մինչև
հաղորդչի
առանցքը եղած ![]() հեռավորությունից
հեռավորությունից
![]() օրենքով,
որտեղ
օրենքով,
որտեղ ![]() -ն
հաստատուն է:
Հաղորդչով
անցնում է
-ն
հաստատուն է:
Հաղորդչով
անցնում է ![]() հոսանք:
Գտնել.1) դաշտի
հոսանք:
Գտնել.1) դաշտի ![]() լարվածությունը
հաղորդչում, 2)
հաղորդչի միավոր
երկարության
դիմադրությունը:
լարվածությունը
հաղորդչում, 2)
հաղորդչի միավոր
երկարության
դիմադրությունը:
Լուծում:
1) Դաշտի ![]() լարվածությունն
ըստ Օհմի
օրենքի
կապված է հոսանքի
լարվածությունն
ըստ Օհմի
օրենքի
կապված է հոսանքի
![]() խտության
հետ, իսկ
խտության
հետ, իսկ ![]() -ն
-ն
![]() հոսանքի
հետ, ուստի
կարելի է
գրել.
հոսանքի
հետ, ուստի
կարելի է
գրել.

Դաշտի
![]() լարվածությունը
տվյալ
հաղորդչի
կտրվածքի բոլոր
կետերում միատեսակ
է, այսինքն`
կախված չէ
լարվածությունը
տվյալ
հաղորդչի
կտրվածքի բոլոր
կետերում միատեսակ
է, այսինքն`
կախված չէ ![]() -ից:
Դրանում
կարելի է
համոզվել`
օգտագործելով
շրջապտույտի
թեորեմը
-ից:
Դրանում
կարելի է
համոզվել`
օգտագործելով
շրջապտույտի
թեորեմը ![]() վեկտորի
համար:
Այսպիսով,
վեկտորի
համար:
Այսպիսով, ![]() -ն
կարելի է ինտեգրալի
նշանի տակից
դուրս բերել և
ինտեգրման
արդյունքում
կստանանք`
-ն
կարելի է ինտեգրալի
նշանի տակից
դուրս բերել և
ինտեգրման
արդյունքում
կստանանք`
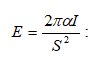
2)
Հաղորդչի
միավոր
երկարության
դիմադրությունը
կարելի է
որոշել ![]() բանաձևով:
Բաժանելով
այս
հավասարման
երկու մասերը
հա-ղորդչի
տեղամասի
երկարությանը,
որին
համապատասխանում
են
բանաձևով:
Բաժանելով
այս
հավասարման
երկու մասերը
հա-ղորդչի
տեղամասի
երկարությանը,
որին
համապատասխանում
են ![]() -ը
և
-ը
և ![]() -ն,
կստանանք`
-ն,
կստանանք`
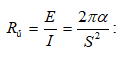
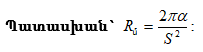
Խնդիր 29.
![]() շառավղով
մետաղական
գունդը
շրջապատված է
շառավղով
մետաղական
գունդը
շրջապատված է ![]() շառավղով
համակենտրոն
բարակ
մետաղական թաղանթով:
Այդ
էլեկտրոդների
միջև
տարածությունը
լցված է
շառավղով
համակենտրոն
բարակ
մետաղական թաղանթով:
Այդ
էլեկտրոդների
միջև
տարածությունը
լցված է ![]() տեսակարար
դիմադրություն
ունեցող
համասեռ
թույլ
հաղորդիչ
միջավայրով:
Գտնել միջէլեկտրոդային
բացակի
դիմադրությունը:
տեսակարար
դիմադրություն
ունեցող
համասեռ
թույլ
հաղորդիչ
միջավայրով:
Գտնել միջէլեկտրոդային
բացակի
դիմադրությունը:
Լուծում:
![]() և
և ![]() շառավիղների
միջև մտովի
առանձնացնենք
գնդային
բարակ շերտ:
Հոսանքի
գծերը այդ
շերտի բոլոր
կետերում
գնում են նրան
ուղղահայաց,
ուստի
այդպիսի
շերտը կարելի
է դիտարկել
որպես լայնական
հատույթի
շառավիղների
միջև մտովի
առանձնացնենք
գնդային
բարակ շերտ:
Հոսանքի
գծերը այդ
շերտի բոլոր
կետերում
գնում են նրան
ուղղահայաց,
ուստի
այդպիսի
շերտը կարելի
է դիտարկել
որպես լայնական
հատույթի ![]() մակերեսով
մակերեսով
![]() երկարություն
ունեցող
գլանային
հաղորդիչ: Օգտվելով
(4.19) բանաձևից,
կունենանք`
երկարություն
ունեցող
գլանային
հաղորդիչ: Օգտվելով
(4.19) բանաձևից,
կունենանք`

Այս
արտահայտությունը
ինտեգրելով
ըստ ![]() -ի
-ի ![]() -ից
մինչև
-ից
մինչև ![]() սահմաններում
կստանանք`
սահմաններում
կստանանք`

Խնդիր 30.
![]() Օմ
ներքին
դիմադրությամբ
միլիամպերետրը
նախատեսված է
չափելու ոչ
ավելի 10մԱ
հոսանքներ:
Ի՞նչ պետք է
անել, որպեսզի
այդ սարքը
կարելի լինի
օգտագործել
չափելու.
Օմ
ներքին
դիմադրությամբ
միլիամպերետրը
նախատեսված է
չափելու ոչ
ավելի 10մԱ
հոսանքներ:
Ի՞նչ պետք է
անել, որպեսզի
այդ սարքը
կարելի լինի
օգտագործել
չափելու.

1) մինչև 1Ա հոսանք, 2) մինչև 1Վ լարում:
Լուծում: 1) Նկ. 12ա-ից ըստ Կիրխհոֆի առաջին կանոնի`
![]()
Արտաքսելով
այս
հավասարումներից
![]() -ը,
կստանանք`
-ը,
կստանանք`

2) Նկ.12բ-ից`

(1)-ից և (2)-ից ստանում ենք.
Պատասխան`![]() Օմ:
Օմ: ![]() Օմ:
Օմ:
Խնդիր 31.
Նկարում
բերված
սխեմայում
հայտնի են
աղբյուրների
ԷլՇՈՒ-ները, ![]() և
և ![]() դիմադրությունները,
ինչպես նաև
կոնդենսատորի
դիմադրությունները,
ինչպես նաև
կոնդենսատորի
![]() ունակությունը:
Աղբյուրների
ներքին
դիմադրությունները
անհամեմատելի
փոքր են:
Գտնել կոնդենսատորի
1 շրջադիրի
վրայի լիցքը:
ունակությունը:
Աղբյուրների
ներքին
դիմադրությունները
անհամեմատելի
փոքր են:
Գտնել կոնդենսատորի
1 շրջադիրի
վրայի լիցքը:

Լուծում: Օգտվենք փակ շղթայի համար Օհմի օրենքից`
![]()
որտեղ
դրական
ուղղություն
ընտրվել է
ժամսլաքի
շարժման
ուղղությունը:
Մյուս կողմից
շղթայի ![]() անհամասեռ
տեղամասի
համար
անհամասեռ
տեղամասի
համար
![]()
իսկ
![]() տեղամասի
համար
տեղամասի
համար
![]()
Գրված հավասարումները համատեղ լուծելով, կստանանք`

Լիցքը
շրջադրի վրա
որոշվում է` ![]() բանաձևով:
բանաձևով:
Հետևաբար, վերջնական արդյունքը`
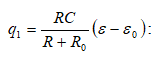
Ստացված
արտահայտությունից
բխում է, որ ![]() դեպքում
դեպքում
![]() և
հակառակը:
և
հակառակը:
Խնդիր 32.
Շղթան
բաղկացած է
հաստատուն ![]() ԷլՇՈԻ-ից
և նրան
հաջորդաբար
միացված
ԷլՇՈԻ-ից
և նրան
հաջորդաբար
միացված ![]() դիմադրությունից
և
դիմադրությունից
և ![]() կոնդենսատորից:
Հոսանքի
աղբյուրի
ներքին դիմադրությունը
անհամեմատելի
փոքր է:
կոնդենսատորից:
Հոսանքի
աղբյուրի
ներքին դիմադրությունը
անհամեմատելի
փոքր է: ![]() պահին
կոնդենսատորի
ունակությունը
արագ փոքրացնում
են
պահին
կոնդենսատորի
ունակությունը
արագ փոքրացնում
են ![]() անգամ:
Գտնել
հոսանքի ուժը
որպես
ժամանակի ֆունկցիա:
անգամ:
Գտնել
հոսանքի ուժը
որպես
ժամանակի ֆունկցիա:
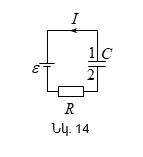
Լուծում:
Գրենք Օհմի
օրենքը
շղթայի ![]() անհամասեռ
տեղամասի
համար (նկ.14).
անհամասեռ
տեղամասի
համար (նկ.14).
![]()


Ածանցելով
այս
հավասարությունն
ըստ ժամանակի,
հաշվի
առնելով, որ (![]() լիցքը
նվազում է)
լիցքը
նվազում է) ![]() կստանանք`
կստանանք`
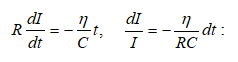
Վերջին հավասարման ինտեգրումը տալիս է .

որտեղ
![]() -ն
որոշվում է (1)
պայմանով:
Իրոք,
-ն
որոշվում է (1)
պայմանով:
Իրոք, ![]() ընդ
որում
ընդ
որում ![]() -ն
կոնդենսատորի
լիցքն է մինչև
նրա
ունակության
փոփոխելը:
Ուստի
-ն
կոնդենսատորի
լիցքն է մինչև
նրա
ունակության
փոփոխելը:
Ուստի


Խնդիր 33.
Երկու
կամայական
ձևի
հաղորդիչներ
գտնվում են ![]() տեսակարար
դիմադրությամբ
և
տեսակարար
դիմադրությամբ
և ![]() դիէլեկտրական
թափանցելիությամբ
համասեռ
անսահման
թույլ
հաղորդիչ
միջավայրում:
Գտնել
դիէլեկտրական
թափանցելիությամբ
համասեռ
անսահման
թույլ
հաղորդիչ
միջավայրում:
Գտնել ![]() արտադրյալի
արժեքը տվյալ
համակարգի
համար, որտեղ
արտադրյալի
արժեքը տվյալ
համակարգի
համար, որտեղ ![]() -ը
հաղորդիչների
միջև
միջավայրի
դիմադրությունն
է,
-ը
հաղորդիչների
միջև
միջավայրի
դիմադրությունն
է, ![]() -ն
հաղորդիչների
փոխադարձ
ունակությունն
է միջավայրի
առկայության
դեպքում:
-ն
հաղորդիչների
փոխադարձ
ունակությունն
է միջավայրի
առկայության
դեպքում:
Լուծում: Մտովի
հաղորդիչները
լիցքավորենք ![]() և
և ![]() լիցքերով:
Քանի որ դրանց
միջև
միջավայրը
թույլ
հաղորդիչ է,
ուրեմն
հաղորդիչների
մակերևույթները
համապոտենցիալ
են, և դաշտի
կոնֆիգուրացիան
նույնպիսին է,
ինչպես և
միջավայրի
բացակայության
դեպքում:
լիցքերով:
Քանի որ դրանց
միջև
միջավայրը
թույլ
հաղորդիչ է,
ուրեմն
հաղորդիչների
մակերևույթները
համապոտենցիալ
են, և դաշտի
կոնֆիգուրացիան
նույնպիսին է,
ինչպես և
միջավայրի
բացակայության
դեպքում:
Դրական
լիցքավորված
հաղորդիչը
շրջապատենք
անմիջականորեն
հաղորդչի
մակերևույթին
հարող ![]() փակ
մակերևույթով
և հաշվենք
առանձին
փակ
մակերևույթով
և հաշվենք
առանձին ![]() -ը
և
-ը
և ![]() -ն:
-ն:

որտեղ
ինտեգրալները
վերցվում են
տրված ![]() մակերևույթով:
մակերևույթով:
![]() -ի
հաշվման
դեպքում
օգտագործվել
է Օհմի
-ի
հաշվման
դեպքում
օգտագործվել
է Օհմի ![]() օրենքը,
օրենքը,
![]() -ի
հաշվման
դեպքում`
Գաուսի թեորեմը:
Ստացված
արտահայտությունների
արտադրյալը`
-ի
հաշվման
դեպքում`
Գաուսի թեորեմը:
Ստացված
արտահայտությունների
արտադրյալը`

Խնդիր 34. Որքա՞ն
ջերմաքանակ
կանջատվի ![]() դիմադրություն
ունեցող
պարույրում
նրանով
դիմադրություն
ունեցող
պարույրում
նրանով ![]() լիցք
անցնելիս, եթե
հոսանքը պարույրում.
լիցք
անցնելիս, եթե
հոսանքը պարույրում.
1)
հավասարաչափ
նվազել է
մինչև զրո ![]() ժամանակի
ընթացքում,
ժամանակի
ընթացքում,
2)
մոնոտոն
նվազել է
մինչև զրո,
այնպես, որ
յուրաքանչյուր
![]() վրկ-ում
այն նվազել է
երկու անգամ:
վրկ-ում
այն նվազել է
երկու անգամ:
Լուծում: 1. Համաձայն Ջոուլ-Լենցի օրենքի

Քանի որ հոսանքը նվազում է հավասարաչափ, ուստի

Երբ
![]() ,
, ![]() , (2)-ից կստանանք
, (2)-ից կստանանք
![]() , հետևաբար
, հետևաբար
![]() :
(3)
:
(3)


(4)-ը տեղադրելով (3)-ի մեջ, կստանանք`

Նկատի ունենալով (5)-ը (1)-ից կստանանք`

2.
Երբ ![]() ,
հոսանքի ուժը
,
հոսանքի ուժը ![]() է,
է, ![]() պահին
պահին
![]() ,
այնպես, որ
,
այնպես, որ ![]() ժամանակից
հետո
ժամանակից
հետո
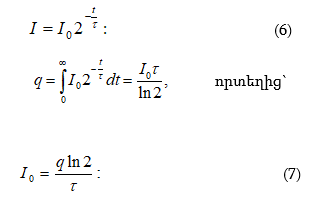
Վերջինը նկատի ունենալով ջերմաքանակի համար կունենանք`
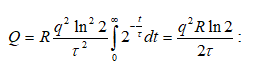
Խնդիր 35.
C
ունակության
կոնդենսատորին
հաղորդում են ![]() լիցք
և այնուհետև
լիցք
և այնուհետև ![]() պահին
փակում են R դիմադրությամբ:
Գտնել
դիմադրության
վրա անջատված
ջերմաքանակը`
կախված
պահին
փակում են R դիմադրությամբ:
Գտնել
դիմադրության
վրա անջատված
ջերմաքանակը`
կախված ![]() ժամանակից:
ժամանակից:

Լուծում: Համաձայն Ջոուլ-Լենցի օրենքի որոնելի ջերմաքանակը`

այստեղից
հետևում է, որ
պետք է գտնել ![]() կախվածությունը:
Այդ նպատակի
համար օգտվենք
Օհմի օրենքից
կախվածությունը:
Այդ նպատակի
համար օգտվենք
Օհմի օրենքից ![]() շղթայի
տեղամասի
համար.
շղթայի
տեղամասի
համար.

(2)-ը ածանցելով ըստ ժամանակի` կստանանք

Անջատելով փոփոխականները` կստանանք հետևյալ արտահայտությունը`

Ինտեգրելով վերջին հավասարումը, կստանանք`
![]()
որտեղ
![]() -ն
որոշվում է (2)
պայմանով,
-ն
որոշվում է (2)
պայմանով, ![]() դեպքում,
այսինքն
դեպքում,
այսինքն ![]() Վերջինը
նկատի
ունենալով
(3)-ից կստանանք
Վերջինը
նկատի
ունենալով
(3)-ից կստանանք
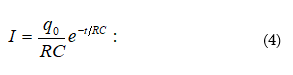
Վերջինը տեղադրելով (1)-ի մեջ և կատարելով ինտեգրումը կստանանք`

Խնդիր 36.
Որոշել
մետաղից
էլեկտրոնի
ելքի
աշխատանքը, եթե
երկէլեկտրոդ
էլեկտրոնային
լամպի հագեցման
հոսանքի խտությունը
![]() ջերմաստիճանում
ջերմաստիճանում
![]() է, իսկ
է, իսկ ![]() ջերմաստիճանում`
ջերմաստիճանում`
![]() է:
է:
Լուծում: Համաձայն Ռիչարդսոն-Դեշմանի բանաձևի
![]()
Բաժանելով իրար կունենանք`
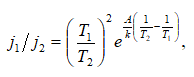
որտեղից

Խնսիր 37.
Ոչ
ինքնուրույն
պարպման
դեպքում
hագեցման հոսանքը`
![]()
![]() Ա:
Գտնել
արտաքին
իոնարարի
ստեղծած
զույգ
իոնների թիվը
Ա:
Գտնել
արտաքին
իոնարարի
ստեղծած
զույգ
իոնների թիվը
![]() վ-ում:
վ-ում:
Լուծում: Իոնների լիցքը`
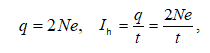
որտեղից

Պատասխան`
![]()
Խնդիր 38.
Որոշել
մագնիսական
դաշտի
ինդուկցիան
հաղորդալարային
![]() սմ
կողմ ունեցող
քառակուսային
շրջանակի կենտրոնում,
եթե
շրջանակով
անցնում է
սմ
կողմ ունեցող
քառակուսային
շրջանակի կենտրոնում,
եթե
շրջանակով
անցնում է ![]() Ա
հոսանք:
Ա
հոսանք:

Լուծում: Արդյունարար դաշտի ինդուկցիան`
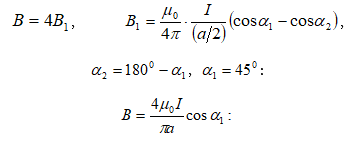
Պատասխան`
![]() մկՏլ:
մկՏլ:
Խնդիր 39.
Երկու անվերջ
երկար
զուգահեռ
հաղորդիչներով,
որոնց միջև
հեռավորությունը`
![]() սմ,
հոսում են
սմ,
հոսում են ![]() Ա և
Ա և ![]() Ա
հակառակ
ուղղություններով
հոսանքներ: Որոշել
մագնիսական
դաշտի
Ա
հակառակ
ուղղություններով
հոսանքներ: Որոշել
մագնիսական
դաշտի ![]() ինդուկցիան
ինդուկցիան
![]() կետում,
որն առաջին
հաղորդչից
հեռացված է
կետում,
որն առաջին
հաղորդչից
հեռացված է ![]() սմ և
երկրորդից`
սմ և
երկրորդից` ![]() սմ:
սմ:
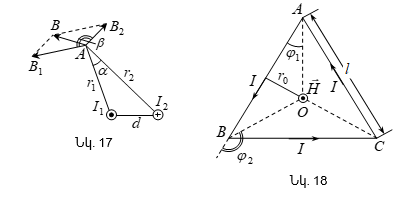
Լուծում:
Համաձայն
դաշտերի
վերադրման
սկզբունքի ![]() կետում`
կետում`
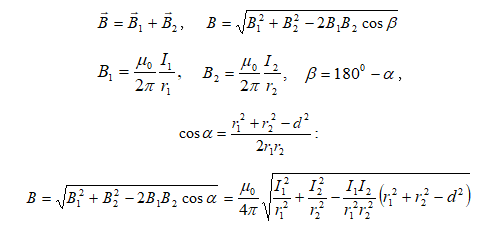
Պատասխան`
![]() մկՏլ:
մկՏլ:
Խնդիր 40.
![]() սմ
երկարություն
ունեցող
հավասարակողմ
եռանկյան
տեսքով ծռված
հաղորդալարով
անցնում է
սմ
երկարություն
ունեցող
հավասարակողմ
եռանկյան
տեսքով ծռված
հաղորդալարով
անցնում է ![]() Ա
հաստատուն
հոսանք: Ի՞նչի
է հավասար
մագնիսական
դաշտի
լարվածությունը
եռանկյան կենտրոնում
(նկ.18):
Ա
հաստատուն
հոսանք: Ի՞նչի
է հավասար
մագնիսական
դաշտի
լարվածությունը
եռանկյան կենտրոնում
(նկ.18):
Լուծում: Եռանկյան կենտրոնում բոլոր վեկտորներն ուղղված են նույն կողմը և մոդուլով իրար հավասար

Նկարից`
![]()
![]() Հետևաբար`
Հետևաբար`
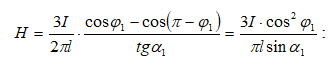
Քանի
որ ![]()
![]() , cos
, cos![]() ,
կստանանք`
,
կստանանք`
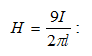
Պատասխան`
![]() Ա/մ:
Ա/մ:
Խնդիր 41.
![]() Ա
հոսանքն
անցնում է
ծռված բարակ
հաղորդալարով,
ինչպես ցույց
է տրված
նկարում:
Հաղորդչի ծռված
մասի
շառավիղը` R=12սմ,
Ա
հոսանքն
անցնում է
ծռված բարակ
հաղորդալարով,
ինչպես ցույց
է տրված
նկարում:
Հաղորդչի ծռված
մասի
շառավիղը` R=12սմ, ![]() Գտնել
մագնիսական
դաշտի
ինդուկցիան
կետում:
Գտնել
մագնիսական
դաշտի
ինդուկցիան
կետում:
Լուծում:
Մագնիսական
դաշտի
ինդուկցիայի
մոդուլը ![]() կետում`
կետում`
![]()
որտեղ
![]() -ը
ուղիղ
տեղամասի
ինդուկցիան
է,
-ը
ուղիղ
տեղամասի
ինդուկցիան
է, ![]() -ը
կորագիծ
մասինը:
-ը
կորագիծ
մասինը:
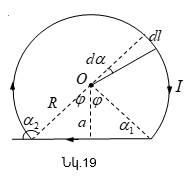

Ըստ
Բիո-Սավար-Լապլասի
օրենքի, քանի
որ ![]() և
և ![]() կարող
ենք գրել
կարող
ենք գրել

կստանանք`
Գումարելով (1)-ը և (2)-ը կստանանք`

Խնդիր 42. ![]() հոսանքն
անցնում է
բարակ
հաղորդչով,
որն ունի
հոսանքն
անցնում է
բարակ
հաղորդչով,
որն ունի ![]() շառավղով
շրջանագծին
ներգծված
կանոնավոր
շառավղով
շրջանագծին
ներգծված
կանոնավոր ![]() անկյան
տեսք: Գտնել
մագնիսական
դաշտի ինդուկցիան
այդպիսի
կոնտուրի
կենտրոնում:
Հետազոտել
ստացված
արտահայտությունը,
երբ
անկյան
տեսք: Գտնել
մագնիսական
դաշտի ինդուկցիան
այդպիսի
կոնտուրի
կենտրոնում:
Հետազոտել
ստացված
արտահայտությունը,
երբ ![]()
Լուծում:
Կոնտուրի կենտրոնում արդյունարար ինդուկցիայի մոդուլը`
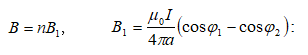
Կանոնավոր
![]() բազմանկյան
յուրաքանչյուր
անկյուն`
բազմանկյան
յուրաքանչյուր
անկյուն`
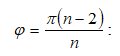
Մեր դեպքի համար

Նկարից`

Այսպիսով,

Երբ ![]() վերջին
արտահայտությունից
ստանում ենք`
վերջին
արտահայտությունից
ստանում ենք`

Խնդիր 43.
Բարակ
(մեկուսացված)
հաղորդալարը
կազմում է ![]() խիտ
կերպով
դասավորված
գալարներով
հարթ պարույր,
որով անցնում
է
խիտ
կերպով
դասավորված
գալարներով
հարթ պարույր,
որով անցնում
է ![]() մԱ
հոսանք:
Ներքին և
արտաքին
գալարների
շառավիղները`
մԱ
հոսանք:
Ներքին և
արտաքին
գալարների
շառավիղները` ![]() մմ,
մմ, ![]() մմ:
Գտնել 1)
պարույրի
կենտրոնում
մագնիսական
դաշտի ինդուկցիան,
2) պարույրի
մմ:
Գտնել 1)
պարույրի
կենտրոնում
մագնիսական
դաշտի ինդուկցիան,
2) պարույրի ![]() մագնիսական
մոմենտը:
մագնիսական
մոմենտը:
Լուծում:

1) ![]() շառավղով
մեկ գալարով
ստեղծված
մագնիսական
դաշտի
ինդուկցիան`
շառավղով
մեկ գալարով
ստեղծված
մագնիսական
դաշտի
ինդուկցիան`

Բոլոր գալարներով`
![]()
որտեղ
![]() -ը
գալարների
թիվն է
-ը
գալարների
թիվն է ![]() միջակայքում:
միջակայքում:

(1)-ը և (3)-ը տեղադրելով (2)-ի մեջ կստանանք`
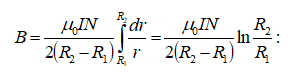
2)
![]() շառավղով
մեկ գալարի
մագնիսական
մոմենտը`
շառավղով
մեկ գալարի
մագնիսական
մոմենտը` ![]()
Բոլոր
գալարների
համար` ![]()


Խնդիր 44.
![]() գ
զանգվածով և
գ
զանգվածով և ![]() սմ
շառավղով
բարակ օղակը
կրում է լիցք,
որը
հավասարաչափ
բաշխված է
սմ
շառավղով
բարակ օղակը
կրում է լիցք,
որը
հավասարաչափ
բաշխված է ![]() Կլ/մ
գծային
խտությամբ:
Օղակը
հավասարաչափ
պտտվում է
Կլ/մ
գծային
խտությամբ:
Օղակը
հավասարաչափ
պտտվում է ![]() վ-1
հաճախությամբ
օղակի
հարթությանն
ուղղահայաց և
օղակի
կենտրոնով
անցնող
առանցքի նկատմամբ:
Որոշել 1) շրջանային
հոսանքի
վ-1
հաճախությամբ
օղակի
հարթությանն
ուղղահայաց և
օղակի
կենտրոնով
անցնող
առանցքի նկատմամբ:
Որոշել 1) շրջանային
հոսանքի ![]() մագնիսական
մոմենտը, 2)
մագնիսական
մոմենտի և
օղակի
իմպուլսի
մոմենտի
հարաբերությունը:
մագնիսական
մոմենտը, 2)
մագնիսական
մոմենտի և
օղակի
իմպուլսի
մոմենտի
հարաբերությունը:
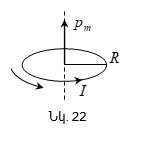
Լուծում: Շրջանային հոսանքի մագնիսական մոմենտը`

![]()
Խնդիր 45. ![]() սմ
շառավղով
բարակ
հաղորդալարային
կիսաօղակով
անցնում է
սմ
շառավղով
բարակ
հաղորդալարային
կիսաօղակով
անցնում է ![]() Ա
հոսանք:
Կիսաօղակի
հարթությանն
ուղղահայաց
գրգռված է
Ա
հոսանք:
Կիսաօղակի
հարթությանն
ուղղահայաց
գրգռված է ![]() Տլ
ինդուկցիայով
համասեռ մագնիսական
դաշտ: Գտնել
կիսաօղակը
ձգող ուժը:
Կիսաօղակի
վրա մատուցող
հաղորդալարերի
մագնիսական
դաշտի ազդեցությունը
և օղակի
առանձին
տարրերի փոխազդեցությունը
հաշվի չառնել:
Տլ
ինդուկցիայով
համասեռ մագնիսական
դաշտ: Գտնել
կիսաօղակը
ձգող ուժը:
Կիսաօղակի
վրա մատուցող
հաղորդալարերի
մագնիսական
դաշտի ազդեցությունը
և օղակի
առանձին
տարրերի փոխազդեցությունը
հաշվի չառնել:

Լուծում: Ըստ Ամպերի օրենքի`
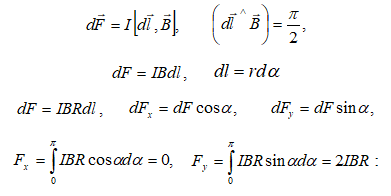
Պատասխան`
![]() Ն:
Ն:
Խնդիր 46.
![]() մ
կողմով
քառակուսի
հոսանքակիր
շրջանակը և անվերջ
երկար
հաղորդալարը
գտնվում են
միևնույն
հարթության
մեջ այնպես,
որ շրջանակի
երկու
կողմերը
զուգահեռ են
հաղորդալարին:
Շրջանակով
հոսում է
մ
կողմով
քառակուսի
հոսանքակիր
շրջանակը և անվերջ
երկար
հաղորդալարը
գտնվում են
միևնույն
հարթության
մեջ այնպես,
որ շրջանակի
երկու
կողմերը
զուգահեռ են
հաղորդալարին:
Շրջանակով
հոսում է ![]() Ա
հոսանք, իսկ
հաղորդալարով
Ա
հոսանք, իսկ
հաղորդալարով
![]() Ա
հոսանք:
Որոշել
շրջանակի վրա
ազդող արդյունարար
ուժի մոդուլը,
եթե շրջանակի
մոտակա կողմից
մինչև լարն
ընկած
հեռավորությունը`
Ա
հոսանք:
Որոշել
շրջանակի վրա
ազդող արդյունարար
ուժի մոդուլը,
եթե շրջանակի
մոտակա կողմից
մինչև լարն
ընկած
հեռավորությունը`
![]() սմ:
Հոսանքների
ուղղությունները
ցույց են տրված
նկարում:
սմ:
Հոսանքների
ուղղությունները
ցույց են տրված
նկարում:
Լուծում:

Արդյունարար ուժը`

Պատասխան`
![]() Ն:
Ն:
Խնդիր 47.
Երկու անվերջ
երկար
հաղորդիչներով
անցնում են
միևնույն
հոսանքները
նույն ուղղությամբ:
Հաղորդիչները
գտնվում են ![]() հեռավորության
վրա: Որպեսզի
դրանք
հեռացվեն
մինչև
հեռավորության
վրա: Որպեսզի
դրանք
հեռացվեն
մինչև ![]() հեռավորությունը
հաղորդչի
յուրաքանչյուր
մեկ
սանտիմետրի
վրա ծախսվում
է
հեռավորությունը
հաղորդչի
յուրաքանչյուր
մեկ
սանտիմետրի
վրա ծախսվում
է ![]() Ջ
աշխատանք:
Որոշել
հաղորդիչներում
հոսանքի ուժը:
Ջ
աշխատանք:
Որոշել
հաղորդիչներում
հոսանքի ուժը:
Լուծում:
![]() տեղափոխության
վրա կատարված
աշխատանքը`
տեղափոխության
վրա կատարված
աշխատանքը`

որտեղից ստանում ենք`


Խնդիր 48. ![]() Վ
պոտենցիալների
տարբերությամբ
արագացված
էլեկտրոնը
շարժվում է
ուղիղ երկար
հաղորդչին
զուգահեռ,
նրանից
Վ
պոտենցիալների
տարբերությամբ
արագացված
էլեկտրոնը
շարժվում է
ուղիղ երկար
հաղորդչին
զուգահեռ,
նրանից ![]() սմ
հեռավորության
վրա: Որոշել
էլեկտրոնի վրա
ազդող ուժը,
եթե
հաղորդչով
բաց է
թողնվում
սմ
հեռավորության
վրա: Որոշել
էլեկտրոնի վրա
ազդող ուժը,
եթե
հաղորդչով
բաց է
թողնվում ![]() Ա հոսանք:
Ա հոսանք:
Լուծում: Էլեկտրական դաշտի ուժերի կատարած աշխատանքը ծախսվում է էլեկտրոնին կինետիկ էներգիա հաղորդելու վրա.
![]()
![]()
![]()

Պատասխան`
![]() Ն:
Ն:
Խնդիր 49.
Էլեկտրոնը
թռչելով, ![]() մՏլ
ինդուկցիայով
համասեռ
մագնիսական
դաշտ,
շարժվում է
մՏլ
ինդուկցիայով
համասեռ
մագնիսական
դաշտ,
շարժվում է ![]() սմ
շառավղով
շրջանային
ուղեծրով:
Որոշել շրջանային
հոսանքին
համարժեք
սմ
շառավղով
շրջանային
ուղեծրով:
Որոշել շրջանային
հոսանքին
համարժեք ![]() մագնիսական
մոմենտը:
մագնիսական
մոմենտը:
Լուծում: Շրջանային հոսանքի մագնիսական մոմենտը`

Պատասխան`
![]() Ա.մ
Ա.մ![]() :
:
Խնդիր 50.
![]() Տլ
մագնիսական
ինդուկցիայով
համասեռ մագնիսական
դաշտի
ինդուկցիայի
գծերին
ուղղահայաց
հաստատուն
արագությամբ
թռչում է
լիցքավորված
մասնիկը:
Տլ
մագնիսական
ինդուկցիայով
համասեռ մագնիսական
դաշտի
ինդուկցիայի
գծերին
ուղղահայաց
հաստատուն
արագությամբ
թռչում է
լիցքավորված
մասնիկը: ![]() մկվ
տևողությամբ
միացվում է
մկվ
տևողությամբ
միացվում է ![]() Վ/մ
լարվածության
էլեկտրական
դաշտը, որի
ուղղությունը
զուգահեռ է
մագնիսական
դաշտին: Որոշել
լիցքավորված
մասնիկի
պարուրագծային
հետագծի
քայլը:
Վ/մ
լարվածության
էլեկտրական
դաշտը, որի
ուղղությունը
զուգահեռ է
մագնիսական
դաշտին: Որոշել
լիցքավորված
մասնիկի
պարուրագծային
հետագծի
քայլը:
Լուծում: Լորենցի ուժը լիցքավորված մասնիկին հաղորդում է կենտրոնաձիգ արագացում`
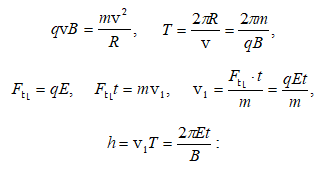
Պատասխան`
![]() սմ:
սմ:
Խնդիր 51.
![]() կգ և
կգ և ![]() կգ
զանգվածներով
երկու իզոտոպների
իոններն
արագացվում
են
կգ
զանգվածներով
երկու իզոտոպների
իոններն
արագացվում
են ![]() Վ
պոտենցիալների
տարբերությամբ,
թռչում են
Վ
պոտենցիալների
տարբերությամբ,
թռչում են ![]() Տլ
ինդուկցիայով
համասեռ
մագնիսական
դաշտ` ինդուկցիայի
գծերին
ուղղահայաց:
Ընդունելով
յուրաքանչյուր
իոնի լիցքը
հավասար տարրական
էլեկտրական
լիցքին`
որոշել, թե,
որքանով կտարբերվեն
իզոտոպների
իոնների
հետագծերի
շառավիղները
մագնիսական
դաշտում:
Տլ
ինդուկցիայով
համասեռ
մագնիսական
դաշտ` ինդուկցիայի
գծերին
ուղղահայաց:
Ընդունելով
յուրաքանչյուր
իոնի լիցքը
հավասար տարրական
էլեկտրական
լիցքին`
որոշել, թե,
որքանով կտարբերվեն
իզոտոպների
իոնների
հետագծերի
շառավիղները
մագնիսական
դաշտում:
Լուծում: Լորենցի ուժը լիցքավորված մասնիկին հաղորդում է կենտրոնաձիգ արագացում.

Պատասխան`
![]() մմ:
մմ:
Խնդիր 52.
Ցիկլոտրոնում
պրոտոններն
արագացվում
են ![]() Տլ
ինդուկցիայով
համասեռ
մագնիսական
դաշտում:
Պրոտոնների
հետագծերի
առավելագույն
կորության
շառավիղը
կազմում է`
Տլ
ինդուկցիայով
համասեռ
մագնիսական
դաշտում:
Պրոտոնների
հետագծերի
առավելագույն
կորության
շառավիղը
կազմում է` ![]() սմ:
Որոշել 1)
պրոտոնների
կինետիկ
էներգիան արագացման
վերջում, 2)
արագացնող
լարման
նվազագույն
հաճախությունը,
որի դեպքում
պրոտոնները
արագացվում
են մինչև
սմ:
Որոշել 1)
պրոտոնների
կինետիկ
էներգիան արագացման
վերջում, 2)
արագացնող
լարման
նվազագույն
հաճախությունը,
որի դեպքում
պրոտոնները
արագացվում
են մինչև ![]() ՄէՎ:
ՄէՎ:
Լուծում: Մագնիսական դաշտում շարժվող պրոտոնների վրա ազդում է Լորենցի ուժը, որը պրոտոններին հաղորդում է կենտրոնաձիգ արագացում.

Պատասխան`
![]() ՄէՎ:
ՄէՎ: ![]() ՄՀց:
ՄՀց:
Խնդիր 53.
Նատրիումային
հաղորդչի
համար Հոլլի
էֆեկտի
ժամանակ
հոսանքի ![]() Ա/սմ2
խտության և
Ա/սմ2
խտության և ![]() Տլ մագնիսական
ինդուկցիայի
դեպքում
լայնական
էլեկտրական
դաշտի
լարվածությունը`
Տլ մագնիսական
ինդուկցիայի
դեպքում
լայնական
էլեկտրական
դաշտի
լարվածությունը`
![]() մՎ/մ է: Որոշել
հաղորդականության
էլեկտրոնների
կոնցենտրացիան,
ինչպես նաև
դրա
հարաբերությունը
այդ
հաղորդչում
ատոմների
կոնցենտրացիային:
Նատրիումի
խտությունը`
մՎ/մ է: Որոշել
հաղորդականության
էլեկտրոնների
կոնցենտրացիան,
ինչպես նաև
դրա
հարաբերությունը
այդ
հաղորդչում
ատոմների
կոնցենտրացիային:
Նատրիումի
խտությունը` ![]() գ/սմ3:
գ/սմ3:
Լուծում: Հաղորդչում լիցքերի հավասարակշռության դեպքում`

![]()
Խնդիր 54. ![]() մմ
հաստության
պղնձե թիթեղի
կտրվածքով
բաց են
թողնում
մմ
հաստության
պղնձե թիթեղի
կտրվածքով
բաց են
թողնում ![]() Ա
հոսանք:
Թիթեղը
տեղադրվում է
Ա
հոսանք:
Թիթեղը
տեղադրվում է ![]() Տլ ինդուկցիայով
համասեռ
մագնիսական
դաշտում
հոսանքի
ուղղությանը
և թիթեղի
կողին
ուղղահայաց:
Հաշվի առնելով,
որ
հաղորդականության
էլեկտրոնների
կոնցենտրացիան
հավասար է
ատոմների
կոնցենտրացիային,
որոշել
թիթեղում
առաջացած
լայնական
պոտենցիալների
տարբերությունը:
Տլ ինդուկցիայով
համասեռ
մագնիսական
դաշտում
հոսանքի
ուղղությանը
և թիթեղի
կողին
ուղղահայաց:
Հաշվի առնելով,
որ
հաղորդականության
էլեկտրոնների
կոնցենտրացիան
հավասար է
ատոմների
կոնցենտրացիային,
որոշել
թիթեղում
առաջացած
լայնական
պոտենցիալների
տարբերությունը:

Լուծում: Լայնական էլեկտրական դաշտը պոտենցիալների տարբերության հետ կապված է հետևյալ առնչությամբ`

![]()
Խնդիր 55.
Մագնիսական
դաշտում, որը
փոփոխվում է
ըստ ![]() օրենքի
(
օրենքի
(![]() Տլ,
Տլ, ![]() վ ),
տեղադրված է
վ ),
տեղադրված է ![]() սմ
կողմ ունեցող
շրջանակը, ընդ
որում` շրջանակի
նորմալը
դաշտի
ուղղությամբ
կազմում է
սմ
կողմ ունեցող
շրջանակը, ընդ
որում` շրջանակի
նորմալը
դաշտի
ուղղությամբ
կազմում է ![]() անկյուն:
Որոշել
անկյուն:
Որոշել ![]() վ
պահին
շրջանակում
առաջացած
մակածման Է
ԷլՇՈՒ-ն:
վ
պահին
շրջանակում
առաջացած
մակածման Է
ԷլՇՈՒ-ն:
Լուծում: Համաձայն Ֆարադեյի օրենքի`

![]()
Խնդիր 56.
Ալյումինե
հաղորդալարով
(![]() Օմ.մ)
օղակը
տեղադրված է
մագնիսական
դաշտում ինդուկցիայի
գծերին
ուղղահայաց:
Օղակի տրամագիծը`
Օմ.մ)
օղակը
տեղադրված է
մագնիսական
դաշտում ինդուկցիայի
գծերին
ուղղահայաց:
Օղակի տրամագիծը`
![]() սմ է,
հաղորդալարի
տրամագիծը`
սմ է,
հաղորդալարի
տրամագիծը` ![]() մմ:
Որոշել
մագնիսական
դաշտի
փոփոխման
արագությունը,
եթե օղակում
հոսանքը`
մմ:
Որոշել
մագնիսական
դաշտի
փոփոխման
արագությունը,
եթե օղակում
հոսանքը` ![]() Ա:
Ա:
Լուծում: Ըստ Ֆարադեյի օրենքի` մակածման ԷլՇՈՒ-ի մոդուլը`

![]()
Խնդիր 57.
Երկու հարթ
փակ առանց
շփման
շարժվող
սահող միջնակապով
հաղորդաձողեր,
որոնց միջև
հեռավորությունը`
![]() սմ,
գտնվում են
կոնտուրի հարթությանն
ուղղահայաց
սմ,
գտնվում են
կոնտուրի հարթությանն
ուղղահայաց ![]() Տլ
ինդուկցիայով
մագնիսական
դաշտում:
Տլ
ինդուկցիայով
մագնիսական
դաշտում: ![]() գ
զանգվածով միջնակապը
սահում է
ներքև
հաստատուն
գ
զանգվածով միջնակապը
սահում է
ներքև
հաստատուն ![]() մ/վ
արագությամբ:
Որոշել
միջնակապի
դիմադրությունը`
անտեսելով
կոնտուրի
ինքնամակածումը
և կոնտուրի
մնացած
մասերի
դիմադրությունը:
մ/վ
արագությամբ:
Որոշել
միջնակապի
դիմադրությունը`
անտեսելով
կոնտուրի
ինքնամակածումը
և կոնտուրի
մնացած
մասերի
դիմադրությունը:
Լուծում:

Համաձայն Ֆարադեյի օրենքի`
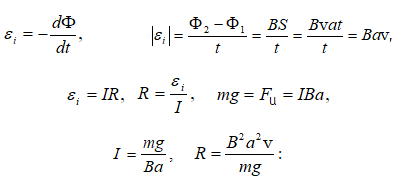
Պատասխան`
![]() Օմ:
Օմ:
Խնդիր 58.
![]() Տլ
ինդուկցիայով
համասեռ
մագնիսական
դաշտում
ուղղաձիգ
առանցքի
շուրջը
պտտվում է
Տլ
ինդուկցիայով
համասեռ
մագնիսական
դաշտում
ուղղաձիգ
առանցքի
շուրջը
պտտվում է ![]() մ
երկարություն
ունեցող
հորիզոնական
ձողը: Պտտման
առանցքն
անցնում է
ձողի ծայրով`
մագնիսական
ինդուկցիայի
գծերին
զուգահեռ:
Որոշել
պտույտների
թիվը մեկ
վայրկյանում,
որի դեպքում
ձողի
ծայրերում
առաջանում է
մ
երկարություն
ունեցող
հորիզոնական
ձողը: Պտտման
առանցքն
անցնում է
ձողի ծայրով`
մագնիսական
ինդուկցիայի
գծերին
զուգահեռ:
Որոշել
պտույտների
թիվը մեկ
վայրկյանում,
որի դեպքում
ձողի
ծայրերում
առաջանում է ![]() Վ
պոտենցիալների
տարբերություն:
Վ
պոտենցիալների
տարբերություն:

Լուծում: Համաձայն Ֆարադեյի օրենքի`

Պատասխան`
![]() վ
վ![]() :
:
Խնդիր 59.
Որոշել ![]() երկարություն
և
երկարություն
և ![]() դիմադրություն
ունեցող
սոլենոիդի
ինդուկտիվությունը,
եթե
սոլենոիդի
փաթույթն
դիմադրություն
ունեցող
սոլենոիդի
ինդուկտիվությունը,
եթե
սոլենոիդի
փաթույթն ![]() զանգվածով
հաղորդալարն
է: Ընդունել
հաղորդալարի
խտությունը և
նրա
տեսակարար
դիմադրությունը
համապատասխանաբար`
զանգվածով
հաղորդալարն
է: Ընդունել
հաղորդալարի
խտությունը և
նրա
տեսակարար
դիմադրությունը
համապատասխանաբար`
![]() և
և
![]()
Լուծում: Երկար սոլենոիդի ինդուկտիվությունը որոշվում է հետևյալ բանաձևով`


Խնդիր
60. ![]() սմ և
սմ և ![]() սմ
լայնական
հատույթի
մակերեսով
սմ
լայնական
հատույթի
մակերեսով ![]() գալարներ
պարունակող
գերհաղորդիչ
սոլենոիդը
միացվել է
գալարներ
պարունակող
գերհաղորդիչ
սոլենոիդը
միացվել է ![]() Վ
ԷլՇՈՒ
ունեցող
աղբյուրին:
Որոշել
հոսանքի ուժը
բանալին
միացնելուց
Վ
ԷլՇՈՒ
ունեցող
աղբյուրին:
Որոշել
հոսանքի ուժը
բանալին
միացնելուց ![]() վ
հետո:
վ
հետո:
Լուծում: Սոլենոիդի ինդուկտիվությունը որոշվում է հետևյալ բանաձևով`

Պատասխան` ![]() Ա:
Ա:
Խնդիր
61. ![]() Հն
ինդուկտիվության
կոճը միացված
է հոսանքի
աղբյուրին:
Որոշել կոճի
Հն
ինդուկտիվության
կոճը միացված
է հոսանքի
աղբյուրին:
Որոշել կոճի ![]() դիմադրությունը,
եթե
դիմադրությունը,
եթե ![]() վ-ում
կոճի միջով
անցնող
հոսանքը
հասնում է իր
սահմանային
արժեքի 80
վ-ում
կոճի միջով
անցնող
հոսանքը
հասնում է իր
սահմանային
արժեքի 80![]() -ին:
-ին:
Լուծում: Հոսանքի ուժը կոճում փոփոխվում է հետևյալ օրենքով`

Պատասխան` ![]() Օմ:
Օմ:
Խնդիր
62. ![]() սմ
տրամագծով
սոլենոիդն
ունի
սմ
տրամագծով
սոլենոիդն
ունի ![]() մմ
տրամագծով
ալյումինե
հաղորդալարի
մեկը մյուսին
խիտ հարող
գալարների
միաշերտ փաթույթ:
Սոլենոիդով
անցնում է
մմ
տրամագծով
ալյումինե
հաղորդալարի
մեկը մյուսին
խիտ հարող
գալարների
միաշերտ փաթույթ:
Սոլենոիդով
անցնում է ![]() Ա
հոսանք:
Որոշել
սոլենոիդով
անցնող
Ա
հոսանք:
Որոշել
սոլենոիդով
անցնող ![]() էլեկտրականության
քանակությունը,
եթե նրա ծայրերը
կարճ միացվեն:
էլեկտրականության
քանակությունը,
եթե նրա ծայրերը
կարճ միացվեն:
Լուծում: Հոսանքի ուժը սոլենոիդում փոփոխվում է հետևյալ օրենքով`

Պատասխան` ![]()
![]() Կլ:
Կլ:
Խնդիր
63. ![]() մմ
տրամագծով
հաղորդալարից
պատրաստված
առանց
միջուկի
միաշերտ փաթույթով
սոլենոիդը
ունի
մմ
տրամագծով
հաղորդալարից
պատրաստված
առանց
միջուկի
միաշերտ փաթույթով
սոլենոիդը
ունի ![]() մ
երկարություն
և
մ
երկարություն
և ![]() սմ2
լայնական
հատույթ: Ի՞նչ
հոսանք է անցնում
փաթույթով
սմ2
լայնական
հատույթ: Ի՞նչ
հոսանք է անցնում
փաթույթով ![]() Վ
լարման
դեպքում, եթե
Վ
լարման
դեպքում, եթե ![]() մվ-ում
փաթույթում
անջատված
ջերմաքանակը
հավասար է
սոլենոիդի
ներսում
մագնիսական
դաշտի
էներգիային:
մվ-ում
փաթույթում
անջատված
ջերմաքանակը
հավասար է
սոլենոիդի
ներսում
մագնիսական
դաշտի
էներգիային:
Լուծում: Համաձայն Ջոուլ-Լենցի օրենքի անջատված ջերմաքանակը`
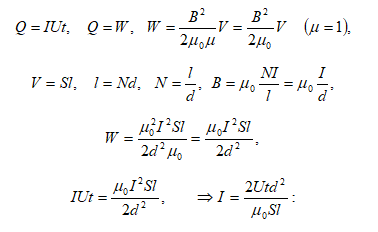
Պատասխան` ![]() Ա:
Ա:
Խնդիր
64.
Օդային միջուկով
տորոիդի 1սմ-ի
վրա կան ![]() գալարներ:
Որոշել
տորոիդում
էներգիայի
ծավալային
խտությունը,
եթե նրա
փաթույթով
անցում է
գալարներ:
Որոշել
տորոիդում
էներգիայի
ծավալային
խտությունը,
եթե նրա
փաթույթով
անցում է ![]() Ա հոսանք:
Ա հոսանք:
Լուծում: Մագնիսական դաշտի էներգիայի ծավալային խտությունը`

Պատասխան`
![]() Ջ/մ
Ջ/մ![]()
Խնդիր
65. Համասեռ
մագնիսական
դաշտում
մտցվում է
երկար վոլֆրամե
ձող (վոլֆրամի
մագնիսական
թափանցելիությունը`![]() Որոշել,
թե այդ ձողում
գումարային
մագնիսական
դաշտի որ մասն
է որոշվում
մոլեկուլային
հոսանքներով:
Որոշել,
թե այդ ձողում
գումարային
մագնիսական
դաշտի որ մասն
է որոշվում
մոլեկուլային
հոսանքներով:
Լուծում: Մագնիսական դաշտի ինդուկցիան և լարվածությունը կապված են իրար հետ հետևյալ բանաձևով`
![]()
![]() ,
, ![]()
![]()
![]()
![]()
Պատասխան` ![]()
Խնդիր
66. ![]() Հն ինդուկտիվության
սոլենոիդը
գտնվում է դիամագնիսական
միջավայրում
և նրա
թափույթով
անցնում է
Հն ինդուկտիվության
սոլենոիդը
գտնվում է դիամագնիսական
միջավայրում
և նրա
թափույթով
անցնում է ![]() Ա
հոսանք:
Սոլենոիդն
ունի
Ա
հոսանք:
Սոլենոիդն
ունի ![]() սմ
երկարություն,
սմ
երկարություն,
![]() սմ2
լայնական
հատույթի
մակերես և
սմ2
լայնական
հատույթի
մակերես և ![]() գալարների
թիվ: Որոշել
սոլենոիդի
ներսում. 1)
մագնիսական
ինդուկցիան, 2)
մագնիսացածությունը:
գալարների
թիվ: Որոշել
սոլենոիդի
ներսում. 1)
մագնիսական
ինդուկցիան, 2)
մագնիսացածությունը:

![]()
Խնդիր
67. ![]() մմ
միջին
տրամագծով
տորոիդի
տեսքով
երկաթյա
միջուկի վրա
փաթաթված է
ընդհանուր
թվով
մմ
միջին
տրամագծով
տորոիդի
տեսքով
երկաթյա
միջուկի վրա
փաթաթված է
ընդհանուր
թվով ![]() գալարներ
ունեցող փաթույթ:
Միջուկում
արված է նեղ
գալարներ
ունեցող փաթույթ:
Միջուկում
արված է նեղ ![]() մմ
լայնության
ճեղք: Տվյալ
պայմաններում
երկաթի
մագնիսական
թափանցելիությունը`
մմ
լայնության
ճեղք: Տվյալ
պայմաններում
երկաթի
մագնիսական
թափանցելիությունը`
![]() :
Որոշել
փաթույթով
անցնող
:
Որոշել
փաթույթով
անցնող ![]() Ա
ուժի հոսանքի
դեպքում. 1)
երկաթում
մագնիսական
դաշտի
լարվածությունը,
2) մագնիսական
դաշտի
Ա
ուժի հոսանքի
դեպքում. 1)
երկաթում
մագնիսական
դաշտի
լարվածությունը,
2) մագնիսական
դաշտի ![]() լարվածությունը
ճեղքում:
լարվածությունը
ճեղքում:

Լուծում: Օգտվենք մագնիսական դաշի լարվածության վեկտորի շրջապտույտի թեորեմից`

![]()
Խնդիր 68. Երկար գլանային կոնդենսատորը լիցքավորվում է ԷլՇՈՒ-ի աղբյուրից: Անտեսելով եզրային էֆեկտները` ապացուցել, որ կոնդենսատորի շրջադիրների միջև տարածությունը լցնող դիէլեկտրիկում շեղման հոսանքը հավասար է շղթայում աղբյուրի ԷլՇՈՒ-ի ստեղծած հոսանքին:

Լուծում:
Որոշակիության
համար ենթադրենք,
որ
կոնդենսատորի
ներքին շրջադիրը
լիցքավորվում
է
դրականապես:
Դիէլեկտրիկում
տանենք ![]() շառավղով
գլանային
կտրվածք:
Նշանակենք
դրա մակերեսը
շառավղով
գլանային
կտրվածք:
Նշանակենք
դրա մակերեսը ![]() -ով:
Դիէլեկտրիկի
այդ
կտրվածքով
շեղման հոսանքը
որոշվում է
հետևյալ
բանաձևով`
-ով:
Դիէլեկտրիկի
այդ
կտրվածքով
շեղման հոսանքը
որոշվում է
հետևյալ
բանաձևով`

որտեղ
![]() -ը
կոնդենսատորի
դաշտի
էլեկտրական
շեղման
-ը
կոնդենսատորի
դաշտի
էլեկտրական
շեղման ![]() վեկտորի
պրոյեկցիան է
վեկտորի
պրոյեկցիան է ![]() տարրի
կտրվածքի
արտաքին
տարրի
կտրվածքի
արտաքին ![]() նորմալի
ուղղության
վրա:
նորմալի
ուղղության
վրա: ![]() վեկտորն
ուղղված է
գլանի
շառավղով նրա
առանցքից
դեպի
վեկտորն
ուղղված է
գլանի
շառավղով նրա
առանցքից
դեպի ![]() տարրը:
Ճիշտ այդպես է
ուղղված նաև
տարրը:
Ճիշտ այդպես է
ուղղված նաև ![]() վեկտորը
վեկտորը
![]() մակերեսի
կետերում,
ուստի
մակերեսի
կետերում,
ուստի ![]() :
Ըստ (1.19)
բանաձևի
կունենանք`
:
Ըստ (1.19)
բանաձևի
կունենանք`

որտեղ
![]() -ն
կոնդենսատորի
ներքին
շրջադիրի վրա
լիցքի գծային
խտությունն է:
Եթե այդ
շրջադիրի
լիցքը
-ն
կոնդենսատորի
ներքին
շրջադիրի վրա
լիցքի գծային
խտությունն է:
Եթե այդ
շրջադիրի
լիցքը ![]() է,
իսկ նրա
բարձրությունը`
է,
իսկ նրա
բարձրությունը`
![]() , ապա
, ապա

![]() մեծությունը
դիտարկվող
կտրվածքի
համար հաստատուն
է, որի համար
էլ
մեծությունը
դիտարկվող
կտրվածքի
համար հաստատուն
է, որի համար
էլ

Կոնդենսատորի
![]() լիցքը
կախված է
միայն
ժամանակից,
այնպես, որ ոչ
մի
տարբերություն
չկա
լիցքը
կախված է
միայն
ժամանակից,
այնպես, որ ոչ
մի
տարբերություն
չկա ![]() -ի
ըստ
-ի
ըստ ![]() -ի մասնակի
և լրիվ
ածանցյաների
միջև.
-ի մասնակի
և լրիվ
ածանցյաների
միջև.

Տեղադրելով այս արտահայտությունը (1)-ի մեջ, կստանանք`
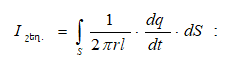
Քանի
որ ![]() -ն
ինտեգրման
-ն
ինտեգրման ![]() փոփոխականից
կախում չունի,
ապա
փոփոխականից
կախում չունի,
ապա

Դիէլեկտրիկի
դիտարկվող
կտրվածքի
մակերեսը` ![]() է,
կոնդենսատորի
լիցքի
փոփոխման
արագությունը`
է,
կոնդենսատորի
լիցքի
փոփոխման
արագությունը`
![]() -ն ոչ
այլ ինչ է, եթե
ոչ
լիցքավորման
-ն ոչ
այլ ինչ է, եթե
ոչ
լիցքավորման ![]() հոսանքը,
այսինքն`
կոնդենսատորը
հոսանքի աղբյուրին
միացնող
շղթայում
հոսանքն է:
Այսպիսով`
հոսանքը,
այսինքն`
կոնդենսատորը
հոսանքի աղբյուրին
միացնող
շղթայում
հոսանքն է:
Այսպիսով` ![]()
Խնդիր
69. ![]() շառավղով
երկար
սոլենոիդի
փաթույթով
անցնող հոսանքը
փոփոխում են
այնպես, որ
սոլենոդի
ներսում
մագնիսական
դաշտն աճում է
ժամանակի
ընթացքում
շառավղով
երկար
սոլենոիդի
փաթույթով
անցնող հոսանքը
փոփոխում են
այնպես, որ
սոլենոդի
ներսում
մագնիսական
դաշտն աճում է
ժամանակի
ընթացքում ![]() օրենքով,
որտեղ
օրենքով,
որտեղ ![]() -ն
հաստատուն է:
Որոշել շեղման
հոսանքի
խտությունը
որպես սոլենոիդի
առանցքից
-ն
հաստատուն է:
Որոշել շեղման
հոսանքի
խտությունը
որպես սոլենոիդի
առանցքից ![]() հեռավորության
ֆունկցիա:
Կառուցել
հեռավորության
ֆունկցիա:
Կառուցել ![]() կախվածության
գրաֆիկը:
կախվածության
գրաֆիկը:

Լուծում: Շեղման հոսանքի խտությունը`


