ԳՏՆՎՈՒՄ Է ՄՇԱԿՄԱՆ ՓՈՒԼՈՒՄ
ՀԱՅԱՍՏԱՆԻ ՀԱՆՐԱՊԵՏՈՒԹՅԱՆ
ԿՐԹՈՒԹՅԱՆ ԵՎ ԳԻՏՈՒԹՅԱՆ ՆԱԽԱՐԱՐՈՒԹՅՈՒՆ
ՀԱՅԱՍՏԱՆԻ ՊԵՏԱԿԱՆ ՃԱՐՏԱՐԱԳԻՏԱԿԱՆ ՀԱՄԱԼՍԱՐԱՆ
ԸՆԴՀԱՆՈՒՐ ԷԼԵԿՏՐԱՏԵԽՆԻԿԱ
Դասագիրք ոչ էլեկտրատեխնիկական մասնագիտությունների համար
ԵՐԵՎԱՆ
ՃԱՐՏԱՐԱԳԵՏ
2011
|
ՀՏԴ |
|
|
ԳՄԴ |
|
|
|
|
Գրախոսներ՝ տ.գ.թ., դոցենտ Մ.Յոնդեմ
տ.գ.թ., դոցենտ Ա.Արզումանյան
Մասնագիտական խմբագիր`
տ.գ.դ, պրոֆեսոր Բ. Մամիկոնյան
Բալաբանյան Հ.
Ընդհանուր էլեկտրատեխնիկա: Դասագիրք/Հ. Բալաբանյան: Մաս. խմբ.`
Բ. Մամիկոնյան; ՀՊՃՀ. - Եր., 2011 - 280 էջ:
Դասագիրքը գրված է ՀՊՃՀ Տեսական և ընդհանուր էլեկտրատեխնիկայի ամբիոնում 2011թ. վերամշակված «Ընդհանուր էլեկտրատեխնիկա» առարկայի ծրագրին համապատասխան: Դասագիրքն ընդգրկում է հաստատուն հոսանքի, սինուսոիդական միաֆազ և եռաֆազ հոսանքի էլեկտրական շղթաների, մագնիսական շղթաների, անցումային պրոցեսների տեսության հիմնական օրենքները և հաշվարկի մեթոդները, ինչպես նաև տրանսֆորմատորների, ասինքրոն, սինքրոն և հաստատուն հոսանքի մեքենաների կառուցվածքին և ընդհանուր տեսությանը նվիրված հիմնական հարցերը: Այն նախատեսվում է ՀՊՃՀ ոչ էլեկտրատեխնիկական մասնագիտությունների (քիմիական, մեքենաշինական, էներգետիկական, քոմփյութերային համակարգերի և ինֆորմատիկայի, լեռնամետալուրգիական, տրանսպորտային, ճարտարագիտա-տնտեսագիտական) ուսանողների համար: Դասագիրքը կարող է օգտակար լինել նաև Հայաստանի այլ բուհերի դասախոսների և ուսանողների համար, որտեղ դասավանդվում է «Ընդհանուր էլեկտրատեխնիկա» առարկան:
|
ՀՏԴ |
621.3 (075.8) |
Երաշխավորված է հրատարակության ՀՊՃՀ Գիտական խորհուրդի 2011թ. հունիսի 29-ի նիստի թիվ 89 որոշմամբ |
|
|
ԳՄԴ |
31.2գ 73 |
||
|
Բ |
200 |
Ó ՃԱՐՏԱՐԱԳԵՏ, 2011
Ó Բալաբանյան Հ. 2011
1. ՀԱՍՏԱՏՈՒՆ ՀՈՍԱՆՔԻ ԷԼԵԿՏՐԱԿԱՆ ՇՂԹԱՆԵՐ
1.1. Էլեկտրական շղթա: Շղթայի տարրերը
1.2. Հաստատուն հոսանքի պարզագույն շղթա
1.3. Էլեկտրական շղթաների ռեժիմները
1.6. Էներգիայի և հզորության արտահայտությունները հաստատուն հոսանքի շղթաներում
1.7. էլեկտրական շղթաների համարժեք ձևափոխությունները
1.8. Քառաթև (Ուիտսթոնի) կամրջակ
1.9. Առավելագույն հզորության փոխանցման թեորեմը
2. ՀԱՍՏԱՏՈՒՆ ՀՈՍԱՆՔԻ ԷԼԵԿՏՐԱԿԱՆ ՇՂԹԱՆԵՐԻ ՀԱՇՎԱՐԿԸ
2.1. Էլեկտրական շղթաների հաշվարկը Կիրխհոֆի օրենքների կիրառությամբ
2.2. Շղթաների հաշվման միջհանգուցային լարման մեթոդը (երկու հանգույցների մեթոդը)
2.3. Կոնտուրային հոսանքների մեթոդը
2.5. Համարժեք գեներատորի մեթոդը (Թևենենի թեորեմը)
2.6. Մեկ աղբյուր պարունակող շղթաների հաշվարկը
2.7. Հաստատուն հոսանքի շղթաների հաշվման օրինակներ
2.8. Քառաբևեռ և դրա հիմնական հավասարումները
2.9. Քառաբևեռի գործակիցների որոշումը:
2.10. Պասիվ քառաբևեռի փոխարինման սխեմաները
2.11. Հաստատուն հոսանքի ոչ գծային շղթաներ
3.1. Ընդհանուր դրույթներ: Սինուսոիդական հոսանքի ստացումը
3.2. Սինուսոիդական մեծությունների գործող և միջին արժեքները
3.3. Սինուսոիդական մեծությունների արտահայտումը պտտվող վեկտորներով և կոմպլեքս թվերով
3.4. Էլեկտրական շղթայի տարրերը փոփոխական հոսանքի դեպքում
3.4.1. Ռեզիստիվ տարրը սինուսոիդական հոսանքի շղթայում
3.4.2. Ինդուկտիվ տարրը սինուսոիդական հոսանքի շղթայում
3.4.3. Ունակային տարրը սինուսոիդական հոսանքի շղթայում
3.5. Ռեզիստիվ, ինդուկտիվ և ունակային տարրերի հաջորդաբար միացումով սինուսոիդական հոսանքի շղթա
3.6. Ռեզիստիվ, ինդուկտիվ և ունակային տարրերի զուգահեռ միացումով շղթա
3.7. Դիմադրությունների և հաղորդականությունների կապը սինուսոիդական հոսանքի շղթայում
3.8. Էներգետիկական երևույթները փոփոխական հոսանքի շղթաներում
3.9. Փոփոխական հոսանքի բարդ շղթաների հաշվարկը
3.10. Սինուսոիդական հոսանքի շղթաների հաշվարկի օրինակներ
3.11. Էլեկտրաէներգիայի սպառիչների հզորության գործակցի բարձրացումը
4.2. Աստղաձև միացված եռաֆազ շղթաներ
4.3. Աստղաձև միացված ոչ սիմետրիկ եռաֆազ շղթա
4.4. Եռանկյունաձև միացված եռաֆազ շղթա
4.5. Հզորության արտահայտությունները եռաֆազ շղթայում
4.6. Աստղաձև և եռանկյունաձև միացված եռաֆազ շղթաների համեմատական բնութագիրը
5. ԱՆՑՈՒՄԱՅԻՆ ՊՐՈՑԵՍՆԵՐԸ ԷԼԵԿՏՐԱԿԱՆ ՇՂԹԱՆԵՐՈՒՄ
5.2. Անցումային պրոցեսները ինդուկտիվ տարր պարունակող հաստատուն հոսանքի շղթաներում
5.2.1. Մագնիսական կոճի միացումը հաստատուն լարման
5.2.2. Հոսանքակիր մագնիսական կոճի կարճ միացումը
5.3. Անցումային պրոցեսները ունակային տարր պարունակող հաստատուն հոսանքի շղթաներում
5.3.1. Կոնդենսատորի լիցքավորումը
5.3.2. Կոնդենսատորի լիցքաթափումը ակտիվ դիմադրության վրա
5.5. Անցումային պրոցեսները R-L-C շղթաներում
5.5.1. Լիցքավորված կոնդենսատորի լիցքաթափումը ինդուկտիվ և ռեզիստիվ տարրերի վրա
5.5.2. Հաջորդաբար միացված R, L, C տարրերով շղթայի միացումը հաստատուն լարման
5.6. Անցումային պրոցեսների հաշվարկի օրինակներ
6.1. Մագնիսական շղթայի տարրերը
6.2. Ֆերոմագնիսական նյութերի հատկությունները
6.3. Պարզագույն մագնիսական շղթայի հաշվարկը
6.4. Ֆերոմագնիսական միջուկով կոճը փոփոխական հոսանքի շղթայում
7. ՊԱՐԲԵՐԱԿԱՆ ՈՉ ՍԻՆՈՒՍՈԻԴԱԿԱՆ ՀՈՍԱՆՔՆԵՐԸ ԷԼԵԿՏՐԱԿԱՆ ՇՂԹԱՆԵՐՈՒՄ
7.1. Պարբերական ոչ սինուսոիդական հոսանքների առաջացման պատճառները
7.2. Պարբերական ոչ սինուսոիդական մեծությունների արտահայտումը Ֆուրյեի շարքով
7.3. Պարբերական ոչ սինուսոիդական մեծությունների գործող արժեքը
7.4. Ոչ սինուսոիդական հոսանքի ակտիվ և լրիվ հզորությունները
7.5. Ոչ սինուսոիդական հոսանքով շղթայի հաշվարկի օրինակներ
8.1. Տրանսֆորմատորների դերն ու նշանակությունը
8.2. Միաֆազ տրանսֆորմատորի կառւցվածքը
8.3. Միաֆազ տրանսֆորմատորի աշխատանքի սկզբունքը
8.4. Տրանսֆորմատորի փաթույթների էլշուները
8.5. Տրանսֆորմատորի հավասարումները
8.6.1. Տրանսֆորմատորի պարապ ընթացքի ռեժիմը
8.6.2. Տրանսֆորմատորի կարճ միացման ռեժիմը
8.7. Տրանսֆորմատորի աշխատանքային ռեժիմը
8.7.1. Տրանսֆորմատորի արտաքին բնութագիծը
8.7.2. Տրանսֆորմատորի հզորության կորուստները և օ.գ.գ.-ն
8.10. Եռակցման տրանսֆորմատորներ
8.11.1. Լարման չափման տրանսֆորմատոր
8.11.2. Հոսանքի չափման տրանսֆորմատոր
9.1. Եռաֆազ ասինքրոն մեքենայի կառուցվածքը
9.2. Պտտվող մագնիսական դաշտի ստացումը ասինքրոն շարժիչում
9.3. Ասինքրոն շարժիչի աշխատանքի սկզբունքը
9.4. Ասինքրոն մեքենայի աշխատանքային ռեժիմները
9.5. Ասինքրոն շարժիչի անվանական պարամետրերը
9.6. Ասինքրոն շարժիչի ստատորի և ռոտորի էլշուները
9.7. Ասինքրոն շարժիչի հզորությունների հաշվեկշիռը
9.8. Ասինքրոն շարժիչի էլեկտրամագնիսական մոմենտը և մեխանիկական բնութագիծը
9.9. Սնող ցանցի լարման ազդեցությունն ասինքրոն շարժիչի աշխատանքի վրա
9.10. Կարճ միացված ռոտորով ասինքրոն շարժիչի գործարկումը
9.11. Ֆազային ռոտորով ասինքրոն շարժիչների գործարկումը
9.12. Բարելավված գործարկման հատկություններով ասինքրոն շարժիչներ
9.13. Ասինքրոն շարժիչի արագության կարգավորումը
10.1. Ընդհանուր տեղեկություններ
10.2. Եռաֆազ սինքրոն մեքենայի կառուցվածքը
10.3. Սինքրոն մեքենայի աշխատանքային ռեժիմները
10.4. Սինքրոն գեներատորի աշխատանքի սկզբունքը
10.5. Սինքրոն գեներատորի ստատորի փաթույթի էլեկտրական վիճակի հավասարումը և փոխարինման սխեման
10.6. Սինքրոն գեներատորի անկյունային բնութագիծը
10. 7. Սինքրոն գեներատորի U-աձև բնութագծերը
10.8. Սինքրոն շարժիչի գործարկումը
10.9. Սինքրոն շարժիչի ստատորի փաթույթի էլեկտրական վիճակի հավասարումը
10.10. Սինքրոն շարժիչի U-աձև բնութագծերը
11. ՀԱՍՏԱՏՈՒՆ ՀՈՍԱՆՔԻ ՄԵՔԵՆԱՆԵՐ
11.1. Ընդհանուր տեղեկություններ
11.2. Հաստատուն հոսանքի մեքենայի կառուցվածքը
11.3. Հաստատուն հոսանքի մեքենայի աշխատանքը որպես գեներատոր
11.4. Հաստատուն հոսանքի մեքենայի աշխատանքը որպես շարժիչ
11.5. Հաստատուն հոսանքի մեքենաների դասակարգումը
11.6. Հաստատուն հոսանքի անկախ գրգռումով գեներատորներ
11.7. Ինքնագրգռման երևույթը հաստատուն հոսանքի գեներատորներում
11.8. Հաստատուն հոսանքի ինքնագրգռումով գեներատորներ
11.9. Հաստատուն հոսանքի շարժիչների գործարկումը
11.10. Հաստատուն հոսանքի անկախ և զուգահեռ գրգռումով շարժիչներ
11.11. Անկախ և զուգահեռ գրգռումով շարժիչների արագության կարգավորումը
11.12. Հաստատուն հոսանքի հաջորդական գրգռումով շարժիչներ
11.13. Հաստատուն հոսանքի խառը գրգռումով շարժիչներ
ՆԱԽԱԲԱՆ
«Ընդհանուր էլեկտրատեխնիկա» առարկայի սույն դասագիրքը նաատեսված է Հայաստանի պետական ճարտարագիտական համալսարանի (Պոլիտեխնիկ) ոչ էլեկտրատեխնիկական մասնագիտությունների գծով մասնագիտացող ուսանողների համար:
Դասագիրքը գրվել է 2001 - 2006 թթ. մի քանի անգամ հրատարակված համանուն ձեռնարկի[1] հիման վրա:
Ձեռնարկի օգտագործման շուրջ 10-ամյա հաջող փորձաշրջանը վստահություն ներշնչեց հեղինակին` այն լրամշակելու, լրացնելու նոր բաժիններով (9.5, 9.10) ու խնդիրներով (2.7, 3.10, 4.7, 9.3, 9.7 բաժիններում), յուրաքանչյուր բաժնին հաջորդող ստուգողական հարցերով և այն հրատարակելու որպես դասագիրք` տեխնիկական բուհերի ոչ էլեկտրատեխնիկական մասնագիտություններով սովորող ուսանողների համար:
Դասագիրքն ընդգրկում է հաստատուն հոսանքի, սինուսոիդական միաֆազ և եռաֆազ հոսանքի էլեկտրական շղթաների, մագնիսական շղթաների, անցումային երևույթների, ոչ սինուսոիդական հոսանքների տեսությունը և հաշվարկի մեթոդները, ինչպես նաև տրանսֆորմատորների, էլեկտրական մեքենաների կառուցվածքին, տեսությանը և օգտագործման բնագավառներին նվիրված բաժինները:
Դասագրքում բերված բազմաթիվ խնդիրների լուծման օրինակները կնպաստեն ուսանողների կողմից առարկայի ավելի խորը յուրացմանն ու ծրագրով նախատեսված հաշվեգրաֆիկական աշխատանքների ինքնուրույն կատարմանը:
Տեսական հարցերի և խնդիրների լուծումների ինքնուրույն յուրացման համար խորհուրդ է տրվում օգտվել նաև հեղինակի` Ընդհանուր էլեկտրատեխնիկա առարկայի համար գրած Թեստային հարցերի և խնդիրների շտեմարանից[2]:
Հեղինակն իր երախտագիտությունն է հայտնում դասագրքի խմբագիր, տեխնիկական գիտությունների դոկտոր, ՀՊՃՀ պատվավոր պրոֆեսոր Բ.Մամիկոնյանին, գրախոսներ, տեխնիկական գիտությունների թեկնածու, դոցենտներ Մ.Յոնդեմին և Ա.Արզումանյանին` ձեռագրի մանրազնին ուսումնասիրման և արժեքավոր դիտողությունների ու առաջարկությունների համար:
Հեղինակն իր շնորհակալությունն է հայտնում նաև ՀՊՃՀ «Տեսական և ընդհանուր էլեկտրատեխնիկա» ամբիոնի դասախոսական անձնակազմին` նախորդ հրատարակություններում նկատված վրիպակները հայտնաբերելու, ինչպես նաև այլ օգտակար խորհուրդների համար:
Հ. Բալաբանյան
«Ընդհանուր էլեկտրատեխնիկա» առարկան ուսումնասիրում է էլեկտրական և մագնիսական երևույթներն ու դրանց օգտագործումը գործնական նպատակներով: Այն ոչ էլեկտրատեխնիկական մասնագիտությունների բակալավրի կրթական ծրագրի ընդհանուր-ճարտարագիտական կրթաբլոկի հիմնական առարկաներից մեկն է:
Դժվար է պատկերացնել ժամանակակից գիտության, տնտեսության և կենցաղի որևէ ոլորտ կամ արդյունաբերության և գյուղատնտեսության որևէ ճյուղ` առանց էլեկտրաէներգիայի օգտագործման:
Էլեկտրաէներգիայի հսկայական դերը մեր կյանքում առաջին հերթին բացատրվում է նրա անվիճելի առավելություններով էներգիայի այլ տեսակների նկատմամբ: Դրանցից գլխավորներն են.
– էլեկտրաէներգիան համեմատաբար հեշտությամբ է ստացվում և փոխակերպվում այլ տեսակի էներգիաների,
– էլեկտրաէներգիան կարելի է արտադրել կենտրոնացված, մեծ հզորություններով և տեղափոխել փոքր կորուստներով` հսկայական տարածությունների վրա,
– էլեկտրաէներգիան հեշտությամբ կարելի է բաշխել բազմապիսի և բազմաբնույթ սպառիչների միջև:
Էլեկտրատեխնիկայի զարգացման սկիզբը վերագրվում է 19-րդ դարի առաջին կեսին: Այն մի կողմից` պայմանավորված էր էլեկտրամագնիսականության ոլորտում ձեռք բերված հաջողություններով, մյուս կողմից` արտադրության բուռն զարգացմանը զուգընթաց էլեկտրաէներգիայի օգտագործման ավելի սուր զգացվող անհրաժեշտությամբ: Դրան մեծապես նպաստեցին մի ամբողջ շարք տաղանդավոր գիտնականների (Գ. Էռստեդ, Ա.Ամպեր, Գ.Օհմ, Մ.Ֆարադեյ, Ջ.Մաքսվել, Գ.Կիրխհոֆ և այլն) կողմից էլեկտրական հոսանքի քիմիական, ջերմային, լուսային և մագնիսական ազդեցություններին նվիրված հայտնագործությունները, էլեկտրական շղթաների կարևորագույն օրենքների ձևակերպումները: Դրանց հիման վրա ստեղծվեցին տարբեր տեսակի էլեկտրական գեներատորներ և շարժիչներ, շիկացման լամպեր, ավտոմատիկայի սարքեր և չափիչ գործիքներ: Արդյունաբերության մեջ էլեկտրաշարժիչներն սկսեցին աստիճանաբար դուրս մղել շոգեմեքենաներին:
Էլեկտրատեխնիկայի զարգացման համար մեծ խթան հանդիսացավ փոփոխական հոսանքի եռաֆազ գեներատորների և տրանսֆորմատորների հայտնագործությունը (Մ. Դոլիվո-Դոբրովոլսկի, Ն. Տեսլա), որով հնարավոր դարձավ կառուցել հզոր էլեկտրակայաններ և ստացված էլեկտրաէներգիան փոքր կորուստներով տեղափոխել հարյուրավոր (ներկայումս նաև հազարավոր) կիլոմետրերի հեռավորության վրա գտնվող բնակավայրերի և արտադրական ձեռնարկությունների սպառիչներին: Մեծագույն նվաճում էր եռաֆազ հոսանքի միջոցով պտտվող մագնիսկան դաշտի ստացումը (Գ.Ֆերարիս, Ն.Տեսլա) և դրա հիման վրա եռաֆազ ասինքրոն շարժիչի ստեղծումը (Մ. Դոլիվո-Դոբրովոլսկի), որը ներկայումս իր անվիճելի արժանիքների շնորհիվ ոչ միայն ամենամեծ կիրառությունն ունեցող էլեկտրաշարժիչն է, այլև ընդհանրապես ամենատարածված էլեկտրաէներգիայի սպառիչներից մեկը:
Էլեկտրաէներգիան մեծ կիրառություն ունի նաև տեխնոլոգիական պրոցեսներում, ինչպիսիք են էլեկտրամետալուրգիան (ինդուկցիոն և աղեղային վառարաններ, ալյումինի էլեկտրալիզի վաննաներ), էլեկտրաթերմիան (դիմադրության էլեկտրական վառարաններ, էլեկտրաեռակցումը) և էլեկտրաքիմիան (սառը էլեկտրալիզ, քիմփայլեցում):
Էլեկտրաէներգիայի արտադրությունն ու կիրառությունը զարգացման իր ուրույն` ավելի քան 100-ամյա պատմությունն ունի նաև Հայաստանում: Այն սկսվել է 1903թ., երբ Ողջի գետի վրա կառուցվեց Հայաստանում առաջին` ընդամենը 75 կՎտ հզորությամբ հիդրո-էլեկտրակայանը (ՀԷԿ), որը կարևոր նշանակություն ունեցավ Սյունիքում սկսված պղնձարդյունաբերության համար:
Խորհրդային Հայաստանում արդյունաբերության զարգացման հետ բուռն կերպով սկսվեց տարբեր հզորությամբ ՀԷԿ-երի կառուցումը: Հրազդան գետի վրա կառուցված վեց խոշոր ՀԷԿ-երը կազմեցին Սևան-Հրազդան կասկադը (ընդհանուր հզորությունը` 556 ՄՎտ), որն ամբողջությամբ գործարկվեց 1960 թ.: Այն հսկայական խթան հանդիսացավ Հայաստանում քիմիական և ալյումինի արտադրության խոշոր էներգատար ձեռնարկությունների զարգացման համար: Սակայն, մյուս կողմից, էներգետիկ նպատակներով մեծ քանակությամբ ջրի բացթողումը Սևանա լճից ծանր հետևանքներ ունեցավ լճի համար. ջրի մակարդակն իջավ գրեթե 20 մետրով:
Սևանի պահպանման և նորանոր արտադրական ձեռնարկություններին էլեկտրաէներգիա մատակարարելու համար գործարկվեցին նոր էլեկտրակայաններ` 1965 թ. շահագործվեցին Երևանի, 1974 թ.` Հրազդանի և 1976թ.` Կիրովականի (Վանաձորի) ջերմաէլեկտրակայանները (ՋԷԿ), որոնց համար անհրաժեշտ էներգակիրները (մազութ, գազ) ներմուծվում էին Ռուսաստանից:
Շարունակվում է հիդրոէներգետիկ շինարարությունը, Որոտան գետի վրա. 1979 թ. գործարկվում է երեք ՀԷԿ-երից կազմված Որոտանի կասկադը (404 Մվտ): Վերջապես, 1976թ. շահագործման է հանձնվում Հայկական ատոմակայանի (ՀԱԷԿ) 1-ին, իսկ 1980թ.` 2-րդ բլոկը` յուրաքանչյուրը 440 ՄՎտ հզորությամբ, ինչի շնորհիվ Հայաստանը էլեկտրաէներգիա ներմուծող երկրից դառնում է էլեկտրաէներգիա արտահանող երկիր:
Հայաստանի էներգետիկ իրավիճակը կտրուկ փոխվեց 1991թ.: Սպիտակի ավերիչ երկրաշարժից հետո` 1989թ., անվտանգության նկատառումներից ելնելով, ՀԱԷԿ-ը կանգնեցվեց և 1991թ. ԽՍՀՄ փլուզումից ու Լեռնային Ղարաբաղի շուրջ ծավալված քաղաքական իրադարձություններից հետո Հայաստանի շրջափակման պատճառով Հանրապետությունը հայտնվեց ծանրագույն էներգետիկական ճգնաժամի մեջ: Էլեկտրաէներգիայի սուր պահանջը հանրապետությունում ստիպեց աննախադեպ միջոցների դիմել. ատոմային էլեկտրակայանների պատմության մեջ առաջին անգամ 1995թ. վերջին հաջողվեց կոնսերվացված ՀԱԷԿ-ի 2-րդ բլոկը վերագործարկել: Ներկայումս ՀԱԷԿ-ի շահագործման ռեսուրսները սպառման մոտ են, և արդեն նախատեսվում է Հայաստանում նոր ատոմակայանի կառուցում: Չնայած Հայաստանը էներգակիրներից աղքատ է (թերևս բացի հիդրոռեսուրսներից), այնուամենայնիվ, ներկայումս մեկ շնչին ընկնող էլեկտրաէներգիայի արտադրության դրվածքային հզորությամբ Հայաստանն առաջատար է տարածաշրջանում:
Ցավոք, հարկ է արձանագրել, որ էլեկտրաէներգիայի արտադրությունը և դրա փոխակերպումը այլ էներգիաների շրջակա միջավայրի աղտոտվածության հիմնական պատճառներից են, ինչը հատկապես վերաբերում է ջերմաէլեկտրակայաններին, որոնք վառելիքի այրման արդյունքում մթնոլորտ են արտանետում մեծ քանակությամբ վնասակար գազեր: Ուստի շրջակա միջավայրի պաշտպանության հարցերը պետք է մշտապես գտնվեն ապագա ճարտարագետների տեսադաշտում: Այս առումով հատկանշական է, որ ներկայումս աշխարհի շատ երկրներում մեծ աշխատանքներ են տարվում շրջակա միջավայրը աղտոտող մեկ այլ գործոնի վերացման` ավտոմեքենաների ներքին այրման շարժիչները էկոլոգիապես ավելի մաքուր էլեկտրաշարժիչներով փոխարինելու ուղղությամբ:
Վերջին տարիներին Հայաստանում նույնպես աշխատանքներ են տարվում բնապահպանական տեսակետից ավելի անվտանգ այլընտրանքային էներգիայի աղբյուրների օգտագործման ուղղությամբ, արդեն գործում են քամու և արևի էներգիայով աշխատող փոքր հզորությամբ տեղակայանքներ, գետերի վրա կառուցվում են բազմաթիվ մինի- և միկրոՀԷԿ-եր, որոնց տեսակարար կշիռն ապագայում մեծանալու միտում ունի:
Ամբողջ աշխարհում ընթացող գիտատեխնիկական առաջընթացը նախատեսում է արտադրական և տեխնոլոգիական պրոցեսների խորը մեքենայացում և ավտոմատացում: Արտադրական պրոցեսներում էլեկտրիֆիկացիայի առավելությունները ստեղծագործաբար կիրառելու, զանազան ավտոմատացված կառավարման համակարգերը ներդնելու և գրագետ շահագործելու համար ցանկացած բնագավառի ապագա ճարտարագետ պետք է ուսումնասիրի և յուրացնի «Ընդհանուր էլեկտրատեխնիկա» դասընթացը, որպեսզի նա, բացի իր բուն մասնագիտական գիտելիքներից ու կարողություններից, նաև էլեկտրատեխնիկայի բնագավառից ձեռք բերի.
ա) Բավարար տեսական գիտելիքներ.
· էլեկտրատեխնիկայի օրենքները, էլեկտրական շղթաների վերլուծության եղանակները,
· էլեկտրատեխնիկական սարքավորումների կառուցվածքը, աշխատանքի սկզբունքը, հատկությունները և կիրառման բնագավառները,
· էլեկտրատեխնիկական տերմիններն ու էլեկտրական սխեմաներում կիրառվող պայմանական նշանները:
բ) Գործնական կարողություններ.
· փորձնական ճանապարհով որոշելու էլեկտրատեխնիկական տարրերի և սարքավորումների պարամետրերն ու բնութագծերը,
· չափելու էլեկտրական հոսանքը, լարումը, հզորությունը,
· կազմելու և հասկանալու էլեկտրական սխեմաները,
· կառավարելու էլեկտրական մեքենաների և չափիչ ու հսկիչ սարքերի աշխատանքը:
1. ՀԱՍՏԱՏՈՒՆ ՀՈՍԱՆՔԻ ԷԼԵԿՏՐԱԿԱՆ ՇՂԹԱՆԵՐ
1.1. Էլեկտրական շղթա: Շղթայի տարրերը
Էլեկտրական շղթայի հասկացությունը էլեկտրատեխնիկայի հիմնարար հասկացություններից մեկն է:
էլեկտրական շղթա է կոչվում միմյանց հետ որոշակի ձևով միացված սարքերի համախումբը, որը նախատեսված է էլեկտրական հոսանք անցկացնելու համար: Շղթան կազմող սարքերը կոչվում են շղթայի տարրեր:
Էլեկտրական շղթայի հիմնական տարրերն են էլեկտրաէներգիայի աղբյուրը (կամ գեներատորը) և էլեկտրաէներգիայի սպառիչը (կամ ընդունիչը):
Էլեկտրաէներգիայի աղբյուրը այն սարքն է, որը ոչ էլեկտրական էներգիան փոխարկում է էլեկտրական էներգիայի (ինչպես օրինակ, էլեկտրակայաններում տեղակայված գեներատորները՝ մեխանիկական էներգիան, ակումուլյատորային մարտկոցները՝ քիմիական էներգիան, ֆոտոէլեմենտները՝ լուսային էներգիան և այլն փոխարկում են էլեկտրական էներգիայի):
Էլեկտրաէներգիայի սպառիչում տեղի է ունենում հակառակ պրոցեսը՝ էլեկտրաէներգիան փոխարկվում է մեխանիկական (էլեկտրական շարժիչներ), ջերմային (ջեռուցիչներ) կամ այլ տեսակի էներգիաների:
Էլեկտրական շղթաներում աղբյուրները և սպառիչները միմյանց հետ միացվում են հաղորդալարերով, որոնք իրականացնում են էլեկտրական էներգիայի տեղափոխությունը աղբյուրից սպառիչին:
Այսպիսով, էլեկտրական շղթայում տեղի է ունենում էլեկտրաէներգիայի ստացման, տեղափոխման և սպառման միաժամանակյա պրոցես:
Էլեկտրական շղթան կարող է պարունակել նաև տարբեր նշանակության օժանդակ տարրեր, ինչպես օրինակ, անջատիչներ, պաշտպանիչ ու չափիչ սարքեր և այլն: Դրանք ծառայում են շղթան կառավարելու, վտանգավոր ռեժիմներից այն պաշտպանելու, դրա աշխատանքը հսկելու և այլ նպատակների համար:
Շղթաների ուսումնասիրությունը պարզեցնելու նպատակով իրական շղթան ներկայացվում է կատարյալ (իդեալական) տարրերից կազմված մոդելով, որը կոչվում է շղթայի փոխարինման սխեմա (կամ, պարզապես, սխեմա): Այն շղթայի գրաֆիկական պատկերումն է դրա տարրերի պայմանական նշանների միջոցով: Էլեկտրական սխեման բավականաչափ ճշգրիտ նկարագրում է իրական էլեկտրական շղթայում ընթացող ֆիզիկական երևույթները:
Ստորև բերված են էլեկտրական շղթայի մի քանի հիմնական տարրերի պայմանական նշանները (նկ.1.1):
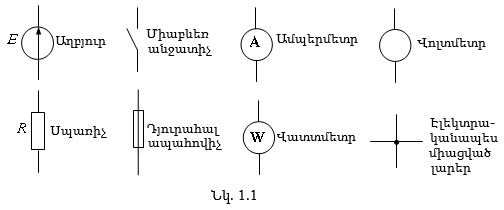
Էլեկտրական շղթաների վերլուծության և հաշվարկի համար էական չէ, թե հատկապես ինչպիսի աղբյուրների և սպառիչների հետ գործ ունենք: Բավական է միայն իմանալ դրանց պարամետրերը և միացման ձևը: Էլեկտրաէներգիայի տարբեր աղբյուրների ընդհանրությունն այն է, որ դրանցում տեղի ունեցող պրոցեսների արդյունքում աղբյուրի սեղմակներում առաջանում է էլեկտրաշարժ ուժ (էլշու), ուստի էլեկտրական սխեմաներում աղբյուրի համար օգտագործվում է շրջանաձև պայմանական նշան, որում սլաքով նշվում է աղբյուրի հիմնական պարամետրի՝ E էլշուի ուղղությունը: Սպառիչների համար, անկախ դրանց տեսակից, ընդունված է ուղղանկյունաձև պայմանական նշանը, որի մոտ նշվում է սպառիչի հիմնական պարամետրը՝ R էլեկտրական դիմադրությունը (նկ.1.1):
Էներգիայի փոխարկման երևույթները աղբյուրներում և սպառիչներում, ինչպես նաև էլեկտրաէներգիայի հաղորդումը հաղորդալարերով ուղեկցվում է էլեկտրաէներգիայի մասնակի (կամ լրիվ) փոխարկումով ջերմային էներգիայի: Դրանով է պայմանավորված այդ տարրերի ջերմաստիճանի բարձրացումը աշխատանքի ընթացքում: Այս պատճառով հաճախ հարկ է լինում շղթայի սխեմայում ներառել նաև աղբյուրների ներքին և էլեկտրահաղորդման գծերի դիմադրությունները:
Ըստ հոսանքի բնույթի` էլեկտրական շղթաները ստորաբաժանվում են հաստատուն հոսանքի շղթաների, փոփոխական հոսանքի միաֆազ և եռաֆազ շղթաների, որոնք, իրենց հերթին, կարող են այլ ստորաբաժանումներ ունենալ (գծային ու ոչ գծային, սինուսոիդական ու ոչ սինուսոիդական, ուժային ու կառավարման և այլն):
1.2. Հաստատուն հոսանքի պարզագույն շղթա
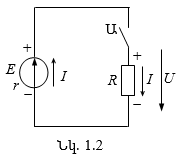
Հաստատուն հոսանքի պարզագույն շղթան պարունակում է մեկական աղբյուր և սպառիչ (նկ. 1.2):
Եթե միացվի Ա անջատիչը, ապա շղթան կփակվի և աղբյուրի E էլեկտրաշարժ ուժի (էլշու) շնորհիվ շղթայով կանցնի I էլեկտրական հոսանք: Ըստ ֆիզիկայի դասընթացի՝ էլեկտրական հոսանք է կոչվում դրական կամ բացասական լիցքավորված մասնիկների ուղղորդված շարժումը: Ներկայումս որպես հոսանքի դրական ուղղություն ընդունված է դրական լիցքավորված մասնիկների շարժման ուղղությունը:
Հաստատուն հոսանքի արժեքը (կամ հոսանքի ուժը) միավոր ժամանակում հաղորդչի լայնական հատույթով անցնող լիցքի քանակությունն է.
![]()
որտեղ t -ն հաղորդչի լայնական հատույթով Q լիցքի անցման ժամանակն է:
Հոսանքի հիմնական միավորն է ամպերը `
[I] = կուլոն/վրկ = ամպեր (Ա).
Ֆիզիկայի դասընթացից հայտնի է. էլշուն թվապես հավասար է այն աշխատանքին, որը կատարում են կողմնակի (ոչ էլեկտրական ծագում ունեցող) ուժերը` միավոր լիցքը աղբյուրի ներսում ցածր պոտենցիալով սեղմակից բարձր պոտենցիալով սեղմակ տեղափոխելու համար: Ուստի, էլշուի, ինչպես նաև աղբյուրով անցնող հոսանքի դրական ուղղությունն է բացասականից դրական (նկ. 1.2):
Այնուհետև, լիցքավորված մասնիկները, շարժվելով սպառիչի միջով, ծախսում են իրենց էներգիան՝ կատարելով աշխատանք և կորցնելով իրենց պոտենցիալը: Ուստի, սպառիչում հոսանքի դրական ուղղությունն է դրականից բացասական:
Շղթայի երկու կետերի միջև պոտենցիալների տարբերությունը կոչվում է լարում այդ կետերի միջև.
![]()
Ըստ ֆիզիկայի դասընթացի` լարումը թվապես հավասար է այն աշխատանքին, որը կատարում է դրական միավոր լիցքը՝ տեղափոխվելով շղթայի բարձր պոտենցիալով կետից ցածր պոտենցիալով կետը, ուստի լարումը միշտ ուղղված է դրականից բացասական:
Ակնհայտ է, որ էլշուն և լարումն ունեն նույն չափման միավորը.
![]()
Շղթայի (նկ. 1.2) սպառիչ պարունակող տեղամասի համար հոսանքի և լարման կապը տրվում է Օհմի օրենքով՝

Այլ խոսքով, սպառիչի հոսանքն ուղիղ համեմատական է նրա սեղմակների միջև լարմանը և հակադարձ համեմատական սպառիչի R դիմադրությանը:
[R] = վոլտ/ամպեր = օհմ (Օմ).
Սպառիչի դիմադրությունը կախված է հաղորդչի նյութից,
նրա ![]() երկարությունից
և S լայնական հատույթի մակերեսից3.
երկարությունից
և S լայնական հատույթի մակերեսից3.
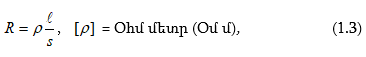
Որտեղ ![]() կոչվում է տեսակարար
դիմադրություն:
կոչվում է տեսակարար
դիմադրություն:
Տարբեր նյութերի համար ![]() արժեքները բերվում են տեղեկատու գրքերում,
արժեքները բերվում են տեղեկատու գրքերում, ![]() փոքր արժեքների դեպքում նյութը համարվում է լավ հաղորդիչ: Մետաղները լավ
հաղորդիչներ են, հատկապես արծաթը, պղինձը, ալյումինը:
փոքր արժեքների դեպքում նյութը համարվում է լավ հաղորդիչ: Մետաղները լավ
հաղորդիչներ են, հատկապես արծաթը, պղինձը, ալյումինը:
Դիմադրության հակադարձ մեծությունը կոչվում է հաղորդականություն.
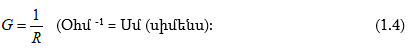
Ֆիզիկայի դասընթացից հայտնի է, որ Օհմի օրենքը փակ շղթայի համար ներկայացվում է հետևյալ բանաձևով՝

որտեղ r -ը աղբյուրի ներքին դիմադրությունն է: Այն հաշվի է առնում, որ աղբյուրի արտադրած էլեկտրական էներգիայի մի մասը ծախսվում է հենց աղբյուրի ներսում՝ վերածվելով ջերմային էներգիայի (օրինակ, գեներատորի փաթույթներով հոսանք անցնելիս դրանք տաքանում են):
Համադրելով (1.2) և (1.5) բանաձևերը` կստանանք
![]()
Հաճախ, էլշու-ի աղբյուրների ներքին դիմադրությունն
այնքան փոքր է, որ գործնականորեն այն կարելի է անտեսել: Այդպիսի աղբյուրները կարող
են ներկայացվել որպես իդեալական աղբյուրներ (կամ լարման աղբյուրներ)` r = 0 ներքին
դիմադրությամբ և բնութագրվում են միայն մեկ պարամետրով՝ ![]() (նկ.1.3ա):
(նկ.1.3ա):
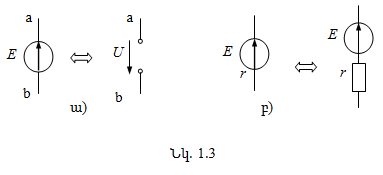
Լարումը իդեալական աղբյուրի սեղմակներում կախված չէ հոսանքից, և էլշուն որոշվում է որպես աղբյուրի սեղմակների միջև պոտենցիալների տարբերություն.
![]()
Իրական աղբյուրի
![]() համարժեք
սխեման
պատկերվում
է
որպես
կատարյալ
(իդեալական) աղբյուրի
և
դրա
r ներքին դիմադրության
հաջորդական
միացում
(նկ. 1.3բ):
համարժեք
սխեման
պատկերվում
է
որպես
կատարյալ
(իդեալական) աղբյուրի
և
դրա
r ներքին դիմադրության
հաջորդական
միացում
(նկ. 1.3բ):
Սխեմայի պարզեցման նպատակով սովորաբար r - ին համապատասխանող պայմանական նշանը չի պատկերվում սխեմայում, այլ պարզապես աղբյուրի պայմանական նշանին կից գրվում է նաև r տառը (նկ.1.2):
Մի շարք դեպքերում, մասնավորապես էլեկտրոնային և կիսահաղորդչային սարքեր պարունակող շղթաներում, աղբյուրի ներքին դիմադրությունը զգալիորեն գերազանցում է սպառիչի դիմադրությունը: Ընդունելով r >> R, այդպիսի աղբյուրի հոսանքի մեծությունը կարելի է համարել հաստատուն.
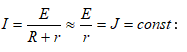
Մեծ ներքին դիմադրությամբ աղբյուրը կարելի է ներկայացնել որպես իդեալական հոսանքի աղբյուր, որի ներքին դիմադրությունը ձգտում է անվերջության: Իրական աղբյուրի համարժեք սխեման կարելի է պատկերել որպես իդեալական հոսանքի աղբյուրի և դրա ներքին դիմադրության զուգահեռ միացում (նկ. 1.4.):
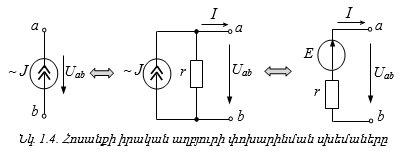
Այս դեպքում`
![]()
1.3. Էլեկտրական շղթաների ռեժիմները
Էլեկտրական շղթայի բոլոր հնարավոր ռեժիմներից առավել կարևորներն են՝ անվանական (նոմինալ) ռեժիմը, պարապ ընթացքի ռեժիմը, կարճ միացման ռեժիմը և համաձայնեցված ռեժիմը:
1.
Անվանական ռեժիմ:
Սա շղթայի այնպիսի ռեժիմ է, որի համար հաշվարկված է շղթան և որի դեպքում այն կարող
է աշխատել տևականորեն, տնտեսապես շահավետ պայմաններով: Անվանական ռեժիմին վերաբերող
մեծությունները կոչվում են անվանական հոսանք ![]() անվանական լարում
անվանական լարում
![]() անվանական հզորություն
անվանական հզորություն ![]() և այլն, որոնք
սովորաբար ստանդարտացված մեծություններ են:
և այլն, որոնք
սովորաբար ստանդարտացված մեծություններ են:
Օրինակ, եթե շիկացման լամպերը նախատեսված և հաշվված
են ![]() անվանական լարման համար, ապա ավելի ցածր լարման դեպքում, ասենք
անվանական լարման համար, ապա ավելի ցածր լարման դեպքում, ասենք ![]() նվազում է լամպերի օ.գ.գ.-ն, իսկ ավելի բարձր լարման դեպքում
նվազում է լամպերի օ.գ.գ.-ն, իսկ ավելի բարձր լարման դեպքում ![]() խիստ կրճատվում է լամպերի ծառայման ժամկետը: Այսպիսով, էլեկտրական լամպը
բավարար չափով երկարատև և շահավետ կարող է աշխատել
խիստ կրճատվում է լամպերի ծառայման ժամկետը: Այսպիսով, էլեկտրական լամպը
բավարար չափով երկարատև և շահավետ կարող է աշխատել ![]() ստանդարտ լարման դեպքում:
ստանդարտ լարման դեպքում:
Գործնականում դժվար է սպառիչների սեղմակներում
ապահովել անվանական արժեքին ճշգրտորեն հավասար լարում, ուստի փաստացի U լարումը այս
կամ այն չափով տարբերվում է անվանականից: Փաստացի և անվանական լարումների տարբերությունը,
արտահայտված տոկոսներով, կոչվում է լարման շեղում ![]()

Սպառիչների մեծամասնության համար,
դրանց նորմալ աշխատանքային պայմաններ ապահովելու նպատակով,
լարման շեղման թույլատրելի արժեքը սահմանված է ![]() այսինքն
այսինքն ![]()
2.
Պարապ ընթացքի ռեժիմ:
Սա շղթայի այնպիսի ռեժիմ է,
երբ սպառիչի հոսանքը զրո է՝
I = 0: Դա կարող է լինել կամ խզված շղթայի դեպքում
(նկ.
1.2-ում Ա անջատիչը բաց է)
և կամ երբ սպառիչի դիմադրությունն անվերջ մեծ է՝ ![]()
Պարապ ընթացքի ռեժիմում
(1.5ա)
-ից հետևում է ![]() այսինքն աղբյուրի պարապ ընթացքի լարումը հավասար է աղբյուրի էլշուին:
Այս հանգամանքը գործնականում օգտագործվում է աղբյուրի էլշուն չափելու համար
(վոլտմետրը միացնելով սպառիչից անջատված աղբյուրի սեղմակներին):
այսինքն աղբյուրի պարապ ընթացքի լարումը հավասար է աղբյուրի էլշուին:
Այս հանգամանքը գործնականում օգտագործվում է աղբյուրի էլշուն չափելու համար
(վոլտմետրը միացնելով սպառիչից անջատված աղբյուրի սեղմակներին):
Էլեկտրատեխնիկայում պարապ ընթացքի ռեժիմը հաճախ դիտարկվում է շղթայի (սարքի) հետազոտման համար (տե՛ս 8.6.1 ենթաբաժինը, տրանսֆորմատորի պարապ ընթացքի ռեժիմը): Գործնականում հանդիպում են սարքեր, որոնց աշխատանքային ռեժիմը մոտ է պարապ ընթացքի ռեժիմին, ինչպես օրինակ, լարման չափման տրանսֆորմատորները (տե՛ս 8.11.1 ենթաբաժինը):
3. Կարճ միացման ռեժիմ: Սա շղթայի այնպիսի ռեժիմ է, երբ փակ շղթայում սպառիչի դիմադրությունը հավասար է զրոյի, R = 0: Այս դեպքում (1.5) -ից ստանում ենք, որ կարճ միացման հոսանքը,
![]()
Քանի որ աղբյուրի r ներքին դիմադրությունը բավականաչափ
փոքր է, ապա կարճ միացման ![]() հոսանքն ստացվում է շատ մեծ: Այն կարող է գերազանցել հոսանքի անվանական
արժեքը մի քանի տասնյակ անգամ, որը շատ վտանգավոր է աղբյուրի և շղթայի մյուս տարրերի
համար: Ուստի կարճ միացման ռեժիմը սովորաբար համարվում է վթարային ռեժիմ և դրանից պաշտպանվելու
համար շղթայում նախատեսում են պաշտպանիչ սարքեր: Ամենատարածված պաշտպանիչ սարքերն են
դյուրահալ ապահովիչները և ավտոմատ անջատիչները, որոնք գերհոսանքների դեպքում արագորեն
խզում են շղթան՝ կանխելով վտանգը:
հոսանքն ստացվում է շատ մեծ: Այն կարող է գերազանցել հոսանքի անվանական
արժեքը մի քանի տասնյակ անգամ, որը շատ վտանգավոր է աղբյուրի և շղթայի մյուս տարրերի
համար: Ուստի կարճ միացման ռեժիմը սովորաբար համարվում է վթարային ռեժիմ և դրանից պաշտպանվելու
համար շղթայում նախատեսում են պաշտպանիչ սարքեր: Ամենատարածված պաշտպանիչ սարքերն են
դյուրահալ ապահովիչները և ավտոմատ անջատիչները, որոնք գերհոսանքների դեպքում արագորեն
խզում են շղթան՝ կանխելով վտանգը:
Դյուրահալ ապահովիչի աշխատանքը հիմնված է հոսանքի ջերմային ազդեցության վրա: Դրա հիմնական մասը դյուրահալ մետաղից պատրաստված թելիկն է, որի միջով անցնում է շղթայի ողջ հոսանքը: Անթույլատրելի մեծ հոսանքների դեպքում այն հալվում է և խզում շղթան:
Ավտոմատ անջատիչը թույլ է տալիս ցանկության դեպքում ձեռքով միացնել և անջատել շղթան, իսկ գերհոսանքների դեպքում՝ ավտոմատորեն անջատել այն: Դրա աշխատանքը հիմնված է հոսանքի առաջացրած մագնիսական դաշտի ուժային ազդեցության վրա: Ավտոմատ անջատիչի հիմնական տարրը էլեկտրամագնիսն է, որի փաթույթով անցնում է շղթայի մուտքային հոսանքը: Երբ հոսանքը թույլատրելի սահմաններում է, էլեկտրամագնիսի ուժը չի բավականացնում ձգելու խարիսխը (շարժական մասը), իսկ գերհոսանքների դեպքում այն ձգում է խարսխը՝ շարժման մեջ դնելով դրա հետ կապված կոնտակտները և խզելով շղթան:
Էլեկտրատեխնիկայում հաճախ կարճ միացման ռեժիմը դիտարկվում է էլեկտրական սարքերի ուսումնասիրման համար (տե՛ս 8.6.2 ենթաբաժինը, տրանսֆորմատորի կարճ միացման ռեժիմը): Գործնականում կիրառվող որոշ էլեկտրական սարքերի աշխատանքը մոտ է կարճ միացման ռեժիմին, ինչպես օրինակ, հոսանքի չափման տրանսֆորմատորը (տե՛ս 8.11.2 ենթաբաժինը), եռակցման տրանսֆորմատորը (տե՛ս 8.10 բաժինը)::
4. Համաձայնեցված ռեժիմ: Շղթայի այս ռեժիմում առավելագույն հզորություն է փոխանցվում աղբյուրից սպառիչին: Այն մանրամասնորեն դիտարկված է 1.9 բաժնում:
Էլեկտրական շղթաների հաշվարկի հիմքում ընկած են Կիրխհոֆի երկու օրենքները: Նախքան այդ օրենքների սահմանումը անհրաժեշտ է ծանոթանալ էլեկտրական շղթայի մի քանի տոպոլոգիական (երկրաչափական) տարրերի հետ:
· Ճյուղ է կոչվում շղթայի այն տեղամասը, որով անցնում է նույն հոսանքը: Ակնհայտ է, որ ճյուղը կազմող տարրերը միացված են հաջորդաբար:
· Հանգույց է կոչվում երեք և ավելի ճյուղերի միացման կետը: Փաստորեն ճյուղը շղթայի երկու հարևան հանգույցների միջև ընկած տեղամասն է:
· Կոնտուր է կոչվում ճյուղերից կազմված փակ ուղին. ընդ որում յուրաքանչյուր ճյուղ կամ հանգույց պետք է վերցնել միայն մեկ անգամ:
Կիրխհոֆի I օրենքը (հոսանքների օրենքը). շղթայի հանգույցում հոսանքների հանրահաշվական գումարը զրո է.
![]()
Կարելի է պայմանավորվել դեպի հանգույց ուղղված հոսանքները վերցնել դրական նշանով, իսկ հանգույցից դուրս ուղղված հոսանքները՝ բացասական նշանով:
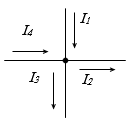
Նկարում պատկերված շղթայի հանգույցի համար (1.8) հավասարումը կգրվի հետևյալ տեքով.
![]()
Ակնհայտ է, որ ճիշտ կլիներ նաև հակառակ պայմանավորվածությունը (այդ դեպքում կստացվեր համարժեք հավասարում, որը բազմապատկված է (– 1) -ով):
Կիրխհոֆի 1-ին օրենքն ունի պարզ ֆիզիկական իմաստ. շղթայի հանգույցում լիցքեր առաջանալ կամ կորչել չեն կարող:
Կիրխհոֆի 2-րդ օրենքը (լարումների օրենքը). էլեկտրական շղթայի կոնտուրում լարումների հանրահաշվական գումարը զրո է.
![]()
Հաշվի առնելով, որ աղբյուրում էլշուի և լարման ուղղությունները հակառակ են` շղթայի էլշու պարունակող կոնտուրի համար (1.9) հավասարումը կարելի է գրել նաև հետևյալ տեսքով.
![]()
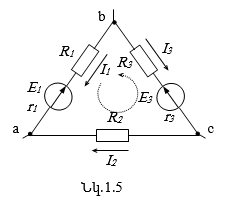
Այսինքն, շղթայի կոնտուրում էլշուների հանրահաշվական գումարը հավասար է լարումների հանրահաշվական գումարին: (1.9) կամ (1.10) հավասարումները ճիշտ կազմելու համար հարմար է ընտրել կոնտուրի շրջանցման կամայական ուղղություն՝ ժամացույցի սլաքների շարժման ուղղությամբ կամ դրան հակառակ: Եթե կոնտուրում լարման, էլշուի կամ հոսանքի ուղղությունները համընկնում են կոնտուրի շրջանցման ընտրված ուղղության հետ, ապա դրանք հավասարման մեջ մտնում են դրական նշանով, հակառակ դեպքում՝ բացասական նշանով:
Օրինակի համար դիտարկենք որևէ շղթայից առանձնացված a-b-c-a կոնտուրը (նկ. 1.5.)՝ որպես շրջանցման ուղղություն ընտրելով ժամսլաքի շարժման հակառակ ուղղությունը: Այդ դեպքում Կիրխհոֆի 2-րդ օրենքի հիման վրա (1. 10) հավասարումը կգրվի հետևյալ տեսքով.
![]()
Լարումը շղթայի որևէ ճյուղի սեղմակների միջև որոշվում է որպես այդ կետերի միջև պոտենցիալների տարբերություն: Շատ խնդիրների լուծման համար հաճախ անհրաժեշտ է լինում ունենալ շղթայի ճյուղի սեղմակների միջև լարման և ճյուղով անցնող հոսանքի կապը:
Նկ. 1.6-ում պատկերված է որևէ էլեկտրական շղթայից
առանձնացված մի ճյուղ, որը պարունակում է հաջորդաբար միացված ![]() էլշուի աղբյուրները և
էլշուի աղբյուրները և ![]() դիմադրությունները:
Տարրերի միացման կետերը նշանակված են a, b, c, d, e տառերով. Որոշենք այդ կետերի պոտենցիալները
a կետի նկատմամբ` ընդունելով հոսանքի դրական ուղղությունը a-ից b:
դիմադրությունները:
Տարրերի միացման կետերը նշանակված են a, b, c, d, e տառերով. Որոշենք այդ կետերի պոտենցիալները
a կետի նկատմամբ` ընդունելով հոսանքի դրական ուղղությունը a-ից b:
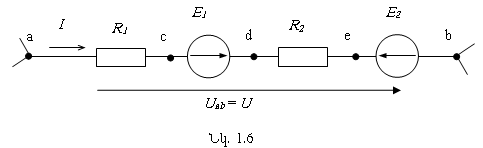
Համաձայն (1.2) բանաձևի,
![]()
Համաձայն (1.6) բանաձևի,
![]()
Համանման ձևով`
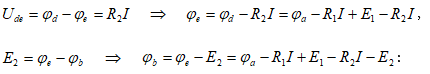
Այստեղից, դիտարկվող ճյուղի սեղմակների միջև լարումը կլինի
![]()
որտեղից ճյուղի հոսանքը`
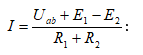
Ստացված բանաձևը Օհմի ընդհանրացված օրենքի արտահայտությունն է դիտարկվող ճյուղի համար:
Ընդհանուր դեպքում, երբ ճյուղը պարունակում է ցանկացած թվով սպառիչներ և աղբյուրներ, Օհմի ընդհանրացված օրենքը կարելի է գրել հետևյալ տեսքով.

Այս բանաձևի համարիչում U լարումը և E էլշուն վերցվում են դրական նշանով, եթե նրանց ուղղությունները համընկնում են հոսանքի նշված ուղղության հետ, հակառակ դեպքում` բացասական նշանով: Հայտարարում` ճյուղի դիմադրությունների թվաբանական գումարն է` ներառյալ աղբյուրների ներքին դիմադրությունները:
1.6. Էներգիայի և հզորության արտահայտությունները հաստատուն հոսանքի շղթաներում
Ինչպես հայտնի է ֆիզիկայի դասընթացից, էներգիան (W) աշխատանք կատարելու ունակությունն է, իսկ հզորությունը (P)՝ միավոր ժամանակում կատարված աշխատանքը՝
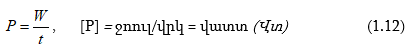
Արտածենք E էլշու և I հոսանք ունեցող աղբյուրի հզորության արտահայտությունը:
Էլշուի սահմանման համաձայն` աղբյուրի a սեղմակից b սեղմակ Q լիցքերի տեղափոխման վրա կողմնակի ուժերի կատարած աշխատանքը (կամ ծախսած էներգիան) կլինի
![]()
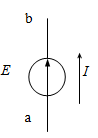
Տեղադրելով այս արտահայտությունը (1.12) բանաձևի մեջ՝ աղբյուրի հզորության համար կստանանք
![]()
Այժմ ստանանք U լարում և I հոսանք ունեցող սպառիչի ծախսած էներգիայի և հզորության բանաձևերը: Լարման սահմանման համաձայն` սպառիչով անցնող Q լիցքերի կատարած աշխատանքը կլինի
![]()
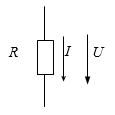
Այստեղից սպառիչի հզորությունը՝
![]()
Հաշվի առնելով (1.2), որ U = RI, կստանանք`

Ֆիզիկայի հիմնարար օրենքը՝ էներգիայի պահպանման և փոխակերպման օրենքը, էլեկտրական շղթաների համար կարելի է վերաձևակերպել հետևյալ կերպ. էլեկտրական շղթայում գործող աղբյուրների հզորությունների գումարը հավասար է շղթայի սպառիչների հզորությունների գումարին: Ուստի (1.13) և (1.14) բանաձևերի հիման վրա կարող ենք գրել.
![]()
Այս հավասարությունը կոչվում է էլեկտրական շղթայի հզորությունների հաշվեկշիռ (բալանս): Հավասարության աջ մասը թվաբանական գումար է. բոլոր անդամները դրական նշանով են, մինչդեռ ձախ մասը` հանրահաշվական գումար է: Ընդ որում, եթե աղբյուրի E էլշուի և I հոսանքի ուղղությունները համընկնում են, ապա EI արտադրյալը (1.15) հավասարության մեջ վերցվում է դրական, հակառակ դեպքում, երբ E-ն և I-ն հակառակ են ուղղված, EI արտադրյալը վերցվում է բացասական նշանով: Վերջինս հնարավոր է, երբ շղթայում գործում են մեկից ավելի աղբյուրներ: Այս դեպքում հնարավոր է, որ դրանցից մեկը կամ մի քանիսը կարող են վերածվել էլեկտրաէներգիայի սպառիչի՝ սնվելով մյուս աղբյուրներից (ինչպես օրինակ, երբ ակումուլյատորային մարտկոցը լիցքավորվում է): Հնարավոր է նաև, որ աղբյուրի I հոսանքը լինի զրո, այդ դեպքում` աղբյուրը կգտնվի պարապ ընթացքի ռեժիմում:
1.7. էլեկտրական շղթաների համարժեք ձևափոխությունները
Էլեկտրական շղթաների ուսումնասիրման և հաշվարկի համար հաճախ նպատակահարմար է շղթան ենթարկել համարժեք ձևափոխության՝ այն պարզեցնելու նպատակով: Շղթայի ձևափոխությունը համարվում է համարժեք, եթե ձևափոխվող տեղամասից դուրս շղթայի ճյուղերում հոսանքները և լարումները մնում են անփոփոխ:
Համարժեք ձևափոխություններ են ֆիզիկայի դասընթացից հայտնի շղթայի հաջորդական և զուգահեռ միացված դիմադրությունները մեկ համարժեք դիմադրությամբ փոխարինելը:
Շղթայի երկու կամ ավելի տարրեր համարվում են հաջորդաբար միացված, եթե նրանք միացված են մեկը մյուսի հետևից և դրանցով անցնում է նույն հոսանքը:
Նկ. 1.7-ում պատկերված շղթայի a-b տեղամասը, որը սպառիչների հաջորդական միացում է, կարելի է փոխարինել մեկ սպառիչով, որի դիմադրությունը որոշվում է որպես հաջորդաբար միացված
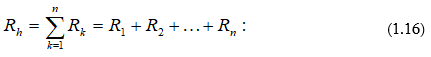
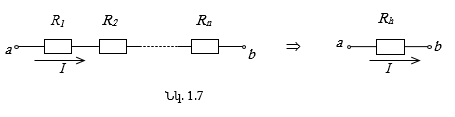
Շղթայի երկու կամ ավելի տարրեր համարվում են զուգահեռ միացված, եթե րանք միացված են շղթայի միևնույն երկու հանգույցներին: Ակնհայտ է, որ բոլոր տարրերի վրա լարումը նույնն է:
Շղթայի n սպառիչների զուգահեռ միացված տեղամասը կարելի է փոխարինել մեկ համարժեք սպառիչով (նկ. 1.8), որի դիմադրությունը որոշվում է հետևյալ բանաձևով.
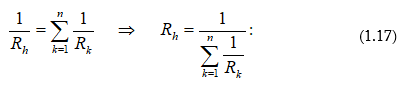
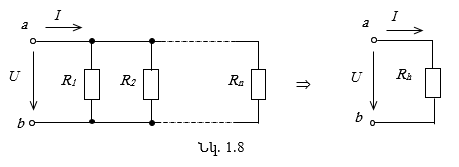
Երկու դիմադրությունների զուգահեռ միացման դեպքում (n = 2).
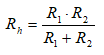
Զուգահեռ միացման դեպքում հաճախ դիմադրությունների փոխարեն հարմար է օգտվել հաղորդականություններից: Այդ դեպքում, նկատի ունենալով (1.4) բանաձևը, համարժեք հաղորդականության համար (1.17) բանաձևը կգրվի հետևյալ տեսքով.

Աստղ-եռանկյուն և եռանկյուն-աստղ համարժեք ձևափոխությունը:
Շղթայի տարրերը (դիմադրությունները) կոչվում են աստղաձև միացված, եթե դրանց մեկական ծայրերը միացված են մի հանգույցում, իսկ մյուս ծայրերը՝ այլ կետերում (նկ. 1.9ա):
Շղթայի երեք տարրեր կոչվում են եռանկյունաձև միացված, եթե դրանցից առաջինի վերջը միացված է երկրորդի սկզբի, երկրորդի վերջը՝ երրորդի սկզբի, երրորդի վերջը՝ առաջինի սկզբի հետ` կազմելով փակ կոնտուր, և միացման կետերը հանդիսանում են շղթայի հանգույցներ (նկ. 1.9բ):
Պարզվում է, որ շղթայի երեք տարրերի աստղաձև միացված տեղամասը կարելի է փոխարինել համարժեք եռանկյունաձև միացումով և հակառակը, եռանկյունաձև միացված տեղամասը՝ համարժեք աստղաձև միացումով:
Վերոհիշյալ համարժեք ձևափոխությունների համար անհրաժեշտ է վերահաշվարկել տարրերի դիմադրությունները՝ օգտվելով հետևյալ բանաձևերից, որոնք բերվում են առանց ապացուցման:
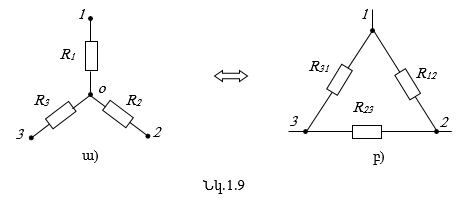
Աստղ-եռանկյուն ձևափոխության համար.
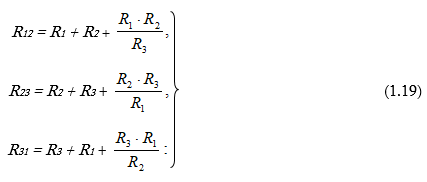
Նկատենք, որ աստղ-եռանկյուն ձևափոխման դեպքում վերանում է աստղաձև միացման “օ” ընդհանուր հանգույցը:
Եռանկյուն-աստղ ձևափոխության համար.
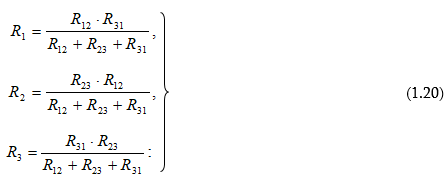
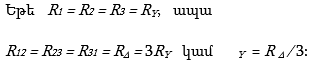
Եռանկյուն - աստղ ձևափոխման դեպքում շղթայում ավելանում է “օ” ընդհանուր հանգույցը:
Աստղաձև և եռանկյունաձև միացումները հատկապես կարևոր են փոփոխական հոսանքի եռաֆազ շղթաների ուսումնասիրման և հաշվարկման ժամանակ:
1.8. Քառաթև (Ուիտսթոնի) կամրջակ
Քառաթև
կամրջակի սխեման պատկերված է նկ. 1.10-ում: Դրա ![]() դիմադրություններով չորս ճյուղերը կոչվում են կամրջակի թևեր, իսկ անկյունագծային
d-b ճյուղի
դիմադրություններով չորս ճյուղերը կոչվում են կամրջակի թևեր, իսկ անկյունագծային
d-b ճյուղի ![]() դիմադրությունը` կամրջակի բեռնվածք:
դիմադրությունը` կամրջակի բեռնվածք:
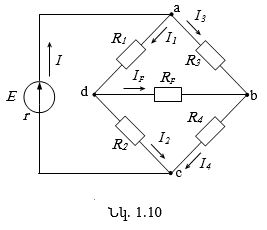
Կամրջակը
միացված է E էլշուով աղբյուրին: Այն համարվում է հավասարակշռված, եթե դրա անկյունագծում
![]() հոսանքը զրո է: Այս դեպքւմ
հոսանքը զրո է: Այս դեպքւմ ![]() ինչպես նաև
ինչպես նաև ![]() դիմադրությունները միացված կլինեն հաջորդաբար, հետևաբար,
դիմադրությունները միացված կլինեն հաջորդաբար, հետևաբար,
![]()
Քանի
որ ![]() ապա b և d հանգույցներն
ունեն պոտենցիալների նույն տարբերությունը (լարումը), համապատասխանաբար, a և c հանգույցների
նկատմամբ
ապա b և d հանգույցներն
ունեն պոտենցիալների նույն տարբերությունը (լարումը), համապատասխանաբար, a և c հանգույցների
նկատմամբ
![]()
Կամ, հաշվի առնելով (1.21)-ը,
![]()
Բաժանելով (1.22) և (1.23) հավասարությունները միմյանց վրա՝ կստանանք կամրջակի հավասարակշռության պայմանը.
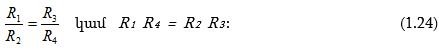
Հենց որ կամրջակի հավասարակշռությունը խախտվի, ասենք՝ թևերից մեկի պարամետրերի փոփոխության պատճառով, ապա անմիջապես հոսանք կհայտնվի դրա անկյունագծում: Ելնելով այդ հոսանքի մեծությունից և ուղղությունից` կարելի է դատել հավասարակշռության խախտման աստիճանի, ինչպես նաև, հետագա վերլուծության միջոցով, այն առաջացրած գործոնի բնույթի և մեծության մասին:
Եթե
ցանկացած երեք թևերի դիմադրությունները և աղբյուրի էլշուն պահվեն հաստատուն, ապա ![]() հոսանքի փոփոխությունը կախված կլինի միայն չորրորդ թևի դիմադրության արժեքից:
Եվ եթե վերջինս կախման մեջ դրվի չափման ենթակա որևէ մեծությունից (ջերմաստիճան, ճնշում,
խոնավություն և այլն), ապա
հոսանքի փոփոխությունը կախված կլինի միայն չորրորդ թևի դիմադրության արժեքից:
Եվ եթե վերջինս կախման մեջ դրվի չափման ենթակա որևէ մեծությունից (ջերմաստիճան, ճնշում,
խոնավություն և այլն), ապա ![]() հոսանքի փոփոխությունները որոշակի մասշտաբով կներկայացնեն այդ մեծությունների
արժեքները: Այս առումով քառաթև կամրջակները կարող են ծառայել ոչ էլեկտրական մեծությունների
չափման համար:
հոսանքի փոփոխությունները որոշակի մասշտաբով կներկայացնեն այդ մեծությունների
արժեքները: Այս առումով քառաթև կամրջակները կարող են ծառայել ոչ էլեկտրական մեծությունների
չափման համար:
Քառաթև կամրջակները լայնորեն օգտագործվում են ավտոմատ կառավորման և հսկման սարքերում որպես հետադարձ կապի կոնտուրներ: Դրանք կարող են օգտագործվել նաև, երբ անհրաժեշտ է մեծ ճշգրտությամբ չափել դիմադրություններ:
1.9. Առավելագույն հզորության փոխանցման թեորեմը
Հաճախ ցանկալի է, որ կապի, էլեկտրոնային, ավտոմատ կառավարման և այլ սարքերում շղթան աշխատի համաձայնեցված ռեժիմում, այսինքն աղբյուրն առավելագույն չափով էներգիա (հզորություն) փոխանցի համապատասխան սպառիչին, քանի որ փոխանցման օ.գ.գ.-ն այս դեպքերում երկրորդական նշանակություն ունի:
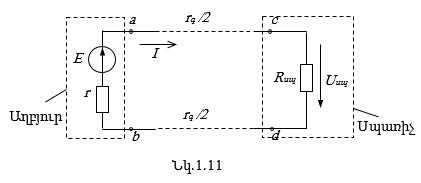
Դիտարկենք մի շղթա, որտեղ աղբյուրը տեղակայված է սպառիչից
որոշ հեռավորության վրա և միացված է դրա հետ ![]() դիմադրությամբ
երկլարանի գծով (նկ. 1.11): Ընդունելով
դիմադրությամբ
երկլարանի գծով (նկ. 1.11): Ընդունելով ![]() Օհմի օրենքի համաձայն, հոսանքի համար
կստանանք
Օհմի օրենքի համաձայն, հոսանքի համար
կստանանք
![]()
Սպառիչի հզորությունը, համաձայն (1.14) -ի,
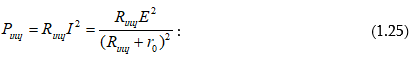
Հզորության փոխանցման ՕԳԳ-ն կլինի`
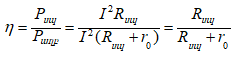
Սպառիչի դիմադրության երկու ծայրագույն արժեքների դեպքում,
երբ ![]() (կարճ
միացում) և
(կարճ
միացում) և ![]() (պարապ ընթացք), բեռնվածքի հզորությունը
զրո է: Հետևաբար սպառիչի առավելագույն հզորությունը համապատասխանում է սպառիչի դիմադրության
որոշակի արժեքին
(պարապ ընթացք), բեռնվածքի հզորությունը
զրո է: Հետևաբար սպառիչի առավելագույն հզորությունը համապատասխանում է սպառիչի դիմադրության
որոշակի արժեքին ![]() միջակայքում: Այն որոշելու համար
զրոյի հավասարեցնենք
միջակայքում: Այն որոշելու համար
զրոյի հավասարեցնենք ![]() ֆունկցիայի ածանցյալն ըստ
ֆունկցիայի ածանցյալն ըստ ![]()
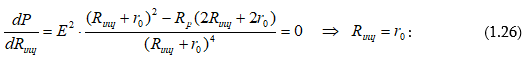
Այսպիսով,
սպառիչին փոխանցվող հզորությունն առավելագույնն է, երբ բեռնվածքի դիմադրությունը հավասար
է գծի և աղբյուրի ներքին դիմադրությունների գումարին՝
![]()
(1.26) հավասարությունը առավելագույն հզորության փոխանցման մաթեմատիկական արտահայտությունն է:
Տեղադրելով (1.25) - ի մեջ ![]() սպառիչին
փոխանցվող առավելագույն հզորության համար կստանանք
սպառիչին
փոխանցվող առավելագույն հզորության համար կստանանք
![]()
Նկ. 1.12-ում պատկերված են աղբյուրի P հզորության,
սպառիչի ![]() լարման
ու
լարման
ու ![]() հզորության
և հզորության փոխանցման
հզորության
և հզորության փոխանցման ![]() օ.գ.գ.-ի
կախվածության կորերը սպառիչի I հոսանքից: Ընդ որում`
օ.գ.գ.-ի
կախվածության կորերը սպառիչի I հոսանքից: Ընդ որում` ![]() ֆունկցիաները
տրվում են հետևյալ բանաձևերով.
ֆունկցիաները
տրվում են հետևյալ բանաձևերով.
![]()
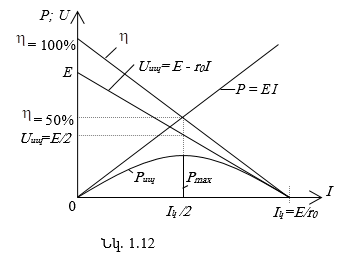
Առավելագույն հզորության փոխանցման դեպքում ընդամենը
![]() Այլ խոսքով
աղբյուրից ստացված հզորության կեսը կորչում է սնող գծերի և աղբյուրի ներքին դիմադրության
վրա:
Այլ խոսքով
աղբյուրից ստացված հզորության կեսը կորչում է սնող գծերի և աղբյուրի ներքին դիմադրության
վրա:
Էլեկտրահաղորդման գծերում, որոնցով փոխանցվում է հսկայական մեծության էլեկտրաէներգիա, իհարկե անհանդուրժելի է ունենալ այսպիսի ցածր օ.գ.գ.: Այդ գծերում հզորության կորուստը չի գերազանցում առկա հզորության 10%-ը: Սակայն վերոհիշյալ սարքերում, որոնցում փոխանցման հզորությունը շատ փոքր է (մի քանի միլիվատտ), ցածր օ.գ.գ.-ն էական չէ և ավելի կարևոր է, որ աղբյուրը բեռնվածքին փոխանցի հնարավոր ամենամեծ հզորությունը:
1. Որո՞նք են էլեկտրական շղթայի հիմնական տարրերը: Պատկերեք դրանց պայմանական նշանները:
2. Թվարկեք շղթայի ոչ հիմնական (օժանդակ) տարրերը և ցույց տվեք դրանց պայմանական նշանները:
3. Տվեք էլեկտրական հոսանքի սահմանումը: Ի՞նչ ուղղություն ունի այն հոսանքի աղբյուրում և սպառիչում: Ո՞րն է հոսանքի չափման միավորը:
4. Ո՞րն է աղբյուրի էլշուի ֆիզիկական իմաստը, ինչպե՞ս է ուղղված այն: Ո՞րն է էլշուի չափման միավորը:
5. Ո՞րն է շղթայի երկու կետերի միջև էլեկտրական լարման ֆիզիկական իմաստը, ինչպե՞ս է ուղղված այն: Ո՞րն է լարման չափման միավորը:
6. Գրեք Օհմի օրենքի արտահայտությունը սպառիչի համար: Ի՞նչ միավորով են չափվում լարումը և դիմադրությունը:
7. Գրեք Օհմի օրենքի արտահայտությունը պարզագույն փակ շղթայի համար: Ի՞նչ ֆիզիկական իմաստ ունի աղբյուրի ներքին դիմադրությունը:
8. Ի՞նչ առնչությամբ է կապված հաղորդականությունը դիմադրության հետ: Ո՞րն է հաղորդականության չափման միավորը:
9. Որո՞նք են շղթայի հիմնական ռեժիմները: Տվեք դրանց սահմանումները:
10. Տվեք շղթայի երկրաչափական տարրերի (ճյուղ, հանգույց, կոնտուր) սահմանումները:
11. Ձևակերպեք Կիրխհոֆի 1-ին օրենքը: Ի՞նչ ֆիզիկական իմաստ ունի այն: Ինչպե՞ս գրել այդ օրենքի հիման վրա հավասարումներ:
12. Ձևակերպեք Կիրխհոֆի 2-րդ օրենքը: Ինչպե՞ս գրել այդ օրենքի հիման վրա հավասարումներ
13. Գրեք շղթայի աղբյուրի և սպառիչի հզորությունների բանաձևերը: Ի՞նչ միավորներով են չափվում էլեկտրական էներգիան և հզորությունը:
14. Գրեք շղթայի հզորությունների հաշվեկշռի հավասարումը: Ինչպե՞ս է այն կազմվում և ի՞նչ ֆիզիկական իմաստ ունի:
15. Տալ էլեկտրական շղթայի համարժեք ձևափոխության սահմանումը և նպատակը:
16. Ի՞նչ է դիմադրությունների հաջորդական միացումը: Ինչպե՞ս է որոշվում շղթայի հաջորդական միացված տեղամասի համարժեք դիմադրությունը:
17. Ի՞նչ է դիմադրությունների զուգահեռ միացումը: Ինչպե՞ս է որոշվում շղթայի զուգահեռ միացված տեղամասի համարժեք դիմադրությունը:
18. Տալ էլեկտրական շղթայի տարրերի աստղաձև և եռանկյունաձև միացումների սահմանումները:
19. Ինչպիսի՞ բանաձևերից պետք է օգտվել «աստղ»-«եռանկյունե համարժեք ձևափոխության համար:
20. Ինչպիսի՞ բանաձևերից պետք է օգտվել «եռանկյուն»-«աստղե համարժեք ձևափոխության համար:
21. Գծեք քառաթև կամրջակի սխեման: Թևերի դիմադրությունների ինչպիսի՞ հարաբերակցության դեպքում կամրջակը կլինի հավասարակշռված (անկյունագծային ճյուղում հոսանքը կլինի զրո):
22. Գործնական ինչպիսի՞ կիրառություններ ունի քառաթև կամրջակը:
23. Սպառիչի դիմադրության ո՞ր արժեքի դեպքում առավելագույն հզորություն կփոխանցվի աղբյուրից սպառիչին:
24. Ինչպիսի՞ն է էլեկտրահաղրդման գծի օ.գ.գ.-ն` սպառիչին առավելագույն հզորության փոխանցման դեպքում:
2. ՀԱՍՏԱՏՈՒՆ ՀՈՍԱՆՔԻ ԷԼԵԿՏՐԱԿԱՆ ՇՂԹԱՆԵՐԻ ՀԱՇՎԱՐԿԸ
Էլեկտրական շղթաների ընդհանուր տեսությունն առնչվում է էլեկտրական շղթաների հաշվարկի երկու հիմնական խնդիրների հետ.
1) Էլեկտրական շղթաների անալիզի խնդիր (շահագործողական խնդիր), երբ տրված է էլեկտրական շղթան իր կառուցվածքով և տարրերի պարամետրերով (E, r, R), անհրաժեշտ է հաշվել հոսանքները, լարումները կամ հզորությունները այդ շղթայի տեղամասերում:
2) Էլեկտրական շղթաների սինթեզի խնդիր (նախագծային խնդիր), երբ տրված են շղթային ներկայացվող պահանջները (օրինակ, ինչպիսի հոսանքներ, լարումներ կամ հզորություններ պետք է լինեն շղթայի մուտքում և ելքում), անհրաժեշտ է կազմել շղթան և հաշվել նրա տարրերի պարամետրերը:
Ակնհայտ է, որ 2-րդ խնդիրը նեղ մասնագիտական է և չի ընդգրկված ոչ էլեկտրատեխնիկական մասնագիտությունների ծրագրում: Այսպիսով, սույն ձեռնարկում դիտարկվում են միայն էլեկտրական շղթաների անալիզի խնդիրները:
2.1. Էլեկտրական շղթաների հաշվարկը Կիրխհոֆի օրենքների կիրառությամբ
Որպես օրինակ դիտարկենք հաստատուն հոսանքի մի շղթա որի բոլոր տարրերի պարամետրերը (E…,r…,R…) տրված են (նկ. 2.1), անհրաժեշտ է որոշել հոսանքներն այդ շղթայի ճյուղերում1:
Առաջարկվում է գործողությունների հետևյալ հաջորդականությունը՝ տվյալ խնդիրը Կիրխհոֆի երկու օրենքների հիման վրա լուծելու համար.
1) Հաշվել շղթայի ճյուղերի m թիվը (նկ. 2.1-ում տրված շղթայի համար m = 6) և դրանցում կամայականորեն նշել անհայտ հոսանքների ուղղությունները:
2) Հաշվել շղթայի հանգույցների n թիվը և ցանկացած n – 1 հանգույցների համար Կիրխհոֆի 1-ին օրենքով կազմել հավասարումներ: Քննարկվող շղթայում n = 4, հետևաբար պետք է կազմել n–1=3 հավասարումներ.
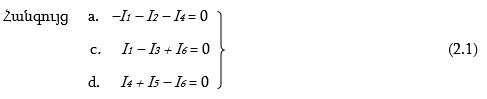
Գումարելով ստացված հավասարումները՝ կստանանք բաց թողնված b հանգույցի համար գրված հավասարմանը համարժեք հավասարում, ինչը վկայում է, որ այն անկախ չէ և, հետևաբար, ավելորդ է:
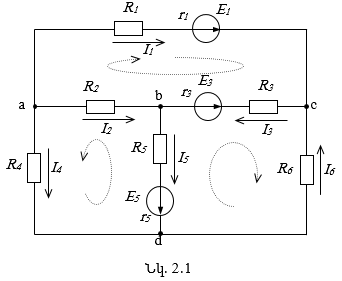
3) Հաշվել շղթայի անկախ կոնտուրների թիվը2 k = m – n + 1 բանաձևով: Փոխադարձ անկախ են կոչվում այն կոնտուրները, որոնցից յուրաքանչյուրը պարունակում է գոնե մեկ (սեփական) ճյուղ, որը չի պատկանում մյուս կոնտուրներին:
Դիտարկվող շղթայի համար k = 6 – 4 + 1 = 3 և որպես անկախ կոնտուրներ` ընտրված են a-c-b-a, a-b-d-a, և b-c-d-b փոխադարձ անկախ կոնտուրները:
Ընտրված կոնտուրներում նշվում են շրջանցման կամավոր ուղղությունները և Կիրխհոֆի 2-րդ օրենքի հիման վրա գրվում են հավասարումներ.
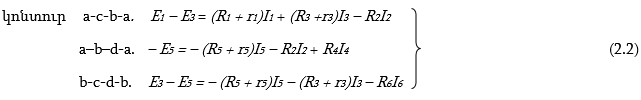
Այսպիսով, ընդհանուր դեպքում, Կիրխհոֆի երկու օրենքների հիման վրա կազմված (2.1) և (2.2) համակարգերում ընդգրկված հավասարումների ընդհանուր թիվը
![]()
Այսինքն՝ ցանկացած շղթայի համար անհայտների թիվը հավասար է անկախ հավասարումների թվին և, հետևաբար, մաթեմատիկորեն այն միշտ միարժեքորեն լուծելի է:
4) Համատեղ լուծելով (2.1) և (2.2) գծային հավասարումների համակարգերը՝ որոշվում են անհայտ հոսանքները շղթայի բոլոր ճյուղերում: Եթե որևէ ճյուղում հոսանքի արժեքն ստացվում է բացասական նշանով, ապա դրա իրական ուղղությունը պետք է լինի սխեմայում նախապես նշված ուղղությանը հակառակ:
Շղթայի հաշվարկի ճշտությունը սովորաբար ստուգվում է հզորությունների հաշվեկշռի հավասարության (1.15) միջոցով, որը դիտարկվող շղթայի համար կգրվի հետևյալ տեսքով.
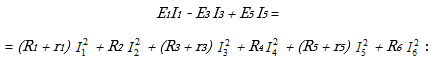
Եթե հոսանքների արժեքները տեղադրելուց հետո հավասարման աջ և ձախ մասերը հավասար են, ապա շղթան ճիշտ է հաշվարկված:
Ընդհանուր դեպքում, (2.1) և (2.2) հավասարումների համակարգի լուծումը բավականաչափ աշխատատար է, այդ պատճառով, որտեղ հնարավոր է, շղթաների հաշվարկի այլ մեթոդներ են կիրառվում: Այդ մեթոդները նույնպես, վերջին հաշվով, հիմնված են Օհմի և Կիրխհոֆի օրենքների վրա:
2.2. Շղթաների հաշվման միջհանգուցային լարման մեթոդը (երկու հանգույցների մեթոդը)
Հաճախ դիտարկվող շղթան պարունակում է միայն երկու հանգույց կամ հեշտությամբ կարող է համարժեքորեն ձևափոխվել երկհանգույց շղթայի: Այդ դեպքում շղթայի հաշվարկի պարզագույն եղանակը միջհանգուցային լարման եղանակն է:
Դիտարկենք երկհանգույց մի շղթա, որտեղ նշված են ճյուղերի
հոսանքների և միջհանգուցային ![]() լարման
ուղղությունները (նկ.2.2):
լարման
ուղղությունները (նկ.2.2):
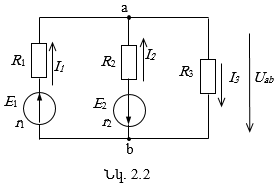
Օգտվելով Օհմի ընդհանրացված օրենքից (1.11), կարող
ենք որոշել ճյուղերի հոսանքները` արտահայտված ![]() լարումով
լարումով
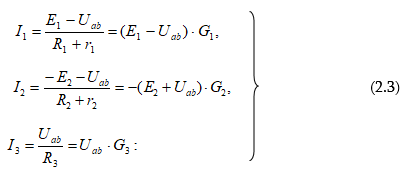
Բանաձևերում ![]() զուգահեռ ճյուղերի հաղորդականություններն
են: Ըստ (1.4) բանաձևի`
զուգահեռ ճյուղերի հաղորդականություններն
են: Ըստ (1.4) բանաձևի`
![]()
Տեղադրելով հոսանքների արժեքները (2.3)-ից a հանգույցի
համար Կիրխհոֆի 1-ին օրենքի հիման վրա կազմված ![]() հավասարման մեջ` կստանանք
հավասարման մեջ` կստանանք
![]()
Այս հավասարումից ստանում ենք միջհանգուցային ![]() լարման
արտահայտությունը`
լարման
արտահայտությունը`

Կամ, ընդհանուր դեպքում,

Բանաձևում Ek էլշուն վերցվում է դրական, եթե այն հակառակ
է ուղղված ![]() լարմանը
(այսինքն` դրանց բևեռականությունները համընկնում են): Միջհանգուցային լարումը որոշելուց
հետո, օգտվելով (2.3) հավասարումներից, հեշտությամբ կարելի է որոշել ճյուղերի հոսանքները:
լարմանը
(այսինքն` դրանց բևեռականությունները համընկնում են): Միջհանգուցային լարումը որոշելուց
հետո, օգտվելով (2.3) հավասարումներից, հեշտությամբ կարելի է որոշել ճյուղերի հոսանքները:
Երկհանգույց շղթաների հաշվարկի համար առաջարկվում է գործողությունների հետևյալ հաջորդականությունը.
§ ճյուղերում կամայականորեն
նշել անհայտ հոսանքների, ինչպես նաև միջհանգուցային ![]() լարման
ուղղությունները,
լարման
ուղղությունները,
§ հաշվել ճյուղերի հաղորդականությունները օգտվելով հետևյալ ընդհանուր բանաձևից
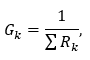
§ հաշվել միջհանգուցային լարումը՝ օգտվելով (2.5) բանաձևից,
§ գտնել անհայտ հոսանքները՝ օգտվելով Օհմի ընդհանրացված օրենքից (2.3):
2.3. Կոնտուրային հոսանքների մեթոդը
Այս մեթոդը հնարավորություն է ընձեռում կրճատել համակարգի մեջ մտնող հավասարումների թիվը՝ զգալիորեն հեշտացնելով շղթայի հաշվարկը:
Կոնտուրային հոսանքների մեթոդով շղթան հաշվելու համար
ընտրվում են շղթայի անկախ կոնտուրները նույն ձևով, ինչ որ դա արվում էր Կիրխհոֆի
2-րդ օրենքով հավասարումների համակարգ կազմելիս (տես 2.1 բաժինը): Այնուհետև ենթադրվում
է, որ յուրաքանչյուր անկախ կոնտուրում գործում է որոշակի հոսանք, որը կոչվում է կոնտուրային
հոսանք: Այն նույնն է տվյալ կոնտուրի բոլոր ճյուղերի համար, և ակնհայտ է, որ մեծությամբ
հավասար է տվյալ կոնտուրի սեփական ճյուղի հոսանքին: Կոնտուրային հոսանքների կամայականորեն
ընտրված դրական ուղղությունները հարմար է ընդունել որպես կոնտուրի շրջանցման ուղղություններ
(նկ. 2.3): Անհայտ կոնտուրային հոսանքները նշանակված են կրկնակի ինդեքսներով ![]()
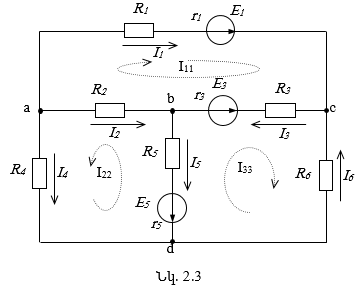
Երեք անկախ կոնտուր պարունակող շղթայում կոնտուրային հոսանքների հաշվման համար հավասարումների համակարգն ունի հետևյալ ընդհանուր տեսքը.
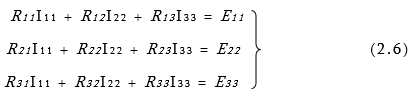
Այստեղ ![]() կոնտուրային էլշուներն են, որոնք
որոշվում են որպես համապատասխան անկախ կոնտուրների էլշուների հանրահաշվական գումար.
կոնտուրային էլշուներն են, որոնք
որոշվում են որպես համապատասխան անկախ կոնտուրների էլշուների հանրահաշվական գումար.
![]()
![]() կոչվում են անկախ կոնտուրների սեփական
դիմադրություններ և որոշվում են որպես կոնտուրի մեջ մտնող ճյուղերի դիմադրությունների
գումար.
կոչվում են անկախ կոնտուրների սեփական
դիմադրություններ և որոշվում են որպես կոնտուրի մեջ մտնող ճյուղերի դիմադրությունների
գումար.
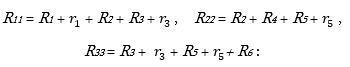
![]() դիմադրությունները կոչվում են փոխադարձ
դիմադրություններ և որոշվում են որպես երկու հարևան կոնտուրների ընդհանուր ճյուղի դիմադրությունների
գումար.
դիմադրությունները կոչվում են փոխադարձ
դիմադրություններ և որոշվում են որպես երկու հարևան կոնտուրների ընդհանուր ճյուղի դիմադրությունների
գումար.
![]()
Վերջինս վերցված է “–“ նշանով, որովհետև տվյալ ճյուղում երկու հարեվան կոնտուրների կոնտուրային հոսանքներն ունեն հակառակ ուղղություններ:
Լուծելով համատեղ (2.6) գծային հավասարումների համակարգը՝
որոշվում են կոնտուրային ![]() հոսանքները:
Որոնց հիման վրա, օգտվելով Կիրխհոֆի օրենքներից, որոշվում են շղթայի ճյուղերի իրական
հոսանքները.
հոսանքները:
Որոնց հիման վրա, օգտվելով Կիրխհոֆի օրենքներից, որոշվում են շղթայի ճյուղերի իրական
հոսանքները.
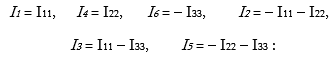
Կոնտուրային հոսանքների մեթոդը կարող է օգտագործվել նաև, երբ շղթան, բացի էլշուի կամ լարման աղբյուրներից, պարունակում է նաև հոսանքի աղբյուրներ: Այս դեպքում հոսանքի աղբյուր պարունակող կոնտուրներում կոնտուրային հոսանքը հայտնի է, ուստի այդ կոնտուրների համար հավասարումներ կազմել պետք չէ: Դրանք կազմվում են միայն մնացած անկախ կոնտուրների համար:
Շղթաների հաշվման վերադրման մեթոդը հիմնված է վերադրման սկզբունքի վրա:
Շղթայի որևէ տարրի սեղմակներում հոսանքը, ըստ Օհմի օրենքի, տրվում է I = U/R բանաձևով: Մինչև այժմ մենք համարել ենք, որ տարրի R դիմադրությունը հաստատուն է և կախված չէ I հոսանքից կամ U արումից: Դա նշանակում է, որ I = f(U) ֆունկցիան գծային է: Այդպիսի տարրերը կոչվում են գծային տարրեր և, համապատասխանաբար, էլեկտրական շղթաները, որոնք պարունակում են միայն գծային տարրեր, կոչվում են գծային շղթաներ:
Գծային շղթաների համար կիրառելի է վերադրման սկզբունքը, որի համաձայն գծային շղթայի որևէ ճյուղի հոսանքը հավասար է շղթայի առանձին աղբյուրների առաջացրած (երբ մյուս աղբյուրները փոխարինված են միայն իրենց ներքին դիմադրություններով) մասնակի հոսանքների հանրահաշվական գումարին:
Վերադրման սկզբւնքը լուսաբանելու համար դիտարկենք նկ. 2.4-ում պատկերված շղթան:
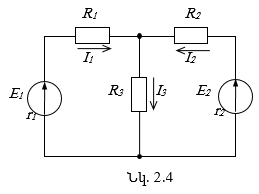
1)
Հեռացվում
է ![]() էլշու-ով աղբյուրը (նկ. 2.5ա), և
այն փոխարինվում դրա ներքին
էլշու-ով աղբյուրը (նկ. 2.5ա), և
այն փոխարինվում դրա ներքին ![]() դիմադրությամբ:
Այդ դեպքում միայն
դիմադրությամբ:
Այդ դեպքում միայն ![]() էլշու-ով պայմանավորված մասնակի
հոսանքները որոշվում են հետևյալ բանաձևերով.
էլշու-ով պայմանավորված մասնակի
հոսանքները որոշվում են հետևյալ բանաձևերով.
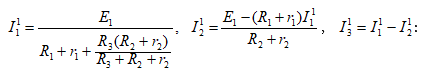
2) Հեռացվում է ![]() էլշու-ով
աղբյուրը (նկ.2.5բ): Համանման ձևով միայն
էլշու-ով
աղբյուրը (նկ.2.5բ): Համանման ձևով միայն ![]() էլշու-ով
պայմանավորված մասնակի հոսանքները կլինեն.
էլշու-ով
պայմանավորված մասնակի հոսանքները կլինեն.
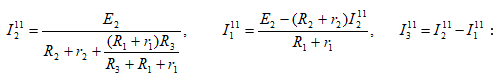
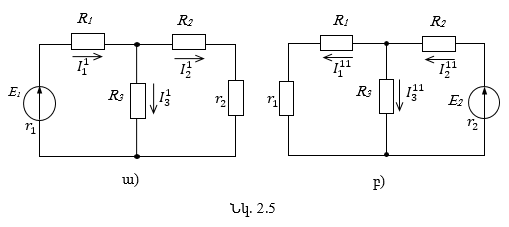
3) Վերադրման սկզբունքի հիման վրա շղթայի ճյուղերի իրական հոսանքները որոշվում են որպես այդ ճյուղերի մասնակի հոսանքների հանրահաշվական գումար.
![]()
Շղթաների հաշվարկի վերադրման սկզբունքն ունի մի էական թերություն. երբ որևէ ճյուղի մասնակի հոսանքները մոտ են արժեքներով և ունեն հակառակ ուղղություններ, ապա հաշվման սխալը կարող է զգալի լինել:
Նշենք, որ շղթայի տեղամասերի հզորությունները չի կարելի
հաշվել վերադրման սկզբունքի կիրառումով. դրանք պետք է հաշվել միայն ![]() իրական
հոսանքների արժեքներով:
իրական
հոսանքների արժեքներով:
2.5. Համարժեք գեներատորի մեթոդը (Թևենենի թեորեմը)
Այս մեթոդը նպատակահարմար է կիրառել այն դեպքերում, երբ անհրաժեշտ է որոշել հոսանքը բարդ շղթայի միայն որևէ մեկ ճյուղում, հատկապես, եթե այդ ճյուղի պարամետրերը ենթակա են փոփոխման:
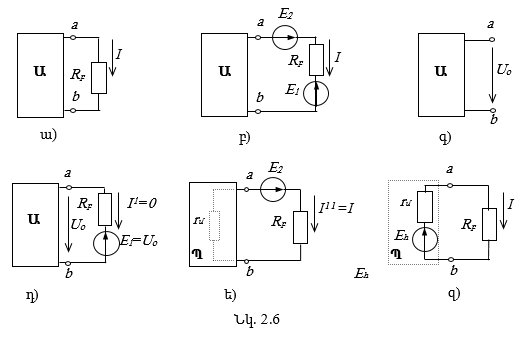
Դիցուք տրված է բարդ շղթա, որը պարունակում է լարման (և/կամ հոսանքի) աղբյուրներ և սպառիչներ: Պահանջվում է որոշել I հոսանքը այդ շղթայի a-b ճյուղում: Այդ ճյուղը առանձնացված է, իսկ շղթայի մնացյալ մասը պատկերված է ուղղանկյան տեսքով և կոչվում է ակտիվ երկբևեռ (Ա) (նկ. 2.6ա), ի տարբերություն պասիվ երկբևեռի (Պ), որը աղբյուրներ չի պարունակում (նկ. 2.6ե):
Երկբևեռի a-b տեղամասին հաջորդաբար միացնենք
երկու միանման, ![]() հավասար
և հակառակ ուղղված էլշուներով աղբյուրներ (նկ. 2.6բ): Ակնհայտ է, որ այդ դեպքում հոսանքը
a-b ճյուղում կմնա անփոփոխ՝ Iab = I, էլշուների ցանկացած արժեքի դեպքում: Ընտրենք
հավասար
և հակառակ ուղղված էլշուներով աղբյուրներ (նկ. 2.6բ): Ակնհայտ է, որ այդ դեպքում հոսանքը
a-b ճյուղում կմնա անփոփոխ՝ Iab = I, էլշուների ցանկացած արժեքի դեպքում: Ընտրենք
![]() որտեղ
որտեղ ![]() ակտիվ երկբևեռի,
այսպես կոչված, պարապ ընթացքի լարումն է: Սա այն լարումն է a և b ծայրակետերի
միջև, երբ a-b ճյուղը խզված է, այսինքն I = 0 (նկ. 2.5գ):
ակտիվ երկբևեռի,
այսպես կոչված, պարապ ընթացքի լարումն է: Սա այն լարումն է a և b ծայրակետերի
միջև, երբ a-b ճյուղը խզված է, այսինքն I = 0 (նկ. 2.5գ):
Դիտարկվող ճյուղի I հոսանքը կարելի է որոշել
վերադրման թեորեմի հիման վրա՝ ներկայացնելով այն որպես երկու մասնակի հոսանքների գումար,
![]() որտեղ
որտեղ ![]() հոսանքը, որը պայմանավորված է ակտիվ
երկբևեռի բոլոր աղբյուրների և
հոսանքը, որը պայմանավորված է ակտիվ
երկբևեռի բոլոր աղբյուրների և ![]() աղբյուրի համատեղ ազդեցությամբ,
ակնհայտորեն զրո է
աղբյուրի համատեղ ազդեցությամբ,
ակնհայտորեն զրո է ![]() իսկ հոսանքի
իսկ հոսանքի
![]() բաղադրիչը պայմանավորված է միայն
բաղադրիչը պայմանավորված է միայն
![]() էլշուով,
և այն գտնելու համար պետք է հեռացնել բոլոր մյուս աղբյուրները՝ փոխարինելով դրանք իրենց
ներքին դիմադրություններով: Որպես արդյունք, ակտիվ երկբևեռը կվերածվի պասիվ երկբևեռի
(նկ. 2.6ե): Պասիվ երկբևեռը, որը պարունակում է միայն որոշակի ձևով միմյանց հետ միացված
դիմադրություններ, կարելի է փոխարինել մեկ համարժեք (կամ մուտքային)
էլշուով,
և այն գտնելու համար պետք է հեռացնել բոլոր մյուս աղբյուրները՝ փոխարինելով դրանք իրենց
ներքին դիմադրություններով: Որպես արդյունք, ակտիվ երկբևեռը կվերածվի պասիվ երկբևեռի
(նկ. 2.6ե): Պասիվ երկբևեռը, որը պարունակում է միայն որոշակի ձևով միմյանց հետ միացված
դիմադրություններ, կարելի է փոխարինել մեկ համարժեք (կամ մուտքային) ![]() դիմադրությամբ: Ակնհայտ է, որ հոսանքի
դիմադրությամբ: Ակնհայտ է, որ հոսանքի
![]() երկրորդ բաղադրիչը, պայմանավորված
միայն
երկրորդ բաղադրիչը, պայմանավորված
միայն ![]() էլշուով
(նկ. 2.6ե), հավասար է տրված շղթայի a-b ճյուղով անցնող որոնելի հոսանքին (նկ.
2.6ա). Համեմատելով 2.6ա և 2.6ե նկարներում պատկերված սխեմաները՝ կարող ենք տեսնել,
որ ակտիվ երկբևեռը կարելի է փոխարինել
էլշուով
(նկ. 2.6ե), հավասար է տրված շղթայի a-b ճյուղով անցնող որոնելի հոսանքին (նկ.
2.6ա). Համեմատելով 2.6ա և 2.6ե նկարներում պատկերված սխեմաները՝ կարող ենք տեսնել,
որ ակտիվ երկբևեռը կարելի է փոխարինել ![]() էլշու և rմ ներքին դիմադրություն
ունեցող աղբյուրով կամ համարժեք գեներատորով (նկ. 2.6զ): Այդ դեպքում որոնելի հոսանքը,
ըստ Օհմի օրենքի (1.5), կլինի
էլշու և rմ ներքին դիմադրություն
ունեցող աղբյուրով կամ համարժեք գեներատորով (նկ. 2.6զ): Այդ դեպքում որոնելի հոսանքը,
ըստ Օհմի օրենքի (1.5), կլինի

Այս բանաձևից բխում է, որ հոսանքը շղթայի որևէ մեկ ճյուղում որոշելու համար բավական է իմանալ ակտիվ երկբևեռի միայն երկու պարամետր՝ լարումը դիտարկվող a-b ճյուղի ծայրերում, երբ հոսանքը դրանում զրո է, և մնացյալ շղթայի (ակտիվ երկբևեռի) մուտքային դիմադրությունը a և b սեղմակների նկատմամբ:
Ակտիվ երկբևեռի նշված պարամետրերը կարելի է որոշել նաև փորձնական ճանապարհով՝ կատարելով հետևյալ գործողությունները.
·
Վոլտմետրի
օգնությամբ չափում են պարապ ընթացքի ![]() լարումը շղթայի a և b սեղմակների
միջև:
լարումը շղթայի a և b սեղմակների
միջև:
·
Կարճ
փակելով a և b սեղմակները ![]() ամպերմետրի
օգնությամբ չափվում է կարճ միացման
ամպերմետրի
օգնությամբ չափվում է կարճ միացման ![]() հոսանքը
a-b տեղամասում:
հոսանքը
a-b տեղամասում:
· Օհմի օրենքով որոշվում է մուտքային դիմադրությունը՝
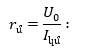
2.6. Մեկ աղբյուր պարունակող շղթաների հաշվարկը
Մեկ աղբյուր պարունակող շղթաների հաշվարկը հարմար է կատարել` կիրառելով շղթաների համարժեք ձևափոխման և պարզեցման եղանակները, պահպանելով հետևյալ հաջորդականությունը:
1) Տրված շղթայի ճյուղերում նշել անհայտ հոսանքների ուղղությունները՝ ելնելով աղբյուրի էլշու-ի (կամ լարման) տրված ուղղությունից: Եթե որևէ ճյուղում դժվար է նախօրոք նշել հոսանքի իրական ուղղությունը, ապա այն նշվում է կամայականորեն: Եթե հաշվարկման արդյունքում այդ հոսանքի արժեքը ստացվի բացասական, նշանակում է դրա իրական ուղղությունը պետք է լինի նախապես նշվածին հակառակ:
2) Աղբյուրից դուրս ամբողջ շղթան ենթարկվում է համարժեք ձևափոխության, աստիճանաբար պարզեցվում է և փոխարինվում մեկ համարժեք դիմադրությամբ:
3) Ստացված պարզագույն շղթայի համար ըստ Օհմի օրենքի գրված (1.2) կամ (1.5) բանաձևի միջոցով որոշվում է աղբյուրի հոսանքը:
4) Աստիճանաբար վերադառնալով սկզբնական շղթային և կիրառելով Օհմի կամ Կիրխհոֆի օրենքները` որոշվում են մյուս անհայտ հոսանքները կամ լարումները:
2.7. Հաստատուն հոսանքի շղթաների հաշվման օրինակներ
Խնդիր 2.1. Որոշել վոլտմետրի ցուցմունքը[3]3 պատկերված շղթայում, եթե հայտնի է, որ ![]()
Լուծում.
Սխեմայի վրա նշում ենք անհայտ հոսանքների դրական ուղղությունները՝
ելնելով աղբյուրի էլշուի տրված ուղղությունից: Կամայականորեն նշում ենք նաև վոլտմետրի
ցուցմունքին համապատասխանող ![]() լարման դրական ուղղությունը:
լարման դրական ուղղությունը:
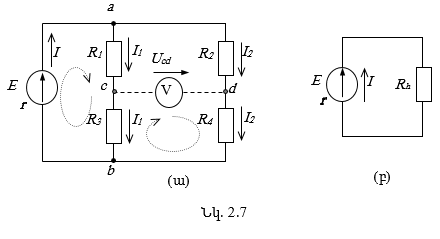
3 Վոլտմետրի ներքին դիմադրությունը համարել անվերջ մեծ:
· Հաշվում ենք շղթայի համարժեք
դիմադրությունը. ![]() ինչպես նաև
ինչպես նաև ![]() դիմադրությունները միացված
են հաջորդաբար, հետևաբար նրանց համարժեք դիմադրությունները կլինեն,
դիմադրությունները միացված
են հաջորդաբար, հետևաբար նրանց համարժեք դիմադրությունները կլինեն,
![]()
Իրենց հերթին, ![]() համարժեք դիմադրությունները միացված են զուգահեռ,
հետևաբար ամբողջ շղթայի համարժեք դիմադրությունը կլինի
համարժեք դիմադրությունները միացված են զուգահեռ,
հետևաբար ամբողջ շղթայի համարժեք դիմադրությունը կլինի
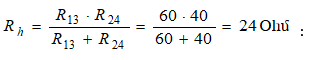
· Ստացված պարզագույն շղթայի համար (նկ. 2.7բ) գրելով Օհմի օրենքի բանաձևը (1.5)` որոշում ենք շղթայի ընդհանուր հոսանքը.
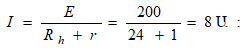
· Տրված շղթայի a-c-b-a կոնտուրի համար (նկ.2.7ա), ընտրելով շրջանցման ուղղություն, ըստ Կիրխհոֆի 2-րդ օրենքի կարելի է գրել.
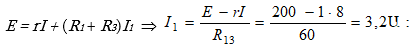
Ըստ Կիրխհոֆի I օրենքի, a հանգույցի համար կարելի է գրել.
![]()
· Վերջապես, c-d-b-c կոնտուրի համար ըստ Կիրխհոֆի 2-րդ օրենքի գրելով հավասարում, ստանում ենք անհայտ լարման արժեքը (վոլտմետրի ցուցմունքը).
![]()
Լարման բացասական նշանը ցույց է տալիս, որ լարման իրական ուղղությունը հակառակ է սխեմայում նախօրոք նշված ուղղությանը:
Խնդիր 2.2. Որոշել ամպերմետրի4 ցուցմունքը
պատկերված շղթայում՝ համարելով աղբյուրի և սպառիչների պարամետրերը ![]() տրված (նկ. 2.8ա):
տրված (նկ. 2.8ա):
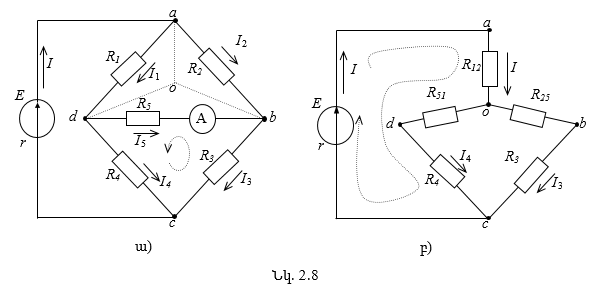
· Անհայտ հոսանքների իրական
ուղղությունները շղթայի ճյուղերում նշված են՝ ելնելով E էլշուի տրված ուղղությունից,
d-b ճյուղում ![]() հոսանքի
ուղղությունն անհնար է նախօրոք որոշել, ուստի այն նշված է կամայականորեն:
հոսանքի
ուղղությունն անհնար է նախօրոք որոշել, ուստի այն նշված է կամայականորեն:
· Տրված շղթայում բացակայում
են դիմադրությունների հաջորդական կամ զուգահեռ միացումները, կան միայն աստղաձև և եռանկյունաձև
միացումներ, հետևաբար շղթան պարզեցնելու համար կարող ենք, օրինակ, ձևափոխել շղթայի
եռանկյունաձև միացված abd տեղամասը համարժեք աստղաձև միացումով: Այդ նպատակով
խորհուրդ է տրվում նախ գծել շղթայի մնացյալ չձևափոխվող տեղամասը, այնուհետև եռանկյունաձև
միացված ![]() դիմադրությունների փոխարեն
գծել աստղաձև միացված
դիմադրությունների փոխարեն
գծել աստղաձև միացված ![]() նոր դիմադրություններ՝ շղթայում ավելացնելով o նոր
հանգույցը (նկ. 2.8բ).
նոր դիմադրություններ՝ շղթայում ավելացնելով o նոր
հանգույցը (նկ. 2.8բ).
· Հաշվել համարժեք ![]() դիմադրությունները` կիրառելով
(1.20) բանաձևերը.
դիմադրությունները` կիրառելով
(1.20) բանաձևերը.
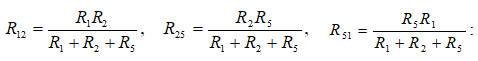
Ձևափոխված շղթայում (նկ. 2.8բ) ![]() ինչպես նաև
ինչպես նաև ![]() դիմադրությունները միացված են հաջորդաբար, դրանց համարժեք
դիմադրությունները՝
դիմադրությունները միացված են հաջորդաբար, դրանց համարժեք
դիմադրությունները՝ ![]() իրենց հերթին, միացված են զուգահեռ, և վերջապես, դրանց
համարժեք դիմադրությունը միացված է
իրենց հերթին, միացված են զուգահեռ, և վերջապես, դրանց
համարժեք դիմադրությունը միացված է ![]() հետ հաջորդաբար: Այսպիսով շղթայի (աղբյուրից դուրս)
համարժեք դիմադրությունը կլինի
հետ հաջորդաբար: Այսպիսով շղթայի (աղբյուրից դուրս)
համարժեք դիմադրությունը կլինի
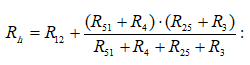
• Ստացված պարզագույն շղթայի համար, Օհմի օրենքի հիման վրա, աղբյուրի հոսանքը կլինի
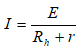
• Կիրխհոֆի 2-րդ օրենքի հիման վրա, a-o-d-c-a կոնտուրի (նկ. 2.8բ) համար, կարելի է գրել
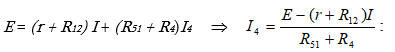
Կիրառելով Կիրխհոֆի I օրենքը o հանգույցի համար՝ կստանանք
![]()
Սկզբնական շղթայի (նկ. 2.7ա) c-b-d-c կոնտուրի համար կիրառելով Կիրխհոֆի 2-րդ օրենքը՝ գտնում ենք ամպերմետրի որոնելի հոսանքը.
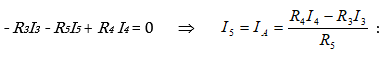
Եթե ստացվում է ![]() հոսանքի բացասական արժեք, ապա դրա իրական
ուղղությունը նշվածին հակառակ է:
հոսանքի բացասական արժեք, ապա դրա իրական
ուղղությունը նշվածին հակառակ է:
Խնդիր 2.3. Պատկերված շղթայում, համարելով տրված աղբյուրների և սպառիչների բոլոր պարամետրերը (E.., r.., R…), որոշել ճյուղերի հոսանքները (նկ. 2.9):
Դիտարկենք այս խնդրի լուծումը տարբեր եղանակներով:
ա) Տրված շղթայի հաշվարկը Կիրխհոֆի օրենքների կիրառությամբ:
· Սխեմայից որոշում ենք շղթայի ճյուղերի թիվը՝ m = 5, և դրանցում կամայականորեն նշում անհայտ հոսանքների ուղղությունները:
· Որոշում ենք հանգույցների թիվը՝ n = 3, և ցանկացած n – 1 = 2 հանգույցի համար ըստ Կիրխհոֆի 1-ին օրենքի կազմում ենք հավասարումներ.
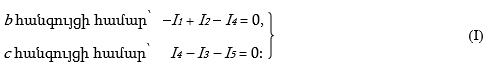
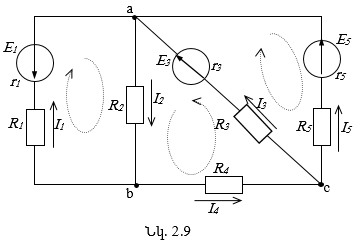
· Հաշվում ենք շղթայի անկախ կոնտուրների թիվը՝ k = m – n + 1 = 3, սխեմայի վրա նշում ենք դրանց շրջանցման ուղղությունները (նկ. 2.9) և ըստ Կիրխհոֆի 2-րդ օրենքի դրանց համար կազմում ենք հավասարումներ.
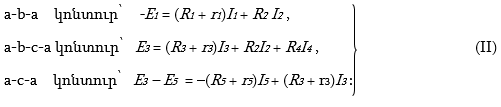
· Համատեղ լուծելով (I) և (II) գծային հավասարումների համակարգը՝ որոշում ենք բոլոր անհայտ հոսանքները: Եթե որևէ ճյուղի հոսանքը ստացվում է “-“ նշանով, ապա դրա իրական ուղղությունը պետք է լինի նշվածին հակառակ:
բ) Տրված շղթայի հաշվարկը կոնտուրային հոսանքների եղանակով:
· Քանի որ տրված շղթան ունի 3 անկախ կոնտուր, ապա կոնտուրային հոսանքների եղանակով պետք է կազմել 3 հավասարումներից կազմված համակարգ, որի ստանդարտ տեսքն է (տես (2.6)).

· Որոշենք այս հավասարումների գործակիցները.
Անկախ կոնտուրների սեփական դիմադրությունները.
![]()
Կոնտուրների փոխադարձ դիմադրությունները.
![]()
Կոնտուրային էլշուները.
![]()
·
Տեղադրելով
գործակիցների արժեքները (III) հավասարումների համակարգի մեջ և լուծելով այն՝ որոշում
են կոնտուրային ![]() հոսանքների
արժեքները:
հոսանքների
արժեքները:
· Կոնտուրների անկախ ճյուղերի հոսանքները կլինեն.
![]()
· Կոնտուրների ընդհանուր ճյուղերի հոսանքներն ըստ (I) համակարգի հավասարումների կլինեն.
![]()
2.8. Քառաբևեռ և դրա հիմնական հավասարումները
Քառաբևեռ է կոչվում այնպիսի էլեկտրական շղթան, որն ունի երկու մուտքային և երկու ելքային սեղմակներ: Տրանսֆորմատորը, էլեկտրահաղորդման գիծը, կամրջակային սխեման և այլն կարելի է դիտարկել որպես քառաբևեռ:
Ընդունված է քառաբևեռը պատկերել ուղղանկյան տեսքով, որից դուրս են գալիս 4 ծայրեր կամ բևեռներ՝ m, n և p, q.
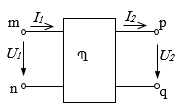
Եթե քառաբևեռը պարունակում է էներգիայի աղբյուր, ապա այն կոչվում է ակտիվ քառաբևեռ, և ուղղանկյան ներսում նշվում է Ա տառը, իսկ եթե չի պարունակում աղբյուր, այն կոչվում է պասիվ և նշվում Պ տառով: Մենք կդիտարկենք միայն պասիվ քառաբևեռները:
Որպես կանոն, մուտքային m-n սեղմակներին միանում է
աղբյուրը, իսկ ելքային p-q սեղմակներին՝ սպառիչը (բեռնվածքը): Փաստորեն քառաբևեռը միջանկյալ
օղակ է սնման աղբյուրի և բեռնվածքի միջև: Մուտքային լարումը և հոսանքը նշանակվում են
![]() իսկ ելքայինները՝
իսկ ելքայինները՝
![]()
Քառաբևեռի տեսության հիմնական նպատակը մուտքի և ելքի
լարումների ու հոսանքների միջև կապի հաստատումն է առանց քառաբևեռի ներքին սխեմայի մանրակրկիտ
ուսումնասիրման: Ցանկացած գծային պասիվ քառաբևեռի մուտքային ![]() մեծությունները
կապված են ելքային
մեծությունները
կապված են ելքային ![]() մեծությունների հետ երկու հիմնական
հավասարումներով.
մեծությունների հետ երկու հիմնական
հավասարումներով.

A, B, C, D –ն հաստատուն գործակիցներ են տվյալ քառաբևեռի համար և դրանց արժեքները կախված են քառաբևեռի ներքին սխեմայից և դիմադրությունների մեծություններից: Քառաբևեռի գործակիցները կարելի է որոշել հաշվարկային կամ փորձնական եղանակով:
Քառաբևեռը կարելի է պատկերացնել որպես երկու անկախ կոնտուր պարունակող շղթա, որի համար մուտքային և ելքային ճյուղերը հանդիսանում են այդ անկախ կոնտուրների սեփական ճյուղեր (նկ. 2.10):
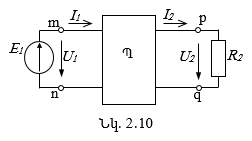
Հետևաբար, oգտվելով կոնտուրային հոսանքների մեթոդից (տես 2.3 բաժինը), կարող ենք կազմել երկու անկախ հավասարում.
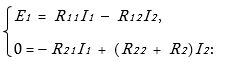
Եթե հավասարումների այս համակարգը լուծենք ![]() հոսանքների
նկատմամբ և նկատի ունենանք, որ
հոսանքների
նկատմամբ և նկատի ունենանք, որ ![]() ապա կստանանք.
ապա կստանանք.
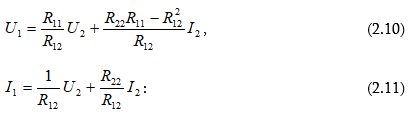
Համեմատելով (2.8) և (2.10), (2.9) և (2.11) հավասարումները՝ կստանանք A, B, C, D գործակիցների արժեքները:
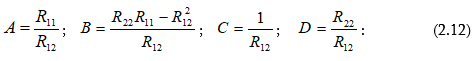
Դժվար չէ համոզվել, որ
![]()
Իսկապես, տեղադրելով գործակիցների արժեքները (2.13)-ի մեջ, կստանանք
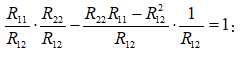
Եթե սնման աղբյուրը միացվի p-q, իսկ բեռնվածքը՝ m-n սեղմակներին (նկ. 2.11), ապա քառաբևեռի հավասարումները կլինեն,
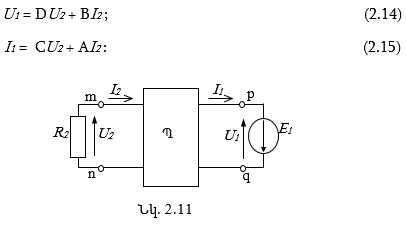
Քառաբևեռը կոչվում է սիմետրիկ, եթե աղբյուրի և բեռնվածքի տեղերը փոխելիս հոսանքները դրանցում չեն փոխվում: Ակնհայտ է, որ սիմետրիկ քառաբևեռի համար A = D:
Եթե (2.8) և (2.9) կամ (2.14) և (2.15) հավասարումներում
չորս մեծություններից ![]() երկուսը հայտնի են, կարելի է
որոշել մյուս երկուսը և ստանալ քառաբևեռի այլ հավասարումներ նույնպես:
երկուսը հայտնի են, կարելի է
որոշել մյուս երկուսը և ստանալ քառաբևեռի այլ հավասարումներ նույնպես:
2.9. Քառաբևեռի գործակիցների որոշումը:
Քառաբևեռի A, B, C, D գործակիցների արժեքները, որոնք մտնում են (2.8) և (2.9) կամ (2.14) և (2.15) հավասարումներում, կարելի է որոշել (2.12) բանաձևերով, եթե քառաբևեռի ներքին սխեման և դրա տարրերի պարամետրերը հայտնի են:
Քառաբևեռի գործակիցները կարելի է որոշել նաև փորձնական եղանակով՝ մուտքին միացված վոլտմետրի և ամպերմետրի միջոցով: Դրա համար անհրաժեշտ է կատարել երեք փորձ:
I փորձ. նկ. 2.10 սխեմայում ելքային
p-q ճյուղը խզված է և ![]() (պարապ ընթացքի ռեժիմ), այս դեպքում (2.8) և
(2.9) հավասարումներից կստանանք.
(պարապ ընթացքի ռեժիմ), այս դեպքում (2.8) և
(2.9) հավասարումներից կստանանք.
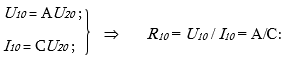
II փորձ. նկ. 2.9 սխեմայում p-q ճյուղը
կարճ է միացված և ![]()
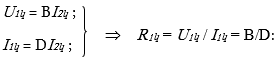
III փորձ. սնումը կատարվում է p-q սեղմակներից
(նկ. 2.11-ի սխեման), ելքային m-n ճյուղը կարճ է միացված և ![]() (2.14) և (2.15) հավասարումներից
կստանանք.
(2.14) և (2.15) հավասարումներից
կստանանք.
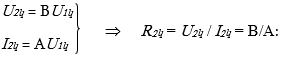
Այսպիսով, քառաբևեռի A, B, C, D գործակիցների որոշման համար (2.13) -ի հետ միասին ունենում ենք անհրաժեշտ չորս հավասարումներ.
![]()
2.10. Պասիվ քառաբևեռի փոխարինման սխեմաները
Փաստորեն քառաբևեռը կարելի է բնութագրել միայն երեք անկախ գործակիցներով (չորրորդը ստացվում է այդ երեքից, (2.13)-ի միջոցով): Ուստի քառաբևեռի փոխարինման համարժեք պարզեցված սխեման նույնպես կարելի է ներկայացնել միայն երեք պարամետրերով (դիմադրություններով): Դա կարող է լինել աստղաձև միացված (կամ T-աձև սխեմա, նկ. 2.12ա) կամ եռանկյունաձև միացված (կամ П-աձև սխեմա, նկ. 2.12բ):
T-աձև կամ П-աձև սխեմաների դիմադրությունները
պետք է հաշվարկվեն այնպես, որպեսզի դրանց A, B, C, D գործակիցները լինեն նույնը, ինչ
որ այն քառաբևեռինը, որը դրանք փոխարինում են: Այդ նպատակով նկ. 2.12 սխեմայում ![]() մուտքային մեծություններն արտահայտենք
մուտքային մեծություններն արտահայտենք ![]() ելքային մեծություններով:
ելքային մեծություններով:
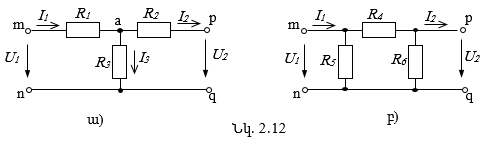
Ըստ Կիրխհոֆի 1-ին և 2-րդ օրենքների, նկ. 2.12ա սխեմայի համար կարող ենք ստանալ.
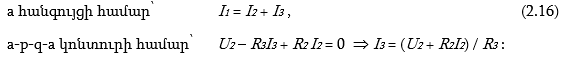
Տեղադրելով ![]() արժեքը ( 2. 16) -ի մեջ՝ կստանանք
արժեքը ( 2. 16) -ի մեջ՝ կստանանք

m-p-q-n-m կոնտուրի համար (նկ.
2.12ա), ըստ Կիրխհոֆի 2-րդ օրենքի` ![]() որտեղից, տեղադրելով
որտեղից, տեղադրելով
![]() ստացված արժեքը, ստանում ենք
ստացված արժեքը, ստանում ենք
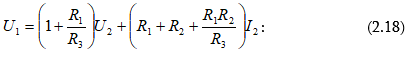
Համեմատելով (2.8)-ը (2.18)-ի հետ և (2.9)-ը (2.17)-ի հետ` կստանանք.
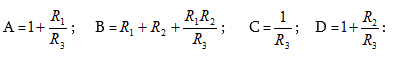
Այստեղից՝
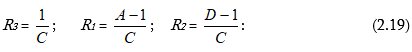
(2.19) բանաձևերը հնարավորություն են տալիս որոշել քառաբևեռի փոխարինման T-աձև սխեմայի (նկ. 2.12ա) դիմադրությունները, երբ քառաբևեռի A, B, C, D գործակիցների արժեքները հայտնի են:
Համանման ձևով П-աձև սխեմայի (նկ. 2.12բ) համար կարելի է ստանալ.
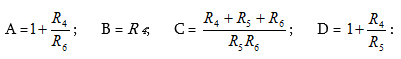
Որտեղից՝
![]()
Եթե քառաբևեռը սիմետրիկ է, ապա A = D և T-աձև սխեմայում`
![]() իսկ П-աձև սխեմայում՝
իսկ П-աձև սխեմայում՝ ![]()
2.11. Հաստատուն հոսանքի ոչ գծային շղթաներ
Մինչև այժմ շղթայի տարրերի պարամետրերը մենք ընդունել ենք որպես հաստատուն մեծություններ, այսինքն համարել ենք, որ դրանցով անցնող հոսանքը կախված է դրանց ծայրերում եղած լարումից գծայնորեն: Սակայն, ընդհանուր դեպքում, իրական շղթայի որևէ տեղամասում հոսանքի և լարման կախվածությունը ոչ գծային է: Որոշ սարքերի համար այդ ոչ գծայնությունն աննշան է հոսանքի և լարման փոփոխության մեծ սահմաններում, ուստի այդպիսի սարքը կարելի է ներկայացնել համարժեք գծային տարրով: Սակայն, գործնականում կիրառվող շատ սարքերի համար հոսանք-լարում կապը էապես ոչ գծային է, և դրանք էլեկտրական շղթայում պատկերվում են որպես ոչ գծային տարրեր: Շղթայի ոչ գծային տարրը բնութագրվում է ոչ թե մի որոշակի պարամետրով (ինչպես օրինակ դիմադրությունն է), այլ այսպես կոչված վոլտամպերային (կամ արտաքին) բնութագծով:

Որպես օրինակ, նկ. 2.13ա-ում պատկերված են շիկացման լամպի (1) և կիսահաղորդիչային դիոդի (2) վոլտ-ամպերային բնութագծերը, իսկ նկ. 2.13բ-ում՝ ոչ գծային տարրի պայմանական նշանը:
Եթե շղթան պարունակում է թեկուզ և մեկ ոչ գծային տարր, ապա այն կոչվում է ոչ գծային շղթա: Ընդհանուր դեպքում ոչ գծային շղթան կարող է պարունակել նաև ոչ գծային լարման կամ հոսանքի աղբյուրներ, որոնց հատկությունները նույնպես բնութագրվում են համապատասխան վոլտ-ամպերային (կամ արտաքին) բնութագծով:
Ոչ գծայնության պատճառով վերադրման թեորեմի վրա հիմնված շղթաների անալիզի մեթոդները դառնում են ոչ պիտանի: Ընդհանուր դեպքում ոչ գծային շղթաները մենք չենք կարող հաշվել կոնտուրային հոսանքների, միջհանգուցային լարման, շղթաների համարժեք ձևափոխման մեթոդներով: Համարժեք գեներատորի եղանակը կիրառելի է միայն այն դեպքերում, երբ ակտիվ երկբևեռը չի պարունակում որևէ ոչ գծային տարր:
Հաստատուն հոսանքի ոչ գծային պարզ շղթաների հաշվարկը սովորաբար կատարվում է գրաֆիկորեն, որի համար անհրաժեշտ է ունենալ ոչ գծային տարրերի վոլտամպերային բնութագծերը:
Դիտարկենք R գծային դիմադրության և ո.գ. ոչ գծային տարրի հաջորդաբար միացված շղթան (նկ. 2.14ա): Ենթադրելով, որ R դիմադրության, աղբյուրի E էլշուի արժեքները և ոչ գծային տարրի վոլտ-ամպերային բնութագիծը տրված են` որոշենք շղթայի հոսանքը:
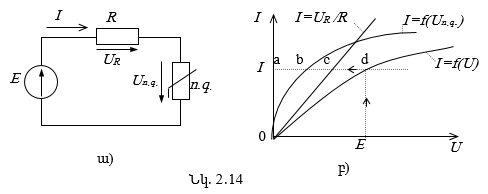
Ոչ գծային դիմադրության վոլտամպերային բնութագիծը տրված
է ![]() կորով
(նկ. 2.14բ), իսկ R գծային դիմադրությունը՝
կորով
(նկ. 2.14բ), իսկ R գծային դիմադրությունը՝ ![]() ուղիղ գծով: Ըստ Կիրխհոֆի 2-րդ օրենքի
ուղիղ գծով: Ըստ Կիրխհոֆի 2-րդ օրենքի
![]() ուստի արդյունարար
ուստի արդյունարար
![]() կորը կառուցելու
համար պետք է ելնել այն բանից, որ հաջորդաբար միացված շղթայում ցանկացած հոսանքի (օրդինատի)
դեպքում տանելով հորիզոնական ուղիղ (ասենք ad), գումարվում են համապատասխան լարումները
(աբսցիսները)՝ ad = ab + ac:
կորը կառուցելու
համար պետք է ելնել այն բանից, որ հաջորդաբար միացված շղթայում ցանկացած հոսանքի (օրդինատի)
դեպքում տանելով հորիզոնական ուղիղ (ասենք ad), գումարվում են համապատասխան լարումները
(աբսցիսները)՝ ad = ab + ac:
Տրված E-ի դեպքում շղթայի հոսանքը որոշելու համար աբսցիսների առանցքի վրա տեղադրվում է E -ին հավասար հատված և ստացված կետից տարվում է օրդինատների առանցքին զուգահեռ ուղիղ մինչև I = f(U) կորի հետ հատվելը (d կետը). այդ կետի օրդինատն էլ (a կետը) կլինի որոնելի հոսանքի արժեքը:
Դիտարկված գծային և ոչ գծային տարրերի զուգահեռ միացման դեպքում (նկ. 2.15ա) նույնպես պահանջվում է որոշել շղթայի ընդհանուր հոսանքը (աղբյուրի հոսանքը) տրված լարման դեպքում:
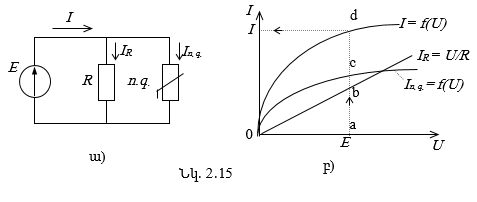
Ըստ Կիրխհոֆի 1-ին օրենքի ![]() հետևաբար
զուգահեռ միացման դեպքում ցանկացած լարման (աբսցիսի) համար գումարվում են ճյուղերի
հոսանքները (օրդինատները). ad = ab + ac (նկ. 2.15բ):
հետևաբար
զուգահեռ միացման դեպքում ցանկացած լարման (աբսցիսի) համար գումարվում են ճյուղերի
հոսանքները (օրդինատները). ad = ab + ac (նկ. 2.15բ):
Համանման ձևով կատարվում է երկուսից ավելի տարրերի հաջորդական, զուգահեռ կամ խառը միացումով ոչ գծային շղթաների հաշվարկը:
1. Որո՞նք են էլեկտրական շղթաների հաշվարկի երկու հիմնարար խնդիրները` շղթայի անալիզը և սինթեզը:
2. Եթե շղթայի ճյուղերի թիվը m է, իսկ հանգույցների թիվը` n, ապա շղթայի հոսանքների հաշվման համար քանի հավասարում պետք է կազմել, համապատասխանաբար, Կիրխոֆի 1-ին և 2-րդ օրենքներով:
3. Տալ շղթայի անկախ կոնտուրների սահմանումը, քանիսն են դրանք:
4. Գրել շղթայի էլշու պարունակող ճյուղի համար հոսանքի և լարման կապը արտահայտող արտահայտությունը (Օհմի ընդհանրացված օրենքը):
5. Երկու հանգույց պարունակող շղթայի համար գրել միջհանգուցային լարման բանաձևը:
6. Օգտվելով կոնտուրային հոսանքների մեթոդից` գրել հավասարումների համակարգը ա) երկու անկախ կոնտուր, բ) երեք անկախ կոնտուր պարունակող շղթայի համար:
7. Գծային էլեկտրական շղթայի համար տալ վերադրման սկզբունքի սահմանումը:
8. Ի՞նչ բանաձևով է որոշվում շղթայի որոշակի ճյուղի հոսանքը` համաձայն համարժեք գեներատորի եղանակի:
9. Տալ ակտիվ և պասսիվ քառաբևեռների սահմանումը: Ինչպե՞ս են դրանք պատկերվում սխեմայում:
10. Ի՞նչ առնչություններով են կապված պասսիվ քառաբևեռի մուտքի լարումն ու հոսանքը ելքի լարման ու հոսանքի հետ:
11. Ի՞նչ առնչությունով են կապված պասիվ քառաբևեռի գործակիցները:
12. Գծել պասիվ քառաբևեռի T-աձև և П-աձև փոխարինման սխեմաները:
13. Փորձնականորեն ինչպե՞ս են որոշվում քառաբևեռի գործակիցները:
14. Տալ էլեկտրական շղթայի ոչ գծային տարրի և ոչ գծային շղթայի սահմանումները:
15. Գծային շղթաների հաշվման ո՞ր մեթոդներն են կիրառելի ոչ գծային շղթաների հաշվարկի համար և որոնք՝ ոչ:
3.1. Ընդհանուր դրույթներ: Սինուսոիդական հոսանքի ստացումը
Ներկայումս էլեկտրաէներգետիկան գլխավորապես հիմնված է փոփոխական հոսանքի օգտագործման վրա: Նույնիսկ որոշ բնագավառներում կիրառվող հաստատուն հոսանքը հիմնականում ստանում են փոփոխական հոսանքից՝ ուղղման միջոցով: Դա պայմանավորված է այն հանգամանքով, որ փոփոխական հոսանքով են աշխատում տրանսֆորմատորները, որոնք ընդունակ են շատ փոքր էներգետիկական կորուստներով բարձրացնել և իջեցնել աղբյուրի լարումը, առանց որի անհնար է պատկերացնել էլեկտրաէներգիայի հաղորդումը մեծ հեռավորությունների վրա:
Սկզբունքորեն փոփոխական է համարվում ժամանակի ընթացքում փոփոխվող ցանկացած հոսանք: Սակայն գործնականում փոփոխական հոսանք ասելով` սովորաբար ենթադրում են սինուսոիդական օրենքով փոփոխվող հոսանքը: Այն ապահովում է էլեկտրաէներգիայի ավելի շահավետ արտադրություն, հաղորդում և բաշխում: Բացի այդ, սինուսոիդական հոսանքը գծային շղթաներում չի փոխում իր սինուսոիդական բնույթը:
Գործնականում սինուսոիդական հոսանքի հիմնական աղբյուրներ են, այսպես կոչված, սինքրոն գեներատորները: նկ. 3.1ա-ում պատկերված է սինքրոն գեներատորի լայնակի հատույթը՝ պարզեցված տեսքով, իսկ նկ. 3.1բ-ում՝ դրա ռոտորի երկայնական տեսքը:
Գեներատորը բաղկացած է անշարժ մասից՝ ստատորից և պտտվող մասից՝ ռոտորից: Ստատորն ունի սնամեջ գլանի տեսք և պատրաստվում է էլեկտրատեխնիկական պողպատի թիթեղներից: Դրա ներքին մակերևույթի վրա արվում են երկայնական փորակներ (ակոսներ) ստատորի փաթույթի տեղադրման համար: Ստատորի փաթույթը կազմված է մեկուսացված պղնձե (երբեմն ալյումինե) հաղորդալարերից: Նկարում, պարզության համար, այն պատկերված է մեկ գալարի տեսքով:
Ռոտորը էլեկտրամագնիս է, որի մագնիսական դաշտը գրգռվում է հաստատուն հոսանքով: Վերջինիս համար որպես աղբյուր է ծառայում գրգռիչը, որը հաստատուն հոսանքի մի փոքր աղբյուր է և միանում է ռոտորի փաթույթին՝ լիսեռին ամրացված, բայց դրանից էլեկտրականապես մեկուսացված երկու պղնձե օղակների և գրաֆիտե խոզանակների միջոցով:
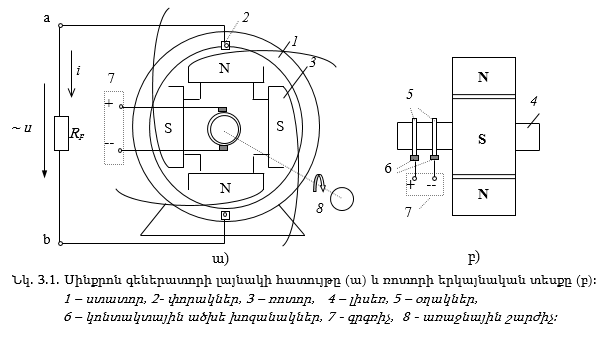
Գեներատորի լիսեռը ռոտորի հետ միասին հաստատուն արագությամբ պտտման մեջ է դրվում առաջնային շարժիչի (տուրբինի) միջոցով: Դրա հետևանքով պտտվում է նաև էլեկտրամագնիսների ստեղծած մագնիսական դաշտը, որի ուժագծերը, հատելով ստատորի փաթույթների գալարները, դրանցում ինդուկտում են էլշու (համաձայն Ֆարադեյի էլեկտրամագնիսական ինդուկցիայի օրենքի)՝
![]()
որտեղ e -ն սինուսոիդական էլշուի ակնթարթային
արժեքն է ժամանակի t պահին, ![]() էլշուի առավելագույն կամ ամպլիտուդային
արժեքը,
էլշուի առավելագույն կամ ամպլիտուդային
արժեքը, ![]() էլշուի սկզբնական փուլը,
էլշուի սկզբնական փուլը,
![]() անկյունային
հաճախությունը:
անկյունային
հաճախությունը:
Մեր օրինակում գեներատորն ունի երկու զույգ մագնիսական բևեռ (նկ. 3.1): Ընդհանուր դեպքում այն կարող է ունենալ p զույգ բևեռ, և այդ դեպքում ինդուկտված էլշուի հաճախությունը (1 վայրկյանում սինուսոիդական ցիկլերի թիվը) կլինի f = pn/60, որտեղ n -ը ռոտորի պտուտաթվերն են (պտ/ր):
Միավորների միջազգային համակարգում (ՄՀ) հաճախության
հիմնական միավորն է հերցը (Հց)՝ ![]()
Հաճախության ստանդարտ արժեքը աշխարհի շատ երկրներում f = 50 Հց է (ԱՄՆ-ում, Կանադայում, Ճապոնիայում՝ 60 Հց): Ավելի ցածր հաճախությունը (25…30 Հց) առաջացնում է աչքի համար նկատելի լույսի թրթռոց, բացի այդ այն նեղացնում է էլեկտրական մեքենաների արագությունների միջակայքը և մեծացնում է դրանց գաբարիտային չափերը: Մյուս կողմից՝ հաճախության ավելի մեծ արժեքների դեպքում առաջանում են էներգիայի լրացուցիչ կորուստներ՝ կապված էլեկտրահաղոդման գծերի, էլեկտրական տարբեր սարքերի ինդուկտիվ դիմադրության (տես բաժին 3.4-ը) մեծացման հետ:
Հաճախության հակադարձ մեծությունը, որը ցույց է տալիս սինուսոիդական մեկ ցիկլի տևողությունը, կոչվում է պարբերություն, T = 1/f (վ):
Եթե գեներատորի a-b սեղմակներին միացվի սպառիչ, ապա սինուսոիդական էլշուի շնորհիվ դրանով կանցնի սինուսոիդական հոսանք՝
![]()
և a-b սեղմակների միջև կհաստատվի սինուսոիդական լարում՝
![]()
Փոփոխական հոսանքի գեներատորը սխեմաներում պատկերվում է հետևյալ պայմանական նշաններով.
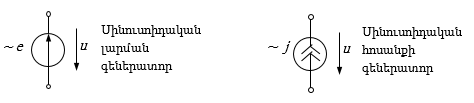
3.2. Սինուսոիդական մեծությունների գործող և միջին արժեքները
Սինուսոիդական օրենքով փոփոխվող հոսանքի մեծությունը գնահատելու համար այն համեմատում են իր ջերմային ազդեցությամբ համարժեք հաստատուն հոսանքի հետ: Սինուսոիդական հոսանքի գործող արժեք է կոչվում այնպիսի հաստատուն հոսանքի ուժը, որն անցնելով որևէ դիմադրության միջով որոշակի ժամանակամիջոցում անջատում է նույնքան ջերմություն, որքան և դիտարկվող սինուսոիդական հոսանքը՝ անցնելով այդ նույն դիմադրության միջով այդ նույն ժամանակամիջոցում:
Հաստատուն I հոսանքի անջատած ջերմության քանակը, երբ այն անցնում է R դիմադրության միջով սինուսոիդական հոսանքի t = T մեկ պարբերության ընթացքում, ըստ (1.12) -ի, կլինի
![]()
իսկ սինուսոիդական հոսանքի առաջացրած ջերմության քանակը, երբ այն անցնում է նույն դիմադրության միջով մեկ պարբերության ընթացքում`
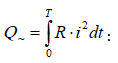
Ըստ սահմանման սինուսոիդական հոսանքի գործող արժեքը
կորոշվի ![]() հավասարությունից՝
հավասարությունից՝
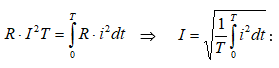
Այսպիսով, սինուսոիդական հոսանքի գործող արժեքը մաթեմատիկորեն
որոշվում է որպես հոսանքի ֆունկցիայի միջին քառակուսային արժեք մեկ պարբերության ընթացքում:
Տեղադրելով ![]() սինուսոիդական
հոսանքի ակնթարթային արժեքի արտահայտությունը վերջին բանաձևի մեջ՝ կստանանք
սինուսոիդական
հոսանքի ակնթարթային արժեքի արտահայտությունը վերջին բանաձևի մեջ՝ կստանանք
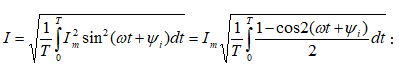
Քանի որ ![]() ապա հոսանքի գործող արժեքը կլինի
ապա հոսանքի գործող արժեքը կլինի

այսինքն՝ սինուսոիդական հոսանքի գործող արծեքը ![]() անգամ փոքր
է իր ամպլիտուդային արժեքից:
անգամ փոքր
է իր ամպլիտուդային արժեքից:
Սինուսոիդական լարման և էլշուի գործող արժեքները որոշվում են համանման ձևով.
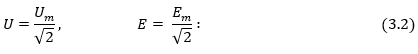
Սինուսոիդական մեծությունների գործող արժեքը գործնական
մեծ կիրառություն ունի: Չափիչ սարքերը, ոպես կանոն, սանդղակավորված են գործող արժեքի
համար: Օրինակ, երբ փոփոխական հոսանքի ցանցին միացված վոլտմետրը ցույց է տալիս 220Վ,
ապա դա լարման գործող արժեքն է, մինչդեռ դրա ամպլիտուդային արժեքը ![]() անգամ ավելի
մեծ է, այսինքն՝
անգամ ավելի
մեծ է, այսինքն՝ ![]()
Սինուսոիդական հոսանքի միջին արժեքը որոշվում
է որպես սինուսոիդական ֆունկցիայի միջին արժեք նրա դրական կես պարբերության ընթացքում:
Ըստ սահմանման, ![]() սինուսոիդական
հոսանքի միջին արժեքը կլինի
սինուսոիդական
հոսանքի միջին արժեքը կլինի
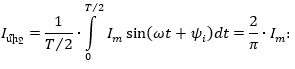
Համանման ձևով, լարման և էլշուի միջին արժեքները կլինեն.
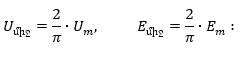
3.3. Սինուսոիդական մեծությունների արտահայտումը պտտվող վեկտորներով և կոմպլեքս թվերով
Փոփոխական հոսանքի շղթաների համար Կիրխհոֆի օրենքների հիման վրա գրված հավասարումներում հոսանքները, լարումները և էլշուները եռանկյունաչափական տեսքով գրված սինուսոիդական ֆունկցիաներ են, որոնցով մաթեմատիկական գործողությունների կատարումը մեծ դժվարությունների հետ է կապված: Ուստի, նպատակահարմար է սինուսոիդական էլեկտրական մեծություններն արտահայտել պտտվող վեկտորներով կամ կոմպլեքս թվերով, դրանով իսկ եռանկյունաչափական արտահայտություններով գործողությունները փոխարինելով, համապատասխանաբար, վեկտորներով կամ կոմպլեքս թվերով կատարվող գործողություններով:
Կոորդինատային հարթության վրա (նկ. 3.2) պատկերենք
![]() շառավիղ
վեկտոր1, որի երկարությունը հավասար է
շառավիղ
վեկտոր1, որի երկարությունը հավասար է
![]()
սինուսոիդական հոսանքի ![]() ամպլիտուդային արժեքին, իսկ հորիզոնական
առանցքի հետ կազմած
ամպլիտուդային արժեքին, իսկ հորիզոնական
առանցքի հետ կազմած ![]() անկյունը՝
սկզբնական փուլին: Սա վեկտորի սկզբնական (t = 0) դիրքն է, և դրա պրոյեկցիան
OY առանցքի վրա կլինի
անկյունը՝
սկզբնական փուլին: Սա վեկտորի սկզբնական (t = 0) դիրքն է, և դրա պրոյեկցիան
OY առանցքի վրա կլինի ![]()
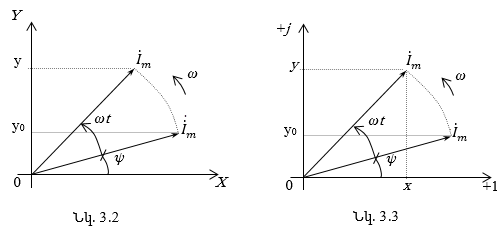
Ենթադրենք ![]() շառավիղ վեկտորը պտտվում է ժամացույցի
սլաքին հակառակ ուղղությամբ
շառավիղ վեկտորը պտտվում է ժամացույցի
սլաքին հակառակ ուղղությամբ ![]() անկյունային արագությամբ: Այդ դեպքում
t ժամանակ հետո այն կպտտվի նախնական դիրքի նկատմամբ
անկյունային արագությամբ: Այդ դեպքում
t ժամանակ հետո այն կպտտվի նախնական դիրքի նկատմամբ![]() անկյունով,
և դրա պրոյեկցիան ուղղաձիգ առանցքի վրա կլինի (նկ. 3.2)
անկյունով,
և դրա պրոյեկցիան ուղղաձիգ առանցքի վրա կլինի (նկ. 3.2)
![]()
Այսպիսով, պտտվող վեկտորի պրոյեկցիան ուղղաձիգ առանցքի վրա ժամանակի որևէ պահին հավասար է սինուսոիդական հոսանքի ակնթարթային արժեքին: Հետևաբար, սինուսոիդական հոսանքը, ինչպես նաև լարումը և էլշուն, կարող են ներկայացվել որպես պտտվող վեկտորներ:
Շղթայի էլեկտրական վիճակը բնութագրող մեծություններին համապատասխանող վեկտորների համախումբը կոչվում է շղթայի վեկտորական դիագրամ:
Քանի որ փոփոխական հոսանքի շղթայում սինուսոիդական
բոլոր մեծություններն ունեն նույն f հաճախությունը, և դրանց համապատասխանող
վեկտորները պտտվում են նույն ![]() անկյունային արագությամբ, ապա վեկտորների
փոխադարձ դիրքը կոորդինատային հարթության վրա ժամանակի ընթացքում մնում է անփոփոխ:
Հետևաբար, այդ վեկտորները կարելի է պայմանականորեն համարել անշարժ: Ուստի, վեկտորական
դիագրամը կառուցելու համար, վեկտորներից մեկը, որն ընդունված է անվանել նախնական վեկտոր,
կարելի է ուղղել կամայականորեն, ասենք հորիզոնական ուղղությամբ, իսկ մնացած վեկտորները
կողմնորոշել նրա նկատմամբ ըստ իրենց սկզբնական փուլերի: Վեկտորական դիագրամում նպատակահարմար
է վեկտորներն արտահայտել գործող արժեքներով՝ դրանց երկարությունները կարճացնելով
անկյունային արագությամբ, ապա վեկտորների
փոխադարձ դիրքը կոորդինատային հարթության վրա ժամանակի ընթացքում մնում է անփոփոխ:
Հետևաբար, այդ վեկտորները կարելի է պայմանականորեն համարել անշարժ: Ուստի, վեկտորական
դիագրամը կառուցելու համար, վեկտորներից մեկը, որն ընդունված է անվանել նախնական վեկտոր,
կարելի է ուղղել կամայականորեն, ասենք հորիզոնական ուղղությամբ, իսկ մնացած վեկտորները
կողմնորոշել նրա նկատմամբ ըստ իրենց սկզբնական փուլերի: Վեկտորական դիագրամում նպատակահարմար
է վեկտորներն արտահայտել գործող արժեքներով՝ դրանց երկարությունները կարճացնելով ![]() անգամ:
անգամ:
Վեկտորական դիագրամն ավելի ակնառու է դարձնում շղթայի էլեկտրական վիճակը և հեշտացնում է դրա վերլուծությունը: Այն թույլ է տալիս սինուսոիդական մեծությունների գումարումն ու հանումը փոխարինել համապատասխան վեկտորների գումարումով ու հանումով:
Սինուսոիդական հոսանքը կոմպլեքս թվով արտահայտելու համար գծենք դրան համապատասխանող պտտվող վեկտորը կոմպլեքս հարթության վրա (նկ. 3.3): Ժամանակի որևէ t պահին պտտվող վեկտորին մաթեմատիկորեն կհամապատասխանի հետևյալ կոմպլեքս թիվը.
![]()
Երևում է, որ գրված կոմպլեքս թվի կեղծ մասի գործակիցը հավասար է սինուսոիդական հոսանքի ակնթարթային արժեքին: Հետևաբար սինուսոիդական հոսանքը (նմանապես լարումը կամ էլշուն) կարող է արտահայտվել համապատասխան կոմպլեքս թվով: Ներկայումս փոփոխական հոսանքի բարդ շղթաների հաշվարկը կոմպլեքս թվերի միջոցով համընդհանուր ճանաչում է գտել որպես ամենաարդյունավետ մեթոդ:
Սինուսոիդական մեծության կոմպլեքս արժեք ասելով սովորաբար հասկանում են դրա կոմպլեքս գործող արժեքը: Սինուսոիդական հոսանքի կոմպլեքս արժեքը կարող է տրվել հետևյալ երեք տեսքերից որևէ մեկով.
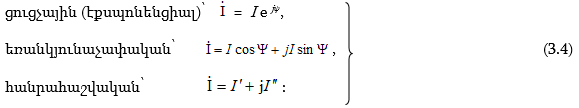
Վերջին արտահայտության մեջ ![]() սինուսոիդական
հոսանքի իրական մասն է, իսկ
սինուսոիդական
հոսանքի իրական մասն է, իսկ ![]() կեղծ մասը:
կեղծ մասը:
Հոսանքի գործող արժեքը որոշվում է որպես կոմպլեքս թվի մոդուլ (բացարձակ արժեք).
![]()
իսկ սկզբնական փուլը՝ որպես կոմպլեքս թվի արգումենտ.

Համանման բանաձևեր են օգտագործվում սինուսոիդական լարումը և էլշուն կոմպլեքս տեսքով ներկայացնելու համար:
Սինուսոիդական մեծությունների արտահայտումը կոմպլեքս թվերով թույլ է տալիս փոփոխական հոսանքի շղթաների հաշվարկի համար կիրառել բոլոր այն մեթոդները, որոնք կիրառվում են հաստատուն հոսանքի շղթաների հաշվարկի դեպքում՝ եռանկյունաչափական ֆունկցիաների միջև գործողությունները փոխարինելով կոմպլեքս թվերով կատարվող հանրահաշվական գործողություններով:
3.4. Էլեկտրական շղթայի տարրերը փոփոխական հոսանքի դեպքում
Փոփոխական հոսանքն անցնելով շղթայի տեղամասերով՝ կարող է առաջացնել հետևյալ երևույթները.
1) էլեկտրաէներգիայի փոխարկում այլ տեսակի էներգիայի,
2) փոփոխական մագնիսական դաշտ և դրա հետ կապված էլեկտրամագնիսական ինդուկցիայի երևույթ,
3) փոփոխական էլեկտրական դաշտ և դրա հետ կապված լիցքերի կուտակման և լիցքաթափման պարբերական պրոցես:
Բոլոր թվարկված երևույթներն էլ հակազդություն են առաջացնում (դիմադրություն են ցուցաբերում) հոսանքին: Ուստի, փոփոխական հոսանքի շղթաների մոդելավորման (համարժեք սխեմայի կազմման) համար, էներգիայի աղբյուրից բացի, ներմուծվում են նաև շղթայի երեք տարբեր տարրեր: Դրանք են` ռեզիստիվ (ա), ինդուկտիվ (բ) և ունակային (գ) տարրերը (նկ. 3.4):
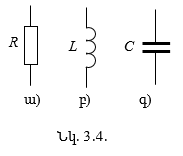
Այս երեք տարրերը համարվում են իդեալական, այսինքն ենթադրվում է, որ դրանցից յուրաքանչյուրում միայն մի երևույթ է տեղի ունենում, իսկ մյուս երկու երևույթները նրանում բացակայում են: Կախված իրական էլեկտրական սարքի ֆիզիկական հատկություններից՝ էլեկտրական սխեմայում այն պատկերվում է նշված տարրերի տարբեր զուգակցումներով:
Օրինակ, տարբեր տեսակի ջեռուցիչ սարքերը սովորաբար պատկերվում են միայն մեկ համարժեք ռեզիստիվ տարրով, որովհետև նրանցում հիմնական երևույթը միայն էներգիայի փոխարկումն է: Էլեկտրական շարժիչները ներկայացնող համարժեք սխեման պետք է պարունակի ռեզիստիվ և ինդուկտիվ տարրեր, քանի որ, բացի էներգիայի փոխարկումից, դրանցում էական է նաև էլեկտրամագնիսական ինդուկցիայի երևույթը: Կոնդենսատորը կարելի է պատկերել միայն ունակային տարրով, քանի որ էներգիայի փոխարկումը և մագնիսական դաշտը գործնականորեն կարելի է անտեսել:
3.4.1. Ռեզիստիվ տարրը սինուսոիդական հոսանքի շղթայում
Դիտարկենք էլեկտրական շղթա, որը պարունակում է միայն ռեզիստիվ տարր (նկ. 3.5): Նրա R պարամետրը կոչվում է ակտիվ դիմադրություն:
Փոփոխական հոսանքի շղթայի վիճակը բնութագրող մեծությունները
(հոսանք, լարում և այլն) պարբերաբար փոխում են իրենց ուղղությունը, այդ պատճառով որպես
դրանց դրական ուղղություն ընդունված է համարել ժամանակի որևէ ակնթարթին համապատասխանող
ուղղությունը: Դիցուք ժամանակի տվյալ ակնթարթին շղթայում հոսանքի և լարման դրական ուղղություններն
ունեն սխեմայում նշված ուղղությունը (նկ. 3.5բ): Այդ դեպքում, եթե ակտիվ դիմադրության
միջով անցնում է ![]() հոսանք,
ապա Օհմի օրենքի համաձայն, ժամանակի որևէ t պահին լարման ակնթարթային արժեքը կլինի
հոսանք,
ապա Օհմի օրենքի համաձայն, ժամանակի որևէ t պահին լարման ակնթարթային արժեքը կլինի
![]()
Այսինքն ռեզիստիվ տարրով սինուսոիդական հոսանք անցնելիս դրա սեղմակների միջև առաջանում է սինուսոիդական լարում, որը փոփոխվում է նույն հաճախությամբ և ունի նույն սկզբնական փուլը, ինչ որ հոսանքը: Այլ խոսքով ռեզիստիվ տարրում հոսանքը և լարումը ըստ փուլի համընկնում են:
Լարման ամպլիտուդային արժեքը
![]()
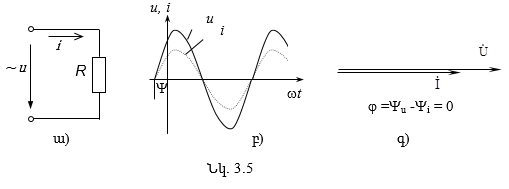
Բաժանելով (3.5) հավասարության երկու կողմերը ![]() -ի վրա՝ կստանանք Օհմի օրենքի
արտահայտությունը ռեզիստիվ տարրի համար` գրված գործող արժեքներով.
-ի վրա՝ կստանանք Օհմի օրենքի
արտահայտությունը ռեզիստիվ տարրի համար` գրված գործող արժեքներով.
![]()
Նկ. 3.5բ-ում պատկերված են դիտարկվող շղթայի լարման և հոսանքի փոփոխման կորերը, իսկ նկ. 3.5գ-ում՝ վեկտորական դիագրամը: Ինչպես երևում է, լարման և հոսանքի սկզբնական փուլերի տարբերությունը կամ,
ինչպես ընդունված է ասել, ![]() փուլային շեղումը, հավասար է զրոյի:
փուլային շեղումը, հավասար է զրոյի:
3.4.2. Ինդուկտիվ տարրը սինուսոիդական հոսանքի շղթայում
Ինչպես հայտնի է ֆիզիկայի դասընթացից, հաղորդալարի շուրջը, երբ դրանով անցնում է հոսանք, առաջանում է մագնիսական դաշտ: Այն պատկերվում է մագնիսական հոսքի ուժագծերով: Ուժեղ մագնիսական դաշտեր ստանալու համար հաղորդալարերից պատրաստվում է փաթույթ (կամ ինդուկտոր):
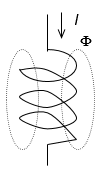
Փաթույթի մագնիսական Փ հոսքի և գալարների w
թվի արտադրյալը կոչվում է փաթույթի հոսքակցում` ![]() Վերջինս ուղիղ համեմատական է փաթույթի
հոսանքին՝
Վերջինս ուղիղ համեմատական է փաթույթի
հոսանքին՝ ![]() որտեղ L-ը փաթույթի ինդուկտիվությունն
է և բնութագրում է դրա հոսք առաջացնելու ընդունակությունը: Ինդուկտիվության հիմնական
միավորն է հենրին (Հն)՝
որտեղ L-ը փաթույթի ինդուկտիվությունն
է և բնութագրում է դրա հոսք առաջացնելու ընդունակությունը: Ինդուկտիվության հիմնական
միավորն է հենրին (Հն)՝ ![]()
Եթե փաթույթի հոսանքը փոփոխվում է, ապա փոփոխվում է նաև դրա հոսքակցումը և, համաձայն էլեկտրամագնիսական ինդուկցիայի օրենքի, փաթույթի գալարներում ինդուկտվում է էլշու, որը կոչվում է ինքնինդուկցիայի էլշու.
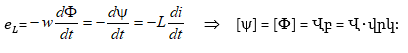
Բանաձևում «-» նշանը ցույց է տալիս, որ ինդուկտված էլշուն հակազդում է հոսանքի փոփոխությանը (Լենցի կանոնը):
Որպես ինդուկտիվ տարր կարելի է դիտարկել իդեալական մագնիսական կոճը, որի համար R = 0 (նկ. 3.6ա):
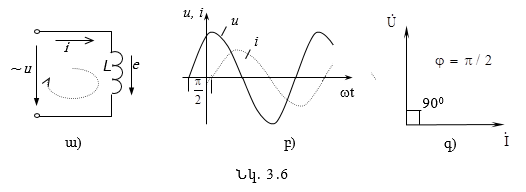
Դիցուք ինդուկտիվ տարրը միացված է փոփոխական հոսանքի
աղբյուրին և դրա միջով անցնում է սինուսոիդական ![]() հոսանք՝ առաջացնելով ինքնինդուկցիայի
էլշու՝
հոսանք՝ առաջացնելով ինքնինդուկցիայի
էլշու՝ ![]()
Ժամանակի որևէ ակնթարթի համար, համաձայն Կիրխհոֆի 2-րդ օրենքի, կարելի է գրել
![]()
որտեղից`
![]()
![]()
Այսինքն ինդուկտիվ տարրով սինուսոիդական հոսանք անցնելիս
դրա ծայրերում առաջանում է սինուսոիդական լարում, որը փոփոխվում է նույն հաճախությամբ,
ինչ որ հոսանքը, բայց առաջ է ընկած դրանից ըստ փուլի ![]() Ընդ որում,
լարման ամպլիտուդային արժեքը կլինի
Ընդ որում,
լարման ամպլիտուդային արժեքը կլինի
![]()
իսկ սկզբնական փուլը՝ ![]()
Բաժանելով (3.7) հավասարության երկու կողմերը ![]() -ի վրա, կստանանք Օհմի օրենքի
արտահայտությունn ինդուկտիվ տարրի համար՝ գրված գործող արժեքներով.
-ի վրա, կստանանք Օհմի օրենքի
արտահայտությունn ինդուկտիվ տարրի համար՝ գրված գործող արժեքներով.
![]()
Այստեղ ![]() -ն ունի դիմադրության
չափողականություն և կոչվում է ինդուկտիվ դիմադրություն:
-ն ունի դիմադրության
չափողականություն և կոչվում է ինդուկտիվ դիմադրություն:
Հաստատուն հոսանքի դեպքում (երբ f = 0) ![]() Այս պատճառով
փոփոխական հոսանքի համար նախատեսված էլեկտրական սարքավորումները (ասենք տրանսֆորմատորը)
չպետք է միացվեն հաստատուն հոսանքի աղբյուրին, խուսափելու համար մեծ հոսանքներից, որը
կարող է դրանց այրվելու պատճառ դառնալ:
Այս պատճառով
փոփոխական հոսանքի համար նախատեսված էլեկտրական սարքավորումները (ասենք տրանսֆորմատորը)
չպետք է միացվեն հաստատուն հոսանքի աղբյուրին, խուսափելու համար մեծ հոսանքներից, որը
կարող է դրանց այրվելու պատճառ դառնալ:
Նկ. 3.6բ-ում պատկերված են դիտարկվող շղթայի լարման
և հոսանքի փոփոխման կորերը, իսկ նկ. 3.6գ-ում՝ վեկտորական դիագրամը, որտեղից երևում
է, որ ինդուկտիվ տարրի համար լարումը առաջ է ընկած հոսանքից (կամ, ինչ որ նույնն է,
հոսանքը hետ է ընկած լարումից) ![]() Այլ խոսքով, լարման և հոսանքի փուլային
շեղումը ինդուկտիվ տարրի համար
Այլ խոսքով, լարման և հոսանքի փուլային
շեղումը ինդուկտիվ տարրի համար
![]()
3.4.3. Ունակային տարրը սինուսոիդական հոսանքի շղթայում
Ֆիզիկայի դասընթացից հայտնի է, որ պարզագույն կոնդենսատորը մի սարք է, որը կազմված է երկու զուգահեռ շրջադիրներից, որոնք իրարից բաժանված են մեկուսիչի նեղ շերտով:
Կոնդենսատորը հաստատուն ![]() լարման միացնելիս,
յուրաքանչյուր շրջադիրի վրա կուտակվում է մեծությամբ հավասար, բայց նշանով հակառակ
լարման միացնելիս,
յուրաքանչյուր շրջադիրի վրա կուտակվում է մեծությամբ հավասար, բայց նշանով հակառակ
![]() լիցք, որի
բացարձակ արժեքը համեմատական է կիրառված
լիցք, որի
բացարձակ արժեքը համեմատական է կիրառված ![]() լարմանը`
լարմանը`
![]()
որտեղ C - ն համեմատականության գործակիցն է, որը բնութագրում է կոնդենսատորի լիցք կուտակելու ընդունակությունը և կոչվում է կոնդենսատորի ունակություն: Հարթ կոնդենսատորի համար
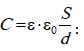
Այստեղ ![]() էլեկտրական հաստատունն է,
էլեկտրական հաստատունն է, ![]() մեկուսիչի
(դիէլեկտրիկի) հարաբերական դիէլեկտրիկական թափանցելիությունը, S-ը՝ մեկ շրջադիրի
մակերեսը, d-ն՝ շրջադիրների միջև հեռավորությունը:
մեկուսիչի
(դիէլեկտրիկի) հարաբերական դիէլեկտրիկական թափանցելիությունը, S-ը՝ մեկ շրջադիրի
մակերեսը, d-ն՝ շրջադիրների միջև հեռավորությունը:
Ունակության հիմնական միավորն է ֆարադը (Ֆ)՝
![]()
Եթե կոնդենսատորին կիրառված լարումը փոփոխվում է, շրջադիրների Q = q լիցքը նույնպես փոփոխվում է` առաջացնելով հոսանք, որի ակնթարթային արժեքը, նկատի ունենալով (3.9)-ը, կլինի

Որպես ունակային տարր կարելի է դիտարկել իդեալական կոնդենսատորը, որի ակտիվ դիմադրությունը՝ R = 0 (նկ. 3.7ա):
Դիցուք ունակային տարրը միացված է սինուսոիդական լարման
և դրա միջով անցնում է ![]() սինուսոիդական հոսանք: (3.10) արտահայտությունից
սինուսոիդական հոսանք: (3.10) արտահայտությունից
![]() որտեղից հետևում
է
որտեղից հետևում
է
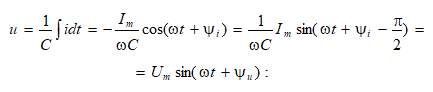
Այստեղից լարման ամպլիտուդային արժեքը կլինի
![]()
իսկ լարման սկզբնական փուլը՝ ![]()
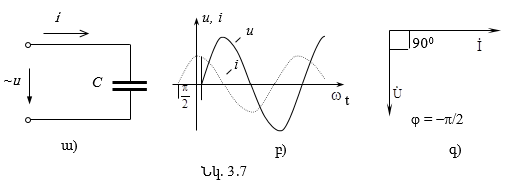
Բաժանելով (3.11) հավասարությունը ![]() վրա` կստանանք Օհմի օրենքի արտահայտությունը ունակային տարրի համար` գրված գործող արժեքներով.
վրա` կստանանք Օհմի օրենքի արտահայտությունը ունակային տարրի համար` գրված գործող արժեքներով.
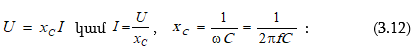
Բանաձևում ![]() մեծությունն ունի դիմադրության չափողականություն
և կոչվում է ունակային դիմադրություն:
մեծությունն ունի դիմադրության չափողականություն
և կոչվում է ունակային դիմադրություն:
Ի տարբերություն ինդուկտիվ դիմադրության, ունակային դիմադրությունը հակադարձ համեմատական է հաճախությանը: Հաստատուն հոսանքի դեպքում (f = 0) ունակային դիմադրությունը անվերջ մեծ է և, հետևաբար, դրանով հաստատուն հոսանք չի անցնում:
Նկ. 3.7ա-ում պատկերված շղթայի լարման և հոսանքի փոփոխման կորերից
(նկ. 3.7բ) և վեկտորական դիագրամից (նկ. 3.7գ) երևում է, որ ունակային տարրի համար
լարումը հետ է ընկած հոսանքից (կամ, որ նույնն է, հոսանքը առաջ է ընկած լարումից)
![]() Այլ խոսքով, ունակային տարրի
համար լարման և հոսանքի փուլային շեղումը՝
Այլ խոսքով, ունակային տարրի
համար լարման և հոսանքի փուլային շեղումը՝
![]()
3.5. Ռեզիստիվ, ինդուկտիվ և ունակային տարրերի
հաջորդաբար միացումով սինուսոիդական հոսանքի շղթա
Ընդհանուր դեպքում փոփոխական հոսանքի չճյուղավորված (միակոնտուր) շղթան պարունակում է սինուսոիդական լարման (կամ էլշուի) աղբյուր, ինչպես նաև հաջորդաբար միացված ռեզիստիվ, ինդուկտիվ և ունակային տարրեր (նկ. 3.8):
Աղբյուրի ![]() սինուսոիդական էլշուն շղթայում առաջ է բերում սինուսոիդական
հոսանք՝
սինուսոիդական էլշուն շղթայում առաջ է բերում սինուսոիդական
հոսանք՝ ![]() որն էլ, իր հերթին, ստեղծում
է
որն էլ, իր հերթին, ստեղծում
է ![]() սինուսոիդական լարումներ
համապատասխանաբար ռեզիստիվ, ինդուկտիվ և ունակային տարրերի վրա: Դիտարկվող շղթայում
բոլոր սինուսոիդական մեծությունների դրական ուղղությունները նշված են ժամանակի որևէ
ակնթարթի համար (նկ. 3.8):
սինուսոիդական լարումներ
համապատասխանաբար ռեզիստիվ, ինդուկտիվ և ունակային տարրերի վրա: Դիտարկվող շղթայում
բոլոր սինուսոիդական մեծությունների դրական ուղղությունները նշված են ժամանակի որևէ
ակնթարթի համար (նկ. 3.8):
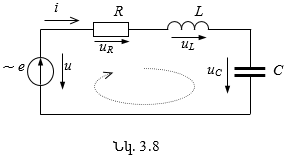
Ըստ Կիրխհոֆի 2-րդ օրենքի, գրված ժամանակի նույն ակնթարթի համար,
![]()
Համաձայն բաժին 3.3-ի դրույթների, սինուսոիդական մեծությունների այս գումարը կարող է փոխարինվել լարումների համապատասխան վեկտորների վեկտորական գումարով.
![]()
Աղբյուրի ![]() լարման վեկտորը գտնելու համար կառուցենք շղթայի վեկտորական
դիագրամը: Քանի որ հոսանքը նույնն է բոլոր տարրերի համար, ապա հարմար է որպես սկզբնական
վեկտոր վերցնել հոսանքի վեկտորը և ուղղել այն հորիզոնական ուղղությամբ (նկ.
3.9): Ռեզիստիվ տարրի վրա
լարման վեկտորը գտնելու համար կառուցենք շղթայի վեկտորական
դիագրամը: Քանի որ հոսանքը նույնն է բոլոր տարրերի համար, ապա հարմար է որպես սկզբնական
վեկտոր վերցնել հոսանքի վեկտորը և ուղղել այն հորիզոնական ուղղությամբ (նկ.
3.9): Ռեզիստիվ տարրի վրա ![]() լարման վեկտորն ուղղված է
լարման վեկտորն ուղղված է ![]() վեկտորի ուղղությամբ
(տես նկ. 3.5գ), ինդուկտիվության վրա
վեկտորի ուղղությամբ
(տես նկ. 3.5գ), ինդուկտիվության վրա ![]() լարման վեկտորն առաջ է ընկած (նկ. 3.6գ), իսկ ունակության
վրա
լարման վեկտորն առաջ է ընկած (նկ. 3.6գ), իսկ ունակության
վրա ![]() լարման վեկտորը հետ է ընկած
հոսանքի վեկտորից
լարման վեկտորը հետ է ընկած
հոսանքի վեկտորից ![]() (նկ. 3.7գ):
(նկ. 3.7գ):
Աղբյուրի ![]() լարման վեկտորը կառուցվում է համաձայն (3.13) վեկտորական
հավասարման:
լարման վեկտորը կառուցվում է համաձայն (3.13) վեկտորական
հավասարման:
Վեկտորական դիագրամի (նկ. 3.9) լարումների եռանկյունուց կարելի
է որոշել ![]() վեկտորի բացարձակ արժեքը
կամ, որ նույնն է, աղբյուրի լարման գործող արժեքը.
վեկտորի բացարձակ արժեքը
կամ, որ նույնն է, աղբյուրի լարման գործող արժեքը.
![]()
որտեղ ![]() Լարումների այս արժեքները տեղադրելով վերջին հավասարման
մեջ` կստանանք
Լարումների այս արժեքները տեղադրելով վերջին հավասարման
մեջ` կստանանք
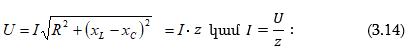
Այս հավասարումը Օհմի օրենքի արտահայտությունն է ռեզիստիվ, ինդուկտիվ և ունակային տարրերի հաջորդաբար միացումով փոփոխական հոսանքի շղթայի համար, որտեղ
![]()
մեծությունը կոչվում է շղթայի լրիվ դիմադրություն, իսկ ![]() ռեակտիվ դիմադրություն:
ռեակտիվ դիմադրություն:
Լարումների նույն եռանկյունուց (նկ. 3.9) կարելի է որոշել նաև շղթայի լարման և հոսանքի փուլային շեղումը.
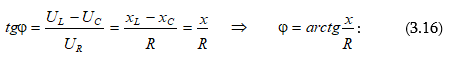
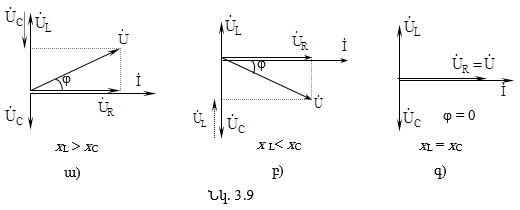
Այսպիսով, ինչպես բխում է (3.16) բանաձևից, լարման և հոսանքի միջև
![]() փուլային շեղումը
կախված չէ լարման կամ հոսանքի մեծություններից, այլ կախված է միայն շղթայի ակտիվ և
ռեակտիվ դիմադրությունների հարաբերությունից:
փուլային շեղումը
կախված չէ լարման կամ հոսանքի մեծություններից, այլ կախված է միայն շղթայի ակտիվ և
ռեակտիվ դիմադրությունների հարաբերությունից:
Ելնելով (3.15) և (3.16) բանաձևերից` դժվար չէ տեսնել, որ շղթայի R, x և z դիմադրությունները կարելի է ներկայացնել որպես ուղղանկյուն եռանկյան կողմեր (նկ. 3.10), ինչը թույլ կտա գտնել նաև այլ կապեր նշված մեծությունների միջև, ինչպես օրինակ,
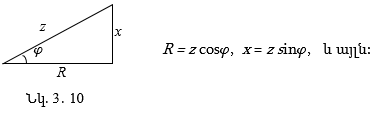
Դիտարկվող շղթայում հնարավոր են հետևյալ երեք բնորոշ դեպքերը:
1) Երբ ![]() շղթան ունի ինդուկտիվ բնույթ և աղբյուրի I
հոսանքը հետ է ընկած U լարումից (կամ լարումն առաջ է հոսանքից) ըստ փուլի
շղթան ունի ինդուկտիվ բնույթ և աղբյուրի I
հոսանքը հետ է ընկած U լարումից (կամ լարումն առաջ է հոսանքից) ըստ փուլի ![]() անկյունով, (նկ.
3.9ա):
անկյունով, (նկ.
3.9ա):
2) Երբ ![]() շղթան ունի ունակային բնույթ և աղբյուրի I
հոսանքը առաջ է ընկած U լարումից (կամ լարումը հետ է հոսանքից) ըստ փուլի
շղթան ունի ունակային բնույթ և աղբյուրի I
հոսանքը առաջ է ընկած U լարումից (կամ լարումը հետ է հոսանքից) ըստ փուլի ![]() անկյունով (նկ.
3.9բ):
անկյունով (նկ.
3.9բ):
3) Երբ ![]() շղթայում առկա է այսպես կոչված լարումների ռեզոնանս,
և աղբյուրի հոսանքն ու լարումը ըստ փուլի համընկնում են (նկ. 3.9գ): Ռեզոնանսային շղթան,
չնայած ինդուկտիվ և ունակային տարրերի առկայությանը, ամբողջությամբ վերցրած, իրեն պահում
է որպես ռեզիստիվ տարր:
շղթայում առկա է այսպես կոչված լարումների ռեզոնանս,
և աղբյուրի հոսանքն ու լարումը ըստ փուլի համընկնում են (նկ. 3.9գ): Ռեզոնանսային շղթան,
չնայած ինդուկտիվ և ունակային տարրերի առկայությանը, ամբողջությամբ վերցրած, իրեն պահում
է որպես ռեզիստիվ տարր:
Ռեզոնանսային շղթայի լրիվ դիմադրությունը հավասար է շղթայի միայն
ակտիվ դիմադրությանը, հետևաբար դրա արժեքը փոքրագույնն է, ![]() իսկ հոսանքի գործող արժեքը,
տրված լարման դեպքում, առավելագույնը՝
իսկ հոսանքի գործող արժեքը,
տրված լարման դեպքում, առավելագույնը՝ ![]() Լարումների ռեզոնանսի դեպքում
լարումները ինդուկտիվ և ունակային տարրերի վրա ըստ գործող արժեքի հավասար են
Լարումների ռեզոնանսի դեպքում
լարումները ինդուկտիվ և ունակային տարրերի վրա ըստ գործող արժեքի հավասար են
![]() բայց հակառակ են ըստ փուլի
(նկ. 3.9գ). Ուստի աղբյուրի լարումը հավասար է ռեզիստիվ տարրի լարմանը՝
բայց հակառակ են ըստ փուլի
(նկ. 3.9գ). Ուստի աղբյուրի լարումը հավասար է ռեզիստիվ տարրի լարմանը՝ ![]()
Այն հաճախությունը, որի դեպքում տեղի է ունենում լարումների ռեզոնանս,
կոչվում է շղթայի ռեզոնանսային հաճախություն: Դրա արժեքը կարելի է գտնել ռեզոնանսի
պայմանից՝ ![]() կամ, ըստ (3.8) և (3.12)
բանաձևերի՝
կամ, ըստ (3.8) և (3.12)
բանաձևերի՝
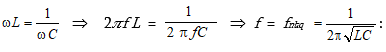
Եթե շղթայի ակտիվ դիմադրությունը շատ փոքր է ռեակտիվ դիմադրությունների
համեմատ, այսինքն ![]() ապա ռեզոնանսային հաճախության դեպքում շղթայի հոսանքը
կտրուկ մեծանում է այլ հաճախությունների դեպքում հոսանքի արժեքների համեմատ: Այս հատկության
շնորհիվ ռեզոնանսի երևույթը լայնորեն օգտագործվում է ռադիոհեռուստատեսային հաղորդակցության
և ավտոմատ կառավարման համակարգերում, տեխնիկայի այլ բնագավառներում:
ապա ռեզոնանսային հաճախության դեպքում շղթայի հոսանքը
կտրուկ մեծանում է այլ հաճախությունների դեպքում հոսանքի արժեքների համեմատ: Այս հատկության
շնորհիվ ռեզոնանսի երևույթը լայնորեն օգտագործվում է ռադիոհեռուստատեսային հաղորդակցության
և ավտոմատ կառավարման համակարգերում, տեխնիկայի այլ բնագավառներում:
Միևնույն ժամանակ կարևոր է գիտենալ, որ ռեզոնանսային շղթայում`
![]()
պայմանի դեպքում, շղթայի առանձին տեղամասերի լարումը կարող է շատ անգամ գերազանցել աղբյուրի լարումը: Իրոք, բազմապատկելով գրված անհավասարությունը I հոսանքի արժեքով,
![]()
Այսինքն` նշված պայմանի դեպքում լարումներն ինդուկտիվ և ունակային տարրերի վրա գերազանցում են աղբյուրի լարումը, ինչը կարող է լուրջ վտանգ ներկայացնել ինչպես մարդկանց, այնպես էլ շղթայում միացված սարքերի համար:
3.6. Ռեզիստիվ, ինդուկտիվ և ունակային տարրերի
զուգահեռ միացումով շղթա
Դիտարկենք շղթա, որում իդեալական ռեզիստիվ, ինդուկտիվ
և ունակային տարրերը միացված են զուգահեռ (նկ. 3.11): Ենթադրենք տարրերի R, L,
C պարամետրերը և աղբյուրի սինուսոիդական ![]() լարումը տրված են:
լարումը տրված են:
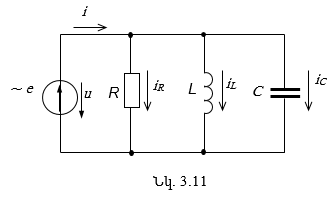
Ժամանակի որևէ ակնթարթի համար, համաձայն Կիրխհոֆի 1-ին օրենքի, կարելի է գրել
![]()
Սինուսոիդական հոսանքների այս գումարը փոխարինենք համապատասխան վեկտորների գումարով.
![]()
Կառուցենք դիտարկվող շղթայի վեկտորական դիագրամը՝ ընտրելով
լարման ![]() վեկտորը
որպես սկզբնական վեկտոր և ուղղելով այն հորիզոնական ուղղությամբ (նկ. 3.12).
վեկտորը
որպես սկզբնական վեկտոր և ուղղելով այն հորիզոնական ուղղությամբ (նկ. 3.12).
Ռեզիստիվ տարրի ![]() հոսանքի վեկտորը համընկնում է լարման
հոսանքի վեկտորը համընկնում է լարման
![]() վեկտորի
հետ: Դրա երկարությունը (գործող արժեքը), համաձայն Օհմի օրենքի,
վեկտորի
հետ: Դրա երկարությունը (գործող արժեքը), համաձայն Օհմի օրենքի,
![]()
որտեղ ![]() մեծությունը կոչվում է ակտիվ
հաղորդականություն:
մեծությունը կոչվում է ակտիվ
հաղորդականություն:
Ինդուկտիվ տարրի ![]() հոսանքի վեկտորը hետ է ընկած
հոսանքի վեկտորը hետ է ընկած ![]() վեկտորից
վեկտորից
![]() Դրա երկարությունը՝
Դրա երկարությունը՝
![]() որտեղ
որտեղ ![]() մեծությունը կոչվում է ինդուկտիվ
հաղորդականություն:
մեծությունը կոչվում է ինդուկտիվ
հաղորդականություն:
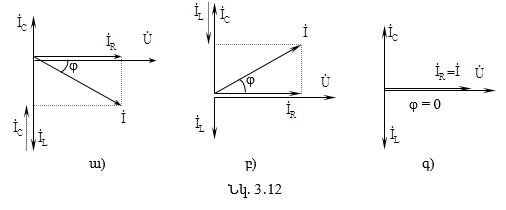
Եվ, վերջապես, ունակային տարրի ![]() հոսանքի
վեկտորն առաջ է ընկած
հոսանքի
վեկտորն առաջ է ընկած ![]() վեկտորից
վեկտորից ![]() և դրա երկարությունն
է
և դրա երկարությունն
է ![]() որտեղ
որտեղ ![]() մեծությունը
կոչվում է ունակային հաղորդականություն:
մեծությունը
կոչվում է ունակային հաղորդականություն:
Աղբյուրի հոսանքի![]() վեկտորը
կառուցվում է ըստ (3.17) վեկտորական հավասարման: Դրա գործող արժեքը որոշվում է որպես
վեկտորը
կառուցվում է ըստ (3.17) վեկտորական հավասարման: Դրա գործող արժեքը որոշվում է որպես
![]() վեկտորի երկարություն.
վեկտորի երկարություն.
![]()
Որտեղ
![]()
մեծությունը կոչվում է շղթայի լրիվ հաղորդականություն:
Այսպիսով, Օհմի օրենքը փոփոխական հոսանքի զուգահեռ շղթայի համար կգրվի`
![]()
Վեկտորական դիագրամի (նկ. 3.12) հոսանքների եռանկյան համար կարելի է գրել.
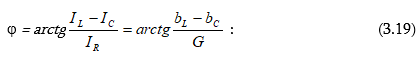
Փոփոխական հոսանքի զուգահեռ միացված շղթաներում նույնպես հնարավոր են երեք բնորոշ դեպքեր.
1) Երբ ![]() շղթան ինդուկտիվ բնույթ ունի, և
աղբյուրի հոսանքը հետ է մնում լարումից
շղթան ինդուկտիվ բնույթ ունի, և
աղբյուրի հոսանքը հետ է մնում լարումից ![]() անկյունով
(նկ. 3.12ա):
անկյունով
(նկ. 3.12ա):
2) Երբ ![]() շղթան ունակային բնույթ ունի, և
աղբյուրի հոսանքը առաջ է ընկնում լարումից
շղթան ունակային բնույթ ունի, և
աղբյուրի հոսանքը առաջ է ընկնում լարումից ![]() անկյունով
(նկ. 3.12բ):
անկյունով
(նկ. 3.12բ):
3) Երբ ![]() Շղթայի այսպիսի ռեժիմը կոչվում է
հոսանքների ռեզոնանս: Ռեզոնանսի դեպքում ինդուկտիվ և ունակային տարրերի հոսանքներն
ըստ գործող արժեքների հավասար են, բայց փոփոխվում են հակառակ փուլերով (նկ. 3.12գ),
իսկ աղբյուրի հոսանքը հավասար է ռեզիստիվ տարրի հոսանքին և, հետևաբար, փոքրագույնն
է տրված U լարման դեպքում.
Շղթայի այսպիսի ռեժիմը կոչվում է
հոսանքների ռեզոնանս: Ռեզոնանսի դեպքում ինդուկտիվ և ունակային տարրերի հոսանքներն
ըստ գործող արժեքների հավասար են, բայց փոփոխվում են հակառակ փուլերով (նկ. 3.12գ),
իսկ աղբյուրի հոսանքը հավասար է ռեզիստիվ տարրի հոսանքին և, հետևաբար, փոքրագույնն
է տրված U լարման դեպքում.
![]()
3.7. Դիմադրությունների և հաղորդականությունների կապը սինուսոիդական հոսանքի շղթայում
Ինչպես հայտնի է, մագնիսական կոճով փոփոխական հոսանք անցնելիս տեղի են ունենում երկու հիմնական երևույթներ. ջերմության անջատում՝ շնորհիվ կոճի R ակտիվ դիմադրության և ինքնինդուկցիայի երևույթ՝ շնորհիվ կոճի L ինդուկտիվության: Հետևաբար, մագնիսական կոճը կարելի է պատկերել (մոդելավորել) ռեզիստիվ և ինդուկտիվ տարրերի միջոցով: Ընդ որում, այն կարող է ներկայացվել ինչպես այդ տարրերի դիմադրությունների հաջորդական միացումով, այնպես էլ դրանց հաղորդականությունների զուգահեռ միացումով (նկ. 3.13): Գործնական շատ խնդիրների լուծման համար կարևոր է կապ հաստատել երկու սխեմաների դիմադրությունների և հաղորդականությունների միջև:
Նկ. 3.13ա սխեմայի համար շղթայի z լրիվ դիմադրությունը (3.15) և նկ.3.13բ սխեմայի համար y լրիվ հաղորդականությունը (3.18) համապատասխանաբար կլինեն
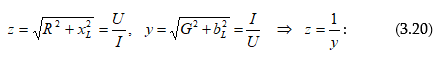
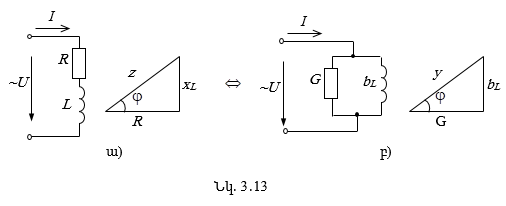
Դիմադրությունների (նկ. 3.13ա) և հաղորդականությունների (նկ.3.13բ) եռանկյունների համար կարող ենք գրել.

Տեղադրելով (3.20)-ից z -ի արժեքը (3.21)-ի մեջ և y -ի արժեքը (3.22)-ի մեջ` կստանանք դիմադրությունների և հաղորդականությունների միջև փոխադարձ կապը, համապատասխանաբար,
· հաջորդաբար շղթան զուգահեռ շղթայով փոխարինելիս՝
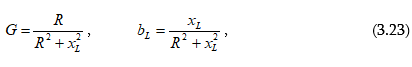
· զուգահեռ շղթան հաջորդաբար շղթայով փոխարինելիս՝
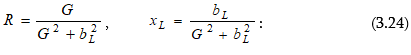
Համանման բանաձևերով որոշվում են նաև R – C հաջորդաբար շղթայի դիմադրությունների և նրան զուգահեռ շղթայի հաղորդականությունների կապը:
3.8. Էներգետիկական երևույթները փոփոխական հոսանքի շղթաներում
Դիցուք տրված է ռեզիստիվ, ինդուկտիվ և ունակային տարրեր պարունակող ցանկացած բարդության սինուսոիդական հոսանքի շղթա, որը ներկայացված է պասիվ (աղբյուր չպարունակող) երկբևեռի տեսքով (նկ.3.14).
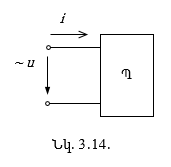
Ենթադրենք երկբևեռը միացված է ![]() սինուսոիդական
լարման աղբյուրին և դրանով անցնում է
սինուսոիդական
լարման աղբյուրին և դրանով անցնում է ![]() սինուսոիդական հոսանքը: Այդ դեպքում
շղթայի ակնթարթային հզորությունը, ըստ (1.12) բանաձևի, կլինի
սինուսոիդական հոսանքը: Այդ դեպքում
շղթայի ակնթարթային հզորությունը, ըստ (1.12) բանաձևի, կլինի
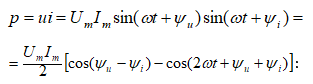
![]()
Այսպիսով, տրված երկբևեռի ակնթարթային հզորության արտահայտությունը
կազմված է երկու բաղադրիչից. ![]() հաստատուն բաղադրիչից, որը կախված
չէ ժամանակից և փոփոխական բաղադրիչից, որը ժամանակից կախված կրկնակի հաճախությամբ
հաստատուն բաղադրիչից, որը կախված
չէ ժամանակից և փոփոխական բաղադրիչից, որը ժամանակից կախված կրկնակի հաճախությամբ ![]() փոփոխվող
սինուսոիդական ֆունկցիա է:
փոփոխվող
սինուսոիդական ֆունկցիա է:
Դիտարկվող երկբևեռի լարման, հոսանքի և հզորության ակնթարթային
արժեքների փոփոխման կորերը կառուցելիս (նկ. 3.15), պարզության համար ընդունված է ![]() իսկ շղթան՝ ինդուկտիվ բնույթի (հոսանքը
hետ է մնում լարումից ըստ փուլի
իսկ շղթան՝ ինդուկտիվ բնույթի (հոսանքը
hետ է մնում լարումից ըստ փուլի ![]() անկյունով):
Հզորության կորով սահմանափակված մակերեսները (մգացված մակերեսները) որոշակի մասշտաբով
ներկայացնում են էլեկտրական էներգիա: Ընդ որում դրական մակերեսները համեմատական են
այն էներգիային, որը երկբևեռը վերցնում է աղբյուրից, իսկ բացասական մակերեսները՝ այն
էներգիային, որը երկբևեռը պարբերաբար վերադարձնում է աղբյուրին՝ ի հաշիվ ինդուկտիվ
և ունակային տարրերում կուտակված մագնիսական և էլեկտրական դաշտերի էներգիաների:
անկյունով):
Հզորության կորով սահմանափակված մակերեսները (մգացված մակերեսները) որոշակի մասշտաբով
ներկայացնում են էլեկտրական էներգիա: Ընդ որում դրական մակերեսները համեմատական են
այն էներգիային, որը երկբևեռը վերցնում է աղբյուրից, իսկ բացասական մակերեսները՝ այն
էներգիային, որը երկբևեռը պարբերաբար վերադարձնում է աղբյուրին՝ ի հաշիվ ինդուկտիվ
և ունակային տարրերում կուտակված մագնիսական և էլեկտրական դաշտերի էներգիաների:
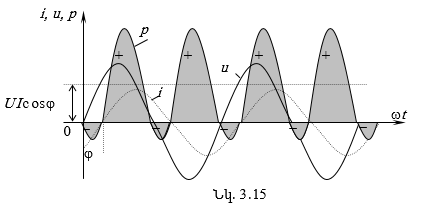
Քանի որ դրական մակերեսները գերազանցում են բացասականները, ապա նշանակում է, որ էլեկտրական էներգիայի մի մասը, որը կոչվում է ակտիվ էներգիա, անվերադարձ ծախսվում է երկբևեռում՝ ռեզիստիվ տարրերի վրա փոխարկվելով այլ տեսակի էներգիաների: Մնացած էներգիան (ռեակտիվ էներգիա) պարբերաբար փոխանցվում է աղբյուրից երկբևեռին և երկբևեռից աղբյուրին:
Ակտիվ էներգիայի հզորությունը որոշվում է որպես հզորության ֆունկցիայի միջին արժեք t = T մեկ պարբերության ընթացքում և կոչվում է շղթայի ակտիվ հզորություն.
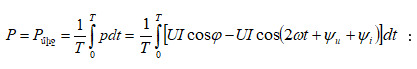
Ինտեգրումից հետո կստանանք
![]()
Բանաձևից հետևում է, որ շղթայի ակտիվ հզորությունը
հավասար է լարման և հոսանքի գործող արժեքների և դրանց միջև փուլային շեղման անկյան
կոսինուսի արտադրյալին: Վերջինս ![]() կոչվում է շղթայի հզորության
գործակից: Պետք է նշել, որ ակտիվ հզորությունը միշտ դրական նշան ունի` անկախ փուլային
շեղման
կոչվում է շղթայի հզորության
գործակից: Պետք է նշել, որ ակտիվ հզորությունը միշտ դրական նշան ունի` անկախ փուլային
շեղման ![]() անկյան նշանից
անկյան նշանից ![]()
Քանի որ շղթայի ակտիվ հզորությունը ռեզիստիվ տարրերի վրա անվերադարձ ծախսված էներգիայի հզորությունն է, ապա այն կարելի է որոշել նաև որպես շղթայի բոլոր ռեզիստիվ տարրերի հզորությունների գումար.
![]()
Պարբերաբար աղբյուրին վերադարձվող էներգիայի հզորությունը կոչվում է երկբևեռի ռեակտիվ հզորություն: Այն որոշվում է հետևյալ բամաձևով.
![]()
Ինդուկտիվ տարրի x ռեակտիվ դիմադրությունը
(3.26)-ում վերցվում է դրական նշանով, իսկ ունակային տարրինը՝ բացասական նշանով: Հետևաբար,
երկբևեռի ռեակտիվ հզորությունը կարող է լինել դրական, բացասական կամ զրո: Ռեզոնանսային
շղթայի ռեակտիվ հզորությունը զրո է, քանի որ ![]()
Լարման և հոսանքի գործող արժեքների արտադրյալը կոչվում է երկբևեռի լրիվ հզորություն.
![]()
Չնայած շղթայի ակտիվ, ռեակտիվ և լրիվ հզորություններն ունեն նույն չափողականությունը, սակայն նրանց միավորներն ունեն տարբեր անվանումներ. ակտիվ հզորության միավորն է վատտ (Վտ), ռեակտիվ հզորության միավորը՝ վոլտ-ամպեր-ռեակտիվ (ՎԱռ), լրիվ հզորության միավորը՝ վոլտ-ամպեր (ՎԱ):
Գործնականում այնպիսի սարքերի հզորությունը, ինչպիսիք են լուսավորման, ջեռուցման սարքերը, էլեկտրաշարժիչները, գեներատորները, նշվում է որպես ակտիվ հզորություն և արտահայտվում է Վտ-ով (կամ կՎտ-ով): Հզոր մագնիսական կոճերի (ռեակտորների) և կոնդենսատորային մարտկոցների հզորությունը նշվում է որպես ռեակտիվ հզորություն՝ ՎԱռ (կՎԱռ): Տրանսֆորմատորների հզորությունը նշվում է որպես լրիվ հզորություն՝ ՎԱ (կՎԱ):
Համեմատելով (3.25)...(3.27) արտահայտությունները` դժվար չէ նկատել, որ ակտիվ, ռեակտիվ և լրիվ հզորությունների արժեքները կարելի է ներկայացնել որպես ուղղանկյուն եռանկյան կողմեր (նկ. 3.16), որի հիման վրա կարող ենք գրել.
![]()
Երբ շղթան ունի զուտ ակտիվ բնույթ, լարումն ու հոսանքը
ըստ փուլի համընկնում են, և հզորության գործակիցը՝ ![]() Այս դեպքում ակնթարթային հզորությունը
միշտ դրական է (նկ.3.17), հետևաբար բացակայում է էներգիայի փոխանակումը աղբյուրի և
շղթայի միջև:
Այս դեպքում ակնթարթային հզորությունը
միշտ դրական է (նկ.3.17), հետևաբար բացակայում է էներգիայի փոխանակումը աղբյուրի և
շղթայի միջև:

Մյուս ծայրագույն դեպքում, երբ շղթան կազմված է միայն
իդեալական ինդուկտիվ և/կամ ունակային տարրերից, լարումն ու հոսանքը ըստ փուլի շեղված
են ![]() (նկ.
3.18): Ուստի մեկ կիսապարբերության ընթացքում աղբյուրից վերցված էներգիան հաջորդ կիսապարբերության
ընթացքում ամբողջովին հետ է վերադարձվում աղբյուրին: Այս դեպքում էներգիայի անվերադարձ
ծախս չկա, և ակտիվ հզորությունը` P = 0, իսկ Q = S:
(նկ.
3.18): Ուստի մեկ կիսապարբերության ընթացքում աղբյուրից վերցված էներգիան հաջորդ կիսապարբերության
ընթացքում ամբողջովին հետ է վերադարձվում աղբյուրին: Այս դեպքում էներգիայի անվերադարձ
ծախս չկա, և ակտիվ հզորությունը` P = 0, իսկ Q = S:
3.9. Փոփոխական հոսանքի բարդ շղթաների հաշվարկը
Օհմի օրենքը կոմպլեքս տեսքով
Փոփոխական հոսանքի շղթայի լարման և հոսանքի կոմպլեքս արժեքների հարաբերությունը կոչվում է շղթայի լրիվ դիմադրության կոմպլեքս արժեք կամ պարզապես կոմպլեքս դիմադրություն:
Սինուսոիդական ![]() լարման և սինուսոիդական
լարման և սինուսոիդական ![]() հոսանքի
կոմպլեքս արժեքներն ըստ (3.4) հավասարման, համապատասխանաբար, կլինեն.
հոսանքի
կոմպլեքս արժեքներն ըստ (3.4) հավասարման, համապատասխանաբար, կլինեն.
![]()
Հետևաբար շղթայի կոմպլեքս դիմադրությունը կլինի
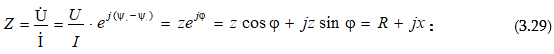
Այսպիսով, կոմպլեքս դիմադրությունը մի կոմպլեքս թիվ է, որի իրական մասը շղթայի ակտիվ դիմադրությունն է, իսկ կեղծ մասի գործակիցը՝ ռեակտիվ դիմադրությունը:
Այստեղից, Օհմի օրենքը կոմպլեքս տեսքով կլինի

Կիրխհոֆի 1-ին օրենքը կոմպլեքս տեսքով
Ժամանակի որևէ ակնթարթին շղթայի ցանկացած հանգույցի
համար ըստ Կիրխհոֆի 1-ին օրենքի կարելի է գրել ![]() այնուհետև, փոխարինելով սինուսոիդական
մեծությունների այս գումարը համապատասխան վեկտորների գումարով, կստանանք Կիրխհոֆի
1-ին օրենքի արտահայտությունը կոմպլեքս տեսքով.
այնուհետև, փոխարինելով սինուսոիդական
մեծությունների այս գումարը համապատասխան վեկտորների գումարով, կստանանք Կիրխհոֆի
1-ին օրենքի արտահայտությունը կոմպլեքս տեսքով.
![]()
Կիրխհոֆի 2-րդ օրենքը կոմպլեքս տեսքով
Ժամանակի որևէ ակնթարթին շղթայի ցանկացած կոնտուրի
համար ըստ Կիրխհոֆի 2-րդ օրենքի կարելի է գրել ![]() կամ, կոմպլեքս տեսքով,
կամ, կոմպլեքս տեսքով, ![]() Այստեղից,
տեղադրելով (3.30)-ից
Այստեղից,
տեղադրելով (3.30)-ից ![]() ստանում ենք Կիրխհոֆի 2-րդ օրենքի
արտահայտությունը կոմպլեքս տեսքով.
ստանում ենք Կիրխհոֆի 2-րդ օրենքի
արտահայտությունը կոմպլեքս տեսքով.
![]()
Այսպիսով, Օհմի և Կիրխհոֆի օրենքները կոմպլեքս տեսքով ունեն այն տեսքը, ինչպիսին դրանք ունեին հաստատուն հոսանքի շղթաների դեպքում: Հետևաբար, սինուսոիդական հոսանքի շղթաների անալիզի համար կարող են կիրառվել բոլոր այն մեթոդները, որոնք կիրառվում են հաստատուն հոսանքի շղթաների անալիզի համար, եթե բոլոր գործողությունները կատարվեն կոմպլեքս թվերով:
Շղթայի լրիվ հզորության կոմպլեքս արժեքը
Սինուսոիդական շղթաների անալիզի համար ներմուծվում
է նաև կոմպլեքս հզորություն հասկացությունը: Շղթայի կոմպլեքս հզորություն է կոչվում
լարման կոմպլեքս արժեքի և հոսանքի կոմպլեքս արժեքի ![]() համալուծի
արտադրյալը.
համալուծի
արտադրյալը.
![]()
Այսինքն, կոմպլեքս հզորությունը մի կոմպլեքս թիվ է, որի իրական մասը շղթայի ակտիվ հզորությունն է, իսկ կեղծ մասի գործակիցը՝ ռեակտիվ հզորությունը:
3.10. Սինուսոիդական հոսանքի շղթաների հաշվարկի օրինակներ
Խնդիր 3.1. Փոփոխական հոսանքի շղթայի համար տրված են (նկ. 3.19).
![]()
Անհրաժեշտ է որոշել ամպերմետրի ցուցմունքը:
Լուծում.
Աղբյուրի էլշուի տրված արտահայտությունից հետևում է,
որ ![]()
Որոշենք ունակային դիմադրությունն ըստ (3.12) –ի.
![]()
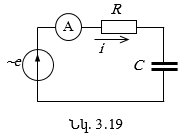
Ամպերմետրը ցույց է տալիս հոսանքի գործող արժեքը, հետևաբար
այն որոշելու hամար պետք է օգտվել Օհմի օրենքից՝ գրված գործող արժեքների համար`
![]()
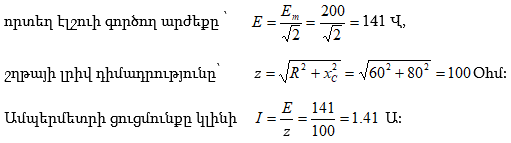
Խնդիր 3.2. Որոշել վոլտմետրի ցուցմունքը
նկ. 3.20-ում բերված շղթայում, որտեղ ![]()
Լուծում.
Շղթայի լրիվ դիմադրությունը
![]()
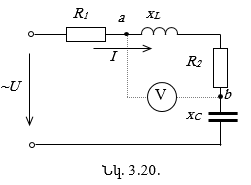
Օգտվելով Օհմի օրենքից՝ որոշում ենք շղթայի հոսանքը.
![]()
Գրելով Օհմի օրենքը շղթայի a-b տեղամասի համար՝
որոշում ենք ![]() լարման
գործող արժեքը, որն էլ կներկայացնի վոլտմետրի ցուցմունքը.
լարման
գործող արժեքը, որն էլ կներկայացնի վոլտմետրի ցուցմունքը.
![]()
Խնդիր 3.3. Որոշել ամպերմետրի ցուցմունքը
նկ. 3.21-ում բերված շղթայում, որտեղ ![]()
Լուծում.
Տրված ակտիվ և ռեակտիվ դիմադրությունների խառը միացված շղթան (նկ.3.21ա) ձևափոխենք հաղորդականությունների զուգահեռ շղթայի (նկ. 3.21բ):
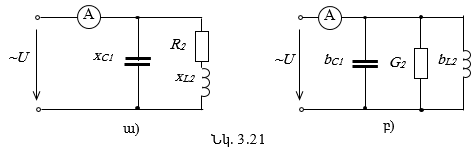
Ըստ 3.23 բանաձևերի`
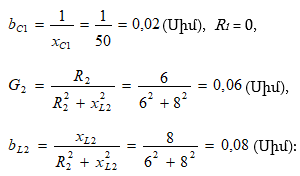
Զուգահեռ շղթայի լրիվ հաղորդականությունը, ըստ (3.18) բանաձևի`
![]()
Ամպերմետրի ցուցմունքը (շղթայի ընդհանուր հոսանքը), ըստ Օհմի օրենքի (3.18’)`
![]()
Խնդիր 3.4. Որոշել շղթայի ակտիվ և ռեակտիվ
հզորությունները, եթե տրված են շղթայի (պասիվ երկբևեռի) մուտքային լարումը և հոսանքը`
![]()
Լուծում.
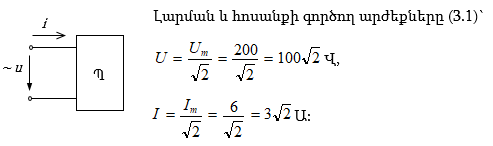
Լարման և հոսանքի փուլային շեղումը`
![]()
Շղթայի ակտիվ և ռեակտիվ հզորությունները (3.25, 3.26)`
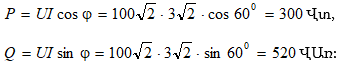
Խնդիր 3.5. Նախորդ խնդրի շղթայի համար որոշել թե դրա համարժեք պարզագույն սխեման ի՞նչ տարրերով պետք է ներկայացնել:
Լուծում.
Լարման և հոսանքի կոմպլեքս արժեքները (3.4)`
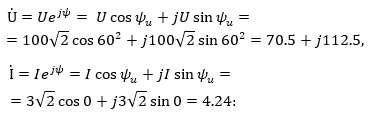
Շղթայի կոմպլեքս դիմադրությունը (3.30)`
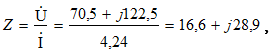
որտեղից հետևում է, որ համարժեք սխեման պետք է պարունակի
հաջորդաբար միացված R = 16,6 Օհմ ակտիվ դիմադրություն և ![]() ինդուկտիվ
դիմադրություն (քանի որ կոմպլեքս դիմադրության կեղծ մասը դրական է):
ինդուկտիվ
դիմադրություն (քանի որ կոմպլեքս դիմադրության կեղծ մասը դրական է):
Խնդիր 3.6. Սինուսոիդական հոսանքի ճյուղավորված
շղթայում (նկ. 3.22ա) տրված են աղբյուրի լարման գործող արժեքը (U) և սկզբնական փուլը
![]() բոլոր տարրերի
պարամետրերը
բոլոր տարրերի
պարամետրերը ![]() ակտիվ դիմադրությունները,
ակտիվ դիմադրությունները, ![]() ինդուկտիվությունը և
ինդուկտիվությունը և ![]() ունակությունը):
ունակությունը):
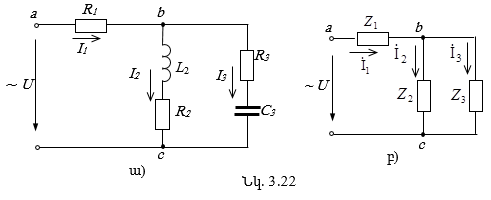
Անհրաժեշտ է հաշվարկել հոսանքների և լարումների գործող արժեքները ճյուղերում, շղթայի ակտիվ, ռեակտիվ և լրիվ հզորությունները:
Լուծում.
Տրված ճյուղավորված շղթայի հաշվարկը հարմար է իրականացնել կոմպլեքս թվերի եղանակով՝ հետևյալ հաջորդականությամբ.
1) Հաշվել շղթայի ռեակտիվ դիմադրությունները՝ օգտվելով (3.8) և (3.12) բանաձևերից.
![]()
Եթե հաճախությունը տրված չէ, պետք է այն վերցնել f = 50 Հց:
2) Տրված մեծություններն արտահայտել կոմպլեքս թվերով.
· Աղբյուրի լարման կոմպլեքս արժեքը, ըստ (3.4) բանաձևի2,
![]()
· Շղթայի ճյուղերի կոմլեքս դիմադրությունները (ըստ 3.29 բանաձևի)
![]()
Հետագա գործողությունների համար կարելի է նկ. 3.22ա-ում տրված շղթան փոխարինել նկ. 3.22բ-ում պատկերված շղթայով, որի բոլոր պարամետրերը կոմպլեքս թվեր են: Այն մեկ աղբյուր պարունակող շղթա է, ուստի դրա հաշվարկը, ինչպես և հաստատուն հոսանքի շղթաների դեպքում, նպատակահարմար է կատարել համարժեք ձևափոխությունների միջոցով:
3) Որոշվում է շղթայի համարժեք կոմպլեքս դիմադրությունը:
Ակնհայտ է, որ ![]() կոմպլեքս դիմադրությունները միացված
են զուգահեռ (նկ.3.22բ), հետևաբար դրանց համարժեք կոմպլեքս դիմադրությունը կլինի
կոմպլեքս դիմադրությունները միացված
են զուգահեռ (նկ.3.22բ), հետևաբար դրանց համարժեք կոմպլեքս դիմադրությունը կլինի
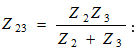
Ամբողջ շղթայի համարժեք կոմպլեքս դիմադրությունը կլինի
![]() դիմադրությունները
միացված են հաջորդաբար).
դիմադրությունները
միացված են հաջորդաբար).
![]()
որտեղ ստացված կոմպլեքս թվի իրական մասը շղթայի համարժեք
ակտիվ դիմադրությունն է, ![]() իսկ կեղծ մասի գործակիցը՝ համարժեք
ռեակտիվ դիմադրությունը,
իսկ կեղծ մասի գործակիցը՝ համարժեք
ռեակտիվ դիմադրությունը, ![]()
Կախված շղթայի համարժեք կոմպլեքս դիմադրության կեղծ մասի գործակցի արժեքից` հնարավոր են երեք դեպքեր (նկ. 3.23).
· Եթե B > 0, շղթան ունի ակտիվ-ինդուկտիվ բնույթ, և այն կարելի է փոխարինել ռեզիստիվ և ինդուկտիվ տարրերի հաջորդաբար միացված պարզագույն համարժեք սխեմայով (նկ.3. 23ա):
· Եթե B < 0, շղթան ունի ակտիվ-ունակային բնույթ, և այն կարելի է փոխարինել ռեզիստիվ և ունակային տարրերի հաջորդաբար միացված պարզագույն համարժեք սխեմայով (նկ. 3.23բ):
· Եթե B = 0, շղթայում տեղի ունի ռեզոնանսի երևույթ և համարժեք պարզագույն սխեման կազմված է միայն ռեզիստիվ տարրից (նկ. 3.23գ):
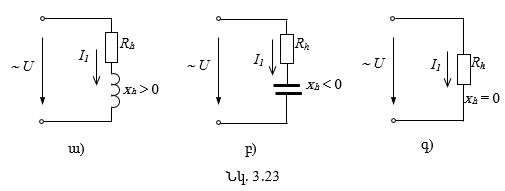
4) Ստացված պարզագույն շղթայի համար (նկ. 3.23), գրելով Օհմի օրենքը կոմպլեքս տեսքով, որոշում ենք աղբյուրի հոսանքի կոմպլեքս արժեքը.

որտեղից հոսանքի գործող արժեքը`
![]()
5) Համաձայն Օհմի օրենքի, որոշում ենք շղթայի զուգահեռ տեղամասի լարումը (նկ. 3.22).
![]()
6) Զուգահեռ ճյուղերից յուրաքանչյուրի համար գրելով Օհմի օրենքը՝ որոշում ենք դրանց հոսանքները.
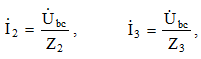
Հոսանքների գործող արժեքները որոշում ենք համանման (3.37) բանաձևի:
7) Հզորությունների հաշվարկը:
Ըստ (3.33) բանաձևի, օգտագործելով (3.34)-ի և (3.36)-ի արդյունքները, որոշում ենք աղբյուրի կոմպլեքս հզորությունը
![]()
որտեղ P -ն աղբյուրի ակտիվ հզորությունն է, Q - ն՝ ռեակտիվ հզորությունը:
Մյուս կողմից, շղթայի ակտիվ հզորությունը կարելի է որոշել որպես շղթայի ռեզիստիվ տարրերի հզորությունների գումար.
![]()
իսկ ռեակտիվ հզորությունը՝ որպես ինդուկտիվ և ունակային տարրերի հզորությունների հանրահաշվական գումար.
![]()
![]() (ակտիվ հզորությունների հաշվեկշիռ)
և
(ակտիվ հզորությունների հաշվեկշիռ)
և ![]() (ռեակտիվ հզորությունների
հաշվեկշիռ) հավասարությունները կարող են հավաստել, որ շղթայի հաշվարկը ճիշտ է կատարված:
(ռեակտիվ հզորությունների
հաշվեկշիռ) հավասարությունները կարող են հավաստել, որ շղթայի հաշվարկը ճիշտ է կատարված:
8) Շղթայի հզորության գործակիցը որոշվում է հետևյալ բանաձևերից որևէ մեկով.
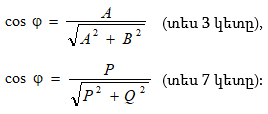
9) Աղբյուրի լարման և հոսանքի ակնթարթային արժեքների որոշումը:
Հաշվի առնելով, համապատասխանաբար, (3.34) և (3.37) արտահայտությունները, համաձայն (3.1) բանաձևի, որոշում ենք լարման և հոսանքի ամպլիտուդային արժեքները`
![]()
Լարման ![]() սկզբնական
փուլը տրված է, իսկ հոսանքի սկզբնական փուլը, համաձայն (3.4բ) բանաձևի,
սկզբնական
փուլը տրված է, իսկ հոսանքի սկզբնական փուլը, համաձայն (3.4բ) բանաձևի,
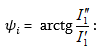
Տեղադրելով ստացված մեծությունները՝ որոշում ենք լարման և հոսանքի ակնթարթային արժեքները
![]()
3.11. Էլեկտրաէներգիայի սպառիչների հզորության գործակցի բարձրացումը
Ինչպես ասվեց 3.8 բաժնում, ռեակտիվ հզորությունը կապված չէ էներգիայի անվերադարձ ծախսի հետ, այն բնութագրում է աղբյուրի և շղթայի միջև էներգիայի հոսքի տատանումները, որոնք, սակայն, շղթան սնող գծերում և տրանսֆորմատորներում առաջացնում են էներգիայի զգալի կորուստներ: Այս պատճառով անհրաժեշտություն է առաջանում փոքրացնել էլեկտրաէներգիայի սպառիչների (ընդունիչների) ռեակտիվ հզորությունը՝ բարձրացնելով դրանց հզորության գործակիցը:
Սպառիչի ակտիվ հզորությունը
![]()
որտեղ U -ն սնող ցանցի լարումն է, I
-ն՝ սպառիչի հոսանքը, ![]() սպառիչի հզորության գործակիցը:
սպառիչի հզորության գործակիցը:
Սպառիչի հոսանքը, որը որոշվում է (3.38) բանաձևից, սնող գծերում առաջացնում է հզորության կորուստ՝

որտեղ ![]() սնող գծի ակտիվ դիմադրությունն է:
սնող գծի ակտիվ դիմադրությունն է:
Ինչպես հետևում է (3.39) բանաձևից, սպառիչի տվյալ լարման
և հզորության դեպքում, որքան փոքր է դրա ![]() այնքան ավելի մեծ է հզորության
(էներգիայի) կորուստը սնող գծերում, այնքան ավելի թանկ արժե էլեկտրաէներգիայի հաղորդումը
գեներատորից սպառիչին: Հետևաբար, էներգետիկական սարքավորումների շահավետությունը բարձրացնելու
համար անհրաժեշտ է միջոցներ ձեռնարկել սպառիչների հզորության գործակցի բարձրացման համար:
այնքան ավելի մեծ է հզորության
(էներգիայի) կորուստը սնող գծերում, այնքան ավելի թանկ արժե էլեկտրաէներգիայի հաղորդումը
գեներատորից սպառիչին: Հետևաբար, էներգետիկական սարքավորումների շահավետությունը բարձրացնելու
համար անհրաժեշտ է միջոցներ ձեռնարկել սպառիչների հզորության գործակցի բարձրացման համար:
Արտադրական ձեռնարկություններում ![]() արժեքը
նախ փորձում են բարձրացնել բնական ճանապարհով՝ կարգավորելով էլեկտրասարքավորումների
էներգետիկական ռեժիմը, բարձրացնելով դրանց բեռնվածության աստիճանը և այլն: Եթե այդ
միջոցառումները անբավարար են լինում, ապա դիմում են հզորության գործակցի բարձրացմանն
ուղղված արհեստական միջոցների՝ օգտագործելով ռեակտիվ հզորությունը կոմպենսացնող
(չեզոքացնող) սարքեր:
արժեքը
նախ փորձում են բարձրացնել բնական ճանապարհով՝ կարգավորելով էլեկտրասարքավորումների
էներգետիկական ռեժիմը, բարձրացնելով դրանց բեռնվածության աստիճանը և այլն: Եթե այդ
միջոցառումները անբավարար են լինում, ապա դիմում են հզորության գործակցի բարձրացմանն
ուղղված արհեստական միջոցների՝ օգտագործելով ռեակտիվ հզորությունը կոմպենսացնող
(չեզոքացնող) սարքեր:
Ներկայումս կիրառվող Էլեկտրաէներգիայի սպառիչները մեծ
մասամբ ակտիվ-ինդուկտիվ բնույթի են (ասինքրոն շարժիչներ, տրանսֆորմատորներ և այլն),
որոնց հոսանքն ըստ փուլի hետ է ընկած սնող ցանցի լարումից ![]() անկյունով: Հետևաբար
անկյունով: Հետևաբար ![]() փոքրացնելու
փոքրացնելու
![]() մեծացնելու)
համար անհրաժեշտ է այդ սպառիչներին զուգահեռ միացնել այնպիսի սարքեր, որոնց հոսանքն
առաջ է ընկած լարումից և կարող է կոմպենսացնել (չեզոքացնել) հոսանքի ինդուկտիվ բնույթ
ունեցող ռեակտիվ բաղադրիչը: Մասնավորապես, այդպիսի սարքեր են կոնդենսատորային մարտկոցները,
որոնք կարելի է ներկայացնել որպես ունակային տարրեր, որոնց հոսանքն ըստ փուլի առաջ
է ընկած լարումից
մեծացնելու)
համար անհրաժեշտ է այդ սպառիչներին զուգահեռ միացնել այնպիսի սարքեր, որոնց հոսանքն
առաջ է ընկած լարումից և կարող է կոմպենսացնել (չեզոքացնել) հոսանքի ինդուկտիվ բնույթ
ունեցող ռեակտիվ բաղադրիչը: Մասնավորապես, այդպիսի սարքեր են կոնդենսատորային մարտկոցները,
որոնք կարելի է ներկայացնել որպես ունակային տարրեր, որոնց հոսանքն ըստ փուլի առաջ
է ընկած լարումից ![]()
Նկ. 3.24ա-ում պատկերված սխեման և նկ. 3.24բ-ում՝
նրա վեկտորական դիագրամը, լուսաբանում են կոնդենսատորների օգնությամբ ![]() բարձրացման
սկզբունքը:
բարձրացման
սկզբունքը:
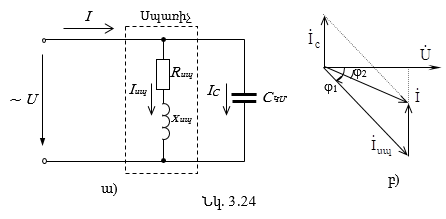
Մինչև կոնդենսատորային մարտկոցի միացնելը սնման գծով
անցնող հոսանքը հավասար է սպառիչի ![]() հոսանքին, որն ըստ փուլի hետ է մնում
U լարումից
հոսանքին, որն ըստ փուլի hետ է մնում
U լարումից ![]() անկյունով: Կոնդենսատորային մարտկոցի
միացման դեպքում սնող գծերով անցնող հոսանքը, ըստ Կիրխհոֆի 1-ին օրենքի, կորոշվի որպես
սպառիչի և կոնդենսատորային մարտկոցի հոսանքների վեկտորական գումար՝
անկյունով: Կոնդենսատորային մարտկոցի
միացման դեպքում սնող գծերով անցնող հոսանքը, ըստ Կիրխհոֆի 1-ին օրենքի, կորոշվի որպես
սպառիչի և կոնդենսատորային մարտկոցի հոսանքների վեկտորական գումար՝
![]()
Վեկտորական դիագրամից (նկ. 3.24բ) հետևում է, որ շնորհիվ
կոնդենսատորային մարտկոցի միացման, սնման գծի հոսանքը և դրա փուլային շեղումը լարման
նկատմամբ փոքրանում են՝ ![]() հետևաբար, հզորության գործակիցը
մեծանում է՝
հետևաբար, հզորության գործակիցը
մեծանում է՝ ![]()
Սպառիչի ռեակտիվ հզորությունը, ըստ (3.26) բանաձևի,
կլինի ![]() իսկ
իսկ ![]() հզորությամբ կոնդենսատորային
մարտկոցը սպառիչին զուգահեռ միացնելուց հետո, շղթայի ռեակտիվ հզորությունը՝
հզորությամբ կոնդենսատորային
մարտկոցը սպառիչին զուգահեռ միացնելուց հետո, շղթայի ռեակտիվ հզորությունը՝
![]()
Հատկանշական է, որ կոնդենսատորային մարտկոցը մասամբ
կամ լրիվ կոմպենսացնելով սպառիչի ռեակտիվ հզորությունը, չի ազդում դրա P ակտիվ
հզորության վրա, որը մնում է անփոփոխ: Ուստի, ըստ (3.28) բանաձևի, որոշելով ![]() ռեակտիվ
հզորությունները, (3.42) -ից կստանանք կոնդենսատորային մարտկոցի
ռեակտիվ
հզորությունները, (3.42) -ից կստանանք կոնդենսատորային մարտկոցի ![]() հզորության
այն արժեքը, որն անհրաժեշտ է հզորության գործակիցը
հզորության
այն արժեքը, որն անհրաժեշտ է հզորության գործակիցը ![]() դարձնելու
համար՝
դարձնելու
համար՝
![]()
Եթե սպառիչի հզորությունը արտահայտված է կՎտ-երով,
ապա ![]() -ը կարտահայտվի
կՎԱռ-ներով:
-ը կարտահայտվի
կՎԱռ-ներով:
Սովորաբար կոնդենսատորային մարտկոցների միջոցով շղթայի
ռեակտիվ հզորության լրիվ կոմպենսացիա ![]() չի կատարվում, և հզորության գործակցի
արժեքը հասցվում է մինչև 0,9…0,95: Դրանից ավելի բարձրացնելու համար պահանջվող լրացուցիչ
կոնդենսատորային մարտկոցների արժեքը տնտեսապես չի արդարացնում իրեն:
չի կատարվում, և հզորության գործակցի
արժեքը հասցվում է մինչև 0,9…0,95: Դրանից ավելի բարձրացնելու համար պահանջվող լրացուցիչ
կոնդենսատորային մարտկոցների արժեքը տնտեսապես չի արդարացնում իրեն:
Մեծ հզորության էլեկտրաէներգետիկական համակարգերում հզորության գործակցի բարձրացման համար կիրառվում են սինքրոն կոմպենսատորներ, որոնք հատուկ ռեժիմով աշխատող սինքրոն շարժիչներ են:
Հզորության գործակցի բարձրացումը, բացի էներգիայի կորուստների փոքրացումից, էապես բարելավում է էլեկտրամատակարարման համակարգի ռեժիմները, փոքրացնում է լարման անկումները էլեկտրական ցանցերում, մեծացնում է էլեկտրահաղորդման գծերի և տրանսֆորմատորների թողունակությունը (թույլ տալով ավելի մեծ ակտիվ էներգիա հաղորդել դրանցով) կամ թույլ է տալիս փոքրացնել ինչպես կաբելային և օդային գծերի հատույթի մակերեսը, այնպես էլ տրանսֆորմատորների հզորությունը կամ թիվը:
Էներգետիկական սարքավորումների հզորության գործակցի
բարձրացումը տնտեսական կարևոր խնդիր է, ուստի այս միջոցառումների խթանման համար շատ
երկրներում սահմանվում են էլեկտրաէներգիայի տարբերակված սակագներ տարբեր ձեռնարկությունների
համար: Որքան մոտ է ![]() արժեքը տվյալ ձեռնարկության համար
նախասահմանված օպտիմալ արժեքին, այնքան ցածր է 1 կՎտ-ժամ էլեկտրաէներգիայի արժեքը այդ
ձեռնարկության համար:
արժեքը տվյալ ձեռնարկության համար
նախասահմանված օպտիմալ արժեքին, այնքան ցածր է 1 կՎտ-ժամ էլեկտրաէներգիայի արժեքը այդ
ձեռնարկության համար:
1. Ինչու՞ գործնականում փոփոխական հոանքն ունի գերակշռող կիրառություն:
2. Ի՞նչ կառուցվածքային մասերից է կազմված սինքրոն գեներատորը:
3. Գրեք սինուսոիդական հոսանքի (լարման, էլշուի) արտահայտությունը: Տվեք սինուսոիդական հոսանքը (լարմումը, էլշուն) բնութագրող մեծությունների (ամպլիտուդային արժեք, հաճախություն, պարբերություն, սկզբնական փուլ)ի սահմանումները:
4. Սահմանել սինուսոիդական մեծության գործող և միջին արժեքները: Ի՞նչ առնչությամբ են դրանք կապված ամպլիտուդային արժեքի հետ:
5. Տալ սինուսոիդական մեծությանը համապատասխանող պտտվող վեկտորի հասկացությունը:
6. Ի՞նչ է շղթայի վեկտորական դիագրամը:
7. Ինչպե՞ս է սինուսոիդական մեծությունը արտահայտվում կոմպլեքս թվով:
8. Ի՞նչ պասիվ տարրերով է պատկերվում փոփոխական հոսանքի շղթան: Ցույց տալ դրանց պայմանական նշանները և նշել պարամետրերը:
9. Գրեք Օհմի օրենքի արտահայտությունը ռեզիստիվ (ինդուկտիվ, ունակային) տարրերի համար:
10. Պատկերեք շղթայի լարման և հոսանքի վեկտորների փոխադարձ դասավորությունը ռեզիստիվ (ինդուկտիվ, ունակային) տարրերի համար:
11. Գրեք R-L-C տարրերի հաջորդաբար միացված շղթայի լրիվ դիմադրության բանաձևը:
12. Գրեք R-L-C տարրերի հաջորդաբար միացված շղթայի համար լարման և հոսանքի փուլային շեղման բանաձևը: Պատկերել դիմադրությունների եռանկյունը:
13. Ինչպիսի՞ երեք բնութագրական դեպքեր են հնարավոր R-L-C հաջորդական շղթայում: Կառուցել շղթայի վեկտորական դիագրամները այդ դեպքերի համար:
14. Ի՞նչ է լարումների ռեզոնանսը և ի՞նչ առանձնահատկություն ունի շղթան այդ դեպքում:
15. Գրեք R-L-C տարրերի զուգահեռ միացված շղթայի լրիվ հաղորդականության բանաձևը:
16. Գրեք R-L-C տարրերի զուգահեռ միացված շղթայի լարման և հոսանքի փուլային շեղման բանաձևը: Պատկերել հաղորդականությունների եռանկյունը:
17. Ինչպիսի՞ երեք բնութագրական դեպքեր են հնարավոր R-L-C զուգահեռ շղթայում: Կառուցել շղթայի վեկտորական դիագրամները այդ դեպքերի համար:
18. Ի՞նչ է հոսանքների ռեզոնանսը, և ի՞նչ առանձնահատկություն ունի շղթան այդ դեպքում:
19. Գրեք փոփոխական հոսանքի շղթայի դիմադրությունների և հաղորդա-կանությունների համարժեք կապերն արտահայտող բանաձևերը:.
20. Ի՞նչ է շղթայի ռեզոնանսային հաճախությունը և ինչպես է այն որոշվում:
21. Գրել փոփոխական հոսանքի շղթայի ակտիվ հզորության բանաձևը:
22. Ի՞նչ է շղթայի հզորության գործակիցը և ինչպե՞ս է այն որոշվում:
23. Գրել փոփոխական հոսանքի շղթայի ռեակտիվ և լրիվ հզորությունների բանաձևերը: Ի՞նչ միավորներով են դրանք չափվում:
24. Պատկերել հզորությունների եռանկյունը:
25. Տալ փոփոխական հոսանքի շղթայի կոմպլեքս դիմադրության և կոմպլեքս հզորության սահմանումները և գրել դրանց որոշման բանաձևերը:
26. Ինչո՞վ է պայմանավորված սպառիչների հզորության գործակցի բարձրացման անհրաժեշտությունը:
27. Էլեկտրական ցանցի հզորության գործակցի բարձրացմանն ուղղված ինչպիսի՞ միջոցառումներ են կիրառվում:
4.1. Ընդհանուր դրույթներ
Եռաֆազ են կոչվում այն էլեկտրական շղթաները, որոնցում
գործում են մեկ գեներատորով ստացված երեք սինուսոիդական էլշուներ, որոնց գործող արժեքները
հավասար են, բայց շեղված են միմյանց նկատմամբ ըստ փուլի ![]()
Ներկայումս էլեկտրաէներգետիկայում գլխավորապես կիրառվում են եռաֆազ շղթաները: Գործնականում հանդիպող միաֆազ շղթաները պարզապես հանդիսանում են եռաֆազ համակարգի մի մասը: Դա պայմանավորված է եռաֆազ շղթաների՝ միաֆազ շղթաների նկատմամբ ունեցած, հետևյալ առավելություններով.
· Եռաֆազ էլեկտրական սարքերն ու ապարատներն ունեն ավելի փոքր չափեր, ավելի ցածր ինքնարժեք և ավելի բարձր օ.գ.գ., քան նույն հզորության միաֆազ պատրաստվածները:
· Եռաֆազ շղթան հնարավորություն է տալիս օգտագործել էժան և պարզ կառուցվածք ունեցող եռաֆազ ասինքրոն շարժիչներ, որոնք ներկայումս էլեկտրաէներգիայի ամենատարածված սպառիչներից են:
· Էլեկտրաէներգիայի հաղորդումը եռաֆազ գծերով տնտեսապես ավելի շահավետ է, որովհետև թույլ է տալիս կրճատել հզորության կորուստները և խնայել հաղորդիչ նյութը::
Եռաֆազ շղթաներում էլեկտրաէներգիայի աղբյուրը եռաֆազ
գեներատորն է: Ժամանակակից էներգետիկայում եռաֆազ էլշուների համակարգը հիմնականում
ստանում են էլեկտրակայաններում տեղադրված եռաֆազ սինքրոն գեներատորների միջոցով: Եռաֆազ
գեներատորի կառուցվածքը սկզբունքորեն նույնն է, ինչ միաֆազ գեներատորի կառուցվածքը
(տես 3.1 բաժինը): Տարբերությունը միայն այն է, որ այստեղ ստատորի վրա մեկի փոխարեն
երեք փաթույթներ են տեղադրվում, որոնց առանցքները միմյանց նկատմամբ տարածականորեն դասավորված
են ![]() շեղված (նկ. 4.1):
շեղված (նկ. 4.1):
Երբ ռոտորը պտտում են առաջնային շարժիչի (տուրբինի)
միջոցով, պտտվում է նաև դրա մագնիսական դաշտը՝ յուրաքանչյուր փաթույթում ինդուկտելով
սինուսոիդական էլշու: Քանի որ փաթույթները լրիվ միատեսակ են, ապա ինդուկտված էլշուների
![]() ամպլիտուդային (հետևաբար նաև E
գործող) արժեքները կլինեն միմյանց հավասար: Սակայն ռոտորը հատում է փաթույթները ժամանակի
տարբեր պահերին, ուստի նրանցում ինդուկտված էլշուները շեղված կլինեն ըստ փուլի
ամպլիտուդային (հետևաբար նաև E
գործող) արժեքները կլինեն միմյանց հավասար: Սակայն ռոտորը հատում է փաթույթները ժամանակի
տարբեր պահերին, ուստի նրանցում ինդուկտված էլշուները շեղված կլինեն ըստ փուլի ![]()
![]() ռադիանով):
ռադիանով):
Եռաֆազ համակարգ կազմող էլշուները և մյուս էլեկտրական մեծություններն ինդեքսավորվում են A, B, C լատինական տառերով:
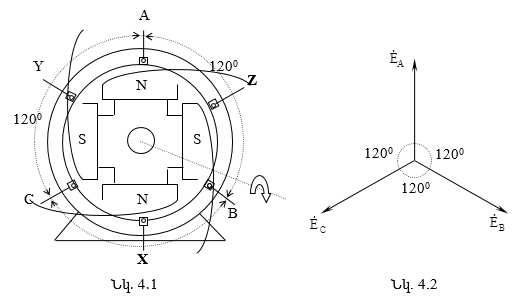
Գեներատորում ինդուկտված եռաֆազ էլշուների ակնթարթային արժեքները ներկայացվում են հետևյալ եռանկյունաչափական տեսքով (էլշուներից մեկի սկզբնական փուլը վերցված է զրո).
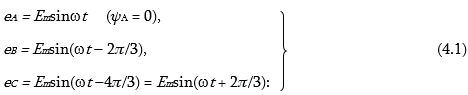
Այս էլշուները կարող են պատկերվել համապատասխան երեք
վեկտորների միջոցով, որոնք ունեն հավասար երկարություններ ![]() և միմյանց
հետ կազմում են
և միմյանց
հետ կազմում են ![]() անկյուններ (նկ. 4.2):
անկյուններ (նկ. 4.2):
Եռաֆազ սինուսոիդական էլշուները, ըստ (3.4)-ի, կարող են ներկայացվել նաև կոմպլեքս տեսքով.
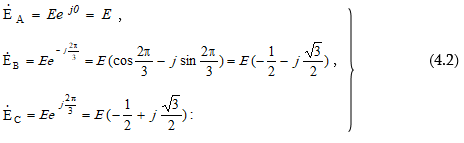
Մաթեմատիկական պարզ գործողությունները ցույց են տալիս, որ եռաֆազ էլշուների ինչպես ակնթարթային, այնպես էլ վեկտորական և կոմպլեքս արժեքների գումարը հավասար է զրոյի.
![]()
Եռաֆազ շղթան փաստորեն երեք միաֆազ շղթաների կամ ֆազերի միավորում է: Եռաֆազ շղթա կազմելու համար գոյություն ունի ֆազերի միացման երկու հիմնական եղանակ. աստղաձև և եռանկյունաձև (տես՝ 1.7 բաժինը):
4.2. Աստղաձև միացված եռաֆազ շղթաներ
Դիտարկենք եռաֆազ շղթա, որի եռաֆազ գեներատորի փաթույթները
և եռաֆազ սպառիչի ֆազերի դիմադրությունները միացված են աստղաձև (նկ. 4.3): A-a,
B-b, C-c հաղորդալարերը, որոնցով էլեկտրաէներգիան գեներատորից փոխանցվում է սպառիչին,
կոչվում են գծային հաղորդալարեր: Դրանցով անցնող ![]() հոսանքները՝ գծային հոսանքներ,
դրանց միջև
հոսանքները՝ գծային հոսանքներ,
դրանց միջև ![]() լարումները՝ գծային լարումներ:
Աստղաձև միացման ընդհանուր հանգույց ներկայացնող N և n կետերը կոչվում են զրոյական
կամ չեզոք կետեր, դրանք միացնող N-n հաղորդալարը՝ չեզոք հաղորդալար, իսկ դրանով
անցնող
լարումները՝ գծային լարումներ:
Աստղաձև միացման ընդհանուր հանգույց ներկայացնող N և n կետերը կոչվում են զրոյական
կամ չեզոք կետեր, դրանք միացնող N-n հաղորդալարը՝ չեզոք հաղորդալար, իսկ դրանով
անցնող ![]() հոսանքը զրոյական կամ չեզոք հոսանք:
Հոսանքների միջև կապը տրվում է Կիրխհոֆի 1-ին օրենքով՝ գրված կոմպլեքս տեսքով:
հոսանքը զրոյական կամ չեզոք հոսանք:
Հոսանքների միջև կապը տրվում է Կիրխհոֆի 1-ին օրենքով՝ գրված կոմպլեքս տեսքով:
Շղթայի n հանգույցի համար
![]()
Գեներատորի փաթույթներով կամ սպառիչի դիմադրություններով
անցնող հոսանքները կոչվում են ֆազային հոսանքներ: Ակնհայտ է, որ աստղաձև միացման դեպքում
համապատասխան գծային և ֆազային հոսանքները հավասար են՝ ![]() Գեներատորի փաթույթների ծայրերում
Գեներատորի փաթույթների ծայրերում
![]() և սպառիչի դիմադրությունների ծայրերում
և սպառիչի դիմադրությունների ծայրերում
![]() լարումները
կոչվում են ֆազային լարումներ
լարումները
կոչվում են ֆազային լարումներ
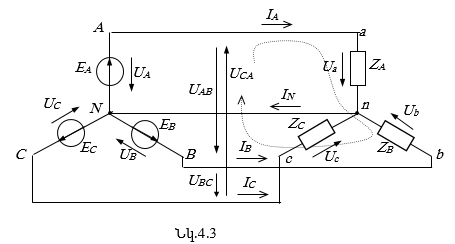
Սխեմայում (նկ. 4.3) կետագծով նշված, ինչպես նաև համանման մյուս երկու կոնտուրների համար, Կիրխհոֆի 2-րդ օրենքի հիման վրա գրենք կոմպլեքս տեսքով հավասարումներ.
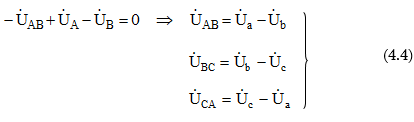
Սպառիչի յուրաքանչյուր ֆազի համար Օհմի օրենքը կոմպլեքս տեսքով կլինի.
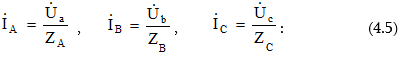
Կառուցենք տրված եռաֆազ շղթայի (նկ.4.3) վեկտորական դիագրամը: Եթե անտեսենք հաղորդալարերի և գեներատորի փաթույթների ներքին դիմադրությունները, ապա սպառիչի ֆազային լարումները հավասար կլինեն աղբյուրի համապատասխան էլշուներին.
![]()
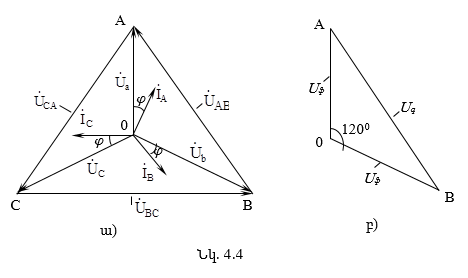
Այսինքն ֆազային լարումների ![]() վեկտորները,
ինչպես էլշուների
վեկտորները,
ինչպես էլշուների ![]() վեկտորները, կլինեն չափով միմյանց
հավասար, բայց ըստ փուլի շեղված
վեկտորները, կլինեն չափով միմյանց
հավասար, բայց ըստ փուլի շեղված ![]() (նկ. 4.4ա): Գծային
լարումների վեկտորները կառուցվում են (4.4) վեկտորական հավասարումների հիման վրա:
(նկ. 4.4ա): Գծային
լարումների վեկտորները կառուցվում են (4.4) վեկտորական հավասարումների հիման վրա:
Եռաֆազ սպառիչը (հետևաբար և եռաֆազ շղթան) կոչվում է սիմետրիկ, եթե դրա երեք ֆազերի կոմպլեքս դիմադրությունները հավասար են.
![]()
Սա նշանակում է, որ եռաֆազ սպառիչը սիմետրիկ է, եթե
դրա և՛ ակտիվ դիմադրություններն են հավասար, և՛ ռեակտիվ դիմադրությունները: Սիմետրիկ
սպառիչի դեպքում յուրաքանչյուր ֆազային հոսանք նույն` ![]() անկյունով
է շեղված համապատասխան ֆազային լարումից, hետևաբար այդ հոսանքների գործող արժեքները
հավասար են և նույնպես շեղված են իրար նկատմամբ ըստ փուլի
անկյունով
է շեղված համապատասխան ֆազային լարումից, hետևաբար այդ հոսանքների գործող արժեքները
հավասար են և նույնպես շեղված են իրար նկատմամբ ըստ փուլի ![]() Այդպիսի
հոսանքների վեկտորական գումարը, հետևաբար և չեզոք հաղորդալարի
Այդպիսի
հոսանքների վեկտորական գումարը, հետևաբար և չեզոք հաղորդալարի ![]() հոսանքը, ըստ (4.3)-ի, նույնպես
հավասար է զրոյի, նշանակում է, որ սիմետրիկ սպառիչի դեպքում զրոյական հաղորդալարն ավելորդ
է: Սիմետրիկ սպառիչի օրինակ է եռաֆազ շարժիչը, որի սնման համար օգտագործվում է միայն
երեք հաղորդալար:
հոսանքը, ըստ (4.3)-ի, նույնպես
հավասար է զրոյի, նշանակում է, որ սիմետրիկ սպառիչի դեպքում զրոյական հաղորդալարն ավելորդ
է: Սիմետրիկ սպառիչի օրինակ է եռաֆազ շարժիչը, որի սնման համար օգտագործվում է միայն
երեք հաղորդալար:
Վեկտորական դիագրամից (նկ. 4.4ա) առանձնացված AOB հավասարասրուն
եռանկյունից (նկ. 4.4բ) հետևում է, որ աստղաձև միացման դեպքում ֆազային լարումը ![]() անգամ փոքր
է գծային լարումից.
անգամ փոքր
է գծային լարումից.

Օրինակ, եթե գծային լարումը ![]() ապա ֆազային լարումը կլինի
ապա ֆազային լարումը կլինի ![]()
4.3. Աստղաձև միացված ոչ սիմետրիկ եռաֆազ շղթա
Եթե աստղաձև միացված եռաֆազ համակարգն ունի չեզոք հաղորդալար, ապա (4.6) և (4.8) արտահայտությունները ճիշտ են նաև ոչ սիմետրիկ սպառիչների համար: Հետևաբար շղթայի լարումների վեկտորական դիագրամը (նկ. 4.6ա) չի տարբերվի սիմետրիկ շղթայի վեկտորական դիագրամից (նկ. 4.4):
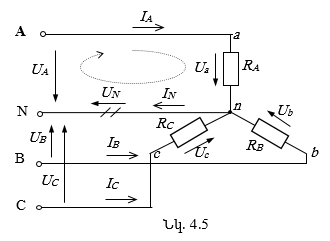
Հոսանքների վեկտորները կառուցելիս պարզության համար
ընդունենք, որ շղթայի երեք ֆազերում էլ սպառիչն ունի ակտիվ բնույթ` այսինքն` ![]() (նկ. 4.5): Ուստի յուրաքանչյուր
ֆազի հոսանք կհամընկնի համապատասխան ֆազային լարման հետ: Քանի որ հոսանքների մեծությունները
տարբեր են, ապա դրանց վեկտորական գումարը հավասար չէ զրոյի, և, հետևաբար, չեզոք հաղորդալարով
անցնում է
(նկ. 4.5): Ուստի յուրաքանչյուր
ֆազի հոսանք կհամընկնի համապատասխան ֆազային լարման հետ: Քանի որ հոսանքների մեծությունները
տարբեր են, ապա դրանց վեկտորական գումարը հավասար չէ զրոյի, և, հետևաբար, չեզոք հաղորդալարով
անցնում է ![]() հոսանք (4.3)՝
հոսանք (4.3)՝
![]()
Եթե չեզոք հաղորդալարը բացակայում է կամ կտրված է,
ապա (4.6) և (4.8) արտահայտություններն իրավացի են միայն սիմետրիկ սպառիչի դեպքում:
Ոչ սիմետրիկ սպառիչի դեպքում եռաֆազ գեներատորի և սպառիչի չեզոք կետերի միջև առաջանում
է պոտենցիալների տարբերություն՝ ![]() լարում
(նկ. 4.5), որի պատճառով սպառիչի ֆազային լարումներն արդեն հավասար չեն լինում գեներատորի
համապատասխան ֆազային լարումներին: Դրանց միջև կապը գտնելու համար օգտվենք Կիրխհոֆի
2-րդ օրենքից՝ գրված A – a – n - N կոնտուրի, ինչպես նաև համանման մյուս երկու կոնտուրների
համար՝
լարում
(նկ. 4.5), որի պատճառով սպառիչի ֆազային լարումներն արդեն հավասար չեն լինում գեներատորի
համապատասխան ֆազային լարումներին: Դրանց միջև կապը գտնելու համար օգտվենք Կիրխհոֆի
2-րդ օրենքից՝ գրված A – a – n - N կոնտուրի, ինչպես նաև համանման մյուս երկու կոնտուրների
համար՝
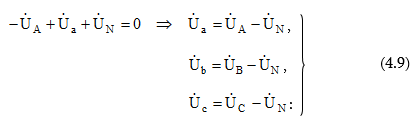
![]() լարման կոմպլեքս արժեքը կարելի է
որոշել որպես միջհանգուցային լարում (համանման (2.5) բանաձևի).
լարման կոմպլեքս արժեքը կարելի է
որոշել որպես միջհանգուցային լարում (համանման (2.5) բանաձևի).
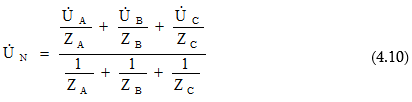
Նկ. 4.6բ-ում պատկերված է աստղաձև միացված ոչ սիմետրիկ շղթայի լարումների վեկտորական դիագրամը՝ չեզոք հաղորդալարի բացակայության դեպքում: Սպառիչի ֆազային լարումների վեկտորները կառուցվում են ըստ (4.9) վեկտորական հավասարությունների:
Ինչպես երևում է լարումների դիագրամից (նկ. 4.6բ), սպառիչի ֆազային լարումները փոփոխվել են, և խախտվել է դրանց (4.8) կապը գծային լարումների հետ:
B և C ֆազերում սպառիչի լարումը մեծացել է ![]() իսկ A ֆազում,
ընդհակառակը, փոքրացել է
իսկ A ֆազում,
ընդհակառակը, փոքրացել է ![]() Այսպես, եթե ֆազերի սպառիչները նախատեսված
էին 220 Վ անվանական լարման համար, ապա սպառիչների մի մասի մոտ այն կարող է հասնել,
ասենք, 300Վ, իսկ մյուսների մոտ՝ 150 Վ: Երկու դեպքերն էլ վտանգավոր են, ուստի չեզոք
հաղորդալարի բացակայությունը կամ խզվելը դիտվում է որպես վթարային դեպք: Չեզոք հաղորդալարի
խզումը կանխելու համար սնող ենթակայաններում և բաշխիչ կետերում չեզոք հաղորդալարի վրա
անջատիչ կամ պաշտպանիչ սարք (ապահովիչ, ավտոմատ անջատիչ) չի նախատեսվում:
Այսպես, եթե ֆազերի սպառիչները նախատեսված
էին 220 Վ անվանական լարման համար, ապա սպառիչների մի մասի մոտ այն կարող է հասնել,
ասենք, 300Վ, իսկ մյուսների մոտ՝ 150 Վ: Երկու դեպքերն էլ վտանգավոր են, ուստի չեզոք
հաղորդալարի բացակայությունը կամ խզվելը դիտվում է որպես վթարային դեպք: Չեզոք հաղորդալարի
խզումը կանխելու համար սնող ենթակայաններում և բաշխիչ կետերում չեզոք հաղորդալարի վրա
անջատիչ կամ պաշտպանիչ սարք (ապահովիչ, ավտոմատ անջատիչ) չի նախատեսվում:
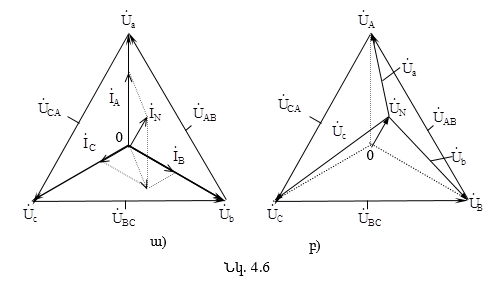
Աստղաձև միացված ոչ սիմետրիկ քառալար շղթայի օրինակ է լուսավորման ցանցը (նկ. 4.7):
Ինչպես երևում է սխեմայից, չեզոք հաղորդալարի վրա ապահովիչ չի դրված: Գծային հաղորդալարի հետ որևէ վթարի (ասենք կարճ միացման) դեպքում անջատվում է դրա վրա դրված համակարգի ապահովիչը և հոսանքազրկվում են միայն այդ ֆազից սնվող սպառիչները, իսկ մյուս երկու ֆազերից սնվող սպառիչները, շնորհիվ չեզոք հաղորդալարի առկայության, շարունակում են նորմալ աշխատանքը: Բնակարանի միաֆազ ցանցում կարճ միացում լինելու դեպքում՝ անջատվում են միայն բնակարանային ապահովիչները՝ հոսանքազրկելով միայն տվյալ բնակարանը: Ակնհայտ է, որ դրա համար բնակարանային ապահովիչների անվանական հոսանքը մի քանի կարգ պետք է փոքր լինի համակարգային ապահովիչների անվանական հոսանքից:
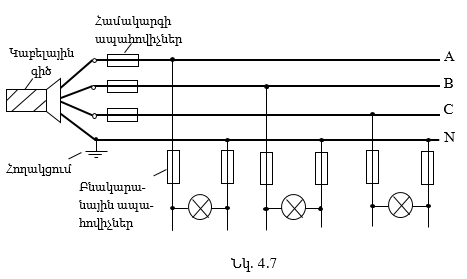
Որպես կանոն, անվտանգության նկատառումներից ելնելով, եռաֆազ համակարգի չեզոք հաղորդալարը հողակցվում է:
4.4. Եռանկյունաձև միացված եռաֆազ շղթա
Եռանկյունաձև միացված եռաֆազ շղթայում չեզոք հաղորդալար չի օգտագործվում: Նկ. 4.8-ում պատկերված եռաֆազ շղթայում եռաֆազ գեներատորը և եռաֆազ սպառիչը միացված են եռանկյունաձև (նկ. 4.8):
Գեներատորի եռանկյունաձև միացված երեք էլշուները կազմում են փակ կոնտուր, սակայն սպառիչի բացակայության դեպքում գեներատորի փաթույթներով շրջանցիկ հոսանքներ չեն անցնում, որովհետև ժամանակի ցանկացած ակնթարթին այդ էլշուների գումարը զրո է`
![]()
Ինչպես երևում է սխեմայից (նկ.4.8), եռանկյունաձև միացման
դեպքում եռաֆազ շղթայի գծային և ֆազային լարումները հավասար են՝ ![]()
Եթե անտեսենք գծերի և աղբյուրի փաթույթների ներքին դիմադրությունները, ապա կարող ենք գրել.

Սակայն, գծային ![]() և ֆազային
և ֆազային ![]() հոսանքները,
ի տարբերություն աստղաձև միացման, իրար հավասար չեն: Դրանց միջև կապը գտնելու նպատակով
a, b և c հանգույցների համար (նկ. 4.8) գրենք Կիրխհոֆի I օրենքի հիման վրա կոմպլեքս
տեսքով հավասարումներ.
հոսանքները,
ի տարբերություն աստղաձև միացման, իրար հավասար չեն: Դրանց միջև կապը գտնելու նպատակով
a, b և c հանգույցների համար (նկ. 4.8) գրենք Կիրխհոֆի I օրենքի հիման վրա կոմպլեքս
տեսքով հավասարումներ.
![]()
Յուրաքանչյուր ֆազի համար, ըստ Օհմի օրենքի կոմպլեքս տեսքով, կարելի է գրել.
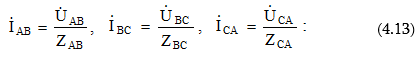
Սիմետրիկ սպառիչի դեպքում, երբ ![]() բոլոր ֆազային
հոսանքները կունենան նույն գործող արժեքը, բայց ըստ փուլի շեղված կլինեն համապատասխան
լարումներից
բոլոր ֆազային
հոսանքները կունենան նույն գործող արժեքը, բայց ըստ փուլի շեղված կլինեն համապատասխան
լարումներից ![]() անկյունով:
անկյունով:
Եռանկյունաձև միացված եռաֆազ շղթայի վեկտորական դիագրամը (նկ. 4.9) պատկերված է, երբ սպառիչը սիմետրիկ է և ունի ակտիվ-ինդուկտիվ բնույթ:
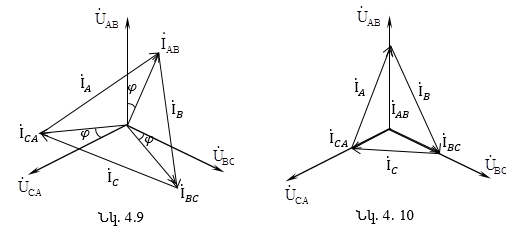
Ինչպես հետևում է վեկտորական դիագրամից, սիմետրիկ բեռնվածքի
դեպքում գծային հոսանքների վեկտորները կազմում են հավասարակողմ եռանկյուն, և ըստ գործող
արժեքի դրանք ![]() անգամ մեծ
են ֆազային հոսանքներից.
անգամ մեծ
են ֆազային հոսանքներից.
![]()
Եթե սպառիչը ոչ սիմետրիկ է, ապա գծային և ֆազային լարումների հավասարությունը չի խախտվում, սակայն հոսանքների միջև (4.14) առնչությունը խախտվում է:
Նկ. 4.10-ում բերված է եռանկյունաձև միացված ոչ սիմետրիկ շղթայի վեկտորական դիագրամը, երբ սպառիչն ակտիվ բնույթի է (երեք ֆազերում էլ ֆազային հոսանքը և լարումը ըստ փուլի համընկնում են):
4.5. Հզորության արտահայտությունները եռաֆազ շղթայում
Քանի որ եռաֆազ շղթան երեք միաֆազ շղթաների (ֆազերի) միավորում է, ապա եռաֆազ շղթայի ակտիվ հզորությունը հավասար է երեք ֆազերի ակտիվ հզորությունների գումարին.
![]()
Համանման ձևով եռաֆազ շղթայի ռեակտիվ հզորությունը.
![]()
Վերջին երկու բանաձևերում ![]() – եռաֆազ շղթայի ֆազային լարումներն են,
– եռաֆազ շղթայի ֆազային լարումներն են, ![]() ֆազային հոսանքները, իսկ
ֆազային հոսանքները, իսկ ![]() - համապատասխանաբար, դրանց
միջև փուլային շեղումները:
- համապատասխանաբար, դրանց
միջև փուլային շեղումները:
Սիմետրիկ եռաֆազ շղթայի դեպքում, անկախ դրա միացման ձևից, հզորությունները նույնը կլինեն բոլոր երեք ֆազերի համար, հետևաբար,
P = 3Pֆ = 3Uֆ Iֆ cos և Q = 3Qֆ = 3Uֆ Iֆ sin, (4.15)
որտեղ ![]() ֆազային լարման և
ֆազային լարման և ![]() ֆազային հոսանքի միջև փուլային շեղումն
է:
ֆազային հոսանքի միջև փուլային շեղումն
է:
Գործնականում նպատակահարմար է եռաֆազ շղթայի հզորություններն
արտահայտել ոչ թե ֆազային, այլ գծային մեծություններով, որոնք ավելի մատչելի են չափման
համար: Այդ նպատակով, տեղադրելով (4-15)-ում, աստղաձև միացման դեպքում ![]() իսկ եռանկյունաձև միացման դեպքում՝
իսկ եռանկյունաձև միացման դեպքում՝
![]() ակտիվ, ռեակտիվ և լրիվ հզորությունների
համար կստանանք նույն արտահայտությունները, որոնք կախված չեն միացման ձևից1.
ակտիվ, ռեակտիվ և լրիվ հզորությունների
համար կստանանք նույն արտահայտությունները, որոնք կախված չեն միացման ձևից1.
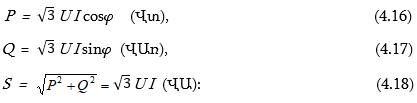
4.6. Աստղաձև և եռանկյունաձև միացված եռաֆազ շղթաների համեմատական բնութագիրը
Աստղաձև միացման դեպքում եռաֆազ շղթաներն ունեն հետևյալ առավելությունները.
1. Նույն շղթայում առկա են երկու անվանական լարումներ`
![]() ինչը թույլ է տալիս նույն շղթայից
սնել տարբեր լարումների համար նախատեսված սպառիչներ, օրինակ՝ 220 Վ և 380 Վ:
ինչը թույլ է տալիս նույն շղթայից
սնել տարբեր լարումների համար նախատեսված սպառիչներ, օրինակ՝ 220 Վ և 380 Վ:
2. Նույն գծային լարման դեպքում ֆազային լարումը ստացվում
է ![]() անգամ ավելի
փոքր, ինչը հնարավորություն է տալիս.
անգամ ավելի
փոքր, ինչը հնարավորություն է տալիս.
2.1. Բարձրացնել անվտանգությունը ցածր լարման (մինչև 660Վ) շղթաներում, որոնց հետ մարդիկ անմիջականորեն գործ ունեն (օրինակ, 220 վոլտն ավելի քիչ վտանգավոր է, քան 380 վոլտը):
2.2. Փոքրացնել մեկուսացման մակարդակը բարձր լարման
շղթաներում ![]() Որքան
բարձր է լարումը, այնքան ավելի հուսալի պետք է մեկուսացնել հաղորդիչները, ուստի լարման
Որքան
բարձր է լարումը, այնքան ավելի հուսալի պետք է մեկուսացնել հաղորդիչները, ուստի լարման
![]() անգամ փոքրացումը
կարող է բերել մեկուսիչ նյութի զգալի խնայողության:
անգամ փոքրացումը
կարող է բերել մեկուսիչ նյութի զգալի խնայողության:
Եռանկյունաձև միացման դեպքում եռաֆազ շղթաներն ունեն հետևյալ առավելությունները.
1. Չեզոք հաղորդալարը բացակայում է շղթայում ոչ միայն սիմետրիկ, այլև ոչ սիմետրիկ բեռնվածքների դեպքում:
2. Նույն գծային հոսանքի դեպքում ֆազային հոսանքը ստացվում
է ![]() անգամ փոքր,
ինչը թույլ է տալիս փոքրացնել էլեկտրական սարքերի ֆազային հաղորդիչների, փաթույթների
գալարների լայնական հատույթները` խնայելով հաղորդիչ նյութը:
անգամ փոքր,
ինչը թույլ է տալիս փոքրացնել էլեկտրական սարքերի ֆազային հաղորդիչների, փաթույթների
գալարների լայնական հատույթները` խնայելով հաղորդիչ նյութը:
Այսպիսով, կատարված վերլուծությունը թույլ է տալիս եզրակացնել, որ հավասար տեխնիկական պայմանների դեպքում աստղաձև միացումը ավելի շահավետ է կիրառել ցածր (մինչև 660 Վ) և շատ բարձր (110 կՎ և ավելի) լարումների դեպքում, իսկ եռանկյունաձև միացումը` մնացած դեպքերում:
Սակայն գործնականում այս կամ այն միացման օգտագործումը հաճախ պայմանավորված է լինում զուտ տեխնիկական նկատառումներով:
Եռաֆազ շղթաները սինուսոիդական հոսանքի շղթաներ են, ուստի դրանց հաշվարկը և ուսումնասիրությունը կատարվում են նույն եղանակներով, որոնք քննարկված են նախորդ` 3-րդ գլխում:
Սիմետրիկ եռաֆազ շղթայի հաշվարկը բերվում է միաֆազ
շղթայի հաշվարկի՝ դիտարկելով միայն մի ֆազը, և ստացված արդյունքները տարածելով մյուս
ֆազերի վրա: Այս դեպքում ակնհայտ է, որ հոսանքները մյուս ֆազերում, ըստ գործող արժեքների,
կլինեն հավասար, իսկ ըստ փուլի՝ շեղված ![]()
Հաճախ, հատկապես էլեկտրաէներգետիկայում, եռաֆազ սիմետրիկ շղթաները պարզության համար պատկերվում են միագիծ սխեմայով: Միագիծ սխեմաներում երեք միատեսակ գծային հաղորդալարերի փոխարեն պատկերվում է միայն մեկ հաղորդալար, իսկ եռաֆազ գեներատորը և եռաֆազ սպառիչը՝ պատկերվում են միայն մեկ ֆազով (տե’ս նկ.8.1-ի սխեման):
Ոչ սիմետրիկ շղթաների հաշվարկը ստորև դիտարկվում է կոնկրետ օրինակներով:
Խնդիր 4.1. Տրված շղթայում (նկ.
4.11) որոշել չեզոք լարի ![]() հոսանքը, եթե գծային լարումը
հոսանքը, եթե գծային լարումը ![]()
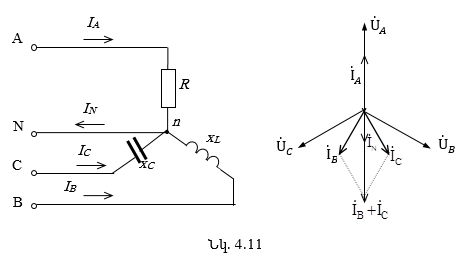
Լուծում: Չեզոք լարի
IN հոսանքը, որոշվում է ըստ (4.3) վեկտորական հավասարման՝ ![]()
Բոլոր երեք ֆազերում էլ հոսանքի գործող արժեքը նույնն է և որոշվում է Օհմի օրենքով.
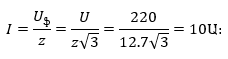
Կառուցենք տրված շղթայի վեկտորական դիագրամը. A ֆազի
ռեզիստիվ դիմադրության ![]() հոսանքի վեկտորի ուղղությունը համընկնում
է
հոսանքի վեկտորի ուղղությունը համընկնում
է ![]() լարման
վեկտորի ուղղության հետ,
լարման
վեկտորի ուղղության հետ, ![]() հետ է մնում
հետ է մնում ![]() առաջ է ընկած
առաջ է ընկած ![]() Այսպիսով
Այսպիսով ![]() միմյանց
հետ կազմում են
միմյանց
հետ կազմում են ![]() անկյուն, հետևաբար նրանց վեկտորական
գումարը կլինի
անկյուն, հետևաբար նրանց վեկտորական
գումարը կլինի ![]() Այն ուղղված է
Այն ուղղված է ![]() հակառակ, ուստի չեզոք լարի հոսանքի
գործող արժեքը կլինի.
հակառակ, ուստի չեզոք լարի հոսանքի
գործող արժեքը կլինի.
![]()
Խնդիր 4.2. Որքա՞ն պետք է լինի դիմադրության
արժեքը A ֆազում (խնդիր 1-ի նախնական պայմանների դեպքում), որպեսզի չեզոք հաղորդալարի
հոսանքը ![]() (նկ. 4.11):
(նկ. 4.11):
Լուծում: Հոսանքը չեզոք
հաղորդալարում կլինի զրո, եթե ![]() հոսանքի վեկտորը, որն ուղղված է
հոսանքի վեկտորը, որն ուղղված է
![]() վեկտորին
հակառակ, մոդուլով հավասար լինի
վեկտորին
հակառակ, մոդուլով հավասար լինի ![]() Այդ դեպքում A ֆազի R
դիմադրության արժեքը ըստ Օհմի օրենքի կլինի
Այդ դեպքում A ֆազի R
դիմադրության արժեքը ըստ Օհմի օրենքի կլինի
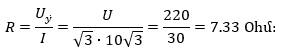
Խնդիր 4.3. Աստղաձև միացված եռաֆազ շղթայում
(նկ. 4.12ա) տրված են եռաֆազ աղբյուրի գծային լարման գործող արժեքը՝ U = 380
Վ, և սպառիչի ֆազերի դիմադրությունները՝ ![]()
Անհրաժեշտ է որոշել հոսանքները ֆազերում և չեզոք հաղորդալարում, ֆազերի և ամբողջ շղթայի ակտիվ ու ռեակտիվ հզորությունները:
Լուծում: Նպատակահարմար է այս խնդիրը լուծել անալիտիկորեն:
1) Ֆազերի կոմպլեքս դիմադրությունները ըստ (3.29)՝
![]()
2) Եռաֆազ շղթայի ֆազային լարման գործող արժեքը ըստ (4.5)-ի.
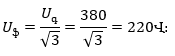
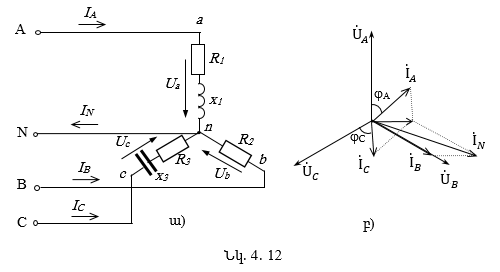
Ֆազային լարումների կոմպլեքս արժեքները ըստ (4.2)-ի.
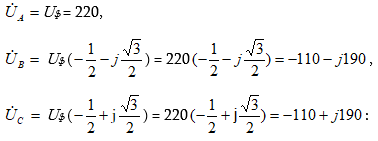
3) Յուրաքանչյուր ֆազի համար ըստ Օհմի օրենքի կոմպլեքս տեսքով (4.5).
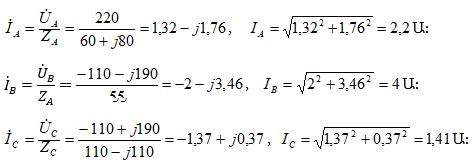
4) Չեզոք լարի հոսանքը (4.3)
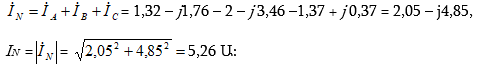
5) Ֆազերի ակտիվ հզորությունները .
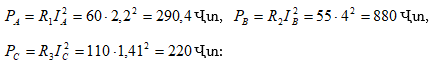
Եռաֆազ շղթայի ակտիվ հզորությունը.
![]()
6) Դիտարկվող շղթայի վեկտորական դիագրամը (նկ.4.12բ)
ավելի ակնառու է դարձնում չեզոք լարի հոսանքի որոշումը: A ֆազում սպառիչը ակտիվ-ինդուկտիվ
բնույթի է, հետևաբար ![]() հոսանքի վեկտորը ետ է մնում
հոսանքի վեկտորը ետ է մնում ![]() լարման վեկտորից
լարման վեկտորից
![]() անկյունով:
B ֆազում, որի սպառիչը ակտիվ բնույթի է,
անկյունով:
B ֆազում, որի սպառիչը ակտիվ բնույթի է, ![]() համընկնում է
համընկնում է ![]() հետ, իսկ
C ֆազում, որի սպառիչը ակտիվ-ունակային բնույթի է,
հետ, իսկ
C ֆազում, որի սպառիչը ակտիվ-ունակային բնույթի է, ![]() որպես ունակային
հոսանք, առաջ է ընկած
որպես ունակային
հոսանք, առաջ է ընկած ![]() անկյունով: Չեզոք լարի
անկյունով: Չեզոք լարի ![]() հոսանքի
վեկտորը կառուցվում է ըստ (4.3) վեկտորական հավասարման:
հոսանքի
վեկտորը կառուցվում է ըստ (4.3) վեկտորական հավասարման:
Խնդիր 4.4. Որոշել A1 և A2 ամպերմետրի ցուցմունքները
B հաղորդալարի խզման դեպքում, եթե եռաֆազ շղթայի գծային լարումը` ![]() (նկ. 4.13):
(նկ. 4.13):
Լուծում: Գծային հաղորդալարի
խզման դեպքում ունենում ենք U լարմանը միացված 2 զուգահեռ ճյուղեր` ab և acb, որոնցից
առաջինի լրիվ դիմադրությունը` ![]() իսկ երկրորդինը`
իսկ երկրորդինը` ![]() (քանի որ
(քանի որ ![]() ճյուղում
տեղի ունի լարումների ռեզոնանս): Հոսանքները դրանցում որոշվում են Օհմի օրենքով.
ճյուղում
տեղի ունի լարումների ռեզոնանս): Հոսանքները դրանցում որոշվում են Օհմի օրենքով.
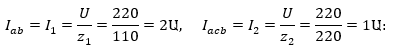
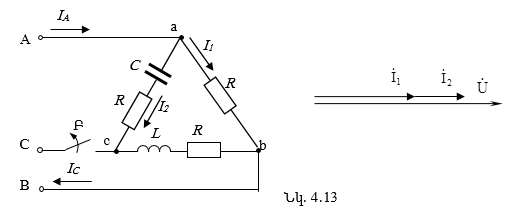
Գծային
![]() հոսանքները
որոշվում են Կիրխոֆի 1-ին օրենքի հիման վրա a հանգույցի համար գրված վեկտորական հավասարումով.
հոսանքները
որոշվում են Կիրխոֆի 1-ին օրենքի հիման վրա a հանգույցի համար գրված վեկտորական հավասարումով.
![]() Շղթայի
վեկտորական դիագրամից (նկ.4.13) հետևում է, որ վեկտորական այս գումարը կարելի է փոխարինել
համապատասխան հանրահաշվական գումարով, որից էլ կորոշվեն անհայտ հոսանքները.
Շղթայի
վեկտորական դիագրամից (նկ.4.13) հետևում է, որ վեկտորական այս գումարը կարելի է փոխարինել
համապատասխան հանրահաշվական գումարով, որից էլ կորոշվեն անհայտ հոսանքները.
![]()
Խնդիր 4.5. Եռաֆազ ցանցին միացված է եռանկյունաձև միացված
եռաֆազ սիմետրիկ սպառիչ, որի ակտիվ հզորությունը` P = 2,9 կՎտ, հզորության գործակիցը`
![]() (ինդուկտիվ բնույթի),
ցանցի գծային լարումը` U = 220 Վ: Որոշել սպառիչի պարամետրերը (R, x) և ֆազային ու
գծային հոսանքները:
(ինդուկտիվ բնույթի),
ցանցի գծային լարումը` U = 220 Վ: Որոշել սպառիչի պարամետրերը (R, x) և ֆազային ու
գծային հոսանքները:
Լուծում: Եռաֆազ սպառիչի մի ֆազի հզորությունը`
![]()
Այստեղից սպառիչի ֆազային հոսանքը՝ ![]()
Գծային
հոսանքը` ![]()
Մի ֆազի լրիվ դիմադրությունը՝ ![]()
Ֆազի ակտիվ և ռեակտիվ դիմադրությունները` ![]()
Խնդիր 4.6. Եռաֆազ ցանցին, որի գծային
լարումը U = 220 Վ է, միացված են եռանկյունաձև միացված էներգիայի սպառիչներ՝ ![]() (նկ. 4.14): Որոշել, թե
ինչպիսի լարման տակ կգտնվեն սպառիչները B հաղորդալարի ապահովիչի այրման դեպքում:
(նկ. 4.14): Որոշել, թե
ինչպիսի լարման տակ կգտնվեն սպառիչները B հաղորդալարի ապահովիչի այրման դեպքում:
Լուծում: Ապահովիչի այրման դեպքում AB և BC ֆազերի սպառիչները կմիանան հաջորդաբար և նրանցով անցնող հոսանքը կլինի.
![]()
Լարումերը սպառիչների սեղմակներում կլինեն.
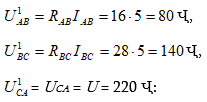
1. Ո՞րն է միաֆազ և եռաֆազ սինքրոն գեներատորի կառուցվածքային տարբերությունը:
2. Գրել էլշուների եռաֆազ համակարգի արտահայտությունները եռանկյունաչափական տեսքով:
3. Գրել էլշուների եռաֆազ համակարգի արտահայտությունները կոմպլեքս տեսքով:
4. Ի՞նչ պայմանի դեպքում եռաֆազ շղթան կոչվում է սիմետրիկ:
5. Գրել գծային ու ֆազային լարումների և գծային ու ֆազային հոսանքների միջև կապը աստղաձև միացված եռաֆազ շղթայի համար:
6. Գծել աստղաձև միացված սիմետրիկ եռաֆազ շղթայի վեկտորական դիագրամը:
7. Երբ է աստղաձև միացված եռաֆազ շղթան եռալար և երբ` քառալար:
8. Գծել աստղաձև միացված ոչ սիմետրիկ եռաֆազ շղթայի վեկտորական դիագրամը` ա) չեզոք լարի առկայության և բ) չեզոք լարի բացակայության դեպքերում:
9. Բացատրել, թե ի՞նչ հետևանք կունենա գծային լարերից մեկի կտրվելը քառալար եռաֆազ շղթայում:
10. Ինչու՞ չեզոք լարի կտրվելը քառալար եռաֆազ շղթայում դիտվում է որպես վթար:
11. Գրել գծային ու ֆազային լարումների և գծային ու ֆազային հոսանքների միջև կապը եռանկյունաձև միացված եռաֆազ շղթայի համար:
12. Գծել եռանկյունաձև միացված սիմետրիկ (ոչ սիմետրիկ) եռաֆազ շղթայի վեկտորական դիագրամը:
13. Բացատրել, թե ի՞նչ հետևանք կունենա գծային լարերից մեկի կտրվելը եռանկյունաձև միացված եռաֆազ շղթայում:
14. Գրել սիմետրիկ եռաֆազ շղթայի ակտիվ, ռեակտիվ և լրիվ հզորությունների արտահայտությունները:
15. Ի՞նչ առավելություններ ունի աստղաձև միացված եռաֆազ շղթան և ե՞րբ է ավելի նպատակահարմար այն կիրառել:
16. Ի՞նչ առավելություններ ունի եռանկյունաձև միացված եռաֆազ շղթան և ե՞րբ է ավելի նպատակահարմար այն կիրառել:
5. ԱՆՑՈՒՄԱՅԻՆ ՊՐՈՑԵՍՆԵՐԸ ԷԼԵԿՏՐԱԿԱՆ ՇՂԹԱՆԵՐՈՒՄ
5.1. Ընդհանուր դրույթներ
Անցումային են կոչվում այն պրոցեսները, որոնք առաջանում են, երբ էլեկտրական շղթան մի կայուն վիճակից (ռեժիմից) անցնում է մի այլ կայուն վիճակի: Անցումային պրոցեսների պատճառ կարող են լինել շղթայում կատարվող փոփոխությունները՝ անջատիչ սարքի անջատումները և միացումները, ինչպես նաև շղթայի տեղամասերում տարբեր պատճառներով առաջացած պարապ ընթացքը կամ կարճ միացումը:
Անցումային պրոցեսները տեղի են ունենում շնորհիվ շղթայում առկա ինդուկտիվ և ունակային տարրերի, որոնց վրա կարող են կուտակվել, համապատասխանաբար, մագնիսական և էլեկտրական դաշտի էներգիաներ: Սովորաբար անցումային երևույթները շատ արագ են ընթանում: Գործնականում դրանց տևողությունը կազմում է վայրկյանի տասնորդական մասերից մինչև հազարերորդական մասեր: Այնուամենայնիվ, անցումային պրոցեսների ուսումնասիրությունը շատ կարևոր է, որովհետև հնարավորություն է տալիս պարզել շղթայի տարբեր տեղամասերում հոսանքի կամ լարման թեկուզ և կարճատև, բայց զգալի թռիչքները, և դա հաշվի առնել էլեկտրական սարքերի նախագծման և ընտրության ժամանակ: Անցումային պրոցեսների ուսումնասիրությունը նույնպես թույլ է տալիս պարզել էլեկտրական ազդանշանների ձևի և մեծության փոփոխության օրինաչափությունները, երբ դրանք անցնում են տարբեր սարքերով (ուժեղարարներով, ֆիլտրերով և այլն):
Ցանկացած անցումային պրոցեսի ժամանակ հոսանքը շղթայի ինդուկտիվ տարրում և լարումը ունակային տարրի վրա չեն կարող թռիչքաձև փոփոխվել: Այս երկու հիմնական դրույթներից հետևում են կոմուտացիայի երկու կանոնները: Այս դեպքում ընդունված է համարել, որ շղթայում կոմուտացիան տեղի է ունենում ակնթարթորեն, ժամանակի t պահին:
Կոմուտացիայի 1-ին կանոնը: Ինդուկտիվության հոսանքը կոմուտացիայից անմիջապես առաջ և անմիջապես հետո մնում է նույնը: Եթե կոմուտացիան տեղի է ունենում ժամանակի t պահին, ապա ժամանակը կոմուտացիայից անմիջապես առաջ նշանակելով t-, իսկ դրանից անմիջապես հետո՝ t+, կոմուտացիայի 1-ին կանոնը կգրվի
![]()
Այս դրույթն ապացուցելու համար օգտվենք ֆիզիկայի դասընթացից
հայտնի ինդուկտիվության վրա կուտակված մագնիսական դաշտի էներգիայի բանաձևից՝ ![]() Այնուհետև
ենթադրենք, որ ժամանակի
Այնուհետև
ենթադրենք, որ ժամանակի ![]() ակնթարթին
հոսանքը ինդուկտիվ տարրում
ակնթարթին
հոսանքը ինդուկտիվ տարրում ![]() է, իսկ
է, իսկ ![]() ակնթարթին՝
ակնթարթին՝ ![]() : Այդ դեպքում ինդուկտիվության
վրա կուտակված մագնիսական դաշտի էներգիայի փոփոխման արագությունը (կամ, որ նույնն է,
զարգացրած հզորությունը) կլինի.
: Այդ դեպքում ինդուկտիվության
վրա կուտակված մագնիսական դաշտի էներգիայի փոփոխման արագությունը (կամ, որ նույնն է,
զարգացրած հզորությունը) կլինի.
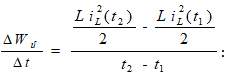
Երբ ![]() իսկ
իսկ ![]() ապա կստացվի,
որ ինդուկտիվ տարրի զարգացրած հզորությունն անվերջ մեծ է, ինչը անհնար է: Հետևաբար
(5.1) պայմանը ճիշտ է:
ապա կստացվի,
որ ինդուկտիվ տարրի զարգացրած հզորությունն անվերջ մեծ է, ինչը անհնար է: Հետևաբար
(5.1) պայմանը ճիշտ է:
Կոմուտացիայի 2-րդ կանոնը. Լարումը ունակային տարրի վրա կոմուտացիայից անմիջապես առաջ և անմիջապես հետո մնում է նույնը.
![]()
Համանման ձևով, ֆիզիկայի դասընթացից հիշելով, որ ունակության
վրա կուտակված էլեկտրական դաշտի էներգիան՝ ![]() էլեկտրական դաշտի էներգիայի փոփոխման
արագության (կամ ունակային տարրի հզորության) համար կստանանք հետևյալ արտահայտությունը.
էլեկտրական դաշտի էներգիայի փոփոխման
արագության (կամ ունակային տարրի հզորության) համար կստանանք հետևյալ արտահայտությունը.
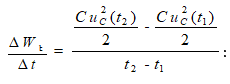
Երբ ![]() իսկ
իսկ ![]() ապա կստացվի, որ ունակային տարրի
զարգացրած hզորությունն անվերջ մեծ է, ինչը նույնպես անհնար է, և հետևաբար, (5.2) պայմանը
ճիշտ է:
ապա կստացվի, որ ունակային տարրի
զարգացրած hզորությունն անվերջ մեծ է, ինչը նույնպես անհնար է, և հետևաբար, (5.2) պայմանը
ճիշտ է:
Գծային էլեկտրական շղթայի անցումային պրոցեսները բնութագրվում են գծային դիֆերենցիալ հավասարումներով, որոնք կազմվում են հետկոմուտացիոն շղթայի համար՝ ըստ Կիրխհոֆի օրենքների: Ընդ որում դիֆերենցիալ հավասարումները կարող են լինել անհամասեռ, եթե հետկոմուտացիոն շղթան պարունակում է լարման կամ հոսանքի աղբյուր և համասեռ՝ եթե այն որևէ աղբյուր չի պարունակում: Մշակված են դիֆերենցիալ հավասարումների լուծման տարբեր եղանակներ: Սույն ձեռնարկում, որը նախատեսված է ոչ էլեկտրատեխնիկական մասնագիտությունների համար, անցումային երևույթները դիտարկվում են միայն պարզ շղթաների համար, երբ շղթայում գործում է միայն հաստատուն լարման կամ հոսանքի աղբյուր: Ուստի ստորև բերվում է միայն դիֆերենցիալ հավասարումների լուծման դասական եղանակը, որն ավելի պարզ է և ակնառու:
Մաթեմատիկայի դասընթացից հայտնի է, որ գծային անհամասեռ
դիֆերենցիալ հավասարումների ընդհանուր լուծումը (տվյալ դեպքում ինդուկտիվության հոսանքը
կամ ունակության լարումը) համասեռ հավասարման (երբ դիֆերենցիալ հավասարման աջ մասը
զրո է) ընդհանուր լուծման և անհամասեռ հավասարման մասնակի լուծման գումարն է: Համասեռ
հավասարման ընդհանուր լուծումը ընդունված է անվանել անցումային կամ ազատ
բաղադրիչ, իսկ անհամասեռ հավասարման մասնավոր լուծումը՝ հարկադրական բաղադրիչ:
Վերջինը կոմուտացիայից հետո շղթայում հաստատված հոսանքի կամ լարման արժեքն է, որը հաշվվում
է հայտնի եղանակներով: Անհրաժեշտ է նկատի ունենալ, որ այստեղ հաստատուն հոսանքի (f
= 0) շղթայի կայունացված ռեժիմների դեպքում ինդուկտիվ դիմադրությունը հավասար է
զրոյի՝ ![]() իսկ ունակային
դիմադրությունը՝ անսահմանության,
իսկ ունակային
դիմադրությունը՝ անսահմանության, ![]()
Շղթայի ինդուկտիվության ![]() հոսանքը
և ունակության
հոսանքը
և ունակության ![]() լարումը, որոնք գոյություն ունեն
կոմուտացիայից առաջ, կոչվում են շղթայի անկախ սկզբնական պայմաններ: Եթե
լարումը, որոնք գոյություն ունեն
կոմուտացիայից առաջ, կոչվում են շղթայի անկախ սկզբնական պայմաններ: Եթե ![]() ապա ընդունված է ասել, որ շղթան ունի զրոյական
սկզբնական պայմաններ, իսկ հակառակ դեպքում՝ ոչ զրոյական սկզբնական պայմաններ:
ապա ընդունված է ասել, որ շղթան ունի զրոյական
սկզբնական պայմաններ, իսկ հակառակ դեպքում՝ ոչ զրոյական սկզբնական պայմաններ:
5.2. Անցումային պրոցեսները ինդուկտիվ տարր պարունակող հաստատուն հոսանքի շղթաներում
5.2.1. Մագնիսական կոճի միացումը հաստատուն լարման
Դիտարկվող շղթայում մագնիսական կոճը պատկերված է ռեզիստիվ և ինդուկտիվ տարրերի հաջորդական միացումով (նկ. 5.1):
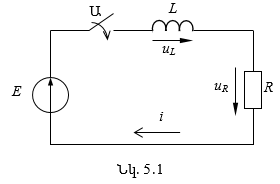
Ժամանակի t = 0 պահին Ա անջատիչի միացումից
(կոմուտացիայից) հետո շղթայով կանցնի i հոսանք և ռեզիստիվ ու ինդուկտիվ տարրերի
վրա կառաջանան համապատասխանաբար, ![]() լարումներ.
լարումներ.
![]()
Կոմուտացիայից հետո, տրված շղթայի համար գրելով Կիրխհոֆի 2-րդ օրենքով հավասարում ակնթարթային արժեքների համար՝ կստանանք
![]()
կամ
![]()
Ստացվածը առաջին կարգի անհամասեռ դիֆերենցիալ հավասարում է, որի ընդհանուր լուծումը հավասար է հոսանքի հարկադրական (կայունացված) և ազատ (կամ անցումային) բաղադրիչների գումարին.
![]()
Հոսանքի հարկադրական բաղադրիչը հաստատուն հոսանք է,
որը հաստատվում է շղթայում, երբ անցումային պրոցեսները լրիվ մարում են1:
Քանի որ հաստատուն հոսանքի դեպքում ![]() ապա
ապա
![]()
Հոսանքի ազատ բաղադրիչը որոշվում է որպես

համասեռ դիֆերենցիալ հավասարման ընդհանուր լուծում: Ինչպես հայտնի է մաթեմատիկայից, այն տրվում է հետևյալ ցուցչային ֆունկցիայի տեսքով.
![]()
որտեղ ![]() բնութագրիչ հավասարման արմատն է:
բնութագրիչ հավասարման արմատն է:
Այսպիսով, հաշվի առնելով (5.5) և (5.7) արտահայտությունները, կստանանք (5.3) անհամասեռ դիֆերենցիալ հավասարման լրիվ լուծումը

Ինտեգրման A հաստատունը որոշելու համար օգտվենք
սկզբնական պայմաններից ![]() և կոմուտացիայի 1-ին կանոնից
(5.1)` համարելով, որ անջատիչը փակվում է t=0 պահին: Քանի որ ինդուկտիվության հոսանքը
չի կարող փոփոխվել թռիչքաձև, և կոմուտացիային նախորդող
և կոմուտացիայի 1-ին կանոնից
(5.1)` համարելով, որ անջատիչը փակվում է t=0 պահին: Քանի որ ինդուկտիվության հոսանքը
չի կարող փոփոխվել թռիչքաձև, և կոմուտացիային նախորդող ![]() պահին այն
զրո է, ապա կարող ենք գրել
պահին այն
զրո է, ապա կարող ենք գրել
![]()
Տեղադրելով A-ի արժեքը (5.8) հավասարման մեջ` կստանանք տրված շղթայում հոսանքի աճը նկարագրող արտահայտությունը

որի գրաֆիկը պատկերված է նկ. 5.2-ում:
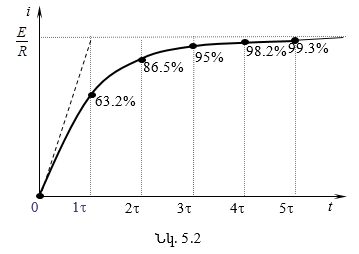
Այստեղ ![]() մեծությունն ունի ժամանակի չափողականություն
(հենրի/օհմ = վրկ) և կոչվում է շղթայի ժամանակի հաստատուն: Այն բնութագրում է շղթայում
հոսանքի փոփոխման արագությունը և ունի որոշակի ֆիզիկական իմաստ. եթե հոսանքի փոփոխման
արագությունը պահպանվեր նույնը, ինչ եղել է անցումային պրոցեսի սկզբնական ակնթարթին,
ապա անցումային պրոցեսը կավարտվեր
մեծությունն ունի ժամանակի չափողականություն
(հենրի/օհմ = վրկ) և կոչվում է շղթայի ժամանակի հաստատուն: Այն բնութագրում է շղթայում
հոսանքի փոփոխման արագությունը և ունի որոշակի ֆիզիկական իմաստ. եթե հոսանքի փոփոխման
արագությունը պահպանվեր նույնը, ինչ եղել է անցումային պրոցեսի սկզբնական ակնթարթին,
ապա անցումային պրոցեսը կավարտվեր ![]() ժամանակում:
ժամանակում:
Գործնականում ընդունված է համարել, որ անջատիչի միացումից
![]() ժամանակ
հետո շղթայում անցումային երևույթները լրիվ մարում են, ինչպես դա երևում է հոսանքի
փոփոխությունն արտահայտող ֆունկցիայի գրաֆիկից (նկ. 5.2). ժամանակի
ժամանակ
հետո շղթայում անցումային երևույթները լրիվ մարում են, ինչպես դա երևում է հոսանքի
փոփոխությունն արտահայտող ֆունկցիայի գրաֆիկից (նկ. 5.2). ժամանակի ![]() պահին հոսանքը
հասնում է իր վերջնական արժեքի 99.3%-ին:
պահին հոսանքը
հասնում է իր վերջնական արժեքի 99.3%-ին:
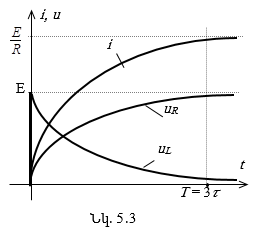
Հոսանքի ֆունկցիայի (5.10) արտահայտության հիման վրա հեշտությամբ որոշվում են նաև ռեզիստիվ և ինդուկտիվ տարրերի վրա ժամանակից կախված լարման ֆունկցիաները, որոնց գրաֆիկաները բերված են նկ. 5.3-ում.
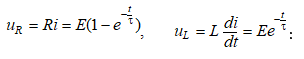
5.2.2. Հոսանքակիր մագնիսական կոճի կարճ միացումը
Դիտարկենք անցումային պրոցեսը հոսանքակիր մագնիսական կոճում` երբ այն կարճ է միացվում: Մասնավորապես, այսպիսի վիճակ կարող է առաջանալ էլեկտրական մեքենաների և ապարատների փաթույթներում:
Մագնիսական կոճը ներկայացնենք ռեզիստիվ և ինդուկտիվ տարրերի հաջորդաբար միացումով (նկ. 5.4):
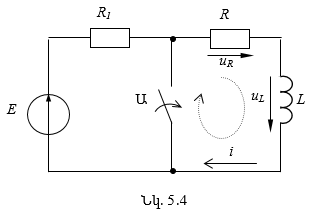
Գրենք անցումային պրոցեսի դիֆերենցիալ հավասարումը Ա անջատիչի միացումից հետո.
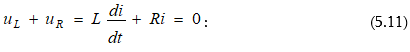
Քանի որ (5.11) դիֆերենցիալ հավասարումը համասեռ է և համընկնում է (5.6) հավասարման հետ, ապա դրա լրիվ լուծումը պարունակում է միայն ազատ բաղադրիչը (5.7)`
![]()
որտեղ ![]() շղթայի ժամանակի հաստատունն է:
շղթայի ժամանակի հաստատունն է:
Ինտեգրման A հաստատունը որոշվում է ինդուկտիվ տարրի համար կոմուտացիայի պայմանից: Մինչև կոմուտացիան կոճով անցնող հաստատուն հոսանքի արժեքը պահպանվում է նաև կոմուտացիայից անմիջապես հետո, ուստի կարելի է գրել .

Տեղադրելով A-ի արժեքը (5.12)-ի մեջ` կստանանք ժամանակից կախված կոճի հոսանքի փոփոխության ֆունկցիան անցումային պրոցեսի ընթացքում.
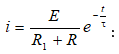
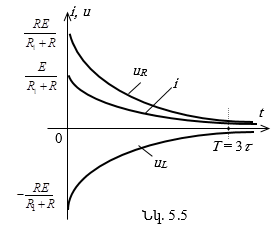
Կոմուտացիայից հետո կոճում հոսանքը պահպանվում է միմիայն ի հաշիվ կոճում կուտակված մագնիսական դաշտի էներգիայի: Ունենալով հոսանքի ֆունկցիայի արտահայտությունը` կարելի է որոշել ռեզիստիվ և ինդուկտիվ տարրերի վրա լարման փոփոխության ֆունկցիաները (նկ.5.5).
5.3. Անցումային պրոցեսները ունակային տարր պարունակող հաստատուն հոսանքի շղթաներում
5.3.1. Կոնդենսատորի լիցքավորումը
Որպես օրինակ դիտարկենք ռեզիստիվ և ունակային տարրերի հաջորդական շղթան, որը միացվում է հաստատուն էլշուի աղբյուրին (նկ. 5.6):
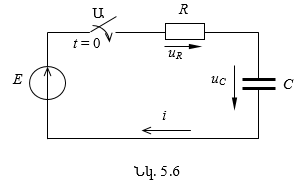
Ընդունենք, որ նախքան Ա անջատիչի միացնելը կոնդենսատորը
չէր լիցքավորված, ![]() t = 0 ակնթարթին անջատիչը միանում է, և կոնդենսատորը սկսում է լիցքավորվել:
t = 0 ակնթարթին անջատիչը միանում է, և կոնդենսատորը սկսում է լիցքավորվել:
Նկատի ունենալով, որ ![]() դիտարկվող
շղթայի համար ըստ Կիրխհոֆի II օրենքի կարող ենք գրել
դիտարկվող
շղթայի համար ըստ Կիրխհոֆի II օրենքի կարող ենք գրել
![]()
Այս անհամասեռ դիֆերենցիալ հավասարման լրիվ լուծումը
![]() լարման նկատմամբ
հավասար է լարման հարկադրական և ազատ բաղադրիչների գումարին.
լարման նկատմամբ
հավասար է լարման հարկադրական և ազատ բաղադրիչների գումարին.
![]()
Ակնհայտ է, որ հարկադրական բաղադրիչը, որը ունակային
տարրի լարումն է լրիվ լիցքավորումից հետո, հավասար է աղբյուրի էլշուին, ![]()
Դիֆերենցիալ հավասարման ազատ կամ անցումային բաղադրիչը
կլինի uա ![]() որտեղ
p-ն՝ RCp + 1 = 0 բնութագրիչ հավասարման արմատն է.
որտեղ
p-ն՝ RCp + 1 = 0 բնութագրիչ հավասարման արմատն է. ![]()
Այսպիսով, (5.14) դիֆերենցիալ հավասարման լրիվ լուծումը կլինի
![]()
Ինտեգրման A հաստատունի որոշման համար կիրառենք կոմուտացիայի 2-րդ կանոնը (5.2)` ընդունելով, որ նախքան անջատիչի փակվելը, t = 0- պահին, կոնդենսատորը լիցքավորված չէր.
![]()
Տեղադրելով A -ի այս արժեքը (5.14) հավասարման մեջ, կգտնենք ունակային տարրի վրա ժամանակից կախված լարման ֆունկցիան լիցքավորման ընթացքում (նկ. 5.7).
![]()
Այստեղ ![]() մեծությունն ունի ժամանակի չափողականություն
մեծությունն ունի ժամանակի չափողականություն ![]() և կոչվում
է
և կոչվում
է ![]() շղթայի
ժամանակի հաստատուն: Այն բնութագրում է լիցքավորման պրոցեսի արագությունը:
շղթայի
ժամանակի հաստատուն: Այն բնութագրում է լիցքավորման պրոցեսի արագությունը:
Այժմ, ունենալով ![]() ֆունկցիան, կարող ենք հեշտությամբ
ստանալ շղթայի i հոսանքի և ռեզիստիվ տարրի վրա
ֆունկցիան, կարող ենք հեշտությամբ
ստանալ շղթայի i հոսանքի և ռեզիստիվ տարրի վրա ![]() լարման
ժամանակային ֆունկցիաները (նկ.5.7).
լարման
ժամանակային ֆունկցիաները (նկ.5.7).
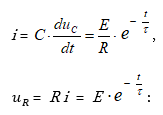
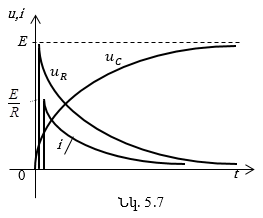
Այստեղ պետք է նկատել, որ անմիջապես անջատիչի միանալուց
հետո (t = 0+ պահին) շղթայի հոսանքը ![]() ինչը նշանակում է, որ ունակային
տարրը դիմադրություն չի ցուցաբերում հոսանքին: Այս պատճառով R դիմադրության
փոքր արժեքների դեպքում շղթայում հնարավոր է հոսանքի արժեքի զգալի թռիչք:
ինչը նշանակում է, որ ունակային
տարրը դիմադրություն չի ցուցաբերում հոսանքին: Այս պատճառով R դիմադրության
փոքր արժեքների դեպքում շղթայում հնարավոր է հոսանքի արժեքի զգալի թռիչք:
Գործնականում կոնդենսատորը ![]() շղթայում կարելի է համարել
լրիվ լիցքավորված
շղթայում կարելի է համարել
լրիվ լիցքավորված ![]() ժամանակից հետո:
ժամանակից հետո:
5.3.2. Կոնդենսատորի լիցքաթափումը ակտիվ դիմադրության վրա
Լիցքավորված կոնդենսատորը օժտված է էլեկտրական դաշտի էներգիայով, որի շնորհիվ այն կարող է որոշ ժամանակ հանդես գալ որպես էներգիայի աղբյուր:
Դիտարկենք նկ. 5.8-ում պատկերված էլեկտրական շղթան,
որի ունակային տարրը (կոնդենսատորը) լիցքավորված է ![]() լարումով աղբյուրից (Փ փոխանջատչը
1 դիրքում է): Երբ Փ փոխանջատիչը բերվում է 2 դիրքի, լիցքավորված կոնդենսատորը միանում
է R ակտիվ դիմադրությանը, տեղի է ունենում կոնդենսատորի լիցքաթափում, և դրա
q լիցքի փոփոխությունը շղթայում առաջ է բերում հոսանք՝
լարումով աղբյուրից (Փ փոխանջատչը
1 դիրքում է): Երբ Փ փոխանջատիչը բերվում է 2 դիրքի, լիցքավորված կոնդենսատորը միանում
է R ակտիվ դիմադրությանը, տեղի է ունենում կոնդենսատորի լիցքաթափում, և դրա
q լիցքի փոփոխությունը շղթայում առաջ է բերում հոսանք՝

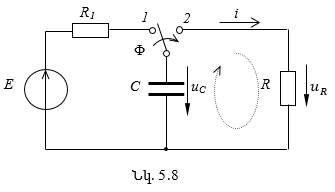
Այստեղ բացասական նշանը ցույց է տալիս, որ i
լիցքաթափման հոսանքի ուղղությունը (նշված է կետագծերով) հակառակ է ![]() լարման
ուղղությանը (նկ. 5.8):
լարման
ուղղությանը (նկ. 5.8):
Նկատի ունենալով (5.16) արտահայտությունը, նշված կոնտուրի համար (նկ.5.8) Կիրխհոֆի 2-րդ օրենքի հիման վրա կարող ենք ստանալ հետևյալ դիֆերենցիալ հավասարումը.
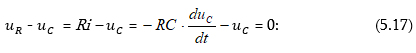
Քանի որ լիցքաթափման շղթան էներգիայի աղբյուր չի պարունակում և (5.17) հավասարման աջ կողմը զրո է, ապա այն հանդիսանում է համասեռ դիֆերենցիալ հավասարում, որի լուծումը կազմված է միայն ազատ (անցումային) բաղադրիչից.

Ինտեգրման A հաստատունի որոշման համար կիրառենք
կոմուտացիայի կանոնը ունակային տարրի համար (5.2). Նախքան փոխանջատումը, այսինքն
t = 0- պահին, կոնդենսատորը լիցքավորված էր, և դրա սեղմակների միջև հաստատվել էր
![]() լարում,
հետևաբար
լարում,
հետևաբար
![]()
Տեղադրելով A-ի արժեքը (5.18) հավասարման մեջ, կստանանք մի բանաձև, որը բնութագրում է ունակային տարրի վրա լարման փոփոխությունը լիցքաթափման ընթացքում (նկ. 5.9).
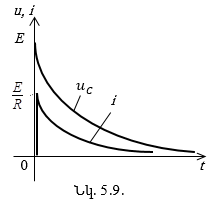
![]()
որտեղ ![]() լիցքաթափման շղթայի ժամանակի հաստատունն
է:
լիցքաթափման շղթայի ժամանակի հաստատունն
է:
Լիցքաթափման հոսանքը, ըստ (5.16) արտահայտության, կլինի

Լիցքաթափման հոսանքը սկզբում գրեթե ակնթարթային աճում
է զրոյից մինչև ![]() որից հետո,
փոքրանալով էքսպոնենցիալ օրենքով, ձգտում է զրոյի (նկ. 5.9):
որից հետո,
փոքրանալով էքսպոնենցիալ օրենքով, ձգտում է զրոյի (նկ. 5.9):
Կոնդենսատորի լիցքաթափման և լիցքավորման պրոցեսները, որոնք կոչվում են ռելաքսացիոն պրոցեսներ, լայնորեն օգտագործվում են ոչ սինուսոիդական պարբերական լարման գեներատորներում: Այդպիսի ռելաքսացիոն գեներատորները ծառայում են, օրինակ, սղոցաձև լարման ստացման համար, որն օգտագործվում է օսցիլոգրաֆների և որոշ այլ սարքերի աշխատանքի համար:
Ռելաքսացիոն գեներատորի աշխատանքի սկզբունքը հիմնված
է կոնդենսատորի պարբերաբար կրկնվող լիցքավորման և լիցքաթափման պրոցեսների վրա: Սղոցաձև
լարման պարզագույն գեներատորի սխեմայում (նկ. 5.10ա) բերված C ունակությամբ
կոնդենսատորի լիցքավորումը կատարվում է մեծ արժեք ունեցող ![]() դիմադրության միջոցով, իսկ լիցքաթափումը՝
փոքր դիմադրությամբ օժտված կարգավորվող սարքով: Որպես այդպիսին դիտարկվող սխեմայում
օգտագործված է կիսահաղորդչային սարք՝ տիրիստոր (Տ): Տիրիստորն ունի այն հատկությունը,
որ ցածր լարումների դեպքում դրա դիմադրությունը շատ մեծ է, իսկ որոշակի լարումից սկսած,
որը կոչվում է բացման լարում
դիմադրության միջոցով, իսկ լիցքաթափումը՝
փոքր դիմադրությամբ օժտված կարգավորվող սարքով: Որպես այդպիսին դիտարկվող սխեմայում
օգտագործված է կիսահաղորդչային սարք՝ տիրիստոր (Տ): Տիրիստորն ունի այն հատկությունը,
որ ցածր լարումների դեպքում դրա դիմադրությունը շատ մեծ է, իսկ որոշակի լարումից սկսած,
որը կոչվում է բացման լարում ![]() այն թռիչքաձև փոքրանում է՝ ընդունելով
շատ փոքր արժեքներ:
այն թռիչքաձև փոքրանում է՝ ընդունելով
շատ փոքր արժեքներ:
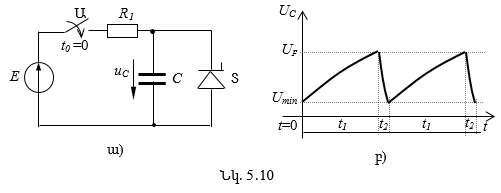
Երբ E էլշու-ով աղբյուրը միացվում է շղթային,
C կոնդենսատորը լիցքավորվում է ![]() դիմադրության
միջով, և
դիմադրության
միջով, և ![]() լարումը
աճում է էքսպոնենցիալ օրենքով,
լարումը
աճում է էքսպոնենցիալ օրենքով, ![]() ժամանակի հաստատունով: Երբ այն հասնում
է
ժամանակի հաստատունով: Երբ այն հասնում
է ![]() լարման
արժեքին, Տ տիրիստորը բացվում է, և կոնդենսատորն սկսում է արագորեն լիցքաթափվել
լարման
արժեքին, Տ տիրիստորը բացվում է, և կոնդենսատորն սկսում է արագորեն լիցքաթափվել
![]() ժամանակի
հաստատունով՝ բացված տիրիստորի
ժամանակի
հաստատունով՝ բացված տիրիստորի ![]() փոքր դիմադրության
միջոցով: Քանի որ
փոքր դիմադրության
միջոցով: Քանի որ ![]() ապա լիցքաթափման
ապա լիցքաթափման ![]() ժամանակը շատ կարճ է լիցքավորման
ժամանակը շատ կարճ է լիցքավորման
![]() ժամանակից: Երբ կոնդենսատորի լարումը
փոքրանալով հասնում է
ժամանակից: Երբ կոնդենսատորի լարումը
փոքրանալով հասնում է ![]() արժեքին, տիրիստորը փակվում է, վերականգնվում
է դրա մեծ դիմադրությունը, C կոնդենսատորը դարձյալ սկսում է լիցքավորվել
արժեքին, տիրիստորը փակվում է, վերականգնվում
է դրա մեծ դիմադրությունը, C կոնդենսատորը դարձյալ սկսում է լիցքավորվել ![]() դիմադրության միջով, և այդպես շարունակ:
Վերը նկարագրված պրոցեսը պարբերաբար կրկնվում է այնքան ժամանակ, քանի դեռ Ա անջատիչը
միացված է:
դիմադրության միջով, և այդպես շարունակ:
Վերը նկարագրված պրոցեսը պարբերաբար կրկնվում է այնքան ժամանակ, քանի դեռ Ա անջատիչը
միացված է:
Եթե կոնդենսատորի լիցքավորման t1 ժամանակը զգալիորեն
փոքր է ![]() ժամանակի
հաստատունից, ապա կարելի է ընդունել, որ այդ
ժամանակի
հաստատունից, ապա կարելի է ընդունել, որ այդ ![]() ժամանակահատվածում
ժամանակահատվածում ![]() ֆունկցիան
համարյա գծային է (նկ. 5.10բ):
ֆունկցիան
համարյա գծային է (նկ. 5.10բ):
Շղթայում փոփոխելով ![]() և C
-ի արժեքները՝ հնարավոր է կարգավորել
և C
-ի արժեքները՝ հնարավոր է կարգավորել ![]() լարման գծայնության աստիճանը, ինչպես
նաև սղոցաձև ազդանշանների տևողությունը:
լարման գծայնության աստիճանը, ինչպես
նաև սղոցաձև ազդանշանների տևողությունը:
5.5. Անցումային պրոցեսները R-L-C շղթաներում
5.5.1. Լիցքավորված կոնդենսատորի լիցքաթափումը ինդուկտիվ և ռեզիստիվ տարրերի վրա
Գործնական մեծ նշանակություն ունի լիցքավորված կոնդենսատորի լիցքաթափումը հաջորդաբար միացված ինդուկտիվ և ռեզիստիվ տարրերի վրա (օրինակ, իմպուլսային լարման գեներատորներում):
Ենթադրենք նկ.5.11-ում պատկերված շղթայում Փ փոխանջատիչը դրված է 1 դիրքում և ունակային տարրը նախապես լիցքավորված է հաստատուն էլշուի աղբյուրից մինչև U= E լարումը: Այնուհետև եթե Փ փոխանջատիչը 1 դիրքից բերվի 2 դիրքի, ապա ունակային C տարրը կմիանա հաջորդաբար միացված L ինդուկտիվ և R ռեզիստիվ տարրերին:
Ըստ Կիրխհոֆի 2-րդ օրենքի` կետագծով նշված կոնտուրի համար կարող ենք գրել հետևյալ հավասարումը.
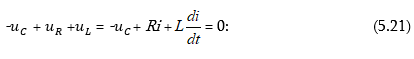
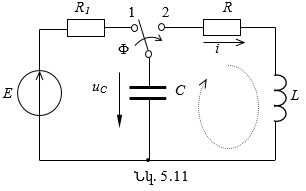
Տեղադրելով (5.16)-ից i-ի արժեքը (5.21)-ի մեջ` կստանանք II կարգի համասեռ դիֆերենցիալ հավասարում.
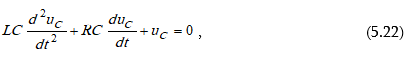
որի բնութագրիչ հավասարումը կլինի
![]()
Համասեռ դիֆերենցիալ հավասարման ընդհանուր լուծումը կազմված
է միայն ազատ բաղադրիչից.
![]()
որտեղ ![]() ինտեգրման հաստատուններն
են, իսկ
ինտեգրման հաստատուններն
են, իսկ ![]() (5.23)
բնութագրիչ հավասարման արմատներն են:
(5.23)
բնութագրիչ հավասարման արմատներն են:
Հաշվի առնելով (5.16) -ը՝ (5.24)-ից կստանաք հոսանքի փոփոխման ֆունկցիան.
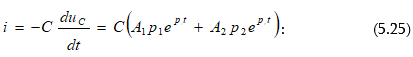
Ինտեգրման ![]() հաստատունները
որոշելու համար, ինչպես և նախորդ դեպքերում, օգտվենք կոմուտացիայի կանոններից: Մինչև
կոմուտացիան, t = 0- պահին լարումը ունակային տարրի վրա
հաստատունները
որոշելու համար, ինչպես և նախորդ դեպքերում, օգտվենք կոմուտացիայի կանոններից: Մինչև
կոմուտացիան, t = 0- պահին լարումը ունակային տարրի վրա ![]() և հոսանքը՝ i = 0: Հետևաբար, (5.24)-ից ըստ կոմուտացիայի I կանոնի կարող
ենք գրել
և հոսանքը՝ i = 0: Հետևաբար, (5.24)-ից ըստ կոմուտացիայի I կանոնի կարող
ենք գրել
![]()
Իսկ (5.25)-ից ըստ կոմուտացիայի II կանոնի`
![]()
Համատեղ լուծելով (5.26) և (5.27) հավասարումները՝ գտնում ենք ինտեգրման հաստատունների արժեքները.

Բնութագրիչ (5.23) հավասարման արմատները կլինեն
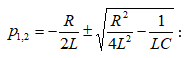
Այստեղ հնարավոր է երեք դեպք.
1) ![]() այսինքն շղթայի R դիմադրության համեմատաբար
մեծ արժեքների դեպքում (5.23) բնութագրիչ հավասարման երկու արմատներն էլ իրական են
և կոնդենսատորի լիցքաթափումը ոչ պարբերական (ապերիոդիկ) բնույթ ունի.
այսինքն շղթայի R դիմադրության համեմատաբար
մեծ արժեքների դեպքում (5.23) բնութագրիչ հավասարման երկու արմատներն էլ իրական են
և կոնդենսատորի լիցքաթափումը ոչ պարբերական (ապերիոդիկ) բնույթ ունի. ![]() ֆունկցիաները էքսպոնենցիալ օրենքով են փոփոխվում (նկ. 5.12):
ֆունկցիաները էքսպոնենցիալ օրենքով են փոփոխվում (նկ. 5.12):
2) ![]() ապա արմատները
հավասար են և իրական՝
ապա արմատները
հավասար են և իրական՝ ![]() Դիտարկվող շղթայում
սա համապատասխանում է ոչ պարբերական պրոցեսի սահմանային դեպքին:
Դիտարկվող շղթայում
սա համապատասխանում է ոչ պարբերական պրոցեսի սահմանային դեպքին:
3) ![]() այսինքն R դիմադրության համեմատաբար փոքր արժեքների
դեպքում, (5.23) բնութագրիչ հավասարման երկու արմատները կոմպլեքս են և համալուծ՝
այսինքն R դիմադրության համեմատաբար փոքր արժեքների
դեպքում, (5.23) բնութագրիչ հավասարման երկու արմատները կոմպլեքս են և համալուծ՝
![]()
![]()
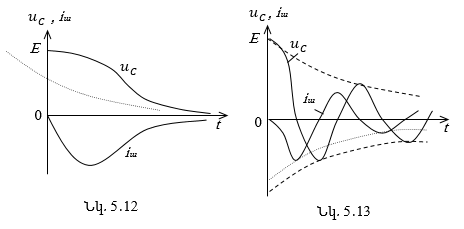
Տեղադրելով (5.28)-ից ![]() կոմպլեքս արմատները (5.24)-ի մեջ, կիրառելով Էյլերի ձևափոխությունը և կատարելով
անհրաժեշտ պարզեցումներ` կստանանք
կոմպլեքս արմատները (5.24)-ի մեջ, կիրառելով Էյլերի ձևափոխությունը և կատարելով
անհրաժեշտ պարզեցումներ` կստանանք
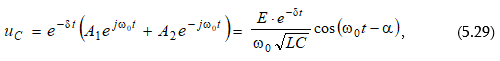
![]()
Այսպիսով, (5.29) արտահայտությունը նկարագրում
է ազատ տատանողական պրոցես, որը տեղի է ունենում ![]() մարման գործակցով
և
մարման գործակցով
և ![]() անկյունային հաճախությամբ (նկ. 5.13):
անկյունային հաճախությամբ (նկ. 5.13):
Հոսանքի ֆունկցիայի արտահայտությունն այս դեպքի համար կարելի է ստանալ (5.25)-ից (նկ. 5.13).
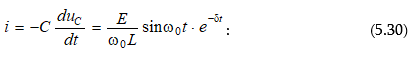
5.5.2. Հաջորդաբար միացված R, L, C տարրերով շղթայի միացումը հաստատուն լարման
Ա անջատիչի միացման դեպքում (նկ.5.14) շղթայի էլեկտրական վիճակը անցումային ռեժիմում նկարագրվում է Կիրխհոֆի II օրենքի հիման վրա կազմված հետևյալ հավասարումով.
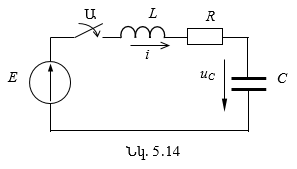
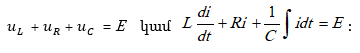
![]()
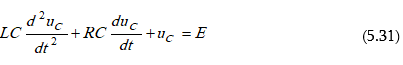
դիֆերենցիալ հավասարումը, որի լրիվ լուծումը կլինի
![]()
Այստեղ ![]() (5.31) դիֆերենցիալ հավասարման
լուծման հարկադրական բաղադրիչն է`
(5.31) դիֆերենցիալ հավասարման
լուծման հարկադրական բաղադրիչն է` ![]() իսկ
իսկ ![]() (5.22)
համասեռ դիֆերենցիալ հավասարման ընդհանուր լուծումն է, որը տրվում է (5.24) բանաձևով:
(5.22)
համասեռ դիֆերենցիալ հավասարման ընդհանուր լուծումն է, որը տրվում է (5.24) բանաձևով:
Այսպիսով,
![]()
Այս դեպքում ինտեգրման ![]() հաստատունների որոշման համար, եթե ընդունենք, որ կոնդենսատորը մինչև կոմուտացիան
լիցքավորված չէր, ապա t=0 պահի համար (5.32) և (5.25) արտահայտություններից
կստանանք
հաստատունների որոշման համար, եթե ընդունենք, որ կոնդենսատորը մինչև կոմուտացիան
լիցքավորված չէր, ապա t=0 պահի համար (5.32) և (5.25) արտահայտություններից
կստանանք
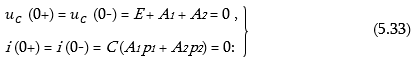
Համատեղ լուծելով հավասարումների այս համակարգը` կստանանք
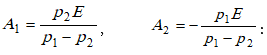
5.6. Անցումային պրոցեսների հաշվարկի օրինակներ
Խնդիր 5.1.
Դիտարկենք էլեկտրական շղթա (նկ.5.15ա), որի համար տրված են. ![]()
Որոշել շղթայի i հոսանքի և ինդուկտիվ տարրի վրա uL լարման փոփոխման ֆունկցիաները Ա անջատիչի միացման հետևանքով առաջացած անցումային պրոցեսի ժամանակ:
Լուծում: Ըստ Կիրխհոֆի 2-րդ օրենքի,

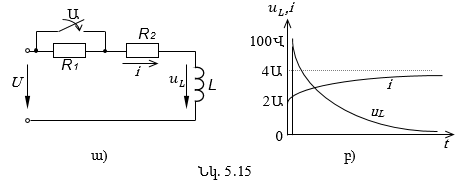
Այս դիֆերենցիալ հավասարման լուծման հարկադրական բաղադրիչը (հոսանքի արժեքը, երբ անցումային պրոցեսները լրիվ մարում են) կլինի
![]()
Գրենք դիֆերենցիալ հավասարման բնութագրիչ հավասարումը՝
![]()
Այսպիսով, (5.31) հավասարման լրիվ լուծումը, որը հարկադրական և ազատ բաղադրիչների գումարին է հավասար, կլինի`

Ինտեգրման հաստատունը որոշենք կոմուտացիայի I կանոնից.
![]()
Տեղադրելով այս արժեքը (5.32) -ի մեջ, կստանանք շղթայի հոսանքի փոփոխման ֆունկցիան (նկ. 5.15բ).
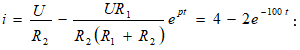
Ինդուկտիվության վրա լարման ֆունկցիան կլինի (նկ.5.13բ)
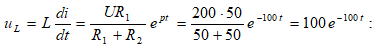
Խնդիր 5.2.
Շղթայի համար տրված են. ![]() (նկ. 5.16ա): Որոշել ունակային
տարրի վրա
(նկ. 5.16ա): Որոշել ունակային
տարրի վրա ![]() լարման և շղթայի i հոսանքի փոփոխման ֆունկցիաները Ա անջատիչի անջատման
հետևանքով առաջացած անցումային պրոցեսի ժամանակ:
լարման և շղթայի i հոսանքի փոփոխման ֆունկցիաները Ա անջատիչի անջատման
հետևանքով առաջացած անցումային պրոցեսի ժամանակ:
Լուծում: Կիրխհոֆի 2-րդ օրենքի համաձայն, հետկոմուտացիոն շղթայի համար, կարող ենք գրել
![]()
Այս դիֆերենցիալ հավասարման լուծման հարկադրական
բաղադրիչը ![]() լարման արժեքը, երբ անցումային երևույթները լրիվ մարում են) կլինի
լարման արժեքը, երբ անցումային երևույթները լրիվ մարում են) կլինի ![]()
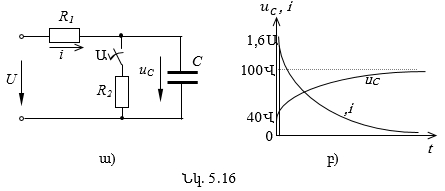
Գրենք համասեռ դիֆերենցիալ հավասարման բնութագրիչ հավասարումը՝
![]()
Այսպիսով (5.36) հավասարման լրիվ լուծումը, որը հավասար է հարկադրական և ազատ բաղադրիչների գումարին, կլինի
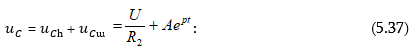
Ինտեգրման հաստատունը որոշենք կոմուտացիայի 2-րդ կանոնից.
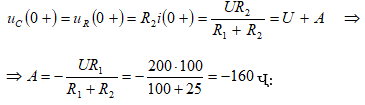
Տեղադրելով այս արժեքը (5.37) –ի մեջ՝ կստանանք
ժամանակից կախված ![]() լարման ֆունկցիան (նկ. 5.11բ).
լարման ֆունկցիան (նկ. 5.11բ).
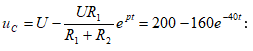
Շղթայի հոսանքի ժամանակից կախված ֆունկցիայի արտահայտությունը, ըստ (5.37)-ի, կլինի (նկ. 5.16բ)
![]()
Խնդիր 5.3.
Գծագրւմ պատկերված է ժամանակի ռելե: Հաշվել, թե ակտիվ դիմադրության ի՞նչ արժեքի դեպքում
ռելեն կգործի անջատիչի միացումից 10 վայրկյան հետո, եթե ռելեի գործողության համար լարման
ներքին շեմը` ![]() աղբյուրի էլշուն` E = 20 Վ, կոնդենսատորի ունակությունը` C =200 մկՖ:
աղբյուրի էլշուն` E = 20 Վ, կոնդենսատորի ունակությունը` C =200 մկՖ:
Լուծում. Անջատիչը միացնելիս տեղի է ունենում կոնդենսատորի լիցքավորում և կոնդենսատորի սեղմակներում լարման աճ, ըստ (5.15) ժամանակային ֆունկցիայի,
![]()
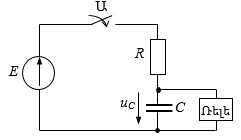
Ռելեն զուգահեռ է միացված կոնդենսատորին, հետևաբար
այն կգործի, երբ կոնդենսատորի վրա լարումը հասնի 12Վ, ինչն ըստ խնդրի պայմանի պետք
է տեղի ունենա 10վ հետո: Տեղադրելով ![]() t = 10վ և E = 20 Վ`
(5.38) բանձևից կորոշենք
t = 10վ և E = 20 Վ`
(5.38) բանձևից կորոշենք ![]() շղթայի ժամանակի
հաստատունը`
շղթայի ժամանակի
հաստատունը` ![]()
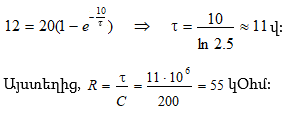
1. Ե՞րբ է էլեկտրական շղթայում տեղի ունենում անցումային պրոցես:
2. Որո՞նք են անցումային պրոցեսի առաջացման պատճառները:
3. Որո՞նք են անցումային պրոցեսների վերլուծության համար հիմք հանդիսա-ցող երկու կանոնները (կոմուտացիայի կանոնները)
4. Որո՞նք են անցումային պրոցեսների սկզբնական պայմանները:
5. Ինչպիսի՞ հավասարումներով է նկարագրվում շղթայի անցումային վիճակը:
6. Ինչպե՞ս է որոշվում անհամասեռ դիֆերենցիալ հավասարման լրիվ լուծումը:
7. Տվեք դիֆերենցիալ հավասարման լուծման ստիպողական և ազատ բաղադրիչների սահմանումը:
8. Ինչպե՞ս է որոշվում ![]() հաջորդական շղթայի ժամանակի հաստատունը և ի՞նչ ֆիզիկական իմաստ ունի այն:
հաջորդական շղթայի ժամանակի հաստատունը և ի՞նչ ֆիզիկական իմաստ ունի այն:
9. Ինչպե՞ս է որոշվում ![]() հաջորդական շղթայի ժամանակի հաստատունը:
հաջորդական շղթայի ժամանակի հաստատունը:
10. Գրել ինդուկտիվ կոճի հոսանքի` ժամանակից կախված ֆունկցիայի արտահայտությունը, երբ կոճը միացվում է հաստատուն լարման աղբյուրին: Գծել այդ ֆունկցիայի գրաֆիկը:
11. Գրել հոսանքակիր ինդուկտիվ կոճի հոսանքի ժամանակից կախված ֆունկցիայի արտահայտությունը, երբ կոճը կարճ է փակվում: Գծել այդ ֆունկցիայի գրաֆիկը:
12. Գրել կոնդենսատորի վրա լարման` ժամանակից կախված ֆունկցիայի արտահայտությունը, երբ այն հաջորդաբար միացված ակտիվ դիմադրությամբ միանում է հաստատուն լարման: Գծել այդ ֆունկցիայի գրաֆիկը:
13. Գրել կոնդենսատորի վրա լարման` ժամանակից կախված ֆունկցիայի արտահայտությունը, երբ այն լիցքաթափվում է ակտիվ դիմադրության վրա: Գծել այդ ֆունկցիայի գրաֆիկը:
14. Ի՞նչ դիֆերենցիալ հավասարումով է նկարագրվում անցումային պրոցեսը, երբ լիցքավորված կոնդենսատորը լիցքաթափվում է ինդուկտիվ կոճի վրա:
15.Նախորդ կետում նկարագրված շղթայի պարամետրերի ի՞նչ հարաբերակցության դեպքում անցումային պրոցեսը ունենում է ոչ պարբերական (ապերիոդիկ) բնույթ և ի՞նչ հարաբերակցության դեպքում` պարբերական բնույթ:
6.1. Մագնիսական շղթայի տարրերը
Տեխնիկայի տարբեր բնագավառներում լայն կիրառություն ունեն էլեկտրամագնիսական զանազան մեխանիզմներ ու սարքեր, (տրանսֆորմատորներ, էլեկտրական մեքենաներ, ռելեներ և այլն), որոնց որոշակի տեղամասերում ստեղծվում են տրված պարամետրերով մագնիսական դաշտեր, որն իրականացվում է մագնիսական շղթայի միջոցով:
Մագնիսական շղթան տարրերի համախումբ է, որը նախատեսված է էլեկտրատեխնիկական սարքի որոշակի տեղամասերում պահանջվող մեծությամբ և ձևի մագնիսական դաշտ ստեղծելու համար: Մագնիսական շղթայի կազմի մեջ են մտնում ինդուկտորը (հաստատուն մագնիս կամ մագնիսական փաթույթ)՝ մագնիսական դաշտ գրգռող սարքը և մագնիսական հոսքի համար փակ ուղի ապահովող մագնիսահաղորդիչները (ֆերոմագնիսական և ոչ ֆերոմագնիսական մասերը) (նկ. 6.1 և նկ. 6.2):
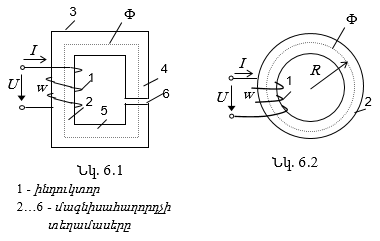
Ֆիզիկայի դասընթացից
հայտնի
է,
որ
մագնիսական
դաշտի
յուրաքանչյուր
կետ
բնութագրվում
է
որոշակի
![]() ինդուկցիայի
վեկտորով (-ի
միավորն
է
տեսլան (Տլ)):
Իսկ
Փ մագնիսական
հոսքը (մագնիսական
ինդուկցիայի
վեկտորի
հոսքը)
փակ
կոնտուրի
S մակերևույթով որոշվում
է
հետևյալ
բանաձևով.
ինդուկցիայի
վեկտորով (-ի
միավորն
է
տեսլան (Տլ)):
Իսկ
Փ մագնիսական
հոսքը (մագնիսական
ինդուկցիայի
վեկտորի
հոսքը)
փակ
կոնտուրի
S մակերևույթով որոշվում
է
հետևյալ
բանաձևով.
![]()
որտեղ ![]() վեկտորի և S մակերևույթին
տարված ուղղահայացի (նորմալի) միջև անկյունն է:
վեկտորի և S մակերևույթին
տարված ուղղահայացի (նորմալի) միջև անկյունն է:
Եթե մագնիսական դաշտը համասեռ է և ![]() (ինդուկցիայի
վեկտորը ուղղությամբ համընկնում է S մակերևույթի նորմալի հետ), ապա
(ինդուկցիայի
վեկտորը ուղղությամբ համընկնում է S մակերևույթի նորմալի հետ), ապա
![]()
Մագնիսական դաշտի B ինդուկցիայի (հետևաբար նաև Փ հոսքի) արժեքը կախված է ինչպես ինդուկտորի հոսանքից, այնպես էլ մագնիսահաղորդչի նյութի հատկություններից: Դրանց միջև կապ հաստատելու համար ներմուծվում է մագնիսական դաշտի լարվածության հասկացությունը, որն անմիջականորեն կախված է ինդուկտորի պարամետրերից և հոսանքից: Այդ կախվածությունը տրվում է լրիվ հոսանքի օրենքով, համաձայն որի մագնիսական դաշտի լարվածության վեկտորի գծային ինտեգրալը որևէ փակ կոնտուրով (դաշտի լարվածության վեկտորի ցիրկուլյացիան) հավասար է այդ կոնտուրով սահմանափակված մակերևույթով անցնող հոսանքների հանրահաշվական գումարին:
![]()
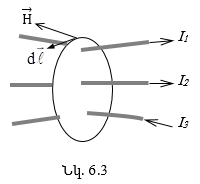
Հավասարման աջ կողմում հոսանքը վերցվում է դրական նշանով, եթե դրա առաջացրած մագնիսական դաշտի լարվածության ուղղությունը (որոշվում է խցանահանի կանոնով) համընկնում է կոնտուրի ընտրված շրջանցման ուղղության հետ: Նկ. 6.3-ում պատկերված կոնտուրի համար լրիվ հոսանքի օրենքը կգրվի հետևյալ տեսքով.
![]()
Ինչպես հետևում է (6.1) հավասարումից, մագնիսական դաշտի H լարվածության միավորն է ամպեր՝ բաժանած մետրի (Ա/մ):
Ինտեգրման կոնտուրով սահմանափակված մակերևույթով անցնող
հոսանքների հանրահաշվական գումարը ՝ ![]() կոչվում է մագնիսաշարժ ուժ
(մշու):
կոչվում է մագնիսաշարժ ուժ
(մշու):
Շատ դեպքերում կարելի է համարել, որ մագնիսական շղթան
կազմված է այնպիսի տեղամասերից, որոնցից յուրաքանչյուրում մագնիսական դաշտը համասեռ
է, այսինքն H = const և ![]() ուղղությունները համընկնում են
(օրինակ, նկ. 6.1-ում պատկերված մագնիսական շղթան): Այդպիսի մագնիսական շղթաների համար
(6.1) հավասարման ինտեգրալը կարելի է փոխարինել գումարով: Եթե մագնիսական դաշտը գրգռվում
է w գալարների թիվ ունեցող ինդուկտորով, որով անցնում է I հոսանքը,
ապա լրիվ հոսանքի օրենքը կգրվի հետևյալ տեսքով.
ուղղությունները համընկնում են
(օրինակ, նկ. 6.1-ում պատկերված մագնիսական շղթան): Այդպիսի մագնիսական շղթաների համար
(6.1) հավասարման ինտեգրալը կարելի է փոխարինել գումարով: Եթե մագնիսական դաշտը գրգռվում
է w գալարների թիվ ունեցող ինդուկտորով, որով անցնում է I հոսանքը,
ապա լրիվ հոսանքի օրենքը կգրվի հետևյալ տեսքով.

Այստեղ
![]() մագնիսական
շղթայի կոնտուրի k-րդ տեղամասում մագնիսական դաշտի լարվածության արժեքն է, իսկ
մագնիսական
շղթայի կոնտուրի k-րդ տեղամասում մագնիսական դաշտի լարվածության արժեքն է, իսկ
![]() այդ տեղամասի
մագնիսական ուժագծերի միջին երկարությունը:
այդ տեղամասի
մագնիսական ուժագծերի միջին երկարությունը:
Մասնավորապես, օղակաձև մագնիսական շղթայի (տորոիդի) համար (նկ. 6.2), որի միջուկը (մագնիսահաղորդիչը) կազմված է S լայնական հատույթի մակերեսով և R շառավղով համասեռ ֆերոմագնիսական օղակից, լրիվ հոսանքի օրենքի միջոցով կարելի է ստանալ դաշտի լարվածության արժեքը տորոիդի միջուկում.
6.2. Ֆերոմագնիսական նյութերի հատկությունները
Եթե մագնիսական դաշտն առաջանում է վակուումում, ապա մագնիսական դաշտի B ինդուկցիայի և H լարվածության միջև կապը գծային է.
![]()
որտեղ ![]() և կոչվում է մագնիսական հաստատուն: Այն բնութագրում
է վակուումի մագնիսական հատկությունները:
և կոչվում է մագնիսական հաստատուն: Այն բնութագրում
է վակուումի մագնիսական հատկությունները:
Եթե մագնիսական դաշտն առաջանում է նյութական միջավայրում, ապա
![]()
որտեղ ![]() տվյալ միջավայրի բացարձակ, իսկ
տվյալ միջավայրի բացարձակ, իսկ ![]() հարաբերական մագնիսական
թափանցելիությունն է:
հարաբերական մագնիսական
թափանցելիությունն է:
Բնության մեջ հանդիպող նյութերի գերակշռող մասի համար ![]() Էլեկտրատեխնիկական սարքերի
համար գործնական մեծ նշանակություն ունեն ֆերոմագնիսական նյութերը, որոնց համար
Էլեկտրատեխնիկական սարքերի
համար գործնական մեծ նշանակություն ունեն ֆերոմագնիսական նյութերը, որոնց համար ![]() Այդպիսի նյութերի թվին են
պատկանում պողպատի համաձուլվածքները, որոնցից պատրաստվում են տրանսֆորմատորների, էլեկտրական
մեքենաների, էլեկտրամագնիսների և այլ սարքերի միջուկները:
Այդպիսի նյութերի թվին են
պատկանում պողպատի համաձուլվածքները, որոնցից պատրաստվում են տրանսֆորմատորների, էլեկտրական
մեքենաների, էլեկտրամագնիսների և այլ սարքերի միջուկները:
Ֆերոմագնիսական նյութերի համար ընդհանուր դեպքում B-ն ոչ գծայնորեն է կապված H-ի հետ. Այդ պատճառով B = f(H) կապը գլխավորապես տրվում է գրաֆիկորեն (նկ. 6.4):
Դիտարկենք oղակաձև տորոիդի (նկ. 6.2) ֆերոմագնիսական միջուկում մագնիսական դաշտի B ինդուկցիայի կախումը H լարվածությունից, երբ ինդուկտորի հոսանքը աստիճանաբար փոփոխվում է:
Դիտարկենք oղակաձև տորոիդի (նկ. 6.2) ֆերոմագնիսական միջուկում մագնիսական դաշտի B ինդուկցիայի կախումը H լարվածությունից, երբ ինդուկտորի հոսանքը աստիճանաբար փոփոխվում է:
Եթե ֆերոմագնիսական նյութի սկզբնական վիճակին համապատասխանում է H = 0 (I = 0) և B = 0, ապա H-ի (I-ի) մեծացման դեպքում միջուկում B-ն նախ աճում է համարյա գծայնորեն, այնուհետև աստիճանաբար այդ գծայնությունը խախտվում է, և սկսած H-ի որոշակի արժեքից, B-ն դադարում է աճել՝ պահպանելով նույն Bmax արժեքը (նկ. 6.4): Այս երևույթը կոչվում է միջուկի հագեցում:
Մագնիսահաղորդչի սկզբնական մագնիսացմանը համապատասխանող կորը (նկ. 6.4-ում նշված է կետագծով) կոչվում է սկզբնական մագնիսացման կոր: Եթե հագեցման հասնելուց հետո H-ը սկսենք փոքրացնել, ապա B-ի արժեքները նույնպես կփոքրանան, սակայն մնացորդային մագնիսականության պատճառով B(H) կորը արդեն չի համընկնի սկզբնական մագնիսացման կորի հետ:
Երբ ինդուկտորի հոսանքը դառնում է զրո (նմանապես H = 0),
ֆերոմագնիսական միջուկը պահպանում է որոշ մագնիսականություն՝ ![]() ինդուկցիայով, որը կոչվում
է մնացորդային ինդուկցիա: Միջուկում
ինդուկցիայով, որը կոչվում
է մնացորդային ինդուկցիա: Միջուկում![]() ինդուկցիան վերացնելու համար անհրաժեշտ է փոխել ինդուկտորի
հոսանքի ուղղությունը և ստեղծել հակառակ ուղղված
ինդուկցիան վերացնելու համար անհրաժեշտ է փոխել ինդուկտորի
հոսանքի ուղղությունը և ստեղծել հակառակ ուղղված ![]() լարվածություն, որը կոչվում է կոէրցիտիվ ուժ:
լարվածություն, որը կոչվում է կոէրցիտիվ ուժ:
Մեծացնելով հոսանքի արժեքը հակառակ ուղղությամբ՝ ֆերոմագնիսական նյութը դարձյալ կհասնի հագեցման` այս դեպքում մագնիսական ինդուկցիայի հակառակ ուղղությանբ: Դարձյալ փոքրացնելով հոսանքը մինչև զրո և այնուհետև փոխելով դրա ուղղությունը և մեծացնելով մինչև միջուկի հագեցումը` կստանանք մեկ լրիվ ցիկլ և կոորդինատների սկզբնակետի նկատմամբ համաչափ փակ B(H) կոր, որը կոչվում է հիսթերեզիսի ստատիկ սահմանային օղակ (նկ. 6.4-ի հոծ գծված կորը):
Եթե H-ի փոփոխման վերոհիշյալ ցիկլը կրկնվի առանց միջուկը հագեցման հասցնելու, ապա ստացված համաչափ, բայց չափերով ավելի փոքր B(H) օղակը կկոչվի ֆերոմագնիսական նյութի հիսթերեզիսի մասնակի օղակ:
Ըստ ![]() կոէրցիտիվ ուժի արժեքի` ֆերոմագնիսական նյութերը բաժանվում
են երկու մեծ խմբի՝ մագնիսափափուկ նյութերի, որոնց համար
կոէրցիտիվ ուժի արժեքի` ֆերոմագնիսական նյութերը բաժանվում
են երկու մեծ խմբի՝ մագնիսափափուկ նյութերի, որոնց համար ![]() և մագնիսակոշտ նյութերի,
որոնց համար
և մագնիսակոշտ նյութերի,
որոնց համար ![]() երջիններս կիրառվում են հիմնականում
հաստատուն մագնիսների պատրաստման համար:
երջիններս կիրառվում են հիմնականում
հաստատուն մագնիսների պատրաստման համար:
Մագնիսափափուկ նյութերն, իրենց հերթին, ըստ B(H) կախվածության
գրաֆիկի, կարող են լինել համարյա ուղղանկյունաձև հիսթերեզիսի օղակով (նկ. 6.5ա), կորագծային
հիսթերեզիսի օղակներով (նկ. 6.5բ) և գծային (նկ. 6.5գ): Վերջին դեպքում ![]() ֆերոմագնիսական նյութի հարաբերական
մագնիսական թափանցելիությունն է
ֆերոմագնիսական նյութի հարաբերական
մագնիսական թափանցելիությունն է ![]()
Զանազան հատկություններով ֆերոմագնիսական նյութերի միջուկները պատրաստվում
են կամ ֆերոմագնիսական տարբեր համաձուլվածքներից, կամ ֆերոմագնիսական կերամիկայից
(ֆերիտներից): Ֆերիտները, ի տարբերություն ֆերոմագնիսական համաձուլվածքների, օժտված
են էլեկտրական մեծ դիմադրությամբ, որի շնորհիվ դրանք կիրառվում են փոփոխական հոսանքի
բարձր հաճախությունների դեպքում ![]()
Ուղղանկյունաձև սահմանային հիսթերեզիսի B(H) օղակով նյութերը լայնորեն օգտագործվում են համակարգիչներում (որպես օպերատիվ հիշող սարքերի միջուկներ), մագնիսական ուժեղարարներում և ավտոմատիկայի այլ սարքերում:
Կորագծային սահմանային B(H) օղակով նյութեր են, մասնավորապես, ածխածնային թերթավոր պողպատները (էլեկտրատեխնիկական պողպատները), որոնք օգտագործվում են տրանսֆորմատորների, փոփոխական հոսանքի էլեկտրական մեքենաների և ապարատների միջուկների պատրաստման համար: Այսպիսի սարքերի մագնիսահաղորդիչները աշխատում են սիմետրիկ մասնակի ցիկլերով վերամագնիսացման ռեժիմում: Դրանց հաշվարկի համար սիմետրիկ մասնակի ցիկլերը փոխարինվում են ֆերոմագնիսական նյութի հիմնական մագնիսացման կորով (նկ. 6.6-ում հոծ գծված կորը), որն ստացվում է՝ մասնակի սիմետրիկ ցիկլերի B(H) օղակների գագաթները միացնելով:
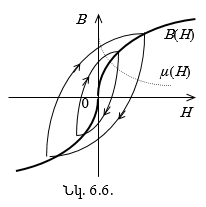
Օգտվելով ֆերոմագնիսական նյութի հիմնական մագնիսացման կորից՝ կարելի է ստանալ դրա բացարձակ մագնիսական թափանցելիությունը (6.4)՝
![]()
որպես ֆունկցիա մագնիսական H լարվածությունից (նկ. 6.6-ում կետագծով պատկերված կորը):
Գծային B(H) կախվածություն ունեցող ֆերոմագնիսական նյութերը մեծ կիրառություն ունեն ռադիոհեռուստատեխնիկական տարբեր սարքերում (հաղորդիչներ, ընդունիչներ)` որպես տատանողական կոնտուրների ինդուկտիվ կոճերի միջուկներ:
Երբ մագնիսական կոճը միացվում է սինուսոիդական լարմանը (նկ.6.9), փաթույթով անցնում է փոփոխական հոսանք, միջուկում գրգռվում է փոփոխական մագնիսական հոսք, և տեղի է ունենում ֆերոմագնիսական նյութի անընդհատ պարբերական (ցիկլիկ) վերամագնիսացում: Այս դեպքում յուրաքանչյուր ցիկլին համապատասխանող B(H) օղակը կոչվում է հիսթերեզիսի դինամիկ օղակ: Մագնիսական ինդուկցիայի նույն առավելագույն արժեքի դեպքում այն մի փոքր ավելի լայն է, քան հիսթերեզիսի ստատիկ օղակը (նկ. 6.4-ում պատկերված է ընդհատ գծով):
Փոփոխական մագնիսական դաշտը ֆերոմագնիսական միջուկներում առաջ է բերում որոշակի էներգիայի կորուստ, որն անջատվում է ջերմության ձևով, տաքացնելով միջուկը և, հետևաբար, ամբողջ սարքը: Էներգիայի անջատումը պայմանավորված է երկու պատճառներով՝ հիսթերեզիսի երևույթով և ֆերոմագնիսական նյութում ինդուկտված մրրկային հոսանքներով:
Մագնիսացման մեկ ցիկլի ընթացքում մագնիսահաղորդչի միավոր ծավալում հիսթերեզիսի հետևանքով անջատված էներգիան համեմատական է B(H) ստատիկ օղակով սահմանափակված մակերեսին: Էլեկտրատեխնիկական պողպատները, որոնք օգտագործվում են փոփոխական հոսանքի սարքերի միջուկների պատրաստման համար, ունեն հիսթերեզիսի նեղ ստատիկ օղակ և համեմատաբար փոքր կորուստներ են առաջացնում:
Մրրկային հոսանքները ինդուկտվում են մագնիսահաղորդչում փոփոխական մագնիսական դաշտի ազդեցության տակ: Դրանց մեծությունը կախված է հոսանքի հաճախությունից, մագնիսահաղորդչի նյութի տեսակարար դիմադրությունից և ինդուկցիայի ամպլիտուդային արժեքից: Մրրկային հոսանքներից առաջացած էներգիայի կորուստները համեմատական են հիսթերեզիսի դինամիկ և ստատիկ օղակների մակերեսների տարբերությանը: Մրրկային հոսանքների փոքրացման համար փոփոխական հոսանքի էլեկտրատեխնիկական սարքերի միջուկները հավաքվում են էլեկտրատեխնիկական պողպատի բարակ թիթեղներից, որոնք մեկուսացված են միմյանցից լաքի բարակ շերտով: f = 50 Հց հաճախության դեպքում թիթեղների հաստությունը 0,35...0.5 մմ է, իսկ ավելի բարձր հաճախությունների դեպքում՝ ավելի բարակ:
Մագնիսահաղորդչում (ֆերոմագնիսական միջուկում) հզորության գումարային
կորուստները գործնական հաշվարկներում կարելի է համարել համեմատական մագնիսական ինդուկցիայի
ամպլիտուդային արժեքի քառակուսուն` ![]()
6.3. Պարզագույն մագնիսական շղթայի հաշվարկը
Մեծ մասամբ մագնիսական շղթայի հաշվարկը հանգում է փաթույթի F=Iw մագնիսաշարժ ուժի որոշմանը, որն անհրաժեշտ է մագնիսահաղորդչի որոշակի տեղամասում անհրաժեշտ մեծության մագնիսական Փ հոսք (կամ B ինդուկցիա) ստանալու համար:
Դիտարկենք ուղղանկյուն շրջանակի տեսք ունեցող պարզագույն մագնիսական
շղթա (նկ. 6.7), որտեղ ցույց են տրված մագնիսահաղորդչի տեղամասերի չափերը՝ լայնական
հատույթի մակերեսները, մագնիսական գծերի միջին երկարությունները: Մագնիսահաղորդիչը
կազմված է ֆերոմագնիսական նյութից, որի մագնիսական հատկությունները տրված են B(H)
հիմնական մագնիսացման և ![]() կախվածության կորերով (նկ.6.8), ինչպես նաև օդային
բացակից (ինչպիսին առկա է ասենք էլեկտրական մեքենայի անշարժ և շարժական մասերի միջև):
կախվածության կորերով (նկ.6.8), ինչպես նաև օդային
բացակից (ինչպիսին առկա է ասենք էլեկտրական մեքենայի անշարժ և շարժական մասերի միջև):
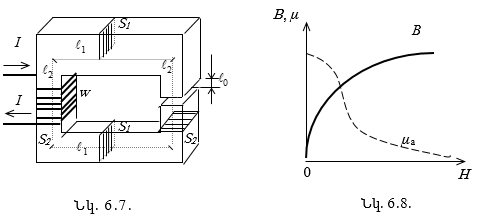
Լրիվ հոսանքի օրենքի համաձայն (6.2)
![]()
որտեղ ![]() մագնիսական դաշտի լարվածություններն են մագնիսահաղորդիչի
մագնիսական դաշտի լարվածություններն են մագնիսահաղորդիչի
![]() միջին երկարությամբ և
միջին երկարությամբ և ![]() լայնական հատույթի մակերես
ունեցող տեղամասերում, իսկ
լայնական հատույթի մակերես
ունեցող տեղամասերում, իսկ ![]() մագնիսական դաշտի լարվածությունը
մագնիսական դաշտի լարվածությունը ![]() լայնությամբ օդային
բացակում:
լայնությամբ օդային
բացակում:
Օդային
բացակում մագնիսական դաշտի ![]() ինդուկցիան և
ինդուկցիան և ![]() լարվածությունը կապված
են (6.3) բանաձևով:
լարվածությունը կապված
են (6.3) բանաձևով:
![]()
Չճյուղավորված մագնիսահաղորդչում, ինչպիսին է դիտարկվող մագնիսահաղորդիչը, մագնիսական հոսքը նույնն է դրա ցանկացած կտրվածքում
![]()
Եթե տրված է մագնիսական Փ հոսքը, ապա ըստ (6.7)-ի կստանանք ինդուկցիաների
![]() արժեքները: Մագնիսական լարվածության
արժեքները: Մագնիսական լարվածության
![]() արժեքները որոշվում են մագնիսահաղորդչի
հիմնական մագնիսացման կորով (նկ. 6.7), իսկ օդային բացակում
արժեքները որոշվում են մագնիսահաղորդչի
հիմնական մագնիսացման կորով (նկ. 6.7), իսկ օդային բացակում ![]() լարվածությունը
(6.6) բանաձևի միջոցով՝
լարվածությունը
(6.6) բանաձևի միջոցով՝ ![]() Այնուհետև, ըստ (6.5) հավասարման որոշվում է մագնիսական
շղթայի F մշուի որոնելի արժեքը:
Այնուհետև, ըստ (6.5) հավասարման որոշվում է մագնիսական
շղթայի F մշուի որոնելի արժեքը:
Տեղադրելով մագնիսահաղորդչի տեղամասերի լարվածությունների
![]() արժեքները (6.5) հավասարման մեջ` կստանանք.
արժեքները (6.5) հավասարման մեջ` կստանանք.
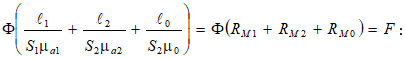
Ընդհանուր դեպքում

որտեղ ![]() - մագնիսահաղորդչի k-րդ տեղամասի մագնիսական
դիմադրությունն է, որը ոչ գծային մեծություն է,
- մագնիսահաղորդչի k-րդ տեղամասի մագնիսական
դիմադրությունն է, որը ոչ գծային մեծություն է, ![]() - oդային բացակի մագնիսական
դիմադրությունն է, որը գծային մեծություն է:
- oդային բացակի մագնիսական
դիմադրությունն է, որը գծային մեծություն է:
Չնայած օդային բացակի ![]() երկարությունը սովորաբար շատ փոքր է,
բայց դրա
երկարությունը սովորաբար շատ փոքր է,
բայց դրա ![]() մագնիսական
դիմադրությունն իր արժեքով մեծ մասամբ գերազանցում է մագնիսահաղորդչի մյուս տեղամասերի
մագնիսական դիմադրությունները (քանի որ
մագնիսական
դիմադրությունն իր արժեքով մեծ մասամբ գերազանցում է մագնիսահաղորդչի մյուս տեղամասերի
մագնիսական դիմադրությունները (քանի որ ![]()
RMk ոչ գծային մագնիսական դիմադրության համար կարելի է կառուցել
վեբերամպերային բնութագիծը, Փ=f(I), որը ստացվում է հիմնական մագնիսացման կորից՝
դրա օրդինատը բազմապատկելով մագնիսահաղորդչի տեղամասի լայնական հատույթի S մակերեսով
(Փ= BS), իսկ աբսցիսը` բազմապատկելով այդ տեղամասի երկարությամբ և բաժանելով
փաթույթի w գալարների թվի վրա ![]()
Ավելի մեծ ջանքեր են պահանջվում մագնիսական շղթաների հաշվման հակառակ խնդրի լուծման համար, երբ տրված է F մագնիսաշարժ ուժը և անհրաժեշտ է որոշել մագնիսական հոսքը մագնիսահաղորդչի տեղամասերում: Այս խնդիրն ավելի պակաս գործնական կարևորություն ունի, ուստի սույն ձեռնարկում այն չի քննարկվում:
6.4. Ֆերոմագնիսական միջուկով կոճը փոփոխական հոսանքի շղթայում
Փոփոխական հոսանքի էլեկտրատեխնիկական սարքերի (էլեկտրամագնիսներ, ռելեներ, կոնտակտորներ, շարժիչներ, գեներատորներ, տրանսֆորմատորներ և այլն) մագնիսական շղթաները շատ բազմազան են և՛ իրենց կառուցվածքով, և՛ ֆունկցիոնալ նշանակությամբ: Ստորև դիտարկվում է դրանցից պարզագույնը՝ ֆերոմագնիսական չճյուղավորված միջուկով կոճը (նկ. 6.9):
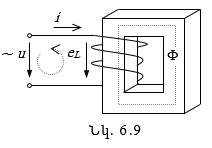
Երբ մագնիսական կոճը միացվում է ![]() սինուսոիդական լարման աղբյուրին
(նկ.6.9), i փոփոխական հոսանք է անցնում փաթույթով, և միջուկում գրգռվում է
Փ փոփոխական մագնիսական հոսք, որն էլ, իր հերթին, կոճում ինդուկտում է ինքնինդուկցիայի
էլշու
սինուսոիդական լարման աղբյուրին
(նկ.6.9), i փոփոխական հոսանք է անցնում փաթույթով, և միջուկում գրգռվում է
Փ փոփոխական մագնիսական հոսք, որն էլ, իր հերթին, կոճում ինդուկտում է ինքնինդուկցիայի
էլշու ![]()
Եթե անտեսենք փաթույթի ակտիվ դիմադրությունը և ենթադրենք, որ մագնիսական բոլոր ուժագծերը փակվում են միջուկով (կամ, ինչպես ասում են, ցրման հոսքը բացակայում է), ապա Կիրխհոֆի 2-րդ օրենքի հիման վրա կետագծով նշված կոնտուրի համար (նկ. 6.9) կարող ենք գրել
![]()
![]()
![]()
Այսպիսով, մագնիսական հոսքը նույնպես սինուսոիդական ֆունկցիա է, անկախ միջուկի նյութի հատկություններից,
![]()
որը փոփոխվում է նույն հաճախությամբ, ինչ որ լարումը, բայց ըստ
փուլի ետ է ընկած դրանից ![]() Սինուսոիդական Փ հոսքի ամպլիտուդային արժեքը, ըստ
(6.10)-ի, կլինի
Սինուսոիդական Փ հոսքի ամպլիտուդային արժեքը, ըստ
(6.10)-ի, կլինի
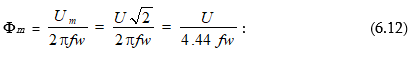
Ինչպես հետևում է (6.9) և (6.12) արտահայտություններից`
![]()
Այս բանաձևը կիրառվում է տրանսֆորմատորի փաթույթներում ինդուկտված էլշուների որոշման համար, ուստի այն կոչվում է տրանսֆորմատորային էլշուի հավասարում:
Չնայած որ միջուկի հոսքը սինուսոիդական է, սակայն մագնիսացնող i հոսանքը փաթույթում ոչ սինուսոիդական մեծություն է:
Նկ. 6.10-ում պատկերված են դիտարկվող կոճի Փ = f (i) վեբեր-ամպերային բնութագիծը, որն ստացվում է մագնիսահաղորդչի նյութի տրված հիսթերեզիսի օղակից (նկ. 6.4) և սինուսոիդական մագնիսական հոսքի Փ=f(t) ժամանակից կախված գրաֆիկը: Համադրելով այդ երկու կորերը` գրաֆիկորեն կառուցված է փաթույթի i = f(t) հոսանքի ժամանակից կախված կորը, որն էլ վկայում է, որ սինուսոիդական հոսքի (նաև կոճին կիրառված սինուսոիդական լարման) դեպքում Փ = f (i) բնութագծի ոչ գծայնության հետևանքով կոճի հոսանքը ոչ սինուսոիդական է:
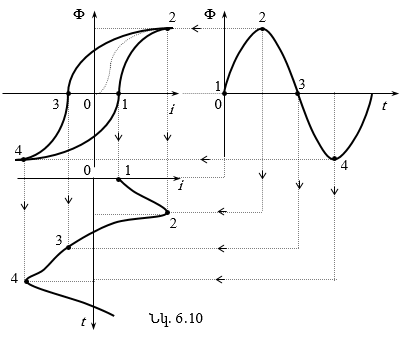
Որքան մեծ է միջուկի հագեցվածությունը, այնքան ավելի զգալի է փաթույթի հոսանքը տարբերվում սինուսոիդականից:
Մագնիսական հոսքի որոշման ժամանակ հաշվի չառնվեց փաթույթի ակտիվ դիմադրությունը և այնպիսի մագնիսական գծերի առկայությունը, որոնք չեն փակվում կամ մասնակիորեն են անցնում մագնիսահաղորդչով, որովհետև դրանք էական ազդեցություն չեն թողնում հոսքի փոփոխման բնույթի վրա: Սակայն, որոշ հանգամանքներում, այդ երկու գործոնները անհրաժեշտ է հաշվի առնել:
Մագնիսական գծերի իրական պատկերը հտևյալն է (նկ. 6.11ա). ինդուկտորի
(փաթույթի) i հոսանքով պայմանավորված մագնիսական հոսքի մեծ մասը փակվում է ֆերոմագնիսական
միջուկով և կոչվում է հիմնական մագնիսական հոսք՝ ![]() Հոսքի գծերի մի փոքր մասը, որը կոչվում
է ցրման հոսք՝
Հոսքի գծերի մի փոքր մասը, որը կոչվում
է ցրման հոսք՝ ![]() ընդգրկում է առանձին գալարները՝
փակվելով օդով կամ մասնակիորեն անցնելով մագնիսահաղորդչով: Ընդ որում
ընդգրկում է առանձին գալարները՝
փակվելով օդով կամ մասնակիորեն անցնելով մագնիսահաղորդչով: Ընդ որում ![]() կախվածությունը (վեբեր-ամպերային
բնութագիծը) որոշվում է մագնիսահաղորդչի հատկություններով: Ցրման
կախվածությունը (վեբեր-ամպերային
բնութագիծը) որոշվում է մագնիսահաղորդչի հատկություններով: Ցրման ![]() հոսքը գրեթե կախված
չէ մագնիսահաղորդչի հատկություններից և հոսանքից կախված գծային ֆունկցիա է, հետևաբար
այն կարելի է հաշվի առնել ինդուկտիվությամբ՝
հոսքը գրեթե կախված
չէ մագնիսահաղորդչի հատկություններից և հոսանքից կախված գծային ֆունկցիա է, հետևաբար
այն կարելի է հաշվի առնել ինդուկտիվությամբ՝
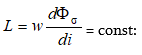
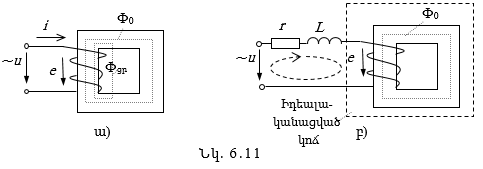
Ուստի, իրական մագնիսական կոճում, հաշվի առնելով փաթույթի r
ակտիվ դիմադրությունը և ![]() ցրման հոսքով պայմանավորված L ինդուկտիվությունը,
ըստ Կիրխհոֆի 2-րդ օրենքի նկ. 6.11ա-ում պատկերված կոճի կոնտուրի համար կարելի է գրել.
ցրման հոսքով պայմանավորված L ինդուկտիվությունը,
ըստ Կիրխհոֆի 2-րդ օրենքի նկ. 6.11ա-ում պատկերված կոճի կոնտուրի համար կարելի է գրել.
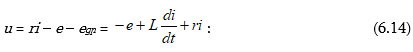
Ըստ (6.14) հավասարման, միջուկով կոճը (նկ. 6.11ա) կարելի է փոխարինել համարժեք սխեմայով (նկ. 6.11բ), որի մի մասը վերը դիտարկված իդեալականացված կոճն է` առանց ցրման հոսքի և ակտիվ դիմադրության:
1. Գրել մագնիսկան հոսքի և մագնիսական ինդուկցիայի կապն արտահայտող բանաձևը: Նշել դրանց չափման միավորները միջազգային համակագում:
2. Սահմանել լրիվ հոսանքի օրենքը և գրել դրա մաթեմատիկական արտահայտությունը:
3. Ի՞նչ է մագնիսաշարժ ուժը և ի՞նչ միավորով է այն չափվում:
4. Գրել մագնիսական ինդուկցիայի և մագնիսկան դաշտի լարվածության կապն արտահայտող բանաձևը: Նշել դրանց չափման միավորները:
5. Գնահատել բացարձակ և հարաբերական մագնիսական թափանցելիության արժեքները ֆերրոմագնիսական և ոչ ֆերրոմագնիսական նյութերի համար:
6. Դեկարտյան կոորդինատային հարթության վրա պատկերել ֆերրոմագնիսական նյութի հիսթերեզիսի օղակը և գրաֆիկի վրա ցույց տալ մնացորդային ինդուկցիայի և կոէռցիտիվ ուժի մեծությունները: Ո՞րն է հիմնական մագնիսացման կորը:
7. Ինչպիսի՞ ֆերրոմագնիսական նյութերն են կոչվում մագնիսակոշտ (մագնիսափափուկ) նյութեր:
8. Որո՞նք են փոփոխական մագնիսական դաշտի ազդեցության տակ ֆերրոմագնիսական նյութերի տաքացման պատճառները: Ի՞նչ միջոցներ են կիրառվում փոքրացնելու համար ջերմային կորուստները ֆերրոմագնիսական նյութերում:
9. Տալ մագնիսական շղթայի սահմանումը: Որոնք են մագնիսական շղթայի տարրերը:
10. Գրեք լրիվ հոսանքի օրենքի գործնականում կիրառվող արտահայտությունը չճյուղավորված ուղղանկյունաձև մագնիսական շղթայի համար:
11. Գրեք սինուսոիդական լարմանը միացված ֆերրոմագնիսկան միջուկով կոճում ինդուկտված էլշուի արտահայտությունը:
12. Ինչու՞ սինուսոիդական լարմանը միացված ֆերրոմագնիսկան միջուկով կոճում առաջանում է ոչ սինուսոիդական հոսանք:
7. ՊԱՐԲԵՐԱԿԱՆ ՈՉ ՍԻՆՈՒՍՈԻԴԱԿԱՆ ՀՈՍԱՆՔՆԵՐԸ ԷԼԵԿՏՐԱԿԱՆ ՇՂԹԱՆԵՐՈՒՄ
7.1. Պարբերական ոչ սինուսոիդական հոսանքների առաջացման պատճառները
Նախորդ գլուխներում դիտարկվում էին սինուսոիդական հոսանքի շղթաների տեսությունը և հաշվարկը: Սակայն գործնականում էլեկտրաէներգիայի ստացման, տրանսֆորմացիայի, հեռահաղորդման և օգտագործման ժամանակ հաճախ առաջ են գալիս էլշուների, լարումների և հոսանքների սինուսոիդական ձևի աղավաղումներ: Այդպիսի աղավաղումները կամ ոչ սինուսոիդական պարբերական հոսանքների և լարումների առաջացումը պայմանավորված է հետևյալ հիմնական պատճառներով:
· Հաստատուն և սինուսոիդական էլշուի աղբյուրների ոչ կատարյալ լինելը: Խիստ մոտեցման դեպքում կարելի է ասել, որ գործնականում բացարձակ հաստատուն կամ բացարձակ սինուսոիդական էլշուի աղբյուրներ գոյություն չունեն:
· Էլեկտրական շղթայում ոչ սինուսոիդական լարման հատուկ գեներատորների առկայությունը: Հաշվողական տեխնիկայի, ավտոմատ կառավարման և այլ բնագավառներում մեծ կիրառություն ունեն զանազան ազդանշանային (իմպուլսային) գեներատորները, որոնք նախատեսված են տարբեր տեսքի պարբերական ազդանշաններ ստանալու համար: Այդպիսի գեներատորների ելքում ստացվում են ուղղանկյունաձև (նկ. 7.1ա), եռանկյունաձև (նկ. 7.1բ), սեղանաձև (նկ. 7.1գ) կամ մի այլ տեսքի ազդանշաններ: Այս բնույթի ամենատարածված գեներատորներից մեկն էլ սղոցաձև լարման գեներատորն է, որը քննարկվեց 5.4 բաժնում:
· Էլեկտրական շղթաներում ոչ գծային տարրերի առկայությունը: Եթե նույնիսկ ընդունենք, որ շղթայում գործող աղբյուրների էլշուն (կամ լարումը) բացարձակ սինուսոիդական է, ապա դրանք ոչ գծային տարրերում առաջացնում են ոչ սինուսոիդական հոսանքներ:
Ոչ գծային տարրերը լայնորեն կիրառվում են ավտոմատիկայի, կառավարման, ռելեական պաշտպանության և այլ շղթաներում: Ինչպես հայտնի է, գործնականում հաստատուն հոսանքը գլխավորապես ստացվում է սինուսոիդական հոսանքի ուղղման միջոցով: Ընդ որում տարբեր տեսակի ուղղիչների սխեմաներում կիրառվում են խիստ արտահայտված ոչ գծային տարրեր (դիոդներ, տիրիստորներ): Մասնավորապես ոչ գծային տարր է նաև տարբեր սարքերում կիրառվող ֆերոմագնիսական միջուկով կոճը, որը քննարկվեց նախորդ գլխում:
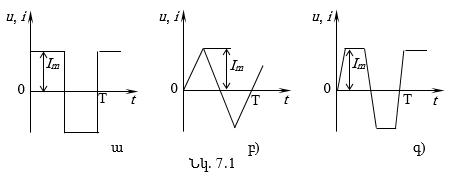
Ոչ սինուսոիդական հոսանքների և լարումների առաջանալը էլեկտրական շղթաներում կարող է ունենալ միանգամայն անցանկալի հետևանքներ՝ հզորության լրացուցիչ կորուստներ, էլեկտրաշարժիչների աշխատանքի վատթարացում, աղավաղումներ կապի գծերում և այլն:
7.2. Պարբերական ոչ սինուսոիդական մեծությունների արտահայտումը Ֆուրյեի շարքով
Մաթեմատիկայի դասընթացից հայտնի է, որ ժամանակից կախված պարբերական ֆունկցիան բավարարում է
![]()
պայմանին, որտեղ T -ն ֆունկցիայի պարբերությունն է՝ այն ամենափոքր ժամանակահատվածը, որից հետո ամբողջ պրոցեսը նույնությամբ կրկնվում է, k-ն ցանկացած ամբողջ թիվ է: Այդպիսի պարբերական ֆունկցիան կարող է ներկայացվել Ֆուրյեի եռանկյունաչափական շարքով:
Այսպես օրինակ, u(t) ոչ սինուսոիդական պարբերական լարման համար կարող ենք գրել.
![]()
որտեղ
![]() լարման
հաստատուն բաղադրիչն է,
լարման
հաստատուն բաղադրիչն է, ![]() - լարման առաջին (կամ հիմնական) հարմոնիկն է,
որի հաճախությունը հավասար է ոչ սինուսոիդական պարբերական ֆունկցիայի հաճախությանը,
- լարման առաջին (կամ հիմնական) հարմոնիկն է,
որի հաճախությունը հավասար է ոչ սինուսոիդական պարբերական ֆունկցիայի հաճախությանը,
![]() բարձր հարմոնիկ
բաղադրիչների ամպլիտուդային արժեքներն են,
բարձր հարմոնիկ
բաղադրիչների ամպլիտուդային արժեքներն են, ![]() հարմոնիկ բաղադրիչների սկզբնական
փուլերը:
հարմոնիկ բաղադրիչների սկզբնական
փուլերը:
Այսպիսով u(t) ոչ սինուսոիդական պարբերական լարումը հավասար է հաստատուն լարման և տարբեր հաճախություններով սինուսոիդական լարումների գումարին: Գործնականում, կախված հաշվարկի պահանջվող ճշտությունից, Ֆուրյեի շարքի անդամների թիվը վերցվում է վերջավոր (սովորաբար 3...7 անդամ):
Եթե գծային էլեկտրական շղթային կիրառված է u(t) ոչ սինուսոիդական լարում, ապա շղթայի հոսանքների հաշվարկի համար նպատակահարմար է կիրառել վերադրման սկզբունքը (տես 2.4 բաժինը): Այսինքն՝ շղթայի յուրաքանչյուր ճյուղի ակնթարթային հոսանք որոշվում է որպես լարման ակնթարթային արժեքի առանձին բաղադրիչներով պայմանավորված հոսանքների գումար: Հաշվարկը կատարվում է յուրաքանչյուր հարմոնիկի համար առանձին՝ կիրառելով շղթաների հաշվարկի հայտնի մեթոդները:
Սկզբում
հաշվում են լարման ![]() հաստատուն բաղադրիչով պայմանավորված
հոսանքները՝ հաշվի առնելով, որ այս դեպքում շղթայի ինդւկտիվ դիմադրությունները հավասար
են զրոյի, իսկ ունակային դիմադրությունները՝ անվերջության: Այնուհետև հաշվում են առաջին
հարմոնիկով պայմանավորված հոսանքները, ապա՝ երկրորդ, երրորդ և այլն: Շղթայի ինդուկտիվ
և ունակային տարրերի ռեակտիվ դիմադրությունները, որոնց արժեքները կախված են հաճախությունից,
լարման տարբեր հարմոնիկների համար կունենան տարբեր արժեքներ: Ընդհանուր դեպքում, ոչ
սինուսոիդական լարման k-րդ հարմոնիկի համար ինդուկտիվ և ունակային դիմադրությունները
կլինեն.
հաստատուն բաղադրիչով պայմանավորված
հոսանքները՝ հաշվի առնելով, որ այս դեպքում շղթայի ինդւկտիվ դիմադրությունները հավասար
են զրոյի, իսկ ունակային դիմադրությունները՝ անվերջության: Այնուհետև հաշվում են առաջին
հարմոնիկով պայմանավորված հոսանքները, ապա՝ երկրորդ, երրորդ և այլն: Շղթայի ինդուկտիվ
և ունակային տարրերի ռեակտիվ դիմադրությունները, որոնց արժեքները կախված են հաճախությունից,
լարման տարբեր հարմոնիկների համար կունենան տարբեր արժեքներ: Ընդհանուր դեպքում, ոչ
սինուսոիդական լարման k-րդ հարմոնիկի համար ինդուկտիվ և ունակային դիմադրությունները
կլինեն.
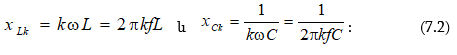
7.3. Պարբերական ոչ սինուսոիդական մեծությունների գործող արժեքը
Ինչպես և սինուսոիդական մեծությունների դեպքում (տես բաժին 3.3), ոչ սինուսոիդական էլշուների, լարումների և հոսանքների գործող արժեքը որոշվում է որպես ոչ սինուսոիդական պարբերական ֆունկցիայի միջին քառակուսային արժեք մեկ պարբերության ընթացքում:
Հոսանքի համար
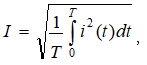
Որտեղ
![]()
Ինտեգրումից և պարզ ձևափոխություններից հետո i(t) ոչ սինուսոիդական պարբերական հոսանքի գործող արժեքի համար վերջնականորեն կստանանք
![]()
որտեղ
![]() հոսանքի
համապատասխան հարմոնիկների գործող արժեքներն են`
հոսանքի
համապատասխան հարմոնիկների գործող արժեքներն են`
![]()
Այսպիսով, ոչ սինուսոիդական պարբերական հոսանքի գործող արժեքը հավասար է դրա հաստատուն և հարմոնիկ բաղադրիչների գործող արժեքների քառակուսիների գումարին՝ քառակուսի արմատի տակ:
Համանման ձևով ոչ սինուսոիդական պարբերական էլշուի և լարման գործող արժեքները կլինեն
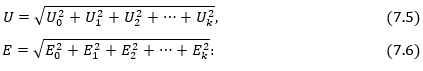
Ոչ սինուսոիդական հոսանքի շղթայում միացված ամպերմետրերը և վոլտմետրերը ցույց են տալիս համապատասխանաբար հոսանքի և լարման գործող արժեքները:
7.4. Ոչ սինուսոիդական հոսանքի ակտիվ և լրիվ հզորությունները
Հզորության
ակնթարթային արժեքի ![]() արտահայտությունը ճիշտ է u(t)
լարման և i(t) հոսանքի ցանկացած տեսքի ֆունկցիաների համար: Ինչպես արդեն ասվել
է 3.8 բաժնում, պարբերական հոսանքի ակտիվ հզորությունը որոշվում է որպես հզորության
ֆունկցիայի միջին արժեք մեկ պարբերության ընթացքում.
արտահայտությունը ճիշտ է u(t)
լարման և i(t) հոսանքի ցանկացած տեսքի ֆունկցիաների համար: Ինչպես արդեն ասվել
է 3.8 բաժնում, պարբերական հոսանքի ակտիվ հզորությունը որոշվում է որպես հզորության
ֆունկցիայի միջին արժեք մեկ պարբերության ընթացքում.
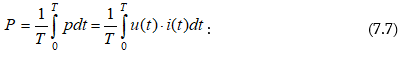
Տեղադրելով (7.1)-ից u(t)-ի արժեքը և (7.3)-ից i(t)-ի արժեքը (7.7) արտահայտության մեջ և կատարելով ինտեգրում՝ կստանանք ոչ սինուսոիդական հոսանքի ակտիվ հզորության բանաձևը.
![]()
կամ
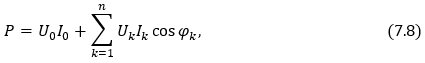
որտեղ
![]() հարմոնիկի
լարման և հոսանքի գործող արժեքներն են,
հարմոնիկի
լարման և հոսանքի գործող արժեքներն են, ![]() լարման և հոսանքի համապատասխան հարմոնիկների
միջև փուլային շեղումն է:
լարման և հոսանքի համապատասխան հարմոնիկների
միջև փուլային շեղումն է:
Այսպիսով, ոչ սինուսոիդական հոսանքի ակտիվ հզորությունը հավասար է դրա հաստատուն բաղադրիչի հզորության և բոլոր հարմոնիկների ակտիվ հզորությունների գումարին:
Ոչ սինուսոիդական հոսանքի լրիվ հզորությունը հավասար է ոչ սինուսոիդական հոսանքի և ոչ սինուսոիդական լարման գործող արժեքների արտադրյալին.
![]()
7.5. Ոչ սինուսոիդական հոսանքով շղթայի հաշվարկի օրինակներ
Խնդիր 7.1. Որոշել շղթայի ակտիվ և լրիվ հզորությունները, լարման և հոսանքի հետևյալ արտահայտությունների դեպքում.
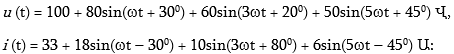
Լուծում:
Որոշենք լարման և հոսանքի գործող արժեքները, համապատասխանաբար, ըստ (7.5) և (7.4) բանաձևերի.
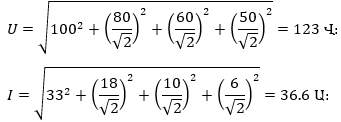
Որոշենք լարման և հոսանքի համապատասխան հարմոնիկների փուլային շեղումները.
![]()
Շղթայի ակտիվ հզորությունը, ըստ (7.8) -ի կլինի,
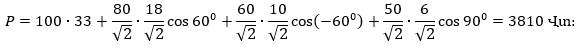
Շղթայի լրիվ հզորությունը. ըստ (7.9) -ի
![]()
Խնդիր 7.2. Որոշել ամպերմետրի ցուցմունքը նկ. 7.2-ում բերված
շղթայում, եթե տրված են` R=50 Օհմ, C=200 մկՖ, ![]()
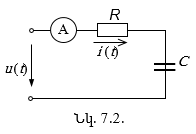
Լուծում: Ակնհայտ է, որ ունակային
տարրի պատճառով դիտարկվող շղթայում հոսանքի հաստատուն բաղադրիչը հավասար է զրոյի` ![]()
Ըստ Օհմի օրենքի, տրված շղթայի հոսանքի գործող արժեքը k-րդ հարմոնիկը
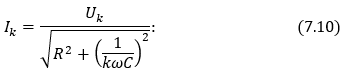
Օգտվելով (7.10)-ից` որոշում ենք շղթայի հոսանքի հարմոնիկների գործող արժեքները.
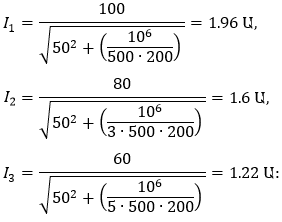
Ամպերմետրի ցուցմունքը, որը հավասար է ոչ սինուսոիդական հոսանքի գործող արժեքին, ըստ (7.4)-ի կլինի
![]()
1. Որոնք են էլեկտրական շղթաներում ոչ սինուսոիդական պարբերական հոսանքների և լարումների առաջացման հիմնական պատճառները:
2. Ի՞նչ բացասական ազդեցություն կարող են ունենալ ոչ սինուսոիդական հոսանքներն ու լարումները:
3. Ինչպե՞ս է ներկայացվում ոչ սինուսոիդական պարբերական մեծությունը Ֆուրյեի շարքով:
4. Ինչպե՞ս է վերադրման սկզբունքը կիրառվում ոչ սինուսոիդական հոսանքի շղթաների հաշվարկի համար:
5. Ինչ բանաձևով է որոշվում ոչ սինուսոիդական հոսանքի (լարման) գործող արժեքը:
6. Ինչ բանաձևեր են կիրառվում ոչ սինուսոիդական հոսանքի (լարման) դեպքում շղթայի ակտիվ (ռեակտիվ, լրիվ) հզորության հաշվարկի համար:
8.1. Տրանսֆորմատորների դերն ու նշանակությունը
Տրանսֆորմատորը էլեկտրամագնիսական սարք է, որը հիմնականում նախատեսված է փոփոխական լարման և հոսանքի գործող արժեքները փոփոխելու համար: Լարումների և հոսանքների տրանսֆորմացիան անհրաժեշտ է` էլեկտրաէներգիան մեծ հեռավորությունների վրա շահավետ տեղափոխելու համար:
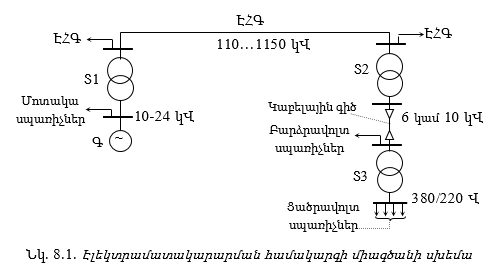
Տրանսֆորմատորը էլեկտրամատակարարման համակարգի կարևորագույն տարրերից մեկն է: Էլեկտրակայաններում արտադրված էլեկտրաէներգիան գեներատորներից սպառիչներին հասցնելու ճանապարհին ենթարկվում է 3 -…5 - ապատիկ տրանսֆորմացիայի:
Դիտարկենք էլեկտրամատակարարման եռաֆազ համակարգի պարզեցված միագծանի սխեման (Նկ. 8.1): Էլեկտրակայաններում տեղակայված սինքրոն գեներատորները նախատեսված են մինչև 24 կՎ լարման համար: Այդպիսի լարումը բավարար է միայն էլեկտրակայանին համեմատաբար մոտ գտնվող (մինչև 10…15 կմ) սպառիչները սնելու համար: Էլեկտրաէներգիան մեծ հեռավորությունների վրա տեղափոխելու համար լարումը տրանսֆորմատորի միջոցով (Տ1) բարձրացվում է՝ հասցնելով 35, 110, 220, 330, 500, 750 կամ 1150 կՎ-ի (կախված հեռավորությունից): Այնուհետև վերերկրյա էլեկտրահաղորդման գծերով (ԷՀԳ) այն տեղափոխվում է մեծ հեռավորությունների վրա (մինչև հարյուրավոր, նույնիսկ` հազարավոր կիլոմետրեր):
Տեղափոխված էներգիայի լարումը շրջանային խոշոր ենթակայաններում իջեցնող տրանսֆորմատորների միջոցով (Տ2) վերափոխվում է 6 կամ 10 կՎ լարման, որտեղից էլ, հիմնականում ստորգետնյա մալուխային (կաբելային) գծերով, էլեկտրաէներգիան բաշխվում է քաղաքի կամ ձեռնարկության տարածքում՝ սնելով փոքր հզորության բազմաթիվ տրանսֆորմատորային ենթակայանները (Տ3), որոնք տեղադրվում են հիմնական սպառիչներին անմիջականորեն մոտ: Գերհզոր սպառիչները (շարժիչներ, էլեկտրական վառարաններ) աշխատում են 6 կամ 10կՎ լարումով: Սակայն սպառիչների գերակշռող մեծամասնությունը նախատեսված է 380 Վ (հազվադեպ 660 Վ) գծային կամ 220 Վ (380 Վ) ֆազային լարման համար:
Ուժային տրանսֆորմատորների անվանական հզորությունը համապատասխանում է դրա լրիվ հզորությանը, ուստի այն արտահայտվում է ՎԱ-ով կամ կՎԱ-ով: Տարբեր տեսակի տրանսֆորմատորների անվանական հզորությունը կարող է փոփոխվել շատ լայն սահմաններում. ռադիոէլեկտրոնային սարքերում կիրառվող տրանսֆորմատորների մի քանի ՎԱ հզորությունից մինչև էլեկտրաէներգետիկայում կիրառվող եռաֆազ տրանսֆորմատորների մինչև 1000 ՄՎԱ հզորությունը:
Տրանսֆորմատորի վահանակի (պիտակի) վրա նշվում են դրա անվանական հզորությունը (ՎԱ կամ կՎԱ), անվանական լարումները (Վ կամ կՎ), անվանական հոսանքները (Ա), հաճախությունը, ֆազերի թիվը, միացման սխեման (եռաֆազ տրանսֆորմատորների համար) և հովացման եղանակը:
Տրանսֆորմատորների գերակշիռ մասը նախատեսված է f = 50 Հց հաճախության համար: Երբ անհրաժեշտ է փոքրացնել տրանսֆորմատորի զանգվածը (օրինակ, թռչող սարքերում, նավերում), օգտագործում են 400Հց կամ 500Հց հաճախություն:
Տրանսֆորմատորները լայնորեն օգտագործվում են նաև էլեկտրաեռակցման համար (եռակցման տրանսֆորմատորներ), բարձր լարումներ և մեծ հոսանքներ չափելու համար (չափման տրանսֆորմատորներ):
8.2. Միաֆազ տրանսֆորմատորի կառւցվածքը
Չնայած տրանսֆորմատորների բազմազանությանը, բոլոր թվարկված տրանսֆորմատորներն ունեն սկզբունքորեն նույն կառուցվածքը. բաղկացած են փակ ֆերոմագնիսական միջուկից (մագնիսահաղորդչից) և դրա վրա տեղադրված երկու կամ ավելի փաթույթներից (նկ. 8.2):
Փաթույթների միջև ինդուկտիվ կապն ուժեղացնելու և մրրկային հոսանքները փոքրացնելու համար միջուկը պատրաստում են մագնիսական մեծ թափանցելիություն ունեցող էլեկտրատեխնիկական պողպատի թիթեղներից, որոնք մեկուսացված են միմյանցից լաքի բարակ շերտով: f = 50Հց հաճախության դեպքում թիթեղները պատրաստվում են 0,35 - 0.5 մմ հաստությամբ: f = 400Հց հաճախության դեպքում դրանց հաստությունը ընդամենը 0,1 մմ է: Շատ բարձր հաճախությունների դեպքում (f > 20 կՀց) միջուկն ընդհանրապես բացակայում է (օդային տրանսֆորմատոր):
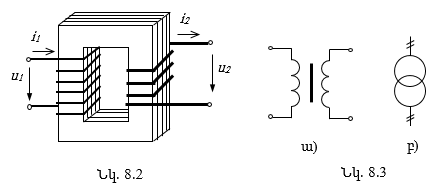
Փաթույթներից մեկը, որը կոչվում է առաջնային փաթույթ, միացվում է փոփոխական հոսանքի աղբյուրին կամ ցանցին (դրան վերաբերող մեծությունները նկ. 8.2-ում նշված են “1” ինդեքսով): Մյուս փաթույթը, որին միացվում են փոփոխական հոսանքի սպառիչները, կոչվում է երկրորդային փաթույթ (դրան վերաբերող մեծությունները նկ. 8.2-ում նշված են “2” ինդեքսով): Փաթույթները տարբերում են նաև ըստ լարման՝ բարձր լարման փաթույթ, ցածր լարման փաթույթ (եռափաթույթ տրանսֆորմատորներում կարող է լինել նաև միջին լարման փաթույթ):
Փաթույթների ցրման հոսքերը փոքրացնելու նպատակով սովորաբար առաջնային և երկրորդային փաթույթները տեղադրվում են միջուկի միևնույն ուղղաձիգ ձողի վրա՝ տալով դրանց համակենտրոն դասավորություն: Միջուկին ավելի մոտ տեղադրվում է ցածր լարման փաթույթը, իսկ դրա վրա՝ բարձր լարման փաթույթը:
Նկ. 8.3-ում բերված են միաաֆազ տրանսֆորմատորի պայմանական նշանները` սկզբունքային (ա) և միագծանի սխեմաներում:
Տրանսֆորմատորի հովացումը կարևոր տեխնիկական խնդիր է, քանի որ նրա միավոր ծավալում անջատվում է մեծ քանակությամբ ջերմային էներգիա, որը բերում է ջերմաստիճանի զգալի բարձրացման: Այն թույլատրելի սահմաններում պահելու համար նախատեսում են զանազան միջոցներ տրանսֆորմատորի հովացման համար: Որքան մեծ է տրանսֆորմատորի անվանական հզորությունը, այնքան մեծ է դրա միավոր ծավալում անջատվող ջերմությունը և այնքան ավելի բարդ է դրա հովացման համակարգը: Գործնականում առավել մեծ կիրառություն ունեն այսպես կոչված յուղային տրանսֆորմատորները:
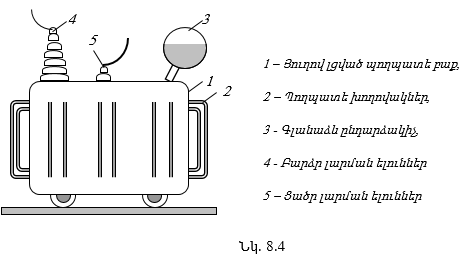
Նկ.8.4-ում պատկերված է միջին հզորության բնական շրջապտույտով (ցիրկուլյացիա) յուղային տրանսֆորմատորի արտաքին տեսքը: Տրանսֆորմատորի միջուկը փաթույթների հետ միասին խորասուզվում է հանքային հատուկ յուղով լցված պողպատե բաքի (1) մեջ: Յուղը կատարում է երկու դեր.
ա) շրջապտույտ կատարելով պողպատյա խողովակներով (2)՝ նպաստում է տրանսֆորմատորի հովացմանը,
բ) մեկուսիչ է փաթույթների և գալարների միջև:
Գլանաձև ընդարձակիչը (3) ջերմաստիճանի մեծ սահմաններում փոփոխվելու դեպքում թույլ է տալիս յուղի մակարդակի ազատ փոփոխություններ՝ պահպանելով բաքի մեջ յուղի անհրաժեշտ մակարդակը:
8.3. Միաֆազ տրանսֆորմատորի աշխատանքի սկզբունքը
Երբ տրանսֆորմատորի առաջնային փաթույթը միացվում
է փոփոխական ![]() լարմանը, նրանով անցնում է
լարմանը, նրանով անցնում է ![]() փոփոխական հոսանք,
որն, իր հերթին, առաջացնում է
փոփոխական հոսանք,
որն, իր հերթին, առաջացնում է ![]() փոփոխական մագնիսական
հոսք: Վերջինս բաղկացած է երկու բաղադրիչից (նկ. 8.4).
փոփոխական մագնիսական
հոսք: Վերջինս բաղկացած է երկու բաղադրիչից (նկ. 8.4).
![]()
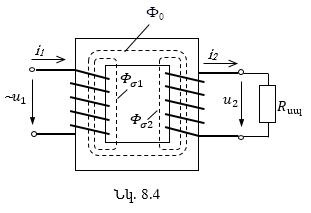
Բաղադրիչներից մեկը ![]() որը կազմում է
որը կազմում է ![]() հոսքի գերակշռող մասը (մոտ 95%), փակվում է ֆերոմագնիսական միջուկով՝ հարակցելով
առաջնային և երկրորդային փաթույթները և մագնիսական կապ ստեղծելով դրանց միջև: Այն
կոչվում է տրանսֆորմատորի հիմնական մագնիսական հոսք: Մագնիսական հոսքի մյուս
բաղադրիչը
հոսքի գերակշռող մասը (մոտ 95%), փակվում է ֆերոմագնիսական միջուկով՝ հարակցելով
առաջնային և երկրորդային փաթույթները և մագնիսական կապ ստեղծելով դրանց միջև: Այն
կոչվում է տրանսֆորմատորի հիմնական մագնիսական հոսք: Մագնիսական հոսքի մյուս
բաղադրիչը ![]() փակվում է միայն առաջնային
փաթույթի գալարների շուրջը և կոչվում է առաջնային փաթույթի ցրման հոսք:
փակվում է միայն առաջնային
փաթույթի գալարների շուրջը և կոչվում է առաջնային փաթույթի ցրման հոսք:
Հիմնական մագնիսական հոսքը առաջնային և երկրորդային փաթույթների յուրաքանչյուր գալարում ինդուկտում է
![]()
էլեկտրաշարժ ուժ: Հետևաբար առաջնային և երկրորդային փաթույթներում ինդուկտված էլշուները կլինեն, համապատասխանաբար,
![]()
որտեղ ![]() համապատասխանաբար`
այդ փաթույթների գալարների թվերն են:
համապատասխանաբար`
այդ փաթույթների գալարների թվերն են:
Եթե երկրորդային փաթույթին միացվի սպառիչ, ապա
![]() էլշուի շնորհիվ դրա
միջով կանցնի փոփոխական
էլշուի շնորհիվ դրա
միջով կանցնի փոփոխական ![]() հոսանք և սպառիչի սեղմակներում կհաստատվի
հոսանք և սպառիչի սեղմակներում կհաստատվի ![]() փոփոխական լարում:
Այսպիսով առաջնային փաթույթին կիրառված
փոփոխական լարում:
Այսպիսով առաջնային փաթույթին կիրառված ![]() փոփոխական լարումը
տրանսֆորմատորը կերպափոխում է
փոփոխական լարումը
տրանսֆորմատորը կերպափոխում է ![]() փոփոխական լարման:
Երկրորդային փաթույթի կողմից տրանսֆորմատորը հանդես է գալիս որպես էներգիայի աղբյուր,
մինչդեռ առաջնային փաթույթի կողմից այն հանդիսանում է սպառիչ:
փոփոխական լարման:
Երկրորդային փաթույթի կողմից տրանսֆորմատորը հանդես է գալիս որպես էներգիայի աղբյուր,
մինչդեռ առաջնային փաթույթի կողմից այն հանդիսանում է սպառիչ:
Սպառիչի առկայության դեպքում երկրորդային փաթույթի
հոսանքը նույնպես առաջացնում է մագնիսական հոսք, որի գերակշիռ մասը փակվում է ֆերոմագնիսական
միջուկով և հակազդում է առաջնային փաթույթի հոսքին, իսկ հոսքի մի փոքր մասը հանդիսանում
է ցրման հոսք ![]() փակվելով միայն երկրորդային փաթույթի շուրջը:
փակվելով միայն երկրորդային փաթույթի շուրջը:
Փաթույթների էլշուների գործող արժեքների հարաբերությունը,
որը, ակնհայտ է, հավասար կլինի գալարների թվի հարաբերությանը, կոչվում է տրանսֆորմացիայի
գործակից ![]()
Եթե ![]() ապա երկրորդային լարման
գործող արժեքը բարձր է առաջնայինից՝
ապա երկրորդային լարման
գործող արժեքը բարձր է առաջնայինից՝ ![]() և տրանսֆորմատորը
կոչվում է բարձրացնող տրանսֆորմատոր: Հակառակ դեպքում, երբ
և տրանսֆորմատորը
կոչվում է բարձրացնող տրանսֆորմատոր: Հակառակ դեպքում, երբ ![]() տրանսֆորմատորը կոչվում է իջեցնող (ցածրացնող) տրանսֆորմատոր:
տրանսֆորմատորը կոչվում է իջեցնող (ցածրացնող) տրանսֆորմատոր:
8.4. Տրանսֆորմատորի փաթույթների էլշուները
Տրանսֆորմատորի փաթույթների առաջացրած ![]() փոփոխական հոսքերը ինդուկտում են համապատասխան էլշուներ տրանսֆորմատորի փաթույթներում:
փոփոխական հոսքերը ինդուկտում են համապատասխան էլշուներ տրանսֆորմատորի փաթույթներում:
Առաջնային փաթույթում՝
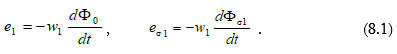
Երկրորդային փաթույթում՝
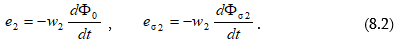
Որոշենք այս էլշուների գործող արժեքները:
Ինչպես ցույց է տրվել սույն ձեռնարկի (6.4 պարագրաֆում),
եթե առաջնային փաթույթին կիրառված է ![]() սինուսոիդական լարում,
ապա
սինուսոիդական լարում,
ապա ![]() հոսքերը, ինչպես նաև նրանցով ինդուկտված
հոսքերը, ինչպես նաև նրանցով ինդուկտված ![]() էլշուները,
նույնպես կփոփոխվեն սինուսոիդական օրենքով:
էլշուները,
նույնպես կփոփոխվեն սինուսոիդական օրենքով:
Ընդունելով
![]()
կստանանք
![]()
Այսպիսով, 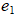 էլշուն, նմանապես և
էլշուն, նմանապես և 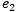 էլշուն, հետ են մնում
էլշուն, հետ են մնում 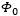 հոսքից ըստ փուլի
հոսքից ըստ փուլի 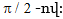 Այդ էլշուների
գործող արժեքները կլինեն, համապատասխանաբար,
Այդ էլշուների
գործող արժեքները կլինեն, համապատասխանաբար,
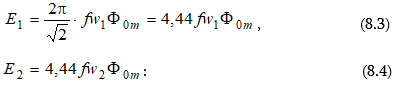
Տրանսֆորմատորի փաթույթների այս բանաձևերը կիրառվում
են տրանսֆորմատորի նախագծման և հաշվարկման ժամանակ: Մասնավորապես, դրանց միջոցով հաշվարկում
են փաթույթների գալարների ![]() թվերը:
թվերը:
Ցրման ![]() հոսքերով ինդուկտված
հոսքերով ինդուկտված
![]() ինքնինդուկցիայի էլշուները կարելի է դիտել որպես լարման անկումներ տրանսֆորմատորի
համապատասխան փաթույթների ինդուկտիվ դիմադրությունների վրա (տես ձեռնարկի առաջին մասի
3.4.2 բաժինը ) .
ինքնինդուկցիայի էլշուները կարելի է դիտել որպես լարման անկումներ տրանսֆորմատորի
համապատասխան փաթույթների ինդուկտիվ դիմադրությունների վրա (տես ձեռնարկի առաջին մասի
3.4.2 բաժինը ) .
![]()
որտեղ
![]() -
համապատասխանաբար, առաջնային և երկրորդային փաթույթների ինդուկտիվ դիմադրություններն
են:
-
համապատասխանաբար, առաջնային և երկրորդային փաթույթների ինդուկտիվ դիմադրություններն
են:
Ինչպես հետևում է (8.3) և (8.4) բանաձևերից, տրանսֆորմացիայի գործակիցը

8.5. Տրանսֆորմատորի հավասարումները
Մի կողմից տրանսֆորմատորի փաթույթները ստեղծում
են ![]() ցրման հոսքեր, ինչը նշանակում է, որ դրանք օժտված են ինդուկտիվությամբ՝ համապատասխանաբար
ցրման հոսքեր, ինչը նշանակում է, որ դրանք օժտված են ինդուկտիվությամբ՝ համապատասխանաբար
![]() ինդուկտիվ դիմադրություններով, մյուս կողմից` դրանցով անցնող
ինդուկտիվ դիմադրություններով, մյուս կողմից` դրանցով անցնող ![]() հոսանքները առաջացնում են ջերմության անջատում, ինչն իր հերթին նշանակում է,
որ փաթույթներն օժտված են նաև
հոսանքները առաջացնում են ջերմության անջատում, ինչն իր հերթին նշանակում է,
որ փաթույթներն օժտված են նաև ![]() ակտիվ դիմադրություններով:
Հետևաբար, տրանսֆորմատորը կարելի է ներկայացնել համապատասխան համարժեք սխեմայի տեսքով
(նկ. 8.6):
ակտիվ դիմադրություններով:
Հետևաբար, տրանսֆորմատորը կարելի է ներկայացնել համապատասխան համարժեք սխեմայի տեսքով
(նկ. 8.6):
Համաձայն Կիրխհոֆի 2-րդ օրենքի, առաջնային փաթույթի համար կոմպլեքս տեսքով կարելի է գրել
![]()
Այստեղից ստացվում է տրանսֆորմատորի առաջնային փաթույթի էլեկտրական վիճակի հավասարումը՝
![]()
որտեղ
![]() -
առաջնային փաթույթի կոմպլեքս դիմադրությունն է:
-
առաջնային փաթույթի կոմպլեքս դիմադրությունն է:
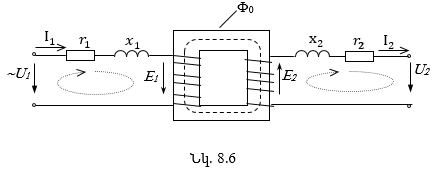
Համանման ձևով, ստացվում է երկրորդային փաթույթի էլեկտրական վիճակի հավասարումը՝
![]()
որտեղ
![]() երկրորդային փաթույթի կոմպլեքս դիմադրությունն է:
երկրորդային փաթույթի կոմպլեքս դիմադրությունն է:
Ստացված (8.7) և (8.8) հավասարումները կոչվում
են տրանսֆորմատորի էլեկտրական վիճակի հավասարումներ: Դրանցում ![]() արտադրյալները կոչվում են տրանսֆորմատորի ներքին լարման անկումներ, համապատասխանաբար,
առաջնային և երկրորդային փաթույթների վրա: Դրանց գործող արժեքները չեն գերազանցում
համապատասխան
արտադրյալները կոչվում են տրանսֆորմատորի ներքին լարման անկումներ, համապատասխանաբար,
առաջնային և երկրորդային փաթույթների վրա: Դրանց գործող արժեքները չեն գերազանցում
համապատասխան ![]() լարումների գործող
արժեքների 5…10%-ը: Հետևաբար (8.3) և (8.7) հավասարումների հիման վրա կարելի է գրել
լարումների գործող
արժեքների 5…10%-ը: Հետևաբար (8.3) և (8.7) հավասարումների հիման վրա կարելի է գրել
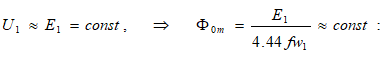
Այսպիսով ![]() հիմնական մագնիսական
հոսքը գործնականորեն կախված է միայն առաջնային փաթույթի
հիմնական մագնիսական
հոսքը գործնականորեն կախված է միայն առաջնային փաթույթի ![]() լարումից և գրեթե
կախված չէ տրանսֆորմատորի բեռնվածքից (փաթույթների
լարումից և գրեթե
կախված չէ տրանսֆորմատորի բեռնվածքից (փաթույթների ![]() հոսանքներից):
հոսանքներից):
Երբ տրանսֆորմատորի երկրորդային փաթույթին բեռնվածք
չի միացված և ![]() (պարապ
ընթացքի ռեժիմ), ապա
(պարապ
ընթացքի ռեժիմ), ապա ![]() մագնիսական հոսքը
պայմանավորված է միայն
մագնիսական հոսքը
պայմանավորված է միայն ![]() հոսանքով (
հոսանքով (![]() մագնիսաշարժ ուժով): Բեռնվածքի առկայության դեպքում, երբ
մագնիսաշարժ ուժով): Բեռնվածքի առկայության դեպքում, երբ ![]() հոսքը պայմանավորված է
հոսքը պայմանավորված է ![]() հոսանքների
հոսանքների ![]() մշուների) համատեղ ազդեցությամբ: Այստեղից հետևում է`
մշուների) համատեղ ազդեցությամբ: Այստեղից հետևում է`
![]()
Բաժանելով (8.9) հավասարման երկու մասերը ![]() կստանանք
կստանանք

որտեղ k-ն տրանսֆորմացիայի գործակիցն է:
Առաջնային և երկրորդային փաթույթների հոսանքներով ստեղծած մագնիսաշարժ ուժերի միջև կապ հաստատող (8.9) կամ (8.10) հավասարումը կոչվում է տրանսֆորմատորի մագնիսական վիճակի հավասարում:
Գործնականում նորմալ գործող տրանսֆորմատորը կարող է գտնվել հետևյալ ռեժիմներից մեկում:
1. Անվանական ռեժիմ. Սա տրանսֆորմատորի,
ինչպես նաև ցանկացած այլ էլեկտրական սարքի, այնպիսի ռեժիմն է, որի համար այն նախագծված
և հաշվարկված է: Անվանական ռեժիմին համապատասխանող մեծությունները կոչվում են համապատասխանաբար
տրանսֆորմատորի անվանական լարում ![]() անվանական հոսանք
անվանական հոսանք
![]() անվանական հզորություն
անվանական հզորություն ![]() և այլն:
և այլն:
2. Աշխատանքային ռեժիմ, երբ տրանսֆորմատորի
առաջնային փաթույթին կիրառված լարումը մոտ է կամ հավասար անվանական լարմանը ![]() իսկ առաջնային փաթույթով անցնող
իսկ առաջնային փաթույթով անցնող ![]() հոսանքը կարող է փոփոխվել`
կախված տրանսֆորմատորի բեռնվածքից:
հոսանքը կարող է փոփոխվել`
կախված տրանսֆորմատորի բեռնվածքից:
Բացի անվանական պարամետրերից (հոսանք, լարում, հզորություն), տրանսֆորմատորը բնութագրվում է նաև այլ պարամետրերով, որոնք կարող են որոշվել տրանսֆորմատորի պարապ ընթացքի և կարճ միացման ռեժիմների փորձերով: Վերջիններս անհրաժեշտ են տրանսֆորմատորի այնպիսի շահագործողական բնութագրերի որոշման համար, ինչպիսիք են լարման շեղման մեծությունը, հզորության կորուստները, օգտակար գործողության գործակիցը և այլն: Այս պատճառով անհրաժեշտ է դիտարկել տրանսֆորմատորի երկու ծայրագույն ռեժիմները` պարապ ընթացքի ռեժիմը և կարճ միացման ռեժիմը: Այս ռեժիմները կարող են նաև հանկարծակի առաջանալ տրանսֆորմատորի աշխատանքի ժամանակ՝ բեռնվածքի անջատման, սխալ գործողության կամ վնասվածքի հետևանքով:
8.6.1. Տրանսֆորմատորի պարապ ընթացքի ռեժիմը
Տրանսֆորմատորի այնպիսի ռեժիմը, երբ առաջնային
փաթույթը միացված է ![]() անվանական լարման,
իսկ երկրորդային փաթույթը բաց է
անվանական լարման,
իսկ երկրորդային փաթույթը բաց է ![]() կոչվում է տրանսֆորմատորի
պարապ ընթացքի ռեժիմ (նկ. 8.7):
կոչվում է տրանսֆորմատորի
պարապ ընթացքի ռեժիմ (նկ. 8.7):
Պարապ ընթացքի (կամ մագնիսացնող) ![]() հոսանքը, որն ամենափոքր
հոսանքն է
հոսանքը, որն ամենափոքր
հոսանքն է ![]() լարման դեպքում,
սովորաբար արտահայտվում է տոկոսներով
լարման դեպքում,
սովորաբար արտահայտվում է տոկոսներով ![]() անվանական հոսանքի
նկատմամբ.
անվանական հոսանքի
նկատմամբ.
![]()
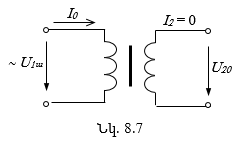
Որքան մեծ է տրանսֆորմատորի հզորությունը, այնքան
փոքր է ![]() հոսանքի տոկոսային
բաժինը:
հոսանքի տոկոսային
բաժինը:
Տրանսֆորմատորի (8.7) և (8.8) հավասարումներից
հետևում է, որ պարապ ընթացքի ռեժիմի դեպքում` ![]() փոքր արժեքի շնորհիվ
ընդունելով
փոքր արժեքի շնորհիվ
ընդունելով ![]()
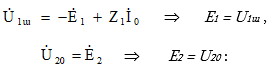
Այսինքն տրանսֆորմատորի պարապ ընթացքի ռեժիմում լարումների գործող արժեքները գործնականորեն հավասար են համապատասխան էլշուների գործող արժեքներին: Ուստի, տրանսֆորմատորի պարապ ընթացքի փորձը կարելի է օգտագործել տրանսֆորմացիայի գործակցի որոշման համար.
![]()
Տրանսֆորմացիայի գործակիցը նշվում է տրանսֆորմատորի պիտակի վրա` որպես պարապ ընթացքի ռեժիմում անվանական լարումների հարաբերություն (օրինակ, 6000/230Վ) :
Ընդհանուր դեպքում տրանսֆորմատորում հզորության
կորուստները որոշվում են որպես միջուկի կորուստների և փաթույթների կորուստների գումար:
Պարապ ընթացքի ռեժիմում տրանսֆորմատորի կորուստները գոյանում են միջուկի կորուստներից
և առաջնային փաթույթում ![]() կորուստներից: Քանի
որ
կորուստներից: Քանի
որ ![]() հոսանքը շատ փոքր է
հոսանքը շատ փոքր է ![]() անվանական հոսանքից,
ապա դրանով պայմանավորված փաթույթի հզորության կորուստները աննշան են միջուկի կորուստների
նկատմամբ, և այն կարելի է անտեսել:
անվանական հոսանքից,
ապա դրանով պայմանավորված փաթույթի հզորության կորուստները աննշան են միջուկի կորուստների
նկատմամբ, և այն կարելի է անտեսել:
Տրանսֆորմատորի միջուկի կորուստները կախված են
միջուկի մագնիսական հոսքից և, հետևաբար, գործնականորեն մնում են հաստատուն ցանկացած
աշխատանքային, ինչպես նաև պարապ ընթացքի ռեժիմներում (բոլոր այն դեպքերում, երբ առաջնային
լարումը մոտ է կամ հավասար ![]() անվանական լարմանը):
Այսպիսով տրանսֆորմատորի
անվանական լարմանը):
Այսպիսով տրանսֆորմատորի ![]() ակտիվ հզորությունը, որը կարելի է չափել վատտմետրի միջոցով, իրենից ներկայացնում
է տրանսֆորմատորի
ակտիվ հզորությունը, որը կարելի է չափել վատտմետրի միջոցով, իրենից ներկայացնում
է տրանսֆորմատորի ![]() միջուկի կորուստները
ցանկացած աշխատանքային ռեժիմում.
միջուկի կորուստները
ցանկացած աշխատանքային ռեժիմում.
![]()
Տրանսֆորմատորի միջուկի ![]() կորուստները կազմում են անվանական հզորության մի չնչին մասը (1%-ից էլ պակաս),
սակայն այդ կորուստները կարևոր գործոն են ուժային տրանսֆորմատորների համար, քանի որ
բաշխիչ ցանցերում կիրառվող տրանսֆորմատորները շատ հազվադեպ են անջատվում էլեկտրական
ցանցից:
կորուստները կազմում են անվանական հզորության մի չնչին մասը (1%-ից էլ պակաս),
սակայն այդ կորուստները կարևոր գործոն են ուժային տրանսֆորմատորների համար, քանի որ
բաշխիչ ցանցերում կիրառվող տրանսֆորմատորները շատ հազվադեպ են անջատվում էլեկտրական
ցանցից:
8.6.2. Տրանսֆորմատորի կարճ միացման ռեժիմը
Տրանսֆորմատորի այնպիսի ռեժիմը, երբ առաջնային փաթույթը միացված է էներգիայի աղբյուրին, իսկ երկրորդային փաթույթը կարճ է փակված (պարզապես փաթույթի ծայրերը իրար են միացված), կոչվում է տրանսֆորմատորի կարճ միացման ռեժիմ: Տարբերում են երկու տիպի կարճ միացում. վթարային և փորձարարական:
Վթարային կարճ միացումը տեղի է ունենում հանկարծակի, մարդկանց կամքից անկախ, որևէ վնասվածքի (ասենք` տևական գերտաքացման պատճառով առաջացած) կամ անձնակազմի սխալ գործողության հետևանքով: Այս դեպքում փաթույթներով անցնող կարճ միացման հոսանքները 10…40 անգամ գերազանցում են համապատասխան անվանական հոսանքների արժեքները և կարող են ավերիչ ազդեցություն ունենալ տրանսֆորմատորի համար, ահա թե ինչու այն համարվում է վթարային ռեժիմ:
Վթարային կարճ միացումներից պաշտպանվելու համար օգտագործում են դյուրահալ ապահովիչներ կամ ավտոմատ անջատիչներ՝ տրանսֆորմատորը հնարավորին չափ արագ ցանցից անջատելու համար: Այդ նույն նպատակով ցանցային հզոր տրանսֆորմատորների համար նախատեսվում են ռելեական պաշտպանության բարդ համակարգեր:
Փորձարարական կարճ միացումը
կատարվում է լաբորատոր պայմաններում՝ տրանսֆորմատորի փաթույթները բնութագրող մի քանի
պարամետրերի որոշման համար: Այս դեպքում երկրորդային փաթույթի սեղմակները միացվում
են զրոյին մոտ դիմադրությամբ հաղորդալարով, իսկ առաջնային փաթույթին կիրառում են այնպիսի
![]() լարում, որ երկրորդային փաթույթի հոսանքը հավասարվի անվանական արժեքին՝
լարում, որ երկրորդային փաթույթի հոսանքը հավասարվի անվանական արժեքին՝ ![]() լարումը կոչվում է տրանսֆորմատորի կարճ միացման լարում և սովորաբար
արտահայտվում է տոկոսներով՝ առաջնային փաթույթի անվանական լարման նկատմամբ.
լարումը կոչվում է տրանսֆորմատորի կարճ միացման լարում և սովորաբար
արտահայտվում է տոկոսներով՝ առաջնային փաթույթի անվանական լարման նկատմամբ.
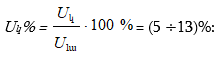
Կարճ միացման ![]() լարման արժեքը տրանսֆորմատորի
կարևորագույն պարամետրերից մեկն է և տարբեր տիպի տրանսֆորմատորների համար տրվում է
տեղեկատու գրքերում:
լարման արժեքը տրանսֆորմատորի
կարևորագույն պարամետրերից մեկն է և տարբեր տիպի տրանսֆորմատորների համար տրվում է
տեղեկատու գրքերում:
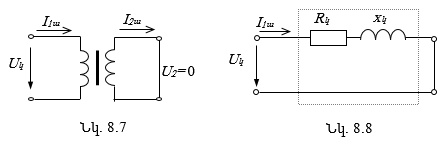
Փորձարարական կարճ միացման ժամանակ կարելի է ընդունել,
որ առաջնային փաթույթի հոսանքը նույնպես անվանական է՝ ![]() Այդ դեպքում տրանսֆորմատորի (8.7) - (8.9) հավասարումները կարելի է գրել հետևյալ
տեսքով.
Այդ դեպքում տրանսֆորմատորի (8.7) - (8.9) հավասարումները կարելի է գրել հետևյալ
տեսքով.
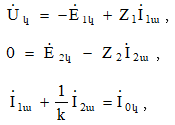
որտեղ ![]() պարապ ընթացքի հոսանքն
է առաջնային փաթույթի
պարապ ընթացքի հոսանքն
է առաջնային փաթույթի ![]() լարման դեպքում: Այն շատ փոքր մեծություն է և կարելի է անտեսել՝
լարման դեպքում: Այն շատ փոքր մեծություն է և կարելի է անտեսել՝ ![]() հետևաբար վերջին հավասարման հիման վրա կարող ենք որոշել տրանսֆորմատորի տրանսֆորմացիայի
գործակիցը.
հետևաբար վերջին հավասարման հիման վրա կարող ենք որոշել տրանսֆորմատորի տրանսֆորմացիայի
գործակիցը.

Քանի որ առաջնային փաթույթին կիրառված ![]() կարճ միացման լարումը
շատ փոքր է, ապա միջուկի
կարճ միացման լարումը
շատ փոքր է, ապա միջուկի ![]() մագնիսական հոսքը,
որը համեմատական է այդ լարմանը, նույնպես կլինի շատ փոքր: Հետևաբար միջուկի կորուստները,
որոնք համեմատական են այդ հոսքի քառակուսուն, կլինեն այնքան փոքր, որ կարելի է դրանք
անտեսել: Այսպիսով տրանսֆորմատորի կարճ միացման ռեժիմում առաջնային փաթույթի
մագնիսական հոսքը,
որը համեմատական է այդ լարմանը, նույնպես կլինի շատ փոքր: Հետևաբար միջուկի կորուստները,
որոնք համեմատական են այդ հոսքի քառակուսուն, կլինեն այնքան փոքր, որ կարելի է դրանք
անտեսել: Այսպիսով տրանսֆորմատորի կարճ միացման ռեժիմում առաջնային փաթույթի ![]() ակտիվ հզորությունը,
որը կարելի է չափել վատտմետրով, հավասար կլինի տրանսֆորմատորի փաթույթներում ծախսվող
հզորության կորուստներին անվանական ռեժիմի դեպքում.
ակտիվ հզորությունը,
որը կարելի է չափել վատտմետրով, հավասար կլինի տրանսֆորմատորի փաթույթներում ծախսվող
հզորության կորուստներին անվանական ռեժիմի դեպքում.
![]()
Կարճ միացման ռեժիմում առաջնային փաթույթի կողմից տրանսֆորմատորի մուտքային դիմադրությունը կոչվում է կարճ միացման դիմադրություն.

Քանի որ տրանսֆորմատորն ունի ակտիվ-ինդուկտիվ բնույթ, ապա կարճ միացման դեպքում այն կարելի է փոխարինել ռեզիստիվ և ինդուկտիվ տարրերի հաջորդաբար միացված շղթայով (նկ. 8.8), ընդ որում
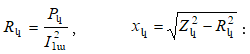
Այս բանաձևերում ![]() ակտիվ դիմադրությունը
պայմանավորված է փաթույթներում առաջացող ջերմային կորուստներով, իսկ
ակտիվ դիմադրությունը
պայմանավորված է փաթույթներում առաջացող ջերմային կորուստներով, իսկ ![]() ռեակտիվ դիմադրությունը՝
ցրման մագնիսական հոսքերով:
ռեակտիվ դիմադրությունը՝
ցրման մագնիսական հոսքերով:
8.7. Տրանսֆորմատորի աշխատանքային ռեժիմը
8.7.1. Տրանսֆորմատորի արտաքին բնութագիծը
Մենք բոլորս նկատել ենք, որ սնման ցանցին որևէ հզոր սպառիչի միացումը բերում է լամպի լույսի թուլացման, որը արդյունք է ցանցի լարման փոքրացման:
Համաձայն տրանսֆորմատորի երկրորդային փաթույթի լարումների (8.8) հավասարման,
![]()
Այստեղից հետևում է, որ տրանսֆորմատորի սպառիչի
![]() հոսանքի մեծացումը
(նոր սպառիչի միացումը) առաջ է բերում
հոսանքի մեծացումը
(նոր սպառիչի միացումը) առաջ է բերում ![]() լարման փոքրացում:
Երկրորդային փաթույթի
լարման փոքրացում:
Երկրորդային փաթույթի ![]() լարման
լարման ![]() հոսանքից ունեցած կախման կորը կոչվում է տրանսֆորմատորի արտաքին բնութագիծ:
հոսանքից ունեցած կախման կորը կոչվում է տրանսֆորմատորի արտաքին բնութագիծ:
Նկ.8.9-ում պատկերված են տրանսֆորմատորի արտաքին
բնութագծերը` բեռնվածքի ![]() հզորության գործակցի տարբեր արժեքների դեպքում: Ինչպես հետևում է բնութագծերի
տեսքից, տրանսֆորմատորի բեռնվածքի (
հզորության գործակցի տարբեր արժեքների դեպքում: Ինչպես հետևում է բնութագծերի
տեսքից, տրանսֆորմատորի բեռնվածքի (![]() հոսանքի) փոփոխությունը
առաջ է բերում դրա
հոսանքի) փոփոխությունը
առաջ է բերում դրա ![]() լարման զգալի փոփոխություն, հատկապես ակտիվ-ինդուկտիվ բնույթի սպառիչի դեպքում,
եթե
լարման զգալի փոփոխություն, հատկապես ակտիվ-ինդուկտիվ բնույթի սպառիչի դեպքում,
եթե ![]() արժեքը զգալիորեն փոքր է մեկից:
արժեքը զգալիորեն փոքր է մեկից:
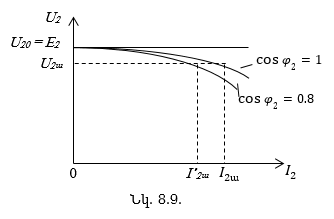
Տրանսֆորմատորի ![]() լարման փոփոխությունը
դրա
լարման փոփոխությունը
դրա ![]() անվանական արժեքի նկատմամբ, արտահայտված տոկոսներով, կոչվում է լարման շեղում
(տես 1.7 բանաձևը).
անվանական արժեքի նկատմամբ, արտահայտված տոկոսներով, կոչվում է լարման շեղում
(տես 1.7 բանաձևը).

Լարման շեղման արժեքը կարելի է արտահայտել և հաշվել կարճ միացման դիմադրությունների միջոցով.
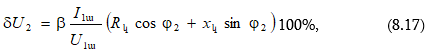
որտեղ ![]() երկրորդային փաթույթի
հոսանքի ու այդ փաթույթի անվանական հոսանքի հարաբերությունն է և կոչվում է տրանսֆորմատորի
բեռնվածության գործակից, այսինքն`
երկրորդային փաթույթի
հոսանքի ու այդ փաթույթի անվանական հոսանքի հարաբերությունն է և կոչվում է տրանսֆորմատորի
բեռնվածության գործակից, այսինքն` ![]() Որոշ մոտավորությամբ
կարելի է համարել, որ նույնանման հարաբերությունը ճիշտ է նաև առաջնային փաթույթի հոսանքի
համար՝
Որոշ մոտավորությամբ
կարելի է համարել, որ նույնանման հարաբերությունը ճիշտ է նաև առաջնային փաթույթի հոսանքի
համար՝ ![]()
(8.17)
արտահայտությունը ցույց է տալիս, որ լարման շեղումը ուղիղ համեմատական է բեռնվածքի
![]() գործակցին և կախված
է սպառիչի
գործակցին և կախված
է սպառիչի ![]() հզորության գործակցից:
հզորության գործակցից:
Ունենալով
![]() լարման շեղման արժեքը՝
ըստ (8.17)-ի կարելի է որոշել տրանսֆորմատորի երկրորդային փաթույթի լարումը.
լարման շեղման արժեքը՝
ըստ (8.17)-ի կարելի է որոշել տրանսֆորմատորի երկրորդային փաթույթի լարումը.

Լարման շեղումը անցանկալի է սպառիչների համար,
ուստի դրանց նորմալ աշխատանքն ապահովելու համար այն չպետք է գերազանցի որոշակի ![]() թույլատրելի արժեքը: Սպառիչների գերակշիռ մասի նորմալ աշխատանքն ապահովելու
համար,
թույլատրելի արժեքը: Սպառիչների գերակշիռ մասի նորմալ աշխատանքն ապահովելու
համար, ![]() արժեքը սահմանված է
արժեքը սահմանված է ![]() այսինքն`
այսինքն` ![]()
Օրինակ, եթե ![]() ապա սպառիչի լարումը
(տրանսֆորմատորի երկրորդային լարումը) պետք է լինի
ապա սպառիչի լարումը
(տրանսֆորմատորի երկրորդային լարումը) պետք է լինի ![]() սահմաններում:
սահմաններում:
Լարման շեղումը փոքրացնելու նպատակով տրանսֆորմատորները
սովորաբար նախագծում են այնպես, որ երկրորդային փաթույթի պարապ ընթացքի լարումը
5%-ով ավելի բարձր լինի անվանական լարումից՝ ![]() Այսպես, եթե
Այսպես, եթե ![]() ապա
ապա ![]() կամ
կամ ![]() ապա
ապա ![]() և այլն: Եթե դա էլ
բավարար չէ, ապա կիրառում են լարման կարգավորում՝ փոփոխելով փաթույթներից մեկի (սովորաբար
բարձր լարման փաթույթի, որի հոսանքն ավելի փոքր է) գալարների թիվը՝ դրանով իսկ փոփոխելով
տրանսֆորմացիայի գործակիցը և, հետևաբար,
և այլն: Եթե դա էլ
բավարար չէ, ապա կիրառում են լարման կարգավորում՝ փոփոխելով փաթույթներից մեկի (սովորաբար
բարձր լարման փաթույթի, որի հոսանքն ավելի փոքր է) գալարների թիվը՝ դրանով իսկ փոփոխելով
տրանսֆորմացիայի գործակիցը և, հետևաբար, ![]() լարումը:
լարումը:
Ժամանակակից ուժային տրանսֆորմատորները օժտված են հատուկ սարքով, որը թույլ է տալիս կատարել լարման կարգավորում բեռի տակ` առանց հոսանքի շղթան անջատելու:
Խնդիր 8.1. Ինչպիսի՞ն կլինի լարումը
միաֆազ տրանսֆորմատորին միացված սպառիչի սեղմակներում, եթե տրանսֆորմատորի անվանական
հզորությունը ![]() լարումները՝ 6000/230 Վ, կարճ միացման հզորությունը՝
լարումները՝ 6000/230 Վ, կարճ միացման հզորությունը՝ ![]() կարճ միացման լարումը՝
կարճ միացման լարումը՝ ![]() իսկ սպառիչի ակտիվ
հզորությունը, P = 42 կՎտ է, անվանական լարումը՝ 230 Վ, հզորության գործակիցը՝
իսկ սպառիչի ակտիվ
հզորությունը, P = 42 կՎտ է, անվանական լարումը՝ 230 Վ, հզորության գործակիցը՝ ![]() (ինդուկտիվ բնույթի):
(ինդուկտիվ բնույթի):
Լուծում: Տրանսֆորմատորի անվանական հոսանքները
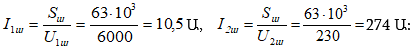
Սպառիչի հոսանքը
![]()
Տրանսֆորմատորի բեռնվածության գործակիցը
![]()
Տրանսֆորմատորի կարճ միացման դիմադրությունները
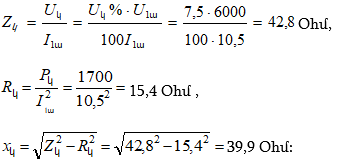
Համապատասխանաբար, լարման շեղումը ըստ (8.17)-ի և երկրորդային փաթույթի լարումը ըստ (8.18)-ի.

8.7.2. Տրանսֆորմատորի հզորության կորուստները և օ.գ.գ.-ն
Տրանսֆորմատորում
հզորության լրիվ կորուստները, ինչպես արդեն ասվել է 8.6.1 և 8.6.2 կետերում, գոյանում
են միջուկում ![]() և փաթույթներում
և փաթույթներում ![]() եղած կորուստներից.
եղած կորուստներից.
![]()
Տեղադրելով
![]() արժեքները (8.14) արտահայտության մեջ` փաթույթների կորուստների համար կստանանք
արժեքները (8.14) արտահայտության մեջ` փաթույթների կորուստների համար կստանանք
![]()
Տեղադրելով (8.12) և (8.20) արտահայտությունները (8.19)-ի մեջ, կստանանք բանաձև տրանսֆորմատորում հզորության կորուստները հաշվելու համար.
![]()
Տվյալ տրանսֆորմատորում ![]() արժեքները հայտնի են, ուստի, ինչպես հետևում է (8.21) բանաձևից, տրանսֆորմատորում
հզորության կորուստները հաշվելու համար բավական է ունենալ բեռնվածության
արժեքները հայտնի են, ուստի, ինչպես հետևում է (8.21) բանաձևից, տրանսֆորմատորում
հզորության կորուստները հաշվելու համար բավական է ունենալ բեռնվածության ![]() գործակցի արժեքը
գործակցի արժեքը ![]()
Տրանսֆորմատորի երկրորդային փաթույթի ![]() ակտիվ հզորության (ելքային հզորության) և առաջնային փաթույթի
ակտիվ հզորության (ելքային հզորության) և առաջնային փաթույթի ![]() ակտիվ հզորության
(մուտքային հզորություն) հարաբերությունը կոչվում է տրանսֆորմատորի օգտակար գործողության
գործակից (օ.գ.գ.).
ակտիվ հզորության
(մուտքային հզորություն) հարաբերությունը կոչվում է տրանսֆորմատորի օգտակար գործողության
գործակից (օ.գ.գ.).
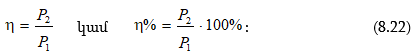
Տրանսֆորմատորի օ.գ.գ.-ն շատ բարձր է, այն հասնում
է 99%-ի և նույնիսկ ավելի բարձր՝ շատ մեծ հզորության տրանսֆորմատորների համար: Այս
պատճառով տրանսֆորմատորի օ.գ.գ.-ն գործնականում երբեք չի որոշվում ![]() հզորությունների անմիջական չափման միջոցով (վատտմետրերի հարաբերական սխալանքն
ավելի մեծ, է քան
հզորությունների անմիջական չափման միջոցով (վատտմետրերի հարաբերական սխալանքն
ավելի մեծ, է քան ![]() հզորությունների տարբերության
տոկոսային չափը): Գործնականում, ավելի ճշգրիտ օ.գ.գ.-ն ընդունված է հաշվել տրանսֆորմատորի
հզորությունների տարբերության
տոկոսային չափը): Գործնականում, ավելի ճշգրիտ օ.գ.գ.-ն ընդունված է հաշվել տրանսֆորմատորի
![]() պարապ ընթացքի և
պարապ ընթացքի և ![]() կարճ միացման հզորությունների
միջոցով` օգտագործելով տրանսֆորմատորում հզորությունների կորստի (8.21) բանաևը:
կարճ միացման հզորությունների
միջոցով` օգտագործելով տրանսֆորմատորում հզորությունների կորստի (8.21) բանաևը:
Ակնհայտ
է, որ ![]() հետևաբար, ըստ (8.22)-ի`
հետևաբար, ըստ (8.22)-ի`

Տրանսֆորմատորի ելքային ակտիվ հզորությունը
![]()
Հետևաբար
![]()
Այս
արտահայտության մեջ ![]() սպառիչի հզորության
գործակիցն է, իսկ
սպառիչի հզորության
գործակիցն է, իսկ ![]() տրանսֆորմատորի անվանական
հզորությունը, որը նշվում է դրա պիտակի վրա:
տրանսֆորմատորի անվանական
հզորությունը, որը նշվում է դրա պիտակի վրա:
Տեղադրելով (8.21) և (8.24) արտահայտությունները (8.23)-ի մեջ՝ կստանանք հարմար բանաձև տրանսֆորմատորում հզորության կորուստների հաշվման համար
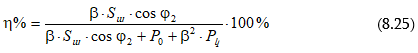
Ինչպես
հետևում է (8.25) բանաձևից, տրանսֆորմատորի օ.գ.գ.-ն կախված է բեռնվածքի ![]() գործակցից և բեռնվածքի
գործակցից և բեռնվածքի
![]() հզորության գործակցից:
հզորության գործակցից:
Եթե տրանսֆորմատորի բեռնվածքը համասեռ է՝ ![]() ապա դրա օ.գ.գ.-ն կախված կլինի միայն
ապա դրա օ.գ.գ.-ն կախված կլինի միայն ![]() գործակցից: Նկ.
8.9-ում բերված են
գործակցից: Նկ.
8.9-ում բերված են ![]() կախվածության կորերը
կախվածության կորերը
![]() տարբեր արժեքների դեպքում: Հավասարեցնելով զրոյի
տարբեր արժեքների դեպքում: Հավասարեցնելով զրոյի ![]() ֆունկցիայի առաջին ածանցյալն ըստ
ֆունկցիայի առաջին ածանցյալն ըստ ![]() կարելի է որոշել բեռնվածքի
գործակցի այն
կարելի է որոշել բեռնվածքի
գործակցի այն ![]() արժեքը, որի դեպքում տրանսֆորմատորի օ.գ.գ.-ն ընդունում է առավելագույն արժեք:
արժեքը, որի դեպքում տրանսֆորմատորի օ.գ.գ.-ն ընդունում է առավելագույն արժեք:
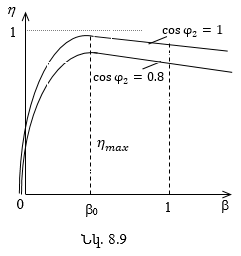
Պարզ ձևափոխությունների միջոցով ստացվում է.
![]()
Այսինքն` տրանսֆորմատորի օ.գ.գ.-ն ընդունում է առավելագույն արժեք, երբ փաթույթի (կամ էլեկտրական) կորուստները հավասարվում են միջուկի (կամ մագնիսական) կորուստներին:
Բանաձև (8.26)-ից`

Գործնականում էլեկտրական ցանցերի ուժային տրանսֆորմատորները նախագծում են այնպես, որ առավելագույն օ.գ.գ.-ն ստացվի դրանց անվանական բեռնվածքի մոտավորապես կեսի դեպքում: Դա պայմանավորված է դրանով, որ այդ տրանսֆորմատորները ընդամենը օրվա մի քանի ժամ են աշխատում անվանական (կամ դրան մոտ) բեռնվածքով:
Չնայած շատ բարձր օ.գ.գ.-ին, տրանսֆորմատորների հսկայական հզորության դեպքում դրանցում եղած հզորության կորուստները հասնում են զգալի չափերի:
Խնդիր 8.2. Նախորդ` խնդիր 8.1-ում դիտարկվող տրանսֆորմատորի համար որոշել օ.գ.գ.-ն, եթե պարապ ընթացքի հզորությունը՝ P0 = 650Վտ:
Լուծում. (8.25) բանաձևի հիման վրա
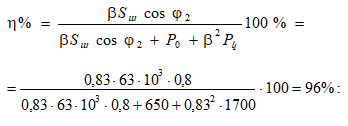
Մինչև այժմ դիտարկվում էին միաֆազ տրանսֆորմատորները, սակայն այն բոլորը, ինչ ասվել է դրանց վերաբերյալ 8.1…8.7 պարագրաֆներում, հավասարապես կարելի է վերագրել նաև եռաֆազ տրանսֆորմատորների յուրաքանչյուր ֆազին: Ուստի ստորև քննարկվում են միայն այն առանձնահատկությունները, որոնք հատուկ են միայն եռաֆազ տրանսֆորմատորներին:
Գործնականում եռաֆազ տրանսֆորմատոր կարելի է ստանալ երկու տարբերակով.
1) երեք միատեսակ միաֆազ տրանսֆորմատորների միջոցով, որոնք հանդես են գալիս որպես համագործակցված մեկ միավոր (նկ. 8.10),
2) մեկ համակցված եռաֆազ մագնիսական միջուկով տրանսֆորմատորի միջոցով (նկ. 8.11):
Առաջին տարբերակի տրանսֆորմատորը (նկ.8.10) ավելի թանկարժեք է, ավելի մեծ մակերես է զբաղեցնում և ավելի ցածր օ.գ.գ.-ով է օժտված (ի հաշիվ միջուկի ծավալի և, հետևաբար, միջուկի հզորության կորուստների մեծացման), քան անվանական նույն հզորությամբ և նույն լարումներով երկրորդ տարբերակի տրանսֆորմատորը (նկ.8.11): Դրա շնորհիվ վերջիններս ամենալայն գործնական կիրառությունն ունեն, մանավանդ փոքր և միջին հզորությունների դեպքում:
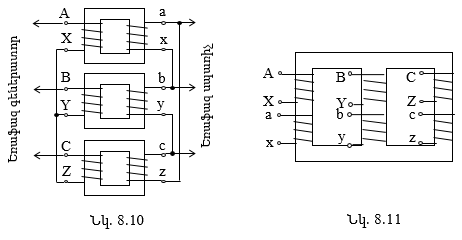
Սակայն, մյուս կողմից, առաջին տարբերակի տրանսֆորմատորների տեղափոխումը և տեղակայումը, մանավանդ հսկայական չափեր ունեցող մեծ հզորությունների դեպքում, և՛ տնտեսապես, և՛ տեխնիկապես ավելի նպատակահարմար է: Բացի դրանից, վթարի կամ պլանային վերանորոգման դեպքում ռեզերվային (պահեստային) տրանսֆորմատոր ունենալու անհրաժեշտության դեպքում, բավական է ռեզերվում ունենալ միայն մեկ միաֆազ տրանսֆորմատոր՝ մեկ ամբողջ եռաֆազի փոխարեն, որովհետև գործնականորեն անհավանական է, որ վթար տեղի ունենա երկու, առավել ևս երեք ֆազերում միաժամանակ:
Եռաֆազ տրանսֆորմատորների փաթույթները կարող են
միացվել աստղաձև (Y) կամ եռանկյունաձև ![]() Նկ.8.10-ում պատկերված
տրանսֆորմատորի մոտ, օրինակ, առաջնային փաթույթը միացված է աստղաձև, իսկ երկրորդային
փաթույթը՝ եռանկյունաձև:
Նկ.8.10-ում պատկերված
տրանսֆորմատորի մոտ, օրինակ, առաջնային փաթույթը միացված է աստղաձև, իսկ երկրորդային
փաթույթը՝ եռանկյունաձև:
Եռաֆազ տրանսֆորմատորներում փաթույթների ֆազային
լարումների ![]() հարաբերությունը մոտավորապես հավասար է գալարների թվի
հարաբերությունը մոտավորապես հավասար է գալարների թվի ![]() հարաբերությանը: Գծային լարումների հարաբերությունը կախված է փաթույթների միացման
ձևից: Հետևաբար, տրանսֆորմատորի փաթույթների միացման ձևի փոփոխությունը բերում է երկրորդային
փաթույթի գծային լարման փոփոխության:
հարաբերությանը: Գծային լարումների հարաբերությունը կախված է փաթույթների միացման
ձևից: Հետևաբար, տրանսֆորմատորի փաթույթների միացման ձևի փոփոխությունը բերում է երկրորդային
փաթույթի գծային լարման փոփոխության:
Եթե երկու կամ ավելի թվով տրանսֆորմատորներ պետք է աշխատեն զուգահեռ, ապա խիստ անհրաժեշտ է, որպեսզի դրանց փաթույթների միացման ձևը լինի միատեսակ կամ, ինչպես ասում են, դրանք ունենան միացման նույն խումբը: Այս պատճառով եռաֆազ տրանսֆորմատորները բնութագրվում են նաև միացման խմբերով: Ստանդարտացման նպատակով գործնականում տրանսֆորմատորները արտադրվում են երեք միացման խմբերով, որոնք են.
·
![]() այսինքն առաջնային փաթույթի աստղաձև - երկրորդայինի եռանկյունաձև միացումով,
այսինքն առաջնային փաթույթի աստղաձև - երկրորդայինի եռանկյունաձև միացումով,
·
![]() առաջնային փաթույթի աստղաձև դուրս բերված չեզոք կետով - եռանկյունաձև միացումով,
առաջնային փաթույթի աստղաձև դուրս բերված չեզոք կետով - եռանկյունաձև միացումով,
·
![]() աստղաձև - աստղաձև չեզոք լարով:
աստղաձև - աստղաձև չեզոք լարով:
Միացման խմբերի 11 կամ 0 թվերը ցույց են տալիս առաջնային և երկրորդային փաթույթների գծային լարումների միջև փուլային շեղումը: Ընդ որում 11 թիվը համապատասխանում է 300 կամ 3300, իսկ 0 - ն՝ 00 փուլային շեղմանը:
![]() միացման խմբի տրանսֆորմատորները
օգտագործվում են էլեկտրական ցանցերում որպես բաշխիչ տրանսֆորմատորներ՝ 10 կամ 6 կՎ
առաջնային լարումով, 400 Վ երկրորդային լարումով (380/220 Վ ցածրավոլտ սպառիչների համար)
և մինչև 2500 կՎԱ անվանական հզորությամբ (նկ. 8.1):
միացման խմբի տրանսֆորմատորները
օգտագործվում են էլեկտրական ցանցերում որպես բաշխիչ տրանսֆորմատորներ՝ 10 կամ 6 կՎ
առաջնային լարումով, 400 Վ երկրորդային լարումով (380/220 Վ ցածրավոլտ սպառիչների համար)
և մինչև 2500 կՎԱ անվանական հզորությամբ (նկ. 8.1):
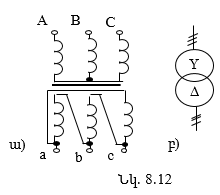
Եռաֆազ տրանսֆորմատորները սկզբունքային էլեկտրական սխեմաներում պատկերվում են նկ.8.12ա-ում ցույց տրված պայմանական նշանով, իսկ եռաֆազ միագծանի սխեմաներում՝ նկ.8.12բ-ում պատկերված պայմանական նշանով, որի վրա նշվում է եռաֆազ փաթույթների միացման ձևը:
Ավտոտրանսֆորմատոր է կոչվում այնպիսի տրանսֆորմատորը, որի առաջնային և երկրորդային փաթույթները էլեկտրականապես միացված են: Փաստորեն ավտոտրանսֆորմատորն ունի միայն մեկ՝ բարձր լարման, փաթույթ, որի մի մասը ծառայում է որպես երկրորդային փաթույթ (նկ. 8.13): Դրա շնորհիվ էլեկտրաէներգիան առաջնային փաթույթից երկրորդային փաթույթին է փոխանցվում ոչ միայն մագնիսական ճանապարհով, ինչպես սովորական տրանսֆորմատորներում, այլև էլեկտրական ճանապարհով:
Ավտոտրանսֆորմատորներն ավելի հաճախ կիրառվում են որպես ցածրացնող տրանսֆորմատորներ, ինչպես ցույց է տրված նկ. 8.13-ում, բայց կարող են լինել նաև բարձրացնող:
Ավտոտրանսֆորմատորի տրանսֆորմացիայի գործակիցը
որոշվում է ![]() բանաձևով, որտեղ
բանաձևով, որտեղ ![]() համապատասխանաբար
փաթույթի a-b և b-c տեղամասերի գալարների թիվն է:
համապատասխանաբար
փաթույթի a-b և b-c տեղամասերի գալարների թիվն է:
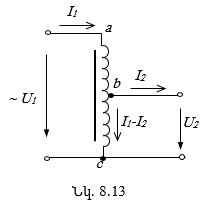
Փաթույթի առաջնային և երկրորդային կողմերի համար
ընդհանուր b-c տեղամասում հոսանքը հավասար է երկու կողմերի ![]() հոսանքների տարբերությանը: Այս հոսանքների միջև փուլային շեղումը շատ չնչին
է, ուստի կարելի է ընդունել
հոսանքների տարբերությանը: Այս հոսանքների միջև փուլային շեղումը շատ չնչին
է, ուստի կարելի է ընդունել
![]()
Նշված առանձնահատկությունների շնորհիվ ավտոտրանսֆորմատորն ունի հետևյալ առավելությունները սովորական տրանսֆորմատորի նկատմամբ.
· այն ունի ընդամենը մեկ փաթույթ երկուսի փոխարեն և, հետևաբար, ավելի փոքր արժեք և չափեր,
·
ընդհանուր b-c տեղամասում հոսանքն ստացվում է ավելի
փոքր, քանի որ ![]() ինչը թույլ է տալիս այդ տեղամասում օգտագործել ավելի փոքր կտրվածքով հաղորդալար՝
հասնելով հաղորդիչ նյութի լրացուցիչ խնայողության:
ինչը թույլ է տալիս այդ տեղամասում օգտագործել ավելի փոքր կտրվածքով հաղորդալար՝
հասնելով հաղորդիչ նյութի լրացուցիչ խնայողության:
Ընդ որում ավտոտրանսֆորմատորի 2-րդ առավելությունն այնքան ավելի է արտահայտված, որքան b-c տեղամասը մեծ է կամ, ինչ որ նույնն է, տրանսֆորմացիայի գործակիցը մոտ է մեկին:
Սակայն ավտոտրանսֆորմատորն ունի նաև մի էական թերություն. քանի որ նրա առաջնային և երկրորդային շղթաները էլեկտրականապես միացված են, ապա անհրաժեշտ է երկու կողմերի մեկուսացումն էլ հաշվարկել բարձր լարման համար: Այն այնքան ավելի զգալի է, որքան լարումների տարբերությունը մեծ է:
Գործնականում ուժային ավտոտրանսֆորմատորի կիրառությունը
արդարացված է, երբ տրանսֆորմացիայի գործակիցը մոտ է մեկին կամ ![]()
Էլեկտրաէներգետիկայում ավտոտրանսֆորմատորները կիրառվում են, օրինակ, երկու տարբեր լարումներ ունեցող ցանցերը միմյանց կապելու համար՝ (ասենք, 220 կՎ ցանցը 330 կՎ ցանցին կամ վերջինս 500 կՎ ցանցին միացնելու համար):
Փոքր հզորության ավտոտրանսֆորմատորները լայնորեն
կիրառվում են որպես լարումը սահուն կերպով փոփոխող սարքեր (ԼԱՏՐ` լաբորատոր ավտոտրանսֆորմատոր):
Այդ նպատակով երկրորդային շղթայի ծայրակետերից մեկը (նկ. 8.13-ում b հանգույցին միացված)
ներկայացնում է շարժական կոնտակտ, որի տեղաշարժման միջոցով կարելի է երկրորդային ![]() լարումը սահուն փոփոխել
լարումը սահուն փոփոխել
![]() սահմաններում:
սահմաններում:
8.10. Եռակցման տրանսֆորմատորներ
Սովորական տրանսֆորմատորները աղեղնային եռակցման համար ամենևին պիտանի չեն, քանի որ եռակցման ժամանակ տրանսֆորմատորը գտնվում է կարճ միացմանը մոտ ռեժիմում, երբ փաթույթների հոսանքները 10-20 անգամ գերազանցում են անվանական արժեքը:
Մյուս կողմից եռակցման աշխատանքների համար անհրաժեշտ
է, որ տրանսֆորմատորը նախագծվի այնպես, որ դրա կարճ միացման հոսանքը լինի ոչ շատ մեծ
(ընդամենը 20-30%-ով գերազանցի անվանական արժեքը) և երկրորդային ![]() լարման զգալի փոփոխությունների
դեպքում, որը պայմանավորված է էլեկտրական աղեղի ոչ հաստատուն դիմադրությամբ, եռակցման
լարման զգալի փոփոխությունների
դեպքում, որը պայմանավորված է էլեկտրական աղեղի ոչ հաստատուն դիմադրությամբ, եռակցման
![]() հոսանքը մնա գրեթե
հաստատուն: Այդ նպատակին կարելի է հասնել մեծացնելով երկրորդային փաթույթի
հոսանքը մնա գրեթե
հաստատուն: Այդ նպատակին կարելի է հասնել մեծացնելով երկրորդային փաթույթի ![]() ցրման հոսքերը՝ դրանով իսկ մեծացնելով այդ հոսքերով պայմանավորված երկրորդային
փաթույթի
ցրման հոսքերը՝ դրանով իսկ մեծացնելով այդ հոսքերով պայմանավորված երկրորդային
փաթույթի ![]() ինդուկտիվ դիմադրությունը: Ցրման հոսքերի մեծացման համար սովորաբար երկրորդային
փաթույթին հաջորդաբար միացվում է լրացուցիչ, այսպես կոչված, ռեակտիվ փաթույթ, իսկ այդ
փաթույթի միջուկը ունենում է օդային բացակ (Նկ.8.14):
ինդուկտիվ դիմադրությունը: Ցրման հոսքերի մեծացման համար սովորաբար երկրորդային
փաթույթին հաջորդաբար միացվում է լրացուցիչ, այսպես կոչված, ռեակտիվ փաթույթ, իսկ այդ
փաթույթի միջուկը ունենում է օդային բացակ (Նկ.8.14):
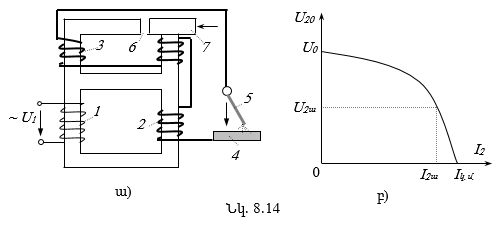
Գործնականում օգտագործվող եռակցման տրանսֆորմատորները ունեն տարբեր կառուցվածքներ: Նկ. 8.14ա-ում պատկերված է առավել մեծ կիրառություն ունեցող եռակցման տրանսֆորմատորի կառուցվածքային սխեման, իսկ նկ. 8.14բ-ում բերված է դրա արտաքին բնութագիծը:
Եռակցման տրանսֆորմատորի առաջնային փաթույթը
(1) միացվում է 220Վ կամ 380Վ լարման: Երկրորդային փաթույթը (2), որին հաջորդաբար
միացված է լրացուցիչ ռեակտիվ փաթույթը (3), ապահովում է պարապ ընթացքում ![]() լարում, իսկ եռակցման պրոցեսում՝
լարում, իսկ եռակցման պրոցեսում՝ ![]() լարում՝ ապահովելով
լարում՝ ապահովելով ![]() աշխատանքային հոսանք:
Երկրորդային փաթույթի մի ծայրը միացվում է եռակցվող առարկային (4), իսկ մյուս մասը՝
էլեկտրոդին (5): Ռեակտիվ փաթույթի միջուկի շարժական մասը (7) տեղափոխելու միջոցով փոփոխվում
է օդային բացակի (6) մեծությունը՝ դրանով իսկ փոփոխելով
աշխատանքային հոսանք:
Երկրորդային փաթույթի մի ծայրը միացվում է եռակցվող առարկային (4), իսկ մյուս մասը՝
էլեկտրոդին (5): Ռեակտիվ փաթույթի միջուկի շարժական մասը (7) տեղափոխելու միջոցով փոփոխվում
է օդային բացակի (6) մեծությունը՝ դրանով իսկ փոփոխելով ![]() ինդուկտիվ դիմադրությունը
և, հետևաբար կարգավորելով նաև եռակցման հոսանքի
ինդուկտիվ դիմադրությունը
և, հետևաբար կարգավորելով նաև եռակցման հոսանքի ![]() արժեքը:
արժեքը:
Չափման տրանսֆորմատորները կիրառվում են բարձրավոլտ կամ մեծ հոսանքով շղթաներում էլեկտրական չափումներ կատարելու համար: Չափման տրանսֆորմատորները թույլ են տալիս. 1) չափումները դարձնել մարդկանց համար անվտանգ և 2) ամենատարբեր շղթաներում չափումներ կատարելու համար օգտագործել միատեսակ և էժան չափիչ գործիքներ:
Չափման տրանսֆորմատորները լինում են երկու տեսակի՝ լարման և հոսանքի չափման տրանսֆորմատորներ:
8.11.1. Լարման չափման տրանսֆորմատոր
Լարման չափման տրանսֆորմատորը կամ, պարզապես,
լարման տրանսֆորմատորը (ԼՏ) իր կառուցվածքով նման է փոքր հզորության ուժային տրանսֆորմատորի:
Նկ. 8.15-ում պատկերված է ԼՏ-ի միացման սխեման: Դրա առաջնային փաթույթը միացվում է
զուգահեռ այն բարձրավոլտ տեղամասին, որի լարումն անհրաժեշտ է չափել: Երկրորդային փաթույթին,
նույնպես զուգահեռ, միացվում են այնպիսի չափիչ գործիքներ կամ սարքեր, ինչպիսիք են վոլտմետրը,
վատտմետրի կամ հաշվիչի լարման փաթույթը, լարման ռելեն և այլն: Նմանատիպ բոլոր սարքերի
ներքին դիմադրությունը չափազանց մեծ է, և ԼՏ-ի երկրորդային փաթույթի ![]() հոսանքը ստացվում
է զրոյին մոտ, որի պատճառով ԼՏ-ի աշխատանքային ռեժիմը մոտ է սովորական տրանսֆորմատորի
պարապ ընթացքի ռեժիմին:
հոսանքը ստացվում
է զրոյին մոտ, որի պատճառով ԼՏ-ի աշխատանքային ռեժիմը մոտ է սովորական տրանսֆորմատորի
պարապ ընթացքի ռեժիմին:
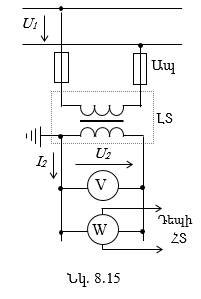
Պարապ ընթացքի ռեժիմի դեպքում, ըստ (8.11) բանաձևի,
կարող ենք գրել ![]()
![]()
Այսպիսով չափելով ![]() լարումը և այն բազմապատկելով
հաստատուն
լարումը և այն բազմապատկելով
հաստատուն ![]() գործակցով, որոշվում
է անհայտ
գործակցով, որոշվում
է անհայտ ![]() լարման արժեքը: Հաճախ, գործնականում, գործիքների թվատախտակը նախօրոք բազմապատկվում
է
լարման արժեքը: Հաճախ, գործնականում, գործիքների թվատախտակը նախօրոք բազմապատկվում
է ![]() և վոլտմետրը անմիջականորեն ցույց է տալիս անհայտ
և վոլտմետրը անմիջականորեն ցույց է տալիս անհայտ ![]() լարումը:
լարումը:
Եթե ԼՏ-ին միացող սարքերի թիվը մեծ է, ապա ![]() հոսանքի արժեքը դառնում
է զգալի, և ԼՏ-ի աշխատանքային ռեժիմը շատ է տարբերվում պարապ ընթացքից:
հոսանքի արժեքը դառնում
է զգալի, և ԼՏ-ի աշխատանքային ռեժիմը շատ է տարբերվում պարապ ընթացքից:
Դրա հետևանքով խախտվում է (8.30) ուղիղ համեմատական կապը և մեծանում է չափման սխալանքը: Հետևաբար որքան մեծ է միացված սարքերի թիվը, այնքան մեծ է չափման սխալանքը:
Գործնականում բոլոր տեսակի լարման տրանսֆորմատորների
երկրորդային փաթույթը նախատեսված է 100Վ անվանական լարման համար: Ուստի լարման տրանսֆորմատորը
բնութագրվում է միայն առաջնային փաթույթի լարումով, որը կարող է լինել ![]()
Լարման տրանսֆորմատորների երկրորդային փաթույթի մի ծայրը, անվտանգության նկատառումներից ելնելով, հողակցվում է (նկ. 8.15): Եթե որևէ վնասվածքի պատճառով առաջնային և երկրորդային շղթաների միջև էլեկտրական կապ առաջանա, և երկրորդային շղթան հայտնվի բարձր լարման տակ, ապա առաջնային շղթան կմիանա հողին՝ պարզապես ստեղծելով կարճ միացում, և ապահովիչները (նկ.8.15) լարման տրանսֆորմատորը կանջատեն բարձր լարման ցանցից` կանխելով վտանգը:
8.11.2. Հոսանքի չափման տրանսֆորմատոր
Նկ.8.16-ում պատկերված է հոսանքի չափման տրանսֆորմատորի կամ պարզապես հոսանքի տրանսֆորմատորի (ՀՏ) միացման սխեման:
ՀՏ-ի առաջնային փաթույթը, որն իրենից ներկայացնում է լայնական հատույթի մեծ մակերեսով հաղորդչի մի քանի գալար, հաջորդաբար է միացվում այն տեղամասին, որի հոսանքը անհրաժեշտ է չափել: Երկրորդային փաթույթին, նույնպես հաջորդաբար, միացվում են այնպիսի չափիչ գործիքներ և սարքեր, ինչպիսիք են ամպերմետրը, վատտմետրի հոսանքի փաթույթը, հոսանքի ռելեն և այլն, որոնց ներքին դիմադրությունը շատ փոքր է: Հետևաբար, հոսանքի տրանսֆորմատորների աշխատանքային ռեժիմը մոտ է կարճ միացման ռեժիմին:
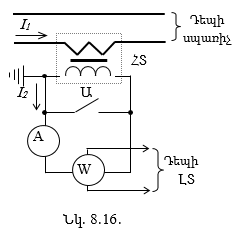
Կարճ միացման ռեժիմի դեպքում, ըստ (8.13) բանաձևի, կարող ենք գրել
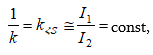
որտեղից
![]()
Այսպիսով, չափելով ![]() հոսանքը և այն բազմապատկելով
հաստատուն
հոսանքը և այն բազմապատկելով
հաստատուն ![]() գործակցով, որոշվում
է անհայտ
գործակցով, որոշվում
է անհայտ ![]() հոսանքի արժեքը: Հաճախ, գործնականում, գործիքների թվատախտակը նախօրոք բազմապատկվում
է
հոսանքի արժեքը: Հաճախ, գործնականում, գործիքների թվատախտակը նախօրոք բազմապատկվում
է ![]() և ամպերմետրը անմիջականորեն ցույց է տալիս անհայտ
և ամպերմետրը անմիջականորեն ցույց է տալիս անհայտ ![]() հոսանքը:
հոսանքը:
Եթե ՀՏ-ին միացող սարքերի թիվը մեծ է, ապա երկրորդային շղթայի դիմադրությունը դառնում է զգալի և ՀՏ-ի աշխատանքային ռեժիմը շատ է տարբերվում կարճ միացման ռեժիմից: Դրա հետևանքով խախտվում է (8.31) ուղիղ համեմատական կապը և մեծանում է չափման սխալանքը: Հետևաբար որքան մեծ է միացված սարքերի թիվը, այնքան մեծ է չափման սխալանքը:
Հատկանշական է, որ ՀՏ-ի առաջնային ![]() հոսանքը պայմանավորված
է միայն սպառիչով և ամենևին կախված չէ երկրորդային
հոսանքը պայմանավորված
է միայն սպառիչով և ամենևին կախված չէ երկրորդային ![]() հոսանքից, ինչպես
դա տեղի ուներ սովորական ուժային տրանսֆորմատորներում: Ուստի, եթե ՀՏ-ի երկրորդային
փաթույթում հոսանքը բացակայի (պարապ ընթացքի ռեժիմ), ապա կվերանա դրա մագնիսաթափող
ազդեցությունը միջուկի հիմնական մագնիսական հոսքի վրա, և վերջինս կտրուկ կմեծանա` երկրորդային
փաթույթում առաջացնելով մարդկանց և սարքերի համար վտանգավոր լարումներ: Այս պատճառով,
սովորաբար, ՀՏ-ի երկրորդային շղթայում նախատեսում են կարճ միացնող Ա անջատիչ. եթե ինչ
որ պատճառով երկրորդային շղթան անհրաժեշտ է խզել (ասենք, չափիչ գործիքը շղթային միացնելու
կամ շղթայից հանելու դեպքում), ապա նախօրոք միացնում են Ա աջատիչը` կարճ փակելով երկրորդային
շղթան:
հոսանքից, ինչպես
դա տեղի ուներ սովորական ուժային տրանսֆորմատորներում: Ուստի, եթե ՀՏ-ի երկրորդային
փաթույթում հոսանքը բացակայի (պարապ ընթացքի ռեժիմ), ապա կվերանա դրա մագնիսաթափող
ազդեցությունը միջուկի հիմնական մագնիսական հոսքի վրա, և վերջինս կտրուկ կմեծանա` երկրորդային
փաթույթում առաջացնելով մարդկանց և սարքերի համար վտանգավոր լարումներ: Այս պատճառով,
սովորաբար, ՀՏ-ի երկրորդային շղթայում նախատեսում են կարճ միացնող Ա անջատիչ. եթե ինչ
որ պատճառով երկրորդային շղթան անհրաժեշտ է խզել (ասենք, չափիչ գործիքը շղթային միացնելու
կամ շղթայից հանելու դեպքում), ապա նախօրոք միացնում են Ա աջատիչը` կարճ փակելով երկրորդային
շղթան:
Գործնականում հոսանքի տրանսֆորմատորների երկրորդային
փաթույթը նախատեսված է 5 Ա անվանական հոսանքի համար: Հոսանքի տրանսֆորմատորները բնութագրվում
են առաջնային ![]() հոսանքով և առաջնային շղթայի
հոսանքով և առաջնային շղթայի ![]() լարումով:
լարումով:
Առաջնային ![]() հոսանքի մեծ արժեքների
դեպքում ՀՏ-ի առաջնային փաթույթը պարզապես բացակայում է և երկրորդային փաթույթի կոճը
միջուկով հանդերձ հագցվում է անմիջականորեն
հոսանքի մեծ արժեքների
դեպքում ՀՏ-ի առաջնային փաթույթը պարզապես բացակայում է և երկրորդային փաթույթի կոճը
միջուկով հանդերձ հագցվում է անմիջականորեն ![]() հոսանքով հաղորդչի
վրա: Այս սկզբունքով են աշխատում նաև այսպես կոչված աքցանային տիպի ՀՏ-ով ամպերմետրերը,
որոնք թույլ են տալիս չափել հաղորդչի հոսանքը առանց այն խզելու:
հոսանքով հաղորդչի
վրա: Այս սկզբունքով են աշխատում նաև այսպես կոչված աքցանային տիպի ՀՏ-ով ամպերմետրերը,
որոնք թույլ են տալիս չափել հաղորդչի հոսանքը առանց այն խզելու:
Անվտանգության նկատառումներից ելնելով, ինչպես ԼՏ-ն, ՀՏ-ի երկրորդային փաթույթի մի ծայրը հողակցվում է:
1. Ո՞րն է տրանսֆորմատորի հիմնական նշանակությունը:
2. Որո՞նք են տրանսֆորմատորի հիմնական կառուցվածքային մասերը:
3. Ինչպիսի՞ կառուցվածք ունի տրանսֆորմատորի մագնիսական միջուկը
4. Ինչու՞ է տրանսֆորմատորի միջուկը հավաքվում էլեկտրատեխնիկական պողպատի թերթերից:
5. Ինչպիսի՞ կառուցվածք ունեն տրանսֆորմատորի փաթույթները:
6. Ի՞նչ հիմնական պարամետրերով է բնութագրվում տրանսֆորմատորը:
7. Տրանսֆորմատորի ո՞ր փաթույթն է կոչվում առաջնային և որը` երկրորդային:
8. Ի՞նչ դեր է կատարում յուղը յուղային տրանսֆորմատորներում:
9. Գծեք տրանսֆորմատորի պարզեցված պատկերը և ցույց տվեք հիմնական մագնիսական և ցրման հոսքերի ուժագծերը:
10. Ինչպե՞ս պետք է նախագծել տրանսֆորմատորը, որպեսզի այն լինի բարձրացնող (իջեցնող):
11. Գրեք տրանսֆորմատորի փաթույթների էլշուների ակնթարթային և գործող արժեքների արտահայտությունները:
12. Գրեք տրանսֆորմատորի էլեկտրական վիճակը բնութագրող հավասարումները:
13. Գրեք տրանսֆորմատորի մագնիսկան վիճակը պատկերող հավասարումները:
14. Ինչպե՞ս է իրականացվում տրանսֆորմատորի պարապ ընթացքի ռեժիմի փորձը:
15. Ո՞րն է տրանսֆորմատորի պարապ ընթացքի ռեժիմի ուսումնասիրության նպատակը:
16. Ինչպե՞ս է իրականացվում տրանսֆորմատորի կարճ միացման ռեժիմի փորձը և ո՞րն է դրա նպատակը:
17. Գրեք տրանսֆորմատորի կորուստների որոշման բանաձևը:
18. Գործնականում ո՞ր բանաձևն են օգտագործում տրանսֆորմատորի օ.գ.գ.-ն որոշելու համար:
19. Գծել տրանսֆորմատորի օ.գ.գ.-ի կախման կորը տրանսֆորմատորի բեռնվածքից: Ի՞նչ պայմանի դեպքում տրանսֆորմատորի օ.գ.գ.-ն առավելագույն արժեք է ստանում:
20. Գծեք տրանսֆորմատորի արտաքին բնութագիծը: Ինչու՞ բեռնվածքի մեծացման հետ երկրորդային փաթույթի լարումը փաքրանում է:
21. Ինչպիսի՞ կառուցվածքով եռաֆազ տրանսֆորմատորներ են կիրառվում: Համեմատեք դրանց արժանիքները և նշեք, թե ո՞ր դեպքերում է նպատակահարմար դրանք կիրառել:
22. Բացատրեք, թե ի՞նչ է եռաֆազ տրանսֆորմատորի միացման խումբը: Փաթույթների ինչպիսի՞ ստանդարտ միացման խմբեր կան:
23. Ինչպիսի՞ կառուցվածք ունի ավտոտրանսֆորմատորը, ի՞նչ առավելություններով և թերություններով է այն օժտված և ե՞րբ է նպատակահարմար այն կիրառել:
24. Ինչպիսի՞ կառուցվածքային առանձնահատկություն ունի եռակցման տրանսֆորմատորը:
25. Գծեք եռակցման տրանսֆորմատորի արտաքին բնութագիծը և բացատրեք դրա աշխատանքը:
26. Ինչու՞ են օգտագործվում չափման տրանսֆորմտորները:
27. Գծեք լարման տրանսֆորմատորի միացման սխեման: Ի՞նչ սարքեր կարող են միացվել լարման տրանսֆորմատորին:
28. Գծեք հոսանքի տրանսֆորմատորի միացման սխեման: Ի՞նչ սարքեր կարող են միացվել հոսանքի տրանսֆորմատորին:
29. Ինչու՞ են չափման տրանսֆորմատորների երկրորդային փաթույթները հողանցվում:
Ինչպես ցանկացած էլեկտրական մեքենա, ասինքրոն մեքենաները նույնպես շրջելի են. նույն մեքենան կարող է աշխատել և՛ որպես գեներատոր, և՛ որպես շարժիչ: Գործնականում, սակայն, ասինքրոն մեքենաները կիրառվում են գլխավորապես որպես շարժիչներ: Ասինքրոն շարժիչները, շնորհիվ իրենց արժանիքների, ներկայումս ոչ միայն ամենատարածված շարժիչներն են, այլև էլեկտրաէներգիայի ամենատարածված սպառիչներից են:
Եռաֆազ հոսանքի լայն կիրառությունը մասամբ պայմանավորված է նաև հուսալի և էժան եռաֆազ ասինքրոն շարժիչների օգտագործման հնարավորությամբ:
Մեծ հզորության ասինքրոն շարժիչները պատրաստվում են եռաֆազ, իսկ փոքր հզորության դեպքում (մինչև 500 Վտ)՝ սովորաբար միաֆազ և երկֆազ: Վերջիններս օգտագործվում են ավտոմատիկայի, բժշկական և այլ սարքավորումներում, ինչպես նաև կենցաղային էլեկտրական սարքերում (սառնարան, լվացքի մեքենա):
9.1. Եռաֆազ ասինքրոն մեքենայի կառուցվածքը
Դիտարկենք ասինքրոն մեքենայի լայնական հատույթը` պարզեցված տեսքով (նկ. 9.1ա):
Ասինքրոն մեքենան կազմված է երկու հիմնական մասերից՝ անշարժ ստատորից և պտտվող ռոտորից:
Ասինքրոն մեքենայի ստատորը իրենից ներկայացնում
է սնամեջ գլան, որը, ինչպես և տրանսֆորմատորի միջուկը (տե՛ս բաժին 8.2), հավաքվում
է միմյանցից լաքի բարակ շերտով մեկուսացված էլեկտրատեխնիկական պողպատի թերթերից: Ստատորի
ներքին մակերևույթի վրա արված երկայնական փորակներում տեղադրվում են միմյանց նկատմամբ
![]() տարածականորեն շեղված ստատորի երեք ֆազային փաթույթները՝ կազմված պղնձե (հազվադեպ՝
ալյումինե) մեկուսացված հաղորդալարի գալարներից: Ստատորը մամլվում է իրանի (պատյանի)
մեջ, որը մեքենայի հենքն է հանդիսանում և օժտված է բավարար մեխանիկական ամրությամբ:
Փոքր հզորության դեպքում այն պատրաստվում է ալյումինից, մեծ հզորության դեպքում՝ չուգունից
կամ պողպատից:
տարածականորեն շեղված ստատորի երեք ֆազային փաթույթները՝ կազմված պղնձե (հազվադեպ՝
ալյումինե) մեկուսացված հաղորդալարի գալարներից: Ստատորը մամլվում է իրանի (պատյանի)
մեջ, որը մեքենայի հենքն է հանդիսանում և օժտված է բավարար մեխանիկական ամրությամբ:
Փոքր հզորության դեպքում այն պատրաստվում է ալյումինից, մեծ հզորության դեպքում՝ չուգունից
կամ պողպատից:
Ասինքրոն մեքենայի ռոտորը կազմված է գլանաձև միջուկից, որը նույնպես հավաքվում է էլեկտրատեխնիկական պողպատի թերթերից: Այն ամուր նստեցվում է պողպատե լիսեռին, որը իր հերթին, երկու կողմերից հենվում է առանցքակալների վրա: Ռոտորի մակերևույթի վրա (կամ մակերևույթին մոտ) արված երկայնական փորակներում տեղադրվում է ռոտորի փաթույթը:
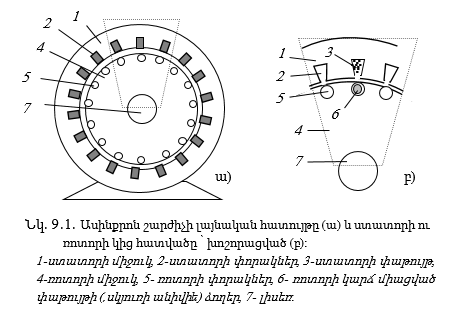
Ասինքրոն մեքենաները, ըստ ռոտորի կառուցվածքի, լինում են երկու տեսակ՝ կարճ միացված ռոտորով և ֆազային ռոտորով (կամ կոնտակտային օղակներով):
Գործնականում առավել մեծ կիրառություն ունեն կարճ միացված ռոտորով ասինքրոն շարժիչները, որոնց ռոտորի թմբուկաձև փաթույթը կազմված է կլոր կամ երկարավուն կտրվածքով ալյումինե կամ պղնձե ձողերից, որոնք տեղադրվում են ռոտորի փորակներում առանց մեկուսացման: Ձողերը երկու կողմերից միացվում են միմյանց հետ նույն նյութից պատրաստված ճակատային օղակներով՝ կազմելով այսպես կոչված «սկյուռի անիվ (կամ վանդակ)ե (նկ.9.2ա): Ալյումինե այսպիսի փաթույթ ստանալու համար, պարզապես ռոտորի փորակները լցնում են հալած ալյումինով: Այս ձևով ստացվում են և՛ «սկյուռի անիվիե ձողերը, և՛ դրանք երկու կողմից կարճ փակող օղակները:
Շնորհիվ ռոտորի այսպիսի կառուցվածքի, որում բացակայում են արագ մաշվող կամ վնասվող մասերը (ինչպես այլ շարժիչներում կոլեկտորը և խոզանականերն են), կարճ միացված ռոտորով շարժիչները ներկայումս համարվում են գործնականում կիրառվող ամենաէժան և հուսալի էլեկտրաշարժիչները:
Ֆազային ռոտորով ասինքրոն շարժիչների
դեպքում ռոտորի (նկ. 9.2բ) փաթույթը պատրաստվում է մեկուսացված պղնձե հաղորդալարից:
Այն, ինչպես և ստատորը, կազմված է երեք ֆազային փաթույթներից, որոնք ռոտորի վրա տեղադրվում
են միմյանց նկատմամբ ![]() շեղված: Որպես կանոն,
ռոտորի փաթույթները միացվում են աստղաձև հենց ռոտորի վրա, իսկ երեք ազատ ծայրերը միացվում
են լիսեռին (7) ագուցված, բայց դրանից էլեկտրականապես մեկուսացված, երեք կոնտակտային
օղակներին (8): Վերջիններիս, զսպանակների միջոցով, հպվում են ածխե (գրաֆիտե) անշարժ
խոզանակները (9): Օղակների և խոզանակների միջոցով ռոտորի փաթույթը միանում է եռաֆազ
ռեոստատին (R):
շեղված: Որպես կանոն,
ռոտորի փաթույթները միացվում են աստղաձև հենց ռոտորի վրա, իսկ երեք ազատ ծայրերը միացվում
են լիսեռին (7) ագուցված, բայց դրանից էլեկտրականապես մեկուսացված, երեք կոնտակտային
օղակներին (8): Վերջիններիս, զսպանակների միջոցով, հպվում են ածխե (գրաֆիտե) անշարժ
խոզանակները (9): Օղակների և խոզանակների միջոցով ռոտորի փաթույթը միանում է եռաֆազ
ռեոստատին (R):
Այսպիսով, հնարավորություն է ստեղծվում անհրաժեշտության դեպքում ռոտորի շղթա մտցնել լրացուցիչ ակտիվ դիմադրություն և դրանով իսկ էապես բարելավել շարժիչի գործարկման պայմանները. այն կարող է զարգացնել զգալիորեն ավելի մեծ գործարկման մոմենտ՝ համեմատաբար փոքր գործարկման հոսանքի դեպքում (տես բաժին 9.7): Ռեոստատի առկայությունը թույլ է տալիս նաև սահուն կարգավորել (փոփոխել) ռոտորի արագությունը:
Սակայն, կոնտակտային օղակների և խոզանակների առկայությունը ֆազային ռոտորով ասինքրոն շարժիչին զրկում է կարճ միացված ռոտորով շարժիչներին հատուկ մի շարք արժանիքներից: Մասնավորապես, այն ավելի թանկարժեք է և պակաս հուսալի, ուստի և ավելի սահմանափակ կիրառություն ունի:
Նկ. 9.3-ում բերված են կարճ միացված ռոտորով (ա) և ֆազային ռոտորով (բ) ասինքրոն շարժիչների պայմանական նշանները:
9.2. Պտտվող մագնիսական դաշտի ստացումը ասինքրոն շարժիչում
Ինչպես արդեն ասվեց, ասինքրոն մեքենայի ստատորի
փորակներում տեղադրվում են երեք ֆազային փաթույթներ, որոնց մագնիսական առանցքները տարածականորեն
միմյանցից շեղված են ![]() (նկ. 9.4):
(նկ. 9.4):

Երբ ստատորի փաթույթները միացվում են եռաֆազ ցանցին,
դրանցով անցնում են նույն մեծությամբ, բայց ըստ փուլի միմյանց նկատմամբ ![]() շեղված սինուսոիդական հոսանքներ.
շեղված սինուսոիդական հոսանքներ.
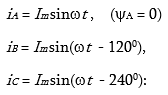
Ֆազային փաթույթների հոսանքները ստեղծում են մագնիսական
դաշտեր, որոնց ինդուկցիայի վեկտորների Bm բացարձակ արժեքները հավասար են, բայց շեղված
են միմյանց նկատմամբ ![]() .
.
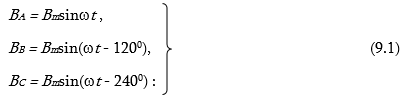
Մագնիսական ինդուկցիաների վեկտորներից յուրաքանչյուրն ուղղված է համապատասխան փաթույթի առանցքով (նկ. 9.4):
Մեքենայի արդյունարար մագնիսական դաշտն ստացվում է երեք մագնիսական դաշտերի վերադրումից, հետևաբար արդյունարար դաշտի ինդուկցիայի վեկտորը`
![]()
Որոշենք ![]() վեկտորի պրոյեկցիան
հորիզոնական x առանցքի վրա.
վեկտորի պրոյեկցիան
հորիզոնական x առանցքի վրա.
![]()
Տեղադրելով ինդուկցիաների արժեքները (9.1)-ից և կատարելով եռանկյունաչափական պարզ ձևափոխություններ` կստանանք.
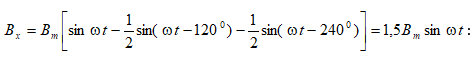
Համանման ձևով որոշվում է ![]() վեկտորի պրոյեկցիան
ուղղաձիգ y առանցքի վրա.
վեկտորի պրոյեկցիան
ուղղաձիգ y առանցքի վրա.
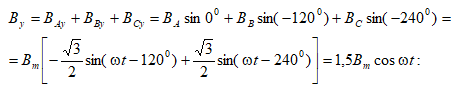
Արդյունարար մագնիսական դաշտի ինդուկցիայի մեծությունը կլինի
![]()
իսկ ![]() վեկտորի կազմած անկյունը
x առանցքի հետ`
վեկտորի կազմած անկյունը
x առանցքի հետ`
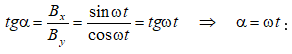
Այսպիսով, ասինքրոն մեքենայի ստատորի փաթույթներով
ստեղծված արդյունարար մագնիսական դաշտի ինդուկցիայի վեկտորը մեծությամբ մնալով հաստատուն՝
![]() պտտվում է մեքենայի լիսեռի (առանցքի) շուրջը
պտտվում է մեքենայի լիսեռի (առանցքի) շուրջը ![]() անկյունային արագությամբ, որտեղ f -ը ցանցի լարման հաճախությունն է
(f = 50 Հց): Ընդ որում վեկտորի ուղղությունը տվյալ պահին համընկնում է այն ֆազի ստեղծած
մագնիսական դաշտի ինդուկցիայի վեկտորի ուղղության հետ, որի հոսանքն ունի առավելագույն
արժեք: Եթե երեք սնող հաղորդալարերից ցանկացած երկուսի տեղերը փոխվեն, ապա ստատորի
ստեղծած մագնիսական դաշտը կպտտվի սկզբնականի նկատմամբ հակառակ ուղղությամբ:
անկյունային արագությամբ, որտեղ f -ը ցանցի լարման հաճախությունն է
(f = 50 Հց): Ընդ որում վեկտորի ուղղությունը տվյալ պահին համընկնում է այն ֆազի ստեղծած
մագնիսական դաշտի ինդուկցիայի վեկտորի ուղղության հետ, որի հոսանքն ունի առավելագույն
արժեք: Եթե երեք սնող հաղորդալարերից ցանկացած երկուսի տեղերը փոխվեն, ապա ստատորի
ստեղծած մագնիսական դաշտը կպտտվի սկզբնականի նկատմամբ հակառակ ուղղությամբ:
Սինուսոիդական մեկ պարբերության ընթացքում այսպիսով
ստացված երկբևեռ դաշտը կկատարի մեկ պտույտ, հետևաբար f = 50 Հց հաճախության դեպքում
մեկ րոպեում ստատորի մագնիսական դաշտի պտուտաթվերը կլինեն ![]() Գործնականում, ավելի փոքր արագություններ ստանալու համար, կիրառում են ստատորի
բազմաբևեռ փաթույթներ: Այդ նպատակով յուրաքանչյուր ֆազային փաթույթ տրոհվում է ընդհանուր
դեպքում հաջորդաբար կամ զուգահեռ միացված p հավասար մասերի (p-ն կոչվում է զույգ
բևեռների թիվ), և դրանց դաշտերի վերադրումից առաջացած արդյունարար մագնիսական դաշտը
ստացվում է p-բևեռանի, իսկ պտտման
Գործնականում, ավելի փոքր արագություններ ստանալու համար, կիրառում են ստատորի
բազմաբևեռ փաթույթներ: Այդ նպատակով յուրաքանչյուր ֆազային փաթույթ տրոհվում է ընդհանուր
դեպքում հաջորդաբար կամ զուգահեռ միացված p հավասար մասերի (p-ն կոչվում է զույգ
բևեռների թիվ), և դրանց դաշտերի վերադրումից առաջացած արդյունարար մագնիսական դաշտը
ստացվում է p-բևեռանի, իսկ պտտման ![]() արագությունը փոքրանում
է p անգամ՝
արագությունը փոքրանում
է p անգամ՝
![]()
Գործնականում կիրառվող ասինքրոն շարժիչների գերակշռող մասի համար p = 1, 2, 3 և 4, որոնց դեպքում այդ շարժիչների դաշտերի պտուտաթվերը (պտ/ր), համապատասխանաբար, կունենան հետևյալ արժեքները՝ 3000, 1500, 1000 և 750:
9.3. Ասինքրոն շարժիչի աշխատանքի սկզբունքը
Ասինքրոն շարժիչում ընթացող էլեկտրամագնիսական
պրոցեսները ուսումնասիրելու համար դիտարկենք դրա ստատորի և ռոտորի մի հատվածը խոշոր
պլանով (նկ. 9.1բ և նկ. 9.5): Ինչպես արդեն ասվեց, երբ ասինքրոն շարժիչի ստատորի եռաֆազ
փաթույթները միացվում են եռաֆազ սնման ցանցին, շարժիչում առաջանում է պտտվող մագնիսական
դաշտ: Ենթադրենք դաշտի ինդուկցիայի վեկտորը ժամանակի տվյալ պահին ունի նկ.9.5-ում նշված
ուղղությունը և պտտվում է ժամացույցի սլաքի շարժման ուղղությամբ ![]() արագությամբ: Դրա
հետևանքով դաշտի ուժագծերը, հատելով անշարժ ռոտորի փաթույթների հաղորդիչ գալարները
(կամ «սկյուռի անիվի» ձողերը), համաձայն էլեկտրամագնիսական ինդուկցիայի երևույթի, դրանցում
ինդուկտում են
արագությամբ: Դրա
հետևանքով դաշտի ուժագծերը, հատելով անշարժ ռոտորի փաթույթների հաղորդիչ գալարները
(կամ «սկյուռի անիվի» ձողերը), համաձայն էլեկտրամագնիսական ինդուկցիայի երևույթի, դրանցում
ինդուկտում են ![]() էլեկտրաշարժ ուժ, որի ուղղությունը որոշվում է աջ ձեռքի կանոնով: Ընդ որում`
աջ ձեռքի բթամատը պետք է ուղղել դաշտի պտտման հակառակ ուղղությամբ, այսինքն դաշտի նկատմամբ
հաղորդիչների հարաբերական շարժման ուղղությամբ: Դիտարկվող օրինակում
էլեկտրաշարժ ուժ, որի ուղղությունը որոշվում է աջ ձեռքի կանոնով: Ընդ որում`
աջ ձեռքի բթամատը պետք է ուղղել դաշտի պտտման հակառակ ուղղությամբ, այսինքն դաշտի նկատմամբ
հաղորդիչների հարաբերական շարժման ուղղությամբ: Դիտարկվող օրինակում ![]() էլշուն ուղղված է
դեպի ընթերցողը և նկ. 9.5-ում նշված է կետով:
էլշուն ուղղված է
դեպի ընթերցողը և նկ. 9.5-ում նշված է կետով:
Ինդուկտված ![]() էլշուն, իր հերթին,
ռոտորի հաղորդիչներում առաջացնում է նույն ուղղությամբ անցնող
էլշուն, իր հերթին,
ռոտորի հաղորդիչներում առաջացնում է նույն ուղղությամբ անցնող ![]() հոսանք: Այս հոսանքի
և ստատորի դաշտի փոխազդեցության շնորհիվ ռոտորի հաղորդիչների վրա ազդում են մեխանիկական
F ուժեր, որոնց ուղղությունը որոշվում է ձախ ձեռքի կանոնով (Ամպերի օրենքը): Դժվար
չէ համոզվել (նկ. 9.5), որ այդ ուժերը մեքենայի լիսեռի վրա կառաջացնեն M պտտող մոմենտ՝
ուղղված ստատորի մագնիսական դաշտի պտտման ուղղությամբ:
հոսանք: Այս հոսանքի
և ստատորի դաշտի փոխազդեցության շնորհիվ ռոտորի հաղորդիչների վրա ազդում են մեխանիկական
F ուժեր, որոնց ուղղությունը որոշվում է ձախ ձեռքի կանոնով (Ամպերի օրենքը): Դժվար
չէ համոզվել (նկ. 9.5), որ այդ ուժերը մեքենայի լիսեռի վրա կառաջացնեն M պտտող մոմենտ՝
ուղղված ստատորի մագնիսական դաշտի պտտման ուղղությամբ:
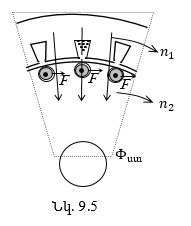
Ինդուկտված ![]() էլշուն, իր հերթին,
ռոտորի հաղորդիչներում առաջացնում է նույն ուղղությամբ անցնող
էլշուն, իր հերթին,
ռոտորի հաղորդիչներում առաջացնում է նույն ուղղությամբ անցնող ![]() հոսանք: Այս հոսանքի
և ստատորի դաշտի փոխազդեցության շնորհիվ ռոտորի հաղորդիչների վրա ազդում են մեխանիկական
F ուժեր, որոնց ուղղությունը որոշվում է ձախ ձեռքի կանոնով (Ամպերի օրենքը): Դժվար
չէ համոզվել (նկ. 9.5), որ այդ ուժերը մեքենայի լիսեռի վրա կառաջացնեն M պտտող մոմենտ՝
ուղղված ստատորի մագնիսական դաշտի պտտման ուղղությամբ:
հոսանք: Այս հոսանքի
և ստատորի դաշտի փոխազդեցության շնորհիվ ռոտորի հաղորդիչների վրա ազդում են մեխանիկական
F ուժեր, որոնց ուղղությունը որոշվում է ձախ ձեռքի կանոնով (Ամպերի օրենքը): Դժվար
չէ համոզվել (նկ. 9.5), որ այդ ուժերը մեքենայի լիսեռի վրա կառաջացնեն M պտտող մոմենտ՝
ուղղված ստատորի մագնիսական դաշտի պտտման ուղղությամբ:
Եթե պտտող M մոմենտն իր մեծությամբ գերազանցում
է մեքենայի լիսեռի վրա եղած հակազդող (արգելակող) ![]() մոմենտը, ապա ռոտորը
կստանա արագացող շարժում դաշտի պտտման ուղղությամբ: Ռոտորի
մոմենտը, ապա ռոտորը
կստանա արագացող շարժում դաշտի պտտման ուղղությամբ: Ռոտորի ![]() արագության մեծացմանը
զուգընթաց կփոքրանա նրա հաղորդիչների և պպտվող մագնիսական դաշտի
արագության մեծացմանը
զուգընթաց կփոքրանա նրա հաղորդիչների և պպտվող մագնիսական դաշտի ![]() հարաբերական արագությունը, կփոքրանան նաև դրանցում ինդուկտված էլշուները,
հոսանքները և, հետևաբար, M պտտող մոմենտը:
հարաբերական արագությունը, կփոքրանան նաև դրանցում ինդուկտված էլշուները,
հոսանքները և, հետևաբար, M պտտող մոմենտը:
Երբ վերջինս հավասարվի լիսեռի վրա ![]() հակազդող մոմենտին, շարժիչի ռոտորը կպտտվի
հակազդող մոմենտին, շարժիչի ռոտորը կպտտվի ![]() հաստատուն արագությամբ,
որը, սակայն, փոքր կլինի դաշտի
հաստատուն արագությամբ,
որը, սակայն, փոքր կլինի դաշտի ![]() արագությունից:
արագությունից:
Ասինքրոն մեքենայի տեսության հիմնական հասկացություններից մեկը մեքենայի s սահքն է, որը կապ է հաստատում ռոտորի և ստատորի դաշտի արագությունների միջև.
![]()
Շարժիչը սնող ցանցի տրված լարման դեպքում սահքը
կախված է շարժիչի բեռնվածքից (լիսեռին կիրառված ![]() մոմենտից): Ընդհանուր
օգտագործման ասինքրոն շարժիչների համար անվանական բեռնվածքների դեպքում
մոմենտից): Ընդհանուր
օգտագործման ասինքրոն շարժիչների համար անվանական բեռնվածքների դեպքում ![]() Օրինակ, եթե ասինքրոն շարժիչի ստատորի դաշտի պտտման արագությունը
Օրինակ, եթե ասինքրոն շարժիչի ստատորի դաշտի պտտման արագությունը ![]() ապա, ըստ (9.3) բանաձևի, ռոտորի պտտման արագությունը անվանական բեռնվածքի դեպքում
տարբեր շարժիչների համար կտատանվի
ապա, ըստ (9.3) բանաձևի, ռոտորի պտտման արագությունը անվանական բեռնվածքի դեպքում
տարբեր շարժիչների համար կտատանվի ![]() սահմաններում, իսկ
եթե
սահմաններում, իսկ
եթե ![]()
Պարապ ընթացքի դեպքում սահքը շատ փոքր է՝ ![]()
Խնդիր 9.1.
Որոշել ասինքրոն շարժիչի զույգ բևեռների թիվը և սահքը, եթե շարժիչին կիրառված փոփոխական
լարման հաճախությունը 50Հց է, իսկ ռոտորի պտտման արագությունը` ![]()
Լուծում.
(9.2) բանաձևից հետևում է, որ ստատորի դաշտի պտտման արագությունը պետք է լինի 950-ին
մոտակա այն մեծ թիվը, որի վրա անմնացորդ բաժանվում է ![]() այսինքն
այսինքն ![]() Այդ դեպքում շարժիչի
զույգ բևեռների թիվը ըստ (9.2) բանաձևի կլինի`
Այդ դեպքում շարժիչի
զույգ բևեռների թիվը ըստ (9.2) բանաձևի կլինի`
![]()
Ասինքրոն շարժիչի սահքը որոշվում է (9.2) բանաձևով`
![]()
9.4. Ասինքրոն մեքենայի աշխատանքային ռեժիմները
Կախված սահքի արժեքից՝ ասինքրոն մեքենան կարող է աշխատել երեք ռեժիմներում. շարժիչի, գեներատորի և էլեկտրամագնիսական արգելակի ռեժիմներում:
Երբ 0 < s < 1, ասինքրոն մեքենան աշխատում
է շարժիչի ռեժիմում՝ ցանցից վերցրած էլեկտրական էներգիան լիսեռի վրա փոխարկելով
մեխանիկական էներգիայի: Շարժիչի ռոտորը պտտվում է ստատորի դաշտի պտտման ուղղությամբ,
բայց նրանից ավելի փոքր արագությամբ՝ ![]() Շարժիչի զարգացրած
պտտող մոմենտը հավասարակշռում է շարժիչի բեռնվածքի (շարժիչին միացված մեխանիզմի) և
շփման ուժերի առաջացրած հակազդող մոմենտը:
Շարժիչի զարգացրած
պտտող մոմենտը հավասարակշռում է շարժիչի բեռնվածքի (շարժիչին միացված մեխանիզմի) և
շփման ուժերի առաջացրած հակազդող մոմենտը:
Երբ s < 0, ասինքրոն մեքենան աշխատում է գեներատորի
ռեժիմում՝ փոխարկելով լիսեռին հաղորդված մեխանիկական էներգիան էլեկտրականի: Այս
դեպքում առաջնային շարժիչով մեքենայի ռոտորը պտտման մեջ է դրվում ստատորի դաշտի պտտման
ուղղությամբ ![]() արագությամբ: Ռոտորի հաղորդիչներում փոխվում է ինդուկտված հոսանքների ուղղությունը,
և այդ հոսանքների ու ստատորի մագնիսական դաշտի փոխազդեցությունից լիսեռի վրա առաջանում
է հակազդող (ռոտորի պտտմանը հակառակ ուղղված) մոմենտ, որը հաղթահարվում է առաջնային
շարժիչի հաղորդած պտտող մոմենտով:
արագությամբ: Ռոտորի հաղորդիչներում փոխվում է ինդուկտված հոսանքների ուղղությունը,
և այդ հոսանքների ու ստատորի մագնիսական դաշտի փոխազդեցությունից լիսեռի վրա առաջանում
է հակազդող (ռոտորի պտտմանը հակառակ ուղղված) մոմենտ, որը հաղթահարվում է առաջնային
շարժիչի հաղորդած պտտող մոմենտով:
Երբ s > 1, ասինքրոն մեքենան աշխատում է այսպես կոչված էլեկտրամագնիսական արգելակի (ԷՄԱ) ռեժիմում: Մեքենայի ռոտորը պտտվում է ստատորի մագնիսական դաշտի պտտման հակառակ ուղղությամբ, և լիսեռի վրա առաջացած հակազդող մոմենտը ձգտում է կանգնեցնել ռոտորը: Այս ռեժիմում ռոտորի հաղորդիչների հարաբերական շարժման արագությունը գերազանցում է դաշտի պտտման արագությունը, որի պատճառով կտրուկ մեծանում են հզորության կորուստները ստատորի և ռոտորի փաթույթներում և միջուկներում:
Այսպիսով, բոլոր ռեժիմներում էլ ասինքրոն մեքենայի ստատորի մագնիսական դաշտը և ռոտորը պտտվում են տարբեր արագություններով՝ ոչ սինքրոն կամ ասինքրոն, որով էլ պայմանավորված է մեքենայի անվանումը՝ ասինքրոն մեքենա:
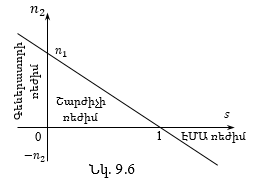
Նկ. 9.6 - ում բերված է ռոտորի պտտման արագության
կախումը մեքենայի սահքից՝ ![]() և ցույց են տրված
ասինքրոն մեքենայի ռեժիմներին համապատասխանող միջակայքերը:
և ցույց են տրված
ասինքրոն մեքենայի ռեժիմներին համապատասխանող միջակայքերը:
9.5. Ասինքրոն շարժիչի անվանական պարամետրերը
Ասինքրոն շարժիչը բնութագրվում է անվանական ռեժիմին համապատասխանող մի շարք պարամետրերով, որոնց համար նախագծված և հաշվարկված է ասինքրոն շարժիչը և որոնք տրվում են շարժիչի պիտակի (անձնագրի) վրա:
·
Էլեկտրաշարժիչի համար, թերևս, ամենակարևոր պարամետրը
շարժիչի ![]() անվանական հզորությունն է: Դա մեխանիկական այն հզորությունն
է, որ շարժիչը զարգացնում է լիսեռի վրա` անվանական բեռնվածքի և սնող ցանցի անվանական
լարման դեպքում: Անվանական հզորությամբ երկարատև աշխատելիս ջերմային կորուստների հետևանքով
շարժիչի ջերմաստիճանի բարձրացումը չի գերազանցում թույլատրելի սահմանային արժեքը:
անվանական հզորությունն է: Դա մեխանիկական այն հզորությունն
է, որ շարժիչը զարգացնում է լիսեռի վրա` անվանական բեռնվածքի և սնող ցանցի անվանական
լարման դեպքում: Անվանական հզորությամբ երկարատև աշխատելիս ջերմային կորուստների հետևանքով
շարժիչի ջերմաստիճանի բարձրացումը չի գերազանցում թույլատրելի սահմանային արժեքը:
· Ասինքրոն շարժիչի անվանական օ.գ.գ.-ն որոշվում է

բանաձևով, որտեղ ![]() անվանական բեռնվածքի դեպքում շարժիչի էլեկտրական ակտիվ հզորությունն է, որ
վերցնում է շարժիչը սնող ցանցից և կոչվում է շարժիչի սպառման հզորություն:
անվանական բեռնվածքի դեպքում շարժիչի էլեկտրական ակտիվ հզորությունն է, որ
վերցնում է շարժիչը սնող ցանցից և կոչվում է շարժիչի սպառման հզորություն:
Ժամանակակից ասինքրոն շարժիչների օ.գ.գ.-ի արժեքը անվանական ռեժիմի դեպքում հասնում է 0,80…0,95 կամ, տոկոսներով արտահայտված, (80…95)%. Ընդ որում՝ օ.գ.գ.-ի բարձր արժեքները համապատասխանում են մեծ հզորություն ունեցող շարժիչներին:
· Եռաֆազ ասինքրոն շարժիչի սպառման հզորությունը որոշվում է, համաձայն (4.16) բանաձևի`
![]()
որտեղ
![]() համապատասխանաբար, շարժիչին մատուցված անվանական գծային լարումը և գծային հոսանքն
են, իսկ
համապատասխանաբար, շարժիչին մատուցված անվանական գծային լարումը և գծային հոսանքն
են, իսկ ![]() անվանական հզորության գործակիցը:
անվանական հզորության գործակիցը:
·
Եռաֆազ շարժիչները, այդ թվում նաև եռաֆազ ասինքրոն
շարժիչները, կարող են աշխատել` սնվելով 2 տարբեր անվանական գծային լարումներ ունեցող
ցանցերից: Այսպես, ստատորի ֆազային փաթույթների աստղաձև միացման դեպքում` ![]() լարումով, իսկ ստատորի ֆազային փաթույթների եռանկյունաձև միացման դեպքում`
լարումով, իսկ ստատորի ֆազային փաթույթների եռանկյունաձև միացման դեպքում` ![]() լարումով ցանցերից:
լարումով ցանցերից:
Օրինակ, եթե շարժիչի պիտակի վրա նշված է ![]() ապա նշանակում է, որ նույն շարժիչը կարելի է միացնել 380 Վ գծային լարումով
եռաֆազ ցանցին, եթե ստատորի ֆազային փաթույթները միացվեն աստղաձև կամ 220Վ գծային լարումով
եռաֆազ ցանցին, եթե այդ փաթույթները միացվեն եռանկյունաձև:
ապա նշանակում է, որ նույն շարժիչը կարելի է միացնել 380 Վ գծային լարումով
եռաֆազ ցանցին, եթե ստատորի ֆազային փաթույթները միացվեն աստղաձև կամ 220Վ գծային լարումով
եռաֆազ ցանցին, եթե այդ փաթույթները միացվեն եռանկյունաձև:
· Եռաֆազ ասինքրոն շարժիչի անվանական հոսանքը, ըստ (9.4) և (9.5) բանաձևերի,
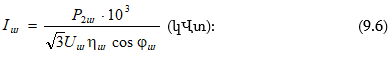
·
Եռաֆազ ասինքրոն շարժիչների անվանական հզորության
գործակիցը բավականաչափ բարձր է` ![]() սակայն անվանական
բեռնվածքի կեսի դեպքում այն արդեն կազմում է
սակայն անվանական
բեռնվածքի կեսի դեպքում այն արդեն կազմում է ![]() իսկ բեռնվածքի բացակայության դեպքում՝ ընդամենը
իսկ բեռնվածքի բացակայության դեպքում՝ ընդամենը ![]() Այս պատճառով այն արտադրամասերում, որտեղ գործում են մեծ թվով ասինքրոն շարժիչներ,
սնող ցանցի ընդհանուր հզորության գործակիցը ստացվում է բավականաչափ ցածր, որի հետևանքով
ցանցում առաջանում են հզորության լրացուցիչ կորուստներ: Ուստի այդպիսի արտադրամասերում
նախատեսում են հատուկ միջոցառումներ՝ ցանցի հզորության գործակցի բարձրացման համար:
Այդ նպատակին ծառայող ամենապարզ և տարածված միջոցը՝ նույն ցանցին զուգահեռ կոնդենսատորային
մարտկոցներ միացնելն է (տե՛ս 3.11 բաժինը):
Այս պատճառով այն արտադրամասերում, որտեղ գործում են մեծ թվով ասինքրոն շարժիչներ,
սնող ցանցի ընդհանուր հզորության գործակիցը ստացվում է բավականաչափ ցածր, որի հետևանքով
ցանցում առաջանում են հզորության լրացուցիչ կորուստներ: Ուստի այդպիսի արտադրամասերում
նախատեսում են հատուկ միջոցառումներ՝ ցանցի հզորության գործակցի բարձրացման համար:
Այդ նպատակին ծառայող ամենապարզ և տարածված միջոցը՝ նույն ցանցին զուգահեռ կոնդենսատորային
մարտկոցներ միացնելն է (տե՛ս 3.11 բաժինը):
Ասինքրոն շարժիչի անվանական մեխանիկական պարամետրերից կարևոր են ռոտորի անվանական արագությունը և լիսեռի վրա զարգացրած անվանական մոմենտը:
· Ասինքրոն շարժիչի ռոտորի անվանական արագությունը`
![]()
որտեղ ![]() շարժիչի անվանական
սահքն է, որի արժեքը տարբեր շարժիչների մոտ (2 … 6)%-ի սահմաններում է:
շարժիչի անվանական
սահքն է, որի արժեքը տարբեր շարժիչների մոտ (2 … 6)%-ի սահմաններում է:
· Լիսեռի վրա ասինքրոն շարժիչի զարգացրած անվանական մեխանիկական մոմենտը, ըստ ֆիզիկայի դասընթացի,
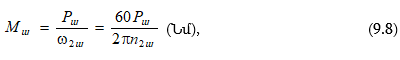
որտեղ ![]() ռոտորի պտտման անկյունային
արագությունն է:
ռոտորի պտտման անկյունային
արագությունն է:
9.6. Ասինքրոն շարժիչի ստատորի և ռոտորի էլշուները
Մեքենայի պտտվող մագնիսական դաշտի ինդուկցիան
(հետևաբար և ![]() հոսքը) ռոտորի շրջագծի երկայնքով բաշխվում է սինուսոիդական օրենքով, ուստի
ռոտորի և ստատորի փաթույթներում ինդուկտված էլշուները կլինեն սինուսոիդական մեծություններ,
որոնց գործող արժեքները կորոշվեն տրանսֆորմատորային էլշուներին համանման (տես
7.3 բաժինը): Տարբերությունը միայն այն է, որ ասինքրոն մեքենայի և՛ ստատորի, և՛ ռոտորի
փաթույթների տարբեր փորակներում տեղադրված գալարներում ինդուկտված էլշուները միմյանց
նկատմամբ ունեն որոշ փուլային շեղում, որի պատճառով փաթույթի ընդհանուր էլշուն փոքր
է բոլոր գալարներում ինդուկտված էլշուների թվաբանական գումարից: Այս հանգամանքը հաշվի
է առնվում, համապատասխանաբար, ստատորի և ռոտորի փաթույթների
հոսքը) ռոտորի շրջագծի երկայնքով բաշխվում է սինուսոիդական օրենքով, ուստի
ռոտորի և ստատորի փաթույթներում ինդուկտված էլշուները կլինեն սինուսոիդական մեծություններ,
որոնց գործող արժեքները կորոշվեն տրանսֆորմատորային էլշուներին համանման (տես
7.3 բաժինը): Տարբերությունը միայն այն է, որ ասինքրոն մեքենայի և՛ ստատորի, և՛ ռոտորի
փաթույթների տարբեր փորակներում տեղադրված գալարներում ինդուկտված էլշուները միմյանց
նկատմամբ ունեն որոշ փուլային շեղում, որի պատճառով փաթույթի ընդհանուր էլշուն փոքր
է բոլոր գալարներում ինդուկտված էլշուների թվաբանական գումարից: Այս հանգամանքը հաշվի
է առնվում, համապատասխանաբար, ստատորի և ռոտորի փաթույթների ![]() գործակիցների միջոցով:
գործակիցների միջոցով:
Այսպիսով, ստատորի փաթույթում ինդուկտված էլշուն կլինի
![]()
որտեղ ![]() սինուսոիդական էլշուի
հաճախությունն է և որոշվում է ըստ բանաձև (9.2)-ի՝
սինուսոիդական էլշուի
հաճախությունն է և որոշվում է ըստ բանաձև (9.2)-ի՝ ![]() ստատորի փաթույթի գալարների թիվն է, իսկ
ստատորի փաթույթի գալարների թիվն է, իսկ ![]() փաթույթի գործակիցը (սովորաբար
փաթույթի գործակիցը (սովորաբար ![]()
Համանմանորեն, ռոտորի փաթույթում ինդուկտված էլշուն
![]()
որտեղ ![]() էլշուի հաճախությունն
է: Կարճ միացված ռոտորի համար`
էլշուի հաճախությունն
է: Կարճ միացված ռոտորի համար` ![]()
Քանի որ ռոտորը պտտվում է ստատորի դաշտի ուղղությամբ,
ապա պտտվող դաշտի հոսքի հարաբերական արագությունը ռոտորի հաղորդիչների նկատմամբ կլինի
![]() Ուստի ռոտորի
Ուստի ռոտորի ![]() էլշուի հաճախությունը,
հաշվի առնելով (9.2) և (9.3) բանաձևերը, կլինի
էլշուի հաճախությունը,
հաշվի առնելով (9.2) և (9.3) բանաձևերը, կլինի
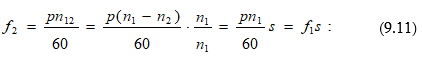
Հետևաբար (9.10) -ից ստանում ենք
![]()
որտեղ ![]() ռոտորի փաթույթի էլշուն
է անշարժ ռոտորի դեպքում (երբ s = 1):
ռոտորի փաթույթի էլշուն
է անշարժ ռոտորի դեպքում (երբ s = 1):
Այսպիսով, ռոտորի ![]() էլշուն փոխվում է սահքին ուղիղ համեմատական, այսինքն՝ այն կախված է շարժիչի
բեռնվածությունից:
էլշուն փոխվում է սահքին ուղիղ համեմատական, այսինքն՝ այն կախված է շարժիչի
բեռնվածությունից:
Ռոտորի փաթույթում ![]() էլշուն առաջ է բերում հոսանք՝
էլշուն առաջ է բերում հոսանք՝

որտեղ ![]() ռոտորի փաթույթի ակտիվ,
իսկ
ռոտորի փաթույթի ակտիվ,
իսկ ![]() ռեակտիվ դիմադրություններն են:
ռեակտիվ դիմադրություններն են:
Ռոտորի հոսանքը ստեղծում է իր սեփական պտտվող
մագնիսական դաշտը: Քանի որ ռոտորն ինքն էլ պտտվում է ![]() արագությամբ, ապա
նրա ստեղծած դաշտի պտտման արդյունարար արագությունը կլինի
արագությամբ, ապա
նրա ստեղծած դաշտի պտտման արդյունարար արագությունը կլինի
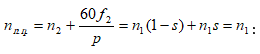
Հետևաբար, ցանկացած բեռնվածքի դեպքում (այսինքն
անկախ սահքի արժեքից) ստատորի և ռոտորի մագնիսական դաշտերը պտտվում են նույն արագությամբ,
և մեքենայի արդյունարար դաշտը ստացվում է այդ երկու դաշտերի վերադրումից: Այսպիսով,
ինչպես և տրանսֆորմատորներում, բեռնվածքի փոփոխությունը բերում է ռոտորի ![]() և ստատորի
և ստատորի ![]() հոսանքների համապատասխան
փոփոխության, որի հետևանքով մեքենայի արդյունարար դաշտի հոսքը մնում է գրեթե անփոփոխ:
հոսանքների համապատասխան
փոփոխության, որի հետևանքով մեքենայի արդյունարար դաշտի հոսքը մնում է գրեթե անփոփոխ:
Տեղադրելով ![]() արժեքները
(9.13)-ի մեջ՝ կստանանք
արժեքները
(9.13)-ի մեջ՝ կստանանք
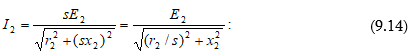
Վերջին արտահայտությունից հետևում է, որ հաշվարկների
համար, պտտվող ասինքրոն շարժիչը կարող է փոխարինվել պայմանականորեն անշարժ համարժեք
շարժիչով, որի ռոտորի փաթույթի մեկ ֆազի շղթան պարունակում է ![]() ակտիվ և
ակտիվ և ![]() ռեակտիվ դիմադրությունները:
ռեակտիվ դիմադրությունները:
Բանաձև (9.13)-ում ![]() մեծությունը կարելի է համարել ռոտորի փաթույթի
մեծությունը կարելի է համարել ռոտորի փաթույթի ![]() և սահքից կախված
և սահքից կախված ![]() ակտիվ դիմադրությունների գումար՝
ակտիվ դիմադրությունների գումար՝
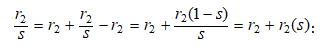
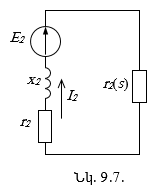
Այսպիսով, ռոտորի փաթույթի ֆազը կարելի է ներկայացնել
համարժեք սխեմայով (նկ.9.7), որտեղ ![]() դիմադրությունը հաշվի
է առնում ռոտորի փաթույթում էներգիայի կորուստները, որոնք վերածվում են ջերմային էներգիայի,
իսկ
դիմադրությունը հաշվի
է առնում ռոտորի փաթույթում էներգիայի կորուստները, որոնք վերածվում են ջերմային էներգիայի,
իսկ ![]() դիմադրությունը հաշվի է առնում այն էներգիան, որը շարժիչում փոխարկվում է էլեկտրականից՝
մեխանիկականի:
դիմադրությունը հաշվի է առնում այն էներգիան, որը շարժիչում փոխարկվում է էլեկտրականից՝
մեխանիկականի:
9.7. Ասինքրոն շարժիչի հզորությունների հաշվեկշիռը
Շարժիչի ![]() ակտիվ հզորությունը
որոշվում է որպես եռաֆազ ցանցից վերցրած այն էներգիայի միջին հզորություն, որի հիմնական
մասը շարժիչում անվերադարձ փոխակերպվում է մեխանիկական էներգիայի, իսկ մի մասն էլ՝
ջերմային կորուստների:
ակտիվ հզորությունը
որոշվում է որպես եռաֆազ ցանցից վերցրած այն էներգիայի միջին հզորություն, որի հիմնական
մասը շարժիչում անվերադարձ փոխակերպվում է մեխանիկական էներգիայի, իսկ մի մասն էլ՝
ջերմային կորուստների:
Ըստ բանաձև (4.16)-ի,
![]()
որտեղ U -ն սնման ցանցի գծային լարումն է, I
-ն՝ գծային հոսանքը, ![]() շարժիչի հզորության
գործակիցը:
շարժիչի հզորության
գործակիցը:
Ասինքրոն շարժիչի էներգետիկական դիագրամը ցույց է տալիս, թե ինչպես է տեղի ունենում էներգիայի փոխարկումը շարժիչում (նկ. 9.8):
Ցանցից վերցրած ![]() ակտիվ հզորության
մի մասը
ակտիվ հզորության
մի մասը ![]() ծախսվում է ստատորի փաթույթներում՝ վերածվելով ջերմային կորուտների: Մնացած
ծախսվում է ստատորի փաթույթներում՝ վերածվելով ջերմային կորուտների: Մնացած
![]() հզորությունը պտտվող մագնիսական դաշտի հզորությունն է:
հզորությունը պտտվող մագնիսական դաշտի հզորությունն է:
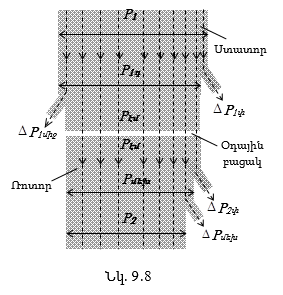
Մագնիսական դաշտը ստատորի միջուկում առաջացնում
է ![]() հզորության կորուստ, որը պայմանավորված է մրրկային հոսանքներով և հիսթերեզիսի
երևույթով: Ռոտորի միջուկում կորուստները գործնականորեն կարելի է անտեսել, քանի որ
ռոտորում մագնիսական հոսքի փոփոխման
հզորության կորուստ, որը պայմանավորված է մրրկային հոսանքներով և հիսթերեզիսի
երևույթով: Ռոտորի միջուկում կորուստները գործնականորեն կարելի է անտեսել, քանի որ
ռոտորում մագնիսական հոսքի փոփոխման ![]() փոքր հաճախության
պատճառով (ըստ բանաձև 9.11-ի,
փոքր հաճախության
պատճառով (ըստ բանաձև 9.11-ի, ![]() մրրկային հոսանքներով
և հիսթերեզիսով պայմանավորված կորուստներն աննշան են:
մրրկային հոսանքներով
և հիսթերեզիսով պայմանավորված կորուստներն աննշան են:
Ռոտորին փոխանցվող էլեկտրամագնիսական հզորությունը, ըստ դիագրամի, կլինի
![]()
Հանելով ![]() հզորությունից ռոտորի
հաղորդիչներում
հզորությունից ռոտորի
հաղորդիչներում ![]() հզորության կորուստները՝
կստանանք շարժիչի զարգացրած
հզորության կորուստները՝
կստանանք շարժիչի զարգացրած ![]() մեխանիկական հզորությունը.
մեխանիկական հզորությունը.
![]()
Լիսեռի վրա շարժիչի զարգացրած ![]() օգտակար մեխանիկական
հզորությունն ստանալու համար անհրաժեշտ է
օգտակար մեխանիկական
հզորությունն ստանալու համար անհրաժեշտ է ![]() հզորությունից հանել
շփումների (առանցքակալներում և օդի հետ) հետևանքով առաջացած
հզորությունից հանել
շփումների (առանցքակալներում և օդի հետ) հետևանքով առաջացած ![]() մեխանիկական կորուստները՝
մեխանիկական կորուստները՝ ![]()
Շարժիչի լիսեռի վրա զարգացրած ![]() մեխանիկական հզորության
հարաբերությունը սնող ցանցից վերցրած
մեխանիկական հզորության
հարաբերությունը սնող ցանցից վերցրած ![]() էլեկտրական հզորությանը,
կոչվում է շարժիչի օգտակար գործողության գործակից՝
էլեկտրական հզորությանը,
կոչվում է շարժիչի օգտակար գործողության գործակից՝

Ակնհայտ է, որ շարժիչի էլեկտրական և մեխանիկական հզորությունների տարբերությունը կներկայացնի շարժիչում հզորության գումարային կորուստները՝
![]()
Ասինքրոն շարժիչի ![]() ռեակտիվ հզորությունը պայմանավորված է պտտվող մագնիսական
դաշտի էներգիայով, որը պարբերաբար փոխանցվում է ցանցից՝ շարժիչ և շարժիչից՝ սնող ցանց:
Ռեակտիվ հզորության առկայությունը զգալիորեն փոքրացնում է շարժիչի հզորության գործակիցը
ռեակտիվ հզորությունը պայմանավորված է պտտվող մագնիսական
դաշտի էներգիայով, որը պարբերաբար փոխանցվում է ցանցից՝ շարժիչ և շարժիչից՝ սնող ցանց:
Ռեակտիվ հզորության առկայությունը զգալիորեն փոքրացնում է շարժիչի հզորության գործակիցը

սակայն անհնար է դրանից խուսափել, քանի որ առանց պտտվող մագնիսական դաշտի անհնար է ասինքրոն շարժիչի աշխատանքը:
Պտտվող մագնիսական դաշտով պայմանավորված ![]() մագնիսական հոսքը մոտավորապես հաստատուն է և կախված չէ շարժիչի բեռնվածքից,
ուստի
մագնիսական հոսքը մոտավորապես հաստատուն է և կախված չէ շարժիչի բեռնվածքից,
ուստի ![]() ռեակտիվ հզորությունը նույնպես հաստատուն է: Հետևաբար, ինչպես հետևում է բանաձև
(9.17)-ից, շարժիչի բեռնվածքի փոքրացումը բերում է նաև հզորության գործակցի փոքրացման:
Ուստի, սնող ցանցերում հզորության ավելորդ կորուստներից խուսափելու համար, անհրաժեշտ
է լրիվ օգտագործել շարժիչի անվանական հզորությունը` հնարավորության դեպքում խուսափելով
թերբեռնումներից:
ռեակտիվ հզորությունը նույնպես հաստատուն է: Հետևաբար, ինչպես հետևում է բանաձև
(9.17)-ից, շարժիչի բեռնվածքի փոքրացումը բերում է նաև հզորության գործակցի փոքրացման:
Ուստի, սնող ցանցերում հզորության ավելորդ կորուստներից խուսափելու համար, անհրաժեշտ
է լրիվ օգտագործել շարժիչի անվանական հզորությունը` հնարավորության դեպքում խուսափելով
թերբեռնումներից:
Խնդիր 9.2.
Որոշել եռաֆազ ասինխրոն շարժիչի էլեկտրական հզորությունը և օ.գ.գ.-ն, եթե գծային լարումը
U = 380 Վ, շարժիչի մեխանիկական հզորությունը` ![]() հոսանքը
սնող գծերում` I = 22 Ա և հզորության գործակիցը`
հոսանքը
սնող գծերում` I = 22 Ա և հզորության գործակիցը` ![]()
Լուծում. Օգտվելով (9.5) բանաձևից` որոշում ենք եռաֆազ ցանցից շարժիչի վերցրած ակտիվ հզորությունը`

9.8. Ասինքրոն շարժիչի էլեկտրամագնիսական մոմենտը և մեխանիկական բնութագիծը
Շարժիչի ![]() էլեկտրամագնիսական
հզորությունը կարելի է արտահայտել մեխանիկական մեծություններով՝
էլեկտրամագնիսական
հզորությունը կարելի է արտահայտել մեխանիկական մեծություններով՝
![]()
որտեղ M -ը շարժիչի զարգացրած էլեկտրամագնիսական
մոմենտն է, իսկ ![]() պտտվող դաշտի անկյունային արագությունը:
պտտվող դաշտի անկյունային արագությունը:
Համաձայն էներգետիկական դիագրամի (նկ. 9.8), կորուստները ռոտորի փաթույթում
![]()
Այսինքն՝ ռոտորի փաթույթում հզորության կորուստները համեմատական են սահքին (բեռնվածքին): Ստացված արտահայտությունից`

Մյուս կողմից` ![]() կորուստները, հաշվի առնելով (9.13) բանաձևը, կարելի է ներկայացնել հետևյալ
տեսքով՝
կորուստները, հաշվի առնելով (9.13) բանաձևը, կարելի է ներկայացնել հետևյալ
տեսքով՝
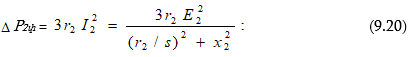
Տեղադրելով (9.20)-ը (9.19)-ի մեջ՝ շարժիչի զարգացրած մոմենտի համար կստանանք
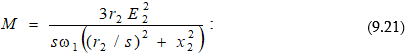
Անշարժ ռոտորի փաթույթում ինդուկտված ![]() էլշուն ուղիղ համեմատական
է պտտվող դաշտի հոսքին, որն էլ, իր հերթին, ուղիղ համեմատական է ստատորի փաթույթին
կիրառված U լարմանը, ուստի շարժիչի զարգացրած մոմենտը, ըստ (9.21)-ի, ուղիղ համեմատական
կլինի U լարման քառակուսուն: Այսպիսով, շարժիչի զարգացրած մոմենտը, տրված U լարման
դեպքում, կախված է միայն սահքից: Այդ կախվածության M(s) կորը բերված է նկ. 9.9-ում:
էլշուն ուղիղ համեմատական
է պտտվող դաշտի հոսքին, որն էլ, իր հերթին, ուղիղ համեմատական է ստատորի փաթույթին
կիրառված U լարմանը, ուստի շարժիչի զարգացրած մոմենտը, ըստ (9.21)-ի, ուղիղ համեմատական
կլինի U լարման քառակուսուն: Այսպիսով, շարժիչի զարգացրած մոմենտը, տրված U լարման
դեպքում, կախված է միայն սահքից: Այդ կախվածության M(s) կորը բերված է նկ. 9.9-ում:
Ածանցելով M(s) ֆունկցիան ըստ s-ի և լուծելով
![]() հավասարումը՝ կարելի է որոշել սահքի այն
հավասարումը՝ կարելի է որոշել սահքի այն ![]() արժեքը, որի դեպքում շարժիչը զարգացնում է առավելագույն կամ կրիտիկական
արժեքը, որի դեպքում շարժիչը զարգացնում է առավելագույն կամ կրիտիկական ![]() մոմենտ.
մոմենտ.
![]()
Ասինքրոն շարժիչների մեծ մասի համար ![]()
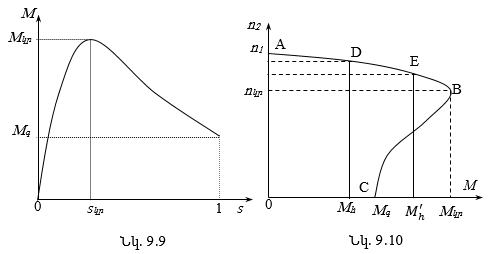
Տեղադրելով (9.22) -ից ![]() արժեքը (9.21) -ի մեջ՝ կստանանք
արժեքը (9.21) -ի մեջ՝ կստանանք

Ուշագրավ է, որ ասինքրոն շարժիչի առավելագույն
![]() մոմենտը նույնպես կախված է սնող ցանցի լարման քառակուսուց, բայց կախված չէ
ռոտորի փաթույթի ֆազի
մոմենտը նույնպես կախված է սնող ցանցի լարման քառակուսուց, բայց կախված չէ
ռոտորի փաթույթի ֆազի ![]() ակտիվ դիմադրությունից:
ակտիվ դիմադրությունից:
Հաշվի առնելով (9.22) և (9.23) բանաձևերը՝ մոմենտի (9.21) բանաձևը հարմար է գրել հետևյալ պարզեցված տեսքով.

Եթե ասինքրոն շարժիչի անվանական պարամետրերը հայտնի
են, ապա M(s) բնութագիծը կարող է կառուցվել (9.24) պարզեցված բանաձևի օգնությամբ: Առավելագույն
մոմենտի արժեքը որոշվում է ![]() բանաձևով, որտեղ
բանաձևով, որտեղ ![]() անվանական մոմենտն է, իսկ
անվանական մոմենտն է, իսկ ![]() կոչվում է շարժիչի
գերբեռնման գործակից, որի արժեքը տրվում է տեղեկատուներում: Կախված շարժիչի աշխատանքի
ռեժիմից՝
կոչվում է շարժիչի
գերբեռնման գործակից, որի արժեքը տրվում է տեղեկատուներում: Կախված շարժիչի աշխատանքի
ռեժիմից՝ ![]()
Շարժիչի շահագործման հետ կապված էլեկտրամագնիսական
պրոցեսների ուսումնասիրման տեսակետից ավելի հարմար է գիտենալ ռոտորի պտտման արագության
և զարգացրած մոմենտի կապը՝ ![]() կախվածության գրաֆիկը,
որը կոչվում է մեխանիկական բնութագիծ (նկ. 9.10):
կախվածության գրաֆիկը,
որը կոչվում է մեխանիկական բնութագիծ (նկ. 9.10):
Ռոտորի այն արագությունը, որի դեպքում շարժիչը
զարգացնում է առավելագույն ![]() մոմենտ, կոչվում է
կրիտիկական արագություն: Ակնհայտ է, որ
մոմենտ, կոչվում է
կրիտիկական արագություն: Ակնհայտ է, որ
![]()
Անշարժ ռոտորի դեպքում ![]() շարժիչի զարգացրած
շարժիչի զարգացրած ![]() մոմենտը կոչվում է
գործարկման մոմենտ: Այդպիսի մոմենտ է զարգացնում ասինքրոն շարժիչը գործարկման առաջին
ակնթարթին: Տեղադրելով (9.21) բանաձևում s = 1, գործարկման մոմենտի համար կստանանք`
մոմենտը կոչվում է
գործարկման մոմենտ: Այդպիսի մոմենտ է զարգացնում ասինքրոն շարժիչը գործարկման առաջին
ակնթարթին: Տեղադրելով (9.21) բանաձևում s = 1, գործարկման մոմենտի համար կստանանք`
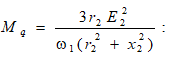
Գործարկման մոմենտի մեծությունը կարելի է որոշել
նաև ![]() բանաձևով, որտեղ
բանաձևով, որտեղ ![]() գործակիցը տվյալ շարժիչի համար տրվում է տեղեկատուներում: Այն ցույց է տալիս,
թե գործարկման առաջին ակնթարթին շարժիչն անվանական մոմենտից քանի անգամ մեծ մոմենտ
կարող է զարգացնել: Կախված գործարկման պայմաններից՝ տարբեր շարժիչների համար
գործակիցը տվյալ շարժիչի համար տրվում է տեղեկատուներում: Այն ցույց է տալիս,
թե գործարկման առաջին ակնթարթին շարժիչն անվանական մոմենտից քանի անգամ մեծ մոմենտ
կարող է զարգացնել: Կախված գործարկման պայմաններից՝ տարբեր շարժիչների համար ![]()
Դիտարկենք ասինքրոն շարժիչի աշխատանքը մեխանիզմի
հետ: Դիցուք՝ մեխանիզմը (բեռնվածքը) շարժիչի լիսեռի վրա ստեղծում է հաստատուն ![]() հակազդող մոմենտ (նկ.9.10): Շարժիչն այսպիսի բեռնվածքով կարող է գործարկվել,
քանի որ շարժիչի զարգացրած գործարկման մոմենտը գերազանցում է հակազդող մոմենտը՝
հակազդող մոմենտ (նկ.9.10): Շարժիչն այսպիսի բեռնվածքով կարող է գործարկվել,
քանի որ շարժիչի զարգացրած գործարկման մոմենտը գերազանցում է հակազդող մոմենտը՝ ![]() Գործարկվելով՝ ռոտորի արագությունը կմեծանա, և այն կպտտվի այնպիսի հաստատուն
արագությամբ, որի դեպքում լիսեռի վրա M պտտող և
Գործարկվելով՝ ռոտորի արագությունը կմեծանա, և այն կպտտվի այնպիսի հաստատուն
արագությամբ, որի դեպքում լիսեռի վրա M պտտող և ![]() հակազդող մոմենտները կհավասարվեն (բնութագծի D կետը):
հակազդող մոմենտները կհավասարվեն (բնութագծի D կետը):
Ասինքրոն շարժիչները, ինչպես և մյուս էլեկտրական մեքենաները օժտված են ինքնակարգավորման հատկությամբ: Եթե փոփոխվում է բեռնվածքի առաջացրած հակազդող մոմենտը, ավտոմատորեն փոփոխվում է նաև մեքենայի պտտող մոմենտը և լիսեռի վրա վերականգնվում է մոմենտների խախտված հավասարակշռությունը:
Ասինքրոն շարժիչում մոմենտների հավասարակշռությունը
հետևյալ կերպ է տեղի ունենում. լիսեռի վրա բեռնվածքը մեծացնելիս ![]() հակազդող մոմենտը դառնում է ավելի մեծ, քան M պտտող մոմենտը, որի հետևանքով
ռոտորի
հակազդող մոմենտը դառնում է ավելի մեծ, քան M պտտող մոմենտը, որի հետևանքով
ռոտորի ![]() արագությունը փոքրանում է, իսկ սահքը, ըստ (9.3)-ի, մեծանում է: Ինչպես երևում
է մեխանիկական բնութագծից (նկ. 9.10),
արագությունը փոքրանում է, իսկ սահքը, ըստ (9.3)-ի, մեծանում է: Ինչպես երևում
է մեխանիկական բնութագծից (նկ. 9.10), ![]() փոքրացումը բերում
է պտտող մոմենտի մեծացման, և հավասարակշռությունը վերականգնվում է ավելի փոքր արագության
(ավելի մեծ սահքի) դեպքում: Սահքի մեծացման հետ մոմենտների հավասարակշռությունն ավտոմատորեն
վերականգնվում է այնքան ժամանակ, քանի դեռ
փոքրացումը բերում
է պտտող մոմենտի մեծացման, և հավասարակշռությունը վերականգնվում է ավելի փոքր արագության
(ավելի մեծ սահքի) դեպքում: Սահքի մեծացման հետ մոմենտների հավասարակշռությունն ավտոմատորեն
վերականգնվում է այնքան ժամանակ, քանի դեռ ![]() Երբ արգելակող մոմենտը
հավասարվում է
Երբ արգելակող մոմենտը
հավասարվում է ![]() ապա բեռի հետագա մեծացման
հետ սահքի մեծացումը բերում է միայն պտտող մոմենտի փոքրացման, որը խախտում է դինամիկ
հավասարակշռությունը, շարժիչը արգելակվում է և կանգ է առնում (բնութագծի C կետը):
ապա բեռի հետագա մեծացման
հետ սահքի մեծացումը բերում է միայն պտտող մոմենտի փոքրացման, որը խախտում է դինամիկ
հավասարակշռությունը, շարժիչը արգելակվում է և կանգ է առնում (բնութագծի C կետը):
Այսպիսով, շարժիչի կայուն աշխատանքը հնարավոր
է միայն բնութագծի A-B տեղամասում և, հետևաբար, ռոտորի արագությունը կարող է փոփոխվել
միայն ![]() միջակայքում
միջակայքում ![]() նկատմամբ մոտ 10%
-15% սահմաններում):
նկատմամբ մոտ 10%
-15% սահմաններում):
Եթե շարժիչի լիսեռին կիրառվի ![]() հաստատուն հակազդող մոմենտ, ապա, ակնհայտ է, որ շարժիչը այդ բեռնվածքով չի
կարող գործարկվել: Սակայն, եթե շարժիչը գործարկվի առանց բեռնվածքի (պարապ ընթացքով)
և ապա կիրառվի
հաստատուն հակազդող մոմենտ, ապա, ակնհայտ է, որ շարժիչը այդ բեռնվածքով չի
կարող գործարկվել: Սակայն, եթե շարժիչը գործարկվի առանց բեռնվածքի (պարապ ընթացքով)
և ապա կիրառվի ![]() ապա շարժիչը կկարողանա
աշխատեցնել այդ մեխանիզմը՝ զարգացնելով
ապա շարժիչը կկարողանա
աշխատեցնել այդ մեխանիզմը՝ զարգացնելով ![]() պտտող մոմենտ (E կետը):
պտտող մոմենտ (E կետը):
9.9. Սնող ցանցի լարման ազդեցությունն ասինքրոն շարժիչի աշխատանքի վրա
Ինչպես ասվեց նախորդ բաժնում, ասինքրոն շարժիչի
առավելագույն ![]() մոմենտը կախված է սնող ցանցի լարման քառակուսուց, իսկ այդ մոմենտին համապատասխանող
մոմենտը կախված է սնող ցանցի լարման քառակուսուց, իսկ այդ մոմենտին համապատասխանող
![]() սահքը, ըստ բանաձև (9.22)-ի, կախված չէ լարումից, ուստի կրիտիկական
սահքը, ըստ բանաձև (9.22)-ի, կախված չէ լարումից, ուստի կրիտիկական ![]() արագությունը նույնպես
կախված չէ լարումից: Հետևաբար ասինքրոն շարժիչի տարբեր լարումներին համապատասխանող
մեխանիկական բնութագծերը կունենան նկ 9.11-ում պատկերված տեսքը:
արագությունը նույնպես
կախված չէ լարումից: Հետևաբար ասինքրոն շարժիչի տարբեր լարումներին համապատասխանող
մեխանիկական բնութագծերը կունենան նկ 9.11-ում պատկերված տեսքը:
Ցանցի ![]() անվանական լարմանը
համապատասխանող բնութագիծը կոչվում է բնական մեխանիկական բնութագիծ:
անվանական լարմանը
համապատասխանող բնութագիծը կոչվում է բնական մեխանիկական բնութագիծ:
Դիցուք՝ շարժիչի լիսեռին կիրառված է ![]() հաստատուն հակազդող մոմենտը: Եթե շարժիչին կիրառված լարումը շատ չի տարբերվում
անվանական արժեքից, ապա այն կգործարկվի, քանի որ
հաստատուն հակազդող մոմենտը: Եթե շարժիչին կիրառված լարումը շատ չի տարբերվում
անվանական արժեքից, ապա այն կգործարկվի, քանի որ ![]()
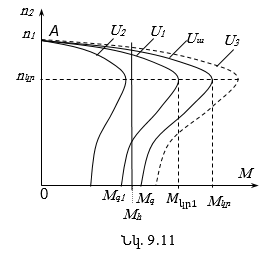
Երբ ցանցի լարումն ընկնի մինչև ![]() անվանական արժեքից (10…20)% ցածր (նկ.9.11-ում
անվանական արժեքից (10…20)% ցածր (նկ.9.11-ում ![]() համապատասխանող կորը), ապա շարժիչում կառաջանան մի շարք բացասական երևույթներ.
համապատասխանող կորը), ապա շարժիչում կառաջանան մի շարք բացասական երևույթներ.
·
շարժիչը չի գործարկվի կիրառված ![]() բեռնվածքի դեպքում, քանի որ
բեռնվածքի դեպքում, քանի որ ![]()
·
նույն ակտիվ հզորությունը ![]() զարգացնելու համար կմեծանա շարժիչի
զարգացնելու համար կմեծանա շարժիչի ![]() հոսանքը, որն, իր
հերթին, կբերի փաթույթներում
հոսանքը, որն, իր
հերթին, կբերի փաթույթներում ![]() հզորության կորստի
քառակուսային մեծացման և, հետևաբար, շարժիչի գերտաքացման և դրա ծառայության ժամկետի
կրճատման,
հզորության կորստի
քառակուսային մեծացման և, հետևաբար, շարժիչի գերտաքացման և դրա ծառայության ժամկետի
կրճատման,
·
կփոքրանա շարժիչի գերբեռնման գործակիցը՝ ![]() և նրա աշխատանքը կդառնա անկայուն կարճատև գերբեռնումների դեպքում:
և նրա աշխատանքը կդառնա անկայուն կարճատև գերբեռնումների դեպքում:
Երբ ցանցի լարումն ավելի է ընկնում, հասնելով
![]() (կամ
(կամ ![]() ցածր), ասինքրոն շարժիչը
ընդհանրապես ի վիճակի չի լինի աշխատել
ցածր), ասինքրոն շարժիչը
ընդհանրապես ի վիճակի չի լինի աշխատել ![]() բեռնվածքով, քանի
որ
բեռնվածքով, քանի
որ ![]()
Ցանցի լարման բարձրացումը, չնայած անմիջականորեն
չի վատացնում շարժիչի շահագործողական հատկությունները, սակայն նույնպես ցանկալի չէ.
այն առաջացնում է շարժիչի գերտաքացում՝ միջուկում կորուստների մեծացման պատճառով, չնայած
փաթույթներում հոսանքի որոշ նվազմանը: Բացի այդ, երբ ![]() փոքրանում է շարժիչի հզորության գործակիցը
փոքրանում է շարժիչի հզորության գործակիցը ![]() սնող ցանցում պատճառելով ավելի մեծ հզորության կորուստներ:
սնող ցանցում պատճառելով ավելի մեծ հզորության կորուստներ:
Այսպիսով, վերլուծությունը ցույց է տալիս, որ
ասինքրոն շարժիչները շատ զգայուն են սնող ցանցի լարման նկատմամբ, ուստի դրանց համար
լարման շեղումը անվանականից չպետք է գերազանցի 5%-ից, այսինքն, ![]() Որոշ դեպքերում նշված միջակայքը թույլատրվում է ընդլայնել մինչև +10%:
Որոշ դեպքերում նշված միջակայքը թույլատրվում է ընդլայնել մինչև +10%:
9.10. Կարճ միացված ռոտորով ասինքրոն շարժիչի գործարկումը
Ընդհանրապես շարժիչի գործարկում է կոչվում անցումային այն պրոցեսը, որը տեղի է ունենում շարժիչը սնող ցանցին միացնելու առաջին ակնթարթից մինչև լրիվ արագություն ձեռք բերելը: Գրեթե բոլոր էլեկտրական շարժիչներին հատուկ է գործարկման մեծ հոսանքը, որը փոքրանում է արագություն ձեռք բերելուն զուգընթաց: Բացառություն չէ նաև ասինքրոն շարժիչը:
Գործարկման առաջին պահին, երբ ստատորի եռաֆազ
փաթույթը միացված է ցանցին, իսկ ռոտորը իր իներցիայի պատճառով դեռևս անշարժ է, ասինքրոն
շարժիչը նման է վթարային կարճ միացման ռեժիմում գտնվող տրանսֆորմատորի. այս դեպքում
ստատորի փաթույթը հանդես է գալիս որպես առաջնային փաթույթ, իսկ ռոտորի կարճ միացված
փաթույթը («սկյուռի անիվը»)՝ որպես երկրորդային փաթույթ: Սակայն, ի տարբերություն տրանսֆորմատորի,
որի վթարային կարճ միացման հոսանքը 10…20 անգամ էր գերազանցում անվանական արժեքը (տե՛ս
բաժին 8.6.2), ասինքրոն շարժիչի գործարկման հոսանքը միայն 5…7 անգամ է գերազանցում
անվանական արժեքը՝ ![]() Դա հիմնականում պայմանավորված
է շարժիչի համեմատաբար մեծ ինդուկտիվությամբ, որն, իր հերթին, պայմանավորված է ստատորի
և ռոտորի մագնիսահաղորդիչների միջև առկա օդային բացակով:
Դա հիմնականում պայմանավորված
է շարժիչի համեմատաբար մեծ ինդուկտիվությամբ, որն, իր հերթին, պայմանավորված է ստատորի
և ռոտորի մագնիսահաղորդիչների միջև առկա օդային բացակով:
Եթե գործարկումները հաճախակի չեն, ապա այսպիսի հոսանքն իր կարճատևության պատճառով1 վտանգ չի ներկայացնում գործարկվող շարժիչի համար, սակայն սնող գծերում այն կարող է առաջացնել մեծ լարման անկումներ, որի հետևանքով լարումը այդ ցանցից սնվող սպառիչների սեղմակներում կարող է անթույլատրելիորեն փոքրանալ և բացասաբար անդրադառնալ դրանց աշխատանքի վրա, հատկապես եթե դրանք աշխատող ասինքրոն շարժիչներ են (տե՛ս բաժին 9.9): Բացասական հետևանքներն այնքան ավելի մեծ կլինեն, որքան մեծ է գործարկվող շարժիչի հզորությունը և որքան փոքր է սնող ցանցի հզորությունը: Ժամանակակից արդյունաբերական ցանցերում թույլատրվում է անմիջականորեն գործարկել մինչև 100 կՎտ հզորությամբ շարժիչները, իսկ առանձին գերհզոր ցանցերում՝ նույնիսկ մինչև 1000 կՎտ:
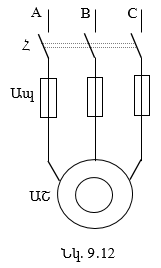
Նկ. 12-ում ցույց է տրված կարճ միացված ռոտորով ասինքրոն շարժիչի անմիջական գործարկման սխեման, ինչի համար անհրաժեշտ է պարզապես միացնել Հ հատիչը (եռաբևեռ անջատիչը): Շատ կարևոր է, որ հատիչի 3 կոնտակտները (դանակները) միաժամանակ միանան սնող ցանցին: Եթե որևէ պատճառով դրանցից միայն 2-ը միանան, ապա շարժիչը կհայտնվի «2 ֆազի տակ», նրանում պտտվող դաշտ չի առաջա-նա, ռոտորը չի պտտվի, իսկ շարժիչի առնվազն 2 փաթույթներով անցնող գործարկման մեծ և երկարատև հոսանքը առաջ կբերի շարժիչի համար վտանգավոր գերտաքացման:
Էլեկտրաշարժիչների պաշտպանության համար օգտագործում են դյուրահալ ապահովիչներ (Ապ) կամ ավտոմատ անջատիչներ, որոնց հոսանքն ընտրվում է ըստ հետևյալ 2 պայմանների.
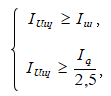
որտեղ ![]() ապահովիչի (կամ ավտոմատ
անջատիչի) անվանական հոսանքն է, այսինքն այն հոսանքը, որ երկարատև կարող է անցնել դրա
միջով` չանջատելով այն,
ապահովիչի (կամ ավտոմատ
անջատիչի) անվանական հոսանքն է, այսինքն այն հոսանքը, որ երկարատև կարող է անցնել դրա
միջով` չանջատելով այն, ![]() շարժիչի անվանական,
իսկ
շարժիչի անվանական,
իսկ ![]() գործարկման հոսանքներն են, երկրորդ արտահայտության 2,5 գործակիցը հաշվի է առնում
գործարկման հոսանքի կարճատևությունը:
գործարկման հոսանքներն են, երկրորդ արտահայտության 2,5 գործակիցը հաշվի է առնում
գործարկման հոսանքի կարճատևությունը:
Եռաֆազ ասինքրոն շարժիչի ռոտորի պտտման ուղղությունը փոխելու (ռևերսի) համար բավական է փոխել ցանկացած 2 ֆազերի տեղերը:
Կարճ միացված ռոտորով ասինքրոն շարժիչների գործարկման հոսանքի սահմանափակման համար մշակված են մի շարք եղանակներ. լրացուցիչ ակտիվ կամ ինդուկտիվ դիմադրությունների հաջորդական միացում ստատորի փաթույթներին, գործարկում ավտոտրանսֆորմատորի միջոցով, ստատորի եռաֆազ փաթույթների միացման ձևի փոփոխություն (աստղաձևից՝ եռանկյունաձև) և այլն:
Սակայն թվարկված բոլոր եղանակներն էլ ունեն մի էական թերություն. գործարկման հոսանքի փոքրացումը փաստորեն իրագործվում է այս կամ այն ձևով ստատորի ֆազային փաթույթի սեղմակներում լարումը փոքրացնելով, որն անխուսափելիորեն բերում է շարժիչի զարգացրած գործարկման մոմենտի քառակուսային փոքրացման: Հետևաբար անհնար է դառնում շարժիչների կիրառումը գործարկման քիչ թե շատ ծանր պայմանների դեպքում, ուստի երբ անհրաժեշտ է զարգացնել մեծ գործարկման մոմենտ ոչ մեծ գործարկման հոսանքի դեպքում, կիրառում են ֆազային ռոտորով ասինքրոն շարժիչներ:
9.11. Ֆազային ռոտորով ասինքրոն շարժիչների գործարկումը
Ինչպես նշվեց բաժին 9.1-ում, ֆազային ռոտորով
շարժիչների կառուցվածքը թույլ է տալիս անհրաժեշտության դեպքում ![]() լրացուցիչ ակտիվ դիմադրություն
միացնել ռոտորի փաթույթին (նկ. 9.13ա):
լրացուցիչ ակտիվ դիմադրություն
միացնել ռոտորի փաթույթին (նկ. 9.13ա):
Ռոտորի շղթայում լրացուցիչ դիմադրություններ մտցնելը
փոխում է ռոտորի արագության և պտտող մոմենտի միջև ![]() կախվածության բնույթը.
hամաձայն (9.17)-ի և (9.18)-ի, շարժիչի զարգացրած առավելագույն
կախվածության բնույթը.
hամաձայն (9.17)-ի և (9.18)-ի, շարժիչի զարգացրած առավելագույն ![]() մոմենտը չի փոխվում,
բայց այն զարգացվում է ավելի մեծ
մոմենտը չի փոխվում,
բայց այն զարգացվում է ավելի մեծ ![]() կրիտիկական սահքի
(ավելի փոքր
կրիտիկական սահքի
(ավելի փոքր ![]() արագության) դեպքում: Այդ պատճառով ասինքրոն շարժիչի մեխանիկական բնութագծերը
ռոտորի շղթայի տարբեր դիմադրությունների դեպքում կունենան նկ. 9.13բ-ում պատկերված
տեսքը:
արագության) դեպքում: Այդ պատճառով ասինքրոն շարժիչի մեխանիկական բնութագծերը
ռոտորի շղթայի տարբեր դիմադրությունների դեպքում կունենան նկ. 9.13բ-ում պատկերված
տեսքը:
Դիտարկենք ֆազային ռոտորով ասինքրոն շարժիչի
գործարկման պրոցեսը՝ ընդունելով, որ դրա լիսեռին միացված է մեխանիկական բեռնվածք ![]() հակազդող հաստատուն մոմենտով: Գործակման ընթացքը պատկերող բնութագիծը նկ.
9.13բ-ում ցույց է տրված հաստ գծով:
հակազդող հաստատուն մոմենտով: Գործակման ընթացքը պատկերող բնութագիծը նկ.
9.13բ-ում ցույց է տրված հաստ գծով:
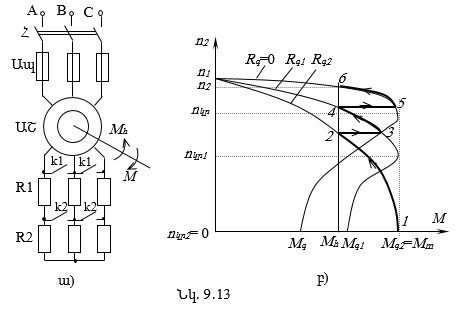
Շարժիչի գործարկման համար անհրաժեշտ է k1 և
k2 բանալիների բաց վիճակում միացնել Հ եռաֆազ հատիչը (նկ. 9.13ա): Այս դեպքում շարժիչը
կգործարկվի, երբ ռոտորի փաթույթի ֆազերին հաջորդաբար միացված ![]() գործարկման դիմադրություններով: Այդ դիմադրություններն ընտրում են այն հաշվով,
որ ռոտորի շղթայում գումարային ակտիվ դիմադրությունը հավասար լինի ինդուկտիվ դիմադրությանը`
գործարկման դիմադրություններով: Այդ դիմադրություններն ընտրում են այն հաշվով,
որ ռոտորի շղթայում գումարային ակտիվ դիմադրությունը հավասար լինի ինդուկտիվ դիմադրությանը`
![]() Այդ դեպքում, ըստ (9.22)-ի,
Այդ դեպքում, ըստ (9.22)-ի, ![]() և շարժիչը լիսեռի
վրա կզարգացնի առավելագույն մոմենտին հավասար գործարկման մոմենտ
և շարժիչը լիսեռի
վրա կզարգացնի առավելագույն մոմենտին հավասար գործարկման մոմենտ ![]() (նկ. 9.13բ-ում 1 կետը):
(նկ. 9.13բ-ում 1 կետը):
Երբ շարժիչի լիսեռի վրա ազդող պտտող և հակազդող
մոմենտները հավասարվեն (նկ. 9.13բ-ում 2 կետը), և ռոտորի արագությունը կայունանա, միացնում
են k2 բանալին և ռոտորի շղթայում միացված գործարկման դիմադրությունը փոքրանում է` դառնալով
![]() Քանի որ ռոտորի արագությունը չի կարող ակնթարթորեն փոխվել, ապա նույն արագության
դեպքում գործարկման պրոցեսը 2 կետից տեղափոխվում է 3 կետ, շարժիչի պտտող մոմենտը մեծանում
է, և այն արագանում է` մինչև նոր հավասարակշռություն է հաստատվում պտտող և հակազդող
մոմենտների միջև (4 կետը):
Քանի որ ռոտորի արագությունը չի կարող ակնթարթորեն փոխվել, ապա նույն արագության
դեպքում գործարկման պրոցեսը 2 կետից տեղափոխվում է 3 կետ, շարժիչի պտտող մոմենտը մեծանում
է, և այն արագանում է` մինչև նոր հավասարակշռություն է հաստատվում պտտող և հակազդող
մոմենտների միջև (4 կետը):
Վերջապես, միացնելով k1 բանալին, գործարկման դիմադրությունները
դուրս են բերվում ռոտորի շղթայից ![]() որի արդյունքում շարժիչը
աշխատում է
որի արդյունքում շարժիչը
աշխատում է ![]() բեռով՝ զարգացնելով
բեռով՝ զարգացնելով
![]() արագություն (6 կետը):
Գործնականում, սովորաբար, գործարկման նկարագրված պրոցեսը ավտոմատացվում է:
արագություն (6 կետը):
Գործնականում, սովորաբար, գործարկման նկարագրված պրոցեսը ավտոմատացվում է:
Որպեսզի գործարկման դիմադրության ռեզիստիվ տարրերը շատ չտաքանան, դրանց հզորությունը պետք է գրեթե նույն կարգի լինի, ինչ որ շարժիչի հզորությունը: Իհարկե, գործարկման դիմադրության կիրառումը էապես բարելավում է գործարկման պայմանները, սակայն, մյուս կողմից, այն զգալիորեն բարձրացնում է շարժիչի արժեքը, բարդացնում դրա շահագործումը: Ուստի ֆազային ռոտորով ասինքրոն շարժիչները կիրառվում են միայն խիստ անհրաժեշտության դեպքում:
9.12. Բարելավված գործարկման հատկություններով ասինքրոն շարժիչներ
Վերջին ժամանակներս այն մեխանիզմների համար, որոնք ունեն գործարկման ծանր պայմաններ (պահանջվում է մեծ գործարկման մոմենտ) լայն կիրառություն են գտել բարելավված գործարկման հատկություններով կարճ միացված ռոտորով ասինքրոն շարժիչները, որոնք զարգացնում են ավելի մեծ գործարկման մոմենտ և ունեն ավելի փոքր գործարկման հոսանք, քան ընդհանուր օգտագործման շարժիչները: Այս շարժիչները, չնայած իրենց բազմազանությանը, տարբերվում են վերջիններից միայն ռոտորի կարճ միացված փաթույթի կառուցվածքով («սկյուռի անիվով»):
Նկ. 9.14-ում պատկերված են այդպիսի շարժիչների երկու տարբերակներ, որոնցից մեկում ռոտորի վրա տեղադրված են համակենտրոն դասավորված երկու անկախ «սկյուռի անիվներ» (նկ. 9.14ա), իսկ մյուսում՝ նեղ և երկար ուղղանկյունաձև ձողերով մեկ «սկյուռի անիվ» (նկ. 9.14բ):
Նկ. 9.14ա-ում կրկնակի «սկյուռի անիվներից» արտաքինը (1) գործարկման փաթույթն է, ներքինը (2)՝ աշխատանքայինը:
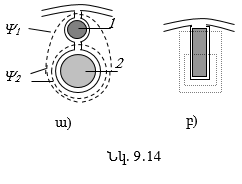
Արտաքին «սկյուռի անիվի» ձողերը պատրաստվում
են փոքր լայնական հատույթով մեծ տեսակարար դիմադրություն ունեցող հաղորդչից (օրինակ,
մանգանի և անագի համաձուլվածքից), իսկ ներքինը՝ ավելի մեծ հատույթի լավ հաղորդիչ նյութից
(օրինակ, պղնձից): Այդ պատճառով արտաքին ձողերի ակտիվ դիմադրությունը զգալիորեն ավելի
մեծ է, քան ներքին ձողերինը՝ ![]() Սակայն,
այսպիսի դասավորության շնորհիվ արտաքին անիվի ձողերի ինդուկտիվությունը ստացվում է
շատ ավելի փոքր, քան ներքինինը՝
Սակայն,
այսպիսի դասավորության շնորհիվ արտաքին անիվի ձողերի ինդուկտիվությունը ստացվում է
շատ ավելի փոքր, քան ներքինինը՝ ![]() որովհետև
օդային բացակի պատճառով հոսքակցումը առաջինների մոտ կլինի ավելի փոքր՝
որովհետև
օդային բացակի պատճառով հոսքակցումը առաջինների մոտ կլինի ավելի փոքր՝ ![]() (նկ. 9.14ա):
(նկ. 9.14ա):
Գործարկման առաջին ակնթարթին, երբ ռոտորը դեռ անշարժ է, դրա փաթույթում ինդուկտված հոսանքի հաճախությունը նույնն է, ինչ որ ցանցի լարման հաճախությունը: Այս պայմաններում ներքին ձողերի լրիվ դիմադրությունը գերազանցում է արտաքին ձողերի լրիվ դիմադրությունը, ի հաշիվ ինդուկտիվ մեծ դիմադրության: Հետևաբար, հոսանքը հիմնականում անցնում է արտաքին՝ ավելի մեծ ակտիվ դիմադրություն ունեցող, ձողերով, որով և պայմանավորված է շարժիչի զարգացրած համեմատաբար մեծ գործարկման մոմենտը ավելի փոքր գործարկման հոսանքի դեպքում:
Երբ շարժիչը արագություն է ձեռք բերում, ռոտորի ձողերում հոսանքի հաճախությունը, հետևաբար նաև ձողերի ինդուկտիվությունը, դառնում է աննշան, և հոսանքը հիմնականում անցնում է փոքր ակտիվ դիմադրությամբ ներքին ձողերով:
Համանման երևույթներ են տեղի ունենում նաև խորը փորակով ասինքրոն շարժիչներում (նկ. 9.14բ): Գործարկման պահին ձողերի ներքին մասերի հոսքակցումը և, հետևաբար, ինդուկտիվությունը մեծանում է, և հոսանքը դուրս է մղվում ձողերի արտաքին շերտերը, որի պատճառով հոսանքի անցման էֆեկտիվ մակերեսը փոքրանում է, և ակտիվ դիմադրությունը ստացվում է մեծ: Գործարկումից հետո ձողերի ինդուկտիվ դիմադրությունը դառնում է աննշան, հոսանքն անցնում է ամբողջ մակերեսով, և հոսանքին ցուցաբերված ակտիվ դիմադրությունը փոքրանում է:
Այսպիսով, դիտարկված շարժիչներում գործարկման ժամանակ ավտոմատորեն ապահովվում են գրեթե նույն պայմանները, ինչը ֆազային ռոտորով ասինքրոն շարժիչներում իրականացվում էր կոնտակտային օղակների և լրացուցիչ դիմադրությունների միջոցով: Այս շարժիչների կառուցվածքը մի փոքր բարդանում, և արժեքը մեծանում է, սակայն նրանք հիմնականում պահպանում են կարճ միացված ռոտորով շարժիչների արժանիքները, որով էլ պայմանավորված է դրանց ավելի լայն կիրառությունը:
9.13. Ասինքրոն շարժիչի արագության կարգավորումը
Կարգավորել շարժիչի արագությունը նշանակում է կարողանալ փոփոխել այն տեխնոլոգիայի պահանջներին համապատասխան կամ այն պահել հաստատուն: Մեծ մասամբ եռաֆազ ասինքրոն շարժիչները կիրառվում են այնպիսի մեխանիզմների հետ, որոնք չեն պահանջում պտտման արագության կարգավորում: Սակայն ասինքրոն շարժիչները, ինչպես արդեն նշվել է, օժտված են մի շարք արժանիքներով, ինչպիսիք են կառուցվածքի պարզությունը, հուսալիությունը, ցածր ինքնարժեքը և բարձր օ.գ.գ.-ն: Ուստի ձգտում են այդ շարժիչներն օգտագործել նաև կարգավորվող պտտման արագությամբ մեխանիզմների հետ:
Ըստ (9.2) և (9.3) բանաձևերի, ասինքրոն շարժիչի ռոտորի պտուտաթվերը
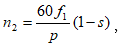
որտեղից երևում է, որ n2 արագությունը կարելի
է կարգավորել` փոփոխելով կամ մեքենայի s սահքը կամ ստատորի փաթույթների p զույգ բևեռների
թիվը (բևեռային կարգավորում) կամ սնող ցանցի լարման ![]() հաճախությունը (հաճախականային
կարգավորում):
հաճախությունը (հաճախականային
կարգավորում):
Սահքի փոփոխությունը
տրված բեռնվածքի դեպքում հնարավոր է իրականացնել կամ շարժիչին կիրառված U լարման փոփոխությամբ,
ինչպես այն հետևում է նկ. 9.11-ի մեխանիկական բնութագծերից, կամ ռոտորի շղթային միացված
![]() ակտիվ դիմադրությունների
մեծության փոփոխությամբ (նկ. 9.13բ):
ակտիվ դիմադրությունների
մեծության փոփոխությամբ (նկ. 9.13բ):
Առաջին դեպքում ![]() արագությունը կարելի
է փոփոխել միայն նեղ միջակայքում
արագությունը կարելի
է փոփոխել միայն նեղ միջակայքում ![]() ընդ որում այդ միջակայքում
ընդ որում այդ միջակայքում
![]() փոքր արժեքների դեպքում, որն ստացվում է U լարման արժեքը փոքրացնելով, շարժիչի
շահագործողական հատկությունները զգալիորեն վատանում են (տես բաժին 9.9), որի պատճառով
արագության կարգավորման այս մեթոդը գործնականում շատ սահմանափակ կիրառություն ունի:
փոքր արժեքների դեպքում, որն ստացվում է U լարման արժեքը փոքրացնելով, շարժիչի
շահագործողական հատկությունները զգալիորեն վատանում են (տես բաժին 9.9), որի պատճառով
արագության կարգավորման այս մեթոդը գործնականում շատ սահմանափակ կիրառություն ունի:
Երկրորդ տարբերակը կիրառելի է միայն ֆազային
ռոտորով ասինքրոն շարժիչների համար: Չնայած այս դեպքում ![]() կարելի է փոփոխել բավական լայն սահմաններում, սակայն
կարելի է փոփոխել բավական լայն սահմաններում, սակայն ![]() փոքր արժեքներ ստանալու համար հարկ է լինում ռոտորի շղթա մտցնել համեմատաբար
մեծ
փոքր արժեքներ ստանալու համար հարկ է լինում ռոտորի շղթա մտցնել համեմատաբար
մեծ ![]() ակտիվ դիմադրություն, որի միջով անցնում է ռոտորի փաթույթի
ակտիվ դիմադրություն, որի միջով անցնում է ռոտորի փաթույթի ![]() ամբողջ հոսանքը՝ պատճառելով
ամբողջ հոսանքը՝ պատճառելով
![]() զգալի հզորության կորուստ և, որպես հետևանք, շարժիչի օ.գ.գ.-ի կտրուկ նվազում:
զգալի հզորության կորուստ և, որպես հետևանք, շարժիչի օ.գ.գ.-ի կտրուկ նվազում:
Բևեռային կարգավորում: Արագության կարգավորման այս եղանակը հիմնված է ստատորի պտտվող մագնիսական դաշտի զույգ բևեռների թվի փոփոխման վրա: Համաձայն (9.2) բանաձևի, ստատորի դաշտի արագությունը կապված է դրա զույգ բևեռների թվի հետ, որը որոշվում է փաթույթի կառուցվածքով:
Զույգ բևեռների թվի փոփոխությունն ամենապարզ ձևով կարելի է իրականացնել փոխանջատելով յուրաքանչյուր ֆազային փաթույթում նրա բաղադրիչ մասերի՝ սեկցիաների միացման ձևը: Այդպիսի փոխանջատման օրինակ է բերված նկ. 9.15-ում:
Մի դեպքում յուրաքանչյուր ֆազի երկու սեկցիաները միացված են հաջորդաբար (ա), մյուս դեպքում՝ զուգահեռ (բ): Կետեգծերով նշված են սեկցիաներով անցնող հոսանքներով պայմանավորված մագնիսական դաշտի ուժագծերի տեսքը և ուղղությունը յուրաքանչյուր դեպքի համար: Ինչպես երևում է սխեմաներից, կատարելով փոխանջատում հաջորդաբար միացումից զուգահեռ միացման, p զույգ բևեռների թիվը փոխվում է 2-ից 1-ի, իսկ ստատորի դաշտի n1 արագությունը՝ 1500 պտ/ր-ից՝ 3000 պտ/ր:
Կիրառելով այլ տեսակի միացումներ՝ կարելի է ստանալ նաև p = 3 և p = 4:
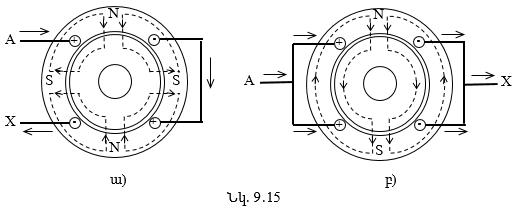
Երբեմն, երկու տարբեր արագություններ ստանալու
համար, ստատորի փորակներում տեղադրվում են երկու միմյանցից անկախ փաթույթներ՝ համապատասխանաբար
![]() զույգ բևեռների թվով: Արագությունը փոխելու համար բավական է եռաբևեռ փոխանջատիչի
միջոցով անջատելով լարման տակ գտնվող փաթույթը՝ նույն լարմանը միացնել մյուս փաթույթը:
Այս դեպքում մեկ ավելորդ փաթույթի առկայությունը և շարժիչի տրամագծի որոշ չափով մեծացումը
զգալիորեն մեծացնում են շարժիչի ընդհանուր արժեքը:
զույգ բևեռների թվով: Արագությունը փոխելու համար բավական է եռաբևեռ փոխանջատիչի
միջոցով անջատելով լարման տակ գտնվող փաթույթը՝ նույն լարմանը միացնել մյուս փաթույթը:
Այս դեպքում մեկ ավելորդ փաթույթի առկայությունը և շարժիչի տրամագծի որոշ չափով մեծացումը
զգալիորեն մեծացնում են շարժիչի ընդհանուր արժեքը:
Համակցելով բևեռային կարգավորման երկու եղանակները՝ կարելի է ասինքրոն շարժիչից ստանալ մինչև չորս տարբեր արագություններ:
Հաճախականային կարգավորում: Առավել կատարյալ արագության կարգավորում կարելի է ստանալ փոփոխելով շարժիչին սնող լարման հաճախությունը: Վերջին ժամանակներս, շնորհիվ կիսահաղորդչային սարքերի լայն կիրառման, ասինքրոն շարժիչների հաճախականային կարգավորումը մեծ կիրառություն է գտել գործնականում:
Նկ. 9.15-ում տրված է ասինքրոն շարժիչների հաճախականային կարգավորման բլոկ-սխեման:
Մասնավորապես այդպիսի հնարավորություն են տալիս հաճախության տիրիստորային ձևափոխիչները: Նկ. 9.16-ում պատկերված է հաճախականային կարգավորում ունեցող ասինքրոն շարժիչի բլոկ-սխեման: Դրա բաղադրիչ մասերից մեկը եռաֆազ ուղղիչն է, որի հիմնական տարրերը կառավարվող դիոդներն են՝ տիրիստորները: Ուղղիչի ելքում ստացվում է հաստատուն լարում, որի մեծությունը, կախված տիրիստորին տրվող ազդանշանի փուլից, կարելի է փոփոխել: Ստացված հաստատուն լարումը տրվում է ինվերտոր կոչված սարքին, որի հիմնական տարրերը նույնպես տիրիստորներ կամ տրանզիստորներ են:
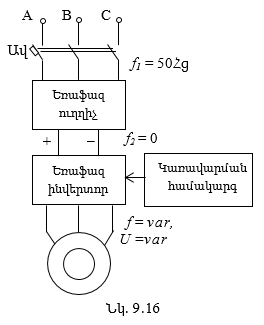
Ինվերտորը հաստատուն լարումը ձևափոխում է դարձյալ եռաֆազ լարումների համակարգի, որի և' մեծությունը, և' հաճախությունը կարելի է փոփոխել փոփոխելով տիրիստորներին տրվող ազդանշանների հաճախությունը և մեծությունը:
Փոփոխելով հաճախությունը` կարելի է ռոտորի արագությունը
սահուն փոփոխել այնպես, որ շարժիչի առավելագույն արագությունը տասնյակ կամ նույնիսկ
հարյուրավոր անգամներ գերազանցի նվազագույն արագությունը: Հաճախականային կարգավորման
դեպքում շատ կարեվոր է, որպեսզի շարժիչի ![]() կրիտիկական մոմենտը
պահպանվի հաստատուն, ինչի համար անհրաժեշտ է ինվերտորն այնպես նախագծել, որ U լարման
և
կրիտիկական մոմենտը
պահպանվի հաստատուն, ինչի համար անհրաժեշտ է ինվերտորն այնպես նախագծել, որ U լարման
և ![]() հաճախության հարաբերությունը մնա հաստատուն:
հաճախության հարաբերությունը մնա հաստատուն:
1. Թվարկեք ասինքրոն շարժիչի առավելությունները:
2. Որո՞նք են եռաֆազ ասինքրոն շարժիչի կառուցվածքային մասերը:
3. Գծեք և նկարագրեք կարճ միացված ռոտորով ասինքրոն շարժիչի կառուցվածքը:
4. Գծեք և նկարագրեք ֆազային ռոտորով ասինքրոն շարժիչի կառուցվածքը:
5. Ասինքրոն շարժիչում ինչպե՞ս է ստացվում պտտվող մագնիսական դաշտը: Գրեք դաշտի պտտման արագության բանաձևը:
6. Գծեք ասինքրոն շարժիչի պարզեցված տեսքը և նկարագրեք, թե ինչպե՞ս և ի՞նչ ուղղությամբ է պտտվում ռոտորը:
7. Գրեք ասինքրոն շարժիչի սահքի բանաձևը: Ի՞նչ սահմաններում է փոփոխվում սահքի արժեքը ասինքրոն մեքենայի աշխատանքային տարբեր ռեժիմներում (շարժիչ, գեներատոր, էլեկտրամագնիսական արգելակ):
8. Ինչպե՞ս է սահմանվում ասինքրոն շարժիչի անվանական հզորությունը: Ո՞րն է շարժիչի սպառման հզորությունը:
9. Ինչպե՞ս է որոշվում ասինքրոն շարժիչի օ.գ.գ.-ն:
10. Ինչպե՞ս է փոփոխվում ասինքրոն շարժիչի հզորության գործակիցը կախված բեռնվածքից և ցանցի լարումից:
11. Գծեք ասինքրոն շարժիչի էներգետիկ դիագրամը: Հզորության ինչպիսի՞ կորուստներ են առաջանում ասինքրոն շարժիչում:
12. Կախված ստատորի փաթույթների միացման ձևից` ի՞նչ լարումներով կարող է աշխատել ասինքրոն շարժիչը:
13. Գրեք ասինքրոն շարժիչի լիսեռի վրա զարգացրած մեխանիկական մոմենտի արտահայտությունը: Ի՞նչից է կախված այդ մոմենտի մեծությունը:
14. Գծեք ասինքրոն շարժիչի մեխանիկական բնութագիծը: Բնութագծի վրա ցույց տվեք շարժիչի զարգացրած առավելագույն և գործարկման մոմենտները, կրիտիկական արագությունը:
15. Գործնականորեն ի՞նչ սահմաններում կարող է փոփոխվել ասինքրոն շարժիչի սահքի արժեքը:
16. Ինչպե՞ս են որոշվում ասինքրոն շարժիչի գերբեռնման և գործարկման մոմենտի գործակիցները:
17. Ի՞նչ բացասական հետևանք են ունենում սնող ցանցի լարման շեղումները ասինքրոն շարժիչի աշխատանքի վրա:
18. Ի՞նչ է էլեկտրական շարժիչի գործարկումը:
19. Ինչու՞ կարճ միացված ռոտորով ասինքրոն շարժիչները գործարկելիս առաջանում են շատ մեծ գործարկման հոսանքներ: Ի՞նչ բացասական հետևանք կարող են դրանք ունենալ:
20. Նկարագրեք ֆազային ռոտորով ասինքրոն շարժիչների գործարկման պրոցեսը և նշեք գործարկման առավելությունները:
21. Ինչպե՞ս կարելի է բարելավել կարճ միացված ռոտորով ասինքրոն շարժիչների գործարկման հատկությունները:
22. Ի՞նչ մեծություններից է կախված ասինքրոն շարժիչի ռոտորի արագությունը:
23. Ասինքրոն շարժիչի արագության կարգավորման ի՞նչ եղանակներ են կիրառվում: Նշել դրանց առանձնահատկությունները:
10.1. Ընդհանուր տեղեկություններ
«Սինքրոն» անվանումն են կրում փոփոխական հոսանքի այն մեքենաները, որոնց ռոտորը և ստատորի փաթույթի ստեղծած մագնիսական դաշտը պտտվում են սինքրոն, այսինքն միևնույն արագությամբ: Եթե հոսանքի հաճախությունը հաստատուն է, ապա անկախ մեքենայի բեռնվածքից, ռոտորը պտտվում է խիստ հաստատուն անկյունային արագությամբ:
Սինքրոն մեքենաները գործնականում կիրառվում են որպես գեներատորներ, շարժիչներ և այսպես կոչված սինքրոն կոմպենսատորներ: Հատկապես լայն կիրառություն ունեն սինքրոն գեներատորները, որոնք ներկայումս տեղակայված են գրեթե բոլոր տեսակի էլեկտրակայաններում և փոփոխական հոսանքի էլեկտրաէներգիայի հիմնական աղբյուրներն են: Եռաֆազ սինքրոն գեներատորներն ամենահզոր էլեկտրական մեքենաներն են: Ժամանակակից մեկ եռաֆազ սինքրոն գեներատորի հզորությունը հասնում է մինչև 1500 ՄՎտ: Համեմատաբար ավելի փոքր հզորությամբ (մինչև մի քանի հարյուր կՎտ) սինքրոն գեներատորները կիրառվում են որպես էլեկտրաէներգիայի ավտոնոմ աղբյուրներ՝ պտտման մեջ դրվելով ներքին այրման շարժիչների, հողմակների և այլ առաջնային շարժիչների միջոցով:
Սինքրոն շարժիչները սովորաբար կիրառվում են մեծ հզորության (մինչև մի քանի տասնյակ ՄՎտ) պոմպեր, կոմպրեսորներ, օդափոխիչներ և այլ սարքավորումներ աշխատացնելու համար, որտեղ չեն պահանջվում հաճախակի գործարկումներ և արագության կարգավորում: Փոքր հզորության սինքրոն շարժիչները անփոխարինելի են այն տեղերում, որտեղ պահանջվում է ապահովել ռոտորի պտտման խիստ հաստաատուն արագություն (գրանցող սարքերում, ձայնատեսագրման սարքերում և այլն):
Սինքրոն կոմպենսատորները
պարապ ընթացքում աշխատող հատուկ տեսակի սինքրոն շարժիչներ են, որոնք ցանցին տալիս են
ռեակտիվ էներգիա: Դրանք տեղակայվում են էլեկտրաէներգետիկական համակարգերում և ծառայում
են ցանցի հզորության գործակցի ![]() բարձրացման (տես
բաժին 3.11), ինչպես նաև ցանցի լարման կարգավորման համար:
բարձրացման (տես
բաժին 3.11), ինչպես նաև ցանցի լարման կարգավորման համար:
Եռաֆազ սինքրոն գեներատորները, շարժիչները և կոմպենսատորներն ունեն սկզբունքորեն նույն կառուցվածքը:
10.2. Եռաֆազ սինքրոն մեքենայի կառուցվածքը
Նկ. 10.1-ում բերված է սինքրոն մեքենայի լայնական հատույթի սխեմատիկ պատկերը:

Սինքրոն մեքենայի անշարժ մասը՝ ստատորն ունի գրեթե
նույն ձևը և կառուցվածքը (բացի չափերից), ինչ որ ասինքրոն մեքենայի ստատորը (տես
9.1 բաժինը): Դրա միջուկը նույնպես հավաքվում է էլեկտրատեխնիկական պողպատի թերթերից,
իսկ դրա ներքին մակերևույթի վրա արված փորակներում տեղադրվում են երեք միատեսակ ֆազային
փաթույթներ, որոնց մագնիսական առանցքները տարածականորեն շեղված են միմյանց նկատմամբ
![]() Ստատորն ամրացվում է պողպատից կամ չուգունից պատրաստված իրանի մեջ:
Ստատորն ամրացվում է պողպատից կամ չուգունից պատրաստված իրանի մեջ:
Սինքրոն մեքենայի պտտվող մասը՝ ռոտորը, հաստատուն էլեկտրամագնիս է, որի զույգ բևեռների թիվը հավասար է ստատորի փաթույթի ստեղծած մագնիսական դաշտի p զույգ բևեռների թվին: Ռոտորի միջուկը պատրաստվում է հոծ պողպատից: Ռոտորի փորակներում տեղադրվում է գրգռման փաթույթը կամ ինդուկտորը, որը սնվում է հաստատուն հոսանքով: Գրգռման փաթույթը հաստատուն հոսանքի աղբյուրին (կամ գրգռիչին) միացնելու համար մեքենայի լիսեռին ամրացվում են միմյանցից և լիսեռից էլեկտրականապես մեկուսացված երկու կոնտակտային օղակներ, որոնց, զսպանակների միջոցով, հպվում են երկու գրաֆիտե խոզանակներ:
Սովորաբար մեծ հզորության սինքրոն մեքենաների
գրգռման փաթույթը սնելու համար որպես գրգռիչ է ծառայում նույն լիսեռին միացված հաստատուն
հոսանքի գեներատորը: Ներկայումս սինքրոն մեքենաներում հաստատուն մագնիսական դաշտ գրգռելու
համար կիրառվում են կիսահաղորդչային ուղղիչներ, որոնք փոփոխական հոսանքը ձևափոխում
են հաստատուն հոսանքի: Գրգռման փաթույթի սնման համար պահանջվող հզորությունը չի գերազանցում
մեքենայի ակտիվ հզորության ![]()
Մինչև մի քանի տասնյակ վատտ հզորությամբ սինքրոն միկրոմեքենաներում էլեկտրամագնիսների փոխարեն կիրառվում են հաստատուն մագնիսներ:
Ինչպես և ասինքրոն մեքենայի, այնպես էլ սինքրոն
մեքենայի զույգ բևեռների p թիվը և ռոտորի պտտման n արագությունը կապված են (9.2) բանաձևով`
![]() որտեղ
հոսանքի ստանդարտ հաճախությունը՝ f = 50 Հց: Հատուկ դեպքերում (ինքնաթիռներում, սուզանավերում
և այլն), գեներատորի չափերի փոքրացման նպատակով, դրանք նախատեսվում են f = 400 Հց
հաճախության համար:
որտեղ
հոսանքի ստանդարտ հաճախությունը՝ f = 50 Հց: Հատուկ դեպքերում (ինքնաթիռներում, սուզանավերում
և այլն), գեներատորի չափերի փոքրացման նպատակով, դրանք նախատեսվում են f = 400 Հց
հաճախության համար:
Կախված բևեռների p թվից (կամ ռոտորի պտտման n արագությունից)` սինքրոն մեքենայի ռոտորը լինում է երկու տեսակ. ոչ բացահայտ բևեռներով և բացահայտ բևեռներով: Արագընթաց մեքենաներում, որոնց համար n = 3000 կամ n = 1500 պտ/ր (համապատասխանաբար, p = 1 կամ p = 2), իներցիայի մոմենտները փոքրացնելու նպատակով, ռոտորը պատրաստվում է ոչ բացահայտ բևեռներով (ինչպես պատկերված է նկ. 10.1ա-ում): Դանդաղընթաց մեքենաներում (p > 2) ռոտորը բացահայտ բևեռներով է (նկ. 10.1բ,5): Վեջինիս փաթույթը պատրաստվում է կոճերի տեսքով, որոնք հագցվում են պարզորոշ երևացող մագնիսական բևեռների վրա:
Գործնականում կիրառվող հզոր սինքրոն մեքենաների կառուցվածքը շատ ավելի բարդ է: Մասնավորապես դրանք օժտված են հովացման, լարման կարգավորման, ռելեական պաշտպանության և այլ բարդ համակարգերով:
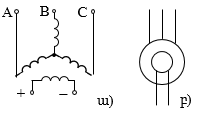
Նկարում պատկերված են եռաֆազ սինքրոն մեքենայի սկզբունքային էլեկտրական սխեման (ա) և պայմանական նշանը (բ):
10.3. Սինքրոն մեքենայի աշխատանքային ռեժիմները
Սինքրոն մեքենայի աշխատանքային ռեժիմները ուսումնասիրելու
համար նպատակահարմար է նախապես ենթադրել, որ այն միացված է եռաֆազ էլեկտրական ցանցին
(համակարգին): Այս դեպքում դրա ստատորի ֆազային փաթույթներով անցնող հոսանքները, որոնք
ըստ փուլի միմյանց նկատմամբ ![]() շեղված են, ինչպես
և ասինքրոն մեքենայում, կառաջացնեն
շեղված են, ինչպես
և ասինքրոն մեքենայում, կառաջացնեն ![]() արագությամբ պտտվող մագնիսական դաշտ: Ենթադրենք,
որ ռոտորը, որը նույն p զույգ բևեռներով էլեկտրամագնիս է, նույնպես պտտվում է նույն
ուղղությամբ և արագությամբ: Այսինքն՝ ստատորի և ռոտորի մագնիսական դաշտերի առանցքների
փոխադարձ դասավորությունը անփոփոխ է:
արագությամբ պտտվող մագնիսական դաշտ: Ենթադրենք,
որ ռոտորը, որը նույն p զույգ բևեռներով էլեկտրամագնիս է, նույնպես պտտվում է նույն
ուղղությամբ և արագությամբ: Այսինքն՝ ստատորի և ռոտորի մագնիսական դաշտերի առանցքների
փոխադարձ դասավորությունը անփոփոխ է:
Եթե սինքրոն մեքենայում անտեսվեն տարբեր տեսակի կորուստները, ապա բեռնվածքի (լիսեռի վրա ազդող մոմենտի) բացակայության դեպքում ռոտորի և ստատորի տարանուն մագնիսական բևեռների առանցքները կհամընկնեն (նկ.10.3ա). մեքենան կաշխատի իդեալական պարապ ընթացքի ռեժիմում, և էներգիայի փոխարկում չի լինի:
Որպեսզի էլեկտրական ցանցին միացված սինքրոն մեքենան
աշխատի գեներատորի ռեժիմում, անհրաժեշտ է առաջնային շարժիչի (տուրբինի) միջոցով պտտող
մոմենտ հաղորդել մեքենայի լիսեռին: Այդ դեպքում ռոտորի մագնիսական բևեռների առանցքները
կթեքվեն ռոտորի պտտման ուղղությամբ և առաջ կընկնեն ստատորի համապատասխան մագնիսական
բևեռների առանցքներից ![]() անկյունով (նկ. 10.3բ): Ռոտորի և ստատորի մագնիսական դաշտերի վերադրումից ստացված
արդյունարար մագնիսական դաշտը կփոփոխվի: Այն ստատորի փաթույթներում կինդուկտի եռաֆազ
սինուսոիդական էլշուներ, և սինքրոն մեքենան կաշխատի որպես գեներատոր՝ ցանցին տալով
էլեկտրական էներգիա, ի հաշիվ առաջնային շարժիչից ստացված մեխանիկական էներգիայի:
անկյունով (նկ. 10.3բ): Ռոտորի և ստատորի մագնիսական դաշտերի վերադրումից ստացված
արդյունարար մագնիսական դաշտը կփոփոխվի: Այն ստատորի փաթույթներում կինդուկտի եռաֆազ
սինուսոիդական էլշուներ, և սինքրոն մեքենան կաշխատի որպես գեներատոր՝ ցանցին տալով
էլեկտրական էներգիա, ի հաշիվ առաջնային շարժիչից ստացված մեխանիկական էներգիայի:
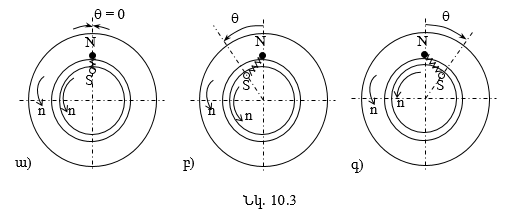
Գեներատորի ռեժիմում ստատորի մագնիսական հոսքը փոխազդելով գրգռման փաթույթի հոսանքակիր հաղորդիչների հետ՝ վերջիններիս վրա կառաջացնի էլեկտրամագնիսական մոմենտ, որն ուղղված կլինի ռոտորի պտտման ուղղությանը հակառակ և կհանդիսանա արգելակող մոմենտ: Ընդ որում, որքան մեծ է գեներատորի տված էլեկտրաէներգիան, այնքան մեծ կլինի արգելակող մոմենտը: Որպեսզի ռոտորը շարունակի պտտվել նախկին արագությամբ, անհրաժեշտ է հաղթահարել լիսեռի վրա հակազդող էլեկտրամագնիսական մոմենտը՝ մեծացնելով առաջնային շարժիչի մեխանիկական հզորությունը՝ ավելացնելով վառելիքի ծախսը ջերմային տուրբիններում կամ ջրի հոսքը հիդրոտուրբիններում:
Եթե այժմ մեքենայի լիսեռին պտտող մոմենտի փոխարեն
կիրառվի մեխանիկական բեռնվածք՝ արգելակող մոմենտ, ապա ռոտորի բևեռների առանցքներըը
կթեքվեն ստատորի բևեռների համապատասխան առանցքների նկատմամբ որոշ ![]() անկյունով՝ այս անգամ
ռոտորի պտտման հակառակ ուղղությամբ: Ստատորի փաթույթներում հոսանքների ուղղությունը
կփոխվի և դրանց փոխազդեցությունը ռոտորի դաշտի հետ այս դեպքում կառաջացնի պտտող մոմենտ:
Դրա շնորհիվ ցանցից վերցրած էլեկտրական էներգիան կփոխարկվի լիսեռի վրա մեխանիկական
էներգիայի. սինքրոն մեքենան կաշխատի որպես շարժիչ (նկ. 10.3գ):
անկյունով՝ այս անգամ
ռոտորի պտտման հակառակ ուղղությամբ: Ստատորի փաթույթներում հոսանքների ուղղությունը
կփոխվի և դրանց փոխազդեցությունը ռոտորի դաշտի հետ այս դեպքում կառաջացնի պտտող մոմենտ:
Դրա շնորհիվ ցանցից վերցրած էլեկտրական էներգիան կփոխարկվի լիսեռի վրա մեխանիկական
էներգիայի. սինքրոն մեքենան կաշխատի որպես շարժիչ (նկ. 10.3գ):
Այսպիսով, սինքրոն մեքենայի լիսեռի վրա մեխանիկական փոխազդեցությունից կախված, մեքենայի աշխատանքի ռեժիմը փոփոխվում է գեներատորից շարժիչ և հակառակը: Ընդ որում էլեկտրամագնիսական ուժերը խաղում են յուրօրինակ առաձգական կապի դեր ռոտորի և ստատորի մագնիսական բևեռների միջև: Կարելի է պատկերացնել, որ դրանք կապված են երևայական մեխանիկական զսպանակով, ինչպես ցույց է տրված նկ. 10.3-ում: Ընդ որում, որքան մեծ է մեքենայի բեռնվածքը, այնքան ավելի է մեծանում բևեռների շեղումը միմյանց նկատմամբ (մեծանում է «զսպանակների» ձգվածությունը):
10.4. Սինքրոն գեներատորի աշխատանքի սկզբունքը
Սինքրոն մեքենան որպես գեներատոր աշխատեցնելու
համար անհրաժեշտ է մեքենայում գրգռել հաստատուն մագնիսական դաշտ՝ ռոտորի փաթույթը միացնելով
հաստատուն հոսանքի աղբյուրին և միաժամանակ ռոտորը պտտել առաջնային շարժիչի (տուրբինի)
միջոցով: Ռոտորի գրգռման փաթույթով անցնող հաստատուն հոսանքը գրգռում է մեքենայում
![]() հիմնական մագնիսական
հոսք: Ռոտորի պտտման հետ կպտտվի նաև
հիմնական մագնիսական
հոսք: Ռոտորի պտտման հետ կպտտվի նաև ![]() հոսքը, որի ուժագծերը
(նկ. 10.1-ում պատկերված են կետագծերով) հատելով ստատորի փաթույթների գալարները, դրանցում
կինդուկտեն էլշուներ (տես 3.1 բաժինը): Քանի որ ստատորի ֆազային փաթույթները միատեսակ
են և դրանց մագնիսական առանցքները տարածականորեն շեղված են միմյանց նկատմամբ
հոսքը, որի ուժագծերը
(նկ. 10.1-ում պատկերված են կետագծերով) հատելով ստատորի փաթույթների գալարները, դրանցում
կինդուկտեն էլշուներ (տես 3.1 բաժինը): Քանի որ ստատորի ֆազային փաթույթները միատեսակ
են և դրանց մագնիսական առանցքները տարածականորեն շեղված են միմյանց նկատմամբ ![]() , ապա դրանցում
կինդուկտվեն միատեսակ ամպլիտուդով և հաճախությամբ երեք էլշուներ, որոնք շեղված կլինեն
միմյանց նկատմամբ ըստ փուլի նույնպես
, ապա դրանցում
կինդուկտվեն միատեսակ ամպլիտուդով և հաճախությամբ երեք էլշուներ, որոնք շեղված կլինեն
միմյանց նկատմամբ ըստ փուլի նույնպես ![]()
Որպեսզի ինդուկտված էլշուները փոփոխվեն սինուսոիդական օրենքով, անհրաժեշտ է, որ ռոտորի մագնիսական դաշտի ստեղծած ինդուկցիան ստատորի և ռոտորի մագնիսահաղորդիչների միջև օդային բացակի երկայնքով նույնպես բաշխվի սինուսոիդական օրենքով: Արտահայտված բևեռներով մեքենաներում դրան հասնում են բևեռների տակ օդային բացակն անելով ոչ հավասարաչափ, իսկ ոչ արտահայտված բևեռներով մեքենաներում, որտեղ օդային բացակը հավասարաչափ է, ռոտորի շրջագծի երկայնքով գրգռման փաթույթի գալարների համապատասխան բաշխման միջոցով:
Գեներատորում ինդուկտված եռաֆազ էլշուների ակնթարթային արժեքները ներկայացվում են հետևյալ եռանկյունաչափական տեսքով (էլշուներից մեկի սկզբնական փուլը վերցված է զրո).
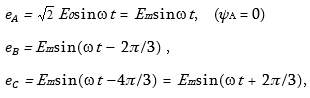
Էլշուների ![]() գործող արժեքը և
f հաճախությունը կարելի է որոշել ասինքրոն շարժիչների համար ստացված (9.3) և (9.1)
համանման բանաձևերով.
գործող արժեքը և
f հաճախությունը կարելի է որոշել ասինքրոն շարժիչների համար ստացված (9.3) և (9.1)
համանման բանաձևերով.

որտեղ k-ն փաթույթի գործակիցն է, w-ն՝ ֆազի փաթույթի գալարների թիվը:
Եթե ստատորի եռաֆազ փաթույթի A, B և C սեղմակներին միացվի էլեկտրաէներգիայի սպառիչ (նկ. 10.1ա), ապա էլշուի ազդեցությամբ ստատորի ֆազերում կառաջանան սինուսոիդական հոսանքներ. սինքրոն մեքենան կաշխատի որպես գեներատոր՝ էլեկտրական էներգիա տալով սպառիչին, ի հաշիվ առաջնային շարժիչից ստացած մեխանիկական էներգիայի:
Ստատորի փաթույթներով անցնող հոսանքները, որոնք
ըստ փուլի շեղված են ![]() , կառաջացնեն պտտվող մագնիսական
դաշտ, որի պտտման արագությունը հավասար է ռոտորի պտտման արագությանը՝
, կառաջացնեն պտտվող մագնիսական
դաշտ, որի պտտման արագությունը հավասար է ռոտորի պտտման արագությանը՝ ![]() , ուստի
ստատորի և ռոտորի մագնիսական դաշտերի առանցքների փոխադարձ դասավորությունը կմնա նույնը:
, ուստի
ստատորի և ռոտորի մագնիսական դաշտերի առանցքների փոխադարձ դասավորությունը կմնա նույնը:
Պտտման տարբեր արագությունների դեպքում ![]() ստանդարտ հաճախություն ստանալու համար սինքրոն գեներատորները պատրաստվում
են տարբեր զույգ բևեռների թվով: Այսպես, տուրբոգեներատորները, որոնք տեղակայվում են
ջերմային և ատոմային էլեկտրակայաններում և պտտման մեջ են դրվում արագընթաց ջերմային
տուրբիններով 3000 պտ/ր արագությամբ, ունեն մեկ զույգ բևեռ՝ p = 1: Մեխանիկական ամրությունը
մեծացնելու համար այս մեքենաների երկարությունը զգալիորեն գերազանցում է տրամագծից,
և ռոտորը ոչ բացահայտ բևեռներով է:
ստանդարտ հաճախություն ստանալու համար սինքրոն գեներատորները պատրաստվում
են տարբեր զույգ բևեռների թվով: Այսպես, տուրբոգեներատորները, որոնք տեղակայվում են
ջերմային և ատոմային էլեկտրակայաններում և պտտման մեջ են դրվում արագընթաց ջերմային
տուրբիններով 3000 պտ/ր արագությամբ, ունեն մեկ զույգ բևեռ՝ p = 1: Մեխանիկական ամրությունը
մեծացնելու համար այս մեքենաների երկարությունը զգալիորեն գերազանցում է տրամագծից,
և ռոտորը ոչ բացահայտ բևեռներով է:
Հիդրոգեներատորները, որոնք տեղակայվում են հիդրոէլեկտրակայաններում
և պտտման մեջ են դրվում հիդրավլիկ տուրբինների միջոցով, ունենում են տարբեր թվով
զույգ բևեռներ՝ ![]() կախված ջրի ճնշումից (որքան մեծ է ջրի ճնշումը, այնքան ավելի արագընթաց է հիդրոտուրբինը
և, հետևաբար դրան միացած գեներատորը): Հիդրոգեներատորները պատրաստվում են բացահայտ
բևեռներով և սովորաբար նրանց տրամագիծը1 ավելի մեծ է երկարությունից, այդ պատճառով
մեծ հզորության հիդրոգեներատորները նպատակահարմար է տեղակայել՝ լիսեռին տալով ուղղաձիգ
դիրք:
կախված ջրի ճնշումից (որքան մեծ է ջրի ճնշումը, այնքան ավելի արագընթաց է հիդրոտուրբինը
և, հետևաբար դրան միացած գեներատորը): Հիդրոգեներատորները պատրաստվում են բացահայտ
բևեռներով և սովորաբար նրանց տրամագիծը1 ավելի մեծ է երկարությունից, այդ պատճառով
մեծ հզորության հիդրոգեներատորները նպատակահարմար է տեղակայել՝ լիսեռին տալով ուղղաձիգ
դիրք:
10.5. Սինքրոն գեներատորի ստատորի փաթույթի էլեկտրական վիճակի հավասարումը և փոխարինման սխեման
Սինքրոն գեներատորում հիմնական մագնիսական դաշտը
գրգռվում է ռոտորի փաթույթի ![]() հոսանքով: Երբ սինքրոն մեքենան բեռնավորված է, դրա ստատորի փաթույթի կամ, ինչպես
ընդունված է անվանել, խարսխի ֆազերով անցնում են I հոսանքներ, որոնք գրգռում են մեքենայում
իրենց մագնիսական դաշտը, որը վերադրվելով հիմնական դաշտին, որոշակիորեն փոփոխում է
այն: Այս երևույթն ընդունված է անվանել խարսխի (այդպես են անվանում սինքրոն
մեքենայի ստատորի փաթույթները) հակազդեցություն: Ստատորի փաթույթի ֆազի x ինդուկտիվ
դիմադրությունը պայմանավորված է ինչպես խարսխի հակազդեցության
հոսանքով: Երբ սինքրոն մեքենան բեռնավորված է, դրա ստատորի փաթույթի կամ, ինչպես
ընդունված է անվանել, խարսխի ֆազերով անցնում են I հոսանքներ, որոնք գրգռում են մեքենայում
իրենց մագնիսական դաշտը, որը վերադրվելով հիմնական դաշտին, որոշակիորեն փոփոխում է
այն: Այս երևույթն ընդունված է անվանել խարսխի (այդպես են անվանում սինքրոն
մեքենայի ստատորի փաթույթները) հակազդեցություն: Ստատորի փաթույթի ֆազի x ինդուկտիվ
դիմադրությունը պայմանավորված է ինչպես խարսխի հակազդեցության ![]() մագնիսական հոսքով
մագնիսական հոսքով
![]() այնպես էլ
այնպես էլ ![]() ցրման հոսքով
ցրման հոսքով ![]()
Մեքենայի արդյունարար ![]() մագնիսական հոսքը ինդուկտում է ստատորի փաթույթի ֆազում
մագնիսական հոսքը ինդուկտում է ստատորի փաթույթի ֆազում ![]() սինուսոիդական էլշու:
Բեռնվածքի առկայության դեպքում փաթույթով անցնում է հոսանք, որը լարման անկումներ է
առաջացնում փաթույթի r ակտիվ և x ինդուկտիվ դիմադրությունների վրա: Սինքրոն մեքենաներում
ցրման հոսքերը բավական զգալի մաս են կազմում, որի պատճառով փաթույթի ինդուկտիվ դիմադրության
արժեքը զգալիորեն գերազանցում է ակտիվ դիմադրության արժեքը՝ x >> r, և վերջինս
կարելի է անտեսել: Հետևաբար, սինքրոն գեներատորը կարելի է դիտարկել որպես x ինդուկտիվ
ներքին դիմադրությամբ
սինուսոիդական էլշու:
Բեռնվածքի առկայության դեպքում փաթույթով անցնում է հոսանք, որը լարման անկումներ է
առաջացնում փաթույթի r ակտիվ և x ինդուկտիվ դիմադրությունների վրա: Սինքրոն մեքենաներում
ցրման հոսքերը բավական զգալի մաս են կազմում, որի պատճառով փաթույթի ինդուկտիվ դիմադրության
արժեքը զգալիորեն գերազանցում է ակտիվ դիմադրության արժեքը՝ x >> r, և վերջինս
կարելի է անտեսել: Հետևաբար, սինքրոն գեներատորը կարելի է դիտարկել որպես x ինդուկտիվ
ներքին դիմադրությամբ ![]() էլշու-ով աղբյուր՝ և դրա փաթույթի ֆազը ներկայացնել նկ. 10.4ա -ում պատկերված
փոխարինման սխեմայով:
էլշու-ով աղբյուր՝ և դրա փաթույթի ֆազը ներկայացնել նկ. 10.4ա -ում պատկերված
փոխարինման սխեմայով:
Գրելով Կիրխհոֆի 2-րդ օրենքի հիման վրա հավասարում նկ.10.4ա-ի սխեմայի համար՝ կստանանք ստատորի փաթույթի ֆազի էլեկտրական վիճակի հավասարումը .
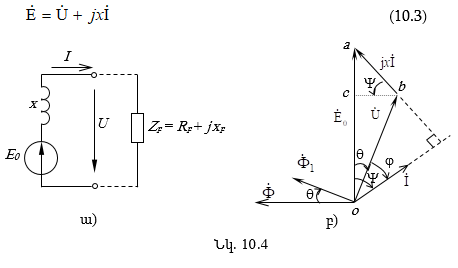
Ըստ նկ. 10.4ա-ի սխեմայի կառուցենք փաթույթի ֆազի
վեկտորական դիագրամը (նկ. 10.4բ): Որպես սկզբնական վեկտոր ընտրենք ![]() հիմնական մագնիսական
հոսքի վեկտորը և ուղղենք այն դեպի ձախ հորիզոնական ուղղությամբ: Այդ հոսքով ինդուկտված
հիմնական մագնիսական
հոսքի վեկտորը և ուղղենք այն դեպի ձախ հորիզոնական ուղղությամբ: Այդ հոսքով ինդուկտված
![]() էլշու-ն հետ է մնում
էլշու-ն հետ է մնում
![]() Ստատորի
Ստատորի ![]() հոսանքը հետ է մնում
հոսանքը հետ է մնում ![]() անկյունով, որի մեծությունը
կախված է ինչպես գեներատորի, այնպես էլ բեռնվածքի ակտիվ դիմադրություններից.
անկյունով, որի մեծությունը
կախված է ինչպես գեներատորի, այնպես էլ բեռնվածքի ակտիվ դիմադրություններից.
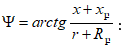
Լարման ![]() վեկտորը կառուցելու
համար անհրաժեշտ է
վեկտորը կառուցելու
համար անհրաժեշտ է ![]() վեկտորից հանել
վեկտորից հանել ![]() վեկտորը, որն առաջ
է ընկած
վեկտորը, որն առաջ
է ընկած ![]() Գեներատորի լարման և հոսանքի միջև
Գեներատորի լարման և հոսանքի միջև ![]() փուլային շեղումը
պայմանավորված է միայն բեռնվածքի
փուլային շեղումը
պայմանավորված է միայն բեռնվածքի ![]() ինդուկտիվ և
ինդուկտիվ և ![]() ակտիվ դիմադրությունների
հարաբերությամբ: Հատկանշական է, որ
ակտիվ դիմադրությունների
հարաբերությամբ: Հատկանշական է, որ ![]() վեկտորների կազմած
վեկտորների կազմած
![]() անկյունը հավասար
է ստատորի և ռոտորի մագնիսական բևեռների միջև
անկյունը հավասար
է ստատորի և ռոտորի մագնիսական բևեռների միջև ![]() վեկտորների միջև) եղած շեղման անկյանը:
վեկտորների միջև) եղած շեղման անկյանը:
10.6. Սինքրոն գեներատորի անկյունային բնութագիծը
Եռաֆազ սինքրոն գեներատորի զարգացրած էլեկտրամագնիսական հզորությունը, ըստ նկ. 10.4ա-ի սխեմայի,
![]()
իսկ սպառիչին տրված ակտիվ հզորությունը
![]()
Եթե անտեսենք ստատորում առկա հզորության կորուստները,
ապա ![]() հզորությունների մեծությունները կարելի է ընդունել մոտավորապես հավասար՝
հզորությունների մեծությունները կարելի է ընդունել մոտավորապես հավասար՝ ![]()
Նկ. 10.4բ-ի վեկտորական դիագրամում տանենք ![]() ուղղահայաց bc հատվածը: Ստացված abc ուղղանկյուն եռանկյունուց ստանում ենք
ուղղահայաց bc հատվածը: Ստացված abc ուղղանկյուն եռանկյունուց ստանում ենք
![]()
Հետևաբար,
![]()
Ընդունելով գեներատորի էլեկտրամագնիսական հզորությունը
հավասար տուրբինի ![]() մեխանիկական հզորությանը՝
կարող ենք (10.6)-ին համանման արտահայտություն գրել նաև էլեկտրամագնիսական մոմենտի
համար՝
մեխանիկական հզորությանը՝
կարող ենք (10.6)-ին համանման արտահայտություն գրել նաև էլեկտրամագնիսական մոմենտի
համար՝
![]()
որտեղ M-ը գեներատորի էլեկտրամագնիսական մոմենտն
է, ![]() ռոտորի անկյունային արագությունը, որը հաստատուն մեծություն է:
ռոտորի անկյունային արագությունը, որը հաստատուն մեծություն է:
Այսպիսով ստացվում է, որ սինքրոն մեքենայի հզորությունը
(կամ էլեկտրամագնիսական մոմենտը) ուղիղ համեմատական է ![]() էլշուին և ստատորի
ու ռոտորի բևեռների առանցքների միջև շեղման
էլշուին և ստատորի
ու ռոտորի բևեռների առանցքների միջև շեղման ![]() անկյան սինուսին:
անկյան սինուսին:
Նկ. 10.5-ում (10.7) արտահայտության հիման վրա
պատկերված է ![]() ֆունկցիայի գրաֆիկը Iգ գրգռման հոսանքի տարբեր արժեքների դեպքում, որն ունի
սինուսոիդի տեսք և կոչվում է սինքրոն գեներատորի անկյունային բնութագիծ: Էլեկտրամագնիսական
մոմենտի
ֆունկցիայի գրաֆիկը Iգ գրգռման հոսանքի տարբեր արժեքների դեպքում, որն ունի
սինուսոիդի տեսք և կոչվում է սինքրոն գեներատորի անկյունային բնութագիծ: Էլեկտրամագնիսական
մոմենտի ![]() (կամ
հզորության
(կամ
հզորության ![]() ամպլիտուդային արժեքը, որը մեքենան զարգացնում է
ամպլիտուդային արժեքը, որը մեքենան զարգացնում է ![]() անկյան դեպքում, կարելի է կարգավորել՝ ռոտորի գրգռման հոսանքի միջոցով փոփոխելով
անկյան դեպքում, կարելի է կարգավորել՝ ռոտորի գրգռման հոսանքի միջոցով փոփոխելով
![]() էլշու-ն:
էլշու-ն:
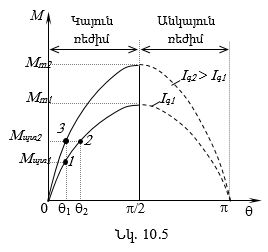
Անկյունային բնութագիծը թույլ է տալիս վերլուծել սինքրոն մեքենայում ընթացող պրոցեսները բեռնվածքի փոփոխության դեպքում:
Դիցուք՝ էլեկտրական ցանցին միացված գեներատորի
լիսեռի վրա ազդում է առաջնային շարժիչի (տուրբինի) ![]() պտտող մոմենտը: Առաջնային
շարժիչից ստացած մեխանիկական էներգիան գեներատորը փոխարկում է էլեկտրական էներգիայի՝
առաջացնելով M էլեկտրամագնիսական արգելակող մոմենտ: Գեներատորի աշխատանքը կհամապատասխանի
այնպիսի
պտտող մոմենտը: Առաջնային
շարժիչից ստացած մեխանիկական էներգիան գեներատորը փոխարկում է էլեկտրական էներգիայի՝
առաջացնելով M էլեկտրամագնիսական արգելակող մոմենտ: Գեներատորի աշխատանքը կհամապատասխանի
այնպիսի ![]() անկյան, որի դեպքում պտտող և արգելակող մոմենտները հավասար են՝
անկյան, որի դեպքում պտտող և արգելակող մոմենտները հավասար են՝ ![]() (նկ.10.5-ում 1 կետը): Առաջնային շարժիչի պտտող մոմենտի մեծացման դեպքում
(նկ.10.5-ում 1 կետը): Առաջնային շարժիչի պտտող մոմենտի մեծացման դեպքում
![]() գեներատորի ռոտորը առաջ ընկնելով կմեծացնի
գեներատորի ռոտորը առաջ ընկնելով կմեծացնի ![]() անկյունը, շարժիչի
և գեներատորի մոմենտների հավասարակշռությունը տեղի կունենա
անկյունը, շարժիչի
և գեներատորի մոմենտների հավասարակշռությունը տեղի կունենա ![]() անկյան դեպքում (նկ. 10.5-ում 2 կետը):
անկյան դեպքում (նկ. 10.5-ում 2 կետը):
Սինքրոն գեներատորի աշխատանքը կայուն է, երբ ![]() փոփոխվում է
փոփոխվում է ![]() միջակայքում:
միջակայքում: ![]() միջակայքում գեներատորի աշխատանքն անկայուն է, որովհետև տուրբինի հզորության
հետագա աճի դեպքում գեներատորը չի կարողանում ստեղծել դրա պտտող մոմենտին հավասար արգելակող
մոմենտ, խզվում է ռոտորի և ստատորի բևեռների միջև կապը (խզվում են նկ. 10.3-ի մոդելում
պատկերված երևակայական զսպանակները), ռոտորի արագությունն աճում է, և մեքենան դուրս
է ընկնում սինքրոնիզմից:
միջակայքում գեներատորի աշխատանքն անկայուն է, որովհետև տուրբինի հզորության
հետագա աճի դեպքում գեներատորը չի կարողանում ստեղծել դրա պտտող մոմենտին հավասար արգելակող
մոմենտ, խզվում է ռոտորի և ստատորի բևեռների միջև կապը (խզվում են նկ. 10.3-ի մոդելում
պատկերված երևակայական զսպանակները), ռոտորի արագությունն աճում է, և մեքենան դուրս
է ընկնում սինքրոնիզմից:
Գեներատորի կայուն աշխատանքն ապահովելու համար
անհրաժեշտ է ունենալ կայունության որոշ պաշար՝ ապահովելու համար մեքենայի սինքրոնիզմը՝
առաջնային շարժիչի հզորության զգալի փոփոխությունների դեպքում (դրա համար գործնականում
![]() արժեքը չի գերազանցում
արժեքը չի գերազանցում ![]() Այս պատճառով, գեներատորի
բեռնվածքի մեծացման դեպքում, երբ մեծանում է առաջնային շարժիչի պտտող մոմենտը, միաժամանակ
անհրաժեշտ է մեծացնել գրգռման հոսանքը, որը թույլ կտա մեծացնել գեներատորի էլեկտրամագնիսական
մոմենտի առավելագույն արժեքը
Այս պատճառով, գեներատորի
բեռնվածքի մեծացման դեպքում, երբ մեծանում է առաջնային շարժիչի պտտող մոմենտը, միաժամանակ
անհրաժեշտ է մեծացնել գրգռման հոսանքը, որը թույլ կտա մեծացնել գեներատորի էլեկտրամագնիսական
մոմենտի առավելագույն արժեքը ![]() և մոմենտների նոր
հավասարակշռություն հաստատել ավելի փոքր
և մոմենտների նոր
հավասարակշռություն հաստատել ավելի փոքր ![]() անկյան դեպքում՝ ապահովելով
կայունության անհրաժեշտ պաշարը (նկ. 10.5-ում 3 կետը):
անկյան դեպքում՝ ապահովելով
կայունության անհրաժեշտ պաշարը (նկ. 10.5-ում 3 կետը):
10. 7. Սինքրոն գեներատորի U-աձև բնութագծերը
Հզոր էլեկտրահամակարգին միացված սինքրոն գեներատորի ռեակտիվ հզորությունը (կամ ռեակտիվ հոսանքը) կարելի է կարգավորել գրգռման հոսանքի փոփոխման միջոցով:
Եթե սինքրոն գեներատորի մեխանիկական ![]() հզորությունը և ցանցի U լարումը հաստատուն են, ապա, ըստ (10.5) և (10.6) բանաձևերի,
ստանում ենք
հզորությունը և ցանցի U լարումը հաստատուն են, ապա, ըստ (10.5) և (10.6) բանաձևերի,
ստանում ենք
![]()
Այսինքն, ստատորի փաթույթի ֆազի ![]() հոսանքի
հոսանքի ![]() ակտիվ բաղադրիչը կախված
չէ
ակտիվ բաղադրիչը կախված
չէ ![]() գրգռման հոսանքից: Հետևաբար գրգռման հոսանքի փոփոխության դեպքում I հոսանքի
փոփոխությունը կատարվում է միայն ի հաշիվ նրա
գրգռման հոսանքից: Հետևաբար գրգռման հոսանքի փոփոխության դեպքում I հոսանքի
փոփոխությունը կատարվում է միայն ի հաշիվ նրա ![]() ռեակտիվ բաղադրիչի
փոփոխության:
ռեակտիվ բաղադրիչի
փոփոխության:
Նկ. 10.6ա-ում բերված է սինքրոն գեներատորի ստատորի
ֆազի վեկտորական դիագրամների համախումբը ![]() գրգռման հոսանքի տարբեր
արժեքների դեպքում, երբ P = const, U = const: Իսկ նկ. 10.6բ-ում բերված են ստատորի
հոսանքի կախման կորերը գրգռման հոսանքից` սինքրոն գեներատորի հզորության տարբեր արժեքների
դեպքում:
գրգռման հոսանքի տարբեր
արժեքների դեպքում, երբ P = const, U = const: Իսկ նկ. 10.6բ-ում բերված են ստատորի
հոսանքի կախման կորերը գրգռման հոսանքից` սինքրոն գեներատորի հզորության տարբեր արժեքների
դեպքում:
Այդ կորերը կոչվում են U-աձև բնութագծեր: Գրգռման
հոսանքի փոքր արժեքների դեպքում, երբ ![]() սինքրոն գեներատորի
կայունությունը կխախտվի: Որքան մեծ է սինքրոն գեներատորի ակտիվ հզորությունը, այնքան
սինքրոն գեներատորի
կայունությունը կխախտվի: Որքան մեծ է սինքրոն գեներատորի ակտիվ հզորությունը, այնքան
![]() հոսանքի ավելի մեծ
արժեքների դեպքում գեներատորը կկորցնի կայունությունը:
հոսանքի ավելի մեծ
արժեքների դեպքում գեներատորը կկորցնի կայունությունը:
Եթե առաջնային շարժիչի պտտող մոմենտը՝ M = 0, ապա անտեսելով գեներատորում առկա կորուստները, կարելի է համարել, որ սինքրոն գեներատորի հոսանքը միայն ռեակտիվ բաղադրիչ ունի:
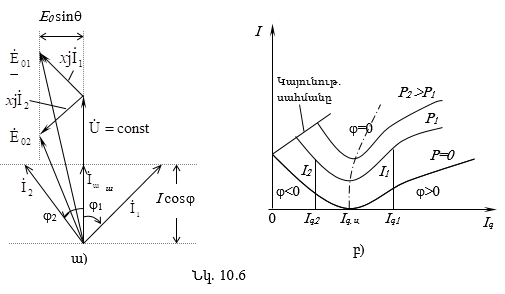
Էլեկտրական համակարգին միացված հաստատուն P ակտիվ
հզորությամբ աշխատող սինքրոն գեներատորի ![]() ռեակտիվ հզորությունը
կարելի է կարգավորել
ռեակտիվ հզորությունը
կարելի է կարգավորել ![]() գրգռման հոսանքի փոփոխությամբ: Եթե Iգ գրգռման հոսանքը փոքր է որոշակի Iգ.ս.
սահմանային արժեքից, ապա սինքրոն գեներատորի I հոսանքը ըստ փուլի առաջ կընկնի լարումից,
և դրա ռեակտիվ բաղադրիչը (նկ. 10.6-ում I2 հոսանքը), հետևաբար նաև Q ռեակտիվ հզորությունը,
կունենան ունակային բնույթ: Երբ
գրգռման հոսանքի փոփոխությամբ: Եթե Iգ գրգռման հոսանքը փոքր է որոշակի Iգ.ս.
սահմանային արժեքից, ապա սինքրոն գեներատորի I հոսանքը ըստ փուլի առաջ կընկնի լարումից,
և դրա ռեակտիվ բաղադրիչը (նկ. 10.6-ում I2 հոսանքը), հետևաբար նաև Q ռեակտիվ հզորությունը,
կունենան ունակային բնույթ: Երբ ![]() ապա Q -ն ունի ինդուկտիվ
բնույթ, իսկ երբ
ապա Q -ն ունի ինդուկտիվ
բնույթ, իսկ երբ ![]()
Գործնականում սինքրոն գեներատորի սովորական ռեժիմը համապատասխանում է ինդուկտիվ բնույթին, որն անհրաժեշտ է լայն տարածում գտած ասինքրոն շարժիչների ռեակտիվ հզորության պահանջարկը բավարարելու համար:
10.8. Սինքրոն շարժիչի գործարկումը
Սինքրոն շարժիչների գործարկումն ունի որոշ առանձնահատկություններ: Երբ ստատորի փաթույթը միացվում է եռաֆազ ցանցին, ապա ստատորի արագ պտտվող մագնիսական դաշտի և մեծ իներցիայով օժտված և դեռևս անշարժ ռոտորի հաստատուն մագնիսական դաշտի փոխազդեցությունից լիսեռի վրա առաջանում է ըստ ուղղության արագ փոփոխվող ուժ, որի պատճառով լիսեռի նկատմամբ պտտող մոմենտի միջին արժեքը ստացվում է զրո, և ռոտորը մնում է անշարժ:
Սինքրոն շարժիչի զարգացրած էլեկտրամագնիսական մոմենտը կարող է ստիպել ռոտորին հաղթահարել իներցիան և հետևել ստատորի մագնիսական դաշտին կամ, ինչպես ընդունված է ասել, ներքաշվել սինքրոնիզմի մեջ, եթե ստատորի մագնիսական դաշտի բևեռները բավականաչափ դանդաղ տեղափոխվեն ռոտորի բևեռների նկատմամբ: Այդպիսի պայմաններ կարելի է ստեղծել, եթե ռոտորին նախօրոք այս կամ այն ձևով հաղորդվի ստատորի դաշտի արագությանը մոտ արագություն: Ժամանակակից սինքրոն շարժիչներում ռոտորի վրա տեղադրում են «սկյուռի անիվի» տիպի գործարկման փաթույթ՝ շարժիչի ասինքրոն գործարկման համար (նկ. 10.7): Գործարկման փաթույթի ալյումինե կամ պղնձե ձողերը տեղադրվում են ռոտորի բևեռների միջուկների մեջ և ճակատային մասերում միացվում են կարճ փակող օղակներով:
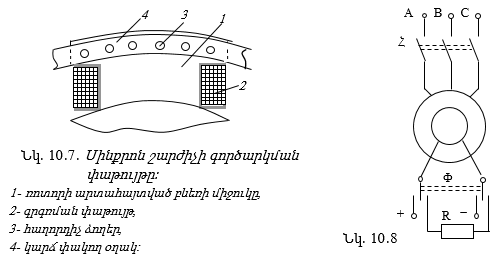
Սինքրոն շարժիչի գործարկումը իրականացվում է երկու փուլով՝ ըստ նկ. 10.8-ում պատկերված սխեմայի.
Առաջին փուլ: Ռոտորի գրգռման փաթույթը Փ փոխանջատիչով միացվում է R ակտիվ դիմադրությանը, որից հետո Հ եռաբևեռ հատիչը միացվում է եռաֆազ ցանցին: Սինքրոն շարժիչը գործարկվում է որպես ասինքրոն շարժիչ: Ռոտորն արագանալով պտտվում է ստատորի դաշտի պտտման արագությանը մոտ արագությամբ: Եթե գրգռման փաթույթը չմիացվի R դիմադրության և մնա բաց, ապա գործարկման պահին դրա սեղմակների միջև կառաջանա լարման անվանական արժեքը տասնյակներ անգամ գերազանցող գերլարում, որը վտանգավոր է գրգռման փաթույթի մեկուսիչի համար:
Երկրորդ փուլ: Գրգռման փաթույթը Փ փոխանջատիչի միջոցով անջատում են R դիմադրությունից և միացնում հաստատուն հոսանքի աղբյուրին: Ռոտորում գրգռվում է հաստատուն մագնիսական դաշտ և առաջանում է սինքրոն էլեկտրամագնիսական մոմենտ, որի շնորհիվ մի փոքր էլ արագանալով ռոտորը մտնում է սինքրոնիզմի մեջ և պտտվում է ստատորի դաշտի արագությամբ:
Շարժիչի բեռնվածքի տատանումների դեպքում, երբ լիսեռի վրա մոմենտների փոփոխություն է առաջանում, ռոտորի կարճ միացված փաթույթում ինդուկտված հոսանքները նպաստում են ռոտորի ճոճումների մարմանը:
Գործարկման համեմատաբար բարդ պրոցեսը և ռոտորի շղթայում հատուկ սարքերի կիրառման անհրաժեշտությունը զգալիորեն թանկացնում են սինքրոն շարժիչների ինքնարժեքը: Այդ պատճառով դրանց կիրառությունը դառնում է նպատակահարմար միայն բավականաչափ մեծ հզորությունների դեպքում (100 կՎտ և ավելի) և երբ չի պահանջվում հաճախակի գործարկումներ (օրինակ, մեծ հզորության պոմպեր, կոմպրեսորներ և օդափոխիչներ աշխատեցնելու համար):
10.9. Սինքրոն շարժիչի ստատորի փաթույթի էլեկտրական վիճակի հավասարումը
Բեռնվածքով աշխատող սինքրոն շարժիչում ռոտորի
բևեռների առանցքները ![]() անկյունով հետ են մնում պտտվող դաշտի բևեռների առանցքից, և շարժիչի զարգացրած
M պտտող մոմենտը հավասարակշռվում է լիսեռին կիրառված բեռնվածքի
անկյունով հետ են մնում պտտվող դաշտի բևեռների առանցքից, և շարժիչի զարգացրած
M պտտող մոմենտը հավասարակշռվում է լիսեռին կիրառված բեռնվածքի ![]() հակազդող (արգելակող)
մոմենտով՝
հակազդող (արգելակող)
մոմենտով՝ ![]()
Սինքրոն շարժիչի ստատորի ֆազի էլեկտրական վիճակի հավասարումը կարելի է ստանալ գեներատորի համար ստացված (10.3) համանման հավասարումից՝ հաշվի առնելով, որ ստատորի հոսանքի ուղղությունը հակառակ է ինդուկտված էլշուի ուղղությանը.
![]()
Այս հավասարմանը համապատասխանում են նկ. 10.9ա-ում պատկերված փոխարինման սխեման և նկ. 10.9բ-ում պատկերված վեկտորական դիագրամը:
Սինքրոն գեներատորի համար ստացված էլեկտրամագնիսական
մոմենտի (10.7) արտահայտությունը ճիշտ է նաև շարժիչի ռեժիմի համար: Հաշվի առնելով,
որ ստատորի դաշտի կամ նույն արագությամբ պտտվող ռոտորի անկյունային արագությունը՝ ![]() կստանանք շարժիչի պտտող մոմենտի և հզորության արտահայտությունները
կստանանք շարժիչի պտտող մոմենտի և հզորության արտահայտությունները
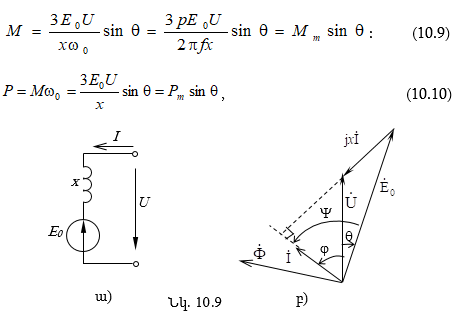
Քանի որ ցանցի U լարումը և f հաճախությունը հաստատուն
մեծություններ են, ապա ![]() գրգռման հոսանքի անփոփոխ արժեքի դեպքում M-ը և P-ն կախված են միայն
գրգռման հոսանքի անփոփոխ արժեքի դեպքում M-ը և P-ն կախված են միայն ![]() անկյունից:
անկյունից: ![]() ֆունկցիաների գրաֆիկները, որոնք կոչվում են սինքրոն շարժիչի անկյունային բնութագծեր,
ունեն նույն տեսքը, ինչ որ սինրոն գեներատորի համապատասխան բնութագծերը (նկ.
10.5):
ֆունկցիաների գրաֆիկները, որոնք կոչվում են սինքրոն շարժիչի անկյունային բնութագծեր,
ունեն նույն տեսքը, ինչ որ սինրոն գեներատորի համապատասխան բնութագծերը (նկ.
10.5):
Շարժիչի լիսեռին կիրառված ![]() հակազդող մոմենտը
մեծացնելիս մեքենայի ռոտորը մի փոքր դանդաղում է, մեծանում է ստատորի և ռոտորի բևեռների
միջև
հակազդող մոմենտը
մեծացնելիս մեքենայի ռոտորը մի փոքր դանդաղում է, մեծանում է ստատորի և ռոտորի բևեռների
միջև ![]() անկյունը, որի շնորհիվ մեծանում է M պտտող մոմենտը, մինչև որ մոմենտների միջև
հաստատվում է նոր հավասարակշռություն
անկյունը, որի շնորհիվ մեծանում է M պտտող մոմենտը, մինչև որ մոմենտների միջև
հաստատվում է նոր հավասարակշռություն ![]() անկյան դեպքում (նկ.
10.5): Մեքենայի կայունության անհրաժեշտ պաշար ապահովելու համար հարկ է մեծացնել
անկյան դեպքում (նկ.
10.5): Մեքենայի կայունության անհրաժեշտ պաշար ապահովելու համար հարկ է մեծացնել ![]() գրգռման հոսանքը,
որը կբերի
գրգռման հոսանքը,
որը կբերի ![]() անկյան համապատասխան փոքրացման:
անկյան համապատասխան փոքրացման:
Եթե սինքրոն շարժիչի լիսեռին կիրառվի ![]() հակազդող մոմենտ, ապա տվյալ
հակազդող մոմենտ, ապա տվյալ ![]() հոսանքի դեպքում
հոսանքի դեպքում ![]() անկյան մեծությունը
կգերազանցի
անկյան մեծությունը
կգերազանցի ![]() կխզվի բևեռների միջև
առաձգական կապը (նկ. 10.3-ում երևակայական զսպանակները կխզվեն) և շարժիչը դուրս կընկնի
սինքրոնիզմից: Որքան մեծ է
կխզվի բևեռների միջև
առաձգական կապը (նկ. 10.3-ում երևակայական զսպանակները կխզվեն) և շարժիչը դուրս կընկնի
սինքրոնիզմից: Որքան մեծ է ![]() արժեքը, այնքան ավելի
մեծ է շարժիչի զարգացրած առավելագույն
արժեքը, այնքան ավելի
մեծ է շարժիչի զարգացրած առավելագույն ![]() մոմենտը և այնքան
ավելի մեծ
մոմենտը և այնքան
ավելի մեծ ![]() բեռնվածքի
դեպքում տեղի կունենա բևեռների միջև կապի խզումը:
բեռնվածքի
դեպքում տեղի կունենա բևեռների միջև կապի խզումը:
Գործնականում մեծ հզորության սինքրոն շարժիչները
օժտված են հատուկ կարգավորող սարքով, որը թույլ է տալիս շարժիչի P հզորության փոփոխության
դեպքում համապատասխան չափով ավտոմատորեն փոփոխել ![]() արժեքը և ապահովել
շարժիչի համար անհրաժեշտ կայունության պաշարը:
արժեքը և ապահովել
շարժիչի համար անհրաժեշտ կայունության պաշարը:
10.10. Սինքրոն շարժիչի U-աձև բնութագծերը
Գրգռման հոսանքի մեծությունն ազդում է սինքրոն շարժիչի ոչ միայն կայունության պաշարի վրա, այլև, ինչպես և սինքրոն գեներատորում էր, դրա ստատորի հոսանքի ռեակտիվ բաղադրիչի վրա:
Շարժիչի լիսեռի վրա ![]() հաստատուն արգելակող մոմենտի դեպքում դրա
հաստատուն արգելակող մոմենտի դեպքում դրա ![]() մեխանիկական հզորությունը նույնպես հաստատուն է և, ինչպես հետևում է
(10.9) և (10.10) բանաձևերից,
մեխանիկական հզորությունը նույնպես հաստատուն է և, ինչպես հետևում է
(10.9) և (10.10) բանաձևերից,
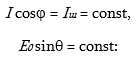
Նկ. 10.10-ում բերված են վեկտորական դիագրամների
համախումբը (ա) և ![]() բնութագծերի ընտանիքը
(բ)՝
բնութագծերի ընտանիքը
(բ)՝ ![]() հոսանքի տարբեր արժեքների դեպքում, երբ
հոսանքի տարբեր արժեքների դեպքում, երբ ![]()
Ինչպես հետևում է դիագրամներից և բնութագծերից,
![]() հոսանքի փոքրացման
դեպքում
հոսանքի փոքրացման
դեպքում ![]() անկյունն աճում է այնքան ժամանակ, մինչև որ սինքրոն շարժիչը կորցնի իր կայունությունը:
Միաժամանակ երևում է նաև, որ ստատորի հոսանքի բնույթը և մեծությունը կախված են
անկյունն աճում է այնքան ժամանակ, մինչև որ սինքրոն շարժիչը կորցնի իր կայունությունը:
Միաժամանակ երևում է նաև, որ ստատորի հոսանքի բնույթը և մեծությունը կախված են ![]() հոսանքից: Երբ
հոսանքից: Երբ ![]() փոքր է որոշակի Iգս. սահմանային արժեքից, I-ն ունի ինդուկտիվ բնույթ և հետ
է մնում ցանցի U լարումից: Երբ
փոքր է որոշակի Iգս. սահմանային արժեքից, I-ն ունի ինդուկտիվ բնույթ և հետ
է մնում ցանցի U լարումից: Երբ ![]() ունի ունակային բնույթ
և առաջ է ընկած U-ից: Վերջին դեպքում, փաստորեն, սինքրոն շարժիչը կարելի է ներկայացնել
որպես ակտիվ և ունակային տարրեր պարունակող շղթա:
ունի ունակային բնույթ
և առաջ է ընկած U-ից: Վերջին դեպքում, փաստորեն, սինքրոն շարժիչը կարելի է ներկայացնել
որպես ակտիվ և ունակային տարրեր պարունակող շղթա:
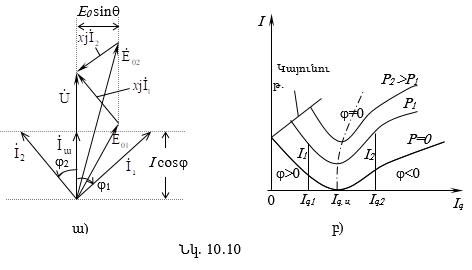
Այսպիսով, փոփոխելով գրգռման հոսանքը, կարելի
է փոփոխել սինքրոն շարժիչի հզորության գործակիցը՝ ![]() Այս հատկության շնորհիվ
սինքրոն շարժիչները դրականորեն տարբերվում են ասինքրոն շարժիչներից, որոնք ունեին ինդուկտիվ
բնույթի
Այս հատկության շնորհիվ
սինքրոն շարժիչները դրականորեն տարբերվում են ասինքրոն շարժիչներից, որոնք ունեին ինդուկտիվ
բնույթի ![]() համեմատաբար ցածր արժեքներ: Սինքրոն շարժիչում կարելի է
համեմատաբար ցածր արժեքներ: Սինքրոն շարժիչում կարելի է ![]() արժեքը ոչ միայն հասցնել 1-ի, այլև, աշխատեցնելով այն գերգրգռման ռեժիմում
արժեքը ոչ միայն հասցնել 1-ի, այլև, աշխատեցնելով այն գերգրգռման ռեժիմում
![]() դարձնել ունակային բնույթի սպառիչ
դարձնել ունակային բնույթի սպառիչ ![]() նպաստելով ամբողջ
ցանցի
նպաստելով ամբողջ
ցանցի ![]() բարձրացմանը և դրանով իսկ սնող գծերում էներգիայի կորուստների նվազեցմանը
(տես 3.11 պարագրաֆը):
բարձրացմանը և դրանով իսկ սնող գծերում էներգիայի կորուստների նվազեցմանը
(տես 3.11 պարագրաֆը):
1. Ի՞նչ ռեժիմներում կարող է աշխատել սինքրոն մեքենան:
2. Որո՞նք են եռաֆազ սինքրոն մեքենայի կառուցվածքային մասերը:
3. Սինքրոն մեքենան ի՞նչ կառուցվածքային նմանություններ և տարբերություններ ունի ասինքրոն մեքենայի համեմատ:
4. Բացատրեք սինքրոն մեքենայի աշխատանքի սկզբունքը գեներատորային ռեժիմում: Գրեք գեներատորում ինդուկտված սինուսոիդական էլշուի հաճախության բանաձևը:
5.Ո՞րն է հիդրոգեներատորների և տուրբոգեներատորների կառուցվածքային տարբերությունը:
6. Գծեք սինքրոն գեներատորի անկյունային բնութագիծը: Ինչպե՞ս է ապահովվում գեներատորի կայուն աշխատանքը բեռնվածքների փոփոխության դեպքում:
7. Ինչպե՞ս է կարգավորվում սինքրոն գեներատորի ռեակտիվ հզորությունը: Պատկերեք գեներատորի U-աձև բնութագծերը:
8. Բացատրեք սինքրոն մեքենայի աշխատանքի սկզբունքը շարժիչի ռեժիմում: Սինքրոն շարժիչի գործարկման ի՞նչ եղանակներ գիտեք:
9. Պատկերեք սինքրոն շարժիչի U-աձև բնութագծերը: Ինչպե՞ս կարելի է օգտագործել սինքրոն շարժիչը` բարձրացնելու համար էլեկտրական ցանցի հզորության գործակիցը:
11. ՀԱՍՏԱՏՈՒՆ ՀՈՍԱՆՔԻ ՄԵՔԵՆԱՆԵՐ
11.1. Ընդհանուր տեղեկություններ
Չնայած փոփոխական հոսանքի համընդհանուր կիրառությանը, այնուամենայնիվ հաստատուն հոսանքի մեքենաները բավական լայնորեն օգտագործվում են գործնականում և’ որպես գեներատորներ, և’ որպես շարժիչներ:
Ի տարբերություն փոփոխական հոսանքի էլեկտրական շարժիչների, հաստատուն հոսանքի շարժիչները հնարավորություն են տալիս պարզ սարքերի միջոցով բավական մեծ սահմանններում սահուն կերպով փոփոխել ռոտորի արագությունը, գործարկման ժամանակ ի վիճակի են զարգացնել մեծ մոմենտներ: Այս արժանիքների շնորհիվ, հաստատուն հոսանքի շարժիչները լայնորեն օգտագործվում են էլեկտրատրանսպորտային մեքենաներում (էլեկտրաքարշ, տրամվայ, տրոլեյբուս և այլն) և որոշ այլ սարքավորումներում (գլանման հաստոններ, վերամբարձ սարքավորումներ, էքսկավատորներ և այլն):
Հաստատուն հոսանքի գեներատորները հիմնականում կիրառվում են որպես հաստատուն հոսանքի էլեկտրաէներգիայի ավտոնոմ աղբյուրներ՝ հաստատուն հոսանքի շարժիչների, էլեկտրալիզային վաննաների, բարձրորակ էլեկտրաեռակցման սարքերի, էլեկտրամագնիսների սնման, ակումուլյատորային մարտկոցների լիցքավորման և այլ նպատակների համար:
Փոքր հզորության հաստատուն հոսանքի մեքենաները հիմնականում կիրառվում են ավտոմատ կառավարման համակարգերում՝ որպես գործադիր մեխանիզմներ աշխատեցնող շարժիչներ, պտտման արագության չափման սարքերում՝ որպես հայտնիչներ:
Հաստատուն հոսանքի մեքենաներին հատուկ ընդհանուր թերությունը կապված է դրանց այսպես կոչված կոլեկտորա-խոզանակային հանգույցի հետ, որի պատճառով ոչ միայն բարդանում է մեքենաների կառուցվածքը, այլև դրանց աշխատանքն ուղեկցվում է կայծարձակումով, որն իր հերթին, նվազեցնում է մեքենայի հուսալիությունը, պահանջում հատուկ խնամք, շրջապատում առաջացնում է ռադիոալիքային խափանումներ: Պայթյունավտանգ միջավայրերում այս մեքենաների կիրառությունը դառնում է անհնար:
Հաստատուն հոսանքի շարժիչների կիրառությունը զգալիորեն սահմանափակվում է նաև այն պատճառով, որ դրանց սնման համար անհրաժեշտ է հաստատուն հոսանքի աղբյուր, այսինքն լրացուցիչ կայանք, որը կարող է լինել կամ հաստատուն հոսանքի գեներատոր կամ փոփոխական հոսանքը հաստատունի վերափոխող ուղղիչ:
11.2. Հաստատուն հոսանքի մեքենայի կառուցվածքը
Հաստատուն հոսանքի մեքենան, ինչպես և ցանկացած էլեկտրական մեքենա, կազմված է երկու հիմնական մասերից. անշարժ մասից՝ ստատորից և պտտվող մասից՝ ռոտորից (նկ. 11.1):

Ստատորն ունի սնամեջ գլանի տեսք և պատրաստվում է ձուլածո պողպատից, քանի որ մագնիսական հոսքը դրանում հաստատուն է: Ստատորը երկու դեր է կատարում. հանդիսանում է մագնիսական շղթայի (մագնիսահաղորդչի) մի մասը և, միաժամանակ, ծառայում է որպես իրան (կորպուս): Ստատորին, դրա ներսի կողմից, ամրացվում են մեքենայի գլխավոր և օժանդակ մագնիսական բևեռները: Տեխնոլոգիական և այլ նկատառումներից ելնելով՝ բևեռները հաճախ պատրաստվում են թերթավոր, իսկ երբեմն էլ, հոծ պողպատից: Գլխավոր բևեռների վրա տեղադրվում է մեկ (կամ երկու) գրգռման փաթույթ: Մեքենայի գրգռման փաթույթը սնվում է հաստատուն հոսանքով՝ մեքենայում հիմնական մագնիսական դաշտ գրգռելու համար, որի ուժագծերը նկ. 11.1ա-ում պայմանականորեն պատկերված են ընդհատ գծերով:
Հաստատուն հոսանքի մեքենայի ռոտորը կամ, ինչպես ընդունված է անվանել խարիսխը, ունի հոծ գլանի տեսք և, վերամագնիսացման ու մրրկային հոսանքներով պայմանավորված հզորության կորուստները փոքրացնելու համար, հավաքվում է էլեկտրատեխնիկական պողպատի թերթերից: Խարսխի մակերևույթի վրա արված փորակներում տեղադրվում է խարսխի փաթույթը: Ինչպես և բևեռների փաթույթները, այն պատրաստվում է մեկուսացված պղնձե հաղորդալարից: Խարսխի փաթույթը կազմված է սեկցիաներից, որոնց ծայրերը միացվում են կոլեկտորի շրջադիրներին:
Կոլեկտորը մի սնամեջ գլան է, որը հավաքվում է միմյանցից մեկուսացված պղնձե սեպաձև շրջադիրներից և ամրացվում է պողպատյա լիսեռին, որից նույնպես էլեկտրականապես մեկուսացված է: Կոլեկտորին զսպանակների միջոցով հպվում են ածխագրաֆիտային կամ մետաղագրաֆիտային խոզանակները: Կոլեկտորի և խոզանակների միջոցով պտտվող խարսխի փաթույթը միանում է արտաքին էլեկտրական շղթային:
Խարսխի պտտման ընթացքում, երբ խոզանակները հերթականությամբ հպվում են կոլեկտորի մի շրջադիրից մյուսին, հպման տեղում առաջանում է կայծարձակում (կոմուտացիա)՝ դրանից բխող մի շարք բացասական երևույթներով: Լրացուցիչ բևեռները ծառայում են կոմուտացիան թուլացնելու համար, որի համար օժանդակ բևեռների փաթույթը միացվում է հաջորդաբար խարսխի փաթույթին:
Գլխավոր բևեռների ծայրամասերին տալիս են այնպիսի կորաձև տեսք, որ խարսխի երկայնքով օդային բացակը գլխավոր բևեռների և խարսխի միջև լինի նույնը, ինչն անհրաժեշտ է խարսխի եզրագծի մեծ մասում միատեսակ մագնիսական ինդուկցիա, իսկ խարսխի փաթույթներում` հաստատուն էլշու ստանալու համար:
Նկ. 11.1ա-ում պատկերված հաստատուն հոսանքի մեքենան երկբևեռ է: Հզորությունից և լարումից կախված մեքենան կարող է ունենալ ավելի մեծ թվով գլխավոր բևեռներ:
Նույն հաստատուն հոսանքի մեքենան կարող է աշխատել և’ որպես գեներատոր, և’ որպես շարժիչ:
11.3. Հաստատուն հոսանքի մեքենայի աշխատանքը որպես գեներատոր
Հաստատուն հոսանքի մեքենայի աշխատանքի սկզբունքը բացատրելու նպատակով հարմար է այն ներկայացնել պարզեցված պայմանական մոդելով, համարելով, որ խոզանակները անմիջականորեն հպվում են խարսխի փաթույթի սեկցիաներին (նկ. 11.2):
Մեքենան որպես գեներատոր աշխատեցնելու համար անհրաժեշտ է որևէ առաջնային շարժիչի միջոցով դրա խարիսխը պտտել n հաստատուն արագությամբ և, գրգռման փաթույթը միացնելով հաստատուն հոսանքի աղբյուրին, մեքենայում գրգռել հաստատուն մագնիսական դաշտ:
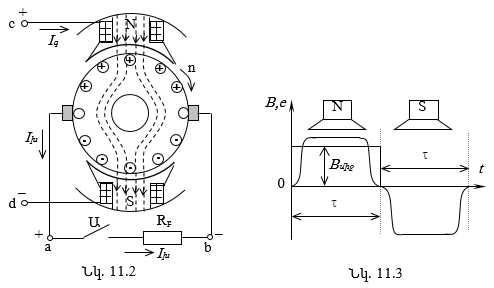
Պտտման հետևանքով խարսխի փաթույթների հաղորդիչները հատում են մագնիսական դաշտի ուժագծերը, որի շնորհիվ դրանցում ինդուկտվում է էլշու՝
![]()
որտեղ ![]() մագնիսական հոսքի
նորմալ (ուղղահայաց) բաղադրիչն է օդային բացակում, v-ն` խարսխի հաղորդիչների գծային
արագությունը,
մագնիսական հոսքի
նորմալ (ուղղահայաց) բաղադրիչն է օդային բացակում, v-ն` խարսխի հաղորդիչների գծային
արագությունը, ![]() խարսխի հաղորդիչների
ակտիվ մասի երկարությունը:
խարսխի հաղորդիչների
ակտիվ մասի երկարությունը:
Ինդուկտված էլշուի ուղղությունը որոշվում է աջ
ձեռքի կանոնով: Կիրառելով այդ կանոնը դիտարկվող մոդելի համար՝ կարելի է համոզվել,
որ հյուսիսային (N) բևեռի շրջանում էլշուն բոլոր հաղորդիչներում ուղղված է դիտորդից
դեպի գիրքը (նկ. 11.2-ում նշված է (+) նշանով), իսկ հարավային բևեռի (S) շրջանում՝
դեպի դիտորդը (նշված է ![]() նշանով): Երբ հաղորդիչներն անցնում են խոզանակների տակով՝ հատելով բևեռները
բաժանող համաչափության առանցքը, դրանցում էլշու չի ինդուկտվում, որովհետև դրանք ոչ
թե հատում են ուժագծերը, այլ սահում են դրանց զուգահեռ:
նշանով): Երբ հաղորդիչներն անցնում են խոզանակների տակով՝ հատելով բևեռները
բաժանող համաչափության առանցքը, դրանցում էլշու չի ինդուկտվում, որովհետև դրանք ոչ
թե հատում են ուժագծերը, այլ սահում են դրանց զուգահեռ:
Բևեռների ծայրապանակներին տալիս են այնպիսի ձև,
որ B մագնիսական ինդուկցիայի բաշխումը օդային բացակի երկայնքով փոփոխվի «սեղանաձև»
(նկ. 11.3): Այլ մասշտաբով, բայց նույն օրենքով կփոփոխվի նաև յուրաքանչյուր սեկցիայում
ինդուկտված ![]() էլշուն:
էլշուն:
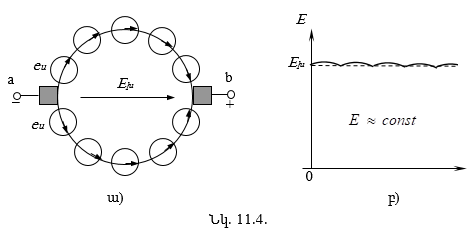
Այսպիսով, յուրաքանչյուր սեկցիայում ինդուկտված
![]() էլշուն պարբերաբար
փոխում է իր ուղղությունը, սակայն, շնորհիվ կոլեկտորի և խոզանակների, մեքենայի խարսխի
a-b սեղմակների միջև հաստատվում է հաստատուն
էլշուն պարբերաբար
փոխում է իր ուղղությունը, սակայն, շնորհիվ կոլեկտորի և խոզանակների, մեքենայի խարսխի
a-b սեղմակների միջև հաստատվում է հաստատուն ![]() էլշու: Դրանում կարելի
է համոզվել դիտելով նկ. 11.4ա-ում պատկերված խարսխի փաթույթի փոխարինման սխեման: Խարսխին
հպվող խոզանակները բաժանում են դրա փաթույթը երկու զուգահեռ միացված մասերի (ճյուղերի),
որոնցից յուրաքանչյուրը կազմված է միևնույն թվով հաջորդաբար միացված սեկցիաներից (կամ
դրանցում ինդուկտված էլշուներից): Ցանկացած պահին զուգահեռ ճյուղերից յուրաքանչյուրում
էլշուների ուղղությունները մնում են անփոփոխ (նկ. 11.4ա): Հետևաբար, մեքենայի a-b սեղմակների
միջև առաջացած
էլշու: Դրանում կարելի
է համոզվել դիտելով նկ. 11.4ա-ում պատկերված խարսխի փաթույթի փոխարինման սխեման: Խարսխին
հպվող խոզանակները բաժանում են դրա փաթույթը երկու զուգահեռ միացված մասերի (ճյուղերի),
որոնցից յուրաքանչյուրը կազմված է միևնույն թվով հաջորդաբար միացված սեկցիաներից (կամ
դրանցում ինդուկտված էլշուներից): Ցանկացած պահին զուգահեռ ճյուղերից յուրաքանչյուրում
էլշուների ուղղությունները մնում են անփոփոխ (նկ. 11.4ա): Հետևաբար, մեքենայի a-b սեղմակների
միջև առաջացած ![]() էլշուն, որը հավասար է մեկ ճյուղում գործող e էլշուների գումարին, կլինի հաստատուն:
էլշուն, որը հավասար է մեկ ճյուղում գործող e էլշուների գումարին, կլինի հաստատուն:
Քանի որ մի սեկցիայից մյուսը (կոլեկտորի մի շրջադիրից
մյուսը) անցումը սահուն չի կատարվում, ապա ինդուկտված արդյունարար ![]() էլշուն ստացվում է
որոշ չափով բաբախող` ոչ կատարյալ հաստատուն (նկ. 11.4բ): Որքան մեծ լինի խարսխի շրջադիրների
թիվը, այնքան բաբախումների ամպլիտուդը կլինի փոքր և
էլշուն ստացվում է
որոշ չափով բաբախող` ոչ կատարյալ հաստատուն (նկ. 11.4բ): Որքան մեծ լինի խարսխի շրջադիրների
թիվը, այնքան բաբախումների ամպլիտուդը կլինի փոքր և ![]() էլշուն մոտ կլինի
հաստատունի, սակայն, մյուս կողմից` չի կարելի կոլեկտորի թիթեղների թիվը ցանկացած չափով
մեծացնել, քանի որ այն բերում է մի շրջադիրի մակերեսի փոքրացման, որի մեծությունը պայմանավորված
է խարսխի հոսանքով:
էլշուն մոտ կլինի
հաստատունի, սակայն, մյուս կողմից` չի կարելի կոլեկտորի թիթեղների թիվը ցանկացած չափով
մեծացնել, քանի որ այն բերում է մի շրջադիրի մակերեսի փոքրացման, որի մեծությունը պայմանավորված
է խարսխի հոսանքով:
Ընդհանուր դեպքում հաստատուն հոսանքի գեներատորի
էլշուի արտահայտությունը ստանալու համար ենթադրենք, որ խարսխի փաթույթը կազմված է
N սեկցիաներից և a զուգահեռ ճյուղերից: Այդ դեպքում մեկ զուգահեռ ճյուղը կպարունակի
![]() սեկցիաներ, հետևաբար
մեքենայի էլշուն, հաշվի առնելով (10,1) բանաձևը, կլինի
սեկցիաներ, հետևաբար
մեքենայի էլշուն, հաշվի առնելով (10,1) բանաձևը, կլինի
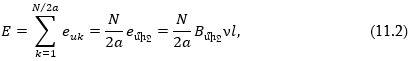
որտեղ ![]() մեկ սեկցիայում ինդուկտված
էլշուի միջին արժեքն է, երբ այն տեղափոխվում է
մեկ սեկցիայում ինդուկտված
էլշուի միջին արժեքն է, երբ այն տեղափոխվում է ![]() մեկ բևեռային բաժանմունքի չափով, D-ն խարսխի տրամագիծն է, p-ն՝ մեքենայի զույգ
բևեռների թիվը,
մեկ բևեռային բաժանմունքի չափով, D-ն խարսխի տրամագիծն է, p-ն՝ մեքենայի զույգ
բևեռների թիվը, ![]() ինդուկցիայի միջին
արժեքը մեկ բևեռային բաժանմունքում:
ինդուկցիայի միջին
արժեքը մեկ բևեռային բաժանմունքում:
Արտահայտելով խարսխի հաղորդիչների գծային արագությունը
խարսխի n պտտման հաճախությամբ` ![]() և մագնիսական ինդուկցիայի
միջին արժեքը
և մագնիսական ինդուկցիայի
միջին արժեքը ![]() մագնիսական հոսքով՝
մագնիսական հոսքով՝

և տեղադրելով դրանց արժեքները (11.2)-ի մեջ՝ կստանանք
![]()
որտեղ ![]() էլշուի գործակիցն
է, որը կախված է մեքենայի կառուցվածքային առանձնահատկություններից:
էլշուի գործակիցն
է, որը կախված է մեքենայի կառուցվածքային առանձնահատկություններից:
Եթե մեքենայի խարսխի a-b սեղմակներին միացվի
R դիմադրությամբ սպառիչ, ապա E էլշուի շնորհիվ դրանով կանցնի ![]() հաստատուն հոսանք: Այսպիսով առաջնային շարժիչի հաղորդած մեխանիկական էներգիան
հաստատուն հոսանքի մեքենան կփոխարկի էլեկտրական էներգիայի, մեքենան կաշխատի որպես գեներատոր:
հաստատուն հոսանք: Այսպիսով առաջնային շարժիչի հաղորդած մեխանիկական էներգիան
հաստատուն հոսանքի մեքենան կփոխարկի էլեկտրական էներգիայի, մեքենան կաշխատի որպես գեներատոր:
Գեներատորի էլշուի համար ստացված (11.4) բանաձևը կիրառելի է նաև հաստատուն հոսանքի շարժիչի խարսխում ինդուկտված էլշուն որոշելու համար: Սակայն, ի տարբերություն գեներատորի, որտեղ էլշուն համընկնում է խարսխի հոսանքի հետ, ինքն է այդ հոսանք առաջացնողը, շարժիչի դեպքում այն ուղղված է խարսխի հոսանքին հակառակ և հանդիսանում է հակազդող էլշու:
11.4. Հաստատուն հոսանքի մեքենայի աշխատանքը որպես շարժիչ
Հաստատուն հոսանքի մեքենայի աշխատանքը որպես շարժիչ դիտարկելու համար դարձյալ օգտվենք մեքենայի պարզեցված մոդելից (նկ. 11.5):
Մեքենան որպես շարժիչ աշխատեցնելու համար անհրաժեշտ
է միաժամանակ հաստատուն հոսանքի աղբյուրին միացնել մեքենայի և′ գրգռման, և′ խարսխի փաթույթները:
Այս դեպքում գրգռման փաթույթով անցնող ![]() հոսանքը մեքենայում
կգրգռի
հոսանքը մեքենայում
կգրգռի ![]() հոսքով հաստատուն մագնիսական դաշտ, իսկ խարսխի փաթույթի սեկցիաներում կառաջանա
հոսքով հաստատուն մագնիսական դաշտ, իսկ խարսխի փաթույթի սեկցիաներում կառաջանա
![]() հոսանք: Խարսխի
հոսանք: Խարսխի ![]() հոսանքի և
հոսանքի և ![]() հոսքի փոխազդեցության
շնորհիվ (Ամպերի օրենքը) խարսխի հաղորդիչների վրա կազդի F մեխանիկական ուժ, որն ըստ
Ամպերի օրենքի, կորոշվի
հոսքի փոխազդեցության
շնորհիվ (Ամպերի օրենքը) խարսխի հաղորդիչների վրա կազդի F մեխանիկական ուժ, որն ըստ
Ամպերի օրենքի, կորոշվի

բանաձևով, որտեղ ![]() սեկցայով անցնող հոսանքն է՝ հավասար զուգահեռ ճյուղի հոսանքին,
սեկցայով անցնող հոսանքն է՝ հավասար զուգահեռ ճյուղի հոսանքին, ![]() խարսխի փաթույթի ընդհանուր հոսանքն է:
խարսխի փաթույթի ընդհանուր հոսանքն է:
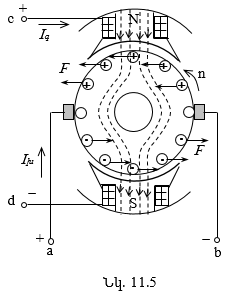
Դիցուք՝ մագնիսական դաշտի բևեռականությունը և
սեկցիաներում ![]() հոսանքի ուղղությունները այնպիսին են, ինչպես նշված են նկ.11.5-ում: Կիրառելով
ձախ ձեռքի կանոնը՝ կարելի է որոշել հաղորդիչների վրա ազդող F ուժերի ուղղությունը:
Ինչպես երևում է նկ. 11.5-ից, խոզանակները միացնող առանցքի տարբեր կողմերում F ուժերն
ունեն տարբեր ուղղություններ, որի շնորհիվ խարսխի վրա կառաջացնեն M պտտող մոմենտ, և
դիտարկվող օրինակում անշարժ խարիսխը լիսեռի հետ միասին կպտտվի ժամսլաքի պտտմանը հակառակ
ուղղությամբ:
հոսանքի ուղղությունները այնպիսին են, ինչպես նշված են նկ.11.5-ում: Կիրառելով
ձախ ձեռքի կանոնը՝ կարելի է որոշել հաղորդիչների վրա ազդող F ուժերի ուղղությունը:
Ինչպես երևում է նկ. 11.5-ից, խոզանակները միացնող առանցքի տարբեր կողմերում F ուժերն
ունեն տարբեր ուղղություններ, որի շնորհիվ խարսխի վրա կառաջացնեն M պտտող մոմենտ, և
դիտարկվող օրինակում անշարժ խարիսխը լիսեռի հետ միասին կպտտվի ժամսլաքի պտտմանը հակառակ
ուղղությամբ:
Այսպիսով, խարսխի փաթույթների միջոցով մեքենային տրված էլեկտրական էներգիան լիսեռի վրա կփոխարկվի մեխանիկական էներգիայի. մեքենան կաշխատի որպես շարժիչ:
Քանի որ խարսխի պտտման ժամանակ B ինդուկցիայի (նկ. 11.3), հետևաբար նաև F ուժերի, արժեքները փոփոխվում են, ապա պտտող մոմենտի որոշման համար կարելի է օգտվել մեկ սեկցիայի վրա ազդող ուժի միջին արժեքից.
![]()
Այդ դեպքում, օգտվելով (11.3) և (11.6) բանաձևերից, կարող ենք որոշել լիսեռի վրա մեքենայի զարգացրած մոմենտը.
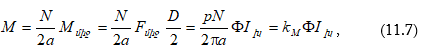
որտեղ ![]() տվյալ մեքենայի համար
հաստատուն գործակից է և կախված է միայն մեքենայի կառուցվածքային առանձնահատկություններից:
տվյալ մեքենայի համար
հաստատուն գործակից է և կախված է միայն մեքենայի կառուցվածքային առանձնահատկություններից:
Այսպիսով, հաստատուն հոսանքի մեքենայի զարգացրած մոմենտը ուղիղ համեմատական է մեքենայի հիմնական մագնիսական հոսքին և խարսխի հոսանքին:
Հաստատուն հոսանքի շարժիչի համար ստացված (11.7) բանաձևի միջոցով որոշվում է նաև հաստատուն հոսանքի գեներատորի խարսխի վրա ազդող մոմենտը: Սակայն, ի տարբերություն շարժիչի, որտեղ մոմենտը պտտող է՝ համընկնում է խարսխի պտտման ուղղության հետ, գեներատորում առաջացած մոմենտը արգելակող է՝ հակառակ է ուղղված խարսխի պտտման ուղղությանը: Դրանում հեշտ է համոզվել` համեմատելով նկ. 11.2 և նկ. 11.5 նկարները. նույն պայմաններում առաջացած մոմենտը, որն ուղղված է ժամսլաքին հակառակ, գեներատորի դեպքում արգելակող է առաջնային շարժիչի համար, որը պտտում է խարիսխը ժամսլաքի ուղղությամբ:
11.5. Հաստատուն հոսանքի մեքենաների դասակարգումը
Հաստատուն հոսանքի մեքենայի գրգռման և խարսխի փաթույթները տարբեր ձևերով կարող են միացվել միմյանց հետ և ցանցին: Կախված դրանց միացման ձևից` տարբերում են չորս տեսակի հաստատուն հոսանքի մեքենաներ.
1) Անկախ գրգռումով մեքենաներ, որոնցում գրգռման և խարսխի փաթույթները միացվում են հաստատուն հոսանքի տարբեր աղբյուրների (նկ. 11.6ա)1:
2) Զուգահեռ գրգռումով (կամ շունտային)
մեքենաներ, որոնցում գրգռման փաթույթը զուգահեռ է միացվում խարսխի փաթույթին (նկ.
11.6բ): Ընդ որում, գրգռման փաթույթը պատրաստվում է փոքր տրամագծով հաղորդալարի մեծ
թվով գալարներից, որի պատճառով գրգռման փաթույթի դիմադրությունը շատ անգամ ավելի մեծ
է, քան խարսխի փաթույթի դիմադրությունը՝ ![]()
3) Հաջորդական գրգռումով (սերիեսային)
մեքենաներ, որոնցում գրգռման փաթույթը միացվում է հաջորդաբար խարսխի փաթույթին (նկ.
11.6գ): Այս դեպքում գրգռման փաթույթը պատրաստվում է մեծ տրամագծով հաղորդալարի մի
քանի գալարներից, և գրգռման փաթույթի դիմադրությունը զգալիորեն ավելի փոքր է, քան խարսխի
փաթույթի դիմադրությունը՝ ![]()
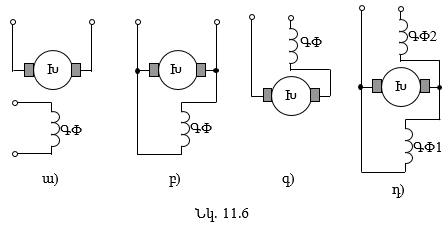
4) Խառը գրգռումով (կոմպաունդային) մեքենաներ (նկ. 11.6դ), որոնց յուրաքանչյուր բևեռի վրա տեղադրվում են գրգռման երկու փաթույթներ: Դրանցից մեկը (ԳՓ1), որն ունի մեծ դիմադրություն, միանում է խարսխի փաթույթին զուգահեռ, իսկ երկրորդը (ԳՓ2) ունի շատ փոքր դիմադրություն և միանում է խարսխի փաթույթին հաջորդաբար:
Վերջին երեք մեքենաները, որոնց գրգռման փաթույթը այս կամ այն ձևով միացված է խարսխի փաթույթին, կոչվում են նաև ինքնագրգռումով մեքենաներ:
Բոլոր թվարկված մեքենաներում գրգռման շղթայի համար անհրաժեշտ հզորությունը շատ փոքր է և կազմում է մեքենայի անվանական հզորության միայն 1-3%-ը:
Գրգռման փաթույթի միացման ձևը խարսխի փաթույթի հետ մեծ ազդեցություն է թողնում գեներատորի էլեկտրական հատկությունների և շարժիչի մեխանիկական հատկությունների վրա:
11.6. Հաստատուն հոսանքի անկախ գրգռումով գեներատորներ
Անկախ գրգռումով գեներատորի գրգռման շղթան միացվում
է անկախ հաստատուն հոսանքի աղբյուրի և էլեկտրականապես մեկուսացված է խարսխի շղթայից
(նկ. 11.7), ուստի ![]() գրգռման հոսանքը կախված չէ գեներատորի U լարումից: Դրա շնորհիվ, գրգռման շղթայում
միացված
գրգռման հոսանքը կախված չէ գեներատորի U լարումից: Դրա շնորհիվ, գրգռման շղթայում
միացված ![]() ռեոստատի միջոցով փոփոխելով
ռեոստատի միջոցով փոփոխելով ![]() գրգռման հոսանքը,
հնարավոր է լայն սահմաններում փոփոխել մեքենայի
գրգռման հոսանքը,
հնարավոր է լայն սահմաններում փոփոխել մեքենայի ![]() հիմնական մագնիսական
հոսքը և, դրանով իսկ խարսխի փաթույթում ինդուկտված
հիմնական մագնիսական
հոսքը և, դրանով իսկ խարսխի փաթույթում ինդուկտված ![]() էլշուն:
էլշուն:
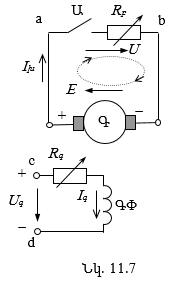
Էլշուի կախումը գրգռման հոսանքից՝ երբ խարսխի
հոսանքը ![]() կոչվում է գեներատորի պարապ ընթացքի բնութագիծ՝
կոչվում է գեներատորի պարապ ընթացքի բնութագիծ՝ ![]() (նկ.
11.8ա):
(նկ.
11.8ա):
Երբ գրգռման շղթան բաց է՝ ![]() ապա շնորհիվ այն բանի, որ մեքենայի ստատորը պահպանում է որոշ մնացորդային մագնիսականություն,
պտտվող խարսխի փաթույթում ինդուկտվում է պարապ ընթացքի
ապա շնորհիվ այն բանի, որ մեքենայի ստատորը պահպանում է որոշ մնացորդային մագնիսականություն,
պտտվող խարսխի փաթույթում ինդուկտվում է պարապ ընթացքի ![]() փոքր էլշու: Եթե գրգռման
փաթույթը միացվի
փոքր էլշու: Եթե գրգռման
փաթույթը միացվի ![]() հաստատուն լարման և ռեոստատի միջոցով
հաստատուն լարման և ռեոստատի միջոցով ![]() հոսանքը աստճանաբար
մեծացվի, ապա էլշուն կմեծանա հոսքին ուղիղ համեմատական (10.4): Սակայն ինչ-որ
հոսանքը աստճանաբար
մեծացվի, ապա էլշուն կմեծանա հոսքին ուղիղ համեմատական (10.4): Սակայն ինչ-որ ![]() արժեքից սկսած՝ ստատորի ֆերրոմագնիսական միջուկը կհագենա, և հոսքը, հետևաբար
նաև էլշուն, այլևս չեն աճի: Այժմ եթե գրգռման հոսանքը աստիճանաբար փոքրացվի, ապա նույն
արժեքից սկսած՝ ստատորի ֆերրոմագնիսական միջուկը կհագենա, և հոսքը, հետևաբար
նաև էլշուն, այլևս չեն աճի: Այժմ եթե գրգռման հոսանքը աստիճանաբար փոքրացվի, ապա նույն
![]() համապատասխանող էլշուի արժեքները հիսթերեզիսի երևույթի հետևանքով մի փոքր ավելի
մեծ կստացվեն, քան ստացվել էին հոսանքը մեծացնելիս, և
համապատասխանող էլշուի արժեքները հիսթերեզիսի երևույթի հետևանքով մի փոքր ավելի
մեծ կստացվեն, քան ստացվել էին հոսանքը մեծացնելիս, և ![]() կորն ավելի բարձրից կանցնի:
կորն ավելի բարձրից կանցնի:
Գեներատորների շահագործման համար կարևոր նշանակություն
ունի արտաքին բնութագիծը, որը խարսխի (բեռնվածքի) լարման կախումն է հոսանքից՝ ![]() (նկ.
11.8բ):
(նկ.
11.8բ):
Ըստ Կիրխհոֆի 2-րդ օրենքի գրելով հավասարում խարսխի շղթայի համար՝ կստանանք.
![]()
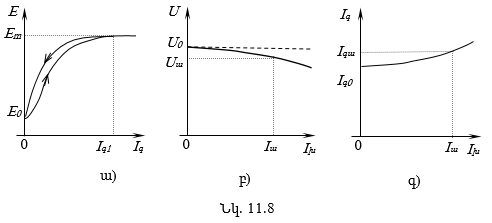
Գրված հավասարումից հետևում է, որ պարապ ընթացքի
ռեժիմում ![]() լարումը հավասար է էլշուին՝
լարումը հավասար է էլշուին՝ ![]() Եթե էլշուն լիներ
հաստատուն, ապա
Եթե էլշուն լիներ
հաստատուն, ապա ![]() ֆունկցիայի գրաֆիկը
կլիներ ուղիղ գիծ (նկ. 11.8բ-ում ընդհատ գիծը): Իրականում, երբ խարսխի փաթույթով հոսանք
է անցնում, այն առաջացնում է իր մագնիսական դաշտը, որը վերադրվելով հիմնական մագնիսական
դաշտին, որոշակիորեն փոփոխում է այն: Այս երևույթը, որը կոչվում է խարսխի հակազդեցություն,
փոքրացնում է էլշու-ի արժեքը, և
ֆունկցիայի գրաֆիկը
կլիներ ուղիղ գիծ (նկ. 11.8բ-ում ընդհատ գիծը): Իրականում, երբ խարսխի փաթույթով հոսանք
է անցնում, այն առաջացնում է իր մագնիսական դաշտը, որը վերադրվելով հիմնական մագնիսական
դաշտին, որոշակիորեն փոփոխում է այն: Այս երևույթը, որը կոչվում է խարսխի հակազդեցություն,
փոքրացնում է էլշու-ի արժեքը, և ![]() գրաֆիկը մի փոքր ավելի
է թեքվում դեպի աբսցիսների առանցքը:
գրաֆիկը մի փոքր ավելի
է թեքվում դեպի աբսցիսների առանցքը:
Լարման զգալի շեղումը ![]() անվանական արժեքից
անցանկալի է որևէ բեռնվածքի համար, ուստի սպառիչների նորմալ աշխատանքն ապահովելու համար
անհրաժեշտ է լարումը պահել հաստատուն՝ հնարավորին չափ մոտ
անվանական արժեքից
անցանկալի է որևէ բեռնվածքի համար, ուստի սպառիչների նորմալ աշխատանքն ապահովելու համար
անհրաժեշտ է լարումը պահել հաստատուն՝ հնարավորին չափ մոտ ![]() Հաստատուն հոսանքի գեներատորներում այն իրականացվում է
Հաստատուն հոսանքի գեներատորներում այն իրականացվում է ![]() ռեոստատի միջոցով
կարգավորելով
ռեոստատի միջոցով
կարգավորելով ![]() գրգռման հոսանքը: Խարսխի պտտման հաստատուն արագության դեպքում բեռնվածքի մեծացման
հետ, երբ U լարումը փոքրանում է, անհրաժեշտ է մեծացնել
գրգռման հոսանքը: Խարսխի պտտման հաստատուն արագության դեպքում բեռնվածքի մեծացման
հետ, երբ U լարումը փոքրանում է, անհրաժեշտ է մեծացնել ![]() որը կբերի E-ի մեծացման, և U -ի արժեքը կվերականգնվի:
որը կբերի E-ի մեծացման, և U -ի արժեքը կվերականգնվի:
Գրգռման հոսանքի այնպիսի կախումը խարսխի հոսանքից, երբ գեներատորի սեղմակներում լարումը մնում է հաստատուն, կոչվում է գեներատորի կարգավորման բնութագիծ (նկ. 11.8գ):
11.7. Ինքնագրգռման երևույթը հաստատուն հոսանքի գեներատորներում
Գեներատորների ինքնագրգռման առաջին նախապայմանը
մեքենայի մագնիսահաղորդչում մնացորդային մագնիսական դաշտի պահպանումն է: Այդ նպատակով
գործարանում պատրաստի գեներատորի մագնիսական շղթան նախապես մագնիսացնում են՝ գրգռման
փաթույթը կարճատև միացնելով հաստատուն հոսանքի աղբյուրին: Փաթույթն անջատելուց հետո
մեքենայի մագնիսահաղորդչում պահպանվում է մնացորդային ![]() հոսք, որը կազմում
է մեքենայի անվանական հոսքի ընդամենը (2-3)%-ը:
հոսք, որը կազմում
է մեքենայի անվանական հոսքի ընդամենը (2-3)%-ը:
Գեներատորի իքնագրգռման երևույթը հարմար է դիտարկել զուգահեռ գրգռումով գեներատորի օրինակի վրա (նկ. 11.9):
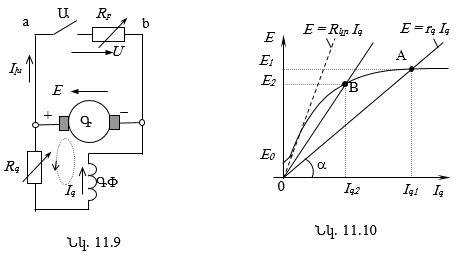
Եթե առաջնային շարժիչի օգնությամբ գեներատորի
խարիսխը պտտման մեջ դրվի հաստատուն n արագությամբ, ապա ![]() հոսքի շնորհիվ դրա
փաթույթում կինդուկտվի
հոսքի շնորհիվ դրա
փաթույթում կինդուկտվի ![]() փոքր էլշու (մի քանի
վոլտ): Քանի որ խարսխի և գրգռման փաթույթները կազմում են փակ շղթա, ապա
փոքր էլշու (մի քանի
վոլտ): Քանի որ խարսխի և գրգռման փաթույթները կազմում են փակ շղթա, ապա ![]() էլշուն բավական է,
որ գրգռման փաթույթում առաջացնի
էլշուն բավական է,
որ գրգռման փաթույթում առաջացնի ![]() փոքր հոսանք: Վերջինս
մեքենայում կգրգռի իր մագնիսական հոսքը, որը գումարվելով
փոքր հոսանք: Վերջինս
մեքենայում կգրգռի իր մագնիսական հոսքը, որը գումարվելով ![]() կուժեղացնի մեքենայի մագնիսական դաշտը: Դրա հետևանքով խարսխի փաթույթում կինդուկտվի
ավելի մեծ էլշու, այն կառաջացնի ավելի մեծ գրգռման հոսանք, դա էլ, իր հերթին, ավելի
ուժեղ մագնիսական դաշտ և այլն: Ինքնագրգռման այս պրոցեսը չի կարող անվերջ շարունակվել,
քանի որ ի վերջո մեքենայի մագնիսահաղորդիչը հագենում է, անցումային պրոցեսն ավարտվում
է, և գեներատորի սեղմակներում հաստատվում է որոշակի մեծությամբ E էլշու:
կուժեղացնի մեքենայի մագնիսական դաշտը: Դրա հետևանքով խարսխի փաթույթում կինդուկտվի
ավելի մեծ էլշու, այն կառաջացնի ավելի մեծ գրգռման հոսանք, դա էլ, իր հերթին, ավելի
ուժեղ մագնիսական դաշտ և այլն: Ինքնագրգռման այս պրոցեսը չի կարող անվերջ շարունակվել,
քանի որ ի վերջո մեքենայի մագնիսահաղորդիչը հագենում է, անցումային պրոցեսն ավարտվում
է, և գեներատորի սեղմակներում հաստատվում է որոշակի մեծությամբ E էլշու:
Օգտվելով գեներատորի պարապ ընթացքի բնութագծից՝
որոշենք գեներատորի սեղմակներում հաստատված էլշուի արժեքը (նկ. 11.10): Քանի որ խարսխի
փաթույթի ![]() դիմադրությունը շատ փոքր է գրգռման փաթույթի
դիմադրությունը շատ փոքր է գրգռման փաթույթի ![]() դիմադրությունից,
ապա անտեսելով այն, ըստ Կիրխհոֆի 2-րդ օրենքի, ինքնագրգռման անցումային պրոցեսի ընթացքում
գրգռման շղթայի համար կարող ենք գրել
դիմադրությունից,
ապա անտեսելով այն, ըստ Կիրխհոֆի 2-րդ օրենքի, ինքնագրգռման անցումային պրոցեսի ընթացքում
գրգռման շղթայի համար կարող ենք գրել
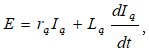
որտեղ ![]() գրգռման փաթույթի
ինդուկտիվությունն է: Երբ ինքնագրգռման պրոցեսն ավարտվի, գրգռման հոսանքը կլինի հաստատուն
և
գրգռման փաթույթի
ինդուկտիվությունն է: Երբ ինքնագրգռման պրոցեսն ավարտվի, գրգռման հոսանքը կլինի հաստատուն
և ![]() Ուստի
Ուստի ![]() գծային ֆունկցիայի
և պարապ ընթացքի բնութագծի հատման A կետի օրդինատը կլինի էլշուի
գծային ֆունկցիայի
և պարապ ընթացքի բնութագծի հատման A կետի օրդինատը կլինի էլշուի ![]() կայունացված արժեքը,
իսկ աբսցիսը՝ գրգռման հոսանքի
կայունացված արժեքը,
իսկ աբսցիսը՝ գրգռման հոսանքի ![]() կայունացված արժեքը
(նկ. 11.10): Ընդ որում`
կայունացված արժեքը
(նկ. 11.10): Ընդ որում` ![]() գծի թեքության
գծի թեքության ![]() անկյան տանգենսը համեմատական
է
անկյան տանգենսը համեմատական
է ![]() դիմադրությանը:
դիմադրությանը:
Եթե փոքրացնենք ![]() արժեքը, օրինակ, գրգռման շղթային միացնելով
արժեքը, օրինակ, գրգռման շղթային միացնելով ![]() դիմադրությամբ ռեոստատ,
ապա
դիմադրությամբ ռեոստատ,
ապա ![]() անկյունը կմեծանա
անկյունը կմեծանա ![]() և գրաֆիկները կհատվեն
էլշուի ավելի փոքր
և գրաֆիկները կհատվեն
էլշուի ավելի փոքր ![]() արժեքին համապատասխանող B կետում: Այսպիսով
արժեքին համապատասխանող B կետում: Այսպիսով ![]() ռեոստատի միջոցով
կարելի է փոփոխել գեներատորի էլշուի, հետևաբար նաև U լարման արժեքները:
ռեոստատի միջոցով
կարելի է փոփոխել գեներատորի էլշուի, հետևաբար նաև U լարման արժեքները:
Գրգռման շղթայի դիմադրության բավականաչափ մեծ
![]() արժեքի դեպքում, որը
կոչվում է կրիտիկական դիմադրություն, գեներատորի ինքնագրգռումը դառնում է անհնար:
արժեքի դեպքում, որը
կոչվում է կրիտիկական դիմադրություն, գեներատորի ինքնագրգռումը դառնում է անհնար:
Ամփոփելով՝ կարելի է ասել, որ հաստատուն հոսանքի գեներատորների ինքնագրգռումը հնարավոր է հետևյալ երեք պայմանների բավարարման դեպքում.
1) մեքենայի մագնիսահաղորդչում մնացորդային մագնիսական դաշտի առկայություն,
2) գրգռման և խարսխի փաթույթների համաձայնեցված միացում, որպեսզի գրգռման փաթույթի ստեղծած մագնիսական դաշտի ուղղությունը հաընկնի մնացորդային դաշտի ուղղության հետ և դրանց հոսքերը գումարվեն,
3) գրգռման շղթայի ընդհանուր դիմադրությունը պետք
է փոքր լինի որոշակի ![]() կրիտիկական դիմադրությունից:
կրիտիկական դիմադրությունից:
11.8. Հաստատուն հոսանքի ինքնագրգռումով գեներատորներ
Անկախ գրգռումով գեներատորների նկատմամբ այս գեներատորների առավելությունն այն է, որ դրանցում հիմնական մագնիսական դաշտ գրգռելու համար չի պահանջվում հաստատուն հոսանքի լրացուցիչ աղբյուր, որը էապես նվազեցնում է դրանց ինքնարժեքը և պազեցնում սպասարկումը:
Նկ. 11.9-ում պատկերված են զուգահեռ գրգռումով, իսկ նկ. 11.12-ում՝ խառը գրգռումով գեներատորների միացման սխեմաները:
Զուգահեռ և խառը գրգռումով գեներատորների պարապ ընթացքի բնութագծերը գործնականորեն չեն տարբերվում անկախ գրգռումով գեներատորի բնութագծից (նկ. 11.8ա):
Նույնը կարելի է ասել նաև դրանց կարգավորման բնութագծերի մասին:
Սակայն դրանց արտաքին բնութագծերը տարբեր են, որով և պայմանավորված է դրանց առանձնահատկությունները:
Զուգահեռ գրգռումով գեներատորի արտաքին բնութագիծը
(նկ. 11.11, 1 կորը) զգալիորեն ավելի ցածր է անցնում քան համեմատության համար բերված
անկախ գրգռումով գեներատորի արտաքին բնութագիծը (2 կորը): Դա բացատրվում է նրանով,
որ բեռնվածքի մեծացման հետ, երբ փոքրանում է գեներատորի խարսխի լարումը, փոքրանում
է նաև խարսխին զուգահեռ միացված գրգռման փաթույթի ![]() հոսանքը, որի հետևանքով
փոքրանում է խարսխի էլշուն (10.4)՝ լրացուցիչ փոքրացնելով լարումը (10.8): Լարման փոքրացումը
անվանական բեռնվածքի դեպքում հասնում է
հոսանքը, որի հետևանքով
փոքրանում է խարսխի էլշուն (10.4)՝ լրացուցիչ փոքրացնելով լարումը (10.8): Լարման փոքրացումը
անվանական բեռնվածքի դեպքում հասնում է ![]() պարապ ընթացքի
պարապ ընթացքի ![]() լարման նկատմամբ:
լարման նկատմամբ:
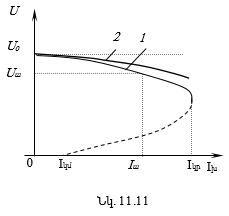
Բեռնվածքի հետագա մեծացման հետ լարման փոքրացումը
բերում է գրգռման հոսանքի, հետևաբար և մեքենայի հիմնական մագնիսական դաշտի ավելի փոքրացման,
որն էլ իր հերթին, բերում է էլշուի փոքրացման, այնպես որ բեռնվածքի հոսանքը, հասնելով
իր առավելագույն ![]() կրիտիկական արժեքին, ինքնիրեն փոքրանում է լարման հետ. տեղի է ունենում գեներատորի
ինքնամագնիսաթափում, և դրանց արժեքները հավասարվում են զրոյի: Այսպիսով, զուգահեռ գրգռումով
գեներատորները անկայուն են գերբեռնումների նկատմամբ: Մեքենայի կայուն աշխատանքի համար
անհրաժեշտ է, որ
կրիտիկական արժեքին, ինքնիրեն փոքրանում է լարման հետ. տեղի է ունենում գեներատորի
ինքնամագնիսաթափում, և դրանց արժեքները հավասարվում են զրոյի: Այսպիսով, զուգահեռ գրգռումով
գեներատորները անկայուն են գերբեռնումների նկատմամբ: Մեքենայի կայուն աշխատանքի համար
անհրաժեշտ է, որ ![]()
Հաջորդական գրգռումով գեներատորները չունեն գործնական կիրառություն, ուստի այստեղ չեն դիտարկվում:
Խառը գրգռումով գեներատորներում մեքենայի հիմնական մագնիսական հոսքը գրգռվում է խարսխի հետ միացված զուգահեռ (ԳՓ1) և հաջորդաբար (ԳՓ2) գրգռման փաթույթներով (նկ.11.12):
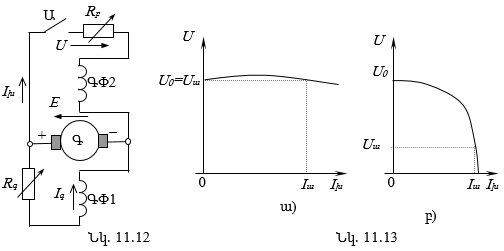
Լրացուցիչ հաջորդաբար փաթույթը, որի միջով անցնում է խարսխի հոսանքը, ստեղծում է լրացուցիչ մագնիսական հոսք, որը թույլ է տալիս չեզոքացնել զուգահեռ փաթույթի հոսանքի փոքրացումով պայմանավորված հիմնական հոսքի փոքրացումը՝ դրանով իսկ զգալիորեն մեծացնելով խառը գրգռումով գեներատորի արժանիքները զուգահեռ գրգռումով գեներատորի նկատմամբ:
Համապատասխան ձևով ընտրելով հաջորդական փաթույթի գալարների թիվը՝ կարելի է չեզոքացնել բեռնվածքից կախված գեներատորի լարման անկումը և լարման արժեքը գործնականորեն պահել հաստատուն, երբ բեռնվածքը փոփոխվում է զրոից մինչև անվանական արժեքը (նկ. 11.13ա):
Եթե խառը գրգռումով գեներատորի զուգահեռ և հաջորդական գրգռումով փաթույթները միացվեն հանդիպակաց, ապա նրանց մագնիսական դաշտերը միմյանցից կհանվեն, և բեռնվածքից կախված լարումը կտրուկ կընկնի, ինչպես դա երևում է նկ. 11.13բ-ում պատկերված արտաքին բնութագծից: Այսպիսի բնութագծով գեներատորը շատ հարմար է բարձրորակ եռակցման աշխատանքներում օգտագործելու համար:
11.9. Հաստատուն հոսանքի շարժիչների գործարկումը
Հաստատուն հոսանքի շարժիչների աշխատանքի համար անհրաժեշտ է դրանցում ստեղծել հաստատուն մագնիսական դաշտ (բևեռների հոսքերը) և խարիսխի փաթույթով բաց թողնել հոսանք: Դա իրագործելու համար շարժիչը համապատասխան սխեմայով միացվում է աղբյուրին և գործարկվում: Գործարկման ժամանակ շարժիչի արագությունը զրոյից հասնում է մինչև որոշակի արժեքի: Գործարկումը տևում է վայրկյանի մասերից (փոքր շարժիչների մոտ) մինչև մի քանի վայրկյան (խոշոր շարժիչների մոտ):
Հաստատուն հոսանքի շարժիչների գործարկումը դիտարկենք զուգահեռ գրգռումով շարժիչի օրինակի վրա (նկ. 11.15):
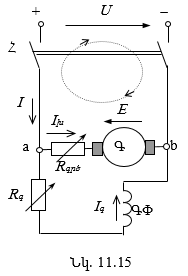
Երբ շարժիչը Հ հատիչի միջոցով միացվում է հաստատուն
U լարման, նրա խարսխի և գրգռման փաթույթներով անցնում են համապատասխանաբար ![]() հոսանքներ, և խարսխի փաթույթում ինդուկտվում է E հակազդող էլշու, որը հակառակ
է ուղղված
հոսանքներ, և խարսխի փաթույթում ինդուկտվում է E հակազդող էլշու, որը հակառակ
է ուղղված ![]()
Ըստ Կիրխհոֆի 1-ին և 2-րդ օրենքների գրենք հավասարումներ, համապատասխանաբար, b հանգույցի և կետագծով նշված կոնտուրի համար.

Հաշվի առնելով, որ ![]() գրված հավասարումներից որոշենք խարսխի հոսանքը.
գրված հավասարումներից որոշենք խարսխի հոսանքը.

Գործարկման առաջին պահին, երբ շարժիչը միացված
է հաստատուն հոսանքի աղբյուրին, իսկ ռոտորը իր մեծ իներցիայի պատճառով դեռևս անշարժ
է՝ n = 0, խարսխի փաթույթում չի ինդուկտվում հակազդող էլշու՝ ![]() ինչպես հետևում է (11.10) հավասարւմից, խարսխի հոսանքը անթույլատրելիորեն մեծանում
է՝
ինչպես հետևում է (11.10) հավասարւմից, խարսխի հոսանքը անթույլատրելիորեն մեծանում
է՝
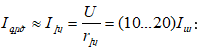
Այսպիսի հոսանքը վտանգավոր է ոչ միայն շարժիչը սնող ցանցի, այլև հենց շարժիչի համար, քանի որ այս դեպքում շարժիչում առաջացած մեխանիկական մեծ ուժերը կարող են լրջորեն վնասել այն: Դա է պատճառը, որ անմիջականորեն ցանցին միացնելով կարելի է գործարկել միայն փոքր հզորության (մինչև 1 կՎտ) շարժիչները, որոնց խարսխի դիմադրությունը համեմատաբար մեծ է:
Հաստատուն հոսանքի շարժիչների գործարկման ամենատարածված
եղանակը ![]() գործարկման ռեոստատի օգտագործումն է, որը գործարկման ընթացքում միացվում է
խարսխին հաջորդաբար (նկ.10.15): Սովորաբար դրա
գործարկման ռեոստատի օգտագործումն է, որը գործարկման ընթացքում միացվում է
խարսխին հաջորդաբար (նկ.10.15): Սովորաբար դրա ![]() դիմադրությունն ընտրվում է այն հաշվով, որ գործարկման առաջին ակնթարթի Iգրծ
հոսանքն ընդամենը
դիմադրությունն ընտրվում է այն հաշվով, որ գործարկման առաջին ակնթարթի Iգրծ
հոսանքն ընդամենը ![]() անգամ գերազանցի
անգամ գերազանցի ![]() անվանական արժեքը2: Գործարկումից
հետո, խարսխի արագանալուն զուգընթաց, մեծանում է նաև հակազդող էլշուն՝ փոքրացնելով
շարժիչի հոսանքը և զարգացրած մոմենտը: Շարժիչի գործարկվելուց հետո ռեոստատը դուրս է
բերվում շարժիչի շղթայից:
անվանական արժեքը2: Գործարկումից
հետո, խարսխի արագանալուն զուգընթաց, մեծանում է նաև հակազդող էլշուն՝ փոքրացնելով
շարժիչի հոսանքը և զարգացրած մոմենտը: Շարժիչի գործարկվելուց հետո ռեոստատը դուրս է
բերվում շարժիչի շղթայից:
Որպեսզի գործարկման ժամանակ շարժիչի զարգացրած
մոմենտը հնարավորին չափ մեծ ստացվի, նպատակահարմար է, որ գործարկման ընթացքում գրգռման
շղթայի ![]() ռեոստատը լրիվ դուրս
բերվի շղթայից՝ առավելագույն գրգռման հոսանք, հետևաբար և առավելագույն մագնիսական հոսք
ստանալու համար`
ռեոստատը լրիվ դուրս
բերվի շղթայից՝ առավելագույն գրգռման հոսանք, հետևաբար և առավելագույն մագնիսական հոսք
ստանալու համար` ![]()
11.10. Հաստատուն հոսանքի անկախ և զուգահեռ գրգռումով շարժիչներ
Ինչպես արդեն ասվել է նախորդ գլուխներում, էլեկտրաշարժիչների կարևորագույն բնութագծերից մեկը մեխանիկական բնութագիծն է՝ n = f (M) ֆունկցիայի գրաֆիկը, որտեղ հաստատուն հոսանքի շարժիչների համար n -ը խարսխի պտտման արագությունն է, M -ը՝ լիսեռի վրա զարգացրած մոմենտը:
Նկ.11.16-ում պատկերված է անկախ գրգռումով գեներատորի միացման սխեման: Ըստ Կիրխհոֆի 2-րդ օրենքի, խարսխի շղթայի համար կարող ենք գրել.
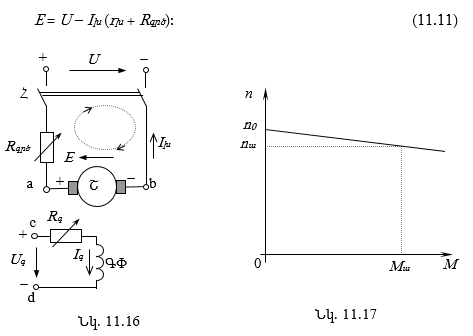
Այս հավասարումը ճիշտ է նաև նկ. 11.15-ում պատկերված
զուգահեռ գրգռումով շարժիչի համար, քանի որ ![]()
Մեխանիկական բնութագծի արտահայտությունը ստանալու նպատակով մեքենայի E էլշուի համար ստացված (11.4) և (11.11) բանաձևերից որոշենք խարսխի պտտման n արագությունը՝
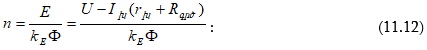
Մեքենայի M մոմենտի համար ստացված (11.7) ![]() հավասարումից, որոշելով
հավասարումից, որոշելով ![]() հոսանքի արժեքը և
տեղադրելով (11.12)-ի մեջ, կստանանք մեխանիկական բնութագծի հավասարումը.
հոսանքի արժեքը և
տեղադրելով (11.12)-ի մեջ, կստանանք մեխանիկական բնութագծի հավասարումը.
![]()
Հաստատուն հոսանքի շարժիչի մեխանիկական բնութագծի
տեսքը կախված է մեքենայում մագնիսական ![]() հոսքի գրգռման եղանակից:
հոսքի գրգռման եղանակից:
Անկախ
և զուգահեռ գրգռումով շարժիչներում մեքենայի ![]() հոսքը գործնականորեն
հաստատուն է, այդ պատճառով, ինչպես հետևում է (11.13) հավասարումից, դրանց մեխանիկական
բնութագիծն ուղիղ գիծ է, որի թեքությունը որոշվում է
հոսքը գործնականորեն
հաստատուն է, այդ պատճառով, ինչպես հետևում է (11.13) հավասարումից, դրանց մեխանիկական
բնութագիծն ուղիղ գիծ է, որի թեքությունը որոշվում է ![]() անկյունային գործակցով:
անկյունային գործակցով:
Այն
մեխանիկական բնութագիծը, որը համապատասխանում է լարման և հոսքի անվանական արժեքներին՝
![]() իսկ գործարկման ռեոստատը դուրս է բերված շղթայից՝
իսկ գործարկման ռեոստատը դուրս է բերված շղթայից՝ ![]() կոչվում է շարժիչի բնական մեխանիկական բնութագիծ (նկ. 11.17): Այն ուղիղ գիծ
է, որը գրեթե հորիզոնական է, այսինքն բավականաչափ «կոշտ» է:
կոչվում է շարժիչի բնական մեխանիկական բնութագիծ (նկ. 11.17): Այն ուղիղ գիծ
է, որը գրեթե հորիզոնական է, այսինքն բավականաչափ «կոշտ» է:
11.11. Անկախ և զուգահեռ գրգռումով շարժիչների արագության կարգավորումը
Մեխանիկական բնութագծի (11.13) հավասարումից հետևում
է, որ անկախ և զուգահեռ գրգռումով շարժիչների արագությունը կարելի է կարգավորել փոփոխելով
մեքենայի ![]() հոսքը (բևեռային կարգավորում), գործարկման ռեոստատի
հոսքը (բևեռային կարգավորում), գործարկման ռեոստատի ![]() դիմադրությունը (ռեոստատային կարգավորում) և շարժիչին կիրառված U լարումը:
դիմադրությունը (ռեոստատային կարգավորում) և շարժիչին կիրառված U լարումը:
Բևեռային կարգավորում: Պարապ ընթացքում, երբ շարժիչի լիսեռին կիրառված մոմենտը M = 0, շարժիչի պտտման արագությունը, համաձայն (11.13) բանաձևի, կլինի
![]()
Այսինքն՝ պարապ ընթացքի ռեժիմում հաստատուն հոսանքի
շարժիչի պտտման արագությունը հակադարձ համեմատական է գրգռման հոսքին, որն էլ իր հերթին
կախված է Iգ հոսանքի արժեքից: Նկ. 11.18-ում բերված են ![]() հոսքի և
հոսքի և ![]() արագության կախման
կորերը
արագության կախման
կորերը ![]() հոսանքի արժեքից:
հոսանքի արժեքից:
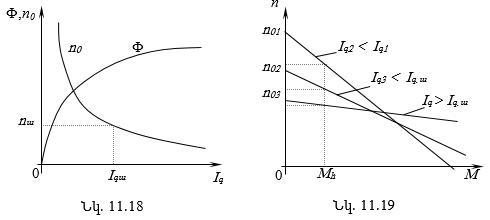
![]() ֆունկցիայի գրաֆիկը,
երբ շարժիչին կիրառված հակազդող մոմենտը՝ M=0, կոչվում է հաստատուն հոսանքի շարժիչի
պարապ ընթացքի կարգավորման բնութագիծ: Գրգռման հոսանքի բավականաչափ փոքրացման
կամ առավել ևս գրգռման շղթայի խզման
ֆունկցիայի գրաֆիկը,
երբ շարժիչին կիրառված հակազդող մոմենտը՝ M=0, կոչվում է հաստատուն հոսանքի շարժիչի
պարապ ընթացքի կարգավորման բնութագիծ: Գրգռման հոսանքի բավականաչափ փոքրացման
կամ առավել ևս գրգռման շղթայի խզման ![]() դեպքում խարսխի հոսանքը
և պտտման արագությունը խիստ մեծանում են, որը կարող է հանգեցնել շարժիչի լուրջ մեխանիկական
վնասվածքների: Այս երևույթը կանխելու համար նախատեսվում է պաշտպանություն, որն անջատում
է շարժիչը ցանցից (սովորաբար, երբ
դեպքում խարսխի հոսանքը
և պտտման արագությունը խիստ մեծանում են, որը կարող է հանգեցնել շարժիչի լուրջ մեխանիկական
վնասվածքների: Այս երևույթը կանխելու համար նախատեսվում է պաշտպանություն, որն անջատում
է շարժիչը ցանցից (սովորաբար, երբ ![]()
Բեռնավորված հաստատուն հոսանքի շարժիչի արագության
բևեռային կարգավորումը նույնպես հիմնված է ![]() գրգռման հոսանքի փոփոխման
միջոցով մեքենայի բևեռների
գրգռման հոսանքի փոփոխման
միջոցով մեքենայի բևեռների ![]() հոսքի փոփոխման վրա:
Գրգռման հոսանքի (նաև հոսքի) փոքրացումը բերում է, ըստ (11.13)-ի,
հոսքի փոփոխման վրա:
Գրգռման հոսանքի (նաև հոսքի) փոքրացումը բերում է, ըստ (11.13)-ի, ![]() անկյունային գործակցի մեծացման և հակառակը: Շարժիչի արհեստական մեխանիկական
բնութագծերը գրգռման տարբեր հոսանքների դեպքում բերված են նկ. 11.19-ում:
անկյունային գործակցի մեծացման և հակառակը: Շարժիչի արհեստական մեխանիկական
բնութագծերը գրգռման տարբեր հոսանքների դեպքում բերված են նկ. 11.19-ում:
Ինչպես երևում է բնութագծերից, լիսեռին կիրառված
նույն ![]() հակազդող մոմենտի
դեպքում
հակազդող մոմենտի
դեպքում ![]() հոսանքի միջոցով փոփոխելով մեքենայի
հոսանքի միջոցով փոփոխելով մեքենայի ![]() մագնիսական հոսքը,
կարելի է բավական լայն սահմաններում սահուն կերպով փոփոխել խարսխի պտտման n արագությունը:
Այսպիսի կարգավորումը առավել արդյունավետ է իրագործել համեմատաբար փոքր
մագնիսական հոսքը,
կարելի է բավական լայն սահմաններում սահուն կերպով փոփոխել խարսխի պտտման n արագությունը:
Այսպիսի կարգավորումը առավել արդյունավետ է իրագործել համեմատաբար փոքր ![]() բեռնվածքների դեպքում:
Եթե
բեռնվածքների դեպքում:
Եթե ![]() մոտ է
մոտ է ![]() անվանական մոմենտին, ապա հոսքի փոքրացման դեպքում, որն անհրաժեշտ է n արագության
մեծացման համար, խարսխի հոսանքը կգերազանցի անվանական արժեքը, որը երկարատև ռեժիմի
դեպքում անթույլատրելի է, որովհետև կբերի շարժիչի գերտաքացման:
անվանական մոմենտին, ապա հոսքի փոքրացման դեպքում, որն անհրաժեշտ է n արագության
մեծացման համար, խարսխի հոսանքը կգերազանցի անվանական արժեքը, որը երկարատև ռեժիմի
դեպքում անթույլատրելի է, որովհետև կբերի շարժիչի գերտաքացման:
Հոսքը չի կարելի չափից ավելի փոքրացնել, որովհետև, հակառակ դեպքում, խարսխի n արագությունը կարող է այնքան մեծանալ, որ շարժիչը լուրջ մեխանիկական վնասվածքների կենթարկվի:
Բևեռային կարգավորումը շատ շահավետ է և հարմար.
քանի որ ![]() հոսանքը շատ փոքր
է, ուստի
հոսանքը շատ փոքր
է, ուստի ![]() ռեոստատը ստացվում է փոքր չափսերի, և դրանում հզորության կորուստները նույնպես
փոքր են:
ռեոստատը ստացվում է փոքր չափսերի, և դրանում հզորության կորուստները նույնպես
փոքր են:
Ռեոստատային կարգավորում:
Շարժիչի արագության կարգավորման այս եղանակի դեպքում փոփոխվում է խարսխի շղթային հաջորդաբար
միացված ռեոստատի ![]() դիմադրությունը, երբ
U = const և
դիմադրությունը, երբ
U = const և ![]() Ըստ (11.13) հավասարման
շարժիչի պարապ ընթացքի
Ըստ (11.13) հավասարման
շարժիչի պարապ ընթացքի ![]() արագությունը չի փոխվում, սակայն մեծանում է k անկյունային գործակիցը, և բնութագծերը
ստանում են ավելի մեծ թեքություն (նկ. 11.20)՝ դառնում են ավելի «փափուկե, քան բնական
մեխանիկական բնութագիծն է
արագությունը չի փոխվում, սակայն մեծանում է k անկյունային գործակիցը, և բնութագծերը
ստանում են ավելի մեծ թեքություն (նկ. 11.20)՝ դառնում են ավելի «փափուկե, քան բնական
մեխանիկական բնութագիծն է ![]()
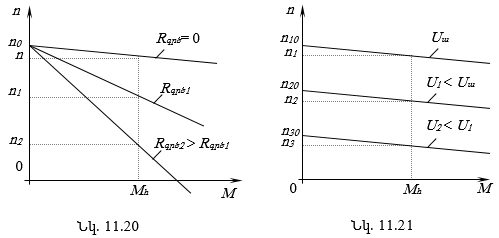
Ակնհայտ է, որ ռեոստատային կարգավորման դեպքում խարսխի n արագությունը կարելի է միայն փոքրացնել դրա անվանական արժեքի նկատմամբ: Ընդ որում արագության փոփոխման միջակայքն այնքան ավելի մեծ է, որքան մեծ է շարժիչի բեռնվածքը:
Հաստատուն հոսանքի շարժիչների ռեոստատային կարգավորումը
կապված է ![]() ռեոստատի վրա հզորության մեծ կորստի հետ՝
ռեոստատի վրա հզորության մեծ կորստի հետ՝ ![]() որն այնքան ավելի մեծ է, որքան փոքր է խարսխի n արագությունը: Բացի դրանից,
եթե
որն այնքան ավելի մեծ է, որքան փոքր է խարսխի n արագությունը: Բացի դրանից,
եթե ![]() ռեոստատը պետք է օգտագործվի արագության կարգավորման համար, այսինքն երկարատև
աշխատանքի համար, ապա այն պետք է ունենա ավելի մեծ չափեր և արժեք: Այս պատճառով այն
հիմնականում կիրառվում է փոքր հզորության շարժիչների արագության կարգավորման համար:
ռեոստատը պետք է օգտագործվի արագության կարգավորման համար, այսինքն երկարատև
աշխատանքի համար, ապա այն պետք է ունենա ավելի մեծ չափեր և արժեք: Այս պատճառով այն
հիմնականում կիրառվում է փոքր հզորության շարժիչների արագության կարգավորման համար:
Լարման միջոցով կարգավորումը կիրառվում է միայն անկախ գրգռումով շարժիչների համար, որովհետև դրանց գրգռման հոսանքի և հոսքի արժեքները կախված չեն շարժիչի խարսխին կիրառված U լարումից (նկ. 11.16):
Փոփոխելով U լարումը, հնարավոր է ստանալ անկախ
գրգռումով շարժիչի պտտման արագության սահուն կարգավորում շարժիչի տարբեր բեռնվածքների
դեպքում, քանի որ փոփոխվում է միայն պարապ ընթացքի ![]() արագության արժեքը,
իսկ արհեստական մեխանիկական բնութագծերի թեքության անկյունը մնում է անփոփոխ. բնութագծերն
ունեն նույն «կոշտությունը», ինչ որ բնական մեխանիկական բնութագիծը (նկ. 11.17):
արագության արժեքը,
իսկ արհեստական մեխանիկական բնութագծերի թեքության անկյունը մնում է անփոփոխ. բնութագծերն
ունեն նույն «կոշտությունը», ինչ որ բնական մեխանիկական բնութագիծը (նկ. 11.17):
Լարման միջոցով կարգավորման թերությունն այն է, որ պահանջվում է հաստատուն լարումը սահուն փոփոխող սարք: Վերջին ժամանակներս որպես կարգավորվող (փոփոխվող) լարման աղբյուրներ առավելապես կիրառվում են կիսահաղորդչային (տիրիստորային) ձևափոխիչները: Նախկինում օգտագործվող թանկարժեք և մեծ տեղ զբաղեցնող շարժիչ-գեներատոր-շարժիչ մեքենայական ագրեգատները ներկայումս պահպանվել են միայն մետալուրգիական արտադրությունում` հզոր շարժիչների արագության կարգավորման համար:
Լարման փոփոխմամբ արագության կարգավորման դեպքում գործարկման ռեոստատը դառնում է ավելորդ, քանի որ գործարկման հոսանքը փոքրացնելու համար կարելի է պարզապես շարժիչը գործարկել ցածր լարման տակ:
11.12. Հաստատուն հոսանքի հաջորդական գրգռումով շարժիչներ
Հաջորդաբար գրգռումով շարժիչներում, որտեղ գրգռման
փաթույթը միացված է հաջորդաբար խարսխի փաթույթին, գրգռման հոսանքը հավասար է խարսխի
հոսանքին (նկ. 11.22ա): Դրա շնորհիվ մեքենայի ![]() հոսքը փոփոխվում է
հոսքը փոփոխվում է
![]() խարսխի հոսանքին համեմատական, հետևաբար մեքենայի զարգացրած M մոմենտը, ըստ
(11.7) բանաձևի, կփոփոխվի այդ հոսանքի քառակուսուն համեմատական՝
խարսխի հոսանքին համեմատական, հետևաբար մեքենայի զարգացրած M մոմենտը, ըստ
(11.7) բանաձևի, կփոփոխվի այդ հոսանքի քառակուսուն համեմատական՝
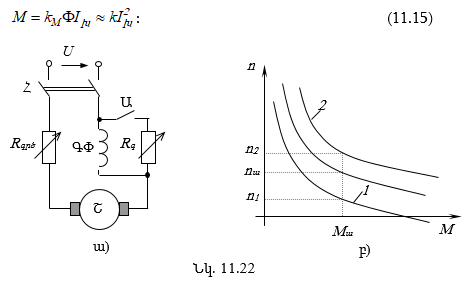
Մեխանիկական բնութագծի (11.13) հավասարումից հետևում
է, որ խարսխի պտտման n արագությունը հակադարձ համեմատական է մեքենայի ![]() հոսքին, հետևաբար,
հաջորդական գրգռումով շարժիչներում n -ը հակադարձ համեմատական կլինի նաև (եթե միջուկը
հագեցած չէ) մեքենայի զարգացրած M մոմենտին, և դրա մեխանիկական բնութագծերը կունենան
նկ. 11.22բ -ում պատկերված տեսքը: Շարժիչի մեխանիկական բնութագիծը շատ «փափուկ» է՝
մոմենտի փոփոխությունը խիստ ազդում է խարսխի պտտման n արագության վրա:
հոսքին, հետևաբար,
հաջորդական գրգռումով շարժիչներում n -ը հակադարձ համեմատական կլինի նաև (եթե միջուկը
հագեցած չէ) մեքենայի զարգացրած M մոմենտին, և դրա մեխանիկական բնութագծերը կունենան
նկ. 11.22բ -ում պատկերված տեսքը: Շարժիչի մեխանիկական բնութագիծը շատ «փափուկ» է՝
մոմենտի փոփոխությունը խիստ ազդում է խարսխի պտտման n արագության վրա:
Հաջորդաբար գրգռումով շարժիչների առանձնահատկությունները
բխում են հենց դրա մեխանիկական բնութագծից: Այս շարժիչները գործարկման ժամանակ կամ
փոքր արագությունների դեպքում զարգացնում են բավական մեծ պտտող մոմենտ: Մյուս կողմից,
բեռնվածքի փոքրացման դեպքում խարսխի ![]() հոսանքը փոքրանում
է դանդաղ, իսկ դրա պտտման n արագությունը մեծանում է շատ արագ: Փոքր բեռնվածքների դեպքում
հոսանքը փոքրանում
է դանդաղ, իսկ դրա պտտման n արագությունը մեծանում է շատ արագ: Փոքր բեռնվածքների դեպքում
![]() շարժիչի արագությունն անթույլատրելիորեն կարող է մեծանալ, որը վտանգավոր է
շարժիչի համար: Այս պատճառով հաջորդաբար գրգռումով շարժիչները չի կարելի գործարկել
առանց բեռի կամ փոքր բեռի տակ:
շարժիչի արագությունն անթույլատրելիորեն կարող է մեծանալ, որը վտանգավոր է
շարժիչի համար: Այս պատճառով հաջորդաբար գրգռումով շարժիչները չի կարելի գործարկել
առանց բեռի կամ փոքր բեռի տակ:
Հաջորդական գրգռումով շարժիչները լավ են դիմանում
տևական գերբեռնումներին, քանի որ M մոմենտի մեծացումը բերում է խարսխի ![]() հոսանքի համեմատաբար
ավելի քիչ չափով մեծացմանը (ըստ (11.15)-ի,
հոսանքի համեմատաբար
ավելի քիչ չափով մեծացմանը (ըստ (11.15)-ի, ![]() համեմատական է
համեմատական է ![]() և գերբեռնումների դեպքում շարժիչը չի գերտաքանում:
և գերբեռնումների դեպքում շարժիչը չի գերտաքանում:
Հաջորդաբար գրգռումով շարժիչի արագությունը կարգավորելու
համար օգտագործվում է ինչպես ![]() գործարկման ռեոստատը,
որը չնայած շահավետ չէ, բայց թույլ է տալիս ստանալ անվանականից ավելի փոքր արագություններ
(նկ. 11.22բ-ում 1 կորը), այնպես էլ հատուկ
գործարկման ռեոստատը,
որը չնայած շահավետ չէ, բայց թույլ է տալիս ստանալ անվանականից ավելի փոքր արագություններ
(նկ. 11.22բ-ում 1 կորը), այնպես էլ հատուկ ![]() կարգավորման ռեոստատ,
որը զուգահեռ է միացվում գրգռման փաթույթին (նկ. 11.22ա): Վերջինիս միացման ժամանակ
խարսխի գրեթե նույն հոսանքի դեպքում փոքրանում է միայն
կարգավորման ռեոստատ,
որը զուգահեռ է միացվում գրգռման փաթույթին (նկ. 11.22ա): Վերջինիս միացման ժամանակ
խարսխի գրեթե նույն հոսանքի դեպքում փոքրանում է միայն ![]() հոսքը և մեծանում
է շարժիչի պտտման արագությունը (նկ. 11.22բ-ում 2 կորը):
հոսքը և մեծանում
է շարժիչի պտտման արագությունը (նկ. 11.22բ-ում 2 կորը):
Հաջորդաբար գրգռումով շարժիչները, շնորհիվ «փափուկ» մեխանիկական բնութագծի, գերբեռնումներին դիմանալու իրենց ունակության և արագության կարգավորման հնարավորություններով, անփոխարինելի են տրանսպորտային մեքենաներում (քաղաքային և երկաթուղային էլեկտրատրանսպորտ, վերամբարձ սարքեր):
Էլեկտրատրանսպորտի էլեկտրամատակարարման համար տեղակայվում են հատուկ ձևափոխիչային ենթակայաններ՝ որոնցում հզոր կիսահաղորդչային ուղղիչների միջոցով փոփոխական հոսանքը վերափոխվում է հաստատուն հոսանքի:
11.13. Հաստատուն հոսանքի խառը գրգռումով շարժիչներ
Զուգահեռ գրգռումով շարժիչն ունի «կոշտ» մեխանիկական բնութագիծ, իսկ հաջորդական գրգռումով շարժիչը՝ «փափուկե մեխանիկական բնութագիծ: Որոշ դեպքերում հարկ է լինում ունենալ միջանկյալ տեսքի բնութագիծ, որն ստանալու ամենահարմար միջոցը խառը գրգռումով շարժիչի կիրառությունն է:
Խառը գրգռումով շարժիչներում մագնիսական դաշտը գրգռվում է երկու գրգռման փաթույթներով, որոնցից մեկը համարվում է հիմնական փաթույթ և ապահովում է մեքենայի ընդհանուր հոսքի մոտ 70%-ը, իսկ մյուսը՝ օժանդակ փաթույթը, տալիս է հոսքի 30%-ը:
Եթե շարժիչի հիմնական գրգռման փաթույթը զուգահեռ փաթույթն է, ապա շարժիչը ձեռք է բերում զուգահեռ գրգռումով շարժիչի առանձնահատկությունները: Օժանդակ հաջորդական փաթույթի առկայությունը կայունացնում է մեքենայի մագնիսական հոսքը և մի փոքր փափկացնում է դրա մեխանիկական բնութագիծը: Զուգահեռ գրգռման փաթույթի խզումը վտանգավոր չէ այս շարժիչների համար, քանի որ հաջորդական փաթույթի հոսքը բավարար է, որպեսզի խարսխի պտտման արագությունը չափից ավելի չմեծանա:
Եթե շարժիչի հիմնական գրգռման փաթույթը հաջորդական փաթույթն է, ապա շարժիչը ձեռք է բերում հաջորդական գրգռումով շարժիչի առանձնահատկություններ: Այս դեպքում շարժիչը կարող է աշխատել նաև փոքր բեռնվածքների կամ պարապ ընթացքի դեպքում, որովհետև օժանդակ զուգահեռ փաթույթի շնորհիվ խարսխի պտտման արագությունը չի գերազանցում թույլատրելի սահմանային արժեքը:
1. Ո՞րն է հաստատուն հոսանքի մեքենայի նշանակությունը և որո՞նք են կիրառման բնագավառները:
2. Որո՞նք են եռաֆազ հաստատուն հոսանքի մեքենայի կառուցվածքային մասերը:
3. Բացատրեք հաստատուն հոսանքի մեքենայի աշխատանքի սկզբունքը գեներատորի ռեժիմում:
4. Բացատրեք հաստատուն հոսանքի մեքենայի աշխատանքի սկզբունքը շարժիչի ռեժիմում:
5. Թվարկեք հաստատուն հոսանքի մեքենայի տեսակները:
6. Տվեք հաստատուն հոսանքի անկախ և զուգահեռ գրգռումով գեներատորների համեմատական բնութագիրը:
7. Պատկերեք անկախ գրգռումով գեներատորի պարապ ընթացքի, արտաքին և կարգավորման բնութագրերը:
8. Բացատրեք ինքնագրգռման երևույթը զուգահեռ գրգռումով օրինակի վրա: Ի՞նչ պայմանների առկայության դեպքում է հնարավոր ինքնագրգռումը:
9. Գծեք խառը գրգռումով գեներատորի արտաքին բնութագծերը` գրռման փաթույթների հակառակ և համաձայն միացման դեպքում: Նշեք դրանց կիրառման բնագավառները:
10. Զուգահեռ գրգռումով շարժիչի օրինակի վրա բացատրեք շարժիչի գործարկման ընթացքը: Ինչո՞վ է վտանգավոր գործարկման մեծ հոսանքը:
11. Գծեք անկախ և զուգահեռ գրգռումով հաստատուն հոսանքի շարժիչի բնական մեխանիկական բնութագիծը: Ինչո՞վ է այն առանձնահատուկ:
12. Անկախ և զուգահեռ գրգռումով հաստատուն հոսանքի շարժիչի արագության կարգավորման ի՞նչ եղանակներ գիտեք:
13. Ի՞նչ հատկություններ ունեն հաջորդական և խառը գրգռումով շարժիչները և ո՞ր դեպքերում են դրանք կիրառվում:
1. Герасимов В.Г. Электротехника. Учебное пособие. М. <<Высшая школа>> 1983, 480 с.
2. Касаткин А. С., Немцов М.В. Электротехника (2-х книгаь). 5-ое изд., М. Энергоиздат, 1995, 240ր. И 305ր.
3. Касаткин А. С., Немцов М.В. Электротехника. Учебник. М. <<Высшая школа>> . 1986, 2002.
4. ИвановИ.И., Лукин А.Ф., Соловьев Г. И. Электротехника.Основные положение, примеры и задачи. Учебник.Из-во“Лань”. 2002.
5. Paul C.R., Nasar S.A., Unnewehr L.E. Introduction to Electrical Engineering. New York 1992.
6. David E. Johnson, John Hilburn. Basic Electric Circuit Analysis. Third Edition. New Jersey 1986.
7. Բալաբանյան Հ. Ընդհանուր էլեկտրատեխնիկա: Թեստային հարցերի և խնդիրների շտեմարան: ՀՊՃՀ, 2010, 75 էջ*:
8. Սարգսյան Ա. Ընդհանուր էլեկտրատեխնիկա: Հաշվեգրաֆիկական աշխատանքների մեթոդական ցուցումներ: ՀՊՃՀ, 2006, 37 էջ:
9. Ազատյան Լ., Բայբուրտյան Մ., Բալաբանյան Հ., Հովհաննիսյան Ժ. Ընդհանուր էլեկտրատեխնիկա: Լաբորատոր աշխատանքներ: ՀՊՃՀ 2005, 50 էջ:
10. Սարգսյան Ա., Պլուզյան Է., Արզումանյան Ա., Արամյան Մ. Տեսական և ընդհանուր էլեկտրատեխնիկա: Վիրտուալ լաբորատոր աշխատանքներ: Մաս1: ՀՊՃՀ, 2009, 80 էջ:
11. Սարգսյան Ա., Պլուզյան Է.,Արզումանյան Ա., Արամյան Մ. Տեսական և ընդհանուր էլեկտրատեխնիկա: Վիրտուալ լաբորատոր աշխատանքներ: Մաս 2: ՀՊՃՀ, 2010, 88 էջ: