ԲՈՎԱՆԴԱԿՈՒԹՅՈՒՆ

1. Տեսական հիմնադրույթները

1.1 Հսկման և արատորոշման հասկացությունները

1.2 Թեստային   հսկման    և  արատորոշման   հասկացությունը

1.3 Թեստային   հսկման    և  արատորոշմանմաթեմատիկական մոդելը

1.4 Ըստ մոդուլի ապարատային հսկման նկարագրությունը

1.5 Թվաբանական գործողությունների թվային հսկումը ըստ մոդուլի

2. Տրամաբանական սխեմաների թեստերի կառուցում

2.1. Տրամաբանական ցանցեր

2.2. Տրամաբանական ցանցերի տեսակները

2.3. ՏՑ-երի թեստի կառուցման սկզբունքները

3. Համարժեք նորմալ ձևի մեթոդ

4. d- ալգորիթմի մեթոդ

5. Թվաբանական-տրամաբանական սարքի հսկում

6. Հսկման կոդիձևավորման գումարիչներ

6.1. Հսկման կոդերի բազմապատկիչներ

1. Տեսական հիմնադրույթները

1.1. Հսկման և արատորոշման հասկացությունները

Ցանկացած տեխնիկական համակարգի կամ սարքի, այդ թվում համակարգչի հսկում ասելով հասկանում ենք նրանում առկա անսարքությունների (սխալների) փաստի հայտնաբերումը, իսկ արատորոշում ասելով` անսարքության տեղի որոշումը: Հսկումը և արատորոշումը կատարվում է լրացուցիչ  ինֆորմացիայի կիրառմամբ, որն իրականացվում է կամ ապարատային եղանակով ավելցուկային սարքավորում ներդնելու, կամ ծրագրային, թեստային եղանակով լրացուցիչ ժամանակ ծախսելու միջոցով: Առաջինն արագագործ է, սակայն թանկ, քանի որ լրացուցիչ ֆինանսական ներդրում է պահանջում, իսկ երկրորդը դանդաղագործ է, սակայն էժան: Համակարգիչներում երկու եղանակներն էլ լայն կիրառում են ստացել: Ապարատայինը նպատակահարմար է օգտագործել հիշասարքերում ինֆորմացիայի պահպանման, գրանցման և ընթերցման, համակարգչի տարբեր հանգույցների միջև ինֆորմացիայի փոխանակման, թվաբանական գործողությունների հսկման և արատորոշման համար, իսկ թեստայինը` տրամաբանական սխեմաների, հանգույցների հսկման և արատորոշման«  ինքնաստուգման« կանխարգելիչ միջոցառումների համար:

      Ցանկացած  տեխնիկական,այդ  թվում  հաշվողական համակարգ  կամ  սարք,  այսուհետև   համակարգ,  բնութագրվում    է   բնութագրերի   շարքով, որոնց  մի մասը  հիմնական   է, մյուսները` երկրորդական: Առաջինները   բնութագրում  են համակարգի  կողմից   իրենց  տրված   գործառույթների  կատարումը, իսկ  երկրորդականները` շահագործման  հարմարությունը, արտաքին   տեսքը   և   այլն: Համակարգը   կոչվում    է   սարքին, եթե   այն   համապատասխանում    է   իրեն առաջադրված   բոլոր  պահանջներին, այսինքն՝ բոլոր  հիմնական   և   երկրորդական   բնութագրերը   գտնվում   են   թույլատրելի  սահմաններում, հակառակ դեպքում  այն  կոչվում  է  անսարք: Համակարգը  աշխատունակ  է, եթե  հիմնական  բնութագրերը  գտնվում  են  թույլատրելի  սահմաններում,հակառակ  դեպքում՝ այն  անաշխատունակ  է: Աշխատունակության  կորուստը  կոչվում  է  անսարքություն: Վերը  շարադրված   հասկացությունները  հավասարապես  վերաբերում   են  նաև   համակարգի  բաղկացուցիչ  մասերին` հանգույցներին, բլոկներին  և  տարրերին: Համակարգի   ցանկացած   բաղկացուցիչի  անսարքությունը   ներկայացնում  է նաև  համակարգի  անսարքություն   և  հանգեցնում  նրա   աշխատունակության կորստին: Աշխատունակ  համակարգը   կարող  է  լինել  սարքին  կամ  անսարք: Սարքին համակարգը   միշտ   աշխատունակ   է: Անսարք  համակարգը   կարող   է  լինել աշխատունակ  կամ  անաշխատունակ: Անաշխատունակ   համակարգը   միշտ   անսարք  է:

>>

1.2. Թեստային   հսկման    և  արատորոշման   հասկացությունը

Համակարգի  աշխատունակության   ստուգման   առավել   տարածված  եղանակներից  է  փորձարկող  ծրագրերի միջոցով  իրականացվող  թեստային  հսկումը: Թեստի  կատարման  ընթացքում  համակարգը  ելակետային  տվյալների նկատմամբ   իրականացնում    է  որոշակի  գործողություններ, ստացված  արդյունքները   համեմատում   աշխատունակ    համակարգի  համար  որոշված  համանման  արդյունքների  հետ  և  դրանց  չհամընկնման  դեպքում  հայտնաբերում անսարքությունները:

 Բնույթով  թեստերը  լինում  են  երկու  տիպի` հսկող և  արատորոշող: Հսկող  թեստերը  նախատեսված   են  համակարգում   անսարքության   առկայության  փաստը  հայտնաբերելու  համար: Արատորոշող   թեստերը  նախատեսված են  անսարքության, այսինքն՝  անսարքտեղը  որոշելու, ընդ  որում  նպատակահարմար   է   նաև   փոխարինման   ենթակա   տարրը   կամ   տարրերի   խումբը մատնանշելու  համար: Արատորոշող  թեստերը  անսարքությունների  տեղերի որոնումները  ավտոմատացնելու  առավել  արդյունավետ  միջոցներն  են: Արատորոշող  թեստերը  նպատակահարմար   է  կիրառել  հսկող  թեստերով անսարքության փաստը  հայտնաբերելուց  հետո: Արատորոշող թեստերը կառուցվում   են “տիրույթի  նեղացման   սկզբունքի”   հիման   վրա   համակարգի փոխարինվող    բաղկացուցիչի   ճշգրտությամբ:  Ըստ    այդ   սկզբունքի   արատորոշումը   կատարվում    է  հաջորդաբար  իրականացվող  ենթաթեստերով, որոնցից  յուրաքանչյուրը  նեղացնում   է  նախորդ  ենթաթեստով  որոշված  փոխարինման  ենթակա  տարրերի  շրջանակը:

>>

1.3. Թեստային   հսկման    և  արատորոշմանմաթեմատիկական մոդելը

Դիտարկենք  թեստերի  կառուցման  սկզբունքները: Կատարենք  հետևյալ  նշանակումները`

G= {g₁,g₂,...  g_n } –  համակարգի     բոլոր   միակի   անսարքությունների բազմություն,

 s₀ -  համակարգի   աշխատունակ   վիճակ,

S = { s₁, s₂, ... s_m} – համակարգի  անաշխատունակ  վիճակների  բազմություն,

π = {π₁, π₂, ...π_k} – համակարգի  փորձարկումների, ստուգումների  բազմություն:

  Թեստերի  կառուցումը  կարելի  է  կատարել  պարզեցված, առավել  հավանական  և  բարդ, նվազ   հավանական  տարբերակներով: Առաջինում  ընդունվում է համակարգում ընդամենը  մեկ  որևէ միակի անսարքության  առկայություն: Այդ  դեպքում n=m  և  G ու S  բազմությունները նույնացված  են: Երկրորդում  ընդունվում է մեկից  ավելի  ընդհուպ  մինչև  բոլոր  հնարավոր  միաժամանակ  անսարքությունների  առկայություն: Այդ  դեպքում  m >n: Ինչ  վերաբերում  է փորձարկումներին, ապա յուրաքանչյուր հայտնաբերում   է, այսինքն՝   ստուգում   է առնվազն մեկ  անսարքության առկայություն, հետևաբար  անաշխատունակ  վիճակ:

կանվանենք  հսկող  թեստ, եթե  նրանով  հայտնաբերվում   են   բոլոր հնարավոր  անաշխատունակ  վիճակները, այսինքն  կատարվում  է  s₀  և  ցանկացած  վիճակների  տարբերակում:  կանվանենք  արատորոշող թեստ, եթե  նրանով  տարբերվում  են  անաշխատունակ  վիճակների  բոլոր հնարավոր  զույգերը, այսինքն՝  ցանկացած    և անաշխատունակ  վիճակ: T_հ( T_ա )  կանվանենք  փակուղային  կամ  տարրական  թեստ, եթե  ցանկացած  թեստ  չէ: Փակուղային  (տարրական)   թեստերից  նվազագույն հզորություն, այսինքն՝ ստուգումների  քանակ  պարունակող  թեստը կանվանենք  նվազագույն  թեստ:

  Կառուցենք  աղյուսակ, որի  տողերը  համապատասխանում  են  անաշխատունակ   վիճակներին, իսկ   սյունակները` ստուգումներին  և   անվանենք  այն  անսարքությունների  աղյուսակ: i-րդ   տողի   և  j –րդ  սյունակի  հատման   վանդակում  կատարվում  է  նշում, գրվում  է   “1“  թվանշան, եթե  s_i   անաշխատունակ վիճակը ստուգվում  է   π_j   ստուգումով, հակառակ  դեպքում՝  նշում  չի  կատարվում   կամ   գրվում   է     “0”  թվանշան, որը   դիտարկելիության  առումով  նպատակահարմար  է  չկատարել:

     Աղյուսակ 2.3.1-ում  բերված  է  

բազմությունների  համար  անսարքությունների  աղյուսակի  օրինակ:

 Անսարքությունների աղյուսակի  միջոցով  հսկող  թեստի  կառուցումը  հանգեցվում  է  սյունակների  այնպիսի ենթաբազմության  որոշմանը, որում  յուրաքանչյուր տող  առնվազն  մեկ  նշում  ունի: Ընդ  որում, եթե  այն  այնպիսին  է, որ  դրանից  առնվազն  մեկ  սյունակի հեռացումը  հանգեցնում  է  վերը  նշված  հատկության  կորստին, ապա  այն  ներկայացնում  է  փակուղային, իսկ  նվազագույն  հզորության  դեպքում  նաև  նվազագույն  հսկող  թեստ:

 Նախքան   թեստերի   կառուցումը  նպատակահարմար   է  կատարել  անսարքության  աղյուսակի  պարզեցում` հեռացնելով   ավելցուկային  տողերը  և  սյունակները:

Եթե  s_i  և  s_j   տողերը  այնպիսին  են, որ  s_j -ն  պարունակում  է  s_i-ի  նշումները կամ   նույն   և   լրացուցիչ   նշումներ, ապա   s_j –ն  հեռացվում   է: Եթե   π_i   և  π_j սյունակները   այնպիսին  են, որ   π_j-ն   պարունակում    է  π _i -ի նշումները  կամ նույն  և  լրացուցիչ  նշումներ, ապա  π _i –ն  հեռացվում  է:

  Այս պարզեցումները  կատարվում  են  հաջորդաբար  մինչև  ստացված  աղյուսակի   համար   նրա  կիրառումը  հնարավոր լինելը: Այսպիսի  աղյուսակը  կանվանենք  փակուղային` չպարզեցվող:

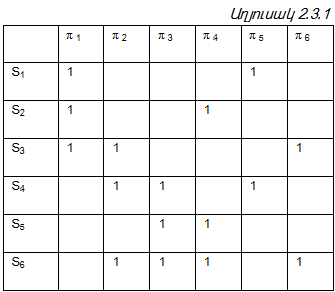
 Աղյուսակ 2.3.1-ի   դեպքում   s₅   և   s₆   տողերի  համեմատման   արդյունքում   հեռացվում է s₆ –ը, իսկ   π ₂  և  π ₆  սյունակների    համեմատման  արդյունքում` π ₆-ը:

Աղյուսակ  2.3.1-ի  պարզեցումից  ստացվում  է  աղյուսակ 2.3.2-ը:

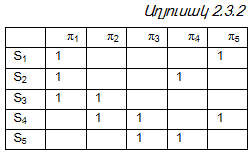Նվազագույն  հսկող  թեստը  կարելի  է կառուցել  հետևյալ  եղանակով: Ընդունելով   ստուգումները   որպես   բուլյան  (տրամաբանական)   փոփոխական` անսարքության   աղյուսակի  յուրաքանչյուր  տող  ներկայացնենք  նշումներին  համապատասխանող  ստուգումներից   կազմված  դիզյունկցիայի  տեսքով, այնուհետև  դրանք   միավորենք  կոնյունկցիայով  և  ստացված     արտահայտությունը    պարզեցնենք: Յուրաքանչյուր    դիզյունկտիվ    անդամում   ընդգրկված   ստուգումների   ենթաբազմությունը   կներկայացնի  փակուղային   հսկող  թեստ, որոնցից  նվազագույն  հզորություն   պարունակողը  կներկայացնի  նվազագույն հսկող  թեստ:

  Կիրառելով  վերը  շարադրվածը՝  աղյուսակ 2.3.2-ի  համար  կստանանք`

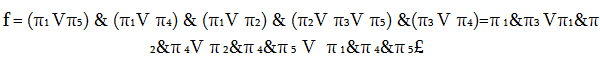
       Հետևաբար  հսկող  թեստեր  են  հետևյալ  ենթաբազմությունները`

որոնցից  առաջինը` նվազագույն հսկող  թեստ  է:

 Նկարագրված  եղանակը   գործողությունների   առումով  աշխատատար   է  և գործնականում   նվազ  կիառելի: Առավել  տարածված   են   այն  եղանակները, որոնք  առավել  պարզ  են   և  հանգեցնում  են  նվազագույնին   մոտ, ընդ  որում հնարավոր  է նաև  նվազագույն, հսկող  թեստերի  կառուցմանը:

Տարածված  եղանակների  ընդհանրացված  տարբերակի  կատարման   փուլերն  են.

1) Անսարքությունների   աղյուսակի  պարզեցում` հեռացնելով  ավելցուկային տողերը  և  սյունակները:

2) Էական  ստուգումների  ընդգրկում  հսկող  թեստում, այդ  ստուգումների  ու դրանցով   ստուգվող   անաշխատունակ   վիճակների   հեռացում   աղյուսակից: Էական  կոչվում  է  այն  ստուգումը, որը  պարունակում   է  առնվազն  մեկ   այնպիսի  նշում, որը  համապատասխան  տողում  միակն  է: Էական  ստուգումները ընդգրկված  են  բոլոր  հնարավոր  փակուղային, հետևաբար  նաև  նվազագույն հսկող  թեստերում  և  ներկայացնում  են  դրանց  միարժեքորեն  որոշվող  մասը:

3)  Հաջորդական  քայլերով  ընդունված  չափանիշներով ստուգումների  ընտրում  և  դրանց  ընդգրկում  հսկող  թեստում, ընտրված  ստուգումների  և  դրանցով   ստուգվող  վիճակների  հեռացում   աղյուսակից   մինչ  դրանց  սպառումը, որի  արդյունքում  ամբողջապես  կձևավորվի  հսկող  թեստը:

 Այժմ  անդրադառնանք  արատորոշման  թեստերի  կառուցմանը: Ստուգումների  արդյունքներով  զույգ  առ  զույգ  համեմատելով  բոլոր անաշխատունակ   վիճակները` կառուցվում էարատորոշման  աղյուսակ, որի  տողերը  ներկայացնում  են  անաշխատունակ  վիճակների  զույգերը, իսկ  սյունակները` ստուգումները: Եթե    π_k  ստուգման   արդյունքները   s_i   և  s_j   անաշխատունակ  վիճակների   համար   համարժեք   չեն, ապա  արատորոշման  աղյուսակի  (s_i, s_j )   զույգին   համապատասխան   տողի   և   π_k  սյունակի  հատման վանդակում  նշում   է   կատարվում, հակառակ  դեպքում, եթե  ստուգման  արդյունքները   համարժեք   են, նշում    չի   կատարվում: Նշումներ չպարունակող տողերին համապատասխանող  զույգերի անաշխատունակ  վիճակները  չտարբերվող  են, հետևաբար  այդ   զույգերը  աղյուսակից   դուրս  են   բերվում: Աղյուսակի  հետագա  պարզեցումը  կատարվում  է  դարձյալ  ավելցուկային  տողերի  և   սյունակների  հեռացումով: Արատորոշման   թեստ   է  հանդիսանում  սյունակների (ստուգումների)   այնպիսի  ենթաբազմությունը, որում  յուրաքանչյուր   տող  առնվազն  մեկ   նշում   ունի, այսինքն   բոլոր   անաշխատունակ  վիճակները  զույգ   առ   զույգ   տարբերակվում  են: Արատորոշման  աղյուսակի  կիրառմամբ` վերը  շարադրված   եղանակներով   կարելի   է   ստանալ նվազագույն  կամ  նվազագույնին  մոտ  արատորոշող  թեստ, որի  կիրառման արդյունքով, ելնելով  անսարքության  աղյուսակից, կարելի  է  որոշել  անաշխատունակ  վիճակը:

Հսկող և արատորոշող թեստերը կիրառվում են հաջորդաբար: Նախ հսկող թեստի կիրառմամբ որոշվում է անաշխատունակ վիճակի փաստը: Եթե այն առկա է, միայն դրանից հետո է կիրառվում արատորոշման թեստը և հայտնաբերվում անաշխատունակ վիճակը:     

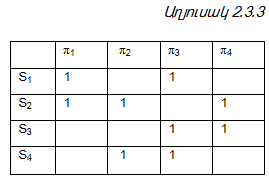
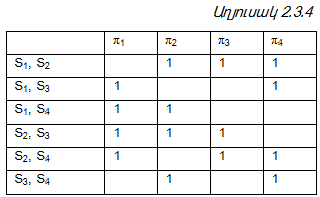
Աղյուսակ  2.3.3-ի  տողերի  զույգ   առ   զույգ  համեմատման   արդյունքում   ստացվում  է  աղյուսակ  2.3.4-ում  բերված  հետևյալ  արատորոշման  աղյուսակը:

Ելնելով  աղյուսակ  2.3.4-ից  կարելի  է  նկատել, որ  նվազագույն  արատորոշման     թեստեր   են ստուգումների   հետևյալ   ենթաբազմությունները`{π₁, π₂}, {π₁, π₄},  {π₂, π₄}: Միաժամանակ, նշենք, որ   նվազագույն  հսկող  թեստեր  են  {π₁, π₃},  {π₂,π ₃}, {π₃,π ₄}  ենթաբազմությունները:

Օրինակ, եթե  հաջորդաբար  կիրառվեն    {π₁, π₃}  հսկող   և   {π₁, π₂}  արատորոշող   թեստերը   և  արդյունքում   ստացվեն   01   և  00   տարբերակներ, ուրեմն  առկա  է  անաշխատունակ  վիճակ,  և  դա  S₃-ն  է:

>>

1.4 Ըստ մոդուլի ապարատային հսկման նկարագրությունը

Թվերի տեսությունից հայտնի է, որ ցանկացած թիվ կարելի է ներկայացնել հետևյալ համարժեքության տեսքով.

որն ընթերցվում է այսպես` A-ն համեմատելի է կամ նույնացված էq մոդուլով r_a մնացորդի հետ և հանգեցնում է A,r_a,q թվերի միջև գոյություն ունեցող հետևյալ կապին

որտեղ. A,q,a, r_a –ն  ամբողջ թվեր են,

A-ն ցանկացած n կարգանի հսկվող թիվ է,

q-ն մոդուլն է,

a-ն քանորդն է:

r_a-A թվի մոդուլի և  q-ի հարաբերությունից ստացված մնացորդն է (A թվի հսկման կոդը):

Այն դեպքում, երբ A₁ և A₂ թվերը ունեն  նույն  մնացորդները, դրանք ըստ q մոդուլի համեմատելի են, որն էլ գրվում է հետևյալ կերպ.

Օրինակ` 6 և 11 թվերը համեմատելի են ըստ մոդուլ 5-ի, քանի որ     6 mod 5=1 և 11mod5=1: Այստեղից հետևում է, որ

Հարկ է նշել, որ r_a-ն ներկայացնում է ամենափոքր մնացորդը: Այլ կերպ` այն կարող է ստացվել նաև A թվից հաջորդաբար q հանելով մինչև արդյունքը կդառնա q-ից փոքր: r_a-ի հնարավոր արժեքների թիվը հավասար է q-ի: Հետևաբար համարժեքության դասերի թիվը, որոնց տրոհվում է ամբողջ դրական A թվերի բազմությունը, հավասար է q: Այստեղից հետևում է, որ ինչքան մեծ է q-ն, որքան շատ են համարժեքության դասերը, այնքան փոքր է յուրաքանչյուր դասի հզորությունը և այդքան փոքր է այն բանի հավանականությունը, որ որևէ սխալի հետևանքով թիվը մնում է այն նույն համարժեքության դասում, որտեղ որ կար (դրա արդյունքում սխալը չի հայտնաբերվում): Այսպիսով, q-ի մեծ արժեքները ապահովում են հսկման ամբողջությունը: q մոդուլի մեծությունը սահմանափակ է՝ q=2,3,…,s: q=1-ի դեպքում հսկումը իմաստ չունի, քանի որ 1-ի բաժանված բոլոր թվերի մնացորդները հավասար են 0-ի: Մոդուլի վերին սահմանը սահմանափակվում է հսկման սխեմաների հուսալիության դատողություններով, քանի որ մեծ մոդուլների ժամանակ հսկման սարքավորումները կտրուկ մեծանում են, և հետևաբար փոքրանում է հուսալիությունը:

r_a մնացորդը կարող է գտնվել հետևյալ սահմաններում.  

Կարելի է նաև կիրառել այնպիսի r_a-եր, որոնք գտնվում են հետևյալ սահմաններում.

Ինչպես արդեն նշել ենք, ըստ մոդուլի հսկումը իրականացվում է ինֆորմացիայի ավելցուկության հաշվին: Յուրաքանչյուր n կարգանի հսկվող A թվին ավելացվում են m լրացուցիչ կարգեր, որտեղ գրվում է հսկող կոդը: Ըստ մոդուլի հսկման ժամանակ պետք է ապահովվի հետևյալ պայմանը՝ m<<n, հակառակ դեպքում հսկող ապարատի մեծ ծավալի պատճառով հսկվող համակարգի հուսալիությունը կնվազի:

Թվերի տեսությունից հայտնի են հետևյալ արտահայտությունները, որոնք լայնորեն կիրառվում են թվաբանական գործողությունների հսկման ընթացքում:

Տարբերում են ըստ մոդուլի հսկման երկու եղանակ՝

1.թվային

2.թվանշանային

Ընդհանուր դեպքում r_a հսկման կոդը, որպես A թվի ֆունկցիա, կարելի է ներկայացնել հետևյալ տեսքով.

Ըստ մոդուլի հսկման դեպքում կարելի է դիտարկել այդ ֆունկցիայի երկու արժեք: Առաջինը, երբ f(A)=A և r_a հսկող կոդ, կապված A թվի հետ, կարելի է ներկայացնել հետևյալ ձևով.

Այսինքն այս դեպքում ունենք թվային հսկում: Այս հսկման ժամանակ թվի հսկման կոդըմնացորդն է, որը ստացվում է A թիվը modq-ի բաժանելիս: Այս հսկմանը համապատասխանում են (4) և (5) արտահայտությունները: f(A)=r_a modq արտահայտության մեջ մոդուլը կարող է հավասար լինել հաշվողական համակարգի հիմքին (q=p), և կարող է հավասար չլինել դրան (q≠p): Եթե (q=p), ուրեմն A=a₁ modq, և հսկումը իմաստ չունի, քանի որ այս դեպքում հսկվում է A թվի միայն a₁ ցածր կարգը, իսկ բարձր կարգերը չեն մասնակցում մնացորդի ձևավորմանը, և այդ կարգում սխալները չեն հայտնաբերվում: Այս նույն դատողությամբ էլ նպատակահարմար չէ q=2^m դեպքը, քանի որ երկուական կոդի յուրաքանչյուր կարգը 2^m տեսքի թիվ է, և ցանկացած սխալ, որը կգտնվի m-րդ կարգից բարձր կարգում, չի հայտնաբերվի: Այսպիսի հսկման արդյունքում չեն հայտնաբերվի նույնիսկ եզակի սխալները, այսինքն՝ հսկումը կլինի ոչ արդյունավետ:

Թվանշանային հսկման դեպքում հսկման կոդը որոշվում է հսկվող թվի թվանշանների նկատմամբ իրականացվող գործողություններով, մասնավորապես, թվանշանների գումարով և այս դեպքում

 որտեղ a_i-ն A թվի թվանշաններն են:

     Ի տարբերություն թվային հսկման` այս հսկումը լայն կիրառություն է գտել: Այս դեպքում հսկման կոդըմասնավորապեսA թվի թվանշանների գումարը modq-ի բաժենելիս ստացված մնացորդն է: Քանի որ մեծ թվի թվանշանների գումարի կարգայնությունը բավականին փոքր է այդ թվի կարգայնությունից, մնացորդի հաշվումը պարզեցվում է, չնայած լրացուցիչ պահանջվում է թվի թվանշանների գումարի հաշվարկման  գործողությունը: Սակայն (4) և (5) արտահայտությունները թվանշանային հսկման համար կիրառելի չեն, բացառությամբ ստորև դիտարկվող մասնավոր դեպքերի: Հետևաբար թվանշանային հսկումը առավել տարածված է թվերի պահպանման և փոխանցման համար:

  Թվանշանային հսկումը հատկապես իրականացվում է երկուական թվերի դեպքում, երբ modq=2: Այդպիսի հսկումը կոչվում է հսկում ըստ զույգության կամ կենտության: Այս դեպքում թվանշանների գումարի մնացորդը հավասար է կամ ‘0’ կամ ‘1’, ելակետային կոդում մեկերի քանակի զույգությունիցկախված: Որպես հսկման կոդ, բավական է ունենալ մեկ լրացուցիչ կարգ:  Խոսքի կոդի ձևավորման ժամանակ հսկման կարգում գրանցվում է ‘0’ կամ ’1’, այնպես, որ մեկերի քանակը խոսքում, ավելցուկային կարգը ներառյալ, լինի զույգ (ըստ զույգության հսկելիս) կամ կենտ (ըստ կենտության հսկելիս):

Հետագայում բոլոր փոխանցումների ժամանակ (ներառյալ գրանցումը հիշողություն և ընթերցումը) խոսքը փոխանցվում է իր հսկման կարգի հետ միասին: Եթե ինֆորմացիայի փոխանցման ժամանակ ընդունող սարքը հայտնաբերում է, որ ընդունված խոսքում հսկման կարգի արժեքը չի համապատասխանում խոսքում մեկերի գումարի զույգությանը, ապա դա ընկալվում է որպես սխալի հայտանիշ:

Ըստ զույգության հսկելիս հսկման կարգում գրվում է այնպիսի թվանշան« որպեսզի բոլոր ինֆորմացիոն և հսկման կարգերում թվանշանների գումարը միասին ըստ մոդուլ 2-ի լինի 0« այլ կերպ՝ 1 նիշերի ընդհանուր քանակը լինի զույգ: Ըստ կենտության հսկման դեպքում կատարվում է հակառակը« այսինքն` թվանշանների գումարը ըստ մոդուլ 2-ի լինի 1« այլ կերպ 1 նիշերի ընդհանուր քանակը լինի կենտ: Այսպիսի հսկումները կարելի է իրականացնել պարզ եղանակներով: Անհրաժեշտ է ըստ mod2-ի գումարմանտրամաբանական տարրի միջոցով գումարել ինֆորմացիոն կարգերը և հսկման կարգում գրել ստացված արժեքը ըստ զույգության հսկելիս և գրել ստացված արդյունքի հակադարձ (ինվերս) արժեքը ըստ կենտության հսկելիս:  

Թվային հսկման ժամանակ modq-ն պետք է 3-ից փոքր չլինի, հակառակ դեպքում` սխալը հայտնաբերվում է երկուական թվի միայն ցածր կարգում, քանի որ մյուս կարգերում կշռային գործակիցները զույգ են, որոնք կարգերում ըստ mod2-ի (ըստ զույգության հայտնիշի) չեն հայտնաբերվում:

Հարկ է նաև նշել, որ զրոյական կոդերի հսկման համար նպատակահարմար է ավելցուկային կարգը ձևավորել այնպես, որ ավելցուկային և ինֆորմացիոն կարգերի գումարը ըստ mod2-ի հավասար լինի մեկի, այսինքն` հարմար է կիրառել ըստ կենտության հսկումը:

Դիտարկենք ըստ կամայական մոդուլի մնացորդի ձևավորման գործընթացը.

Հնարավոր են հսկման q մոդուլի և հաշվարկման համակարգի p հիմքի հարաբերության հետևյալ երեք դեպքերը`

Դիտարկենք մնացորդի ձևավորումը երկրորդ դեպքի համար, երբ q=p: Այս դեպքում

p=q-γ-ումγ=0, և ինչպես հետևում է

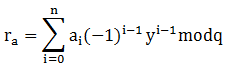
-ից, բոլոր  i≥2 կարգերի համար կշիռային ֆունկցիաները վերածվում են 0-ի: Այդ իսկ պատճառով r_a=a₁, դիտարկումները կատարենք երկուական(p=2) թվերի համար: Երբ  p=q=2 դեպքըվերը շարադրվածումարդեն դիտարկվել է: Հետևաբար  r_a=a_1, որն իմաստ չունի, քանի որ  ընդգրկում է միայն մեկ ցածր կարգը, և բարձր կարգերում սխալները չեն հայտնաբերվում: Այս դեպքի համար կիրառվում է թվանշանային հսկումը, որը p=q=2-ի դեպքում վերածվում է հսկվող 2-ական թվի կոդում մեկերի` ըստ զույգության (կամ կենտության) հսկմանը:

Մնացորդի ձևավորման երրորդ դեպքը գործնական կիրառում չունի, քանի որ p =2, q =1, որն անիմաստ է:

Ինչ վերաբերում է առաջին դեպքին, երբ q>p, ապա գործնականում տարածում են ստացել q=p^m-1 և q=p^m+1 դասերի մասնավոր դեպքերը, որոնցում բոլոր կարգերի կշռային քաշերը վերածվում են մեկերի` հանգեցնելով թվային և թվանշանային հսկումների համարժեքությանը: Հետևաբար, ի տարբերություն թվայինի, կիրառելով ավելի պարզ թվանշանային հսկում` հնարավոր է դառնում, բացի թվերի պահպանման և փոխանցման հսկումներից, կատարել նաև թվաբանական գործողությունների կատարման հսկումներ:

Դիտարկենք յուրաքանչյուր դասի համար հսկման եղանակը: Առաջինում, երբ q=p^m-1, նախ  A  հսկվող թիվը p-ական հաշվարկման համակարգից փոխադրվում է P=p^m համակարգ` ներկայացվելով հետևյալ տեսքով.

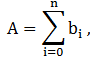
որտեղ b_i(i = 1…k) – P-ական համակարգի թվանշաններն են k=n/m, ըստ որում, եթե n կարգերը չեն բավարարում m կարգերից կազմված լրիվ խմբավորում կատարելուն, ձախից ավելացվում են անհրաժեշտ քանակով 0-ներ:

Այնուհետև այդ տեսքով ներկայացված թվի թվանշանները գումարվում են ըստ մոդուլ q-ի, որի արդյունքը

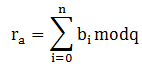
ներկայացնում է A թվի հսկման կոդը ըստ մոդուլ q-ի:

Համակարգչային իրականացման առումով P-ական թվանշանները ներկայացվում են m p-ական կարգերով: Հետևաբար A թվի թվանշաններին ավելացվում են լրացուցիչ m հսկման կարգերը: Նկատի ունենալով հաշվողական գումարող սարքում (գումարիչում) 2 գումարելիներով գումարման հանգամանքը՝ 2-ից ավելի թվանշանների գումարումը կարելի է կատարել երկու եղանակով` հաջորդական և զուգահեռ: Առաջինում, նախ գումարվում են 2 թվանշան, արդյունքին գումարվում է երրորդ թվանշանը և այսպես շարունակ: Երկրորդում` բոլոր թվանշանները բաժանվում են զույգերի և գումարվում միաժամանակ, այնուհետև ստացված արդյունքները նորից զույգերով միաժամանակ գումարվում են: Առաջինում փոքր է լրացուցիչ սարքավորման ծախսը, ինչպես նաև արագագործությունը, երկրորդում՝ ընդհակառակը:

Վերըշարադրվածը դիտարկենք հետևյալ օրինակով.

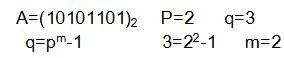
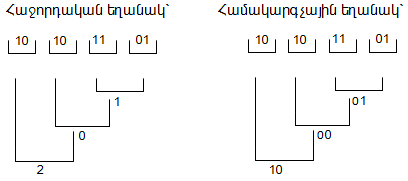
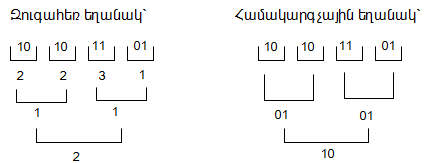
Երկրորդում, երբ q=p^m+1, նախ դարձյալ A հսկվող թիվը p-ական հաշվարկման համակարգից փոխադրվում է P=p^m համակարգ: Այնուհետև P-ական թվանշանները աջից ձախ, 1 համարից սկսած, համարակալվում են:

Առանձին-առանձին կենտ և զույգ համարներով թվանշանները գումարվում են ըստ մոդուլ q-ի, և որոշվում է դրանց տարբերությունը: Եթե այն դրական է, ներկայացնում է հսկման կոդը, իսկ եթե բացասական է, հսկման կոդ է ներկայացնում նրա լրացումը մինչև q:

Կատարելով հետևյալ նշանակումները`

S_կ–կենտ համարներով թվանշանների գումարը ըստ մոդուլ q-ի;

S_զ -զույգ համարներով թվանշանների գումարը ըստ մոդուլ q-ի՝

S_տ=S_կ-S_զ

կստանանք

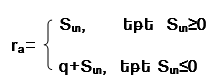
Դիտարկենք այս դասի մոդուլով հսկումը հետևյալ օրինակով`

>>

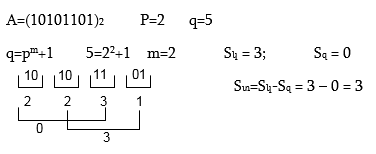
1.5 Թվաբանական գործողությունների թվային հսկումը ըստ մոդուլի

  Ըստ մոդուլի հսկումը հնարավորություն է ընձեռում հսկել նաև թվաբանական գործողությունները: Այդպիսի հսկումը կարելի է իրականացնել` հիմնվելով երկու թեորեմների վրա, որոնք բերվում են առանց ապացույցի.

Թեորեմ 1.

թվերի գումարը համեմատական է ըստ q մոդուլի այդ  նույն թվի r_ai մնացորդների գումարին, այսինքն.

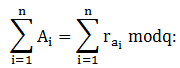
Թեորեմ 2.

թվերի արտադրյալը համեմատական է ըստ q մոդուլի այդ իսկ թվերի r_ai մնացորդների ատադրյալին, այսինքն.

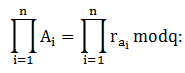
Վերը շարադրվածը 2 օպերանդների դեպքում համարժեք է հետևյալ արտահայտությունների իրականացմանը:

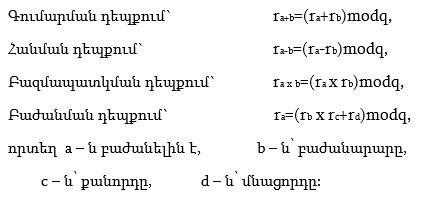
  Թվաբանական գործողությունների հսկումը ըստ մոդուլի կատարվում է հետևյալ կերպ: Թվաբանական գործողությանը մասնակցող յուրաքանչյուր թվի (օպերանդի) համար որոշվում է հսկման կոդը ըստ modq-ի: Թվաբանական գործողության կատարմանը զուգընթաց իրականացվում են հսկման կոդերի նկատմամբ թվաբանական գործողություններ ըստ վերը դիտարկված համապատասխան բանաձևերի: Հիմնական թվաբանական գործողության արդյունքի համար որոշվում է հսկման կոդը և համեմատվում հսկման կոդերի նկատմամբ իրականացված գործողությունների արդյունքի հետ: Չհամընկնելը վկայում է սխալի առկայության մասին:

Դիտարկենք օրինակներ.

0=0 սխալը բացակայում է:

 Ընդունենք գումարման արդյունքում աջից 4-րդ կարգում 1-ի փոխարեն ստացվել է 0, այսինքն

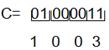
Հետևաբար r_c=mod₃(1+3)=1

1≠0, և առկա է սխալ

     1=1    սխալը բացակայում է:

Ընդունենք բազմապատկման արդյունքում աջից 3-րդ կարգում 0-ի փոխարեն ստացվել է 1, այսինքն՝

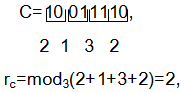
        2≠1,    և առկա է սխալ:

>>

2. Տրամաբանական սխեմաների թեստերի կառուցում

Տրամաբանական սխեմաների (ՏՍ) թեստային հսկման հարցերի տեսական վերլուծությունը ենթադրում է որոշակի իդեալացում, որի դեպքում առանձնացվում են իրական ՏՍ-ի թեստային հսկման տեսանկյունից էական առանձնահատկությունները, իսկ երկրորդականները` հեռացվում: Այսինքն՝ իրական ՏՍ-ը  և  դրանում  առկա  անսարքությունները   փոխարինվում  են  համապատասխան   մաթեմատիկական   մոդելով: Այդպիսի   մոդելներ    են    տրամաբանական ցանցերը (ՏՑ): Իրական սխեմաների և ՏՑ-երի միջև առկա է  որոշակի համապատասխանություն՝ նկարագրման միևնույն հարաբերակցության առումով:

2.1. Տրամաբանական ցանցեր

ՏՑ-ն տարրերից և մուտքային ու ելքային  բևեռներից բաղկացած որոշակի օբյեկտ է: Տարրերը ՏՑ-ի հետագա չմասնատվող բաղադրամասերն են և իրականացնում են տրամաբանական հանրահաշվի գործառույթներ: Հետագայում կդիտարկվեն սխեմաներ և ցանցեր՝ կառուցված «և», «կամ», «ոչ», «և-ոչ», «կամ-ոչ» գործառնական տարրերի հիմքի վրա: Մուտքային  բևեռներով ինֆորմացիան ընդունվում է ցանց, իսկ ելքային բևեռներով` դուրս բերվում: ՏՑ-ի կառուցվածքը պատկերվում է կողմնորոշված  գրաֆի տեսքով, որի գագաթները  համապատասխանում են տրամաբանական տարրերին, կողերը` դրանց միջև միացումներին, բևեռները` մուտքերին և ելքերին: Գագաթները պատկերվում են կետերով, բևեռները` օղակներով: Գագաթի աջ կողմում նշվում է տրամաբանական տարրին համապատասխանող նիշը, իսկ ձախ կողմում` տարրին վերագրված համարը: ՏՑ-ի և նրա համապատասխան  գրաֆի միջև կա  որոշակի կառուցվածքային իզոֆորմիզմ, որը հնարավորություն է ընձեռում օգտվել գրաֆների տեսության հասկացություններից և սահմանումներից՝  պարզեցնելով   ՏՑ-ի ուսումնասիրումը:

>>

2.2. Տրամաբանական ցանցերի տեսակները

Թեստերի կառուցման խնդիրները կդիտարկենք միայն համակցումային  ՏՑ-ի համար, քանի որ դիտարկվող խնդիրը հիշողությամբ  ՏՑ-երի համար բավականին բարդ է, և պահանջում է հատուկ հետազոտություններ: Կան  նաև հետադարձ կապով  և առանց հետադարձ կապի, ոչ ճիշտ և ճիշտ, չկրկնվող և կրկնվող, ճյուղավորված և առանց ճյուղավորումների  ՏՑ-ներ:  Հետադարձ կապով  (առանց հետադարձ կապի) ՏՑ-ի R գրաֆում կա (չկա) գոնե մեկ կողմնորոշված ցիկլ: Ոչ ճիշտ (ճիշտ) ՏՑ-ի R գրաֆում կա  (չկա) առնվազն մեկ զույգ կողմնորոշված երթուղի` միանման սկզբնական և վերջավոր վերջնական գագաթներով կամ առնվազն մեկ կողմնորոշված ցիկլ: Չկրկնվող ՏՑ-ում յուրաքանչյուր մուտքային բևեռ կամ գագաթ միացվում է ՏՑ-ի միայն մեկ գագաթի հետ, հակառակ դեպքում՝ այն կոչվում է կրկնվող: Ճյուղավորված ՏՑ-ում առնվազն մեկ գագաթ միացված է ՏՑ-ի՝ մեկից ավելի գագաթների հետ: Հակառակ դեպքում՝ այն կոչվում է չճյուղավորված ՏՑ:  Հետագայում կդիտարկենք միայն առանց հետադարձ կապի համակցումային  ՏՑ-եր, քանի որ առաջին հերթին գործնականում շատ հազվադեպ են հանդիպում հետադարձ կապով համակցումային  սխեմաներ, երկրորդը, եթե նույնիսկ այդպիսիք հանդիպում են, դրանք կարելի է նախագծել այնպես, որ հսկման ժամանակ հետադարձ կապերի շղթաները հնարավոր լինի խզել:

>>

2.3. ՏՑ-երի թեստի կառուցման սկզբունքները

ՏՑ-երի անսարքություններնառաջանում են սխեմայի տարրերի և դրանց միջև միացումների անսարքություններից: Սահմանափակվենք տրամաբանորեն հաստատուն 0(const-0) և հաստատուն 1(const-1) տիպի անսարքություններով, որոնք ֆիզիկական են,  առավել իրական  և տարածված: Հետազոտությունները ցույց են տալիս, որ այդպիսի անսարքությունների ստուգումը հանգեցնում  է նաև տրամաբանական բոլոր հնարավոր անսարքությունների գերակշռող մասի ստուգմանը:

  Նշանակենք C_i-0(1)-ով՝ i-րդ տարրի ելքիconst-0 (1), C_ij-0(1)-ով՝ i-րդ տարրի j-րդ  մուտքի const-0 (1), S_k-0(1)-ով՝ k-րդ միացման  const-0 (1) անսարքությունները: Տարրի մուտքային հավաքածուն կկոչվի  էական մուտքային՝  փոփոխականի համար, եթե արժեքներից ցանկացածի փոփոխումը հակառակով փոխում է տարրի ելքի արժեքը: Գործառնական  տարրերից յուրաքանչյուրի համար գոյություն ունի միայն մեկ էական հավաքածու բոլոր մուտքային փոփոխականների համար և մեկ  էական հավաքածու՝ մեկ մուտքային փոփոխականի համար: Յուրաքանչյուր տարրի C_ij-0(1) անսարքության համար գոյություն ունի փոփոխականների  միայն մեկ մուտքային հավաքածու, որով  ստուգվում է անսարքությունը: Յուրաքանչյուր գործառնական  տարրի մուտքերի անսարքությունների նկատմամբ  հսկող թեստը (ՀԹ) ՀԹ է ամբողջ տարրի համար:

Վերը  շարադրվածի հիման վրա կարելի է անել հետևյալ եզրակացությունը .  մուտքերով տարրի համար գոյություն ունի (m+1) երկարությամբ  միակ  նվազագույն  հսկող թեստ (ՆՀԹ) , որը միաժամանակ միակ նվազագույն  արատորոշող թեստն է  (ՆԱԹ): Տարրի ՆՀԹ-ը ստուգում է նաև  տարրի տրամաբանական անսարքությունների մեծամասնությունը: Թեստերի կառուցման համար բավական է դիտարկել բոլոր տարրերի մուտքային և միայն  ճյուղավորվող տարրերի համար՝  ելքային անսարքությունները: Հեշտ է նկատել, որ յուրաքանչյուր C_ij-0(1)  անսարքություն համընկնում է j-րդ մուտքին միացած  կողի S_k-0(1) անսարքության հետ: Հետևաբար, ՀԹ-ն  կառուցելիս կարելի է սահմանափակվել ՏՑ-ի կողերի անսարքությունների դիտարկմամբ,   ՏՍ-ի  թեստային հսկումն իրականացվում է միևնույն մուտքային ազդանշանների դեպքում՝ սխեմայի ելքերից առնվազն մեկում չափանմուշային  և սխալ արժեքների համեմատման միջոցով: Հետևաբար սխեմայի i-րդ ելքում մուտքային ազդանշանների e_k հավաքածուի միջոցով j-րդ անսարքությունը կարելի է ստուգել, եթե , որտեղ  -ն  i-րդ ելքում e_k հավաքածուի դեպքում համապատասխանաբար աշխատունակ և j-րդ անսարքությամբ անաշխատունակ սխեմաների  i-րդ ելքի արժեքներն են: Վերոհիշյալ եղանակով հսկումը կատարվում է դեպի սխեմայի ելքերից առնվազն մեկն անսարքությունների փոխանցման  կամ, ինչպես ընդունված է անվանել, ազդանշանների անցման համապատասխան ճանապարհների ակտիվացման (զգայուն դարձնելու) միջոցով: Նկատենք, որ մուտքային և ելքային բևեռները միացնող բոլոր հնարավոր ուղիների  ակտիվացման հավաքածուների բազմությունը ներկայացնում է  ՏՑ-ի, հետևաբար ՏՍ-ի համար՝ ՀԹ: Թեստերի  կառուցման  առավել  տարածված երկու հիմնական մեթոդ կա.

1. Համարժեք  նորմալ  ձևի  (Դ. Արմսթրոնգի) մեթոդ:

2. d  ալգորիթմի  կամ  d  խորանարդների (Ջ. Ռոտի) մեթոդ:

>>

3. Համարժեք նորմալ ձևի մեթոդ

Այս  մեթոդով կազմվում է կառուցվածքային և գործառնական  առումով սխեմային համապատասխան համարժեք նորմալ ձև (ՀՆՁ)[3,5]: ՀՆՁ-ի փոփոխականի (տառի) ստուգումը համարժեք է այդ փոփոխականը ելքի հետ միացնող ճանապարհի ակտիվացմանն ու զգայունացմանը: Հետևաբար,  ՀՆՁ-ի բոլոր տառերի ստուգումը հանգեցնում է սխեմայի հնարավոր ճանապարհների, այսինքն նաև՝ հնարավոր անսարքությունների ստուգմանը: Համաձայն [3]-ի, ՀՆՁ-ն ձևավորվում է սխեմային համարժեք տրամաբանական արտահայտության տեսքով, սակայն այն առանձնահատկությամբ, որ դրանում  տառերն ինդեքսավորվում են դրանք՝ ելքերի հետ միացնող համապատասխան ուղիների  տարրերի թվային համարների հաջորդականություններով: Դիտարկենք ՀՆՁ-ի ձևավորումը նկ.4.1-ում բերված  ՏՍ-ի (ա) և նրան համարժեք ՏՑ-ի (բ) համար:  ՀՆՁ-ն ձևավորվում է հետևյալ կերպ

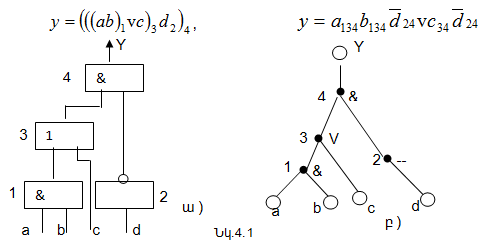
ՀՆՁ-ի պարզեցման և թեստերի համակարգչային կառուցման դեպքում հիշողության տարողության նվազեցման նպատակով առաջարկվում  է ինդեքսավորումը կիրառել միայն ճյուղավորվող փոփոխականների և տարրերի դեպքում [7]: Ելնելով վերոհիշյալից՝ դիտարկվող օրինակում ինդեքսները կբացակայեն: Ստուգող հավաքածուների գեներացումը կատարվում է հետևյալ կերպ.

ՀՆՁ  ստուգող հավաքածու      ստուգվող տառեր

որտեղ a-0(1)-ը նշանակում է a տառի const-0(cons-1) սխալ:

Թեստերի գեներացման համար կարելի է կիրառել նաև հակադարձ ՀՆՁ(ՀՀՆՁ), որը դիտարկվող օրինակում կլինի հետևյալը՝

[3] մեթոդով կիրառվում է 22 նիշ, իսկ առաջարկվող մեթոդով՝ 10 նիշ:Հիշողության ծախսը առավել նվազեցնելու նպատակով առաջարկվում է նաև ճյուղավորվող ՏՑ-երըներկայացնել ենթացանցերի տեսքով, կիրառելով ներքին փոփոխականներ՝ վերագրված ճյուղավորվող տարրերի ելքերին: Դիտարկենք նկ.4.2-ում բերված ՏՑ-ն:

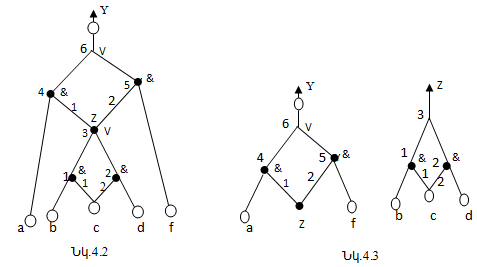
[3]  մեթոդով ՀՆՁ-ն հետևյալն է՝

  Դիտարկվող ՏՑ–ն ներկայացնենք նկար 4.3-ում բերված ենթացանցերով:

   Առաջարկվող մեթոդով կիրառվում է 2 ՀՆՁ: Առաջին ՀՆՁ-ն կոչվում է գլխավոր և որոշվում է y ելքային փոփոխականի համար, երկրորդ ՀՆՁ-ն կոչվում է երկրորդական և որոշվում`  z ներքին փոփոխականի համար՝ վերագրված ճյուղավորվող տարրին՝ , որտեղ c₁ և c₂ c մուտքային փոփոխականի ճյուղավորումներն են, իսկ z₁ և z₂-ը՝   z ներքին փոփոխականի ճյուղավորումները: [1]  մեթոդով կիրառվում է 57 նիշ, իսկ առաջարկվող մեթոդով՝18 նիշ, այսինքն՝ 3 անգամից ավելի պակաս: Կարևորվում է նաև ստուգող հավաքածուների ձևավորման (գրանցման) հաջորդականությունը,որը [3]  մեթոդում որոշվում է կամայական ալգորիթմով, իսկ առաջարկվող մեթոդում՝ պայմանական ալգորիթմով: Այս առումով սահմանվում է «էական տառ» հասկացությունը: Էական է կոչվում այն տառը, որը ՀՆՁ-ի կամ ՀՀՆՁ-ի ընդամենը 1 թերմում է կիրառվում: Ստուգող հավաքածուները գեներացվում են 2 փուլով: Առաջին փուլում ստուգվում են էական տառերը և դրանց հետ միաժամանակ ստուգվող տառերը: Հարկ է նշել, որ ձևավորված ստուգվող հավաքածուները ընդգրկված են բոլոր հնարավոր փակուղային, (չպարզեցվող) և նվազագույն ՀԹ-երում: Երկրորդ փուլում ստուգվում են մնացած չստուգված տառերը, ընդ  որում՝ յուրաքանչյուր հերթական քայլում ձգտելով ստուգել հնարավորին միաժամանակ ստուգվող տառեր: Առաջարկվող ալգորիթմը հանգեցնում է կեղծ նվազագույն, իսկ հաճախ նաև՝ նվազագույն  ՀԹ-եր:

>>

4. d- ալգորիթմի մեթոդ

Այս մեթոդը ներառում է հետևյալ երկու գործընթացները.

1) կիրառվող տարրերի համար d խորանարդների ձևավորում

2) d խորանարդների հատումների միջոցով ճանապարհների ակտիվացում

Տրամաբանական  տարրի  համար  d  խորանարդը  ստուգող խորանարդի, (հավաքածուի) կրճատ ունիվերսալ տարբերակն է:

 Ձևավորենք  տարածված  տարրերի  համար  հսկող  խորանարդները: Պարզության համար ելքային անսարքությունները չեն դիտարկվում, քանի որ մուտքային անսարքությունների ստուգումը միաժամանակ հանգեցնում է համապատասխան ելքային անսարքության ստուգմանը:

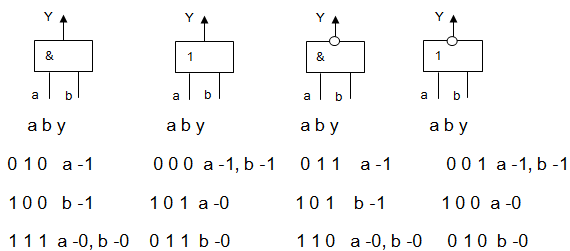
Ներկայացված   խորանարդները  փոխարինվում  են  հետևյալ  d  խորանարդներով:

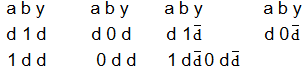
Հետևաբար տարրի երեք ստուգող խորանարդների փոխարեն կիրառվում է երկու d խորանարդ, որտեղ d-ն կարող է ընդունել 0 կամ 1 արժեք:

Ճանապարհների ակտիվացումն իրականացվում է տարրերի d խորանարդների հատման, այսինքն՝ համեմատման և համաձայնեցման միջոցով անհրաժեշտ արժեքների ապահովման վերընթաց, (դեպի ելք) և վարընթաց (դեպի մուտք)  գործողություններով:

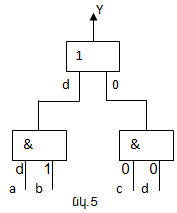
Օրինակ, տրված սխեմայի (նկ.5) “կամ” տարրի առաջին մուտքի ստուգման համար անհրաժեշտ է կիրառել d 0 խորանարդը, որի ապահովման համար կատարվում են հատումներ “և” տարրի համապատասխան d խորանարդների հետ: Արդյունքում ձևավորվում է   հավաքածուն, որը ներառում է երկու ստուգում` d=0 դեպքում նշված մուտքի const-1 անսարքության ստուգում և d=1 դեպքում նույն մուտքի const-0 ստուգում:

>>

5. Թվաբանական-տրամաբանական սարքի հսկում

Թվաբանական-տրամաբանական սարքը (ԹՏՍ) նախատեսված է՝ որոշակի կոդով ներկայացվող թվերով թվաբանական և տրամաբանական գործողություններ կատարելու համար: Նկար 6-ում բերված է ԹՏՍ-ի և նրա հսկման միջոցների գործառնական բլոկ-սխեման: ԹՏՍ-ն բաղկացած է ՄՌ-մուտքային ռեգիստրից, Ռ1, Ռ2, Ռ3 օպերանդների ռեգիստրներից, Գ կոմբինացիոն գումարիչից:

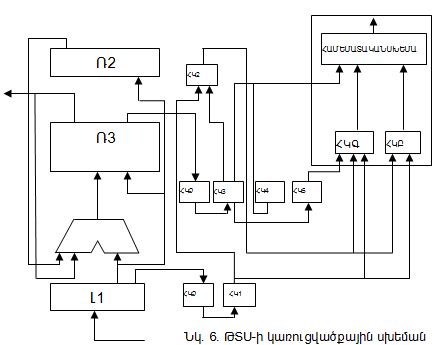
    Հիշողությունից օպերանդները ՄՌ-ով են ներանցվում ԹՏՍ և այնուհետև ուղարկվում մյուս հանգույցներ: ՄՌ-ում գրանցված օպերանդի համար ձևավորվում է Հեմինգի կոդը և կատարվում հսկում: Միայնակ սխալի հայտնաբերման դեպքում կատարվում է արատորոշում և սխալի ուղղում և այնուհետև ուղղված, ճշգրիտ օպերանդը ուղարկվում է համապատասխան հանգույց: Այս գործընթացով կատարվում է հիշողությունից ԹՏՍ օպերանդների հաղորդման և ընդունման հսկում, արատորոշում և ուղղում: Կարելի է պարզեցնել վերոհիշյալ գործընթացը՝ կիրառելով ըստ կենտության կամ զույգության հսկում, չօգտագործելով առանձնացված մուտքային ռեգիստր, այդ նպատակին ծառայեցնելով ԹՏՍ-ի ռեգիստրներից մեկը, ինչպես ներքոհիշյալ տարբերակում Ռ1-ը:

Ռ1, Ռ2-ը հանրահաշվական գումարման և բազմապատկման դեպքում պահպանում են օպերանդները ընդհուպ մինչև գործողությունների ավարտը: Գումարումը կատարվում է կոմբինացիոն գումարիչի միջոցով, որի ելքին միացված է Ռ3 ռեգիստրը, և վերջինս կատարում է կուտակիչի դեր: Այն ԹՏՍ–ում ելքային ռեգիստր է, այսինքն՝ այդ ռեգիստորի միջոցով դուրս է բերվում ԹՏՍ-ից գործողության արդյունքը: Հանրահաշվական գումարման դեպքում Ռ1-ում գրվում է առաջին գումարելին, Ռ2-ում` երկրորդ գումարելին: Բազմապատկման դեպքում Ռ1-ում գրվում է բազմապատկվող թիվը, իսկ Ռ2-ում` բազմապատկող թիվը, արտադրյալը գրվում է Ռ3-ում: Բաժանման դեպքում Ռ3-ում գրվում է բաժանելին, Ռ1-ում բաժանարարը, Ռ2-ում ձևավորվում է քանորդը, իսկ բաժանման ավարտից հետո Ռ3-ում ստացվում է մնացորդը:

Աղյուսակ 6-ում բերված են ռեգիստրների պարունակությունները թվաբանական գործողությունների կատարման ընթացքում.

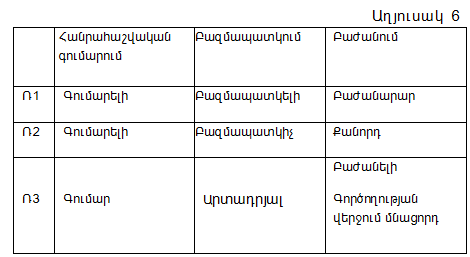
ԹՏՍ-ում հսկման միջոցներ են հանդիսանում՝

- ՀԿՁ՝ հսկման կոդի ձևավորիչներ,

- ՀԿ1, ՀԿ2, ՀԿ3, ՀԿ4, ՀԿ5՝ հսկման կոդի    պահպանման (հիշող) հանգույցները,

- ՀԿԳ՝ հսկման կոդերի գումարիչը, ՀԿԲ՝ հսկման կոդերի բազմապատկիչը, համեմատման սխեման, որոնց ներկայացնում են հսկման կոդերի թվաբանական սարքը (ՀԿԹՍ),

ՀԿՁ-ով ձևավորվում է Ռ1-ի և Ռ3 պարունակությունների հսկման կոդերը: Հանրահաշվական գումարման դեպքում նախ ձևավորվում է Ռ1-ում գրված առաջին գումարելիի հսկման կոդը և գրանցվում՝ Հկ1, այնուհետև ուղարկվում է Ռ2, իսկ ՀԿ1՝ ՀԿ2: Հետո որոշվում է Ռ1-ում գրված երկրորդ գումարելիի հսկման կոդը և գրանցվում ՀԿ1: Կատարվում է գումարում, որոշվում է Ռ3-ում գրված արդյունքի հսկման կոդը և գրանցվում ՀԿ3-ում: ՀԿԳ-ով կատարվում է  (ՀԿ1 x ՀԿ2) mod q գործողությունը և համեմատման սխեմայով կատարվում ՀԿ3-ի հետ համեմատում և չհամընկման դեպքում տրվում է սխալի ազդանշան: Բազմապատկման դեպքում կատարվում են նմանատիպ գործողություններ բազմապատկելիի, բազմապատկիչի և արտադրյալի նկատմամբ ու ՀԿԲ-ով կատարվում է  (ՀԿ1 x ՀԿ2) mod q գործողությունը և դարձյալ համեմատվում ՀԿ3-ի հետ:

Բաժանման դեպքում, բացի նշված երեք հանգույցներից, կիրառվում են նաև լրացուցիչ ՀԿ4 և ՀԿ5 հանգույցները: Բաժանման սկզբում ՀԿ1-ում գրանցվում են բաժանարարի, ՀԿ3-ում՝ բաժանելիի հսկման կոդերը: Բաժանման գործողության ավարտից հետո ՀԿ3-ը ուղարկվում է Հկ4, ձևավորվում է Հկ3-ում ներկայացված մնացորդի հսկման կոդը և ուղարկվում Հկ3, իսկ այնուհետև Հկ5: Ռ2-ից քանորդն ուղարկվում էՌ3, ձևավորվում է նրա հսկման կոդը և ուղարկվում ՀԿ3, իսկ այնուհետև՝ ՀԿ2: Վերջում Հկ4-ն ուղարկվում է ՀԿ3: Այսպիսով, արդյունքում նշված հանգույցներում գրանցվում են հետևյալ հսկման կոդերը` ՀԿ1-ում՝ բաժանարարի, ՀԿ2-ում՝ քանորդի, ՀԿ3-ում՝ բաժանելիի, ՀԿ5-ում՝ մնացորդի: Կատարվում է (ՀԿ1 x ՀԿ2+ՀԿ5)mod q գործողությունը և համեմատվում ՀԿ3-ի հետ:

>>

6. Հսկման կոդիձևավորման գումարիչներ

 Հսկման կոդի ձևավորման կարևոր գործընթացներից է տրված մոդուլով գումարման իրականացումը: Առավել պարզ է ըստ կենտության կամ զույգության դեպքում մոդուլ 2-ով գումարումը, որն իրականացվում է համապատասխան տրամաբանական տարրով: Մնացած դեպքերում կիրառվում են տարածված մոդուլներով գումարման կոմբինացիոն կամ կուտակող տիպի գումարիչներ:

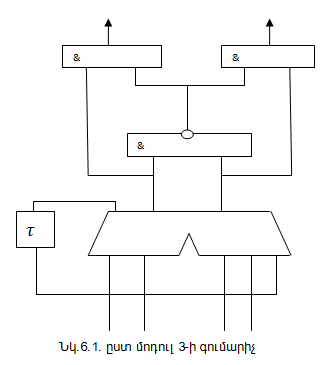
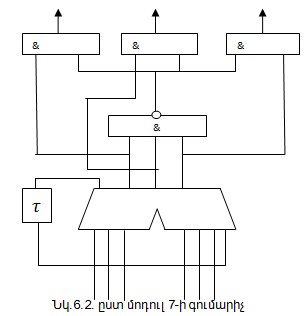
 Դիտարկենք երկուական գումարիչների դեպքում  q=p^m-1 մոդուլով գումարման իրականացումը: Հայտնի է, որ n կարգանի երկուական գումարիչը իրականացնում է 2ⁿ     մոդուլով գումարում: Հետևաբար (2ⁿ- 1) մոդուլով գումարման դեպքում անհրաժեշտ բարձր կարգից առաջացած փոխանցումը կորցնելու փոխարեն, որը համարժեք է 2ⁿ   արժեքով հանմանը, այն հետադարձ կապով, ցիկլիկ փոխանցման շղթայով գումարել գումարիչի պարունակությանը: Ստորև բերված են 3, 7, 15 մոդուլներով գումարիչների գործառնական սխեմաները(նկ.6.1; նկ.6.2; նկ.6.3):  հապաղման տարրը կիրառվում է սխալ փոխանցումների չառաջացման նպատակով: Գումարիչի ելքում հավաքված տրամաբանական սխեման նախատեսված է՝ գումարման 3, 7, 15 արդյունքների դեպքում գումարիչից 0 արժեք դուրս բերելու համար:

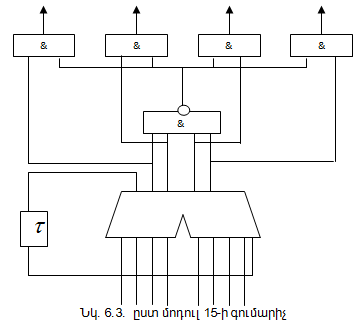
 Ըստ մոդուլ 15-ի գումարումը կատարվում է 4 կարգանի գումարիչի միջոցով: Ինչպես հայտնի է, այդպիսի գումարիչը իրականացնում է ըստ մոդուլ16-ի գումարում: Հետևաբար, ըստ մոդուլ15-ի գումարում իրականացնելու համար բարձր կարգից առաջացած փոխանցումը ոչ թե պետք է կորցնել, այլ որոշ ուշացումով հետադարձ կապով հաղորդել ցածր կարգ և գումարել: Այսպիսի փոխանցումը կոչվում է ցիկլային փոխանցում: Արդյունքում, բարձր կարգից առաջացած փոխանցման դեպքում ստացված գումարը կնվազի ոչ թե 16-ով (այն դեպքում, երբ փոխանցումը կանտեսվեր), այլ մեկով պակաս: Երբ գումարման արդյունքը 15 է, այն պետք է փոխարինվի 0-ով, այսինքն՝ գումարիչից պետք է ստացվի 0 արդյունք: Նկար 6.3-ում բերված է ըստ մոդուլ 15-ի գումարիչի ֆունկցիոնալ սխեման: τ տառով նշված է հապաղման տարրը, որպես այդպիսին կարող է օգտագործվել D տրիգեր: Գումարիչի քառակարգ ելքերը տրված են «և-ոչ» տարրին, գումարիչից 15 գումարային արդյունք ստանալու դեպքում 0 դուրս բերելու համար:

Անդրադառնանք (2^m+1) մոդուլով գումարմանը, որն իրականացվում է հետևյալ կերպ.

1. Կիրառվում է (n+1) կարգանի գումարիչ:

2. Բարձր կարգից փոխանցման դեպքում գումարիչի պարունակությանը գումարվում է   (2ⁿ⁺¹- q) արժեք:

3. Փոխանցում է ձևավորվում և գումարիչի պարունակությանը գումարվում է  (2ⁿ⁺¹-q) արժեք նաև գումարման հետևյալ x արդյունքի դեպքում   qx2^{n +1}:

4. Փոխանցումները հետադարձ կապով ցիկլիկ փոխանցման շղթայով գումարիչի մուտք են հաղորդվում հապաղմամբ:

5. Գումարման q արդյունքի դեպքում գումարիչից դուրս է բերվում 0 արժեք:

>>

6.1. Հսկման կոդերի բազմապատկիչներ

q=p^m-1 մոդուլով բազմապատկումը իրականացվում է n=m կարգանի բազմապատկիչով: Երբ հսկման կոդերի բազմապատկման արդյունքը հավասար է q-ի, ապա բազմապատկիչից դուրս է բերվում 0 արդյունք: Երբ բազմապատկման արդյունքը n թվանշանային կարգից ավելի է, ապա n կարգից բարձր թվանշաններով ձևավորված օպերանդը գումարվում է ստացված արդյունքին: Եթե այն դարձյալ հավասար է q-ի, ապա բազմապատկիչից դուրս է բերվում 0 արդյունք:

q=p^m+1 մոդուլով բազմապատկումն առավել բարդ է: Հետևաբար նպատակահարմար է այն իրականացնել q=p^m+1 մոդուլով գումարիչի միջոցով q մոդուլով հաջորդական գումարումներով:

     Որպես օրինակ դիտարկենք քառակարգ թվերի բազմապատկիչով ըստ մոդուլ 15-ի բազմապատկումը:Երբ բազմապատկման արդյունքը ստացվում է չորս թվանշանային կարգից ավելի, ապա 4 կարգից բարձր թվանշանը ներկայացվելով որպես քառակարգ օպերանդ՝ գումարվում է ստացված արդյունքին: Այսպիսով, իրականացվում է երկու քառակարգ օպերանդների բազմապատկում ըստ մոդուլ 15- ի, եթե արդյունքում ստացվում է 15, ապա բազմապատկիչից դուրս է բերվում 0 թվանշանը` նկատի ունենալով, որ ըստ մոդուլ 15-ի մնացորդը 0 է: Վերը նշվածը ներկայացնենք հետևյալ օրինաով.

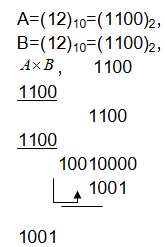
 Իրոք (11001100)mod15=9:

     Ինչ վերաբերում է քառակարգ բազմապատկիչին, ապա նախընտրելի է կիրառել Բրաունի բազմապատկիչը, որի պատկերը բերված է նկար 7.1.1-ում: Առանց նշանի A  և B n-կարգանի ամբողջական թվերի p բազմապատկման արդյունքը կարելի է գրանցել     հետևյալ կերպ.

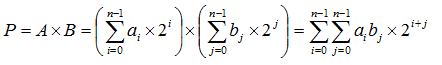
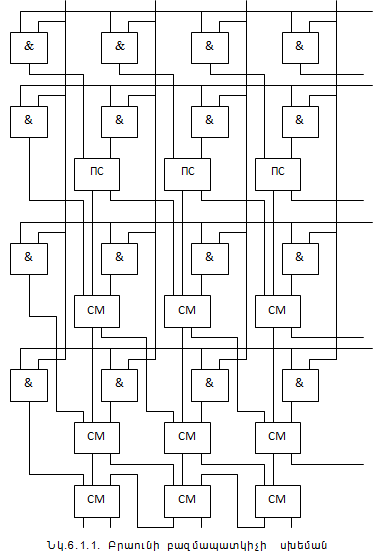
  Բազմապատկումը հանգեցնում է nn-կարգանի մասնակի արտադրյալներից բիտերի զուգահեռ կազմավորման, իրենց հետագա գումարումով գումարիչների մատրիցի օգնությամբ, որի կազմությունը համապատասխանում է նշված բազմապատկման մատրիցին: Այս սխեման ճանաչված է որպես Բրաունի բազմապատկիչ: Մասնակի մնացորդի բիտերը a_i b_j տիպի ձևավորում են «և» էլեմենտի միջոցով: Մասնակի մնացորդի գումարման համար օգտագործում են միակարգ գումարիչների երկու տեսակ` կիսագումարիչներ և լրիվ գումարիչներ: մատրիցային բազմապատկիչը պարունակում է «և», ո կիսագումարիչ և (n<sup>2</sup>-2n) գումարիչ: Եթե համարենք, որ կիսագումարիչի իրականացման համար անհրաժեշտ է երկու տրամաբանական տարր, իսկ լրիվ գումարիչին` հինգ, ապա ընդհանուր քանակը կազմում է n²+2n+5 (n²-2n)=6ո²-8ո:

     Բազմապատկիչի արագագործությունը որոշվում է ազդանշանի տարածման ավելի երկար ճանապարհով, որը ամենավատ դեպքում ներառում է մեկ  «և» սխեմա, երկու կիսագումարիչ և (2n-4) գումարիչ: Համարելով հապաղումը «և» սխեմայում և կիսագումարիչում՝ D, լրիվ գումարիչում՝ 2D, ընդհանուր հապաղումը կարելի է գնահատել՝ (4n-5)D: Սրա տևողության կրճատման համար հաջորդական փոխանցումով ո կարգանի գումարիչը բազմապատկիչի ներքևի տողում կարելի է փոխանցել գումարիչի ավելի արագ տարբերակով: Սակայն այն ավելացնում է տրամաբանական տարրերի քանակը և դրանով խափանում սխեմայի կանոնակարգությունը:

     Մատրիցային  բազմապատկիչի  էությունը  ներկայացնենք  հետևյալ  եղանակով.

Դիցուք  տրված  է երկու  քառակարգ  բազմապատկիչ.         

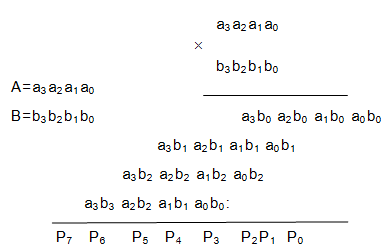
դրանց  բազմապատկման  արդյունքում  կատարվում  են  հետևյալ  կարգային  զույգերի  բազմապատկումներ,  որոնցով  ձևավորված  միջանկյալ  արտադրյալները  միմյանցից  շեղված  են  դեպի  ձախ մեկ  կարգով: 

Նկատի  ունենալով,  որ բազմապատկիչների  կարգերը  երկուական  են,  ցանկացած  զույգ  կարգերի  բազմապատկում  կարող  է  ներկայացվել  «և»  տրամաբանական  սխեմայի  միջոցով:

     Նկատի  ունենալով,  որ  երկու  կարգերի  միաժամանակ  1  լինելու  դեպքում  ձևավորվում  է  փոխանցում  հաջորդ  կարգ,  բազմապատկիչում  օգտագործվում  են  կիսագումարիչներ, որոնց  ելքերում  ստացվում  են կարգային  գումարները  և  հաջորդ  կարգ  տրվող  փոխանցումները:

     Վերը  շարադրվածի  իրականացման  արդյունքում  ձևավորվում  են  «և»  սխեմաներից  և  կիսագումարիչներից  կազմված  կոմբինացիոն  սխեմաներ,  որոնց  ելքերում առաջանում  է  բազմապատկման  P₇P₆P₅P₄P₃P₂P₁P₀   արդյունքը:

     Այդպիսի  մատրիցաով,  փաստորեն  կատարվում  է  ըստ  մոդուլ  16-ի  երկու  16-ական  թվանշանների  բազմապատկում,  մինչդեռ  ըստ  մոդուլ  15-ի  հսկում  կատարելու  նպատակով  անհրաժեշտ  է  կատարել   ըստ  մոդուլ  15-ի  բազմապատկում: Այդ նպատակով բազմապատկման  արդյունքում  ստացված  8  կարգանի  2-ական  կոդի   P₇P₆P₅P₄4-ական  կոդը  ըստ  էության,  ներկայացնում  է  այն  ուղղող  մեծությունը,  որը  գումարվելով  P₃P₂P₁P₀4-ական  կոդին,  արդյունքում  ձևավորում  է  ըստ  մոդուլ  15-ի  բազմապատկման  արդյունքը:

      Հիշեցնենք,  որ  քառակարգ  թվերի՝  ըստ  մոդուլ  15-ի  բազմապատկման  դեպքում բարձր  կարգից  առաջացած  փոխանցումը  ոչ  թե  կորսվում  է,  այլ ուղարկվում  է ցածր  կարգ  և  գումարվում    գումարման  արդյունքին:

     Նկատի  ունենալով,  որ  բազմապատկումը  բազմաքայլ  գումարում  է, հետևաբար քառակարգ  ձախ  ձևավորվող  կոդը  ներկայացնում  է  քառակարգ  կոդից   բարձր  կարգից  փոախնցունմերի  արդյունքը,  որն  էլ  ինչպես  արդեն  նշվեց`  ուղղող կոդի  մեծությունն է: