
ԲՈՎԱՆԴԱԿՈՒԹՅՈՒՆ
ԳԼՈՒԽ XI. ՓՈՓՈԽԱԿԱՆ ԲԱՂԱԴՐՈՒԹՅԱՄԲ ՀԱՄԱԿԱՐԳԵՐԻ ԹԵՐՄՈԴԻՆԱՄԻԿԱՆ: ԼՈՒԾՈՒՅԹՆԵՐ
XI-2. ՄԻՋՄՈԼԵԿՈՒԼԱՅԻՆ ՓՈԽԱԶԴԵՑՈՒԹՅՈՒՆՆԵՐԸ ԼՈՒԾՈՒՅԹՆԵՐՈՒՄ
XI-3. ԲԱԶՄԱԿՈՄՊՈՆԵՆՏ ՀԱՄԱԿԱՐԳԵՐԻ ԹԵՐՄՈԴԻՆԱՄԻԿԱՆ: ՔԻՄԻԱԿԱՆ ՊՈՏԵՆՑԻԱԼԻ ԿԱՐԵՎՈՐՈՒԹՅՈՒՆԸ
XI-4. ԴՅՈՒՀԵՄ–ՄԱՐԳՈՒԼԵՍԻ ՀԱՎԱՍԱՐՈՒՄԸ
XI.5. ԼՈՒԾՈՒՅԹՆԵՐԻ ԹԵՐՄՈԴԻՆԱՄԻԿԱԿԱՆ ԴԱՍԱԿԱՐԳՈՒՄԸ
XI-5:2. Ոչիդեալական լուծույթներ
XI-7. ԼՈՒԾՈՒՅԹՆԵՐԻ ԹԵՐՄՈԴԻՆԱՄԻԿԱՅԻ ՄԻ ՔԱՆԻ ՀԱՐՑԵՐ
XI-7:1. Հավելյալ թերմոդինամիկական մեծություններ
XI-7:2. Լուծույթի մոլային ծավալ: Որոշման մեթոդներ
XI-7:3. Հարաբերական պարցիալ մոլային մեծություններ: Հարաբերական պարցիալ մոլային էնտալպիա
ԳԼՈՒԽ XII. ԼՈՒԾՈՒՅԹՆԵՐԻ ԿՈԼԻԳԱՏԻՎ ՀԱՏԿՈՒԹՅՈՒՆՆԵՐԸ
XII-1. ՌԱՈՒԼԻ ՕՐԵՆՔԸ: ԿԱՏԱՐՅԱԼ ԼՈՒԾՈՒՅԹՆԵՐ
XII-1:1. Հեղուկ լուծույթի վրա գոլորշու ընդհանուր ճնշման կախումը հեղուկի բաղադրությունից: Դիագրամներ
XII-1:2. Հեղուկ լուծույթի վրա գոլորշու ընդհանուր ճնշման կախումը գոլորշու բաղադրությունից
XII-2. ՇԵՂՈՒՄՆԵՐ ՌԱՈՒԼԻ ՕՐԵՆՔԻՑ
XII-2:2. Վան Լաարի հավասարումը: Ռաուլի օրենքից շեղման պատճառները
XII-3. ![]() ԴԻԱԳՐԱՄՆԵՐԻ ԿԻՐԱՌԱԿԱՆ ՆՇԱՆԱԿՈՒԹՅՈՒՆԸ
ԴԻԱԳՐԱՄՆԵՐԻ ԿԻՐԱՌԱԿԱՆ ՆՇԱՆԱԿՈՒԹՅՈՒՆԸ
XII-3:1. Կոտորակային (ֆրակցիոն) թորում: Ռեկտիֆիկացում: Ազեոտրոպ խառնուրդներ
XII-4:ա. ԳԻԲՍ-ԿՈՆՈՎԱԼՈՎԻ ԿԱՆՈՆՆԵՐԸ
XII-5. ՋԵՐՄԱՍՏԻՃԱՆԻ ԱԶԴԵՑՈՒԹՅՈՒՆԸ ԻՐԱՐ ՄԵՋ ՍԱՀՄԱՆԱՓԱԿ ԼՈՒԾՎՈՂ ՀԵՂՈՒԿՆԵՐԻ ՓՈԽԱԴԱՐՁ ԼՈՒԾԵԼԻՈՒԹՅԱՆ ՎՐԱ:
ԼՈՒԾՄԱՆ ԿՐԻՏԻԿԱԿԱՆ ՋԵՐՄԱՍՏԻՃԱՆ
XII-6. ԹՈՐՈՒՄ ՋՐԱՅԻՆ ԳՈԼՈՐՇԻՆԵՐՈՎ
XII-7. ԵՐՐՈՐԴ ՆՅՈՒԹԻ ԲԱՇԽՈՒՄՆ ԻՐԱՐ ՄԵՋ ՉԼՈՒԾՎՈՂ ԵՐԿՈՒ ՀԵՂՈՒԿՆԵՐՈՒՄ: ԱՐՏԱԼՈՒԾՈՒՄ (ԷՔՍՏՐԱԿՑՈՒՄ): ԲԱՇԽՄԱՆ ԳՈՐԾԱԿԻՑ
XII-8. ԻԴԵԱԼԱԿԱՆ ԼՈՒԾՈՒՅԹՆԵՐԻ ԿՈԼԻԳԱՏԻՎ ՀԱՏԿՈՒԹՅՈՒՆՆԵՐԸ
XII-8:1. Լուծույթի սառեցման ջերմաստիճանի կախումը լուծույթի կոնցենտրացիայից: Կրիոսկոպիա
XII.8:2. Լուծույթի եռման ջերմաստիճանի կախումը լուծույթի կոնցենտրացիայից: Էբուլոսկոպիա:
XII.8:3. Օսմոս: Օսմոտիկական ճնշում
ԳԼՈՒԽ XIII. ՖԱԶԱՅԻՆ ՀԱՎԱՍԱՐԱԿՇՌՈՒԹՅՈՒՆԸ ՄԻԱԿՈՄՊՈՆԵՆՏ ԵՎ ԲԱԶՄԱԿՈՄՊՈՆԵՆՏ ՀԱՄԱԿԱՐԳԵՐՈՒՄ: ԳԻԲՍԻ ՖԱԶԵՐԻ ԿԱՆՈՆԸ
XIII-1. ԸՆԴՀԱՆՈՒՐ ՀԱՍԿԱՑՈՒԹՅՈՒՆՆԵՐ
XIII-3. ԳԻԲՍԻ ՖԱԶԵՐԻ ԿԱՆՈՆԻ ԿԻՐԱՌՈՒԹՅՈՒՆԸ
XIII-3:1. Միակոմպոնենտ համակարգերի նկատմամբ
XIII-3:2. Երկկոմպոնենտ կոնդենսված համակարգեր ուսումնասիրելու ֆիզիկաքիմիական անալիզի հիմունքները
XIII-3:2(Ա) Երկու բաղադրիչների միջև բացակայում է քիմական փոխազդեցությունը
XIII-3:2 (Բ) Երկու բաղադրիչներն իրար հետ ռեակցում են
XIII-4. ԵՌԿՈՄՊՈՆԵՆՏ ՀԱՄԱԿԱՐԳԵՐ: ՈՒՍՈՒՄՆԱՍԻՐՈՒԹՅԱՆ ՄԵԹՈԴՆԵՐԸ: ԳԻԲՍԻ ՖԱԶԵՐԻ ԿԱՆՈՆԻ ԿԻՐԱՌՈՒՄԸ ԱՅԴ ՀԱՄԱԿԱՐԳԵՐԻ ՆԿԱՏՄԱՄԲ
XIII-4:1. Փոխուղղահայաց կոորդինատների մեթոդ
XIII-4:2. Գիբսի եռանկյան մեթոդ
ԳԼՈՒԽ XI
ՓՈՓՈԽԱԿԱՆ ԲԱՂԱԴՐՈՒԹՅԱՄԲ ՀԱՄԱԿԱՐԳԵՐԻ ԹԵՐՄՈԴԻՆԱՄԻԿԱՆ: ԼՈՒԾՈՒՅԹՆԵՐ
Լուծույթը փոփոխական բաղադրությամբ ֆազ է: Նշանակում է, որ լուծույթը հոմոգեն համակարգ է, որի բաղադրությունը կարելի է փոփոխել պահպանելով հոմոգենությունը:
Լուծույթն ըստ էության բազմակոմպոնենտ համակարգ է: Պարզագույն դեպքում երկկոմպոնենտ է. կազմված է լուծիչից և լուծված նյութից: Այն նյութը, որը քանակապես շատ է լուծույթում և լուծման պրոցեսում պահպանվում է դրա ֆազային վիճակը, համարվում է լուծիչ: Կարող են մեկից ավելի լուծված նյութեր լինել:
Մոլեկուլային (իոնական)
է
այն
լուծույթը,
որում
լուծված
նյութը
մանրասփռված
(դիսպերսված) է
մինչև
մոլեկուլի
(իոնի) չափսերը ![]()
Լուծույթների հատկանիշներից են.
1. Լուծույթը քիմիական միացություն չէ, որովհետև դրա առաջացման ընթացքում չեն պահպանվում քիմիայի դասական` բաղադրության, համարժեքների և բազմապատիկ հարաբերությունների օրենքները:
2. Թերմոդինամիկորեն լուծույթը կայուն համակարգ է:
3. Լուծույթում բաղադրիչները պահպանում են իրենց անհատականությունը, որի շնորհիվ հնարավոր է ֆիզիկական մեթոդներով բաղադրիչներն իրարից անջատել:
4. Ընդհանրապես լուծույթի առաջացումը ջերմաչեզոք պրոցես չէ, որովհետև լուծույթի առաջացումը լուծիչ – լուծված նյութ միջմասնիկային փոխազդեցությունների հետևանք է:
Կախված լուծիչի ագրեգատային վիճակից լուծույթները կարող են լինել գազային, օրինակ, ![]() խառնուրդը, հեղուկ, օրինակ, ջուրը լուծված էթանոլում և հակառակը, պինդ, օրինակ, ջրածինը լուծված պլատինում, ոսկին պղնձի մեջ և այլն:
խառնուրդը, հեղուկ, օրինակ, ջուրը լուծված էթանոլում և հակառակը, պինդ, օրինակ, ջրածինը լուծված պլատինում, ոսկին պղնձի մեջ և այլն:
Թերմոդինամիկայի տեսանկյունից լուծույթի վիճակը բնութագրվում է ջերմաստիճանով, ճնշումով, և կոնցենտրացիայով: Այս վերջինի փոխարեն հաճախ օգտագործվում է «բաղադրություն» եզրը (տերմինը):
Կոնցենտրացիայի միջոցով է արտահայտվում լուծիչ/լուծված նյութ քանակական հարաբերությունը, որից մեծ չափով կախված են լուծույթի թերմոդինամիկական հատկությունները:
Շատ կարևոր է «լուծելիություն» հասկացությունը: Դա լուծված նյութի այն քանակն է, որը տվյալ ջերմաստիճանում (սովորաբար 298,15K-ում) կարող է 100 գ լուծիչում լուծվել: Այս պայմանի դեպքում լուծույթը համարվում է հագեցած: Հագեցած լուծույթում հավասարակշռության մեջ է լուծույթը նստվածքի հետ: Եթե տվյալ ջերմաստիճանում լուծված նյութի քանակը նվազ է լուծելիությունից, ապա լուծույթը համարվում է չհագեցած: Լուծույթը կոչվում է գերհագեցած, երբ լուծված նյութի քանակը լուծելիությունից ավելի է: Գերհագեցած լուծույթը թերմոդինամիկորեն անկայուն է: Նույնիսկ փոքր ցնցումը բավական է, որ լուծույթը դառնա հագեցած: Բնական է, որ լուծույթից կանջատվի այնքան լուծված նյութ, որքանով այն գերազանցել էր լուծելիությունը:
Այս ամփոփ շարադրանքը բավական է համոզվելու համար, որ լուծույթի կոնցենտրացիան կարևոր քանակական պարամետր է:
Կոնցենտրացիան կարելի է արտահայտել տարբեր ձևերով: Հենց ընտրված ձևից էլ կախված է կոնցենտրացիայի չափողականությունը:
Կոնցենտրացիայի արտահայտման համար երկու սկզբունք գոյություն ունի. վերաբերել լուծված նյութի քանակը կամ զանգվածը. ա. լուծույթի քանակի, զանգվածի կամ ծավալի միավորին և բ. լուծիչի միավոր քանակին:
I – Լուծված նյութի քանակը, զանգվածը վերաբերում են յուծույթի քանակի, զանգվածի կամ ծավալի միավորին:
1. Զանգվածային բաժին ![]() Ցույց է տալիս, թե 1 գ լուծույթի մեջ քանի՞ գրամ է տվյալ լուծված նյութը: Եթե i-րդ լուծված նյութի զանգվածը
Ցույց է տալիս, թե 1 գ լուծույթի մեջ քանի՞ գրամ է տվյալ լուծված նյութը: Եթե i-րդ լուծված նյութի զանգվածը ![]() լուծույթինը G
գրամ, ապա
լուծույթինը G
գրամ, ապա
![]()
Զանգվածային բաժինը 100-ով բազմապատկելով այն կարտահայտվի տոկոսով: ![]() ցույց է տալիս, թե 100 գ լուծույթում տվյալ նյութից քանի գրամ է լուծված: Բնական է, որ
ցույց է տալիս, թե 100 գ լուծույթում տվյալ նյութից քանի գրամ է լուծված: Բնական է, որ ![]() չափողականություն չունի և
չափողականություն չունի և ![]()
2. Մոլային բաժին. ![]() Նորից վերացական, չափողականություն չունեցող մեծություն է և ցույց է տալիս, թե 1 մոլ լուծույթում տվյալ նյութից քանի՞ մոլ
Նորից վերացական, չափողականություն չունեցող մեծություն է և ցույց է տալիս, թե 1 մոլ լուծույթում տվյալ նյութից քանի՞ մոլ ![]() կա:
կա:
Ըստ սահմանումի.
![]()
Այս դեպքում էլ. ![]() Հետևաբար.
Հետևաբար.
![]()
և
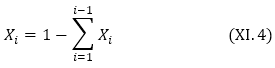
Օրինակ, եթե լուծույթը կազմված է լուծիչից և լուծված նյութից, ապա
![]()
![]() էլ կարելի է տոկոսներով արտահայտել:
էլ կարելի է տոկոսներով արտահայտել:
3. Ծավալային բաժին ![]() Ըստ սահմանումի.
Ըստ սահմանումի.
![]()
Սա ճիշտ է այն դեպքում, երբ քննարկվող խառնուրդը իդեալական է, այսինքն եթե ունենք ![]() ապա
ապա ![]() Հակառակ դեպքում
Հակառակ դեպքում
![]()
Օրինակ, ![]() :
:
Նախորդների նման ![]() չափողականություն չունի:
չափողականություն չունի: ![]() տվյալ խառնուրդում i -
րդ բաղադրիչի ծավալային բաժինն է` արտահայտված տոկոսներով:
տվյալ խառնուրդում i -
րդ բաղադրիչի ծավալային բաժինն է` արտահայտված տոկոսներով:
5.
Մոլային (մոլյար) կոնցենտրացիա ![]() : Ցույց է տալիս, թե 1 լ լուծույթում տվյալ նյութից քանի՞ մոլ է լուծված:
: Ցույց է տալիս, թե 1 լ լուծույթում տվյալ նյութից քանի՞ մոլ է լուծված:
![]()
Լուծույթի մոլյարությունը
խորհրդանշվում
է
M տառով: 1 M լուծույթ
նշանակում
է
մի
լուծույթ,
որի 1 լ-ում
1 մոլ քննարկվող
նյութ
է
լուծված:
![]() չափողականություն
ունի.
մոլ.լ–1
(մոլ.դմ–3):
չափողականություն
ունի.
մոլ.լ–1
(մոլ.դմ–3):
Եթե լուծված
նյութի
զանգվածն
արտահայտվում
է
գ.համարժեքով
![]() այդ
դեպքում լուծույթի կոնցենտրացիան
կարտահայտվի
նորմալությամբ
այդ
դեպքում լուծույթի կոնցենտրացիան
կարտահայտվի
նորմալությամբ
![]() գ
գ ![]() Միջազգային
միավորների
ընդունման
պատճառով
նորմալությունն
այժմ
գործնականորեն
չի
կիրառվում:
Տիտրը
լուծված
նյութի
զանգվածն
է
(գրամներով) 1 մլ
լուծույթում:
Միջազգային
միավորների
ընդունման
պատճառով
նորմալությունն
այժմ
գործնականորեն
չի
կիրառվում:
Տիտրը
լուծված
նյութի
զանգվածն
է
(գրամներով) 1 մլ
լուծույթում:
II – Լուծված նյութի քանակը վերաբերում են յուծիչի քանակին:
1. Մոլալ
լուծույթ.
խորհրդանշվում
է
m-ով: Ցույց
է
տալիս,
թե
1000 գ կամ 1 կգ
լուծիչում
տվյալ
նյութից
քանի
մոլ
է
լուծված:
Կարևոր
է
նշել,
որ
![]()
![]()
Թերմոդինամիկական քննարկումներում սա կոնցենտրացիայի արտահայտման առավել կիրառական ձևն է:
2. Մոլային հարաբերություն
![]()
![]()
Չափողականություն չունեցող մեծություն է: Ցույց է տալիս, թե 1 մոլ լուծիչում տվյալ նյութից քանի՞ մոլ է լուծված:
XI-2. ՄԻՋՄՈԼԵԿՈՒԼԱՅԻՆ ՓՈԽԱԶԴԵՑՈՒԹՅՈՒՆՆԵՐԸ ԼՈՒԾՈՒՅԹՆԵՐՈՒՄ
Խոսքը վերաբերելու է լուծիչ–լուծիչ, լուծված նյութ–լուծված նյութ և լուծիչ–լուծված նյութ (սոլվատացում, հիդրատացում) փոխազդեցություններին:
Լուծույթում կուլոնյան, ինչպես նաև վալենտական փոխազդեցությունների բացակայության դեպքում հիմնական փոխազդեցությունները վան դեր Վաալսյան բնույթի են (տե՛ս գլուխ VI):
Այս դասի
բոլոր
տեսակի
փոխազդեցությունների
ուժը
![]() (r-ը
միջմասնիկային
հեռավորությունն
է):
Կախված
r-ից փոխազդեցությունները
կարող
են
լինել
ինչպես
ձգողական,
այնպես
էլ
վանողական:
(r-ը
միջմասնիկային
հեռավորությունն
է):
Կախված
r-ից փոխազդեցությունները
կարող
են
լինել
ինչպես
ձգողական,
այնպես
էլ
վանողական:
Միջմասնիկային փոխազդեցությունների
բնույթը
քննարկելիս
անհնար
է
անտեսել
յուրահատուկ
սոլվատացման
դերը,
որն
իր
բնույթով
քիմիական
է:
Օրինակ,
դա
կարող
է
լինել
արդյունքը
մոլեկուլների
միջև
H-ական կապի,
լիցքի
տեղաշարժով
և
![]() առաջացման:
Այս
առումով
յուրահատուկ
սոլվատացումը
շատ
ավելի
ուժեղ
և
ըստ
էության
վալենտական
փոխազդեցություն
է,
քան
վան
դեր
Վաալսյանը:
Այս
հարցին
կանդրադառնանք
XXIV գլխում, երբ
քննարկման
նյութ
կհանդիսանա
լուծույթում
ընթացող
ռեակցիաների
կինետիկան:
առաջացման:
Այս
առումով
յուրահատուկ
սոլվատացումը
շատ
ավելի
ուժեղ
և
ըստ
էության
վալենտական
փոխազդեցություն
է,
քան
վան
դեր
Վաալսյանը:
Այս
հարցին
կանդրադառնանք
XXIV գլխում, երբ
քննարկման
նյութ
կհանդիսանա
լուծույթում
ընթացող
ռեակցիաների
կինետիկան:
XI-3. ԲԱԶՄԱԿՈՄՊՈՆԵՆՏ ՀԱՄԱԿԱՐԳԵՐԻ ԹԵՐՄՈԴԻՆԱՄԻԿԱՆ:
ՔԻՄԻԱԿԱՆ ՊՈՏԵՆՑԻԱԼԻ ԿԱՐԵՎՈՐՈՒԹՅՈՒՆԸ
Բնական է,
որ
նշված
դասի
համակարգերում
չի
կարելի
անտեսել
Գիբսյան
պոտենցիալի
կախումը
համակարգի
բաղադրությունից:
Այս
դեպքում
![]()
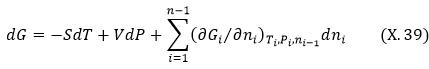
Հաշվի պետք է առնել այս հավասարումից բխող արդեն քննարկված հետևությունները:
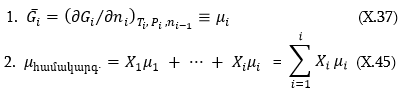
Այս արտահայտության
հիման
վրա
նշվեց,
որ
![]() ինտենսիվ պարամետր
է:
ինտենսիվ պարամետր
է:
3. Երբ T = const և P = const
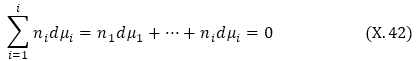
Սա Գիբս-Դյուհեմի հավասարումն է:
4. Խառնման պրոցեսի, մասնավոր դեպքում լուծույթի առաջացման ընթացքում համակարգի էնտրոպիայի և Գիբսյան պոտենցիալի փոփոխությունները հետևյալ հավասարումներով են նկարագրվում.
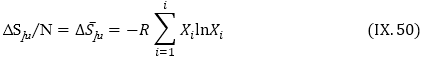
և
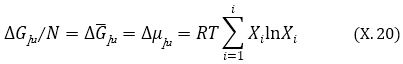
Գրաֆիկական մեթոդով քննարկենք խառնման ընթացքում թերմոդինամիկական (Գիբսի) պոտենցիալի (G) փոփոխությունը
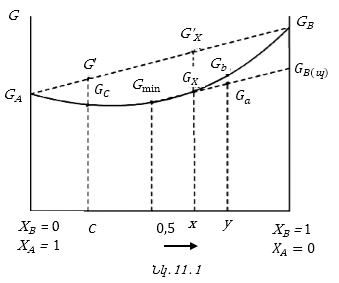
![]()
![]() մաքուր
A և B հեղուկ
նյութերի
մոլային
Գիբսյան
պոտենցիալներն
են:
Հնարավոր
է
երկու
դեպք.
մաքուր
A և B հեղուկ
նյութերի
մոլային
Գիբսյան
պոտենցիալներն
են:
Հնարավոր
է
երկու
դեպք.
1. A և B նյութերն իրար հետ չեն փոխազդում և իրար մեջ չեն լուծվում: Այս դեպքում կպահպանվի հատկությունների ադիտիվությունը:
2. A-ն
և
B-ն իրար
մեջ
լուծվում
են
անսահմանափակ:
Խառնման
էնտրոպիան
քննարկելիս
(տե’ս գլուխ
IX) ցույց տրվեց,
որ
խառնման
հետևանքով
համակարգի
էնտրոպիան
աճում
է
![]() ,
հետևաբար
պետք
է
նվազի
Գիբսյան
պոտենցիալը
,
հետևաբար
պետք
է
նվազի
Գիբսյան
պոտենցիալը
Եզրակացություն.
ցանկացած X բաղադրությամբ
լուծույթի
G-ն պետք
է
լինի`
![]() Օրինակ,
եթե
ստացվող
խառնուրդի
(լուծույթի) բաղադրությունը
C է, ապա
Օրինակ,
եթե
ստացվող
խառնուրդի
(լուծույթի) բաղադրությունը
C է, ապա ![]()
Եթե մասնավոր
դեպքում
B-ն պինդ
նյութ
է,
ապա
B-ի ինչ
որ
մի
քանակի
դեպքում
տվյալ
ջերմաստիճանում
լուծույթը
պետք
է
հագենա:
Դիցուք
X-ը համապատասխանում
է
A հեղուկում B-ի
լուծելիությանը:
Եթե
![]() ,
օրինակ
Y, ապա համակարգը
կլինի
երկֆազ.
հագեցած
լուծույթ
(հ) և B (պ):
B-ի քանակի
աճի
հետ
անընդհատ
կաճի
նստվածքի
(պինդ ֆազի)
քանակը:
Համակարգի
թերմոդինամիկական
պոտենցիալը
կաճի
,
օրինակ
Y, ապա համակարգը
կլինի
երկֆազ.
հագեցած
լուծույթ
(հ) և B (պ):
B-ի քանակի
աճի
հետ
անընդհատ
կաճի
նստվածքի
(պինդ ֆազի)
քանակը:
Համակարգի
թերմոդինամիկական
պոտենցիալը
կաճի
![]() ուղիղին
համապատասխան:
ուղիղին
համապատասխան:
![]() հագեցած լուծույթի
Գիբսյան
պոտենցիալն
է:
հագեցած լուծույթի
Գիբսյան
պոտենցիալն
է:
Իսկ եթե լուծելիությունից ավելի է լուծվում հագեցած լուծույթում, ապա կստացվի գերհագեցած լուծույթ: Պինդ նյութի լուծման հակառակ պրոցեսը բյուրեղացումն է:
Եթե համակարգի
ելային
բաղադրությունը
Y է, ապա
![]() (հագեցած
լուծույթ
+ նստվածք)
(հագեցած
լուծույթ
+ նստվածք) ![]() (գերհագեցած
լուծույթ):
Նշանակում
է,
որ
գերհագեցած
լուծույթն
ինքնաբերաբար
կվերածվի
հագեցածի`
նստվածքի
առաջացումով:
Հետևաբար,
թերմոդինամիկան
«արգելում է»
հագեցած
լուծույթ
– նստվածք
(գերհագեցած
լուծույթ):
Նշանակում
է,
որ
գերհագեցած
լուծույթն
ինքնաբերաբար
կվերածվի
հագեցածի`
նստվածքի
առաջացումով:
Հետևաբար,
թերմոդինամիկան
«արգելում է»
հագեցած
լուծույթ
– նստվածք ![]() գերհագեցած
լուծույթ
ինքնաբերաբար
անցումը:
գերհագեցած
լուծույթ
ինքնաբերաբար
անցումը:
XI-4. ԴՅՈՒՀԵՄ–ՄԱՐԳՈՒԼԵՍԻ ՀԱՎԱՍԱՐՈՒՄԸ
Գրենք Գիբս–Դյուհեմի հավասարումը.
![]()
Բաժանելով ![]() վրա կստացվի.
վրա կստացվի.
![]()
Քանի որ ![]() ապա
ապա ![]()
Հետևաբար, լուծույթի բաղադրության փոփոխության հետ պետք է փոխվի նաև ![]() Ուրեմն, j-րդ
Ուրեմն, j-րդ ![]() բաղադրիչի քանակի փոփոխության հետևանքով համակարգի քիմիական պոտենցիալը կփոփոխվի: Այդ փոփոխության մեջ j-րդ բաղադրիչի քիմիական պոտենցիալի փոփոխության բաժինը (լուման) կլինի.
բաղադրիչի քանակի փոփոխության հետևանքով համակարգի քիմիական պոտենցիալը կփոփոխվի: Այդ փոփոխության մեջ j-րդ բաղադրիչի քիմիական պոտենցիալի փոփոխության բաժինը (լուման) կլինի.
![]()
Եթե համակարգը (լուծույթը) մասնավոր դեպքում երկբաղադրիչ է (լուծիչ + մեկ հատ լուծված նյութ), այդ դեպքում.
![]()
Տեղադրենք (XI.11) -ի մեջ.
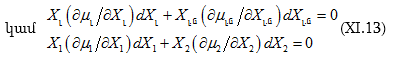
Նորից հաշվի առնելով, որ ![]() կստացվի.
կստացվի.
![]()
Եթե քննարկվում է իդեալական գազ.
![]()
![]()
(XI.15)-ի մեջ ![]() տվյալ ջերմաստիճանում (1) և (2) հեղուկների գոլորշիների պարցիալ ճնշումներն են այն դեպքում, երբ համակարգը գտնվում է հավասարակշռության մեջ, իսկ
տվյալ ջերմաստիճանում (1) և (2) հեղուկների գոլորշիների պարցիալ ճնշումներն են այն դեպքում, երբ համակարգը գտնվում է հավասարակշռության մեջ, իսկ ![]() էլ` լուծույթում այդ երկու հեղուկների մոլային բաժիններն են համապատասխանաբար:
էլ` լուծույթում այդ երկու հեղուկների մոլային բաժիններն են համապատասխանաբար:
Եթե քննարկվող գազը ռեալ է, ապա անհրաժեշտ է գազի ճնշումը
![]() փոխարինել ցնդելիությամբ
փոխարինել ցնդելիությամբ ![]() Այս հանգամանքը նկատի առնելով
(XI.15)-ի փոխարեն կստացվի.
Այս հանգամանքը նկատի առնելով
(XI.15)-ի փոխարեն կստացվի.
![]()
(XI.15) և (XI.16) հավասարումները հայտնի են որպես Դյուհեմ-Մարգուլեսի հավասարումներ: Կիրառելի են ցանկացած լուծույթի նկատմամբ:
XI.5. ԼՈՒԾՈՒՅԹՆԵՐԻ ԹԵՐՄՈԴԻՆԱՄԻԿԱԿԱՆ ԴԱՍԱԿԱՐԳՈՒՄԸ
Հայտնի է, որ վիճակի փոփոխության հետ փոխվում է նաև նյութի (համակարգի) քիմիական պոտենցիալը: Այս առումով ![]()
Ըստ Լյուիսի առաջարկի ![]() կոչվել է i-րդ նյութի ակտիվության գործակից: Տեղադրելով (X.61)
-ի մեջ կստացվի.
կոչվել է i-րդ նյութի ակտիվության գործակից: Տեղադրելով (X.61)
-ի մեջ կստացվի.
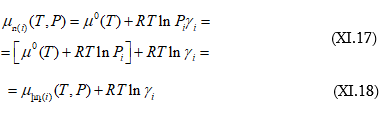
Եթե քննարկվող նյութը ոչ թե գազ է, այլ հեղուկ P-ն պետք է փոխարինել c-ով (կոնցենտրացիա), ![]() a-ով (ակտիվություն) և
a-ով (ակտիվություն) և
![]()
Սա կիրառելի է նաև պինդ լուծույթների նկատմամբ:
Հետևաբար.
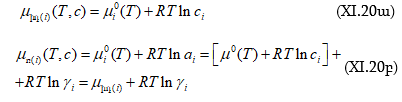
Նշված արտահայտություններից կհետևի.
![]()
![]() աշխատանք է: Ըստ էության դա այն աշխաանքն է, որն անհրաժեշտ է կատարել հաղթահարելու համար համակարգում առկա միջմոլեկուլային (միջմասնիկային) փոխազդեցությունները, որի հետևանքով համակարգը կդառնա իդեալական: Կարելի է եզրակացնել,որ ակտիվությունը ուղղված կոնցենտրացիա է
աշխատանք է: Ըստ էության դա այն աշխաանքն է, որն անհրաժեշտ է կատարել հաղթահարելու համար համակարգում առկա միջմոլեկուլային (միջմասնիկային) փոխազդեցությունները, որի հետևանքով համակարգը կդառնա իդեալական: Կարելի է եզրակացնել,որ ակտիվությունը ուղղված կոնցենտրացիա է
![]()
Սա նշանակում է, որ հաստատուն ջերմաստիճանում միջմասնիկային փոխազդեցությունների և բնույթից և սաստկությունից է կախված G-ն (H-ը և S-ը):
Սա վերաբերում
է
մասնավոր
դեպքում
նաև
խառնման
պրոցեսին
![]()
Միջմասնիկային փոխազդեցությունների չափը կախված է ինչպես դրանց բնույթից (իոն–իոն, իոն–դիպոլ, դիպոլ–դիպոլ, իոն–ապոլյար մոլեկուլ և այլն), այնպես էլ դրանց սաստկությունից (իոնի լիցքի և շառավիղի հարաբերությունից, դիպոլ մոմենտից և այլն):
Յուրաքանչյուր դեպքի
համար
![]() որոշակի
ֆունկցիոնալ
կախման
մեջ
է
գտնվում
այդ
փոխազդեցությունների
ուժը
պայմանավորող
պարամետրերից:
Այս
հարցին
ավելի
հանգամանալի
կանդրադառնանք
XXIV գլխում:
որոշակի
ֆունկցիոնալ
կախման
մեջ
է
գտնվում
այդ
փոխազդեցությունների
ուժը
պայմանավորող
պարամետրերից:
Այս
հարցին
ավելի
հանգամանալի
կանդրադառնանք
XXIV գլխում:
Լուծույթների դասակարգման հիմքում վերցվում են նշված թերմոդինամիկական ֆունկցիաները և խառնման (այսինքն լուծույթի առաջացման) ընթացքում դրանց կրած ինչպես որակական, այնպես էլ քանակական փոփոխությունները: Հետևաբար լուծույթների թերմոդինամիկական դասակարգման հիմքում դրված են լուծույթում բաղադրիչների քիմիական պոտենցիալներն արտահայտող հավասարումները:
XI-5:1. Իդեալական լուծույթներ
ա. Կատարյալ լուծույթներ
Ցույց տրվեց, որ միջմոլեկուլային փոխազդեցությունների բացակայության պարագային.
![]()
(կամ ![]()
Գրված արտահայտություններից հետևում է, որ S-ը, G-ն (իզոթերմ–իզոբարային էներգիա), F-ը (իզոթերմ–իզոխորային էներգիա), ընդհանրապես Y, ֆունկցիա են X-ից. Այսինքն Y = f (X): Զուգորդելով (IX.50) և (X.20)-ը (X.19)-ի հետ
![]()
կստացվի.
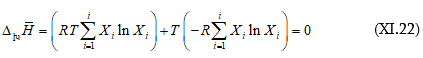
[![]() օգտագործելիս կստացվի
օգտագործելիս կստացվի
![]()
և
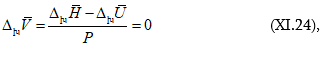
որովհետև
![]()
Եզրակացություն. Եթե լուծույթի առաջացման ընթացքում ![]() այդ դեպքում առաջացած լուծույթը իդեալական է: Կարելի է նաև ասել հետևյալը: Իդեալական է այն լուծույթը, որի առաջացումը ջերմաչեզոք է, ինչպես նաև առաջացած լուծույթի ծավալը հավասար է վերցված բաղադրիչների ծավալների գումարին
այդ դեպքում առաջացած լուծույթը իդեալական է: Կարելի է նաև ասել հետևյալը: Իդեալական է այն լուծույթը, որի առաջացումը ջերմաչեզոք է, ինչպես նաև առաջացած լուծույթի ծավալը հավասար է վերցված բաղադրիչների ծավալների գումարին
![]()
Եթե նշված օրինաչափությունները պահպանվում են լուծույթի կոնցենտրացիոն ողջ տիրույթում այդպիսի իդեալական լուծույթը կոչվում է կատարյալ: Կատարյալ լուծույթները ենթարկվում են Ռաուլի օրենքին:
բ. Անսահման նոսր լուծույթներ:
Այդպիսի օրինաչափություններ դիտվում են նաև այն դեպքում, երբ առաջանում է անսահման նոսր լուծույթ:
Երբ ![]()
Նշանակում է, որ անսահման նոսր լուծույթներում միջմոլեկուլային փոխազդեցություններն այնքան փոքր են, որ կարելի է անտեսել: Այս պայմաններում համակարգը իրեն պահում է որպես իդեալական: Անսահման նոսր լուծույթները ենթարկվում են Հենրիի օրենքին:
XI-5:2. Ոչիդեալական լուծույթներ
Ոչիդեալական են այն լուծույթները, որոնց առաջացման ընթացքում (XI.22![]() 24) օրինաչափություններից գոնե մեկը չի պահպանվում:
24) օրինաչափություններից գոնե մեկը չի պահպանվում:
ա. ռեալ լուծույթներ:
Եթե լուծույթի առաջացման պայմանները սահմանային չեն, ապա այդ երեք օրինաչափություններն էլ չեն պահպանվի, այսինքն. ![]() որը հետևանք է միջմոլեկուլային զգալի փոխազդեցությունների գոյության: Այս պայմաններում առաջացած լուծույթը ռեալ է:
որը հետևանք է միջմոլեկուլային զգալի փոխազդեցությունների գոյության: Այս պայմաններում առաջացած լուծույթը ռեալ է:
Ինչպես նշվեց, եթե առկա են միջմոլեկուլային փոխազդեցություններ այդ դեպքում պետք է ճնշումը փոխարինել ցնդելիությամբ, կոնցենտրացիան էլ` ակտիվությամբ:
Հետևաբար, եթե
![]()
ապա
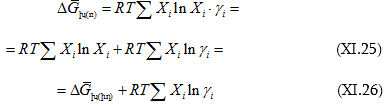
Ցույց է տված, որ
![]()
Ուրեմն, եթե պետք է որոշել ռեալ լուծույթի առաջացման ընթացքում էնտրոպիայի փոփոխությունը հարկավոր է
(XI.26)-ը ածանցել ըստ ջերմաստիճանի նկատի առնելով. Որ ![]()
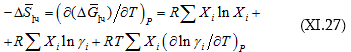
Էնտրոպիայի փոփոխության իմացումը հնարավորություն կտա որոշել նաև ![]() որովհետև
որովհետև
![]()
(XI.28)-ի մեջ տեղադրենք (XI.25)-ը և (XI.27)-ը.
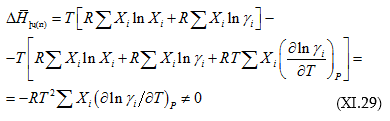
![]() օգտագործելիս կստացվի
օգտագործելիս կստացվի
![]() :
:
Եզրակացություն. եթե խառնման հետևանքով ռեալ լուծույթ է առաջանում, ապա (XI.22-24)-ի փոխարեն կստացվի
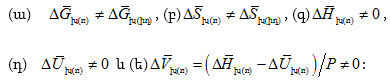
բ. Աթերմալ լուծույթներ – Լուծույթը աթերմալ է կոչվում, երբ ![]()
Ըստ (XI.21)-ի.
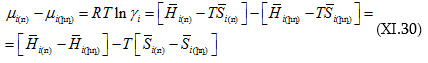
Քանի որ ըստ սահմանումի
![]() այդ պատճառով էլ.
այդ պատճառով էլ.
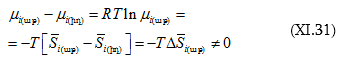
Այսպիսով, աթերմալ լուծույթների առաջացումը պայմանավորված է ոչ թե էներգիական
![]() այլ էնտրոպիական բաղադրիչի փոփոխությամբ
այլ էնտրոպիական բաղադրիչի փոփոխությամբ ![]() այսինքն ի հաշիվ խառնման հետևանքով ստացված լուծույթում մասնիկների շարժման «անկարգության» աստիճանի մեծացման:
այսինքն ի հաշիվ խառնման հետևանքով ստացված լուծույթում մասնիկների շարժման «անկարգության» աստիճանի մեծացման:
Աթերմալ լուծույթ կարելի է ստանալ պոլիմերը իր հիդրված մոնոմերի մեջ լուծելով:
գ. Կանոնավոր (ռեգուլյար) լուծույթներ – Այս հասկացությունը 1929-ին առաջարկել է Հիլդեբրանդը:
Կանոնավոր է կոչվում է այն լուծույթը, որում լուծիչի և լուծված(ների) մոլեկուլների բաշխումը և իրար նկատմամբ փոխադարձ կողմնորոշումը (օրիենտացումը) միանգամայն պատահական են: Անտեսվում են մոլեկուլների ասոցումը և քիմիական փոխազդեցությունը: Հետևաբար, առաջացող լուծույթը կանոնավոր է, եթե
![]()
Այստեղից հետևում է.
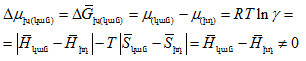
այսինքն.
![]()
Նշվածից կարելի է եզրակացնել, որ
![]()
![]() -դա մի հավելյալ աշխատանք է, որը կատարվում է կանոնավոր լուծույթում համեմատած իդեալականի հետ:
-դա մի հավելյալ աշխատանք է, որը կատարվում է կանոնավոր լուծույթում համեմատած իդեալականի հետ:
Ցույց է տված, որ եթե մոլեկուլները մոտավորապես իրար հավասար շառավիղներով գնդիկներ են, ապա
![]()
![]() միջմոլեկուլային փոխազդեցությունների մի հանրագումար է, որի ֆիզիկական էությունը կպարզվի հետագա քննարկումների ընթացքում:
միջմոլեկուլային փոխազդեցությունների մի հանրագումար է, որի ֆիզիկական էությունը կպարզվի հետագա քննարկումների ընթացքում:
Օգտվենք հեղուկների կառուցվածքի բջջային մոդելից (տե՛ս էջ 154): Ընդունենք նաև, որ յուրաքանչյուր մոլեկուլ շրջապատված է Z հատ մոլեկուլներով, իսկ բջիջներն իրարից անկախ գոյացություններ են:
Պայմանականորեն ընդունենք, որ լուծույթում կան բջիջներ. ![]() տիպի (տեսակի) մոլեկուլներից
տիպի (տեսակի) մոլեկուլներից ![]() հատ և b
տիպի մոլեկուլներից`
հատ և b
տիպի մոլեկուլներից` ![]() հատ: Մինչև խառնումը a
և b
մոլեկուլներից կազմված 2 նյութերը իրարից մեկուսացված համակարգեր են, հետևաբար.
հատ: Մինչև խառնումը a
և b
մոլեկուլներից կազմված 2 նյութերը իրարից մեկուսացված համակարգեր են, հետևաբար.
![]()
![]() 2 հատ միանման մասնիկների միջև գործող փոխազդեցության էներգիան է:
2 հատ միանման մասնիկների միջև գործող փոխազդեցության էներգիան է: ![]() գործակիցը մտցվում է այն նկատառումով, որ
գործակիցը մտցվում է այն նկատառումով, որ ![]() այսինքն 2 հատ a
մոլեկուլների միջև առկա փոխազդեցությունը, օրինակ բախումը մեկ հատ է:
այսինքն 2 հատ a
մոլեկուլների միջև առկա փոխազդեցությունը, օրինակ բախումը մեկ հատ է:
Խառնումից հետո սկսվում են բախվել նաև ![]() և
և ![]() մոլեկուլները: Բնական է, որ a +
b, (կամ b + a) բախումների հավանականությունը պետք է համեմատական լինի խառնուրդում a
և b
մոլեկուլների բաժինների արտադրյալին: Ուրեմն, խոսքը վերաբերվում է
մոլեկուլները: Բնական է, որ a +
b, (կամ b + a) բախումների հավանականությունը պետք է համեմատական լինի խառնուրդում a
և b
մոլեկուլների բաժինների արտադրյալին: Ուրեմն, խոսքը վերաբերվում է ![]() արտադրյալներին:
արտադրյալներին:
Քանի որ փոխազդեցության էներգիան պայմանավորված է բախումներով, այդ պատճառով էլ ![]() փոխազդեցության էներգիան պետք է ընդունել.
փոխազդեցության էներգիան պետք է ընդունել. ![]() համար`
համար` ![]() համար`
համար` ![]() համար էլ`
համար էլ` ![]()
Նկատի առնելով այն հանգամանքը, որ խառնումից հետո համակարգում մասնիկների թիվը կլինի ![]() և ընդունելով, որ անկախ մոլեկուլների բնույթից բջիջների կազմը նույնն է` Z
մոլեկուլ մեկ բջիջում , կարող ենք գրել.
և ընդունելով, որ անկախ մոլեկուլների բնույթից բջիջների կազմը նույնն է` Z
մոլեկուլ մեկ բջիջում , կարող ենք գրել.
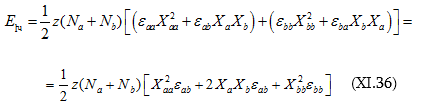
Որտեղ ![]()
Հաշվի առնելով այս նշանակումը (XI.36)-ի մեջ համապատասխան փոփոխություն կատարենք.
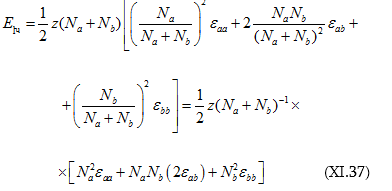
Բնական է, որ.
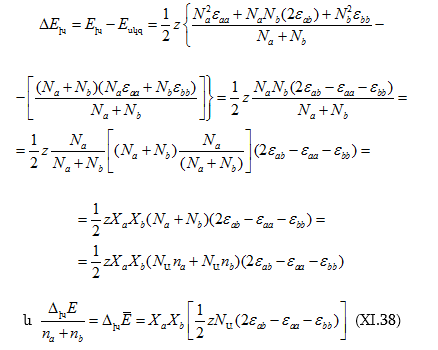
(XI.38)-ը հենց այն հավելյալ էներգիան է, որի գոյությունը միջմոլեկուլային փոխազդեցությունների հետևանք է:
իսկ
![]()
Համեմատությունից կստացվի, որ
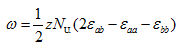
Նկատի առնելով այն հանգամանքը, որ կանոնավոր լուծույթների առաջացումը հիմնականում վերագրվում է վան դեր վաալսյան ուժերով պայմանավորված փոխազդեցություններին, մոլեկուլները համարվում են գնդաձև և փոխազդեցություններում նախապատվությունը տալով միայն ձգողական ուժերին ակտիվության գործակցի համար Լեյդլերը առաջարկել է հետևյալ հավասարումը.
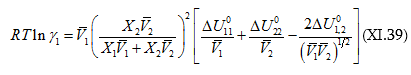
որտեղ ![]() մաքուր հեղուկներում միջմոլեկուլային փոխազդեցություններն են:
մաքուր հեղուկներում միջմոլեկուլային փոխազդեցություններն են: ![]() ծավալային բաժին է:
ծավալային բաժին է:
Առաջին մոտավորությամբ կարելի է գրել.
![]()
և ![]() (հիշել Ամագայի օրենքը): Այս պայմանների համար կստացվի.
(հիշել Ամագայի օրենքը): Այս պայմանների համար կստացվի.
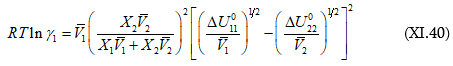
Եթե (2) ինդեքսը վերաբերում է լուծիչին և լուծույթն էլ նոսր է, ապա ![]()
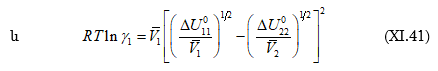
Վիճակի թերմոդինամիկական (X.34)
հավասարման քննարկումից ստացվեց, որ ![]()
հետևաբար
![]()
Այս հավասարումից հետևում է, որ լուծույթը կլինի իդեալական, եթե.
1.
բացակայում են միջմոլեկուլային փոխազդեցությունները ![]()
2.
իրար են հավասար բաղադրիչների ներքին ճնշումները. ![]()
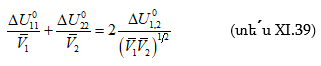
որտեղ
![]()
XI-6. ԼՐԻՎ ՊՈՏԵՆՑԻԱԼ
Մինչև հիմա քննարկվեցին այնպիսի համակարգեր, որոնց վիճակը բնութագրող Գիբսյան պոտենցիալը դիտվում էր միայն ֆունկցիա T-ից, P-ից և n-ից:
Բայց եթե համակարգը գտնվում է էլեկտրական և մագնիսական դաշտերում կամ զգալի է երկրագնդի գրավիտացիոն դաշտի ազդեցությունը, ապա ![]() փոխարեն պետք է
փոխարեն պետք է ![]() գրել
գրել ![]() տակ հասկանալով տարբեր մեծությունների ունեցած լուման
տակ հասկանալով տարբեր մեծությունների ունեցած լուման ![]() մեջ:
մեջ:
Օրինակ, եթե էլեկտրաքիմիական պրոցես է տեղի ունենում, ապա
![]()
որտեղ n-ը էլեկտրաքիմիական պրոցեսին մասնակցող էլեկտրոնների թիվն է, F-ը Ֆարադեյի թիվն է ![]() իսկ
իսկ ![]() երկու էլեկտրոդների միջև գոյություն ունեցող պոտենցիալների տարբերությունն է:
երկու էլեկտրոդների միջև գոյություն ունեցող պոտենցիալների տարբերությունն է:
Եթե քիմիական համակարգի վիճակը կախված է գրավիտացիոն դաշտից, այդ դեպքում
![]()
(XI.43 ա)-ն և (XI.43 բ)-ն կարելի է գրել 1 մոլ նյութի համար, որի դեպքում խոսքը կվերաբերի քիմիական պոտենցիալին:
Ուրեմն երևույթի քննարկմանն ավելի խիստ մոտենալու դեպքում բացի ընդունելուց
T = const, V(P) = const, m = const անհրաժեշտ է ընդունել առհասարակ ընդհանրացված տեսքով ներկայացվող` ![]() պոտենցիալի մեծության հաստատունությունը, որի դեպքում միայն կարելի է հաստատապես խոսել համակարգի հավասարակշռական վիճակում գտնվելու հավաստիության մասին: Այդ
պոտենցիալի մեծության հաստատունությունը, որի դեպքում միայն կարելի է հաստատապես խոսել համակարգի հավասարակշռական վիճակում գտնվելու հավաստիության մասին: Այդ ![]() կոչվում է «լրիվ պոտենցիալ»:
կոչվում է «լրիվ պոտենցիալ»:
Բնական է, որ սովորական պայմաններում, երբ ուսումնասիրվող համակարգի վրա չեն ազդում առանձին, հատուկ նշանակության դաշտեր, ուժի մեջ է այն, ինչը շարադրվել է:
XI-7. ԼՈՒԾՈՒՅԹՆԵՐԻ ԹԵՐՄՈԴԻՆԱՄԻԿԱՅԻ ՄԻ ՔԱՆԻ ՀԱՐՑԵՐ
XI-7:1. Հավելյալ թերմոդինամիկական մեծություններ
Ցույց տրվեց, որ եթե խառնման հետևանքով իդեալական լուծույթ է ստացվում, ապա այդ պրոցեսի ընթացքում
![]()
իսկ եթե առաջացած լուծույթը իդեալական չէ պետք է օգտվել ակտիվությունից`
![]() որտեղ
որտեղ ![]() լուծույթում i-րդ բաղադրիչի ակտիվության գործակիցն է: Հետևաբար.
լուծույթում i-րդ բաղադրիչի ակտիվության գործակիցն է: Հետևաբար.
![]()
իսկ
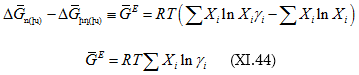
![]() կոչվում է Գիբսի հավելյալ էներգիա: Հիշենք, որ
կոչվում է Գիբսի հավելյալ էներգիա: Հիշենք, որ ![]()
Բնութագրական ֆունկցիաները քննարկելիս ցույց տրվեց, որ
![]()
Նմանակությամբ կարող ենք գրել.
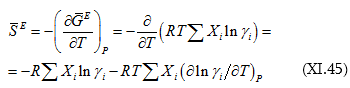
![]() հավելյալ մոլային էնտրոպիան է:
հավելյալ մոլային էնտրոպիան է:
իսկ
![]()
որտեղից.
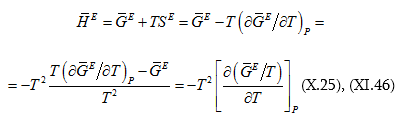
![]() համար կարելի է նաև այլ արտահայտություն ստանալ.
համար կարելի է նաև այլ արտահայտություն ստանալ.
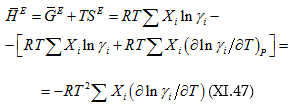
Վերջապես ![]() (հավելյալ ծավալ) (X.16),
(XI.48)
(հավելյալ ծավալ) (X.16),
(XI.48)
![]()
Հավելյալ մեծությունները կարող են լինել և դրական և բացասական: Եթե ![]() ապա
ապա ![]() (կանոնավոր լուծույթներ)
(կանոնավոր լուծույթներ) ![]() ապա
ապա ![]() (աթերմալ լուծույթներ):
(աթերմալ լուծույթներ):
XI-7:2. Լուծույթի մոլային ծավալ: Որոշման մեթոդներ
Քննարկենք մի լուծույթ, որը կազմված է լուծիչից [նշանակենք (1) ինդեքսով] և մի հատ լուծված նյութից, որը նշանակում ենք (2) ինդեքսով:
Եթե լուծույթի ծավալը V
լիտր է և պարունակում է ![]() մոլ նյութ, ապա (տես III-1:4
բաժինը)
մոլ նյութ, ապա (տես III-1:4
բաժինը)
![]()
![]() բաղադրիչի պարցիալ մոլային ծավալն է: Ըստ իմաստի.
բաղադրիչի պարցիալ մոլային ծավալն է: Ըստ իմաստի.
![]()
Պետք է նշել, որ պարցիալ մոլային մեծությունը ոչ թե հատկություն է, այլ համակարգի (լուծույթի) հատկության փոփոխությունն է, երբ ![]() պայմանում լուծույթին i-րդ բաղադրիչից 1 մոլ է ավելացվում: Ինչպե՞ս իրականացնել. ա) կամ անվերջ մեծ ծավալով լուծույթին է ավելացվում i-րդ նյութից 1 մոլ կամ բ) V ծավալով լուծույթին ավելացվում է
պայմանում լուծույթին i-րդ բաղադրիչից 1 մոլ է ավելացվում: Ինչպե՞ս իրականացնել. ա) կամ անվերջ մեծ ծավալով լուծույթին է ավելացվում i-րդ նյութից 1 մոլ կամ բ) V ծավալով լուծույթին ավելացվում է ![]()
(XI.50)-ից կստացվի.
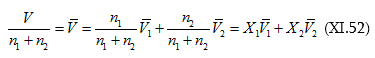
Յուրաքանչյուր բաղադրիչի կշռային բաժինը նշանակենք
![]()
![]()
որտեղից
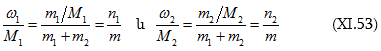
![]() բաղադրիչի զանգվածն է (գ կամ կգ),
բաղադրիչի զանգվածն է (գ կամ կգ), ![]() մոլային զանգվածը (գ/մոլ կամ կգ/մոլ): Պարզ է, որ
մոլային զանգվածը (գ/մոլ կամ կգ/մոլ): Պարզ է, որ ![]() (սա V ծավալով լուծույթի զանգվածն է),
(սա V ծավալով լուծույթի զանգվածն է), ![]() (մոլերի թիվ) և
(մոլերի թիվ) և ![]()
Գումարելով կստանանք.
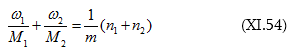
Լուծույթի խտությունը նշանակենք ![]() Տեղադրենք
(XI.54)-ի մեջ.
Տեղադրենք
(XI.54)-ի մեջ.
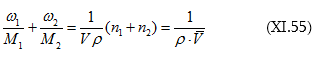
որտեղ ![]() : Եվ վերջապես.
: Եվ վերջապես.
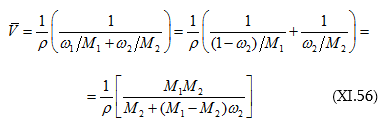
Այս հավասարումը հնարավորություն է տալիս լուծվածի տվյալ զանգվածային բաժնի համար որոշել լուծույթի մոլային ծավալը:
(XI.52)-ից կստացվի.
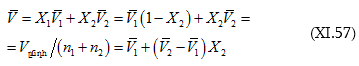
Այս հավասարումը հնարավորություն կտա լուծույթի տվյալ բաղադրության համար ![]() որոշել
որոշել ![]() Երկու դեպք է հնարավոր.
Երկու դեպք է հնարավոր.
![]() ա) լուծիչի և լուծվածի պարցիալ մոլային ծավալներն անկախ են լուծույթի բաղադրությունից (իդեալական դեպք):
ա) լուծիչի և լուծվածի պարցիալ մոլային ծավալներն անկախ են լուծույթի բաղադրությունից (իդեալական դեպք): ![]() ֆունկցիան կարտահայտվի
ֆունկցիան կարտահայտվի ![]() ուղիղ գծի հավասարման տեսքով, որտեղ
ուղիղ գծի հավասարման տեսքով, որտեղ ![]()
բ) եթե ![]() ֆունկցիան գծային չէ, ապա
ֆունկցիան գծային չէ, ապա ![]() կոորդինատներով կառուցվածը կլինի կորագիծ: Կորագծի վրա տվյալ
կոորդինատներով կառուցվածը կլինի կորագիծ: Կորագծի վրա տվյալ ![]() կոորդինատներով կետին շոշափող տանելով կարելի է որոշել
կոորդինատներով կետին շոշափող տանելով կարելի է որոշել ![]() Այս մեծությունը տեղադրելով
(XI.57)-ի մեջ կարելի է տվյալ
Այս մեծությունը տեղադրելով
(XI.57)-ի մեջ կարելի է տվյալ ![]() բաղադրության համար հաշվել
բաղադրության համար հաշվել ![]() այնուհետև
այնուհետև
![]() Այսպես են վարվում այլ բաղադրությունների համար:
Այսպես են վարվում այլ բաղադրությունների համար:
Ուրեմն ունենք «փաստացի» վիճակ, երբ ![]() (a) և «սպասվելիք» վիճակ (b).
(a) և «սպասվելիք» վիճակ (b).
![]()
և
![]()
Բնականաբար. ![]() ( հավելյալ ծավալ)
( հավելյալ ծավալ)
Հետևաբար.
![]()
Նկատի առնելով, որ ![]() կստացվի.
կստացվի.
![]()
Մաքուր նյութի համար ![]() Եթե հայտնի է
Եթե հայտնի է ![]() (տես վերևում շարադրվածը) և
(տես վերևում շարադրվածը) և ![]() կարելի է որոշել
կարելի է որոշել ![]() մեծությունը և նշանը պատկերացում են տալիս լուծիչ + լուծված նյութ փոխազդեցության և’ բնույթի և’ սաստկության մասին:
մեծությունը և նշանը պատկերացում են տալիս լուծիչ + լուծված նյութ փոխազդեցության և’ բնույթի և’ սաստկության մասին:
![]() -ն կարելի է նաև հետևյալ կերպ որոշել.
-ն կարելի է նաև հետևյալ կերպ որոշել.
![]()
և
![]()
որտեղից.
![]()
(բ)-ից հանենք (ա)-ն.
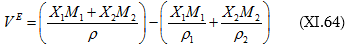
Հավելյալ մեծությունների գոյությունը պատճառ է հանդիսացել մտցնելու ևս մի հասկացություն. «թվացյալ մեծություն», նաև «թվացյալ մոլային մեծություն», օրինակ, «թվացյալ մոլային ծավալ», «թվացյալ մոլային էնտալպիա» և այլն:
Իմաստը հետևյալն է: եթե ընդունենք, որ օրինակ, ռեալ համակարգում անկախ բաղադրությունից լուծիչի պարցիալ մոլային ծավալը հաստատուն է, այդ դեպքում լուծվածի պարցիալ մոլային ծավալը տվյալ ![]() բաղադրության համար կունենա
բաղադրության համար կունենա ![]() արժեքը: Սա նշանակում է, որ
արժեքը: Սա նշանակում է, որ
![]()
Եթե լուծույթը դարձնենք անվերջ նոսր, ապա ![]()
Եզրակացություն. անվերջ նոսր լուծույթներում իրար հավասար են լուծվածի պարցիալ և թվացյալ մոլային ծավալները:
Թվացյալ պարցիալ մոլային մեծությունների կարևորությունը հարց է առաջ բերում. ինչպե՞ս դրանք որոշել: Որոշման մատչելի մեթոդներից մեկի հիմքում (XI.65)-ն է.
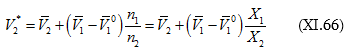
(![]() որոշման հարցն արդեն քննարկված է):
որոշման հարցն արդեն քննարկված է):
Կարելի է որոշել նաև լուծույթի խտության ![]() միջոցով: Վերցվում է 1000գ լուծիչ
միջոցով: Վերցվում է 1000գ լուծիչ ![]()
![]()
որտեղից.
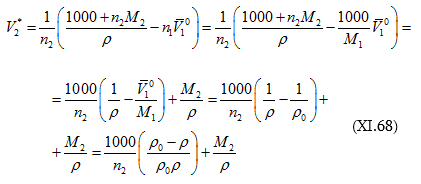
(![]() մաքուր լուծիչի խտությունն է):
մաքուր լուծիչի խտությունն է):
Ըստ սահմանումի ![]() (մոլ/1կգ) դա լուծվածի (լուծույթի) մոլալ կոնցենտրացիան է.
(մոլ/1կգ) դա լուծվածի (լուծույթի) մոլալ կոնցենտրացիան է. ![]() Տեղադրելով կստացվի.
Տեղադրելով կստացվի.
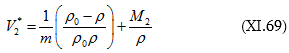
![]()

Մատչելի է նաև պարցիալ մոլային մեծությունների որոշման գրաֆիկական մեթոդը, որը կոչվում է «իրար հատող ուղիղների մեթոդ»: Այս եղանակը հնարավորություն է տալիս միաժամանակ որոշել երկու բաղադրիչների պարցիալ մոլային մեծությունները ![]() որտեղ
որտեղ ![]() ընդհանրցված մի պարամետր է. կարող է լինել ծավալ, H, G և այլն):
ընդհանրցված մի պարամետր է. կարող է լինել ծավալ, H, G և այլն):
Քննարկենք ներկայացված գծագիրը:
![]()
![]()
![]() Նշանակենք.
Նշանակենք. ![]()
![]()
![]()
![]() դա աբսցիսին զուգահեռ է, իսկ BDF
ուղիղը D
կետին տարված շոշափողն է): Ըստ ածանցյալի երկրաչափական իմաստի.
դա աբսցիսին զուգահեռ է, իսկ BDF
ուղիղը D
կետին տարված շոշափողն է): Ըստ ածանցյալի երկրաչափական իմաստի.
![]()
Քննարկման համար վարվում են հետևյալ կերպ. վերցնում են ![]() և փոխում
և փոխում ![]() Քանի որ
Քանի որ ![]() այդ պատճառով էլ
այդ պատճառով էլ ![]()
Դիֆերենցենք
![]()
իսկ ըստ (XI.70)-ի
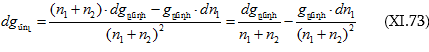
Բաժանելով իրար վրա կստացվի.
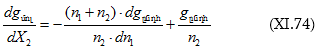
որտեղից.
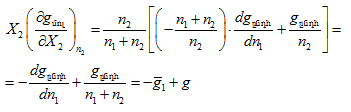
Տեղադրենք (XI.71)-ի մեջ. ![]() ինչ որ պետք էր ապացուցել:
ինչ որ պետք էր ապացուցել:
Նույն ձևով կարելի է ցույց տալ, որ ![]()
![]() կարելի է որոշել նաև օգտվելով
կարելի է որոշել նաև օգտվելով ![]() արտահայտելու փորձարարական (էմպիրիկ) հավասարումներից, որոնք ներկայացվում են շարքի տեսքով.
արտահայտելու փորձարարական (էմպիրիկ) հավասարումներից, որոնք ներկայացվում են շարքի տեսքով.
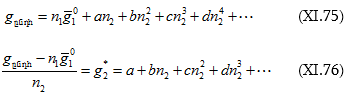
Կազմելով ![]() կոորդինատներով գրաֆիկ և կորի տվյալ կետին շոշափող տանելով կարելի է որոշել տվյալ
կոորդինատներով գրաֆիկ և կորի տվյալ կետին շոշափող տանելով կարելի է որոշել տվյալ ![]() համար
համար ![]() Նույնը կարելի է կատարել
Նույնը կարելի է կատարել
![]() կորի հետ: Հեշտ է ցույց տալ, որ
կորի հետ: Հեշտ է ցույց տալ, որ ![]() կամ
կամ ![]() (կազմել գրաֆիկ
(կազմել գրաֆիկ
![]() կոորդինատներով):
կոորդինատներով):
Կարելի է օգտվել նաև ԷՀՄ-ից նշված շարքերի գործակիցները որոշելու համար (թվային լուծում):
Շարքերի կիրառումը ամրացնելու համար լուծենք հետևյալ խնդիրը.
Խնդիր – Ինչի՞ է հավասար 25oC-ում 1 մոլալանոց (m = 1) NaCl-ի ջրային լուծույթի պարցիալ մոլային ծավալը, եթե
![]()
(երբ m > 0,25 մոլ/կգ) հաշված 1000 գ ջրի համար: 25oC
-ում մաքուր ջրի ![]() մլ/մոլ է:
մլ/մոլ է:
Լուծում – նշված պայմաններում տվյալ լուծույթի պարցիալ մոլային ծավալը կլինի.
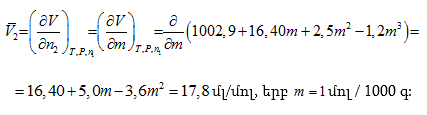
Ծավալը կրճատվեց: Իսկ
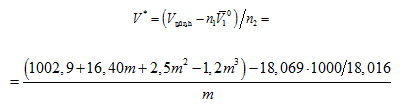
![]()
Երբ m = 1 մոլ/1000 գ, այդ դեպքում.
![]()
XI-7:3. Հարաբերական պարցիալ մոլային մեծություններ:
Հարաբերական պարցիալ մոլային էնտալպիա
Սա թեև շատ կարևոր է, բայց վերաբերում է լուծույթների թերմոդինամիկային և ըստ էության նեղ մասնագիտական հարց է: Այդ պատճառով այն քննարկվելու է մակերեսորեն հարցի մասին ընդհանուր պատկերացում կազմելու համար:
Ըստ ընդհանուր սահմանումի ![]() H-ի բացարձակ արժեքն անհնար է իմանալ: Կարելի է պարզապես նշել, որ տվյալ վիճակում գտնվող նյութի էնթալպիան ինչքանով է տարբեր, եթե այդ նյութը գտնվեր մի այլ վիճակում, օրինակ այլ կոնցենտրացիայով, բայց նույն լուծիչում: Այս նկատառումով էլ թերմոդինամիկայում կարևորվել է «ստանդարտ վիճակի» հարցը:
H-ի բացարձակ արժեքն անհնար է իմանալ: Կարելի է պարզապես նշել, որ տվյալ վիճակում գտնվող նյութի էնթալպիան ինչքանով է տարբեր, եթե այդ նյութը գտնվեր մի այլ վիճակում, օրինակ այլ կոնցենտրացիայով, բայց նույն լուծիչում: Այս նկատառումով էլ թերմոդինամիկայում կարևորվել է «ստանդարտ վիճակի» հարցը:
Հիշենք, որ ոչ էլեկտրոլիտների լուծույթների դեպքում կիրառվում է ստանդարտ վիճակ ընտրելու սիմետրիկ համակարգը: Այս պարագային լուծույթի երկու բաղադրիչների համար ստանդարտ վիճակ է համարվում, երբ նյութը գտնվում է մաքուր վիճակում, որի ակտիվությունը պայմանականորեն ընդունվում է հավասար 1-ի. ![]() հետևաբար
հետևաբար ![]()
Էլեկտրոլիտների լուծույթների դեպքում կիրառվում է ստանդարտ վիճակ ընտրելու ոչսիմետրիկ համակարգը: Այս դեպքում քննարկվողը լուծված նյութն է: Լուծույթի վիճակը համարվում է ստանդարտ, եթե լուծույթն ըստ լուծվածի 1 մոլալանոց է: Ընդունելի է նաև 1 մոլյարանոց լուծույթը:
Այս նկատառումով, եթե i-րդ նյութի պարցիալ մոլային էնթալպիան
![]() է ինչ որ մի վիճակում և
է ինչ որ մի վիճակում և ![]() է ստանդարտ վիճակում, ապա ըստ սահմանումի
է ստանդարտ վիճակում, ապա ըստ սահմանումի
![]() տարբերությունը կոչվում է հարաբերական պարցիալ մոլային
տարբերությունը կոչվում է հարաբերական պարցիալ մոլային
![]() էնթալպիա: Եթե լուծույթը անսահման նոսր է և գտնվում է ստանդարտ վիճակում, ապա ունենք
էնթալպիա: Եթե լուծույթը անսահման նոսր է և գտնվում է ստանդարտ վիճակում, ապա ունենք ![]() Եթե որպես ստանդարտ վիճակ վերցվում է նյութը մաքուր վիճակում, ապա գրում ենք
Եթե որպես ստանդարտ վիճակ վերցվում է նյութը մաքուր վիճակում, ապա գրում ենք ![]()
Հետևաբար, լուծիչի համար. ![]() և լուծվածի համար.
և լուծվածի համար. ![]() Պարզ է, որ եթե լուծույթն անվերջ նոսր է, ապա
Պարզ է, որ եթե լուծույթն անվերջ նոսր է, ապա ![]()
Եթե լուծույթում կա ![]() մոլ լուծիչ և
մոլ լուծիչ և ![]() մոլ լուծված նյութ, ապա.
մոլ լուծված նյութ, ապա.
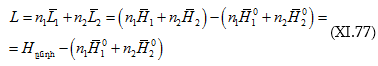
այսինքն.
![]()
որն իր տեսքով հիշեցնում է (XI.50)-ը:
Նույն դատողությամբ կարելի է գրել.
![]()
Պրոցեսների ջերմությունը քննարկելիս ցույց է տրվել, որ ընդհանրապես
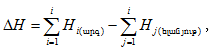 լուծման համար մասնավորաբար.
լուծման համար մասնավորաբար.
![]()
իսկ
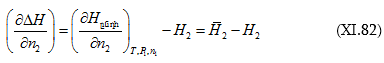
(XI.82)-ը կարելի է գրել
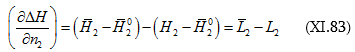
![]() տվյալ լուծույթում լուծվածի հարաբերական պարցիալ էնթալպիան է, իսկ
տվյալ լուծույթում լուծվածի հարաբերական պարցիալ էնթալպիան է, իսկ ![]() մաքուր լուծվածինը:
մաքուր լուծվածինը:
Ըստ իմաստի ![]() լուծման պարցիալ կամ դիֆերենցիալ ջերմությունն է:
լուծման պարցիալ կամ դիֆերենցիալ ջերմությունն է:
1. Որոշել ըստ զանգվածի 36 % HCl պարունակող աղաթթվի լուծույթում HCl -ի մոլային բաժինը:
2. 5,0 գ տոլուոլը լուծել են 225 գ բենզոլի մեջ: Ստացված լուծույթի
![]() գ/մլ:
Կոնցենտրացիան արտահայտել.
գ/մլ:
Կոնցենտրացիան արտահայտել.
ա) մոլալությամբ,
բ) մոլերով լիտրում,
գ) մոլային և
դ) զանգվածային բաժիններով:
3. Հաշվել Bi-ի լուծելիությունը Cd-ում
![]() և 200oC - ներում
օգտվելով Շրեդերի բանաձևից: 273oC -ում
և 200oC - ներում
օգտվելով Շրեդերի բանաձևից: 273oC -ում ![]() Ընդունել, որ առաջանում է իդելական լուծույթ: Շրեդերի բանաձևն է.
Ընդունել, որ առաջանում է իդելական լուծույթ: Շրեդերի բանաձևն է.
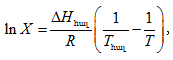
որտեղ X-ը մոլային բաժին է:
ԳԼՈՒԽ XII
ԼՈՒԾՈՒՅԹՆԵՐԻ ԿՈԼԻԳԱՏԻՎ ՀԱՏԿՈՒԹՅՈՒՆՆԵՐԸ
Կոլիգատիվ են կոչվում այն հատկությունները, որոնք կախված չեն լուծված նյութի բնույթից, այլ կախված են մի ընդհանուր մեծությունից. տվյալ քանակով լուծիչում լուծված նյութից առաջացած մասնիկների թվից: Այդ բառի հիմքում լատիներենից վերցված կո-միասին նախածանցն է և լիգատե-կապել բայն է: Այսինքն, իրար հետ են կապված լուծույթում առկա մասնիկների թիվը և լուծույթի որոշ հատկություններ:
Լուծույթների կոլիգատիվ հատկություններից են լուծույթի վրա գոլորշիների ճնշման, լուծույթի սառեցման և եռման ջերմաստիճանների, օսմոտիկական ճնշման կախումը լուծույթի կոնցենտրացիայից, այսինքն լուծված նյութի մոլերի և վերջին հաշվով լուծված նյութի այդ քանակից առաջացած մասնիկների թվից:
XII-1. ՌԱՈՒԼԻ ՕՐԵՆՔԸ: ԿԱՏԱՐՅԱԼ ԼՈՒԾՈՒՅԹՆԵՐ
Փորձը ցույց է տալիս, որ մաքուր հեղուկի վրա տվյալ նյութի սեփական գոլորշիների ճնշումն ավելի մեծ է քան երբ այդ հեղուկում լուծված նյութ կա:
Եթե տվյալ ջերմաստիճանում տվյալ հեղուկի գոլորշիների հավասարակշռական ճնշումը ![]() մթն է և այդ հեղուկից ստացված լուծույթի վրա`
մթն է և այդ հեղուկից ստացված լուծույթի վրա` ![]() մթն, ապա
մթն, ապա ![]() կոչվում է գոլորշիների ճնշման բացարձակ նվազում, իսկ
կոչվում է գոլորշիների ճնշման բացարձակ նվազում, իսկ ![]() հարաբերությունը` գոլորշիների ճնշման հարաբերական նվազում: Այն ցույց է տալիս, թե հեղուկում ինչ որ քանակով նյութ լուծելիս մաքուր հեղուկի (լուծիչի) սեփական գոլորշիների ճնշման
հարաբերությունը` գոլորշիների ճնշման հարաբերական նվազում: Այն ցույց է տալիս, թե հեղուկում ինչ որ քանակով նյութ լուծելիս մաքուր հեղուկի (լուծիչի) սեփական գոլորշիների ճնշման ![]() յուրաքանչյուր միավորը ինչ փոփոխություն կկրի:
յուրաքանչյուր միավորը ինչ փոփոխություն կկրի:
Համադրելով գրականական հայտնի տվյալներ` Ռաուլը (1887) բացահայտեց, որ տվյալ հեղուկի վրա գոլորշիների հարաբերական նվազումը հավասար է լուծույթում լուծված նյութի մոլային բաժնին (X0)
Եթե T ջերմաստիճանում № 1 մաքուր նյութի սեփական գոլորշիների ճնշումը ![]() է և լուծույթի վրա`
է և լուծույթի վրա` ![]() իսկ այդ լուծույթում 2-րդ (լուծված) նյութի մոլային բաժինը
իսկ այդ լուծույթում 2-րդ (լուծված) նյութի մոլային բաժինը ![]() է, ապա ըստ Ռաուլի օրենքի.
է, ապա ըստ Ռաուլի օրենքի.
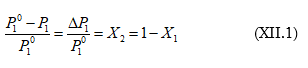
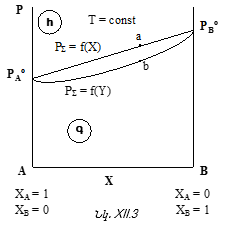
Սա Ռաուլի օրենքի մաթեմատիկական արտահայտությունն է:
Նկ.XII.1-ից հետևում է. ![]()
և ընդհանրապես
![]()
Սա նույնպես Ռաուլի օրենքի մաթեմատիակական արտահայտությունն է, ըստ որի լուծույթի վրա լուծույթում գտնվող որևէ i հեղուկի սեփական գոլորշիների ճնշումը գծային կախման մեջ է լուծույթում իր մոլային բաժնից:
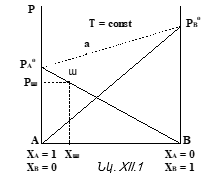
Նկ. XII.1-ը Ռաուլի օրենքի գրաֆիկական պատկերումն է այն դեպքի համար, երբ լուծույթը բաղկացած է A
և B
հեղուկներից: Այսպիսի համակարգը կոչվում է բինար: ![]() ուղիղը ցույց է տալիս թե հաստատուն ջերմաստիճանում լուծույթի վրա ինչպես է փոխվում B
հեղուկի սեփական գոլորշիների ճնշումը լուծույթում իր մոլային բաժնից
ուղիղը ցույց է տալիս թե հաստատուն ջերմաստիճանում լուծույթի վրա ինչպես է փոխվում B
հեղուկի սեփական գոլորշիների ճնշումը լուծույթում իր մոլային բաժնից ![]()
![]() վերաբերում է A
հեղուկին: Նկ.XII.1-ը կոչվում է
վերաբերում է A
հեղուկին: Նկ.XII.1-ը կոչվում է ![]() դիագրամ
(T=const):
դիագրամ
(T=const):
Այս նկարից հետևում է նաև, որ AB բինար լուծույթի (խառնուրդի) կոնցենտրացիոն ողջ տիրույթում ![]() ֆունկցիան նկարագրվում է Ռաուլի օրենքով: Այդպիսի լուծույթները կոչվում են կատարյալ և իդեալական լուծույթի տիպական օրինակներն են:
ֆունկցիան նկարագրվում է Ռաուլի օրենքով: Այդպիսի լուծույթները կոչվում են կատարյալ և իդեալական լուծույթի տիպական օրինակներն են:
Չնայած այն բանին, որ Ռաուլը օրենքը ձևակերպել է բացառապես հրատարակված փորձնական տվյալները համադրելու և քննարկելու հիման վրա, բայց և այնպես այն կարելի է արտածել տեսականորեն` օգտվելով հավասարակշռության ընդհանուր պայմանից, ըստ որի.
![]()
Օրինակ, (ա) կետում ![]() բաղադրության լուծույթի հետ հավասարակշռության մեջ է
բաղադրության լուծույթի հետ հավասարակշռության մեջ է ![]() պարցիալ ճնշումով A նյութը (տե’ս նկ.XII.1):
պարցիալ ճնշումով A նյութը (տե’ս նկ.XII.1):
Այդ պայմանը բխում է թերմոդինամիկայի հիմնադրույթներից. հավասարակշռական վիճակում գտնվող համակարգի յուրաքանչյուր բաղադրիչի քիմիական պոտենցիալը նույն արժեքն ունի հավասարակշռության մեջ գտնվող բոլոր ֆազերում: Այս պայմանը քննարկվելու է XIII գլխում:
Այս հանգամանքը հնարավորություն կտա ապացուցելու, որ (XII.2)-ը ճիշտ է լուծույթում եղած ցանկացած բաղադրիչի համար:
Վերցնենք երկբաղադրիչ լուծույթ, մեկը պայմանականորեն համարելով լուծիչ: Զուգորդենք (XII.2)-ը և (XII.3)-ը:
![]()
ընդունելով գոլորշին որպես իդեալական գազ և ![]() որտեղ
որտեղ ![]() քննարկվող մաքուր հեղուկի վրա (X
= 1) տվյալ ջերմաստիճանում սեփական գոլորշիների ճնշումն է, իսկ
քննարկվող մաքուր հեղուկի վրա (X
= 1) տվյալ ջերմաստիճանում սեփական գոլորշիների ճնշումն է, իսկ ![]() այդ նյութի քիմիական պոտենցիալը ստանդարտ վիճակում:
այդ նյութի քիմիական պոտենցիալը ստանդարտ վիճակում:
Եթե գոլորշին առաջացած լիներ միայն մաքուր հեղուկից (այսինքն լուծված նյութ չկա) (X = 1), այդ դեպքում կստացվեր.
![]()
(XII.4)-ից և (XII.5)-ից կստացվի
![]()
կամ
![]()
Դիցուք սա վերաբերում է լուծիչին, որը խորհրդանշել ենք «լ» ինդեքսով: Թող «լն» վերաբերվի լուծված նյութին: Նույն արդյունքը կստացվի, եթե լուծիչի փոխարեն «լն» վերցվի:
Հիշենք Գիբս-Դյուհեմի հավասարումը.
![]()
որտեղից
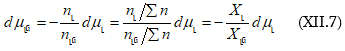
Քանի որ ![]()
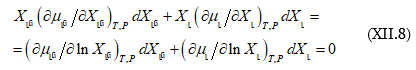
որտեղից.
![]()
և
![]()
Եթե նկատի առնենք, որ իդեալական գազի դեպքում ![]() (XII.10)-ը կվերածվի Դյուհեմ-Մարգուլեսի հավասարմանը
(XI.15)
(XII.10)-ը կվերածվի Դյուհեմ-Մարգուլեսի հավասարմանը
(XI.15)
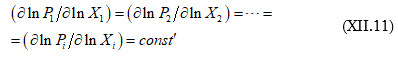
որտեղից ![]()
Երբ
![]()
Սա փաստորեն Ռաուլի օրենքի տեսական արտածումն է:
Ռաուլի օրենքը կարելի է արտածել նաև ընդունելով, որ հավասարակշռական որևէ վիճակում ![]() Օրինակ, (ա) վիճակի համար.
Օրինակ, (ա) վիճակի համար.
![]()
![]()
և
![]()
(a)-ի և (b)-ի զուգորդումից կստացվի.
![]()
որտեղից
![]()
XII-1:1. Հեղուկ լուծույթի վրա գոլորշու ընդհանուր ճնշման կախումը
հեղուկի բաղադրությունից: ![]() դիագրամներ
դիագրամներ
Դիցուք A-ից և B-ից է կազմված քննարկվող լուծույթը:
![]()
Օգտվելով Դալտոնի օրենքից կարող ենք գրել.
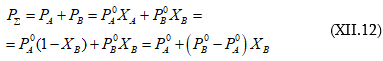
Սա y = a+bx տիպի ուղիղ գծի հավասարումն է, որը նկ. XII.1-ի վրա արտահայտված է ![]() ուղիղով:
ուղիղով:
(XII.12)-ը արտահայտում է լուծույթի վրա գոլորշիների ընդհանուր ճնշման ![]() կախումը ելային լուծույթի (հեղուկի) բաղադրությունից:
կախումը ելային լուծույթի (հեղուկի) բաղադրությունից:
Ըստ քննարկվող դեպքի ![]() (տե’ս նկ.XII.1):
Սա նշանակում է, որ
(տե’ս նկ.XII.1):
Սա նշանակում է, որ ![]() քանի որ հեղուկը կեռա այն պահին, երբ սեփական գոլորշիների ճնշումը հավասարվի մթնոլորտային ճնշմանը:
քանի որ հեղուկը կեռա այն պահին, երբ սեփական գոլորշիների ճնշումը հավասարվի մթնոլորտային ճնշմանը: ![]() ըստ էության ֆազային դիագրամ է:
ըստ էության ֆազային դիագրամ է:
XII-1:2. Հեղուկ լուծույթի վրա գոլորշու ընդհանուր ճնշման կախումը
գոլորշու բաղադրությունից
Իրար վրա բաժանենք երկու բաղադրիչների պարցյալ ճնշումները.
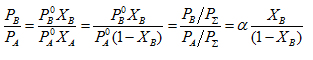
որտեղ ![]() Ըստ Դալտոնի օրենքի
Ըստ Դալտոնի օրենքի ![]() բաղադրիչի մոլային բաժինն է գազ ֆազում): Հետևաբար.
բաղադրիչի մոլային բաժինն է գազ ֆազում): Հետևաբար.
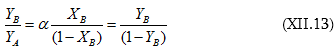
(XII.13)-ից կստացվի.
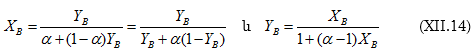
Քննարկենք հնարավոր դեպքերը.
1. ![]() Սա այն դեպքն է, երբ երկու հեղուկները միևնույն եռման ջերմաստիճանն ունեն
Սա այն դեպքն է, երբ երկու հեղուկները միևնույն եռման ջերմաստիճանն ունեն ![]()
(XII.14)-ից կստացվի ![]() Այս պայմանն արտահայտվում է Aad
ուղիղով: Երբ
Այս պայմանն արտահայտվում է Aad
ուղիղով: Երբ ![]() (տե՛ս նկ.XII.2):
(տե՛ս նկ.XII.2):
2. ![]() Ինչպես նշվեց, ըստ այս պայմանի
Ինչպես նշվեց, ըստ այս պայմանի ![]()
Քննարկենք մասնավոր դեպք, օրինակ, ![]() Տեսնենք ի՞նչ օրինաչափություն
կստացվի:
Ըստ
(XII.14)-ի.
Տեսնենք ի՞նչ օրինաչափություն
կստացվի:
Ըստ
(XII.14)-ի.
![]()
(հիշել, որ ![]() Նշված տիրույթում
Նշված տիրույթում ![]() -ին տալով կամայական արժեքներ կարելի է հաշվել
-ին տալով կամայական արժեքներ կարելի է հաշվել ![]() -ի համապատասխան արժեքները:
-ի համապատասխան արժեքները:
Այդպիսի տվյալներ բերված են աղյուսակ XII.1-ում:
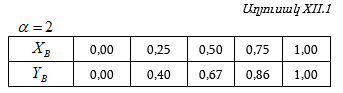
Այս տվյալներից հետևում է, որ հեղուկ ֆազում ![]() (այսինքն լուծույթում – հեղուկ ֆազում B-ի տվյալ բաղադրությանը) համապատասխանող գոլորշի ֆազում
(այսինքն լուծույթում – հեղուկ ֆազում B-ի տվյալ բաղադրությանը) համապատասխանող գոլորշի ֆազում ![]() այսինքն գոլորշում B-ին համապատասխանող մոլային բաժինն ավելի մեծ արժեք ունի (օրինակ, երբ
այսինքն գոլորշում B-ին համապատասխանող մոլային բաժինն ավելի մեծ արժեք ունի (օրինակ, երբ ![]() ): Այդ կախումը կարտահայտվի Abd
կորով:
): Այդ կախումը կարտահայտվի Abd
կորով:
3.
![]() այսինքն B-ի հետ համեմատած A-ն ավելի դյուրաեռ է: Քննարկելու համար, այս անգամ վերցնենք
այսինքն B-ի հետ համեմատած A-ն ավելի դյուրաեռ է: Քննարկելու համար, այս անգամ վերցնենք ![]() Նման հաշվումներ կատարելով կստացվեն արժեքներ, որոնք գրաֆիկորեն կպատկերվեն Acd
կորով:
Նման հաշվումներ կատարելով կստացվեն արժեքներ, որոնք գրաֆիկորեն կպատկերվեն Acd
կորով:
Այժմ պարզենք, թե ինչպես է կախված հեղուկի վրա գոլորշիների գումարային ճնշումը
![]() գոլորշու բաղադրությունից
գոլորշու բաղադրությունից ![]() այսինքն, պարզենք
այսինքն, պարզենք ![]() ֆունկցիայի տեսքը:
ֆունկցիայի տեսքը:
(XII.12)-ի և (XII.14)-ի զուգորդումից կստացվի.
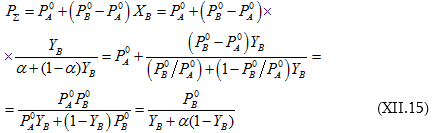
Այսպիսով, լուծույթի վրա գոլորշիների գումարային ճնշման կախումը հեղուկի (լուծույթի) բաղադրությունից արտահայտվում է (XII.12) և գոլորշու բաղադրությունից` (XII.15) հավասարումներով:
Այդ երկու ֆունկցիաները միևնույն նկարի վրա գրաֆիկորեն պատկերելու համար օգտվենք հետևյալ աղյուսակում բերված հաշվարկային տվյալներից, որոնք ստացված են հետևյալ մասնավոր դեպքի համար. ![]() Պետք է նշել, որ ստացված օրինաչափության բնույթը կախված չէ այն բանից, թե քննարկման համար հիմքում որ բաղադրիչն է վերցվում:
Պետք է նշել, որ ստացված օրինաչափության բնույթը կախված չէ այն բանից, թե քննարկման համար հիմքում որ բաղադրիչն է վերցվում:

Այս աղյուսակի տվյալներից միանշանակ հետևում է, որ հեղուկ և գոլորշի ֆազերում B բաղադրիչի միևնույն բաղադրության դեպքում (օրինակ, ![]() այսինքն
այսինքն ![]() (տե՛ս նկ.XII.3): Այսինքն,
(տե՛ս նկ.XII.3): Այսինքն, ![]() կորը
կորը ![]() -ից ավելի ցածրից է անցնում:
-ից ավելի ցածրից է անցնում:
Երկրորդ եզրակացությունն այն է, որ ![]() ֆունկցիան ուղղագծային է [որը հետևում է
(XII.12)-ից], իսկ
ֆունկցիան ուղղագծային է [որը հետևում է
(XII.12)-ից], իսկ ![]() -ը կորագծային:
-ը կորագծային:
Երրորդ եզրակացությունը վերաբերում է հետևյալին: ![]() ֆունկցիաները կազմելիս X-ը դիտվել է որպես միայն հեղուկ ֆազի բաղադրություն և Y-ն էլ` որպես միայն գոլորշի ֆազի բաղադրություն` իրարից անկախ և ոչ թե որպես հեղուկի ելային բաղադրություն:
ֆունկցիաները կազմելիս X-ը դիտվել է որպես միայն հեղուկ ֆազի բաղադրություն և Y-ն էլ` որպես միայն գոլորշի ֆազի բաղադրություն` իրարից անկախ և ոչ թե որպես հեղուկի ելային բաղադրություն:
Այս առումով ![]() ուղիղը ցույց է տալիս թե հաստատուն ջերմաստիճանի տակ ինչպես է փոխվում լուծույթի վրա գոլորշու ընդհանուր ճնշումը հեղուկ ֆազի և ոչ թե ելային լուծույթի բաղադրությունից: Իհարկե ավելի լավ կլիներ առանձին նկարների վրա պատկերել այդ երկու ֆունկցիաները. աբսցիսը մի դեպքում կլիներ X-ը, մյուսում` Y-ը: Երկու դեպքում էլ
ուղիղը ցույց է տալիս թե հաստատուն ջերմաստիճանի տակ ինչպես է փոխվում լուծույթի վրա գոլորշու ընդհանուր ճնշումը հեղուկ ֆազի և ոչ թե ելային լուծույթի բաղադրությունից: Իհարկե ավելի լավ կլիներ առանձին նկարների վրա պատկերել այդ երկու ֆունկցիաները. աբսցիսը մի դեպքում կլիներ X-ը, մյուսում` Y-ը: Երկու դեպքում էլ ![]()
Բայց գործնական խնդիրներ լուծելու համար հարկավոր է այդ երկու կորերը պատկերել միայն մի նկարի վրա, օգտագործելով միայն մի աբսցիս, որի վրա ներկայացվի ողջ համակարգի (հեղուկ + գոլորշի) բաղադրությունը, այսինքն հեղուկի ելային բաղադրությունը (X):
Բնական է, որ հեղուկ ֆազը կայուն է բարձր ճնշումների տակ, այսինքն ![]() ուղիղից վերև, իսկ գոլորշին` ցածր (
ուղիղից վերև, իսկ գոլորշին` ցածր (![]() կորից ներքև): Եթե համակարգը հեղուկ վիճակում է (
կորից ներքև): Եթե համակարգը հեղուկ վիճակում է (![]() -ից վերև), ապա իզոթերմային պայմանում P-ն նվազեցնելիս, երբ հասնում ենք, օրինակ, a
վիճակին կնկատվի պղպջակների առաջացում: Երբ համակարգը գոլորշի վիճակում է (
-ից վերև), ապա իզոթերմային պայմանում P-ն նվազեցնելիս, երբ հասնում ենք, օրինակ, a
վիճակին կնկատվի պղպջակների առաջացում: Երբ համակարգը գոլորշի վիճակում է (![]() կորից ներքև), ապա ներքևից բարձրանալիս (T=const),
օրինակ b
կետում կնկատվի գոլորշում հեղուկի կաթիլների առաջացում: Նշված երկու կորերի արանքում հեղուկը և գոլորշին միատեղ են հանդես գալիս` իրար հետ հավասարակշռված:
կորից ներքև), ապա ներքևից բարձրանալիս (T=const),
օրինակ b
կետում կնկատվի գոլորշում հեղուկի կաթիլների առաջացում: Նշված երկու կորերի արանքում հեղուկը և գոլորշին միատեղ են հանդես գալիս` իրար հետ հավասարակշռված:
Ուրեմն, ![]() կորերը առանձին-առանձին ֆազեր բաժանող կորեր չեն, այլ արտահայտում են T=const
պայմանում հավասարակշռության մեջ գտնվող երկու ֆազերի բաղադրությունների կախումը ընդհանուր ճնշումից և ընդհակառակը:
կորերը առանձին-առանձին ֆազեր բաժանող կորեր չեն, այլ արտահայտում են T=const
պայմանում հավասարակշռության մեջ գտնվող երկու ֆազերի բաղադրությունների կախումը ընդհանուր ճնշումից և ընդհակառակը:
Բերված բոլոր նկարները ![]() դիագրամներ են:
դիագրամներ են: ![]() դիագրամ ստանալու համար հիմնական պայման է փորձերը կատարել իզոթերմային պայմանում (T=const
):
դիագրամ ստանալու համար հիմնական պայման է փորձերը կատարել իզոթերմային պայմանում (T=const
):
XII-1:3.
![]() դիագրամներ
դիագրամներ
Գործնական խնդիրներ լուծելու համար առավել մատչելի, հետևաբար առավել կիրառական են ![]() դիագրամները:
դիագրամները:
Այս դեպքում փորձերը կատարվում են իզոբարային պայմանում, օրինակ, մթնոլորտային ճնշման տակ որոշելով
![]() բաղադրության լուծույթների եռման կետերը: Այս դեպքում ևս աբսցիսը լուծույթի (հեղուկի) ելային բաղադրությունն է:
բաղադրության լուծույթների եռման կետերը: Այս դեպքում ևս աբսցիսը լուծույթի (հեղուկի) ելային բաղադրությունն է:
Բնականաբար, տվյալ դեպքում հեղուկ ֆազը կայուն է ցածր ջերմաստիճաններում, իսկ գազ (գոլորշի) ֆազը` համեմատաբար բարձր ջերմաստիճաններում: ![]() կորի ներսում համակարգը հետերոգեն է: Հավասարակշռության մեջ են (հեղուկ
կորի ներսում համակարգը հետերոգեն է: Հավասարակշռության մեջ են (հեղուկ ![]() գոլորշի) հեղուկ և գոլորշի ֆազերը:
գոլորշի) հեղուկ և գոլորշի ֆազերը:
Ուշագրավ է հետևյալ դիտողությունը: Նկ.XII.3 ![]() դիագրամի վրա ներկայացված
դիագրամի վրա ներկայացված
![]() ուղիղը նկ.XII.4-ի վրա դարձել է
ուղիղը նկ.XII.4-ի վրա դարձել է ![]() կոր: Պատճառն այն է, որ P =
f(t) ֆունկցիան ուղղագծային չէ (հիշել Կլաուզիուս-Կլապեյրոնի հավասարումը):
կոր: Պատճառն այն է, որ P =
f(t) ֆունկցիան ուղղագծային չէ (հիշել Կլաուզիուս-Կլապեյրոնի հավասարումը):
Մենք շարունակում ենք քննարկել հեղուկներից ստացվող այնպիսի լուծույթներ, որոնք ենթարկվում են Ռաուլի օրենքին, այսինքն իդեալական (կատարյալ) են: Այդպիսիք են.
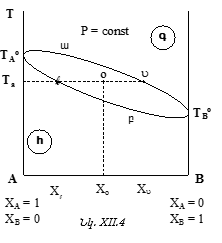
Նկ.XII.4-ը, որը ![]() դիագրամ է (P=const)
կոչվում է վիճակի դիագրամ: Այն հնարավորություն է տալիս հեշտությամբ որոշել հավասարկշռության մեջ գտնվող երկու ֆազերի բաղադրությունները: Ինչպե՞ս:
դիագրամ է (P=const)
կոչվում է վիճակի դիագրամ: Այն հնարավորություն է տալիս հեշտությամբ որոշել հավասարկշռության մեջ գտնվող երկու ֆազերի բաղադրությունները: Ինչպե՞ս:
Վերցնենք A և B հեղուկներից ![]() ելային բաղադրությամբ մի լուծույթ և տաքացնենք մինչև
ելային բաղադրությամբ մի լուծույթ և տաքացնենք մինչև ![]() ջերմաստիճան
ջերմաստիճան ![]() Ելային հեղուկի մի մասը կանցնի գոլորշի ֆազ. կստեղծվի
Ելային հեղուկի մի մասը կանցնի գոլորշի ֆազ. կստեղծվի ![]() հավասարակշռություն:
հավասարակշռություն:
Հեղուկ և գոլորշի ֆազերի բաղադրությունները որոշելու համար ![]() կետից աբսցիսին զուգահեռ տանենք: Այն
կետից աբսցիսին զուգահեռ տանենք: Այն ![]() կորերը կհատի
կորերը կհատի ![]() կետերում:
կետերում: ![]() գծի վրա է գտնվում O կետը, որին համապատասխանում է ելային լուծույթի
գծի վրա է գտնվում O կետը, որին համապատասխանում է ելային լուծույթի ![]() բաղադրությունը: Այդ խառնուրդում A-ի մոլային բաժինը
բաղադրությունը: Այդ խառնուրդում A-ի մոլային բաժինը ![]() է, իսկ B-ինը`
է, իսկ B-ինը` ![]() Նշվեց, որ
Նշվեց, որ ![]() ջերմաստիճանում ելային լուծույթը երկու ֆազերի է տրոհվում:
ջերմաստիճանում ելային լուծույթը երկու ֆազերի է տրոհվում: ![]() կորը բնութագրում է
կորը բնութագրում է ![]() ֆունկցիան: Ուրեմն, ֆազի բաղադրությունը որոշելու համար
ֆունկցիան: Ուրեմն, ֆազի բաղադրությունը որոշելու համար ![]() աբսցիսին ուղղահայց իջեցնենք: Հատման կետը
աբսցիսին ուղղահայց իջեցնենք: Հատման կետը ![]() Հետևաբար,
Հետևաբար, ![]() ջերմաստիճանում հեղուկ ֆազում A-ի մոլային բաժինը
ջերմաստիճանում հեղուկ ֆազում A-ի մոլային բաժինը ![]()
Նույն դատողությամբ ![]() գտնվում է
գտնվում է ![]() ֆունկցիան պատկերող կորի վրա: Հետևաբար
ֆունկցիան պատկերող կորի վրա: Հետևաբար ![]() իջեցրած ուղղահայացը, որն աբսցիսը հատում է
իջեցրած ուղղահայացը, որն աբսցիսը հատում է ![]() կետում, հնարավորություն կտա
կետում, հնարավորություն կտա ![]() ջերմաստիճանում որոշել գոլորշու բաղադրությունը: Գոլորշում A-ի մոլային բաժինը
ջերմաստիճանում որոշել գոլորշու բաղադրությունը: Գոլորշում A-ի մոլային բաժինը
![]()
Երկու կորերը հատող աբսցիսին զուգահեռը, օրինակ ![]() կոչվում է նոդ:
կոչվում է նոդ:
Ստացված մեծությունների համեմատությունից կարելի է եզրակացնել, որ գոլորշի ֆազն ավելի հարուստ է ավելի ցածր եռման ջերմաստիճան ունեցող B բաղադրիչով:
XII-1:4. Լծակի կանոնը
Այս կանոնը հնարավորություն է տալիս հեշտությամբ որոշել երկու ֆազերում բաշխված միևնույն բաղադրիչի քանակների հարաբերությունը:
Դիցուք վերցվել է A և B նյութերից կազմված մեկ մոլ լուծույթ: Դրանում B – ն ![]() մոլ % է: Ենթադրենք այդ 1 մոլից m մոլ նյութ (A-ի և B-ի խառնուրդ) մնացել է հեղուկ ֆազում, հետևաբար
(1 - m) մոլ խառնուրդ անցել է գոլորշի ֆազ: Ըստ նկ.XII.4-ի հեղուկում B-ի մոլային բաժինը
մոլ % է: Ենթադրենք այդ 1 մոլից m մոլ նյութ (A-ի և B-ի խառնուրդ) մնացել է հեղուկ ֆազում, հետևաբար
(1 - m) մոլ խառնուրդ անցել է գոլորշի ֆազ: Ըստ նկ.XII.4-ի հեղուկում B-ի մոլային բաժինը
![]() է: Ուրեմն, B-ն m մոլ հեղուկի
է: Ուրեմն, B-ն m մոլ հեղուկի
![]() և (1-m
) մոլ գոլորշում էլ`
և (1-m
) մոլ գոլորշում էլ` ![]() մոլ % -ն է: Իսկ 1 մոլ ելային խառնուրդի
մոլ % -ն է: Իսկ 1 մոլ ելային խառնուրդի ![]()
որտեղից.
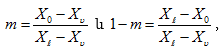
բաժանենք իրար վրա, կստանանք
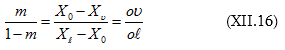
Սա լծակի կանոնի մաթեմատիկական արտահայտությունն է: Այն հնարավորություն
է
տալիս չափելով ![]() երկարությունները որոշել m
/ (1-m) հարաբերությունը:
երկարությունները որոշել m
/ (1-m) հարաբերությունը:
(XII.16)-ը կարելի է ստանալ նաև առանց պայմանական ընդունելության` կապված 1 մոլ ելային խառնուրդ վերցնելու պայմանի հետ:
Այսպես. վերցված է ![]() մոլ A նյութից և
մոլ A նյութից և ![]() մոլ էլ B-ից կազմված ելային լուծույթ:
մոլ էլ B-ից կազմված ելային լուծույթ: ![]() Այդ լուծույթը ինչ որ մինչև
Այդ լուծույթը ինչ որ մինչև ![]() ջերմաստիճան տաքացնելիս
ջերմաստիճան տաքացնելիս
![]() մոլ նյութ անցել է գոլորշի ֆազ, իսկ
մոլ նյութ անցել է գոլորշի ֆազ, իսկ ![]() մոլ ընդհանուր քանակով լուծույթ` մնացել է հեղուկ: Հետևաբար.
մոլ ընդհանուր քանակով լուծույթ` մնացել է հեղուկ: Հետևաբար.
![]()
Ելային խառնուրդում B-ի մոլային բաժինը` ![]() որտեղից
որտեղից
![]()
Դիցուք B-ի ![]() մնացել է հեղուկում, հետևաբար
մնացել է հեղուկում, հետևաբար
![]() անցել է գոլորշի ֆազ:
անցել է գոլորշի ֆազ:
Հեղուկում B-ի մոլային բաժինը կլինի
![]()
և գոլորշի ֆազում`
![]()
Մի կողմից ![]() որտեղից.
որտեղից. ![]()
մյուս կողմից էլ ըստ (բ)-ի և ըստ (ա)-ի
![]()
որտեղից ![]()
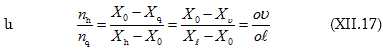
(XII.17)-ից կստացվի.
![]()
Զուգորդելով (XII.17)-ի հետ և օգտվելով (դ)-ից կստացվի.
![]()
որտեղից.
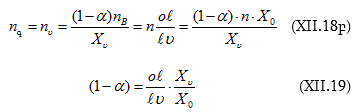
Նկ.XII.4-ից որոշելով ![]() կարելի է հաշվել
կարելի է հաշվել ![]() որից էլ
որից էլ ![]() այսինքն պարզել, թե B - ի քանի տոկոսն է անցել գոլորշի ֆազ և քանի տոկոսն է մնացել հեղուկ ֆազում:
այսինքն պարզել, թե B - ի քանի տոկոսն է անցել գոլորշի ֆազ և քանի տոկոսն է մնացել հեղուկ ֆազում:
XII-2. ՇԵՂՈՒՄՆԵՐ ՌԱՈՒԼԻ ՕՐԵՆՔԻՑ
Իդեալական չեն Ռաուլի օրենքին չենթարկվող լուծույթները:
Օրինակներ.
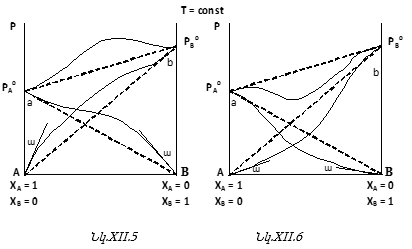
Նկ.XII.5-ի վրա պատկերված դեպքը կոչվում է «Ռաուլի օրենքից դրական շեղում», իսկ նկ.XII.6-ը պատկերում է «Ռաուլի օրենքից բացասական շեղումը»: Բերված են համապատասխան օրինակներ:
Քննարկենք նշված երկու դեպքերից միայն մեկը, քանի որ բացատրության հիմքում միևնույն սկզբունքն է լինելու. միջմոլեկուլային փոխազդեցությունների առկայությունը, բնույթը և սաստկությունը:
Ստացված կորերի քննարկումից հետևում է նաև, որ երբ լուծույթը ձգտում է անսահման նոսրության փորձնական կորը ձուլվում է Ռաուլի կորի հետ (տե՛ս
![]() մարզերը):
մարզերը):
Քննարկենք մի դեպք, երբ ![]() այսինքն
այսինքն ![]() Այս պայմանը հիմք է տալիս ընդունելու, որ տվյալ դեպքում B-ն լուծիչն է, իսկ A-ն` լուծված նյութը (
Այս պայմանը հիմք է տալիս ընդունելու, որ տվյալ դեպքում B-ն լուծիչն է, իսկ A-ն` լուծված նյութը (![]() մարզ): Սա փաստորեն համարժեք է այն պայմանին ըստ որի ըստ A-ի լուծույթը անսահման նոսր է: Ինչպես գծագրերից երևում է, այդ վիճակում համակարգը ենթարկվում է Ռաուլի օրենքին, այսինքն իդեալական է, բայց ոչ կատարյալ: Նույնը կարելի է ասել
մարզ): Սա փաստորեն համարժեք է այն պայմանին ըստ որի ըստ A-ի լուծույթը անսահման նոսր է: Ինչպես գծագրերից երևում է, այդ վիճակում համակարգը ենթարկվում է Ռաուլի օրենքին, այսինքն իդեալական է, բայց ոչ կատարյալ: Նույնը կարելի է ասել ![]() մարզի համար. ոչ մի սկզբունքային տարբերություն չկա:
մարզի համար. ոչ մի սկզբունքային տարբերություն չկա:
Սկսած ![]() կետից դեպի աջ շարժվելիս լուծույթում B-ի մոլային բաժինը մեծանում է: Տվյալ դեպքում B-ն հանդես է գալիս որպես լուծվող նյութ (A-ն դեռ մնում է որպես լուծիչ): Հեշտ է նկատել, որ
կետից դեպի աջ շարժվելիս լուծույթում B-ի մոլային բաժինը մեծանում է: Տվյալ դեպքում B-ն հանդես է գալիս որպես լուծվող նյութ (A-ն դեռ մնում է որպես լուծիչ): Հեշտ է նկատել, որ ![]() մեծացման հետ մեծանում է նաև
մեծացման հետ մեծանում է նաև ![]() Ճիշտ է նաև հակառակ դիտողությունը. լուծույթի վրա B
նյութի պարցիալ ճնշումը մեծացնելիս լուծույթում մեծանում է B-ի մոլային բաժինը:
Ճիշտ է նաև հակառակ դիտողությունը. լուծույթի վրա B
նյութի պարցիալ ճնշումը մեծացնելիս լուծույթում մեծանում է B-ի մոլային բաժինը:
Ընդհանրապես դրական շեղման դեպքում ![]() Բացասական շեղման դեպքում պատկերը հակառակն է:
Բացասական շեղման դեպքում պատկերը հակառակն է:
Եթե մասնավոր դեպքում B-ն ջրում վատ լուծվող գազ է և A-ն ջուր (սկզբունքորեն A-ն կարող է նաև այլ հեղուկ լինել), ապա մենք կառնչվենք մեզ քաջ հայտնի մի երևույթի հետ. հեղուկի վրա գազի ճնշման մեծացման հետ տվյալ հեղուկում գազի լուծելիությունը մեծանում է: Այստեղ հարցը վերաբերում է տվյալ հեղուկում քիչ լուծվող գազին, որից ստացվող լուծույթը նոսր է, նույնիսկ շատ նոսր:
Ուշադրության արժանի է հետևյալ փաստը: Կոնցենտրացիոն նեղ (փոքր) տիրույթում ուռուցիկ կորերի սկզբնական մարզերը ուղղագծային են ![]() և ձուլված են Ռաուլի օրենքով նկարագրվող ուղիղ գծի հետ: Եթե դա A-ին է վերաբերում, ապա A-ն լուծիչն է և ըստ B-ի շատ նոսր լուծույթ է (B-ի դեպքում` B-ն է լուծիչը և A-ն լուծվող նյութը): Երկու դեպքերում էլ լուծույթները անսահման նոսր են:
և ձուլված են Ռաուլի օրենքով նկարագրվող ուղիղ գծի հետ: Եթե դա A-ին է վերաբերում, ապա A-ն լուծիչն է և ըստ B-ի շատ նոսր լուծույթ է (B-ի դեպքում` B-ն է լուծիչը և A-ն լուծվող նյութը): Երկու դեպքերում էլ լուծույթները անսահման նոսր են:
XII-2:1. Հենրիի օրենքը
Այժմ քննարկենք հակառակ դեպքը. նույն A-ն (կամ B-ն) լուծվող նյութն է ![]() Կորերի սկզբնական նեղ մարզերը ուղիղ գծային են (տե°ս ա մարզերը): Յուրաքանչյուրը նկարագրվում է
Կորերի սկզբնական նեղ մարզերը ուղիղ գծային են (տե°ս ա մարզերը): Յուրաքանչյուրը նկարագրվում է ![]() տիպի հավասարումով.
տիպի հավասարումով.
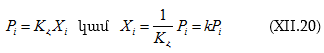
Սա Հենրիի օրենքն է: ![]() կոչվում է Հենրիի գործակից: Ունի ճնշման չափողականություն:
(XII.20)-ից նույնպես հետևում է, որ անսահման նոսր լուծույթները իդեալական են:
կոչվում է Հենրիի գործակից: Ունի ճնշման չափողականություն:
(XII.20)-ից նույնպես հետևում է, որ անսահման նոսր լուծույթները իդեալական են:
Ընդհանրացնելով կարող ենք գրել.
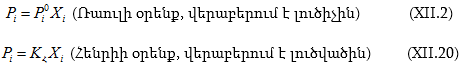
Ռաուլի օրենքից դրական շեղման դեպքում
![]() բացասականի դեպքում`
բացասականի դեպքում` ![]()
Հեղուկում գազերի լուծելիությունը սովորաբար արտահայտում են Բունզենի աբսորբցիոն գործակցի ![]() միջոցով:
միջոցով: ![]() ցույց է տալիս, թե
ցույց է տալիս, թե ![]() (կամ 0,101 ՄՊա, 760 մմ սնդիկի սյուն) ճնշման տակ և
(կամ 0,101 ՄՊա, 760 մմ սնդիկի սյուն) ճնշման տակ և ![]() (0oC )
(0oC ) ![]() լուծիչում i
գազից քանի՞
լուծիչում i
գազից քանի՞ ![]() լուծվում: Ի՞նչ կապ կա Հենրիի
լուծվում: Ի՞նչ կապ կա Հենրիի ![]() և Բունզենի
և Բունզենի ![]() գործակիցների միջև:
գործակիցների միջև:
Երբ ![]() մթն, ապա
մթն, ապա
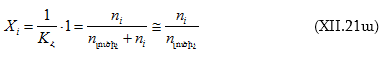
( ![]() լուծիչում լուծված նյութի մոլերի թիվն է):
լուծիչում լուծված նյութի մոլերի թիվն է):
Եթե ![]() լուծիչի զանգվածը m
գ է, ապա
լուծիչի զանգվածը m
գ է, ապա ![]() [M-ը լուծիչի մոլային
զանգվածն
է (գ/մոլ), d-ն լուծիչի խտությունն է
[M-ը լուծիչի մոլային
զանգվածն
է (գ/մոլ), d-ն լուծիչի խտությունն է
![]() ]:
]:
Գրվածից հետևում է, որ
![]()
Ընդունելով, որ լուծվող գազը իդեալական է հաշվենք այն ծավալը, որն զբաղեցնում է ![]() մոլ գազը, երբ նա գտնվում է 1 մթն ճնշման տակ և
273,15 K - ում:
մոլ գազը, երբ նա գտնվում է 1 մթն ճնշման տակ և
273,15 K - ում: ![]()
որտեղից
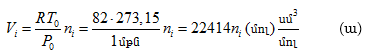
Ըստ իմաստի ![]() (կլանման գործակից), որովհետև այն ցույց է տալիս, թե նշված պայմաններում
(կլանման գործակից), որովհետև այն ցույց է տալիս, թե նշված պայմաններում ![]() լուծիչը քանի սմ3 գազ է կլանել:
լուծիչը քանի սմ3 գազ է կլանել:
Հետևաբար ![]()
(բ)-ն տեղադրենք (XII.21բ)-ի մեջ.
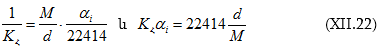
երբ ճնշումն արտահայտվում է մթն-ներով: Կա նաև լուծման Օստվալդի գործակից` ![]() որը վերաբերում է 1
որը վերաբերում է 1 ![]() լուծիչի կլանած V
լուծիչի կլանած V ![]() գազին, որը որոշված է փորձի ջերմաստիճանում
գազին, որը որոշված է փորձի ջերմաստիճանում ![]() և P ճնշման տակ: Գործնական տեսակետից ավելի հարմար է
և P ճնշման տակ: Գործնական տեսակետից ավելի հարմար է ![]() օգտվել:
օգտվել:
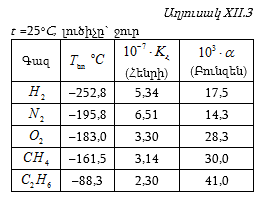
Աղյուսակ 3-ում բերված են մի քանի գազերի համար ![]() և
և ![]() արժեքները (
արժեքները (![]() արժեքները հաշված են այն դեպքի համար, երբ
արժեքները հաշված են այն դեպքի համար, երբ ![]() սնդիկի սյուն):
սնդիկի սյուն): ![]() տված են մմ Hg
սյունով:
տված են մմ Hg
սյունով:
Գազի լուծելիությունը իմանալով կարելի է հաշվել ցանկացած լուծված գազի կոնցենտրացիան 25oC-ում (298,15 K):
Քննարկենք ![]() դեպքը:
դեպքը: ![]() լուծույթի վրա
լուծույթի վրա ![]() պարցիալ ճնշումն է:
պարցիալ ճնշումն է:
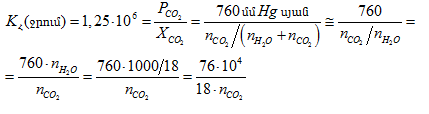
որտեղից
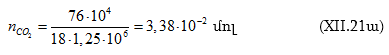
Բայց քանի որ ջրի քանակը որոշվել էր ![]() հարաբերությամբ, ուրեմն
հարաբերությամբ, ուրեմն ![]() լուծված է
լուծված է ![]() ջրում:
ջրում:
![]() կարելի է որոշել
(XII.20) արտահայտության միջոցով: Մի քանի անգամ նշվել է, որ նման դեպքերում նպատակահարմար է օգտվել վիրիալ հավասարումներից: Տվյալ պարագայում
(XII.20)-ը կարելի է ներկայացնել.
կարելի է որոշել
(XII.20) արտահայտության միջոցով: Մի քանի անգամ նշվել է, որ նման դեպքերում նպատակահարմար է օգտվել վիրիալ հավասարումներից: Տվյալ պարագայում
(XII.20)-ը կարելի է ներկայացնել. ![]() հավասարման տեսքով, որտեղից
հավասարման տեսքով, որտեղից
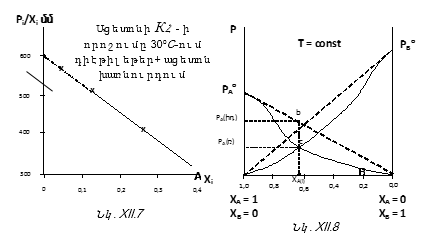
![]() (տե’ս նկ.XII.7):
(տե’ս նկ.XII.7):
Նորից վերադառնանք Ռաուլի օրենքից շեղման երևույթին:
Ռաուլի օրենքից շեղման չափը որոշելով կարելի է հաշվել ակտիվության գործակիցը ![]() նկատի առնելով, որ գազի ցնդելիությունը`
նկատի առնելով, որ գազի ցնդելիությունը` ![]() Տվյալ դեպքում
Տվյալ դեպքում ![]() նույնացվում է ճնշման փաստացի արժեքի հետ
նույնացվում է ճնշման փաստացի արժեքի հետ ![]() Նկ.XII.8-ի վրա
Նկ.XII.8-ի վրա ![]() մոլային բաժնով A նյութ պարունակող լուծույթի վրա այդ փաստացի ճնշումն արտահայտվում է C կետով: Եթե լուծույթը իդեալական լիներ, այդպիսի բաղադրությամբ լուծույթի վրա
մոլային բաժնով A նյութ պարունակող լուծույթի վրա այդ փաստացի ճնշումն արտահայտվում է C կետով: Եթե լուծույթը իդեալական լիներ, այդպիսի բաղադրությամբ լուծույթի վրա ![]() պիտի արտահայտվեր b
կետով, որը գտնվում է Ռաուլի օրենքով նկարագրվող
պիտի արտահայտվեր b
կետով, որը գտնվում է Ռաուլի օրենքով նկարագրվող ![]() ուղիղի վրա:
ուղիղի վրա:
Նկարից հետևում է, որ.
![]()
Նման ձևով կարելի է հաշվել ![]() բաղադրության համար տվյալ B նյութի ակտիվության գործակիցը և այսպես ցանկացած բաղադրության համար
բաղադրության համար տվյալ B նյութի ակտիվության գործակիցը և այսպես ցանկացած բաղադրության համար ![]()
Հեշտ է նկատել, որ Ռաուլի օրենքից (-) շեղում ցուցաբերող զույգի համար ![]() իսկ (+) շեղման դեպքում`
իսկ (+) շեղման դեպքում` ![]()
Ընդհանրացնենք.
![]()
որտեղից
![]()
![]() բաղադրիչի ակտիվությունն է, երբ լուծույթի բաղադրությունը (կոնցենտրացիան) արտահայտվում է մոլային բաժնով: Եթե կոնցենտրացիան մոլալությամբ (m)
է արտահայտված
այդ դեպքում.
բաղադրիչի ակտիվությունն է, երբ լուծույթի բաղադրությունը (կոնցենտրացիան) արտահայտվում է մոլային բաժնով: Եթե կոնցենտրացիան մոլալությամբ (m)
է արտահայտված
այդ դեպքում.
![]()
իսկ մոլային կոնցենտրացիայից օգտվելիս`
![]()
XII-2:2. Վան Լաարի հավասարումը: Ռաուլի օրենքից շեղման պատճառները
Բինար (երկբաղադրիչ) լուծույթների թերմոդինամիկան վիճակագրական թերմոդինամիկայի մեթոդներով քննարկելով Վան Լաարը ցույց է տվել, որ
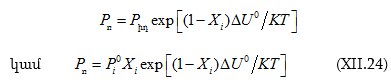
![]() անվանվել է փոխադարձ փոխանակման էներգիա: Ո՞րն է ֆիզիկական իմաստը:
անվանվել է փոխադարձ փոխանակման էներգիա: Ո՞րն է ֆիզիկական իմաստը:
Դիցուք երկբաղադրիչ լուծույթը կազմված է ![]() տեսակի մոլեկուլներից:
տեսակի մոլեկուլներից: ![]() նշանակենք տարանուն մոլեկուլների միջև գործող փոխազդեցությունների (ադհեզիոն) էներգիան, իսկ նույնանունների (կոհեզիոն) համար`
նշանակենք տարանուն մոլեկուլների միջև գործող փոխազդեցությունների (ադհեզիոն) էներգիան, իսկ նույնանունների (կոհեզիոն) համար` ![]()
Ըստ Վան Լաարի ![]() Քննարկենք հնարավոր դեպքերը.
Քննարկենք հնարավոր դեպքերը.
1. ![]() Նշանակում է, որ նույնանուն և տարանուն մոլեկուլների միջև գործող փոխազդեցությունների էներգիաներն իրար հավասար են, այսինքն իրար հավասար են կոհեզիոն և ադհեզիոն ուժերը:
Նշանակում է, որ նույնանուն և տարանուն մոլեկուլների միջև գործող փոխազդեցությունների էներգիաներն իրար հավասար են, այսինքն իրար հավասար են կոհեզիոն և ադհեզիոն ուժերը:
Այս դեպքում.
![]()
Ստացվեց Ռաուլի օրենքի մաթեմատիկական արտահայտությունը:
Այս նույնը կստացվի նաև եթե ![]() այսինքն, երբ բացակայում են կոհեզիոն և ադհեզիոն ուժերը:
այսինքն, երբ բացակայում են կոհեզիոն և ադհեզիոն ուժերը:
2. ![]() այսինքն
այսինքն ![]() Այս պայմանից հետևում է. կոհեզիոն ուժեր > ադհեզիոն ուժեր:
Այս պայմանից հետևում է. կոհեզիոն ուժեր > ադհեզիոն ուժեր:
Հետևանքը.
![]()
Եզրակացություն. Եթե գերակշռում են կոհեզիոն ուժերը (ուժերը նույնանուն մոլեկուլների միջև) այդ դեպքում Ռաուլի օրենքից (+) շեղում կդիտվի: Իսկ երբ ![]() , ապա համակարգը կդառնա երկֆազ. հեղուկները կշերտավորվեն: Օրինակ,
, ապա համակարգը կդառնա երկֆազ. հեղուկները կշերտավորվեն: Օրինակ, ![]() և այլն:
և այլն:
3. ![]() Ուրեմն, գերակշռում են ադհեզիոն ուժերը: Սա համապատասխանում է այն դեպքին, երբ վերցված երկու հեղուկները իրար նկատմամբ քիմիական խնամակցություն ունեն, օրինակ
Ուրեմն, գերակշռում են ադհեզիոն ուժերը: Սա համապատասխանում է այն դեպքին, երբ վերցված երկու հեղուկները իրար նկատմամբ քիմիական խնամակցություն ունեն, օրինակ ![]() Այս դեպքում կդիտվի (-) շեղում Ռաուլի օրենքից: Սահմանային դեպքում`
Այս դեպքում կդիտվի (-) շեղում Ռաուլի օրենքից: Սահմանային դեպքում` ![]() Հետևանքը կարող է լինել
Հետևանքը կարող է լինել ![]() քիմիական միացության առաջացում:
քիմիական միացության առաջացում:
Հետևաբար Ռաուլի օրենքից շեղումների պատճառը մեկն է. միջմոլեկուլային փոխազդեցությունների առկայություն: Դրանց բնույթը և սաստկությունն էլ որոշում են շեղման տեսակը և խորությունը:
Այս տեսանկյունից խնդրին մոտենալով կարելի է որակապես կանխատեսել ![]() ֆունկցիաների տեսքն ու բնույթը:
ֆունկցիաների տեսքն ու բնույթը:
![]()
[նկ.XII.9. aeb ուղիղը, ab ուղիղը ըստ XII.10 նկարի]
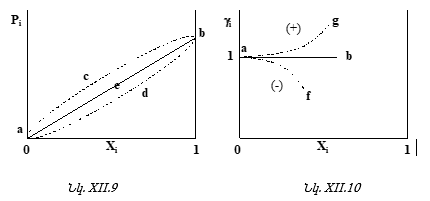
2. ![]() [նկ.XII.9.
acb կորը, ag կորը
(+) շեղման դեպքում. XII.10]
[նկ.XII.9.
acb կորը, ag կորը
(+) շեղման դեպքում. XII.10]
3. ![]() [նկ.XII.9.
adb կորը, af կորը (-) շեղման դեպքում.
XII.10]
[նկ.XII.9.
adb կորը, af կորը (-) շեղման դեպքում.
XII.10]
XII-3. ![]() ԴԻԱԳՐԱՄՆԵՐԻ
ԿԻՐԱՌԱԿԱՆ ՆՇԱՆԱԿՈՒԹՅՈՒՆԸ
ԴԻԱԳՐԱՄՆԵՐԻ
ԿԻՐԱՌԱԿԱՆ ՆՇԱՆԱԿՈՒԹՅՈՒՆԸ
XII-3:1. Կոտորակային (ֆրակցիոն) թորում: Ռեկտիֆիկացում: Ազեոտրոպ խառնուրդներ
ա) Կոտորակային (ֆրակցիոն) թորում:
Վերցնենք ![]() բաղադրությամբ A
և B
հեղուկներից բաղկացած լուծույթ: Մինչև
բաղադրությամբ A
և B
հեղուկներից բաղկացած լուծույթ: Մինչև ![]() ջերմաստիճան լուծույթը տաքացնելիս այն կտրոհվի
ջերմաստիճան լուծույթը տաքացնելիս այն կտրոհվի ![]() բաղադությամբ հեղուկի և
բաղադությամբ հեղուկի և ![]() բաղադրությամբ գոլորշու (տե՛ս նկ.XII.11,
a և b կետերը և աբսցիսի վրա համապատասխան նշանակումները):
բաղադրությամբ գոլորշու (տե՛ս նկ.XII.11,
a և b կետերը և աբսցիսի վրա համապատասխան նշանակումները):
Այստեղ սկզբունքային նշանակություն ունի հետևյալ դիտողությունը. յուրաքանչյուր ջերմաստիճանում հեղուկի և գոլորշու բաղադրություններն իրարից զգալիորեն տարբեր են (տե՛ս a և b, c և d, e և f, g և h կետերը): Սա հիմնական նախադրյալ է, որի առկայության դեպքում միայն հնարավոր է կոտորակային (ֆրակցիոն) թորման միջոցով A և B հեղուկներն իրարից բաժանել:
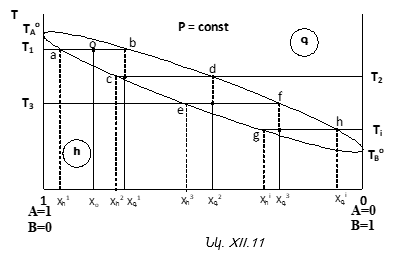
Առավել պարզ պրոցես է այսպես կոչված «պարզ թորումը»: Այս պրոցեսի էությունը հետևյալն է. ցածր ջերմաստիճանում եռացող բաղադրիչը անընդհատ հեռացնում են համակարգից. լուծույթն անընդհատ հարստանում է դժվարաեռ բաղադրիչով: Ի վերջո թորման անոթում միայն այդ հեղուկը կմնա: Հավաքում են նաև հաստատուն ջերմաստիճանում թորվող ֆրակցիան:
Երբ արդեն մնացել է A-ն, այն կսկսի թորվել հաստատուն
![]() ջերմաստիճանում և գոլորշին կոնդեսացնելով այն կստացվի մաքուր վիճակում:
ջերմաստիճանում և գոլորշին կոնդեսացնելով այն կստացվի մաքուր վիճակում:
Այս պրոցեսի դեպքում ֆրակցիաների կորուստն անխուսափելի է: Կոտորակային (ֆրակցիոն) թորումը զերծ է այս թերություններից:
Վերադառնանք նկ.XII.11-ին: ![]() ջերմաստիճանում ստացված
ջերմաստիճանում ստացված
![]() բաղադրությամբ գոլորշին մինչև
բաղադրությամբ գոլորշին մինչև ![]() ջերմաստիճան կոնդենսացնելիս կստացվի մի լուծույթ, որը նորից կտրոհվի հեղուկ և գոլորշի ֆազերի, բայց նախկիններից տարբեր բաղադրությամբ
ջերմաստիճան կոնդենսացնելիս կստացվի մի լուծույթ, որը նորից կտրոհվի հեղուկ և գոլորշի ֆազերի, բայց նախկիններից տարբեր բաղադրությամբ ![]() Այս անգամ
Այս անգամ ![]() գոլորշին մինչև
գոլորշին մինչև ![]() ջերմաստիճան կոնդենսացնելով կստացվի
ջերմաստիճան կոնդենսացնելով կստացվի ![]() բաղադրություններով նոր` հեղուկ և գոլորշի ֆազեր: Հեշտ է նկատել, որ յուրաքանչյուր կոնդենսատ ավելի է հարստանում դյուրաեռ հեղուկով և աղքատանում դժվարաեռով:
բաղադրություններով նոր` հեղուկ և գոլորշի ֆազեր: Հեշտ է նկատել, որ յուրաքանչյուր կոնդենսատ ավելի է հարստանում դյուրաեռ հեղուկով և աղքատանում դժվարաեռով: ![]() ջերմաստիճանում խառնուրդն արդեն համարյա B-ից է բաղկացած: Պարզ է, որ այս պրոցեսը շարունակելով ի վերջո կստացվի B-ն և անոթում կմնա A-ն:
ջերմաստիճանում խառնուրդն արդեն համարյա B-ից է բաղկացած: Պարզ է, որ այս պրոցեսը շարունակելով ի վերջո կստացվի B-ն և անոթում կմնա A-ն:
բ) Ռեկտիֆիկացում – Թորման այս պրոցեսն է իրականացվում արտադրության մեջ անընդհատորեն և ավտոմատացված: Ռեկտիֆիկացումը կատարվում է «ափսեներ» պարունակող` ռեկտիֆիկացիոն աշտարակում: Սարքի ուրվագիծը ներկայացված է նկ. XII.12-ում: Ռեկտիֆիկացիոն աշտարակի կառուցվածքը հետևյալն է:
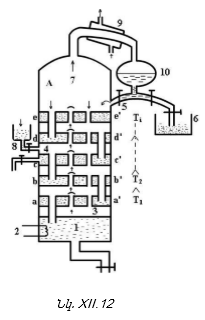
Սկզբնական լուծույթի տարողություն (1), լուծույթը տաքացնող հարմարանք (2): A-ն թորման աշտարակն է, որի մեջ որոշակի թվով «ափսեներ» են դասավորված. ![]() (3)-ից գոլորշին աշտարակ է մտնում: Ներքևից վերև ափսեների ջերմաստիճանը նվազում է: Գոլորշին կոնդենսանում է (4) ափսեներում: Յուրաքանչյուր ափսե նոր բաղադրությամբ գոլորշիացման օջախ է:
(3)-ից գոլորշին աշտարակ է մտնում: Ներքևից վերև ափսեների ջերմաստիճանը նվազում է: Գոլորշին կոնդենսանում է (4) ափսեներում: Յուրաքանչյուր ափսե նոր բաղադրությամբ գոլորշիացման օջախ է: ![]() ափսեից մինչև
ափսեից մինչև ![]() ափսեն լուծույթը հարստանում է դյուրաեռ բաղադրիչով:
ափսեն լուծույթը հարստանում է դյուրաեռ բաղադրիչով:
Նկ. XII.12-ի վրա ![]() հորիզոնականները ափսեներ են հիշեցնում:
հորիզոնականները ափսեներ են հիշեցնում: ![]() փաստորեն համարյա B է պարունակում, որի գոլորշին վերջնականորեն կոնդենսանում է (9) սառնարանի միջով անցնելիս: Կոնդենսատը հավաքվում է (10) ծավալում: Մի մասը (5)-ից որպես ֆլեգմա հետ է դառնում աշտարակ: Մաքուր B-ն հավաքվում է (6) ընդունարանում: Ի վերջո (1)-ում դժվարաեռ A-ն է մնում: Լուծույթի նոր մասնաբաժինները (1) տարողության մեջ ավելացնում են (8)-ից:
փաստորեն համարյա B է պարունակում, որի գոլորշին վերջնականորեն կոնդենսանում է (9) սառնարանի միջով անցնելիս: Կոնդենսատը հավաքվում է (10) ծավալում: Մի մասը (5)-ից որպես ֆլեգմա հետ է դառնում աշտարակ: Մաքուր B-ն հավաքվում է (6) ընդունարանում: Ի վերջո (1)-ում դժվարաեռ A-ն է մնում: Լուծույթի նոր մասնաբաժինները (1) տարողության մեջ ավելացնում են (8)-ից:
«Բաժանման գործակցի» (a) մեծությամբ է որոշվում թորման ճանապարհով հեղուկների իրարից բաժանման արդյունավետությունը: Ինչքան a-ն տարբեր է մեկից, այնքան ավելի արդյունավետ է բաժանումը:
a-ն որոշվում է օգտագործելով արդեն հայտնի (XI.15) հավասարումը:
![]()
(հիշել, որ ![]()
Ըստ Դալտոնի օրենքի.
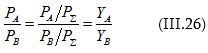
Եթե ![]() հեղուկում
հեղուկում ![]() բաղադրիչի մոլային բաժինն է, ապա
բաղադրիչի մոլային բաժինն է, ապա ![]() նույն բաղադրիչի մոլային բաժինն է գոլորշում:
նույն բաղադրիչի մոլային բաժինն է գոլորշում:
(ա)-ից կստացվի.
![]()
Աջ և ձախ մասերը բաժանենք
![]()

Նորից ըստ Դալտոնի օրենքի. ![]() (III.26)
և
(XII.27ա)
(III.26)
և
(XII.27ա)
Ածանցենք ըստ ![]()
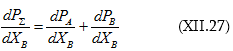
Զուգորդելով (XII.25), (XII.26) և (XII.27) հավասարումները կստացվի.
գ) Ազեոտրոպ խառնուրդներ.
Հանդիպում են դեպքեր, երբ ![]() դիագրամների վրա էքստրեմում է դիտվում:
դիագրամների վրա էքստրեմում է դիտվում: ![]() դիագրամի վրա max-ին
դիագրամի վրա max-ին ![]() դիագրամի վրա, այդ նույն
դիագրամի վրա, այդ նույն ![]() բաղադրության տակ կորը մինիմումի վրայով է անցնում և ընդհակառակը:
բաղադրության տակ կորը մինիմումի վրայով է անցնում և ընդհակառակը:
Ազեոտրոպ են կոչվում այն լուծույթները (խառնուրդները), որոնց ![]() կամ
կամ ![]() դիագրամների վրա էքստրեմում է դիտվում:
դիագրամների վրա էքստրեմում է դիտվում:
Այն պատճառները, որոնք պայմանավորում են Ռաուլի օրենքից (+) և (-) շեղումները, այդ նույն պատճառները առկա են նաև ազեոտրոպ խառնուրդներում: Փաստորեն ![]() դիագրամի վրա max է դիտվում, երբ ազեոտրոպ խառնուրդը (+) շեղում է ցուցաբերում Ռաուլի օրենքից, min-ի դեպքում (-):
դիագրամի վրա max է դիտվում, երբ ազեոտրոպ խառնուրդը (+) շեղում է ցուցաբերում Ռաուլի օրենքից, min-ի դեպքում (-):
Աղյուսակ 4-ում ներկայացված են ազեոտրոպ խառնուրդների օրինակներ: Ջերմաստիճանները նշված են ցելսիուսի սանդղակով:
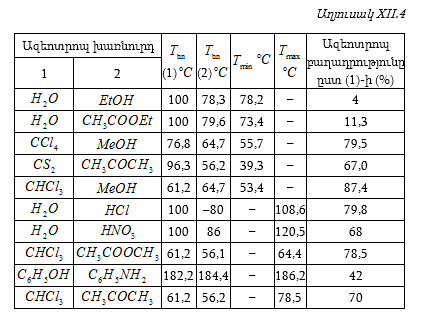
Ոչ ազեոտրոպ և ազեոտրոպ խառնուրդների ![]() (կամ
(կամ ![]() ) դիագրամները իրար հետ համեմատած սկզբունքային տարբերություն ունեն:
) դիագրամները իրար հետ համեմատած սկզբունքային տարբերություն ունեն:
Ոչ ազեոտրոպ խառնուրդների դեպքում կոնցենտրացիոն ողջ տիրույթում ![]() հեղուկ և գոլորշի ֆազերի բաղադրություններն իրարից զգալիորեն տարբեր են (տե’ս նկ.XII.11):
Հենց այս է այն պատճառը, որը հնարավորություն է տալիս թորման միջոցով երկու բաղադրիչ հեղուկներն իրարից բաժանել:
հեղուկ և գոլորշի ֆազերի բաղադրություններն իրարից զգալիորեն տարբեր են (տե’ս նկ.XII.11):
Հենց այս է այն պատճառը, որը հնարավորություն է տալիս թորման միջոցով երկու բաղադրիչ հեղուկներն իրարից բաժանել:
Ինչ վերաբերում է ազեոտրոպ խառնուրդների ![]() կամ
կամ ![]() դիագրամներին, ապա էքստրեմում կետում հեղուկ և գոլորշի ֆազերի բաղադրություններն իրար հավասար են: Հետևաբար, այդ բաղադրության հեղուկն անցնելով գոլորշի ֆազ և կոնդենսանալով ելային բաղադրության հեղուկն է առաջացնում: Բնական է, որ այս դեպքում անհնար է թորման միջոցով այդ հեղուկներն իրարից բաժանել:
դիագրամներին, ապա էքստրեմում կետում հեղուկ և գոլորշի ֆազերի բաղադրություններն իրար հավասար են: Հետևաբար, այդ բաղադրության հեղուկն անցնելով գոլորշի ֆազ և կոնդենսանալով ելային բաղադրության հեղուկն է առաջացնում: Բնական է, որ այս դեպքում անհնար է թորման միջոցով այդ հեղուկներն իրարից բաժանել:
Քաջ հայտնի է ![]() լուծույթը որպես ազեոտրոպ խառնուրդ: Եթե ելային լուծույթը ջրով շատ է հարուստ, ապա թորման ընթացքում նախ ջուրն է հեռանում մինչև, որ
լուծույթը որպես ազեոտրոպ խառնուրդ: Եթե ելային լուծույթը ջրով շատ է հարուստ, ապա թորման ընթացքում նախ ջուրն է հեռանում մինչև, որ ![]() (սա ազեոտրոպի բաղադրությունն է) (տե՛ս աղյուսակ
XII.4): Հենց, որ խառնուրդի բաղադրությունը դարձավ 96:4 այս բաղադրությամբ էլ խառնուրդը կսկսի թորվել: Եթե ելային խառնուրդի բաղադրությունը
(սա ազեոտրոպի բաղադրությունն է) (տե՛ս աղյուսակ
XII.4): Հենց, որ խառնուրդի բաղադրությունը դարձավ 96:4 այս բաղադրությամբ էլ խառնուրդը կսկսի թորվել: Եթե ելային խառնուրդի բաղադրությունը ![]() այս դեպքում նախ էթանոլը կսկսի թորվել այնքան, մինչև որ բաղադրությունը հավասարվի ազեոտրոպի բաղադրությանը, որից հետո հեղուկը կսկսի թորվել 96:4 հաստատուն բաղադրությամբ:
այս դեպքում նախ էթանոլը կսկսի թորվել այնքան, մինչև որ բաղադրությունը հավասարվի ազեոտրոպի բաղադրությանը, որից հետո հեղուկը կսկսի թորվել 96:4 հաստատուն բաղադրությամբ:
Ազեոտրոպ խառնուրդի հաստատուն բաղադրություն և հաստատուն եռման ջերմաստիճան ունենալու հանգամանքը իրավունք չի տալիս այն դիտելու որպես քիմիական միացություն:
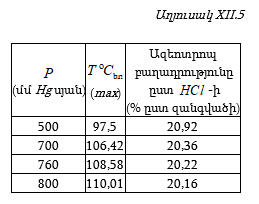
Աղյուսակ XII.5-ում բերված տվյալներից հետևում է, որ ճնշման փոփոխության հետ, թեև քիչ չափով, այնուամենայնիվ ազեոտրոպի բաղադրությունը փոխվում է: Քանի որ չի պահպանվում բաղադրության հաստատունության օրենքը, այդ պատճառով էլ ազեոտրոպ խառնուրդը քիմիական միացություն չէ:
XII-4:ա. ԳԻԲՍ-ԿՈՆՈՎԱԼՈՎԻ ԿԱՆՈՆՆԵՐԸ
Այս կանոնները հնարավորություն են տալիս քննարկելու բինար լուծույթներում հեղուկ և գոլորշի ֆազերի բաղադրությունների հարաբերությունը:
Կոնավալովը զուտ փորձարարական ճանապարհով երեք կանոններ է ձևակերպել:
1. Հեղուկ ![]() գոլորշի հավասարակշռական վիճակում հագեցած գոլորշին կհարստանա այն բաղադրիչով, որի ավելացման հետևանքով հեղուկի վրա եղած գոլորշու ընդհանուր ճնշումը կմեծանա:
գոլորշի հավասարակշռական վիճակում հագեցած գոլորշին կհարստանա այն բաղադրիչով, որի ավելացման հետևանքով հեղուկի վրա եղած գոլորշու ընդհանուր ճնշումը կմեծանա:
2. ![]() դիագրամի վրա եթե էքստրեմում կա, ապա այդ կետում իրար հավասար են հեղուկ և գոլորշի ֆազերի բաղադրությունները:
դիագրամի վրա եթե էքստրեմում կա, ապա այդ կետում իրար հավասար են հեղուկ և գոլորշի ֆազերի բաղադրությունները:
3. Եթե համակարգը գտնվում է հաստատուն ջերմաստիճանում և ճնշման տակ, ապա հեղուկ և գոլորշի ֆազերի բաղադրությունները կփոխվեն իրար սիմբատ: Մաթեմատիկայի
լեզվով,
նշվածը կարտահայտվի հետևյալ անհավասարումով
![]()
Գիբսի որոշ դրույթներ օգտագործելով կարելի է նշված կանոնները տեսականորեն հիմնավորել: Այս պատճառով էլ նշված կանոնները կոչվում են Գիբս-Կոնովալովի:
Իդեալական լուծույթների համար Դալտոնի և Ռաուլի օրենքները զուգորդելով
կստացվի. ![]() որտեղից.
որտեղից.

![]() պայմանականորեն վերաբերվում է երկու A
և B
նյութերից այն նյութին, որի համար
պայմանականորեն վերաբերվում է երկու A
և B
նյութերից այն նյութին, որի համար ![]() (ըստ նկ.XII.3-ի
(ըստ նկ.XII.3-ի ![]() Այդ նկարը քննարկելիս նշվեց, որ B-ն A-ից դյուրաեռ է: Հեշտ է նկատել, որ A-ին B
ավելացնելիս
Այդ նկարը քննարկելիս նշվեց, որ B-ն A-ից դյուրաեռ է: Հեշտ է նկատել, որ A-ին B
ավելացնելիս ![]() մեծանում է, բայց միշտ պահպանվում է
մեծանում է, բայց միշտ պահպանվում է ![]() այսինքն
այսինքն ![]() պայմանը:
(XII.30)-ը տվյալ կոնկրետ դեպքի համար կիրառելիս կստացվի
պայմանը:
(XII.30)-ը տվյալ կոնկրետ դեպքի համար կիրառելիս կստացվի
![]() այսինքն ելային խառնուրդը հարստացնելով
ավելի
ցածր եռման կետ ունեցող (տվյալ դեպքում B-ով) նյութով միշտ տեղի կունենա
այսինքն ելային խառնուրդը հարստացնելով
ավելի
ցածր եռման կետ ունեցող (տվյալ դեպքում B-ով) նյութով միշտ տեղի կունենա
![]() պայմանը:
պայմանը:
Այս հետևությունը համընկնում է Կոնովալովի առաջին կանոնի հետ, որը հետևում է նաև (XII.28)-ից.
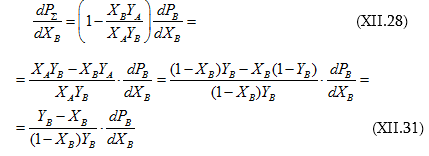
Այս հավասարման աջ մասում գտնվող երեք մեծություններն էլ դրական են ![]()
Հայտնի է.
![]()
Ուրեմն, ![]() մեծացման հետ
մեծացման հետ ![]() էլ է մեծանում, մյուս կողմից
էլ է մեծանում, մյուս կողմից
![]() հետևաբար.
հետևաբար.
![]()
Եզրակացությունը միանշանակ է. Եթե ![]() ուրեմն.
ուրեմն. ![]() Սա Կոնովալովի առաջին կանոնն է:
Սա Կոնովալովի առաջին կանոնն է:
Նկատի առնելով, որ ![]() (XII.25)-ից կստացվի.
(XII.25)-ից կստացվի.
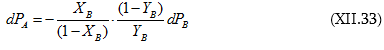
Դիֆերենցենք (XII.27ա)-ն. ![]()
Եթե ![]() վերաբերում է էքստրեմումին, ապա
վերաբերում է էքստրեմումին, ապա ![]() որտեղից.
որտեղից.
![]()
Տեղադրենք (XII.25)-ի մեջ.
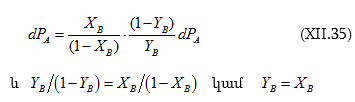
Իրոք էքստրեմում կետում հեղուկ և գոլորշի ֆազերի բաղադրություններն իրար հավասար են:
Ինչ վերաբերում է Կոնովալովի երրորդ կանոնին, ապա այն անմիջապես հետևում է համակարգի թերմոդինամիկական կայունության պայմանից: Այդ պայմանը (XII.32)-ն է: Այն հավասարապես վերաբերվում է և հեղուկ և գոլորշի ֆազերին.
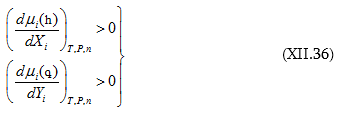
Հայտնի է նաև, որ ըստ ֆազային հավասարակշռության պայմանի.
![]()
Հաշվի առնելով (XII.37)-ը և իրար վրա բաժանելով (XII.36) անհավասարությունները կստանանք.
![]()
Ստացվեց այն, ինչը պետք էր ապացուցել. երբ T = const և P = const, ապա ինչ ուղղությամբ, որ փոխվի հեղուկի բաղադրությունը, նույն ուղղությամբ էլ կփոխվի գոլորշու բաղադրությունը:
բ) Վրևսկու կանոնները. Ազեոտրոպ խառնուրդների մասին խոսելիս նշվեց, որ ազեոտրոպի բաղադրությունը ինչ որ չափով կապված է ճնշման, նաև ջերմաստիճանի հետ: Ջերմաստիճանի ազդեցությունը որակապես արտահայտվում է Վրևսկու երեք կանոններով:
1. Եթե գոլորշու հետ հավասարակշռության մեջ գտնվող հաստատուն ![]() բաղադրությամբ լուծույթի ջերմաստիճանը բարձրացնենք, ապա գոլորշին կհարստանա այն բաղադրիչով, որի գոլորշիացման պարցիալ մոլային ջերմությունն ավելի մեծ է:
բաղադրությամբ լուծույթի ջերմաստիճանը բարձրացնենք, ապա գոլորշին կհարստանա այն բաղադրիչով, որի գոլորշիացման պարցիալ մոլային ջերմությունն ավելի մեծ է:

2. Եթե ազեոտրոպ խառնուրդը հավասարակշռական վիճակում է, ապա ջերմաստիճանի բարձրացման հետ ![]() դիագրամի մաքսիմումը կտեղաշարժվի այնպես, որ ազեոտրոպ խառնուրդը հարստանա այն կոմպոնենտով, որի գոլորշիացման պարցիալ մոլային ջերմությունն ավելի մեծ է: Եթե
դիագրամի մաքսիմումը կտեղաշարժվի այնպես, որ ազեոտրոպ խառնուրդը հարստանա այն կոմպոնենտով, որի գոլորշիացման պարցիալ մոլային ջերմությունն ավելի մեծ է: Եթե ![]() դիագրամի վրա մինիմում կա, ապա նշված պայմաններում ազեոտրոպը կաղքատանա այդ բաղադրիչով:
դիագրամի վրա մինիմում կա, ապա նշված պայմաններում ազեոտրոպը կաղքատանա այդ բաղադրիչով:
3. Նորից քննարկենք մաքսիմումի հարցը: Ջերմաստիճանի բարձրացման հետ և գոլորշի ֆազի և ազեոտրոպի բաղադրությունները կփոխվեն նույն ուղղությամբ: Երկուսն էլ կաճեն: Եթե խոսքը մինիմումին է վերաբերվում, այդ երկու բաղադրությունները նորից նույն ուղղությամբ կփոխվեն, բայց դեպի նվազում: (տե՛ս նկ. XII15 ա և բ):
XII-5. ՋԵՐՄԱՍՏԻՃԱՆԻ ԱԶԴԵՑՈՒԹՅՈՒՆԸ ԻՐԱՐ ՄԵՋ ՍԱՀՄԱՆԱՓԱԿ ԼՈՒԾՎՈՂ ՀԵՂՈՒԿՆԵՐԻ
ՓՈԽԱԴԱՐՁ ԼՈՒԾԵԼԻՈՒԹՅԱՆ ՎՐԱ: ԼՈՒԾՄԱՆ ԿՐԻՏԻԿԱԿԱՆ ՋԵՐՄԱՍՏԻՃԱՆ
Ընդհանրացումներ կատարենք մասնավոր դեպքերի քննարկումներից ստացված արդյունքների հիման վրա:
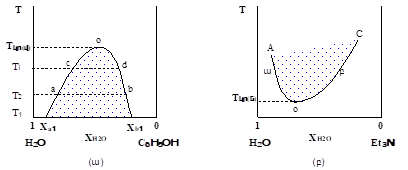
Նկ. XII.16
1. Նկ.XII.16ա-ի վրա ներկայացված է ջրի և ֆենոլի փոխադարձ լուծելիության կախումը ջերմաստիճանից:
Դիցուք ![]() ջերմաստիճանում որոշ քանակով ջուր է վերցված, որին ֆենոլ է ավելացվում: Երբ
ջերմաստիճանում որոշ քանակով ջուր է վերցված, որին ֆենոլ է ավելացվում: Երբ ![]() պղտորություն է նկատվում: Ֆենոլի քանակի հետագա ավելացման հետ նկատվում է ֆենոլային շերտի առաջացում և այդ շերտի ծավալի (քանակի) աճ: Ուրեմն, սկսած
պղտորություն է նկատվում: Ֆենոլի քանակի հետագա ավելացման հետ նկատվում է ֆենոլային շերտի առաջացում և այդ շերտի ծավալի (քանակի) աճ: Ուրեմն, սկսած ![]() համակարգը դարձել է երկշերտ (հետերոգեն): Երբ խառնուրդում
համակարգը դարձել է երկշերտ (հետերոգեն): Երբ խառնուրդում ![]() ապա ֆենոլի չնչին քանակի հետագա ավելացման հետևանքով շերտերի բաժանման մակերեսը վերանում է. համակարգը դառնում է միաշերտ (հոմոգեն): Ֆենոլի քանակի հետագա ավելացումն արդեն չի խաթարում համակարգի հոմոգենությունը:
ապա ֆենոլի չնչին քանակի հետագա ավելացման հետևանքով շերտերի բաժանման մակերեսը վերանում է. համակարգը դառնում է միաշերտ (հոմոգեն): Ֆենոլի քանակի հետագա ավելացումն արդեն չի խաթարում համակարգի հոմոգենությունը:
Երևույթի բացատրությունը.
![]() ջերմաստիճանում
ջերմաստիճանում ![]() տիրույթում առաջանում է ֆենոլի ջրային լուծույթ: Երբ
տիրույթում առաջանում է ֆենոլի ջրային լուծույթ: Երբ ![]() և
և ![]() ջուրը հագենում է ֆենոլով: Իմանալով
ջուրը հագենում է ֆենոլով: Իմանալով ![]() -ը կարելի է որոշել ջրում ֆենոլի լուծելիությունը
-ը կարելի է որոշել ջրում ֆենոլի լուծելիությունը ![]()
![]() տիրույթում համակարգը երկշերտ է մնում: Արդեն, երբ
տիրույթում համակարգը երկշերտ է մնում: Արդեն, երբ ![]() ֆենոլն է դառնում լուծիչ և ջուրը` լուծվող նյութ:
ֆենոլն է դառնում լուծիչ և ջուրը` լուծվող նյութ: ![]() պայմանը ցույց է տալիս, որ այս անգամ ֆենոլն է հագեցել ջրով: Օգտվելով այդ պայմանից կարելի է որոշել ջրի լուծելիությունը ֆենոլում նորից
պայմանը ցույց է տալիս, որ այս անգամ ֆենոլն է հագեցել ջրով: Օգտվելով այդ պայմանից կարելի է որոշել ջրի լուծելիությունը ֆենոլում նորից ![]() Երբ
Երբ ![]() ունենք ջրի ֆենոլային լուծույթ:
ունենք ջրի ֆենոլային լուծույթ:
Կատարելով նույն փորձը տարբեր ջերմաստիճաններում` ![]() կորերն իրար են միանում 0 կետում, ըստ որում
կորերն իրար են միանում 0 կետում, ըստ որում ![]() կստանանք համապատասխանաբար a
և b,
c և d կետերը:
կստանանք համապատասխանաբար a
և b,
c և d կետերը:
Ի վերջո, երբ ![]() ապա
ապա ![]() ցանկացած հարաբերության համար համակարգը (լուծույթ) մնում է հոմոգեն:
ցանկացած հարաբերության համար համակարգը (լուծույթ) մնում է հոմոգեն:
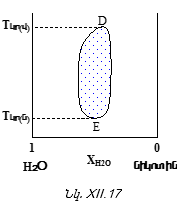
Սա նշանակում է, որ երբ ![]() ջուրն ու ֆենոլը իրար մեջ լուծվում են անսահմանափակ: Այդ սահմանային ջերմաստիճանը`
ջուրն ու ֆենոլը իրար մեջ լուծվում են անսահմանափակ: Այդ սահմանային ջերմաստիճանը` ![]() կոչվում է լուծման վերին կրիտիկական ջերմաստիճան:
կոչվում է լուծման վերին կրիտիկական ջերմաստիճան:
Այսպիսով, ![]() կորով սահմանափակված մարզում համակարգը երկշերտ է: Ներքևինը ջրով հագեցած ֆենոլային շերտն է
կորով սահմանափակված մարզում համակարգը երկշերտ է: Ներքևինը ջրով հագեցած ֆենոլային շերտն է ![]() իսկ վերևինը` ֆենոլով հագեցած ջրային շերտը: Հետևաբար
իսկ վերևինը` ֆենոլով հագեցած ջրային շերտը: Հետևաբար ![]() կորը ցույց է տալիս թե ջերմաստիճանից ինչպես է կախված ջրում ֆենոլի լուծելիությունը, իսկ
կորը ցույց է տալիս թե ջերմաստիճանից ինչպես է կախված ջրում ֆենոլի լուծելիությունը, իսկ ![]() կորն էլ համապատասխանաբար ցույց է տալիս ֆենոլում ջրի լուծելիության կախումը ջերմաստիճանից:
կորն էլ համապատասխանաբար ցույց է տալիս ֆենոլում ջրի լուծելիության կախումը ջերմաստիճանից:
2. Նկ.XII.16բ-ն վերաբերում է ջրի և տրիէթիլամինի իրար մեջ փոխադարձ լուծելիության կախմանը ջերմաստիճանից: Ի տարբերություն
![]() համակարգին հատուկ է լուծման ներքին կրիտիկական ջերմաստիճան: Սա նշանակում է, որ այս դեպքում փոխադարձ լուծելիությունն անսահմանափակ է, երբ
համակարգին հատուկ է լուծման ներքին կրիտիկական ջերմաստիճան: Սա նշանակում է, որ այս դեպքում փոխադարձ լուծելիությունն անսահմանափակ է, երբ ![]() Այս դեպքում AաOբC կորով սահմանափակված մարզում համակարգը երկշերտ է:
Այս դեպքում AաOբC կորով սահմանափակված մարզում համակարգը երկշերտ է:
3. Ջուր–նիկոտին համակարգը վերաբերում է երրորդ դեպքին, երբ ի հայտ են գալիս լուծման և վերին և ներքին կրիտիկական ջերմաստիճաններ: Կորի ներսում համակարգը երկշերտ է, իսկ կորից դուրս` փոխադարձ լուծելիությունն անսահմանափակ է (նկ.XII.17):
XII-6. ԹՈՐՈՒՄ ՋՐԱՅԻՆ ԳՈԼՈՐՇԻՆԵՐՈՎ
Այս հարցն ունի գործնական նշանակություն:
Հաճախ ենք գործ ունենում օրգանական միացությունների հետ, որոնք եռման ջերմաստիճանում կամ քայքայվում են կամ խեժանում, մասնավոր դեպքում` պոլիմերվում:
Եթե կարիք է լինում մեզ հետաքրքրող այդպիսի օրգանական նյութեր թորման ճանապարհով խառնուրդից բաժանել, այդ դեպքում շատ մատչելի մեթոդներից մեկը «ջրային գոլորշիներով թորումն» է:
Վերցնենք ab միջնորմով իրարից բաժանված A և B իրար մեջ գործնականորեն անլուծելի հեղուկներ: Համակարգը թերմոստատացված է:
Եթե ab միջնորմը վերացնենք, կստացվի երկշերտ հետերոգեն մի համակարգ: Դիցուք A
հեղուկի սեփական գոլորշիների ճնշումը ![]() B-ինը`
B-ինը` ![]() Այդ երկշերտ խառնուրդի վրա գոլորշիների ընդհանուր ճնշումը
Այդ երկշերտ խառնուրդի վրա գոլորշիների ընդհանուր ճնշումը ![]() կլինի.
կլինի.
![]()
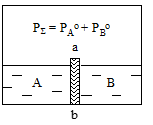
Նորից կիրառենք Դալտոնի օրենքը. ![]()
![]() գոլորշի ֆազում համապատասխանաբար A
և B
նյութերի մոլային բաժիններն են:
գոլորշի ֆազում համապատասխանաբար A
և B
նյութերի մոլային բաժիններն են:
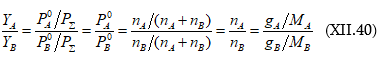
Որտեղ ![]() վերցված
հեղուկի
զանգվածն
է
(գ) և
վերցված
հեղուկի
զանգվածն
է
(գ) և ![]() էլ`
դրա
մոլային
զանգվածը
(գ/մոլ):
(XII.40)-ից կստացվի.
էլ`
դրա
մոլային
զանգվածը
(գ/մոլ):
(XII.40)-ից կստացվի.

Ընդունենք, որ
![]() և
A-ն` ջրում
անլուծելի
հետազոտվող
հեղուկն
է,
օրինակ,
անիլին:
[Այս բաժնում
g-ն զանգված
է
(գրամ)]:
և
A-ն` ջրում
անլուծելի
հետազոտվող
հեղուկն
է,
օրինակ,
անիլին:
[Այս բաժնում
g-ն զանգված
է
(գրամ)]:
Հայտնի է, որ որևէ հեղուկ կսկսի եռալ այն դեպքում, երբ իր սեփական գոլորշիների ճնշումը (քննարկվող դեպքում տվյալ փակ համակարգում ստեղծվածը) կհավասարվի մթնոլորտային ճնշմանը:
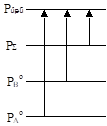
Կից բերված նկարից հետևում է, որ նախ, B-ն A-ից դյուրաեռ է և, երկրորդ, խառնուրդի վրա գոլորշիների գումարային ճնշումը ավելի մոտ է մթնոլորտայինին, քան ![]()
![]() առանձին-առանձին վերցրած:
առանձին-առանձին վերցրած:
Հետևաբար, եթե ջրում անլուծելի այդ օրգանական A նյութի մեջ ջրային (B) գոլորշի մղվի այնպես, որ ![]() այդ դեպքում ջրային գոլորշին իր հետ կտանի գոլորշի ֆազում գտնվող A-ն: A-ի նոր քանակ հեղուկից կանցնի գոլորշի և այսպես շարունակ, մինչև A-ն լրիվ տեղափոխվի ընդունարան, որտեղ կառաջանա երկշերտ համակարգ` կազմված ջրից և A-ից: Այդ շերտն իրարից անջատելով կարելի է առանձնացնել մեզ հետաքրքրող A նյութը: Ուրեմն, այդ A նյութը խառնուրդից կհեռացվի իր եռման ջերմաստիճանից զգալիորեն ցածր ջերմաստիճանում:
այդ դեպքում ջրային գոլորշին իր հետ կտանի գոլորշի ֆազում գտնվող A-ն: A-ի նոր քանակ հեղուկից կանցնի գոլորշի և այսպես շարունակ, մինչև A-ն լրիվ տեղափոխվի ընդունարան, որտեղ կառաջանա երկշերտ համակարգ` կազմված ջրից և A-ից: Այդ շերտն իրարից անջատելով կարելի է առանձնացնել մեզ հետաքրքրող A նյութը: Ուրեմն, այդ A նյութը խառնուրդից կհեռացվի իր եռման ջերմաստիճանից զգալիորեն ցածր ջերմաստիճանում:
Քննարկենք կոնկրետ մի դեպք: Լուծույթում նիտրոբենզոլը վերականգնելով անիլին է ստացվել: Այն հարկավոր է խառնուրդից անջատել:
Հայտնի է, որ 1 մթն (760 մմ սնդիկի սյուն) ճնշման տակ ![]() Այդ ջերմաստիճանում
Այդ ջերմաստիճանում ![]() սյուն:
սյուն:
Ուրեմն, եթե անիլին պարունակող խառնուրդի մեջ 98,4օC ջերմաստիճանի տակ ջրային գոլորշի մղենք, խառնուրդի վրա կստեղծվի հետևյալ գումարային ճնշումը. 718+42=760 մմ սնդիկի սյուն, որն էլ հավասար է 1 մթն: Սա բավարար պայման է, որ (XII.41) հավասարումն օգտագործելով կարելի լինի հաշվել, թե ցանկալի քանակով անիլին խառնուրդից հեռացնելու համար քանի՞ գրամ ջրային գոլորշի է պետք մղել ելային խառնուրդի մեջ:
Լուծենք հակադարձ խնդիրը: 98,4оC-ի տակ խառնուրդի մեջ է մղվել 100 գ ջրային գոլորշի (այս քանակը կարելի է ծավալով արտահայտել ընդունելով ջրային գոլորշին որպես իդեալական գազ): Ինչքա՞ն անիլին կտեղափոխվի: Այն որոշենք օգտվելով
(XII.41)-ից, որտեղ ![]()
![]()
Փաստորեն որպես կոնդենսատ կստացվի 100գ ջուր + 31գ անիլին = 131գ երկշերտ խառնուրդ, որից կարելի է հեշտությամբ անջատել օրգանական շերտը (անիլինը):
XII-7. ԵՐՐՈՐԴ ՆՅՈՒԹԻ ԲԱՇԽՈՒՄՆ ԻՐԱՐ ՄԵՋ ՉԼՈՒԾՎՈՂ ԵՐԿՈՒ ՀԵՂՈՒԿՆԵՐՈՒՄ:
ԱՐՏԱԼՈՒԾՈՒՄ (ԷՔՍՏՐԱԿՑՈՒՄ): ԲԱՇԽՄԱՆ ԳՈՐԾԱԿԻՑ
Ջուր + քլորոֆորմ երկշերտ խառնուրդին յոդ ավելացնենք: Երկու շերտերն էլ կգունավորվեն, բայց քլորոֆորմային շերտի գույնն ավելի մուգ է: Սա նշանակում է, որ ավելացված յոդը բաշխվել է երկու հեղուկների միջև, բայց ավելի շատ քլորոֆորմում: Հաստատուն ջերմաստիճանի տակ շերտերում յոդի քանակը կմնա անփոփոխ: Հետևաբար համակարգում հավասարակշռություն է ստեղծվել.
![]()
Հաշվի առնելով (XII.42)-ը և ընդունելով, որ համակարգը իդեալական է կստացվի.
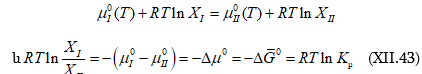
![]() -ն այն քիմիական պոտենցիալն է, որ պիտի ունենա հիպոթետիկ (անկախ) վիճակում գտնվող մաքուր յոդը: Այն կախված է լուծիչի բնույթից:
-ն այն քիմիական պոտենցիալն է, որ պիտի ունենա հիպոթետիկ (անկախ) վիճակում գտնվող մաքուր յոդը: Այն կախված է լուծիչի բնույթից:
Ըստ նշանակման.
![]()
որտեղ ![]() մոլային բաժիններն են քլորոֆորմում և ջրում:
մոլային բաժիններն են քլորոֆորմում և ջրում: ![]() կոչվում է բաշխման գործակից, որը տվյալ լուծիչում ֆունկցիա է միայն ջերմաստիճանից
կոչվում է բաշխման գործակից, որը տվյալ լուծիչում ֆունկցիա է միայն ջերմաստիճանից ![]()
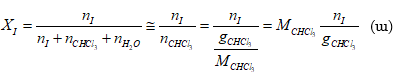
![]() լուծված ջրի քանակն է, որը գործնականորեն համեմատական է տվյալ ջերմաստիճանում քլորոֆորմում ջրի լուծելիությանը: Այն շատ փոքր մեծություն է, այսինքն.
լուծված ջրի քանակն է, որը գործնականորեն համեմատական է տվյալ ջերմաստիճանում քլորոֆորմում ջրի լուծելիությանը: Այն շատ փոքր մեծություն է, այսինքն. ![]() Քանի որ
Քանի որ ![]() համար
համար ![]() լուծիչ է, այս պատճառով էլ
լուծիչ է, այս պատճառով էլ ![]()
Նույն դատողությունների հիման վրա կարելի է գրել.
![]()
(ա)-ն և (բ)-ն իրար վրա բաժանելով կստանանք.
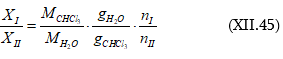
Ըստ մեր նշանակումների ![]() իսկ 1000 գ-ում` թող լինի
իսկ 1000 գ-ում` թող լինի ![]() մոլ: Ուրեմն
մոլ: Ուրեմն ![]() քլորոֆորմում, նույն ձևով ջրում, որտեղից.
քլորոֆորմում, նույն ձևով ջրում, որտեղից.
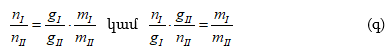
Բնական է, որ տվյալ դեպքում ![]() մոլալ կոնցենտրացիա է: Տեղադրենք (գ)-ն
(XII.45)-ի մեջ.
մոլալ կոնցենտրացիա է: Տեղադրենք (գ)-ն
(XII.45)-ի մեջ.
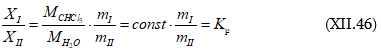
և
![]()
![]() կոնցենտրացիան կարելի է արտահայտել մոլյարությամբ (մոլ/լ): Ընդունելով, որ
կոնցենտրացիան կարելի է արտահայտել մոլյարությամբ (մոլ/լ): Ընդունելով, որ ![]() կստացվի.
(XII.47բ)
կստացվի.
(XII.47բ)
![]() (XII.47բ):
(XII.47բ):
Սա Ներնստի բաշխման օրենքն է: Քանի որ ![]() (V-ն լուծույթի ծավալն է լ-երով) և
(V-ն լուծույթի ծավալն է լ-երով) և ![]() հետևաբար
հետևաբար
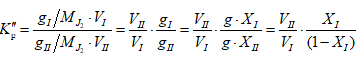 (XII.48):
(XII.48):
որովհետև.
![]()
![]() -ն
-ն ![]() -ի սկզբնական քանակն է: Տվյալ փորձի համար հաստատուն մեծություն է, իսկ
-ի սկզբնական քանակն է: Տվյալ փորձի համար հաստատուն մեծություն է, իսկ ![]()
1.
![]() վերցված ջրի ծավալն է լ-երով,
վերցված ջրի ծավալն է լ-երով, ![]() քլորոֆորմինը, որի մեջ է անցել
քլորոֆորմինը, որի մեջ է անցել ![]()
(XII.48)-ից ունենք. ![]()
![]()
և ![]() (XII.48)-ից կստացվի.
(XII.48)-ից կստացվի.
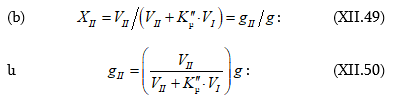
Հիշենք, որ
(XII.50)-ի մեջ ![]() ջրում լուծված
ջրում լուծված ![]() զանգվածն է (գ), g - ն վերցված
զանգվածն է (գ), g - ն վերցված ![]() զանգվածն է,
զանգվածն է, ![]() ջրի ծավալն է (լ),
ջրի ծավալն է (լ), ![]() քլորոֆորմինը:
քլորոֆորմինը:
Լուծենք հետևյալ խնդիրը: ![]() ջրում և պետք է այն արտալուծել
ջրում և պետք է այն արտալուծել ![]() օգտագործելով:
օգտագործելով:
Վերցնենք կոնկրետ դեպք: 1 լ ջրում 1 գ յոդ կա: Այս նպատակով օգտագործվելու է ![]() Խնդիրը գործնականորեն կարելի է լուծել երկու ճանապարհով. (ա)
1 լ
Խնդիրը գործնականորեն կարելի է լուծել երկու ճանապարհով. (ա)
1 լ ![]() միանվագ ավելացնելով: Ընդունենք, որ
միանվագ ավելացնելով: Ընդունենք, որ ![]() Օգտվենք
(XII.50)-ից.
Օգտվենք
(XII.50)-ից.
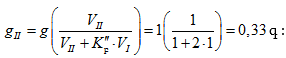
Ուրեմն ջրում մնաց 0,33 գ յոդ և քլորոֆորմի մեջ անցավ 1-
0,33 =0,67 գ, այսինքն այս ճանապարհով ![]() 67%-ը (2/3-ը) արտալուծվեց.
67%-ը (2/3-ը) արտալուծվեց.
(բ) այդ
1 լ
![]() կարելի է մաս-մաս ավելացնել, դիցուք 10 անգամով, յուրաքանչյուր անգամ
0,1 լ ավելացնելով: Առաջին էքստրակցիայից հետո ունեինք
կարելի է մաս-մաս ավելացնել, դիցուք 10 անգամով, յուրաքանչյուր անգամ
0,1 լ ավելացնելով: Առաջին էքստրակցիայից հետո ունեինք ![]() ջրում: Ավելացվեց
ջրում: Ավելացվեց ![]() Դիցուք ջրում մնաց
Դիցուք ջրում մնաց ![]() Ուրեմն.
Ուրեմն. ![]() անցել է
անցել է ![]() մեջ:
մեջ:
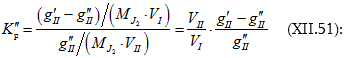
որտեղից
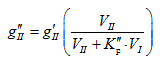
իսկ
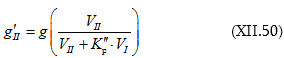
Հետևաբար
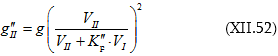
Եթե այս գործողությունը i անգամ կրկնենք կստացվի.
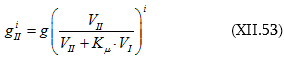
Եթե վերցրել ենք 1 լ ![]() և ամեն անգամ 0,1 լ ենք ավելացնում, ուրեմն արտալուծումը 10 անգամ ենք կրկնել:
և ամեն անգամ 0,1 լ ենք ավելացնում, ուրեմն արտալուծումը 10 անգամ ենք կրկնել:
Այստեղից
Եզրակացություն.
1 լ ![]() միանվագ օգտագործելու դեպքում
միանվագ օգտագործելու դեպքում ![]() արտալուծվեց, իսկ այդ նույն 1 լ ծավալով
արտալուծվեց, իսկ այդ նույն 1 լ ծավալով ![]() 0,1 լ-ով 10 անգամով ավելացնելիս կարտալուծվի 1 –
0,15 =0,85 գ կամ 85%:
0,1 լ-ով 10 անգամով ավելացնելիս կարտալուծվի 1 –
0,15 =0,85 գ կամ 85%:
Հետևաբար նպատակահարմար է որոշակի ծավալով արտալուծող լուծիչը մաս-մաս ավելացնել:
XII-8. ԻԴԵԱԼԱԿԱՆ ԼՈՒԾՈՒՅԹՆԵՐԻ ԿՈԼԻԳԱՏԻՎ ՀԱՏԿՈՒԹՅՈՒՆՆԵՐԸ
XII-8:1. Լուծույթի սառեցման ջերմաստիճանի կախումը լուծույթի կոնցենտրացիայից: Կրիոսկոպիա
Արդեն քննարկել ենք Ռաուլի օրենքը:
Նախ քննարկենք հետևյալ ընդհանուր հարցը: Ջերմաստիճանի բարձրացման հետ ինչպե՞ս է փոխվում որևէ նյութի քիմիական պոտենցիալը, եթե մի դեպքում այն մաքուր է, մյուս դեպքում, երբ լուծված նյութ է պարունակում:
Այդ կախումը ներկայացված է նկ. XII.18-ի վրա:
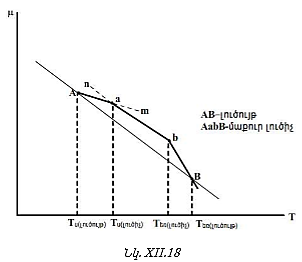
Հայտնի է, որ ջերմաստիճանի բարձրացման հետ նյութի (համակարգի) էնտրոպիան
աճում
է
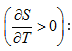 Քանի որ
Քանի որ ![]() ապա ջերմաստիճանի
բարձրացման հետ քիմիական պոտենցիալը նվազելու է:
ապա ջերմաստիճանի
բարձրացման հետ քիմիական պոտենցիալը նվազելու է:
Քննարկումը մասնավորեցնենք ջրի օրինակի համար (տե՛ս նկ. XII.18): Aa մարզում ջուրը գտնվում է պինդ վիճակում (սառույց): a -ին համապատասխանում է ![]() Ջերմաստիճանի բարձրացման հետ սառույցը հալվում է: b կետին համապատասխանում է
Ջերմաստիճանի բարձրացման հետ սառույցը հալվում է: b կետին համապատասխանում է ![]() Երբ P=1 մթն այդ ջերմաստիճանում ջուրը կսկսի եռալ: bB մարզը վերաբերում է գոլորշու տաքացմանը:
Երբ P=1 մթն այդ ջերմաստիճանում ջուրը կսկսի եռալ: bB մարզը վերաբերում է գոլորշու տաքացմանը:
an-ը և am-ը համապատասխանում են անկայուն վիճակների: Չնայած այն բանին, որ am մարզում ![]() ջուրը դեռ պինդ (սառույց) է մնում: Ասում են, որ ջուրը գտնվում է գերտաք բյուրեղական վիճակում («գերտաք սառույց»): Իսկ an մարզում, երբ
ջուրը դեռ պինդ (սառույց) է մնում: Ասում են, որ ջուրը գտնվում է գերտաք բյուրեղական վիճակում («գերտաք սառույց»): Իսկ an մարզում, երբ ![]() ջուրը հեղուկ է մնացել: Այս դեպքում «գերցուրտ հեղուկ» ունենք:
ջուրը հեղուկ է մնացել: Այս դեպքում «գերցուրտ հեղուկ» ունենք:
Ցույց է տված, որ ![]() Ուրեմն, ջրային լուծույթում ջրի քիմիական պոտենցիալն ավելի փոքր է, քան մաքուր ջրինը: Հետևաբար, վ
ֆունկցիան պատկերող կորը պետք է AabB-ից ցածրով անցնի:
Ուրեմն, ջրային լուծույթում ջրի քիմիական պոտենցիալն ավելի փոքր է, քան մաքուր ջրինը: Հետևաբար, վ
ֆունկցիան պատկերող կորը պետք է AabB-ից ցածրով անցնի:
AB-ն ջրային լուծույթում ջրի քիմիական պոտենցիալի ջերմաստիճանից ունեցած կախումն է արտահայտում: Այս առումով A կետին համապատասխանում է ջրային լուծույթից սառույցի անջատման ջերմաստիճանը ![]() Նույն դատողությամբ կարելի է ասել, որ B կետին համապատասխանողը ջրային լուծույթի եռման ջերմաստիճանն է
Նույն դատողությամբ կարելի է ասել, որ B կետին համապատասխանողը ջրային լուծույթի եռման ջերմաստիճանն է ![]() Հետևաբար, լուծույթի սառեցման կետը ավելի ցածր է, քան մաքուր ջրինը
Հետևաբար, լուծույթի սառեցման կետը ավելի ցածր է, քան մաքուր ջրինը ![]() իսկ եռման կետն ավելի բարձր է
իսկ եռման կետն ավելի բարձր է ![]() (մ-մաքուր և լ-լուծույթ):
(մ-մաքուր և լ-լուծույթ):
Նույն եզրակացությանը կարելի է հանգել, եթե ջրի վիճակի դիագրամը քննարկենք ![]() կոորդինատային համակարգ օգտագործելով (տե՛ս նկ.
XII.19): Ներկայացվածը ջրի վիճակի պարզեցված դիագրամն է, երբ հաշվի չեն առնված սառույցի բյուրեղական այլափոխությունները:
կոորդինատային համակարգ օգտագործելով (տե՛ս նկ.
XII.19): Ներկայացվածը ջրի վիճակի պարզեցված դիագրամն է, երբ հաշվի չեն առնված սառույցի բյուրեղական այլափոխությունները:
COA մարզում ջուրը գտնվում է հեղուկ վիճակում, BOC մարզում պինդ է (սառույց), իսկ BOA կորից ներքև` գոլորշի: Դիագրամը սահմանափակվում է ![]() բարձրացված ուղղահայացով, որովհետև երբ
բարձրացված ուղղահայացով, որովհետև երբ ![]() Գոլորշին արդեն գազ է և այն չի կարելի հեղուկացնել (տե՛ս նկ.III.12
և հարակից բացատրությունները):
Գոլորշին արդեն գազ է և այն չի կարելի հեղուկացնել (տե՛ս նկ.III.12
և հարակից բացատրությունները):

A կետին համապատասխանում է 1 մթն ճնշման տակ ջրի եռման ջերմաստիճանը (373,15
К, 100оC ): OA կորը պատկերում է ![]() հավասարակշռությունը: OC-ն իրարից բաժանում է հեղուկ և պինդ ֆազերը. այն վերաբերում է
հավասարակշռությունը: OC-ն իրարից բաժանում է հեղուկ և պինդ ֆազերը. այն վերաբերում է ![]() հավասարակշռությանը, իսկ OB-ն
հավասարակշռությանը, իսկ OB-ն ![]() O կետում նշված երեք ֆազերը գտնվում են փոխադարձ հավասարակշռության մեջ:
O կետում նշված երեք ֆազերը գտնվում են փոխադարձ հավասարակշռության մեջ:
O կետին ոչ թե 0oC (273,15 K) է համապատասխանում, այլ 0,01oC-ով բարձր (273,16 K): Սառույցի վրա սեփական գոլորշիների ճնշումը 4,6 մմ սնդիկի սյուն է:
Ինչպես նշվել է պայմանականորեն է ընդունվել
![]()
![]() այն էլ միայն այն դեպքում, երբ
այն էլ միայն այն դեպքում, երբ ![]() մթն (տե՛ս նկ.XII.19-ը): Բնական է, որ այս պայմանում ջրում լուծված օդ կա:
մթն (տե՛ս նկ.XII.19-ը): Բնական է, որ այս պայմանում ջրում լուծված օդ կա:
Ըստ Ռաուլի օրենքի տվյալ ջերմաստիճանում մաքուր հեղուկի (լուծիչի) սեփական գոլորշիների ճնշումն ավելի մեծ է, քան երբ դրանում լուծված նյութ կա: Սա նշանակում է, որ մաքուր ջրի փոխարեն ջրային լուծույթ վերցնելիս ![]() կախումն արտահայտող կորը պետք է OA-ից ներքևով անցնի
կախումն արտահայտող կորը պետք է OA-ից ներքևով անցնի ![]() կետում լուծույթից սառույցի բյուրեղներ կսկսեն անջատվել: Եթե լուծույթը գտնվում է 1 մթն ճնշման տակ, ապա այդ պրոցեսը կսկսի
կետում լուծույթից սառույցի բյուրեղներ կսկսեն անջատվել: Եթե լուծույթը գտնվում է 1 մթն ճնշման տակ, ապա այդ պրոցեսը կսկսի ![]() ջերմաստիճանում:
ջերմաստիճանում:
Ուրեմն, ինչպես պետք էր սպասել` նկ.XII.19-ից ևս հետևում է, որ ![]()
Այս բոլորը նախապատրաստությունն էր թերմոդինամիկական մեթոդով քննարկելու ![]() հավասարակշռությունները:
հավասարակշռությունները:
Պետք է նշել, որ նշված օրինաչափությունները ընդհանուր են ցանկացած նյութի, մասնավորաբար ջրի համար:
Նախ և առաջ քննարկենք ![]() հավասարակշռությունը:
հավասարակշռությունը:
Փաստորեն քննարկվում է ջրային լուծույթ, որի մեջ լողում են սառույցի բյուրեղներ հաստատուն ջերմաստիճանում և 1 մթն ճնշման տակ:
Գրենք հավասարակշռության պայմանը կոնկրետ այս օրինակի համար.
![]()
![]() ջրի քիմիական պոտենցիալն է, X-ը լուծույթում ջրի մոլային բաժինն է, իսկ
ջրի քիմիական պոտենցիալն է, X-ը լուծույթում ջրի մոլային բաժինն է, իսկ ![]() սառույցի քիմիական պոտենցիալն է, որն X-ից անկախ է, որովհետև սառույցը մաքուր ջուր է և լուծված նյութ չի պարունակում:
սառույցի քիմիական պոտենցիալն է, որն X-ից անկախ է, որովհետև սառույցը մաքուր ջուր է և լուծված նյութ չի պարունակում:
Հայտնի է, որ
![]()
որովհետև, ինչպես նշվեց, սառույցը մաքուր ջուր է և կոնդենսված ֆազում գտնվող ցանկացած մաքուր նյութի ակտիվությունը 1-ի է հավասար (a = 1): Իսկ
![]()
Ուրեմն.
![]()
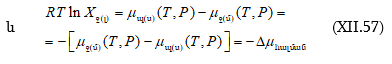
Ըստ ընդունված կարգի
(XII.57)-ում փակագծի մեջ ներկայացվածը վերաբերում է ![]() տարբերությանը: Մեր դեպքում պրոցեսի արգասիքը հեղուկն է, իսկ ելայինը` սառույցը: Ուրեմն, խոսքը վերաբերում է
տարբերությանը: Մեր դեպքում պրոցեսի արգասիքը հեղուկն է, իսկ ելայինը` սառույցը: Ուրեմն, խոսքը վերաբերում է ![]() անցմանը, այսինքն հալման պրոցեսին:
(XII.57)-ից կստացվի.
անցմանը, այսինքն հալման պրոցեսին:
(XII.57)-ից կստացվի.
![]()
Գրվածից հետևում է, որ ![]() Ածանցնենք ըստ T-ի.
Ածանցնենք ըստ T-ի.
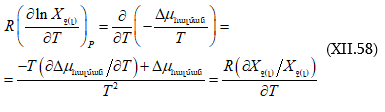
Հայտնի է, որ ![]() Հետևաբար,
Հետևաբար,
![]()
Ուրեմն.
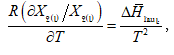
որտեղից
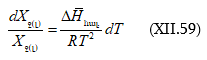
Դիցուք վերցված է 1000 գ =1 կգ ջուր (լուծիչ): Ըստ իմաստի
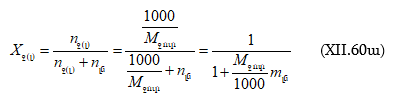
(լն-լուծված նյութ): ![]() , որը կոնկրետ
1000 գ (1 կգ) լուծիչում լուծված նյութի մոլերի թիվն է:
, որը կոնկրետ
1000 գ (1 կգ) լուծիչում լուծված նյութի մոլերի թիվն է:
(XII.60ա)-ն ածանցենք ըստ ![]()
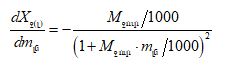
և

(XII.60բ)-ն և (XII.60ա)-ն իրար վրա բաժանելով կստացվի.
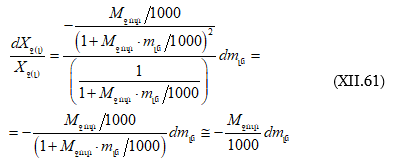
որովհետև լուծիչի մոլային զանգվածը` ![]() (ջրի դեպքում
(ջրի դեպքում ![]() իսկ
իսկ ![]() 1000գ լուծիչում լուծված նյութի քանակն է և քննարկվում են իդեալական (նոսր) լուծույթներ: Բնական է, որ
1000գ լուծիչում լուծված նյութի քանակն է և քննարկվում են իդեալական (նոսր) լուծույթներ: Բնական է, որ ![]() (ջուրը այլ լուծիչով փոխարինելով
օրինաչափությունը չի փոխվի):
(ջուրը այլ լուծիչով փոխարինելով
օրինաչափությունը չի փոխվի):
(XII.61)-ը տեղադրենք (XII.59)-ի մեջ.
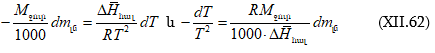
Քանի որ ![]() փոքր մեծություն է, ապա ջերմաստիճանի փոփոխության տիրույթում կարելի է ընդունել, որ
փոքր մեծություն է, ապա ջերմաստիճանի փոփոխության տիրույթում կարելի է ընդունել, որ ![]()
Հաշվի առնելով այս հանգամանքը ինտեգրենք (XII.62)-ը.
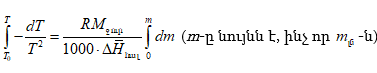
![]() կոնցենտրացիայով լուծույթի սառեցման կետը:
կոնցենտրացիայով լուծույթի սառեցման կետը:
Ինտեգրման արդյունքն է.
![]()
որովհետև ![]() Օրինակ, եթե ջրի համար t = 0oC, ապա 0,1 մոլալ լուծույթի համար
Օրինակ, եթե ջրի համար t = 0oC, ապա 0,1 մոլալ լուծույթի համար ![]() Եթե
Եթե ![]() ապա նշված դեպքում T
= 273,00 K:
ապա նշված դեպքում T
= 273,00 K:
(XII.63)-ից կստացվի.
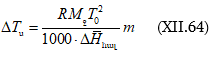
Տվյալ լուծիչի համար m-ի գործակիցը հաստատուն մեծություն է: Այն նշանակենք
![]()
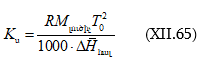
որտեղ
![]() լուծիչի մոլային զանվածն է,
լուծիչի մոլային զանվածն է, ![]() դրա սառեցման ջերմաստիճանը և
դրա սառեցման ջերմաստիճանը և ![]() հալման մոլային ջերմությունը:
հալման մոլային ջերմությունը:
Օգտվելով (XII.65) նշանակումից կստանանք.
![]()
![]() -ն կոչվում է կրիոսկոպիական հաստատուն կամ լուծույթի սառեցման կետի մոլալ անկում (դեպրեսիա): Չափողականությունն է. աստ(կգ/մոլ): Այն ցույց է տալիս, թե ինչի է հավասար 1 մոլալ m=1
մոլ/կգ) լուծույթի սառեցման կետի նվազումը կամ 1 մոլալ տվյալ լուծույթի սառեցման ջերմաստիճանը քանի՞ աստիճանով է ցածր մաքուր լուծիչի սառեցման կետից
-ն կոչվում է կրիոսկոպիական հաստատուն կամ լուծույթի սառեցման կետի մոլալ անկում (դեպրեսիա): Չափողականությունն է. աստ(կգ/մոլ): Այն ցույց է տալիս, թե ինչի է հավասար 1 մոլալ m=1
մոլ/կգ) լուծույթի սառեցման կետի նվազումը կամ 1 մոլալ տվյալ լուծույթի սառեցման ջերմաստիճանը քանի՞ աստիճանով է ցածր մաքուր լուծիչի սառեցման կետից ![]() :
:
Օրինակ, փորձը ցույց է տալիս, որ շաքարի 1 մոլալ լուծույթը սառչում է -1,86oC-ում:
Հետևաբար
![]() :
:
Սա ջրի կրիոսկոպիական հաստատունն է:
(XII.65)-ը հնարավորություն է տալիս ցանկացած լուծիչի համար հաշվել ![]() Օրինակ, ջրի համար
Օրինակ, ջրի համար ![]() կալ/(մոլ.աստ): Որտեղից.
կալ/(մոլ.աստ): Որտեղից.
![]()
Այս բոլորը ճիշտ է, եթե քննարկվող լուծույթը իդեալական է:
Աղյուսակ XII.6-ում բերված են մի քանի լուծիչների (դա կախված չէ ագրեգատային վիճակից) կրիոսկոպիական հաստատունները:

երված տվյալներից հետաքրքիր է կամֆորան, որի ![]() անսովոր մեծ արժեք ունի: Այս հանգամանքը հնարավորություն է տալիս կամֆորայի լուծույթում կրիոսկոպիական մեթոդով մոլային զանգված որոշելու համար օգտվել 0,1o
ճշտությամբ ջերմաչափից:
անսովոր մեծ արժեք ունի: Այս հանգամանքը հնարավորություն է տալիս կամֆորայի լուծույթում կրիոսկոպիական մեթոդով մոլային զանգված որոշելու համար օգտվել 0,1o
ճշտությամբ ջերմաչափից:
Այս վերջին պարբերությունից հետևում է, որ կրիոսկոպիան կարելի է օգտագործել անհայտ նյութի մոլային զանգված որոշելու համար:
Նախքան այս գործնական նշանակություն ունեցող հարցը քննարկելը անհրաժեշտ ենք համարում ավելի մանրամասն քննարկել ![]() -ի չափողականության հարցը որոշ թյուրիմացություններից խուսափելու համար:
(XII.64)-ը կարելի է ներկայացնել նաև հետևյալ հավասարումով.
-ի չափողականության հարցը որոշ թյուրիմացություններից խուսափելու համար:
(XII.64)-ը կարելի է ներկայացնել նաև հետևյալ հավասարումով.
![]()
որտեղ ![]()
Տեղադրենք (XII.64ա)-ի մեջ.
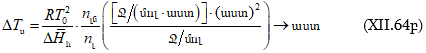
![]() Տեղադրենք
(XII.64բ)-ի մեջ կստացվի.
Տեղադրենք
(XII.64բ)-ի մեջ կստացվի.
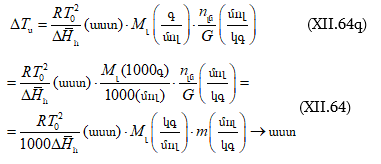
որովհետև ![]()
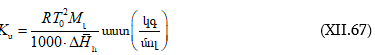
Եթե ![]() մոլային զանգվածով նյութից
մոլային զանգվածով նյութից ![]() գ նյութ է լուծված
գ նյութ է լուծված
![]() գ լուծիչում, ապա ըստ պայմանի 1000 գ լուծիչում ունենք m
մոլ լուծված նյութ: Ուրեմն,
գ լուծիչում, ապա ըստ պայմանի 1000 գ լուծիչում ունենք m
մոլ լուծված նյութ: Ուրեմն, ![]() Տեղադրենք
(XII.66)-ի մեջ.
Տեղադրենք
(XII.66)-ի մեջ.
![]()
(XII.68)-ից հետևում է, որ ![]() որտեղ
որտեղ ![]() (
(![]() լուծված անհայտ նյութի մոլային զանգվածն է) և
լուծված անհայտ նյութի մոլային զանգվածն է) և
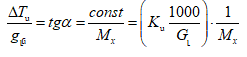
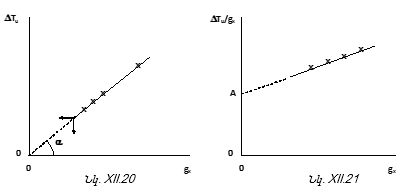
[տե՛ս նկ.XII.20]:
Այստեղ միակ անհայտը ![]()
Կարելի է և հակադարձ խնդիրը լուծել: Եթե վերցվի հայտնի նյութ, ապա կարելի է անհայտ ![]() որոշել:
որոշել:
Բայց միշտ չէ, որ ![]() կախումն ուղիղ գծային է: Շեղումը ցույց է տալիս, որ քննարկվող լուծույթը ռեալ է (իդելական չէ):
կախումն ուղիղ գծային է: Շեղումը ցույց է տալիս, որ քննարկվող լուծույթը ռեալ է (իդելական չէ):
Ռեալ գազերի վիճակը նկարագրելու համար բացի Վան դեր Վաալսի հավասարումից կարելի է օգտվել նաև վիճակի վիրիալ հավասարումից (III.43):
Օգտվելով նմանակությունից (անալոգիայից) կարող ենք գրել.
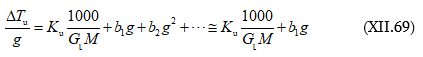
Սա արդեն ոչ թե ![]() տիպի հավասարում է: (տե՛ս նկ.XII.21):
Եթե
տիպի հավասարում է: (տե՛ս նկ.XII.21):
Եթե ![]() նշանակում է, որ
նշանակում է, որ ![]() և լուծույթը իդեալական է: Ինչպես
(III.43)-ում, (XII.69)-ում էլ
և լուծույթը իդեալական է: Ինչպես
(III.43)-ում, (XII.69)-ում էլ ![]() վիրիալ գործակիցներ են, որոնք բնութագրում են լուծիչ-լուծված նյութ փոխազդեցության սաստկությունը:
վիրիալ գործակիցներ են, որոնք բնութագրում են լուծիչ-լուծված նյութ փոխազդեցության սաստկությունը:
Այստեղ կարելի է կարևոր եզրակացության հանգել:
(XII.66) հավասարման միջոցով տվյալ կոնցենտրացիայով տվյալ լուծված նյութի համար կարելի է հաշվել ![]() Այն նշանակենք
Այն նշանակենք ![]() և այն որոշել փորձով
և այն որոշել փորձով ![]()
Եթե ![]() ապա լուծույթն իդեալական է: Այսպիսի արդյունք կստացվի, եթե վերցնենք եղեգնաշաքարի 0,1 մոլալանոց լուծույթ: Եղեգնաշաքարը կերակրի աղով (NaCl)
փոխարինելիս կնկատենք, որ
ապա լուծույթն իդեալական է: Այսպիսի արդյունք կստացվի, եթե վերցնենք եղեգնաշաքարի 0,1 մոլալանոց լուծույթ: Եղեգնաշաքարը կերակրի աղով (NaCl)
փոխարինելիս կնկատենք, որ ![]()
Հետևությունը միակն է. կերակրի աղի ջրային լուծույթը իդեալական չէ:
Քացախաթթվի մոլային զանգվածը 60 է: Եթե փորձենք այն որոշել կրիոսկոպիական մեթոդով օգտագործելով բենզոլային լուծույթ, կստացվի. ![]() Ուրեմն, բենզոլում քացախաթթուն (ՔԹ) միաժամանակ գտնվում է և մոնոմերային
Ուրեմն, բենզոլում քացախաթթուն (ՔԹ) միաժամանակ գտնվում է և մոնոմերային ![]() ձևերով (այսինքն մասամբ ասոցված վիճակում): Բենզոլային լուծույթում
ձևերով (այսինքն մասամբ ասոցված վիճակում): Բենզոլային լուծույթում
![]() Եթե վերցնենք ջրային լուծույթ, ապա
Եթե վերցնենք ջրային լուծույթ, ապա ![]() Նույնը դիտվեց NaCl-ի լուծույթի հետ: Բացատրությունը հետևյալն է. ջրային լուծույթում երկուսն էլ դիսոցված են, NaCl
-ը շատ ավելի մեծ չափով:
Նույնը դիտվեց NaCl-ի լուծույթի հետ: Բացատրությունը հետևյալն է. ջրային լուծույթում երկուսն էլ դիսոցված են, NaCl
-ը շատ ավելի մեծ չափով:
Նշանակենք.
![]()
i - ն կոչվում է Վանդ Հոֆֆի գործակից: Եթե i =1, ապա լուծույթը իդեալական է: Եթե i >1, ապա տվյալ լուծիչում լուծված նյութը դիսոցված է և եթե i <1, ապա լուծված նյութն ասոցված է:
Այստեղից հետևում է, որ կրիոմետրիան հարմար և մատչելի մեթոդ է լուծիչում (օրինակ, ջրում) լուծված նյութի դիսոցման կամ ասոցման աստիճանը որոշելու համար:
Եթե 1 մոլ լուծված նյութից ![]() մոլը դիսոցվել է և յուրաքանչյուր դիսոցված մոլեկուլից
մոլը դիսոցվել է և յուրաքանչյուր դիսոցված մոլեկուլից ![]() իոն է առաջացել, ապա լուծույթում լուծված նյութի հետ կապված բոլոր տեսակի մասնիկների քանակը կլինի.
իոն է առաջացել, ապա լուծույթում լուծված նյութի հետ կապված բոլոր տեսակի մասնիկների քանակը կլինի. ![]() մոլ չդիսոցված
մոլ չդիսոցված ![]() (մոլ դիսոցումից առաջացած իոններ)
(մոլ դիսոցումից առաջացած իոններ)
![]() Երբ
Երբ ![]() այդ դեպքում
այդ դեպքում
![]()
Հետևաբար.
![]()
Փորձով i-ն որոշելով և իմանալով
![]() [օրինակ,
[օրինակ, ![]() դեպքում
դեպքում ![]() կարելի է
(XII.71)-ի օգնությամբ հաշվել
կարելի է
(XII.71)-ի օգնությամբ հաշվել ![]() (լուծույթում տվյալ լուծված նյութի դիսոցման կամ ասոցման աստիճանը):
(լուծույթում տվյալ լուծված նյութի դիսոցման կամ ասոցման աստիճանը):
XII.8:2. Լուծույթի եռման ջերմաստիճանի կախումը
լուծույթի կոնցենտրացիայից: Էբուլոսկոպիա
Նկ.XII.18 և 19-ից հետևում է, որ լուծույթի եռման ջերմաստիճանն ավելի բարձր է, քան մաքուր լուծիչինը:
Երևույթի քանակական բացատրության հիմքում այն սկզբունքային դատողություններն են, որոնք հիմք ծառայեցին լուծույթի սառեցման կետի նվազման մեծությունը լուծույթի կոնցենտրացիայի հետ կապելու համար:
Տվյալ դեպքում պետք է քննարկել ![]() հավասարակշռությունը: Ուրեմն, հարկավոր է պարզապես հալման մոլային թաքնված ջերմությունը
հավասարակշռությունը: Ուրեմն, հարկավոր է պարզապես հալման մոլային թաքնված ջերմությունը ![]() փոխարինել գոլորշիացման մոլային թաքնված ջերմությամբ
փոխարինել գոլորշիացման մոլային թաքնված ջերմությամբ ![]() Նմանօրինակ մոտեցում ցուցաբերելով կստացվի.
Նմանօրինակ մոտեցում ցուցաբերելով կստացվի.
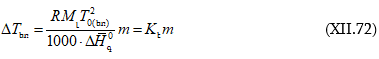
որտեղ ![]() 1 մթն ճնշման տակ մաքուր լուծիչի եռման ջերմաստիճանն է: Ջրի համար
1 մթն ճնշման տակ մաքուր լուծիչի եռման ջերմաստիճանն է: Ջրի համար ![]() Այս դեպքում ևս.
Այս դեպքում ևս.

![]() կոչվում է էբուլոսկոպիական հաստատուն և տվյալ լուծիչի համար հաստատուն մեծություն է:
կոչվում է էբուլոսկոպիական հաստատուն և տվյալ լուծիչի համար հաստատուն մեծություն է:
Աղյուսակ XII.7-ում մի քանի տվյալներ են ներկայացված:
Ջրի համար ![]() նշանակում է, որ եթե 1 մթն ճնշման տակ ջուրը 100oC-ում է եռում, ապա գլյուկոզի 1 մոլալանոց լուծույթը կեռա 100,51oC-ում: Պետք է միշտ նկատի ունենալ, որ
նշանակում է, որ եթե 1 մթն ճնշման տակ ջուրը 100oC-ում է եռում, ապա գլյուկոզի 1 մոլալանոց լուծույթը կեռա 100,51oC-ում: Պետք է միշտ նկատի ունենալ, որ ![]() արժեքը ֆունկցիա է ճնշումից:
արժեքը ֆունկցիա է ճնշումից:
Այս դեպքում էլ ուժի մեջ է (XII.72)-ը:
Էբուլոսկոպիան ևս կիրառվում է անհայտ նյութի մոլային զանգված որոշելու համար:
XII.8:3. Օսմոս: Օսմոտիկական ճնշում:
Նյութի քննարկումն սկսենք հետևյալ փորձի նկարագրությունից:
Ջրով և ջրային լուծույթով լցված Ա և Բ անոթները իրար հետ կոնտակտի մեջ են be կիսաթափանց թաղանթի միջոցով: Ներկայացված սարքը կոչվում է օսմոմետր: Հեղուկները համապատասխանաբար լցված են մինչև a և c նիշերը: Օսմոմետրը տեղադրված է թերմոստատի մեջ:
Փորձը ցույց է տալիս, որ Բ մասում` մազական խողովակի մեջ հեղուկը կբարձրանա մինչև ինչ որ մի d մակարդակ, որը կախված է լուծույթի կոնցենտրացիայից և ջերմաստիճանից:
Նկարագրված փորձից 3 հարց է առաջանում: Ինչու՞.
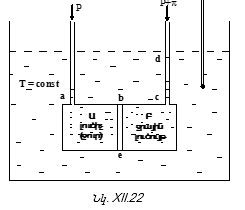
(ա) լուծիչն է be կիսաթափանց թաղանթով միակողմանիորեն անցնում Ա-ից Բ և ոչ թե հակառակը:
(բ) ի վերջո կանգ է առնում լուծիչի ներթափանցումը լուծույթի մեջ:
(գ) լուծույթի կոնցենտրացիայի աճի և ջերմաստիճանի բարձրացման հետ մեծանում է cd սյան բարձրությունը:
Այդ 3 հարցերի պատասխանը տալիս է թերմոդինամիկան:
Հիշենք, որ ըստ փորձնական տվյալների (Բ) մասում հեղուկի ծավալը մեծանում է և ի վերջո այդ աճը դադարում է: Սա նշանակում է, որ տեղի է ունեցել (1) միակողմանի պրոցես. ինչ որ մի քանակով ջուր (Ա) մասից տեղափոխվել է (Բ) մաս անցնելով be թաղանթով և (2) ի վերջո ստեղծվել է հավասարակշռություն:
Հավասարակշռության ստեղծման ընդհանուր պայմանն է.
![]()
Փաստորեն քննարկվելու է բաց համակարգ, որովհետև տեղի ունի նյութի (ջրի) տեղափոխություն:
![]() նշանակենք Ա մասում գտնվող մաքուր ջրի քիմիական պոտենցիալը,
նշանակենք Ա մասում գտնվող մաքուր ջրի քիմիական պոտենցիալը, ![]() թող լինի Բ մասում լուծույթը բաղկացնող ջրի (լուծիչի) քիմիական պոտենցիալը:
թող լինի Բ մասում լուծույթը բաղկացնող ջրի (լուծիչի) քիմիական պոտենցիալը:
Կարող ենք գրել.
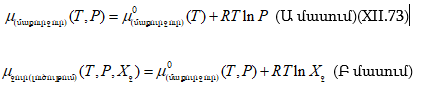
Տվյալ դեպքում ![]() կարելի է նույնացնել ջրի հիդրոստատիկ ճնշման հետ:
կարելի է նույնացնել ջրի հիդրոստատիկ ճնշման հետ:
Սկզբում (մինչև ջրի տրանսպորտը)
![]()
որովհետև ![]()
Պարզված է, որ ցանկացած պրոցես ինքնաբերաբար կընթանա միայն G-ի (կամ ![]() ուղղությամբ): Այս է պատճառը, որ ջուրն է Ա-ից անցնում Բ և ոչ թե հակառակը:
ուղղությամբ): Այս է պատճառը, որ ջուրն է Ա-ից անցնում Բ և ոչ թե հակառակը:
Փորձի սկզբում be թաղանթը գտնվում էր P հիդրոստատիկ ճնշման տակ:
Ջուրը Ա-ից Բ տեղափոխվելով Բ-ում հիդրոստատիկ ճնշումը աճեց և P-ից դարձավ ![]() , որի հետևանքով Բ-ում P-ն մեծացավ, հետևաբար և
, որի հետևանքով Բ-ում P-ն մեծացավ, հետևաբար և ![]() -ն:
-ն:
Եթե սկզբում ![]() էր, ապա հավասարակշռություն ստեղծվելու պահից
էր, ապա հավասարակշռություն ստեղծվելու պահից ![]() (
(![]() գործնականորեն հաստատուն է մնում, որովհետև շատ փոքր է տեղափոխված ջրի քանակը):
գործնականորեն հաստատուն է մնում, որովհետև շատ փոքր է տեղափոխված ջրի քանակը):
Բ մասում վերջում.
![]()
(տե’ս XII.73)-ը: Ջրի տրանսպորտը դադարում է այն պահին, երբ.
![]()
Հետևաբար.
![]()
որտեղից.
![]()
Իզոթերմային պրոցեսի դեպքում
![]()
Ինտեգրելով կստանանք.
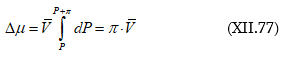
![]() լուծույթի մոլային ծավալն է: Քանի որ լուծույթը նոսր է և տեղափոխված ջրի քանակն էլ փոքր է կարելի է ընդունել, որ
լուծույթի մոլային ծավալն է: Քանի որ լուծույթը նոսր է և տեղափոխված ջրի քանակն էլ փոքր է կարելի է ընդունել, որ ![]() լուծիչի մոլային ծավալն է, այսինքն.
լուծիչի մոլային ծավալն է, այսինքն.
![]()
Զուգորդելով
(XII.76) և (XII.77) հավասարումները և նկատի առնելով, որ ![]() կստացվի.
կստացվի.
![]()
Նոսր լուծույթների դեպքում ![]() Հետևաբար.
Հետևաբար.

Արդեն այս հավասարման մեջ c - ն լուծված նյութի մոլային կոնցենտրացիան է (մոլ/լ):
Ամփոփենք քննարկված նյութը:
Շնորհիվ մաքուր ջրում և ջրային լուծույթում ջրի քիմիական պոտենցիալների տարբերությանը մաքուր ջրից ջուրը միակողմանիորեն կիսաթափանց թաղանթի միջով անցնում է դեպի ջրային լուծույթ: Այս երևույթը կոչվում է օսմոս: Այն վերջիվերջո դադարում է, որովհետև լուծույթի կողմից թաղանթի վրա հիդրոստատիկ ճնշումը դառնում է ![]() այն ինչ մաքուր ջրի կողմից այն գործնականորեն մնացել է P:
Այդ հավելյալ
այն ինչ մաքուր ջրի կողմից այն գործնականորեն մնացել է P:
Այդ հավելյալ ![]() կոչվում է օսմոտիկական ճնշում, որը և արգելակում է օսմոսը:
(XII.80)-ից հետևում է, որ
կոչվում է օսմոտիկական ճնշում, որը և արգելակում է օսմոսը:
(XII.80)-ից հետևում է, որ ![]()
Այսպիսով առաջադրված երեք հարցերն էլ ստացան իրենց հիմնավորված պատասխանները: (XII.80)-ը հայտնի է Վանդ Հոֆֆի անունով:
Փորձերը ցույց են տալիս, որ ![]() որը նույնն է ինչ որ գազային ունիվերսալ հաստատունը:
որը նույնն է ինչ որ գազային ունիվերսալ հաստատունը:
Հետևաբար, (XII.80)-ը նույնանում է իդեալական գազերի վիճակի հավասարման հետ: Այս փաստը հնարավորություն է տալիս հետևյալ կերպ մեկնաբանել օսմոտիկական ճնշումը: ![]() այն ճնշումն է, որով կներգործի n
մոլ նյութը, եթե լինի իդեալական գազ և T
K -ում զբաղեցնի V
ծավալ:
այն ճնշումն է, որով կներգործի n
մոլ նյութը, եթե լինի իդեալական գազ և T
K -ում զբաղեցնի V
ծավալ:
Եթե փորձենք մթնոլորտային ճնշումը փոխանակ սնդիկի` ջրի սյունով արտահայտել, ապա այն կհամապատասխանի.
![]()
որտեղից
![]()
Ուրեմն, 1 մթն ճնշումը հավասար է 10,2 մ ջրի սյան ցուցաբերած հիդրոստատիկ ճնշմանը:
Այժմ տեսնենք, թե 298,2К-ում 1M շաքարի լուծույթը ինչպիսի՞ օսմոտիկական ճնշում է ստեղծում. ![]() Այս ճնշումը համարժեք է
Այս ճնշումը համարժեք է ![]() Այս է պատճառը, որ լուծույթի օսմոտիկական ճնշումը որոշելու համար անհրաժեշտ է օգտագործել շատ նոսր լուծույթներ: Այսպես, սենյակային ջերմաստիճանում
Այս է պատճառը, որ լուծույթի օսմոտիկական ճնշումը որոշելու համար անհրաժեշտ է օգտագործել շատ նոսր լուծույթներ: Այսպես, սենյակային ջերմաստիճանում ![]() լուծույթի ստեղծած օսմոտիկական ճնշումը կլինի
լուծույթի ստեղծած օսմոտիկական ճնշումը կլինի ![]() որը միանգամայն չափելի մեծություն է (նկ.XII.22-ում cd բարձրության առավելագույն արժեքը կլինի):
որը միանգամայն չափելի մեծություն է (նկ.XII.22-ում cd բարձրության առավելագույն արժեքը կլինի):
Օսմոսի հետևանքով և մազական խողովակով (մազական երևույթներ) ջրի բարձրացումով է ապահովվում բույսերում, այդ թվում շատ բարձր ծառերի բոլոր մասերի մատակարարումը ջրով և տարբեր նյութերի ջրային լուծույթներով: (Այստեղ չենք քննարկելու «Կապիլյարային էֆեկտը»):
Օսմոսի կարևորությունն ակնհայտ է նաև կենդանի օրգանիզմի կենսագործունեության համար:
Կենդանական բջիջները յուրահատուկ քիմիական ռեակտորներ են, որոնք շրջապատից բաժանված են հատուկ կառուցվածքի կենսաբանական մեմբրանով:
Աղի բան ուտելու հետևանքով բջիջներից դուրս համեմատաբար խիտ լուծույթ է առաջանում: Ըստ վերևում շարադրվածի ջուրը նոսր լուծույթից ավելի խիտն է տեղափոխվում. բջիջները ջրազրկվում են, որի հետևանքով ջուր խմելու անհրաժեշտություն` ծարավի զգացմունք է առաջանում: Կամ վարունգը աղաջրի մեջ դնելուց կնճռոտվում է, որը հետևանք է ջրազրկման:
Ներարկվող դեղերը ջրային լուծույթներ են: Ներարկման պահին տեղական նոսրացում է առաջանում: Ասվածի համաձայն, այս դեպքում ջուրը պետք է թափանցի բջիջների մեջ: Բջիջում այն աստիճանի կարող է աճել օսմոտիկական ճնշումը, որ այն պատճառ դառնա բջիջի պատռվելուն: Այս խիստ վտանգավոր երևույթը կանխելու համար ներարկման համար ֆիզիոլոգիական լուծույթ է օգտագործվում ![]() Հաշվի է առնվում նաև լուծույթի pH-ը: Ֆիզիոլոգիական լուծույթի ստեղծած օսմոտիկական ճնշումը գործնականորեն հավասար է օրգանիզմի առանձին մասերի, օրինակ, արյունատար անոթների ցուցաբերած օսմոտիկական ճնշմանը:
Հաշվի է առնվում նաև լուծույթի pH-ը: Ֆիզիոլոգիական լուծույթի ստեղծած օսմոտիկական ճնշումը գործնականորեն հավասար է օրգանիզմի առանձին մասերի, օրինակ, արյունատար անոթների ցուցաբերած օսմոտիկական ճնշմանը:
Այն լուծույթները, որոնք հավասար օսմոտիկական ճնշում են ցուցաբերում կոչվում են իզոտոնիկ: Հիպերտոնիկ է այն լուծույթը, որը ցուցաբերում է ավելի մեծ օսմոտիկական ճնշում, քան պայմանականորեն ստանդարտ լուծույթի օսմոտիկական ճնշումն է: Հակառակ դեպքում լուծույթը կոչվում է հիպոտոնիկ:
Իդեալական է համարվում այն լուծույթը, որի ցուցաբերած օսմոտիկական ճնշումը ներկայացվում է (XII.80) հավասարումով: Եթե չի նկարագրվում, ապա այդպիսի լուծույթը համարվում է ոչ իդեալական: Այս դեպքում (XII.80)-ի փոխարեն պիտի գրել.
![]()
որտեղ i-ն` Վանդ Հոֆֆի գործակիցն է, որի իմաստն արդեն քննարկվել է: Այն կոչվում է նաև օսմոտիկական գործակից:
Այս գլխում քննարկված բոլոր երևույթներում ![]() մի ընդհանրություն կա. փորձով որոշվող այդ մեծությունների արժեքներն անմիջապես կախված են լուծված նյութի քանակից, հետևաբար և լուծույթում առկա մասնիկների (մոլեկուլներ, իոններ) թվից` անկախ լուծված նյութի բնույթից: Հենց այս հատկությունն է, որը համարվում է կոլիգատիվ:
մի ընդհանրություն կա. փորձով որոշվող այդ մեծությունների արժեքներն անմիջապես կախված են լուծված նյութի քանակից, հետևաբար և լուծույթում առկա մասնիկների (մոլեկուլներ, իոններ) թվից` անկախ լուծված նյութի բնույթից: Հենց այս հատկությունն է, որը համարվում է կոլիգատիվ:
Նորից վերադառնանք (XII.80) հավասարմանը:
Այն մեծ կիրառություն ունի տարբեր նյութերի, մասնավորաբար արհեստական և բնական, նաև կենսաբանական պոլիմերների այսպես կոչվող «միջին թվային մոլեկուլային զանգվածը» որոշելու համար:
![]()
որտեղ m-ը քննարկվող նյութի զանգվածն է (գ կամ կգ), d-ն հետազոտվող լուծույթի խտությունն ![]() Հեշտ է նկատել, որ կազմելով
Հեշտ է նկատել, որ կազմելով
![]() գրաֆիկ պետք է ուղիղ գիծ ստացվի, որի անկյան գործակցից կարելի է հեշտությամբ որոշել
գրաֆիկ պետք է ուղիղ գիծ ստացվի, որի անկյան գործակցից կարելի է հեշտությամբ որոշել ![]()
Ռեալ համակարգերի նկատմամբ կրիոսկոպիայի կիրառումը ապահովելու համար առաջարկվում է օգտագործել վիրիալ հավասարում (XII.69):
Այս դեպքում ևս պետք է օգտվել վիրիալ հավասարումից.
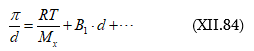
Հաճախ բավարար է առաջին երկու անդամներից օգտվելը: Այս դեպքում
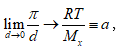 որտեղ а
–ն y=a+bx
տիպի հավասարման ազատ անդամն է:
որտեղ а
–ն y=a+bx
տիպի հավասարման ազատ անդամն է:
Ինչ վերաբերում է ![]() վիրիալ գործակցին, ապա այդ անդամի մեծությունը պատկերացում կարող է տալ լուծված-լուծիչ փոխազդեցության մասին:
վիրիալ գործակցին, ապա այդ անդամի մեծությունը պատկերացում կարող է տալ լուծված-լուծիչ փոխազդեցության մասին:
1. Ա և Բ հեղուկները իդեալական լուծույթ են առաջացնում: 25օC-ում մաքուր A-ի սեփական գոլորշիների ճնշումը հավասար է 100,00 մմ սնդիկի սյան: Միևնույն ջերմաստիճանում 1,00 գ B և 10,0 գ A պարունակող լուծույթի վրա գոլորշիների ճնշումը 95,00 մմ սնդիկի սյան է հավասար: Ինչպիսի՞ն է լուծույթում B և A նյութերի մոլային զանգվածների հարաբերությունը:
2.
Որոշել ![]() լուծույթում
լուծույթում ![]() -ի ակտիվության գործակիցը, եթե հայտնի է, որ 0,0250
մոլ բաժին
-ի ակտիվության գործակիցը, եթե հայտնի է, որ 0,0250
մոլ բաժին ![]() և 0,9750
մոլ բաժին
և 0,9750
մոլ բաժին ![]() պարունակող լուծույթի վրա
պարունակող լուծույթի վրա ![]() մմ սնդիկի սյուն: Փորձի ջերմաստիճանում
մմ սնդիկի սյուն: Փորձի ջերմաստիճանում ![]() մմ սնդիկի սյուն: Ընդունել, որ մաքուր հեղուկ բրոմը գտնվում է ստանդարտ վիճակում:
մմ սնդիկի սյուն: Ընդունել, որ մաքուր հեղուկ բրոմը գտնվում է ստանդարտ վիճակում:
3.
Աղյուսակում բերված տվյալները վերաբերում են 20oC-ում ![]() լուծույթի վրա առանձին բաղադրիչների սեփական գոլորշիների ճնշումներին` կախված լուծույթում էթանոլի բաղադրությունից` արտահայտված զանգվածային բաժնով (տոկոսներով):
լուծույթի վրա առանձին բաղադրիչների սեփական գոլորշիների ճնշումներին` կախված լուծույթում էթանոլի բաղադրությունից` արտահայտված զանգվածային բաժնով (տոկոսներով):
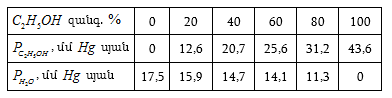
Որոշել ըստ զանգվածի 40%![]() պարունակող լուծույթում յուրաքանչյուր բաղադրիչի ակտիվությունը և ակտիվության գործակիցը: Մաքուր վիճակում յուրաքանչյուր բաղադրիչի վիճակը համարել «ստանդարտ»:
պարունակող լուծույթում յուրաքանչյուր բաղադրիչի ակտիվությունը և ակտիվության գործակիցը: Մաքուր վիճակում յուրաքանչյուր բաղադրիչի վիճակը համարել «ստանդարտ»:
4.
80oC-ում էթիլենգլիկոլի մոնոմեթիլեթերի և մոնոէթիլեթերի գոլորշիների ճնշումներն են. 154,4
և 102,2 մմ սնդիկի սյուն: Կոնցենտրացիոն ամբողջ տիրույթի համար որոշել գազ ֆազի բաղադրությունը (Y)
որպես ֆունկցիա հեղուկ ֆազի բաղադրությունից (X)
ընդունելով, որ այդ երկկոմպոնենտ լուծույթը իդեալական է: Քննարկել ![]() դիագրամը:
դիագրամը:
5. Էթիլբենզոլ + ստիրոլ զույգը ենթարկվում է Ռաուլի օրենքին: Պարզված է, որ
Էթիլբենզոլ (ԷԲ) համար
![]()
ստիրոլ (Ս) համար
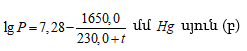
Այս տվյալների հիման վրա
գրաֆիկորեն քննարկել ![]() կախումները:
կախումները: ![]() հեղուկ ֆազի
բաղադրությունն է,
հեղուկ ֆազի
բաղադրությունն է, ![]() գազ ֆազի: Ընդունել,
որ
գազ ֆազի: Ընդունել,
որ ![]() սնդիկի սյան ճնշման տակ
սնդիկի սյան ճնշման տակ ![]()
6.
760 մմ սնդիկի սյան ճնշման տակ ![]() խառնուրդի համար ջերմաստիճանից կախված
ստացված են հետևյալ հավասարակշռական բաղադրությունները: Նշված ջերմաստիճաններում են
որոշվել հեղուկների վրա գոլորշիների ճնշումները.
խառնուրդի համար ջերմաստիճանից կախված
ստացված են հետևյալ հավասարակշռական բաղադրությունները: Նշված ջերմաստիճաններում են
որոշվել հեղուկների վրա գոլորշիների ճնշումները.
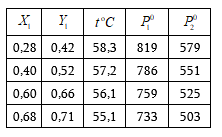
(ա) ցույց տալ, որ այս լուծույթը իդեալական չէ,
(բ) հաշվել նշված բաղադրությունների համար այդ 2 նյութերի ակտիվության գործակիցները:
7. Ճշգրիտ չափումները ցույց են տվել, որ 20,036oC
-ում մաննիտի 0,5 մոլալ ջրային լուծույթի վրա ջրային գոլորշիների ճնշումը 0,156 մմ
սնդիկի սյունով սպասվելիքից ցածր է ![]() Հաշվի առնելով,
որ 20,036oC –ում
Հաշվի առնելով,
որ 20,036oC –ում ![]() սնդիկի սյուն,
ցույց տալ, որ այդ լուծույթը ենթարկվում է Ռաուլի օրենքին:
սնդիկի սյուն,
ցույց տալ, որ այդ լուծույթը ենթարկվում է Ռաուլի օրենքին:
8.
Հալման կետում (86,9oC)
պ - ![]() հալման
թաքնված ջերմությունը 3160 կալ/մոլ է: Ինչպիսի՞ն է 20oC -ում բենզոլում
պ-դիբրոմբենզոլի լուծելիությունը, եթե ստացվող լուծույթը իդեալական է:
հալման
թաքնված ջերմությունը 3160 կալ/մոլ է: Ինչպիսի՞ն է 20oC -ում բենզոլում
պ-դիբրոմբենզոլի լուծելիությունը, եթե ստացվող լուծույթը իդեալական է:
9.
Հայտնի է, որ ![]() խառնուրդը իդեալական լուծույթ է:
30oC –ում
խառնուրդը իդեալական լուծույթ է:
30oC –ում ![]()
![]() Որոշել
այդ 2 հեղուկների պարցիալ ճնշումները, եթե հավասարակշռության մեջ գտնվող համակարգում
հեղուկ ֆազում 2 բաղադրիչների զանգվածներն իրար հավասար են:
Որոշել
այդ 2 հեղուկների պարցիալ ճնշումները, եթե հավասարակշռության մեջ գտնվող համակարգում
հեղուկ ֆազում 2 բաղադրիչների զանգվածներն իրար հավասար են: ![]() և
և ![]()
10.
Նավթալինը հալվում է 80,2օC -ում: Հալման թաքնված
մոլային ջերմությունը 4540 կալ/մոլ է: Ինչի՞ է հավասար նավթալինի լուծելիությունը իդեալական լուծիչում 20օC -ում ![]() Բենզոլում
Բենզոլում
![]() տոլուոլում`
0,224:
տոլուոլում`
0,224:
11. 35օC -ում ացետոն + քլորոֆորմ խառնուրդների համար որոշված է և ացետոնի և քլորոֆորմի գոլորշիների ճնշման կախումը լուծույթում քլորոֆորմի մոլային բաժնից
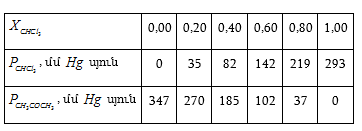
(ա) ենթարկվու՞մ է արդյոք այս զույգը Ռաուլի օրենքին: Եթե ոչ ապա ինչպիսի՞ն է շեղումը,
(բ) Գրաֆիկորեն որոշել Հենրիի հաստատունը:
12. 19,94oC-ում ջրում ![]() աբսորբցիայի Բունզենի գործակիցը հավասար է 0,031 մթն-ի: 1 մթն
ճնշման տակ գտնվող 21%
աբսորբցիայի Բունզենի գործակիցը հավասար է 0,031 մթն-ի: 1 մթն
ճնշման տակ գտնվող 21% ![]() և 79%
և 79% ![]() (ըստ ծավալի) բաղադրությամբ օդից քանի՞ մոլ
(ըստ ծավալի) բաղադրությամբ օդից քանի՞ մոլ ![]() կլուծվի 1 լ ջրում:
կլուծվի 1 լ ջրում:
13. 30oC--ում և 1 մթն ճնշման տակ 244,0 մլ ջրում
2,265 մլ He է լուծվում: Նշված պայմանում He-ի համար որոշել Բունզենի
գործակիցը ![]()
14.
0oC -ում և
10oC -ում ջրում ![]() համար աբսորբցիայի
Բունզենի գործակիցը համապատասխանաբար 0,0489 և 0,0380
համար աբսորբցիայի
Բունզենի գործակիցը համապատասխանաբար 0,0489 և 0,0380 ![]() Որոշել
ջրում թթվածնի լուծման ջերմությունը
Որոշել
ջրում թթվածնի լուծման ջերմությունը ![]()
15.
Ջրագազի բաղադրությունն է. ![]() 20oC-ում և 1
մթն ճնշման տակ յուրաքանչյուր գազից քանի՞ գ կլուծվի
20oC-ում և 1
մթն ճնշման տակ յուրաքանչյուր գազից քանի՞ գ կլուծվի ![]()
Հենրիի գործակիցներն են ![]()
![]()
![]()
16.
25oC-ում և 1 մթն ճնշման տակ 100 գ ջրում
0,00515 գ Ar է լուծվում: Օգտվելով Բունզենի գործակցից որոշել նշված պայմաններում
Ar –ի լուծելիությունը ջրում: ![]()
17. 25oC -ում հեղուկ էթանի գոլորշիների ճնշումը 42 մթն է: Ինչի՞ է հավասար այդ ջերմաստիճանում և 1 մթն ճնշման տակ որևէ հեղուկում լուծված հեղուկ էթանի մոլային բաժինը, եթե իդեալական լուծույթ է առաջանում:
18.
Ռեակցիոն միջավայրից խինոլինը հեռացնելու համար օգտագործվել է ջրային
գոլորշիներով թորման մեթոդը: (1)-ով նշանակենք ջրային գոլորշիները և (2)-ով խինոլինինը
![]() Ստացվել
են հետևյալ տվյալները.
Ստացվել
են հետևյալ տվյալները.
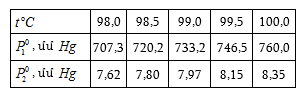
(ա) Որոշել 740 մմ Hg սյան ընդհանուր ճնշման տակ գտնվող խառնուրդի եռման ջերմաստիճանը
(բ) 1000 գ ջրային գոլորշիով քա՞նի գրամ խինոլին
կարելի է տեղափոխել: Ջուրը և խինոլինը գործնականորեն իրար մեջ չեն լուծվում: ![]()
19.
18oC-ում քլորոֆորմում
մեթիլամինի լուծելիությունը 8,5 անգամ ավելի մեծ է քան ջրում: Քանի՞ գ ![]() կմնա 1000 մլ
կմնա 1000 մլ ![]() -ում եթե օգտագործելով
800 մլ ջուր կատարենք հաջորդական արտալուծում: Ելային լուծույթի բաղադրությունն է.
-ում եթե օգտագործելով
800 մլ ջուր կատարենք հաջորդական արտալուծում: Ելային լուծույթի բաղադրությունն է.
![]()
(ա) յուրաքանչյուր անգամ 200 մլ ջուր օգտագործելով 4 անգամ
(բ) յուրաքանչյուր անգամ 400 մլ ջուր օգտագործելով 2 անգամ
20.
0,0961 գ կամֆորային 0,0113 գ ֆենանտրեն են խառնել: Կամֆորայի հալման
ջերմաստիճանը նվազել է 27oC-ով: Ինչի՞ է հավասար ֆենանտրենի մոլային
զանգվածը: Կամֆորայի կրիոսկոպիական հաստատունը` ![]()
21.
Տետրաիզոամիլամոնիումի թիոցիանատի 0,077 մոլալանոց բենզոլային լուծույթը
պնդացել է 0,016օC -ում: Ի՞նչ եզրակացության կարելի է հանգել այս
տվյալների քննարկումից: ![]()
22. Ուսումնասիրված է քացախաթթվի բենզոլային լուծույթների սառեցման կետի կախումը քացախաթթվի կոնցենտրացիայից.
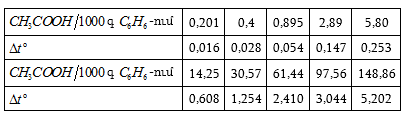
![]() Յուրաքանչյուր լուծույթի համար որոշել
քացախաթթվի թվացող մոլային զանգվածը: Ի՞նչ եզրակացության կարելի է հանգել:
Յուրաքանչյուր լուծույթի համար որոշել
քացախաթթվի թվացող մոլային զանգվածը: Ի՞նչ եզրակացության կարելի է հանգել: ![]() և
և ![]()
23. Բենզոլը հալվում է 5,4oC -ում, իսկ հալման
թաքնված ջերմությունը 30,2 կալ/գ է: Տրիֆենիլ մեթանի բենզոլային լուծույթը, որը ստացվել
է 1000 գ բենզոլում 6,054 գ ![]() լուծելիս,
սառչում է մաքուր բենզոլի սառեցման կետից 0,1263oC-ով ավելի ցածր
ջերմաստիճանում: Որոշել լուծված նյութի մոլային զանգվածը:
լուծելիս,
սառչում է մաքուր բենզոլի սառեցման կետից 0,1263oC-ով ավելի ցածր
ջերմաստիճանում: Որոշել լուծված նյութի մոլային զանգվածը: ![]() գ/մոլ:
գ/մոլ:
24.
Էլեմենտային անալիզը ցույց է տվել, որ ինչ որ մի անհայտ նյութի
պարզագույն բանաձևը ![]() Այդ նյութից 1 գ 100 գ ջրում լուծելով
ստացված լուծույթը սառչում է -0,103oC -ում: (ա) որոշել այդ նյութի
մոլային զանգվածը և (բ) պարզել այդ նյութի մոլեկուլային բանաձևը:
Այդ նյութից 1 գ 100 գ ջրում լուծելով
ստացված լուծույթը սառչում է -0,103oC -ում: (ա) որոշել այդ նյութի
մոլային զանգվածը և (բ) պարզել այդ նյութի մոլեկուլային բանաձևը: ![]()
25.
28oC-ում ջրային լուծույթի վրա ջրային գոլորշիների
ճնշումը 28,00 մմ է, իսկ նույն ջերմաստիճանում մաքուր ջրի համար ![]() Գնահատել
այդ լուծույթի սառեցման և եռման ջերմաստիճանները:
Գնահատել
այդ լուծույթի սառեցման և եռման ջերմաստիճանները:
26.
Նավթալինի հալման ջերմաստիճանը 80,1oC է: Երբ
20 գ նավթալինում լուծված է 0,1106 գ անտրանիլաթթու (օրթո-ամինոբենզոյական թթու),
լուծույթի սառեցման կետը նվազում է 0,278օ -ով: Որոշել նավթալինի կրիոսկոպիական
հաստատունը: ![]()
27.
Անհայտ նյութը պարունակում է 10,13% C և 89,87%Cl:
Այդ նյութի մոլային զանգվածը որոշել են էբուլոսկոպիական մեթոդով: Որպես լուծիչ վերցվել
է 96,8 գ ![]() որի համար
որի համար
![]() Ստացվել
են հետևյալ տվյալները.
Ստացվել
են հետևյալ տվյալները.
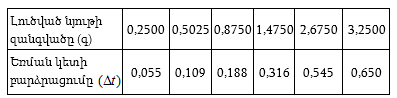
Որոշել (ա) այդ նյութի մոլային զանգվածը (բ) ի՞նչ նյութ է:
28.
Նյութի մոլային զանգվածը որոշել են օսմոմետրիայով: Այլ մեթոդներ
օգտագործելով ստացվել է. M = 25000: 25oC-ում 100 մլ լուծույթի ![]() Քանի՞ գ
նյութ է լուծված եղել 100 մլ լուծույթում:
Քանի՞ գ
նյութ է լուծված եղել 100 մլ լուծույթում:
29. 25oC -ում որոշվել է պոլիվինիլքլորիդի ցիկլոհեքսանային լուծույթի օսմոտիկական ճնշումը: Ստացվել են հետևյալ տվյալները.

d - ն ցույց է տալիս, թե 1լ լուծիչում քանի՞ գրամ պոլիմեր է լուծված:
h - ը օսմոմետրի մազական խողովակով
բարձրացած լուծույթի բարձրությունն է: Լուծույթի միջին խտությունը` ![]() Հաշվել
պոլիվինիլքլորիդի միջին մոլային զանգվածը:
Հաշվել
պոլիվինիլքլորիդի միջին մոլային զանգվածը:
30. Հեմոգլոբինի մոլային զանգվածը որոշել են 298 K-ում 1 լ ջրում 20 գ հեմոգլոբին պարունակող լուծույթի օսմոտիկական ճնշումը չափելով: Հավասարակշռություն է ստեղծվել, երբ օսմոմետրի մազական խողովակում լուծույթը բարձրացել է 77,8 մմ (7,78 սմ): Այս տվյալների օգնությամբ հաշվել (որոշել) հեմոգլոբինի մոլային զանգվածը:
31.
Որոշել ![]() լուծույթի և հավասարակշռության մեջ
գտնվող գոլորշու բաղադրությունները: Այդ լուծույթը P = 1 մթն ճնշման տակ եռում է 100oC-ում:
100oC-ում
լուծույթի և հավասարակշռության մեջ
գտնվող գոլորշու բաղադրությունները: Այդ լուծույթը P = 1 մթն ճնշման տակ եռում է 100oC-ում:
100oC-ում ![]()
32.
Անհայտ մոլային զանգվածով 0,250 գ ինչ որ
չցնդող մի նյութ լուծել են 40,0 գ ![]() մեջ: Լուծիչի
եռման կետը բարձրացել է 0,357oC-ով: Ինչի՞ է
հավասար այդ անհայտ նյութի մոլային զանգվածը:
մեջ: Լուծիչի
եռման կետը բարձրացել է 0,357oC-ով: Ինչի՞ է
հավասար այդ անհայտ նյութի մոլային զանգվածը: ![]() աստ(կգ/մոլ):
աստ(կգ/մոլ):
33.
25օC-ում (298 K) արյան օսմոտիկական ճնշումը
![]() 7,7 մթն է: Գլյուկոզի
7,7 մթն է: Գլյուկոզի ![]() ի՞նչ կոնցենտրացիայի
լուծույթը կլինի իզոտոնիկ: Կոնցենտրացիան արտահայտել մոլ/լ-ով (M) և զանգվածային
բաժնով (G): Լուծույթի խտությունը
ի՞նչ կոնցենտրացիայի
լուծույթը կլինի իզոտոնիկ: Կոնցենտրացիան արտահայտել մոլ/լ-ով (M) և զանգվածային
բաժնով (G): Լուծույթի խտությունը ![]() է: Ինչպիսի՞ն կլինեն տվյալները,
եթե գլյուկոզը փոխարինվի NaCl-ով:
է: Ինչպիսի՞ն կլինեն տվյալները,
եթե գլյուկոզը փոխարինվի NaCl-ով:
34.
![]() -ում 0,2 գ հեմոգլոբինը լուծել են 20,0 մլ ջրում: Այդ լուծույթի ցուցաբերած օսմոտիկական
ճնշումը`
-ում 0,2 գ հեմոգլոբինը լուծել են 20,0 մլ ջրում: Այդ լուծույթի ցուցաբերած օսմոտիկական
ճնշումը` ![]() սյան է
հավասար: Որոշել հեմոգլոբինի մոլային զանգվածը:
սյան է
հավասար: Որոշել հեմոգլոբինի մոլային զանգվածը:
35.
100 գ էթիլենգլիկոլը ![]() լուծել
են 900 գ ջրում: Որոշել այդ լուծույթի
սառեցման և եռման ջերմաստիճանները (
լուծել
են 900 գ ջրում: Որոշել այդ լուծույթի
սառեցման և եռման ջերմաստիճանները (![]() և
և ![]() ): Ջրի համար
): Ջրի համար
![]() աստ(կգ/մոլ)
և
աստ(կգ/մոլ)
և ![]() աստ(կգ/մոլ):
աստ(կգ/մոլ):
ԳԼՈՒԽ XIII
ՖԱԶԱՅԻՆ ՀԱՎԱՍԱՐԱԿՇՌՈՒԹՅՈՒՆԸ ՄԻԱԿՈՄՊՈՆԵՆՏ ԵՎ ԲԱԶՄԱԿՈՄՊՈՆԵՆՏ
ՀԱՄԱԿԱՐԳԵՐՈՒՄ: ԳԻԲՍԻ ՖԱԶԵՐԻ ԿԱՆՈՆԸ
XIII-1. ԸՆԴՀԱՆՈՒՐ ՀԱՍԿԱՑՈՒԹՅՈՒՆՆԵՐ
Նորից վերադառնանք «ֆազ» հասկացությանը:
Ֆազը հետերոգեն համակարգի հոմոգեն մասն է: Այն համակարգի միևնույն բաղադրությամբ և քանակից անկախ, վիճակը բնութագրող միևնույն ինտենսիվ հատկություններ ունեցող մասերի ամբողջությունն է: Հոմոգեն համակարգի զբաղեցրած ծավալում նշված հատկությունները կամ հաստատուն են, կամ փոխվում են անընդհատորեն:
Ֆազը կազմված է շատ մեծ թվով մասնիկներից և կոնտակտի մեջ գտնվող այլ ֆազերից սահմանազատված է որոշակի մակերեսով (մակերևույթով): Ֆազերն իրարից տարբերվում են նաև իրենց օպտիկական հատկություններով:
Եթե ցանկացած թվով նյութերից և ֆազերից կազմված համակարգը գտնվում է հավասարակշռական վիճակում, ապա իրար հետ միաժամանակ գոյակցող ֆազերի թիվը որոշվում է Գիբսի ֆազերի կանոնով: Այս կանոնից հետևում է, որ իրար հետ հավասարակշռության մեջ գտնվող ֆազերի թիվը կամայական չի կարող լինել:
Համակարգի բաղադրիչ մաս է կոչվում տվյալ համակարգի կազմության մեջ մտնող մակրոսկոպիական մաքուր նյութը, որը համակարգից դուրս էլ գոյություն պետք է ունենա: Օրինակ, NaCl-ի ջրային լուծույթը կազմված է ջրից և նատրիումի քլորիդից: Բայց լուծույթում կան նաև ![]() իոններ: Սակայն այս իոնները բաղադրիչներ չեն, որովհետև համակարգից դուրս չեն կարող առանձին-առանձին գոյություն ունենալ:
իոններ: Սակայն այս իոնները բաղադրիչներ չեն, որովհետև համակարգից դուրս չեն կարող առանձին-առանձին գոյություն ունենալ:
Եթե համակարգում քիմիական ռեակցիա չի ընթանում, ապա դրանում յուրաքանչյուր բաղադրիչի քանակը (կոնցենտրացիան) անկախ է մյուս բաղադրիչների քանակներից: Այս դեպքում հավասարակշռության մեջ գտնվող յուրաքանչյուր ֆազի բաղադրությունը որոշվում է բոլոր բաղադրիչների քանակով: Մասնավոր դեպքում, երբ համակարգի բաղադրությունն արտահայտվում է մոլային բաժիններով, ապա.
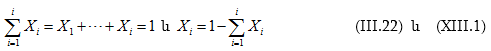
Եթե տվյալ համակարգում քիմիական հավասարակշռություն է ստեղծված, այդ դեպքում որևէ մի բաղադրիչի քանակի փոփոխությունը առաջ կբերի ռեակցիային մասնակցող մյուս բաղադրիչների քանակների փոփոխություն:
Անկախ են կոչվում այն բաղադրիչները, որոնց քանակները (կոնցենտրացիաները) պայմանավորում են հավասարակշռության վիճակում գտնվող յուրաքանչյուր ֆազի բաղադրությունը: Անկախ բաղադրիչները նաև կոմպոնենտ են կոչվում: Համակարգում անկախ բաղադրիչների ընտրությունը կամայական է:
Համակարգի թերմոդինամիկական հատկությունները որոշվում են կոմպոնենտների թվով և ոչ թե դրանց քիմիական բնույթով, այսինքն նրանով, թե որ՞ նյութն է (նյութերն են) ընտրված որպես կոմպոնենտ:Օրինակ, ![]() նյութերից կազմված համակարգում 3 բաղադրիչ կա: Բայց այդ երեքից միայն երկուսը կարող են լինել անկախ, բայց որ՞ երկուսը, դա որոշիչ չէ:
նյութերից կազմված համակարգում 3 բաղադրիչ կա: Բայց այդ երեքից միայն երկուսը կարող են լինել անկախ, բայց որ՞ երկուսը, դա որոշիչ չէ:
Եթե համակարգում քիմիական ռեակցիա չի ընթանում, ապա.
![]()
Օրինակ, ![]() Սա երկկոմպոնենտ համակարգ է:
Սա երկկոմպոնենտ համակարգ է:
Իսկ եթե համակարգում քիմիական ռեակցիա է ընթանում, այդ դեպքում.
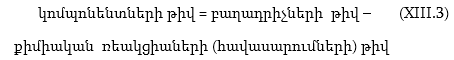
Քիմիական ռեակցիաների թիվը որոշվում է համակարգում բաղադրիչների հավասարակշռական կոնցենտրացիաներն (քանակներն) իրար հետ կապող հավասարումների թվով:
«Կոմպոնենտների թիվ» ասելով կարելի է հասկանալ նաև բաղադրիչների այն նվազագույն թիվը, որը բավարար է որոշելու համար հավասարակշռական վիճակում գտնվող համակարգի ցանկացած ֆազի բաղադրությունը:
Քննարկենք մի քանի դեպքեր նշված հասկացություններն ավելի շոշափելի դարձնելու համար:
1. ![]() ջրալուծելի, չհիդրոլիզվող աղ (էլեկտրոլիտ) է: Ըստ (XIII.2)-ի այս համակարգում կոմպոնենտների թիվը երկուսի է հավասար (բինար կամ երկկոմպոնենտ համակարգ): Եթե նույնիսկ հաշվի առնենք այդ աղի դիսոցումը.
ջրալուծելի, չհիդրոլիզվող աղ (էլեկտրոլիտ) է: Ըստ (XIII.2)-ի այս համակարգում կոմպոնենտների թիվը երկուսի է հավասար (բինար կամ երկկոմպոնենտ համակարգ): Եթե նույնիսկ հաշվի առնենք այդ աղի դիսոցումը. ![]() (ա) որպես քիմիական ռեակցիա (հավասարում), ապա էլեկտրոլիտի լուծույթի չեզոքությունից մի հավասարում էլ է հետևում.
(ա) որպես քիմիական ռեակցիա (հավասարում), ապա էլեկտրոլիտի լուծույթի չեզոքությունից մի հավասարում էլ է հետևում. ![]() (բ): Ուրեմն, պետք է ստացվեր 4 բաղադրիչ
(բ): Ուրեմն, պետք է ստացվեր 4 բաղադրիչ ![]() և 2 հավասարում. (ա) և (բ): Ըստ (XIII.3)-ի նորից կստացվի.
և 2 հավասարում. (ա) և (բ): Ըստ (XIII.3)-ի նորից կստացվի.
կոմպոնենտների թիվ = 4 – 2 = 2
2. ![]()
Այս դեպքում 3 բաղադրիչ ունենք. ![]() Բայց ունենք մի կոմպոնենտ, որովհետև երկու հավասարում ունենք, որոնք իրար հետ են կապում բաղադրիչների հավասարակշռական կոնցենտրացիաները.
Բայց ունենք մի կոմպոնենտ, որովհետև երկու հավասարում ունենք, որոնք իրար հետ են կապում բաղադրիչների հավասարակշռական կոնցենտրացիաները.
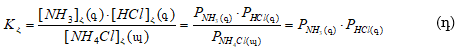
որովհետև ինչպես նշվել է կոնդենսված ֆազի ակտիվությունը (տվյալ դեպքում ![]() ) հավասար է մեկի: (դ)-ի մեջ
) հավասար է մեկի: (դ)-ի մեջ ![]() -ն հավասարակշռական ճնշում է:
-ն հավասարակշռական ճնշում է:
![]() -ի (հավասարակշռության հաստատուն) ֆիզիկական իմաստը կպարզաբանվի հաջորդ գլխում:
-ի (հավասարակշռության հաստատուն) ֆիզիկական իմաստը կպարզաբանվի հաջորդ գլխում:
Ըստ ստեխիոմետրիայի.
![]()
Նորից, ըստ (XIII.3)-ի.
![]()
Հետևաբար, այս 3 բաղադրիչներից կազմված համակարգը միակոմպոնենտ է:
Ստացված արդյունքը կարելի է մեկնաբանել նաև նկատի առնելով, որ տվյալ դեպքում պինդ և գազ ֆազերը նույն բաղադրությունն ունեն.
![]()
Կարծեք թե պարզապես ֆազային անցում է տեղի ունենում:
Ի՞նչ է նշանակում տվյալ դեպքում «միակոմպոնենտություն»: Եթե հայտնի է այդ երեքից միայն մեկի հավասարակշռական կոնցենտրացիան, ապա օգտվելով ![]() արժեքից կարելի է հաշվել մյուս երկուսի հավասարակշռական կոնցենտրացիաները, այսինքն պարզել երկու ֆազերի [(պ) և (գ)] բաղադրությունները:
արժեքից կարելի է հաշվել մյուս երկուսի հավասարակշռական կոնցենտրացիաները, այսինքն պարզել երկու ֆազերի [(պ) և (գ)] բաղադրությունները:
Պատկերը կփոխվի, եթե քննարկենք.
![]()
ռեակցիան: Այս համակարգը միայն մասնավոր դեպքում կլինի միակոմպոնենտային, եթե ելային խառնուրդը էկվիմոլային է ![]() Ընդհանրապես, եթե
Ընդհանրապես, եթե ![]() համակարգը երկկոմպոնենտ է, որովհետև (ե)-ն կբացակայի.
համակարգը երկկոմպոնենտ է, որովհետև (ե)-ն կբացակայի.
![]()
3. Փակ անոթում իրականացվում է հետևյալ դարձելի ռեակցիան.
![]()
որտեղից
![]()
որովհետև ինչպես նշվել է ![]() Այս ընդունելությունը ճիշտ է միայն այն դեպքում, երբ պինդ նյութերն իրար հետ չեն փոխազդում, օրինակ, չեն առաջացնում պինդ լուծույթ: Ուրեմն, այս համակարգը երկկոմպոնենտ է.
Այս ընդունելությունը ճիշտ է միայն այն դեպքում, երբ պինդ նյութերն իրար հետ չեն փոխազդում, օրինակ, չեն առաջացնում պինդ լուծույթ: Ուրեմն, այս համակարգը երկկոմպոնենտ է.
![]()
Հետաքրքիր է այն իրողությունը, որ ![]() միայն
միայն ![]() ճնշումից է կախված:
ճնշումից է կախված:
Ուրեմն պինդ և գազ ֆազերի բաղադրություններն իմանալու համար բացի ![]() պետք է երկու բաղադրիչների քանակներն իմանալ:
պետք է երկու բաղադրիչների քանակներն իմանալ:
Պարզաբանենք:
Հայտնի է, որ 1073 K-ում ![]() մթն: Եթե փոփոխենք
մթն: Եթե փոփոխենք ![]() ելային քանակը, նորից պետք է այնքան
ելային քանակը, նորից պետք է այնքան ![]() քայքայվի, որ առաջացած
քայքայվի, որ առաջացած ![]() ստեղծի
ստեղծի ![]() ճնշում: Եթե համակարգին սկզբից CaO
ավելացվի, նորից (ժ)-ն կմնա անփոփոխ, որովհետև
ճնշում: Եթե համակարգին սկզբից CaO
ավելացվի, նորից (ժ)-ն կմնա անփոփոխ, որովհետև ![]()
![]() - ն կարելի է փոխել փոխելով համակարգի ջերմաստիճանը և այն ճնշումը, որի տակ է գտնվում տվյալ համակարգը:
- ն կարելի է փոխել փոխելով համակարգի ջերմաստիճանը և այն ճնշումը, որի տակ է գտնվում տվյալ համակարգը:
XIII-2. ԳԻԲՍԻ ՖԱԶԵՐԻ ԿԱՆՈՆԸ
Այս կանոնը հիմնարար նշանակություն ունի: Այն հնարավորություն է տալիս թերմոդինամիկական մեթոդով ուսումնասիրելու հավասարակշռության վիճակում գտնվող համակարգերը:
Դիցուք քննարկվող համակարգը բաղկացած է n հատ կոմպոնենտից և հավասարակշռության մեջ գտնվող ֆազերի թիվն էլ հավասար է K-ի:
Բազմիցս նշվել է, որ եթե որևէ համակարգ գտնվում է հավասարակշռական վիճակում, ապա յուրաքանչյուր բաղադրիչի քիմիական պոտենցիալը ![]() բոլոր ֆազերում պետք է միևնույն արժեքն ունենա: Հետևաբար.
բոլոր ֆազերում պետք է միևնույն արժեքն ունենա: Հետևաբար.

Վերևում՝ փակագծի մեջ գրվածը վերաբերում է կոմպոնենտի համարին, իսկ ներքևի ինդեքսը՝ ֆազին: Օրինակ, ![]() նշանակում է համար 1 կոմպոնենտի քիմիական պոտենցիալը համար 2 ֆազում:
նշանակում է համար 1 կոմպոնենտի քիմիական պոտենցիալը համար 2 ֆազում:
Քննարկենք հետևյալ կոնկրետ օրինակը: Վերցված է ջուր, բենզոլ և յոդ: Համակարգը երկշերտ է և եռաֆազ. ջուր հագեցած բենզոլով, բենզոլ հագեցած ջրով, յոդը բաշխված երկու շերտերի միջև և գոլորշի ֆազ կազմված ջրի, բենզոլի և յոդի գոլորշիներից:
Համակարգը գտնվում է հաստատուն ջերմաստիճանում (T = const) և հաստատուն ճնշման տակ (P = const):
Եթե նշված համակարգում հավասարակշռություն է ստեղծված, դա նշանակում է, որ.

մյուս կողմից.
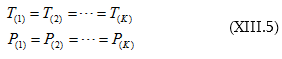
(XIII.4)-ը հավասարումներ են, իսկ (XIII.5)-ը՝ նույնություններ:
Որոշենք հավասարումների և անհայտների թիվը: (XIII.4) հավասարումների համակարգի յուրաքանչյուր տողում (K-1) հավասարում կա, իսկ տողերի թիվը հավասար է n - ի: Ուրեմն, ունենք n (K-1) հատ հավասարում: Այսինքն, յուրաքանչյուր կոմպոնենտի համար (K-1) հատ հավասարում կա:
Յուրաքանչյուր սյունակում (այսինքն յուրաքանչյուր ֆազում) n
հատ փոփոխական (անհայտ) կա: Եթե մոլային բաժինը ![]() է, ապա ըստ
(XIII.1)-ի բավական է (n -1)
հատ կոմպոնենտների մոլային բաժիններն իմանալ, իսկ n
-րդինը արդեն կարելի է
(XIII.1) հավասարումով որոշել:
է, ապա ըստ
(XIII.1)-ի բավական է (n -1)
հատ կոմպոնենտների մոլային բաժիններն իմանալ, իսկ n
-րդինը արդեն կարելի է
(XIII.1) հավասարումով որոշել:
Ուրեմն յուրաքանչյուր ֆազում (n - 1) հատ փոփոխական կա, իսկ ֆազերի թիվն էլ հավասար է K-ի: Հետևաբար համակարգում K (n -1) հատ փոփոխական (անհայտ) կա: Այս փոփոխականներից բացի ևս 2 փոփոխական ունենք. T-ն և P-ն, որոնք ինտենսիվ պարամետրեր են և հավասարակշռական վիճակում գտնվող ամբողջ համակարգի համար պարտադրաբար պետք է հաստատուն լինեն:
Լուծումը միանշանակ կլինի, եթե հավասարումների և անհայտների թվերն իրար հավասար են, այսինքն.
![]()
(2-ը T-ն և P-ն են):
Բայց սկզբունքորեն այնպիսի դեպքեր են հնարավոր, երբ փոփոխելով փոփոխականների թիվը հավասարակշռությունը չի խախտվի: Այս հնարավորությունը ցույց է տրվելու: Սա նշանակում է, որ փոփոխականների (անհայտների) թիվը կարող է հավասարումների թվից մեծ լինել, այսինքն.
![]()
Անհավասարության նշանը հավասարման նշանով փոխարինելու համար անհրաժեշտ է ձախ մասում ինչ որ մի դրական F մեծություն ավելացնել.
![]()
որտեղից
![]()
Սա Գիբսի ֆազերի կանոնի մաթեմատիկական արտահայտությունն է: F-ը կոչվում է բազմաֆազ (հետերոգեն) համակարգի ազատության աստիճանների թիվ: F-ը կապված է ընդհանրացված ուժերի (T, P ) հետ, որոնք ինտենսիվ պարամետրեր են: Ցույց է տալիս, թե քանի՞ հատ ինտենսիվ պարամետր կարելի է ազատորեն փոփոխել առանց խախտելու գոյություն ունեցող հավասարակշռությունը, այսինքն հավասարակշռության մեջ գտնվող ֆազերի թիվը:
Եթե բացի T-ից և P-ից, էլի կան ինտենսիվ պարամետրեր, որոնց փոփոխությունը կարող է խախտել գոյություն ունեցող հավասարակշռությունը, ինչպիսիք մագնիսական, էլեկտրական, գրավիտացիոն և այլ դաշտերն են, այդ պարամետրը (պարամետրերը) ևս հաշվի առնելով (XIII.8)-ի մեջ երկուսի փոխարեն պետք է այլ թիվ գրել: Իսկ եթե հետազոտվողը այնպիսի համակարգ է, որի վիճակի վրա ճնշումն էական ազդեցություն չի կարող ունենալ, օրինակ, եթե հետերոգեն համակարգը կազմված է իրար հետ քիմիապես չփոխազդող մետաղներից, հալույթներից, այդ դեպքում (XIII.8)-ի մեջ 2-ի փոխարեն պետք է 1 գրել
![]()
XIII-3. ԳԻԲՍԻ ՖԱԶԵՐԻ ԿԱՆՈՆԻ ԿԻՐԱՌՈՒԹՅՈՒՆԸ
XIII-3:1. Միակոմպոնենտ համակարգերի նկատմամբ
Սա այն դեպքն է, երբ n = 1: Ուրեմն. F = (1-K)+2=3-K:
Այս արդյունքից հետևում է, որ միակոմպոնենտ համակարգում առավելագույնը 3 ֆազեր կարող են գտնվել հավասարկշռության մեջ.
Քննարկենք մի նյութ, որը փակ համակարգում կարող է հանդես գալ իրար հետ փոխկապակցված տարբեր ագրեգատային վիճակներով: Իրար հետ փոխհարաբերող վիճակները կարելի է գրաֆիկորեն պատկերել օգտագործելով ![]() դիագրամներ, որոնք կոչվում են ֆազային կամ վիճակի դիագրամներ: Այդ դիագրամը հնարավորություն կտա որոշելու թե տվյալ պայմաններում ո՞ր ֆազն է կայուն, ո՞ր ֆազերն են գտնվում իրար հետ հավասարակշռության մեջ:
դիագրամներ, որոնք կոչվում են ֆազային կամ վիճակի դիագրամներ: Այդ դիագրամը հնարավորություն կտա որոշելու թե տվյալ պայմաններում ո՞ր ֆազն է կայուն, ո՞ր ֆազերն են գտնվում իրար հետ հավասարակշռության մեջ:
ա) Ջրի վիճակի դիագրամը – նկ.XIII.1-ի վրա պատկերված է ջրի ֆազային (վիճակի) դիագրամը առանց նկատի առնելու սառույցի տարբեր մոդիֆիկացիաներով հանդես գալու հնարավորությունը.
![]() կորից ներքև (ցածր ճնշումներ և բարձր ջերմաստիճաններ) ջուրը գտնվում է գոլորշի վիճակում. այդ ֆազն է կայուն: Ուրեմն,
կորից ներքև (ցածր ճնշումներ և բարձր ջերմաստիճաններ) ջուրը գտնվում է գոլորշի վիճակում. այդ ֆազն է կայուն: Ուրեմն, ![]() և այլն վիճակներում միայն գոլորշի ունենք: Այդ մարզի նկատմամբ կիրառենք
(XIII.8)-ը: n = 1 և K =
1: Որտեղից. F
= (1-1)+2 = 2: Հետևաբար, այդ մարզում այդ միակոմպոնենտ համակարգը բիվարիանտ է (F
= 2), այսինքն ազատության աստիճանների թիվը երկուսի է հավասար: Նշանակում է, որ որոշակի տիրույթում ազատորեն կարելի է փոփոխել այդ 2 ինտենսիվ պարամետրերը (P-ն և T-ն) պահպանելով համակարգի միաֆազությունը: Օրինակ,
և այլն վիճակներում միայն գոլորշի ունենք: Այդ մարզի նկատմամբ կիրառենք
(XIII.8)-ը: n = 1 և K =
1: Որտեղից. F
= (1-1)+2 = 2: Հետևաբար, այդ մարզում այդ միակոմպոնենտ համակարգը բիվարիանտ է (F
= 2), այսինքն ազատության աստիճանների թիվը երկուսի է հավասար: Նշանակում է, որ որոշակի տիրույթում ազատորեն կարելի է փոփոխել այդ 2 ինտենսիվ պարամետրերը (P-ն և T-ն) պահպանելով համակարգի միաֆազությունը: Օրինակ, ![]() կարելի է
կարելի է
![]() վիճակին անցնել միաժամանակ փոխելով և T-ն և P-ն. այնուամենայնիվ կպահպանվի համակարգի միաֆազությունը: Նույնը կարելի է ասել COA
հեղուկ մարզի և այդ մարզում գտնվող
վիճակին անցնել միաժամանակ փոխելով և T-ն և P-ն. այնուամենայնիվ կպահպանվի համակարգի միաֆազությունը: Նույնը կարելի է ասել COA
հեղուկ մարզի և այդ մարզում գտնվող ![]() ինչպես նաև BOC
պինդ (սառույց) մարզի և այդ մարզում գտնվող
ինչպես նաև BOC
պինդ (սառույց) մարզի և այդ մարզում գտնվող
![]() վիճակների մասին:
վիճակների մասին:
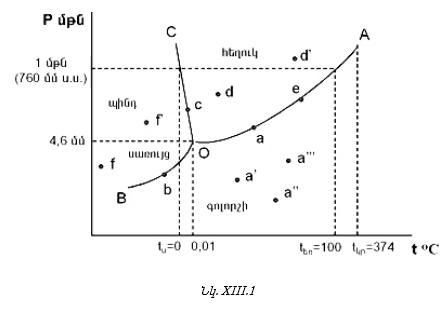
OA կորը իրարից սահմանազատում է հեղուկ և գոլորշի ֆազերը: Ուրեմն a վիճակում գտնվող համակարգում հավասարակշռության մեջ են հեղուկ և գոլորշի ֆազերը: a կետում (վիճակում) n = 1 և K = 2: Հետևաբար ըստ (XIII.8)-ի F = 1: Այս դեպքում համակարգը մոնովարիանտ է: Նշանակում է, որ կարելի է ազատորեն միայն մի պարամետր փոփոխել (կամ P-ն, կամ T-ն) պահպանելով 2 ֆազերի համագոյությունը: Եթե T-ն ենք փոփոխում, ապա P-ն պետք է այնպես փոփոխվի, որ a կետը տեղաշարժվի OA կորով, օրինակ, անցնի e վիճակի: Եթե P-ն ենք փոփոխում, ապա T-ն պետք է փոփոխվի ըստ P = f (T) ֆունկցիայի [հիշել Կլաուզիուս-Կլապեյրոնի հավասարումը (X.88)]: Եթե T-ն և P-ն փոփոխենք կամայականորեն այնպես, որ a-ն տեղափոխվի վերև կամ ներքև, ապա երկֆազ համակարգը կդառնա միաֆազ (հեղուկ կամ գոլորշի):
Նույնը վերաբերում է BOC մարզին և c (պ-հ) և b (պ-գ) վիճակներին:
O կետում 3 ֆազեր են գտնվում հավասարակշռության մեջ.
O-ն կոչվում է եռյակ կետ: Այդ վիճակում ըստ (XIII.8)-ի F=(1-3)+2=0 : Ասում են, որ այս վիճակում համակարգը նոնվարիանտ է, այսինքն ոչ մի պարամետր չի կարելի փոխել առանց խախտելու գոյություն ունեցող հավասարակշռությունը, այսինքն հավասարակշռության մեջ գտնվող ֆազերի թիվը:
բ) Ծծմբի վիճակի դիագրամը: Էնանտիոտրոպիա և մոնոտրոպիա
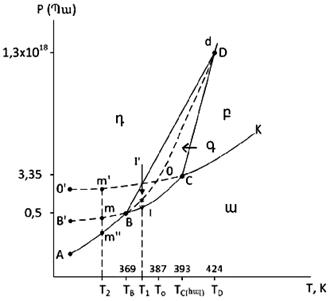
Նկ. XIII.2
Նկ.XIII.2-ի վրա պատկերված է ծծմբի ֆազային (վիճակի) դիագրամը:
ABCK կորից ներքևը S-ը գտնվում է գոլորշի վիճակում ![]() (օրինակ, ա վիճակը): Այս մարզում համակարգը միաֆազ է (հոմոգեն):
(օրինակ, ա վիճակը): Այս մարզում համակարգը միաֆազ է (հոմոգեն):
dDCK մարզում համակարգը նորից միաֆազ է. ծծումբը գտնվում է հեղուկ վիճակում ![]() (օրինակ, բ վիճակ): DBC
մարզում S-ը գտնվում է բյուրեղական վիճակում (մոնոկլինային ծծումբ,
(օրինակ, բ վիճակ): DBC
մարզում S-ը գտնվում է բյուրեղական վիճակում (մոնոկլինային ծծումբ, ![]() օրինակ, գ վիճակ): ABDd-ից ձախ ծծումբը նորից բյուրեղական վիճակում է, բայց բյուրեղական այլ կառուցվածքով. ռոմբային ծծումբ
օրինակ, գ վիճակ): ABDd-ից ձախ ծծումբը նորից բյուրեղական վիճակում է, բայց բյուրեղական այլ կառուցվածքով. ռոմբային ծծումբ ![]() օրինակ, դ վիճակ:
օրինակ, դ վիճակ:
AB, BC, BD, CK և CD կորերը սահմանազատում են հավասարակշռության մեջ գտնվող երկու կայուն ֆազեր: Այսպես.
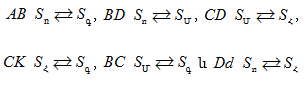
Փաստորեն այդ կորերը ցույց են տալիս, թե ֆազային անցման ջերմաստիճանները ինչպես են կախված ճնշումից:
B, C և D կետերը եռյակ կետեր են: Այդ կետերը այնպիսի վիճակների են համապատասխանում, երբ 3 ֆազեր գտնվում են հավասարակշռության մեջ և նոնվարիանտ են:

O-ն նույնպես եռյակ կետ է: Այդ կետում են հատվում OB, OC և OD կորերը: Բայց այդ կորերը վերաբերում են երեք ֆազերի միջև ստեղծված անկայուն հավասարակշռությանը:
OC-ն KC-ի շարունակությունն է: C
կետում
(393 K) պետք է սկսվեր հեղուկ ծծումբի բյուրեղացումը մոնոկլինային ծծումբի առաջացումով: Բայց մինչև O
կետը ![]() ծծումբը հեղուկ է մնում: Քանի որ
ծծումբը հեղուկ է մնում: Քանի որ ![]() այդ պատճառով ասում ենք, որ ծծումբը գտնվում է «գերցուրտ (գց) հեղուկ» վիճակում:
այդ պատճառով ասում ենք, որ ծծումբը գտնվում է «գերցուրտ (գց) հեղուկ» վիճակում:
![]()
BO-ն AB-ի շարունակությունն է: Հետագա տաքացումով B-ից պիտի սկսվեր ռոմբային ծծումբի վերածվելը մոնոկլինայինի, բայց մինչև O
կետը պրոցեսը ձգձգվում է: ![]() այս պատճառով էլ ռոմբային ծծումբը գտնվում է «գերտաք պինդ» վիճակում: Իսկ BB’
կորը պատկանում է հետևյալ մետաստաբիլ հավասարակշռությանը.
այս պատճառով էլ ռոմբային ծծումբը գտնվում է «գերտաք պինդ» վիճակում: Իսկ BB’
կորը պատկանում է հետևյալ մետաստաբիլ հավասարակշռությանը.
![]()
Ինչ վերաբերում է DO-ին, ապա դա սահմանազատում է «գերտաք ռոմբային» ծծումբը գց ![]() Այսպիսով.
Այսպիսով.
(a)
BO-ն վերաբերում է ![]() (գերտաք)
(գերտաք) ![]() (գերհագեցած
(գերհագեցած ![]() նկատմամբ)
նկատմամբ)
(b)
CO-ն` ![]() (գերցուրտ)
(գերցուրտ) ![]() (գերհագեցած
(գերհագեցած ![]() նկատմամբ)
նկատմամբ)
(c)
DO-ն` ![]() (գերտաք)
(գերտաք) ![]() (գերցուրտ)
(գերցուրտ)
Ինչպես նշվեց, BC
կորը վերաբերում է ![]() հավասարակշռությանը: Բայց OC
կորի քննարկումից հետևեց
հավասարակշռությանը: Բայց OC
կորի քննարկումից հետևեց ![]() բացակայությունը [տե'ս (b)-ն]:
բացակայությունը [տե'ս (b)-ն]:
(a)-ի, (b)-ի և (c)-ի համադրումից կարելի է եզրակացնել, որ O կետում 3 անկայուն ֆազեր գտնվում են կեղծ հավասարակշռության մեջ.
Այդ O կետը գտնվում է BDC
մարզում, որտեղ կայուն պետք է լինի ![]() ֆազը: Ուրեմն, բավական է T-ի կամ P-ի շատ փոքր փոփոխություն, որ այդ անկայուն (մետաստաբիլ) վիճակը կայունանա
ֆազը: Ուրեմն, բավական է T-ի կամ P-ի շատ փոքր փոփոխություն, որ այդ անկայուն (մետաստաբիլ) վիճակը կայունանա ![]() առաջացումով:
առաջացումով:
Նկ.XIII.2-ի վրա հետաքրքիր մի իրավիճակ էլ կա:
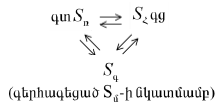
BDO մարզում, որտեղ ![]() գտնվում է գերտաք վիճակում
գտնվում է գերտաք վիճակում ![]() Պայմանական
Պայմանական ![]() ջերմաստիճանում BC
կորի վրա ունենք I
վիճակը, իսկ OB-ի վրա՝ I'
վիճակը: Բնական է, որ պետք է տեղի ունենա
ջերմաստիճանում BC
կորի վրա ունենք I
վիճակը, իսկ OB-ի վրա՝ I'
վիճակը: Բնական է, որ պետք է տեղի ունենա ![]() անցում
անցում ![]()
Իսկ ![]() ջերմաստիճանում իրավիճակը հակառակն է.
ջերմաստիճանում իրավիճակը հակառակն է.
![]()
Այս դեպքում տեղի կունենա ![]() անցում
անցում ![]()
Տվյալ նյութի բյուրեղային մի կառուցվածքից մի այլ կառուցվածքի անցումը կոչվում է պոլիմորֆային, օրինակ, ![]() Որոշակի այլ պայմանում հակառակ անցումն է հնարավոր դառնում
Որոշակի այլ պայմանում հակառակ անցումն է հնարավոր դառնում ![]() Այսպիսի դարձելի պոլիմորֆային անցումը կոչվում է էնանտիոտրոպային, իսկ երևույթը՝ էնանտիոտրոպիա:
Այսպիսի դարձելի պոլիմորֆային անցումը կոչվում է էնանտիոտրոպային, իսկ երևույթը՝ էնանտիոտրոպիա:
Եզրակացություն. ֆազային անցումներն ինքնաբերաբար ընթանում են աստիճանաբար նվազ կայուն վիճակից դեպի առավել կայունը: Սա Օստվալդի կանոնն է:
Պետք է նշել նաև, որ էնանտիոտրոպային փոխակերպումը հնարավոր է միայն այն դեպքում, երբ երկու բյուրեղային կառուցվածքների միջև անցումային ջերմաստիճանը ցածր է դրանց հալման ջերմաստիճաններից: Քննարկված օրինակների համար
![]()
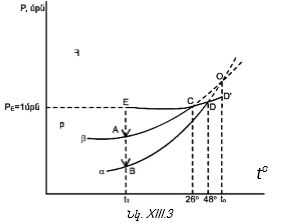
Պոլիմորֆային անցումը մոնոտրոպային է կոչվում այն դեպքում, երբ այդ պրոցեսը դարձելի չէ, այլ միակողմանի է: Ուրեմն, թերմոդինամիկորեն թույլատրելի է միայն անցման մի ուղղությունը. նվազ կայունից առավել կայունը: Չկա մի պայման, երբ առավել կայունը հանդես գա նվազ կայունից ավելի նվազ կայուն վիճակում: Առավել կայուն վիճակից ավելի նվազ կայուն վիճակի անցումը ![]() արգելված է:
արգելված է:
Ասվածը ավելի հիմնավոր ձևով ցույց տանք բենզոֆենոնի օրինակով: Այդ նյութը երկու մոդիֆիկացիա ունի. ![]() (նվազ կայուն): Դա կախված է երկու ֆենիլ խմբերի տարածական դիրքերից. թերթին ուղղահայաց և թերթին զուգահեռ:
(նվազ կայուն): Դա կախված է երկու ֆենիլ խմբերի տարածական դիրքերից. թերթին ուղղահայաց և թերթին զուգահեռ: ![]() մոդիֆիկացիայի հալման ջերմաստիճանն է (26oC) և D-ն`
մոդիֆիկացիայի հալման ջերմաստիճանն է (26oC) և D-ն` ![]() (48oC):
(48oC):
Նկ.XIII.3-ից հետևում է, որ ողջ ջերմաստիճանային տիրույթում ![]() հետևաբար
հետևաբար ![]()
Եզրակացություն. միայն ![]() անցումն է հնարավոր: E
կետում բենզոֆենոնը գտնվում է գերցուրտ վիճակում: Այդ դեպքում անցումը միակողմանի է.
անցումն է հնարավոր: E
կետում բենզոֆենոնը գտնվում է գերցուրտ վիճակում: Այդ դեպքում անցումը միակողմանի է.
![]()
Չկա մի տիրույթ, որտեղ ![]() ինչպիսին կար
ինչպիսին կար ![]() անցումների դեպքում: Այդպիսի միակողմանի անցումը կոչվում է մոնոտրոպային:
անցումների դեպքում: Այդպիսի միակողմանի անցումը կոչվում է մոնոտրոպային:
O-ն տեսական կետ է. փորձով չի ստացվի: AC և BD կորերը էքստրապոլելով կհատվեն O կետում, որին համապատասխանող հիպոթետիկ ջերմաստիճանը նշանակված է ![]() Հենց այդ ջերմաստիճանից բարձր հնարավոր պետք է լիներ
Հենց այդ ջերմաստիճանից բարձր հնարավոր պետք է լիներ ![]() անցումը: Բայց այդ պրոցեսը անհնար է իրականացնել: Հարցը նրանումն է, որ հալման կետից ավելի բարձր ջերմաստիճանում անհնար է բյուրեղային վիճակ պահպանել, այսինքն ստանալ գերտաք բյուրեղ: Երբ նորից վերադառնանք նկ.XIII.2-ին ուշադրություն դարձնելով քննարկված հարցի վրա կնկատենք, որ S-ի դեպքում, երբ
անցումը: Բայց այդ պրոցեսը անհնար է իրականացնել: Հարցը նրանումն է, որ հալման կետից ավելի բարձր ջերմաստիճանում անհնար է բյուրեղային վիճակ պահպանել, այսինքն ստանալ գերտաք բյուրեղ: Երբ նորից վերադառնանք նկ.XIII.2-ին ուշադրություն դարձնելով քննարկված հարցի վրա կնկատենք, որ S-ի դեպքում, երբ ![]() :
:
XIII-3:2. Երկկոմպոնենտ կոնդենսված համակարգեր ուսումնասիրելու
ֆիզիկաքիմիական անալիզի հիմունքները
Երբ խոսքը վերաբերում է երկու կոմպոնենտներից կազմված կոնդենսված համակարգերին, երկու սահմանային դեպքերի կարելի է հանդիպել: Երկու կոմպոնենտների միջև փոխազդեցություն չկա (ա) և կա (բ):
Ֆիզիկաքիմիական անալիզի մեթոդի կիրառումը հնարավորություն է տալիս Գիբսի ֆազերի կանոնից օգտվելով որոշել հավասարակշռության մեջ գտնվող ֆազերի բնույթը և բաղադրությունը: Այդ մեթոդի հիմքն է. որոշել համակարգը բնութագրող ֆիզիկական որևէ մի հատկության կախումը համակարգի բաղադրությունից և ստացված փորձնական տվյալների հիման վրա որոշել ֆազերի և բնույթը և բաղադրությունը:
Որպես համակարգի բաղադրությունից կախված ֆիզիկական մեծություն կարելի է վերցնել համակարգի հալման (կամ սառեցման) ջերմաստիճանը, էլեկտրահաղորդականությունը, մածուցիկությունը, մագնիսական ընկալելիությունը, դիէլեկտրիկական թափանցելիությունը և այլն: Իսկ համակարգի բաղադրությունն արտահայտելու առավել հարմարը դա մոլային (X),
զանգվածային բաժինների օգտագործումն է, որովհետև երկու դեպքերում էլ դրանք անտարչափ մեծություններ են և փոփոխվում են ![]() տիրույթում:
տիրույթում:
Ֆիզիկական հատկություն – բաղադրություն դիագրամի վերծանման հիմքում գտնվում է Կուռնակովի կողմից առաջադրված անընդհատության և համապատասխանելիության սկզբունքները:
Ըստ անընդհատության սկզբունքի համակարգի վիճակը պայմանավորող երեք պարամետրերը (T, P, X) անընդհատորեն փոխելիս անընդհատորեն փոխվում են նաև հավասարակշռության մեջ գտնվող առանձին ֆազերի քննարկվող հատկությունները: Բայց հենց որ տեղի է ունենում ֆազերի թվի կամ բնույթի փոփոխություն չափվող (որոշվող) հատկությունը փոխվում է թռիչքաձև:
Իսկ ըստ համապատասխանելիության սկզբունքի ստացված հատկություն-բաղադրություն դիագրամի վրա գոյություն ունեն երկրաչափական որոշակի տիրույթներ: Տիրույթը վերաբերում է համակարգի յուրաքանչյուր կոնկրետ վիճակի: Հետևաբար դիագրամի վրա յուրաքանչյուր կետ համապատասխանում է համակարգի կոնկրետ մի վիճակի, որի թերմոդինամիկական որոշ հատկություններ կարելի է պարզաբանել օգտվելով Գիբսի ֆազերի կանոնից:
Մեթոդական առումով շատ մատչելի է որպես համակարգի վիճակն արտահայտող ֆիզիկական հատկություն վերցնել հալման (սառեցման) ջերմաստիճանը: Այդ դեպքում կիրառվում է թերմիկ անալիզի մեթոդը:
XIII-3:2(Ա) Երկու բաղադրիչների միջև բացակայում է
քիմական փոխազդեցությունը
ա) Դեպք առաջին. էվտեկտիկական կետ: Առաջանում է մի հատ էվտեկտիկական խառնուրդ:
Մեթոդի հիմքում տարբեր բաղադրությամբ խառնուրդների ցրտեցման կորերի ստացումն է: Ցրտեցման կորը հալույթի ջերմաստիճան-ժամանակ կախումն արտահայտող գրաֆիկն է [նկ. XIII.4] և ստացված կորերի հիման վրա հալման (սառեցման) ջերմաստիճան-բաղադրություն երկչափ դիագրամի պատկերումը [նկ. XIII.5]:
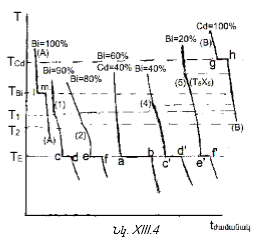
Շարադրվածը փորձենք նյութականացնել ուսումնասիրելով Cd - Bi երկկոմպոնենտ համակարգը, որը լիովին համապատասխանում է «դեպք 1»-ում նշված պայմաններին: Այս զույգին հատուկ է այն, որ հեղուկ վիճակում իրար մեջ լուծվում են անսահմանափակ, այսինքն դրանց միահալույթը լուծույթ է, իսկ պինդ վիճակում իրար մեջ չեն լուծվում:

(Նկ.XIII.5-ի վրա X-ի տակ կարելի է հասկանալ նաև զանգվածային բաժին)
Նախ վերցնում են մաքուր բաղադրչները. տվյալ դեպքում Bi(A)
և Cd(B):
Bi-ը (Cd-ը) հալելուց հետո ժամանակի տարբեր պահերին գրանցում են հալույթի ջերմաստիճանը: Երբ ![]() հալույթում ի հայտ են գալիս Bi-ի (Cd-ի) բյուրեղներ [տես A(B)
կորերը]: Սկսած I(g)
պահից համակարգի ջերմաստիճանը անփոփոխ է մնում մինչև m(h)
կետին համապատասխանող պահը, երբ մետաղի (Bi-ի կամ Cd-ի) բյուրեղացումն ավարտվում է: Ջերմաստիճանի անփոփոխության պատճառն այն է, որ մի կողմից ջերմություն է ցրվում, մյուս կողմից բյուրեղացման հետևանքով ջերմություն է անջատվում և այդ երկու պրոցեսներն իրար փոխհատուցում են: Բյուրեղացման ավարտից հետո համակարգի ջերմաստիճանը նորից է սկսում նվազել: A(I)
և B(G)
տիրույթներում համակարգը հեղուկ է, իսկ mA
և hB
տիրույթներում՝ պինդ: Բայց Im
և hg
տիրույթներում համակարգը երկֆազ (հետերոգեն) է. հեղուկ + պինդ: Ցրտեցման կորերի վրա արձանագրված կանգառների երկարությունը կախված է համակարգի զանգվածից:
հալույթում ի հայտ են գալիս Bi-ի (Cd-ի) բյուրեղներ [տես A(B)
կորերը]: Սկսած I(g)
պահից համակարգի ջերմաստիճանը անփոփոխ է մնում մինչև m(h)
կետին համապատասխանող պահը, երբ մետաղի (Bi-ի կամ Cd-ի) բյուրեղացումն ավարտվում է: Ջերմաստիճանի անփոփոխության պատճառն այն է, որ մի կողմից ջերմություն է ցրվում, մյուս կողմից բյուրեղացման հետևանքով ջերմություն է անջատվում և այդ երկու պրոցեսներն իրար փոխհատուցում են: Բյուրեղացման ավարտից հետո համակարգի ջերմաստիճանը նորից է սկսում նվազել: A(I)
և B(G)
տիրույթներում համակարգը հեղուկ է, իսկ mA
և hB
տիրույթներում՝ պինդ: Բայց Im
և hg
տիրույթներում համակարգը երկֆազ (հետերոգեն) է. հեղուկ + պինդ: Ցրտեցման կորերի վրա արձանագրված կանգառների երկարությունը կախված է համակարգի զանգվածից:
Այժմ ուսումնասիրենք տարբեր բաղադրության խառնուրդներ: Քննարկենք (1)-ը, որը վերաբերում է ըստ զանգվածի 90%Bi + 10%Cd բաղադրությամբ խառնուրդին, որին համապատասխանում է որոշակի ցրտեցման կոր: Քանի որ Bi-ն քանակապես Cd-ից շատ է, ապա այդ հալույթի (լուծույթի) մեջ Bi-ն լուծիչն է և Cd-ն՝ լուծված նյութը: ![]() ջերմաստիճանում հալույթից սկսում են լուծիչի (Bi)
բյուրեղներ անջատվել: Հետևաբար, ժամանակի ընթացքում լուծիչի (Bi)
քանակը նվազում է և լուծույթը ավելի կոնցենտրիկ է դառնում:
ջերմաստիճանում հալույթից սկսում են լուծիչի (Bi)
բյուրեղներ անջատվել: Հետևաբար, ժամանակի ընթացքում լուծիչի (Bi)
քանակը նվազում է և լուծույթը ավելի կոնցենտրիկ է դառնում:
Լուծույթների կոլիգատիվ հատկություններն ուսումնասիրելիս ցույց տրվեց, որ լուծույթի սառեցման կետի անկումը՝![]() , որտեղ m -
ը լուծույթի մոլալությունն է: Քանի որ տվյալ դեպքում ժամանակի ընթացքում լուծույթի կոնցենտրացիան մեծանում է, այդ պատճառով
, որտեղ m -
ը լուծույթի մոլալությունն է: Քանի որ տվյալ դեպքում ժամանակի ընթացքում լուծույթի կոնցենտրացիան մեծանում է, այդ պատճառով
![]() ջերմաստիճանը հաստատուն չի մնում և անընդհատ նվազում է: Իսկ ընդհանրապես
ջերմաստիճանը հաստատուն չի մնում և անընդհատ նվազում է: Իսկ ընդհանրապես ![]() (լուծիչը լուծույթում)
(լուծիչը լուծույթում) ![]() (մաքուր լուծիչ), դրա համար էլ
(մաքուր լուծիչ), դրա համար էլ ![]()
Սառեցման ջերմաստիճանը ի վերջո հավասարվում է ինչ որ մի ![]() ջերմաստիճանի և որոշ ժամանակ հաստատուն է մնում, այսինքն սառեցման կորի վրա կանգառ է դիտվում:
ջերմաստիճանի և որոշ ժամանակ հաստատուն է մնում, այսինքն սառեցման կորի վրա կանգառ է դիտվում:
Փորձը ցույց է տալիս, որ այդ ![]() ջերմաստիճանում մնացած հեղուկը սկսում է պնդանալ: Պարզվում է, որ
ջերմաստիճանում մնացած հեղուկը սկսում է պնդանալ: Պարզվում է, որ ![]() ջերմաստիճանում պնդացող հեղուկն ունի որոշակի բաղադրություն. 60%
Bi և 40% Cd:
cd կանգառի ընթացքում այդ բաղադրությունն էլ անփոփոխ է մնում: d
կետում անբողջ համակարգն արդեն պինդ (բյուրեղական) վիճակում է, որն սկսում է աստիճանաբար սառչել:
ջերմաստիճանում պնդացող հեղուկն ունի որոշակի բաղադրություն. 60%
Bi և 40% Cd:
cd կանգառի ընթացքում այդ բաղադրությունն էլ անփոփոխ է մնում: d
կետում անբողջ համակարգն արդեն պինդ (բյուրեղական) վիճակում է, որն սկսում է աստիճանաբար սառչել:
Ստացված փորձնական տվյալների քննարկումը հեշտացնելու համար վերցվում է հաստատուն զանգվածով ելային նմուշ, օրինակ, 100 գ: Սկզբում վերցվել է 100 գ Bi (և 100 գ Cd): Հաջորդ №1 խառնուրդում 90 գ Bi կա և 10 գ Cd:
80 գ Bi-ից և
20 գ Cd-ից կազմված ելային խառնուրդի սառեցման կորը (2)-ն է: Ինչպես պետք էր սպասել
![]() իսկ (2) ցրտեցման կորը որակապես չպիտի տարբերվեր (1)-ից: Այստեղ հետաքրքրականն այն է, որ նորից նույն
իսկ (2) ցրտեցման կորը որակապես չպիտի տարբերվեր (1)-ից: Այստեղ հետաքրքրականն այն է, որ նորից նույն ![]() ջերմաստիճանում է սկսվում պնդանալ մի հալույթ, որը կազմված է 60%
Bi-ից և 40% Cd-ից: Ընդհանրացնելով կարող ենք ասել, որ
ջերմաստիճանում է սկսվում պնդանալ մի հալույթ, որը կազմված է 60%
Bi-ից և 40% Cd-ից: Ընդհանրացնելով կարող ենք ասել, որ ![]() ջերմաստիճանում պնդացող հեղուկի բաղադրությունը հաստատուն է. տվյալ դեպքում 60%
Bi և 40% Cd:
Այժմ երբ ելային բաղադրությունը
60 գ Bi +
40 գ Cd
է, այս դեպքում մինչև
ջերմաստիճանում պնդացող հեղուկի բաղադրությունը հաստատուն է. տվյալ դեպքում 60%
Bi և 40% Cd:
Այժմ երբ ելային բաղադրությունը
60 գ Bi +
40 գ Cd
է, այս դեպքում մինչև ![]() ջերմաստիճան ոչ մի էֆեկտ չի դիտվում: Նույն այդ
ջերմաստիճան ոչ մի էֆեկտ չի դիտվում: Նույն այդ ![]() ջերմաստիծանում այդ 100 գ խառնուրդը (հալույթը) սկսում է պնդանալ:
ջերմաստիծանում այդ 100 գ խառնուրդը (հալույթը) սկսում է պնդանալ:
Այդ հաստատուն բաղադրությամբ խառնուրդը, որն ունի հաստատուն սառեցման (հալման) կետ կոչվում է էվտեկտիկական խառնուրդ, որը միաֆազ չէ, իսկ ![]() էվտեկտիկական ջերմաստիճան (կետ):
էվտեկտիկական ջերմաստիճան (կետ):
Նկ.XIII.4-ի վրա պատկերված ցրտեցման կորերից հետևում է, որ ![]() և այլն:
և այլն:
Նշվեց, որ կանգառի տևողությունը կախված է պնդացող խառնուրդի զանգվածից: Այս հարցը քննարկենք: (1) ելային նմուշի բաղադրությունն էր. 90գBi + 10գCd, իսկ էվտեկտիկը՝ 60%Bi + 40%Cd, այսինքն էվտեկտիկ խառնուրդում
Bi/Cd=3/2: Եթե ելային բաղադրությունն է 90գ
Bi/10գ Cd, ապա ![]() ջերմաստիճանում պիտի առաջանա հետևյալ խառնուրդը. x/10=3/2,
որտեղից x =15
գ: Ուրեմն, մինչև
ջերմաստիճանում պիտի առաջանա հետևյալ խառնուրդը. x/10=3/2,
որտեղից x =15
գ: Ուրեմն, մինչև ![]() ջերմաստիճան № 1 ելային խառնուրդից պետք է անջատվի. 90-15 =75 գ Bi, որպեսզի մնա Bi(15գ) /Cd (10գ)=3/2 խառնուրդ, որի զանգվածը կլինի 15+10
= 25 գ: Այս 25գ-ը էվտեկտիկ խառնուրդն է, որն սկսում է որպես մի ամբողջություն պնդանալ: № 2 ելային խառնուրդի համար կստացվի Bi(x)/Cd(20)=3/2,
որտեղից x
= 30 գ: Ուրեմն, պիտի հալույթից անջատվի
80-30 = 50 գ Bi, որպեսզի ստացվի 3:2 հարաբերությամբ 30 -
20=50 գ էվտեկտիկ խառնուրդ: Իսկ երբ ելային խառնուրդի բաղադրությունը համապատասխանում է էվտեկտիկին՝ 60գ Bi +
40գ Cd,
այս դեպքում էվտեվտիկական խառնուրդի զանգվածը կլինի 100գ:
ջերմաստիճան № 1 ելային խառնուրդից պետք է անջատվի. 90-15 =75 գ Bi, որպեսզի մնա Bi(15գ) /Cd (10գ)=3/2 խառնուրդ, որի զանգվածը կլինի 15+10
= 25 գ: Այս 25գ-ը էվտեկտիկ խառնուրդն է, որն սկսում է որպես մի ամբողջություն պնդանալ: № 2 ելային խառնուրդի համար կստացվի Bi(x)/Cd(20)=3/2,
որտեղից x
= 30 գ: Ուրեմն, պիտի հալույթից անջատվի
80-30 = 50 գ Bi, որպեսզի ստացվի 3:2 հարաբերությամբ 30 -
20=50 գ էվտեկտիկ խառնուրդ: Իսկ երբ ելային խառնուրդի բաղադրությունը համապատասխանում է էվտեկտիկին՝ 60գ Bi +
40գ Cd,
այս դեպքում էվտեվտիկական խառնուրդի զանգվածը կլինի 100գ:
Այսպիսով 100 գ ելային խառնուրդում.
№ 1 խառնուրդ. էվտեկտիկական խառնուրդը 25 գ էր
№ 2 ––“–– ––“–– ––“–– 50 գ
ելային խառնուրդ 60 գ Bi + 40 գ Cd 100 գ
Բնական է, որ նշված հերթականությամբ էլ պետք է մեծանա էվտեկտիկական խառնուրդի սառեցման կանգառը:
Եթե այժմ վերցնենք խառնուրդներ, որոնք Cd-ով են հարուստ, նորից կդիտվի նույն օրինաչափությունը: Օրինակ, վերցված է 70գ Cd + 30 գ Bi: Պետք է նստի (բյուրեղանա) այնքան Cd, որ մնացած հալույթի բաղադրությունը լինի x/30=2/3,
x = 20 գ, այսինքն նստի 70-20=50 գ Cd: Մնացած խառնուրդի (էվտեկտիկ) զանգվածը կլինի. 20 +
30=50 գ ![]() գ:
գ:
Այսպիսով, պարզվեց կանգառների տևողությունների հետ դիտված օրինաչափությունների պատճառը:
Հարցի այդ մասի քննարկումը ավարտելու համար լուծենք նաև հետևյալ խնդիրը: Հալույթի ջերմաստիճանի նվազման պատճառը, այսինքն լուծույթից անջատումը ո՞ր բաղադրիչի բյուրեղացումն է: Խնդրի լուծման հիմքում Էվտեկտիկ խառնուրդի բաղադրության հաստատունությունն է: Հալույթից առաջինն անջատվում է ոչ թե այն բաղադրիչը, որն ավելի շատ է, այլ այն, որի զանգվածն ավելի մեծ է, քան այն, որը համապատասխանում է էվտեկտիկ խառնուրդի բաղադրությանը:
Ասվածը հիմնավորենք հաշվումով: Նորից վերադառնանք (Bi+Cd) զույգին, որի էվտեկտիկական խառնուրդի բաղադրությունն էր ըստ զանգվածի 60%Bi+40%Cd::
Վերցնենք հետևյալ խառնուրդը ![]() Պարզ է, որ այս խառնուրդը Bi-ով ավելի հարուստ է և թվում է, որ պետք է նախ Bi -ն անջատվի հալույթից: Բայց այս դեպքում Cd-ն է սկսում բյուրեղանալ: Ինչու՞: Օգտվենք նույն հարաբերությունից.
Պարզ է, որ այս խառնուրդը Bi-ով ավելի հարուստ է և թվում է, որ պետք է նախ Bi -ն անջատվի հալույթից: Բայց այս դեպքում Cd-ն է սկսում բյուրեղանալ: Ինչու՞: Օգտվենք նույն հարաբերությունից. ![]() որտեղից
որտեղից ![]() այնինչ վերցվել էր 43գ Cd: Հետևաբար էվտեկտիկականի համեմատ Cd-ն է ավելցուկով և ոչ թե Bi-ը: Ուրեմն, ելային խառնուրդից պետք է անջատվի
այնինչ վերցվել էր 43գ Cd: Հետևաբար էվտեկտիկականի համեմատ Cd-ն է ավելցուկով և ոչ թե Bi-ը: Ուրեմն, ելային խառնուրդից պետք է անջատվի ![]() որպեսզի մնացած խառնուրդի բաղադրությունը համապատասխանի էվտեկտիկին: Ուրեմն, թեև ելային խառնուրդում Bi-ի զանգվածը Cd-ից մեծ է, բայց Cd-ն է սկսում բյուրեղանալ (խառնուրդից անջատվել):
որպեսզի մնացած խառնուրդի բաղադրությունը համապատասխանի էվտեկտիկին: Ուրեմն, թեև ելային խառնուրդում Bi-ի զանգվածը Cd-ից մեծ է, բայց Cd-ն է սկսում բյուրեղանալ (խառնուրդից անջատվել):
Այժմ տեսնենք թե ցրտեցման կորերի հիման վրա ինչպե՞ս պետք է կառուցել Bi - Cd բինար (երկկոմպոնենտ) համակարգի դիագրամը: Նշենք, որ բաղադրությունն արտահայտող աբսցիսը բաժանված է հավասար (առավել ձեռնտու է, երբ 10) մասերի: Իսկ օրդինատը խառնուրդի հալման (սառեցման) ջերմաստիճանն է:
Ցրտեցման կորերի վրա նշված բեկումնային կետերը (1, 2, 4, 5 և այլն) տեղափոխում ենք ![]() հարթության վրա հաշվի առնելով յուրաքանչյուր կետի կոորդինատները [օրինակ, (1)
հարթության վրա հաշվի առնելով յուրաքանչյուր կետի կոորդինատները [օրինակ, (1) ![]() և այլն]: Նշվում են նաև
և այլն]: Նշվում են նաև ![]() և այլն կետերը, որոնք համապատասխանում են
և այլն կետերը, որոնք համապատասխանում են ![]() ջերմաստիճանին և գտնվում են աբսցիսին զուգահեռ ուղիղի վրա: Այդ կետերն իրար հետ միացնելով կստացվի այն նկարը, որը ներկայացված է նկ.XIII.5-ի վրա: Այն կոչվում է A
-B (տվյալ դեպքում Bi –
Cd) բինար (երկբաղադրիչ) համակարգի վիճակի դիագրամ:
ջերմաստիճանին և գտնվում են աբսցիսին զուգահեռ ուղիղի վրա: Այդ կետերն իրար հետ միացնելով կստացվի այն նկարը, որը ներկայացված է նկ.XIII.5-ի վրա: Այն կոչվում է A
-B (տվյալ դեպքում Bi –
Cd) բինար (երկբաղադրիչ) համակարգի վիճակի դիագրամ:
A-ն և B-ն կարող են լինել ինչպես պարզ նյութեր, այնպես էլ տարբեր քիմիական միացություններ:
Այժմ քննարկենք ստացված դիագրամը: Ամբողջ հարթությունը կարելի է բաժանել իրարից սահմանազատված հինգ տիրույթների: ![]() կորից վերև խառնուրդը միաֆազ է. հալույթ: Այս պատճառով նշված կորը կոչվում է լիկվիդուս
(liquid-հեղուկ):
կորից վերև խառնուրդը միաֆազ է. հալույթ: Այս պատճառով նշված կորը կոչվում է լիկվիդուս
(liquid-հեղուկ):
Քննարկումն սկսենք AT օրդինատից, որի վրա ջերմաստիճաններն են նշված: Ա կետում ![]() զանգվածային բաժինն է:
զանգվածային բաժինն է: ![]() հալման ջերմաստիճանն է: Հետևաբար, երբ
հալման ջերմաստիճանն է: Հետևաբար, երբ ![]() (օրինակ,
(օրինակ, ![]() ) վերցված Bi-ը գտնվում է հեղուկ վիճակում: Երբ
) վերցված Bi-ը գտնվում է հեղուկ վիճակում: Երբ ![]() հալված Bi-ն սկսում է պնդանալ (բյուրեղանալ): Ամբողջ զանգվածը պնդանալուց հետո բյուրեղացած Bi-ը կսկսի սառչել: B կետում
հալված Bi-ն սկսում է պնդանալ (բյուրեղանալ): Ամբողջ զանգվածը պնդանալուց հետո բյուրեղացած Bi-ը կսկսի սառչել: B կետում ![]()
Վերցնենք ![]() բաղադրությամբ խառնուրդ, որը պարունակում է
բաղադրությամբ խառնուրդ, որը պարունակում է ![]() (ըստ զանգվածի): Տաքացնենք մինչև
(ըստ զանգվածի): Տաքացնենք մինչև ![]() ջերմաստիճան, խառնուրդը կհալվի (Ա կետ): Թողնենք, որ հալույթն ինքն իրեն սառչի: Երբ
ջերմաստիճան, խառնուրդը կհալվի (Ա կետ): Թողնենք, որ հալույթն ինքն իրեն սառչի: Երբ ![]() կնկատենք Bi-ի բյուրեղների անջատում. նշանակում է, որ
կնկատենք Bi-ի բյուրեղների անջատում. նշանակում է, որ ![]() ջերմաստիճանում հալույթը հագեցած է Bi-ով: Ուրեմն, y կետից մի փոքր վերև համակարգը միաֆազ է (հեղուկ) և մի փոքր ներքև՝ երկֆազ (հալույթ +Bi (բյուրեղներ)): Քանի որ այս մասնավոր դեպքում Bi-ն է լուծիչը այդ պատճառով ժամանակի ընթացքում լուծույթի կոնցենտրացիան կմեծանա, կնվազի սառեցման կետը և ջերմաստիճանը կսահի yME կորով
ջերմաստիճանում հալույթը հագեցած է Bi-ով: Ուրեմն, y կետից մի փոքր վերև համակարգը միաֆազ է (հեղուկ) և մի փոքր ներքև՝ երկֆազ (հալույթ +Bi (բյուրեղներ)): Քանի որ այս մասնավոր դեպքում Bi-ն է լուծիչը այդ պատճառով ժամանակի ընթացքում լուծույթի կոնցենտրացիան կմեծանա, կնվազի սառեցման կետը և ջերմաստիճանը կսահի yME կորով ![]() օրենքին համապատասխան: Նշեցինք, որ
օրենքին համապատասխան: Նշեցինք, որ ![]() էվտեկտիկ խառնուրդի սառեցման (հալման) ջերմաստիճանն է: Այն հաստատուն է յուրաքանչյուր նման զույգի համար: Հետևաբար,
էվտեկտիկ խառնուրդի սառեցման (հալման) ջերմաստիճանն է: Այն հաստատուն է յուրաքանչյուր նման զույգի համար: Հետևաբար, ![]() կորը ցույց է տալիս հալույթի Bi-ով հագեցման կախումը ջերմաստիճանից:
կորը ցույց է տալիս հալույթի Bi-ով հագեցման կախումը ջերմաստիճանից: ![]() նույնն է Cd-ի համար:
նույնն է Cd-ի համար:
Նորից վերցնենք ![]() բաղադրությամբ հալույթ
բաղադրությամբ հալույթ ![]() և այդ խառնուրդն արագ սառեցնենք մինչև
և այդ խառնուրդն արագ սառեցնենք մինչև ![]() ջերմաստիճան: Այս պայմանում համակարգի վիճակը կնկարագրվի K
կետով: Արդեն այս վիճակում համակարգը երկֆազ է (հալույթ + Bi(պ)): Երկու ֆազերի բաղադրությունը որոշելու համար K-ով աբսցիսին զուգահեռ (նոդ կամ կոնոդ) տանենք: Նոդը կհատի լիկվիդուսը M կետում: Այդ կետից իջեցնենք ուղղահայաց, որը կոչվում է իզոպլետ: Աբսցիսը կհատի
ջերմաստիճան: Այս պայմանում համակարգի վիճակը կնկարագրվի K
կետով: Արդեն այս վիճակում համակարգը երկֆազ է (հալույթ + Bi(պ)): Երկու ֆազերի բաղադրությունը որոշելու համար K-ով աբսցիսին զուգահեռ (նոդ կամ կոնոդ) տանենք: Նոդը կհատի լիկվիդուսը M կետում: Այդ կետից իջեցնենք ուղղահայաց, որը կոչվում է իզոպլետ: Աբսցիսը կհատի ![]() կետում: Հետևաբար,
կետում: Հետևաբար, ![]() ջերմաստիճանում հալույթը կպարունակի
ջերմաստիճանում հալույթը կպարունակի ![]() Իմանալով ելային բաղադրությունը կարելի է որոշել Bi-ի %-ը. քանի՞ գրամ Bi է գտնվում հալույթում բյուրեղական ձևով: Նման ձևով կարելի է քննարկել դիագրամի աջ ճյուղը:
Իմանալով ելային բաղադրությունը կարելի է որոշել Bi-ի %-ը. քանի՞ գրամ Bi է գտնվում հալույթում բյուրեղական ձևով: Նման ձևով կարելի է քննարկել դիագրամի աջ ճյուղը:
Սառեցումը շարունակելով կհասնենք ![]() ջերմաստիճանին (E կետ): Այս ընթացքում շարունակվում է Bi-ի անջատումը: Արդեն E կետում մնացած հալույթի բաղադրությունը հավասարվում է էվտեկտիկին: Երբ
ջերմաստիճանին (E կետ): Այս ընթացքում շարունակվում է Bi-ի անջատումը: Արդեն E կետում մնացած հալույթի բաղադրությունը հավասարվում է էվտեկտիկին: Երբ ![]() այդ խառնուրդը որպես մի ամբողջություն կսկսի պնդանալ: Հետևաբար, երբ
այդ խառնուրդը որպես մի ամբողջություն կսկսի պնդանալ: Հետևաբար, երբ ![]() ցանկացած բաղադրությամբ խառնուրդ գտնվում է պինդ վիճակում. E-ից ձախ ունենք Bi +
էվտեկտիկ և E-ից աջ՝ Cd +
էվտեկտիկ:
ցանկացած բաղադրությամբ խառնուրդ գտնվում է պինդ վիճակում. E-ից ձախ ունենք Bi +
էվտեկտիկ և E-ից աջ՝ Cd +
էվտեկտիկ:
Էվտեկտիկ խառնուրդի միկրոսկոպիական անալիզը ցույց է տալիս, որ հոմոգեն չէ. իրարից տարբերվում են Bi-ի և Cd-ի բյուրեղները: Ուրեմն դա երկֆազ, հետերոգեն խառնուրդ է:
Այժմ կարող ենք քննարկել նկ.XIII.5-ի վրա նշված հինգ տիրույթները:
I-ն տիրույթում համակարգը միաֆազ է, հեղուկ (հալույթ).
II-րդ տիրույթը հետերոգեն է. հալույթ+ (Bi (պ)
III-րդ տիրույթը հետերոգեն է. հալույթ + Cd(պ)
II-րդ և III-րդ տիրույթների ներսում յուրաքանչյուր կետում գոյություն ունի ![]() հավասարակշռություն:
հավասարակշռություն:
IV-րդ և V-րդ տիրույթներում համակարգը նորից հետերոգեն է (թեև պինդ) Bi + էվտեկտիկ (IV) և Cd + էվտեկտիկ (V):
Այս քննարկումից հետևում է, որ համակարգում ![]() ավելի ցածր հալման ջերմաստիճան ունեցող խառնուրդ չկա, այստեղից էլ կոչումը` էվտեկտիկական, որը հունարեն նշանակում է հեշտ հալվող:
ավելի ցածր հալման ջերմաստիճան ունեցող խառնուրդ չկա, այստեղից էլ կոչումը` էվտեկտիկական, որը հունարեն նշանակում է հեշտ հալվող:
![]() կետից աբսցիսին տարված զուգահեռի վրա դրան ուղղահայաց տեղադրենք նկ.XIII.4-ի վրա ներկայացված էվտեկտիկական խառնուրդի սառեցման ընթացքում ստացված կանգառները՝ համեմատական երկարություններով
կետից աբսցիսին տարված զուգահեռի վրա դրան ուղղահայաց տեղադրենք նկ.XIII.4-ի վրա ներկայացված էվտեկտիկական խառնուրդի սառեցման ընթացքում ստացված կանգառները՝ համեմատական երկարություններով ![]() և այլն):
և այլն):
Պարզվում է, որ այդ ուղղահայացների ծայրերը միացնելով կստացվի եռանկյուն ![]() Քանի որ սկզբնակետերը համապատասխանում են մաքուր նյութերին (Bi
և Cd), ուրեմն խոսք չի կարող լինել էվտեկտիկ խառնուրդի, հետևաբար և դրա կանգառի մասին (այն 0-ի է հավասար): Ստացված եռանկյունը հայտնի է Տամանի անունով:
Քանի որ սկզբնակետերը համապատասխանում են մաքուր նյութերին (Bi
և Cd), ուրեմն խոսք չի կարող լինել էվտեկտիկ խառնուրդի, հետևաբար և դրա կանգառի մասին (այն 0-ի է հավասար): Ստացված եռանկյունը հայտնի է Տամանի անունով:
Պարզվում է, որ այդպիսի քննարկումների ընթացքում ստացված եռանկյունների թիվը՝ n կապված է համակարգում ընթացող քիմիական ռեակցիաների թվի՝ N հետ. ![]()
Քննարկվող օրինակի համար n = 1, հետևաբար N = 0, այսինքն Bi- ի և Cd-ի միջև քիմիական ռեակցիա չի ընթանում:
Համակարգի վիճակի դիագրամի օգնությամբ կարելի է որոշել դիագրամի յուրաքանչյուր տիրույթում համակարգի ազատության աստիճանների թիվը, որի իմացումը հնարավորություն կտա կողմնորոշվելու, թե ինչպես կարելի է ստեղծված հավասարակշռությունը պահպանել:
Օգտվենք Գիբսի ֆազերի կանոնից.
![]()
որը տարբերվում է (XIII.8)-ից: Պատճառը բացատրված է:
Տիրույթ I-ում n = 2 (Bi և Cd), k-ն հավասար է 1(հեղուկ), հետևաբար. F=(2-1)+1=2. այսինքն լայն տիրույթում կարելի է կամայականորեն փոփոխել բաղադրությունը և ջերմաստիճանը առանց փոխելու համակարգի միաֆազությունը (հեղուկ):
Լիկվիդուսի վրա երկու ֆազեր են գտնվում հավասարակշռության մեջ. պինդ և հեղուկ: Հետևաբար. F=(n-2)+1=1: Նշանակում է, որ կարելի է միայն մի պարամետր փոխելով համակարգի երկֆազությունը պահպանել: Եթե T-ն ենք փոխում, ապա X-ը կփոխվի այնպես, որ ֆիգուրատիվ կետը տեղաշարժվի լիկվիդուսի վրայով: Տիրույթ II-ն (նաև III-րդ) ունի մի առանձնահատկություն:
Համակարգը թեև երկֆազ է, բայց պինդ ֆազի բաղադրությունը փոփոխական չէ. պարզապես զանգվածը կարող է փոփոխվել (օրինակ, եթե Bi + հալույթ համակարգի մասին է խոսքը, ապա T-ն կամ X-ը առանձին կամ միաժամանակ փոխելիս միայն հալույթի բաղադրությունն է փոխվում, իսկ պինդ ֆազը, որը միայն Bi-ից է կազմված, կենթարկվի միայն քանակական փոփոխության): Ուրեմն, միայն մի հատ ֆազ կա, որի բաղադրությունը փոփոխական է: Հետևաբար F = 2:
Էվտեկտիկ կետը (E) ըստ էության եռյակ կետ է: Այդ վիճակում երեք ֆազեր են գտնվում հավասարակշռության մեջ.
![]()
Ուրեմն F=(2-3)+1=0: Հետևաբար, էվտեկտիկ կետում համակարգը նոնվարիանտ է, այսինքն հնարավոր չէ փոփոխել պարամետրերից թեկուզ մեկը (T-ն կամ X-ը) առանց խախտելու գոյություն ունեցող հավասարակշռությունը:
Եզրակացություն. վիճակի դիագրամի միջոցով կարելի է պարզել (ա) քիմիական փոխազդեցություն կա՞ թե ոչ բաղադրիչների միջև, (բ) ի՞նչ ֆազեր են գտնվում հավասարակշռության մեջ, (գ) որոշել յուրաքանչյուր ֆազի բաղադրությունը. (դ) ինչպե՞ս և ի՞նչ ուղղությամբ կարելի է փոխել հավասարակշռությունը:
Մասնավոր դեպքում երկկոմպոնենտ համակարգը կարող է չհիդրոլիզվող աղի ջրային լոուծույթ լինել, օրինակ, ![]() Այս դեպքում կստացվի նկ.
XIII.6-ի վրա պատկերված դիագրամը:
Այս դեպքում կստացվի նկ.
XIII.6-ի վրա պատկերված դիագրամը:
Քանի, որ NaCl -ի հալման ջերմաստիճանը շատ բարձր է, այդ պատճառով էլ EA կորը գործնականորեն անավարտ է մնում: E կետով բնութագրվող էվտեկտիկ խառնուրդը տվյալ դեպքում կրիոհիդրատ է կոչվում, որը հալվում է -21,1օ-ում: Այս է պատճառը, որ ձմռանը սառցակալած ճանապարհների վրա աղ են շաղ տալիս, որպեսզի սառույցը հալվի: Բայց եթե օդի ջերմաստիճանը -22օ -ից ցածր է, ապա NaCl-ը արդյունավետ չէ այդ նպատակի համար:
բ) Դեպք երկրորդ. Երկու բաղադրիչներն իրար հետ պինդ լուծույթ են առաջացնում:
Սա այն դեպքն է, երբ երկու բաղադրիչներն իրար հետ տարբեր բաղադրությամբ պինդ լուծույթներ են առաջացնում. այն որ լուծիչ էր աստիճանաբար լուծված նյութ կդառնա:
Պինդ լուծույթներ կարող են առաջացնել ինչպես մետաղները, օրինակ, ![]() այնպես էլ աղերը.
այնպես էլ աղերը. ![]()
Տվյալ դեպքում պետք է հիշել, որ «լուծույթը փոփոխական բաղադրության ֆազ է», այսինքն հոմոգեն համակարգ է:

Պինդ լուծույթի առաջացման երկու մեխանիզմ կա.
1. Տեղակալման մեխանիզմ. սա այն դեպքն է, երբ երկու բաղադրիչները միևնույն կառուցվածքի բյուրեղավանդակ են առաջացնում և բյուրեղավանդակի հանգույցներում տեղավորված մասնիկների (ատոմների, իոնների) շառավիղներն էլ մոտավորապես իրար հավասար են: Այս պարագայում երկու բաղադրիչների մասնիկները կարող են իրար փոխարինել բյուրեղավանդակի հանգույցներում: Այս դեպքում պինդ (բյուրեղական) վիճակում այդ երկու նյութերն իրար մեջ անսահմանափակ կլուծվեն:
2. Ներկալման մեխանիզմ: Հնարավոր է, որ բյուրեղացման ժամանակ նյութերից մեկը ներկալվի մյուսի բյուրեղացանցի մեջ: Բնական է, որ այս դեպքում ներկալումը անսահման չի կարող լինել. ի վերջո բյուրեղավանդակներից մեկը կհագենա մյուս՝ ներկալվող նյութով: Փաստորեն (ա)-ի բյուրեղավանդակը կհագենա (բ)-ով և (բ)-ինն էլ (ա)-ով: Պայման չէ, որ երկուսի համար հագեցման աստիճանները նույնը լինեն:
Նկ.XIII.7-ի վրա պատկերվածը վերաբերում է տեղակալման մեխանիզմով պինդ լուծույթի առաջացման դեպքին:
Քննարկենք այն: ![]() Այս դեպքում էվտեկտիկական խառնուրդ չի կարող առաջանալ, հետևաբար ցրտեցման կորի վրա կանգառ չի լինի (տե՛ս նկ.XIII.8):
ab տիրույթում միայն հալույթ ունենք (միաֆազ համակարգ): b-ում սկսվում է ինչ որ մի բաղադրությամբ պինդ լուծույթի առաջացում: Բյուրեղացման ընթացքում փոխվում է պինդ լուծույթի բաղադրությունը: Բյուրեղացումն ավարտվում է c կետում, երբ առաջացած պինդ լուծույթն ունի բոլորովին այլ բաղադրություն, ինչ b կետում: b կետում որպես լուծիչ հանդես եկողը c-ն դառնում է լուծված նյութ: c-ում ամբողջ զանգվածը արդեն բյուրեղական վիճակում է և սկսում է սառել: bc մարզում համակարգը երկֆազ է. հալույթ + պինդ լուծույթ (պ): ab և cd մարզերում համակարգը միաֆազ է:
Այս դեպքում էվտեկտիկական խառնուրդ չի կարող առաջանալ, հետևաբար ցրտեցման կորի վրա կանգառ չի լինի (տե՛ս նկ.XIII.8):
ab տիրույթում միայն հալույթ ունենք (միաֆազ համակարգ): b-ում սկսվում է ինչ որ մի բաղադրությամբ պինդ լուծույթի առաջացում: Բյուրեղացման ընթացքում փոխվում է պինդ լուծույթի բաղադրությունը: Բյուրեղացումն ավարտվում է c կետում, երբ առաջացած պինդ լուծույթն ունի բոլորովին այլ բաղադրություն, ինչ b կետում: b կետում որպես լուծիչ հանդես եկողը c-ն դառնում է լուծված նյութ: c-ում ամբողջ զանգվածը արդեն բյուրեղական վիճակում է և սկսում է սառել: bc մարզում համակարգը երկֆազ է. հալույթ + պինդ լուծույթ (պ): ab և cd մարզերում համակարգը միաֆազ է:
![]() վերև համակարգը հեղուկ է (ab-ն ցրտեցման կորի վրա),
վերև համակարգը հեղուկ է (ab-ն ցրտեցման կորի վրա), ![]() - ներքև նորից համակարգը միաֆազ է, թեև պինդ: Այս պատճառով
- ներքև նորից համակարգը միաֆազ է, թեև պինդ: Այս պատճառով ![]() -ը կոչվում է լիկվիդուս, իսկ
-ը կոչվում է լիկվիդուս, իսկ ![]() սոլիդուս
(solid-պինդ):
սոլիդուս
(solid-պինդ):
Վերցնենք ![]() բաղադրությամբ (նորից արտահայտված զանգվածային բաժիններով) խառնուրդ և այն տաքացնենք մինչև
բաղադրությամբ (նորից արտահայտված զանգվածային բաժիններով) խառնուրդ և այն տաքացնենք մինչև ![]() ջերմաստիճան: Այն կտրոհվի երկու. [հեղուկ (հալույթ
ջերմաստիճան: Այն կտրոհվի երկու. [հեղուկ (հալույթ ![]() բաղադրությամբ) և պինդ (պինդ լուծույթ
բաղադրությամբ) և պինդ (պինդ լուծույթ ![]() բաղադրությամբ)] ֆազերի: Այս պինդ լուծույթում լուծիչը Ni-ն է: Եթե վերցնենք
բաղադրությամբ)] ֆազերի: Այս պինդ լուծույթում լուծիչը Ni-ն է: Եթե վերցնենք ![]() բաղադրությամբ ելային խառնուրդ, ապա հալույթի հետ
բաղադրությամբ ելային խառնուրդ, ապա հալույթի հետ ![]() ջերմաստիճանում հավասարակշռության մեջ գտնվող պինդ լուծույթում լուծիչը կլինի Cu-ը
ջերմաստիճանում հավասարակշռության մեջ գտնվող պինդ լուծույթում լուծիչը կլինի Cu-ը ![]()
Փաստորեն լիկվիդուսը ցույց է տալիս հալույթի, իսկ սոլիդուսը՝ պինդ լուծույթի բաղադրությունների կախումը ջերմաստիճանից: Այս դեպքում ևս կիրառելի է լծակի կանոնը:
Այս դեպքի տարատեսակներից մեկը ազեոտրոպ խառնուրդի առաջացումն է: Էքստրեմում կետում հալույթի և պինդ լուծույթի բաղադրություններն իրար հավասար են: (Տե՛ս նկարներ XIII.9 և XIII.10): Մեզ արդեն հայտնի երկու դեպքերն էլ հանդիպում են: Cu - Au համակարգը նույնպես առաջացնում է ազեոտրոպ խառնուրդ՝ հալման կետի մինիմումով:

Դեպք 3: Այժմ քննարկենք այն դեպքը, երբ երկու բաղադրիչները հեղուկ վիճակում իրար մեջ անսահմանափակ են լուծվում, և պինդ վիճակում առաջացնում են իրար մեջ սահմանափակ լուծվող պինդ լուծույթներ: Լավ օրինականեր են Sn –Pb և ![]() զույգերը:
զույգերը:

Նկ.XIII.11-ի վրա ներկայացված է Sn -Pb զույգի վիճակի դիագրամը:
Մեր ունեցած գիտելիքների հիման վրա քննարկենք դիագրամը ըստ տիրույթների:
![]() լիկվիդուսն է, հետևաբար I տիրույթում ունենք Sn
–Pb զույգի հալույթ (միաֆազ համակարգ):
լիկվիդուսն է, հետևաբար I տիրույթում ունենք Sn
–Pb զույգի հալույթ (միաֆազ համակարգ):
Վերցնենք ![]() ելային բաղադրությամբ խառնուրդ և տաքացնենք մինչև
ելային բաղադրությամբ խառնուրդ և տաքացնենք մինչև ![]() ջերմաստիճանը: Համակարգի վիճակը կբնութագրվի K ֆիգուրատիվ կետով: Թողնենք, որ հալույթը ինքն իրեն սառչի: l կետից սկսվում է պինդ ֆազի անջատում և սառեցման կետի աստիճանական նվազում: Տվյալ դեպքում հալույթից նստում է պինդ լուծույթ: Քանի որ նշված դեպքում անագի քանակն է գերակշռում, այս պատճառով խոսքը վերաբերում է այն պինդ լուծույթին, որն առաջանում է երբ կապարն է լուծվում անագի մեջ: Այս տիպի լուծույթը պայմանականորեն կոչվում է a պինդ լուծույթ: Հետևաբար, II տիրույթում ունենք հետերոգեն (երկֆազ) համակարգ. Հալույթ
ջերմաստիճանը: Համակարգի վիճակը կբնութագրվի K ֆիգուրատիվ կետով: Թողնենք, որ հալույթը ինքն իրեն սառչի: l կետից սկսվում է պինդ ֆազի անջատում և սառեցման կետի աստիճանական նվազում: Տվյալ դեպքում հալույթից նստում է պինդ լուծույթ: Քանի որ նշված դեպքում անագի քանակն է գերակշռում, այս պատճառով խոսքը վերաբերում է այն պինդ լուծույթին, որն առաջանում է երբ կապարն է լուծվում անագի մեջ: Այս տիպի լուծույթը պայմանականորեն կոչվում է a պինդ լուծույթ: Հետևաբար, II տիրույթում ունենք հետերոգեն (երկֆազ) համակարգ. Հալույթ ![]() պինդ լուծույթ: Նույն դատողություններով III տիրույթում ունենք հալույթ
պինդ լուծույթ: Նույն դատողություններով III տիրույթում ունենք հալույթ ![]() պինդ լուծույթ (այս պինդ լուծույթի լուծիչը կապարն է, իսկ լուծվածը՝ անագը):
պինդ լուծույթ (այս պինդ լուծույթի լուծիչը կապարն է, իսկ լուծվածը՝ անագը):
Այժմ K վիճակում գտնվող հալույթը արագ սառեցնենք մինչև ![]() ջերմաստիճան կամ
ջերմաստիճան կամ ![]() ելային բաղադրությամբ խառնուրդը տաքացնենք մինչև մինչև
ելային բաղադրությամբ խառնուրդը տաքացնենք մինչև մինչև ![]() ջերմաստիճան: Համակարգն անմիջապես կտրոհվի հեղուկ (հալույթ) և պինդ (
ջերմաստիճան: Համակարգն անմիջապես կտրոհվի հեղուկ (հալույթ) և պինդ (![]() լուծույթ) ֆազերի: Երկու ֆազերի բաղադրությունները որոշելու համար f-ից տանենք նոդ: nfm
ուղիղը կհատի սոլիդուսը n
կետում և լիկվիդուսը՝ m
կետում: n-ից և m-ից իջեցված ուղղահայցների (իզոպլետների) միջոցով կարելի է որոշել երկու ֆազերի բաղադրությունները: Այս դեպքում ևս կիրառելի է լծակի կանոնը: n
կետը ցույց է տալիս, որ
լուծույթ) ֆազերի: Երկու ֆազերի բաղադրությունները որոշելու համար f-ից տանենք նոդ: nfm
ուղիղը կհատի սոլիդուսը n
կետում և լիկվիդուսը՝ m
կետում: n-ից և m-ից իջեցված ուղղահայցների (իզոպլետների) միջոցով կարելի է որոշել երկու ֆազերի բաղադրությունները: Այս դեպքում ևս կիրառելի է լծակի կանոնը: n
կետը ցույց է տալիս, որ ![]() ջերմաստիճանում հավասարակշռության մեջ է հալույթը
ջերմաստիճանում հավասարակշռության մեջ է հալույթը ![]() լուծույթի հետ: Հետևաբար, IV տիրույթում ունենք տարբեր բաղադրությամբ
լուծույթի հետ: Հետևաբար, IV տիրույթում ունենք տարբեր բաղադրությամբ ![]() պինդ լուծույթներ: Նման ձևով քննարկելով խնդիրը կարող ենք ասել, որ V տիրույթում ունենք փոփոխական բաղադրությամբ
պինդ լուծույթներ: Նման ձևով քննարկելով խնդիրը կարող ենք ասել, որ V տիրույթում ունենք փոփոխական բաղադրությամբ ![]() լուծույթ: Եթե
լուծույթ: Եթե ![]() ելային բաղադրությամբ խառնուրդը
ելային բաղադրությամբ խառնուրդը ![]() ջերմաստիճանից մինչև
ջերմաստիճանից մինչև ![]() ջերմաստիճան սառեցնենք, համակարգը նորից կտրոհվի երկու ֆազերի, բայց այս անգամ երկու ֆազերն էլ պինդ են: E
կետում առաջանում է էվտեկտիկական խառնուրդ՝ կազմված
ջերմաստիճան սառեցնենք, համակարգը նորից կտրոհվի երկու ֆազերի, բայց այս անգամ երկու ֆազերն էլ պինդ են: E
կետում առաջանում է էվտեկտիկական խառնուրդ՝ կազմված ![]() պինդ լուծույթներից: E-ն եռյակ կետ է. իրար հետ հավասարակշռության մեջ են հալույթը և երկու պինդ լուծույթները: Այդ վիճակը նոնվարիանտ է, որովհետև.
պինդ լուծույթներից: E-ն եռյակ կետ է. իրար հետ հավասարակշռության մեջ են հալույթը և երկու պինդ լուծույթները: Այդ վիճակը նոնվարիանտ է, որովհետև.
![]()
Ըստ նկ.XIII.11-ի էվտեկտիկական խառնուրդը կազմված է 70% Sn-ից և 30% Pb-ից: Բայց Sn-ը և Pb-ը չեն գտնվում մաքուր մետաղների ձևով: Ֆազերից մեկը ![]() բաղադրությամբ
բաղադրությամբ
![]() լուծույթն է, իսկ մյուս ֆազը՝
լուծույթն է, իսկ մյուս ֆազը՝ ![]() բաղադրությամբ
բաղադրությամբ
![]() լուծույթը: Այդ երկու պինդ լուծույթների զանգվածների հարաբերությունը որոշակի է:
լուծույթը: Այդ երկու պինդ լուծույթների զանգվածների հարաբերությունը որոշակի է: ![]() գիծը պատկերում է
գիծը պատկերում է ![]() լուծույթի բաղադրության կախումը ջերմաստիճանից:
լուծույթի բաղադրության կախումը ջերմաստիճանից: ![]() վերաբերում է
վերաբերում է ![]() լուծույթին: Բայց այդ բաղադրությունները որոշվում են իրար մեջ փոխադարձ լուծելիությամբ: Հետևաբար, ara՛-ը ցույց է տալիս թե ջերմաստիճանից ինչպե՞ս է կախված Pb-ի լուծելիությունը Sn-ում, իսկ
լուծույթին: Բայց այդ բաղադրությունները որոշվում են իրար մեջ փոխադարձ լուծելիությամբ: Հետևաբար, ara՛-ը ցույց է տալիս թե ջերմաստիճանից ինչպե՞ս է կախված Pb-ի լուծելիությունը Sn-ում, իսկ ![]() էլ՝ անագինը կապարում:
էլ՝ անագինը կապարում:
XIII-3:2 (Բ) Երկու բաղադրիչներն իրար հետ ռեակցում են
ա) Դեպք առաջին - կոնգրուենտ հալման կետով քիմիական միացության առաջացում:
Քննարկվելու է այն դեպքը, երբ առաջացող միացությունը հեղուկ վիճակում անսահմանափակ լուծվում է երկու ելանյութերի մեջ: Բայց պինդ վիճակում գործնականորեն իրար մեջ չեն լուծվում: Ստացվող ![]() բաղադրությամբ քիմիական միացությունն իր հալման ջերմաստիճանում ոչ դիսոցվում է, ոչ էլ քայքայվում:
բաղադրությամբ քիմիական միացությունն իր հալման ջերմաստիճանում ոչ դիսոցվում է, ոչ էլ քայքայվում:
Նկ. XIII.12-ից հետևում է, որ այդ դիագրամը կարելի է դիտել որպես երկու հատ իրարից անկախ երկկոմպոնենտ համակարգերի մի զուգորդում (տե՛ս նկ.XIII.5-ը, որը վերաբերում է Bi-Cd զույգին): Դիագրամներից մեկը ![]() է, որը վերաբերում է
է, որը վերաբերում է ![]() զույգին և մյուսը՝
զույգին և մյուսը՝ ![]() դիագրամն է, որը վերաբերվում է
դիագրամն է, որը վերաբերվում է ![]() զույգին:
զույգին:
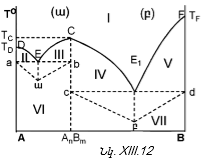
![]() ռեակցիայի արգասիքի բանաձևն է: n-ը և m-ը ստեխիոմետրական գործակիցներն են.
ռեակցիայի արգասիքի բանաձևն է: n-ը և m-ը ստեխիոմետրական գործակիցներն են. ![]()
Ըստ տիրույթների անալիզի արդյունքները.
I տիրույթում ունենք հալույթ: 1(ա) մասում հալույթ կազմված ![]() խառնուրդից, 1(բ) մասում հալույթ կազմված
խառնուրդից, 1(բ) մասում հալույթ կազմված
![]() խառնուրդից:
խառնուրդից:
II տիրույթում. հալույթ ![]() (բյուրեղներ)
(բյուրեղներ)
III տիրույթում. հալույթ ![]() (բյուրեղներ)
(բյուրեղներ)
IV տիրույթում. հալույթ ![]() (բյուրեղներ)
(բյուրեղներ)
V տիրույթում. հալույթ ![]() (բյուրեղներ)
(բյուրեղներ)
VI տիրույթում. պինդ վիճակ. Էվտեկտիկ
![]()
VII տիրույթում. պինդ վիճակ. էվտեկտիկ ![]()
E-ն էվտեկտիկական խառնուրդ է կազմված A-ից և ![]() նույնպես էվտեկտիկական խառնուրդ է, բայց կազմված B-ից և
նույնպես էվտեկտիկական խառնուրդ է, բայց կազմված B-ից և ![]() E
կետում հավասարակշռության մեջ են. հալույթը, A-ն (պ) և
E
կետում հավասարակշռության մեջ են. հալույթը, A-ն (պ) և ![]() (պ), իսկ
(պ), իսկ ![]() հալույթը, B-ն(պ) և
հալույթը, B-ն(պ) և ![]() (պ):
(պ):
![]() ջերմաստիճանից կախված պինդ նյութով
ջերմաստիճանից կախված պինդ նյութով ![]() հալույթի հագեցման կորերն են:
հալույթի հագեցման կորերն են:
C կետը, որը ![]() իրարից անկախ գոյություն ունեցող 2 կորերի հատման արդյունքն է` կոչվում է սինգուլյար կետ: Նման սուր մաքսիմումի գոյությունը ցուցանիշն է այն բանի, որ A-ի և B-ի փոխազդեցությունից առաջացած
իրարից անկախ գոյություն ունեցող 2 կորերի հատման արդյունքն է` կոչվում է սինգուլյար կետ: Նման սուր մաքսիմումի գոյությունը ցուցանիշն է այն բանի, որ A-ի և B-ի փոխազդեցությունից առաջացած
![]() բաղադրությամբ քիմիական միացությունը
բաղադրությամբ քիմիական միացությունը ![]() ջերմաստիճանում հալվում է բաղադրության պահպանումով (կոնգրուենտ հալման կետ):
ջերմաստիճանում հալվում է բաղադրության պահպանումով (կոնգրուենտ հալման կետ):
Նշված պայմաններին բավարարում են հետևյալ զույգերը. ![]() և այլն:
և այլն:
Ինչպես նախորդ դեպքերում, այս դեպքում ևս ![]() կետերը եռյակ են, 3 ֆազեր են գտնվում հավասարակշռության մեջ: E կետում. A(պ)+հալույթ
կետերը եռյակ են, 3 ֆազեր են գտնվում հավասարակշռության մեջ: E կետում. A(պ)+հալույթ ![]() իսկ
իսկ ![]() -ում՝ B(պ)+հալույթ
-ում՝ B(պ)+հալույթ![]() (պ): Այդ երկու կետերին համապատասխանում են էվտեկտիկական խառնուրդներ
(պ): Այդ երկու կետերին համապատասխանում են էվտեկտիկական խառնուրդներ ![]()
Հեշտ է նկատել, որ երկու հատ Տամանի եռանկյուն է ստացվում, հետևաբար համակարգում ![]() հատ քիմիական ռեակցիա է ընթանում:
հատ քիմիական ռեակցիա է ընթանում:
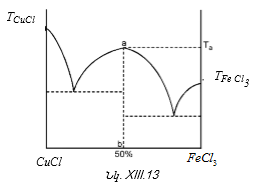
Հնարավոր է այնպիսի քիմիական միացության առաջացում, որն իր հալման ջերմաստիճանում մասամբ դիսոցվում է: Այդպիսի օրինակ է հետևյալ ռեակցիան.
![]()
![]() հալման ջերմաստիճանում առաջացած արգասիքը մասամբ դիսոցվում է:
հալման ջերմաստիճանում առաջացած արգասիքը մասամբ դիսոցվում է:
բ) Դեպք երկրորդ. Պերիտեկտիկ կետով քիմիական միացության առաջացում:
Քննարկվելու է այն դեպքը, երբ քիմիական միացությունը չհասած իր հալման ջերմաստիճանին քայքայվում է: Այսպես, երբ
![]()
(ա)-ն (բ)-ից տարբերվում է ռեակցիայի դարձելիությամբ:
Նկ.XIII.15 տիպի վիճակի դիագրամը վերաբերում է կիրառական որոշակի հետաքրքրություն ներկայացնող ![]() համակարգին: Այս երկու քիմիական տարրերն իրար հետ ռեակցում են՝ առաջացնելով
համակարգին: Այս երկու քիմիական տարրերն իրար հետ ռեակցում են՝ առաջացնելով ![]() բաղադրությամբ քիմիական միացություն, որը չհասած հալման ջերմաստիճանին քայքայվում է: Այս դեպքում հալումը ոչ կոնգրուենտ է: Նշանակում է, որ բաղադրությունը չի պահպանվում:
բաղադրությամբ քիմիական միացություն, որը չհասած հալման ջերմաստիճանին քայքայվում է: Այս դեպքում հալումը ոչ կոնգրուենտ է: Նշանակում է, որ բաղադրությունը չի պահպանվում:
Քննարկենք այս դեպքը. ![]()
Առաջին եզրակացությունն այն է, որ ![]() քիմիական միացությունը կայուն է միայն 7oC-ից ցածր ջերմաստիճաններում:
քիմիական միացությունը կայուն է միայն 7oC-ից ցածր ջերմաստիճաններում:
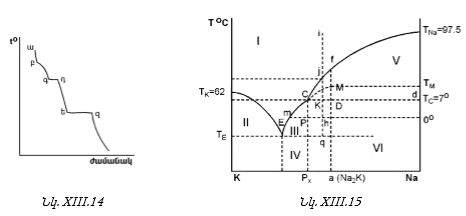
Տիրույթ I-ում համակարգը գտնվում է հեղուկ վիճակում (միաֆազ հալույթ):
Տիրույթ II-ը հետերոգեն (երկֆազ) համակարգ է: Այն կազմված է հալույթից ![]() և մետաղական K-ից (պինդ ֆազ): E-ն K-ից և
և մետաղական K-ից (պինդ ֆազ): E-ն K-ից և ![]() կազմված էվտեկտիկական խառնուրդն է:
կազմված էվտեկտիկական խառնուրդն է:
0oC –ում ![]() բաղադրությամբ ելային խառնուրդը երկու ֆազերի կտրոհվի. ֆազերից մեկը m բաղադրությամբ հալույթ է, իսկ մյուսը՝ պինդ
բաղադրությամբ ելային խառնուրդը երկու ֆազերի կտրոհվի. ֆազերից մեկը m բաղադրությամբ հալույթ է, իսկ մյուսը՝ պինդ ![]() քիմիական միացություն:
քիմիական միացություն:
IV տիրույթում կա K(պ) և ![]() (պ), նաև էվտեկտիկական խառնուրդ կազմված K-ից և
(պ), նաև էվտեկտիկական խառնուրդ կազմված K-ից և ![]() -ից:
-ից:
Այժմ դիագրամը քննարկենք կոնկրետ ֆիգուրատիվ կետի հիման վրա:
Սկսենք a-ից, որը նշում է քիմիական միացության բաղադրությունը: Մինչև 7oC
տաքացնենք այն: Նախքան հալվելը արդեն D
կետում ![]() միացությունն սկսում է քայքայվել [(գ)-ին հակադիր ռեակցիան է]: Ստացվում է հալույթ (Na+K)
(հ) (C
կետում) և Na (պ) (d
կետում): Քանի որ ընդհանուր խառնուրդից Na
է անջատվել, դա նշանակում է, որ խառնուրդը հարստացել է K-ով (C
կետ): C-ն կոչվում է պերիտեկտիկ կետ (հունարեն՝ շուրջ բոլորը հալված):
միացությունն սկսում է քայքայվել [(գ)-ին հակադիր ռեակցիան է]: Ստացվում է հալույթ (Na+K)
(հ) (C
կետում) և Na (պ) (d
կետում): Քանի որ ընդհանուր խառնուրդից Na
է անջատվել, դա նշանակում է, որ խառնուրդը հարստացել է K-ով (C
կետ): C-ն կոչվում է պերիտեկտիկ կետ (հունարեն՝ շուրջ բոլորը հալված):
![]()
Հետևաբար C կետում նորից 3 ֆազեր են գտնվում հավասարակշռության մեջ [տե՛ս (դ)-ն]:
Եթե ![]() արդեն քիմիական միացություն չկա: V տիրույթում համակարգը երկֆազ է. հալույթ+Na (պ):
արդեն քիմիական միացություն չկա: V տիրույթում համակարգը երկֆազ է. հալույթ+Na (պ): ![]() այն ենթադրական ջերմաստիճանն է, որի տակ պիտի հալվեր քիմիական միացությունը, եթե այդ ջերմաստիճանում կայուն լիներ, չքայքայվեր:
այն ենթադրական ջերմաստիճանն է, որի տակ պիտի հալվեր քիմիական միացությունը, եթե այդ ջերմաստիճանում կայուն լիներ, չքայքայվեր:
Քննարկենք i վիճակում գտնվող միաֆազ համակարգը: Այդ կետին համապատասխանող բաղադրությունը չի ապահովում Na-ի համար պահանջվող ստեխիոմետրական քանակը (համեմատել a
բաղադրության հետ) որպեսզի վերցված ամբողջ կալիումը ռեակցիայի մեջ մտնի: j
կետում հալույթը հագեցած է Na-ով, որից կսկսի Na-ի բյուրեղացումը. համակարգը երկֆազ է: Ցրտեցման կորը կպատկերվի բգ կորով [տես նկ.XIII.14]:
K կետում արդեն կայուն քիմիական միացություն է առաջանում [այդ պիտի առաջանար թերևս ավելի բարձր՝ ![]() ջերմաստիճանում]: Այդ կետից է սկսվում
ջերմաստիճանում]: Այդ կետից է սկսվում ![]() բյուրեղացումը: Ցրտեցման կորի վրա այն արտահայտվում է գդ կանգառով: h վիճակում համակարգը նորից երկֆազ է ինչպիսին էր p
վիճակում: Մինչև
բյուրեղացումը: Ցրտեցման կորի վրա այն արտահայտվում է գդ կանգառով: h վիճակում համակարգը նորից երկֆազ է ինչպիսին էր p
վիճակում: Մինչև ![]() ջերմաստիճանի հետագա նվազման հետևանքով կառաջանա նոր խառնուրդ, որը կազմված կլինի էվտեկտիկականից և քիմիական միացությունից: Ինչ վերաբերում է VI տիրույթին, ապա այդ մարզում առաջանում է մի խառնուրդ, որը կազմված է Na-ից (պ) և քիմիական միացությունից (պ):
ջերմաստիճանի հետագա նվազման հետևանքով կառաջանա նոր խառնուրդ, որը կազմված կլինի էվտեկտիկականից և քիմիական միացությունից: Ինչ վերաբերում է VI տիրույթին, ապա այդ մարզում առաջանում է մի խառնուրդ, որը կազմված է Na-ից (պ) և քիմիական միացությունից (պ):
գ) Դեպք երրորդ. Քիմիական միացությունը սահմանափակ լուծելիությամբ լուծույթներ է առաջացնում ելանյութերի հետ: Դալտոնիդներ և Բերթոլիտներ:
Առաջացող քիմիական միացությունը սահմանափակ լուծելիությամբ պինդ լուծույթներ է առաջացնում երկու ելանյութերի (A և B) հետ:
Հաշվի առնելով մինչև այս էջը շարադրված նյութը պետք՝ ակնկալել, որ այս դեպքում ֆազային դիագրամը կազմված կլինի իրար հետ միացված երկու հատ նկ.XIII.11
դիագրամներից, այնպես որ առաջին կեսում ![]() քիմիական միացությունը կգրավի B-ի տեղը և երկրորդ կեսը կավարտվի B-ով: Աբսցիսի վրա M-ին համապատասխանող կետը կարտահայտի առաջացող քիմիական միացության բաղադրությունը
(
քիմիական միացությունը կգրավի B-ի տեղը և երկրորդ կեսը կավարտվի B-ով: Աբսցիսի վրա M-ին համապատասխանող կետը կարտահայտի առաջացող քիմիական միացության բաղադրությունը
(![]() ):
):
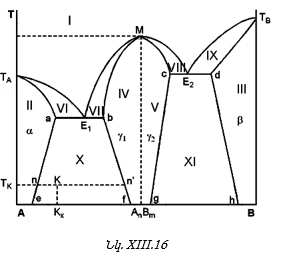
![]() կորից (լիկվիդուս) վերև համակարգը միաֆազ է և գտնվում է հեղուկ վիճակում (տիրույթ I): II
տիրույթում գտնվում է a
պինդ լուծույթը, որում լուծիչը A-ն է և լուծված նյութը՝ քիմիական միացությունը: Բաղադրությունը փոփոխական է: Տիրույթ III-ում
կորից (լիկվիդուս) վերև համակարգը միաֆազ է և գտնվում է հեղուկ վիճակում (տիրույթ I): II
տիրույթում գտնվում է a
պինդ լուծույթը, որում լուծիչը A-ն է և լուծված նյութը՝ քիմիական միացությունը: Բաղադրությունը փոփոխական է: Տիրույթ III-ում ![]() պինդ լուծույթ, որի լուծիչը B-ն է և լուծված նյութը՝ նորից քիմիական միացությունն է: IV և V տիրույթներում էլ պինդ լուծույթներ ունենք: IV-ում և V-ում լուծիչը քիմիական միացությունն է, իսկ լուծվածը՝ A-ն (IV մարզ) և B-ն՝ V-ում: Երբեմն այդ երկուսը միացնում են
պինդ լուծույթ, որի լուծիչը B-ն է և լուծված նյութը՝ նորից քիմիական միացությունն է: IV և V տիրույթներում էլ պինդ լուծույթներ ունենք: IV-ում և V-ում լուծիչը քիմիական միացությունն է, իսկ լուծվածը՝ A-ն (IV մարզ) և B-ն՝ V-ում: Երբեմն այդ երկուսը միացնում են ![]() անվան տակ: VI-IX
տիրույթներում համակարգը հետերոգեն է:
անվան տակ: VI-IX
տիրույթներում համակարգը հետերոգեն է:
![]() էվտեկտիկական կետեր են
էվտեկտիկական կետեր են ![]() խառնուրդները): X և XI տիրույթներում համակարգը պինդ է, բայց երկֆազ: Եթե
խառնուրդները): X և XI տիրույթներում համակարգը պինդ է, բայց երկֆազ: Եթե ![]() ջերմաստիճանում վերցնենք
ջերմաստիճանում վերցնենք ![]() լային բաղադրությամբ խառնուրդ, ապա այն կտրոհվի կոնկրետ բաղադրություններով
լային բաղադրությամբ խառնուրդ, ապա այն կտրոհվի կոնկրետ բաղադրություններով ![]() երկու պինդ լուծույթների: Իրավիճակը նման է XI տիրույթում:
երկու պինդ լուծույթների: Իրավիճակը նման է XI տիրույթում:
Կախված հալման ջերմաստիճանում առաջացող քիմիական միացության կայունությունից քննարկված դեպքերի հիման վրա կարելի է կատարել հետևյալ ընդհանրացումը: Այն վերաբերում է վիճակի դիագրամի վրա առաջացող մաքսիմումի տեսքին.

Նախ նշենք, որ մաքսիմում կետին համապատասխանող բաղադրությունը հենց առաջացող քիմիական միացության ստեխիոմետրական բաղադրությունն է: Բոլոր դեպքերում ռեակցիայի արգասիքը չի քայքայվում հալման ջերմաստիճանում:
I [(ա) և (բ)] նկարները վերաբերում են այն դեպքերին, երբ արգասիքը՝ տվյալ համակարգում պինդ լուծույթներ չի առաջացնում:
(ա) դեպքում քիմիական միացությունը հալվում է առանց դիսոցվելու, իսկ (բ) դեպքում՝ այն դիսոցվում է:
II [(ա) և (բ)] նկարներից հետևում է, որ խիստ որոշակի է պինդ լուծույթներ առաջացնող քիմիական միացության բաղադրությունը:
Հետաքրքրական է II (գ) դեպքը: Բացակայում է սուր «մաքսիմում”. այն փռված է: Հետևաբար առաջացող քիմիական միացության բաղադրությունը որոշակի չէ, փոփոխական է:
Ֆիզիկաքիմիական անալիզի հիմունքները քննարկելիս նշվեց, որ ուսումնասիրության այդ մեթոդը կոնկրետ պայմանների համար պարզելով բաղադրությունից ֆիզիկական մի հատկության կախումը տեղեկություն է տալիս համակարգի վիճակի մասին:
Նշված մեթոդով ուսումնասիրելով այն համակարգերը, որոնք համապատասխանում են II(ա) և II(բ) դեպքերին (տե՛ս նկ.XIII.17) պարզվել է, որ մաքսիմում կետում էքստրեմալ արժեք ունի նույնպես համակարգի ևս մի հատկություն, օրինակ, էլեկտրահաղորդականությունը:
Բայց երբ քննարկվող համակարգը II(գ) դեպքին է վերաբերում, ապա կոնցենտրացիոն այդ տիրույթում, երբ մաքսիմումի փոխարեն փռված (ճապաղված) «զանգակ” է ստացվում, կոնցենտրացիոն այդ նույն տիրույթում համակարգի էլեկտրահաղորդականությունը նույնպես չունի էքստրեմալ արժեք:
Եզրակացությունը հետևյալն է. Կոնցենտրացիոն այդ տիրույթում քիմիական միևնույն տարրերից տարբեր քանակական հարաբերություններով քիմիական միացություններ են առաջանում: Կուռնակովի առաջարկությամբ (IIա) և (IIբ) դեպքերին համապատասխանող նյութերը կոչվել են «դալտոնիտներ» (հաստատուն բաղադրությամբ միացություններ) ի պատիվ Ջ.Դալտոնի, իսկ (IIգ)-ին համապատասխանողները՝ «բերթոլիտներ» (փոփոխական բաղադրությամբ միացություններ) ի պատիվ Բերթոլեի: Նյութաբանության տեսակետից այս վերջին միացությունները որոշակի հետաքրքրություն են ներկայացնում:
XIII-4. ԵՌԿՈՄՊՈՆԵՆՏ ՀԱՄԱԿԱՐԳԵՐ: ՈՒՍՈՒՄՆԱՍԻՐՈՒԹՅԱՆ ՄԵԹՈԴՆԵՐԸ: ԳԻԲՍԻ ՖԱԶԵՐԻ ԿԱՆՈՆԻ ԿԻՐԱՌՈՒՄԸ
ԱՅԴ ՀԱՄԱԿԱՐԳԵՐԻ ՆԿԱՏՄԱՄԲ
Եռկոմպոնենտ համակարգի մասնավոր դեպքեր են երկու աղերից ![]() և ջրից կազմված լուծույթները: Տեխնիկական առումով համակարգի այսպիսի քննարկումը բարդ է: Քանի որ հավասարակշռական վիճակը կախված է նաև T-ից և P-ից, այդ պատճառով էլ հարցի քննարկումը պարզեցնելու համար ուսումնասիրությունները կատարում են հաստատուն ճնշման տակ իզոթերմային պայմաններում:
և ջրից կազմված լուծույթները: Տեխնիկական առումով համակարգի այսպիսի քննարկումը բարդ է: Քանի որ հավասարակշռական վիճակը կախված է նաև T-ից և P-ից, այդ պատճառով էլ հարցի քննարկումը պարզեցնելու համար ուսումնասիրությունները կատարում են հաստատուն ճնշման տակ իզոթերմային պայմաններում:
Տվյալ դեպքի համար կիրառելի է Գիբսի ֆազերի կանոնը (XIII.8) տեսքով:
![]()
Ուրեմն, տվյալ համակարգը կայուն հավասարակշռական վիճակում կգտնվի, եթե 5 ֆազեր գտնվեն փոխադարձ հավասարակշռության մեջ ![]()
Նպատակահարմար է բաղադրիչների կոնցենտրացիաներն արտահայտել մոլային կամ զանգվածային բաժիններով, որպեսզի փոփոխությունը սահմանափակվի 0-ից մինչև 1 տիրույթում:
Մի հարց էլ կա, որը կբարդացնի համակարգը: Եթե, օրինակ, վերցվում է ջուր և երկու հատ չհիդրոլիզվող աղ ![]() և
և ![]() , ապա ջրային լուծույթում անխուսափելի է հետևյալ դարձելի փոխանակման ռեակցիան.
, ապա ջրային լուծույթում անխուսափելի է հետևյալ դարձելի փոխանակման ռեակցիան.
![]()
օրինակ, ![]()
Փաստորեն ջուրը գոլորշիացնելուց հետո այդ չորս աղերը կհայտնվեն խառնուրդում: Ուրեմն, համակարգը կդառնա քառակոմպոնենտ. ![]() մեկ քիմիական հավասարում:
մեկ քիմիական հավասարում:
Որպեսզի համակարգն ըստ էության եռակոմպոնենտ լինի, պետք է վերցնել երկու այնպիսի աղեր, որոնք բացի չհիդրոլիզվելուց ունենան կամ ընդհանուր կատիոն կամ ընդհանուր անիոն: Օրինակ, ![]() և այլն:
և այլն:
Եռկոմպոնենտ համակարգերն ուսումնասիրլու երկու մատչելի մեթոդ կա.
1. փոխուղղահայաց կոորդինատների և
2. Գիբսի եռանկյունի մեթոդ։
XIII-4:1. Փոխուղղահայաց կոորդինատների մեթոդ
Այս մեթոդն օգտագործելու համար պետք է ջրի հաստատուն քանակ վերցնել. N մոլ=const:
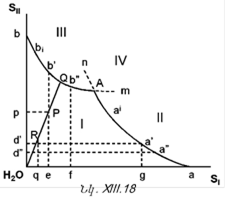
Նախ ![]() աղի բացակայությամբ այդ N
մոլ ջրի մեջ աստիճանաբար լուծում են
աղի բացակայությամբ այդ N
մոլ ջրի մեջ աստիճանաբար լուծում են ![]() քանակներով:
քանակներով:
Երբ ![]() լուծույթը նշված պայմաններում հագենում է
լուծույթը նշված պայմաններում հագենում է ![]() աղով: Երբ
աղով: Երբ
![]() ապա նստվածք կառաջանա:
ապա նստվածք կառաջանա:
Նման դատողությամբ կարելի է ասել, որ b-ն տվյալ պայմաններում ![]() աղի այն քանակն է, որը N
մոլ ջուրը հագեցնում է:
աղի այն քանակն է, որը N
մոլ ջուրը հագեցնում է:
Հաջորդ փորձերը կատարվում են հետևյալ պայմաններում: N
մոլ ջրում նախօրոք լուծում են ![]() աղի որոշակի քանակ՝
աղի որոշակի քանակ՝ ![]() և այդ լուծույթներում հարաճուն ավելացնում են
և այդ լուծույթներում հարաճուն ավելացնում են ![]() աղից: Այս փորձերից կստացվեն
աղից: Այս փորձերից կստացվեն ![]() կետերը, որոնք ցույց են տալիս
կետերը, որոնք ցույց են տալիս ![]() աղի ներկայությամբ N մոլ ջուրը
աղի ներկայությամբ N մոլ ջուրը ![]() հագեցումը: Նման ձևով կստացվեն
հագեցումը: Նման ձևով կստացվեն
![]() կետերը: Այս դեպքում
կետերը: Այս դեպքում
![]() աղի ջրային լուծույթը հագենում է
աղի ջրային լուծույթը հագենում է ![]() աղով:
աղով:
![]() կորերը կհատվեն A
կետում: Այսպիսով, վիճակի դիագրամի վրա 4 որոշակի տիրույթներ են ստացվում:
կորերը կհատվեն A
կետում: Այսպիսով, վիճակի դիագրամի վրա 4 որոշակի տիրույթներ են ստացվում:
I տիրույթում լուծույթն ըստ երկու աղերի չհագեցած է: II տիրույթում ըստ ![]() լուծույթը հագեցած է, լուծույթում
լուծույթը հագեցած է, լուծույթում
![]() նստվածք կա, իսկ ըստ
նստվածք կա, իսկ ըստ ![]() ոչ: III տիրույթում ընդհակառակը: Այս դեպքում լուծույթում
ոչ: III տիրույթում ընդհակառակը: Այս դեպքում լուծույթում
![]() աղի նստվածք կա: IV տիրույթը վերաբերում է այն վիճակին, երբ լուծույթը ոչ միայն հագեցած է ըստ երկու աղերի, այլև լուծույթում երկու աղերի նստվածքներ կան:
աղի նստվածք կա: IV տիրույթը վերաբերում է այն վիճակին, երբ լուծույթը ոչ միայն հագեցած է ըստ երկու աղերի, այլև լուծույթում երկու աղերի նստվածքներ կան:
Հետևաբար, aA կորը ցույց է տալիս, թե տվյալ ջերմաստիճանում և ճնշման տակ ![]() աղի լուծելիությունն ինչպես է կախված լուծույթում
աղի լուծելիությունն ինչպես է կախված լուծույթում ![]() աղի կոնցենտրացիայից: bA-ն նույնն է
աղի կոնցենտրացիայից: bA-ն նույնն է ![]() աղի համար:
աղի համար:
Եթե վերցնում են R
ելային բաղադրությամբ լուծույթ և ենթարկում են իզոթերմային գոլորշիացման, ապա 2 աղերի քանակների հարաբերությունը հաստատուն մնալու պայմաններում համակարգի վիճակը կփոխվի ORPQ
ուղիղով: Հենց որ լուծույթը ![]() աղով հագենա (Q
կետ), այդ աղը կսկսի աստիճանաբար նստել: Լուծույթը կսկսի
աղով հագենա (Q
կետ), այդ աղը կսկսի աստիճանաբար նստել: Լուծույթը կսկսի ![]() աղով աղքատանալ և ջրի գոլորշիացմանը զուգահեռ կմեծանա լուծույթի ըստ
աղով աղքատանալ և ջրի գոլորշիացմանը զուգահեռ կմեծանա լուծույթի ըստ ![]() կոնցենտրացիան: Վիճակը կփոխվի QA
կորով: A
կետում լուծույթն արդեն կհագենա նաև
կոնցենտրացիան: Վիճակը կփոխվի QA
կորով: A
կետում լուծույթն արդեն կհագենա նաև ![]() աղով և ի վերջո համակարգը կտեղափոխվի IV տիրույթ: Ջրի լրիվ գոլորշիացման հետ կստացվի R
հարաբերությամբ
աղով և ի վերջո համակարգը կտեղափոխվի IV տիրույթ: Ջրի լրիվ գոլորշիացման հետ կստացվի R
հարաբերությամբ
![]() աղերի խառնուրդ:
աղերի խառնուրդ:
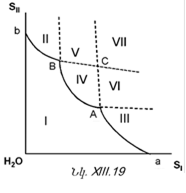
Եթե երկու աղերն իրար հետ փոխազդում են, օրինակ, կրկնակի աղ է առաջանում, ապա դիագրամի վրա լրացուցիչ AB
կորն է ավելանում (տես նկ.XIII.19):
Այն ցույց է տալիս, թե տվյալ պայմաններում լուծույթում
![]() աղերի քանակներն ինչպես են ազդում կրկնակի աղի լուծելիության վրա:
աղերի քանակներն ինչպես են ազդում կրկնակի աղի լուծելիության վրա:
I տիրույթում չհագեցած լուծույթ ունենք: II տիրույթում լուծույթը հագեցած է ըստ ![]() կա
կա ![]() նստվածք և չի հագեցած կրկնակի աղով: III-ում նույնը ըստ
նստվածք և չի հագեցած կրկնակի աղով: III-ում նույնը ըստ ![]() V-ում լուծույթը հագեցած է
V-ում լուծույթը հագեցած է ![]() և կրկնակի աղերով, լուծույթում այդ երկու աղերից նստվածք կա, չի հագեցած ըստ
և կրկնակի աղերով, լուծույթում այդ երկու աղերից նստվածք կա, չի հագեցած ըստ ![]() VI-ում նույնը ըստ
VI-ում նույնը ըստ ![]() IV տիրույթում (BCA
մարզ) լուծույթը միայն ըստ կրկնակի աղի է հագեցած և այս վերջինից նստվածք է պարունակում: Իսկ VII տիրույթում լուծույթը հագեցած է ըստ երեք աղերի և նստվածքում այդ երեք աղերից էլ կան:
IV տիրույթում (BCA
մարզ) լուծույթը միայն ըստ կրկնակի աղի է հագեցած և այս վերջինից նստվածք է պարունակում: Իսկ VII տիրույթում լուծույթը հագեցած է ըստ երեք աղերի և նստվածքում այդ երեք աղերից էլ կան:
XIII-4:2. Գիբսի եռանկյան մեթոդ
Քննարկված մեթոդի թերություններից մեկն այն է, որ հնարավոր չէ 3 բաղադրիչներն էլ (ներառյալ ջուրը) միաժամանակ փոփոխել, այնուհետև պարզել, թե եթե համակարգում փոխազդեցություն կա, ապա դա ինչ բնույթի է, օրինակ, կրկնակի աղ է գոյանում, թե բյուրեղահիդրատ:
Գիբսի մեթոդը վերացնում է այդ թերությունները:
1. Եռանկյան կողմերն իրար հավասար են: Յուրաքանչյուրը կարելի է, օրինակ, 10 հավասար մասերի բաժանել:
2. Եռանկյան գագաթներից յուրաքանչյուրը մեկ կոմպոնենտ է ներկայացնում, օրինակ, A-ն ջուրն է, B-ն ![]() աղը, C-ն
աղը, C-ն ![]() ը:
ը:
3. Եռանկյան ներսում գտնվող համակարգի վիճակը նկարագրող որևէ մի a
կետից երեք կողմերին իջեցրած ուղղահայացների գումարը հավասար է եռանկյան բարձրությանը, որը նույնպես 10 հավասար մասերի է բաժանված: Այսպիսով եռանկյան 3 կողմերին a կետից ուղղահայացներ տանելով կարելի է միանգամաից երեք բաղադրիչների բաղադրությունները որոշել: Բերված օրինակի համար ![]() վերաբերում է A-ին (տվյալ դեպքում ջրին),
վերաբերում է A-ին (տվյալ դեպքում ջրին), ![]()
4. Եռանկյան յուրաքանչյուր կողմը երկկոմպոնենտ համակարգ է ներկայացնում: Օրինակ, ![]() գագաթներում
գագաթներում
![]() Այսպես մյուսների համար:
Այսպես մյուսների համար:
Պետք է նշել, որ բաղադրություն որոշելու համար կա նաև Ռոզեբոմի եղանակը. a կետից 3 գագաթներին զուգահեռներ տանել. ըստ bc-ի ![]() 20% է, ըստ ef-ի ջուրը 50% է և ըստ gh-ի
20% է, ըստ ef-ի ջուրը 50% է և ըստ gh-ի ![]() 30% է:
30% է:
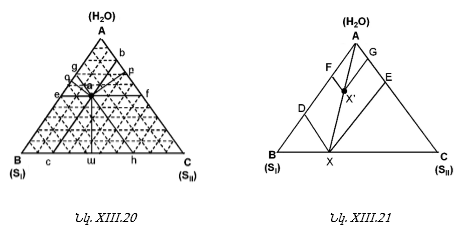
Ռոզեբոմի մեթոդն ունի հետևյալ առավելությունը:
Վերցնենք X բաղադրությամբ B-ից և C-ից կազմված բինար խառնուրդ: X-ից AB-ին տանենք XE և AC-ին DX զուգահեռները (տե՛ս նկ.XIII.21):
X-ը միացնենք երրորդ կոմպոնենտը խորհրդանշող A գագաթին: X՛-ից նորից զուգահեռներ տանենք AC և AB կողմերին (FX՛- և X՛-G ) :
Այսպիսով կստացվեն նման եռանկյուններ, որոնց համեմատությունից կստացվի.
![]()
Սա նշանակում է, որ AX
ուղիղի վրա ցանկացած կետի (որի միջոցով են որոշվում 3 բաղադրիչների քանակները) համար համապատասխան երկու բաղադրիչների հարաբերությունը հաստատուն է: Այսպես, եթե վերցնենք X՛
բաղադրությամբ ![]() աղեր պարունակող ջրային լուծույթ, ապա ջուրը իզոթերմորեն գոլորշիացնելիս լուծույթի կոնցենտրացիան ըստ երկու աղերի աստիճանաբար կմեծանա, բայց լուծույթում այդ աղերի զանգվածների կամ մոլերի հարաբերությունը հաստատուն կմնա նույնիսկ երբ ջրի վերջին կաթիլը գոլորշիանա:
աղեր պարունակող ջրային լուծույթ, ապա ջուրը իզոթերմորեն գոլորշիացնելիս լուծույթի կոնցենտրացիան ըստ երկու աղերի աստիճանաբար կմեծանա, բայց լուծույթում այդ աղերի զանգվածների կամ մոլերի հարաբերությունը հաստատուն կմնա նույնիսկ երբ ջրի վերջին կաթիլը գոլորշիանա:
Գիբսի մեթոդով քննարկենք այն դեպքերը, որոնք քննարկել ենք փոխուղղահայաց կոորդինատների մեթոդով:
Դեպք 1: Ջուր և 2 հատ ընդհանուր իոնով իրար հետ չփոխազդող աղեր են վերցվել:
T=const և P=const: Ելային բաղադրությունը համապատասխանում է a ֆիգուրատիվ կետին: Սկզբնական պայմանն այնպիսին է, որ լուծույթը ըստ երկու աղերի չհագեցած է (տիրույթ I):
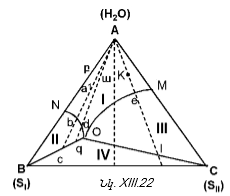
Լուծույթը ենթարկենք իզոթերմային գոլորշիացման:
Վերևում նշված երկրաչափական հատկանիշի համաձայն համակարգի (լուծույթի) կոնցենտրացիան (բաղադրությունը) պիտի փոխվի ըստ Aabc
ուղիղի: b
կետում լուծույթը ըստ ![]() հագենում է: Եթե վերցնենք ելային (ա) բաղադրությամբ լուծույթ, ապա նշված պայմաններում այն կհագենա d
կետում: Այս երևույթը կհաստատվի հետևյալով. ջրի մի փոքր գոլորշիացման հետևանքով նստվածք կառաջանա:
հագենում է: Եթե վերցնենք ելային (ա) բաղադրությամբ լուծույթ, ապա նշված պայմաններում այն կհագենա d
կետում: Այս երևույթը կհաստատվի հետևյալով. ջրի մի փոքր գոլորշիացման հետևանքով նստվածք կառաջանա:
Եթե վերցնենք միայն ![]() աղի ջրային լուծույթ, ապա հագեցում կնկատվի N կետում: N-ից, b-ից և d-ից սկսվում է
աղի ջրային լուծույթ, ապա հագեցում կնկատվի N կետում: N-ից, b-ից և d-ից սկսվում է ![]() աղի նստեցումը: c և q կետերում լուծույթը սկսում է հագենալ նաև
աղի նստեցումը: c և q կետերում լուծույթը սկսում է հագենալ նաև ![]() աղով: M-ով որոշվում է ջրում
աղով: M-ով որոշվում է ջրում ![]() լուծելիությունը: Եթե ելային լուծույթի բաղադրությունը որոշվում է K
կետով, ապա ջուրն իզոթերմորեն գոլորշիացնելիս նորից կմեծանա լուծույթի կոնցենտրացիան և e
կետում այն կհագենա
լուծելիությունը: Եթե ելային լուծույթի բաղադրությունը որոշվում է K
կետով, ապա ջուրն իզոթերմորեն գոլորշիացնելիս նորից կմեծանա լուծույթի կոնցենտրացիան և e
կետում այն կհագենա ![]() աղով մնալով ըստ
աղով մնալով ըստ ![]() չհագեցած: l կետում լուծույթը կհագենա նաև
չհագեցած: l կետում լուծույթը կհագենա նաև ![]() աղով:
աղով:
Այսպիսով, տիրույթ I-ում լուծույթը ըստ երկու աղերի չհագեցած է: NbdO
կորը ցույց է տալիս ![]() աղի լուծելիության կախումը լուծույթում
աղի լուծելիության կախումը լուծույթում ![]() աղի կոնցենտրացիայից, MeO-ն նույնն է
աղի կոնցենտրացիայից, MeO-ն նույնն է ![]() աղի համար: Հետևաբար, II տիրույթում (NOB)
լուծույթն ըստ
աղի համար: Հետևաբար, II տիրույթում (NOB)
լուծույթն ըստ ![]() աղի հագեցած է, ըստ
աղի հագեցած է, ըստ ![]() չհագեցած է և լուծույթը պարունակում է
չհագեցած է և լուծույթը պարունակում է ![]() նստվածք: III տիրույթում (MOC)
լուծույթը հագեցած է ըստ
նստվածք: III տիրույթում (MOC)
լուծույթը հագեցած է ըստ ![]() չհագեցած է ըստ
չհագեցած է ըստ ![]() պարունակում է
պարունակում է ![]() նստվածք:
նստվածք:
OգB-ն վերաբերում է լուծույթի նաև ![]() հագեցմանը, իսկ OlC-ն՝ լուծույթի հագեցմանը նաև ըստ
հագեցմանը, իսկ OlC-ն՝ լուծույթի հագեցմանը նաև ըստ ![]() Ուրեմն BOC
(IV) տիրույթում լուծույթը հագեցած է և ըստ
Ուրեմն BOC
(IV) տիրույթում լուծույթը հագեցած է և ըստ ![]() և ըստ
և ըստ ![]() և այդ երկու աղերից նստվածք է պարունակում:
և այդ երկու աղերից նստվածք է պարունակում:
Ինչպես նշվեց N
և M
կետերով տվյալ պայմաններում որոշվում է մաքուր ![]() աղերի լուծելիությունը ջրում:
աղերի լուծելիությունը ջրում:
Դեպք 2. Աղերից առնվազն մեկը բյուրեղահիդրատ է առաջացնում: Եթե միայն ![]() աղն է բյուրեղահիդրատ առաջացնում, ապա կստացվի նկ.XIII.23-ը:
աղն է բյուրեղահիդրատ առաջացնում, ապա կստացվի նկ.XIII.23-ը:
N կետում լուծույթը հագենում է բյուրեղահիդրատով: H
կետում ![]() հարաբերությունը համապատասխանում է բյուրեղահիդրատի բաղադրությանը
հարաբերությունը համապատասխանում է բյուրեղահիդրատի բաղադրությանը ![]() Այդ կետում լուծույթում բացի բյուրեղահիդրատից
Այդ կետում լուծույթում բացի բյուրեղահիդրատից
![]() էլ կա, որը նույնպես սկսում է նստել:
էլ կա, որը նույնպես սկսում է նստել:
Նորից վերցնենք a բաղադրությամբ ըստ ![]() չ հագեցած լուծույթ և իրականացնենք իզոթերմային գոլորշիացում:
չ հագեցած լուծույթ և իրականացնենք իզոթերմային գոլորշիացում:

b կետում լուծույթը կհագենա ![]() բյուրեղահիդրատով: bc
ուղիղի վրա շարունակվում է բյուրեղահիդրատի անջատումը որպես նստվածք: c
կետում լուծույթը նաև
բյուրեղահիդրատով: bc
ուղիղի վրա շարունակվում է բյուրեղահիդրատի անջատումը որպես նստվածք: c
կետում լուծույթը նաև ![]() աղով է հագենում:
աղով է հագենում:
e կետում լուծույթը հագենում է նաև ![]() աղով, որովհետև ջուրն այնքան է նվազել, որ բյուրեղահիդրատ չի կարող առաջանալ:
աղով, որովհետև ջուրն այնքան է նվազել, որ բյուրեղահիդրատ չի կարող առաջանալ:
f կետում լուծույթը հագենում է ![]() աղով, g
կետում նաև բյուրեղահիդրատով:
աղով, g
կետում նաև բյուրեղահիդրատով:
Դիագրամը քննարկենք ըստ տիրույթների: I տիրույթում լուծույթը չհագեցած է: II-ում (NOH)
լուծույթը հագեցած է ըստ ![]() բյուրեղահիդրատի և պարունակում է նաև դրա նստվածքը: III տիրույթում (MOC)
հագեցած լուծույթ ըստ
բյուրեղահիդրատի և պարունակում է նաև դրա նստվածքը: III տիրույթում (MOC)
հագեցած լուծույթ ըստ ![]() որը պարունակում է դրա նստվածքը: IV-ում (HOC)
լուծույթը պարունակում է ինչպես բյուրեղահիդրատի այնպես էլ
որը պարունակում է դրա նստվածքը: IV-ում (HOC)
լուծույթը պարունակում է ինչպես բյուրեղահիդրատի այնպես էլ ![]() նստվածք: V-ում (HBC)
ըստ բոլոր աղերի հագեցած լուծույթ, որը պարունակում է այդ երեք աղերի նստվածքները:
նստվածք: V-ում (HBC)
ըստ բոլոր աղերի հագեցած լուծույթ, որը պարունակում է այդ երեք աղերի նստվածքները:
Օրինակ, եթե վերցված է ջուր ![]() , ապա HBC-ում կլինի հագեցած լուծույթ,
, ապա HBC-ում կլինի հագեցած լուծույթ, ![]() նստվածքներ:
նստվածքներ:
d կետում համակարգը նշված 3 աղերի խառնուրդ է (ջուր չկա):
Դեպք 3. Ուսումնասիրման առարկա երկու աղերն իրար հետ փոխազդում են, օրինակ, կրկնակի աղ են առաջացնում:
Նախ քննարկենք այն դեպքը, երբ ինչպես ելային այնպես էլ այդ աղերի փոխազդեցության արգասիք հանդիսացող կրկնակի աղը բյուրեղահիդրատներ չեն առաջացնում: Հանդիպող երկու դեպքեր են ներկայացված նկ.XIII.24-ի վրա:
b կետում լուծույթը հագեցած է ![]() աղով և F
բաղադրությամբ կրկնակի աղով: c
կետում լուծույթն հագեցած է
աղով և F
բաղադրությամբ կրկնակի աղով: c
կետում լուծույթն հագեցած է ![]() աղով և կրկնակի աղով:
աղով և կրկնակի աղով:
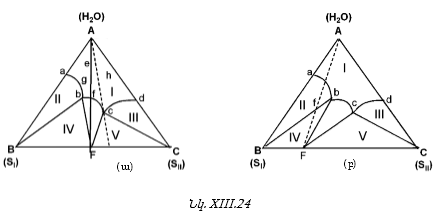
II տիրույթը (abB).
լուծույթը հագեցած է ![]() պարունակում է նաև վերջինիս նստվածքը: III տիրույթը (dcC)
նույնն է
պարունակում է նաև վերջինիս նստվածքը: III տիրույթը (dcC)
նույնն է ![]() աղի համար: f
կետում լուծույթը հագեցած է կրկնակի աղով, իսկ (bcF)
մարզում լուծույթը պարունակում է կրկնակի աղի նստվածք:
աղի համար: f
կետում լուծույթը հագեցած է կրկնակի աղով, իսկ (bcF)
մարզում լուծույթը պարունակում է կրկնակի աղի նստվածք:
IV տիրույթը (BbF)
լուծույթը հագեցած է ![]() աղով և կրկնակի աղով պարունակում է դրանց նստվածքները: V տիրույթը (FcC)
նման է IV-ին` միայն
աղով և կրկնակի աղով պարունակում է դրանց նստվածքները: V տիրույթը (FcC)
նման է IV-ին` միայն ![]() պետք է փոխարինել
պետք է փոխարինել ![]()
Չնայած արտաքին նմանությանը, այնուամենայնիվ (ա) և (բ) ենթադեպքերն իրար նկատմամբ սկզբունքային տարբերություն ունեն:
Կարելի է երկու ճանապարհով ստանալ լուծելիություն արտահայտող եռկոմպոնենտ համակարգի ֆազային դիագրամ.
1. ![]() բաղադրություններով չհագեցած լուծույթները իզոթերմորեն գոլորշիացնելով կամ
բաղադրություններով չհագեցած լուծույթները իզոթերմորեն գոլորշիացնելով կամ
2. որոշակի բաղադրությամբ աղերի խառնուրդին աստիճանաբար ջուր ավելացնելով:
Քննարկենք 2-րդ դեպքը: Վերցնենք F բաղադրությամբ կրկնակի աղ և աստիճանաբար ջուր ավելացնենք:
Վիճակը նկարագրող ֆիգուրատիվ կետերը կշարվեն AF ուղիղի վրա (այս հարցն արդեն քննարկված է):
Ենթադրենք (ա) – կրկնակի աղին ջուր ավելացնելիս կհասնենք f կետը. լուծույթն ըստ կրկնակի աղի հագեցած է և պարունակում է կրկնակի աղի նստվածք: Ջրի հետագա ավելացումով արդեն լուծույթն ըստ կրկնակի աղի, ![]() կդառնա չհագեցած: Հետևաբար, Ff ուղիղի վրա տեղի է ունենում կրկնակի աղի կոնգրուենտ լուծում: Երևույթը կոչվում է կրկնակի աղի կոնգրուենտ հագեցում:
կդառնա չհագեցած: Հետևաբար, Ff ուղիղի վրա տեղի է ունենում կրկնակի աղի կոնգրուենտ լուծում: Երևույթը կոչվում է կրկնակի աղի կոնգրուենտ հագեցում:
Հեշտ է նկատել, որ (բ) ենթադեպքում նշված պայմանում F
բաղադրությամբ չոր կրկնակի աղին ջուր ավելացնելիս այն միանգամից խառնվում է ![]() աղի հետ, առաջանում է
աղի հետ, առաջանում է ![]() աղի նստվածք պարունակող հագեցած լուծույթ. մաքուր կրկնակի աղի նստվածք չկա: Այս դեպքում կրկնակի աղով լուծույթի հագեցումը ոչկոնգրուենտ է, այսինքն կրկնակի աղի լուծման ընթացքում կրկնակի աղը (բաղադրությունը) չի պահպանվում:
աղի նստվածք պարունակող հագեցած լուծույթ. մաքուր կրկնակի աղի նստվածք չկա: Այս դեպքում կրկնակի աղով լուծույթի հագեցումը ոչկոնգրուենտ է, այսինքն կրկնակի աղի լուծման ընթացքում կրկնակի աղը (բաղադրությունը) չի պահպանվում:
Դեպք 4. Եռկոմպոնենտ համակարգը կարող է կազմված լինել նաև միայն հեղուկ նյութերից: Այդպիսի մի օրինակ է.
![]()
(վինիլացետատ) համակարգը:
Վերցնենք D բաղադրությամբ ջրի և վինիլացետատի խառնուրդ: I տիրույթում համակարգը երկշերտ է: aB-ն արտահայտում է ջրով հագեցած վինիլացետատի լուծույթ, իսկ bC-ն՝ վինիլացետատով հագեցած ջրային լուծույթ:
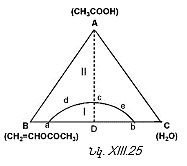
D բաղադրությամբ այդ խառնուրդին աստիճանաբար քացախաթթու ավելացնենք: adceb տիրույթը մնում է երկշերտ: Յուրաքանչյուր շերտի բաղադրությունը փոփոխական է: Քացախաթթվի ներկայությամբ պարզապես մեծանում է ջրի և վինիլացետատի փոխադարձ լուծելիությունը: Արդեն II մարզում համակարգը միաշերտ է. լուծույթ, հետևաբար և հոմոգեն:
Այդ դիագրամի օգնությամբ կարելի է հեշտությամբ որոշել այդ 3 բաղադրիչների այն հարաբերությունները, որոնք ապահովում են հոմոգեն համակարգի ստացումը:
1. Օգտվելով Գիբսի ֆազերի կանոնից որոշել հետևյալ համակարգերի ազատության աստիճանների թիվը (T=const):
ա) ջրային լուծույթ, որը պարունակում է ![]() լուծված
և որպես նստվածք: Լուծույթը հավասարակշռության մեջ է նաև ջրային գոլորշիների հետ,
լուծված
և որպես նստվածք: Լուծույթը հավասարակշռության մեջ է նաև ջրային գոլորշիների հետ,
բ) երկու աղերի ջրային լուծույթ, որը հավասարակշռության մեջ է ջրային գոլորշիների և սառույցի հետ,
գ) երկու աղերի ջրային լուծույթ, որը պարունակում է այդ աղերի նստվածքները, սառույց և հավասարակշռության մեջ գտնվող ջրային գոլորշիներ:
2. Գծել Sb-Pb բինար խառնուրդի վիճակի դիագրամը օգտվելով հետևյալ տվյալներից.
ա) Ելային բաղադրությունը

բ) Այդ համակարգում առաջանու՞մ է արդյոք քիմիական միացություն:
գ) Ի՞նչ բաղադրություն ունի էվտեկտիկական խառնուրդը: Ո՞ր ջերմաստիճանում է հալվում:
դ) Ինչի՞ է հավասար համակարգի ազատության աստիճանների թիվը a, c և E վիճակներում (a - ն լիկվիդուսից վերև է, c-ն լիկվիդուսի վրա է և E-ն համապատասխանում է էվտեկտիկական խառնուրդին):
ե) 430oC-ում վերցված է 2 կգ
ելային խառնուրդ, որի 40%-ը ![]() Այդ վիճակում համակարգը հոմոգե՞ն
է, թե հետերոգեն: Պատասխանը հիմնավորել: Եթե հոմոգեն է, ապա քանի՞ կգ է հալույթը և
քանի՞ կգ է պինդ ֆազը: Ի՞նչ է իրենից ներկայացնում պինդ ֆազը: Այս հարցը լուծել նաև
կիրառելով լծակի կանոնը:
Այդ վիճակում համակարգը հոմոգե՞ն
է, թե հետերոգեն: Պատասխանը հիմնավորել: Եթե հոմոգեն է, ապա քանի՞ կգ է հալույթը և
քանի՞ կգ է պինդ ֆազը: Ի՞նչ է իրենից ներկայացնում պինդ ֆազը: Այս հարցը լուծել նաև
կիրառելով լծակի կանոնը:
3. ա) Բերված ցրտեցման կորերի հիման վրա գծել Pt -Cu բինար համակարգի վիճակի դիագրամը.
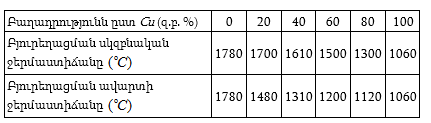
բ) Ի՞նչ կարելի է ասել այդ համակարգի մասին:
գ) Ինչպե՞ս է կոչվում վերևի կորը և ինչպե՞ս` ներքևինը:
դ) Ըստ փորձնական տվյալների վիճակի դիագրամի վրա երեք տիրույթ է ստացվում: Ինչպիսի՞ն է յուրաքանչյուր տիրույթին վերաբերող ֆազի բաղադրությունը:
ե) Վերցված է ըստ զանգվածի
![]() Cu պարունակող խառնուրդ և
տաքացված է մինչև 1400oC: Այդ վիճակում քանի՞ ֆազ է գտնվում հավասարակշռության
մեջ: Որոշել յուրաքանչյուր ֆազի բաղադրությունը:
Cu պարունակող խառնուրդ և
տաքացված է մինչև 1400oC: Այդ վիճակում քանի՞ ֆազ է գտնվում հավասարակշռության
մեջ: Որոշել յուրաքանչյուր ֆազի բաղադրությունը:
4. Mg-Si բինար համակարգի տարբեր բաղադրությունների համար տրված են ցրտեցման կորերը:
ա) Գծել վիճակի դիագրամը: Ի՞նչ կարելի է եզրակացնել:
բ) Որոշել առաջացող քիմիական միացության բաղադրությունը և հալման ջերմաստիճանը: Կայու՞ն է արդյոք այդ քիմիական միացությունը հալման ջերմաստիճանում: Ինչպե՞ս է կոչվում այդպիսի հալման ջերմաստիճանը:
գ) Քանի՞ հատ էվտեկտիկական խառնուրդ է առաջանում: Որոշել յուրաքանչյուրի բաղադրությունը և հալման ջերմաստիճանը:
5. Տրված է հետևյալ վիճակի դիագրամը: Վերցված է 200 գ խառնուրդ:
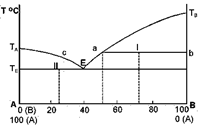
ա) Որոշել I կետին համապատասխանող ելային բաղադրությունը, հավասարակշռության մեջ գտնվող ֆազերի թիվը և յուրաքանչյուր ֆազի բաղադրությունը:
բ) Որոշել II կետում հավասարակշռության մեջ գտնվող ֆազերի թիվը և յուրաքանչյուրի բաղադրությունը:
