ՀՏԴ

Ատոմա-մոլեկուլային ուսմունք:  Ատոմի կառուցվածքը: Ուսումնական ձեռնարկ Ֆ.Գրիգորյան, Ա.Գրիգորյան: Հայաստանի պետական ճարտարագիտական համալսարան: Երևան, 2005 թ., 48 էջ:

Նախատեսված է Քիմիա-տեխնոլոգիական և բնապահպանական ճարտարագիտություն մասնագիտության ուսանողների, մագիստրանտների և ասպիրանտների համար:

 

Գրախոսներ`                 Հ Մխիթարյան

                                       Ռ.Միրզախանյան

 

Խմբագիր`                      Ն. Խաչատրյան

 

 

1. Ներածություն

1.1. Քիմիան և բնագիտությունը

1.2. Քիմիան ճշգրիտ գիտություն է

1.3. Քիմիան և ժամանակակից հասարակության խնդիրները

2. Ատոմամոլեկուլային ուսմունք

2.1 Մոլեկուլ, ատոմ, տարր

2.2. Պարզ և բարդ նյութեր: Ալոտրոպիա:

2.3. Քիմիական տարրերի նշանները: Քիմիական բանաձևերը

2.4. Ատոմի զանգված: Հարաբերական ատոմային և մոլեկուլային զանգվածներ

2.5. Նյութի մոլ քանակություն

2.6. Գազային նյութերի մոլեկուլային զանգվածի որոշումը

Ամփոփում

Սովորելու նպատակը

Հիմնական հասկացություններ

3. Ատոմի  կառուցվածքը

3.1.Ատոմի միջուկային մոդելը

3.2. Միջուկի բաղադրությունը

3.3. Զանգվածային թիվ

3.4. Կարգահամարի ֆիզիկական իմաստը: Իզոտոպներ

3.5. Սպեկտրոգրաֆի աշխատանքի սկզբունքը

3.6. Ջրածնի ատոմի սպեկտրը

3.7. Գաղափար լուսային քվանտների մասին

3.8. Բորի տեսությունը ջրածնի ատոմի համար

3.9. Բորի տեսության մաթեմատիկական հետևությունները

3.10. Ջրածնի ատոմի սպեկտրի բացատրությունն ըստ Բորի

3.11. Բորի - Զոմերֆելդի տեսության հակասությունները

4. Քվանտային մեխանիկայի տարրերը

4.1. Ալիքներ և մասնիկներ

4.2. Լույսի ալիքամասնիկային երկվությունը

4.3. Դե-Բրոյլի տեսությունը

4.4. Հայզենբերգի անորոշության սկզբունքը

4.5. Շրյոդինգերի հավասարումը

4.6. Ալիքային ֆունկցիան, դրա ֆիզիկական իմաստը և նկարագրման եղանակները

4.7. Շրյոդինգերի հավասարման լուծումը: Միաչափ պոտենցիալ տուփ

4.8. Ջրածնի ատոմի կառուցվածքը ըստ քվանտային մեխանիկայի

4.9. Չորս քվանտային թվեր

Բազմաէլեկտրոն ատոմներ

4.10. Էլեկտրոնների լրացման հաջորդականությունը բազմաէլեկտրոն ատոմներում

4.11. Էլեկտրոնային բանաձևեր, էլեկտրոնային դիագրամներ

Ամփոփում

Սովորելու նպատակը

Հիմնական հասկացություններ

 

 

 

1. Ներածություն

1.1. Քիմիան և բնագիտությունը

Քայլե՞լ եք դուք աշնանային անտառով, զարմացե՞լ եք տերևների գույների փոփոխությունից, նստե՞լ եք իրիկնային խարույկի շուրջն ու զմայլվել բոցի գույներով: Այդ երևույթները քիմիական փոփոխությունների արդյունք են: Քիմիան գործ ունի բոլոր նյութերի հետ, և դրանց հետ կատարվող փոփոխությունները, որ տեսնում ենք մեր շրջապատում, դարձնում են աշխարհը բազմազան ու գեղեցիկ, երբեմն էլ խորհրդավոր: Դրանով է բացատրվում է մետաղի ժանգոտումը, քաղցրավենիքի մարսումը, հ ացի թխումը, մարդու ծերացումը և այլն:

Ձեզանից շատերը ուսումնասիրում են քիմիան, քանի որ այն ընդգրկված է ուսումնական ծրագրերում: Ձեր հիմնական մասնագիտությունը կարող է լինել էլեկտրատեխնիկան, երկրաբանությունը, բժշկությունն ու շինարարությունը, սակայն քիմիայի ուսումնասիրությունն անհրաժեշտ է: Պատճառն այն է, որ մարդկային գործունեության  ցանկացած բնագավառ, որը կապված է նյութական աշխարհի հետ, կարիք ունի հասկանալու, թե ինչպե՞ս են նյութերը փոխազդում իրար և շրջապատի հետ,  ինչպե՞ս են նյութերը փոփոխվում: Այդ պատճառով քիմիան կարևոր դեր ունի Ձեր ապագա մասնագիտության մեջ: Դուք կլինեք ավելի բազմակողմանի և ստեղծագործ անձ, եթե հասկանաք Ձեր աշխատանքին վերաբերող քիմիական հասկացությունները և կարողանաք անհրաժեշտության դեպքում օգտագործել դրանք:

Քիմիական ուսումնասիրությունների արդյունքում ստեղծվել և օգտագործվում են այնպիսի նյութեր, որպիսիք չի ստեղծել բնությունը և առանց որոնց չէին կարող զարգանալ գիտությունը և արդյունաբերության բոլոր բնագավառները: Ժամանակակից մարդ լինելու համար Դուք կարիք կունենաք տեղեկացված լինելու քիմիայի շատ համապարփակ հարցերի, քիմիական նյութերի օգտագործման մասին: Այս գիրքը կծանոթացնի Ձեզ հիմնական քիմիական հասկացություններին, կօգնի հասկանալու շրջապատող աշխարհը` հնարավորությունները և պահանջները:

Այն ամենը, ինչ մենք տեսնում ենք մեզ շրջապատող աշխարհում մեկ ընդհանուր անունով կոչվում է մատերիա: Մատերիան գտնվում է անընդհատ շարժման` փոփոխությունների մեջ:  Մատերիայի  շարժման պարզագույն տեսակը մեխանիկական շարժումն է` մի մարմնի տեղափոխությունը մյուսի նկատմամբ: Շարժմա ն այս պարզագույն տեսակը մարդը յուրացրել է ամենից վաղ և դրա օրինաչափությունները ուսումնասիրող բնական գիտությունը կոչվում է մեխանիկա: Ավելի ուշ մարդը յուրացրեց մատերիայի շարժման մի նոր ավելի բարդ տեսակ` ֆիզիկական շարժումը, երբ փոխվում է նյութի ձևը, չափը, ագրեգատային վիճակը: Այս շարժման օրինաչափությունը ուսումնասիրում է ֆիզիկա բնական գիտությունը: Զարգացման շատ ավելի բարձր փուլում (մոտ երկու-երեք հարյուրամյակ առաջ) մարդը ճանաչեց մատերիայի շարժման մի նոր, ավելի բարդ տեսակ, երբ նյութը փոխվում է բաղադրությամբ, երբ մեկ կամ մի քանի նյութերից ստացվում են նոր նյութեր: Այդպիսի շարժումը կոչվում է քիմիական շարժում և դրա օրինաչափությունները ուսումնասիրող բնական գիտությունը կոչվում է քիմիա: Եթե ջրի հոսելը մարդը ճանաչել և օգտագործել էր դեռ նախնադարում, ջրի գոլորշիանալը` ավելի ուշ, ապա այն բանը, որ ջուրը կարող է քայքայվել, առաջացնելով նոր նյութեր` ջրածին և թթվածին, մարդը հասկացել է մոտ երկու հարյուր տարի առաջ միայն: Հետևաբար,

    Քիմիան բնական գիտություն է, որն ուսումնասիրում է նյութերի փոխարկումները և դրանց օրինաչափությունները:

Մատերիայի շարժման հաջորդ տեսակը կենսաբանական շարժումն է, կենդանի օրգանիզմի ծագումը, զարգացումը և մահացումը, որն ուսումնասիրում է կենսաբանություն բնական գիտությունը և հասարակական շարժումը, մատերիայի ամենաբարձր կազմակերպված տեսակի` մարդկային հասարակության շարժումը, որը ուսումնասիրում է հասարակագիտությունը:

Մատերիան գոյություն ունի երկու վիճակներում` նյութի և դաշտի: Նյութի օրինակ են մի կտոր կավիճը, մի բաժակ ջուրը, շրջապատող առարկաները: Դաշտի օրինակ են էլեկտրական, մագնիսական, գրավիտացիոն դաշտերը: Դաշտը և նյութը ունեն մի շարք ինչպես ընդհանուր, այնպես էլ տարբեր հատկանիշներ: Օրինակ` ընդհանուր հատկանիշ է այն, որ և’ դաշտը, և’ նյութը տեղափոխում են էներգիա: Երկար ժամանակ կար կարծիք, որ նյութի և դաշտի միջև տարբերությունն այն է, որ նյութը ունի զանգված, իսկ դաշտը` ոչ: 20-րդ դարի սկզբում Էյնշտեյնը ցույց տվեց, որ էներգիան ևս ունի զանգված, և ձգողական ուժի ազդեցության տակ լույսը ձգվում է նյութի կողմից:

Զանգվածի մեծությունը կապված է էներգիայի հետ Էյնշտեյնի բանաձևով.

E=mc²,

որտեղ E-n` էներգիայի քանակն է (Ջոուլ), m-ը` զանգվածը (կգ),

c-ն` լույսի արագությունը (մ×վրկ^-1):

Լույսի արագությունը բնության կարևոր հասկացություններից է և հավասար է c=2.9979×10⁸ մ×վրկ^-1:

Դաշտը իրականացնում է նյութի առանձին մասերի կապը և փոխազդեցությունը:

Պայմանականորեն քիմիան բաժանվել է չորս բաղադրիչ մասերի, օրգանական, անօրգանական, ֆիզիկական և անալիտիկ քիմիայի:

Օրգանական քիմիայի ավանդական բնագավառը կապված է ածխածնի ջրածնական միացությունների ուսումնասիրման հետ, իսկ անօրգանական քիմիան գործ ունի մնացած բոլոր տարրերի և ածխածնի մնացած միացությունների հետ:

Ցանկացած քիմիական ռեակցիա ուղեկցվում է նաև բազմաթիվ ֆիզիկական երևույթներով: Փոխվում է նյութի չափը, անջատվում է լույս, ջերմություն, առաջանում է դետոնացիոն ալիք` պայթյուն: Ցանկացած քիմիական երևույթ կոմպլեքսային բնույթ ունի և այդ պատճառով այն պետք է ուսումնասիրել ոչ միայն քիմիայի, այլ նաև մնացած գիտությունների տեսանկյունից:

Կիբեռնետիկայի հայրը` Նորբերտ Վիները նշել է, որ եթե քիմիական հիմնախնդի լուծման դժվարությունը   մաթեմատիկայում է, ապա տասը քիմիկոս ավելի քիչ բան կանեն, քան մեկ մաթեմատիկոս: Սա նշանակում է, որ գիտության բաժանումը մեր կողմից ինչ-որ չափով արհեստական է: Այդ պատճառով տարբեր գիտությունների սահմանագծում առաջացել են նոր գիտություններ` ֆիզիկական քիմիա, քիմիական ֆիզիկա, էլեկտրաքիմիա, կենսաքիմիա, տիեզերական քիմիա և այլն: 

>>

 

 

 

1.2. Քիմիան ճշգրիտ գիտություն է

Բոլոր ճշգրիտ գիտություններին բնորոշ են հետևյալ երեք տարբերիչ գծերը.

ա) վերացական դատողությունների առկայությունը,

բ) փորձնական փաստերի կրկնությունը,

գ) գործնական կիրառությունը:

Քիմիայում վերացական դատողությունների դերը կատարում են հասկացությունները, հիպոթեզները, օրենքները և տեսությունները, որոնք մշակված են այնպես, որ համապատասխանեն լաբորատոր դիտարկումներով հաստատված փաստերին: Եթե հայտնաբերվում են երևույթներ, որոնք կրկնվում են փորձից փորձ, և այդ դիտարկումը բերում է ընդհանրացման, ապա այս կերպ հայտնաբերվում է օրենքը:

Օրենքը փորձի ընդհանրացումն է տվյալ երևույթի նկատմամբ, որը կրկնվում է անկախ ժամանակից: Տարբեր հասկացությունների և օրենքների համախումբը, որը բացատրում է տվյալ երևույթների շարքը, կոչվում է տեսություն:

Օրենքը սահմանելուց հետո անհրաժեշտ է այն բացատրել: Սա ստեղծագործական առումով գիտության ամենահետաքրքիր մասն է: Օրենքի բացատրությունը սկսվում է վարկածով:

Վարկածը օգտակար է միայն այն դեպքում, եթե նրա հիման վրա կարելի է անել ենթադրություն, որը կարելի է ստուգել և ժխտել կամ հաստատել:

Վարկածը, որը ստուգվել է բազմաթիվ փորձերով և հաստատվել է, կոչվում է տեսություն: Տեսությունը ծառայում է փաստերի ընդհանրացմանը, որոնք տրված են լայն տիրույթում, ինչպես նաև օրենքների բացատրությանը:

Այդպիսի տեսություններ են` ատոմամոլեկուլային ուսմունքը, նյութի ատոմային կառույցը և այլն:

>>

 

 

 

1.3. Քիմիան և ժամանակակից հասարակության խնդիրները

Հաճախ խնդրի հայտնաբերումը խիստ կարևոր է, որովհետև դրա լուծումից հետո կարող է պարզվել, որ այն խիստ մեծ նշանակություն ունի:

Վերջերս մի խումբ խոշոր գիտնականներ ձևակերպել են ամենաարդիական խնդիրները, որոնց հետ շփվում է մարդկությունը: Նրանք առանձնացրել են այդ խնդիրներից այնպիսիք, որոնց լուծման հարցում քիմիկոսները լուրջ ներդրում կարող են ունենալ: Բերենք այդ չլուծված խնդիրների շարքը:

1. Սննդամթերքի խնդիրը:  Աշխարհի այն մասերում, որտեղ 25 տարին մեկ կրկնապատկվում է բնակչության թիվը, իսկ սննդամթերքի արտադրությունը համարյա չի փոխվում, առաջանում է սովի հիմնախնդիր: Քիմիկոսների խնդիրն է ստեղծել բույսերի հիվանդությունների դեմ պայքարի նոր միջոցներ, ինչպես նաև մշակել ավելի արդյունավետ պարարտանյութեր: Անհրաժեշտ է ստեղծել նոր գյուղատնտեսական ծագում ունեցող արհեստական սննդի տեխնոլոգիա:

2. Հումքի օվկիանոսային աղբյուր: Մինչև այժմ մարդկությունը օվկիանոսի հսկայական ռեսուրսների չնչին մասն է օգտագործում գործնական նպատակների համար: Իհարկե օվկիանոսից սպացվում է սնունդ և որոշ միներալներ, սակայն դա կազմում է օվկիանոսի ռեսուրսների չնչին մասը: Բացի դրանից, աշխարհի որոշ մասերում զգացվում է ջրի պակաս, որը  օվկիանոսից քաղցրահամ ջրի ստացումը դարձնում է արդիական:

3. Շրջապատող միջավայիրի պաշտպանությունը: Բոլորին հայտնի է օդի և ջրի աղտոտման խնդիրը: Մինչդեռ մինչև այժմ էլ այն չի գտել ընդունելի լուծում: Շրջապատող միջավայրի աղտոտումը պայմանավորված է մարդու գործունեության հետ կապված երկու պատճառներով. բնական և արհեստական: Մենք սովորաբար քիչ ուշադրություն ենք դարձնում աղտոտման բնական պրոցեսներին, մասնավորապես այն պատճառով, որ չենք կարող էականորեն ազդել դրանց վրա: Մարդու գործունեությամբ պայմանավորված պրոցեսները կապված են հիմնականում տրանսպորտի և արդյունաբերության հետ: Տրանսպորտի արտանետումները պակասացնելու համար անհրաժեշտ է ստեղծել նոր վառելիքներ, նոր շարժիչներ, նոր կատալիզատորներ: Լուրջ խնդիրներ կան արդյունաբերության, հատկապես քիմիական  արդյունաբերության մեջ արտանետումները նվազեցնելու խնդրում:

4. Կենսաքիմիական պրոցեսներ: Հետազոտման քիմիական մեթոդների կիրառումը կենսաքիմիական պրոցեսներում հանգեցրել է զգալի ձեռքբերումների կենդանի օրգանիզմում նյութափոխանակության, ֆոտոսինթեզի և այլ կենսաբանական երևույթների: Գիտության այդ բնագավառում կան մեծ քանակով չլուծված պրոբլեմներ: Դրանց թվին են պատկանում, մտածելու երևույթի քիմիական մեխանիզմը, ժառանգականությունը, դեղանյութերի ազդեցությունը մարդու օրգանիզմի վրա, կյանքի առաջացումը:

5. Էներգիայի նոր աղբյուրներ: Նավթի, գազի և ածխի պաշարների սպառմանը զուգընթաց մարդկությունը ավելի շատ ուշադրություն պետք է դարձնի միջուկային, արևային և քամու էներգիաների օգտագործմանը:

6. Նոր նյութեր: Մարդկության առաջընթացը թելադրում է նոր նյութերի անհրաժեշտությունը: Արդեն ստեղծվում են կիսահաղորդչային  և գերհաղորդչային նյութեր, ջերմակայուն պլաստիկներ, նոր կոմպոզիցիոն պոլիմերներ: Նման խնդիրների լուծումը անհնարին է առանց քիմիկոսի միջամտության:

7. Տեսական հետազոտություններ: Ցանկացած գործնական խնդրի լուծումը թելադրում է որոշակի, տվյալ բնագավառին վերաբերվող նոր տեսական խնդիրների առաջացումը և լուծումը:

>>

 

 

 

2. Ատոմամոլեկուլային ուսմունք

2.1 Մոլեկուլ, ատոմ, տարր

Բոլոր նյութերը բաժանվում են երկու մեծ խմբի` մոլեկուլային և ոչ-մոլեկուլային կառուցվածքի նյութեր:

Մոլեկուլային կառուցվածքի նյութեր կոչվում են այն նյութերը, որոնք կազմված մոլեկուլներից: Օրինակ.  շաքարը, ջուրը, թթվածինը:

Ոչ-մոլեկուլային կառուցվածքի նյութերը կազմված են ոչ թե մոլեկուլներից, այլ կառուցվածքային այլ միավորներից (ատոմներից, դրական և բացասական լիցքավորված իոններից, դրական իոններից և ընդհանրացված էլեկտրոններից): Օրինակ. ալմաստը կազմված է ածխածնի ատոմներից, սեղանի աղը` նատրիումի դրական և քլորի բացասական իոններից, երկաթը և ընդհանրապես բոլոր մետաղները` դրական լիցքավորված իոններից և բացասական լիցքավորված ընդհանրացված էլեկտրոններից: Նյութի հատկությունները պայմանավորված են այն կառուցվածքային միավորների հատկություններով, որոնցից կազմված է այն:

Մոլեկուլը` մոլեկուլային կառուցվածքով նյութերի փոքրագույն մասնիկն է, որն ունի դրա բաղադրությունը, պահպանում է դրա քիմիական հատկությունները և որոշում է այդ հատկությունները:

 Միևնույն նյութի մոլեկուլներն ունեն նույն բաղդրությունն ու հատկությունները, տարբեր նյութերի մոլեկուլները տարբերվում են ինչպես բաղադրությամբ, այնպես էլ կառուցվածքով և հատկություններով:

Քիմիական հատկությունը նյութերի քիմիական ռեակցիայի մեջ մտնելու ունակությունն է:

Մոլեկուլը կազմված է ատոմներից, որոնք միացած են իրար որոշակի հաջորդականությամբ:

 Տարրը որոշակի  հատկություններ ունեցող ատոմների տարատեսակն է, որն ունի միջուկի միևնույն լիցքը: Օրինակ. H, O, Cl: 

 Ատոմը տարրի փոքրագույն, քիմիապես անբաժանելի մասնիկն է, որը պահպանում է տարրի քիմիական հատկությունները: 

Ատոմը էլեկտրաչեզոք մասնիկ է, որը կազմված է դրական լիցքավորված միջուկից և դրա շուրջը շարժվող բացասական լիցքավորված էլեկտրոններից: Ամբողջությամբ վերցրած` ատոմը էլեկտրաչեզոք մասնիկ է:

>>

 

 

2.2. Պարզ և բարդ նյութեր: Ալոտրոպիա:

Տարրերը բնության մեջ հանդես են գալիս պարզ նյութերի ձևով և բարդ նյութերի բաղադրության մեջ: 

Պարզ կոչվում են այն նյութերը, որոնք կազմված են միևնույն տարրի ատոմներից:

Օրինակ, H₂ մոլեկուլը կազմված է միայն ջրածին տարրի ատոմներից, հետևաբար պարզ նյութ է:

Բարդ կոչվում  են այն նյութերը, որոնք կազմված են տարբեր տարրի ատոմներից:

Օրինակ, ջուրը H₂Օ կազմված է ջրածին և թթվածին տարրերի ատոմներց, հետևաբար ջուրը բարդ նյութ է:

Յուրաքանչյուր տարր բնության մեջ առաջացնում է առնվազն մեկ պարզ նյութ: Սակայն կան տարրեր, որոնք առաջացնում են մի քանի պարզ նյութեր:

Միևնույն տարրը, օրինակ թթվածինը` O-ն կարող է առաջացնել երկու պարզ նյութ` O₂ և O₃, որոնք ունեն տարբեր հատկություններ:

Այն երևույթը, երբ միևնույն տարրը առաջացնում է մի քանի պարզ նյութեր, կոչվում է ալոտրոպիա, իսկ  առաջացած պարզ նյութերը` ալոտրոպ ձևափոխություններ:

Ալլոտրոպիայի երևույթը պայմանավորված է երկու պատճառով.

1. Մոլեկուլում ատոմների տարբեր թվով (օրինակ, O₂, O₃),

2. բյուրեղավանդակի տարբեր կառուցվածքներով (օրինակ, ածխածնի տարբեր ալոտրոպ ձևափոխություններն են ալմաստը, գրաֆիտը, ֆուլերոնը, կարբինը, պոլիկումուլենը):

>>

 

 

 

2.3. Քիմիական տարրերի նշանները: Քիմիական բանաձևերը

Քիմիական տարրերը նշանակվում են տվյալ տարրի լատիներեն անվան առաջին տառով կամ նաև հաջորդ տառերից մեկով, եթե առաջին տառը տարբեր տարրերի անվան մեջ համընկնում է:

Օրինակ, թթվածին` oxigenium – Օ, օսմիում` osmium – Os:

 Քիմիական տարրերի  լատիներեն անվանումների այդ տառերը կոչվում են քիմիական նշաններ:

Քիմիական նշանը ցույց է տալիս.

1. տվյալ քիմիական տարրը, օրինակ, H – ջրածին, C –ածխածին:

2. տվյալ քիմիական տարրի մեկ ատոմը:

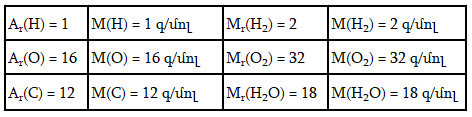
3. տվյալ քիմիական տարրի հարաբերական ատոմական զանգվածը: Օրինակ Ar(H) =1, Ar(C) =12:

4. տվյալ քիմիական տարրի ատոմների մեկ մոլ քանակը: Օրինակ`

5. տվյալ տարրի մոլային զանգվածը M(H) =1 գ/մոլ, M(C) =12 գ/մոլ:

Քիմիական նշանների և ինդեքսների միջոցով նյութի որակական և քանակական բաղադրության պայմանական գրառումը կոչվում է բանաձև:

Քիմիական բանաձևի կամ նշանի առջև դրած թվերը կոչվում են գործակիցներ և ցույց են տալիս տվյալ բանաձևին համապատասխանող կառուցվածքային միավորների թիվը: Քիմիական նշանի ներքևի աջ մասում գրված թիվը կոչվում է ինդեքս և ցույց է տալիս ատոմների թիվը մոլեկուլում:

Բանաձևը ցույց է տալիս.

1. նյութը, օրինակ, H₂O – ջուր, CaCl₂ –կալցիումի քլորիդ:

2. տվյալ նյութի մեկ մոլեկուլուլը կամ կառուցվածքային միավորը:

3. որակական բաղադրությունը, այսինքն ի՞նչ տարրերից է բաղկացած: Օրինակ H₂O -ն բաղկացած է H և O տարրերից:

4. քանակական բաղադրությունը: Օրինակ H₂O մոլեկուլը բաղկացած է 2 ատոմ ջրածնից և 1 ատոմ թթվածնից:

5. հարաբերական մոլեկուլային զանգվածը. Mr (H₂O) =18 մոլ:

6. կառուցվածքային միավորների մեկ մոլ քանակը.  

7. կառուցվածքային միավորի մեկ մոլ քանակի զանգվածը M(H₂O) =18 գ/մոլ:

>>

 

 

 

2.4. Ատոմի զանգված: Հարաբերական ատոմային և մոլեկուլային զանգվածներ

Տարբեր տարրերի ատոմները իրարից տարբերվում են ոչ միայն միջուկի լիցքի մեծությամբ, այլ նաև զանգվածներով: Ատոմների և մոլեկուլների զանգվածները սովորական միավորներով (գ, կգ) չափելը հարմար չէ, որովհետև ստացվում են շատ փոքր թվեր: Օրինակ, ջրածնի ատոմի զանգվածը  Այդ պատճառով ատոմի և մոլեկուլի զանգվածները չափելու համար ստեղծվել է նոր, ավելի փոքր միավոր:

Ածխածնի ¹²C իզոտոպի ատոմի զանգվածի 1/12 մասը կոչվում է զանգվածի ատոմական միավոր:  

Այդ դեպքում ջրածնի  ատոմի զանգվածը ստացվում է 1.008 զ.ա.մ.: Գործնականում ատոմի զանգածի փոխարեն կիրառվում է հարաբերական ատոմային զանգվածը:

 Քիմիական տարրի (Ar) հարաբերական ատոմային զանգվածը ցույց է տալիս,թե տվյալ քիմիական տարրի ատոմի զանգվածը քանի անգամ է մեծ ածխածնի  իզոտոպի զանգվածի 1/12 մասից:

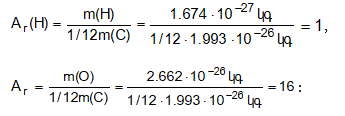
Ինչպես երևում է գրվածից, հարաբերական ատոմային զանգվածը չափողականություն չունեցող մեծություն է: Չպետք է շփոթել հարաբերական ատոմային զանգվածը ատոմի զանգվածի հետ

Տարրերի հարաբերական ատոմային զանգվածները բերված են պարբերական համակարգում:

Օրինակ.  

Նյութի հարաբերական մոլեկուլային զանգվածը` Mr -ը ցույց է տալիս, թե տվյալ նյութի մոլեկուլի զանգվածը քանի անգամ է մեծ ածխածնի  իզոտոպի ատոմի զանգվածի 1/12 մասից:

Նյութի հարաբերական մոլեկուլային զանգվածը նույնպես չափողականություն չունեցող մեծություն է: Նյութի հարաբերական մոլեկուլային զանգվածը այդ մոլեկուլի կազմի մեջ մտնող բոլոր ատոմների հարաբերական ատոմային զանգվածների գումարն է:

>>

 

 

 

 

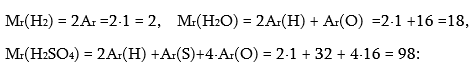
2.5. Նյութի մոլ քանակություն

Միավորների SI համակարգում գոյություն ունի «Նյութի քանակ» հասկացությունը: «Քանակ» նշանակում է կառուցվածքային մասնիկների թիվ:

Քիմիայում որպես նյութի քանակի չափ ընդունված է մոլը:

 Մոլը նյութի այն քանակն է, որը պարունակում է այնքան կառուցվածքային միավոր (ատոմ, մոլեկուլ, իոն, ռադիկալ, էլեկտրոն), որքան ատոմ կա 0.012 կգ (12 գ) ածխածնի  իզոտոպում:

12 գրամ ածխածնի մեջ կա  Այդ թիվը (N_A) կոչվում է Ավոգադրոյի թիվ: Հետևաբար`

 Մոլը նյութի այնպիսի քանակն է, որը պարունակում է  կառուցվածքային մասնիկ:        

Քանի որ մոլեկուլները և ատոմները մենք չենք տեսնում և հաշվել չենք կարող, մոլը օգտագործելու համար անհրաժեշտ է իմանալ մոլի զանգվածը: 

Տվյալ նյութի մեկ մոլի զանգվածը կոչվում է մոլային զանգված (M) և չափվում է գ/մոլ միավորներով:

 Մոլային զանգվածը նյութի գրամների այն քանակն է, որը թվապես հավասար է հարաբերական ատոմային կամ մոլեկուլային զանգվածին:

Ցանկաված նյութի N_A հատ մոլեկուլների գումարային զանգվածը այնքան գրամ է, որքան այդ նյութի մոլեկուլային զանգվածն է:

Հետևաբար Ավոգադրոյի թիվը փաստորեն ցույց է տալիս, թե գրամը զանգվածի ատոմական միավորից քանի անգամ է մեծ:

Այսպիսով, նյութի քանակը ելնելով զանգվածից, կարելի է հաշվել հետևյալ բանաձևով.

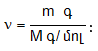
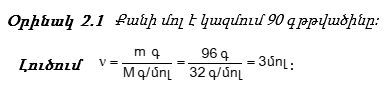
1811 թ. իտալացի գիտնական Ավոգադրոն մտցրեց մոլեկուլի գաղափարը որպես նյութի փոքրագույն մասնիկի և տվեց մի հիպոթեզ, որը այժմ կոչվում է օրենք:

 Տարբեր գազերի հավասար ծավալներում միևնույն պայմաններում պարունակվում են հավասար թվով մոլեկուլներ:

Քանի որ տարբեր գազերի մեկական մոլերը պարունակում են նույն թվով (N_A) մոլեկուլներ, ապա ըստ Ավոգադրոյի օրենքի` դրանք պետք է գրավեն նույն ծավալը: Այդ ծավալը կոչվում է մոլային ծավալ (V₀) և նորմալ պայմաններում հավասար է 22.4 մոլ/լ-ի:  

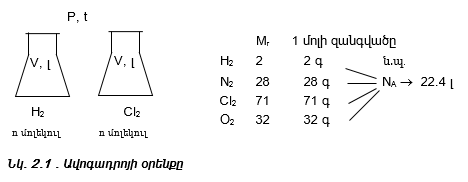
Հետևաբար նյութի քանակը` ելնելով ծավալից կարելի է հաշվել

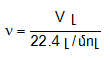
բանաձևով:

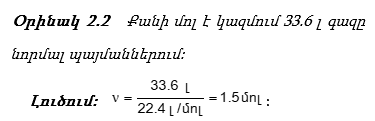
Եթե գազը գտնվում է ոչ նորմալ պայմաններում, ապա մոլային ծավալը կարելի է հաշվել գազային միացյալ հավասարումով`

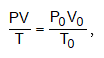
որտեղ զրո ինդեքսով նշված են ճնշումը, ծավալը և ջերմաստիճանը նորմալ պայմաններում (P₀ =101.3 կՊա, T₀= 273 Կ):

Քանի որ նյութի մեկ մոլում կա N_A հատ մասնիկ, ապա նյութի քանակը կարելի է հաշվել` ելնելով մասնիկների թվից

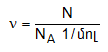
բանաձևով:

Նկ.2.2-ում ցույց է ընդհանրացված կապը նյութի քանակի զանգվածի (m), ծավալի (V) և մասնիկների թվի (N) միջև հնարավոր տասներկու հաշվարկներով:

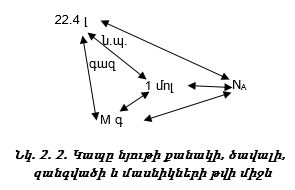
Այսպիսով նյութի քանակի, ծավալի, զանգվածի և մասնիկների թվի միջև կա հետևյալ կապը`

Հայտարարում ունենք մեկ մոլին ընկնող մեծություններ` M - 1 մոլի զանգվածը, N_A-1 մոլում մասնիկների թիվը, V₀-22.4լ/մոլ-1 մոլ գազի ծավալը:

Իմանալով Ավոգադրոյի թվի արժեքը` կարելի է գտնել ցանկացած տարրի մեկ ատոմի զանգվածը գրամներով և գնահատել ատոմի չափերը:

>>

 

 

 

2.6. Գազային նյութերի մոլեկուլային զանգվածի որոշումը

Նյութի հարաբերական մոլեկուլային զանգվածները փորձնականորեն որոշելու համար գտնում են դրանց թվապես հավասար մոլային զանգվածները: Ակնհայտ է, որ գազերի խտությունները, ինչպես նաև որևէ ծավալի զանգվածները, պետք է հարաբերեն իրար այնպես, ինչպես մոլային զանգվածները, քանի որ խտությունները (d) մեկական լիտրերի զանգվածներն են, իսկ մոլային զանգվածները` 22.4-ական լիտրերինը:

Հետևաբար

 հարաբերությունը կոչվում է առաջին գազի հարաբերական խտությունը ըստ երկրորդի`  հետևաբար`  որտեղից  այսինքն գազի մոլային (մոլեկուլային) զանգվածը հավասար է մի այլ գազի նկատմամբ դրա հարաբերական խտության և այդ գազի մոլային (մոլեկուլային) զանգվածի արտադրյալին:

Եթե հայտնի գազը ջրածինն է, ապա բանձևը կընդունի հետևյալ տեսքը  եթե թթվածինը` ապա  և այլն:

Գազային նյութերի մոլային զանգվածը կարելի է որոշել` օգտվելով նաև մոլային ծավալ հասկացությունից: Եթե հայտնի է գազի որևէ ծավալի զանգվածը նորմալ պայմաններում, ապա հաշվում ենք այդ նյութի 22.4 լ-ի զանգվածը:

Ընդհանրապես գազերի ծավալները չափվում են ոչ-նորմալ պայմաններում: Այդ դեպքում, ինչպես նշվեց վերը, նման հաշվարկ կատարելուց առաջ ծավալը պետք է բերել նորմալ պայմանների` օգտվելով Բոյլ-Մարիոտտի և Գեյ-Լյուսակի միացյալ հավասարումից`  Մեկ մոլի համար  մեծությունը հաստատուն է և նշանակվում է R-ով: Այն կոչվում է գազային ունիվերսալ հաստատուն և հավասար է  Այդ դեպքում բանաձևը կընդունի հետևյալ տեսքը PV=RT: Որևէ  մոլի համար, ընդունելով, որ  բանաձևը կընդունի  տեսքը: Այդ բանաձևը կոչվում է Մենդելեև-Կլայպերոնի հավասարում, իմանալով ցանկացած պայմաններում գազի որևէ ծավալի զանգվածը, այդ բանաձևով կարելի է հաշվել դրա մոլի (մոլեկուլի զանգվածը):

>>

 

Ամփոփում

Քիմիական տարրը  միջուկի միևնույն լիցք ունեցող ատոմների տեսակ է: Տարրերը բնության մեջ գոյություն ունեն պարզ նյութերի ձևով և բարդ նյութերի բաղադրության մեջ: Ատոմը` տարրի, մոլեկուլը` նյութի փոքրագույն մասնիկներն են, որոնք պահպանում են դրանց հատկությունները: Ատոմների և մոլեկուլների զանգվածները չափվում են զանգվածի ատոմական միավորներով (զ.ա.մ.), որը ածխածնի ¹²C իզոտոպի ատոմի զանգվածի 1/12 մասն է: Նյութի քանակ նշանակում է կառուցվածքային մասնիկների թիվ, դրա միավորը մոլն է: Նյութի մեկ մոլում պարունակվում է 6.02×10²³ հատ  կառուցվածքային մասնիկ: Մոլի զանգվածը նյութի գրամների այն քանակն է, որը թվապես հավասար է այդ նյութի հարաբերական մոլեկուլային զանգվածին: Գազային նյութերի մեկ մոլը նորմալ պայմաններում գրավում է 22.1 լ ծավալ:

 

Սովորելու նպատակը

Այս բաժինը սովորելուց հետո դուք պետք է կարողանաք.

1. Ձևակերպել և ճշգրիտ օգտագործել տարր, ատոմ, մոլեկուլ, պարզ և բարդ նյութեր հասկացությունները:

2. Որոշել տարրի կամ նյութի մոլի զանգվածը, կատարել հաշվումներ մոլի զանգվածի, դրանում եղած մասնիկների թվի, գազային նյութերի դեպքում դրանց ծավալի միջև, հաշվել տարրի մեկ ատոմի, նյութի մեկ մոլեկուլի զանգվածը և ծավալը:

 

 

Հիմնական հասկացություններ

Քիմիական տարր կոչվում է միջուկի միևնույն լիցք ունեցող ատոմների տեսակը:

Ալոտրոպիան տվյալ տարրի մի քանի պարզ նյութեր առաջացնելու երևույթն է:

Զանգվածի ատոմական միավորը ( Զ.ա.մ.) ածխածնի ¹²C իզոտոպի ատոմի զանգվածի 1/12 մասն է:

Ատոմի զանգվածը կարող է չափվել գրամներով, կգ-երով և զանգվածի ատոմական միավորներով:

Հարաբերական ատոմական զանգվածը ատոմի զանգվածի հարաբերությունն է զանգվածի ատոմական միավորներին: Այն չունի չափողականություն:

Նյութի քանակ`  նշանակում է կառուցվածքային մասնիկների թիվ:

Մոլ կոչվում է նյութի այն քանակը, որը պարունակում է է 6.02.10²³ հատ  կառուցվածքային մասնիկ:

Մոլի զանգվածը նյութի գրամների այն քանակն է, որը թվապես հավասար է այդ նյութի հարաբերական մոլեկուլային  զանգվածին:

>>

 

 

 

3. Ատոմի  կառուցվածքը

3.1.Ատոմի միջուկային մոդելը

1911 թ. Ռեզերֆորդն առաջարկեց ատոմի կառույցի փորձով հիմնավորված մոդել: Ըստ նրա ատոմը կազմված է դրական լիցքավորված միջուկից և դրա դաշտում, զգալի հեռավորության վրա, դրա շուրջը պտտվող բացասական լիցքավորված էլեկտրոններից: Միջուկի չափերը (10^-13մկմ) շատ փոքր են ատոմի չափերի հետ (10^-8մկմ) համեմատած: Միջուկի լիցքը թվապես հավասար է էլեկտրոնների գումարային լիցքին, այսինքն` ատոմը էլեկտրաչեզոք է: Միջուկի զանգվածը շատ մեծ է էլեկտրոնների զանգվածից և միջուկում է կենտրոնացված  ատոմի համարյա ամբողջ զանգվածը: Ատոմի կառուցվածքի այս մոդելը նման է արեգակնային համակարգին և հաճախ կոչվում է մոլորակային մոդել:

>>

 

 

 

3.2. Միջուկի բաղադրությունը

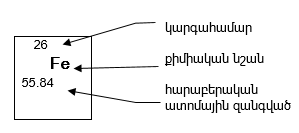
Միջուկը կազմված է դրական լիցքավորված պրոտոններից և էլեկտրաչեզոք նեյտրոններից` բացառությամբ ջրածնի թեթև իզոտոպի ատոմի, որի միջուկը կազմված է մեկ պրոտոնից: Պրոտոնները և նեյտրոնները այլ կերպ կոչվում են նուկլոններ: Աղյուսակ 3.1-ում բերված են նուկլոնների և էլեկտրոնների հիմնական բնութագրերը:

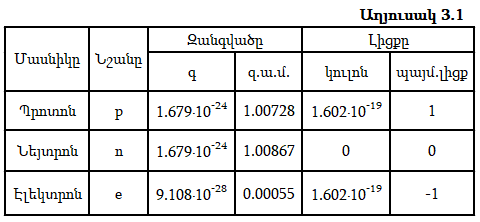
Պրոտոնի և նեյտրոնի զանգվածները համարյա նույնն են և մոտ են մեկ զ.ա.մ.-ին: Դրանք համապատասխանաբար մեծ են էլեկտրոնի զանգվածից 1836.12 և 1838.65 անգամ: Քանի որ էլեկտրոնի զանգվածը շատ փոքր է միջուկի զանգվածից, ապա այն պտտվում է միջուկի շուրջը: Նուկլոնների միջև գործում են հզոր ձգողական ուժեր` միջուկային ուժեր: Այդ ուժերը պայմանավորված չեն լիցքով, հազարավոր անգամ գերազանցում են էլեկտրոստատիկ ձգողության ուժերին և գործում են փոքր (10-15մ) հեռավորության վրա: Դրանց բնույթը հայտնի չէ: Միջուկային ուժերով է պայմանավորված միջուկի հսկայական էներգիան: Այն ռեակցիները, որոնց ընթացքում քայքայվում կամ առաջանում են նոր միջուկներ, կոչվում են միջուկային ռեակցիաներ: Այս ռեակցիաների էներգիան հազարավոր անգամ գերազանցում է քիմիական ռեակցիաների էներգիային:

>>

 

 

 

3.3. Զանգվածային թիվ

Միջուկը բնորոշվում է երկու մեծություններով` կարգահամարով (Z) և  զանգվածային թվով (A):

Զանգվածային թիվը որոշվում է միջուկում պարունակվող նուկլոնների (պրոտոնների և նեյտրոնների) թվերի գումարով, իսկ կարգահամարը` միջուկում պրոտոնների թվով:

որտեղ N-ը նեյտրոնների թիվն է: Միջուկի բնութագրերը գրանցվում են տարրի քիմիական նշանի ձախ մասում: Ներքևում գրվում է կարգահամարը, վերևում` զանգվածային թիվը: Օրինակ, ածխածնի ատոմի միջուկի բնութագրերը  նշանակվում են  որը նշանակում է, որ միջուկի լիցքը (հետևաբար և պրոտոնների թիվը) հավասար է +6-ի, իսկ զանգվածային թիվը` 12-ի: Նեյտրոնների թիվը հավասար է զանգվածային թվի և միջուկի լիցքի տարբերությանը: N=A–Z=12-6=6:

Քանի որ պրոտոնի և նեյտրոնի զանգվածները շատ քիչ են տարբերվում իրարից, ապա զանգվածային թիվը մոտավորապես ցույց է տալիս նաև միջուկի հարաբերական զանգվածը և միշտ ամբողջ թիվ է: Պրոտոնի և նեյտրոնի միջև կա որոշակի փոխադարձ կապ: Որոշակի պայմաններում պրոտոնը կարող է վերածվել նեյտրոնի և հակառակը:

>>

 

 

 

3.4. Կարգահամարի ֆիզիկական իմաստը: Իզոտոպներ

Կարգահամարը ցույց է տալիս.

1. Տարրի հերթական համարը պարբերական համակարգում:

2. Միջուկի դրական լիցքի մոծությունը:

3. Պրոտոնների թիվը մրջուկում:

4. Միջուկի շուրջը պտտվող էլեկտրոնների թիվը:

Ելնելով զանգվածային թվի պատկերացումներից` ստացվում է, որ ատոմային զանգվածները պետք է արտահայտվեն ամբողջ թվերով:

1910թ. Սոդիի կողմից հաստատվել է, թր ռադիոակտիվ քայքայման ժամանակ կարող են առաջանալ միևնույն տարրի ատոմներ, որոնք ունենալով միևնույն միջուկի լիցքը, ունեն տարբեր զանգվածներ, այիսինքն` ունեն նույն կարգահամարը, բայց տարբեր զանգվածային թվեր: Այդպիսի ատոմները կոչվեցին իզոտոպներ:

 Ատոմների տարատեսակները, որոնք ունեն միևնույն թվով պրոտոններ, այսինքն միևնույն միջուկի լիցքը, բայց տարբեր թվով նեյտրոններ, հետևաբար տարբեր զանգվածային թվեր, կոչվում են իզոտոպներ:

Օրինակ, ջրածին տարրն ունի երեք իզոտոպ:

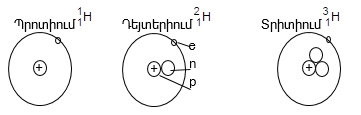
Բնության մեջ բոլոր տարրերը հանդիպում են իզոտոպների խառնուրդի ձևով:

Հարաբերական ատոմային զանգվածը ցույց է տալիս տարրի` բնության մեջ գոյություն ունեցող բոլոր իզոտոպների զանգվածային թվերի միջին մեծությունը, ուստի չի արտահայտվում ամբողջ թվերով:

Տարրի միջին հարաբերական զանգվածը որոշվում է հետևյալ բանաձևով.

որտեղ  իզոտոպի զանգվածային բաժինն է, A -ն զանգվածային թիվը:

Լինում են տարբեր տարրերի ատոմներ, որոնք ունեն միևնույն զանգվածային թիվը: Այդպիսի ատոմները կոչվում են իզոբարներ: Օրինակ.

>>

 

 

 

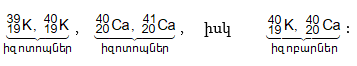
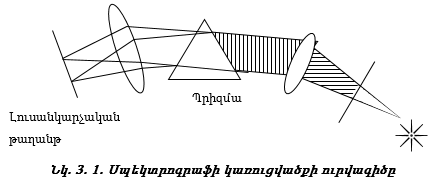
3.5. Սպեկտրոգրաֆի աշխատանքի սկզբունքը

Ատոմների էլեկտրոնային թաղանթների կառուցվածքի պարզաբանման փորձարարական հինքը քիմիական տարրերի սպեկտրների մասին տվյալներն են: Սպեկտրոգրաֆում լույսի փունջը անցնելով իր ալիքի երկարության հետ համաչափելի ճեղքի միջով` ենթարկվում է ցրման (դիֆրակցիայի) և բաղադրիչ ճառագայթները, ընկնելով լուսանկարչային թաղանթի վրա, գրանցվում են ըստ ալիքի երկարության: Տեսանելի և ուլտրամանուշակագույն ճառագայթներն ուսումնասիրելու նպատակով սովորաբար օգտագործում են օպտիկական սպեկտրոգրաֆներ, որոնցում ճառագայթները բաժանում են` անցկացնելով ապակե պրիզմայի միջով` տեսանելի մարզի, կամ կվարցե պրիզմայի միջով` ուլտրամանուշակագույն մարզի համար: Սպեկտրոգրաֆի սկըզբունքային սխեման բերված է նկ. 3.1-ում: Պրիզմայի միջոցով լույսի բաժանումը պայմանավորված է նրանով, որ բեկման ցուցիչը կախված է լույսի ալիքի երկարությունից:

Մարմնի կողմից արձակված լույսի ճառագայթների բաժանման միջոցով ստացված սպեկտրները կոչվում են էմիսիոն սպեկտրներ: Դրանք լինում են անընդհատ, գծային և շերտավոր: Անընդհատ սպեկտրներ առաջացնում են շիկացած պինդ կամ հեղուկ մարմինների արձակած ճառագայթները: Գազերը կարող են ճառագայթել տաքացման կամ էլեկտրական պարպման միջոցով: Դրանց ճառագայթումը տալիս է գծային սպեկտր` կազմված առանձին գծերից, կամ շերտավոր սպեկտր` կազմված շերտերից: Ներկայումս հաստատված է, որ գծային սպեկտրերը ստացվում են ատոմների ճառագայթումից, իսկ շերտավորը` մոլեկուլների: Յուրաքանչյուր տարրի ատոմ և յուրաքանչյուր նյութի մոլեկուլ ունի իր բնորոշ սպեկտրը, որը որոշակի գծերի կամ շերտերի հավաքածու է: Եթե ճառագայթման աղբյուրը տեղադրենք մագնիսական դաշտում, ապա առանձին գիծը վեր է ածվում մի քանի գծի (Զեմանի էֆեկտ): Նման պատկեր է ստացվում, եթե ճառագայթման աղբյուրը տեղավորենք էլեկտրական դաշտում:

>>

 

 

3.6. Ջրածնի ատոմի սպեկտրը

Տեսանելի մարզում ջրածնի սպեկտրն ունի ընդամենը չորս գիծ: Դրան հարող ուլտրամանուշակագույն մարզում կան ևս մի քանի գծեր, որոնք միասին կազմում են Բալմերի սերիան (նկ. 3.2):

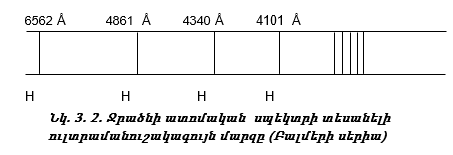
Բալմերը ցույց է տվել, որ այդ սերիայի գծերի ալիքային թիվը`   կարելի է հաշվել հետևյալ բանաձևով`

որտեղ n=3, 4, 5 …

Ալիքային թիվը ալիքի երկարության հակադարձ մեծությունն է, այսինքն` մեկ սանտիմետրի վրա ալիքների թիվը: Հավասարման մեջ մտնող R հաստատունը կոչվում է Ռիդբերգի հաստատուն:

R=109678 սմ^-1:

Ջրածնի ատոմի սպեկտրի ուսումնասիրումը ուլտրամանուշակագույն և ինֆրակարմիր մարզում հայտնաբերել է ևս մի քանի գծերի սերիաներ, որոնք կոչվում են Լայմանի, Պաշենի, Բրեկետի, Պֆունցի սերիաներ (նկ. 3.3):

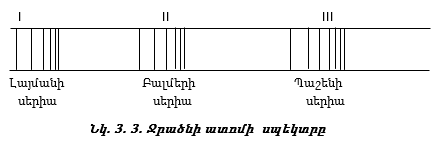
Պարզվել է, որ այդ սերիաների գծերի ալիքային թվերը որոշվում են Բալմերի բանաձևին նման մի ընդհանուր բանաձևով` 

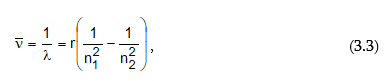
որտեղ n₁ և n₂–ը ամբողջ թվեր են, ընդ որում` n<sub>1</sub> > n<sub>2</sub> –ից: n<sub>1</sub>-ին և n<sub>2</sub>-ին  արժեքներ տալով` կարելի է հաշվել բոլոր սերիաների գծերին համապատասխանող ալիքի երկարությունները: n₁=1; n₂=2,3,4… - Լայմանի սերիան, n1=2; n2=3,4,5… - Բալմերի սերիան և այլն: Եթե հավասարման երկու մասերը բազմապատկենք c-ով (լույսի արագություն) և h-ով (Պլանկի հաստատուն), ապա կստանանք

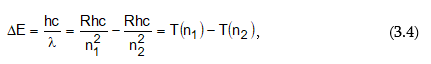
Այսպիսով ստացվեց, որ ճառագայթված էներգիան միշտ կարելի է արտահայտել n₁ և n₂ ամբողջ թվերից կախված ֆունկցիաների (T) տարբերությամբ: Այդ ֆունկցիաները կոչվում են թերմեր: R-ի և n-ի ֆիզիկական իմաստը պարզվեց միայն Բորի տեսության ստեղծումից հետո:

>>

 

 

 

3.7. Գաղափար լուսային քվանտների մասին

1900 թ. Պլանկը ցույց տվեց, որ տաքացած մարմինների լույս արձակելու հատկությունը կարելի է քանակապես ճիշտ նկարագրել միայն ենթադրելով, որ ատոմների կողմից էներգիան արձակվում կամ կլանվում է ոչ թե անընդհատ, այլ առանձին փոքրագույն բաժիններով` քվանտներով

որտեղ  արձակված կամ կլանված էներգիան է, E-ն մեկ քվանտի  էներգիան է, n-ը` ամբողջ թիվ է` 1,2,3,…:                                                                          

 

Քվանտի  էներգիան ճառագայթված լույսի հաճախության հետ կապված է

հավասարումով, որը կոչվում է Պլանկի հավասարում, որտեղ ν-ն լույսի հաճախությունն է, c-ն` լույսի արագությունը, h-ը` Պլանկի հաստատունը. հ=6.625×10-34 Ջ×վրկ:

>>

 

 

 

3.8. Բորի տեսությունը ջրածնի ատոմի համար

Ոեզերֆորդի մոդելը չէր կարող բացատրել ջրածնի ատոմի սպերտրը, որովհետև այդ մոդելն ուներ հակասություններ:

1. Ըստ էլեկտրադինամիկայի օրենքների պտտվող լիցքը, տվյալ դեպքում` էլեկտրոնը, պետք է ճառագայթեր էներգիա: Ճառագայթելով դրա էներգիան պետք է պակասի, աստիճանաբար պտտման շառավիղը պետք է փոքրանա, էլեկտրոնը պետք է ընկնի միջուկի վրա: Սակայն այս պատկերը չի համընկնում փորձի հետ:

2. Քանի որ էլեկտրոնի էներգիան պետք է անընդհատ նվազի, ապա նրա առաջացրած սպեկտրը պետք է լինի անընդհատ: Փորձը ցույց է տալիս, որ ջրածնի սպեկտրը ընդհատ է:

Այս հակասությունները պարզաբանվեցին Բորի կողմից: Նա տվեց նոր տեսություն ջրածնի ատոմի կառուցվածքի վերաբերյալ (1913թ.):

Բորն իր տեսությունը տվել է երեք կանխադրույթների (պոստուլատների) ձևով:

Առաջին  կանխադրույթ. Էլեկտրոնը պտտվում է միջուկի շուրջը ոչ թե կամայական ուղեծրերով, այլ քվանտային տեսությանը բավարարող` որոշակի ուղեծրերով: Այդ ուղեծրերը կոչվում են ստացիոնար կամ “թույլատրված”ուղեծրեր:

Երկրորդ  կանխադրույթ. Էլեկտրոնը պտտվելով “թույլատրված” ուղեծրերից որևէ մեկով, չի ճառագայթում և չի կլանում էներգիա: Առաջին ուղեծիրը կոչվում է հիմնական  ուղեծիր, մնացածները` գրգռված: Գրգռված վիճակում Էլեկտրոնը մնում է ոչ ավելի, քան t=10^-8վրկ:

Երրորդ կանխադրույթ.  Էլեկտրոնը կարող է մեկ “թույլատրված” ուղեծրից տեղափոխվել մյուսի վրա: Հեռավոր ուղեծրից ավելի մոտ ուղեծիր տեղափոխվելիս  ճառագայթում է էներգիա` մեկ քվանտի ձևով:

Բորի կանխադրույթները խիստ հակասում են դասական էլեկտրադինամիկայի օրենքներին: Ըստ դասական էլեկտրադինամիկայի օրենքների` էլեկտրամագնիսական դաշտում պտտվող լիցքը ճառագայթում է էներգիա: Սակայն այս կանխադրույթներն իրենց արդարացումը ստացան այն արդյունքներում, որոնք Բորը ստացել էր ջրածնի ատոմի սպեկտրը հաշվելիս:

>>

 

 

 

3.9. Բորի տեսության մաթեմատիկական հետևությունները

Ըստ Բորի Էլեկտրոնը պտտվում է ստացիոնար ուղեծրերով, եթե դրա շարժման քանակի մոմենտը բազմապատիկ է 

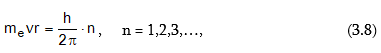
որտեղ m_e–ն Էլեկտրոնի զանգվածն է, v-ն Էլեկտրոնի արագությունը, r-ը ուղեծրի շառավիղն է:

Շարժման քանակի մոմենտը  վեկտորի և  վեկտորի վեկտորական արտադրյալն է`

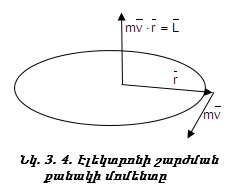
 մեծությունն ընդունված է նշանակել  Այսպիսով, կստանանք

Էլեկտրոնի արագությունը, ցանկացած պահի համընկնում է շրջանային ուղեծրի շոշափողի հետ (նկ. 3.5) և փոփոխվում է ուղեծրով էլեկտրոնի շարժմանը զուգահեռ:

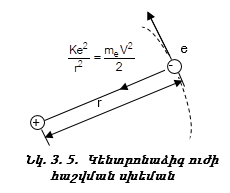
Դրա համար անհրաժեշտ է Էլեկտրոնի վրա, դեպի միջուկն ուղղված ուժ, որը կառաջացնի դեպի միջուկն ուղղված արագացում: Ըստ ուրվագծի այն հավասար է  Այդ ուժը կուլոնյան ձգողական ուժն է: Այսպիսով, կստանանք`

որտեղ K-ն հաստատուն մեծություն է: Փաստորեն ունենք երկու հավասարում երկու անհայտով (r,V): (3.9) և (3.10) հավասարումների համակարգի լուծումը տալիս է Էլեկտրոնի շարժման արագությունը`

 և շառավղի արտահայտություններ`

Տեղադրելով մեծությունների արժեքները` կստանսնք

և

Այսպիսով, ջրածնի ատոմում առաջին ուղեծրի  շառավիղը  a₀ = 0.53×10^-10 մ է, իսկ արագությունը`  v = 2.188×10⁶/ մ/վրկ (նկ. 3.6):

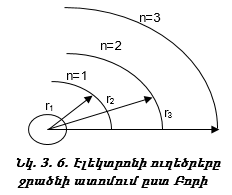
Բորը հաշվել է Էլեկտրոնի էներգիան տարբեր պայմաններում:  

Էլեկտրոնի լրիվ էներգիան  հավասար է կինետիկ`   պոտենցիալ էներգիաների գումարին`

 

:                                     (3.15)

Տեղադրելով r –ի և V –ի արժեքները` կստանանք

Քանի որ ջրածնի ատոմում Էլեկտրոնի էներգիան քվանտացվում է, ապա ջրածնի ատոմում կան  էներգետիկ մակարդակներ (նկ. 3.7): 

>>

 

 

 

 

3.10. Ջրածնի ատոմի սպեկտրի բացատրությունն

ըստ Բորի

1. Որակական բացատրություն. Առաջին` Լայմանի սերիայի գծերն առաջանում են, երբ Էլեկտրոնը մնացած բոլոր ուղեծրերից անցնում է առաջին ուղեծիր (նկ. 3.7):

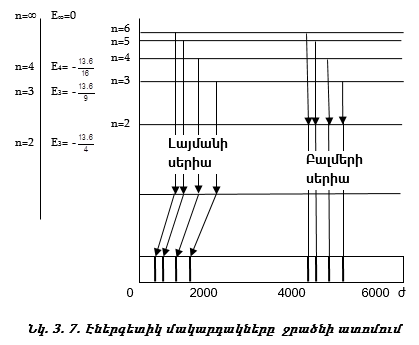
Յուրաքանչյուր թռիչքին համապատասխանում է որոշակի ալիքի երկարությամբ մեկ ֆոտոն: Երկրորդ (Բալմերի) սերիայի գծերն առաջանում են, երբ Էլեկտրոնը մնացած բոլոր ուղեծրերից (3,4,5) թռչում է երկրորդ ուղեծիր:

2. Քանակական բացատրություն. Ըստ երրորդ պոստուլատի ունենք

Տեղադրելով E_հ և E_մ արժեքները (3.4) հավասարման մեջ և տեղափոխելով հավասարումը` կստանանք.

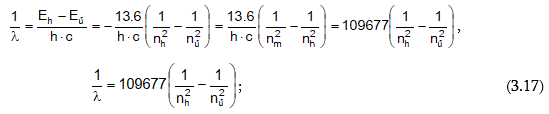
Ստացվեց նույն բանաձևը ինչ-որ Բալմերինը: n₁ –ը Բալմերի բանաձևում մոտակա ուղեծրի համարն է,  n₂ –ը` հեռավոր ուղեծրի համար, λ -ն ճառագայթված ալիքի երկարությունն է:

 այն ալիքի երկարության հակադարձ մեծությունն է, երբ էլեկտրոնը անվերջ հեռու ուղեծրից թռչում է առաջին ուղեծիր:

 

Այսպիսով ջրածնի ատոմի սպեկտրալ գծերն առաջանում են հետևյալ կերպ.

n_մ =1; n_h =2,3,4, … - Լայմանի սերիա,

n_մ =2; n_h =3,4,5, … - Բալմերի սերիա,

n_մ =3; n_h =4,5,6, … - Պաշենի սերիա:

>>

 

 

 

3.11. Բորի - Զոմերֆելդի տեսության հակասությունները

Բորը բացատրեց ջրածնի ատոմի կառուցվածքի օրինաչափությունները: Հետագայում Զոմերֆելդը զարգացրեց Բորի տեսությունը և մշակեց բազմաէլեկտրոն ատոմների կառուցվածքի տեսությունը: Ըստ այդ տեսության` ատոմների ստացիոնար ուղեծրերը, ոչ միայն շրջանաձև են, այլ նաև էլիպսաձև և դասավորված են տարածության մեջ տարբեր ձևերով: Սակայն Բորի - Զոմերֆելդի տեսությունը չի բավարարում գիտության ներկայիս պահանջներին:

Չնայած   Բորի - Զոմերֆելդի տեսությունը բացատրեց ատոմների սպեկտրների շատ առանձնահատկություններ, սակայն այն ունի մի շարք անհաղթահարելի հակասություններ:

Այս տեսության գիխավոր հակասություններն են.

1. Տեսության հիմքը քվանտացման կանոններն են, որոնք չեն բխում մեխանիկայի և էլեկտրադինամիկայի օրենքներից;

2. Այս տեսությունը չի կարողանում բացատրել սպեկտրալ բնութագրերի որոշ նրբությունները;

3. Բազմաէլեկտրոն ատոմների էներգիան հաշվելիս տալիս է փորձի հետ չհամընկնող տվյալներ (նույնիսկ պարզագույն դեպքի`  He – ի ատոմի համար);

4. Տեսությունը չի բացատրում քիմիական կապի առաջացումը:

>>

 

 

 

 

4. Քվանտային մեխանիկայի տարրերը

4.1. Ալիքներ և մասնիկներ

Ալիքներն ու մասնիկներն ունեն մի շարք ընդհանուր և տարբեր հատկանիշներ, երկուսն էլ տեղափոխում են էներգիա: Մասնիկներն ունեն դադարի զանգված, իմպուլս: Ալիքներն ունեն ալիքի երկարություն (λ), տատանման հաճախականություն (ν) և ամպլիտուդ (A):

Ավելի լավ հասկանալու համար ալիքների և մասնիկների տարբերությունը` կատարենք երկու փորձ.

1. Բաց թողնենք մասնիկների փունջը նեղ ճեղքով: Մասնիկներն անցնելով ճեղքով` կընկնեն էկրանի A կետը (նկ.4.2 ա): A կետի երկու կողմերում ընկնող մասնիկների թիվը կնվազի: Նրբագծված մասը համեմատական է մասնիկների թվին:

2. Կատարենք նույն փորձը ալիքների համար: Բաց թողնենք ալիքների փունջ նեղ ճեղքով,որի լայնությունը համեմատական է ալիքի երկարությանը: Ի տարբերություն մասնիկների` ալիքներն անցնելով ճեղքով, ենթարկվում են դիֆրակցիայի (նկ.4.2 բ): Դիֆրակցիան  արգելքի շրջանցումն է ալիքի կողմից:

>>

 

 

 

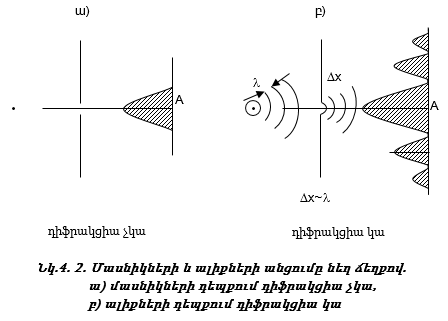
4.2. Լույսի ալիքամասնիկային երկվությունը

Լույսը էլեկտրամագնիսական ալիք է, սակայն տարածվում է առանձին մասնիկիների` ֆոտոնների ձևով: Ըստ Էնշտեյնի հավասարման մեկ ֆոտոնի էներգիան`

E = mc²

որտեղ` m-ը ֆոտոնի զանգվածն է, C –ն` լույսի արագությունը: Մյուս կողմից լույսն ունի ալիքային բնույթ, ենթարկվում է դիֆրակցիայի: Որպես ալիք ֆոտոնի էներգիան որոշվում է Պլանկի բանաձևով.

Վերջին երկու հավասարումներից հետևում է, որ

Մարմնի զանգվածի և արագության արտադրյալը կոչվում է շարժման քանակ  կամ իմպուլս: P = mC, տեղադրելով ( 4.1)-ում` վերջնականորեն կստանանք

Այս հավասարումն արտահայտում է ֆոտոնի ալիքամասնիկային երկվությունը, որովհետև հավասարման ձախ մասում ունենք ալիոային բնութագիր - λ, աջ մասում մասնիկային` P=mc:

Լույսի մասնիկային բնույթը հաստատվում է ֆոտոէֆեկտի, իսկ ալիքային հատկությունը` դիֆրակցիայի երևույթով:

>>

 

 

 

 

4.3. Դե-Բրոյլի տեսությունը

1924 թ Լուի Դե-Բրոյլը (Ֆրանսիա) առաջարկեց, որ ալիքամասնիկային երկվությունը բնորոշ է ոչ միայն ֆոտոններին, այլ նաև ցանկացած նյութական մասնիկներին: Ցանկացած նյութական մասնիկի շարժումը կարելի է դիտել որպես ալիքային պրոցես և ալիքի երկարությունը որոշվում է Դե-Բրոյլի բանաձևով`

որտեղ m–ը նյութի զանգվածն է, v–ն` արագությունը, h–ը` Պլանկի հաստատունը:

Շարժվող մասնիկին համապատասխանող ալիքները ստացել են Դե-Բրոյլի ալիքներ անվանումը:

Հետագայում Դե-Բրոյլի ենթադրությունը հաստատվեց, հայտնաբերվեց էլեկտրոնների դիֆրակցիայի երևույթը, իսկ դիֆրակցիան ալիքային պրոցեսի բնութագիր է: Էլեկտրոնների փունջը դիֆրակցիոն ցանցով անցկացնելիս ֆոտոթաղանթի վրա նկատվում է նույնպիսի դիֆրակցիոն պատկեր, ինչպես ճառագայթների անցման ժամանակ: Որպես դիֆրակցիոն ցանց` օգտագործվել են մետաղների բյուրեղները: Ատոմները բյուրեղում դասավորված են կանոնավոր կարգով` առաջացնելով բնական դիֆրակցիոն ցանց:

1927թ Ջերմերը և Դևիսոնը (ԱՄՆ), Թոմսոնը (Անգլիա) և Տարտակովսկին (ԽՍՀՄ) առաջին անգամ փորձնականորեն հաստատեցին էլեկտրոնների դիֆրակցիան:

Ներկայումս էլեկտրոնների դիֆրակցիան օգտագործում են նյութի կառուցվածքը ուսումնասիրելու նպատակով: Սարքը, որում նկատվում է այդ երևույթը, կոչվում է էլեկտրոնագրաֆ:

Յգտվելով (4.3) հավասարումից օգնությամբ կարող ենք հաշվել λ-ի արժեքը զանազան մարմինների համար (օրինակ 4.1):

Մակրոմարմինների  ալիքային հատկությունները ոչնչով չեն արտահայտվում: Եթե ալիքի երկարությունը զգալիորեն փոքր է ատոմի չափերից  ապա հնարավոր չէ պատրաստել այդ չափի դիֆրակցիոն ցանց կամ ճեղք: Այլ է պատկերը միկրոմասնիկների համար: (4.3) հավասարման համաձայն  էլեկտրոնի ալիքի երկարությունը այսինքն` այն ատոմի չափերի կարգի մեծություն է: Այդ չափի դիֆրակցիոն ցանց պատրաստել անհնարին է: Բարեբախտաբար բնության մեջ կան այդպիսի ցանցեր: Պինդ նյութի, մասնավորապես մետաղների բյուրեղային ցանցում ատոմների հեռավորությունը մի քանի անգստրեմ է  այսինքն` բավարարում է դիֆրակցիայի պայմանին:

>>

 

 

 

 

4.4. Հայզենբերգի անորոշության սկզբունքը

Էլեկտրոնի փունջը նեղ ճեղքով անցկացնելիս էկրանի վրա ստացվում է նույն պատկերը, ինչ որ ալիքների դեպքում:

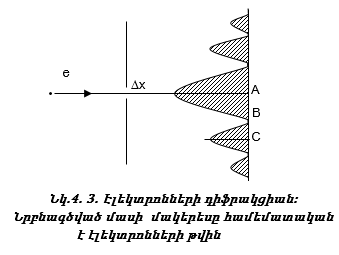
Իսկ ի՞նչ կարելի է ասել էլեկտրոնի մասին, ո՞ր կետը կընկնի: Մեծ հավանականությամբ կարելի է ասել, որ կընկնի A կետը, հնարավոր է նաև C կետը, բայց B կետը չի ընկնի:

Այսպիսով էլեկտրոնների փնջի տեղը ճշգրիտ կարող ենք որոշել, սակայն մեկ էլեկտրոնի տեղը և արագությունը միաժամանկ չենք կարող որոշել: Սա քվանտային մեխանիկայի հիմնական սկզբունքներից մեկն է և կոչվում է Հայզենբերգի անորոշության սկզբունք:

 Հնարավոր չէ միաժամանակ ճշգրիտ որոշել մասնիկի տեղը և դրա իմպուլսը (p = mv): Որքան ճշգրիտ որոշենք մասնիկի տեղը, այնքան անորոշ է դառնում դրա իմպուլսը, և հակառակը:

Անորոշության  առնչությունն ունի հետևյալ տեսքը.

կամ

որտեղ մասնիկի տեղի, կոորդինատի անորոշությունն է,   կոորդինատի ուղղությամբ  իմպուլսի և  արագության անորոշությունն է:

Քանի որ  մեծությունը, որը մտնում է անորոշության առնչության մեջ, փոքր մեծություն է, ապա մակրոօբյեկտների համար  էլ ավելի փոքր կլինի և հետևաբար կոորդինատի և իմպուլսի անորոշությունը չնչին է: Դրանց տեղը և արագությունը միաժամանակ կարելի է որոշել մեծ ճշտությամբ: Հետևաբար, դրանց նկատմաբ կարելի է կիրառել դասական մեխանիկան:

Անորոշությունը հետևանք է տարրական մասնիկների ալիքային հատկության, այլ ոչ թե մեր սարքերի անճշտության:

>>

 

 

 

4.5. Շրյոդինգերի հավասարումը

1925-26 թթ. Շրյոդինգերը (Ավստրիա) և Հայզենբերգը (Գերմանիա) ստեղծեցին միկրոմասնիկների շարժումը նկարագրող նոր մեխանիկա, որը կոչվեց քվանտային մեխանիկա: Նյուտոնի օրենքների հիման վրա ստեղծված մեխանիկան, որը կիրառվում է մակրոմարմինների համար կոչվեց դասական մեխանիկա: Քվանտային մեխանիկայի հիման վրա ստացված արդյունքները լրիվ համապատասխանում են փորձին:

Քվանտային մեխանիկայում մակրոմասնիկների շարժումը նկարագրվում է Շրյոդինգերի հավասարումով: Այն կատարում է նույն դերը քվանտային մեխանիկայում, ինչ որ Նյուտոնի օրենքները դասական մեխանիկայում:

Ինչպես և Նյուտոնի օրենքները, Շրյոդինգերի հավասարումը չի կարելի դուրս բերել ավելի ընդհանուր, հիմնարար դրույթներից:

Շրյոդինգերի հավասարումը մասնակի ածանցյալներով դիֆերենցիալ հավասարում է: Ստացիոնար, այսինքն ժամանակից չկախված վիճակի դեպքում մեկ մասնիկի համար այդ հավասարումը ունի հետևյալ տեսքը.

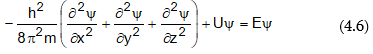
որտեղ m-ը` մասնիկի զանգվածն է, h-ը`Պլանկի հաստատունը, U-ն` պոտենցիլ էներգիան, E-ն` կինետիկ էներգիան, x,y,z-ը` մասնիկի կոորդինատներն են:

 փոփոխականը կոչվում է ալիքային ֆունկցիա: Դրա ֆիզիկական իմաստը կբացատրենք ստորև:

Լուծել Շրյոդինգերի հավասարումը նշանակում է գտնել տվյալ մասնիկին համապատասխանող  ֆունկցիաները և դրանց համապատասխանող լրիվ էներգիաները` E₁, E₂, E₃:

>>

 

 

 

4.6. Ալիքային ֆունկցիան, դրա ֆիզիկական իմաստը և նկարագրման եղանակները

Քանի որ էլեկտրոնի շարժումն ունի ալիքային բնույթ, քվանտային մեխանիկան այդ շարժումը ատոմում նկարագրում է  ալիքային ֆունկցիայի օգնությամբ: Ատոմական տարածության տարբեր կետերում այդ ֆունկցիան ունի տարբեր արժեքներ: Մաթեմատիկորեն այդ ֆունկցիան գրվում է (x,y,z) արտահայտության տեսքով, որտեղ x,y,z-ը` կետի կոորդինատներն են: Ալիքային ֆունկցիայի քառակուսին ունի որոշակի ֆիզիկական իմաստ:  ցույց է տալիս դիտարկվող մասնիկի dV ծավալում գտնվելու հավանականությունը:  մեծությունը կոչվում է հավանականության խտություն  կամ էլեկտրոնային խտություն  (էլեկտրոնի դեպքում):

Ալիքային ֆունկցիան պետք է բավարարի հետևյալ պայմաններին, այն պետք է լինի.

1. անընդհատ,

2. վերջավոր,

3. միանշանակ,

4. պետք է դառնա 0 այն կետերում, որտեղ մասնիկը չի կարող գտնվել (օրինակ անվերջ հեռու կետում):

Ալիքային ֆունկցիան, ավելի ճիշտ դրա քառակուսին` () կարելի է ներկայացնել հետևյալ եղանակներով.

1. անալիտիկ եղանակով`  =Ae^-kr,

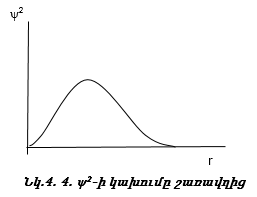
2. Գրաֆիկական եղանակով (նկ. 4.4),

3. Աղյուսակի ձևով,

4. Էլեկտրոնային ամպի եղանակով: Տարածության այն մասերում, որտեղ էլեկտրոնի գտնվելու հավանականությունը, այսինքն  -ն մեծ է, դրվում են խիտ կետեր, որտեղ փոքր է` նոսր կետեր:

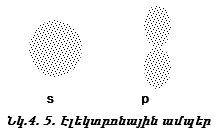
5. Սահմանային մակերևույթի եղանակ: Այս դեպքում գծվում է ծավալ, որտեղ մասնիկի գտնվելու հավանականությունը մոտ 90 % է:

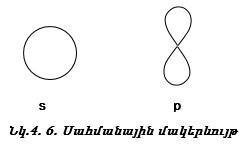
Միջուկաշուրջ տարածության այն մասը, որտեղ էլեկտրոնի գտնվելու հավանականությունը մեծ է  կոչվում է օրբիտալ:

>>

 

 

 

 

 

4.7. Շրյոդինգերի հավասարման լուծումը: Միաչափ պոտենցիալ տուփ

Ատոմի և մոլեկուլի համար Շրյոդինգերի հավասարման  լուծումը բարդ է, և այստեղ չենք քննարկի, կքննարկվեն միայն պատրաստի լուծումները:

Այդ լուծումներն ստանալու համար քննարկենք Շրյոդինգերի հավասարման լուծումը ավելի պարզ օրինակների դեպքում:

Քննարկենք Շրյոդինգերի հավասարման  լուծումը միաչափ պոտենցիալ տուփի համար:

Այս մոդելում մասնիկը (օրինակ էլեկտրոնը) կարող է շարժվել միայն մի ուղղությամբ, օրինակ x առանցքի ուղղությամբ x = 0-ից  x = a hատվածում:

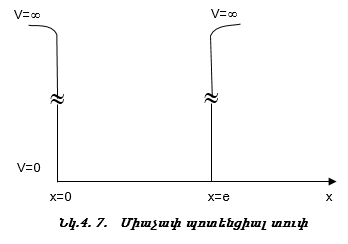
 Այդ հատվածի սահմաններում մասնիկի U պոտենցիալ էներգիան հաստատուն է: Հարմար է այն ընդունել հավասար զրոյի:

Տվյալ հատվածի սահմաններից դուրս մասնիկի վրա ազդող v պոտենցիալը անվերջ մեծ Է: Դա նշանակում է, որ մասնիկը 0 < x < a hատվածից դուրս գալ չի կարող, որովհետև կպահանջվի անվերջ մեծ էներգիա` E:

Շրյոդինգերի հավասարումը միաչափ պոտենցիալ տուփի համար կընդունի հետևյալ տեսքը.

Այս հավասարումը լուծելու համար անհրաժեշտ է գտնել  ալիքային ֆունկցիան և E էներգիայի արժեքները, որոնք բավարարում են նշված հավասարմանը:  ալիքային ֆունկցիան պետք է լինի վերջավոր, միանշանակ և անընդհատ: Այն պետք է դառնա զրո x = 0 և x=a դեպքում, քանի որ այդ կետերում մասնիկը չի կարող գտնվել, հետևաբար -ն  հատվածից դուրս պետք է հավասար լինի զրոյի:

Նշված պայմաններին բավարարում է

որտեղ n =1,2,3, …, իսկ А -ն հաստատուն մեծություն է: n = 0 արժեքը բացառված է, որովհետև դա կնշանակի մասնիկի բացակայությունը տուփում ( = 0):  Տեղադրենք (4.7) -ը (4.8) հավասարման մեջ և դիֆերենցենք ձախ մասը

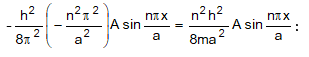
Աջ մասը`

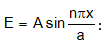
Հավասարեցնելուց և կրճատելուց հետո կստանանք `

որտեղ  n = 1, 2, 3:

Այսպիսով, մենք գտանք (4.7) հավասարմանը բավարարող  ֆունկցիան և էներգիայի արժեքը, այսինքն` լուծեցինք Շրյոդինգերի հավասարումը միաչափ պոտենցիալ տուփի համար: Քննարկենք ստացված լուծումը:

Նախ ընդգծենք, որ ստացված արդյունքը կտրուկ տարբերվում է նման խնդրից, երբ մասնիկը ենթարկվում է դասական մեխանիկայի օրենքներին:

Ակնհայտ է, որ մակրոմասնիկի էներգիան կարող է ընդունել ցանկացած արժեք, և x առանցքի վրա դրա գտնվելու հավանականությունը  նույնը կլինի: Ընդհակռակը, մասնիկը, որի համար ճշգրիտ են քվանտային մեխանիկայի օրենքները, ընդունում է խիստ որոշակի արժեքներ, կախված n -ից (նկ. 4.8):

Այսպիսով, մասնիկի էներգիան միաչափ պոտենցիալ տուփում քվանտացված է:

Քանի որ m զանգվածը (4.9) բանաձևում գտնվում է հայտարարում, ապա մեծ զանգված ունեցող մասնիկների համար, այսինքն` մակրոմարմինների համար, էներգիան կստացվի շատ փոքր և քվանտացում չի նկատվի: (4.9) բանաձևից երևում է, որ տուփի չափը նույնպես գտնվում է հայտարարում: Դա նշանակում է, որ մեծ տուփերում քվանտացումը նորից չի նկատվի:

Այսպիսով, քվանտային մեխանիկան բացատրում է ատոմներում և մոլեկուլներում էլեկտրոնի դիսկրետ էներգետիկ մակարդակների առկայությունը:

Քննարկենք մասնիկի գտնվելու հավանականությունը միաչափ տուփում (նկ.4.9).

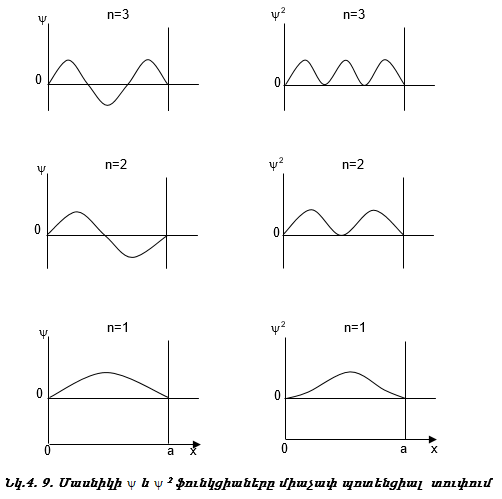
-ի կախումը x –ից համանման է երկու կողմից ամրացված լարի տատանումներին, որի դեպքում լարի երկարությամբ տեղավորվում են ամբողջ թվով կիսաալիքներ: Ինչպես երևում է նկ.4.9 –ից, -ն, այսինքն` մասնիկի գտնվելու հավանականությունը տուփի տարբեր մասերում տարբեր է, ի տարբերություն դասական դեպքի: Բացի դրանից, n>1 արժեքների դեպքում, տուփի ներսի որոշ կետերում մասնիկի գտնվելու հավանականությունը զրո է, արդյունք, որը բոլորովին հնարավոր չէ դասական մեխանիկայի տեսանկյունից:

Այն կետերը, որտեղ մասնիկի գտնվելու հավանականությունը զրո է, կոչվում են հանգուցային կետեր, իսկ n-ը` գլխավոր քվանտային թիվ:

 Գլխավոր քվանտային թիվը` n-ը, ցույց է տալիս

1. միաչափ տուփ a երկարության մեջ տեղավորված կես ալիքների թիվը,

2. էներգետիկ մակարդակի համարը,

3. դրա յուրաքանչյուր արժեքին համապատասխանում է որոշակի էներգիա, էներգիան կախված է n-ից:

4. հանգուցային կետերի թիվը, այն հավասար է (n+1)-ի:

Մասնիկի էներգիան միաչափ պոտենցիալ տուփում կարելի է հաշվել նաև առանց Շրյոդինգերի հավասարման` օգտագործելով կանգուն ալիքների գաղափարը:

Կանգուն ալիք առաջանում է այն դեպքում, երբ a երկարության մեջ տեղավորվում են ամբողջ թվով կես ալիքներ:

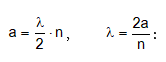
Մյուս կողմից ըստ Դե-Բրոյլի`

Վերջին երկու հավասարումների աջ մասերը հավասարեցնելով իրար` կստանանք

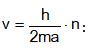
ՈՒնենալով մասնիկի v արագությունը` հաշվենք կինետիկ էներգիան.

>>

 

 

 

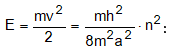
4.8. Ջրածնի ատոմի կառուցվածքը ըստ քվանտային մեխանիկայի

Ջրածնի ատոմն ունի ամենապարզ կառուցվածքը: Այն ունի մեկ էլեկտրոն, որը շարժվում է միջուկի դաշտում: Այդ համակարգի պոտենցիալ էներգիայի ֆունկցիան, որը մտնում է Շրյոդինգերի հավասարման մեջ, ունի հետևյալ տեսքը.

r-ը էլեկտրոնի հեռավորությունն է միջուկից:

Տեղադրենք այս արժեքը Շրյոդինգերի հավասարման մեջ:

Հավասարման լուծումը ջրածնի ատոմի համար ստացվում է շատ բարդ, այդ պատճառով լուծում չենք բերի, կքննարկենք միայն պատրաստի լուծումները: Մասնիկը միաչափ տուփում քննարկելիս տեսանք, որ լուծումը պարունակում է մեկ քվնտային թիվ, որովհետև մասնիկն ունի մեկ ազատության աստիճան: Ատոմում էլեկտրոնն ունի երեք ազատության աստիճան և հետևաբար անհրաժեշտ է երեք քվանտային թիվ: Հետագայում պարզվեց, որ էլեկտրոնը կատարում է ևս մի շարժում, որի շնորհիվ ձեռք է բերում շարժման քանակի սեփական մոմենտ: Այդ շարժումը նկարագրելու համար մտցվեց չորրորդ քվանտային թիվ` սպինային քվանտային թիվը: Այսպիսով, էլեկտրոնի վիճակը ատոմում նկարագրելու համար անհրաժեշտ է 4 քվանտային թիվ:

>>

 

 

 

 

4.9. Չորս քվանտային թվեր

Էլեկտրոնի վիճակը ատոմում նկարագրվում է 4 քվանտային թվերով: Էլեկտրոնի վիճակ ասելով` հասկանում ենք էլեկտրոնի էներգիան, էլեկտրոնային ամպի ձևը, չափերը, տարածական դասավորությունը, էլեկտրոնի շարժման քանակի մոմենտը միջուկի նկատմամբ, սեփական առանցքի նկատմամբ և այլն: Էլեկտրոնի վիճակը ատոմում լրիվ նկարագրվում է չորս թվերով, որոնք կոչվում են քվանտային թվեր` գլխավոր (n), օրբիտալ (l), մագնիսական (m) և սպինային (s): 

1. Գլխավոր քվանտային թիվ  - n, ընդունում է ամբողջ արժեքներ, նշանակվում է նաև տառերով.

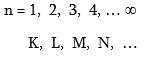
Գլխավոր քվանտային թիվը` n-ը, ցույց է տալիս.

ա) էլեկտրոնի էներգիան: Օրինակ Շրյոդինգերի հավասարման լուծումը ջրածնի ատոմի համար տալիս է.

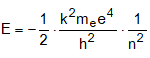
n-ի մեծացման հետ E-ն աճում է (նկ. 4.10):

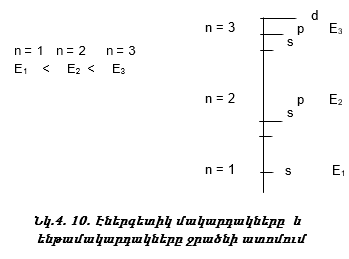
բ) էլեկտրոնային ամպի կամ օրբիտալի չափը, օրինակ

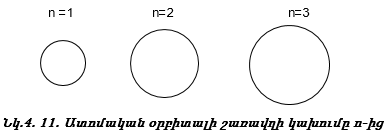
գ) հանգուցային մակերևույթների թիվը: Հանգուցային մակերևույթը, տվյալ դեպում գունդ, այն կետերն են, որտեղ  = 0, այսինքն` մասնիկը չի գտնվում: Հանգուցային մակերևույթը հասկանալու համար քննարկենք թմբուկի թաղանթի տատանումները.

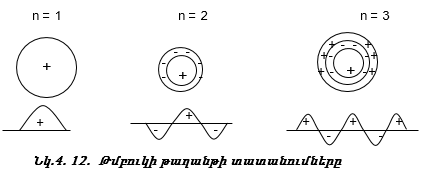
Պլյուս  (+) նշանով նշանակվում է թաղանթի ուռչումը, մինուս (-) նշանով` փոս ընկնելը: n=1 դեպքում կա մեկ,  n=2 դեպքում` երկու, n=3 դեպքում` երեք հանգուցային գնդաձև մակերևույթ: Այս տատանումները կոչվում են շառավղային տատանումներ: Այժմ քննարկենք նույն ատոմների, մասնավորապես` ջրածնի ատոմի համար:

 

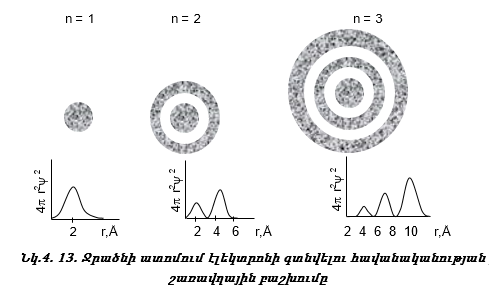
Ինչպես արդեն նշել ենք, հավանականությունը, որ էլեկտրոնը գտնվում է dv ծավալում, հավասար  Տվյալ դեպքում dv ծավալը dr հաստությամբ գնդային ծավալն է, այսինքն`   Բազմապատկելով  կստանանք էլեկտրոնի գտնվելու հավանականություն r շառավիղ ունեցող և dr հաստություն ունեցող գնդաձև շերտում  Նկ. 4.13-ում բերված է այդ հավանականության կախումը r-ից: n=1 դեպքում գնդային շերտի շառավիղը, որտեղ էլեկտրոնի գտնվելու հավանականությունը առավելագույնն է,  Այդ արժեքը համապատասխանում է Բորի տեսությամբ ստացված ուղեծրի շառավղին, երբ n=1: Սակայն օրբիտալի տեսքը խիստ տարբերվում է Բորի ստացված արդյունքից: Ըստ Բորի էլեկտրոնը գտնվում է միայն այդ հեռավորության վրա, ըստ քվանտային մեխանիկայի` ցանկացած կետում, բայց տարբեր հավանականությամբ:

դ) ենթամակարդակների թիվը:

2. Օրբիտալ քվանտային թիվ:  Նշանակվում է  l  տառով:

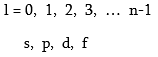
Օրբիտալ քվանտային թվի` l – ի արժեքները կախված են n-ի արժեքներից: Այն ընդունում է 0-ից մինչև n-1 միջակայքի բոլոր ամբողջ թվերի արժեքները:

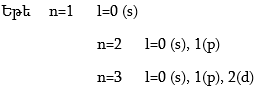
Օրբիտալ քվանտային թիվը ցույց է տալիս

ա) ենթամակարդակի էներգիան (նկ. 4.10);

 բ) էլեկտրոնային ամպի ձևը;

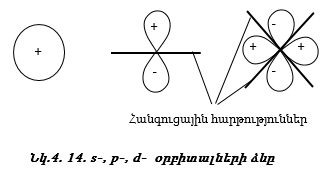
գ) կենտրոնով անցնող հանգուցային հարթությունների թիվը: Նորից քննարկենք թմբուկի թաղանթի տատանումները, սակայն այս անգամ` անկյունային տատանումները  (նկ. 4.15):

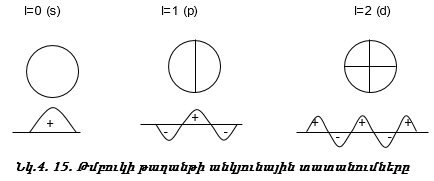
Դրական նշանը ցույց է տալիս ուռուցիկ լինելը, բացասական նշանը` փոս լինելը:  Թմբուկի տատանումները նշանակենք l = 0, 1, 2, 3, …: l-ի արժեքները ցույց են տալիս թմբուկի կենտրոնով անցնող հանգուցային հարթությունների քանակը: Հանգուցային հարթության վրա տատանում չկա: l=0 (s) տատանման դեպքում հանգուցային հարթությունների քանակը զրո է, l=1 (p) տատանման դեպքում` մեկ, l=2 (d) տատանման դեպքում` երկու:

Ճիշտ նույն կերպ էլեկտրոնը կատարում է անկյունային տատանողական շարժում (նկ. 4.14): Միջուկով անցնող հանգուցային հարթությունների թիվը s ամպի համար զրո է, p ամպի համար` մեկ, d ամպի համար` երկու:

դ) էլեկտրոնի շարժման քանակի մոմենտը միջուկի նկատմամբ (օրբիտալ մոմենտ).

3. Մագնիսական քվանտային թիվ: Նշանակվում է  տառով և ընդունում է հետևյալ միջակայքի բոլոր ամբողջ արժեքները, ներառյալ զրոն:

Մագնիսական քվանտային թիվը ցույց է տալիս.

ա) էլեկտրոնային օրբիտալի դիրքը տարածության մեջ: Օրինակ. 

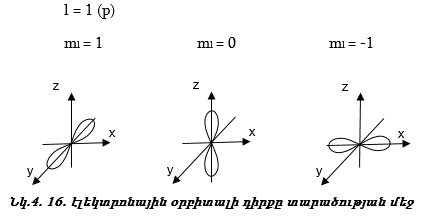
բ) Օրբիտալ շարժման քանակի մոմենտի պրոյեկցիան որևէ առանցքի ուղղությամբ, օրինակ` z առանցքի նկատմամբ

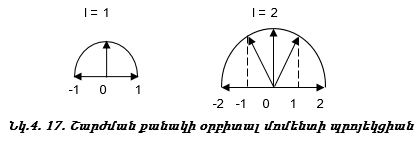
Այսպիսով s վիճակին համապատասխանում է մեկ օրբիտալ,p վիճակին` երեք, d վիճակին` հինգ,  f վիճակին` յոթ: 

4. Սպինային քվանտային թիվ: Նշանակվում է S տառով: Ընդունում է երկու արժեք

Սպինային քվանտային թիվը ցույց է տալիս

ա) էլեկտրոնի շարժման քանակի մոմենտը սեփական առանցքի նկատմամբ

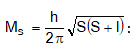
բ) Մագնիսական մոմենտը,

գ) Պարզեցված` էլեկտրոնի պտույտը սեփական առանցքի  նկատմամբ:                   

Քանի որ էլեկտրոնն ունի լիցք, ապա նրա պտույտն առաջացնում է մագնիսական դաշտ` մագնիսական մոմենտ: Էլեկտրոնն ունի երկու մագնիսական մոմենտ, սեփական առանցքի նկատմամբ` սպինային մոմենտ, միջուկի նկատմամբ` օրբիտալ մոմենտ:

>>

 

 

 

 

Բազմաէլեկտրոն ատոմներ

Ինչպես և ջրածնի ատոմում, բազմաէլեկտրոն ատոմներում յուրաքանչյուր էլեկտրոնի վիճակը որոշվում է չորս քվանտային թվերի ` n,l,m,s արժեքներով: Այդ թվերը կարող են ընդունել նույն արժեքները, ինչ որ ջրածնի ատոմի համար:

Բազմաէլեկտրոն ատոմներում էլեկտրոնը շարժվում է ոչ միայն միջուկի դաշտում, այլ նաև մնացած էլեկտրոնների դաշտում: Այդ գործոնի ազդեցությունը բերում է նրան, որ միևնույն n, բայց տարբեր l ունեցող էլեկտրոնների էներգիան դառնում է տարբեր: Այսպիսով, բազմաէլեկտրոն ատոմներում  էլեկտրոնի էներգիան որոշվում է երկու քվանտային թվերի` n -ի և l -ի արժեքներով: Այսինքն` էներգիան աճում է ինչպես n -ի, այնպես էլ l -ի արժեքների մեծացման հետ:

էլեկտրոնի վիճակը բազմաէլեկտրոն ատոմներում ենթարկվում է Պաուլիի կողմից սահմանված քվանտամեխանիկական սկզբունքին:

 Ատոմում չի կարող լինել երկու էլեկտրոն նույն չորս քվանտային թվերով  (Պաուլիի արգելման սկզբունքը):

Այդ սկզբունքի ֆիզիկական իմաստն այն է, որ տարածության միևնույն կետում միաժամանակ չի կարող լինել երկու էլեկտրոն: Քանի որ տվյալ օրբիտալում գտնվող էլեկտրոնների համար n–ի, l–ի և m–ի արժեքները նույնն են, ապա դրանք պետք է տարբերվեն գոնե S–ի արժեքով, իսկ վերջինս ունի երկու արժեք, ուստի յուրաքանչյուր օրբիտալում կարող է լինել երկու էլեկտրոն, որոնք պետք է  ունենան հակառակ սպիններ, այսինքն` սպինային քվանտային թվերի արժեքները պետք է լինեն տարբեր:

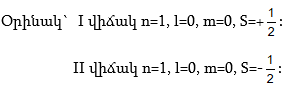
Էլեկտրոնների առավելագույն թիվը n մակարդակում 2n² է (Աղյուսակ 1):

Ատոմում n –ի նույն արժեքները ունեցող էլեկտրոնների համախումբըը կոչվում է էներգետիկ մակարդակ: Էլեկտրոնները, որոնք ունեն նույն n–ի և l–ի արժեքները, կոչվում են էներգետիկ ենթամակարդակ: Էլեկտրոնների առավելագույն թիվը  ենթամակարդակում հավասար է l(2l+1):

Այժմ էներգետիկ մակարդակներն ու ենթամակարդակները նկարագրենք էներգետիկ դիագրամների ձևով: Ատոմական օրբիտալը պայմանականորեն նշանակենք քառակուսի վանդակի ձևով, որի երեք կողմերում նշենք երեք քվանտային թվերը: 

Մեկ օրբիտալում կարող են լինել կա՛մ մեկ, կա՛մ երկու էլեկտրոն, բայց տարբեր սպիներով:

 

Ելնելով քվանտային թվերի հատկություններից` կառուցենք բազմաէլեկտրոն ատոմի էներգետիկ դիագրամը:

>>

 

 

 

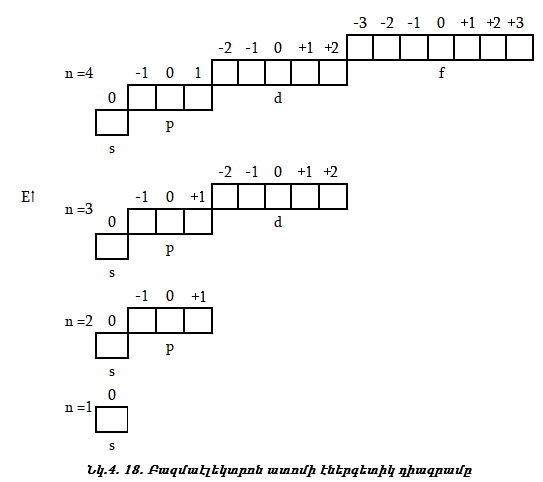
4.10. Էլեկտրոնների լրացման հաջորդականությունը բազմաէլեկտրոն ատոմներում

Էլեկտրոնների լրացումը ատոմների էներգետիկական մակարդակներում և ենթամակարդակներում կատարվում է հետևյալ հաջորդականությամբ (աուֆբատ - սկզբունք):

1. Էլեկտրոնը, առաջին հերթին, լրացնում է այն մակարդակը,իսկ մակարդակում նախ այն ենթամակարդակը, որի էներգիան ամենափոքրն է (նվազագույն էներգիայի սկզբունք):

2. Օրբիտալներում էլեկտրոնները լրանում են ըստ Պաուլիի սկզբունքի: Տվյալ օրբիտալում կարող է լինել մեկ էլեկտրոն, կամ երկու էլեկտրոն հակառակ սպիններով:

3. Էլեկտրոնների լրացումը տվյալ ենթամակարդակում  կատարվում է ըստ Հունդի կանոնի:

 Ատոմական օրբիտալները էլեկտրոններով լրանում են այնպես, որ ատոմը ունենա սպինային թվերի գումարի առավելագույն բացարձակ արժեք:

Դա նշանակում է, որ տվյալ ենթամակարդակում սկզբում լրանում է մեկական էլեկտրոն, սպինների նույն ուղղությամբ, հետո նոր զույգավորվում են:

4. Էլեկտրոնների լրացումը կատարվում է ըստ Կլեչկովսկու երկու կանոնների:

 I կանոն Էլեկտրոնը առաջին հերթին լրանում է այն ենթամակարդակում, որի համար n+l գումարը ավելի փոքր է:

II կանոն եթե երկու օրբիտալների համար n+l գումարը նույնն է, ապա էլեկտրոնը առաջին հերթին  լրանում է  այն ենթամակարդակում, որի n-ը ավելի փոքր է:

Ջրածնի ատոմի համար էլեկտրոնի էներգիան կախված է միայն n-ից, մացած ատոմների համար` նաև l-ից, հետևյալ պատճառով: Էլեկտրոնները, որոնք ձգվում են միջուկի կողմից, նաև վանվում են ներքին շերտերի էլեկտրոնների կողմից, այսինքն` տեղի է ունենում արտաքին շերտի էլեկտրոնների էկրանացում ներքին շերտերի էլեկտրոնների կողմից:

>>

 

 

 

 

4.11. Էլեկտրոնային բանաձևեր, էլեկտրոնային դիագրամներ

Տարրերի ատոմների էլեկտրոնային կոնֆիգուրացիան կարելի է նկարագրել երեք եղանակով`էլեկտրոնային բանաձևերով, էներգետիկ դիագրամներով և էլեկտրոնային ամպերի տեսքով:

Փոքր պարբերության տարրեր: Պարբերական համակարգի առաջին պարբերությունը կազմված է 2 տարրերից: Էլեկտրոնը ջրածնի ատոմում գտնվում է առաջին էներգետիկ մակարդակի s  ենթամակարդակում: s -էլեկտրոնային ամպն ունի գնդի ձև:

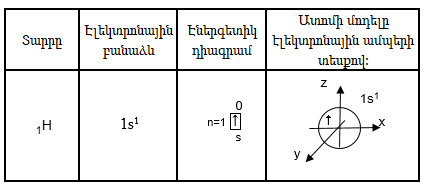
Պաուլիի սկզբունքի համաձայն մեկ օրբիտալում կարող է լինել առավելագույնը երկու էլեկտրոն` հակառակ սպիններով: Երկու էլեկտրոն պարունակող օրբիտալը ներկայացնենք նրբագծված տեսքով:

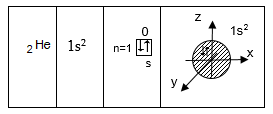
Երկրորդ և երրորդ պարբերությունները պարունակում են ութական տարր:

Երկրորդ պարբերության տարրերի մոտ լրանում է n=2 շերտը, սկզբում 2s – օրբիտալը, հետո երեք p -  օրբիտալները: Ստորև բերված են մի քանի օրինակներ:

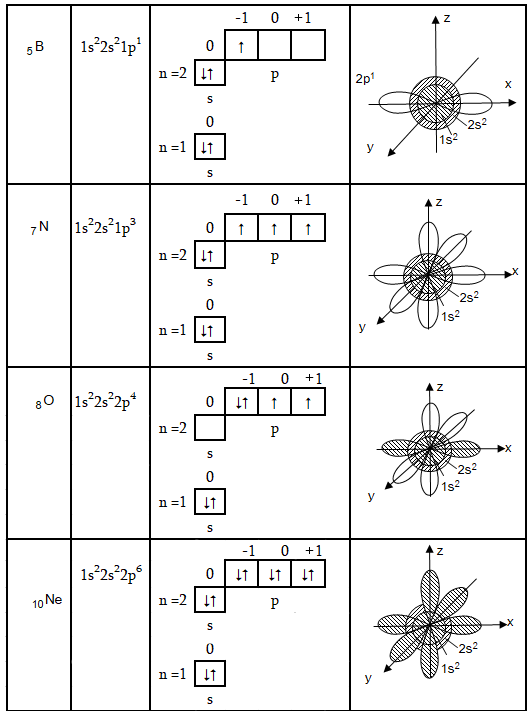
Նեոնի ատոմում երկրորդ էլեկտրոնային շերտում էլեկտրոնների թիվը հասնում է առավելագույնի: Այսպիսով, տարրերի ընդհանուր թիվը երկրորդ պարբերությունում հավասար է երկրորդ էներգետիկ մակարդակի էլեկտրոնների թվին:

Երրորդ պարբերության տարրերի մոտ լրանում է n=3 շերտը, որը կազմված է 3s-, 3p-, 3d-, օրբիտալներից: Ինչպես և երկրորդ պարբերությունում, առաջին երկու տարրերի (Na, Mg)  ատոմներում լրանում են  s - օրբիտալները, վերջին վեց տարրերի մոտ (Al – Ar) - p - օրբիտալները, օրինակ.

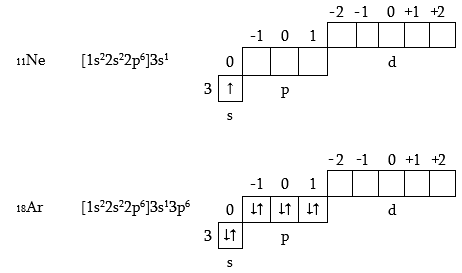
Na և Ar տարրերում մոտ n=1,  n=2 շերտերում կրկնվում է նեոնի ատոմի կառուցվածքը, այդ պատճառով պարզության համար բերված ուրվագծերում ցույց է տրված միայն արտաքին շերտի լրացումը: Երրորդ պարբերության վերջին տարրի` արգոնի Ar (ինչպես նաև Ne) մոտ լրանում են s- և p- օրբիտալները, այսինքն` վերջին շերտը  չորս երկէլեկտրոնային ամպերն են (մեկ գնդաձև, երեքը` հանտելաձև): Ի տարբերություն երկրորդ պարբերության երրորդ պարբերությունում մնում են դատարկ 3d- օրբիտալները:

Մեծ պարբերության տարրերը: Չորրորդ և հինգերորդ պարբերությունները պարունակում են 18 տարր: Չորրորդ պարբերության ատոմներում էլեկտրոնների լրացումը սկսվում է n=4 շերտի 4s- օրբիտալներից: Ինչպես արդեն նշել ենք, 4s- օրբիտալներլում էլեկտրոնի լրացումը 3d դատարկ օրբիտալի առկայությամբ, պայմանավորված է 3s²3p⁶ շերտի միջոցով միջուկի էկրանացմամբ: Այդ պատճառով կալիումի 19-րդ էլեկտրոնի և կալցիումի 20-րդ էլեկտրոնի համար ավելի ձեռնտու է 4s- վիճակը: Իսկապես, ըստ Կլեչկովսկու առաջին կանոնի, և՛ կալիումի,  և՛ կալցիումի համար n+l  գումարը 4s- օրբիտալի համար ավելի փոքր է , քան 3d- օրբիտալի համար:

Ըստ Կլեչկովսկու երկրորդ  կանոնի, սկզբում լրանում է 3d- օրբիտալը, իսկ հետո` 4p-  օրբիտալը:

Սկանդիումի ատոմում սկսվում է 3d- օրբիտալի լրացումը.

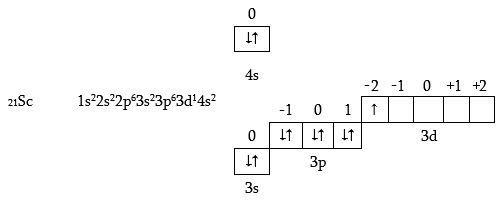
3d- օրբիտալի լրացումը ավարտվում է Zn-ի ատոմում.

 

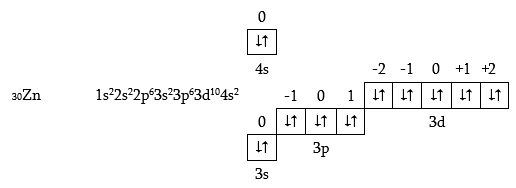
Տասը d-տարրերը, սկսած սկանդիումից և վերջացած ցինկով, կոչվում են անցողիկ տարրեր:

Այս տարրերի էլեկտրոնային թաղանթների կառուցվածքի առանձնահատկությունը նախորդների (s- և p- տարրեր) համեմատությամբ այն է, որ յուրաքանչյուր հաջորդ d- տարրին անցնելիս, նոր էլեկտրոնը լրացնում է ոչ թե արտաքին n = 4, այլ նախավերջին n = 3 էլեկտրոնային շերտը: Կարևոր է նշել, որ տարրերի քիմիական հատկությունները որոշվում են ատոմի արտաքին էլեկտրոնային թաղանթի կառուցվածքով և քիչ են կախված նախավերջին շերտի կառուցվածքից: Բոլոր անցողիկ տարրերի ատոմների արտաքին թաղանթում կա մեկ s– կամ երկու s– էլեկտրոն: Այդ պատճառով բոլոր d- տարրերը մետաղներ են, և դրանց հատկությունները քիչ են փոխվում կարգահամարի մեծացման հետ պարբերություններում, մինչդեռ p- տարրերի հատկությունները  փոխվում են տիպիկ մետաղականից  տիպիկ ոչ-մետաղականի:

3d- ենթամակարդակի (n=3, l=2) լրացումից հետո  էլեկտրոնները Կլեչկովսկու երկրորդ կանոնի համաձայն, զբաղեցնում են 4p- ենթամակարդակը (n=4, l=1): Այդ պրոցեսը սկսվում գալիումի (Z=31) և վերջանում կրիպտոնի ատոմով  (Z=36):

Ինչպես նախորդ ազնիվ գազերի` նեոնի և արգոնի ատոմները, կրիպտոնի ատոմը բնորոշվում է արտաքին էլեկտրոնային շերտի ns²np⁶ կառուցվածքով, որտեղ n-ը գլխավոր քվանտային թիվն է (նեոն 2s²2p⁶, արգոն 3s²3p⁶, կրիպտոն 4s²4p⁶): Դրանով է մասնավորապես պայմանավորված այդ ատոմների իներտությունը:

Հինգերորդ պարբերությունն սկսվում է Ռուբիդիումով, որի ատոմում լրանում է 5s- ենթամակարդակը: Ստրոնցիումի ատոմի (Z=38) 5s- ենթամակարդակը  լրացվում է երկու էլեկտրոնով, որից հետո տեղի է ունենում 4d- ենթամակարդակի լրացում, ընդամենը տասը անցողիկ տարր:

Այնուհետև ինդիումից մինչև քսենոն ազնիվ գազը լրանում է վեց տարրերի P- ենթամակարդակը: Դրանով ավարտվում է հինգերորդ պարբերությունը, որը նման է չորրորդ պարբերությանը:

Վեցերորդ պարբերությունը նախորդների նման սկսվում է երկու S- տարրերով: Այն լրանալուց հետո սկսում է լրանալ 4f- ենթամակարդակը, ըստ Կլեչկովսկու կանոնի:

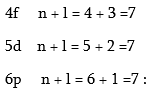
Բոլոր երեք դեպքերում էլ n + l գումարը հավասար է յոթի, սակայն n–ի ամենափոքր արժեքը համապատասխանում է 4f ենթամակարդակին: Իրականում լանթանի (Z = 57) ատոմում լրանում է ոչ թե 4f, այլ 5d ենթամակարդակը

Սակայն հաջորդ  ցերիումի  (Z = 58) ատոմում սկսվում է 4f- ենթամակարդակի լրացումը: 5d- էլեկտրոնը, որը կար լանթանի ատոմում, անցնում է 4f-ի վրա: Ցերիումի ատոմի էլեկտրոնային կառուցվածքն է`

Փաստորեն լանթանի ատոմում Կլեչկովսկու կանոնի խախտումը բացառություն է: Այսպիսով, վեցերորդ պարբերությունում տեղավորված են 14 լանթանոիդներ, որոնց ատոմներում վերջին և նախավերջին էլեկտրոնային թաղանթները նույնն են:

Յուրաքանչյուր հաջորդ տարրի ատոմում էլեկտրոնը լրանում է վերջից հաշված երրորդ էլեկտրոնային թաղանթի f-  ենթամակարդակում: Դրա շնորհիվ լանթանոիդների հատկությունները քիչ են տարբերվում:

Յոթերորդ անավարտ պարբերությունը նման է վեցերորդին:

Վերը բերված Կլեչկովսկու կանոնի խախտումը միակը չէ:

Այն դեպքերում, երբ  d- ենթամակարդակում պակասում է մեկ էլեկտրոն, կիսով չափ կամ լրիվ լրանալու համար, մեկ էլեկտրոն 4S-ենթամակարդակից անցնում է 3d- ենթամակարդակ:

Այդպիսի վիճակը էներգետիկ տեսակետից ավելի կայուն է: Այդ երևույթը կոչվում է “գլորման’’ երևույթ: Օրինակ, քրոմի և պղնձի ատոմներում 4s- ենթամակարդակում կա ոչ թե երկու, այլ մեկ էլեկտրոն: Արտաքին s-էլեկտրոններից մեկը “գլորվում” է նախավերջին  d- ենթամակարդակը: Քրոմի ատոմում էլեկտրոնի  գլորումը բերում է d- ենթամակարդակի լրացմանը կիսով չափ (d⁵), իսկ պղնձի մոտ` լրիվ (d¹⁰): Գլորման երևույթը հանդիպում է առաջին խմբում Cr, Mo տարրերի մոտ: Բացի նշված դեպքերից, կան ուրիշ բացառություններ ևս:

Այսպիսով, ատոմների էլեկտրոնային կառուցվածքները որոշում են պարբերական համակարգում տարրերի հատկությունների փոփոխման գլխավոր օրինաչափությունները:

1. Առաջին պարբերության տարրերը, որոնց ատոմներում լրացված է առաջին էլեկտրոնային շերտը, շատ հատկություններով բացառիկ են: Ավելին, դրանց որոշ հատկությունները (H+ իոնի հատկությունները, հեղուկ  He) չկան այլ տարրերի մոտ:

2. Երկրորդ պարբերության տարրերը, որոնց ատոմներում լրացվում է երկրորդ էլեկտրոնային շերտը, խիստ տարբերվում են մնացած տարրերից: Դա բացատրվում է նրանով, որ էլեկտրոնների էներգիան երկրորդ  շերտում զգալի փոքր է հաջորդ շերտերի  էլեկտրոնների   էներգիայից և նրանով, որ երկրորդ  շերտում չի կարող լինել ութից ավելի էլեկտրոն:

3. d- տարրերը, որոնց ատոմներում էլեկտրոնը լրանում է d- ենթամակարդակում, զգալիորեն քիչ են  տարբերվում իրարից, քան գլխավոր ենթախմբի տարրերը:

4. Լանթանոիդների հատկությունների տարբերությունն աննշան է, որովհետև էլեկտրոնները լրանում են վերջից հաշված երրորդ f- ենթամակարդակում:

>>

 

 

Ամփոփում

Ատոմը կազմված է դրական միջուկից և դրա շուրջը պտտվող էլեկտրոններից: Միջուկը կազմված է դրական լիցքավորված պրոտոններից և չեզոք նեյտրոններից: Էլեկտրոնը ֆոտոնի նման ունի երկակի` մասնիկային և ալիքային բնույթ: Որպես ալիք էլեկտրոնը միջուկի շուրջն առաջացնում է էլեկտրոնային ամպ:

Էլեկտրոնի վիճակը բնութագրվում է չորս քվանտային թվերով: Գլխավոր քվանտային թիվը ցույց է տալիս էլեկտրոնի էներգիայի մեծությունը: Երկրորդական (ուղեծրային) քվանտային թիվը ցույց է տալիս էլեկտրոնային ամպի ձևը: Մագնիսական քվանտային թիվը ցույց է տալիս էլեկտրոնային ամպի դիրքը տարածության մեջ:  Սպինային քվանտային թիվը ցույց է տալիս էլեկտրոնի պտտման ուղղությունը սեփական առանցքի շուրջը: Էլեկտրոնային թաղանթների լրացումը կատարվում է էներգիայի նվազագույն լինելու սկզբունքով այսինքն` լրանում է նախ այն շերտը, իսկ շերտում նախ այն ենթա շերտը, որտեղ էլեկտրոնի էներգիան ավելի փոքր է:

Էլեկտրոնային թաղանթների կառուցվածքի արտահայտությունը քվանտային թվերի օգնությամբ կոչվում  են էլեկտրոնային բանաձևեր:

Ատոմական օրբիտալների լրացումը կատարվում է Հունդի կանոնի համաձայն, այսինքն` այնպես, որ ատոմում լինեն առավելագույն թվով կենտ էլեկտրոններ:

>>

 

 

Սովորելու նպատակը

Այս բաժինը սովորելուց հետո դուք պետք է կարողանաք.

1. Տարբերել տարրական մասնիկները, իմանալ էլեկտրոնի, նեյտրոնի, պրոտոնի զանգվածը, լիցքը:

2. Հասկանալ էլեկտրոնի երկակի բնույթի իմաստը, օգտագործել  հարաբերակցությունը:

3. Բացատրել էլեկտրոնային ամպ, ամպի խտություն, էլեկտրոնի տվյալ ծավալում գտնվելու հավանականություն, հավանականության խտություն հասկացությունները:

4. Իմանալ էլեկտրոնի վիճակը բնութագրող չորս քվանտային թվերի իմաստները, արժեքները:

5. Իմանալ էլեկտրոնային թաղանթների լրացման հերթականությունը, կազմել տարրերի էլեկտրոնային բանաձևերը, իմանալ հունդի կանոնը, կազմել ատոմների էլեկտրոնային թաղանթների էներգետիկ դիագրամները:

 

Հիմնական հասկացություններ

1. Ատոմը կազմված է միջուկից և դրա շուրջը պտտվող էլեկտրոններից:

2. Միջուկը կազմված է պրոտոններից  և նեյտրոններից:

3. Էլեկտրոնն ունի երկակի` ինչպես մասնիկի, այնպես էլ ալիքի հատկություններ:

4. Որպես ալիք` էլեկտրոնը միջուկի շուրջը առաջացնում է էլեկտրոնային ամպ:

5. Էլեկտրոնի վիճակը բնութագրվում է  չորս քվանտային թվերով.

ա) Գլխավոր քվանտային թիվ (n)` ցույց է տալիս էլեկտրոնի էներգիայի մեծությունը,

բ) Երկրորդական քվանտային թիվ (l)` ցույց է տալիս էլեկտրոնի ամպի ձևը,

գ) Մագնիսական քվանտային թիվ (m)` ցույց է ամպի դիրքը տարածության մեջ,

դ) Սպինային քվանտային թիվ (s)` ցույց է տալիս էլեկտրոնի պտտման ուղղությունը սեփական առանցքի շուրջը:

6. էլեկտրոնային թաղանթների լրացումը էլեկտրոններով կատարվում է էներգիայի նվազագույն լինելու սկզբունքով:

7. Էլեկտրոնային բանաձևերն արտահայտում են էլեկտրոնային թաղանթների կառուցվածքը քվանտային թվերի օգնությամբ:

8. Ատոմական օրբիտալները էլեկտրոններով լրացվում են այնպես, որ ատոմում էլեկտրոնների սպինային թվերի գումարային բացարձակ արժեքը լինի առավելագույնը` այսինքն լինեն առավելագույն թվով կենտ էլեկտրոններ (Հունդի կանոն):